Задачи по гидравлике с решениями.
Решение задач по гидравлике
Решение задач с использованием закона Архимеда
Задача
Баркас массой mб = 250 кг изготовлен в форме параллелепипеда шириной b = 1 м, длиной l = 3 м, высота бортов h = 0,3 м.
Определить, сколько человек могут разместиться в баркасе, не потопив его.
Средняя масса человека mч = 70 кг, плотность воды ρ = 1000 кг/м3.
Правильное решение:
Определим водоизмещение баркаса Мmax, которое равно массе воды, вытесненной им при полном погружении (по обрез бортов).
Для этого определим объем корпуса баркаса и умножим полученный результат на плотность воды:
Мmax = b×l×h×ρ = 1×3×0,3×1000 = 900 кг.
Чтобы найти грузоподъемность Мгр баркаса, необходимо из полученного результата вычесть массу самого баркаса:
Мгр = Мmax – mб = 900 – 250 = 650 кг.
Разделив полученную максимальную грузоподъемность на среднюю массу человека, и округлив результат до целого числа, получим допустимое количество пассажиров баркаса:
n = Мгр/mч = 650/70 = 9 человек.
Ответ: баркас может принять на борт не более 9 человек.
***
Задача
Медный шар диаметром d = 100 мм весит в воздухе G1 = 45,7 Н, а при погружении в жидкость его вес стал равен G2 = 40,6 Н.
Определить плотность жидкости.
Правильное решение:
Вес шара в жидкости меньше, чем его вес в воздухе, поскольку в жидкости на него действует выталкивающая архимедова сила, равная весу вытесненной шаром жидкости.
Очевидно, что вес вытесненной шаром жидкости будет равен разности между весом шара в воздухе и его весом в жидкости:
Gж = G1 – G2 = 45,7 – 40,6 = 5,1 Н.
Чтобы определить плотность жидкости, необходимо ее массу разделить на объем, который равен объему шара, определяемого по формуле:
Vш = πd3/6 = 3,14×0,13/6 = 0,00052 м3.
Массу жидкости можно определить, зная ее вес:
mж = Gж/g = 5,1/9,81 ≈ 0,52 кг.
Определив массу и объем, находим плотность жидкости:
ρ = mж/Vш = 0,52/0,00052 = 1000 кг/м3.
Ответ: плотность жидкости равна 1000 кг/м3 (судя по плотности, жидкость – вода).
***
Задача
Баржу, имеющую форму параллелепипеда, загрузили песком в количестве 18 тонн. Ее осадка (глубина погружения) составила h0 = 0,5 м.
Определить массу пустой баржи, если ее размеры: длина l = 12 м; ширина b =
Какова полная грузоподъемность баржи, если высота ее бортов h = 1 м.
Плотность воды принять равной 1000 кг/м3.
Правильное решение:
В соответствии с законом Архимеда, на баржу со стороны воды действует выталкивающая сила, равная весу воды, вытесненной погруженной частью баржи. Этот вес (обозначим его GВ) можно определить, зная ширину, длину и осадку баржи, а также плотность воды:
GВ = mg = b×l×h0×ρ×g = 4×12×0,5×1000×9,81 = 235400 Н.
Итак, на баржу действует выталкивающая сила, равная 235400 Н, удерживая ее в равновесном состоянии на поверхности воды. Следовательно, вес G
mБГ = GБГ/g = 235400/9,81 ≈ 24000 кг.
Чтобы найти массу пустой баржи, необходимо из массы груженой баржи вычесть массу груза:
mБ = mБГ – mГ = 24000 – 18000 = 6000 кг.
Очевидно, что при полном погружении баржи в воду (по самые борта), выталкивающая архимедова сила увеличится в два раза по сравнению с рассмотренным нами случаем, т.
Данная сила характеризует водоизмещение баржи, т. е. максимальное количество вытесняемой ее корпусом воды.
Однако, эта величина не характеризует полную грузоподъемность баржи, поскльку она сама имеет вес.
Исходя из этого, полная грузоподъемность баржи может быть подсчитана, как разница между массой вытесненной баржой воды и массой баржи:
Мmax = mВ – mБ = 47080 – 6000 = 41080 кг.
Ответ: пустая баржа весит 6 тонн, а ее полная грузоподъемность – 41 тонна.
***
Задача
Для переправы грузов через реку построен плот из 25 штук пустых железных бочек.
Масса одной бочки m = 50 кг.
Определить грузоподъемность плота Мmax при условии его полного погружения.
Плотность воды принять равной ρ = 1000 кг/м3.

Правильное решение:
Определим объем бочек, из которых изготовлен плот:
V = 25 h πd2/4 = 25×1,3×3,14×0,82/4 = 16,33 м3.
Масса этих бочек: mБ = 25m = 25 × 50 = 1250 кг.
Масса воды, вытесняемой бочками при полном погружении плота, равна произведению плотности воды на объем бочек:
mВ = ρVБ = 1000×1,664 = 16330 кг.
Грузоподъемность плота равна массе вытесняемой бочками воды с учетом массы самих бочек:
Мmax = mВ – mБ = 16330 – 1250 = 15080 кг.
Ответ: максимальная грузоподъемность плота равна 15080 кг.
***
Решение задач с применением основного уравнения гидростатики
Задача
На рисунке изображены три сосуда разной формы, в каждый из которых налита вода на одинаковую высоту Н.
Площадь свободной поверхности в сосуде а больше площади свободной поверхности в сосуде в в два раза, но в два раза меньше площади свободной поверхности в сосуде б.
Площадь дна во всех трех сосудах одинакова и равна S.
Во сколько раз сила давления на дно в сосуде а будет отличаться от силы давления на дно в сосуде в?
Ответ обоснуйте основным уравнением гидростатики.
Решение:
В соответствии с основным уравнением гидростатики p = p0 + γ(z0 – z), т. е. давление в любой точке объема жидкости зависит от внешнего давления p0 и глубины погружения рассматриваемой точки.
Поскольку внешнее давление для всех трех сосудов равно атмосферному давлению, т. е. одинаково, то давление на каждую из точек поверхности дна зависит только от уровня Н (т. е. глубины, равной z
Тогда и сила давления на дно, определяемая, как произведение площади дна на величину давления, во всех трех сосудах будет одинакова, несмотря на то, что они имеют разную форму.
***
Задача
Определить избыточное давление в забое скважины глубиной h = 85 м, которая заполнена глинистым раствором плотностью ρ =
Правильное решение:
Избыточное давление – это давление, которое оказывает столб жидкости на единицу площади на данной глубине без учета внешнего давления (атмосферы) на поверхности жидкости, и определяется, как произведение удельной плотности жидкости на высоту столба (глубины погружения).
Удельная плотность жидкости определяется, как произведение абсолютной плотности на ускорение свободного падения.
Тогда избыточное давление в скважине исходя из условий задачи можно записать так:
pизб = γh = ρgh = 1250×9,81×85 = 1040000 Па ≈ 1 МПа.
Ответ: избыточное давление в забое скважины составляет примерно 1 МПа.
***
Задача
Водолазы при подъеме затонувшего судна работали в море на глубине h = 50 м.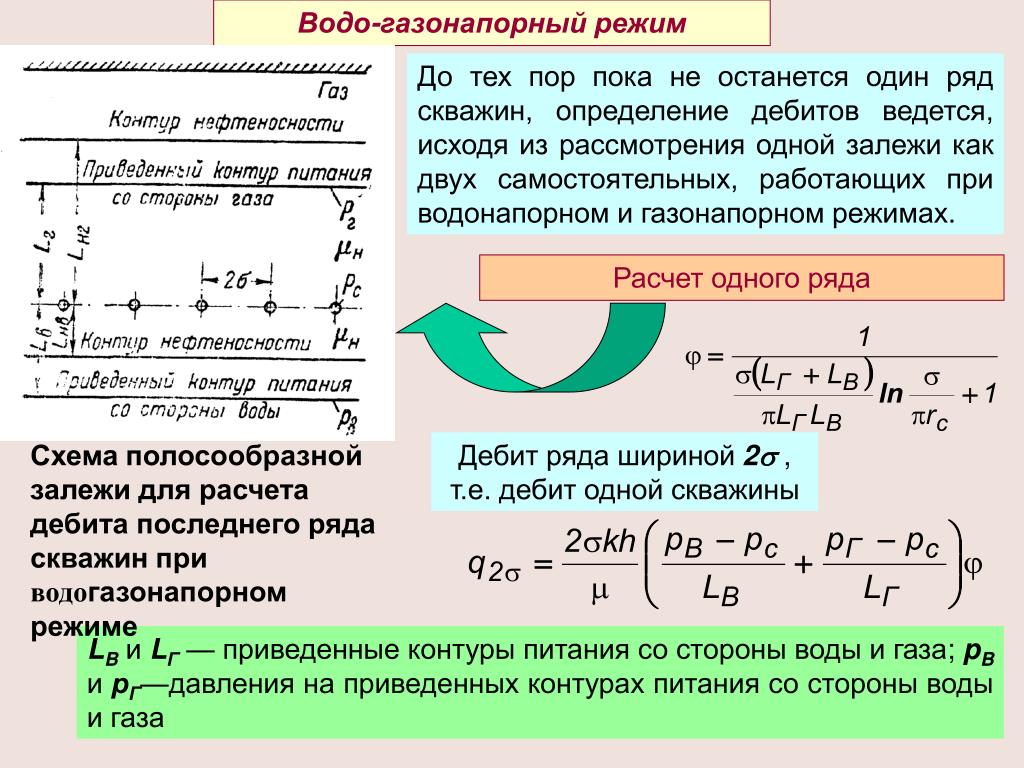
Определите давление воды на этой глубине и силу давления на скафандр водолаза, если площадь поверхности S скафандра равна 2,5 м2.
Атмосферное давление считать равным p0 = 1,013×105 Па, плотность воды ρ = 1000 кг/м3.
Правильное решение:
Давление воды на глубине 50 м складывается из атмосферного давления p0 и избыточного давления, обусловленного столбом воды высотой 50 м:
p = p0 + ρgh = 1,013×105 + 1000×9,81×50 = 5,918×105 Па.
Сила давления воды на скафандр водолаза равна произведению площади скафандра на избыточное давление (внутри скафандра давление равно атмосферному, поэтому p0 не учитывается) и определяется по формуле:
F = ρgh×S = 1000×9,81×50×2,5 = 1226250 Н ≈ 1226 кН.
Ответ: давление воды на глубине 50 м равно 591 МПа, а сила давления на скафандр равна 1226 кН.
***
Задача
После сжатия воды в цилиндре под поршнем давление в ней увеличилось на 3 кПа.
Необходимо определить конечный объем V2 воды в цилиндре, если ее первоначальный объем составлял V1 = 2,55 л.
Коэффициент объемного сжатия воды βV = 4,75 • 10-10 Па-1.
Правильное решение:
Приведем исходные данные задачи к системе единиц СИ: V1 = 2,55л = 2,25х10-3 м3, Δp = 3 кПа = 3000 Па.
Тогда конечный объем воды в цилиндре будет равен сумме первоначального объема V1 и уменьшения объема ΔV в результате сжатия:
V2 = V1 + ΔV = (2,25×10-3) + (2,25×10-3×3000×4,75×10-10) = 2,25000320625×10-3 м3 = 2,2500032625 л.
Ответ: конечный объем воды 2,2500032625 л, т. е. изменился ничтожно мало.
***
Задачи по гидродинамике и определению параметров насосов
Скачать задачи по гидравлике с вариантами решений
(в формате Word, размер файла 324 кБ – 27 задач с решениями и вопросы по насосам)
Скачать теоретические вопросы к экзаменационным билетам по дисциплине “Основы гидравлики и теплотехники”
(в формате Word, размер файла 68 кБ)
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Примеры решения задач по гидравлике
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Задача 1.
Центробежный насос откачивает воду из сборного колодца в резервуар с постоянным уровнем H по трубопроводам размерами l1, d1 и l2, d2. Эквивалентная шероховатость поверхности труб Δ, плотность воды ρ=1000 кг/м3, кинематический коэффициент вязкости ν=0. 01 см2/с, расстояние a=1 м.
01 см2/с, расстояние a=1 м.
Характеристики насоса представлены следующими параметрами :
|
Q, л/с |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Hн, м |
45 |
47.5 |
48.5 |
48 |
47 |
45 |
40 |
35 |
30 |
22. |
15 |
|
Hдопвак, м |
– |
– |
8.2 |
8 |
7.6 |
7 |
6.6 |
6 |
5.5 |
4.75 |
4 |
При расчетах принять суммарные коэффициенты местных сопротивлений на всасывающей линии ξ1=10, на напорной линии ξ2=6.
Требуется определить :
1. На какой глубине h установится уровень воды в колодце, если приток в него Q?
2. Вакуумметрическую высоту всасывания при входе в насос Hвак, выраженную в метрах водяного столба (м в. ст.).
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе.
Дано : H=20 м ; l1=7 м ; l2=30 м ; d1=125 мм ; d2=100 мм ; Δ=1.5 мм ; Q=17 л/с ; ρ=1000 кг/м3 ; ν=0.01 см2/с ; a=1 м ; ξ1=10 ; ξ2=6.
Найти : h, Hвак, Hдопг.вс
Решение.
Пользуясь заданными в таблице параметрами, построим характеристики насоса : Hн=f(Q) и Hдопвак=f(Q).
По построенным кривым, определяем, при заданном значении Q=6 л/с величины Hн=27 м, Hдопвак=5 м.
1. Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту Hг=H+h и преодоление потерь напора во всасывающей и нагнетательной линиях :
Hн=Hг+h2+h3=H+h+h2+h3
Отсюда глубина, на котором установится уровень воды в колодце :
h=Hн-h2-h3 (1)
где Hн – напор, развиваемый насосом при заданном расходе Q (определяется по графику) ; h2 и h3 – потери напора во всасывающей и нагнетательной линиях.
Потери напора состоят из потерь напора по длине и в местных сопротивлениях :
h2=hℓ1+hм1 ; h3=hℓ2+hм2
Потери напора по длине определим по формуле Дарси :
hℓ1= ; hℓ2=
где λ – гидравлический коэффициент трения. Определяем по формуле Альштуля :
λ1= ; λ2=
где Re – число Рейнольдса.
Скорость движения воды во всасывающей линии :
v1= м/с.
Скорость движения жидкости в нагнетающей линии :
v2= м/с.
Число Рейнольдса для всасывающей линии :
Re1=
Число Рейнольдса для нагнетающей линии :
Re2=
Гидравлический коэффициент трения для всасывающей линии :
λ1=
Гидравлический коэффициент трения для нагнетающей линии :
λ2=
Потери напора по длине трубопровода для всасывающей линии :
hℓ1= м.
Потери напора по длине трубопровода для нагнетающей линии :
hℓ2= м.
Потери в местных сопротивлениях по формуле Вейсбаха :
для всасывающей линии :
hм1= м ;
для нагнетающей линии :
hм2= м.
Общие потери во всасывающей линии :
h2=0.22+0.98=1.2 м.
Общие потери в нагнетающей линии :
h3=2.88+1.44=4.32 м.
Тогда, искомая глубина, на которой установится уровень воды в колодце :
h=27-1.2-4.32=21.48 м.
2. Вакуумметрическую высоту всасывания при входе в насос определяем из уравнения Бернулли, составленного для сечений 1 – 1 и 2 – 2, приняв за горизонтальную плоскость сравнения сечение 1 – 1 :
Hвс= (2)
Вычисления по формуле (2) дают :
Hвс= Па.
или в метрах водного столба :
Hвс=23836 мм. в. ст.=23.8 м. в. ст.
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе определим по формуле :
(3)
где – допустимая вакуумметрическая высота всасывания (определяется по графику =5 м) ; h2 – потеря напора ; – скоростной напор во всасывающей линии ; α1 – коэффициент кинетической энергии потока (примем α1=1).
Вычисления по формуле (3) дают :
м.
Ответ : h=21.48 м ; Hвс=23.8 м. в. ст. ; =3.7 м.
Задача 2.
Жидкость плотностью ρ=900 кг/м3 поступает в левую полость цилиндра через дроссель с коэффициентом расхода μ=0.62 и диаметром d под избыточным давлением pн ; давление на сливе pс. Поршень гидроцилиндра диаметром D под действием разности давлений в левой и правой полостях цилиндра движется слева направо с некоторой скоростью v.
Требуется определить значение силы F, преодолеваемой штоком гидроцилиндра диаметром dш при движении его против нагрузки со скоростью v.
Дано : D=110 мм ; dш=55 мм ; d=2 мм ; pн=28 МПа ; pc=0.8 МПа ; v=5 см/с ; ρ=900 кг/м3 ; μ=0.62.
Найти : F.
Решение.
Силу, действующую на поршень определим, составив уравнение равновесия сил, действующих на поршень слева и справа :
F+pcS/=pрабS
или F+ ;
F+ (1)
где pраб – давление в левой полости цилиндра ; S – площадь поршня в левой полости ; pc – давление в правой полости ; S/ – площадь поршня в правой полости.
Используя формулу расхода при истечении из отверстия определим давление p2, под действием которого происходит истечение через дроссель. Это давление равно разности давлений на входе в дроссель и в левой полости цилиндра p2=pн-pраб :
Q= (2)
Расход через дроссель равен расходу через цилиндр и определяется по формуле :
Q=vS= (3)
где v – скорость движения поршня.
Приравнивая правые части уравнений (2) и (3), получим :
Отсюда находим давление в левой полости цилиндра :
pраб= (4)
С учётом (4) формула (1) примет вид :
Отсюда значение силы :
F= (5)
Вычисления по формуле (5) дают :
F= Н=7.5 кН
Ответ : F=7.5 кН.
Задача 3.
Определить давление, создаваемое насосом, если длины трубопроводов до и после гидроцилиндра, равны l ; их диаметры d ; диаметр поршня D ; диаметр штока dш ; сила на шток F ; подача насоса Q ; вязкость рабочей жидкости ν=0.5 см2/с ; плотность ρ=900 кг/м3.
Потери напора в местных сопротивлениях не учитывать.
Дано : l=13 м ; d=12 мм ; D=70 мм ; dш=40 мм ; F=2 кН ; Q=1. 7 л/с ; ν=0.5 см2/с ; ρ=900 кг/м3.
7 л/с ; ν=0.5 см2/с ; ρ=900 кг/м3.
Найти : pн.
Решение.
Давление, создаваемое насосом pн, затрачивается на преодоление потери давления Δp1 в подводящей линии и создание давления pп перед поршнем в цилиндре :
pн=Δp1+pп (1)
Необходимую величину давления перед поршнем pп найдём из условия равенства сил, действующих на поршень слева и справа :
pпSп=pш(Sп-Sш)+F
где pш – давление в цилиндре со стороны штока, равное потере давления в отводящей линии (pш=Δp2) ; Sп и Sш – соответственно площади поршня и штока.
Отсюда давление перед поршнем :
pп= (2)
С учётом (2) формула (1) примет вид :
pн= (3)
Скорость движения жидкости в подводящей линии :
v1= м/с.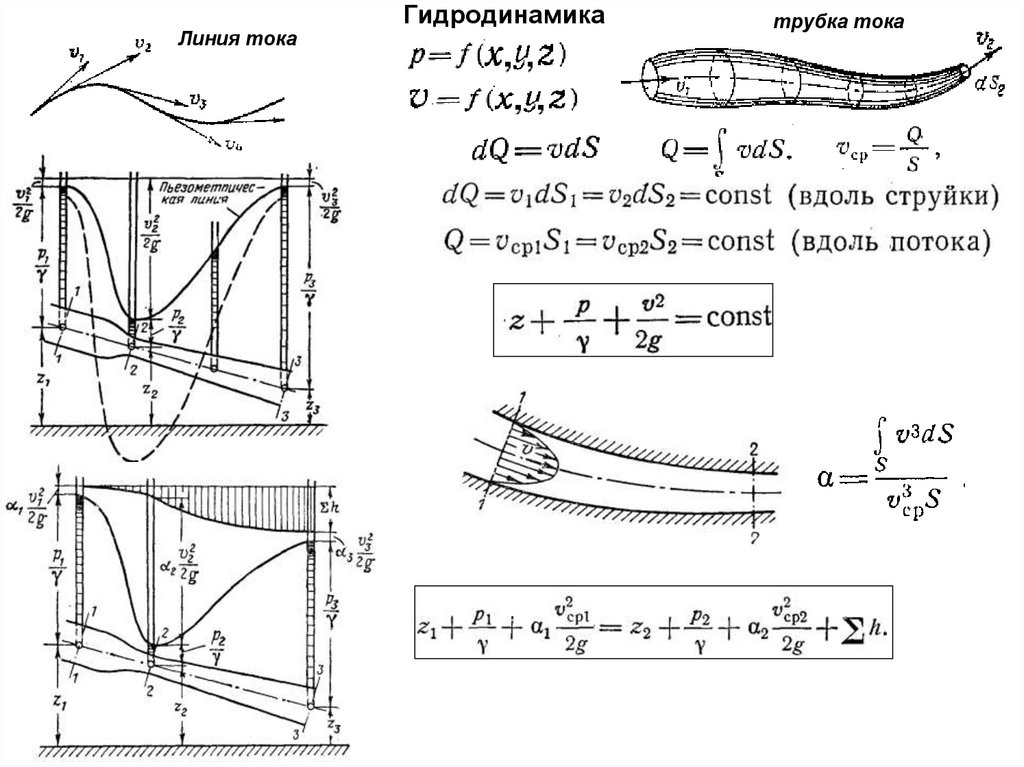
где S – площадь сечения подводящей линии.
Скорость перемещения поршня :
vп= м/с.
Расход жидкости, вытесняемой из штоковой области :
Qш=
= м3/с.
Скорость движения жидкости в отводящей линии :
v2= м/с.
где S – площадь сечения отводящей линии.
Числа Рейнольдса соответствующие скоростям движения жидкости v1 и v2 :
Re1= ; Re2=
Так как, полученные числа Re1 и Re2 больше критического Reкр=2320, то движение жидкости в обоих случаях будет турбулентным. Поэтому гидравлический коэффициент трения λ определяем по формуле :
λ1=0.3164/Re10.25=0.3164/36100.25=0.041 ; λ2=0.3164/Re20.25=0.3164/24190.25=0.045
Потери давления в подводящей линии :
Δp1= Па.
Δp2= Па.
Тогда вычисления по формуле (3), окончательно, дают :
pн= Па=6.5 МПа.
Ответ : pн=6.5 МПа.
Гидродинамика, теория и примеры задач
Общие понятия гидродинамики
Описывает взаимодействие жидкости (реального газа) с движущимися и неподвижными поверхностями.
Перемещение жидкости принципиально отличается от движения твердых тел. В своем движении жидкость не может сохранять неизменным расстояние между ее частицами. Если рассматривать движение элементарного объема жидкости, то его можно представить как сумму трех движений: поступательного и вращательного перемещения всего объема жидкости как целого, и движение разных частиц рассматриваемого объема по отношению друг к другу. При движении жидкости следует учитывать массовые силы и силы трения (вязкость).
Задачи гидродинамики
Жидкость, находящаяся в движении обычно характеризуется при помощи двух параметров: скорости течения () и гидродинамического давления (). Следовательно, к основным задачам гидродинамики относят определения этих параметров при известной системе действующих внешних сил.
В процессе движения жидкости и способны изменяться в зависимости от времени и точки в пространстве. При этом выделяют два типа движения жидкости установившееся и неустановившееся.
Движение, при котором и являются постоянными во времени для любой точки жидкости в пространстве и являются функция координат, называют установившимся. При неустановившемся течении скорость и давление являются функциями и от времени и от координат.
В гидродинамике используют понятие жидкой частицы. Это условно выделяемый элементарный объем жидкости, изменением формы которого можно пренебречь. Частица жидкости при своем движении описывает кривую, которая носит название траектории движения.
Потоком жидкости считают перемещающуюся массу жидкости, которая полностью или частично ограничена поверхностями. Эти поверхности могут образовываться самой жидкостью на фазовой границе или быть твердыми. Границы потоков – это стенки трубы, канала, поверхность, которую жидкость обтекает, открытая поверхность жидкости.
Небольшая сжимаемость жидкости позволяет во многих случаях полностью пренебречь изменением ее объема. Тогда говорят о несжимаемой жидкости. Это идеализация, которую часто используют. Говорят, что несжимаемая жидкость – предельный случай сжимаемой жидкости, когда для получения бесконечно больших давлений, достаточно бесконечно малых сжатий.
Жидкость, в которой при любом ее движении не возникают силы внутреннего трения, называют идеальной. Иначе говоря, в идеальной жидкости существуют только силы нормального давления, которые однозначно определяются степенью сжатия и температурой жидкости. Модель идеальной жидкости используют тогда, когда скорости изменения деформаций в жидкости малы.
Физическая величина, которая определяется нормальной силой, с которой жидкость действует на единицу площади поверхности, называют давлением ():
Давление при равновесии жидкости подчиняется закону Паскаля:
Давление в любой точке покоящейся жидкости одинаково во всех направлениях. Давление одинаково передается во всем объеме, которое жидкость занимает.
Сила давления на нижние слои жидкости больше, чем на верхние. Вследствие этого на тело, погруженное в жидкость (газ) действует выталкивающая сила, называемая силой Архимеда ():
где – плотность жидкости; – объем тела, погруженного в жидкость.
В состоянии равновесия жидкости (газа) давление () меняется в зависимости от плотности ( и температуры () и однозначно определено ими. Соотношение:
в состоянии равновесия называют уравнением состояния.
Основные уравнения равновесия и движения жидкостей
Силы, действующие в жидкости, обычно разделяют на массовые (объемные) и поверхностные. Примером массовых сил может служить сила тяжести. Обозначим – объемную плотность массовых сил. Поверхностные силы – это силы, которые действуют на каждый объем жидкости, благодаря нормальным и касательным напряжениям, действующим на его поверхности со стороны соседних частей жидкости.
Основным уравнением гидростатики является выражение:
Уравнение (4) показывает, что при равновесии жидкости плотность силы, действующая на единицу объема жидкости ( есть градиент скалярной функции. Это необходимое и достаточное условие консервативности плотности силы . Получается, что для равновесия жидкости надо, чтобы поле сил, в котором находится жидкость, было консервативным. В неконсервативных силовых полях равновесие не возможно.
В координатной форме формулу (4) запишем как:
Основным уравнением гидродинамики идеальной жидкости является выражение:
где ускорение жидкости в рассматриваемой точке. Уравнение (6) называется уравнением Эйлера.
Уравнением Бернулли получено швейцарским физиком Д. Бернулли в 1738 г. Это выражение закона сохранения энергии относительно установившегося течения идеальной жидкости:
где – статическое давление – давление жидкости на поверхности тела, которое она обтекает; — динамическое давление; — гидростатическое давление; — высота столба жидкости.
Графически движение жидкости изображают при помощи линий тока. Их проводят так, что касательные к ним совпадают по направлению с вектором скорости в соответствующих точках пространства. Жидкость, ограниченную линиями тока называют трубкой тока. При стационарном течении жидкости форма и расположение линий тока не изменяется.
Движение несжимаемой жидкости подчиняется уравнению неразрывности, которое записывают как:
и – сечения трубки тока.
Примеры решения задач
Гидравлика решение задач онлайн. Заказать решение задач по гидравлике онлайн
Спасибо за скорость и качество!
Понравилось обслуживание в личном кабинете на сайте. Все очень быстро, чётко. Отвечали оперативно на все мои вопросы и быстро подготовили решение. Мне нужно было не срочно получить задачки, до конца сессии просто сдать. Но получилось так, что я принесла все листики уже через пару дней!)
5,0 rating based on 521 ratingsСпасибо большое!
В работу вносятся правки, и это отлично! Мое счастье, что вовремя сообразила. В первый раз сдавала, препод не принял ответы без проставленных методов решения. Типа, надо объяснять, как я пришла к такому выводу. Написала менеджеру на сайте, вопрос был решен через день, добавили развернутые ответы.
5,0 rating based on 521 ratingsОоочень благодарна Вам!
Уважаемые сотрудника сайта. Я ооочень рада что Вы мне помогаете с учёбой. Постоянно у Вас заказываю решение по сопромату, термодинамике, матанализу и другим непонятным предметам))). Вообщем спасибо огромное, вы мне помогаете получить высшее образование. Еще хотелось бы Вас попросить о скидках ))
5,0 rating based on 521 ratingsЗаочникам тоже помогут! Спасибо
Пришлось сдать вступительные и начать учиться на заочке. Честно – я уже в возрасте и уделять время на учебу нет желания. Решил воспользоваться – написал на решаем онлайн, сотрудники быстро ответили, проконсультировали. Теперь заказываю решение задач только у них
5,0 rating based on 521 ratingsНа удивление недорого и качественно!
Только поступил на 1-ый курс. Наткнулся на проблему – никто не хотел мне помогать с учёбой и домашнем заданием. Решил обратиться к интернету. Очень долго искал подходящий сайт по решение домашних задач. Но везде очень много берут денег и не понятно за что. Самый недорогой сервис – решаем онлайн.
5,0 rating based on 521 ratingsЗаказываю все решения по эконом теории только в решаем онлайн
Что в школе, что в университете училась на пять. Но тут наткнулась на предмет, с который у меня ну ни как не выходит разобраться, а тем более понять. Тут у наших ребят подслушала, что решения по различным предметам заказывают, где то в сети. Обратилась и заказываю все решения по эконом теории у вас!
5,0 rating based on 521 ratingsУбедился в качественном сервисе 5+
Заказывал решение задач на разных сайтах. Постоянно были проблемы с выполнением. То преподаватели были не довольны, при этом мне не переделывали решение. То не вовремя скинут задачу и опять же не были довольны мной преподы. Наткнулся на сайт решаемонлайн – стал систематично заказывать только тут.
5,0 rating based on 521 ratingsСкорость и удобство порадовали
Меня смутило, что некуда приложить условия, на сайте только email и имя. Однако после открылся личный кабинет, где я нашла все нужые вкладки. Отправила фотографию с заданием и села ждать. Ответили моментально, прислали цену и сказали, что нашли автора. Я в восторге от скорости.
5,0 rating based on 521 ratingsМорока с Гражданским правом решена на отлично!
Работаю, воспитываю двоих детей одна. Параллельно учусь на заочке. Времени катастрофически не хватает ни на что. На учебе была на гране вылета из-за предмета гражданское право, накопилось много хвостов. Подружка посоветовала обратиться к ребятам из решаемонлайн. В общем они еще и диплом написали!
5,0 rating based on 521 ratingsСессия для Бухгалтера теперь без проблем ребята!)
Катастрофически не хватает времени! Учусь на бухгалтера и каждую сессию получаю эти пресловутые задачки. Спасибо вам за помощь с работами! Я всегда оформлялась за несколько дней до сдачи, чтобы успеть получить, проверить, распечатать и сдать. Радуют цены, т.к. за учебу итак плачу денежку немалую.
5,0 rating based on 521 ratingsКто не любит писать сочинения тогда вам сюда!
Очень люблю точные науки. С цифрами мне проще работать. Поэтому я поступил на физмат. Но оказывается весь первый курс у нас продолжают преподавать школьную программу по русскому языку и литературе. Ненавижу писать сочинения. Спасибо однокурснику – показал сайт на котором быстро, качественно!
5,0 rating based on 521 ratingsНезаменимые помощники!
После 9 класса поступил в колледж. Случайно узнал о сайте решаемонлайн – делают за тебя всю домашнюю работу быстро и не дорого. Одногруппники о таком сайте не знают. Стал всем ребятам предлагать помощь в домашнем задании, при этом перенаправляю на работников сайта!
5,0 rating based on 521 ratingsЗакрыл сессию на отлично благодаря Вам!
Спасибо вам, дорогие друзья, за помощь! Для меня было жизненно важно закрыть сессию и сдать все экзамены, чтобы получить стипендию. Но я вообще, ну никак не успевала сдать парочку задач по макроэкономике, списывать было не вариант. Мне решили все за один день, по демократичной цене!
5,0 rating based on 521 ratingsМастера на все руки!
Всю свою сознательную жизнь программировал на С++, а тут преподаватель задал задачку на языке Phynton. Не стал долго заморачиваться и написал ребятам из решаемонлайн – был очень удивлен когда они взялись за работу и через день прислали решение задачи. При этом денег практически не взяли!
5,0 rating based on 521 ratingsОперативный сервис!
На последних курсах просто некогда заниматься заданиями, которые выдаются на дом. Итак куча дел, а я должен видеть ночами и помимо основной работы и диплома писать задачки. Нашел сайт, где буду заказывать ответы для галочки, а получил настоящих друзей со скидками и супербыстрой реакцией! Спасибо!
5,0 rating based on 521 ratingsСпасибо! Очень выручили
Компьютер для меня – это настоящая черная дыра, умею только то, что делает среднестатистический пользователь. Задали сделать видео с музыкой из своих фоток, а я только накачала вирусов, пока искала программку. Посоветовали обратиться к специалистам, нашла ваш сайт. Спасибо за готовое задание!
5,0 rating based on 521 ratingsВаш выпускник!)
На втором курсе учиться очень сложно. Я не успевал ничего из-за новых предметов и жуткого расписания занятий. Именно тогда с вами познакомился и стал заказывать мелкие задачки, которые делать не хотелось (или попросту не хватало часов в сутках). Сейчас выпускаюсь и хочу сказать спасибо за поддержку
5,0 rating based on 521 ratingsОбратился впервые – компания не подвела!
На потоке знакомый подкинул идею – что бы самому не заморачиваться с выполнением задач по термодинамики, можно заказать где-то в интернете. Наткнулся на reshaemonline. Предоставил всю методичку, решения скидывают по мере необходимости, еще ни разу не подводили.
5,0 rating based on 521 ratingsТеперь матанализ не зло!
Мне нужно было срочно решить несколько задач по матанализу, иначе ждало отчисление. От безысходности полез в интернет и начал оставлять заявки везде, где предлагаются услуги помощи студентам. Тут мне ответили быстрее всех, я оформил заказ и получил файлик с готовым решением в этот же день. Спасибо!
5,0 rating based on 521 ratingsБольшое спасибо!
Медикам особенно тяжело учиться… я частенько обращаюсь за помощью, чтобы закрыть неважные предметы и уделить время учебе по специальности. Задачи по генетике – это зло, но мне не пришлось ими заниматься. 🙂 Я просто передал специалистам нежелаемые дела и получил море свободного времени для написания
5,0 rating based on 521 ratingsБлагодарю за помощь!
Медикам особенно тяжело учиться… я частенько обращаюсь за помощью, чтобы закрыть неважные предметы и уделить время учебе по специальности. Задачи по генетике – это зло, но мне не пришлось ими заниматься. 🙂 Я просто передал специалистам нежелаемые дела и получил море свободного времени для написания
5,0 rating based on 521 ratingsКак выбрать модель турбулентности для решения задач вычислительной гидродинамики?
Для моделирования турбулентных течений в пакете COMSOL Multiphysics® реализованы несколько моделей турбулентности: L-VEL, yPlus, Спаларта-Аллмараса, k-ε, k-ω, низкорейнольдсовая k-ε, SST и v2-f. Все эти модели доступны при использовании модуля «Вычислительная гидродинамика» (CFD Module), а модели L-VEL, yPlus, k-ε и низкорейнольдсовая k-ε доступны также при использовании модуля «Теплопередача» (Heat Transfer Module). В настоящей статье рассматриваются вопросы, связанные с выбором и эффективной реализацией модели турбулентности.
Первая редакция статьи была опубликована в 2013 году. Материал был обновлен после выхода COMSOL® версии 5.3, поскольку в модуль «Вычислительная гидродинамика» была добавлена новая модель турбулентности.
Описание турбулентности. Краткое введение
Рассмотрим задачу об обтекании плоской пластины потоком жидкости (см. рисунок). На поверхности пластины, начиная от передней кромки, формируется пограничный слой — область течения, в которой происходит основное изменение скорости жидкости. На передней части пластины течение в погранслое ламинарное. Профиль скорости в этой области легко рассчитать. Но начиная с некоторого расстояния от передней кромки малые хаотические возмущения в потоке усиливаются, в результате чего поток теряет устойчивость, и режим течения в погранслое меняется с ламинарного на переходный, а затем и на турбулентный.
Переход между тремя режимами течения в погранслое определяется числом Рейнольдса, Re=\rho v L/\mu, где \rho — плотность жидкости, v — скорость, L — характерный линейный размер (в данном случае, расстояние от передней кромки пластины) и \mu — динамический коэффициент вязкости. Будем рассматривать течение ньютоновской жидкости, то есть такой жидкости, вязкость которой не зависит от скорости сдвига. Многие важные для инженерной практики жидкости и газы, в том числе вода и воздух, являются ньютоновскими. Плотность жидкости может зависеть от давления, однако будем считать, что жидкость несжимаемая, то есть число Маха для рассматриваемого потока не превышает 0.3. Параметр Weakly compressible flow (Слабо сжимаемая жидкость) в настройках гидродинамических интерфейсов COMSOL Multiphysics позволяет пренебречь зависимостью плотности среды от давления и волн сжатия.
При ламинарном режиме течения поле скорости может быть найдено из решения стационарных уравнений Навье-Стокса, которые описывают распределение скорости и давления в потоке жидкости. Можно предположить, что скорость жидкости не изменяется во времени, и получить точное описание характеристик потока. В качестве примера можно привести решение задачи Блазиуса о ламинарном течении в пограничном слое. Когда поток начинает переходить к турбулентности, в потоке появляются колебания, несмотря на то, что скорость потока на входе не меняется со временем. Предположение о том, что характеристики течения не зависят от времени, больше не применимо. В этом случае, необходимо решать нестационарную задачу, а расчетная сетка должна быть достаточно мелкой, чтобы на ней можно было разрешить (описать) самые мелкие вихри, образующиеся в потоке, то есть размер элементов сетки должен быть сопоставим с размером самых мелких вихрей. Примером подобной задачи является учебная модель обтекания горизонтального цилиндра. Отметим, что течение нестационарно, но при этом все еще сохраняется ламинарных режим течения. Для решения стационарных и нестационарных задач о ламинарном течении дополнительные модули не требуются, достаточно только базового модуля COMSOL Multiphysics.
С ростом числа Рейнольдса характерный размер вихревых структур в потоке уменьшается, а временной масштаб пульсаций скорости и давления становится столь коротким, что численное решение уравнений Навье-Стокса для большинства практических задач практически невозможно. Для описания таких режимов течения мы можем использовать осредненные по Рейнольдсу уравнения Навье-Стокса (уравнения Рейнольдса, RANS), в которых мгновенные значения скорости u представлены в виде суммы пульсационной u’ и осредненной по времени U составляющих. В одно- и двухпараметрических моделях вводятся дополнительные уравнения переноса для характеристик турбулентности, одной из которых является кинетическая энергия (переменная k в k-ε и k-ω моделях турбулентности).
В алгебраических моделях используются алгебраические уравнения для турбулентной вязкости, описывающие ее зависимость от поля осредненной скорости и, в некоторых случаях, расстояния от твердых стенок. Найденные значения турбулентных переменных затем используются для расчета турбулентной (вихревой) вязкости, котороая прибавляется к молекулярной вязкости жидкости. Импульс, который мог бы переноситься малыми вихревыми структурами, наоборот, диссипирует за счет вязких эффектов. Турбулентная диссипация обычно превосходит вязкую диссипацию во всех области течения, за исключением вязкого подслоя вблизи твердых стенок. Модель турбулентности должна описывать непрерывное снижение степени турбулентности потока по мере приближения к стенке, как это делают низкорейнольдсовые модели. Либо должны быть рассчитаны новые граничные условия с помощью пристеночных функций.
Низкорейнольдсовые модели турбулентности
Название “низкорейнольдсовая модель турбулентности” может показаться противоречивым, поскольку турбулентный режим течения наблюдается только при достаточно высоких значениях числа Рейнольдса. Однако термин “низкорейнольдсовая” относится не ко всей области течения, а только к пристеночной области, где доминируют вязкие эффекты, то есть к области вязкого подслоя, показанного на рисунке выше. Низкорейнольдсовая модель турбулентности — это модель, которая позволяет корректно рассчитать асимптотическое поведение различных характеристик потока, когда расстояние от стенки стремится к нулю. Например, низкорейнольдсовая модель должна описывать зависимость кинетической энергии турбулентности от расстояния от стенки как k~y2 при y→0. Корректная асимптотика означает, что модель турбулентности может использоваться для расчета течения по всей толщине погранслоя, в том числе в вязком подслое и буферном слое.
Почти все модели, содержащие уравнение для ω, являются низкорейнольдсовыми по определению. Однако стандартная и другие распространенные формулировки k-ε модели не являются низкорейнольдсовыми. Тем не менее некоторые из них могут быть дополнены так называемыми демпфирующими функциями, которые позволяют дают корректную ассимптотику. Такие модели называются низкорейнольдсовыми k-ε моделями.
Зачастую низкорейнольдсовые модели позволяют очень точно рассчитать течение в погранслое. Для разрешения значительных градиентов вблизи стенки, однако, требуется очень плотная расчетная сетка, что, в свою очередь, приводит к повышенным требованиям к вычислительным ресурсам. По этой причине для расчета течения вблизи твердых стенок при решении инженерных задач часто используются альтернативные методы.
Пристеночные функции
В турбулентном погранслое у плоской твердой поверхности можно выделить четыре характерных области. Непосредственно на стенке скорость жидкости равна нулю, а в очень тонком слое у стенки скорость линейно зависит от расстояния от стенки. Этот слой называется вязким или ламинарным подслоем. За ним следует область, которая называется буферным слоем. В этой области начинается переход к турбулентности, а заканчивается этот слой областью развитой турбулентности, где средняя скорость течения определяется логарифмической зависимостью от расстояния от стенки. Эта часть турбулентного погранслоя называется областью логарифмического закона. При дальнейшем удалении от стенки мы переходим в область свободного течения. Вязкий и буферный слои очень тонкие. Если обозначить их суммарную толщину как \delta, то толщина области логарифмического закона составит приблизительно 100\delta.
Уравнения Рейнольдса можно использовать для расчета поля скорости во всех четырех областях турбулентного погранслоя. Однако, так как толщина вязкого и буферного слоев очень мала, решить уравнения в области этих слоев может быть крайне затруднительно. С помощью использования пристеночных функций можно отказаться от решения уравнений Рейнольдса в буферной области и аналитически рассчитать скорость вблизи стенки. Таким образом, мы должны иметь аналитическое выражение для расчета скорости в вязком подслое, тогда требования к вычислительным ресурсам, необходимым для решения уравнений Рейнольдса, можно существенно снизить. Данный подход очень полезен для решения многих инженерных задач.
В случае, когда необходима более высокая точность решения, превосходящая точность пристеночных функций, нужно использовать модель турбулентности, которая позволяет рассчитать характеристики потока во всей области течения, как это позволяют сделать, например, низкорейнольдсовые модели турбулентности, упомянутые выше. Например, если нужно определить силу сопротивления и подъемную силу, действующие на объект, или рассчитать теплообмен между жидкостью и стенкой.
Автоматический выбор модели для пристеночной области
Автоматический выбор модели пристеночной области, реализованный в COMSOL Multiphysics версии 5.3, объединяет достоинства обоих подходов — низкорейнольдсовых моделей и пристеночных функций. Автоматический выбор модели пристеночной области адаптируется под имеющуюся расчетную сетку, обеспечивая, таким образом, и устоцчивость, и точность расчета. К примеру, для грубой погранслойной сетки при использовании автоматического выбора модели пристеночной области будет задействованы пристеночные функции. Если же сетка в пределах погранслоя достаточно плотная, автоматический выбор будет сделан в пользу низкорейнольдсовой модели для расчета поля скорости непосредственно во всей области течения вплоть до самой стенки.
Переход от низкорейнольдсовой формулировки к пристеночным функциям осуществляется непрерывно и гладко. Алгоритмы, реализованные в программном обеспечении, “склеивают” две формулировки на погранслойных элементах сетки. Рассчитывается расстояние узлов погранслойных элементов сетки от стенки (в безразмерных единицах). Затем в качестве граничного условия используется комбинированная формулировка модели турбулентности.
Все физические интерфейсы расчета турбулентных течений, реализованные в COMSOL Multiphysics, за исключением интерфейса страндартной k-ε модели, поддерживают возможность автоматического выбора модели пристеночной области. Таким образом, теперь для решения инженерных задач можно использовать низкорейнольдосовые модели, при этом их собственно низкорейнольдсовые формулировки будут реализованы только если разрешение расчетной сетки будет достаточным.
Коротко о различных моделях турбулентности
Восемь моделей турбулентности, основанные на использовании уравнений Рейнольдса, различаются подходами к описанию течения в пристеночной области, количеством и физическим смыслом дополнительных неизвестных переменных, определяющих характеристики турбулентного течения. Во всех этих моделях в уравнениях Навье-Стокса появляется дополнительное слагаемое для турбулентной вихревой вязкости, однако рассчитывается это слагаемое в разных моделях по-разному.
L-VEL и yPlus
Алгебраические модели турбулентности L-VEL и yPlus позволяют рассчитать коэффициент турбулентной вязкости в зависимости от локальной скорости жидкости и расстояния от стенки. Никаких дополнительных уравнений переноса в этих моделях решать не требуется. При этом они могут использоваться для расчета всей области течения. Из всех восьми перечисленных моделей они отличаются наибольшей устойчивостью и самой низкой требовательностью к вычислительным ресурсам. Несмотря на то, что это наименее точные модели, полученные с их помощью результаты являются хорошим приближением для внутренних течений, особенно в задачах расчета охлаждения электронного оборудования.
Модель Спаларта-Аллмараса
Эта модель относится к классу однопараметрических моделей турбулентности. Здесь появляется только одно дополнительное уравнение для расчета кинематического коэффициента вихревой вязкости. Это низкорейнольдсовая модель, которая описывает всю область течения, включая пристеночные слои. Изначально модель была предложена для решения аэродинамических задач. Ее выгодно отличают относительно хорошая устойчивость и надежность, а также не слишком высокие требования к плотности расчетной сетки. Опыт показывает, что данная модель не очень хорошо описывает сдвиговые и отрывные течения, а также затухание турбулентности. Преимуществом этой модели является ее устойчивость и хорошая сходимость.
k-ε модель турбулентности
В k-ε модели турбулентности записываются два дополнительных уравнения для расчета кинетической энергии турбулентности k и скорости диссипации кинетической энергии ε. Буферный слой не моделируется, для расчета скорости у стенки используются пристеночные функции. Благодаря быстрой сходимости и относительно низким требованиям к объему памяти k-ε модель очень популярна при решении промышленных задач. Она не очень точна при моделировании течений с положительным градиентом давления, струйных течений и течений в области с сильно искривленной геометрией. Модель хорошо подходит для решения задач внешнего обтекания тел сложной геометрической формы. Например, k-ε модель можно использовать для моделирования потока вблизи плохо обтекаемого тела.
Модели турбулентности, перечисленные ниже, отличаются более высокой степенью нелинейности по сравнению со стандартной k-ε моделью, и поэтому зачастую в расчетах на основе этих моделей бывает трудно добиться сходимости, если только не воспользоваться хорошим начальным приближением. Результаты расчета, полученные с помощью стандартной k-ε модели, могут послужить таким начальным приближением. Решите задачу, используя стандартную k-ε модель, а затем воспользуйтесь новым инструментом «Настроить новый интерфейс турбулентного течения» (Generate New Turbulence Interface), который появился в модуле «Вычислительная гидродинамика» пакета COMSOL Multiphysics версии 5.3.
k-ω модель турбулентности
Модель k-ω похожа на k-ε, только здесь решается уравнение для удельной скорости диссипации кинетической энергии ω. Эта модель относится к низкорейнольдсовым, но она также может быть использована совместно с пристеночными функциями. Она отличается более высокой степенью нелинейности, а потому хуже сходится, чем стандартная k-ε модель, а кроме того, достаточно чувствительна к начальному приближению. Использование k-ω модели дает хорошие результаты в тех задачах, где k-ε модель недостаточно точна, например, при моделировании внутренних течений, течений по сильно искривленным каналам, отрывных и струйных течений. Хорошим примером применения k-ω модели является задача о течении жидкости через колено трубопровода.
Низкорейнольдсовая k-ε модель
В отличие от стандартной k-ε модели в низкорейнольдсовой модификации этой модели пристеночные функции не используются; модель применима ко всей области течения. Она является логическим продолжением стандартной k-ε модели и сохраняет многие ее преимущества, однако для ее реализации, как правило, требуется более плотная расчетная сетка, причем не только в пристеночной области, но везде, где низкорейнольдсовые свойства играют роль и подавляют турбулентность. Часто рекомендуется использовать стандартную k-ε модель для расчета хорошего начального приближения для решения уравнений низкорейнольдсовой модели. Альтернативой может стать использование автоматического выбора модели пристеночной области и последовательное измельчение сетки в погранслое в ключевых зонах расчетной области.
С помощью низкорейнольдсовой k-ε модели расчет силы сопротивления и подъемной силы, а также плотности теплового потока может быть выполнен с более высокой точностью, чем при использовании стандартной k-ε модели. В некоторых случаях эта модель также дает хорошие результаты моделирования отрыва и повторного присоединения потока.
SST-модель
SST-модель представляет собой комбинацию k-ε и k-ω моделей турбулентности: для расчета течения в свободном потоке используются уравнения k-ε модели, а в области вблизи стенок — уравнения k-ω модели. Это низкорейнольдсовая модель, которая стала своего рода стандартом для инженерных приложений. Требования к плотности сетки здесь те же, что и у k-ω модели и низкорейнольдсовой k-ε модели, однако эта модель лишена некоторых недостатков исходных k-ω и k-ε моделей. В учебной модели для расчета обтекания крылового профиля NACA 0012 используется SST-модель турбулентности. Полученные результаты хорошо согласуются с экспериментальными данными.
v2-f модель турбулентности
Около твердых стенок интенсивность флуктуаций скорости в направлении по касательной к стенке обычно намного превышает интенсивность флуктуаций в направлении по нормали к стенке. Другими словами, флуктуациям скорости свойственна анизотропия. По мере удаления от стенки интенсивность флуктуаций во всех направлениях становится одинаковой. Флуктуации скорости становятся однородными или изотропными.
Анизотропия турбулентных флуктуаций в погранслое описывается v2-f моделью турбулентности за счет введения двух дополнительных уравнений, решаемых совместно с уравнениями для кинетической энергии турбулентности (k) и скорости диссипации кинетической энергии (ε). Первое дополнительное уравнение описывает перенос турбулентных флуктуаций скорости в направлении по нормали к линиям тока. Второе уравнение учитывает нелокальные эффекты, а именно обусловленное стенкой демпфирование перераспределения кинетической энергии между нормальным и касательным направлениями.
Эту модель следует использовать для расчета внутренних течений в системах с искривленными границами, например, при моделировании циклонов-сепараторов.
Некоторые замечания о расчетной сетке
Решение любых гидродинамических задач, будь то задачи о ламинарном или турбулентном течениях, требуют значительных вычислительных ресурсов. Как правило, моделирование проводится на относительно плотных расчетных сетках и требует решения уравнений для многих переменных. Даже при использовании очень быстрого компьютера с большим объемом оперативной памяти решение подобных задач для крупных трехмерных моделей может занимать много времени — от нескольких часов до нескольких дней. Поэтому, желательно использовать как можно более простую сетку, которая, тем не менее, сохраняет все детали моделируемого течения.
Если вернуться к самому первому рисунку этой статьи, можно увидеть, что для плоской пластины (а также для большинства гидродинамических задач) интенсивность изменения скорости в поперечном (по нормали к поверхности) направлении намного превышает интенсивность изменения скорости в продольном направлении (по касательной к поверхности), особенно в области буферного слоя. Это наблюдение позволяет нам использовать погранслойную сетку. Данный тип сеток (который используется по умолчанию при активации автоматических, адаптированных к физической модели, алгоритмов построения сетки) состоит из тонких четырехугольников (в двумерном случае) или треугольных призм (в трехмерном случае) вблизи стенки. Данный тип сильно вытянутых конечных элементов хорошо подходит для разрешения изменения скорости течения в направлении по нормали к поверхности, при этом позволяет сократить количество расчетных узлов в продольном направлении.
Погранслойная сетка (выделена пурпурным цветом) вокруг крылового профиля и треугольная сетка (выделена голубым цветом) для двумерной задачи.
Погранслойная сетка (выделена пурпурным цветом) вокруг плохо обтекаемого тела и тетраэдральная сетка для трехмерной задачи.
Анализ результатов моделирования турбулентности
После получения результатов моделирования с помощью той или иной выбранной модели турбулентности естественно возникает желание удостовериться в том, что полученное решение верно. Конечно, как и при решении любой другой задачи, можно проводить расчет на сетках разной плотности и следить за изменением результатов. Как только решение перестанет меняться в зависимости от параметров сетки в пределах требуемой точности, можно считать, что параметры сетки заданы оптимально. Тем не менее, есть некоторые дополнительные параметры, которые следует отслеживать при моделировании турбулентности.
Если используется модель с пристеночными функциями, желательно контролировать значение безразмерного расстояния сеточных узлов от стенки (этот график добавляется в результаты автоматически). Эта величина позволяет определить, как далеко расчетная область отдалена от стенки, и значение этой величины не должно быть слишком велико. В случае, если в некоторых зонах расчетной области безразмерное расстояние от стенки превышает несколько сотен, следует увеличить плотность сетки в направлении по нормали к стенке. Вторая величина, которую нужно контролировать при использовании пристеночных функций — это расстояние от стенки, выраженное в размерных единицах. Эта величина связана с предполагаемой толщиной вязкого подслоя и должна быть достаточно малой по сравнению с характерным линейным масштабом расчетной области. В тех областях, где это условие не выполняется, сетку необходимо сделать более плотной.
Максимальное безразмерное расстояние от стенки меньше 100, поэтому нет необходимости увеличивать плотность сетки в погранслое.
При решении задач с помощью одной из низкорейнольдсовых моделей без использования автоматического выбора модели пристеночной области контролируйте величину безразмерного расстояния от стенки до центра ячейки, график для которой также создается автоматически. Для алгебраических моделей значение этой величины должно быть порядка единицы во всей расчетной области, а для двухпараметрических моделей и v2-f модели значение не должно превышать 0.5. Необходимо увеличить плотность сетки в тех зонах расчетной области, где эти условия не выполняются.
Заключительные примечания
В этой статье обсуждались различные модели турбулентности, реализованные в пакете COMSOL Multiphysics, и были даны некоторые рекомендации по использованию этих моделей в задачах вычислительной гидродинамики. Настоящая сила пакета COMSOL® заключается в том, что с его помощью можно комбинировать моделирование течения жидкости с решением других физических задач, например, расчетом механических напряжений, возникающих в солнечной панели при сильном ветре, моделированием вынужденной конвекции в теплообменных аппаратах или расчетом массопереноса в устройствах смешения и т.п.
Если Вы заинтересовались применением пакета COMSOL Multiphysics® для решения задач вычислительной гидродинамики и мультифизического моделирования, или у Вас возникли вопросы, которые здесь не обсуждались, пожалуйста, напишите нам.
Решение задач по гидравлике. Помощь c работами по гидравлике онлайн на Mentro24
Коротко об услуге
Ментор24 > Заказать Решение задач по гидравлике
Гидравлика – наука, которая изучает законы движения, равновесие жидкостей, а также способы применения получаемых результатов на практике (например, при решении задач инженерного характера). Эта вузовская дисциплина – не проходящий предмет, а один из основных, поэтому заучиванием теории наизусть знакомство с ней не ограничится. Решение задач по гидравлике – важный этап, на котором преподаватель проверяет, насколько студенты усвоили материал. Тут у многих возникают трудности. Во-первых, одно дело – материал выучить и совсем другое – его понимать. Во-вторых, большинство студентов любит отложить решение задач по гидравлике на потом, вспоминая про них накануне сессии. Тогда приходится выбирать: все бросать и садиться за решение или спокойно готовиться к экзаменам, доверившись специалистам. Не хотите лишиться стипендии и получить отличные оценки по предмету? Мы поможем!
Решение задач по гидравлике любой сложности
Гидравлика – предмет не только сложный, но и разнообразный. Если одну тему вы усвоили хорошо и уверены в своих силах, то по другой можете “плавать” или вовсе не понимать ничего. Наши авторы готовы решить за вас самые разные задачи по гидравлике и разделам (гидродинамике, гидростатике):
- на определение режимов течения,
- на выявление физических свойств жидкостей,
- на истечение жидкостей и газов из отверстий и насадок,
- по расчетам трубопроводов,
- по подбору насосных установок и т.д.
Пускай вы сами не будете участвовать в процессе, исполнитель mentor24.ru проконсультирует вас, объяснит все непонятные моменты, и впоследствии вы сможете решать задачи сами по аналогии с готовым решением. Сотрудничество с нами принесет вам разгрузку во время сессии и гарантирует отличные оценки. Мы тщательно следим за выполнением заказов и осуществляем решение задач по гидравлике “под ключ”: вы размещаете заказ, а дальше все делает выбранный вами специалист – решает задачи в строго оговоренные сроки, вносит коррективы при необходимости и сопровождает заказ до защиты.
Задачи гидродинамики – Энциклопедия по машиностроению XXL
Значительное упрощение исходных уравнений, описывающих движение идеальной жидкости в случаях, когда имеют место интегралы уравнений движения, открывает широкие возможности для решения конкретных задач гидродинамики. [c.256]В общем случае задачей гидродинамики является определение скоростей и давлений для данного момента времени в любых точках пространства, через которое проходит поток жидкости (метод Эйлера), или для отдельных ( отмеченных ) частиц жидкости, заданных начальными параметрами (метод Лагранжа). Последующее решение задач технической гидродинамики осуществляется по методу Эйлера, причем в ряде случаев задача сводится к одноразмерной с введением необходимых поправок. [c.70]
Обтекание тел потоком жидкости или газа, как уже указывалось, является одной из основных задач гидродинамики и аэродинамики ). Мы начнем рассмотрение этих задач с простейшего случая обтекания цилиндра, ось которого перпендикулярна к потоку. При этом мы пока ограничимся задачами, в которых силами вязкости можно пренебречь (когда соблюдены условия, приведенные в 125). Для цилиндра, расположенного перпендикулярно к потоку жидкости, опыт дает изображенную на рис. 324 картину распределения токовых линий в потоке, обтекающем цилиндр. Поскольку мы пренебрегли вязкостью, то для потока справедлив закон Бернулли. Согласно этому закону в точке А, где скорость потока близка к нулю, давление в жидкости [c.545]
Задачи гидродинамики вязко жидкости решаются обычно приближенно путем отбрасывания в уравнениях Навье — Стокса членов, которые в тех или иных конкретных условиях могут быть малы по сравнению с другими членами. [c.69]
Ввиду невозможности получить точное решение уравнений Навье — Стокса и уравнения энергии для подавляющего большинства задач гидродинамики и газовой динамики прибегают либо к приближенным решениям, либо к экспериментам на моделях. В последнем случае возникает вопрос об условиях подобия для обтекания натурного объекта и его модели. [c.75]
Как показывают многочисленные эксперименты, механизм действия сил сопротивления существенно различен при разных граничных условиях и разных режимах движения жидкости. В этой главе рассмотрены основные закономерности сопротивлений, которые возникают в потоках, ограниченных твердыми стенками (внутренняя задача гидродинамики). [c.138]
Решение общей задачи гидродинамики наталкивается на математические трудности. Большое значение поэтому приобретает получение из уравнений движения некоторых частных соотношений, устанавливающих связи между параметрами движения, [c.92]
В этой главе рассмотрены основные закономерности сопротивлений, которые возникают в потоках, ограниченных твердыми стенками (внутренняя задача гидродинамики). [c.151]
Следует, однако, иметь в виду, что течений жидкости, строго отвечающих условиям потенциальности, в природе и технике не встречается. Представление о безвихревом характере движения является идеализацией, которая лишь с большей или меньшей степенью достоверности воспроизводит отдельные классы реальных течений. И тем не менее эта идеализация имеет важнейшее не только теоретическое, но и прикладное значение. Оно обусловлено тем, что вязкость жидкости, являющаяся первопричиной (для несжимаемой жидкости единственной) возникновения вихрей, проявляется, как правило, в ограниченных областях вблизи твердых поверхностей или в относительно узкой полосе за обтекаемым телом. В остальной части потока его завихренность может оказаться настолько малой, что поток можно считать потенциальным. Разумеется, встречается немало случаев, когда поток является сплошь завихренным и ни в какой его части влияние вязкости нельзя считать малосущественным. Такой поток может быть рассчитан только методами теории вязкой жидкости. Однако в тех случаях, когда допущение о потенциальности обосновано, его использование может значительно облегчить решение основной задачи гидродинамики. К числу таких случаев относится, например практически важная задача об обтекании твердых тел безграничным потоком (так называемая внешняя задача гидроаэродинамики). [c.225]
Идея Жуковского заменить крыло одним или несколькими присоединенными вихрями, неподвижно связанными с крылом и создающими в потоке такую же циркуляцию скорости по любому замкнутому контуру, какую в действительности создает крыло, позволяет решать многие практические задачи гидродинамики крыла бесконечного размаха. [c.161]
Очень важным для решения задач гидродинамики и вынужденной конвекции является безразмерный комплекс, показывающий [c.179]
В большинстве задач гидродинамики (внешнее обтекание тел, движение жидкостей и газа в трубах и др.) величины давления и скорости в любой точке потока однозначно определяются числом Re. Следовательно, число Ей в этих случаях не является критерием подобия и его значение полностью зависит от других чисел подобия. Например, при движении жидкости в трубах число Ей представляет собой безразмерную величину сопротивления и зависит лишь от числа Re [c.229]
Основной задачей гидродинамики является изучение законов движения жидкости. В гидродинамике широко используется понятие об идеальной жидкости. Решения, полученные для идеальной жидкости, применяются и для реальной с внесением необходимых поправок на ее свойства — в первую очередь на вязкость, а также иногда и на сжимаемость. Исследования в области гидродинамики заключаются преимущественно в нахождении основных величин — скоростей течения и давлений, возникающих в движущейся жидкости. [c.64]
Как указывалось выше, основной задачей гидродинамики является изучение движения жидкости, характеризующегося скоростями движения частиц и давлением в различных точках потока. [c.72]
В различных точках движущейся жидкости в результате действия внешних сил возникает давление, называемое гидродинамическим в отличие от гидростатического, свойственного жидкости, находящейся в равновесии, Поэтому одной из задач гидродинамики является определение величин гидродинамического давления, возникающего внутри жидкости, а также скоростей движения жидкости в различных точках пространства, занятого движущейся жидкостью. Для решения этих задач необходимо составить уравнения движения жидкости, связывающие между собой скорости и ускорения с силами, действующими на жидкость. Рассмотрим движение элементарного жидкого тела в виде параллелепипеда, выделенного в потоке идеальной жидкости (рис. 3.8). Введем следующие обозначения р — гидродинамическое давление и — скорость движения жидкости в точке пространства с координатами х, у, z и , и — составляющие скорости и по осям координат (рис. 3.8). [c.72]
Достаточно удовлетворительно подтвержденное опытом теоретическое решение задачи гидродинамики удавалось найти только в тех случаях, когда было возможно пренебречь силами трения по сравнению с другими силами, определяющими динамику рассматриваемого потока (силой тяжести, силой давления). [c.9]
Такой подход к исследованию задач гидродинамики позволил получить вполне удовлетворительные теоретические зависимости, раскрывающие закономерности сопротивлений, возникающих при обтекании тел (крыла и фюзеляжа самолета, лопатки турбины, кораблей различных форм и т. д.) жидкостью, и найти ряд эффективных решений этих задач. [c.10]
Гидродинамика рассматривает законы движения жидкости. Скорость и давление — параметры, характеризующие движение, изменяются в потоке жидкости в пространстве и во времени. Основная задача гидродинамики состоит в исследовании изменения этих параметров. [c.25]
Две разных задачи гидродинамики. Рассматривая движущуюся жидкость, различают [c.71]
При движении потока реальной жидкости происходят потери напора, так как часть удельной энергии потока затрачивается на преодоление различных гидравлических сопротивлений. Количественное определение этих потерь напора является одной из важнейших задач гидродинамики, без решения которой невозможно использование уравнения Бернулли для конкретных инженерных задач. [c.57]
Наличие потенциала скоростей существенно облегчает решение математических задач гидродинамики и в то же время потенциальные течения представляют собой очень важный ( )изический класс течений. [c.153]
Определение истинных значений параметров двухфазного потока в различных сечениях канала является одной из основных задач гидродинамики. Без этих величин нельзя рассчитать теплопередачу и, следовательно, выбрать необходимые параметры сред и размеры поверхностей теплообмена, определить сопротивления на различных участках течения потока, [c.20]
Таким образом, задачи гидродинамики и методы их исследования играют роль более широкую, чем только исследование движения жидкостей и газов, что и выдвигает гидродинамику в разряд общетеоретических дисциплин наряду с другими частями кпяссиче-ской механики. [c.276]
Общая задача гидродинамики состоит в отыскании функции Л1 Иу. г1 Р Р и р с помощью СИСТ6МЫ уравнений Навье—Стокса (5-8) или (5-9), уравнения неразрывности (2-14) или (2-17) и дополнительных соотнощений, замыкающих систему. [c.91]
Вместе с тем, чтобы упростить решение задач гидродинамики, здесь вводят особое понятие – понятие г идродинамического давления в точке р, и условно считают, что р в данной точке движущейся реальной жидкости, являясь также скалярной величиной (как и в гидростатике), не зависит от ориентировки площадки действия и равняется [c.69]
Общий подход к решению задач гидродинамики состоит, в следзпощем. При осесимметричной постановке и предположении о постоянстве физических свойств среды вводятся в рассмотрение. функция тока ф и азимутальная составляющая вихря со согласно уравнениям [c.99]
Динамика жидкости – AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Гидродинамика – проблемы и решения Решенные задачи по фундаментальной физике
СТАТЬИ На главную »Решенные задачи по основам физики» Динамика жидкости – проблемы и решения Гидродинамика – проблемы и решения
Теорема Торричелли
- Емкость, наполненная водой и имеющая отверстие, как показано на рисунке ниже.Если ускорение свободного падения составляет 10 м / с, какова скорость воды через это отверстие? Известный : Высота (h) = 85 см – 40 см = 45 см = 0. метры
Ускорение свободного падения (g) = 10 м / с 2 Разыскивается: скорость воды (v) Решение : Теорема Торричелли утверждает, что вода покидает отверстие с той же скоростью, что и объект. свободное падение с одинаковой высоты. Высота (h) = 85 см – 40 см = 45 см = 0,45 метра Скорость воды рассчитывается по уравнению свободного падения:
vt 2 = 2 г в час
vt 2 = 2 г h = 2 (10) (0.45) = 9 vt = √9 = 3 м / с
Чтение: определение результата в линейном векторе
- Емкость, наполненная водой и имеющая отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 м / с, какова скорость воды через это отверстие. Известный : Высота (h) = 1,5 м – 0,25 м = 1,25 метра
Ускорение свободного падения (g) = 10 м / с 2 Разыскивается: скорость воды (v) Решение:
vt 2 = 2 г h = 2 (10) (1,25) = 25 vt = √25 = 5 м / с
СТАТЬИ Уроки физики (103) Решенные задачи по основам физики (246)
- Емкость, наполненная водой, с отверстием, как показано на рисунке ниже.Если ускорение свободного падения составляет 10 м / с, какова скорость воды через это отверстие. Известный : Высота (h) = 1 м – 0,20 м = 0,8 метра
Ускорение свободного падения (g) = 10 м / с 2 Разыскивается: скорость воды (v) Решение:
vt 2 = 2 г h = 2 (10) (0,8) = 16 vt = √16 = 4 м / с
Прочтите: Первый закон термодинамики – проблемы и решения
- Емкость, наполненная водой и имеющая отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 м / с, какова скорость воды через это отверстие.Известный : Высота (h) = 20 см = 0,2 метра
Ускорение свободного падения (g) = 10 м / с 2 Разыскивается: скорость воды (v) Решение:
- Емкость, наполненная водой, с двумя отверстиями, как показано на рисунке ниже. Какое отношение x1 к x2? Решение
Интервал времени свободного падения воды из скважины 1:
ч = 1/2 а т 2
0,8 = 1/2 (10) т 2
0,8 = 5 т 2
т 2 = 0,8 / 5 = 0. t = 0,4 секунды Интервал времени свободного падения воды из лунки 2:
ч = 1/2 а т 2
0.5 = 1/2 (10) т 2
0,5 = 5 т 2
т 2 = 0,5 / 5 = 0. t = √0,1 секунды
- Вода течет по трубе разного диаметра, как показано на рисунке ниже. Если область 1 (A 1) = 8 см 2, A 2 = 2 см 2 и скорость воды в трубе 2 = v 2 = 2 м / с, тогда какова скорость воды в трубе 1 = v 1. Известно:
Площадь 1 (A 1) = 8 см 2
Площадь 2 (A 2) = 2 см 2 Скорость воды в трубе 2 (v 2) = 2 м / с Разыскивается: скорость воды в трубе 1 (v 1) Решение : Уравнение неразрывности: А 1 v 1 = А 2 v 2 8 v 1 = (2) (2) 8 v 1 = 4 v 1 = 4/8 = 0.5 м / с 9. Если диаметр большей трубы в 2 раза больше диаметра меньшей трубы, какой скорость жидкости в трубе меньшего размера. Известный : Диаметр большей трубы (d 1) = 2 Радиус большей трубы (r 1) = ½ d 1 = ½ (2) = 1
Площадь большей трубы (A 1) = π r 12 = π (1) 2 = π (1) = π Диаметр меньшей трубы (d 2) = 1 Радиус меньшей трубы (r 2) = ½ d 2 = ½ (1) = ½
Площадь меньшей трубы (A 2) = π r 22 = π (1/2) 2 = π (1/4) = ¼ π Скорость жидкости в большей трубе (v 1) = 4 м / с. Требуется: скорость жидкости в трубе меньшего размера (v 2) Решение : Уравнение неразрывности: А 1 v 1 = А 2 v 2 π 4 = ¼ π (v 2) 4 = ¼ (v 2) v 2 = 8 м / с
Читайте: Выталкивающая сила – проблемы и решения
Принцип и уравнение Бернулли 10.Вода перекачивается компрессором на 120 кПа, поступает в нижнюю трубу (1) и течет. вверх со скоростью 1 м / с. Ускорение свободного падения составляет 10 м / с, а плотность воды составляет 1000 кг / м-3. Какое давление воды в верхней трубе (II). Известно:
Радиус нижней трубы (r 1) = 12 см Радиус нижней трубы (r 2) = 6 см. Давление воды в нижнем патрубке (p 1) = 120 кПа = 120000 Паскалей Скорость воды в нижней трубе (v 1) = 1 м.с Высота нижней трубы (h 1) = 0 м. Высота верхней трубы (h 2) = 2 м
Ускорение свободного падения (g) = 10 м.с-
Плотность воды = 1000 кг.м- Требуется: Давление воды в трубе 2 (p 2) Решение : Скорость воды в трубе 2 рассчитывается по уравнению неразрывности:
Давление воды в трубе 2 рассчитывается по уравнению Бернулли:
Читать: Принцип работы механической энергии – проблемы и решения
- Большая труба на высоте 5 метров над землей и маленькая труба на высоте 1 метра над землей. Скорость воды в большой трубе – 36 км / ч при давлении 9.1 х 10 5 Па, в то время как давление в малой трубе составляет 2,10 5 Па. Какова скорость воды в малой трубе? трубка? Плотность воды = 10 3 кг / м 3 Известно:
Давление воды в большой трубе (p 1) = 9,1 x 10 5 Паскалей = 910 000 Паскалей
Давление воды в малой трубе (p 2) = 2 x 10 5 Паскаль = 200 000 паскалей
Скорость воды в большой трубе (v 1) = 36 км / ч = 36 (1000) / (3600) = 36000/3600 = 10 м / с
О нас | Контакты | Ссылки | Конфиденциальность Авторские права © Физика.Gurumuda.Net Все права защищены.
Статьи
Поделиться: Twitter Skype Facebook LinkedIn Reddit Tumblr Pinterest Telegram Pocket WhatsApp Print
Похожие сообщения Сила тяжести и гравитационное поле – проблемы и решения
- Два объекта m1 и m2 каждый массой 6 кг и 9 кг, разделенные расстоянием 5 … Параболическое движение, работа и кинетическая энергия, количество движения, линейное и угловое движение – проблемы и решения
- Мяч брошен сверху здания с начальной скоростью 8 м / с под углом… Поперечные волны – проблемы и решения
- Расстояние между двумя впадинами поверхностных волн на воде – 20 м. Объект плавает на поверхность … Скорость механических волн – проблемы и решения
- Скорость поперечной волны на веревке длиной 25 метров – 50 м / с. Сила натяжения веревка … Простое гармоническое движение – проблемы и решения
- Объект вибрирует с частотой 5 Гц вправо и влево. Объект движется из точка равновесия…
Кинематика потока жидкости: примечания, методы, типы, проблемы и решения
Кинематика потока жидкости: примечания, методы, проблемы и решения! Эта статья поможет вам получить вероятные ответы на вопросы, связанные с кинематикой потока жидкости.
Кинематика потока жидкости имеет дело с движением частиц жидкости без учета фактора, производящего движение. Это касается геометрии движения жидких частиц.Это также касается скорости и ускорения движущихся частиц жидкости. Движение жидкости можно анализировать по тем же принципам, что и движение твердого тела.
Однако существует принципиальная разница между движением твердого тела и движением жидкости. Твердое тело компактно и движется как одна масса. Между частицами твердого тела нет относительного движения. Следовательно, мы изучаем движение всего тела, и нет необходимости изучать движение какой-либо частицы твердого тела.
Но в случае жидкого тела все частицы жидкости по отдельности подвижны и независимо двигаются. Частица жидкости может иметь движение, отличное от движения окружающих ее. Однако можно получить взаимосвязь между движениями соседних частиц жидкости.
Кинематика потока жидкости: заметки, методы, проблемы и решения
Методы описания движения жидкости :Мы знаем, что каждая частица движущейся жидкости в любой момент имеет определенное значение своих свойств, таких как плотность, скорость, ускорение и т. Д.По мере продвижения жидкости значения этих свойств будут время от времени изменяться от одного положения к другому.
Таким образом, можно понять, что возможны два метода описания движения жидкости. В первом методе, называемом методом Лагранжа, мы изучаем скорость, ускорение и т. Д. Отдельной жидкой частицы в каждый момент времени, когда частица перемещается в разные положения.
Этот метод изучения свойств отдельной жидкой частицы – очень утомительный процесс, и поэтому этот метод обычно не применяется.Во втором методе, называемом методом Эйлера, мы описываем поток, исследуя скорость, ускорение, давление, плотность и т. Д. В фиксированной точке пространства. Из-за простоты применения этот метод используется чаще всего.
Пусть x, y и z обозначают пространственные координаты, а t время. Пусть V – результирующая скорость в любой точке пространства жидкого тела. Пусть u, v и w – компоненты результирующей скорости V в любой точке в направлениях осей x, y и z.На рис. 6.1 показаны обозначения.
Линия потока :Линия потока – это непрерывная линия в жидкости, которая показывает направление скорости жидкости в каждой точке вдоль линии. Касательная к линии потока в любой ее точке соответствует направлению скорости в этой точке. Частицы жидкости, лежащие на линии потока, в мгновение ока движутся вдоль линии потока.
Когда жидкость находится в движении, имеется много линий потока, и эти линии потока указывают структуру потока в этот конкретный момент.Например, когда жидкость обтекает цилиндрическое тело, рисунок линий тока будет таким, как показано на рис. 6.3. В установившемся потоке скорость в точке не меняется ни по величине, ни по направлению.
Следовательно, нет изменения направления вектора скорости в точке. Другими словами, линия потока зафиксирована на месте. И наоборот, если рисунок линий потока остается постоянным, поток остается постоянным. В случае нестационарного течения направление скорости меняется со временем в каждой точке.Это означает, что положение линии потока непостоянно. Положение линии потока меняется от момента к моменту.
Линия пути :Линия пути означает путь или линию, фактически описываемую отдельной жидкой частицей, когда она движется в течение определенного периода времени. Линия пути указывает направление скорости одной и той же жидкой частицы в последовательные моменты времени.
В случае установившегося потока из-за отсутствия колебаний скорости линия пути совпадает с линией потока.В случае нестационарного потока линии потока меняют свое положение в каждый момент, и, таким образом, линия пути может колебаться между разными линиями потока в течение определенного интервала времени.
На рис. 6.4 показана линия пути конкретной жидкой частицы. Это геометрическое место положения одной и той же частицы, когда она движется.
На рис. 6.5 показаны линии пути, описанные тремя частицами, которые прошли через начало координат в моменты времени t 0 , t 1 и t 2 .Рассмотрим частицу, прошедшую через начало координат в момент времени до. На рис. 6.5 показаны положения, занимаемые частицей в моменты времени t 0 + ∆t, t 0 + 2∆t, t 0 + 3∆t и т. Д., Когда она проследила линию своего пути.
Streak Line :Штриховая линия – это геометрическое место положений частиц жидкости, которые последовательно прошли через заданную точку. Предположим, что A, B, C, D… жидкие частицы, прошедшие через контрольную точку, одну за другой, в начале координат.Эти частицы описали свои собственные траектории. Предположим, что в момент времени t эти частицы A, B, C, D… находятся в точке P a ,
.P b , P c , P d …. Линия P a , P b , P c , P d …. – штриховая линия в момент времени t.
Потоковая трубка :Трубка потока – это воображаемое трубчатое пространство, образованное рядом линий потока. Это сборка или набор линий потока, образующих табличное пространство.Поверхность водопроводной трубы состоит из линий тока. Скорость жидкой частицы на поверхности трубки потока вдоль линии потока над поверхностью трубки потока. Это означает, что не может быть потока через стенки водопроводной трубы.
В любом сечении струйной трубки скорость в центре тяжести сечения представляет собой среднюю скорость потока через струйную трубу в этом сечении. На рис. 6.7 показана струйная трубка. Поскольку не может быть потока через стенки струйной трубки, должно быть ясно, что количество текучей среды, поступающей в струйную трубу, равно количеству текучей среды, покидающей струйную трубу.
Потенциальные линии :На поверхности, состоящей из линий потока, мы можем представить линии, идущие перпендикулярно линиям потока. Такие линии называются потенциальными линиями, см. Рис. 6.8.
Набор линий тока и потенциальных линий составляет сеть потока.
Типы потока :Встречаются следующие типы потоков:
(i) Ламинарный поток и турбулентный поток.
(ii) Устойчивый поток и нестационарный поток.
(iii) Равномерный и неравномерный поток.
(iv) Вращательный и безвихревой поток.
(i) Ламинарный и турбулентный поток :
Ламинарный поток:
Это тип потока, в котором частицы жидкости движутся слоями, плавно позолочая соседние слои. Транспортировка жидких частиц из одного слоя в другой отсутствует. Частицы жидкости в любом слое движутся по четко определенным линиям тока.
Пути отдельных частиц не пересекаются. Этот тип потока также называется потоком по линии потока или вязким потоком. Это плавное перетекание одного слоя жидкости поверх другого. Этот тип течения возникает в вязких жидкостях, где вязкость влияет на течение.
Турбулентный поток:
Это наиболее распространенный вид течения в природе. Этот поток характеризуется случайным, беспорядочным, непредсказуемым движением частиц жидкости, которое приводит к возникновению вихревых токов.В движении происходит общее перемешивание частиц жидкости. Скорость меняется по направлению и величине от точки к точке.
Между частицами происходит непрерывное столкновение, приводящее к передаче импульса между ними. Вихревые токи вызывают значительные потери энергии по сравнению с потерями энергии в ламинарном потоке. Эта большая потеря энергии происходит из-за того, что турбулентные напряжения сдвига намного больше, чем напряжение ламинарного сдвига, определяемое законом вязкости Ньютона.
В турбулентном потоке отличительной особенностью турбулентности является ее неравномерность, неопределенная частота и отсутствие определенной наблюдаемой картины. Этот тип потока не может быть полностью математически проанализирован, и любой анализ возможен путем статистической оценки. Течение воды в реках обычно бурное. Течение воды в трубах с высокой скоростью является турбулентным. Течение густой нефти в узких трубках, течение грунтовых вод, кровоток в кровеносных сосудах ламинарное.
По мере постепенного увеличения скорости воды в трубе поток будет меняться с ламинарного на турбулентный.Скорость, с которой поток в трубе меняется с ламинарного на турбулентный, называется критической скоростью. Тип потока, который существует в любом случае, зависит от значения безразмерного числа dν / γ, называемого числом Рейнольдса, где d – диаметр трубы, ν – средняя скорость потока в трубе, а γ – величина кинематическая вязкость жидкости.
Когда число Рейнольдса меньше 2000, поток обычно ламинарный. Когда число Рейнольдса больше 2800, поток обычно турбулентный.Если число Рейнольдса находится между указанными выше пределами, поток может быть ламинарным или турбулентным. Таким образом, критическая скорость не имеет фиксированного или определенного значения.
Скорость, соответствующая числу Рейнольдса, равному 2000, называется нижней критической скоростью, а скорость, соответствующая числу Рейнольдса, равному 2800, называется верхней критической скоростью.
(ii) Устойчивый поток и нестационарный поток :
Устойчивый поток:
Если такие характеристики потока, как скорость, плотность, давление и т. Д.в данной точке текущая масса жидкости не изменяется с течением времени, поток называется устойчивым. Напротив, если эти характеристики потока в данной точке меняются во времени, поток называется нестационарным.
Поскольку скорость является общепринятой характеристикой потока, вполне достаточно считать поток устойчивым, если скорость в данной точке не изменяется во времени.
Предположим, что V – это скорость в точке (x 1 , y 1 , z 1 ).В этот момент, если V остается постоянным все время, поток будет постоянным. Но если в этот момент V изменяется со временем, поток будет нестационарным, т.е.
(iii) Равномерный и неравномерный поток :
Если характеристики потока, такие как скорость, плотность, давление и т. Д., В данный момент остаются неизменными во всех точках, поток однороден. Если V выбирается в качестве характеристики потока, то в данный момент V имеет одинаковое значение во всех точках и не зависит от положения в пространстве.Если характеристики потока имеют разные значения в разных точках в данный момент времени, поток является неравномерным.
Мы часто используем термины «равномерный» и «неравномерный поток» в связи с открытыми каналами. В канале, где сечение канала однородно, а глубина потока одинакова, поток будет однородным, так как скорость будет одинаковой на всех участках. Но если размеры сечения канала разные на разных участках, то глубина потока на разных участках будет разной.
Очевидно, что скорость будет разной на разных участках, и поток будет неоднородным, независимо от того, является ли поток однородным или неоднородным, если скорость потока постоянна, поток будет постоянным и если скорость потока изменяется со временем, поток неустойчивый. Таким образом, мы можем встретить устойчивый или нестационарный, равномерный или неравномерный поток. Любой тип потока может существовать независимо от другого.
Также возможна комбинация двух типов потока.
Некоторые комбинации:
а.Стабильный равномерный поток.
г. Устойчивый неравномерный поток.
г. Неустойчивый равномерный поток.
г. Неустойчивый неравномерный поток.
(iv) Вращательные и безвихревые потоки :
При движении жидкости частицы жидкости могут подвергаться поступательным или вращательным перемещениям. Предположим, что частица, которая движется вдоль линии тока, вращается вокруг своей оси, тогда говорят, что частица имеет вращательное движение. Если же частица при движении вдоль линии потока не вращается вокруг своей оси, то говорят, что частица имеет безвихревое движение.
На рис. 6.11 (a) показано вращательное движение. Рассмотрим жидкую частицу AB. Когда эта частица движется вдоль линии потока, она также вращается вокруг своей оси. Рис. 6.11 (b) показывает безвихревое движение. Жидкая частица AB в этом случае при движении вдоль линии тока не вращается вокруг собственной оси.
Различные типы движений жидкости :Элемент жидкости может совершать четыре типа движений, а именно:
(i) Чистый перевод,
(ii) линейная деформация,
(iii) Чистое вращение,
(iv) Угловая (сдвигающая) деформация
(i) Чистый перевод:
Рис.6.12 показано движение жидкого элемента за счет чистого перевода.
Фигура сплошной линией представляет собой очень маленький элемент жидкости в определенный момент. После чистого перевода положение жидкостного элемента показано пунктирными линиями. Во время этого смещения размеры жидкостного элемента не изменяются и продолжают сохранять свою первоначальную ориентацию.
(ii) Линейная деформация:
На рис. 6.13 показано движение элемента жидкости за счет линейной деформации.
В этом случае элемент жидкости изменил свою форму. Но направления главных осей элемента жидкости не изменились.
(iii) Чистое вращение:
Рис. 6.14 (a) и (b) показывают чистое вращение элемента жидкости.
Элемент жидкости повернулся на угол θ без какой-либо деформации.
(iv) Угловая деформация или деформация сдвига:
Одно-, двух- и трехмерные потоки :
Это еще один способ описания движения жидкости.Скорость жидкого элемента в самом общем случае зависит от его положения. Если любую точку в пространстве определить в терминах пространственных координат (x, y, z), то в любой данный момент скорость в этой точке определяется выражением V = ƒ (x, y, z). Течение в таком случае называется трехмерным потоком.
Иногда условие потока может быть таким, что скорость в любой точке зависит только от двух пространственных координат, например (x, y) в данный момент, то есть, в данном случае, в данный момент V = ƒ (x, y) .В этом случае условия потока являются потенциальными в плоскостях, перпендикулярных оси Z. Этот тип течения называется двумерным потоком.
В двумерном потоке течение идентично в параллельных плоскостях. На рис. 6.16 показан двумерный поток. На этом рисунке показан канал, стенки которого перпендикулярны плоскости схемы. Обратите внимание на векторы скорости в секциях 1-1 и 2-2. На участке 1-1 скорость меняется по каналу. Аналогично на участке 2-2 скорость меняется по каналу.Но течение одинаково во всех плоскостях, параллельных плоскости рисунка.
Нет компонента скорости, перпендикулярного плоскости рисунка. В целом ряде случаев движение принято считать одномерным. Без сомнения, это упрощение по сравнению с двумерным и трехмерным движением жидкости. В этом типе потока скорость V в данный момент является функцией одной пространственной координаты, скажем только x, то есть в данный момент V = ƒ (x)
Рис.6.17 показывает одномерный поток. На участке 1-1 скорость постоянна на всем участке. Точно так же на участке 2-2 скорость постоянна на всем участке.
Одномерный, двухмерный или трехмерный поток может быть стационарным или нестационарным потоком.
Эти типы потоков можно выразить следующим образом:
Скорость потока или нагнетания :
Количество жидкости, протекающей в единицу времени через любой участок трубы или канала, называется скоростью потока или выпуска.Скорость потока может быть выражена как вес текучей среды, протекающей через секцию в секунду, или как масса текучей среды, протекающей через секцию за секунду, или как объем текучей среды, протекающей через секцию за секунду. Соответственно, скорость потока может быть выражена в таких единицах, как (i) N в секунду, (ii) кг в секунду, (iii) кубический метр в секунду (iv) литры в секунду.
В этом случае потока несжимаемой жидкости скорость потока обычно выражается как объем жидкости, протекающей через секцию в секунду.В случае сжимаемых жидкостей скорость потока обычно выражается как вес жидкости, протекающей через секцию в секунду.
Контрольный объем :Это некая четко очерченная часть пространства. Чтобы понять изменения, происходящие в характеристиках жидкости, мы можем ввести контрольный объем, чтобы мы могли сравнивать характеристики потока жидкости непосредственно перед тем, как она входит в контрольный объем, и сразу после того, как она покидает контрольный объем.
Уравнение непрерывности :Это уравнение, основанное на принципе сохранения массы. Предположим, мы рассматриваем струйную трубку. Поскольку струйная труба всегда заполнена текучей средой, количество текучей среды, поступающей в струйную трубу на одном конце в единицу времени, должно быть равно количеству текучей среды, покидающей струйную трубу на другом конце в единицу времени.
Пусть V – средняя скорость в любом сечении, а A – площадь сечения.Если w – удельный вес жидкости, количество жидкости, протекающей в секунду через секцию
.Уравнение непрерывности в трех измерениях :
Рассмотрим бесконечно малый параллелепипед пространства в жидком теле. Пусть стороны параллелепипеда имеют длину dx, dy и dz соответственно. См. Рис. 6.20. Пусть u, v и w – компоненты скорости на входе в направлениях осей X, Y и Z. Масса жидкости, поступающей в левую грань = ρu dy dz.Масса жидкости, выходящей из правой грани
Скорость и ускорение :В наиболее общем случае движения жидкости результирующая скорость V в любой точке является функцией не только смещения s вдоль линии тока, но и времени t, то есть –
Скоростной потенциал и функции потока :Потенциальная функция скорости:
Это функция, разработанная для ускорения аналитического исследования полей скорости.Если ɸ – некоторая функция координат x и y в двумерном потоке, такая что
Эквипотенциальная линия : Линия потока :Физическая концепция функции потока :
Рассмотрим двумерное установившееся течение несжимаемой жидкости. На рис. 6.26 показаны две линии потока PP ’и QQ’, расположенные рядом друг с другом.
Мы знаем, что линия потока – это линия постоянной функции потока. Пусть координаты P и Q равны (x, y) и [(x + dx), (y + dy)].
Рассмотрим поток через любую линию от P до Q, скажем, через линию PRQ. Если поток устойчивый, поток через линию PRQ или любую такую линию должен быть таким же. Считайте поток в положительном направлении X как положительный, а поток в положительном направлении Y как положительный, мы имеем поток через линию PRQ = – udy + vdx
Следовательно, dΨ численно представляет поток через линию PRQ, т.е.е., dΨ представляет собой поток между линиями потока PP ’и QQ’. Таким образом, мы заключаем, что поток через линию, соединяющую две точки, равен изменению функции тока между этими двумя точками.
Обращение :
Рассмотрим замкнутую линию или контур в двумерном потоке. Пусть V представляет результирующую скорость в любой точке контура. Пусть θ – угол между скоростью V и элементарным элементом контура ds. Интеграл от произведения (длина контура ds x составляющая скорости в направлении ds) называется линейным интегралом.Линейный интеграл скорости вокруг замкнутого контура называется циркуляцией (обычно обозначается γ).
Обращение сторон прямоугольника :Домашнее задание
Online Fluid Mechanics Homework Help | Репетиторы по механике жидкостей
О механике жидкости
Гидравлическая механика – это изучение жидкости в движении (гидродинамика) или в состоянии покоя (статика жидкости) и последующее воздействие жидкости на границы, которые могут быть либо твердой поверхностью, либо границами с другими жидкостями.
С точки зрения механики жидкостей, вся материя состоит только из двух состояний: жидкости и твердого тела.
Твердое тело может противостоять напряжению сдвига за счет статической деформации; жидкость не может. Любое напряжение сдвига, приложенное к жидкости, независимо от того, насколько оно мало, приведет к движению этой жидкости. Жидкость непрерывно движется и деформируется, пока прикладывается напряжение сдвига.
Есть две разные точки зрения на анализ задач в механике. Первая точка зрения, соответствующая механике жидкостей, связана с полем течения и называется эйлеровым методом описания.В эйлеровом методе мы вычисляем поле давления p (x, y, z, t) картины течения, а не изменение давления p (t), которое испытывает частица при движении через поле. Второй метод, который отслеживает движение отдельной частицы в потоке, называется лагранжевым описанием. Лагранжев подход больше подходит для механики твердого тела.
Термодинамические свойства жидкости:
- Давление: Давление – это напряжение (сжатия) в точке статической жидкости.
- Температура: Температура T является мерой уровня внутренней энергии жидкости.
- Плотность: плотность жидкости – это ее масса на единицу объема.
- Вязкость: Когда жидкость сдвигается, она начинает двигаться со скоростью деформации, обратно пропорциональной свойству, называемому ее коэффициентом вязкости µ.
Неньютоновские жидкости:
Жидкости, которые не подчиняются линейному закону, называются неньютоновскими жидкостями.
Схема потока:
- Линия тока: это линия, касающаяся вектора скорости в данный момент времени.
- Линия пути: это фактический путь, пройденный данной жидкой частицей.
- Штриховая линия: это геометрическое место частиц, которые ранее прошли через заданную точку.
- Временная шкала: это набор жидких частиц, образующих линию в данный момент.
Линия обтекания, штриховая линия и траектория идентичны в установившемся потоке.
Плавучесть:
- Тело, погруженное в жидкость, испытывает вертикальную выталкивающую силу, равную весу вытесненной жидкости.
- Плавающее тело перемещает собственный вес в жидкости, в которой оно плавает.
Поток без трения: уравнение Бернулли
Он тесно связан с уравнением энергии установившегося потока и является соотношением между давлением, скоростью и высотой в потоке без трения = const.Допущения для уравнения Бернулли:
- Устойчивый поток
- Несжимаемый поток
- Поток без трения
- Обтекание по линии тока
- Нет работы на валу
- Нет теплопередачи
Вязкий поток в воздуховодах:
Ламинарный поток характеризуется плавными линиями тока и высокоупорядоченным движением.Турбулентный поток характеризуется колебаниями скорости и сильно неупорядоченным движением.
Номер Рейнольдса:
Переход от ламинарного к турбулентному потоку зависит от геометрии, шероховатости поверхности, скорости потока, температуры поверхности, типа жидкости. Отношение силы инерции к силе вязкости называется № Рейнольдса.
Для проточной трубы,
Re
2300
Re> 4000 турбулентный поток
Поверхностное натяжение:
Жидкость, неспособная свободно расширяться, образует поверхность раздела с вторичной жидкостью или газом.Молекулы глубоко внутри жидкости отталкиваются друг от друга из-за их плотной упаковки. Молекулы на поверхности менее плотные и притягиваются друг к другу. Поскольку половина их соседей отсутствует, механический эффект заключается в том, что они находятся в напряжении. Если разрез длиной dl выполняется на межфазной поверхности, равные и противоположные силы величины Ydl подвергаются действию перпендикулярно разрезу и параллельно поверхности, где Y называется коэффициентом поверхностного натяжения.
Ссылки:
· Механика жидкости, 4-е издание – Франк М.Белый
· Механика жидкости – Юнус А. Ценгель
Онлайн-справка по домашнему заданию по механике жидкостей на Tutorbin
Онлайн-помощь в домашнем задании по гидравлической механике – это способ найти ответы на все ваши вопросы в сжатые сроки. Вы можете просто отправить запросы онлайн-преподавателям по гидравлической механике и в течение определенного периода времени получить решения для домашних заданий по гидравлической механике.Онлайн-помощь в домашнем задании по гидравлической механике идеально подходит для вас, если вы находитесь в затруднительном положении и нуждаетесь в быстрых 100% правильных решениях в короткие сроки. Получите быстрые, четкие, подробные и высококачественные решения для заданий и домашних заданий по любым темам механики жидкости с помощью простых, новейших и передовых методов электронного обучения с нашими наставниками по гидродинамике, чтобы повысить свои оценки.
Мы гордимся тем, что с нами работают преподаватели по механике жидкостей. Наши онлайн-наставники по механике жидкости и наставники по гидродинамике приезжают со всех уголков мира и не связаны географическими границами.Мы стремимся преодолеть границы, чтобы помочь студентам получить лучшую домашнюю помощь и онлайн-обучение по механике жидкостей со всего мира.
14,5 Динамика жидкости – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Опишите характеристики потока
- Рассчитать расход
- Опишите взаимосвязь между расходом и скоростью
- Объясните последствия уравнения неразрывности для сохранения массы
Первая часть этой главы посвящена статике жидкости, изучению жидкости в состоянии покоя.Остальная часть этой главы посвящена гидродинамике, изучению движущихся жидкостей. Даже самые простые формы движения жидкости могут быть довольно сложными. По этой причине мы ограничиваем наше исследование идеальной жидкостью – во многих примерах. Идеальная жидкость – жидкость с незначительной вязкостью. Вязкость – это мера внутреннего трения в жидкости; мы исследуем его более подробно в разделе «Вязкость и турбулентность». На нескольких примерах мы исследуем несжимаемую жидкость – ту, для которой требуется чрезвычайно большая сила, чтобы изменить объем, – поскольку плотность в несжимаемой жидкости постоянна на всем протяжении.
Характеристики потока
Векторы скорости часто используются для иллюстрации движения жидкости в таких приложениях, как метеорология. Например, ветер – жидкое движение воздуха в атмосфере – может быть представлен векторами, указывающими скорость и направление ветра в любой заданной точке на карте. (Рисунок) показывает векторы скорости, описывающие ветры во время урагана Артур в 2014 году.
Рис. 14.24 Векторы скорости показывают поток ветра во время урагана Артур. Обратите внимание на циркуляцию ветра вокруг очага урагана.Самые высокие скорости ветра у глаз. Цвета представляют относительную завихренность, меру вращения или вращения воздуха.Другой метод представления движения жидкости – это линия обтекания . Линия тока представляет собой путь небольшого объема жидкости, когда она течет. Скорость всегда тангенциальна к линии тока. На схемах (Рисунок) линии тока используются для иллюстрации двух примеров движения флюидов по трубе. Первая жидкость демонстрирует ламинарный поток (иногда описываемый как устойчивый поток), представленный плавными параллельными линиями тока.Обратите внимание, что в примере, показанном в части (а), скорость жидкости наибольшая в центре и уменьшается у стенок трубы из-за вязкости жидкости и трения между стенками трубы и жидкостью. Это особый случай ламинарного потока , где трение между трубой и жидкостью велико, что известно как граничные условия отсутствия проскальзывания. Вторая диаграмма представляет турбулентный поток, в котором линии тока нерегулярны и меняются со временем. В турбулентном потоке пути потока текучей среды нерегулярны, поскольку разные части текучей среды смешиваются вместе или образуют небольшие круглые области, напоминающие водовороты.Это может произойти, когда скорость жидкости достигает определенной критической скорости.
Рис. 14.25 (a) Ламинарный поток можно представить как слои жидкости, движущиеся параллельными регулярными путями. (b) В турбулентном потоке области жидкости движутся по нерегулярным, сталкивающимся траекториям, что приводит к перемешиванию и завихрению.Расход и его связь со скоростью
Объем жидкости, проходящей через заданное место через область в течение периода времени, называется расходом Q , или, точнее, объемным расходом .В символах это записывается как
., где V – объем, а т – прошедшее время. На (Рисунок) объем цилиндра составляет Ax , поэтому расход равен
. Рис. 14.26 Расход – это объем жидкости, протекающей мимо точки через область A в единицу времени. Здесь заштрихованный цилиндр жидкости обтекает точку P по однородной трубе за время t.Единица СИ для расхода –
., но несколько других единиц для Q широко используются, например, литры в минуту (л / мин).Обратите внимание, что литр (L) равен 1/1000 кубического метра или 1000 кубических сантиметров
Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, рассмотрим скорость течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера и формы реки. Быстрый горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. (Рисунок) показывает объемный расход.Объемный расход
где
– это площадь поперечного сечения трубы, а v – величина скорости.
Точное соотношение между расходом Q и средней скоростью v составляет
, где A – площадь поперечного сечения, а
– средняя скорость. Это соотношение говорит нам, что скорость потока прямо пропорциональна средней скорости жидкости и площади поперечного сечения реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. (Рисунок) иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем
., которая проходит мимо точки P за время t . Разделив обе стороны этого отношения на т, дает
Отметим, что
и средняя скорость
. Таким образом, уравнение принимает вид
.
(рисунок) показывает несжимаемую жидкость, текущую по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. Поток является непрерывным, потому что они не являются источниками или стоками, которые добавляют или удаляют массу, поэтому масса, втекающая в трубу, должна быть равна массе, вытекающей из трубы. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться.Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для произвольных точек 1 и 2
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости (с постоянной плотностью). Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью – это и есть назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища.Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.
Рис. 14.27 Когда труба сужается, тот же объем занимает большую длину. Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим. Если жидкость течет в обратном направлении, ее скорость уменьшается при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не масштабированы.)Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример
Расчет скорости жидкости через сопло
Насадка диаметром 0,500 см присоединяется к садовому шлангу радиусом 0,900 см. Расход через шланг и насадку составляет 0,500 л / с. Рассчитайте скорость воды (а) в шланге и (б) в форсунке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы используем индекс 1 для шланга и 2 для сопла.
Решение
- Решаем уравнение расхода для скорости и используем
за площадь поперечного сечения шланга, получив
Подставляя значения и используя соответствующие преобразования единиц, получаем
- Мы можем повторить этот расчет, чтобы найти скорость в сопле.
, но мы используем уравнение неразрывности, чтобы дать несколько иное представление.Уравнение утверждает:
Решение для
и заменяющий
по площади поперечного сечения дает
Подстановка известных значений,
Значение
Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга с форсункой. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Сохранение массы
Скорость потока жидкости также может быть описана массовым расходом или массовым расходом. Это скорость, с которой масса жидкости движется мимо точки.Еще раз обратитесь к (Рисунок), но на этот раз рассмотрите массу в заштрихованном объеме. Масса определяется по плотности и объему:
Тогда массовый расход будет
где
– плотность, A, – площадь поперечного сечения, и v – величина скорости. Массовый расход является важной величиной в гидродинамике и может использоваться для решения многих задач.Рассмотрим (рисунок). Труба на рисунке начинается на входе с площадью поперечного сечения
.и сужается к выходу с меньшей площадью поперечного сечения
. Масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу. По этой причине скорость на выходе
больше, чем скорость на входе
. Используя тот факт, что масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу, мы можем найти связь между скоростью и площадью поперечного сечения, взяв скорость изменения массы в трубе и массы из:
(рисунок) также известно как уравнение неразрывности в общем виде.Если плотность жидкости остается постоянной из-за сужения, то есть жидкость несжимаема, тогда плотность сокращается из уравнения неразрывности,
Уравнение сокращается, чтобы показать, что объемный расход в трубе равен объемному расходу из трубы.
Рисунок 14.28 Геометрия для вывода уравнения неразрывности. Количество жидкости, поступающей в площадь поперечного сечения (заштрихованную), должно равняться количеству жидкости, покидающей площадь поперечного сечения, если жидкость несжимаема.Резюме
- Расход Q определяется как объем V , протекающий через момент времени т , или
, где V – объем, а т – время. Единица измерения расхода в системе СИ –
., но можно использовать и другие значения, например л / мин.
- Расход и скорость связаны соотношением
, где A – площадь поперечного сечения потока, а v – его средняя скорость.
- Уравнение неразрывности гласит, что для несжимаемой жидкости масса, втекающая в трубу, должна равняться массе, вытекающей из трубы.
Концептуальные вопросы
На многих рисунках в тексте показаны обтекаемые формы. Объясните, почему скорость жидкости максимальна там, где линии тока находятся ближе всего друг к другу. ( Подсказка: Учитывайте взаимосвязь между скоростью жидкости и площадью поперечного сечения, через которую она течет.)
[show-answer q = ”fs-id1170959940734 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1170959940734 ″]
Рассмотрим две разные трубы, подключенные к одной трубе меньшего диаметра, при этом жидкость течет из двух труб в меньшую трубу.Поскольку жидкость проталкивается через меньшую площадь поперечного сечения, она должна двигаться быстрее по мере того, как линии потока становятся ближе друг к другу. Точно так же, если труба с большим радиусом входит в трубу с малым радиусом, линии потока станут ближе друг к другу, и жидкость будет двигаться быстрее.
[/ hidden-answer]
Проблемы
Какой средний расход в
бензина в двигатель автомобиля, движущегося со скоростью 100 км / ч, если в среднем 10.0 км / л?
[show-answer q = ”fs-id1170957599093 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1170957599093 ″]
2,77
[/ hidden-answer]
Сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5,00 л / мин. (а) Преобразуйте это в
. (б) Что это за ставка в
?
Водопад Хука на реке Вайкато – одна из самых посещаемых природных достопримечательностей Новой Зеландии.В среднем река имеет скорость потока около 300 000 л / с. В ущелье река сужается до 20 метров в ширину и в среднем до 20 метров в глубину. а) Какова средняя скорость реки в ущелье? b) Какова средняя скорость воды в реке ниже водопада, когда она расширяется до 60 м, а глубина увеличивается в среднем до 40 м?
[показывать-ответ q = ”fs-id1170960142461 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170960142461 ″]
а. 0,75 м / с; б.0,13 м / с
[/ hidden-answer]
(a) Оцените время, необходимое для наполнения частного бассейна емкостью 80 000 л с использованием садового шланга с расходом 60 л / мин. (b) Сколько бы времени это заняло, если бы вы могли изменить направление реки среднего размера, текущая в
?в бассейн?
Какова скорость жидкости в пожарном шланге диаметром 9 см, пропускающем 80,0 л воды в секунду? б) Какая скорость потока в кубических метрах в секунду? (c) Вы бы ответили иначе, если бы соленая вода заменила пресную воду в пожарном шланге?
[показывать-ответ q = ”fs-id1170960089546 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170960089546 ″]
а.12,6 м / с; б.
; c. Нет, расход и скорость не зависят от плотности жидкости.
[/ hidden-answer]
Вода движется со скоростью 2,00 м / с по шлангу с внутренним диаметром 1,60 см. а) Какая скорость потока в литрах в секунду? (b) Скорость жидкости в сопле этого шланга составляет 15,0 м / с. Каков внутренний диаметр сопла?
Докажите, что скорость несжимаемой жидкости через сужение, например, в трубке Вентури, увеличивается в раз, равный квадрату коэффициента уменьшения диаметра.(Обратное верно для потока из сужения в область большего диаметра.)
[показывать-ответ q = ”fs-id1170959803647 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170959803647 ″]
Если жидкость несжимаемая, расход через обе стороны будет равен:
или
[/ hidden-answer]
Вода выходит прямо из крана диаметром 1,80 см со скоростью 0 °.500 м / с. (Из-за конструкции крана скорость потока не меняется.) (A) Какая скорость потока в
? (б) Каков диаметр ручья на 0,200 м ниже крана? Пренебрегайте эффектами поверхностного натяжения.
Глоссарий
- расход
- сокращенно Q , это объем V , который проходит мимо определенной точки в течение времени t , или
- идеальная жидкость
- жидкость с пренебрежимо малой вязкостью
- ламинарный поток
- вид потока жидкости, в котором слои не смешиваются
- турбулентный поток
- Тип потока жидкости, в котором слои смешиваются друг с другом посредством завихрений и завихрений
- вязкость
- Измерение внутреннего трения в жидкости
Эффективное решение задач гидродинамики за счет комбинации метод
Мы изучаем технику комбинации разреженных сеток как эффективный метод. для решения задач гидродинамики.Комбинированная техника требует Только O (h –1 n (log (h –1 n )) d – 1 ) точки сетки для задач с размерностью d вместо O (h –d n ) точек сетки, используемых методом полной сетки. Здесь h n = 2 –n обозначает ширину сетки сеток. Кроме того, при условии, что решение достаточно гладкое, точность (относительно L 2 – и L ∞ ‐norm) решения комбинации разреженных сеток является O (h α n (log (h –1 n )) d – 1 ), что лишь немного хуже, чем O (h α n ) полученное методом полной сетки.Здесь α включает порядок лежащая в основе схема дискретизации, а также влияние особенностей. Таким образом, комбинированный метод очень экономичен для обоих требований к хранению. и время вычислений, но достигает почти такой же точности, как и обычный полный сеточное решение. Еще одно преимущество комбинированной техники состоит в том, что только необходимы простые структуры данных. Где нужны другие методы разреженной сетки иерархические структуры данных и, следовательно, специально разработанные решатели, Комбинированный метод обрабатывает всего d -мерных массивов.Таким образом, реализация техники комбинирования может быть основана на любом «черном». коробочный решатель ». Однако из соображений эффективности подходящая многосеточная должен использоваться решатель. Часто задачи гидродинамики приходится решать на довольно сложные домены. Обычный подход – разделить домен на блоки, чтобы облегчить решение проблемы. Мы показываем, что Комбинированная техника работает и на таких блочно-структурированных сетках. Когда имея дело со сложными областями, часто желательно оценивать сетку вокруг особенности.Градуированные сетки также поддерживаются комбинацией техника. Наконец, мы представляем первые результаты численных экспериментов. для применения комбинированного метода к задачам CFD . Там, мы рассматриваем двумерные задачи ламинарного течения с умеренными Числа Рейнольдса и обсудите преимущества комбинации метод.
Цифровые решения для проблем потока жидкости в нефтегазовой отрасли
Нефтегазовая отрасль сталкивается с множеством проблем, от начала разведки до добычи нефти и природного газа, работая в экстремальных условиях с растущими полномочиями по минимизации капитальных и операционных затрат, уделяя приоритетное внимание безопасности при одновременном сокращении времени простоя и выбросов.Роль передовых технологий моделирования потоков очень важна для преодоления этих проблем, особенно в условиях нынешнего прогресса в цифровую эпоху. Точное цифровое представление операций вверх и вниз по потоку требует мультидисциплинарного подхода, начиная от простых корреляций до высокоточного численного анализа, такого как вычислительная гидродинамика (CFD). Объем и потребность в моделировании CFD приобрели значительный импульс в отрасли и быстро растут, предлагая возможность максимизировать инновационные и инженерные разработки при сокращении времени и затрат.
Этот симпозиум направлен на предоставление обзора того, как численное моделирование и анализ могут быть успешно применены для решения проблем потока жидкости для нефтегазовой промышленности в широком спектре приложений, включая, помимо прочего, моделирование призабойной зоны скважины, бурение и Заканчивание, обеспечение потока, безопасность технологических процессов, шельфовые и глубоководные работы, нефтепереработка и нефтехимия. Этот симпозиум в дальнейшем станет местом встречи экспертов из промышленности и академических кругов для обмена опытом и извлеченными уроками.
Программа включает технические презентации по различным темам механики жидкостей, некоторые из этих тем следующие –
- Моделирование в упрощенном порядке и цифровые двойники
- Интеграция машинного обучения и анализа данных с CFD
- Проблемы целостности, такие как эрозия, коррозия и вибрация, вызванная потоком
- Мультифизическое, многофазное и многомасштабное моделирование
- Численное моделирование волн для морского строительства
- Моделирование потока в скважинных инструментах
- CFD в химических и нефтехимических процессах
ПРОГРАММА
7:00 – 7:45 Регистрация / завтрак
7:45 – 8:00 Приветствие / Введение
8:00 – 8:30 Основной доклад: Спикер TBD , BP
8:30 – 10:00 Сессия-1
- Аналитика данных и машинное обучение в обеспечении потока данных , Prabu Parthasarathy, Wood Plc
- Моделирование на основе моделирования автономного устройства контроля притока циклонного типа для регулирования воды и газа, Gocha Chochua, Schlumberger
- Ускорение инноваций в новых источниках энергии: применение вычислительных методов, Сантош Шанкар, Shell
- Достижения в CFD-моделировании многорежимных многофазных потоков, Саймон Ло, Siemens PLM Software
10:00 – 10:15 Кофе-брейк
10:15 – 12:00 Сессия-2
- Ключи к приложениям отвода твердых частиц: от моделирования CFD до геомеханического моделирования, Jian Huang, Weatherford
- Выбор правильного масштаба для создания эффективных цифровых двойников в обрабатывающих отраслях, Нандакумар, Университет штата Луизиана
- Цифровые двойники на основе моделирования для улучшенного управления эксплуатацией и техническим обслуживанием активов , Anchal Jatale, ANSYS
- CFD-моделирование в инструментах для заканчивания скважин , Bin Zhu, Baker
- Моделирование полидисперсных многофазных потоков квадратурными методами моментов в OpenQBMM , Альберто Пассалаква и Родни Фокс, Университет штата Айова
12:00 – 13:00 Перерыв на обед
13:00 – 14:45 Сессия-3
- Модель нейронной сети на основе CFD для разделения нефти / воды в горизонтальных трубопроводах, Kuochen Tsai, Shell
- Роль моделирования CFD в концепции цифрового двойника для нефтегазовой промышленности, Али Марзбан, ноябрь
- Структурная целостность: почему я должен беспокоиться о моделировании потока жидкости, Matt Straw, Norton Straw Consultants
- Многофазная вычислительная гидродинамика в Exascale , Мадхава Шьямлал и Уильям Роджерс, NETL
- Оценка эрозии трубопроводов с использованием методов Data Science, Erosion Science и CFD , Praveen Gonuguntla и Damodaran Vedapuri, Tridiagonal
14:45 – 15:00 Перерыв на кофе
15:00 – 16:50 Сессия-4
- Гибридный цифровой двойник: проблемы в сочетании основанных на данных и физических методов для создания и моделирования цифрового двойника , Srinath Madasu, Landmark – Halliburton
- CFD – Муфта DEM для моделирования потока жидкости с точным представлением частиц, Маркус Рейс и Кловис Малиска, ESSS
- Примеры мультифизического моделирования и прогнозной аналитики для приложений нефтяной инженерии, Mayank Tyagi, Университет штата Луизиана
- Прагматический подход к моделированию потоков газа и твердых веществ в промышленных масштабах , Sreekanth Pannala, SABIC
- Расширенные инструменты моделирования CFD для точного и эффективного прогнозирования сложных опасных явлений на крупных нефтехимических предприятиях , Скотт Дэвис, Gexcon US
16:50 – 17:00 Заключительное слово
.
 5
5