Решение задач по квантовой механике
Для многих студентов квантовая механика — все равно что китайская грамота. Почему данная наука вызывает непонимание, а каждое домашнее или контрольное задание становится труднопреодолимым испытанием?
Причины бывают самые разные в зависимости от того, к какому виду относится тот или иной студент. Без лукавства можно сказать, что самой распространенной из них является элементарная лень. Большинство студентов не имеют желания тратить время и усилия на освоение науки, сильно отличной от всех и потому требующей большего внимания. Другие страдают от нехватки базовых знаний в области математики и физики, ведь, согласитесь, сложно решать квантовомеханические дифференциальные уравнения, не имея хороших навыков дифференцирования и интегрирования. Вызван дефицит знаний ленью или “плохой школой” — уже другая история.
Конечно, бывает и такoй фактор, как преподавание предмета плохим лектором, неспособным грамотно, логически структурированно пояснить фундаментальные основы квантовой механики.
Квантовая механика не является чем-то недоступным для человеческого понимания. На самом деле, при наличии желания понять данный предмет и должном усердии можно достичь больших успехов (что справедливо, впрочем, и для любого другого предмета).
Желающим приложить усилия и изучить квантовую механику как следует можем дать следующие рекомендации. Итак, краткая инструкция:
- Восполните пробелы в своих знаниях по линейной алгебре: линейные пространства, базисы, детерминанты, матрицы. Без этих знаний вам будет сложной понять математический аппарат квантовой механики. Рекомендую доступную в плане изложения книгу —
- Вспомните, как решать дифференциальные уравнения. Если не умеете, научитесь!
- К сожалению, хороших русскоязычных учебников по квантовой механике мало. Традиционно, для курса квантовой механики используют следующий учебник: Л.Д. Ландау и Е.
 М. Лифшица «Квантовая механика». Можно воспользоваться такими книгами, как Мессиа А. « Квантовая механика». Если есть возможность, то лучше ознакомиться с хорошим западным учебником, например, Claude Cohen-Tannoudji, Bernard Diu , Frank Laloe
М. Лифшица «Квантовая механика». Можно воспользоваться такими книгами, как Мессиа А. « Квантовая механика». Если есть возможность, то лучше ознакомиться с хорошим западным учебником, например, Claude Cohen-Tannoudji, Bernard Diu , Frank Laloe - Читать хорошо, но надо и практиковаться, решать задачки и выполнять некие математические выкладки для понимания того, что и откуда выводится. Для этих целей хорошо подходят следующие задачники:
- В.М.Галицкий, Б.М.Карнаков, В.И.Коган. «Задачи по квантовой механике».
- З. Флюгге . «Задачи по квантовой механике» (содержит и теорию).
Для желающих заработать хорошую оценку при меньших усилиях, есть хорошая новость. За исключением отдельных физических специализаций на отдельных факультетах, большинство проходит неполный курс ознакомительного характера.
Квантовый мир устроен немного иначе. И вам надо понять основные различия между квантовой механикой и теоретической: получить представление о вероятностном характере движения электрона, уяснить принцип неопределенности Гейзенберга и его последствия, и т.д.
Типичные вопросы, на которых ловят нерадивых студентов:
- Почему движущийся с ускорением электрон не падает на ядро, теряя энергию при излучении электромагнитных волн?
- Схоже ли движение электрона вокруг ядра с движением Луны вокруг солнца (нет, поймите почему)?
- Может ли частица проскочить через барьер с энергией меньшей, чем высота барьера (вероятность туннелирования маленькая, но не нулевая)?
- В чем отличие квантового гармонического осциллятора от классического гармоническом осцилляторе из курса теоретической механики (обязательно поясните для себя, в чем состоит различие между двумя этими задачами)?
Решение квантовой механики на заказ
 У нас можно заказать подробное решение задач по квантам. Нужно только прикрепить задание и указать сроки.
У нас можно заказать подробное решение задач по квантам. Нужно только прикрепить задание и указать сроки.УЗНАТЬ СТОИМОСТЬ РЕШЕНИЯ
Семинары по квантовой механике
Семинары по квантовой механике Материалы: [Осень 2021] [Весна 2021] [Осень 2020] [Весна 2020] [Осень 2019] [Весна 2019] [Осень 2018] [Весна 2018] [Осень 2017] [Весна 2017] [Осень 2016] [Весна 2016] [Осень 2015]- Где: 515 ГК
- Когда: Суббота, 10:45 — 12:10
- Дополнительное время: 122 ЛК, Суббота, 12:45 — 14:00
- Контакты: Тихонов Константин
Программа
Семинар 1: Общее введение. Принцип суперпозиции, операторы и наблюдаемые (Тихонов К.)
5 сентября 2015 г.- [обязательно] Учебник: Ландау — Глава 1: Основные понятия квантовой механики
- [обязательно] Учебник: Ландау — Глава 2: Энергия и импульс
- [обязательно] Учебник: Ландау — Глава 3§17: Уравнение Шредингера
- [обязательно] Учебник: Дирак — Глава 1: Принцип суперпозиции
- [рекомендовано] Учебник: Дирак — Глава 2: Динамические переменные и наблюдаемые
- [рекомендовано] Задачи: Галицкий — Глава 1: Операторы в квантовой механике
- [дополнительно]
Видео: S.
 R. Coleman, Quantum Mechanics in Your Face
R. Coleman, Quantum Mechanics in Your Face
Семинар 2: Одномерное движение (Тихонов К.)
12 сентября 2015 г.- [обязательно] Учебник: Ландау — Глава 3: Уравнение Шредингера
- [обязательно] Учебник: Дирак — Глава 3: Представления
- [рекомендовано] Задачи: Галицкий — Глава 2§1: Стационарные состояния дискретного спектра
- [рекомендовано] Задачи: Галицкий — Глава 2§2: Уравнение Шредингера в импульсном представлении. Интегральная форма уравнения Шредингера
- [рекомендовано]
Задачи: Галицкий — Глава 2§4: Системы с несколькими степенями свободы.

- [дополнительно] Учебник: Базь — Глава VI§1-3: Точные решения нестационарных задач для осциллятора
Семинар 3: Теория возмущений (Тихонов К.)
19 сентября 2015 г.- [обязательно] Книга: Ландау — Глава 6: Теория возмущений
- [обязательно] Задачи: Галицкий — Глава 8§1: Стационарная теория возмущений (дискретный спектр)
- [обязательно] Задачи: Галицкий — Глава 8§3: Стационарная теория возмущений (непрерывный спектр)
- [обязательно] Задачи: Галицкий — Глава 8§4: Нестационарная теория возмущений. Переходы в непрерывном спектре
- [рекомендовано] Книга: Мигдал — Глава 2§1: Теория возмущений в непрерывном спектре
- [рекомендовано] Книга: Мигдал — Глава 2§6: Теория возмущений в случае близких уровней
Семинар 4: Адиабатическое приближение (Тихонов К.
 ) 26 сентября 2015 г.
) 26 сентября 2015 г.- [обязательно] Книга: Мигдал — Глава 2§5: Быстрая и медленная подсистемы
- [обязательно] Задачи: Галицкий — Глава 8§6а: Адиабатическое приближение в нестационарных задачах
- [обязательно] Задачи: Галицкий — Глава 8§6б: Адиабатическое приближение в стационарных задачах
Семинар 5: Квазиклассическое приближение (Тихонов К.)
24 октября 2015 г.- [обязательно] Книга: Ландау — Глава 8: Квазиклассический случай
- [обязательно] Задачи: Галицкий — Глава 9: Квазиклассическое приближение
- [рекомендовано]
Книга: Мигдал — Глава 3§1: Квазиклассическое приближение.
 Одномерная задача
Одномерная задача - [рекомендовано] Статья: В. Л. Покровский — Semiclassical and Adiabatic Approximation in Quantum Mechanics
Семинар 6: Теория рассеяния – 1. Формула Ландауэра (Антоненко Д.)
31 октября 2015 г.- [обязательно] Книга: Ландау — Глава 17: Упругие столкновения
- [обязательно] Задачи: Галицкий — Глава 13§1: Борновское приближение
- [обязательно] Задачи: Галицкий — Глава 13§2: Фазовая теория рассеяния
- [рекомендовано] Заметки: Д. Антоненко — Формула Ландауэра
- [дополнительно]
Книга: Y.
 V. Nazarov, Y. M. Blanter — Quantum Transport: Introduction to Nanoscience
V. Nazarov, Y. M. Blanter — Quantum Transport: Introduction to Nanoscience
Семинар 7: Надбарьерное отражение – 1 (Степанов Н.)
7 ноября 2015 г.Семинар 8: Теория рассеяния – 2 (Побойко И.)
21 ноября 2015 г.- [обязательно] Книга: Ландау — Глава 17: Упругие столкновения
- [обязательно] Книга: Дирак — Глава 8: Задачи о столкновениях
- [обязательно] Книга: Базь — Глава 2: Непрерывный спектр
- [обязательно] Задачи: Галицкий — Глава 13§1: Борновское приближение
- [обязательно] Задачи: Галицкий — Глава 13§2: Фазовая теория рассеяния
- [рекомендовано]
Заметки: И.
 Побойко — Теория рассеяния
Побойко — Теория рассеяния - [дополнительно] Книга: Базь — Глава 3: Аналитические свойства волновой функции
- [дополнительно] Задачи: Галицкий — Глава 13§6: Аналитические свойства и унитарность амплитуды рассеяния
Семинар 9: Надбарьерное отражение – 2 (Тихонов К.)
12 декабря 2015 г.Задания
Даты:
- Промежуточный экзамен 1: 10 Октября
- Сдача заданий 1 – 4: 3 Октября
- Сдача заданий 5 – 9: 19 Декабря
Оценка:
- Задания: 40%
- Промежуточные экзамены: 30%
- Экзамен: 30%
Математический минимум:
- Обязательно: Ландау — Математические дополнения
- Обязательно: Мигдал — Глава 1§1: Методы оценки математических выражений
- Рекомендовано: Уиттекер Э.
 Т., Ватсон Дж.Н. “Курс современного анализа” – М.: Гл. ред. физ.-мат.лит, 1963
Т., Ватсон Дж.Н. “Курс современного анализа” – М.: Гл. ред. физ.-мат.лит, 1963 - Упражнения
Задачи:
Экзамены
Литература
- [обязательно] Л.Д. Ландау, Е.М. Лифшиц “Квантовая механика (нерелятивистская теория)”, 5-е изд., ФИЗМАТЛИТ, 2002
- [обязательно] В.М. Галицкий, Б.М. Карнаков, В.И. Коган “Задачи по квантовой механике”, 3-е изд., Едиториал УРСС, 2001
- [рекомендовано] П.А.М. Дирак “Принципы квантовой механики”, Наука, 1979
- [рекомендовано] А.Б. Мигдал, “Качественные методы в квантовой теории”, Наука, 1975
- [рекомендовано] А.И. Базь, Я.Б. Зельдович, А.М. Переломов “Рассеяние, реакции и распады в нерелятивистской квантовой механике”, Наука, 1971
- [рекомендовано] З. Флюгге “Задачи по квантовой механике (в 2 томах)”, Мир, 1974
Powered by Lektor
© Copyright 2017 by Igor Poboiko.

(PDF) Квантовая механика и статистическая физика
38
5.3. Распределения Максвелла и Больцмана
1. Для максвелловского распределения скоростей найти:
а) среднюю скорость;
б) среднюю квадратичную скорость;
в) наиболее вероятную скорость.
2. Чему равна наиболее вероятная кинетическая энергия молекулы,
описываемой максвелловским распределением скоростей? Равна ли она
2/2mυ, где υ − наиболее вероятная скорость молекулы?
3. Газ, состоящий из молекул с массой m, находится в равновесии при
абсолютной температуре Τ. Обозначим через υ скорость молекулы, а че-
рез
υ, y
υ, z
υ − ее декартовские проекции. Найти следующие средние: a)
υ; б) 2
υ; в) 2y
υυ ; г) 2
y
υυ ; д) 2n
y
υ+bυ, где b− постоянная. Соображения
симметрии и теорема о равнораспределении энергии по степеням свободы
дают возможность получить эти средние без сложных вычислений.
4. Какая доля молекул газа (газ находится в тепловом равновесии) об-
ладает кинетической энергией:
а) большей, чем средняя тепловая;
б) в 3 раза большей, чем средняя тепловая;
в) в 10 раз большей, чем средняя тепловая?
5. Молекулы одноатомного газа вылетают из щели в стенке сосуда,
находящегося при абсолютной температуре Т. Как соотносятся средняя
кинетическая энергия вылетевших молекул 0
и средняя кинетическая
энергия молекул, находящихся внутри сосуда i
?
6. Найти отношение средней длины волны де Бройля к среднему рас-
стоянию между частицами для воздуха при нормальных условиях.
7. Оценить типичные максимальную и минимальную скорости моле-
кул (ту скорость, которую имеет в среднем одна-единственная молекула) в
литре воздуха при нормальных условиях.
8. Газ из атомов, имеющих массу m, находится внутри сосуда при аб-
солютной температуре Т. Атомы испускают свет, который выходит из со-
суда в направлении
через окно в его стенке. Свет, испускаемый атомом,
Свет, испускаемый атомом,
имеет определенную частоту 0
ν. Однако благодаря эффекту Доплера час-
тота света, испущенного атомом, не равна частоте 0
ν. Приближенное зна-
чение частоты равно
0
1,
x
v= v + v /c где c − скорость света. В результате
Урок физики “Решение задач по теме: «Квантовые явления»” (9 класс)
Тема: Решение задач по теме: «Квантовые явления» Цели и задачи:
обобщить и систематизировать материал по основам квантовой физики;
научить выявлять положительные и отрицательные стороны научных исследований, открытий и технологических достижений;
продолжить формирование интереса к научным познаниям;
Оборудование: компьютер,,портреты учёных, словарь физических терминов.
План урока:
Актуализация знаний
Обобщение ранее изученного
Разноуровневая самостоятельная работа
Работа учащихся с КиМ “Физика”, раздел «Квантовая физика»
Подведение итогов урока
Итоговое обобщение
I . Актуализация знаний
Актуализация знаний
Допишите формулы:
… = hν
Р = m…
Е = …c2
hc/λ = А + …
… = Ек – Еp
λm = hc/…
νmin = А/…
Озаглавьте записанные формулы.
Ответьте на вопросы:
1.Назовите факты, опыты и явления, подтверждающие квантовые свойства света.
2. Что понимают под внешним фотоэффектом?
3. В 1905 году А. Эйнштейн дал простое уравнение, вскрывающее сущность фотоэффекта. Если А1 –работа, потребная для вырывания электронов из атома и А2 –работа, необходимая для выведения электронов сквозь поверхностный слой вещества, то кинетическая энергия фотоэлектронов, вырывающихся наружу, будет:
Ек = hν – ( A1+A2)
Исходя из этого уравнения, объясните:
А) Как зависит Ек от частоты излучения?
Б) Чем будет отличаться механизм фотоэффекта при облучении вещества рентгеновскими лучами УФ излучением?
4. Как объяснить резкое увеличение электропроводности селена под воздействием радиации?
Как объяснить резкое увеличение электропроводности селена под воздействием радиации?
Ответ: если электроны под воздействием радиации вырываются из атомов, но при этом остаются внутри тела, а не вырываются наружу, то электропроводность вещества возрастает. На этом основан принцип селенового фотоэлемента.
II. Обобщение изученного ранее.
Проблемный вопрос.
В чём отличие классического понятия реальности от понимания реальности и измерения в квантовой физике?
В ходе урока попытаемся дать ответ на этот вопрос при подведении итогов.
Тепловые детекторы и фотодетекторы.
Тепловые детекторы предшествовали квантовым. Их история началась в 1800 году, когда Уильям Гершель /1738 – 1822/, используя призму и ртутный термометр, открыл инфракрасное излучение. Но первый настоящий детектор появился лишь в 1830 году, когда итальянские физики Леопольдо Нобели и Македонио Меллони сконструировали первые термоэлементы, которые представляют собой совокупность термопар, соединённых вместе. В качестве фотодетектора может служить селеновый фотоэлемент.
В качестве фотодетектора может служить селеновый фотоэлемент.
2. Фотоэффект
Физические механизмы излучения света достаточно многообразны. Попытки с классической точки зрения объяснить излучение абсолютно чёрного тела потерпели неудачу, приведя к известному закону излучения Планка и квантовой теории.
Макс Планк пытается примерить два начала термодинамики с теорией электромагнетизма. Однако за хорошую упаковку надо платить. Чтобы закон излучения удовлетворял экспериментальным данным по излучению чёрного тела, Планк в 1900 году вынужден ввести новую постоянную величину ( постоянную Планка h = 6,63-34Дж∙ с).
Какую гипотезу выдвигает Планк об излучении?
Ответ: электромагнитное излучение происходит не непрерывно, а отдельными порциями – квантами.
Ни План.к, никто другой не понимают в тот момент, что, завершив построение основ термодинамики, они стали родоначальниками новых представлений об энергии и оказались на пороге нового мира – квантовой физики.
Открытие фотоэффекта взбудоражило умы многих учёных, среди которых был А. Г. Столетов (краткое сообщение ученика об открытии фотоэффекта).
У вас есть уникальная возможность смоделировать опыты Столетова, используя компьютер, и ответить на вопросы, мучившие учёного многие месяцы.
Работа учащихся с КиМ “Физика”, раздел «Квантовая физика».
Начальный уровень – выполняется в виде тестов с выбором ответа;
Средний уровень – включает в себя несложные задачи, при решении которых необходимо получить ответ. /Тесты прилагаются /.
Зная ответы, можно быстро оценить работы учащихся, предложив предварительно провести проверку в парах.
Подведение итогов.
А. Эйнштейн, который так и не принял до конца философию квантовой теории, тем не менее, заложил начало двум фундаментальным положениям: понятию фотона / 1905г. / и стимулированного излучения / 1917г. /. Без этих понятий нельзя, например, описать работу лазера. Нильс Бор – наиболее страстный приверженец квантовой теории, создал первую квантовую модель атома. Многие учёные внесли свой вклад в создание квантовой теории.
Нильс Бор – наиболее страстный приверженец квантовой теории, создал первую квантовую модель атома. Многие учёные внесли свой вклад в создание квантовой теории.
Итоговое обобщение.
Изучение фундаментальных опытов – это один из способов научного познания, который позволил нам на уроке вести научный поиск проблемного характера.
Словарь новых терминов.
Релаксация – постепенное возвращение в состояние равновесия какой-либо системы после прекращения действия возмущения.
Фотон ( гр. свет ) – элементарная частица – квант электромагнитного поля.
Лазер – прибор для получения чрезвычайно интенсивных и узконаправленных пучков монохроматического излучения.
Инверсия – нарушение нормального порядка двух элементов в перестановке.
Основные этапы создания квантовой механики.
Квантование энергии: Макс Планк, 1900г. (премия 1918) (слайд 17)
Фотоны: Альберт Эйнштейн,1905г.
 (премия 1921г.)
(премия 1921г.)Атомные уровни: Нильс Бор, 1913 г. (премия 1922г.)
Корпускулярно-волновой дуализм: Луи де Бройль, 1923-1924гг. (премия 1929г.)
Принцип запрета: Вольфганг Паули, 1924-1925гг. (премия 1945г.
Матричная механика и принцип неопределённости: Вернер Гейзенберг, 1925г. и 1927г. (премия 1932г.)
Волновая функция: Эрвин Шрёдингер, 1926г. и Поль Дирак 1926-27гг. (совместная премия 1933г.)
Вероятностная интерпретация волновой функции: Макс Борн, 1926г. (премия 1954г.)
Математически строгая формулировка квантовой механики: Джон фон Нейман, 1927-1932гг Рефлексия. Задание на дом:
задачи по физике, примеры решения
Столкнувшись с задачами по физике на внутреннюю энергию, главное, основательно разобраться во всех процессах, указанных в условиях, и использовать ранее изученные формулы по этой теме.
Каким образом можно изменить внутреннюю энергию в физике
Чтобы условия задачи всегда были ясны, важно детально разобраться с понятием, точно знать, что это такое, от чего зависит и на что влияет.
Понятие, определение
Внутренней энергией называется энергия движения и взаимодействия частиц, составляющих тело, соответственно, она складывается из кинетической энергии, возникающей при движении молекул тела, и потенциальной энергии взаимодействия его частиц.
В международной системе обозначается большой латинской буквой U и измеряется в Джоулях.
Внутренняя энергия тела зависит:
- От температуры. Чем выше температура тела, тем активнее движутся частицы внутри него, тем больше его внутренняя энергия.
- От его массы.
- От агрегатного состояния вещества (вода/лед).
Изменить внутреннюю энергию можно:
- С помощью работы, совершаемой над телом или совершенной им. Причем, внутренняя энергия объекта уменьшается, если он совершает работу, и, наоборот, увеличивается, если работа совершается над ним.
- При помощи теплопередачи.
Теплопередача — это один из способов изменения внутренней энергии объекта, при котором происходит передача энергии от объекта к объекту или от одной части тела к другой без совершения работы.
Основные формулы и их применение
Основными формулами, которые понадобятся для решения задач по данной теме, являются:
- \(U=E_к+E_п\), где \(E_к\) — кинетическая энергия, а \(E_п\) — потенциальная.
- \(\Delta U=A+Q\), где \(A\) — это работа, \(Q\) — количество теплоты. Данное уравнение выражает первый закон термодинамики: изменение внутренней энергии при переходе системы из одного состояния в другое будет равняться сумме работы внешних сил и количества теплоты переданной системе.
Примеры решения качественных задач по теме
Для решения задач по данной теме термодинамики чаще всего нужны следующие формулы:
Источник: infourok.ruЧтобы окончательно разобраться с темой, рассмотрим решение нескольких типовых задач.
Задача №1
Какова внутренняя энергия гелия, который заполняет аэростат объемом 50 м3 при давлении в нем 80 кПа?
Решение
- Записываем известные нам данные: p=80 кПа, V=50 м3, U=?
- Приводим единицы измерения давления к общепринятым — Па, p=8х104 Па.
- Для одноатомного идеального газа U вычисляется по формуле: \(U=\frac32\times\frac mM\times R\times T\)
- Для решения этой задачи нам понадобится уравнение Менделеева-Клапейрона: \(p\times V=\frac mM\times R\times T\)
- Соответственно, \(U=V=\frac32\times p\times V\)
- Подставляем числовые значения в формулу и получаем ответ: 6 МДж.
Задача №2
Насколько изменилась внутренняя энергия гелия, если его масса 200 грамм, а температура увеличилась на 20 Кельвинов?
Решение
- Записываем вводные данные: m= 200 гр., T=20 К, R=8,31 Дж х моль/К, M=0,004 кг/моль, U=?
- Для решения данной задачи потребуется одна формула — для идеального газа: \(U=\frac32\times\frac mM\times R\times T\)
- Производим несложные математические действия и получаем ответ: 12,5 кДж.
Задача №3
Газ находится в закрытом баллоне. При охлаждении газа его внутренняя энергия снизилась на 500 Дж. Какое количество теплоты при этом отдал газ и совершал ли он работу?
Решение
- Это задача скорее теоретическая, поэтому давайте рассуждать: так как газ находится в закрытом баллоне, следовательно, его объем не меняется, т.е. \(\Delta V=0\)
- Работа определяется по формуле: \(\Delta V=0\), \(А=0\), а это значит, что газ работу не совершал.
- По первому закону термодинамики, \(Q=A+\Delta U=\Delta U= — 500\) Дж.
Если тема по-прежнему кажется сложной, а вам предстоит подготовить доклад или решить с десяток задач по ней, не спешите отчаиваться! Специалисты онлайн-сервиса Феникс.Хелп рады будут помочь с любой темой по физике или другому предмету.
задач квантовой механики | SpringerLink
Это второе издание чрезвычайно хорошо принятой книги представляет более 250 задач нерелятивистской квантовой механики различной сложности с целью предоставить студентам дидактический материал доказанной ценности, позволяющий им проверить свое понимание и овладение каждым предметом. Охват чрезвычайно широк: от тем, связанных с кризисом классической физики через достижения в рамках современной атомной физики, до оживленных, интригующих аспектов, касающихся, например, парадокса ЭПР, эффекта Ааронова-Бома и квантовой телепортации.По сравнению с первым изданием был внесен ряд улучшений и включены дополнительные темы, представляющие интерес, особенно с упором на элементарное потенциальное рассеяние. Сами проблемы варьируются от стандартных и простых до сложных, но могут считаться важными, поскольку они касаются вопросов выдающейся важности или аспектов, которые обычно упускаются из виду в учебниках. Книга предлагает студентам как отличный инструмент для самостоятельного обучения, так и готовое справочное руководство, к которому они могут вернуться позже в своей карьере.Проблемы квантовой механики с решениями Учебник по квантовой физике Взаимодействие излучения и материи Элементарный потенциал Рассеяние Старая квантовая теория Волны и частицы Уравнение Шредингера Эффекты спинового и магнитного поля Электромагнитные переходы ЭПР-парадокс Эффект Ааронова-Бома Квантовая телепортация
Об авторах
Эмилио д’Эмилио ранее был научным сотрудником факультета физики Пизанского университета, Италия.Он читал курсы по физике в Пизанском и Сиенском университетах, включая аналитическую механику, элементарную квантовую механику, промежуточную квантовую механику и квантовую электродинамику. Доктор д’Эмилио публиковался в международных журналах по калибровочным квантовым теориям поля, феноменологии элементарных частиц и математической физике. Он также сотрудничал с L.E. Пикассо за публикацию лекций по квантовой механике (2016) со Спрингером.
Э. Пикассо ранее был профессором теоретической физики в Пизанском университете, Италия.Он читал курсы по физике и математике, включая Введение в квантовую механику и дополнения к физике. Доктор Пикассо имеет множество публикаций, посвященных его имени. Он внес вклад в Энциклопедию сложности и системных наук (Springer) и является соавтором вместе с Э. д’Эмилио книги Лекции по квантовой механике (Springer, 2016).
3.2: Несвязанные задачи в квантовой механике
Затем мы решим не зависящее от времени уравнение Шредингера в некоторых интересных одномерных случаях, связанных с задачами рассеяния.
Бесконечный барьер
Сначала рассмотрим потенциал, показанный на рисунке \ (\ PageIndex {1} \). Мы рассматриваем два случая:
- Случай A. Система (частица) имеет полную энергию, превышающую потенциальный барьер \ (E> V_H \).
- Случай Б. Энергия меньше потенциального барьера \ (E
Давайте сначала рассмотрим классическую задачу.{2}} {2 m} = E-V_ {H} \), что дает просто приведенную скорость частицы. Если вместо этого E
В квантовой механике нам нужно решить уравнение Шредингера, чтобы найти волновую функцию, описывающую частицу в любом положении.{2}} = \ left (E-V_ {H} \ right) \ psi (x) \ text {в области II}
\ end {array} \ right. \ nonumber \]
Эти два случая различаются, поскольку в Области II разность энергий \ (\ Delta E = E-V_ {H} \) либо положительна, либо отрицательна.
Положительная энергия
Давайте сначала рассмотрим случай, когда \ (\ Delta E = E-V_ {H}> 0 \). В обеих областях частица ведет себя как свободная частица с энергией E I = E и E II = E – V H . Мы уже видели решения такого дифференциального уравнения.{-i k x} \) как волна, бегущая справа налево. Затем мы рассмотрим случай, аналогичный классическому, когда мяч был направлен к преграде. Тогда частица первоначально описывается как волна, движущаяся слева направо в области I. На потенциальном барьере частица может либо отражаться, вызывая волну, бегущую справа налево в области I, либо передаваться, давая волну путешествуя слева направо в Регионе II. Это решение описывается приведенными выше уравнениями, если мы полагаем D = 0, подразумевая, что нет волны, исходящей далеко справа.
Поскольку волновая функция должна описывать физическую ситуацию, мы хотим, чтобы она была непрерывной функцией и с непрерывной производной. Таким образом, мы должны согласовать значения решения и их производные на границе x = 0. {\ prime}} A \ nonumber \]
Мы можем найти A, интерпретируя волновую функцию в терминах потока частиц.{\ prime}} {k} \ end {align *} \]
Тогда легко увидеть, что \ (T + R = 1 \), и мы можем интерпретировать коэффициенты отражения и передачи как вероятность отражения и передачи соответственно.
В соответствии с вероятностной природой квантовой механики мы видим, что решение уравнения Шредингера не дает нам точного местоположения частицы. Вместо этого он описывает вероятность нахождения частицы в любой точке пространства. Зная волновую функцию, найденную выше, мы можем затем вычислить различные интересующие нас величины, такие как вероятность того, что частица будет иметь заданный импульс, положение и энергию.{2}} = k \ nonumber \]
В терминах потока мы можем записать это соотношение как \ (\ Gamma = \ Gamma_ {R} \), что подразумевает R = 1 и T = 0. Таким образом, у нас нет передачи, только идеальное отражение, хотя есть проникновение вероятности в запрещенной области. Это можно назвать исчезающей прошедшей волной .
Конечная преграда
Теперь рассмотрим другой потенциал, который создает конечный барьер высотой V H между x = 0 и L. Как показано на рисунке \ (\ PageIndex {2} \), этот потенциал делит пространство на 3 области.Снова рассмотрим два случая, когда полная энергия частицы больше или меньше V H . Классически мы рассматриваем шар сначала в Области I. Затем в случае, когда
Рисунок \ (\ PageIndex {2} \): Конечный барьерный потенциал (CC BY-NC-ND; Паола Каппелларо) E> V H шар может перемещаться везде, во всех трех областях, а для E
В частности, нас интересует вероятность прохождения пучка через преграду в область III. {ikx}
\ end {array} \ nonumber \]
Разница здесь в том, что возможна конечная передача через барьер и коэффициент передачи не равен нулю.Действительно, из полного решения задачи с граничными условиями мы можем найти, как и в предыдущем случае, коэффициенты T и R, и мы имеем T + R = 1.
Таким образом, существует вероятность того, что частица туннелирует через конечный барьер и появится в Области III, а затем продолжит движение до x → ∞.
Обс. Хотя мы описывали ситуацию в терминах волны, распространяющейся в одном или другом направлении, то, что мы здесь описываем, не является проблемой, зависящей от времени.В этой задаче вообще нет зависимости от времени (все решения являются функцией только от x, а не от времени). Это та же ситуация, что и стационарные волны, например, в канате. Состояние системы не меняется. Он всегда (в любое время) описывается одними и теми же волнами, и поэтому в любое время мы будем иметь одинаковые результаты и вероятностные результаты для любого измерения.
Оценки и масштабирование
Вместо того, чтобы точно решать задачу для второго случая, мы пытаемся сделать некоторые оценки в случае очень малой вероятности туннелирования.В этом случае мы имеем следующие приближения для коэффициентов A, B, C и D.
- Предполагая T ≪ 1, мы ожидаем D ≈ 0, поскольку, если существует очень малая вероятность того, что частица окажется в области III, вероятность возврата от нее через барьер должна быть еще меньше (другими словами, если \ ( D \ neq 0 \) вероятность выхода волны из преграды возрастала).
- Кроме того, T ≪ 1 означает R ≈ 1. Это означает, что B / A ≈ 1 или B ≈ A.
- Согласовав волновую функцию при x = 0, мы имеем C = A + B ≈ 2A.{-2 \ kappa L} \ nonumber \]
Таким образом, вероятность передачи зависит от длины потенциального барьера (чем длиннее барьер, тем меньше пропускание, как это интуитивно понятно) и от коэффициента \ (\ kappa \). Обратите внимание, что \ (\ kappa \) зависит от разницы между энергией частицы и потенциальной силой: если энергия частицы находится около края потенциального барьера (то есть ΔE ≈ 0), то \ (\ kappa \) ≈ 0 и есть большая вероятность туннелирования. Однако этот случай противоречит нашим первым предположениям о малом туннелировании (поэтому мы получаем нефизический результат, что T ≈ 4 !!).Вместо этого мы рассматриваем случай, когда энергия частицы мала по сравнению с потенциалом, так что \ (\ kappa \) велико, и частица имеет очень низкую вероятность туннелирования.
(PDF) Уравнения релятивистской и квантовой механики и точные решения некоторых задач
УРАВНЕНИЯ РЕЛЯТИВИСТСКОЙ И КВАНТОВОЙ МЕХАНИКИ
21
ЖУРНАЛ СОВРЕМЕННОЙ ФИЗИКИ (АН АРМ.) Том. 53 № 1 2018
Представлены решения задачи о движении заряда в постоянном электрическом поле, задачи
частицы в потенциальной яме, задачи о проникновении частицы через потенциальный барьер и задачи
проблемы атома водорода.
Анализ решений показывает полное соответствие принципам релятивистской и квантовой механики
, а решения лишены каких-либо ограничений на природу и величину взаимодействий
.
СПИСОК ЛИТЕРАТУРЫ
1. Бор Н. Филос. Mag., 1913, т. 26, стр. 1; 476; 857.
2. Uhlenbeck, G.E. и Гоудсмит, С., Naturwissenschaften, 1925, т. 47, стр. 953; Природа, 1926, т. 117, стр. 264.
3.Зоммерфельд, А., Ann. Физ., 1916, т. 51, стр. 1; Phys. З., 1916, т. 17, стр. 491.
4. Грановский Ю.И. // Успехи физ. Наук. 47, стр. 523.
5. Dirac, P.A.M., Proc. Королевское общество А, 1928, стр. 117, стр. 610.
6. Де Бройль, M.L., Comptes Rendus, 1923, vol. 177, стр. 507.
7. Hoffman, D., Erwin Schrödinger, Leipzig: Teubner, 1984.
8. Schrödinger, E., Ann. Physik., 1926, т. 79, стр. 389.
9. Клейн О. З. Phys. 1926. Т.37, стр. 895.
10. Фок В., З. Физика, 1926, т. 38, стр. 242.
11. Гордон, В., З. Phys., 1926, т. 40, стр. 117.
12. Гейзенберг В., Джордан П., Zeits. Физ., 1926, т. 37, стр. 263.
13. Thomas, L.H., Nature, 1926, vol. 117, стр. 514; Фил. Mag., 1927, т. 3, стр. 1.
14. Соколов А.А., Тернов И.М., Килмистер Ч.В., Излучение релятивистских электронов, Нью-Йорк: Американский институт физики
, 1986.
15.Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая электродинамика, Оксфорд: Пергамон, 1984.
16. Маделунг Э., Mathematische Hilfsmtittel des Physikers, 3-е изд., Берлин: Springer, 1936.
17. Ахиезер А.И., Берестецкий В.Б. Квантовая электродинамика, John Wiley & Sons, 1965.
18. Дирак П.А. Труды института истории естествознания и техники, 1959, вып. 22, стр. 32.
19. Мехитарян В.М., J. Contemp. Phys. (Армянский ак. Наук.), 2012, т. 47, стр. 249.
20. Ландау, Л.Д. , Лифшиц Е.М. // Механика. 1, 3-е изд., Баттерворт – Хайнеман, 1976.
21. Мехитарян В.М., J. Contemp. Phys. АН СССР, 2013, т. 48, стр. 1.
22. Ландау, Л.Д. и Лифшиц Е.М., Классическая теория полей, Баттерворт – Хайнеман, 1975.
23. Мехитарян В.М., J. Contemp. Phys. АН СССР, 2016, т. 51, стр. 108.
24. Ландау, Л.Д. а также. Лифшиц Е.М. Квантовая механика: нерелятивистская теория.3, 3-е изд., Pergamon
Press, 1977.
Просмотр статистики публикации Просмотр статистики публикации Просмотр статистики публикации Просмотр статистики публикации
Содержание
Следующая: Предисловие Up: Квантовая физика 130 Предыдущая: Квантовая физика 130- Краткое содержание курса
- Проблемы классической физики
- Мысленные эксперименты по дифракции
- Амплитуды вероятности
- Волновые пакеты и неопределенность
- Операторы
- Ожидаемые значения
- Коммутаторы
- Уравнение Шредингера
- Собственные функции, собственные значения и векторные пространства
- Частица в коробке
- Кусочно-постоянные потенциалы в одном измерении
- Гармонический осциллятор в одном измерении
- Возможности дельта-функции в одном измерении
- Решение гармонического осциллятора с операторами
- Больше удовольствия с операторами
- Две частицы в трех измерениях
- Идентичные частицы
- Некоторые трехмерные задачи, разделимые в декартовых координатах
- Угловой момент
- Решения радиального уравнения для постоянных потенциалов
- Водород
- Решение трехмерной задачи HO в сферических координатах
- Матричное представление операторов и состояний
- Исследование Операторы и собственные функции
- Спин 1/2 и другие системы с двумя состояниями
- Квантовая механика в электромагнитном поле
- Локальная фазовая симметрия в квантовой механике и калибровочная симметрия
- Добавление углового момента
- Теория возмущений, не зависящая от времени
- Тонкая структура водорода
- Сверхтонкая структура
- Атом гелия
- Атомная физика
- Молекулы
- Теория возмущений, зависящая от времени
- Излучение в атомах
- Классическая теория поля
- Классическое электромагнитное поле
- Квантование электромагнитного поля
- Рассеяние фотонов
- Собственная энергия электрона
- Уравнение Дирака
- Уравнение Дирака
- Проблемы классической физики
- Излучение черного тела *
- Фотоэлектрический эффект
- Атом Резерфорда *
- Атомные спектры *
- Выводы и вычисления
- Примеры
- Пример задач теста
- Дифракция
- Дифракция на двух щелях
- Дифракция на одной щеле
- Дифракция на кристаллах
- Длина волны ДеБрогли
- Двойственность волновых частиц (мысленные эксперименты)
- Примеры
- Пример задач теста
- Решение: амплитуды вероятностей
- Выводы и вычисления
- Пример задач теста
- Волновые пакеты
- Построение локализованного одночастичного волнового пакета
- Два примера локализованных волновых пакетов
- Принцип неопределенности Гейзенберга
- Пространство позиций и пространство импульсов
- Временная развертка пакета гауссовской волны *
- Выводы и вычисления
- Примеры
- Пример задач теста
- Операторы
- Операторы в позиционном пространстве
- Операторы в Momentum Space
- Ожидаемые значения
- Обозначение Дирака Браке
- Коммутаторы
- Выводы и вычисления
- Примеры
- Пример задач теста
- Уравнение Шредингера
- Вывод уравнения с помощью операторов
- Поток вероятности *
- Волновое уравнение Шредингера
- Независимое от времени уравнение Шредингера
- Выводы и вычисления
- Примеры
- Пример задач теста
- Собственные функции, собственные значения и векторные пространства
- Уравнения на собственные значения
- Эрмитовский конъюгат оператора
- Эрмитские операторы
- Собственные функции и векторное пространство
- Частица в одномерном ящике
- Собственные функции импульса
- Выводы и вычисления
- Примеры
- Пример задач теста
- Одномерные потенциалы
- Кусочно-постоянные потенциалы в 1D
- Одномерный гармонический осциллятор
- Дельта-функция потенциала *
- Модель молекулы с дельта-функцией *
- Модель кристалла с дельта-функцией *
- Квантовый ротор
- Выводы и вычисления
- Примеры
- Пример задач теста
- Решение для гармонического осциллятора с использованием операторов
- Представляем а также
- Коммутаторы , а также
- Использование коммутаторов для получения энергии HO
- Ожидаемые значения а также
- Волновая функция для основного состояния HO
- Примеры
- Пример задач теста
- Больше удовольствия с операторами
- Операторы в векторном пространстве
- Полный набор операторов, перемещающихся между собой
- Принцип неопределенности для операторов, не выезжающих на работу
- Временная производная от ожидаемых значений *
- Оператор развития времени *
- Изображение Гейзенберга *
- Примеры
- Пример задач теста
- Расширение QM до двух частиц и трех измерений
- Квантовая механика двух частиц
- Квантовая механика в трех измерениях
- Две частицы в трех измерениях
- Идентичные частицы
- Пример задач теста
- 3D-задачи, разделяемые в декартовых координатах
- Частица в 3D-коробке
- Трехмерный гармонический осциллятор
- Пример задач теста
- Угловой момент
- Вращательная симметрия
- Алгебра углового момента: операторы подъема и опускания
- Собственные функции углового момента
- Выводы и вычисления
- Примеры
- Пример задач теста
- Радиальное уравнение и постоянные потенциалы *
- Радиальное уравнение *
- Поведение в исходной точке *
- Сферические функции Бесселя *
- Частица в сфере *
- Связанные состояния в сферической потенциальной яме *
- Анализ рассеяния частичных волн *
- Рассеяние на сферической яме *
- Радиальное уравнение для *
- Пример задач теста
- Водород
- Решения радиальных волновых функций
- Спектр водорода
- Вычисления и расчеты
- Примеры
- Пример задач теста
- Трехмерный симметричный HO в сферических координатах *
- Матрицы операторов и спин
- Матричное представление операторов и волновых функций
- Матрицы углового момента *
- Задачи на собственные значения с матрицами
- An Система в магнитном поле *
- Разделение собственных состояний с помощью Штерна-Герлаха
- Операторы вращения для *
- А Аппарат Штерна-Герлаха с вращением *
- Вращение
- Другие системы с двумя состояниями *
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Домашние задания 130A
- ДОМАШНИЕ 1
- Домашнее задание 2
- Домашнее задание 3
- Домашнее задание 4
- Домашнее задание 5
- Домашнее задание 6
- Домашнее задание 7
- Домашнее задание 8
- Домашнее задание 9
- Электроны в электромагнитном поле
- Обзор классических уравнений электричества и магнетизма в единицах CGS
- Квантовый гамильтониан, включающий B-поле
- Калибровочная симметрия в квантовой механике
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Сложение углового момента
- Сложение спинов двух электронов
- Полный угловой момент и взаимодействие спиновой орбиты
- Добавление вращения к целочисленному орбитальному угловому моменту
- Спектроскопические обозначения
- Общее сложение углового момента: серия Клебша-Гордана
- Симметрия обмена для состояний с идентичными частицами
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Теория возмущений, не зависящая от времени
- Серия возмущений
- Теория возмущений вырожденного состояния
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Тонкая структура в водороде
- Тонкая структура водорода
- Атом водорода в слабом магнитном поле
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Сверхтонкая структура
- Сверхтонкое расщепление
- Сверхтонкое расщепление в B-поле
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Атом гелия
- Общие характеристики состояний гелия
- Основное состояние гелия
- Первое возбужденное состояние (а)
- Вариационный принцип (приближение Рэлея-Ритца)
- Вариационная энергия основного состояния гелия
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Атомная физика
- Модель атомной оболочки
- Уравнения Хартри
- Правила Хунда
- Периодическая таблица
- Модель ядерной оболочки
- Примеры
- Домашние задания
- Пример задач теста
- Молекулярная физика
- Ион
- Молекула
- Важность неспаренных валентных электронов
- Молекулярные орбитали
- Колебательные состояния
- Вращательные состояния
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Теория нестационарных возмущений
- Общие зависящие от времени возмущения
- Синусоидальные возмущения
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Излучение в атомах
- Поле фотона в квантовом гамильтониане
- Скорость распада фотонов
- Фазовое пространство: плотность конечных состояний
- Общая скорость затухания с использованием фазового пространства
- Правила приближения и выбора электрического диполя
- Явная скорость затухания от 2p до 1s
- Общее неполяризованное начальное состояние
- Угловые распределения
- Векторные операторы и теорема Вигнера Эккарта
- Экспоненциальное затухание
- Срок службы и ширина линии
- Явления радиационной теории
- Примеры
- Выводы и вычисления
- Домашние задания
- Пример задач теста
- Рассеяние
- Рассеяние на экранированном кулоновском потенциале.
- Рассеяние на твердой сфере
- Домашние задания
- Пример задач теста
- Классические скалярные поля
- Простые механические системы и поля
- Классическое скалярное поле в четырех измерениях
- Классические поля Максвелла
- Рационализированные единицы Хевисайда-Лоренца
- Тензор электромагнитного поля
- Лагранжиан электромагнитных полей
- Калибровочная инвариантность может упростить уравнения
- Квантовая теория излучения
- Поперечные и продольные поля
- Фурье-разложение генераторов излучения
- Гамильтониан радиационного поля.
- Канонические координаты и моменты
- Квантование осцилляторов
- Фотонные состояния
- Операторы Фермиона
- Поле квантованного излучения
- Время развития полевых операторов
- Отношения неопределенности и среднеквадратичные колебания поля
- Излучение и поглощение фотонов атомами
- Обзор излучения фотонов
- Спектр излучения черного тела
- Рассеяние фотонов
- Резонансное рассеяние
- Упругое рассеяние
- Рэлеевское рассеяние
- Томсоновское рассеяние
- Рамановский эффект
- Электронная коррекция собственной энергии
- Баранина Сдвиг
- Уравнение Дирака
- Мотивация Дирака
- Гамильтониан Шредингера-Паули
- Уравнение Дирака
- Сохраненный ток вероятности
- Нерелятивистский предел уравнения Дирака
- Решение уравнения Дирака для свободной частицы.
- Решения с отрицательной энергией: теория дыр
- Эквивалентность двухкомпонентной теории
- Релятивистская ковариация
- Четность
- Билинейные коварианты
- Константы движения свободной частицы.
- Гамильтониан релятивистского взаимодействия
- Явления состояний Дирака
- Решение уравнения Дирака для водорода.
- Томсоновское рассеяние
- Теория дырок и конъюгация зарядов
- Зарядно-сопряженные волны
- Квантование поля Дирака
- Квантованное поле Дирака с позитронными спинорами
- Поляризация вакуума
- Лагранжиан и калибровочная инвариантность QED
- Взаимодействие со скалярным полем
- Формулы
Джим Брэнсон 2013-04-22Фундаментальная проблема квантовой физики
БЕРКЛИ, Калифорния – Более полувека теоретики пытались и не смогли предоставить полное решение рассеяния в квантовой системе из трех заряженных частиц, одного из самых фундаментальных явлений в атомной физике. .Такие взаимодействия есть везде; ионизация электронным ударом, например, ответственна за свечение люминесцентных ламп и за ионные лучи, которые гравируют кремниевые чипы.
Теперь сотрудники Национальной лаборатории Лоуренса Беркли Министерства энергетики, Ливерморской национальной лаборатории Лоуренса и Калифорнийского университета в Дэвисе использовали суперкомпьютеры для получения полного решения проблемы ионизации атома водорода при столкновении с электроном, простейшего нетривиального решения. пример последнего нерешенного компонента проблемы.Они сообщают о своих выводах в выпуске журнала Science от 24 декабря 1999 года.
Репрезентативная радиальная волновая функция двух электронов, рассеянных при столкновении электрона с атомом водорода.
Их прорыв основан на математическом преобразовании волнового уравнения Шредингера, которое позволяет рассматривать уходящие частицы не так, как если бы их волновые функции простирались до бесконечности – как с ними следует обращаться традиционно – а вместо этого, как будто они просто исчезают на больших расстояниях. из ядра.
«Используя это преобразование, мы вычисляем точные решения квантово-механической волновой функции исходящих частиц, и из этих решений мы извлекаем всю динамическую информацию о взаимодействии», – говорит Билл МакКерди, заместитель директора лаборатории Berkeley Lab по вычислительным наукам и главный автор научной статьи.
Маккарди и его давний соавтор Томас Ресиньо, штатный физик Ливерморской лаборатории, и их соавторы, докторант Марк Бэртши из Калифорнийского университета в Дэвисе и постдокторант Уильям Айзекс из Беркли лаборатории использовали SGI / Cray T3E в Национальном научном центре энергетических исследований. Вычислительный центр (NERSC) в лаборатории Беркли и компьютер IBM Blue Pacific в лаборатории Ливермора за решение задачи рассеяния трех заряженных тел.
«Точное решение волновой функции атома водорода из первых принципов имело жизненно важное значение для создания новой квантовой теории в 1920-х годах», – говорит Решиньо. «Но даже сегодня для систем с тремя или более заряженными частицами не существует аналитических решений», то есть нет явных решений уравнения Шредингера для таких систем.
Rescigno отмечает, что «только в конце 1950-х с использованием первых компьютеров были получены точные решения даже для связанных состояний гелия», атома с двумя электронами, близко вращающимися вокруг ядра.«Проблемы с рассеянием намного сложнее».
Как и все проблемы с рассеянием, электронная ионизация атома водорода начинается с частицы, летящей с определенной скоростью. Этот электрон взаимодействует с атомом, и два электрона вылетают под углом друг к другу, оставляя протон позади. Вероятность того, что конкретное входящее состояние приведет к исходящему состоянию с частицами под определенными углами и энергиями, является «поперечным сечением» этого результата.
Сечения квантово-механических процессов выводятся из волновой функции системы, решений уравнения Шредингера, которые дают вероятности нахождения сущностей, вовлеченных в определенное состояние.В задачах рассеяния волновые функции не локализованы, а распространяются по всему пространству.
Более того, говорит МакКарди об электромагнитных силах между заряженными частицами, «кулоновские взаимодействия вечны». Эти бесконечности не позволяют точно определить конечное состояние рассеяния. «Форма волновой функции, в которой все три частицы широко разделены, настолько трудноразрешима, что никакой компьютерный численный подход не смог включить ее в явном виде».
Но, как отмечает Ресциньо, «это, очевидно, не остановило людей от работы с плазмой и другими явлениями ионизации.С математической точки зрения они придумали невероятно хитрые уловки, и некоторые из них, кажется, даже работают ».
Ранее в этом году, однако, в Proceedings of the Royal Society Колм Т. Уилан из Кембриджского университета и его коллеги опубликовали свой вывод о том, что все такие приближения работают непоследовательно и что те немногие случаи, которые, как представляется, дают хорошее согласие с экспериментом, “в значительной степени являются удачно “.
Напротив, метод, разработанный МакКарди и Рессиньо и их соавторами, позволяет вычислить высокоточную волновую функцию для исходящего состояния, которую можно запросить на предмет деталей входящего состояния и взаимодействия таким же образом, как экспериментатор опросил бы физическая система.
Они начинаются с преобразования уравнения Шредингера, называемого «внешнее комплексное масштабирование», изобретенного Барри Саймоном из Калифорнийского технологического института в 1979 году для доказательства формальных теорем теории рассеяния. Преобразование оставляет решение неизменным в областях, которые соответствуют физической реальности, создавая правильную исходящую форму волны, основанную на угловом расстоянии и расстоянии двух электронов от ядра.
После того, как волновая функция вычислена, она должна быть проанализирована путем вычисления «квантово-механического потока», средства нахождения распределения плотностей вероятности, которое датируется 1920-ми годами.Этот вычислительно-интенсивный процесс может дать вероятность получения электронов с определенными энергиями и направлениями от ионизированного атома. (Поскольку электроны идентичны, нет возможности отличить изначально связанный электрон от изначально свободного).
Исследователи признают важные достижения, сделанные ранее другими исследователями, такими как Игорь Брей и Андрес Стелбовичс, чьи методы могли дать полное сечение ионизации реакции рассеяния, но не смогли дать конкретных данных, таких как направления или энергии исходящих электронов.В отличие от этого, говорит Ресчиньо, «наша работа дает абсолютные ответы на высочайшем уровне детализации».
Предсказанные сечения рассеянных электронов (сплошные кривые) и экспериментальные измерения (точки) почти точно совпадают.
Сравнение с реальными экспериментами по рассеянию, такими как недавно опубликованные J. Röder et al., Который рассеял входящие электроны напряжением 17,6 электронвольт от атомов водорода и измерил углы и энергии уходящих электронов, доказывает точность нового метода.Точки экспериментальных данных с поразительной точностью совпадают с графиком поперечных сечений, рассчитанных Rescigno, Baertschy, Isaacs и McCurdy.
«Даже если конкретные методы изменились, квантовая химия была основана, когда был решен атом гелия с двумя связанными электронами – она показала, что эти проблемы в принципе решаемы», – говорит МакКарди. «То, что мы сделали, аналогично. Детали нашего метода, вероятно, не сохранятся, но мы сделали большой шаг к рассмотрению ионизирующих столкновений электронов с более сложными атомами и молекулами.«
«Столкновительный распад в квантовой системе из трех заряженных частиц», авторы TN Rescigno, M. Baertschy, WA Isaacs и CW McCurdy, опубликованы в журнале Science от 24 декабря 1999 г. В заключение авторы отмечают, что необходимы те же вычислительные мощности и инструменты. для исследования сложности все более крупных систем также необходимо «ответить на основной физический вопрос для одной из простейших систем, которые можно вообразить в физике и химии».
Решение измерительной задачи
22 декабря Квантовая теория поля – решение «проблемы измерения»
Отправлено в 00:51 в квантовой теории поля Родни БруксОпределение «задачи измерения»
Главный вопрос в физике сегодня – это «проблема измерения », также известная как «коллапс« волновой функции ».Проблема возникла на заре квантовой механики из-за вероятностной природы уравнений. Поскольку волновая функция QM описывает только вероятности, результат физического измерения может быть рассчитан только как вероятность. Это, естественно, приводит к вопросу: когда производится измерение, в какой момент «определяется» окончательный результат. Некоторые люди считали, что роль наблюдателя имеет решающее значение и что «решение» принимается, когда кто-то смотрит. Это побудило Шредингера предложить свой знаменитый эксперимент с кошкой, чтобы показать, насколько нелепа такая идея.Это не является общеизвестным, но Эйнштейн также предложил эксперимент с бомбой по той же причине, заявив, что « своего рода смесь еще не взорванных и уже взорванных систем … не может быть реальным положением дел, поскольку в действительности существует просто нет посредника между взорванным и невзорвавшимся. ». Позднее Эйнштейн прокомментировал:« Существует ли Луна, только когда я смотрю на нее? ”
Споры продолжаются и по сей день, некоторые люди все еще верят, что кошка Шредингера представляет собой суперпозицию мертвого и живого, пока кто-то не посмотрит.Однако большинство людей считает, что волновая функция QM «схлопывается» в какой-то более ранний момент, прежде чем неопределенность достигнет макроскопического уровня – ключевым вопросом является определение «макроскопического» (например, теория GRW, интерпретация Пенроуза, форум по физике). Некоторые люди придерживаются точки зрения «множества миров», в которой нет «коллапса», а есть разделение на разные миры, содержащие все возможные истории и варианты будущего. Был проведен ряд экспериментов, направленных на решение этого вопроса, например.г., «К квантовой суперпозиции зеркала».
Теперь мы увидим, что однозначный ответ на этот вопрос дает квантовая теория поля. Однако, поскольку эта теория игнорировалась или неправильно понималась многими физиками, мы должны сначала определить, что мы подразумеваем под КТП.
Определение квантовой теории поля
Квантовая теория поля, упоминаемая в этой статье, является версией Швингера, в которой нет частиц, есть только поля, а не версией Фейнмана, основанной на частицах.* Две версии математически эквивалентны, но концепции, лежащие в их основе, очень разные, и именно версия Фейнмана используется большинством физиков, занимающихся квантовой теорией поля.
* По словам Фрэнка Вильчека, Фейнман в конце концов передумал: «Фейнман сказал мне, что, когда он понял, что его теория фотонов и электронов математически эквивалентна обычной теории, это разбило его самые сокровенные надежды … Он сдался, когда … он обнаружил поля, введенные для удобства, начинают жить своей собственной жизнью.”
В квантовой теории поля, в дальнейшем мы будем использовать этот термин, мир состоит из полей и только полей. Поля определяются как свойства пространства или, иначе говоря, пространство состоит из полей. Концепция поля была введена Майклом Фарадеем в 1845 году как объяснение электрических и магнитных сил. Однако людям было нелегко принять эту концепцию, и поэтому, когда Максвелл показал, что эти уравнения предсказывают существование электромагнитных волн, была введена идея эфира, переносящего волны.Однако сегодня принято считать, что пространство может иметь свойства:
Отрицать эфир – значит предполагать, что пустое пространство не имеет никаких физических качеств. Основные факты механики не согласуются с этой точкой зрения. – А. Эйнштейн ( R2003 , стр. 75)
Более того, само пространство-время стало динамической средой – эфиром, если он когда-либо существовал. – Ф. Вильчек («Постоянство эфира», Physics Today, январь 1999 г., стр.11).
Хотя уравнение Шредингера является нерелятивистским пределом уравнения Дирака для полей материи, между квантовой теорией поля и квантовой механикой существует важное и фундаментальное различие. Один описывает силу поля в данной точке, другой описывает вероятность того, что частицы могут быть найдены в этой точке или что данное состояние существует.
Однако поля квантовой теории поля не являются классическими полями; они квантованные поля.Каждый квант – это часть поля, которое, будучи разбросанным в пространстве, действует как единое целое. Он живет и умирает отдельно от других квантов. (Именно эта квантовая природа приводит к поведению, подобному частицам.) Термин квант был введен в 1900 году Планком, который сказал в своей Нобелевской речи: « Это было нечто совершенно новое, о котором раньше никогда не слышали, что казалось призванным в основном пересмотреть все наше физическое мышление ». Как он был прав.
Quanta может быть как свободным, так и связанным вместе.Примеры свободных квантов – фотон, испускаемый лампой, или электрон, испускаемый катодом. Примером связанных квантов являются протоны и нейтроны в атомном ядре или электронное поле, окружающее ядро. Существуют также собственные или прикрепленные поля, которые не являются квантами, но создаются квантами – например, электромагнитное поле вокруг электрона или сильное поле вокруг нуклона. Эти поля не имеют собственной жизни, но остаются привязанными к своему источнику.
Поля квантовой теории поля обладают внутренним свойством, называемым вращением или спиральностью.Поля материи имеют спин 1/2, из которого следует принцип исключения Паули, в то время как силовые (или бозонные) поля могут накладываться друг на друга даже до классического предела. Другой важной особенностью квантовой теории поля является то, что, как и спин в QM, напряженности поля описываются векторами в (бесконечномерном) гильбертовом пространстве, а динамика полей описывается операторами в этом гильбертовом пространстве. Это означает, что напряженность поля описывается суперпозицией значений, поэтому, когда мы говорим о напряженности поля в данной точке, мы можем говорить только об ожидаемых значениях.Тот факт, что квантовые поля отличаются от классических полей, беспокоит некоторых людей, но, начиная с эксперимента Штерна-Герлаха в 1922 году, у нас было почти сто лет, чтобы привыкнуть к идее, что физические величины квантуются (что и приводит к использование гильбертова пространства). Конечно, когда мы берем классический предел, как мы можем поступить с силовыми полями, уравнения для математического ожидания сводятся к классическим уравнениям электромагнитной теории и общей теории относительности.
Поля квантовой теории поля ведут себя детерминированно в соответствии с уравнениями поля, за одним исключением:
Квантовый коллапс
Квантовый коллапс происходит, когда квант поля внезапно вкладывает свою энергию (или импульс) в поглощающий атом.Это сильно отличается от «коллапса волновой функции» в КМ: это физическое событие , а не изменение вероятностей. Когда это происходит, квант, каким бы обширным он ни был, исчезает из космоса. Хотя нет теории, описывающей это, мы должны помнить, что это необходимо, если квант должен действовать как неделимая единица. Коллапс также происходит, если некоторая энергия (или импульс) передается другому веществу. Это также может происходить с несколькими связанными вместе квантами, например, когда атом или молекула захватываются детектором.
Как уже говорилось, квантовый коллапс не описывается уравнениями поля. На самом деле не существует теории, которая могла бы сказать нам, когда, где и как это происходит. Однако мы знаем, что вероятность связана с напряженностью поля в данной точке. Некоторых это беспокоит, но даже если у нас нет теории для чего-то, это не значит, что этого не может быть. История физики наполнена примерами наблюдений, которые в то время не имели объяснения или теории. Другой тревожный факт заключается в том, что квантовый коллапс нелокален.Однако нелокальность была доказана во многих экспериментах, и это не приводит к каким-либо противоречиям или парадоксам.
В теории многих миров коллапса нет. Вместо этого происходит разделение на два разных мира: один, в котором происходит перенос или поглощение, и другой, в котором этого не происходит. Однако с точки зрения наблюдателя в нашем мире эффектом является коллапс, поэтому, как бы он ни назывался, наступает момент, когда «решение» – точка невозврата – достигается.
Решение – квантовая теория поля
Квантовый коллапс – это ответ квантовой теории поля на проблему измерения .В случае с кошкой Шредингера, если излучаемый квант захватывается атомом счетчика Гейгера, он запускает необратимую цепочку событий, которая приводит к смерти кошки. Если его не захватить, то кошка живет (по крайней мере, до следующего радиоактивного выброса).
Кто-то теперь может спросить: «Хорошо, но разве не возможно, что схлопывание / расщепление произойдет в более позднее время, ближе к точке, когда происходит измерение (макроскопическое изменение)?» Проблема в следующем: эти изменения не могут продолжаться дальше «вверх по линии», если энергия или импульс не будут переданы поглощающему атому.Например, в эксперименте с кошками не может быть разряда Таунсенда, если атом не был ионизирован, а ионизация может произойти только в случае квантового коллапса. [Это правда?] Все остальное неизбежно следует (с небольшими микроскопическими вариациями). По словам Шредингера, «счетчик разряжается и через реле выпускает молоток, который разбивает небольшую колбу с синильной кислотой», которая убивает кошку. Это похоже на устройство Руба Голдберга, где вы бросаете мяч в желоб на одном конце, а после серии действий на другом конце появляется торт.
Также нет никакого эксперимента, который мог бы исключить приведенное выше описание коллапса / расщепления. В любом эксперименте, предназначенном для изучения коллапса, в какой-то момент должно быть макроскопическое обнаружение события. Но это обнаружение может только определить, что произошло обрушение. Он не может определить, насколько далеко по цепочке событий продвинулась предполагаемая суперпозиция.
Квантовая теория поля – решение
Квантовая теория поля – это элегантная теория, основанная на прочном математическом фундаменте.Он разрешает или объясняет многие парадоксы специальной теории относительности и квантовой механики, которые сбивают с толку так много людей *. И, как показано здесь, он дает простой и уникальный ответ на текущую проблему в физике. Нет запутываний, нет суперпозиций, нет квантовых «состояний». Существует просто квант поля, который коллапсирует (вкладывает часть или всю свою энергию или импульс) в поглощающий атом. И еще раз: тот факт, что у нас нет теории, чтобы описать это, не означает, что этого не происходит.Можно только удивляться, почему эту теорию не приняли и не преподают во всех школах. Может быть, физикам пора проснуться и почувствовать запах квантовых полей.
Buy Fields of Color: Теория, от которой ускользнул Эйнштейн на Amazon или Kindle!
границ | Численное решение квантово-механических задач на собственные значения
1. Введение
Уравнение Шредингера было центральной частью «современной» физики на протяжении почти столетия. При широком толковании его можно сформулировать множеством способов [1].Здесь мы в основном ограничиваем наше обсуждение нерелятивистской, не зависящей от времени формой,
[-Δq + V (q)] ψ (q) = Eψ (q). (1)Это составляет проблему собственных значений для E (есть много случаев, когда оператор, определяемый уравнением (1), допускает непрерывный спектр значений E , но это не будет напрямую влиять на обработку конечных дискретизаций таких систем. ). В уравнении (1) q обозначает координату пространства конфигурации для системы из одной или нескольких частиц в одном или нескольких пространственных измерениях, а Δ q является оператором Лапласа в этом пространстве конфигурации. V ( q ) – потенциал взаимодействия, а E – параметр собственного значения, интерпретируемый как разрешенная энергия для квантовой системы.
Несмотря на то, что оно выглядит как одночастичное уравнение, уравнение (1) также может использоваться для моделирования систем частиц N , где q = ( r 1 ,…, r N ) и Δ q = ( c 1 Δ 1 ,…, c N Δ N ).Здесь каждый Δ k – это обычный оператор Лапласа плоского пространства, а c k – числовой коэффициент, обратно пропорциональный массе m k частицы k ; эта масса может отличаться от частицы к частице. При соответствующем масштабировании каждой координаты r k можно математически преобразовать все c k в (например) единицу.Но такие преобразования могут затруднить понимание физических интерпретаций координат и сделать математические формулировки более подверженными ошибкам.
Как решить задачи на собственные значения, такие как (1)? К счастью для быстрого начального развития квантовой механики, для многих важных физических случаев [таких как атом водорода [2, 3] и гармонические осцилляторы [4]] он мог быть сведен к набору одномерных задач на собственные значения путем разделения метод переменных. Более того, все возникающие одномерные задачи могут быть решены точно аналитическими методами.Истоки такого удачного положения вещей неизменно можно проследить в расширенном наборе симметрий. Однако не каждая представляющая физический интерес система обладает высокой степенью симметрии. Даже большинство одномерных задач вида (1) не имеют известного аналитического решения. Популярной и широко исследуемой системой является ангармонический осциллятор
. [-d2dx2 + μx2 + εx4] ψ (x) = Eψ (x). (2)Эта модель часто использовалась как теоретическая лаборатория [5, 6], например, для исследования поведения и свойств пертурбативных [7, 8] и других [9–12] разложений, а также альтернативных методов решения [13–15].
В этой статье мы описываем некоторые попытки упростить численных решений задач на собственные значения, таких как (1). Наш подход основан на стандартных численных алгоритмах, уже закодированных и свободно доступных в пакетах Python, таких как numpy [16] и scipy [17, 18]. Основная цель состоит в том, чтобы автоматизировать преобразование (1) в вызовы функций, принимаемые численными решателями собственных значений. В рамках вышеупомянутого класса моделей проблема полностью определяется вектором коэффициентов ( c 1 , c 2 ,…, c N ) и реальной функцией V ( q ).В принципе, это должен быть единственный пользовательский ввод, необходимый для численного решения.
На практике должны быть приняты некоторые дополнительные решения, например, как возможно бесконечное конфигурационное пространство должно быть уменьшено до области конечной протяженности, как следует обрабатывать границы этой области и как эта область должна быть аппроксимирована конечной решеткой. Другие варианты включают выбор численных подходов, например, следует ли использовать решатели для плотных или итерационных разреженных матриц. Такие решения имеют последствия для многих «тривиальных» деталей числовых программ, но они могут быть предоставлены в форме параметров и селекторов, автоматически реализованных без дальнейшего утомительного и подверженного ошибкам вмешательства человека.Даже многие из указанных выше решений могут в конечном итоге быть переданы системам искусственного интеллекта, но это выходит за рамки наших текущих возможностей.
2. Доступные процедуры Python для численного решения
Численные подходы к решению подобных задач в принципе просты: оператор
, определяемый уравнением (1), аппроксимируется конечной вещественной симметричной матрицей
, где мы ввели обозначение T = – Δ q .Для плотно определенных матриц M H доступно несколько стандартных числовых решателей собственных значений, например eig и eigval в пакете scipy.linalg . Матрица чисел двойной точности размером 10 4 × 10 4 требует 800 Мб дискового пространства; это указывает на масштабы проблем, с которыми можно справиться с помощью методов плотной матрицы (например) на современных ноутбуках. То есть у таких компьютеров более чем достаточно памяти для численного решения одномерных задач, и обычно также достаточно памяти для двумерных.
Для задач более высокой размерности можно использовать разреженную природу M H для поиска решений с помощью итерационных процедур, таких как решатель собственных значений eigsh в пакете scipy.sparse.linalg . Этот решатель не требует явного построения матрицы M H , а только функции LinearOperator , которая возвращает вектор M H ψ для любого входного вектора ψ.В рассматриваемых нами представлениях M V всегда диагональ, а M T может быть сделана диагональной с помощью быстрого преобразования Фурье (БПФ) или некоторых его дискретных тригонометрических вариантов. Это открывает возможность обрабатывать проблемы с неразреженной матрицей, где T заменяется более общими выражениями F ( T ) с помощью тех же процедур. Например, функция F , которая включает дробные и / или обратные степени своих аргументов.
3. Необходимые параметры и селекторы
В этом разделе мы описываем дополнительные величины, которые пользователь должен ввести для полной спецификации числовой задачи. Они предполагают, что конфигурационное пространство было смоделировано прямоугольной точечной решеткой с выбором возможных граничных условий.
3.1. Форма решетки
Самым основным элементом численной модели является дискретная решетка, аппроксимирующая соответствующую область конфигурационного пространства.Для прямоугольных аппроксимаций это определяется параметром shape , кортежем Python ,
shape = (s0, s1,…, sd-1), (3), где каждые s k – положительное целое число, определяющее количество точек решетки в k ‘-м направлении, а d – (эффективное) измерение пространства конфигурации. Для моделей с непрерывной симметрией (например, вращательной) эффективный размер может быть выбран меньшим, чем физический, путем разделения переменных.Аналогичным образом можно использовать дискретные симметрии для уменьшения размера конфигурационного пространства, которое эта решетка должна аппроксимировать.
В программах на Python такие величины, как волновая функция ψ и потенциал V , определяются как массивы NumPy с плавающей запятой формы и формы .
3.2. Длины кромок и смещения
Геометрический экстент выбранной области определяется длиной ее краев xe . Это массив положительных чисел с плавающей запятой NumPy,
xe = [e0, e1,…, ed-1].(4)Вторичная величина, полученная из xe и формы , является элементарной ячейкой решетки,
dx = xe / shape = [e0 / s0, e1 / s1,…, ed-1 / sd-1]. (5)Абсолютное позиционирование области относительно некоторой фиксированной системы координат определяется массивом чисел с плавающей запятой NumPy,
xo = [x0, x1,…, xd-1]. (6)Это определяется как положение «левого нижнего» угла выбранной области. Размещение точек решетки в пределах области все еще необходимо указать, как будет описано ниже.
3.3. Граничные условия
Ограничение конечными областями пространства требует наложения граничных условий. Для областей прямоугольной формы (обобщенных до произвольных размеров), как здесь рассматривается, возможно, самый простой выбор – это периодических граничных условий в каждом направлении. Это можно рассматривать как топологическое свойство самого конфигурационного пространства. Другие граничные условия на самом деле являются свойствами функций, определенных в этом пространстве, как спецификации того, как функции должны быть расширены за границу.Два естественных варианта – это симметричных и антисимметричных расширений. С помощью решеточного приближения можно сделать еще одно различие, связанное с тем, как точки решетки расположены относительно границы.
В этой связи естественно рассмотреть случаи, которыми занимаются тригонометрические родственники быстрого преобразования Фурье (БПФ). В одномерном случае расширение может быть симметричным или антисимметричным по отношению к границе, которая расположена либо (i) в точке решетки, либо (ii) посередине между двумя точками решетки.Таким образом, на каждой границе имеется матрица возможностей 2 × 2, как показано в Таблице 1.
Таблица 1 . Индивидуальные граничные условия покрываются стандартными дискретными тригонометрическими преобразованиями ( DCT и DST ).
С двумя границами всего 4 × 4 = 16 возможностей. Однако подпрограммы в scipy.fftpack ( dct и dst типов I – IV) реализуют только те случаи, когда оба параметра взяты из одной строки таблицы 1.С периодическим расширением P в дополнение к этому мы получаем набор из девяти возможностей в каждом направлении:
ℬ = {′ PP ′, ′ SS ′, ′ SA ′, ′ AS ′, ′ AA ′, ′ ss ′, ′ sa ′, ′ as ′, ′ aa ′}. (7)Следовательно, числовая модель должна быть дополнительно определена кортежем Python из двухсимвольных строк, определяющим выбранное граничное условие во всех направлениях,
bc = (b0, b1,…, bd-1) (8)с каждым bk∈B (или в расширенном наборе возможностей).
3.4. Позиции решетки. Позиции двойной решетки в квадрате
Если задано bc , можно автоматически вычислить положения всех узлов решетки
xlat = (X0, X1,…, Xd-1), (9)при условии, что форма , xe и xo также известны.В уравнении (9) свойство xlat является кортежем одномерных массивов. Для иллюстрации рассмотрим случай трехмерной решетки формы ( s x , s y , s z ). Тогда xlat – кортеж Python ( X, Y, Z ), где X – массив формы numpy ( s x , 1, 1), Y представляет собой массив формы numpy (1, s y , 1), а Z – массив формы numpy (1, 1, s z ).Все это одномерные массивы, но информация об их форме подразумевает, что (например) выражение Python X * Y автоматически вычисляется как массив формы numpy ( s x , s л , 1).
Функция Python V ( x, y, z ), определенная выражением, которое может включать «стандартные» функции, затем может быть вычислена на всей решетке с помощью короткого и простого выражения V (* xlat ).Когда V зависит от всех своих аргументов, результатом будет массив формы numpy ( s x , s y , s z ).
В общем случае, когда преобразование Фурье периодической функции f ( x ), где x принимает значения на некоторой дискретной решетке, результатом становится другая периодическая функция f ~ (k), где k принимает значения на другой дискретной решетке (двойная решетка / обратное пространство).По модулю общего масштабирования можно определить набор из k -значений (маркировка точек некоторого полного минимального субдомена, расширяемого периодичностью) так, чтобы f ( x + a ) преобразуется в e-ik · af ~ (k). Естественным выбором для этой минимальной области является, говоря языком физиков, первая зона Бриллюэна (этот выбор все же может оставить несколько произвольный выбор граничных точек, которые необходимо включить). В этой подобласти дуальной решетки производные могут быть определены как операторы умножения −i k .Но эти операторы по-прежнему должны быть продолжены на полную дуальную решетку по периодичности. Общие выражения Стенсила для производных решетки соответствуют младшим компонентам Фурье (периодически расширенного) оператора умножения −i k .
Для других (дискретных тригонометрических) преобразований возникает сложность, потому что вывод также вызывает транспонирование граничных условий в B. Однако два вывода в одном и том же направлении оставляют граничные условия неизменными и, следовательно, могут быть представлены как оператор умножения q на преобразованные функции.Пусть ∂ k будет сокращенной записью для ∂ / ∂ x k . Из предыдущего вывода следует, что все операторы вида F (∂02, ∂12,…, ∂d-12) могут быть вычислены с помощью умножений и быстрых дискретных преобразований,
F (∂02, ∂12,…, ∂d-12) = T-1F (q0, q1,…, qd-1) T. (10)Мы реализовали код, который выполняет T и T-1 через последовательность дискретных тригонометрических или быстрых преобразований Фурье, в зависимости от bc и других параметров.Аналогично массивам позиций решетки xlat (уравнение 9), можно автоматически вычислять аналогичные массивы квадратов позиций для обратной решетки,
qlat = (Q0, Q1,…, Qd-1). (11)3,5. Решеточный лапласиан. Представительства Stensil
Вместо того, чтобы полагаться на преобразования типа БПФ, можно напрямую построить дискретные аппроксимации (шаблоны) оператора Лапласа и подобных дифференциальных операторов. Простейшая реализация решеточного лапласиана в одномерном измерении получается с использованием формулы
d2ψdx2 (xn) ≈ψ (xn + δx) -2ψ (xn) -ψ (xn-δx) δx2, (12), где δ x – расстояние между ближайшими соседними точками решетки.Формальная ошибка дискретизации этого приближения имеет порядок δ x 2 . Суммируя такое выражение в d ортогональных направлениях, можно найти выражение (2 d + 1) -напряжения для решеточного лапласиана.
Более точное приближение – трафарет (4 d + 1),
Δφ (xn) ≈∑k = 0d-1-φ (xn + 2δk) + 16φ (xn + δk) -30φ (xn) + 16φ (xn-δk) -φ (xn-2δk) 12 | δk | 2. (13)Здесь δ k обозначает вектор длины | δ k | указывая в положительном направлении k .
Произвольный (ближний) оператор, не зависящий от положения O , в общем случае может быть представлен стенсилом s O ( b ) таким образом, что
(Oψ) (xn) = ∑bsO (b) ψ (xn-b). (14)Когда n – b выпадает за пределы решетки, значение ψ ( x n – b ) должно интерпретироваться в соответствии с граничными условиями bc .Это снова можно автоматизировать. Мы реализовали алгоритм для этого, в настоящее время только для 5 из 9 случаев в B в каждом направлении, но для произвольного количества направлений.
Различные способы аппроксимации оператора Лапласа или, в более общем смысле, оператора кинетической энергии доступны через селектор ke , значение которого в настоящее время ограничено набором опций {‘2dplus1’, ‘4dplus1’, ‘fftk2’ }. Последний из этих вариантов обсуждается в разделе 5.
4.Простые приложения
В этом разделе мы продемонстрируем некоторые применения нашего автоматического кода. Основное требование состоит в том, что в каждом случае должен быть предоставлен только набор параметров и селекторов, без необходимости кодирования самого приложения. Этого должно быть достаточно для генерации собственных значений E n по запросу, а также, необязательно, связанных с ними собственных функций (проблема, которую мы еще не тестировали).
4.1. Пример: одномерный гармонический осциллятор
Рассмотрим задачу на собственные значения одномерного гармонического осциллятора,
-ψn ″ (x) + x2ψn (x) = Enψn (x).(15)Собственные значения: E n = 2 n + 1 для n = 0, 1,…, и степень волновой функции ψ n ( x ) может быть оценена из требования, что классическая частица с энергией E n ограничена величиной x2≤En. Квантовая частица требует немного больше места, чем классически ограниченная.
Для численного анализа мы предоставляем параметры
shape = (128,), bc = (′ a ′, a ′), xe = (25,), xo = (- 12.5), V = лямбда x: x ** 2,выбирает приближение 3-стенсиля для T (выбор по умолчанию) и решатель плотной матрицы eigvalsh (выбор по умолчанию). Это мгновенно возвращает 128 собственных значений, как показано на рисунке 1. Мы можем легко изменить форму на (1024) для гораздо лучшего результата. Возможность дополнительных исследований без какого-либо кодирования должна быть очевидна.
Рисунок 1 . 128 наименьших собственных значений уравнения (15), вычисленных с помощью стандартного приближения 3-стенсила для оператора Лапласа (здесь кинетическая энергия T ).Параметры выбраны для иллюстрации двух типичных эффектов: с граничными условиями bc = ( a, a ) потенциал гармонического осциллятора эффективно изменяется до В = ∞ для x ≥ 12,5, тем самым изменяя поведение расширенные (сильно возбужденные) состояния. Эффект этого заключается в увеличении собственной энергии таких состояний до поведения, более похожего на поведение частиц в ящике. Это видно для n ≳ 80. Эффект от использования приближения 3-стенсила для T заключается в изменении спектра этого оператора с k 2 на (более медленный рост) (2 / δ x ) 2 sin 2 ( kδx /2).Это видно по сублинейному росту спектра для N = 2 7 .
Для лучшей количественной оценки полученной точности мы нанесем некоторые разности энергий, En (точный) -En, на рис. 2.
Рисунок 2 . Ошибка дискретизации собственных значений энергии при использовании стандартного приближения 3-стенсила для одномерного оператора Лапласа (здесь кинетическая энергия T ). В E 90 нет улучшений за пределами определенного размера решетки N , потому что соответствующее состояние осциллятора слишком велико для геометрической области.Следовательно, для повышения точности более высоких собственных значений следует вместо этого увеличить xe , сохраняя при этом xo = – xe /2. Для других состояний улучшение согласуется с ожиданием ошибки, пропорциональной δ x 2 . Это предсказывает улучшение точности на величину 2 12 = 4096, когда количество узлов решетки увеличивается с N = 2 7 до N = 2 13 для фиксированной геометрии.Собственные значения вычисляются с помощью подпрограммы для плотной матрицы eigvalsh из scipy.linalg .
Этот метод перебора приводит к резкому увеличению требований к памяти с увеличением размера решетки. Для решетки с N = 2 м узлов матрица требует хранения 4 м чисел двойной точности (8 байт). Для м = 13 это соответствует примерно 12 ГБ памяти, для м = 14 примерно 2 ГБ.Ситуация становится еще хуже в высших измерениях.
Предполагая, что нас интересуют только некоторые из самых низких собственных значений, альтернативным подходом является их вычисление с помощью итерационной процедуры eigsh из scipy.sparse.linalg . Это позволяет расширить до более крупных решеток, как показано на рисунке 3.
Рисунок 3 . Ошибка дискретизации, вычисленная программой eigsh из scipy.sparse.linalg . Для фиксированного размера решетки ошибка дискретизации по существу такая же, как и для подпрограмм с плотной матрицей.Однако при потребности в памяти, пропорциональной размеру решетки (а не ее квадрату), становится возможным перейти к решеткам гораздо большего размера. Этот рисунок также демонстрирует ( E 70 ), что ошибка может быть ограничена граничными эффектами вместо конечной длины дискретизации δ x .
При использовании решателя с разреженными собственными значениями расчет становится ограниченным доступным временем вычисления, что во многих случаях является гораздо более слабым ограничением: при правильном планировании и организации вычислений соответствующая шкала времени – это время для анализа и публикации результатов (т.е., недели или месяцы). Тем не менее, представляет интерес время расчета (оно не должно составлять годы). Мы измерили время настенных часов, использованное для выполнения вычислений для рисунков 2, 3, выполненных на Mac Mini 2012 года с 16 ГБ памяти и оснащенном распараллеленной библиотекой scipy . Следовательно, подпрограммы eigvalh и eigsh работают с четырьмя потоками. Результаты представлены на Рисунке 4.
Рисунок 4 . Время настенных часов используется для нахождения 128 наименьших собственных значений для различных систем и методов.Мы также использовали подпрограмму для плотной матрицы eigvalsh для вычисления собственных значений двумерной решетки 2 7 × 2 7 ( N = 2 14 ); Не удивительно, что это занимает то же время, что и для одномерной решетки 2 14 . Несколько удивительно то, что с eigsh гораздо быстрее найти собственные значения для двумерной решетки, чем для одномерной с тем же числом узлов, и несколько быстрее найти собственные значения для трехмерной решетки, чем для двух -мерные с таким же количеством сайтов.
Здесь мы использовали процедуру eigsh самым простым способом, используя настройки по умолчанию для большинства параметров. Это означает, в частности, что начальный вектор для итерации (и последующий набор пробных векторов) не может быть выбран оптимальным образом для нашей категории задач. Интересно отметить, что eigsh лучше работает для задач более высокой размерности. В (краткой) документации scipy [17] говорится, что лежащие в основе процедуры лучше всего работают при вычислении собственных значений наибольшей величины, которые не представляют физического интереса для нашего типа задач.По нашему опыту, предложенная стратегия использования режима shift-invert вместо этого не работает сразу после установки для задач интересного размера (то есть, когда нельзя использовать плотные решатели). Мы были несколько удивлены, заметив, что время вычисления может уменьшиться на на , если количество вычисленных собственных значений увеличится (см. Рисунок 5).
Рисунок 5 . Можно подумать, что для вычисления большего количества собственных значений требуется больше времени. Это не всегда так, когда количество собственных значений невелико, как показано на этом рисунке.По умолчанию eigsh вычисляет k = 6 собственных значений. Для наших двумерных и трехмерных задач это значение выглядит близко к оптимальному, но слишком мало для одномерной задачи.
4.2. Пример: осцилляторы 2- и 3-мерных гармоник
Генератор гармонических колебаний d
[-Δ + r2] ψn (r) = Enψn (r), (16)имеет собственные значения E n = ( d + 2 n ), для n = 0, 1,….Вырождение уровня энергии E n составляет g n = ( n + 1) в двух измерениях, а gn = 12 (n + 1) (n + 2) в три измерения . Это вырождение может быть существенно нарушено численным приближением. Для численного решения достаточно немного изменить предыдущие параметры:
shape = (128,) * dim, bc = ((′ a ′, ′ a ′),) * dim, xe = (25,) * dim, xo = (- 12,5,) * dim, (17a) V = лямбда x, y: x ** 2 + y ** 2 (dim = 2), (17b) V = лямбда x, y, z: x ** 2 + y ** 2 + z ** 2 (dim = 3), (17c)для dim = 2, 3.
Как уже обсуждалось, подпрограмма eigsh работает несколько быстрее в более высоких измерениях, чем в одном измерении (для тех же общее число N точек решетки). Соответствующие ошибки дискретизации показаны на рисунках 6, 7.
Рисунок 6 . Ошибка дискретизации собственных значений энергии при использовании стандартного приближения 5-стенсила для двумерного оператора Лапласа. Точно, состояния E 78 и E 90 являются двумя краями 13-членного мультиплета с энергией 26, а состояние E 12 является средним членом 5-членного мультиплета. с энергией 10.При выбранных параметрах все состояния считаются хорошо ограниченными геометрической областью; следовательно, мы не наблюдаем никаких эффектов граничной коррекции.
Рисунок 7 . Ошибка дискретизации собственных значений энергии при использовании стандартного 7-стенсилового приближения для трехмерного оператора Лапласа. Точно, состояния E 56 и E 83 являются двумя краями 28-членного мультиплета с энергией 15, а состояние E 15 является средним членом 10-членного мультиплета. с энергией 9.
Ошибка дискретизации продолжает масштабироваться как δ x 2 . Это означает, что уменьшение этой ошибки в 2 раза 2 = 4 требует увеличения количества узлов решетки в 2 раза d в d измерениях. Это означает, что становится более актуальным использование лучшего представления оператора Лапласа в более высоких измерениях. К счастью, как мы увидим в следующих разделах, для нашего типа проблем доступны лучшие представления.
5. Вычисление БПФ оператора Лапласа
Одним из улучшений является использование симметрии отражения каждой оси ( x → – x , y → – y и т. Д.) Для уменьшения размера пространственной области. Это уменьшает δ x вдвое без изменения количества узлов решетки.
Гораздо более значительным улучшением является использование некоторого варианта быстрого преобразования Фурье (БПФ): после преобразования Фурье ψ (r) → ψ ~ (k) оператор Лапласа превращается в оператор умножения,
Это означает, что применение оператора Лапласа может быть представлено (i) преобразованием Фурье, за которым следует (ii) умножение на k 2 и, наконец, (iii) обратное преобразование Фурье.По сути, такая же процедура работает для связанных тригонометрических преобразований.
Для прямоугольных решеток эти варианты также могут быть реализованы как практические процедуры благодаря существованию эффективных и точных алгоритмов для дискретных преобразований Фурье и тригонометрических преобразований. Время выполнения вышеуказанной процедуры не намного больше, чем соответствующих операций стенсила. Преимущество состоит в том, что оператор Лапласа становится точным в пространстве функций, которые могут быть представлены модами, включенными в дискретное преобразование.
Мы закодировали это представление типа БПФ оператора Лапласа для различных типов граничных условий, перечисленных в таблице 1. Эта возможность может быть выбрана в качестве опции для селектора кинетической энергии, ke . Достигаемая точность с помощью этой опции резко возрастает, как показано на рисунках 8–11. Как показано на рисунке 8, уменьшение длины решетки δ x не обязательно приводит к более точному результату. Мы связываем это с увеличением числа ошибок округления.
Рисунок 8 . С представлением БПФ оператора Лапласа ошибка дискретизации падает исключительно быстро с δ x ∝ N -1 . Когда он становится «достаточно маленьким», становится заметен эффект числового округления; последнее приводит к увеличению ошибки на на при δ x . Результаты на этом рисунке относятся к одномерной решетке, но поведение одинаково во всех измерениях. Урок состоит в том, что мы должны сделать δ x «достаточно маленьким» (которое в целом может быть трудно определить априори ), но не меньше.Также возможно переписать проблему собственных значений в форме с меньшим увеличением ошибок округления.
Рисунок 9 . Точность вычисленных собственных значений для осциллятора 1 D с использованием приближения БПФ для кинетической энергии T . Эта цифра может предполагать, что увеличение числа решеток с размером N приведет к точной обработке состояний с более высокими n . Наши выводы таковы, что это , а не : результаты для N = 2 7 и N = 2 8 имеют практически такое же поведение, что и для N = 2 6 .
Рисунок 10 . Точность вычисленных собственных значений для осциллятора 2 D с использованием приближения БПФ для кинетической энергии T . Как можно видеть, большое количество наименьших собственных значений может быть вычислено с абсолютной точностью в диапазоне 10 −14 –10 −12 с размером решетки 2 6 × 2 6 . Мы не наблюдаем улучшения при переходе к решетке 2 7 × 2 7 , но и никакого вреда (за исключением увеличения времени выполнения настенных часов примерно с 3 до 30 с для каждой комбинации граничных условий).
Рисунок 11 . Точность вычисленных собственных значений для осциллятора 3 D с использованием приближения БПФ для кинетической энергии T . Как видно, большое количество наименьших собственных значений может быть вычислено с абсолютной точностью в диапазоне от 10 −14 до 10 −12 с размером решетки 2 6 × 2 6 × 2 6 . Мы не наблюдаем никаких улучшений при переходе к решетке 2 7 × 2 7 × 2 7 , но и никакого вреда (за исключением увеличения времени выполнения настенных часов примерно с 6 до 95 минут для каждой комбинации граничных условий ).
Может оказаться, что системы гармонических осцилляторов особенно подходят для применения представления БПФ. Одной из важных особенностей является то, что компоненты Фурье волновых функций гармонического осциллятора исчезают экспоненциально быстро, например e – k 2 /2 , с увеличением волновых чисел k 2 . Эта особенность характерна для всех собственных функций полиномиальных потенциальных уравнений Шредингера, но обычно с разными степенями k в показателе степени, что количественно приводит к несколько иному поведению.Кроме того, начало экспоненциального затухания будет происходить при больших значениях k 2 для более возбужденных состояний (т.е. с большими собственными числами).
Для систем с сингулярными волновыми функциями соответствующие компоненты Фурье могут исчезнуть только алгебраически с k 2 . В таких случаях нельзя ожидать столь же значительного повышения точности.
6. Ангармонические осцилляторы
Наша общая установка допускает любой вычислимый потенциал, просто изменяя определение функции, присвоенной V (это не означает, что каждый потенциал приведет к успешному вычислению собственных значений).В целях демонстрации и сравнения, как здесь, возникает проблема, заключающаяся в том, что точные ответы больше не известны. Это затрудняет оценку точности и других качеств кода. В качестве примера, где возможны некоторые поучительные сравнения, мы рассматриваем двумерный ангармонический осциллятор, подчиняющийся уравнению Шредингера,
12 (-d2dx2-d2dy2 + x4 + 6x2y2 + y4) ΨE (x, y) = EΨ (x, y). (18)По построению эта задача имеет разделимые решения вида
ΨE (x, y) = ψm (ξ) ψn (η), где ξ = (x + y) / 2, η = (x-y) / 2, (19), где множители ψ подчиняются одномерному уравнению,
(-d2dξ2 + ξ4) ψm (ξ) = εmψm (ξ), (20)и E = ε м + ε n .Как упоминалось во введении, уравнения, подобные последнему, довольно интенсивно изучались в литературе. Точные значения собственных значений четной четности уравнения (20) можно, например, найти в таблице 1 в [9]. В таблице 2 мы перечисляем 10 наименьших собственных значений с точностью до 30 знаков после запятой, вычисленных с помощью метода очень высокой точности, описанного в [14]. Следовательно, для практических целей все интересующие значения ε m можно считать точно известными. Это означает, что собственные значения E уравнения (18) также можно считать точно известными.Мы перечисляем 22 самых низких из них в таблице 3. Это значения, которые мы хотим сравнить со стандартными методами решения. Последние не используют свойство разделимости задачи, которое в любом случае разрушается решеточным приближением.
Таблица 2 . 10 наименьших собственных значений квантового ангармонического осциллятора, вычисленных с высокой точностью методом, описанным в [14], из уравнения Шредингера (-d2dξ2 + ξ4) ψn (ξ) = εnψn (ξ).
Таблица 3 .Отображаются 22 наименьших собственных значения E двумерного квантового ангармонического осциллятора, как определено уравнением Шредингера 12 (-d2dx2-d2dy2 + x4 + 6x2y2 + y4) ΨE (x, y) = EΨE (x, y). с точностью до 30 знаков после запятой.
Первый столбец таблицы 3 связывает классификацию симметрии ( P x , P y ) с каждым собственным значением E , или, скорее, с его соответствующей собственной функцией Ψ E ( х, у ).Поскольку уравнение (18) инвариантно относительно отражений,
Px: x → -x или Py: y → -y,все собственные функции могут быть сконструированы для симметричного (S) или антисимметричного (A) преобразования при таких отражениях. Для м < n такая конструкция составляет
Ψmn (±) (x, y) = 12 [ψm (ξ) ψn (η) ± ψn (ξ) ψm (η)]. (21а)Для м = n есть только одна возможность,
Ψmm (x, y) = ψm (ξ) ψm (η). (21b)Используя свойства, которые
ψm (-ξ) = (- 1) m-1ψ (ξ), Px: (ξ, η) → – (η, ξ) и Py: (ξ, η) → (η, ξ),находим, что
Ψmn (±) (- x, y) = ± (-1) m + nΨmn (±) (x, y) и mn (±) (x, -y) = ± Ψmn (±) (x, y).(22)и далее мм (- x, y ) = Ψ мм ( x , – y ) = Ψ мм ( x, y ). Вывод состоит в том, что при точном расчете состояния Ψ mn будут дважды вырожденными при m ≠ n , с четностями ( P x , P y ) равны ( S, S ) и ( A, A ), когда m, n оба четные или оба нечетные, в противном случае с четностями ( S, A ) и ( A, S ).Состояния Ψ мм являются синглетами с четностями ( S, S ). Первый столбец Таблицы 3 построен в соответствии с этими правилами.
Таблица 4 показывает результаты некоторых стандартных численных решений уравнения (18), «автоматически» сгенерированных таким же образом, как и предыдущие обработки гармонических (линейных) осцилляторов. Во втором столбце мы показываем результаты использования минимальной 5-точечной аппроксимации stensil оператора Лапласа на решетке 1 024 × 1 024 (аппроксимация всего пространства).Результирующая численная задача решается с помощью разреженного решателя eigsh . Числовая точность обозначается подчеркиванием первой неточной позиции с учетом правильного округления: точные и числовые результаты округляются до одинакового количества цифр и сравниваются; подчеркивание указывает на первую позицию, где результаты различаются.
Таблица 4 . Численные расчеты низших собственных значений двумерного квантового ангармонического осциллятора с использованием различных приближений и размеров решетки.
Как видно, результаты не впечатляют, если учесть объем затраченных вычислительных усилий. Одним из простых улучшений является использование отражательной симметрии задачи для уменьшения масштабов проблемы (с тем же размером ячейки решетки δ x 2 ) в 4 раза или уменьшения размера ячейки решетки δ x 2 (с той же величиной проблемы) в 4 раза. Другой вариант – использовать приближение stensil более высокого порядка, например (13).Однако, как уже обсуждалось в разделе 5, еще лучшим вариантом (для этого класса задач) является использование типа БПФ аппроксимации оператора Лапласа. Полученные собственные значения перечислены в столбцах 3–5 для различных размеров решетки, приближающихся к верхнему правому квадранту ( x ≥ 0, y ≥ 0) пространства. Для каждого размера решетки задача должна быть решена 4 раза с симметричными ( S ) и антисимметричными ( A ) граничными условиями на осях x = 0 и y = 0.
По симметрии при замене, x ↔ y , мы ожидаем, что ( S, A ) и ( A, S ) дадут идентичные результаты (если приближение решетки соблюдает эту симметрию). Как можно видеть, численные результаты удовлетворяют симметрии с точностью до нескольких × 10 −12 , независимо от того, насколько результаты близки к точным значениям. Вырождение состояний с симметрией ( S, S ) соответственно ( A, A ) не может быть выведено таким же образом из аппроксимируемой решёткой задачи.В формулировке бесконечного пространства проблема сепарабельна, что, в свою очередь, подразумевает это вырождение. Однако решеточное приближение вводит нефакторизуемые границы по (ξ, η) -координатам. Это означает, что проблема больше не отделима в решеточном приближении. В результате вырождение энергий ( S, S ) и ( A, A ) делится на гораздо большую величину, того же порядка, что и разница между точными и численными результатами. (В этом случае проблема решетки может быть отделена поворотом ориентации решетки на 45 градусов.)
Мы видим, что даже решетка 2 4 × 2 4 с «аппроксимированным БПФ» оператором Лапласа обеспечивает почти такие же точные результаты, как решетка 2 10 × 2 10 с приближением 5-стенсиля. Результаты для решетки 2 5 × 2 5 кажутся более чем достаточными для практических целей (скажем, по сравнению с полученной экспериментально точностью), и мало что можно получить от дальнейшего уменьшения длины решетки δ x .
Время вычисления для «приближения БПФ» составляет около 0,06, 0,8 и 75 с для размеров решетки соответственно 16 × 16, 32 × 32 и 128 × 128. Для того же количества узлов решетки 5-стенсил может привести к несколько более короткому времени вычислений. Но это полностью компенсируется необходимостью работать с гораздо большим количеством узлов решетки: время вычисления для приближения стенсила размером 1 024 × 1 024 составляло около 30 минут.
Пакет Python, описанный в этой статье, доступен по адресу [19].
Заявление о доступности данныхНеобработанные данные [19], подтверждающие выводы этой статьи, будут предоставлены авторами без излишних оговорок.
Авторские взносы
Все перечисленные авторы внесли существенный, прямой и интеллектуальный вклад в работу и одобрили ее к публикации.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Ранняя версия этой работы была представлена на Международной мультиконференции инженеров и компьютерных ученых IAENG, Гонконг, 18–20 марта 2015 г., как описано в [20].
AM благодарит Исследовательская группа по преподаванию и обучению математике в рамках Департамент математики, Будё, Северный университет за частичную поддержку.
Сноски
Список литературы
1. Dirac PAM. Основные уравнения квантовой механики. Proc R Soc A . (1925) 109: 642–53. DOI: 10.1098 / RSPA.1925.0150
CrossRef Полный текст | Google Scholar
2. Шредингер Э. Волнообразная теория механики атомов и молекул. Phys Ред. . (1926) 28: 1049–70. DOI: 10.1103 / PhysRev.28.1049
CrossRef Полный текст | Google Scholar
3. Паули В. Убер die Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. Zeitsch Phys . (1926) 36: 336–63.
Google Scholar
4.Гейзенберг В. Квантово-теоретическая интерпретация кинематических и механических соотношений. Zeitsch Phys . (1925) 33: 879–93.
Google Scholar
5. Бендер CM, Wu TT. Аналитическая структура уровней энергии в теоретико-полевой модели. Phys Rev Lett. (1968) 21: 406–9. DOI: 10.1103 / PhysRevLett.21.406
CrossRef Полный текст | Google Scholar
7. Бендер CM, Wu TT.Большой порядок теории возмущений. Phys Rev Lett. (1971) 27: 461–5. DOI: 10.1103 / PhysRevLett.27.461
CrossRef Полный текст | Google Scholar
8. Бендер CM, Wu TT. Ангармонический осциллятор. II. Изучение теории возмущений в большом порядке. Phys Rev D. (1973) 7: 1620–36. DOI: 10.1103 / PhysRevD.7.1620
CrossRef Полный текст | Google Scholar
9. Бендер С.М., Олауссен К., Ван П.С. Нумерологический анализ приближения ВКБ в большом порядке. Phys Rev D. (1977) 16: 1740–8. DOI: 10.1103 / PhysRevD.16.1740
CrossRef Полный текст | Google Scholar
10. Zinn-Justin J, Jentschura UD. Мульти-инстантоны и точные результаты I: предположения, ВКБ-разложения и инстантонные взаимодействия. Ann Phys. (2004) 313: 197–267. DOI: 10.1016 / j.aop.2004.04.004
CrossRef Полный текст | Google Scholar
11. Zinn-Justin J, Jentschura UD. Мультиинстантоны и точные результаты II: частные случаи, эффекты высших порядков и численные расчеты. Ann Phys. (2004) 313: 269–325. DOI: 10.1016 / j.aop.2004.04.003
CrossRef Полный текст | Google Scholar
12. Норин А., Олауссен К. Расширение квантовой петли до высоких порядков, расширенное суммирование по Борелю и сравнение с точными результатами. Phys Rev Lett. (2013) 111: 040402. DOI: 10.1103 / PhysRevLett.111.040402
PubMed Аннотация | CrossRef Полный текст | Google Scholar
13. Янке В., Кляйнерт Х. Сходящиеся разложения сильной связи из расходящейся теории возмущений слабой связи. Phys Rev Lett. (1995) 75: 2787–91. DOI: 10.1103 / PhysRevLett.75.2787
PubMed Аннотация | CrossRef Полный текст | Google Scholar
14. Муштак А., Норин А., Олауссен К., Овербо И. Решения одного класса уравнений типа Шредингера с очень высокой точностью. Comput Phys Commun. (2011) 182: 1810–3. DOI: 10.1016 / j.cpc.2010.12.046
CrossRef Полный текст | Google Scholar
15. Норин А., Олауссен К. Рядные решения дифференциальных уравнений высокой точности: обыкновенные и регулярные особые точки ОДУ второго порядка. Comput Phys Commun . (2012) 183: 2291–7. DOI: 10.1016 / j.cpc.2012.05.015
CrossRef Полный текст | Google Scholar
16. Ван Дер Уолт С., Колберт С. К., Вароко Г. Массив NumPy: структура для эффективных численных вычислений. Comput Sci Eng . (2011) 13: 22–30. DOI: 10.1109 / MCSE.2011.37
CrossRef Полный текст | Google Scholar
17. Джонс Э., Олифант Т., Петерсон П. SciPy: Научные инструменты с открытым исходным кодом для Python .(2014). Доступно в Интернете по адресу: http://www.scipy.org/
19. Муштак А., Норин А., Олауссен А. Пакет Python для численного решения квантово-механических задач на собственные значения (2020). DOI: 10.6084 / m9.figshare.127655
CrossRef Полный текст
20. Норин А., Олауссен А. Класс питона для многомерных уравнений Шредингера. В: Proceedings of the International MultiConference of Engineers and Computer Scientists IMECS 2015 . Гонконг (2015).п. 206–11.
- Краткое содержание курса

 М. Лифшица «Квантовая механика». Можно воспользоваться такими книгами, как Мессиа А. « Квантовая механика». Если есть возможность, то лучше ознакомиться с хорошим западным учебником, например, Claude Cohen-Tannoudji, Bernard Diu , Frank Laloe
М. Лифшица «Квантовая механика». Можно воспользоваться такими книгами, как Мессиа А. « Квантовая механика». Если есть возможность, то лучше ознакомиться с хорошим западным учебником, например, Claude Cohen-Tannoudji, Bernard Diu , Frank Laloe 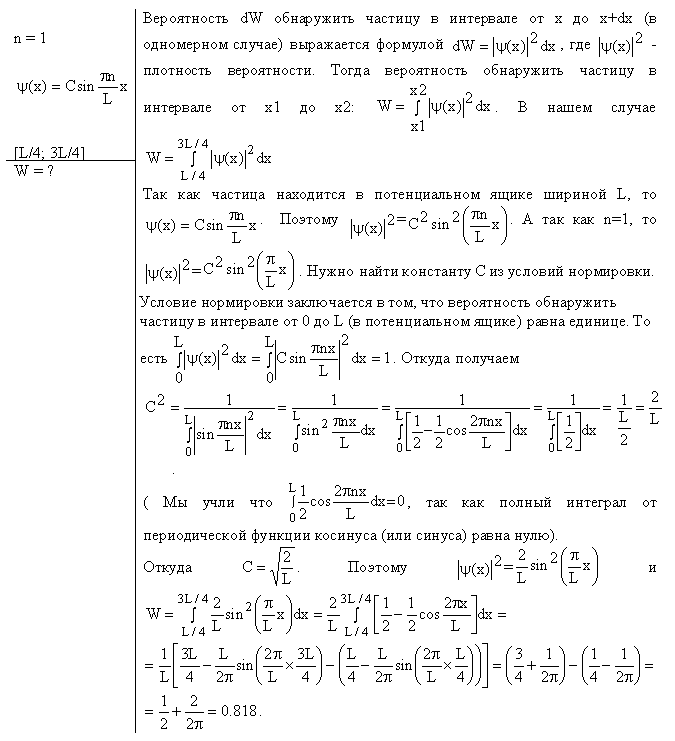 R. Coleman, Quantum Mechanics in Your Face
R. Coleman, Quantum Mechanics in Your Face
 Одномерная задача
Одномерная задача V. Nazarov, Y. M. Blanter — Quantum Transport: Introduction to Nanoscience
V. Nazarov, Y. M. Blanter — Quantum Transport: Introduction to Nanoscience Побойко — Теория рассеяния
Побойко — Теория рассеяния Т., Ватсон Дж.Н. “Курс современного анализа” – М.: Гл. ред. физ.-мат.лит, 1963
Т., Ватсон Дж.Н. “Курс современного анализа” – М.: Гл. ред. физ.-мат.лит, 1963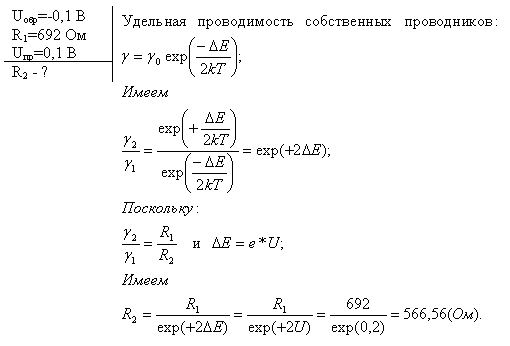 (премия 1921г.)
(премия 1921г.)