Задачи производные с решениями: Примеры решения производных с ответами

7$.

9. -1,5.

10. 236.

11. $x∈(-\sqrt{6}; \sqrt{6})$.

12. $x=\frac{\pi}{24}; \frac{11\pi}{24}; \frac{13\pi}{24}; \frac{23\pi}{24}; \frac{25\pi}{24}; \frac{35\pi}{24}; \frac{37\pi}{24}; \frac{47\pi}{24}; \frac{49\pi}{24}; \frac{59\pi}{24}; \frac{61\pi}{24}; \frac{71\pi}{24}; \frac{73\pi}{24}; \frac{83\pi}{24}; \frac{85\pi}{24}; \frac{95\pi}{24}; \frac{97\pi}{24}$.

Таблица производных, правила нахождения производных

Таблица производных основных функций

---

Основные правила нахождения производной

---

Если  – постоянная и ,  – функции, имеющие производные, то

 

1) Производная от постоянного числа равна нулю. 

 

2) Производная от переменной равна единице

 

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

3) Производная суммы равна сумме производных

Пример 1

Найдем производную функции

4) Производная произведения постоянной на некоторую функцию равна произведению этой постоянной на производную от заданной функции.

Пример 2

Найдем производную функции

5) Производная произведения функций

Пример 3

Найдем производную функции

6) Производная частного:

Пример 4

Найдем производную функции

Правило дифференцирования сложной функции

---

или в других обозначениях:

Пример 5

Найдем производную функции 

Пример 6

Найдем производную функции

Логарифмическая производная

---

Логарифмической производной функции  называется производная от логарифма этой функции, то есть:

Применение предварительного логарифмирования функции иногда упрощает нахождение ее производной.

Пример 7

Найдем производную функции 

Прологарифмируем заданную функцию:

Искомая производная:

Производная обратной функции

---

Если для функции  производная , то производная обратной функции  есть

или в других обозначениях:

Пример 8

Найдем производную , если

Имеем:

Следовательно:

Производная функции, заданной параметрически

---

Если зависимость функции  и аргумента  задана посредством параметра

то

или в других обозначениях:

Пример 9

Найдем производную функции 

 

Воспользуемся формулой:

Производная неявной функции

Если зависимость между  и  задана в неявной форме

    (*)

то для нахождения производной  в простейших случаях достаточно:

1) вычислить производную по  от левой части равенства (*), считая  функцией от ;

2) приравнять эту производную к нулю, то есть положить:

3) решить полученное уравнение относительно .

 

Пример 10

Найдем производную  функции   

Вычисляем производную от левой части равенства:

Решаем уравнение относительно :

Искомая производная:

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК

сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.

Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.

4.1.4. Примеры решения задач по теме «Производная по направлению.

Градиент»

Задача 1.

Составить уравнение касательной плоскости к поверхности

Указание

Уравнение касательной плоскости к поверхности

В точке (Х

0, Y0, Z0) имеет вид:

Решение

Подставим эти значения в уравнение касательной плоскости:

Ответ:

Задача 2.

Составить уравнение касательной плоскости к поверхности

В точке (1,2,-1).

Указание

Найдите частные производные Z по Х и У как производные неявной функции:

Решение

Уравнение касательной плоскости:

Ответ:

Задача 3.

Составить уравнения нормали к поверхности

В точке (0,4,2).

Указание

Будем называть нормалью прямую, проходящую через данную точку перпендикулярно касательной плоскости, проведенной через эту точку. Тогда канонические уравнения нормали выглядят так:

Решение

Следовательно, канонические уравнения нормали:

Ответ:

Задача 4.

Найти производную функции

И точке М(2,-4) по направлению вектора MN, если N(-1,-8).

Указание

Производная функции Z = F (X, Y) в точке (Х0, У0) по направлению L, заданному вектором А = (Ха, Уа, Za), имеет вид:

Направляющие косинусы направления L.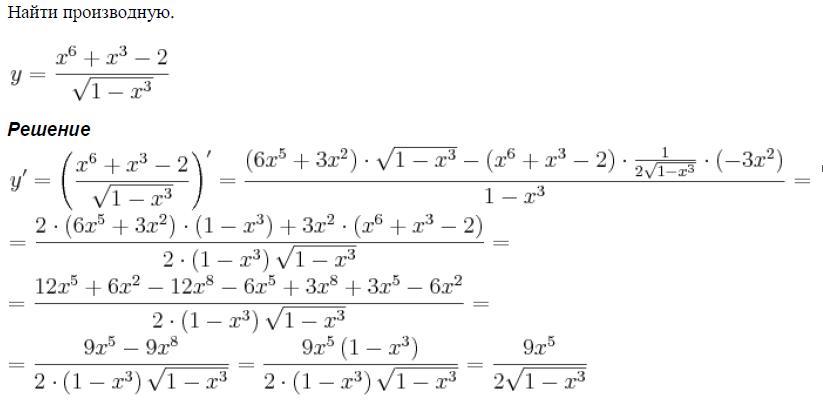

Решение

Ответ: 9,2.

Задача 5.

Найти производную функции

В точке (3,2,1) по направлению, образующему с координатными осями равные тупые углы.

Указание

Причем

Решение

Найдем направляющие косинусы направления L, используя свойство направляющих косинусов:

(поскольку косинус тупого угла отрицателен).

Тогда

Ответ:

Задача 6.

Найти градиент функции

В точке А(6,10,-5).

Указание

Воспользуйтесь формулой

Решение

Ответ:

< Предыдущая		Следующая >

Применение производной к решению математических задач практического содержания (Останькович Т.

Э.)

Разработка  урока ( 2*45 мин.)

в 10 классе с профильным изучением  математики  по  теме:

«Применение производной к решению математических задач

практического содержания.»

Останькович Татьяна Эдгаровна- учитель высшей категории.

Цель:    формирование  практических  навыков  применения теоретических  знаний  и общеучебных компетенций учащихся.

Задачи:

·                  познавательный аспект- расширение общего кругозора школьников,  стимулирование познавательной деятельности, умение находить и обрабатывать информацию;

·                  учебный аспект- активизация мыслительной деятельности учащихся при решении задач прикладного характера, алгоритмизация деятельности;

·                  воспитательный аспект- развитие умения работать в команде, активно слушать, уважать чужое мнение, формировать потребности в самовыражении и научном творчестве.

Математические задачи с практическим содержанием – это такие задачи, которые связаны с                 применением математики в технике, химии, экономике, медицине, экологии, а так же в быту. Мы рассмотрим задачи, которые можно решить с помощью производной . Эти задачи не совсем обычны как по форме изложения, так и по применяемым методам решения.

Одним из важнейших понятий математического анализа является производная функции. Производная характеризует скорость изменения функции по отношению к изменению независимой переменной. В геометрии производная характеризует крутизну графика, в механике – скорость неравномерного прямолинейного движения, в биологии – скорость размножения колонии микроорганизмов, в экономике – отзывчивость производственной функции (выход продукта на единицу затрат), в химии – скорость химической реакции.

В приложениях математики к решению конкретных задач приходится иметь дело с величинами, числовые значения которых получены путем измерений и, следовательно, точное их значение неизвестно. Если исходные данные содержат погрешности измерений, то применение точных методов измерения не целесообразно. Для упрощения и облегчения вычислений в таких случаях лучше использовать приближенные методы. Теоретической основой одного из простейших приемов приближенных значений вычислений является понятие дифференциала. Приближенное значение приращение функции называется дифференциалом функции и обозначается dy, причем dy=y’(x)dx.

Среди многих задач, решаемых с помощью производной, наиболее важной является задача нахождения экстремума функции и связанная с ней задача нахождения наибольшего (наименьшего) значения соответствующих функций. Рассмотрим некоторые из них. ( Образцы задач может приводить как сам учитель, так и заранее подготовленные ученики).

Задача №1

Докажите, что уравнение  3×5 – 25×3 + 60x + 15 = 0 имеет только один действительный корень.

Решение:

Рассмотрим функцию f(x) = 3×5 – 25×3 + 60x + 15 = 0 и найдем её интервалы монотонности. Имеем: f’(x) = 15×4 – 75×2 + 60 = 15(x + 2)(x + 1)(x – 1)(x – 2).

Производная f’(x) обращается в нуль в четырех точках: -2, -1, 1, 2. Эти точки разбивают числовую прямую на пять промежутков: (- ∞; -2), (-2; -1), (-1; 1), (1; 2), (2; +∞).

На каждом из указанных промежутков производная сохраняет постоянный знак. Отсюда заключаем, что на каждом из этих промежутков функция y = f(x) монотонна, т.е. или возрастает или убывает. Тогда график функции на каждом из указанных промежутков может пересекать ось абсцисс не более∞ чем в одной точке. Это значит, что функция y = f(x) на каждом из рассматриваемых промежутков может иметь не более одного корня, причем корни функции могут быть в тех и только тех промежутках, на концах которых функция имеет разные по знаку значения. Имеем

lim f(x) = – ∞, f(- 2) < 0, f(- 1) < 0,  f(1) > 0, f(2) > 0, lim f(x) = +∞

x → – ∞                                                                      x → +∞

 

f(1) > 0, f(2) > 0, lim f(x) = +∞

x → + ∞

Так как f(x) имеет различные знаки только на концах промежутка (-1; 1), то заданное уравнение имеет лишь один действительный корень, лежащий внутри этого интервала.

Задача №2.  При извержении вулкана камни горной породы выбрасываются перпенди-  кулярно вверх с начальной скоростью 120 м/ с. Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь?

Решение: Вещество выбрасывается перпендикулярно вверх. Высота камня h, функция времени-

h(t) = Vо t -1/2gt2 .Откуда следует: h(t)= v(t)= vо–gt. Следовательно, 0= 120-9,8t и t≈13 сек. Тогда h=745м, т.е. камни горной породы достигают уровня 720 м от края вулкана.

 

Задача №3. Нагруженные сани движутся по горизонтальной поверхности под действием силы  F, приложенной к центру  тяжести. Какой угол α должна составлять линия действия силы F с горизонтом, чтобы равномерное движение саней происходило под действием наименьшей силы? Коэффициент трения саней о снег равен к.

Решение: Разложим силу F на горизонтальную и вертикальную составляющие. Сила нормального движения саней и вертикальной составляющей силы  F:N=P-F sinα, поэтому сила трения  F тр =kN=

=k(P-Fsinα). Сани будут двигаться равномерно при условии компенсации горизонтальных сил:

Fx=Fтр., то есть Fcosα=k (P-Fsinα). Далее находим силу   как функцию угла α:

F(α)= kP/(ksinα+cosα).   F′(α) =kP(sinα-kcosα)/(ksinα+cosα)2. Тогда F′(α)=0 при k=tgα.

Определим знак второй производной в этой точке…

 

Из  решения этой задачи можно сделать практический вывод: когда необходимо везти на санях груз по дороге с большим коэффициентом трения, нужно тянуть сани за короткую веревку. Если же коэффициент  трения мал, веревка должна быть длинной.

 

Задача№4. Расход горючего легкового автомобиля (литр на 100 км) в зависимости от скорости х км/ч при движении на четвертой передачи приблизительно описывается функцией

f(x)=0,0017х-0,18х+10,2; х>30. При какой скорости расход горючего будет наименьший? Найдите этот расход.

Решение:  Исследуем расход горючего с помощью производной: f′(х)=0,0034х-0,18.Тогда f′(х)=0 при

х≈53. Определим знак второй производной в критической точке: f′′(х)=0,0034>0, следовательно, рас-

ход горючего при скорости 53 км/ч будет наименьшим. f(53)≈5,43 л.

 

Задача№5. Оборот предприятия за истекший год описывается через функцию  U(t)=0,15t2 – 2t2 + 200, где t –месяцы,  U-миллионы. Исследуйте оборот предприятия.

Решение. Исследуем оборот предприятия с помощью производной:U′(t)=0,45t2 – 4t  U′′(t)=0,9t-4

U″′(t)=0,9. Момент наименьшего оборота при U(t)=0, т.е.при  t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U(t)=0 следует t=4,4.Так как U″′(t)>0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение.

Так, например, по решению предложенной задачи можно сделать выводы:

1.В начале исследуемого периода у предприятия было снижение оборота;

2.Предприятие пыталось выйти из этого состояния и для этого использовало определенные средства.

На пятом месяце ( точка перегиба) что-то было предпринято и предприятие стало выходить из

кризиса, а на девятом месяце стало набирать обороты.

 

Задачи из биологии и химии

Биологический смысл производной.  Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у=p(t). Пусть ∆t-промежуток времени от некоторого начального значения t до t+∆t. Тогда у+∆у=p(t+∆t)- новое значение численности популяции, соответствующее моменту t+∆t, а  ∆y+p(t+∆t)-p(t)-изменение числа особей

организмов.

Химический смысл производной. Пусть дана функция m=m(t),где m-количество некоторого вещества, вступившего в химическую реакцию в момент времени t. Приращению времени ∆t будет соответствовать приращение ∆m  величины  m. Отношение ∆m/∆t- есть средняя скорость химической реакции за промежуток времени ∆t. Предел этого отношения при стремлении t∆ к нулю- есть скорость химической реакции в данный момент времени .

 

Р а с с м о т р и м   н е с к о л ь к о   з а д а ч

 

Задача №6. Зависимость между количеством х вещества, получаемого в результате некоторой

химической реакции и временем t выражается уравнением  Х=А(1+е) Определите скорость химической реакции в момент времени t.

 

Задача №7. Закон накопления сухой биомассы у винограда сорта Шалса определяется уравнением  y=0,003x-0,0004x  , где x- число дней от распускания почек, y-накопление биомассы в кг на 1 куст. Равенство отражает зависимость величин x и y как средний результат массовых

наблюдений. Выясните, как изменится сухая биомасса при изменении от 50 до 60 дней.

 

Задача №8. Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, уменьшения температуры тела, изменении пульса или других физиологических показателей. степень реакции зависит от назначенного лекарства, его дозы. Предположим, что Х обозначает дозу назначенного лекарства, У – функция степени реакции. У=f(x)=x2(a-x) ,где а – некоторая положительная постоянная. При каком значении Х реакция максимальна?

Решение: 0<x<а. Значит f′(x)=2ax-3×2  . Тогда  f′(x)=0 при x=⅔ а. В этой точке f″(⅔ а)= -2а<0, то х=⅔-а – тот уровень дозы, который дает максимальную реакцию.

Точки перегиба важны в биохимии, так как они определяют условия, при которых некоторая величина, например скорость процесса, наиболее ( или наименее) чувствительна к каким-либо

воздействиям.

 

Предлагается творческое задание (при наличии времени на уроке, если имеем в наличии сдвоенные уроки. Если такая возможность отсутствует, творческое задание выполняется дома).

Задача №9. За последние 10 лет численность грызунов в городе Н выросла в 5 рази достигла 1

миллиона особей: по одной крысе на каждого жителя. За год одна пара крыс способна воспроизвести 50 штук себе подобных. По словам эпидемиологов, крысы являются переносчиками многих болезней – чумы, бешенства, энцефалита. Составьте задачу по приведенным данным и решите её.

 

Задача №10. Зависимость суточного удой У в литрах от возраста коров Х в годах определяется

уравнением У(х)= -9,3+6,86х-0,49х , где х>2.Найдите возраст дойных коров, при котором суточный удой будет наибольшим.

Подведение  итогов.

 

Примеры решения производных

Пример. Производная суммы функций.

Дано: сумма функций .
Найти:
Вычислить производную суммы функций

Решение:
Исходя из того, что производная алгебраической суммы (разности) функций, имеющих производную, равна такой же сумме (разности) производных этих функций: используя формулы производных (ссылка), вычислим производную, заданной в условии задачи суммы функций:

Ответ: производная суммы функций равна

Пример. Производная произведения функций.

Дано: произведение функций .
Найти:
Вычислить производную произведения функций

Решение:
Исходя из того, что производная двух функций, имеющих производную, вычисляется по формуле: найдем производную, заданного в условии задачи произведения функций:

Ответ: производная произведения функций равна

Пример. Производная отношения функций.

Дано: отношение функций .
Найти:
Вычислить производную отношения функций

Решение:
Исходя из того, что производная отношения двух функций, имеющих производную, вычисляется по формуле: определим производную, заданного в условии задачи отношения функций:

Ответ: производная отношения функций равна

Пример. Производная сложной функций.

Дано: сложная функция .
Найти:
Вычислить производную сложной функции

Решение:
Исходя из того, что функция имеет производную в точке а функция имеет производную в точке причем сложная функция будет иметь производную в точке и в нашем случае получаем следующее а Тогда а значит

Ответ: производная сложной функции равна

Пример. Производная функции заданной параметрически.

Дано: функция заданная параметрически .
Найти:
Вычислить производную функции заданной параметрически.

Решение:
Исходя из того, что производная функции, заданной параметрически, то есть в виде соотношения где изменяется в пределах некоторого множества, определяется по формуле вычислим производную, заданной в задаче функции:

Производная параметрически заданной функции будет тоже функция, заданная параметрически:

Ответ: производная параметрически заданной функции равна

Материалы к уроку решения задач по физике с помощью производной

Здравствуйте! Здравствуйте, дорогие любители экспериментов и научных знаний!

11/24/18

Физика – книга о природе, но написана эта книга языком математики

Применение производной к решению задач физики

Ε i (t)= – Φ′ (∆ t)

Повторяем

2

3

1

физика

5

4

5

4

2

3

1

математика

Формула скорости равноускоренного движения

1

1

 х =  0х + а х t

Формула координаты равноускоренного движения

2

2

x = х 0 +  0х t + а х

 

Формула импульса тела

3

3

P х = m  х

II закон Ньютона

4

4

F x = ma x

Уравнение колебательного движения

5

5

x = x max cos 2πνt

Найти производную функции

y = x 3 + 4x + 2

yʹ = 3 x 2 + 4

1

1

Найти производную функции

y = cos5x

yʹ = – 5sin5x

2

2

Найти производную функции

y = cosx

yʹ = – sinx

3

3

Найти производную функции

y = – 3sinx

yʹ = – 3cosx

4

 

Найти производную функции

y = sin

yʹ = cos

 

5

5

Проба сил

№ 81 (Р)

Движения четырёх тел заданы следующими уравнениями

• x = 10t + 0,4t 2
• x = – t – 6t 2
• x = – 4t + 2t 2
• x = 2t – t 2

Написать уравнение  х =  х (t) для каждого тела

Проба сил

Привычные формулы «бастуют»

В момент времени 1с найти проекцию равнодействующих сил, действующих на тело массой 2 кг , движение которого описывается уравнением

x = – 6 + 2t – t 2 + t 3 – cosπt

Проба сил

№ 1. 2.12 (С)

Мальчик надувает шарик. При радиусе шарика 10 см скорость увеличения радиуса равна 0,1 см/с.

Какой объём воздуха ежесекундно выдыхает мальчик?

Раньше мы эту задачу решали сложным путём.

Раньше мы эту задачу решали сложным путём.

Теперь решаем так: для неизменного объёма мы имеем

Теперь решаем так: для неизменного объёма мы имеем

V ш = 3 . В процессе надувания объём меняется с известной скоростью увеличения радиуса. Где здесь спрятана зависимость 𝗋(t) ? (конечно в 3 ).

V ш = 𝟒/𝟑 𝛑𝗿 3 . В процессе надувания объём меняется с известной скоростью увеличения радиуса. Где здесь спрятана зависимость 𝗋(t) ? (конечно в 𝘳 3 ).

Мы имеем дело со сложной функцией, где 𝗋(t) – внутренняя функция. Тогда V(t) = 𝟒/𝟑 𝛑(𝗿(𝐭)) 3 . Дифференцируем.

Мы имеем дело со сложной функцией, где 𝗋(t) – внутренняя функция. Тогда V(t) = 3 . Дифференцируем.

Скорость роста объёма Vʹ= (𝟒/𝟑 𝛑𝗿 3 )ʹ𝗋ʹ= 𝟒/𝟑 𝛑𝟑𝗿 2 𝗋ʹ= 40π см 3 /с

Скорость роста объёма Vʹ( 3 )ʹ𝗋ʹ= 2 𝗋ʹ= 40π см 3 /с

(справа: производная объёма по радиусу на производную радиуса по времени). Видите, как быстро решена задача! ( сложная функция по правилу:производная функции на производную аргумента)

(справа: производная объёма по радиусу на производную радиуса по времени). Видите, как быстро решена задача!

14

Проба сил

Экспериментальная задача

Оборудование :

Груз известной массы, пружина, штатив, линейка, секундомер

Что будем определять?

Рабочая формула

P(t) = m  (t)

 (t) =хʹ = (x max cos2πνt)ʹ= – x max 2πνsin2πνt

P(t) = – m x max 2πνsin2πνt

14

Тест

Помощница производная

осилим

Проверяем как научились

Правильные ответы

физика

1

вариант

2

48 Н

вариант

80 Н

 х = 25 м/с;

 х = 10 м/с;

P x = 2500 кг·м/с

P x = 1000 кг • м/ c

Критерии оценок

Количество правильных ответов

физика

Качество научения

0

1

неудовлетворительное

Оценка

2

1,5

удовлетворительное

3

хорошее

2

4

отличное

5

Поразмышляем

• достигнуты ли цели урока ?
• что вспомнили,
• чему научились,
• выполнили ли все поставленные задачи?
• понравилось ли вам решать известные вам задачи новым способом?

Проба сил дома

• № 75 (Р) – с помощью производной
• Составить 2 задачи на движение для решения с помощью производной
• *** для подготовки к ЕГЭ – № 8. 4 (Г.) http://egefizika5.com/egef5.htm

Это задача на второй закон Ньютона, в которой для

исследования полученного уравнения силы примените производную

Завершая урок

Шёл мудрец, а навстречу ему три человека, которые везли под солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу.

У первого спросил: «Что ты делал целый день?» И тот ответил, что целый день возил проклятые камни.

У второго мудрец спросил: «А ты, что делал целый день?» и тот ответил: «А я добросовестно выполнял свою работу».

А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма».

А что ответил бы ты ?

Спасибо за работу!

Использованная литература

Анимация к титульному слайду https :// matematuka2015.files.wordpress. com/2016/01/giphy.gif?w=640

Анимация генератора http:// nataliia-shchegelska.kh.sch.in.ua/files2/images/fizika-2.gif?size=10

Гонщики https:// pxhst.co/avaxhome/fa/04/004004fa_medium.jpg

Мальчик с шариком http :// img.dni.ru/binaries/v2_articlepic/575736.jpg

Анимация к пробе сил http:// zaryad.com/forum/proxy.php?image=http%3A%2F%2Fwww.physicscentral.org%2Fexplore%2Faction%2Fimages%2FCoriolis-Effect-animation.gif&hash=bf2e228a4f3a3289998f4831e85ff840

Анимация маятника http:// oplib.ru/image.php?way=oplib/baza14/355100078345.files/image004.gif

Рымкевич А.П. Сборник задач по физике М.: Просвещение, 2015

Анимация синусоиды

https://files3.adme.ru/files/news/part_76/760860/19dc7998a45cf2cf7233af6438831897.gif

Проба сил

Практическая работа



Оборудование :

Шарик на нити, штатив,

секундомер

Решение:

Решение:

Период колебаний математического маятника определяется по формуле:

Период колебаний математического маятника определяется по формуле:

T = 2. (−1/2)· 1/𝑔 = 𝜋√(𝑔/𝑙)· 1/𝑔 = 𝜋/𝑙 √(𝑙/𝑔).

Ответ:

Ответ: 𝜋/𝑙 √(𝑙/𝑔)

Что будем определять?

Каково изменение периода колебаний математического маятника при изменении его длины?

28

Применение производной к решению задач физики

 х (t) = xʹ

http://s4.postimg.org/q0wvddly5/image.png

 х (t) = xʹ

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию. 2} \\ [8px] & = \ dfrac {{\ Big [\ text {(производная от числителя)} \ times \ text {(знаменатель)} \ Big] – \ Big [\ text {(числитель)} \ times \ text {(производная от знаменателя )}} \ Big]} {\ text {все разделено на [знаменатель, в квадрате]}}
   \ end {align *}

   Многие студенты помнят правило частного, думая о числителе как о «привет», а о демонинаторе – как «Lo», производное от «d», а затем пение

   «lo d-hi minus hi d-lo over lo-lo»

   [свернуть]

   страница не найдена – Williams College

   ’62 Центр Театра и Танца, 62 Центр
   Касса	597-2425
   Магазин костюмов	597-3373
   Менеджер мероприятий / Ассистент менеджера	597-4808	597-4815 факс
   Производство		597-4474 факс
   Магазин сцен	597-2439
   ’68 Центр карьерного роста, Мирс	597-2311	597-4078 факс
   Академические ресурсы, Парески	597-4672	597-4959 факс
   Служба поддержки инвалидов, Парески	597-4672
   Прием, Вестон-холл	597-2211	597-4052 факс
   Программа позитивных действий, Хопкинс-холл,	597-4376
   Africana Studies, Hollander	597-2242	597-4222 факс
   Американские исследования, Шапиро	597-2074	597-4620 факс
   Антропология и социология, Холландер	597-2076	597-4305 факс
   Архивы и специальные коллекции, Sawyer	597-4200	597-2929 факс
   Читальный зал	597-4200
   Искусство (История, Студия), Spencer Studio Art / Lawrence	597-3578	597-3693 факс
   Архитектурная студия, Spencer Studio Art	597-3134
   Фотостудия, Spencer Studio Art	597-2030
   Студия гравюры, Студия Спенсера Арт	597-2496
   Студия скульптуры, Студия Спенсера Арт	597-3101
   Senior Studio, Spencer Studio Art	597-3224
   Видео / фотостудия, Spencer Studio Art	597-3193
   Азиатские исследования, Hollander	597-2391	597-3028 факс
   Астрономия / астрофизика, Thompson Physics	597-2482	597-3200 факс
   Департамент легкой атлетики, физическое воспитание, отдых, Lasell	597-2366	597-4272 факс
   Спортивный директор	597-3511
   Лодочный домик, Озеро Онота	443-9851
   Автобусы	597-2366
   Фитнес-центр	597-3182
   Hockey Rink Ice Line, Lansing Chapman	597-2433
   Intramurals, Спортивный центр Чандлера	597-3321
   Физическая культура	597-2141
   Pool Wet Line, Спортивный центр Чандлера	597-2419
   Спортивная информация, Хопкинс-холл	597-4982	597-4158 факс
   Спортивная медицина	597-2493	597-3052 факс
   Площадки для игры в сквош	597-2485
   Поле для гольфа Taconic	458-3997
   Биохимия и молекулярная биология, Thompson Biology	597-2126
   Биоинформатика, геномика и протеомика, Бронфман	597-2124
   Биология, Thompson Biology	597-2126	597-3495 факс
   Охрана и безопасность кампуса, Хопкинс-холл	597-4444	597-3512 факс
   Карты доступа / системы сигнализации	597-4970 / 4033
   Служба сопровождения, Хопкинс Холл	597-4400
   Офицеры и диспетчеры	597-4444
   Секретарь, удостоверения личности	597-4343
   Коммутатор	597-3131
   Центр развития творческого сообщества, 66 Stetson Court	884-0093
   Центр экономики развития, 1065 Main St	597-2148	597-4076 факс
   Компьютерный зал	597-2522
   Вестибюль	597-4383
   Центр экологических исследований, выпуск 1966 г. Экологический центр	597-2346	597-3489 факс
   Лаборатория экологических наук, Морли	597-2380
   Экологические исследования	597-2346
   Лаборатория ГИС	597-3183
   Центр иностранных языков, литератур и культур, Холландер	597-2391	597-3028 факс
   Арабоведение, Hollander	597-2391	597-3028 факс
   Сравнительная литература, Hollander	597-2391
   Критические языки, Hollander	597-2391	597-3028 факс
   Языковая лаборатория	597-3260
   Россия, Hollander	597-2391
   Центр обучения в действии, Brooks House	597-4588	597-3090 факс
   Библиотека редких книг Чапина, Сойер	597-2462	597-2929 факс
   Читальный зал	597-4200
   Офис капелланов, Парески	597-2483	597-3955 факс
   Еврейский религиозный центр, Стетсон-Корт, 24,	597-2483
   Молельная мусульманская, часовня Томпсона (нижний уровень)	597-2483
   Католическая часовня Ньюмана, часовня Томпсона (нижний уровень)	597-2483
   Химия, Thompson Chemistry	597-2323	597-4150 факс
   Классика (греческий и латинский), Hollander	597-2242	597-4222 факс
   Когнитивные науки, Бронфман	597-4594
   Маршал колледжа, Thompson Physics	597-2008
   Отношения с колледжем	597-4057
   25-я программа воссоединения, Фогт	597-4208	597-4039 факс
   Программа 50-го воссоединения, Фогт	597-4284	597-4039 факс
   Advancement Operations, Мирс-Вест	597-4154	597-4333 факс
   Мероприятия для выпускников, Vogt	597-4146	597-4548 факс
   Фонд выпускников	597-4153	597-4036 факс
   Связи с выпускниками, Мирс-Уэст	597-4151	597-4178 факс
   Почтовые службы для выпускников / разработчиков, Мирс-Уэст	597-4369
   Разработка, Vogt	597-4256
   Отношения с донорами, Vogt	597-3234	597-4039 факс
   Офис по планированию подарков, Vogt	597-3538	597-4039 факс
   Офис грантов, Мирс-Уэст	597-4025	597-4333 факс
   Программа крупных подарков, Vogt	597-4256	597-4548 факс
   Фонд родителей, Фогт	597-4357	597-4036 факс
   Prospect Management & Research, Мирс	597-4119	597-4178 факс
   Выпускные и академические мероприятия, Jesup	597-2347	597-4435 факс
   Коммуникации, Хопкинс Холл	597-4277	597-4158 факс
   Спортивная информация, Хопкинс-холл	597-4982	597-4158 факс
   Веб-группа, Саутвортская школа
   Williams Magazines (ранее Alumni Review), Хопкинс-холл	597-4278
   Компьютерные науки, Thompson Chemistry	597-3218	597-4250 факс
   Conferences & Events, Парески	597-2591	597-4748 факс
   Запросы Elm Tree House, Mt.Ферма Надежды	597-2591
   Офис диспетчера, Хопкинс Холл	597-4412	597-4404 факс
   Счета к оплате и ввод данных, Хопкинс-холл	597-4453
   Bursar & Cash Receipts, Hopkins Hall	597-4396
   Финансовые информационные системы, Хопкинс Холл	597-4023
   Карты закупок, Хопкинс Холл	597-4413
   Студенческие ссуды, Хопкинс Холл	597-4683
   Танец, 62 Центр	597-2410
   Дэвис-центр (бывший мультикультурный центр), Дженнесс	597-3340	597-3456 факс
   Харди Хаус	597-2129
   Jenness House	597-3344
   Райс Хаус	597-2453
   Декан колледжа, Хопкинс-холл	597-4171	597-3507 факс
   Декан факультета, Хопкинс Холл	597-4351	597-3553 факс
   Столовая, капельницы	597-2121	597-4618 факс
   ’82 Гриль, Парески	597-4585
   Булочная, Пареский	597-4511
   Общественное питание, факультет	597-2452
   Driscoll Dining Hall, Дрисколл	597-2238
   Эко-кафе, Научный центр	597-2383
   Grab ‘n Go, Парески	597-4398
   Lee Snack Bar, Парески	597-3487
   Обеденный зал Mission Park, Mission Park	597-2281
   Whitmans ‘, Парески	597-2889
   Экономика, Шапиро	597-2476	597-4045 факс
   английский, Hollander	597-2114	597-4032 факс
   Сооружения, здание бытового обслуживания	597-2301
   Запрос на автомобиль в колледже	597-2302
   Аварийная ситуация вечером / в выходные дни	597-4444
   Запросы на работу оборудования		597-4141 факс
   Особые события	597-4020
   Склад	597-2143	597-4013 факс
   Клуб преподавателей, Дом факультетов / Центр выпускников	597-2451	597-4722 факс
   Бронирование	597-3089
   Fellowships Office, Hopkins Hall	597-3044	597-3507 факс
   Financial Aid, Weston Hall	597-4181	597-2999 факс
   Науки о Земле, Кларк Холл	597-2221	597-4116 факс
   Немецко-Русский, Hollander	597-2391	597-3028 факс
   Глобальные исследования, Холландер	597-2247
   Магистерская программа по истории искусств, Кларк		458-2317 факс
   Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health	597-2206	597-2982 факс
   Медицинское просвещение	597-3013
   Услуги интегративного благополучия (консультирование)	597-2353
   Чрезвычайные ситуации с опасностью для жизни	Позвоните 911
   Медицинские услуги	597-2206
   История, Hollander	597-2394	597-3673 факс
   История науки, Бронфман		597-4116 факс
   Лес Хопкинса	597-4353
   Розенбург-центр	458-3080
   Отдел кадров, B&L Building	597-2681	597-3516 факс
   Услуги няни, корпус B&L	597-4587
   Преимущества	597-4355
   Программа помощи сотрудникам	800-828-6025
   Занятость	597-2681
   Заработная плата	597-4162
   Ресурсы для супруга / партнера	597-4587
   Занятость студентов	597-4568
   Погодная линия (ICEY)	597-4239
   Humanities, Schapiro	597-2076
   Информационные технологии, Jesup	597-2094	597-4103 факс
   Пакеты для чтения курсов, ящик для сообщений офисных услуг	597-4090
   Центр ссуды на оборудование, приложение Додда	597-4091
   Служба поддержки преподавателей / сотрудников, [электронная почта]	597-4090
   Медиауслуги и справочная система	597-2112
   Служба поддержки студентов, [электронная почта]	597-3088
   Телекоммуникации / телефоны	597-4090
   Междисциплинарные исследования, Hollander	597-2552
   Международное образование и учеба, Хопкинс-холл	597-4262	597-3507 факс
   Инвестиционный офис, Хопкинс Холл	597-4447
   Бостонский офис	617-502-2400	617-426-5784 факс
   Еврейские исследования, Мазер	597-3539
   Правосудие и закон, Холландер	597-2102
   Latina / o Studies, Hollander	597-2242	597-4222 факс
   Исследования лидерства, Шапиро	597-2074	597-4620 факс
   Морские исследования, Бронфман	597-2297
   Математика и статистика, Bascom	597-2438	597-4061 факс
   Музыка, Бернхард	597-2127	597-3100 факс
   Concertline (записанная информация)	597-3146
   Неврология, Thompson Biology	597-4107	597-2085 факс
   Окли Центр, Окли	597-2177	597-4126 факс
   Управление институционального разнообразия и справедливости, Хопкинс-холл	597-4376	597-4015 факс
   Управление счетов студентов, Хопкинс-холл	597-4396	597-4404 факс
   Performance Studies, ’62 Центр	597-4366
   Философия, Шапиро	597-2074	597-4620 факс
   Физика, Thompson Physics	597-2482	597-4116 факс
   Планетарий / Обсерватория Хопкинса	597-3030
   Театр старой обсерватории Хопкинса	597-4828
   Бронирование	597-2188
   Политическая экономия, Шапиро	597-2327
   Политология, Шапиро	597-2168	597-4194 факс
   Офис президента, Хопкинс Холл	597-4233	597-4015 факс
   Дом Президента	597-2388	597-4848 факс
   Услуги печати / почты для преподавателей / сотрудников, ’37 House	597-2022
   Программа обучения, Бронфман	597-4522	597-2085 факс
   Офис Провоста, Хопкинс Холл	597-4352	597-3553 факс
   Психология, психологические кабинеты и лаборатории	597-2441	597-2085 факс
   Недвижимость, корпус B&L	597-2195 / 4238	597-5031 факс
   Ипотека для преподавателей / сотрудников	597-4238
   Аренда жилья для преподавателей / сотрудников	597-2195
   Офис регистратора, Хопкинс Холл	597-4286	597-4010 факс
   Религия, Холландер	597-2076	597-4222 факс
   Romance Languages, Hollander	597-2391	597-3028 факс
   Планировщик помещений	597-2555
   Соответствие требованиям безопасности и охраны окружающей среды, класс ’37, дом	597-3003
   Библиотека Сойера, Сойер	597-2501	597-4106 факс
   Службы доступа	597-2501
   Поступления / серийные номера	597-2506
   Услуги каталогизации / метаданных	597-2507
   Межбиблиотечный абонемент	597-2005	597-2478 факс
   Исследовательские и справочные службы	597-2515
   Стеллаж	597-4955	597-4948 факс
   Системы	597-2084
   Научная библиотека Schow, Научный центр	597-4500	597-4600 факс
   Исследования в области науки и технологий, Бронфман	597-2239
   Научный центр, Бронфман		597-4116 факс
   Магазин электроники	597-2205
   Машинно-модельный цех	597-2230
   Безопасность	597-4444
   Специальные академические программы, Харди	597-3747	597-4530 факс
   Спортивная информация, Хопкинс-холл	597-4982	597-4158 факс
   Студенческая жизнь, Парески	597-4747
   Планировщик помещений	597-2555
   Управление студенческими центрами	597-4191
   Организация студенческих мероприятий	597-2546
   Студенческий корпус, Пареский	597-2555
   Участие студентов	597-4749
   Программы проживания в старших классах	597-4625
   Студенческая почта, Паресский почтовый кабинет	597-2150
   Устойчивое развитие / Центр Зилха, Харпер	597-4462
   Коммутатор, Хопкинс Холл	597-3131
   Книжный магазин Williams	458-8071	458-0249 факс
   Театр, 62 Центр	597-2342	597-4170 факс
   Trust & Estate Administration, Sears House	597-4259
   Учебники	597-2580
   Вице-президент по вопросам жизни в кампусе, Хопкинс-холл	597-2044	597-3996 факс
   Вице-президент по связям с колледжем, Мирс	597-4057	597-4178 факс
   Вице-президент по финансам и администрированию, Хопкинс Холл	597-4421	597-4192 факс
   Центр визуальных ресурсов, Лоуренс	597-2015	597-3498 факс
   Детский центр Williams College, Детский центр Williams	597-4008	597-4889 факс
   Музей искусств колледжа Уильямс (WCMA), Лоуренс	597-2429	597-5000 факс
   Подготовка музея	597-2426
   Служба безопасности музея	597-2376
   Музейный магазин	597-3233
   Williams International	597-2161
   Williams Outing Club, Парески	597-2317
   Оборудование / Студенческий стол	597-4784
   Проект Уильямса по экономике высшего образования, Мирс-Вест	597-2192
   Уильямс Рекорд, Парески	597-2400	597-2450 факс
   Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет	011-44-1865-512345
   Программа Williams-Mystic, Mystic Seaport Museum	860-572-5359	860-572-5329 факс
   Исследования женщин, гендера и сексуальности, Шапиро	597-3143	597-4620 факс
   Написание программ, Хопкинс Холл	597-4615
   Центр экологических инициатив «Зилха», Харпер	597-4462

   Производные от экспоненциальных функций

   На этой странице мы рассмотрим, как различать экспоненциальные функции.2}}} \ ln 4.} \]

   Wolfram | Примеры альфа: производные

   ---

   Производные

   Дифференцировать выражение по заданной переменной.

   Вычислить производную функции:

   Другие примеры

   ---

   Производные высшего порядка

   Вычислить производные высшего порядка.

   Вычислить производные высшего порядка:

   Другие примеры

   ---

   Неявная дифференциация

   Дифференцируйте функции, неявно определяемые уравнениями.

   Продифференцируйте уравнение:

   Вычислить производную, используя неявное дифференцирование:

   Другие примеры

   ---

   Частные производные

   Найдите частную производную по одной переменной или вычислите смешанные частные производные.

   Вычислить частные производные:

   Вычислить частные производные высшего порядка:

   Другие примеры

   ---

   Направленные производные

   Вычислить производную многомерной функции в заданном направлении.

   Вычислить производную по направлению:

   Другие примеры

   ---

   Производные абстрактных функций

   Найдите производную произвольной функции.

   Вычислить производные с использованием абстрактных функций:

   Вычислить частные производные абстрактных функций:

   Другие примеры

   ---

   Дифференцируемость

   Проверить, дифференцируемы ли функции над полем действительных чисел.

   Проверить дифференцируемость функции:

   Другие примеры

   ---

   Производные приложения

   Изучите множество приложений деривативов.

   Найдите интервалы монотонности:

   Изучите примечательные точки кривых:

   Вычислить экстремальные значения одномерных и многомерных функций:

   Вычислить касательную к уравнению в заданной точке:

   Другие примеры

   Правил дифференциации | Дифференциальное исчисление

   \ (\ frac {dy} {dx} = – 20x ^ {4} \)

   \ (g ‘(x) = – 32x ^ {- 3} = – \ frac {32} {x ^ {3}} \)

   \ (f (x) = \ frac {1} {3} x ^ {3} – x ^ {2} + \ frac {2} {5} \)

   \ (f ‘(x) = x ^ {2} -2x \)

   \ (y = 3x ^ {\ frac {3} {2}} – 4x + 20 \)

   \ (\ frac {dy} {dx} = \ frac {9} {2} x ^ {\ frac {1} {2}} – 4 \)

   \ (g (x) = x ^ {2} + 7x \\ д ‘(х) = 2х + 7 \)

   \ (p (x) = 200 [x ^ {3} – \ frac {1} {2} x ^ {2} + \ frac {1} {5} x-40] \)

   \ (p ‘(x) = 200 [3x ^ {2} -x + \ frac {1} {5}] \\ p ‘(x) = 600x ^ {2} -200x + 40 \)

   \ (y = 14 (x-1) \ left [\ frac {1} {2} + x ^ {2} \ right] \)

   \ (y = 14 (x ^ {3} – x ^ {2} + \ frac {1} {2} x – \ frac {1} {2}) \\ \ поэтому \ frac {dy} {dx} = 14 \ left (3x ^ {2} – 2x + \ frac {1} {2} \ right) \\ = 42x ^ {2} -28x + 7 \)

   Найдите \ ({f} ‘\ left (x \ right) \), если \ (f \ left (x \ right) = \ frac {{x} ^ {2} -5x + 6} {x-2} \ ).{\ frac {3} {2}}} \ end {выровнять *}

   6. Производные продукты и коэффициенты

   М. Борна

   ПРАВИЛО ПРОДУКТА

   Если u и v – две функции от x , то производная от произведения uv дается как …

   `(d (uv)) / (dx) = u (dv) / (dx) + v (du) / dx`

   На словах это можно запомнить как:

   “Производная произведения двух функций – это первое, умноженное на производное второго, плюс второе, умноженное на производное первого.«

   Откуда взялась эта формула? Как и все встречающиеся нам формулы дифференцирования, она основана на производных от первых принципов.

   Пример 1

   Если у нас есть такой товар, как

   y = (2 x ² + 6 x ) (2 x ³ + 5 x ² )

   мы можем найти производную, не умножая выражение справа.2) `(в главе« Дифференциация трансцендентных функций ».) Это выражение нельзя умножить почленно, поэтому нам нужен метод, чтобы дифференцировать произведения таких функций.

   Примечание

   Мы можем написать правило продукта разными способами:

   `(d (uv)) / (dx) = uv’ + vu’`

   ИЛИ

   `(d (fg)) / (dx)` `= f (x) d / (dx) g (x) + g (x) d / (dx) f (x)`… и т. Д.

   ЧАСТНОЕ ПРАВИЛО

   (частное – это всего лишь дробь.2) `

   4.3 Частные производные – том 3 исчисления

   Цели обучения

   • 4.3.1 Вычислить частные производные функции двух переменных.
   • 4.3.2 Вычислить частные производные функции более двух переменных.
   • 4.3.3. Определите производные высшего порядка функции двух переменных.
   • 4.3.4 Объясните значение уравнения в частных производных и приведите пример.

   Теперь, когда мы изучили пределы и непрерывность функций двух переменных, мы можем перейти к изучению производных.Нахождение производных функций двух переменных – ключевая концепция в этой главе, которая имеет такое же множество приложений в математике, науке и технике, как и дифференциация функций одной переменной. Однако мы уже видели, что ограничения и непрерывность функций с несколькими переменными имеют новые проблемы и требуют новой терминологии и идей для их решения. Это также переносится на дифференциацию.

   Производные функции двух переменных

   При изучении производных функций одной переменной мы обнаружили, что одна из интерпретаций производной – это мгновенная скорость изменения yy как функции от x.Икс. Обозначение Лейбница для производной – dy / dx, dy / dx, что означает, что yy – зависимая переменная, а xx – независимая переменная. Для функции z = f (x, y) z = f (x, y) двух переменных, xx и yy – независимые переменные, а zz – зависимая переменная. Сразу возникает два вопроса: как адаптировать обозначения Лейбница для функций двух переменных? Кроме того, какова интерпретация производной? Ответ кроется в частных производных.

   Определение

   Пусть f (x, y) f (x, y) – функция двух переменных.Тогда частная производная ff по x, x, записанная как ∂f / ∂x, ∂f / ∂x или fx, fx, определяется как

   ∂f∂x = limh → 0f (x + h, y) −f (x, y) h. ∂f∂x = limh → 0f (x + h, y) −f (x, y) h.

   (4,12)

   Частная производная ff по y, y, записанная как ∂f / ∂y, ∂f / ∂y или fy, fy, определяется как

   ∂f∂y = limk → 0f (x, y + k) −f (x, y) k. ∂f∂y = limk → 0f (x, y + k) −f (x, y) k.

   (4,13)

   Это определение уже показывает два различия. Во-первых, обозначения меняются в том смысле, что мы все еще используем версию обозначений Лейбница, но dd в исходных обозначениях заменяется символом ∂.∂. (Это округленное «d» «d» обычно называют «частичным», поэтому ∂f / ∂x∂f / ∂x произносится как «частичное ff по отношению к x».) X ».) Это первое намек на то, что мы имеем дело с частными производными. Во-вторых, теперь у нас есть две разные производные, которые мы можем взять, поскольку есть две разные независимые переменные. В зависимости от того, какую переменную мы выберем, мы можем получить разные частные производные, что часто и происходит.

   Пример 4.14

   Расчет частных производных от определения

   Используйте определение частной производной как предел для вычисления ∂f / ∂x∂f / ∂x и ∂f / ∂y∂f / ∂y для функции

   f (x, y) = x2−3xy + 2y2−4x + 5y − 12.f (x, y) = x2−3xy + 2y2−4x + 5y − 12.

   Решение

   Сначала вычислите f (x + h, y) .f (x + h, y).

   f (x + h, y) = (x + h) 2−3 (x + h) y + 2y2−4 (x + h) + 5y − 12 = x2 + 2xh + h3−3xy − 3hy + 2y2−4x −4h + 5y − 12. f (x + h, y) = (x + h) 2−3 (x + h) y + 2y2−4 (x + h) + 5y − 12 = x2 + 2xh + h3− 3xy − 3hy + 2y2−4x − 4h + 5y − 12.

   Затем подставьте это в уравнение 4.12 и упростите:

   ∂f∂x = limh → 0f (x + h, y) −f (x, y) h = limh → 0 (x2 + 2xh + h3−3xy − 3hy + 2y2−4x − 4h + 5y − 12) – ( x2−3xy + 2y2−4x + 5y − 12) h = limh → 0x2 + 2xh + h3−3xy − 3hy + 2y2−4x − 4h + 5y − 12 − x2 + 3xy − 2y2 + 4x − 5y + 12h = limh → 02xh + h3−3hy − 4hh = limh → 0h (2x + h − 3y − 4) h = limh → 0 (2x + h − 3y − 4) = 2x − 3y − 4.∂f∂x = limh → 0f (x + h, y) −f (x, y) h = limh → 0 (x2 + 2xh + h3−3xy − 3hy + 2y2−4x − 4h + 5y − 12) – ( x2−3xy + 2y2−4x + 5y − 12) h = limh → 0x2 + 2xh + h3−3xy − 3hy + 2y2−4x − 4h + 5y − 12 − x2 + 3xy − 2y2 + 4x − 5y + 12h = limh → 02xh + h3−3hy − 4hh = limh → 0h (2x + h − 3y − 4) h = limh → 0 (2x + h − 3y − 4) = 2x − 3y − 4.

   Чтобы вычислить ∂f∂y, ∂f∂y, сначала вычислите f (x, y + h): f (x, y + h):

   f (x, y + h) = x2−3x (y + h) +2 (y + h) 2−4x + 5 (y + h) −12 = x2−3xy − 3xh + 2y2 + 4yh + 2h3−4x + 5y + 5h − 12. f (x, y + h) = x2−3x (y + h) +2 (y + h) 2−4x + 5 (y + h) −12 = x2−3xy − 3xh + 2y2 + 4yh + 2h3−4x + 5y + 5h − 12.

   Затем подставьте это в уравнение 4.13 и упростите:

   ∂f∂y = limk → 0f (x, y + h) −f (x, y) k = limk → 0 (x2−3xy − 3xk + 2y2 + 4yk + 2k2−4x + 5y + 5k − 12) – ( x2−3xy + 2y2−4x + 5y − 12) k = limk → 0x2−3xy − 3xk + 2y2 + 4yk + 2k2−4x + 5y + 5k − 12 − x2 + 3xy − 2y2 + 4x − 5y + 12k = limk → 0−3xk + 4yk + 2k2 + 5kk = limk → 0h (−3x + 4y + 2k + 5) k = limk → 0 (−3x + 4y + 2k + 5) = – 3x + 4y + 5.∂f∂y = limk → 0f (x, y + h) −f (x, y) k = limk → 0 (x2−3xy − 3xk + 2y2 + 4yk + 2k2−4x + 5y + 5k − 12) – ( x2−3xy + 2y2−4x + 5y − 12) k = limk → 0x2−3xy − 3xk + 2y2 + 4yk + 2k2−4x + 5y + 5k − 12 − x2 + 3xy − 2y2 + 4x − 5y + 12k = limk → 0−3xk + 4yk + 2k2 + 5kk = limk → 0h (−3x + 4y + 2k + 5) k = limk → 0 (−3x + 4y + 2k + 5) = – 3x + 4y + 5.

   КПП 4.12

   Используйте определение частной производной как предел для вычисления ∂f / ∂x∂f / ∂x и ∂f / ∂y∂f / ∂y для функции

   f (x, y) = 4×2 + 2xy − y2 + 3x − 2y + 5. f (x, y) = 4×2 + 2xy − y2 + 3x − 2y + 5.

   Идея, которую следует иметь в виду при вычислении частных производных, заключается в том, чтобы рассматривать все независимые переменные, кроме переменной, по которой мы производим дифференцирование, как константы.Затем переходите к дифференцированию, как с функцией одной переменной. Чтобы понять, почему это так, сначала зафиксируйте yy и определите g (x) = f (x, y) g (x) = f (x, y) как функцию от x.x. Тогда

   g ′ (x) = limh → 0g (x + h) −g (x) h = limh → 0f (x + h, y) −f (x, y) h = ∂f∂xg ′ (x) = limh → 0g (x + h) −g (x) h = limh → 0f (x + h, y) −f (x, y) h = ∂f∂x.

   То же самое верно и для вычисления частной производной ff по y.y. На этот раз зафиксируйте xx и определите h (y) = f (x, y) h (y) = f (x, y) как функцию от y.y. Тогда

   h ′ (x) = limk → 0h (x + k) −h (x) k = limk → 0f (x, y + k) −f (x, y) k = ∂f∂y.h ′ (x) = limk → 0h (x + k) −h (x) k = limk → 0f (x, y + k) −f (x, y) k = ∂f∂y.

   Применяются все правила дифференциации из Введение в производные финансовые инструменты.

   Пример 4.15

   Расчет частных производных

   Вычислить ∂f / ∂x∂f / ∂x и ∂f / ∂y∂f / ∂y для следующих функций, удерживая противоположную переменную постоянной и затем дифференцируя:

   1. f (x, y) = x2−3xy + 2y2−4x + 5y − 12f (x, y) = x2−3xy + 2y2−4x + 5y − 12
   2. g (x, y) = sin (x2y − 2x + 4) g (x, y) = sin (x2y − 2x + 4)

   Решение

   1. Чтобы вычислить ∂f / ∂x, ∂f / ∂x, рассматривайте переменную yy как константу.Затем продифференцируйте f (x, y) f (x, y) относительно xx, используя правила суммы, разности и мощности:
      ∂f∂x = ∂∂x [x2−3xy + 2y2−4x + 5y − 12] = ∂∂x [x2] −∂∂x [3xy] + ∂∂x [2y2] −∂∂x [4x] + ∂∂x [5y] −∂∂x [12] = 2x − 3y + 0−4 + 0−0 = 2x − 3y − 4. ∂f∂x = ∂∂x [x2−3xy + 2y2−4x + 5y −12] = ∂∂x [x2] −∂∂x [3xy] + ∂∂x [2y2] −∂∂x [4x] + ∂∂x [5y] −∂∂x [12] = 2x − 3y + 0−4 + 0−0 = 2x − 3y − 4.
      Производные третьего, пятого и шестого членов равны нулю, потому что они не содержат переменных x, x, поэтому они рассматриваются как постоянные члены. Производная второго члена равна коэффициенту при x, x, который равен −3y.−3y. Вычисление ∂f / ∂y: ∂f / ∂y:
      ∂f∂y = ∂∂y [x2−3xy + 2y2−4x + 5y − 12] = ∂∂y [x2] −∂∂y [3xy] + ∂∂y [2y2] −∂∂y [4x] + ∂∂y [5y] −∂∂y [12] = – 3x + 4y − 0 + 5−0 = −3x + 4y + 5. ∂f∂y = ∂∂y [x2−3xy + 2y2−4x + 5y −12] = ∂∂y [x2] −∂∂y [3xy] + ∂∂y [2y2] −∂∂y [4x] + ∂∂y [5y] −∂∂y [12] = – 3x + 4y −0 + 5−0 = −3x + 4y + 5.
      Это те же ответы, что и в примере 4.14.
   2. Чтобы вычислить ∂g / ∂x, ∂g / ∂x, рассматривайте переменную y как константу. Затем дифференцируйте g (x, y) g (x, y) относительно x , используя правило цепочки и правило мощности:
      ∂g∂x = ∂∂x [sin (x2y − 2x + 4)] = cos (x2y − 2x + 4) ∂∂x [x2y − 2x + 4] = (2xy − 2) cos (x2y − 2x + 4 ).∂g∂x = ∂∂x [sin (x2y − 2x + 4)] = cos (x2y − 2x + 4) ∂∂x [x2y − 2x + 4] = (2xy − 2) cos (x2y − 2x + 4 ).
      Чтобы вычислить ∂g / ∂y, ∂g / ∂y, рассматривайте переменную xx как константу. Затем дифференцируйте g (x, y) g (x, y) относительно yy, используя цепное правило и правило мощности:
      ∂g∂y = ∂∂y [sin (x2y − 2x + 4)] = cos (x2y − 2x + 4) ∂∂y [x2y − 2x + 4] = x2cos (x2y − 2x + 4) .∂g∂ y = ∂∂y [sin (x2y − 2x + 4)] = cos (x2y − 2x + 4) ∂∂y [x2y − 2x + 4] = x2cos (x2y − 2x + 4).

   КПП 4.13

   Вычислить ∂f / ∂x∂f / ∂x и ∂f / ∂y∂f / ∂y для функции f (x, y) = tan (x3−3x2y2 + 2y4) f (x, y) = tan ( x3−3x2y2 + 2y4), удерживая противоположную переменную постоянной, а затем производя дифференцирование.

   Как мы можем интерпретировать эти частные производные? Напомним, что график функции двух переменных – это поверхность в ℝ3.ℝ3. Если мы удалим предел из определения частной производной по x, x, то разностное отношение останется:

   f (x + h, y) −f (x, y) h.f (x + h, y) −f (x, y) h.

   Это похоже на коэффициент разности производной функции одной переменной, за исключением наличия переменной yy. На рис. 4.21 изображена поверхность, описываемая произвольной функцией z = f (x, y).г = е (х, у).

   Рис. 4.21. Секущая линия, проходящая через точки (x, y, f (x, y)) (x, y, f (x, y)) и (x + h, y, f (x + h, y)). (x + h, y, f (x + h, y)).

   На рис. 4.21 значение hh положительное. Если построить график f (x, y) f (x, y) и f (x + h, y) f (x + h, y) для произвольной точки (x, y), (x, y), то наклон секущей линии, проходящей через эти две точки, равен

   . f (x + h, y) −f (x, y) h.f (x + h, y) −f (x, y) h.

   Эта линия параллельна оси x. Оси x. Следовательно, наклон секущей линии представляет собой среднюю скорость изменения функции ff, когда мы движемся параллельно оси x.ось абсцисс. Когда hh приближается к нулю, наклон секущей линии приближается к наклону касательной.

   Если мы решим изменить yy вместо xx на то же значение приращения h, h, то секущая линия параллельна оси y, как и касательная. Следовательно, ∂f / ∂x∂f / ∂x представляет собой наклон касательной, проходящей через точку (x, y, f (x, y)) (x, y, f (x, y)), параллельную Ось x ось x и ∂f / ∂y∂f / ∂y представляет собой наклон касательной линии, проходящей через точку (x, y, f (x, y)) (x, y, f (x, y) ) параллельно оси ординат.ось y. Если мы хотим найти наклон касательной, проходящей через ту же точку в любом другом направлении, нам понадобится так называемая производная по направлению , , которую мы обсуждаем в разделе «Производные по направлению и градиент».

   Теперь вернемся к идее контурных карт, которую мы представили в разделе «Функции нескольких переменных». Мы можем использовать контурное отображение для оценки частных производных функции g (x, y) .g (x, y).

   Пример 4.16

   Частные производные от контурной карты

   Используйте контурную карту, чтобы оценить ∂g / ∂x∂g / ∂x в точке (5,0) (5,0) для функции g (x, y) = 9 − x2 − y2.д (х, у) = 9-х2-у2.

   Решение

   На следующем графике представлена ​​контурная карта для функции g (x, y) = 9 − x2 − y2.g (x, y) = 9 − x2 − y2.

   Рисунок 4.22. Контурная карта для функции g (x, y) = 9 − x2 − y2, g (x, y) = 9 − x2 − y2, используя c = 0,1,2, c = 0,1,2, и 33 (c = 3 (c = 3 соответствует началу координат).

   Внутренний круг на контурной карте соответствует c = 2c = 2, а следующий круг соответствует c = 1.c = 1. Первый круг задается уравнением 2 = 9 − x2 − y2; 2 = 9 − x2 − y2; вторая окружность задается уравнением 1 = 9 − x2 − y2.1 = 9 − x2 − y2. Первое уравнение упрощается до x2 + y2 = 5×2 + y2 = 5, а второе уравнение упрощается до x2 + y2 = 8.×2 + y2 = 8. Пересечение x-точки первой окружности равно (5,0) (5,0), а пересечение x-точки второй окружности равно (22,0). (22,0). Мы можем оценить значение ∂g / ∂x∂g / ∂x, вычисленное в точке (5,0) (5,0), используя формулу наклона:

   ∂g∂x | (x, y) = (5,0) ≈g (5,0) −g (22,0) 5−22 = 2−15−22 = 15−22≈ − 1.688.∂g∂ x | (x, y) = (5,0) ≈g (5,0) −g (22,0) 5−22 = 2−15−22 = 15−22≈ − 1,688.

   Чтобы вычислить точное значение ∂g / ∂x∂g / ∂x, вычисленное в точке (5,0), (5,0), мы начнем с нахождения ∂g / ∂x∂g / ∂x с использованием цепочки правило.Сначала перепишем функцию как g (x, y) = 9 − x2 − y2 = (9 − x2 − y2) 1 / 2g (x, y) = 9 − x2 − y2 = (9 − x2 − y2) 1. / 2, а затем дифференцировать по xx при постоянном yy:

   ∂g∂x = 12 (9 − x2 − y2) −1/2 (−2x) = – x9 − x2 − y2. ∂g∂x = 12 (9 − x2 − y2) −1/2 (−2x) = −x9 − x2 − y2.

   Затем мы оцениваем это выражение, используя x = 5x = 5 и y = 0: y = 0:

   ∂g∂x | (x, y) = (5,0) = – 59− (5) 2− (0) 2 = −54 = −52≈ − 1.118.∂g∂x | (x, y) = (5,0) = – 59− (5) 2− (0) 2 = −54 = −52≈ − 1,118.

   Оценка частной производной соответствует наклону секущей линии, проходящей через точки (5,0, g (5,0)) (5,0, g (5,0)) и (22,0, g (22,0)).(22,0, г (22,0)). Он представляет собой аппроксимацию наклона касательной к поверхности через точку (5,0, g (5,0)), (5,0, g (5,0)), которая параллельна оси x- ось. ось x.

   КПП 4.14

   Используйте контурную карту, чтобы оценить ∂f / ∂y∂f / ∂y в точке (0,2) (0,2) для функции

   f (x, y) = x2 − y2. f (x, y) = x2 − y2.

   Сравните это с точным ответом.

   Функции более двух переменных

   Предположим, у нас есть функция трех переменных, например w = f (x, y, z).w = f (x, y, z). Мы можем вычислить частные производные ww по любой из независимых переменных, просто как расширение определений частных производных функций двух переменных.

   Определение

   Пусть f (x, y, z) f (x, y, z) – функция трех переменных. Тогда частная производная ff по x, , записанная как ∂f / ∂x, ∂f / ∂x или fx, fx, определяется как

   ∂f∂x = limh → 0f (x + h, y, z) −f (x, y, z) h.∂f∂x = limh → 0f (x + h, y, z) −f (x, у, г) з.

   (4,14)

   Частная производная от ff по y, y, записанная как ∂f / ∂y, ∂f / ∂y или fy, fy, определяется как

   ∂f∂y = limk → 0f (x, y + k, z) −f (x, y, z) k.∂f∂y = limk → 0f (x, y + k, z) −f (x, y, z) k.

   (4,15)

   Частная производная от ff относительно z, z, записанная как ∂f / ∂z, ∂f / ∂z или fz, fz, определяется как

   ∂f∂z = limm → 0f (x, y, z + m) −f (x, y, z) m.∂f∂z = limm → 0f (x, y, z + m) −f (x, у, г) м.

   (4,16)

   Мы можем вычислить частную производную функции трех переменных, используя ту же идею, которую мы использовали для функции двух переменных. Например, если у нас есть функция ff от x, y и z, x, y и z, и мы хотим вычислить ∂f / ∂x, ∂f / ∂x, то мы обрабатываем две другие независимые переменные, как если бы они являются константами, то дифференцируем по x.Икс.

   Пример 4.17

   Расчет частных производных для функции трех переменных

   Используйте определение предела частных производных для вычисления ∂f / ∂x∂f / ∂x для функции

   f (x, y, z) = x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z.f (x, y, z) = x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z.

   Затем найдите ∂f / ∂y∂f / ∂y и ∂f / ∂z∂f / ∂z, установив две другие переменные постоянными и проведя соответствующее дифференцирование.

   Решение

   Сначала мы вычисляем ∂f / ∂x∂f / ∂x, используя уравнение 4.14, затем мы вычисляем две другие частные производные, оставляя оставшиеся переменные постоянными. Чтобы использовать уравнение для нахождения ∂f / ∂x, ∂f / ∂x, нам сначала нужно вычислить f (x + h, y, z): f (x + h, y, z):

   f (x + h, y, z) = (x + h) 2−3 (x + h) y + 2y2−4 (x + h) z + 5yz2−12 (x + h) + 4y − 3z = x2. + 2xh + h3−3xy − 3xh + 2y2−4xz − 4hz + 5yz2−12x − 12h + 4y − 3zf (x + h, y, z) = (x + h) 2−3 (x + h) y + 2y2 −4 (x + h) z + 5yz2−12 (x + h) + 4y − 3z = x2 + 2xh + h3−3xy − 3xh + 2y2−4xz − 4hz + 5yz2−12x − 12h + 4y − 3z

   и напомним, что f (x, y, z) = x2−3xy + 2y2−4zx + 5yz2−12x + 4y − 3z.f (x, y, z) = x2−3xy + 2y2−4zx + 5yz2−12x + 4y − 3z.Затем мы подставляем эти два выражения в уравнение:

   ∂f∂x = limh → 0 [x2 + 2xh + h3−3xy − 3hy + 2y2−4xz − 4hz + 5yz2−12x − 12h + 4y − 3zh − x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3zh ] = limh → 0 [2xh + h3−3hy − 4hz − 12hh] = limh → 0 [h (2x + h − 3y − 4z − 12) h] = limh → 0 (2x + h − 3y − 4z − 12) = 2x − 3y − 4z − 12. ∂f∂x = limh → 0 [x2 + 2xh + h3−3xy − 3hy + 2y2−4xz − 4hz + 5yz2−12x − 12h + 4y − 3zh − x2−3xy + 2y2− 4xz + 5yz2−12x + 4y − 3zh] = limh → 0 [2xh + h3−3hy − 4hz − 12hh] = limh → 0 [h (2x + h − 3y − 4z − 12) h] = limh → 0 (2x + h − 3y − 4z − 12) = 2x − 3y − 4z − 12.

   Затем мы находим ∂f / ∂y∂f / ∂y, удерживая постоянные xandzxandz. Следовательно, любой член, не включающий переменную yy, является постоянным, а его производная равна нулю.Мы можем применить правила суммы, разности и мощности для функций одной переменной:

   ∂∂y [x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z] = ∂∂y [x2] −∂∂y [3xy] + ∂∂y [2y2] −∂∂y [4xz] + ∂ ∂y [5yz2] −∂∂y [12x] + ∂∂y [4y] −∂∂y [3z] = 0−3x + 4y − 0 + 5z2−0 + 4−0 = −3x + 4y + 5z2 + 4. ∂∂y [x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z] = ∂∂y [x2] −∂∂y [3xy] + ∂∂y [2y2] −∂∂y [4xz] + ∂∂y [5yz2] −∂∂y [12x] + ∂∂y [4y] −∂∂y [3z] = 0−3x + 4y − 0 + 5z2−0 + 4−0 = −3x + 4y + 5z2 + 4.

   Чтобы вычислить ∂f / ∂z, ∂f / ∂z, мы держим константы x и y и применяем правила суммы, разности и степени для функций одной переменной:

   ∂∂z [x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z] = ∂∂z [x2] −∂∂z [3xy] + ∂∂z [2y2] −∂∂z [4xz] + ∂ ∂z [5yz2] −∂∂z [12x] + ∂∂z [4y] −∂∂z [3z] = 0−0 + 0−4x + 10yz − 0 + 0−3 = −4x + 10yz − 3.∂∂z [x2−3xy + 2y2−4xz + 5yz2−12x + 4y − 3z] = ∂∂z [x2] −∂∂z [3xy] + ∂∂z [2y2] −∂∂z [4xz] + ∂ ∂z [5yz2] −∂∂z [12x] + ∂∂z [4y] −∂∂z [3z] = 0−0 + 0−4x + 10yz − 0 + 0−3 = −4x + 10yz − 3.

   КПП 4.15

   Используйте определение предела частных производных для вычисления ∂f / ∂x∂f / ∂x для функции

   f (x, y, z) = 2×2−4x2y + 2y2 + 5xz2−6x + 3z − 8. f (x, y, z) = 2×2−4x2y + 2y2 + 5xz2−6x + 3z − 8.

   Затем найдите ∂f / ∂y∂f / ∂y и ∂f / ∂z∂f / ∂z, установив две другие переменные постоянными и проведя соответствующее дифференцирование.

   Пример 4.18

   Расчет частных производных для функции трех переменных

   Вычислите три частные производные следующих функций.

   1. f (x, y, z) = x2y − 4xz + y2x − 3yzf (x, y, z) = x2y − 4xz + y2x − 3yz
   2. g (x, y, z) = sin (x2y − z) + cos (x2 − yz) g (x, y, z) = sin (x2y − z) + cos (x2 − yz)
   .

   Решение

   В каждом случае трактуйте все переменные как константы, кроме той, частную производную которой вы вычисляете.

   1. ∂f∂x = ∂∂x [x2y − 4xz + y2x − 3yz] = ∂∂x (x2y − 4xz + y2) (x − 3yz) – (x2y − 4xz + y2) ∂∂x (x − 3yz ) (x − 3yz) 2 = (2xy − 4z) (x − 3yz) – (x2y − 4xz + y2) (1) (x − 3yz) 2 = 2x2y − 6xy2z − 4xz + 12yz2 − x2y + 4xz − y2 ( x − 3yz) 2 = x2y − 6xy2z − 4xz + 12yz2 + 4xz − y2 (x − 3yz) 2∂f∂x = ∂∂x [x2y − 4xz + y2x − 3yz] = ∂∂x (x2y − 4xz + y2 ) (x − 3yz) – (x2y − 4xz + y2) ∂∂x (x − 3yz) (x − 3yz) 2 = (2xy − 4z) (x − 3yz) – (x2y − 4xz + y2) (1) (x − 3yz) 2 = 2x2y − 6xy2z − 4xz + 12yz2 − x2y + 4xz − y2 (x − 3yz) 2 = x2y − 6xy2z − 4xz + 12yz2 + 4xz − y2 (x − 3yz) 2
      ∂f∂y = ∂∂y [x2y − 4xz + y2x − 3yz] = ∂∂y (x2y − 4xz + y2) (x − 3yz) – (x2y − 4xz + y2) ∂∂y (x − 3yz) ( x − 3yz) 2 = (x2 + 2y) (x − 3yz) – (x2y − 4xz + y2) (- 3z) (x − 3yz) 2 = x3−3x2yz + 2xy − 6y2z + 3x2yz − 12xz2 + 3y2z (x −3yz) 2 = x3 + 2xy − 3y2z − 12xz2 (x − 3yz) 2∂f∂y = ∂∂y [x2y − 4xz + y2x − 3yz] = ∂∂y (x2y − 4xz + y2) (x − 3yz ) – (x2y − 4xz + y2) ∂∂y (x − 3yz) (x − 3yz) 2 = (x2 + 2y) (x − 3yz) – (x2y − 4xz + y2) (- 3z) (x − 3yz ) 2 = x3−3x2yz + 2xy − 6y2z + 3x2yz − 12xz2 + 3y2z (x − 3yz) 2 = x3 + 2xy − 3y2z − 12xz2 (x − 3yz) 2
      ∂f∂z = ∂∂z [x2y − 4xz + y2x − 3yz] = ∂∂z (x2y − 4xz + y2) (x − 3yz) – (x2y − 4xz + y2) ∂∂z (x − 3yz) ( x − 3yz) 2 = (- 4x) (x − 3yz) – (x2y − 4xz + y2) (- 3y) (x − 3yz) 2 = −4×2 + 12xyz + 3x2y2−12xyz + 3y3 (x − 3yz) 2 = −4×2 + 3x2y2 + 3y3 (x − 3yz) 2∂f∂z = ∂∂z [x2y − 4xz + y2x − 3yz] = ∂∂z (x2y − 4xz + y2) (x − 3yz) – (x2y− 4xz + y2) ∂∂z (x − 3yz) (x − 3yz) 2 = (- 4x) (x − 3yz) – (x2y − 4xz + y2) (- 3y) (x − 3yz) 2 = −4×2 + 12xyz + 3x2y2−12xyz + 3y3 (x − 3yz) 2 = −4×2 + 3x2y2 + 3y3 (x − 3yz) 2
   2. ∂f∂x = ∂∂x [sin (x2y − z) + cos (x2 − yz)] = (cos (x2y − z)) ∂∂x (x2y − z) – (sin (x2 − yz)) ∂∂x (x2 − yz) = 2xycos (x2y − z) −2xsin (x2 − yz) ∂f∂y = ∂∂y [sin (x2y − z) + cos (x2 − yz)] = (cos (x2y −z)) ∂∂y (x2y − z) – (sin (x2 − yz)) ∂∂y (x2 − yz) = x2cos (x2y − z) + zsin (x2 − yz) ∂f∂z = ∂∂ z [sin (x2y − z) + cos (x2 − yz)] = (cos (x2y − z)) ∂∂z (x2y − z) – (sin (x2 − yz)) ∂∂z (x2 − yz) = −cos (x2y − z) + ysin (x2 − yz) ∂f∂x = ∂∂x [sin (x2y − z) + cos (x2 − yz)] = (cos (x2y − z)) ∂∂x (x2y − z) – (sin (x2 − yz)) ∂∂x (x2 − yz) = 2xycos (x2y − z) −2xsin (x2 − yz) ∂f∂y = ∂∂y [sin (x2y − z ) + cos (x2 − yz)] = (cos (x2y − z)) ∂∂y (x2y − z) – (sin (x2 − yz)) ∂∂y (x2 − yz) = x2cos (x2y − z) + zsin (x2 − yz) ∂f∂z = ∂∂z [sin (x2y − z) + cos (x2 − yz)] = (cos (x2y − z)) ∂∂z (x2y − z) – (sin (x2 − yz)) ∂∂z (x2 − yz) = – cos (x2y − z) + ysin (x2 − yz)
   .

   Контрольно-пропускной пункт 4.16

   Вычислить ∂f / ∂x, ∂f / ∂x, ∂f / ∂y, ∂f / ∂y и ∂f / ∂z∂f / ∂z для функции f (x, y, z) = sec (x2y) −tan (x3yz2) .f (x, y, z) = sec (x2y) −tan (x3yz2).

   Частные производные высшего порядка

   Рассмотрим функцию

   f (x, y) = 2×3−4xy2 + 5y3−6xy + 5x − 4y + 12. f (x, y) = 2×3−4xy2 + 5y3−6xy + 5x − 4y + 12.

   Его частные производные:

   ∂f∂x = 6×2−4y2−6y + 5and∂f∂y = −8xy + 15y2−6x − 4. ∂f∂x = 6×2−4y2−6y + 5and∂f∂y = −8xy + 15y2−6x− 4.

   Каждая из этих частных производных является функцией двух переменных, поэтому мы можем вычислить частные производные этих функций.Как и в случае с производными функций одной переменной, мы можем называть эти производными второго порядка, производными третьего порядка и так далее. В общем, они называются частными производными более высокого порядка. Для любой функции существует четыре частных производных второго порядка (при условии, что все они существуют):

   ∂2f∂x2 = ∂∂x [∂f∂x], ∂2f∂x∂y = ∂∂x [∂f∂y], ∂2f∂y∂x = ∂∂y [∂f∂x], ∂ 2f∂y2 = ∂∂y [∂f∂y] .∂2f∂x2 = ∂∂x [∂f∂x], ∂2f∂x∂y = ∂∂x [∂f∂y], ∂2f∂y ∂x = ∂∂y [∂f∂x], ∂2f∂y2 = ∂∂y [∂f∂y].

   Альтернативное обозначение для каждого из них – fxx, fyx, fxy, fxx, fyx, fxy и fyy, fyy соответственно.Частные производные высшего порядка, вычисляемые по различным переменным, таким как fxyfxy и fyx, fyx, обычно называются смешанными частными производными.

   Пример 4.19

   Расчет вторых частных производных

   Вычислить все четыре вторые частные производные функции

   f (x, y) = xe − 3y + sin (2x − 5y). f (x, y) = xe − 3y + sin (2x − 5y).

   Решение

   Чтобы вычислить ∂2f / dx2∂2f / dx2 и ∂2f / ∂y∂x, ∂2f / ∂y∂x, сначала вычислим ∂f / ∂x: ∂f / ∂x:

   ∂f∂x = e −3y + 2cos (2x − 5y).∂f∂x = e − 3y + 2cos (2x − 5y).

   Чтобы вычислить ∂2f / dx2, ∂2f / dx2, продифференцируйте ∂f / ∂x∂f / ∂x по x: x:

   ∂2f∂x2 = ∂∂x [∂f∂x] = ∂∂x [e − 3y + 2cos (2x − 5y)] = – 4sin (2x − 5y). ∂2f∂x2 = ∂∂x [∂f ∂x] = ∂∂x [e − 3y + 2cos (2x − 5y)] = – 4sin (2x − 5y).

   Чтобы вычислить ∂2f / ∂y∂x, ∂2f / ∂y∂x, продифференцируйте ∂f / ∂x∂f / ∂x по y: y:

   ∂2f∂y∂x = ∂∂y [∂ f∂x] = ∂∂y [e − 3y + 2cos (2x − 5y)] = – 3e − 3y + 10sin (2x − 5y) .∂2f∂y∂x = ∂∂y [∂f∂x] = ∂∂y [e − 3y + 2cos (2x − 5y)] = – 3e − 3y + 10sin (2x − 5y).

   Чтобы вычислить ∂2f / ∂x∂y∂2f / ∂x∂y и ∂2f / dy2, ∂2f / dy2, сначала вычислите ∂f / ∂y: ∂f / ∂y:

   ∂f∂y = −3xe − 3y − 5cos (2x − 5y).∂f∂y = −3xe − 3y − 5cos (2x − 5y).

   Чтобы вычислить ∂2f / ∂x∂y, ∂2f / ∂x∂y, продифференцируйте ∂f / ∂y∂f / ∂y по x: x:

   ∂2f∂x∂y = ∂∂x [∂ f∂y] = ∂∂x [−3xe − 3y − 5cos (2x − 5y)] = – 3e − 3y + 10sin (2x − 5y) .∂2f∂x∂y = ∂∂x [∂f∂y] = ∂∂x [−3xe − 3y − 5cos (2x − 5y)] = – 3e − 3y + 10sin (2x − 5y).

   Чтобы вычислить ∂2f / ∂y2, ∂2f / ∂y2, продифференцируйте ∂f / ∂y∂f / ∂y по y: y:

   ∂2f∂y2 = ∂∂y [∂f∂y] = ∂∂y [−3xe − 3y − 5cos (2x − 5y)] = 9xe − 3y − 25sin (2x − 5y). ∂2f∂y2 = ∂∂ y [∂f∂y] = ∂∂y [−3xe − 3y − 5cos (2x − 5y)] = 9xe − 3y − 25sin (2x − 5y).

   КПП 4.17

   Вычислить все четыре вторые частные производные функции

   f (x, y) = sin (3x − 2y) + cos (x + 4y).f (x, y) = sin (3x − 2y) + cos (x + 4y).

   Здесь мы должны заметить, что как в примере 4.19, так и в контрольной точке верно, что ∂2f / ∂x∂y = ∂2f / ∂y∂x.∂2f / ∂x∂y = ∂2f / ∂y ∂x. При определенных условиях это всегда так. Фактически, это прямое следствие следующей теоремы.

   Теорема 4.5

   Равенство смешанных частных производных (теорема Клеро)

   Предположим, что f (x, y) f (x, y) определена на открытом диске DD, содержащем точку (a, b). (A, б). Если функции fxyfxy и fyxfyx непрерывны на D, D, то fxy = fyx.fxy = fyx.

   Теорема Клеро гарантирует, что до тех пор, пока смешанные производные второго порядка непрерывны, порядок, в котором мы выбираем дифференцировать функции (т.е. какая переменная идет первой, затем второй и т. Д.), Не имеет значения. Его также можно распространить на производные более высокого порядка. Доказательство теоремы Клеро можно найти в самых продвинутых книгах по математике.

   Две другие частные производные второго порядка могут быть вычислены для любой функции f (x, y) .f (x, y). Частная производная fxxfxx равна частной производной fxfx по x, x, а fyyfyy равна частной производной fyfy по y.у.

   Уравнения в частных производных

   Во введении в дифференциальные уравнения мы изучали дифференциальные уравнения, в которых неизвестная функция имела одну независимую переменную. Уравнение в частных производных – это уравнение, которое включает неизвестную функцию более чем одной независимой переменной и одной или нескольких ее частных производных. Примеры дифференциальных уравнений в частных производных:

   ut = c2 (uxx + uyy) ut = c2 (uxx + uyy)

   (4,17)

   (уравнение теплопроводности в двух измерениях)

   utt = c2 (uxx + uyy) utt = c2 (uxx + uyy)

   (4.18)

   (волновое уравнение в двух измерениях)

   (уравнение Лапласа в двух измерениях)

   В первых двух уравнениях неизвестная функция uu имеет три независимые переменные: t, x, andyt, x, andy, а cc – произвольная константа. Независимые переменные xandyxandy считаются пространственными переменными, а переменная tt представляет время. В уравнении Лапласа неизвестная функция uu имеет две независимые переменные xandy.xandy.

   Пример 4.20

   Решение волнового уравнения

   Убедитесь, что

   u (x, y, t) = 5sin (3πx) sin (4πy) cos (10πt) u (x, y, t) = 5sin (3πx) sin (4πy) cos (10πt)

   – решение волнового уравнения

   utt = 4 (uxx + uyy).utt = 4 (uxx + uyy).

   (4,20)

   Решение

   Сначала мы вычисляем utt, uxx, utt, uxx и uyy: uyy:

   utt = ∂∂t [∂u∂t] = ∂∂t [5sin (3πx) sin (4πy) (- 10πsin (10πt))] = ∂∂t [−50πsin (3πx) sin (4πy) sin (10πt) ] = – 500π2sin (3πx) sin (4πy) cos (10πt) uxx = ∂∂x [∂u∂x] = ∂∂x [15πcos (3πx) sin (4πy) cos (10πt)] = – 45π2sin (3πx) sin (4πy) cos (10πt) uyy = ∂∂y [∂u∂y] = ∂∂y [5sin (3πx) (4πcos (4πy)) cos (10πt)] = ∂∂y [20πsin (3πx) cos ( 4πy) cos (10πt)] = – 80π2sin (3πx) sin (4πy) cos (10πt) .utt = ∂∂t [∂u∂t] = ∂∂t [5sin (3πx) sin (4πy) (- 10πsin ( 10πt))] = ∂∂t [−50πsin (3πx) sin (4πy) sin (10πt)] = – 500π2sin (3πx) sin (4πy) cos (10πt) uxx = ∂∂x [∂u∂x] = ∂ ∂x [15πcos (3πx) sin (4πy) cos (10πt)] = – 45π2sin (3πx) sin (4πy) cos (10πt) uyy = ∂∂y [∂u∂y] = ∂∂y [5sin (3πx) (4πcos (4πy)) cos (10πt)] = ∂∂y [20πsin (3πx) cos (4πy) cos (10πt)] = – 80π2sin (3πx) sin (4πy) cos (10πt).

   Затем мы подставляем каждый из них в правую часть уравнения 4.20 и упрощаем:

   4 (uxx + uyy) = 4 (−45π2sin (3πx) sin (4πy) cos (10πt) + – 80π2sin (3πx) sin (4πy) cos (10πt)) = 4 (−125π2sin (3πx) sin (4πy) cos (10πt)) = – 500π2sin (3πx) sin (4πy) cos (10πt) = utt.4 (uxx + uyy) = 4 (−45π2sin (3πx) sin (4πy) cos (10πt) + – 80π2sin (3πx) sin) (4πy) cos (10πt)) = 4 (−125π2sin (3πx) sin (4πy) cos (10πt)) = – 500π2sin (3πx) sin (4πy) cos (10πt) = utt.

   Это подтверждает решение.

   КПП 4.18

   Убедитесь, что u (x, y, t) = 2sin (x3) sin (y4) e − 25t / 16u (x, y, t) = 2sin (x3) sin (y4) e − 25t / 16 является решением уравнение теплопроводности

   ut = 9 (uxx + uyy).ut = 9 (uxx + uyy).

   (4,21)

   Поскольку решение двумерного уравнения теплопроводности является функцией трех переменных, создать визуальное представление решения непросто. Мы можем построить график решения для фиксированных значений t , что составляет моментальные снимки распределения тепла в фиксированные моменты времени. Эти снимки показывают, как тепло распределяется по двумерной поверхности с течением времени. График предыдущего решения в момент времени t = 0t = 0 показан на следующем рисунке.Со временем крайности выравниваются, приближаясь к нулю, а t приближается к бесконечности.

   Рисунок 4.23

   Если рассматривать уравнение теплопроводности в одном измерении, то можно построить график решения во времени. Уравнение теплопроводности в одном измерении становится

   , где c2c2 представляет коэффициент температуропроводности рассматриваемого материала. Решение этого дифференциального уравнения можно записать в виде

   um (x, t) = e − π2m2c2tsin (mπx) um (x, t) = e − π2m2c2tsin (mπx)

   (4.22)

   , где мм – любое положительное целое число. График этого решения с m = 1m = 1 показан на рис. 4.24, где начальное распределение температуры по проводу длиной 11 дается формулой u (x, 0) = sinπx.u (x, 0) = sinπx. Обратите внимание, что со временем провод остывает. Это видно, потому что слева направо самая высокая температура (которая возникает в середине провода) уменьшается и меняет цвет с красного на синий.

   Рис. 4.24. Одномерный график решения уравнения теплопроводности с течением времени.

   Студенческий проект

   Лорд Кельвин и эпоха Земли

   Рис. 4.25 (а) Уильям Томсон (лорд Кельвин), 1824–1907, был британским физиком и инженером-электриком; (b) Кельвин использовал уравнение диффузии тепла для оценки возраста Земли (кредит: модификация работы НАСА).

   В конце 1800-х годов ученые новой области геологии приходили к выводу, что Земле должны быть «миллионы и миллионы» лет. Примерно в то же время Чарльз Дарвин опубликовал свой трактат по эволюции.Дарвин считал, что для эволюции необходимы многие миллионы лет, и он смело заявил, что меловые поля Уилда, где были обнаружены важные окаменелости, были результатом эрозии в течение 300–300 миллионов лет.

   В то время выдающийся физик Уильям Томсон (лорд Кельвин) использовал важное дифференциальное уравнение в частных производных, известное как уравнение диффузии тепла , чтобы оценить возраст Земли, определив, сколько времени потребуется Земле, чтобы охладиться от расплавленной породы до какого у нас было в то время.Его вывод был в диапазоне от 20 до 40020 до 400 миллионов лет, но, скорее всего, около 5050 миллионов лет. На протяжении многих десятилетий провозглашение этой неопровержимой иконы науки не нравилось геологам или Дарвину.

   Кельвин сделал разумные предположения, основанные на том, что было известно в его время, но он также сделал несколько предположений, которые оказались неверными. Одно неверное предположение заключалось в том, что Земля твердая и поэтому охлаждение происходило только за счет теплопроводности, что оправдывает использование уравнения диффузии.Но самая серьезная ошибка была простительной – упущение того факта, что Земля содержит радиоактивные элементы, которые постоянно поставляют тепло под мантию Земли. Открытие радиоактивности было ближе к концу жизни Кельвина, и он признал, что его расчет придется изменить.

   Кельвин использовал простую одномерную модель, примененную только к внешней оболочке Земли, и получил возраст из графиков и примерно известного градиента температуры у поверхности Земли. Давайте посмотрим на более подходящий вариант уравнения диффузии в радиальных координатах, который имеет вид

   ∂T∂t = K [∂2T∂2r + 2r∂T∂r].∂T∂t = K [∂2T∂2r + 2r∂T∂r].

   (4,23)

   Здесь T (r, t) T (r, t) – температура как функция от rr (отсчитывается от центра Земли) и времени t.t. KK – теплопроводность, в данном случае для расплавленной породы. Стандартный метод решения такого уравнения с частными производными – разделение переменных, где мы выражаем решение как произведение функций, содержащих каждую переменную отдельно. В этом случае мы бы записали температуру как

   T (r, t) = R (r) f (t). T (r, t) = R (r) f (t).
   1. Подставьте эту форму в уравнение 4.13 и, отмечая, что f (t) f (t) постоянна по отношению к расстоянию (r) (r) и R (r) R (r) постоянна по отношению к времени (t), (t), показать, что
      1f∂f∂t = KR [∂2R∂r2 + 2r∂R∂r]. 1f∂f∂t = KR [∂2R∂r2 + 2r∂R∂r].
   2. Это уравнение представляет собой разделение переменных, которые мы хотим. Левая часть является функцией только tt, а правая часть – только функцией r, r, и они должны быть равны для всех значений randt.randt. Следовательно, они оба должны быть равны константе. Назовем эту константу −λ2. − λ2.(Удобство такого выбора видно при замене.) Итак, имеем
      1f∂f∂t = −λ2 и KR [∂2R∂r2 + 2r∂R∂r] = – λ2.1f∂f∂t = −λ2 иKR [∂2R∂r2 + 2r∂R∂r] = – λ2.
      Теперь мы можем проверить путем прямой подстановки для каждого уравнения, что решениями являются f (t) = Ae − λ2tf (t) = Ae − λ2t и R (r) = B (sinαrr) + C (cosαrr), R (r) = B (sinαrr) + C (cosαrr), где α = λ / K.α = λ / K. Обратите внимание, что f (t) = Ae + λn2tf (t) = Ae + λn2t также является допустимым решением, поэтому мы могли бы выбрать + λ2 + λ2 в качестве нашей постоянной. Вы понимаете, почему это не годится для этого случая по мере увеличения времени?
   3. Теперь применим граничные условия.
      1. Температура должна быть конечной в центре Земли, r = 0.r = 0. Какая из двух констант, BB или C, C, должна быть равна нулю, чтобы RR оставалось конечным при r = 0? R = 0? (Напомним, что sin (αr) / r → α = sin (αr) / r → α = при r → 0, r → 0, но cos (αr) / rcos (αr) / r ведет себя совершенно иначе.)
      2. Кельвин утверждал, что, когда магма достигает поверхности Земли, она очень быстро остывает. Часто человек может прикоснуться к поверхности в течение нескольких недель после течения. Таким образом, поверхность очень рано достигла умеренной температуры и оставалась почти постоянной при температуре поверхности Ts.Ц. Для простоты положим T = 0atr = RET = 0atr = RE и найдем αα так, чтобы это была температура за все время t.t. (Кельвин принял значение равным 300K≈80 ° F, 300K≈80 ° F. Мы можем добавить эту константу 300K300K к нашему решению позже.) Чтобы это было правдой, аргумент синуса должен быть равен нулю при r = RE.r = RE. Отметим, что αα имеет бесконечный ряд значений, удовлетворяющих этому условию. Каждое значение αα представляет собой допустимое решение (каждое со своим собственным значением для A) .A). Общее или общее решение – это сумма всех этих решений.
      3. При t = 0, t = 0, мы предполагаем, что вся Земля находилась при начальной горячей температуре T0T0 (Кельвин принял это за около 7000 К.) 7000 К.) Применение этого граничного условия включает более сложное применение коэффициентов Фурье. . Как отмечено в части b. каждое значение αnαn представляет собой допустимое решение, а общее решение представляет собой сумму всех этих решений. В результате получается серийное решение:
         T (r, t) = (T0REπ) ∑n (−1) n − 1ne − λn2tsin (αnr) r, где αn = nπ / RE.T (r, t) = (T0REπ) ∑n (−1) n− 1ne − λn2tsin (αnr) r, где αn = nπ / RE.

   Обратите внимание, как значения αnαn берутся из граничного условия, примененного в части b. Член −1n − 1n − 1n − 1n – это константа AnAn для каждого члена в ряду, определенная с применением метода Фурье. Положив β = πRE, β = πRE, исследуем первые несколько членов этого решения, показанного здесь, и обратите внимание, как λ2λ2 в экспоненте заставляет старшие члены быстро уменьшаться с течением времени:

   T (r, t) = T0REπr (e − Kβ2t (sinβr) −12e − 4Kβ2t (sin2βr) + 13e − 9Kβ2t (sin3βr) −14e − 16Kβ2t (sin4βr) + 15e − 25Kβ2t (sin5βr)…). T (r, t) = T0REπr (e − Kβ2t (sinβr) −12e − 4Kβ2t (sin2βr) + 13e − 9Kβ2t (sin3βr) −14e − 16Kβ2t (sin4βr) + 15e − 25Kβ2t (sin5βr) … ).

   Вблизи момента времени t = 0, t = 0 для точности требуется много членов решения. Подставляя значения для проводимости KK и β = π / REβ = π / RE для времени, приближающегося всего к тысячам лет, только первые несколько членов вносят значительный вклад. Кельвину нужно было только посмотреть на раствор у поверхности Земли (рис. 4.26) и, спустя долгое время, определить, какое время лучше всего дает расчетный градиент температуры, известный в его эпоху (1 ° F (увеличение на 1 ° F на 50 футов).50 футов). Он просто выбрал диапазон времен с градиентом, близким к этому значению. На рис. 4.26 решения нанесены на график и масштабированы с добавлением температуры поверхности 300-K300-K. Обратите внимание, что центр Земли был бы относительно прохладным. В то время считалось, что Земля должна быть твердой.

   Рис. 4.26. Зависимость температуры от радиального расстояния от центра Земли. (а) Результаты Кельвина в масштабе. (b) Крупный план результатов на глубине 4,0–4,0 мили ниже поверхности Земли.

   Эпилог

   20 мая 1904–201904 физик Эрнест Резерфорд выступил в Королевском институте, чтобы объявить пересмотренный расчет, который включал вклад радиоактивности как источника тепла Земли.По словам Резерфорда:

   «Я вошел в комнату, которая была полутемной, и тут же заметил лорда Кельвина в аудитории и понял, что меня ждут неприятности в последней части моей речи, посвященной возрасту Земли, где мои взгляды расходились. с его. К моему облегчению, Кельвин крепко заснул, но когда я подошел к важному моменту, я увидел, как старая птица села, открыла глаз и бросила на меня злобный взгляд.

   Затем внезапно пришло вдохновение, и я сказал, что лорд Кельвин ограничил возраст Земли, при условии, что не будет обнаружен новый источник [ тепла ] .Это пророческое высказывание относилось к тому, что мы сейчас рассматриваем сегодня вечером, – к радию! Вот! Старик сиял на меня ».

   Резерфорд рассчитал, что возраст Земли составляет около 500–500 миллионов лет. Сегодняшнее принятое значение возраста Земли составляет около 4,64,6 миллиарда лет.

   Раздел 4.3. Упражнения

   Для следующих упражнений вычислите частную производную, используя только определения пределов.

   112.

   ∂z∂x∂z∂x для z = x2−3xy + y2z = x2−3xy + y2

   113.

   ∂z∂y∂z∂y для z = x2−3xy + y2z = x2−3xy + y2

   Для следующих упражнений вычислите знак частной производной, используя график поверхности.

   Для следующих упражнений вычислите частные производные.

   118.

   ∂z∂x∂z∂x для z = sin (3x) cos (3y) z = sin (3x) cos (3y)

   119.

   ∂z∂y∂z∂y для z = sin (3x) cos (3y) z = sin (3x) cos (3y)

   120.

   ∂z∂x∂z∂x и ∂z∂y∂z∂y для z = x8e3yz = x8e3y

   121.

   ∂z∂x∂z∂x и ∂z∂y∂z∂y для z = ln (x6 + y4) z = ln (x6 + y4)

   122.

   Найдите fy (x, y) fy (x, y) для f (x, y) = exycos (x) sin (y). F (x, y) = exycos (x) sin (y).

   123.

   Пусть z = exy.z = exy. Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.

   124.

   Пусть z = ln (xy) .z = ln (xy). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.

   125.

   Пусть z = tan (2x − y) .z = tan (2x − y). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.

   126.

   Пусть z = sh (2x + 3y) .z = sh (2x + 3y). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.

   127.

   Пусть f (x, y) = arctan (yx). F (x, y) = arctan (yx). Вычислите fx (2, −2) fx (2, −2) и fy (2, −2) .fy (2, −2).

   128.

   Пусть f (x, y) = xyx − y.f (x, y) = xyx − y. Найдите fx (2, −2) fx (2, −2) и fy (2, −2) .fy (2, −2).

   Вычислить частные производные в точке P (0,1).Р (0,1).

   129.

   Найдите ∂z∂x∂z∂x в точке (0,1) (0,1) для z = e − xcos (y) .z = e − xcos (y).

   130.

   Для заданного f (x, y, z) = x3yz2, f (x, y, z) = x3yz2 найдите ∂2f∂x∂y∂2f∂x∂y и fz (1,1,1) .fz (1 , 1,1).

   131.

   Дано f (x, y, z) = 2sin (x + y), f (x, y, z) = 2sin (x + y), найти fx (0, π2, −4), fx (0, π2 , −4), fy (0, π2, −4), fy (0, π2, −4) и fz (0, π2, −4). Fz (0, π2, −4).

   132.

   Площадь параллелограмма со смежными сторонами, равными aandb, aandb, а угол между этими двумя сторонами равен θ, θ, задается функцией A (a, b, θ) = бассейн (θ).A (a, b, θ) = бассейн (θ). Найдите скорость изменения площади параллелограмма относительно следующего:

   1. Сторона a
   2. Сторона b
   3. Угол θ Угол θ
   133.

   Выразите объем правого кругового цилиндра как функцию двух переменных:

   1. радиусом rr и высотой h.h.
   2. Покажите, что скорость изменения объема цилиндра относительно его радиуса является произведением его окружности, умноженной на его высоту.
   3. Покажите, что скорость изменения объема цилиндра относительно его высоты равна площади круглого основания.
   134.

   Вычислить ∂w∂z∂w∂z для w = zsin (xy2 + 2z) .w = zsin (xy2 + 2z).

   Найдите указанные частные производные высшего порядка.

   135.

   fxyfxy для z = ln (x − y) z = ln (x − y)

   136.

   fyxfyx для z = ln (x − y) z = ln (x − y)

   137.

   Пусть z = x2 + 3xy + 2y2.z = x2 + 3xy + 2y2. Найдите ∂2z∂x2∂2z∂x2 и ∂2z∂y2.∂2z∂y2.

   138.

   Для z = extany, z = extany найти ∂2z∂x∂y∂2z∂x∂y и ∂2z∂y∂x.∂2z∂y∂x.

   139.

   Дано f (x, y, z) = xyz, f (x, y, z) = xyz, найдите fxyy, fyxy, fxyy, fyxy и fyyx.fyyx.

   140.

   Дано f (x, y, z) = e − 2xsin (z2y), f (x, y, z) = e − 2xsin (z2y), покажем, что fxyy = fyxy.fxyy = fyxy.

   141.

   Покажите, что z = 12 (ey − e − y) sinxz = 12 (ey − e − y) sinx является решением дифференциального уравнения ∂2z∂x2 + ∂2z∂y2 = 0. ∂2z∂x2 + ∂2z∂y2 = 0.

   142.

   Найдите fxx (x, y) fxx (x, y) для f (x, y) = 4x2y + y22x.f (x, y) = 4x2y + y22x.

   143.

   Пусть f (x, y, z) = x2y3z − 3xy2z3 + 5x2z − y3z.f (x, y, z) = x2y3z − 3xy2z3 + 5x2z − y3z. Найдите fxyz.fxyz.

   144.

   Пусть F (x, y, z) = x3yz2−2x2yz + 3xz − 2y3z.F (x, y, z) = x3yz2−2x2yz + 3xz − 2y3z. Найдите Fxyz.Fxyz.

   145.

   Дано f (x, y) = x2 + x − 3xy + y3−5, f (x, y) = x2 + x − 3xy + y3−5, найти все точки, в которых fx = fy = 0fx = fy = 0 одновременно.

   146.

   Дано f (x, y) = 2×2 + 2xy + y2 + 2x − 3, f (x, y) = 2×2 + 2xy + y2 + 2x − 3, найти все точки, в которых ∂f∂x = 0∂f∂ x = 0 и ∂f∂y = 0∂f∂y = 0 одновременно.

   147.

   Дано f (x, y) = y3−3yx2−3y2−3×2 + 1, f (x, y) = y3−3yx2−3y2−3×2 + 1, найти все точки на ff, в которых fx = fy = 0fx = fy = 0 одновременно.

   148.

   Дано f (x, y) = 15×3−3xy + 15y3, f (x, y) = 15×3−3xy + 15y3, найти все точки, в которых fx (x, y) = fy (x, y) = 0fx (x , y) = fy (x, y) = 0 одновременно.

   149.

   Покажите, что z = exsinyz = exsiny удовлетворяет уравнению ∂2z∂x2 + ∂2z∂y2 = 0. ∂2z∂x2 + ∂2z∂y2 = 0.

   150.

   Покажите, что f (x, y) = ln (x2 + y2) f (x, y) = ln (x2 + y2) решает уравнение Лапласа ∂2z∂x2 + ∂2z∂y2 = 0. ∂2z∂x2 + ∂2z∂ у2 = 0.

   151.

   Покажите, что z = e − tcos (xc) z = e − tcos (xc) удовлетворяет уравнению теплопроводности ∂z∂t = −e − tcos (xc) .∂z∂t = −e − tcos (xc).

   152.

   Найдите limΔx → 0f (x + Δx) −f (x, y) ΔxlimΔx → 0f (x + Δx) −f (x, y) Δx для f (x, y) = – 7x − 2xy + 7y.f ( х, у) = – 7x − 2xy + 7y.

   153.

   Найдите limΔy → 0f (x, y + Δy) −f (x, y) ΔylimΔy → 0f (x, y + Δy) −f (x, y) Δy для f (x, y) = – 7x − 2xy + 7y.f (x, y) = – 7x − 2xy + 7y.

   154.

   Найдите limΔx → 0ΔfΔx = limΔx → 0f (x + Δx, y) −f (x, y) ΔxlimΔx → 0ΔfΔx = limΔx → 0f (x + Δx, y) −f (x, y) Δx для f (x, y) = x2y2 + xy + yf (x, y) = x2y2 + xy + y.

   155.

   Найдите limΔx → 0ΔfΔx = limΔx → 0f (x + Δx, y) −f (x, y) ΔxlimΔx → 0ΔfΔx = limΔx → 0f (x + Δx, y) −f (x, y) Δx для f (x, y) = sin (xy). f (x, y) = sin (xy).

   156.

   Функция P (T, V) = nRTVP (T, V) = nRTV дает давление в точке газа как функцию температуры TT и объема V.V. Буквы nandRnandR являются константами. Найдите ∂P∂V∂P∂V и ∂P∂T, ∂P∂T и объясните, что представляют собой эти величины.

   157.

   Уравнение теплового потока в xy-planexy-плоскости: ∂f∂t = ∂2f∂x2 + ∂2f∂y2.∂f∂t = ∂2f∂x2 + ∂2f∂y2. Докажите, что f (x, y, t) = e − 2tsinxsinyf (x, y, t) = e − 2tsinxsiny – решение.

   158.

   Основное волновое уравнение: ftt = fxx.ftt = fxx. Убедитесь, что f (x, t) = sin (x + t) f (x, t) = sin (x + t) и f (x, t) = sin (x − t) f (x, t) = sin (x − t) – решения.

   159.

   Закон косинусов можно рассматривать как функцию трех переменных. Пусть x, y, x, y и θθ – две стороны любого треугольника, где угол θθ – это угол между двумя сторонами. Тогда F (x, y, θ) = x2 + y2−2xycosθF (x, y, θ) = x2 + y2−2xycosθ дает квадрат третьей стороны треугольника. Найдите ∂F∂θ∂F∂θ и ∂F∂x∂F∂x, когда x = 2, y = 3, x = 2, y = 3 и θ = π6.θ = π6.

   160.

   Предположим, что стороны прямоугольника меняются во времени. Первая сторона меняется со скоростью 22 дюйма./ сек, тогда как вторая сторона изменяется со скоростью 44 дюйма / сек. Насколько быстро изменяется диагональ прямоугольника, если длина первой стороны составляет 1616 дюймов, а второй – 2020 дюймов? (Округлите ответ до трех знаков после запятой.)

   161.

   Производственная функция Кобба-Дугласа: f (x, y) = 200×0,7y0,3, f (x, y) = 200×0,7y0,3, где xandyxandy представляет количество доступного труда и капитала. Пусть x = 500x = 500 и y = 1000.y = 1000. Найдите δfδxδfδx и δfδyδfδy при этих значениях, которые представляют предельную производительность труда и капитала соответственно.

   162.

   Показатель кажущейся температуры – это мера ощущения температуры, и он основан на двух переменных: h, h, которая представляет собой относительную влажность, и t, t, которая представляет собой температуру воздуха.

   A = 0,885t − 22,4h + 1,20th − 0,544.A = 0,885t − 22,4h + 1,20th − 0,544. Найдите ∂A∂t∂A∂t и ∂A∂h∂A∂h, когда t = 20 ° Ft = 20 ° F и h = 0,90.h = 0,90.

   .