Простая физика – EASY-PHYSIC
Задача 1. К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .
Рисунок 1
Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона
Откуда найдем ускорение системы:
Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего и нижнего грузов:
Откуда
Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:
Ответ: Н, Н, Н.
Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н.
Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?
Рисунок 2
Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:
Теперь можно написать уравнения:
Вычитаем уравнения:
Ответ: м/с.
Задача 3.
Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.
Рисунок 3
Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:
Сложим уравнения:
Откуда
Теперь можно найти и силу натяжения нити:
Сила давления на блок равна :
Ответ: , ,
.
Задача 4.
Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами .
Одновременно на каждый из грузов кладут по перегрузку: справа массой , слева (рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
Рисунок 4
Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:
Сложение уравнений даст нам
Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:
Определим силу давления меньшего перегрузка массой на груз :
Для большего перегрузка
Ответ: , , , .
Задача 5.
Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.
Рисунок 5
Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:
Для правого грузика
Складываем уравнения:
Определим силу натяжения нити между грузиками.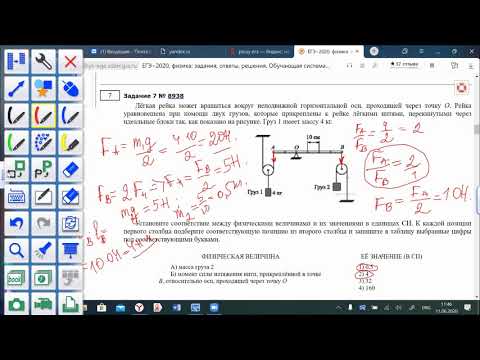
Обозначим ее . Тогда для самого нижнего грузика слева:
Определяем путь грузиков за 4 с:
Ответ: м/с, Н, м.
Задача 6.
Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.
Рисунок 6
Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это груз массой справа и слева. Силу натяжения основной нити обозначим :
Складываем уравнения:
Тогда
Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа
Осталось определить и . Для верхнего грузика слева
Откуда
А для нижнего грузика слева
Ответ: , , , , .
Задача 7.
Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.
). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.
Рисунок 7
Записываем уравнение по второму закону:
Тогда
Ответ: .
Задача 8.
Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.
Рисунок 8
Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение по второму закону с учетом наличия силы трения:
Складывая уравнения, имеем:
Откуда
Но, если бы , тогда
Тогда, чтобы учесть обе возможности, запишем ответ так:
Ответ: .
Задача 9.
Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.
). С каким ускорением движется кольцо, если груз неподвижен?
Рисунок 9
Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза
А для кольца
Ответ: 6 м/с.
Простая физика – EASY-PHYSIC
Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «статика». Поговорим про блоки, посчитаем силы, установим равновесие.
Задача 1.
Черный ящик, привязанный через систему блоков и нитей к стенке, покоится на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть его с места, непосредственно к нему необходимо приложить горизонтальную силу чуть больше Н. Какую минимальную силу надо прикладывать к черному ящику, чтобы он оставался неподвижным, если к веревке приложена сила Н? Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Рисунок 1
Расставим силы:
Рисунок 2
Теперь видно, что на блок действуют три силы , поэтому общая сила равна 45 Н.
16 из них «съест» сила трения, поэтому, чтобы удержать такой ящик, не хватает Н.
Ответ: 29 Н.
Задача 2.
Все блоки в системе, представленной на рисунке − невесомые. Масса левого тела кг. При какой массе правого тела система останется в равновесии? Ответ дать в килограммах, округлив до целых. Считать, что м/c.
Рисунок 3
Расставим силы:
Рисунок 4
Теперь запишем условия равновесия:
Откуда
И
Ответ: 2 кг.
Задача 3.
Спасатели с помощью веревок, перекинутых через систему блоков, перемещают равномерно и прямолинейно массивную плиту так, как показано на рисунке. С какой результирующей силой верёвки действуют на плиту? Спасатели тянут свой конец веревки с силой Н. Массами веревок и блоков пренебречь. Ответ дать в Н, округлив до целых. Считать, что м/c.
Замечание: требуется найти только силу, с которой нити действуют непосредственно на плиту.
Силу, действующую на плиту со стороны верхнего крепления в ответ включать не надо.
Рисунок 5
Расставим силы:
Рисунок 6
Теперь видно, что «за нитки» плиту тянут Н, а полная сила (с учетом верхнего крепления – Н.
Ответ: 600 Н.
Задача 4.
Какую горизонтальную силу надо прикладывать к шкафу, чтобы удержать его на месте? Массы грузов равны кг, кг. Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Рисунок 7
На шкаф действуют две силы тяжести: первого груза (20 Н) и второго (50 Н). Итого 70 Н.
Ответ: 70 Н.
Задача 5.
Два ящика покоятся на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть с места левый ящик, к нему необходимо приложить горизонтальную силу чуть больше 26 Н. Чтобы сдвинуть правый − чуть больше 14 Н. Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.
Рисунок 8
Расстояние будет уменьшаться при сдвиге любого из ящиков, поэтому нужно выяснить, какой легче сдвинуть. Для этого расставляем силы:
Рисунок 9
Теперь видно, что на левый ящик действует сила , а на правый – . Если
То Н, а если
То Н. Поэтому ответ – 7 Н. Этого будет достаточно, чтобы сдвинуть правый ящик и тем самым сократить расстояние.
Блоки в решении задачи ранжирования лифта (Освоение физики, глава 04: Сила и движение)
В книге: Физика
Внутри лифта три блока уложены друг на друга, как показано на рисунке. Ответьте на следующие вопросы со ссылкой на восемь сил, определенных следующим образом.
A. сила блока 3 кг на блок 2 кг, F3 на блок 2,
B. сила блока 2 кг на блок 3 кг, F2 на блок 3,
C. сила блока 3 кг блок на 1 кг блок, F3 на 1,
D. сила блока 1 кг на блок 3 кг, F1 на 3,
E. сила блока 2 кг на блок 1 кг, F2 на 1,
F. сила блока 1 кг на блок 2 кг, F1 на 2,
Г.
сила блока 1 кг на пол, F1 на пол и
Н. сила пола на блок 1 кг, Fпол на 1,
Предположим, лифт отдыхает. Ранжируйте величину сил.
Ранжируйте от большего к меньшему. Чтобы ранжировать элементы как эквивалентные, наложите их друг на друга.
Решения
Понятия и разум
Необходимыми понятиями для решения данного вопроса являются второй закон движения Ньютона и силы, действующие на каждый брусок.
Сначала рассмотрим силы, действующие на каждый из блоков в разных вариантах, приведенных в вопросе. Позже рассчитайте силы, действующие в каждом случае. Наконец, сравните величины полученных сил и после ранжируйте их от наибольшей к наименьшей.
Основы
Сила может быть определена как внезапный толчок или притяжение, которые могут изменить направление объекта. Второй закон Ньютона гласит, что ускорение объекта, создаваемое результирующей силой, прямо пропорционально величине результирующей силы и обратно пропорционально массе объекта.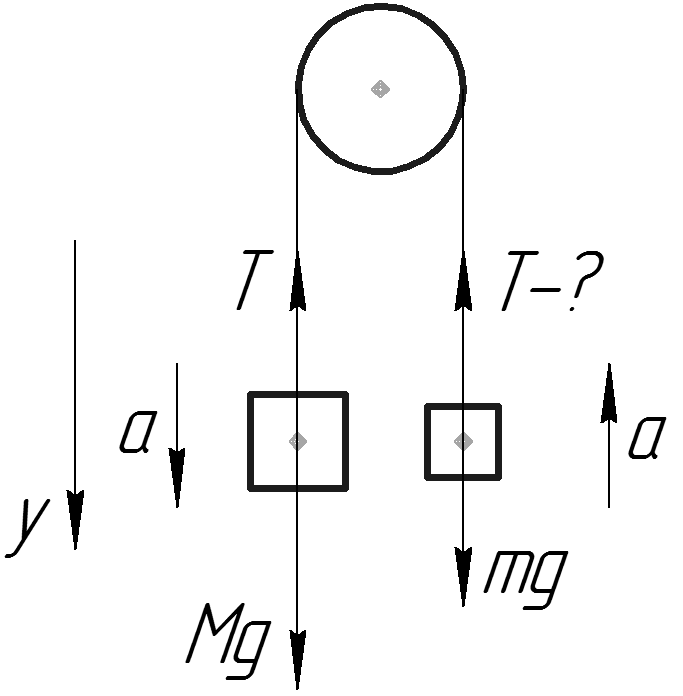
Вес объекта равен произведению массы на ускорение под действием силы тяжести объекта. Математическое выражение для веса объекта: \(W=m g\) 9{\prime} g \\ &=3 \times 9.8 \end{aligned} $$
\(=29.4 \mathrm{~N}\)
Сила, действующая на блок массой 3 кг со стороны блока массой 1 кг,
\(F_{31}=0 \mathrm{~N}\)
Это потому, что нет контакта между блоком 1 и блоком 3. Сила, действующая на брусок 1 кг со стороны бруска 2 кг,
\(F_{13}=0 \mathrm{~N}\)
Сила, действующая на брусок 1 кг со стороны бруска 2 кг,
\( F_{12}=\left(m_{2}+m_{3}\right) g\)
Замените \(2 \mathrm{~kg}\) на \(m_{2} 3 \mathrm{~kg) }\) для \(m_{3}\) и \(9{2}\right) \\ &=58,8 \mathrm{~N} \end{aligned} $$
Из значений сил, полученных в результате расчета, можно представить как
$$ F_{\text {этаж, } 1}=F_{1, \text { ,hoor }}>F_{21}=F_{12}>F_{23}=F_{32}>F_{31}=F_{13} $$
Силы могут быть выражены в виде }>F_{31}=F_{13}\).
Вес тела действует вниз.
Пол испытывает большую силу, чем другие блоки. Это потому, что веса всех блоков действуют вниз. В свою очередь пол прикладывает такое же усилие к блоку 1, который с ним соприкасается. Это объясняет третий закон движения Ньютона. Силы всегда встречаются в паре как силы действия и противодействия, и это можно выразить как \(F_{21}=-F_{12}\).
Силы могут быть выражены как, \(F_{\text {этаж,}, 1}=F_{1, \text{этаж}}>F_{21}=F_{12}>F_{23}=F_{ 32}>F_{31}=F_{13}\)
Следующая > < Предыдущая
Связанные решения
Два блока и решение со шкивом (Освоение физики, глава 04: Сила и движение)
Блок 1, из Масса m1 = 0,650 кг соединена через идеальный (безмассовый и без трения) шкив с блоком 2 массой m2, как показано на рисунке. При угле θ = 30,0° и коэффициенте кинетического трения между блоком 2 и плоскостью μ = 0,200 для блока 2 наблюдается ускорение величиной a = 0,450 м/с2. Часть А Найдите массу блока 2, м2.
Толкание газонокосилки Решение(Мастерство физики, глава 04: Сила и движение)
Рассмотрим газонокосилку весом w, которая может скользить по горизонтальной поверхности с коэффициентом трения μ.
В этой задаче газонокосилку толкают невесомой ручкой, образующей угол тета с горизонтом. Предположим, что Fh, сила, действующая на ручку, параллельна ручке.
Возьмите положительное направление x вправо, а положительное направление y — вверх.
Часть А
Найдите величину Fh требуемой силы…
Решение Mechanical Advantage (Мастерство физики, глава 04: Сила и движение)
Система шкивов, показанная на рисунке, используется для подъема 52-килограммового ящика. Обратите внимание, что одна цепь соединяет верхний шкив с потолком, а вторая цепь соединяет нижний шкив с ящиком. Предположим, что массы цепей, шкивов и канатов пренебрежимо малы. Часть А Определить силу F, необходимую для подъема ящика с постоянной скоростью. Часть Б Определить натяжение верхней цепи. Часть С Определить натяжение нижней цепи.
Книга на столе Решение(Мастерство физики Глава 04: Сила и движение)
Книга весом 5 Н лежит на столе.
Часть А
На книгу действует направленная вниз сила величиной 5 Н.
Таблица
сила тяжести
инерция
Часть Б
На _____ со стороны стола действует направленная вверх сила _____.
6 н/стол
5 н/стол
5 н/кн.
6 н/кн.
Часть С
Сделайте направленную вниз силу в Части A и направленную вверх силу в Части…
Решение Mechanical Advantage (Mastering Physics Chapter 04: Force and Motion)
Решение для подвески динамика (Mastering Physics Chapter 04: Force and Motion)
Громкоговоритель массой 24,0 кг подвешен на расстоянии h = 1,00 ниже потолка на двух тросах, образующих с потолком равные углы. Каждый кабель имеет длину l = 3,10.
Часть А
Чему равно натяжение T каждого троса? Используйте 9,80 м/с2 для величины ускорения свободного падения.
Гимнастка на веревке Решение (Мастерство физики, глава 04: Сила и движение)
Гимнастка массой 50,0 кг висит на вертикальной веревке, прикрепленной к потолку. Вы можете пренебречь весом веревки и считать, что веревка не растягивается. Часть А Вычислите силу натяжения T в скакалке, если гимнаст неподвижно висит на скакалке. Ответ выразите в ньютонах. Часть Б Вычислите силу натяжения T в скакалке, если гимнаст поднимается по скакалке с постоянной скоростью. Выразите ответ в ньютонах. Часть С Рассчитать натяжение…
Решение для подвесной люстры (Мастерство физики, глава 04: Сила и движение)
Люстра массой m прикреплена к потолку большого концертного зала двумя тросами. Поскольку потолок покрыт замысловатыми архитектурными украшениями (на рисунке они не указаны, используется более скромное изображение), рабочие, которые вешали люстру, не могли прикрепить кабели к потолку прямо над люстрой. Вместо этого они прикрепили кабели к потолку возле стен. Трос 1 имеет натяжение T1 и образует с потолком угол θ1.
Кабель…
Вопрос 4.10 Решение (Мастерство физики Глава 04: Сила и движение)
Часть A Кирпич попадает в оконное стекло. Кирпич разбивает стекло, поэтому: Величина силы кирпича на стекле больше, чем сила силы стекла на кирпиче. Величина силы кирпича на стекле равна силе силы стекла на кирпиче. Величина силы кирпича на стекле меньше, чем величина…
Задачи двух тел
В разделе “Законы Ньютона” введена тема “Задачи двух тел”. Пара стратегий решения проблем была обсуждена и применена для решения трех примеров проблем. Такие задачи двух тел обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельных объектов для определения силы, передаваемой между объектами. Вторая стратегия заключалась в использовании анализа двух отдельных объектов для разработки системы двух уравнений для решения двух неизвестных величин.
При необходимости найдите время, чтобы просмотреть страницу, посвященную решению задач двух тел. Эта страница будет основываться на уроках, полученных ранее в разделе «Законы Ньютона».
В этом уроке мы будем анализировать задачи двух тел, в которых объекты движутся в разных направлениях. В этих задачах два объекта соединены нитью, которая передает силу одного объекта другому объекту. Струна наматывается на шкив, который изменяет направление действия силы без изменения ее величины. В качестве иллюстрации того, как работает шкив, рассмотрите диаграмму справа. Объект A связан с объектом B цепочкой. Веревка наматывается на шкив в конце стола. Объект А подвешен в воздухе, а объект Б лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец веревки, к которой он подключен. Согласно закону действия-противодействия Ньютона, этот нижний конец нити будет тянуть вверх объект А. Противоположный конец нити соединен с объектом В. Этот конец нити тянет вправо объект В.
Таким образом, струна соединение двух объектов означает притяжение обоих объектов с одинаковой силой, но в разных направлениях. Струна тянет вверх объект А и вправо объект В. Блок изменил направление приложения силы.
Задачи, связанные с двумя объектами, соединительными струнами и шкивами, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях. Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при подходе к таким проблемам становится важным выбрать другую систему отсчета и систему координат для каждого объекта. Следует уделить внимание выбору такой системы координат, чтобы оба объекта ускорялись вдоль оси в положительном направлении. С правильно определенными осями для каждого отдельного объекта можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы составить систему из двух уравнений для решения двух неизвестных. Этот процесс решения проблем будет продемонстрирован для трех различных примеров задач.
Пример задачи 1
Груз массой 200,0 грамм (m 1 ) и груз массой 50,0 грамм (m 2 ) соединены нитью. Нить натянута на шкив. Определить ускорение масс и натяжение нити.
Как это часто бывает, в этом примере задачи запрашивается информация о двух неизвестных — ускорении объектов и силе, действующей между объектами. В ситуации, подобной этой, с двумя объектами, подвешенными на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат выбрана для m 
Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.
Уравнение второго закона Ньютона (F net = m•a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражаться как сила, направленная в направлении ускорения, за вычетом силы, противодействующей ему. Таким образом, для массы 200,0 грамм F нетто записывается как 1,960 N – F десяток . Для массы 50,0 грамм F нетто записывается как F десятки – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 грамм и 50,0 грамм. (Обратите внимание, что перед использованием в уравнениях значения массы преобразуются в стандартные килограммы. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
1,960 – F десятков = 0,2000•a
F десятков – 0,490 = 0,0500•a
С этого момента несколько шагов алгебры приводят к ответам на задачу.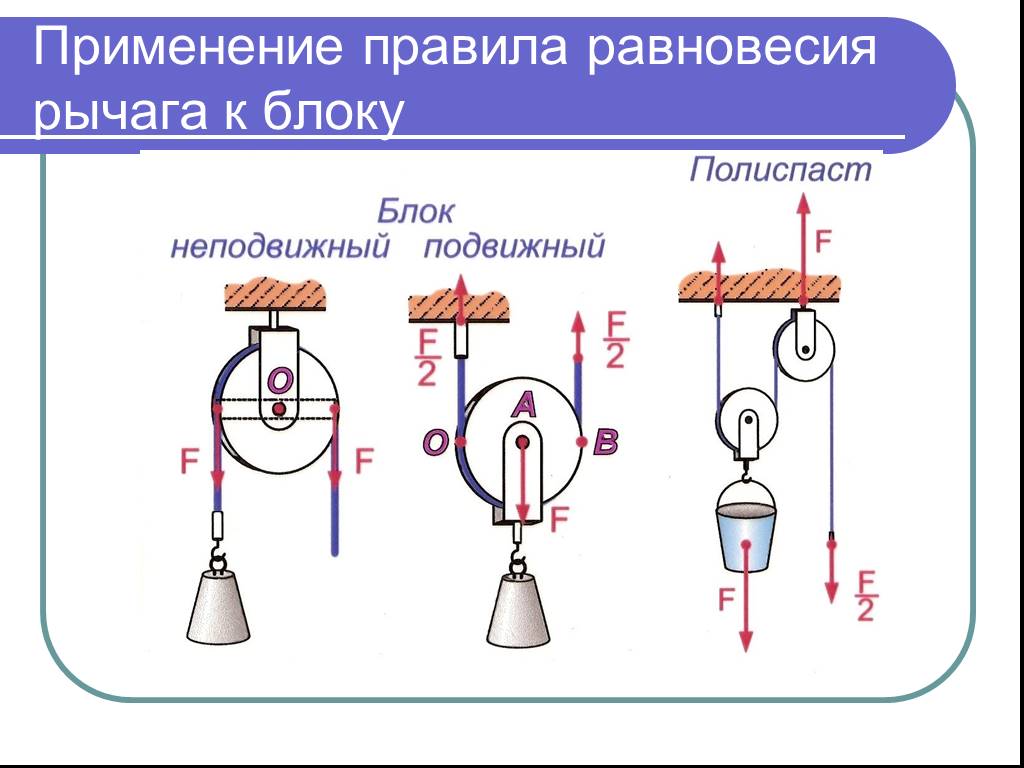
Уравнение 2 можно изменить, чтобы получить выражение для F десятков , записанное через ускорение.
F десятков = 0,0500•a + 0,490
Теперь это выражение для F десятков можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.
1,96 – (0,0500•а + 0,490) = 0,2000•а
1,96 – 0,0500•а – 0,490 = 0,2000•а
1,47 = 0,2500•а
a = 1,47/0,2500 = 5,88 м/с 2
Теперь, когда ускорение найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.
F десятки = 0,0500•(5,88) + 0,490
F десятки = 0,784 N
Рассматриваемую здесь систему шкивов иногда называют машиной Атвуда. Подход к решению проблем — это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных.
Пример задачи 2
Рассмотрим ситуацию с двумя телами справа. Подвесной груз массой 20,0 грамм (m 2 ) прикреплен к планеру с воздушной гусеницей массой 250,0 грамм (m 1 ). Определить ускорение системы и натяжение нити.
Как и в примере задачи 1, эту систему необходимо сначала проанализировать концептуально, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Так как нечего толкать м 
При таком выборе осей направление ускорения будет положительным для каждого объекта.
Диаграмма свободного тела для каждой отдельной массы показана ниже. На каждый объект действует направленная вниз сила тяжести (F
Уравнение второго закона Ньютона (F net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражена как сила в направлении ускорения за вычетом всех противодействующих сил.
F десятки = 0,2500•a
0,196 – F десятков = 0,0200•a
С этого момента несколько шагов алгебры приводят к ответам на задачу. Уравнение 4 выражает F десятки значение с точки зрения ускорения. Это выражение для F десятков можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным.
Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.
0,196 – 0,2500•а = 0,0200•а
0,196 = 0,2700•а
а = 0,196/0,2700 = 0,72593 м/с 2
a = ~0,726 м/с 2
Теперь, когда ускорение найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.
F десятки = 0,2500•(0,72593) = 0,18148
F десятки = ~0,181 N
Систему шкивов, проанализированную в примере задачи 2, иногда называют модифицированной машиной Этвуда. Анализ немного сложнее, чем анализ машины Этвуда из примера задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Этвуда с наклонной поверхностью, как показано ниже. Подход к решению проблемы будет таким же.
Пример задачи 3
Рассмотрим ситуацию с двумя телами справа.
Ящик размером 2,50×10 3 кг (m 1 ) опирается на наклонную плоскость и соединен тросом с массой 4,00×10 3 кг (m 2 ). Эта вторая масса (m 2 ) подвешена на шкиве. Угол наклона составляет 30,0°, поверхность не имеет трения. Определить ускорение системы и натяжение троса.
Как и в предыдущей задаче, первая задача включает анализ ситуации, чтобы определить, в каком направлении будут ускоряться объекты. Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m 2 ) могла ускоряться вверх или вниз. Направление, в котором он ускоряется, зависит от сравнения его веса (силы тяжести) с противодействующей силой, действующей на другую массу (m 1 ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена вниз (как обычно) и рассчитывается как m 1 •г. Нормальная сила направлена перпендикулярно поверхности (как обычно).
Сила натяжения направлена вверх и вправо – параллельно наклонной плоскости и вдоль той же ориентации, что и струна, создающая эту силу. Как обсуждалось на предыдущей странице, объекты, расположенные на наклонных плоскостях, анализируются путем разделения силы тяжести на две составляющие. Одна компонента направлена параллельно плоскости (и вниз под этим углом), а другая компонента направлена перпендикулярно плоскости (и вверх под этим углом). Именно параллельная составляющая силы тяжести пытается притянуть m 1 вниз по наклонной плоскости. Как упоминалось ранее, эту составляющую можно рассчитать, умножив вес объекта (m 1 •g) на синус угла наклона (30°). Значение для F параллельно составляет
F параллельно = m 1 •g•sine(θ) = (2500 кг)•(9,8 Н/кг)•sine(30°)
F параллельно = 12250 N
Эта параллельная составляющая силы тяжести пытается тянуть m 1 вниз по наклонной плоскости.
С м 1 крепится кабелем к m 2 , с ним будет тянуться подвесная масса. Однако существует противоположное действие силы тяжести, тянущей m 2 вниз; это противодействующее действие, если оно преобладает, будет тянуть объект m 1 вверх по наклонной плоскости. Сила тяжести на м 2 равна
F грав-2 = м 2 •g = (4000 кг)•(9,8 Н/кг) = 39200 Н
Эта сила тяжести на м 2 является доминирующей силой. И так м 1 будет ускоряться вверх по наклонной плоскости, а m 2 будет ускоряться вниз. Оси координат назначаются соответствующим образом, чтобы каждый объект имел положительное ускорение.
На рисунках ниже показаны эти координатные оси и силы, действующие на два объекта. Три силы на m 1 уже обсуждались. На диаграмме показаны два компонента F grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как
F перпендикулярно = м 1 •g•cosθ = (2500 кг)•(9,8 Н/кг)•cos(30°)
F перпендикулярно = 21218 Н
Нормальная сила (F норма ), действующая на m 1 , уравновешивает перпендикуляр F так, что ускорение перпендикулярно наклонной плоскости отсутствует.
Значение нормы F также равно 21218 Н. Подвешенная масса (m 2 ) испытывает только две силы – направленную вниз силу тяжести и восходящую силу растяжения.
Теперь уравнение второго закона Ньютона (F net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F выражается как сила в направлении ускорения за вычетом всех сил, противодействующих ему. Для массы 2500 кг на склоне (м 1 ) F нетто представляет собой просто силу натяжения (F десяток ) за вычетом параллельной составляющей силы тяжести. Для подвесной массы 4000 кг (м 2 ), F нетто – сила тяжести (39200 Н) минус сила натяжения (F десяток ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m 1 и m 2 . (Обратите внимание, что единицы измерения опущены, чтобы уравнения читались более четко.
)
F десятки – 12250 = 2500•a
39200 – F десятки = 4000•a
С этой точки a несколько шагов алгебры приводят к ответам на проблему. Уравнение 6 можно изменить, чтобы создать выражение для F десятков , выраженное через ускорение.
F десятков = 2500•a + 12250
Это выражение для F десятков можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.
39200 – (2500•а + 12250) = 4000•а
39200 – 2500•а – 12250 = 4000•а
26950= 6500•а
а = 26950/6500 = 4,1462 м/с 2
a = ~4,15 м/с 2
Теперь, когда ускорение найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F десяток ).
F tens = 2500•a + 12250 = 2500•(4.
1462) + 12250 = 22615 N
F tens = ~2.26 x 10 4 N
Two-body problems like these three примеры проблем могут быть довольно сложной задачей. Наличие системного подхода, применяемого к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона являются важными составляющими успеха.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора Atwood’s Machine Simulator. Вы можете найти его в разделе Physics Interactives на нашем сайте. Тренажер позволяет исследовать двухмассовые системы, ускоряемые подвешенной массой.