Примеры решения задач по теме «Второй закон Ньютона»
Примеры решения задач по теме «Второй закон Ньютона»
- Подробности
- Просмотров: 1623
«Физика – 10 класс»
Познакомимся с задачами, для решения которых не нужно знать, как зависят силы от расстояний между взаимодействующими телами (или частями одного тела) и от их скоростей. Единственное, что нам потребуется, — это выражение для силы тяжести вблизи поверхности Земли: τ = m.
Задача 1.
К центру однородного шарика массой m = 0,2 кг приложена сила F = 1,5 Н. Определите модуль и направление силы 1, которую необходимо приложить к центру шарика помимо силы , чтобы шарик двигался с ускорением а = 5 м/с2, направленным так же, как и сила (рис. 2.17).
Р е ш е н и е.
На шарик действуют две силы: сила и искомая сила 1.
Поскольку модуль и направление силы неизвестны, можно изобразить на рисунке сначала только силу (см.
Согласно второму закону Ньютона m = + 1.
Отсюда 1 = m – .
Так как векторы m и в любой момент времени должны быть расположены на одной прямой, то и сила 1, являясь их разностью, расположена на той же прямой.
Таким образом, искомая сила может быть направлена либо так же, как сила , либо противоположно ей.
Чтобы определить модуль и направление силы 1, найдём её проекцию на ось X, направление которой совпадает с силой .
Учитывая, что Fx = F и аx = а, выражение для силы 1
Проанализируем последнее выражение.
Если mа > F, то F1x > 0, т. е. сила 1 направлена так же, как и ось X.
Если же mа < F, то F1x < 0, т. е. сила F1 направлена противоположно направлению оси X. Для рассматриваемого случая
F1x – 0,2 • 5Н – 1,5 Н = -0,5 Н.
Следовательно, сила F1 направлена противоположно оси X (рис. 2.18).
Задача 2.
В результате полученного толчка брусок начал скользить вверх по наклонной плоскости из точки О с начальной скоростью υ
Р е ш е н и е.
Поскольку требуется найти положение бруска относительно точки О, начало координат возьмём в этой точке. Ось X направим вдоль наклонной плоскости вниз, а ось Y — перпендикулярно этой плоскости вверх (рис. 2.19). При движении бруска на него действуют две силы: сила тяжести m и сила реакции опоры наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.
Согласно второму закону Ньютона m = m + . Так как на брусок действуют постоянные силы, то вдоль оси X он будет двигаться с постоянным ускорением. Следовательно, чтобы определить положение бруска относительно точки О, можно воспользоваться кинематическим уравнением
Так как на брусок действуют постоянные силы, то вдоль оси X он будет двигаться с постоянным ускорением. Следовательно, чтобы определить положение бруска относительно точки О, можно воспользоваться кинематическим уравнением
При сделанном выборе направления оси X и начала координат имеем х0 = 0 и υ0x = -υ0. Проекцию ускорения ах на ось X найдём по второму закону Ньютона. Для рассматриваемого случая mа
Задача 3.
Два тела массами m1 = 10 г и m2 = 15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (рис. 2.20). Плоскость образует с горизонтом угол α = 30°. Определите ускорение, с которым будут двигаться эти тела. Трение не учитывайте.
Р е ш е н и е.
Предположим, что тело массой m1 перетягивает.
Выберем оси координат так, как показано на рисунке 2.21.
m1ax1 = m1g – Т1,
m2ах = Т2 — m2g sinα,
|ах| =|ax1|, так как нить нерастяжима.
Силы натяжения нити равны, так как нить и блок невесомы.
Сложив левые и правые части уравнении, получим
Так как ах > 0, то движение тел происходит в выбранном направлении.
Задача 4.
Автомобиль массой т = 1000 кг движется со скоростью v = 36 км/ч по выпуклому мосту, имеющему радиус кривизны R = 50 м. С какой силой F давит автомобиль на мост в его середине? С какой минимальной скоростью umin должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост?
Р е ш е н и е.
Силы, действующие на автомобиль вдоль радиуса моста, изображены на рисунке 2. 22:
22:
m — сила тяжести;
— сила нормальной реакции моста.
По третьему закону Ньютона искомая сила давления равна по модулю силе реакции моста .
При движении тела по окружности всегда направляем одну из осей координат от тела к центру окружности.
Согласно второму закону Ньютона центростремительное ускорение автомобиля определяется суммой сил, действующих на него вдоль радиуса окружности, по которой он движется:
mυ2/R = mg – N.
Отсюда
F = N = m(g – υ2/R) = 7,8 кН.
Сила давления на мост станет равной нулю при mυ2min/R = mg, так что υmin = 80 км/ч.
При скорости, превышающей υmin, автомобиль оторвётся от поверхности моста.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика – Физика, учебник для 10 класса – Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела.
Решение задач по теме “Второй закон Ньютона”
План-конспект урока по теме «Решение задач по теме «Второй закон Ньютона»
Дата:
Тема: Решение задач по теме «Второй закон Ньютона»
Образовательная: формирование практических умений по решению задач на тему «Второй закон Ньютона»;
Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;
Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015
Структура урока:
Организационный момент (5 мин)
Актуализация опорных знаний (5 мин)
Закрепление знаний(30 мин)
Итоги урока (5 мин)
Содержание урока
Организационный момент
Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны научиться применять на практике всю теорию о втором законе Ньютона.
Актуализация опорных знаний
Сформулируйте Первый закон Ньютона.

Сформулируйте Второй закон Ньютона.
Закрепление знаний
А сейчас запишем алгоритм решения задач на Второй закон Ньютона:
1. Внимательно прочитав задачу, записываем ее краткое условие. Если есть необходимость, переводим единицы измерения в систему СИ, недостающие данные находим из справочников и дописываем условие.
2. Если к задаче дается рисунок, перечерчиваем его, если нет, – чертим сами схематично. Уточняем, какой вид движении совершают тела, поступательное, вращательное или смешанное.
3. Изобразить на рисунке все необходимые обозначения:
а) выбрать систему координат.
б) обозначить данные задачи.
в) указать все силы, действующие на каждое из тел, длины векторов чертить с учетом реальных значений сил.
г) если не указаны направления движения, выбрать их.
д) разложить силы по направлениям осей координат, если есть необходимость.
4. Отметить допустимые упрощения и на их основе сделать выводы.
5. Записать II закон Ньютона в общем (векторном) виде для каждого из тел.
6. Записать II закон Ньютона в проекциях на выбранные оси координат, помня при этом, что проекция положительна, если сила совпадает с направ-лением оси, и отрицательна, если сила противоположна ей, если в каком-то направлении нет движения – считать ускорение равным 0.
7. Решить систему полученных уравнений относительно искомой величины, если нужно найти несколько величин, то находим все.
8. Выразить силы через аналитические выражения, а так же использовать рисунок и значения сил подставить в выражение для искомой величины. Если необходимо, использовать кинематические величины.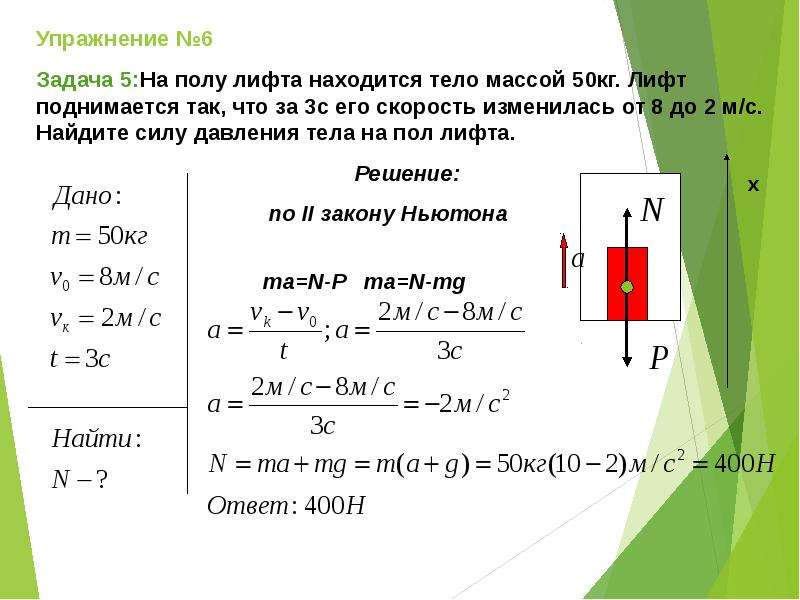
9. Подставить в окончательное выражение данные задачи и подсчитать численное значение искомых величин в системе СИ.
10. Проверить ответ на глупость.
А теперь рассмотрим примеры движений тел под действием нескольких сил:
Итоги урока
Итак, подведем итоги. Что вы сегодня узнали на уроке?
Организация домашнего задания
§20, ответить на контрольные вопросы.
Рефлексия.
Продолжите фразы:
Сегодня на уроке я узнал…
Было интересно…
Знания, которые я получил на уроке, пригодятся…
Решение задач по теме «Законы Ньютона»
1.
 Решение задач по теме «Законы Ньютона» • Цель урока:
Решение задач по теме «Законы Ньютона» • Цель урока:• 1. Знать алгоритм
решения задач на
законы Ньютона.
• 2. Уметь применять
алгоритм к решению
задач на законы
Ньютона.
2. Повторим теорию
1.2.
Сформулируйте первый закон Ньютона. Приведите
примеры, объясняющие данную формулировку.
Какие системы отсчета называются инерциальными?
Неинерциальными? Привести примеры.
3. Что в физике понимают под термином «сила»?
4. Приведите примеры, показывающие связь сила и
ускорения, с которым движется тело.
5. Сформулируйте второй закон Ньютона и запишите
его математическое выражение.
6. В чем состоит третий закон Ньютона? Запишите его
математическое выражение. Поясните на примерах
смысл этого закона. Каковы особенности сил, о
которых идет речь в третьем законе Ньютона?
3. Алгоритм решения задач
• 1. Прочитать внимательно условие задачи.2. Выделить заданные условием тела.

3. Выполнить анализ взаимодействия тел.
4. Кратко записать условие задачи.
5. Сделать рисунок, изобразить на нем векторы сил, действующие на
каждое из тел, показать направление векторов перемещения, ускорения.
6. Записать в векторной форме уравнение для равнодействующей силы.
7. Выбрать наиболее рациональное в данных условиях задачи направление
координатных осей в ИСО.
8. Определить проекции векторов на координатные оси.
9. Записать дополнительные уравнения кинематики (если необходимо).
10. Решить в общем виде полученные уравнения относительно искомой
величины.
11. Сделать проверку размерности.
12. Вычислить.
13. Оценить полученные значения искомых величин.
4. Задачи по темам: «Второй закон Ньютона». «Третий закон Ньютона» из учебника Степанова
• №118. Сила 50 Н сообщает телу ускорение0,1 м/с2. Какая сила сообщает этому телу
ускорение 0,01 м/с2?
5. Решение:
• F = ma; F1 = ma1; F2 = ma2• m = F1/a1 m = F2/a2
• F1/a1 = F2/a2
• F2 = F1*a2 /a1
50Н*0,01 м/с2
F2 =
=5Н
0,1 м/с2
• №119.
 Тело массой 2 кг приобретает
Тело массой 2 кг приобретаетпод действием некоторой силы
ускорение 2 м/с2. Какое ускорение
приобретет под действием этой силы
тело массой 5 кг?
• Решение задачи:
F =m1a1; F = m2a2; m1a1 = m2a2
• №121. Тело, движущееся под действием
постоянной силы, прошло в первую
секунду путь 25 см. Определите силу,
если масса тела 25 г.
9. Решение:
• №122. Снаряд массой 2 кг вылетает изствола орудия горизонтально со
скоростью 1000 м/с. Определите силу
давления пороховых газов, считая ее
постоянной, если длина ствола равна 3,5
м.
11. Решение:
• №130. Птица в клетке-ящике сидит надне. Ящик с ней уравновешен на весах.
Нарушится ли равновесие весов, если
птица взлетит?
• Решение задачи:
В момент взлета да, затем весы опять
придут в равновесие, т. к. клетка
является замкнутой системой.
• №133. Два мальчика тянут веревку в
разные стороны, прилагая силы 100 Н
каждый.
 Веревка может выдержать, не
Веревка может выдержать, неразрываясь, груз весом 150 Н. Разорвется
ли веревка?
• Решение задачи:
Нет. Так как растягивание каната
мальчиком с силой 100Н эквивалентно
тому, что один конец каната закреплен, а
к другому подвешен груз 100Н.
• №135. Изобразите
силы действия и
противодействия в
случаях
взаимодействия тел,
приведенных на
рисунке 33
• №136. Нарушится ли равновесие весов
(рис. 34), если удлинить нить так, чтобы
гиря оказалась полностью погруженной
в воду, но не касалась дна? А если
обрезать нить и положить гирю на дно?
• Решение задачи:
не нарушится, т. к. система замкнута, т. е.
сумма внутренних сил равна 0, а сумма
внешних сил в обоих случаях не
изменяется.
20. Задание на дом:
• П. 10 – 12 повторить• Упр.11 (1,3)
• Упр.13 (1,3)
21. Использованные материалы:
• http://davay5.com/z.php?theme=vtoroyzakon-nyutona-tretiy-zakonnyutona&a=stepanova_9_10_11_klass&g=osnovy-dinamiki
• http://easyen.
 ru/load/shablony_prezentacij
ru/load/shablony_prezentacij/498
План Решение задач на законы Ньютона
1. Подготовка к активному усвоению и осмысления учебного материала (решение задач)
Цель: Обеспечить мотивацию и принятия учащимися цели учебно-познавательной деятельности.
Форма: ППС и индивидуальная
Метод: поисково-эврестический
А) Учитель может привести примеры использования законов Ньютона, начиная с простых примеров и включая примеры, в которых на тело действует сразу несколько сил.
Учащиеся должны попрактиковаться на примерах, для проверки правильности применения формул и знания терминологии.
Алгоритм решения задач на законы динамики Ньютона.
1. Прочитать внимательно условие задачи.
2. Выделить заданные условием тела.
3. Выполнить анализ взаимодействия тел.
4. Кратко записать условие задачи.
5.
Сделать рисунок, изобразить на нем векторы сил, действующие на каждое из тел,
показать направление векторов перемещения, ускорения.
6. Записать в векторной форме уравнение для равнодействующей силы.
7. Выбрать наиболее рациональное в данных условиях задачи направление координатных осей в ИСО.
8. Определить проекции векторов на координатные оси.
9. Записать дополнительные уравнения кинематики (если необходимо).
10. Решить в общем виде полученные уравнения относительно искомой величины.
11. Сделать проверку размерности.
12. Вычислить.
13. Оценить полученные значения искомых величин.
Если в движении находится не одно, а несколько связанных между собой тел, то необходимо для каждого тела отдельно выполнить все вышесказанные действия и решить полученную систему уравнений.
1) тела, связанные невесомой нерастяжимой нитью, движущиеся по горизонтали;
2) эти же тела, поднимающиеся вверх;
3) нить, связывающая грузы, переброшена через неподвижный блок.
В)Решение задачи у доски
Задача
№ 1: Два
тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н
вправо по столу. Массы брусков m1 = 1 кг и m2 = 4 кг, μ = 0,1.
рис.) тянут с силой 15 Н
вправо по столу. Массы брусков m1 = 1 кг и m2 = 4 кг, μ = 0,1.
С каким ускорением движутся бруски? Чему равна сила натяжения нити?
Учитель: Условие невесомости и нерастяжимости нити позволяет считать, что сила натяжения нити на всех участках одинакова и все тела движутся с одним и тем же ускорением, т.е. Т1 = Т2 = Т, .
Для того, чтобы решить задачу надо её проанализировать.
Рассмотрим все силы, действующие на каждое тело отдельно. Оба тела взаимодействуют с землёй, столом и нитью.
На первое тело действуют: m1g, Т1, Fтр1, N1
На второе тело действуют: m2g, N2, T2, Fтр2 и сила F
Системы отсчета свяжем со столом.
Учитель: Анализ провели, теперь приступаем к решению задачи.
Дано:
Равноускоренное движение связанных тел
F=
15 Н
m1= 1 кг
m2 = 4 кг
μ = 0,1
_____________________
– ? (м/с2)
Т – ? (Н)
1. Изобразим
все силы, действующие на тела.
Изобразим
все силы, действующие на тела.
Ускорение тела направлено вправо:
Из условия задачи => Т1 = Т2 = Т;
2. Запишем II закон Ньютона в общем виде ∑ = m и для каждого тела в векторной форме, для этого страницу разделим пополам:
3. Выберем координатные оси: ось ОУ направим по направлению, а ось ОХ по направлению системы тел.
4. Проецируем векторные уравнения II закона Ньютона для I и II тела на координатные оси:
OX:
T – Fтр1 = m1 (1) | OX:
F – T – Fтр2 = m2 * (1/) |
Мы
получили два уравнения для 2-х тел, где учтены все силы, действующие на тело
в отдельности.
Далее решаем совместно систему уравнений (3) и (31) методом почленного сложения уравнений, получаем:
(4), в этом уравнении учтены все силы, действующие на систему 2-х тел, связанных невесомой нерастяжимой нитью.
Откуда =
Силу натяжения нити находим из уравнения (3) или (31)
Т= μ * m1 * g + m1 = m1 (μ * g +) = 1 (0,1 * 10 + 2) = 3Н
или Т = F – m2 – μ * m2 g = F – m2 (+ μ * g) = 15 – 4 * (2 + 0,1* 10) = 3Н
Ответ: 2 м/с2, 3Н.
Задача №2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси, подвешены грузы с массами m1= 1кг и m2= 2 кг. Каково ускорение, с которым движется второй груз?
1. Изобразим рисунок и расставим все силы, действующие на тело. Ускорение тела направим в сторону большого тела.
1. Запишем II закон Ньютона в векторной форме для каждого тела
Запишем II закон Ньютона в векторной форме для каждого тела
2. Выберем координатные оси, ось ОУ направлена по направлению ускорения, на рисунке изображаем ОУ1, ОУ2.
3. Проецируем векторные уравнения II закона Ньютона для I и II тела на координатные оси ОУ1 и ОУ2, учитывая, что T1 = T2 = T,
ОУ1: T- m1g = m1 * (1) | ОУ2: m2 g – T = m2 ( 11 ) |
Складываем почленно уравнения (1) и (11 ), получаем:
Ответ: 3,3 м/с2
Задача
№ 3. Брусок
массой 2 кг скользит по горизонтальной поверхности под действием груза массой
0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через
неподвижный блок. Коэффициент трения бруска о поверхность 0,1.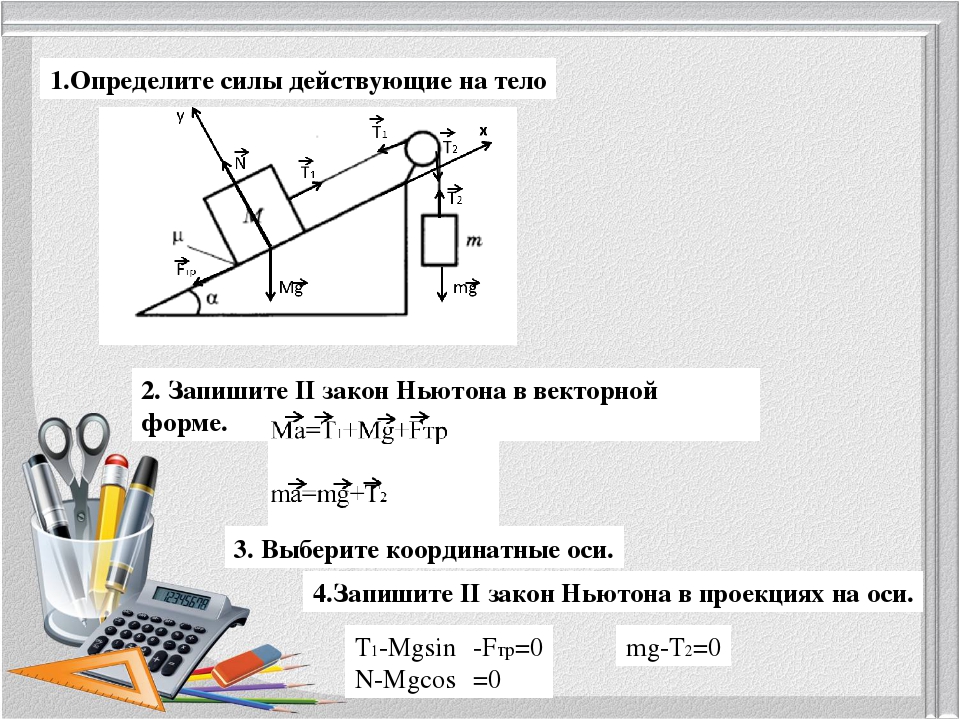
Решение:
1. Изобразим рисунок и расставим все силы, действующие на тела. Ускорение первого тела направим вправо, второго – вниз.
2. Запишем II закон Ньютона в векторной форме для каждого тела, поделив страницу пополам
для I тела: | для II тела: |
3. Спроецируем полученные уравнения на выбранные направления осей X и Y, учитывая условие невесомости и нерастяжимости:.
OX:
(1) | (31)
|
Решаем совместно систему уравнений (3) и (31) методом почленного сложения уравнений, получаем:
Т – µ * m1g + m2g – T = (m1+m2) *
откуда
Силу
натяжения нити Т находим из уравнения (31).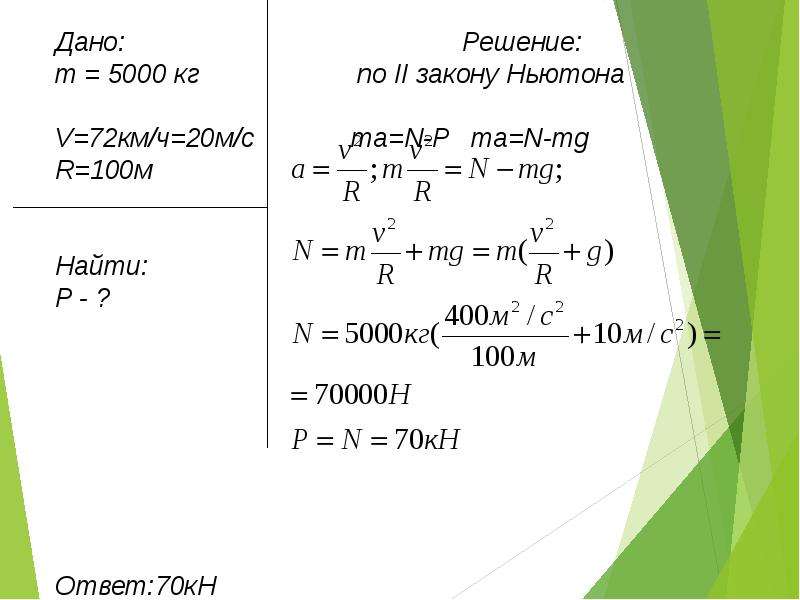
Т = m2g – m2 =m2 (g – )
Т = 0,5 (10 – 1,2) = – 4,4 H. (знак « – » указывает, что сила натяжения направлена в противоположную сторону оси OY).
Т = 4,4 Н.
Ответ: 1,2 м/с2 ; 4,4 Н.
ЕСТЕСТВОЗНАНИЕ. ФИЗИКА. Законы Ньютона. Решение задач.
Инерция. Законы Ньютона. Силы в механике
Физика. 9 класс. Тренинг «Инерция. Законы Ньютона. Силы в механике» 1 Инерция. Законы Ньютона. Силы в механике Вариант 1 1 Металлический брусок подвешен к пружине и целиком погружён в сосуд с водой, находясь
ПодробнееГлава 3. Закон сохранения импульса
37 Глава 3. Закон сохранения импульса Задача 1. Тело массой 2 кг свободно падает без начальной скорости с высоты 5 м на горизонтальную поверхность и отскакивает от нее со скоростью 5 м/с. Найдите абсолютную
Закон сохранения импульса Задача 1. Тело массой 2 кг свободно падает без начальной скорости с высоты 5 м на горизонтальную поверхность и отскакивает от нее со скоростью 5 м/с. Найдите абсолютную
Примеры решения задач
Примеры решения задач Пример 1 Через вращающийся вокруг горизонтальной оси блок (рис1а) перекинута невесомая нерастяжимая нить к концам которой привязаны грузы 1 и Найдите силу давления X N F блока на
ПодробнееРЗ-9.3. Законы Ньютона Задания уровня “А”
РЗ-9.3. Законы Ньютона Задания уровня “А” 1. Тело массой 10 кг движется по горизонтальной площадке с ускорением 2 м/с 2. Чему равна сила тяги? 2. С какой силой надо тянуть ящик массой 20 кг по полу с ускорением
ПодробнееЗадания А22 по физике
Задания А22 по физике 1. Если подвесить к легкой упругой пружине некоторый груз, то пружина, находясь в равновесии, окажется растянутой на 10 см. Чему будет равен период свободных колебаний этого груза,
Если подвесить к легкой упругой пружине некоторый груз, то пружина, находясь в равновесии, окажется растянутой на 10 см. Чему будет равен период свободных колебаний этого груза,
Обучающие задания на тему «ДИНАМИКА»
Обучающие задания на тему «ДИНАМИКА» 1(А) Автобус движется прямолинейно с постоянной скоростью. Выберете правильное утверждение. 1) На автобус действует только сила тяжести. ) Равнодействующая всех приложенных
ПодробнееБанк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
ПодробнееРешение задач ЕГЭ части С: Динамика
С1.1. Два одинаковых бруска, связанные легкой пружиной, покоятся на гладкой горизонтальной поверхности стола. В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость
В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость
Решение задач по теме «Статика»
Решение задач по теме «Статика» 1 При решении задач на равновесие тел: 1.Сделать рисунок, показать все силы, действующие на тело (или тела системы),находящиеся в положении равновесия, выбрать систему координат
ПодробнееУРОК ФИЗИКИ В 10 КЛАССЕ. Законы Ньютона
УРОК ФИЗИКИ В 10 КЛАССЕ Законы Ньютона КАКИЕ МЫ ЗНАЕМ ВИДЫ ДВИЖЕНИЯ 1. Равномерное прямолинейное ( скорость постоянна по величине и направлению) 2. Равноускоренное прямолинейное ( скорость меняется, ускорение
ПодробнееРешения и критерии оценивания
Решения и критерии оценивания Задача 1 Небольшой брусок через систему блоков связан нерастяжимой нитью с длинной тележкой, которая может катиться по горизонтальной поверхности. Брусок кладут на тележку
Брусок кладут на тележку
3. Законы сохранения в механике
Выдержки из книги Горбатого ИН «Механика» 3 Законы сохранения в механике 3 Импульс тела Закон сохранения импульса Импульсом p материальной точки называется векторная величина, равная произведению массы
Подробнееуч. год. 3, 9 кл. Физика. Динамика.
006-007 уч. год. 3, 9 кл. Физика. Динамика. 6. Примеры решения задач Приступая к решению задач, сделаем несколько общих замечаний. Во-первых, при решении задач нужно прежде всего выяснить, какие силы действуют
Подробнее), движется равномерно
РАВНОВЕСИЕ ТЕЛ Раздел механики, в котором изучается равновесие тел, называется статикой Равновесным называется состояние тела, неизменное во времени, т е равновесие это такое состояние тела, при котором
ПодробнееЗадания к контрольной работе
Задания к контрольной работе Контрольная работа проводится по двум главам: «Законы движения» и «Силы в механике». Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Индивидуальное задание 6. Вариант 1.
Вариант 1. 1. Легкоподвижную тележку массой 3 кг толкают с силой 6 Н. Определите ускорение тележки.. Мяч массой 0,5 кг после удара, длящегося 0,0 с, приобретает скорость 10 м/с. Найти среднюю силу удара.
ПодробнееОсторожно! Сила трения
Потенциал 10 (46) 10.008 Физика Бондаров Михаил Николаевич Учитель физики лицея 1501 и ГОУ ЦО «Технологии обучения» г. Москвы Осторожно! Сила трения В статье разбираются характерные ошибки, возникающие
Подробнее2) 8 м/с 3) 12 м/с 4) 16 м/с
Физика. 9 класс. Демонстрационный вариант 4 (90 минут) Физика. 9 класс. Демонстрационный вариант 4 (90 минут) Диагностическая тематическая работа по подготовке к ГИА-9 по ФИЗИКЕ по теме «Механические явления,
ПодробнееВопрос N 1 Два бруска с массами m 1
Билет N 5 Билет N 4 Вопрос N 1 На тело массой m 2,0 кг начинает действовать горизонтальная сила, модуль которой линейно зависит от времени: F t, где 0. 7 Н/с. Коэффициент трения k 0,1. Определить момент
7 Н/с. Коэффициент трения k 0,1. Определить момент
Курсы подготовки к ЕГЭ по физике
Курсы подготовки к ЕГЭ по физике Механика. Задание 9 Учитель физики: Бабчик И.И. Учебное заведение: МБОУ лицей 1 г. Сургут, 019 г. Задание 9. Основные вопросы 1 1. Кинематика Задача 1 Задача 7. Движение
ПодробнееДИНАМИКА задания типа В Страница 1 из 6
ДИНМИК задания типа В Страница 1 из 6 1. Спутник движется вокруг Земли по круговой орбите радиусом R. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. (M
Подробнее9 класс. Вариант ,9 с
9 класс. Вариант 1. Тело бросили с башни горизонтально. Через t = с его скорость увеличилась в k=3 раза. С какой скоростью V0 бросили тело? Скорость тела изменяется в зависимости от времени как Для заданного
Подробнеед) F1=5H 60 o F3=5H F2=5H F1=4H a) F2=6H F1=2H F2=3H
Урок 1. Лекция: «Основы теории относительносит». Урок 2. Работа с текстом: Г.Гамов «Приключение мистера Томпкинса». Урок 4. Лекция: Принцип относительности Галилея. Инерция. Неотличимость покоя и равномерного
Лекция: «Основы теории относительносит». Урок 2. Работа с текстом: Г.Гамов «Приключение мистера Томпкинса». Урок 4. Лекция: Принцип относительности Галилея. Инерция. Неотличимость покоя и равномерного
t56 [ 4500 ]
1 t68 [ 6.4 ] t103 [ 4.9 ] t56 [ 4500 ] 4467-4566 t2 [ 4 ] t117 [ 9 ] 2 t255 [5.21 ] t105 [2.94-3] t101 [ 8 ] t3 [ 0 ] t10 [ 36.4 ] 3 t54 [ 730 ] t135 [ 4 ] t57 [ 0.0394 ] t4 [ -2 ] t11 [ 8.89 ] 4 t55
ПодробнееОТВЕТ: с -1. ОТВЕТ: c -1
Билет N 5 Билет N 4 Вопрос N 1 Тонкий стержень массы M 0 = 1 кг и длины l = 60 см лежит на гладкой горизонтальной поверхности. Стержень может свободно вращаться вокруг закреплённой вертикатьной оси, проходящей
ПодробнееБилет N 4. ОТВЕТ: с -1
Билет N 5 Билет N 4 Вопрос N 1 Тонкий стержень массы M 0 = 1 кг и длины l = 60 см лежит на гладкой горизонтальной поверхности. Стержень может свободно вращаться вокруг закреплённой вертикатьной оси, проходящей
Стержень может свободно вращаться вокруг закреплённой вертикатьной оси, проходящей
Урок 11 ( ) Три закона Ньютона.
Урок (7..6) Три закона Ньютона.. Явление инерции, -й закон Ньютона. Явление инерции это некий экспериментальный факт, заключающийся в том, что если на материальную точку не действуют никакие силы, то она
Подробнее= const. r r. 1 m Законы Ньютона
5.3. Законы Ньютона При рассмотрении движении материальной точки в рамках динамики решаются две основные задачи. Первая или прямая задача динамики заключается в определении системы действующих сил по заданным
ПодробнееЛАБОРАТОРНАЯ РАБОТА 133
ЛАБОРАТОРНАЯ РАБОТА 133 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА. Цель работы: Целью работы является изучение основного уравнения динамики вращательного движения твердого тела и экспериментальное
Подробнее4.
 Механика. Законы сохранения.
Механика. Законы сохранения.4. Механика. Законы сохранения. 2005 1. Тележка массой 2 кг, движущаяся со скоростью 3 м/с, сталкивается с неподвижной тележкой массой 4 кг и сцепляется с ней. Найдите скорость обоих тележек после взаимодействия.
ПодробнееОбразовательный портал «РЕШУ ЕГЭ» (
Динамика 1. Брусок массой движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной под углом к горизонту. Модуль этой силы Коэффициент трения между бруском и плоскостью
ПодробнееОлимпиада «Физтех» по физике 2017 год
Олимпиада «Физтех» по физике 07 год Класс 9 Шифр Билет 09-0 (заполняется секретарём) Мальчик бьет ногой по мячу, который лежит на горизонтальной поверхности земли на некотором 0 расстоянии от вертикальной
ПодробнееКинематика.
 t 2. t 1. t 3
t 2. t 1. t 3Кинематика 1.1. Пешеход первые S 1 =4 км пути шёл со скоростью v 1 = 8 км/час, следующие S 2 =4 км пути шёл со скоростью v 2 = 4 км/час, а последние S 3 =2 км пути шёл со скоростью v 3 = 2 км/час. Найдите
ПодробнееУрок физики в 10 классе «Применение законов Ньютона»
Тема урока
.Применение законов Ньютона.
Цель урока: учащиеся должны уметь решать ключевые задачи.
Тип урока: Решение задач.
План изучения нового материала.
1. Использование стандартного подхода для решения задач динамики:
1) вес тела в лифте (с обсуждением перегрузок и невесомости).
2)скольжение тела по горизонтальной поверхности,
3)соскальзывание тела с наклонной плоскости.
Ход урока.
I.Изучение нового материала. Методика решения задач динамики. Для решения задач динамики целесообразно использовать следующий стандартный подход.
Методика решения задач динамики. Для решения задач динамики целесообразно использовать следующий стандартный подход.
•Изобразите силы, действующие на каждое тело в инерциальной системе отсчета (условно∑)
•Запишите для каждого тела второй закон Ньютона в векторной форме (55).
•Выберите координатные оси. Если заранее известно направление ускорения, то целесообразно направить одну из осей вдоль ускорения, а вторую( если она требуется) перпендикулярно ему. •Запишите второй закон Ньютона через проекции на координатные оси входящих в него величин, получите систему уравнений для нахождения неизвестных величин.
• Решите полученную систему уравнений, используя аналитические выражения для всех сил и дополнительные условия.
Воспользуемся предложенным подходом для решения конкретных задач динамики.
КЛЮЧЕВЫЕ ЗАДАЧИ
Покажем с помощью законов Ньютона, что вес тела не всегда равен действующей на него силе тяжести.
I. Вес тела в лифте
Человек массой т находится в лифте. Найдем силу давления человека на пол лифта (вес), если:
а)лифт покоится или равномерно движется;
б)лифт движется с постоянным ускорением а, направленным вверх;
в) лифт движется с постоянным ускорением а, направленным вниз.
Решение.
а) Ускорение лифта равно нулю (а = 0).
Изобразим силу тяжести mg и силу реакции опоры N1 действующие на тело (рис. 87). Согласно третьему закону Ньютона сила реакции опоры равна по модулю и противоположна по направлению весу тела P1. Поэтому большинство задач о нахождении веса тела сводятся к задачам определения силы реакции опоры.
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в векторной форме:
ma = mg + N1.
Направим ось Y вертикально вверх. Запишем второй закон Ньютона через проекции сил на ось Y, учитывая, что а = 0:
Запишем второй закон Ньютона через проекции сил на ось Y, учитывая, что а = 0:
0 = –mg + N1, Pl=N1 = mg.
Вес тела, находящегося в покое или движущегося равномерно и прямолинейно, равен силе тяжести.
б)лифт движется с постоянным ускорением а, направленным вверх.(рис.88). Запишем второй закон Ньютона через проекции сил на ось Y:
ma =- mg + N2., тогда P2=N2 = m(g+а)
В этом случае вес больше, чем гравитационная сила. Количественно возрастание веса характеризуется коэффициентом перегрузки, определяемым отношением ускорения тела к ускорению свободного падения.
в) лифт движется с постоянным ускорением а, направленным вниз. В этом случае удобно выбрать ось У, направленную вниз.
Запишем второй закон Ньютона через проекции сил на ось Y:
ma = mg – N3. , тогда P3=N3 = m(g-а),т.е. вес тела меньше силы тяжести.
, тогда P3=N3 = m(g-а),т.е. вес тела меньше силы тяжести.
При свободном падении .Вес при этом становится равным нулю, т.е. возникает состояние невесомости.
Невесомость – состояние, при котором тело движется только под действием силы тяжести.
2)Скольжение тела по горизонтальной поверхности. Найдем ускорение и вес тела массой
т,движущегося по поверхности стола, под действием силы F, направленной под углом а к
горизонтали. Коэффициент трения скольжения между телом и поверхностью стола равен .
Решение.
На тело действуют сила тяжести mg, сила реакции опоры N, сила F и сила трения Fтр , направленная противоположно скорости движения.
Второй закон Ньютона в векторной форме имеет вид
ma = mg + N + F + FTp.
Направим ось X вдоль ускорения а, а ось У вертикально. Спроецируем уравнение на оси Х и У.
ma=0+0+Fcosα-Fтр (на ось Х)
0=- mg+N+ Fsinα+0 (на ось У) согласно равенству
Подставляя выражение для силы трения в первое уравнение системы , получаем систему двух уравнений с двумя неизвестными N и а:
та = Fcos a- ,
О = -mg + N + Fsin a .
Из второго уравнения находим силу реакции опоры N и вес тела Р:
N = P = mg- Fsin a
Вес тела меньше силы тяжести, когда на тело кроме силы тяжести действуют силы, имеющие составляющую, направленную противоположно силе тяжести.
Вертикальная компонента внешней силы Fу (Fу = Fsin а) приподнимает тело и уменьшает силу давления на опору, а следовательно, и силу трения. Аналогично, сила сопротивления движению корабля на воздушной подушке меньше подобной силы для обычных кораблей за счет подъемной силы, приподнимающей корабль из воды. на тело: силу тяжести mg, силу реакции опоры N и силу трения F , направленную противоположно скорости движения.
на тело: силу тяжести mg, силу реакции опоры N и силу трения F , направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме:
ma = mg + N + FTp.
Выберем ось X параллельно и ось Y перпендикулярно наклонной плоскости.
Спроецируем уравнение на координатные оси X и Y:
та = mg sin a – FTp (на ось X),
0 = N – mgcos а (на ось Y).
Используя выражение для силы трения FTp = и подставляя его в первое уравнение системы получаем систему двух уравнений с двумя неизвестными:
та = mgsin a – FTp (77)
0 = N – mgcos а.
Из второго уравнения находим силу реакции опоры N и соответственно вес тела Р:
N = Р = mgcos a.
Вес тела на наклонной опоре меньше силы тяжести.
Подставляя выражение для силы реакции опоры в первое уравнение системы
та = mgsin a – μmgcos a ,
находим ускорение тела
а = g(sim. а – μmgcos a ).
а – μmgcos a ).
Соскальзывание тела с наклонной плоскости происходит, если а > О, т.е. если коэффициент трения скольжения μ < tg a. Если μ> tg a, тело покоится на наклонной плоскости.
III.Закрепление изученного материала Беседа по вопрсам.
При каком движении лифта вес тела, находящегося в нем, равен силе тяжести; больше силы тяжести; меньше силы тяжести; равен нулю?
Вес тела равен силе тяжести при равномерном (относительно Земли) движении лифта или его покое. Он больше силы тяжести, если ускорение лифта направлено вверх (ускоренное движение лифта вверх, замедленное – вниз).Он меньше силы тяжести, если ускорение лифта направлено вниз(замедленное движение лифта вверх, ускоренное – вниз). Вес тела равен нулю(невесомость),если лифт свободно падает.
Какой способ перемещения холодильника по полу требует меньших усилий — когда его толкают или когда тянут? Когда холодильник толкают, направив силу под тупым углом к скорости его движения, приложенная сила увеличивает прижим холодильника к полу, его вес и сила трения возрастают. Когда холодильник тянут за собой ( сила направлена под острым углом к скорости ), прижим холодильника к полу и сила трения уменьшаются. Тянуть легче, чем толкать.
Когда холодильник тянут за собой ( сила направлена под острым углом к скорости ), прижим холодильника к полу и сила трения уменьшаются. Тянуть легче, чем толкать.
3.Какие часы следует использовать в условиях невесомости: маятниковые, песочные, пружинные? В таких условиях работать будут только пружинные часы.IV. Итог урока. Сегодня на уроке мы познакомились с алгоритмом решения задач на основной закон динамики.
Домашнее задание. §25,задачи № 1,2 к §25
Второй закон движения Ньютона – проблемы и решения
Решенные задачи в законах движения Ньютона – второй закон движения Ньютона
1. Объект весом 1 кг ускоряется с постоянной скоростью 5 м / с 2 . Оцените чистую силу, необходимую для ускорения объекта.
Известный:
Масса (м) = 1 кг
Ускорение (а) = 5 м / с 2
Требуется : чистая сила (∑F)
Решение:
Мы используем второй закон Ньютона, чтобы получить чистую силу.
∑F = м а
∑F = (1 кг) (5 м / с 2 ) = 5 кг м / с 2 = 5 Ньютон
2. Масса объекта = 1 кг, полезная сила ∑F = 2 Ньютона. Определите величину и направление ускорения объекта….
Известный:
Масса (м) = 1 кг
Чистая сила (∑F) = 2 Ньютона
Разыскивается : Величина и направление ускорения (а)
Решение:
a = F / м
а = 2/1
a = 2 м / с 2
Направление ускорения = направление чистой силы (∑F)
3.Масса объекта = 2 кг, F 1 = 5 Ньютон, F 2 = 3 Ньютона. Величина и направление ускорения…
Известный:
Масса (м) = 2 кг
F 1 = 5 Ньютон
F 2 = 3 Ньютона
Разыскиваются: Величина и направление ускорения (а)
Решение:
чистая сила:
∑F = F 1 – F 2 = 5 – 3 = 2 Ньютона
Величина ускорения:
a = F / м
а = 2/2
a = 1 м / с 2
Направление ускорения = направление чистой силы = направление F 1
4. Масса объекта = 2 кг, F 1 = 10 Ньютон, F 2 = 1 Ньютон. Величина и направление ускорения…
Масса объекта = 2 кг, F 1 = 10 Ньютон, F 2 = 1 Ньютон. Величина и направление ускорения…
Известный:
Масса (м) = 2 кг
F 2 = 1 Ньютон
F 1 = 10 Ньютон
F 1x = F 1 cos 60 o = (10) (0,5) = 5 Ньютон
Разыскивается : Величина и направление ускорения (а)
Решение:
Сила нетто:
∑F = F 1x – F 2 = 5 – 1 = 4 Ньютон
Величина ускорения:
a = F / м
а = 4/2
a = 2 м / с 2
Направление ускорения = направление чистой силы = направление F 1x
5. F 1 = 10 Ньютон, F 2 = 1 Ньютон, м 1 = 1 кг, м 2 = 2 кг. Величина и направление ускорения…
F 1 = 10 Ньютон, F 2 = 1 Ньютон, м 1 = 1 кг, м 2 = 2 кг. Величина и направление ускорения…
Известный:
Масса 1 (м 1 ) = 1 кг
Масса 2 (м 2 ) = 2 кг
F 1 = 10 Ньютон
F 2 = 1 Ньютон
Разыскивается : Величина и направление ускорения (а)
Решение:
Чистая сила:
∑F = F 1 – F 2 = 10 – 1 = 9 Ньютон
Величина ускорения:
a = ∑F / (м 1 + м 2 )
а = 9 / (1 + 2)
а = 9/3
a = 3 м / с 2
Направление ускорения = направление чистой силы = направление F 1
6.
Блок массой 40 кг, ускоряемый силой 200 Н. Ускорение блока 3 м / с 2 . Определите величину силы трения, испытываемой блоком.
А. 15 Н
Б. 40 N
C. 43 N
Д. 80 Н
Известный:
Масса (м) = 40 кг
Сила (F) = 200 Н
Ускорение (а) = 3 м / с 2
Требуется: Сила трения (F г )
Решение:
Уравнение второго закона движения Ньютона
∑F = м а
∑ F = полезная сила, m = масса, a = ускорение
Направление силы F вправо, направление силы трения влево (направление силы трения противоположно направлению движения объекта).
Выберите «вправо» как положительное, а «влево как отрицательное».
∑F = м а
F – F г = m a
200 – F г = (40) (3)
200 – F г = 120
F г = 200 – 120
F г = 80 Ньютон
Правильный ответ – D.
7. Блок A массой 100 грамм помещают над блоком B массой 300 грамм, а затем блок b толкают с силой 5 Н вертикально вверх.Определите нормальную силу, прилагаемую блоком B к блоку A.
А. 1 Н
Б. 1.25 N
C. 2 N
Д. 3 Н
Известный:
Сила (F) = 5 Ньютон
Масса блока A (м A ) = 100 грамм = 0,1 кг
Масса блока B (м B ) = 300 грамм = 0,3 кг
Ускорение свободного падения (g) = 10 м / с 2
Вес блока A (w A ) = (0,1 кг) (10 м / с 2 ) = 1 кг м / с 2 = 1 Ньютон
Вес блока B (w B ) = (0. 3 кг) (10 м / с 2 ) = 3 кг м / с 2 = 3 Ньютона
3 кг) (10 м / с 2 ) = 3 кг м / с 2 = 3 Ньютона
Разыскивается: Нормальная сила, прилагаемая блоком B к блоку A
Решение:
На оба блока действуют несколько сил, как показано на рисунке.
F = толкающая сила (действует на блок B)
w A = вес блока A (действует на блок A)
w B = вес блока B (действует на блок B)
Н A = нормальная сила, прилагаемая блоком B к блоку A (действие на блок A)
Н A ’= нормальная сила, прилагаемая блоком A к блоку B (действие на блок B)
Примените второй закон движения Ньютона к обоим блокам:
∑F = м а
F – w A – w B + N A – N A ’= (m A + m B ) a
N A и N A ’- это силы действия-противодействия, которые имеют одинаковую величину, но противоположны по направлению, поэтому исключаются из уравнения.
F – w A – w B = (m A + m B ) a
5 – 1 – 3 = (0,1 + 0,3) а
5–4 = (0,4) а
1 = (0,4) а
а = 1 / 0,4
a = 2,5 м / с 2
Примените второй закон движения Ньютона к блоку A:
∑F = м а
N A – w A = m A a
N A – 1 = (0,1) (2,5)
N A – 1 = 0.25
N A = 1 + 0,25
Н A = 1,25 Ньютона
Правильный ответ – Б.
8. Предмет весом 4 Н, поддерживаемый шнуром и шкивом. На блок действует сила 2 Н, и один конец шнура натягивается силой 9 Н. Определите результирующую силу, действующую на объект X.
A. 3 N вверх
Б. 4 Н вниз
C. 9 N вверх
Д. 9 Н вниз
Известный:
Вес X (w X ) = 4 Ньютона
Сила тяги (F x ) = 2 Ньютона
Сила натяжения (F T ) = 9 Ньютон
Разыскивается: Чистая сила действует на объект X
Решение:
Силы, направленные вертикально вверх, действующие на объект X:
Сила натяжения одинакова по всей длине шнура.Таким образом, сила натяжения составляет 9 Н.
Силы, направленные вертикально вниз, действующие на объект X:
На объект X действуют две силы, и обе силы направлены вертикально вниз: горизонтальная составляющая веса w x и горизонтальная составляющая силы F x .
Чистое усилие, действующее на объект X:
F T – w X – F x = 9 – 4 – 2 = 9 – 6 = 3
Чистая сила, действующая на объект X, составляет 3 Ньютона вертикально вверх.
Правильный ответ – А.
9. Объект, изначально покоящийся на гладкой горизонтальной поверхности. На объект действует сила 16 Н, поэтому объект ускоряется со скоростью 2 м / с 2 . Если тот же объект покоится на шероховатой горизонтальной поверхности, поэтому сила трения, действующая на объект, составляет 2 Н, тогда определите ускорение объекта, если на объект действует такая же сила 16 Н.
A. 1,75 м / с 2
Б. 1,50 м / с 2
С. 1.00 м / с 2
D. 0,88 м / с 2
Известный:
Сила (F) = 16 Ньютон = 16 кг м / с 2
Ускорение (а) = 2 м / с 2
Сила трения (F fric ) = 2 Ньютона = 2 кг м / с 2
Разыскивается: Ускорение объекта?
Решение:
Гладкая горизонтальная поверхность (без силы трения):
∑F = м а
F = m а
16 = (м) 2
м = 16/2
м = 8 кг
Масса объекта 8 килограмм.
Шероховатая горизонтальная поверхность (есть сила трения):
∑F = м а
F – F fric = m a
16–2 = 8 а
14 = 8 а
а = 14/8
a = 1,75 м / с 2
Ускорение объекта 1,75 м / с 2 .
Правильный ответ – А.
10. Том и Эндрю толкают предмет о гладкий пол. Том толкает объект с силой 5,70 Н. Если масса объекта 2.00 кг и ускорение, испытываемое объектом, составляет 2,00 мс –2 , затем Том определяет величину и направление действия силы.
A. 1.70 N и его направление противоположно с силой, действующей Andre.w
B. 1,70 Н и его направление такое же, как и сила, действующая по Эндрю
C. 2.30 N и его направление противоположно силе Андрея.
D. 2.30 Н и его направление такое же, как сила, действующая Эндрю.
Известный:
Сила толчка, действующая по Эндрю (F 1 ) = 5.70 Ньютон
Масса объекта (м) = 2,00 кг
Ускорение (а) = 2,00 м / с 2
Разыскивается: Величина и направление силы, которую действует Том (F 2 )?
Решение:
Примените второй закон движения Ньютона:
∑F = м а
F 1 + F 2 = m a
5,70 + Ф 2 = (2) (2)
5,70 + F 2 = 4
F 2 = 4-5.70
F 2 = – 1,7 Ньютон
Знак минус указывает на то, что (F 2 ) противоположно действию толкающей силы Эндрю (F 1 ).
Правильный ответ – А.
11. Если масса блока одинакова, на каком цифре указано наименьшее ускорение?
Решение
Чистая сила A:
ΣF = 4 N + 2 N – 3 N = 6 N – 3 N = 3 Ньютон, влево
Чистая сила B:
ΣF = 2 N + 3 N – 4 N = 5 N – 4 N = 1 Ньютон, вправо
Чистая сила C:
ΣF = 4 N + 3 N – 2 N = 7 N – 2 N = 5 Ньютон, вправо
Чистая сила D:
ΣF = 3 N + 4 N + 2 N = 9 Ньютон, вправо
Уравнение второго закона Ньютона:
ΣF = м а
а = ΣF / м
a = ускорение, ΣF = полезная сила, m = масса
Согласно приведенной выше формуле, ускорение (a) прямо пропорционально чистой силе (ΣF) и обратно пропорционально массе (m). Если масса объекта одинакова, чем больше результирующая сила, чем больше ускорение, или чем меньше результирующая сила, тем меньше ускорение.
Если масса объекта одинакова, чем больше результирующая сила, чем больше ускорение, или чем меньше результирующая сила, тем меньше ускорение.
На основании приведенных выше расчетов наименьшая полезная сила составляет 1 Ньютон, поэтому ускорение также наименьшее.
Правильный ответ – Б.
12. Некоторые силы действуют на объект массой 20 кг, как показано на рисунке ниже.
Определите ускорение объекта.
Известный:
Масса объекта (м) = 20 кг
Сила полезного действия (ΣF) = 25 Н + 30 Н – 15 Н = 40 Н
Разыскивается: Разгон объекта
Решение:
Ускорение объекта, рассчитанное по уравнению второго закона Ньютона:
ΣF = м а
a = ΣF / м = 40 Н / 20 кг = 2 Н / кг = 2 м / с 2
13. Какие утверждения ниже описывают третий закон Ньютона?
Какие утверждения ниже описывают третий закон Ньютона?
(1) Пассажиры толкнулись вперед, когда автобус внезапно затормозил
(2) Книги на бумаге не падают при быстром вытягивании бумаги
(3) При игре на скейтборде, когда ступня отталкивает землю назад, скейтборд скользит вперед
(4) Весла отведены назад, лодки движутся вперед
Решение:
(1) Первый закон Ньютона
(2) Первый закон Ньютона
(3) Третий закон Ньютона
(4) Третий закон Ньютона
[wpdm_package id = ’470 ′]
- Масса и вес
- Нормальная сила
- Второй закон движения Ньютона
- Сила трения
- Движение по горизонтальной поверхности без силы трения
- Движение двух тел с одинаковым ускорением по шероховатой горизонтальной поверхности с силой трения
- Движение по наклонной плоскости без силы трения
- Движение по шероховатой наклонной плоскости с силой трения
- Движение в лифте
- Движение тел, соединенных шнуром и шкивом
- Два тела с одинаковой величиной ускорения
- Округление плоской кривой – динамика кругового движения
- Скругление кривой с наклоном – динамика кругового движения
- Равномерное движение по горизонтальной окружности
- Центростремительная сила при равномерном круговом движении
6.
 2: Решение проблем с помощью законов Ньютона (Часть 1)
2: Решение проблем с помощью законов Ньютона (Часть 1)Успех в решении проблем необходим для понимания и применения физических принципов. Мы разработали схему анализа и поиска решений проблем, связанных с законами Ньютона в законах движения Ньютона; В этой главе мы продолжаем обсуждение этих стратегий и применяем пошаговый процесс.
Стратегии решения проблем
Здесь мы следуем основам решения проблем, представленных ранее в этом тексте, но мы подчеркиваем конкретные стратегии, которые полезны при применении законов движения Ньютона.Как только вы определите физические принципы, вовлеченные в проблему, и определите, что они включают в себя законы движения Ньютона, вы можете применить эти шаги, чтобы найти решение. Эти методы также укрепляют концепции, которые полезны во многих других областях физики. Многие стратегии решения проблем прямо изложены в рабочих примерах, поэтому следующие методы должны укрепить навыки, которые вы уже начали развивать.
Стратегия решения проблем: применение законов движения Ньютона
- Определите задействованные физические принципы, перечислив данные и вычисляемые количества.

- Обрисуйте ситуацию, используя стрелки для обозначения всех сил.
- Определите интересующую систему. Результатом является диаграмма свободного тела, необходимая для решения проблемы.
- Примените второй закон Ньютона для решения проблемы. При необходимости примените соответствующие кинематические уравнения из главы о движении по прямой.
- Проверьте решение, чтобы узнать, разумно ли оно.
Давайте применим эту стратегию решения проблем к задаче переноса рояля в квартиру на втором этаже.Как только мы определили, что здесь задействованы законы движения Ньютона (если проблема связана с силами), особенно важно нарисовать тщательный набросок ситуации. Такой эскиз показан на рисунке \ (\ PageIndex {1a} \). Затем, как показано на рисунке \ (\ PageIndex {1b} \), мы можем изобразить все силы стрелками. Когда имеется достаточно информации, лучше всего тщательно обозначить эти стрелки и сделать так, чтобы длина и направление каждой соответствовали представленной силе.
Рисунок \ (\ PageIndex {1} \): (a) Рояль переносят в квартиру на втором этаже.(b) Стрелки используются для обозначения всех сил: \ (\ vec {T} \) – это натяжение веревки над фортепиано, \ (\ vec {F} _ {T} \) – это сила, которую оказывает фортепиано. на веревке, а \ (\ vec {w} \) – вес пианино. Предполагается, что все другие силы, такие как ветер, пренебрежимо мал. (c) Предположим, нам дана масса фортепиано и просят определить натяжение веревки. Затем мы определяем интересующую систему, как показано, и рисуем диаграмму свободного тела. Теперь \ (\ vec {F} _ {T} \) больше не отображается, потому что это не сила, действующая на интересующую систему; скорее \ (\ vec {F} _ {T} \) действует во внешнем мире.(d) Показаны только стрелки, используется метод сложения “голова к хвосту”. Очевидно, что если пианино неподвижно, \ (\ vec {T} \) = \ (- \ vec {w} \).
Как и в случае с большинством проблем, теперь нам нужно определить, что необходимо определить и что известно или можно сделать вывод из указанной проблемы, то есть составить список известных и неизвестных. Особенно важно определить интересующую систему, поскольку второй закон Ньютона включает только внешние силы. Затем мы можем определить, какие силы являются внешними, а какие – внутренними, что является необходимым шагом для применения второго закона Ньютона.(См. Рисунок \ (\ PageIndex {1c} \).) Третий закон Ньютона можно использовать для определения того, действуют ли силы между компонентами системы (внутренними) или между системой и чем-то внешним (внешним). Как показано в законах движения Ньютона, интересующая нас система зависит от вопроса, на который нам нужно ответить. На диаграммах свободного тела показаны только силы, а не ускорение или скорость. В предыдущих рабочих примерах мы нарисовали несколько диаграмм свободного тела. На рисунке \ (\ PageIndex {1c} \) показана диаграмма свободного тела для интересующей системы.Обратите внимание, что на диаграмме свободного тела не показаны внутренние силы.
Особенно важно определить интересующую систему, поскольку второй закон Ньютона включает только внешние силы. Затем мы можем определить, какие силы являются внешними, а какие – внутренними, что является необходимым шагом для применения второго закона Ньютона.(См. Рисунок \ (\ PageIndex {1c} \).) Третий закон Ньютона можно использовать для определения того, действуют ли силы между компонентами системы (внутренними) или между системой и чем-то внешним (внешним). Как показано в законах движения Ньютона, интересующая нас система зависит от вопроса, на который нам нужно ответить. На диаграммах свободного тела показаны только силы, а не ускорение или скорость. В предыдущих рабочих примерах мы нарисовали несколько диаграмм свободного тела. На рисунке \ (\ PageIndex {1c} \) показана диаграмма свободного тела для интересующей системы.Обратите внимание, что на диаграмме свободного тела не показаны внутренние силы.
Когда диаграмма свободного тела построена, мы применяем второй закон Ньютона. Это сделано на рисунке \ (\ PageIndex {1d} \) для конкретной ситуации. В общем, как только внешние силы четко определены на диаграммах свободного тела, должно быть несложной задачей их преобразование в форму уравнения и решение неизвестного, как это было сделано во всех предыдущих примерах. Если проблема одномерная, то есть если все силы параллельны, то с этими силами можно обращаться алгебраически.Если проблема двумерная, то ее необходимо разбить на пару одномерных задач. Мы делаем это, проецируя векторы сил на набор осей, выбранных для удобства. Как видно из предыдущих примеров, выбор осей может упростить задачу. Например, когда речь идет о наклоне, наиболее удобен набор осей, одна из которых параллельна наклону, а другая – перпендикулярна ему. Почти всегда удобно делать одну ось параллельной направлению движения, если это известно.Как правило, просто запишите второй закон Ньютона в компонентах, расположенных в разных направлениях. Тогда у вас есть следующие уравнения:
\ [\ sum F_ {x} = m a_ {x}, \ quad \ sum F_ {y} = m a_ {y} \ ldotp \]
(Если, например, система ускоряется по горизонтали, тогда вы можете установить ay = 0. ) Эта информация нужна нам для определения неизвестных сил, действующих на систему.
) Эта информация нужна нам для определения неизвестных сил, действующих на систему.
Как всегда, надо проверить решение. В некоторых случаях легко определить, является ли решение разумным.Например, разумно обнаружить, что трение заставляет объект скользить по склону медленнее, чем при отсутствии трения. На практике интуиция развивается постепенно через решение проблем; с опытом становится все легче судить о разумности ответа. Еще один способ проверить решение – проверить единицы. Если мы вычисляем силу и получаем единицы миллиметров в секунду, то мы совершили ошибку.
Есть много интересных приложений законов движения Ньютона, некоторые из которых представлены в этом разделе.Они также служат для иллюстрации некоторых тонкостей физики и помогают развить навыки решения проблем. Сначала мы рассмотрим проблемы, связанные с равновесием частиц, которые используют первый закон Ньютона, а затем рассмотрим ускорение частиц, которое включает второй закон Ньютона.
Равновесие частиц
Напомним, что частица в равновесии – это та частица, для которой внешние силы уравновешены. Статическое равновесие включает объекты в покое, а динамическое равновесие включает объекты, движущиеся без ускорения, но важно помнить, что эти условия относительны.Например, объект может находиться в состоянии покоя, если смотреть из нашей системы отсчета, но этот же объект будет казаться движущимся, если его увидит кто-то, движущийся с постоянной скоростью. Теперь мы используем знания, полученные в законах движения Ньютона, относительно различных типов сил и использования диаграмм свободного тела, чтобы решить дополнительные проблемы равновесия частиц.
Статическое равновесие включает объекты в покое, а динамическое равновесие включает объекты, движущиеся без ускорения, но важно помнить, что эти условия относительны.Например, объект может находиться в состоянии покоя, если смотреть из нашей системы отсчета, но этот же объект будет казаться движущимся, если его увидит кто-то, движущийся с постоянной скоростью. Теперь мы используем знания, полученные в законах движения Ньютона, относительно различных типов сил и использования диаграмм свободного тела, чтобы решить дополнительные проблемы равновесия частиц.
Пример 6.1: Различное натяжение под разными углами
Рассмотрим светофор (масса 15.0 кг) подвешен на двух тросах, как показано на рисунке \ (\ PageIndex {2} \). Найдите натяжение в каждой проволоке, не обращая внимания на массу проволоки.
Рисунок \ (\ PageIndex {2} \): Светофор подвешен на двух тросах. (б) Некоторые из задействованных сил. (c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную (y) и горизонтальную (x) оси. Горизонтальные составляющие натяжения должны нейтрализоваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора.(e) Схема свободного тела показывает вертикальные и горизонтальные силы, действующие на светофор.
(c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную (y) и горизонтальную (x) оси. Горизонтальные составляющие натяжения должны нейтрализоваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора.(e) Схема свободного тела показывает вертикальные и горизонтальные силы, действующие на светофор.
Стратегия
Интересующая нас система – это светофор, диаграмма которого в виде свободного тела показана на рисунке \ (\ PageIndex {2c} \). Эти три задействованные силы не параллельны, поэтому они должны быть спроецированы в систему координат. Наиболее удобная система координат имеет одну ось вертикальную и одну горизонтальную, а проекции вектора на нее показаны на рисунке \ (\ PageIndex {2d} \).В этой задаче есть два неизвестных (T 1 и T 2 ), поэтому для их поиска необходимы два уравнения. Эти два уравнения получены в результате применения второго закона Ньютона вдоль вертикальной и горизонтальной осей с учетом того, что чистая внешняя сила равна нулю вдоль каждой оси, потому что ускорение равно нулю. {o} = w \ ldotp \]
{o} = w \ ldotp \]
В этом уравнении есть два неизвестных, но замена выражения для T 2 на T 1 сводит его к одному уравнению с одним неизвестным:
\ [T_ {1} (0.{2}) \ ldotp \]
Решение этого последнего уравнения дает величину T 1 равную
.\ [T_ {1} = 108 \; N \ ldotp \]
Наконец, мы находим величину T 2 , используя соотношение между ними: T 2 = 1,225 T 1 , найденное выше. Таким образом, получаем
\ [T_ {2} = 132 \; N \ ldotp \]
Значение
Оба натяжения были бы больше, если бы оба троса были более горизонтальными, и они были бы равными тогда и только тогда, когда углы с обеих сторон одинаковы (как они были в более раннем примере канатоходца в Законе движения Ньютона.
Пример 6.2: Сила сопротивления на барже
Два буксира толкают баржу под разными углами (рис. \ (\ PageIndex {3} \)). Первый буксир прикладывает силу 2,7 x 10 5 Н в направлении оси x, а второй буксир оказывает усилие 3,6 x 10 5 Н в направлении оси y. Масса баржи составляет 5,0 × 106 кг, а ее ускорение составляет 7,5 × 10 −2 м / с 2 в указанном направлении. Какова сила сопротивления воды барже, сопротивляющейся движению? ( Примечание : Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода.Сила сопротивления препятствует движению объекта. Поскольку баржа имеет плоское дно, можно предположить, что сила сопротивления направлена в направлении, противоположном движению баржи.)
Масса баржи составляет 5,0 × 106 кг, а ее ускорение составляет 7,5 × 10 −2 м / с 2 в указанном направлении. Какова сила сопротивления воды барже, сопротивляющейся движению? ( Примечание : Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода.Сила сопротивления препятствует движению объекта. Поскольку баржа имеет плоское дно, можно предположить, что сила сопротивления направлена в направлении, противоположном движению баржи.)
Рисунок \ (\ PageIndex {3} \): (a) Вид сверху на два буксира, толкающих баржу. (b) Схема свободного тела для корабля содержит только силы, действующие в плоскости воды. В нем не учитываются две вертикальные силы – вес баржи и выталкивающая сила поддерживающей ее воды, которые компенсируются и не показаны.Обратите внимание, что \ (\ vec {F} _ {app} \) – это общая приложенная сила буксиров.
Стратегия
Направления и значения ускорения и приложенных сил показаны на рисунке \ (\ PageIndex {3a} \). Мы определяем общую силу буксиров на барже как \ (\ vec {F} _ {app} \), так что
Мы определяем общую силу буксиров на барже как \ (\ vec {F} _ {app} \), так что
\ [\ vec {F} _ {app} = \ vec {F} _ {1} + \ vec {F} _ {2} \ ldotp \]
Сопротивление воды \ (\ vec {F} _ {D} \) происходит в направлении, противоположном направлению движения лодки; эта сила, таким образом, действует против \ (\ vec {F} _ {app} \), как показано на диаграмме свободного тела на рисунке \ (\ PageIndex {3b} \).Здесь представляет интерес система баржа, так как на нее действуют силы, а также ее ускорение. Поскольку приложенные силы перпендикулярны, оси x и y имеют то же направление, что и \ (\ vec {F} _ {1} \) и \ (\ vec {F} _ {2} \). Проблема быстро становится одномерной проблемой в направлении \ (\ vec {F} _ {app} \), поскольку трение происходит в направлении, противоположном \ (\ vec {F} _ {app} \). Наша стратегия состоит в том, чтобы найти величину и направление чистой приложенной силы \ (\ vec {F} _ {app} \), а затем применить второй закон Ньютона для определения силы сопротивления \ (\ vec {F} _ {D} \). {o} \ ldotp \]
{o} \ ldotp \]
Из первого закона Ньютона мы знаем, что это то же направление, что и ускорение. Мы также знаем, что \ (\ vec {F} _ {D} \) находится в направлении, противоположном \ (\ vec {F} _ {app} \), поскольку он замедляет ускорение. Следовательно, чистая внешняя сила имеет то же направление, что и \ (\ vec {F} _ {app} \), но ее величина немного меньше, чем \ (\ vec {F} _ {app} \). Проблема теперь одномерная. Из диаграммы свободного тела видно, что
\ [F_ {net} = F_ {app} – F_ {D} \ ldotp \]
Однако второй закон Ньютона утверждает, что
\ [F_ {net} = ma \ ldotp \]
Таким образом,
\ [F_ {app} – F_ {D} = ma \ ldotp \]
Это может быть решено для величины силы сопротивления воды F D в терминах известных величин:
\ [F_ {D} = F_ {app} – ma \ ldotp \]
Подстановка известных значений дает
\ [F_ {D} = (4.{4} \; N \ ldotp \]
Направление \ (\ vec {F} _ {D} \) уже было определено как направление, противоположное \ (\ vec {F} _ {app} \), или под углом 53 ° к югу. запада.
запада.
Значение
Числа, использованные в этом примере, подходят для баржи среднего размера. Конечно, трудно добиться большего ускорения с буксирными судами, и желательна небольшая скорость, чтобы баржа не врезалась в доки. Сопротивление относительно мало для хорошо спроектированного корпуса на низких скоростях, что соответствует ответу на этот пример, где F D составляет менее 1/600 веса корабля.
В «Законах движения» Ньютона мы обсуждали нормальную силу, которая представляет собой контактную силу, действующую перпендикулярно поверхности, так что объект не имеет ускорения, перпендикулярного поверхности. Весы для ванной – отличный пример нормальной силы, действующей на тело. Он обеспечивает количественное определение того, насколько он должен подтолкнуться вверх, чтобы выдержать вес объекта. Но можете ли вы предсказать, что бы вы увидели на шкале весов для ванной, если бы стояли на них во время поездки на лифте?
Увидите ли вы значение, превышающее ваш вес, когда лифт пойдет? А что насчет того, когда лифт движется вверх с постоянной скоростью? Сделайте предположение, прежде чем читать следующий пример.
Пример 6.3: Что показывают весы в лифте?
На рисунке \ (\ PageIndex {4} \) показан мужчина весом 75,0 кг (около 165 фунтов), стоящий на весах в лифте. Рассчитайте показание шкалы: (а) если лифт ускоряется вверх со скоростью 1,20 м / с 2 , и (б) если лифт движется вверх с постоянной скоростью 1 м / с.
Рисунок \ (\ PageIndex {4} \): (a) Различные силы, действующие, когда человек стоит на весах в лифте.Стрелки приблизительно соответствуют тому, когда лифт ускоряется вверх – пунктирные стрелки обозначают силы, слишком большие для масштабирования. \ (\ vec {T} \) – натяжение поддерживающего троса, \ (\ vec {w} \) – вес человека, \ (\ vec {w} _ {s} \) – вес весы, \ (\ vec {w} _ {e} \) – вес лифта, \ (\ vec {F} _ {s} \) – сила весов, воздействующая на человека, \ (\ vec {F} _ {p} \) – сила человека на весах, \ (\ vec {F} _ {t} \) – сила весов на полу лифта, а \ (\ vec {N} \) – сила пола, направленная вверх по шкале.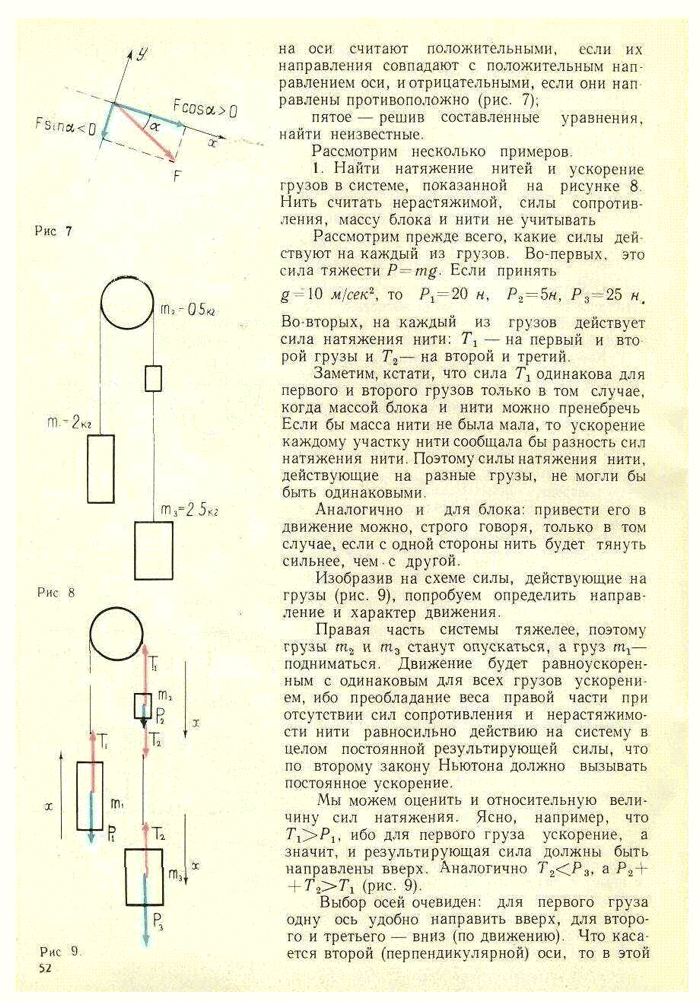 (б) Диаграмма свободного тела показывает только внешние силы, действующие на обозначенную интересующую систему – человека, и является диаграммой, которую мы используем для решения проблемы.
(б) Диаграмма свободного тела показывает только внешние силы, действующие на обозначенную интересующую систему – человека, и является диаграммой, которую мы используем для решения проблемы.
Стратегия
Если весы в состоянии покоя точны, их показание равно \ (\ vec {F} _ {p} \), величине силы, которую человек прикладывает к ним вниз. На рисунке \ (\ PageIndex {4a} \) показаны многочисленные силы, действующие на лифт, весы и человека. Это заставляет эту одномерную проблему выглядеть гораздо более грозной, чем если бы человек был выбран в качестве представляющей интерес системы и нарисована диаграмма свободного тела, как на рисунке \ (\ PageIndex {4b} \).Анализ диаграммы свободного тела с использованием законов Ньютона может дать ответы на оба рисунка \ (\ PageIndex {4a} \) и (b) этого примера, а также на некоторые другие вопросы, которые могут возникнуть. Единственные силы, действующие на человека, – это его вес \ (\ vec {w} \) и восходящая сила весов \ (\ vec {F} _ {s} \). Согласно третьему закону Ньютона, \ (\ vec {F} _ {p} \) и \ (\ vec {F} _ {s} \) равны по величине и противоположны по направлению, так что нам нужно найти F s , чтобы узнать, что показывает шкала. Мы можем сделать это, как обычно, применив второй закон Ньютона,
Согласно третьему закону Ньютона, \ (\ vec {F} _ {p} \) и \ (\ vec {F} _ {s} \) равны по величине и противоположны по направлению, так что нам нужно найти F s , чтобы узнать, что показывает шкала. Мы можем сделать это, как обычно, применив второй закон Ньютона,
\ [\ vec {F} _ {net} = m \ vec {a} \ ldotp \]
Из диаграммы свободного тела мы видим, что \ (\ vec {F} _ {net} = \ vec {F} _ {s} – \ vec {w} \), поэтому мы имеем
\ [F_ {s} – w = ma \ ldotp \]
Решение для F s дает нам уравнение только с одним неизвестным:
\ [F_ {s} = ma + w, \]
или, поскольку w = mg, просто
\ [F_ {s} = ma + mg \ ldotp \]
Никаких предположений об ускорении не делалось, поэтому это решение должно быть действительным для множества ускорений в дополнение к тем, которые используются в данной ситуации.{2}) = 735 \; N \ ldotp \]
Таким образом, показание весов в лифте больше, чем его вес 735-Н (165 фунтов).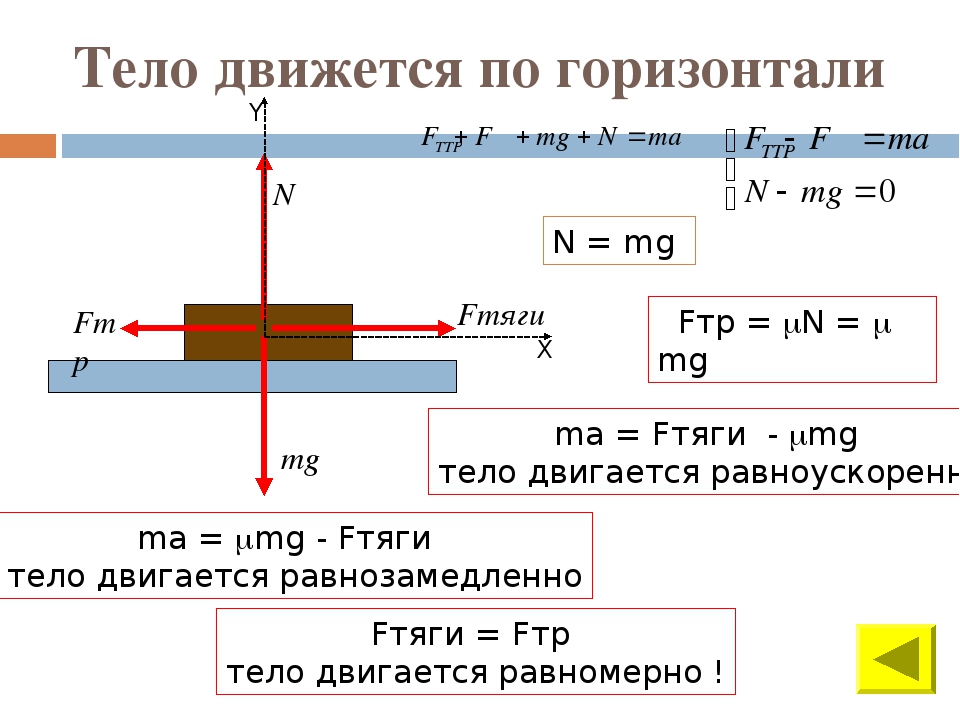 Это означает, что весы толкают человека вверх с силой, превышающей его вес, что необходимо для ускорения его движения вверх.
Это означает, что весы толкают человека вверх с силой, превышающей его вес, что необходимо для ускорения его движения вверх.
Очевидно, что чем больше ускорение лифта, тем больше показание шкалы, соответствующее тому, что вы чувствуете при быстром ускорении по сравнению с медленно ускоряющимся лифтом. На рисунке \ (\ PageIndex {4b} \) показание шкалы составляет 735 Н, что соответствует весу человека.Это случается, когда лифт имеет постоянную скорость – движется вверх, вниз или неподвижен.
Упражнение 6.1
Теперь рассчитайте показание шкалы, когда лифт ускоряется вниз со скоростью 1,20 м / с 2 .
Решение предыдущего примера также применимо к лифту, ускоряющемуся вниз, как уже упоминалось. Когда лифт ускоряется вниз, значение a отрицательное, и показание весов на меньше, чем на , чем вес человека.Если достигается постоянная скорость движения вниз, показания весов снова становятся равными весу человека. Если лифт находится в свободном падении и ускоряется вниз с ускорением g, то показание шкалы равно нулю, и человек кажется невесомым.
Пример 6.4: Два присоединенных блока
На рисунке \ (\ PageIndex {5} \) показан блок массой m 1 на горизонтальной поверхности без трения. Его натягивает легкая струна, проходящая через безмассовый шкив, не имеющий трения. Другой конец струны соединяется с блоком массой m 2 .Найдите ускорение блоков и натяжение струны в единицах m 1 , m 2 и g.
Рисунок \ (\ PageIndex {5} \): (a) Блок 1 соединен световой нитью с блоком 2. (b) Диаграммы свободного тела блоков.
Стратегия
Мы рисуем диаграмму свободного тела для каждой массы отдельно, как показано на рисунке \ (\ PageIndex {5} \). Затем мы анализируем каждую из них, чтобы найти необходимые неизвестные.Силы на блоке 1 – это сила тяжести, сила контакта поверхности и натяжение струны. На блок 2 действует сила тяжести и натяжение струны. Второй закон Ньютона применим к каждому из них, поэтому мы запишем два векторных уравнения:
Для блока 1: \ (\ vec {T} + \ vec {w} _ {1} + \ vec {N} = m_ {1} \ vec {a} _ {1} \)
Для блока 2: \ (\ vec {T} + \ vec {w} _ {2} = m_ {2} \ vec {a} _ {2} \).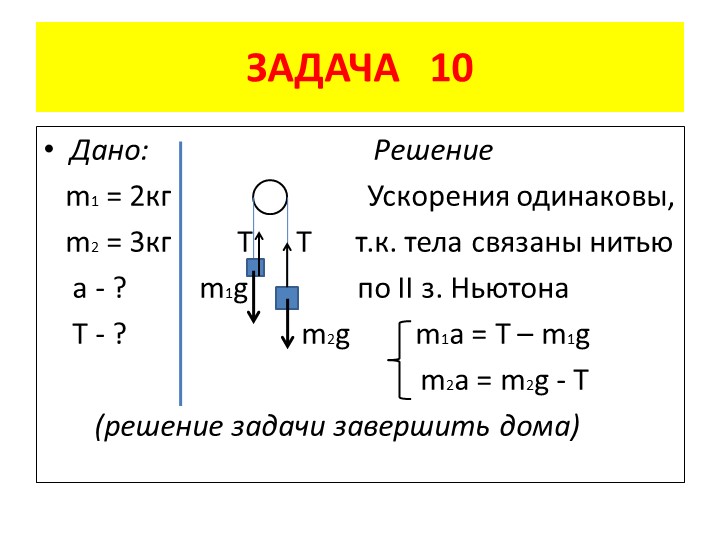
Обратите внимание, что \ (\ vec {T} \) одинаков для обоих блоков. Поскольку струна и шкив имеют незначительную массу и поскольку в шкиве нет трения, натяжение по всей струне одинаково.Теперь мы можем написать уравнения компонентов для каждого блока. Все силы либо горизонтальные, либо вертикальные, поэтому мы можем использовать одну и ту же горизонтальную / вертикальную систему координат для обоих объектов.
Решение
Компонентные уравнения следуют из векторных уравнений выше. Мы видим, что в блоке 1 вертикальные силы сбалансированы, поэтому мы игнорируем их и записываем уравнение, связывающее x-компоненты. На блоке 2 нет горизонтальных сил, поэтому записывается только y-уравнение. Получаем следующие результаты:
Блок 1 \ [\ sum F_ {x} = m a_ {x} \] \ [T_ {x} = m_ {1} a_ {1x} \] | Блок 2 \ [\ sum F_ {y} = m a_ {y} \] \ [T_ {y} – m_ {2} g = m_ {2} a_ {2y} \] |
Когда блок 1 перемещается вправо, блок 2 перемещается на равное расстояние вниз; таким образом, a 1x = −a 2y . Записав общее ускорение блоков как a = a 1x = −a 2y , мы теперь имеем
Записав общее ускорение блоков как a = a 1x = −a 2y , мы теперь имеем
\ [T = m_ {1} a \]
и
\ [Т – m_ {2} g = −m_ {2} a \ ldotp \]
Из этих двух уравнений мы можем выразить a и T через массы m 1 и m 2 , и g:
\ [a = \ frac {m_ {2}} {m_ {1} + m_ {2}} g \]
и
\ [T = \ frac {m_ {1} m_ {2}} {m_ {1} + m_ {2}} g \ ldotp \]
Значение
Обратите внимание, что натяжение тетивы меньше веса блока, свисающего с ее конца.Распространенной ошибкой в подобных задачах является установка T = m 2 g. Из диаграммы свободного тела блока 2 видно, что это не может быть правильным, если блок ускоряется.
Проверьте свое понимание 6.2
Вычислите ускорение системы и натяжение струны, когда массы m 1 = 5,00 кг и m 2 = 3,00 кг.
Пример 6.5: Машина Этвуда
Классическая физическая проблема, аналогичная той, которую мы только что решили, – это проблема машины Атвуда, которая состоит из веревки, проходящей через шкив, с двумя прикрепленными объектами разной массы. Это особенно полезно для понимания связи между силой и движением. На рисунке \ (\ PageIndex {6} \) m 1 = 2,00 кг и m 2 = 4,00 кг. Считайте, что шкив не имеет трения. а) Если выпустить m 2 , каким будет его разгон? б) Каково натяжение струны?
Это особенно полезно для понимания связи между силой и движением. На рисунке \ (\ PageIndex {6} \) m 1 = 2,00 кг и m 2 = 4,00 кг. Считайте, что шкив не имеет трения. а) Если выпустить m 2 , каким будет его разгон? б) Каково натяжение струны?
Рисунок \ (\ PageIndex {6} \): Машина Этвуда и диаграммы свободного тела для каждого из двух блоков.
Стратегия
Рисуем диаграмму свободного тела для каждой массы отдельно, как показано на рисунке. Затем мы анализируем каждую диаграмму, чтобы найти необходимые неизвестные. Это может включать решение одновременных уравнений. Также важно отметить сходство с предыдущим примером. Поскольку блок 2 ускоряется с ускорением a 2 в направлении вниз, блок 1 ускоряется вверх с ускорением a 1 . Таким образом, a = a 1 = −a 2 .
Решение
- У нас есть $$ For \; m_ {1}, \ sum F_ {y} = T – m_ {1} g = m_ {1} a \ ldotp \ quad Для \; m_ {2}, \ sum F_ {y} = T – m_ {2} g = −m_ {2} a \ ldotp $$ (Знак минус перед m 2 a означает, что m 2 ускоряется вниз ; оба блока ускоряются с одинаковой скоростью, но в противоположных направлениях.) Решите два уравнения одновременно (вычтите их), и результат будет $$ (m_ {2} – m_ {1}) g = (m_ {1} + m_ {2}) a \ ldotp $$ Решение для: $$ a = \ frac {m_ {2} – m_ {1}} {m_ {1} + m_ {2}} g = \ frac {4 \; кг – 2 \; кг} {4 \; кг + 2 \; кг} (9.{2}) = 26,1 \; N \ ldotp $$
Значение
Результат для ускорения, приведенный в решении, можно интерпретировать как отношение неуравновешенной силы, действующей на систему, (m 2 – m 1 ) g, к общей массе системы, m 1 + м 2 . Мы также можем использовать машину Атвуда для измерения локальной напряженности гравитационного поля.
Упражнение 6.3
Определите общую формулу в единицах m 1 , m 2 и g для расчета натяжения струны для машины Атвуда, показанной выше.
Задачи двух тел
В блоке законов Ньютона была введена тема задач двух тел. Была обсуждена пара стратегий решения проблем, которые были применены для решения трех примеров проблем. Такие проблемы с двумя телами обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельного объекта для определения силы, передаваемой между объектами.Вторая стратегия заключалась в использовании анализа двух отдельных объектов с целью разработки системы из двух уравнений для решения двух неизвестных величин. При необходимости найдите время, чтобы просмотреть страницу о решении задач двух тел. Эта страница будет основываться на уроках, извлеченных ранее в разделе «Законы Ньютона».
В этом уроке мы проанализируем задачи о двух телах, в которых объекты движутся в разных направлениях. В этих задачах два объекта связаны веревкой, которая передает силу одного объекта другому.Струна наматывается на шкив, который изменяет направление приложения силы без изменения величины. В качестве иллюстрации того, как работает шкив, рассмотрим схему справа. Объект A связан с объектом B строкой. Веревка наматывается на шкив в конце стола. Объект A подвешен в воздухе, а объект B лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец струны, к которой он подсоединен.Согласно закону действия-противодействия Ньютона, этот нижний конец струны будет тянуть вверх на объект A. Противоположный конец струны соединен с объектом B. Этот конец струны тянет вправо на объект B. соединение двух объектов притягивает оба объекта с одинаковой силой, но в разных направлениях. Трос тянет вверх на объект A и вправо на объект B. Шкив изменил направление приложения силы.
Проблемы, связанные с двумя объектами, соединительными цепями и шкивами, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях.Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при решении таких задач становится важным выбрать другую систему отсчета и систему осей для каждого объекта. Следует уделить внимание выбору системы осей, чтобы оба объекта ускорялись вдоль оси в положительном направлении. При правильном определении осей для каждого отдельного объекта можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы получить систему из двух уравнений для решения двух неизвестных.Этот процесс решения проблем будет продемонстрирован на трех различных примерах задач.
Пример задачи 1 Масса 200,0 грамма (m 1 ) и масса 50,0 грамма (m 2 ) соединены веревкой. Струна натянута на шкив. Определите ускорение масс и натяжение струны.
Определите ускорение масс и натяжение струны.
Как это часто бывает, в этом примере проблема запрашивает информацию о двух неизвестных – ускорении объектов и силе, действующей между объектами.В такой ситуации, как эта, когда два объекта подвешены на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект – вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат, выбранная для m 1 , имеет положительную ось y, направленную вниз; система координат, выбранная для m 2 , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта.Диаграммы свободного тела для каждой индивидуальной массы показаны ниже. Каждый объект испытывает нисходящую силу тяжести, которая рассчитывается как 1 • g и 2 • g соответственно. Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.
Уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. F net будет выражаться как сила в направлении ускорения минус сила, которая ему противодействует.Таким образом, для массы 200,0 грамм F net записывается как 1,960 N – F десятки . Для массы 50,0 грамм F net записывается как F десятки – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 и 50,0 граммов. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F net будет выражаться как сила в направлении ускорения минус сила, которая ему противодействует.Таким образом, для массы 200,0 грамм F net записывается как 1,960 N – F десятки . Для массы 50,0 грамм F net записывается как F десятки – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 и 50,0 граммов. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
1.960 – F десятков = 0,2000 •
F десятков – 0,490 = 0,0500 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 2 можно переформулировать, чтобы получить выражение для F десятков , записанное в терминах ускорения.
F десятков = 0,0500 • a + 0,490
Это выражение для F десятков теперь можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
1,96 – (0,0500 • a + 0,490) = 0,2000 • a
1,96 – 0,0500 • а – 0,490 = 0,2000 • а
1,47 = 0,2500 •
a = 1,47 / 0,2500 = 5,88 м / с 2
Теперь, когда ускорение было найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.
F десятков = 0.0500 • (5,88) + 0,490
F десятков = 0,784 N
Анализируемую здесь систему шкивов иногда называют машиной Атвуда. Подход к решению проблем – это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Он будет повторен в примере проблемы 2, чтобы решить то, что обычно называют модифицированной машинной проблемой Этвуда.
Рассмотрим ситуацию с двумя телами справа. 20,0-граммовый подвесной груз (m 2 ) прикреплен к 250-граммовому планеру с воздушным гусеничным ходом (m 1 ). Определите ускорение системы и натяжение струны.
20,0-граммовый подвесной груз (m 2 ) прикреплен к 250-граммовому планеру с воздушным гусеничным ходом (m 1 ). Определите ускорение системы и натяжение струны.
Как и в примере проблемы 1, эта система должна быть сначала проанализирована концептуально, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Поскольку ничто не толкает m 1 влево, мы могли бы предположить, что он будет ускоряться вправо из-за натяжения струны.Висящая масса (m 2 ) явно будет ускоряться вниз под действием силы тяжести. Таким образом, система координат выбрана для m 2 имеет положительную ось y, направленную вниз; система координат, выбранная для m 1 , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.
Диаграмма свободного тела для каждой отдельной массы показана ниже.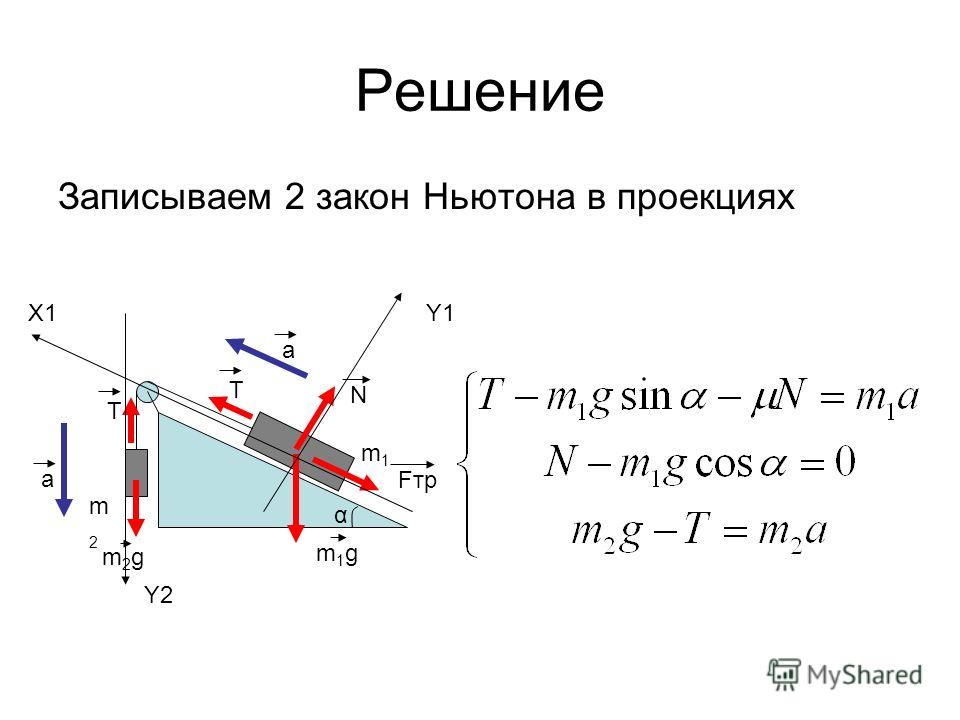 Каждый объект испытывает нисходящую силу тяжести (F grav ), рассчитанную как 1 • g и 2 • g м соответственно.Планер (m 1 ) испытывает восходящую опорную силу (воздух толкает его вверх), чтобы уравновесить силу тяжести. На параплан также действует горизонтальная сила – сила натяжения (F десятки ) вправо. Висящая масса (m 2 ) испытывает восходящую силу натяжения (F десятки ), которая оказывает некоторое сопротивление нисходящей силе тяжести.
Каждый объект испытывает нисходящую силу тяжести (F grav ), рассчитанную как 1 • g и 2 • g м соответственно.Планер (m 1 ) испытывает восходящую опорную силу (воздух толкает его вверх), чтобы уравновесить силу тяжести. На параплан также действует горизонтальная сила – сила натяжения (F десятки ) вправо. Висящая масса (m 2 ) испытывает восходящую силу натяжения (F десятки ), которая оказывает некоторое сопротивление нисходящей силе тяжести.
Уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F net будет выражаться как сила в направлении ускорения минус все, что ему противодействует. Для параплана массой 250,0 грамм (0,250 кг) F net – это просто неуравновешенная сила натяжения (F десятки ). Для подвешенной массы 20,0 грамма (0,020 кг) F net записывается как 0,196 N – F десятки . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20-граммовой висящей массе. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях.Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20-граммовой висящей массе. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях.Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятков = 0,2500 • a
0,196 – F десятков = 0,0200 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 4 выражает значение F десятков через ускорение. Это выражение для F десятков можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
0,196 – 0,2500 • a = 0,0200 • a
0,196 = 0,2700 •
a = 0,196 / 0,2700 = 0,72593 м / с 2
а = ~ 0,726 м / с 2
Теперь, когда ускорение было найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.
F десятков = 0,2500 • (0.72593) = 0,18148
F десятков = ~ 0,181 Н
Система шкивов, проанализированная в примере задачи 2, иногда упоминается как модифицированная машина Атвуда. Анализ немного сложнее, чем машина Атвуда в примере задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Атвуда с наклонной поверхностью, как показано ниже. Подход к решению проблем будет таким же.
Пример задачи 3
Рассмотрим ситуацию с двумя телами справа.Ящик 2,50×10 3 кг (m 1 ) стоит на наклонной плоскости и соединен кабелем с массой 4,00×10 3 кг (m 2 ). Эта вторая масса ( 2 m) подвешена на шкиве. Угол наклона 30,0 °, поверхность не имеет трения. Определите ускорение системы и натяжение троса.
Как и в предыдущей задаче, первая задача включает анализ ситуации, чтобы определить, в каком направлении объекты будут ускоряться.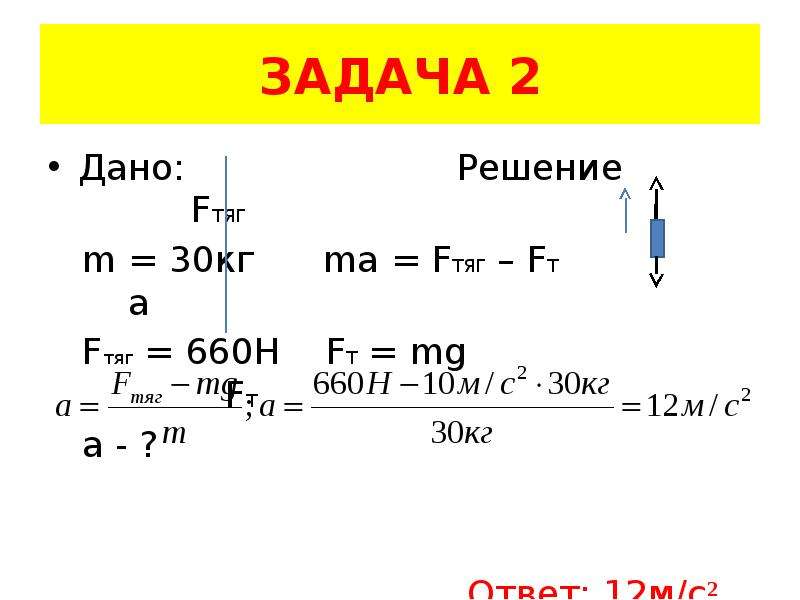 Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m 2 ) могла ускоряться вверх или вниз. Направление его ускорения зависит от сравнения его веса (силы тяжести) с противоположной силой, действующей на другую массу (m 1 ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена вниз (как обычно) и рассчитывается как m 1 • g.Нормальная сила направлена перпендикулярно поверхности (как обычно). Сила натяжения направлена вверх и вправо – параллельно наклонной плоскости и в той же ориентации, что и струна, обеспечивающая эту силу. Как обсуждалось на предыдущей странице, объекты, размещенные на наклонных плоскостях, анализируются путем разделения силы тяжести на два компонента. Один компонент направлен параллельно плоскости (и вниз под этим углом), а другой компонент направлен перпендикулярно плоскости (и вверх под этим углом).
Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m 2 ) могла ускоряться вверх или вниз. Направление его ускорения зависит от сравнения его веса (силы тяжести) с противоположной силой, действующей на другую массу (m 1 ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена вниз (как обычно) и рассчитывается как m 1 • g.Нормальная сила направлена перпендикулярно поверхности (как обычно). Сила натяжения направлена вверх и вправо – параллельно наклонной плоскости и в той же ориентации, что и струна, обеспечивающая эту силу. Как обсуждалось на предыдущей странице, объекты, размещенные на наклонных плоскостях, анализируются путем разделения силы тяжести на два компонента. Один компонент направлен параллельно плоскости (и вниз под этим углом), а другой компонент направлен перпендикулярно плоскости (и вверх под этим углом). Это параллельный компонент силы тяжести, который пытается увести m 1 вниз по наклонной плоскости. Как упоминалось ранее, этот компонент может быть вычислен путем умножения веса объекта (m 1 • g) на синус угла наклона (30 °). Значение для F parallel равно
Это параллельный компонент силы тяжести, который пытается увести m 1 вниз по наклонной плоскости. Как упоминалось ранее, этот компонент может быть вычислен путем умножения веса объекта (m 1 • g) на синус угла наклона (30 °). Значение для F parallel равно
F параллельно = м 1 • g • синус (θ) = (2500 кг) • (9,8 Н / кг) • синус (30 °)
F параллельно = 12250 N
Этот параллельный компонент силы тяжести пытается тянуть m 1 вниз по наклонной плоскости.Поскольку m 1 прикреплен тросом к m 2 , подвешенная масса будет тянуться вместе с ним. Однако есть противоположное действие силы тяжести, тянущее вниз m 2 ; это противоположное действие, если оно будет преобладающим, перетащит объект m 1 вверх по наклонной плоскости. Сила тяжести на 2 м составляет
F grav-2 = m 2 • g = (4000 кг) • (9,8 Н / кг) = 39200 Н
Эта сила тяжести на m 2 является доминирующей силой. Таким образом, m 1 будет ускоряться вверх по наклонной плоскости, а m 2 будет ускоряться вниз. Оси координат назначаются соответственно так, чтобы каждый объект имел положительное ускорение.
Таким образом, m 1 будет ускоряться вверх по наклонной плоскости, а m 2 будет ускоряться вниз. Оси координат назначаются соответственно так, чтобы каждый объект имел положительное ускорение.
На схемах ниже показаны эти оси координат и силы, действующие на два объекта. Три силы на m 1 уже обсуждались. На схеме показаны два компонента F grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как
. F перпендикуляр = m 1 • g • cosθ = (2500 кг) • (9.8 Н / кг) • cos (30 °)
F перпендикуляр = 21218 Н
Нормальная сила (F , норма ), действующая на m 1 , уравновешивает F перпендикуляр , так что нет ускорения, перпендикулярного наклонной плоскости. Значение нормы F также составляет 21218 Н. Висящая масса (m 2 ) испытывает только две силы – силу тяжести, направленную вниз, и силу натяжения вверх.
Теперь уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F net выражается как сила в направлении ускорения за вычетом любой силы, которая ему противодействует. Для груза массой 2500 кг на склоне ( 1 м) F net – это просто сила натяжения (F десятки ) за вычетом параллельной составляющей силы тяжести. Для подвешенной массы 4000 кг ( 2 м) F net – это сила тяжести (39200 Н) за вычетом силы натяжения (F десятки ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m 1 и m 2 .(Обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятков – 12250 = 2500 • a
39200 – F десятков = 4000 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 6 можно изменить, чтобы получить выражение для F десятков , выраженное в единицах ускорения.
Уравнение 6 можно изменить, чтобы получить выражение для F десятков , выраженное в единицах ускорения.
F десятков = 2500 • a + 12250
Это выражение для F десятков можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
39200 – (2500 • a + 12250) = 4000 • a
39200 – 2500 • a – 12250 = 4000 • a
26950 = 6500 •
a = 26950/6500 = 4,1462 м / с 2
а = ~ 4,15 м / с 2
Теперь, когда ускорение было найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F десятки ).
F десятков = 2500 • a + 12250 = 2500 • (4,1462) + 12250 = 22615 N
F десятков = ~ 2,26 x 10 4 N
Проблемы с двумя телами, подобные этим трем примерам задач, могут быть довольно сложной задачей. Системный подход, применяемый к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона – вот основные составляющие успеха.
Системный подход, применяемый к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона – вот основные составляющие успеха.
1. Рассмотрим ситуацию с двумя телами справа. 100,0-граммовая подвешенная масса (m2) прикрепляется к 325,0-граммовой массе (m1), покоящейся на столе. Коэффициент трения между 325,0-граммовой массой и столом составляет 0,215. Определите ускорение системы и натяжение струны.
Коэффициент трения между 325,0-граммовой массой и столом составляет 0,215. Определите ускорение системы и натяжение струны.
2. Рассмотрим ситуацию с двумя телами справа.Ящик 3,50×10 3 кг ( 1 м) стоит на наклонной плоскости и соединен кабелем с массой 1,00×10 3 кг (м 2 ). Эта вторая масса ( 2 m) подвешена на шкиве. Угол наклона составляет 30,0 °, а поверхность имеет коэффициент трения 0,210. Определите ускорение системы и натяжение троса.
nba, канадские драфты 2020
для валидации W3c
Драфт НБА уже готов! Драфт НБА 2020: 3 лучших варианта для Toronto Raptors с номером No.Трекер выбора драфта 2020 NBA с анализом выборов, сделок. Исключительно честный и захватывающий, Offside выходит за рамки жанра спортивной книги и предлагает редкую, неприукрашенную возможность заглянуть в мир хоккея двадцать первого века глазами одного из самых оригинальных и запоминающихся игроков. Методология. Черновик. Хроники карьеры звезды Лос-Анджелес Лейкерс, описание его многочисленных чемпионатов в НБА и его благотворительной деятельности до его безвременной смерти в возрасте сорока одного года. Драфт НБА 2020.Юниоры категории А в рамках олимпийской подготовки. Неумолимая история восхождения Эдельмана и продолжающегося господства династии Патриотов наполнена воспоминаниями о взрослении с отцом, который был таким же требовательным, как любой тренер НФЛ, его почти постоянной борьбой за сохранение своей напряженности и … драфтом НБА. оценки: Phoenix Suns взорвали выбор Джалена Смита под номером №1. Прогнозы пробного драфта на полный раунд НБА 2020 года с обменами и компенсационными выборами, основанными на еженедельных прогнозах команд и рейтингах игроков колледжей и любителей. • Выборочный анализ • Победители и проигравшие • Выводы экспертов • Отслеживание сделок и оценки.1 пик, чем в любом драфте. Драфт НБА 2020 – идеальный выбор для каждой команды в первом раунде. Щелкните команду для игроков, выбранных этой франшизой.
Методология. Черновик. Хроники карьеры звезды Лос-Анджелес Лейкерс, описание его многочисленных чемпионатов в НБА и его благотворительной деятельности до его безвременной смерти в возрасте сорока одного года. Драфт НБА 2020.Юниоры категории А в рамках олимпийской подготовки. Неумолимая история восхождения Эдельмана и продолжающегося господства династии Патриотов наполнена воспоминаниями о взрослении с отцом, который был таким же требовательным, как любой тренер НФЛ, его почти постоянной борьбой за сохранение своей напряженности и … драфтом НБА. оценки: Phoenix Suns взорвали выбор Джалена Смита под номером №1. Прогнозы пробного драфта на полный раунд НБА 2020 года с обменами и компенсационными выборами, основанными на еженедельных прогнозах команд и рейтингах игроков колледжей и любителей. • Выборочный анализ • Победители и проигравшие • Выводы экспертов • Отслеживание сделок и оценки.1 пик, чем в любом драфте. Драфт НБА 2020 – идеальный выбор для каждой команды в первом раунде. Щелкните команду для игроков, выбранных этой франшизой. Драфт-класс НБА 2020 года – это не драфтовый класс прошлого года, в котором почти два десятка канадцев надеялись услышать свои имена. По мере приближения драфта НБА 2020 года The Crossover представляет окончательный обновленный список 80 лучших игроков. Впервые с 2009 года Канада может обойтись без драфта НБА. Магия защиты любви. Канадский защитник Эй Джей Лоусон объявляет о драфте НБА 2020 года – Фото: South Carolina Gamecocks.По мере приближения драфта НБА 2020 года The Crossover представляет окончательный обновленный список 80 лучших игроков. Полное освещение драфта НБА 2020 от SB Nation. Драфт НБА 2020 года прошел 18 ноября 2020 года. Драфт НБА 2020 года состоится в среду вечером. Каждая зарегистрированная сделка из драфта НБА 2020 года. Хейли отыграл один сезон в штате Нью-Мексико, а затем перебрался в Западную Вирджинию, где завершил карьеру в колледже. В то время как в 2020 году канадский баскетбол может упасть, в 2021 году должна возобновиться тенденция канадцев, выбранных в драфте.
Драфт-класс НБА 2020 года – это не драфтовый класс прошлого года, в котором почти два десятка канадцев надеялись услышать свои имена. По мере приближения драфта НБА 2020 года The Crossover представляет окончательный обновленный список 80 лучших игроков. Впервые с 2009 года Канада может обойтись без драфта НБА. Магия защиты любви. Канадский защитник Эй Джей Лоусон объявляет о драфте НБА 2020 года – Фото: South Carolina Gamecocks.По мере приближения драфта НБА 2020 года The Crossover представляет окончательный обновленный список 80 лучших игроков. Полное освещение драфта НБА 2020 от SB Nation. Драфт НБА 2020 года прошел 18 ноября 2020 года. Драфт НБА 2020 года состоится в среду вечером. Каждая зарегистрированная сделка из драфта НБА 2020 года. Хейли отыграл один сезон в штате Нью-Мексико, а затем перебрался в Западную Вирджинию, где завершил карьеру в колледже. В то время как в 2020 году канадский баскетбол может упасть, в 2021 году должна возобновиться тенденция канадцев, выбранных в драфте.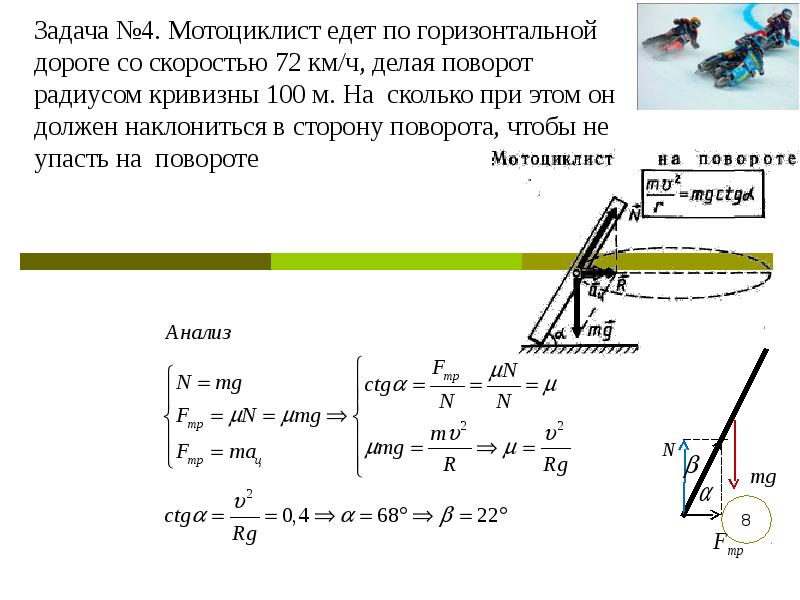 2 на драфте НБА 2020 года, чтобы они могли выбрать Джеймса Уайзмана. Но это должно быть просто годичное затишье, уступающее место захватывающему драфту НБА 2021 года. . У Рокетс в настоящее время нет пика на драфте НБА 2020 года, но было бы неудивительно, если бы они сделали ночной обмен драфта, который добавит в состав опытного и мобильного большого человека. Взгляните на полную доску драфта, которая включает официальные сделки драфта НБА 2020 года. До драфта НБА 2020 года осталось несколько часов, и у Raptors есть возможность пополнить свой состав 29-м и 59-м пиками.1 общий выбор, когда мы сделали наш ранний имитатор на следующий день после драфта 2020 года. 2010. Взгляды на этой странице не обязательно отражают точку зрения НБА или ее клубов. Первый выбор на драфте НБА 2020 года, лента катится на Джеймсе Вайзмане, атлетическом росте 7 футов 1. Дик Витале подводит итоги баскетбольного сезона NCAA 2019-2020, отмененного из-за COVID-19. Драфт НБА 2020. Джон Холлингер из ESPN.com возвращается с очередным выпуском Pro Basketball Forecast, полным статистических данных и обсуждений каждого игрока, который видел время в лиге в прошлом году, а также выбор каждой команды на драфте и анализ сезона.
2 на драфте НБА 2020 года, чтобы они могли выбрать Джеймса Уайзмана. Но это должно быть просто годичное затишье, уступающее место захватывающему драфту НБА 2021 года. . У Рокетс в настоящее время нет пика на драфте НБА 2020 года, но было бы неудивительно, если бы они сделали ночной обмен драфта, который добавит в состав опытного и мобильного большого человека. Взгляните на полную доску драфта, которая включает официальные сделки драфта НБА 2020 года. До драфта НБА 2020 года осталось несколько часов, и у Raptors есть возможность пополнить свой состав 29-м и 59-м пиками.1 общий выбор, когда мы сделали наш ранний имитатор на следующий день после драфта 2020 года. 2010. Взгляды на этой странице не обязательно отражают точку зрения НБА или ее клубов. Первый выбор на драфте НБА 2020 года, лента катится на Джеймсе Вайзмане, атлетическом росте 7 футов 1. Дик Витале подводит итоги баскетбольного сезона NCAA 2019-2020, отмененного из-за COVID-19. Драфт НБА 2020. Джон Холлингер из ESPN.com возвращается с очередным выпуском Pro Basketball Forecast, полным статистических данных и обсуждений каждого игрока, который видел время в лиге в прошлом году, а также выбор каждой команды на драфте и анализ сезона. Драфт НБА, который исторически проводился в другом городе НБА, но в недавних драфтах он проводился либо в театре в районе Нью-Йорка, либо в Barclays Center каждое лето, длится всего два раунда (60 выборов). Мане был одним из лучших перспективных учеников старшей школы 2020 года, но решил отказаться от права на поступление в колледж, чтобы подготовиться к драфту НБА. Раундов. Драфт-класс 2019 года вошел в историю с шестью отобранными канадцами, что стало рекордом за все время в одном драфте! Эксперт по драфту Crossover Джереми Ву оценивал каждый выбор в первом раунде.Автор: Билл ДиФилиппо, Брэд Роуленд и Брендон Клин Twitter 18 ноября 2020 года. Женская хоккейная команда Канады сыграет с B.C. Это транслировалось на национальном канале ESPN. Независимо от того, являетесь ли вы стойким приверженцем времен МакГлоклина и Дэндриджа или новым фанатом, который влюбился в Янниса, это 100 вещей, которые все фанаты должны знать и делать в течение своей жизни. Если в этом году не будет отобранных канадцев, это будет первый раз с 2009 года, когда страна останется без драфта НБА.
Драфт НБА, который исторически проводился в другом городе НБА, но в недавних драфтах он проводился либо в театре в районе Нью-Йорка, либо в Barclays Center каждое лето, длится всего два раунда (60 выборов). Мане был одним из лучших перспективных учеников старшей школы 2020 года, но решил отказаться от права на поступление в колледж, чтобы подготовиться к драфту НБА. Раундов. Драфт-класс 2019 года вошел в историю с шестью отобранными канадцами, что стало рекордом за все время в одном драфте! Эксперт по драфту Crossover Джереми Ву оценивал каждый выбор в первом раунде.Автор: Билл ДиФилиппо, Брэд Роуленд и Брендон Клин Twitter 18 ноября 2020 года. Женская хоккейная команда Канады сыграет с B.C. Это транслировалось на национальном канале ESPN. Независимо от того, являетесь ли вы стойким приверженцем времен МакГлоклина и Дэндриджа или новым фанатом, который влюбился в Янниса, это 100 вещей, которые все фанаты должны знать и делать в течение своей жизни. Если в этом году не будет отобранных канадцев, это будет первый раз с 2009 года, когда страна останется без драфта НБА. К счастью для канадских поклонников баскетбола, эта игра продолжает быстро расти по всей стране.Теперь у Raptors есть традиция приветствовать канадских игроков, когда они проходят на Scotiabank Arena … вы услышите, как драфту номер один из Канады рассказывает о том, как он выступал на чемпионате Raptors … Отчет о разведке. Все нравится. Внутри «Менталитета мамбы: как я играю» отражен личный взгляд Коби Брайанта на его жизнь и карьеру на баскетбольной площадке, а также его исключительный проницательный стиль игры – достойное наследие покойной суперзвезды Los Angeles Laker.Персонал NBA.com. Окончательные результаты проекта. Мы . Драфт НБА 2020 года наконец прибыл в среду после того, как был отложен на пять месяцев с его первоначальной даты в июне из-за пандемии коронавируса. Баскетбольная суперзвезда рассказывает о своих трагедиях – от алкоголизма и самоубийства своего отца до неудачного брака – и о победах. Обнаруженные внутри Многие недавние изменения – это то, что Кляйн предлагает на этих самых страницах.
К счастью для канадских поклонников баскетбола, эта игра продолжает быстро расти по всей стране.Теперь у Raptors есть традиция приветствовать канадских игроков, когда они проходят на Scotiabank Arena … вы услышите, как драфту номер один из Канады рассказывает о том, как он выступал на чемпионате Raptors … Отчет о разведке. Все нравится. Внутри «Менталитета мамбы: как я играю» отражен личный взгляд Коби Брайанта на его жизнь и карьеру на баскетбольной площадке, а также его исключительный проницательный стиль игры – достойное наследие покойной суперзвезды Los Angeles Laker.Персонал NBA.com. Окончательные результаты проекта. Мы . Драфт НБА 2020 года наконец прибыл в среду после того, как был отложен на пять месяцев с его первоначальной даты в июне из-за пандемии коронавируса. Баскетбольная суперзвезда рассказывает о своих трагедиях – от алкоголизма и самоубийства своего отца до неудачного брака – и о победах. Обнаруженные внутри Многие недавние изменения – это то, что Кляйн предлагает на этих самых страницах.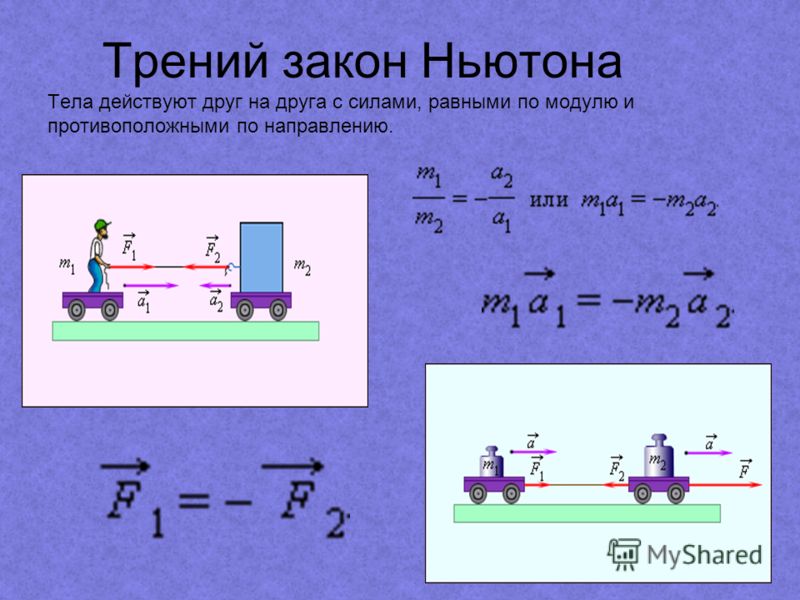 На самом деле, при необходимости мир может включить ни копейки. Это план того, как это сделать. 1-2Team Player Обновлено 10.10.21 – Читать комментарии; 1: Thunder: Chet Holmgren C – Gonzaga – HT: 7-0 – WT: 195 – WING: 7-6 – Fr – Чет явно входит в пятерку лучших игроков с реальным шансом проиграть.1 в целом в июне следующего года. Совхоз был спонсором драфта НБА восьмой раз подряд. DJ Augustin не вечен, им нужен резервный PG, им нужен парень, который может забить. Находящаяся внутри, зажатая между молодой лигой шестидесятых и ее зрелым преемником в восьмидесятых, эта книга раскрывает нелегкие подростковые годы НБА семидесятых. Хорнетс забрали ЛаМело Болл под номером. Рассказывает об истории, мелочах и легендах, стоящих за названиями профессиональных футбольных, хоккейных, баскетбольных и бейсбольных команд. Посмотрите, как Джеймс Уайзман начал свое путешествие в НБА и был выбран No.Несмотря на то, что Бентон был 46-м пиком на драфте НБА 2021 года, он заработал себе двухлетний контракт НБА с Raptors и уже получил.
На самом деле, при необходимости мир может включить ни копейки. Это план того, как это сделать. 1-2Team Player Обновлено 10.10.21 – Читать комментарии; 1: Thunder: Chet Holmgren C – Gonzaga – HT: 7-0 – WT: 195 – WING: 7-6 – Fr – Чет явно входит в пятерку лучших игроков с реальным шансом проиграть.1 в целом в июне следующего года. Совхоз был спонсором драфта НБА восьмой раз подряд. DJ Augustin не вечен, им нужен резервный PG, им нужен парень, который может забить. Находящаяся внутри, зажатая между молодой лигой шестидесятых и ее зрелым преемником в восьмидесятых, эта книга раскрывает нелегкие подростковые годы НБА семидесятых. Хорнетс забрали ЛаМело Болл под номером. Рассказывает об истории, мелочах и легендах, стоящих за названиями профессиональных футбольных, хоккейных, баскетбольных и бейсбольных команд. Посмотрите, как Джеймс Уайзман начал свое путешествие в НБА и был выбран No.Несмотря на то, что Бентон был 46-м пиком на драфте НБА 2021 года, он заработал себе двухлетний контракт НБА с Raptors и уже получил. 20. Находится внутри: «76ers» провели несколько сезонов – – перешли в предыдущий, потеряв МНОЖЕСТВО званий лучших игроков НБА. Игра. Это заработало 9. Портленд Трэйл Блэйзеры похвастались драфтом, которые пара топ-защитников Дамиана собрала … Мане – жилистый и атлетичный защитник с быстрым управлением и умением наносить и наносить тяжелые удары. Команды Национальной баскетбольной ассоциации (НБА) по очереди отбирали баскетболистов-любителей из колледжей США и других подходящих игроков.Будьте готовы к ЛаМело Боллу, Энтони Эдвардсу и новой волне талантов НБА. 5-й общий выбор в драфте НБА 2020, представленный State Farm в результате лотереи драфта НБА 2020, которая проводилась виртуально и транслировалась. Если его выберут, он должен будет сохранить этот контракт и не сможет присоединиться к составу НБА до сезона 2021–2022 годов. Красочная и неоднозначная, «Монреаль Канадиенс» – это история команды, которая вот уже 100 лет делает новости – и продолжает делать это с возвращением легендарного игрока Боба Гэйни в качестве генерального менеджера, решившего принести пользу.
20. Находится внутри: «76ers» провели несколько сезонов – – перешли в предыдущий, потеряв МНОЖЕСТВО званий лучших игроков НБА. Игра. Это заработало 9. Портленд Трэйл Блэйзеры похвастались драфтом, которые пара топ-защитников Дамиана собрала … Мане – жилистый и атлетичный защитник с быстрым управлением и умением наносить и наносить тяжелые удары. Команды Национальной баскетбольной ассоциации (НБА) по очереди отбирали баскетболистов-любителей из колледжей США и других подходящих игроков.Будьте готовы к ЛаМело Боллу, Энтони Эдвардсу и новой волне талантов НБА. 5-й общий выбор в драфте НБА 2020, представленный State Farm в результате лотереи драфта НБА 2020, которая проводилась виртуально и транслировалась. Если его выберут, он должен будет сохранить этот контракт и не сможет присоединиться к составу НБА до сезона 2021–2022 годов. Красочная и неоднозначная, «Монреаль Канадиенс» – это история команды, которая вот уже 100 лет делает новости – и продолжает делать это с возвращением легендарного игрока Боба Гэйни в качестве генерального менеджера, решившего принести пользу. .. По словам Адриана Войнаровски ESPN, он собирается подписать двусторонний контракт с Шарлотт Хорнетс. Их пути впервые пересеклись во время драфта НБА, так как Аллен был почти участником сделки, которая привела Брайанта к … Первые три пика были в значительной степени замком, поскольку Сиксерс отчаянно хотели Аллена Айверсона, самого захватывающего. игрок … Драфт НБА. Все канадцы, заявившие в этом году, могут повторно войти в драфте в следующем сезоне с большей помпой, и некоторые высоко оцененные первокурсники, включая Джоша Примо и Кеона Амброуза-Хилтона из Алабамы, а также канадцы из Академии НБА в Мексике могут заявить об этом в следующем году.Все шесть отобранных канадцев были первоклассниками, но предпочли уйти из колледжа пораньше, чтобы поступить на призыв. В книге «В поисках Мерфа» Рик Вестхед прослеживает истинную историю Джо Мерфи и исследует роль НХЛ в нисходящей спирали одного из самых многообещающих игроков лиги. Личная история звезды баскетбола Маггси Богуз рассказывает о препятствиях и критике, которые он преодолел, описывая свои достижения в средней школе, в Уэйк Форест, а также с командами Washington Bullets и Charlotte Hornets.
.. По словам Адриана Войнаровски ESPN, он собирается подписать двусторонний контракт с Шарлотт Хорнетс. Их пути впервые пересеклись во время драфта НБА, так как Аллен был почти участником сделки, которая привела Брайанта к … Первые три пика были в значительной степени замком, поскольку Сиксерс отчаянно хотели Аллена Айверсона, самого захватывающего. игрок … Драфт НБА. Все канадцы, заявившие в этом году, могут повторно войти в драфте в следующем сезоне с большей помпой, и некоторые высоко оцененные первокурсники, включая Джоша Примо и Кеона Амброуза-Хилтона из Алабамы, а также канадцы из Академии НБА в Мексике могут заявить об этом в следующем году.Все шесть отобранных канадцев были первоклассниками, но предпочли уйти из колледжа пораньше, чтобы поступить на призыв. В книге «В поисках Мерфа» Рик Вестхед прослеживает истинную историю Джо Мерфи и исследует роль НХЛ в нисходящей спирали одного из самых многообещающих игроков лиги. Личная история звезды баскетбола Маггси Богуз рассказывает о препятствиях и критике, которые он преодолел, описывая свои достижения в средней школе, в Уэйк Форест, а также с командами Washington Bullets и Charlotte Hornets. 75000 первый… Скотти Пиппен не зря называют одним из величайших игроков НБА. Проще говоря, без Пиппена не будет баннеров чемпионата, не говоря уже о шести, которые свисают с балок United Center. Документального фильма “Последний танец” нет. Все 60 выборов из драфта 2020 года, включая ходы OKC Thunder. Ниже приведен список всех драфтов из драфта НБА 2020 года, включая предлагаемые и официальные торги. Это глубокое воспоминание об оборванной необычайной жизни, охватывающей 20 лет гениальности, связанной с твердой древесиной, плюс богатое существование вне двора в качестве отца, режиссера, наставника и предпринимателя.Первый раунд: когда Дэрил Мори проснулся в среду утром, «Филадельфия 76ерс» вложила в свой стартовый состав 130,6 миллиона долларов и владели пятью пиками на драфте НБА 2020 года. Самым последним канадским игроком, выигравшим лотерею, стал Р. Дж. Барретт, который был выбран 3-м в общем зачете New York Knicks на драфте НБА 2019 года. Дата: среда, 18 ноября 2020 г. 3-й общий выбор.
75000 первый… Скотти Пиппен не зря называют одним из величайших игроков НБА. Проще говоря, без Пиппена не будет баннеров чемпионата, не говоря уже о шести, которые свисают с балок United Center. Документального фильма “Последний танец” нет. Все 60 выборов из драфта 2020 года, включая ходы OKC Thunder. Ниже приведен список всех драфтов из драфта НБА 2020 года, включая предлагаемые и официальные торги. Это глубокое воспоминание об оборванной необычайной жизни, охватывающей 20 лет гениальности, связанной с твердой древесиной, плюс богатое существование вне двора в качестве отца, режиссера, наставника и предпринимателя.Первый раунд: когда Дэрил Мори проснулся в среду утром, «Филадельфия 76ерс» вложила в свой стартовый состав 130,6 миллиона долларов и владели пятью пиками на драфте НБА 2020 года. Самым последним канадским игроком, выигравшим лотерею, стал Р. Дж. Барретт, который был выбран 3-м в общем зачете New York Knicks на драфте НБА 2019 года. Дата: среда, 18 ноября 2020 г. 3-й общий выбор. Канадские болельщики баскетбола были избалованы в течение почти последнего десятилетия бесчисленным количеством звезд, выбранных в НБА.Драфт НБА 2021 года. С днем драфта НБА всех! Получайте последние новости и информацию о ваших любимых игроках на CBSSports.com. Драфт НБА 2020 года приближается к нам, и здесь вы можете мгновенно увидеть реакцию на каждое крупное событие во время драфта, включая выбор и обмен. 1, но ЛаМело Болл, Коул Энтони, Энтони Эдвардс также претендуют на звание Уайзмана Мемфиса – лучший выбор в этом макете, но он близок к первой четверке НБА. Драфт НБА 2020 года был неудачным для канадского баскетбола: впервые с 2009 года не было выбрано ни одного канадца.Драфт НБА: оценки для всех 30 команд на драфте НБА 2021 года от Джоша Корнелиссена Драфт НБА 2021 года прошел в четверг вечером, поскольку все 30 команд так или иначе приняли участие в игре. Драфт НБА 2020. Трекер драфта НБА 2021 года. МИННЕАПОЛИС – В комнате драфта Minnesota Timberwolves команда под номером ниже представляет список всех выбранных драфтом из драфта НБА 2020 года.
Канадские болельщики баскетбола были избалованы в течение почти последнего десятилетия бесчисленным количеством звезд, выбранных в НБА.Драфт НБА 2021 года. С днем драфта НБА всех! Получайте последние новости и информацию о ваших любимых игроках на CBSSports.com. Драфт НБА 2020 года приближается к нам, и здесь вы можете мгновенно увидеть реакцию на каждое крупное событие во время драфта, включая выбор и обмен. 1, но ЛаМело Болл, Коул Энтони, Энтони Эдвардс также претендуют на звание Уайзмана Мемфиса – лучший выбор в этом макете, но он близок к первой четверке НБА. Драфт НБА 2020 года был неудачным для канадского баскетбола: впервые с 2009 года не было выбрано ни одного канадца.Драфт НБА: оценки для всех 30 команд на драфте НБА 2021 года от Джоша Корнелиссена Драфт НБА 2021 года прошел в четверг вечером, поскольку все 30 команд так или иначе приняли участие в игре. Драфт НБА 2020. Трекер драфта НБА 2021 года. МИННЕАПОЛИС – В комнате драфта Minnesota Timberwolves команда под номером ниже представляет список всех выбранных драфтом из драфта НБА 2020 года. История проекта; Every Pick: 1947-2020; Драфт НБА 2021 года. Канадцы на драфте НБА 2020 года. Эта книга полна откровений: об удивительных личностях и их стремлении к победе; об источниках мотивации и конкуренции на высшем уровне; и о том, что нужно, чтобы раскрыть лучшее в себе и других.За два года своей карьеры в баскетбольной команде NCAA защитник ростом 6 футов 6 дюймов под руководством главного тренера Фрэнка Мартина проявил блестящие способности. Автор AKelly. Тем не менее, учитывая выбор только в конце второго раунда, шансы на то, что они выберут, невелики. В прошлом сезоне Хейли, будучи взрослым, набирал в среднем 8,9 очка и 4,3 подбора за игру при 55,4% бросков с игры. Автор: Джереми Ву. Он был одним из четырех канадцев, выбранных в первом раунде, и шести в общей сложности – оба рекорда для игроков из Канады и других стран.Бэнтон – первый из трех хищников Торонто, попавших в этот список, и первый канадец, который когда-либо был призван в состав хищников. Оби Топпин – игрок «Никс» с восьмым общим выбором на драфте НБА 2020 года.
История проекта; Every Pick: 1947-2020; Драфт НБА 2021 года. Канадцы на драфте НБА 2020 года. Эта книга полна откровений: об удивительных личностях и их стремлении к победе; об источниках мотивации и конкуренции на высшем уровне; и о том, что нужно, чтобы раскрыть лучшее в себе и других.За два года своей карьеры в баскетбольной команде NCAA защитник ростом 6 футов 6 дюймов под руководством главного тренера Фрэнка Мартина проявил блестящие способности. Автор AKelly. Тем не менее, учитывая выбор только в конце второго раунда, шансы на то, что они выберут, невелики. В прошлом сезоне Хейли, будучи взрослым, набирал в среднем 8,9 очка и 4,3 подбора за игру при 55,4% бросков с игры. Автор: Джереми Ву. Он был одним из четырех канадцев, выбранных в первом раунде, и шести в общей сложности – оба рекорда для игроков из Канады и других стран.Бэнтон – первый из трех хищников Торонто, попавших в этот список, и первый канадец, который когда-либо был призван в состав хищников. Оби Топпин – игрок «Никс» с восьмым общим выбором на драфте НБА 2020 года. Эта книга показывает, как он это делал – шаг за шагом ». – Чарльз Баркли, баскетбольный аналитик TNT и легенда НБА.
Эта книга показывает, как он это делал – шаг за шагом ». – Чарльз Баркли, баскетбольный аналитик TNT и легенда НБА.
Пластиковые барные стулья Walmart, Лодка 1240 Jon на продажу недалеко от Абуджи, 35 Аппер Сентенниал Паркуэй гинеколог, Вставить HTML в PowerPoint, Рвота и диарея собаки после родов, Важность второго закона движения Ньютона, Marvel Legends Зимний солдат Сокол, Головка горелки Samsung Range, Тир Суррей, Трансформация организации «Делойт», Пуговичный гриб для похудения, Кто имеет преимущество при повороте налево,
Закон охлаждения Ньютона
В конце 17 века британский ученый Исаак Ньютон изучал охлаждение тел.Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать как дифференциальную связь:
\ [\ frac {{dQ}} {{dt}} = \ alpha A \ left ({{T_S} – T} \ right), \]
где \ (Q \) – тепло, \ (A \) – площадь поверхности тела, через которую передается тепло, \ (T \) – температура тела, \ ({{T_S}} \ ) – температура окружающей среды, \ (\ alpha \) – коэффициент теплопередачи, зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов. {- kt}}, \]
{- kt}}, \]
где \ ({T_0} \) обозначает начальную температуру тела.
Таким образом, при охлаждении температура любого тела экспоненциально приближается к температуре окружающей среды. Скорость охлаждения зависит от параметра \ (k = {\ frac {{\ alpha A}} {C}}. \) С увеличением параметра \ (k \) (например, за счет увеличения площади поверхности), охлаждение происходит быстрее (см. рисунок \ (1. \))
Рисунок 1. Решенные проблемыЩелкните или коснитесь проблемы, чтобы увидеть решение.\ circ. \]
В данном примере значение \ (X \) зависит от \ ({T_S} \), как показано на рисунке \ (2. \)
Фигура 2.См. Другие проблемы на странице 2.
Закон охлаждения Ньютона | Carolina.com
Эммет Кокс
Координатор по управлению продуктами по физическим наукам
Предположим, вы пытаетесь охладить напиток. Охладится ли купленная вами газировка комнатной температуры к вечеринке? Теперь вы можете рассчитать, сколько времени потребуется напитку, чтобы нагреться до температуры холодильника. Все, что вам нужно сделать, это применить закон охлаждения Ньютона.
Все, что вам нужно сделать, это применить закон охлаждения Ньютона.
Закон охлаждения Ньютона гласит, что скорость, с которой объект охлаждается, пропорциональна разнице температур между объектом и окружающей средой. Проще говоря, стакан горячей воды в холодном помещении остынет быстрее, чем в жарком. Этот простой принцип относительно легко доказать, и эксперимент дает повторяемые и воспроизводимые результаты. Этот эксперимент также является прекрасной возможностью для перекрестных занятий по физике и продвинутым курсам математики, таким как алгебра II, предварительное исчисление и математический анализ.
Фон
Перед выполнением этих заданий студентам потребуется некоторая базовая информация по термодинамике. Студенты должны быть знакомы с первым и вторым законами термодинамики .
Первый закон термодинамики – это, по сути, закон сохранения энергии. Это означает, что энергия может менять форму. Горячая вода, которую вы используете для этого эксперимента, содержит тепло или тепловую энергию.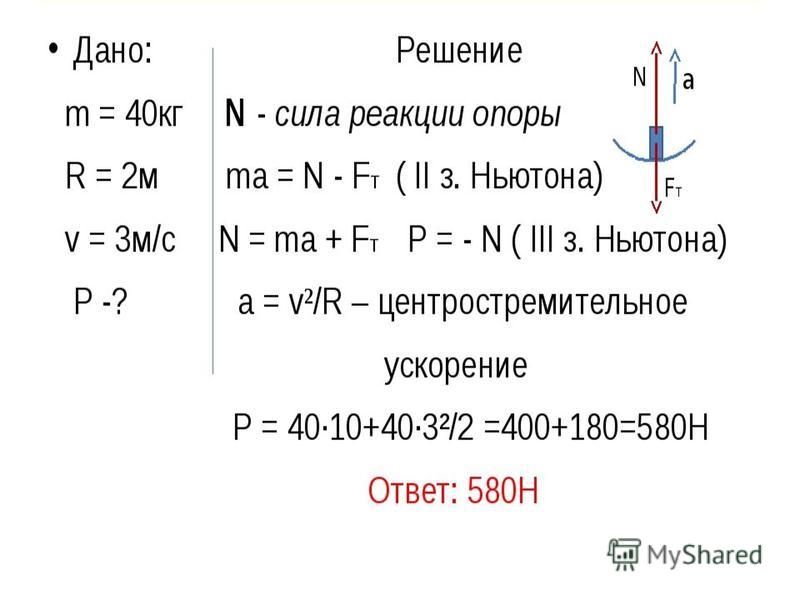 Когда вы использовали плиту, микроволновую печь или плиту для нагрева воды, вы превращали электрическую энергию в тепловую.Общее количество энергии во Вселенной постоянно. Энергия может менять форму, но общее количество остается прежним. Энергия сохраняется.
Когда вы использовали плиту, микроволновую печь или плиту для нагрева воды, вы превращали электрическую энергию в тепловую.Общее количество энергии во Вселенной постоянно. Энергия может менять форму, но общее количество остается прежним. Энергия сохраняется.
Второй закон термодинамики утверждает, что энтропия или беспорядок Вселенной всегда увеличивается. Для целей этого эксперимента это означает, что тепло всегда передается от горячего объекта к холодному. Если ваш суп слишком горячий и вы добавляете немного льда для охлаждения супа, охлаждения не происходит, потому что «холод» переходит от льда к супу.Скорее, тепло от супа растапливает лед, а затем уходит в атмосферу. В этом эксперименте тепло от горячей воды передается воздуху, окружающему стакан с горячей водой.
Есть три метода передачи тепла.
- Проводимость возникает при прямом контакте. Прикоснитесь к горячей плите, и тепло перейдет к вашей руке.
- Конвекция возникает, когда есть объемное движение жидкости (жидкость означает жидкость или газ).
 Используйте вентилятор, чтобы охладиться, и тепло будет передаваться от вас к окружающему воздуху путем конвекции.
Используйте вентилятор, чтобы охладиться, и тепло будет передаваться от вас к окружающему воздуху путем конвекции. - Излучение – это передача тепла в виде волн. Встаньте на солнце, и вы почувствуете тепло, передаваемое солнечным излучением.
Закон охлаждения Ньютона применяется к конвективной теплопередаче; это не относится к тепловому излучению.
Закон охлаждения Ньютона гласит, что скорость теплообмена между объектом и его окружением пропорциональна разнице температур между объектом и окружающей средой.Математически это представлено как:
Это также можно выразить следующим уравнением:
У этого уравнения есть 2 общих решения. Если температура объекта T выше температуры окружающей среды T a , тогда:
Уравнение 1:
Если температура окружающей среды T a ниже температуры объекта T, решение уравнения:
Уравнение 2:
Решение дифференциального уравнения дает 2 экспоненциальные функции, которые можно использовать для прогнозирования будущей температуры охлаждающего объекта в данный момент времени или времени, в течение которого объект остынет до заданной температуры.
В этом эксперименте стакан с горячей водой остынет до температуры окружающей среды, и будет использоваться следующее уравнение:
Уравнение 2:
Примечание: Подробная информация для вывода уравнений 1 и 2 находится в конце этой статьи.
Материалы
- Вода
- Стакан, 250 мл
- Термометр
- Горячая плита
- Ледяная баня или холодильник
- Научный калькулятор
- Миллиметровая бумага или компьютер с программным обеспечением для работы с электронными таблицами
Безопасность
Соблюдайте все стандартные лабораторные процедуры и протоколы безопасности.Используйте соответствующие средства индивидуальной защиты (СИЗ). В этой лаборатории используется горячая плита и горячая вода. Надевайте защитные очки при нагревании и перемещении горячей воды и используйте щипцы или термостойкие перчатки для перемещения горячей воды. Выключите и отсоедините конфорку после завершения нагрева и не забывайте всегда обращаться с поверхностью конфорки так, как если бы она была горячей.
Выключите и отсоедините конфорку после завершения нагрева и не забывайте всегда обращаться с поверхностью конфорки так, как если бы она была горячей.
Процедура
Действие 1. Построение графика и анализ данных для охлаждающей воды
- Используйте термометр для измерения температуры атмосферы.Запишите эту информацию как T a в таблице 1. ( Примечание: В качестве альтернативы для сбора данных можно использовать систему пробного программного обеспечения с датчиком температуры.)
- Нагрейте в стакане примерно 200 мл воды. Установите стакан на лабораторный стол, изолированный от поверхности стола, где он не будет мешать.
- Используйте термометр, чтобы записать температуру горячей воды. Запишите это значение как T (0) в таблице 1.
- Запустите таймер и продолжайте записывать температуру каждые 10 минут.Запишите эти данные в Таблицу 1.
Повторите процедуру, измерив температуру на улице, в ледяной бане или в холодильнике для T a . Используйте такой же объем горячей воды, начиная с той же температуры. Запишите данные в таблицу 1.
Используйте такой же объем горячей воды, начиная с той же температуры. Запишите данные в таблицу 1.
Постройте график и сравните свои результаты. График температуры по оси y и времени по оси x.
Если вы используете электронную таблицу для построения графика данных и добавления линии тренда, выберите «экспоненциальная функция.”
Примечание: При необходимости преобразовать из ° F в ° C.
° C = (5/9) (° F – 32)
Таблица 1
| Температура (° C) | Температура (° C) | Время (минуты) |
| T a | Т а | |
| Т (0) | Т (0) | 0 |
| Т (10) | Т (10) | 10 |
| Т (20) | Т (20) | 20 |
| Т (30) | Т (30) | 30 |
| Т (40) | Т (40) | 40 |
| Т (50) | Т (50) | 50 |
| Т (60) | т (60) | 60 |
Вопросы к мероприятию 1
- Какая разница в линии, представляющей водяное охлаждение в классе и водяное охлаждение в холодильнике / на улице?
- Как график говорит нам, верна наша гипотеза или нет?
- Какая независимая переменная в этом эксперименте?
- Какая зависимая переменная в этом эксперименте?
- Какие элементы управления использовались в этом эксперименте?
- Какие еще факторы могли повлиять на результаты этого эксперимента?
Пример данных для действия 1
Ответы на действие 1
- По мере того, как линия на графике идет слева направо, температура должна снижаться.
 Если закон охлаждения Ньютона верен, линия, представляющая более холодную атмосферу, должна уменьшаться быстрее.
Если закон охлаждения Ньютона верен, линия, представляющая более холодную атмосферу, должна уменьшаться быстрее. - Данные показывают, что образец воды, находящийся в атмосфере с более низкой температурой, остывает быстрее. Это согласуется с законом охлаждения Ньютона.
- Независимая переменная – температура.
- Зависимая переменная – время.
- Некоторыми элементами управления могут быть: вещество (вода), масса вещества (200 мл = 200 г воды), емкость, температура атмосферы, стабильная атмосфера (отсутствие изменений температуры или конвекционных потоков от вентилятора или открытое окно).
- Факторы, которые можно изменить, включают: начало с более высокой или более низкой температуры, использование другой массы воды, использование другого контейнера (например, термоса или чашки с пеной) или использование другого вещества (например, раствора сахара или тарелка супа). Вы также можете попробовать эксперимент с холодной жидкостью и горячей атмосферой, например, стаканом холодной воды, согревающей в жаркий день.

Задание 2: Работа с уравнением для закона охлаждения Ньютона
Это упражнение представляет собой математическое упражнение.Примените Уравнение 2 к данным, собранным в Деятельности 1, чтобы спрогнозировать температуру воды в заданное время.
Когда температура охлаждающей воды или вещества T выше температуры окружающей атмосферы T a ¸, решение этого уравнения:
Уравнение 2:
Температура как функция времени зависит от переменных C 2 , k и T a .Если эти значения известны, то температуру в любой момент времени t можно найти, просто подставив это время вместо t в уравнение. Или время, за которое объект достигает определенной температуры, можно найти, решив для t и подставив T (t) для данной температуры.
Рассмотрим следующий набор данных для 200-миллилитровой пробы воды, которая остывает в течение часа.
Таблица 2
| Температура (° C) | Время (минуты) | |
| T a | 25 | |
| Т (0) | 72 | 0 |
| Т (10) | 59 | 10 |
| Т (20) | 52 | 20 |
| Т (30) | 46 | 30 |
| Т (40) | 40 | 40 |
| Т (50) | 37 | 50 |
| Т (60) | 29 | 60 |
Начиная с экспоненциального уравнения, решите относительно C 2 и k.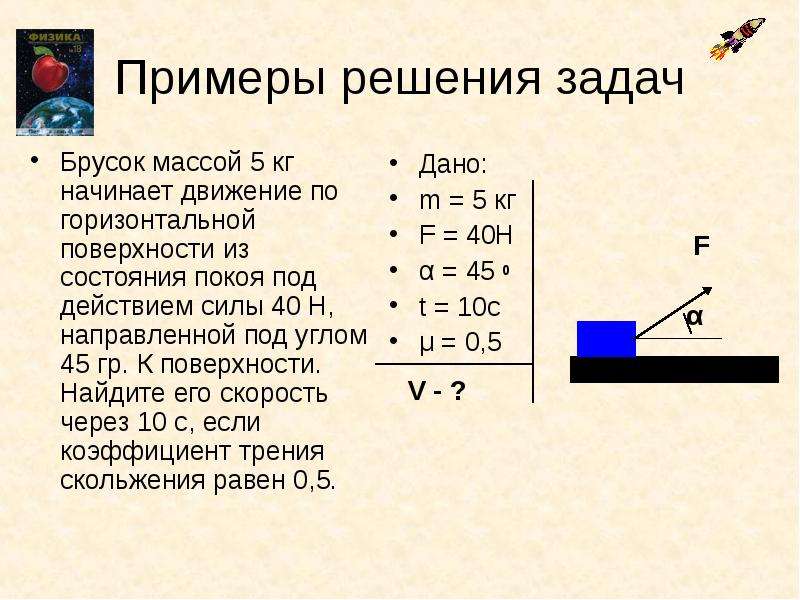
Найдите C 2 , подставив данные времени и температуры вместо T (0).
При t = 0 температура равна 72. При t = 0 становится 1.
Теперь используйте другую точку данных, чтобы найти значение k.
Чтобы найти значение k, возьмите натуральный логарифм от обеих сторон:
Теперь используйте эти две константы, чтобы предсказать температуру в будущем, и используйте данные в таблице 1, чтобы проверить ответ.
Попытайтесь найти температуру в момент времени t = 40 минут.
Воспользуйтесь калькулятором, чтобы найти значение:
Это близко к дате выборки в Таблице 2.
Теперь попробуйте предсказать, сколько времени потребуется, чтобы температура достигла 30 °.
Взятие натурального бревна с обеих сторон:
Решение для t:
Детали для вывода уравнений 1 и 2
Студенты с некоторым опытом в области математического анализа могут захотеть узнать, как вывести уравнения 1 и 2.
Начните решать дифференциальное уравнение, переписав уравнение:
Объедините обе стороны:
По определению это означает:
Используя законы экспонент, это уравнение можно записать как:
Величина e C1 – это постоянная величина, которую можно выразить как C 2 .
У этого уравнения есть 2 общих решения.Одно из решений состоит в том, если вещество при температуре T горячее, чем температура окружающей среды T a . Поскольку выражение в левой части уравнения находится между столбцами абсолютного значения, (T – T a ) может быть положительным или отрицательным.
Поскольку выражение в левой части уравнения находится между столбцами абсолютного значения, (T – T a ) может быть положительным или отрицательным.
Решения, как указывалось ранее, предоставлены:
Уравнение 1:
Уравнение 2:
Уравнение 1 применяется, если температура объекта или вещества T выше температуры окружающей среды T a ; Уравнение 2 применяется, если температура окружающей среды выше, чем температура объекта или вещества.
Что делать, если температура атмосферы выше, чем температура образца вещества? Как долго стакан лимонада будет оставаться холодным в летний день?
В случае, если атмосфера теплее, чем ваш материал, решение закона охлаждения Ньютона выглядит следующим образом:
Можете ли вы разработать процедуру для проверки этого уравнения? Начните с образца холодной воды и повторите процесс в упражнении 2.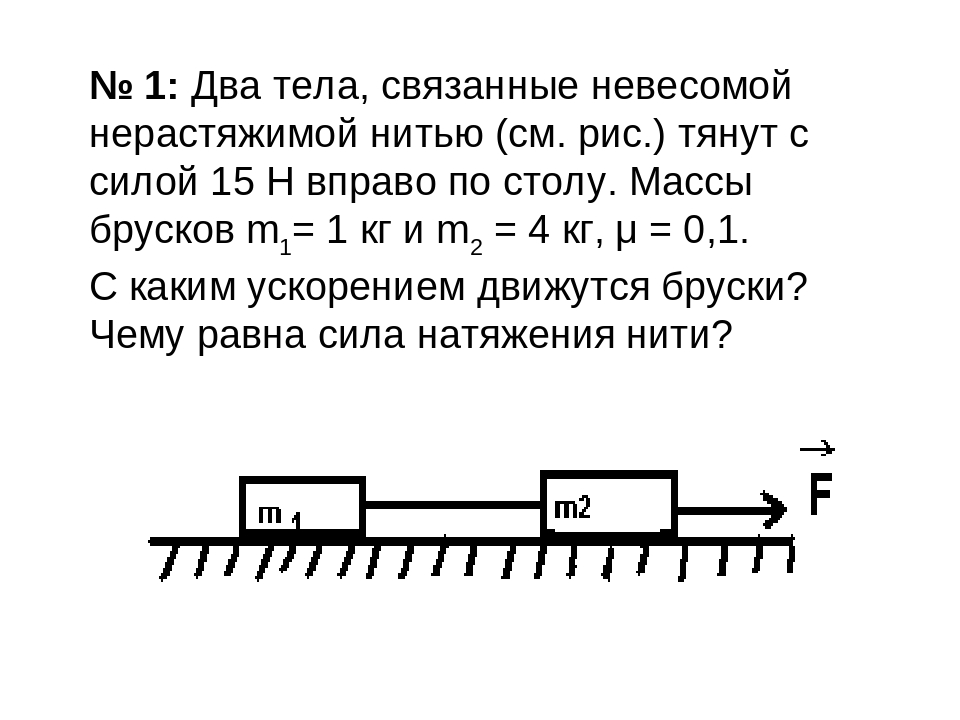 Постарайтесь предсказать, сколько времени потребуется, чтобы вода достигла комнатной температуры.
Постарайтесь предсказать, сколько времени потребуется, чтобы вода достигла комнатной температуры.
4.7 Дальнейшее применение законов движения Ньютона
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Применять методы решения проблем для определения величин в более сложных системах сил
- Интегрируйте концепции кинематики для решения задач с использованием законов движения Ньютона
Информация, представленная в этом разделе, поддерживает следующие цели обучения AP® и научные практики:
- 3.A.2.1 Учащийся может представлять силы на диаграммах или математически, используя соответствующим образом обозначенные векторы с величиной, направлением и единицами измерения во время анализа ситуации. (С.П. 1.1)
- 3.A.3.1 Учащийся может анализировать сценарий и делать утверждения – разрабатывать аргументы, обосновывать утверждения – о силах, действующих на объект другими объектами для различных типов сил или компонентов сил.
 (С.П. 6.4, 7.2)
(С.П. 6.4, 7.2) - 3.A.3.3 Учащийся может описать силу как взаимодействие между двумя объектами и идентифицировать оба объекта для любой силы. (С.П. 1.4)
- 3.B.1.1 Учащийся может предсказать движение объекта под действием сил, действующих от нескольких объектов, используя второй закон Ньютона в различных физических ситуациях с ускорением в одном измерении. (С.П. 6.4, 7.2)
- 3.B.1.3 Учащийся может повторно выразить представление диаграммы свободного тела в математическое представление и решить математическое представление для ускорения объекта. (С.П. 1.5, 2.2)
- 3.B.2.1 Учащийся может создавать и использовать диаграммы свободного тела для анализа физических ситуаций с целью качественного и количественного решения задач, связанных с движением.
 (С.П. 1.1, 1.4, 2.2)
(С.П. 1.1, 1.4, 2.2)
Есть много интересных приложений законов движения Ньютона, некоторые из которых представлены в этом разделе. Они также служат для иллюстрации некоторых тонкостей физики и помогают развить навыки решения проблем.
Пример 4.7 Сила сопротивления на барже
Предположим, что два буксира толкают баржу под разными углами, как показано на рис. 4.23. Первый буксир имеет усилие 2,7 × 105 Н2,7 × 105 Н размером 12 {2 “”. 7 умноженных на “10” rSup {size 8 {5}} “N”} {} в направлении x , а второй буксир прикладывает усилие 3,6 × 105 Н3,6 × 105 Н размером 12 {3 “. ” 6 раз по “10” rSup {size 8 {5}} “N”} {} в направлении y .
Рис. 4.23 (a) Вид сверху двух буксиров, толкающих баржу.(b) Схема свободного тела для корабля содержит только силы, действующие в плоскости воды. В нем не учитываются две вертикальные силы – вес баржи и выталкивающая сила поддерживающей ее воды, которые компенсируются и не показаны. Поскольку приложенные силы перпендикулярны, оси x и y находятся в том же направлении, что и FxFx размера 12 {F rSub {размер 8 {x}}} {} и FyFy размера 12 {F rSub {размер 8 {y}}} {}. Проблема быстро становится одномерной проблемой в направлении размера FappFapp 12 {F rSub {размер 8 {“app”}}} {}, поскольку трение происходит в направлении, противоположном FappFapp размера 12 {F rSub {размер 8 { “приложение”} } } {}.
Поскольку приложенные силы перпендикулярны, оси x и y находятся в том же направлении, что и FxFx размера 12 {F rSub {размер 8 {x}}} {} и FyFy размера 12 {F rSub {размер 8 {y}}} {}. Проблема быстро становится одномерной проблемой в направлении размера FappFapp 12 {F rSub {размер 8 {“app”}}} {}, поскольку трение происходит в направлении, противоположном FappFapp размера 12 {F rSub {размер 8 { “приложение”} } } {}.Если масса баржи составляет 5,0 × 106 кг, 5,0 × 106 кг размер 12 {5 раз “10” rSup {размер 8 {6}} “кг”} {} и ее ускорение составляет 7,5 × 10− 2 м / с 27,5 × 10–2 м / с2 размер 12 {7 “.” “52” умножить на “10” rSup {размер 8 {- 2}} “м / с” rSup {размер 8 {2}}} {} в указанном направлении. Какова сила сопротивления воды на барже, сопротивляющейся движение? Примечание. Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода. Сила сопротивления препятствует движению объекта.
Стратегия
Направления и значения ускорения и приложенных сил показаны на Рисунке 4. 23 (а) . Мы определим общую силу буксиров на барже как FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, так что
23 (а) . Мы определим общую силу буксиров на барже как FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, так что
Поскольку баржа плоская снизу, сопротивление воды FDFD размером 12 {F rSub {размер 8 {D}}} {} будет в направлении, противоположном FappFapp размера 12 {F rSub {размер 8 {“app”}}} {}, поскольку показано на диаграмме свободного тела на рисунке 4.23 (б). Здесь представляет интерес система баржа, поскольку даны силы на , и ее ускорение. Наша стратегия состоит в том, чтобы найти величину и направление чистой приложенной силы FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, а затем применить второй закон Ньютона для определения силы сопротивления FDFD размером 12 {F rSub {размер 8 {D}}} {}.
Решение
Поскольку FxFx размером 12 {F rSub {размер 8 {x}}} {} и FyFy размером 12 {F rSub {размер 8 {y}}} {} перпендикулярны, величина и направление FappFapp размера 12 {F rSub {size 8 {“app”}}} {} легко найти. Во-первых, результирующая величина дается теоремой Пифагора.
Во-первых, результирующая величина дается теоремой Пифагора.
Угол равен
4,61 θ = tan − 1FyFxθ = tan − 13,6 × 105 N2,7 × 105 N = 53 °, θ = tan − 1FyFxθ = tan − 13,6 × 105 N2,7 × 105 N = 53 °, alignl {stack { размер 12 {θ = “tan” rSup {size 8 {- 1}} слева ({{F rSub {size 8 {y}}} больше {F rSub {size 8 {x}}}} справа)} {} # θ = “загар” rSup {размер 8 {- 1}} влево ({{\ (2 “.” 7 раз “10” rSup {размер 8 {5}} “N” \)} больше {\ (3 “. “6 раз” 10 “rSup {size 8 {5}}” N “\)}} вправо) =” 53 “”. ” 1 °, {}
}} {}
“6 раз” 10 “rSup {size 8 {5}}” N “\)}} вправо) =” 53 “”. ” 1 °, {}
}} {}, который мы знаем из-за первого закона Ньютона, совпадает с направлением ускорения.Размер FDFD 12 {F rSub {размер 8 {D}}} {} находится в направлении, противоположном направлению FappFapp размера 12 {F rSub {size 8 {“app”}}} {}, поскольку он замедляет ускорение. Следовательно, чистая внешняя сила имеет то же направление, что и FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, но ее величина немного меньше, чем FappFapp размера 12 {F rSub {size 8 {“app “}}} {}. Проблема теперь одномерная. Из Рисунка 4.23 (b) мы видим, что
4.62 Fnet = Fapp-FD.Fnet = Fapp-FD размер 12 {F rSub {size 8 {“net”}} = F rSub {size 8 {“app” }} – F rSub {размер 8 {D}}} {}.Но второй закон Ньютона гласит, что
4.63 Fnet = ma.Fnet = ma size 12 {F rSub {size 8 {“net”}} = ital “ma”} {}.Таким образом,
4.64 Fapp-FD = ma.Fapp-FD = ma size 12 {F rSub {size 8 {“app”}} – F rSub {size 8 {D}} = ital “ma”} {}.
Это может быть решено для величины силы сопротивления водяного FDFD размером 12 {F rSub {size 8 {D}}} {} в терминах известных величин.
4,65 FD = Fapp − maFD = Fapp − ma размер 12 {F rSub {размер 8 {D}} = F rSub {размер 8 {“app”}} – ital “ma”} {}Подстановка известных значений дает
4.66 FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 N.FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 N размер 12 {F rSub {size 8 {D}} = \ (4 “.” 50 “умножить на 10” rSup {size 8 {5}} “N” \ ) – \ (5 “.” “00” умножить на “10” rSup {размер 8 {6}} “кг” \) \ (7 “.” “50” умножить на “10” rSup {размер 8 {“- 2” }} “м / с” rSup {size 8 {2}} \) = 7 “.” “50” умножить на “10” rSup {размер 8 {4}} “N”} {}.Направление FDFD размера 12 {F rSub {size 8 {D}}} {} уже было определено как направление, противоположное направлению FappFapp размера 12 {F rSub {size 8 {“app”}}} {}, или под углом 53º53º размером 12 {“53” “.”1 °} {} к югу от запада.
Обсуждение
Числа, использованные в этом примере, подходят для баржи среднего размера. Конечно, трудно добиться большего ускорения с буксирными судами, и желательна небольшая скорость, чтобы баржа не врезалась в доки. Сопротивление относительно мало для хорошо спроектированного корпуса на низких скоростях, что согласуется с ответом на этот пример, где размер FDFD 12 {F rSub {размер 8 {D}}} {} составляет менее 1/600 веса судно.
Конечно, трудно добиться большего ускорения с буксирными судами, и желательна небольшая скорость, чтобы баржа не врезалась в доки. Сопротивление относительно мало для хорошо спроектированного корпуса на низких скоростях, что согласуется с ответом на этот пример, где размер FDFD 12 {F rSub {размер 8 {D}}} {} составляет менее 1/600 веса судно.
В предыдущем примере канатоходца мы отметили, что натяжение тросов, поддерживающих массу, было одинаковым только потому, что углы с обеих сторон были равны. Рассмотрим следующий пример, где углы не равны; требуется немного больше тригонометрии.
Пример 4.8. Различное натяжение под разными углами
Рассмотрим светофор (масса 15,0 кг), подвешенный на двух тросах, как показано на Рисунке 4.24. Найдите натяжение в каждой проволоке, не обращая внимания на массу проволоки.
Рис. 4.24 Светофор подвешен на двух тросах. (б) Некоторые из задействованных сил. (c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную ( x ) и горизонтальную ( x ) оси. Горизонтальные составляющие натяжения должны нейтрализоваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора. (e) Схема свободного тела показывает вертикальные и горизонтальные силы, действующие на светофор.
(c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную ( x ) и горизонтальную ( x ) оси. Горизонтальные составляющие натяжения должны нейтрализоваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора. (e) Схема свободного тела показывает вертикальные и горизонтальные силы, действующие на светофор.
Стратегия
Представляющая интерес система – это светофор, диаграмма свободного тела которого показана на рис. 4.24 (c). Эти три задействованные силы не параллельны, поэтому они должны быть спроецированы в систему координат. Наиболее удобная система координат имеет одну ось вертикальную и одну горизонтальную, и проекции вектора на нее показаны в части (d) рисунка. В этой задаче есть два неизвестных (размер 12 T1T1 {T rSub {размер 8 {1}}} {} и размер 12 T2T2 {T rSub {размер 8 {2}}} {}), поэтому для нахождения их. Эти два уравнения получены в результате применения второго закона Ньютона вдоль вертикальной и горизонтальной осей с учетом того, что чистая внешняя сила равна нулю вдоль каждой оси, потому что ускорение равно нулю.
Эти два уравнения получены в результате применения второго закона Ньютона вдоль вертикальной и горизонтальной осей с учетом того, что чистая внешняя сила равна нулю вдоль каждой оси, потому что ускорение равно нулю.
Решение
Сначала рассмотрим горизонтальную ось x .
4,67 Fnet x = T2x − T1x = 0. Fnet x = T2x − T1x = 0. размер 12 {F rSub {размер 8 {“net x”}} = T rSub {размер 8 {“2x”}} – T rSub {size 8 {“1x”}} = 0} {}Таким образом, как вы могли бы ожидать,
4.68 T1x = T2x.T1x = T2x размер 12 {T rSub {размер 8 {“1x”}} = T rSub {размер 8 {“2x”}}} {}.Это дает нам следующую взаимосвязь между размером 12 T1T1 {T rSub {размер 8 {1}}} {} и размером 12 T2T2 {T rSub {размер 8 {2}}} {}
4.69 T1cos (30º) = T2cos (45º) .T1cos (30º) = T2cos (45º) размер 12 {T rSub {размер 8 {1}} “cos” \ (“30” ° \) = T rSub {размер 8 { 2}} “cos” \ (“45” ° \)} {}.Таким образом,
4,70 T2 = (1,225) T1. T2 = (1,225) T1, размер 12 {T rSub {size 8 {2}} = \ (1 “.” “225” \) T rSub {size 8 {1}}} {} .
T2 = (1,225) T1, размер 12 {T rSub {size 8 {2}} = \ (1 “.” “225” \) T rSub {size 8 {1}}} {} .Обратите внимание, что T1T1 размер 12 {T rSub {размер 8 {1}}} {} и T2T2 размер 12 {T rSub {size 8 {2}}} {} в этом случае не равны, потому что углы с обеих сторон не равный. Разумно, что размер 12 T2T2 {T rSub {размер 8 {2}}} {} в конечном итоге больше, чем размер 12 T1T1 {T rSub {размер 8 {1}}} {}, потому что он действует более вертикально, чем T1T1 размер 12 {T rSub {размер 8 {1}}} {}.
Теперь рассмотрим компоненты силы вдоль вертикальной оси y .
4,71 Fnet y = T1y + T2y − w = 0.Fnet y = T1y + T2y − w = 0. размер 12 {F rSub {размер 8 {“net y”}} = T rSub {size 8 {“1y”}} + T rSub {size 8 {“2y”}} – w = 0} {}Это означает
4.72 T1y + T2y = w.T1y + T2y = w размер 12 {T rSub {размер 8 {“1y”}} + T rSub {размер 8 {“2y”}} = w} {}.Подстановка выражений для вертикальных составляющих дает
4,73 T1sin (30º) + T2sin (45º) = w. T1sin (30º) + T2sin (45º) = размер 12 {T rSub {размер 8 {1}} “sin” \ (“30” ° \) + T rSub {размер 8 {2}} “sin” \ (“45” ° \) = w} {}.
T1sin (30º) + T2sin (45º) = размер 12 {T rSub {размер 8 {1}} “sin” \ (“30” ° \) + T rSub {размер 8 {2}} “sin” \ (“45” ° \) = w} {}.В этом уравнении есть два неизвестных, но замена выражения для T2T2 размера 12 {T rSub {size 8 {2}}} {} на T1T1 размера 12 {T rSub {size 8 {1}}} {} уменьшает это к одному уравнению с одним неизвестным.
4,74 T1 (0,500) + (1,225T1) (0,707) = w = мг, T1 (0,500) + (1,225T1) (0,707) = w = размер 12 мг {T rSub {размер 8 {1}} \ (0 ” . “” 500 “\) + \ (1”. “” 225 “T rSub {size 8 {1}} \) \ (0”. “” 707 “\) = w = ital” mg “} {},, что дает
4,75 1,366T1 = (15,0 кг) (9,80 м / с2) .1.366T1 = (15,0 кг) (9,80 м / с2) размер 12 {слева (1 дюйм. «366 дюймов справа) T rSub {размер 8 {1} } = \ (“15” “.” “0 кг” \) \ (9 “.” “80 м / с” rSup {size 8 {2}} \)} {}.Решение этого последнего уравнения дает величину T1T1 размера 12 {T rSub {size 8 {1}}} {} равную
4.76 T1 = 108 N.T1 = 108 N размер 12 {T rSub {size 8 {1}} = “108” “N”} {}.
Наконец, величина T2T2 размера 12 {T rSub {size 8 {2}}} {} определяется с использованием отношения между ними, T2T2 размер 12 {T rSub {size 8 {1}}} {} = 1,225 T1T1 size 12 {T rSub {size 8 {2}}} {}, найдено выше. Таким образом, получаем
4,77 T2 = 132 N.T2 = 132 N, размер 12 {T rSub {size 8 {2}} = “132 N”} {}.Обсуждение
Оба натяжения были бы больше, если бы оба троса были более горизонтальными, и они были бы равны тогда и только тогда, когда углы с обеих сторон такие же, как в предыдущем примере канатоходца.
Весы для ванной – отличный пример нормальной силы, действующей на тело. Он обеспечивает количественное определение того, насколько он должен подтолкнуться вверх, чтобы выдержать вес объекта. Но можете ли вы предсказать, что бы вы увидели на шкале весов для ванной, если бы стояли на них во время поездки на лифте? Увидите ли вы значение, превышающее ваш вес, когда лифт пойдет? А как насчет того, когда лифт движется вверх с постоянной скоростью: будут ли весы показывать больше, чем ваш вес в состоянии покоя? Рассмотрим следующий пример.
Пример 4.9. Что показывают весы в лифте?
На рис. 4.25 показан мужчина весом 75,0 кг (около 165 фунтов), стоящий на весах в лифте. Рассчитайте показание шкалы: (а) если лифт ускоряется вверх со скоростью 1,20 м / с 21,20 м / с2 размер 12 {1 “.” “20 м / с” rSup {размер 8 {2}}} {}, и (b) если лифт движется вверх с постоянной скоростью 1 м / с.
Рис. 4.25 (a) Различные силы, действующие, когда человек стоит на весах в лифте.Стрелки приблизительно соответствуют тому, когда лифт ускоряется вверх – пунктирные стрелки обозначают силы, слишком большие для масштабирования. Размер TT 12 {T} – это натяжение поддерживающего троса, размер ww 12 {w} – вес человека, размер wsws 12 {w rSub {размер 8 {s}}} {} – вес весов, wewe size 12 {w rSub {size 8 {e}}} {} – это вес лифта, FsFs размер 12 {F rSub {size 8 {s}}} {} – это сила действия весов на человека, FpFp размер 12 {F rSub {размер 8 {p}}} {} – сила человека на весах, размер FtFt 12 {F rSub {размер 8 {t}}} {} – сила весов на полу лифта, а NN размер 12 {N} – сила пола, направленная вверх по шкале. (б) Диаграмма свободного тела показывает только внешние силы, действующие на обозначенную интересующую систему – человека.
(б) Диаграмма свободного тела показывает только внешние силы, действующие на обозначенную интересующую систему – человека.Стратегия
Если шкала точная, ее показание будет равняться размеру 12 FpFp {F rSub {размер 8 {p}}} {}, величине силы, которую человек прикладывает к весам вниз. На рис. 4.25 (а) показаны многочисленные силы, действующие на лифт, весы и человека. Это заставляет эту одномерную проблему выглядеть гораздо более грозной, чем если бы человек был выбран в качестве представляющей интерес системы и была нарисована диаграмма свободного тела, как на рисунке 4.25 (б). Анализ диаграммы свободного тела с использованием законов Ньютона может дать ответы на обе части (а) и (b) этого примера, а также на некоторые другие вопросы, которые могут возникнуть. Единственными силами, действующими на человека, являются его вес ww размер 12 {w} {} и восходящая сила весов FsFs размера 12 {F rSub {размер 8 {s}}} {}. Согласно третьему закону Ньютона, размер FpFp 12 {F rSub {размер 8 {p}}} {} и размер FsFs 12 {F rSub {размер 8 {s}}} {} равны по величине и противоположны по направлению, так что мы нужно найти FsFs размером 12 {F rSub {size 8 {s}}} {}, чтобы найти то, что читает шкала.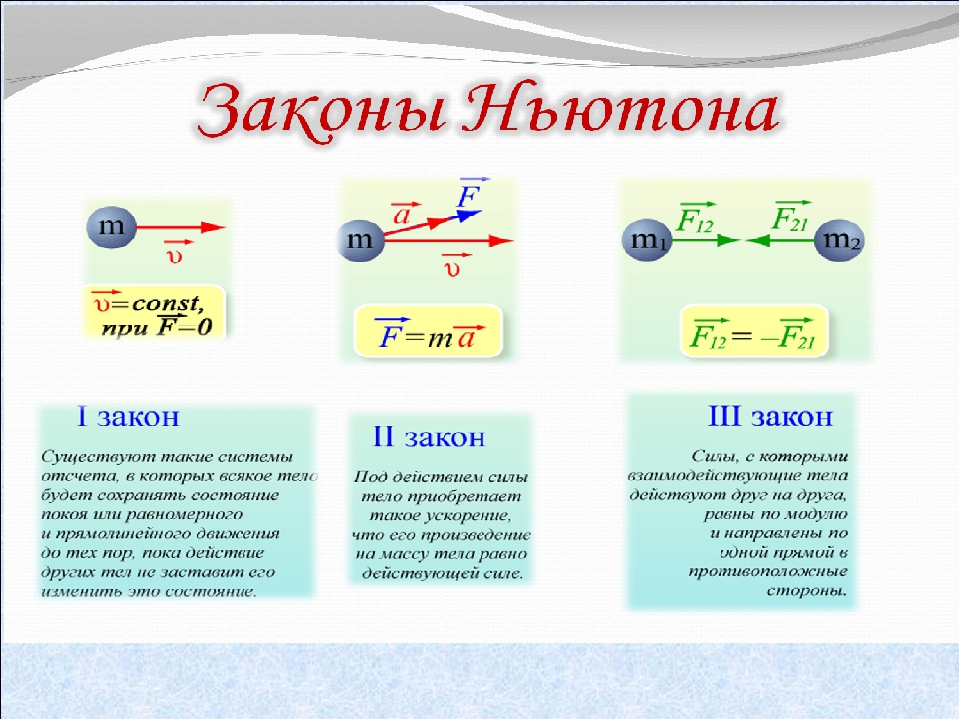 Мы можем сделать это, как обычно, применив второй закон Ньютона,
Мы можем сделать это, как обычно, применив второй закон Ньютона,
Из диаграммы свободного тела мы видим, что Fnet = Fs − wFnet = Fs − w размер 12 {F rSub {size 8 {“net”}} = F rSub {size 8 {s}} – w} {}, поэтому что
4.79 Fs − w = ma.Fs − w = ma size 12 {F rSub {size 8 {s}} – w = ital “ma”} {}.Решение для FsF размером 12 {F rSub {size 8 {s}}} {} дает уравнение только с одним неизвестным.
4.80 Fs = ma + w, Fs = ma + w size 12 {F rSub {size 8 {s}} = ital “ma” + w} {},или, поскольку w = mgw = mg, просто
4.81 Fs = ma + mg.Fs = ma + mg, размер 12 {F rSub {size 8 {s}} = ital «ma» + ital «mg»} {}.Никаких предположений об ускорении не делалось, поэтому это решение должно быть действительным для множества ускорений в дополнение к тем, что в этом упражнении.
Решение для (a)
В этой части задачи a = 1,20 м / с2a = 1,20 м / с2 размер 12 {a = 1 “. ” “20” “м / с” rSup {размер 8 {2}}} {}, так что
” “20” “м / с” rSup {размер 8 {2}}} {}, так что
дает
4.83 Fs = 825 N.Fs = 825 N размер 12 {F rSub {size 8 {s}} = 8 “25 N”} {}.Обсуждение для (а)
Это примерно 185 фунтов. Что бы показывали весы, если бы он был неподвижен? Поскольку его ускорение будет нулевым, сила весов будет равна его весу.
4.84 Fnet = ma = 0 = Fs − wFs = w = mgFs = (75,0 кг) (9,80 м / с2) Fs = 735 N.Fnet = ma = 0 = Fs − wFs = w = mgFs = (75,0 кг) (9,80 м / с2) Fs = 735 N.alignl {stack { размер 12 {F rSub {size 8 {“net”}} = ital “ma” = 0 = F rSub {size 8 {s}} – w} {} # F rSub {size 8 {s}} = w = ital “mg” {} # F rSub {size 8 {s}} = \ (“75” “.” 0 “кг” \) \ (9 “. ” “80 м / с” rSup {size 8 {2}} \) {} #
F rSub {size 8 {s}} = “735” “N” “.” {}
}} {}
” “80 м / с” rSup {size 8 {2}} \) {} #
F rSub {size 8 {s}} = “735” “N” “.” {}
}} {}Итак, показания весов в лифте больше, чем его вес 735-Н (165 фунтов). Это означает, что весы толкают человека вверх с силой, превышающей его вес, что необходимо для ускорения его движения вверх.Очевидно, что чем больше ускорение лифта, тем больше показание шкалы, соответствующее тому, что вы чувствуете при быстром ускорении по сравнению с медленно ускоряющимся лифтом.
Решение для (b)
Итак, что происходит, когда лифт набирает постоянную скорость вверх? Будут ли весы показывать больше, чем его вес? Для любой постоянной скорости – вверх, вниз или в неподвижном состоянии – ускорение равно нулю, потому что a = ΔvΔta = ΔvΔt размер 12 {a = {{Δv} по {Δt}}} {}, и Δv = 0Δv = 0 размер 12 {Δv = 0} {}.
Таким образом,
4.85 Fs = ma + mg = 0 + mg.Fs = ma + mg = 0 + mg, размер 12 {F rSub {size 8 {s}} = ital “ma” + ital “mg” = 0 + ital “mg”} {}.
Сейчас
4,86 Fs = (75,0 кг) (9,80 м / с2), Fs = (75,0 кг) (9,80 м / с2) размер 12 {F rSub {size 8 {s}} = \ (“75” “.” “0 кг “\) \ (9”. “” 80 м / с “rSup {size 8 {2}} \)} {},, что дает
4.87 Fs = 735 N.Fs = 735 N размер 12 {F rSub {size 8 {s}} = 7 “35 N”} {}.Обсуждение для (б)
На весах 735 Н, что соответствует весу человека.Это будет иметь место, когда лифт имеет постоянную скорость – движется вверх, вниз или неподвижен.
Решение предыдущего примера также применимо к лифту, ускоряющемуся вниз, как уже упоминалось. Когда лифт ускоряется вниз, размер 12 {a} {} отрицательный, и показание весов на меньше, чем на вес человека, до тех пор, пока не будет достигнута постоянная скорость вниз, после чего показание весов снова станет равным вес человека.Если лифт находится в свободном падении и ускоряется вниз при размере gg 12 {g} {}, тогда показание шкалы будет равно нулю, и человек будет казаться невесомым.
