Задачи с решениями по гидрогазодинамике: Решебник 18 (Гидрогазодинамика) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решебник 18 (Гидрогазодинамика) –

Решение задач по гидрогазодинамике часть 2

Задача 1

По трубопроводу диаметром d = 200мм движется жидкость плотностью p=950кг/м3. Массовый расход ее равен M = 200т/ч. Определить 1) при каком давлении P в сечении, расположенном на высоте Z = 2м, гидравлический (полный) напор равен H = 28м; 2) пьезометрический и скоростной напоры в данном сечении.
Скачать решение задачи 1 (цена 70р)

Задача 2

По трубопроводу диаметром d = 100мм движется жидкость плотностью 970кг/м³. В сечении, расположенном на высоте Z = 3 м, давление Р = 0,16 МПа. Определить 1) при каком массовом расходе М гидравлический напор в этом сечении равен Н = 20 м; 2) пьезометрический и скоростной напоры в данном сечении.
Скачать решение задачи 2 (цена 80р)

Задачи 3 – 8

На напорном водопроводе постоянного диаметра в водопроводных колодцах А и В, расположенных на расстоянии 1 друг от друга, установлены манометры МА и МВ (рис.

19), показывающие давление РА и РВ. Гидравлический уклон равен i, пьезометрический ip. Высота колодцев ZA и ZB. Пользуясь данными таблицы 6, определить величины, отмеченные в ней знаком вопроса

№	ZA, м	ZB, м	РА, кПа	РВ, кПа	L, км	i	ip	Направление течения
3	43	50	510	500	1,1	?	–	?	Скачать задачу 3 (цена 90р)
4	62	80	380	250	2,1	–	?	?	Скачать задачу 4 (цена 90р)
5	110	120	470	400	1,8	?	–	?	Скачать задачу 5 (цена 90р)
6	115	120	416	?	1,5		0,002	От А к В
7	80	?	420	386	2		0,0018	От А к В	Скачать задачу 7 (цена 90р)
8	93	95	?	320	1,6		0,0019	От А к В

Задачи 9 – 12

Газ находится в баллоне при темпе¬ратуре tвн и вытекает из него через насадок со скоростью и в атмосферу (рис.

20). Принимаем процесс адиабатическим (у=1,4). потерями напора пренебрегаем. Температура струи tc. Пользуясь данными таблицы 7, определите величины, отмеченные в ней знаком вопроса.

Задачи 13 – 16

Воздух плотности р, имея скорость на подходе к зданию, равную UA, над коньком здания имеет скорость, равную UB, причем UA < UB (рис.21). Давление на подходе к зданию и в самом здании равно атмосферному, благодаря этому в фонаре здания В создается тяга р вентиляционного потока. Потерями напора пренебрегаем. Пользуясь данными таблицы 8, определить величины, отмеченные в ней знаком вопроса.

Задачи 17 – 24

Определите расход воды. протекающий через насадок (рис.22) по данным таблицы 9. Во всех вариантах задан диаметр входного сечения. Значение давления дано в атмосферах. РА=1атм=101325Па.

№	Тип насадка	Н1, м	Н2, м	d, мм	l, мм	Q град	Р1, атм	Р2, атм
17	Цилиндр	2	6	20	60	0	РА	Ризб=0,2	Скачать задачу 17 (цена 100р)
18	Цилиндр	6	–	30	90	0	РА	Рабс=1,2	Скачать задачу 18 (цена 100р)
19	Цилиндр	7	–	20	80	0	Рвак=0,3	РА	Скачать задачу 19 (цена 100р)
20	Цилиндр	9	2	30	120	0	Ризб=0,2	РА	Скачать задачу 20 (цена 100р)
21	Сход конус	16	–	30	100	13°24	РА	Ризб=0,7	Скачать задачу 21 (цена 100р)
22	Расход конус	2	–	30	90	6	Рабс=1,2	РА
23	Расход конус	9	5	20	60	6	РА	РА	Скачать задачу 23 (цена 100р)
24	Расход конус	12	–	30	120	6	РА	Рвак

Задачи по гидродинамике и расчету параметров насосов.

Решение задач по гидродинамике

На этой странице приведена подборка несложных задач по гидродинамике жидкостей и теплотехнике, которые могут быть использованы для текущего контроля освоения дисциплины студентами.
К каждой задаче прилагается вариант решения с ответом.
Следует отметить, что решение большинства подобных задач возможно с использованием разных способов и алгоритмов, поэтому приведенные примеры решений не являются эталоном. Тем не менее, при разных методах решения задачи, результат решения (ответ) должен быть одинаковым.

***

Задача

Определить скорость движения жидкости в подводящей линии и скорость поршня, если известны:

диаметр трубопровода d = 0,012 м;
диаметр поршня D = 0,07 м;
подача насоса Q = 1,7х10^-3 м³/с.

Потери напора в местных сопротивлениях не учитывать.

Правильное решение:

Скорость движения жидкости в подводящей линии:

v_ж = Q/S_труб = 4Q/πd² = (4×1,7×10^-3)/(3,14×0,012²) = 15,04 м/с.

где S_труб = πd²/4 – площадь сечения трубопровода подводящей линии.

Скорость перемещения поршня:

v_п = Q/S_п = 4Q/πD² = (4×1,7×10^-3)/(3,14×0,07²) = 0,44 м/с.

Ответ: скорость движения жидкости в подводящей линии – 15,04 м/с, скорость поршня – 0,44 м/с.

***

Задача

Определить режимы движения рабочей жидкости в питающей и отводящей линии гидропривода, изображенного на схеме в приведенной выше задаче.
Исходные данные:
Скорость движения жидкости в питающей линии v₁ = 15,04 м/с;
скорость движения жидкости в отводящей линии v₂ = 10,08 м/с;
вязкость жидкости v = 0,5×10^-4 м²/с;
диаметр трубопроводов d = 0,012 м;
критическое число Рейнольдса для рабочей жидкости равно Re_кр = 2320.
Потери напора в местных сопротивлениях и трубопроводах не учитывать.

Правильное решение:

Числа Рейнольдса, характеризующее режим движения жидкости, определяется по формуле:

Re = vd/v,

где:
v – скорость движения жидкости в трубопроводе;
d – диаметр трубопровода;
v – кинематическая вязкость жидкости.

Тогда для питающей и отводящей линии число Рейнольдса будет соответственно равно:

Re₁ = v₁d /v = (15,04×0,012)/(0,5×10^-4) = 3610;
Re₂ = v₂d /v = (10,08×0,012)/(0,5×10^-4) = 2419.

Так как, полученные числа Re₁ и Re₂ больше критического Re_кр = 2320, то движение жидкости в обоих случаях будет турбулентным.

Ответ: в питающей и отводящей линии режим движения жидкости будет турбулентным.

***

Задача

Определить режим движения нефти в трубопроводе диаметром d = 400 мм при скорости движения v = 0,13 м/с.
Кинематическая вязкость нефти v = 0,3×10^-4 м²/с, критерий Рейнольдса для нефти, определяющий переход от ламинарного движения к турбулентному Re_кр = 2000…2300.

Правильное решение:

Приведем исходные данные к системе единиц СИ: d = 0,4 м.
Чтобы определить режим движения нефти в трубопроводе, вычислим число Рейнольдса для данного диаметра труб и скорости потока:

Re = vd/v = 0,13×0,4/0,3×10^-4 = 1733.

Ответ: поскольку число Рейнольдса менее критического значения, движение нефти в трубопроводе будет осуществляться в ламинарном режиме.

***

Задача

В дне бака высотой H = 4 м проделано отверстие площадью S = 4 см².
Бак наполнен водой доверху, при этом уровень воды поддерживается постоянным благодаря пополнению из водопровода.
Определите, какую подачу воды должен обеспечить водопровод, чтобы ее уровень в баке оставался неизменным.
Коэффициент расхода отверстия равен μ_s = 0,6.

Правильное решение:

Подача (расход) воды определяется произведением площади отверстия S на скорость v истекающей из отверстия струи, поскольку объем вытекающей из отверстия воды должен компенсироваться водой из водопровода.
При истечении воды из малого отверстия в баке с постоянно поддерживаемым напором скорость струи v может быть определена по формуле Торричелли:

v = μ_s √(2gH) (м/с),

где: g = 9,81 м/с² – ускорение свободного падения, Н = 4 м – напор (уровень отверстия).

Тогда, с учетом формулы Торричелли, получим требуемую подачу воды из водопровода:

Q = Sv = S μ_s √(2gH) = 4×10^-4×0,6√(2×9,81×4) ≈ 2,126×10^-3 м³/с ≈ 2,1 л/с.

Ответ: требуемый расход воды из водопровода примерно равен 2,1 л/с.

***

Задача

Вода вытекает из бака через конический сходящийся насадок с минимальным пропускным сечением S = 2 см² в ведро емкостью V = 10 л.
Коэффициент расхода насадка μ_s = 0,96.
Уровень воды в баке поддерживается постоянным от водопроводной сети.
Центр сечения насадка расположен на глубине H = 1,2 м от поверхности воды в баке.
Определить время t заполнения ведра водой.

Правильное решение:

При истечении жидкости из насадка при постоянном напоре объемный расход определяется по формуле:

Q = μ_s S√(2gH) (м³/с),

где: g = 9,81 м/с² – ускорение свободного падения.

Приведем исходные данные к системе единиц СИ (S = 0,0002 м², V = 0,01 м³), и, подставив известные величины в формулу, получим:

Q = μ_s S√(2gH) = 0,96×0,0002×√(2×9,81×1,2) ≈ 0,00093 м³/с.

Чтобы определить время заполнения ведра водой необходимо объем ведра разделить на полученный объемный расход жидкости:

t = V/Q = 0,01/0,00093 ≈ 10,75 с.

Ответ: ведро наполнится водой через 10,75 секунд.

***

Задачи по расчету параметров насосов

Задача

При частоте вращения вала 1000 мин^-1 центробежный насос потребляет 4 кВт энергии, подает 20 литров воды в секунду под напором 10 метров.
Определить, как изменятся рабочие параметры насоса, если частоту вращения вала увеличить до 3000 мин^-1.

Правильное решение:

Зависимость рабочих параметров насоса от частоты вращения вала выражается уравнениями:

n₁/n₂ = Q₁/Q₂; n₁²/n₂² = H₁/H₂; n₁³/n₂³ = N₁/N₂,

т. е. при увеличении частоты вращения вала насоса в три раза, его подачу, напор и потребляемую мощность можно определить по формулам:

Q₂ = Q₁ n₂/n₁ = 3Q₁ = 60 л/с; H₂ = H₁ √(n₂/n₁) ≈ 17,3 м; N₂ = ³√(n₂/n₁)N₁ ≈ 11,95 кВт.

Ответ: при увеличении частоты вращения до 3000 мин^-1 подача насоса составит 60 л/с, напор – приблизительно 17,3 м, а потребляемая мощность – приблизительно 11,95 кВт.

***

Задача

Определите, какова объемная подача двухцилиндрового поршневого насоса, если диаметр его поршней d = 0,1 м, рабочий ход поршней l = 0,1 м, частота вращения вала приводного электродвигателя n = 960 мин^-1.
Объемные потери не учитывать.

Правильное решение:

Объемная подача поршневого насоса может быть определена, как рабочий объем всех его цилиндров, умноженный на количество рабочих циклов за единицу времени.
Частота вращения вала насоса n = 960 мин^-1 = 16 с^-1, т. е. за одну секунду двухцилиндровый насос совершает 2×16 рабочих циклов (каждый цилиндр за один оборот совершает 1 цикл).
Рабочий объем одного цилиндра: V_ц = l πd²/4 (м³).

Тогда объемная подача насоса (без учета потерь) при данной частоте вращения составит:

Q = 2×16×l πd²/4 = 2×16×0,1×3,14×0,1²/4 = 0,02512 м³/с.

Ответ: объемная подача насоса составляет чуть более 25 л/с.

***

Задача

Определить диаметр поршней d аксиально-поршневого насоса, если известны параметры:

диаметр окружности, на которой размещены поршни D = 80 мм;
количество поршней в насосе z = 6;
угол наклона диска (шайбы насоса) к оси цилиндров γ = 45˚;
подача насоса Q равна 0,001 м³/с при частоте вращения вала n = 50 с^-1.

Правильное решение:

Подача аксиально-поршневого насоса определяется по формуле:

Q = znD tg γ πd²/4.

С учетом того, что tg γ = tg 45˚ = 1, а диаметр D в системе единиц СИ равен 0,08 м, выразим и определим из этой формулы диаметр поршней d:

d = √(4Q/πznD tg γ) = √(4×0,001/3,14×6×50×0,08×1) ≈ 0,0073 м ≈7,3 мм.

Ответ: диаметр поршней насоса приблизительно равен 7,3 мм.

***

Задача

Определите, какую мощность должен иметь электродвигатель привода водяного насоса, если насос при подаче Q = 0,05 м³/с создает напор Н = 40 м, а его полный КПД η = 0,6.
Плотность воды принять равной ρ = 1000 кг/м³.

Правильное решение:

Полезная мощность любого насоса может быть определена по формуле:

N_п = ρgQH,

где g = 9,81 м/с² – ускорение свободного падения.

Потребляемая мощность N_п, т. е. мощность, которую на работу насоса затрачивает электродвигатель N_эд (без учета потерь в приводе), равна полезной мощности с учетом КПД:

N_эд = N_п/η = ρgQH/η = 1000×9,81×0,05×40/0,6 = 32700 Вт = 32,7 кВт.

Ответ: для обеспечения работы насоса в заданном режиме
необходим электродвигатель мощностью 32,7 кВт.

***

Задача

Привод водяного насоса обеспечивает частоту вращения его вала n₁ = 15 с^-1, при этом подача насоса составляет Q₁ = 0,01 м³/с, а напор H₁ = 20 м.
Определите, какова должна быть частота вращения вала насоса, если потребуется увеличить его напор до 80 м.
Как изменится при этом подача насоса?

Правильное решение:

Зависимость рабочих параметров насоса от частоты вращения его вала выражается уравнениями:

n₁/n₂ =Q₁/Q₂; n₁²/n₂² = H₁/H₂,

т. е. для увеличения напора в четыре раза, частота вращения вала насоса должна возрасти в два раза:

n₂ = n₁ √(H₂/H₁) = n₁√4 = 2n₁.

В соответствии с первой формулой, при увеличении частоты вращения вала насоса в два раза его подача тоже возрастет в два раза, и составит Q₂ = 0,02 м³/с.

Ответ: для увеличения напора до 80 м (т. е. в четыре раза)
вал насоса должен вращаться с частотой 30 с^-1, при этом подача насоса возрастет в два раза.

***

Задача

Определите по приведенной здесь графической характеристике поршневого насоса, какова будет потребляемая им мощность и полный КПД, если подача равна 0,52 л/с.
Какое давление в системе при этом насос развивает?
Охарактеризуйте форму кривой, отображающей график зависимости Q = f(p).

Правильный ответ:

При подаче Q = 0,52 л/с насос потребляет мощность примерно равную 1,2 кВт, его КПД составляет 0,65 (максимальное значение).
Давление в системе при этом равно 1,6 МПа.

Зависимость подачи насоса от давления в системе отображает кривая Q = f(p), которая показывает, что с нарастанием давления в системе подача уменьшается, при этом резкий спад величины подачи начинается при увеличении давления от точки на графике, характеризующей максимальный КПД насоса.

***

Примеры решения задач по гидравлике и теплотехнике

Скачать задачи по гидравлике с вариантами решений
(в формате Word, размер файла 324 кБ – 27 задач с решениями и вопросы по насосам)

Скачать теоретические вопросы к экзаменационным билетам по дисциплине “Основы гидравлики и теплотехники”
(в формате Word, размер файла 68 кБ)

Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

Механика жидкостей и газов. № 4.

1 – 4.20. Решения задач из сборника волькенштейна – 26 Октября 2012 – Блог

4.1. Найти скорость v течения углекислого газа по трубе, если известно, что за время t = 30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа р = 7,5 кг/м³. Диаметр трубы D = 2 см.

Решение:

4.2. В дне цилиндрического сосуда диаметром D = 0,5 м име круглое отверстие диаметром d = 1см. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти значение этой скорости для высоты h = 0,2 м.

Решение:

4.3. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на рас h₁ от дна сосуда и на расстоянии h₂ от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии l от сосуда ( по горизонтали) струя воды падает на стол в случае, если: a) h₁ = 25 см, h₂=16см ; б) h₁ =16 см, h₂ = 25 см?

Решение:

4.4. Сосуд, наполненный водой, сообщается с атмосферой через стеклянную трубку, закрепленную в горлышке сосуда. Кран К находится на расстоянии h₂ = 2 см от дна сосуда. Найти скорость v вытекания воды из крана в случае, если расстояние между нижним концом трубки и дном сосуда: а) h₁ = 2 см; б) h₁ =7,5 см; в) h₁ =10 см.

Решение:

4.5. Цилиндрической бак высотой h = 1 м наполнен до краев водой. За какое время t вся вода выльется через отверстие, расположенное у дна бака, если площадь S₂ поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака? Сравнить это время с тем, которое понадобилось бы для вытекания того же объема воды, если бы уровень воды в баке поддерживался постоянным на высоте h = 1 м от отверстия.

Решение:

4.6. В сосуд льется вода, причем за единицу времени наливается объем воды V₁ = 0,2 л/с. Каким должен быть диаметр d отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h = 8,3 см?

Решение:

4.7. Какое давление р создает компрессор в краскопульте, если струя жидкой краски вылетает из него со скоростью v = 25 м/с? Плотность краски р = 0,8 • 10³ кг/м³.

Решение:

4.8. По горизонтальный трубе АВ течет жидкость. Разность уровней этой жидкости в трубах а и b равна dh = 10 см. Диаметры трубок а и b одинаковы. Найти скорость v течения жидкости в трубе АВ.

Решение:

4.9. Воздух продувается через трубку АВ. За единицу времени через трубку АВ протекает объем воздуха V₁ = 5 л/мин. Площадь поперечного сечения широкой части трубки АВ равна S₁ = 2 см², а узкой ее части и трубки abc равна S₂ = 0,5 см². Найти разность уровней dh воды, налитой в трубку abc. Плотность воздуха р = 1,32 кг/м³.

Решение:

4.10. Шарик всплывает с постоянной скоростью v в жид, плотность р₁которой в 4 раза больше плоскости мате шарика. Во сколько раз сила трения F_тр, действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?

Решение:

4.11. Какой наибольшей скорости v может достичь дождевая капля диаметром d = 0,3 мм, если динамическая вязкость воз n= 1,2-10^-5 Па*с?

Решение:

4.12. Стальной шарик диаметром d = 1мм падает с посто скоростью v = 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость n касторо масла.

Решение:

4.13. Смесь свинцовых дробинок с диаметрами d₁ = 3 мм и d₂ = 1 мм опустили в бак с глицерином высотой h = 1 м. На сколько позже упадут на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра? Динамическая вязкость глицерина n = 1,47 Па*с.

Решение:

4.14. Пробковый шарик радиусом r = 5 мм всплывает в сосуде, наполненном касторовым маслом. Найти динамическую и кинематическую вязкости касторового масла, если шарик всплывает с постоянной скоростью v = 3,5 см/с.

Решение:

4.15. В боковую поверхность цилиндрического сосуда радиусом R = 2 см вставлен горизонтальный капилляр, внутренний радиус r = 1 мм которого и длина l = 2 см. В сосуд налито касторовое масло, динамическая вязкость которого n = 1,2Па*с. Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h = 26 см.

Решение:

4.16. В боковую поверхность сосуда вставлен горизон капилляр, внутренний радиус которого r = 1 мм и длина l = 1,5 см. В сосуд налит глицерин, динамическая вязкость которого n = 1,0Па*с. Уровень глицерина в сосуде поддержи постоянным на высоте h = 0,18м выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина V = 5 см³?

Решение:

4.17. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте h₁ = 5 см от дна сосуда. Внутренний радиус капилляра r = 1 мм и длина l = 1 см. В сосуд налито машинное масло, плотность которого р = 0,9 • 10³ кг/м³ и динамическая вязкость n = 0,5 Па*с. Уровень масла в сосуде поддерживается постоянным на высоте h₂ – 50 см выше капилляра. На каком расстоянии L от конца капилляра (по горизонтали) струя масла падает на стол?

Решение:

4.18. Стальной шарик падает в широком сосуде, напол трансформаторным маслом, плотность которого р — 0,9 • 10³ кг/ m³ и динамическая вязкость n= 0,8Па*с. Считая, что закон Стокса имеет место при числе Рейнольдса Re < 0,5 (если при вычислении Re в качестве величины D взять диаметр шарика), найти предельное значение диаметра D шарика.

Решение:

4.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Rе<3000 (если при вычислении Re в качестве величины D взять диаметр трубы), показать, что условия задачи 4. 1 соответствуют ламинарному движению. Кинематическая вязкость газа v = 1,33 • 10^-6 м²/с.

Решение:

4.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды V₁ = 200см³/с. Динамическая вязкость воды n = 0,001 Па*с. При каком предельном значении диаметра D трубы движение воды остается ламинарным? (Смотри условие предыдущей задачи.)

Решение:

Autodesk Simulation CFD 2012 — комплекс инструментов для решения задач гидрогазодинамики

Антон Лепестов

Комплекс Autodesk Simulation CFD предоставляет пользователям полный набор гибких инструментов, позволяющих моделировать потоки жидкостей и процессы теплопередачи. Быстрый анализ и точные расчеты возможны на самых ранних этапах разработки изделий, когда принятие верных решений особенно важно. Специальная среда изучения проектных вариантов обеспечивает исследование эксплуатационных характеристик различных вариантов изделия, тем самым повышая качество разрабатываемой продукции. Simulation CFD позволяет применять технологию цифровых прототипов в области архитектуры и строительства, при производстве товаров промышленного назначения и потребительской продукции, а также при разработке систем охлаждения электронной аппаратуры.

Предисловие

Сегодня нелегко найти простой в применении программный комплекс для инженерного анализа, способный удовлетворить растущие с каждым днем запросы пользователя. Проблема становится еще сложнее, когда дело касается комплекса задач из области гидромеханики и теплопроводности, поскольку такие задачи очень специфичны и разнообразны и для их решения требуются огромный опыт и глубокие знания. Тем более что развитие данной отрасли всегда связано с практической применимостью изделий, будь то парус, весло, насос или сложные газо и гидромеханические механизмы.

Прогресс не стоит на месте. Вместе с другими областями человеческого знания динамично развивается и техническая механика жидкости (гидравлика). Появилась соответствующая измерительная аппаратура — пьезометры, трубки Пито, вертушки Вольтмана и т.п. Вслед за идеей использования материальных (вещественных) моделей тех или иных гидравлических явлений для их изучения и проектирования соответствующих инженерных сооружений пришли идеи теоретического построения приближенных расчетных зависимостей с введенными эмпирическими коэффициентами.

Однако главной проблемой гидрогазодинамики как научнотехнической дисциплины традиционно является взаимодействие между средой и движущимися или покоящимися в ней телами. С течением времени эта проблема только усложняется. Если раньше она ограничивалась в основном решением задач транспортировки воздуха и воды, то сегодня основное внимание уделяется изучению движения вязких жидкостей, для которых эмпирические методы и зависимости неприменимы. Кроме того, всё более насущной становится необходимость наблюдения и предупреждения таких эффектов, как падение давления, кавитация, конвекция и т. д. Всё это требует совершенствования методов и средств расчета гидрогазодинамических явлений. И успехи здесь очевидны.

Simulation CFD 2012

С недавнего времени в семействе продуктов для инженерного анализа Autodesk появился комплекс Simulation CFD 2012 (Computational fluid dynamics), ранее известный под названием CFdesign. Он предоставляет пользователям полный набор инструментов для моделирования потоков жидкостей и процессов теплопередачи, позволяющих существенно расширить возможности технологии «цифровых прототипов» и выполнять различные сценарии анализа проекта.

Комплекс Autodesk Simulation CFD базируется на основных уравнениях неразрывности, НавьеСтокса и сохранения энергии, обеспечивающих эффективное сопоставление результатов расчетов компьютерного анализа с реальностью. Расчет потоков среды (газа или жидкости) посредством данного программного комплекса применим в архитектуре, приборостроении, общем машиностроении, автомобилестроении, авиастроении и др. С помощью Autodesk Simulation CFD можно осуществлять учет влияния движения воздушных масс в системе вентиляции, определять аэродинамические характеристики автомобиля, исследовать температурные поля электрических приборов во время их работы, распределять давление в трубопроводах… Этот список можно продолжать и продолжать. Не будет преувеличением сказать, что комплекс позволяет решать практически все задачи, связанные с гидрогазодинамикой.

Autodesk Simulation CFD предоставляет полный набор инструментов для исследования течения потоков жидкости:

ламинарных;
турбулентных;
несжимаемых;
стационарных.

По сравнению с Autodesk Simulation CFD возможности исследования физических процессов в Autodesk Simulation CFD Advanced расширены: анализ потоков дополнен инструментами анализа переходных состояний, сжимаемых потоков, кавитации, двухфазных потоков (газожидкостные смеси), а также добавлены расчет процессов теплопередачи эффектов излучения, расчет влияния солнечного излучения и т. д.

Это позволяет инженерам в области конструирования машиностроительной продукции:

моделировать запуск потока для прогнозирования распространения волн давления через изделие;
собирать данные о давлении в переходном режиме и развитии потока;
прогнозировать падение давления и распределение скоростей сверхзвуковых потоков газа в пневмораспределителях;
моделировать смешивание двух схожих жидкостей с использованием скалярного условия.

Этот модуль будет полезен и изготовителям электронных приборов, поскольку одна из основных проблем, с которой они сталкиваются, заключается в поддержании рабочего температурного диапазона компонентов. Проектировщики же систем освещения получат возможность эффективнее осуществлять термоуправление светодиодами, значительная часть общей энергии которых преобразуется в тепло, что требует обеспечения их намного более низкими температурами, чем для других типов ламп.

Autodesk Simulation CFD Advanced будет полезен при расчетах искусственной и естественной вентиляции, внешнего обтекания (ветровой нагрузки) и зон комфорта для людей.

Autodesk CFD Motion обеспечивает моделирование взаимодействия компонентов изделия и дополняет задачу необходимым перемещением в среде твердого тела. Это позволяет более точно моделировать работу насосов, вентиляторов, нагнетателей, компрессоров, задвижек и других механических устройств в условиях, близких к реальным. Данный пакет позволяет учитывать:

возникающие усилия;
крутящий момент;
скорость вращения;
линейную скорость перемещения;
угловую скорость;
линейную деформацию изделия;
угловую деформацию;
скачки/падения давления;
скачки/падения температуры;
изменение скорости потока.

Развитые возможности комплекса Autodesk Simulation CFD позволяют пользователю выбрать необходимый набор специализированных инструментов для решения задач гидроаэродинамики и принять оптимальные конструкторские решения.

Работа с САПРплатформами

Важное преимущество Autodesk Simulation CFD — возможность при ассоциативном моделировании потоков жидкости и процессов теплопередачи взаимодействовать с различными САПР. Входящий в поставку специальный модуль Connection for… позволяет осуществлять интеграцию с:

Autodesk Inventor;
Autodesk Revit;
Siemens NX;
PTC Pro/ENGINEER;
PTC CoCreate;
Siemens Solid Edge;
SolidWorks;
SpaceClaim;
CATIA.

Заключение

Autodesk Simulation CFD предоставляет инновационные возможности для проведения быстрого анализа и осуществления точных расчетов как на ранних этапах разработки изделий, так и при оформлении окончательного варианта проекта. Специальная среда изучения эксплуатационных характеристик проектных вариантов позволяет существенно повысить качество разрабатываемой продукции. Возможность применения технологии цифровых прототипов обеспечит значительный рост производительности в области архитектуры и строительства, при производстве товаров промышленного назначения и потребительской продукции, а также при разработке систем охлаждения электронной аппаратуры.

САПР и графика 5`2012

ANSYS CFD | Архивные версии продуктов ANSYS

Решатели гидрогазодинамики общего назначения

Технология ANSYS CFD открывает доступ к хорошо известным программным продуктам ANSYS FLUENT и ANSYS CFX. Это основные продукты для задач гидрогазодинамики общего назначения, предлагаемые компанией ANSYS, Inc.

Оба решателя разрабатывались в течение десятилетий независимо друг от друга и обладают несколькими существенными отличиями, несмотря на некоторые схожие черты. Оба модуля основаны на методе контрольных объемов, дающем высокую точность, и используют решатель по давлению, что позволяет применять эти продукты для решения широкого круга инженерных задач. Основные отличия состоят в способе интегрирования уравнений течения жидкостей и в стратегиях решения уравнений.

Решатель ANSYS CFX использует сетку конечных элементов (числовые значения в узлах сетки), схожую с теми, что используется в анализе прочности, для дискретизации области. В отличие от ANSYS CFX, решатель ANSYS FLUENT использует сетку конечных объемов (числовые значения в центрах ячеек). В итоге оба подхода формируют уравнения для конечных объемов, которые обеспечивают сохранение значений потока, что является необходимым условием для точных решений задач гидрогазодинамики. В ANSYS CFX особый упор сделан на решение основных уравнений движения (сопряженная алгебраическая сетка), а ANSYS FLUENT предлагает несколько подходов к решению (метод на основе плотности, расщепленный метод на основе давления, сопряженный метод на основе давления). Оба решателя содержат в себе самые ценные возможности физического моделирования для получения максимально точных результатов.

ANSYS CFD-Post предоставляет мощные количественные и графические возможности постобработки и создания отчетов

Модуль ANSYS CFD является высокомасштабируемым. Время разработки продукта может быть сокращено благодаря функции высокопроизводительного расчета ANSYS CFD HPC. Она позволяет делать расчеты больших моделей на параллельных расчетных кластерах. Линейная масштабируемость была продемонстрирована на более чем тысяче процессоров.

На создание решателей ANSYS для течений жидкостей и газов потрачено более тысячи человеко-лет исследований и разработок. Эти усилия выгодно отличают программные продукты ANSYS от конкурентов благодаря опыту, надежности, широкому набору продуктов и максимальной аналитической глубине. Решатели для гидрогазодинамики компании ANSYS широко используются компаниями по всему миру.

Специализированные инструменты для анализа жидкостей и газов

Гибкость и общеприменимость решателей важны, но иногда они не требуются для решения конкретных специализированных задач. В дополнение к инструментам для решения задач гидрогазодинамики общего назначения ANSYS предлагает узкоспециализированные решения для анализа жидкостей и газов. Эти решения часто называют вертикальными приложениями из-за способа интеграции всех шагов системы анализа специфического типа в программный модуль. Технологии ANSYS предлагают специфические отраслевые функции и терминологию.

Контуры давления на внешних поверхностях вертолета, находящегося в режиме зависания

Турбомашиностроение – один из самых удачных примеров вертикально интегрированной задачи анализа жидкостей и газов, поскольку геометрии и физические процессы во всех областях вращающихся машин схожи. Технология ANSYS для турбосистем включает в себя специализированные инструменты для работы с геометрией и сеткой, а также специализированные модели.

В конечном итоге пользователи могут создавать собственные вертикальные приложения в рамках продуктов моделирования жидкостей/газов общего назначения. Модуль ANSYS CFX предлагает настраиваемый мастер установок и язык описания; ANSYS FLUENT – определяемые пользователем функции.

Совместно с инструментами написания сценариев, доступными во всех приложениях ANSYS Workbench, они могут быть использованы для создания специализированных вертикальных приложений. Не редки случаи, когда аналитический отдел создает подобное вертикальное приложение, которое используется и в конструкторском отделе. Основное преимущество такого подхода – повторяемое с высокой точностью управление процессом моделирования и, следовательно, контроль качества любых гидрогазодинамических процессов.

Преимущества решений компании ANSYS для моделирования жидкостей и газов

Технология анализа течений жидкостей и газов компании ANSYS позволяет выполнять глубокий анализ механики жидкости во многих типах изделий и процессов, что дает возможность не только снизить необходимость дорогостоящих прототипов, но и получить исчерпывающие данные, которые не всегда доступны при проведении экспериментальных исследований. Моделирование жидкостей и газов может служить дополнением к физическому эксперименту. Некоторые разработчики используют моделирование для анализа новых систем перед принятием решения о том, какие эксперименты проводить и в каком количестве. Во время поиска неисправностей вызывающие трудности задачи решаются быстрее и точнее, поскольку анализ гидрогазодинамики выделяет не только следствие неисправности, но и ее причину. Во время оптимизации конструкции нового оборудования за короткий промежуток времени можно выполнить много аналитических вычислений типа «что-если». Результатом этого становится лучшее соответствие продукта, увеличенная производительность, надежность. ANSYS продолжит внедрять инновации в свои разработки, чтобы пользователи могли заменить традиционные капиталоемкие процессы разработки на процесс разработки продукта, на основе инженерных расчетов.

Решения задач

Решения задач Математического праздника

Тридцатый второй Математический праздник (18 апреля 2021 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс
«Математический праздник в Математической вертикали»: 6 класс, 7 класс
Рабочие критерии проверки: 6 класс, 7 класс

Тридцатый первый Математический праздник (09 февраля 2020 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс
«Математический праздник в Математической вертикали»: 6 класс, 7 класс

Тридцатый Математический праздник (17 февраля 2019 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать девятый Математический праздник (18 февраля 2018 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать восьмой Математический праздник (19 февраля 2017 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать седьмой Математический праздник (21 февраля 2016 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать шестой Математический праздник (15 февраля 2015 года)
Решения в формате PDF
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать пятый Математический праздник (16 февраля 2014 года)
Решения в формате PDF (555 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать четвёртый Математический праздник (17 февраля 2013 года)
Решения в формате PDF (308 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать третий Математический праздник (19 февраля 2012 года)
Решения в формате PDF (486 К, 12 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать второй Математический праздник (13 февраля 2011 года)
Решения в формате PDF (141 К, 16 страниц)
Рабочие критерии проверки: 6 класс, 7 класс

Двадцать первый Математический праздник (14 февраля 2010 года)
Решения в формате PDF (96 К, 12 страниц)

Двадцатый Математический праздник (15 февраля 2009 года)
Решения в формате PDF (102 К, 12 страниц)

Девятнадцатый Математический праздник (17 февраля 2008 года)
Решения в формате PDF (132 К, 8 страниц)

Восемнадцатый Математический праздник (11 февраля 2007 года)
6 класс
7 класс
Решения в формате PDF (98 Кб, 8 страниц)

Семнадцатый Математический праздник (12 февраля 2006 года)
6 класс
7 класс
Решения в формате PDF (551 Кб, 8 страниц)

Шестнадцатый Математический праздник (13 февраля 2005 года)
6 класс
7 класс
Решения в формате PDF (217 Кб, 8 страниц)

Пятнадцатый Математический праздник (15 февраля 2004 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 7 страниц)

Четырнадцатый Математический праздник (16 февраля 2003 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 8 страниц)

Тринадцатый Математический праздник (17 февраля 2002 года)
6 класс
7 класс
Решения в формате PDF (131 Кб, 8 страниц)

Двенадцатый Математический праздник (18 февраля 2001 года)
6 класс
7 класс
Решения в формате PDF (183 Кб, 4*2 страниц)

Одиннадцатый Математический праздник (13 февраля 2000 года)
6 класс
7 класс
Решения в формате PDF (88 Кб, 6 страниц)

Десятый Математический праздник (21 февраля 1999 года)
6 класс
7 класс

Дата последнего изменения: 19 апреля 2021 года

Ночь решения задач в Вышке

Любите ли вы решать задачи так же, как любим это мы?

В преддверии нового года и сессии мы решили отметить первое и морально подготовиться ко второму. И если Дед Мороз раздаёт подарки за добрые дела и хорошее поведение, то мы в университете раздаём подарки за количество решённых задач. Всего на мероприятии будет три площадки: анализ данных, алгоритмы и математика. На каждой из площадок вам предложат задачи разной степени сложности для решения, но в целом они будут рассчитаны на людей, обучающихся в вузе или уже имеющих профильное образование. Среднее время решения задач одной площадки — 1,5 часа, поэтому вы сможете попробовать свои силы во всех категориях, получая за решения баллы и подарки. Чем больше баллов, тем выше место в рейтинге по итогам мероприятия и больше интереса к вам со стороны компаний-партнеров, которые всегда заинтересованы в талантах.

Помимо задач в программе: лекции о работе с Kaggle, чат-ботах, технологических конкурсах, встреча с работодателями, настольные игры, новогодняя атмосфера и многое другое.

21:30

Регистрация участников

Регистрация проходит в холле здания Высшей школы экономики на Мясницкой 9/11

22:00

Открытие Ночи решения задач

22:30 – 06:00

Решение задач

Задача по анализу данных

Для решения предлагается задача определения спроса в объектах общественного питания.

Решение задач будет проходить на своём ноутбуке, поэтому нужно заранее установить все необходимые инструменты.

Начальные требования и рекомендации: владение инструментами анализа данных — например, Python или R с соответствующими библиотеками. Решение задач будет проходить на своём ноутбуке, поэтому нужно заранее установить все необходимые инструменты. До мероприятия нужно пройти регистрацию на Kaggle.

Задачи по математике

На площадке будет предложен ряд задач различной сложности: от простых до олимпиадных. За правильное решение каждой из задач вручаются памятные подарки. Также предусмотрен разбор решений.

Задачи по алгоритмам

Для решения предлагается набор из пяти задач классического олимпиадного программирования: от простых задач до самых сложных.
Решение задач будет происходить на своих ноутбуках, по этому нужно заранее позаботиться, чтобы все необходимые для вас среды разработки были у вас установлены.
Сдача решений происходит через систему Яндекс.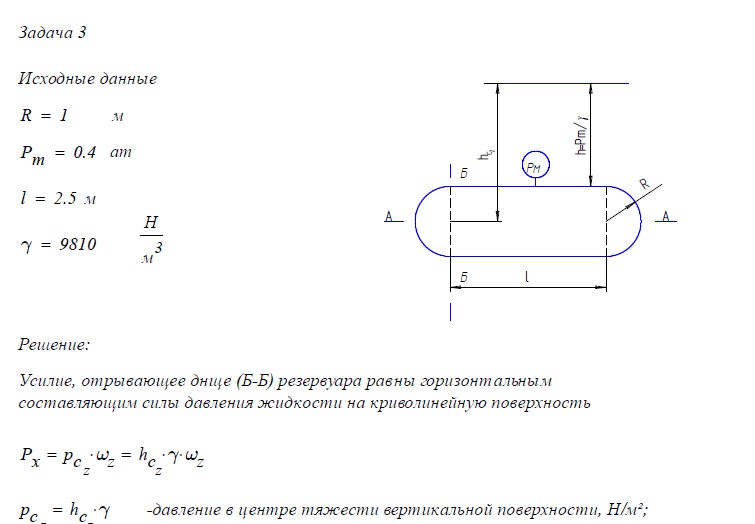 Контест, где происходит автоматическая проверка. Доступные языки: Python, C/C++, Pascal, Java.
Судьями гарантируется существование решения на языке C++, укладывающееся в ограничении по памяти и времени работы, указанное в условиях задач.

22:30-00:30

Серия лекций про технологии и стажировки

22:30-23:00

Лекция “Продвинутые фичи, а также знания полезные в конкурсах на Kaggle и не только”

Спикер: Дмитрий Ульянов, выпускник МГУ ВМК и аспирант Сколтеха. Работает в исследовательском отделе Яндекса. Активно участвовал в соревнованиях по анализу данных, в которых больше 10 раз занимал призовые места. Дмитрий является организатором и лектором курса про соревновательный анализ данных на Coursera.

23:00-23:40

Лекция “Вопросно-ответные системы”

Михаил Гильмутдинов и Роман Лучков, Тинькофф Банк

23:50-00:30

О стажировках из первых уст

01:00-06:00

Настолки, фильмы и многое другое

Гидродинамика – проблемы и решения

Теорема Торричелли

1. Емкость, наполненная водой и имеющая отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс ^-2, какова скорость воды через это отверстие?

Известный:

Высота (h) = 85 см – 40 см = 45 см = 0,45 метра

Ускорение свободного падения (g) = 10 м / с ²

Разыскивается: Скорость воды (v)

Решение:

Теорема Торричелли утверждает, что вода покидает отверстие с той же скоростью, что и объект, свободно падающий с той же высоты.Высота (h) = 85 см – 40 см = 45 см = 0,45 метра

Скорость воды рассчитывается по уравнению свободного падения:

v _t ² = 2 g h

v _t ² = 2 г h = 2 (10) (0,45) = 9

v _t = √9 = 3 м / с

2. Емкость, наполненная водой, с отверстием, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс ^-2, какова скорость воды через это отверстие?

Известный:

Высота (h) = 1,5 м – 0,25 м = 1,25 метра

Ускорение свободного падения (g) = 10 м / с ²

Разыскивается: Скорость воды (v)

Решение:

v _t ² = 2 г h = 2 (10) (1,25) = 25

v _t = √25 = 5 м / с

3. Емкость, наполненная водой, с отверстием, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс ^-2, какова скорость воды через это отверстие?

Известный:

Высота (h) = 1 м – 0,20 м = 0,8 метра

Ускорение свободного падения (g) = 10 м / с ²

Разыскивается: Скорость воды (v)

Решение:

v _t ² = 2 г h = 2 (10) (0,8) = 16

v _t = √16 = 4 м / с

4. Емкость, наполненная водой, с отверстием, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс ^-2, какова скорость воды через это отверстие?

Известный:

Высота (h) = 20 см = 0,2 метра

Ускорение свободного падения (g) = 10 м / с ²

Разыскивается: Скорость воды (v)

Решение:

5. Емкость с водой, в которой есть два отверстия, как показано на рисунке ниже. Каково отношение x ₁ к x ₂?

Soluti на

Интервал времени свободного падения воды из скважины 1:

ч = 1/2 а т ²

0.8 = 1/2 (10) т ²

0,8 = 5 т ²

т ² = 0,8 / 5 = 0,16

t = 0,4 секунды

Интервал времени свободного падения воды из лунки 2:

ч = 1/2 а т ²

0,5 = 1/2 (10) т ²

0,5 = 5 т ²

т ² = 0,5 / 5 = 0,1

t = √0,1 секунды

Расстояние по горизонтали (x):

x ₁ = v ₁ t ₁ = (2) (0.4) = 0,8 метра

x ₂ = v ₂ t ₂ = (√10) (√0,1) = (10) (0,1) = 1 метр

Соотношение x ₁ к x ₂:

x ₁ _: x ₂ = 0,8: 1 = 8: 10 = 4: 5

Уравнение неразрывности

6. Вода течет по трубе разного диаметра, от А к В, а затем к С. Отношение А к С составляет 8: 3. Если скорость воды в трубе А равна v, какова скорость воды в трубе? С.

Известный:

Площадь A (A _A) = 8

Площадь C (A _C) = 3

Скорость воды в трубе A (v _A) = v

Разыскивается: Скорость воды в трубе C (v _C)

Решение:

Уравнение неразрывности:

A _A v _A = A _C v _C

8 v = 3 v _C

v _C = 8/3 v

7.Если скорость воды в трубе диаметром 12 см составляет 10 см / с, какова скорость воды в трубе диаметром 8 см?

Известный:

Диаметр 1 (d ₁) = 12 см, радиус 1 (r ₁) = 6 см

Диаметр 2 (d ₂) = 8 см, радиус 2 (r ₂) = 4 см

Скорость воды 1 (v ₁) = 10 см / с

Разыскивается: Скорость воды 2 (v ₂)

Решение:

Площадь 1 (A ₁) = π r ² = π 6 ² = 36π см ²

Площадь 2 (A ₂) = π r ² = π 4 ² = 16π см ²

Уравнение неразрывности:

A ₁ v ₁ = A ₂ v ₂

(36π) (10) = (16π) v ₂

(36) (10) = (16) против ₂

360 = (16) против ₂

против ₂ = 360/16

v ₂ = 22.5 см / с

8. Вода течет по трубе разного диаметра, как показано на рисунке ниже. Если площадь 1 (A ₁) = 8 см ², A ₂ = 2 см ² и скорость воды в трубе 2 = v ₂ = 2 м / с, то какова скорость вода в трубе 1 = v ₁.

Известный:

Площадь 1 (A ₁) = 8 см ²

Площадь 2 (A ₂) = 2 см ²

Скорость воды в трубе 2 (v ₂) = 2 м / с

Требуется: скорость воды в трубе 1 (v ₁)

Решение:

Уравнение неразрывности:

A ₁ v ₁ = A ₂ v ₂

8 против ₁ = (2) (2)

8 против ₁ = 4

против ₁ = 4/8 = 0.5 м / с

9. Если диаметр большей трубы в 2 раза больше диаметра меньшей трубы, какова скорость жидкости в меньшей трубе.

Известный:

Диаметр большей трубы (d ₁) = 2

Радиус большей трубы (r ₁) = ½ d ₁ = ½ (2) = 1

Площадь большей трубы ( A ₁) = π r ₁ ² = π (1) ² = π (1) = π

Диаметр меньшей трубы (d ₂) = 1

Радиус меньшей трубы (r ₂) = ½ d ₂ = ½ (1) = ½

Площадь меньшей трубы ( A ₂) = π r ₂ ² = π (1/2) ² = π (1/4) = ¼ π

Скорость жидкости в большей трубе ( v ₁) = 4 м / с

Требуется: Скорость жидкости в меньшей трубе ( v ₂)

Решение:

Уравнение неразрывности:

A ₁ v ₁ = A ₂ v ₂

π 4 = ¼ π (v ₂)

4 = ¼ (v ₂)

v ₂ = 8 м / с

Принцип и уравнение Бернулли

10.Вода перекачивается компрессором на 120 кПа, поступая в нижнюю трубу (1) и течет вверх со скоростью 1 м / с. Ускорение свободного падения 10 м / с, плотность воды 1000 кг / м ^-3. Какое давление воды в верхней трубе (II).

Известный:

Радиус нижней трубы (r ₁) = 12 см

Радиус нижней трубы (r ₂) = 6 см

Давление воды в нижней трубе (p ₁) = 120 кПа = 120000 Паскалей

Скорость воды в нижней трубе (v ₁) = 1 м.с ^-1

Высота нижней трубы (h ₁) = 0 м

Высота верхней трубы (h ₂) = 2 м

Ускорение свободного падения (g) = 10 м.с ^-2

Плотность воды = 1000 кг.м ^-3

Требуется: Давление воды в трубе 2 (п. ₂)

Решение:

Скорость воды в трубе 2 рассчитывается по уравнению неразрывности:

Давление воды в трубе 2 рассчитывается по уравнению Бернулли:

11.Большая труба на высоте 5 метров над землей и маленькая труба на высоте 1 метра над землей. Скорость воды в большой трубе составляет 36 км / ч при давлении 9,1 x 10 ⁵ Па, а давление в малой трубе составляет 2,10 ⁵ Па. Какова скорость воды в маленькой трубе? Плотность воды = 10 ³ кг / м ³

Известный:

Давление воды в большой трубе (p ₁) = 9,1 x 10 ⁵ Паскаль = 910 000 Паскаль

Давление воды в малой трубе (p ₂) = 2 x 10 ⁵ Паскаль = 200000 Паскалей

Скорость воды в большой трубе (v ₁) = 36 км / ч = 36 (1000) / (3600) = 36000/3600 = 10 м / с

Высота большой трубы (h ₁) = -4 метра

Высота малой трубы (h ₂) = 0 метров

Ускорение свободного падения (g) = 10 м.с ^-2

Плотность воды = 1000 кг / м ³

Разыскивается: Скорость воды в малой трубе (v ₂)

Решение:

Скорость воды в маленькой трубе (v ₂) рассчитывается по уравнению Бернулли:

12. Труба радиусом 15 см соединена с другой трубой радиусом 5 см. Оба находятся в горизонтальном положении. Скорость потока воды в большой трубе составляет 1 м / с при давлении 10 ⁵ Н / м ².Какое давление воды на малой трубе (1 г · см ^-3)

Известный:

Радиус большой трубы (r ₁) = 15 см = 0,15 м

Радиус малой трубы (r ₂) = 5 см = 0,05 м

Давление воды в большой трубе (p ₁) = 10 ⁵ Н · м ^-2 = 100,000 Н · м ^-2

Скорость воды в большой трубе (v ₁) = 1 м с ^-1

Ускорение свободного падения (g) = 10 м.с ^-2

Плотность воды = 1 г · см ^-3 = 1000 кг · м ^-3

Перепад высот (Δh) = 0.

Требуется: Давление в малой трубе (п. ₂)

Решение:

Скорость воды в трубе 2 рассчитывается по уравнению неразрывности:

Давление воды в малой трубе (стр. ₂) рассчитывается по уравнению Бернулли:

Решение задач гидродинамики в усеченных вычислительных областях

I.Орлански, “Простое граничное условие для неограниченных гиперболических потоков”, Журн. Вычисл. Phys. 21 , 251–269 (1976).

Артикул МАТЕМАТИКА Google Scholar

Г. В. Хедстром, «Неотражающие граничные условия для нелинейных гиперболических систем», Журн. Вычисл. Phys. 30 , 222–237 (1979).