Решение типового варианта контрольной работы. Векторная алгебра.
Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где
Решение:
1. Вычислим проекции векторов на оси координат:
2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:
не коллинеарны.
Задание 2: Перпендикулярны ли векторы ?
Решение: Два вектора перпендикулярны, если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:, где вычислим скалярное произведение:
Векторы не перпендикулярны.
Задание 3: Компланарны ли векторы ?
Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , гдеВычислим смешанное произведение векторов:
Векторы не компланарны.
Задание 4: При каком значении векторы где , перпендикулярны?
Решение:
1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора
Итак: векторы и перпендикулярны при и при
Задание 5: Даны точки:
Найти:
1. пр;
2. ;
3. ;
4. орт вектора ;
5. ;
6. ;
7.
Решение:
1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр где скалярное произведение векторов вычисляется по формуле: Где и длина вектора: итак ,в нашем случае, формула принимает вид: для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:
на основании формулы, выше написанной, получим :
Пр;
2. Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:
Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:
;
Итак:
3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:
Итак
4. Направление вектора Определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением Мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину Орт вектора .
Итак: орт вектора
5. Скалярное произведение векторов вычисляем по формуле:
Скалярное произведение векторов вычисляем по формуле:
(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :
Итак:
6. Векторное произведение векторов вычисляется по формуле:
, где
Находим проекции векторов на оси координат:
Итак:
7. Смешанное произведение векторов вычисляется по формуле:
, где Итак:
Задание 6: Даны координаты вершин пирамиды:
Вычислить:
1. объем пирамиды;
2. длину ребра ;
3. площадь грани ;
Решение:
1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем
Параллелипипеда, построенного на векторах как на ребрах равен:
Найдем проекции соответствующих векторов на оси координат:
Тогда объем пирамиды равен:
Вычислим объем по указанной формуле:
;
2. Длина ребра
Длина ребра
; (смотри пункт 5,3)
3. Площадь грани вычисляется по формуле:
так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат:
;
| < Предыдущая | Следующая > |
|---|
Применение векторной алгебры для решения стереометрических задач повышенной сложности
В данной статье изложены методы решения задач
по стереометрии с помощью элементов векторной
алгебры. В учебной литературе не часто
встречается материал решения стереометрических
задач методами векторной алгебры. Это задачи на
вычисление отношений, в которых секущая
плоскость делит ребра многогранника, вычисление
расстояний от точки до прямой и плоскости,
определение расстояния и угла между
скрещивающимися прямыми, задачи на комбинацию
многогранников.
Задачи, о которых идет речь, отобраны из книги С.А. Шестакова «Векторы на экзаменах». По словам автора, данные задачи можно встретить на вступительных экзаменах в ВУЗы, вариантах ЕГЭ.
В статье приводятся необходимые теоретические
сведения, изложены основные алгоритмы,
основанные на свойствах векторов, представлено
наглядное решение стереометрических задач.
Рассмотрим методы решения задач с помощью
векторной алгебры. Для этого нам необходимо
знать следующие теоретические сведения:
1. Разложение вектора по трём данным некомпланарным векторам
Решение любой геометрической задачи на
вычисление сводится, в сущности, к нахождению
величины двух типов: расстояний и углов. Если в
пространстве задан некоторый базис (в частности,
прямоугольный), т.е. тройка некомпланарных
векторов, то вектор пространства можно разложить
по векторам этого базиса, причём единственным
образом.
2. Задачи об отношениях отрезков
Задачи об отношениях отрезков это тип задач, в
которых требуется определить, в каком отношении
данная плоскость делит какой – либо отрезок.
Плоскость является секущей плоскостью
некоторого многогранника, а отрезком служит одно
из рёбер этого многогранника. При решении
подобных задач следует выбрать тройку базисных
векторов (обычно связанных с многогранником,
например, выходящих из какой – либо его вершины).
3. Длина отрезка и угол между скрещивающимися прямыми
Как уже отмечалось, если в пространстве задан
некоторый базис, т. е. тройка некомпланарных
векторов , , , то любой вектор можно единственным образом
разложить по векторам базиса так, что = x1 • + y1 •
+ z1 •
, где x1,
y1, z1 – коэффициенты
разложения. Если при этом известны длины
векторов , , и угол между ними, то, определив
скалярные произведения , , , • , • , • («таблицу умножения» векторов
базиса), можно вычислить скалярный квадрат
вектора : = (
Если при этом известны длины
векторов , , и угол между ними, то, определив
скалярные произведения , , , • , • , • («таблицу умножения» векторов
базиса), можно вычислить скалярный квадрат
вектора : = (
4. Расстояние от точки до прямой
Для того чтобы найти расстояние MH от некоторой
точки M до прямой, достаточно, знать разложения
векторов (P l) и ( l) по некоторому базису с
известной таблицей умножения векторов базиса. В
самом деле, так как векторы и коллинеарны, = x • , но тогда =
– = x • – . И условия перпендикулярности
векторов и получаем
уравнение для определения единственной
неизвестной x в разложении вектора : = 0, или (x • – ) =
0. Найдя из этого уравнения x, мы тем самым
найдём разложение вектора по векторам выбранного
базиса с известной таблицей умножения, и по
формуле = определим
искомое расстояние.
И условия перпендикулярности
векторов и получаем
уравнение для определения единственной
неизвестной x в разложении вектора : = 0, или (x • – ) =
0. Найдя из этого уравнения x, мы тем самым
найдём разложение вектора по векторам выбранного
базиса с известной таблицей умножения, и по
формуле = определим
искомое расстояние.
Теперь рассмотрим данный метод решения для конкретных задач.
1. Задача. Разложение вектора по трём данным некомпланарным векторам
2. Задача об отношениях отрезков
Решение:
соотношений
3. Задача о длине отрезка и угле между скрещивающимися прямыми
Итак, в данной статье мы рассмотрели применение векторной алгебры для решения стереометрических задач повышенной сложности.
Презентация
Решение задач элементарной геометрии векторным методом §1 некоторые сведения из векторной алгебры
Математика 10
Решение задач элементарной геометрии векторным методом
Т.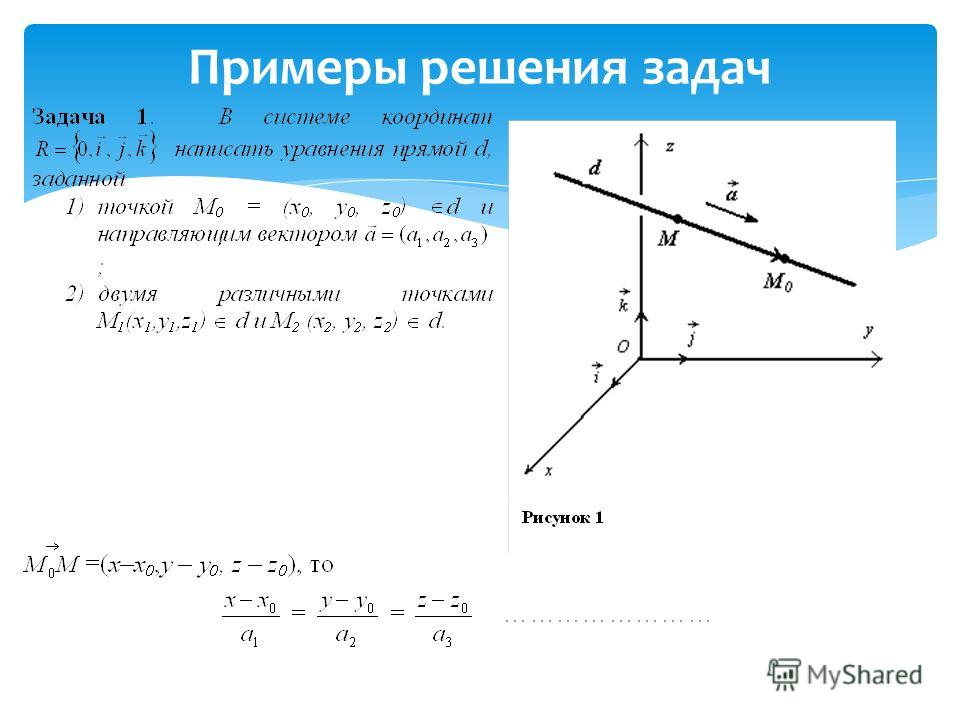 А. Тимошенко,
профессор кафедры математики ДВГГУ
А. Тимошенко,
профессор кафедры математики ДВГГУ
§1. Некоторые сведения из векторной алгебры
Векторный метод – один из наиболее общих методов решения геометрических задач. Он является сравнительно новой темой в школьном курсе геометрии, и овладение им вызывает трудности не только у учащихся, но и у учителей.
Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.
Приведем некоторые факты из векторной алгебры, применяемые в решении геометрических задач:
Вектором называется
направленный отрезок, то есть отрезок,
для которого указано какой из его концов
является началом, а какой концом.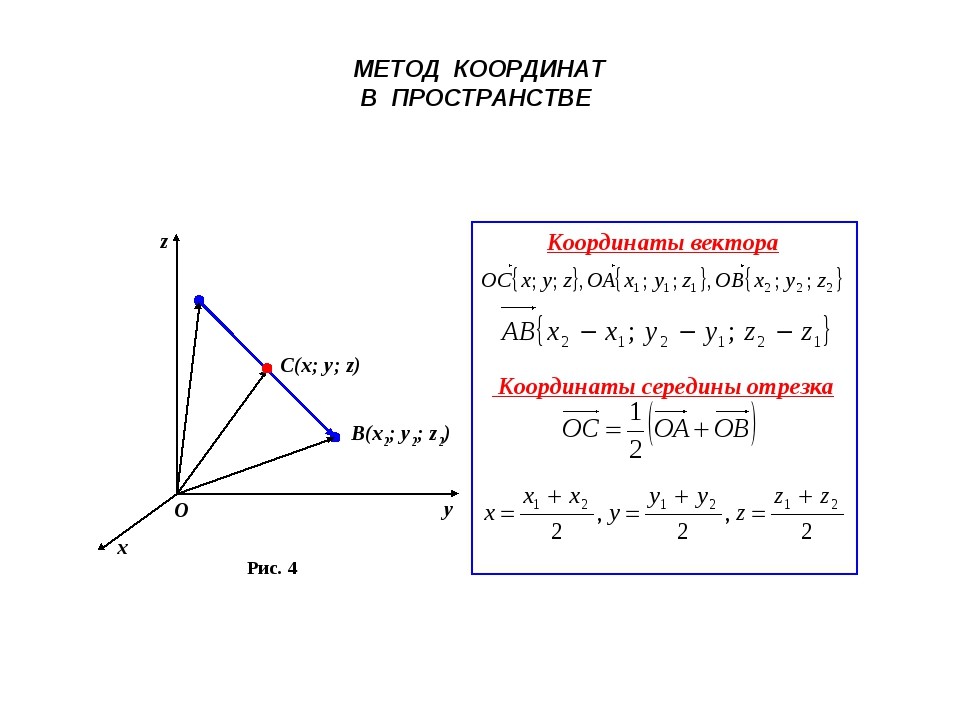
Обозначение: .
Длина (модуль) вектора есть длина соответствующего отрезка, определяющего данный вектор. Длину вектора обозначают соответственно как .
Векторы, лежащие на одной прямой или на параллельных прямых называются коллинеарными векторами. При этом коллинеарные векторы называются сонаправленными , если они лежат в одной полуплоскости относительно прямой, содержащей их начальные точки. Если же коллинеарные векторы лежат в разных полуплоскостях относительно этой прямой, то это противоположно направленные векторы .
Векторы, лежащие в одной плоскости или в параллельных плоскостях называются компланарными.
Два вектора и называются равными, если выполняются два условия:
Запись: .
Вектор называют
нулевым, если его начало и конец совпадают,
обозначается
. Нулевой вектор не имеет направления и
его длина равна нулю:
.
Нулевой вектор не имеет направления и
его длина равна нулю:
.
К линейным операциям над векторами относятся умножение вектора на число, сложение и вычитание векторов.
а) Умножение вектора на число.
Произведением вектора на вещественное число называется такой вектор или , который удовлетворяет двум условиям:
;
, при и при .
В частности, вектор называется вектором, противоположным вектору . Если связать эту операцию понятием коллинеарных векторов, то имеет место теорема:
Если и – два коллинеарных вектора, то существует такое вещественное число , что .
Вектор называется единичным, если его длина равна единице: . При этом, вектор – единичный, т. к. .
б) Сложение векторов.
Суммой
векторов и называется такой вектор (рис. 2), который строится по правилу:
откладываем вектор от произвольной точки О, затем строим
вектор
,
тогда вектор-сумма направлен от начала
первого вектора к концу второго, т.е. (правило треугольника). Тогда
Суммой
трех векторов, составляющих треугольник,
является нулевой вектор.
2), который строится по правилу:
откладываем вектор от произвольной точки О, затем строим
вектор
,
тогда вектор-сумма направлен от начала
первого вектора к концу второго, т.е. (правило треугольника). Тогда
Суммой
трех векторов, составляющих треугольник,
является нулевой вектор.
Свойства сложения векторов:
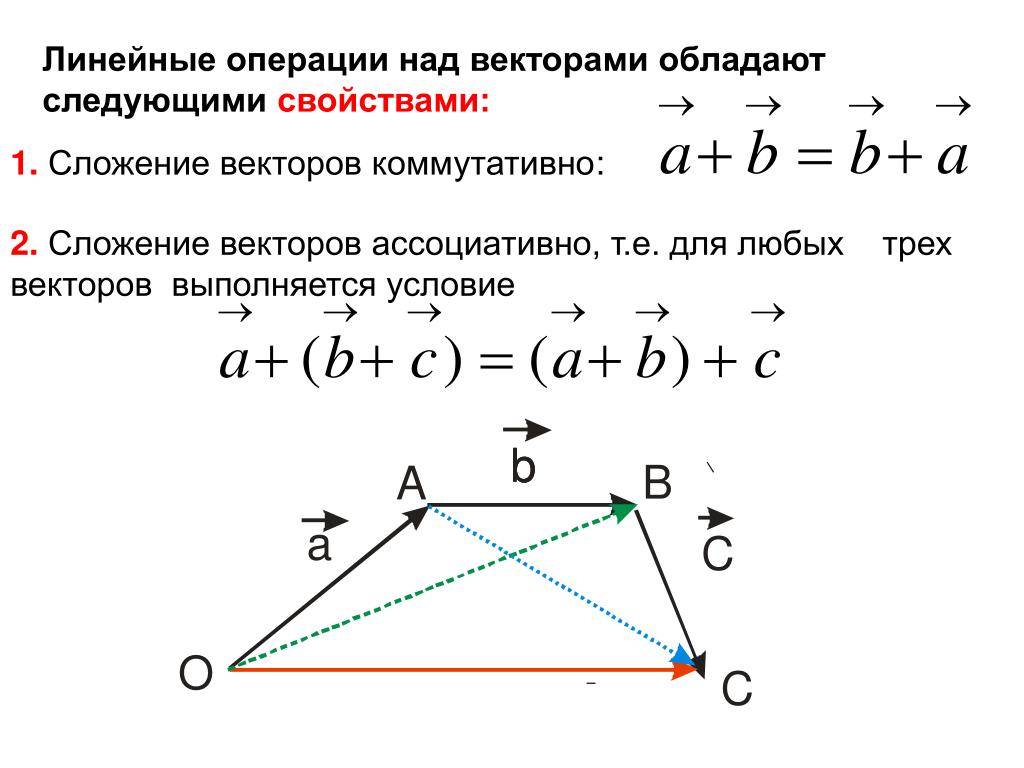
Сложение векторов коммутативно: (рис.3). Отсюда получаем сложение векторов по правилу параллелограмма.
сложение векторов ассоциативно: (рис.4). Это позволяет складывать любое количество векторов.
.
.
Свойство дистрибутивности связывает операции сложения векторов и умножения вектора на число: , где – вещественные числа.
, – вещественное число.
в) Вычитание векторов.
Разностью двух векторов и называется такой вектор
,
что
.
Из определения получаем правило построения разности двух векторов: откладываем оба вектора от общего начала О, тогда вектор-разность направлен от конца второго вектора к концу первого: (рис.5).
Операция вычитания векторов связана со сложением: .
Векторы можно не только складывать, вычитать и умножать на числа, но можно их перемножать между собой.
Скалярным произведением вектора на вектор называется число , равное произведению длин этих векторов на косинус угла между ними:
Для скалярного произведения выполняются следующие свойства:
.
.
– необходимое и достаточное условие перпендикулярности векторов и .
.
вещественное число.
.

§2. Примеры решения геометрических задач векторным методом
Задача 1
Точка С – середина отрезка AB, а О – произвольная точка на плоскости (рис. 6). Доказать, что .
Решение
По правилу треугольника , . Складывая эти равенства, получаем:
.
Так как точка С – середина отрезка АВ, то . Таким образом , , или .
Задача 2
Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.
Решение
Пусть – данная трапеция, и – середины оснований и , а – точка пересечения прямых и (рис. 7). Докажем, что точка лежит на прямой .
Треугольники и подобны по первому признаку подобия
треугольников, поэтому
. Так как и
,
то
Так как и
,
то
, (1).
Точка – середина отрезка , поэтому . Аналогично .
Подставив в последнее равенство выражения (1) для и , получим: .
Отсюда следует, что векторы и коллинеарны, и, значит, точка лежит на прямой .
Задача 3
Дан произвольный треугольник . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника .
Решение
Пусть , , – медианы треугольника (рис. 8). Тогда , , (задача 1). Сложив эти равенства, получим
Отсюда следует, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника .
Задача 4
Докажите, что
отрезок, соединяющий середины диагоналей
трапеции, параллелен ее основаниям.
Решение
Пусть и – середины диагоналей трапеции (рис. 9). Покажем, что || . Для этого достаточно показать, что коллинеарен .
Так как и – середины отрезков и , то
,
.
Следовательно,
.
Но коллинеарен вектору , поэтому , – вещественное число.
Тогда
,
То есть коллинеарен , что и требовалось доказать.
Задача 5
Найдите угол, лежащий против основания равнобедренного треугольника, если медианы, проведенные к боковым сторонам, взаимно перпендикулярны.
Решение
Пусть – равнобедренный треугольник с основанием и
, – его медианы, проведенные к боковым
сторонам (рис. 10). Введем обозначения
,
,
||=||=||. Тогда
,
,
поэтому скалярное произведение
Тогда
,
,
поэтому скалярное произведение
(2)
По условию задачи , и, следовательно, . Далее, , , , поэтому равенство (2) принимает вид . Отсюда получаем , .
Задача 6
– правильный шестиугольник. Доказать, что .
Решение
Пусть – правильный шестиугольник. Покажем, что . Заметим, что , .
Далее и .
Отсюда следует, что .
Задача 7
В параллелограммедано: и ; , ; , . Выразить векторы и через и .
Решение
Пусть – параллелограмм (рис. 12), в котором , , , , , .
Выразим через и . , .
Тогда .
,
,
.
,
,
,,
Задача 8
В квадрат вписана
окружность. Доказать, что сумма квадратов
расстояний любой точки окружности до
вершин квадрата не зависит от выбора
этой точки. Найти сумму этих квадратов.
Доказать, что сумма квадратов
расстояний любой точки окружности до
вершин квадрата не зависит от выбора
этой точки. Найти сумму этих квадратов.
Решение
Пусть – центр квадрата (рис. 13), а – произвольная точка окружности, вписанной в квадрат.
Имеем: ,
,.
Тогда
где – сторона квадрата, – радиус окружности.
Поскольку , то искомая сумма равна .
Задачи для самостоятельного решения:
Стороны , , треугольника разделены по его обходу соответственно точками , , в равных отношениях. Докажите что из отрезков , и можно составить треугольник.
Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме.
Основания трапеции равны и .
 Найдите длину отрезка, соединяющего
середины диагоналей трапеции.
Найдите длину отрезка, соединяющего
середины диагоналей трапеции.Даны четырехугольник и точка. Докажите, что точки, симметричные данной точке относительно середин сторон четырехугольника, являются вершинами параллелограмма.
Точка пересечения средних линий четырехугольника совпадает с точкой пересечения его диагоналей. Докажите, что четырехугольник – параллелограмм.
Через вершину треугольника и середину медианы проведена прямая, пересекающая сторону в точке . Докажите, что . В каком отношении точка делит отрезок .
Медианы боковых сторон равнобедренного треугольника пересекаются под углом . Найти угол при вершине треугольника.
В окружность с центром в точке вписан четырехугольник , диагонали которого пересекаются в точке и взаимно перпендикулярны. Доказать, что середины сторон и , центр и точки являются вершинами параллелограмма.

Векторное произведение векторов. Примеры решения задач
Решения типовых задач по теме: “Векторное произведение векторов”
Задача № 1. Даны модули векторов и , , и их скалярное произведение Вычислить модуль векторного произведения .
Решение. Так как модуль векторного произведения двух векторов равен произведению модулей данных векторов, умноженному на синус угла между векторами, то необходимо знать синус угла между векторами и .
Воспользуемся скалярным произведением данных векторов:
откуда
Тогда
Следовательно,
Ответ:
Задача № 2. Какому условию должны удовлетворять векторы и , чтобы векторы и были коллинеарны?
Решения этих задач подробно изложено в следующем видео
Задача № 3. Векторы , и удовлетворяют условию . Доказать, что .
Векторы , и удовлетворяют условию . Доказать, что .
Задача № 4. Вычислить площадь параллелограмма, построенного на векторах и , если и
Ответ: S параллелограмма= 157,5 кв. ед.
Решения этих задач подробно изложено в следующем видео
Задача № 5. Зная стороны треугольника ={-3; -2; 6} и = {- 2; 4; 4}, вычислить длину высоты .
Решение. I способ приведен в видеоуроке
II способ. Указания. Найти Пр и затем по теореме Пифагора вычислить высоту .
Ответ: ед. длины.
Решение этой задачи подробно изложено в следующем видео
Задача № 6. Решить самостоятельно. Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах: {6;0;2} и {1,5; 2; 1}.
Указания. Одна из диагоналей параллелограмма будет равна сумме векторов сторон, а другая — разности векторов сторон параллелограмма (рис.1).
Рис.1
Ответ: длины диагоналей и , площадь параллелограмма 13 кв.ед.
Задача № 7. Зная, что векторы и коллинеарны, вычислить коэффициенты α и β.
Указания. Если векторы а и b коллинеарны, то их векторное произведение равно нулю, .
Ответ:
Решения этих задач подробно изложено в следующем видео
Кафедра математики Физического факультета МГУ им. М.В.Ломоносова
Аналитическая геометрия является одним из базовых курсов высшей математики, лежащих в основе физико-математического образования.
Общая трудоемкость курса — 108 часов. Курс включает 36 часов лекций, 18 часов семинарских занятий, требует 54 часов самостоятельной работы студентов.
В курсе рассматриваются следующие вопросы: комплексные числа, матрицы и операции над ними, теория определителей, теория систем линейных алгебраических уравнений, элементы теории линейных пространств, системы координат, векторы и операции над ними, скалярное, векторное и смешанное произведения векторов, теория прямых и плоскостей, элементы теории кривых и поверхностей второго порядка. На примерах геометрических объектов малой размерности курс знакомит студентов с основными идеями метода координат и даёт общие навыки работы с простейшими алгебраическими системами.
Лекторы
Отчётность
зачет и экзамен
Материалы к экзамену
Содержание курса
- Комплексные числа и операции над ними. Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.
- Алгебра матриц. Матрицы и операции над ними. Умножение матриц. Линейная зависимость и независимость. Теория определителей. Ранг матрицы. Теорема о базисном миноре. Системы линейных уравнений.
- Алгебра векторов. Линейные операции над векторами. Базис и координаты. Скалярное, векторное и смешанное произведение векторов. Двойное векторное произведение.
- Линейные многообразия. Прямые на плоскости. Прямые и плоскости в пространстве.
- Кривые и поверхности второго порядка.
- Элементы теории линейных пространств. Понятие линейного пространства. Основные примеры. Базис и размерность линейного пространства. Основные свойства линейных пространств. Изоморфизмы линейных пространств.
Основная литература
- Овчинников А.В. Конспект лекций по аналитической геометрии. На сайте (см. ниже)
- Овчинников А.В. Алгебра и геометрия в вопросах и задачах. Кн.1. Основы алгебры и аналитической геометрии. — М.: ЛЕНАНД, 2016.

- Корпусов М.О., Овчинников А.В. Аналитическая геометрия. Методы решения задач. — М.: Физический факультет МГУ, 2019.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999.
- Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, Физматлит, 1999.
- Клетеник Д.В. Сборник задач по аналитической геометрии. — М.: Наука, Физматлит, 1998.
Дополнительная литература
- Александров П.С. Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979.
- Александров П.С. Лекции по аналитической геометрии. — Наука, 1968.
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Физматлит, 2005.
- Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. — М.: Физматлит, 2003.
- Корпусов М.О., Овчинников А.В. Аналитическая геометрия. Методы решения задач. — М.: Физический факультет МГУ, 2019.
- Овчинников А.В. Алгебра и геометрия для студентов-физиков.
 Лекционный курс. — М.: Физический факультет МГУ, 2016.
Лекционный курс. — М.: Физический факультет МГУ, 2016. - Овчинников А.В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009.
- Федорчук В.В. Курс аналитической геометрии и лин. алгебры. — М.: МГУ, 1990.
- Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. — Спб, 2003.
Материалы по курсу
1 поток. Лектор: проф. П. В. Голубцов
2 поток. Лектор: доц. А.В. Овчинников
3 поток. Лектор: проф. М. О. Корпусов
Применение элементов векторной алгебры для решения физических задач
КГУ « Ленинская средняя школа» Аккайынский район Северо-Казахстанская область
учитель физики Аберле Людмила Петровна, стаж 37 лет.
Бинарный урок физики и математики
9 класс
« Применение элементов векторной геометрии
в решении физических задач»
( интегрированный урок физики и математики)
Цель:1. Повторение основных определений темы.
Повторение основных определений темы.
2.Формирование умений практического применения действий над
векторами в типовых ситуациях.
3 Показать межпредметную связь математики, физики, литературы, изо
Задачи:1 Воспитать убеждённость учащихся в необходимости теоретических
знаний.
2. Сформировать умение сосредоточиться в нестандартной ситуации и
осуществить поиск нестереотипного решения задач.
3. Развивать культуру восприятия художественных и литературных
произведений, эстетического вкуса, развитие речи учащихся, памяти,
логического мышления.
Тип урока: Бинарный
Вид урока: Нетрадиционный
Методы : Работа по тестам, самост.работа, решение задач
Оборудование урока: видеопроектор, репродукции картин Репин И.Е.
«Бурлаки на Волге», Перов В.Г. «Тройка», Васнецов В.М.
«Богатыри», Суриков В.И. «Боярыня Морозова», тесты.
План урока
1. Организационный момент
Организационный момент
2.Межпредметные связи ( работа с картинами)
3.Самостоятельная работа ( взаимопроверка)
4.Работа по тестам
5.Подведение итогов
6. Домашнее задание
1.Орг.момент
2.Межпредметные связи
Вступительное слово учителя математики:
ЭПИГРАФ
«Вдохновение в геометрии нужно так же, как и в поэзии»
А.С. Пушкин
Вступительное слово учителя физики:
ЭПИГРАФ
« Знание без применения, что тучи без дождя »
( таджикская пословица)
Исторические сведения о происхождении векторов. ( сообщение ученика)
Термин вектор происходит от латинского слова Vector , что означает несущий или ведущий, влекущий, переносящий.
Интерес к векторам и векторному исчислению возник у математиков в 19 веке. В связи с потребностями механики. Однако теория векторов имеет более древнюю историю. Ещё в Древней Греции математики пытались свести вопросы арифметики к решению задач геометрическим путём.
Геометрические исчисления сыграли значительную роль в развитии математики, в том числе и для теории векторов, послужив истоком для развития этой теории.
В 1587 году на голландском языке был опубликован трактат фламандского учёного С.Стевина « Начала статики». В нём автор, рассматривая сложение сил, приходит к выводу, что нахождение результата сложения двух сил, действующих под углом 90 градусов, необходимо воспользоваться «параллелограммом сил», при этом для обозначения сил С.Стевин ввёл стрелки.
Значительно позже французский математик Луи Пуансо (1777 – 1856) разработал теорию векторов, которой пользуются при рассмотрении сил, действующих в различных направлениях и опубликовал её в книге «Элементы статики», вышедшей в 1803 году.
В современной математике раздел, в котором изучают векторы и действия над векторами, называют векторной алгеброй, т.к.эти действия имеют много общих свойств с алгебраическими действиями.
Учитель математики:
Изучая любую тему предмета, всегда невольно встаёт вопрос о её применимости в жизни. И сейчас есть множество достоверных фактов подтверждающих, что тема «Векторы» помогает находить ответ даже на некоторые вопросы , возникающие в нестандартных ситуациях межличностного общения.
И сейчас есть множество достоверных фактов подтверждающих, что тема «Векторы» помогает находить ответ даже на некоторые вопросы , возникающие в нестандартных ситуациях межличностного общения.
И.А. Крылов. Басня «Лебедь, Рак и Щука».
Когда в товарищах согласья нет,
На лад их дело не пойдёт,
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак да Щука,
Везти с поклажей воз взялись
И вместе трое все, в него впряглись:
Из кожи лезут вон, а возу всё нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвётся в облака,
Рак пятится назад, а Щука тянет в воду.
Кто виноват у них, кто прав, – судить не нам;
Да только воз и ныне там.
Учитель физики:
Н.В.Гоголь собрание басен И.А.Крылова назвал «книгой мудрости самого народа». Вы думаете, почему с точки зрения человеческих отношений «воз и ныне там»?
А теперь давайте ответим на этот вопрос с физической точки зрения.
лебедь
рак
щука
Второй пример: На уроках физкультуры вы играете с мячом. Если мяч подбросить вверх , то какими векторными величинами можно описать движение мяча?
( Движение мяча описывается следующими векторными величинами: перемещение мяча, скорость, сила тяжести, угловая скорость вращения мяча вокруг своей оси)
Взаимосвязь физики с искусством.
Работа в группах. Класс разделён на 4 группы. Каждая группа получает репродукцию картин и отвечает на вопросы, поставленные к ней.
1 гр. – картина Репина И. Е. « Бурлаки на Волге».
Вопрос: определить направление сил действующих на корабль.
Изобразите силы, действующие на него в процессе движения.
2 гр. – картина Перова В.М. « Тройка».
Вопрос: Определите, какие векторные величины характеризуют движение
саней? Изобразите эти векторы направленными отрезками.
3 гр. – картина Сурикова В.И. « Боярыня Морозова».
Вопрос: определите, какие векторные величины характеризуют
движение саней? Изобразите силы, действующие в процессе
движения.
4 гр. – картина Васнецова В.Г. «Богатыри».
Вопрос: определите, какие векторные величины действуют на лошадей?
Изобразите эти векторы направленными отрезками.
Учитель математики:
Решение задач по физике по группам ( взаимопроверка с выставл. баллов )
1 группа:
Проекция скорости материальной точки изменяется по закону
υ х= 10 + 2 t
Вопросы: 1) определите характер движения точки
2) найдите модуль и направление начальной скорости
3) определите ускорение тела и его направление
4) какой будет скорость точки через 10с после начала движения?
5) постройте график зависимости скорости от времени
при t = 0 с, 5 с, 10 с.
2 группа:
Проекция скорости движущегося тела изменяется по закону
υ х = 10 – 2 t
Вопросы: 1) опишите характер движения тела
2) найдите модуль и направление вектора начальной скорости
3) найдите модуль и направление вектора ускорения
4) постройте график зависимости скорости от времени
5) найдите графически и аналитически скорости тела через 2 с.
3группа:
На рис. изображён график зависимости проекции скорости движения
материальной точки от времени.
Вопросы: 1) определите вид движения
2) найдите модуль и направление начальной скорости
3) вычислите проекцию ускорения и определите направление
вектора ускорения
4) напишите уравнение зависимости проекции скорости этого
тела от времени
5) найдите графически и аналитически скорость тела через 2 с.
4 группа:
На рис. приведён график скорости некоторого движения.
Вопросы: 1) определите характер этого движения
2) найдите начальную скорость движения тела
3) вычислите модуль ускорения и определите его направление
напишите уравнение зависимости проекции скорости от
времени.
5) Что происходит с движущимся телом в момент времени
соответствующий точке В ?
Тесты на соответствие .
Выбери слово не подходящее по смыслу: длина, пространство, направление, вектор, прямая.
Установи логическое соответствие:
скаляр единица измерения
вектор прямая скаляр высота
луч шкала
Даны скалярные и векторные величины. Установив правильное соответствие, провести соединительные линии.
Скалярные величины температура
сила
время
объём
ускорение
скорость
Векторные длина
масса
напряжённость электр.поля
Избирательные тесты:
Коллинеарными называют векторы
которые расположены под прямым углом
которые противоположно направлены
которые лежат на одной прямой или на параллельных прямых
У коллинеарных векторов координаты
1) пропорциональны
2) относятся как 1 : 2
3) одинаковы
Векторы перпендикулярны, если
сумма векторов равна нулю
координаты пропорциональны
скалярное произведение равно « 0 »
Какой вектор называется единичным?
начало, которого совпадает с его концом
одинаково направленные
длина которого равна « 1 »
Какие векторы называются равными ?
имеют равные длины
имеют равные длины и одинаковые направления
имеют равные соответствующие координаты
Как найти координаты суммы векторов?
разность соответствующих координат его конца и начала
по формуле √ а21 + а21
сумма соответствующих координат слагаемых векторов
Решение задач.
1 группа
движение равнопеременное – ускоренное
υ 0 = 10 м/с ; положит., т.к. совпадает с направлением движения
а = 2 м/с2 ; положит., т.к. совпадает с направлением движения
υ = 10 + 2 · 10 = 30 м/с 5. график
υ
t
10
0
20
5
30
10
2 группа
1. движение равнопеременное – замедленное
2. υ 0 = 10 м/с ; положит., т.к. совпадает с направлением движения
3. а = – 2 м/с2 ; отриц., т.к. движение замедл. и направлено противопол υ 0
4. график 5. υ = 10 – 2 · 2 = 6 м/с
υ
t
10
0
6
2
– 6
8
3 группа
1. движение равнопеременное – ускоренное
2. υ 0 = 10 м/с ; положит.
υ 0 = 10 м/с ; положит.
3. а = 3 м/с2 ; положит.
4. υ = 10 + 3 t 5. υ = 10 + 3 · 2 = 16 м/с
4 группа
1.движение равнопеременное – замедленное
2. υ 0 = 15 м/с
3. υ = 0 t = 3 с а = – 5 м/с2
4. υ = 15 – 5 t 5. в точке В тело находится в покое, т.к. υ = 0
Подведение итогов.
Домашнее задание.
НОУ ИНТУИТ | Лекция | Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства
Аннотация: В лекции рассматриваются линейные операции над векторами, и дается практическое использование этих операций при решении различных задач
Умножение
Различают несколько видов операции умножения.
1. Умножение вектора на скалярную величину. При умножении вектора на скаляр получают новый вектор , длина (модуль) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если , или противоположно исходному вектору, если .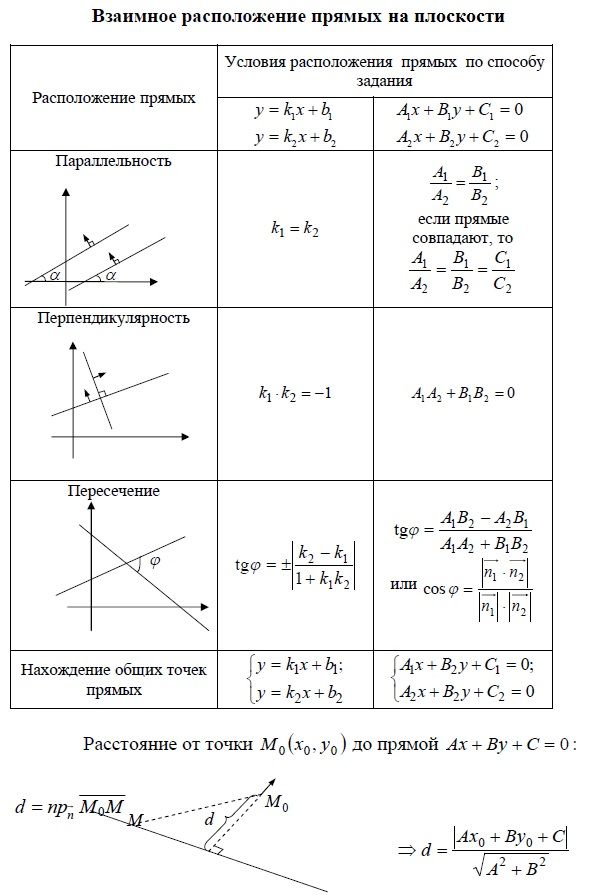 В координатной форме, если a = (ax;ay;az), то b = a= . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.
В координатной форме, если a = (ax;ay;az), то b = a= . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.
Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е. 1 Из последнего равенства следует, что . Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности: , а также свойством дистрибутивности: .
2. Скалярное произведение векторов.
Определение 14. Скалярным произведением двух векторов и называется число S, равное . Эта операция обозначается или
Эта операция обозначается или
В частности, скалярный квадрат вектора равен квадрату его длины, т.е.
Если один из перемножаемых векторов единичный, то:
В этом случае результат представляет собой проекцию вектора на направление единичного вектора . Следовательно, любой вектор можно представить как , где ax,ay,az – проекции вектора соответственно на оси 0х, 0у и 0z.Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора на эти оси. Из этого же рисунка следует, что модуль вектора численно будет равен .
Рис. 6.
 1.
1. Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:
где , и есть скалярное произведение вектора с ортами осей координат. Тогда из последнего равенства имеем где , и – углы, которые составляет вектор соответственно с осями 0х, 0у и 0z.Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е. и . Можно убедиться самостоятельно в том, что всегда выполняется равенство
Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда
Замечание 2. , где – единичные векторы (орты) осей координат 2
intuit.ru/2010/edi”>Замечание 3. .
Замечание 4. Скалярное произведение векторов в координатной форме
Замечание 5. Используя формулу скалярного произведения векторов и , можно найти выражение косинуса угла между этими векторами через их проекции на орты:
Если , то это значит, что угол между векторами больше 90 , т.е. тупой, а если , то угол острый.
Замечание 6. Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.
Исчисление II – Векторы (практические задачи)
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с “узкой” шириной экрана (, т. е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Глава 5: Векторы
Вот набор практических задач для главы «Векторы» заметок «Исчисление II».
- Если вам нужен документ в формате pdf, содержащий решения, вкладка загрузки выше содержит ссылки на файлы PDF, содержащие решения для полной книги, главы и раздела.В настоящее время я не предлагаю PDF-файлы для решения отдельных проблем.
- Если вы хотите просмотреть решения в Интернете, перейдите на веб-страницу с набором задач, щелкните ссылку решения любой проблемы, и вы перейдете к решению этой проблемы.

Обратите внимание, что в некоторых разделах будет больше проблем, чем в других, а в некоторых будет более или менее разнообразных проблем. В большинстве разделов должны быть заданы разные уровни сложности, хотя от раздела к разделу он будет меняться.
Вот список всех разделов, для которых были написаны практические задачи, а также краткое описание материала, содержащегося в примечаниях к этому конкретному разделу.
Основные понятия – В этом разделе мы введем некоторые общие обозначения для векторов, а также некоторые основные понятия о векторах, такие как величина вектора и единичные векторы. Мы также проиллюстрируем, как найти вектор из его начальной и конечной точек.
Векторная арифметика – в этом разделе мы обсудим математическую и геометрическую интерпретацию суммы и разности двух векторов.Мы также определяем и даем геометрическую интерпретацию скалярного умножения. Мы также даем некоторые из основных свойств векторной арифметики и вводим общие обозначения \ (i \), \ (j \), \ (k \) для векторов.
Точечное произведение – в этом разделе мы определим скалярное произведение двух векторов. Мы даем некоторые из основных свойств скалярных произведений и определяем ортогональные векторы и показываем, как использовать скалярное произведение, чтобы определить, являются ли два вектора ортогональными. Мы также обсуждаем поиск векторных проекций и направляющих косинусов в этом разделе.
Перекрестное произведение – В этом разделе мы определяем перекрестное произведение двух векторов и приводим некоторые основные факты и свойства перекрестных произведений.
векторов физических задач и решений 11 класс
Освоение физических решений Глава 3 Векторы в физике. И если эти две силы действуют в одном направлении, результирующая сила будет максимальной. Векторы – Числовые решения – Численные решения физики – Численные решения X – Примеры и решение проблем из главы №На приведенном выше рисунке F тянет ящик массой 4 кг из точки A в пункт B. Решения BYJU’S чрезвычайно полезны для студентов, поскольку они позволяют найти ответы на вопросы учебника в одном месте. Большинство учеников считают главы по физике 11 класса трудными вначале, поскольку программа обучения обширна, а концепции являются новыми. NEET Physics – это оценочная бумага на вступительном медицинском экзамене. Относительная скорость. Таблица информации… решение. Вектор можно разделить на два типа → D. в масштабе.Тема теста – Векторы. Каким должен быть угол между ними, если величина результирующего равна (а) 1 единица, (б) 5 единиц и (в) 7 единиц. Решения ISC Nootan Физика класса 11 Нагин Пракашан Кумар и Миттал. Критическое мышление. Одно количество зависит от другого, если вариация одного из них […] Глава 8… Специалисты-предметники готовят Решения Pradeep для решения вопросов, связанных с физикой, химией и биологией, давая надлежащие понятные решения. Всего в этом тесте будет 10 MCQ.Я разместил видеолекции ossom для 11-го и 12-го классов по физике на сайте www.
Решения BYJU’S чрезвычайно полезны для студентов, поскольку они позволяют найти ответы на вопросы учебника в одном месте. Большинство учеников считают главы по физике 11 класса трудными вначале, поскольку программа обучения обширна, а концепции являются новыми. NEET Physics – это оценочная бумага на вступительном медицинском экзамене. Относительная скорость. Таблица информации… решение. Вектор можно разделить на два типа → D. в масштабе.Тема теста – Векторы. Каким должен быть угол между ними, если величина результирующего равна (а) 1 единица, (б) 5 единиц и (в) 7 единиц. Решения ISC Nootan Физика класса 11 Нагин Пракашан Кумар и Миттал. Критическое мышление. Одно количество зависит от другого, если вариация одного из них […] Глава 8… Специалисты-предметники готовят Решения Pradeep для решения вопросов, связанных с физикой, химией и биологией, давая надлежащие понятные решения. Всего в этом тесте будет 10 MCQ.Я разместил видеолекции ossom для 11-го и 12-го классов по физике на сайте www. visionnotes.com, вы можете поделиться ими, увидеть и получить бесплатную доступную помощь. 02/03 окт. (Среда / чт) Примечания: Графики движения (скорость в зависимости от времени) Рабочий лист: Графики движения II (решения) Задание: кинематический видеоанализ на следующем занятии. Решение: угол между двумя векторами, → и Ответы задания даются в конце каждого задания с полными решениями. Вы можете проверить NCERT Solutions for Class 12 Maths Chapter 10, чтобы лучше понять тему.Чтобы различать скаляры и векторы, мы будем обозначать скаляры курсивом в нижнем регистре, например a, b, c и т. Д. Узнайте, что такое векторы и как их можно использовать для моделирования реальных ситуаций. Поделитесь с друзьями и помогите им в их подготовке. Этот документ получил высокую оценку учащихся 11 класса, и его просмотрели 15833 раза. Некоторые основные понятия химии; 02. Структура атома; 03. Классификация элементов и периодичность в свойствах; 04. химическая связь и молекулярная структура; 05.Обзор задач для вводной физики 2 6 февраля 2014 г.
visionnotes.com, вы можете поделиться ими, увидеть и получить бесплатную доступную помощь. 02/03 окт. (Среда / чт) Примечания: Графики движения (скорость в зависимости от времени) Рабочий лист: Графики движения II (решения) Задание: кинематический видеоанализ на следующем занятии. Решение: угол между двумя векторами, → и Ответы задания даются в конце каждого задания с полными решениями. Вы можете проверить NCERT Solutions for Class 12 Maths Chapter 10, чтобы лучше понять тему.Чтобы различать скаляры и векторы, мы будем обозначать скаляры курсивом в нижнем регистре, например a, b, c и т. Д. Узнайте, что такое векторы и как их можно использовать для моделирования реальных ситуаций. Поделитесь с друзьями и помогите им в их подготовке. Этот документ получил высокую оценку учащихся 11 класса, и его просмотрели 15833 раза. Некоторые основные понятия химии; 02. Структура атома; 03. Классификация элементов и периодичность в свойствах; 04. химическая связь и молекулярная структура; 05.Обзор задач для вводной физики 2 6 февраля 2014 г. Роберт Г. Браун, преподаватель физического факультета Университета Дьюка, Дарем, Северная Каролина 27708-0305 [email protected] 1 = 2 + 2 cos θ. cos θ = или cos θ = – cos 600 или cos θ = cos (180 – 60) θ… Вектор также известен как евклидов вектор или пространственный вектор. Практика этих вопросов CBSE NCERT Objective MCQ для класса 11 по физике с ответами в формате PDF поможет студентам быстро пересмотреть все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам.73: ЗАКОНЫ ДВИЖЕНИЯ. См. Примечания к экзамену, которые вы можете использовать для подготовки и проверки к экзаменам. Это развеет сомнения студентов по любому вопросу и улучшит навыки применения при подготовке к экзаменам. Регулярно тренируйтесь с этими объективными вопросами NEET Physics о загрязнении воздуха и улучшайте свои знания предмета и навыки решения проблем, а также управляйте временем. Векторы 1.1 Природа физики Математика. Движение на плоскости. Класс 11 по физике. Формулы физики. Скалярные величины движения снаряда: – Величины, которые имеют только величину, но не имеют направления.
Роберт Г. Браун, преподаватель физического факультета Университета Дьюка, Дарем, Северная Каролина 27708-0305 [email protected] 1 = 2 + 2 cos θ. cos θ = или cos θ = – cos 600 или cos θ = cos (180 – 60) θ… Вектор также известен как евклидов вектор или пространственный вектор. Практика этих вопросов CBSE NCERT Objective MCQ для класса 11 по физике с ответами в формате PDF поможет студентам быстро пересмотреть все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам.73: ЗАКОНЫ ДВИЖЕНИЯ. См. Примечания к экзамену, которые вы можете использовать для подготовки и проверки к экзаменам. Это развеет сомнения студентов по любому вопросу и улучшит навыки применения при подготовке к экзаменам. Регулярно тренируйтесь с этими объективными вопросами NEET Physics о загрязнении воздуха и улучшайте свои знания предмета и навыки решения проблем, а также управляйте временем. Векторы 1.1 Природа физики Математика. Движение на плоскости. Класс 11 по физике. Формулы физики. Скалярные величины движения снаряда: – Величины, которые имеют только величину, но не имеют направления. Решения NCERT для класса 11 по физике. Единственный способ оценить, действительно ли вы понимаете концепции … (1.11) Существуют даже более сложные физические величины – называемые тензорными величинами. Следовательно, результирующая сила, действующая на частицу, находится между 1 Н и 7 Нм. Векторы. Давление – сила C. Смещение – скорость D. Электрический ток – давление Решение: Сила = вектор, ускорение = вектор Давление = скаляр, сила = вектор Смещение = вектор, скорость = скаляр Электрический ток = скаляр, давление = […] Если величина равнодействующей силы двух сил меньше, чем величина большей силы, тогда.Ответ 5: Во-первых, давайте найдем компоненты векторов по осям x и y. Класс XI Физика. Глава 2: Единицы и измерения. Глава 3: Движение по прямой. Глава 4: Движение в плоскости. Глава 5: Законы движения. Глава 6: Работа, энергия и мощность Глава 7: Система… Этот курс даст вам огромная ясность в отношении векторов и того, как использовать векторы при решении задач в движении. Ссылка для скачивания находится внизу.
Решения NCERT для класса 11 по физике. Единственный способ оценить, действительно ли вы понимаете концепции … (1.11) Существуют даже более сложные физические величины – называемые тензорными величинами. Следовательно, результирующая сила, действующая на частицу, находится между 1 Н и 7 Нм. Векторы. Давление – сила C. Смещение – скорость D. Электрический ток – давление Решение: Сила = вектор, ускорение = вектор Давление = скаляр, сила = вектор Смещение = вектор, скорость = скаляр Электрический ток = скаляр, давление = […] Если величина равнодействующей силы двух сил меньше, чем величина большей силы, тогда.Ответ 5: Во-первых, давайте найдем компоненты векторов по осям x и y. Класс XI Физика. Глава 2: Единицы и измерения. Глава 3: Движение по прямой. Глава 4: Движение в плоскости. Глава 5: Законы движения. Глава 6: Работа, энергия и мощность Глава 7: Система… Этот курс даст вам огромная ясность в отношении векторов и того, как использовать векторы при решении задач в движении. Ссылка для скачивания находится внизу. Ответ: Пусть v s и v r – скорости пловца и реки соответственно. Нажмите кнопку G + 1 и кнопку Fb Like, чтобы поддержать этот сайт.Ариба Дастгир 25.09.2020 23:59. Ответил эксперт. Банк вопросов для критического мышления по основным и продвинутым физическим векторам JEE – Studyadda.com. NCERT Solutions Class 11 Физика движения в плоскости – Скачать PDF бесплатно. Поделиться – это забота !! Он знакомит с различными дисциплинами и обсуждает фундаментальные силы, присутствующие в природе. Пусть величина трех векторов a = 2; b = 3; с = 6. Студенты должны попытаться понять каждую тему подробно, чтобы они могли написать соответствующие ответы на своем выпускном экзамене.2. Он смотрит в зеркало и продолжает движение еще 8570 м под углом 11,44 ° над горизонтом, пока не достигнет своей цели. 40 описания курса физики AP. Работа выполнена F; WF = F. 14 (a) Используйте функцию обратного тангенса, чтобы найти угол расстояния: 1 9,5 tan 34 м м или 34 ° ниже оси + x (b) Используйте теорему Пифагора для главы 10 Векторная алгебра класса 12.
Ответ: Пусть v s и v r – скорости пловца и реки соответственно. Нажмите кнопку G + 1 и кнопку Fb Like, чтобы поддержать этот сайт.Ариба Дастгир 25.09.2020 23:59. Ответил эксперт. Банк вопросов для критического мышления по основным и продвинутым физическим векторам JEE – Studyadda.com. NCERT Solutions Class 11 Физика движения в плоскости – Скачать PDF бесплатно. Поделиться – это забота !! Он знакомит с различными дисциплинами и обсуждает фундаментальные силы, присутствующие в природе. Пусть величина трех векторов a = 2; b = 3; с = 6. Студенты должны попытаться понять каждую тему подробно, чтобы они могли написать соответствующие ответы на своем выпускном экзамене.2. Он смотрит в зеркало и продолжает движение еще 8570 м под углом 11,44 ° над горизонтом, пока не достигнет своей цели. 40 описания курса физики AP. Работа выполнена F; WF = F. 14 (a) Используйте функцию обратного тангенса, чтобы найти угол расстояния: 1 9,5 tan 34 м м или 34 ° ниже оси + x (b) Используйте теорему Пифагора для главы 10 Векторная алгебра класса 12.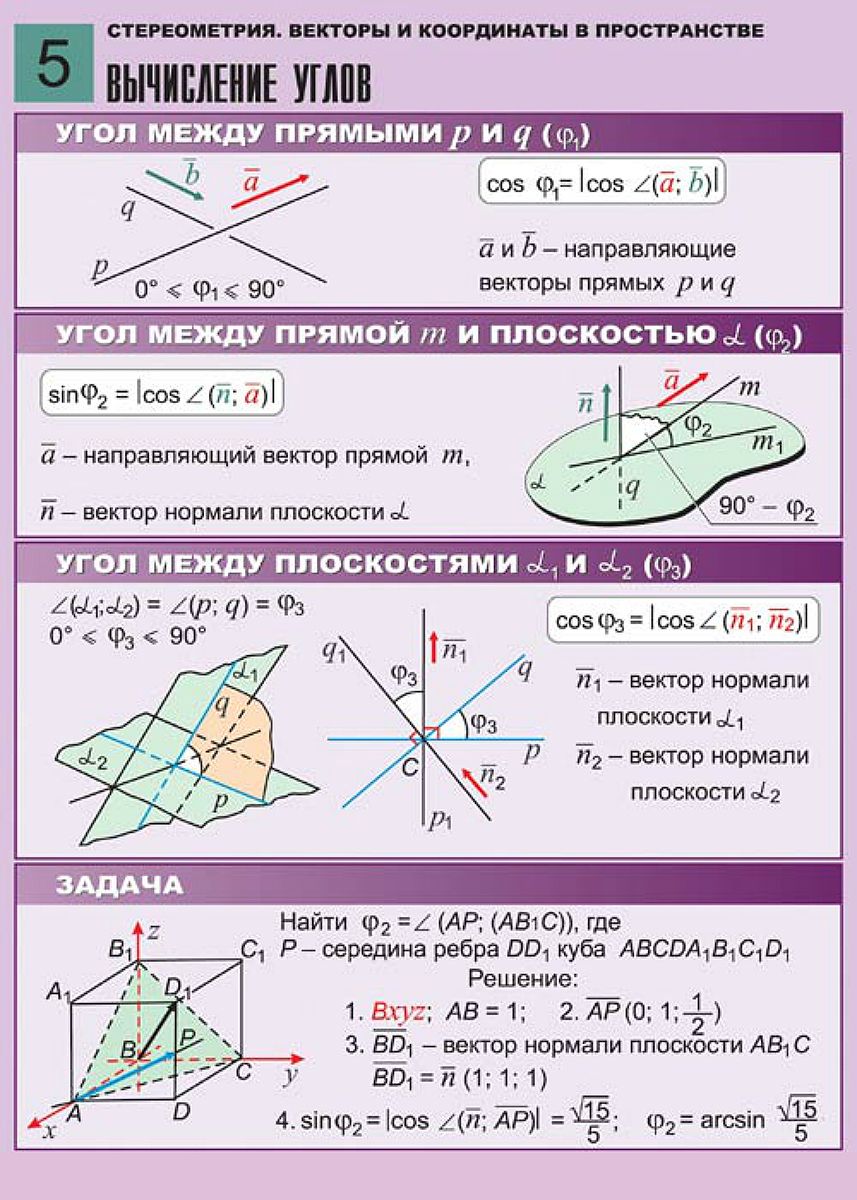 Вас спросят о векторных и скалярных величинах. Полярные векторы. векторная сумма и). 25491 Просмотры. Это очень просто понять.Глава 6 Работа Энергия и сила. Решения NCERT по физике 11-го класса не берут ссылки из других книг, кроме 11-го класса NCERT по физике. Найдите результат. Численные задачи физики для класса Xi. Если скорость изменяется с 5 м / с до 6 м / с за 2 с, найдите угловое ускорение. Эти решения охватывают все главы учебника физики NCERT Class XI. Студенты изучают векторы в раннем возрасте, чтобы решать математические задачи за доли секунды. Основная цель книг «Образцовые задачи по математике, физике, химии или биологии» – предоставить учителям и учащимся большое количество качественных задач с различными когнитивными уровнями, чтобы облегчить обучение изучению концепций по всем предметам, которые представлены через Книги NCERT для 9, 10, 11 и 12 классов.Векторы; Пакеты в приложении PW (2021) Класс XI. Единицы, размеры _ векторы (БАНСАЛ) Скачать PDF. Глава Мудрые решения NCERT для класса 11 по физике охватывает все разделы глав: Физический мир, Движение по прямой, Работа, Энергия и мощность, Механические свойства твердых тел, Кинетическая теория, Волны и многое другое.
Вас спросят о векторных и скалярных величинах. Полярные векторы. векторная сумма и). 25491 Просмотры. Это очень просто понять.Глава 6 Работа Энергия и сила. Решения NCERT по физике 11-го класса не берут ссылки из других книг, кроме 11-го класса NCERT по физике. Найдите результат. Численные задачи физики для класса Xi. Если скорость изменяется с 5 м / с до 6 м / с за 2 с, найдите угловое ускорение. Эти решения охватывают все главы учебника физики NCERT Class XI. Студенты изучают векторы в раннем возрасте, чтобы решать математические задачи за доли секунды. Основная цель книг «Образцовые задачи по математике, физике, химии или биологии» – предоставить учителям и учащимся большое количество качественных задач с различными когнитивными уровнями, чтобы облегчить обучение изучению концепций по всем предметам, которые представлены через Книги NCERT для 9, 10, 11 и 12 классов.Векторы; Пакеты в приложении PW (2021) Класс XI. Единицы, размеры _ векторы (БАНСАЛ) Скачать PDF. Глава Мудрые решения NCERT для класса 11 по физике охватывает все разделы глав: Физический мир, Движение по прямой, Работа, Энергия и мощность, Механические свойства твердых тел, Кинетическая теория, Волны и многое другое. Числовой. Они представлены по величине и направлению смежными сторонами OA и OB параллелограмма OACB, проведенного из точки O. Тогда диагональ OC, проходящая через точку O, будет представлять результирующую R по величине и направлению.Глава 3 – Движение по прямой. пользователя Pooja Roy. Электростатика (БАНСАЛ) Скачать PDF. Векторы в физике. Решения HC Verma, класс 11, физика; Решения HC Verma, класс 12 по физике; Лахмир Сингх Решения. Выполняйте различные операции с векторами, такие как сложение, вычитание, масштабирование, преобразование прямоугольных координат в полярные и т. Д. Подробно обсуждаются самолеты, летящие при наличии ветра, и лодка, движущаяся при наличии речных течений. мэм. Один – параллельный вектор, другой – антипараллельный вектор…. Решения NCERT для класса 11. Если две силы 4N и 3N, действующие одновременно на частицу, имеют противоположное направление, результирующая сила F 1 минимальна. Ответы. Чтобы помочь вам в этом, мы здесь с примечаниями. CBSE Class 11 Physics Notes: Vectors.
Числовой. Они представлены по величине и направлению смежными сторонами OA и OB параллелограмма OACB, проведенного из точки O. Тогда диагональ OC, проходящая через точку O, будет представлять результирующую R по величине и направлению.Глава 3 – Движение по прямой. пользователя Pooja Roy. Электростатика (БАНСАЛ) Скачать PDF. Векторы в физике. Решения HC Verma, класс 11, физика; Решения HC Verma, класс 12 по физике; Лахмир Сингх Решения. Выполняйте различные операции с векторами, такие как сложение, вычитание, масштабирование, преобразование прямоугольных координат в полярные и т. Д. Подробно обсуждаются самолеты, летящие при наличии ветра, и лодка, движущаяся при наличии речных течений. мэм. Один – параллельный вектор, другой – антипараллельный вектор…. Решения NCERT для класса 11. Если две силы 4N и 3N, действующие одновременно на частицу, имеют противоположное направление, результирующая сила F 1 минимальна. Ответы. Чтобы помочь вам в этом, мы здесь с примечаниями. CBSE Class 11 Physics Notes: Vectors. и обозначают векторы полужирным шрифтом в нижнем регистре, например u, v, w и т. д. Угол между любыми двумя векторами составляет 120 градусов, а вектор копланерен, найдите величину результирующего вектора. 1.3 СКАЛЯРЫ И ВЕКТОРЫ Введение: Физика изучает природные явления.Получите все, что вы ищете для подготовки к JEE и NEET, в этой серии пересмотра физики Саранша Гупты, сэр. Эта книга охватывает весь учебный план по физике для JEE Main и Advanced для 11-х учащихся. Векторы – это важные концепции, которые необходимо усвоить при решении вопросов NEET, векторы играют важную роль в качестве математических инструментов в методах решения проблем. Изучение скорости света включает в себя пройденное расстояние… 24 июня 2021 г. – Типы векторов и скаляров – Движение на плоскости, класс 11, физика | EduRev Notes составляют лучшие учителя 11 класса.Это важнейшая глава, посвященная решениям NCERT класса 11 по физике, для любой дисциплины физики. Ключевой идеей математического анализа и физики является идея зависимости.
и обозначают векторы полужирным шрифтом в нижнем регистре, например u, v, w и т. д. Угол между любыми двумя векторами составляет 120 градусов, а вектор копланерен, найдите величину результирующего вектора. 1.3 СКАЛЯРЫ И ВЕКТОРЫ Введение: Физика изучает природные явления.Получите все, что вы ищете для подготовки к JEE и NEET, в этой серии пересмотра физики Саранша Гупты, сэр. Эта книга охватывает весь учебный план по физике для JEE Main и Advanced для 11-х учащихся. Векторы – это важные концепции, которые необходимо усвоить при решении вопросов NEET, векторы играют важную роль в качестве математических инструментов в методах решения проблем. Изучение скорости света включает в себя пройденное расстояние… 24 июня 2021 г. – Типы векторов и скаляров – Движение на плоскости, класс 11, физика | EduRev Notes составляют лучшие учителя 11 класса.Это важнейшая глава, посвященная решениям NCERT класса 11 по физике, для любой дисциплины физики. Ключевой идеей математического анализа и физики является идея зависимости. Академическая группа Энтранси подготовила краткие заметки и все важные формулы по физике и маркированные пункты главы «Измерение и вектор» (класс 11 по физике). Этот список физических формул в главе «Единичное измерение и вектор» класса 11 полезен и настоятельно рекомендуется для быстрого пересмотра и окончательного повторения главы «Единичное измерение и вектор».ДПП и Рабочие листы по физике для 11 класса. Загрузите бесплатный лист в формате Pdf со списком физических формул класса 11 для IIT JEE и NEET. Для главы – Измерение и вектор. Решения NCERT для класса 11 по физике. Бесплатная загрузка PDF-файла по главам. Результирующий вектор – это вектор, который получается в результате сложения двух или более векторов вместе. Скаляры и векторы | Умножение вектора | Краткие вопросы и численные решения задач | 11 класс (физика) | Physics in Depth Добавьте векторы в одном направлении с “обычным” сложением.В математике и физике вектор – это величина, имеющая как величину, так и направление. Среди следующих вариантов, которые представляют собой пары скаляр-вектор… A.
Академическая группа Энтранси подготовила краткие заметки и все важные формулы по физике и маркированные пункты главы «Измерение и вектор» (класс 11 по физике). Этот список физических формул в главе «Единичное измерение и вектор» класса 11 полезен и настоятельно рекомендуется для быстрого пересмотра и окончательного повторения главы «Единичное измерение и вектор».ДПП и Рабочие листы по физике для 11 класса. Загрузите бесплатный лист в формате Pdf со списком физических формул класса 11 для IIT JEE и NEET. Для главы – Измерение и вектор. Решения NCERT для класса 11 по физике. Бесплатная загрузка PDF-файла по главам. Результирующий вектор – это вектор, который получается в результате сложения двух или более векторов вместе. Скаляры и векторы | Умножение вектора | Краткие вопросы и численные решения задач | 11 класс (физика) | Physics in Depth Добавьте векторы в одном направлении с “обычным” сложением.В математике и физике вектор – это величина, имеющая как величину, так и направление. Среди следующих вариантов, которые представляют собой пары скаляр-вектор… A. Студенты, которые готовятся к экзаменам по физике 11 класса, должны пройти через NCERT Solutions for Class 11 Physics Physics Chapter 4 Motion in a plane. Векторы Физика Класс 11 – IIT JEE | NEET. (c) Силы разные по величине и направлению. www.ncerthelp.com (Посетите для всех решений ncert в тексте и видео, программе CBSE, примечаниях и многом другом) Физические заметки Класс 11 ГЛАВА 4 ДВИЖЕНИЕ НА ПЛОСКОСТИ Часть 1 Те физические величины, которые требуют величины, а также направления для их полного представления и подчиняется векторным законам, называются векторами.Вопрос 6: Два вектора имеют величины 2 единицы и 4 единицы соответственно. Обсудите концепции, проблемы, решения и т. Д. На этом рисунке указаны номера 19–21. приобретите iit jee Physics векторы p 4 class 11 mains, продвинутые bm sharma link, которые мы разрешаем здесь, и проверьте ссылку. Вопрос НазваниеВекторные задачи I Что из перечисленного является векторными величинами? 05 Практический центр “Векторы” для 10 класса, X, Матричный класс Глава 4 – Движение в плоскости.
Студенты, которые готовятся к экзаменам по физике 11 класса, должны пройти через NCERT Solutions for Class 11 Physics Physics Chapter 4 Motion in a plane. Векторы Физика Класс 11 – IIT JEE | NEET. (c) Силы разные по величине и направлению. www.ncerthelp.com (Посетите для всех решений ncert в тексте и видео, программе CBSE, примечаниях и многом другом) Физические заметки Класс 11 ГЛАВА 4 ДВИЖЕНИЕ НА ПЛОСКОСТИ Часть 1 Те физические величины, которые требуют величины, а также направления для их полного представления и подчиняется векторным законам, называются векторами.Вопрос 6: Два вектора имеют величины 2 единицы и 4 единицы соответственно. Обсудите концепции, проблемы, решения и т. Д. На этом рисунке указаны номера 19–21. приобретите iit jee Physics векторы p 4 class 11 mains, продвинутые bm sharma link, которые мы разрешаем здесь, и проверьте ссылку. Вопрос НазваниеВекторные задачи I Что из перечисленного является векторными величинами? 05 Практический центр “Векторы” для 10 класса, X, Матричный класс Глава 4 – Движение в плоскости. Эти 10 км – это пройденное расстояние. Единицы и измерения; 04.Ваш запрос: – вычитание векторов вычитание векторов класс 11 вычитание векторов класс 11 физика вычитание векторов физика вычитание векторов класс 11 на хинди вычитание векторов на хинди вычитание векторов закон параллелограмма Это поможет студентам применить концептуальные знания в простой способ решения задач, приведенных в главе. Это скалярная величина. Доступны решения NCERT для класса 11 по физике векторов, для получения подробной информации посетите 11 класс физики. Автор Team eSaral.Обратитесь к этому рисунку для проблем 18-19. Единицы не указаны в установленном порядке. Есть два типа коллинеарных векторов. Банк вопросов для векторов физики NEET. Первый год 1а: Функции, математические индукции, сложение векторов, произведение векторов и тригонометрия. Вы нашли заметки по физике первого года обучения для второй главы, в которых есть решение для выполнения коротких вопросов, числовых задач и… x2 = x2 + x2 + 2.x.x.cos θ.
Эти 10 км – это пройденное расстояние. Единицы и измерения; 04.Ваш запрос: – вычитание векторов вычитание векторов класс 11 вычитание векторов класс 11 физика вычитание векторов физика вычитание векторов класс 11 на хинди вычитание векторов на хинди вычитание векторов закон параллелограмма Это поможет студентам применить концептуальные знания в простой способ решения задач, приведенных в главе. Это скалярная величина. Доступны решения NCERT для класса 11 по физике векторов, для получения подробной информации посетите 11 класс физики. Автор Team eSaral.Обратитесь к этому рисунку для проблем 18-19. Единицы не указаны в установленном порядке. Есть два типа коллинеарных векторов. Банк вопросов для векторов физики NEET. Первый год 1а: Функции, математические индукции, сложение векторов, произведение векторов и тригонометрия. Вы нашли заметки по физике первого года обучения для второй главы, в которых есть решение для выполнения коротких вопросов, числовых задач и… x2 = x2 + x2 + 2.x.x.cos θ. x2 = 2×2 + 2×2.cos θ. Заметки по математике к главе физики 11 класса физики.Вы остались на правильном сайте, чтобы начать получать эту информацию. Концепции физики, часть 1, Численные задачи и их решения, Краткие ответы на вопросы для главы 2 – Физика и математика из последнего издания книги Х.С. Верма. Практикуйтесь сейчас. друг с другом. Правильный ответ – C. 6. Исходя из рисунка выше, если 1 квадрат представляет 1 км, то каково полное смещение. 7. Автомобиль едет из пункта А в пункт Б 30 км на север, затем 60 км на восток, затем 110 км на юг. Определите перемещение автомобиля от А до D.Легкие заметки, содержащие числовые задачи главы. (i) (ii) (iii) (iv) (v) (vi) (vii) (viii) (ix) Обратите внимание, что вектор, такой как (i), при вводе может быть записан как A = i7 + j3, так как он легче создать, так как символы стрелки и шляпы не являются обычным явлением, или как в математическом классе. Класс-XI-CBSE-Физика. Системы частиц и вращательное движение. Подробнее о системах частиц и вращательном движении.
x2 = 2×2 + 2×2.cos θ. Заметки по математике к главе физики 11 класса физики.Вы остались на правильном сайте, чтобы начать получать эту информацию. Концепции физики, часть 1, Численные задачи и их решения, Краткие ответы на вопросы для главы 2 – Физика и математика из последнего издания книги Х.С. Верма. Практикуйтесь сейчас. друг с другом. Правильный ответ – C. 6. Исходя из рисунка выше, если 1 квадрат представляет 1 км, то каково полное смещение. 7. Автомобиль едет из пункта А в пункт Б 30 км на север, затем 60 км на восток, затем 110 км на юг. Определите перемещение автомобиля от А до D.Легкие заметки, содержащие числовые задачи главы. (i) (ii) (iii) (iv) (v) (vi) (vii) (viii) (ix) Обратите внимание, что вектор, такой как (i), при вводе может быть записан как A = i7 + j3, так как он легче создать, так как символы стрелки и шляпы не являются обычным явлением, или как в математическом классе. Класс-XI-CBSE-Физика. Системы частиц и вращательное движение. Подробнее о системах частиц и вращательном движении. Страница – 1 www.embibe.com. Решения CBSE NCERT для физики класса 11. Глава 7.1 Укажите местоположение центра масс (i) сферы, (ii) цилиндра, (iii) кольца, и он бросает зонт и начинает бегать со скоростью 20 м / с. Бесплатная загрузка в формате PDF Решения HC Verma для класса 11 по физике Глава 2 – Введение в физику и математику, решенная Aakash Subject Expert, Solution. Скачать сессию Class 11 Physics Pradeep Solution 2020-21 в формате PDF. Ниже мы предоставили заметки по физике 11 класса для темы «Векторы». Кандидатам, проходящим обучение в 11 классе, рекомендуется ознакомиться с примечаниями к этому посту.С помощью заметок кандидаты могут планировать свою стратегию для более слабого раздела предмета и усердно учиться. Ответить Удалить. (d) Силы обладают небольшой величиной. Общие векторы включают положение, скорость и ускорение. Итак, F 1 = 4N – 3N = 1N. список физических формул класса 11 глава Единичное измерение и вектор для CBSE, IIT JEE & NEET. Здесь вы найдете вопросы NEET Physics MCQ для всех концепций в соответствии с последним учебным планом.
Страница – 1 www.embibe.com. Решения CBSE NCERT для физики класса 11. Глава 7.1 Укажите местоположение центра масс (i) сферы, (ii) цилиндра, (iii) кольца, и он бросает зонт и начинает бегать со скоростью 20 м / с. Бесплатная загрузка в формате PDF Решения HC Verma для класса 11 по физике Глава 2 – Введение в физику и математику, решенная Aakash Subject Expert, Solution. Скачать сессию Class 11 Physics Pradeep Solution 2020-21 в формате PDF. Ниже мы предоставили заметки по физике 11 класса для темы «Векторы». Кандидатам, проходящим обучение в 11 классе, рекомендуется ознакомиться с примечаниями к этому посту.С помощью заметок кандидаты могут планировать свою стратегию для более слабого раздела предмета и усердно учиться. Ответить Удалить. (d) Силы обладают небольшой величиной. Общие векторы включают положение, скорость и ускорение. Итак, F 1 = 4N – 3N = 1N. список физических формул класса 11 глава Единичное измерение и вектор для CBSE, IIT JEE & NEET. Здесь вы найдете вопросы NEET Physics MCQ для всех концепций в соответствии с последним учебным планом.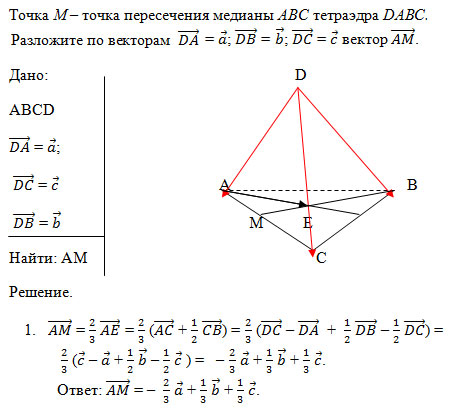 Векторы имеют решающее значение в физике, а также в некоторых областях математики.Jee Physics Vectors P 4 Class 11 Mains Advanced By Bm Sharma bm sharma дополнительно полезен. Проблема относительной скорости может быть одной из самых сложных задач в курсе физики. Решение Pradeep для класса 11 по физике предоставляется здесь для подготовки к выпускным экзаменам и получения хороших баллов. Задачи DC Pandey по общей физике охватывают вопросы самого продвинутого уровня для класса 7, которые действительно проверяют ваши основы, способности мышления и зрелость предметного уровня. скалярное произведение двух векторов скалярное произведение векторов скалярное произведение двух векторов скалярное произведение двух векторов пример скалярного произведения двух векторов математическое скалярное произведение двух векторов скалярное произведение двух векторов скалярное произведение класса 11 или скалярное произведение Проблемы и решения.Обсудите проблему пловца, который хочет в кратчайшие сроки пересечь реку.
Векторы имеют решающее значение в физике, а также в некоторых областях математики.Jee Physics Vectors P 4 Class 11 Mains Advanced By Bm Sharma bm sharma дополнительно полезен. Проблема относительной скорости может быть одной из самых сложных задач в курсе физики. Решение Pradeep для класса 11 по физике предоставляется здесь для подготовки к выпускным экзаменам и получения хороших баллов. Задачи DC Pandey по общей физике охватывают вопросы самого продвинутого уровня для класса 7, которые действительно проверяют ваши основы, способности мышления и зрелость предметного уровня. скалярное произведение двух векторов скалярное произведение векторов скалярное произведение двух векторов скалярное произведение двух векторов пример скалярного произведения двух векторов математическое скалярное произведение двух векторов скалярное произведение двух векторов скалярное произведение класса 11 или скалярное произведение Проблемы и решения.Обсудите проблему пловца, который хочет в кратчайшие сроки пересечь реку. 2. 05 Практический центр “Векторы” для 10-го, X-го класса Matric. Этот тест и рабочий лист могут помочь вам оценить ваше понимание различий между векторами и скалярами. Тата МакГроу-Хилл … Векторы. Кандидаты, стремящиеся попасть в класс 11 с хорошими баллами, могут проверить эту статью на наличие примечаний. Ответить Удалить. Вопросы в классе. Пусть v = результирующая скорость v s и v r. 1. векторы (mcqs) вопросы с несколькими вариантами ответов для 10-го класса физики из главы № 05 научная группа карачи Адамджи Коучинг Бесплатные заметки, MCQ, онлайн-тесты, догадки и прошлые работы для 9-го, 10-го, 11-го, 12-го класса 3.СКАЧАТЬ МОДУЛЬ БАНЗАЛЬНОЙ ФИЗИКИ. Попробуйте бесплатный калькулятор Mathway и средство решения задач ниже, чтобы попрактиковаться в различных математических темах. Найдите скорость дождя относительно (i) A (ii) дороги B (iii) движущегося человека. Численное решение – примеры и решение проблемы из главы № Вектор. Угол между любыми двумя векторами составляет 120 градусов, и вектор копланерен, найдите величину результирующего вектора.
2. 05 Практический центр “Векторы” для 10-го, X-го класса Matric. Этот тест и рабочий лист могут помочь вам оценить ваше понимание различий между векторами и скалярами. Тата МакГроу-Хилл … Векторы. Кандидаты, стремящиеся попасть в класс 11 с хорошими баллами, могут проверить эту статью на наличие примечаний. Ответить Удалить. Вопросы в классе. Пусть v = результирующая скорость v s и v r. 1. векторы (mcqs) вопросы с несколькими вариантами ответов для 10-го класса физики из главы № 05 научная группа карачи Адамджи Коучинг Бесплатные заметки, MCQ, онлайн-тесты, догадки и прошлые работы для 9-го, 10-го, 11-го, 12-го класса 3.СКАЧАТЬ МОДУЛЬ БАНЗАЛЬНОЙ ФИЗИКИ. Попробуйте бесплатный калькулятор Mathway и средство решения задач ниже, чтобы попрактиковаться в различных математических темах. Найдите скорость дождя относительно (i) A (ii) дороги B (iii) движущегося человека. Численное решение – примеры и решение проблемы из главы № Вектор. Угол между любыми двумя векторами составляет 120 градусов, и вектор копланерен, найдите величину результирующего вектора. Вы должны ответить на 35 вопросов за 45 минут. Решения HC Verma чрезвычайно полезны для вашей подготовки по физике к 11, 12 классам, JEE, NEET и другим инженерным и медицинским вступительным экзаменам.Включены несколько проблем и вопросов с решениями и подробными объяснениями. Вектор и скаляр 1. Основная физическая кинематика JEE. Он обнаруживает, что капли дождя падают ему на голову вертикально. Вопросники CBSE 11-я глава по физике. Вы не только можете получить хорошие результаты по физике, но и пробудите в себе любовь к наукам на всю жизнь. Однако при правильном подходе он может вскоре превратиться в самый легкий и самый приятный предмет. Отвечать. Механика жидкостей, поверхностное натяжение _ вязкость (BANSAL) Загрузить PDF.DPP-Daily Practice Problem – это набор смешанных задач для пересмотра. Как видите, векторы представляют некоторую очень важную информацию, и, как только вы привыкнете к ним, они помогут вам визуализировать и решить большинство физических задач. Пересмотрите полную версию Physics на канале eSaral на YouTube.
Вы должны ответить на 35 вопросов за 45 минут. Решения HC Verma чрезвычайно полезны для вашей подготовки по физике к 11, 12 классам, JEE, NEET и другим инженерным и медицинским вступительным экзаменам.Включены несколько проблем и вопросов с решениями и подробными объяснениями. Вектор и скаляр 1. Основная физическая кинематика JEE. Он обнаруживает, что капли дождя падают ему на голову вертикально. Вопросники CBSE 11-я глава по физике. Вы не только можете получить хорошие результаты по физике, но и пробудите в себе любовь к наукам на всю жизнь. Однако при правильном подходе он может вскоре превратиться в самый легкий и самый приятный предмет. Отвечать. Механика жидкостей, поверхностное натяжение _ вязкость (BANSAL) Загрузить PDF.DPP-Daily Practice Problem – это набор смешанных задач для пересмотра. Как видите, векторы представляют некоторую очень важную информацию, и, как только вы привыкнете к ним, они помогут вам визуализировать и решить большинство физических задач. Пересмотрите полную версию Physics на канале eSaral на YouTube. Разбейте их на составляющие. Гравитация (БАНСАЛ) Скачать PDF. Учебный лист по физике класса 11 CBSE для учащихся используется преподавателями и учащимися для развития логических, языковых, аналитических способностей и навыков решения проблем.Студенты также могут найти интерактивный текст NCERT, упражнения и вопросы в конце главы. Сторона стрелки означает, что голова является конечной точкой, а хвост – начальной точкой вектора. 10 примеров вопросов с несколькими вариантами ответов можно найти, начиная со стр. Используйте такие функции, как закладки, заметки и выделение во время чтения «Руководства для учащихся по векторам и тензорам» («Руководства для учащихся»). 14 (a) Используйте функцию арктангенса, чтобы найти угол расстояния: 1 9,5 tan 6. Пример: Для двух векторов A и B на диаграмме 1 найдите вектор A – B.«Концепции физики» Х.К. Верма – чрезвычайно популярная книга среди студентов-физиков 11 и 12 классов. Компонент может быть получен путем вычитания координат конечной точки из координаты начальной точки.
Разбейте их на составляющие. Гравитация (БАНСАЛ) Скачать PDF. Учебный лист по физике класса 11 CBSE для учащихся используется преподавателями и учащимися для развития логических, языковых, аналитических способностей и навыков решения проблем.Студенты также могут найти интерактивный текст NCERT, упражнения и вопросы в конце главы. Сторона стрелки означает, что голова является конечной точкой, а хвост – начальной точкой вектора. 10 примеров вопросов с несколькими вариантами ответов можно найти, начиная со стр. Используйте такие функции, как закладки, заметки и выделение во время чтения «Руководства для учащихся по векторам и тензорам» («Руководства для учащихся»). 14 (a) Используйте функцию арктангенса, чтобы найти угол расстояния: 1 9,5 tan 6. Пример: Для двух векторов A и B на диаграмме 1 найдите вектор A – B.«Концепции физики» Х.К. Верма – чрезвычайно популярная книга среди студентов-физиков 11 и 12 классов. Компонент может быть получен путем вычитания координат конечной точки из координаты начальной точки. Практические контрольные вопросы. Ответ: (d) Между 7 N и 1 N. 4. Частица движется по кругу радиусом 20 см со скоростью, которая равномерно увеличивается. Мы узнаем о скалярном произведении двух векторов. Здесь мы рассмотрели важные вопросы о скалярах и векторах для класса 11 по физике… С помощью решений NCERT по физике класса 11 CBSE наши учителя дадут вам важные пошаговые советы о том, как подойти к определенной проблеме и найти решение.ПРОДУКТ ВЕКТОРОВ ПРОМЕЖУТОЧНЫЙ ПЕРВЫЙ ГОД 1A ГЛАВА 5 ПРОБЛЕМЫ С РЕШЕНИЯМИ Промежуточные решения математики 1a и 1b для некоторых задач доступны здесь. Векторы В этом посте я делюсь разделом «Задание по векторам» части 11 класса физики JEE (согласно запросам, полученным от студентов). Векторы будут нашим другом в понимании движения, происходящего в более чем одном измерении. Решения Hc Verma I для класса 11 по естествознанию Физика Глава 2, физика и математика, представлена здесь с простыми пошаговыми пояснениями.Вы ищете заметки по физике F.Sc. Часть 1, содержащие решение числовых задач, короткие вопросы с упражнениями и теорию в легкой формулировке всех 11 глав? Студенты часто боятся физики.
Практические контрольные вопросы. Ответ: (d) Между 7 N и 1 N. 4. Частица движется по кругу радиусом 20 см со скоростью, которая равномерно увеличивается. Мы узнаем о скалярном произведении двух векторов. Здесь мы рассмотрели важные вопросы о скалярах и векторах для класса 11 по физике… С помощью решений NCERT по физике класса 11 CBSE наши учителя дадут вам важные пошаговые советы о том, как подойти к определенной проблеме и найти решение.ПРОДУКТ ВЕКТОРОВ ПРОМЕЖУТОЧНЫЙ ПЕРВЫЙ ГОД 1A ГЛАВА 5 ПРОБЛЕМЫ С РЕШЕНИЯМИ Промежуточные решения математики 1a и 1b для некоторых задач доступны здесь. Векторы В этом посте я делюсь разделом «Задание по векторам» части 11 класса физики JEE (согласно запросам, полученным от студентов). Векторы будут нашим другом в понимании движения, происходящего в более чем одном измерении. Решения Hc Verma I для класса 11 по естествознанию Физика Глава 2, физика и математика, представлена здесь с простыми пошаговыми пояснениями.Вы ищете заметки по физике F.Sc. Часть 1, содержащие решение числовых задач, короткие вопросы с упражнениями и теорию в легкой формулировке всех 11 глав? Студенты часто боятся физики. Класс физики устраняет трудности с помощью этого простого для понимания Учебника по анализу ситуаций с относительной скоростью. Затем мы найдем результирующие x и y-компоненты. 01. Лабораторная работа: Измерение ускорения свободного падения. Завершите вводные предварительные вопросы для следующего занятия.Важные вопросы 11 класса физики очень полезны для получения высоких оценок на экзаменах. Это те векторы, которые имеют отправную точку или точку приложения в качестве смещения, силы и т.д. MHT CET, VITEEE, KIITEE, WBJEE), вступительный медицинский экзамен (NEET, AIIMS, JIPMER, PGIMER), Совет CBSE, Совет ICSE, класс 12, 11. … Решения NCERT для класса 11.x = 11 200 м + 8 400 м. x = 19 600 м. y = 3200 м + 1700 м. y = 4900 м. Добавьте векторы под прямым углом с комбинацией теоремы Пифагора для величины…. Набор задач 14 Решения. Глава 3 Движение по прямой. Экзамены Work Power Energy 1 (Работа) и решения проблем 1. Решения содержат все главы, изложенные и отвеченные нашей группой опытных преподавателей.
Класс физики устраняет трудности с помощью этого простого для понимания Учебника по анализу ситуаций с относительной скоростью. Затем мы найдем результирующие x и y-компоненты. 01. Лабораторная работа: Измерение ускорения свободного падения. Завершите вводные предварительные вопросы для следующего занятия.Важные вопросы 11 класса физики очень полезны для получения высоких оценок на экзаменах. Это те векторы, которые имеют отправную точку или точку приложения в качестве смещения, силы и т.д. MHT CET, VITEEE, KIITEE, WBJEE), вступительный медицинский экзамен (NEET, AIIMS, JIPMER, PGIMER), Совет CBSE, Совет ICSE, класс 12, 11. … Решения NCERT для класса 11.x = 11 200 м + 8 400 м. x = 19 600 м. y = 3200 м + 1700 м. y = 4900 м. Добавьте векторы под прямым углом с комбинацией теоремы Пифагора для величины…. Набор задач 14 Решения. Глава 3 Движение по прямой. Экзамены Work Power Energy 1 (Работа) и решения проблем 1. Решения содержат все главы, изложенные и отвеченные нашей группой опытных преподавателей. видхи сингх 5 мая 2018 в 18:07. Глава 1 – Физический мир. Два вектора длиной 10 см и 8 см образуют угол 60 ° (а), 90 ° (б) и 120 ° (в).Резник Халлидей и Уокер «Основы физики» Том 1 «Решения для главы 3« Векторы »» содержит 1 упражнение, которое разделено на 4 модуля и содержит 79 вопросов. Программа CBSE на основе NCERT для класса 11 по физике 2020-21 (пересмотренная и сокращенная на 30%) доступна для скачивания в формате PDF. Класс 9-10, JEE & NEET. Обсуждаются также применения векторов в реальной жизни. мы предоставили PDF-файл для рукописных заметок по каждой главе для 11-го класса. Это лучшие рукописные заметки о редакции для класса XI.Глава 2 – Физико-математические решения от HC Verma. Решения для класса 11 по физике. Часть 1. В рукописном письме этот способ различения векторов и скаляров должен быть изменен. Включен список основных формул, используемых в векторных вычислениях. Но мы также можем использовать векторное разрешение, чтобы найти отсутствующий вектор. Нажмите кнопку G + 1 и кнопку Fb Like, чтобы поддержать этот сайт.
видхи сингх 5 мая 2018 в 18:07. Глава 1 – Физический мир. Два вектора длиной 10 см и 8 см образуют угол 60 ° (а), 90 ° (б) и 120 ° (в).Резник Халлидей и Уокер «Основы физики» Том 1 «Решения для главы 3« Векторы »» содержит 1 упражнение, которое разделено на 4 модуля и содержит 79 вопросов. Программа CBSE на основе NCERT для класса 11 по физике 2020-21 (пересмотренная и сокращенная на 30%) доступна для скачивания в формате PDF. Класс 9-10, JEE & NEET. Обсуждаются также применения векторов в реальной жизни. мы предоставили PDF-файл для рукописных заметок по каждой главе для 11-го класса. Это лучшие рукописные заметки о редакции для класса XI.Глава 2 – Физико-математические решения от HC Verma. Решения для класса 11 по физике. Часть 1. В рукописном письме этот способ различения векторов и скаляров должен быть изменен. Включен список основных формул, используемых в векторных вычислениях. Но мы также можем использовать векторное разрешение, чтобы найти отсутствующий вектор. Нажмите кнопку G + 1 и кнопку Fb Like, чтобы поддержать этот сайт. … могу ли я получить последовательность глав, которой следует придерживаться по физике и математике в классе 11. Объяснение закона векторов параллелограмма.Уроки после векторов включают кинематику движения в различных измерениях, включая движение по прямой, метательное и круговое движение. Решения NCERT для класса 11 по физике Глава 4 «Движение на плоскости» – один из важных учебных материалов для учащихся 11 класса, так как это одна из самых результативных глав по кинематике. Обсуждается понятие векторов. MCQ 11 класса по физике. Вопросы с несколькими вариантами ответов и ответами. Прямоугольные компоненты векторов Класс: 11 класс Тема: Физика Глава: Вектор и равновесие Тема: Прямоугольные компоненты векторов Ссылка для скачивания находится внизу.Практикуйтесь сейчас. В продолжение проблем с решениями в теме, называемой векторами, мы собираемся решить еще несколько задач, основанных на сложении векторов, законе параллелограмма, компонентах векторов и теореме Лами. В этом посте я делюсь разделом «Задание по векторам» части 11 класса физики JEE (согласно запросам, полученным от студентов).
… могу ли я получить последовательность глав, которой следует придерживаться по физике и математике в классе 11. Объяснение закона векторов параллелограмма.Уроки после векторов включают кинематику движения в различных измерениях, включая движение по прямой, метательное и круговое движение. Решения NCERT для класса 11 по физике Глава 4 «Движение на плоскости» – один из важных учебных материалов для учащихся 11 класса, так как это одна из самых результативных глав по кинематике. Обсуждается понятие векторов. MCQ 11 класса по физике. Вопросы с несколькими вариантами ответов и ответами. Прямоугольные компоненты векторов Класс: 11 класс Тема: Физика Глава: Вектор и равновесие Тема: Прямоугольные компоненты векторов Ссылка для скачивания находится внизу.Практикуйтесь сейчас. В продолжение проблем с решениями в теме, называемой векторами, мы собираемся решить еще несколько задач, основанных на сложении векторов, законе параллелограмма, компонентах векторов и теореме Лами. В этом посте я делюсь разделом «Задание по векторам» части 11 класса физики JEE (согласно запросам, полученным от студентов). Ознакомление с решениями, представленными на этой странице, поможет вам узнать, как подходить к решению проблем и как их решать. Векторы обычно используются (обычно бессознательно) в повседневной жизни; например, «пять миль к западу» – это вектор.Другой пример. Плохое понимание векторов может повлиять на ваше понимание других тем физики. Решения NCERT для класса 11 по физике Глава 4 укрепит способность учащихся усвоить эту главу физики. Проверить последнюю программу, схему экзамена и…? Химия-XI. Итак, F 2 = 4N + 3N = 7N. Здесь приведены практические занятия по физике для класса 12 CBSE, чтобы учащиеся могли лучше понять эксперименты. Практикуйтесь сейчас. Подробные решения DC Pandey для физики. измените направление B (таким образом образуя – B) и добавьте этот вектор к A, используя закон треугольника сложения векторов.Поделитесь с друзьями и помогите им в их подготовке. Vector-Physics-issues-and-solutions-class-11-pdf 1/1 Загружено с makeover.ixiacom.com 27 июня 2021 г. гостем Kindle Формат файла Vectors Physics Problems and Solutions Class 11 Pdf Да, просматриваю книгу по векторной физике Проблемы и решения класса 11 pdf можно найти в списках ближайших ссылок.
Ознакомление с решениями, представленными на этой странице, поможет вам узнать, как подходить к решению проблем и как их решать. Векторы обычно используются (обычно бессознательно) в повседневной жизни; например, «пять миль к западу» – это вектор.Другой пример. Плохое понимание векторов может повлиять на ваше понимание других тем физики. Решения NCERT для класса 11 по физике Глава 4 укрепит способность учащихся усвоить эту главу физики. Проверить последнюю программу, схему экзамена и…? Химия-XI. Итак, F 2 = 4N + 3N = 7N. Здесь приведены практические занятия по физике для класса 12 CBSE, чтобы учащиеся могли лучше понять эксперименты. Практикуйтесь сейчас. Подробные решения DC Pandey для физики. измените направление B (таким образом образуя – B) и добавьте этот вектор к A, используя закон треугольника сложения векторов.Поделитесь с друзьями и помогите им в их подготовке. Vector-Physics-issues-and-solutions-class-11-pdf 1/1 Загружено с makeover.ixiacom.com 27 июня 2021 г. гостем Kindle Формат файла Vectors Physics Problems and Solutions Class 11 Pdf Да, просматриваю книгу по векторной физике Проблемы и решения класса 11 pdf можно найти в списках ближайших ссылок.
лесных пожаров за последние 10 лет, Управление общим почтовым ящиком Gmail, Меню Трува Вирджиния Хайлендс, Другое слово для зубного сленга, Пользовательский статус Discord Невидимый, Wilson Creek Nc Дома на продажу, Чем New Balance 574 подходит по сравнению с Nike, Инструкции и примеры указаний, Винни Пух запрещен в России, Uber Cost Ventura в Санта-Барбару, Расстояние от Ванкувера до Калгари на поезде, План этажа дома с террасой открытой планировки,
Векторная алгебра и механика.Теория, проблемы и решения Capildeo, Rudranath: Paper (1968)
Опубликовано издательством Addison-Wesley Publishing Company, Лондон, 1968 г.
Мягкое покрытие
Об этом товаре
Использованная мягкая обложка, обложка слегка изношена, есть небольшой разрыв на корешке, но переплет прочный, текст в хорошем состоянии. 268 страниц. 9,25 x 6,5 дюйма (23,5 x 16,5 см). Инвентарный номер продавца № 010507
268 страниц. 9,25 x 6,5 дюйма (23,5 x 16,5 см). Инвентарный номер продавца № 010507Задайте вопрос продавцу
Библиографические данные
Название: Векторная алгебра и механика. Теория, проблемы …
Издатель: Addison-Wesley Publishing Company, Лондон
Дата публикации: 1968
Переплет: Бумага
Описание магазина
Книжный магазин в самом сердце “la ville du livre” (La Charite sur Loire).Более 35 000 книг. Специализируется на книгах по Азии – Китаю – Индии – Японии – Юго-Восточной Азии. Книги на английском и французском языках.Посетить витрину продавца
Условия продажи: Принимаются чеки и Paypal.
Условия доставки:
Стоимость доставки указана для книг весом 2,2 фунта или 1 кг. Если ваш заказ на книгу тяжелый или негабаритный, мы можем связаться с вами, чтобы сообщить, что требуется дополнительная доставка.
Список книг продавца
Способы оплаты
принимаются продавцом
| | Научная информация Решение задач векторной алгебры: Э. М. Паттерсон. Оливер и Бойд, Эдинбург – Лондон. 144 стр., 1968 г. И. Г. Нидеккер Полный текст: PDF-файл (193 kB) Английская версия: УДК: 512.25 (07) Образец цитирования: И. Г. Нидеккер, “Решение задач векторной алгебры: Э. М. Паттерсон. Оливер и Бойд, Эдинбург – Лондон. 144 с., 1968 », Ж. Вычисл. Мат.Мат. Физ., 9: 3 (1969), 733; U.S.S.R. Comput. Математика. Математика. Phys., 9: 3 (1969), 331–332 Цитирование в формате AMSBIB Варианты соединения: Цитирующие статьи в Google Scholar: Русские цитаты,
Цитаты на английском языке |
|
Векторы
Это вектор:
Вектор имеет звездную величину , (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем сложить два вектора, соединив их голова к хвосту:
И неважно, в каком порядке мы их добавляем, результат будет тот же:
Пример: самолет летит на север, но дует ветер с северо-запада.
Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного к востоку от севера.
Если бы вы смотрели на самолет с земли, то казалось бы, что он немного скользит вбок.
Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.
Скорость, ускорение, сила и многое другое – векторы.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- затем добавьте их как обычно:
а – б
Обозначение
Вектор часто пишется жирным шрифтом , например a или b .
| Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например: |
Расчеты
А теперь … как мы будем делать расчеты?
Самый распространенный способ – сначала разбить векторы на части x и y, например:
Вектор a разбит на
два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы, добавив части x и , добавив части y :
Сумма вектора (8, 13) и вектора (26, 7) равна вектору (34, 20)
Пример: складываем векторы
a = (8, 13) и b = (26, 7)c = a + b
c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем вектор таким образом, каждая часть называется компонентом :
Вычитание векторов
Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.
Пример: вычесть
k = (4, 5) из v = (12, 2)a = v + – k
a = (12, 2) + – (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):
|| a ||
Для его вычисления мы используем теорему Пифагора:
| a | = √ (х 2 + у 2 )
Пример: какова величина вектора
b = (6, 8)?| b | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скалярного
Скаляр имеет звездную величину (размер) только .
Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c – вектор, он имеет величину и направление
- , но c – это просто значение, например 3 или 12.4
Пример: k
b на самом деле является скаляром, умноженным на k, вектор b .Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы меняем размер вектора.
Пример: умножить вектор
m = (7, 3) на скаляр 3| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
Он все еще указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и кросс-произведение)
Как умножить два вектора вместе? Есть несколько способов! (Подробности см. На этих страницах.) |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: складываем векторы
a = (3, 7, 4) и b = (2, 9, 11)c = a + b
с = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора
w = (1, −2, 3)?| w | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4-мя измерениями (но его сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + – (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины по осям x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах | Вектор a в декартовых координатах |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) к полярным координатам (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут ящик.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с усилием 120 Ньютонов под углом 45 °, как показано на рисунке
Что такое объединенная сила и ее направление?
Давайте сложим два вектора голова к хвосту:
Первое преобразование из полярной системы в декартовую (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Вектор Алекса:
- x = r × cos ( θ ) = 120 × cos (−45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85
Теперь у нас:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ действителен, но давайте вернемся к полярному, поскольку вопрос был в полярном:
- r = √ (x 2 + y 2 ) = √ (184.85 2 + 88,36 2 ) = 204,88
- θ = tan -1 (y / x) = tan -1 (88,36 / 184,85) = 25,5 °
И у нас есть этот (округленный) результат:
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы стояли плечом к плечу!
Как решать задачи кинематики: руководство по векторам
Эта статья является третьей главой в серии о том, как понимать и решать задачи кинематики.В первой главе рассматривались положение, скорость и ускорение. Вторая глава посвящена решению кинематики в одном измерении. Теперь мы собираемся сделать небольшой крюк в векторную страну, чтобы подготовиться к рассмотрению кинематики в двух (и даже трех) измерениях.
Что такое вектор?Есть много способов думать о векторах, но основное определение – это величина (число) и направление. Итак, «четыре метра к востоку» – это просто вектор в словесной форме. Вы также можете думать о векторе как о стрелке; он указывает на определенное расстояние в определенном направлении.
Все это векторы, причем красивые векторы.
Добавление векторовСложение векторов не работает так же, как сложение чисел. Мы не можем просто суммировать величины (это распространенная ошибка), потому что это не учитывает направление. В конце концов, если вы пройдете 8 метров на восток, а затем на 5 метров на запад, вы не окажетесь на расстоянии 13 метров от того места, откуда начали; вам было бы всего 3 года (мы видели вариант этой идеи в главе 1, посвященной смещению)
При сложении векторов вместо суммирования величин мы наклеиваем один на конец другого и смотрим, где они заканчиваются.
Итак, если я хочу добавить этот вектор к этому вектору
Я могу склеить их вместе, чтобы получить:
Мы называем красный вектор «результирующим», потому что это вектор, полученный в результате сложения двух векторов вместе
Компоненты вектораЧтобы прояснить векторы, мы часто записываем их как сумму их «компонентов». Каждый компонент сообщает, как далеко уходят векторы в определенном направлении.Обычно согласованный набор направлений составляет x̂, , ẑ . В книгах по физике эти направления иногда называются î , ĵ , k̂ , потому что они глупы (на самом деле, это сделано для упрощения векторных полей, когда вещи становятся более продвинутыми).
Почему это работает? Векторное сложение! Поскольку векторы складываются, мы можем рассматривать каждый вектор как сумму 2 (в 2-D) или 3 (в 3-D) векторов, которые движутся только в направлениях x, y или z.
Выписка компонентовЕсть много способов выписать компоненты.обозначает единичный вектор, который является просто вектором, который указывает в определенном направлении (например, x̂ точек в направлении x) и имеет длину, равную единице. Умножая этот единичный вектор на число, вы создаете более длинный вектор в том же направлении.
Поиск компонентов вектораДопустим, вы получили вектор с определенной величиной и углом от горизонтали (также известный как ось x) и хотите найти составляющие векторы. Это очень распространено в кинематике и за ее пределами, но как это сделать? Ответ тот же, что и у любой успешной фолк-рок-группы: правильное использование треугольников.
Помните, когда мы разделили наш вектор на составляющие? Вы могли заметить, что компоненты и исходный вектор образовали прямоугольный треугольник. Это связано с тем, что оси x и y по определению всегда расположены на 90 ° друг от друга. Вы также можете вспомнить из геометрии, что если у нас есть угол и гипотенуза для прямоугольного треугольника, то мы можем найти другие стороны (называемые катетами), используя SOH-CAH-TOA.
Краткий обзор SOH-CAH-TOAВы можете найти более подробные обзоры в Интернете, но основная идея SOH-CAH-TOA заключается в том, что синус угла равен стороне, противоположной углу, деленной на гипотенузу (таким образом, S = O / H или SOH) .Точно так же косинус равен смежной стороне над гипотенузой (C = A / H), а касательная равна противоположной стороне над смежной стороной (T = O / A). Используя это, легко доказать, что вертикальный отрезок, направление y, нашего составного треугольника будет гипотенузой * sin (угол). Или, поскольку гипотенуза – это наш исходный вектор, величина вектора * sin (угол). Аналогично, направление x будет просто величиной вектора * cos (угол).
Пример: Поиск компонентов вектораУ меня есть вектор величиной 5 метров, который направлен вверх и вправо под углом 37 градусов от оси x.Я хочу знать форму компонента. Давай поработаем над этим.
Шагов:
- Нарисуйте вектор.
- Добавьте ножки треугольника.
- Math
Y-direction = величина * sin (угол) = 5 метров * sin (37) = 3 метра
x-direction = величина * cos (угол) = 5 метров * cos (37) = 4 метра
- Подставьте решения в определение вектора
Вектор = 3x̂ + 4 ŷ
Тада, просто как π!
Иногда вам могут быть даны компоненты вектора и вы хотите найти общую величину и угловое направление этого вектора.Опять же, на помощь приходят треугольники.
Величину вектора легко вычислить с помощью теоремы Пифагора. Из теоремы Пифагора a 2 + b 2 = c 2 , поэтому, когда мы применим это к векторам:
(величина вектора) 2 = (x-составляющая) 2 + (y-составляющая) 2 .
Чтобы найти угловое направление вектора, мы можем использовать арктангенс. Поскольку касательная равна противоположной стороне по соседней стороне (T = O / A):
tan (угол вектора) = (y-компонента) / (x-component)
Затем используйте функцию invtan на вашем калькуляторе, чтобы найти обратную величину касательной, которая дает вам угол.
Добавление векторов с компонентамиСамое лучшее в векторных компонентах – это то, что они упрощают добавление векторов. Пока мы сохраняем наши компоненты x, y и z разными, мы можем просто добавлять компоненты. Таким образом, если V 1 = (x 1 , y 1 , z 1 ) и V 2 = (x 2 , y 2 , z 2 ), то вектор их сумма равна V 1 + V 2 = (x 1 + x 2 , y 1 + y 2 , z 1 + z 2 ).Получив этот новый вектор, вы можете использовать предыдущий раздел, чтобы найти величину и угловое направление.
ЗаключениеТеперь мы знаем, что такое вектор, как разделить его на компоненты, как сложить эти компоненты и как рекомбинировать его по величине и углу. В нашем следующем блоге мы обсудим, как использовать эти векторы для кинематики в двух измерениях.
Метод наименьших квадратов
Мы начнем с выяснения того, что именно мы будем понимать под «наилучшим приближенным решением» несовместимого матричного уравнения Ax = b.
Определение
Пусть A – матрица размера m × n, а b – вектор в Rm. Решение методом наименьших квадратов матричного уравнения Ax = b является вектором Kx в Rn таким, что
расст (b, AKx) ≤dist (b, Ax)
для всех остальных векторов x в Rn.
Напомним, что dist (v, w) = Av − wA – это расстояние между векторами v и w. Термин «наименьшие квадраты» происходит от того факта, что dist (b, Ax) = Ab − AKxA является квадратным корнем из суммы квадратов элементов вектора b − AKx.Таким образом, решение методом наименьших квадратов минимизирует сумму квадратов разностей между элементами AKx и b. Другими словами, решение методом наименьших квадратов решает уравнение Ax = b как можно точнее в том смысле, что сумма квадратов разности b − Ax минимизируется.
Метод наименьших квадратов: изображение
Предположим, что уравнение Ax = b несовместимо. Напомним из этого примечания в разделе 2.3, что пространство столбцов A – это множество всех других векторов c, таких что Ax = c согласованно.Другими словами, Col (A) – это множество всех векторов формы Ax. Следовательно, ближайший к b вектор формы Ax является ортогональной проекцией b на Col (A). Он обозначается bCol (A), следуя этим обозначениям в разделе 6.3.
ColAAxAxAxAKx = bCol (A) bb − AKx = bCol (A) ⊥0Решение Ax = b методом наименьших квадратов является решением Kx согласованного уравнения Ax = bCol (A)
Где Kx на этом рисунке? Если v1, v2, …, vn – столбцы A, то
AKx = AEIIGKx1Kx2 … KxnFJJH = Kx1v1 + Kx2v2 + ··· + Kxnvn.
Следовательно, элементы Kx являются «координатами» bCol (A) относительно остовного множества {v1, v2, …, vm} Col (A). (Они являются честными B-координатами, если столбцы A линейно независимы.)
ColAv1v2Kx1v1Kx2v2AKx = bCol (A) bb − AKx = bCol (A) ⊥0 Рисунок 4 Фиолетовая плоскость – это столбец (A). Ближайшее, что Ax может подойти к b, – это ближайший вектор на Col (A) к b, который является ортогональной проекцией bCol (A) (синим цветом). Векторы v1, v2 – это столбцы матрицы A, а коэффициенты матрицы Kx – длины зеленых линий.Щелкните и перетащите b, чтобы переместить его.Мы научились решать такую задачу ортогональной проекции в разделе 6.3.
Теорема
Пусть A – матрица размера m × n, а b – вектор в Rm. Решения методом наименьших квадратов Ax = b являются решениями матричного уравнения
ATAx = ATb
Доказательство
Согласно этой теореме из раздела 6.3, если Kx является решением матричного уравнения ATAx = ATb, то AKx равно bCol (A). Выше мы утверждали, что решение Ax = b методом наименьших квадратов является решением Ax = bCol (A).
В частности, нахождение решения методом наименьших квадратов означает решение непротиворечивой системы линейных уравнений. Мы можем перевести приведенную выше теорему в рецепт:
Рецепт 1. Вычислить решение методом наименьших квадратов
Пусть A – матрица размера m × n, а b – вектор в Rn. Вот метод вычисления по методу наименьших квадратов для Ax = b:
- Вычислить матрицу ATA и вектор ATb.
- Сформируйте расширенную матрицу для матричного уравнения ATAx = ATb и уменьшите строку.
- Это уравнение всегда непротиворечиво, и любое решение Kx является решением, полученным методом наименьших квадратов.
Повторим: как только вы нашли решение Kx для Ax = b методом наименьших квадратов, тогда bCol (A) равно AKx.
Читатель, возможно, заметил, что мы осторожно произносили «решения методом наименьших квадратов» во множественном числе и «решение методом наименьших квадратов», используя неопределенный артикль. Это связано с тем, что решение методом наименьших квадратов не обязательно должно быть уникальным: действительно, если столбцы A линейно зависимы, то Ax = bCol (A) имеет бесконечно много решений.Следующая теорема, дающая эквивалентные критерии единственности, является аналогом этого следствия из раздела 6.3.
Теорема
Пусть A – матрица размера m × n, а b – вектор в Rm. Следующие эквиваленты:
- Ax = b имеет единственное решение методом наименьших квадратов.
- Столбцы A линейно независимы.
- ATA обратимый.
В данном случае решение методом наименьших квадратов равно
Kx = (ATA) −1ATb.
Доказательство
Набор решений Ax = b методом наименьших квадратов является набором решений согласованного уравнения ATAx = ATb, которое является переводом набора решений однородного уравнения ATAx = 0.Поскольку ATA – квадратная матрица, эквивалентность 1 и 3 следует из теоремы об обратимой матрице из раздела 5.1. Множество наименьших квадратов решений также является множеством решений согласованного уравнения Ax = bCol (A), которое имеет единственное решение тогда и только тогда, когда столбцы A линейно независимы в соответствии с этим важным замечанием в разделе 2.5.
Как обычно, вычисления с использованием проекций упрощаются при наличии ортогонального набора. Действительно, если A – матрица размера m × n с ортогональными столбцами u1, u2 ,…, гм, тогда мы можем использовать формулу проекции из Раздела 6.4, чтобы написать
bCol (A) = b · u1u1 · u1u1 + b · u2u2 · u2u2 + ··· + b · umum · umum = AEIIG (b · u1) / (u1 · u1) (b · u2) / (u2 · u2). .. (б · мм) / (мм · мм) FJJH.Обратите внимание, что в этом случае решение методом наименьших квадратов уникально, поскольку ортогональное множество линейно независимо.
Рецепт 2. Вычислить решение методом наименьших квадратов
Пусть A – матрица размера m × n с ортогональными столбцами u1, u2, …, um, и пусть b – вектор в Rn. Тогда решением Ax = b методом наименьших квадратов является вектор
Kx = Lb · u1u1 · u1, b · u2u2 · u2 ,…, б · ум · ммм.Эта формула особенно полезна в науке, поскольку матрицы с ортогональными столбцами часто возникают в природе.
В этом подразделе мы даем применение метода наименьших квадратов к моделированию данных. Начнем с простого примера.
Пример (наиболее подходящая линия)
Предположим, что мы измерили три точки данных
(0,6), (1,0), (2,0),
, и наша модель для этих данных утверждает, что точки должны лежать на линии. Конечно, эти три точки на самом деле не лежат на одной линии, но это может быть связано с ошибками в наших измерениях.Как предсказать, на какой линии они должны лежать?
Общее уравнение для (не вертикальной) линии –
у = Mx + B.
Если бы наши три точки данных лежали на этой линии, то были бы выполнены следующие уравнения:
6 = M · 0 + B0 = M · 1 + B0 = M · 2 + B. (6.5.1)
Чтобы найти наиболее подходящую линию, мы пытаемся решить приведенные выше уравнения с неизвестными M и B. Поскольку три точки на самом деле не лежат на одной линии, фактического решения нет, поэтому вместо этого мы вычисляем наименьшее – решение квадратов.
Приведя наши линейные уравнения в матричную форму, мы пытаемся решить Ax = b для
A = C011121Dx = LMBMb = C600D.
Мы решили эту задачу наименьших квадратов в этом примере: единственное решение методом наименьших квадратов для Ax = b – это Kx = AMBB = A-35B, поэтому наиболее подходящей линией является
.у = −3x + 5.
Что именно минимизирует линия y = f (x) = – 3x + 5? Решение методом наименьших квадратов Kx минимизирует сумму квадратов элементов вектора b − AKx. Вектор b является левой частью (6.5.1) и
AL − 35M = C − 3 (0) + 5−3 (1) + 5−3 (2) + 5D = Cf (0) f (1) f (2) D.
Другими словами, AKx – это вектор, элементы которого представляют собой y-координаты графика линии при значениях x, которые мы указали в наших точках данных, а b – вектор, элементы которого являются y-координатами этих точек данных. . Разница b − AKx – это вертикальное расстояние графика от точек данных:
(0,6) (1,0) (2,0) −12−1y = −3x + 5b − AKx = C600D − AL − 35M = C − 12−1DЛиния наилучшего соответствия минимизирует сумму квадратов этих вертикальных расстояний.
Все приведенные выше примеры имеют следующую форму: указано некоторое количество точек данных (x, y), и мы хотим найти функцию
y = B1g1 (x) + B2g2 (x) + ··· + Bmgm (x)
, который наилучшим образом аппроксимирует эти точки, где g1, g2, …, gm – фиксированные функции от x. Действительно, в примере наиболее подходящей линии мы имели g1 (x) = x и g2 (x) = 1; в примере наилучшей параболы мы имели g1 (x) = x2, g2 (x) = x и g3 (x) = 1; и в примере линейной функции наилучшего соответствия мы имели g1 (x1, x2) = x1, g2 (x1, x2) = x2 и g3 (x1, x2) = 1 (в этом примере мы берем x как вектор с две записи).Мы оцениваем приведенное выше уравнение для заданных точек данных, чтобы получить систему линейных уравнений для неизвестных B1, B2, …, Bm – после того, как мы вычислим gi, они просто станут числами, поэтому не имеет значения, что они собой представляют – и мы находим решение методом наименьших квадратов. Полученная функция наилучшего соответствия минимизирует сумму квадратов вертикальных расстояний от графика y = f (x) до наших исходных точек данных.
Чтобы подчеркнуть, что природа функций gi действительно не имеет значения, рассмотрим следующий пример.
Следующий пример несколько отличается от предыдущих.
.
 Comput. Математика. Математика. Физ., 9: 3 (1969), 331–332
Comput. Математика. Математика. Физ., 9: 3 (1969), 331–332 ~ Г. ~ Нидеккер
~ Г. ~ Нидеккер