Задания с ответами пределы: Примеры пределов с решениями - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Задания для практических занятий с вариантами ответов по теме “Вычисление пределов функции” | Тест по алгебре (11 класс) на тему:

Опубликовано 03.03.2017 – 13:07 – Кувшинова Елена Григорьевна

Задания предназначены для использования на уроках математики, изучаемой на 1 курсе техникума. Их можно применять как в процессе отработки навыков вычисления пределов определенного типа, так и при проверке умений вычислять пределы функций. Кроме того, задания позволяют расширить кругозор студентов, так как ключом к ответам являются фамилии ученых или название следующей темы из курса дисциплины.

Скачать:

Предварительный просмотр:

Задание: Вычислить пределы функции.

Задание 1. Вычислить предел функции

-1

0,6

0,125

-0,75

Критерии оценок:

Количество баллов	Оценка
11	5 «отлично»
8-10	4 «хорошо»
6-7	3 «удовлетворительно»
менее 6	2 «неудовлетворительно»

Задание 2. Вычислить предел функции

-1

1,5

-1

-5

-2

0,4

0,5

-2

-5

-0,5

4,5

3,5

2,5

-8

4,5

-1

-3

-20

-4

-0,5

Задание 3. Вычислить предел функции

ПРИМЕР

Вычислить .

РЕШЕНИЕ:

Пределы числителя и знаменателя при равны нулю, т.е. имеем неопределённость вида . Для вычисления предела этой функции нужно умножить числитель и знаменатель на сопряжённый знаменателю множитель и затем, сократив дробь на х, получим

Задания для самостоятельного решения

0,5

-32

108

-1

4/9

-2

2/3

1/8

1/3

-2

0,5

-1/2

-1

1/2

-1

1/5

1/3

-1/3

1/3

-3

Во время Великой Отечественной войны этот выдающийся математик, используя свои работы по теории вероятностей, разработал теорию наивыгоднейшего рассеивания артиллерийских снарядов.

Полученные им результаты помогли повысить меткость стрельбы и тем самым увеличить эффективность действия артиллерии, которую заслуженно называли богом войны.

По теме: методические разработки, презентации и конспекты

Карточки – задания к практическим занятиям

Наглядный материал по физической культуре…

СБОРНИК ЗАДАНИЙ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ «ИСТОРИЯ»

Рабочая программа учебной дисциплины «История» для изучения истории в ГБОУ СПО «Сочинский колледж поликультурного образования» Краснодарского края при освоении образовательной программы среднего (полн…

Технологическая карта практического занятия по математике на тему: Вычисление пределов функции. Предел функции на . Два замечательных предела. Вычисление числа «е»

В технологической карте содержится описание заняти со всеми необходимыми пояснениями…

Презентация к практическому занятию по математике на тему: Вычисление пределов функции. Предел функции на .

Два замечательных предела. Вычисление числа «е»

В презентации содержится материал к занятию…

Практическое занятие на тему “Расчет лекарственных средств – процентная функция”

Данное практическое занятие предназначено для формирования у обучающихся по специальности 34.02.01 “Сестринское дело” умение применять электронные таблицы для расчета лекарственных сре…

Задание 24 Практическая работа 2 варианта 11 класс ЕГЭ

Задание 24 Практическая работа 2 варианта 11 класс ЕГЭ…

Задание 24 Практическая работа 2 варианта 11 класс ЕГЭ

Задание 24…

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7	8	9	10	11	12	13
Правильный ответ	1	2	3	1	2	4	3	1	2	2, 4	2	3	4

Номер теста	14	15	16	17	18	19	20	21
Правильный ответ	1	2	1	2	4	2	2	3

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств. Под множествами будут пониматься числовые множества, т. е. множества, состоящие из действительных чисел.

Определение. Если каждому элементу х из некоторого множества Х поставлен в соответствие по определенному правилу f некоторый единственный элемент у из множества У (рисунок 23), то говорят, что на множестве Х задана функция у = f(х), х  Х.

Рисунок 23

Элемент х называется независимой переменной, или аргументом, а у – зависимой, или функцией.

Множество Х называется областью определения данной функции и обозначается D(f ), а У – множеством (областью) значений функции и обозначается Е(f).

Задать функцию f – значит указать, как по каждому значению аргумента х находить соответствующее ему значение функции f(х). Существуют три основных способа задания функций: аналитический, графический, табличный.

Аналитический способ заключается в том, что зависимость между переменными величинами определяется с помощью формулы, указывающей, какие действия нужно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

Пример 1. Формула y = х² задает функцию, областью определения которой является числовая прямая (–; +), а множеством значений – полупрямая [0; +) (рисунок 24). Формула у = задает функцию, областью определения которой является отрезок [–1; 1], а множеством значений – отрезок [0; 1] (рисунок 25).

Рисунок 24

Рисунок 25

При графическом способе задается график функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.

Преимуществом графического задания является его наглядность, недостатком – его неточность.

При табличном способе функция задается таблицей ряда значений аргумента и соответствующих значений функции (например, известные таблицы значений тригонометрических функций, логарифмические таблицы).

Определение. Графиком функции

у = f(х) в прямоугольной системе координат Оху называется множество всех точек, плоскости с координатами (х; у), х  D(f).

Например, графиком функции у = является верхняя полуокружность радиуса R = 1 с центром в О(0; 0) (рисунок 25).

Пусть функция у = f(u) определена на множестве D, а функция u = (x) – на множестве D₁, причем длях  D₁ соответствующее значение u = (х)  D.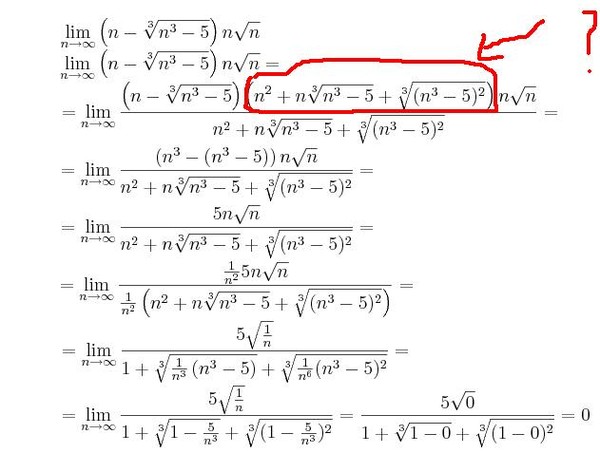

Тогда на множестве D₁ определена функция u = f((х)), которая называется сложной функцией от х (или функцией от аргумента, или суперпозицией заданной функции).

Переменную u = (х) называют промежуточным аргументом сложной функции.

Например, функция у = sin 2x есть суперпозиция двух функций у = sin u и и = 2х.

Основными элементарными функциями называют следующие:

1. Постоянная функция

y = c, c – const.

2. Степенная функция y = x^,  – любое действительное число.

3. Показательная функция y = a^x (0 < a  1).

4. Логарифмическая функция y = log_ax (0 < a  1).

5. Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x.

6. Обратные тригонометрические функции

у = arcsin x, y = arcos x, y = arctg x, y = arcctg x.

Функцию, аналитическое выражение которой можно получить при помощи конечного числа арифметических операций над основными элементарными функциями, а также при помощи операции взятия функции от функции, назовем элементарной функцией.

Определение. Число называется пределом функцииy = f(x) при x, стремящемся к a (или в точке a), если для любого наперед заданного положительного числа ^¹ (хотя бы и сколь угодно малого) можно найти такое положительное число 

² (вообще говоря, зависящее от ;  = ()), что для всех значений x, входящих в область определения функции, отличных от a и удовлетворяющих неравенству

(1)

имеет место неравенство

(2)

Если число a является пределом функции f(x) в точке a, то этот факт символически записывают следующим образом:

или при

С помощью логических символов определение имеет вид

Отметим, что неравенства можно записать в виде

Данное определение называют определением предела функции по Коши^¹, или «на языке–».

Смысл определения предела функции f(x) в точке а состоит в том, что для всех значений х, достаточно близких к а, значения функции f(x) как угодно мало отличаются от числа А (по абсолютной величине).

Пример 2. Пользуясь определением Коши, доказать, что

Доказательство. Пусть  > 0. Найдем число (), такое, что для всех х из промежутка выполняется неравенство

Поскольку для всехх  1, то в качестве () мы можем взять .

Итак, для произвольного числа  > 0 мы нашли число () = , такое, что для всех из промежуткавыполняется неравенство

Это означает, что

Следует заметить, что нахождение пределов функций, пользуясь определением предела по Коши, чаще всего затруднительно. Поэтому позже укажем некоторые приемы нахождения предела функции.

Если при стремлении х к а переменная х принимает лишь значения, меньшие а, или наоборот, лишь значения, большие а, и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах функции f(x) соответственно слева f(x) и справа f(x).

Определение этих пределов будет аналогично рассмотренному выше при х  а.

Здесь вместо значений х, удовлетворяющих условию (1), при которых верно неравенство (2), необходимо рассматривать значения х, такие, что прих  а – 0 (слева), или значения х, такие, что прих  а + 0 (справа).

Замечание. Еслиf(x) =f(x) =А, тоf(x) =А. Если в точке а функция f(x) имеет конечные левый и правый пределы и они равны между собой, то это число является пределом функции в точке а.

Пример 3. Найти односторонние пределы функции

f(x) в точкеа = 3 (рисунок 26).

Решение

Вычислим

f(x) =

Так как односторонние пределы существуют, то

f(x)  f(x) в точке а = 3 функция предела не имеет.

Рисунок 26

Кроме рассмотренных понятий предела функции при и односторонних пределов существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение. Число называетсяпределом функции y = f(x) при x, стремящемся к бесконечности, если для любого (сколь угодно малого) положительного числа  > 0 найдется такое положительное число S > 0 (зависящее от ), что для всех x, таких, что верно неравенство

(3)

Предел функции f(x) в бесконечности обозначается

f(x) = А или f(x)  А при

С помощью логических символов определение имеет вид

Смысл определения состоит в том, что при достаточно больших по модулю значениях xзначения функцииf(x) как угодно мало отличаются от числаA(по абсолютной величине).

Пример 4.Доказать, что

Решение

Пусть  > 0 – произвольное число. Найдем такое число S(), что для всех x, таких, что верно неравенствоПреобразуем последнее неравенство, получимили

Итак, для любого существует числочто для всехх, таких, что будет верно неравенствогдеЭто означает, что

Вычисление пределов значительно упрощается, если использовать ряд утверждений.

Свойства пределов следующие:

1) предел постоянной равен самой постоянной, т. е.

2) еслиисуществуют;

3) еслиисуществуют;

4) еслиисуществуют и

5) постоянный множитель можно выносить за знак предела, т. е.

Теорема. Предел элементарной функции в точке а, принадлежащей ее области определения, равен значению данной функции в рассматриваемой точке, т. е.

Теорема. Если то предел сложной функции

Пример 5. Найти предел

Решение

Воспользовавшись свойствами 1, 2, 5, получим:

Тест 1. Предел равен:

1) 5;

2) 7;

3) 31;

4) 1;

5) 15.

Пример 6. Найти предел

Решение

Так как здесь отыскивается предел частного, то, прежде чем применить соответствующее свойство 4, надо проверить, не обращается ли в нуль знаменатель дроби при х  3.

Применив свойства 1, 2, 5, будем иметь:

Следовательно,

Тест 2. Предел равен:

1) 5;

2) 4;

3) 31;

4) 1;

5) 15.

Бесконечно малые и бесконечно большие функции. Функция f(x) называется бесконечно малой при х  а, если .

Функция f(x) называется бесконечно большой при х  а, если

Аналогично формулируются определения при х  .

Заметим, что если функция (х) является бесконечно малой (бесконечно большой) при х  а (х  ), то – бесконечно большая (бесконечно малая) прих  а (х  ).

Пример 7. Функция прих  0 является бесконечно малой, так как

Пример 8. Функция прих  0 – бесконечно большая, поскольку

Неопределенности. Если вычисление пределов приводит к неопределенным выражениям вида, необходимо провести дополнительные исследования, т. е. раскрывать неопределенности.

Раскрыть неопределенность – значит найти предел соответствующего выражения, если он существует.

Методика раскрытия неопределенностей изложена ниже.

 Первый замечательный предел. Если угол u выражен в радианах, то

Многие задачи нахождения пределов приводят к использованию первого замечательного предела.

Первый замечательный предел можно применять в ряде случаев для раскрытия неопределенностей вида

Пример 9. Найти предел

Решение

Предел знаменателя равен нулю, нулю равен и предел числителя.

Для нахождения данного предела умножим числитель и знаменатель на 5 с целью получения отношения синуса к его аргументу:

Тест 3. Пределравен:

3) 7;

4) 5;

Пример 10. Найти предел

Решение

Имеем неопределенность

Следовательно, предварительно преобразуем данное выражение

Пример 11. Найти предел

Решение

Имеем неопределенность

Следовательно, предварительно преобразуем данное выражение

= 1  1 = 1.

Замечание. Можно доказать, что

Тест 4. Предел равен:

3) 3;

4) 5;

5) 1.

 Второй замечательный предел.

где – иррациональное число, называемое числом Л. Эйлера.

Оно играет большую роль в математике так же, как и число (е = 2,718 281 828 459 045 235 3 ).

Логарифмы с основанием называются натуральными и обозначаются

С помощью второго замечательного предела раскрывают неопределенность вида .

Пример 12. Найти предел

Решение

Выполним некоторые преобразования

Пример 13. Найти предел

Решение

Тест 5. Предел равен:

1) ;

2) е³;

3) е;

4) е²;

5) 1.

Основные приемы раскрытия неопределенностей приведены ниже.

1. Раскрытие неопределенности вида Неопределенное выражение вида получаем при нахождении еслиf(x) является дробью.

Способы раскрытия неопределенности зависят от вида f(x).

· Пусть f(x) – рациональная дробь.

В этом случае числитель и знаменатель дроби разлагают на множители.

Пример 14. Найти предел

Решение

Пример 15. Найти предел

Решение

Имеем неопределенность Разложим числитель и знаменатель на множители, воспользовавшись формулой

где и– корни уравнения

Тогда,

Следовательно,

Тест 6. Предел равен:

4) 15;

5) 2.

· Пусть f(x) – дробь, содержащая иррациональные выражения.

В этом случае умножаем числитель и знаменатель дроби на выражение, сопряженное к числителю или знаменателю, а иногда и к тому и другому (избавляемся от иррациональности), с целью применения формул сокращенного умножения:

(множители слева – сопряженные выражения).

Пример 16. Найти предел

Решение

· Пусть f(x) – дробь, содержащая тригонометрические функции.

Для раскрытия неопределенности в этом случае используют первый замечательный предел.

Пример 17. Найти предел

Решение

2. Раскрытие неопределенности вида Пусть следует найти предел , гдеи– многочленыn–й и m-й степени соответственно.

В этом случае необходимо руководствоваться следующим:

Пусть

где a_i и b_i – некоторые постоянные.

Тогда

Таким образом, для раскрытия неопределенности целесообразно числитель и знаменатель разделить на наивысшую степеньx из числа слагаемых одночленов числителя и знаменателя, а затем перейти к пределу.

Пример 18. Найти предел

Решение

Разделим числитель и знаменатель на х², получим:

Однако, так как степень многочлена числителя равна степени многочлена знаменателя (m = 2), то можно было записать, что

Пример 19. Найти предел

Решение

Степень многочлена числителя (n = 7) больше степени многочлена знаменателя (m = 3), следовательно,

Тест 7. Предел равен:

1) ;

2) –5;

3) 3;

4) –;

5) 2.

Тест 8. Предел равен:

3) 0;

4) 5;

5) –4.

3. Раскрытие неопределенности вида Неопределенное выражение вида сводится к неопределенности вида или

Методику раскрытия этой неопределенности покажем на примере.

Пример 20. Найти предел

Решение

Имеем неопределенность Преобразовав данное выражение, получим неопределенность вида

4. Раскрытие неопределенности вида Неопределенное вы- ражение вида раскрывается путем преобразования соответствующих выражений и сведения их к неопределенности вида или

Пример 21. Найти предел

Решение

Выполним преобразование и получим неопределенность вида

5. Раскрытие неопределенности вида Неопределенное выражение вида получаем при вычислении пределов

если а

В этом случае для раскрытия неопределенности применяют второй замечательный предел.

Пример 22. Найти предел

Решение

AC Ответы на действия

$\require{marginnote}\newcommand{\dollar}{\$} \DeclareMathOperator{\erf}{erf} \DeclareMathOperator{\arctanh}{arctanh} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} $

Это приложение содержит ответы на все действия в тексте. Ответы на предварительные действия не включены.

Раздел 1.1 Как мы измеряем скорость?

Подраздел 1.1.1 Положение и средняя скорость

Мероприятие 1.1.2

Ответить

Подраздел 1.1.2 Мгновенная скорость

Мероприятие 1.1.3

Ответить

Мероприятие 1.1.4

Ответить

Раздел 1.2 Понятие предела

Подраздел 1.2.1 Понятие предела

Мероприятие 1.2.2

Ответить

Подраздел 1.2.2 Мгновенная скорость

Мероприятие 1.2.3

Ответить

Мероприятие 1.2.4

Ответить

Раздел 1.3 Производная функции в точке

Подраздел 1.3.1 Производная функции в точке

Мероприятие 1.3.2

Ответить

Мероприятие 1.3.3

Ответить

Мероприятие 1.3.4

Ответить

Раздел 1.4 Производная функция

Подраздел 1.4.1 Как производная сама по себе является функцией

Мероприятие 1.

4.2

Ответить

Мероприятие 1.4.3

Ответить

Раздел 1.5 Интерпретация, оценка и использование производной

Подраздел 1.5.2 К более точным оценкам производных

Мероприятие 1.5.2

Ответить

Мероприятие 1.5.3

Ответить

Мероприятие 1.5.4

Ответить

Раздел 1.6 Вторая производная

Подраздел 1.6.3 Вогнутость

Мероприятие 1.6.2

Ответить

Мероприятие 1.6.3

Ответить

Мероприятие 1.6.4

Ответить

Раздел 1.7 Пределы, непрерывность и дифференцируемость

Подраздел 1.7.1 Наличие предела в точке

Мероприятие 1.7.2

Ответить

Подраздел 1.7.2 Непрерывность в точке

Мероприятие 1.7.3

Ответить

Подраздел 1.7.3 Дифференцируемость в точке

Мероприятие 1.7.4

Ответить

Раздел 1.8 Аппроксимация касательной линии

Подраздел 1.

8.2 Локальная линеаризация

Мероприятие 1.8.2

Ответ

Мероприятие 1.8.3

Ответить

Раздел 2.1 Элементарные производные правила

Подраздел 2.1.2 Постоянные, степенные и экспоненциальные функции

Мероприятие 2.1.2

Ответить

Подраздел 2.1.3 Постоянные кратные и суммы функций

Мероприятие 2.1.3

Ответить

Мероприятие 2.1.4

Ответить

Раздел 2.2 Функции синуса и косинуса

Подраздел 2.2.1 Функции синуса и косинуса

Мероприятие 2.2.2

Ответить

Мероприятие 2.2.3

Ответить

Мероприятие 2.2.4

Ответить

Раздел 2.3 Правила произведения и частного

Подраздел 2.3.1 Правило продукта

Мероприятие 2.3.2

Ответить

Подраздел 2.3.2 Факторное правило

Мероприятие 2.3.3

Ответить

Подраздел 2.3.3 Объединение правил

Мероприятие 2.

3.4

Ответ

Раздел 2.4 Производные других тригонометрических функций

Подраздел 2.4.1 Производные функций котангенса, секанса и косеканса

Мероприятие 2.4.2

Ответить

Мероприятие 2.4.3

Ответить

Мероприятие 2.4.4

Ответить

Раздел 2.5 Цепное правило

Подраздел 2.5.1 Цепное правило

Мероприятие 2.5.2

Ответить

Подраздел 2.5.2 Использование нескольких правил одновременно

Мероприятие 2.5.3

Ответить

Мероприятие 2.5.4

Ответить

Раздел 2.6 Производные обратных функций

Подраздел 2.6.2 Производная функции натурального логарифма

Мероприятие 2.6.2

Ответить

Подраздел 2.6.3 Обратные тригонометрические функции и их производные

Мероприятие 2.6.3

Ответить

Мероприятие 2.6.4

Ответить

Раздел 2.7 Производные функций, заданных неявно

Подраздел 2.

7.1 Неявное дифференцирование

Мероприятие 2.7.2

Ответить

Мероприятие 2.7.3

Ответить

Мероприятие 2.7.4

Ответить

Раздел 2.8 Использование производных для оценки лимитов

Подраздел 2.8.1 Использование производных для оценки неопределенных пределов формы $\frac{0}{0}\text{.}$

Мероприятие 2.8.2

Ответить

Мероприятие 2.8.3

Ответ

Подраздел 2.8.2 Ограничения, связанные с $\infty$

Мероприятие 2.8.4

Ответить

Раздел 3.1 Использование производных для определения экстремальных значений

Подраздел 3.1.1 Критические числа и проверка первой производной

Мероприятие 3.1.2

Ответить

Подраздел 3.1.2 Тест второй производной

Мероприятие 3.1.3

Ответить

Мероприятие 3.1.4

Ответить

Раздел 3.2 Использование производных для описания семейств функций

Подраздел 3.

2.1 Описание семейств функций в терминах параметров

Мероприятие 3.2.2

Ответить

Мероприятие 3.2.3

Ответить

Мероприятие 3.2.4

Ответить

Раздел 3.3 Глобальная оптимизация

Подраздел 3.3.1 Глобальная оптимизация

Мероприятие 3.3.2

Ответить

Мероприятие 3.3.3

Ответить

Подраздел 3.3.2 Движение к приложениям

Мероприятие 3.3.4

Ответить

Раздел 3.4 Прикладная оптимизация

Подраздел 3.4.1 Более прикладные задачи оптимизации

Мероприятие 3.4.2

Ответить

Мероприятие 3.4.3

Ответить

Мероприятие 3.4.4

Ответить

Мероприятие 3.4.5

Ответить

Раздел 3.5 Связанные ставки

Подраздел 3.5.1 Проблемы со связанными ставками

Мероприятие 3.5.2

Ответить

Мероприятие 3.5.3

Ответить

Мероприятие 3.

5.4

Ответить

Мероприятие 3.5.5

Ответить

Раздел 4.1 Определение пройденного пути по скорости

Подраздел 4.1.1 Площадь под графиком функции скорости

Мероприятие 4.1.2

Ответить

Подраздел 4.1.2 Два подхода: площадной и антидифференцировочный

Мероприятие 4.1.3

Ответ

Подраздел 4.1.3 Когда скорость отрицательна

Мероприятие 4.1.4

Ответить

Раздел 4.2 Суммы Римана

Подраздел 4.2.1 Сигма-нотация

Мероприятие 4.2.2

Ответить

Подраздел 4.2.2 Суммы Римана

Мероприятие 4.2.3

Ответить

Подраздел 4.2.3 Когда функция иногда отрицательна

Мероприятие 4.2.4

Ответить

Раздел 4.3 Определенный интеграл

Подраздел 4.3.1 Определение определенного интеграла

Мероприятие 4.3.2

Ответить

Подраздел 4.

3.2 Некоторые свойства определенного интеграла

Мероприятие 4.3.3

Ответить

Подраздел 4.3.3. Как определенный интеграл связан со средним значением функции.

Мероприятие 4.3.4

Ответить

Раздел 4.4. Основная теорема исчисления.

Подраздел 4.4.1. Основная теорема исчисления.

Мероприятие 4.4.2

Ответить

Подраздел 4.4.2 Основные первообразные

Мероприятие 4.4.3

Ответить

Подраздел 4.4.3 Теорема о полной замене

Мероприятие 4.4.4

Ответить

Раздел 5.1 Построение точных графиков первообразных

Подраздел 5.1.1 Построение графика первообразной

Мероприятие 5.1.2

Ответить

Подраздел 5.1.3 Функции, определяемые интегралами

Мероприятие 5.1.4

Ответить

§ 5.2. Вторая фундаментальная теорема исчисления.

Подраздел 5.2.1. Вторая основная теорема исчисления.

Мероприятие 5.2.2

Ответить

Подраздел 5.2.2 Понимание интегральных функций

Мероприятие 5.2.3

Ответить

Подраздел 5.2.3. Дифференцирование интегральной функции.

Мероприятие 5.2.4

Ответить

Раздел 5.3 Интеграция путем замены

Подраздел 5.3.1 Отмена цепного правила: первые шаги

Мероприятие 5.3.2

Ответить

Подраздел 5.3.2 Обратное цепное правило: $u$-подстановка

Мероприятие 5.3.3

Ответить

Подраздел 5.3.3. Вычисление определенных интегралов с помощью $u$-подстановки

Мероприятие 5.3.4

Ответить

Раздел 5.4 Интеграция по частям

Подраздел 5.4.1 Отмена правила продукта: интеграция по частям

Мероприятие 5.4.2

Ответить

Подраздел 5.4.2 Некоторые тонкости интегрирования по частям

Мероприятие 5.4.3

Ответить

Подраздел 5.

4.3 Многократное использование интегрирования по частям

Мероприятие 5.4.4

Ответить

Раздел 5.5 Другие варианты поиска алгебраических первообразных

Подраздел 5.5.1 Метод частных дробей

Мероприятие 5.5.2

Ответ

Подраздел 5.5.2 Использование интегральной таблицы

Мероприятие 5.5.3

Ответить

Раздел 5.6 Численное интегрирование

Подраздел 5.6.1 Правило трапеций

Мероприятие 5.6.2

Ответить

Подраздел 5.6.3 Правило Симпсона

Мероприятие 5.6.3

Ответить

Подраздел 5.6.4 Общие наблюдения относительно $L_n\text{,}$ $R_n\text{,}$ $T_n\text{,}$ $M_n\text{,}$ и $ S_{2n}\text{.}$

Мероприятие 5.6.4

Ответить

Раздел 6.1 Использование определенных интегралов для нахождения площади и длины

Подраздел 6.1.1 Площадь между двумя кривыми

Мероприятие 6.

1.2

Ответить

Подраздел 6.1.2 Поиск площади с помощью горизонтальных срезов

Мероприятие 6.1.3

Ответить

Подраздел 6.1.3 Нахождение длины кривой

Мероприятие 6.1.4

Ответить

Раздел 6.2 Использование определенных интегралов для нахождения объема

Подраздел 6.2.1 Объем тела вращения

Мероприятие 6.2.2

Ответить

Подраздел 6.2.2 Вращение вокруг оси $y$

Мероприятие 6.2.3

Ответить

Подраздел 6.2.3 Вращение вокруг горизонтальных и вертикальных линий, отличных от осей координат

Мероприятие 6.2.4

Ответить

Раздел 6.3 Плотность, масса и центр масс

Подраздел 6.3.1 Плотность

Мероприятие 6.3.2

Ответить

Подраздел 6.3.2 Средневзвешенные значения

Мероприятие 6.3.3

Ответить

Подраздел 6.3.3 Центр масс

Мероприятие 6.

3.4

Ответить

Раздел 6.4 Физические приложения: работа, сила и давление

Подраздел 6.4.1 Работа

Мероприятие 6.4.2

Ответить

Подраздел 6.4.2 Работа: откачка жидкости из бака

Мероприятие 6.4.3

Ответить

Подраздел 6.4.3 Сила гидростатического давления

Мероприятие 6.4.4

Ответить

Раздел 6.5 Несобственные интегралы

Подраздел 6.5.1 Несобственные интегралы, включающие неограниченные интервалы

Мероприятие 6.5.2

Ответить

Подраздел 6.5.2 Конвергенция и дивергенция

Мероприятие 6.5.3

Ответить

Подраздел 6.5.3 Несобственные интегралы, включающие неограниченные интегранты

Мероприятие 6.5.4

Ответить

Раздел 7.1. Введение в дифференциальные уравнения

Подраздел 7.1.1 Что такое дифференциальное уравнение?

Мероприятие 7.1.2

Ответить

Подраздел 7.

1.2 Дифференциальные уравнения в окружающем нас мире

Мероприятие 7.1.3

Ответить

Подраздел 7.1.3 Решение дифференциального уравнения

Мероприятие 7.1.4

Ответить

Раздел 7.2 Качественное поведение решений ДУ

Подраздел 7.2.1 Уклонные поля

Мероприятие 7.2.2

Ответить

Подраздел 7.2.2 Равновесные решения и устойчивость

Мероприятие 7.2.3

Ответить

Раздел 7.3 Метод Эйлера

Подраздел 7.3.1 Метод Эйлера

Мероприятие 7.3.2

Ответить

Мероприятие 7.3.3

Ответить

Раздел 7.4 Разделимые дифференциальные уравнения

Подраздел 7.4.1 Решение разделимых дифференциальных уравнений

Мероприятие 7.4.2

Ответить

Мероприятие 7.4.3

Ответить

Мероприятие 7.4.4

Ответить

Раздел 7.5 Моделирование с помощью дифференциальных уравнений

Подраздел 7.

5.1 Составление дифференциального уравнения

Мероприятие 7.5.2

Ответить

Мероприятие 7.5.3

Ответить

Раздел 7.6 Рост населения и логистическое уравнение

Подраздел 7.6.1 Население Земли

Мероприятие 7.6.2

Ответить

Подраздел 7.6.2 Решение логистического дифференциального уравнения

Мероприятие 7.6.3

Ответить

Раздел 8.1 Последовательности

Подраздел 8.1.1 Последовательности

Мероприятие 8.1.2

Ответить

Мероприятие 8.1.4

Ответить

Раздел 8.2 Геометрические ряды

Подраздел 8.2.1 Геометрические суммы

Мероприятие 8.2.2

Ответ

Мероприятие 8.2.3

Ответить

Мероприятие 8.2.4

Ответить

Раздел 8.3 Серии действительных чисел

Подраздел 8.3.1 Бесконечная серия

Мероприятие 8.3.2

Ответить

Подраздел 8.

3.2 Тест на дивергенцию

Мероприятие 8.3.3

Ответить

Мероприятие 8.3.4

Ответить

Подраздел 8.3.3 Интегральный тест

Мероприятие 8.3.5

Ответ

django – Celery Ограничение количества задач, выполняемых на пользователя

У меня есть задача в Celery, которая выглядит так:

 @app.task(name='task_one')
def task_one(user_id, *args, **kwargs):
    # Длительная задача

Эта задача создается в представлениях каждый раз, когда пользователь отправляет форму, задача требует много ресурсов и занимает в среднем около 10 минут.

 (просмотры.py)
...
если request.method == 'POST':
    task_one.delay(user.id)
...

Я хочу ограничить количество task_one задач, созданных для каждого пользователя, до одной (активной или зарезервированной)

Пока что я проверяю, есть ли задача активная или зарезервированная для этого пользователя перед созданием задача:

 def user_created_task (active_tasks, зарезервированные_задачи, user_id):
  для задачи в списке(active_tasks. values())[0] + list(reserved_tasks.values())[0]:
    если task['name'] == 'task_one' и task['args'][0] == user_id:
      # Проверяем, создана ли для пользователя задача `task_one`
      вернуть Истина
  
  вернуть ложь
def user_tasks_already_running_or_reserved (user_id):
  проверить = приложение.control.inspect()
  active_tasks = проверить.активный()
  зарезервированные_задачи = проверить.зарезервировано()
  если для active_tasks установлено значение None, а для Reserved_tasks установлено значение None:
    # Работники Celery отключены
    вернуть ложь
  вернуть user_created_task (active_tasks, зарезервированные_задачи, user_id)
(просмотры.py)
...
если request.method == 'POST':
    если не user_tasks_already_running_or_reserved(user.id):
        task_one.delay(user.id)
...

Мне было интересно, есть ли более эффективный способ сделать это, вместо того, чтобы проверять всех рабочих по каждому запросу пользователя, может быть, есть способ добавить это условие в Celery перед запуском задачи, пока я ничего не нашел в документации.

джанго
сельдерей
джанго-сельдерей
сельдерей-задача

Ситуация, которую вы описываете, требует использования распределенной блокировки (поскольку n = 1), но в более общем смысле ее можно описать как распределенный семафор. Грубо говоря, эти замки и механизмы выходят за рамки того, что встроено в сельдерей.

Как упоминалось комментаторами (подсказка: @bernhard vallan), простая реализация распределенной блокировки обычно использует что-то вроде таблицы в базе данных или redis rlock/redlocks.

Чтобы использовать одну общую реализацию, вы можете сделать следующее:

 from redlock import MultipleRedlockException, Redlock
из настроек импорта django.conf
@app.task(name='task_one', autoretry_for=(MultipleRedlockException, ), retry_kwargs={'max_retries': 5})
def task_one(user_id, *args, **kwargs):
 # предполагается, что вы используете Redis для кеша django с указанием местоположения
 # установить URL-адрес Redis
 lock_manager = Redlock([ settings.