Тело погруженное в жидкость вытесняет чей закон. Как проявляется сила Архимеда. Как Архимед открыл свой закон
Почему мы можем лежать на поверхности моря, не опускаясь на дно? Почему плавают на поверхности воды тяжелые корабли?
Наверное, существует какая-то сила, которая выталкивает людей и кораблики, то есть, все тела из воды и позволяет плавать на поверхности.
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы,или иначе силы Архимеда, действующей на любое тело, погруженное в жидкость или газ. Рассмотрим силу Архимеда подробнее на примере.
Все мы пускали кораблики по лужам. А какой кораблик без капитана? Что мы наблюдали? Кораблик под весом капитана погружается глубже. А если мы мы размещали на нашем кораблике пять или восемь капитанов? Наш кораблик опускался на дно.
Что же мы можем извлечь полезного из данного опыта? Когда увеличивался вес кораблика, то мы видели, что кораблик ниже опускался в воду.
Когда же вес тела превысил величину выталкивающей силы, то кораблик под действием этой силы опустился на дно. То есть, существует выталкивающая сила, одинаковая для конкретного тела, но разная для различных тел.
Выталкивающая сила, она же сила Архимеда, действующая на тело, погружённое в жидкость, равна весу жидкости, вытесненной этим телом.
Кирпич, как всем известно, пойдет на дно в любом случае, а вот деревянная дверь не только будет плавать на поверхности, но и может еще удержать пару пассажиров. Сила эта и называется архимедовой силой и выражается формулой:
Fвыт = g*m ж = g* ρ ж * V ж = P ж,
где m ж – это масса жидкости,
а P ж – вес вытесненной телом жидкости.
А так как масса у нас равна: m ж = ρ ж * V ж, то из формулы архимедовой силы мы видим, что она не зависит от плотности погруженного тела, а только от объема и плотности вытесненной телом жидкости.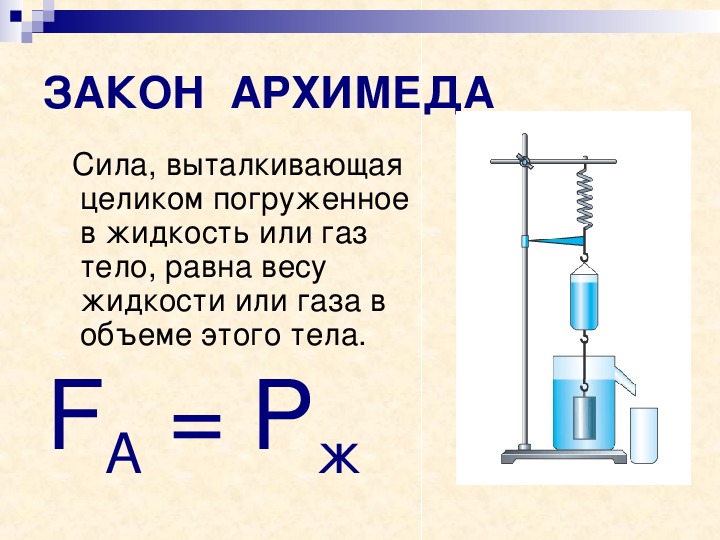
Архимедова сила – это векторная величина. Причина существования выталкивающей силы – разница в давлении на верхнюю и нижнюю часть тела.Указанное на рисунке давление P 2 > P 1 из-за большей глубины. Для возникновения силы Архимеда достаточно того, чтобы тело было погружено в жидкость хотя бы частично.
Так, если тело плывёт по поверхности жидкости, значит выталкивающая сила, действующая на погружённую в жидкость часть этого тела равна силе тяжести всего тела. Если плотность тела больше плотности жидкости, то тело тонет, если меньше – то всплывает.
Тело же, погруженное в жидкость, теряет в своем весе ровно столько, сколько весит вытесненная им вода. Поэтому, естественно предположить, что если вес тела меньше веса воды такого же объема, то оно будет плавать на поверхности, а если больше – то утонет.
Если же вес тела и воды будет равен, то тело может замечательно плавать в толще воды, как и поступают все водные обитатели. Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела.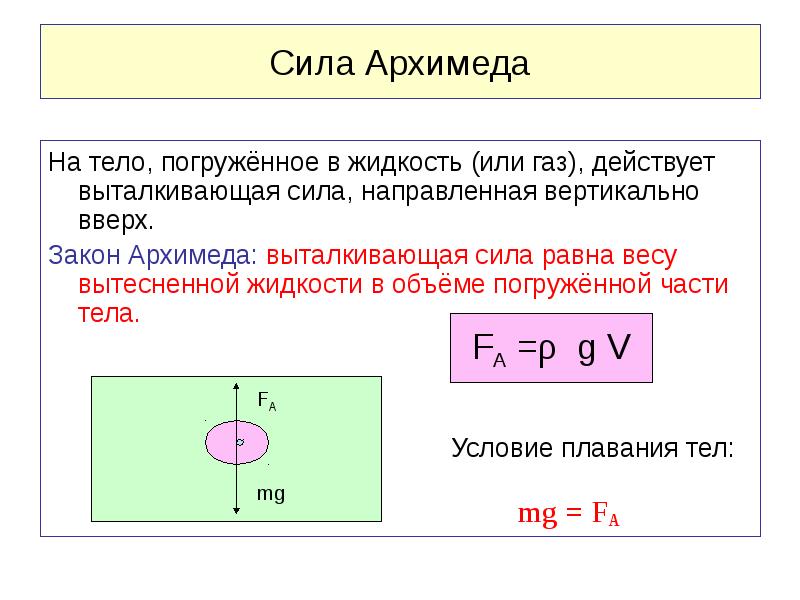 Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемоезаконом Архимеда , справедливо для тел любой формы.
При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg , а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела
 Если же ρ т ρ
(или по–другому mg F
A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Если же ρ т ρ
(или по–другому mg F
A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.Плавание тел
Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: V погр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.
Основные теоретические сведения
Импульс тела
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р . Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Импульс обозначается р . Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела
где: p н – импульс тела в начальный момент времени, p к – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой .
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось.
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Эмпирически еще в древней Греции было получено, что тело, погруженное в жидкость, весит меньше, чем находящееся в воздухе. На тело в жидкости со всех сторон она оказывает давление. Силы давления направлены перпендикулярно поверхности тела в каждой его точке. В том случае, если все силы, действующие на тело, были бы равны по модулю, то это тело испытывало только всестороннее сжатие. Мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.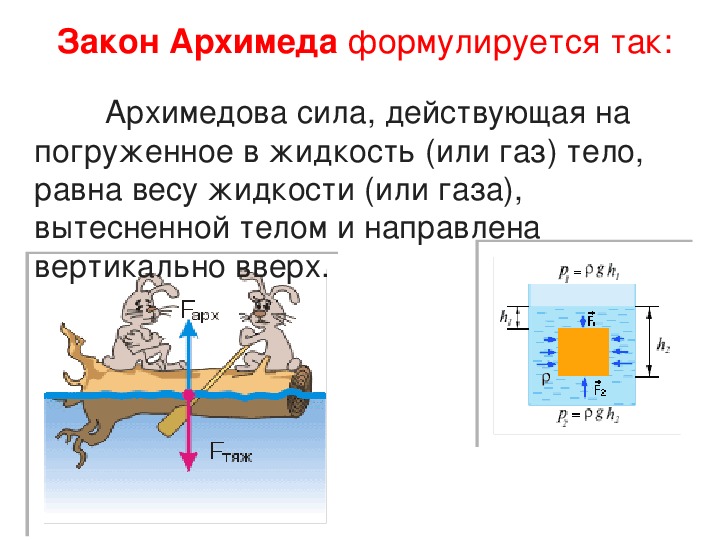
Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.
Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Величина силы Архимеда
Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.
Рассмотрим тело в виде прямоугольного параллелепипеда полностью находящееся в жидкости рис.1. Предположим, что верхнее и нижнее основания располагаются параллельно горизонту.
Силы давления, действующие на боковые грани параллелепипеда, попарно уравновешены (например, ${\overline{F}}_{12}$=$-{\overline{F}}_{21}$). Они только сжимают параллелепипед. Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:
Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:
где $\rho $ – плотность жидкости; $S$ – площадь основания; $h_1$ – высота столба жидкости над верхним основанием параллелепипеда.$\ p_0-$ давление атмосферы на поверхность жидкости.
Сила давления жидкости на нижнее основание параллелепипеда:
где $h_2$ – высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль результирующей силы, действующей на тело со стороны жидкости:
Если обозначить высоту параллелепипеда как $h=h_2-h_1$, получим:
где $V$ – объем параллелепипеда. При нахождении тела в жидкости (газе) частично, то под V понимают объем погруженный в вещество (жидкость, газ). Правую часть выражения (4) еще называют весом жидкости, которую вытесняет тело, погруженное в нее.
На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.
Сила Архимеда направлена вертикально вверх.
Закон Архимеда (4) выполняется для тел любой формы.
Сила Архимеда дает возможность плавать разного рода кораблям, несмотря на то, что плотность материала, из которого изготовлен корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.
Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.
Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. Если тело примыкаем ко дну сосуда или его стенке, то равнодействующая сил гидростатического давления станет прижимать тело ко дну или стенке. {-2}$Н
{-2}$Н
Пример 2
Задание. Чему равна сила натяжения каната (N), при помощи которого из пресного водоема равномерно двигая, поднимают тело плотностью $\rho $ и объемом V? Плотность воды считайте известной (${\rho }_g$). Движение рассмотрите в жидкости.
Решение. Рассмотрим силы, действующие на тело, поднимаемое из воды (рис.2).
В соответствии со вторым законом Ньютона равнодействующая всех сил, приложенных к телу равна нулю, так как тело поднимают равномерно:
\[\overline{N}+m\overline{g}+{\overline{F}}_A=0\ \left(2.1\right).\]
В проекции на ось Y инерциальной системы отсчета, которую мы связали с Землей, уравнение (2.1) даст нам следующее скалярное выражение:
Масса поднимаемого тела может быть найдена как:
Силу Архимеда определим как:
Подставим правые части выражений (2.3) и (2.4) в формулу (2.2) вместо соответствующих величин, выразим силу натяжения каната:
Ответ. $N=\left(\rho -{\rho }_g\right)Vg$
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра.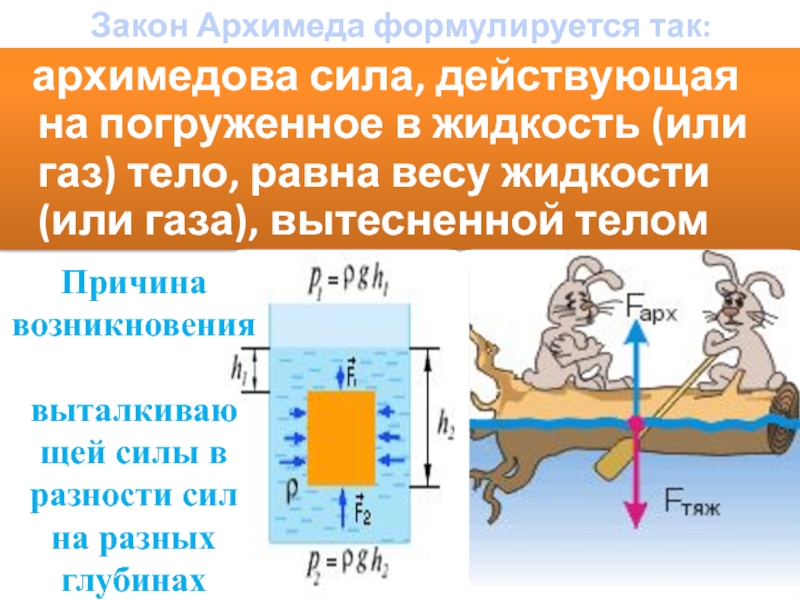 Это и есть история открытия закона Архимеда.
Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н.э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном.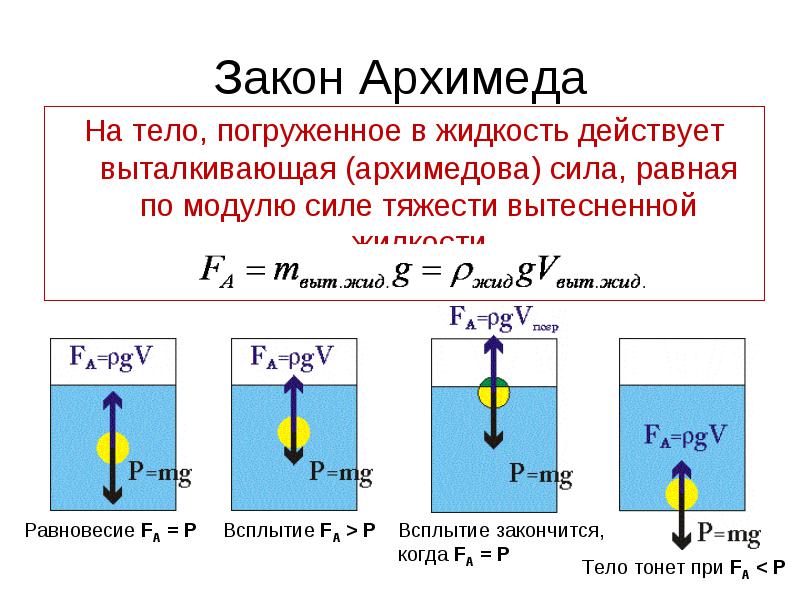 Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал
закон, впоследствии названный законом Архимеда.
Существует предание, что идея этого закона
посетила Архимеда, когда он принимал ванну, с
возгласом “Эврика!” он выскочил из ванны и нагим
побежал записывать пришедшую к нему научную
истину. Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом
в трактате “О плавающих телах”. Архимед
писал: “тела более тяжелые, чем жидкость,
опущенные в эту жидкость, будут опускаться пока
не дойдут до самого низа, и в жидкости станут
легче на величину веса жидкости в объеме, равном
объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и
объема тела или его погруженной части и не
зависит от плотности тела, его веса и объема
жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости. Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
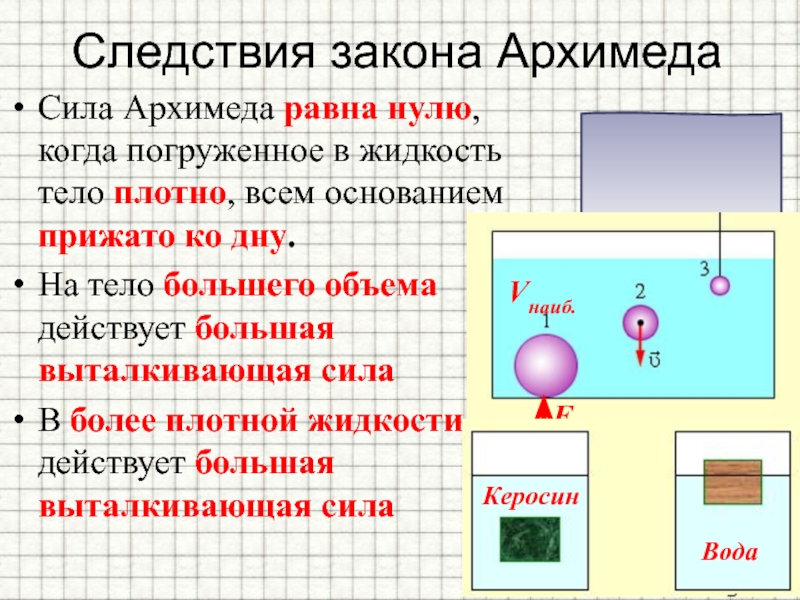
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и
воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.
Закон архимеда сообщение.
 Старт в науке
Старт в наукеКазалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.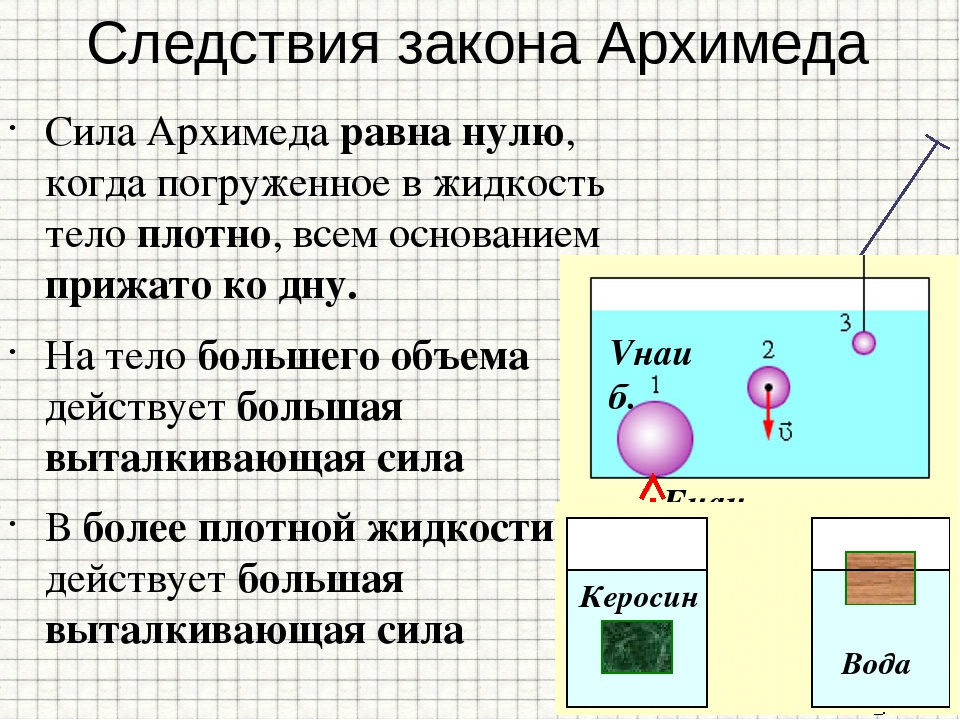
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали:
Сила Архимеда
Плотность жидкости
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Жидкостей и газов, согласно которому на всякое тело, пог-руженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.
Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.
Ниже приведены выводы, следующие из закона Архимеда .
Действие жидкости и газа на погруженное в них тело.
Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а ). В каж-дой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростати-ческое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.
Если заменить все силы давления , приложенные к погруженному в воду телу, одной (резуль-тирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как F A .
На рисунке б она обозначена как F A .
Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глу-бинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.
Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном про-странстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.
Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).
Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P 0 , то его вес в воздухе равен:
,
где F´ A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что P возд. =P 0 =mg .
е. можно считать, что P возд. =P 0 =mg .
Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе P возд. =P 0 , то вес тела в жидкости равен P жидк = Р 0 — F A . Здесь F A — архимедова сила, действующая в жидкости. Отсюда следует, что
Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.
Другими словами, учитывая формулу (1.32), можно сказать:
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.
Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем пра-во это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):
Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):
Но сила тяжести равна весу вытесненной жидкости Р ж . Таким образом.
Учитывая, что масса жидкости равна произведению ее плотности ρ ж на объем, формулу (1.33) можно записать в виде:
где V ж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погру-жена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем V ж вытесненной жидкости меньше объема V тела (рис. 1.39).
Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом слу-чае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.
С учетом вышеизложенного закон Архимеда можно сформулировать так:
На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или га-за), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).
Выталкивающая сила. Закон Архимеда – Класс!ная физика
Выталкивающая сила. Закон Архимеда
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит …. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg.
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
Найден трактат Архимеда – смотреть
Архимедова сила и киты – смотреть
Архимед (из книги Я. Голованова “Этюды об ученых”) – смотреть
Голованова “Этюды об ученых”) – смотреть
Тонна дерева и тонна железа – смотреть
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря , сокращая или расслабляя мышцы.
___
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся.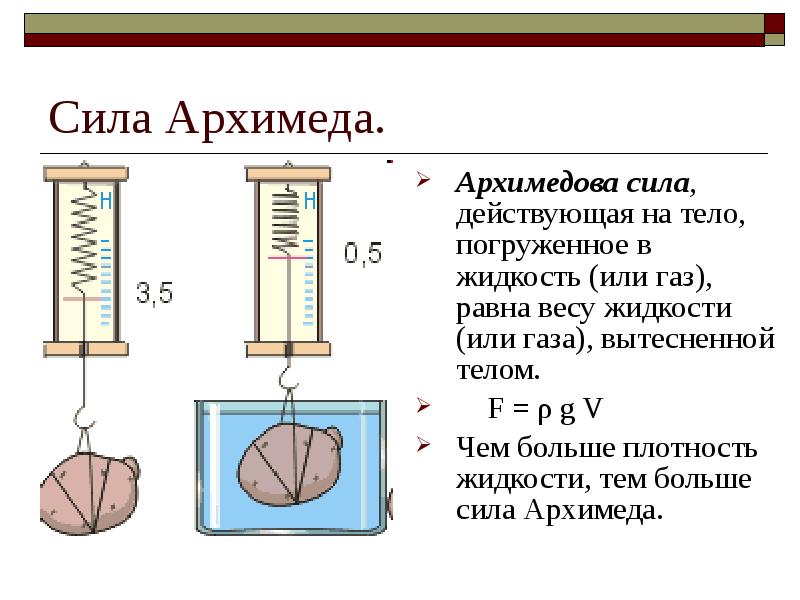 После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.
Включаем соображалку
1. Плотность тела определяется взвешиванием его в воздухе и в воде. При погружении небольшого тела в воду на его поверхности удерживаются пузырьки воздуха, из-за которых получается ошибка в определении плотности. Больше или меньше получается при этом значение плотности?
2. Какое заключение можно сделать о величине архимедовой силы, проводя соответствующие опыты на Луне, где сила тяжести в шесть раз меньше, чем на Земле?
3. Действуют ли на искусственном спутнике Земли архимедова сила и закон Паскаля?
Вывод полного закона Архимеда – Завершение формирования комплекса законов физики
Вывод полного закона Архимеда
Мы живём в мире, где век географических открытий в мире может смениться веком открытий в самом себе. Для новых открытий в окружающем нас мире не нужно готовить экспедиции в неизведанные страны. Самая неизведанная страна это сам человек. Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Любознательность позволит познавать окружающий мир без фундаментальных затрат в самых неожиданных местах.
Для новых открытий в окружающем нас мире не нужно готовить экспедиции в неизведанные страны. Самая неизведанная страна это сам человек. Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Любознательность позволит познавать окружающий мир без фундаментальных затрат в самых неожиданных местах.
Физика это одна из основных наук, изучающих природу. Но даже первый закон физики – закон Архимеда, за 23 века своего существования до сих пор окончательно не сформулирован. Под этим названием в учебниках физики изучается правило Архимеда для выталкивающей силы. В этом законе отсутствует как формулировка, так и основное уравнение, без чего физических законов не бывает.
Всем известная формулировка: “на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной жидкости” является формулировкой правила Архимеда для определения выталкивающей силы. Но нигде не определено, что потом с этой силой делать.
Но нигде не определено, что потом с этой силой делать.
Если мы попытаемся узнать конечный результат – что произойдёт с телом, погруженным в жидкость (решить физическую задачу), то увидим, что нам это определение мало что даёт. Для того чтобы узнать, что произойдёт с телом, нужно ещё знать объём тела, вес этого тела, удельный вес выталкивающей среды. Причём проблема закона Архимеда состоит не в том, что он не правильно описывает архимедову силу, а в том что он не имеет алгоритма, что потом с ней делать. В дополнение к этим проблемам, закон Архимеда для жидкостей и газов в учебниках по физике рассматривается раздельно, что усложняет его понимание. Полный закон Архимеда был опубликован в http://drjukow.narod.ru/.
Решение задач в школе по закону Архимеда происходит без единой методики. Показывается буквально на пальцах, что делать с архимедовой силой в одном случае, что в другом. Этот подход значительно усложняет как преподавание этого предмета, так и его усвоение. Не проще ли один раз вывести общее уравнение (формулу) закона Архимеда, включающую архимедову силу и решать все примеры по закону Архимеда одним способом, по одной формуле?
Для вывода основного уравнения (формулы) закона Архимеда рассмотрим общий случай тела, погруженного в выталкивающую среду.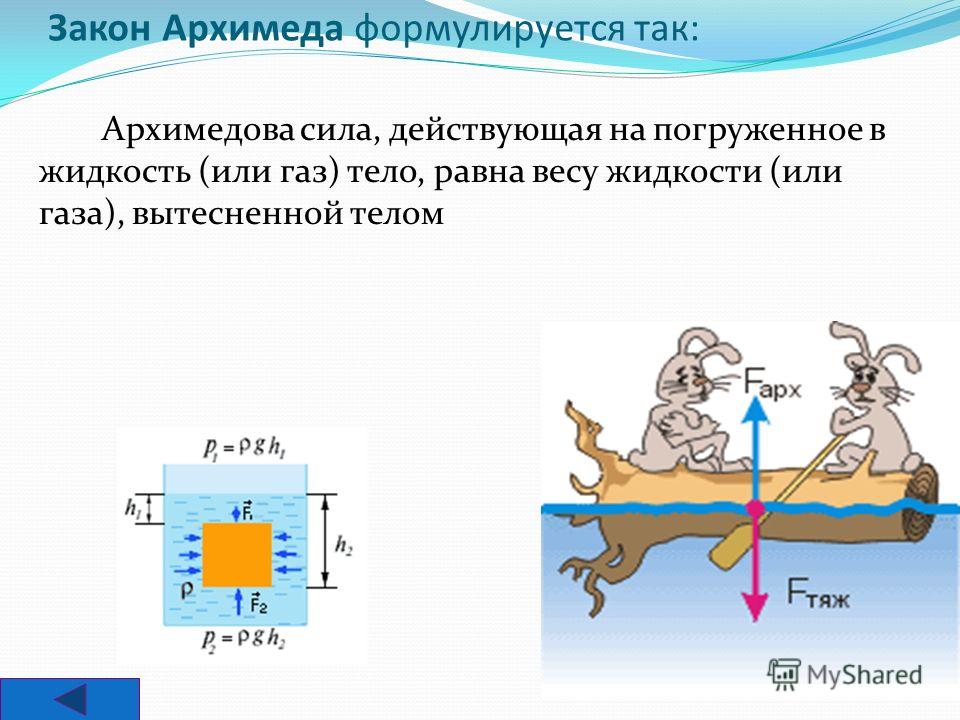
На это тело действуют три силы:
Первая сила – архимедова сила , равная весу вытесненной среды.
Вторая сила – вес тела .
Но есть ещё третья сила, не очень известная в теории. Это архимедова сила, не задействованная для плавания – запас плавучести . В судостроении эта величина называется грузоподъёмностью.
Если к телу, не полностью погруженному в выталкивающую среду, добавить вес, по величине равный , тело полностью погрузится.
В этом случае тело будет уравновешенно в выталкивающей среде, и мы можем написать основное уравнение (формулу) закона Архимеда. Закон Архимеда определяет условие плавания тел (рис.1).
,
Где – максимально возможная архимедова сила (в судостроении называется
водоизмещением),
– архимедова сила, используемая для плавания (равна весу судна Р).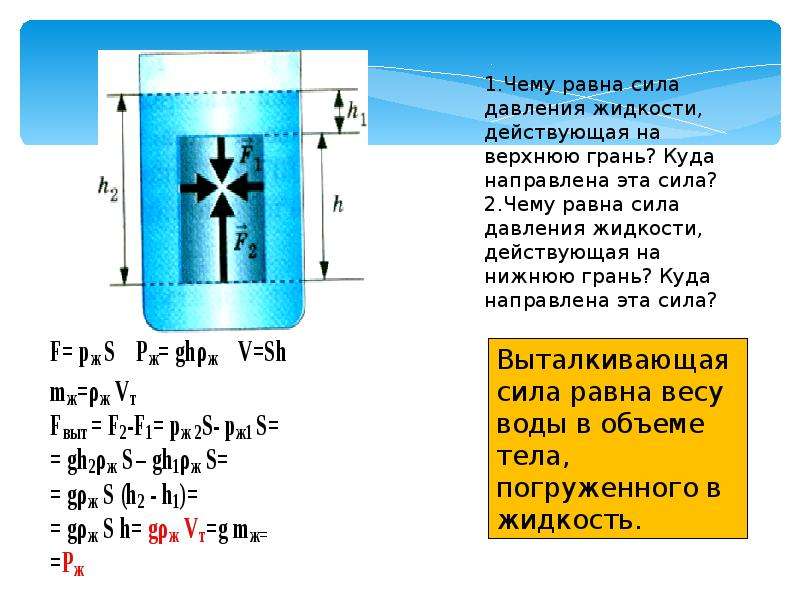
– запас плавучести (в судостроении называется грузоподъёмностью).
Рис.1. У не полностью погруженного тела запас плавучести .
Основное уравнение закона Архимеда можно также составить относительно веса погруженного тела , равного и противоположного архимедовой силе , но смысла это не меняет.
Физическое определение полного закона Архимеда можно вывести из его основного уравнения: максимально возможная архимедова сила погруженного тела равна сумме архимедовой силы и запаса плавучести, и равна весу жидкости в объёме тела.
Без учёта запаса плавучести невозможно узнать конечный результат погружения тела в выталкивающую среду. Именно её величина определяет поведение погруженного тела в выталкивающей среде:
1) При погруженное тело висит неподвижно, или сохраняет направление своего движения (при отсутствии других сил).
2) При , погруженное тело всплывает (при отсутствии других сил).
3) При , погруженное тело тонет (при отсутствии других сил).
Строители кораблей на практике давно поняли, что закон Архимеда не полный. Они ввели понятие водоизмещения, имеющего смысл максимально возможной выталкивающей силы , грузоподъёмности , и собственного веса корабля , равного архимедовой силе и противоположно ей направленного.
Это показывает, что в судостроении давно пользуются основным уравнением Архимеда. Однако это уравнение выводят каждый раз, исходя из здравого смысла. Это же самое делают и в школе. Не проще ли один раз вывести уравнение и потом им пользоваться?
1. Дрюков В.М. О чём молчат физики. Тула. 2004.
2. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021
3. http://sciteclibrary.ru/rus/catalog/pages/9433. html
html
Сила Архимеда – это… Что такое Сила Архимеда?
- Сила Архимеда
Wikimedia Foundation. 2010.
- Сила (физика)
- Сила Уорд
Архимеда закон — Архимеда закон: F выталкивающая сила; P сила тяжести, действующая на тело. АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх, равная весу вытесненной им жидкости и приложенная к центру… … Иллюстрированный энциклопедический словарь
АРХИМЕДА ЧИСЛО — подобия критерий двух гидродинамич. или тепловых явлений, при к рых определяющими явл. выталкивающая (архимедова) сила (см. АРХИМЕДА ЗАКОН) и сила вязкости. где l характерный линейный размер, v коэфф.
 кинематич. вязкости, r и r1 плотность среды в … Физическая энциклопедия
кинематич. вязкости, r и r1 плотность среды в … Физическая энциклопедияАРХИМЕДА ЗАКОН — закон статики жидкостей и газов, согласно к рому на всякое тело, погружённое в жидкость (или газ), действует со стороны этой жидкости (газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и… … Физическая энциклопедия
СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… … Большая политехническая энциклопедия
СИЛА — в физическом смысле способность изменять форму материальных масс, вызывать их движение, менять направление и скорость движения или приводить тело в состояние покоя. «Живая» сила (редко употребляемое теперь выражение), или действующая сила, – сила … Философская энциклопедия
АРХИМЕДА ЗАКОН — АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости.
 Закон Архимеда справедлив и для газов … Энциклопедический словарь
Закон Архимеда справедлив и для газов … Энциклопедический словарьАрхимеда закон — на всякое тело, погружённое в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости. В несколько иной формулировке впервые был установлен древнегреческим учёным Архимедом в III в. до н. э. Доказывается на основе уравнений… … Энциклопедия техники
Архимеда закон — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) поддерживающая сила, равная весу вытесненной телом жидкости (газа), направленная вверх и… … Большая советская энциклопедия
Архимеда закон{:} — на всякое тело, погружённое в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Архимеда закон справедлив и для газов … Энциклопедический словарь
АРХИМЕДА ЗАКОН — [по имени древнегреч.
 учёного Архимеда (ок. 287 212 до н. э.)] закон гидро и аэростатики. Согласно А. з., на тело, погруж. в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости (или… … Большой энциклопедический политехнический словарь
учёного Архимеда (ок. 287 212 до н. э.)] закон гидро и аэростатики. Согласно А. з., на тело, погруж. в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости (или… … Большой энциклопедический политехнический словарь
Смотреть что такое “Сила Архимеда” в других словарях:
%d0%b0%d1%80%d1%85%d0%b8%d0%bc%d0%b5%d0%b4%d0%b0 — со всех языков на все языки
Все языкиАнглийскийРусскийКитайскийНемецкийФранцузскийИспанскийИтальянскийЛатинскийФинскийГреческийИвритАрабскийСуахилиНорвежскийПортугальскийВенгерскийТурецкийИндонезийскийШведскийПольскийЭстонскийЛатышскийДатскийНидерландскийАрмянскийУкраинскийЯпонскийСанскритТайскийИрландскийТатарскийСловацкийСловенскийТувинскийУрдуИдишМакедонскийКаталанскийБашкирскийЧешскийГрузинскийКорейскийХорватскийРумынский, МолдавскийЯкутскийКиргизскийТибетскийБелорусскийБолгарскийИсландскийАлбанскийНауатльКомиВаллийскийКазахскийУзбекскийСербскийВьетнамскийАзербайджанскийБаскскийХиндиМаориКечуаАканАймараГаитянскийМонгольскийПалиМайяЛитовскийШорскийКрымскотатарскийЭсперантоИнгушскийСеверносаамскийВерхнелужицкийЧеченскийГэльскийШумерскийОсетинскийЧеркесскийАдыгейскийПерсидскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)МикенскийКвеньяЮпийскийАфрикаансПапьяментоПенджабскийТагальскийМокшанскийКриВарайскийКурдскийЭльзасскийФарерскийАбхазскийАрагонскийАрумынскийАстурийскийЭрзянскийКомиМарийскийЧувашскийСефардскийУдмурдскийВепсскийАлтайскийДолганскийКарачаевскийКумыкскийНогайскийОсманскийТофаларскийТуркменскийУйгурскийУрумскийБурятскийОрокскийЭвенкийскийМаньчжурскийГуараниТаджикскийИнупиакМалайскийТвиЛингалаБагобоЙорубаСилезскийЛюксембургскийЧерокиШайенскогоКлингонский
Все языкиРусскийАнглийскийНемецкийЛатинскийИвритИспанскийНорвежскийКитайскийФранцузскийУкраинскийИтальянскийПортугальскийВенгерскийТурецкийПольскийДатскийТатарскийКурдскийСловенскийГреческийИндонезийскийВьетнамскийМаориТагальскийУрдуИсландскийХиндиИрландскийФарерскийБолгарскийЛатышскийАлбанскийАрабскийФинскийПерсидскийМонгольскийНидерландскийШведскийПалиЯпонскийКорейскийЭстонскийГрузинскийТаджикскийЛитовскийРумынский, МолдавскийХорватскийСуахилиКазахскийМакедонскийТайскийБелорусскийГалисийскийКаталанскийЧеченскийКарачаевскийСловацкийЧешскийСербскийАрмянскийАзербайджанскийУзбекскийКечуаГаитянскийМайяАймараШорскийЭсперантоКрымскотатарскийОсетинскийАдыгейскийЯкутскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)ТамильскийКвеньяАварскийАфрикаансПапьяментоМокшанскийЙорубаЭльзасскийИдишАбхазскийЭрзянскийИнгушскийИжорскийМарийскийЧувашскийУдмурдскийВодскийВепсскийАлтайскийКумыкскийТуркменскийУйгурскийУрумскийЛожбанЭвенкийскийБашкирскийМалайскийМальтийскийЛингалаПенджабскийЧерокиЧаморроКлингонскийБаскскийПушту
На тело погруженное.
 Архимедова сила
Архимедова сила Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Если принять вес тела в вакууме за Р о, то его вес в воздушной среде может быть описан такой формулой: Р в =Р о – F а;
здесь Р о – вес в вакууме;
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
Это и есть закон Архимеда.
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.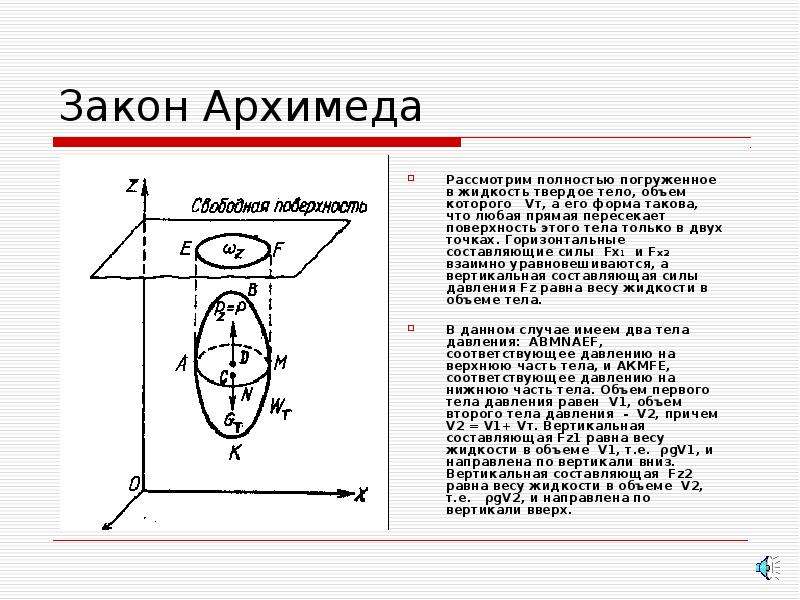
Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :
где
– плотностьжидкости (газа),
– ускорение
свободного падения, а
– объём погружённого тела (или часть
объёма тела, находящаяся ниже поверхности).
Если тело плаваетна поверхности или равномерно движется
вверх или вниз, то выталкивающая сила
(называемая также архимедовой силой)
равна по модулю (и противоположна по
направлению) силе тяжести, действовавшей
на вытесненный телом объём жидкости
(газа), и приложена кцентру
тяжестиэтого объёма.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Тело,
погруженное (полностью или частично) в
жидкость, испытывает со стороны жидкости
суммарное давление, направленное снизу
вверх и равное весу жидкости в объеме
погруженной части тела.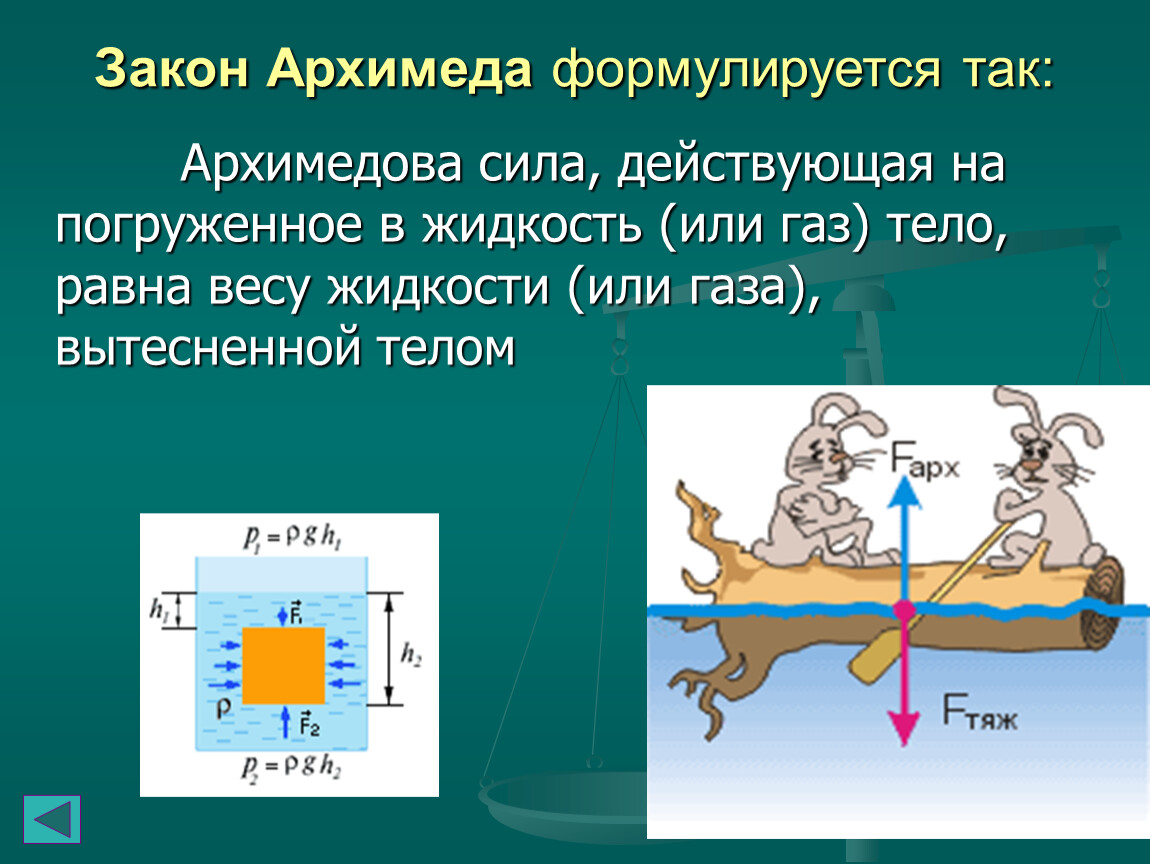 P выт =
ρ ж gV погр
P выт =
ρ ж gV погр
Для однородного тела плавающего на поверхности справедливо соотношение
где: V – объем плавающего тела; ρ m – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью . Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением , а точку приложения равнодействующей давления (т.е. центр давления) – центром водоизмещения . При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O”-O” , представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть
под влиянием внешних сил судно наклонилось
на некоторый угол α, часть судна KLM вышла
из жидкости, а часть K”L”M” ,
наоборот, погрузилось в нее. При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если h
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Проделаем простой эксперимент: возьмем слабо надутый резиновый мяч и «притопим» его в воде. Если глубина погружения будет даже 1-2 метра, то нетрудно видеть, что его объем уменьшится, т. е. со всех сторон мяч обжала некая сила. Обычно говорят, что здесь «виновато» гидростатическое давление – физический аналог силы, действующей в неподвижных жидкостях на погруженное тело. Гидростатические силы действуют на тело со всех сторон, а их результирующая, известная как архимедова сила, еще называется выталкивающей, что соответствует ее направлению действия на погруженное в жидкость тело.
е. со всех сторон мяч обжала некая сила. Обычно говорят, что здесь «виновато» гидростатическое давление – физический аналог силы, действующей в неподвижных жидкостях на погруженное тело. Гидростатические силы действуют на тело со всех сторон, а их результирующая, известная как архимедова сила, еще называется выталкивающей, что соответствует ее направлению действия на погруженное в жидкость тело.
Архимед открыл свой закон чисто экспериментально, а его теоретическое обоснование ждало еще почти 2000 лет до того, как Паскаль открыл для неподвижной жидкости. Согласно этому закону давление передается через жидкость по всем направлениям независимо от площади, на которую оно действует, на все плоскости, ограничивающие жидкость, а его величина P пропорциональна поверхности S и направлена по нормали к ней. Паскаль открыл и проверил этот закон на опыте в 1653 г. В соответствии с ним, на поверхность погруженного в жидкость тела со всех сторон действует гидростатическое давление.
Допустим, что в сосуд с водой погружено тело в форме куба с ребром L на глубину H – расстояние от поверхности воды до верхней грани. При этом нижняя грань находится на глубине H+L. Вектор силы F1, действующей на верхнюю грань, направлен вниз и F1 = r * g * H * S, где r – плотность жидкости, g – ускорение
При этом нижняя грань находится на глубине H+L. Вектор силы F1, действующей на верхнюю грань, направлен вниз и F1 = r * g * H * S, где r – плотность жидкости, g – ускорение
Вектор силы F2, действующей на нижнюю плоскость, направлен вверх, а ее величина определяется выражением F2 = r * g * (H+L) * S .
Векторы сил, действующих на боковые поверхности, взаимно уравновешиваются, поэтому в дальнейшем из рассмотрения исключаются. Архимедова сила F2 > F1 и направлена снизу вверх, и приложена к нижней грани куба. Определим ее величину F:
F = F2 – F1 = r * g * (H+L) * S – r * g * H * S = r * g * L * S
Заметим, что L * S – это объем куба V, а т. к. r * g = p представляет собой вес единицы жидкости, то формула архимедовой силы определяет вес объема жидкости, равный объему куба, т.е. это как раз и есть вес вытесненной телом жидкости. Интересно, что говорить о возможно только для среды, где присутствует сила тяжести – в условиях невесомости закон не работает. Окончательно формула закона Архимеда имеет следующий вид:
F = p * V, где p – удельный вес жидкости.
Архимедова сила может служить основанием для анализа плавучести тел. Условием для анализа служит соотношение веса погруженного тела Рт и веса жидкости Рж с объемом, равным объему погруженной в жидкость части тела. Если Рт = Рж, то тело плавает в жидкости, а если Рт > Рж, то тело тонет. В противном случае тело всплывает, пока выталкивающая сила не сравняется с весом вытолкнутой утопленной частью тела воды.
Закон Архимеда и его использование имеют длинную историю в технике, начиная с классического примера применения во всех известных плавсредствах и до воздушных шаров и дирижаблей. Здесь сыграло роль то, что газ относится к такому состоянию вещества, которое вполне моделирует жидкость. При этом, в воздушной среде на любые предметы действует архимедова сила, сродни такой же, как в жидкости. Первые попытки осуществить воздушный полет на воздушном шаре предприняли братья Монгольфьер – они наполняли воздушный шар теплым дымом, благодаря чему вес заключенного в шаре воздуха был меньше, чем вес такого же объема холодного воздуха. Это и было причиной появления а ее величина определялась как разность веса этих двух объемов. Дальнейшим усовершенствованием воздушных шаров была горелка, которая непрерывно подогревала воздух внутри шара. Понятно, что дальность полета зависела от длительности работы горелки. Позже на дирижаблях применялся для наполнения газ с удельным весом меньше, чем у воздуха.
Это и было причиной появления а ее величина определялась как разность веса этих двух объемов. Дальнейшим усовершенствованием воздушных шаров была горелка, которая непрерывно подогревала воздух внутри шара. Понятно, что дальность полета зависела от длительности работы горелки. Позже на дирижаблях применялся для наполнения газ с удельным весом меньше, чем у воздуха.
Жидкостей и газов, согласно которому на всякое тело, пог-руженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.
Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.
Ниже приведены выводы, следующие из закона Архимеда .
Действие жидкости и газа на погруженное в них тело.
Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а ). В каж-дой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростати-ческое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.
Если заменить все силы давления , приложенные к погруженному в воду телу, одной (резуль-тирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как F A .
На рисунке б она обозначена как F A .
Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глу-бинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.
Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном про-странстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.
Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).
Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P 0 , то его вес в воздухе равен:
,
где F´ A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что P возд. =P 0 =mg .
е. можно считать, что P возд. =P 0 =mg .
Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе P возд. =P 0 , то вес тела в жидкости равен P жидк = Р 0 — F A . Здесь F A — архимедова сила, действующая в жидкости. Отсюда следует, что
Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.
Другими словами, учитывая формулу (1.32), можно сказать:
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.
Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем пра-во это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано.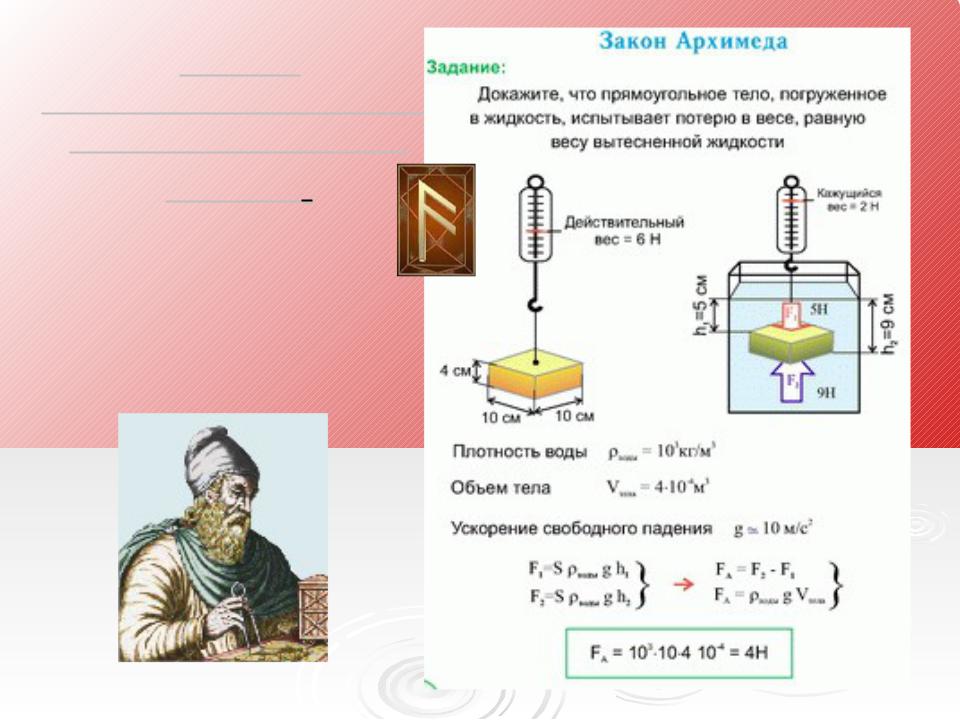 Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):
Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):
Но сила тяжести равна весу вытесненной жидкости Р ж . Таким образом.
Учитывая, что масса жидкости равна произведению ее плотности ρ ж на объем, формулу (1.33) можно записать в виде:
где V ж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погру-жена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем V ж вытесненной жидкости меньше объема V тела (рис. 1.39).
Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом слу-чае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.
С учетом вышеизложенного закон Архимеда можно сформулировать так:
На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или га-за), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).
Рекомендуем также
Что такое плавучесть – Принцип Архимеда
ЧТО ТАКОЕ ПЛАВУЧИЕ?
Плавучесть – это сила, создаваемая жидкостью или
газ, противодействующий весу объекта. Плавучесть также может быть
заявлен как вес вытесненной жидкости. Давление в жидкости
увеличивается с глубиной в результате веса вышележащих
жидкость (см. гидростатический
давление). Таким образом, объект, погруженный в жидкость, испытывает
большее давление внизу жидкости, чем вверху.Эта разница в давлении приводит к чистой силе, которая стремится
для ускорения объекта вверх. Величина этой силы
пропорциональна разнице давлений между
верх и низ столбца, а также эквивалентны
к весу жидкости, которая в противном случае занимала бы
столбец, т. е. вытесненная жидкость. По этой причине
объект, плотность которого больше, чем у жидкости
то, что он погружен в воду, утонет.Принцип Архимеда позволяет
для экспериментального определения плотности путем обеспечения
простой и точный метод определения объема
объект неправильной формы. См. Также: Масса,
Объемная плотность..для интерактивных занятий.
е. вытесненная жидкость. По этой причине
объект, плотность которого больше, чем у жидкости
то, что он погружен в воду, утонет.Принцип Архимеда позволяет
для экспериментального определения плотности путем обеспечения
простой и точный метод определения объема
объект неправильной формы. См. Также: Масса,
Объемная плотность..для интерактивных занятий.
Принцип Архимеда назван в честь Архимеда из Сиракуз, который первым открыл этот закон в 212 г. до н. э. Архимед’ принцип можно выразить таким образом в силе:
Любой объект, полностью или частично погруженный в жидкости, поддерживается силой, равной весу жидкость, вытесняемая объектом.
– Архимед Сиракузский
ОБ АРХИМЕДЕ
– Архимед был сыном астронома. |
Для объектов, плавающих и затонувших, а также в газы, а также жидкости, принцип Архимеда может быть сформулирован в силе:
Любой объект, полностью или частично погруженный в воду. в жидкости поддерживается силой, равной весу жидкости, вытесненной объектом.с разъяснениями что для затонувшего объекта объем вытесненной жидкости равен объем объекта, а для плавающего объекта на жидкости, вес вытесненной жидкости – это вес объекта.
Принцип Архимеда указывает что восходящая выталкивающая сила, действующая на тело, полностью или частично погруженное в жидкость погруженный, равен весу жидкости, которая тело смещается. Обратите внимание, что действующие силы увеличиваются с глубиной жидкости. равнодействующая всех сил вверх называется плавучестью и равен весу вытесненная жидкость. |
Принцип Архимеда допускает плавучесть объекта, частично или полностью погруженного в жидкость, подлежащую рассчитано.Сила, направленная вниз на объект, – это просто его масса. Восходящая или плавучая сила, действующая на объект, такова, что утверждается принципом Архимеда, приведенным выше. Таким образом, чистая вверх сила на объекте – это разница между плавучестью сила и ее вес. Если эта результирующая сила положительна, объект плавает; если отрицательный, объект тонет; и если ноль, объект имеет нейтральную плавучесть, то есть остается на месте без либо поднимается, либо опускается.Простыми словами принцип Архимеда утверждает, что когда тело частично или полностью погружено в жидкости он испытывает очевидную потерю веса, которая равна массе жидкости, вытесненной погруженным часть тела.
Примечание: принцип Архимеда не учитывать поверхностное натяжение (капиллярность), действующее на тело но эта дополнительная сила изменяет только количество жидкости смещен, так что принцип Плавучесть = вес вытесненная жидкость остается в силе.
Рассмотрим куб, погруженный в жидкость, с его стороны параллельны направлению силы тяжести .. Только силы на верхней и нижней гранях куба будут способствовать к плавучести. Разница давлений между днищем и верхняя грань прямо пропорциональна высоте (разница в глубине). Умножение разницы давлений на площадь грани дает чистую силу на куб – , плавучесть , или вес вытесняемой жидкости.
ФОРМУЛЫ Для полностью погруженного объект, принцип Архимеда можно сформулировать как следует: кажущаяся полная масса = вес объекта – вес вытесненной жидкости плотность объекта / плотность жидкости = вес / (вес вытесненной жидкости) плотность объекта / плотность жидкости = вес / (вес – кажущийся погруженный вес) __________________________ “Плавучесть” сила »на погруженном в воду теле направлена в направлении, противоположном силе тяжести, и равно по величине до: (плотность жидкости) (Объем вытесняемой жидкости) (ускорение) |
Когда объект всплывет или воздушный шар повышаться?
Объект будет плавать в жидкости, если плотность этого объекта меньше плотности жидкости.
Пример: если вы уроните дерево в воду, плавучесть будет держать его на плаву. Древесина менее плотная, чем вода.
Воздушные шары поднимаются в воздух, потому что плотность воздуха (более теплый воздух) внутри воздушного шара составляет менее плотный, чем воздух за пределами воздушного шара (более прохладный воздух). Баллон и корзина вытесняют более тяжелую жидкость. чем воздушный шар и корзина, поэтому он обладает выталкивающей силой действуя на систему.Воздушные шары, как правило, лучше летают по утрам, когда окружающий воздух прохладный.
ОБРАЗЕЦ ПРОБЛЕМА
Стальной блок плотностью 7800 кг / м3
подвешивается на веревке в стакане с водой
, так что блок полностью погружен, но не находится в состоянии покоя
снизу. Блок представляет собой куб
со сторонами 3 см (0,03 м).
Подъемная сила = вес вытесненной воды
= масса воды * ускорение свободного падения
= плотность воды * объем куба * г
= 1×10 3 кг / м 3 * 27 * 10-6 м3 9.8 м / с2
= 2,65 * 10-1 Н = 0,265 Н
вес
блока = масса г
W = мг = 2,106 x 10-1 кг x 9,8 м / с2 = 2,106×9,8 x 10-1 кг * м / с2
= 20,64 x 10-1 Н
= 2,064 Н кг * м / с2 = Н (Ньютон)
Проверьте свой Понимание:
Принцип Архимеда – AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Buoyancy – The Physics Hypertextbook
Обсуждение
Подъемные силы действуют на фундаменты зданий. Станции токийского метрополитена необходимо закрепить, чтобы не выскакивать на поверхность из-за подъемных сил, вызванных повышением уровня воды.
| B = F низ – F верх B = P низ A – P верх A B = B gh низ – ρ жидкость gh верх ) A B = ρ жидкость г ∆ hA = ρ 9016 жидкость g г B = W жидкость |
Принцип Архимеда : Выталкивающая сила ( B ) на объект, погруженный в жидкость, равна весу вытесненной жидкости.
Архимед Сиракузский (287–212 гг. До н.э.) был уполномочен королем Сиракуз Иеро II определить, изготовлена ли для него золотая корона из чистого золота или из сплава низкого качества, как он подозревал. Проблема заключалась в том, как определить содержание золота, не повредив корону. Как гласит история, Архимед решил, что приятная расслабляющая ванна поможет ему думать. Он погрузился в воду и почувствовал себя немного легче – событие, которое пережили миллиарды других людей бесчисленное количество раз. Что уникально в расслабляющей ванне Архимеда, так это то, что он осознал, возможно, впервые в истории человечества, что эта жизненная сила, которую он испытывал, может быть использована для определения качества королевской короны.
Эврика – совершенная указательная форма слова ευρισκω [eurisko] – найти. Относится к английскому слову эвристика, относящемуся к методам, используемым для поиска решений проблем.
Буй – « Boiæ genus vinculorum tam ferreæ quam ligneæ ». – Фестус (словарь Вебстера 1913 г.). что-то делать с привязкой ремнями? ( boiæ ?)
Кажущийся вес ( W ′) объекта, погруженного в жидкость, определяется как…
| W ′ = W – B W ′ = м объект г – м жидкость г W ′ = (ρ объект – ρ жидкость V ) g W ′ = (ρ объект – ρ жидкость ) gV W ′ = ρ16 где… ρ ′ = ρ объект – ρ жидкость – это относительная плотность . Когда…
Плотность выбранных материалов (~ 20 ° C, 1 атм)
Понимание принципа Архимеда – урок для учащихсяАрхимед открыл принцип плавучести, который используется в различных приложениях, включая корабли. Это позволяет им плавать, когда вес вытесняемой воды равен весу корабля. Все, что имеет форму, позволяющую вытеснять воду под собственным весом до того, как достигнет точки, в которой она погрузится в воду, обязательно будет плавать. Сегодня вы познакомитесь с определением, применением, формулой, выводом, экспериментами, примерами и расчетами принципа Архимеда. Подробнее: Electric force Что такое принцип Архимеда?Принцип Архимеда касается сил, приложенных к объекту окружающими его жидкостями. Эта приложенная сила уменьшает чистый вес объекта, погруженного в жидкость. Этот принцип также можно рассматривать как физический закон плавучести, который помогает нам понять, как корабли плавают в воде.Другими словами, любой объект, полностью или частично погруженный в жидкость или жидкость, подпитывается силой, равной весу жидкости, вытесняемой объектом. В данном случае принцип Архимеда позволяет вычислить плавучесть любого плавающего объекта, частично или полностью погруженного в жидкость. Сила, направленная вниз на объект, – это то, что мы называем весом. Восходящая или поднимающая сила на объект – это то, что утверждал принцип Архимеда. Таким образом, результирующая сила, действующая на объект, – это разница между величиной выталкивающей силы и его весом.Если эта результирующая сила отрицательна, объект обязательно тонет, а если положительная, объект поднимается. Если объект равен нулю, объект имеет нейтральную плавучесть, то есть остается на месте, не опускаясь или не поднимаясь. Подробнее: Как сила меняет состояние движения Посмотрите видео ниже, чтобы узнать больше о принципе Архимеда:
Проще говоря, принцип Архимеда гласит, что когда тело полностью или частично погружено в жидкость, оно испытывает очевидную потерю веса.Этот вес равен весу жидкости, вытесняемой погруженной частью тела. Этот принцип можно сформулировать так: восходящая выталкивающая сила, действующая на тело, погруженное в жидкость, частично или полностью погруженное в жидкость, равна весу жидкости, которую вытесняет тело, и действует в направлении вверх в центре масс. вытесненная жидкость. Подробнее: Взаимосвязь силы и движения Принцип Архимеда – это физический закон, фундаментальный для механики жидкости. Применение принципа АрхимедаНиже показано применение принципа Архимеда в различных областях: Подводная лодка:Применение Архимеда в подводных лодках настолько распространено из-за их связи с морем. Они могли оставаться под водой из-за компонента, называемого балластным танком, который позволяет воде течь в него. Это заставляет подводную лодку находиться под водой, поскольку ее вес превышает подъемную силу. Ареометр:Для измерения относительной плотности жидкостей используется ареометр.Он сделан из свинцовой дроби, которая заставляет их плавать вертикально по жидкости. Когда ареометр опускается ниже, плотность жидкости будет меньше. Подробнее: Понимание механики жидкости Воздушный шар:Воздушные шары способны парить в воздухе благодаря тому, что подъемная сила у воздушного шара меньше, чем у окружающего воздуха. Таким образом, воздушный шар опустится, когда подъемная сила будет больше. Это достигается за счет изменения количества горячего воздуха в воздушном шаре. Формула принципа АрхимедаКак было сказано ранее, закон Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, вытесняемой объектом. Математически это записывается как: F b = ρ x g x V где: F b – подъемная сила P – плотность жидкости В – погружной объем g – ускорение свободного падения. Подробнее: Понимание различных типов потока жидкости Вывод принципа АрхимедаМасса вытесненной жидкости составляет. Масса = Плотность × Объем = ρ × В Это связано с тем, что плотность (ρ) определяется как Плотность, ρ = Масса Объем = MV Таким образом, вес вытесненной жидкости равен: Вес = Масса × Ускорение свободного падения W = M × g = ρ × V × g Таким образом, из принципа Архимеда можно записать: Кажущаяся потеря веса = вес вытесненной воды = ρ × V × г Таким образом, сила тяги равна, Тяга = ρ × V × g Где:
Подробнее: Что нужно знать о насосе Сила тяги также известна как выталкивающая сила, потому что она отвечает за плавание объектов.Таким образом, это уравнение еще называют законом плавучести. Решенные примеры принципа Архимеда1 кв. Рассчитайте результирующую силу, если стальной шарик радиусом 6 см погрузить в воду.Ответ: Дано, Радиус стального шара = 6 см = 0,06 м Объем стального шара, V = 43πr3 В = 43π0,063 ∴V = 9,05 × 10 -4 м 3 Плотность воды ρ = 1000 кг.м -3 Ускорение свободного падения, g = 9,8 м.с -2 Формула из принципа Архимеда F b = ρ × g × V F b = (1000 кг.м -3 ) (9,8 м.с -2 ) (9,05 × 10 -4 м 3 ) ∴F b = 8,87 Н Подробнее: Понятие о поршневом насосе 2 кв. Рассчитайте выталкивающую силу, если плавающее тело погружено в воду на 95%.Плотность воды 1000 кг.м -3 . Ответ: Дано, F b = ρ × g × V или В b × ρ b × g = ρ × g × V Где: ρ, g и V – плотность, ускорение свободного падения и объем воды. V b , ρ b , а g – объем, плотность и ускорение под действием силы тяжести погруженного тела Преобразование уравнения, ρb = VρVb Так как 95% тела погружено в воду, 0.95 × V b = V ∴ρ b = 950 кг.м -3 ЗаключениеПринцип Архимеда касается сил, приложенных к объекту окружающими его жидкостями. Эта приложенная сила уменьшает чистый вес объекта, погруженного в жидкость. Этот принцип также можно рассматривать как физический закон плавучести, который помогает нам понять, как корабли плавают в воде. Это все для этого поста, в котором обсуждались определение, приложения, формула, вывод, эксперименты, пример и расчет принципа Архимеда.Обязательно посмотрите встроенное видео, чтобы узнать больше о том, как работает принцип Архимеда Я надеюсь, что вы многое почерпнули из этого поста, если да, любезно поделитесь с другими студентами. Спасибо за чтение, увидимся в следующий раз! 14.4 Принцип Архимеда и плавучесть – University Physics Volume 1Learning ObjectivesК концу этого раздела вы сможете:
При помещении в жидкость некоторые объекты плавают под действием выталкивающей силы.Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары (рис. 14.19)? Фигура 14,19 (а) Даже тонущие предметы, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (c) наполненные гелием воздушные шары тянут вверх свои струны, демонстрируя плавучесть воздуха.(Фото b: модификация работы Allied Navy; кредит c: модификация работы Crystl / Flickr) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта. На любой объект в любой жидкости действует восходящая или выталкивающая сила (рис. 14.20). Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает.Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости. Плавучая силаВыталкивающая сила – это сила, направленная вверх на любой объект в любой жидкости. Фигура 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что p = hpgp = hpg.Это изменение давления и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра. Разница в силе приводит к выталкивающей силе FBFB. (Горизонтальные силы отменяются.)Принцип АрхимедаНасколько велика сила подъема? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на рисунке 14.21. Если бы объект не находился в жидкости, пространство, которое занимал объект, было бы заполнено жидкостью, имеющей вес wfl.wfl. Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться wfl, wfl, весу жидкости, вытесняемой объектом. Принцип АрхимедаВыталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда – , где FBFB – выталкивающая сила, а wflwfl – вес жидкости, вытесняемой объектом. Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок.287–212 гг. До н.э.), которые сформулировали этот принцип задолго до того, как концепции силы были хорошо установлены. Фигура 14.21 (а) Объект, погруженный в жидкость, испытывает подъемную силу FB.FB. Если FBFB больше веса объекта, объект поднимается. Если FBFB меньше веса объекта, объект тонет. (b) Если объект удален, он заменяется жидкостью, имеющей вес wfl.wfl. Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться массе вытесняемой жидкости.Принцип Архимеда относится к силе плавучести, которая возникает, когда тело погружается в жидкость, частично или полностью. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила, создаваемая давлением внизу, направлена вверх, тогда как вверху сила, обусловленная давлением, направлена вниз; силы из-за давления по бокам направлены внутрь тела. Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на рисунке 14.20. Следовательно, на тело действует чистая направленная вверх сила. Эта направленная вверх сила и есть сила плавучести, или просто плавучесть . Плотность и принцип АрхимедаЕсли вы уроните кусок глины в воду, он утонет. Но если вылепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем кусок, и испытывает большую выталкивающую силу, хотя ее масса такая же. То же самое и со стальными кораблями. Средняя плотность объекта – это то, что в конечном итоге определяет, плавает ли он.Если средняя плотность объекта меньше, чем у окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, выталкивающая сила, равная весу вытесняемой жидкости, превышает вес объекта. Точно так же утонет объект, более плотный, чем жидкость. Степень погружения плавающего объекта в воду зависит от того, как плотность объекта сравнивается с плотностью жидкости.На рис. 14.22, например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем при загрузке. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или . погруженная фракция = VsubVobj = VflVobj. погруженная часть = VsubVobj = VflVobj.Погруженный объем равен объему вытесненной жидкости, который мы называем VflVfl. Теперь мы можем получить соотношение между плотностями, подставив в выражение ρ = mVρ = mV.Это дает VflVobj = mfl / ρflmobj / ρobj, VflVobj = mfl / ρflmobj / ρobj,где ρobjρobj – средняя плотность объекта, а ρflρfl – плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя погруженная фракция = ρobjρfl. погруженная часть = ρobjρfl.Мы можем использовать это соотношение для измерения плотности. Фигура 14,22 Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b). Пример 14,4Расчет средней плотностиПредположим, женщина весом 60,0 кг плавает в пресной воде с погружением 97,0% ее объема, когда ее легкие полны воздуха. Какая у нее средняя плотность?СтратегияПлотность женщины можно найти, решив уравнение погруженная фракция = ρobjρfфракция погруженная = ρobjρflдля плотности объекта. Это дает ρobj = ρperson = (часть погруженных) · ρfl.ρobj = ρperson = (часть погруженных) · ρfl.Нам известны и доля погруженной воды, и плотность воды, поэтому мы можем вычислить плотность женщины. РешениеВводя известные значения в выражение для ее плотности, получаем ρчеловек = 0,970 · (103кгм3) = 970кгм3. ρчеловек = 0,970 · (103кгм3) = 970кгм3.ЗначениеПлотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе, ” назвать несколько.Менее очевидный пример – горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками. Измерение плотностиОдин из наиболее распространенных методов определения плотности показан на рис. 14.23. Фигура 14,23 (а) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты. Предмет, в данном случае монета, взвешивается на воздухе, а затем снова взвешивается, будучи погруженным в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на принципе Архимеда, который гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что при погружении объект кажется меньше весит; мы называем это измерение кажущимся весом объекта.Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости. Принцип Архимеда – (Обновлено в период с 2021 по 2022 год) | CoolGyan.OrgПринцип Архимеда касается сил, приложенных к объекту окружающими его жидкостями.Эта приложенная сила уменьшает чистый вес объекта, погруженного в жидкость. Также этот физический закон плавучести помогает нам понять, как корабли плавают в воде. FormulaDerivationApplicationsExperimentSolved Примеры Что такое принцип Архимеда?Принцип Архимеда гласит:
Значение силы тяги определяется законом Архимеда, который был открыт Архимедом Сиракузским в Греции. Когда объект частично или полностью погружен в жидкость, кажущаяся потеря веса равна весу вытесненной им жидкости. Объяснение принципа АрхимедаЕсли вы посмотрите на рисунок, вес из-за силы тяжести противостоит силе, создаваемой жидкостью. Объект внутри жидкости ощущает только общую силу, действующую на него, как на вес.Поскольку действительная гравитационная сила уменьшается за счет подъема жидкости вверх, объект чувствует, как будто его вес уменьшился. Таким образом, кажущийся вес определяется как:
Принцип Архимеда говорит нам, что эта потеря веса равна весу жидкости, которую вытесняет объект. . Если объект имеет объем V, то он вытесняет объем жидкости V, когда он полностью погружен. Если погружена только часть объема, объект может вытеснить только это количество жидкости. Формула принципа АрхимедаВ простой форме закон Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, вытесняемой объектом. Математически записывается как: Где
Принцип Архимеда Эксперимент
Вывод по принципу АрхимедаМасса вытесненной жидкости составляет. \ (Масса \) = \ (Плотность ~ × ~ Объем \) = \ (ρ ~ × ~ V \) Это потому, что плотность (ρ) определяется как \ (Плотность, ρ \) = \ (\ frac {Mass} {Volume} \) = \ (\ frac {M} {V} \) Таким образом, вес вытесненной жидкости равен: \ (Weight \) = \ (Масса ~ × ~ Ускорение ~ из-за ~ ~ гравитации \) \ (W \) = \ (M ~ × ~ g \) = \ (ρ ~ × ~ V ~ × ~ g \) Таким образом, из принципа Архимеда, мы можем напишите: Кажущаяся потеря веса = вес вытесненной воды = ρ × V × g Таким образом, сила тяги равна, \ (Thrust \) = \ (ρ ~ × ~ V ~ × ~ g \) Где,
Сила тяги также называется выталкивающей силой, поскольку она отвечает за плавание объектов.Таким образом, это уравнение еще называют законом плавучести. Статьи по теме: Принцип Архимеда ПриложенияНиже приведены приложения принципа Архимеда: Подводная лодка:Причина, по которой подводные лодки всегда находятся под водой, заключается в том, что у них есть компонент, называемый балластным баком, который позволяет воде чтобы войти, заставляя подводную лодку находиться под водой, поскольку вес подводной лодки больше, чем подъемная сила. Воздушный шар:Причина, по которой воздушные шары поднимаются и плавают в воздухе, заключается в том, что подъемная сила воздушного шара меньше, чем у окружающего воздуха. Когда подъемная сила воздушного шара больше, он начинает снижаться. Это достигается изменением количества горячего воздуха в воздушном шаре. Ареометр:Ареометр – это прибор, используемый для измерения относительной плотности жидкостей. Ареометр состоит из свинцовых дробинок, которые заставляют их плавать вертикально по жидкости.{3} \) ∴V = 9,05 × 10 -4 м 3 Плотность воды, ρ = 1000 кг.м -3 Ускорение свободного падения, g = 9,8 мс – 2 Из формулы принципа Архимеда, F b = ρ × g × V F b = (1000 кг.м -3 ) (9,8 мс -2 ) (9,05 × 10 -4 м 3 ) ∴F b = 8,87 Н Q2. Рассчитайте выталкивающую силу, если плавающее тело погружено в воду на 95%.Плотность воды 1000 кг.м -3 . Ответ: Дано, или V b × ρ b × g = ρ × g × V Где, ρ, g и V – плотность, ускорение свободного падения и объем воды V b , ρ b , а g – объем, плотность и ускорение от силы тяжести погруженного тела. Переставив уравнение, \ (\ rho _ {b} = \ frac {V \ rho} {V_ {b}} \)Поскольку Погружено 95% тела, 0.95 × V b = V ∴ρ b = 950 кг.м -3
Часто задаваемые вопросы – Часто задаваемые вопросыЧто утверждает принцип Архимеда?Принцип Архимеда гласит, что объект, погруженный в жидкость, полностью или частично, испытывает восходящую выталкивающую силу, которая по величине равна силе тяжести на вытесненной жидкости. Кто открыл принцип Архимеда?Греческий математик Архимед открыл принцип Архимеда. Как принцип Архимеда применим к кораблям?Архимед продолжал проводить больше экспериментов и придумал принцип плавучести, согласно которому корабль будет плавать, когда вес вытесняемой им воды равен весу корабля, и все будет плавать, если оно имеет форму, позволяющую вытеснять собственный вес воды раньше. он достигает точки, в которой он погрузится в воду. Где используется принцип Архимеда?Принцип Архимеда используется в принципе проектирования кораблей и подводных лодок. В основе ареометров лежит принцип Архимеда. Как можно использовать принцип Архимеда для определения плотности?Вес вытесненной жидкости равен выталкивающей силе, действующей на погруженный объект. Полученная таким образом масса, разделенная на объем, дает меру средней плотности объекта. Следите за обновлениями с CoolGyan’S, чтобы узнавать больше интересных тем с помощью увлекательных видео! 1.НАЗНАЧЕНИЕ: Для исследования различных методов измерения плотности твердых тел и жидкостей с использованием принципа Архимеда. 2. АППАРАТ: Штангенциркуль для микрометра, штангенциркуль с нониусом, две полуметровые штанги, тройные балансиры над головой с платформой для измерения удельного веса, двойной поворотной шкалой (опция), переливным баком с уловителем, ареометры (для легких и тяжелых жидкостей), баллон для измерения плотности (пикнометр), градуировка 250 мл, различные мензурки, прямая стеклянная трубка, стеклянная U-образная трубка, резиновая трубка. Неизвестных: а) Различные образцы металлов. 3. ТЕОРИЯ: Прочтите материал о принципе Архимеда, плотности и удельном весе в любом учебник. I. Принцип Архимеда: когда тело полностью или частично погружено в жидкость, это тело испытывает восходящую силу (выталкивающую силу), равную весу вытесненная жидкость.Вытесненная жидкость – это объем жидкости, равный объему тела под поверхностью воды. В некоторых методах измерения потребуется другой принцип. II. Когда любые две точки в одной и той же жидкости находятся на разной высоте, давление в нижняя точка, p 1 , и давление в верхней точке, p 2 , связаны соотношением где ρ – плотность жидкости, g – ускорение свободного падения, h – расстояние между точками по вертикали.Фраза “в той же жидкости” очень важно и означает, что можно провести путь между две точки, этот путь никогда не покидает жидкость. III.Когда экспериментальная ситуация включает в себя как жидкости, так и газы, оказывающие давление на друг друга, можно предположить, что любые две точки в одном и том же газе имеют по существу одинаковое давление, независимо от высоты. Это потому, что плотность газов настолько высока. намного меньше плотности жидкостей, поскольку перепад давления в газе из-за высоты различия незначительны по сравнению с перепадами давления в жидкостях. 4. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ: A. Прямое определение плотности по массе и по объему- мент. масса легко определяется взвешиванием. Объемы жидкостей легко определяется с помощью градуированного цилиндра. Объемы твердых тел простой формы (сферы, цилиндров, кубиков) могут быть определены прямым измерением их размеров с помощью линейки или штангенциркули микрометра и нониуса. Единственная новая техника, которая вам понадобится, – это когда объем твердого тела неправильной формы нужно найти. Здесь можно использовать перелив, при этом жидкость переливается через боковую стенку. носик. Наполняйте банку до ее перелива. Затем прикрепите веревку к твердому телу и опустите ее в банку. до тех пор, пока он полностью не погрузится в воду, улавливая переливную жидкость в стакан. Теперь найдите объем переливную жидкость любым подходящим способом. Если эта жидкость – вода, это может быть просто навеска на 1 мл воды имеет объем 1 см 3 и массу 1 г.
B. Удельный Плотность бутылка (пикнометр). Этот особенный Бутылка используется для сравнения веса точно равных объемов двух жидкостей. Бутылка имеет специальная стеклянная пробка с точным сопряжением с матовым стеклом. Пробки НЕ взаимозаменяемы между бутылками; не путайте их. Пробка с отверстием который позволяет жидкости перетекать при вставке пробки, обеспечивая точное полное заполнение каждые время. Бутылку необходимо сначала взвесить насухо . Затем взвесьте его, наполненный неизвестным жидкость. Тщательно просушите (ополаскивание спиртом быстро высушит). Затем взвесьте его, наполненный водой. Снова просушите. C. Манометр методы . В этих методах используются принципы II и III. для сравнения плотностей двух жидкостей. Рис. 1-3 иллюстрируют несколько возможностей, и предоставьте студенту возможность провести математический анализ.Метод, показанный на рис. 1, можно использовать только с несмешивающимися жидкостями. На рис. 2 и 3 две жидкости разделены воздухом и никогда не смешиваются (если будете осторожны!). На рис. 2 показан особенно удобный метод. Два U-образных отвода такой формы, что в каждую U можно вставить полуметровую палку для прямого измерения высоты различия.
На рис. 4 есть запорный кран или пробка в точке S, где может быть применено пониженное давление для вытяжки. вверх жидкости в трубках.Y-образный соединитель с тремя резиновыми трубками и зажимом. зажим работает хорошо. Для этого метода требуются мерные стержни, которые не повреждаются при погружении. в жидкостях. Во всех случаях длина a измеряется для материала A, а длина b – для материала. B. Формула, относящаяся к плотности: Хотя это уравнение одинаково для всех трех случаев, вывод уравнения различается. в каждом случае.Студент должен получить этот результат для каждого случая, начиная с первого. принципы. D. Архимеда Принцип . Этот принцип фигурирует во многих самые точные и практичные приборы для измерения плотности. Основная цель этого эксперимента состоит в том, чтобы исследовать некоторые из этих методов. Другие методы (от A до C выше) могут использоваться для проверьте свои результаты. 5. ПРОЦЕДУРА:
(1) Поместите стакан с водой на балансировочные весы с двумя чашами. Сбалансируйте инструмент Весы. Как вы думаете, что произойдет, если вы погрузите палец в воды, не касаясь стакана. Проанализируйте ситуацию и сделайте свое предположение до вы попробуете, используя принцип Архимеда. Если это не имеет смысла, перед продолжением проконсультируйтесь со своим инструктором. (2) Удельный вес латуни 8,4. Каков объем латунной гирьки 500 г (из набора веса)? Предскажите , что произойдет, если этот груз будет подвешен веревку и опускаем в воду на ваших весах (как на рис. 5. Предскажите , сколько массу необходимо добавить или удалить с другой чаши, чтобы сбалансировать весы под эти условия. Проверьте свой прогноз экспериментально. Вы можете проверить свой расчет объема с помощью переливной банки. (3) Получите неизвестное твердое тело неправильной формы. Вы воспользуетесь методом, который у вас только что обнаружили, чтобы определить его плотность. Взвесьте неизвестное твердое тело обычным способом. Взвесьте стакан с водой, уравновесив весы. Подвесьте неизвестное твердое тело в воды и определите, сколько веса необходимо добавить, чтобы сбалансировать весы. Анализ: Поскольку вода оказывает выталкивающую силу B вверх на твердое тело, то по третьему закону Ньютона твердое тело прилагает силу B вниз к воды.Это выводит весы из равновесия на величину B , а массу, имеющую вес B необходимо добавить, чтобы сбалансировать их. Таким образом, этот добавленный вес равен плавучести. сила, а принцип Архимеда позволяет рассчитать объем твердого тела. Проверьте измерение объема с помощью переливного баллона, понимая, что он не будет таким, как точен, как метод принципа Архимеда.
(4) Подвесные балансиры (рис. 6) обычно имеют платформу, которую можно расположить над одну кастрюлю, чтобы на нее можно было поставить стакан с жидкостью. Эта функция предусмотрена специально для измерения плотности по принципу Архимеда. Подвесьте неизвестный твердый объект на веревке, как показано, и уравновесите весы. Теперь поставьте стакан с водой на платформу и отрегулируйте высоту платформы до твердого состояния. полностью погружен в воду.Перебалансируйте весы. The chang e в масштабе показания представляют собой подъемную силу. Первоначальное показание шкалы – это просто вес твердого тела. Рассчитайте плотность неизвестного твердого тела по этим измерениям. (5) Возьмите химический стакан с легкой неизвестной жидкостью и поместите в нем неизвестное твердое вещество. Используя то, что вы узнали, постройте формулу для расчета плотности неизвестного жидкость из только эти данные : показания шкалы с неизвестным твердым веществом свободно висит, показания шкалы с твердым веществом, погруженным в воду, считывание шкалы с твердым веществом, погруженным в неизвестной жидкости.Плотность твердого тела в расчет не входит, и вам даже не нужно знаю, что это такое. Найдите плотность неизвестной жидкости по вашей формуле. Этот метод является принцип стандартного прибора, известного как весы Мора-Вестфала. Проверьте этот результат с помощью ареометра. Поместите большой образец жидкости в высокий градуировать и медленно опускать в него ареометр, пока он не начнет свободно плавать. Считайте ареометр накипь на уровне жидкости. Ареометры часто имеют странные шкалы для специального использования, поэтому вы должны определить, какой из них представляет удельный вес.Многие ареометры производятся в Европа, и они часто используют запятую для десятичной точки. (6) Возьмите прямоугольный деревянный брусок. Взвесьте его и измерьте его размеры, тем самым вычисляя его объем и плотность напрямую. Предсказать , какая часть его объема будет быть ниже уровня воды, если бы он находился на воде (снова воспользуйтесь принципом Архимеда). Проверьте свои прогноз. (7) Имеется большой резервуар с водой. Предскажите , сколько веса вы могли бы положите на деревянный брусок, прежде чем он утонет.Проверьте свой прогноз.
(8) Основной метод погружения (процедуры 3 и 4) прост для измерения плотность предметов тяжелее воды. Но объекты легче воды будут плавать. Просто требуется изменение процедуры. Найдите пробку или кусок дерева для использования в качестве «неизвестного» твердого тела. Сначала взвесьте его насухо.Получать металлический груз с крючком (возможно, свинцовое грузило). Подвесьте пробку на веревочке (как вы это делали в процедуре 3 или 4) и повесьте груз чуть ниже него. Теперь сделайте два измерения с вашими весами, один с только свинцовым грузом под водой, а другой со свинцом и пробкой под водой. Разница в весе – это подъемная сила на пробке. Этот метод, очевидно, работает с экспериментальной установкой или (из процедура 3 или 4), а металлический груз просто служит для удержания пробки под водой.Мы не нужно что-нибудь знать о весе металлического грузила. (9) Если у вас останется время, вы, возможно, захотите изучить некоторые методы манометра для сравнение плотностей жидкостей. 6. ЧТО СЛЕДУЕТ ДУМАТЬ: (1) Во многих книгах принцип Архимеда формулируется следующим образом: «Подъемная сила на теле это потеря веса тела при погружении в жидкость ». Теперь фраза «потеря веса» должна вас немного беспокоить.Если вес определяется как ” сила, действующая на объект под действием силы тяжести, “тогда тело не” теряет “вес при погружении, сила тяжести на нем одинакова, независимо от того, находится ли он в воздухе, в жидкости или просто сидит на столе. Так что означает под «потерей веса»? Возможно, приведенное выше утверждение Принцип Архимеда предполагает, что мы используем (стандартный) метод процедуры (4). Там мы «взвешиваем» объект в воздухе, затем «взвешиваем» его в жидкости и берем разницу в «весах». по шкале весов .Но второе показание шкалы – это не “вес” по обычное определение, это просто натяжение струны, поддерживающей тело. Различия в этих двух натяжений – подъемная сила. Поскольку мы обычно относимся к любому чтению от весов как «показание веса», что может объяснить это странное утверждение Принцип Архимеда. Некоторые авторы предложили, чтобы мы определяли вес по-другому. Они предполагают: «вес» – это сила, необходимая для поддержки покоящегося объекта в его раме. ссылка.”При таком определении вес предмета, лежащего на столе, как и прежде, составляет мг. «Вес» нашего объекта, погруженного в жидкость, – это просто натяжение поддерживающей струны, согласованное с изложением принципа Архимеда выше. “Вес” космонавта на орбите космический шаттл равен нулю. Астронавт падает так же быстро, как его космическая капсула, и нет сила опоры требуется для удержания космонавта в состоянии покоя относительно космоса шаттл системы отсчета. (2) Вы, наверное, заметили, что все методы, использующие принцип Архимеда с весы требовали вычитания двух показаний шкалы. Балансы сравнивают силы (веса), но их весы показывают единицы массы (граммы). Если мы рассмотрим анализ Процедура (4) мы видим, что это не имеет значения.
Но принцип Архимеда говорит нам, что: B = ρ 2 Vg T 1 – T 2 = ρ w Vg T 2 ρ с Vg r с ——————— = ———— = —— = с с T 1 - T 2 ρ w Vg r w Таким образом, удельный вес образца зависит от напряжений T2 и T1 поддерживающая струна.Шкала баланса напрямую считывает эти напряжения. Но поскольку наша формула имеет коэффициент напряжений , они могут быть измерены в любых согласованных единиц “даже в” граммах “. 7. ВОПРОСЫ, НА КОТОРЫЕ НЕОБХОДИМО ОТВЕТИТЬ ПЕРЕД ПРИХОДОМ В ЛАБОРАТОРИЮ: (Инструктор проверит эти ответы, прежде чем вы сможете начать эксперимент.) (1) Выведите уравнение для удельного веса, определенного методом Процедуры (4).Составьте уравнение распространения случайной ошибки. Используйте это, чтобы определить, сколько граммов потребуется образец латуни для получения его удельного веса до 1%, если весы могут читать с точностью до 0,1 грамма. (2) На весах в ванной стоит ведро с водой. Показания шкалы записываются. А брусок плавает на воде. Насколько меняется показание шкалы, когда блок добавлен? Теперь подумайте о том, чтобы осторожно надавить на деревянный брусок рукой, пока он не встанет. «просто» затопленный (его верхняя поверхность на уровне поверхности воды).От чего зависит ванная шкала чтения сейчас? Покажите, как можно использовать три показания шкалы для определения конкретного тяжесть дерева. 8. ВОПРОСЫ, НА КОТОРЫЕ НЕОБХОДИМО ОТВЕТИТЬ В ОТЧЕТЕ ВАШЕЙ ЛАБОРАТОРИИ: (3) Повлияет ли добавленный вес строки на результаты процедуры (4)? Будет, если повлияет результаты процедуры (3), если она не была включена в расчет? (4) Один килограмм железа и один килограмм латуни подвешены на отдельных весах. весы, каждый металл полностью погружен в воду.Как сравнивать показания весов? выражать ваш ответ как функция плотности двух материалов. (5) Две емкости для перелива заполнены разными жидкостями. Деревянный блок будет плавать в либо жидкость. Сравните объемы, которые переполняются, когда блок плавает в каждом из бидоны переполнения. Соотнесите это с плотностями жидкостей. Также сравните переполнение весит . (6) Один см 3 латуни и один см 3 алюминия каждый взвешивают в воздухе, а затем в воды.Сравните их «потерю веса». Соотнесите это с плотностями двух материалов. (7) Точность считывания шкалы ареометра определяется расстоянием между маркировка на его стебле. Чувствительность может быть увеличена, а расстояние между отметками увеличено, сделав ареометр с большей грушей и / или меньшим штоком. Объясните, почему это так. (8) Что на рисунке 3 определяет высоту c? Выразите свой ответ в виде формулы. Ввиду из этого, правильно ли нарисована фигура? (9) [MMG] Можете ли вы увидеть из своего анализа какое-либо общее соотношение, которое всегда должно существуют между плотностью плавающего тела, объемом тела, объемом, который под поверхностью и плотностью жидкости? (10) Вы использовали грузило, чтобы погрузить кусок пробки под воду, чтобы определить плотность пробки.Почему не было необходимости знать плотность грузила? (11) Дежурный в подсобном помещении предлагает вам два ареометра, подходящие для данной серии. удельного веса, который необходимо измерить. У одного стержень большего диаметра, чем у другого. Зная только этот факт, какой из двух вы выберете для наибольшей точности? (12) Используйте принцип Архимеда, чтобы доказать следующее: «Когда тело плывет на жидкость, он вытесняет массу жидкости, равную ее собственному весу. |


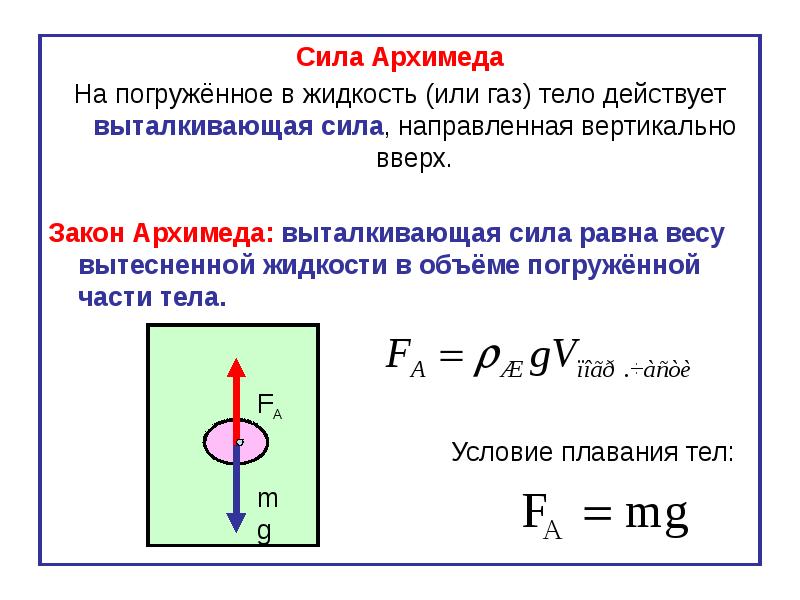 кинематич. вязкости, r и r1 плотность среды в … Физическая энциклопедия
кинематич. вязкости, r и r1 плотность среды в … Физическая энциклопедия Закон Архимеда справедлив и для газов … Энциклопедический словарь
Закон Архимеда справедлив и для газов … Энциклопедический словарь учёного Архимеда (ок. 287 212 до н. э.)] закон гидро и аэростатики. Согласно А. з., на тело, погруж. в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости (или… … Большой энциклопедический политехнический словарь
учёного Архимеда (ок. 287 212 до н. э.)] закон гидро и аэростатики. Согласно А. з., на тело, погруж. в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости (или… … Большой энциклопедический политехнический словарь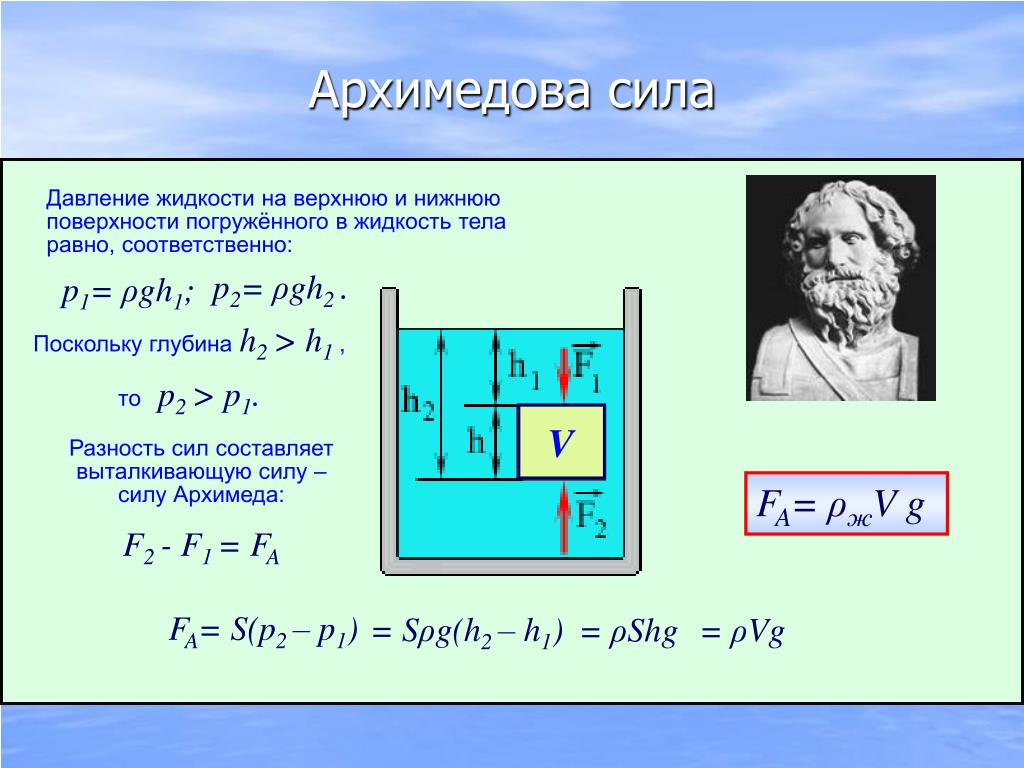 Он путешествовал
в Александрию, Египет, место великой учебы, где
он изучал работы некоторых других математиков, например
Евклид и Конон. Архимед помог своему другу королю
Hiero II, создав машины для королевской армии.В
шкив был одним из этих изобретений, но Архимед думал
изучение математики было самым важным делом
он мог сделать. Архимед написал несколько книг по математике,
в том числе на плавающих телах. Архимед умер
во время осады Сиракуз, когда он был убит
Римский солдат, несмотря на приказ, чтобы он не пострадал
Он путешествовал
в Александрию, Египет, место великой учебы, где
он изучал работы некоторых других математиков, например
Евклид и Конон. Архимед помог своему другу королю
Hiero II, создав машины для королевской армии.В
шкив был одним из этих изобретений, но Архимед думал
изучение математики было самым важным делом
он мог сделать. Архимед написал несколько книг по математике,
в том числе на плавающих телах. Архимед умер
во время осады Сиракуз, когда он был убит
Римский солдат, несмотря на приказ, чтобы он не пострадал