Закон архимеда на тело погруженное в жидкость. Закон Архимеда: определение и формула
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :
где – плотностьжидкости (газа), – ускорение свободного падения, а – объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует
заметить, что тело должно быть полностью
окружено жидкостью (либо пересекаться
с поверхностью жидкости). Так, например,
закон Архимеда нельзя применить к
кубику, который лежит на дне резервуара,
герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Для однородного тела плавающего на поверхности справедливо соотношение
где: V –
объем плавающего тела; ρ m –
плотность тела.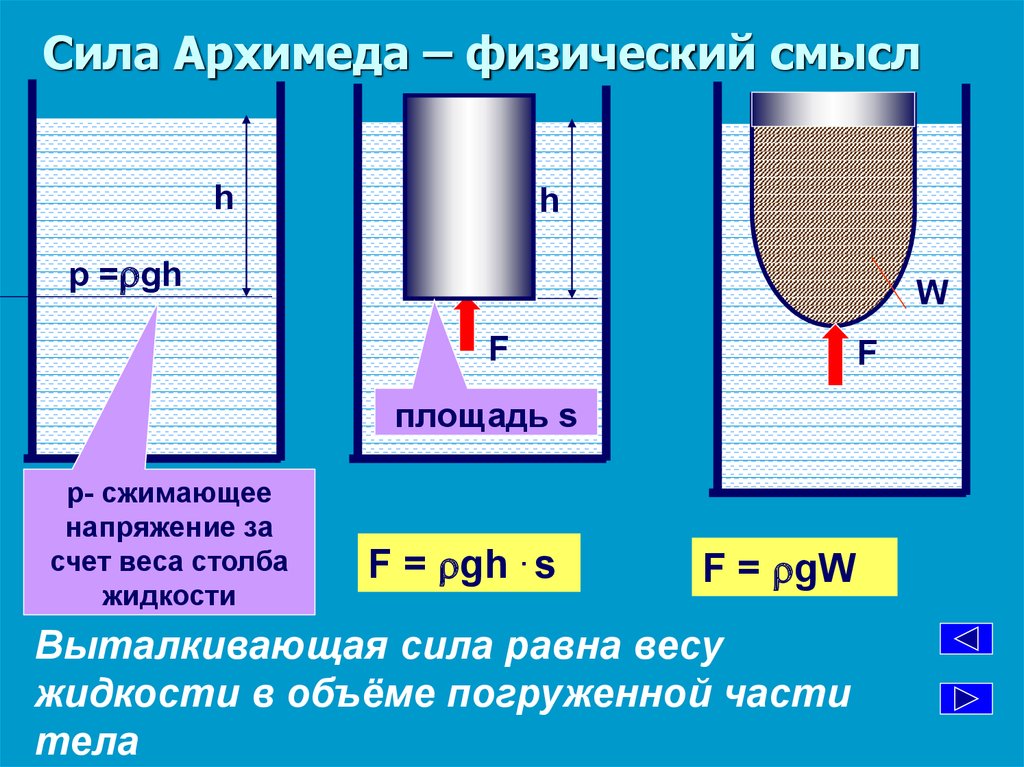
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K”L”M” , наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d” . Приложим к точке
 Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться.
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.
Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела.Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Продолжим изучение архимедовой силы. Проделаем опыты. К коромыслу весов подвесим два одинаковых шара. Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Второй опыт. Подвесим к динамометру большую картофелину. Вы видите, что её вес равен 3,5 Н. Погрузим картофелину в воду. Мы обнаружим, что её вес уменьшился и стал равен 0,5 Н.
Вычислим изменение веса картофеля:
DW = 3,5 Н – 0,5 Н = 3 Н
Почему же вес картофеля уменьшился именно на 3 Н? Очевидно потому, что в воде на картофель подействовала выталкивающая сила такой же величины. Другими словами, сила Архимеда равна изменению веса т ела:
Эта формула выражает способ измерения архимедовой силы: нужно дважды измерить вес тела и вычислить его изменение. Полученное значение равно силе Архимеда.
Для вывода следующей формулы проделаем опыт с прибором «ведёрко Архимеда». Основные его части следующие: пружина со стрелкой 1, ведёрко 2, тело 3, отливной сосуд 4, стаканчик 5.
Сначала пружину, ведёрко и тело подвешивают к штативу (рис. «а») и отмечают положение стрелки жёлтой меткой. Затем тело помещают в отливной сосуд. По мере погружения тело вытесняет некоторый объём воды , который сливается в стаканчик (рис. «б»). Вес тела становится меньше, пружина сжимается, и стрелка поднимается выше жёлтой метки.
Перельём воду, вытесненную телом, из стаканчика в ведёрко (рис. «в»). Самое удивительное в том, что когда вода будет перелита (рис «г»), стрелка не просто опустится вниз, а укажет точно на жёлтую метку! Значит, вес влитой в ведёрко воды уравновесил архимедову силу . В виде формулы этот вывод запишется так:
Обобщая результаты двух опытов, получим закон Архимеда : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объёме этого тела и направлена противоположно вектору веса.
В § 3-б мы указали, что сила Архимеда обычно направлена вверх. Поскольку она противонаправлена вектору веса, а он не всегда направлен вниз, архимедова сила также не всегда действует вверх. Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
Закон Архимеда, теория и онлайн калькуляторы
Закон Архимеда, теория и онлайн калькуляторыЕсли тело погрузить в жидкость, то на это тело со всех сторон действуют силы давления жидкости. Эти силы направлены перпендикулярно поверхности тела в каждой его точке. Если бы все силы, действующие на тело, были одинаковы по величине, то оно испытывало бы только всестороннее сжатие. Однако мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.
Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.
Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Благодаря действию силы Архимеда всплывают тела в жидкости, могут летать воздушные шары. Из-за выталкивающей силы вес каждого тела в жидкости меньше, чем в воздухе. Уменьшение веса тела произойдет, если перенести тело из вакуума в любой газ. Если вес тела в вакууме равен $P$, то его вес в жидкости или газе равен:
\[P’=P-F_A\left(1\right).\]
Формулировка закона Архимеда
Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.
Сила выталкивания не зависит от вещества, из которого состоит тело, как от него не зависит давление окружающих тело слоев жидкости. Пусть погруженное в жидкость тело состоит из этой же жидкости. Данное жидкое тело, как и другая часть окружающей его жидкости, будет находиться в равновесии. Это означает, что приложенная к нему сила Архимеда, уравновешивается силой тяжести:
Это означает, что приложенная к нему сила Архимеда, уравновешивается силой тяжести:
\[F_A=m_gg\ \left(2\right),\]
где $m_g={\rho }_gV$ – масса жидкости в объеме рассматриваемого тела; ${\rho }_g$ – плотность жидкости. Но, сила тяжести $(m_gg)$ равна весу вытесненной жидкости $P$, следовательно:
\[F_A=P\left(3\right).\]
Это означает, что выражение (2) можно переписать в виде:
\[F_A={\rho }_gV\ g\left(4\right),\]
где $V$- объем вытесненной телом жидкости. Если тело находится в жидкости целиком, то это объем тела. Если тело частично погружено в жидкость, то V – часть тела, находящаяся в жидкости.
Закон Архимеда в виде (4) выполняется и для газов.
Закон Архимеда на сегодняшний день можно формулировать так: На любое тело, которое погружено в жидкость (газ), находящуюся в состоянии равновесия, действует со стороны жидкости (газа) сила выталкивания, равная произведению плотности вещества в котором находится тело, на ускорение свободного падения и на объем погруженной части тела.
Примеры задач на закон Архимеда
Пример 1
Задание. Чему равна сила Архимеда, если тело плавает на границе раздела двух жидкостей с разными плотностями?
Решение. Если тело плавает на границе раздела двух жидкостей, имеющих разные плотности, то силу Архимеда найдем как:
\[F_A=g\left[{\rho }_1V_1+{\rho }_2V_2\right]\ ,\]
где ${\rho }_1$ – плотность первой жидкости; ${\rho }_2$ – плотность второй жидкости; $V_1$ – объем тела, находящийся в первой жидкости; $V_2$ – объем тела во второй жидкости.
Пример 2
Задание. Вес тела в воздухе равен $P_1$, его же вес в жидкости, плотность которой равна ${\rho }_g$, равен $P_2$. Какова плотность тела ($\rho $)?
Решение. Сделаем рисунок.
Вес тела по третьему закону Ньютона равен по величине силе натяжения нити и направлен в противоположную сторону: ($\overline{N}=-\overline{P}$). Сила натяжения нити на нашем рисунке обозначается буквой N. В соответствии со вторым законом Ньютона сила натяжения нити в воздухе (рис.1(а)) равна:
Сила натяжения нити на нашем рисунке обозначается буквой N. В соответствии со вторым законом Ньютона сила натяжения нити в воздухе (рис.1(а)) равна:
\[{\overline{N}}_1=-m\overline{g}\to Y:\ N_1=mg\ \to P_1=mg\left(2.1\right).\]
Запишем второй закон Ньютона для сил, которые действуют на тело во втором случае (рис.1(b)):
\[m\overline{g}+{\overline{N}}_2+{\overline{F}}_A=0\ \left(2.2\right).\]
В проекции на ось Y выражения (2.2) имеем:
\[F_A+N_2-mg=0\ \left(2.3\right).\]
Масса рассматриваемого тела равна:
\[m=\rho V\ \left(2.4\right),\]
где $V$ – объем тела. Сила Архимеда, действующая на тело (рис.1(b)):
\[F_A={\rho }_gVg\ \left(2.5\right).\]
Выразим вес тела из (2.3), учтем выражения (2.4) и (2.5):
\[N_2=\rho Vg-{\rho }_gVg=P_2\ \left(2. 6\right).\]
6\right).\]
Найдем отношение выражений (2.6) к (2.1):
\[\frac{P_2}{P_1}=\frac{\rho Vg-{\rho }_gVg\ }{\rho Vg}=1-\frac{{\rho }_g}{\rho }\left(2.7\right).\]
Из формулы (2.7) получим выражение для плотности тела:
\[\rho =\frac{{\rho }_g}{P_1-P_2}P_1.\]
Ответ. $\rho =\frac{{\rho }_g}{P_1-P_2}P_1$
Читать дальше: формула второго закона Ньютона.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Закон Архимеда для неподвижных т
Закон Архимеда для неподвижных тЗакон Архимеда для неподвижных тел
Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными
приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую
из жидкости погруженное в нее тело.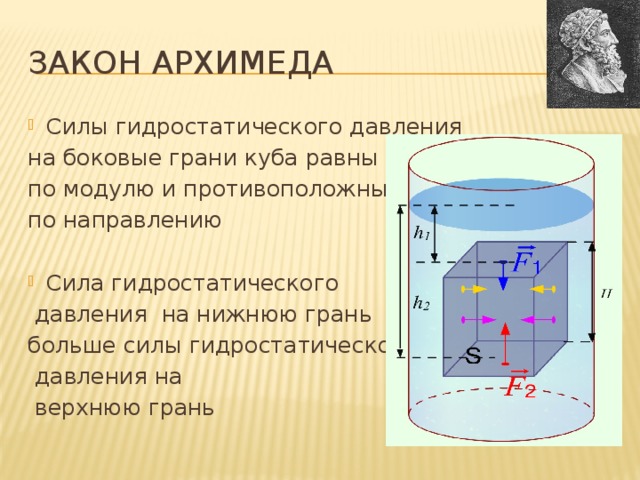
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью rдействует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (rgh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкости в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде – для тел любой формы!
Попробуем восстановить ход рассуждений Архимеда и вывести его
закон.
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести mg= Vg и сила гидростатического давления F. Выделенный объем находится в равновесии, следовательно, сила, действующих на жидкость в этом объеме, равны: F=rVg.
Отсюда следует выражение для силы гидростатического давления: F=rVg.
Мы нашли силу, действующую на поверхность жидкости,
заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с
поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное
выражение и есть “выталкивающая” сила – сила Архимеда
FАрх=rgV.
Это равенство и носит название закон Архимеда.
Сила Архимеда. Условие плавания тел.
|
1.В сосуде с водой плавает брусок из льда, на котором лежит деревянный шар. Плотность вещества шара меньше плотности воды. Изменится ли уровень воды в сосуде, если лед растает? |
|
|
2.В сосуде с водой плавает железный коробок, ко дну которого при помощи нити подвешен стальной шар. Шар не касается дна сосуда. Как изменится высота уровня воды в сосуде, если нить, удерживающая шар, оборвется? |
|
|
3.В сосуде с водой плавает деревянный диск, в центре которого укреплен шарик из свинца (см.рис.) Из-менится ли уровень воды в сосуде относительно его дна, если диск перевернуть? |
|
|
4. |
|
|
5.На левой чаше весов находится сосуд с водой, а на правой—штатив, к перекладине которого подвешено на нити какое-нибудь тело. Пока тело не погружено в воду, весы находятся в равновесии (см. рис.). Затем нить удлиняют так, что тело полностью погружается в воду (не касаясь дна сосуда). При этом равновесие весов нарушается. Какой груз и на какую чашу весов нужно положить, чтобы восстановить равновесие? |
|
Решение задачи №1
Способ №1
Вспомним условие плавание тел: вес вытесненной жидкости равен весу плавающего
тело. На основе этого в данной задаче можно утверждать, что:
На основе этого в данной задаче можно утверждать, что:
- Когда в сосуд опустили лед с шариком, уровень воды в нем поднялся на столько, чтобы вытеснялся вес воды равный весу льда и шарика.
- Вес той части воды, которая вытеснялась за счет веса льда, имеет равный ему вес.
Поэтому:
- когда лед растает, и соответствующая часть воды уже не будет вытесняться, ее место займет равное количество талой воды.
- Вода, вытесненная за счет веса шарика, останется в прежнем количестве.
Следовательно, уровень воды останется прежним
Способ №2
Рассуждаем так:
- Уровень воды в сосуде определяет давление на дно по
формуле:
p=rgh. - Давление определяет силу давления на дно сосуда по
формуле:
F=pS, где S – площадь дна сосуда.
- Сила давления на дно сосуда – это просто вес его содержимого.
Так как вес содержимого не изменился после того, как лед растаял, то сила давления на дно осталась прежней, и, следовательно, давление на дно осталось прежним, и, следовательно, уровень воды остался прежним.
Решение задачи №2
Так как тело плавает, вес вытесненной воды будет равен весу шарика с диском (условие плавания тел).
Будем считать, что при перевороте диска, свинцовый шарик продолжает плавать вместе с ним. Следовательно, вес вытесненной воды не изменится и уровень воды в сосуде тоже.
Решение задачи №3
Шар и коробок плавают вместе: они вытесняют вес воды равный сумме веса коробка и веса шара.
Коробок плавает, а шар лежит на дне: вытесняется вес воды равный весу коробка и вес воды в объеме шара.
Вес стального шара больше веса воды в объеме этого шара. Следовательно, в первом случае вытесняется больше воды, чем во втором и
уровень воды понизится.
Следовательно, в первом случае вытесняется больше воды, чем во втором и
уровень воды понизится.
Решение задачи №5
Что происходит с правой чашкой весов?
После полного погружения тела в воду, на него будет действовать выталкивающая сила (сила Архимеда) и оно станет легче на величину веса воды в объеме тела (закон Архимеда). Следовательно, вес на правой чашке на эту величину станет меньше.
Что происходит с левой чашкой весов?
Уровень воды в сосуде повысится, увеличится давление на дно, следовательно, возрастет сила давления на дно сосуда и, следовательно, вес на левой чашке возрастет.
На какую величину возрастет вес на левой чашке?
Полностью погруженное тело вытесняет вес воды в объеме тела. Легко
сообразить, что именно вытесненная вода оказывает дополнительное давление на дно
сосуда и создает дополнительный вес равный собственному весу. Следовательно, вес
на левой чашке увеличится на вес воды в объеме погруженного тела.
Следовательно, вес
на левой чашке увеличится на вес воды в объеме погруженного тела.
(К такому же выводу можно прийти и быстрее: на тело со стороны воды действует выталкивающая сила равная весу в объеме тела, но действие одного тела на другое всегда носит характер взаимодействия. Следовательно, со стороны тела на жидкость действует такая же по величине сила, направленная в противоположную сторону.)
Поэтому, чтобы уравновесить весы надо на правую чашку положить гирю, имеющую удвоенный вес воды в объеме погруженного тела.
Решение задачи №4
Так как содержимое сосуда не меняется, то остается неизменной сила давления на дно сосуда. Посчитаем силу давления на дно до того, как растаял лед:
F=pS, p=r 2gH
F=Sr 2gH (где H – уровень воды в сосуде до того, как лед растаял).
После того, как лед растает, сила давления на дно складывается из силы гидростатического давления(F1)и веса шарика, лежащего на дне (F2):
F= F1+ F2
F1= Sr
2g(H-h), уровень воды понизился на
h по условию задачи.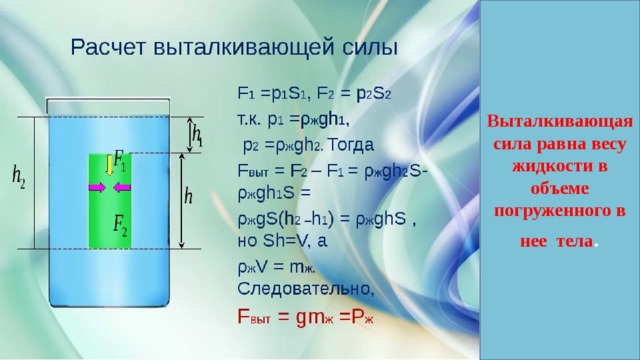
Вес шарика, полностью погруженного в воду (F2), вычисляется как разность силы тяжести (Mg=r1gVшарика) и действующей на него силы Архимеда (Fарх=r 2gVшарика), поэтому :
F2=Mg - r2gVшарика=r1gVшарика-r2gVшарика=(r1-r2)gVшарика
Но силы давления на дно до и после равны, поэтому получаем следующее уравнение:
Sr 2gH = Sr2g(H-h)+(r1-r2)gVшарика
Из этого уравнения можно легко найти объем шарика (Vшарика), а потом и его массу:
M=r1Vшарика
Некоторые формулы и законы
Запомни, пожалуйста, как связаны между собой масса (M), плотность (r )и объем (V):
M=r V, r =M/V, V=M/r
Сила тяжести
F=Mg, где g=9,8Н/кг
Вес тела
Вес тела – сила, действующая на опору или подвес. Мы ее, пока, вычисляем по
формуле:
Мы ее, пока, вычисляем по
формуле:
P=mg
Закон Архимеда (сила Архимеда)
На тело в жидкости или газе действует выталкивающая сила равная весу газа или жидкости в погруженном в жидкость или газ объеме тела.
Если жидкость (газ) одна (однородна), то формула получается такой:
F=r gV,
где V – объем части тела, погруженной в жидкость (газ).
Если тело находится на границе двух жидкостей (газов), тогда формула получается такой:
F=r 1gV1+r 2gV2,
где r 1 и V1 – плотность первой жидкости и часть объема тела, погруженного в нее, а r 2 и V2плотность второй жидкости и часть объема тела, погруженного в нее.
Подъемная сила
Подъемной силой называется равнодействующая силы Архимеда и силы тяжести,
действующих на тело. Формула получается такой:
Формула получается такой:
Fпод=Fарх - Mg
Механическая работа
Механическая работа:
A=Fs, где F- сила, s – путь в направлении действия силы
Если сила противоположна перемещению тела, то формула будет такой:
A=-Fs
Если сила перпендикулярна перемещению, то
A=0
К уроку
Сайт создан в системе uCoz
Давление на тело погруженное в жидкость. Выталкивающая сила
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам – очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.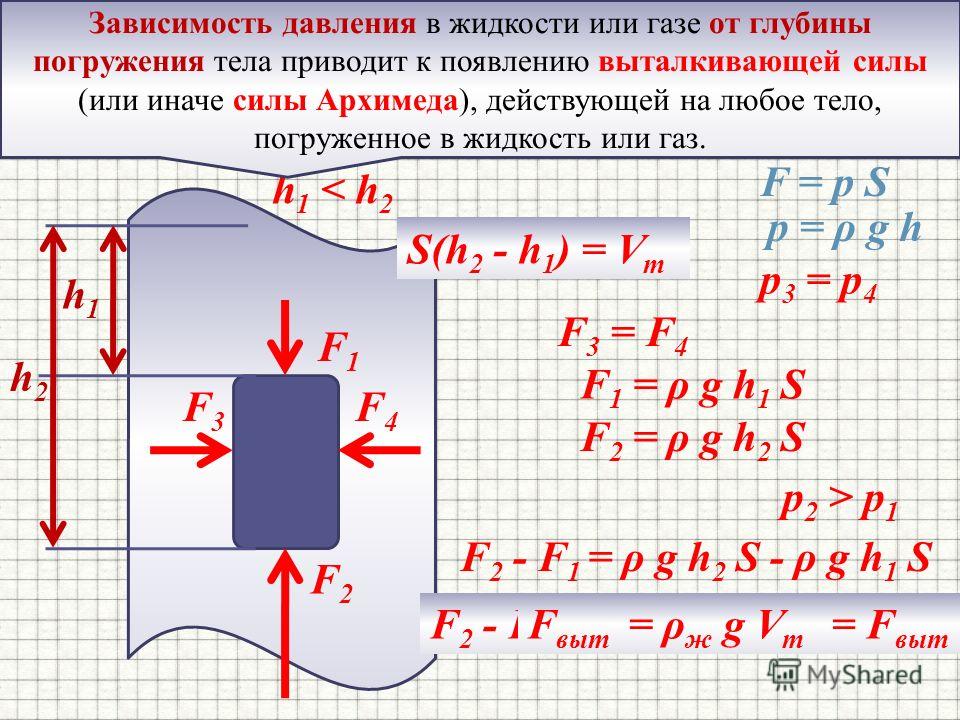
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали.
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела.
Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытесняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к нашим специалистам . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит…. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg .
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.
Наблюдая за полетом воздушных шаров и за движением кораблей по морской глади, многие люди задаются вопросом: что заставляет подниматься в небеса или держит на поверхности воды эти транспортные средства? Ответом на этот вопрос является выталкивающая сила. Рассмотрим подробнее ее в статье.
Рассмотрим подробнее ее в статье.
Текучие среды и статическое давление в них
Текучими называются два агрегатных состояния вещества: газ и жидкость. Воздействие любой касательной силы на них заставляет смещаться одни слои вещества относительно других, то есть материя начинает течь.
Жидкости и газы состоят из элементарных частиц (молекул, атомов), которые не имеют определенного положения в пространстве, как, например, у твердых тел. Они постоянно движутся в разных направлениях. В газах это хаотичное движение является более интенсивным, чем в жидкостях. Благодаря отмеченному факту текучие субстанции могут передавать оказываемое на них давление по всем направлениям одинаково
Поскольку все направления движения в пространстве являются равноправными, то суммарное давление на любой элементарный объем внутри текучего вещества равно нулю.
Ситуация в корне изменяется, если рассматриваемое вещество поместить в гравитационное поле, например, в поле тяжести Земли. В этом случае каждый слой жидкости или газа имеет некоторый вес, с которым он давит на лежащие ниже слои. Это давление называется статическим. Оно возрастает прямо пропорционально глубине h. Так, в случае жидкости с плотностью ρ l гидростатическое давление P определяется по формуле:
Это давление называется статическим. Оно возрастает прямо пропорционально глубине h. Так, в случае жидкости с плотностью ρ l гидростатическое давление P определяется по формуле:
Здесь g = 9,81 м/с 2 – ускорение свободного падения вблизи поверхности нашей планеты.
Гидростатическое давление ощущал на себе каждый человек, который хотя бы один раз нырял на несколько метров под воду.
Гидростатическое давление и закон Архимеда
Поставим следующий простой опыт. Возьмем тело правильной геометрической формы, например, куб. Пусть длина стороны куба равна a. Погрузим этот куб в воду так, что его верхняя грань окажется на глубине h. Какое давление оказывает вода на куб?
Чтобы ответить на поставленный выше вопрос, необходимо рассмотреть величину гидростатического давления, которое действует на каждую грань фигуры. Очевидно, что суммарное давление, действующее на все боковые грани, будет равно нулю (давление на левую грань будет компенсироваться давлением на правую). Гидростатическое давление на верхнюю грань будет равно:
Это давление направлено вниз. Соответствующая ему сила равна:
Соответствующая ему сила равна:
F 1 = P 1 *S = ρ l *g*h*S.
Где S – площадь квадратной грани.
Сила, связанная с гидростатическим давлением, которая действует на нижнюю грань куба, будет равна:
F 2 = ρ l *g*(h+a)*S.
Сила F 2 направлена вверх. Тогда результирующая сила будет направлена также вверх. Ее значение равно:
F = F 2 – F 1 = ρ l *g*(h+a)*S – ρ l *g*h*S = ρ l *g*a*S.
Заметим, что произведение длины ребра на площадь грани S куба – это его объем V. Этот факт позволяет переписать формулу следующим образом:
Такая формула выталкивающей силы говорит о том, что значение F не зависит от глубины погружения тела. Так как объем тела V совпадает с объемом жидкости V l , которую оно вытеснило, то можно записать:
Формулу выталкивающей силы F A принято называть математическим выражением закона Архимеда. Его впервые установил древнегреческий философ в III веке до нашей эры. Закон Архимеда принято формулировать так: если тело погружено в текучую субстанцию, то на него действует направленная вертикально вверх сила, которая равна весу вытесненной телом рассматриваемой субстанции. Выталкивающую силу также называют силой Архимеда или подъемной силой.
Закон Архимеда принято формулировать так: если тело погружено в текучую субстанцию, то на него действует направленная вертикально вверх сила, которая равна весу вытесненной телом рассматриваемой субстанции. Выталкивающую силу также называют силой Архимеда или подъемной силой.
Силы, оказывающие действие на твердое тело, погруженное в текучую субстанцию
Эти силы важно знать, чтобы ответить на вопрос, будет тело плавать или тонуть. В общем случае их всего две:
- сила тяжести или вес тела F g ;
- выталкивающая сила F A .
Если F g >F A , тогда с уверенностью можно сказать, что тело утонет. Наоборот, если F g
Подставляя формулы для названных сил в указанные неравенства, можно получить математическое условие плавания тел. Оно выглядит так:
Здесь ρ s – средняя плотность тела.
Демонстрацию действия записанного выше условия на практике провести несложно. Достаточно взять два металлических куба, один из которых сплошной, а другой – полый. Если бросить их в воду, то первый утонет, а второй будет плавать на поверхности воды.
Если бросить их в воду, то первый утонет, а второй будет плавать на поверхности воды.
Применение выталкивающей силы на практике
Все транспортные средства, которые движутся на поверхности воды или под водой, используют принцип Архимеда. Так, водоизмещение кораблей рассчитывается исходя из знания максимальной выталкивающей силы. Подводные лодки, изменяя свою среднюю плотность с помощью специальных балластных камер, могут всплывать или погружаться.
Ярким примером изменения средней плотности тела является использование человеком спасательных жилетов. Они значительно увеличивают общий объем и при этом практически не изменяют вес человека.
Подъем воздушного шара или накачанных гелием детских шариков в небе – это яркий пример действия выталкивающей архимедовой силы. Ее появление связано с разностью между плотностью горячего воздуха или газа и холодного воздуха.
Задача на вычисление архимедовой силы в воде
Полый шар полностью погружен в воду.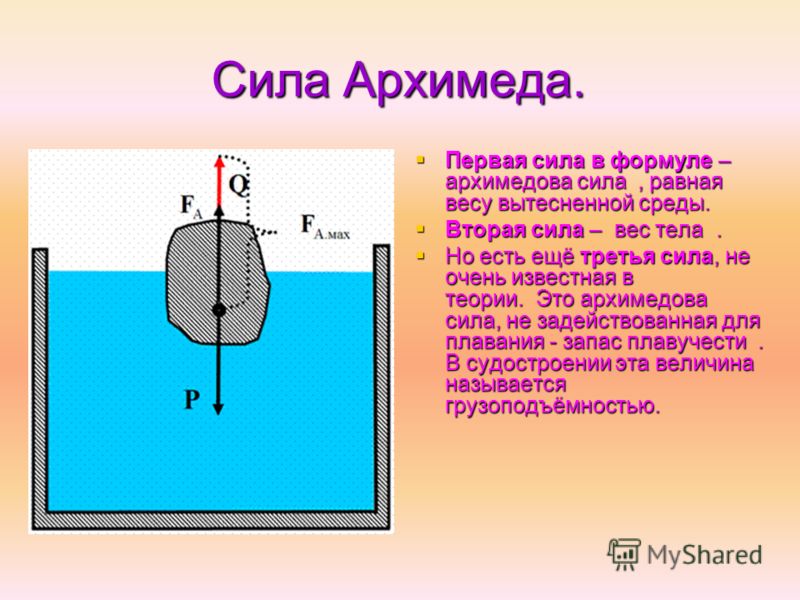 Радиус шара равен 10 см. Необходимо вычислить выталкивающую силу воды.
Радиус шара равен 10 см. Необходимо вычислить выталкивающую силу воды.
Для решения этой задачи не требуется знать, из какого материала изготовлен шар. Необходимо лишь найти его объем. Последний вычисляется по формуле:
Тогда выражение для определения архимедовой силы воды запишется в виде:
F A = 4/3*pi*r 3 *ρ l *g .
Подставляем радиус шара и плотность воды (1000 кг/м 3), получаем, что выталкивающая сила равна 41,1 Н.
Задача на сравнение архимедовых сил
Имеется два тела. Объем первого равен 200 см 3 , а второго – 170 см 3 . Первое тело погрузили в чистый этиловый спирт, а второе – в воду. Необходимо определить, одинаковы ли выталкивающие силы, действующие на эти тела.
Соответствующие архимедовы силы зависят от объема тела и от плотности жидкости. Для воды плотность равна 1000 кг/м 3 , для этилового спирта – 789 кг/м 3 . Рассчитаем выталкивающую силу в каждой жидкости, используя эти данные:
для воды: F A = 1000*170*10 -6 *9,81 ≈ 1,67 Н;
для спирта: F A = 789*200*10 -6 *9,81 ≈ 1,55 Н.
Таким образом, в воде архимедова сила оказывается на 0,12 Н больше, чем в спирте.
Несмотря на явные различия свойств жидкостей и газов, во многих случаях их поведение определяется одними и теми же параметрами и уравнениями, что позволяет использовать единый подход к изучению свойств этих веществ.
В механике газы и жидкости рассматривают как сплошные среды. Предполагается, что молекулы вещества распределены непрерывно в занимаемой ими части пространства. При этом плотность газа значительно зависит от давления, в то время как для жидкости ситуация иная. Обычно при решении задач этим фактом пренебрегают, используя обобщенное понятие несжимаемой жидкости, плотность которой равномерна и постоянна.
Определение 1
Давление определяется как нормальная сила $F$, действующая со стороны жидкости на единицу площади $S$.
$ρ = \frac{\Delta P}{\Delta S}$.
Замечание 1
Давление измеряется в паскалях. Один Па равен силе в 1 Н, действующей на единицу площади 1 кв. м.
м.
В состояние равновесия давление жидкости или газа описывается законом Паскаля, согласно которому давление на поверхность жидкости, производимое внешними силами, передается жидкостью одинаково во всех направлениях.
При механическом равновесии, давление жидкости по горизонтали всегда одинаково; следовательно, свободная поверхность статичной жидкости всегда горизонтальна (кроме случаев соприкосновения со стенками сосуда). Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.
Представим некоторый объем жидкости, ограниченный вертикальным цилиндром. Поперечное сечение столба жидкости обозначим $S$, его высоту $h$, плотность жидкости $ρ$, вес $P=ρgSh$. Тогда справедливо следующее:
$p = \frac{P}{S} = \frac{ρgSh}{S} = ρgh$,
где $p$ – давление на дно сосуда.
Отсюда следует, что давление меняется линейно, в зависимости от высоты. При этом $ρgh$ – гидростатическое давление, изменением которого и объясняется возникновение силы Архимеда.
Формулировка закона Архимеда
Закон Архимеда, один из основных законов гидростатики и аэростатики, гласит: на тело, погруженное в жидкость или газ, действует выталкивающая или подъемная сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Замечание 2
Возникновение Архимедовой силы связано с тем, что среда – жидкость или газ – стремится занять пространство, отнятое погруженным в нее телом; при этом тело выталкивается из среды.
Отсюда и второе название для этого явление – выталкивающая или гидростатическая подъемная сила.
Выталкивающая сила не зависит от формы тела, также как и от состава тела и прочих его характеристик.
Возникновение Архимедовой силы обусловлено разностью давления среды на разных глубинах. Например, давление на нижние слои воды всегда больше, чем на верхние слои.
Проявление силы Архимеда возможно лишь при наличии тяжести. Так, например, на Луне выталкивающая сила будет в шесть раз меньше, чем на Земле для тел равных объемов.
Возникновение Силы Архимеда
Представим себе любую жидкую среду, например, обычную воду. Мысленно выделим произвольный объем воды замкнутой поверхностью $S$. Поскольку вся жидкость по условию находится в механическом равновесии, выделенный нами объем также статичен. Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.
Теперь обозначим, что вместо этой условного ограниченной жидкости в среду было помещено любое твердое тело соответствующего объема. 2$.
2$.
Выталкивающая сила, действующая на тело, противоположна по направлению силе тяжести, поэтому поведение погруженного тела в среде зависит от соотношения модулей силы тяжести $F_T$ и Архимедовой силы $F_A$. Здесь возможны три случая:
- $F_T$ > $F_A$. Сила тяжести превышает выталкивающую силу, следовательно, тело тонет/падает;
- $F_T$ = $F_A$. Сила тяжести уравнивается с выталкивающей силой, поэтому тело «зависает» в жидкости;
- $F_T$
К чему приложена сила архимеда. Выталкивающая сила
F A = ρ g V , {\displaystyle F_{A}=\rho gV,}Описание
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести , прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление
p
{\displaystyle p}
на глубине
h
{\displaystyle h}
, оказываемое жидкостью плотностью
ρ
{\displaystyle \rho }
на тело, есть
p
=
ρ
g
h
{\displaystyle p=\rho gh}
. Пусть плотность жидкости (
ρ
{\displaystyle \rho }
) и напряжённость гравитационного поля (
g
{\displaystyle g}
) – постоянные величины, а
h
{\displaystyle h}
– параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS}
. На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. {**}grad(h)=\nabla h={\vec {e}}_{z}.}
{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Замечание . Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погруженного тела на жидкость, приводит к изменению ее потенциальной энергии:
A = F Δ h = m ж g Δ h = Δ E p {\displaystyle \ A=F\Delta h=m_{\text{ж}}g\Delta h=\Delta E_{p}}
где m ж − {\displaystyle m_{\text{ж}}-} масса вытесненной части жидкости, Δ h {\displaystyle \Delta h} – перемещение ее центра масс. Отсюда модуль вытесняющей силы:
F = m ж g {\displaystyle \ F=m_{\text{ж}}g}
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит…. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg .
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.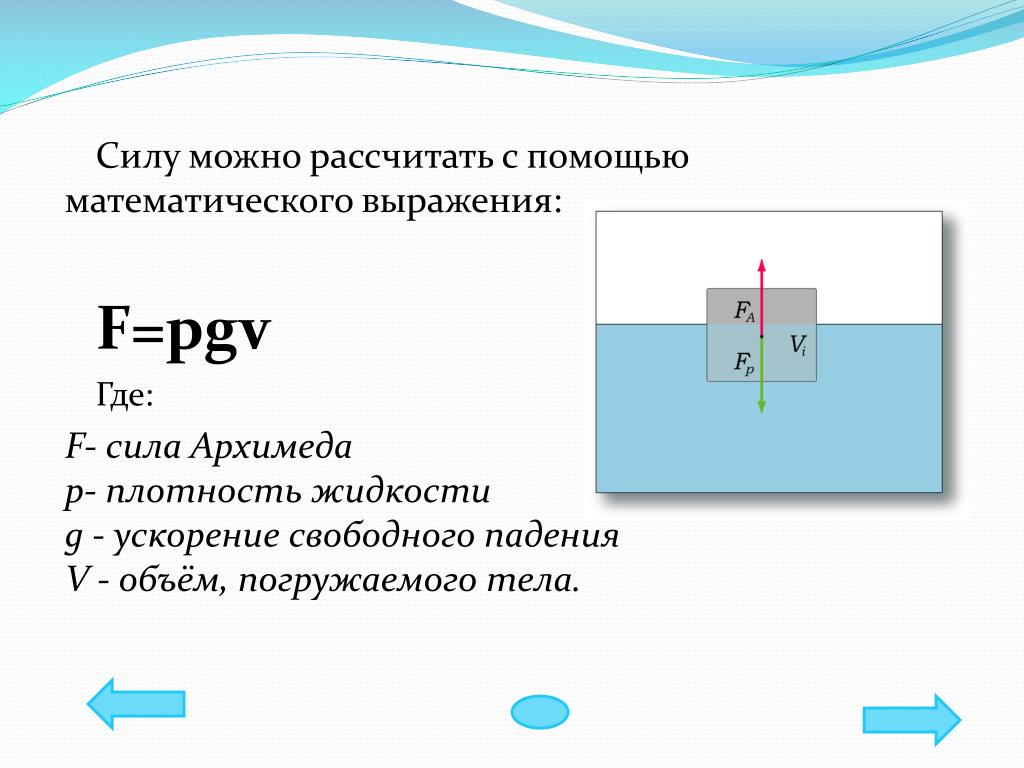
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.
На поверхность твердого тела, погруженного в жидкость, действуют, как мы знаем, силы давления. Так как давление увеличивается с глубиной погружения, то силы давления, действующие на нижнюю часть тела и направленные вверх, больше, чем силы, действующие на верхнюю его часть и направленные вниз, и мы можем ожидать, что равнодействующая сил давления будет направлена вверх. Опыт подтверждает это предположение.
Рис. 258. Если груз погружен в воду, показание динамометра уменьшается
Рис. 259. Пробка, погруженная в воду, натягивает нитку
Если,
например, гирю, подвешенную к крючку динамометра, опустить в воду, то показание
динамометра уменьшится (рис. 258).
258).
Равнодействующая сил давления на тело, погруженное в жидкость, называется выталкивающей силой. Выталкивающая сила может быть больше силы тяжести, действующей на тело; например, кусок пробки, привязанный к дну сосуда, наполненного водой, стремясь всплыть, натягивает нитку (рис. 259). Выталкивающая сила возникает и в случае частичного погружения тела. Кусок дерева, плавающий на поверхности воды, не тонет именно благодаря наличию выталкивающей силы, направленной вверх.
Если тело, погруженное в жидкость, предоставить самому себе, то оно тонет, остается в равновесии или всплывает на поверхность жидкости в зависимости от того, меньше ли выталкивающая сила силы тяжести, действующей на тело, равна ей или больше ее. Выталкивающая сила зависит от рода жидкости, в которую, погружено тело. Например, кусок железа тонет в воде, но плавает в ртути; значит, в воде выталкивающая сила, действующая на этот кусок меньше, а в ртути – больше силы тяжести.
Найдем
выталкивающую силу, действующую на твердое тело, погруженное в жидкость.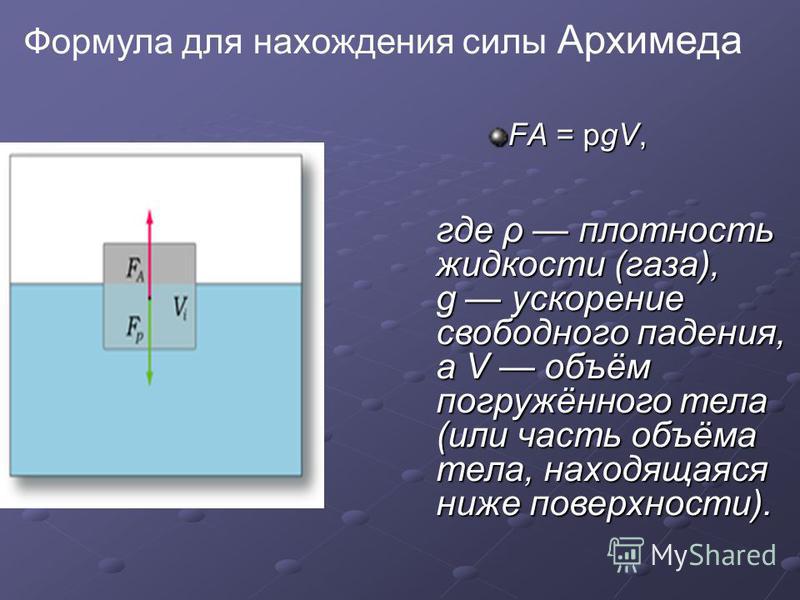
Рис. 260. а) Тело находится в жидкости, б) Тело заменено жидкостью
Выталкивающая
сила, действующая на тело (рис. 260 а), есть равнодействующая сил давления
жидкости на его поверхность. Представим себе, что тело удалено и его место
занято той же жидкостью (рис. 260, б). Давление на поверхность такого мысленно
выделенного объёма будет таким же, каким было давление на поверхность самого тела.
Значит, и равнодействующая сила давления на тело (выталкивающая сила) равна
равнодействующей сил давления на выделенный объем жидкости. Но выделенный объем
жидкости находится в равновесии. Силы, действующие на него, – это сила тяжести и выталкивающая
сила (рис.
261, а). Значит, выталкивающая сила равна по модулю силе тяжести, действующей
на выделенный объем жидкости, и направлена вверх. Точкой приложения этой силы
должен быть центр тяжести выделенного объема. В противном случае равновесие
нарушилось бы, так как сила тяжести и выталкивающая сила образовали бы пару сил
(рис. 261, б). Но, как уже сказано, выталкивающая сила для выделенного объема
совпадает с выталкивающей силой тела. Мы приходим, таким образом, к закону
Архимеда:
Но, как уже сказано, выталкивающая сила для выделенного объема
совпадает с выталкивающей силой тела. Мы приходим, таким образом, к закону
Архимеда:
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю силе тяжести, действующей на жидкость в объеме, занимаемом телом (вытесненный объем), направлена вертикально вверх и приложена в центре тяжести этого объема. Центр тяжести вытесненного объема называют центром давления.
Рис. 261. а) Равнодействующая сил давления на поверхность погруженного тела равна силе тяжести, действующей на жидкость, объем которой равен объему тела, б) Если бы точка приложения равнодействующей силы не совпадала с центром тяжести вытесненного объема жидкости, то получилась бы пара сил и равновесие этого объема было бы невозможным
Для
тела, имеющего простую форму, можно вычислить выталкивающую силу, рассмотрев
силы давления на его поверхность. Пусть, например, тело, погруженное в
жидкость, имеет форму прямого параллелепипеда и расположено так, что две его
противолежащие грани горизонтальны (рис. 262). Площадь его основания обозначим
через ,
высоту – через ,
а расстояние от поверхности до верхней грани – через .
262). Площадь его основания обозначим
через ,
высоту – через ,
а расстояние от поверхности до верхней грани – через .
Равнодействующая сил давления жидкости составляется из сил давления на боковую поверхность параллелепипеда и на его основания. Силы действующие на боковые грани, взаимно уничтожаются, так как для противолежащих граней силы давления равны по модулю и противоположны по направлению. Давление на верхнее основание равно , на нижнее основание равно . Следовательно, силы давления на верхнее и на нижнее основания равны соответственно
причем сила направлена вниз, а сила – вверх. Таким образом, равнодействующая всех сил давления на поверхность параллелепипеда (выталкивающая сила) равна разности модулей сил и :
и направлена вертикально вверх. Но – это объем параллелепипеда, а – масса вытесненной телом жидкости. Значит, выталкивающая сила действительно равна по модулю силе тяжести, действующей на вытесненный объем жидкости.
Рис. 262. К вычислению выталкивающей силы
Рис. 263.
Опытная проверка закона Архимеда при помощи «ведерка Архимеда»
263.
Опытная проверка закона Архимеда при помощи «ведерка Архимеда»
Если тело, подвешенное к чашке весов, погрузить в жидкость, то весы показывают разность между весом тела и выталкивающей силой, т. е. весом вытесненной жидкости. Поэтому закону Архимеда придают иногда следующую формулировку: тело, погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость.
Для иллюстрации справедливости этого вывода сделаем следующий опыт (рис. 263): пустое ведерко («ведерко Архимеда») и сплошной цилиндр , имеющий объем, в точности равный вместимости ведерка, подвесим к динамометру. Затем, подставив сосуд с водой, погрузим цилиндр в воду; равновесие нарушится, и растяжение динамометра уменьшится. Если теперь наполнить ведерко водой, то динамометр снова растянется до прежней длины. Потеря в весе цилиндра как раз равна весу воды в объеме цилиндра.
По
закону равенства действия и противодействия выталкивающей силе, с которой жидкость
действует на погруженное тело, соответствует сила, с которой тело действует на
жидкость. Эта сила направлена вертикально вниз и равна весу жидкости,
вытесненной телом. Следующий опыт демонстрирует сказанное (рис. 264). Неполный
стакан с водой уравновешивают на весах. Затем в стакан погружают тело,
подвешенное на штативе; при этом чашка со стаканом опускается, и для
восстановления равновесия приходится добавить на другую чашку гирю, вес которой
равен весу воды, вытесненной телом.
Эта сила направлена вертикально вниз и равна весу жидкости,
вытесненной телом. Следующий опыт демонстрирует сказанное (рис. 264). Неполный
стакан с водой уравновешивают на весах. Затем в стакан погружают тело,
подвешенное на штативе; при этом чашка со стаканом опускается, и для
восстановления равновесия приходится добавить на другую чашку гирю, вес которой
равен весу воды, вытесненной телом.
Рис. 264. Вес гири, которую нужно положить на левую чашку весов, равен весу воды, вытесненной телом
160.1. Найдите выталкивающую силу, действующую на погруженный в воду камень массы 3 кг, если его плотность равна .
160.2. Куб с ребром 100 мм погружен в сосуд, наполненный водой, поверх которой налит керосин так, что линия раздела обеих жидкостей проходит посередине ребра куба. Найдите выталкивающую силу, действующую на куб. Плотность керосина равна .
160.3 . Кусок пробки массы 10 г, обмотанный медной
проволокой с поперечным сечением , остается в равновесии в воде, не
погружаясь и не всплывая (табл. 1). Найдите длину проволоки.
1). Найдите длину проволоки.
160.4. Что произойдет с весами, находящимися в равновесии, если в стакане с водой, стоящий на чашке весов, погрузить палец, не прикасаясь пальцем ни к дну, ни к стенкам стакана?
160.5. К чашкам весов подвешены на нитках кусок меди и кусок железа массы 500 г каждый (табл. 1). Нарушится ли равновесие, если медь погрузить в воду, а железо – в керосин плотности . Гирю какой массы и на какую чашку весов нужно поставить, чтобы восстановить равновесие?
В воде некоторые тела не тонут. Если попытаться их силой переместить в толщу воды, то они все-равно всплывут на поверхность. Другие тела погружаются в воду, но почему-то становятся легче.
В воздухе на тела действует сила тяжести. Она никуда не девается и в воде, оставаясь прежней. Но если кажется, что вес тела уменьшается, значит силе тяжести противодействует, то есть действует в противоположном направлении, еще какая-то сила. Это выталкивающая сила , или архимедова сила (сила Архимеда ).
Выталкивающая сила возникает в любой жидкой или газовой среде. Однако в газах она намного меньше, чем в жидкостях, так как их плотность намного меньше. Поэтому при решении ряда задач выталкивающую силу газов не учитывают.
Что создает выталкивающую силу? В воде есть давление, которое создает силу давления воды. Именно эта сила давления воды создает выталкивающую силу. Когда тело погружено в воду, на него со всех сторон, перпендикулярно поверхностям тела, действуют силы давления воды. Равнодействующая всех этих сил давления воды создает выталкивающую силу для определенного тела.
Равнодействующая сил давления воды оказывается направленной вверх. Почему? Как известно, давление воды с глубиной увеличивается. Поэтому на нижнюю поверхность тела будет действовать сила давления воды по величине больше, чем сила, действующая на верхнюю поверхность (если тело полностью погружено в воду).
Так как силы направлены перпендикулярно поверхности, то та, что действует снизу направлена вверх, а та, что действует сверху, направлена вниз. Но действующая снизу сила больше по модулю (по числовому значению). Поэтому равнодействующая сил давления воды направлена вверх, создавая выталкивающую силу воды.
Но действующая снизу сила больше по модулю (по числовому значению). Поэтому равнодействующая сил давления воды направлена вверх, создавая выталкивающую силу воды.
Силы давления, действующие на боковые стороны тела обычно уравновешивают друг друга. Например, та, что действует справа, уравновешивается той, что действует слева. Поэтому эти силы можно не учитывать при расчете выталкивающей силы.
Однако, когда тело плавает на поверхности, то на него действует только сила давления воды снизу. Сверху силы давления воды нет. В данном случае вес тела на поверхности воды оказывается меньше, чем выталкивающая сила. Поэтому тело не погружается в воду.
Если же тело тонет, то есть опускается на дно, то это значит, что его вес оказывается больше выталкивающей силы.
Когда тело полностью погружено в воду, то увеличивается ли выталкивающая сила в зависимости от того, как глубоко погружено тело? Нет, не увеличивается. Ведь вместе с увеличивающейся силой давления на нижнюю поверхность, увеличивается сила давления на верхнюю. Разница между верхним и нижним давлением всегда определяется высотой тела. Высота тела с глубиной не меняется.
Разница между верхним и нижним давлением всегда определяется высотой тела. Высота тела с глубиной не меняется.
Выталкивающая сила, действующая на определенное тело в определенной жидкости, зависит от плотности жидкости и объема тела. При этом объем тела при погружении в жидкость вытесняет равный ему объем воды. Поэтому, можно сказать, что выталкивающая сила определенной жидкости зависти от ее плотности и вытесняемого телом ее объема.
Тема 8. ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
Сплошной считается среда, для которой характерно равномерное распределение вещества – т.е. среда с одинаковой плотностью. Таковыми являются жидкости и газы.
Поэтому в этом разделе мы рассмотрим основные законы, которые выполняются в этих средах.
СТАТИКА ЖИДКОСТЕЙ
ЗАКОН АРХИМЕДА
Рассмотрим рисунок 1, на котором изображен сосуд с водой, в который погружено некое тело произвольной формы. В процессе погружения очевидно, что
Рис. 1 уровень воды поднимается, т. е. тело
е. тело
вымещает определенное количество
Воды. Понятно также, что это количество
Vт воды равно объему погруженного тела.
С На это тело действует в данных
А условиях действует 2 силы:
1). Сила тяжести F т, которая направлена
вертикально вниз и приложена к
Точке С, которая называется центром
тяжести тела.
2). Некая сила, которая направлена вертикально вверх и приложена к точке А, которая называется центром плавучести тела. Эта сила была обнаружена и рассчитана древнегреческим математиком Архимедом, поэтому названа в его честь архимедовой силой. Архимедова сила имеет формулу:
F Α = ρ ж gV т,
где F Α – сила Архимеда, ρ ж – плотность жидкости, в которую погружено тело, g=9,8 м/с 2 V т – объем тела.
Если погруженный объем меняется, то будет меняться и выталкивающая сила, действующая на тело. Тогда последняя формула примет дифференциальный вид:
dF Α = ρ ж gdV т ,
Но что же такое центр плавучести? Это точка, которая является центром тяжести вытесненной жидкости. Т.е. если бы на месте тела была жидкость, то у этого объема жидкости был бы свой центр тяжести – в этом месте находится центр плавучести тела. Центр плавучести находится в геометрическом центре погруженного объема тела, тогда как центр тяжести не всегда находится в геометрическом центре тела, т.к. плотность внутри твердого тела может быть распределена неравномерно.
Т.е. если бы на месте тела была жидкость, то у этого объема жидкости был бы свой центр тяжести – в этом месте находится центр плавучести тела. Центр плавучести находится в геометрическом центре погруженного объема тела, тогда как центр тяжести не всегда находится в геометрическом центре тела, т.к. плотность внутри твердого тела может быть распределена неравномерно.
Итак, закон Архимеда формулируется следующим образом: На тело, погруженное в жидкость, действует сила, равная весу вытесненной жидкости и приложенная к центру плавучести тела.
Из соотношения сил, действующих на тело, погруженное в жидкость, легко получить условие плавания тел :
Если F т > F А , то тело тонет;
Если F т , то тело всплывает;
Если F т = F А , то тело плавает на том уровне, где эти силы уравнялись.
Рис. 2 Возможные направления
Из рис. 1 видно, что Архимедова сила направлена вертикально вверх. И если тело со всех сторон омывается жидкостью, то F А имеет именно такое направление. Но, в случае, когда между телом и дном нет водной прослойки( т.е. тело плотно лежит на дне– см. рис.2), то Архимедова сила направлена перпендикулярно поверхности дна .
И если тело со всех сторон омывается жидкостью, то F А имеет именно такое направление. Но, в случае, когда между телом и дном нет водной прослойки( т.е. тело плотно лежит на дне– см. рис.2), то Архимедова сила направлена перпендикулярно поверхности дна .
На рис.3 изображен опыт, подтверждающий выше
Рис. 3 упомянутое утверждение. Дно стеклянного сосуда
покрыто тонким слоем парафина. На него кладут
кусок парафина с гладким основанием и осторожно
наливают в сосуд воду. Кусок парафина не
всплывает на поверхность воды, хотя плотность
его меньше плотности воды. Слегка наклоняя сосуд,
можно заставить кусок парафина передвигаться по
дну, но он не всплывает. Но если наклонить кусок парафина так, чтобы вода проникла под его нижнюю поверхность, то выталкивающая сила заставит парафин всплывать вертикально вверх. Известно, что подводная лодка, легшая на мягкий грунт, иногда не может оторваться от него, даже полностью высвободив свои балластные отсеки от воды. Это также объясняется тем, что вода не может проникнуть под корпус лодки, плотно прилегшему к грунту.
Это также объясняется тем, что вода не может проникнуть под корпус лодки, плотно прилегшему к грунту.
Архимедова сила. 7 класс. Физика. – Объяснение нового материала.
Комментарии преподавателяСИЛА АРХИМЕДА
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы (или иначе силы Архимеда ), действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме. Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
ИНТЕРЕСНО, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Мы уже знаем, что сила Архимеда — это равнодействующая сил давления жидкости на все участки тела. На рис. 1, а схематически изображены силы, действующие на участки одинаковой площади для тела произвольной формы. С увеличением глубины эти силы увеличиваются — поэтому равнодействующая всех сил давления и направлена вверх.
Рис.1. К доказательству закона Архимеда для тела произвольной формы
Заменим теперь мысленно погруженное в жидкость тело этой же жидкостью, которая «отвердела», сохранив свою плотность (рис. 1, б). На это «тело» будет действовать такая же сила Архимеда, что и на данное тело: ведь поверхность этого «тела» совпадает с поверхностью выделенного объема жидкости, а силы давления на различные участки поверхности остались такими же.
Выделенный объем жидкости, «плавая» внутри той же жидкости, находится в равновесии. Значит, действующие на него сила тяжести Fт и сила Архимеда FA уравновешивают друг друга, то есть равны по модулю и направлены противоположно (рис. 1, в). Для покоящегося тела сила тяжести равна весу — значит, сила Архимеда равна весу выделенного объема жидкости. А это и есть объем погруженной части тела: ведь именно его мы мысленно заменяли жидкостью.
Итак, мы доказали, что на тело произвольной формы действует сила Архимеда, равная по модулю весу жидкости в объеме, занятом телом.
Проведенное доказательство — пример мысленного эксперимента. Это излюбленный прием рассуждений многих ученых. Особенно любил мысленные эксперименты Галилей. Но выводы, полученные в результате мысленного эксперимента, надо обязательно проверить на настоящем эксперименте: ведь при рассуждениях и допущениях, неизбежных в любом мысленном эксперименте, можно допустить ошибку. Поэтому мы не ограничимся приведенным теоретическим доказательством закона Архимеда и проверим его на столь же красивом опыте.
Поставим опыт
Подвесим к пружине пустое ведерко (его называют ведерком Архимеда), а к нему — небольшой камень произвольной формы (рис.2,а). Отметим удлинение пружины и подставим под камень сосуд, в который налита вода до уровня отливной трубки (рис.2,б). При полном погружении камня вытесненная им вода выльется по отливной трубке в стакан. Мы заметим, что удлинение пружины, благодаря действию выталкивающей силы, уменьшилось.
Рис. 2. Опыт показывает, что сила Архимеда равна весу воды, вытесненной телом
Выльем теперь вытесненную камнем воду из стакана в ведерко Архимеда — этим мы добавим к весу камня как раз вес вытесненной им воды. И мы увидим, что удлинение пружины стало таким же, каким оно было до погружения камня в воду (рис. 2, в). Значит, сила Архимеда действительно равна по модулю весу вытесненной камнем воды!
Если мы повторим опыт, погрузив камень в воду лишь частично, то увидим, что и в этом случае сила Архимеда равна по модулю весу вытесненной камнем воды.
Задание 1. Ответь на вопросы.
- Сформулируйте закон Архимеда.
- Какова природа силы Архимеда?
- Действует ли сила Архимеда на тело, которое тонет в воде? Если да, то почему тогда тело тонет?
- Плотность тела определяется взвешиванием его в воздухе и в воде. При погружении небольшого тела в воду на его поверхности удерживаются пузырьки воздуха, из-за которых получается ошибка в определении плотности. Больше или меньше получается при этом значение плотности?
- Какое заключение можно сделать о величине архимедовой силы, проводя соответствующие опыты на Луне, где сила тяжести в шесть раз меньше, чем на Земле?
Задание 2. Реши ребус.
К занятию прикреплен файл «Это интересно!». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
http://www.tepka.ru/fizika_7 , http://class-fizika. narod.ru
narod.ru
Закон Архимеда для тела, погруженного в жидкость. Закон Архимеда: определение и формула
Закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа), вытесненной этим телом. Сила называется силой Архимеда :
где – плотность жидкости (газа), – ускорение свободного падения, – объем погруженного тела (или часть объема тела ниже уровня воды). поверхность). Если тело плавает на поверхности или движется равномерно вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по абсолютной величине (и противоположна по направлению) силе тяжести, действующей на объем жидкости (газа). вытесняется телом и приложена к центру тяжести этого объема.
Тело всплывает, если сила Архимеда уравновешивает силу тяжести тела.
Следует отметить, что тело должно быть полностью окружено жидкостью (или пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубу, который лежит на дне бака, герметично касаясь дна.
Что касается тела, находящегося в газе, например, в воздухе, то для нахождения подъемной силы необходимо плотность жидкости заменить плотностью газа. Например, воздушный шар с гелием летит вверх из-за того, что плотность гелия меньше плотности воздуха.
Закон Архимеда можно объяснить с помощью разности гидростатических давлений на примере прямоугольного тела.
, где P A , P B – Точки давления A и B , ρ – плотность жидкости, H – Разница между уровнями между точками A и B , уровня между точками A и B , уровня. S – площадь горизонтального сечения корпуса, V – объем погруженной части корпуса.
18. Равновесие покоящегося тела в жидкости
На тело, погруженное (полностью или частично) в жидкость, действует полное давление со стороны жидкости, направленное вверх и равное весу жидкости в объеме погруженная часть тела. P ты т знак равно ρ колодец гВ захоронение
Для плавающего на поверхности однородного тела соотношение
где: V – объем плавающего тела; стр. м – плотность тела.
м – плотность тела.
Существующая теория плавающего тела достаточно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из равновесия, вновь вернуться в это состояние называется устойчивостью . Массу жидкости, взятой в объеме затопленной части корабля, называют водоизмещением , а точку приложения равнодействующего давления (т.е. центр давления) – центр смещения . В нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной линии О”-О” , представляющей собой ось симметрии судна и называемой осью плавания ( рис. 2.5).
Пусть под действием внешних сил корабль накренился на некоторый угол α, часть корабля КЛМ вышла из жидкости, а часть К”Л”М” , наоборот, погрузилась в нее При этом было получено новое положение центра смещения d” . Приложить к точке d” подъемную силу R и продолжить ее линию действия до пересечения с осью симметрии О”-О” . Полученную точку м назвали метацентром , а отрезок mC = h назвал метацентрической высотой . Считаем h положительным, если точка m лежит выше точки C , и отрицательным в противном случае.
Полученную точку м назвали метацентром , а отрезок mC = h назвал метацентрической высотой . Считаем h положительным, если точка m лежит выше точки C , и отрицательным в противном случае.
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия корабля:
1) если ч > 0, то корабль возвращается в исходное положение; 2) если ч = 0, то это случай индифферентного равновесия; 3) если ч
Следовательно, чем ниже центр тяжести и больше метацентрическая высота, тем больше остойчивость судна.
Архимед — греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед учился в Александрии (Египет), которая в то время была культурным и научным центром. Там он встретил Эратосфен — греческий математик, астроном, географ и поэт, ставший наставником Архимеда и долгое время покровительствовавший ему.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основоположником теоретической механики и гидростатики, разработал методы нахождения площадей и объемов поверхностей различных фигур и тел.
Согласно легенде, Архимеду принадлежит множество удивительных технических изобретений, снискавших ему известность среди современников. Считается, что Архимед, используя зеркала и отражая солнечные лучи, смог поджечь римский флот, осадивший Александрию. Этот случай — наглядный пример отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, строительство планетария, в котором двигались планеты. Ученый создал винт для подъема воды (винт Архимеда), который используется до сих пор и представляет собой водоподъемную машину, вал с винтовой поверхностью, расположенный в наклонной трубе, погруженной в воду. При вращении винтовая поверхность вала перемещает воду по трубе на разную высоту.
Архимед написал множество научных работ: “О спиралях”, “О коноидах и сфероидах”, “О шаре и цилиндре”, “О рычагах”, “О плавающих телах”. А в трактате «О песчинках» он подсчитал количество песчинок в объеме земного шара.
А в трактате «О песчинках» он подсчитал количество песчинок в объеме земного шара.
Архимед открыл свой знаменитый закон при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел знать, смешивали ли ювелиры золото с серебром, когда делали корону. Для этого необходимо определить не только массу, но и объем венца, чтобы рассчитать плотность металла. Определить объем изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Решение пришло в голову Архимеду, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело ученого опустили в воду. То есть объем его тела вытеснил равный объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не удосужившись одеться. Он опускал венец в воду и определял объем вытесненной жидкости. Проблема решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, то оно вытеснит объем жидкости, равный объему части тела, погруженной в жидкость. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которой оно находится.
Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которой оно находится.
Принцип Архимеда гласит, что на любое тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной им жидкости или газа.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Один из первых физических законов, изучаемых старшеклассниками. Хотя бы приблизительно этот закон помнит любой взрослый человек, как бы он ни был далек от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, о которых можно было забыть.
Что говорит закон Архимеда?
Существует легенда, что древнегреческий ученый открыл свой знаменитый закон, принимая ванну. Погрузившись в сосуд, наполненный водой до краев, Архимед заметил, что вода при этом выплеснулась наружу, – и испытал озарение, моментально сформулировав суть открытия.
Скорее всего, в действительности дело обстояло иначе, и открытию предшествовали длительные наблюдения. Но это не столь важно, ибо в любом случае Архимеду удалось открыть следующую закономерность:
Но это не столь важно, ибо в любом случае Архимеду удалось открыть следующую закономерность:
- погруженные в какую-либо жидкость тела и предметы испытывают сразу несколько разнонаправленных сил, но направленных перпендикулярно их поверхности;
- конечный вектор этих сил направлен вверх, поэтому любой предмет или тело, находясь в покоящейся жидкости, испытывает выталкивание;
- в этом случае выталкивающая сила в точности равна коэффициенту, который получится, если произведение объема предмета и плотности жидкости умножить на ускорение свободного падения.
Итак, Архимед установил, что тело, погруженное в жидкость, вытесняет такой объем жидкости, который равен объему самого тела. Если в жидкость погрузить только часть тела, то оно вытеснит жидкость, объем которой будет равен объему только той части, которая погружена.
Та же картина и с газами – только здесь объем тела надо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, выталкивающая некий предмет из жидкости или газа, в точности равна весу жидкости или газа, вытесняемого этим предметом при погружении.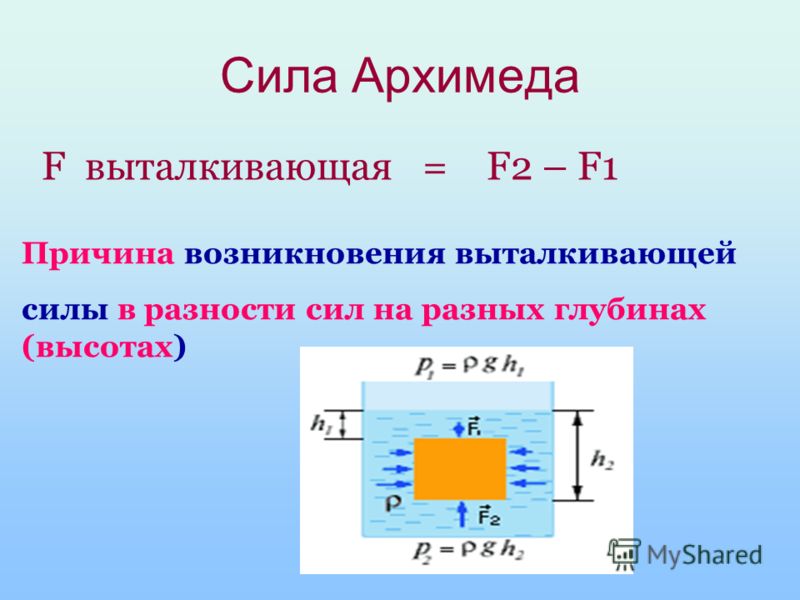
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, обнаруженная древнегреческими учеными, проста и совершенно очевидна. Но в то же время его значение для повседневной жизни трудно переоценить.
Именно благодаря знаниям об изгнании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что в их конструкции учитывается закон Архимеда и его многочисленные следствия – они построены так, что могут плавать на поверхности воды, а не тонуть. По аналогичному принципу действуют воздухоплавательные средства – они используют плавучесть воздуха, становясь как бы легче его во время полета.
Закон Архимеда — закон статики жидкостей и газов, согласно которому на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу жидкости в объеме тела.
Фон
“Эврика!” («Найден!») — такое восклицание, по легенде, издал древнегреческий ученый и философ Архимед, открывший принцип перемещения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, сделана ли его корона из чистого золота, не повредив при этом саму царскую корону. Архимеду не составило труда взвесить корону, но этого было недостаточно – необходимо было определить объем короны, чтобы вычислить плотность металла, из которого она была отлита, и определить, было ли это чистое золото . Далее, по преданию, Архимед, озабоченный мыслями о том, как определить объем венца, окунулся в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый понял, что объем его тела вытеснил равный объем воды, следовательно, корона, если ее опустить в наполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение проблемы было найдено и, по самой распространенной версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не удосужившись одеться.
Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, сделана ли его корона из чистого золота, не повредив при этом саму царскую корону. Архимеду не составило труда взвесить корону, но этого было недостаточно – необходимо было определить объем короны, чтобы вычислить плотность металла, из которого она была отлита, и определить, было ли это чистое золото . Далее, по преданию, Архимед, озабоченный мыслями о том, как определить объем венца, окунулся в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый понял, что объем его тела вытеснил равный объем воды, следовательно, корона, если ее опустить в наполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение проблемы было найдено и, по самой распространенной версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не удосужившись одеться.
Однако, что правда, то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, то оно вытеснит объем жидкости, равный объему части тела, погруженной в жидкость. Давление, которое раньше действовало на вытесняемую жидкость, теперь будет действовать и на вытеснившее ее твердое тело. А если выталкивающая сила, действующая вертикально вверх, больше силы тяжести, тянущей тело вертикально вниз, то тело будет плавать; иначе он пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Давление, которое раньше действовало на вытесняемую жидкость, теперь будет действовать и на вытеснившее ее твердое тело. А если выталкивающая сила, действующая вертикально вверх, больше силы тяжести, тянущей тело вертикально вниз, то тело будет плавать; иначе он пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярная кинетическая теория
В покоящейся жидкости давление создается ударами движущихся молекул. При вытеснении твердого тела определенного объема жидкости восходящий импульс молекулярных ударов будет приходиться не на молекулы жидкости, вытесняемые телом, а на само тело, что объясняет давление, оказываемое на него снизу и толкающее его навстречу поверхность жидкости. Если тело полностью погружено в жидкость, то на него все равно будет действовать выталкивающая сила, так как с увеличением глубины давление возрастает, и нижняя часть тела подвергается большему давлению, чем верхняя, от чего и возникает выталкивающая сила . Это объяснение выталкивающей силы на молекулярном уровне.
Это объяснение выталкивающей силы на молекулярном уровне.
Этот образец плавучести объясняет, почему корабль, сделанный из стали, которая намного плотнее воды, остается на плаву. Дело в том, что объем вытесненной кораблем воды равен объему погруженной в воду стали плюс объем воздуха, содержащегося внутри корпуса корабля ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри него, то получится, что плотность корабля (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате восходящих импульсов удара молекул воды оказывается выше силы гравитационного притяжения Земли, тянущей корабль ко дну, и корабль плывет.
Формулировки и пояснения
То, что на тело, погруженное в воду, действует определенная сила, всем хорошо известно: тяжелые тела как бы становятся легче – например, наше собственное тело при погружении в ванну. Плавая в реке или в море, можно легко поднимать и перемещать по дну очень тяжелые камни — те, которые невозможно поднять на суше. В то же время легкие тела сопротивляются погружению в воду: нужна сила и ловкость, чтобы утопить шарик размером с небольшой арбуз; шар диаметром в полметра погрузить скорее всего не получится. Интуитивно ясно, что ответ на вопрос, почему одно тело плавает (а другое тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые тонут: стальная пластина, конечно, утонет в воде, но если сделать из нее ящик, то она может плавать; при этом ее вес не изменился.
В то же время легкие тела сопротивляются погружению в воду: нужна сила и ловкость, чтобы утопить шарик размером с небольшой арбуз; шар диаметром в полметра погрузить скорее всего не получится. Интуитивно ясно, что ответ на вопрос, почему одно тело плавает (а другое тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые тонут: стальная пластина, конечно, утонет в воде, но если сделать из нее ящик, то она может плавать; при этом ее вес не изменился.
Наличие гидростатического давления приводит к тому, что на любое тело в жидкости или газе действует выталкивающая сила. Впервые величину этой силы в жидкостях экспериментально определил Архимед. Закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу количества жидкости или газа, вытесненного погруженной частью тела.
Формула
Сила Архимеда, действующая на тело, погруженное в жидкость, может быть рассчитана по формуле: F A = ρ w gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vpt – объем части тела, погруженной в жидкость.
Поведение тела в жидкости или газе зависит от соотношения модулей силы тяжести Ft и архимедовой силы FA, действующих на это тело. Возможны следующие три случая:
1) Ft > FA – тело тонет;
2) Ft = FA – тело плавает в жидкости или газе;
3) Футов
Продолжим изучение архимедовой силы. Проведем эксперименты. К бревну подвешиваем два одинаковых мяча. Их вес одинаков, поэтому коромысло уравновешено (рис. «а»). Подставьте пустой стакан под правый шар. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).
Второй опыт. Подвесим к динамометру большую картофелину. Вы видите, что его вес составляет 3,5 Н. Опустим картофель в воду. Мы обнаружим, что его вес уменьшился до 0,5 Н.
Рассчитайте изменение веса картофеля:
DW = 3,5 Н – 0,5 Н = 3 Н
Почему вес картофеля уменьшился ровно на 3 Н? Очевидно, потому что в воде на картофель действовала выталкивающая сила такой же величины. Иными словами, сила Архимеда равна изменению веса m ate:
Иными словами, сила Архимеда равна изменению веса m ate:
Эта формула выражает способ измерения архимедовой силы: нужно дважды измерить массу тела и вычислить ее изменение. Полученное значение равно силе Архимеда.
Для вывода следующей формулы проведем опыт с прибором “ковш Архимеда”. Основные его части следующие: пружина со стрелой 1, ковш 2, корпус 3, разливочный сосуд 4, стакан 5.
Сначала к треноге подвешивают пружину, ковш и корпус (рис. » а”), а положение стрелки отмечено желтой меткой. Затем тело помещают в сосуд для заливки. Когда тело тонет, оно вытесняет определенный объем воды. , который сливается в стакан (рис. «б»). Вес корпуса становится меньше, пружина сжимается, а стрелка поднимается выше желтой отметки.
Выливаем вытесненную телом воду из стакана в ведро (рис. «в»). Самое удивительное, что при наливании воды (рис. “г”) стрелка не просто пойдет вниз, а будет указывать точно на желтую метку! Значит, вес воды, налитой в ведро, уравновешивал архимедову силу . В виде формулы этот вывод запишется так:
В виде формулы этот вывод запишется так:
Суммируя результаты двух опытов, получаем закон Архимеда : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объеме этого тела и направлен против вектора весов.
В § 3-б мы указывали, что сила Архимеда обычно направлена вверх. Поскольку он противоположен вектору веса и не всегда направлен вниз, архимедова сила также не всегда действует вверх. Например, в вращающейся центрифуги в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.
Принцип Архимеда – Описание и факты
Принцип Архимеда касается силы тяги, которая была открыта и объяснена Архимедом из Греции, всемирно известным математиком. Принцип Архимеда гласит, что когда объект частично или полностью погружен в жидкость, уменьшение веса эквивалентно весу вытесненной жидкости.
Принцип Архимеда гласит, что «Выталкивающая сила, действующая на тело, погруженное в жидкость, частично или полностью погруженное, равна весу жидкости, которую тело вытесняет и действует в направлении вверх в центре масс вытесняемой жидкости».
Сила тяги прикладывается к объекту жидкостью.
Эта сила уменьшает вес объекта, погруженного в жидкость. Закон позволяет нам понять, как корабли и лодки плавают по водоемам.
Описать закон АрхимедаПредположительно, мяч погружен в банку с водой; две постоянные силы будут влиять на положение мяча.
Сила тяги толкает мяч вверх, а сила тяжести тянет мяч вниз. Если вы посмотрите на такое зрелище, вы увидите, что вес мяча из-за гравитации постоянно сталкивается с силой, создаваемой жидкостью (в данном случае водой).
Сила гравитации усиливается за счет выталкивающей силы жидкости. Здесь фактический вес объекта кажется уменьшенным.
В этом случае кажущийся вес объекта объясняется следующим образом:
Кажущийся вес = Вес объекта (мяча) в воздухе – Сила тяги (плавучесть)
Принцип Архимеда описывает, что уменьшение вес объекта эквивалентен весу жидкости, вытесненной этим объектом. Предположительно, объект обладает объемом B; он заменяет тот же объем B, когда объект погружен в жидкость.
Когда объект частично погружен в воду, он вытесняет только этот объем жидкости.
Закон плавучестиЗакон плавучести — открытие Архимеда. Принцип Архимеда также известен как физический закон плавучести. Закон плавучести гласит, что когда вы помещаете объект в какую-либо жидкость или газ, он теряет часть веса.
Когда мы находимся в воздухе, наш вес уменьшается из-за замены воздуха. В случае жидкости потеря веса объекта эквивалентна вытесненной жидкости. Согласно закону, выталкивающая сила — это то, сколько веса тело теряет в жидкости или воздухе.
Принципиальная формула Архимеда Принципиальная формула Архимеда говорит, что выталкивающая сила, действующая на тело, аналогична весу жидкости или воздуха, отводимого в сторону объектом.
Математически уравнение закона Архимеда записывается так:
Вывод закона Архимеда
В этом разделе мы обсудим вывод закона Архимеда в математических терминах. Вывод подразумевает массу вытесненной жидкости или воздуха.
Вывод подразумевает массу вытесненной жидкости или воздуха.
Масса = Плотность × Объем = p × V
P = Плотность
Плотность (p) определяется как
Плотность, p = Масса/Объем = M/V
2 902 вес вытесненной жидкости равен
Вес = масса × ускорение свободного падения
W = M × g = p × V × g
Из закона Архимеда можно написать:
Потеря вес объекта = вес вытесненной жидкости = p × V × g
Следовательно, сила тяги равна
Сила тяги = p × V × g
Здесь «P» обозначает плотность жидкости, а «V» обозначает объем вытесненной жидкости.
Применение принципа АрхимедаВ предыдущих подразделах мы узнали о местонахождении принципа Архимеда. В этом сегменте мы поговорим о нескольких применениях принципа Архимеда.
Ареометр Ареометр используется для измерения относительной плотности жидкостей. Инструмент изготовлен из свинцовой дроби. Свинцовые дроби позволяют ареометру плавать вертикально в жидкости. Чем меньше становится плотность жидкости, тем ниже опускается ареометр.
Инструмент изготовлен из свинцовой дроби. Свинцовые дроби позволяют ареометру плавать вертикально в жидкости. Чем меньше становится плотность жидкости, тем ниже опускается ареометр.
Принцип Архимеда помогает подводным лодкам всегда оставаться под водой благодаря наличию оборудования, называемого балластной цистерной. Балластная цистерна помогает воде удерживать подводную лодку. Подводная лодка может постоянно двигаться под водой, так как вес подводной лодки больше, чем выталкивающая сила внешнего водоема. Корабли плавают по воде по тому же закону Архимеда.
ЛактометрТочно так же, как и ареометр, лактометр работает так же. Лактометр был создан под руководством закона Архимеда, где равная сила веса молока вытесняется погруженной частью взвешенных веществ.
Аналогично, чем меньше плотность, тем больше тонет ареометр. Ученые изобрели лактометр для измерения уровня чистоты молока.
Воздушные шары плавают и постоянно парят в воздухе за счет выталкивающей силы.
Выталкивающая сила воздушного шара меньше, чем у наружного воздуха. Когда выталкивающая сила в воздушном шаре начинает увеличиваться, воздушный шар начинает опускаться.
Изменение количества горячего воздуха в воздушном шаре влияет на плавающий уровень воздушного шара.
Примеры принципа Архимеда:В этом разделе вам будет представлен пример принципа Архимеда с помощью математических решений.
Рассчитайте результирующую силу, если теннисный мяч с радиусом 6 см погрузить в аквариум.
Ответ: Радиус стального шара = 6 см = 0,06 м
Объем стального шара, V =4/3 πr3
V = 4/3 π 0,063
V = 9,05 × 10-4 м3
Плотность воды в бассейне, p = 1000 кг.м-3
Ускорение силы тяжести, g= 9,8 м.с-2
Теперь по формуле Архимеда,
F b = p × g × V
F b = (1000 кг. м-3) (9,8 м.с-2) (9,05 × 10-4 м3)
м-3) (9,8 м.с-2) (9,05 × 10-4 м3)
F b = 8,87 Н
В заключение,В блоге обсуждались различные аспекты Принципы Архимеда с приложениями и примерами.
Блог посвящен Закону плавучести, в частности, чтобы передать идею формулы Архимеда с большей ясностью и лучшим пониманием.
Eduauraa поможет вам разобраться в различных математических и вычислительных теориях. Если вы студент, Euauraa окажется для вас очень полезным.
Надеюсь, этот блог поможет вам ясно понять принципы Архимеда.
11.7 Принцип Архимеда – College Physics: OpenStax
Глава 11 Статика жидкости
Резюме
- Определение выталкивающей силы.
- Государственный закон Архимеда.
- Поймите, почему объекты плавают или тонут.
- Поймите взаимосвязь между плотностью и принципом Архимеда.
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой предмет в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
(См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
ВЫПЛУЧИВАЮЩАЯ СИЛА
Выталкивающая сила – это чистая направленная вверх сила, действующая на любой объект в любой жидкости.
Рис. 2. Давление из-за веса жидкости увеличивается с глубиной, так как P=hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B . (Горизонтальные силы компенсируются.)
Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рис. 3.9.0005 Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. то есть F B = w fl , формулировка закона Архимеда.
3.9.0005 Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. то есть F B = w fl , формулировка закона Архимеда.
Пространство, которое он занимает, заполнено жидкостью, имеющей вес[латекс]\boldsymbol{w _{\textbf{fl}}}.[/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/латекс]
, где [латекс]\boldsymbol{F_{\textbf{B}}}[/latex]является выталкивающей силой, а[латекс]\boldsymbol{w_{\textbf{fl}}}[/latex]является весом жидкость, вытесненная объектом. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
ПРИНЦИП АРХИМЕДА
Согласно этому принципу выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/latex]
, где[латекс]\boldsymbol{F_{\textbf{B}}}[ /latex] – выталкивающая сила, а [latex]\boldsymbol{w _{\textbf{fl}}}[/latex] – вес жидкости, вытесненной объектом.
Humm … Высокотехнологичные боди-купальники были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Бросьте кусок глины в воду. Он утонет. Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями. 93}[/latex]воды?
Стратегия для (a)
Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Решение для (a)
Сначала мы используем определение плотности [латекс]\boldsymbol{\rho=\frac{m}{V}}[/латекс], чтобы найти объем стали, а затем мы замените значения массы и плотности. Это дает 97\textbf{ N}},[/latex]что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (b)
Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды.
Решение для (b)
Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. то есть 98\textbf{ N.}} \end{array}[/latex]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, без тонет.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{V _{\textbf{sub}}}{V _{\textbf{obj}}}} [/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{V _{\textbf{fl}}}{V _{\textbf{obj}}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]\boldsymbol{V_{\textbf{fl}}}.[/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[латекс]\boldsymbol{\frac{V _{\textbf{fl}}}{V_{\textbf{obj}}}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\ жирный символ {\ гидроразрыва {m _ {\ textbf {fl}}/\ rho _ {\ textbf {fl}}} {m _ {\ textbf {obj}}/\ bar {\ rho} _ {\ textbf {obj}}}} ,[/латекс]
, где [латекс]\boldsymbol{\bar{\rho}_{\textbf{obj}}}[/latex] — средняя плотность объекта, а [латекс]\boldsymbol{\rho _{\textbf{fl}} }[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}_{\textbf{obj}}}{\rho _{\ textbf{fl}}}}.[/latex]
Рис. 4. Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
.[латекс]\boldsymbol{\textbf{удельный вес}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}}{\rho _{\textbf{w}}}}, [/латекс]
, где[латекс]\boldsymbol{\bar{\rho}}[/латекс]является средней плотностью объекта или вещества, а[латекс]\boldsymbol{\rho _{\textbf{w}}}[/латекс]является плотность воды при 4,00°С. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для [латекс]\жирныйсимвол{\ро}. [/латекс]Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
[/латекс]Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
УДЕЛЬНЫЙ ВЕС
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Рис. 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
 3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]
3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рисунок 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, что является частью определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Один из наиболее распространенных методов определения плотности показан на рис. 7.
Рис. 7. (а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
[латекс]\boldsymbol{\textbf{очевидная потеря веса}=\textbf{вес вытесненной жидкости}}[/латекс]
или
[латекс]\boldsymbol{\textbf{кажущаяся потеря массы}=\textbf{масса вытесненной жидкости.}}[/латекс]
Следующий пример иллюстрирует использование этой техники.
Пример 3. Расчет плотности: является ли монета подлинной?
Масса древнегреческой монеты определена на воздухе как 8,630 г. Когда монета погружена в воду, как показано на рисунке 7, ее кажущаяся масса составляет 7800 г. Вычислите его плотность, учитывая, что плотность воды составляет[латекс]\boldsymbol{1,000\textbf{ г/см}^3}[/латекс]и что эффекты, вызванные проволокой, подвешивающей монету, незначительны. 3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
Обсуждение
Из таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
ИССЛЕДОВАНИЯ PHET: ПЛАВУЧОСТЬ
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Рис. 8. Плавучесть- Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости. 93}?[/latex]
2: Иногда бревна плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой.
 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?3: Найдите плотность жидкости, в которой плавает ареометр с плотностью [латекс]\boldsymbol{0,750\textbf{ г/мл}}[/латекс]с [латексом]\boldsymbol{92,0\% }[/latex] его объема погружено.
93}?[/latex]5: В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и обнаруживает, что ее масса равна[latex]\boldsymbol{45.0\textbf{g}}[/latex], а видимая масса в погруженном состоянии составляет[latex]\boldsymbol{3.60\textbf {g}}[/latex](кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
6: Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
7: Принцип Архимеда можно использовать для расчета плотности как жидкости, так и твердого тела.
 Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.8: При иммерсионном измерении плотности женщины установлено, что ее масса в воздухе составляет 62,0 кг, а кажущаяся масса 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
9: Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить морской окунь массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела составляет[latex]\boldsymbol{1015\textbf{ кг/м}^3}?[/latex]
10: (a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона.
 (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.11: (a) Какова плотность женщины, плавающей в пресной воде с [латексом]\жирным символом{4,00\%}[/латекс] ее объема над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде? 93}[/latex](за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
13: Можно сделать простой компас, поместив небольшой стержневой магнит на плавающую в воде пробку. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
14: Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
15: Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама.
 С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?16: Двуспальный надувной матрас для кемпинга имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
17: По рисунку 3 докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна[латекс]\boldsymbol{F_2-F_1}[/latex]и что концы цилиндра имеют одинаковую площадь[латекс]\boldsymbol{A}.[/latex]Обратите внимание, что объем цилиндр (и вытесняемая им жидкость) равен [латекс]\boldsymbol{(h_2-h_1)A}.[/latex]
18: (a) Мужчина массой 75,0 кг плавает в пресной воде, [latex]\boldsymbol{3,00\%}[/latex] его объема над водой, когда его легкие пусты, и[latex]\boldsymbol{ 5,00\%}[/latex] его объема над водой, когда его легкие полны.
 Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
14.4 Закон Архимеда и плавучесть
Цели обучения
К концу этого раздела вы сможете:
- Давать определение выталкивающей силе
- Государственный принцип Архимеда
- Опишите связь между плотностью и принципом Архимеда
При помещении в жидкость некоторые объекты всплывают благодаря выталкивающей силе. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров ((Рисунок))?
Рис.
 14.19 (a) Даже объекты, которые тонут, например этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)
14.19 (a) Даже объекты, которые тонут, например этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. На любой объект в любой жидкости действует направленная вверх сила или выталкивающая сила ((Рисунок)). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.
 Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.Выталкивающая сила
Выталкивающая сила — это направленная вверх сила, действующая на любой объект в любой жидкости.
Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что [латекс] p=hpg [/латекс]. Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ text {B}} [/латекс]. (Горизонтальные силы компенсируются.)
Закон Архимеда
Насколько велика выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке. Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}.
 [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex] {w}_{\text{fl}}, [/latex] весу жидкости, вытесненной объектом.
[/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex] {w}_{\text{fl}}, [/latex] весу жидкости, вытесненной объектом.Закон Архимеда
Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс] {F} _ {\ text {B}} = {w} _ {\ text {fl}}, [/latex]
, где [латекс] { F}_{\text{B}} [/latex] — выталкивающая сила, а [latex] {w}_{\text{fl}} [/latex] — вес жидкости, вытесненной объектом.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. до н. э.), который сформулировал этот принцип задолго до того, как понятие силы стало общепризнанным.
Рис. 14.21 (a) На объект, погруженный в жидкость, действует выталкивающая сила [латекс] {F} _ {\ text {B}}. [/latex] Если [латекс] {F}_{\text{B}} [/латекс] больше, чем вес объекта, объект поднимается.
 Если [латекс] {F}_{\text{B}} [/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.
Если [латекс] {F}_{\text{B}} [/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.Принцип Архимеда относится к силе плавучести, которая возникает, когда тело полностью или частично погружено в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила давления внизу направлена вверх, а сила давления вверху направлена вниз; силы из-за давлений по бокам направлены внутрь тела.
Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на (рис.). Следовательно, на тело действует направленная вверх сила. Эта направленная вверх сила есть сила плавучести, или просто плавучесть .

Восклицание «Эврика» (означающее «Я нашел это») часто приписывают Архимеду, когда он сделал открытие, которое привело к принципу Архимеда. Некоторые говорят, что все началось в ванной. Чтобы прочитать историю, посетите NASA или откройте журнал Scientific American, чтобы узнать больше.
Плотность и закон Архимеда
Если вы бросите кусок глины в воду, он утонет. Но если вы слепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу, хотя ее масса одинакова. То же самое и со стальными кораблями.
Средняя плотность объекта определяет, будет ли он плавать. Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта.
 Точно так же объект, более плотный, чем жидкость, утонет.
Точно так же объект, более плотный, чем жидкость, утонет.Степень погружения плавучего объекта зависит от того, как плотность объекта соотносится с плотностью жидкости. На (Рисунок), например, незагруженный корабль имеет меньшую плотность и меньше его погружено по сравнению с тем же кораблем, когда он загружен. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \text{фракция погружена}=\frac{{V}_{\text{sub}}}{{V}_{\text{obj}}}=\frac{{V}_{\ текст{fl}}}{{V}_{\text{объект}}}. [/latex]
Погруженный объем равен объему вытесненной жидкости, которую мы называем [латекс] {V}_{fl} [/латекс]. Теперь мы можем получить соотношение между плотностями, подставив в выражение [латекс] \rho =\frac{m}{V} [/латекс]. Это дает
[латекс] \frac{{V}_{\text{fl}}}{{V}_{\text{obj}}}=\frac{{m}_{\text{fl}} \text{/}{\rho}_{\text{fl}}}{{m}_{\text{obj}}\text{/}{\rho}_{\text{obj}}}, [ /латекс]
, где [latex] {\rho }_{\text{obj}} [/latex] — средняя плотность объекта, а [latex] {\rho }_{\text{fl}} [/latex] — плотность жидкости.
 Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается[латекс] \text{фракция под водой}=\frac{{\rho} _{\text{obj} }}{{\rho}_{\text{fl}}}. [/latex]
Мы можем использовать это отношение для измерения плотности.
Рисунок 14.22 Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).
Пример
Расчет средней плотности
Предположим, что женщина весом 60,0 кг плавает в пресной воде, при этом 97,0% ее объема погружено в воду, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Плотность женщины можно найти, решив уравнение \text{fl}}} [/latex]
для плотности объекта. Это дает
[латекс] {\rho}_{\text{obj}}={\rho}_{\text{person}}=\text{(фракция погружена)}·{\rho}_{\text {фл}}. [/латекс] 9{3}}. [/latex]
Значимость
Плотность женщины меньше плотности жидкости.
 Мы ожидаем этого, потому что она плавает.
Мы ожидаем этого, потому что она плавает.Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе». ,” назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на (Рисунок).
Рисунок 14.23 (a) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости.
 Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.Все эти расчеты основаны на принципе Архимеда, согласно которому выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что погруженный в воду объект кажется менее весящим; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Резюме
- Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет.
 Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Концептуальные вопросы
Чтобы вытащить пробку из полной ванны, требуется больше усилий, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Показать решение
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ. 9{3} [/латекс]?
Показать решение
Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела.
 Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее.Показать решение
Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Объемом резины пренебречь.
Какова плотность женщины, плавающей в пресной воде с [латексом] 4,00\text{%} [/латекс] ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой.) (b) Какой процент ее объема находится над поверхностью, когда она плавает в морской воде? 9{3} [/latex] (исключая воздух в легких).
 а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
Показать решение
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
Ссылаясь на (рисунок), докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна [латекс] {F}_{2}-{F}_{1} [/латекс] и что концы цилиндра имеют равные площади[латекс] А [/латекс]. Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс] ({ч}_{2}-{ч}_{1})А [/латекс].

Показать решение
Человек массой 75,0 кг плавает в пресной воде, при этом 3,00 % его объема над водой, когда его легкие пусты, и 5,00 % его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости из-за разницы давлений на разных глубинах
ПРИНЦИП АРХИМЕДА И ЗАКОН ФЛОТАЦИИ
Принцип Архимеда и закон флотации
Закон Архимеда
Рассмотрим диаграмму ниже.
Когда кусок дерева, погруженный в жидкость, всплывает из-за выталкивающая сила или выталкивающая сила.
 Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется выше
Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется вышеПринцип Архимеда
Принцип Архимеда также называется законом плавучести , который заявить, что
” Когда тело частично или полностью погружено в жидкость он испытывает подъем, равный весу вытесненной жидкости ”
Соотношение между реальным весом и кажущимся весом
Рассмотрим диаграмму массы (веса) объекта ниже
Реальный вес – вес объекта
U = R – A
Где:
U = Аптраст или кажущаяся потеря веса
A = кажущийся вес
R = реальный вес
я.
 жидкость обычно
оказывает аптраст
жидкость обычно
оказывает аптрастII. Аптраст имеет тенденцию к уменьшить массу тела
III. 1 г воды = 0,01 н. воды
IV. 1 г воды = 1 см3 = 1 мл воды
Пример,
Данный вес тела в воздухе равен 10,10 Н веса тела, когда в воде составляет 9,2 н. Найдите аптраст.
Данные предоставлены
Реальный вес, R =10,10 Н
Кажущийся вес, А = 9,2 Н
Аптраст, U = ?
Решение
Из : U = R – A
Ш = 10,10 – 9,2
Ш = 0,9 Н
Пример,
Вес тела, полностью погруженного в жидкость, равен 4,2 Н, если вес вытесненной жидкости равен 2,5 Н.
 Найдите массу тела
в воздухе.
Найдите массу тела
в воздухе.Данные предоставлены
Кажущийся вес, А = 4,2 Н
Упор, U = 2,5 Н
Реальный вес, R = ?
Решение
Из : U = R – A – сделать тему W1
Р = У + А
R = 2,5 + 4,2
R = 6,7 Н
Пример,
Когда тело полностью погружено в воду, его вес равен записывается как 3,1 Н, если его вес в воздухе равен 4,9 Н. Найдите аптраст.
Данные предоставлены
Реальный вес, R =4,9 Н
Кажущийся вес, А = 3,1 Н
Аптраст, U = ?
Раствор
U = 1,8 Н
Пример,
Тело, погруженное в воду, вытеснило 1,1 н жидкости, если его вес белого в воде 3,3Н.
 Найдите их вес в воздухе.
Найдите их вес в воздухе.Данные предоставлены
Кажущийся вес, А = 1,1 Н
Упор, U = 3,3 Н
Реальный вес, R = ?
Решение
Из : U = R – A – сделать тему W1
Р = У + А
R = 3,3 + 1,1
R = 4,4N
Относительная плотность по закону Архимеда
Рассмотрим формулу ниже
Р.Д = msmw (Vw=Vs)
RD = Ms x gmw x g
Где:
я. mw x g = тяга вверх = У
II.
 Ms x g = реальный
вес =
Ms x g = реальный
вес =р. III. RD = относительный плотность
IV. ms = масса вещество
v. mw (vw = vw) = масса равного объема воды или масса вытесненная вода
R.D = 𝑅U
Но: U = R – A
R.D = 𝑹R−A
Пример,
Вес куска стекла в воздухе 1,2 Н и 0,7 Н в полностью погруженный в воду, рассчитайте это.
(а) Относительная плотность
(b) Плотность стекла
Данные приведены
Масса тела в воздухе, R = 1,2 Н
Масса тела в воде, А = 0,7 Н
Плотность воды, ρw = 10000 кг/м3
Относительная плотность стекла, R.
 D = ?
D = ?Плотность стекла, ρg = ?
Раствор
(а) Относительная плотность стекла, RD = ?
Из : R.D = R/(R – A) = 1,2/ (1,2 – 0,7) = 2,4
Р.Д = 2,4
(б) Плотность стекла, d = ?
Из : RD = ρg/ρw = сделать ρg предметом
ρg = R.D x dw = 2,4 x 1000
ρg = 2400
ρg = 2400 кг/м3
Относительная плотность другой жидкости из воды по твердому вещество в Законе Архимеда
При погружении твердого тела в жидкость и воду относительная плотность задается вытеснением жидкости над вытесненной водой
Математически
R.
 D = вес вытесненной жидкости Вес вытесненной воды
D = вес вытесненной жидкости Вес вытесненной водыRD = вес объекта в воздухе – вес объекта в жидкий вес объекта в воздухе − вес объекта в воде
RD = напор на жидкостинапор на воде = 𝑈𝑙𝑈𝑤
RD = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤
Где:
𝑈𝑙= аптраст на жидкости
𝑈𝑤 =напор на воде
𝐴𝑙= Кажущийся вес на жидкости
𝐴𝑤 = Кажущийся вес на воде
Пример,
В эксперименте по определению относительной плотности жидкий, твердый Q, взвешенный следующим образом:
Вес Q в воздухе, R = 8,6 Н
Вес Q в воде, AW = 6,0 Н
Масса Q в жидкости, AL = 5,4 Н
Приведены данные
Вес корпуса Q в воздухе, R = 8,6 Н
Вес корпуса Q в воде, AW = 6,0 Н
Вес корпуса Q в жидкости, AL = 5,4 Н
Раствор
RD = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤
R.
 D = 8,6 − 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2
D = 8,6 − 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2R.D = 1,2
Пример,
Используя приведенные ниже данные, определите относительную плотность жидкости
Данные приведены
Масса тела в воздухе, R = 15 Н
Масса тела в воде, Aw = 11N
Масса тела в жидкости, Al = 9N
Относительная плотность, R.D = ?
Раствор
RD = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤
R.D = 15 − 9 18 – 11 = 6/7 = 1,5
R.D = 1,5
Пример,
Вес тела в воздухе 0,52 Н.
 Полное погружение в воду
весит всего 0,32 Н, в то время как его вес при погружении в другую жидкость составляет 0,36 Н.
Плотность воды 1000 кг/м3 . Какова плотность другого
жидкость?
Полное погружение в воду
весит всего 0,32 Н, в то время как его вес при погружении в другую жидкость составляет 0,36 Н.
Плотность воды 1000 кг/м3 . Какова плотность другого
жидкость?Данные предоставлены
Масса тела в воздухе, R = 0,52 Н
Масса тела в воде, Aw = 0,32 Н
Масса тела в жидкости, Al = 0,36 Н
Плотность воды ρw = 1000 кг/м3
Относительная плотность, R.D = ?
Плотность жидкости, ρl = ?
Раствор
RD = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤
RD = 0,52−0,360,52−0,32 = 0,16/0,2 = 0,8
R.D = 0,8
Но : R.D = ρl/ ρw – сделать ρl подлежащим
ρl = RD x ρw = 0,8 x 1000 = 800
ρ l = 800 кг/м3
приведенное ниже видео поможет получить больше информации о принципе Архимеда и относительной плотности тела
ytimg.com/vi/05WkCPORlj4/0.jpg” frameborder=”0″ src=”https://www.youtube.com/embed/05WkCPORlj4?feature=player_embedded”>
ПОГРУЖЕНИЕ И ПЛАВАНИЕ
Погружение объект для падения или падения на более низкие уровни в жидкости
Условия для погружения
я. Аптраст, вызванный жидкость меньше веса объекта
II. Объект плотнее жидкости означает, что объект имеет большую плотность чем жидкость
Плавающая
Определение: Плавание – это тенденция объект должен быть подвешен (остаться) на поверхности жидкости из-за аптраст
Способность объекта плавать называется Плавучесть
Состояние плавучести
я.
 Напор, создаваемый жидкостью, должен быть равен или больше
реальный вес объекта
Напор, создаваемый жидкостью, должен быть равен или больше
реальный вес объектаNb : кажущийся вес приблизительно равен нулю
А ≈ 0 Н
II. Плотность тела должно быть меньше, чем у жидкости
III. Объем затопленного объекта должен быть достаточно большим, чтобы вытеснить много жидкости
На видео ниже показаны условия погружения и всплытия
НИЗКАЯ ПЛАВУЩОСТЬ
Закон гласит, что
«Плавающее тело вытесняет жидкость под собственным весом в который плавает»
Применение флотации
Закон о плавании является заявителем в различных веществах, включая
я.
 Наполнение воздушных шаров
Наполнение воздушных шаровII. Заполнение горячим воздухом баллон
III. Подводные лодки
IV. Корабли
v. Ареометр
Воздушные шары
Рассмотрим диаграмму ниже. vt/vs) x 100
Но : R = U
Тогда : ρs x vs x g = ρf x vf x g
Ρs x vs x g = ρf x %S x vf x g
Ρs = ρf x %S
R = реальный вес вещества
U = W = вес вытесненной жидкости
Ms = масса вещества
Ρs = плотность вещества
Vs = объем вещества
Mf = масса вытесненной жидкости
Ρf = плотность вытесненной жидкости
Vf = объем вытесненной жидкости
%S= процент погруженного вещества
Vt = погруженный объем
Воздушные шары
Рассмотрим диаграмму ниже
Где :
F = принудительный дрейф вверх ниже
U = подъем
R = вес баллона
Механизм
Воздушные шары наполнены легким газом, например.
 гелий который
вытеснить объем воздуха, равный его объему. Так как заполненный газ имеет свет или
имеет низкую плотность по сравнению с вытесняемым воздухом, поэтому воздушный шар дрейфует с силой
гелий который
вытеснить объем воздуха, равный его объему. Так как заполненный газ имеет свет или
имеет низкую плотность по сравнению с вытесняемым воздухом, поэтому воздушный шар дрейфует с силойВоздушный шар
Механизм
При нагревании воздуха в оболочке увеличивается количество газа внутри расширяться так, что его объем увеличивается, а масса газа внутри оболочки остается постоянной поэтому его плотность снижена, как если бы вы сравнивали с внешним газом (холодным воздухом). Этот разные по плотности дрейфуют воздушный шар и его пассажиры в воздух
Рассмотрим схему ниже
Для плавучего вещества R = U
But : U = Mt x g
U = (MB + Mc + mh) x g
Но: mh = vh x ρh
Тогда: U = (Mt + vh x ρh) x g – – – – – 1
Также: R = mc x g
Но: mc = vc x ρc x g
Тогда: R = vc x ρc x g – – – – – 2
Но: vc = vh = v
0 90: 90 уравнение 1 = уравнение 2 (U = R)
(Mt + vh x ρh) x g = vc x ρc x g
(Mt + vh x ρh) = vc x ρc
Mt + v x ρh = v x ρc ce : mf = ρf x vf
Mt + v x ρh = v x ρc – сделать v предметом
v = Mt/(ρc – ρh)
v = (ml + mb)/Δρ
Общая масса = mt = (MB + Mc + mh)
Объем горячего воздуха = vh
Объем холодного воздуха = vc
Масса горячего воздуха = mh
Масса холодного воздуха = mc
Масса баллона = мб
Плотность горячего воздуха = ρh
Плотность холодного воздуха = ρc
Пример,
Воздушный шар, включая конверт, гондолу, горелку и топлива и один пассажир имеет общую массу 450кг.
 Температура воздуха снаружи воздушного шара составляет 20 ℃.
и имеет плотность 1,29 кг/м3, воздух внутри при температуре 120 ℃ имеет плотность
0,90 кг/м3. До какого объема должна расшириться оболочка, чтобы просто поднять воздушный шар
в воздух?
Температура воздуха снаружи воздушного шара составляет 20 ℃.
и имеет плотность 1,29 кг/м3, воздух внутри при температуре 120 ℃ имеет плотность
0,90 кг/м3. До какого объема должна расшириться оболочка, чтобы просто поднять воздушный шар
в воздух?Данные предоставлены
Полная масса, т = 450 кг
Плотность при 120℃, ρ2 = 0,90 кг/м3
Плотность при 20℃, ρ1 = 1,29 кг/м3
Объем вытесненного воздуха, v1 = ?
Раствор
Из : v = (мл + мб) / Δρ
v = 450 кг /(1,29-0,9)
v = 450 кг /(1,29-0,9)
v = 450/0,39 = 1,15
v = 1,15 м3
Пример,
Воздушный шар имеет объем 20 м3 и наполнен водород.
 Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0,089кг/м3
и плотность воздуха 1,29 кг/м3)
Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0,089кг/м3
и плотность воздуха 1,29 кг/м3)Данные приведены
Общая масса = мт = мл + мб
Вместимость, v = 20м3
Объем холодного воздуха, v1 =20м3
Масса баллона, мб = 2,5 кг
Плотность при v2, ρ2 = 0,089 кг/м3
Плотность при v1, ρ1 = 1,29 кг/м3
Масса прибора), мл = ?
Раствор
Из : v = (мл + мб)/Δρ – сделать мл предмет
Ml = (v x Δρ) – mb)
Мл = (20 х (1,29 – 0,089)) – 2,5
Мл = (20 х 1,201) – 2,5
Ml = 24,02 – 2,5
Ml = 21,52 кг
Sub Marine
Рассмотрим схему ниже
Механизм
Подводная лодка, состоящая из пустого пространства, заполненного воздухом, называется балласта, чтобы увеличить его объем, чтобы придумать плотность подводной лодки и наоборот
Когда вода заполнила балласт, подводная лодка погрузилась и при допуске баллона в спеццистерну и при заполнении балласта воздух подводная лодка плавает, как и другие корабли
Когда количество воды увеличивается/заливается в дутье, уменьшить объем, следовательно, увеличить плотность подводной лодки.

Корабль сделан из стали и, как ожидается, затонет из-за его масса. он содержит полость, которая увеличивает объем корабля, что помогает на делает менее плотным, чем вода
Но когда груз помещается на корабль, он имеет тенденцию к увеличению плотности. и массе корабля, при перегрузке корабль тонет полностью. Чтобы проверить более Забродные суда отмечены линией или отметкой, называемой отметкой Plimsoll.
Линия кроссовок
Линия плимсолла на корабле, используемая для обозначения минимальной высоты (максимальной плотность) над разными типами воды в разных морях, как показано на схема ниже
Где:
F = для пресной воды
S = для моря в летнее время
W = для моря в воде время
TF = тропическая пресная вода
WNA = зима в Атлантике
T = тропический
Ареометр
Defn: ареометр — используемый прибор.
 для измерения плотности жидкостей или ареометр – это прибор, используемый для
определить относительную плотность жидкостей.
для измерения плотности жидкостей или ареометр – это прибор, используемый для
определить относительную плотность жидкостей.Структура ареометра
я. Тяжелое грузило (колба): содержит ртутные или свинцовые дроби, держите ареометр в вертикальном положении, когда он плавает
II. Воздушная груша: увеличивает объем вытесняемой жидкости и преодолевает вес грузила
III. Стебель: стебель тонкий, поэтому небольшие изменения плотности (высота) дают большие различия в показаниях
IV. Шкала: внутри штока градуировка по плотности
v. Изготовлены из стекла для предотвращения впитывания жидкости
Чем больше плотность жидкости, тем короче стержень Аретометр погрузился
Как использовать Aretometer
ytimg.com/vi/t9XAiRbL7t4/0.jpg” frameborder=”0″ src=”https://www.youtube.com/embed/t9XAiRbL7t4?feature=player_embedded”>
Относительная плотность
Относительная плотность жидко я. Когда ареометр плавает над водой, вес ареометра (wg) должно равняться весу вытесненной воды (ww)
wg = ww
II. Когда ареометр плавает над жидкостью, вес ареометр (wg) должен равняться весу вытесненной жидкости (wl)
wg = wl
III. так как относительная плотность жидкости определяется отношением плотности жидкости (ρl) к плотности воды (ρw)
R.D = ρl/ρw = wl/vl ÷ ww/vw
Где:
vl = объем вытесненной жидкости
vw = объем вытесненной воды
wl = ww
Тогда: RD = vw/vl
IV.
 так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погружены в них
так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погружены в нихR.D = lw/ll
Где:
Lw = длина погруженного в воду ареометра
Ll = длина ареометра, погруженного в жидкость0974 Рассмотрим схему ниже
Где:
Объем пара, v1 = Ач
Объем колбы, v2 = v
Общий объем, vt = v1 + v = Ah + v2
Но: R = U
Где:
U = взброс в жидкости
ρmn = минимальная плотность
ρmx = максимальная плотность
R = вес ареометра
U = vt x ρmn x g
R = v x ρmx x g
Бут : Р = У
Тогда: vt x ρmn x g = v x ρmx x g
(Ah + v) x ρmn x g = v x ρmx x g
(Ah + v) x ρmn = v x ρmx
Ah x ρmn + v x ρmn = v x ρmx – сделать v2 субъектом
v x ρmx – v x ρmn = Ah x ρmn
v x (ρmx – ρmn) = Ah x ρmn
v = (Ah x ρmn)/(ρmx – ρmn
v = (Ah x ρmn)/(ρmx – ρmn)
Пример,
Рассмотрим приведенную ниже диаграмму, используемую для измерения плотности жидкости.
 от 1 г/см3 до 0,81 г/см3 (площадь поперечного сечения стебля составляет 0,5 см2).
Найдите объем ареометра менее 1,0 г/см3 с градуировкой
от 1 г/см3 до 0,81 г/см3 (площадь поперечного сечения стебля составляет 0,5 см2).
Найдите объем ареометра менее 1,0 г/см3 с градуировкойДанные предоставлены
Площадь поперечного сечения стержня, A = 0,5 см2
Высота пара, h=16 см
Объем пара, v1 = Ah = 8 см3
Общий объем, vt = (8 + v2) см3
Минимальная плотность, ρмн = 0,8 г/см3
Максимальная плотность, ρmx = 1,0 г/см3
Объем колбы, v2 = ?
Раствор
Объем колбы, v2 = ?
Из : v2 = (Ah x ρmn)/(ρmx – ρmn)
v2 = (8 х 0,8)/(1 – 0,8)
v2 = 6,4/0,2
v2 = 32 см3
Пример: NECTA форма IV 2012 QN: 4
а) Что делает твердое тело масса тела на воздухе больше, чем при погружении в жидкость?
(б) Обыкновенный ареометр массой 27 г всплывает на 4 см над водой.
 Если крест
площадь сечения ствола 0,75см2 рассчитать
Если крест
площадь сечения ствола 0,75см2 рассчитатья. Общий объем стержень прямо под поверхностью жидкости
II. Относительная плотность жидкости
Данные приведены (б):
Масса ареометра, mh = 27 г
Масса вытесненной воды, mw = 27 г
Площадь стержня, A = 0,75 см2
Высота стебля, h = 4см
Плотность воды, ρw = 1 г/см3
Плотность жидкости, ρl = ?
Раствор
я. Общий объем, vt = v1 + v
Объем штока, v1 = Ah = 3 см3
Объем колбы, v = mw x ρw = 27 см3
vt = v1 + v
vt = Ah + mw x ρw
vt = (3 + 27) см3
vt = 30 см3
II.
 Относительная плотность, R.D = ?
Относительная плотность, R.D = ?Из: R.D = ρl/ρw
, но: ρl = мл/VT = 27/30 = 0,9 г/см3
Тогда: R.d = ρl/ρw 0,9/1 = 0,
3 3. R.D = 0,9
Пример,
Баллон объемом 2000м3 наполнен водородом плотностью 0,09 кг/м3. Если масса ткани 100 кг, а масса пилота 75 кг,
я. Что будет максимальная масса оборудования, которое можно перевозить при работе в воздухе 1,25 кг/м3?
II. Как бы изменилась эта цифра, если бы гелий, имеющий дважды плотность водорода при тех же условиях, должны были быть использованы?
Раствор
я. Для водорода
Приведены данные
Общая масса Mt = mt = (мл + мб)
Объем водорода, v2 = 2000м3
Объем окружающий, v1 =20000м3
Масса баллона, мб = (75+100) = 175 кг
Плотность при v2, ρ2 = 0,09 кг/м3
Плотность при v1, ρ1 = 1,25 кг/м3
Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,09) = 1,16 кг/м3
Раствор
Масса прибора), мл = ?
Откуда: v = (ml + mb) / Δρ – сделать мл предметом
Ml = (v x Δρ) – мб
Мл = (2000 х 1,16) – 175
Ml = 2320 – 175
Ml = 2145 кг
II.
 Для гелия
Для гелия Данные приведены
Общая масса Mt = mt = (мл + мб)
Объем гелия, v2 = 2000м3
Объем окружающий, v1 =20000м3
Масса баллона, мб = (75+100) = 175 кг
Плотность при v2, ρ2 = 0,18 кг/м3
Плотность при v1, ρ1 = 1,25 кг/м3
Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,18) = 1,07 кг/м3
Раствор
Масса прибора), мл = ?
v = (ml + mb) / Δρ – сделать мл подлежащим
Ml = (v x Δρ) – мб
Мл = (2000 х 1,07) – 175
Мл = 2140 – 175
Ml = 1965 кг
Пример,
Масса куска пробки (0,25 г/см3) равна 20 г.
 Какая дробь
пробки погружается, когда она плавает в воде?
Какая дробь
пробки погружается, когда она плавает в воде?Данные предоставлены
Масса пробки, mc = 20 г
Плотность пробки, ρc = 0,25 г/см3
Плотность воды, ρw = 1 г/см3
Пробка Фракция погружена, x = ?
Объем вытесненной воды, vw = ?
Объем погруженной пробки, vc = ?
Решение
Откуда: принцип плавучести (vw = vc)
Mc = масса воды, mw
20 = vw x 1
Vw = vc = 20 см3
Но: x = vc/vt
Где: Объем пробки, vt = ?
Откуда: ρc = mc/vt
Vt = mc/ ρc = 20/0,25 = 80 см3
Vt = 80 см3
Х = 20/80 = 1/4
X = 1/4
Пример,
Масса куска пробки (0,25 г/см3) равна 20 г.
 какая
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
составляет 0,8 г/см3)
какая
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
составляет 0,8 г/см3)Приведены данные
Масса пробки, mc = 20 г
Плотность пробки, ρc = 0,25 г/см3
Плотность спирта, ρa = 0,8 г/см3
Пробка Фракция погружена, x = ?
Объем вытесненного спирта, ва = ?
Объем погруженной пробки, vc = ?
Решение
Откуда: принцип плавучести (va = vc)
Mc = масса воды, mw
20 = vw x 0,8
Vw = va = 25 см3
Но: x = vc/vt
Где: Объем пробки, vt = ?
Откуда: ρc = mc/vt
Vt = mc/ ρc = 20/0,25 = 80 см3
Vt = 80 см3
Х = 25/80 = 5/16
X = 5/16
Пример,
Однородный карандаш плавает вертикально в воде, его длина 8 см.
 длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)?
длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)?Данные предоставлены
Длина карандаша, погруженного в воду, lw = 8 см
Плотность глицерина, ρg = 1,3 г/см3
Плотность воды, ρw = 1 г/см3
Длина карандаша, погруженного в глицерин, lg = ?
Раствор
Но: R.D глицерина = lw/lg
Тогда: lg = lw/R.D = 8/1,3 = 6,2 см
lg = 6,2 см
Пример,
Воздушный шар и газ в нем имеют массу 450 г. объем 500 литров. Какой максимальный груз он может поднять в воздухе с плотностью 1,3 г/см3?
Данные предоставлены
Общая масса, мт = (мл + мб)
Масса баллона, мб = 450г
Плотность газа, ρg = 1,3 г/см3
Изменение плотности, Δρ = 1,3 г/см3
Объем баллона, vb = 500 литров
Максимальная загрузка, мл = ?
Раствор
Максимальная загрузка, мл = ?
Откуда: v = ( мл + мб) / Δρ – сделать мл предмет
Ml = (v x Δρ) – мб
Мл = (500 х 1,3) – 450
Мл = 650 – 450
Мл = 200 г
Пример: NECTA 2012
На приведенной ниже диаграмме показана форма используемого мной ареометра.
 для измерения плотности жидкости в диапазоне от 0,8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определить
для измерения плотности жидкости в диапазоне от 0,8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определитьа) Объем ареометр ниже 1,00 с градуировкой
(b) Положение деления 0,90
Данные предоставлены
Площадь поперечного сечения стержня, A = 0,5 см2
Высота пара, h=18 см
Объем пара, v1 = Ah = 9 см3
Общий объем, vt = (9 + v2) см3
Минимальная плотность, ρмн = 0,8 г/см3
Максимальная плотность, ρmx = 1,0 г/см3
Объем колбы, v2 = ?
Раствор
(а) Объем колбы, v2 = ?
Из: v2 = (Ah x ρmn)/(ρmx – ρmn)
v2 = (9 х 0,8)/(1 – 0,8)
v2 = 7,2/0,2
v2 = 36 см3
б) Какова высота h3 ареометра при смещении на меру 0,9? г/см3
Но: вес ареометра никогда не менять
V3 x 0,9 x 0,01 Н = 0,36 Н
V3 = 40 3
V3 = Ah3
h3 = 8 см
ПРИНЦИП АРКМЕДА И ЗАКОН ПЛАВУЧЕСТИ – моя ссылка
ПРИНЦИП АРКМЕДА И ЗАКОН ПЛАВУЩЕЙ МОЩНОСТИ
1. ПРИНЦИП АРХИМЕДА
ПРИНЦИП АРХИМЕДА
Кажущийся вес :Вес тела, когда он частично или полностью погружены в жидкость.
Подъемное усилие – восходящая сила, действующая со стороны жидкости на тело.
Жидкость – жидкость или газ.
ЭКСПЕРИМЕНТ
- Галстук твердое тело на веревке и подвесить его на пружине.
- Найти вес тела в воздухе, назовите его W 1 .
- Найти вес тела при его частичном погружении в воду, содержащуюся в стакан, назовите его W 2.
- Найти вес тела, полностью погруженного в воду, обозначим W 3 .
- Удалить тело из воды, высушите его и найдите его вес, назовите его W 4 .
- Это можно заметить, что W 1 > W 2 > W 3 .
Также Ш 1 = Ш 4
- Это
показывает, что вес тела, погруженного в воду, равен его
веса после погружения в воду.

- Это результат показывает, что наблюдается очевидная потеря веса тела, когда он частично или полностью погружены в воду.
- Тот потеря веса не является реальной потерей.
- Ан кажущаяся потеря = масса тела – кажущаяся масса тела в жидкости.
Из этого эксперимента
Очевидная потеря = Вт 1 — Вт 2 Жидкость действует на тело с направленной вверх силой, когда оно частично или полностью погрузился в него.
Тяга вверх = кажущаяся потеря веса = W 1 —W 2
Пример:
1. Масса тела в воздухе составляет 3,0 Н. Когда это полностью (полностью) погруженный в жидкость, он весит 2,2 Н. Найдите толчок, испытываемый телом.
Данные:
Вес в воздухе (w 1 ) = 3.N
Вес в вода (W 2 ) = 2,2NВыброс = ?
Решение
Тяга вверх = вес в воздухе – кажущийся вес
= ш 1 — ш 2
= 3,0 Н – 2,2 Н
=0,8 Н
Пример
2.
 Масса тела 4,6 Н на воздухе и 3,1 Н при погружении в воду.
Найдите силу тяги, действующей на тело со стороны воды.
Масса тела 4,6 Н на воздухе и 3,1 Н при погружении в воду.
Найдите силу тяги, действующей на тело со стороны воды.Данные:
Вес в воздухе (W 1 ) = 4,6 Н
Вес в вода (W 2 ) = 3,1 NПодъем =?
Раствор :
Подъемная тяга = вес в воздухе – кажущийся вес
= Ш 1 — Ш 2
= 4,6 – 3,1 = 1,5 Н
Пример:
3. Тело, полностью погруженное в жидкость, весит 3,2 Н. Это весит 6,8 Н в воздухе. Вычислить толчок тела вверх.
Данные :
Вес в воздухе (W 1 ) = 6,8 Н
Вес в вода (W 2 ) = 3,2NВыброс =?
Решение :
Подъем = вес в = кажущийся вес
= Ш 1 —Ш 2
= 6,8 – 3,2 = 3,6 Н
тяга = 3,6 Н
ДЕМОНСТРАЦИЯ ПОТЕРИ В ВЕСЕ
Эксперимент:
- Найти
вес тела в воздухе с помощью пружинных весов.

- Залить воду в эврику можно до носика.
- Взять любую сухую мензурку, взвесьте ее и поместите под носик банки eureka.
- Найти вес тела при полном погружении в воду.
- вода, вытесненная телом, перетекает через носик в утяжеленный стакан.
- Удалить стакан и вес.
Результаты следующие;
- Вес тела в воздухе -W 1
- Вес тела в воде – W 2
- Вес пустого стакана – W 3
- Вес стакана и вытесненной воды -W 4
Упор = W 1 — W 2 и вес вытеснить воду = W 4 — W 3.
- It будет замечено, что тяга равна весу смещенного вода.
- Это
результат известен как принцип Архимеда , который гласит, что « Когда
тело частично или полностью погружено в жидкость, в которой оно испытывает
выталкивающая сила, равная весу вытесненной жидкости
вес 4,2Н.
 Найдите толчок, испытываемый телом.
Найдите толчок, испытываемый телом.Данные :
Вес тела в воздухе (W 1 ) = 6.0N
Видимый вес (W 2 ) = 4,2 Н
знак равноРешение
Подъем = вес в воздухе (w 1 ) – кажущийся вес (Ш 2 )
= 6,0 Н — 4,2 Н
Выброс = 1,8 Н
ОТНОСИТЕЛЬНАЯ ПЛОТНОСТЬ ПО ПРИНЦИПУ АРХИМЕДА
Относительный Плотность по закону Архимеда можно получить, взяв вес тело в воздухе разделить на явная потеря веса тела .
РД = вес в воздухе — кажущийся вес
Пример
1. Вес тела в воздухе составляет 5 Н, а при полном погружении в воду он весит 3 Н. Находить его РД.
Данные :
Вес в воздухе (W 1 ) = 5N
Вес в воде (W 2 ) = 3NRD =?
Решение
RD = 2,52.
 Найдите относительную плотность тела, масса которого в воздухе 7,5 Н, а на воздухе 6,0 Н.
при погружении в воду.
Найдите относительную плотность тела, масса которого в воздухе 7,5 Н, а на воздухе 6,0 Н.
при погружении в воду.Данные :
Вес в воздухе (W 1 ) = 7,5 Н
Вес в воде ( W 2 ) = 6,0 НРД знак равно
Раствор
RD = 5УПРАЖНЕНИЕ
- Тело гири 0,8 Н на воздухе и 0,5 Н при полном погружении в воду, Рассчитать;
- Выброс
- Относительная плотность тела.
Данные :
Вес в воздухе (W 1 ) = 0,8
Вес в воде (W 2 ) = 0,5РД знак равно
Решение
RD = 2 ,66
2. ЗАКОН ПЛАВАЮЩАЯ
ПЛАВАЮЩАЯ :
A тело будет плавать в жидкости, если тяга вверх будет равна его весу. Мы можем заключить говоря это;
- Тело всплывает, если
Тяга вверх = его вес
U = W
- Тело утонет if
Тяга вверх меньше его веса т.
 е. U <
W
е. U <
W - Тело поднимется если тяга вверх больше веса, т. е. U> W
ПОЛОЖЕНИЕ О ЗАКОНЕ ПЛАВАНИЯ
Закон плавучести гласит, что: « Плавающее тело вытесняет собственный вес жидкости, в которой он плавает ”.
ПРИМЕНЕНИЕ ЗАКОНА ПЛАВАНИЯ
законы плавучести применяются в различных ситуациях нашей повседневной жизни. Ниже приведены некоторые из ситуаций.
- Корабли
- Подводная лодка
- Аэростаты
- Ареометр
ПЛАВАЮЩИЙ СУДОВ
А Часто можно задать вопрос: «Почему монета тонет в воде, а корабль, сделанный из плавает сталь». Ответ на этот распространенный вопрос таков: «Корабль плавает, потому что он очень большой и полый, структура которого позволяет использовать большую часть его объема. быть заполненным воздухом, который делает корабль менее плотным, чем вода.

средняя плотность корабля становится меньше плотности воды. Когда груз загружается в корабль, масса корабля увеличивается, что увеличивает его плотность, Там корабль тонет до тех пор, пока вес вытесненной воды не станет равным вес корабля и груза, то корабль плавает.
NB . Ограниченный вес разрешено перевозить груз на судне, иначе возникнет опасность перегрузки и заставляя его полностью утонуть.
ШАРЫ
А Воздушный шар представляет собой легкий мешок, наполненный газообразным водородом или гелием. Эти газы менее плотнее воздуха. Воздушный корабль представляет собой большой воздушный шар с мотором и плавником. управлять им. Сила, направленная вниз в воздушном шаре, равна весу мешок плюс вес газа в нем.
Примечание что : Воздушный шар поднимается, если тяга вверх больше силы, направленной вниз.
АРЕОМЕТР
А ареометр плавучий прибор для измерения плотности жидкости.
 Например. Молоко,
пиво, вина, кислоты в автомобильных маслах и т. д.
Например. Молоко,
пиво, вина, кислоты в автомобильных маслах и т. д.Измерение выполняется путем определения того, насколько глубоко в них он тонет. Ареометр состоит из длинной стеклянной трубки с колбой на дне, в колбе находится ртутная или свинцовая дробь, так что ареометр плавает вертикально, стержень тонкий и градуированный. Он может тонуть в другой жидкости, даже если находится в одном и том же положении.
КАК ИСПОЛЬЗОВАНИЕ АРЕРОМЕТРА
Когда ареометр осторожно опускают в объем жидкости и дают ему отстояться, он может плавать в жидкости глубже или мельче. Он плавает глубже в менее плотной жидкости или неглубоко в плотной жидкости.
Примеры
1. Плотность льда 920 кг/м 3 и плотность морской воды 1030 кг/м 3 . Какой объем айсберга обнажен?Раствор
Дано:
Плотность морской воды = 1030 кг/м 3
Плотность льда = 920 кг/м 3
Вес тела = Вес вытесненной жидкости
вытесненная водаV лед × ρ лед × g = ρ Water × V Вода смещен × g
V ICE × 920 = 1030 × V DISLACED WATER
Объем фракции.


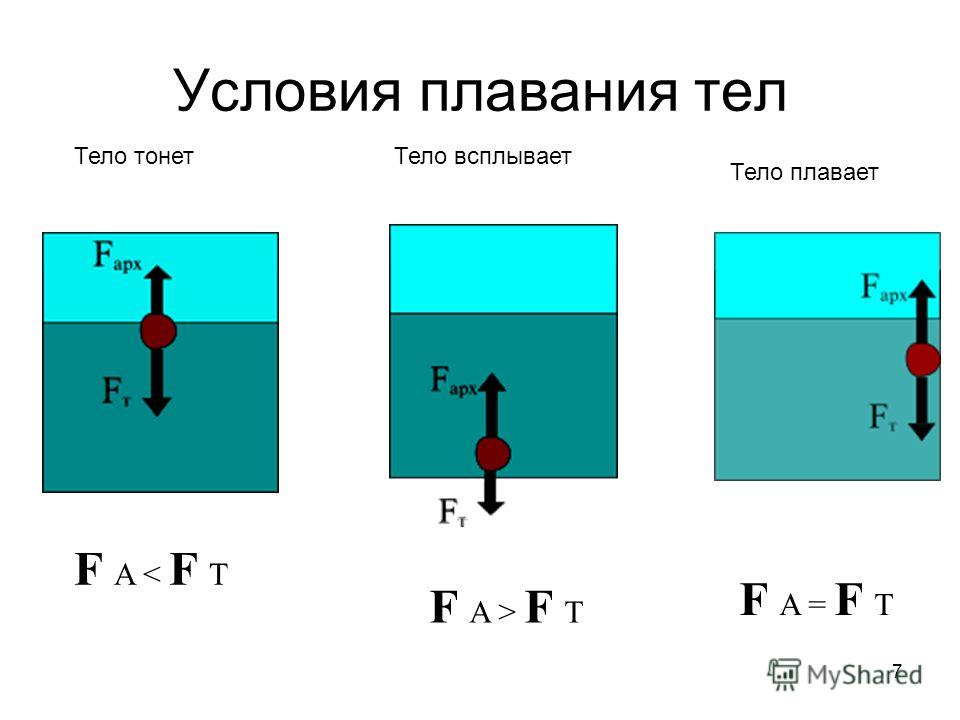
 Кусок льда, внутри которого вморожен шарик из
свинца, плавает в цилиндрическом сосуде с водой.
Пло-щадь дна сосуда S. Какова масса
шарика, если после полного таяния льда уровень воды в сосуде понизился
на h? Плотность свинца
r1, воды
r2.
Кусок льда, внутри которого вморожен шарик из
свинца, плавает в цилиндрическом сосуде с водой.
Пло-щадь дна сосуда S. Какова масса
шарика, если после полного таяния льда уровень воды в сосуде понизился
на h? Плотность свинца
r1, воды
r2.


 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой? Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины. С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото? Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым? 14.19 (a) Даже объекты, которые тонут, например этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)
14.19 (a) Даже объекты, которые тонут, например этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr)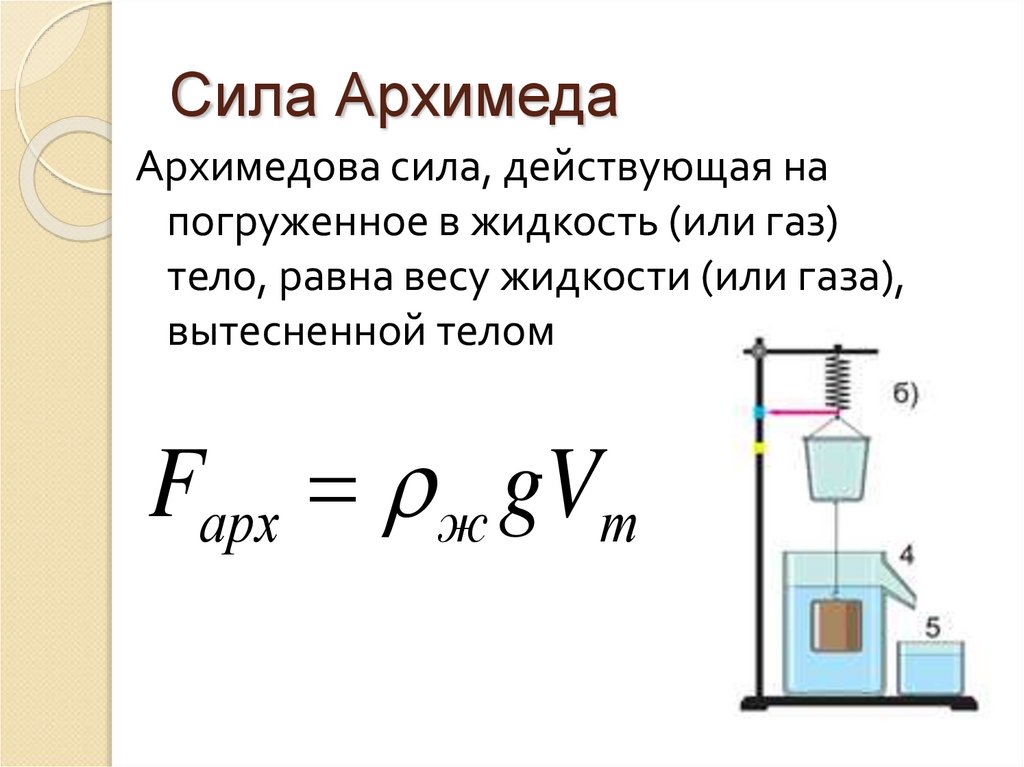 Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости. [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex] {w}_{\text{fl}}, [/latex] весу жидкости, вытесненной объектом.
[/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex] {w}_{\text{fl}}, [/latex] весу жидкости, вытесненной объектом. Если [латекс] {F}_{\text{B}} [/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.
Если [латекс] {F}_{\text{B}} [/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости.
 Точно так же объект, более плотный, чем жидкость, утонет.
Точно так же объект, более плотный, чем жидкость, утонет.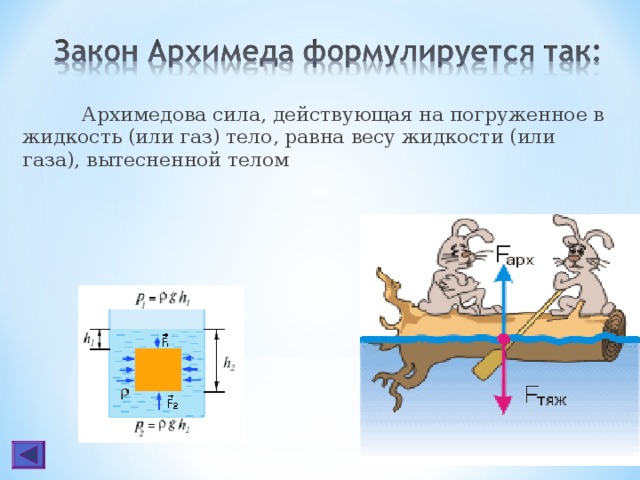 Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается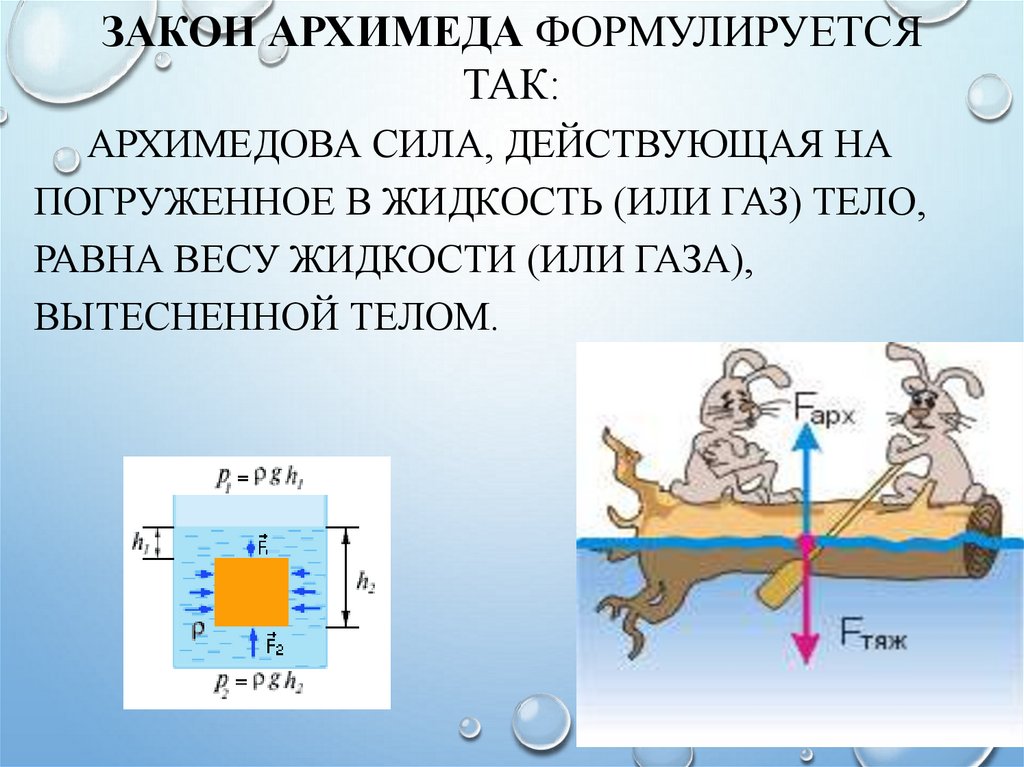 Мы ожидаем этого, потому что она плавает.
Мы ожидаем этого, потому что она плавает. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, указанную на (рис.)? в) Рассчитайте плотность жидкости и определите ее. а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
 Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется выше
Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется выше жидкость обычно
оказывает аптраст
жидкость обычно
оказывает аптраст Найдите массу тела
в воздухе.
Найдите массу тела
в воздухе. Найдите их вес в воздухе.
Найдите их вес в воздухе. Ms x g = реальный
вес =
Ms x g = реальный
вес =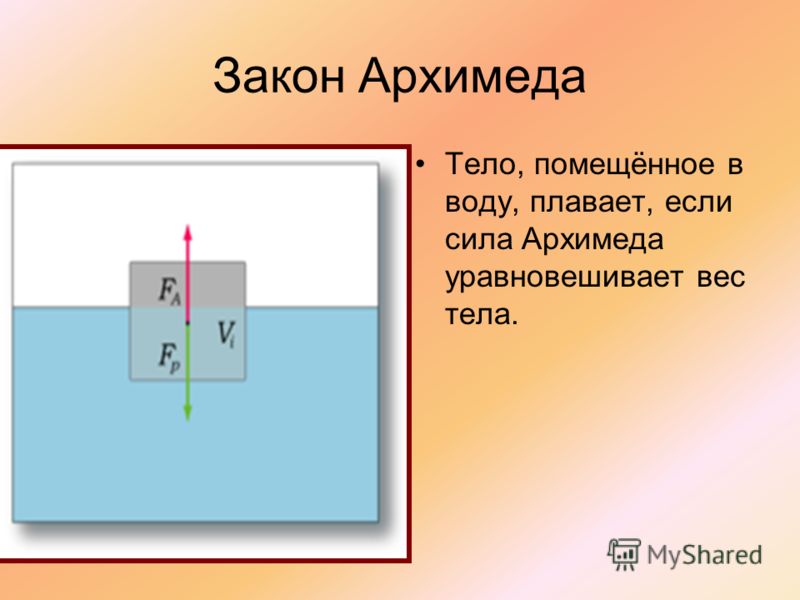 D = ?
D = ? D = вес вытесненной жидкости Вес вытесненной воды
D = вес вытесненной жидкости Вес вытесненной воды D = 8,6 − 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2
D = 8,6 − 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2 Полное погружение в воду
весит всего 0,32 Н, в то время как его вес при погружении в другую жидкость составляет 0,36 Н.
Плотность воды 1000 кг/м3 . Какова плотность другого
жидкость?
Полное погружение в воду
весит всего 0,32 Н, в то время как его вес при погружении в другую жидкость составляет 0,36 Н.
Плотность воды 1000 кг/м3 . Какова плотность другого
жидкость? Напор, создаваемый жидкостью, должен быть равен или больше
реальный вес объекта
Напор, создаваемый жидкостью, должен быть равен или больше
реальный вес объекта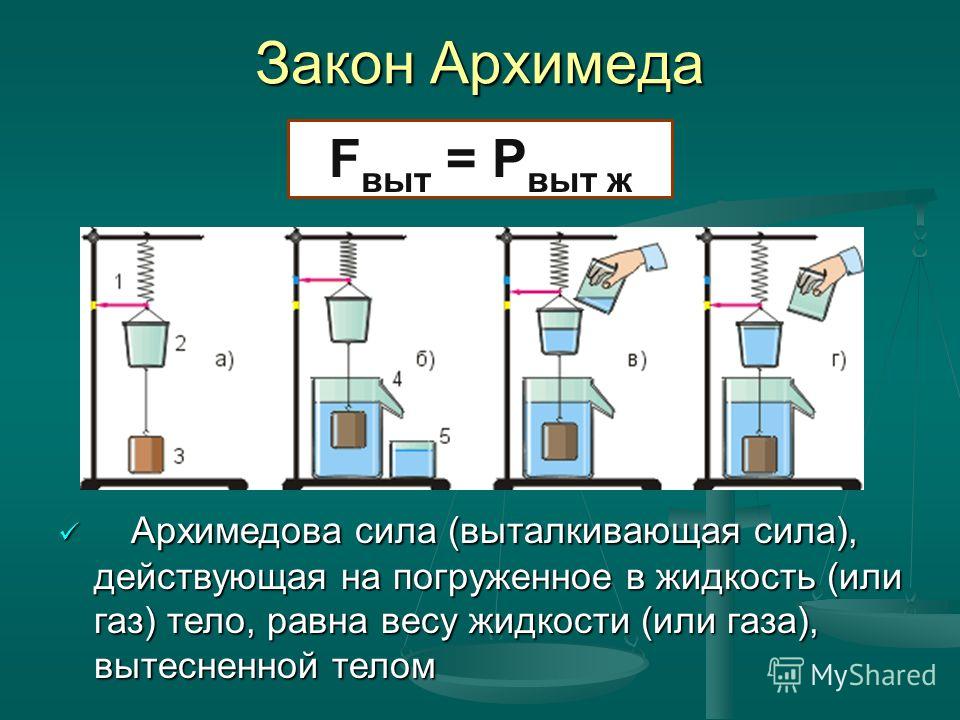 Наполнение воздушных шаров
Наполнение воздушных шаров гелий который
вытеснить объем воздуха, равный его объему. Так как заполненный газ имеет свет или
имеет низкую плотность по сравнению с вытесняемым воздухом, поэтому воздушный шар дрейфует с силой
гелий который
вытеснить объем воздуха, равный его объему. Так как заполненный газ имеет свет или
имеет низкую плотность по сравнению с вытесняемым воздухом, поэтому воздушный шар дрейфует с силой Температура воздуха снаружи воздушного шара составляет 20 ℃.
и имеет плотность 1,29 кг/м3, воздух внутри при температуре 120 ℃ имеет плотность
0,90 кг/м3. До какого объема должна расшириться оболочка, чтобы просто поднять воздушный шар
в воздух?
Температура воздуха снаружи воздушного шара составляет 20 ℃.
и имеет плотность 1,29 кг/м3, воздух внутри при температуре 120 ℃ имеет плотность
0,90 кг/м3. До какого объема должна расшириться оболочка, чтобы просто поднять воздушный шар
в воздух? Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0,089кг/м3
и плотность воздуха 1,29 кг/м3)
Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0,089кг/м3
и плотность воздуха 1,29 кг/м3)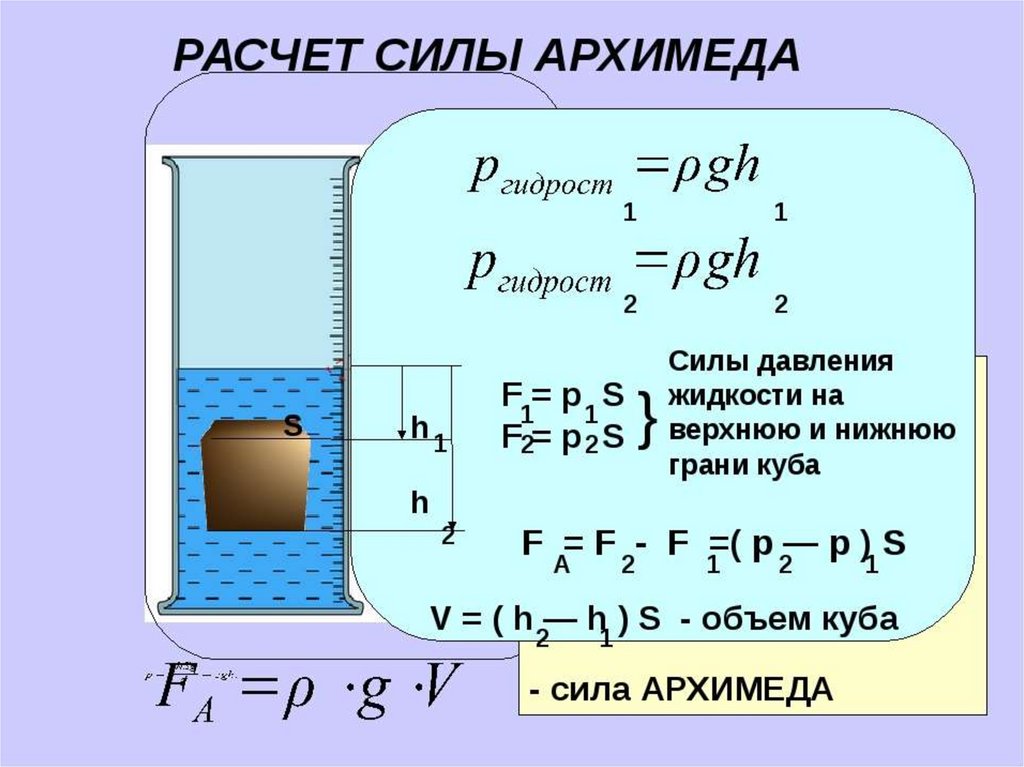
 для измерения плотности жидкостей или ареометр – это прибор, используемый для
определить относительную плотность жидкостей.
для измерения плотности жидкостей или ареометр – это прибор, используемый для
определить относительную плотность жидкостей.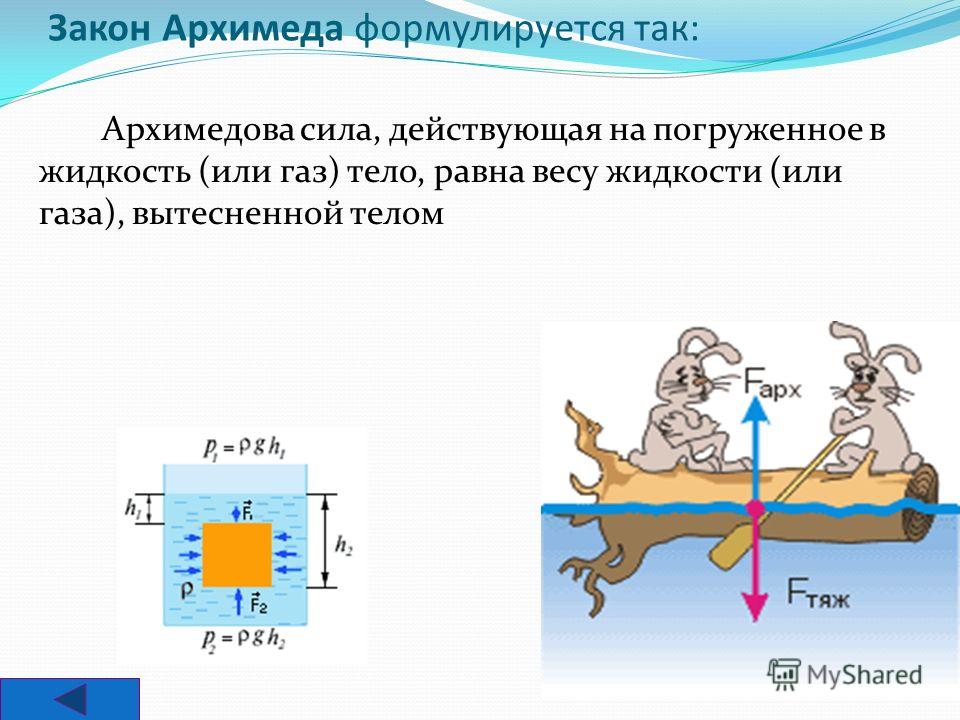 так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погружены в них
так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погружены в них от 1 г/см3 до 0,81 г/см3 (площадь поперечного сечения стебля составляет 0,5 см2).
Найдите объем ареометра менее 1,0 г/см3 с градуировкой
от 1 г/см3 до 0,81 г/см3 (площадь поперечного сечения стебля составляет 0,5 см2).
Найдите объем ареометра менее 1,0 г/см3 с градуировкой Если крест
площадь сечения ствола 0,75см2 рассчитать
Если крест
площадь сечения ствола 0,75см2 рассчитать Относительная плотность, R.D = ?
Относительная плотность, R.D = ? Для гелия
Для гелия  Какая дробь
пробки погружается, когда она плавает в воде?
Какая дробь
пробки погружается, когда она плавает в воде? какая
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
составляет 0,8 г/см3)
какая
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
составляет 0,8 г/см3) длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)?
длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)? для измерения плотности жидкости в диапазоне от 0,8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определить
для измерения плотности жидкости в диапазоне от 0,8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определить ПРИНЦИП АРХИМЕДА
ПРИНЦИП АРХИМЕДА 
 Масса тела 4,6 Н на воздухе и 3,1 Н при погружении в воду.
Найдите силу тяги, действующей на тело со стороны воды.
Масса тела 4,6 Н на воздухе и 3,1 Н при погружении в воду.
Найдите силу тяги, действующей на тело со стороны воды.
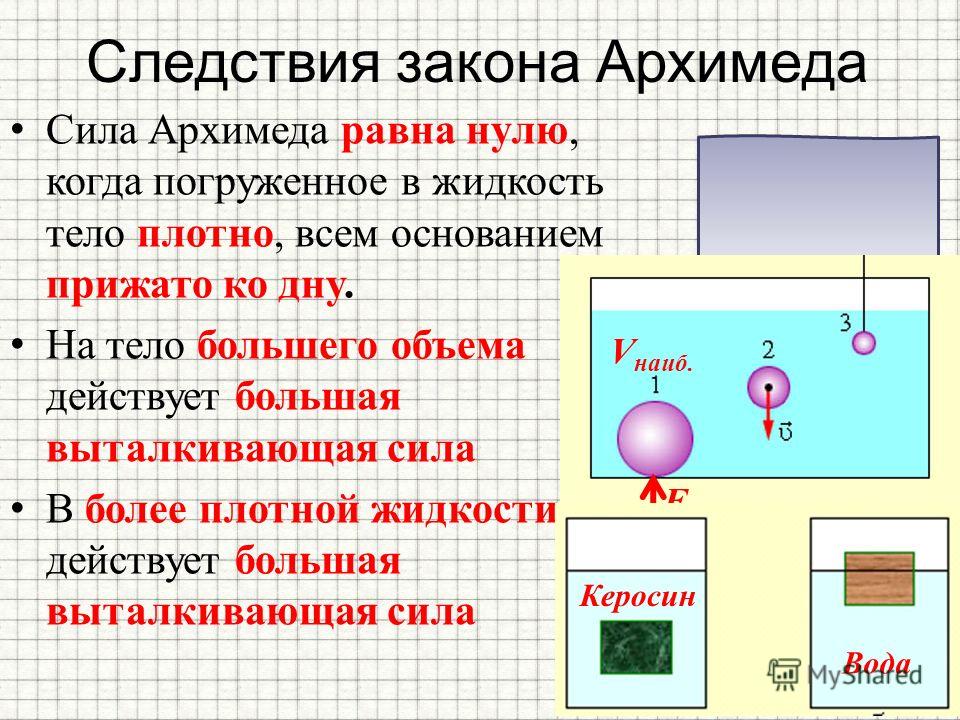 Найдите толчок, испытываемый телом.
Найдите толчок, испытываемый телом. Найдите относительную плотность тела, масса которого в воздухе 7,5 Н, а на воздухе 6,0 Н.
при погружении в воду.
Найдите относительную плотность тела, масса которого в воздухе 7,5 Н, а на воздухе 6,0 Н.
при погружении в воду. е. U <
W
е. U <
W 
 Например. Молоко,
пиво, вина, кислоты в автомобильных маслах и т. д.
Например. Молоко,
пиво, вина, кислоты в автомобильных маслах и т. д.