Архимедова сила. Закон Архимеда – Технарь
Силу, с которой тело, находящееся в жидкости, выталкивается ею; можно рассчитать. Но проще определить ее на опыте, используя для этого прибор, изображенный на рисунке 138.
К пружине подвешивают небольшое ведерко и цилиндрической формы тело. Растяжение пружины отмечает стрелка на штативе (рис. 138, а), показывая вес тела в воздухе. Приподняв тело, под него подставляют отливной сосуд с жидкостью и погружают тело целиком в жидкость (рис. 138, б). При этом часть жидкости, равная по объему тела, выливается из отливного сосуда в стакан, указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, кроме силы тяжести, действует еще и сила, выталкивающая его из жидкости. Если вылить в ведерко жидкость из стакана, то указатель пружины возвратится к своему начальному положению (рис. 138, в).
На основании этого опыта можно заключить, что сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела. Если бы подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Если бы подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Силу, выталкивающую тело из жидкости или газа, называют архимедовой силой, в честь древнегреческого ученого Архимеда, который впервые указал на ее существование и рассчитал ее значение.
Если вес тела в вакууме Р= gm, где m — масса тела, то вес этого же тела в жидкости (или газе) Р1, будет меньше на архимедову силу FA, т. е.
P1 = P—FA, или Р1 =gm—gm1,
здесь m1 — масса жидкости или газа в объеме тела, находящегося в жидкости (газе). Поэтому иногда говорят, что тело, находящееся в жидкости (или газе), теряет в своем весе столько, сколько весит жидкость (или газ) в объеме, вытесненном телом. Так обычно формулируется закон Архимеда.
Подсчитаем архимедову силу, действующую на тело объемом V в жидкости, плотность которой р.
Архимедова сила равна весу жидкости в объеме тела. Значит, FA = Р = gm. Массу жидкости m, вытесняемую телом, можно выразить через ее плотность и объем m = рЖV. Тогда получим:
Значит, FA = Р = gm. Массу жидкости m, вытесняемую телом, можно выразить через ее плотность и объем m = рЖV. Тогда получим:
FA = gpЖV.
Пример. Определить выталкивающую силу, действующую на камень объемом 1,6 м3 в морской воде.
Вопросы.
- Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
- Чему равна эта сила?
- Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
- Как подсчитать архимедову силу?
- Как формулируется закон Архимеда?
Упражнение.
- К коромыслу весов подвешены два цилиндра одинаковой массы: 28 свинцовый, и алюминиевый. Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду? спирт? Ответ обоснуйте. Проверьте его на опыте.
 Как зависит выталкивающая сила от объема тела?
Как зависит выталкивающая сила от объема тела? - К коромыслу весов подвешены два одинаковых по объему алюминиевых цилиндра. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, другой — в спирт? Ответ обоснуйте. Проверьте его на опыте. Зависит ли выталкивающая сила от плотности жидкости?
- К коромыслу весов подвешены два цилиндра одинакового объема: железный и алюминиевый. С помощью дополнительного груза весы уравновешены. Нарушится ли равновесие весов, если оба цилиндра погрузить в воду? Ответ обоснуйте.
- Объем куска железа 0,1 дм3. Какая выталкивающая сила будет на него действовать при полном погружении в воду? в керосин?
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.

Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть – глубина погружения верхней грани, – плотность жидкости, – ускорение силы тяжести; тогда давление на верхнюю грань равно
А на нижнюю
Сила давления равна давлению, умноженному на площадь, т.е.
,
,
где – ребро кубика, причем сила направлена вниз, а сила – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – и и определяется их разностью, которая и является выталкивающей силой:
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина равна объему тела (кубика) , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см).
 Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.
Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.Если тело произвольной формы (рис. 2) занимает внутри жидкости объем , то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема . Так как вес жидкости в объеме тела равен и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме , т.
 е. .
е. .Сделав мысленно обратную замену – поместив в объеме данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» ,
т.е. веса единицы объема вещества: ;
если принять, что для воды ,
то сплошное тело из вещества, у которого утонет, а при будет плавать на поверхности; при тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Архимед из Сиракуз / Archimedes of Siracuse, ок. 287–212 г. до н. э.
Древнегреческий математик, изобретатель и натурфилософ. О его жизни известно мало. Доказал ряд основополагающих математических теорем, прославился благодаря изобретению различных механизмов, до сих пор находящих широкое применение как в быту, так и в оборонной промышленности. Легенда гласит, что Архимед умер насильственной смертью, пав от руки римского воина во время осады Сиракуз, не пожелав укрыться в доме, поскольку был всецело поглощен геометрической задачей, начертанной им на прибрежном песке.
| Комментарии: 1 |
Николай Горькавый
Началось с того, что царь Гиерон II пригласил Архимеда к себе во дворец, налил ему лучшего вина, спросил про здоровье, а потом показал золотую корону, изготовленную для правителя придворным ювелиром. – Я не разбираюсь в ювелирном деле, но разбираюсь в людях, – сказал Гиерон. – И думаю, что ювелир меня обманывает. Царь взял со стола слиток золота. – Я дал ему точно такой же слиток, и он сделал из него корону. Вес у короны и слитка одинаковый, мой слуга проверил это. Но меня не оставляют сомнения, не подмешано ли в корону серебро? Ты, Архимед, самый великий учёный Сиракуз, и я прошу тебя это проверить, ведь, если царь наденет фальшивую корону, над ним будут смеяться даже уличные мальчишки…
– Я не разбираюсь в ювелирном деле, но разбираюсь в людях, – сказал Гиерон. – И думаю, что ювелир меня обманывает. Царь взял со стола слиток золота. – Я дал ему точно такой же слиток, и он сделал из него корону. Вес у короны и слитка одинаковый, мой слуга проверил это. Но меня не оставляют сомнения, не подмешано ли в корону серебро? Ты, Архимед, самый великий учёный Сиракуз, и я прошу тебя это проверить, ведь, если царь наденет фальшивую корону, над ним будут смеяться даже уличные мальчишки…
Движение физического тела в одном измерении не зависит от его движения в двух других измерениях. Например, траектория полета пушечного ядра представляет собой совокупность двух независимых траекторий движения: равномерного движения по горизонтали со скоростью, приданной ядру пушкой, и равноускоренного движения по вертикали под воздействием земного притяжения.
Вам, возможно, доводилось испытывать странные физические ощущения в скоростных лифтах: когда лифт трогается вверх (или тормозит при движении вниз), вас придавливает к полу, и вам кажется, что вы на мгновение потяжелели; а в момент торможения при движении вверх (или старта при движении вниз) пол лифта буквально уходит у вас из-под ног.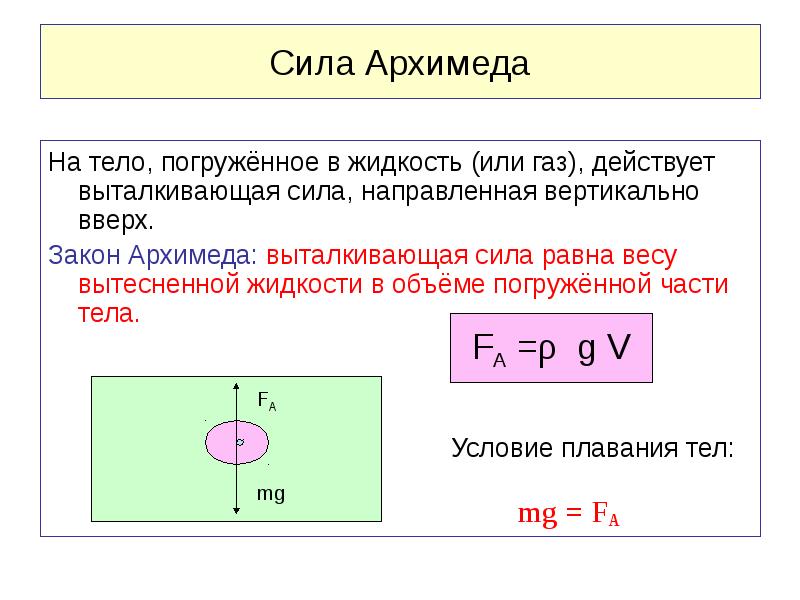 Сами, возможно, того не сознавая, вы испытываете при этом на себе действие принципа эквивалентности инертной и гравитационной масс. Когда лифт трогается вверх, он движется с ускорением, которое приплюсовывается к ускорению свободного падения в неинерциальной (движущейся с ускорением) системе отсчета, связанной с лифтом, и ваш вес увеличивается. Однако, как только лифт набрал «крейсерскую скорость», он начинает двигаться равномерно, «прибавка» в весе исчезает, и ваш вес возвращается к привычному для вас значению. Таким образом, ускорение производит тот же эффект, что и гравитация.
Сами, возможно, того не сознавая, вы испытываете при этом на себе действие принципа эквивалентности инертной и гравитационной масс. Когда лифт трогается вверх, он движется с ускорением, которое приплюсовывается к ускорению свободного падения в неинерциальной (движущейся с ускорением) системе отсчета, связанной с лифтом, и ваш вес увеличивается. Однако, как только лифт набрал «крейсерскую скорость», он начинает двигаться равномерно, «прибавка» в весе исчезает, и ваш вес возвращается к привычному для вас значению. Таким образом, ускорение производит тот же эффект, что и гравитация.
В классической механике Ньютона любая сила – это всего лишь сила притяжения или отталкивания, вызывающая изменение характера движения физического тела. В современных квантовых теориях, однако, понятие силы (трактуемое теперь как взаимодействие между элементарными частицами) интерпретируется несколько иначе. Силовое взаимодействие теперь считается результатом обмена частицей-носителем взаимодействия между двумя взаимодействующими частицами. При таком подходе электромагнитное взаимодействие между, например, двумя электронами, обусловлено обменом фотоном между ними, и аналогичным образом обмен другими частицами-посредниками приводит к возникновению трех прочих видов взаимодействий.
При таком подходе электромагнитное взаимодействие между, например, двумя электронами, обусловлено обменом фотоном между ними, и аналогичным образом обмен другими частицами-посредниками приводит к возникновению трех прочих видов взаимодействий.
Законы Ньютона – в зависимости от того, под каким углом на них посмотреть, – представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки – блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.
Начав двигаться, тело имеет тенденцию продолжать движение. Первый закон механики Ньютона гласит: если тело движется, то при отсутствии внешних воздействий оно так и будет двигаться дальше прямолинейно и равномерно до тех пор, пока оно не подвергнется воздействию внешней силы. Эту тенденцию называют линейным импульсом. Аналогично вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться, поскольку вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения.
Эту тенденцию называют линейным импульсом. Аналогично вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться, поскольку вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения.
Стандартной моделью сегодня принято называть теорию, наилучшим образом отражающую наши представления об исходном материале, из которого изначально построена Вселенная. Она же описывает, как именно материя образуется из этих базовых компонентов, и силы и механизмы взаимодействия между ними.
Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял – в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки
Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.
Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения. Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)
И статики газов.
Энциклопедичный YouTube
1 / 5
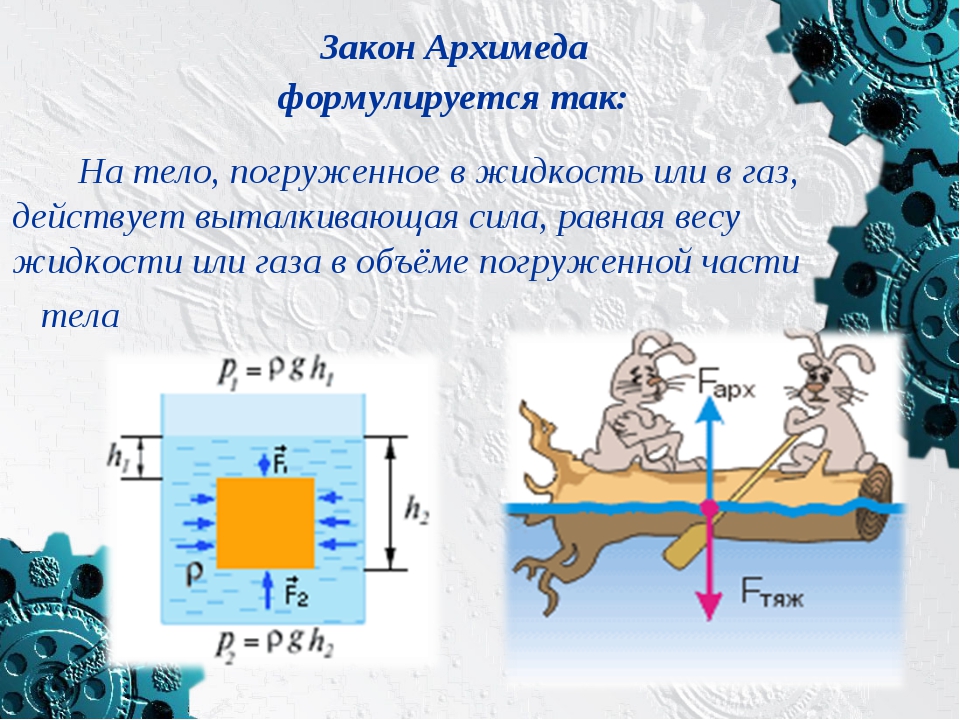
Закон Архимеда формулируется следующим образом : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела .
F A = ρ g V , {\displaystyle {F}_{A}=\rho {g}V,} Сила называется силой Архимеда :
Сила называется силой Архимеда :где ρ {\displaystyle \rho } – плотность жидкости (газа), g {\displaystyle {g}} – ускорение свободного падения , а V {\displaystyle V} – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа.
 Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
P B − P A = ρ g h {\displaystyle P_{B}-P_{A}=\rho gh} F B − F A = ρ g h S = ρ g V , {\displaystyle F_{B}-F_{A}=\rho ghS=\rho gV,}где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
F A = ∬ S p d S {\displaystyle {F}_{A}=\iint \limits _{S}{p{dS}}} ,где S {\displaystyle S} – площадь поверхности, p {\displaystyle p} – давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости , закон Архимеда не работает.
 Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине h {\displaystyle h} есть p = ρ g h {\displaystyle p=\rho gh} . При этом считаем ρ {\displaystyle \rho } жидкости и напряжённость гравитационного поля постоянными величинами, а h {\displaystyle h} – параметром.
 Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) {\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z})}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса .
 {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Другая формулировка (где ρ t {\displaystyle \rho _{t}} – плотность тела, ρ s {\displaystyle \rho _{s}} – плотность среды, в которую оно погружено).
Равновесие тела, погруженного в жидкость. Закон Архимеда
из “Гидравлика насосы и компрессоры”
Погруженное в жидкость тяжелое тело, например камень, опустится на дно сосуда. Тело более легкое, например пустотелый металлический шар, будет плавать на поверхности жидкости, будучи несколько погруженным в жидкость. Рассмотрим условия равновесия тел в жидкости. [c.24]Пусть тело массой М полностью погружено в жидкость (рис.
 11). [c.24]
11). [c.24]
На верхнюю часть поверхности АВС тела жидкость давит с силой, равной весу заштрихованного столба жидкости QgV АВСС А А). [c.24]
На нижнюю часть поверхности АВС тела жидкость давит с силой, равной pgV (АА С СОА). [c.24]
Сила N называется архимедовой подъемной силой. Равенство (21) носит название закона Архимеда. [c.24]
Согласно закону Архимеда на всякое тело, погруженное в жид-жость, действует со стороны этой я идкости подъемная сила, направленная вверх и равная весу вытесненной телом жидкости. [c.24]
Так как давление жидкости с глубиной погружения увеличивается, сила давления жидкости, действующая на нижние элементы поверхности тела, всегда больше, чем сила давления, действующая на верхние элементы. Результирующая всех этих сил давления оказывается направленной вверх и называется подъемной силой. [c.24]
Сила веса тела направлена вниз и противоположна направлению подъемной силы.
 [c.24]
[c.24]
Если вес тела больше, чем подъемная сила gM N), то тело будет опускаться на дно сосуда. [c.24]
Если вес тела будет меньше, чем архимедова сила gM М), то тело будет всплывать. [c.24]
Здесь масса плавающего тела, равна массе воды, вытесненной телом из объема F . Объем меньше объема всего тела. [c.25]
Вернуться к основной статье
Архимед погружал его в жидкость. Архимедова сила
ЗАКОН АРХИМЕДА –закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.
Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, r – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно
r · g · h = p 1
а на нижнюю
r · g (h+a ) = p 2
Сила давления равна давлению, умноженному на площадь, т.е.
F 1 = p 1 · a \up122, F 2 = p 2 · a \up122 , где a – ребро кубика,
причем сила F 1 направлена вниз, а сила F 2 – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F 1 и F 2 и определяется их разностью, которая и является выталкивающей силой:
F 2 – F 1 =r · g · (h+a ) a \up122 – r gha ·a 2 = pga 2
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F 2 – F 1 = pga 3 равна объему тела (кубика) a 3 , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед , один из величайших ученых Земли.
Величина F 2 – F 1 = pga 3 равна объему тела (кубика) a 3 , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед , один из величайших ученых Земли.
Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V , то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V . Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V , т.е. pgV .
Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V , т.е. pgV .
Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g , т.е. веса единицы объема вещества: g = pg ; если принять, что для воды g = 1
, то сплошное тело из вещества, у которого g > 1
утонет, а при g g = 1
тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Владимир Кузнецов
Причина возникновения архимедовой силы – разность давлений среды на разной глубине. Поэтому сила Архимеда возникает только в при наличии силы тяжести. На Луне она будет вшестеро, а на Марсе – в 2,5 раза меньше, чем на Земле.
В невесомости архимедовой силы нет. Если представить себе, что сила тяжести на Земле вдруг пропала, то все корабли в морях, океанах и реках от малейшего толчка уйдут на любую глубину. А вот подняться вверх им не даст не зависящее от силы тяжести поверхностное натяжение воды, так что взлететь они не смогут, все потонут.
Как проявляется сила Архимеда
Величина архимедовой силы зависит от объема погруженного тела и плотности среды, в которой оно находится. Его точная в современном представлении: на погруженное в жидкую или газовую среду тело в поле силы тяжести действует выталкивающая сила, в точности равная весу вытесненной телом среды, то есть F = ρgV, где F – сила Архимеда; ρ – плотность среды; g – ускорение свободного падения; V – объем вытесненной телом или погруженной его частью жидкости (газа).
Если в пресной воде на каждый литр объема погруженного тела действует выталкивающая сила в 1 кг (9,81 н), то в морской воде, плотность которой 1,025 кг*куб. дм, на тот же литр объема будет действовать сила Архимеда в 1 кг 25 г. Для человека средней комплекции разность силы поддержки морской и пресной водой составит почти 1,9 кг. Поэтому плавать в море легче: представьте себе, что вам нужно переплыть хотя бы пруд без течения с двухкилограммовой гантелью за поясом.
От формы погруженного тела архимедова сила не зависит. Возьмите железный цилиндр, измерьте силу его из воды. Затем раскатайте этот цилиндр в лист, погрузите в воду плашмя и ребром. Во всех трех случаях сила Архимеда окажется одинаковой.
На первый взгляд странно, но, если погружать лист плашмя, то уменьшение разности давлений для тонкого листа компенсируется увеличением его площади, перпендикулярной поверхности воды. А при погружении ребром – наоборот, малая площадь ребра компенсируется большей высотой листа.
Если вода очень сильно насыщена солями, отчего ее плотность стала выше плотности человеческого тела, то в ней не утонет и человек, не умеющий плавать. В Мертвом море в Израиле, например, туристы могут часами лежать на воде, не шевелясь. Правда, ходить по нему все равно нельзя – площадь опоры получается малой, человек проваливается в воду по горло, пока вес погруженной части тела не сравняется с весом вытесненной им воды. Однако при наличии некоторой доли фантазии сложить легенду о хождении по воде можно. А вот в керосине, плотность которого всего 0,815 кг*куб. дм, не сможет удержаться на поверхности и очень опытный пловец.
В Мертвом море в Израиле, например, туристы могут часами лежать на воде, не шевелясь. Правда, ходить по нему все равно нельзя – площадь опоры получается малой, человек проваливается в воду по горло, пока вес погруженной части тела не сравняется с весом вытесненной им воды. Однако при наличии некоторой доли фантазии сложить легенду о хождении по воде можно. А вот в керосине, плотность которого всего 0,815 кг*куб. дм, не сможет удержаться на поверхности и очень опытный пловец.
Архимедова сила в динамике
То, что суда плавают благодаря силе Архимеда, известно всем. Но рыбаки знают, что архимедову силу можно использовать и в динамике. Если на попалась большая и сильная рыбина (таймень, например), то медленно подтягивать ее к сачку (вываживать) нет: оборвет леску и уйдет. Нужно сначала дернуть слегка, когда она уходит. Почувствовав при этом крючок, рыба, стремясь освободиться от него, метнется в сторону рыбака. Тогда нужно дернуть очень сильно и резко, чтобы леска не успела порваться.
В воде тело рыбы почти ничего не весит, но его масса с инерцией сохраняются. При таком способе ловли архимедова сила как бы наддаст рыбе в хвост, и добыча сама плюхнется к ногам рыболова или к нему в лодку.
Архимедова сила в воздухе
Архимедова сила действует не только в жидкостях, но и в газах. Благодаря ей летают воздушные шары и дирижабли (цеппелины). 1 куб. м воздуха при нормальных условиях (20 градусов Цельсия на уровне моря) весит 1,29 кг, а 1 кг гелия – 0,21 кг. То есть 1 кубометр наполненной оболочки способен поднять груз в 1,08 кг. Если оболочка диаметром в 10 м, то ее объем будет 523 куб. м. Выполнив ее из легкого синтетического материала, получим подъемную силу около полутонны. Архимедову силу в воздухе аэронавты называют сплавной силой.
Если из аэростата откачать воздух, не дав ему сморщиться, то каждый его кубометр потянет вверх уже все 1,29 кг. Прибавка более 20% к подъемной силе технически весьма соблазнительна, да гелий дорог, а водород взрывоопасен. Поэтому проекты вакуумных дирижаблей время от времени появляются на свет. Но материалов, способных при этом выдержать большое (около 1 кг на кв. см) атмосферное давление снаружи на оболочку, современная технология создать пока не способна.
Поэтому проекты вакуумных дирижаблей время от времени появляются на свет. Но материалов, способных при этом выдержать большое (около 1 кг на кв. см) атмосферное давление снаружи на оболочку, современная технология создать пока не способна.
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
И статики газов.
Энциклопедичный YouTube
1 / 5
Закон Архимеда формулируется следующим образом : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела . Сила называется силой Архимеда :
F A = ρ g V , {\displaystyle {F}_{A}=\rho {g}V,}где ρ {\displaystyle \rho } – плотность жидкости (газа), g {\displaystyle {g}} – ускорение свободного падения , а V {\displaystyle V} – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
 Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
P B − P A = ρ g h {\displaystyle P_{B}-P_{A}=\rho gh} F B − F A = ρ g h S = ρ g V , {\displaystyle F_{B}-F_{A}=\rho ghS=\rho gV,}где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме:
F A = ∬ S p d S {\displaystyle {F}_{A}=\iint \limits _{S}{p{dS}}} ,где S {\displaystyle S} – площадь поверхности, p {\displaystyle p} – давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости , закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине h {\displaystyle h} есть p = ρ g h {\displaystyle p=\rho gh} . При этом считаем ρ {\displaystyle \rho } жидкости и напряжённость гравитационного поля постоянными величинами, а h {\displaystyle h} – параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат O x y z {\displaystyle Oxyz} , причём выберем направление оси z совпадающим с направлением вектора g → {\displaystyle {\vec {g}}} . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку d S {\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела, d F → A = − p d S → {\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}} . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) {\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z})}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса .
 {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Другая формулировка (где ρ t {\displaystyle \rho _{t}} – плотность тела, ρ s {\displaystyle \rho _{s}} – плотность среды, в которую оно погружено).
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :
где – плотностьжидкости (газа), – ускорение свободного падения, а – объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма.

Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
 P выт =
ρ ж gV погр
P выт =
ρ ж gV погр Для однородного тела плавающего на поверхности справедливо соотношение
где: V – объем плавающего тела; ρ m – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью . Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением , а точку приложения равнодействующей давления (т.е. центр давления) – центром водоизмещения . При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O”-O” , представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K”L”M” , наоборот, погрузилось в нее.
 При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если h
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Рекомендуем также
Закон Архимеда для газа – Энциклопедия по машиностроению XXL
Изменение скорости газа от первой до второй критической, сопровождаемое сильным расширением слоя, увеличит долю пустот, что в свою очередь катастрофически отразится на плотности кипящего слоя, которая упадет практически до нуля или, вернее, до величины, близкой к плотности газа. Другими словами, если, например, в стадии однородного псевдоожижения плотность слоя, состоящего из применяемой в топках кипящего слоя смеси угля и доломита, существенно превышает плотность воды знаменитого Мертвого моря в Палестине, в котором, не нарушая закона Архимеда, нельзя утонуть, то при псевдоожижении, когда доля пустот начнет приближаться к 70 %, даже профессиональному пловцу вряд ли удастся удержаться на поверхности. В таком море судам пришлось бы постоянно менять ватерлинию в зависимости от скорости фильтрации газа.
[c.75]
Другими словами, если, например, в стадии однородного псевдоожижения плотность слоя, состоящего из применяемой в топках кипящего слоя смеси угля и доломита, существенно превышает плотность воды знаменитого Мертвого моря в Палестине, в котором, не нарушая закона Архимеда, нельзя утонуть, то при псевдоожижении, когда доля пустот начнет приближаться к 70 %, даже профессиональному пловцу вряд ли удастся удержаться на поверхности. В таком море судам пришлось бы постоянно менять ватерлинию в зависимости от скорости фильтрации газа.
[c.75]
Левая часть уравнения (8-25) представляет собой подъемную силу, создаваемую потоком газов по отношению к частице, а правая часть — вес частицы с поправкой на вытесняемый объем газов (по закону Архимеда). [c.236]
Закон Архимеда. Всякое тело объемом V, погруженное в жидкость (или газ), выталкивается с силой Q, равной весу вытесненной жидкости (газа)
[c. 10]
10]
Приведем здесь также формулировку известного из школьного курса физики закона Архимеда на всякое погруженное в жидкость (или газ) тело действует выталкивающая (архимедова) сила, равная весу жидкости, вытесненной этим телом, и приложенная к центру тяжести (или центру масс) вытесненного телом объема жидкости. [c.267]
Физически ясно появление критерия подобия Аг и зависимости от него величины теплопередачи при кипении. Пузырьки газа увеличиваются при движении их к поверхности нод действием выталкивающей силы в соответствии с законом Архимеда. Эта сила зависит от разности плотностей жидкости и пара, от величины пузырька с газом и от величины ускорения силы тяжести. Очевидно, на движение пузырька в реальной жидкости окажет влияние ее вязкость, характеризуемая коэффициентом кинематической вязкости V. Можно, следовательно, утверждать, что если в двух различных испарительных системах с разными жидкостями критерии 1 [c.16]
Подъемная сила аэростата. Применение закона Архимеда к газам дает возможность ввести понятие о подъемной силе всякого газа, помещенного в атмосферу другого гааа, более тяжелого, чем он сам. Обозначив уд. весовые плотности этих газов через Ув и где Уз — для атмосферного воздуха и у, — для газа легче воздуха величина подъемной силы 1 м легкого газа будет
[c.66]
Применение закона Архимеда к газам дает возможность ввести понятие о подъемной силе всякого газа, помещенного в атмосферу другого гааа, более тяжелого, чем он сам. Обозначив уд. весовые плотности этих газов через Ув и где Уз — для атмосферного воздуха и у, — для газа легче воздуха величина подъемной силы 1 м легкого газа будет
[c.66]
Тело, погруженное в жидкость или газ (и омываемое со всех сторон), испытывает действие выталкивающей силы, равное весу вытесненной им жидкости или газа (закон Архимеда). [c.44]
ПЛАВАНИЕ ТЕЛ — состояние равновесия твёрдого тела, частично или полностью погружённого в жидкость (или газ). Осн. задача теории П, т.— определение равновесия тела, погружённого в жидкость, выяснение условий устойчивости равновесия. Простейшие условия П. т. указывает Архимеда закон. [c.592]
Тело, погруженное полностью или отчасти в жидкость (или газ), испытывает действие подъемной силы со стороны окружающей жидкости или газа. Еще Архимедом (III век до н. э.) был найден основной закон всякое тело, погруженное в жидкость (или газ), испытывает со стороны окружающей среды действие силы, равной весу вытесненной телом жидкости (или газа) эта сила направлена вверх и проходит через центр масс вытесненной жидкости (или газа).
[c.343]
Еще Архимедом (III век до н. э.) был найден основной закон всякое тело, погруженное в жидкость (или газ), испытывает со стороны окружающей среды действие силы, равной весу вытесненной телом жидкости (или газа) эта сила направлена вверх и проходит через центр масс вытесненной жидкости (или газа).
[c.343]
Критерий подобия Аг носит имя первооткрывателя закона, определяющего подъемную силу , действующую на всякое тело, погруженное в жидкость или газ, имя величайшего ученого древней Греции — Архимеда (3 в. до н. э.) [c.16]
В основе полета летательных аппаратов легче воздуха лежит закон, открытый Архимедом сила, выталкивающая целиком погруженное в жидкость (или газ) тело, равна весу жидкости (или газа) в объеме этого тела. Эта сила направлена вертикально вверх и приложена в центре объема погруженной части тела. [c.44]
Решение. Подъемная сила воздуха Рвыт, действующая на щар по закону Архимеда, уравновешивается весом шара О я весом газа в нем ргё [см. формулу (1.15)]
[c.40]
формулу (1.15)]
[c.40]
Так как за единицу массы в G -системе (абсолютной системе физич. величин) выбрана масса 1 см чистой воды, равная 1 г при ее наибольшей плотности (3,99°), то П. воды при 4° равна 1, и уд. в. любого тела по отношению к воде при 4°, как к стандарту, численно равен плотности этого тала при1)о= 1, -P D.U. газа по отношению к водороду или к воздуху часто называют (не вполне правильно) уд. в. этого газа относительно водорода или воздуха, взятых при тех же условиях. П. твердых тел и жидкостей обычно измеряют или по методу гидростатич. взвешивания (пользуясь законом Архимеда) или же пикнометром (см.). К первому же способу относится и наиболее употребительное в технике измерение П. с помощью ареометра. [c.371]
Если иижняя часть жидкости или газа иагрега сильнее, чем верхняя, то от иагреваиия вещество расширяется и плотиость внизу становится меньше плотности наверху. По закону Архимеда, более легкая жидкость стремится вверх, в результате чего возникает макроскопическое движение более нагретой жидкости вверх, а более холодной—вниз. Это явление называют конвекцией. В результате такого взаимного макроскопического движения температура жидкости стремится выравняться. Вообще говоря, Этот процесс протекает более интенсивно, нежели выравнивание температуры вследствие теплопроводности жидкости и возникающего потока теплоты снизу вверх. Отметим, что в конвективных процессах сколько-нибудь существенной сжимаемости вещества не происходит, так что все результаты относятся к газам в той же мере, что и к жидкостям.
[c.161]
Это явление называют конвекцией. В результате такого взаимного макроскопического движения температура жидкости стремится выравняться. Вообще говоря, Этот процесс протекает более интенсивно, нежели выравнивание температуры вследствие теплопроводности жидкости и возникающего потока теплоты снизу вверх. Отметим, что в конвективных процессах сколько-нибудь существенной сжимаемости вещества не происходит, так что все результаты относятся к газам в той же мере, что и к жидкостям.
[c.161]
Обобщим уравнение Навье—Стокса, учтя в нем силу Архимеда. Прн этом мы ограничимся стацноиарными течениями. Выталкивающая сила, действующая на единичный объем вещества, по закону Архимеда равна Р=р , где р — разность плотностей нагретой и холодной жидкостей (или газов), д — ускорение свободного падения. Малую разность р можно выразить через малую разность температур Т нагретой и холодной жидкостей [c.161]
Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), со стороны этой жидкости (или газа) действует вытал кивающая сила, направленная по вертикали вверх и приложенная к центру тяжести вытесненного объема. Выталкивающую силу называют Архимедовой или гидростатической подъемной силой.
[c.121]
Выталкивающую силу называют Архимедовой или гидростатической подъемной силой.
[c.121]
Тело, погруженное в жидкость (или газ), испытьюает действие выталкивающей силы, направленной вверх и равной весу вытесненной им жидкости (закон Архимеда). [c.160]
АРХИМЕДА ЗАКОН — закон статики жидкостей и газов, согласно к-рому на всякое тело, погружённое в жидкость (или газ), действует со стороны, 9Toii жидкости (газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру тяжести вытесненного объёма. Выталкивающую силу наз. тайнее архимедовой или гидростатич. подъемной силой. Давление, действующее на погружённое в жидкость те.ю, увеличивается с глубиной погружения, позтому сила давления на ниж. элементы поверхности тела больше, чем на верхние. В результате сложения всех сил, действующих на каждый элемент поверхности, получается равнодействующая F, направленная по вертикали вверх.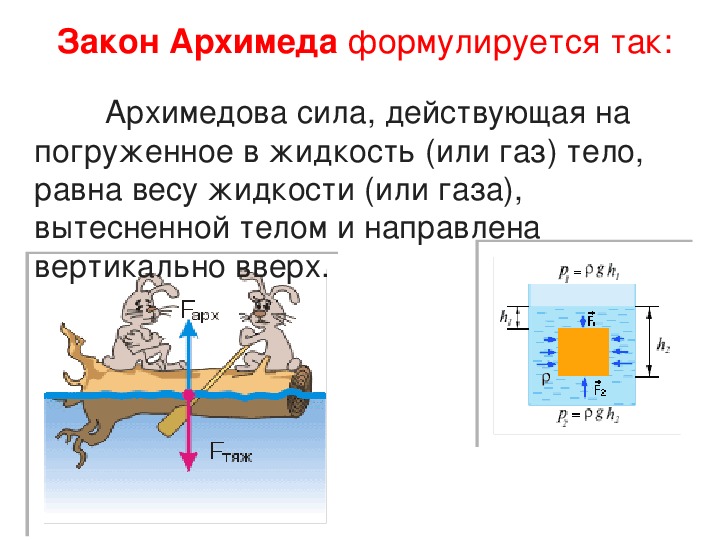 Если же тело плотно лежит на дне, то давление жидкости только сильнее прижимает его ко дну.
[c.123]
Если же тело плотно лежит на дне, то давление жидкости только сильнее прижимает его ко дну.
[c.123]
КОНВЕКЦИОННЫЙ ТОК, перенос электрич. зарядов, осуществляемый перемещением заряж. макроскопич. тела. С точки зрения электронной теории, любой перенос зарядов в конечном счёте обусловлен конвекцией (перемещением) заряж. микрочастиц. Этим объясняется полная тождественность магн. св-в К. т. и тока проводимости (упорядоченного движения эл-нов, ионов и т.п.), установленная в опытах амер. физика Г. Роуланда (1879) и А. А. Эйхенвальда (1903). КОНВЕКЦИЯ (от лат. сопуес11о — принесение, доставка), перенос теплоты в жидкостях, газах или сыпучих средах потоками в-ва. Естественная (свободная) К. возникает в поле силы тяжести при неравномерном нагреве (нагреве снизу) текучих или сыпучих в-в. Нагретое в-во под действием архимедовой силы Р(Др — разность плотности нагретого в-ва и окружающей среды, V — его объём, д — ускорение свободного падения см. Архимеда закон) перемещается относительно менее нагретого в-ва в направлении, противоположном направлению силы тяжести. К. приводит к выравниванию темп-ры в-ва. При стационарном подводе теплоты к в-ву в нём возникают стационарные конвекц. потоки. Интенсивность К. зависит от разности темп-р между слоями, теплопроводности и вязкости среды.
[c.307]
К. приводит к выравниванию темп-ры в-ва. При стационарном подводе теплоты к в-ву в нём возникают стационарные конвекц. потоки. Интенсивность К. зависит от разности темп-р между слоями, теплопроводности и вязкости среды.
[c.307]
7 Сила Архимеда. Плавание тел
Сила Архимеда. Плавание тел
2.5.1. Закон Архимеда
Закон Архимеда – это закон, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) поддерживающая сила, равная весу вытесненной телом жидкости (газа), направленная вверх и приложенная к центру тяжести вытесненного объёма (рис. 2.12).
(2.19)
где W – объем погруженного тела.
Рис. 2.12. Поддерживающая сила
Сила F называется поддерживающей силой; ее также называют также архимедовой, или силой водоизмещения, илигидростатической подъёмной силой.
Рекомендуемые файлы
ДЗ№2. Вариант№7. Расчет ламинарного пограничного слоя на пластине + MathCAD
Механика жидкости и газа (МЖГ или Гидравлика)
В установке гидравлического пресса насос 3 всасывает жидкость Ж, температура которой tоС, из бака 1 и через трехпозиционный распределитель 4 нагнетает ее в пресс. При прессовании по нагнетательным трубопроводам l1 и l2 жидкость подается в правую стор
При прессовании по нагнетательным трубопроводам l1 и l2 жидкость подается в правую стор
Гидравлика
Исполнительный механизм силового цилиндра совершает возвратно-поступательное движение, обеспечивает n=24 двойных ходов в минуту. Размеры цилиндра: ход поршня L=0,8м, диаметр поршня D=0,14м, левого штока d1=0,1м, правого – d2=0,07м. Уплотнение в гидро
Гидравлика
Задача 9-7
Куколевский (Гидравлика)
Определить расход воды (ρ=1000кг/м3, ν=1∙10-6 м2/с) в трубопроводе длиной l=17м и диаметром d=100мм для подачи ее на высоту Н=5. Располагаемое давление ррас=0,2МПа. Коэффициенты сопротивления: задвижки поворота , выхода в бак – Шероховатость трубы Δ
Гидравлика
Задача 13-7
Куколевский (Гидравлика)
Если вес тела P меньше поддерживающей силы F, тело всплывает на поверхность жидкости до тех пор, пока вес вытесненной погруженной частью тела жидкости не станет равным поддерживающей силе. Если вес тела больше поддерживающей силы, тело тонет; если же вес тела равен поддерживающей силе, тело плавает внутри жидкости
2.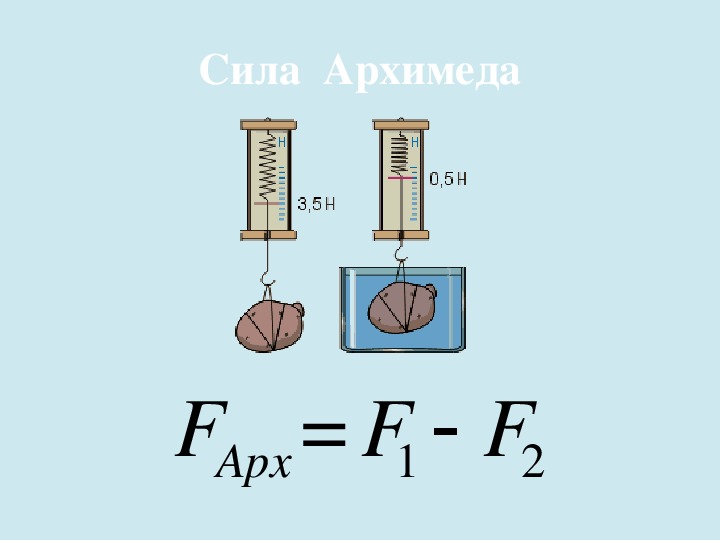 5.2. Плавание тел
5.2. Плавание тел
Плавание тел – это состояние равновесия твёрдого тела, частично или полностью погруженного в жидкость (или газ). Основная задача теории плавания тел – определение положений равновесия тела, погруженного в жидкость, выяснение условий устойчивости равновесия. Простейшие условия плавания тел указывает закон Архимеда.
Для однородного тела плавающего на поверхности справедливо соотношение
где: V – объем плавающего тела; ρm – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) – центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O”, представляющей ось симметрии судна и называемой осью плавания (рис. 2.14).
2.14).
Рис. 2.14. Поперечный профиль судна
Люди также интересуются этой лекцией: 8.4 Приспособление (уступка, коллаборационизм).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O”. Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным – в противном случае.
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Как был открыт закон Архимеда? Исследование границ применимости закона архимеда.
Разные предметы в жидкости ведут себя по-разному. Одни тонут, другие остаются на поверхности и плавают. Почему так происходит, объясняет закон Архимеда, открытый им при весьма необычных обстоятельствах и ставший основным законом гидростатики.
Как Архимед открыл свой закон
Легенда рассказывает нам, что Архимед открыл свой закон случайно. И этому открытию предшествовало следующее событие.
Царь Сиракуз Гиерон, правивший в 270-215 г.г. до н.э., заподозрил своего ювелира в том, что тот подмешал в заказанную ему золотую корону некоторое количество серебра. Чтобы развеять сомнения, он попросил Архимеда подтвердить или опровергнуть свои подозрения. Как истинного учёного, Архимеда увлекла эта задача. Для её решения нужно было определить вес короны. Ведь если в неё подмешано серебро, то её вес отличался бы от того, как если бы она была сделана из чистого золота. Удельный вес золота был известен. Но как вычислить объём короны? Ведь она имела неправильную геометрическую форму.
Ведь если в неё подмешано серебро, то её вес отличался бы от того, как если бы она была сделана из чистого золота. Удельный вес золота был известен. Но как вычислить объём короны? Ведь она имела неправильную геометрическую форму.
Согласно легенде, однажды Архимед, принимая ванну, размышлял над задачей, которую ему предстояло решить. Неожиданно учёный обратил внимание на то, что уровень воды в ванне стал выше после того, как он в неё погрузился. Когда он поднялся, уровень воды снизился. Архимед заметил, что своим телом вытесняет из ванны какое-то количество воды. И объём этой воды равнялся объёму его собственного тела. И тут он понял, как решить задачу с короной. Достаточно лишь погрузить её в сосуд, наполненный водой, и измерить объём вытесненной воды. Говорят, что он так обрадовался, что с криком «Эврика!» («Нашёл!») выскочил из ванны, даже не одевшись.
Так ли это было на самом деле или нет, значения не имеет. Архимед нашёл способ измерения объёма тел со сложной геометрической формой. Он впервые обратил внимание на свойства физических тел, которые называют плотностью, сопоставив их не друг с другом, а с весом воды. Но самое главное, им был открыт принцип плавучести .
Он впервые обратил внимание на свойства физических тел, которые называют плотностью, сопоставив их не друг с другом, а с весом воды. Но самое главное, им был открыт принцип плавучести .
Закон Архимеда
Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Е сли в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
А на само тело в жидкости действует сила, которая выталкивает его на поверхность. Её величина равна весу вытесненной им жидкости. Эту силу называют силой Архимеда .
Для жидкости закон Архимеда выглядит так: на тело, погружённое в жидкость, действует выталкивающая сила, направленная вверх, и равная весу вытесненной этим телом жидкости.
Величина силы Архимеда вычисляется следующим образом:
F A = ρ ɡ V ,
где ρ – плотность жидкости,
ɡ – ускорение свободного падения
V – объём погружённого в жидкость тела, или часть объёма тела, находящаяся ниже поверхности жидкости.
Сила Архимеда всегда приложена к центру тяжести объёма и направлена противоположно силе тяжести.
Следует сказать, что для выполнения этого закона должно соблюдаться одно условие: тело либо пересекается с границей жидкости, либо со всех сторон окружено этой жидкостью. Для тела, которое лежит на дне и герметично касается его, закон Архимеда не действует. Так, если мы положим на дно кубик, одна из граней которого будет плотно соприкасаться с дном, закон Архимеда для него мы не сможем применить.
Силу Архимеда называют также выталкивающей силой .
Эта сила по своей природе – сумма всех сил давления, действующих со стороны жидкости на поверхность тела, погружённого в неё. Выталкивающая сила возникает из-за разности гидростатического давления на разных уровнях жидкости.
Рассмотрим эту силу на примере тела, имеющего форму куба или параллелограмма.
P 2 – P 1 = ρ ɡ h
F A = F 2 – F 1 = ρɡhS = ρɡhV
Закон Архимеда действует и для газов. Но в этом случае выталкивающая сила называется подъёмной, а для её вычисления плотность жидкости в формуле заменяют на плотность газа.
Но в этом случае выталкивающая сила называется подъёмной, а для её вычисления плотность жидкости в формуле заменяют на плотность газа.
Условие плавания тела
От соотношения значений силы тяжести и силы Архимеда зависит, будет ли тело плавать, тонуть или всплывать.
Если сила Архимеда и сила тяжести равны по величине, то тело в жидкости находится в состоянии равновесия, когда оно не всплывает и не погружается. Говорят, что оно плавает в жидкости. В этом случае F T = F A .
Если же сила тяжести больше силы Архимеда, тело погружается, или тонет.
Здесь F T ˃ F A .
А если значение силы тяжести меньше силы Архимеда, тело всплывает. Это происходит, когда F T ˂ F A .
Но всплывает оно не бесконечно, а лишь до того момента, пока сила тяжести и сила Архимеда не сравняются. После этого тело будет плавать.
Почему не все тела тонут
Если положить в воду два одинаковых по форме и размерам бруска, один из которых сделан из пластмассы, а другой из стали, то можно увидеть, что стальной брусок утонет, а пластмассовый останется на плаву. Так же будет, если взять любые другие предметы одинаковых размеров и формы, но разные по весу, например, пластмассовый и металлический шарики. Металлический шарик пойдёт ко дну, а пластмассовый будет плавать.
Так же будет, если взять любые другие предметы одинаковых размеров и формы, но разные по весу, например, пластмассовый и металлический шарики. Металлический шарик пойдёт ко дну, а пластмассовый будет плавать.
Но почему же ведут себя по-разному пластмассовый и стальной бруски? Ведь их объёмы одинаковы.
Да, объёмы одинаковы, но сами бруски сделаны из разных материалов, которые имеют разную плотность. И если плотность материала выше плотности воды, то брусок утонет, а если меньше – будет всплывать до тех пор, пока не окажется на поверхности воды. Это справедливо не только для воды, но и для любой другой жидкости.
Если обозначить плотность тела P t , а плотность среды, в которой оно находится, как P s , то если
P t ˃ Ps (плотность тела выше плотности жидкости) – тело тонет,
P t = Ps (плотность тела равна плотности жидкости) – тело плавает в жидкости,
P t
˂ Ps (плотность тела меньше плотности жидкости) – тело всплывает, пока не окажется на поверхности. После чего оно плавает.
После чего оно плавает.
Не выполняется закон Архимеда и в состоянии невесомости. В этом случае отсутствует гравитационное поле, а, значит, и ускорение свободного падения.
Свойство тела, погруженного в жидкость, оставаться в равновесии, не всплывая и не погружаясь дальше, называется плавучестью .
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Если принять вес тела в вакууме за Р о, то его вес в воздушной среде может быть описан такой формулой: Р в =Р о – F а;
здесь Р о – вес в вакууме;
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
Это и есть закон Архимеда.
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи.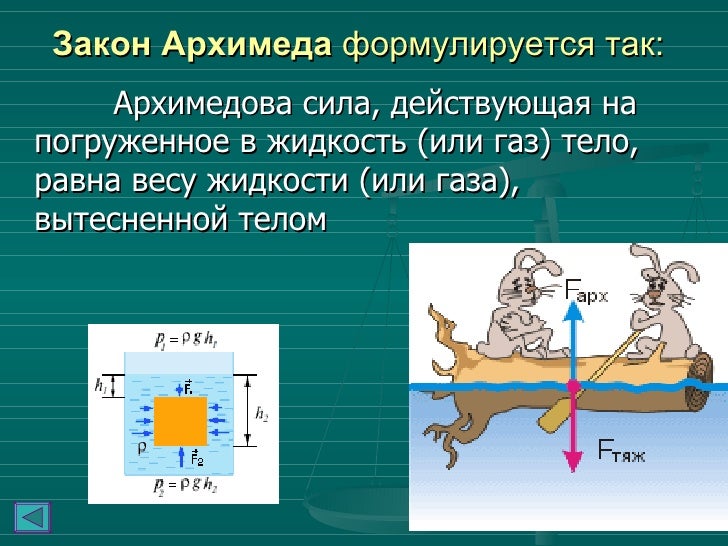 Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.
Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.
Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
Несмотря на явные различия свойств жидкостей и газов, во многих случаях их поведение определяется одними и теми же параметрами и уравнениями, что позволяет использовать единый подход к изучению свойств этих веществ.
В механике газы и жидкости рассматривают как сплошные среды. Предполагается, что молекулы вещества распределены непрерывно в занимаемой ими части пространства. При этом плотность газа значительно зависит от давления, в то время как для жидкости ситуация иная. Обычно при решении задач этим фактом пренебрегают, используя обобщенное понятие несжимаемой жидкости, плотность которой равномерна и постоянна.
Определение 1
Давление определяется как нормальная сила $F$, действующая со стороны жидкости на единицу площади $S$.
$ρ = \frac{\Delta P}{\Delta S}$.
Замечание 1
Давление измеряется в паскалях. Один Па равен силе в 1 Н, действующей на единицу площади 1 кв. м.
В состояние равновесия давление жидкости или газа описывается законом Паскаля, согласно которому давление на поверхность жидкости, производимое внешними силами, передается жидкостью одинаково во всех направлениях.
При механическом равновесии, давление жидкости по горизонтали всегда одинаково; следовательно, свободная поверхность статичной жидкости всегда горизонтальна (кроме случаев соприкосновения со стенками сосуда). Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.
Представим некоторый объем жидкости, ограниченный вертикальным цилиндром. Поперечное сечение столба жидкости обозначим $S$, его высоту $h$, плотность жидкости $ρ$, вес $P=ρgSh$. Тогда справедливо следующее:
$p = \frac{P}{S} = \frac{ρgSh}{S} = ρgh$,
где $p$ – давление на дно сосуда.
Отсюда следует, что давление меняется линейно, в зависимости от высоты. При этом $ρgh$ – гидростатическое давление, изменением которого и объясняется возникновение силы Архимеда.
Формулировка закона Архимеда
Закон Архимеда, один из основных законов гидростатики и аэростатики, гласит: на тело, погруженное в жидкость или газ, действует выталкивающая или подъемная сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Замечание 2
Возникновение Архимедовой силы связано с тем, что среда – жидкость или газ – стремится занять пространство, отнятое погруженным в нее телом; при этом тело выталкивается из среды.
Отсюда и второе название для этого явление – выталкивающая или гидростатическая подъемная сила.
Выталкивающая сила не зависит от формы тела, также как и от состава тела и прочих его характеристик.
Возникновение Архимедовой силы обусловлено разностью давления среды на разных глубинах. Например, давление на нижние слои воды всегда больше, чем на верхние слои.
Проявление силы Архимеда возможно лишь при наличии тяжести. Так, например, на Луне выталкивающая сила будет в шесть раз меньше, чем на Земле для тел равных объемов.
Возникновение Силы Архимеда
Представим себе любую жидкую среду, например, обычную воду. Мысленно выделим произвольный объем воды замкнутой поверхностью $S$. Поскольку вся жидкость по условию находится в механическом равновесии, выделенный нами объем также статичен. Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.
Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.
Теперь обозначим, что вместо этой условного ограниченной жидкости в среду было помещено любое твердое тело соответствующего объема. Если соблюдается условие механического равновесия, то со стороны окружающей среды никаких изменений не произойдет, в том числе останется прежним давление, действующее на поверхность $S$. Таким образом мы можем дать более точную формулировку закона Архимеда:
Замечание 3
Если тело, погруженное в жидкость, находится в механическом равновесии, то со стороны окружающей его среды на него действует выталкивающая сила гидростатического давления, численно равная весу среды в объеме, вытесненным телом. 2$.
2$.
Выталкивающая сила, действующая на тело, противоположна по направлению силе тяжести, поэтому поведение погруженного тела в среде зависит от соотношения модулей силы тяжести $F_T$ и Архимедовой силы $F_A$. Здесь возможны три случая:
- $F_T$ > $F_A$. Сила тяжести превышает выталкивающую силу, следовательно, тело тонет/падает;
- $F_T$ = $F_A$. Сила тяжести уравнивается с выталкивающей силой, поэтому тело «зависает» в жидкости;
- $F_T$
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
аэродинамика | гидромеханика | Britannica
аэродинамика , раздел физики, изучающий движение воздуха и других газообразных жидкостей, а также силы, действующие на тела, проходящие через такую жидкость. Аэродинамика стремится, в частности, объяснить принципы полета самолетов, ракет и ракет. Он также занимается проектированием автомобилей, высокоскоростных поездов и кораблей, а также строительством таких сооружений, как мосты и высотные здания, для определения их сопротивления сильным ветрам.
Наблюдения за полетом птиц и снарядов вызвали у древних спекуляции относительно задействованных сил и способа их взаимодействия.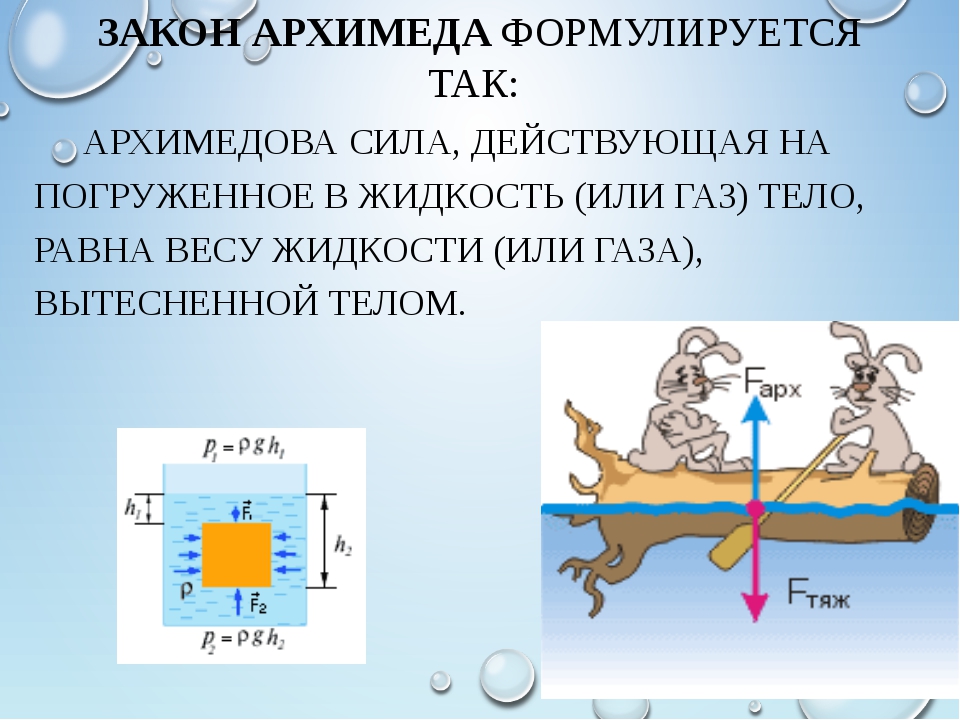 Однако у них не было реальных знаний о физических свойствах воздуха и они не пытались систематически изучать эти свойства. Большинство их идей отражало веру в то, что воздух обеспечивает поддерживающую или движущую силу. Эти представления в значительной степени основывались на принципах гидростатики (учения о давлении жидкостей) в их тогдашнем понимании.Так, в ранние времена считалось, что толкающая сила снаряда связана с силами, действующими на основание при замыкании потока воздуха вокруг тела. Эта концепция воздуха как вспомогательной среды, а не противодействующей силы сохранялась на протяжении столетий, хотя в 16 веке было признано, что энергия движения снаряда сообщается ему катапультирующим устройством.
Однако у них не было реальных знаний о физических свойствах воздуха и они не пытались систематически изучать эти свойства. Большинство их идей отражало веру в то, что воздух обеспечивает поддерживающую или движущую силу. Эти представления в значительной степени основывались на принципах гидростатики (учения о давлении жидкостей) в их тогдашнем понимании.Так, в ранние времена считалось, что толкающая сила снаряда связана с силами, действующими на основание при замыкании потока воздуха вокруг тела. Эта концепция воздуха как вспомогательной среды, а не противодействующей силы сохранялась на протяжении столетий, хотя в 16 веке было признано, что энергия движения снаряда сообщается ему катапультирующим устройством.
Подробнее по этой теме
Самолет: Аэродинамика
На самолет в горизонтальном полете без ускорения действуют четыре силы.(В повороте, пикировании или полете с набором высоты дополнительно. ..
..
Ближе к концу 15 века Леонардо да Винчи заметил, что воздух оказывает сопротивление движению твердого тела, и объяснил это сопротивление эффектами сжимаемости. Позже Галилей экспериментально установил факт сопротивления воздуха и пришел к выводу, что сопротивление пропорционально скорости проходящего через него тела. В конце 17 века Христиан Гюйгенс и сэр Исаак Ньютон определили, что сопротивление воздуха движению тела пропорционально квадрату скорости.
Работа Ньютона по изложению законов механики положила начало классическим теориям аэродинамики. Давление, действующее на наклонную пластину, он рассматривал как возникающее при столкновении частиц со стороной пластины, обращенной к воздушному потоку. Его формулировка дала результат, что давление, действующее на пластину, пропорционально произведению плотности воздуха, площади пластины, квадрата скорости и квадрата синуса угла наклона.Это не учитывало влияние потока на верхнюю поверхность пластины, где существует низкое давление и из которой создается основная часть подъемной силы крыла. Представление о воздухе как о континууме с полем давления, простирающимся на большие расстояния от пластины, должно было появиться гораздо позже.
Представление о воздухе как о континууме с полем давления, простирающимся на большие расстояния от пластины, должно было появиться гораздо позже.
В 18 и 19 веках были сделаны различные открытия, которые способствовали лучшему пониманию факторов, влияющих на движение твердых тел в воздухе. Связь сопротивления с вязкими свойствами жидкости, например, была частично осознана к началу 1800-х годов, а эксперименты британского физика Осборна Рейнольдса в 1880-х годах прояснили значение эффектов вязкости.
Современная аэродинамика возникла примерно в то же время, когда братья Райт совершили свой первый полет с двигателем (1903 г.). Через несколько лет после их исторической работы британский инженер Фредерик У. Ланчестер предложил циркуляционную теорию подъемной силы аэродинамического профиля бесконечного размаха и вихревую теорию подъемной силы крыла конечного размаха. Немецкий физик Людвиг Прандтль, которого обычно считают отцом современной аэродинамики, независимо пришел к тем же гипотезам, что и Ланчестер, и разработал математическую трактовку. Работа Прандтля, уточненная и дополненная последующими исследователями, сформировала теоретическую основу этой области. Среди других, сыгравших заметную роль в развитии современной аэродинамики, был инженер венгерского происхождения Теодор фон Карман, чей вклад привел к крупным достижениям в таких областях, как теория турбулентности и сверхзвуковой полет.
Работа Прандтля, уточненная и дополненная последующими исследователями, сформировала теоретическую основу этой области. Среди других, сыгравших заметную роль в развитии современной аэродинамики, был инженер венгерского происхождения Теодор фон Карман, чей вклад привел к крупным достижениям в таких областях, как теория турбулентности и сверхзвуковой полет.
Закон Архимеда для тела, погруженного в жидкость. Закон Архимеда: определение и формула
Закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа), вытесненной этим телом.Мощность называется по степени Архимеда :
где – плотность жидкости (газа), – ускорение свободного падения, – объем погруженного тела (или часть объема тела, которая находится ниже поверхности). Если тело плавает на поверхности или движется равномерно вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по величине (и противоположна по направлению) силе тяжести, действующей на объем жидкости (газа), вытесняемый тела, и приложена к центру тяжести этого объема.
Тело всплывает, если сила Архимеда уравновешивает силу притяжения тела.
Следует отметить, что тело должно быть полностью окружено жидкостью (или пересекаться с поверхностью жидкости). Например, закон Архимеда нельзя применить к кубу, который лежит на дне бака, герметично касаясь дна.
Что касается тела, находящегося в газе, например, в воздухе, то для нахождения подъемной силы необходимо плотность жидкости заменить плотностью газа.Например, воздушный шар с гелием летит вверх из-за того, что плотность гелия меньше плотности воздуха.
Закон Архимеда можно объяснить, используя разность гидростатических давлений на примере прямоугольного тела.
, где P A A , P B – точки давления A и B , ρ – плотность жидкости, ч – разница на уровне между точками A и B , S – площадь горизонтального сечения корпуса, V – объем подводной части корпуса.
18.
 Равновесие покоящегося тела в жидкости
Равновесие покоящегося тела в жидкостиНа тело, погруженное (полностью или частично) в жидкость, действует полное давление со стороны жидкости, направленное снизу вверх и равное весу жидкости в объеме погружаемой части корпуса. P ты т знак равно ρ f gV погребение
Для плавающего на поверхности однородного тела справедливо соотношение:
где: V – объем плавающего тела; ρ m – плотность тела.
Существующая теория плавающего тела достаточно обширна, поэтому ограничимся рассмотрением только гидравлической сущности этой теории.
Способность плавучего тела, выведенного из равновесия, снова вернуться в это состояние называется остойчивостью … Вес жидкости, взятой в объеме погруженной части судна, называется водоизмещением , и точкой приложения результирующего давления (т.е. центром давления) является центр смещения … При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной линии О”-О” , представляющей ось симметрии судна и называемой навигационной осью (рис. 2.5).
2.5).
Пусть под действием внешних сил корабль накренился на некоторый угол α, часть корабля KLM вышла из жидкости, а какая-то K”L”M” , наоборот, погрузилась в е. При этом мы получили новое положение центра смещения d” … Прикладываем к точке d” подъем R и продолжаем ее линию действия до пересечения с осью симметрии O”-O” … Полученная точка m называется метацентром , а линия отрезок мС = h называется метацентрической высотой … h считаем положительным, если точка м лежит выше точки С , и отрицательным в противном случае
Рис. 2.5. Сечение сосуда
Теперь рассмотрим условия равновесия корабля:
1) если ч > 0, то корабль возвращается в исходное положение, 2) если ч = 0, то это случай безразличного равновесия; 3) если ч
Следовательно, чем ниже центр тяжести и выше метацентрическая высота, тем больше остойчивость судна.
Архимед — греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед учился в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и долгое время покровительствовал ему.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основоположником теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
Согласно легенде, Архимеду принадлежит множество удивительных технических изобретений, снискавших ему известность среди современников. Считается, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, осаждавший Александрию. Этот случай является ярким примером превосходных оптических навыков.
Этот случай является ярким примером превосходных оптических навыков.
Архимеду также приписывают изобретение катапульты, военной метательной машины и строительство планетария, в котором двигались планеты. Ученый создал движитель для подъема воды (движитель Архимеда), который используется до сих пор и представляет собой водоподъемную машину, представляющую собой вал с винтовой поверхностью, расположенный в наклонной трубе, погруженной в воду. При вращении винтовая поверхность вала перемещает воду по трубе на разную высоту.
Архимед написал множество научных работ: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объеме земного шара.
Архимед открыл свой знаменитый закон при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не смешали ли ювелиры серебро с золотом, когда делали корону. Для этого необходимо определить не только массу, но и объем короны, чтобы вычислить плотность металла. Определить объем изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Определить объем изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Решение пришло в голову Архимеду, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело ученого опустили в воду. То есть объем его тела вытеснил равный объем воды. Кричать “Эврика!” Архимед побежал во дворец, даже не удосужившись одеться. Он опускал венец в воду и определял объем вытесненной жидкости.Проблема была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему части тела, погруженной в жидкость. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую оно было помещено.
Закон Архимеда гласит: на любое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.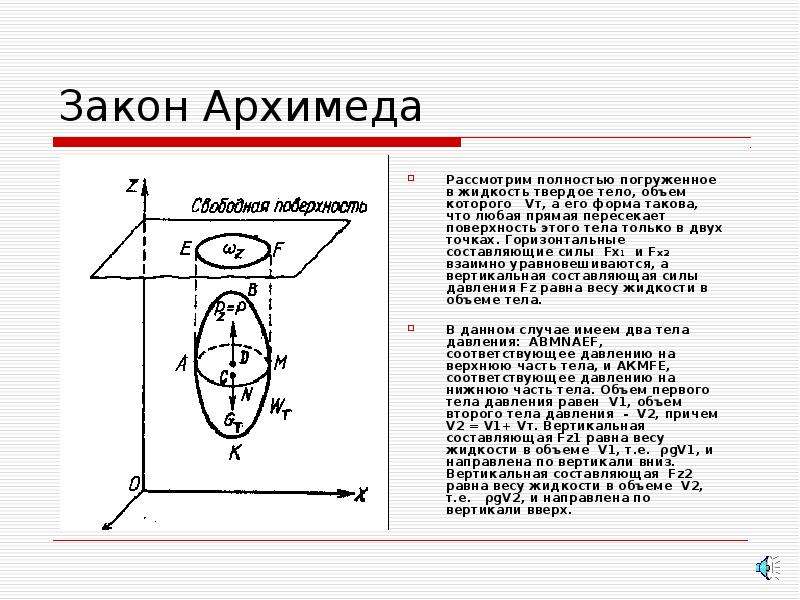
Один из первых законов физики, изученных старшеклассниками. Хотя бы приблизительно этот закон помнит любой взрослый человек, как бы он ни был далек от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, которые могли быть забыты.
Что говорит закон Архимеда?
Существует легенда, что древнегреческий ученый открыл свой знаменитый закон, принимая ванну.Окунувшись в сосуд, наполненный водой до краев, Архимед заметил, что вода при этом выплеснулась наружу, – и испытал озарение, моментально сформулировав суть открытия.
Скорее всего, в действительности дело обстояло иначе, и открытию предшествовали длительные наблюдения. Но это не так важно, ведь в любом случае Архимеду удалось обнаружить следующую закономерность:
- погружаясь в любую жидкость, тела и предметы испытывают сразу несколько разнонаправленных сил, но направленных перпендикулярно их поверхности;
- конечный вектор этих сил направлен вверх, поэтому любой предмет или тело, находясь в покоящейся жидкости, испытывает выталкивание;
- в этом случае толкающая сила в точности равна коэффициенту, который получится, если произведение объема предмета и плотности жидкости умножить на ускорение свободного падения.

Итак, Архимед установил, что тело, погруженное в жидкость, вытесняет такой объем жидкости, который равен объему самого тела. Если в жидкость погрузить только часть тела, то оно вытеснит жидкость, объем которой будет равен объему только той части, которая погружена.
То же правило относится и к газам – только здесь объем тела надо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, выталкивающая некий предмет из жидкости или газа, в точности равна весу жидкости или газа, вытесняемого этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, обнаруженная древнегреческим ученым, проста и совершенно очевидна. Но в то же время его значение для повседневной жизни трудно переоценить.
Именно благодаря знаниям об изгнании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что в их конструкции учитывается закон Архимеда и многочисленные следствия из него – они построены таким образом, что могут оставаться на поверхности воды, а не идти ко дну . По похожему принципу действует воздухоплавание — они используют выталкивающие возможности воздуха, становясь как бы легче в полете.
Тяжелые металлические корабли не тонут благодаря тому, что в их конструкции учитывается закон Архимеда и многочисленные следствия из него – они построены таким образом, что могут оставаться на поверхности воды, а не идти ко дну . По похожему принципу действует воздухоплавание — они используют выталкивающие возможности воздуха, становясь как бы легче в полете.
Закон Архимеда — закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История выпуска
“Эврика!” («Нашел!») — именно такое восклицание, по преданию, издал древнегреческий ученый и философ Архимед, открывший принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, сделана ли его корона из чистого золота, не повредив при этом саму царскую корону. Архимеду не составило труда взвесить корону, но этого было недостаточно – необходимо было определить объем короны, чтобы вычислить плотность металла, из которого она была отлита, и определить, было ли это чистое золото . Далее, по преданию, Архимед, озабоченный мыслями о том, как определить объем венца, окунулся в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тогда ученый понял, что объем его тела вытеснил равный объем воды, следовательно, корона, если ее опустить в наполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение проблемы было найдено и, по самой популярной версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не удосужившись одеться.
Далее, по преданию, Архимед, озабоченный мыслями о том, как определить объем венца, окунулся в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тогда ученый понял, что объем его тела вытеснил равный объем воды, следовательно, корона, если ее опустить в наполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение проблемы было найдено и, по самой популярной версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не удосужившись одеться.
Однако, что верно, то верно: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему части тела, погруженной в жидкость. Давление, которое раньше действовало на вытесняемую жидкость, теперь будет действовать и на вытеснившее ее твердое тело. А если выталкивающая сила, действующая вертикально вверх, окажется больше силы тяжести, тянущей тело вертикально вниз, то тело всплывет; иначе он утонет (утонет).Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление создается ударом движущихся молекул. При вытеснении некоторого объема жидкости твердым телом восходящий импульс ударов молекул будет приходиться не на молекулы жидкости, вытесняемой телом, а на само тело, чем и объясняется оказываемое на него давление снизу и толкает его к поверхности жидкости.Если тело полностью погружено в жидкость, на него все равно будет действовать выталкивающая сила, так как с глубиной давление возрастает, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Это объяснение плавучести на молекулярном уровне.
Эта схема толкания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объем воздуха, содержащегося внутри корпуса судна ниже ватерлинии.Если усреднить плотность оболочки корпуса и воздуха внутри нее, то окажется, что плотность корабля (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате всплытия вверх импульсы удара молекул воды оказываются выше силы гравитационного притяжения Земли, тянущей корабль ко дну – и корабль плывет.
Формулировки и пояснения
То, что на тело, погруженное в воду, действует определенная сила, всем хорошо известно: тяжелые тела как бы становятся легче — например, наше собственное тело при погружении в ванну.Купаясь в реке или в море, можно легко поднимать и перемещать по дну очень тяжелые камни — те, которые невозможно поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить шарик размером с небольшой арбуз, требуется и сила, и ловкость; шар диаметром в полметра погрузить скорее всего не получится. Интуитивно ясно, что ответ на вопрос, почему одно тело плавает (а другое тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые тонут: стальная пластина, конечно, утонет в воде, но если сделать из нее ящик, то она может плавать; однако ее вес не изменился.
Наличие гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила.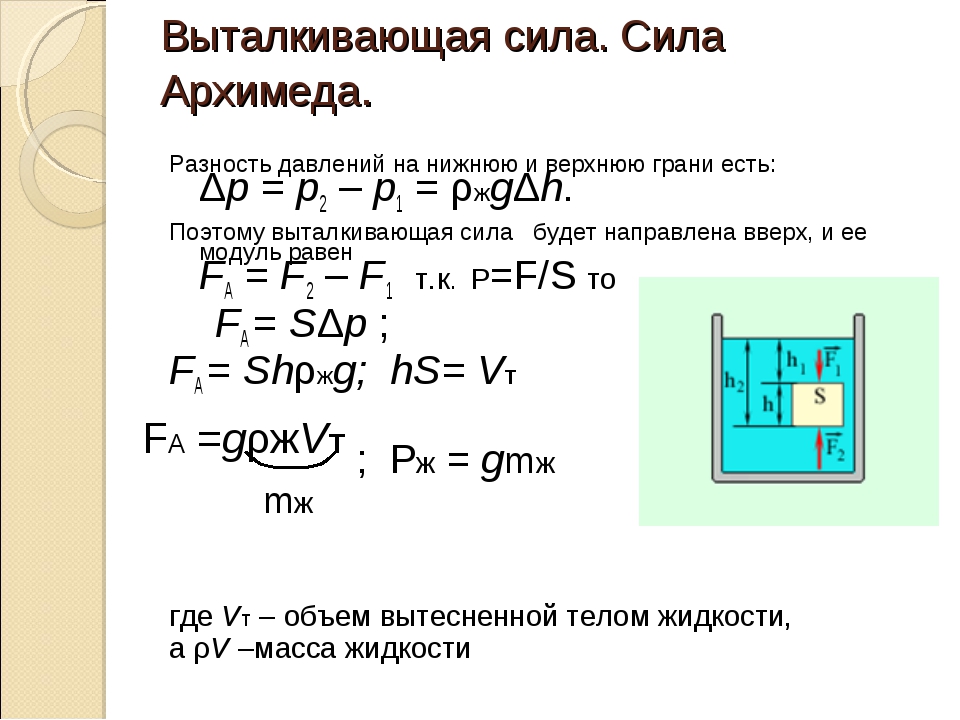 Впервые величину этой силы в жидкостях экспериментально определил Архимед. Закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу количества жидкости или газа, вытесненного погруженной частью тела.
Впервые величину этой силы в жидкостях экспериментально определил Архимед. Закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу количества жидкости или газа, вытесненного погруженной частью тела.
Формула
Сила Архимеда, действующая на тело, погруженное в жидкость, может быть рассчитана по формуле: F A = ρ w гВ Пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем части тела, погруженной в жидкость.
Поведение тела в жидкости или газе зависит от соотношения модулей силы тяжести Fт и архимедовой силы FA, действующих на это тело. Возможны следующие три случая:
1) Fт> FA – тело тонет;
2) Ft = FA – тело плавает в жидкости или газе;
3) Фт
Продолжим изучение архимедовой силы. Проведем эксперименты. Подвесьте два одинаковых мяча к бревну.Их вес одинаков, поэтому коромысло находится в равновесии (рис. «А»). Поместите пустой стакан под шар справа. Вес шаров от этого не изменится, поэтому баланс сохранится (рис. «Б»).
Подвесьте два одинаковых мяча к бревну.Их вес одинаков, поэтому коромысло находится в равновесии (рис. «А»). Поместите пустой стакан под шар справа. Вес шаров от этого не изменится, поэтому баланс сохранится (рис. «Б»).
Второй опыт. Прикрепим к динамометру большую картофелину. Вы видите, что его вес равен 3,5 Н. Погрузим картофель в воду. Найдем, что его вес уменьшился до 0,5 Н.
Рассчитаем изменение веса картофеля:
DW = 3.5 Н – 0,5 Н = 3 Н
Почему вес картофелины уменьшился ровно на 3 Н? Очевидно, потому что в воде на картошку действовала выталкивающая сила такой же величины. Другими словами, сила Архимеда равна изменению веса т ели:
Эта формула выражает способ измерения выталкивающей силы: нужно дважды измерить массу тела и вычислить ее изменение. Полученное значение равно силе Архимеда.
Для вывода следующей формулы проделаем опыт с прибором “ковш Архимеда”. Его основные части следующие: пружина со стрелой 1, ковш 2, корпус 3, литейный сосуд 4, стакан 5.
Сначала пружина, ковш и корпус подвешиваются к треноге (рис. . “A”), а положение стрелки отмечено желтой меткой. Затем тело помещают в литейный сосуд. Во время погружения тело вытесняет некоторый объем воды. , которую наливают в стакан (рис.«б»). Масса тела становится меньше, пружина сжимается, а стрелка поднимается выше желтой отметки.
Слейте вытесненную телом воду из стакана в ведро (рис. «С»). Самое удивительное, что при наливании воды (рис “г”) стрелка не просто пойдет вниз, а будет указывать точно на желтую метку! Значит, вес воды, налитой в ведро, уравновешивал архимедову силу … В виде формулы этот выход запишется так:
Суммируя результаты двух опытов, получаем Архимеда закон : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объеме этого тела, и направлена противоположно вектору веса.
В § 3-б мы указали, что сила Архимеда обычно направлена вверх. Поскольку он противоположен вектору веса и не всегда направлен вниз, архимедова сила также не всегда действует вверх. Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут не всплывать, а отклоняться к оси вращения.
Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут не всплывать, а отклоняться к оси вращения.
плавучесть.htm
Изобретатели вечного двигателя очарован плавучестью, предполагая, что плавучесть обладает какой-то «волшебной» способность производить движение против силы тяжести без затрат энергия.Учебники плавучести обычно основаны на принципе Архимеда: «На тело, погруженное в жидкость, действует восходящая сила, к жидкости размером, равным весу вытесненной жидкости». Более проницательный (но эквивалентный) подход выглядит следующим образом:
Рассмотрим тело массой m и объемом V , которое имеет меньшую плотность, чем вода.
Если его толкнуть под воду и отпустить,
он движется вверх. При движении вверх из положения А в положение В вода
должен двигаться вниз.Объем V в позиции А, которую занимало тело, теперь должен
быть заменена водой, и вода, которая была в пространстве, которое она теперь занимает
в положении B должны быть смещены. Чистый эффект заключается в том, что объем V тело движется из положения А в положение В, равный объем V воды
перемещается из положения В в положение А.
Чистый эффект заключается в том, что объем V тело движется из положения А в положение В, равный объем V воды
перемещается из положения В в положение А.
|
Всякий раз, когда масса движется в гравитационном поле, над телом может совершаться работа. полем или на источник поля телом.Эта работа имеет размеры F h , где F – величина силы, действующей на тело со стороны поля и ч расстояние, пройденное по вертикали. Когда тело движется вверх в поле (напротив
к силе гравитации) это
работа над источником поля. При движении тела вниз в поле (в
направление гравитационной силы)
поле источника поля действует на тело.
полем или на источник поля телом.Эта работа имеет размеры F h , где F – величина силы, действующей на тело со стороны поля и ч расстояние, пройденное по вертикали. Когда тело движется вверх в поле (напротив
к силе гравитации) это
работа над источником поля. При движении тела вниз в поле (в
направление гравитационной силы)
поле источника поля действует на тело.
Запишем силу и работу на тело (масса м ) и на равный объем воды (масса M ).Поскольку тело легче воды, м < м . Сеть работа, совершаемая телом, движущимся вверх в жидкости, равна (M-m)gh = (Mg-mg)h . Мы определяем Mg как величину Выталкивающей силы, и мг как сила тяжести, действующая на тело массой м .
Mgh – работа силы тяжести над водой при движении вниз. -mgh – это работа, совершаемая над перемещением тела зажигалки вверх.
Итак, мы видим, что движение тела в жидкости — это просто движение двух масс. меняясь местами в окружающей жидкости. Здесь нет ничего таинственного.
Более того, мы можем посмотреть на это в свете третьего закона Ньютона. Если
тело м испытывает силу от действующей на него жидкости, жидкость испытывает
равная и противоположная сила тела m, действующая на жидкость. Следует
что работа, совершаемая жидкостью над массой, равна работе, совершаемой
масса на жидкости.Единственный агент, выполняющий какую-либо другую работу на любом из них.
является гравитация.
меняясь местами в окружающей жидкости. Здесь нет ничего таинственного.
Более того, мы можем посмотреть на это в свете третьего закона Ньютона. Если
тело м испытывает силу от действующей на него жидкости, жидкость испытывает
равная и противоположная сила тела m, действующая на жидкость. Следует
что работа, совершаемая жидкостью над массой, равна работе, совершаемой
масса на жидкости.Единственный агент, выполняющий какую-либо другую работу на любом из них.
является гравитация.
Короче говоря, машины, использующие жидкости, просто еще один пример перетасовки масс вокруг. Массы по-прежнему подчиняются законам Ньютона, так что вы ничего не получите просто так. Это еще хуже. Жидкости вносят вязкость, которая неизменно снижает производительность, потому что это энергорассеивающий процесс.
Обычное изложение этого учебника рассматривает только силы на подводном
объект.Сила тяжести м г действует вниз. g – это величина ускорения свободного падения. Выталкивающая сила B действует вверх. Чистая восходящая сила равна B – м г .
По закону Архимеда размер B равен B = rgV , где r – массовая плотность
жидкости V – объем погруженного тела.Это правильно, но
это затемняет понимание того, что когда погруженное тело движется вверх на равную
объем жидкости должен двигаться вниз. Изобретатели вечного двигателя
очень часто забывают включить это движение воды в свое мышление.
Выталкивающая сила B действует вверх. Чистая восходящая сила равна B – м г .
По закону Архимеда размер B равен B = rgV , где r – массовая плотность
жидкости V – объем погруженного тела.Это правильно, но
это затемняет понимание того, что когда погруженное тело движется вверх на равную
объем жидкости должен двигаться вниз. Изобретатели вечного двигателя
очень часто забывают включить это движение воды в свое мышление.
Плавучие колеса и ремни

Вот более простое на вид устройство, работающее по тому же принципу. Он также работает под водой. К колесу прикреплены сильфоны со свинцовыми грузиками. Воздух во всех мехах передается через трубки в восьми плечах в камеру в ступице.
Изобретатель помнит принцип Архимеда из школьного курса физики.В нем говорится, что когда тело погружается в жидкость, жидкость действует и направленная вверх выталкивающая сила, действующая на это тело, размеры которого равны жидкости тела вытесняет». «Вытесненная» жидкость — это просто объем жидкости, равный к объему тела.
Таким образом, в этих устройствах грузы уменьшают объем воздуха в
поршни или сильфоны на одной стороне оси, увеличивая объем в
те, что с другой стороны оси.Поэтому поршни или сильфоны
на стороне с повышенным
объем испытывает большую выталкивающую силу, чем на другой стороне
колеса. Поэтому оба этих устройства должны вращаться против часовой стрелки.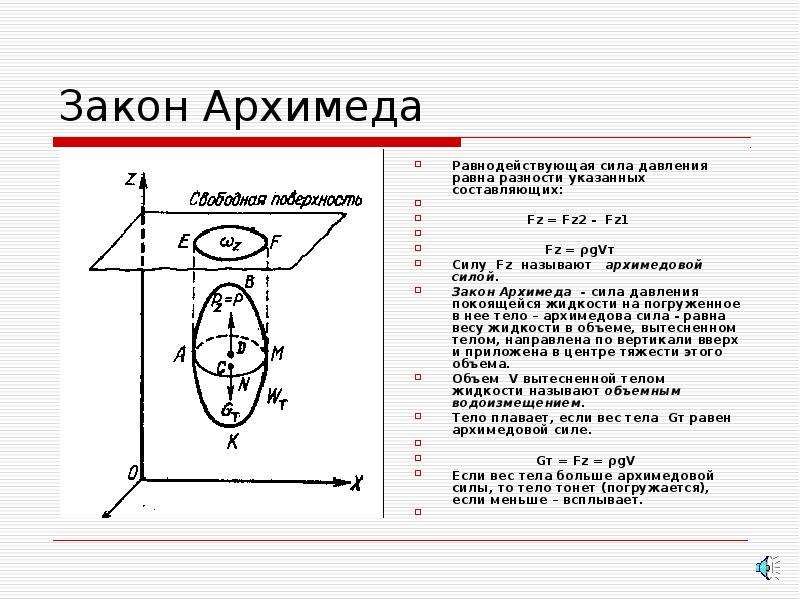
Выталкивающая сила, действующая на свинцовые грузы, везде одинакова. случается. Выталкивающие силы на цилиндры, сильфоны и другие детали системы четко сбалансированы. Эти аргументы очень соблазнительны, чтобы привести можно подумать, что эти устройства будут постоянно вращаться.
Рассмотрим это более простое расположение всего двух поршней. жизнерадостный силы обозначены B 1 и B 2 . с В 2 > В 1 . гравитационный силы с обеих сторон равны, поэтому этот дисбаланс выталкивающей силы должен заставить правую сторону подняться.
Но будет ли это движение продолжаться вокруг полного цикла? Поршни должны перейти на другую сторону колеса.Изобретатель внушил нам самодовольство, обращая внимание на неуравновешенную выталкивающую силу, поэтому мы соблазн пренебречь тем, что происходит при «переходе».
Минимальный объем внутри поршневой камеры составляет V 1 .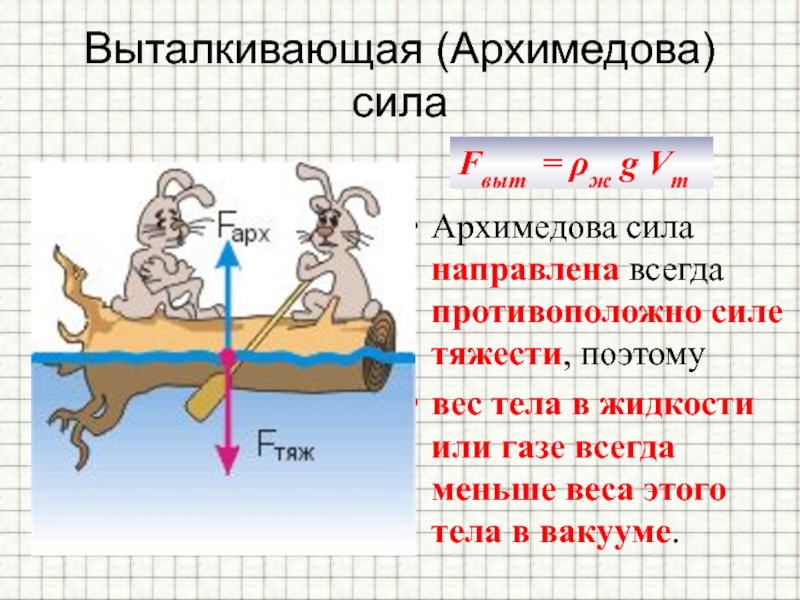 Максимальный объем внутри поршневой камеры составляет V 2 .
Разница между ними заключается в разнице в количестве
жидкости, смещенной влево/вправо, составляет В = В 2 – В 1 .Чистая выталкивающая сила воды, действующая на пару
поршни, один из которых движется вверх, а другой вниз. B = rgV .
Совершенная работа равна Bh = rgVh . Когда эти две соединенные поршневые камеры перемещаются на другую сторону,
свинцовые гири
принудительное изменение количества воздуха в каждой поршневой камере.
Это происходит, когда верхний поршень начинает двигаться вниз и во время его
путь по изогнутой дуге вокруг шкива. Это движение соответствует
при движении нижнего поршня вверх по криволинейной дуге
его шкив.В это время воздух нагнетается вверх через
трубка от нижнего поршня к верхнему. Поршневая камера
вверху набирает объем воздуха V . Тот, что внизу
теряет объем воздуха V . При этом
оба поршня перемещаются в своих камерах на одинаковое расстояние, причем верхний, однако,
находится под меньшим давлением воды, чем нижний.
Максимальный объем внутри поршневой камеры составляет V 2 .
Разница между ними заключается в разнице в количестве
жидкости, смещенной влево/вправо, составляет В = В 2 – В 1 .Чистая выталкивающая сила воды, действующая на пару
поршни, один из которых движется вверх, а другой вниз. B = rgV .
Совершенная работа равна Bh = rgVh . Когда эти две соединенные поршневые камеры перемещаются на другую сторону,
свинцовые гири
принудительное изменение количества воздуха в каждой поршневой камере.
Это происходит, когда верхний поршень начинает двигаться вниз и во время его
путь по изогнутой дуге вокруг шкива. Это движение соответствует
при движении нижнего поршня вверх по криволинейной дуге
его шкив.В это время воздух нагнетается вверх через
трубка от нижнего поршня к верхнему. Поршневая камера
вверху набирает объем воздуха V . Тот, что внизу
теряет объем воздуха V . При этом
оба поршня перемещаются в своих камерах на одинаковое расстояние, причем верхний, однако,
находится под меньшим давлением воды, чем нижний. Разность давлений верх/низ
равно P =r gh , где h равно
разница в высоте между верхом и низом.Таким образом, чистая работа, совершаемая водой на движущихся поршнях в этом процессе
отрицательно: PV = – rgVh .
Разность давлений верх/низ
равно P =r gh , где h равно
разница в высоте между верхом и низом.Таким образом, чистая работа, совершаемая водой на движущихся поршнях в этом процессе
отрицательно: PV = – rgVh .
Теперь пересмотрите полную версию с поршневыми камерами на ремне над двумя шкивами. Каждая пара поршней получает энергию, двигаясь по прямой части ремня, но теряет такое же количество энергии обход шкивов на другую сторону аппарата.
Опытному физику или инженеру не терпится такая длинная алгебраический анализ, для которого мы только набросали основные моменты.Из законов сохранения следует вывод, который, как известно, должен результат, даже без хлопот по подробным расчетам. Некоторым даже нравится думать об этом в следующем концептуальном ключе:
.
На этом рисунке показано, что происходит, когда один поршень проходит через сверху, а другой пересекает снизу. Мы предполагаем, что это колесо вращалось против часовой стрелки.Это совершенно гениальное устройство, то ли в ковшовой цепи, то ли в колесе. форма. Он имеет несколько форм неправильного направления:То следующее, что произойдет, это то, что верхний вес вызовет его поршень, чтобы уменьшить его объем, в то время как нижний вызовет его поршень, чтобы увеличить его объем.При этом нижний выталкивает воду из своего открытого конца, а верхний набирает воду в свой открытый конец. Этот процесс заставляет объем воды двигаться снизу вверх. (схематично показано изогнутой стрелкой). Это требует работы, как всегда случай, когда масса перемещается в более высокое положение против действия силы сила тяжести. И угадайте, что? Работа, необходимая для этого, точно равна работе выталкивающих сил (в идеализированном случае без диссипативные процессы с потерей энергии), так же, как мы нашли в подробном анализ.
- Вы легко не замечаете, что происходит сверху и снизу.
- Вы легко замечаете воду, которая окружает все вокруг.
- Вы полагаете, что вода создает только выталкивающую силу, не требуя
любые затраты энергии.

Модификации
Как только мы видим недостаток мышления, общий для всех этих устройств, мы понимаем, что неважно, соединены ли поршни по воздуху линиями попарно или общим воздушным резервуаром. На самом деле, не имеет значения, есть ли какие-либо перекрестные связи между колесо или ремень, либо по воздуху, либо с помощью механической связи. Так же видим бесперспективность версии с жидкостью в поршнях
и соединительные шланги, как показано на этой модификации картинки deAth.Возможно, это был исторический предшественник обсуждаемых устройств.
выше, ибо он близок к классическому перебалансированному колесу с переключением
масса. Здесь вес, смещенный по осям, – это вода (синяя).
Изобретатель полагает, что поскольку вес воды больше слева
колесо должно вращаться против часовой стрелки.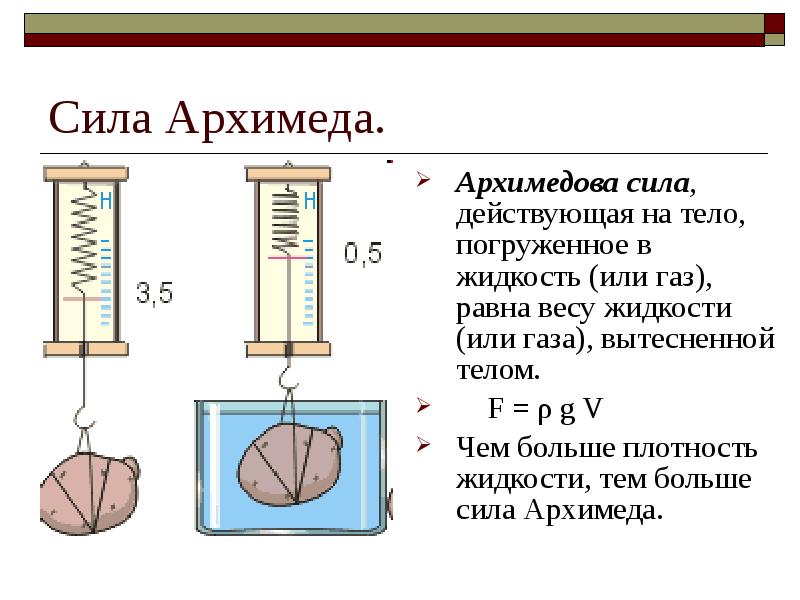 Вес больше, конечно,
но когда этот верхний поршень движется справа налево, вода должна
поднимается по шлангу от поршня внизу,
что требует столько же работы, сколько система получает от каждой пары
поршней, движущихся вверх/вниз по прямым участкам цепи.
Вес больше, конечно,
но когда этот верхний поршень движется справа налево, вода должна
поднимается по шлангу от поршня внизу,
что требует столько же работы, сколько система получает от каждой пары
поршней, движущихся вверх/вниз по прямым участкам цепи.
Давайте рассмотрим это подробно, как мы это делали ранее.
Когда эти две соединенные поршневые камеры перемещаются на другую сторону,
свинцовые гири
принудительное изменение количества жидкости в каждой поршневой камере.
Это происходит, когда верхний поршень начинает двигаться вниз и во время его
путь по изогнутой дуге вокруг шкива. Это движение соответствует
при движении нижнего поршня вверх по криволинейной дуге
его шкив. За это время вода нагнетается вверх через
трубка от нижнего поршня к верхнему.Поршневая камера
вверху набирает объем воды V . Тот, что внизу
теряет объем воды V . При этом
оба поршня перемещаются в своих камерах на одинаковое расстояние, причем верхний, однако,
находится под меньшим давлением воды, чем нижний. Разность давлений верх/низ
равно P =r gh , где h равно
разница в высоте между верхом и низом.
Таким образом, чистая работа, совершаемая водой на движущихся поршнях в этом процессе
отрицательно: PV = – rgVh .
Разность давлений верх/низ
равно P =r gh , где h равно
разница в высоте между верхом и низом.
Таким образом, чистая работа, совершаемая водой на движущихся поршнях в этом процессе
отрицательно: PV = – rgVh .
Вы можете заметить, что это описание идентично описанию для наполненные воздухом камеры, за исключением того, что слово «воздух» заменено на «вода» кроме последнего предложения. Разница давлений сверху/снизу в воздухе равна незначительно из-за малой плотности воздуха. Становится немного интереснее если камеры заполнены жидкостью и весь аппарат погружен в другой жидкости. Мы оставляем это в качестве упражнения для читателя. Но лежащие в основе физические принципы, которые гарантируют, что это не будет вечным двигателем машина все та же во всех этих устройствах.Зависимость давления от высоты в любой жидкости помешает изобретателю на каждом (воображаемом) виртуальном повороте.
Это устройство является одним из лучших для наглядной иллюстрации
тщетность идеи разбалансированного колеса. Можно представить, что эта версия была построена в какой-то исторический момент,
с большими надеждами на успех. Но повторяющиеся неудачи ведут беспокойный
задумайтесь, может ли он работать лучше, погруженный в резервуар с водой,
«использовать выталкивающую силу».«И по сей день урок
до сих пор не изучены подающими надежды изобретателями.
Можно представить, что эта версия была построена в какой-то исторический момент,
с большими надеждами на успех. Но повторяющиеся неудачи ведут беспокойный
задумайтесь, может ли он работать лучше, погруженный в резервуар с водой,
«использовать выталкивающую силу».«И по сей день урок
до сих пор не изучены подающими надежды изобретателями.
Все это иллюстрирует, что геометрия является основной причиной почему перебалансированные колеса не подойдут. Вы действительно можете получить толчок от дисбаланса массы, но в циклическом процессе эта масса должен быть перемещен обратно туда, где он начал повторять цикл, и вот где вы теряете то, что вы приобрели.
Еще примеры жизнерадостного оптимизма.
Я пренебрег целым классом иллюзий о вечных двигателях, считая их слишком тривиальными или явно неработоспособными для изложения здесь.Но мой почтовый ящик постоянно получает примеры от людей, которые серьезно думают, что они могут сработать. И многочисленные сайты подтверждают, что эта идея никогда не умирает.
Рассмотрим этот пример. Я не указал сайт и имя автора.
Идея состоит в том, чтобы нагнетать воздух в нижнюю часть резервуара для воды, который поднимается в камеры колеса и заставляет колесо вращаться до тех пор, пока воздух не выйдет в верхней части. Конечно, энергия должна извлекаться из вращения колеса.
Это не было предложено как устройство сверхединицы, а только как метод извлечения энергии (которая в противном случае была бы потрачена впустую) сжатых выхлопных газов из производственных процессов. Достаточно справедливая и достойная цель. Но это оказывается очень неэффективным способом сделать это.
Одна очевидная проблема – эти воздушные камеры. Изобретатель, кажется, понимает, что воздух должен временно задерживаться внутри некоторых из них. А теперь давайте перерисуем картинку, чтобы показать воду и посмотреть, как это работает.
Сейчас это не выглядит так многообещающе, не так ли. Тем не менее, часть воздуха остается в ловушке и может заставить колесо вращаться, подобно тому, как насос сжатого воздуха в аквариуме вращает погруженное водяное колесо. Но сколько энергии мы можем ожидать от вращающегося колеса?
Но сколько энергии мы можем ожидать от вращающегося колеса?
Это легко. Самое большее , если предположить идеализированный случай нулевого трения и вязкости, мы получим не больше энергии, необходимой для нагнетания воздуха на дно резервуара против давления воды.С настоящим колесом в вязкой воде производительность была бы намного хуже. Если вы хотите, чтобы двигатель приводился в движение сжатым воздухом, вы можете это сделать. Есть устройства (маленькие турбины), которые неплохо с этим справляются. Но делать это, погружая систему в воду, просто глупо.
Парень, у которого есть это на его веб-сайте, утверждает, что он инженер-консультант. Я бы не нанял его. Вы понимаете, почему я не назвал ни его имени, ни URL-адреса его веб-сайта. Я делаю ему одолжение.
Еще один изобретатель-оптимист прислал мне устройство для подводного пояса, использующее тот же ошибочный принцип.Он любезно приводит расчеты, что если бы его подводный конвейер находился на глубине 700 футов (для сравнения с плотиной Гувера), он бы выдавал 800 лошадиных сил вместо ничтожных 30 лошадиных сил, используемых воздушным компрессором для нагнетания воздуха на дно. С энергоэффективностью 800/30 = 26,67 я бы не хотел находиться рядом с этой штукой, если бы она работала так, как он утверждает. Он нагнетает воздух в складные контейнеры (подушки безопасности?) и говорит, что они должны быть обтекаемыми, чтобы уменьшить сопротивление. Но он не учитывает того факта, что для наполнения каждого мешка воздухом требуется энергия, так как при наполнении он вытесняет воду под большим давлением (более 21 атм на глубине 700 футов).Он просит меня проверить его расчеты. За такие услуги я беру гонорар консультанта (оплачивается заранее). Он может правильно складывать, умножать и делить, но плохо использует физику и часто считает крутящий момент, работу и мощность эквивалентными вещами.
С энергоэффективностью 800/30 = 26,67 я бы не хотел находиться рядом с этой штукой, если бы она работала так, как он утверждает. Он нагнетает воздух в складные контейнеры (подушки безопасности?) и говорит, что они должны быть обтекаемыми, чтобы уменьшить сопротивление. Но он не учитывает того факта, что для наполнения каждого мешка воздухом требуется энергия, так как при наполнении он вытесняет воду под большим давлением (более 21 атм на глубине 700 футов).Он просит меня проверить его расчеты. За такие услуги я беру гонорар консультанта (оплачивается заранее). Он может правильно складывать, умножать и делить, но плохо использует физику и часто считает крутящий момент, работу и мощность эквивалентными вещами.
Он не может должным образом объяснить два факта:
- Работа, необходимая для нагнетания воздуха на дно водяного столба, работающего против давления воды там.
- Работа, затраченная на увеличение размеров контейнеров с поднимающимся воздухом. dW = PdV .

Вернуться наверх.
Вернитесь к плавучим сильфонным двигателям.
Вернитесь в главную галерею музея.
Вернитесь на главную страницу Дональда Симанека.
14.4 Принцип Архимеда и плавучесть – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определение выталкивающей силы
- Состояние закона Архимеда
- Опишите связь между плотностью и принципом Архимеда
При помещении в жидкость некоторые объекты всплывают благодаря выталкивающей силе. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Поддерживает ли ваше тело атмосфера или только воздушные шары с гелием (рисунок)?
Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Поддерживает ли ваше тело атмосфера или только воздушные шары с гелием (рисунок)?
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. На любой объект в любой жидкости действует направленная вверх сила, или выталкивающая сила (рисунок). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает.Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает.Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила
Выталкивающая сила — это направленная вверх сила, действующая на любой объект в любой жидкости.
Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что [латекс]p=hpg[/латекс].Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс]. (Горизонтальные силы компенсируются.)
Закон Архимеда
Насколько велика выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке. Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}.[/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex]{w}_{\text{fl}},[/latex] весу жидкости, вытесненной объектом.
Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}.[/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [latex]{w}_{\text{fl}},[/latex] весу жидкости, вытесненной объектом.
Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения Принцип Архимеда равен
.[латекс] {F} _ {\ text {B}} = {w} _ {\ text {fl}}, [/ латекс]
, где [латекс]{F}_{\text{B}}[/латекс] — выталкивающая сила, а [латекс]{w}_{\текст{фл}}[/латекс] — вес вытесненной жидкости. по объекту.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. до н. э.), который сформулировал этот принцип задолго до того, как понятие силы стало общепринятым.
Рисунок 14.21 (a) На объект, погруженный в жидкость, действует выталкивающая сила [латекс] {F} _ {\ text {B}}. [/latex] Если [латекс] {F} _ {\ text {B} }[/latex] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет.(b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости.
[/latex] Если [латекс] {F} _ {\ text {B} }[/latex] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет.(b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости.Принцип Архимеда относится к силе плавучести, возникающей, когда тело полностью или частично погружено в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила давления внизу направлена вверх, а сила давления вверху направлена вниз; силы из-за давлений по бокам направлены внутрь тела.
Поскольку нижняя часть тела находится на большей глубине, чем верхняя часть тела, давление в нижней части тела выше, чем давление в верхней части, как показано на рисунке. Следовательно, на тело действует направленная вверх сила. Эта направленная вверх сила является силой плавучести, или просто плавучестью .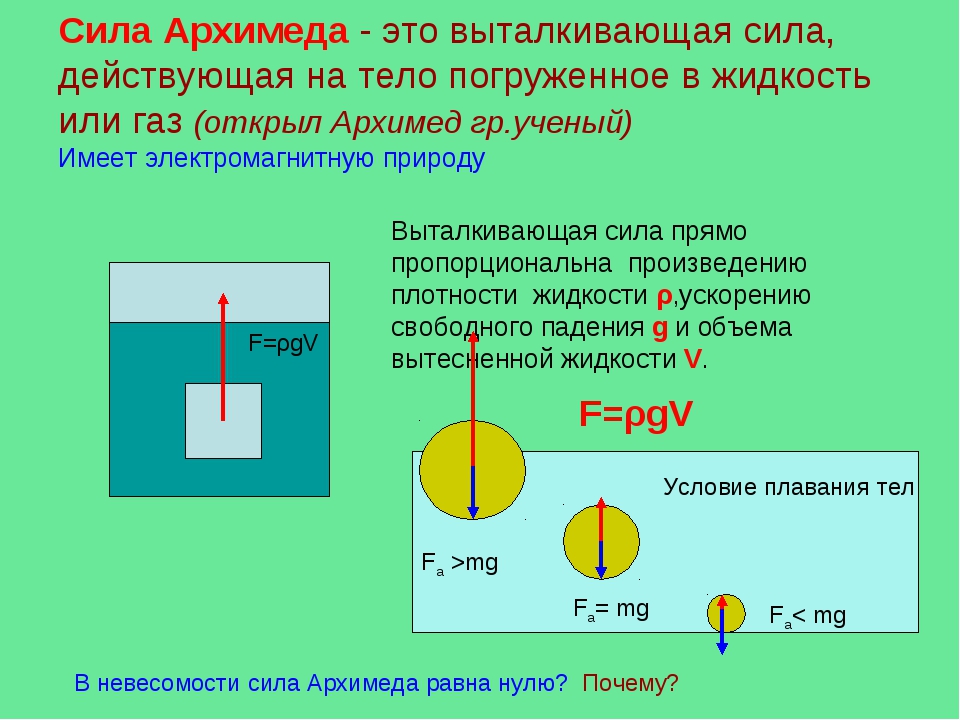
Плотность и закон Архимеда
Если бросить в воду кусок глины, он утонет. Но если вы слепите из того же куска глины форму лодки, она будет плавать.Из-за своей формы глиняная лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу, хотя ее масса одинакова. То же самое и со стальными кораблями.
Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта.Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта соотносится с плотностью жидкости. На рисунке, например, незагруженный корабль имеет меньшую плотность и меньше его погружено в воду по сравнению с тем же кораблем, когда он загружен.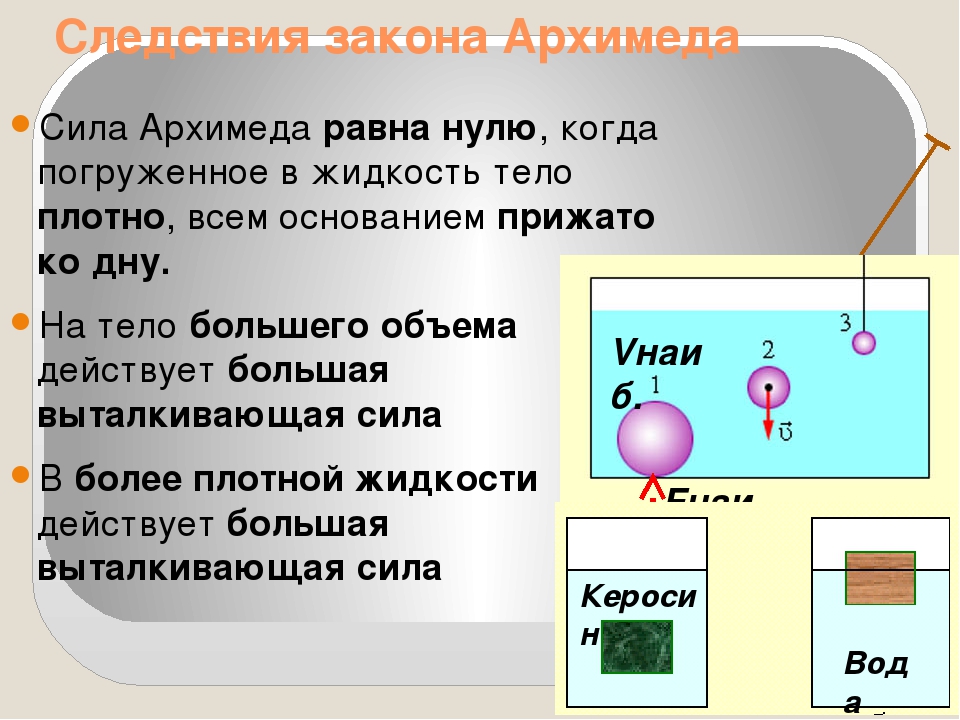 Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \ text {фракция погружена} = \ frac {{V} _ {\ text {sub}}} {{V} _ {\ text {obj}}} = \ frac {{V} _ {\ text {fl}}}{{V}_{\text{объект}}}.[/латекс]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]{V}_{фл}[/латекс]. Теперь мы можем получить связь между плотностями, подставив в выражение [латекс]\ро =\фрак{м}{В}[/латекс]. Это дает
[латекс] \ frac {{V} _ {\ text {fl}}} {{V} _ {\ text {obj}}} = \ frac {{m} _ {\ text {fl}} \ text { /}{\rho}_{\text{fl}}}{{m}_{\text{obj}}\text{/}{\rho}_{\text{obj}}},[/latex]
, где [latex]{\rho }_{\text{obj}}[/latex] — средняя плотность объекта, а [latex]{\rho }_{\text{fl}}[/latex] — плотность жидкости.Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\текст{фракция погружена}=\фракция{{\rho}_{\text{obj}}}{{\rho}_{\text{fl}}}.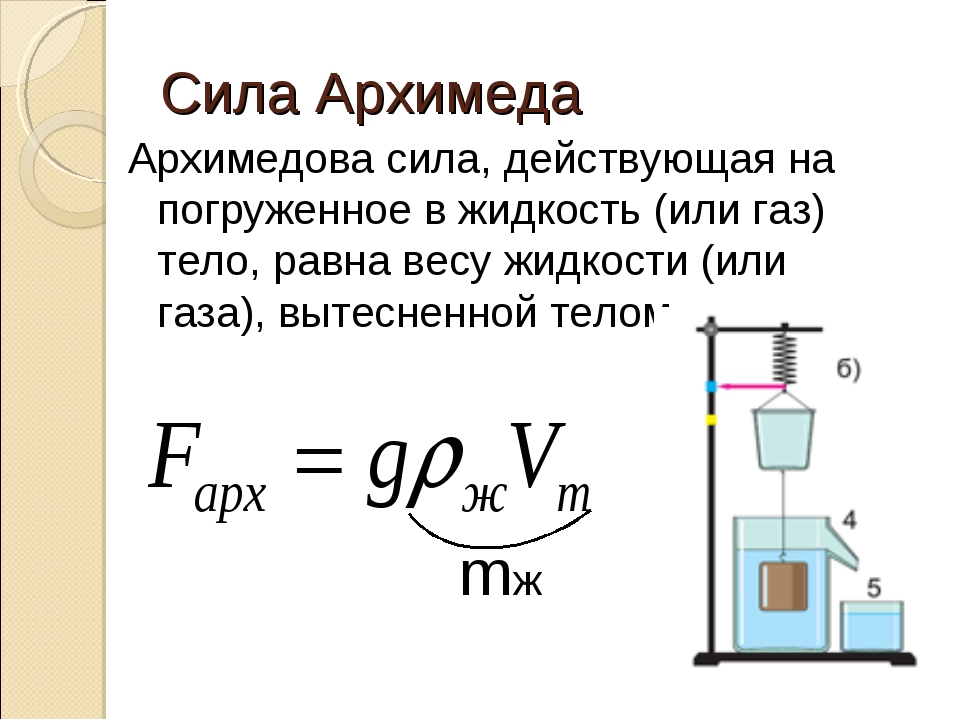 [/latex]
[/latex]
Мы можем использовать это соотношение для измерения плотности.
Рисунок 14.22 Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).Пример
Расчет средней плотности
Предположим, что женщина весом 60,0 кг плавает в пресной воде с силой 97.0% ее объема погружено под воду, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение
[латекс]\текст{фракция погружена}=\фракция{{\rho}_{\text{obj}}}{{\rho}_{\text{fl}}}[/latex]
для плотности объекта. Это дает
[латекс] {\ rho} _ {\ text {obj}} = {\ rho } _ {\ text {человек}} = \ text {(фракция погружена)} \ cdot {\ rho} _ {\ text {fl }}.[/латекс]
Нам известна и доля погруженного в воду, и плотность воды, поэтому мы можем вычислить плотность женщины.{3}}.[/латекс]
Значение
Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.
Мы ожидаем этого, потому что она плавает.
Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе», ” назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на рисунке.
Рис. 14.23 (a) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты. Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Все эти расчеты основаны на принципе Архимеда, согласно которому выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что погруженный в воду объект кажется менее весящим; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости.То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Резюме
- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет.
 Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Концептуальные вопросы
Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Показать РешениеВовсе нет. Принцип Паскаля гласит, что изменение давления осуществляется через жидкость.Причина, по которой полная ванна требует большего усилия, чтобы вытащить пробку, заключается в весе воды над пробкой.
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ. {3}[/латекс]?
{3}[/латекс]?
а.погружено на 99,5 %; б. 96,9 % под водой
Установлено, что камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350.{3}[/латекс]; этиловый спирт
Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Объемом резины пренебречь.
Какова плотность женщины, плавающей в пресной воде с [латексом]4,00\текст{%}[/латекс] ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой.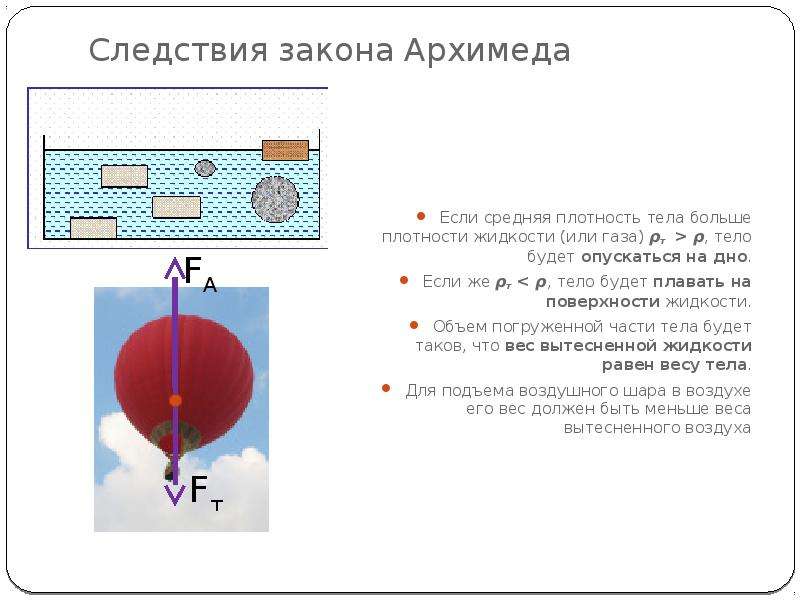 {3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
{3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
Показать решениеа.0,24; б. 0,68; в. Да, пробка будет плавать в этиловом спирте.
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
С помощью рисунка докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна [латекс]{F}_{2}-{F}_{1}[/латекс] и что концы цилиндра имеют равные площади [латекс]А[/латекс]. Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]({ч}_{2}-{ч}_{1})А[/латекс].
Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]({ч}_{2}-{ч}_{1})А[/латекс].
[латекс]\begin{array}{ccc}\text{net}\,F\hfill & =\hfill & {F}_{2}-{F}_{1}={p}_{ 2}A-{p}_{1}A=({p}_{2}-{p}_{1})A=({h}_{2}{\rho}_{\text{fl }}g-{h}_{1}{\rho}_{\text{fl}}g)A\hfill \\ & =\hfill & ({h}_{2}-{h}_{1 }){\rho}_{\text{fl}}gA,\,\text{где}\,{\rho}_{\text{fl}}=\text{плотность жидкости}\text{.} \hfill \\ \text{net}\,F\hfill & =\hfill & ({h}_{2}-{h}_{1})A{\rho}_{\text{fl}}g = {V} _ {\ text {fl}} {\ rho} _ {\ text {fl}} g = {m} _ {\ text {fl}} g = {w} _ {\ text {fl}} \hfill \end{массив}[/латекс]
А 75.Человек массой 0 кг плавает в пресной воде так, что 3,00% его объема над водой, когда его легкие пусты, и 5,00% его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости из-за разницы давлений на разных глубинах
Принцип Архимеда – Принцип Архимеда – Эксперимент, Viva Voce ЭКСПЕРИМЕНТ Цель Установить
Закон Архимеда – Эксперимент, Viva Voce
ЭКСПЕРИМЕНТ
Цель
Установить связь между потерей веса твердого тела при полном погружении в
1. вода водопроводная
вода водопроводная
2. Сильносоленая вода, с массой вытесненной ею воды за счет взятия не менее двух
различных твердых веществ.
Теория
1. Жидкости: Газы и жидкости текут и поэтому называются жидкостями.
2. Плавучесть: Восходящая сила, с которой жидкости действуют на кого-либо, называется выталкивающей
силой, и это явление известно как плавучесть.
3. Тяга: Сила, действующая на тело перпендикулярно его поверхности, называется тягой.
С.I. единицей является Ньютон.
4. Давление: Упор на единицу площади называется давлением.
Давление =
Единица S.I. = или Нм-2. Эту единицу (Нм-2) также называют Паскаль,
.’. 1 Паскаль (Па) = 1 Нм-2
5. Вес тела = Масса x ускорение свободного падения
Вт = мг
6. Когда тело погружается в воду или жидкость, оно вытесняет некоторое количество жидкости.
7. Объем вытесненной жидкости = общий объем твердого вещества.
8.Масса вытесненной жидкости может быть измерена как:
Масса вытесненной жидкости = Объем x Плотность
M = V x D
9. Вес вытесненной жидкости = Объем x Плотность xg (ускорение свободного падения)
Вес вытесненной жидкости = Объем x Плотность xg (ускорение свободного падения)
W = V x D xg
10. Тело немного теряет в весе при погружении в жидкость, его можно найти следующим образом:
Вес тела в воздухе = W1
Вес тела при погружении в жидкость = W2
11 Следовательно, потеря веса = W2 -W1
Насколько велика будет эта восходящая сила/выталкивающая сила, зависит от плотности жидкости
, в которую он погружен.Аптраст больше за счет более плотных жидкостей.
12. Закон Архимеда: когда тело полностью или частично погружено в жидкость, на него
действует направленная вверх сила, равная весу вытесненной им жидкости.
Необходимые материалы
Пружинные весы, металлический боб, хлопковая нить, переливной бак, стеклянный стакан, кран
вода, соленая вода, железная подставка.
ПРИНЦИП АРХИМЕДА И ЗАКОН ПЛАВУЧЕСТИ
Принцип Архимеда и закон флотации Рассмотрим схему ниже Когда кусок дерева погружается в жидкость, он всплывает из-за выталкивающая сила или выталкивающая сила.
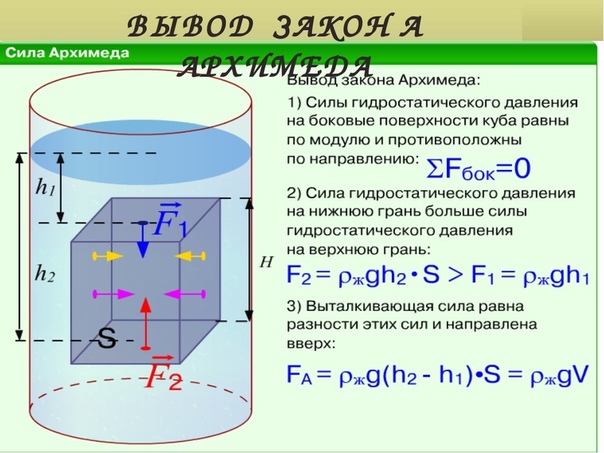 Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется выше Принцип Архимеда также называется законом плавучести , который
утверждать, что ” Когда тело частично или полностью погружено в жидкость
он испытывает подъем, равный весу вытесненной жидкости ” Соотношение между реальным весом и кажущимся весом
Где по выталкивающей силе восходящая сила позволяет
объект парит или хотя бы кажется выше Принцип Архимеда также называется законом плавучести , который
утверждать, что ” Когда тело частично или полностью погружено в жидкость
он испытывает подъем, равный весу вытесненной жидкости ” Соотношение между реальным весом и кажущимся весом Рассмотрим диаграмму массы (веса) объекта ниже
Реальный вес вес объекта в воздухе и кажущийся вес вес объекта в жидкости U = Аптраст или кажущаяся потеря веса я.жидкость обычно оказывает аптраст II. Аптраст имеет тенденцию к уменьшить массу тела III. 1 г воды = 0,01 н воды IV. 1 г воды = 1 см3 = 1 мл воды Данный вес тела в воздухе равен 10,10 Н веса тела, когда в воде составляет 9,2 н. Найдите аптраст. Кажущийся вес, А = 9,2 Н Вес тела, полностью погруженного в жидкость, равен 4,2 Н, если вес вытесненной жидкости равен 2,5 Н. Найдите массу тела в воздухе.
 Кажущийся вес, А = 4,2 Н Из : U = R – A – сделать субъектом W1 Когда тело полностью погружено в воду, его вес равен
записано как 3.1 Н, если его вес в воздухе равен 4,9 Н. Найдите аптраст. Кажущийся вес, А = 3,1 Н Тело, погруженное в воду, вытеснило 1,1 н жидкости, если его
вес белого в воде 3,3Н. Найдите их вес в воздухе. Кажущийся вес, А = 1,1 Н Из : U = R – A – сделать субъектом W1 Относительная плотность с использованием закона Архимеда Рассмотрим формулу ниже II. Ms x g = реальный
вес = R III. RD = относительный
плотность IV. ms = масса
вещество v. mw (vw = vw) = масса равного объема воды или масса
вытесненная вода Вес куска стекла в воздухе 1.2Н и 0,7Н при полном
погруженный в воду, рассчитайте это. Масса тела в воздухе, R = 1,2 Н. Масса тела в воде, А = 0,7 Н. Плотность воды, ρw = 10000 кг/м3 Относительная плотность стекла, R.D = ? Плотность стекла, ρg = ? (а) Относительная плотность стекла, RD = ? Из : R.
Кажущийся вес, А = 4,2 Н Из : U = R – A – сделать субъектом W1 Когда тело полностью погружено в воду, его вес равен
записано как 3.1 Н, если его вес в воздухе равен 4,9 Н. Найдите аптраст. Кажущийся вес, А = 3,1 Н Тело, погруженное в воду, вытеснило 1,1 н жидкости, если его
вес белого в воде 3,3Н. Найдите их вес в воздухе. Кажущийся вес, А = 1,1 Н Из : U = R – A – сделать субъектом W1 Относительная плотность с использованием закона Архимеда Рассмотрим формулу ниже II. Ms x g = реальный
вес = R III. RD = относительный
плотность IV. ms = масса
вещество v. mw (vw = vw) = масса равного объема воды или масса
вытесненная вода Вес куска стекла в воздухе 1.2Н и 0,7Н при полном
погруженный в воду, рассчитайте это. Масса тела в воздухе, R = 1,2 Н. Масса тела в воде, А = 0,7 Н. Плотность воды, ρw = 10000 кг/м3 Относительная плотность стекла, R.D = ? Плотность стекла, ρg = ? (а) Относительная плотность стекла, RD = ? Из : R. D = R/(R – A) = 1,2/ (1,2 –
0,7) = 2,4 (б) Плотность стекла, d = ? Из : RD = ρg/ρw = подчинить ρg ρg = R.D x dw = 2,4 x 1000 Относительная плотность другой жидкости из воды по твердому
вещество в Законе Архимеда При погружении твердого тела в жидкость и воду относительная плотность
дается жидкостью, вытесненной над водой, вытесненной Р.D = вес вытесненной жидкости Вес вытесненной воды RD = вес объекта в воздухе – вес объекта в
жидкий вес предмета в воздухе — вес предмета в воде RD = напор на жидкостинапор на воде = 𝑈𝑙𝑈𝑤 RD = 𝑅−
𝐴𝑙𝑅−
𝐴𝑤 𝑈𝑙=
аптраст на жидкости 𝑈𝑤
= напор на воде 𝐴𝑙=
Кажущийся вес на жидкости 𝐴𝑤
= Кажущийся вес на воде В эксперименте по определению относительной плотности
жидкий, твердый Q, взвешенный следующим образом: Вес Q в воздухе, R = 8,6 Н Вес Q в воде, AW=6.0Н Вес Q в жидкости, AL = 5,4 Н Вес корпуса Q в воздухе, R = 8,6 Н Вес корпуса Q в воде, AW = 6,0 Н Масса корпуса Q в жидкости, AL = 5,4 Н RD = 𝑅−
𝐴𝑙𝑅−
𝐴𝑤 Р.
D = R/(R – A) = 1,2/ (1,2 –
0,7) = 2,4 (б) Плотность стекла, d = ? Из : RD = ρg/ρw = подчинить ρg ρg = R.D x dw = 2,4 x 1000 Относительная плотность другой жидкости из воды по твердому
вещество в Законе Архимеда При погружении твердого тела в жидкость и воду относительная плотность
дается жидкостью, вытесненной над водой, вытесненной Р.D = вес вытесненной жидкости Вес вытесненной воды RD = вес объекта в воздухе – вес объекта в
жидкий вес предмета в воздухе — вес предмета в воде RD = напор на жидкостинапор на воде = 𝑈𝑙𝑈𝑤 RD = 𝑅−
𝐴𝑙𝑅−
𝐴𝑤 𝑈𝑙=
аптраст на жидкости 𝑈𝑤
= напор на воде 𝐴𝑙=
Кажущийся вес на жидкости 𝐴𝑤
= Кажущийся вес на воде В эксперименте по определению относительной плотности
жидкий, твердый Q, взвешенный следующим образом: Вес Q в воздухе, R = 8,6 Н Вес Q в воде, AW=6.0Н Вес Q в жидкости, AL = 5,4 Н Вес корпуса Q в воздухе, R = 8,6 Н Вес корпуса Q в воде, AW = 6,0 Н Масса корпуса Q в жидкости, AL = 5,4 Н RD = 𝑅−
𝐴𝑙𝑅−
𝐴𝑤 Р.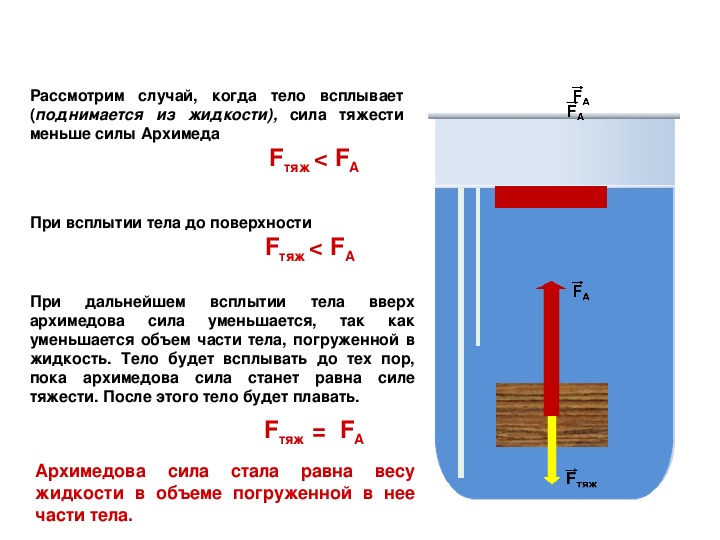 Д = 8,6 – 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2 Используя приведенные ниже данные, определите относительную плотность
жидкости
Д = 8,6 – 5,4 8,6 – 6,0 = 3,2/2,6 = 1,2 Используя приведенные ниже данные, определите относительную плотность
жидкости Вес тела в воздухе, R = 15 Н Масса тела в воде, Aw = 11 Н. Масса тела в жидкости, Al = 9N Относительная плотность, R.D = ? RD = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤 Р.Д = 15 – 9 18 – 11 = 6/7 = 1,5 Пример,
Вес тела в воздухе 0,52 Н. Полное погружение в воду весит всего 0,32 Н, в то время как его вес при погружении в другую жидкость составляет 0,36 Н. Плотность воды 1000 кг/м3 . Какова плотность другого жидкость? Масса тела в воздухе, R = 0,52 Н. Масса тела в воде, Aw = 0,32 Н. Масса тела в жидкости, Al = 0,36 Н. Плотность воды ρw = 1000 кг/м3 Относительная плотность, R.D = ? Плотность жидкости, ρl = ? Р.D = 𝑅− 𝐴𝑙𝑅− 𝐴𝑤 RD = 0,52−0,360,52−0,32 = 0,16/0,2 = 0,8 Но : R.D = ρl/ ρw – подчинить ρl ρl = R.D x ρw = 0,8 x 1000 = 800 ρ л = 800 кг/м3
Видео ниже полезно, чтобы получить больше информации о принципе Архимеда и реальной плотности тела
ytimg.com/vi/05WkCPORlj4/0.jpg” frameborder=”0″ src=”https://www.youtube.com/embed/05WkCPORlj4?feature=player_embedded”/>
ПОГРУЖЕНИЕ И ПЛАВАНИЕ
Погружение Defn: Тонуть – это тенденция объект, чтобы упасть или упасть на более низкие уровни в жидкости я.Аптраст, вызванный жидкость меньше веса объекта II. Объект плотнее жидкости означает, что объект имеет большую плотность чем жидкость
Defn: Плавающая тенденция объект должен быть подвешен (остаться) на поверхности жидкости из-за вскидывать Способность объекта плавать называется Плавучесть я. Напор, создаваемый жидкостью, должен быть равен или больше реальный вес объекта Nb : кажущийся вес приблизительно равен нулю II.Плотность тела должно быть меньше, чем у жидкости III. Объем затопленного объекта должен быть достаточно большим, чтобы вытеснить много жидкости
На видео ниже показаны условия погружения и плавания
ytimg.com/vi/nMlXU97E-uQ/0.jpg” frameborder=”0″ src=”https://www.youtube.com/embed/nMlXU97E-uQ?feature=player_embedded”/>
НИЗКИЙ ПЛАВОК
«Плавающее тело вытесняет жидкость под собственным весом в который, если плавает» Закон о плавании является заявителем в различных веществах, включая II. Заполнение горячим воздухом воздушный шар Рассмотрим схему нижеСледовательно, : U = ρf x vf x g Затем : ρs x vs x g = ρf x vf x g Ρs x vs x g = ρf x %S x vf x g R = реальный вес вещества U = W = вес вытесненной жидкости Ρs = плотность вещества Mf = масса вытесненной жидкости Ρf = плотность вытесняемой жидкости Vf = объем вытесненной жидкости %S= процент погруженного вещества Рассмотрим схему ниже
Воздушные шары наполнены легким газом e.г. гелий который вытеснить объем воздуха, равный его объему. Так как заполненный газ имеет свет или имеет низкую плотность, чем вытесненный воздух, поэтому воздушный шар дрейфует силой Воздушный шар
При нагревании воздуха в оболочке увеличивается количество газа внутри расширяться так, что его объем увеличивается, а масса газа внутри оболочки остается постоянной поэтому его плотность снижена, как если бы вы сравнивали с внешним газом (холодным воздухом).
 Этот
разный по плотности дрейф воздушного шара и его пассажиров в воздух Рассмотрим схему ниже
Этот
разный по плотности дрейф воздушного шара и его пассажиров в воздух Рассмотрим схему ниже Чтобы вещество плавало, R = U Тогда: U = (Mt + vh x ρh) x g – – – – – 1 Тогда: R = vc x ρc x g – – – – – 2 Тогда: уравнение 1 = уравнение 2 (U = R) (Mt + vh x ρh) x g = vc x ρc x g (Mt + vh x ρh) = vc x ρc Mt + v x ρh = v x ρc ce : mf = ρf x vf Mt + v x ρh = v x ρc – сделать v подчиненным Общая масса = mt = (MB + Mc + mh) Воздушный шар, включая конверт, гондолу, горелку и топлива и один пассажир имеет общую массу 450кг.Температура воздуха снаружи воздушного шара составляет 20 ℃. и имеет плотность 1,29 кг/м3, воздух внутри при температуре 120 ℃ имеет плотность 0,90 кг/м3. До какого объема должна расшириться оболочка, чтобы просто поднять воздушный шар в воздух? Плотность при 120℃, ρ2 = 0,90 кг/м3 Плотность при 20℃, ρ1 = 1,29 кг/м3 Объем вытесненного воздуха, v1 = ? Воздушный шар имеет объем 20 м3 и наполнен водород.
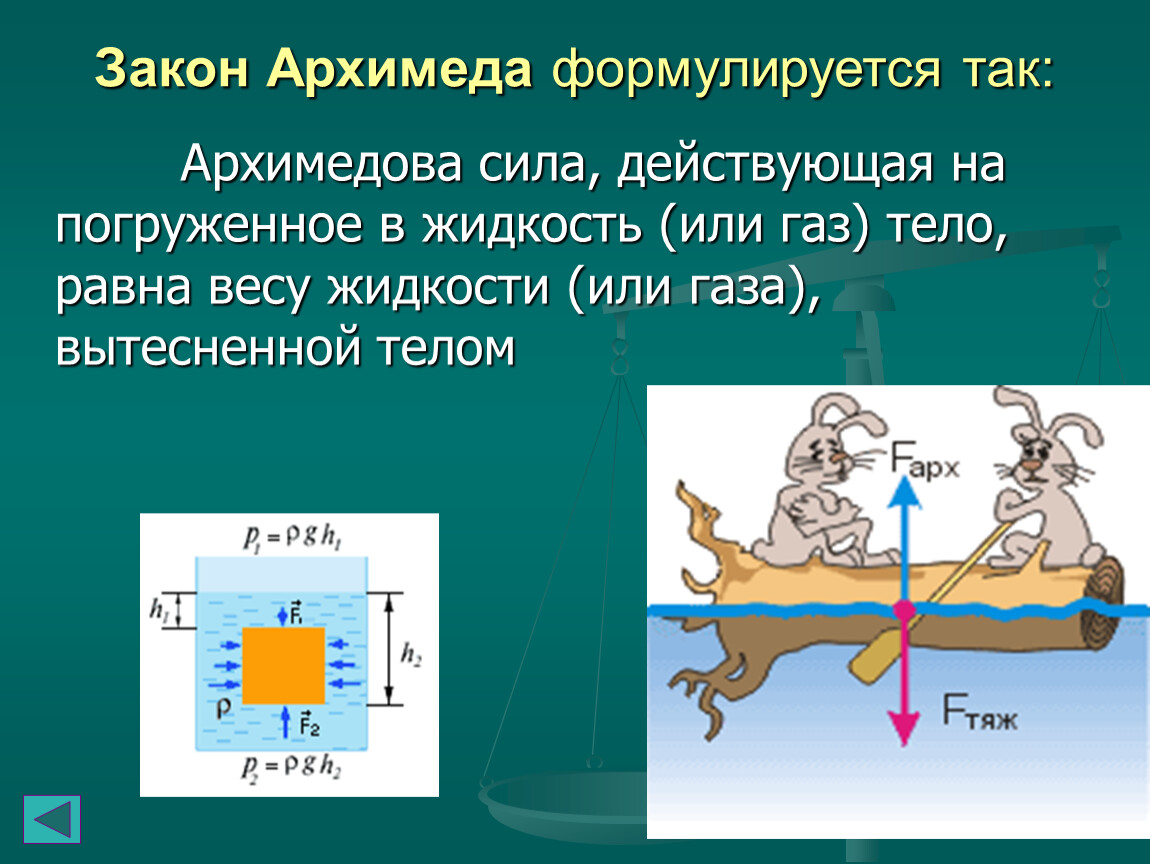 Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0.089кг/м3
и плотность воздуха 1,29 кг/м3) Общая масса = мт = мл + мб Объемная вместимость, v = 20м3 Объем холодного воздуха, v1=20м3 Масса баллона, мб = 2,5 кг Плотность при v2, ρ2 = 0,089 кг/м3 Плотность при v1, ρ1 = 1,29 кг/м3 Масса прибора), мл = ? Из : v = (мл + мб)/Δρ – сделать мл
предмет Мл = (20 х (1,29 – 0,089)) – 2,5 Мл = (20 х 1,201) – 2,5 Рассмотрим схему ниже
Ткань баллона и контейнер имеют массу 2,5 кг. Какая масса
инструментов можно поднять на воздушном шаре? (Плотность водорода = 0.089кг/м3
и плотность воздуха 1,29 кг/м3) Общая масса = мт = мл + мб Объемная вместимость, v = 20м3 Объем холодного воздуха, v1=20м3 Масса баллона, мб = 2,5 кг Плотность при v2, ρ2 = 0,089 кг/м3 Плотность при v1, ρ1 = 1,29 кг/м3 Масса прибора), мл = ? Из : v = (мл + мб)/Δρ – сделать мл
предмет Мл = (20 х (1,29 – 0,089)) – 2,5 Мл = (20 х 1,201) – 2,5 Рассмотрим схему ниже Подводная лодка, состоящая из пустого пространства, заполненного воздухом, называется балласта, чтобы увеличить его объем, чтобы придумать плотность подводной лодки и наоборот
Когда вода заполнила балласт, подводная лодка погрузилась и при допуске баллона в спеццистерну и при заполнении балласта воздух подводная лодка плавает, как и другие корабли Когда количество воды увеличивается/заливается в дутье, уменьшить объем, следовательно, увеличить плотность подводной лодки.
 Корабль сделан из стали и, как ожидается, затонет из-за его
масса. он содержит полость, которая увеличивает объем корабля, что помогает на
делает менее плотным, чем вода
Корабль сделан из стали и, как ожидается, затонет из-за его
масса. он содержит полость, которая увеличивает объем корабля, что помогает на
делает менее плотным, чем вода Но когда груз помещается на корабль, он имеет тенденцию к увеличению плотности. и массе корабля, при перегрузке корабль тонет полностью. Чтобы проверить более Забродные суда отмечены линией или отметкой, называемой отметкой Plimsoll. Линия плимсолла на корабле, используемая для обозначения минимальной высоты (максимальной плотность) над разными типами воды в разных морях, как показано на схема ниже
S = для моря в летнее время W = время моря в воде TF = тропическая пресная вода Defn: ареометр – используемый прибор для измерения плотности жидкостей или ареометр – это прибор, используемый для определить относительную плотность жидкостей.
я. Тяжелое грузило (колба): содержит ртутные или свинцовые дроби, держите ареометр в вертикальном положении, когда он плавает II. Воздушная груша: увеличивает объем вытесняемой жидкости и преодолевает вес грузила III.
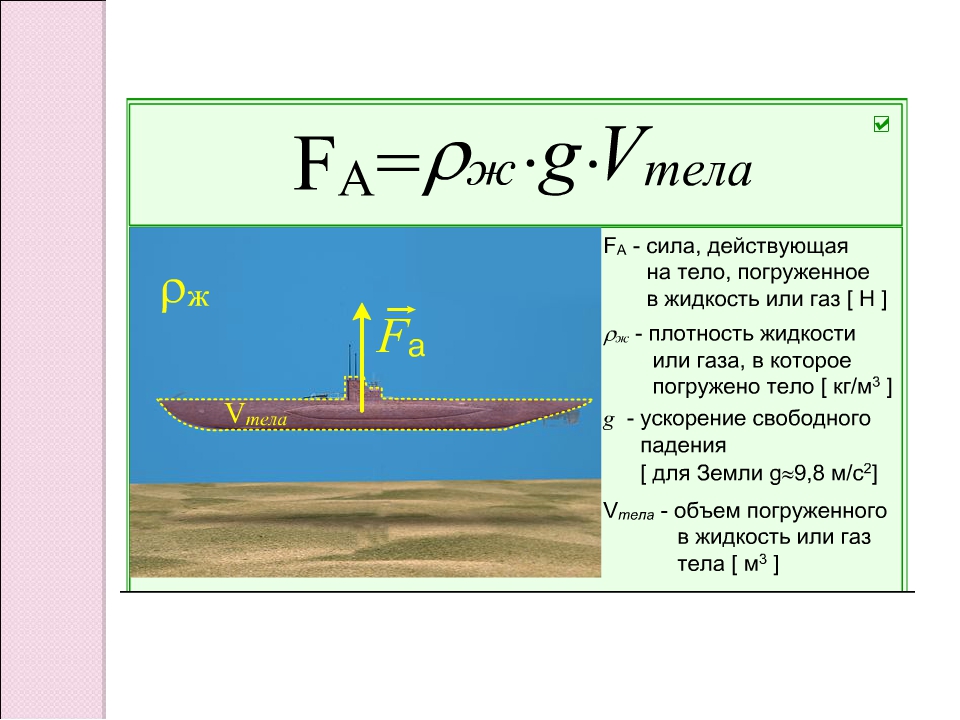 Стебель: стебель тонкий, поэтому небольшие изменения плотности
(высота) дают большие различия в чтении IV. Шкала: внутри стержня градуировка по плотности v. Изготовлены из стекла, чтобы жидкость не впитывалась Чем больше плотность жидкости, тем короче стержень
погружной ареометр
Стебель: стебель тонкий, поэтому небольшие изменения плотности
(высота) дают большие различия в чтении IV. Шкала: внутри стержня градуировка по плотности v. Изготовлены из стекла, чтобы жидкость не впитывалась Чем больше плотность жидкости, тем короче стержень
погружной ареометр КАК ПОЛЬЗОВАТЬСЯ АРЕРОМЕТРОМ
ОТНОСИТЕЛЬНАЯ ПЛОТНОСТЬ Относительная плотность жидкости по ареометру я.Когда ареометр плавает над водой, вес ареометра (wg) должно равняться весу вытесненной воды (ww) II. Когда ареометр плавает над жидкостью, вес ареометр (wg) должен равняться весу вытесненной жидкости (wl) III. так как относительная плотность жидкости определяется отношением плотность жидкости (ρl) к плотности воды (ρw) R.D = ρl/ρw = wl/vl ÷ ww/vw vl = объем вытесненной жидкости vw = объем вытесненной воды IV.
 так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погруженный в них Lw = длина погруженного в воду ареометра Ll = длина ареометра, погруженного в жидкость
так как площадь поперечного сечения ареометра одинакова,
объемы воды и вытесненной жидкости пропорциональны длинам
погруженный в них Lw = длина погруженного в воду ареометра Ll = длина ареометра, погруженного в жидкость КАК ПОЛЬЗОВАТЬСЯ АРЕОМЕТРОМ Рассмотрим схему ниже
Где: Общий объем, vt = v1 + v = Ah + v2 Тогда: vt x ρmn x g = v x ρmx x g (Ah + v) x ρmn x g = v x ρmx x g (Ah + v) x ρmn = v x ρmx Ah x ρmn + v x ρmn = v x ρmx – подчинить v2 v x ρmx – v x ρmn = Ah x ρmn v x (ρmx – ρmn) = Ah x ρmn v = (Ah x ρmn)/(ρmx – ρmn v = (Ач x ρмн)/(ρмх – ρмн) Рассмотрим приведенную ниже диаграмму, используемую для измерения плотности жидкости. от 1 г/см3 до 0.81 г/см3 (площадь поперечного сечения стебля 0,5 см2). Найдите объем ареометра менее 1,0 г/см3 с градуировкой
Площадь поперечного сечения стебля, А = 0,5см2 Высота пара, h = 16 см Объем пара, v1 = Ah = 8 см3 Общий объем, vt = (8 + v2) см3 Минимальная плотность, ρмн = 0,8 г/см3 Максимальная плотность, ρmx = 1,0 г/см3 Объем колбы, v2 = ? Объем колбы, v2 = ? Из : v2 = (Ah x ρmn)/(ρmx – ρmn) v2 = (8 х 0,8)/(1 – 0,8) Пример: NECTA форма IV 2012 QN: 4 а) Что делает твердое тело масса тела на воздухе больше, чем при погружении в жидкость? (б) Обыкновенный ареометр массой 27 г всплывает на 4 см над водой.
 Если крест
площадь сечения стебля 0,75см2 рассчитать я. Общий объем
стержень прямо под поверхностью жидкости II. Относительная плотность жидкости Масса ареометра, mh = 27г Масса вытесненной воды, mw = 27г Площадь стебля, А = 0,75 см2 Плотность воды, ρw = 1 г/см3 Плотность жидкости, ρl = ? я. Общий объем, vt = v1 + v Объем штока, v1 = Ah = 3 см3 Объем колбы, v = mw x ρw = 27 см3 II. Относительная плотность, R.D = ? Но: ρл = мл/вт = 27/30 = 0,9 г/см3 Потом: р.D = ρl/ρw 0,9/1 = 0,9 Баллон объемом 2000м3 наполнен водородом плотностью
0,09 кг/м3. Если масса ткани 100 кг, а пилота 75 кг, я. Что будет
максимальная масса оборудования, которое можно перевозить при работе в воздухе
1,25 кг/м3? II. Как бы изменилась эта цифра, если бы гелий, имеющий дважды
плотность водорода при тех же условиях, должны были быть использованы? Общая масса Mt = mt = (мл + мб) Объем водорода, v2 = 2000м3 Объем окружающий, v1=20000м3 Масса баллона, мб = (75+100) = 175кг Плотность при v2, ρ2 = 0.
Если крест
площадь сечения стебля 0,75см2 рассчитать я. Общий объем
стержень прямо под поверхностью жидкости II. Относительная плотность жидкости Масса ареометра, mh = 27г Масса вытесненной воды, mw = 27г Площадь стебля, А = 0,75 см2 Плотность воды, ρw = 1 г/см3 Плотность жидкости, ρl = ? я. Общий объем, vt = v1 + v Объем штока, v1 = Ah = 3 см3 Объем колбы, v = mw x ρw = 27 см3 II. Относительная плотность, R.D = ? Но: ρл = мл/вт = 27/30 = 0,9 г/см3 Потом: р.D = ρl/ρw 0,9/1 = 0,9 Баллон объемом 2000м3 наполнен водородом плотностью
0,09 кг/м3. Если масса ткани 100 кг, а пилота 75 кг, я. Что будет
максимальная масса оборудования, которое можно перевозить при работе в воздухе
1,25 кг/м3? II. Как бы изменилась эта цифра, если бы гелий, имеющий дважды
плотность водорода при тех же условиях, должны были быть использованы? Общая масса Mt = mt = (мл + мб) Объем водорода, v2 = 2000м3 Объем окружающий, v1=20000м3 Масса баллона, мб = (75+100) = 175кг Плотность при v2, ρ2 = 0. 09кг/м3 Плотность при v1, ρ1 = 1,25 кг/м3 Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,09) = 1,16 кг/м3 Масса прибора), мл = ? Откуда: v = (ml + mb) / Δρ – сделать мл подлежащим Мл = (2000 х 1,16) – 175 Общая масса Mt = mt = (мл + мб) Объем гелия, v2 = 2000м3 Объем окружающий, v1=20000м3 Масса баллона, мб = (75+100) = 175кг Плотность при v2, ρ2 = 0,18 кг/м3 Плотность при v1, ρ1 = 1,25 кг/м3 Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,18) = 1,07 кг/м3 Масса прибора), мл = ? v = (ml + mb) / Δρ – сделать мл подлежащим Мл = (2000 х 1.07) – 175 Масса куска пробки (0,25 г/см3) равна 20 г. Какая дробь
пробки погружается, когда она плавает в воде? Плотность пробки, ρc = 0,25 г/см3 Плотность воды, ρw = 1 г/см3 Пробка Фракция погружена, x = ? Объем вытесненной воды, vw = ? Объем погруженной пробки, vc = ? Из: принцип плавучести (vw = vc) Где: Объем пробки, vt = ? Vt = mc/ ρc = 20/0,25 = 80 см3 Масса куска пробки (0,25 г/см3) равна 20 г.
09кг/м3 Плотность при v1, ρ1 = 1,25 кг/м3 Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,09) = 1,16 кг/м3 Масса прибора), мл = ? Откуда: v = (ml + mb) / Δρ – сделать мл подлежащим Мл = (2000 х 1,16) – 175 Общая масса Mt = mt = (мл + мб) Объем гелия, v2 = 2000м3 Объем окружающий, v1=20000м3 Масса баллона, мб = (75+100) = 175кг Плотность при v2, ρ2 = 0,18 кг/м3 Плотность при v1, ρ1 = 1,25 кг/м3 Изменение плотности, Δρ = (ρ2-ρ1) = (1,25 – 0,18) = 1,07 кг/м3 Масса прибора), мл = ? v = (ml + mb) / Δρ – сделать мл подлежащим Мл = (2000 х 1.07) – 175 Масса куска пробки (0,25 г/см3) равна 20 г. Какая дробь
пробки погружается, когда она плавает в воде? Плотность пробки, ρc = 0,25 г/см3 Плотность воды, ρw = 1 г/см3 Пробка Фракция погружена, x = ? Объем вытесненной воды, vw = ? Объем погруженной пробки, vc = ? Из: принцип плавучести (vw = vc) Где: Объем пробки, vt = ? Vt = mc/ ρc = 20/0,25 = 80 см3 Масса куска пробки (0,25 г/см3) равна 20 г.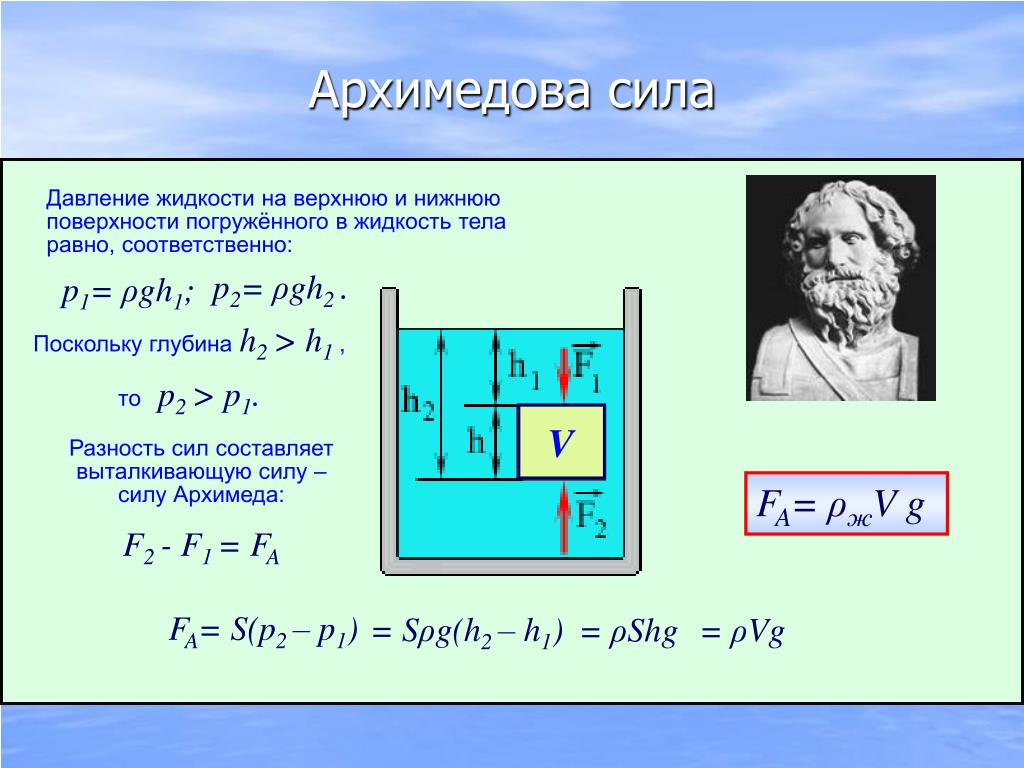 Что
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
равно 0.8 г/см3) Плотность пробки, ρc = 0,25 г/см3 Плотность спирта, ρa = 0,8 г/см3 Пробка Фракция погружена, x = ? Объем вытесненного спирта, ва = ? Объем погруженной пробки, vc = ? Из: принцип флотации (va = vc) Где: Объем пробки, vt = ? Vt = mc/ ρc = 20/0,25 = 80 см3 Однородный карандаш плавает вертикально в воде, его длина 8 см.
длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)? Длина карандаша, погруженного в воду, lw = 8 см. Плотность глицерина, ρg = 1.3 г/см3 Плотность воды, ρw = 1 г/см3 Длина карандаша, погруженного в глицерин, lg = ? Но: R.D глицерина = lw/lg Тогда: lg = lw/R.D = 8/1,3 = 6,2 см Воздушный шар и газ в нем имеют массу 450 г.
объем 500 литров. Какой максимальный груз он может поднять в воздухе с плотностью
1,3 г/см3? Общая масса, мт = (мл + мб) Масса баллона, мб = 450г Плотность газа, ρg = 1,3 г/см3 Изменение плотности, Δρ = 1,3 г/см3 Объем баллона, vb = 500 литров Откуда: v = ( мл + мб) / Δρ –
сделай мл тему На приведенной ниже диаграмме показана форма используемого мной ареометра.
Что
какая часть пробки погружается, когда она плавает в спирте? (плотность спирта
равно 0.8 г/см3) Плотность пробки, ρc = 0,25 г/см3 Плотность спирта, ρa = 0,8 г/см3 Пробка Фракция погружена, x = ? Объем вытесненного спирта, ва = ? Объем погруженной пробки, vc = ? Из: принцип флотации (va = vc) Где: Объем пробки, vt = ? Vt = mc/ ρc = 20/0,25 = 80 см3 Однородный карандаш плавает вертикально в воде, его длина 8 см.
длина погружена. На какую длину погружается, когда плавает в глицерине (плотность
глицерина составляет 1,3 г/см3)? Длина карандаша, погруженного в воду, lw = 8 см. Плотность глицерина, ρg = 1.3 г/см3 Плотность воды, ρw = 1 г/см3 Длина карандаша, погруженного в глицерин, lg = ? Но: R.D глицерина = lw/lg Тогда: lg = lw/R.D = 8/1,3 = 6,2 см Воздушный шар и газ в нем имеют массу 450 г.
объем 500 литров. Какой максимальный груз он может поднять в воздухе с плотностью
1,3 г/см3? Общая масса, мт = (мл + мб) Масса баллона, мб = 450г Плотность газа, ρg = 1,3 г/см3 Изменение плотности, Δρ = 1,3 г/см3 Объем баллона, vb = 500 литров Откуда: v = ( мл + мб) / Δρ –
сделай мл тему На приведенной ниже диаграмме показана форма используемого мной ареометра. для измерения плотности жидкости в диапазоне 0.от 8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определите
для измерения плотности жидкости в диапазоне 0.от 8 до 1,00 г/см3. Если
площадь поперечного сечения стержня 0,5 см2, а расстояние между
а 100 делений это 18см определите а) Объем ареометр ниже 1,00 градуированный (b) Положение деления 0,90 Площадь поперечного сечения стебля, А = 0,5см2 Высота пара, h = 18 см Объем пара, v1 = Ah = 9 см3 Общий объем, vt = (9 + v2) см3 Минимальная плотность, ρмн = 0,8 г/см3 Максимальная плотность, ρmx = 1,0 г/см3 Объем колбы, v2 = ? (а) Объем колбы, v2 = ? Из: v2 = (Ah x ρmn)/(ρmx – ρmn) v2 = (9 х 0.8)/(1 – 0,8) б) Какова высота h3 ареометра при смещении на меру 0,9? г/см3 Но: вес ареометра никогда не меняется
(PDF) Использование поверхностных интегралов для проверки закона Архимеда о плавучести
Проверка справедливости закона Архимеда 13
[15] Дж. Бирман и Э. Кинканон, «Пересмотр принципа Архимеда», Phys. Учат. 41, 340–344
(2003).
[16] CE Mungan, «Какова выталкивающая сила на блоке на дне стакана с водой?». ” APS
” APS
Форум по образованию, весна/2006 г. – Информационный бюллетень. Доступно по адресу:
\protect\vrule width0pt\protect\href{http://units.aps.org/units/fed/newsletters/spring2006/mungan
[17] FMS Lima и GT Brasil, «A ‘downward’ эксперимент с выталкивающей силой», Представлено в Eur. J.
Физ. (2011).
[18] К. Голд, «Еще раз принцип Архимеда», Austral. науч. Учат. Журнал 43(2), 48 (1997).
[19] Дж. Кейси, «Принцип жесткости», Arch.гист. Точные науки 43, 329–383 (1992).
[20] Дж. М. Уоллес и П. В. Хоббс, Наука об атмосфере, 2-е изд. (Academic Press, Нью-Йорк, 2006 г.),
, стр. 67–71.
[21] Для малых глубин большинство жидкостей ведут себя как практически несжимаемые жидкости. Например, плотность
морской воды увеличивается всего на 0,5% при увеличении (абсолютного) давления от 1 до 100 атм
(на глубине 1000 м).
[22] Э. Крейзиг, Высшая инженерная математика, 9-е изд.(Уайли, Нью-Йорк, 2006 г.), стр. 458–459.
458–459.
[23] В. Каплан, Advanced Calculus, 5-е изд. (Аддисон-Уэсли, Бостон, Массачусетс, 2003 г.), гл. 5.11.
[24] А. Алтинтас, «Принцип Архимеда как приложение теоремы о дивергенции», IEEE Trans.
Учеб. 33, 222 (1990).
[25] Эта более общая версия теоремы о расходимости используется здесь, поскольку она справедлива для кусочно
гладких поверхностей, охватывая таким образом, например, случаи прямоугольных блоков и цилиндров, в которых Sis
не является гладким во всех своих проявлениях. точки.
[26] Строго говоря, все жидкости демонстрируют некоторое увеличение плотности с глубиной, но скорость увеличения для
жидкостей намного меньше, чем для газов.
[27] Б. Леруа, «Принцип Архимеда: простой вывод», Eur. Дж. Физ. 6, 56–57 (1985).
[28] Р. Э. Вермиллион, «Выводы принципа Архимеда», Am. Дж. Физ. 59, 761 (1991).
[29] B. C. Reed, «Закон Архимеда представляет собой хороший пример минимизации энергии», Phys. Образовательный 39, 322–323
Образовательный 39, 322–323
(2004).
[30] Б. Л. Лан, «Не бегайте пока голым и не кричите «Эврика!»», Phys. Учат. 38, 125–126 (2000).
[31] Архимед определенно знал о существовании воздуха, который был открыт Эмпедоклом (490-430
до н.э.), но, как указывает Роррес, сомнительно, чтобы он знал о плавучести
воздуха . См. примечание 4 в: C. Rorres, «Завершение книги II Архимеда о плавающих телах», Math.
Intelligencer 26, 32–42 (2004).
[32] На самом деле, для большинства приложений, включающих пары жидкость-воздух, второй член в уравнении.(19) представляет только
небольшую поправку к наивному приближению в уравнении. (17) потому что плотность воздуха обычно намного
меньше, чем типичная плотность жидкости. Например, на уровне моря плотность воздуха составляет всего 1,2 кг/м3
, тогда как плотность пресной воды составляет около 1000 кг/м3.
[33] Б. Киббл, «Возвращение к Архимеду — дальнейшие мысли от заместителя редактора», Phys. Образовательный 35, 285–
Образовательный 35, 285–
286 (2000).
[34] А. Шарма, «Обобщение, основанное на количественной неадекватности принципа Архимеда в экспериментах на воздушном шаре
», Speculations in Science and Technology 20, 297–300 (1997).
[35] Предположение об однородном гравитационном поле является очень хорошим приближением для точек вблизи
поверхности Земли. Однако для задач, связанных с большими глубинами/высотами флюидов (например, подводная
добыча нефти, изостазия в глубоких слоях земной коры и др.), затухание гравитационного поля
с расстоянием до центра Земли должно быть принято во внимание. Для этих приложений необходимо разработать более точную модель (с учетом уравнений (4) и (5)).
[36] Для однородной жидкости имеем ρ(r) = ρ= const., что сводит интеграл в уравнении (9) к
ρ g RRRVfdV ˆ
k=ρ g Vfˆ
k=ρ g V ˆ
k, что, как и ожидалось, согласуется с АП.
[37] К. М. Р. Фаулер, Твердая Земля, введение в глобальную геофизику, 2-е изд.

 Как зависит выталкивающая сила от объема тела?
Как зависит выталкивающая сила от объема тела?
 Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
 Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
 Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.
Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.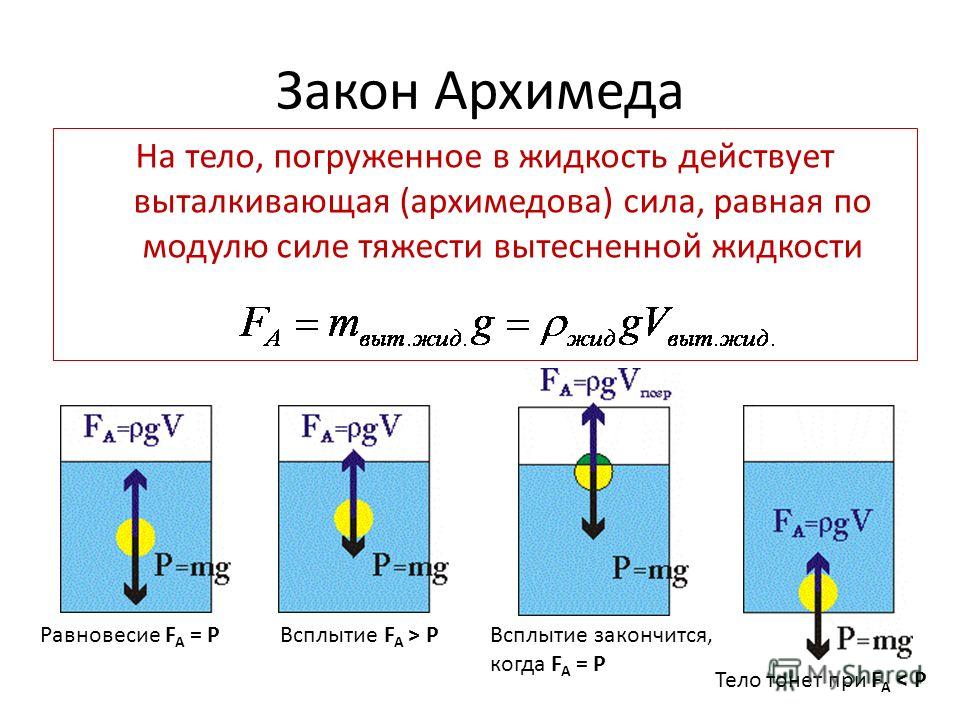

 Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что
Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что 


 Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.

 В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1). Сила называется силой Архимеда :
Сила называется силой Архимеда :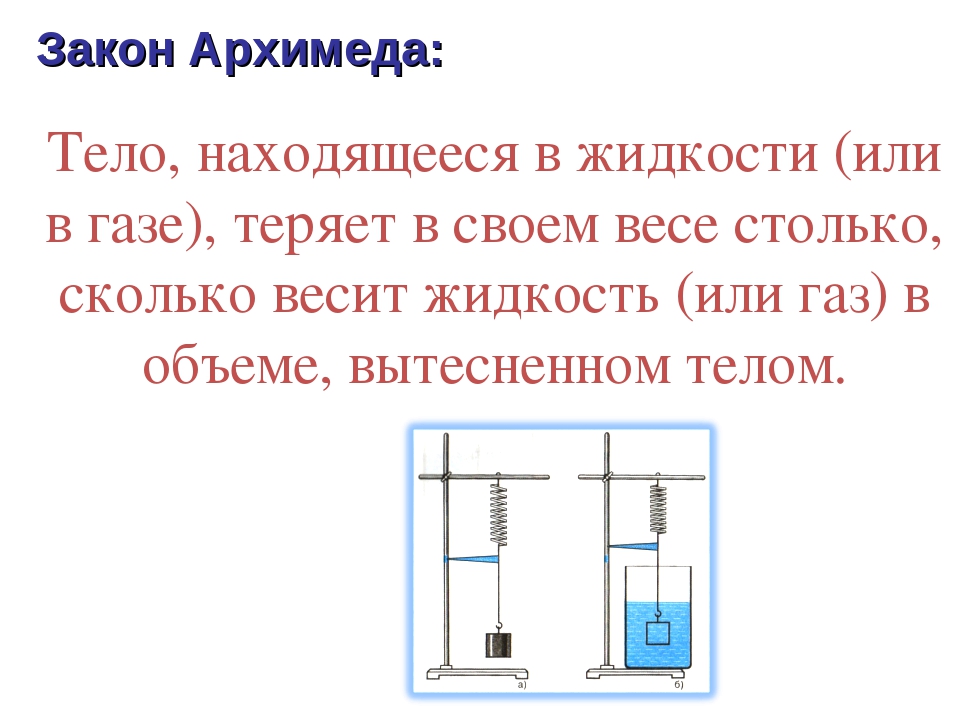 Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .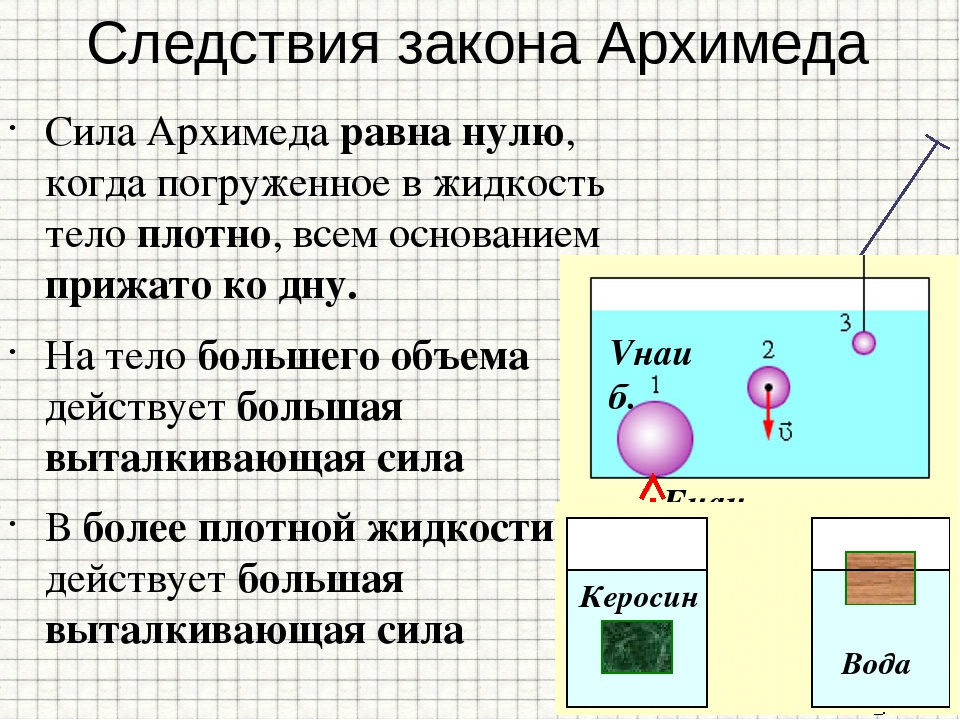 Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности: {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}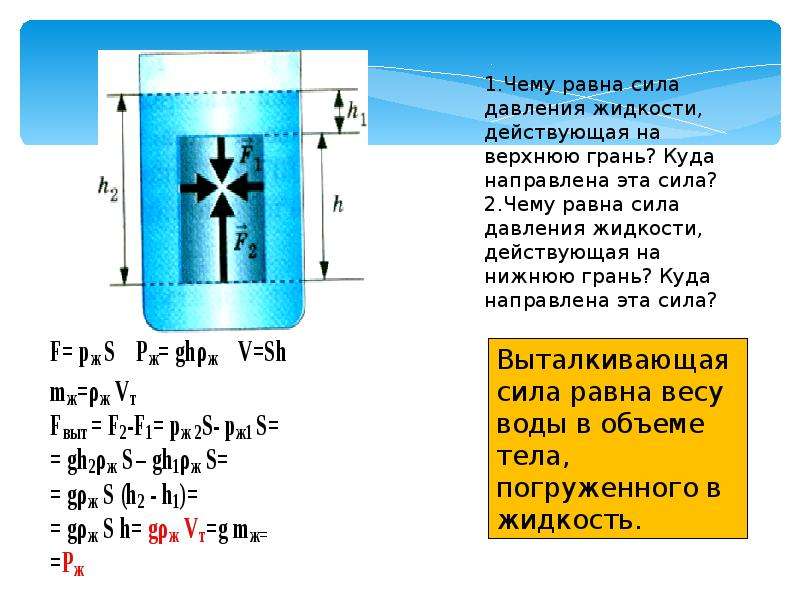 Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

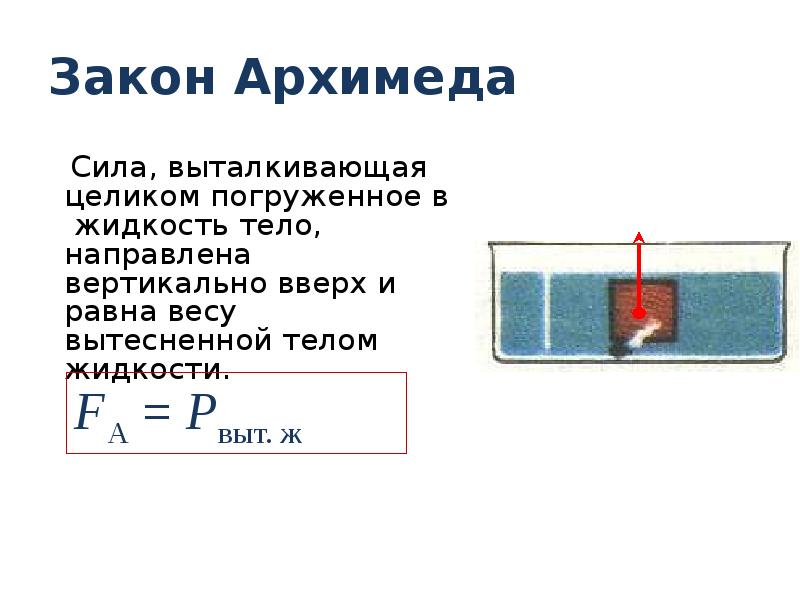 {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}
 P выт =
ρ ж gV погр
P выт =
ρ ж gV погр  При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.
При этом
получили новое положении центра
водоизмещения d” .
Приложим к точке d” подъемную
силу R и
линию ее действия продолжим до пересечения
с осью симметрии O”-O” .
Полученная точка m называется метацентром ,
а отрезок mC
= h называется метацентрической
высотой .
Будем считать h положительным,
если точка m лежит
выше точки C ,
и отрицательным – в противном случае.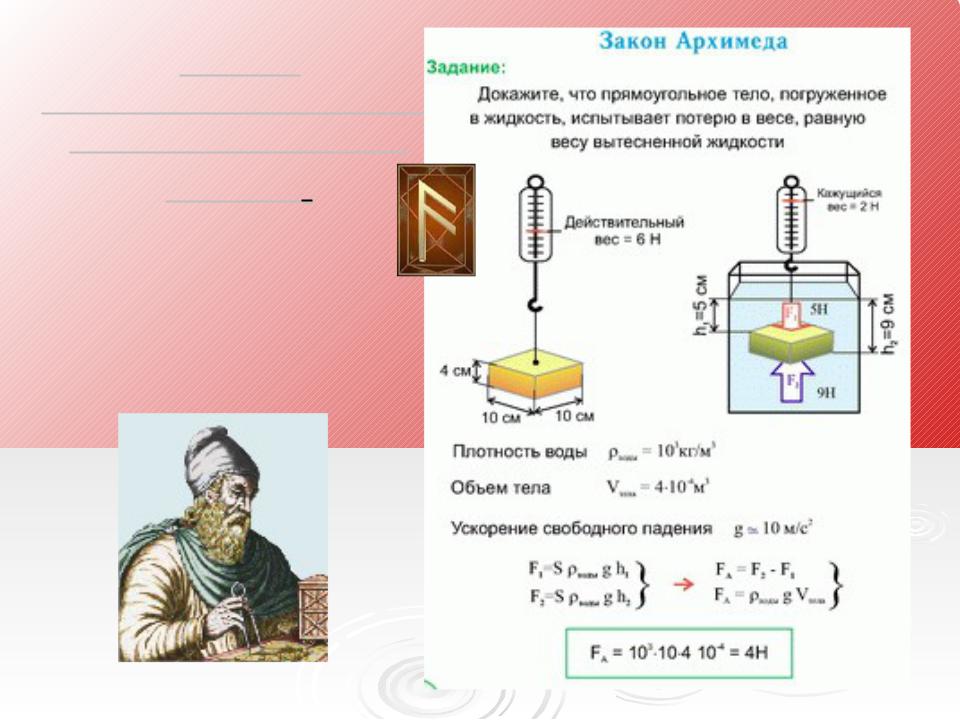
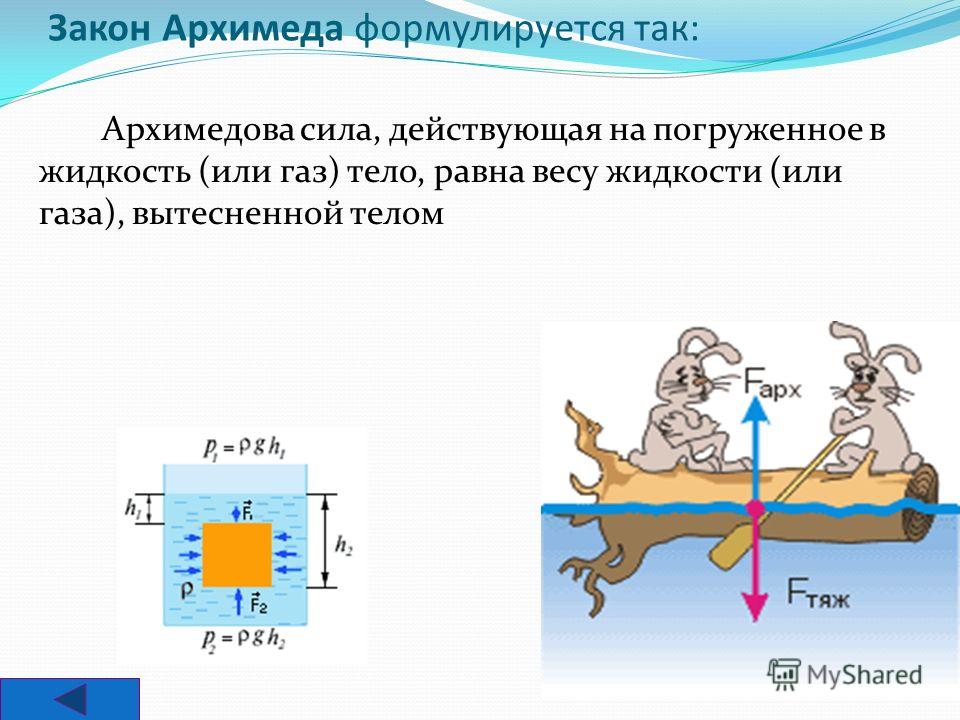
 То
следующее, что произойдет, это то, что верхний вес вызовет
его поршень, чтобы уменьшить его объем, в то время как нижний вызовет
его поршень, чтобы увеличить его объем.При этом нижний
выталкивает воду из своего открытого конца, а верхний набирает воду в свой открытый конец.
Этот процесс заставляет объем воды двигаться снизу вверх.
(схематично показано изогнутой стрелкой). Это требует работы, как всегда
случай, когда масса перемещается в более высокое положение против действия силы
сила тяжести. И угадайте, что? Работа, необходимая для этого, точно равна
работе выталкивающих сил (в идеализированном случае без
диссипативные процессы с потерей энергии), так же, как мы нашли в подробном
анализ.
То
следующее, что произойдет, это то, что верхний вес вызовет
его поршень, чтобы уменьшить его объем, в то время как нижний вызовет
его поршень, чтобы увеличить его объем.При этом нижний
выталкивает воду из своего открытого конца, а верхний набирает воду в свой открытый конец.
Этот процесс заставляет объем воды двигаться снизу вверх.
(схематично показано изогнутой стрелкой). Это требует работы, как всегда
случай, когда масса перемещается в более высокое положение против действия силы
сила тяжести. И угадайте, что? Работа, необходимая для этого, точно равна
работе выталкивающих сил (в идеализированном случае без
диссипативные процессы с потерей энергии), так же, как мы нашли в подробном
анализ.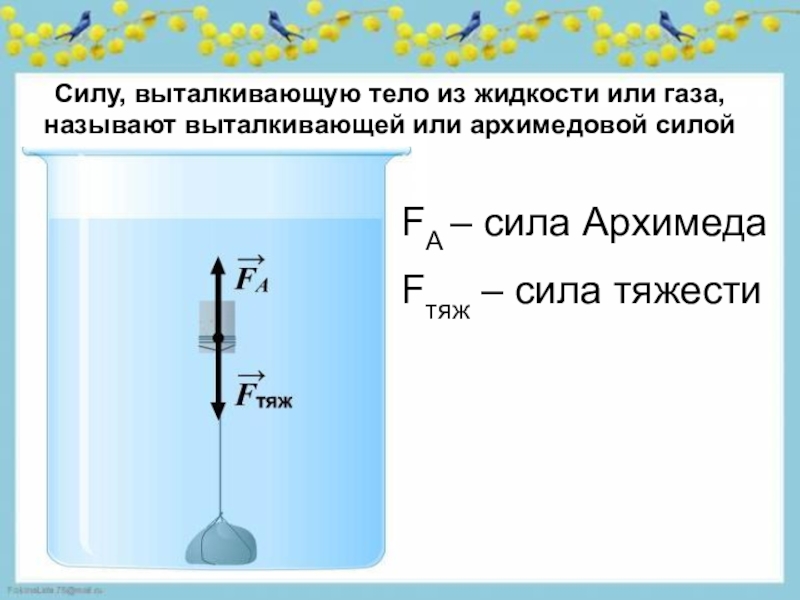

 Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.