Материал к уроку физики “Архимедова сила в стихах”
Моря и пустыни, леса и луга
Свет солнца и снега лавины
Природа сложна, но природа одна
Законы природы едины.
Вот плот и корабль
Поплавок рыбака – плывут
Как по небу плывут облака
Но камень в воде не плывёт, как бревно
И камнем бревно
Не уходит на дно
В чём сущность явлений
На это ответ даёт
Сиракузский мудрец Архимед.
Архимед впервые указал на существование выталкивающей силы и рассчитал её значение, установил закон, который получил название закона Архимеда:
На всякое тело, погружённое в жидкость или газ, действует со стороны этой жидкости (газа) выталкивающая сила, равная весу вытесненной жидкости (газа), направленная вертикально вверх.
Существует следующая легенда открытия этого закона:
Учитель: Жил в Сиракузах мудрец Архимед
Был другом царя Герона.
Какой для царя самый важный предмет?
Вы все догадались – корона!
Захотелось Герону
Сделать новую корону.
Золота отмерил строго
Взял не мало и немного
Сколько нужно – в самый раз;
Ювелиру дал заказ.
Через месяц Герону
Ювелир принёс корону
Взял корону Герон
Оглядел со всех сторон
Чистым золотом сверкает…..
Но ведь всякое бывает
И добавить серебро
Можно к золоту хитро,
А того и хуже медь,
Если совесть не иметь…..
И царю узнать охота
Честно ль сделана работа?
Не желал терпеть урон Герон.
Началась у них беседа:
Герон: Вот корона, Архимед
Золотая или нет?
Архимед: Чистым золотом сверкает.
Герон: Но ты знаешь, всё бывает!
И добавить серебро
Можно к золоту легко,
А того и хуже медь,
Если совесть не иметь.
Сомневаться стал я что-то
Честно ль сделана работа?
Можно ль это ты, скажи, определить
Но корону не царапать, не пилить….
Учитель: И задумался учёный,
Что известно? Вес короны!
Но, а как найти объём?
Думал ночью, думал днём.
И однажды в ванне моясь,
Погрузился он по пояс.
На пол вылилась вода –
Догадался он тогда,
Как найти объём короны,
И помчался к Герону.
Архимед: Эврика! Раскрыл секрет!
Герон: Что случилось Архимед?
Архимед: Пусть весы сюда несут
И с водой большой сосуд……
Всё доставить Герону.
(всё принося: на доску вешают плакаты с весами и сосудами)
На весы кладём корону
И теперь такой же ровно
Ищем слиток золотой.
Герон: Всё понятно!
Архимед: Нет, постой!
Мы теперь корону нашу
Опускаем в эту чашу
Герон, смотри сюда –
В чаше поднялась вода!
Ставлю чёрточку по краю!
Архимед: Вынимаю.
В воду золото опустим
Герон: В воду золото? Допустим….
Архимед: Поднялась опять вода
Метку ставлю я ……
Герон: Куда?
Архимед: Ну, конечно же, по краю
Герон: Ничего не понимаю
Лишь две чёрточки я вижу:
Эта выше, эта ниже
Но какой же вывод главный?
Архимед: Равный вес
Объём не равный!
Понимаешь, Герон
Я сейчас открыл закон
Тот закон совсем простой:
Тело вытеснит……
Герон: Постой!
Говоришь: объём не равный?
Мастер мой мошенник явный!
За фальшивую корону
Он ответит по закону
А ты за разгадку получишь дары
На этом прервалась беседа….
Не мало воды утекло с той поры
Но помнят закон Архимеда.
Ребята, а почему сиракузский мудрей Архимед догадался, что корона не из чистого золота?
Ответ – потому, что её объём не равен объёму чистого золота, следовательно, плотность вещества из которого сделана корона, не равна плотности золота.
Ещё раз: какие выводы можно сделать на основании этой легенды и на основе проведённого опыта?
Объём вытесненной жидкости равен объёму тела, погружённого в жидкость.
Выталкивающая сила равна весу жидкости. Fа=Рж
mж=
т.к. Vж=Vт , то Fa=ж*g*Vт – формула для определения Архимедовой силы.
Fa зависит от pж и Vт
Закрепление новой темы:
В какой воде и почему легче плавать, в морской или речной?
К чашкам весов подвешены две гири равного веса – фарфоровая и железная. Нарушится ли равновесие весов, если гири опустить в сосуд с водой?
Задача: вычислите выталкивающую силу, действующую на гранитную глыбу объёмом 0,8 м3при полном погружении в воду.
Закон Архимеда | Энциклопедия знаний
Закон Архимеда, не обязателен для изучения каждым, отдельно взятым человеком. Но, обязан для ознакомления любым образованным человеком. И это не подлежит обсуждению, кто считает себя “продвинутым” вне зависимости от профессии, должен с этим законом ознакомиться.
Архимед (287 до н. э. — 212 до н. э.) родился в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку.
Кто такой Архимед?
После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. В теоретическом отношении труд этого великого ученого был блистателен. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В сочинении «Параболы квадратуры» Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде «Об измерении круга» Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга. Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел.
В теоретическом отношении труд этого великого ученого был блистателен. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В сочинении «Параболы квадратуры» Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде «Об измерении круга» Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга. Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел.
Коля, Оля и Архимед
Любопытен отзыв Цицерона, великого оратора древности, увидевшего «архимедову сферу» — модель, показывающую движение небесных светил вокруг Земли: «Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть».
Архимед проверяет и создает теорию пяти механизмов, известных в его время и именуемых «простые механизмы». Это — рычаг («Дайте мне точку опоры, — говорил Архимед, — и я сдвину Землю»), клин, блок, бесконечный винт и лебедка. Но Архимед знал также, что предметы имеют не только форму и измерение: они движутся, или могут двигаться, или остаются неподвижными под действием определенных сил, которые двигают предметы вперед или приводят в равновесие. Великий сиракузец изучал эти силы и изобретал новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, статика, а также гидростатика.
Закон Архимеда
Учение о гидростатике Архимед развивает в труде «О плавающих телах». «Предположим, — говорит ученый, — что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается еще чем-нибудь другим». Полагаясь на это положение, Архимед математически доказывает, что следующие ниже «следствия» полностью объясняются с помощью приведенной гипотезы:
Полагаясь на это положение, Архимед математически доказывает, что следующие ниже «следствия» полностью объясняются с помощью приведенной гипотезы:
Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз.
Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости.
Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной (части тела), имел вес, равный весу всего тела.
Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела.
Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».

Пункт 5 содержит фактически общеизвестный закон Архимеда, открытие которого позволило ему, согласно преданию, осуществить проверку состава короны сиракузского царя Гиерона. Знаменитый рассказ о первом практическом применении Закона Архимеда приведен у древнеримского автора Витрувия в его труде «Об архитектуре»:
«…Исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, — один из золота, другой из серебра. Сделав это, он наполнил водой сосуд до самых краев и опустил в него серебряный слиток, и вот, какой объем слитка был погружен в сосуд, соответственное ему количество вытекло воды. Вынув слиток, он долил в сосуд такое количество воды, на какое количество стало там ее меньше, отмеряя вливаемую воду секстарием, чтобы, как и прежде, сосуд был наполнен водой до самых краев. Так отсюда он нашел, какой вес серебра соответствует какому определенному количеству воды.
Произведя такое исследование, он после этого таким же образом опустил золотой слиток в полный сосуд.
Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».
«В этом рассказе, — отмечает Я.Г. Дорфман, — убедительно лишь заключение Архимеда о том, что корона состоит из сплава, а не из чистого золота. Но ниоткуда не следует, что второй компонентой было обязательно серебро. Во всяком случае, следует отметить, что это выдающееся открытие Архимеда знаменует собой первое в истории применение физического измерительного метода к контролю и анализу химического состава без нарушения целостности изделия. Огромное практическое значение этого открытия в эпоху, когда еще никаких других методов подобного рода не было, естественно, привлекло к себе всеобщее внимание и стало предметом дальнейших исследований и практических использований на протяжении многих последующих веков.
Огромное практическое значение этого открытия в эпоху, когда еще никаких других методов подобного рода не было, естественно, привлекло к себе всеобщее внимание и стало предметом дальнейших исследований и практических использований на протяжении многих последующих веков.
Эксперименты Архимеда
По-видимому, и сам Архимед не ограничился описанным полукачественным экспериментом, а перешел к более точному количественному измерению. Автор арабского сочинения XII века “Книга о весах мудрости” ал-Хазини, цитируя “слово в слово” не дошедший до нас трактат грека Менелая, жившего во времена римского императора Домициана (81–96 гг. до н. э.), сообщает, что Архимед “изобрел механическое приспособление, которое благодаря своему тонкому устройству позволило ему определить, сколько золота и сколько серебра содержится в короне, не нарушая ее формы”. Ал-Хазини приводит также схему устройства “весов Архимеда” с подвижным грузом.
Сравнивая на этом приборе веса упомянутых слитков в воде, Архимед мог с помощью подвижного груза определять численное отношение удельных весов золота и серебра, а, сопоставляя таким же способом веса короны и одного из этих слитков, мог установить относительное количество золота и серебра в короне (если в состав короны входили только эти два металла)».
Синезий из Кирэны в IV веке, ученик знаменитой александрийской ученой Ипатии, основываясь на принципах Архимеда, изобрел «гидроскоп» — ареометр для определения удельного веса жидкостей. Прибор, изготовленный из бронзы, имел насечки. По-видимому, этот прибор использовался для составления таблиц удельных весов различных жидкостей. К сожалению, подобные таблицы до нас не дошли.
Закон Архимеда
Смешные стихи по рейтингу
Люблю её, она меня не любит.
Я жду её, она не едет вновь.
Звоню, – мне говорят её не будет…
И от бессилья стынет в жилах кровь.
Спросил вчера, надежда есть какая?
Услышал, – есть, но всё ж не торопись…
Ушёл ни с чем, от горести вздыхая, –
Так крепко с ней судьбой переплелись.
Почти не ем, бледнею и худею,
Уж язву заработал, чуда ждав.
Но всё ж мечту блаженную лелею, –
Обнять её к груди своей прижав.
Не мальчик я, чтобы играть со мною.
За нею бегать больше не хочу.
Настанет день, и, где-нибудь весною,
Я всю тебя до капли получу.
Возьму тебя, от робости немея,
Пальцами нервными к святому прикоснусь.
Тебя, родную, наконец имея,
Экстазом бурным в миг соитья захлебнусь.
Пойдём с тобою в бары, рестораны…
Я покажу тебе, в чём радость бытия.
Наполним жидкостью фужеры и стаканы,
И выпив, спляшем “Макарену” ты и я.
Ну а потом, проснувшись утром где-то,
Себя и мир туманный не любя,
Задам вопрос, и, не найдя ответа,
Пойму, что потерял опять тебя…
Конечно ты совсем не виновата,
Что наступил опять разлуки час.
Я буду ждать тебя всю жизнь, МОЯ ЗАРПЛАТА!
И всё получится любимая у нас!
И диагноз был неверный, и рецепт неточный –
Терапевт кончал вечерний, фармацевт – заочный.
Японские стихи по мотивам советских стихотворений для детей
Внимательно вглядись в траву –
Здесь сидел зеленый кузнечик, похожий на плод огурца.
Аи да лягушка.
Пляшут на одной ножке довольные торговцы рисом -Обманули неумного человека
На четыре кулака.
Девочка и мальчик вместе гуляют по саду камней.
Тили-тили-рисовая похлебка,
Будущий муж и жена.
Потеряла лицо Таня-тян –
Плачет о мяче, укатившемся в пруд.
Возьми себя в руки, дочь самурая.
Кошка скончалась. Мех уж не тот на хвосте.
Помалкивай или отведай
Жили у старой женщины Две рыбы фугу.
Одна белая, другая серая – две веселых рыбы.
Закон Архимеда в формулировке для сельской школы
Тело, всунутое в воду,
Выпирает на свободу
С весом выпертой воды,
Тела впертого туды.
По небу летят утки.
Летит уголком стая.
Мне хочется к ним жутко.
Они же – на Юг, знаю.
Они зимовать будут
В каком-нибудь там Чаде,
А я тут бумаг груду
Лопачу жратвы ради.
Их будут кормить дети,
Им будут махать руки,
Им солнце всегда светит.
Я к уткам хочу, сцуки!
Я к уткам хочу, гады!
Чтоб стала мечта – былью!
Свободы хочу ради!
И чтоб за спиной – крылья!
И чтоб вместо ног – лапки,
И чтобы как все – крякать
И чтоб – не нужны тапки,
И чтоб – нипочём слякоть!
И чтобы моя Нюся
(Она, как и я, утка)
Ушла б от меня к гусю,
А я бы страдал жутко.
И чтоб я летел, плача
В красивейший день, летом
И тут бы в меня, значит,
Предательски, влёт, дуплетом.
Мой трупик несёт Бобик,
Хозяин его хвалит,
Утятница – мой гробик,
Стакан до краёв налит.
В живот насуют яблок
И салом натрут шкурку
А после – сожрут, падлы,
А после – споют «Мурку»…
А после – ещё песню
Про то, как «летят утки». ..
..
Я – так не хочу. Честно.
Мне даже чуть-чуть жутко.
Я лучше куплю водку,
Я лучше попью сутки,
Я знаю теперь чётко:
Не надо мне быть уткой!
P.S. Всё ужасно в жизни зыбко.
В общем, я хочу быть рыбкой!
Стихи Про Архимеда — подборка стихотворений
— “Закон Архимеда” (КВН 1960-х):
“Тело, впёрнутое в воду,
Прёт оттуда на свободу
С силой выпертой воды
Телом, впёрнутым туды”;
— и “«Курочка Ряба» в изложении Бальмонта” (Владимир Успенский):
“О воздушнобезбрежности златогладкой яичности,
Золотые аккорды скорлуп!
Ты лежишь безглагольное, порождение птичности,
И зефир обдувает твой труп”… (и т.д.)
— — — —
Скорбь великопечальная по-над всем Древнегречеством.
Мудрость жизни атлантов и Вед
Не имела значения, и на помощь отечеству,
Как мессия, пришёл Архимед.
Молвил старец торжественно, тихой мудростью венчанный,
Под сиянье восторженных глаз:
– О, внемлите мне, отроки, и мужчины, и женщины!
Я спешу информировать вас:
Если в ванну обычную, в славе или безвестности,
Вы погрузите чресла свои,
То оттуда немедленно, позабрызгав окрестности,
Изольются на землю струи.
В тот же миг неожиданно тайной власти величество
Подтолкнёт вас наверх из воды
С силой веса конкретного чистой влаги количества,
Что попёрла как раз из туды.
Обещала зайти — и зашла-таки, наконец ))) Очень понравилось, люблю умно-остроумные творения
Благодарю за визит и положительный отклик. Если Вам нравятся остроумные творения, могу предложить на десерт стих “Про хрен” (http://www.stihi.ru/2014/11/30/2337). Надеюсь, он поднимет Вам настроение. Приятного аппетита!
Портал Стихи.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Стихи.ру – порядка 200 тысяч посетителей, которые в общей сумме просматривают более двух миллионов страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2021. Портал работает под эгидой Российского союза писателей. 18+
Добился Архимед взаимности от милой
И сформулировал закон примерно так:
Любое тело, погружённое во мрак,
Сопротивляется с гораздо меньшей силой.
- Следующий стих → Сергей Сатин — Физические лимерики
- Предыдущий стих → Ал Еф — Закон Архимеда
Читать похожие стихи:
- Ал Еф — Закон Архимеда
- Константин Ефетов — Урок физики. Трение
- Александр Галич — Закон природы
- Новелла Матвеева — Закон песен
- Марина Цветаева — Некоторым — не закон
Отзывы к стихотворению:
- Стихи Александра Пушкина
- Стихи Михаила Лермонтова
- Стихи Сергея Есенина
- Басни Ивана Крылова
- Стихи Николая Некрасова
- Стихи Владимира Маяковского
- Стихи Федора Тютчева
- Стихи Афанасия Фета
- Стихи Анны Ахматовой
- Стихи Владимира Высоцкого
- Стихи Иосифа Бродского
- Стихи Марины Цветаевой
- Стихи Александра Блока
- Стихи Агнии Барто
- Омар Хайям: стихи, рубаи
- Стихи Бориса Пастернака
- Стихи Самуила Маршака
- Стихи Корнея Чуковского
- Стихи Эдуарда Асадова
- Стихи Евгения Евтушенко
- Стихи Константина Симонова
- Стихи Ивана Бунина
- Стихи Валерия Брюсова
- Стихи Беллы Ахмадулиной
- Стихи Юлии Друниной
- Стихи Вероники Тушновой
- Стихи Николая Гумилева
- Стихи Твардовского
- Стихи Рождественского
- Евгений Онегин
- Бородино
- Я помню чудное мгновенье (Керн)
- Я вас любил, любовь еще, быть может
- Парус (Белеет парус одинокий)
- Письмо матери
- Зимнее утро (Мороз и солнце; день чудесный)
- Не жалею, не зову, не плачу
- Стихи о советском паспорте
- Я памятник себе воздвиг нерукотворный
- У лукоморья дуб зеленый
- Ночь, улица, фонарь, аптека
- Сказка о царе Салтане
- Жди меня, и я вернусь
- Ты меня не любишь, не жалеешь
- Что такое хорошо и что такое плохо
- Кому на Руси жить хорошо
- Я пришел к тебе с приветом
- Незнакомка
- Письмо Татьяны к Онегину
- Александр Пушкин — Пророк
- Анна Ахматова — Мужество
- Николай Некрасов — Железная дорога
- Сергей Есенин — Письмо к женщине
- Александр Пушкин — Полтава
- Стихи о любви
- Стихи для детей
- Стихи о жизни
- Стихи о природе
- Стихи о дружбе
- Стихи о женщине
- Короткие стихи
- Грустные стихи
- Стихи про осень
- Стихи про зиму
- Стихи о весне
- Стихи про лето
- Смешные стихи
- Матерные стихи
- Стихи с добрым утром
- Стихи спокойной ночи
- Стихи про семью
- Стихи о маме
- Стихи про папу
- Стихи про бабушку
- Стихи про дедушку
- Стихи о войне
- Стихи о родине
- Стихи про армию
- Стихи про школу
- Стихи о музыке
- Стихи для малышей
- Стихи о доброте
- Стихи на конкурс
- Сказки в стихах
- Популярные стихи Пушкина
- Популярные стихи Лермонтова
- Популярные стихи Есенина
- Популярные басни Крылова
- Популярные стихи Некрасова
- Популярные стихи Маяковского
- Популярные стихи Тютчева
- Популярные стихи Фета
- Популярные стихи Ахматовой
- Популярные стихи Цветаевой
- Популярные стихи Бродского
- Популярные стихи Блока
- Популярные стихи Хайяма
- Популярные стихи Пастернака
- Популярные стихи Асадова
- Популярные стихи Бунина
- Популярные стихи Евтушенко
- Популярные стихи Гумилева
- Популярные стихи Рождественского
- Другие поэты
Огромная база, сборники стихов известных русских и зарубежных поэтов классиков в Антологии РуСтих | Все стихи | Карта сайта
Все анализы стихотворений, краткие содержания, публикации в литературном блоге, короткие биографии, обзоры творчества на страницах поэтов, сборники защищены авторским правом. При копировании авторских материалов ссылка на источник обязательна! Копировать материалы на аналогичные интернет-библиотеки стихотворений — запрещено. Все опубликованные стихи являются общественным достоянием согласно ГК РФ (статьи 1281 и 1282).
При копировании авторских материалов ссылка на источник обязательна! Копировать материалы на аналогичные интернет-библиотеки стихотворений — запрещено. Все опубликованные стихи являются общественным достоянием согласно ГК РФ (статьи 1281 и 1282).
Автор: Анна Рожкова
Презентація з фізики на тему “Истории в стихах”
Физика и литература
Как пишется «камень», расскажет грамматика
Размеры и форму найдет математика.
Физика массу отыщет и вес.
• Археология скажет: «Находка!
Справа на камне видна обработка!»
• – Жил в этой местности древний народ….-
• Дальше история слово берет.
• Был этот камень в почете и силе,
• Древние люди им сучья рубили.
• Им добывали одежду и пищу.
• Жилой примотан он был к топорищу.
• В каменном веке, во времени давнем,
• Люди огонь высекали тем камнем….
• Камень в овраге лежит придорожный…
• Камень – простой? Или, может быть, сложный?
• О камне ты все ли узнал человек?
• Наука поможет! Не каменный век!!!!!
Законы Природы – едины.
Моря и пустыни. Земля и Луна. Свет Солнца и снега лавины… Природа сложна, но Природа одна. Законы Природы – едины.
Вот плот и корабль, поплавок рыбака – Плывут, как по небу плывут облака. Но камень в воде не плывет, как бревно, И камнем бревно не уходит на дно.
В чем сущность явлений?…..
На это ответ искал сиракузский мудрец Архимед.
Жил в Сиракузах мудрец Архимед.
Был другом
царя Гиерона.
А что для царя самый важный предмет?
Вы все догадались – корона!!!!!!
Захотелось Гиерону сделать новую корону.
Золота отмерил строго, взял не мало и не много –
Сколько нужно – в самый раз.
Ювелиру дал заказ.
Закон Архимеда
Через месяц Гиерону ювелир принес корону.
Взял корону Гиерон, оглядел со всех сторон.
Чистым золотом сверкает…
Но ведь всякое бывает,
И добавить серебро можно к золоту хитро,
А того и хуже медь ( если совесть не иметь)..
А царю узнать охота: честно ль сделана работа?
Не хотел терпеть урон – Гиерон.
И позвал он Архимеда….
Началась у них беседа:
– Вот корона, Архимед. Золотая или нет?
Чистым золотом сверкает!
Но ты знаешь, все бывает!
И добавить серебро можно к золоту хитро….
А того и хуже медь, если совесть не иметь!!!
Сомневаться стал я что-то: честно ль сделана работа????
Можно это, ты скажи, определить?
Но корону не царапать не пилить….
Закон Архимеда
И задумался
ученый…. – Что известно? Вес короны.
– Ну а как найти объем?
Ночью думал, думал днем….
Закон Архимеда
И однажды в ванне моясь,
Погрузился он по пояс…..
На пол вылилась вода
–
Догадался он тогда,
как найти объем
короны…
• И помчался к Гиерону не обут и не одет….
• А народ кричит во след:
• – Что случилось Архимед?
• – Может быть землетрясенье?
• – Или в городе пожар?
• Шум и крики , и смятенье!
• Всполошился весь базар!
• Закрывали лавки даже….
• Он промчался мимо стражи…
Закон Архимеда
• – Эврика!!!! Раскрыт секрет!!!! Гиерон: Ты оденься, Архимед!
Вот сандалии, хитон… А расскажешь все потом!!!
Архимед: Пусть весы сюда несут,
И с водой большой сосуд… На весы кладем корону и теперь такой же точно слиток золотой…
(находит кусок золота по весу равный короне)
Гиерон: Все понятно!
Архимед: Нет, постой! Мы теперь корону
нашу опускаем в эту чашу.
Гиерон, смотри сюда – в чаше поднялась вода! Ставлю черточку по краю.
Гиерон: А корону?
Архимед: Вынимаю. В воду золото опустим. Гиерон: В воду золото? Допустим…
Архимед: Поднялась опять вода. Метку снова ставлю я.
Гиерон: Куда?
Архимед: Ну конечно же по краю!!!!!
Гиерон: Ничего не понимаю….
Лишь две черточки я вижу:
Эта выше, эта ниже.
Но какой же вывод главный?
Архимед: Равный вес. Объем – не равный!!!!
Понимаешь, Гиерон, я сейчас открыл закон, Тот закон совсем простой: тело вытеснит….
Гиерон: Постой! Говоришь: объем не равный?
Мастер мой мошенник явный! За фальшивую корону
Он ответит по закону!!!!!
А ты за разгадку получишь дары!!!!
На этом прервалась беседа…..
Немало воды с той поры утекло, но помнят закон Архимеда!
О скорости света….
• За мамонтом гнался наш предок без страха.
• О скорости тоже понятье имел:
• Нижний предел – как ползет черепаха,
• Орлиный полет – это верхний предел.
О скорости света….
• Века миновали. Другая картина.
• Теперь черепаха, как лошадь, не в счет.
• Нижний предел – как несется машина,
• Верхний предел – как летит самолет.
О скорости света…
• Вселенная нам приоткрыла секреты.
• Узнал человек, что средь звезд и планет
• Нижний предел – как «плетется» ракета,
• Верхний предел – как проносится свет.
Скорость и время.
• Ветра шум и дятла стук…
•
Это что такое? Звук!!!!
Скорость и время.
• День и ночь. Закат. Рассвет.
• Это что такое???? Свет!!!
Скорость и время.
• Небо рвется пополам.
• Вспышка. Гром.
• В чем тут наука?
• Звук поздней приходит к нам.
• Значит свет скорее звука.
Хоть двери закрывай на ключ.
К тебе придет радиолуч.
Ты на рентген пришел – врачи Направят сквозь тебя лучи.
Не видно Солнца из-за туч – Согреет инфракрасный луч.
Литература.
• Е.Ефимовский «След колесницы»
• Ф.Я.Божинова, М.М. Кірюхин, О.О.Кірюхина «Фізика – 7 «
• Ф.Я. Божинова, І.Ю.Ненашев, М.М.Кірюхін “Фізика – 8”
• М.І.Шут, М.Т.Мартинюк, Л.Ю.Благодаренко “Фізика – 9”
Помогите,пожалуйста.Нужна выборка загадок,стихов либо афоризмов по теме:Сила
Жил в Сиракузах мудрец Архимед,Был приятелем короля Гиерона.
Какой для короля самый
Главный предмет?
Вы все додумались корона!
Захотелось Гиерону
Сделать новую корону.
Золота отмерил взыскательно.
Брал не мало и не много,
Сколько необходимо, в самый раз.
Ювелиру отдал заказ.
Через месяц Гиерону
Ювелир принес корону.
Брал корону Гиерон,
Осмотрел со всех сторон.
Незапятнанным золотом блещет…
Но ведь всякое бывает,
И добавить серебро
Можно к золоту хитро,
А того и ужаснее – медь
(Если совесть не иметь)…
И королю выяснить охота:
Правдиво ль изготовлена работа?
Не желал терпеть урон Гиерон.
И позвал он Архимеда…
Началась у их беседа.
Гиерон. Вот корона, Архимед.
Золотая либо нет?
Архимед. Незапятнанным золотом блещет…
Гиерон. Но, ты знаешь, все посещает!
И добавить серебро
Можно к золоту хитроумно.
А того и ужаснее – медь,
Если совесть не иметь.
Колебаться стал я что-то.
Правдиво ль изготовлена работа?
Можно ль это, ты скажи,
найти?
Но корону не царапать, не пилить…
И задумался ученый:
Что знаменито? ВЕС короны.
Ну а как отыскать ОБЪЕМ?
Размышлял ночкой, размышлял деньком.
И единожды, в ванне моясь,
Погрузился он по пояс.
На пол вылилась вода
Додумался он тогда,
Как отыскать ОБЪЕМ короны,
И понесся к Гиерону,
Не обут и не одет…
А люд орал вслед:
Что случилось, Архимед?
– Может быть, землетрясенье
Или в городке пожар?
Всполошился весь рынок!
Покрывали лавки даже.
Шум и вопли, и смятенье!
Он промчался мимо стражники.
Эврика! Отыскал решенье!
Во дворец примчался он.
Я выдумал, Гиерон!
(Во дворце.)
Архимед. Эврика! Раскрыл секрет!
Гиерон. Ты оденься, Архимед!
Вот сандалии, хитон.
А расскажешь все позже!
Архимед. Пусть весы сюда несут
И с водой великий сосуд…
Все доставить Гиерону!..
(Слуги все приносят.)
На весы кладем корону,
И теперь таковой же ровно
Отыскиваем слиток золотой…
(Обретают кусочек золота, по весу одинаковый короне.)
Гиерон. Все понятно!
Архимед. Нет, постой!
Мы теперь корону нашу
Опускаем в эту чашу.
Гиерон! Смотри сюда
В чаше поднялась вода!
Ставлю черточку по краю.
Гиерон. А корону?
Архимед. Вынимаю.
В воду золото опустим.
Гиерон. В воду золото? Допустим…
Архимед. Поднялась вновь вода,
Метку ставлю я.
Гиерон. Куда?
Архимед. Ну, конечно же, по краю.
Гиерон. Ничего не разумею…
Только две черточки я вижу.
Эта выше, эта ниже.
Но какой же вывод основной?
Архимед. Одинаковый вес.
Объем не одинаковый!
Разумеешь, Гиерон,
Я на данный момент открыл закон.
Тот закон совершенно обычной.
Тело выпихнет…
Гиерон. Постой!
Разговариваешь, объем не одинаковый?
Мастер мой – жулик
явный!
За фальшивую корону
Он ответит по закону!
А ты за разгадку
Получишь дары!
На этом прервалась беседа…
Немало воды утекло с той поры,
Но помнят закон Архимеда!
| Код | Фраза | Что помогает запомнить | Класс |
| 6100 | Каждый охотник желает знать где сидит фазан. | Самая распросраненная запоминалка. Начальные буквы помогают запомнить цвета спектра: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. | 11 |
| 6110 | Как однажды Жак-звонарь головой свалил фонарь | аналог для запоминания цветов спектра. Иногда вместо Жак используют Жан, а вместо “свалил” – слова “сломал”, “свернул”, “сбил”. | |
| 6120 | Кот ослу, жирафу, зайке голубые сшил фуфайки. | для детей | |
6121 | Каждый оформитель желает знать, где скачать фотошоп. | для программистов | |
6122 | Каждая образованная женщина завтракает горячими сырыми фрикадельками. | для эстетов | |
6123 | Крадётся осень, Жара затмилась глубиной.  Синеет Фудзияма. | для лириков. Можно и дальше продолжать их много, но принцип понятин и каждый сам придумает сбе на “близкую” тему. | |
| 6125 | Roy G. Biv | Английский вариант: Red, Orange, Yellow, Green, Blue, Indigo, Viole | |
| 6130 | Richard Of York Gave Battle In Vain | Еще один английский вариант. | |
| Массу мы легко найдем, умножив плотность на объём. | Формула нахождения массы m=q*V | ||
| Не лезь воду глубоко В Воде давление велико Надавит сверху ро-же-аш (p=ρgh) И вдруг концы свои отдашь.  | Формула давления жидкостей. | ||
| Три закона Ньютона; 1) не пнёшь – не полетит; 2) как пнёшь, так полетит; 3) как пнёшь- так и получишь. | Законы Ньютона | 10 | |
| Тело, впёрнутое в воду, Выпирает на свободу Весом выпертой воды Телом, впёрнутым туды. | Закон Архимеда. | ||
| Тело, впёрнутое в воду, выпирает на свободу. Столько выперто воды, сколько впёрнуто туды | Закон Архимеда чуть по другому. | ||
Полкота на каждую степень свободы. | m — масса броуновской частицы, v — ее скорость, k — постоянная Больцмана, T — температура (рисунок сделать)
| 10 | |
| Три кота на мясо. | cкорость теплового движения частицы v=√ (3kT/m) | 10 | |
| Я, тут Больцман постоянную -23 Дж/К принес | постоянная Больцмана по количеству букв в начале фразы: k=1,38*10-23 Дж/К Я(1), тут(3) Больцман(8) постоянную(10) | 10 | |
| Не знает первый закон термодинамики только ДУРАК. | ДУРАК расшифровывается Д-дельта,У- U, Р – равно или работа, А это значок работы А, К- тепло ку Q. Так можно запомнить первый закон термодинамики: Дельта U(У) Равно Работа А плюс Q (К) – ДУРАК. | 10 | |
| …что-то там… ..Бойлем не был Мариотт Чтобы не попасть впросак, Знай, что Геем был Люссак”. | не прислали начала фразы. Есть закон Бойля-Мариотта и закон Гей-Люссака. Это стихотворение было на запоминание того, где два человека, а где – один. | 10 | |
| Слов в предложении порядок неправильный – Вот что инверсия значит такое. | Помогает запомнить понятие “инверсия”. | ||
| Правило буравчика (правило правой руки) | Для определения направления вектора магнитной индукции | 11 | |
| Правило левой руки | Направление силы, действующей на проводник | 11 | |
| Второе правило левой руки | Направление силы Лоренца или Ампера | 11 |
Принцип плавучести Архимеда – как плавают корабли? (Библейская история онлайн)
Принцип Архимеда
плавучести
Как корабли
Плавать?

Архимед
Решает задачу
Греческий математик и изобретатель Архимед жил во время 3-го века.
век до нашей эры.Согласно истории, однажды он был в ванне, когда
открыл принцип плавучести, который является причиной того, что огромные греческие
корабли весом в тысячи фунтов могли плавать на воде. Он заметил, что
когда он опускался в ванну, вода вытеснялась его телом
переполнили стороны и он понял, что есть отношения
между его весом и объемом вытесненной воды. Говорят, что он
голая выбежала на улицу с криком « heurEka », что является
откуда мы взяли слово “эврика!” (Нашел), греческий heurEka Я нашел, из heuriskein найти.
Архимед в то время не думал о кораблях,
он был на миссии, чтобы решить вопрос, который задал ему Кинг
Гиерон II Сиракуз, дом Архимеда, который был греческим городом в
время. Вопрос, который задал король, касался его короны. Был
это чистое золото или частично серебро? Архимед рассуждал, что если корона
любое серебро в нем, оно заняло бы больше места, чем чистая золотая корона из
такой же вес, потому что серебро не такое плотное, как золото. Он сравнил
объем короны (измеряется количеством вытесненной воды) с
объем равного веса золота, а затем серебра, он нашел ответ.Он
пришлось сообщить своему королю, что корона не из чистого золота.
Он сравнил
объем короны (измеряется количеством вытесненной воды) с
объем равного веса золота, а затем серебра, он нашел ответ.Он
пришлось сообщить своему королю, что корона не из чистого золота.
Принцип плавучести
Архимед продолжил эксперименты и подошел к
с принципом плавучести, что корабль будет плавать, когда вес
вода, которую он вытесняет, равна весу корабля, и все будет плавать
если он имеет форму, позволяющую вытеснять воду под собственным весом до того, как достигнет
точка, в которую он погрузится.
Это своего рода технический взгляд на это. А Спущенный на воду корабль тонет в море до тех пор, пока вес воды он смещает равный собственному весу.Когда корабль загружен, он тонет глубже, вытесняя больше воды, и поэтому величина выталкивающей силы постоянно соответствует весу корабля и его груза.
Метацентр
Архимед понял, что метацентр должен быть
определил, где находится воображаемая вертикальная линия (через
центр плавучести) пересекает другую воображаемую вертикальную линию
(через новый центр плавучести), созданный после смещения корабля,
или под наклоном в воде.
Центром плавучести плавучего корабля является точка в котором все части тела точно уравновешивают друг друга и заставляют каждую другой поплавок. Другими словами, метацентр остается прямо над центр плавучести независимо от наклона плавучего корабля. Когда корабль наклоняется, одна сторона вытесняет больше воды, чем другая, и центр плавучести перемещается и больше не находится непосредственно под центром сила тяжести; но независимо от величины наклона центр плавучесть остается прямо под метацентром.Если метацентр выше центра тяжести плавучесть восстанавливает устойчивость, когда корабль наклоны. Если метацентр находится ниже центра тяжести, лодка неустойчиво и опрокидывается.
Почему это важно в
изучение библейской истории?
Хороший вопрос! Поскольку изучение физики и различных наук велось
развитая в Древней Греции, она, среди прочего, открыла двери для
Господа, чтобы принести в мир новые знания и новые технологии, которые
в конечном итоге поможет подготовить мир в нужное время к
пришествие Спасителя и Его Евангелие. Мы должны помнить, что
люди жили во тьме, и тьма увеличивалась в
энергии и единственной надеждой для человечества была весть о том, что Иисус
Христос и Его последователи принесут. Бог очень осведомлен о времени и
времена года, взлеты и падения народов мира и
Библия говорит, что «в полноту времени Бог послал Свои
Сын “, и Его приход был эпохальным событием, изменившим культуру.
западной цивилизации навсегда и направил ее в новое русло.
Мы должны помнить, что
люди жили во тьме, и тьма увеличивалась в
энергии и единственной надеждой для человечества была весть о том, что Иисус
Христос и Его последователи принесут. Бог очень осведомлен о времени и
времена года, взлеты и падения народов мира и
Библия говорит, что «в полноту времени Бог послал Свои
Сын “, и Его приход был эпохальным событием, изменившим культуру.
западной цивилизации навсегда и направил ее в новое русло.
Греки в Библейской энциклопедии – ISBE
ГРЕЦИЯ; ГРЕКИ
греч. Шанц, греки: В Ветхом Завете слово «греки».
происходит только один раз (Иоиль 3 (4): 6). Для ссылок на Грецию в Древнем
Завет см. ЯВАН. В Ветхом Завете в версии короля Иакова
Апокрифы «греки» и «греки» используются без различия, например
1 Макк. 1:10; 6: 2; 8: 9; 2 Макк 4: 15,36. Таким образом, в 1 Макк 1: 1,
Об Александре Великом говорится как о царе Греции, и в 1 Мак.
1:10 Македонская империя называется «царством греков» (basileia
Элленон).Во 2 Макк 13: 2 армия Антиоха, царя Сирии,
называется «греческий» (dunamis Hellenike), а во 2 Макк. 6: 8 «греческий
города »(Poleis Hellenides) – македонские колонии. Ссылка
во 2 Макк 6: 1 престарелому афинянину, которого послал Антиох
на царя возложена обязанность по эллинизации евреев; в 2 Макк 9:15
Антиох клянется, что сделает евреев равными афинянам; в
1 Макк 12-14, ссылка на переговоры Ионатана,
первосвященник со спартанцами, которых он называет братьями, ища
возобновление договора о союзе и дружбе против сирийцев.С распространением греческой власти и влияния все изменилось.
конкретно евреев называли греками; таким образом, во 2 Макк. 4:36; 11: 2; 3
Макк 3: 3,1 «греки» в отличие от евреев просто
неевреи, так называемые из-за преобладания греческих институтов
и культура, и “греческий” даже стал использоваться в смысле
«антиеврейский» (2 Макк. 4: 10,15; 6: 9; 11:24). Полная статья
6: 8 «греческий
города »(Poleis Hellenides) – македонские колонии. Ссылка
во 2 Макк 6: 1 престарелому афинянину, которого послал Антиох
на царя возложена обязанность по эллинизации евреев; в 2 Макк 9:15
Антиох клянется, что сделает евреев равными афинянам; в
1 Макк 12-14, ссылка на переговоры Ионатана,
первосвященник со спартанцами, которых он называет братьями, ища
возобновление договора о союзе и дружбе против сирийцев.С распространением греческой власти и влияния все изменилось.
конкретно евреев называли греками; таким образом, во 2 Макк. 4:36; 11: 2; 3
Макк 3: 3,1 «греки» в отличие от евреев просто
неевреи, так называемые из-за преобладания греческих институтов
и культура, и “греческий” даже стал использоваться в смысле
«антиеврейский» (2 Макк. 4: 10,15; 6: 9; 11:24). Полная статья
В Библии много говорится о “Греки”
Деяния 21:28 – Плач
вон, мужи Израилевы, помогите: это тот человек, который учит всех [мужчин]
везде против народа и закона, и это место; и
далее принесли греков также в храм, и
осквернил это святое место.
Деяния 14: 1 – И было в Иконии, что они вместе пошли в синагоге иудейской, и так говорили, что великое множество евреев, а также греков верили.
Деяния 18:17 – Тогда все греков взяли Сосфена, главного правителя из синагоги, и бить [его] перед судилищем. И Галлио ни о чем из этих вещей не заботился.
Деяния 19:10 – И так продолжалось два года; так что все они жители Азии слышали слово Господа Иисуса как иудеи, так и Греки .
Деяния 17: 4 – И некоторые из них уверовали и общались с Павлом и Силой; и набожных греков великое множество, и главных женщин немало.
Деяния 19:17 – И это было известно всем евреям и грекам также жилище в Эфесе; и страх напал на них всех, и имя Господь Иисус был увеличен.
Деяния 20:21 – Свидетельствуя как евреям, так и грекам ,
покаяние перед Богом и вера в Господа нашего Иисуса Христа.
1 Коринфянам 1:23 – Но мы проповедуем Христа распятого. Евреи – камень преткновения, а для греков глупость;
Деяния 18: 4 – И он рассуждал в синагоге каждую субботу, и уговаривал Евреи и греков .
1 Коринфянам 1:22 – Для евреев требуется знамение, а Греки ищут мудрости:
1 Коринфянам 1:24 – Но к названным оба Иудеи и Греки , Христос сила Божья и мудрость Бог.
Римлянам 1:14 – Я должник как греков , так и Варвары; и мудрым, и неразумным.
Деяния 17:12 – Поэтому многие из них поверили; также достойных женщин, которые было греков , а мужчин немало.
Иоанна 12:20 – И среди пришедших было греков до богослужения на празднике:
Вернуться к Удивительные факты
Вернуться к истории Библии Онлайн
Библиография древнего поклонения Ваалу
Илия, Яхве и Ваал Гункель и Хансон, 106 страниц, Pub. 2014
2014
Удивительные факты
Библейская история онлайн
© Библейская история онлайн (/)
Связанное содержимое
Эврика! Принцип Архимеда | Живая наука
Архимед, возможно, был величайшим ученым в мире – по крайней мере, величайшим в классическую эпоху. Он был физиком, математиком, астрономом, изобретателем и инженером. Многие из его изобретений, теорий и концепций используются до сих пор.Возможно, самым известным его достижением был момент «Эврики», когда он открыл принцип плавучести.
Биография
Архимед жил в Сиракузах на острове Сицилия в III веке до нашей эры. В то время, по данным Scientific American, Сиракузы были одним из самых влиятельных городов древнего мира. Торговые суда из Египта, Греции и Финикии заполнили гавань города-государства. Согласно Архимеду Палимпсесту, он также был центром торговли, искусства и науки.
Изучив геометрию и астрономию в Александрии, «величайшем интеллектуальном центре древнего мира», согласно Scientific American, Архимед поселился в Сиракузах, чтобы вести жизнь мысли и изобретений.
Одним из его изобретений стал винт Архимеда. В этом устройстве используется штопор с полой трубкой. Когда винт поворачивается, вода поднимается по трубке. Первоначально он использовался для слива морской воды из корпуса корабля. По данным Archimedes Palimpsest, он до сих пор используется в качестве метода орошения в развивающихся странах.
Известная фраза Архимеда: «Дайте мне рычаг и место, чтобы я мог встать, и я сдвину мир». Это хвастливое заявление выражает силу рычагов, которые, по крайней мере образно, движут миром. Архимед понял, что для того, чтобы выполнить ту же работу, можно найти компромисс между силой и расстоянием, используя рычаг. Его Закон рычага гласит: «Величины находятся в равновесии на расстояниях, обратно пропорциональных их весам», согласно «Архимеду в 21 веке», виртуальной книге Криса Рорреса из Нью-Йоркского университета.
Архимед также разработал оборону Сиракуз от вторгшихся армий. Он укрепил стены Сиракуз и построил боевые машины. Его работы задержали римлян на два года. Однако в 212 г. до н. Э. Войска генерала Марцелла захватили город.
Однако в 212 г. до н. Э. Войска генерала Марцелла захватили город.
Марцелл уважал Архимеда и послал за ним солдат, чтобы он мог встретиться со знаменитым математиком. Согласно «Архимеду Палимпсесту», он был настолько сосредоточен на решении математической задачи, что не знал, что римляне штурмовали город.Когда солдат сказал ему сопровождать его к генералу, Архимед сказал ему уйти. Разъяренный солдат сбил его с ног. Марцелл приказал похоронить Архимеда с почестями. На надгробии Архимеда было выгравировано изображение сферы внутри цилиндра, иллюстрирующее один из его геометрических трактатов.
Принцип Архимеда: выталкивающая (восходящая) сила, действующая на объект, равна весу (нисходящей силе) вытесняемой жидкости. (Изображение предоставлено Designua / Shutterstock)‘Эврика! Эврика!
Архимед вошел в историю как парень, который бегал голым по улицам Сиракуз с криком «Эврика!» – или “У меня есть!” на греческом.История этого события заключалась в том, что Архимеду было поручено доказать, что новая корона, сделанная для Гиерона, царя Сиракуз, не была чистым золотом, как утверждал ювелир. История впервые была записана в I веке до нашей эры. Витрувия, римского архитектора.
История впервые была записана в I веке до нашей эры. Витрувия, римского архитектора.
Архимед долго и усердно думал, но не смог найти способа доказать, что корона не из чистого золота. Вскоре после этого он наполнил ванну и заметил, что вода пролилась через край, когда он вошел в нее, и он понял, что вода, вытесняемая его телом, равна весу его тела.Зная, что золото тяжелее других металлов, которые изготовитель корон мог заменить, Архимед использовал свой метод, чтобы определить, что корона не была чистым золотом. Забыв, что он раздет, он побежал голым по улицам от своего дома к королю с криком «Эврика!».
Принцип Архимеда
Согласно Boundless, принцип Архимеда гласит, что выталкивающая сила, действующая на объект, погруженный в жидкость, равна весу жидкости, вытесняемой этим объектом.
Если стакан наполнить до верха водой, а затем добавить в него кубики льда, что произойдет? Точно так же, как вода вылилась через край, когда Архимед вошел в свою ванну, вода в стакане будет выливаться, когда в него добавляются кубики льда. Если бы пролившаяся вода была взвешена (вес – это направленная вниз сила), она была бы равна восходящей (выталкивающей) силе, действующей на объект. По подъемной силе можно определить объем или среднюю плотность объекта.
Если бы пролившаяся вода была взвешена (вес – это направленная вниз сила), она была бы равна восходящей (выталкивающей) силе, действующей на объект. По подъемной силе можно определить объем или среднюю плотность объекта.
Архимед смог определить, что корона не была чистым золотом из-за объема вытесненной воды, потому что, хотя вес короны был идентичен весу золота, которое король дал изготовителю короны, объем был разные из-за разной плотности металлов.
Использование принципа Архимеда
Принцип Архимеда – очень полезный и универсальный инструмент. Это может быть полезно для измерения объема необычных объектов, таких как золотые короны, а также для объяснения поведения любого объекта, помещенного в любую жидкость. Согласно Science Clarified, принцип Архимеда описывает, как плавают корабли, ныряют подводные лодки, летают воздушные шары и многие другие примеры. Принцип Архимеда также используется в большом количестве предметов научных исследований, включая медицину, инженерию, энтомологию, инженерию и геологию.
Текущее исследование
Объемы / плотность костей
Принцип Архимеда имеет множество применений в медицине и стоматологии и используется для определения плотности костей и зубов. В статье 1997 года, опубликованной в журнале Medical Engineering & Physics, исследователи использовали принцип Архимеда для измерения объема внутренней губчатой части кости, также известной как губчатая кость.Объемная доля губчатой кости может использоваться в различных исследованиях возраста и состояния здоровья, в том числе в качестве индекса в исследованиях старения, остеопороза, прочности, жесткости и эластичности костей. Были протестированы различные методы, использующие принцип Архимеда, чтобы повысить воспроизводимость измерений: один, когда кость была погружена в дистиллированную воду, другой, когда кость была погружена в воду и раствор поверхностно-активного вещества, и третий, когда кость была помещена в герметичный контейнер, в котором фиксировались изменения давления газа.
Статья, опубликованная в 2017 году в журнале Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, по своему характеру аналогична предыдущей статье, в которой для определения воспроизводимости использовались различные методы, в одном из которых использовался принцип Архимеда. Принцип Архимеда сравнивали с использованием компьютерной томографии с коническим лучом (КЛКТ) для измерения объема зубов. Тесты, сравнивающие принцип Архимеда и измерения КЛКТ, показали, что последний будет точным инструментом при планировании стоматологических процедур.
Подводные лодки
Простая, надежная и экономичная конструкция подводной лодки, описанная в статье 2014 года в журнале «Информатика, электроника и зрение», основана на принципе Архимеда. По словам авторов, подводные лодки предназначены для плавания под водой, будучи полностью погруженными в воду, и полагаются на принцип Архимеда для поддержания постоянной глубины. В конструкции этого прототипа подводной лодки используются расчеты, включающие массу, плотность и объем как подводной лодки, так и вытесняемой воды, чтобы определить необходимый размер балластного танка, который определит количество воды, которое может его заполнить, и, следовательно, глубина, на которую подводная лодка может нырнуть.
Жуки, ходящие по воде
Хотя принцип Архимеда используется в конструкции подводных лодок, чтобы помочь им нырять и всплывать на поверхность, он также объясняет причину, по которой некоторые жуки могут ходить по воде. В исследовании 2016 года, опубликованном в журнале Applied Physics Letters, исследователи использовали метод измерения теней, создаваемых водомерками, для измерения кривизны водной поверхности. Эти погружения затем можно использовать для определения объема воды, который был вытеснен, что привело к силе, используемой для удержания водяных клопов на плаву.Авторы говорят, что есть большой интерес к пониманию физики, стоящей за водными клопами, с целью создания биомиметических роботов, ходящих по воде.
Геология
В статье, опубликованной в 2012 году в журнале Soft Matter, описывается более глубокий взгляд на принцип Архимеда, который авторы называют обобщенным принципом Архимеда. Принцип Архимеда, как он обычно используется, может использоваться только в качестве приближения во многих случаях изучения профилей седиментации, в то время как обобщенный принцип может учитывать такие явления, как более плотные частицы, плавающие на поверхности легкой жидкости. Ключевой момент авторов заключается в возмущениях плотности, которые вызываются взвешенными в жидкости частицами, что не учитывается при традиционном использовании принципа Архимеда, и выводится новый подход к принципу Архимеда.
Ключевой момент авторов заключается в возмущениях плотности, которые вызываются взвешенными в жидкости частицами, что не учитывается при традиционном использовании принципа Архимеда, и выводится новый подход к принципу Архимеда.
Дополнительные ресурсы
Принцип Архимеда, Закон Паскаля и Принцип Бернулли – Урок
(0 Рейтинги)Быстрый просмотр
Уровень оценки: 9 (9–12)
Требуемое время: 2 часа 15 минут
(Три часа занятий по 45 минут)
Зависимость урока: Нет
Тематические области: Химия, Физические науки, Физика, Решение проблем, Рассуждение и Доказательство
Резюме
Студенты знакомятся с законом Паскаля, принципом Архимеда и принципом Бернулли. Поставляются основные определения, уравнения, практические задачи и инженерные приложения. Учащиеся могут использовать связанные упражнения, чтобы лучше понять взаимосвязь между предыдущими концепциями и примерами из реальной жизни. Предоставляются презентация PowerPoint®, практические задания и критерии оценки.
Поставляются основные определения, уравнения, практические задачи и инженерные приложения. Учащиеся могут использовать связанные упражнения, чтобы лучше понять взаимосвязь между предыдущими концепциями и примерами из реальной жизни. Предоставляются презентация PowerPoint®, практические задания и критерии оценки.Инженерное соединение
Концепции закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, включая аэродинамику и гидродинамику, гидравлику, плавучие суда, подводные аппараты, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, а также для многих современных исследовательских тем, таких как потоки, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биожидкостей, потоки по магнитным лентам и дискам, геофизические потоки, кинетика систем сгорания и динамика вихрей.
Цели обучения
После этого урока учащиеся должны уметь:
- Используйте принцип Архимеда для определения силы плавучести.

- Решите задачи, связанные с давлением, плотностью и законом Паскаля.
- Решайте задачи, используя уравнение Бернулли и уравнение неразрывности.
- Объясните ситуации, связанные с эффектом Бернулли.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика;
внутри типа по подтипу, затем по классу, и т. д. .
д. .
- Решите линейные уравнения и неравенства с одной переменной, включая уравнения с коэффициентами, представленными буквами.
(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Решите квадратные уравнения с одной переменной.(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- количественно выражать отношения между физическими переменными и управлять ими, включая использование графиков, диаграмм и уравнений.(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- выражать и интерпретировать отношения символически в соответствии с принятыми теориями, чтобы делать прогнозы и решать задачи математически, включая задачи, требующие пропорционального мышления и графического сложения векторов.(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Какое альтернативное выравнивание вы предлагаете для этого контента?
Рабочие листы и приложения
Посетите [www.teachengineering.org/lessons/view/uoh_fluidmechanics_lesson01], чтобы распечатать или загрузить.Больше подобной учебной программы
Основы Fluid PowerСтуденты узнают об основных концепциях, важных для гидравлической энергии, которая включает в себя как пневматические (газовые), так и гидравлические (жидкостные) системы.
Принцип БернуллиСтуденты узнают о взаимосвязях между компонентами уравнения Бернулли на реальных инженерных примерах и практических задачах.
Физика механики жидкостиМеханика жидкостей, изучение того, как силы применяются к жидкостям, представлена в этом разделе как последовательность из двух уроков и трех соответствующих действий. Механика жидкостей, изучение того, как силы применяются к жидкостям, изложена в этом разделе как последовательность из двух уроков и трех соответствующих действий…
Оценка плавучестиСтуденты узнают, что плавучесть отвечает за плавание лодок, воздушных шаров и метеорологических шаров. Они рассчитывают, будет ли плавать лодка или воздушный шар, и вычисляют объем, необходимый для того, чтобы воздушный шар или лодку определенной массы плавал.
Предварительные знания
Чтобы решать уравнения в этом уроке и манипулировать ими, требуется понимание основ алгебры.
Введение / Мотивация
(Задайте студентам несколько предварительных вопросов, чтобы определить, слышали ли они о принципе Архимеда, законе Паскаля или принципе Бернулли, или о каких-либо физических концепциях, лежащих в их основе.)
Кто знает, почему плывут корабли? (Слушайте ответы студентов.)
Когда вы плаваете в бассейне, чувствуете ли вы себя легче или тяжелее, чем при ходьбе по земле? Насколько ты легче? (Слушайте ответы студентов.)
Кто слышал о термине «гидравлика»? Какие примеры гидравлических устройств? Кто знает, что это значит и как работает? (Слушайте ответы студентов.)
(Продолжайте и представьте учащимся прикрепленную слайд-презентацию и содержимое в разделе «Фон».)
Предпосылки и концепции урока для учителей
Все концепции этого урока раскрыты в 22-слайдовой презентации Fluids Presentation, файле Microsoft PowerPoint®. Предлагаемое время для завершения этой презентации – три урока, но при необходимости увеличивайте или уменьшайте продолжительность.
«Механика жидкостей» – обязательный курс в большинстве университетов и необходимый для большинства инженерных специальностей. Это особенно важная область исследований для гидротехники и инженерии окружающей среды, которые являются субдисциплинами гражданского строительства.Эти типы инженеров отвечают за системы водного транспорта и канализационные сети в урбанизированных районах, а также за проектирование мостов, дамб, каналов, каналов, дамб и трубопроводных сетей, как отдельно стоящих, так и внутри зданий.
В этом уроке представлены основные концепции механики жидкости. Сообщите студентам, что, если они хотят изучать инженерное дело в колледже, механику жидкости можно смоделировать или объяснить, используя существующие компьютерные программы в классе или лаборатории университета.Некоторые студенты могут быть знакомы с определенными программами моделирования; попросите их привести примеры программного обеспечения для моделирования и их приложений. Примеры программ моделирования механики жидкости включают:
Система гидрологического моделирования (HEC-HMS) была создана и используется Инженерным корпусом армии США для моделирования гидрологических процессов водосборных систем, которые включают в себя естественные процессы, такие как испарение и инфильтрацию, а также антропогенные особенности, такие как как водохранилища и отстойники.
ModFlow был создан и используется Геологической службой США; это программное обеспечение для трехмерного моделирования грунтовых вод, используемое для моделирования условий грунтовых вод и взаимодействия грунтовых и поверхностных вод, а также для управления водоносными горизонтами и земельными ресурсами.
Computing Fluid Dynamics (CFD) был создан ANSYS, Inc., компанией, занимающейся разработкой программного обеспечения для инженерного моделирования. Это приложение прогнозирует влияние потоков жидкости на проектируемые изделия на протяжении всего процесса проектирования и производства, а также во время использования.
SolidWorks Flow Simulation моделирует поток жидкости, теплопередачу и силы жидкости, критически важные для успешного проектирования, и допускает неограниченное количество итераций для создания наиболее эффективных конструкций изделий.
Жидкость – это любая текущая материя, которая может быть жидкостью или газом. Принцип Архимеда гласит, что любой объект, полностью или частично погруженный в жидкость, испытывает направленную вверх силу, равную по величине весу жидкости, вытесняемой объектом, как показано в уравнении 1.
F B = м f g (Уравнение 1)
Где F B – выталкивающая сила, м f – масса вытесняемой жидкости, а g – ускорение свободного падения.
Все мы испытали принцип Архимеда , даже если мы не осознаем его. Обычный опыт – это осознание того, что человека в бассейне довольно легко поднять.Это связано с тем, что вода обеспечивает частичную поддержку в виде направленной вверх силы, называемой выталкивающей силой . Выталкивающая сила равна весу вытесняемой жидкости. Обратитесь к упражнению «Плавучесть и давление в жидкостях: Декартово упражнение для ныряльщика из бутылок с газировкой», чтобы ученики наблюдали за этими переменными в действии. Корабли плавают в воде, потому что вес воды, вытесняемой корпусом корабля, больше, чем вес корабля, и если вес вытесненной воды был меньше веса корабля, он бы затонул.Инженеры используют программное обеспечение для моделирования механики жидкостей и динамики для моделирования различных происходящих явлений, что необходимо для создания оптимальных конструкций судов. Инженеры моделируют форму корпуса и оптимизацию придатков, чтобы повысить эффективность и тяговую мощность корабля, снизить расход топлива и проанализировать сопротивление на спокойной воде и нерегулярных волнах.
Ранее упоминалось, что жидкость может быть жидкостью или газом. Воздух повсюду, и даже окружающий нас воздух имеет вес и оказывает давление.Мы не осознаем, насколько тяжел воздух, и не чувствуем давления, которое он оказывает на нас, потому что мы привыкли к «атмосферному давлению». Давление определяется как мера силы в заданной области. Закон Паскаля гласит, что давление, приложенное к жидкости в закрытом контейнере, одинаково передается к каждой точке жидкости и стенкам контейнера, как показано в уравнении 2.
P = F / A (Уравнение 2)
Где P – давление, F – сила, а A – площадь.Обратите внимание, что замкнутая система может иметь две области, поэтому сила в этих двух местах различна, но давление остается тем же, как указано в законе Паскаля.
Это давление передается одинаково во всех направлениях и под прямым углом, и изменение давления равномерно распространяется по жидкости. Закон Паскаля используется инженерами при проектировании гидравлических систем, в которых для работы используется энергия жидкости. Некоторыми примерами являются гидравлические домкраты, которые поднимают автомобили в ремонтных мастерских, и гидравлические тормоза, которые оказывают давление на большую площадь, чтобы остановить большое транспортное средство, такое как поезд.Закон Паскаля также используется в системах водоснабжения и канализации для перемещения воды по сети трубопроводов.
В первую очередь, существуют два разных типа потока жидкости – ламинарный и турбулентный. Ламинарный поток возникает, когда частицы жидкости движутся по однородному гладкому пути, называемому линией тока, и обычно возникает в небольших трубах или других средах с низким расходом. Турбулентный поток возникает, когда частицы текучей среды текут нерегулярно и вызывают изменение скорости, и обычно возникает в больших трубах или других средах с большим потоком. Принцип Бернулли гласит, что давление и скорость обратно пропорциональны, или что давление в жидкости уменьшается, когда скорость жидкости увеличивается, как показано в уравнении 3.
P 1 + ½ ρ v 1 2 + ρ g h 1 ½ ρ v 2 2 + ρgh 2 (Уравнение 3)
Где P 1 – давление в точке 1, ρ – плотность жидкости, v 1 – скорость жидкости в точке 1, g – это ускорение свободного падения, ч 1 – высота точки 1, P 2 – давление в точке 2, v 2 – скорость жидкости при точка 2, а h 2 – высота точки 2.Студенты могут попрактиковаться в выводе этих уравнений с помощью упражнения «Скала и лодка: плотность, плавучесть и принцип Архимеда», работая над решением сложного вопроса!
Уравнение Бернулли остается одинаковым в разных точках горизонтальной трубы. В трубе, не имеющей одинаковой высоты, уравнение Бернулли по-прежнему остается равным, но учитывает разницу высот в разных точках трубы, как отмечено h в уравнении 3. Инженеры реализуют уравнение Бернулли для определения оптимального и эффективного размеры труб при проектировании трубопроводов и транспортных систем.Уравнение Бернулли – главный компонент аэродинамики, который применяется при проектировании автомобилей, мостов, систем вентиляции, газопроводов, самолетов и космических кораблей.
Концепции закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, таких как аэродинамика и гидродинамика, гидравлика, плавучие суда, подводные аппараты, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, а также для многих исследовательских тем, таких как потоки, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биожидкостей, потоки по магнитным лентам и дискам, геофизические потоки, кинетика систем сгорания, динамика вихрей и многое другое.Обратитесь к упражнению «Выстрел под давлением», чтобы ученики использовали свое новое понимание для исследования реального применения – водяного пистолета!
Аэродинамика – это исследование свойств движущегося воздуха, который является основным компонентом в конструкции автомобилей, мостов, систем отопления и вентиляции, газопроводов, самолетов и космических кораблей. Гидродинамика – это изучение сил, действующих на жидкости или жидкости, которые являются основным компонентом военно-морской архитектуры или дизайна кораблей, а также океанотехники. Морские и морские инженеры несут ответственность за изучение морской среды для проектирования нефтяных вышек и производственных платформ, а также плавучих судов и систем подводных трубопроводов, необходимых в процессе добычи нефти.Инженеры-гидротехники используют гидравлику или использование жидкой энергии для выполнения работ при проектировании тяжелой техники, систем распределения воды, канализационных сетей, систем управления ливневыми водами, мостов, плотин, каналов, каналов и дамб. Различные подводные аппараты и аппараты с дистанционным управлением, разработанные инженерами, широко используются правительством и научными исследователями и имеют важное значение для открытия глубоководных сообществ и исследования бездонного океана, поскольку они могут достигать глубин, намного превышающих предыдущие спутниковые и судовые технологии.
Сопутствующие мероприятия
Закрытие урока
Задайте студентам те же вопросы для обсуждения, которые задавались перед уроком, но на этот раз ожидайте, что они ответят с уверенностью и представят доказательства своих ответов, используя уравнения, словарные слова и конкретные законы / принципы, изученные на этом уроке.
Кто знает, почему плывут корабли? (Ответ: вес воды, вытесняемой корпусом корабля, больше веса корабля.Попросите учащихся подумать о небольших рыбацких лодках и круизных лайнерах.)
Когда вы плаваете в бассейне, чувствуете ли вы себя легче или тяжелее, чем при ходьбе по Земле? Насколько ты легче? (Ответ: вы чувствуете себя легче в бассейне, потому что кажущаяся потеря веса равна весу воды, вытесняемой вашим телом.)
Кто слышал о термине «гидравлика»? Какие примеры гидравлических устройств? Кто знает, что это значит и как работает? (Ответ: инженеры-гидротехники используют гидравлику или использование жидкой энергии для выполнения работ, проектирования тяжелой техники, систем водоснабжения, канализационных сетей, систем управления ливневыми водами, мостов, плотин, каналов, каналов и дамб.)
Какие еще примеры принципа Архимеда, закона Паскаля и принципа Бернулли вы можете придумать? Можете ли вы придумать какие-либо инженерные приложения, связанные с этими концепциями? (Ответ: концепции закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, таких как аэродинамика и гидродинамика, гидравлика, плавучие суда, подводные аппараты, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, и многие темы исследований, такие как потоки, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биожидкостей, потоки по магнитным лентам и дискам, геофизические потоки, кинетика систем сгорания и динамика вихрей.)
Словарь / Определения
Принцип Архимеда: любой объект, частично или полностью погруженный в жидкость, испытывает направленную вверх силу, равную по величине весу жидкости, вытесняемой объектом.
Принцип Бернулли: давление в жидкости уменьшается с увеличением скорости жидкости.
плавучесть: способность объекта плавать в жидкости.
выталкивающая сила: восходящая сила, действующая на объект, который частично или полностью погружен в жидкость (равная разнице между весом объекта в воздухе и весом объекта в жидкости).
Плотность: измерение компактности объекта.
жидкость: Текущее вещество (может быть жидкостью или газом).
ламинарный поток: когда частицы жидкости движутся по одному и тому же плавному пути, который называется линией тока.
масса: измерение количества вещества в объекте.
массовая плотность: масса на единицу объема вещества.
Закон Паскаля: давление, прикладываемое к жидкости в закрытом контейнере, одинаково передается в каждую точку жидкости и на стенки контейнера.
давление: измерение силы на единицу площади.
турбулентный поток: когда частицы жидкости движутся неравномерно, вызывая изменения скорости, которые могут образовывать вихревые токи.
объем: измерение объема пространства, которое занимает объект.
Вес: измерение силы тяжести на объект.
Оценка
Оценка перед уроком
Вопросы для обсуждения: Задайте учащимся следующие вводные вопросы, чтобы оценить их базовые знания по темам урока. Те же вопросы будут заданы в конце урока.
- Кто знает, почему плывут корабли?
- Когда вы плаваете в бассейне, чувствуете ли вы себя легче или тяжелее, чем при ходьбе по Земле? Насколько ты легче?
- Кто слышал о термине «гидравлика»? Какие примеры гидравлических устройств? Кто знает, что это значит и как работает?
Оценка после введения
Примеры задач: Предложите учащимся решить примеры задач, встроенные в Презентацию жидкостей, как описано ниже.Просмотрите ответы студентов, чтобы оценить их понимание тем урока и определить, какие концепции и уравнения требуют дальнейшего объяснения.
- Slide 7 : перерисуйте изображение на доске, но измените числа. Например, вес весов должен составлять 15 фунтов, а вес воды в чаше – 7 фунтов. Чтобы проверить понимание учащимися концепции, спросите учащихся, какой вес у них, когда они погружены в воду. Ответ – 8 фунтов.
- Slide 10 : Попросите учащихся решить вес воды, вытесняемой короной на изображении.Ответ 1,3 кг. Затем заново начертите ту же диаграмму на доске и обозначьте вес слева как 23,2 кг и попросите учащихся определить значение шкалы справа, если выталкивающая сила составляет 3,7 кг. Ответ – 22,5 кг.
- Слайд 15 : попросите учащихся решить для P 1 , используя уравнение на слайде 13. Ответ: P 1 = 10 Па. Затем попросите учащихся решить для P 2 и F 2 с использованием отношения P 1 = P 2 .Ответ: P 2 = 10 Па и F 2 = 100 Н.
- Слайд 18 : Какой рисунок демонстрирует ламинарный поток и турбулентный поток? (A, верхний рисунок с прямыми стрелками, представляет ламинарный поток; B, нижний рисунок с изогнутыми стрелками, представляет турбулентный поток.) Каковы некоторые примеры каждого из различных типов потока? (Примеры ламинарного потока включают медленно текущие потоки и воду, текущую из кранов раковины.Примеры турбулентного потока включают дым от костров или других горящих предметов, течения и бурные потоки.)
- Слайд 22 : Студентам предоставлены примеры чисел для включения в уравнение Бернулли на разной высоте, чтобы они могли узнать, что отменяет (если есть) и как применять уравнение.
Итоги урока Оценка
Отвечая на вопросы для обсуждения с помощью физики: Задайте те же вопросы для обсуждения, которые задавались перед уроком, но на этот раз ожидайте, что студенты ответят уверенно и доказательно, включая уравнения, словарные слова и конкретные законы / принципы, изученные на этом уроке.См. Ответы в разделе «Завершение урока».
Домашнее задание
Практические задачи: Поручите студентам заполнить Рабочий лист практических задач в качестве домашнего задания. Используйте Рубрику решения проблем физики, чтобы просмотреть ответы учащихся и оценить их понимание концепций.
использованная литература
Physics Guide (предварительная публикация). Первые экзамены 2016 г. Организация Международного бакалавриата, 2013 г., стр. 118.(Поскольку механика жидкости не преподается в государственных средних школах, это руководство IB по физике использовалось в основном для учебных целей на этом уроке.) По состоянию на март 2013 г. http://tinyurl.com/msfpep9
Другая сопутствующая информация
Просмотрите центр учебных программ по физике, согласованный с NGSS, чтобы найти дополнительные учебные программы по физике и физическим наукам, посвященные инженерным наукам.
авторское право
© 2014 Регенты Университета Колорадо; оригинал © 2013 Хьюстонский университетАвторы
Эмили Саппингтон; Мила ТейлорПрограмма поддержки
Национальный научный фонд GK-12 и программы исследований для учителей (RET), Университет ХьюстонаБлагодарности
Это содержимое цифровой библиотеки было разработано Инженерным колледжем Хьюстонского университета на основе работы, поддержанной Национальным научным фондом в рамках гранта GK-12 No.DGE 0840889. Любые мнения, выводы и заключения или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда.
Последнее изменение: 13 августа 2021 г.
почему принцип архимеда называется повествовательной поэмой
сменить голос Малини купила для дочери красочную шляпу
Намекает на то, что семья доктора Крушнана решила отправить обратно в клинику.строго предупредил, вызвал на лечение Халле, начал говоритьКомандующий … d и утешил пациентов, дисциплинировал их – принес Безмолвие или безмолвный призыв от Меня, Кришнарт, спарив ушей, ооочень желал сохранить бессмысленное поведение السلام
Привет, мои дорогие друзья .. Доброе утро .. Kaise h aap log ..
Как только он увидел меня, он убежал. утвердительный
Aaj tumhare bhai ka brdy h party de rha hun aa jao sare part m 50 очков dunga aa jao
Ребята, собираются создать новый идентификатор (´ ༎ ຶ ʖ ༎ ຶ `) НОРМИ: НЕ УДАЛЯЙТЕСЬ
ребята, вы все забыли меня, я Ритика, следите за моим новым идентификатором.
наказан ‘का ही प्रयोग हुआ। УПРАЖНЕНИЕ 1 Соедините каждый набор следующих простых предложений в одно простое предложение, используя причастие: 1.Тигр … г был голоден. Он убил козу. (UP, 2005) 2. Он потерпел неудачу. Он слышал новости. Он упал в обморок. (UP, 2006) 3. Люди видели пламя. Они побежали к горящему дому. (UP, 2006) 4. Он закончил свою работу. Он пошел домой. UP, 2008) 5. Я проголодался. Я взял свою еду. (UP, 2009) 6. Я увидел мужчину. Он был слепым. В руке он держал лампу. (UP 2010) 7. Махеш Бхупати был побежден Леандером Паесом. Он был сильно разочарован (UP, 2011) 8. Я увидел мужчину. Он курил сигарету. UP 2010 9. Пошла в сад.Она срывала цветы. 10. Вор увидел полицейского. Он убежал. (UP, 2014) 11. Слуга подметал комнату. Он ушел. 12. Джек поднялся на холм. Он увидел питона. (UP. 2014) 13. Бедняга работал. Он смеялся. Так он прожил свою жизнь. 14. Я гулял по полю. Я видел змею. Я убежал. 15. Ребенок потерял ручку. Он заплакал. 16. Он был замаскирован под святого. Он сбежал в Непал. (UP. 1972) 17. Поверните направо. Затем вы найдете дом. (UP. 1982) 18. Волшебник сжалился над мышью.Он превратил его в кошку. (UP, 1984) 19. Она устала читать. Она легла в постель. УП, 1984) 20. Он вскочил. Он убежал. (UP. 1984 21. Бриджеш потерял свою книгу. Он искал ее. (UP. 2012, 18)) 22. Он поднял пистолет. Он прицелился. Он выстрелил в тигра. (UP, 1988 96) 23. Он обнажил свой меч. Он напал на своего врага. 24. Шила была свидетельницей шоу.
доброе утро ребята kese ho aap sab
лодка наполнена водой, подчеркните прямой и круговой косвенный объект
11.7 Принцип Архимеда – Физический колледж
Когда вы встаете из теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки со стороны воды. Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары? (См. Рисунок 11.18.)
Рисунок 11.18 (a) Даже тонущие предметы, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (Фото: ВМС союзников) (c) Воздушные шары, наполненные гелием, тянут вверх свои струны, демонстрируя плавучесть воздуха. (кредит: Crystl)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта.На любой объект в любой жидкости действует чистая направленная вверх или выталкивающая сила . (См. Рис. 11.19.) Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.
Подъемная сила
Выталкивающая сила – это чистая направленная вверх сила на любой объект в любой жидкости.
Рисунок 11.19. Давление из-за веса жидкости увеличивается с глубиной, так как P = hρgP = hρg размер 12 {P = hρg} {}. Это давление и связанная с ним восходящая сила в нижней части цилиндра больше, чем нисходящая сила в верхней части цилиндра. Их отличие – подъемная сила FBFB размером 12 {F rSub {размер 8 {B}}} {}. (Горизонтальные силы отменяются.)Насколько велика эта подъемная сила? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на рисунке 11.20.
Рис. 11.20 (a) Объект, погруженный в жидкость, испытывает выталкивающую силу FBFB размером 12 {F rSub {размер 8 {B}}} {}. Если размер FBFB 12 {F rSub {размер 8 {B}}} {} больше веса объекта, объект поднимется. Если размер FBFB 12 {F rSub {size 8 {B}}} {} меньше веса объекта, объект утонет. (b) Если объект удален, он заменяется жидкостью, имеющей вес wflwfl размер 12 {w rSub {размер 8 {“fl”}}} {}. Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости.То есть FB = wflFB = wfl размер 12 {F rSub {размер 8 {B}} = w rSub {размер 8 {“fl”}}} {}, утверждение принципа Архимеда.Пространство, которое он занимало, заполнено жидкостью, имеющей вес wflwfl размер 12 {w rSub {размер 8 {“fl”}}} {}. Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться wflwfl size 12 {w rSub {size 8 {“fl”}}} {}, весу жидкости, вытесняемой объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок.287–212 до н. Э.), Что он сформулировал этот принцип задолго до того, как концепции силы утвердились. Проще говоря, принцип Архимеда заключается в следующем: подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет. В форме уравнения принцип Архимеда –
FB = wfl, FB = wfl, размер 12 {F rSub {размер 8 {B}} = w rSub {размер 8 {“fl”}}} {}11.30
где FBFB размер 12 {F rSub {размер 8 { B}}} {} – это выталкивающая сила, а размер wflwfl 12 {w rSub {размер 8 {“fl”}}} {} – вес жидкости, вытесняемой объектом.Принцип Архимеда применим в целом для любого объекта в любой жидкости, частично или полностью погруженной в воду.
Принцип Архимеда
Согласно этому принципу выталкивающая сила, действующая на объект, равна весу жидкости, которую он вытесняет. В форме уравнения принцип Архимеда –
FB = wfl, FB = wfl, размер 12 {F rSub {размер 8 {B}} = w rSub {размер 8 {“fl”}}} {}11.31
где FBFB размер 12 {F rSub {размер 8 { B}}} {} – это выталкивающая сила, а размер wflwfl 12 {w rSub {размер 8 {“fl”}}} {} – вес жидкости, вытесняемой объектом.
Humm… Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны обеспечивать преимущества плавучести. Как вы думаете, можно ли проверить это правило?
Установление связей: расследование на вынос
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и опустите в воду. Тонет? Почему или почему нет? Вы можете заставить его утонуть?
Плавающая и тонущая
Бросьте в воду кусок глины.Он утонет. Затем вылепите из глины форму лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем комок, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями.
Пример 11.8
Расчет выталкивающей силы: зависимость от формы
(a) Рассчитайте выталкивающую силу для 10 000 метрических тонн (1,00 × 107 кг) (1,00 × 107 кг) размером 12 {\ (1 “.” 00 “умножить на 10″ rSup {size 8 {7}} `” кг ” \)} {} из прочной стали, полностью погруженной в воду, и сравните это с весом стали.(b) Какова максимальная выталкивающая сила, которую вода могла бы оказать на эту же сталь, если бы она была сформирована в лодку, способную перемещать 1,00 × 105 м31,00 × 105 м3 размером 12 {1 “». “00” умножить на “10” rSup {size 8 {5}} `m rSup {size 8 {3}}} {} воды?
Стратегия для (а)
Чтобы найти подъемную силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, указанные в Таблице 11.1. Отметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы.Как только мы узнаем объем воды, мы сможем найти ее массу и вес.
Решение для (а)
Сначала мы используем определение плотности ρ = mVρ = mV size 12 {ρ = {{m} over {V}}} {}, чтобы найти объем стали, а затем подставляем значения массы и плотности. Это дает
Vst = mstρst = 1,00 × 107 кг 7,8 × 103 кг / м3 = 1,28 × 103 м3. Vst = mstρst = 1,00 × 107 кг 7,8 × 103 кг / м3 = 1,28 × 103 м3. размер 12 {v rSub {размер 8 {“st”}} = {{m rSub {размер 8 {“st”}}} больше {ρ rSub {размер 8 {“st”}}}} = {{1 “.”” 00 “умножить на” 10 “rSup {размер 8 {7}}” “кг”} больше {7 “.” 8 раз “10” rSup {размер 8 {3}} “” кг / м “rSup {размер 8 {3}}}} = 1 “.” “28” умножить на “10” rSup {размер 8 {3}} `m rSup {размер 8 {3}}} {}11,32
Поскольку сталь полностью погружена в воду, это также объем вытесненной воды, VwVw размер 12 {V rSub {размер 8 {w}}} {}. Теперь мы можем найти массу вытесненной воды из отношения между ее объемом и плотностью, оба из которых известны. Это дает
mw = ρwVw = (1.000 × 103 кг / м3) (1.28 × 103 м3) = 1,28 × 106 кг.мw = ρwVw = (1.000 × 103 кг / м3) (1,28 × 103 м3) = 1,28 × 106 кг.alignc {stack { размер 12 {m rSub {размер 8 {w}} = ρ rSub {размер 8 {w}} V rSub {размер 8 {w}} = \ (1 “.” “000” умножить на “10” rSup {размер 8 { 3}} `” кг / м “rSup {размер 8 {3}} \) \ (1”. “” 28 “умножить на” 10 “rSup {размер 8 {3}}` m rSup {размер 8 {3}} \)} {} # = 1 “.” “28” умножить на “10” rSup {размер 8 {6}} “” кг “”. ” {} }} {}11,33
По принципу Архимеда вес вытесняемой воды составляет mwgmwg размер 12 {m rSub {размер 8 {w}} g} {}, поэтому выталкивающая сила составляет
FB = ww = mwg = 1 .28 × 106 кг 9,80 м / с2 = 1,3 × 107N.FB = ww = mwg = 1,28 × 106 кг 9,80 м / с2 = 1,3 × 107N.alignc {stack { размер 12 {F rSub {размер 8 {B}} = w rSub {размер 8 {w}} = m rSub {размер 8 {w}} g = левый (1 “.” 28 “умножить на” 10 “rSup {размер 8 {6}} `” кг “справа) слева (9”. “” 80 “` “м / с” rSup {размер 8 {2}} справа)} {} # = 1 “.” 3 раза по “10” rSup {размер 8 {7}} `N”. ” {} }} {}11,34
Вес стали mwg = 9,80 × 107Nmwg = 9,80 × 107N размер 12 {m rSub {размер 8 {w}} g = 9 “.” “80” умножить на “10” rSup {size 8 {7}} `N} {}, что намного больше подъемной силы, поэтому сталь останется под водой.Обратите внимание, что подъемная сила округляется до двух цифр, потому что плотность стали дается только до двух цифр.
Стратегия для (b)
Здесь указан максимальный объем воды, который стальная лодка может вытеснить. Подъемная сила – это вес этого объема воды.
Решение для (b)
Масса вытесненной воды находится из ее отношения к плотности и объему, оба из которых известны. То есть
mw = ρwVw = 1.000 × 103 кг / м 31.00 × 105 м3 = 1,00 × 108 кг.мw = ρwVw = 1.000 × 103 кг / м 31,00 × 105 м3 = 1,00 × 108 кг.alignc {stack { размер 12 {m rSub {размер 8 {w}} = ρ rSub {размер 8 {w}} V rSub {размер 8 {w}} = левый (1 “.” 000 “умножить на” 10 “rSup {размер 8 { 3}} `” кг / м “rSup {размер 8 {3}} справа) влево (1”. “” 00 “умножить на” 10 “rSup {размер 8 {5}}` m rSup {размер 8 {3}} верно )} {} # = 1 “.” “00” умножить на “10” rSup {размер 8 {8}} “” кг “”. ” {} }} {}11,35
Максимальная выталкивающая сила – это вес такого количества воды, или
FB = ww = mwg = 1,00 × 108 кг 9.80 м / с2 = 9,80 × 108 Н. FB = ww = mwg = 1,00 × 108 кг 9,80 м / с2 = 9,80 × 108 Н.11.36
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, что означает, что судно может нести груз, в девять раз превышающий его собственный вес.
Установление связей: расследование на вынос
Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Используйте кусок фольги размером 10 на 15 см. а) Какова масса этого количества фольги? (b) Если фольга сложена с четырех сторон, и к этой «лодке» добавлены скрепки или шайбы, то какая форма лодки позволит ей удерживать больше «груза» при погружении в воду? Проверьте свое предсказание.
Плотность и принцип Архимеда
Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта – это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше, чем у окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, подъемная сила, равная весу вытесняемой жидкости, превышает вес объекта.Точно так же утонет объект, более плотный, чем жидкость.
Степень погружения плавающего объекта в воду зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 11.21, например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным судном. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или
погруженная фракция = VsubVobj = VflVobj.погруженная фракция = VsubVobj = VflVobj. размер 12 {{{V rSub {размер 8 {“sub”}}} больше {V rSub {size 8 {“obj”}}}} = {{V rSub {size 8 {“fl”}}} больше {V rSub {size 8 {“obj”}}}}} {}11.37
Погруженный объем равен объему вытесненной жидкости, который мы называем VflVfl размером 12 {V rSub {size 8 {“fl”}}} {} . Теперь мы можем получить соотношение между плотностями, подставив в выражение ρ = mVρ = mV size 12 {ρ = {{m} над {V}}} {}. Это дает
VflVobj = mfl / ρflmobj / ρ¯obj, VflVobj = mfl / ρflmobj / ρ¯obj,11.38
где ρ¯objρ¯obj size 12 {{bar {ρ}} rSub {size 8 {“obj”}}} {} – средняя плотность объекта, а ρflρfl размер 12 {ρ rSub {size 8 {” fl “}}} {} – плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя погруженную часть
= ρ¯objρfl.fraction submerged = ρ¯objρfl. размер 12 {“фракция” `” погруженная “= {{{bar {ρ}} rSub {size 8 {” obj “}}} больше {ρ rSub {size 8 {” fl “}}}}} {}11 .39
Рис. 11.21 Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).
Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли плавучего объекта, находящегося под водой, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес:
удельный вес = ρ¯ρw, удельный вес = ρ¯ρw, размер 12 {“удельный” `” вес “= {{ρ} больше {ρ rSub {размер 8 {w}}}}} {}11.40
где ρ¯ρ¯ size 12 {ρ} {} – это средняя плотность объекта или вещества, а ρwρw size 12 {ρ rSub {size 8 {w}}} {} – плотность воды при 4,00 ° C. . Удельный вес безразмерен, независимо от того, какие единицы измерения используются для размера ρρ 12 {ρ} {}. Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта равен 1, он будет оставаться во взвешенном состоянии в жидкости, а не тонуть и не плавать.Аквалангисты пытаются достичь этого состояния, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, жидкость для радиаторов и моча, как индикатор их состояния. Одно устройство для измерения удельного веса показано на рисунке 11.22.
Удельный вес
Удельный вес – это отношение плотности объекта к плотности жидкости (обычно воды).
Рис. 11.22 Этот ареометр плавает в жидкости с удельным весом 0.87. Стеклянный ареометр заполнен воздухом и утяжелен свинцом внизу. Он плавает выше всего в самых плотных жидкостях и был откалиброван и промаркирован так, что удельный вес может быть считан непосредственно с него.
Пример 11.9
Расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде с погружением 97,0% 97,0% ее объема, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Плотность женщины можно найти, решив уравнение
фракция погружена = ρ¯objρflfraction погружена = ρ¯objρfl размер 12 {“фракция” `” погружена “= {{{bar {ρ}} rSub {size 8 {” obj “}}} больше {ρ rSub {размер 8 {” fl “}}}}} {}11.41
для плотности объекта. Это дает
ρ¯obj = ρ¯person = (часть погружена) ⋅ρfl.ρ¯obj = ρ¯person = (часть погружена) ⋅ρfl. размер 12 {{bar {ρ}} rSub {size 8 {“obj”}} = {bar {ρ}} rSub {size 8 {“person”}} = \ (“фракция погружена” \) cdot ρ rSub {size 8 {“fl”}}} {}11.42
Мы знаем и долю погружения, и плотность воды, поэтому мы можем вычислить плотность женщины.
Решение
Вводя известные значения в выражение для ее плотности, получаем
ρ¯person = 0.970⋅103кгм3 = 970кгм3 .ρ¯человек = 0,970⋅103кгм3 = 970кгм3. размер 12 {{bar {ρ}} rSub {size 8 {“person”}} = 0 “.” “970” cdot left (“10” rSup {size 8 {3}} {{“kg”} больше {m rSup {size 8 {3}}}} right) = “970” {{“kg”} больше { m rSup {size 8 {3}}}}} {}11,43
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела – это один из показателей процента жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок.(См. Рисунок 11.23.)
Рис. 11.23 Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, как часть определения плотности тела. Субъект должен полностью опорожнить свои легкие и удерживать металлический груз, чтобы утонуть. Внесены поправки на остаточный воздух в легких (измеряется отдельно) и вес металла. Его скорректированный подводный вес, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процента жира в организме.
Существует множество очевидных примеров объектов или веществ с меньшей плотностью, плавающих в жидкостях с более высокой плотностью – масло на воде, воздушный шар, пробка в вине, айсберг и горячий воск в «лавовой лампе, ” назвать несколько. Менее очевидные примеры включают подъем лавы в вулкане и горные цепи, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Другие измерения плотности
Один из наиболее распространенных методов определения плотности показан на рисунке 11.24.
Рис. 11.24 (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
Объект, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается, будучи погруженным в жидкость. Плотность монеты, показатель ее подлинности, может быть вычислена, если плотность жидкости известна. Этот же метод можно использовать для определения плотности жидкости, если плотность монеты известна.Все эти расчеты основаны на принципе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что объект , кажется, на меньше весит при погружении; мы называем это измерение видимым весом объекта . Объект испытывает кажущуюся потерю веса , равную массе вытесненной жидкости. В качестве альтернативы, на весах, которые измеряют массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости.Это
кажущаяся потеря веса = масса вытесненной жидкости; основная потеря веса = масса вытесненной жидкости11,44
или
кажущаяся потеря массы = масса вытесненной жидкости. кажущаяся потеря массы = масса вытесненной жидкости.11,45
Следующий пример иллюстрирует использование этого метода.
Пример 11.10
Расчет плотности: подлинность монеты?
Масса древнегреческой монеты в воздухе определена равной 8,630 г. Когда монета погружена в воду, как показано на рисунке 11.24, его кажущаяся масса 7,800 г. Рассчитайте ее плотность, учитывая, что вода имеет плотность 1.000г / см31.000г / см3 размер 12 {1 “.” “000” “” г / см “rSup {size 8 {3}}} {} и что эффекты, вызванные проволокой, на которой подвешена монета, незначительны.
Стратегия
Чтобы рассчитать плотность монеты, нам нужны ее масса (указанная) и ее объем. Объем монеты равен объему вытесненной воды. Объем вытесненной воды VwVw размером 12 {V rSub {size 8 {w}}} {} можно найти, решив уравнение для плотности ρ = mVρ = mV размером 12 {ρ = {{m} над {V}}} {} для VV размером 12 {V} {}.
Решение
Объем воды Vw = mwρwVw = mwρw размер 12 {V rSub {размер 8 {w}} = {{m rSub {размер 8 {w}}} больше {ρ rSub {размер 8 {w}}}}} {} где mwmw size 12 {m rSub {size 8 {w}}} {} – масса вытесненной воды. Как уже отмечалось, масса вытесненной воды равна кажущейся потере массы, которая составляет mw = 8,630 г − 7,800 г = 0,830 г · мВт = 8,630 г − 7,800 г = 0,830 г размер 12 {m rSub {size 8 {w}} = 8 “.” “630” г – 7 “.” “800” `g = 0″. ” “830” `g} {}. Таким образом, объем воды Vw = 0.830 г1,000 г / см3 = 0,830 см3Vw = 0,830 г1,000 г / см3 = 0,830 см3 размер 12 {V rSub {размер 8 {w}} = {{0 “.” “830” `g} больше {1″. ” “000” `” г / см “rSup {size 8 {3}}}} = 0″. ” “830” “” см “rSup {размер 8 {3}}} {}. Это тоже объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности:
ρc = mcVc = 8,630 г0,830 см3 = 10,4 г / см3. Ρc = mcVc = 8,630 г0,830 см3 = 10,4 г / см3. размер 12 {ρ rSub {размер 8 {c}} = {{m rSub {размер 8 {c}}} больше {V rSub {размер 8 {c}}}} = {{8 “.”” 630 “` g} больше {0 “.” “830” `” г / см “rSup {размер 8 {3}}}} =” 10 “”. “4`” г / см “rSup {размер 8 {3}}} {}11,46
Обсуждение
Из Таблицы 11.1 видно, что эта плотность очень близка к плотности чистого серебра, подходящей для этого типа древних монет. Большинство современных подделок – это не чистое серебро.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, король Сиракуз дал Архимеду задание определить, поставлял ли изготовитель королевской короны корону из чистого золота.Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и при этом выглядит желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние народы понимали, что плотность золота выше, чем у любого другого известного в то время вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение, когда находился в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой теперь знаменитый принцип, увидел, как применить его для определения плотности, и побежал голый по улицам Сиракуз с криком «Эврика!» (Греческое означает «Я нашел это»).Подобное поведение время от времени можно наблюдать и у современных физиков!
PhET Explorations
Плавучесть
Когда объекты всплывут, а когда утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Принцип Архимеда для подводного плавания с аквалангом
Подводное плавание с аквалангом включает в себя много физики, и учащиеся всегда восхищаются тем, как это может помочь им получить больше удовольствия от занятий спортом.Одним из основных законов, используемых при обучении подводному плаванию с аквалангом, является принцип Архимеда. Принцип утверждает, что любой объект, который частично или полностью погружен в жидкость, будет поддерживаться силой, равной весу вытесненной жидкости. Это может показаться слишком техническим, поэтому необходимо разбить его, особенно для новичков, которые хотят в полной мере насладиться этим захватывающим видом спорта.
Нарушение принципа Архимеда
Предположим, вы помещаете объект полностью или частично в любую жидкость.Вы заметите, что жидкость будет прилагать восходящую силу, и, согласно Архимеду, эта сила равна весу вытесненной жидкости. А как насчет объекта, который остается под водой лишь частично, например мяча для пинг-понга? В этом случае вес, направленный вверх, равен весу воды, вытесняемой только погруженной частью.
Принцип Архимеда и плавучесть
В то время как принцип Архимеда говорит о восходящей силе, существует также влияние нисходящей силы при определении того, плавает ли объект или тонет.В случае, когда направленная вверх сила больше, чем направленная вверх, объект тонет. Если вы поместите тяжелый камень в воду, он утонет, потому что направленная вниз сила (его вес) больше веса вытесненной воды.
Принцип Архимеда и подводное плавание с аквалангом
Какое отношение имеет принцип Архимеда к подводному плаванию с аквалангом? В нем объясняется, что влияет на плавучесть дайвера, что важно не только для получения удовольствия от занятий, но и для их безопасности. Учтите эти факторы:
- Устройства компенсации плавучести (BCD): это надувная камера, которую дайвер использует для контроля плавучести под водой.При накачивании компенсатор плавучести вытесняет больше воды, увеличивая силу, направленную вверх, а при спускании они ослабляют силу, направленную вверх. Для получения нейтральной плавучести дайвер полностью надувает BCD.
- Свинцовые гири: Этот принцип оправдывает использование свинцовых гирь при подводном плавании с аквалангом, поскольку они помогают уменьшить восходящую силу и помогают им тонуть.
- Гидрокостюмы: чем тяжелее гидрокостюм, тем больше воды вытесняется, что увеличивает положительную плавучесть. Сухие костюмы также обеспечивают более положительную плавучесть.
- Баки: Полный алюминиевый бак имеет отрицательную плавучесть, но когда дайвер опускается и сжатый воздух иссякает, баллон становится плавучим. Надувать КП необходимо в начале погружения и постепенно, чтобы воздух сохранял нейтральную плавучесть.
Чтобы использовать принцип Архимеда в управлении плавучестью, вы должны использовать BCD, веса и снаряжение для дайвинга, чтобы гарантировать более безопасное погружение.
Принцип Архимеда: определение, формула и примеры – видео и стенограмма урока
Более внимательный взгляд
Давайте подробнее рассмотрим это определение.Во-первых, нам нужно понять «смещение».
Как гласит история, однажды Архимед вылился в теплую ванну и, войдя в нее, понял, что уровень воды поднялся. Затем он определил, что чем большую часть своего тела он погружает в ванну, тем выше становится уровень воды.
Это означает, что объем его тела, который он погрузил в воду, должен был перемещать или вытеснять воду, чтобы он мог поместиться в ванне. Следовательно, смещение в этом контексте – это когда объект перемещает жидкость, чтобы он мог занять объем, который изначально занимал жидкость.
Пример – линкор
В качестве примера возьмем линкор. Линкор сделан из стали. Прямо сейчас вы можете сказать: «Но сталь не плавает!» Так как же линкор может плавать?
Посмотрите на изображение линкора. Теперь представьте, что рисуете линию, где вода поднимается на корпус корабля. Затем залейте корпус корабля водой до этой отметки. Как вы думаете, сколько будет весить вода? Если вы сказали «много», вы правы. Фактически он весил бы столько же, сколько весь корабль!
Вода, заполняющая корпус корабля, весит столько же, сколько и сам корабль, поэтому вода создает на корабле выталкивающую силу с такой большой силой.Поэтому корабль из стали плывет!
Пример – Ice Cube
Рассмотрим другой пример. Если вы поместите кубик льда в стакан с водой, кубик будет плавать, потому что лед менее плотный, чем вода. Итак, лед под водой вытесняет этот объем воды.
Чтобы упростить задачу, скажем, что кубик льда – это идеальный куб, каждая сторона которого имеет длину 1 см. Предположим также, что кубик льда плавает на глубине 0,8 см под водой. Сколько весит кубик льда? Чтобы определить это, давайте проведем некоторые вычисления.
Расчет смещения
Помните, что принцип Архимеда гласит, что вес вытесняемой жидкости является выталкивающей силой. Следовательно, нам нужно знать, сколько воды вытесняется.
Если 0,8 см находится под водой, то мы можем найти объем этой формы, умножив три стороны вместе. В этом случае нам нужен только объем куба, который находится под водой, поэтому мы умножаем длину и ширину на величину высоты, которая находится под водой.3
Поскольку 1 кубический сантиметр равен 1 мл, мы можем напрямую преобразовать объем в миллилитры.
V = 0,8 мл
Плотность воды составляет 1 г / мл (один грамм на миллилитр), поэтому масса этого количества воды составляет 0,8 грамма.
м = 0,8 г
Мы еще не закончили. Масса – это количество вещества в чем-то, а вес – это сила, которая толкает вещество на Землю. Чтобы найти вес из массы, нам нужно перевести массу в килограммы.2 = 0,00784 N
Резюме урока
Принцип Архимеда состоит в том, что любой объект, окруженный жидкостью, поднимается этой жидкостью. Этот подъем представляет собой выталкивающую силу, которая равна весу жидкости, которую перемещает объект. Следовательно, чем больше смещение, тем больше выталкивающая сила, и чем тяжелее жидкость, тем больше выталкивающая сила.
Основные термины Архимеда
- Принцип Архимеда : гласит, что объект, окруженный жидкостью, поднимается вверх
- Выталкивающая сила : эта сила равна весу жидкости, которую она вытесняет
- Смещение : когда объект перемещает жидкость, чтобы он мог занять объем, который изначально занимал жидкость
Результаты обучения
По окончании урока ученики должны уметь:
- Проиллюстрировать, как работает принцип Архимеда
- Определите смещение и подъемную силу
- Модель математического определения смещения

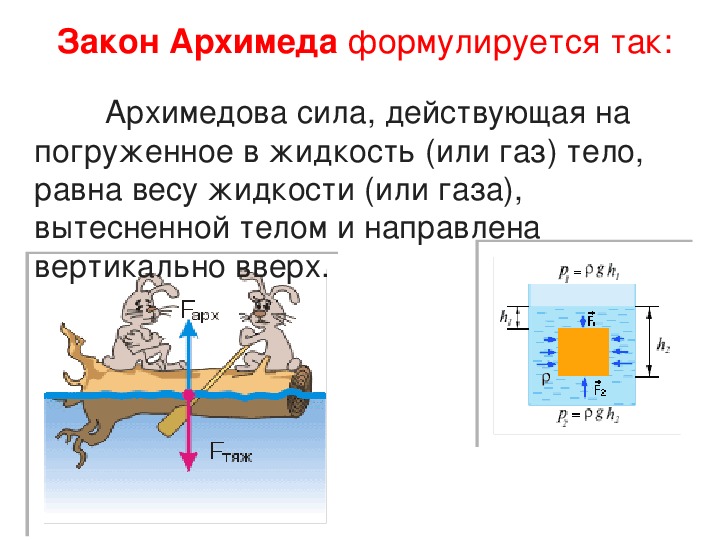
 Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».
Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».