Механика (Зубов В.Г.)
Механика (Зубов В.Г.)
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ I. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ § 1. Основные опыты и наблюдения. Что такое механическое движение? § 2. Относительность движений. Система отсчета § 3. Как определить положение тел друг относительно друга? Радиус-вектор § 4.  § 5°. Другой способ определения положения тел. Координаты § 6°. Как связан радиус-вектор с декартовыми координатами? § 7. Как определить конечный результат движения? Вектор перемещения § 8. Как связан вектор перемещения с приращением радиус-вектора? § 9°. Определение вектора перемещения по координатам § 10. Через какие точки проходило тело во время движения? Траектория § 11. Как связана траектория движения с векторами перемещения? § 12. Как определить положение тела на траектории? Длина пути § 13. Закон движения тела по заданной траектории § 14. Первые итоги. Примеры § 15. Как определить состояние движения в данной точке? Скорость § 17°. Определение скорости по изменению координат тела § 18. Две основные задачи кинематики § 19. Формула закона равномерного движения § 20. Порядок действий при решении задач кинематики § 21. Некоторые особенности практических транспортных задач § 22.  Как количественно определить изменения скорости? Ускорение§ 23. Изменение модуля скорости. Тангенциальное ускорение § 24. Изменение направления скорости. Нормальное ускорение § 25. Формула скорости равнопеременного движения § 26. Формула закона равнопеременного движения § 28. Свободное падение тел. Закон Галилея § 29. Два примера свободного падения тел § 30. Принцип независимого сложения движений § 31°. Расчет криволинейного движения по координатам § 32. Правила перехода от одной системы отсчета к другой. Преобразования Галилея § 33. Поступательное и вращательное движения твердого тела § 34. Некоторые вопросы измерений. Системы единиц § 35°. Кинематика движения тел с большими скоростями § 36. Краткие сведения из истории II. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ДИНАМИКИ § 37. Выбор системы отсчета. Первый закон Ньютона. Инерциальные системы отсчета § 39.  Влияние собственных свойств тела на его ускорение§ 40°. Влияние скорости движения тела на его ускорение § 41. Двусторонний характер действия тел § 42°. Взаимодействия тел и невозможность создания вечного двигателя § 43. Итоги основных опытов и наблюдений § 44. Как количественно определить действия тел друг на друга? Сила § 45. Измерение сил § 46. Сила — вектор. Принцип независимого действия сил § 47. Разложение сил на составляющие § 48. Связь между силой и ускорением § 50. Зависимость ускорения от массы тела § 51. Второй закон Ньютона § 52. Третий закон Ньютона § 53. Полная система законов динамики § 54. Две основные задачи динамики § 55. Порядок действий при решении задач на применение законов Ньютона § 56. Пример решения сложной задачи § 57. Краткие сведения из истории III. МЕХАНИЧЕСКИЕ СВОЙСТВА ТЕЛ. ИСПОЛЬЗОВАНИЕ ИХ В РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ § 58. Как ведут себя тела в свободном состоянии? Способность тел сохранять свою форму и объем § 59.  Определение результата движения частей тела. Деформации§ 60. Силы, возникающие при деформациях. Упругие и пластические деформации § 62. Упругие свойства твердых тел. Закон Гука § 63. Упругие пружины. Динамометры § 64. Упругие свойства жидкостей § 65. Упругие свойства газов. Закон Бойля — Мариотта § 66. Трение в жидкостях и газах § 67. Прыжок с парашютом § 68. Сухое трение § 69. Всемирное тяготение § 70. Пример применения закона всемирного тяготения. Первая космическая скорость § 71. Вес и невесомость § 72. Общий обзор механических свойств тел § 73. Принцип относительности механических явлений § 74°. Основные положения теории относительности IV. ИМПУЛЬС СИЛЫ. КОЛИЧЕСТВО ДВИЖЕНИЯ ТЕЛА. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 76. Преобразование второго закона Ньютона § 77. Упругий удар шара о стенку § 78. Расчет силы давления струи воды на препятствие § 79.  Гидромонитор§ 80. Турбина § 81. Системы тел § 82. Новая форма третьего закона Ньютона. Закон сохранения количества движения § 83. Порядок действий при решении задач на применение закона сохранения количества движения § 84. Реактивная сила тяги § 85. Ракетные и реактивные двигатели § 86°. Применение второго закона Ньютону к движению тел переменной массы § 87°. Уравнение движения тел с большими скоростями § 88. Еще один путь преобразования законов Ньютона § 89. Работа постоянной силы § 90. Работа переменной силы § 91. Кинетическая энергия тела § 92. Еще одна форма второго закона Ньютона § 93. Примеры применения разных форм второго закона Ньютона § 94. Работа силы тяжести § 95. Графический способ расчета работы. Работа упругой силы § 96°. Работа сил всемирного тяготения § 97. Работа силы трения § 98. Потенциальная энергия системы тел § 99°. Потенциальная энергия сил всемирного тяготения.  § 100. Связь между работой внутренних сил и потенциальной энергией § 101. Полная энергия системы тел. Закон сохранения энергии § 102. Значение закона сохранения энергии § 103. Примеры применения закона сохранения энергии § 104. Мощность двигателей § 105. Краткие сведения из истории VI. ВРАЩЕНИЕ ТЕЛ § 106. Угловое перемещение тела § 107. Угловая скорость тела § 108. Угловое ускорение тела § 109. Динамика вращения тел. Основные опыты и наблюдения § 110. Момент силы § 111°. Момент инерции тела § 112°. Уравнение моментов § 113°. Независимое сложение моментов сил § 114°. Примеры применения уравнения моментов § 116. Сводка основных понятий и законов динамики вращения § 117. Общие условия равновесия тел § 118. Пример расчета простых механизмов ЗАКЛЮЧЕНИЕ |
Закон движения тела: определение, формулы
Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни.
Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.
О каких типах движения пойдет речь?
Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:
- Равномерное по прямой линии.
- Равноускоренное (равнозамедленное) по прямой линии.
- Равномерное по окружности.
- Равноускоренное по окружности.
- Движение по эллиптической траектории.
Равномерное движение, или состояние покоя
Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI – начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения – это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).
Законы Ньютона. Второй закон Ньютона. Законы Ньютона -…
Взаимосвязь этих величин изложена в трех закономерностях, выведенных величайшим английским физиком….
Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.
Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:
s = v * t
Где s – расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):
v = s / t; t = s / v
Перемещение по прямой с ускорением
Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:
Импульс силы – что это? Отвечаем на вопрос.
Закон силы…
Часто в физике говорят об импульсе тела, подразумевая при этом количество движения. На самом же…
a = v / t или v = a * t
Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).
Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:
s = a * t2 / 2
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.
Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах.
Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:
v = v0 – a * t
Здесь v0 – начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v0.
Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:
s = v0 * t – a * t2 / 2
Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.
Формулировка третьего закона Ньютона: примеры, связь с…
Движение всех окружающих нас макроскопических объектов описывается с помощью так называемых трех.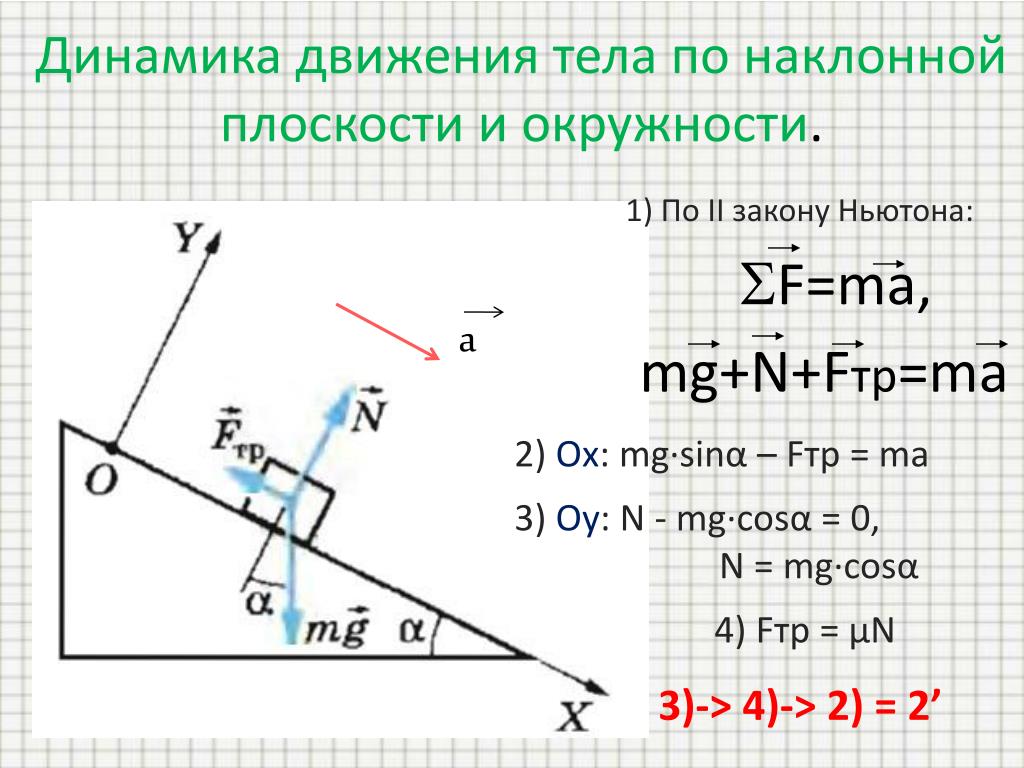
..
В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак “-” на “+”.
Движение по окружности
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:
ac = v2 / r, r – радиус
В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).
Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.
Вращение вокруг оси с постоянной скоростью
Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:
L =I * ω
Здесь L и I – моменты импульса и инерции, соответственно, ω – угловая скорость, которая с линейной связана равенством:
v = ω * r
Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:
θ = ω * t
Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик – это массивный диск, которому очень тяжело придать какое-либо ускорение.
Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.
Вращение вокруг оси с ускорением
Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:
F * d = I * dω / dt
Здесь F – внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.
Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:
ω = α * t, где α = F * d / I – угловое ускорение
В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:
θ = α * t2 / 2
Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:
ω = ω0 + α * t;
θ = ω0 * t + α * t2 / 2
Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.
Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:
I * ω = const
Движение по эллиптической траектории на примере планет Солнечной системы
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:
- Планеты Солнечной системы движутся по эллиптическим орбитам, причем Солнце расположено в одном из фокусов эллипса.
- Радиус-вектор, который соединяет Солнце и планету, за равные промежутки времени описывает одинаковые площади. Этот факт следует из сохранения момента импульса.
- Если поделить квадрат периода обращения на куб большой полуоси эллиптической орбиты планеты, то получается некоторая константа, которая одинакова для всех планет нашей системы. Математически это записывается так:
T2 / a3 = С = const
Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:
C = 4 * pi2 / (G * M)
Где G – гравитационная универсальная константа, а M – масса Солнца.
Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.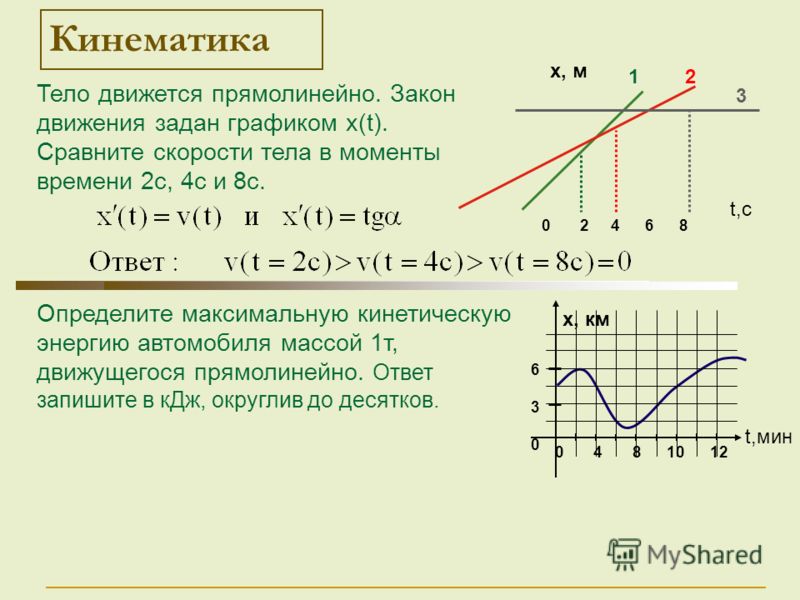
Передвижение – Физика тела: от движения к метаболизму
основан на сочетании законов Ньютона. Тело будет двигаться с постоянной скоростью, пока на него не действует результирующая сила (). Изменение движения тела достигается за счет инициирования сокращения мышц для приложения силы к другому объекту, например к полу или стене. Затем другой объект прикладывает к телу равную и противоположную силу реакции (). Эта сила реакции, действующая на тело, суммируется со всеми другими силами, действующими на тело, и определяет . Чистая сила вызывает ускорение, которое зависит от тела согласно .
Повседневные примеры: ответ на код без поскальзываний
Джолин идет со скоростью 2,5 миль в час по больничному коридору, когда по внутренней связи вызывается код. Она останавливается, затем разворачивается и начинает идти в другом направлении, к комнате, где был вызван код, со скоростью 4,0 миль в час . Если масса Джолин равна 61 кг , и она попыталась сделать это движение очень быстро, например, всего за 0,75 с , какая результирующая сила будет приложена к ней?
В задаче даны только скорости, но для анализа нужно определить направление движения.
(1)
Если мы переведем наш ответ в единицы м/с , мы получим: 6,5 миль в час = 2,9 м/с . (Вы можете проверить это самостоятельно, используя модульный анализ или онлайн-конвертер).
Затем мы вычисляем ускорение Джолин, используя определение среднего ускорения:
Вводя наши значения:
Мы находим, что ускорение Джолин составляет 3,9 м/с, что означает ее скорость / .9 м/с больше положительного каждую секунду. Обратите внимание, что изначально она двигалась в отрицательном направлении, поэтому скорость, которая становится более положительной, означает, что она, должно быть, замедлилась.
Теперь мы можем использовать второй закон Ньютона для расчета средней чистой силы, необходимой для обеспечения этого ускорения:
Теперь мы готовы ввести наши значения:
Трение – единственная горизонтальная сила, способствующая горизонтальному ускорению Джолин опыта, поэтому результирующая сила будет просто равна силе трения. Мы можем выяснить, поскользнется ли Джолин, сравнив требуемую чистую силу с максимально возможной статической силой трения.
Сначала мы начнем с уравнения для максимальной статической силы трения:
Затем мы разделим на нормальную силу, чтобы найти коэффициент трения:
Предположим, что пол ровный и изменяется только горизонтальное движение Джолин, тогда нормальная сила должна уравновешивать вес Джолин (если бы они не были уравновешены, у нее также было бы вертикальное ускорение). Для этого особого случая мы заменим ее вес на нормальную силу:
Наконец, мы вводим наши значения:
Просматривая коэффициенты трения, мы обнаруживаем, что коэффициент трения между резиной и бетоном обычно равен 0,6 или выше, так что Джолин, вероятно, могла бы сделать это движение без проскальзывания.
Прыжки
Каждый день Пример: Прыжки
Когда человек стоит на ровной поверхности, он находится внутри и отталкивание от земли равно его . Чтобы прыгнуть, мышцы ноги сокращаются, чтобы оттолкнуться от пола. Этот толчок вниз приводит к равной реактивной нормальной силе от пола, так что теперь нормальная сила больше, чем вес тела, а есть направленное вверх . Теперь с восходящей чистой силой тело испытает направленное вверх . Следующий график нормальной силы, действующей на человека, был создан путем прыжков и приземлений на силовую пластину, которая, по сути, представляет собой сверхпрочную цифровую шкалу, которая регистрирует то, что она обеспечивает с течением времени.
Нормальная сила воздействия земли на человека во время прыжка, зафиксированная цифровой силовой пластиной во время эксперимента, описанного в следующем тексте. Сначала прыгун наступает на силовую пластину, и он читает их около 800 N . Затем показания пластины падают на пару сотен ньютонов, потому что восходящая нормальная сила уменьшается, когда они приседают, что имеет смысл, потому что они должны ускоряться вниз, чтобы упасть.
Затем сила достигает пика около 1700 N , они сильно отталкиваются, чтобы остановить движение вниз и начать движение вверх. На протяжении всей этой стадии нормальная сила больше, чем вес, чтобы создать это восходящее ускорение. Нормальная сила падает до нуля, когда тело покидает контакт с землей. В то время как в воздухе создается результирующая нисходящая сила, поэтому ускорение направлено вниз, а скорость тела вверх замедляется. (После отрыва от земли ускорение – г = – 9,8 м/с/с ). Тело в конце концов разворачивается, когда восходящая скорость достигает нуля, а затем начинает двигаться обратно к земле. Приземление требует восходящего ускорения, чтобы остановить нисходящую скорость, поэтому создается большая направленная вверх нормальная сила, превышающая 2500 Н . Парашютист пытается совершить «мягкое приземление» и поэтому продолжает приседать во время приземления, что приводит к падению нормальной силы еще на пару сотен ньютонов в конце приземления.
Наконец, нормальная сила снова равняется весу после завершения приземления. В следующих главах мы больше поговорим о «мягкой посадке» и других методах предотвращения травм.
Вождение
Каждый день Пример: вождение автомобиля
Чтобы ваш автомобиль мог двигаться по ровной дороге, он должен иметь результирующую горизонтальную силу. Какая сила действует на ваш автомобиль, чтобы обеспечить эту результирующую силу? Помните, что сила должна действовать на автомобиль от другого объекта, автомобиль не может воздействовать на себя результирующей силой (поэтому ответом не может быть двигатель или какая-либо часть автомобиля). Гравитация и являются внешними силами, воздействующими на автомобиль, но эти силы действуют вертикально и не могут влиять на горизонтальное . Сила, действующая на автомобиль в горизонтальном направлении, называется трением. Когда шины пытаются вращаться, они отталкиваются от земли за счет трения, а земля отталкивается с равной противодействующей силой.
Тогда, согласно , эта сила трения, действующая на автомобиль, заставляет его ускоряться. Цель дроссельной заслонки, двигателя и трансмиссии состоит в том, чтобы заставить шины отталкиваться от дороги, чтобы в ответ получить толчок вперед от дороги.
[1]
, воздух оказывает обратное сопротивление вашему автомобилю. Когда сила сопротивления и сила трения на автомобиле равны, автомобиль достигает постоянной скорости, что-то вроде конечной скорости. Если вы хотите, чтобы автомобиль ехал быстрее, вам нужно увеличить силу трения автомобиля о дорогу, чего вы достигаете, увеличивая силу, с которой шины прижимаются к дороге с помощью дроссельной заслонки, двигателя и трансмиссии.
Ходьба и бег
Каждый день Примеры: ходьба и бег
При ходьбе или беге вы горизонтально отталкиваетесь от пола, а пол отталкивается назад, предоставляя вам необходимое для создания . Ходьба с постоянной средней скоростью достигается чередованием ускорения вперед, вызванного тем, что пол давит на заднюю ногу, и ускорением назад, вызванным тем, что пол давит на переднюю ногу. Эти ускорения в среднем равны нулю, поэтому появляется , но если вы используете датчик, способный выполнять несколько измерений в секунду, то вы можете увидеть характер движения при ходьбе:
Кривая зависимости ускорения от времени для идущего человека.Начальное положительное значение соответствует изменению от нуля на первом шаге. После этого постоянное движение при ходьбе приводит к ускорению, которое колеблется от положительного к отрицательному и усредняется до нуля.
Кривая зависимости скорости от времени для идущего человека. Осциллирующие ускорения приводят к чередованию замедления и ускорения, однако мы видим, что скорость остается положительной, поэтому вы всегда продвигаетесь в том направлении, в котором собираетесь идти.
Мы также видим, что в течение всего цикла ходьбы постоянна, около 0,4 м/с для этого примера, что согласуется с нулевым средним ускорением на предыдущем графике.
По мере вашего прогресса увеличивается примерно линейно со средним значением, равным вашей константе , в данном случае 0,4 м/с . Однако колебания скорости заметны в виде небольших изменений наклона графика положения.
- Адаптировано из Chevrolet Malibu пятого поколения на межштатной автомагистрали 85 в Дареме, Северная Каролина, автор Ильдар Сагдеев (Specious) — собственная работа, CC BY-SA 3.0, через wikimedia commons ↵
Движущееся тело стремится оставаться в движении. Законы движения Ньютона и ваша музыкальная (или художественная) карьера!
Я постоянно говорю это на уроках, наука может МНОГОму научить нас в жизни музыкантов. Как саксофонист, я почти ежедневно обращаюсь к акустике и физике, так как мне интересно наблюдать, как наука и музыка физически взаимодействуют через мой инструмент и мои действия, но я думаю, что мы также можем многое почерпнуть из науки, когда дело касается к тому, как мы подходим к нашей карьере и образу жизни.
Сегодня я воспользуюсь некоторыми законами физики сэра Исаака Ньютона.
Отказ от ответственности: пожалуйста, помните, что я не физик, поскольку мы делаем это. Дело не в том, что я ученый, а в том, чтобы посмотреть на некоторые законы науки, которые могут иметь смысл и в нашей жизни.
НАУКА № 1: ПЕРВЫЙ ЗАКОН НЬЮТОНА:Инерция. Тело в состоянии покоя имеет тенденцию оставаться в покое, а тело в движении имеет тенденцию оставаться в движении, если на него не действует чистая внешняя сила.
Яркий пример: ваша тренировка!
Когда вы делаете перерыв в занятиях на несколько дней/недель/лет (надеюсь, не на годы, если вы планируете сделать карьеру в музыке), насколько сложно вернуться в комнату для занятий и начать ? ТЯЖЕЛО, да? Чем дольше вы находитесь вдали от своего инструмента, тем труднее вернуться к нему. – Тело в состоянии покоя стремится оставаться в покое .
С другой стороны, если у вас есть план регулярных тренировок, и вы постоянно следите за ходом событий, насколько легко продолжать? Движущееся тело стремится оставаться в движении .
БУМ! Наука!Ха! Если бы это было так просто. Но вот в чем дело — вы можете использовать этот закон инерции в своих интересах. Вы когда-нибудь чувствовали, что зашли в тупик и просто НЕ МОЖЕТЕ получить мотивацию, чтобы начать проект, который, как вы знаете, потребует постоянных усилий? Например, блог? Если вы чувствуете это, вы действительно можете активировать эту концепцию « тело в движении имеет тенденцию оставаться в движении 9».0008», сделав что-то очень маленькое. Как только вы сделаете первый шаг к тому, чтобы быть в движении, вам будет легче двигаться вперед. Вам буквально нужно только начать, и вы уже в пути.
Конечно, в мире ничего не дается бесплатно, и проблема с этим возникает, когда вы сталкиваетесь с сопротивлением в процессе — тогда наша мотивация и импульс исчезают — благодаря надоедливому окончанию этого закона — , если только не действует сеть внешняя сила .
Стивен Прессфилд говорит о сопротивлении в своей книге « Война искусства », и я думаю, что он обращается к этой «чистой внешней силе», когда говорит о «сопротивлении». Гей Хендрикс называет это нашей «проблемой верхнего предела», и, честно говоря, с этим регулярно сталкиваемся ВСЕ. Что следует помнить об этом законе, так это то, что если вы испытываете эту чистую внешнюю силу или сопротивление, когда находитесь в движении, совершая действие, Ньютон утверждает, что вы ОСТАНЕТЕСЬ в движении.
НАУКА #2. ВТОРОЙ ЗАКОН НЬЮТОНА:Ускорение объекта, создаваемое результирующей силой, прямо пропорционально величине результирующей силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта. Также известен как F=ma
. Прочитав это как минимум 35 раз (и погуглив «второй закон Ньютона — простое издание», потому что я не изучал никаких наук с 12-го класса), это в основном означает, что величина ускорения вам нужно переместить объект определяется его массой и силой.
Яснее не так ли?
Да, я знаю, позвольте мне объяснить это.
Нам нужно немного разобраться в формуле; F(сила) = m(масса) x a(ускорение) , так что просто держитесь меня.Это уравнение объясняет, что для того, чтобы определить, какую силу вам нужно приложить к объекту, вы должны понимать не только массу или вес объекта, но и направление, в котором вы хотите, чтобы он двигался (ускорение). .
С другой стороны, чтобы ускорить объект в определенном направлении, необходимо учитывать как массу, так и требуемую силу. Например; у вас есть тяжелый валун для перемещения. Чтобы вычислить, какую силу вам нужно приложить, вы должны понять его массу (это валун, сделанный из камня или искусственный валун?), а также направление, в котором вы пытаетесь его направить – движется ли он? в гору, под гору или на ровной поверхности?
Эта формула идеально работает для нас с точки зрения карьерного роста.
Если вы хотите знать, сколько труда/сил вложено в разработку проекта/навыка/образа жизни, вам нужно понять пару вещей: какова масса проекта (насколько он БОЛЬШОЙ?) и что ваша конечная цель? Каково направление/ускорение работы?
Перевернутое, если вы знаете объем/размер проекта (масса) — вам нужно обратить внимание не только на то, насколько усердно работать (сила), но и на то, где эта работа применяется (направление) .
БУМ! Наука! (снова) НАУКА №3: ТРЕТИЙ ЗАКОН НЬЮТОНА:На каждое действие существует равное и противоположное противодействие ЭТА НАУКА – МОЯ ЛЮБИМАЯ ИЗ ВСЕХ НАУК!
Честно говоря, этот третий закон удерживает меня вместе большую часть времени. Ранее я упоминал книгу Гей Хендрикс Большой скачок , и эта книга познакомила меня с идеей сопротивления и помогла мне понять, что прогресс — это ТЯЖЕЛЫЙ (и это нормально).
Закон Ньютона гласит, что на каждое действие, которое вы совершаете, существует столь же противоположная реакция, которая отталкивает вас. Отталкивание или сопротивление в равной степени. Мы все говорим о жизни как о равновесии, и это равновесие ваших действий.
В карьере или в тренировочном зале это переводится как « Чем больше цель, тем тяжелее работа ». Надеюсь, это никого не удивит, но причина, по которой я ЛЮБЛЮ этот третий закон, — это разрешение и свобода, которые он дает мне, когда я натыкаюсь на стену.
Поясню.
Размышляя над этой концепцией, я настроился на свои собственные реакции на многие вещи в моей работе. Одним из них является ощущение, что что-то «твердое». Когда я работаю над чем-то, что кажется трудным, я научил себя меньше думать о том, что это бросает мне вызов, и больше о том, что отпор/сопротивление, которое я чувствую, вызвано тем, что задача, которую я пытаюсь выполнить, больше, чем я испытал ранее.
Когда я получаю большое сопротивление проекту, к которому я достаточно увлечен, чтобы применить науку № 2 выше, это на самом деле признак того, что я делаю успехи. Если я прилагаю к работе много действий, я могу рассчитывать на получение такого же количества противодействия для поддержания равновесия.
Если я перестану давить, сопротивление со временем исчезнет, но если вы помните первый из вышеприведенных законов, вы также будете знать, что, попав в движение, это сопротивление будет продолжать давить, пока вы не давите назад. Это еще одна причина, по которой вам может казаться, что вы отстали от проекта, если остановились, столкнувшись с массовым сопротивлением. Эмоционально, скорее всего, да (по крайней мере временно)!
Итак, причина, по которой я люблю этот закон, заключается в том, что я не только могу предсказать и ожидать сопротивление, когда приступлю к проекту (в целом это делает его менее страшным), я знаю, что в тот момент, когда я начинаю чувствовать это, я на самом деле я достиг достаточного прогресса и достаточного роста, чтобы противоборствующие силы почувствовали необходимость замедлить мой бросок.
Это был первый раз, когда я услышал, как этот закон используется за пределами научной лаборатории, и я сразу же интегрировал его в свое мышление.
