Закон электромагнитная индукция: Ошибка 404: страница не найдена

Электромагнитная индукция – это… Что такое Электромагнитная индукция?

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Майклом Фарадеем 29 августа^{[источник не указан 100 дней]} 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

 — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

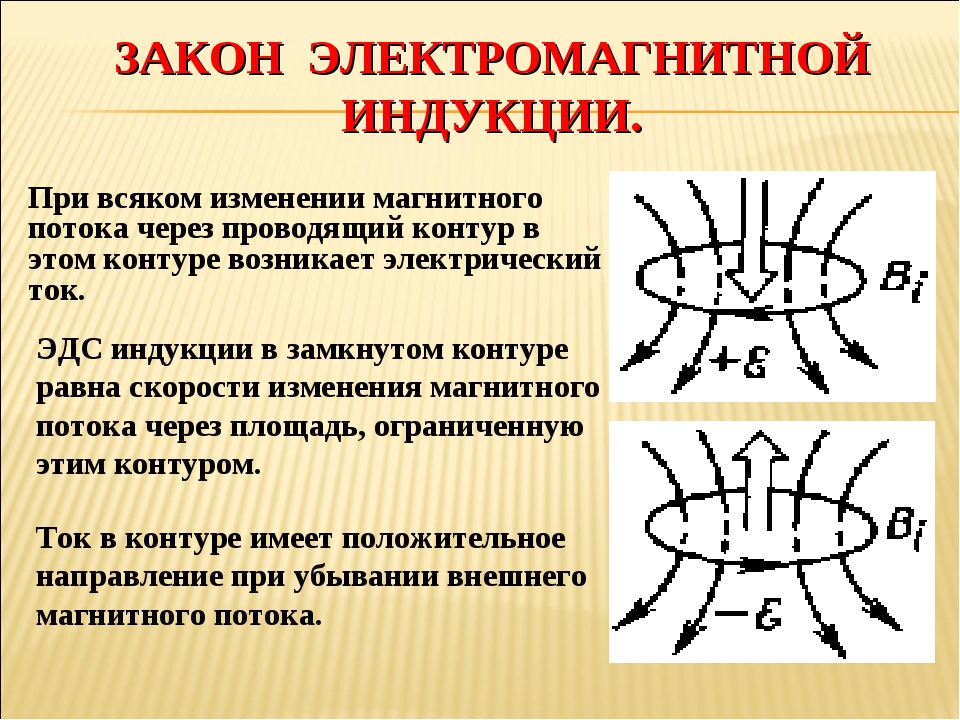
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

Векторная форма

В дифференциальной форме закон Фарадея можно записать в следующем виде:

(в системе СИ)

или

(в системе СГС).

В интегральной форме (эквивалентной):

(СИ)

или

(СГС)

Здесь  — напряжённость электрического поля,  — магнитная индукция,  — произвольная поверхность,  — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

• В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[1].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство продолжает соблюдаться, но ЭДС в левой части теперь не сводится к (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

• Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год^[2] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[3]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
• Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определенных ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединенным к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчета, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчета, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчета мы ее рассчитали.

Потенциальная форма

При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:

(в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).

В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:

История

В 1820 г. Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 г. в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 г.

наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, заключалась в том, что Фарадей изготовил кольцо из мягкого железа примерно 2 см шириной и 15 см диаметром и намотал много витков медной проволоки на каждой половине кольца. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.

В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М.

Фарадея об открытии им электромагнитной индукции.

М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.

См. также

Примечания

1. ↑ Это уравнение Максвелла может быть переписано в эквивалентном виде
   (здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь очевидно не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
2. ↑ М. Лившиц Закон электромагнитной индукции или «правило потока»? // Квант.  — 1998. — № 3. — С. 37—38.
3. ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.

Ссылки

Закон электромагнитной индукции – Класс!ная физика

Закон электромагнитной индукции

Подробности

Просмотров: 442

«Физика – 11 класс»

Опыты Фарадея показали, что сила индукционного тока I_i в проводящем контуре пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром, т.

е. скорости изменения магнитного потока.

ЭДС индукции

В цепи появляется электрический ток, когда на свободные заряды проводника действуют сторонние силы.
Величину, численно равную работе этих сил при перемещении единичного положительного заряда вдоль замкнутого контура, называют электродвижущей силой (ЭДС).

При изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризует ЭДС индукции.
Обозначение ЭДС индукции – .

Согласно закону Ома для замкнутой цепи индукционный ток в контуре

Закон электромагнитной индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца?

Пусть положительное направление обхода контура – против часовой стрелки.
Нормаль к контуру образует правый винт с направлением обхода.

Если магнитная индукция В внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем.
Тогда магнитный поток Ф > 0 и скорость измененеия магнитного потока тоже > 0.
По правилу Ленца индукционный ток создает магнитный поток Ф’ меньше 0.
Индукционный ток I_i по правилу буравчика направлен по часовой стрелке (против направления положительного обхода).
ЭДС индукции отрицательна.
Поэтому в формуле для закона электромагнитной индукции должен стоять знак «-»,
указывающий на то, что ЭДС индукции и скорость изменения магнитного потока имеют разные знаки:

Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитная индукция. Физика, учебник для 11 класса – Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

Электромагнитная индукция. Опыты Фарадея. Закон электромагнитной индукции

ИСХОДНЫЙ МАТЕРИАЛ

План изложения учебного материала по теме

«Электромагнитная индукция. Опыты Фарадея. Закон электромагнитной индукции»

1.     История открытия явления.

2.     Опыты Фарадея.

3.     Изменение направления индукционного тока.

4.     Закон электромагнитной индукции. Магнитный поток.

5.     Возникновение вихревого магнитного поля.

1.     История открытия явления.

До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.

Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.

Рис. 1. Схема опыта Фарадея

На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генриобнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.

Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).

1.     Опыты Фарадея.

Для проведения опыта он взял катушку с большим количеством витков и присоединил ее к миллиамперметру (прибору, измеряющему силу тока). По направлению вверх и вниз ученый передвигал магнит по катушке.

Во время проведения эксперимента, в катушке действительно появлялся электрический ток по причине изменения магнитного поля вокруг нее.

По наблюдениям Фарадея стрелка миллиамперметра отклонялась и указывала на то, что движение магнита порождает собой электрический ток. При остановке магнита стрелка показывала нулевую разметку, т.е. ток не циркулировал по цепи.

Рис. 2 Изменение силы тока в катушке за счет передвижения реостата.

Данное явление, при котором  ток возникает под действием переменного магнитного поля в проводнике, назвали явлением электромагнитной индукции.

1.     Изменение направления индукционного тока.

В своих последующих исследованиях Майкл Фарадей пытался выяснить, что влияет на направление возникающего индукционного электрического тока. Проводя опыты, он заметил, что изменяя числа мотков на катушке или полярность магнитов, направление электрического тока, которое возникает в замкнутой сети, меняется.

1.     Закон электромагнитной индукции. Магнитный поток.

Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.

Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока. Определение магнитного потока:

Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.

Формула магнитного потока:

Ф = BS cosα , здесь α – угол между направлением вектора магнитной индукции B и нормалью к поверхности S.

Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.

А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.

Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 10⁸ мкс. Соответственно 1 мкс = 10^-8 вб.

Магнитный поток является скалярной величиной.

Формула закона электромагнитной индукции Фарадея выглядит следующим образом:

Рис. 3. Формула закона электромагнитной индукции

И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается, существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея.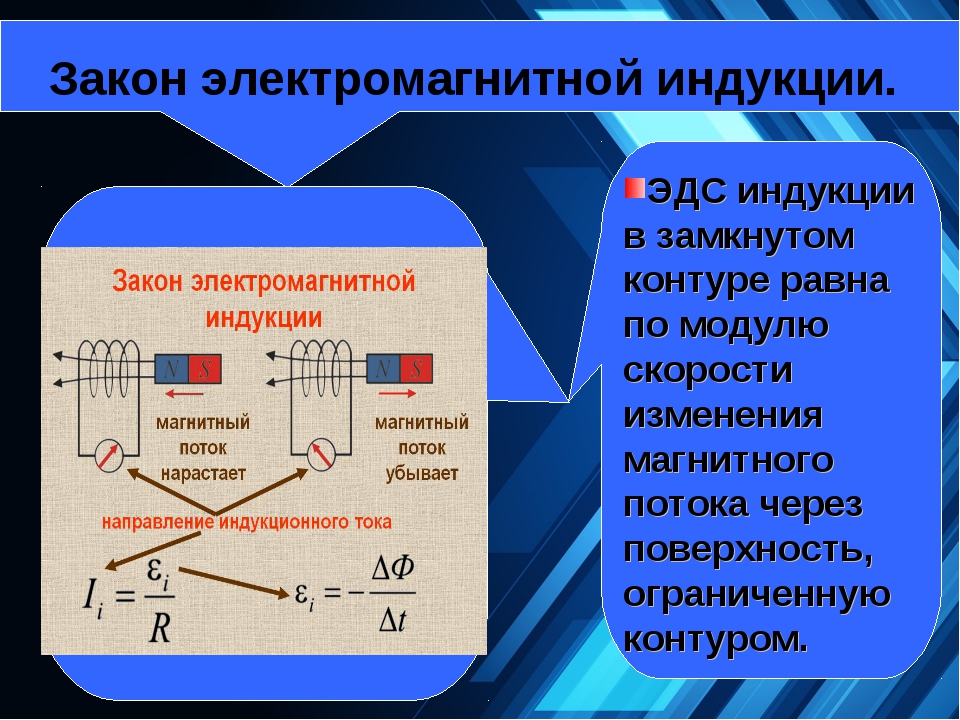 По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.

Закон Фарадея-Максвелла

В 1873 году Дж. К. Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:

Edl = -dФ/dt – уравнение электродвижущей силы

Hdl = -dN/dt – уравнение магнитодвижущей силы.

Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.

1.     Возникновение вихревого магнитного поля.

1 Вб = 1 Тл · 1 м².

Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. Физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:

• если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
• если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.

Рис. 4. Возникновение вихревого магнитного поля

Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.

ПРИЛОЖЕНИЕ №1

КОНТРОЛЬ ЗНАНИЙ ПО ПРЕДЫДУЩЕЙ ТЕМЕ (устно)

«Сила Лоренца. Движение заряженной частицы в магнитных и электрических полях»

1.     Сформулируйте понятие и выведите формулу для нахождения силы Лоренца.

Ответ: Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, может быть выражена через силы, действующие на отдельные носители заряда.

Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: 

Выражение для силы Ампера можно записать в виде: 

F = q n S Δl υB sin α.

Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна 

FЛ = q υ B sin α.

Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью  и вектором магнитной индукции  .

2.     Сформулируйте правило левой руки для нахождения силы Лоренца.

Ответ: Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика.

 ПРАВИЛО ЛЕВОЙ РУКИ для заряженной частицы с целью определения направления силы, действующей на отдельную заряженную частицу, движущуюся в магнитном поле. Если ЛЕВУЮ РУКУ расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной частицы), то отставленный на 90 градусов большой палец покажет направление действующей на частицу силы.

Взаимное расположение векторов ,  и  для положительно заряженной частицы показано на рисунке.

 Модуль силы Лоренца  численно равен площади параллелограмма, построенного на векторах  и  помноженной на заряд q

Сила Лоренца направлена перпендикулярно векторам   и .

3.     Опишите движение заряженной частицы в магнитном поле.

Ответ: При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость  лежит в плоскости, перпендикулярной вектору  то частица будет двигаться по окружности радиуса 

Сила Лоренца в этом случае играет роль центростремительной силы.

Круговое движение заряженной частицы в однородном магнитном поле

Период обращения частицы в однородном магнитном поле равен 

Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.

Угловая скорость движения заряженной частицы по круговой траектории 

называется циклотронной частотой.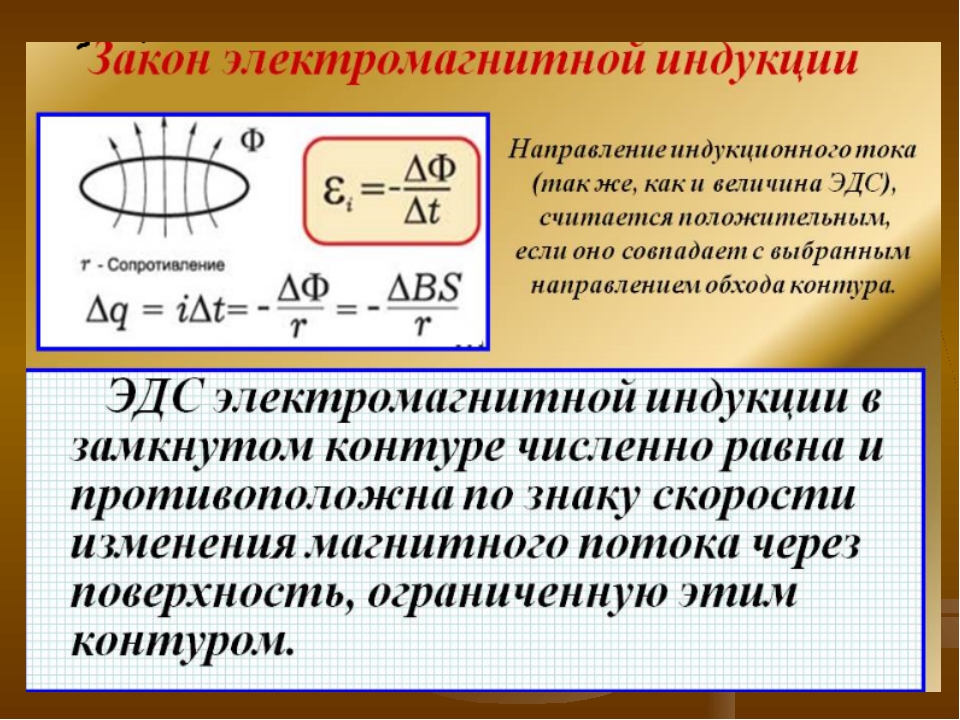 Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рисунке.

Движение заряженных частиц в вакуумной камере циклотрона.

4.     Опишите движение заряженной частицы в электрическом поле.

Ответ: Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость  заряженных частиц направлена перпендикулярно векторам  и 

На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила  и  магнитная сила Лоренца. При условии E = υB. эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью .

Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле  Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов   Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение . В случае изотопов (q₁ = q₂) масс-спектрометр позволяет разделить частицы с разными массами.

Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10^–4.

Критерии оценки:

Оценка «5» – на поставленный вопрос студент дал полный развернутый ответ и ответил на дополнительный вопрос;

Оценка «4» – на поставленный вопрос студент дал полный развернутый ответ, но не ответил на дополнительный вопрос;

Оценка «3» – на поставленный вопрос студент дал неполный ответ и не смог ответить на дополнительный вопрос;

Оценка «2» – не ответил на поставленный вопрос.

ПРИЛОЖЕНИЕ №2

ЗАДАНИЯ ДЛЯ ЗАКРЕПЛЕНИЯ И СИСТЕМАТИЗАЦИИ НОВЫХ ЗНАНИЙ (письменно, не оценивается)

Физика 11 Разноуровневые самостоятельные и контрольные работы А. Кирик стр.4 начальный уровень №1-6, стр. 6 достаточный уровень №1, 2, 3.

Эталоны ответов к заданиям для закрепления и систематизации

Уровень /№	1	2	3	4	5	6
Начальный уровень	Б, В	В	Б, В	Б	А, Б	В
Достаточный уровень	1	2	3
	6 м/с	0,5 м	0,3 Тл

ПРИЛОЖЕНИЕ № 3

ЗАДАНИЯ ДЛЯ ПРЕДВАРИТЕЛЬНОГО КОНТРОЛЯ ЗНАНИЙ

(Устно, не оценивается. Эталоны ответов к вопросам для предварительного контроля знаний содержатся в исходном материале)

1.     Расскажите об истории открытия явления.

2.     Какие еще ученые занимались данным явлением?

3.     Сформулируйте определение электромагнитной индукции.

4.     Опишите опыты Фарадея.

5.     От каких факторов зависит направление индукционного тока?

6.     От чего зависит сила возникающего индукционного тока?

7.     Дайте определение магнитного потока.

8.     При каком условии магнитный поток, пронизывающий контур, будет максимальным?

9.     Сформулируйте закон электромагнитной индукции.

10. На что указывает знак «-» в формуле закона электромагнитной индукции?

11. По какому правилу можно определить направление индукционного тока?

12. Почему возникающее магнитное поле называется вихревым?

ПРИЛОЖЕНИЕ №4

КОНТРОЛИРУЮЩИЙ МАТЕРИАЛ (письменно)

Тест

1.      Кто одновременно с Фарадеем открыл явление электромагнитной индукции?

1.      Джозеф Генри

2.      Э.Х. Ленц

3.      Дж.К. Максвелл

4.      Ш. Кулон

 2.В каком веке было открыто явление электромагнитной индукции?

1.      в XVII

2.      в XVIII

3.      в XIX

4.      в XX

3. Фарадей был уверен, что электрическое и магнитное поле:

1.      не имеют ни какой связи друг с другом

2.      имеют общую природу

3.      ничем не отличаются друг от друга

4.      ни один из ответов не является правдой

4.Для образования индукционного тока необходимо:

1.      изменение магнитного потока

2.      хаотичное движение молекул

3.      неизменность магнитного потока

4.      ни одно из утверждений ни является верным

1.     По закону Фарадея ЭДС:

1.      равна скорости изменения магнитного потока

2.      прямо пропорциональна скорости изменения магнитного потока

3.       обратно пропорциональна скорости изменения магнитного потока

4.      не зависит от скорости изменения магнитного потока

6. Знак «-» в формуле закона электромагнитной индукции указывает:

1.      на направление тока

2.      на уменьшение времени изменения магнитного потока

3.      на направление возникающей ЭДС

4.      ни одно из утверждений не является верным

7. Явление электромагнитной индукции стало:

1.      фундаментом для устройства генераторов всех электростанций

2.      основой для устройства ветряных мельниц

3.      основой для устройства гидростанций

4.      ни одно из утверждений не является верным

8. Скорость распространения электромагнитного поля:

1.      больше скорости света

2.      меньше скорости света

3.      равна скорости распространения света

4.      ни одно из утверждений не является верным

9. При электромагнитной индукции ток возникает:

1.       в замкнутом электропроводящем контуре

2.      в незамкнутом контуре

3.      вне контура

4.      ни одно из утверждений не является верным

10. В каком году Максвелл по-новому изложил теорию электромагнитного поля?

1.      в 1879

2.      в 1765

3.      в 1873

4.      в 1901

Эталоны ответов к заданиям контролирующего материала:

Номер задания	1	2	3	4	5	6	7	8	9	10
Ответы	А	С	В	А	В	С	А	С	А	С

Критерии оценки:

за 7 правильных ответов– «3» балла;

за 8 правильных ответов – «4» балла;

за 9, 10 правильных ответов – «5» баллов.

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ ВНЕАУДИТОРНОЙ РАБОТЫ СТУДЕНТОВ

Цель: Определить объем информации для самостоятельной работы студента, обратить внимание на значимые моменты.

Время для выполнения задания: 45 минут.

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Соцкий, Физика. 11 класс. Учебник для общеобразовательных учреждений (с приложением на электронном носителе). Базовый и профильный уровни – М.: Просвещение, 2016 г., с. 31-35, параграфы 7, 8 прочитать, конспект выучить; подготовить сообщение по теме «Майкл Фарадей».

ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ СООБЩЕНИЯ

1. Сообщение оформляется на компьютере, сдается преподавателю в мультифоре.

2. Шрифт TimesNewRoman, 14 пт, межстрочный интервал – одинарный, поля по 1,5 см справа и слева, текст выравниваются по ширине, заголовок – посредине. Ф.И. автора – по правому краю.

3. Объем сообщения – 2-3 страницы формата А4; время выступления – не более 5 минут.

4. В сообщении не выделяются главы; недопустимы орфографические ошибки, опечатки, записи и исправления ручкой или карандашом.

5. В конце сообщения указывается список информационных источников.

6. Сообщение может сопровождаться мультимедийной презентацией (по желанию автора).

!!! Определите самостоятельно, соответствует ли Ваше сообщение требованиям к оформлению. Для этого внимательно прочтите их и подчеркните каждое выполненное требование. Проведите коррекцию работы по тем требованиям, которые не выполнены.

Критерии оценки:

• студент выучил конспект – «3» балла;
• студент прочитал параграфы и выучил конспект, владеет информацией из учебника – «4» балла;
• студент выучил конспект, владеет информацией из учебника, подготовил сообщение, соответствующее требованиям – «5» баллов.

 

 

 

Список использованных источников

1. Батышев С.Я. Профессиональная педагогика: Учебник для студентов, обучающихся по педагогическим специальностям и направлениям /С.Я.Батышев. – М.: Ассоциация «Профессиональное образование»/, 1997. – 512 с.

2.Батышев С.Я. Реформа профессиональной школы: Опыт, поиск, задачи, пути реализации. – М.: Высшая школа, 1987. –340 с.

3. Болдырев Н. И., Гончаров Н. К., Есипов Б. П. и др. Педагогика. – М.: Наука, 1998.

4. Большой энциклопедический словарь. 2-е изд. перераб. и доп. – М.: «Большая Российская энциклопедия»; СПб.: «Норинт», 2007. – 1456 с.

5. Бордовская Н.В., Реан А.А. Педагогика. Учебник для вузов- CПб.: Питер, 2000.

6. Буланова-Топоркова М.В. Педагогика и психология высшей школы: учебное пособие. – Ростов-на-Дону: Феникс, 2002. – 544 с.

7. Подласый И.П. Педагогика: 100 вопросов – 100 ответов: учеб. пособие для вузов/ И. П. Подласый. – М.: ВЛАДОС-пресс, 2004. – 365 с.

8. Общая и профессиональная педагогика: Учебное пособие для студентов, обучающихся по специальности «Профессиональное обучение»: В 2-х книгах /Под ред. В.Д. Симоненко, М.В. Ретивых. – Брянск: Изд-во Брянского государственного университета/, 2003. – Кн.1 – 174 с.

9. Сластенин В.А. и др. Педагогика: Учеб. пособие для студ. высш. пед. учеб. заведений / В. А. Сластенин, И. Ф. Исаев, Е. Н. Шиянов; Под ред. В.А. Сластенина. – М.: Издательский центр “Академия”, 2002. – 576 с.

10. Смирнов И.П. Проблемы развития профессионального образования в РФ // Стратегия профессионального образования молодежи. – М., 1995.– С.12-22.

11. Стандарты профессионального образования зарубежных стран. – М.: НПО, 2007.-42с.

12. Харламов И.Ф. Педагогика: Учебное пособие. 2-е изд. – М.: Высшая школа, 1990. -576 с.

13. Закон РФ «О высшем и послевузовском профессиональном образовании» //Бюллетень Госкомитета РФ по высшему образованию. – 1996. – №10. – С. 1-59.

14. Зеер Э.Ф. Психология профессионального образования: Учеб. пособие. -Екатеринбург: Изд-во Урал. гос. проф.-пед. ун-та, 2000. – С. 181-224.

15. Зеер Э.Ф. Психология личностно ориентированного профессионального образования. – Екатеринбург: Изд-во Урал. гос. проф.-пед. ун-та, 2000. – С 3-71.

16. Концепция модернизации российского образования на период до 2010 года. Одобрена Распоряжением Правительства РФ №1756-р от 29 декабря 2001 г. // Официальные документы в образовании. – 2002. – №4. – С. 3-31.

17. Маркова А.К. Психология профессионализма. – М., 1996. — С. 49-57; 262-270.

18. Шелтен А. Введение в профессиональную педагогику: Учеб. пособие. -Екатеринбург: Изд-во Урал. гос. проф-пед. ун-та, 1996. – С. 91-106; 154-164.

19. Новиков A.M. Профессиональное образование в России. – М.: Просвещение, 1997. – 254 с.

20. Семушина Л.Г., Ярошенко Н.Г. Содержание и технологии обучения в средних специальных учебных заведениях: учеб. пособие для преп. учреждений сред. проф. образования – М.: Мастерство, 2001. – 272 с.

21. Беляева А.П.Дидактические принципы профессиональной подготовки в профтехучилищах: Методическое пособие.- М.:Высш.шк.,1991.,с.143-184

22. Коменский Я.А. Избранные педагогические сочинения. -М.:1982г.,с.242-404.

23. Педагогика. Учебное пособие для студентов педагогических вузов и педагогических колледжей / Под ред. И.П. Пидкасистый. – М.: Педагогическое общество России, 1998. – 640с., с.129-192.

24.Кукушин В.С. Введение в педагогическую деятельность: учебное пособие. Изд-е 2-е М.: ИКЦ «МарТ», Рост он/Д, 2005 год

25. Под общ. ред. Н. Л. Селивановой. Гуманистические воспитательные системы вчера и сегодня//Под общ. ред. Н. Л. Селивановой. — М.: Пед. об-во России, 1998 г.—336 с.

26. Симоненко В.Д. – Общая и профессиональная педагогика – М.: Вентана-граф, 2006 год

27. Кларин М. В. Технология обучения: идеал и реальность// Кларин М. В.— Рига, «Эксперимент», 1999 г.—180 с.

Internet

1.www.dist-edu.ru

2.www.hse.ru

3.http://ito.bitpro.ru

4.www.ui.usm.ru

5.http://biro.ufanet.ru

6.http://kampi.kcr.ru2.9 Технология дистанционного обучения

7. http://refleader.ru/jgemerrnaujgmer.html

 

Скачано с www. znanio.ru

Формула закона электромагнитной индукции

Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией.

Формула данного закона выглядит следующим образом:

   

где – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.

Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин.

Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.

Знак минус в законе индукции отражает правило Ленца.

В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ).

Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как:

   

Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде:

   

где – потокосцепление.

Результаты применения основного закона электромагнитной индукции

Формулы ЭДС индукции для частных случаев

ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:

   

Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна:

   

где – угол между направлением вектора скорости и направлением вектора магнитной индукции.

Если в однородном магнитном поле вращается плоский контур со скоростью , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:

   

где S – площадь, которую ограничивает виток; – мгновенное значение угла между и вектором нормали к плоскости рамки; – поток самоиндукции витка.

Если в рамке, вращающейся со скоростью в однородном магнитном поле, имеется N витков, то

   

в формуле (6) самоиндукцией витков пренебрегли.

Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как:

   

Примеры решения задач по теме «Закон электромагнитной индукции»

Что такое закон электромагнитной индукции Фарадея простыми словами

Сегодня речь пойдет об одном из основных законов электродинамики — законе электромагнитной индукции Фарадея. Для тех, кто забыл, электродинамика — это раздел физики, который изучает электромагнитное поле во всех его проявлениях.

С чего все начиналось

О явлении электромагнитной индукции мир узнал в 1831 году. Результаты исследования Фарадей получил параллельно с Генри, но успел их опубликовать раньше. Сегодня закон используется в разработке техники, электродвигателей, генераторов, дросселей, трансформаторов.

Суть физического явления заключается в следующем: при изменении магнитного потока через замкнутый проводящий контур в нем возникает электрический ток. Чтобы было понятнее: если скрутить из проволоки рамку и магнитом крутить вокруг нее (создавать переменное магнитное поле), потечет ток, который Фарадей назвал индукционным. Само явление получило название электромагнитной индукции.

Источник: pinterest.ru

Электромагнитная индукция — явление, при котором происходит возникновение в замкнутом контуре электрического тока при изменении магнитного потока, проходящего через контур.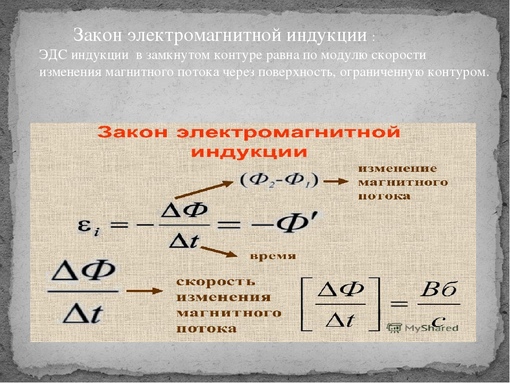

Формулировка закона, который объясняет это физическое явление, звучит так: ЭДС, возникающая в контуре, пропорциональна скорости изменения магнитного потока Ф через контур.

 

Минус в формуле объясняет правило Ленца. Согласно ему, возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Если говорить еще проще, то индукционный ток направлен так, чтобы создавать препятствие причине,его вызвавшей. Чтобы определить вектор его движения, применяют правило буравчика. Иначе — правило правой руки, или правого винта.

Если расположить ладонь правой руки таким образом, чтобы отогнутый большой палец был направлен по движению проводника, то остальные пальцы укажут направление огибающих его линий магнитной индукции.

Источник: pinterest.ru

Как решать задачи: примеры

Закон Фарадея лежит в основе практически всей электрической промышленности. Предлагаем рассмотреть примеры решения задач, где встречается это физическое явление.

Надеемся, наша статья была вам полезна, и с заданиями по физике, касающимися этой темы, вы справитесь без труда. Но если возникнут проблемы, то в ФениксХелп вам всегда помогут.

Закон электромагнитной индукции (закон Фарадея – Максвелла – Ленца) – З – Русский алфавит – Словарь-справочник электрика

Закон электромагнитной индукции, закон Фарадея – Максвелла – Ленца — закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. Эдс электромагнитной индукции, в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Пусть в однородном магнитном поле B помещен прямолинейный отрезок проводника. При передвижении его перпендикулярно к силовым линиям заряды под действием магнитной силы начнут передвигаться вдоль проводника перпендикулярно к направлению движения и вектору поля B. Направление тока легко установить по правилу правой руки. Ток будет течь до тех пор, пока на концах проводника не образуются заряды противоположного знака, которые создадут электрическое поле E, направленное против силы, действующей на заряд. Электрические и магнитные силы уравновесят друг друга, и движение зарядов прекратится. В этот момент E=-q[VB]/q=-[VB]. В рассматриваемом случае заряды накапливаются на концах проводника. Если поместить в магнитное поле замкнутый контур и двигать его так, чтобы плоскость рамки была перпендикулярна к линиям однородного магнитного поля B, то ток пойдет по стороне ab (от a к b) и по dc (от d к c). Две другие стороны можно не рассматривать, так как сила, действующая на заряды, расположенные в проводнике, перпендикулярна к проводу и движение зарядов прекращается. Если токи в сторонах ab и dc текут навстречу друг другу, что приводит к накоплению заряда, замкнутый ток по рамке не пойдет. Величина эдс вдоль рамки равна нулю ΣE_lΔl=E_abl_ab+E_bcl_bc+E_cdl_cd+E_dal_da=(E+0-E+0)Δl=0. При движении рамки в том же направлении сторона dc выйдет из области, занимаемой магнитным полем, и поток последнего через плоскость рамки начнет уменьшаться. В этом случае сила, действовавшая на заряды, принадлежащие стороне dc, исчезнет и заряды, движущиеся от a к b, ничто уравновешивать не будет. По рамке пойдет замкнутый ток. То же самое будет наблюдаться при движении, например, соленоида относительно неподвижно лежащей рамки. Величина эдс в этом случае равна ΣEΔl=E_abl_ab+0+0+0=E_abl_ab=VBΔl. Таким образом, наведенная в проводе эдс электромагнитной индукции пропорциональна величине магнитной индукции поля, в котором движется проводник, длине провода и скорости его движения в направлении, перпендикулярном к магнитным силовым линиям.

Если обозначить скорость V=Δx/Δt где Δx — смещение рамки за время Δt, то ΣEΔl=-BΔxΔl/Δt. Знак минус в правой части равенства объясняется законом Ленца. Так как произведение ΔxΔl равно изменению площади ΔS, пронизываемой магнитным потоком, а ΔSB=ΔΦ — изменение самого магнитного потока за время t, то получим ΣEΔl=-ΔΦ/Δt. Таким образом, при изменении магнитного потока через контур начинает идти ток (индукционный или наведенный), который обязан своим возникновением электрическому полю. Величина эдс поля зависит от скорости изменения магнитного потока.

Электромагнитная индукция. Закон Фарадея. Правило Ленца. Самоиндукция

1. Лекция 9. Электромагнитная индукция

1. Закон Фарадея.
2. Правило Ленца.
3. Самоиндукция.
4. Взаимная индукция.
5. Вихревые токи.
6. Плотность энергии магнитного поля.
7. Энергия и силы в магнитном поле.
8. Магнитное давление.
В 1831-м Майкл Фарадей открыл
электромагнитную индукцию — возникновение
разности электрических потенциалов между
частями проводника, движущегося в магнитном
поле.
На лекциях его не раз спрашивали о возможной
пользе от электромагнитной индукции. История
донесла два ответа: светской даме — «Мадам, а
какова польза от новорождённого младенца?» и
министру финансов — «Когда-нибудь Вы сможете
обложить это налогом».
А.С. Чуев. 2020 г.
2
ФАРАДЕЙ Майкл (1791 – 1867) –
знаменитый английский физик.
Исследования в области
электричества, магнетизма,
магнитооптики, электрохимии.
Создал лабораторную модель
электродвигателя. Открыл экстротоки
при замыкании и размыкании цепи и установил их
направление. Открыл законы электролиза, первый ввел
понятия поля и диэлектрической проницаемости, в 1845
употребил термин «магнитное поле».
Кроме всего прочего М. Фарадей открыл явления диа и
парамагнетизма. Он установил, что все материалы в
магнитном поле ведут себя по-разному: ориентируются по
полю (пара и ферромагнетики) или поперек поля –
А.С. Чуев. 2020 г.
3
диамагнетики.
Сила Лоренца или закон Фарадея? Два разных
объяснения одного и того же явления
e nv j
2
Ф
Ф
ЭДС
[ v, B] dl
[ v, B]l ;
t
t
1
[ v, B ] Е
Первая составляющая ЭДС – закон Фарадея, вторая составляющая – изза сила Лоренца. Для лучшего понимания формулы все части следует
умножить на q.
А.С. Чуев. 2020 г.
4
А.С. Чуев. 2020 г.
5
Известные опыты Фарадея по магнетизму:
катушка и постоянный магнит
Если перемещать магнит относительно катушки,
то в катушке возникнет электрический ток.
А.С. Чуев. 2020 г.
6
То же самое с двумя близко расположенными
катушками: если к одной из катушек подключить
источник переменного тока, то в другой тоже возникает
переменный ток.
А.С. Чуев. 2020 г.
7
Эффект усилится, если две катушки
соединить намагничиваемым
сердечником.
А.С. Чуев. 2020 г.
8
При этом, явление совершенно не зависит от способа
изменения потока вектора магнитной индукции.
Получается, что движущиеся заряды (ток) создают
магнитное поле, а движущееся магнитное поле создает
(вихревое) электрическое поле или индукционный ток
А.С. Чуев. 2020 г.
9
Для многих витков или источников
– потокосцепление
При равенстве потоков
А.С. Чуев. 2020 г.
10
В 1833 г. Ленц установил общее правило
нахождения направления индукционного тока:
индукционный ток всегда направлен так, что
магнитное поле этого тока препятствует
изменению магнитного потока, вызывающего
индукционный ток.
Это утверждение носит название
правило Ленца.
А.С. Чуев. 2020 г.
11
Опыт
Алюминиевое кольцо выталкивается и зависает над
сердечником соленоида, подключенного к генератору
переменного электрического тока.
Сила отталкивания возникает в соответствии с правилом Ленца
– индукционный ток порождает магнитное поле,
препятствующее изменению магнитного потока в контуре
А.С. Чуев. 2020 г.
12

13. Явление самоиндукции

До сих пор мы рассматривали изменяющиеся
магнитные поля не обращая внимание на то, что
является их источником. На практике, чаще всего
магнитные поля создаются с помощью
различного рода соленоидов, т.е. многовитковых
контуров с током.
А.С. Чуев. 2020 г.
13
Здесь возможны два случая:
при изменении тока в контуре
изменяется магнитный поток,
пронизывающий:
а) этот же контур,
б) соседний контур.
А.С. Чуев. 2020 г.
14
• ЭДС индукции, возникающая в самом же контуре
называется ЭДС самоиндукции, а само явление –
самоиндукция.
Если же ЭДС индукции возникает в соседнем
контуре, то говорят о явлении взаимной индукции.
Ясно, что природа явления одна и та же, а разные
названия – чтобы подчеркнуть место возникновения ЭДС
индукции.
А.С. Чуев. 2020 г.
15
Т.к. магнитная индукция В пропорциональна току I
(В = μμ0nI), следовательно
Ψ = LI,
где L – коэффициент пропорциональности, названный
индуктивностью контура.
L = const, если внутри контура нет ферромагнетиков,
т.к. μ = f(I) = f(H)
Индуктивность контура L зависит от геометрии
контура: числа витков, площади витка контура.
А.С. Чуев. 2020 г.
16
За единицу индуктивности в СИ
принимается индуктивность такого
контура, у которого при токе I = 1А
возникает полный поток Ψ = 1Вб.
Эта единица называется Генри (Гн).
Единица измерения индуктивности
L Гн
L Вб В с Ом с 1Гн
I А
А
А.С. Чуев. 2020 г.
17
Индуктивность соленоида L.
Было в лекции 5
Если длина соленоида l гораздо больше его диаметра
d ( l >> d), то к нему можно применить формулы для
бесконечно длинного соленоида.
Из циркуляции вектора В
N
B μμ 0 I
l
Здесь N – число витков.
Поток через каждый из витков Ф = ВS
2
N
N
S
Потокосцепление NBS μμ I NS μμ
I
0
0
l
По определению:
LI
N 2S
L μμ 0
l
А.С. Чуев. 2020 г.
l
L μμ 0 n 2V
18
При изменении тока в контуре в нем
возникает ЭДС самоиндукции, равная
d
d
dI
Ei
IL L
dt
dt
dt
Знак минус в этой формуле обусловлен
правилом Ленца.
dI
Ei L
dt
А.С. Чуев. 2020 г.
19

20. Явление самоиндукции при замыкании и размыкании цепи, содержащей индуктивность

Случай 1. Подключение к источнику цепи с
индуктивностью
По правилу Ленца, токи возникающие в цепях вследствие
самоиндукции всегда направлены так, чтобы
препятствовать изменению
тока,
А.С. Чуев.
2020 г. текущего в цепи.
20
Это приводит к тому, что при замыкании ключа К установление
тока I2 в цепи содержащей индуктивность L ,будет происходить не
мгновенно, а постепенно.
Сила тока в этой цепи будет удовлетворять уравнению
RL t
I 2 I 0 1 e
Скорость возрастания тока будет характеризоваться постоянной
времени цепи
L
τ
R
В цепи, содержащей только активное сопротивление R ток I1
А.С. Чуев. 2020 г.
21
установится практически мгновенно.
Случай 2. Отключение цепи, содержащей
индуктивность L, от источника.
Размыкание цепи в момент времени t0
приводит к резкому возрастанию ЭДС индукции,
определяемой по формуле
dI
Ei L
.
dt
R
Происходит этот скачок напряжения вследствие
большой величины скорости изменения тока dI .
А.С. Чуев. 2020 г.
dt
22
Нельзя резко размыкать цепь,
состоящую из трансформатора и других
индуктивностей.
А.С. Чуев. 2020 г.
23

24. Взаимная индукция

Возьмем два контура, расположенные недалеко друг от
друга
В первом контуре течет ток I1.
Он создает магнитный поток, который пронизывает и
витки второго контура.
2 L21I1
А.С. Чуев. 2020 г.
24
При изменении тока I1 во втором контуре наводится ЭДС
индукции
1 L12 I 2
Аналогично, ток I2 второго контура создает магнитный поток
пронизывающий первый контур
dI1
Ei 2 L21
dt
И при изменении тока I2 наводится ЭДС
Ei1 L12
А.С. Чуев. 2020 г.
dI 2
dt
25
Контуры называются связанными, а явление –
взаимной индукцией.
Коэффициенты L21 и L12 называются взаимной
индуктивностью или коэффициенты взаимной индукции.
Причём
L21 = L12 .
Трансформатор является типичным примером двух
связанных контуров.
А.С. Чуев. 2020 г.
26

27. Устройство трансформатора

Явление взаимной индукции используется в широко
распространенных устройствах – трансформаторах.
Трансформатор был изобретен Яблочковым – русским
ученым, в 1876г. для раздельного питания отдельных
электрических источников света (свечи Яблочкова).
А.С. Чуев. 2020 г.
27

28. Вихревые токи (токи Фуко)

А.С. Чуев. 2020 г.
28

29. Энергия магнитного поля

Рассмотрим случай отключения индуктивности от источника
тока
Считается, что ток в цепи после отключения поддерживается
за счет ранее накопленной энергии магнитного поля
А.С. Чуев. 2020 г.
29
Энергия индуктивности с током
dA = EiIdt
dI
dA L
Idt LIdI
dt
0
LI 2
A L IdI
2
I
LI
W
2
2
А.С. Чуев. 2020 г.
Ф
W
2L
2
30
LI 2
W
2
n – количество витков на единицу длины соленоида
Объемная плотность энергии магнитного поля
μμ 0n VH
μμ 0 H
W
V
2
2
2n
2
2
2
А.С. Чуев. 2020 г.
μμ 0 H 2
W
V
2
31
Магнитное давление
А.С. Чуев. 2020 г.
32
А.С. Чуев. 2020 г.
33

34. Факультативный материал и материал для повторения

А.С. Чуев. 2020 г.
34
А.С. Чуев. 2020 г.
35
А.С. Чуев. 2020 г.
36
А.С. Чуев. 2020 г.
37
А.С. Чуев. 2020 г.
38
А.С. Чуев. 2020 г.
39
А.С. Чуев. 2020 г.
40
Подтверждающие примеры
А.С. Чуев. 2020 г.
41
А.С. Чуев. 2020 г.
42
А.С. Чуев. 2020 г.
43
Парадокс изображения магнитных полей
Закон Б-С-Л не выполняется
0 I [dl , r ]
dB
4
r3
А.С. Чуев. 2020 г.
I [dl , r ]
dН
.
3
4 r
44
Правильные соотношения магнитных
векторов внутри магнетиков
А.С. Чуев. 2020 г.
45
Конец лекции 9
А.С. Чуев. 2020 г.
46

Закон Фарадея и закон электромагнитной индукции Ленца

Законы электромагнитной индукции Фарадея объясняют взаимосвязь между электрической цепью и магнитным полем. Этот закон является основным принципом работы большинства электродвигателей, генераторов, трансформаторов, индукторов и т. Д.

Первый закон Фарадея:

Всякий раз, когда проводник помещается в переменное магнитное поле, ЭДС индуцируется поперек проводника (называемая индуцированной ЭДС), и если проводник представляет собой замкнутую цепь, то индуцированный ток течет через него.
Магнитное поле можно варьировать различными методами –
1. Путем перемещения магнита
2. Перемещая катушку
3. Вращением катушки относительно магнитного поля

Второй закон Фарадея:

Второй закон электромагнитной индукции Фарадея утверждает, что величина наведенной ЭДС равна скорости изменения магнитных связей с катушкой. Магнитопровод представляет собой произведение числа витков и магнитного потока, связанного с катушкой.

Формула закона Фарадея:

Если считать, что проводник движется в магнитном поле, тогда
потокосцепление с катушкой в ​​исходном положении проводника = NΦ ₁ (Wb) (N – скорость двигателя, Φ – поток)
потокосцепление с катушкой в ​​конечном положении проводника = NΦ ₂ (Wb)
изменение потокосцепления с начального на конечное = N (Φ ₁ – Φ ₂ )
пусть Φ ₁ – Φ ₂ = Φ
следовательно, изменение потокосцепления = NΦ
и скорость изменения потокосцепления = NΦ / t
взяв производную от RHS
скорость изменения магнитных связей = N (dΦ / dt)

Согласно закону электромагнитной индукции Фарадея , скорость изменения магнитных связей равна наведенной ЭДС

Итак, E = N (dΦ / dt) (вольт )

Феномен взаимной индукции

Переменный ток, протекающий в катушке, создает вокруг нее переменное магнитное поле.Когда две или более катушек магнитно связаны друг с другом, тогда переменный ток, протекающий через одну катушку, вызывает наведенную ЭДС на других связанных катушках. Это явление называется взаимной индукцией.

Закон Ленца

Закон электромагнитной индукции Ленца гласит, что, когда ЭДС индуцируется в соответствии с законом Фарадея, полярность (направление) этой индуцированной ЭДС такова, что она противодействует причине ее возникновения.

Таким образом, учитывая закон Ленца

E = -N (dΦ / dt) (вольт)

Отрицательный знак показывает, что направление наведенной ЭДС и направление изменения магнитных полей имеют противоположные знаки.

Закон электромагнитной индукции Фарадея – Первый закон, Второй закон

Закон электромагнитной индукции Фарадея

Электромагнитная индукция Процесс был разработан Майклом Фарадеем в 1831 году. поток. он намотал две катушки на железное кольцо и обнаружил, что при включении переключателя на гальванометре наблюдается отклонение. А при размыкании переключателя гальванометр отклонялся в обратном направлении.

Аналогичное отклонение гальванометра было обнаружено при перемещении постоянного магнита по направлению к катушке и от нее.

Таким образом, он пришел к выводу, что электрический ток может быть произведен движением магнитного потока относительно катушки. Величина наведенной э.д.с. пропорциональна скорости изменения магнитного потока, проходящего через катушку.

В качестве альтернативы, мы можем сказать, что когда проводник режет или режется магнитным потоком, э.д.с.м. генерируется в проводнике.Величина создаваемой ЭДС. пропорциональна скорости, с которой проводник режет или разрезается магнитным потоком.

ПЕРВЫЙ ЗАКОН

Первый закон электромагнитной индукции Фарадея гласит, что всякий раз, когда проводник помещается в переменное магнитное поле, индуцируются ЭДС, которая называется индуцированной ЭДС, если цепь проводника замкнута, индуцируется также ток, который называется индуцированным током.

или

Всякий раз, когда проводник вращается в магнитном поле, индуцируется ЭДС, которая является индуцированной ЭДС.

Закон Фарадея Анимация

ВТОРОЙ ЗАКОН

Второй закон электромагнитной индукции Фарадея гласит, что индуцированная ЭДС равна скорости изменения потоковых связей (потокосцепления – это произведение витков n катушки и связанного с ней потока).

РАЗЪЯСНЕНИЕ ЗАКОНА ФАРАДА

Пусть

Начальные потокосцепления = Nφ1

Конечные потокосцепления = Nφ2

Изменение потокосцепления = Nφ2 – Nφ1

= N ((φ2-φ1)

Если (φ2-φ1) = φ

Тогда изменение потокосцепления = Nφ

Скорость изменения потокосцеплений = Nφ / т вес.б / с

Взяв производную от правой части, получаем

Скорость изменения потокосцеплений = Ndφ / dt wb / sec

Rut, согласно законам электромагнитной индукции Фарадея, скорость изменения магнитных связей равна индуцированной ЭДС, следовательно, мы можем написать

= Ndφ / dt вольт

Обычно законы Фарадея записываются как

e = -Ndφ / dt вольт

Где отрицательный знак представляет направление индуцированного тока в проводнике, будет таким, что создаваемое им магнитное поле будет противодействовать глаголу «причина его создания».

Электромагнитная индукция | HowStuffWorks

В магнетизме есть что-то почти волшебное. В детстве мы были очарованы способностью магнита воздействовать на такие металлы, как железо, никель и кобальт, не касаясь их. Мы узнаем о притяжении и отталкивании между магнитными полюсами и становимся свидетелями формы магнитного поля, сформированного в железных опилках, окружающих стержневой магнит. Физики говорят нам, что электромагнетизм, сила, управляющая электричеством и магнетизмом, во много раз сильнее гравитации.Подвешивание поезда на магнитной подвеске над его путями – яркий пример этой силы.

Как следует из названия «электромагнетизм», электричество и магнетизм очень тесно связаны. Эта взаимосвязь позволяет им влиять друг на друга бесконтактно, как в примере с поездом на магнитной подвеске, или посредством электромагнитной индукции. Электромагнитная индукция возникает, когда цепь с протекающим через нее переменным током генерирует ток в другой цепи, просто будучи размещенной поблизости.Переменный ток – это электричество, протекающее по линиям электропередач и домашней электропроводке, в отличие от постоянного тока, который мы получаем от батарей.

Как одна цепь вызывает ток в другой, не касаясь ее, и какое отношение все это имеет к магнетизму? Прежде чем мы перейдем к этому, нам нужно рассмотреть несколько принципов, связывающих магнетизм и электричество:

1. Каждый электрический ток имеет окружающее магнитное поле.
2. Переменные токи имеют переменные магнитные поля.
3. Колеблющиеся магнитные поля заставляют токи течь в проводниках, помещенных в них, что также известно как закон Фарадея.

Сложение этих трех свойств вместе означает, что изменяющийся электрический ток окружен соответствующим изменяющимся магнитным полем, которое, в свою очередь, генерирует изменяющийся электрический ток в проводнике, помещенном внутри него, который имеет собственное магнитное поле… и так далее. Это электромагнитный эквивалент матрешки-матрешки. Таким образом, в случае электромагнитной индукции размещение проводника в магнитном поле, окружающем первый ток, генерирует второй ток.

Индукция – это принцип, который делает возможными электродвигатели, генераторы и трансформаторы, а также предметы, расположенные ближе к дому, такие как перезаряжаемые электрические зубные щетки и устройства беспроводной связи. Если у вас есть рисоварка, скорее всего, вы уже готовите на индукции. Теперь давайте посмотрим, как наведенный ток используется для нагрева индукционных варочных панелей.

Закон электромагнитной индукции Фарадея: уравнение и применение – стенограмма видео и урока

Закон Фарадея

Это открытие было настолько фундаментальным и важным, что теперь известно как Закон Фарадея , который гласит, что величина индуцированного напряжения равна скорости изменения магнитного потока.Это можно представить в виде уравнения как:

Это довольно много, поэтому давайте разберемся, чтобы посмотреть, что здесь происходит.

Сначала нам нужно освежить наш греческий язык. Для этого закона мы собираемся использовать греческую букву эпсилон , чтобы обозначить величину индуцированного напряжения, также известного как ЭДС . Это означает «электродвижущая сила». Думайте об этом как об электрическом токе, вызванном движением силы.Также может быть полезно увидеть, что epsilon выглядит как курсивный E для «EMF». Далее идет буква , дельта , что означает «изменение». Наконец, у нас есть phi , который представляет магнитный поток. Это просто величина магнитного поля, проходящего через заданную площадь поверхности. В случае Фарадея площадь поверхности проходила через катушку с проволокой, в которую он перемещал магнит и из него. Наконец, t в нижней части уравнения обозначает «время».

Теперь, когда мы знаем, как читать закон Фарадея, давайте посмотрим, что именно он означает. Мы можем сказать, просто взглянув на уравнение, что ЭДС и магнитный поток пропорциональны, потому что оба находятся наверху в уравнении. Это означает, что когда одна переменная увеличивается или уменьшается, другая переменная будет изменяться в том же направлении на ту же величину. Изменение времени находится внизу, это означает, что оно обратно пропорционально ЭДС. Изменение здесь будет противоположным. Когда одна переменная увеличивается или уменьшается, другая переменная будет меняться в противоположном направлении на ту же величину.По мере увеличения изменения магнитного потока увеличивается и ЭДС. Но если изменение во времени увеличится, ЭДС уменьшится. Помните: «дельта» означает «изменение», поэтому дело не в величине потока или времени, а в величине изменения одной из тех переменных, которые нас интересуют.

Возьмем катушки с проволокой Фарадея, Например. Если у вас есть магнит, и вы пропустите его через витую проволочную катушку, вы создадите или индуцируете определенное количество напряжения. Но если вы пропустите тот же магнит через катушку с вдвое большим количеством витков, вы создадите в два раза больше напряжения, потому что вы удвоили площадь поверхности, через которую проходит магнитное поле.Если вы пропустите магнит через катушку с 20 петлями, вы наведете в 20 раз больше напряжения. Таким образом, мы можем видеть, как магнитный поток и ЭДС пропорциональны, потому что они изменяются на одинаковую величину.

Мы можем использовать проволочную катушку Фарадея, чтобы увидеть, как время также влияет на ЭДС. При очень медленном перемещении магнита по петлям катушки создается небольшое напряжение, потому что изменение во времени очень велико. Однако быстро перемещайте этот магнит через петлю, и вы создадите большое напряжение, потому что изменение во времени очень мало.Это показывает нам, как эти два обратно пропорциональны – когда один растет, другой опускается на ту же величину. Большое изменение во времени (медленное движение) означает, что создается небольшое напряжение, в то время как небольшое изменение во времени (быстрое движение) означает, что индуцируется большое напряжение.

Применение закона Фарадея

Закон Фарадея выходит далеко за рамки классных лабораторных экспериментов с магнитами и проводами. Реальные применения этого типа индукции напряжения многочисленны, и, знаете ли вы об этом или нет, они окружают вас в повседневной жизни.

И генераторы, и двигатели используют закон Фарадея. Генератор преобразует механическую энергию в электрическую, поэтому он полезен при отключении электроэнергии. Двигатель делает обратное и преобразует электрическую энергию в механическую. Это делает их полезными для питания транспортных средств. Генератор вырабатывает электрический ток, вращая катушку в постоянном магнитном поле. В двигателе через катушку проходит ток, который заставляет его вращаться. В любом случае оба используют катушки с проволокой и магнитные поля для наведения напряжения.Каждый раз, когда вы едете на работу или в школу, вы применяете закон Фарадея!

Индукционная готовка также использует закон Фарадея. Это когда через катушку на плите протекает ток, который создает магнитное поле. Когда другой проводящий материал, такой как сковорода, помещается поверх этой области, на него наводится ток, нагревая его и готовя все, что находится в сковороде. Что действительно приятно в этом, так это то, что сама плита не нагревается, и нет прямой передачи тепла, как в газовой или электрической плите.Сковорода нагревается магнитным полем, поэтому вы можете дотронуться до плиты, не обожгясь!

Электрогитары, трансформаторы и электромагнитные расходомеры также используют закон Фарадея. Как видите, уважение к Фарадею и его творчеству заслужено.

Резюме урока

Майкл Фарадей считается одним из наших величайших ученых, и это очень подходящее название. Изобретатель и первооткрыватель многих вещей, одно из величайших открытий Фарадея заключалось в том, как напряжение может быть индуцировано изменяющимся магнитным полем, известным как электромагнитная индукция .

Закон Фарадея резюмировал электромагнитную индукцию следующим образом: величина индуцированного напряжения равна скорости изменения магнитного потока. Это говорит о том, что величина напряжения равна изменению магнитного потока с течением времени, или, в форме уравнения: Эпсилон = Дельта Фи / Дельта t . Здесь эпсилон, – индуцированное напряжение, или ЭДС, дельта, – «изменение», фи, – магнитный поток, а t – время.Поток и ЭДС пропорциональны, потому что они увеличиваются или уменьшаются на одну и ту же величину.

Увеличение количества витков в катушке с проволокой увеличивает магнитный поток, что, следовательно, увеличивает ЭДС. Время и ЭДС обратно пропорциональны, потому что по мере увеличения изменения времени величина индуцированного напряжения уменьшается. Если вы очень быстро перемещаете магнит через катушку с проволокой, величина индуцированного напряжения увеличивается, потому что изменение во времени уменьшается.

Закон Фарадея применим не только к лабораторным экспериментам, и мы можем видеть его примеры в действии повсюду вокруг нас в повседневной жизни.В генераторах, двигателях, трансформаторах, электрических инструментах и ​​индукционных плитах используется закон Фарадея, который позволяет нам ездить на работу, снабжать электроэнергией дома, готовить еду и, конечно же, зажигать!

Результаты обучения

После этого видеоурока вы сможете:

• Описать, что такое электромагнитная индукция
• Объясните, что такое закон Фарадея, и определите уравнение, которое с ним совпадает
• Обобщите взаимосвязь между магнитным потоком, временем и ЭДС согласно закону Фарадея
• Найдите примеры закона Фарадея в бытовой технике

Что такое закон Фарадея? Законы электромагнитной индукции

Закон электромагнитной индукции Фарадея

Электромагнетизм

Взаимодействие между магнитным полем и электрическим током называется электромагнетизмом.Проводники с током создают магнитное поле, когда через них проходит ток. Движение электронов в проводнике приведет к возникновению электрического тока (дрейфующих электронов), который возникает в результате создания ЭДС в проводнике.

ЭДС, возникающая в проводнике, может быть в форме энергии, хранящейся в химической энергии или в магнитном поле. Проводники с током, помещенные в магнитное поле, будут испытывать механическую силу, в то время как проводники, помещенные в магнитное поле, будут перемещать электроны, что приведет к возникновению электрического тока.

Полевой поток

Два магнита с разными полюсами будут притягиваться друг к другу, в то время как магниты с одинаковыми полюсами будут отталкивать друг друга (то же самое происходит с электрическими зарядами). Каждый магнит окружен силовым полем и представлен воображаемыми линиями, исходящими от северного полюса магнита, переходящего в южный полюс того же магнита.

Прочтите важные термины, связанные с потоком поля и магнитным полем. Заполните формулы здесь.

«Линии, соединяющие северный и южный полюсы магнита, которые представляют силовое поле, которое связывает катушки в трансформаторе, называются магнитным потоком».

Электромагнитная индукция

Электромагнитная индукция – это явление, объясняющее, как ЭДС и ток индуцируются или могут индуцироваться в катушке при взаимодействии катушки и магнитного поля. Это явление «электромагнитной индукции» объясняется законами электромагнитной индукции Фарадея. Направление наведенной ЭДС в катушке или индукторах объясняется законом Ленца и правилом правой руки Флеминга.

Похожие сообщения:

Законы электромагнитной индукции Фарадея

После того, как Андре Мари Ампер (французский математик и физик, известный как отец электромагнетизма) и другие исследовали магнитный эффект тока, Майкл Фарадей попробовал обратное.В ходе своей работы в 1831 году он открыл принцип электромагнитной индукции, согласно которому при изменении магнитного поля, в которое была помещена катушка или индуктор, в катушке индуцировалась ЭДС.

Это происходило только всякий раз, когда он перемещал катушку или магнит, который он использовал в эксперименте. ЭДС индуцировалась в катушке только тогда, когда происходило изменение потока поля (если катушка зафиксирована, перемещение магнита по направлению к катушке или от нее вызывает индукцию ЭДС). Таким образом, законы электромагнитной индукции Фарадея гласят:

Первый закон Фарадея

Первый закон электромагнитной индукции Фарадея гласит, что «ЭДС индуцируется в катушке, когда происходит изменение потока, связанного с катушкой».

Другими словами, всякий раз, когда поток, связанный или связанный с цепями, изменяется. в цепи индуцируется E.M.F. Эта ЭДС длится только до тех пор, пока происходят изменения. Индуцированный ЭДС изменяется как скорость изменения потока.

Второй закон Фарадея

Второй закон Фарадея электромагнитной индукции гласит, что «величина наведенной ЭДС в катушке прямо пропорциональна скорости изменения магнитного потока, связанного с катушкой».

Другими словами, E.МФ, индуцированная в электрической цепи, пропорциональна скорости изменения во времени потока магнитной индукции, связанного с цепью. Величина наведенного ЭДС прямо пропорциональна скорости изменения тока. Короче говоря, чем больше потокосцепление к катушке или проводнику, тем больше наведенная ЭДС (dΦ / dt).

Законы электромагнитной индукции Фарадея можно математически записать в виде уравнения следующим образом.

e = N d Φ / d t

Где

• e = Индуцированная ЭДС
• N = количество витков
• dΦ = Изменение потока
• dt = Изменение во времени

Формула и уравнение закона электромагнитной индукции Фарадея:

Предположим, что катушка содержит N витков, а магнитный поток изменяется от начального значения «Φ ₁ » до конечного значения «Φ _{». 2} »за время« t »секунд.Имейте в виду, что потокосцепление – это произведение связанного потока на количество витков в катушке. т.е.

Начальные потокосцепления = NΦ ₁

Конечные потокосцепления = NΦ ₂

Индуцированная ЭДС

e = NΦ ₁ – NΦ ₂ / т… wb / s или вольт

∴ Индуцированная Уравнение ЭДС «e» преобразовано в дифференциальную форму

e = d / dt (NΦ)… вольт

e = N (dΦ / dt)… вольт

Здесь скорость изменения потока (dΦ) происходит меньше возможное время (dΦ).Знак минус «-» в правой части уравнения показывает, что индуцированная ЭДС направляет ток в таком направлении, где он противодействует его магнитному эффекту, который произвел ЭДС. Проще говоря, индуцированная ЭДС противодействует причине (изменение тока или движение), которая ее производит (ЭДС). Это явление также известно как закон Ленца.

e = – N (dΦ / dt)… вольт

Наконец, эта формула показывает, что ЭДС, индуцированная в катушке, равна скорости изменения потока (dΦ / dt), умноженной на количество витков (Н) в этой катушке.т.е.

e = N (dΦ / dt)… вольт

Объяснение и работа закона Фарадея

На следующем рисунке показаны различные сценарии работы закона Фарадея.

Рис. 1.A показывает, что когда магнит движется вправо, магнитное поле изменяется по отношению к катушке, и возникает ЭДС.

Рис. 1.B показывает, что по мере того, как магнит движется быстрее вправо, магнитное поле изменяется быстрее по отношению к катушке, и индуцируется большая ЭДС.

Рис. 2.A показывает, что магнит движется через катушку и индуцирует ЭДС.

Рис. 2.B показывает, что магнит движется с той же скоростью через катушку с большим количеством витков (петель) и индуцирует большую ЭДС.

На рис. 2 показана основная демонстрация второго закона Фарадея, т.е. величина наведенной ЭДС прямо пропорциональна количеству мелодий в катушке.

Применение закона Фарадея

Самый мощный закон электромагнитной индукции Майкла Фарадея используется в различных приложениях, таких как электрические машины, медицинские поля, промышленность и т. Д.Некоторые из них следующие.

• Электрические трансформаторы (силовые и распределительные т / ф), асинхронные двигатели, генераторы и генераторы переменного тока (для выработки электроэнергии) основаны на взаимной индукции, то есть законе Фарадея.
• Принцип действия электромагнитного расходомера и индукционной плиты основан на законе электромагнетизма Фарадея.
• Он также используется в уравнении Максвелла, основанном на силовых линиях.
• Закон Фарадея также применим к развлечениям и музыкальным инструментам e.грамм. электрическое пианино, скрипка, электрогитара и т. д.
• Магнитная индукция на основе закона Фарадея, используемая в электрических и гибридных транспортных средствах, и транскраниальная магнитная стимуляция.
• Компьютер HD (жесткие диски) и графические планшеты работают на основе магнитной индукции, которая основана на законе Фарадея.

Решенный пример закона электромагнетизма Фарадея

Пример:

Примените закон Фарадея, чтобы найти наведенное напряжение или ЭДС на катушке со 100 витками, которая находится в магнитном поле и которая изменяется со скоростью 5 Вт / с.

Решение:

Приведенные данные:

• Число витков = 100
• Скорость изменения магнитного поля = 5 Вт / с.

Подставляем значения в уравнение закона Фарадея

e = N (dΦ / dt)

e = 100 x (5)

e = 500V.

Похожие сообщения

Что такое электромагнитная индукция? – Вселенная сегодня

Трудно представить мир без электричества. Когда-то электричество было скромным подарком, обеспечивающим человечество неестественным светом, который не зависел от газовых ламп или керосиновых фонарей.Сегодня он превратился в основу нашего комфорта, обеспечивая наше отопление, освещение и климат-контроль, а также питая всю нашу бытовую технику, будь то приготовление пищи, уборка или развлечения. И под большинством машин, которые делают это возможным, находится простой закон, известный как электромагнитная индукция, закон, который описывает работу генераторов, электродвигателей, трансформаторов, асинхронных двигателей, синхронных двигателей, соленоидов и большинства других электрических машин. С научной точки зрения это относится к созданию напряжения через проводник (провод или аналогичный кусок проводящего материала), который движется через магнитное поле.

Хотя считается, что многие люди внесли свой вклад в открытие этого явления, именно Майклу Фарадею приписывают первое открытие в 1831 году. Известный как закон Фарадея, он гласит, что «индуцированная электродвижущая сила (ЭДС) в любом замкнутый контур равен скорости изменения магнитного потока через контур ». На практике это означает, что электрический ток будет индуцироваться в любой замкнутой цепи, когда магнитный поток (то есть величина магнитного поля), проходящий через поверхность, ограниченную проводником, изменяется.Это применимо независимо от того, изменяется ли само поле по силе или через него перемещается проводник.
Тогда как уже было известно, что электрический ток создает магнитное поле, Фарадей показал, что верно и обратное. Короче говоря, он доказал, что можно генерировать электрический ток, пропуская провод через магнитное поле. Чтобы проверить эту гипотезу, Фарадей обернул кусок металлической проволоки вокруг бумажного цилиндра, а затем подключил катушку к гальванометру (устройству, используемому для измерения электрического тока).Затем он перемещал магнит взад и вперед внутри цилиндра и регистрировал с помощью гальванометра, что в проводе индуцировался электрический ток. На основании этого он подтвердил, что движущееся магнитное поле необходимо для индукции электрического поля, потому что, когда магнит прекращает движение, прекращается и ток.
Сегодня электромагнитная индукция используется для питания многих электрических устройств. Одно из наиболее широко известных применений – в электрических генераторах (таких как плотины гидроэлектростанций), где механическая энергия используется для перемещения магнитного поля мимо катушек с проволокой для генерации напряжения.
В математической форме закон Фарадея гласит:? = – d? B / dt, где? – электродвижущая сила, ΔB – магнитный поток, а d и t – расстояние и время.

Мы написали много статей об электромагнитной индукции для Universe Today. Вот статья об электромагнитах, а вот статья о генераторах.

Если вам нужна дополнительная информация об электромагнитной индукции, прочтите эти статьи в All About Circuits and Physics 24/7.

Мы также записали целый эпизод Astronomy Cast, посвященный электромагнетизму.Послушайте, Эпизод 103: Электромагнетизм.

Источники:
http://en.wikipedia.org/wiki/Electromagnetic_induction
http://en.wikipedia.org/wiki/Faraday%27s_law_of_induction
http://en.wikipedia.org/wiki/Mintage_flux
http: //micro.magnet.fsu.edu/electromag/java/faraday2/
http://www.scienceclarified.com/El-Ex/Electromagnetic-Induction.html
http://en.wikipedia.org/wiki/Гальванометр

Нравится:

Нравится Загрузка …

Физика | Бесплатный полнотекстовый | Закон Фарадея и магнитная индукция: причина и следствие, эксперимент и теория

1.Введение

Майкл Фарадей был первым, кто опубликовал экспериментальные результаты по электромагнитной индукции, явлению, которое часто описывается как ток, индуцируемый при изменении магнитного потока, проходящего через проводящую катушку.

Явление компактно описывается математической моделью, связывающей «электродвижущую силу» (ЭДС) V вокруг замкнутой цепи с временными изменениями магнитного потока Φ – интегралом магнитного поля по поверхности, очерченной этим замыканием.Закон индукции Фарадея может быть напрямую связан с векторным уравнением Максвелла – Фарадея ([1], с. 160). Используя обозначение где ∂t≡d / dt, уравнения записываются как

V = −∂tΦ↔∇ × E = −∂tB,

(1)

где E – электрическое поле, а B – магнитное поле. Однако фундаментальный закон причинности требует, чтобы эффекты не могли происходить раньше их причин; и это ожидание имеет математические последствия. Эти следствия приводят, в частности, к знаменитым соотношениям Крамерса-Кронига [2, 3, 4], которые можно использовать для ограничения как спектральных свойств физических величин, так и моделей, используемых для их описания.Здесь мы берем локальный взгляд на причинность, а не глобальный, и используем временную область, наиболее естественную для выражений причинного поведения. В этом случае существует схема [5] для приписывания конкретных причинно-следственных ролей компонентам математических моделей, которые основаны на временных дифференциальных уравнениях (математические подробности см. Также [6,7]). Проще говоря, это означает, что в любом уравнение математической модели – это член производной по времени высшего порядка, который следует рассматривать как следствие, а другие члены – как причины; но обратите внимание, что это также может быть применено к системам связанных уравнений (например,g., уравнения Максвелла ([5], раздел V), а также далее в этой статье в разделе 5.2). В качестве простого примера, поскольку второй закон Ньютона можно записать как ∂tv = F / m, то согласно [5] мы можем утверждать, что сила F вызывает изменение скорости v массы m. Использование этой интерпретации особенно естественно при рассмотрении вычислительного решения динамических физических моделей; см. Приложение A в [8], и где основное внимание уделяется тому, что происходит при обновлении текущего состояния системы [9,10] (т.е., интегрированный вперед во времени), или когда Вселенная расширяется в свое «будущее» (как, например, в подходе причинных множеств [11]). Обратите внимание, что другие обсуждения и подходы к причинности в электродинамике, относящиеся к закону Фарадея существуют [12,13,14]. В частности, одна значительная школа мысли предпочитает связывать все обратно с исходными исходными терминами (см., Например, [12] и примечания в Приложении B к [8]). К сожалению, поскольку закон Фарадея не содержит явных ссылок на исходные обвинения, мы не можем анализировать его в отношении причинно-следственных связей на этой основе – нам потребуется другая модель, которая действительно относилась бы к исходным зарядам и их перемещению (например,g., см. [15]). Следовательно, в дальнейшем мы решаем использовать только локальное и совместимое с Крамерсом-Кронигом определение [5] для того, что составляет причинную интерпретацию математической модели. 5] и во вставке 1, поскольку уравнение (1) не имеет производных по времени, применяемых к V, но имеет одну производную по времени, примененную к Φ, это означает, что ЭДС V следует рассматривать как причину, где изменение потока ∂tΦ является ее следствием. . Как следствие, было бы более интуитивно понятно переписать уравнение (1) как

∂tΦ = −V↔∂tB = −∇ × E,

(2)

где мы также вынуждены описывать пространственные градиенты электрического поля ∇ × E как причину, а результирующие временные изменения поля B как следствие.Несколько беспокоит то, что теперь это означает, что мы не можем интерпретировать нашу математическую модель закона индукции Фарадея как наше предпочтительное причинное утверждение: то есть, когда изменения потока вызывают ЭДС (и, следовательно, управляющие токи) [16,17,18]. Однако, основываясь на нашей математической модели, мы по-прежнему можем сделать более слабое утверждение, когда эти два понятия просто приравниваются или связаны друг с другом [19]. Эта ситуация предполагает, что уравнение (2), несмотря на его полезность, просто не подходит. причинно-следственная репрезентация эксперимента, который мы имели в виду.Чтобы решить эту проблему, нам необходимо провести четкое различие между причинной связью, очевидной в эксперименте, и причинной интерпретацией математической модели, которая обязательно является лишь приближением к этому эксперименту. Хотя мы обычно надеемся, что они согласны, кажется, что в случае с законом Фарадея они не согласны, и в разделе 2 мы обсуждаем, почему (или как) это может быть.

Ясно, что было бы желательно, чтобы наше математическое описание индукции явно показывало, как ЭДС или электрический ток могут генерироваться в проводнике, будь то изменяющиеся свойства магнитного поля или движение проводника внутри этих полей.Далее мы попробуем три (нерелятивистских) подхода к поиску математической модели, которая описывает, как определенное свойство или поведение магнитного потока (или, возможно, просто магнитного поля) явным образом можно отнести к причине ЭМП.

Первый из разделов 3 основан на уравнении Максвелла – Фарадея и не работает. Второй, в разделе 4, вместо этого основан на уравнении Максвелла – Ампера и достигает этой важной цели, но, возможно, не очень удовлетворительным образом. Третий, в Разделе 5, основан на законе силы Лоренца, и мы пробуем как простой абстрактный расчет, так и конкретную установку, распространенную во многих курсах бакалавриата, и выводим модель тока, обусловленного магнитными полями и движением.Наконец, в разделе 6 мы делаем вывод. Вставка 1. Как быть причинной: Рассмотрим простое модельное уравнение ∂tR (t) = Q (t), которое в использованной здесь интерпретации интерпретируется как «Q вызывает изменения R». Используя математическое определение производной, в некоторый произвольный момент времени t0 уравнение модели имеет вид

limδ → 0R (t0 + δ) −R (t0 − δ) 2δ = Q (t0).

(3)

Непосредственно перед переходом к пределу и для некоторого достаточно малого значения δ мы имеем

R (t0 + δ) −R (t0 − δ) 2δ = Q (t0).

(4)

Теперь давайте попробуем использовать это как предсказатель будущего.Мы сразу видим, что самая последняя (или наиболее приближенная к будущему) величина – это R (t0 + δ), поэтому мы переставляем, чтобы поместить это слева, и получаем

R (t0 + δ) = R (t0 − δ) + 2δQ (t0).

(5)

Здесь мы видим, что для обновления наших знаний о R до следующего значения в t + δ требуется (а) прошлое знание R (т. Е. R (t0 − δ)) и (б) текущее знание Q (т. Е. Q ( t0)). Таким образом, ясно, что значение Q вызывает изменения в R. Если бы мы вместо этого хотели вычислить Q, надеясь сказать что-то вроде «R вызывает Q», мы бы сначала переписали уравнение (4) на

Q (t0) = R (t0 + δ) −R (t0 − δ) 2δ,

(6)

но сразу увидим, что Q (t0) зависит от будущего значения R, а именно R (t0 + δ) – и зависимость от будущих значений несовместима со стандартными представлениями о причинности.

Эта презентация уровня бакалавриата, в которой обсуждается магнитная индукция, подчеркивает различие между любой предполагаемой экспериментальной причинностью и той, которая закодирована в ее математической модели. Это показывает, что очевидно полезное определение ЭДС фактически работает против наших попыток создать модель, в которой она вызвана изменениями магнитного потока. Напротив, альтернативный подход к электрическим токам, генерируемым движением или изменением магнитного поля, не имеет таких ограничений.

2.Эксперимент

Рассмотрим пример эксперимента, состоящего из двух частей устройства: (i) магнита и (ii) петли или катушки с присоединенным вольтметром, как показано на рисунке 1. Когда мы перемещаем магнит вблизи петли, мы видим индуцированное напряжение. Поэтому на основе этого экспериментального опыта вполне естественно – и действительно точно – сделать вывод, что перемещение магнита вызвало появление напряжения (или ЭДС). Если мы также изучаем физику, мы могли бы также связать движение магнита с величиной магнитного потока, пересекающего петлю, и, таким образом, наш эксперимент показывает, что «изменение потока вызывает ЭДС».Только что описанная «экспериментальная причинность» не вызывает сомнений. Однако здесь исследуется слияние этого экспериментального опыта причинности с любой причинной интерпретацией математического выражения закона Фарадея, то есть уравнения (2).

Для лучшего понимания нам нужно начать с более ясного понимания того, почему мы можем сделать вывод, что напряжение было вызвано нашими действиями при перемещении магнита. Примечательно, что мы должны понимать, что это не просто потому, что мы видели конечное напряжение, зарегистрированное на вольтметре, поскольку оно могло просто быть плохо обнулено и всегда иметь какое-то конечное показание, или смещено эффектами некоторого внешнего поля, не имеющего отношения к эксперименту индукции. .Вместо этого мы говорим «вызвано», потому что после (и по мере того, как) мы перемещали магнит около петли, напряжение, регистрируемое вольтметром, изменялось. Изменение напряжения – это видимый эффект, который заставляет искать его причину. В таком случае, по крайней мере, мы должны захотеть, чтобы наша причинная модель индукции описывала, как изменения напряжения («ЭДС») происходят из-за внешних стимулов.

Давайте теперь попробуем математически кодифицировать наш эксперимент, учитывая заранее определенный вход (движение магнита), ища результирующий эффект на выходе (ЭДС V).Предположим, для простоты, магнит фиксированной силы с такой же фиксированной ориентацией, единственным входом в нашу модель должна быть только его скорость v (t). Это v (t) – причина; это то, что мы указываем в экспериментальном проекте, а затем реализуем. Мы надеемся или ожидаем, что эта причина приведет к изменениям. Это изменение должно быть видно как влияние на измеряемую ЭДС, так что в один момент она может быть равна нулю, а в следующий будет другой, то есть должна измениться со временем и каким-то образом в результате причины v (t ).Таким образом, мы могли бы написать где L (·) – функция или оператор, который, как считается, содержит всю необходимую информацию об электромагнетизме, структуре поля, создаваемой магнитом, силе Лоренца для зарядов и теории цепей. Теперь мы можем сразу увидеть, что структура математическая модель Уравнение (7) для нашего эксперимента не имеет той же формы, что и закон Фарадея: уравнение (2) явно относится только к изменениям потока ∂tΦ, а не к изменениям ЭДС. В самом деле, это не должно вызывать удивления, поскольку уравнение (2) даже не является попыткой микроскопической модели экспериментального процесса, в которой движущийся магнит создает изменяющееся распределение электромагнитного поля, которое затем влияет на движение электронов, производящие или изменяющие электрические токи (например,g., [15]), и, таким образом, впоследствии вызывает ЭДС. Поскольку в уравнении (2) опущено так много экспериментальных деталей, на первый взгляд неясно, почему мы должны ожидать, что они будут совпадать, не говоря уже об идеальном совпадении.

Тем не менее, в дальнейшем мы попытаемся найти закон Фарадея, который лучше соответствует нашей экспериментальной концепции.

3. Уравнение Максвелла – Фарадея

Сначала рассмотрим стандартный вывод закона индукции Фарадея, начиная с уравнения Максвелла ротора; обратите внимание, однако, что некоторые подходы используют обратный подход, и начинают с индукции и сводят его к уравнению локона.

Мы начинаем с петли материала и рассматриваем эту петлю как границу C некоторой замкнутой поверхности S, и рассматриваем электрическое поле E и магнитное поле B, как показано на рисунке 2. Вывод начинается с уравнения Максвелла – Фарадея. , взяв поверхностный интеграл с обеих сторон, а затем применив теорему Стокса к левой части (lhs), чтобы преобразовать поверхностный интеграл по S в линейный интеграл по элементам dl вдоль C:

∫SdS · ∂tB = −∫SdS · ∇ × E,

(9)

∂t∫SdS · B = −∮Cdl · E,

(10)

Причинная интерпретация этого уравнения должна заключаться в [5], что ЭДС «вызывает» изменения в потоке Φ – на самом деле мы не можем принять общепринятую интерпретацию, согласно которой изменения в потоке индуцируют (или вызывают) ЭДС.Обратите внимание, что это не интерпретация экспериментальных фактов или наблюдений, а интерпретация, основанная на математической модели. Кроме того, обратите внимание, что ЭДС, то есть V = Cdl · E, которая, как предполагается, представляет генерирующий ток потенциал, индуцированный в провод, рассчитывается не так, как мы, возможно, ожидали, т. е. отслеживанием одиночного заряда на его пути вокруг проводящей петли, чтобы вычислить пройденную разность напряжений. Вместо этого мы рассмотрели силы, приложенные к непрерывной линии бесконечно малых зарядов на петле в один момент, и интегрировали эти силы.Без модели движения этих зарядов то, что мы смоделировали, больше похоже на диэлектрическое кольцо со связанными зарядами и токами, привязанными к их собственным местоположениям, а не на проводящую петлю со свободно движущимися зарядами и токами [20]. , с практической точки зрения закон индукции Фарадея, выведенный выше и показанный в уравнении (1), является чрезвычайно полезным выражением и совместим с экспериментальными измерениями. Примечательно, что в электродвигателе или генераторе скорость вращения оси дает нам собственную угловую частоту ω, так что производная потока по времени становится простым умножением на ω; и, кроме того, в таком квазистационарном случае атрибуция причинности становится неважной.Однако его полезность не является гарантией того, что он предоставит математическую модель, инкапсулирующую случайные свойства, на которые мы могли бы надеяться для генерации ЭМП. Тем не менее, позже в разделе 5 мы увидим, что этой трудности нет при нахождении моделей, которые показывают влияние на ток в результате изменений магнитного поля или потока.

4. Уравнение Максвелла – Ампера

В разделе 3 мы увидели, что уравнение Максвелла – Фарадея не дает той причинной интерпретации, которую мы хотели. Следовательно, давайте попробуем альтернативный вывод для модели индукции, начав с уравнения Максвелла ротора, которое представляет закон Ампера.Цель здесь – показать, как какое-то подходящее свойство магнитного поля – надеюсь, связанное с магнитным потоком – явно вызывает изменение ЭДС. Это означало бы, что мы можем решить проблему генерации ЭДС из ничего и использовать это, чтобы мотивировать появление индуцированного тока. Поскольку в предыдущем разделе мы видели, что, согласно [5], уравнение Максвелла – Фарадея является неверным способом создания картины «магнитные поля, вызывающие (индуцирующие) ток»), уравнение Максвелла – Ампера с его обратной ролью для электрического и магнитные вклады могут показаться более многообещающими.Снова возьмем петлю, содержащую заряды, с замкнутой поверхностью S и границей C, и рассмотрим поля электрического смещения и магнитной индукции D и H, как показано на рисунке 3. Вывод начинается с уравнения Максвелла – Ампера, беря поверхностный интеграл с обеих сторон, а затем применив теорему Стокса к правой части (rhs), чтобы преобразовать этот поверхностный интеграл в линейный интеграл:

∫SdS · ∂tD = ∫SdS · ∇ × H − ∫SdS · J,

(13)

ϵ∂t∫SdS · E = μ − 1∮Cdl · B − ∫SdS · J,

(14)

где J – электрический ток.Отсюда сразу видно, что ни ЭДС, ни поток Φ не возникает. Однако некоторые дальнейшие размышления приводят нас к большему успеху, поскольку мы берем локон с обеих сторон перед применением интеграла по поверхности. Поскольку ϵ – диэлектрическая проницаемость, а μ – магнитная проницаемость, мы имеем:

∇ × ∂tD = ∇ × ∇ × H − ∇ × J,

(15)

ϵ∫SdS · ∇ × ∂tE = μ − 1∫SdS · ∇ × ∇ × B − ∫SdS · ∇ × J,

(16)

ϵ∂t∮Cdl · E = μ − 1∫SdS · ∇ × ∇ × B − ∮Cdl · J,

(17)

∂t∮Cdl · E = μϵ − 1∫SdS · ∇ × ∇ × B − ϵ − 1∮Cdl · J.

(18)

Это уравнение теперь дает нам ЭДС от л. С. линейный интеграл, вычисляемый так же, как в разделе 3. Поскольку ∇ · B = 0, а c = 1 / μϵ – скорость света, мы можем записать

∂tV = c2∫SdS · 2B − ϵ − 1∮Cdl · J.

(19)

Этот результат представляет собой уравнение, подобное индукции, которое мы можем дать четко определенную причинную интерпретацию, в которой возникает ЭДС: пространственные вариации B (или, когда они интегрированы, пространственные вариации потока) вызывают изменения ЭДС, как и токи.

Хотя мы могли бы попытаться рассмотреть этот общий случай, поучительно упростить его и взять случай нулевого тока, когда все dS ориентированы вдоль z, а B в основном выровнены вдоль и изменяются в направлении z, так что только его компонента Bz существенный. При соблюдении этих предположений и вычислении эффективного магнитного потока как ΦA = SBz, то есть после перемещения правого колеса. поверхностный интеграл через пространственные производные ∂z в направлении z, мы можем записать упрощенное уравнение

∂tV = −c2∂z2SBz = −c2∂z2ΦA.

(20)

В заключение, в ситуациях, когда разумно заменить c∂z на ∂t, мы также можем восстановить что-то эквивалентное обычной форме, но с дополнительной производной по времени с обеих сторон. Однако с этой заменой поток ΦA снова подвергается воздействию производной по времени наивысшего порядка. Таким образом, индукционная модель также вернулась к той же причинной интерпретации, которая отличается от нашего предпочтения «поток как причина».

5. Закон силы Лоренца

Несмотря на относительно знакомую природу вычислений в разделах 3 и 4, во многих отношениях может показаться более естественным вывести модель индукции тока, исходя из закона силы Лоренца.Поскольку закон магнитной индукции Фарадея не основан на эффектах, связанных с приложенными электрическими полями (см., Например, [1], стр. 160), я начну с импульса p электрического заряда q в чисто магнитном поле.

Это сама по себе модель, в которой изменения импульса заряда вызываются (магнитной) силой Лоренца F. Хотя рассмотрение изменений импульса в контексте индуцированных токов необычно, в приведенных ниже расчетах это удобный способ резюмируя задействованные силы.

Как и в предыдущих расчетах, теперь мы надеемся найти полезным определение величины, подобной ЭДС. Однако в то время как в этих расчетах ЭДС выводилась из линейного интеграла электрического поля, здесь мы вместо этого основываем ее на интеграле по движущимся зарядам; и чтобы подчеркнуть это различие, мы обозначаем его VL, а не просто V.

5.1. Простая петля

Здесь мы применим ее к (одному из) зарядов в нашей проводящей петле. Это более общая формулировка того, что было у Блини и Блини ([1], с.160), но они используют его просто как поддержку для чего-то эквивалентного стандартному вычислению, как это сделано в разделе 3, поскольку VL = W / q для потенциала (ЭДС) VL, работы W и заряда q, а также приращения работы на заряде задается формулой dW = F · dl с силой F вдоль линейного элемента dl, Сначала мы проводим линейное интегрирование по петле (контур C), содержащей заряды q и движущейся в v, чтобы получить полную ЭДС VL,

VL = q − 1∮Cdl · F = ∮Cdl · v × B.

(23)

Затем мы преобразуем r.h.s. линейный интеграл к поверхностному интегралу ротора по теореме Стокса

VL = q − 1∮Cdl · F = ∫SdS · ∇ × v × B,

(24)

так что теперь мы можем использовать стандартное векторное тождество для ∇ × (A × B),

VL = ∫SdS · v∇ · B − B∇ · v + B · v − v · B.

(25)

Первый член равен нулю, поскольку ∇ · B = 0; и мы можем еще больше упростить, удалив второй член, если поле скорости для зарядов (по существу, масштабированный ток) не имеет источников или стоков. Здесь для удобства мы идем дальше и настаиваем на постоянстве поля скоростей v, так что третий член также обращается в нуль. Результат

VL = −∫SdS · v · B.

(26)

Чтобы сделать этот результат более понятным, мы дополнительно упрощаем ситуацию, как показано на рисунке 4, рассматривая квадратную петлю в плоскости xy, которая ограничивает поверхность S, площадь S которой перпендикулярна оси z.Магнитное поле ориентировано вдоль z, так что единственной ненулевой составляющей является Bz, и она изменяется только вдоль x и с фиксированной скоростью. Затем мы перемещаем наш цикл в сторону параллельно оси x с фиксированной скоростью v, так что мы получаем прямое равенство, но без каких-либо производных по времени и, следовательно, без подразумеваемой причинности: Это, по-видимому, наиболее тесно связано с формулировкой Максвелла – Ампера из раздела 4, которая также зависит от пространственных градиентов B. Тем не менее, мы могли бы адаптировать это соотношение, преобразовав часть числителя dx скорости v = dx / dt, и знаменатель dx часть градиента поля dBz / dx, чтобы получить

VL = -SdxdtdBzdx → -SdBzdt,

(28)

что является нормальным выражением закона Фарадея, если мы предположим эквивалентность VL и V, несмотря на то, что они получены из разных отправных точек.Несмотря на это, нам до сих пор не удалось найти математическую модель с причинными свойствами, которые мы ищем, где свойства магнитного поля или его потока вызывают появление или изменение токов.

5.2. П-образный стержень и подвижный стержень

Давайте теперь попробуем добиться большего прогресса, рассматривая конкретную ситуацию, а не абстрактные конструкции. Рассмотрим стандартную систему студенческого стиля длинной прямоугольной проводящей U-образной формы в постоянном магнитном поле с проводящей перемычкой, замыкающей токовую петлю, как показано на рисунке 5.Затем говорят, что стержень скользит по плечам U, таким образом изменяя площадь, ограниченную петлей, и, следовательно, изменяя заключенный поток. Тогда мы могли бы прямо применить закон Фарадея из л. уравнения (1), и использовать скорость изменения потока для расчета ЭДС, а затем (если мы хотим) индуцированного тока, связанного с этой ЭДС. Однако, учитывая наше решение настаивать на конкретной причинной интерпретации, и поскольку закон Фарадея не соответствует этой интерпретации, мы должны выбрать другую математическую модель.Поскольку без допущения пространственных градиентов поля, которые не являются обязательной характеристикой нашего примера, мы не можем использовать выражение на основе Ампера в уравнении (19), мы начнем с закона силы. Однако использование уравнения закона силы Лоренца (21) означает, что мы сразу видим, что здесь действуют две силы на заряды:

Во-первых, это магнитная сила, действующая на заряды в стержне из-за движения стержня. в магнитном поле. Эта сила направляется вдоль стержня, изменяя скорость заряда в стержне, а затем растягивается по всей петле.

Во-вторых, на заряды в стержне действует магнитная сила из-за их продольного движения в магнитном поле. Эта сила толкает заряды перпендикулярно стержню, что может быть связано с эффектом Холла. Здесь мы предполагаем, что этот эффект Холла быстро поляризует стержень в масштабе времени намного быстрее, чем другие процессы, так что результирующий эффект проявляется только в остаточной замедляющей силе на самом стержне.

Это означает, что мы можем использовать закон силы для вычисления (а) того, как ток J в петле реагирует на скорость v стержня, и (b) как движение стержня реагирует на ток J в петле. .Естественно, это будут динамические уравнения с явной причинностью.

Здесь мы считаем провод U неподвижным и жестким, так что любые силы, действующие на него из-за протекания в нем тока и / или наличия электромагнитных полей, не учитываются. Сам провод U имеет произвольно длинные ответвления с разделением и базовой длиной Lbar, каждое с линейной плотностью заряда σ. У стержня есть масса M и скорость v, чтобы дать импульс Pbar. Он установлен перпендикулярно плечам U-образной проволоки на расстоянии L от их основания и (также) имеет плотность заряда σ и длину Lbar.

Ток J состоит из потока зарядов с прямым импульсом Pcur. Он имеет полный заряд Q, но только с q = Lbarσ в стержне, который является единственной частью, которая толкается магнитной силой. Если (эффективная) массовая плотность зарядов [21] равна ρ, скорость зарядов вдоль стержня равна u, а их скорость равна u = Pcur / ρLtot (t), где Ltot (t) = 2Lbar + 2L (t ). Предполагается, что углы U и контакты между U и стержнем отклоняют (например, возможно, за счет упругого отражения) заряды вокруг петли (т.е.е., в их новом направлении), так что Pcur движется либо вперед (по часовой стрелке на рисунке 5), либо назад (против часовой стрелки) по петле; плотность заряда тока также считается фиксированной [22]. Полная сила на стержне возникает только из-за магнитной силы, которую необходимо суммировать по длине Lbar. Обратите внимание, что поле внутри петли здесь не важно, имеет значение его сила в каждой точке стержня в момент интегрирования общей силы. Плотность силы на каждом элементе стержня равна так что в сумме получаем

∂tPbar = LbarσPcurBz / ρLtot (t).

(30)

Полная сила тока – это не только магнитная сила, которую необходимо суммировать по длине стержня Lbar, но также включает линейный резистивный член γ (t), где γ (t) = rLtot (t), а r пропорционально к сопротивлению на единицу длины. Обратите внимание, что (опять же) поле внутри цикла здесь не важно, важна его сила вдоль полосы в его текущем местоположении. Поскольку скорость стержня вдоль проводов равна Pbar / M, плотность силы на каждом элементе тока равна

∂tpcur = −σv∇B − rpcur,

(31)

так что в сумме мы имеем

∂tPcur = −LbarσPbarBz / M − γ (t) Pcur.

(32)

Это два линейных связанных дифференциальных уравнения, которые проще всего объединить, взяв производную по времени от уравнения Pcur и подставив одно в другое. Упрощая уравнения, не отображая явных зависимостей Ltot (t) и γ (t) от времени, получаем

∂t2Pcur = −LbarσBz / M∂tPbar − ∂tγPcur + −LbarσPbar / M∂tBz

(33)

= −LbarσBz / MLbarσPcurBz / ρLtot − ∂tγ (t) Pcur − LbarσPbar / M∂tBz

(34)

= −Lbar2σ2Bz2MρLtotPcur − ∂tγPcur − LbarσPbar / M∂tBz

(35)

= −Ω2Pcur − ∂tγPcur − σLbarPbar / M∂tBz

(36)

= −Ω2Pcur − ∂tγPcur − σLbarv∂tBz,

(37)

куда

Ω (t) = LbarσBzρMLtot (t).

(38)

Обратите внимание, что мы не можем напрямую заменить Pcur на ток J в дифференциальных уравнениях, поскольку они связаны через общую длину проводника Ltot (t). Кроме того, управляющий член, зависящий от ∂tBz, пропорционален v (t) = Pbar (t) / M, который имеет свою собственную динамику: если магнитное поле изменяется во времени, недостаточно пытаться решить только уравнение ( 37), нам также необходимо учитывать уравнение (30).

Поскольку этот результат содержит некоторые сложные взаимозависимости, мы теперь рассмотрим несколько поучительных частных случаев.

5.2.1. Постоянное магнитное поле

Рассмотрим случай, когда магнитное поле является постоянным во всем времени, а также в пространстве, так что ∂tBz = 0, то есть третья r.h.s. член уравнения (37) обращается в нуль. Здесь стержень после первоначального толчка будет колебаться вперед и назад в соответствии с параметром частоты Ω (t), но с амплитудой этих колебаний, затухающей со скоростью, определяемой γ (t). что для небольших изменений L (t) и Ltot (t) параметр частоты будет фактически постоянным и, таким образом, станет истинной частотой колебаний.В этом режиме мы можем просто заменить Pcur на ток J = σPcur / ρLtot и получить

∂t2J = −Ω2J − ∂tγJ.

(39)

Это привело бы к затухающим синусоидальным колебаниям тока и, следовательно, к связанным колебаниям скорости стержня; поскольку ускорение стержня может быть связано с током уравнением (30).

5.2.2. Магнитное поле, изменяющееся во времени,

Уравнение (37) сохранило возможность зависящего от времени Bz. Мы можем видеть, что изменение поля ∂tBz ускоряет ток, но способом, зависящим от Pbar (т.е.е., скорость штанги). Таким образом, ток все еще хочет колебаться, хотя и маловероятно, чтобы это была простая синусоида, с изменениями поля, действующими как движущий член. Обратите внимание, что причинно-следственная связь сохраняется, поскольку влияние на Pcur является вторым порядком по времени, на один порядок больше, чем что на Bz [5,23].

5.2.3. Электродвижущая сила

Теперь мы можем рассмотреть, что уравнение (37) говорит нам об ЭДС, индуцированной в петле; поскольку то, что мы делаем, основано на законе силы Лоренца, мы используем ЭДС VL, а не обычный закон Фарадея V.Поскольку VL – это работа на единицу заряда или линейный (петлевой) интеграл силы, а сила – это просто изменение количества движения, мы имеем VL = σ − 1∂tPcur. Это означает, что для небольших изменений Ltot (t) мы можем почти повторно использовать уравнение (37) напрямую – мы просто применяем другую производную по времени и заменяем Pcur, чтобы получить

∂t2VL = −Ω2VL − ∂tγVL − ∂tLbarv∂tBz.

(40)

На первый взгляд может показаться, что уравнение показывает временные изменения магнитного поля, вызывающие изменения в ЭДС.Конечно, поскольку он содержит больше деталей, зависящих от модели, следует ожидать некоторых отличий от стандартного закона Фарадея в уравнении (2) или альтернативного закона Фарадея в уравнении (19). Прямой результат преобразования из Pcur в VL теперь имеет производную второго порядка по времени, действующую на B, так же, как и левая часть, действующая на VL. Поскольку они имеют равные порядки производной по времени, они имеют один и тот же причинный статус – правильно объединенные вместе, они могут быть интерпретированы как результат действия других членов в уравнении (40), т.е.е. причинноподобные термины VL и ∂tγVL, а также термины, включающие v. Это означает, что уравнение (40) не имеет причинной интерпретации, которую мы искали, например, такой, когда временноподобные изменения первого порядка в магнитном поле вызвали изменения ЭДС второго порядка.

5.3. Обсуждение. ЭДС.Тем не менее, причинно-следственные связи, подобные тому, к которому мы стремились, все еще можно сделать, не ссылаясь на ЭДС, а вместо этого используя такие утверждения, как (изменения) свойств магнитного поля, индуцирующих токи.

6. Выводы

В этой статье мы попытались найти версию или пересмотр закона Фарадея, математическая форма которого имитирует причинную интерпретацию, которую мы хотели бы иметь, а именно: изменения магнитного потока через петлю вызывают изменения ЭДС вокруг этот цикл.Однако обычная математическая форма закона Фарадея несовместима с этим желанием и позволяет нам только сказать, что ЭДС вызывает изменения потока.

Чтобы устранить этот очевидный недостаток, мы вывели закон Фарадея, основанный на уравнении ротора Максвелла-Ампера, который действительно позволил нам говорить об индуцированных изменениях ЭДС, но вместо этого они были вызваны пространственными градиентами магнитного потока, которые не совсем то, на что мы надеялись. Это побудило нас попробовать альтернативный подход, основанный на законе силы Лоренца, микроскопические основы которого показали многообещающие свойства магнитного поля, которые действительно вызывали (вызывали) изменения тока, как в абстрактной, так и в более реалистичной обстановке.Однако, когда математическая модель была преобразована для обозначения индуцированных изменений в величине VL, подобной ЭМП, мы обнаружили, что модель стала несовместимой с желаемой причинно-следственной интерпретацией, подчеркнув, что именно настойчивое использование ЭМП создает трудности.

Таким образом, наше исследование показало, что следует проявлять осторожность при причинной интерпретации процессов магнитной индукции и опасаться зависимости от скрытых или неявных предположений, которые могут привести к ошибочным выводам.Во-первых, следует четко различать интерпретации, относящиеся к эксперименту, и интерпретации, относящиеся к математической модели; различие, которое жизненно важно в случае закона Фарадея.