НОВОСТИ |
Любое открытие нового закона полезно лишь тогда, Из предисловия к русскому изданию книги “Фейнмановские лекции по физике” Большей частью лектор и слушатели – люди разных поколений, и лектору очень трудно уйти от соблазна вести слушателей той знакомой и надежной дорогой, по которой он сам в свое время дошел до желанных высот. Однако старая дорога не вечно остается лучшей. Физика развивается очень быстро, и, чтобы не отставать от нее, надо менять пути ее изучения. Все согласны с тем, что физика – одна из самых интересных наук. В то же время многие учебники физики никак не назовешь интересными. В таких учебниках изложено все, что следует по программе. Там обычно объясняется, какую пользу приносит физика и как важно ее изучать, но из них очень редко можно понять, почему заниматься физикой интересно. Лекции Фейнмана отличаются тем, что они обращены к слушателю, живущему во второй половине ХХ века, который уже многое знает или слышал. Поэтому в лекциях не тратится время на объяснение «ученым языком» того, что и так известно. Что бы ни говорили об этих лекциях-восторгались стилем изложения или сокрушались по поводу ломки старых добрых традиций,- одно остается бесспорным: надо начинать педагогические опыты. Это послужит стимулом к появлению новых книг, в которых получат отражение другие взгляды. Это и есть эксперимент. Кому будет полезна эта книга? Прежде всего – преподавателям, которые ее прочтут целиком: она заставит их задуматься об изменении сложившихся взглядов на то, как начинать обучать физике. Далее, ее прочтут студенты. Они найдут в ней много нового в дополнение к тому, что они узнают на лекциях. Конечно, ее попытаются читать и школьники. Большинству из них будет трудно одолеть все, но и то, что они смогут прочесть и понять, поможет им войти в современную науку, путь в которую всегда бывает трудным, но никогда не бывает скучным. (Я. Смородинский, 1965)
Фейнман в лекциях, в главе, посвященной гравитационному взаимодействию, рассматривает несколько примеров объяснительных и предсказательных возможностей Ньютоновской теории. Самыми убедительными доказательствами корректности и широких предсказательных возможностей приведенными Фейнманом являлись
Каких-либо недостатков и противоречий в теории гравитации Ньютона Фейнман не отмечал. Более того он считал, что эта теория является ярким примером математического подхода к вопросам естествознания или, говоря словами Фейнмана из Нобелевской лекции: «…наверное, наилучший способ создания новой теории – угадывать уравнения, не обращая внимания на физические модели или физическое объяснение». В учебнике Фейнман пишет:
Это определило быстрый, успешный рост науки в последующие годы; у людей появилась надежда, что и в других явлениях мира прячутся такие же простые закономерности. До сих пор мы только описывали, Предлагались многие механизмы тяготения. Интересно рассмотреть один из них, ибо до него время от времени додумывались то один, то другой ученый. Причем каждый сперва воспрянет духом и ходит осчастливленный своим «открытием», но потом начинает понимать, что тут что-то не так. Впервые это открытие произошло примерно в 1750 г. Представьте себе, что в пространстве носится в разных направлениях с огромной скоростью множество частиц, лишь слегка поглощаемых веществом.  И не было предложено ни одного механизма, «объясняющего» тяготение, который бы не предсказывал добавочных, И не было предложено ни одного механизма, «объясняющего» тяготение, который бы не предсказывал добавочных, Рассмотрим еще возможную связь тяготения с прочими силами. В нынешнее время не удается свести тяготение к другим силам. Тяготение отнюдь не проявление электричества или чего-либо подобного; этим его не объяснишь. И все же тяготение похоже на другие силы, и любопытно посмотреть, в чем. К примеру, электрическая сила между двумя заряженными телами чрезвычайно похожа на тяготение: она равна со знаком минус постоянной величине, умноженной на величины зарядов тел, и изменяется обратно квадрату расстояния. Правда, она действует в обратную сторону, т. е. отталкивает. Но замечательно не столько это, сколько одинаковая зависимость от расстояния, входящая в оба закона. Не исключено, что тяготение и электричество связаны значительно сильнее, чем мы думаем. Было сделано много попыток объединить их; так называемая единая теория поля – лишь одна из очень изящных попыток сочетать электричество с тяготением. Если мы измерим в естественных единицах отталкивание двух электронов (возникающее из-за того, что у них есть заряд) и их притяжение (возникающее оттого, что у них есть масса), то мы можем получить и отношение электрического отталкивания к гравитационному притяжению. Отношение это не зависит от расстояния, это фундаментальная мировая константа. Гравитационное притяжение составляет 1/4,17 •10 Как известно, сила тяготения пропорциональна массе, т. Cопоставим тяготение с другими теориями. В последние годы выяснилось, что любая масса обязана своим происхождением мельчайшим частицам, и что существует несколько видов взаимодействия, например ядерные силы и т. п. Ни одна из этих ядерных или электрических сил пока тяготения не объясняет. Квантовомеханические стороны природы мы еще пока не распространили на тяготение. Когда на малых расстояниях начинаются квантовые эффекты, то тяготение оказывается еще настолько слабым, что нужды в квантовой теории тяготения не возникает. С другой стороны, для последовательности наших физических теорий было бы важно понять, должен ли закон Ньютона с внесенным Эйнштейном видоизменением быть изменен и дальше с тем, чтобы согласовываться с принципом неопределенности. Это последнее видоизменение пока не сделано. … Со времен Ньютона и до наших дней никто не смог описать механизм, скрытый за законом тяготения, не повторив того, что уже сказал Ньютон, не усложнив математики или не предсказав явлений, которых на самом деле не существует. «…Если закону противоречит хотя бы один случай, то закон неверен », – это слова Фейнмана. Однако нам трудно представить почему Фейнман ничего не сказал о нижеследующем высказывании Ньютона в «Началах» и о важных открытиях, сделанных после публикации закона гравитации, противоречащих этому закону.
Ньютон говорил, что поддержание настоящего вида Солнечной системы требует вмешательства сверхъестественных сил. За более чем 300 лет, прошедшие после публикации закона гравитации Ньютона, было обнаружено, что его теория гравитации внутренне противоречива. Принятая теория приводит к парадоксальному выводу о том, что некоторые тела под действием собственной силы тяжести должны неудержимо сжиматься и “схлопываться” – практически исчезать из окружающего их пространства. Начиная со второй половины XX века, астрономы стали находить свидетельства того, что огромные звездные скопления нарушают законы Ньютона. Наиболее распространенная гипотеза, объясняющая “неправильное” поведение галактик, предполагает, что законы Ньютона не нарушаются, а наблюдаемое отклонение от законов объясняется наличием темной материи. Этим термином обозначают пока экспериментально не обнаруженное вещество, участвующее в гравитационном взаимодействии, но не участвующее в электромагнитном. Темная материя создает дополнительную массу, которая ответственна за расширение галактик. Наблюдения сверхновых типа Ia, проведённые в 1998 г. в рамках Supernova Cosmology Project показали, что постоянная Хаббла меняется со временем таким образом, что её поведение можно объяснить соответствующим подбором величины космологической постоянной Λ, вносящей вклад ΩΛ в среднюю плотность Ω.
Интерпретация данных по анизотропии реликтового излучения, полученных в ходе работы WMAP (Wilkinson Microwave Anisotropy Probe, 2003 г.) дала следующие результаты: наблюдаемая плотность Ω близка к Ωcrit и распределение Ω = ΩΛ + Ωvis + Ωdark по компонентам: барионная материя Ωvis – 4,4 %, тёмная холодная материя (WIMP) Ωdark – 23 %, «тёмная энергия» ΩΛ – 72,6 %. В нашей Галактике в окрестности Солнца масса темной материи примерно равна массе обычного вещества. Темная энергия – гораздо более странная субстанция, чем темная материя. Начать с того, что она не собирается в сгустки, а равномерно «разлита» во Вселенной. В галактиках и скоплениях галактик её столько же, сколько вне их. Не будет преувеличением сказать, что природа темной энергии – это «математическая» загадка фундаментальной физики XXI века. Масса является исходной сущностью в законе гравитации. Однако физическая природа массы до настоящего времени не известна. Так, согласно академику РАН Л. Б. Окуню природа массы: вопрос № 1 современной физики. До настоящего времени считается, что принятая теория гравитации позволяет рассчитывать плотность Солнца. В работе L. Neslufsan [Queen Mary and West_eld College, Mile End Road, London E1 4NS, UK, Received 19 January 2001г , Accepted 6 April 2001] доказывается, что Солнце заряжено положительным зарядом, и что электростатическое взаимодействие Солнца с другими звездами надо учитывать при расчете гравитационных взаимодействий. Скорость движения электронов на поверхности (в короне) Солнца оценивается в научной литературе сотнями тысяч километров в секунду, а скорость протонов сотнями километров в секунду. Вторая космическая скорость для тела, вращающегося вокруг Солнца в рамках принятой теории гравитации, равна 618 км/сек. Частицы, имеющие скорость большую, должны покинуть Солнце и улететь в космос. Таким образом, наличие на Солнце электронов, двигающихся со скоростью, превышающую вторую космическую, позволяет говорить, что кроме сил гравитации на электроны короны Солнца действуют силы электростатического притяжения. Величины второй космической скрости и скорости электронов на Солнце (расчет по уравнениям в учебника И.В. Савельев т.1 стр.250) позволяют оценить соотношение между электростатическим и гравитационным взаимодействием и заряд Солнца. Рассчитанное отношение сил электростатической к гравитационной составило более 100 раз (даже без учета магнитного взаимодействия), а положительный заряд Солнца, обеспечивающий это соотношение, равен 3. Давайте вернемся непосредственно к электростатическому объяснению гравитации, и еще раз проанализируем какие объективные обстоятельства, мешали, по нашему мнению, принятию этого объяснения гравитации. В настоящее время нам представляется, что основной объективной причиной было отсутствие во всех изученных нами работах даже полуколичественной оценки этого объяснения. В этих работах, включая и наши предыдущие статьи, оценка влияния электрических взаимодействий в лучшем случае ограничивалась сравнением электрических и массовых взаимодействий между электронами. Получившаяся неожиданно большая величина заряда Солнца повергла нас, как сторонников электрического объяснения гравитации, в уныние, несмотря на все перечисленные за, включающие, в том числе наш, казалось бы убийственный аргумент – если бы Ньютон знал. Чтобы удостовериться в корректности рассчетного значения заряда Солнца, мы решили оценить, какова должна быть разница между количеством электронов и количеством протонов, улетевших с Солнца, чтобы оно приобрело заряд 3. 1. Почему скорость электронов в короне Солнца в несколько раз больше второй космической? 2. Почему согласно расчетам, с учетом только гравитационного взаимодействия, рассчитанный удельный вес Солнечного вещества всего в три раза меньше удельного веса Земли, состоящего из водорода (93%) и гелия (7%), нагретых до миллионов градусов? Электростатическое объяснение гравитации оказалось противоречивым. Что же можно сказать сегодня о физической природе сил гравитации? Широко известно, что самым эффективным способом решения частных вопросов является решение общих вопросов. В ходе наших работ мы доказали, что нейтральной материи – материи не несущей зарядов – не существует. И соответственно, существущее объянение ее гравитационных свойств не корректно. Нейтральная масса как мера количества материи была введена Ньютоном вместо веса, используемого до нее, но в настоящее время это архаичная формулировка. Мы считаем гравитацию, как и инерцию, электромагнитным явлением. Электромагнитное происхождение инерциальных свойств материи позволяет ответить на другой вопрос: почему устойчивы системы центростремительных сил? В Законе всемирного тяготения, открытом Ньютоном в 1678 г. В космических и атомных системах, описываемых только законами Ньютона, при малом отклонение тела от положения равновесия возникают силы, стремящиеся увеличить это отклонение, т.к. и гравитационные силы и Кулоновские обратно пропорциональны квадрату расстояния между планетами для космических объектов и атомов, а центробежные силы обратно пропорциональны первой степени расстояния. Т.е при малейшем отклонении электрона, вращающегося вокруг протона (при увеличении или уменьшении расстояния между протоном и электроном), центростремительные и центробежные силы увеличивают это отклонение.
 Г. «Судьба солнечной системы. Популярные очерки по небесной механике». (1969). В предисловии к этой книги мы читаем: “Немногим менее двух столетий отделяет нас от поры, когда выдающиеся французские ученые Жозеф Луи Лагранж и Пьер Симон Лаплас, чьи имена вызывают почтительное и восхищенное уважение ученых всех времен, продолжая великое дело Исаака Ньютона и славной плеяды его последователей, создали величественное здание небесной механики. Около полувека, поддерживая непрерывную связь друг с другом, в духе постоянного творческого соперничества самозабвенно трудились Лагранж и Лаплас над общей проблемой построения теории движения больших планет. Им обоим по праву принадлежит постановка знаменитой задачи механики – задачи об устойчивости Солнечной системы …» Г. «Судьба солнечной системы. Популярные очерки по небесной механике». (1969). В предисловии к этой книги мы читаем: “Немногим менее двух столетий отделяет нас от поры, когда выдающиеся французские ученые Жозеф Луи Лагранж и Пьер Симон Лаплас, чьи имена вызывают почтительное и восхищенное уважение ученых всех времен, продолжая великое дело Исаака Ньютона и славной плеяды его последователей, создали величественное здание небесной механики. Около полувека, поддерживая непрерывную связь друг с другом, в духе постоянного творческого соперничества самозабвенно трудились Лагранж и Лаплас над общей проблемой построения теории движения больших планет. Им обоим по праву принадлежит постановка знаменитой задачи механики – задачи об устойчивости Солнечной системы …»«…Многие десятилетия виднейшие математики и механики штурмовали проблему Лагранжа-Лапласа. Но решение знаменитой проблемы оставалось по-прежнему столь же далеким, как и во времена Лагранжа и Лапласа ». Для объяснения устойчивости орбит рассмотрим легко осуществимый и широко известный эксперимент рис.
В этом эксперименте шарик, имеющий массу М, вращается на пружине. К нему присоединен динамометр, измеряющий силу натяжения пружины. В этой системе мы можем измерить орбитальную скорость движения шарика, центростремительную (Fцс) и центробежную силу (Fцб) и радиус орбиты (R). Т.е. Экспериментально было доказано, что при движении тела в поле центральных сил центробежная сила наглядно проявляется, что ее величина равна по величине центростремительной силе, вызывающей движение тела с ускорением, т.е. Fцс = Fцб.= MV2/R где M,V и R – масса, скорость и радиус круга вращения. При математическом подходе к науке поиск механизма этого равенства не считался задачей. Для нас выяснение механизма (ответ на вопрос почему) является научной целью. В данном случае ответ оказался прост. С увеличением центробежной силы пропорционально растет сила Гука (сила натяжения пружины динамометра). Т.е. имеется обратная связь между центростремительной и центробежной силами. Правда, такое решение далось не сразу. Только 3 года тому назад мы пришли к заключению, что силами, осуществляющими функцию обратной связи в космических и атомных системах, являются силы Лоренца. Изучая движение электронов во внешних полях, Лоренц обобщил наблюдения, выведя силу, действующую на электрон, движущийся одновременно в электрическом и магнитном полях, которую впоследствии назвали его именем. Она имеет вид: Здесь е – заряд частицы, E – напряжённость электрического поля, В – магнитная индукция, v – скорость заряженной частицы относительно системы координат, в которой вычисляются величины F, E, B, а с – скорость света в вакууме. Формула справедлива при любых значениях скорости заряженной частицы. Первый член в правой части формулы – сила, действующая на заряженную частицу в электрическом поле, второй – в магнитном. Магнитная часть силы Лоренца пропорциональна векторному произведению B и v, то есть она перпендикулярна скорости частицы (направлению её движения) и вектору магнитной индукции; следовательно, она не совершает механической работы и только искривляет траекторию движения частицы, не меняя её энергии. Магнитная составляющая силы Лоренца осуществляет обратную связью между движущимися объектами разделенными пространством. Более того, можно сказать, что устойчивость системы доказывает, что в ней действует сила Лоренца, и соответственно, присутствуют электрические и магнитные поля. Учет электромагнитных сил позволяет качественно объяснить противоречия в принятой теории гравитации, роль и природу темной материи и энергии, и такие явления как разбегание галактик без дополнительного введения экспериментально не обнаруживаемых сущностей. Во времена Ньютона единственной центростремительной силой, действующей на расстоянии, существование которой признавалось Коперником, Галлилеем, Гуком и Ньютоном, была сила гравитации. В это время и до настояшего периода в решении физических проблем доминировал математический подход. Значимость теории определялась возможностью в рамках теории, объяснять и рассчитывать явления, до этой поры количественно не описанные. В качестве конкретного примера рассмотрим расчет первой космической скорости (скорость движения спутника по орбите вокруг Земли). Согласно закону гравитации (см. Савельев, Курс общей физики, т.1, стр.249) спутник вращается на постоянной орбите, когда центробежная сила равна центростремительной. Исходное уравнение mv2/R = mg, где m – масса тела, v2/R – центробежное ускорение, mg – сила тяжести, действующая на спутник. Отсюда следует что v = (g R)-0.5 В это уравнение масса тела даже не входит, поэтому замена ньютоновской массы, как исходной сущности, на электромагнитную массу, определяемую зарадом, не окажет влияет на расчеты. Земля является спутником Солнца. Мы знаем ее скорость движения по орбите v и ее расстояние до Солнца R. По уравнению v = (g R)-0.5 мы можем рассчитать gсолнц – ускорение свободного падения на Солнце и вычислить силу притяжения Земли к Солнцу F=mgсолнц. Центростремительная сила в этом случае – сила гравитационного притяжения. Ньютон не смог объяснить устойчивость орбит планет Солнечной системы, и приписывал эту закономерность божественным силам. В рамках математического подхода явления не объясняются. Заряды, из которых состоят все материальные тела, совершают постоянное движение с ускорением (поступательное и вращательное). Движущиеся с ускорением заряды создают переменное магнитное поле и взаимодействуют между собой кулоновскими и магнитными силами, т.е. силами Лоренца. Движение зарядов с ускорением и, соответственно, с переменным магнитным полем вызывает ЭДС, которая действует на движушийся заряд с силой равной по величине и противоположной по направлению силе, вызвавшей движение заряда с ускорением. Количественное равенство центростремительных сил и центробежных является доказательством, что никаких других сил в природе не существует. Также как и не существует материя, не содержащая заряды. |
просто и понятно о значении в физике
ОткрытиеОткрытие
Ни для кого не секрет, что закон всемирного тяготения был открыт великим английским ученым Исааком Ньютоном, по легенде гуляющим в вечернем саду и раздумывающем над проблемами физики. В этот момент с дерева упало яблоко (по одной версии прямо на голову физику, по другой просто упало), ставшее впоследствии знаменитым яблоком Ньютона, так как привело ученого к озарению, эврике. Яблоко, упавшее на голову Ньютону и вдохновило того к открытию закона всемирного тяготения, ведь Луна в ночном небе оставалась не подвижной, яблоко же упало, возможно, подумал ученый, что какая-то сила воздействует как на Луну (заставляя ее вращаться по орбите), так и на яблоко, заставляя его падать на землю.
Сейчас по заверениям некоторых историков науки вся эта история про яблоко лишь красивая выдумка. На самом деле падало яблоко или нет, не столь уж важно, важно, что ученый таки действительно открыл и сформулировал закон всемирного тяготения, который ныне является одним из краеугольных камней, как физики, так и астрономии.
Разумеется, и задолго до Ньютона люди наблюдали, как падающие на землю вещи, так и звезды в небе, но до него они полагали, что существует два типа гравитации: земная (действующая исключительно в пределах Земли, заставляющая тела падать) и небесная (действующая на звезды и Луну). Ньютон же был первым, кто объединил эти два типа гравитации в своей голове, первым кто понял, что гравитация есть только одна и ее действие можно описать универсальным физическим законом.
Определение закона
Согласно этому закону, все материальные тела притягивают друг друга, при этом сила притяжения не зависит от физических или химических свойств тел. Зависит она, если все максимально упростить, лишь от веса тел и расстояния между ними. Также дополнительно нужно принять во внимание тот факт, что на все тела находящиеся на Земле действует сила притяжения самой нашей планеты, получившая название – гравитация (с латыни слово «gravitas» переводиться как тяжесть).
Также дополнительно нужно принять во внимание тот факт, что на все тела находящиеся на Земле действует сила притяжения самой нашей планеты, получившая название – гравитация (с латыни слово «gravitas» переводиться как тяжесть).
Попробуем же теперь сформулировать и записать закон всемирного тяготения максимально кратко: сила притяжения между двумя телами с массами m1 и m2 и разделенными расстоянием R прямо пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними.
Формула
Ниже представляем вашему вниманию формулу закона всемирного тяготения.
G в этой формуле это гравитационная постоянная, равная 6,67408(31)•10−11 эта величина воздействия на любой материальный объект силы гравитации нашей планеты.
Невесомость тел
Открытый Ньютоном закон всемирного тяготения, а также сопутствующий математический аппарат позже легли в основу небесной механики и астрономии, ведь с помощью него можно объяснить природу движения небесных тел, равно как и явление невесомости. Находясь в космическом пространстве на значительном удалении от силы притяжения-гравитации такого большого тела как планета, любой материальный объект (например, космический корабль с астронавтами на борту) окажется в состоянии невесомости, так как сила гравитационного воздействия Земли (G в формуле закона тяготения) или какой-нибудь другой планеты, больше не будет на него влиять.
Находясь в космическом пространстве на значительном удалении от силы притяжения-гравитации такого большого тела как планета, любой материальный объект (например, космический корабль с астронавтами на борту) окажется в состоянии невесомости, так как сила гравитационного воздействия Земли (G в формуле закона тяготения) или какой-нибудь другой планеты, больше не будет на него влиять.
Видео
И в завершение поучительное видео об открытии закона всемирного тяготения.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.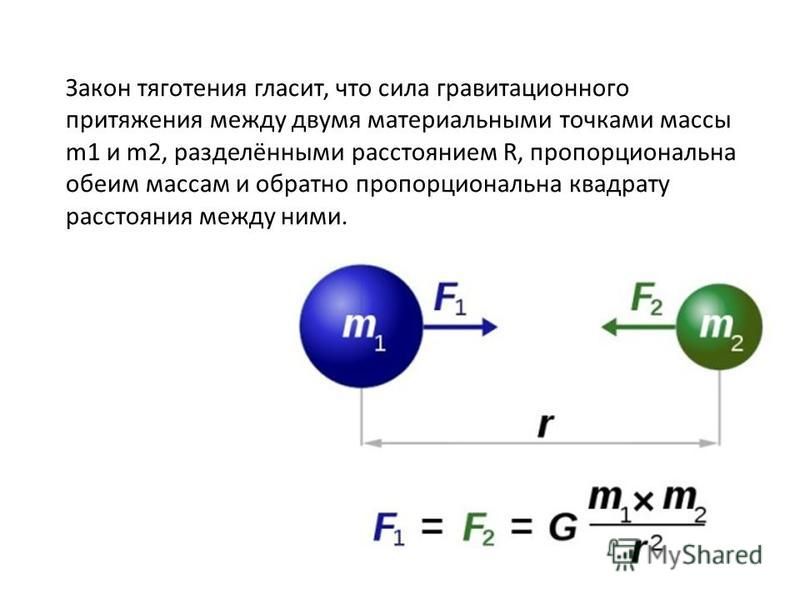
Ученые объяснили, как цепочка из бусин “нарушает” закон гравитации
Ученые нашли объяснение необычному феномену: цепочка бусин, вытянутая из стакана, поднимается над его краем, прежде чем упасть, что на первый взгляд противоречит законам физики.Если положить цепочку из бусин в стакан на некоторой высоте над полом, а потом потянуть за один конец, то под действием силы тяжести цепочка начнет вытягиваться из стакана. При этом она будет не просто “течь” через край, но подниматься над ним, прежде чем упасть, образуя “фонтан”.
Это необычное явление впервые заметил научный фокусник Стив Молд (Steve Mould), демонстрирующий занимательные научные эксперименты в телепрограммах “Би-би-си”. Видео, в котором он продемонстрировал фонтан из бусин, посмотрело более миллиона человек.
Молд пытался объяснить это явление инерцией, однако Джон Биггинс (John Biggins) и Марк Уорнер (Mark Warner) из Кембриджского университета (Великобритания), опубликовавшие статью в журнале Proceedings of the Royal Society A, нашли другое объяснение.
Ученые выяснили, что бусины в цепочке не изолированы друг от друга, а ведут себя, как короткие “бруски”, состоящие из нескольких бусин. Они построили модель, в которой бусины объединяются в бруски по трое. Размер такого бруска вычисляется по количеству бусин, которое нужно для того, чтобы цепь завернулась на 180 градусов (в данном случае — шесть бусин).
Когда конец цепочки вытягивают из стакана вверх, каждый брусок поворачивается так, что его нижний конец начинает давить на стакан и оставшуюся в нем часть цепи, которые в ответ давят на брусок, выталкивая его вверх. Без этого цепь просто “перетекала” бы через край стакана, не образуя “фонтан”, считают ученые. Они продемонстрировали такое поведение, сделав цепь, в которой отдельные бусины прилегали друг к другу не плотно, а были разделены нитью и не могли образовывать бруски.
Биггинс и Уорнер, преподающие физику в Кембридже, изначально наткнулись на “фонтан” из бусин в поисках заданий для своих студентов. Объяснение этого феномена ученым подсказал эксперимент Энди Руины (Andy Ruina) и его коллег из Корнелльского университета в Итаке (США). Они показали, что брошенная цепь падает быстрее, когда ее конец касается поверхности. Это объясняется похожим образом: как только конец первого бруска в цепи касается поверхности, она давит на него вверх, из-за чего брусок переворачивается и другой его конец тянет другие бруски за собой вниз.
Они показали, что брошенная цепь падает быстрее, когда ее конец касается поверхности. Это объясняется похожим образом: как только конец первого бруска в цепи касается поверхности, она давит на него вверх, из-за чего брусок переворачивается и другой его конец тянет другие бруски за собой вниз.
Источник: РИА Новости
Что такое закон всеобщей гравитации?
Закон всемирного тяготения является важнейшим принципом физики. Впервые он был записан сэром Исааком Ньютоном в 1600-х годах. Закон всемирного тяготения гласит, что все объекты притягиваются друг к другу под действием силы тяжести; сила притяжения зависит от массы объектов и уменьшается в зависимости от расстояния между ними. Открытие Ньютона было заменено теорией общей теории относительности Эйнштейна. Это все еще точно, однако, для большинства практических применений.
Ньютон не обнаружил гравитации, как считает распространенное мнение, но расширил работу более ранних ученых, таких как Галилей. Ньютон сослался на этих ученых, когда он, как известно, написал: «Если бы я видел дальше, то стою на плечах гигантов». Падение яблока вдохновило Ньютона на изучение предмета гравитации; однако, яблоко не принесло мгновенного понимания, ударяя его голову. Вместо этого он использовал орбиту Луны вокруг Земли, чтобы проверить и подтвердить свои расчеты в течение 20 лет. Закон всемирного тяготения был подробно описан в его революционной книге Principia Mathematica , опубликованной в 1687 году.
Ньютон сослался на этих ученых, когда он, как известно, написал: «Если бы я видел дальше, то стою на плечах гигантов». Падение яблока вдохновило Ньютона на изучение предмета гравитации; однако, яблоко не принесло мгновенного понимания, ударяя его голову. Вместо этого он использовал орбиту Луны вокруг Земли, чтобы проверить и подтвердить свои расчеты в течение 20 лет. Закон всемирного тяготения был подробно описан в его революционной книге Principia Mathematica , опубликованной в 1687 году.
Книга Ньютона включала математические формулы, описывающие закон всемирного тяготения. По сути, закон гласит, что все объекты оказывают гравитационное воздействие на все другие объекты. Объекты с большой массой имеют более сильные области гравитации или гравитационные поля, поэтому объекты и люди притягиваются к Земле, но не заметно друг к другу. Гравитационное притяжение уменьшается с увеличением расстояния; это уменьшение может быть точно измерено и известно в физике как закон обратных квадратов. Универсальная гравитация – это сила, которая удерживает планеты и спутники на орбите, вместо того, чтобы свободно путешествовать по вселенной.
Универсальная гравитация – это сила, которая удерживает планеты и спутники на орбите, вместо того, чтобы свободно путешествовать по вселенной.
В веках после жизни Ньютона закон всемирного тяготения использовался для предсказания местоположений планет и естественных спутников, которые еще не были обнаружены. Возможные открытия этих небесных тел подтвердили, что закон был правильным. Один аспект закона, который Ньютон не мог объяснить, заключался в том, как сила гравитации передается между объектами. Другие фундаментальные силы, такие как электромагнетизм, работают, потому что субатомные частицы перемещаются между объектами, притягивая их друг к другу. Подобная частица для передачи гравитации, гравитон, была описана в теории, но остается неоткрытой более 300 лет после работы Ньютона.
К 20 веку ученые обнаружили незначительные несоответствия в законе всемирного тяготения. Эти несоответствия были объяснены теорией общей теории относительности Эйнштейна. Эйнштейн понял, что в действительности массы небесных тел влияют не только друг на друга, но и на ткань пространства-времени вокруг них.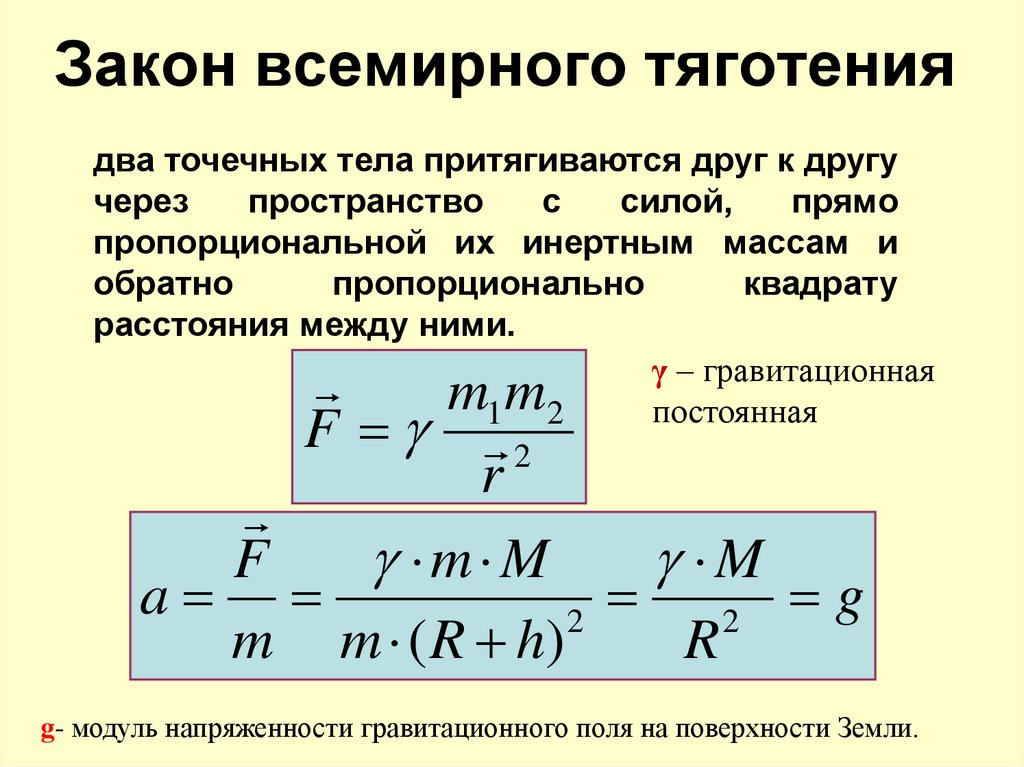 Эти эффекты заметны только при очень точных измерениях и расчетах. Для практических применений, таких как запуск ракет, закон всемирного тяготения все еще точен и его гораздо легче вычислить, чем эффекты относительности.
Эти эффекты заметны только при очень точных измерениях и расчетах. Для практических применений, таких как запуск ракет, закон всемирного тяготения все еще точен и его гораздо легче вычислить, чем эффекты относительности.
ДРУГИЕ ЯЗЫКИ
Законы гравитации не действуют на полет влюбленных людей ▷ Socratify.Net
ПОХОЖИЕ ЦИТАТЫ
ПОХОЖИЕ ЦИТАТЫ
Птицы, рожденные в клетке, думают, что полет – это болезнь.
Алехандро Ходоровский (1)
Кто для других законы составляет,
Джеффри Чосер (10+)
Пусть те законы первым соблюдает.
— Все-таки любовь могучее явление.
Меч в камне (The Sword In The Stone) (5)
— Сильнее гравитации?
— Ну… я бы сказал, это величайшая сила на земле.
Я полон оптимизма.
Станислав Ежи Лец (500+)Человечество преодолело законы морали, почему бы ему не преодолеть законы физики?
Не откладывайте близких людей на потом, потом их не будет.
Неизвестный автор (1000+)
Не тратьте время на людей, у которых нет времени на вас.
Габриэль Гарсиа Маркес (50+)
Когда множатся законы и приказы, растёт число воров и разбойников.
Лао-Цзы (100+)
У каждой поры свои законы. Осенью надеешься, зимой веришь, весной дожидаешься, летом — получаешь.
Я вернусь (Эльчин Сафарли) (100+)
Идеальных людей не бывает, зато бывают идеальные заблуждения на их счёт.
Михаил Казаков (1)
Есть установленные законы бытия, и, если идти им наперекор, добром это не кончится.
Облачный атлас (20+)
Как Ньютон открыл закон всемирного тяготения. Раритетные издания. Наука и техника
Джеймс Э. МИЛЛЕР
Огромный рост числа молодых энергичных работников, подвизающихся на научной ниве, есть счастливое следствие расширения научных исследований в нашей стране, поощряемых и лелеемых Федеральным правительством. Измотанные и задерганные научные руководители бросают этих неофитов на произвол судьбы, и они часто остаются без лоцмана, который мог бы провести их среди подводных камней государственного субсидирования. По счастью, они могут вдохновляться историей сэра Исаака Ньютона, открывшего закон всемирного тяготения. Вот как это произошло.
В 1665 году молодой Ньютон стал профессором математики в Кембриджском университете – своей альма-матер. Он был влюблен в работу, и способности его как преподавателя не вызывали сомнений. Однако нужно заметить, что это ни в коей мере не был человек не от мира сего или же непрактичный обитатель башни из слоновой кости. Его работа в колледже не ограничивалась только аудиторными занятиями: он был деятельным членом Комиссии по Составлению Расписаний, заседал в управлении университетского отделения Ассоциации Молодых Христиан Благородного Происхождения, подвизался в Комитете Содействия Декану, в Комиссии по Публикациям и прочих и прочих комиссиях, которые были необходимы для надлежащего управления колледжем в далеком XVII веке. Тщательные исторические изыскания показывают, что всего за пять лет Ньютон заседал в 379 комиссиях, которые занимались изучением 7924 проблем университетской жизни, из коих решена 31 проблема.
Он был влюблен в работу, и способности его как преподавателя не вызывали сомнений. Однако нужно заметить, что это ни в коей мере не был человек не от мира сего или же непрактичный обитатель башни из слоновой кости. Его работа в колледже не ограничивалась только аудиторными занятиями: он был деятельным членом Комиссии по Составлению Расписаний, заседал в управлении университетского отделения Ассоциации Молодых Христиан Благородного Происхождения, подвизался в Комитете Содействия Декану, в Комиссии по Публикациям и прочих и прочих комиссиях, которые были необходимы для надлежащего управления колледжем в далеком XVII веке. Тщательные исторические изыскания показывают, что всего за пять лет Ньютон заседал в 379 комиссиях, которые занимались изучением 7924 проблем университетской жизни, из коих решена 31 проблема.
Однажды (а было это в 1680 году) после очень напряженного дня заседание комиссии, назначенное на одиннадцать часов вечера – раньше времени не было, не собрало необходимого кворума, ибо один из старейших членов комиссии внезапно скончался от нервного истощения. Каждое мгновение сознательной жизни Ньютона было тщательно распланировано, а тут вдруг оказалось, что в этот вечер ему нечего делать, так как начало заседания следующей комиссии было назначено только на полночь. Поэтому он решил немного пройтись. Эта коротенькая прогулка изменила мировую историю.
Каждое мгновение сознательной жизни Ньютона было тщательно распланировано, а тут вдруг оказалось, что в этот вечер ему нечего делать, так как начало заседания следующей комиссии было назначено только на полночь. Поэтому он решил немного пройтись. Эта коротенькая прогулка изменила мировую историю.
Была осень. В садах многих добрых граждан, живших по соседству со скромным домиком Ньютона, деревья ломились под тяжестью спелых яблок. Все было готово к сбору урожая. Ньютон увидел, как на землю упало очень аппетитное яблоко. Немедленной реакцией Ньютона на это событие – типичной для человеческой стороны великого гения – было перелезть через садовую изгородь и сунуть яблоко в карман. Отойдя на приличное расстояние от сада, он с наслаждением надкусил сочный плод.
Вот тут его и осенило. Вез обдумывания, без предварительных логических рассуждений в мозгу его блеснула мысль, что падение яблока и движение планет по своим орбитам должны подчиняться одному и тому же универсальному закону.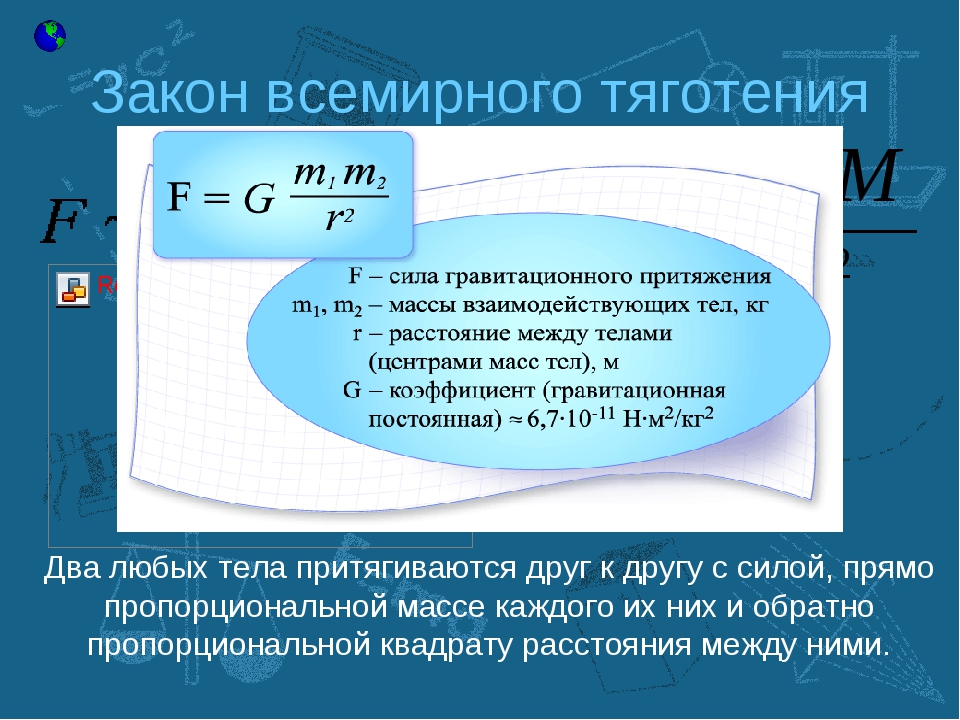 Не успел он доесть яблоко и выбросить огрызок, как формулировка гипотезы о законе всемирного тяготения была уже готова. До полуночи оставалось три минуты, и Ньютон поспешил на заседание Комиссии по Борьбе с Курением Опиума Среди Студентов Неблагородного Происхождения.
Не успел он доесть яблоко и выбросить огрызок, как формулировка гипотезы о законе всемирного тяготения была уже готова. До полуночи оставалось три минуты, и Ньютон поспешил на заседание Комиссии по Борьбе с Курением Опиума Среди Студентов Неблагородного Происхождения.
В последующие недели мысли Ньютона все снова и снова возвращались к этой гипотезе. Редкие свободные минуты между двумя заседаниями он посвящал планам ее проверки. Прошло несколько лет, в течение которых, как показывают тщательные подсчеты, он уделил обдумыванию этих планов 63 минуты 28 секунд. Ньютон понял, что для проверки его предположения нужно больше свободного времени, чем то, на которое он может рассчитывать. Ведь требовалось определить с большой точностью длину одного градуса широты на земной поверхности и изобрести дифференциальное исчисление.
Не имея еще опыта в таких делах, он выбрал простую процедуру и написал краткое письмо из 22 слов королю Карлу, в котором изложил свою гипотезу и указал на то, какие великие возможности она сулит, если подтвердится. Видел ли король это письмо – неизвестно, вполне возможно, что и не видел, так как он ведь был перегружен государственными проблемами и планами грядущих войн. Однако нет никакого сомнения в том, что письмо, пройдя по соответствующим каналам, побывало у всех начальников отделов, их заместителей и заместителей их заместителей, которые имели полную возможность высказать свои соображения и рекомендации.
Видел ли король это письмо – неизвестно, вполне возможно, что и не видел, так как он ведь был перегружен государственными проблемами и планами грядущих войн. Однако нет никакого сомнения в том, что письмо, пройдя по соответствующим каналам, побывало у всех начальников отделов, их заместителей и заместителей их заместителей, которые имели полную возможность высказать свои соображения и рекомендации.
В конце концов письмо Ньютона вместе с объемистой папкой комментариев, которыми оно успело обрасти по дороге, достигло кабинета секретаря ПКЕВИР/КИНИ/ППАБИ (Плановая Комиссия Его Величества по Исследованиям и Развитию, Комитет по Изучению Новых Идей, Подкомитет по Подавлению Антибританских Идей). Секретарь сразу же осознал важность вопроса и вынес его на заседание Подкомитета, который проголосовал за предоставление Ньютону возможности дать показания на заседании Комитета. Этому решению предшествовало краткое обсуждение идеи Ньютона на предмет выяснения, нет ли в его намерениях чего-нибудь антибританского, но запись этой дискуссии, заполнившая несколько томов in quarto, с полной ясностью показывает, что серьезного подозрения на него так и не упало.
Показания Ньютона перед ПКЕВИР/КИНИ следует рекомендовать для прочтения всем молодым ученым, еще не знающим, как вести себя, когда придет их час. Колледж проявил деликатность, предоставив ему на период заседаний Комитета двухмесячный отпуск без сохранения содержания, а зам декана по научно-исследовательской работе проводил его шутливым напутственным пожеланием не возвращаться без «жирного» контракта. Заседание Комитета проходило при открытых дверях, и публики набилось довольно много, но впоследствии оказалось, что большинство присутствующих ошиблось дверью, стремясь попасть на заседание КЕВОРСПВО – Комиссии Его Величества по Обличению Разврата Среди Представителей Высшего Общества.
После того как Ньютон был приведен к присяге и торжественно заявил, что он не является членом Лояльной Его Величества Оппозиции, никогда не писал безнравственных книг, не ездил в Россию и не совращал молочниц, его попросили кратко изложить суть дела. В блестящей, простой, кристально ясной десятиминутной речи, произнесенной экспромтом, Ньютон изложил законы Кеплера и свою собственную гипотезу, родившуюся при виде падающего яблока.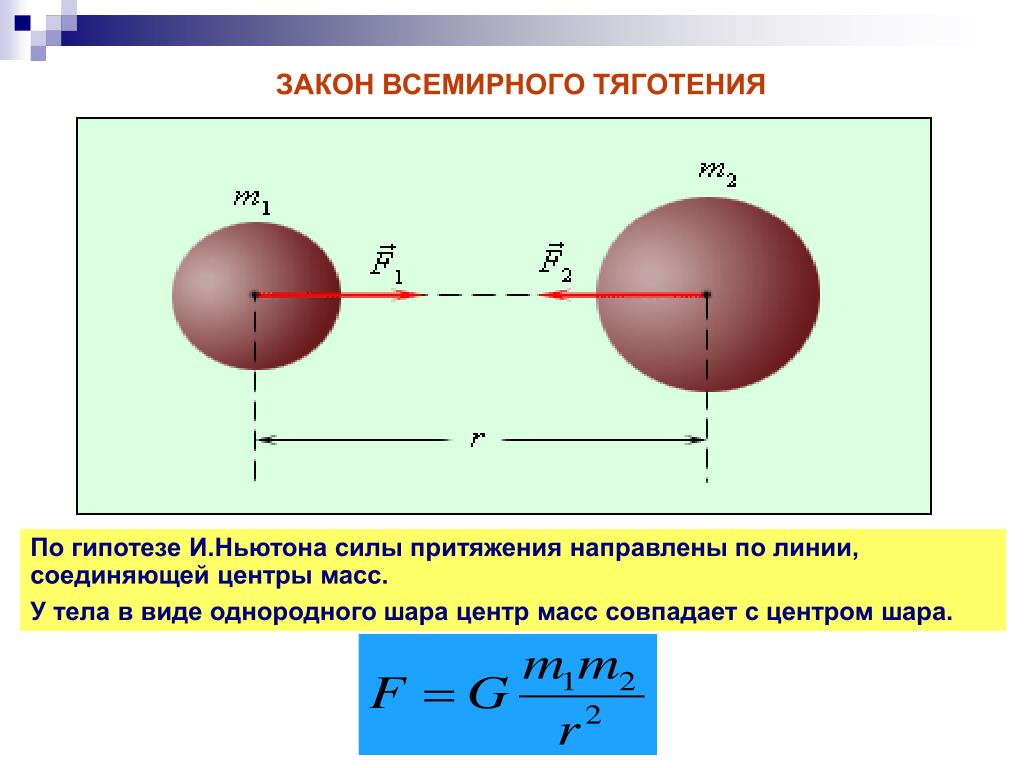 В этот момент один из членов Комитета, импозантный и динамичный мужчина, настоящий человек действия, пожелал узнать, какие средства может предложить Ньютон для улучшения постановки дела по выращиванию яблок в Англии. Ньютон начал объяснять, что яблоко не является существенной частью его гипотезы, но был прерван сразу несколькими членами Комитета, которые дружно высказались в поддержку проекта по улучшению английских яблок. Обсуждение продолжалось несколько недель, в течение которых Ньютон с характерным для него спокойствием и достоинством сидел и ждал, когда Комитет пожелает с ним проконсультироваться. Однажды он опоздал на несколько минут к началу заседания и нашел дверь запертой. Он осторожно постучал, не желая мешать размышлениям членов Комитета. Дверь приотворилась, и привратник, прошептав, что мест нет, отправил его обратно. Ньютон, всегда отличавшийся логичностью мышления, пришел к заключению, что Комитет не нуждается более в его советах, а посему вернулся в свой колледж, где его ждала работа в различных комиссиях.
В этот момент один из членов Комитета, импозантный и динамичный мужчина, настоящий человек действия, пожелал узнать, какие средства может предложить Ньютон для улучшения постановки дела по выращиванию яблок в Англии. Ньютон начал объяснять, что яблоко не является существенной частью его гипотезы, но был прерван сразу несколькими членами Комитета, которые дружно высказались в поддержку проекта по улучшению английских яблок. Обсуждение продолжалось несколько недель, в течение которых Ньютон с характерным для него спокойствием и достоинством сидел и ждал, когда Комитет пожелает с ним проконсультироваться. Однажды он опоздал на несколько минут к началу заседания и нашел дверь запертой. Он осторожно постучал, не желая мешать размышлениям членов Комитета. Дверь приотворилась, и привратник, прошептав, что мест нет, отправил его обратно. Ньютон, всегда отличавшийся логичностью мышления, пришел к заключению, что Комитет не нуждается более в его советах, а посему вернулся в свой колледж, где его ждала работа в различных комиссиях.
Спустя несколько месяцев Ньютон был удивлен, получив объемистый пакет из ПКЕВИР/КИНИ. Открыв его, он обнаружил, что содержимое состоит из многочисленных правительственных анкет, в пяти экземплярах каждая. Природное любопытство – главная черта всякого истинного ученого – заставило его внимательно изучить эти анкеты. Затратив на это изучение определенное время, он понял, что его приглашают подать прошение о заключении контракта на постановку научного исследования для выяснения связи между способом выращивания яблок, их качеством и скоростью падения на землю. Конечной целью проекта, как он понял, было выведение сорта яблок, которые не только имели бы хороший вкус, но и падали бы на землю мягко, не повреждая кожуры. Это, конечно, было не совсем то, что Ньютон имел в виду, когда писал письмо королю. Но он был человеком практичным и понял, что, работая над предлагаемой проблемой, сможет попутно проверить и свою гипотезу. Так он соблюдет интересы короля и позанимается немножко наукой – за те же деньги. Приняв такое решение, Ньютон принялся заполнять анкеты без дальнейших колебаний.
Приняв такое решение, Ньютон принялся заполнять анкеты без дальнейших колебаний.
Однажды в 1865 году точный распорядок дня Ньютона был нарушен. В четверг после обеда он готовился принять комиссию вице-президентов компаний, входивших во фруктовый синдикат, когда пришло повергшее Ньютона в ужас и всю Британию в скорбь известие о гибели всего состава комиссии во время страшного столкновения почтовых дилижансов. У Ньютона, как это уже было однажды, образовалось ничем не занятое «окно», и он принял решение прогуляться. Во время этой прогулки ему пришла (он сам не знает как) мысль о новом, совершенно революционном математическом подходе, с помощью которого можно решить задачу о притяжении вблизи большой сферы. Ньютон понял, что решение этой задачи позволит проверить его гипотезу с наибольшей точностью, и тут же, не прибегая ни к чернилам, ни к бумаге, в уме доказал, что гипотеза подтверждается. Легко можно себе представить, в какой восторг он пришел от столь блестящего открытия.
Вот так правительство Его Величества поддерживало и воодушевляло Ньютона в эти напряженные годы работы над теорией. Мы не будем распространяться о попытках Ньютона опубликовать свое доказательство, о. недоразумениях с редакцией «Журнала садоводов» и о том, как его статью отвергли журналы «Астроном-любитель» и «Физика для домашних хозяек». Достаточно сказать, что Ньютон основал свой собственный журнал, чтобы иметь возможность напечатать без сокращений и искажений сообщение о своем открытии.
Мы не будем распространяться о попытках Ньютона опубликовать свое доказательство, о. недоразумениях с редакцией «Журнала садоводов» и о том, как его статью отвергли журналы «Астроном-любитель» и «Физика для домашних хозяек». Достаточно сказать, что Ньютон основал свой собственный журнал, чтобы иметь возможность напечатать без сокращений и искажений сообщение о своем открытии.
Напечатано в журнале «The American Scientist», 39, №1 (1951).
Дж.Э. Миллер – заведующий кафедрой метеорологии и океанографии Нью-йоркского университета.
Принципы научного администрирования
Оглавление
Дата публикации:
17 августа 2000 года
Отрицать глобализацию — всё равно, что отрицать закон гравитации
27 – 28 мая 2015 года в БФУ им. И. Канта прошёл воркшоп «Глобализация 2.0. Новые подходы к исследованиям и преподаванию». Мероприятие было организовано Международным университетом Венеции (Италия), Российским советом по международным делам и БФУ им. И. Канта и собрало ведущих специалистов из России и Италии по вопросам глобального мира. О целях, перспективах и проблемах глобализации беседуем с Андреем Кортуновым, директором Российского совета по международным делам.
И. Канта и собрало ведущих специалистов из России и Италии по вопросам глобального мира. О целях, перспективах и проблемах глобализации беседуем с Андреем Кортуновым, директором Российского совета по международным делам.
– Говоря о глобализации, в России подразумевают прежде всего вопросы экономики, в последнее время политику, а на конференции обсуждается глобализация в образовании, культуре… Это новая повестка для нашей страны.
– Глобализация — это явление комплексное. Действительно, оно началось, возможно, как явление преимущественно экономическое, хотя и об этом можно спорить. Но сейчас мы говорим о глобализации в культуре, в образе жизни, глобализации как формировании глобального гражданского общества, формирование глобального среднего класса. Т.е. это сложное явление, которое имеет много измерений и не может изучаться инструментами одной дисциплины. Это и экономика, и политология, и культурная антропология, и международные отношения, и в какой-то степени история. Это сложное, противоречивое, неоднозначное явление.
Это сложное, противоречивое, неоднозначное явление.
– Давайте рассмотрим глобализацию в образовании. Это и традиция приглашать учёных (преподавателей) из других вузов и стран, и студенческие обмены. По какой-то причине в отдельно взятой России эти процессы развиты слабее, чем в других развитых странах…
– Ну это как посмотреть. Есть два подхода к вузам.
Первый исходит из того, что, как это и было в Средние века, университеты были интернациональными. Не глобальными, но общеевропейскими. Был общий язык преподавания — латынь, преподаватели мигрировали из одного университета в другой, студенты тоже. Собственно говоря, исторически университеты возникли как некие профсоюзы иностранных студентов преимущественно, если брать итальянские университеты (Болонский и другие).
Если исходить из этого: университет — международная структура, что есть общеевропейская или даже общепланетарная система университетов, то университеты должны быть агентами этой глобализации. Но есть и другое представление об университете, которое возникло позднее, в XIX веке: университет — это носитель национальных традиций, культуры, что образование должно отражать специфику данной страны. И до сих пор идёт борьба между этими точками зрений. И действительно, говорят, что есть особенности российского образования, свои преимущества, которые нельзя игнорировать и тем более искоренять. Но вместе с тем академическая мобильность сейчас растёт. Во всём мире увеличивается количество вузов, в которых преподавание идёт на английском языке.
И до сих пор идёт борьба между этими точками зрений. И действительно, говорят, что есть особенности российского образования, свои преимущества, которые нельзя игнорировать и тем более искоренять. Но вместе с тем академическая мобильность сейчас растёт. Во всём мире увеличивается количество вузов, в которых преподавание идёт на английском языке.
Идёт глобальная конкуренция между университетами. И конечно, наши ведущие университеты должны быть частью этого глобального образовательного сообщества. Если они не будут встраиваться в него, то им будет трудно поддерживать уровень обучения, трудно будет конкурировать.
Вузы, конечно, и без этого останутся, но студенты, лучшие студенты, будут искать лучшие вузы. Поэтому альтернативы глобализации нет, и России надо в той или иной степени в этом участвовать.
– Однако в последние месяцы, наоборот, всё больше говорят об особом пути России, и это, конечно, протест против глобализации, точнее — связанной с ней невозможностью всё контролировать. Ведь в глобальных процессах нет какого-то центра, есть отдельные акторы, но их роль постоянно меняется…
Ведь в глобальных процессах нет какого-то центра, есть отдельные акторы, но их роль постоянно меняется…
– Наверное, в этих настроениях присутствует и разочарование, и страх, связанный с неконтролируемыми процессами. И конечно, глобализация имеет не только позитивную, но и негативную сторону. Для социальных групп, для экономических групп, для целых стран. Не все выигрывают, кто-то и проигрывает. Но отрицать глобализацию — это всё равно, что отрицать закон гравитации: это делать можно, но если прыгнуть с крыши, то всё равно упадёшь, а не взлетишь вверх. Важно понимать, что любой закон любую тенденцию можно использовать себе на пользу. Поэтому здесь должно быть разумное сочетание и какого-то протекционизма, и включённости.
Мне кажется, что в XXI веке выиграет то общество, то государство, которое сможет включиться в процесс глобализации, при этом не потеряв себя, т.е. не превратившись в объект. Это требует искусства, это требует большой скоординированной работы и государства, и бизнеса, и образовательных учреждений, и общественных организаций.
И здесь идеальных ответов нет ни у кого, потому что протесты против глобализации возникают всюду, не только у нас. Конечно, люди боятся: это новое, непривычное, риски растут, подвижность системы возрастает, и есть ностальгия по тем временам, когда всё было проще понятнее, когда всё можно было контролировать на уровне отдельных государств. Теперь этого нет.
– И пути обратно тоже нет?
– Ну, некоторые шаги вспять на каких-то направлениях возможны: протекционизм, скажем, или создание вместо глобальной экономики экономики блоков стран, возможно усиление государств, возможно усиление контроля на границах, сокращение потоков мигрантов, но это всё временные явления, я думаю. А общие тенденции — к объединению, к взаимодействию, к интеграции — будут продолжаться. К этому ведут и технологии, и изменения социальной картины жизни, распространение глобальных стандартов поведения и т.д. То есть я думаю, что с какими-то возможными отступлениями, не всегда с равной скоростью, но процессы глобализации полностью обратить вспять невозможно.
– А если говорить о глобализации образования, то кто игроки, кто задаёт вектор и темп? Государства, работодатели, отдельные вузы, отдельные лаборатории, учёные?
– Образование — это очень большой и неоднородный сектор. Здесь есть, конечно, и бизнес-интересы: есть борьба за студентов с их деньгами, это огромный рынок (для Австралии, Канады и даже США — это большая статья экспорта). Есть конкуренция между университетами, между государствами, но есть конкуренция и внутри университетов: скажем, есть хорошая школа, а есть слабые. Но университет — это не только экономика, он воспитывает человека, он учит человека коммуницировать, социализироваться, он производит граждан, а не просто выпускников. Так что образование — специфическая сфера, где нельзя оперировать только экономическими понятиями. Это не просто бизнес, не продажа нефти и не поставки вооружения, это особая сфера, поэтому образование требует междисциплинарного подхода.
– Относительно недавно, с развитием цифровых технологий, в образовании наметился глобальный тренд — создание массовых онлайн-курсов (MOOC). К знанию получили доступ миллионы пользователей Интернета, вне зависимости от их места жительства. И это тоже проявление глобализации. Насколько этот тренд изменит систему образования?
К знанию получили доступ миллионы пользователей Интернета, вне зависимости от их места жительства. И это тоже проявление глобализации. Насколько этот тренд изменит систему образования?
– Да, это продукт глобализации, но прежде всего, это продукт автоматизации. Как и в любой области (в промышленности или сфере обслуживания), процессы автоматизируются, они упрощаются, ставятся на конвейер, удешевляются и т.д. В образовании это тоже происходит, хотя происходит своеобразно. Думаю, какие-то муки (прим. смеётся) нам всем предстоят, но при этом, чем выше ты на этой образовательной лестнице, тем важнее индивидуальный подход, уникальное знание, повышается роль и значение человеческого фактора. Одно дело — бакалавриат, его можно как-то стандартизировать, а вот с магистратурой уже сложнее, PhD — невозможно.
Так что эти онлайн-курсы ни в коей мере не угрожают университетам, они только помогают распространять какое-то очень стандартное знание, осваивать очень простые навыки, но не более того.
Источник: Балтийский федеральный университет имени Иммануила Канта
Закон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона
Далее: Проблемы Up: Круговое движение и Предыдущая: Центростремительное ускорение
Идея: Универсальный закон тяготения Ньютона гласит, что
любые два объекта
приложить гравитационную силу притяжения к каждому
разное. Направление силы вдоль линии, соединяющей
объекты (см. рис. (7.3)). Величина силы
пропорциональна произведению гравитационных масс
объекты,
и обратно пропорционально квадрату расстояния между
их.Для двух объектов на рисунке 7.3:
Примечание:
- инерционная масса объекта определяет количество
из
сила, необходимая для создания заданного ускорения этого объекта.
 В гравитационная масса определяет силу гравитационного
Привлечение
между двумя телами. В механике Ньютона эти две массы имеют
нет очевидной связи друг с другом.Тем не менее, это было
эмпирически замечено, что они численно равны.
Этот замечательный факт был известен веками, но оставался
необъяснимо до
Общая теория относительности Эйнштейна.
В гравитационная масса определяет силу гравитационного
Привлечение
между двумя телами. В механике Ньютона эти две массы имеют
нет очевидной связи друг с другом.Тем не менее, это было
эмпирически замечено, что они численно равны.
Этот замечательный факт был известен веками, но оставался
необъяснимо до
Общая теория относительности Эйнштейна. - Гравитационная постоянная Ньютона чрезвычайно мала при выражении в объектах лабораторных размеров: гравитационная сила между двумя 1 кг объектов, разделенных 1 кв.м только 6,67 x 10 – 11 Ньютонов.
- Для объекта массой м у поверхности Земли:
где M E = 5.98 x 10 24 кг – масса Земли и R E = 6,38 x 10 6 м – радиус Земли иF грав = – G м = – мг (24)
в соответствии с выражением в главе 3.г G = 9,8 м / с 2 (25) 
Определение: Гравитационная потенциальная энергия
Из-за гравитационной силы притяжения любые два объекта с масс м 1 и м 2 , расположенных на расстоянии r друг от друга, имеют умение делать работу.Следовательно, у них есть потенциальная энергия. В гравитационной потенциальной энергии таких объектов составляет:
| PE грав = – G . | (26) |
Примечание:
Далее: Проблемы Up: Круговое движение и Предыдущая: Центростремительное ускорение [email protected]
09.10.1997
6.5 Универсальный закон тяготения Ньютона – College Physics
Что общего между ноющими ногами, падающим яблоком и орбитой Луны? Каждый из них вызван гравитационной силой. Наши ноги напрягаются, поддерживая наш вес – силу земного притяжения. Яблоко падает с дерева из-за той же силы, действующей на несколько метров над поверхностью Земли. А Луна вращается вокруг Земли, потому что гравитация способна обеспечить необходимую центростремительную силу на расстоянии в сотни миллионов метров.Фактически, одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды – вращаться вокруг центра галактики, а галактики – группироваться вместе. Гравитация – еще один пример простоты, лежащей в основе природы. Это самая слабая из четырех основных сил, существующих в природе, и в некотором смысле наименее понятная. Это сила, которая действует на расстоянии, без физического контакта, и выражается формулой, которая действительна повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.
Наши ноги напрягаются, поддерживая наш вес – силу земного притяжения. Яблоко падает с дерева из-за той же силы, действующей на несколько метров над поверхностью Земли. А Луна вращается вокруг Земли, потому что гравитация способна обеспечить необходимую центростремительную силу на расстоянии в сотни миллионов метров.Фактически, одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды – вращаться вокруг центра галактики, а галактики – группироваться вместе. Гравитация – еще один пример простоты, лежащей в основе природы. Это самая слабая из четырех основных сил, существующих в природе, и в некотором смысле наименее понятная. Это сила, которая действует на расстоянии, без физического контакта, и выражается формулой, которая действительна повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.
Сэр Исаак Ньютон был первым ученым, который точно определил силу гравитации и показал, что она может объяснить как падающие тела, так и астрономические движения. См. Рисунок 6.20. Но Ньютон был не первым, кто подозревал, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движения планет имеют одну и ту же причину. Некоторые современники Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенных успехов в понимании гравитации. Но Ньютон был первым, кто предложил точную математическую форму и использовал ее, чтобы показать, что движение небесных тел должно иметь конические сечения – окружности, эллипсы, параболы и гиперболы.Это теоретическое предсказание стало большим триумфом – с некоторого времени было известно, что луны, планеты и кометы следуют такими путями, но никто не смог предложить механизм, который заставил бы их следовать этим путям, а не другим.
См. Рисунок 6.20. Но Ньютон был не первым, кто подозревал, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движения планет имеют одну и ту же причину. Некоторые современники Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенных успехов в понимании гравитации. Но Ньютон был первым, кто предложил точную математическую форму и использовал ее, чтобы показать, что движение небесных тел должно иметь конические сечения – окружности, эллипсы, параболы и гиперболы.Это теоретическое предсказание стало большим триумфом – с некоторого времени было известно, что луны, планеты и кометы следуют такими путями, но никто не смог предложить механизм, который заставил бы их следовать этим путям, а не другим.
Рис. 6.20. Согласно ранним источникам, Ньютон был вдохновлен на установление связи между падающими телами и астрономическими движениями, когда он увидел яблоко, падающее с дерева, и понял, что если гравитационная сила может распространяться над землей на дерево, она также может достигать солнце. Яблоко Ньютона является частью всемирного фольклора и, возможно, даже основано на фактах. Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку понятию лежащей в основе простоты и единства в природе. Ученые по-прежнему ожидают, что в результате их постоянных исследований природы появится основная простота.
Яблоко Ньютона является частью всемирного фольклора и, возможно, даже основано на фактах. Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку понятию лежащей в основе простоты и единства в природе. Ученые по-прежнему ожидают, что в результате их постоянных исследований природы появится основная простота.
Гравитационная сила относительно проста. Это всегда привлекательно, и это зависит только от вовлеченных масс и расстояния между ними.Выражаясь современным языком, универсальный закон всемирного тяготения Ньютона гласит, что каждая частица во Вселенной притягивает каждую другую частицу с силой, действующей вдоль соединяющей их линии. Сила прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Рис. 6.21 Гравитационное притяжение происходит вдоль линии, соединяющей центры масс этих двух тел. Величина силы одинакова для всех в соответствии с третьим законом Ньютона.
Величина силы одинакова для всех в соответствии с третьим законом Ньютона.
Предупреждение о неправильном представлении
Величина силы, действующей на каждый объект (один имеет большую массу, чем другой), одинакова, что соответствует третьему закону Ньютона.
Тела, с которыми мы имеем дело, имеют тенденцию быть большими. Чтобы упростить ситуацию, мы предполагаем, что тело действует так, как будто вся его масса сосредоточена в одной конкретной точке, называемой центром масс (ЦМ), что будет более подробно изучено в разделах «Линейный импульс и столкновения». Для двух тел с массой 12 мм {m} {} и размером 12 мм {M} {} с расстоянием rr размером 12 {r} {} между их центрами масс уравнение универсального закона всемирного тяготения Ньютона составляет
F. = GmMr2, F = GmMr2, размер 12 {F = G {{ital “mM”} больше {r rSup {size 8 {2}}}}} {}6.40
, где размер FF 12 {F} {} – величина гравитационной силы, а размер GG 12 {G} {} – коэффициент пропорциональности, называемый гравитационной постоянной. GG размера 12 {G} {} – это универсальная гравитационная постоянная, то есть считается, что она одинакова во всей Вселенной. Экспериментально измеренная величина составляет
GG размера 12 {G} {} – это универсальная гравитационная постоянная, то есть считается, что она одинакова во всей Вселенной. Экспериментально измеренная величина составляет
6.41
в единицах СИ. Обратите внимание, что единицы размера GG 12 {G} {} таковы, что сила в ньютонах получается из F = GmMr2F = GmMr2 размер 12 {F = G {{ital “mM”} над {r rSup {размер 8 {2 }}}}} {}, если считать массу в килограммах и расстояние в метрах. Например, две массы по 1.000 кг, разделенные расстоянием 1.000 м, будут испытывать гравитационное притяжение 6,674 × 10–11N6,674 × 10–11N размером 12 {6 “”. “673” умножить на “10” rSup {размер 8 {- “11”}} N} {}. Это необычайно малая сила. Небольшая величина гравитационной силы согласуется с повседневным опытом.Мы не подозреваем, что даже большие объекты, такие как горы, действуют на нас. Фактически, вес нашего тела – это сила притяжения всей Земли на нас с массой 6 × 1024 кг6 × 1024 кг размером 12 {6 раз “10” rSup {size 8 {“24″}} `” кг ” } {}.
Фактически, вес нашего тела – это сила притяжения всей Земли на нас с массой 6 × 1024 кг6 × 1024 кг размером 12 {6 раз “10” rSup {size 8 {“24″}} `” кг ” } {}.
Напомним, что ускорение свободного падения gg размер 12 {g} {} составляет около 9,80 м / с 29,80 м / с2 размер 12 {9 “.” 8` “м / с” rSup {size 8 {2}}} {} на Земле. Теперь мы можем определить, почему это так. Вес объекта мг. – это сила тяжести между ним и Землей.Замена мг на размер FF 12 {F} {} в универсальном законе тяготения Ньютона дает
mg = GmMr2, mg = GmMr2, размер 12 {ital “mg” = G {{ital “mM”} больше {r rSup { размер 8 {2}}}}} {}6.42
, где размер 12 {m} {} мм – масса объекта, размер 12 мм {M} {} – масса Земли, а размер rr 12 { r} {} – это расстояние до центра Земли (расстояние между центрами масс объекта и Землей). См. Рисунок 6.22. Масса mm size 12 {m} {} объекта отменяется, оставляя уравнение для gg size 12 {g} {}:
g = GMr2. г = GMr2. размер 12 {g = G {{M} больше {r rSup {size 8 {2}}}}} {}
г = GMr2. размер 12 {g = G {{M} больше {r rSup {size 8 {2}}}}} {}6,43
Подстановка известных значений массы и радиуса Земли (до трех значащих цифр),
g = 6,67 × 10-11 Н⋅м2 кг2 × 5,98 × 1024 кг (6,38 × 106 м) 2, g = 6,67 × 10-11 Нм2 кг2 × 5,98 × 1024 кг (6,38 × 106 м) 2, размер 12 {g = левый (6 дюймов). “” 67 “умножить на” 10 “rSup {размер 8 {-” 11 “}} {{N cdot m rSup {размер 8 {2}}} больше {” kg “rSup {размер 8 {2}}}} справа) раз {{5 “.” “98” умножить на “10” rSup {размер 8 {“24”}} “кг”} больше {\ (6 “.”” 38 “умножить на” 10 “rSup {size 8 {6}}” m “\) rSup {size 8 {2}}}} {}6,44
и мы получаем значение ускорения падающего тела :
g = 9,80 м / с2. g = 9,80 м / с2. размер 12 {g = 9 “.” “80” “м / с” rSup {размер 8 {2}}} {}6,45
Рис. 6.22. Расстояние между центрами масс Земли и объектом на ее поверхности почти такое же, как и радиус Земли, потому что Земля намного больше, чем объект.
Это ожидаемое значение и не зависит от массы тела . Закон тяготения Ньютона продвигает наблюдение Галилея о том, что все массы падают с одинаковым ускорением, на шаг вперед, объясняя наблюдение с точки зрения силы, заставляющей объекты падать, – фактически, с точки зрения универсально существующей силы притяжения между массами.
Закон тяготения Ньютона продвигает наблюдение Галилея о том, что все массы падают с одинаковым ускорением, на шаг вперед, объясняя наблюдение с точки зрения силы, заставляющей объекты падать, – фактически, с точки зрения универсально существующей силы притяжения между массами.
Эксперимент на вынос
Возьмите шарик, шарик и ложку и бросьте их с одной высоты. Они одновременно падают на пол? Если вы также уроните лист бумаги, будет ли он вести себя так же, как и другие предметы? Объясните свои наблюдения.
Выполнение подключений
Попытки понять гравитационную силу все еще делаются. Как мы увидим в Физике элементарных частиц, современная физика изучает связи гравитации с другими силами, пространством и временем. Общая теория относительности меняет наш взгляд на гравитацию, заставляя нас думать о гравитации как о искривлении пространства и времени.
В следующем примере мы проводим сравнение, подобное тому, которое сделал сам Ньютон. Он отметил, что если гравитационная сила заставила Луну вращаться вокруг Земли, то ускорение свободного падения должно равняться центростремительному ускорению Луны на своей орбите.Ньютон обнаружил, что два ускорения совпадают «почти почти».
Он отметил, что если гравитационная сила заставила Луну вращаться вокруг Земли, то ускорение свободного падения должно равняться центростремительному ускорению Луны на своей орбите.Ньютон обнаружил, что два ускорения совпадают «почти почти».
Пример 6.6
Гравитационная сила Земли – это центростремительная сила, заставляющая Луну двигаться по изогнутой траектории
(a) Найдите ускорение свободного падения Земли на расстоянии Луны.
(b) Рассчитайте центростремительное ускорение, необходимое для удержания Луны на своей орбите (при условии круговой орбиты вокруг неподвижной Земли), и сравните его со значением ускорения, обусловленным земным гравитационным движением, которое вы только что нашли.
Стратегия для (a)
Этот расчет аналогичен вычислению ускорения свободного падения на поверхности Земли, за исключением того, что размер rr 12 {r} {} – это расстояние от центра Земли до центра Луны. Радиус почти круговой орбиты Луны составляет 3,84 × 108 м3,84 × 108 м, размер 12 {3 “”. “84” умножить на “10” rSup {size 8 {8}} `m} {}.
Радиус почти круговой орбиты Луны составляет 3,84 × 108 м3,84 × 108 м, размер 12 {3 “”. “84” умножить на “10” rSup {size 8 {8}} `m} {}.
Решение для (a)
Подставляя известные значения в выражение для размера gg 12 {M} {}, найденное выше, помня, что размер MM 12 {M} {} – это масса Земли, а не Луны, получаем
g = GMr2 = 6.67 × 10−11Нм2кг2 × 5,98 × 1024 кг (3,84 × 108 м) 2 = 2,70 × 10−3 м / с. 2g = GMr2 = 6,67 × 10−11Нм2 кг2 × 5,98 × 1024 кг (3,84 × 108 м) 2 = 2,70 × 10−3м / с.26.46
Стратегия для (б)
Центростремительное ускорение можно рассчитать, используя любую форму
ac = v2rac = rω2} .ac = v2rac = rω2}. размер 12 {не осталось матрицы { a rSub {размер 8 {c}} = {{v rSup {размер 8 {2}}} больше {r}} {} ## a rSub {размер 8 {c}} = rω rSup {размер 8 {2}} } правая rbrace “.” } {}6.47
Мы выбрали вторую форму:
ac = rω2, ac = rω2, размер 12 {a rSub {размер 8 {c}} = rω rSup {размер 8 {2}}} {} 6. 48
48
где ωω размер 12 {ω} {} – угловая скорость Луны относительно Земли.
Решение для (b)
Учитывая, что период (время, необходимое для совершения одного полного оборота) орбиты Луны составляет 27,3 дня, (d) и используя
1 d × 24 часа × 60 минут × 60 минут = 86400 с1, d × 24 часа × 60 минут × 60 секунд = 86 400 s размер 12 {ω = {{Δθ} над {Δt}} = {{2π “rad”} над {\ (“27” “.” “3 d” \) \ (“86 400 s / d” \)} } = 2 “.” “66” умножить на “10” rSup {size 8 {- 6}} {{“rad”} больше {s}}} {}6.49
мы видим, что
ω = ΔθΔt = 2π рад (27,3 д) (86400 с / д) = 2,66 × 10-6рад. Ω = Δθ∆t = 2π рад (27,3 д) (86,400 с / д) = 2,66 × 10 −6рад. размер 12 {ω = {{Δθ} над {Δt}} = {{2π “rad”} над {\ (“27” “.” “3 d” \) \ (“86 400 s / d” \)}} = 2 “.” “66” умножить на “10” rSup {размер 8 {- 6}} {{“rad”} больше {s}}} {}6.50
Центростремительное ускорение составляет
ac = rω2 = (3,84 × 108 м) (2,66 × 10–6рад / с) 2 = 2,72 × 10–3 м / с 2ac = rω2 = (3,84 × 108 м) (2,66 × 10–6рад / с) 2 = 2,72 × 10−3м / с. 2alignl {stack {
размер 12 {a rSub {размер 8 {c}} = rω rSup {размер 8 {2}} = \ (3 “.”” 84 “умножить на” 10 “rSup {размер 8 {8}}” m “\) \ (2”. “” 66 “умножить на” 10 “rSup {размер 8 {- 6}}” рад / с “\) rSup {размер 8 {2}}} {} #
“” = 2 “.” “72” умножить на “10” rSup {размер 8 {- 3}} “м / с” rSup {размер 8 {2}} {}
}} {}
2alignl {stack {
размер 12 {a rSub {размер 8 {c}} = rω rSup {размер 8 {2}} = \ (3 “.”” 84 “умножить на” 10 “rSup {размер 8 {8}}” m “\) \ (2”. “” 66 “умножить на” 10 “rSup {размер 8 {- 6}}” рад / с “\) rSup {размер 8 {2}}} {} #
“” = 2 “.” “72” умножить на “10” rSup {размер 8 {- 3}} “м / с” rSup {размер 8 {2}} {}
}} {}6.51
Направление ускорения – к центру Земли.
Обсуждение
Центростремительное ускорение Луны, найденное на (b), отличается менее чем на 1% от ускорения, вызванного земным притяжением, на (a).Это совпадение является приблизительным, поскольку орбита Луны имеет слегка эллиптическую форму, а Земля не является неподвижной (скорее, система Земля-Луна вращается вокруг своего центра масс, который расположен примерно на 1700 км ниже поверхности Земли). Ясно подразумевается, что гравитационная сила Земли заставляет Луну вращаться вокруг Земли.
Почему Земля не остается неподвижной, когда Луна вращается вокруг нее? Это связано с тем, что, как и ожидалось из третьего закона Ньютона, если Земля воздействует на Луну, то Луна должна оказывать на Землю равную и противоположную силу (см. Рисунок 6.23). Мы не ощущаем влияние Луны на движение Земли, потому что гравитация Луны перемещает наши тела вместе с Землей, но на Земле есть и другие знаки, которые ясно показывают влияние гравитационной силы Луны, как обсуждается в Спутниках и законах Кеплера: аргумент в пользу Простота.
Рисунок 6.23). Мы не ощущаем влияние Луны на движение Земли, потому что гравитация Луны перемещает наши тела вместе с Землей, но на Земле есть и другие знаки, которые ясно показывают влияние гравитационной силы Луны, как обсуждается в Спутниках и законах Кеплера: аргумент в пользу Простота.
Рис. 6.23 (a) Земля и Луна вращаются примерно раз в месяц вокруг своего общего центра масс. (б) Их центр масс вращается вокруг Солнца по эллиптической орбите, но на пути Земли вокруг Солнца есть «изгибы».Подобные колебания на траекториях звезд наблюдались и считаются прямым доказательством того, что планеты вращаются вокруг этих звезд. Это важно, потому что отраженный свет планет часто слишком тусклый, чтобы его можно было наблюдать.
Приливы
Океанские приливы – один из очень заметных результатов гравитации Луны, действующей на Землю. Рисунок 6.24 представляет собой упрощенный рисунок положения Луны относительно приливов и отливов. Поскольку вода легко течет по поверхности Земли, прилив создается на ближайшей к Луне стороне Земли, где гравитационное притяжение Луны наиболее велико. Почему на противоположной стороне Земли бывает прилив? Ответ заключается в том, что Земля тянется к Луне больше, чем вода на обратной стороне, потому что Земля находится ближе к Луне. Таким образом, вода на ближайшей к Луне стороне Земли отводится от Земли, а Земля отводится от воды на дальней стороне. Когда Земля вращается, приливная выпуклость (эффект приливных сил между вращающимся на орбите естественным спутником и основной планетой, вокруг которой он вращается) сохраняет свою ориентацию с Луной. Таким образом, в день бывает два прилива (фактический период составляет около 12 часов 25.2 минуты), потому что Луна тоже каждый день движется по своей орбите).
Почему на противоположной стороне Земли бывает прилив? Ответ заключается в том, что Земля тянется к Луне больше, чем вода на обратной стороне, потому что Земля находится ближе к Луне. Таким образом, вода на ближайшей к Луне стороне Земли отводится от Земли, а Земля отводится от воды на дальней стороне. Когда Земля вращается, приливная выпуклость (эффект приливных сил между вращающимся на орбите естественным спутником и основной планетой, вокруг которой он вращается) сохраняет свою ориентацию с Луной. Таким образом, в день бывает два прилива (фактический период составляет около 12 часов 25.2 минуты), потому что Луна тоже каждый день движется по своей орбите).
Рис. 6.24 Луна вызывает океанические приливы, притягивая воду на ближней стороне больше, чем Земля, и притягивая Землю больше, чем воду на обратной стороне. Расстояния и размеры не в масштабе. Для этого упрощенного представления системы Земля-Луна, есть два прилива и два отлива в день в любом месте, потому что Земля вращается под приливной выпуклостью.
Солнце также влияет на приливы и отливы, хотя оно имеет примерно половину эффекта Луны.Однако самые большие приливы, называемые весенними приливами, происходят, когда Земля, Луна и Солнце выровнены. Наименьшие приливы, называемые непрямыми приливами, происходят, когда Солнце находится под углом 90º90º размером 12 {“90” rSup {size 8 {circ}}} {} к центру Земли и Луны.
Рис. 6.25 (a, b) Весенние приливы: самые высокие приливы происходят, когда Земля, Луна и Солнце выровнены. (c) Ближний прилив: самые низкие приливы происходят, когда Солнце находится под углом 90º90º размером 12 {“90” rSup {size 8 {circ}}} {} к центру Земли и Луны.Обратите внимание, что этот рисунок не в масштабе. Приливы не являются уникальными для Земли, но происходят во многих астрономических системах. Наиболее экстремальные приливы возникают там, где сила гравитации наиболее велика и изменяется наиболее быстро, например, около черных дыр (см. Рис. 6.26). Несколько вероятных кандидатов в черные дыры были обнаружены в нашей галактике. Они имеют массу больше Солнца, но имеют диаметр всего несколько километров. Приливные силы рядом с ними настолько велики, что могут фактически оторвать материю от звезды-компаньона.
Они имеют массу больше Солнца, но имеют диаметр всего несколько километров. Приливные силы рядом с ними настолько велики, что могут фактически оторвать материю от звезды-компаньона.
Рис. 6.26. Черная дыра – это объект с такой сильной гравитацией, что даже свет не может покинуть его. Эта черная дыра была создана сверхновой одной звезды в двухзвездной системе. Приливные силы, создаваемые черной дырой, настолько велики, что отрывают материю от звезды-компаньона. Это вещество сжимается и нагревается, когда оно всасывается в черную дыру, создавая свет и рентгеновские лучи, наблюдаемые с Земли.
«Невесомость» и микрогравитация
В отличие от огромной гравитационной силы около черных дыр, это видимое гравитационное поле, которое испытывают астронавты, вращающиеся вокруг Земли.Как влияет «невесомость» на космонавта, который месяцами находится на орбите? А как насчет влияния невесомости на рост растений? Невесомость не означает, что на космонавта не действует сила гравитации. На орбите космонавта нет «невесомости». Этот термин просто означает, что космонавт находится в свободном падении, ускоряясь с ускорением свободного падения. В случае обрыва троса лифта пассажиры внутри окажутся в свободном падении и испытают невесомость.На некоторых аттракционах в парках развлечений можно испытать непродолжительные периоды невесомости.
На орбите космонавта нет «невесомости». Этот термин просто означает, что космонавт находится в свободном падении, ускоряясь с ускорением свободного падения. В случае обрыва троса лифта пассажиры внутри окажутся в свободном падении и испытают невесомость.На некоторых аттракционах в парках развлечений можно испытать непродолжительные периоды невесомости.
Рис. 6.27 Астронавты в невесомости на борту Международной космической станции. (предоставлено NASA)
Микрогравитация относится к среде, в которой кажущееся чистое ускорение тела мало по сравнению с ускорением, создаваемым Землей на ее поверхности. Многие интересные темы биологии и физики были изучены за последние три десятилетия в условиях микрогравитации.Непосредственное беспокойство вызывает влияние на астронавтов длительного пребывания в космическом пространстве, например, на Международной космической станции. Исследователи заметили, что в этой среде мышцы атрофируются (истощаются). Также происходит соответствующая потеря костной массы. Продолжаются исследования по адаптации сердечно-сосудистой системы к космическим полетам. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за силы тяжести. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, в то время как в горизонтальном положении происходит прямо противоположное.Какая разница в отсутствии этого перепада давления на сердце?
Продолжаются исследования по адаптации сердечно-сосудистой системы к космическим полетам. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за силы тяжести. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, в то время как в горизонтальном положении происходит прямо противоположное.Какая разница в отсутствии этого перепада давления на сердце?
Некоторые открытия в области физиологии человека в космосе могут иметь клиническое значение для лечения болезней на Земле. С другой стороны, космические полеты, как известно, влияют на иммунную систему человека, что, возможно, делает членов экипажа более уязвимыми для инфекционных заболеваний. Эксперименты, проведенные в космосе, также показали, что некоторые бактерии в условиях микрогравитации растут быстрее, чем на Земле. Однако следует отметить, что исследования показывают, что производство микробных антибиотиков может увеличиваться в два раза в культурах, выращиваемых в космосе. Можно надеяться, что сможем понять эти механизмы, чтобы добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белка, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.
Можно надеяться, что сможем понять эти механизмы, чтобы добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белка, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.
Растения эволюционировали под действием силы тяжести и датчиков силы тяжести. Корни растут вниз, а побеги вверх. Растения могли бы обеспечить систему жизнеобеспечения для длительных космических полетов, регенерируя атмосферу, очищая воду и производя пищу.Некоторые исследования показали, что на рост и развитие растений не влияет сила тяжести, но все еще существует неопределенность в отношении структурных изменений растений, выращенных в условиях микрогравитации.
Эксперимент Кавендиша: тогда и сейчас
Как отмечалось ранее, универсальная гравитационная постоянная GG размером 12 {G} {} определяется экспериментально. Это определение впервые было сделано точно Генри Кавендишем (1731–1810), английским ученым, в 1798 году, более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения.Измерение размера GG 12 {G} {} очень простое и важное, потому что оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень трудным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (максимум десятки килограммов), используя прибор, подобный показанному на рис. 6.28. Примечательно, что его значение для размера GG 12 {G} {} отличается менее чем на 1% от лучшего современного значения.
Это определение впервые было сделано точно Генри Кавендишем (1731–1810), английским ученым, в 1798 году, более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения.Измерение размера GG 12 {G} {} очень простое и важное, потому что оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень трудным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (максимум десятки килограммов), используя прибор, подобный показанному на рис. 6.28. Примечательно, что его значение для размера GG 12 {G} {} отличается менее чем на 1% от лучшего современного значения.
Одним из важных следствий знания размера GG 12 {G} {} было то, что наконец можно было получить точное значение массы Земли.Это было сделано путем измерения ускорения свободного падения с максимальной точностью, а затем вычисления массы Земли MM размером 12 {M} {} на основе соотношения, которое дает универсальный закон всемирного тяготения Ньютона
mg = GmMr2, mg = GmMr2, размер 12 {ital “mg” = G {{ital “mM”} больше {r rSup {size 8 {2}}}}} {} 6. 52
52
где размер 12 {m } {} – это масса объекта, размер MM 12 {M} {} – масса Земли, а rr size 12 {r} {} – это расстояние до центра Земли (расстояние между центрами масс объект и Земля).См. Рисунок 6.21. Масса mm size 12 {m} {} объекта отменяется, оставляя уравнение для gg size 12 {g} {}:
g = GMr2.g = GMr2. размер 12 {g = G {{M} больше {r rSup {size 8 {2}}}}} {}6,53
Изменение порядка решения для размера 12 мм {M} {} дает
M = gr2G.M = gr2G. размер 12 {M = {{ital “gr” rSup {size 8 {2}}} больше {G}}} {}6.54
Таким образом, размер MM 12 {M} {} можно рассчитать, потому что все количества справа , включая радиус Земли rr размером 12 {r} {}, известны из прямых измерений.В книге «Спутники и законы Кеплера: аргумент в пользу простоты» мы увидим, что знание размера GG 12 {G} {} также позволяет определять астрономические массы. Интересно, что из всех фундаментальных констант в физике размер GG 12 {G} {} определен гораздо хуже.
Эксперимент Кавендиша также используется для исследования других аспектов гравитации. Один из самых интересных вопросов заключается в том, зависит ли сила тяжести от вещества, а также от массы – например, действует ли один килограмм свинца такое же гравитационное притяжение, что и один килограмм воды.Венгерский ученый по имени Роланд фон Этвеш стал пионером этого исследования в начале 20 века. Он обнаружил с точностью до пяти частей на миллиард, что сила тяжести не зависит от вещества. Такие эксперименты продолжаются и сегодня, они улучшили измерения Этвёша. Эксперименты типа Кавендиша, такие как эксперименты Эрика Адельбергера и других из Вашингтонского университета, также наложили серьезные ограничения на возможность существования пятой силы и подтвердили главное предсказание общей теории относительности – что гравитационная энергия вносит вклад в массу покоя.В текущих измерениях используются торсионные весы и параллельная пластина (а не сферы, как использовал Кавендиш), чтобы проверить, как действует закон всемирного тяготения Ньютона на субмиллиметровых расстояниях.
Один из самых интересных вопросов заключается в том, зависит ли сила тяжести от вещества, а также от массы – например, действует ли один килограмм свинца такое же гравитационное притяжение, что и один килограмм воды.Венгерский ученый по имени Роланд фон Этвеш стал пионером этого исследования в начале 20 века. Он обнаружил с точностью до пяти частей на миллиард, что сила тяжести не зависит от вещества. Такие эксперименты продолжаются и сегодня, они улучшили измерения Этвёша. Эксперименты типа Кавендиша, такие как эксперименты Эрика Адельбергера и других из Вашингтонского университета, также наложили серьезные ограничения на возможность существования пятой силы и подтвердили главное предсказание общей теории относительности – что гравитационная энергия вносит вклад в массу покоя.В текущих измерениях используются торсионные весы и параллельная пластина (а не сферы, как использовал Кавендиш), чтобы проверить, как действует закон всемирного тяготения Ньютона на субмиллиметровых расстояниях. В таком мелком масштабе отклоняются ли гравитационные эффекты от закона обратных квадратов? Пока никаких отклонений не наблюдается.
В таком мелком масштабе отклоняются ли гравитационные эффекты от закона обратных квадратов? Пока никаких отклонений не наблюдается.
7.2 Закон всемирного тяготения Ньютона и общая теория относительности Эйнштейна
Концепции, связанные с законом всемирного тяготения Ньютона
Сэр Исаак Ньютон был первым ученым, который точно определил силу гравитации и показал, что она может объяснить как падающие тела, так и астрономические движения.См. Рисунок 7.8. Но Ньютон был не первым, кто подозревал, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник, Галилео Галилей, утверждал, что падающие тела и движения планет имеют одну и ту же причину. Некоторые современники Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенных успехов в понимании гравитации. Но Ньютон был первым, кто предложил точную математическую форму и использовал ее, чтобы показать, что движение небесных тел должно иметь конические сечения – окружности, эллипсы, параболы и гиперболы.Это теоретическое предсказание стало большим триумфом. В течение некоторого времени было известно, что луны, планеты и кометы следуют такими путями, но никто не смог предложить объяснения механизма, который заставил их следовать этим путям, а не другим.
Его предшественник, Галилео Галилей, утверждал, что падающие тела и движения планет имеют одну и ту же причину. Некоторые современники Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенных успехов в понимании гравитации. Но Ньютон был первым, кто предложил точную математическую форму и использовал ее, чтобы показать, что движение небесных тел должно иметь конические сечения – окружности, эллипсы, параболы и гиперболы.Это теоретическое предсказание стало большим триумфом. В течение некоторого времени было известно, что луны, планеты и кометы следуют такими путями, но никто не смог предложить объяснения механизма, который заставил их следовать этим путям, а не другим.
Рис. 7.8 В популярной легенде о том, что Ньютон внезапно открыл закон всемирного тяготения, когда яблоко упало с дерева и ударило его по голове, есть доля правды. Более вероятно, что он шел через фруктовый сад и задавался вопросом, почему все яблоки падают в одном направлении с одинаковым ускорением. Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку понятию лежащей в основе простоты и единства в природе. Ученые по-прежнему ожидают, что в результате их постоянных исследований природы появится основная простота.
Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку понятию лежащей в основе простоты и единства в природе. Ученые по-прежнему ожидают, что в результате их постоянных исследований природы появится основная простота.
Гравитационная сила относительно проста. Это всегда привлекательно, и это зависит только от вовлеченных масс и расстояния между ними. Выраженный современным языком, универсальный закон всемирного тяготения Ньютона гласит, что каждый объект во Вселенной притягивает любой другой объект с силой, которая направлена вдоль соединяющей их линии.Сила прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Это притяжение показано на рис. 7.9.
Рис. 7.9 Гравитационное притяжение происходит вдоль линии, соединяющей центры масс (ЦМ) двух тел. Величина силы, действующей на каждое тело, одинакова, что соответствует третьему закону Ньютона (действие-противодействие).
Для двух тел массой м и M с расстоянием между их центрами масс r уравнение всемирного закона всемирного тяготения Ньютона составляет
, где F – величина силы тяжести, а G – коэффициент пропорциональности, называемый гравитационной постоянной. G – универсальная постоянная, означающая, что она считается одинаковой во всей Вселенной. Экспериментально определено, что G = 6,673 × 10-11 Н⋅м2 / кг2G = 6,673 × 10-11 Н⋅м2 / кг2.
Если человек имеет массу 60,0 кг, какой будет сила гравитационного притяжения на нем у поверхности Земли? G приведено выше, масса Земли M составляет 5,97 × 10 24 кг, а радиус r Земли составляет 6,38 × 10 6 м. Помещение этих значений в универсальный закон всемирного тяготения Ньютона дает
F = GmMr2 = (6. 673 × 10-11 Н · м2кг2) ((60,0 кг) (5,97 · 1024 кг) (6,38 · 106 м) 2) = 584 НФ = GmMr2 = (6,673 · 10-11 Н · м2 кг2) ((60,0 кг) ( 5,97 × 1024 кг) (6,38 × 106 м) 2) = 584 Н
673 × 10-11 Н · м2кг2) ((60,0 кг) (5,97 · 1024 кг) (6,38 · 106 м) 2) = 584 НФ = GmMr2 = (6,673 · 10-11 Н · м2 кг2) ((60,0 кг) ( 5,97 × 1024 кг) (6,38 × 106 м) 2) = 584 НЭтот результат можно проверить соотношением: F = mg = (60 кг) (9,8 м / с2) = 588 NF = mg = (60 кг) (9,8 м / с2) = 588 Н
Вы можете помнить, что g , ускорение свободного падения, является еще одной важной константой, связанной с гравитацией. Подставляя g на a в уравнение для второго закона движения Ньютона, мы получаем F = mgF = mg. Комбинируя это с уравнением всемирного тяготения, получаем
Исключение массы м с обеих сторон уравнения и заполнение значений гравитационной постоянной, массы и радиуса Земли дает значение г, , которое может выглядит знакомо.
g = GMr2 = (6,67 × 10-11 Н⋅м2 кг2) (5,98 × 1024 кг (6,38 × 106 м) 2) = 9,80 м / с2g = GMr2 = (6,67 × 10-11 Н⋅м2 кг2) (5,98 × 1024 кг (6,38 × 106 м) 2) = 9,80 м / с2 Это хороший момент, чтобы вспомнить разницу между массой и весом. Масса – это количество вещества в объекте; Вес – это сила притяжения между массой двух объектов. Вес может меняться, потому что г различаются на каждой луне и планете. Масса объекта м не меняется, но его вес м г может.
Масса – это количество вещества в объекте; Вес – это сила притяжения между массой двух объектов. Вес может меняться, потому что г различаются на каждой луне и планете. Масса объекта м не меняется, но его вес м г может.
Виртуальная физика
Гравитация и орбиты
Переместите Солнце, Землю, Луну и космическую станцию в этой симуляции, чтобы увидеть, как это влияет на их гравитационные силы и орбитальные траектории. Визуализируйте размеры и расстояния между разными небесными телами. Отключите гравитацию и посмотрите, что будет без нее!
Проверка захвата
Почему Луна не движется по плавному кругу вокруг Солнца?
- На Луну не действует гравитационное поле Солнца.
- На Луну не действует гравитационное поле Земли.

- На Луну действуют гравитационные поля Земли и Солнца, которые всегда аддитивны.
- На Луну действуют гравитационные поля Земли и Солнца, которые иногда складываются, а иногда противоположны.
Snap Lab
Эксперимент на вынос: падающие предметы
В этом упражнении вы изучите влияние массы и сопротивления воздуха на ускорение падающих предметов.Сделайте прогнозы (гипотезы) об исходе этого эксперимента. Запишите их, чтобы потом сравнить с результатами.
Материалы
- Четыре листа бумаги 8-1 / 2 × 118-1 / 2 × 11 дюймов
Порядок действий
- Возьмите четыре одинаковых листа бумаги.
- Скомкайте один в маленький шарик.
- Оставьте один без мятого.
- Возьмите два других и скомкайте их вместе, чтобы получился шар, в два раза превышающий массу другого скомканного шара.

- Теперь сравните, какой шарик из бумаги приземляется первым при одновременном падении с одной и той же высоты.
- Сравните скомканный шарик из одной бумаги со скомканным шариком из двух листов.
- Сравните скомканный бумажный шарик с немятой бумагой.
Проверка захвата
Почему одни объекты падают у поверхности земли быстрее других, если вся масса одинаково притягивается силой тяжести?
- Некоторые объекты падают быстрее из-за сопротивления воздуха, которое действует в направлении движения объекта и оказывает большую силу на объекты с меньшей площадью поверхности.
- Некоторые объекты падают быстрее из-за сопротивления воздуха, которое действует в направлении, противоположном движению объекта, и оказывает большую силу на объекты с меньшей площадью поверхности.
- Некоторые объекты падают быстрее из-за сопротивления воздуха, которое действует в направлении движения объекта и оказывает большую силу на объекты с большей площадью поверхности.

- Некоторые объекты падают быстрее из-за сопротивления воздуха, которое действует в направлении, противоположном движению объекта, и оказывает большую силу на объекты с большей площадью поверхности.
Третий закон Кеплера можно вывести из закона всемирного тяготения Ньютона. Применение второго закона Ньютона к угловому движению дает выражение для центростремительной силы, которое можно приравнять к выражению для силы в уравнении всемирной гравитации. Этим выражением можно манипулировать, чтобы получить уравнение для третьего закона Кеплера. Ранее мы видели, что выражение r 3 / T 2 является константой для спутников, вращающихся вокруг одного и того же массивного объекта.Вывод третьего закона Кеплера из закона всемирного тяготения Ньютона и второго закона движения Ньютона дает эту константу:
, где M – масса центрального тела, вокруг которого вращаются спутники (например, Солнце в нашей солнечной системе). Полезность этого уравнения станет очевидной позже.
Полезность этого уравнения станет очевидной позже.
Универсальная гравитационная постоянная G определена экспериментально. Это определение было впервые дано точно в 1798 году английским ученым Генри Кавендишем (1731–1810), более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения.Измерение G очень простое и важное, поскольку оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень трудным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (максимум десятки килограммов) с помощью прибора, подобного показанному на рис. 7.11. Что примечательно, его стоимость для G отличается от современного значения менее чем на 1%.
Рис. 7.11 Кавендиш использовал подобное устройство для измерения гравитационного притяжения между двумя подвешенными сферами ( m ) и двумя сферами на подставке ( M ), наблюдая за величиной скручивания (скручивания), создаваемого в волокне. Расстояние между массами можно варьировать, чтобы проверить зависимость силы от расстояния. Современные эксперименты этого типа продолжают исследовать гравитацию.
Расстояние между массами можно варьировать, чтобы проверить зависимость силы от расстояния. Современные эксперименты этого типа продолжают исследовать гравитацию.
Общая теория относительности Эйнштейна
Общая теория относительности Эйнштейна объяснила некоторые интересные свойства гравитации, не охваченные теорией Ньютона. Эйнштейн основал свою теорию на постулате о том, что ускорение и гравитация имеют одинаковый эффект и их нельзя отличить друг от друга. Он пришел к выводу, что свет должен падать как в гравитационном поле, так и в ускоряющейся системе отсчета.На рис. 7.12 показан этот эффект (сильно преувеличенный) в ускоряющемся лифте. На рис. 7.12 (a) лифт ускоряется вверх в невесомости. На Рис. 7.12 (b) комната не ускоряется, но подвержена действию силы тяжести. Эффект на свет одинаков: в обоих случаях он «падает» вниз. Человек в лифте не может определить, ускоряется ли лифт в условиях невесомости или он неподвижен и подвержен действию силы тяжести.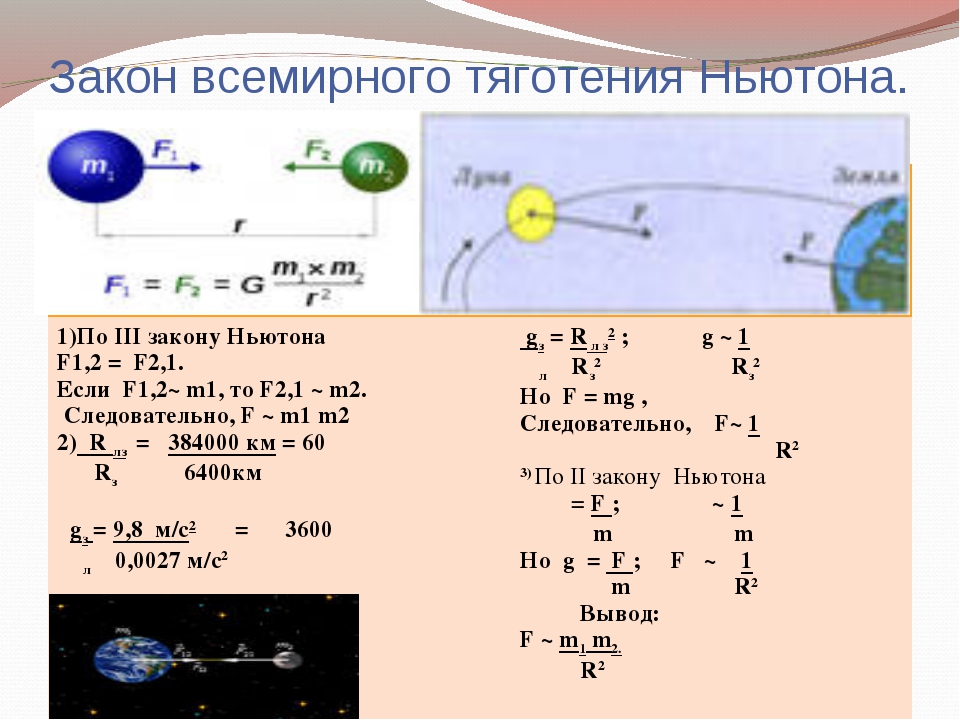 Таким образом, гравитация влияет на путь света, даже если мы думаем, что гравитация действует между массами, в то время как фотоны безмассовые.
Таким образом, гравитация влияет на путь света, даже если мы думаем, что гравитация действует между массами, в то время как фотоны безмассовые.
Рис. 7.12 (a) Луч света выходит из фонарика в лифте, ускоряющемся вверх. Поскольку лифт движется вверх в течение времени, необходимого свету, чтобы достичь стены, луч падает ниже, чем если бы лифт не был ускорен. (b) Гравитация должна иметь такое же влияние на свет, поскольку невозможно определить, ускоряется ли лифт вверх или неподвижен и на него действует сила тяжести.
Общая теория относительности Эйнштейна получила свое первое подтверждение в 1919 году, когда во время солнечного затмения наблюдали свет звезд, проходящий около Солнца.(См. Рис. 7.13.) Во время затмения небо темнеет, и мы можем ненадолго увидеть звезды. Те, кто находится на линии прямой видимости, ближайшей к солнцу, должны иметь смещение в их видимом положении. Этот сдвиг не только наблюдался, но и хорошо согласовывался с предсказаниями Эйнштейна в пределах экспериментальных неопределенностей. Это открытие произвело фурор в науке и общественности. Эйнштейн теперь стал народным героем, а также очень великим ученым. Искривление света материей эквивалентно искривлению самого пространства, когда свет движется по кривой.Это еще одно радикальное изменение в нашем представлении о пространстве и времени. Это также другая связь, что на любую частицу с массой или энергии (например, безмассовые фотоны) действует гравитация.
Это открытие произвело фурор в науке и общественности. Эйнштейн теперь стал народным героем, а также очень великим ученым. Искривление света материей эквивалентно искривлению самого пространства, когда свет движется по кривой.Это еще одно радикальное изменение в нашем представлении о пространстве и времени. Это также другая связь, что на любую частицу с массой или энергии (например, безмассовые фотоны) действует гравитация.
Рис. 7.13 На этой схеме показано, как свет, проходящий рядом с массивным телом, таким как солнце, изгибается к нему. Тогда кажется, что свет, достигающий Земли, исходит из разных мест, отличных от известных положений исходящих звезд. Не только этот эффект наблюдался, но и величина изгиба была в точности тем, что Эйнштейн предсказал в своей общей теории относительности.
Обобщая два взгляда на гравитацию, Ньютон представил гравитацию как перетягивание каната вдоль линии, соединяющей любые два объекта во Вселенной. Напротив, Эйнштейн представлял гравитацию как искривление пространства-времени массой.
Напротив, Эйнштейн представлял гравитацию как искривление пространства-времени массой.
Boundless Physics
Гравитационный зонд НАСА B
Миссия NASA Gravity Probe B (GP-B) подтвердила два ключевых предсказания, основанных на общей теории относительности Альберта Эйнштейна. Зонд, показанный на рис. 7.14, был запущен в 2004 году. В нем было четыре сверхточных гироскопа, предназначенных для измерения двух эффектов, предполагаемых теорией Эйнштейна:
- Геодезический эффект, который представляет собой искривление пространства и времени гравитационным полем массивного тела (в данном случае Земли)
- Эффект перетаскивания кадра, который представляет собой величину, на которую вращающийся объект тянет за собой пространство и время при вращении.
Рисунок 7.14 Художественная концепция космического корабля Gravity Probe B на орбите вокруг Земли. (кредит: NASA / MSFC)
Оба эффекта были измерены с беспрецедентной точностью. Это было сделано путем наведения гироскопов на одну звезду, вращаясь вокруг Земли по полярной орбите. Согласно теории относительности, гироскопы испытали очень небольшие, но измеримые изменения направления их вращения, вызванные притяжением Земли.
Это было сделано путем наведения гироскопов на одну звезду, вращаясь вокруг Земли по полярной орбите. Согласно теории относительности, гироскопы испытали очень небольшие, но измеримые изменения направления их вращения, вызванные притяжением Земли.
Главный исследователь предложил представить себе Землю, вращающуюся в меде.Когда Земля вращается, она увлекает за собой пространство и время, как окружающее море меда.
Проверка захвата
Согласно общей теории относительности, гравитационное поле искривляет свет. При чем здесь время и пространство?
- Гравитация не влияет на пространственно-временной континуум, а гравитация влияет только на движение света.
- Пространственно-временной континуум искажен гравитацией, и гравитация не влияет на движение света.
- Гравитация не влияет ни на пространственно-временной континуум, ни на движение света.

- Пространственно-временной континуум искажен гравитацией, и гравитация влияет на движение света.
Всемирный закон тяготения
Сэр Исаак Ньютон: Всемирный закон тяготенияСэр Исаак Ньютон: Универсальный закон тяготения
Что на самом деле случилось с Apple?
Вероятно, более правильная версия рассказа состоит в том, что Ньютон, наблюдая яблоко упало с дерева, стал думать в следующих направлениях: Яблоко ускоряется, так как его скорость изменяется с нуля, когда он висит на дереве и движется к земле. Таким образом, согласно 2-му закону Ньютона на яблоко должна действовать сила, вызывающая
это ускорение.Давайте
назовем эту силу «гравитацией», а связанное с ней ускорение – «ускорением, обусловленным
к гравитации ».
Затем представьте, что яблоня вдвое выше. Снова,
мы ожидаем, что яблоко будет ускоряться к земле, поэтому это говорит о том, что
эта сила, которую мы называем гравитацией, достигает вершины самого высокого
яблоня.
Таким образом, согласно 2-му закону Ньютона на яблоко должна действовать сила, вызывающая
это ускорение.Давайте
назовем эту силу «гравитацией», а связанное с ней ускорение – «ускорением, обусловленным
к гравитации ».
Затем представьте, что яблоня вдвое выше. Снова,
мы ожидаем, что яблоко будет ускоряться к земле, поэтому это говорит о том, что
эта сила, которую мы называем гравитацией, достигает вершины самого высокого
яблоня.Самая прекрасная идея сэра Исаака
Теперь пришел поистине гениальный Ньютон понимание: если сила тяжести достигает вершины самого высокого дерева, может он не может идти дальше; в частности, может ли он не дойти до конца на орбиту Луны! Затем орбита Луны вокруг Земли могла быть следствием гравитационного силы, потому что ускорение свободного падения может изменить скорость движения Луна так, что двигалась по орбите вокруг земли. Это можно проиллюстрировать мысленным экспериментом, показанным на
следующий рисунок. Предположим, мы стреляем из пушки горизонтально с высокой горы;
снаряд в конечном итоге упадет на землю, о чем свидетельствует самый короткий
траектория на рисунке из-за гравитационного
сила, направленная к центру Земли, и связанное с ней ускорение. (Помните, что ускорение – это
изменение скорости, и эта скорость является вектором, поэтому она имеет как величину
и направление. Таким образом, ускорение происходит, если одна или обе величины
и направление изменения скорости.)
(Помните, что ускорение – это
изменение скорости, и эта скорость является вектором, поэтому она имеет как величину
и направление. Таким образом, ускорение происходит, если одна или обе величины
и направление изменения скорости.)
 постоянная .Это называется «универсальной константой», потому что считается
быть таким же на всех
мест и всегда, и, следовательно, повсеместно
характеризует внутреннюю силу
сила гравитации.
постоянная .Это называется «универсальной константой», потому что считается
быть таким же на всех
мест и всегда, и, следовательно, повсеместно
характеризует внутреннюю силу
сила гравитации.Центр масс для двоичной системы
Если задуматься на мгновение, может показаться немного странным, что у Кеплера Законы Солнце фиксируется в точке в космосе, а планета вращается вокруг нее. Почему у Солнца есть привилегия? Кеплер имел довольно мистические представления о Солнце, наделив его почти богоподобными качествами, оправдавшими его особые место.Однако Ньютон, в значительной степени как следствие своего 3-го закона, продемонстрировал, что ситуация на самом деле была более симметричной, чем у Кеплера. воображали и что Солнце не занимает привилегированного положения; в процессе он модифицировал 3-й закон Кеплера.Рассмотрим диаграмму, показанную справа. Мы можем определить точку, называемую центром масса между двумя объектами через уравнения
где R – полное расстояние между центрами двух объектов. Центр масс знаком каждому, кто хоть раз играл на качелях.Точка опоры
точка, в которой качели точно уравновесят двух человек, сидящих на
любой конец является центром масс для двух людей, сидящих на качелях.
Центр масс знаком каждому, кто хоть раз играл на качелях.Точка опоры
точка, в которой качели точно уравновесят двух человек, сидящих на
любой конец является центром масс для двух людей, сидящих на качелях.Два предельных случая
Мы можем получить дальнейшее представление, рассмотрев положение центра масс в двух пределах. Сначала рассмотрим только что рассмотренный пример, где одна масса намного больше, чем другие. Тогда мы видим, что центр масс для Система практически совпадает с центром массивного объекта: Такова ситуация в Солнечной системе: Солнце настолько массивно по сравнению с любая из планет, центр масс пары Солнце-планета всегда очень близко к центру Солнца.Таким образом, для всех практических целей Солнце почти (но не совсем) неподвижным в центре масс системы, как Кеплер изначально думал. Однако теперь рассмотрим другой предельный случай, когда две массы равны
друг с другом.
Тогда легко увидеть, что центр масс находится на равном расстоянии. из двух масс, и если они гравитационно связаны друг с другом,
каждая масса вращается вокруг общего центра масс для
система, лежащая посередине между ними:
из двух масс, и если они гравитационно связаны друг с другом,
каждая масса вращается вокруг общего центра масс для
система, лежащая посередине между ними:
Эти предельные случаи расположения центра масс возможно знакомы с нашей вышеупомянутой детской площадки опыт. Если на качелях находятся люди равного веса, точка опоры должна быть помещается посередине, чтобы сбалансировать, но если один человек весит намного больше, чем другому человеку, точка опоры должна быть расположена ближе к более тяжелому человеку, чтобы достигать остаток средств.
Круговая скорость и геосинхронная орбита
Как быстро нам нужно лететь на ракете, чтобы оставаться в круговой по орбите вокруг гораздо более массивного тела, такого как Земля? Я приведу здесь ответ без вывода, но он следует из Закон всемирного тяготения Ньютона.
Если предположить, что масса ракеты мала по сравнению с Землей, тогда КРУГОВАЯ СКОРОСТЬ дается квадратным корнем из GM / r, то есть
где G – гравитационная постоянная, R – радиус орбиты, M – масса большего объекта, как Земля, вокруг которой вращается меньший объект. Обратите внимание, что формула не зависит от массы меньшего объекта. (Последний факт следует из теории Ньютона и связано с экспериментальным выводом Галилея о том, что два объекта разной массы упали с одной высоты падают на Землю в то же время.)
Мы можем использовать эту формулу, чтобы вычислить, насколько быстро луна движется в его орбита вокруг Земли. Поглощая массу Земли M = 6 x 10 24 кг, радиус орбиты Луны R = 3,84 x 10 8 метров, и гравитационная постоянная G = 6,67 x 10 -11 Ньютон-метр 2 / кг 2 , тогда величина скорости Луны составляет 1020 м / с. Это примерно 2278 миль в час.
(Эй, так если он движется так быстро, в 5 раз быстрее
чем реактивные самолеты, почему кажется, что реактивные самолеты движутся по небу быстрее, чем луна?
Вам придется ответить на этот вопрос самостоятельно. .)
.)
Поскольку круговая скорость изменяется обратно пропорционально квадратному корню из R, объект в меньшем орбита имеет более высокую скорость, потому что сила тяжести сильнее. Такой же расчет для R = 6578 км над центром Земля говорит нам, что спутник должен двигаться со скоростью 17 400 миль. в час (= 7790 м / с). Таким образом, ракеты должны двигаться невероятно быстро. Ракета должна подняться, а затем повернуться в точку по кругу. орбита с правильной скоростью. Но как только он наберет такую скорость, он оставаться на орбите без последующего движения ракеты.
Поскольку орбитальная скорость спутника зависит от его расстояния
от центра Земли, чем дальше, тем дольше период
орбиты. Около Земли период обращения вокруг Земли составляет около 1,5 часов.
Если уйти на расстояние около 42000 км (26000) миль, период обращения
24 часа. Таким образом, спутник окажется на ГЕОСИНХРОННОЙ ОРБИТЕ.
Представьте себе запуск спутника на восток над экватором Земли.
на геостационарной орбите: тогда спутник останется над той же точкой
на Земле все время на своей орбите.
Открытые и закрытые орбиты
Орбиты, которые замыкаются друг на друга, как круглые или эллиптические. орбиты называются ЗАКРЫТЫМИ ОРБИТАМИ. Объект на таких орбитах всегда возвращается в одно и то же место на орбите. периодически. На круговых орбитах скорость объекта остается то же самое везде на орбите. На эллиптических орбитах скорость тем быстрее, чем объект приближается к ближайшей части своей орбиты и затем замедляется по мере продвижения объекта к дальней части орбиты.
Есть также орбиты, называемые ESCAPE ORBITS или OPEN ORBITS.На этих орбитах объект никогда не возвращается и уходит на большие расстояния. расстояния.
Чтобы увидеть это Представьте себе пушечный выстрел с горы на поверхности Земли (рис. 5-13). Есть 5 качественно разных возможностей в зависимости от того, насколько быстро пушечное ядро. сначала движется относительно круговой скорости.

Скорость убегания
СКОРОСТЬ ПОБЕГА от такого объекта, как Земля, определяется выражением где R – радиус точки запуска объекта. Когда точка запуска находится на поверхности Земли, то R будет радиусом Земли. Эта убегающая скорость является критической скоростью, которую должен иметь объект. для последующего полета к бесконечности при выстреле вверх изнутри гравитационное поле. То есть, если с Земли выстрелила ракета и расходует все свое топливо, чтобы разогнаться до этой скорости, а затем даже после того, как ракета перестанет сжигать топливо, она будет выбегать до бесконечности, и гравитация Земли не может вернуть ракету в Земной шар.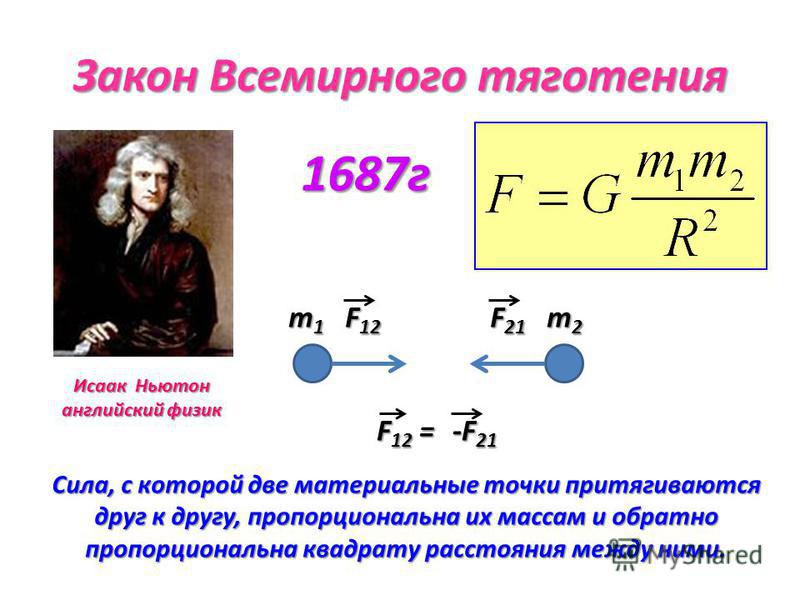
Подсчитывая массу, радиус Земли и G, получаем 11,2 км / с для космической скорости для запущенного объекта с поверхности Земли. Это примерно 25 000 миль в час! Смею вас попытаться сбежать. (Вот вам и беспокойство Аристотеля по поводу птицы, летящие с поверхности Земли – никаких шансов в присутствии силы тяжести.)
Вес и гравитационная сила
Мы видели, что во Всемирном законе тяготения решающее значение имеет масса. В популярном языке масса и вес часто означают одно и то же. вещь; на самом деле они связаны, но совершенно разные вещи.Что мы обычно называют вес на самом деле просто гравитационная сила оказал объект определенной массы. Мы можем проиллюстрировать, выбрав Земля как одна из двух масс в предыдущей иллюстрации Закона всемирного тяготения: Таким образом, получается масса объекта массой м у поверхности Земли. умножив массу m на ускорение свободного падения, г , на поверхности земли. Ускорение свободного падения приблизительно равно произведению универсальная гравитационная постоянная G и масса Земли M , г. деленное на радиус Земли, r в квадрате.(Мы предполагаем, что Земля
сферической и пренебречь радиусом объекта относительно радиуса
Земля в этом обсуждении.) Измеренное ускорение свободного падения на
Скорость поверхности Земли составляет около 9,8 м / с 2 .
деленное на радиус Земли, r в квадрате.(Мы предполагаем, что Земля
сферической и пренебречь радиусом объекта относительно радиуса
Земля в этом обсуждении.) Измеренное ускорение свободного падения на
Скорость поверхности Земли составляет около 9,8 м / с 2 .Масса и вес
Масса – это мера количества материала в объекте, но вес является мерой гравитационная сила, действующая на этот материал в гравитационном поле; таким образом, масса и вес пропорциональны друг другу, с ускорением из-за гравитации как константа пропорциональности.Это следует из того масса объекта постоянна (на самом деле это не совсем так, но мы сохранит этот сюрприз для нашего дальнейшего обсуждения Теория относительности), но вес зависит от расположения объекта. Например, если мы перевезли предыдущий объект массы м до поверхности луны, гравитационное ускорение изменится, потому что радиус и Масса Луны отличается от массы Земли. Таким образом, наш объект имеет массу м как на поверхности Земли, так и на поверхности Луны, но это будет весить на намного меньше на поверхности Луны потому что ускорение свободного падения в 6 раз меньше, чем на поверхности земли.
Вывод законов Кеплера Ньютоном
Обратите внимание, что величина круговой скорости объекта на орбите также равно окружность орбиты, деленная на период обращения. Это:
В
круг = (GM / R) 1/2 = (2 pi R) / P где pi = 3,1415, а P – период обращения. Последнее равенство следует из простого учета того, что величина скорости – это измерение расстояния, пройденного за единицу времени.Пройденное расстояние – это длина окружности орбиты (= 2 пи R), а период P – это время, необходимое для прохождения этого расстояния. Но посмотрите: теперь мы волшебным образом восстановили третий закон Кеплера !: Преобразуя последнее равенство, имеем(GM) P
2 = 4 пи 2 R 3 Дело в том, что P 2 пропорционально R 3 . Это третье место Кеплера. закон, теперь выпадающий прямо из теории Ньютона.Интерпретация законов Кеплера Ньютоном
Потому что для каждого действия есть равное и противоположная реакция, Ньютон понял, что в системе планета-Солнце планета не вращается вокруг неподвижного Солнца. Вместо этого Ньютон предположил, что оба
планета и Солнце вращаются вокруг общего центра масс планеты-Солнца.
система. Затем он модифицировал 3-й закон Кеплера так, чтобы масса
Используемое M теперь является суммой массы Солнца и планеты.
Вместо использования M 1 и M 2 , как указано выше, давайте использовать M s и M p . Тогда мы
иметь M = M s + M p и так
Вместо этого Ньютон предположил, что оба
планета и Солнце вращаются вокруг общего центра масс планеты-Солнца.
система. Затем он модифицировал 3-й закон Кеплера так, чтобы масса
Используемое M теперь является суммой массы Солнца и планеты.
Вместо использования M 1 и M 2 , как указано выше, давайте использовать M s и M p . Тогда мы
иметь M = M s + M p и такG (M
s + M p ) P 2 = 4 пи 2 R 3Но обратите внимание, что происходит в новом уравнении Ньютона, если масса Солнца намного больше массы любой из планет (что всегда так).Тогда сумма двух масс всегда приблизительно равна массе Солнце и так вернулись в
G M
s P 2 = 4 пи 2 R 3 для систем планета-Солнце. Если мы возьмем отношения 3-го закона Кеплера для двух разных планет, масса Солнца затем отменяется из отношения, и мы остаемся с исходная форма 3-го закона Кеплера: Таким образом, 3-й закон Кеплера приблизительно верен, потому что Солнце намного больше массивнее любой из планет и, следовательно, Поправка Ньютона мала. Данные, к которым имел доступ Кеплер, не годились
достаточно, чтобы показать этот небольшой эффект. Тем не мение,
подробные наблюдения, сделанные после Кеплера, показывают, что модифицированная форма Ньютона
3-й закон Кеплера лучше согласуется с данными, чем исходная форма Кеплера.
Данные, к которым имел доступ Кеплер, не годились
достаточно, чтобы показать этот небольшой эффект. Тем не мение,
подробные наблюдения, сделанные после Кеплера, показывают, что модифицированная форма Ньютона
3-й закон Кеплера лучше согласуется с данными, чем исходная форма Кеплера.Закон всемирного тяготения Ньютона
Сила тяжести и гравитационный потенциал
Закон всемирного тяготения был сформулирован Исааком Ньютоном \ (\ left (1643-1727 \ right) \) и опубликован в \ (1687.2}}}}. \)
Сила гравитационного притяжения – это центральная сила, которая направлена вдоль линии, проходящей через центры взаимодействующих тел.
В системе двух тел (рисунок \ (2 \)) сила притяжения \ ({\ mathbf {F} _ {12}} \) второго тела действует на первое тело массы \ ({m_1} . \)
Рис. 2.Аналогичным образом сила притяжения \ ({\ mathbf {F} _ {21}} \) первого тела действует на второе тело массы \ ({m_2}. \) Обе силы \ ({\ mathbf {F} _ {12}} \) и \ ({\ mathbf {F} _ {21}} \) равны и направлены вдоль \ (\ mathbf {r}, \), где
\ [\ mathbf {r} = {\ mathbf {r} _2} – {\ mathbf {r} _1}. 3}}} \ mathbf {r}, \]
3}}} \ mathbf {r}, \]
где \ ({M_ \ text {S}} \) – масса Солнца.
Гравитационное взаимодействие тел происходит через гравитационное поле, которое можно описать скалярным потенциалом \ (\ varphi. \) Сила, действующая на тело массы \ (m, \), помещенное в поле с потенциалом \ ( \ varphi, \) равно
\ [\ mathbf {F} = m \ mathbf {a} = – m \, \ mathbf {\ text {grad}} \, \ varphi. \]
В случае точечной массы \ (M, \) потенциал гравитационного поля определяется выражением
\ [\ varphi = – \ frac {{GM}} {r}. \]
Последняя формула также верна для распределенных тел с центральной симметрией, таких как планета или звезда.
Законы Кеплера
Основные законы движения планет были установлены Иоганном Кеплером \ (\ left (1571-1630 \ right) \) на основе анализа астрономических наблюдений Тихо Браге \ (\ left (1546-1601 \ right) \). В \ (1609, \) Кеплер сформулировал первые два закона. Третий закон был открыт в \ (1619). Позже, в конце \ (17 \) века, Исаак Ньютон математически доказал, что все три закона Кеплера являются следствием закона всемирного тяготения.
Первый закон Кеплера
Орбита каждой планеты Солнечной системы представляет собой эллипс, одним из фокусов которого является Солнце (рис. \ (3 \)).
Рисунок 2.Второй закон Кеплера
Радиус-вектор, соединяющий Солнце и планету, описывает равные области через равные промежутки времени. На рисунке \ (4 \) показаны два сектора эллипса, соответствующие одним и тем же временным интервалам.
Рисунок 2.Согласно второму закону Кеплера, площади этих секторов равны.3}}. \]
См. Решенные проблемы на странице 2.
Является ли гравитация теорией или законом?
Я часто получаю электронные письма с просьбой узнать, является ли гравитация законом или теорией. Этот вопрос вызывает столько других вопросов, что я подумал, что было бы интересно изучить его.
Для этого вам понадобится:
– объект для падения.
Хорошо, выберите предмет, который не сломается, не повредит пол, не вызовет беспорядок или не доставит никому из нас неприятностей. Вытяните его перед собой и отпустите. Что случается? Он падает, если вы не взяли в руки гелиевый шар. В этом случае гравитация заставляет его плыть вверх, притягивая вниз с большей силой воздух вокруг воздушного шара). Гравитационное притяжение между Землей и объектом притягивает его к земле. Но, когда мы проводим этот эксперимент, должны ли мы говорить о Законе гравитации или теории гравитации?
Вытяните его перед собой и отпустите. Что случается? Он падает, если вы не взяли в руки гелиевый шар. В этом случае гравитация заставляет его плыть вверх, притягивая вниз с большей силой воздух вокруг воздушного шара). Гравитационное притяжение между Землей и объектом притягивает его к земле. Но, когда мы проводим этот эксперимент, должны ли мы говорить о Законе гравитации или теории гравитации?
На самом деле, мы должны говорить о обоих. Чтобы понять почему, нам нужно понять научный смысл слов «закон» и «теория».«
На языке науки слово «закон» описывает аналитическое утверждение. Это дает нам формулу, которая говорит нам, что делать. Например, закон всемирного тяготения Ньютона говорит нам:
«Каждая точечная масса притягивает каждую отдельную точечную массу силой, направленной вдоль линии, пересекающей обе точки. Сила прямо пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между точечными массами».
Итак, если мы знаем массу двух объектов и расстояние между центрами масс этих двух объектов, мы можем вычислить гравитационное притяжение между Землей и объектом, который вы уронили, между Солнцем и Марсом или между мной и миска с мороженым.
Мы можем использовать закон всемирного тяготения Ньютона, чтобы вычислить, насколько сильна гравитационная сила между Землей и объектом, который вы уронили, что позволит нам рассчитать его ускорение при падении, сколько времени потребуется, чтобы удариться о землю, как быстро он будет идти при ударе, сколько энергии потребуется, чтобы поднять его снова, и т. д.
Хотя закон позволяет нам довольно много вычислять о том, что происходит, обратите внимание, что он ничего не говорит нам о том, ПОЧЕМУ это происходит. Вот для чего нужны теории.На языке науки , теория – это объяснение того, почему и как все происходит. Что касается гравитации, мы используем общую теорию относительности Эйнштейна, чтобы объяснить, почему вещи падают.
Теория начинается с одной или нескольких гипотез, непроверенных идей о том, почему что-то происходит. Например, я мог бы предложить гипотезу о том, что выпущенный вами объект упал, потому что был притянут магнитным полем Земли. Как только мы начали тестирование, вскоре выяснилось, что моя гипотеза не подтверждается доказательствами. Немагнитные предметы падают с той же скоростью, что и магнитные. Поскольку это не было подтверждено доказательствами, моя гипотеза не получает статуса теории. Чтобы стать научной теорией, идея должна быть тщательно проверена и должна быть точным и предсказуемым описанием мира природы.
Немагнитные предметы падают с той же скоростью, что и магнитные. Поскольку это не было подтверждено доказательствами, моя гипотеза не получает статуса теории. Чтобы стать научной теорией, идея должна быть тщательно проверена и должна быть точным и предсказуемым описанием мира природы.
Хотя законы меняются редко, теории часто меняются по мере обнаружения новых свидетельств. Вместо того, чтобы отвергаться из-за новых свидетельств, теории часто пересматриваются, чтобы включить новые свидетельства в свои объяснения.Общая теория относительности адаптировалась по мере того, как новые технологии и новые свидетельства расширили наш взгляд на Вселенную.
Итак, когда мы обсуждаем гравитацию с научной точки зрения, мы можем говорить о законе гравитации, который описывает притяжение между двумя объектами, и мы также можем говорить о теории гравитации, которая описывает, почему объекты притягиваются друг к другу.
Когда теория становится законом?
Закон тяготения Ньютона: определение и примеры – видео и стенограмма урока
Как работает гравитация?
У меня есть друг, который изобрел нечто замечательное. У него есть место для завтрака, а в местах для завтрака вы должны намазать ОГРОМНОЕ количество тостов маслом. Это становится довольно раздражающим. Поэтому он изобрел нечто под названием «Масляный пистолет». Это ручной пистолет. Вы берете кусок масла и загружаете его. Внутри масляного пистолета есть нагревательные спирали, которые плавят масло. Затем, когда он будет готов, вы направляете пистолет для масла на тост, нажимаете на спусковой крючок и брызгаете, масло вылетает и покрывает ваш тост.
У него есть место для завтрака, а в местах для завтрака вы должны намазать ОГРОМНОЕ количество тостов маслом. Это становится довольно раздражающим. Поэтому он изобрел нечто под названием «Масляный пистолет». Это ручной пистолет. Вы берете кусок масла и загружаете его. Внутри масляного пистолета есть нагревательные спирали, которые плавят масло. Затем, когда он будет готов, вы направляете пистолет для масла на тост, нажимаете на спусковой крючок и брызгаете, масло вылетает и покрывает ваш тост.
Он показал мне это, и я попробовал, но я использовал только один кусок тоста.Итак, ВСЯ пачка масла вылетела и покрыла тосты. Он был практически в дюйм толщиной… так отвратительно! Он сказал мне, что вам нужно отодвинуть ружье подальше и положить несколько ломтиков тоста рядом друг с другом. Если у вас есть четыре тоста, масло будет тоньше. Девять тостов, еще тоньше. Так что вам нужно найти правильный баланс, чтобы получить желаемую толщину.
Когда мой друг показал мне, как это работает, я понял… это что-то вроде физики.


 Зато в них увлекательно рассказывается, как человек изучает окружающую его природу, о достигнутых сегодня границах в познании мира, о том, какие проблемы наука решает сегодня и будет решать завтра.
Зато в них увлекательно рассказывается, как человек изучает окружающую его природу, о достигнутых сегодня границах в познании мира, о том, какие проблемы наука решает сегодня и будет решать завтра.

 Все физические законы отличаются в этом отношении своим абстрактным характером. Закон сохранения энергии – это теорема о величинах, которые нужно вычислить и сложить, не думая о причине этого; точно так же и великие законы механики представляют собой количественные математические закономерности, о внутреннем механизме работы которых никаких данных нет. Почему мы можем пользоваться математикой для описания законов, не зная их причины? Никто и этого не знает. Мы продолжаем идти по этой дороге, потому что на ней все еще происходят открытия.
Все физические законы отличаются в этом отношении своим абстрактным характером. Закон сохранения энергии – это теорема о величинах, которые нужно вычислить и сложить, не думая о причине этого; точно так же и великие законы механики представляют собой количественные математические закономерности, о внутреннем механизме работы которых никаких данных нет. Почему мы можем пользоваться математикой для описания законов, не зная их причины? Никто и этого не знает. Мы продолжаем идти по этой дороге, потому что на ней все еще происходят открытия.

 е. мере инерции тела, или мере того, насколько трудно удержать тело, вращающееся по кругу. Поэтому два тела, тяжелое и легкое, движущиеся бок о бок вокруг массивного тела по одному и тому же кругу с одной скоростью под действием тяготения, будут все время оставаться рядом, потому что движение по кругу требуетдля большего тела и большей силы. Иначе говоря, тяжесть у большей массы больше как раз в нужной пропорции, так что два тела будут вращаться, не удаляясь одно от другого. Если же одно тело находится внутри другого, то оно и останется там; равновесие является совершенным. Поэтому Гагарин и Титов наблюдали невесомость всех предметов внутри космического корабля; выпущенный из руки карандаш, например, вращался вокруг Земли по той же траектории, что и весь корабль, поэтому он замирал, повиснув в воздухе. Любопытно, что эта сила в точности пропорциональна массе; если бы это было не так, то должны были бы наблюдаться явления, в которых инерция и вес отличаются. Отсутствие подобных явлений было с огромной точностью проверено на опыте, выполненном впервые Этвешем в 1909 г.
е. мере инерции тела, или мере того, насколько трудно удержать тело, вращающееся по кругу. Поэтому два тела, тяжелое и легкое, движущиеся бок о бок вокруг массивного тела по одному и тому же кругу с одной скоростью под действием тяготения, будут все время оставаться рядом, потому что движение по кругу требуетдля большего тела и большей силы. Иначе говоря, тяжесть у большей массы больше как раз в нужной пропорции, так что два тела будут вращаться, не удаляясь одно от другого. Если же одно тело находится внутри другого, то оно и останется там; равновесие является совершенным. Поэтому Гагарин и Титов наблюдали невесомость всех предметов внутри космического корабля; выпущенный из руки карандаш, например, вращался вокруг Земли по той же траектории, что и весь корабль, поэтому он замирал, повиснув в воздухе. Любопытно, что эта сила в точности пропорциональна массе; если бы это было не так, то должны были бы наблюдаться явления, в которых инерция и вес отличаются. Отсутствие подобных явлений было с огромной точностью проверено на опыте, выполненном впервые Этвешем в 1909 г. , апозже повторенном Дикке. У всех веществ масса и вес пропорциональны с точностью 1/1 000 000 000 или даже более того. Не правда ли, замечательный эксперимент?
, апозже повторенном Дикке. У всех веществ масса и вес пропорциональны с точностью 1/1 000 000 000 или даже более того. Не правда ли, замечательный эксперимент? Так что до сих пор у нас нет иной модели для теории гравитации, кроме математической.
Так что до сих пор у нас нет иной модели для теории гравитации, кроме математической. В недавно изданной на русском языке книге “Гравитация” американские физики называют “схлопывание в точку” величайшим кризисом физики. Это мнение разделяют многие ученые – физики и философы.
В недавно изданной на русском языке книге “Гравитация” американские физики называют “схлопывание в точку” величайшим кризисом физики. Это мнение разделяют многие ученые – физики и философы. Эта часть скрытой массы получила название тёмной энергии (darkenergy).
Эта часть скрытой массы получила название тёмной энергии (darkenergy).  Самое необычное то, что темная энергия в определенном смысле испытывает антигравитацию. Современными астрономическими методами можно не только измерить нынешний темп расширения Вселенной, но и определить, как он изменялся со временем. Астрономические наблюдения свидетельствуют о том, что сегодня (и в недалеком прошлом) Вселенная расширяется с ускорением: темп расширения растет. В этом смысле и можно говорить об антигравитации: обычное гравитационное притяжение замедляло бы разбегание галактик, а в нашей Вселенной, получается, всё наоборот.
Самое необычное то, что темная энергия в определенном смысле испытывает антигравитацию. Современными астрономическими методами можно не только измерить нынешний темп расширения Вселенной, но и определить, как он изменялся со временем. Астрономические наблюдения свидетельствуют о том, что сегодня (и в недалеком прошлом) Вселенная расширяется с ускорением: темп расширения растет. В этом смысле и можно говорить об антигравитации: обычное гравитационное притяжение замедляло бы разбегание галактик, а в нашей Вселенной, получается, всё наоборот.  Плотность вещества определяется длиной связи между ядрами атомов и количеством нуклонов в этих ядрах. При температурах выше 6000 градусов в водороде и гелии (Солнце состоит на 93% из водорода и 7% – гелия, нагретых до температуры более 10000К) разрываются связи между электронами и ядрами, энергия связи которых порядка 15 электрон вольт. Водород и гелий при температуре 6000 градусов уже находятся в виде плазмы. От разлета этой плазмы на Солнце, в первую очередь, оберегают Кулоновские и магнитные силы, которые отличаются по силе от гравитационных более чем на 40 порядков. Удельный вес Солнца, соответственно, должен быть, как максимум (верхняя граница) меньше удельного веса водорода при нормальных условиях и составлять соответственно величину меньшую чем 0,0000899 (при 273 K=0°C) г/см³, отличающуюся от определяемой по Ньютоновским законам гравитации 2 г /см³ ,более чем в 2000 раз .
Плотность вещества определяется длиной связи между ядрами атомов и количеством нуклонов в этих ядрах. При температурах выше 6000 градусов в водороде и гелии (Солнце состоит на 93% из водорода и 7% – гелия, нагретых до температуры более 10000К) разрываются связи между электронами и ядрами, энергия связи которых порядка 15 электрон вольт. Водород и гелий при температуре 6000 градусов уже находятся в виде плазмы. От разлета этой плазмы на Солнце, в первую очередь, оберегают Кулоновские и магнитные силы, которые отличаются по силе от гравитационных более чем на 40 порядков. Удельный вес Солнца, соответственно, должен быть, как максимум (верхняя граница) меньше удельного веса водорода при нормальных условиях и составлять соответственно величину меньшую чем 0,0000899 (при 273 K=0°C) г/см³, отличающуюся от определяемой по Ньютоновским законам гравитации 2 г /см³ ,более чем в 2000 раз .
 1031 кулонов. Причем, понятно происхождение этого заряда. Электроны улетали быстрей чем протоны с только что родившейся нейтральной звезды Солнце. Этот процесс продолжался до тех пор, пока положительный заряд Солнца не достиг величины, при которой скорости удаления электронов и протонов сравнялись. Это объяснение было изложено без привлечения понятия нейтральной массы и приводилось в контексте наших предыдущих объяснений электромагнитной природы массы.
1031 кулонов. Причем, понятно происхождение этого заряда. Электроны улетали быстрей чем протоны с только что родившейся нейтральной звезды Солнце. Этот процесс продолжался до тех пор, пока положительный заряд Солнца не достиг величины, при которой скорости удаления электронов и протонов сравнялись. Это объяснение было изложено без привлечения понятия нейтральной массы и приводилось в контексте наших предыдущих объяснений электромагнитной природы массы. Величина 4.17.1042 раз действительно завораживала и представлялась достаточно убедительной, по крайней мере, для необходимости учета этой силы в небесной механике. Зная величину отрицательного заряда Земли (-6.105 Кл), мы рассчитали, каким должен быть заряд Солнца, чтобы его сила взаимодействия с Землей была бы соизмерима с гравитационным притяжением этих небесных тел, имеющих массу 2.1030 и 6.1024 кг Солнца и Земли, соответственно. Рассчитанный заряд Солнца составил 3.1029 Кл.
Величина 4.17.1042 раз действительно завораживала и представлялась достаточно убедительной, по крайней мере, для необходимости учета этой силы в небесной механике. Зная величину отрицательного заряда Земли (-6.105 Кл), мы рассчитали, каким должен быть заряд Солнца, чтобы его сила взаимодействия с Землей была бы соизмерима с гравитационным притяжением этих небесных тел, имеющих массу 2.1030 и 6.1024 кг Солнца и Земли, соответственно. Рассчитанный заряд Солнца составил 3.1029 Кл. 1029 Кл. Эта величина вылилась в трудно вообразимую цифру 1048 электронов, кажется, превышающую общее количество электронов на Солнце. Мы решили вычислить количество электронов на Солнце, состоящем, в основном, из ионизированных атомов водорода. Эта величина составила 1,2 .1057 электронов. Т.е. оказалось, что для того, чтобы Солнце приобрело заряд 3.1029 Кл – величину, обеспечивающую электростатическую силу притяжения между планетой Земля и Солнцем, соизмеримую с силой гравитации, Солнцу достаточно потерять электронов лишь на 10-7% от имеющегося у него количества, что представляется вполне достижимой величиной.
1029 Кл. Эта величина вылилась в трудно вообразимую цифру 1048 электронов, кажется, превышающую общее количество электронов на Солнце. Мы решили вычислить количество электронов на Солнце, состоящем, в основном, из ионизированных атомов водорода. Эта величина составила 1,2 .1057 электронов. Т.е. оказалось, что для того, чтобы Солнце приобрело заряд 3.1029 Кл – величину, обеспечивающую электростатическую силу притяжения между планетой Земля и Солнцем, соизмеримую с силой гравитации, Солнцу достаточно потерять электронов лишь на 10-7% от имеющегося у него количества, что представляется вполне достижимой величиной.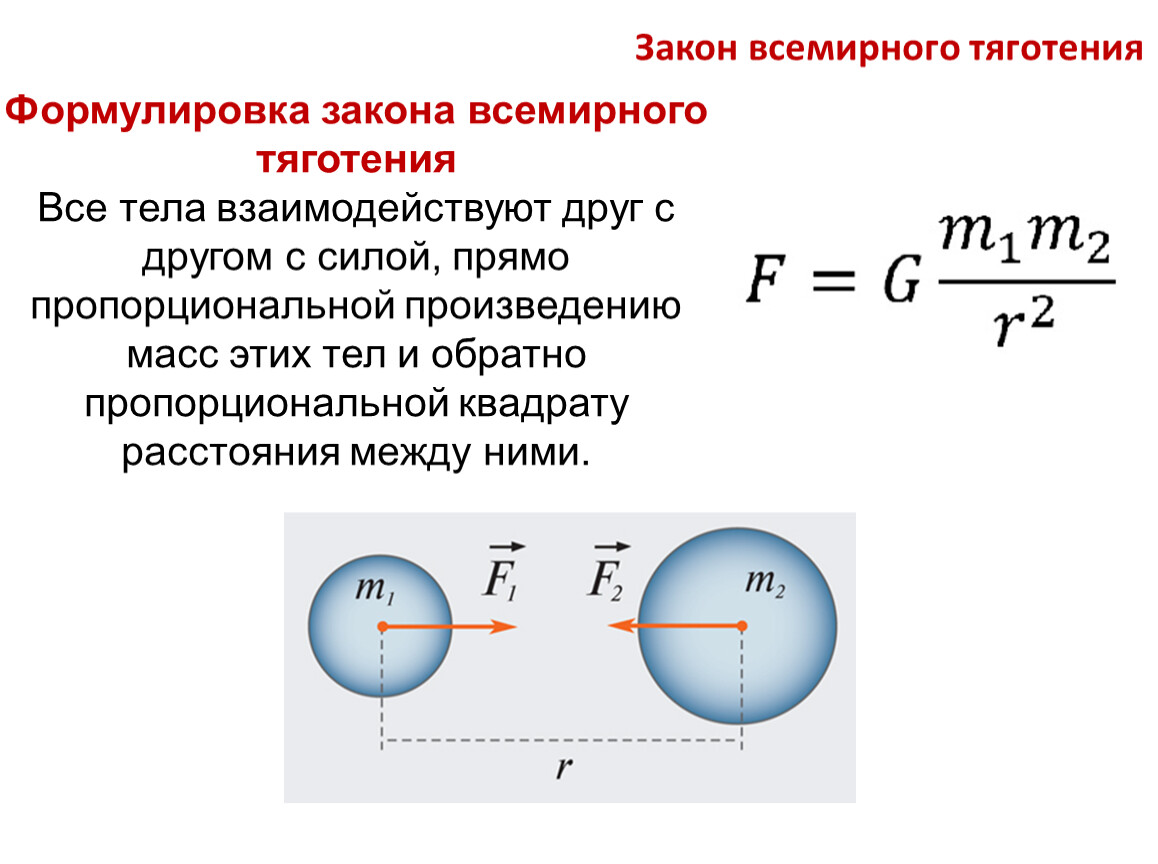 Оно объясняло указанные выше явления, но противоречило факту отрицательного заряда Земли. Электроны должны были приближаться к Земле со скоростями во много раз превышающими вторые космические скорости. Кроме того электростатическое объяснение не разрешило проблему устойчивости Солнечной Системы.
Оно объясняло указанные выше явления, но противоречило факту отрицательного заряда Земли. Электроны должны были приближаться к Земле со скоростями во много раз превышающими вторые космические скорости. Кроме того электростатическое объяснение не разрешило проблему устойчивости Солнечной Системы. , основным недостатком явилось то, что построенные согласно этому закону системы должны быть неустойчивыми, т.е. не могут существовать в принципе.
, основным недостатком явилось то, что построенные согласно этому закону системы должны быть неустойчивыми, т.е. не могут существовать в принципе.  5.
5. 
 В рамках электродинамического объяснения галактики разбегаются, потому что горящие звезды несут избыточный положительный заряд. Темная материя – это облака возбужденных и невозбужденных микрочастиц (электроны, протоны, нейтроны, позитроны, позитронии, анионы позитрониев и т.д).
В рамках электродинамического объяснения галактики разбегаются, потому что горящие звезды несут избыточный положительный заряд. Темная материя – это облака возбужденных и невозбужденных микрочастиц (электроны, протоны, нейтроны, позитроны, позитронии, анионы позитрониев и т.д).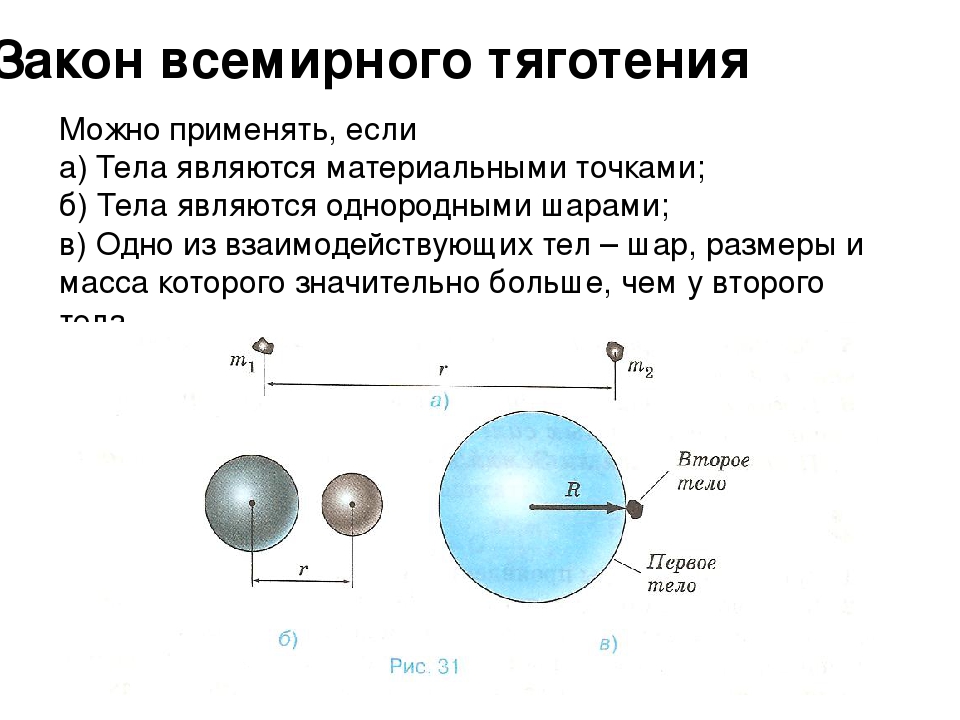
 Равенство центробежных сил центростремительным, приводимые в учебниках, также не объясняют физических причин устойчивости орбит спутников, вращающихся вокруг Земли. Тем не менее, спутники, запущенные в XX – м веке, являются творением мысли и рук человеческих, и их орбиты – устойчивы.
Равенство центробежных сил центростремительным, приводимые в учебниках, также не объясняют физических причин устойчивости орбит спутников, вращающихся вокруг Земли. Тем не менее, спутники, запущенные в XX – м веке, являются творением мысли и рук человеческих, и их орбиты – устойчивы. Устойчивость орбит спутников и космических объектов является независимым дополнительным экспериментальным доказательством корректности вывода, что силы гравитации являются силами Лоренца.
Устойчивость орбит спутников и космических объектов является независимым дополнительным экспериментальным доказательством корректности вывода, что силы гравитации являются силами Лоренца. 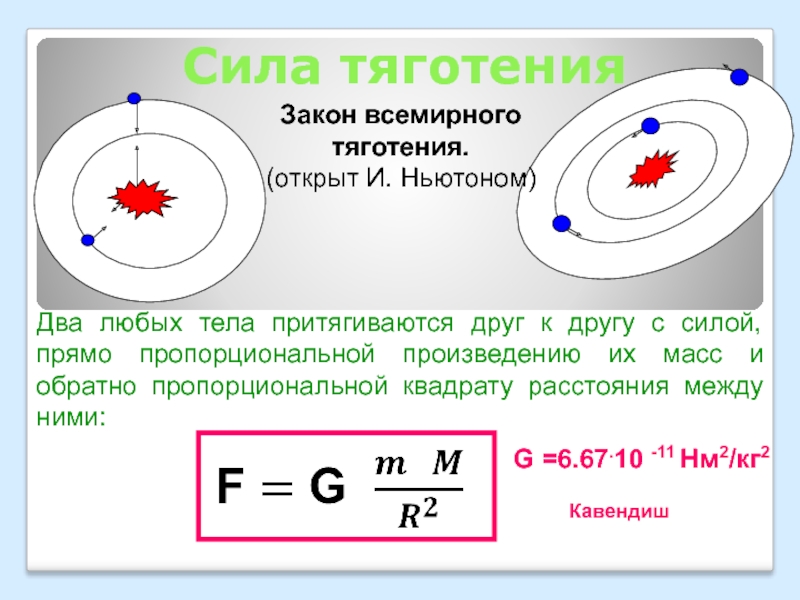 Человечество преодолело законы морали, почему бы ему не преодолеть законы физики?
Человечество преодолело законы морали, почему бы ему не преодолеть законы физики?
 В гравитационная масса определяет силу гравитационного
Привлечение
между двумя телами. В механике Ньютона эти две массы имеют
нет очевидной связи друг с другом.Тем не менее, это было
эмпирически замечено, что они численно равны.
Этот замечательный факт был известен веками, но оставался
необъяснимо до
Общая теория относительности Эйнштейна.
В гравитационная масса определяет силу гравитационного
Привлечение
между двумя телами. В механике Ньютона эти две массы имеют
нет очевидной связи друг с другом.Тем не менее, это было
эмпирически замечено, что они численно равны.
Этот замечательный факт был известен веками, но оставался
необъяснимо до
Общая теория относительности Эйнштейна.



