Применение законов кинематика на практике презентация. Основные понятия кинематики
Краткая историческая справка Ø Ø Ø Развитие кинематики как науки началось еще в древнем мире и связано с таким именем как Галилей, который вводит понятие ускорения. Развитие кинематики в XVIII в. связано с работами Эйлера, заложившего основы кинематики твердого тела и создавшего аналитические методы решения задач механики. Более глубокие исследования геометрических свойств движения тела были вызваны развитием техники в начале XIX в. и, в частности, быстрым развитием машиностроения. Крупные исследования в области кинематики механизмов и машин принадлежат и русским ученым: основоположнику русской школы теории машин и механизмов П. Л. Чебышеву(1821 -1894), Л. В. Ассуру (1878 -1920), Н. И. Мерцалову (1866 -1948), Л. П. Котельникову (1865 -1944) и другим ученым.
Основные понятия кинематики: Кинематика (с греч. κινειν – двигаться) – раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Кинематика – это описание движения тел с математическими ответами на вопросы: 1. Где? 2. Когда? 3. Как? Для получения ответов на поставленные вопросы необходимы следующие понятия:
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
Материальная точка Тело можно считать материальной точкой, если: 1. расстояния, проходимые телом, значительно больше размеров этого тела; 2. тело движется поступательно, т. е. все его точки движутся одинаково в любой момент времени.
Материальная точка – тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь; Траектория – условная линия движения тела в пространстве; Путь – длина траектории; Перемещение – направленный отрезок
Способы задания движения точки Ø естественный При этом способе задают: траекторию точки и закон движения по этой траектории Ø координатный Положение точки относительно некоторой системы отсчета задано ее координатами Уравнения движения точки в прямоугольных координатах x = f 1 (t) , y = f 2 (t) , z = f 3 (t)
Скорость: векторная величина характеризует быстроту движения, показывает, какое перемещение тело совершает в единицу времени Движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Ускорение величина, характеризующая изменение скорости при неравномерном движении тела. Средним ускорением неравномерного движения в интервале от t до t + ∆t называется векторная величина, равная отношению изменения скорости ∆v к интервалу времени ∆t: При свободном падении вблизи поверхности Земли, где
Составляющая аτ вектора ускорения, направленная вдоль касательной к траектории в данной точке, называется тангенциальным (касательным) ускорением. Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор аτ направлен в сторону движения точки при возрастании ее скорости (рисунок – а) и в противоположную сторону – при убывании скорости (рисунок – б).
Тангенциальная составляющая ускорения аτ равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю: Вторая составляющая ускорения, равная: называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют так же центростремительным ускорением). Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих.
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
Тема урока: Основные понятия и уравнения кинематики. Цель урока: повторить основные понятия кинематики – траектория, ускорение, скорость, пройденный путь и перемещение.
2 слайд
Описание слайда:
План Что изучает механика? Её основная задача. Кинематика. Основные понятия: тело отсчета, система координат, система отсчета закон независимости движений материальная точка и абсолютно твердое тело поступательное и вращательное движение траектория, путь, перемещение скорость ускорение Классификация механических движений. Основные уравнения. Графики движений.
Основные уравнения. Графики движений.
3 слайд
Описание слайда:
Что изучает механика? Её основная задача. Раздел физики – механика занимается изучением механического движения тел. Механическим движением называется изменение положения тела (в пространстве) относительно других тел с течением времени. Основная задача механики заключается в определении положения тела в любой момент времени.
4 слайд
Описание слайда:
Кинематика. Основные понятия: Механика состоит из двух основных разделов: кинематики и динамики. Раздел, который не рассматривает причин возникновения механического движения и описывает только его геометрические свойства называется кинематикой. В кинематике используются такие понятия как траектория, путь и перемещение, скорость и ускорение.
5 слайд
Описание слайда:
ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. СИСТЕМА ОТСЧЕТА. Чтобы описать механическое движение тела (точки), нужно знать его координаты в любой момент времени. Для определения координат следует выбрать тело отсчета и связать с ним систему координат. Часто телом отсчета служит Земля, с которой связывается прямоугольная декартова система координат. Для определения положения точки в любой момент времени необходимо также задать начало отсчета времени. Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела
Для определения координат следует выбрать тело отсчета и связать с ним систему координат. Часто телом отсчета служит Земля, с которой связывается прямоугольная декартова система координат. Для определения положения точки в любой момент времени необходимо также задать начало отсчета времени. Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела
6 слайд
Описание слайда:
Движение реальных тел, как правило, сложное. Поэтому для упрощения рассмотрения движений пользуются законом независимости движений: всякое сложное движение можно представить как сумму независимых простейших движений. К простейшим движениям относятся поступательное и вращательное. В физике широко пользуются моделями, которые позволяют из всего многообразия физических свойств выбрать главное, определяющее данное физическое явление. Одним из первых моделей реальных тел являются материальная точка и абсолютно твердое тело.
7 слайд
Описание слайда:
Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого остается постоянным при его движении. Эти модели позволяют исключить деформацию тел при движении. МАТЕРИАЛЬНАЯ ТОЧКА И АБСОЛЮТНО ТВЕРДОЕ ТЕЛО.
8 слайд
Описание слайда:
Поступательное и вращательное движение. Поступательным называется движение, при котором отрезок, соединяющий любые две точки твердого тела, перемещается при движении параллельно самому себе. Из этого следует, что все точки тела при поступательном движении движутся одинаково, т.е. с одинаковыми скоростями и ускорениями. Вращательным называется движение, при котором все точки абсолютно твёрдого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, причем эти окружности лежат в плоскостях, перпендикулярных оси вращения.
9 слайд
Описание слайда:
Поступательное движение Выберите верное утверждение о поступательном движении: Поступательное движение – это движение тела, при котором отрезок прямой, соединяющий две любые точки, принадлежащие этому телу, перемещается, оставаясь параллельным самому себе. При поступательном движении все точки твердого тела движутся одинаково, описывают одинаковые траектории и в каждый момент времени имеют одинаковые скорости и ускорения. Движение парашютиста вниз является примером поступательного движения. Луна вокруг Земли движется поступательно.
10 слайд
Описание слайда:
ТРАЕКТОРИЯ, ПУТЬ, ПЕРЕМЕЩЕНИЕ Траекторией движения называется линия, вдоль которой движется тело. Длина траектории называется пройденным путем. Путь – скалярная физическая величина, сумма длин отрезков траектории, может быть только положительным.
11 слайд
Описание слайда:
ПРИМЕР ВЕКТОРА ПЕРЕМЕЩЕНИЯ Перемещение – есть разность между конечным и начальным положением и обозначается:
12 слайд
Описание слайда:
Скорость Характер движения тела определяется его скоростью. Если скорость постоянна, то движение называют равномерным и уравнение движения выглядит следующим образом: [м/с2] Модуль скорости равен: Если скорость увеличивается на одинаковую величину за одинаковые промежутки времени, то движение называется равноускоренным. Если скорость уменьшается на одинаковую величину за одинаковые промежутки времени, то движение называется равнозамедленным. Такие виды движений называют равнопеременным движением.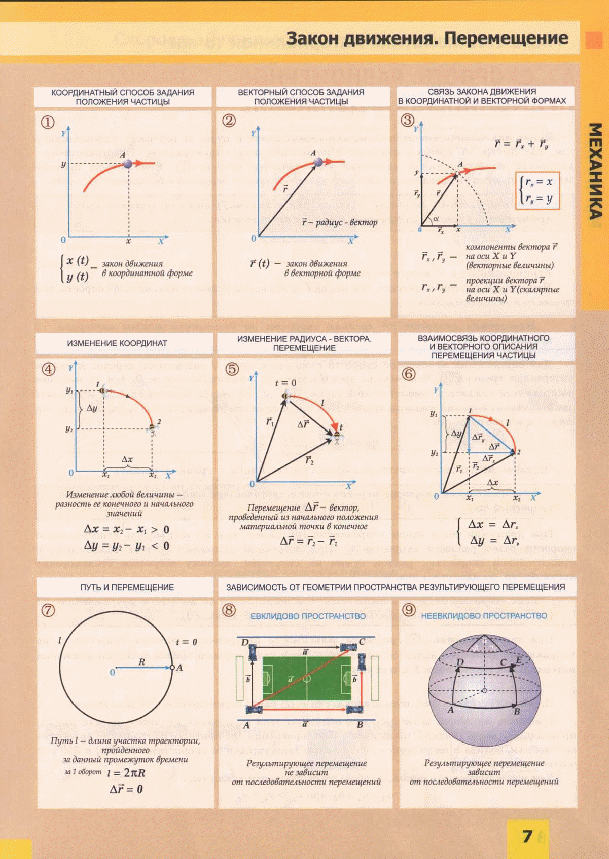
13 слайд
Описание слайда:
СРЕДНЯЯ И МГНОВЕННАЯ СКОРОСТИ Быстрота изменения положения материальной точки в пространстве с течением времени характеризуется средней и мгновенной скоростями. Средняя скорость – векторная величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло: Vср = s/t. Мгновенной скоростью называется предел отношения перемещения s к промежутку времени t, за которое это перемещение произошло, при стремлении t к нулю: Vмгн = limt–>0 s/t.
14 слайд
Описание слайда:
СЛОЖЕНИЕ СКОРОСТЕЙ Рассмотрим перемещение тела в подвижной системе координат. Пусть S1 – перемещение тела в подвижной системе координат, S2– перемещение подвижной системы координат относительно неподвижной, тогда S – перемещение тела в неподвижной системе координат равно: Если перемещения S1 и S2 совершаются одновременно, то: Таким образом т.е скорость тела относительно неподвижной системы отсчета равна сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной. Это утверждение называется классическим законом сложения скоростей.
Это утверждение называется классическим законом сложения скоростей.
15 слайд
Описание слайда:
Ускорение Величина изменения скорости за единицу времени есть ускорение: В процессе движения скорость может измениться, отсутствие изменения скорости приводит к отсутствию ускорения. Неподвижное тело, либо тело движущее с постоянной скоростью обладает нулевым ускорением. Ускорение определяет на сколько скорость увеличилась при равноускоренном движении, и насколько уменьшилась при равнозамедленном движении за 1 секунду.
16 слайд
Описание слайда:
Например: Велосипедист движется с ускорением а=5м/с2, тогда через каждую секунду его скорость будет принимать значения:
17 слайд
Описание слайда:
Среднее и мгновенное ускорение Величина, характеризующая быстроту изменения скорости, называется ускорением. Среднее ускорение – величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: аср = v/t. Если v1 и v2 – мгновенные скорости в моменты времени t1 и t2, то v=v2-v1, t=t2-t1. Мгновенное ускорение – ускорение тела в данный момент времени. Это физическая величина, равная пределу отношения изменения скорости к промежутку времени, за которое это изменение произошло, при стремлении промежутка времени к нулю: aмгн = lim t–>0 v/t.
Если v1 и v2 – мгновенные скорости в моменты времени t1 и t2, то v=v2-v1, t=t2-t1. Мгновенное ускорение – ускорение тела в данный момент времени. Это физическая величина, равная пределу отношения изменения скорости к промежутку времени, за которое это изменение произошло, при стремлении промежутка времени к нулю: aмгн = lim t–>0 v/t.
18 слайд
Описание слайда:
19 слайд
Описание слайда:
Основные уравнения.
Механика
Основные понятия кинематики
Тема: Пространство, время, движение, скорость. Основная задача механики.
Механика (с греч. Искусство постороения машин)
Раздел физики о движении материальных объектов и взаимодействия между ними .
Механика
- Кинематика (движение)
- Динамика (сила)
раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
раздел механики, в котором изучаются причины возникновения механического движения.
Основные понятия кинематики
1. Пространство и время
Окружающий нас мир – материален
Существует объективно и реально т.е. Независимо о нашего сознания и вне его.
Способен действовать на наши органы чувств и вызывать у нас определенные ощущения.
Пространство и время (время скорости развития событий)
Свойство времени: одномерность, непрерывность
Единица времени – секунда
Разность значений любой величины обозначают Δ (дельта), например: Δt – промежуток времени.
Основной пространственной характеристикой является расстояние
Свойства просранства:
– непрерывность
– трехмерность
-евклидовость
Мера расстояния – метр
Существуюет три уровня строения мира:
МЕГАмир (мир галактик)
МАКРОмир (от песчинки до планет Солнечной системы)
МИКРОмир (молекулы, атомы, элементрарные частицы)
2. Система отсчета
Система отсчета
Тело отсчета – тело, относительно которого рассматривается движение других тел.
Система отсчета – совокупность системы координат, тела отсчета, с которым она связана, и прибора для измерения времени.
Системы координат
- Одномерная – координатная прямая
Двумерная – координатная плоскость
Пространственная система
Координат (трехмерная)
3. Механическое движение (МД)
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
4. Материальная точка
Материальная точка – тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело можно считать материальной точкой, если: 1. расстояния, проходимые телом, значительно больше размеров этого тела; 2. тело движется поступательно, т.е. все его точки движутся одинаково в любой момент времени.
5. Основная задача механики
Определение положения частицы в выбранной системе отсчета в любой момент времени
6. Траектория, путь перемещение.
Траектория – воображаемая линия, по которой движется тело
Путь ( S) – длина траектории. Перемещение – вектор, соединяющий начальную и конечную точки траектории.
7. Скорость
Скорость – физическая векторная величина, характеризующая направление и быстроту движения. Показывает, какое перемещение совершило тело в единицу времени:
Мгновенная скорость – скорость тела в данный момент времени или в данной точке траектории. Равна отношению малого перемещения к малому промежутку времени, за которое это перемещение совершено:
Средняя скорость – физическая величина, равная отношению всего пройденного пути ко всему времени:
Решение задач
Задача 1 . Когда можно, когда нельзя принимать за материальную точку: ножницы, автомобиль, ракету?
Когда можно, когда нельзя принимать за материальную точку: ножницы, автомобиль, ракету?
Задача 2. Гуляя молодой человек прошел 3 км на север, где встретился со своей подругой. После встречи они сели на автобус и проехали 4 км в восточном направлении. Определить путь и перемещение, совершенные молодым человеком
Задача 3. Какую величину измеряет счетчик в автомашине: пройденный путь или длину перемещения?
Задача 4. Когда мы говорим, что смена дня и ночи на Земле объясняется вращением Земли вокруг своей оси, то мы имеем в виду систему отсчеа связанную с … а) планетами; б) Солнцем; в) Землей; г) любым телом.
1 уровень.
1) П о заданной траектории движения тела (см.рис) найдите(графически) его перемещение
2) Диктант «Веришь- не веришь»(+ или -):
А) Механика – часть физики, изучающая механические явления;
Б) Механическое движение – это физическая величина;
В) Движение шарика по желобу – механическое явление;
Г) центр колеса велосипеда (при движении по горизонтальной дороге) совершает поступательное движение;
Д) при падении с некоторой высоты мяч совершает поступательное движение.
2 уровень:
А) линейку можно принять за материальную точку, если она совершает вращательное движение на столе;
Б) Траектория конца стрелки часов – окружность;
В) Землю при движении её по орбите можно принять за материальную точку.
3 уровень
3) Расстояние между пунктами А и Б по прямой 6 км. Человек проходит это расстояние туда и обратно за 2 часа. Чему равны путь и перемещение человека за 2ч и 1ч?
4) Велосипедист движется по окружности радиусом 100 ми делает 1 оборот за 2 мин. Определите путь и перемещение велосипедиста за 1 мин и 2 мин.
«Движение тел» – Основные понятия кинематики. И больше 5 мин на графике нет такого промежутка времени. Какое из тел движется с наибольшей скоростью? Интенсивный курс подготовки к Единому государственному экзамену. – М.: Айрис-пресс, 2007. Относительность движения. Пройденный путь l длина траектории, пройденной телом за некоторое время t.
«Равномерное и неравномерное движение» – Особенности данного движения.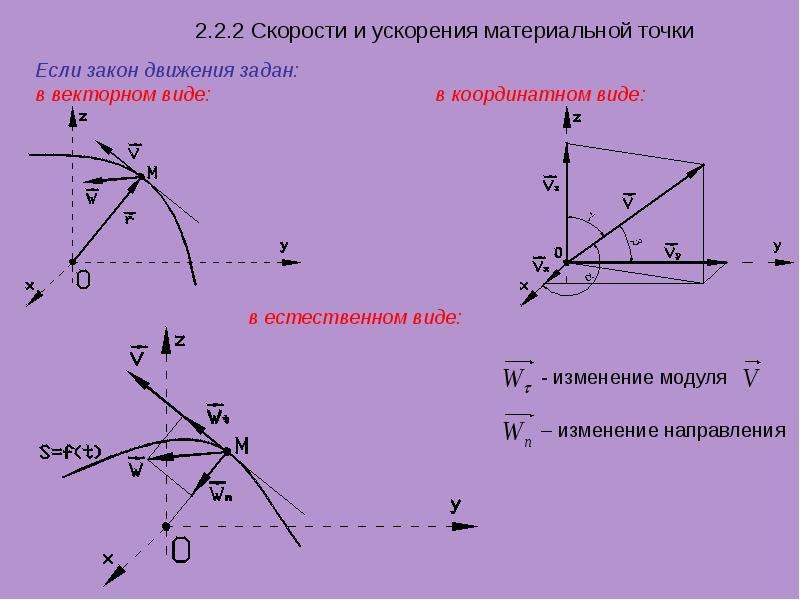 Перемещение (пройденный путь) Время Скорость. Особенности неравномерного движения. Равномерное движение. Скорость тела при равномерном движении можно определить по формуле. Яблоневка. Скорость тела при неравномерном движении можно определить по формуле. Неравномерное движение.
Перемещение (пройденный путь) Время Скорость. Особенности неравномерного движения. Равномерное движение. Скорость тела при равномерном движении можно определить по формуле. Яблоневка. Скорость тела при неравномерном движении можно определить по формуле. Неравномерное движение.
«Понятие кинематики» – Векторные величины. Величина дает число оборотов в единицу времени. Вектор a. Вектор угловой скорости. Единичный вектор. Вектор, соединяющий начальную точку (1) движения с конечной (2). Векторное сложение скоростей. В учебниках векторы обозначаться жирными буквами. Выберем прямоугольную систему координат.
«Изучение движения тела по окружности» – Движение тел по окружности. Выполните тест. Динамика движения тел по окружности. Решите задачу. П.Н.Нестеров. Решите самостоятельно. Проверяем ответы. Базовый уровень. Алгоритм решения задач. Вес тела. Изучение метода решения задач.
«Движение тела по окружности» – С какой линейной скоростью волк бросил шляпу. Период в случае равномерного кругового движения. Минутная стрелка часов в 3 раза длиннее секундной. Ускорение прямо пропорционально скорости движения. С какой минимальной скоростью должен двигаться самолет аттракциона. Угловое перемещение. Угловая скорость.
Минутная стрелка часов в 3 раза длиннее секундной. Ускорение прямо пропорционально скорости движения. С какой минимальной скоростью должен двигаться самолет аттракциона. Угловое перемещение. Угловая скорость.
«Кинематика точки» – Ускорение Кориолиса. Теорема Эйлера. Кинематика твердого тела. Общий случай составного движения тела. Плоскопараллельное движение твердого тела. Сложное движение точки. Угловая скорость и угловое ускорение. Причины возникновения ускорения Кориолиса. Преобразование вращений. Сложное движение твердого тела.
Контрольная работа №1 по теме «Основы кинематики. Законы Ньютона.»
Урок №
тема: Контрольная работа №1 по теме «Основы кинематики. Законы Ньютона.»
тип: урок контроля и учёта знаний и умений
цели:
Ход урока:
Организация начала урока.
Постановка целей и задач урока.

Контрольная работа
Вариант 1
1.С каким ускорением должен затормозить автомобиль, движущийся со
скоростью 36 км/ч, чтобы через 10 с остановиться?
2.За какое время велосипедист проедет 30 м, начиная движение с ускорением
0,75 м/с2?
3.Какую скорость приобретает троллейбус за 5 с, если он трогается с места с
ускорением 1,2 м/с2?
4.С каким ускорением двигался при разбеге реактивный самолёт массой
50 т, если сила тяги двигателей 80 кН?
5.Чему равна сила, сообщающая телу массой 3 кг ускорение 0,4 м/с2?
6..Лыжник массой 60 кг, имеющий в конце спуска скорость 36 км/ч,
остановился через 40 с после окончания спуска. Определите силу
сопротивления его движению.
Вариант – 2
1.Поезд подходит к станции со скоростью 36 км/ч и останавливается
через минуту после начала торможения. С каким ускорением двигался
поезд?
2. Определите, какую скорость развивает мотоциклист за 15 с, двигаясь
Определите, какую скорость развивает мотоциклист за 15 с, двигаясь
из состояния покоя с ускорением 1,3 м/с2?
3.Какой должна быть длина взлетной полосы, если известно, что самолёт
для взлёта должен приобрести скорость 240 км/ч, а время разгона
самолёта равно примерно 30 с?
4.Вагонетка массой 200 кг движется с ускорением 0,2 м/с2. Определите
силу, сообщающую вагонетке это ускорение.
5..Чему равно ускорение, с которым движется тело массой 3 кг, если на
него действует сила 12 Н?
6.Порожний грузовой автомобиль массой 3 т начал движение с
ускорением 0,2 м/с2. Какова масса этого автомобиля вместе с грузом,
если при той же силе тяги он трогается с места с ускорением 0,15м/с2?
Законы кинематики формулы. Кинематика основные понятия, законы и формулы. Свободное падение по вертикали
Для того чтобы понять, что изучает механика, необходимо рассмотреть, что означает движение в самом общем смысле. Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример – экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.
Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример – экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.
Что-то подобное можно наблюдать и в механике. При механическом движении изменяется положение тела в пространстве относительно других предметов с течением времени. Основная задача механики – указать, где находится объект в любой момент, учитывая даже тот, который еще не наступил. То есть, предсказать положение тела в заданное время, а не только узнать, где именно в пространстве оно находилось в прошлом.
Кинематика – это раздел механики, который изучает движение тела, не анализируя его причины. Это значит, что она учит не объяснять, а описывать. То есть, придумать способ, с помощью которого можно было бы задать положение тела в любой момент времени. Основные понятия кинематики включают в себя скорость, ускорение, расстояние, время и перемещение.
Сложность в описании движения
Первая проблема, с которой сталкивается кинематика – это то, что у каждого тела есть определенный размер. Допустим, необходимо описать движение какого-нибудь предмета. Это значит научиться обозначать его положение в любой момент времени. Но каждый предмет занимает в пространстве какое-то место. То есть, что все части этого объекта в один и тот же момент времени занимают разное положение.
Какую точку в таком случае необходимо взять для описания нахождения всего предмета? Если учитывать каждую, то расчеты окажутся слишком сложными. Поэтому решение ответа на этот вопрос можно максимально упростить. Если все точки одного тела движутся в одинаковом направлении, то для описания движения достаточно одной такой, которую содержит это тело.
Виды движения в кинематике
Существует три типа:
- Поступательным называется движение, при котором любая прямая проведенная в теле остается параллельной самой себе. Например, автомобиль, который движется по шоссе, совершает такой вид движения.
- Вращательным называется такое движение тела при котором все его точки движутся по окружностям с центрами, лежащими на одной прямой, называемой осью вращения. Например, вращение Земли относительно своей оси.
- Колебательным называется движение, при котором тело повторяет свою траекторию через определенный отрезок времени. Например, движение маятника.
Основные понятия кинематики – материальная точка
Любое сложное движение можно описать как комбинацию двух простейших видов – поступательного и вращательного. Например колесо автомобиля или юла, стоящая на движущейся прямо платформе, участвуют одновременно в этих двух типах перемещения.
Но что делать, если движение тела нельзя представить в виде комбинации? Например, если автомобиль едет по ухабистой дороге, его положение будет меняться очень сложным образом. Если рассчитывать только то, что этот транспорт перемещается из одного города в другой, то в такой ситуации становится не важно какого размера тело движется из точки А в точку Б и им можно пренебречь. В данном случае важно только за какое время автомобиль прошел определенное расстояние и с какой скоростью двигался.
Однако следует учитывать, что пренебрежение размером допускается не в каждой задаче. Например, если рассчитывать движение при парковке автомобиля, то игнорирование величины данного тела, приведет к пагубным последствием. Поэтому, только в тех ситуациях, когда в рамках конкретной задачи, размерами движущегося объекта можно пренебречь, то такое тело принято называть материальной точкой.
Формулы кинематики
Числа, с помощью которых задается положение точки в пространстве, называются координатами. Чтобы определить его на прямой, достаточно одного числа, когда речь идет о поверхности, то двух, о пространстве – трех. Большего количества чисел в трехмерном мире (для описывания положения материальной точки) не требуется.
Существует три основных уравнения для понятия кинематики, как раздела о движении тел:
- v = u + at.
- S = ut + 1/2at 2 .
- v 2 = u 2 + 2as.
v = конечная скорость,
u = Начальная скорость,
a = ускорение,
s = расстояние, пройденное телом,
Формулы кинематики в одномерном пространстве:
X – X o = V o t + 1/2a t2
V 2 = V o 1 + 2a (X – X o)
X – X o = 1\2 (V o + V) t
Где,
V – конечная скорость (м / с),
V o – начальная скорость (м / с),
a – ускорение (м / с 2),
t – время (с),
X – конечное положение (м),
Формулы кинематики в двумерном пространстве
Поскольку следующие уравнения используются для описания материальной точки на плоскости, стоит рассматривать ось X и Y.
Учитывая направление Х:
a x = constant
V fx = V i x + a x Δt
X f = X i + V i x Δt +1/2a x Δt 2
Δt = V fx -V ix /a x
V fx 2 = V ix 2 + 2ax Δx
X f = X i + 1/2 (V fx + V ix) Δ t .
И учитывая направление y:
a y = constant
V fy = V iy + a y Δt
y f = y i + V iy Δt + 1/2 a x Δt 2
Δt = V fy – V iy /a y
V fy 2 = V iy 2 + 2 ay Δ y
y f = y i +1/2 (V fy + V iy) Δt.
V f – конечная скорость (м / с),
V i – начальная скорость (м / с),
a – ускорение (m / с 2),
t – время (с),
X – конечное положение (м),
X 0 – начальное положение (м).
Перемещение брошенного снаряда – лучший пример для описания движения объекта в двух измерениях. Здесь тело перемещается, как в вертикальном положении У, так и в горизонтальном положении Х, поэтому можно сказать, что предмет имеет две скорости.
Примеры задач по кинематике
Задача 1 : Начальная скорость грузовика равна нулю. Изначально этот объект находится в состоянии покоя. На него начинает действовать равномерное ускорение в течение временного интервала 5,21 секунды. Расстояние, пройденное грузовиком, составляет 110 м. Найти ускорение.
Решение:
Пройденное расстояние s = 110 м,
начальная скорость v i = 0,
время t = 5,21 с,
ускорение a =?
Используя основные понятие и формулы кинематики, можно заключить, что,
s = v i t + 1/2 a t 2 ,
110 м = (0) × (5.21) + 1/2 × a (5.21) 2 ,
a = 8,10 м / с 2 .
Задача 2: Точка движется вдоль оси х (в см), после t секунд путешествия, ее можно представить, используя уравнение x = 14t 2 – t + 10. Необходимо найти среднюю скорость точки, при условии, что t = 3s?
Решение:
Положение точки при t = 0, равно x = 10 см.
При t = 3s, x = 133 см.
Средняя скорость, V av = Δx/Δt = 133-10/3-0 = 41 см / с.
Что такое тело отсчета
О движении можно говорить только если существует что-то, относительно чего рассматривается изменение положения изучаемого объекта. Такой предмет называется телом отсчета и оно условно всегда принимается за неподвижное.
Если в задаче не указано в какой системе отчета движется материальная точка, то телом отсчета считается земля по умолчанию. Однако, это не означает, что за неподвижный в заданный момент времени объект, относительно которого совершается движение, нельзя принять любой другой удобный для расчета. Например, за тело отсчета можно взять движущийся поезд, поворачивающий автомобиль и так далее.
Система отсчета и ее значение в кинематике
Для описания движения необходимы три составляющие:
- Система координат.
- Тело отсчета.
- Прибор для измерения времени.
Тело отсчета, система координат, связанная с ним и прибор для измерения времени образуют систему отсчета. Бессмысленно говорить о движении, если ее не указывать. Правильно подобранная система отсчета, позволяет упростить описание перемещения и, наоборот, усложнить, если она выбрана неудачно.
Именно по этой причине, человечество долго считало, что Солнце движется вокруг Земли и что она находится в центре вселенной. Такое сложное движение светил, связанное с тем, что земные наблюдатели находятся в системе отсчета, которая очень замысловато движется. Земля вращается вокруг свое оси и одновременно вокруг Солнца. На самом деле, если сменить систему отсчета, то все движения небесных тел легко описываются. Это в свое время было сделано Коперником. Он предложил собственное описание мироустройства, в котором Солнце неподвижно. Относительно него описать движение планет гораздо проще, чем если телом отсчета будет являться Земля.
Основные понятия кинематики – путь и траектория
Пусть некоторая точка первое время находилась в положении А, спустя некоторое время она оказалась в положении В. Между ними можно провести одну линию. Но для того, чтобы эта прямая несла больше информации о движении, то есть было понятно откуда и куда двигалось тело, это должен быть не просто отрезок, а направленный, обычно обозначающийся буквой S. Перемещением тела, называется вектор, проведенный из начального положения предмета в конечное.
Если тело изначально находилось в точке А, а затем оказалось в точке В, это не означает, что оно двигалось только по прямой. Из одного положения в другое можно попасть бесконечным количеством способов. Линия, вдоль которой движется тело, является еще одним основным понятием кинематики – траекторией. А ее длина называется путь, который обычно обозначается буквами L или l.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела , объекта или частицы . Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Радиус-вектор точки – это вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой. Радиус-вектор обозначается, как правило, буквой r . К сожалению некоторые авторы обозначают его буквой s . Настоятельно советую не использовать обозначение s для радиус-вектора. Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r – радиус-вектор точки, s – путь, пройденный точкой.
Вектор перемещения (часто говорят просто – перемещение ) – это вектор , начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr . Использование символа Δ очевидно: Δr – это разность между радиус-вектором r конечной точки изучаемого отрезка траектории и радиус-вектором r 0 точки начала этого отрезка (рис. 1), то есть Δr = r − r 0 .
Траектория – это линия, вдоль которой движется тело.
Путь – это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r, мы уже об этом говорили). Запомните! Путь – это положительный скаляр ! Путь в процессе движения может только увеличиваться .
Средняя скорость перемещения v ср
v ср = Δr /Δt.
Мгновенная скорость перемещения v – это вектор, определяемый выражением
v = dr /dt.
Средняя скорость пути v ср – это скаляр, определяемый выражением
V ср = Δs/Δt.
Часто встречаются и другие обозначения, например, .
Мгновенная скорость пути v – это скаляр, определяемый выражением
Модуль мгновенной скорости перемещения и мгновенная скорость пути – это одно и то же, поскольку dr = ds.
Среднее ускорение a
a ср = Δv /Δt.
Мгновенное ускорение (или просто, ускорение ) a – это вектор, определяемый выражением
a =dv /dt.
Касательное (тангенциальное) ускорение a τ (нижний индекс – это греческая строчная буква тау) – это вектор , являющийся векторной проекцией мгновенного ускорения на касательную ось .
Нормальное (центростремительное) ускорение a n – это вектор , являющийся векторной проекцией мгновенного ускорения на ось нормали .
Модуль касательного ускорения
| a τ | = dv/dt,
То есть это – производная модуля мгновенной скорости по времени.
Модуль нормального ускорения
| a n | = v 2 /r,
Где r – величина радиуса кривизны траектории в точке нахождения тела.
Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.
Запомните!
a τ – это вектор касательного ускорения,
a n – это вектор нормального ускорения.
a τ и a n являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,
A τ – это проекция (скалярная!) касательного ускорения на касательную ось,
A n – это проекция (скалярная!) нормального ускорения на ось нормали,
| a τ |- это модуль вектора касательного ускорения,
| a n | – это модуль вектора нормального ускорения.
Особенно не удивляйтесь, если, читая в литературе о криволинейном (в частности, вращательном) движении, Вы обнаружите, что автор под a τ понимает и вектор, и его проекцию, и его модуль. То же самое относится и к a n . Все, как говорится, «в одном флаконе». И такое, к сожалению, сплошь и рядом. Даже учебники для высшей школы не являются исключением, во многих из них (поверьте – в большинстве!) царит полная неразбериха по этому поводу.
Вот так, не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.
Мгновенная угловая скорость (или просто, угловая скорость ) ω – это вектор, определяемый выражением
ω = dφ /dt,
Где dφ – бесконечно малое изменение угловой координаты (dφ – вектор!).
Мгновенное угловое ускорение (или просто, угловое ускорение ) ε – это вектор, определяемый выражением
ε = dω /dt.
Связь между v , ω и r :
v = ω × r .
Связь между v, ω и r:
Связь между | a τ |, ε и r:
| a τ | = ε · r.
Теперь перейдем к кинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть .
Кинематическое уравнение равномерного и прямолинейного движения имеет вид:
r = r 0 + v t,
Где r – радиус-вектор объекта в момент времени t, r 0 – то же в начальный момент времени t 0 (в момент начала наблюдений).
Кинематическое уравнение движения с постоянным ускорением имеет вид:
r = r 0 + v 0 t + a t 2 /2, где v 0 скорость объекта в момент t 0 .
Уравнение для скорости тела при движении с постоянным ускорением имеет вид:
v = v 0 + a t.
Кинематическое уравнение равномерного движения по окружности в полярных координатах имеет вид:
φ = φ 0 + ω z t,
Где φ – угловая координата тела в данный момент времени, φ 0 – угловая координата тела в момент начала наблюдения (в начальный момент времени), ω z – проекция угловой скорости ω на ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).
Кинематическое уравнение движения по окружности с постоянным ускорением в полярных координатах имеет вид:
φ = φ 0 + ω 0z t + ε z t 2 /2.
Кинематическое уравнение гармонических колебаний вдоль оси X имеет вид:
Х = А Cos (ω t + φ 0),
Где A – амплитуда колебаний, ω – циклическая частота, φ 0 – начальная фаза колебаний.
Проекция скорости точки, колеблющейся вдоль оси X, на эту ось равна:
V x = − ω · A · Sin (ω t + φ 0).
Проекция ускорения точки, колеблющейся вдоль оси X, на эту ось равна:
А x = − ω 2 · A · Cos (ω t + φ 0).
Связь между циклической частотой ω, обычной частотой ƒ и периодом колебаний T:
ω = 2 πƒ = 2 π/T (π = 3,14 – число пи).
Математический маятник имеет период колебаний T, определяемый выражением:
В числителе подкоренного выражения – длина нити маятника, в знаменателе – ускорение свободного падения
Связь между абсолютной v абс, относительной v отн и переносной v пер скоростями:
v абс = v отн + v пер.
Вот, пожалуй, и все определения и формулы, которые могут понадобиться при решении задач на кинематику. Приведенная информация носит только справочный характер и не может заменить электронную книгу, где доступно, подробно и, надеюсь, увлекательно изложена теория этого раздела механики.
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины – метр (1 м),
- времени – секунда (1 с),
- массы – килограмм (1 кг),
- количества вещества – моль (1 моль),
- температуры – кельвин (1 К),
- силы электрического тока – ампер (1 А),
- Справочно: силы света – кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой . Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела .
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: L полн – весь путь, который прошло тело, t полн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v 0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t ).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей.
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х » писать «у ». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v 0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v x = v 0 . А вертикальная возрастает по законам ускоренного движения v y = gt . При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали . Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны.
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t . Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T . При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt . Очевидно, что за время равное периоду T тело пройдет угол равный 2π , следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω :
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением , так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v
на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Основы кинематики – презентация онлайн
1. 1 ОСНОВЫ КИНЕМАТИКИ
Механика – часть физики, в которой изучаютсязакономерности механического движения и
причины, вызывающие или изменяющие это
движение.
• Классическая (механика Галилея—Ньютона).
Изучает законы движения макроскопических тел,
скорости которых малы по сравнению со
скоростью распространения света в вакууме.
• Релятивистская. Изучает законы движения
макроскопических тел со скоростями,
сравнимыми со скоростью распространения
света в вакууме (основана на специальной
теории относительности, сформулированной А.
Эйнштейном.)
• Квантовая. Изучает законы движения
микроскопических тел (отдельных атомов и
элементарных частиц).
Разделы механики
• Кинематика. Изучает движение тел, не
рассматривая причины, которые это движение
обусловливают.
• Динамика. Изучает законы движения тел и
причины, которые вызывают или изменяют это
движение.
• Статика. Изучает законы равновесия системы
тел. Если известны законы движения тел, то из них
можно установить и законы равновесия.
• Материальная точка – тело, обладающее
массой, размерами которого в данной задаче
можно пренебречь. Понятие материальной точки
— абстрактное, но его введение облегчает
решение практических задач. Например, изучая
движение планет по орбитам вокруг Солнца,
можно принять их за материальные точки.
• Система материальных точек – произвольное
макроскопическое тело или систему тел можно
мысленно разбить на малые
взаимодействующие между собой части, каждая
из которых рассматривается как материальная
точка. Тогда изучение движения произвольной
системы тел сводится к изучению системы
материальных точек. В механике сначала
изучают движение одной материальной точки, а
затем переходят к изучению движения системы
материальных точек.
• Абсолютно твердое тело – тело, которое ни при
каких условиях не может деформироваться и
при всех условиях расстояние между двумя
точками (точнее, между двумя частицами) этого
тела остается постоянным.
• Абсолютно упругое тело – тело, деформация
которого подчиняется закону Гука, а после
прекращения действия внешних сил принимает
свои первоначальные размеры и форму.
• Абсолютно неупругое тело – тело, полностью
сохраняющее деформированное состояние
после прекращения действия внешних сил.
6. 1.1 МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
Тело отсчетаПроизвольно выбранное тело, относительно
которого определяется положение других
(движущихся) тел. Положение любого движущегося
тела определяется по отношению к телу отсчета,
поэтому механическое движение относительно.
Система координат
Система (в простейшем случае прямоугольная
декартова система xyz), связанная с телом
отсчета.
Система отсчета
Совокупность тела отсчета,
связанной с ним системы
координат и синхронизированных
между собой часов.
Кинематические уравнения движения
материальной точки (закон движения)
Положение материальной точки А в декартовой
системе координат определяется тремя
координатами х,у,z или радиусом-вектором r (он
проводится из начала отсчета координат 0 в точку
А). При движении материальной точки ее
координаты с течением времени изменяются,
поэтому ее движение определяется записанной
системой скалярных уравнений или эквивалентным
ей векторным уравнением.
Пример. Определить закон движения
материальной точки
x=1+0,75t
z=4,9t2
Траектория
Линия, описываемая движущейся материальной
точкой (или телом) относительно выбранной
системы отсчета.
В зависимости от формы траектории различают
прямолинейное движение, криволинейное
движение, движение по окружности и т. д.
♦ Вид траектории зависит от характера движения
материальной точки и от системы отсчета.
Пример. Определить вид траектории тела
падающего в вагоне
• относительно вагона,
• относительно Земли.
Определить вид траектории какой-либо точки
пропеллера движущегося самолета
• относительно самолета,
• относительно Земли.
Вектор перемещения
Вектор r = r2 – r1 проведенный из начального
положения движущейся точки в положение ее в данный
момент времени (приращение радиуса-вектора точки
за рассматриваемый промежуток времени).
Длина пути
Длина участка траектории АВ, пройденного
материальной точкой за данный промежуток времени:
s = s(t) — скалярная функция времени.
При прямолинейном движении
вектор перемещения совпадает
с соответствующим участком
траектории и модуль перемещения
| r | равен пройденному пути
s: | r | = s.
Поступательное движение твердого тела
Движение, при котором любая прямая, жестко
связанная с движущимся телом и проведенная
через две произвольные точки данного тела,
остается параллельной самой себе.
При поступательном движении все точки тела
движутся одинаково, поэтому его поступательное
движение можно охарактеризовать движением
какой-то произвольной точки тела (например,
движением центра масс тела).
Вращательное движение твердого тела
Движение, при котором все точки тела движутся
по окружностям, центры которых лежат на одной
прямой, называемой осью вращения.
Различные точки твердого тела движутся поразному, поэтому его вращательное движение
нельзя охарактеризовать движением какой-то
одной точки.
16. 1.2 КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
СкоростьВекторная величина, которая определяет как
быстроту движения, так и его направление в
данный момент времени.
Средняя скорость
Векторная величина, численно равная отношению
перемещения к промежутку времени t, в течение
которого это перемещение произошло.
Направление вектора средней скорости
совпадает с направлением
перемещения.
Для оценки численного значения средней
скорости на практике иногда пользуются
следующим определением: средняя скорость
равна отношению пройденного пути ко времени
движения.
Определенная таким образом средняя
скорость является скаляром, а не вектором.
Пример. Первую половину пути автомобиль
проехал со скоростью 60 км/ч, а вторую со
скоростью 40 км/ч. Найти среднюю скорость
движения автомобиля.
48 км/ч.
Мгновенная скорость
Векторная величина, определяемая первой
производной радиуса-вектора движущейся точки
по времени. Вектор мгновенной скорости
направлен по касательной к траектории в сторону
движения.
Модуль мгновенной скорости
Равен первой производной пути по времени.
Единица измерения скорости — 1 м/с
1 метр в секунду — скорость прямолинейно и равномерно
движущейся точки, при которой эта точка за время 1 с
перемещается на расстояние 1 м.
Пример. Найти мгновенную скорость точки,
движущейся по закону s(t) = t 3 (s — путь в метрах, t
— время в минутах):
а) в начальный момент движения;
б) через 10 сек после начала движения;
в) в момент t = 5 мин.
а) 0 м/мин
б) 1/12 м/мин
в) 75 м/мин
Проекции вектора скорости на оси координат
x, y, z — соответственно проекции
радиуса-вектора на оси координат.
Движение в одной плоскости
vx, vy — проекции у вектора скорости v на оси
координат.
Ускорение
Характеристика неравномерного движения,
определяющая быстроту изменения скорости по
модулю и направлению.
Среднее ускорение
Векторная величина, равная отношению изменения
скорости v к интервалу времени t, за которое
это изменение произошло.
Мгновенное ускорение
Векторная величина, определяемая первой
производной скорости по времени.
Пример. Найти мгновенное ускорение точки,
движущейся по закону s(t) = t3+2t2 (s — путь в
метрах, t — время в минутах):
а) в начальный момент движения;
б) через 10 сек после начала движения;
в) в момент t = 5 мин.
Составляющие ускорения
• тангенциальная
Характеризует быстроту изменения скорости по
модулю (направлена по касательной к
траектории).
• нормальная
Характеризует быстроту изменения скорости по
направлению (направлена к центру кривизны
траектории).
Полное ускорение при криволинейном движении
— геометрическая сумма тангенциальной и
нормальной составляющих ускорения.
Модуль полного ускорения.
Единица измерения ускорения — 1 м/с2
Классификация движения в зависимости от
тангенциальной и нормальной составляющих
ускорения
28. 1.4 ПРИМЕРЫ РАЗЛИЧНЫХ ВИДОВ ДВИЖЕНИЯ
Пример. Автомобиль движется по прямой улице.На графике представлена зависимость скорости
автомобиля от времени.
В каком интервале времени максимален модуль
ускорения?
Пример. На рисунке приведен график
зависимости проекции скорости тела от времени.
Нарисуйте график проекции ускорения тела в
интервале времени от 30 до 40 с.
Пример. Тело движется прямолинейно вдоль оси х.
На графике представлена зависимость
координаты тела от времени. В какой момент
времени модуль перемещения относительно
исходной точки имел максимальное значение?
Пример. На рисунке представлен график
зависимости модуля скорости автомобиля от
времени t. Найдите путь, пройденный автомобилем
за 5 c.
Свободное падение тел
Пример. Камень падает с высоты h=1200 м.
Сколько секунд продолжается падение?
Движение тела, брошенного вертикально вверх
Пример. На какую высоту поднимется камень,
брошенный вертикально вверх с начальной
скоростью 5 м/с.
Движение тела, брошенного горизонтально
Пример. С башни брошено тело в горизонтальном
направлении со скоростью 40 м/с. Какова
скорость тела через 3 с после начала движения?
Движение тела, брошенного под углом к горизонту
Пример. Снаряд вылетает из орудия с начальной
скоростью 490 м/с под углом 300 к горизонту. Найти
высоту, дальность и время полета снаряда, не
учитывая его вращение и сопротивление воздуха.
47. 1.5 КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Элементарный угол поворота (d )Элементарные (бесконечно малые)
повороты рассматривают как векторы.
Модуль вектора d равен углу поворота, а
его направление совпадает с
направлением поступательного движения
острия винта, головка
которого вращается
в направлении движения
точки по окружности,
т. е. подчиняется правилу
правого винта.
Угловая скорость
Единица измерения угловой
скорости – 1 рад/с
Равномерное движение по окружности
Движение, при котором материальная точка (тело)
за равные промежутки времени проходит равные
по длине дуги окружности.
Угловая скорость = const: = /t( угол
поворота).
Период вращения Т время, за которое
материальная точка совершает один полный
оборот по окружности, т. е. поворачивается на угол
2 .
Частота вращения число полных оборотов,
совершаемых материальной точкой при
равномерном ее движении по окружности, в
единицу времени.
Характерная особенность равномерного
движения по окружности
Равномерное движение по окружности — частный
случай криволинейного движения.
Движение по окружности со скоростью,
постоянной по модулю (v = const), является
ускоренным. Это обусловлено тем, что при
постоянном модуле направление скорости все
время изменяется.
Ускорение материальной точки, равномерно
движущейся по окружности
Тангенциальная составляющая ускорения при
равномерном движении точки по окружности
равна нулю.
Нормальная составляющая ускорения
(центростремительное ускорение) направлена по
радиусу к центру окружности. В любой
точке окружности вектор нормального ускорения
перпендикулярен вектору скорости.
Единица измерения углового ускорения – 1 рад/с2
Пример. Точка движется по кривой с постоянным
тангенциальным ускорением aτ=0,5 м/с2.
Определить полное ускорение a точки на участке
кривой с радиусом кривизны R=3 м, если точка
движется на этом участке со скоростью v=2 м/с.
Угловое ускорение – векторная величина,
определяемая первой производной угловой скорости
по времени.
Направление вектора углового ускорения. При
вращении тела вокруг неподвижной оси вектор
углового ускорения направлен вдоль оси вращения в
сторону вектора элементарного
приращения угловой скорости.
При ускоренном движении вектор
сонаправлен вектору , при замедленном —
противонаправлен ему.
Вектор — псевдовектор.
Основное уравнение кинематики. Кинематика, законы и формулы
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины – метр (1 м),
- времени – секунда (1 с),
- массы – килограмм (1 кг),
- количества вещества – моль (1 моль),
- температуры – кельвин (1 К),
- силы электрического тока – ампер (1 А),
- Справочно: силы света – кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой . Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела .
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: L полн – весь путь, который прошло тело, t полн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v 0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t ).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей.
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х » писать «у ». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v 0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v x = v 0 . А вертикальная возрастает по законам ускоренного движения v y = gt . При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали . Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны.
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t . Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T . При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt . Очевидно, что за время равное периоду T тело пройдет угол равный 2π , следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω :
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением , так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v
на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Для того чтобы понять, что изучает механика, необходимо рассмотреть, что означает движение в самом общем смысле. Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример – экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.
Что-то подобное можно наблюдать и в механике. При механическом движении изменяется положение тела в пространстве относительно других предметов с течением времени. Основная задача механики – указать, где находится объект в любой момент, учитывая даже тот, который еще не наступил. То есть, предсказать положение тела в заданное время, а не только узнать, где именно в пространстве оно находилось в прошлом.
Кинематика – это раздел механики, который изучает движение тела, не анализируя его причины. Это значит, что она учит не объяснять, а описывать. То есть, придумать способ, с помощью которого можно было бы задать положение тела в любой момент времени. Основные понятия кинематики включают в себя скорость, ускорение, расстояние, время и перемещение.
Сложность в описании движения
Первая проблема, с которой сталкивается кинематика – это то, что у каждого тела есть определенный размер. Допустим, необходимо описать движение какого-нибудь предмета. Это значит научиться обозначать его положение в любой момент времени. Но каждый предмет занимает в пространстве какое-то место. То есть, что все части этого объекта в один и тот же момент времени занимают разное положение.
Какую точку в таком случае необходимо взять для описания нахождения всего предмета? Если учитывать каждую, то расчеты окажутся слишком сложными. Поэтому решение ответа на этот вопрос можно максимально упростить. Если все точки одного тела движутся в одинаковом направлении, то для описания движения достаточно одной такой, которую содержит это тело.
Виды движения в кинематике
Существует три типа:
- Поступательным называется движение, при котором любая прямая проведенная в теле остается параллельной самой себе. Например, автомобиль, который движется по шоссе, совершает такой вид движения.
- Вращательным называется такое движение тела при котором все его точки движутся по окружностям с центрами, лежащими на одной прямой, называемой осью вращения. Например, вращение Земли относительно своей оси.
- Колебательным называется движение, при котором тело повторяет свою траекторию через определенный отрезок времени. Например, движение маятника.
Основные понятия кинематики – материальная точка
Любое сложное движение можно описать как комбинацию двух простейших видов – поступательного и вращательного. Например колесо автомобиля или юла, стоящая на движущейся прямо платформе, участвуют одновременно в этих двух типах перемещения.
Но что делать, если движение тела нельзя представить в виде комбинации? Например, если автомобиль едет по ухабистой дороге, его положение будет меняться очень сложным образом. Если рассчитывать только то, что этот транспорт перемещается из одного города в другой, то в такой ситуации становится не важно какого размера тело движется из точки А в точку Б и им можно пренебречь. В данном случае важно только за какое время автомобиль прошел определенное расстояние и с какой скоростью двигался.
Однако следует учитывать, что пренебрежение размером допускается не в каждой задаче. Например, если рассчитывать движение при парковке автомобиля, то игнорирование величины данного тела, приведет к пагубным последствием. Поэтому, только в тех ситуациях, когда в рамках конкретной задачи, размерами движущегося объекта можно пренебречь, то такое тело принято называть материальной точкой.
Формулы кинематики
Числа, с помощью которых задается положение точки в пространстве, называются координатами. Чтобы определить его на прямой, достаточно одного числа, когда речь идет о поверхности, то двух, о пространстве – трех. Большего количества чисел в трехмерном мире (для описывания положения материальной точки) не требуется.
Существует три основных уравнения для понятия кинематики, как раздела о движении тел:
- v = u + at.
- S = ut + 1/2at 2 .
- v 2 = u 2 + 2as.
v = конечная скорость,
u = Начальная скорость,
a = ускорение,
s = расстояние, пройденное телом,
Формулы кинематики в одномерном пространстве:
X – X o = V o t + 1/2a t2
V 2 = V o 1 + 2a (X – X o)
X – X o = 1\2 (V o + V) t
Где,
V – конечная скорость (м / с),
V o – начальная скорость (м / с),
a – ускорение (м / с 2),
t – время (с),
X – конечное положение (м),
Формулы кинематики в двумерном пространстве
Поскольку следующие уравнения используются для описания материальной точки на плоскости, стоит рассматривать ось X и Y.
Учитывая направление Х:
a x = constant
V fx = V i x + a x Δt
X f = X i + V i x Δt +1/2a x Δt 2
Δt = V fx -V ix /a x
V fx 2 = V ix 2 + 2ax Δx
X f = X i + 1/2 (V fx + V ix) Δ t .
И учитывая направление y:
a y = constant
V fy = V iy + a y Δt
y f = y i + V iy Δt + 1/2 a x Δt 2
Δt = V fy – V iy /a y
V fy 2 = V iy 2 + 2 ay Δ y
y f = y i +1/2 (V fy + V iy) Δt.
V f – конечная скорость (м / с),
V i – начальная скорость (м / с),
a – ускорение (m / с 2),
t – время (с),
X – конечное положение (м),
X 0 – начальное положение (м).
Перемещение брошенного снаряда – лучший пример для описания движения объекта в двух измерениях. Здесь тело перемещается, как в вертикальном положении У, так и в горизонтальном положении Х, поэтому можно сказать, что предмет имеет две скорости.
Примеры задач по кинематике
Задача 1 : Начальная скорость грузовика равна нулю. Изначально этот объект находится в состоянии покоя. На него начинает действовать равномерное ускорение в течение временного интервала 5,21 секунды. Расстояние, пройденное грузовиком, составляет 110 м. Найти ускорение.
Решение:
Пройденное расстояние s = 110 м,
начальная скорость v i = 0,
время t = 5,21 с,
ускорение a =?
Используя основные понятие и формулы кинематики, можно заключить, что,
s = v i t + 1/2 a t 2 ,
110 м = (0) × (5.21) + 1/2 × a (5.21) 2 ,
a = 8,10 м / с 2 .
Задача 2: Точка движется вдоль оси х (в см), после t секунд путешествия, ее можно представить, используя уравнение x = 14t 2 – t + 10. Необходимо найти среднюю скорость точки, при условии, что t = 3s?
Решение:
Положение точки при t = 0, равно x = 10 см.
При t = 3s, x = 133 см.
Средняя скорость, V av = Δx/Δt = 133-10/3-0 = 41 см / с.
Что такое тело отсчета
О движении можно говорить только если существует что-то, относительно чего рассматривается изменение положения изучаемого объекта. Такой предмет называется телом отсчета и оно условно всегда принимается за неподвижное.
Если в задаче не указано в какой системе отчета движется материальная точка, то телом отсчета считается земля по умолчанию. Однако, это не означает, что за неподвижный в заданный момент времени объект, относительно которого совершается движение, нельзя принять любой другой удобный для расчета. Например, за тело отсчета можно взять движущийся поезд, поворачивающий автомобиль и так далее.
Система отсчета и ее значение в кинематике
Для описания движения необходимы три составляющие:
- Система координат.
- Тело отсчета.
- Прибор для измерения времени.
Тело отсчета, система координат, связанная с ним и прибор для измерения времени образуют систему отсчета. Бессмысленно говорить о движении, если ее не указывать. Правильно подобранная система отсчета, позволяет упростить описание перемещения и, наоборот, усложнить, если она выбрана неудачно.
Именно по этой причине, человечество долго считало, что Солнце движется вокруг Земли и что она находится в центре вселенной. Такое сложное движение светил, связанное с тем, что земные наблюдатели находятся в системе отсчета, которая очень замысловато движется. Земля вращается вокруг свое оси и одновременно вокруг Солнца. На самом деле, если сменить систему отсчета, то все движения небесных тел легко описываются. Это в свое время было сделано Коперником. Он предложил собственное описание мироустройства, в котором Солнце неподвижно. Относительно него описать движение планет гораздо проще, чем если телом отсчета будет являться Земля.
Основные понятия кинематики – путь и траектория
Пусть некоторая точка первое время находилась в положении А, спустя некоторое время она оказалась в положении В. Между ними можно провести одну линию. Но для того, чтобы эта прямая несла больше информации о движении, то есть было понятно откуда и куда двигалось тело, это должен быть не просто отрезок, а направленный, обычно обозначающийся буквой S. Перемещением тела, называется вектор, проведенный из начального положения предмета в конечное.
Если тело изначально находилось в точке А, а затем оказалось в точке В, это не означает, что оно двигалось только по прямой. Из одного положения в другое можно попасть бесконечным количеством способов. Линия, вдоль которой движется тело, является еще одним основным понятием кинематики – траекторией. А ее длина называется путь, который обычно обозначается буквами L или l.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Определение 1
Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Определение 2
Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Определение 3
Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета .
Определение 4
Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В С И единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Определение 5
Механическое движение называют поступательным , в случае если все части тела перемещаются одинаково.
Пример 1
Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Определение 6
Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Термин “материальная точка” имеет важное значение в механике.
Определение 7
Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.
Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x = x (t) , y = y (t) , z = z (t) или зависимость от времени радиус-вектора r → = r → (t) , проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке 1 . 1 . 1 .
Рисунок 1 . 1 . 1 . Определение положения точки при помощи координат x = x (t) , y = y (t) и z = z (t) и радиус-вектора r → (t) , r 0 → – радиус-вектор положения точки в начальный момент времени.
Определение 8
Перемещение тела s → = ∆ r → = r → – r 0 → – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.
Пройденный путь l равняется длине дуги траектории, преодоленной телом за определенное время t . Путь является скалярной величиной.
Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.
В случае небольшого промежутка времени Δ t преодоленный телом путь Δ l практически совпадает с модулем вектора перемещения ∆ s → . При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок 1 . 1 . 2).
Рисунок 1 . 1 . 2 . Пройденный путь l и вектор перемещения ∆ s → при криволинейном движении тела.
a и b – это начальная и конечная точки пути.
Для описания движения в физике введено понятие средней скорости: υ → = ∆ s → ∆ t = ∆ r → ∆ t .
Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени Δ t , то есть υ → = ∆ s → ∆ t = ∆ r → ∆ t ; ∆ t → 0 .
В математике данный предел называется производная и обозначается d r → d t или r → ˙ .
Мгновенная скорость υ → тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок 1 . 1 . 3 .
Рисунок 1 . 1 . 3 . Средняя и мгновенная скорости. ∆ s 1 → , ∆ s 2 → , ∆ s 3 → – перемещения за время ∆ t 1 соответственно. При t → 0 , υ → с р → υ → .
При перемещении тела по криволинейной траектории скорость υ → меняется по модулю и по направлению. Изменение вектора скорости υ → за какой-то маленький промежуток времени Δ t задается при помощи вектора ∆ υ → (рисунок 1 . 1 . 4).
Вектор изменения скорости ∆ υ → = υ 2 → – υ 1 → за короткий промежуток времени Δ t раскладывается на 2 составляющие: ∆ υ r → , которая направлена вдоль вектора υ → (касательная составляющая) и ∆ υ n → , которая направлена перпендикулярно вектору υ → (нормальная составляющая).
Рисунок 1 . 1 . 4 . Изменение вектора скорости по величине и по направлению. ∆ υ → = ∆ υ → r + ∆ υ → n – изменение вектора скорости за промежуток времени Δ t .
Определение 9
Мгновенное ускорение тела a → – это предел отношения небольшого изменения скорости ∆ υ → к короткому отрезку времени Δ t , в течение которого изменялась скорость: a → = ∆ υ → ∆ t = ∆ υ → τ ∆ t + ∆ υ → n ∆ t ; (∆ t → 0) .
Направление вектора ускорения a → , при криволинейном движении, не совпадает с направлением вектора скорости υ → . Составляющие вектора ускорения a → – это касательные (тангенциальные) a → τ и нормальные a → n ускорения (рисунок 1 . 1 . 5).
Рисунок 1 . 1 . 5 . Касательное и нормальное ускорения.
Касательное ускорение показывает, как быстро меняется скорость тела по модулю: a τ = ∆ υ ∆ t ; ∆ t → 0 .
Вектор a → τ направлен по касательной к траектории.
Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.
Пример 2
Представим криволинейное движение, как движение по дугам окружностей (рисунок 1 . 1 . 6).
Рисунок 1 . 1 . 6 . Движение по дугам окружностей.
Нормальное ускорение находится в зависимости от модуля скорости υ и радиуса R окружности, по дуге которой тело перемещается в определенный момент времени: a n = υ 2 R .
Вектор a n → все время направлен к центру окружности.
По рисунку 1 . 1 . 5 видно, модуль полного ускорения равен a = a τ 2 + a n 2 .
Итак, основные физические величины в кинематике материальной точки – это пройденный путь l , перемещение s → , скорость υ → и ускорение a → .
Путь l – скалярная величина.
Перемещение s → , скорость υ → и ускорение a → – векторные величины.
Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Техническая механика – Тема 1.6. Основные понятия кинематики
Рис.3. Координаты точки М
Материальная точка – тело, размерами которого в данных условиях можно пренебречь.
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Основной задачей кинематики точки является изучение законов движения точки. Зависимость между произвольными положениями движущейся точки в пространстве и времени определяет закон ее движения. Закон движения точки считают известным, если можно определить положение точки в пространстве в произвольный момент времени. Положение точки рассматривается по отношению к выбранной системе координат.
Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом “тело” будем понимать “материальная точка”.
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
Путь s – скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0.Единицы измерения в системе СИ: м (метр).
Перемещение тела за определенный промежуток времени – направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2):
,
где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).
Проекция перемещения на ось Ох: ∆rx =∆х = х-х0, где x0 и x – координаты тела в начальный и конечный моменты времени.
Модуль перемещения не может быть больше пути: ≤s.
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
Понимание кинематики и законов движения Ньютона — Wolfram | Alpha Blog
На протяжении всей истории физики ученые постулировали законы и теории о природе окружающего мира. Некоторые из них оказались ложными, в то время как другие стали основой целых областей исследования. Одной из таких областей является классическая механика, которая описывает наиболее знакомую нам область физики – движение макроскопических объектов, от бейсбольных мячей до планет, от путешествий по холмам до падения из космоса.Эта работа, являющаяся одним из старейших научных предметов, служит основой для менее известных областей, таких как теория относительности и квантовая механика.
Важнейший набор законов классической механики предложен Исааком Ньютоном. «Законы движения Ньютона» лежат в основе всех наших теорий о движении частиц. Его первый закон движения просто гласит, что объект, который не испытывает чистой силы, будет продолжать двигаться с постоянной скоростью, что означает, что если он не движется, он останется неподвижным, а если он движется, он продолжит движение с той же скоростью. темп.Таким образом, если что-то движется со скоростью «20 миль в час в течение 30 минут» и на него не действуют никакие внешние силы, оно переместится на 10 миль.
Второй закон Ньютона более интересен. Он говорит нам, что сила, действующая на объект, будет ускорять этот объект в том же направлении, что и сила, и обратно пропорционально его массе. Это дает нам знакомое уравнение: F = м × a
Ускорение – это просто скорость, с которой скорость объекта изменяется со временем.Из определения ускорения мы можем построить большую часть кинематики. Мы можем определить расстояние до объекта с ускорением «2 метра в секунду в квадрате через 10 минут». Мы можем найти ускорение, работая в обратном направлении, например, в случае объекта, «перемещающегося на 2 мили за 100 секунд с начальной скоростью 5 метров в секунду». Из этих расчетов и первых двух законов Ньютона мы можем вывести множество других уравнений.
Давайте посмотрим на очень распространенную форму ускорения, которому все мы подвержены, – гравитацию.Как известно многим из нас, наша «теория гравитации» также начинается с Исаака Ньютона. Ньютон выяснил, что сила тяжести между двумя объектами пропорциональна их массе и обратно пропорциональна их расстоянию. Однако эта сила довольно мала. «Сила тяжести между 100 кг и 200 кг на расстоянии 10 метров» составляет всего 1,335 × 10 -8 ньютонов. Только с объектами в масштабе планеты («масса Земли» 5,9721986 × 10 24 килограммов) мы можем получить уровень гравитации, который мы ощущаем на Земле.
Возвращаясь ко второму закону движения Ньютона, давайте посмотрим, как гравитация ускоряет объекты здесь, на Земле. В пределах нескольких миль от поверхности Земли «ускорение свободного падения» довольно постоянное. Wolfram | Alpha может сказать вам, как сила гравитации уменьшается над вашим местоположением, например, на высоте 4 миль. Даже на расстоянии 4 миль ускорение свободного падения находится в пределах 1% от значения на уровне земли.
При относительно постоянном ускорении на небольшой высоте мы можем посмотреть, сколько времени нужно, чтобы упасть с заданной высоты.По сути, мы берем неподвижный объект и позволяем силе тяжести перемещать его. В качестве конкретного примера мы найдем «время упасть с Эмпайр-стейт-билдинг».
Конечно, это вычисление для идеализированного мира без сопротивления воздуха. Сила воздуха, ударяющего по нашему падающему объекту, будет противодействовать ускорению свободного падения. Запрос Wolfram | Alpha о «времени, чтобы упасть с Эмпайр-стейт-билдинг с помощью сопротивления» добавляет этот дополнительный фактор. Предполагая, что наш падающий объект представляет собой коробку, нам нужно будет отрегулировать коэффициент сопротивления до 0.8 (падающий куб имеет коэффициент лобового сопротивления от 0,8 до 1,05 в зависимости от его облицовки). Отсюда мы находим, что ящик, падающий с Эмпайр-стейт-билдинг, достигнет предельной скорости, скорость, при которой сила тяжести, тянущая объект вниз, полностью равна силе сопротивления воздуха, толкающей его вверх. В этот момент результирующая сила равна нулю, и по первому закону движения Ньютона ящик движется с постоянной скоростью – до тех пор, пока другая сила не действует на объект, например, на землю.
Далее мы вместе рассмотрим первый и второй законы Ньютона в двухмерном движении.В частности, давайте посмотрим на движение снаряда, например, супергерой прыгает через высокое здание одним прыжком. В этом примере мы пренебрегаем сопротивлением воздуха. Таким образом, если наш супергерой движется вперед и вверх, то восходящая часть его движения будет подвержена гравитации, в то время как движение вперед не будет иметь действующих сил. Таким образом, супергерой будет двигаться вперед с постоянной скоростью, в то время как его движение в вертикальном направлении сначала замедлится, а затем обратное направление, когда он упадет обратно на Землю.
Давайте посмотрим на некоторые цифры. Эмпайр-стейт-билдинг, безусловно, высокое здание, имеет высоту 1250 футов. Если наш супергерой перепрыгнет через нее с начальным углом в 85 градусов, с какой скоростью ему нужно будет двигаться? Wolfram | Alpha сообщает нам, что для прыжка на «максимальную высоту 1250 футов при 85 градусах» требуется начальная скорость 86,77 метра в секунду или примерно 194 миль в час.
Wolfram | Alpha включает инструменты для расчета более сложных форм двумерного движения.Особо следует отметить «массу на наклонной плоскости». График сил:
Здесь мы видим, что сила тяжести находится под углом к наклону. Это дает компонент, который параллелен поверхности наклона и, таким образом, тянет блок вниз и влево. Мы также видим нормальную силу, указанную перпендикулярно поверхности склона. Это вызвано третьим законом Ньютона: каждое действие имеет равную и противоположную реакцию. Если мы посмотрим на силовую диаграмму скользящего блока, мы увидим, что сила тяжести давит на наклон, и, таким образом, наклон толкает назад.
Эта нормальная сила важна как источник трения для предметов, скользящих по склону. Трение бывает двух типов для твердых объектов: статическое трение, когда две поверхности находятся в состоянии покоя относительно друг друга, и кинетическое трение для объектов, скользящих друг мимо друга. Вы можете включить эти силы в формулу Wolfram | Alpha, которая позволяет моделировать блок, удерживаемый силой статического трения, или блок, который замедляется кинетическим трением.
Все эти движения вверх и вниз вызывают еще один ключевой закон физики – сохранение энергии.Закон сохранения энергии гласит, что энергия может быть уничтожена или создана. Энергия может существовать во многих формах, но основное деление – кинетическая и потенциальная энергия. Движущиеся объекты обладают кинетической энергией. Для объектов, движущихся по прямой линии, «кинетическая энергия» определяется как работа, необходимая для ускорения объекта от состояния покоя до его текущей скорости, и определяется формулой K = 1/2 м v 2 , где м – масса объекта, а v – его скорость.
Что происходит с энергией снаряда, когда он подбрасывается в воздух, как наш супергерой в предыдущем примере? Мы можем видеть, что кинетическая энергия (и скорость движения вверх) медленно уменьшается, когда снаряд поднимается выше, и затем возвращается, когда он опускается. Но где это находится между ними?
Здесь энергия преобразуется в потенциальную. Это энергия объекта из-за его расположения, в данном случае его высоты над Землей. Эта потенциальная энергия гравитации примерно равна высоте над Землей (с учетом небольшого ограничения по высоте, которое мы обсуждали ранее).По мере того, как объект поднимается в воздух, а затем замедляется, его кинетическая энергия превращается в потенциальную энергию, пока, наконец, он не упадет обратно на Землю и не обратит процесс вспять.
Для нашего супергероя, прыгающего через высокое здание одним прыжком, если его начальная скорость составляет 86,77 метра в секунду и он весит около 70 килограммов, его начальная кинетическая энергия будет равна 263,5 килоджоулей. Когда он достигнет максимальной высоты чуть выше Эмпайр-стейт-билдинг, его гравитационная потенциальная энергия будет равна 261.5 килоджоулей. Недостающая энергия – это его прямая кинетическая энергия. При этом используется горизонтальная часть его скорости, которая представляет собой «косинус 85 градусов × 86,77 метра в секунду» или 7,563 метра в секунду, что дает кинетическую энергию 2,002 килоджоулей. 261,5 килоджоулей плюс 2,002 килоджоулей равняются 263,5 килоджоулей с нашей точностью.
А как насчет того, чтобы наш блок скользил по наклонной плоскости с трением? Он набирает скорость медленнее, чем теряет потенциальную энергию. Куда уходит энергия? В этом случае трение преобразует часть энергии движения в тепло, возбуждая молекулы и атомы, составляющие поверхность наклона и скользящего объекта.Тепло – это разновидность кинетической энергии, при которой колебания и движение частиц, составляющих плоскость и блок, увеличиваются. Это то, что вызывает ожоги от веревки, скользящей по рукам, или как трение рук на морозе может согреть их быстрее, чем сжимание.
Еще одно важное понятие, связанное с энергией, – это работа. Работа, как уже говорилось о кинетической энергии, может ускорить объект. Он также может увеличить потенциальную энергию объекта, перемещая его в другое положение.Но что такое работа? Работа – это продукт силы и расстояния. Приложение силы в 100 ньютонов, чтобы толкнуть ящик на 10 метров, даст 1 килоджоуль, единицу энергии. Важно то, что главное – это продукт. Вы можете выполнить тот же объем работы с меньшим усилием, если увеличите расстояние, на которое прикладывается сила. Эта идея лежит в основе механизмов многих простых машин, таких как «рычаг».
Наконец, с энергией мы также получаем понятие мощности или скорости передачи энергии. Мощность зависит от скорости выполнения работы и, следовательно, от того, насколько быстро в систему добавляется энергия.Например, мощность, необходимая для перемещения объекта весом 100 кг на 10 метров за 5 секунд, составляет 320 Вт. Но если бы мы сделали это за 2 секунды, нам потребовалось бы 5 киловатт. Эти измерения более знакомы нам по электромагнетизму, где они присутствуют в механике «электрических цепей».
Третий закон движения Ньютона также подразумевает сохранение количества движения. Сила может быть описана с точки зрения количества движения: F = ∂ p / ∂ t
Объединяя это с идеей равных и противоположных реакций, можно показать, что сумма импульсов системы, не подверженной внешним силам, должна оставаться постоянной.Если две частицы сталкиваются, их полный импульс до столкновения должен быть таким же, как после столкновения.
Столкновения обычно делятся на две категории: упругие столкновения, при которых сохраняются кинетическая энергия и импульс, и неупругие столкновения, когда деформации удара вызывают потерю кинетической энергии либо из-за слипания частиц, либо из-за некоторой преобразуемой энергии. в тепло.
Представленные здесь идеи составляют основу современной физики.Идеи о сохранении энергии и количества движения входят в известное уравнение Эйнштейна E = m c 2 . Формулы для кинетической и потенциальной энергии связаны с аналитической механикой и формулировками «лагранжевых» и «гамильтоновых» функций, введенными в восемнадцатом и девятнадцатом веках. Это, в свою очередь, предоставило важнейшие концепции для развития «квантовой механики». «Теория относительности Эйнштейна» и квантовая механика, в свою очередь, касаются почти всех остальных областей физики.
Базовая кинематика – Викиверситет
Кинематика – это исследование движения предметов. Основные кинематические задачи решаются с помощью законов движения Исаака Ньютона.
Ньютон попытался объяснить, как движутся объекты, используя как можно меньше предположений. Эти предположения и есть то, что мы сегодня называем законами Ньютона. Они примечательны тем, что выдержали испытание временем почти для всех движений, кроме движений в самых малых масштабах (квантовая механика) и самых больших масштабах (общая теория относительности).Даже тогда мы в основном просто добавили или изменили некоторые предположения о природе Вселенной, которые мы считали разумными, но три закона в основном остались. Законы используются для вывода фундаментального уравнения, которое мы будем использовать для изучения почти всей классической физики ниже. Формулировки законов немного изменены, чтобы они не раздражали современного студента. Другой перевод оригинальных законов можно найти здесь.
Первый закон Ньютона: Закон инерции [править | править источник]
Каждое тело остается в состоянии покоя или равномерного движения по прямой линии, если только оно не вынуждено изменить это состояние под действием приложенных к нему сил.
На данный момент Ньютон не сказал нам, что такое сила, поэтому этот закон не является описанием движения тел. Вы можете подумать: «Эй, я знаю, что такое сила, я заставляю что-то двигаться, когда я на нее нажимаю». Однако эта «контактная сила» – не единственный тип силы, с которой Ньютон имеет дело. Он в основном использовал это утверждение, чтобы определить, что такое сила: все, что изменяет линейное движение (включая нулевое движение) тела. Это позволяет нам включить гравитацию как силу. Фактически, мы увидим, что классическая физика успешно описывает все силы в терминах полей (подобно тому, как работает гравитация).Ваше нажатие на объект на самом деле является результатом взаимодействия электромагнитного поля между частицами в вашей руке и частицами того, что вы толкаете. На самом деле ваша рука никогда не соприкасается с чем-либо напрямую, в том смысле, что между вашей рукой и другим предметом нет места.
Второй закон Ньютона: Закон ускорения [править | править источник]
Изменение количества движения пропорционально величине силы; и производится в направлении прямой линии, по которой направлена эта сила.
Колыбель Ньютона . Когда вы отпускаете ближний мяч, он передает свой импульс дальнему мячу, который (при условии отсутствия трения или потерь тепла) должен подняться на ту же высоту, на которой вы подняли первый мяч. Ньютон использовал более простой двухшариковый аппарат с шарами разных типов.Этот закон чрезвычайно богат по содержанию, поскольку Ньютон использовал устройства, похожие на то, что мы сегодня называем колыбелью Ньютона, чтобы отметить, что «количество движения», придаваемое концевому шару (при условии идеальных столкновений, когда вся «движущая сила» мяч, который вы поднимаете на одном конце, передается мячу на другом конце) пропорциональна конечной скорости запускаемого вами мяча.Он также отметил, что разные типы шаров придавали большие дуги другим шарам, и поэтому он пришел к выводу, что произведение массы (количество, пропорциональное весу объекта) и скорости является «количеством движения» объекта, которое должно быть сохранено. в идеальных столкновениях. Сегодня мы называем этот продукт импульсом объекта и обычно обозначаем его как
п = mv {\ displaystyle \ mathbf {p} = m \ mathbf {v}}, где p и v имеют как величину, так и направление, как описано законами Ньютона.Управление объектами, имеющими как величину, так и направление (называемые векторами), рассматривается в векторной алгебре, о которой будет рассказано в дополнительном руководстве по обзору. Теперь, если мы обозначим вектор силы как F → {\ displaystyle {\ vec {F}}}, тогда второй закон Ньютона говорит нам, что
F → = dp → dt = ddt (m⋅v →) = mdv → dt {\ displaystyle {\ vec {F}} = {d {\ vec {p}} \ over dt} = {\ frac {d} { dt}} (m \ cdot {\ vec {v}}) = m {d {\ vec {v}} \ over dt}}ddt {\ displaystyle {\ frac {d} {dt}}} – это обычная производная по времени от исчисления.Если вы еще не изучали математический анализ, то приведенное выше также можно записать как
F → = m⋅a → {\ displaystyle {\ vec {F}} = m \ cdot {\ vec {a}}}, где a – изменение скорости во времени, также известное как ускорение.
- Exercise 1: Если вы немного знакомы с расчетами, докажите, что если общая сила, действующая на систему из двух частиц (или шариков пула, если хотите), равна нулю, то импульс постоянен. Обратите внимание, что это тот случай, когда два шара для пула ударяются друг о друга (при идеальных обстоятельствах).Мы говорим, что импульс сохраняется .
Третий закон Ньютона: Закон взаимодействия [править | править источник]
Каждому действию всегда противопоставляется равное противодействие; или взаимные действия двух тел друг на друга всегда равны и направлены в противоположные части.
Суть третьего закона Ньютона: ДЕЙСТВИЕ = РЕАКЦИЯ
Этот закон применяется в первую очередь для идеализированных объектов, таких как сферы и точки, которые действуют на центры движения друг друга.Однако именно импульс позволил нам отделить массу от веса. В символических терминах это означает, что если одно тело оказывает силу F → 1 {\ displaystyle {\ vec {F}} _ {1}} на другое тело, то второе тело оказывает силу F → 2 {\ displaystyle {\ vec {F}} _ {2}} на первом теле, а в векторных терминах F → 1 = −F → 2 {\ displaystyle {\ vec {F}} _ {1} = – {\ vec {F}} _ {2}}. Используя уравнение, полученное нами из второго закона, нетрудно увидеть, что масса затем может быть измерена путем определения одной массы как эталона и использования отношения ускорений как массы второго объекта.
Векторы – это физические величины, которые имеют как величину, так и направление.
Примеры векторов: «сила», «скорость», «ускорение» и т. Д.
Диаграммы свободного тела – чрезвычайно полезный инструмент при анализе физических задач. Приступая к задаче кинематики, первое, что вы должны сделать, это нарисовать диаграмму свободного тела. Что такое диаграмма свободного тела? Это простой набросок, который показывает все силы, действующие на объект («свободное тело»). При рисовании диаграммы свободного тела сначала необходимо изолировать рассматриваемый объект.Затем вы должны определить все силы, действующие на него. Помните, что если объект находится в состоянии покоя, векторная сумма всех сил должна быть равна нулю. Законы Ньютона также говорят нам, что каждое действие имеет равное и противоположное противодействие. Если объект сидит на столе, его вес толкает его вниз, но стол также толкает его вверх (эта сила по отношению к весу объекта называется нормальной силой . Это очень важная концепция в кинематике). Поскольку обе силы равны и противоположны, объект не проваливается через стол и не взлетает в воздух.
Движение частицы [править | править источник]
Теперь мы применим законы Ньютона к идеализированному объекту, одной частице . Частица в классической физике имеет очень четко определенное значение: это объект без каких-либо пространственных измерений; математически это одна точка. Сначала мы изучаем эти простые объекты, а позже рассматриваем более крупные объекты как состоящие из множества частиц. Мы увидим, что сферы (такие объекты, как шары для пула) ведут себя во многом как частицы (классически), как и объекты, которые взаимодействуют вдоль своих центров масс, и поэтому мы будем говорить о сферических объектах, простых взаимодействиях центра масс, и частицы свободно.Мы покажем, что приведенное выше предложение верно, позже, когда мы разработаем инструменты и познакомимся с физикой для этого.
Теперь возьмите мяч и держите его в руке на некотором расстоянии от пола. Если вы перестанете держать мяч, он упадет на пол. Согласно закону инерции Ньютона, мяч не мог бы сделать это, если бы на него не действовала сила (по инерции он должен был оставаться там, где вы его держали). Поскольку вы не толкали мяч вниз, на мяч должна была действовать какая-то другая сила, помимо вас самих.Из-за нашего опыта с другими объектами, падающими на землю, мы предполагаем, что Земля оказывает на ваш мяч силу. Согласно третьему закону Ньютона, мяч также должен оказывать на Землю силу равной величины и противоположного направления.
Вывод основной кинематики пишется ….
с отличием по физике: кинематические уравнения
Разработка набора инструментов
Графики движения, такие как графики положения-времени, скорости-времени и ускорения-времени, являются прекрасным инструментом для понимания движения.Однако бывают случаи, когда графическое отображение движения может быть не самым эффективным или действенным способом понимания движения объекта. Чтобы помочь в этих ситуациях, вы можете добавить набор уравнений для решения проблем в свой набор инструментов физики, известный как кинематические уравнения. Эти уравнения могут помочь вам найти ключевые переменные, описывающие движение объекта при постоянном ускорении. Как только вы узнаете значения любых трех переменных, вы можете использовать кинематические уравнения для решения двух других!
| Переменная | Значение |
|---|---|
| против 0 | Начальная скорость |
| в | Конечная скорость |
| Δx | Рабочий объем |
| Разгон | |
| т | Истекшее время |
Стратегия решения проблем
При использовании этих уравнений для решения задач движения важно позаботиться о настройке анализа, прежде чем приступить к поиску решения.Ключевые шаги для решения кинематических задач включают:
- Маркировка вашего анализа для горизонтального (ось x) или вертикального (ось y) движения.
- Выбор и указание положительного направления (обычно направления начального движения).
- Создание таблицы анализа движения (v 0 , v, Δx, a, t). Обратите внимание, что Δx – это изменение положения или смещения, и его можно переписать как x-x 0 .
- Используйте то, что вы знаете о проблеме, для заполнения ваших «данностей» в таблице.
- Когда вы знаете три элемента в таблице, используйте кинематические уравнения, чтобы найти все неизвестные.
- Убедитесь, что ваше решение имеет смысл.
Взгляните на пример задачи, чтобы увидеть, как можно использовать эту стратегию.
Примеры задач
Эти уравнения и шаги по решению проблем применимы как к задачам горизонтального, так и вертикального движения. Давайте попробуем их:
Эта стратегия решения задач и кинематические уравнения работают также и для задач вертикального движения:
В некоторых случаях у вас может не получиться решить напрямую для «найденного» количества.В этих случаях вы можете сначала найти другую неизвестную переменную, а затем выбрать уравнение, которое даст вам окончательный ответ:
Вопрос: Космонавт роняет молот с высоты 2 метра над поверхностью Луны. Если ускорение свободного падения на Луне составляет 1,62 метра в секунду 2 , сколько времени потребуется, чтобы молот упал на поверхность Луны?
Ответ:
Kinematics and Calculus – The Physics Hypertextbook
Обсуждение
постоянное ускорение
Исчисление – это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения.По определению, ускорение – это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. Это дает нам уравнение скорости-времени. Если мы предположим, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| а | = | ||
| дв | = | и дт | |
| = | |||
| v – v 0 | = | при | |
| в | = | v 0 + at [1] | |
Опять же, по определению, скорость – это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость для определения положения. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| в | = | |||||||||
| DS | = | v dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
| |||||||||
| с – с 0 | = | v 0 t + ½ at 2 | ||||||||
| с | = | с 0 + v 0 т + ½ при 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), и другую производную, равную обратной скорости ( dt ds ).
| дв. | = | дв. | 1 | |
| DS | DS | |||
| дв | = | дв. | дт | |
| DS | DS | дт | ||
| дв | = | дв. | дт | |
| DS | дт | DS | ||
| дв | = | а | 1 | |
| DS | в |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | и DS | ||
| = | ||||
| ½ ( v 2 – v 0 2 ) | = | a ( с – с 0 ) | ||
| в 2 | = | v 0 2 + 2 a ( с – с 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным – постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| против = | v 0 + at | [1] |
| + | ||
| с = | с 0 + v 0 т + ½ при 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( с – с 0 ) | [3] |
постоянный рывок
Показанный выше метод работает даже при непостоянном ускорении.Применим его к ситуации с необычным названием – постоянный рывок. Нет лжи, вот как это называется. Рывок – это скорость изменения ускорения во времени.
Это делает рывком первую производную ускорения, вторую производную скорости и третью производную положения.
| j = | да | = | d 2 v | = | г 3 с |
| дт | дт 2 | дт 3 |
Единица рывка в системе СИ – это метров в секунду в кубе .
| ⎡ ⎢ ⎣ | 903 10 м / с 3 = | м / с 2 | ⎤ ⎥ ⎦ |
| с |
Альтернативная единица – г в секунду .
Jerk – это не просто ответ некоторых мудрых физиков на вопрос: «Ах да, так как вы называете третьей производной от позиции?» Рывок – это значимая величина.
Человеческое тело оснащено датчиками, определяющими ускорение и рывки.Глубоко внутри уха, интегрированные в наш череп, находится серия камер, называемых лабиринтом . Часть этого лабиринта посвящена нашему слуху (улитка , ), а часть – нашему чувству равновесия (вестибулярная система , ). Вестибулярная система оснащена датчиками, определяющими угловое ускорение (полукружные каналы , ) и датчиками, определяющими линейное ускорение (отолиты , ). У нас есть два отолита в каждом ухе – один для определения ускорения в горизонтальной плоскости (мешок ) и один для определения ускорения в вертикальном месте (мешочек , ).Отолиты – это наши собственные встроенные акселерометры.
Слово отолит происходит от греческого οτο ( от ) для уха и λιθος ( lithos, ) для камня. Каждый из наших четырех отолитов состоит из твердой костеподобной пластины, прикрепленной к мату из сенсорных волокон. Когда голова ускоряется, пластина смещается в сторону, изгибая сенсорные волокна. Это посылает в мозг сигнал: «Мы ускоряемся». Поскольку гравитация также действует на пластины, сигнал может также означать, что «это путь вниз».«Мозг довольно хорошо понимает разницу между двумя интерпретациями. Настолько хорош, что мы склонны игнорировать это. Зрение, звук, запах, вкус, прикосновение – где баланс в этом списке? Мы игнорируем его, пока что-то не изменится в необычный, неожиданный или экстремальный способ.
Я никогда не был на орбите и не жил на другой планете. Гравитация всегда одинаково тянет меня вниз. Стоять, ходить, сидеть, лежать – все довольно степенно. А теперь давайте покатаемся на американских горках или займемся не менее захватывающим занятием, например, катанием на горных лыжах, гонками Формулы-1 или ездой на велосипеде в пробках Манхэттена.Ускорение направлено сначала в одну сторону, затем в другую. Вы даже можете испытывать кратковременные периоды невесомости или инверсии. Подобные ощущения вызывают интенсивную умственную деятельность, поэтому нам нравится их выполнять. Они также обостряют нас и удерживают сосредоточенность в моменты, которые, возможно, заканчиваются жизнью, поэтому мы в первую очередь развили это чувство. Ваша способность чувствовать подергивание жизненно важна для вашего здоровья и благополучия. Рывок одновременно увлекателен и необходим.
С постоянным рывком легко справиться математически.В качестве обучающего упражнения выведем уравнения движения для постоянного рывка. Если хотите, можете попробовать более сложные задачи с толчком.
Рывок – это производная от ускорения. Отменить этот процесс. Интегрируйте рывок, чтобы получить ускорение в зависимости от времени. Предлагаю называть это нулевым уравнением движения для постоянного рывка . Причина станет очевидной после того, как мы закончим следующий вывод.
| j = | да | |
| дт | ||
| да = | j dt | |
| а | т | ||
| ⌠ ⌡ | да = | ⌠ ⌡ | j dt |
| а 0 | 0 |
| a – a 0 = | jt | |
| а = | a 0 + jt | [0] |
Ускорение – это производная скорости.Интегрируйте ускорение, чтобы получить скорость как функцию времени. Мы делали этот процесс раньше. Мы назвали результат соотношением скорость-время или первым уравнением движения, когда ускорение было постоянным. Мы должны дать ему похожее имя. Это первое уравнение движения для постоянного рывка .
| а = | ||
| дв = | а дт | |
| дв = | ( a 0 + jt ) dt | |
| в | т | ||
| ⌠ ⌡ | дв = | ⌠ ⌡ | ( a 0 + jt ) dt |
| в 0 | 0 |
| v – v 0 = | a 0 т + ½ jt 2 | ||
| v = | v 0 + a 0 t + ½ jt 2 | [1] | |
Скорость – это производная от смещения.Интегрируйте скорость, чтобы получить смещение как функцию времени. Мы уже делали это раньше. Результирующая зависимость смещения от времени будет нашим вторым уравнением движения для постоянного рывка .
| против = | ||
| DS = | v dt | |
| DS = | ( v 0 + a 0 t + ½ jt 2 ) dt | |
| с | т | ||
| ⌠ ⌡ | дс = | ⌠ ⌡ | ( v 0 + a 0 t + ½ jt 2 ) dt |
| с 0 | 0 |
| с – с 0 = | v 0 т + ½ a 0 т 2 + ⅙ jt 3 | ||
| с = | с 0 + v 0 т + ½ a 0 т 2 + ⅙ jt 3 | [2] | |
Обратите внимание на эти уравнения.Когда рывок равен нулю, все они возвращаются к уравнениям движения для постоянного ускорения. Нулевой рывок означает постоянное ускорение, так что все в порядке с миром, который мы создали. (Я никогда не говорил, что постоянное ускорение реально. Постоянный рывок тоже миф. Однако в мире гипертекстов все возможно.)
Куда мы пойдем дальше? Должны ли мы работать над соотношением скорость-смещение (третье уравнение движения для постоянного рывка)?
| против = | v 0 + a 0 t + ½ jt 2 | [1] |
| + | ||
| с = | с 0 + v 0 т + ½ a 0 т 2 + ⅙ jt 3 | [2] |
| = | ||
| против = | f ( s ) | [3] |
Как насчет зависимости ускорения от смещения (четвертое уравнение движения для постоянного рывка)?
| а = | a 0 + jt | [1] |
| + | ||
| с = | с 0 + v 0 т + ½ a 0 т 2 + ⅙ jt 3 | [2] |
| = | ||
| а = | f ( s ) | [4] |
Я даже не знаю, можно ли их вычислить алгебраически.Я сомневаюсь. Посмотрите на это страшное кубическое уравнение для смещения. Это не может быть нашим другом. На данный момент меня это не беспокоит. Не знаю, расскажет ли мне про это что-нибудь интересное. Я от до знаю, что мне никогда не требовалось третье или четвертое уравнение движения для постоянного рывка – пока нет. Я оставляю эту задачу математикам всего мира.
Это проблема, которая отличает физиков от математиков. Математика не обязательно заботит физическая значимость, и он может просто поблагодарить физика за интересный вызов.Физика не обязательно заботит ответ, если он не окажется полезным, и в этом случае физик обязательно поблагодарит математика за его любопытство.
постоянное ничего
Эта страница в этой книге не о движении с постоянным ускорением, постоянным рывком, постоянным щелчком, треском или треском. Речь идет об общем методе определения количества движения (положения, скорости и ускорения) относительно времени и друг друга для любого вида движения.Для этого используется либо дифференцирование (нахождение производной)…
- Производная положения по времени – это скорость ( v = ds dt ).
- Производная скорости по времени – это ускорение ( a = dv dt ).
или интегрирование (нахождение интеграла)…
- Интеграл ускорения во времени – это изменение скорости (∆ v = ∫ a dt ).
- Интеграл скорости во времени – это изменение положения (∆ с = ∫ v dt ).
Вот как это работает. Некоторая характеристика движения объекта описывается функцией. Можете ли вы найти производную от этой функции? Это дает вам еще одну характеристику движения. Можете ли вы найти его неотъемлемую часть? Это дает вам другую характеристику. Повторите любую операцию столько раз, сколько необходимо. Затем примените методы и концепции, которые вы изучили в исчислении и связанных областях математики, чтобы извлечь больше смысла – диапазон, область, предел, асимптота, минимум, максимум, экстремум, вогнутость, перегиб, аналитический, числовой, точный, приблизительный и т. Д.Я добавил несколько важных примечаний по этому поводу в резюме по этой теме.
Концепция системы – Колледж физики
Цели обучения
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона.Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости.Изменение скорости по определению означает ускорение. Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным – внешняя сила действует извне интересующей системы. Например, на (Рисунок) (а) интересующая система – это вагон плюс ребенок в нем.Две силы, действующие со стороны других детей, – это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на (Рисунок) (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на повозке, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем вы сможете определить, какие силы являются внешними .Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было проверено экспериментально и проиллюстрировано на (Рисунок).В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы – это вес и поддержка земли, а горизонтальная сила – это сила трения. Они будут обсуждаться более подробно в следующих разделах. А пока мы определим трение как силу, которая противодействует движению соприкасающихся объектов друг за другом.(Рисунок) (b) показывает, как векторы, представляющие внешние силы, складываются вместе, образуя результирующую силу,.
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
, где символ означает «пропорционально», а – чистая внешняя сила. (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты.Методы такие же, как и для сложения других векторов, и описаны в «Двумерной кинематике». Эта пропорциональность выражает то, что мы сказали словами – ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы.Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на (Рисунок), та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
., где – масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.
Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Объединение двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе.
В форме уравнения второй закон движения Ньютона равен
.Это часто записывается в более привычной форме
Если рассматривать только величину силы и ускорения, это уравнение просто
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона.Закон – причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
Единиц силы
используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютоном (сокращенно Н) и представляет собой силу, необходимую для ускорения системы весом 1 кг со скоростью. То есть, поскольку,
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 N = 0.225 фунтов
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его весом. Вес можно обозначить как вектор, потому что он имеет направление; вниз по определению является направлением силы тяжести, и, следовательно, вес – это сила, направленная вниз.Величина веса обозначена как . Галилей сыграл важную роль в демонстрации того, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением. Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект с массой, падающей вниз к Земле. Он испытывает только силу тяжести, направленную вниз, которая имеет величину. Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна.
Поскольку на объект действует только сила тяжести, направленная вниз,. Мы знаем, что ускорение объекта под действием силы тяжести равно, или. Подставляя их во второй закон Ньютона, получаем
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении. То есть единственная сила, действующая на объект, – это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.
Ускорение свободного падения немного меняется по поверхности Земли, так что вес объекта зависит от местоположения и не является внутренним свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение только за счет силы тяжести. Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта – это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее.Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике мы называем «свободным падением». Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса – очень разные физические величины, хотя они тесно связаны.Масса – это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес – это сила тяжести, которая зависит от силы тяжести. Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
Распространенные заблуждения: масса против веса
В обиходе масса и вес часто используются как синонимы. Однако в науке эти термины существенно отличаются друг от друга. Масса – это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «слизняк» в английских единицах измерения). С другой стороны, вес – это мера силы тяжести, действующей на объект. Вес равен массе объекта (), умноженной на ускорение свободного падения ().Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах).
Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения. Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с большей или меньшей силой тяжести. Например, ускорение свободного падения на Луне равно (что намного меньше ускорения свободного падения на Земле).Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» гораздо меньше, хотя и не выглядите худее. Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Эксперимент на вынос: масса и вес
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении. Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле.Масса косилки 24 кг. Какое у него ускорение?
Чистое усилие на газонокосилке справа 51 Н. С какой скоростью газонокосилка ускоряется вправо?
Стратегия
Поскольку даны и , ускорение можно вычислить непосредственно из второго закона Ньютона, как указано в.
Решение
Величина ускорения. Ввод известных значений дает
Замена единиц на N дает
Обсуждение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле.В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально). Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку.Такое усилие не будет длиться слишком долго, потому что человек скоро наберет максимальную скорость.
Какая ракетная тяга ускоряет этот снегоход?
До космических полетов с астронавтами, ракетные сани использовались для тестирования самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами. Вычислите величину силы, прилагаемой каждой ракетой, называемой ее тягой, для четырехракетной двигательной установки, показанной на (Рисунок).Начальное ускорение салазок – масса системы – 2100 кг, а сила трения, препятствующая движению, известна как 650 Н.
Стратегия
Несмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с
где – чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует тяге.В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
Таким образом, общая тяга
и индивидуальные тяги
Обсуждение
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийных выбросах реактивных истребителей.Была получена скорость 1000 км / ч с ускорением 45 с. (Напомним, что ускорение свободного падения равно. Когда мы говорим, что ускорение составляет 45 с, это примерно так.) Хотя живые объекты больше не используются, была получена наземная скорость 10 000 км / ч. с ракетными санками. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой.Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Концептуальные вопросы
Какое утверждение верно? (а) Чистая сила вызывает движение. (b) Чистая сила вызывает изменение движения. Объясните свой ответ и приведите пример.
Почему мы можем пренебрегать такими силами, как силы, удерживающие тело вместе, когда мы применяем второй закон движения Ньютона?
Объясните, как выбор «интересующей системы» влияет на то, какие силы следует учитывать при применении второго закона движения Ньютона.
Опишите ситуацию, в которой чистая внешняя сила, действующая на систему, не равна нулю, но ее скорость остается постоянной.
Система может иметь ненулевую скорость, в то время как чистая внешняя сила, действующая на нее , равна нулю. Опишите такую ситуацию.
Камень брошен вверх. Какая чистая внешняя сила действует на скалу, когда она находится на вершине своей траектории?
(a) Приведите пример различных чистых внешних сил, действующих на одну и ту же систему, вызывая разные ускорения.(b) Приведите пример одной и той же чистой внешней силы, действующей на системы разной массы, вызывая разные ускорения. (c) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
Если ускорение системы равно нулю, не действуют ли на нее внешние силы? А как насчет внутренних сил? Объясни свои ответы.
Если к объекту приложена постоянная ненулевая сила, что вы можете сказать о скорости и ускорении объекта?
Сила тяжести, действующая на баскетбольный мяч (рисунок), игнорируется.Если принять во внимание гравитацию , каково направление чистой внешней силы на баскетбольный мяч – выше горизонтали, ниже горизонтали или все еще горизонтально?
Проблемные упражнения
Вы можете предположить, что данные, взятые с иллюстраций, имеют точность до трех цифр.
Спринтер весом 63,0 кг начинает забег с ускорением. Какая чистая внешняя сила действует на него?
Если спринтер из предыдущей задачи разгоняется с такой скоростью на 20 м, а затем сохраняет эту скорость до конца 100-метрового рывка, сколько у него времени для забега?
Уборщик нажимает 4.Тележка для белья весом 50 кг таким образом, чтобы чистая внешняя сила, действующая на нее, составляла 60,0 Н. Рассчитайте величину ее ускорения.
Поскольку астронавты на орбите явно невесомые, необходим умный метод измерения их массы, чтобы отслеживать прирост или потерю массы и корректировать рацион. Один из способов сделать это – приложить известную силу к космонавту и измерить возникающее ускорение. Предположим, что действует чистая внешняя сила 50,0 Н и измеренное ускорение астронавта равно.(а) Рассчитайте ее массу. (b) При приложении силы к космонавту, аппарат, в котором он движется по орбите, испытывает равную и противоположную силу. Обсудите, как это повлияет на измерение ускорения космонавта. Предложите метод, позволяющий избежать отдачи автомобиля.
В (рисунок) чистая внешняя сила на газонокосилку 24 кг заявлена равной 51 Н. Если сила трения, препятствующая движению, равна 24 Н, какую силу (в ньютонах) человек прилагает к косилке? Предположим, косилка движется на 1.5 м / с при снятии силы. Как далеко уйдет косилка до остановки?
Те же ракетные салазки, изображенные на (Рис.), Замедляются со скоростью. Какая сила необходима, чтобы вызвать это замедление? Предположим, что ракеты выключены. Масса системы 2100 кг.
(a) Если салазки ракеты, показанные на (Рисунок), запускаются с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы составляет 2100 кг, тяга T равна N, а сила трения, препятствующая движению, известна как 650 Н.б) Почему ускорение не в четыре раза меньше, чем у всех горящих ракет?
(а).
(b) Ускорение не в четверть от того, что было при горящих ракетах, потому что сила трения все еще такая же большая, как и при горящих всех ракетах.
Какое замедление у ракетных санок, если они останавливаются через 1,1 с со скорости 1000 км / ч? (Из-за такого замедления один испытуемый потерял сознание и временно потерял сознание.)
Предположим, двое детей толкаются горизонтально, но в противоположных направлениях, на третьего ребенка в повозке.Первый ребенок прикладывает силу 75,0 Н, второй – 90,0 Н, трение составляет 12,0 Н, а масса третьего ребенка с повозкой составляет 23,0 кг.
- Какая система представляет интерес, если нужно рассчитывать ускорение ребенка в повозке?
- Нарисуйте диаграмму свободного тела, включая все силы, действующие на систему.
- Рассчитайте ускорение.
- Каким было бы ускорение, если бы трение было 15,0 Н?
- Система – это ребенок в вагоне плюс вагон.
- в направлении толчка второго ребенка.
Мощный мотоцикл может развивать ускорение до 90,0 км / ч. На этой скорости силы сопротивления движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта.) Какова величина силы, которую мотоцикл оказывает в обратном направлении на мотоцикл. земля, чтобы произвести его ускорение, если масса мотоцикла с водителем составляет 245 кг?
Ракетные салазки, показанные на (Рисунок), ускоряются со скоростью.Его пассажирский вес составляет 75,0 кг. (а) Рассчитайте горизонтальную составляющую силы, которую сиденье оказывает на его тело. Сравните это с его весом, используя соотношение. (b) Рассчитайте направление и величину общей силы, которую сиденье оказывает на его тело.
(а). Эта сила в 5 раз больше его веса.
(б)
Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью. В этой задаче силы прилагаются к сиденью и удерживающим ремням.
Вес космонавта и его скафандра на Луне составляет всего 250 Н. Сколько они весят на Земле? Какая масса на Луне? На земле?
Предположим, масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей составляет 30 000 Н. (а) Рассчитайте величину ускорения при вертикальном взлете с Луны. б) Может ли он взлететь с Земли? Если нет, то почему? Если бы это было возможно, вычислите величину его ускорения.
Урок, объединяющий второй закон Ньютона и кинематику
Этот рабочий лист, Второй закон Ньютона и кинематика, содержит множество задач с множественным выбором и задач со словами. Вопросы охватывают материал, данный с самого начала раздела, чтобы напомнить учащимся о том, что они должны знать и уметь делать. Я раздаю рабочий лист и сообщаю студентам, что у них есть 25 минут, чтобы заполнить этот лист, и я забираю его в конце урока. Эта практика помогает студентам развивать знания в содержании и помогает им эффективно решать проблемы.Для более продвинутых студентов я добавляю интересную бонусную задачу в конце рабочего листа.
Пока студенты работают над листом, я хожу по классу и оказываю поддержку там, где это необходимо. Чтобы лучше обслуживать студентов, которым нужна моя помощь, я разработал систему с тремя чашками , которая предупреждает меня о том, кому нужна помощь. Мои ученики сидят за столами группами по четыре человека. За каждым столом по три чашки: красная, желтая и красная (на фото справа).В зависимости от того, как учащиеся справляются с заданием, они будут ставить одну из цветных чашек сверху.
Зеленая чашка : стандартная чашка, все идет хорошо, помощь не нужна.
Желтая чашка : Мы боремся с концепцией, нам нужно, чтобы вы подтвердили, что мы движемся в правильном направлении.
Красная чашка : Помогите! Мы полностью застряли и не можем двигаться дальше.
Пока студенты работают над заданием, я просматриваю комнату. Красные чашки получают приоритет, а затем – желтые.Чашки являются постоянным приспособлением к столам и используются, когда учащиеся занимаются деятельностью, ориентированной на учащихся (рабочие листы, лаборатории, исследования и т. Д.). Если я смотрю вверх и вижу в основном зеленые чашки, значит, все идет хорошо. Однако, если в основном отображаются красные чашки, это говорит мне о том, что я должен прекратить самостоятельную работу и заново обучать концепциям.
У студентов есть 25 минут на решение этих практических задач. Затем, чтобы закончить урок, мы рассматриваем эти практические задачи, чтобы учащиеся сразу получали обратную связь по мере самооценки своего понимания.
Использование законов на основе уравнений в CATIA Kinematics
Юрий Апанович
Это продолжение моей предыдущей публикации «Использование законов на основе эскизов в CATIA Kinematics».
Чтобы освежить память, что это такое…
Функции CATIA Law могут использоваться для связывания всех команд в механизме с одним параметром – временем. Это позволяет моделировать движение механизма, управляя одним параметром времени, поэтому несколько команд могут изменяться одновременно и определяемым пользователем способом.Кроме того, это позволяет рассчитывать в механизме зависящие от времени величины, такие как скорости и ускорения.
В CATIA есть два типа законов – на основе эскизов и на основе уравнений. Законы на основе эскиза (объясненные в моем вышеупомянутом посте) требуют определения профиля движения как эскиза, который во многих случаях хорошо работает. Но у законов, основанных на эскизах, есть свои ограничения.
Рассмотрим задачу: как смоделировать движение маятника? Из физики мы знаем, что движение маятника следует закону синусоидальной волны, но – в рабочей среде Sketcher нет инструмента для рисования синусоидальной волны!
В этом посте я объясню, как использовать законы на основе уравнений, чтобы обойти такие ограничения.
Образец модели показан ниже. Модель состоит из осевой части и маятниковой части. Осевая часть закреплена, а маятник соединен с осью шарниром Revolute , Angle – по команде. Цель состоит в том, чтобы смоделировать движение маятника по синусоидальному закону с амплитудой колебания 30 градусов.
Во-первых, нам нужно записать уравнение движения. Угол поворота при движении маятника описывается следующим уравнением:
Где A – амплитуда качания, t – время, ω – циклическая частота в радианах в секунду, f – частота в циклах в секунду (Герцы) и φ – фаза в радианах.
Например, если маятник совершает одно полное движение вперед и назад за 1 секунду, тогда частота f = 1 Гц. При максимальном размахе 30 градусов и начале движения в крайнем левом положении поворота уравнение движения принимает следующий вид:
Теперь нам нужно создать функцию Закона. Щелкните значок (Закон) на панели инструментов «Знание», чтобы открыть диалоговое окно «Редактор законов». Правая часть позволяет вам создавать формальные параметры, которые будут использоваться в законе («формальные» в том смысле, что они не являются фактическими параметрами в модели CATIA, скорее, они служат в качестве «входных» и «выходных» параметров. в определении закона), левая часть – это окно редакции закона.
Теперь нам нужно выяснить, какие типы формальных параметров нам нужны. В разделе Dictionary прокрутите вниз до главы Law и изучите функцию Evaluate – это функция, которую мы позже будем использовать, чтобы связать команду угла в механизме с законом.
Обратите внимание, что функция требует входного параметра типа Real и также выдает выходное значение типа Real .Поэтому, используя новый параметр типа , создайте два параметра типа Real и переименуйте их как y и t .
Теперь в разделе “Закон” введите следующее уравнение (функцию sin можно найти в главе Math и константу PI в главе Константа в разделе Dictionary ):
y = 30 * sin (2 * PI * t * 1rad – PI / 2 * 1rad)
Обратите внимание на использование единиц в кодексе закона – это очень важно! Если единицы не указаны, CATIA интерпретирует значения в международной системе единиц СИ.Щелкните OK , чтобы завершить определение закона.
Далее нам нужно связать команду в механизме с законом. Дважды щелкните Command.1 в дереве, щелкните правой кнопкой мыши поле Command value и выберите Изменить формулу в контекстном меню.
В редакторе формул введите следующую формулу:
Закройте редактор формул.

