Закон ома для участка цепи переменного тока: Закон Ома для переменного тока - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Закон ома для переменной цепи

После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.

При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

где

I [А] – сила тока,
U [В] – напряжение,
Z [Ом] – полное сопротивление цепи.

В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]).

Полное сопротивление цепи переменного тока можно вычислить по формуле:

где

– индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
– емкостное сопротивление, создается конденсатором.

Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.

Рис.1. Треугольник сопротивлений

Учитывая последние равенства, запишем формулу закона Ома для переменного тока:

– амплитудное значение силы тока.

Рис.2. Последовательная электрическая цепь из R, L, C элементов.

Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:

Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?

Закон Ома – физический закон, определяющий зависимость между электрическими величинами – напряжением, сопротивлением и током для проводников.

Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость.
Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости, стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя.
Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r.

Закон Ома для участка цепи

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.
Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
После сброса ввести два любых известных параметра.

Закон Ома для замкнутой цепи

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.
r – Внутреннее сопротивление источника питания.

Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания.
С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U.
Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.

В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R.
Такой источник питания называют источником напряжения.

Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:

Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.
Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

– комплексная амплитуда тока. = I_ampe jφ
– комплексная амплитуда напряжения. = U_ampe jφ
– комплексное сопротивление. Импеданс.
φ – угол сдвига фаз между током и напряжением.
e – константа, основание натурального логарифма.
j – мнимая единица.
I_amp , U_amp – амплитудные значения синусоидального тока и напряжения.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.
Такие элементы и цепи, в которых они используются, называют нелинейными.

Замечания и предложения принимаются и приветствуются!

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

формулы и объяснение. Закон Ома для переменного тока

Содержание

Классическая формулировка
Принятые единицы измерения
Закон Ома для участка цепи
Закон Ома для параллельной и последовательной цепи
Закон Ома для полной цепи
Формула закона Ома для полной цепи
Закон Ома в дифференциальной и интегральной форме
Закон Ома для переменного тока
Закон Ома для участка цепи с ЭДС
Идеальный источник ЭДС
Внутреннее сопротивление источника ЭДС
Как найти внутреннее сопротивление источника ЭДС
Закон Ома для различных типовых цепей переменного тока
Закон Ома для неоднородного участка
Мнемоническая диаграмма
Практическое использование

Классическая формулировка

Этот простой вариант трактовки, известный нам со школы.

Однородный открытый участок электроцепи

Формула в интегральной форме будет иметь следующий вид:

Формула в интегральной форме

То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.

В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.

Принятые единицы измерения

Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:

напряжение – в вольтах;
ток в амперах
сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.

Закон Ома для участка цепи

Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:

I=U/R

Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.

Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.

Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.

Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

f(x) = ky или f(u) = IR или f(u)=(1/R)*I

Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:

I=12 В/6 Ом=2 А

Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.

Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.

Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:

R_провод=ρ(L/S)

Где ρ – удельное сопротивление в Ом*мм²/м, L – длина в м, S – площадь поперечного сечения.

Закон Ома для параллельной и последовательной цепи

В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:

I=I1=I2

U=U1+U2

R=R1+R2

Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:

U_эл=I*R_{элемента}

Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:

I=I1+I2

U=U1=U2

1/R=1/R1+1/R2

Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.

Закон Ома для полной цепи

Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:

напряжение, если это источник ЭДС;
силу тока, если это источник тока;

Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.

Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:

I=ε/(R+r)

Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.

На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.

Формула закона Ома для полной цепи

R – внешнее сопротивление [Ом];
r – сопротивление источника ЭДС (внутреннее) [Ом];
I – сила тока [А];
ε– ЭДС источника тока [В].

Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.

I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.

По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.

Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?

Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.

Закон Ома в дифференциальной и интегральной форме

Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.

Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.

В интегральной форме:

Закон Ома для переменного тока

При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R_a и реактивное сопротивление X (или R_r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:

Ток в цепи с индуктивностью не может измениться мгновенно.
Напряжение в цепи с ёмкостью не может измениться мгновенно.

Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.

U=I/Z

X_L и X_C – это реактивные составляющие нагрузки.

В связи с этим вводится величина cosФ:

Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.

Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.

Читайте также: Как утилизировать энергосберегающие лампы?

При этом сопротивление представляют в комплексной форме:

Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.

Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».

Закон Ома для участка цепи с ЭДС

Для однозначного определения потенциала любой точки электрической цепи необходимо задать (произвольно) потенциал какой-нибудь одной точки. Выберем для схемы, представленной на рис. 1.7, а, . По определению потенциал точки 3 больше j2 на значение ЭДС:

Ток I во внешней части простейшей электрической цепи, а в общем случае в любом пассивном элементе цепи, а значит, и схемы, направлен, как указывалось, от точки с более высоким потенциалом (3) к точке с более низким (1). Поэтому потенциал j3 больше потенциала j1:

Из (1.9) и (1.10) имеем

Аналогично можно написать формулу для тока участка сложной электрической схемы, состоящего из любого числа последовательно соединенных источников, представленных схемами замещения на рис. 1.7, и приемников при заданной разности потенциалов на концах этого участка (рис. 1.9). Ток I на участке схемы, содержащем источники ЭДС, может быть направлен от точки а к точке b или наоборот. Если направление тока заранее не известно, то для составления выражений, подобных (1.11), нужно выбрать направление тока произвольно. Такое произвольно выбранное направление тока условились называть положительным направлением и обозначать (как и выше действительное направление) стрелкой с просветом или отмечать индексами у буквы I.

Если принять за положительное направление тока I направление от точки а к точке b, то потенциал jb определяется через потенциал jа выражением

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка – это нагрузка, которая обладает сопротивлением.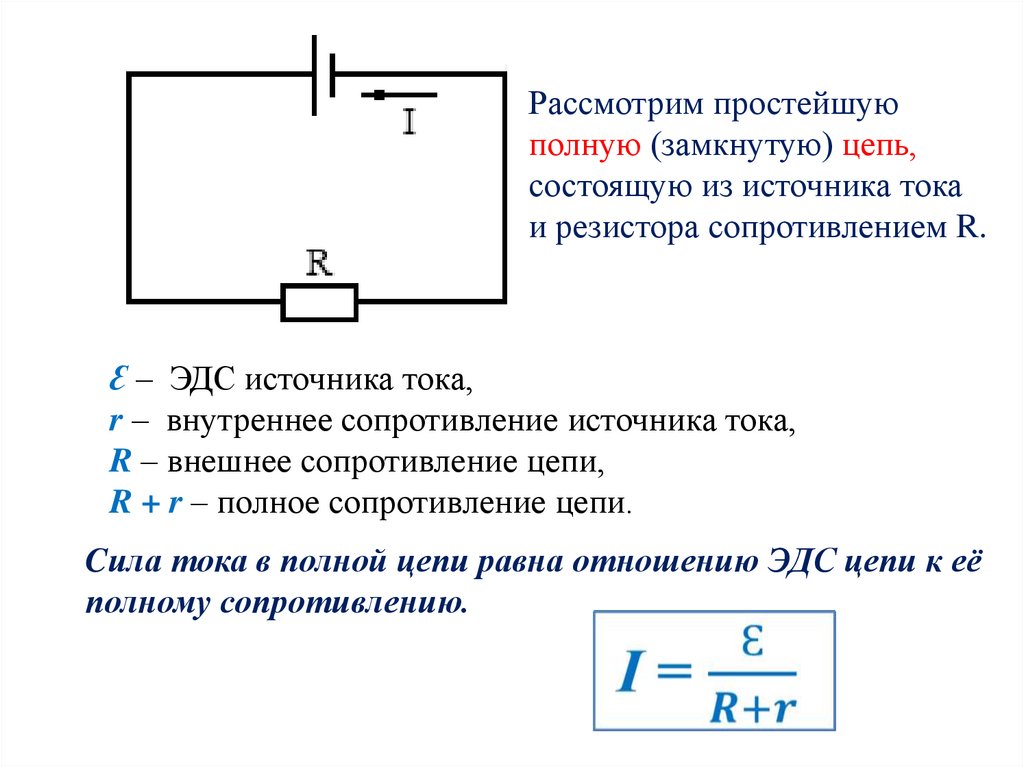 Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Закон Ома для различных типовых цепей переменного тока

Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис.

4.)

Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.

Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:

(6)

где —эффективное значение силы тока в А;

U—эффективное значение напряжения в В;

R—активное сопротивление в Ом;

ωL—индуктивное сопротивление в ом.

Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.

В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.

Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.

А закон Ома для такой цепи принимает вид:

(7)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),

Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.

Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:

(8)

где I-сила тока в А;

U-напряжение в В;

R-активное сопротивление в Ом;

ωL-индуктивное сопротивление в Ом;

1/ωС-емкостное сопротивление в Ом.

Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.

Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).

Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.

Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.

Эквивалентная схема колебательного контура.

Таким образом закон Ома для переменного тока можно сформулировать следующим образом.

Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)

Закон Ома для неоднородного участка

Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .

Подставляем сюда выражения для , и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .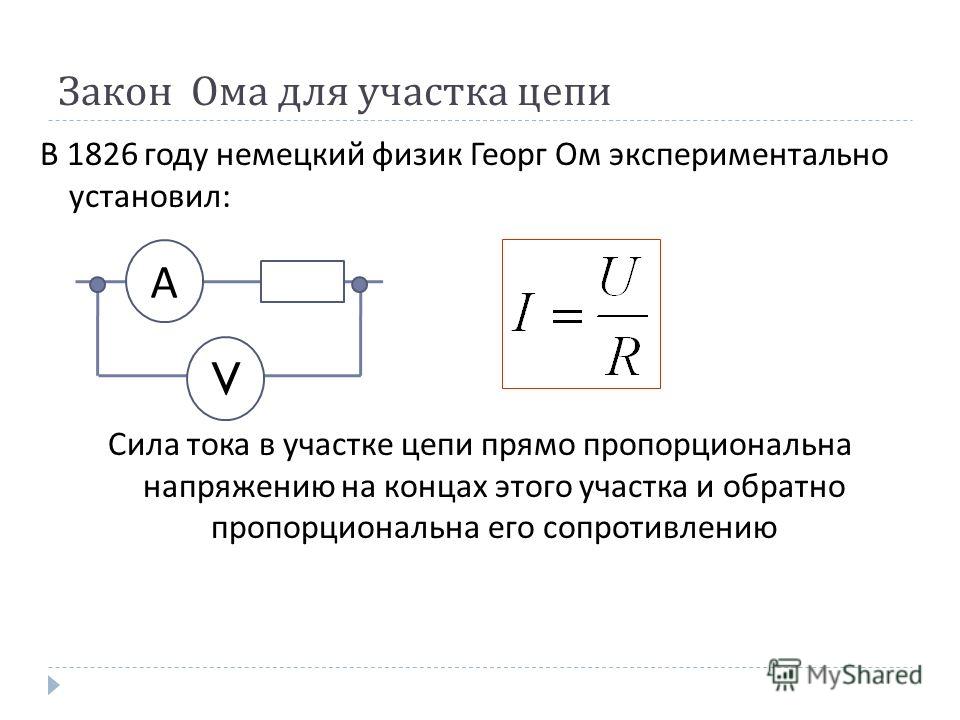

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Мнемоническая диаграмма

Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.

Практическое использование

Видео: Закон Ома для участка цепи — практика расчета цепей.

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.

Применяем закон к любому участку цепи

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

Напряжение – 220 В;
R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

R=0,2 МОм;
U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

R=20 кОм;
I=10 мА.

Преобразуем исходные данные:

20 кОм = 20000 Ом;
10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление.

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров.

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Источники

https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html
https://www.remontostroitel.ru/zakon-oma-dlya-uchastka-tsepi-i-polnoj-tsepi-formuly-i-obyasnenie.html
https://zakon-oma.ru/dlya-polnoj-cepi.php
https://www.ess-ltd.ru/elektro/zakon-oma-uchastok.php
https://www.RusElectronic.com/eds-istochnika-napryazheniya-i-ego-vnutrennee-soprotivlenie/
http://www.sxemotehnika.ru/zakon-oma-dlia-peremennogo-toka.html
https://ege-study.ru/ru/ege/materialy/fizika/eds-zakon-oma-dlya-polnoj-cepi/
https://electroandi.ru/toe/dc/zakon-oma.html

Закон ома для цепи с емкостью. Описание закона ома для электрической цепи переменного тока

Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.

Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.

Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.

Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.

Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.

В результате нового эксперимента Ом пришел к формуле:

Х = a / b + l

Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.

Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи .

Закон Ома для участка цепи

Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.

I = U / R

Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.

Таким образом формула для расчета сопротивления проводника примет вид:

R = p ⋅ l / s

Закон Ома для полной цепи

Отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:

I = U / R + r

Закон Ома для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
В сверхпроводниках;
Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
В вакуумных и газовых радиолампах;
В диодах и транзисторах.

Закон ома для переменного тока в общем случае имеет такой же вид, как и для постоянного. То есть при увеличении напряжения в цепи ток также в ней будет увеличиваться. Отличием же является то, что в цепи переменного тока сопротивление ему оказывают такие элементы как катушка индуктивности и емкость. Учитывая этот факт, запишем закон ома для переменного тока.

Формула 1 — закон ома для переменного тока

где z это полное сопротивление цепи.

Формула 2 — полное сопротивление цепи

В общем случае полное сопротивление цепи переменного тока будет состоять из активного емкостного и индуктивного сопротивления. Проще говоря, ток в цепи переменного тока, зависит не только от активного омического сопротивление, но и от величины емкости и индуктивности.

Рисунок 1 — цепь, содержащая омическое индуктивное и емкостное сопротивление

Если, например, в цепь постоянного тока включить конденсатор то тока в цепи не будет, так как конденсатор на постоянном токе является разрывом цепи. Если же в цепи постоянного тока появится индуктивность, то ток не изменится. Строго говоря, изменится, так как катушка будет обладать омическим сопротивлением. Но изменение будет ничтожным.

Если же конденсатор и катушку включить в цепи переменного тока, то они будут оказывать сопротивление току пропорционально величине ёмкости и индуктивности соответственно. Кроме этого в цепи буде наблюдаться сдвиг фаз между напряжением и током. В общем случае ток в конденсаторе опережает напряжение на 90 градусов. В индуктивности же отстает на 90 градусов.

Емкостное сопротивление зависит от величины емкости и частоты переменного тока. Эта зависимость обратно пропорциональна, то есть с увеличением частоты и ёмкости сопротивление будет уменьшаться.

I [А] – сила тока,
U [В] – напряжение,
Z [Ом] – полное сопротивление цепи.

Полное сопротивление цепи

где

Рис.1. Треугольник сопротивлений

Учитывая последние равенства, запишем формулу закона Ома для переменного тока:

– амплитудное значение силы тока.

Рис.2. Последовательная электрическая цепь из R, L, C элементов.

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах .

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах . Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль .

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах .

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Кстати! Для наших читателей сейчас действует скидка 10% на

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря “участок цепи” мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС , читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего . А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Цель: экспериментально определить импеданс различных нагрузок и сопоставить экспериментальные значения с теоретическими.

Теоретическая часть

Рассмотрим соотношения между током и напряжением в цепи переменного тока при включении в нее различных нагрузок (рис. 29).

Омическое сопротивление. Под этим термином понимают сопротивление проводника постоянному току. В дальнейшем будем рассматривать квазистационарные токи, для которых мгновенные значения силы тока и напряжения, обозначаемые малыми буквами i и u , подчиняются законам Ома и Джоуля-Ленца. Амплитудные значения тока и напряжения будем обозначать I m и U m .

Пусть к омическому сопротивлению приложено напряжение, меняющееся по гармоническому закону:

U = U m сos wt , (31)

где w – циклическая частота колебаний. Согласно закону Ома через R потечет ток силой i :

i = I m сos wt , (33)

Из соотношений (32) и (33) следует:

1) фазы тока и напряжения на омическом сопротивлении совпадают;

2) амплитуды силы тока и напряжения связаны соотношением

Рис. 29. Омическая, индуктивная и емкостная нагрузки

Индуктивное сопротивление. Подадим на катушку, обладающую индуктивностью L и пренебрежимо малым омическим сопротивлением, напряжение, меняющееся по закону (31). В катушке возникает меняющийся ток, создающий переменное магнитное поле. Изменение магнитного потока Ф = Li этого поля возбудит в витках катушки ЭДС самоиндукции

Поскольку подводимое к катушке напряжение играет роль ЭДС, а падение напряжения в цепи отсутствует (R = 0), по второму правилу Кирхгофа для мгновенных значений можем записать:

u + = 0 или .

Последнее перепишем в виде дифференциального уравнения

Или .

Интегрирование этого уравнения дает следующее выражение:

(35)

Из (31) и (35) следует:

1) ток, проходящий через катушку, отстает от напряжения по фазе на p/2 или, что то же самое, напряжение опережает ток по фазе на p/2;

Из сопоставления (36) с (32) следует, что величина wL в цепи с индуктивностью играет роль сопротивления. Величину

X L = wL (37)

называют индуктивным сопротивлением .

Емкостное сопротивление . Конденсатор представляет собой разрыв проводов, поэтому постоянный ток он не пропускает. При изменении напряжения между обкладками меняется и мгновенное значение заряда конденсатора, определяемого формулой

q = Cu , (38)

для чего в подводящих проводах должен протекать ток, приносящий заряд к обкладкам или уносящий от них. Говорят, что конденсатор пропускает переменный ток, хотя в пространстве между обкладками никакой передачи заряда от одной обкладки к другой не происходит.

Проходящий по проводам заряд скапливается на обкладках конденсатора, поэтому его величина равна i = dq/dt , где q – мгновенное значение заряда обкладки. Учитывая (38) и считая подаваемое напряжение меняющимся по закону (31), получаем:

Так как cos (p/2 + wt ) = –sin wt, последнее примет вид:

. (39)

Сопоставляя (31) и (39), имеем:

1) ток в цепи с конденсатором опережает напряжение по фазе на p/2, иначе говоря, напряжение отстает от тока по фазе на p/2;

2) амплитуды тока и напряжения связаны соотношением

. (40)

Величину

называют емкостным сопротивлением .

При измерениях и расчетах цепей переменного тока вместо амплитудных пользуются действующими (эффективными) значениями силы тока I и напряжения U , которые связаны с амплитудными:

Их использование обусловлено тем, что закон Джоуля-Ленца в случае переменного тока принимает такой же вид, как и для постоянного. Соответственно электроизмерительные приборы градуируются на эффективные значения.

Очевидно, что формулы (34), (36) и (40) не изменяются при замене амплитудных значений на эффективные и примут вид:

U R = I × R , U L = I × wL , U C = I /wC , (42)

где индексы R , L и C означают напряжение на соответствующей нагрузке.

Векторные диаграммы . Фазовые соотношения между током и напряжением графически изображены на рис. 30.

Существует и другой способ их представления, позволяющий упростить расчеты цепей со сложной нагрузкой.

Рис. 31

Проведем из некоторой точки О (рис. 31) ось ОХ и отложим из той же точки вектор А под углом j к оси ОХ . Затем приведем этот вектор во вращение вокруг точки О в плоскости рисунка против часовой стрелки с угловой скоростью w. Угол a между А® и ОХ спустя время t будет a = wt + j. Проекция А® на ось ОХ равна

А Х = Х = A cos a

Х = A cos (wt + j). (43)

Вывод: всякое гармоническое колебание можно представить вращением вектора соответствующей длины и ориентации.

Следовательно, если построить вектор U и под соответствующим углом отложить вектор I , то при совместном вращении векторов угол между ними останется неизменным (43). Векторные диаграммы токов и напряжений при различных нагрузках приведены на рис. 32.

Последовательное соединение R , L и С . Для расчета такой цепи воспользуемся методом векторных диаграмм. При последовательном соединении нагрузок мгновенное значение силы тока во всех точках цепи должно быть одинаковым, т.е. фаза тока на всех нагрузках одинакова.

Однако напряжения на нагрузках не совпадают по фазе с током. Напряжение на омическом сопротивлении совпадает по фазе с током, на индуктивном – опережает ток на p/2, на емкостном – отстает на p/2. Таким образом, сложив векторы U R , U L и U C , получим полное напряжение, приложенное к цепи. Поскольку U L и U C противоположны по направлению, удобнее сначала сложить их, а затем вектор U L – U C сложить с U R . В итоге имеем:

Подставляя соотношения (42), получим:

. (44)

В этом выражении роль сопротивления выполняет величина

, (45)

называемая полным сопротивлением цепи переменному току или импедансом . С ее использованием (44) примет вид:

U = I × Z. (46)

Это выражение часто называют законом Ома для переменных токов. Величина

(47)

называется реактивным сопротивлением и является комбинацией индуктивного и емкостного сопротивлений.

Векторная диаграмма (рис. 33) также показывает, что приложенное напряжение и протекающий в цепи ток колеблются не в одинаковой фазе, а имеют между собой сдвиг фаз j, величина которого определяется любой из приведенных ниже формул, следующих из диаграммы:

; ;

Следует отметить, что формула (46) является общей для любого соединения нагрузок, а формулы (45), (47) и (48) справедливы лишь для частного случая последовательного соединения.

Экспериментальная часть

Оборудование: реостат 1000 Ом, ключ, амперметр, вольтметр, реостат 100 Ом, батарея конденсаторов, катушка.

Порядок выполнения работы

Задание 1. Измерение омического сопротивления.

Схема установки приведена на рис. 34.

В этом опыте в качестве нагрузки применяется низкоомный реостат. Высокоомный реостат используется как потенциометр.

1. Измерить ток через нагрузку при трех различных значениях подаваемого на нее напряжения. Результаты измерения занести в табл. 12.

Задание 2. Измерение емкостного сопротивления.

1. В рабочую схему в качестве нагрузки включить батарею конденсаторов. Ток и напряжение на нагрузке измерить аналогично заданию 1. Результаты измерения также внести в табл. 12.

Примечание. Значение емкости батареи рекомендуется выбрать в интервале 20–40 мкФ.

Задание 3. Измерение импеданса катушки.

1. Измерение импеданса катушки проводится аналогично предыдущим заданиям с использованием катушки в качестве нагрузки.

Задание 4. Измерение импеданса последовательного соединения R , L и С.

1. Нагрузкой будут служить соединенные последовательно реостат, батарея конденсаторов и катушка.

2. Ток и напряжение на нагрузке измерить аналогично заданию 1.

3. По результатам каждого измерения вычислить импедансы Z эксп нагрузок.

4. Сравнить экспериментальные результаты с теоретическими или паспортными значениями. Результаты сравнения привести в выводе.

Таблица 12

Номер задания	Напряжение, U	Сила тока, I	Z эксп, Ом	Z экспср , Ом	Z теор, Ом
цена деления	в делениях	в В	цена деления	в делениях	в А
резистор


конденсатор


катушка


4 последовательное соединение

Примечание. Теоретическим для реостата будет его паспортное значение сопротивления. Для конденсатора Z теор определяется по использованному в опыте значению емкости, расчет производится по формуле (41). Катушка обладает и омическим, и индуктивным сопротивлением, поэтому ее импеданс вычисляется по формуле (45), причем в качестве R должна использоваться сумма омических сопротивлений реостата и катушки.

5. Вычисление погрешностей экспериментальных значений произвести по классам точности амперметра и вольтметра, теоретических – по паспортным данным приборов.

Контрольные вопросы и задания

1. Запишите и поясните закон Ома для переменного тока.

2. Как определяется омическое, реактивное и полное сопротивление в цепи переменного тока?

3. Что понимается под эффективными значениями тока и напряжения?

4. Нарисуйте векторную диаграмму для резистора в цепи переменного тока. Сделайте пояснения.

5. Нарисуйте векторную диаграмму для конденсатора в цепи переменного тока. Сделайте пояснения.

6. Нарисуйте векторные диаграммы для идеальной катушки и катушки с заметным омическим сопротивлением в цепи переменного тока. Сделайте пояснения.

7. Нарисуйте векторную диаграмму для последовательного соединения резистора, конденсатора и катушки в цепи переменного тока. Сделайте пояснения. Получите из векторной диаграммы закон Ома.

Лабораторная работа 9 (11)

ИЗМЕРЕНИЕ МОЩНОСТИ

В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Цель: ознакомиться с измерением мощности в цепи переменного тока методом трех вольтметров.

Теоретическая часть

Как всякий проводник, катушка в цепи постоянного тока потребляет энергию, идущую на нагревание проводов. Свойство проводника превращать энергию электрического тока в тепловую характеризуется его омическим сопротивлением R . Мощность тепловых потерь определяется по формуле

где I – сила тока в проводнике.

При включении катушки в цепь переменного тока у нее также происходит выделение тепла по закону (49), но в этом случае I – эффективное значение силы переменного тока.

Если у катушки имеется ферромагнитный сердечник, то проходящий по катушке переменный ток возбуждает в нем вихревые токи (токи Фуко), ведущие к нагреванию сердечника. Кроме того, происходит непрерывное изменение намагниченности сердечника по величине и направлению (перемагничивание), что также приводит к нагреванию сердечника. Эти дополнительные потери энергии эквивалентны возрастанию сопротивления проводника. Совокупные необратимые потери энергии, идущие на нагревание как проводов, так и сердечника, характеризуются активным сопротивлением катушки, определяемым по формуле

Это сопротивление, в отличие от омического, невозможно измерить, его можно лишь рассчитать.

Падение напряжения на активном сопротивлении считается колеблющимся в фазе с током.

Рис. 35

При отсутствии ваттметра мощность, потребляемая катушкой, может быть определена с использованием трех вольтметров. Если катушка обладает индуктивностью L и активным сопротивлением R а, то между током в катушке и напряжением на ней возникает сдвиг фаз j, что иллюстрируется векторной диаграммой (рис. 35), где I – ток через катушку, U а и U L – падения напряжения на активном и индуктивном сопротивлениях катушки, U к – полное напряжение на катушке.

Потребляемую катушкой мощность можно вычислить либо из (49), либо по формуле

. (51)

I и U к измеряют непосредственно, а для определения коэффициента мощности (сos j) последовательно с катушкой включается омическое сопротивление R .

Из векторной диаграммы (рис. 36) полное напряжение в цепи запишется по теореме косинусов:

. (52)

Рис. 36

В этих выражениях U – подаваемое напряжение, U к – напряжение на катушке, U R – напряжение на омическом сопротивлении. Все три напряжения измеримы непосредственно. Далее, поскольку катушка и омическое сопротивление соединены последовательно, сила тока в них одинакова и определяется по формуле

что позволяет обойтись без амперметра.

Экспериментальная часть

Оборудование: автотрансформатор; катушка; реостат; вольтметр 0-50 В; 2 вольтметра 0-150 В; сплошной и наборный сердечники.

Порядок выполнения работы

Задание 1. Измерение мощности катушки без сердечника.

В схеме на рис. 37 подаваемое в цепь напряжение регулируется автотрансформатором. В качестве омического сопротивления используется реостат.

Цепи переменного тока

Цепи переменного тока
Далее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия Цепи переменного тока (AC) состоят из э.д.с. источники и три различные типы пассивных элементов: резисторы, катушки индуктивности, и конденсаторы, резисторы удовлетворяют закону Ома:

(968)

где – сопротивление, ток, протекающий через резистор, и падение напряжения на резисторе (в направлении, в котором ток течет). Катушки индуктивности удовлетворяют

(969)

где индуктивность.

Наконец, конденсаторы подчиняются

(970)

где – емкость, – заряд, накопленный на пластине с наибольшим положительный потенциал, а для . Обратите внимание, что любой пассивный компонент реального электрического Цепь всегда можно представить как комбинацию идеальных резисторов, катушек индуктивности и конденсаторы.

Рассмотрим классическую схему LCR, состоящую из катушки индуктивности, конденсатор , и резистор , соединенные последовательно с ЭДС источник, . Уравнение схемы получается путем установки входного напряжения равным сумма падений напряжения на трех пассивных элементах цепи. Таким образом,

(971)

Это интегро-дифференциальное уравнение, которое, вообще говоря, довольно сложно решить.

решать. Предположим, однако, что и напряжение, и ток колебаться с некоторой фиксированной угловой частотой, так что

			(972)
			(973)

где под физическим решением понимается действительная часть приведенные выше выражения. Предполагаемое поведение напряжения и тока явно относится к электрике схемы питаются от сетевого напряжения (которое колеблется с частотой 60 герц).

Уравнения (971)–(973) дают результат

(974)

давать

(975)

Полезно определить импеданс схемы:

(976)

Импеданс является обобщением понятия сопротивления.

В общем случае импеданс цепи переменного тока составляет сложных величин.

Средняя выходная мощность Э.Д.С. источник

(977)

где среднее значение берется за один период колебаний. Давайте, прежде всего, вычислить мощность, используя реальные (а не комплексные) напряжения и токи. Мы можем написать

			(978)
			(979)

где – фазовое отставание тока по отношению к напряжению.

Это следует из того


			(980)

давать

(981)

поскольку а также . В комплексном представлении напряжение и ток записываются

			(982)
			(983)

Обратите внимание, что

(984)

Это следует из того

(985)

Используя уравнение (976), мы находим, что

(986)

Обратите внимание, что рассеиваемая мощность связана с действительной частью импеданса.

Для частного случая схемы LCR,

(987)

Понятно, что только резистор рассеивает энергию в этой цепи. Индуктор и конденсатор накапливает энергию, но в конечном итоге возвращает ее в цепь без рассеивания.

Согласно уравнению. (976), амплитуда тока, протекающего в цепи LCR для заданной амплитуды входного напряжения данный

(988)

Ответ цепи четко резонансный , достигая пика в , и достижение пикового значения в (при условии, что ). На самом деле схемы LCR используются в радиотюнерах для фильтрации сигналы, частоты которых выходят за пределы заданного диапазона.

Отставание по фазе тока по отношению к напряжению определяется выражением

(989)

Отставание по фазе изменяется от для частот значительно ниже резонансной частоты, к нулю на резонансной частоте ( ), к для частот значительно выше резонансной частоты.

Понятно, что в обычных цепях переменного тока уравнение цепи сводится к простое алгебраическое уравнение, и поведение схемы суммируется по комплексному импедансу. Действительная часть говорит нам о мощности, рассеиваемой в цепи, величина дает отношение пикового тока к пиковое напряжение, а аргумент дает отставание по фазе тока относительно напряжения.

Далее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия

Ричард Фицпатрик 2006-02-02

Противодействие току переменного тока

Существуют три фактора, которые могут создать сопротивление потоку электронов (току) в цепи переменного тока. Сопротивление, как и сопротивление цепей постоянного тока, измеряется в омах и оказывает прямое влияние на переменный ток независимо от частоты. С другой стороны, индуктивное реактивное сопротивление и емкостное реактивное сопротивление противодействуют протеканию тока только в цепях переменного тока, а не в цепях постоянного тока. Поскольку переменный ток постоянно меняет направление и интенсивность, катушки индуктивности и конденсаторы также могут препятствовать протеканию тока в цепях переменного тока. Следует также отметить, что индуктивное реактивное сопротивление и емкостное реактивное сопротивление могут создавать фазовый сдвиг между напряжением и током в цепи переменного тока. При анализе цепи переменного тока очень важно учитывать сопротивление, индуктивное сопротивление и емкостное сопротивление. Все три влияют на ток в этой цепи.

Сопротивление

Как уже упоминалось, сопротивление создает сопротивление току в цепи переменного тока, подобное сопротивлению цепи постоянного тока. Ток через резистивную часть цепи переменного тока обратно пропорционален сопротивлению и прямо пропорционален напряжению, приложенному к этой цепи или части цепи. Уравнения I = E / R и E = I × R показывают, как ток связан как с напряжением, так и с сопротивлением. Следует отметить, что сопротивление в цепи переменного тока не создает фазового сдвига между напряжением и током. На рис. 1 показано, как цепь с сопротивлением 10 Ом пропускает ток силой 11,5 ампер через резистивную цепь переменного тока с напряжением 115 вольт.

Figure 1. Resistance

I =

R
I =

115V

10Ω
I = 11.5 amps

Inductive Reactance

When moving магнит через катушку провода, на катушке индуцируется напряжение. Если обеспечена полная цепь, то ток также будет индуцироваться. Величина индуцированного напряжения прямо пропорциональна скорости изменения магнитного поля по отношению к катушке. И наоборот, ток, протекающий по катушке с проводом, создает магнитное поле. Когда этот провод превращается в катушку, он становится основной катушкой индуктивности.

Основным эффектом катушки является ее свойство противодействовать любому изменению тока через нее. Это свойство называется индуктивностью. Когда ток течет по любому проводнику, магнитное поле начинает расширяться от центра провода. По мере того, как магнитные силовые линии растут наружу через проводник, они индуцируют ЭДС в самом проводнике. Индуцированное напряжение всегда находится в направлении, противоположном направлению приложенного тока. Эффекты этой противодействующей ЭДС должны противодействовать приложенному току. Этот эффект является лишь временным состоянием. Как только ток в проводнике достигает устойчивого значения, магнитные силовые линии больше не расширяются, и противодействующая ЭДС больше не присутствует. Поскольку значение переменного тока постоянно меняется, индуктивность повторяется в цикле, всегда противоположном приложенному напряжению. Следует отметить, что единицей измерения индуктивности является генри (Гн).

Физические факторы, влияющие на индуктивность:

Количество витков — удвоение числа витков в катушке приводит к вдвое более сильному полю при использовании того же тока. Как правило, индуктивность зависит от квадрата числа витков.
Площадь поперечного сечения катушки — индуктивность катушки увеличивается прямо по мере увеличения площади поперечного сечения сердечника. Удвоение радиуса катушки увеличивает индуктивность в четыре раза.
Длина катушки — удвоение длины катушки при сохранении того же числа витков снижает индуктивность вдвое.
Материал сердечника, вокруг которого сформирована катушка — катушки наматываются на магнитные или немагнитные материалы. Некоторые немагнитные материалы включают воздух, медь, пластик и стекло. К магнитным материалам относятся никель, железо, сталь и кобальт, которые обладают проницаемостью, обеспечивающей лучший путь для магнитных силовых линий и допускающей более сильное магнитное поле.

Поскольку переменный ток находится в состоянии постоянного изменения, магнитные поля внутри индуктора также постоянно меняются и создают индуктивное напряжение/ток. Это индуцированное напряжение противодействует приложенному напряжению и известно как противо-ЭДС. Это сопротивление называется индуктивным сопротивлением, обозначается буквой XL и измеряется в омах. Эта характеристика катушки индуктивности также может создавать фазовый сдвиг между напряжением и током в цепи. Фазовый сдвиг, создаваемый индуктивным сопротивлением, всегда приводит к тому, что напряжение опережает ток. То есть напряжение индуктивной цепи достигает своих пиковых значений до того, как ток достигает пиковых значений.

Индуктивность — это свойство цепи сопротивляться любому изменению тока и измеряется в генри. Индуктивное реактивное сопротивление – это мера того, насколько противодействующая ЭДС в цепи противодействует приложенному току. Индуктивное реактивное сопротивление компонента прямо пропорционально индуктивности компонента и приложенной к цепи частоте. При увеличении либо индуктивности, либо приложенной частоты индуктивное реактивное сопротивление также увеличивается и оказывает большее сопротивление току в цепи. Это соотношение задается как XL = 2πfL, где XL = индуктивное сопротивление в омах, L = индуктивность в генри, f = частота в циклах в секунду и π = 3,1416.

На рисунке 2 показана последовательная цепь переменного тока с индуктивностью 0,146 генри и напряжением 110 вольт при частоте 60 циклов в секунду. Индуктивное реактивное сопротивление определяется следующим методом.

. реактивное сопротивление добавляется как последовательное сопротивление в цепи постоянного тока. [Рисунок 3] Общее реактивное сопротивление в показанной цепи равно сумме отдельных реактивных сопротивлений.

Рисунок 3. Индуктивность в серии

XL = XL1 + XL2
XL = 10ω 9 000 9 0002 xlt = XL1 + XL 2
XL = 10ω 9 000 9 0002 XLT = 25,5 -ors = 25,9,9 0,9,9. так же, как полное сопротивление в параллельной цепи. [Рисунок 4] Таким образом, общее реактивное сопротивление индуктивностей, соединенных параллельно, как показано, выражается как:

Рисунок 4. Параллельные индуктивности

Емкостное реактивное сопротивление

Емкость – это способность тела удерживать электрический заряд. Обычно конденсатор состоит из двух параллельных пластин, разделенных изолятором. Изолятор обычно называют диэлектриком. Пластины конденсатора способны накапливать электроны при зарядке от источника напряжения. Конденсатор разряжается, когда приложенное напряжение больше не присутствует, и конденсатор подключен к цепи тока. В электрической цепи конденсатор служит резервуаром или хранилищем для электричества.

Основной единицей измерения емкости является фарад, который обозначается буквой F. По определению, один фарад – это один кулон заряда, хранящегося в одном вольте на пластинах конденсатора. С практической точки зрения, один фарад — это большое количество емкости. Обычно в электронике используются гораздо меньшие единицы. Двумя более распространенными меньшими единицами измерения являются микрофарад (мкФ), равный 10-6 фарад, и пикофарад (пФ), равный 10-12 фарад.

Емкость зависит от физических свойств конденсатора:

Емкость параллельных пластин прямо пропорциональна их площади. Большая площадь пластины дает большую емкость, а меньшая площадь дает меньшую емкость. Если мы удвоим площадь пластин, останется место для вдвое большего заряда.
Емкость параллельных пластин обратно пропорциональна расстоянию между пластинами.
Диэлектрический материал влияет на емкость параллельных пластин. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве справочных, и все другие материалы имеют значения относительно воздуха (вакуума).

Когда в цепь подается переменный ток, заряд на пластинах постоянно меняется. [Рисунок 5] Это означает, что электричество должно течь сначала от Y по часовой стрелке к X, затем от X против часовой стрелки к Y, затем от Y по часовой стрелке к X и так далее. Хотя через изолятор между пластинами конденсатора ток не протекает, он постоянно течет в остальной части цепи между X и Y. Поскольку этот ток попеременно поступает в конденсатор и выходит из него, создается определенная временная задержка. Когда конденсатор заряжается или разряжается через сопротивление, для полного заряда или разряда требуется определенное время. Напряжение на конденсаторе не меняется мгновенно. Скорость зарядки или разрядки определяется постоянной времени цепи. Эта скорость заряда и разряда создает сопротивление протеканию тока в цепях переменного тока, известное как емкостное реактивное сопротивление. Емкостное реактивное сопротивление обозначается XC и измеряется в омах. Эта характеристика конденсатора может также создавать фазовый сдвиг между напряжением и током цепи. Фазовый сдвиг, создаваемый емкостным реактивным сопротивлением, всегда приводит к тому, что ток опережает напряжение. То есть ток емкостной цепи достигает своих пиковых значений до того, как напряжение достигает пиковых значений.

Рис. 5. Конденсатор в цепи переменного тока. Емкостное реактивное сопротивление измеряется в омах. Емкостное реактивное сопротивление цепи косвенно пропорционально емкости цепи и приложенной к цепи частоте. При увеличении емкости или приложенной частоты емкостное сопротивление уменьшается, и наоборот. Это отношение задается как:
XC = 1
2πfC
Где: XC = емкостное реактивное сопротивление в омах, C = емкость в фарадах, f = частота в циклах в секунду и π = 3,1416.
На рисунке 5 показана последовательная цепь, в которой приложенное напряжение составляет 110 вольт при 400 имп/с, а емкость конденсатора составляет 80 мФ. Найти емкостное сопротивление и ток.
Чтобы найти емкостное сопротивление, используйте следующее уравнение:
XC = 1
2πfC
Сначала емкость, 80 мкФ, преобразуют в фарады путем деления 80 на 1 000 000, поскольку 1 миллион микрофарад равен 1 фараду. Это частное равно 0,000080 фарад. Это заменяется в уравнении:
XC = 1
2πfc
XC =
1
2π (400) (0,000080)
xc = 4,97 ОД

0). Цепь переменного тока называется импедансом и обозначается буквой Z. Комбинированные эффекты сопротивления, индуктивного и емкостного реактивного сопротивления составляют импеданс (полное сопротивление току, протекающему в цепи переменного тока). Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока, только если эта цепь содержит только сопротивление и не содержит индуктивности или емкости. Как в последовательных, так и в параллельных цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как и сопротивление, а закон Ома для цепи переменного тока I = E/Z точно такой же, как для цепи постоянного тока. схема. На рис. 6 показана последовательная цепь, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 вольт. Чтобы найти, какой ток протекает при подаче 110 вольт переменного тока, решается следующий пример:
I =
E
Z
I =
110V
11Ω
I = 10 amps
Figure 6. Ohm’s Law applies to AC circuit only when circuit consists of resistance only .
Импеданс (Z) = Сопротивление (R)
Если два значения сопротивления подключены параллельно к переменному напряжению, как показано на рис. 7, импеданс равен общему сопротивлению цепи.
Рисунок 7. Два значения сопротивления, подключенные параллельно к переменному напряжению. Импеданс равен общему сопротивлению цепи
Опять же, вычисления будут проводиться так же, как если бы это была цепь постоянного тока, и будет применяться следующее:
Поскольку это чисто резистивная цепь RT = Z (сопротивление = импеданс)
ZT = RT
ZT = 10 Ом
Для определения тока в цепи используйте уравнение:
I =
E
Z
I =
50 В
10 Ом 10 Ом Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (XL) и/или емкостное реактивное сопротивление (XC) для определения импеданса (Z). В этом случае Z не равно RT. Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя складывать напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рисунок 8] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. Он гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.
Рис. 8. Треугольник импеданса как:
0053
Эту формулу можно использовать для определения импеданса, когда известны значения индуктивного реактивного сопротивления и сопротивления. Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу XC вместо XL. В цепях, содержащих сопротивление как с индуктивным, так и с емкостным реактивным сопротивлением, реактивные сопротивления могут быть объединены; но так как их действие в цепи прямо противоположно, они объединяются вычитанием (меньшее число всегда вычитается из большего):
Z = XL – XC
или
X = XC – XL
На рис. 9 показан пример 1. Здесь последовательная цепь, состоящая из резистора и катушки индуктивности, подключена к источнику 110 вольт со скоростью 60 циклов в секунду. Резистивный элемент представляет собой простой измеритель 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 генри. Каково значение импеданса и тока в цепи?
Решение:
Сначала вычисляется индуктивное сопротивление катушки:
XL = 2π × f × L
XL = 6,28 × 60 × 0,021
XL = 8 Ом, индуктивное сопротивление
Далее вычисляется полное сопротивление: емкостное сопротивление, а не емкость.
После определения импеданса можно рассчитать общий ток.
I = E
Z
I = 110В
10 Ом 10 Ом 10 Ом
Пример 2 представляет собой последовательную цепь, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором сопротивлением 10 Ом. [Рисунок 10] Каково значение импеданса, протекающего тока и падения напряжения на резисторе?
Так как 1 миллион микрофарад равен 1 фараду, то 200 мкФ = 0,000200 фарад.
Далее решите емкостное сопротивление:
Чтобы найти импеданс,

Поскольку эта цепь резистивная и емкостная, есть фазовый сдвиг, где ток опережает напряжение:

Чтобы найти ток:
IT = E
Z
IT =
110V
6,4 Ом
IT = 6,7 А.

, чтобы найти падение напряжения по резистору (ER):
ER = I × R
ER = 6,7A × 10Ом
ER = I × R
ER = 6,7A × 10Ом
ER = I × R
ER = 6,7A × 10Ом
ER = I × R
ER = 6,7A × 10Ом
ER = I × R
.0002 ER = 67 вольт
Чтобы найти падение напряжения на конденсаторе (EC):
EC = I × XC
EC = 6,7 A × 13 Ом
EC = 86,1 вольт

Сумма этих двух напряжений не равна приложенное напряжение, так как ток опережает напряжение. Используйте следующую формулу, чтобы найти приложенное напряжение:
Когда цепь содержит сопротивление, индуктивность и емкость, для определения импеданса используется следующее уравнение.
Пример 3. Чему равно сопротивление последовательной цепи, состоящей из конденсатора с емкостным сопротивлением 7 Ом, дросселя с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 11]
Рис. сдвиг между напряжением и током. В этом примере индуктивное сопротивление больше, чем емкостное сопротивление, поэтому напряжение опережает ток.
Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падение напряжения в любой последовательной цепи переменного тока следует суммировать с помощью векторного сложения. На рис. 12 показаны падения напряжения в последовательной цепи переменного тока, описанной выше в примере 3.
Рис. I × XC
Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть сложено с помощью сложения векторов.

Параллельные цепи переменного тока
При решении параллельных цепей переменного тока необходимо также использовать производную теоремы Пифагора. Уравнение для нахождения импеданса в цепи переменного тока выглядит следующим образом:

Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 13, необходимо сначала определить емкостное и индуктивное сопротивления. (Не забудьте преобразовать микрофарады в Farads.)
Рисунок 13. Общее сопротивление параллельной схемы
Далее. Circuit:
Чтобы определить ток, протекающий по каждому параллельному пути цепи, рассчитайте IR, IL и IC.
Следует отметить, что общий ток параллельных цепей находится путем сложения векторов отдельных токов следующим образом:

Мощность в цепях переменного тока
потребляется как цепями переменного, так и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи. Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой создается реактивным сопротивлением цепи.
Истинная мощность
Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая резистивной частью цепи, и измеряется в ваттах (Вт). Истинная мощность обозначается буквой Р и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:

Полная мощность
Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи. Полная мощность — это мощность, потребляемая всей цепью, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность представляет собой произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:

Связанные посты
Электрическая система самолетов
Закон OHM, ток, напряжение и сопротивление
Электромагнитная генерация Power
. Практика и поиск и устранение неисправностей
Генераторы постоянного тока и средства управления
Средства управления генераторами
Видео с вопросами: Импеданс цепей переменного тока
Стенограмма видео
Цепь переменного тока содержит резистор сопротивлением 25 Ом, катушку индуктивности с индуктивным сопротивлением 32 Ом и конденсатор с емкостным сопротивлением 12,8 Ом. Пиковое напряжение, создаваемое источником переменного напряжения, питающим цепь, составляет 120 вольт. Каков пиковый ток в цепи? Дайте ответ с точностью до одного десятичного знака.
Начнем с наброска этой цепи переменного тока. Здесь у нас есть цепь переменного тока с резистором, катушкой индуктивности и конденсатором. Нам сказали, что резистор имеет сопротивление 25 Ом. И затем, вместо индуктивности и емкости цепи, нам дают то, что называется индуктивным реактивным сопротивлением и емкостным реактивным сопротивлением. Реактивное сопротивление компонента в цепи показывает, насколько этот компонент сопротивляется потоку электрического заряда. Реактивное сопротивление похоже на сопротивление, но немного отличается от него. Однако мы видим, что реактивное сопротивление и сопротивление достаточно похожи, чтобы использовать одни и те же единицы измерения, единицы Ом. Символ, обозначающий реактивное сопротивление, — заглавная 𝑋. Для реактивного сопротивления катушки индуктивности мы будем писать 𝑋 sub 𝐿, а для емкостного сопротивления 𝑋 sub 𝐶.
Нам сообщают, каковы эти два значения, опять же в омах. Теперь, поскольку это цепь переменного тока или переменного тока, это означает, что напряжение, как и ток, изменяется в цепи. Он следует синусоидальной схеме. Нам говорят, что самое высокое значение этого напряжения, назовем его 𝑉 sub P, составляет 120 вольт. Зная все это, первая часть нашего вопроса спрашивает: «Каков пиковый ток в цепи?» Итак, мы знаем пиковое напряжение и хотим найти пиковый ток. Пиковый ток, который мы обозначим как 𝐼 sub P, связан с пиковым напряжением способом, подобным закону Ома.
Напомним, что закон Ома гласит, что разность потенциалов 𝑉 в цепи равна силе тока в цепи 𝐼, умноженной на сопротивление цепи 𝑅. Разделив обе части на 𝑅, мы получим 𝐼 равно 𝑉 над 𝑅. Уравнение, дающее 𝐼 sub P, выглядит так. Оно равно пиковому напряжению, деленному на то, что называется импедансом цепи. В цепи переменного тока импеданс представляет собой величину, объединяющую все величины, противодействующие потоку заряда. Сюда входят все сопротивления и реактивные сопротивления. Чтобы найти полное сопротивление 𝑍 нашей цепи, мы могли бы подумать, что нам просто нужно сложить эти значения, указанные в единицах измерения Ом. Но это немного сложнее.
Давайте освободим место на экране, и мы будем использовать это пространство, чтобы вспомнить математическое уравнение для импеданса 𝑍. Обратите внимание, что это включает сопротивление 𝑅, а также разницу между индуктивным реактивным сопротивлением и емкостным реактивным сопротивлением. К счастью, у нас есть вся эта информация для данной схемы. Подставив эти значения, мы получим полное сопротивление нашей цепи, равное квадратному корню из 25 Ом в квадрате плюс величина 32 Ом минус 12,8 Ом в квадрате. Теперь нам пока не нужно вычислять 𝑍, потому что, помните, мы ищем пиковый ток в цепи. Эта величина равна импедансу 𝑍, деленному на пиковое напряжение. Заменив 120 вольт на 𝑉 sub P, теперь мы готовы рассчитать этот пиковый ток. Округлив до одного десятичного знака, получим 3,8 ампера.
Другими словами, если бы мы увидели, как 𝐼 меняется со временем в этой цепи переменного тока, пиковое значение на этой кривой было бы приблизительно 3,8 ампера. Это наш ответ на первую часть этого вопроса. Теперь перейдем ко второй части.
Каково среднеквадратичное значение тока в цепи? Дайте ответ с точностью до одного десятичного знака.
Давайте начнем с размышлений об идее среднеквадратичного тока. Мы знаем, что сила тока в цепи переменного тока изменяется со временем. Итак, если кто-то спросит: «Какова сила тока в этой цепи?» мы не могли дать только один ответ. Вот тут-то и появляется среднеквадратичное значение тока. Это математическая мера тока, который изменяется синусоидально, поэтому мы можем указать одно единственное репрезентативное значение тока. И это значение остается постоянным во времени.
Чтобы увидеть, как это работает, представьте, что у нас есть этот ток в цепи с течением времени. Если бы нам нужно было одно репрезентативное значение тока для этого переменного тока, мы могли бы указать среднее значение тока. Но тогда это будет просто ноль. Это не лучшее представление этого переменного тока. Идея среднеквадратичного тока заключается в том, что сначала мы возводим в квадрат все отдельные значения тока на нашей кривой. Если бы мы сделали это, мы бы получили кривую, похожую на эту розовую. Обратите внимание, что ни одно из значений на этой кривой не является отрицательным. Все они либо положительные, либо нулевые.
Далее мы находим среднее или среднее значение всех этих точек на нашей розовой кривой. Допустим, это среднее значение где-то здесь. Наконец, что мы делаем, так это извлекаем квадратный корень из этого среднего значения. Это опустило бы линию вниз, чтобы быть, скажем, здесь, где синяя линия. Это значение и есть то, что мы называем среднеквадратичным током в цепи.
Оставить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Поиск:
Рубрики
2019 © Все права защищены. Карта сайта
Меню
Поиск:
Советы абитуриенту
Работа для всех
Востребованные вакансии
Студенческие будни
Обучение за границей