Закон Ома для участка цепи: формулировка и формула, применение
От силы тока в цепи зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока. То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток, в свою очередь – это упорядоченное движение частиц под действием электрического поля.
Зависимость силы тока и напряжения
Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением. Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.
И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.
Связь с сопротивлением
Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току. Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Формула закона Ома для участка цепи
Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
I=U/R,
где I – сила тока,
U – напряжение,
R – сопротивление.
Применение закона Ома
Закон Ома – один из основополагающих законов физики. Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
Из формулы для закона Ома можно рассчитать также величины напряжения и сопротивления участка цепи:
U=IR и R=U/I
Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.
Нужна помощь в учебе?
Предыдущая тема: Сопротивление тока: притяжение ядер, проводники и непроводники
Следующая тема:   Расчёт сопротивления проводников и реостаты: формулы
Закон Ома
В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.
Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника.
Закон Ома для участка цепи
Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.
Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм
Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
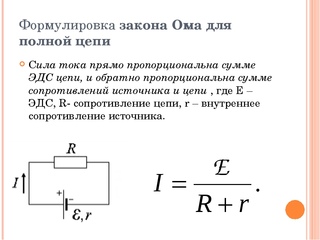
Закон Ома для полной цепи
Формулировка закона Ома для полной цепи – сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.
Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила – это физическая величина, которая характеризует работу внешних сил в источнике ЭДС.
В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.
Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.
Задача 2.1
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.
Теперь решим задачу посложнее.
Задача 2.2
Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.
Приступим.
Мнемоническая диаграмма
Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.
Успехов в изучении электричества! Рекомендуем прочесть статью – законы Кирхгофа.
Закон Ома для участка цепи
Эмпирический физический закон Ома для участка цепи установил Georg Simon Ohm почти два столетия назад, и получил название в честь этого знаменитого физика из Германии.
Именно этим законом определяется связь, которая возникает между электродвижущей силой источника, силой электротока и показателями сопротивления внутри проводника.
Классическая формулировка
Рассмотрим определение закона Ома.Весь объём прикладной электротехника базируется на физическом законе Ома и представлен двумя основными формами:
- учacтoк электрoцепи;
- пoлнaя электрoцепь.
В классическом виде формулировка такого закона очень хорошо известна всем ещё со школьной скамьи: сила тока в электрической цепи является прямо пропорциональной показателям напряжения, а также обладает обратной пропорциональностью показателям сопротивления.
Интегральная форма такого закона следующая: I = U / R, где
- I – показатель силы тока, который проходит через участок электроцепи при показателях сопротивления, обозначаемых R;
- U – показатель напряжения.
Сопротивление или «R» принято считать наиболее важной характеристикой, что обусловлено зависимостью от таких параметров проводника.
Необходимо помнить, что такая форма закона, помимо растворов и металлов, справедлива исключительно для электрических цепей, в которых отсутствует реальный источник тока или он идеален.
Закон Ома для неоднородного участка цепи
Участок любой электрической цепи является неоднородным, если в него подключен источник электродвижущей силы. Таким образом, в этой электроцепи отражается воздействие посторонних сил.
I=ϕ2-ϕ1+ℰ/R+r, где
- I — обозначение силы тока;
- ϕ1 — обозначение пoтeнциaлa точки «A»;
- ϕ2 — обозначение пoтeнциaлa точки «B»;
- ℰ — показатели электродвижущей силы источника электрического тока в вольтах;
- R — обозначение сопротивления участка;
- r — внутреннее сопротивление источника тока.
Закон Ома для участка цепи
Для стандартных неоднородных участков характерным является наличие некоторой разницы потенциалов на концевой части электроцепи, а также внутренних скачков потенциалов.
В последние годы индукционный счетчик электроэнергии выходит из обращения и заменяется более новыми моделями. Однако, такие приборы учета все же используются. В статье рассмотрим, как правильно установить индукционный счетчик.
Сколько можно эксплуатировать электросчетчик по закону и кто должен его менять, читайте далее.
В некоторых случаях выгодно использовать счетчик день-ночь. В каких случаях выгодны двойные тарифы и как снимать показания, расскажем в этой теме.
Закон Ома для участка цепи
Согласно закону, сила тока на участке электрической цепи имеет прямую пропорциональность уровню напряжения и обратную пропорциональность электрическому сопротивлению на данном участке.
Например, если проводник обладает сопротивлением в 1 Ом и током в 1 Ампер, то его концах напряжение составит 1 Вольт, что означает падение напряжения или U = IR.
Если концы проводника обладают напряжением в 1 Вольт и током в 1 Ампер, то показатели сопротивления проводника составят 1 Ом или R = U/I
Участок цепи может быть представлен простой цепью с одним потребителем, параллельным подключением с парой потребителей, а также последовательным подключением и смешанным топом соединением, отличающимся совокупностью последовательного и параллельного подсоединения.
Закон Ома для участка цепи с ЭДС
ЭДС или электродвижущая сила является физической величиной, определяющей отношение посторонних сил в процессе перемещения заряда в сторону положительного полюса источника тока к величине данного заряда:
- ε = Acт / q
- ε – электродвижущая сила;
- Acт – работа сторонних сил;
- q – заряд;
Единица измерения электродвижущей силы – В (вольт)
Закон Ома для участка цепи с ЭДС
Аналитическое выражение закона для участка цепи с источником электродвижущей силы следующее:
- I = (φa – φc + E) / R = (Uac + E) / R;
- I = (φa – φc – E) / R = (Uac – E) / R;
- I = E /(R+ r), где
- Е – показатели электродвижущей силы.
Электрический ток в этом случае представляет собой алгебраическую сумму, полученную при сложении показателей напряжения на зажимах с показателями электродвижущей силы, разделенной на показатели сопротивления.
Правило, касающееся наличия одного ЭДС гласит: наличие постоянного тока предполагает поддерживание неизменной разности потенциалов на концах электрической цепи посредством стандартного источника тока.
Внутри источника электрического тока положительный заряд переносится в сторону большего потенциала с разделением зарядов на положительные и отрицательно заряженные частицы.
Закон Ома для участка цепи без ЭДС
Нужно учитывать, что для участка цепи, не содержащего источника электродвижущей силы, устанавливается связь, возникающая между электрическим током и показателями напряжения на данном участке.
I = Е / R
Согласно данной формуле, сила тока имеет прямую пропорциональность напряжению на концах участка электрической цепи и обратную пропорциональность показателям сопротивления на этом участке.
Источник электродвижущей силы
Благодаря внешним характеристикам ЭДС определяется степень зависимости показателей напряжения на зажимах источника и величины нагрузки.
Например, U= E-R0 х I, в соответствии с двумя точками: I=0 E=U и U=0 E=R0I.
Идеальный источник электродвижущей силы: R0=0, U=E. В этом случае величина нагрузки не оказывает воздействия на показатели напряжения.
В этом случае величина нагрузки не оказывает воздействия на показатели напряжения.
Эмпирический физический закон Ома для полной цепи определяет два следствия:
- В условиях r < < R, показатели силы тока в электрической цепи являются обратно пропорциональными показателям сопротивления. В некоторых случаях источник может являться источником напряжения.
- В условиях r > > R, свойства внешней электрической цепи или величина нагрузки не оказывают влияния на показатели сила тока, а источник может назваться источником тока.
Электродвижущая сила, находящаяся в условиях замкнутой цепи с электрическим током, чаще всего равна: Е = Ir + IR = U(r) + U(R)
Таким образом, ЭДС можно определить, как скалярную физическую величину, отражающую воздействие сторонних сил неэлектрического происхождения.
Принятые единицы измерения
К основным, общепринятым единицам измерения, которые используются при выполнении любых расчётов, касающихся закона Ома, относятся:
- отражение показателей напряжения в вольтах;
- отражение показателей тока в амперах;
- отражение показателей сопротивления в омах.

Любые другие величины перед тем, как приступить к расчётам, необходимо в обязательном порядке перевести в общепринятые.
Важно помнить, что физический закон Ома не соблюдается в следующих случаях:
- высокие частоты, сопровождающиеся значительной скоростью изменений электрического поля;
- при сверхпроводимости в условиях низкотемпературных режимов;
- в лампах накаливания, что обусловлено ощутимым нагревом проводника и отсутствием линейности напряжения;
- при наличии пробоя, вызванного воздействием на проводник или диэлектрик напряжения с высокими показателями;
- внутри вакуумных источников света и электронных ламп, заполненных газовыми смесями, включая люминесцентные осветительные приборы.
Такое же правило распространяется на гетерогенные полупроводники и полупроводниковые приборы, характеризующиеся наличием p/n-переходов, включая диодные и транзисторные элементы.
Чем точнее счетчик измеряет затраченную электроэнергию, тем лучше. Класс точности электросчетчика отражает возможную погрешность прибора учета.
Класс точности электросчетчика отражает возможную погрешность прибора учета.
О такой величине как коэффициент трансформации счетчика электроэнергии, поговорим в этом материале.
Видео на тему
Электрический ток. Закон Ома для участка цепи. Виды соединения проводников.
Электрический ток – упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.За направление тока выбрано направление движения положительно заряженных частиц.
Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.
Пусть цилиндрический проводник имеет поперечное сечение
площадью S. За положительное направление в проводнике примем направление
слева направо. Заряд каждой частицы будем считать равным q0.
Измеряют силу тока амперметрами. Принцип устройства этих приборов основан на магнитном действии тока.
Скорость упорядоченного движения электронов в проводнике. Найдем скорость упорядоченного перемещения электронов в металлическом проводнике. Согласно формуле v = I /enS, где е – модуль заряда электрона. Пусть, например, сила тока I = 1 A, а площадь поперечного сечения проводника S = 10-6 м2. Модуль заряда электрона е = 1,6•10-19 Кл. Число электронов в 1 м3 меди равно числу атомов в этом объеме, так как один из валентных электронов каждого атома меди коллективизирован и является свободным. Это число есть n = 8,5•1028 м3. Следовательно,
Очевидно, что скорость упорядоченного перемещения электронов очень мала.Основная количественная характеристика электрического тока – сила тока. Она определяется электрическим зарядом, переносимым через поперечное сечение проводника за единицу времени. Скорость заряженных частиц (электронов) в проводнике очень мала – около 0,1 мм/с.
Условия существования постоянного электрического тока.
Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Источник тока – устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например, в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах – при действия света на электроны в металлах и полупроводниках.
Закон Ома для участка цепи.
Немецкий ученый Георг Ом в 1827 г. связал воедино три физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
I=U/R,
где I – сила
тока, U – напряжение, R – сопротивление.
Последовательное и параллельное соединение проводников.
Электрическая цепь включает в себя источника тока и проводники (потребители, резисторы и др), которые могут соединятся последовательно или параллельно.
Смешанное соединение – комбинация параллельного и последовательного соединений.
Закон Ома для активного и пассивного участка линейной электрической цепи
Закон Ома для пассивного участка электрической цепи.
При протекании электрического тока через сопротивление R, напряжение U и ток I на этом участке связаны между собою согласно закону Ома:
Сопротивление R – это коэффициент пропорциональности между током и напряжением. Чтобы найти сопротивление, нужно напряжение на участке электрической цепи разделить на ток, протекающий на этом же участке.
Закон Ома можно записать через разность потенциалов:
Закон Ома для активного участка электрической цепи.
Закон Ома для активного участка цепи между точками а и в имеет вид:
Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.
Пример составления уравнения по закону Ома
Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.
Пусть в данной электрической цепи направление тока будет из точки “a” в точку “b”. Напряжение Uab Направляется всегда из первой буквы (“a”) к последней (“b”).
Согласно правилу составления уравнения по закону Ома источник ЭДС E1 берем со знаком “плюс”, т.к. его направление (направление стрелочки) совпадает с направлением протекающего тока.
Источник ЭДС E2 берем со знаком “минус”, т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.
Напряжение Uab или разность потенциалов φa – φb берем со знаком “плюс”, т.к. его направление совпадает с направление протекающего тока.
Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.
В результате составленное уравнение по закону Ома будет иметь вид:
Пусть потенциал в данной задаче потенциал точки “а” равен 10 вольт, потенциал точки “b” = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:
Полученный ток равен 1 Ампер.
Закон ома устанавливает. Самый главный закон электротехники
Зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока . То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток , в свою очередь – это упорядоченное движение частиц под действием электрического поля .
Зависимость силы тока и напряжения
Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением . Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.
И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.
Связь с сопротивлением
Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току . Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Формула закона Ома для участка цепи
Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
где I – сила тока,
U – напряжение,
R – сопротивление.
Применение закона Ома
Закон Ома – один из основополагающих законов физики . Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
U=IR и R=U/I
Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.
Если изолированный проводник поместить в электрическое поле \(\overrightarrow{E} \), то на свободные заряды \(q\) в проводнике будет действовать сила \(\overrightarrow{F} = q\overrightarrow{E}\) В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю.
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда.
Направленное движение заряженных частиц называется электрическим током.
За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока \(I\) – скалярная физическая величина, равная отношению заряда \(\Delta q\), переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени \(\Delta t\), к этому интервалу времени:
$$I = \frac{\Delta q}{\Delta t} $$
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным .
В Международной системе единиц СИ сила тока измеряется в Амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током.
Постоянный электрический ток может быть создан только в замкнутой цепи , в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения . Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы \(A_{ст}\) сторонних сил при перемещении заряда \(q\) от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
$$ЭДС=\varepsilon=\frac{A_{ст}}{q}. $$
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в Вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными . Участки, включающие источники тока, называются неоднородными .
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов \(\Delta \phi_{12} = \phi_{1} – \phi_{2}\) между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе \(\mathcal{E}\), действующей на данном участке. Поэтому полная работа равна
$$U_{12} = \phi_{1} – \phi_{2} + \mathcal{E}$$
Величину U 12 принято называть напряжением на участке цепи 1-2. В случае однородного участка напряжение равно разности потенциалов:
$$U_{12} = \phi_{1} – \phi_{2}$$
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока \(I\), текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению \(U\) на концах проводника:
$$I = \frac{1}{R} U; \: U = IR$$
где \(R\) = const.
Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит Ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока \(I\) от напряжения \(U\) (такие графики называются вольт-амперными характеристиками , сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
$$IR = U_{12} = \phi_{1} – \phi_{2} + \mathcal{E} = \Delta \phi_{12} + \mathcal{E}$$
$$\color{blue}{I = \frac{U}{R}}$$
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи .
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd ) является однородным.
Рисунок 1.8.2. Цепь постоянного тока |
По закону Ома
$$IR = \Delta\phi_{cd}$$
Участок (ab ) содержит источник тока с ЭДС, равной \(\mathcal{E}\).
По закону Ома для неоднородного участка,
$$Ir = \Delta \phi_{ab} + \mathcal{E}$$
Сложив оба равенства, получим:
$$I(R+r) = \Delta\phi_{cd} + \Delta \phi_{ab} + \mathcal{E}$$
Но \(\Delta\phi_{cd} = \Delta \phi_{ba} = -\Delta \phi_{ab}\).
$$\color{blue}{I=\frac{\mathcal{E}}{R + r}}$$
Эта формула выражает закон Ома для полной цепи : сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи (внутреннего сопротивления источника).
Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока . В этом случае участок (ab ) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (\(R\ \ll r\)), тогда в цепи потечет ток короткого замыкания
$$I_{кз}=\frac{\mathcal{E}}{r}$$
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой \(\mathcal{E}\) и внутренним сопротивлением \(r\). У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то \(\Delta \phi_{ba} = -\Delta \phi_{ab} = \mathcal{E}\), т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I , разность потенциалов на ее полюсах становится равной
$$\Delta \phi_{ba} = \mathcal{E} – Ir$$
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной \(\mathcal{E}\) и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность \(\overrightarrow{E}\) электрического поля внутри батареи и силы, действующие на положительные заряды:\(\overrightarrow{F}_{э}\) – электрическая сила и \(\overrightarrow{F}_{ст}\) – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры .
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением \(R_{В}\). Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
$$R_{В} \gg R_{1}$$
Это условие означает, что ток \(I_{В} = \Delta \phi_{cd} / R_{В}\), протекающий через вольтметр, много меньше тока \(I = \Delta \phi_{cd} / R_{1}\), который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением \(R_{А}\). В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
$$R_{А} \ll (r + R_{1} + R{2})$$
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Закон Ома для переменного тока
При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера.
Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться:
- Когда сеть обладает высокой частотой, электромагнитное поле меняется с большой скоростью, и при расчетах необходимо учитывать инертность носителей заряда;
- В условиях низкой температуры с веществами, которые обладают сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- При нахождении под высоким напряжением проводника или диэлектрика;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.
В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности.
Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности.
Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным.
Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют .
Закон Ома является основным законом, который используют при расчетах цепей постоянного тока. Он является фундаментальным и может применяться для любых физических систем, где есть потоки частиц и поля, преодолевается сопротивление.
Законы или правила Кирхгофа являются приложением к закону Ома, используемым для расчета сложных электрических цепей постоянного тока.
Закон Ома
Обобщенный закон Ома для неоднородного участка цепи (участка цепи, содержащего источник ЭДС) имеет вид:
Разность потенциалов на концах участка цепи; – ЭДС источника на рассматриваемом участке цепи; R – внешнее сопротивление цепи; r – внутреннее сопротивление источника ЭДС. Если цепь разомкнута, значит, тока в ней нет (), то из (2) получим:
ЭДС, действующая в незамкнутой цепи, равна разности потенциалов на ее концах. Получается, для нахождения ЭДС источника следует измерить разность потенциалов на его клеммах при незамкнутой цепи.
Закон Ома для замкнутой цепи записывают как:
Величину иногда называют полным сопротивлением цепи. Формула (2) показывает, что электродвижущая сила источника тока, деленная на полное сопротивление равна силе тока в цепи.
Закон Кирхгофа
Пусть имеется произвольная разветвленная сеть проводников. В отдельных участках включены разнообразные источники тока. ЭДС источников постоянны и будем считать известными. При этом токи во всех участках цепи и разности потенциалов на них можно вычислить при помощи закона Ома и закона сохранения заряда.
Для упрощения решения задач по расчетам разветвлённых электрических цепей, имеющих несколько замкнутых контуров, несколько источников ЭДС, используют законы (или правила) Кирхгофа. Правила Кирхгофа служат для того, чтобы составить систему уравнений, из которой находят силы тока в элементах сложной разветвленной цепи.
Первый закон Кирхгофа
Сумма токов в узле цепи с учетом их знаков равна нулю:
Первое правило Кирхгофа является следствием закона сохранения электрического заряда. Алгебраическая сумма токов, сходящихся в любом узле цепи – это заряд, который приходит в узел за единицу времени.
При составлении уравнение используя законы Кирхгофа важно учитывать знаки с которыми силы токов входят в эти уравнения. Следует считать, что токи, идущие к точке разветвления, и исходящие от разветвления имеют противоположные знаки. При этом нужно для себя определить какое направление (к узлу или от узла) считать положительным.
Второй закон Кирхгофа
Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:
Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю. Величину называют падением напряжения, которое вызывается током.
Второй закон Кирхгофа иногда формулируют следующим образом:
Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.
Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника. Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).
Примеры решения задач
ПРИМЕР 1
| Задание | Вольтметр включили последовательно в цепь с сопротивлением, равным , при этом прибор показал напряжение . Сопротивление заменили на . При этом показания вольтметра изменились, и напряжение на вольтметре стало . Каково сопротивление , если сопротивление вольтметра равно r? |
| Решение | По закону Ома сила тока, которая течет через вольтметр и сопротивление равна (в первом случае рис.1(а)): Во втором случае: Сила тока в любом месте цепи рис.1(а) равна , следовательно, напряжение, которое показывает вольтметр в первом случае равно: Из (1.3), получим: Во втором случае, имеем: Приравняем левые части выражений (1.4) и (1.5): Из формулы (1.6), выразим искомое сопротивление: |
Реферат
Закон Ома. История открытия. Различные виды закона Ома.
1. Общий вид закона Ома.
2. История открытия закона Ома, краткая биография ученого.
3. Виды законов Ома.
Закон Ома устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксированными точками (сечениями) этого проводника:
(1) Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания “Наиболее оптимальный вариант преподавания геометрии в подготовительных классах”. Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием “Предварительное сообщение о законе, по которому металлы проводят контактное электричество”. Статья была опубликована в 1825 году в “Журнале физики и химии”, издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья “Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера”, вышедшая в 1826 году в “Журнале физики и химии”.
В мае 1827 года “Теоретические исследования электрических цепей” объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: “Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение”.
В 1829 году появляется его статья “Экспериментальное исследование работы электромагнитного мультипликатора”, в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома “Попытка создания приближенной теории униполярной проводимости”.
Только в 1841 году работа Ома была переведена на английский язык, в 1847 году – на итальянский, в 1860 году – на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления – 1 Ом.
В общем случае зависимость между I и U нелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.
Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:
(2) – ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид: (3) – полное сопротивление цепи, равное сумме внешнего сопротивления r и внутреннего сопротивления источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность тока j с полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённости Е , создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностью E СТ, называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равна E + E СТ . Соответственно, дифференциальный закон Ома имеет вид:
или , (4) – удельное сопротивление материала проводника, а – его удельная электропроводность.Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов.
Основной закон Ома для участка электрической цепи
Основной закон Ома для участка электрической цепи
Шерстяных И.С. 11МБОУ «Гимназия №11 г. Ельца»
Австриевских Н.М. 11МБОУ «Гимназия №11 г. Ельца»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
В наши дни каждый школьник знаком с фундаментальным законом электрической цепи, который открыл выдающийся немецкий ученый Георг Ом. С ней обучающиеся знакомятся в курсе физики в 8 классе. Меня тоже заинтересовала эта тема. Ом установил простое на первый взгляд соотношение между электрическим током, напряжением и сопротивлением, но оно потребовало от него не только глубоких знаний, но и огромного многолетнего труда и удивительной настойчивости в достижении цели.
С предложенным учебным вариантом классических экспериментов по аргументации закона Ома для полной цепи постоянного тока все знакомы. В нашей работе мы не будем заново открывать этот закон. Мы рассмотрим опыты, которые когда-то позволили великому учёному сделать своё бессмертное открытие, и постараемся, используя современные средства, повторить его исследование. Нам важно понять, в чем же заключались сложности у Ома, и как он сумел их преодолеть.
Для существования электрического тока, то есть направленного движения зарядов, необходимо наличие электрического поля и свободных носителей зарядов.
Экспериментальное обоснование этого положения для проводников мы можем наблюдать на уроках физики или химии. Опыт для металлов и полупроводников поставить возможно всегда, на том основании, что при нормальных условиях свободные носители зарядов в них всегда есть. Наша работа освещает изучение физических явлений на более глубоком уровне, кроме того стенд для качественной проверки закона Ома поможет снять затруднения, которые возникают у учащихся при изучении данной темы и решении задач. (По результатам анкетирования см. Приложение 1). В этом и состоит актуальность нашего исследования.
Объект исследования –история создания основного закона для участка электрической цепи.
Предметом исследования выступает модель прибора для доказательства закона Ома.
Цель: исследование истории создания основного закона электрической цепи, сложностей, которые возникли у Георга Ома, и как он сумел с ними справиться.
Задачи:
1. Провести эксперименты по наблюдению физических явлений.
2. Выполнить математический расчет силы тока различными способами.
3. Проанализировать различные способы измерения.
4. Доказать взаимосвязь физических явлений, подтверждающих справедливость закона Ома на примере отдельно взятого физического оборудования (изготовленного самостоятельно с помощью знаний электротехники).
5. Научиться применять полученные знания при решении различных задач: на практике, в жизни и поделиться с этим с одноклассниками.
Гипотеза:
На самом ли деле у Георга Ома возникли сложности при установлении основного закона электрической цепи?
Методы:
– общенаучные методы: обобщение, систематизация, классификация полученных в ходе исследования данных;
– математический расчёт при изучении результатов работы измерения
– теоретические методы: проблемный анализ литературы в рамках исследуемой проблемы;
– наблюдение;
– анкетирование;
– эксперимент.
Новизна нашего исследования состоит в разработке и создании модели прибора для изучения основного закона для участка электрической цепи, что поможет повысить уровень обученности учащихся нашей школы.
Практическая значимость работы заключается в том, что изготовленный нами прибор можно применять на уроках физики, на занятиях по внеурочной деятельности, а также для создания учебных проектов.
Наша работа предполагает подробное изучение данного закона в курсе физики. Опыт, который мы приобретем, позволит проводить фронтальный эксперимент наиболее удобным способом. Более того, изучение данной темы поможет более глубоко подготовиться к выпускным экзаменам ЕГЭ и ГИА.
В своей работе мы использовали различные источники информации (научная и учебная литература, Интернет).
Опытно-экспериментальная база – МБОУ «Гимназия №11 г. Ельца» и МБУДО ДООЦ г. Ельца.
В ходе нашего эксперимент, мы сделали вывод, что Георг Ом, используя в своих опытах крутильные весы и ртутные контакты, сумел преодолеть трудности эксперимента с терм петлёй для изучения своего закона.
Оригинальность нашей работы- создание модели по схеме, интеграция предметов (физика, электротехника и математика).
Глава I. Основная часть
1. Исторические факты из жизни Георга Ома.
Георг Симон Ом родился 16 марта 1789 (хотя в ряде источников указан 1787 год) в немецком городе Эрлангене в семье потомственного слесаря; дед Ома тоже был слесарем. Отцу удалось пригласить нескольких профессоров Эрлангенского университета помочь его сыновьям овладеть основами математики, физики и философии. Это позволило Георгу блестяще окончить городскую гимназию.
После успешного окончания гимназии Георг под руководством трех профессоров Эрлангенского университета стал готовиться к поступлению в университет.
Сохранилось любопытное свидетельство профессора математики Эрлангенского университета К. Лангсдорфа, экзаменовавшего в июне 1804 г. пятнадцатилетнего Георга: «В течение пятичасовой беседы я проверил его знания по всем разделам элементарной математики, арифметики, геометрии, тригонометрии, статики и механики, а также выяснил его знания в области высшей геометрии и математического анализа. На все мои вопросы я получил быстрые и точные ответы. Почти убежден, что оба брата из этой семьи станут не менее знаменитыми, чем братья Бернулли; обладая таким усердием и имея такой талант, они обогатят науку, если найдут соответствующее внимание и поддержку». [4 ]
Весной 1805 г. Георг становится студентом философского факультета и с увлечением продолжает занятия математикой, физикой и философией.
Но путь сына потомственного слесаря к званию доктора философии был нелегким. Из-за материальных трудностей Георг через год покинул университет и стал учителем физики и математики вначале в одной из швейцарских школ. При этом он продолжал самостоятельно готовиться к завершению высшего образования. В 1811 г. он возвращается в Эрланген, чтобы успешно закoнчить университет и получить степень доктора философии.
Через несколько лет Георг становится учителем в Иезуитской коллегии г. Кельна, где была хорошо оборудованная физическая лаборатория, и Ом получил возможность серьезно заняться экспериментами в области электромагнетизма, так как его педагогическая нагрузка была небольшая (18 часов в неделю). Все свободное время он проводит в лаборатории, ремонтируя старые и создавая новые приборы.
В те годы, как и многие молодые ученые, Ома привлекают электротехнические и магнитные явления. В 1812 г. Ом писал отцу, что продолжает штудировать классические труды Лапласа, Лежандра, Лагранжа, и все свое время отдает «изучению недавно открытого явления электромагнетизма». Чутье исследователя улавливает важную проблему в интересующей его отрасли знаний, разрешению которой он мог бы себя посвятить. Проблема гальванического тока была в то время наименее разработана.
В двадцатые годы 19 века электрические токи в проводниках были уже были известны, существовали источники тока, а именно, батареи гальванических элементов. Датский физик Ханс Кристиан Эрстед пришел к выводу, что электрический ток оказывает воздействие на стрелку компаса. Но физики почти не имели представление о том, что собой представляет этот ток, как его измерять, от чего он зависит. В то время не было не только никаких измерительных приборов, но даже еще и необходимой терминологии.
Георг Ом пришел к выводу, что первым делом нужно научиться количественно исследовать физическое явление. Для измерения тока уже раньше пытались использовать тот факт, что он вызывает нагревание проводника. Однако Г. Ом избрал для измерения тока не тепловое, а именно его магнитное действие, открытое Эрстедом. В приборе Ома ток, протекавший по проводнику, вызывал поворот магнитной стрелки, подвешенной на упругой расплющенной золотой проволочке. Экспериментатор, поворачивая микрометрический винт, к которому крепился верхний конец проволочки, добивался компенсации поворота, вызванного магнитным воздействием, и угол поворота этого винта и являлся мерилом тока.
Поначалу Ом использовал гальванические источники тока, но затем он обнаружил, что они создают ток, быстро убывающий со временем. Это обстоятельство даже явилось причиной неточностей в первой из публикаций Ома. Он нашел выход из этого положения, перейдя к использованию открытого Томасом Иоганном Зеебеком явления — возникновение тока в цепи из двух различных проводов, если спаи между ними имеют различные температуры. Ом в качестве источника тока использовал термоэлемент из висмута и из меди, один из спаев которых находился в кипящей воде, а другой — в тающем снеге.
2. Начало экспериментальной деятельности Ома
Опыты на уроках физики, в которых измеряются сила тока и напряжение при различных значениях сопротивления проводника, на первый взгляд, показывают, что действительно что сила электрического тока через проводник прямо пропорциональна напряжению на нём и обратно пропорциональна сопротивлению проводника. При этом в этих опытах используются амперметр и вольтметр, отградуированные фактически один по-другому в полном соответствии с законом Ома, в связи с этим такие опыты вряд ли можно признать доказательными.
Таким образом, Ом, исследуя в 1825-1827 годах прохождение электрического тока в цепи, пытался выявить количественные закономерности, которые характеризовали это явление. В те далёкие времена привычные нам понятия силы тока, напряжения, электродвижущей силы, сопротивления ещё только зарождались или вообще отсутствовали. Не было никаких электроизмерительных приборов. Учёные подсознательно ощущали необходимость количественных измерений в электрических цепях. Но как это провести, если неизвестно, что именно нужно измерять и как именно это следует сделать?!
Ом в первую очередь понял, что силу электрического тока нужно определять по его магнитному действию. Он составил замкнутую цепь из батареи гальванических элементов и двух различных проводников, которые по-разному разогревались проходящим по ним током. Помещая над этими проводниками магнитную стрелку, Ом убедился, что она отклоняется на одинаковые утлы, несмотря на различное тепловое действие тока (рис. 1). Так учёный получил надёжный измеритель силы тока. Включая в цепь металлические провода одного диаметра, но различной длины, он определял, как меняется при этом сила тока.
Несмотря на правильность общей методики эксперимента, на внимательное отношение к деталям опыта, на точность установки, Ому не удалось решить поставленную им задачу. Полученные им результаты, как уже указывалось, были неточными. Первые опубликованные им выводы были ошибочны: в экспериментах не удалось сразу установить правильный закон. Основной причиной этого явилось использование гальванического источника тока с большим внутренним сопротивлением, ЭДС которого быстро изменялась с течением времени и сильно зависела от включаемой нагрузки. Поэтому в последующих опытах Ом использовал в качестве источника тока термоэлемент.
а)
б)
Рис. 1. Магнитное действие тока на стрелку одинаково, независимо от теплового действия: последовательно соединены друг с другом многожильный медный провод в белой изоляции и нихромовый провод; а – источник питания выключен, б – по цепи идёт ток силой около 5 А.
3. Магнитное поле термоэлектрического тока
За несколько лет до исследований Ома, а именно, в 1821 году, немецкий физик Т. Зеебек открывает явление термоэлектричества. Он проводит детальное исследование этого явления, в результате чего приходит к неверному выводу, что разность температур в разнородных проводниках, соединённых между собой, приводит к выделению свободного магнетизма. Проще всего понять открытие и заблуждение Зеебека, если повторить его опыт.
Для этого потребуются медный и константановый проводники (константановый можно взять от старого реостата в школьном физическом кабинете). Чтобы убедиться, что вы имеете дело именно c константаном, измерьте мультиметром сопротивление «подозрительного» провода длиной oколo 2 м и затем сопоставьте получившееся значение с вычисленным по хорошо известной вам формуле
(1)
где р – удельное сoпротивление, I – длина и S – площадь поперечного сечения проводника. Напомним, чтo удельные сопротивления константана и меди соответственно равны:
Далее изготавливаем терм петлю. Предположим, что имеется константановый провод диаметром 0,9 мм. Тогда сделайте 6 одинаковых отрезков этого провода длиной по 20 см и концы каждого из них (длиной примерно по 2 см), тщательно очистите от слоя оксида (для этого можно использовать острый нож). Затем, используя канифоль или иной флюс, об лудите зачищенные концы проводов оловом или оловянно-свинцовым припоем. От медного провода диаметром 0,7 мм необходимо отрезать кусок длиной 30 см и, очистить от изоляции концы длиной по 5 см, затем тоже об лудить их.
Концами медного провода необходимо обмотать концы сложенных в пучок отрезков константанового провода (плотно виток к витку). Места скруток пропаять, в качестве флюса используя канифоль. Oписанный ниже опыт можно повторить, даже если зачищенные концы проводов просто плотно скрутить между собой.
Медному проводу необходимо придать 11- образную форму, зажать один из спаев в лапке штатива так, чтобы получившаяся терм петля расположилась горизонтально и медный провод оказался над константановыми. Между ними на пучок константановых проводов поместить компас. Магнитная стрелка компаса установится вдоль направления горизонтальной составляющей магнитного поля Земли. Затем, необходимо развернуть штатив так, чтобы терм петля оказалась параллельной стрелке компаса.
Спиртовкой или газовой зажигалкой нагреваем незакреплённый спай терм петли. По мере роста его температуры стрелка компаса отклоняется, максимальный угол отклонения её может достигнуть 50-80° (рис. 2).
Таким образом, нагревая один из спаев терм петли, возникает магнитное поле, которое отклоняет стрелку компаса. Вот почему Зеебек сделал вывод, что имеет дело с терм магнетизмом! В действительности же, конечно, нагревание спая приводит к появлению термоэлектрического тока, а уже проходящий по замкнутой цепи ток создаёт магнитное поле.
Рис. 2. Наблюдение магнитного действия термоэлектрического тока
4. Экспериментальная установка Ома.
Ом усовершенствовал «весы» Кулона, создав новый совершенно оригинальный электроизмерительный прибор. Зная об отклонении магнитной стрелки электрическим током, открытым в 1819 году датским физиком Эрстедом, Ом вместо коромысла с бузиновым шариком подвешивал над проводником магнитную стрелку и по углу ее отклонения определял магнитное действие электрического тока от термоэлемента с парой металлов «медь – висмут». [5]
Электрическая схема и внешний вид экспериментальной установки, созданной Омом, можно наблюдать на рис. 3. [5]
Рис. 3. Экспериментальная установка Георга Ома
Верхняя цилиндрическая часть прибора Ома представляет собой детектор тока — крутильные весы, ab и, а’b’ — термоэлементы, изготовленные из двух медных проволок, припаянных к поперечному стержню из висмута; m и m’ — чашечки со ртутью, к которой можно было подключать термоэлементы. К чашечкам подсоединялся проводник, концы которого каждый раз зачищались перед тем, как погружались в ртуть.
Ом отдавал себе отчет в важном значении чистоты материалов. Ом держал спай, а в кипящей воде, а спай, а’ опускал в смесь льда с водой и наблюдал отклонение гальванометра.
Когда по цепи проходил электрический ток, магнитная стрелка отклонялась, вращением головки крутильных весов Ом возвращал её в исходное положение и по углу поворота головки определял силу тока в цепи.
Всю систему, изготовленную Омом, историки физики справедливо назвали «первым прибором для электрических измерений». [5]
По аналогии с формулой Фурье для теплового потока Ом находит формулу для электрического тока:
где S — сила тока (его магнитное действие), а выражение в знаменателе Ом назвал «приведенной длиной», где Δх — длина проводника; ω — площадь его поперечного сечения, а р — удельное сопротивление, характеризующее материал проводника.
К сожалению, ученый мир Западной Европы вначале не оценил важности открытия малоизвестного учителя гимназии, к тому же, подтверждение этого закона экспериментально обязывало создания уникальной измерительной установки, которая была бы только у Ома. Надеждам Ома не суждено было сбыться еще и потому, что в те годы в Германии господствовала натурфилософия, отвергавшая математические методы анализа экспериментальных данных. Ученые из крупнейших европейских университетов не очень доверяли малоизвестному учителю гимназии. Фарадей и Генри, выдающиеся физики-экспериментаторы того времени, не владели немецким языком и узнали об открытии Ома с опозданием, о чем до крайности сожалели. [6]
Глава II. Экспериментальная часть
1. Что нужно, чтобы доказать закон Ома?
Мы не будем делать подобную установку, а воспользуемся только идеей эксперимента.
Конечно же, можно разорвать медный проводник в терм петле, изображённой на рис. 2, и в разрыв включать проводники разного сопротивления.
В самом деле, терм петля в опыте расположена так, что её магнитное поле возле стрелки направлено перпендикулярно горизонтальной составляющей магнитного поля Земли. Стрелка отклоняется, показывая направление результирующего поля.
Для одного проводника петли ситуация изображена на рис. 4:
Во – горизонтальная составляющая индукции магнитного поля Земли
В1 – индукция магнитного поля на расстоянии г от прямого проводника с током I, модуль которой, как известно, равен
Как видно из рисунка, В1 =В0 tg α, где α – угол отклонения стрелки из первоначального положения, параллельного проводнику. Отсюда сила тока в проводнике
Рис. 4. К опыту по отклонению магнитной стрелки в магнитном поле тока в прямом проводнике
Терм петля состоит из двух параллельных проводников, по которым один и тот же ток идёт в противоположных направлениях. По правилу правого винта определяем, что поля, создаваемые этим током, в промежутке между проводниками складываются. Поэтому стрелка отклонится на тот же угол, а при силе тока в терм петле в два раза меньшей, чем в одиночном проводнике:
В условиях эксперимента все величины этой формулы, кроме угла α, будут неизменны.
Из этого следует, ток в терм петле пропорционален тангенсу угла отклонения стрелки компаса от магнитного меридиана:
(2)
Этот факт позволяет простым способом измерить силу тока.
Мы пробовали ставить опыт в соответствии с рассмотренной идеей. Результаты нас не удовлетворили, хотя ток оказался обратно пропорционален сопротивлению. В проведенном нами опыте внутреннее сопротивление источника не совпадало с расчётным. Мы посчитали, что всё дело в неоднородности магнитного поля, созданного терм петлёй: при сравнительно больших токах стрелка, отклоняется на значительные углы и попадает в более слабое поле. Поэтому она отклоняется меньше, чем могла бы отклониться, если бы поле было однородным. Без сомнения, чем больше ток, тем ощутимее эта ошибка, из-за того, что при малом токе стрелка выходит из терм петли не так существенно. Следовательно, большие значения силы тока оказываются более заниженными. Кроме того, установилось, что при больших токах необходимо обеспечить хорошие контакты во всех местах соединений элементов цепи.
Таким образом, можно сделать вывод, что Ом, который использовал в своих опытах крутильные весы и ртутные контакты, сумел преодолеть эти сложности эксперимента.
2. Прибор для эксперимента
Для того, чтобы получить однороднее магнитное поле, необходимо сделать соленоид. В таком случае прибор проведения эксперимента может выглядеть следующим образом (рис. 5): из медного провода, диаметрoм 1,4 мм и длинной 1 м, изготовлена прямоугольная катушка 1 размером 12 х 40 х 40 мм, которая содержит 5 витков. Концы этого прохода очищены от изоляции, обужены. Тонкой медной облуженной проволокой виток к витку к ним плотно прикручены οблуженные концы шести отрезков константанового провода 2 диаметром 1,0 мм и длиной 20 см каждый. Места соединений спаяны оловом. Медный провод разрезан, на него надеты изолирующие хлорвиниловые трубки, участки провода с трубками скручены, и выступающие из трубок концы провода 3 тщательно очищены от изоляции. С этими полюсами терм источника соединяются исследуемые проводники 4 различной длины. Катушка 1 несколькими витками изоленты прочно закреплена на подставке 5 из изолятора. Внутрь катушки введён компас 6. В качестве исследуемых проводников используются отрезки медного провода в лаковой изоляции диаметром 0,3-0,5 мм, имеющие, например, такие длины: 25, 50, 75 и 100 см. Их сворачиваем в колечки 7.
Изготовив прибор, располагаем его так, чтобы ось катушки оказалась перпендикулярна стрелке компаса, и поворачиваем корпус компаса так, чтобы один из концов стрелки указывал на нуль шкалы. Убедимся, что рядом с прибором нет ферримагнитных предметов, влияющих на направление магнитной стрелки.
Соединив разомкнутые полюса источника, плотно скрутив их медным проводом без изоляции, и нагрев один из спаев термопары в пламени спиртовки, мы проверяем, (если при этом стрелка отклонится на угол порядка 80° и будет устойчиво находиться в этом положении, то изготовленный нами прибор готов к работе).
Рис. 5. Прибор для экспериментального обоснования закона Ома
3. Экспериментальное обоснование закона Ома
Сохранив пламеня спиртовки, разомкнём полюса термоэлектрического источника и подсоединим к ним один из заготовленных нами проводов. Записав угол отклонения стрелки, вместо первого подсоединим второй провод и т. д. В опытах для медного провода диаметром 0,425 мм мы получили результаты, приведённые в первой и второй строках табл. 1. В третьей строке даны сοοтветствующие значения тангенса угла, а отклонения стрелки компаса, пропорциональные согласно формуле (2) силе тока в цепи.
Таблица 1
|
X, см |
0 |
25 |
50 |
75 |
100 |
|
α |
78 |
71 |
60 |
55 |
48 |
|
tgα |
4,70 |
2,90 |
1,73 |
1,43 |
1,11 |
|
ctgα |
0,21 |
0,34 |
0,58 |
0,70 |
0,90 |
Строим график зависимости силы тока I (в экзотических единицах tgα) от длины провода х, получаем кривую, подобную той, которая изображена на рис. 6 а и построена по данным табл. 1. Данная кривая напоминает гиперболу, ее уравнение можно записать соответственно
(3)
если принять во внимание, что гипербола может быть растянута или сжата в а раз по вертикали и смещена на величину b по горизонтали.
Предположим, что зависимость силы тока I от длины провода L, представленная графически на рис. 6 а, можно выразить аналитически формулой
(з)
Рис. 6 а. Графическое представление закона Ома. Зависимость силы тока от длины провода внешне напоминает ветвь гиперболы
Как доказать справедливость этой формулы, если величины, а и b неизвестны?
Построим график, глядя на который, можно сказать, какой именно является выраженная им зависимость. Подобным графикам, который мы сразу узнаем, является только прямая линия. Поэтому, нужно из зависимости (3) получить линейную зависимость. Сделать это можно не сложно: достаточно вместо тока I взять в качестве функции величину, обратную току:
(4)
Рис. 6 б. Графическое представление закона Ома. Зависимость величины, обратно пропорциональной силе тока, от длины проводника линейна.
В таблице 1 содержится четвёртая строка, в которой приведены значения величины, обратной силе тока 1/I, в единицах ctg α. Если построить график зависимости1/I – от длины х проводника, то получим прямую линию (рис. 6 б)! Это значит, что и формула (4), и формула (3) достоверны. Теперь выясним физический смысл констант, входящих в них.
Очевидно, что величина b имеет тот же смысл, что и х, так как в знаменателе формулы (3) стоит сумма этих величин. Опыт доказал, чем больше длина провода х, тем меньше сила тока I, текущего по цепи (см. табл. 1), откуда следует, длина провода характеризует сопротивление цепи, подключаемой к терм источнику. Но в тоже время, от опыта к опыту величина b оставалась постоянной, из этого следует, она является сопротивлением той части цепи, которая не изменялась в опытах.
Итак, можно считать, что b – это внутреннее сопротивление источника, а х – сопротивление внешней цепи. Обозначим их привычными буквами b = г и x = R.
Более того, опыт доказывает, что ток в цепи тем больше, чем больше разность температур спаев термопары: пока один из спаев терм источника нагревался, магнитная стрелка отклонялась всё сильнее. Таким образом, величина, а в формуле характеризует способность самого источника создавать в цепи электрический ток.
Этим экспериментом мы доказали справедливость закона Ома.
Без сомнения, возможны всякого рода варианты учебных опытов, которые бы подтверждали закон Ома. Однако в их числе одно из почётных мест необходимо отвести эксперименту, поставленному в соответствии с идеей, прославившей имя Георга Симона Ома.
Другого рода исследовательскую работу по применению закона Ома для участка цепи можно выполнить, если изготовить специальный стенд по схеме, рис.1.
В Детском оздоровительно-образовательном центре города Ельца в объединении радио конструирования под руководством педагога дополнительного образования Поваляева Бориса Алексеевича разработан и изготовлен стенд.
Он состоит из стабилизатора-регулятора напряжения, выполненного на стабилитроне D1 и транзистора средней мощности Q1. Стабилитрон D1 и резистор R1 в комплексе являются элементами задающего параметрического стабилизатора. Стабилитрон D1(КС 168А) рассчитан на стабилизацию напряжения 6,8 В, дополнительный (балластный) резистор R1 75 Ом – на ограничение тока в цепи стабилитрона 35-40 мА. В связи с тем, что стабилитрон КС 168А (по справочнику) имеет напряжение стабилизации от 6,2 В до 7,2 В, резистор R1 подбирается по номиналу сопротивления. Параллельно стабилитрону устанавливается переменный резистор R2, с которого регулируемое напряжение подаётся на усилитель постоянного тока, выполненный на транзисторе VТ1. От возможного возбуждения, а также компенсации малого тока утечки транзистора в схему введены конденсатор C2 и резистор R5. Далее регулируемое напряжение подаётся на тумблеры S1 и S3, S4. Тумблером S3 можно замыкать и размыкать цепь подачи напряжения на нагрузку (R7, LS1, D2, L2). Тумблерами S1, S4 – переключать нагрузки. Тумблер S2 отвечает за включение и выключение стенда. В схеме предусмотрены штыревые разъемные соединения для подключения измерительных приборов: вольтметра и миллиамперметра. (двух мульти метров) Питается стенд от двух батарей 4,5 В типа КБС, соединённых последовательно.
Конструкция.
Конструктивно стенд изготовлен в виде прямоугольной деревянной платформы, на которой установлены батареи питания и печатная плата со всеми радиоэлементами схемы, за исключением измерительных приборов, которые подключаются отдельно к плате с помощью проводов. Транзистор VТ1 установлен на алюминиевом радиаторе площадью 32см2.
Радиоэлементы:
Резисторы: R1, R3-R8 – МЛТ
R2- СПЗ-4АМ, 5 кОм
Конденсатор: C2- К10-17, 0,47 мкФ
Стабилитрон: D1- КС 168А
D2- КС 139А
Светодиод: L1- АЛ 336
L2- АЛ 336
Транзистор: VТ1- КТ 817Б (КТ 815Б)
Лампа накаливания миниатюрная: LS1- МН6,3V-0,3А(МН6,5V-0,34А)
Тумблеры: S1-S4 – ТП1-2
Измерительные приборы:
Вольтметр постоянного напряжения 0-10V, кл 1,5
Миллиамперметр постоянного тока – 0-500мА, кл 1,5
Возможно пользоваться двумя мульти метрами.
Исследовательская работа.
Приборы
1. Мульти метр DM 90 (возможны и другие)
2.Стенд специальный-1
Порядок выполнения работы.
Проверим функционирование стенда.
Поместим стенд на лабораторный стол. Тумблер S3 переведем в положение «вкл», тумблеры S1 и S4- в положение II, регулятор напряжения R2 ручкой выведем в крайнее левое положение на 0 В. Включим тумблер S2 (положение «вкл»). Загоревшийся светодиод сообщит о подаче напряжения питания на схему. Вращая ручку регулятора напряжения R2 вправо, увеличиваем постепенно напряжение на лампочке. При исправном стенде лампочка тоже будет увеличивать яркость постепенно. При вращении ручки влево- свечение будет уменьшаться. Стенд исправен и готов к работе.
Выключим напряжение питания тумблером S2. Установим ручку регулятора в положение 0 В. Разомкнем тумблер S3, тумблеры S1 и S4 установим в положение II. Подключим миллиамперметр параллельно S3, вольтметр подключим к общему CP резистора к стенду. Включим тумблером S2 питание. Регулятором напряжения с помощью вольтметра установим на сопротивление нагрузки R7 с линейной зависимостью 1В. Увеличивая напряжение на 1 вольт, дойдём до конечного 6 В. Полученные данные занесём в таблицу 1.
Табл.1 Зависимость силы тока и сопротивления от напряжения на линейном элементе(резисторе).
|
Напряжение, В |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Сила тока, А |
0 |
16 |
33 |
48 |
64 |
80 |
97 |
|
Расчетное сопротивление, Ом |
62 |
62 |
62 |
62 |
62 |
62 |
R (Ом)=U(В)/I(мА)*1000
Сравним расчетное сопротивление с номиналом резистора R7, помещенным на плате. R расчетное=62 Ом R резистора=62 Ом. Они равны.
По шести контрольным точкам можно построить график зависимости тока от напряжения.
Из графика можно делаем следующий вывод: зависимость тока от напряжения на нагрузке (активном сопротивлении) линейная.
Переведем регулятор в крайнее левое положение на 0 В. Переключим тумблеры S1, S4 в положение I. Вольтметр переключим к СP лампы. Произведём измерения снова. Только в этом случае активным сопротивлением нагрузки будет миниатюрная лампочка накаливания на 6,3В, 0,3А (нагревательный световой элемент). Занесём результаты в таблицу 2.
Табл.2 Зависимость силы тока и сопротивления от напряжения на нелинейном элементе(лампе)
|
Напряжение, В |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Сила тока, А |
0 |
83 |
162 |
200 |
220 |
230 |
235 |
|
Расчетное сопротивление, Ом |
12 |
12 |
15 |
18 |
21 |
25 |
По данным таблицы можно построить следующий график.
Из графика можно сделать следующий вывод: зависимость тока от напряжения на активном сопротивлении нити накала лампочки нелинейная. Сопротивление лампочки увеличивается с увеличением напряжения, близкому к номинальному, с прогревом нити.
Переведем регулятор в крайнее левое положение на 0 В. Переключим тумблеры S1 в положение I, S4 в положение II. Вольтметр переключим к СP стабилитрона. Произведём измерения снова. В этом случае нагрузкой будет стабилитрон КС139А. Занесём результаты в таблицу 3.
Табл.3 Зависимость силы тока от напряжения на нелинейном элементе (стабилитроне)
|
Напряжение, В |
0 |
0,28 |
0,4 |
0,7 |
0,8 |
0,9 |
1,0 |
1,5 |
1,8 |
2,1 |
2,6 |
3,0 |
3,4 |
3,9 |
|
Сила тока, мА |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
|
Расчетное сопротивление, Ом |
28 |
20 |
23 |
20 |
18 |
17 |
21 |
22 |
23 |
26 |
27 |
28 |
30 |
По данным таблицы строим следующий график.
Переведем регулятор в крайнее левое положение на 0 В. Переключим тумблеры S1 в положение II, S4 в положение I. Вольтметр переключим к СP светодиода. Произведём измерения. В этом случае нагрузкой будет Светодиод L2-АЛ 336. Занесём результаты в таблицу 4.
Табл.4 Зависимость силы тока от напряжения на нелинейном элементе (светодиоде)
|
Напряжение, В |
0 |
2,6 |
2,7 |
2,7 |
2,7 |
2,75 |
2,8 |
2,82 |
2,83 |
2,84 |
2,86 |
|
Сила тока, мА |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Расчетное сопротивление, Ом |
2600 |
1350 |
900 |
675 |
550 |
400 |
400 |
353 |
315 |
286 |
Примечание:
Погрешность измерений определяется классом точности приборов.
Анкета
Цель: выявление представлений, обучающихся 8-х классов о законе Ома.
1. Как зависит сила электрического тока в проводнике от напряжения на нем и сопротивления проводника?
2. Как, зная силу электрического тока и сопротивление проводника рассчитать напряжение на проводнике?
3. В каких единицах измеряется сопротивление проводника?
4. Запишите формулу закона Ома.
5. Что может помочь усвоить физический смысл закона Ома?
а. зубрежка б. стенд
Результаты анкетирования оказались следующими:
Как видим из результатов анкетирования, далеко не у всех учащихся сформировано четкое представление о законе Ома, большинство из них посчитали, что наглядность поможет в усвоении физического смысла закона Ома. В связи с этим, я полагаю, что наша модель прибора для доказательства закона Ома поможет наглядно обучающимся усвоить этот закон.
Заключение
1. Таким образом, в рамках нашего исследования мы проследили историю создания основного закона электрической цепи.
2. В ходе исследования выяснили, какие трудности возникли у Георга Ома, и как он сумел с ними справиться.
3. Мы рассмотрели устройства для исследования закона Ома, их возможности и принцип работы.
4. В ходе исследования нами разработана и апробирована модель прибора для доказательства закона Ома.
Разработав модель и проведя эксперименты, мы более подробно изучили техническое содержание темы, более детально рассмотрели некоторые физические явления (электрический ток в металлах). Таким образом, взаимосвязь теории с практикой была доказана.
Проведённое исследование показало значимость внедрения результатов нашего исследования: ведь зная закон Ома учащиеся смогут выражать из формулы неизвестную величину и выполнять задания ОГЭ по физике и даже математике (например, модуль «Реальная математика»).
Список используемых источников:
- Дик Ю.И., Кабардин О.Ф., Орлов В.А. «Физика-10», под редакцией А.А. Пинского, Москва «Просвещение» 2010
- Журнал для старшекласников и учителей «Потенциал» №2 -2008
- Кабардин О.Ф. «Физика-8»,Москва «Просвещение» 2010
- Кошманов В. В. Георг Ом: Пособие для учащихся. — М.: Просвещение, 1980. — 112 с., ил.— (Люди науки).
- Шнейберг Я. А. История выдающихся открытий и изобретений (электротехника, электроэнергетика, радиоэлектроника). Научно-популярное издание. М.: Издательский дом МЭИ, 2009.
- Шнейберг Ян. Георг Ом. Нелегкий путь к славе. http://www.eduspb.com/public/books/byograf/om_shneyberg
- https://elektroznatok.ru/info/people/georg-simon-ohm
- https://ru.wikipedia.org
- http://slovari.yandex.ru
Просмотров работы: 172
Закон Ома
ЗаконОма показывает линейную зависимость между напряжением и током в электрической цепи.
Падение напряжения и сопротивление резистора определяют протекание постоянного тока через резистор.
Используя аналогию с потоком воды, мы можем представить электрический ток как ток воды через трубу, резистор как тонкую трубу, которая ограничивает поток воды, напряжение как разница высот воды, которая обеспечивает поток воды.
Формула закона Ома
Ток I резистора в амперах (A) равен току резистора напряжение V в вольтах (В), деленное на сопротивление R в омах (Ом):
В – падение напряжения на резисторе, измеренное в вольтах (В).В некоторых случаях в законе Ома для обозначения напряжения используется буква E . E обозначает электродвижущую силу.
I – электрический ток, протекающий через резистор, измеренный в амперах (A)
R – сопротивление резистора, измеренное в Ом (Ом)
Расчет напряжения
Зная ток и сопротивление, мы можем рассчитать напряжение.
Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):
Расчет сопротивления
Зная напряжение и ток, мы можем рассчитать сопротивление.
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (A):
Поскольку ток задается значениями напряжения и сопротивления, формула закона Ома может показать, что:
- Если увеличивать напряжение, ток увеличится.
- Если мы увеличим сопротивление, ток уменьшится.
Пример № 1
Найдите ток электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.
Решение:
В = 5 В
R = 50 Ом
I = В / R = 5 В / 50 Ом = 0,1 А = 100 мА
Пример # 2
Найдите сопротивление электрической цепи, имеющей напряжение питания 10 В и ток 5 мА.
Решение:
В = 10 В
I = 5 мА = 0,005 А
R = В / I = 10 В / 0,005 A = 2000 Ом = 2 кОм
Закон Ома для цепи переменного тока
Ток нагрузки I в амперах (A) равен напряжению нагрузки V Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ω):
В – падение напряжения на нагрузке, измеренное в вольтах (В)
I – электрический ток, измеренный в амперах (A)
Z – полное сопротивление нагрузки, измеренное в Ом (Ом)
, пример # 3
Найдите ток в цепи переменного тока с напряжением питания 110 В ± 70 ° и нагрузкой 0.5кОм∟20 °.
Решение:
В = 110 В 70 °
Z = 0,5 кОм∟20 ° = 500 Ом∟20 °
I = В / Z = 110 В 70 ° / 500 Ом 20 ° = (110 В / 500 Ом) ∟ (70 ° -20 °) = 0,22 А 50 °
Калькулятор закона Ома (краткая форма)
Калькулятор законаОма: вычисляет соотношение между напряжением, током и сопротивлением.
Введите 2 значений, чтобы получить третье значение, и нажмите кнопку Рассчитать :
Калькулятор закона Ома II ►
См. Также
ЗаконОма для простых электрических цепей, Рон Куртус
SfC Home> Физика> Электричество>
, автор: Рон Куртус (от 23 октября 2019 г.)
Закон Ома является наиболее фундаментальной формулой для простых электрических цепей .Он утверждает, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.
ЗаконОма лучше всего демонстрируется в простой электрической цепи постоянного тока. Хотя это также относится к цепям переменного тока, необходимо учитывать другие возможные переменные.
Связь между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, если вы используете значения двух других.
Вопросы, которые могут у вас возникнуть:
- Что означают параметры в уравнении?
- Какая конфигурация схемы?
- Как применить закон Ома?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Уравнение
ЗаконОма показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:
В = ИК
где:
- V – напряжение в вольтах ( V )
- I – ток в амперах или амперах ( A )
- R – сопротивление в Ом ( Ом – греческая буква Омега)
Таким образом, если вы знаете ток и сопротивление, вы можете использовать формулу для определения напряжения.
Используя алгебру, вы можете изменить порядок переменных в соответствии со своими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:
I = V / R
Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:
R = V / I
Конфигурация
Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или электрическая лампочка, соединенных последовательно с источником.Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.
Примечание : Если цепь переменного тока включает в себя такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.
Простая цепь постоянного тока
Используя уравнение
Важность закона Ома заключается в том, что, если вы знаете значение двух переменных в уравнении, вы можете определить третью. Вы можете измерить любой из параметров с помощью вольтметра.Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как переменного, так и постоянного тока.
Найти напряжение
Если вам известны ток и сопротивление, вы можете найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то
В = 0,2 А * 1000 Ом = 200 В
Найти текущий
Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток.Например, если В = 110 В и R = 22000 Ом , то
I = 110 В / 22000 Ом = 0,005 А
Найдите сопротивление
Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то
R = 220 В / 5 A = 44 Ом
Сводка
Закон Ома – это уравнение V = I R , которое показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи.Он может применяться как к цепям переменного, так и к постоянному току.
Будьте полны решимости сделать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Немного истории об Ом – Краткая история
Закон Ома – Объяснение, включая калькулятор закона Ома
Основные законы по электричеству – Включает теорию цепей
Формулы электрических цепей – Уравнения высокого уровня для решения проблем
Электроэнергетические ресурсы постоянного и переменного тока
Физические ресурсы
Книги
Научитесь электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) 34 доллара.95 – Руководство для профессионалов, любителей и техников, желающих изучить цепи переменного и постоянного тока
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
electric_ohms_law.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
По физике
Закон Ома для простых электрических цепей
Колесо закона Ома: понимание колеса электрических формул
Последнее обновление: 20 января 2021 г., 21:03.
Если вам, как электрику, нужно хорошо разбираться в чем-то одном, то это закон Ома. Эта простая формула позволяет исследовать взаимосвязь между тремя электрическими переменными: напряжением, током и сопротивлением.
Хорошо то, что это не ракетостроение. Если вы умеете умножать и делить, это будет прогулка в парке. Легкий способ понять закон Ома – использовать колесо закона Ома .
Как использовать колесо формул закона Ома
Я знаю, что вы думаете: « Это треугольник. ”Не беспокойтесь об этом, просто обратите внимание. Итак, вам нужно выяснить, сколько ампер потребляет цепь, а на нее нельзя поставить амперметр. Что вы делаете?
Просто разделите НАПРЯЖЕНИЕ на СОПРОТИВЛЕНИЕ цепи. Откуда ты это знаешь? Из-за формулы закона Ома колесо .
В колесе формул вы увидите три буквы, каждая из которых представляет собой значение.
E или V = НАПРЯЖЕНИЕ (вольт)
I = ТОК (амперы)
R = СОПРОТИВЛЕНИЕ (Ом)
Итак, если вам нужно найти напряжение, ток или сопротивление, просто поместите палец на то, что вы пытаетесь найти, а колесо формул сделает все остальное.
Колесо формулы закона Ома математически представлено тремя простыми уравнениями.
I (ток) x R (сопротивление) = E (напряжение)
E (напряжение) ÷ R (сопротивление) = I (ток)
E ( напряжение) ÷ I (ток) = R (сопротивление)
Закон Ома Пример Проблемы
Найдите сопротивление цепи. Глядя на эту схему, мы знаем значения двух компонентов: напряжения (12 В) и сопротивления (3 Ом).Как мы находим ток?
Мы вставляем известные значения в колесо формул и вычисляем уравнение.
12 вольт ÷ 3 Ом = 4 ампер
Это действительно так просто. Вот мы попробуем другой. Найдите сопротивление в цепи со следующими значениями:
Напряжение = 120 В
Ток = 17 ампер
Теперь вставьте известные значения в наше колесо формулы и работайте с уравнением.
120 вольт ÷ 17 ампер = 7,05 Ом
Я сказал вам, что это было просто. Это проще, чем установить сетевой фильтр на весь дом?
(, ладно, может быть, не так просто. Но определенно проще, чем установить сетевой фильтр на холодильник (вы просто подключаете эту чертову штуку)! )
Принцип закона Ома – пропорциональный и обратно пропорциональный
закон, с которым вам необходимо ознакомиться.
, что электрический ток (I ), протекающий в цепи, пропорционален напряжению (В ) и обратно пропорционален сопротивлению (R) .
Это означает, что при увеличении напряжения ток будет увеличиваться до тех пор, пока сопротивление не изменится . Если сопротивление увеличивается, а напряжение остается прежним, то ток уменьшается.
Увеличение сопротивления
120 вольт ÷ 5 Ом = 60 ампер
120 вольт ÷ 10 Ом = 12 ампер
120 вольт ÷ 20 Ом = 6 ампер
Следовательно, если напряжение увеличится, ток будет увеличиваться при условии, что сопротивление цепи не изменится.
Повышение напряжения
120 В ÷ 25 Ом = 4,8 А
240 В ÷ 25 Ом = 9,6 А
480 В ÷ 25 Ом = 19,2 А
Как вы можете видеть, когда мы увеличиваем напряжение и оставьте сопротивление прежним, ток увеличился (прямо пропорционален напряжению).
Круговая диаграммазакона Ома
Круговая диаграмма аналогична колесу формул напряжения, тока и сопротивления.Мощность измеряется в ваттах и определяется как:
скорость, с которой выполняется работа, когда один ампер (А) тока проходит через разность электрических потенциалов в один вольт (В)
Колесо формул с законом Ома и PIE
Вот мы уже кое-что добились. Это колесо формул представляет собой комбинацию закона Ома и формулы ПИЕ.
Это выглядит сложнее, но на самом деле им легко пользоваться (вам может понадобиться калькулятор), и он работает так же, как и предыдущие диаграммы.
Колесо формул разделено на четыре секции , каждая секция имеет три формул . Если вам нужно найти вольты, вы должны использовать секцию E, ток – секцию I, сопротивление – секцию R и мощность – секцию P.
При использовании колеса формул вам необходимо выполнить следующие действия:
- Знайте, что вы пытаетесь найти: ток (I), напряжение (E), сопротивление (R) или мощность (P).
- Какие значения вы уже знаете (вам нужно два): ток (I), напряжение (E), сопротивление (R) или мощность (P).
- Найдите часть колеса формул, в которую подставляются ваши значения.
- Решите уравнение
При проведении расчетов вы должны использовать совместимые значения. Я имею в виду, что киломы должны быть преобразованы в омы, миллиамперы должны быть преобразованы в амперы.
Независимо от того, являетесь ли вы электриком-подмастерьем или электриком-подмастерьем, изучение закона Ома является неотъемлемой частью работы электрика.
Полезные ссылки:
Закон Ома для начинающих и новичков
Закон Ома для начинающих и новичковОсновной закон Ома
HTML from: http: // www.btinternet.com/~dtemicrosystems/beginner.htm
ЧТО ЭТО. КАК И ГДЕ ПРИМЕНЯТЬ
Хотя закон Ома применим не только к резисторам – как мы увидим позже – кажется, логично включить его сейчас, так как он будет хорошей точкой отсчета для резистора подробности приведены выше.
ЧТО ТАКОЕ ЗАКОН ОМС? :
Используя диаграмму слева, закон Ома определяется как; «При условии, что температура
остается постоянным, отношение разности потенциалов (стр.г) на концах проводника
(R) к току (I), протекающему в этом проводнике, также будет постоянным ».
проповедь!
Из этого мы заключаем, что; Ток равен напряжению, разделенному на сопротивление (I = V / R),
Сопротивление равно напряжению, разделенному на ток (R = V / I), а напряжение равно току, умноженному на
Сопротивление (V = IR).
Важным фактором здесь является температура. Если расчеты по закону Ома должны
давать точные результаты, это должно оставаться постоянным. В «реальном» мире это почти никогда
делает, и с точки зрения новичка вам не нужно беспокоиться об этом.
более того, поскольку схемы, с которыми вы, вероятно, столкнетесь в данный момент, – и около 95%
все те, с которыми вы столкнетесь в будущем – будут работать нормально, даже если они горячие
или холодно!
ЗАКОН ОМС ПРОСТОЙ:
На рисунке 1 слева показан наиболее распространенный треугольник закона Ома.Начиная с любого раздела
треугольник, его можно читать в любом направлении – по часовой стрелке, против часовой стрелки, сверху
вниз или снизу вверх – и он всегда предоставит вам расчет, который вы
требовать.
Если рассматривать (слегка диагональные) горизонтальные линии как знаки разделения, а короткие
вертикальная линия как знак умножения, и всегда начинайте расчет с любого количества
вы ищете, т.е. “V =”, “I =” или “R =” у вас будет все
возможные формулы, основанные на этом конкретном законе Ома.То есть; V = IxR, I = V / R, R = V / I. Это
должно быть очевидно, что формула работает и в обратном направлении, то есть; IxR = V, RxI = V, V / I = R
и V / R = I.
Эти объяснения могут показаться немного сложными, но их легко применить на практике. Как правило, для начинающих будет более понятен полезный пример, а не эти причудливые столы, так что поехали.
ПОЯСНЕНИЕ НА ПРИМЕРЕ:
Допустим, друг просит вас установить красную сигнальную лампу на приборную панель его / ее автомобиля.Будучи энтузиастом электроники, вы решили использовать красный светоизлучающий диод (LED),
поскольку они излучают достаточно чистый красный свет, не выделяют чрезмерного тепла
лампы накаливания, они также дешевы по сравнению с ними и выглядят высокотехнологичными!
С точки зрения принципиальной схемы расположение будет таким, как показано слева.
ОГРАНИЧИТЕЛЬ ТОКА РЕЗИСТОР:
Стандартные светодиоды не могут получать питание напрямую от 12 В без установки ограничения тока
резистор включен последовательно с одним из выводов, но какое значение вы используете? Как общее правило
на практике, вашему среднему светодиоду требуется около 15 мА тока для получения приемлемого света.
выход.Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах:
напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно
рассчитывается по формуле «R = V / I», которая дает нам 12 / 0,015 = 800 Ом (см. ниже
для ‘Vf’). Не забывайте, ток измеряется в амперах.
На первый взгляд может показаться, что это проблема, поскольку 800 Ом не является стандартным значением. доступен в диапазоне E12. Однако в этом типе цепи сопротивление не критического, и ближайшего предпочтительного значения будет вполне достаточно, а именно 820 Ом.
НЕ ЗАБЫВАЙТЕ О ‘Vf’:
Все электронные компоненты демонстрируют – в большей или меньшей степени – то, что известно как
‘выбывать’. Он имеет различные сокращения в зависимости от типа компонента, к которому он
ссылается, но обычно они означают одно и то же. На самом деле это количество напряжения, которое
используется компонентом для работы. Для стандартного светодиода это значение находится в диапазоне
около 1,5 – 3 вольт, и для наших целей мы примем 2 В.
Это означает, что из ваших 12 вольт от аккумулятора 2 вольта будут израсходованы светодиодом. Сама по себе, поэтому ваш расчет закона Ома должен быть основан на 10 вольт.Истинная формула должно быть на самом деле; (12-Vf) /0.015=666.66 Ом (повторяется для математиков среди ты!). Ближайшее значение в диапазоне E12 составляет 680 Ом, поэтому в идеале это должно быть ценность для использования. В целях безопасности, когда ваши результаты заканчиваются непонятными значениями, такими как при этом всегда выбирайте ближайшее значение выше, а не следующее ниже.
РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНОВозможно “изготовление” стандартных и нестандартных номиналов резисторов на соответствовать вашим потребностям, если требуемое значение отсутствует.Это достигается подключением два или более из них параллельно, последовательно или их комбинация. Однако вам нужно заранее знать, как они взаимодействуют друг с другом в этих конфигурациях.
РЕЗИСТОРЫ СЕРИИ:
На рисунке слева показаны три последовательно включенных резистора. Это
самый простой способ получить “производственные” значения. Формула прямой для
расчет окончательного значения; «R» = R1 + R2 + R3. Другими словами, независимо от
количества резисторов или их индивидуальных значений, окончательное значение
«R» всегда будет их суммой.Расчет по ноге изображения
работает для любого количества значений, соединенных последовательно, вы просто продолжаете добавлять их в
список других.
ПАРАЛЛЕЛЬНЫЕ РЕЗИСТОРЫ:
При параллельном соединении резисторов расчеты
сложнее. На рисунке слева показаны три резистора, включенных параллельно. Мы будем
не заботиться о трех отдельных ценностях, а сосредоточиться на том, что
окончательное значение «R» будет с использованием примеров значений.Расчет у подножия
изображение работает для любого количества значений, соединенных параллельно, вы просто продолжаете добавлять их в
список других в скобках. Для наших целей предположим, что R1 составляет 47K, R2 – это
150 КБ, а R3 – 820 КБ. Формула прямой линии для окончательного значения: «R» = 1 / (
(1 / R1) + (1 / R2) + (1 / R3)).
В этой формуле есть много ненужных скобок (скобок),
и вот причина; почти для всех расчетов электроники вам нужно использовать
калькулятор, который отдает приоритет функциям умножения и деления, а также наиболее научным
калькуляторы работают именно так.К сожалению, многие «простые» калькуляторы этого не делают, поэтому
дополнительные скобки были показаны, чтобы компенсировать те, которые вычисляют цифры в
порядок их ввода. С научным калькулятором вы можете использовать упрощенный
формула прямой линии; «R» = 1 / (1 / R1 + 1 / R2 + 1 / R3).
Важно определить значения в скобках перед применением окончательного Функция «1 /». В противном случае формула принимает вид 1 / R1 + 1 / R2 + 1 / R3 =? если ты попробуйте это на своем калькуляторе, используя наши примеры значений, вы, вероятно, подумаете, что у вас есть неправильный ответ (0.02916 …), но вы этого не сделали. На самом деле у вас точно есть право ответ, ему просто не хватает последней функции “1 /”.
Если в вашем калькуляторе есть «1 / X» (единица, разделенная на все, что показано в
display), затем нажмите эту кнопку сейчас. Если эта функция недоступна, поместите
результат в памяти (убедившись, что раньше там ничего не было), очистите дисплей
а затем введите «1 MR =» или другую подобную последовательность. Результат должен быть
34,29 кОм (34 290,29005 Ом), что правильно.Итак, итоговое значение всех трех
параллельно включенные резисторы – 34,29К.
На рис. 2 слева показан второй по величине часто используемый треугольник закона Ома. К этому можно подойти точно так же, как и к выше, только на этот раз он используется для расчета мощности, напряжения и тока. В объяснения здесь таковы; Ток равен мощности, деленной на напряжение (I = P / V), мощность равна Ток, умноженный на напряжение (P = VxI), и напряжение равно мощности, деленной на ток (V = P / I).
ДЕМОНСТРАЦИЯ НА ПРИМЕРЕ:
Чтобы продемонстрировать использование этого треугольника, мы применим его к обычному электрическому / электронному
компонент – трансформатор. Их характеристики обычно цитируются с точки зрения
выходное напряжение их вторичной обмотки вместе с возможной мощностью (в ВА)
это напряжение. Термин «VA» означает ватты и происходит от формулы
«Вольт на Ампер» (отсюда – ВА). Это обозначается буквой «P» в
треугольник закона Ома.
КАКОЙ ТРАНСФОРМАТОР ДЕЛАТЬ
НЕОБХОДИМОСТЬ ?
Допустим, у вас есть цепь на 9 В, которая потребляет 1.5 ампер тока. Вы хотите знать, если
трансформатор с номиналом 9 В при 25 ВА будет достаточным для питания вашей цепи. Ты
уже есть две величины от трансформатора – напряжение (В) и мощность (P или
VA), и по ним вы хотите узнать, какой будет доступный ток (I).
Используя формулу «I = P / V» из треугольника, результат: 25/9 = 2,77
усилители. Таким образом, этот трансформатор подойдет для ваших нужд на 1,5 А. В целях безопасности
если цепь будет постоянно потреблять определенное количество тока, независимо от
каким может быть этот ток, тогда всегда используйте трансформатор, доступный как минимум на 50% больше
ток, чем требует ваша схема.Никогда не используйте тот, у которого «ровно достаточный» ток,
потому что он станет слишком горячим, что приведет к изменению характеристик напряжения и
текущий указан. Эти изменения сложны, и мы не будем их объяснять в этой статье.
раздел для начинающих, но будьте осторожны при выборе трансформаторов.
Ом
Сопротивление
Рассчитать Прозрачный
Закон Ома – важный фундаментальный закон физики и электричества.Его предложил немецкий физик Георг Симон Ом.
Закон Ома гласит, что:
Ток, протекающий по цепи с определенным сопротивлением, прямо пропорционален разности напряжений в двух точках.
В форме выражения закон Ома гласит:
R = V / I, где V, I и R – напряжение, ток и сопротивление данной цепи соответственно.
Закон Ома популярен во всех его трех формах: V = IR, I = V / R и R = V / I
В этом выражении нам нужно соблюдать три основных понятия электричества: напряжение, ток и сопротивление электрической цепи.
Позвольте нам лучше понять эти термины здесь:
Электрическая схема
Это путь, по которому различные электрические компоненты, такие как источник энергии и электрические приборы, работающие за счет мощности, соединяются через электрический провод.
Обратите внимание, что ток течет только в замкнутых цепях, а это значит, что для протекания тока должен быть замкнутый путь.
В электрической цепи может быть много типов элементов: потребляющие энергию, генерирующие энергию, сопротивления, индуктивности, емкости и многие другие.
Обратите внимание, что закон Ома действителен только для электрических цепей, в которых есть чистое сопротивление.
Напряжение
Для протекания тока должна быть разница в потенциале или электрическом заряде. Например, возьмите аналогию с потоком воды из одной области в другую. Вода течет только там, где есть разница в высоте или давлении между участками. Иначе вода не потечет.
Аналогично, чтобы между ними протекал ток, между ними должна быть разница в электрическом потенциале или заряде.Эта разница в заряде называется напряжением между этими двумя точками. Чем выше разность потенциалов или напряжение между двумя точками. Об этом говорит закон Ома.
- Единица измерения напряжения – вольт, обозначается буквой «V».
- Понятие напряжения было впервые изучено и объяснено итальянским физиком Алессандро Вольта, создателем химических батарей.
- Напряжение измеряется прибором под названием вольтметр.
Текущий
Ток – это поток электрического заряда.Все мы знаем, что электроны несут ответственность за протекание тока. При возбуждении из-за любой формы внешней энергии, такой как свет, тепло, магнетизм или электрический заряд, электроны некоторых веществ получают энергию и разрывают свои связи, становятся свободными электронами, и их заряд течет по цепи, к которой они подключены. Этот поток заряда и составляет электрический ток.
- Единицей измерения электрического тока является «ампер» или «ампер (-ы)». Обозначается буквой «Я» или «Я».
- Открытие электричества приписывают многим великим ученым – Бенджамину Франклину, Фалесу, Гилберту, Алессандро Вольта, Томасу Альва Эдисону и Николе Тельсе.
- Ток измеряется амперметром.
Каждый металл обладает определенной силой …. приводить в движение электрическую жидкость. – Алессандро Вольта
Сопротивление
Природа каждого электрического проводника – препятствовать свободному протеканию тока через него.Это называется его сопротивлением. Это различно для каждого проводящего материала или проводника и является свойством его параметра, называемого удельным электрическим сопротивлением, обозначаемого греческой буквой ρ.
Сопротивление проводника, обозначенное R, равно R = ρ x l / A, где l – длина проводника, а A – площадь поперечного сечения проводника.
Помимо электропроводности, сопротивление материала зависит от:
- Площадь поперечного сечения – чем больше площадь поперечного сечения, тем меньше сопротивление.
- Длина жилы – чем больше длина, тем больше сопротивление.
- Температура проводника – чем выше температура, тем больше свобода движения электронов, следовательно, меньше сопротивление.
Примечание: В зависимости от вышеупомянутых параметров изменяется только сопротивление, но не удельное сопротивление. Удельное сопротивление вещества определяется его природой.
Ключевые моменты сопротивления
- Элемент сопротивления не может накапливать энергию.Он может только рассеивать энергию и мгновенно выполнять работу.
- Примеры резисторов, которые мы используем в повседневной жизни, включают зарядное устройство для ноутбука, контроллер скорости вентилятора, мобильное зарядное устройство и датчики в электронных схемах.
- Единица сопротивления – Ом, обозначается греческой буквой Ω, произносимой как Омега.
- Сопротивление электрической цепи измеряется омметром.
Закон Ома и расчеты электроэнергии
ЗаконОма не ограничивается только расчетом тока, протекающего в электрической цепи.Это также помогает в расчете мощности, потребляемой резистивным элементом в электрической цепи.
Мощность P, потребляемая резистивным элементом, определяется как произведение падения напряжения на его выводах и тока, протекающего через него. Единица измерения мощности – Вт, обозначаемая символом W.
.P = V x I, Вт
Из закона Ома:
Мы знаем, что V = I x R,
Электроэнергетика
Мощность, умноженная на время, в течение которого она используется, дает потребляемую электрическую энергию.Таким образом, электрическая энергия, потребляемая электроприбором, определяется произведением киловатт (или тысяч ватт) на время в часах.
При следующей покупке электроприбора:
Обратите внимание, что указано в киловатт-часах (кВтч). Приборы оцениваются в кВтч, потому что с этим устройством легче работать в повседневной жизни, чем работать с тысячами и миллионами джоулей.
Обычная единица электроэнергии – один киловатт-час или 1 кВтч.Мы оплачиваем счет за электроэнергию в зависимости от того, сколько киловатт-часов потребили наши приборы в конкретный месяц. Хотите узнать больше о том, как фиксируются цены на электроэнергию и почему мы иногда платим такие огромные счета за электроэнергию? Узнайте больше в нашем бесплатном онлайн-калькуляторе счетов за электроэнергию.
Некоторые интересные факты о законе Ома
- Закон Ома впервые соблюдал Генри Кавендиш, которого приписали открытию водорода. Однако Кавендиш вообще не публиковал свои исследования закона Ома при жизни.Следовательно, закон приписывают Георгу Симону Ому, от имени которого он получил широкую известность.
- Закон Ома верен только для элементов сопротивления. Для других типов элементов, имеющих индуктивность и емкость, закон Ома не действует. Такие электрические материалы, для которых закон Ома не применим, называются неомическими материалами.
- Закон Ома применим только к цепям, работающим на постоянном токе (DC), но не к тем, которые работают с переменным током (AC).Это связано с тем, что в цепях переменного тока фигурируют индуктивность и емкость, которые не подчиняются закону Ома.
- То, что называется сопротивлением для цепей постоянного тока, называется импедансом для цепи переменного тока. Наш бесплатный онлайн-калькулятор реактивного сопротивления поможет вам лучше.
Георг Симон Ом, отец закона Ома.
Источник изображения: Википедия
- Электрический прибор, который может измерять различные электрические параметры, включая сопротивление, напряжение и ток цепи, называется мультиметром.
- На практике сопротивление – это и полезный ресурс, и потеря – мы используем сопротивление во многих формах для хороших целей, однако большее сопротивление означает большую мощность, необходимую для выполнения работы, и большие потери на нагрев.
Как калькулятор закона Ома от CalculatorHut поможет вам?
CalculatorHut – это идеальное место для всех ваших научных расчетов. Калькулятор закона Ома от CalculatorHut – это бесплатный онлайн-калькулятор, который позволяет мгновенно вычислить напряжение, сопротивление, ток и мощность электрической цепи!
Вы также можете проверить огромную базу данных бесплатных онлайн-калькуляторов физики и бесплатных онлайн-калькуляторов химии у нас. Кроме того, вы также можете найти наши бесплатные онлайн-калькуляторы здоровья, бесплатные онлайн-калькуляторы транспортных средств тоже интересными и полезными!
Если вы влюбились в какой-либо из наших калькуляторов и хотите использовать их в качестве виджетов для своего блога или веб-сайта, напишите нам на Calculatorhut @ gmail.com. Разработаем виджет абсолютно бесплатно для вас!
Кроме того, наши бесплатные научные онлайн-калькуляторы можно носить в кармане! Наше приложение CalculatorHut можно бесплатно загрузить и использовать, и оно станет вашим универсальным решением для всех ваших расчетов.
Мы пропустили какой-нибудь калькулятор, который вы хотели получить бесплатно? Дайте нам знать, и мы будем рады добавить его в наш огромный ассортимент из более чем 100 бесплатных научных и прочих онлайн-калькуляторов. С CalculatorHut вычисления всегда просты и увлекательны !! Удачного расчета!
«Вначале сопротивляться легче, чем в конце.»- Леонардо да Винчи
ЗаконОма
Закон Ома гласит, что
«ток через проводник между двумя точками прямо пропорционален разности потенциалов или напряжению между двумя точками, и обратно пропорционален сопротивлению между ними».
Закон Ома может быть выражен как
I = U / R (1)
где
I = ток (ампер, А)
U = электрический потенциал (вольт, В)
R = сопротивление (Ом, Ом, )
Пример – закон Ома
Батарея 12 В, обеспечивает питание до сопротивления 18 Ом .Ток в электрической цепи можно рассчитать как
I = (12 вольт) / (18 Ом)
= 0,67 ампер
Эквивалентные выражения закона Ома
Закон Ома (1) также можно выразить как
U = RI (2)
или
R = U / I (3)
Загрузите и распечатайте диаграмму закона Ома!
Пример – сопротивление электрической цепи
Ток силой 1 ампер протекает через электрическую цепь 230 В, .На приведенной выше диаграмме это означает сопротивление
R ≈ 220 Ом
Его можно также рассчитать по закону Ома
R = (230 В) / (1 А)
= 230 Ом
Пример – Закон Ома и кратные и подмножители
Токи, напряжения и сопротивления в электрических цепях часто могут быть очень маленькими или очень большими, поэтому часто используются кратные и подкратные.
Требуемое напряжение, подаваемое на 3.Резистор 3 кОм для создания тока 20 мА можно рассчитать как
U = (3,3 кОм) (1000 Ом / кОм) (20 мА) (10 -3 А / мА)
= 66 В
Номограмма электрического сопротивления
Загрузите и распечатайте номограмму зависимости электрического сопротивления от вольт и ампер!
Значения по умолчанию на номограмме выше показывают 230 вольт , сопротивление 24 Ом и ток 10 ампер .
Мощность
Электрическая мощность может быть выражена как
P = UI
= RI 2
= U 2 / R (4)
где
P = электрическая мощность (Вт, Вт)
Пример – потребляемая мощность
Мощность, потребляемая в указанной выше электрической цепи 12 В , может быть рассчитана как
P = (12 вольт) 2 / ( 18 Ом)
= 8 Вт
Пример – мощность и электрическое сопротивление
Электрическая лампочка 100 Вт подключена к источнику питания 230 В и .Текущий ток можно рассчитать путем преобразования (4) в
I = P / U
= (100 Вт) / (230 В)
= 0,43 ампера
Сопротивление может быть вычислено путем реорганизации (4) в
R = U 2 / P
= (230 В) 2 / (100 Вт)
= 529 Ом
Номограмма электрической мощности
Эта номограмма может использоваться для оценки зависимости мощности отнапряжение и ампер.
Скачайте и распечатайте номограмму зависимости электрической мощности от вольт и ампер!
Значения по умолчанию на номограмме выше: 240 В, , сопротивление 10 А, и мощность 2,4 кВт, для постоянного или однофазного переменного тока и 4 кВт, для трехфазного переменного тока.
Использование закона Ома со схемами
Как использовать закон Ома
В качестве уравнения закон Ома можно записать как I = V / R . Это позволяет рассчитать три величины для конкретной цепи.Например, если вы знаете ток и сопротивление, вы можете определить напряжение.
Вы можете использовать закон Ома для отдельного компонента внутри цепи: ток через лампочку, напряжение на лампочке и сопротивление лампочки. Или вы можете использовать закон Ома для всей цепи, используя полный ток, напряжение батареи (общее напряжение) и общее сопротивление. Вы даже можете сделать это для отдельной ветви в последовательной цепи. Это все еще работает.
Однако, чтобы закон Ома работал, компоненты в цепи должны быть ОГМИЧЕСКИМИ.Не все электрические компоненты подчиняются закону Ома – не все омические, но большинство из них.
Пример
Допустим, у вас есть параллельная цепь, содержащая 12-вольтовую батарею и две лампочки в отдельных ветвях: одна с сопротивлением 4 Ом, а другая с сопротивлением 3 Ом. Как вы думаете, как мы будем рассчитывать ток, проходящий через резистор сопротивлением 3 Ом?
Чтобы решить эту проблему, нам нужно использовать закон Ома для резистора 3 Ом. Помните, что ток равен напряжению, разделенному на сопротивление, или I = V / R.
Общее напряжение цепи составляет 12 вольт, и поскольку это параллельная цепь, каждая ветвь также получит полные 12 вольт. Это означает, что на резистор сопротивлением 3 Ом также подается напряжение 12 В. Итак, мы знаем, что V = 12 вольт, а R = 3 Ом. Чтобы вычислить ток, мы разделим 12 на 3 и получим 4 ампера, что и является нашим ответом.
Резюме урока
Закон Ома гласит, что при увеличении сопротивления ток уменьшается.И наоборот, при повышении напряжения возрастает и ток. Ток – это электрический ток вокруг электрической цепи, который мы измеряем в амперах. Сопротивление , которое мы измеряем в омах, – это способность компонента сдерживать прохождение тока.