Закон ома сопротивление: 1. Электрическое сопротивление. Закон Ома для участка электрической цепи

Закон Ома для участка цепи. Сопротивление. Соединение проводников.

Металлический проводник, подключенный к источнику тока является примером однородного участка цепи.

Немецкий физик Георг Симон Ом экспериментально изучил зависимость силы тока в металлических проводниках от напряжения, пришел к выводу: если состояние проводника с течением времени не меняется, а его температура постоянна, то для каждого проводника существует однозначная связь между I и U – вольт-амперная характеристика.

Закон Ома для участка цепи: 

Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Электрическое сопротивление проводника

Это физическая скалярная величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных зарядов.

Сопротивление однородного металлического проводника постоянного сечения зависит от его геометрических размеров, формы и вещества, из которого изготовлен проводник.

Удельное сопротивление проводника  зависит от рода вещества и его состояния, например, температуры. Удельное сопротивление для определенного вещества имеет постоянное табличное значение.

Величина, обратная сопротивлению, называется электрической проводимостью данного проводника.

Параллельное и последовательное соединение проводников

Резистор – элемент электрической цепи, характеризуемый только сопротивлением электрическому току. На схемах резистор обозначается прямоугольником:  Реостат – прибор, служащий для регулировки и получения требуемой величины сопротивления. Обозначение на схемах: 

Резисторы Реoстат

???Вопросы

1. Что называют вольт-амперной зависимостью?
2. Как зависит сила тока от напряжения? от сопротивления?
3. Сформулируйте закон Ома для участка цепи?
4. Что называют сопротивлением?
5. От каких величин зависит сопротивление? Формула?
6. Назовите единицы измерения I, U,R?
7. Какие вы знаете соединения проводников?
8. Какое соединение называют последовательным?
9. Запишите законы последовательного соединения?
10. Какое соединение называют параллельным?
11. Запишите законы параллельного соединения?
12. Какое соединение больше применяется на практике? Почему?
13. Как называется этот прибор? Какова цена деления?

Закон Ома, сопротивление проводников

| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Немецкий физик Г. Ом (1787;—1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению

U на концах проводника:

                                                                    (98.1)

где R — электрическое сопротивление проводника. Уравнение (98.1) выражает закон Ома для участка цепи (не содержащего источника тока): сала тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула (98.1) позволяет установить единицу сопротивления — ом (Ом): 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина

называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.

Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

                                                                (98.2)

где r — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — ом×метр (Ом×м). Наименьшим удельным сопротивлением обладают серебро (1,6×10

–8 Ом×м) и медь (1,7×10^–8 Ом×м). На практике наряду с медными применяются алюминиевые провода. Хотя алюминий и имеет большее, чем медь, удельное сопротивление (2,6×10^–8 Ом×м), но зато обладает меньшей плотностью по сравнению с медью.

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (98.2) в закон Ома (98.1), получим

                                                     (98.3)

где величина, обратная удельному сопротивлению,

называется

удельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что U/l = Е — напряженность электрического поля в проводнике, I/S = j — плотность тока, формулу (98.3) можно записать в виде

                                                                      (98.4)

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу (98.4) можно записать в виде

                                                                      (98.5)

Выражение (98.5) — закон Ома в дифференциальном форме

, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:

где r и r₀, R и R₀ — соответственно удельные сопротивления и сопротивления провод­ника при t и 0°С, a — температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К

–1. Следовательно, температур­ная зависимость сопротивления может быть представлена в виде

где Т — термодинамическая температура.

Качественный ход температурной зависимости сопротивления металла представлен на рис. 147   (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах T_K (0,14—20 К), называемых критическими, характерных для каждого вещества, скачко­образно уменьшается до нуля (кривая 2), т.

е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.

На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют по градуированной взаимо­связи сопротивления от температуры измерять температуру с точностью до 0,003 К. Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, изготовленные по специальной технологии, называются

термисторами. Они позволяют измерять температуры с точностью до миллионных долей кельвин.

---

Закон Ома

Закон Ома показывает линейную зависимость между напряжением и током в электрической цепи.

Падение напряжения и сопротивление резистора определяют протекание постоянного тока через резистор.

Используя аналогию с потоком воды, мы можем представить электрический ток как поток воды через трубу, резистор как тонкую трубу, ограничивающую поток воды, напряжение как разность высот воды, которая позволяет воде течь.

Формула закона Ома

Ток резистора I в амперах (А) равен напряжению резистора V в вольтах (В), деленному на сопротивление R в омах (Ом):

V – падение напряжения на резисторе, измеренное в вольтах (В). В некоторых случаях в законе Ома для обозначения напряжения используется буква E. E обозначает электродвижущую силу.

I – электрический ток, протекающий через резистор, измеряется в амперах (А).

R – сопротивление резистора, измеренное в Ом (Ом).

Расчет напряжения

Зная ток и сопротивление, мы можем рассчитать напряжение.

Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):

Расчет сопротивления

Зная напряжение и ток, мы можем рассчитать сопротивление.

Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (А):

Поскольку ток задается значениями напряжения и сопротивления, формула закона Ома может показать, что:

• Если мы увеличим напряжение, ток увеличится.
• Если мы увеличим сопротивление, ток уменьшится.

Пример # 1

Найдите ток электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.

Решение:

V = 5 В

R = 50 Ом

I = V / R = 5 В / 50 Ом = 0,1 А = 100 мА

Пример # 2

Найдите сопротивление электрической цепи, имеющей напряжение питания 10 В и ток 5 мА.

Решение:

V = 10 В

I = 5 мА = 0,005 А

R = V / I = 10 В / 0,005 A = 2000 Ом = 2 кОм

Закон Ома для цепи переменного тока

Ток нагрузки I в амперах (А) равен напряжению нагрузки V _Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ом):

V – падение напряжения на нагрузке, измеренное в вольтах (В).

I – электрический ток, измеряемый в амперах (А)

Z – полное сопротивление нагрузки, измеренное в Ом (Ом).

Пример # 3

Найдите ток в цепи переменного тока с напряжением питания 110 В ± 70 ° и нагрузкой 0,5 кОм ± 20 °.

Решение:

V = 110V∟70 °

Z = 0,5 кОм∟20 ° = 500 Ом∟20 °

I = V / Z = 110V∟70 ° / 500Ω∟20 ° = (110V / 500Ω) (70 ° -20 °) = 0,22A 50 °

Калькулятор закона Ома (краткая форма)

Калькулятор закона Ома: вычисляет соотношение между напряжением, током и сопротивлением.

Введите 2 значения, чтобы получить третье значение, и нажмите кнопку « Рассчитать» :

 

Калькулятор закона Ома II ►

 

---

Смотрите также

Законы Ома для постоянного и переменного тока

Поиск по вики-сайту о сжатом воздухе

Чтобы получить из обычного воздуха сжатый воздух, требуется энергия. Эта энергия поступает в виде электричества: переменного или постоянного тока. В этой статье мы кратко рассмотрим законы Ома. Эти законы определяют сопротивление в виде отношения между током и напряжением.

Что такое закон Ома для постоянного тока?

Закон Ома утверждает, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению на этих двух точках. Вводя константу пропорциональности, сопротивление, получаем обычное математическое уравнение, которое описывает это соотношение:U = R x IГде I – ток в проводнике, выраженный в амперах, V – напряжение, измеренное на проводнике в вольтах, а R – сопротивление проводника в Омах. Если точнее, закон Ома утверждает, что R в этом соотношении является постоянной величиной и не зависит от тока.

Что такое закон Ома для переменного тока (и что такое самоиндукция)?

Переменный ток, проходящий через катушку, создает увеличение магнитного потока. Этот поток изменяет величину и направление аналогично электрическому току. При изменении потока в катушке генерируется ЭДС (электродвижущая сила) в соответствии с законами индукции.ЭДС направлена против напряжения подключенного полюса. Это явление называется самоиндукцией. Самоиндукция в блоке переменного тока приводит к частичному смещению фазы между током и напряжением, а также частично к индуктивному падению напряжения. Полное сопротивление устройства переменному току становится больше, чем рассчитанное или измеренное при постоянном токе.Смещение фазы между током и напряжением представлено углом φ. Индуктивное сопротивление (так называемое реактивное сопротивление) обозначено X. Сопротивление обозначено R. Полное сопротивление блока или проводника обозначено Z.

Другие статьи по этой теме

Электромонтаж компрессорных систем

В этой статье мы рассмотрим электрическую систему, которая обеспечивает работу компрессора. В нее входят электродвигатели, кабели, системы управления напряжением и защиты от короткого замыкания.

Введение в электричество

Узнайте об основах электричества и о той роли, которую оно играет в сжатии воздуха. Некоторые основные термины и определения.

Электродвигатель

Узнайте об основах электродвигателей и о том, как они используются в современных воздушных компрессорах.

Закон Ома для участка цепи простое объяснение | Энергофиксик

Закон Ома для участка цепи – это базовое знание, которое мы с вами получаем еще в школе. Но зачастую получается так, что мы с вами либо забыли, либо пропустили или банально не понимаем этот закон. В этой статье я постараюсь вам объяснить Закон Ома для участка цепи простым образом, проведя аналогию с водопроводом.

Проводим аналогию

Итак, для того чтобы понять закон Ома давайте проведем аналогию с гидравликой и представим, что:

Напряжение U равно уровню воды в самой обычной водонапорной башне;

Сопротивление R = это отходящая водяная труба;

Сила тока I = некий объем воды протекающий через трубу за определенное время.

Сила тока

Итак, давайте теперь разберемся, что такое сила тока. Для этого представьте колбу, у которой на одной стороне есть три отверстия одного размера, расположенные по вертикали. Если этот сосуд наполнить водой, то из боковых отверстий начнет вытекать вода.

Причем, как видно из рисунка, с самого нижнего отверстия струя воды будет бить дальше всех, а с самого верхнего струя будет самая слабая. Так как наши отверстия идентичные, то сопротивление водному потоку оказывается одинаковое.

За одно и то же время из нижнего отверстия вытечет воды больше, чем с верхнего (так как столб воды «U» оказывает разное давление на отверстия), а объем воды (из вышеописанной аналогии), вытекающий из отверстия за определенное время, есть не что иное, как сила тока «I».

Посмотрите еще раз внимательно на рисунок, не заметили тут определенную закономерность? А она такова: при одинаковом сопротивлении и при возрастании напряжения возрастает и сила тока.

Сопротивление

Итак, давайте теперь разберемся со следующей величиной, а именно силой тока. Вы когда-нибудь видели вот такие штуки:

yandex.ru

yandex.ru

Наверняка, да, так вот эта водонапорная башня. Ее основное назначение в создании давления в водонапорных трубах. Итак, вы пришли домой и решили помыть руки. Открыв кран на полную, поток воды будет существенным и наврятли вас устроит, и вы с помощью краника отрегулируете поток так, чтобы он был для вас комфортен.

А теперь подумайте, что только что было сделано? А вот что: изменив сопротивление потоку, вы отрегулировали его.

Теперь переносим эту аналогию на электричество. Напряжение остается у нас на постоянном уровне, так как мы не можем никоим образом оказать влияние на нашу с вами водонапорную башню, в которой постоянно поддерживается один и тот же уровень воды благодаря системе насосов.

Открыв кран на максимум, мы с вами пустили поток воды на полную, а закрутив его до нужного нам уровня мы изменили сопротивление потоку. И это привело к тому, что ток воды стал слабым. Получается, что мы путем изменения сопротивления отрегулировали количество протекающей воды за определенный отрезок времени.

Теперь вспоминаем, что такое сила тока. Сила тока – определенное количество электронов, проходящих через поперечное сечение проводника за определенное время.

Итак, получается, что, изменяя сопротивление (при неизменном напряжении), мы с вами можем изменять силу тока.

Напряжение

Давайте рассмотрим простейшую систему водоснабжения, где у вас уже есть возможность управлять водонапорной башней:

yandex.ru

yandex.ru

Теперь создаем ситуацию: вам нужно заполнить емкость водой за 1 час, причем время строго регламентировано и в большую или меньшую сторону отклоняться нельзя. И тут на ваш шланг (через который заполняется емкость) наступает человек и вы никак не можете его заставить сойти с него.

По факту человек передавивший шланг стал сопротивлением и в результате этого изменился поток воды. Так как вы не можете убрать это сопротивление нужно действовать по-другому, только вопрос как?

А все просто. Достаточно нам увеличить количество воды в водонапорной башне, это увеличит давление воды в трубах и через наш с вами передавленный шланг потечет больший поток воды. Если, открыв на полную кран, наполняющий башню, вы поняли, что наполните емкость быстрее чем за час, то достаточно прикрыть кран. Это снизит уровень воды в башне, что соответственно уменьшит поток через пережатый шланг.

Возвращаемся к электричеству. Итак, человек, передавивший шланг, увеличил сопротивление и по этой причине сила тока у нас уменьшилась. Для ее восстановления мы с вами увеличили напряжение (уровень воды в водонапорной башне).

Закон Ома для участка цепи

Итак, из всего вышеописанного вы заметили определенные закономерности? Так вот, Г. Ом, проводя ряд простейших опытов, выявил эти закономерности между тремя величинами: сила тока, сопротивление и напряжение и вывел следующий закон:

yandex. ru

yandex.ru

Надеюсь, статья позволила вам понять Закон Ома для участка цепи. Не стесняйтесь оценивать материал пальцем вверх и спасибо за внимание!

«Закон Ома для участка цепи. Электрическое сопротивление проводников. Удельное сопротивление проводников».

«Закон Ома для участка цепи. Электрическое сопротивление проводников.

Удельное сопротивление проводников».

Цель.

Воспитательные: выработать представление у учащихся о необходимости планирования чёткого эксперимента для нахождения и установления физических законов и закономерностей;

Развивающие: учить раскрывать смысл конкретного значения физических величин на основе их определения.

Ход урока

1. Организационный момент. Мотивация учебной деятельности.

Ставится цель урока, намечаются пути её достижения и указываются критерии её достижения.
2. Проверка домашнего задания.

Фронтальный опрос.

1. Что такое электрический ток?

2. Перечислите условия, необходимые для существования электрического тока.

3. Перечислите действия электрического тока.

4. Что называется электродвижущей силой?

5. Что называют силой тока?

6. Дайте определение единице силы тока.

7. Что такое 1 кулон?

8. Что называется напряжением?

9. Что такое 1 вольт?

3.Формирование новых знаний

Определить зависимость силы тока от напряжения.

Демонстрации. Закон Ома для участка цепи.

Понятие о сопротивлении.

R – электрическое сопротивление проводника.

Единица электрического сопротивления в СИ – ом(Ом).

Электрическим сопротивлением 1 Ом обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В. 1 Ом = 1В/1А

Закон Ома для участка цепи.

Экспериментально установленную зависимость силы тока от напряжения и электрического сопротивления участка цепи называют законом Ома (1826 г.) для участка цепи.

Падение напряжения.

Величину IR – называют падением напряжения.

Демонстрация. Соотношение между сопротивлением проводника, его длиной и площадью поперечного сечения.

Формула для расчёта сопротивления.

Удельное сопротивление.

Реостаты.

Демонстрации. Изменение силы тока изменением сопротивления реостата.

4. Закрепление знаний. Решить задачи

5. Применение полученных знаний на практике. Инстр. по ТБ.

Лабораторная работа №4 «Измерение сопротивления с помощью амперметра и вольтметра.»

Цель работы: Научиться измерять сопротивление проводника при помощи амперметра и вольтметра.

Убедиться на опыте, что сопротивление проводника не зависит от силы тока в нем и напряжения на его концах.

Оборудование:  источник тока, амперметр, вольтметр, резистор, реостат, соединительные провода.

Ход работы

1. Соберите цепь, последовательно соединив источник питания, реостат, амперметр, резистор. Начертите схему этой цепи.

2. Измерьте силу тока в цепи.

3. В собранную цепь подключите вольтметр таким образом, чтобы он измерял напряжение на резисторе.

 4. С помощью реостата измените сопротивление в цепи и снова измерьте силу тока и напряжение на исследуемом проводнике.

5. Результаты измерений запишите в таблицу.

№ опыта

Сила тока

I, A

Напряжение

U, B

Сопротивление

R, Oм

1

2

3

6. Используя закон Ома, вычислите сопротивление проводника по данным каждого опыта. Результаты вычислений занесите в таблицу.  

I = U/R –  закон Ома 

7. Сделайте вывод.

5.Домашнее задание.

Лабораторная работа №4 «Измерение сопротивления с помощью амперметра и вольтметра.»

Цель работы: Научиться измерять сопротивление проводника при помощи амперметра и вольтметра. Убедиться на опыте, что сопротивление проводника не зависит от силы тока в нем и напряжения на его концах.

Оборудование:  источник тока, амперметр, вольтметр, резистор, реостат, соединительные провода.

Ход работы

1. Соберите цепь, последовательно соединив источник питания, реостат, амперметр, резистор. Начертите схему этой цепи.

Схема

2.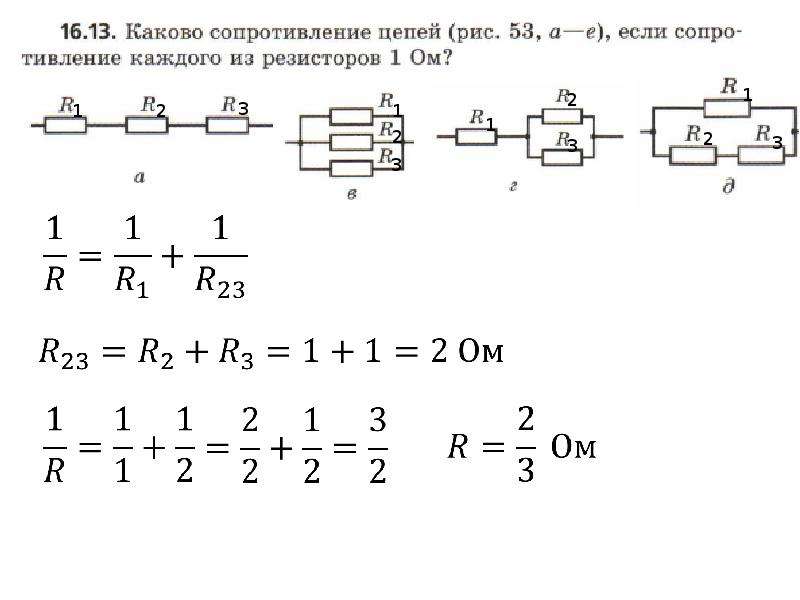 Измерьте силу тока в цепи.

3. В собранную цепь подключите вольтметр таким образом, чтобы он измерял напряжение на резисторе.

 4. С помощью реостата измените сопротивление в цепи и снова измерьте силу тока и напряжение на исследуемом проводнике.

5. Результаты измерений запишите в таблицу.

опыта

Сила тока

I, A

Напряжение

U, B

Сопротивление

R, Oм

1

2

3

6. Используя закон Ома, вычислите сопротивление проводника по данным каждого опыта. Результаты вычислений занесите в таблицу.  

I = U/R –  закон Ома 

R1=

R2=

R3=

7. Сделайте вывод.

Лабораторная работа №4 «Измерение сопротивления с помощью амперметра и вольтметра.»

Цель работы: Научиться измерять сопротивление проводника при помощи амперметра и вольтметра. Убедиться на опыте, что сопротивление проводника не зависит от силы тока в нем и напряжения на его концах.

Оборудование:  источник тока, амперметр, вольтметр, резистор, реостат, соединительные провода.

Ход работы

1. Соберите цепь, последовательно соединив источник питания, реостат, амперметр, резистор. Начертите схему этой цепи.

Схема

2. Измерьте силу тока в цепи.

3. В собранную цепь подключите вольтметр таким образом, чтобы он измерял напряжение на резисторе.

 4. С помощью реостата измените сопротивление в цепи и снова измерьте силу тока и напряжение на исследуемом проводнике.

5. Результаты измерений запишите в таблицу.

опыта

Сила тока

I, A

Напряжение

U, B

Сопротивление

R, Oм

1

2

3

6. Используя закон Ома, вычислите сопротивление проводника по данным каждого опыта. Результаты вычислений занесите в таблицу.  

I = U/R –  закон Ома 

R1=

R2=

R3=

7. Сделайте вывод.

Закон Ома. Электрическое сопротивление. Электрическая проводимость

Рассмотрим участок В — Г замкнутой электрической цепи, содержащей источник э. д. с. (см. рис. 1).

Рис. 1

Пусть потенциал в точке В равен φ_В, а в точке Г — φ_Г. Разность потенциалов между этими точками φ_В — φ_Г равна U_ВГ — напряжению между ними, а расстояние между точками В и Г равно l. Поле внутри проводника однородное. Напряженность поля внутри проводника:
Чем больше напряженность поля внутри проводника, тем больший ток возникает в проводнике. Естественно, что величина тока I в проводнике пропорциональна напряженности поля и площади поперечного сечения s. Величина тока I может быть подсчитана по формуле:
в которой γ (гамма) — коэффициент пропорциональности, зависящий от свойств материала проводника.

Так как в однородном поле (для любого участка цепи), то:
Обозначив — l/γs буквой r, получим формулу:
Величина r, равная — l/γs, называется сопротивлением проводника, а величина l/γ – называется удельным сопротивлением материала и обозначается буквой р (ро).

Удельное сопротивление представляет собой сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм². Наименьшим удельным сопротивлением обладают серебро, медь, платина, золото, алюминий.

Сопротивление проводника, длина которого существенно больше диаметра сечения, может быть подсчитано по формуле:

Величина, обратная сопротивлению, называется проводимостью и обозначается буквой g:
Полученное выражение для тока I = U/r показывает, что величина тока в проводнике прямо пропорциональна напряжению между его концами и обратно пропорциональна сопротивлению проводника. Это соотношение называется законом Ома.

Формулу I = U/r можно написать в виде U=Ir, откуда следует, что падение напряжения в проводнике равно произведению тока на сопротивление проводника.

Вследствие падения напряжения в соединительных проводах любой электрической цепи напряжение на зажимах потребителя всегда меньше, чем на зажимах источника тока. При длинной соединительной линии, когда сопротивление проводов становится достаточно большим, напряжение на зажимах потребителя может снизиться настолько, что нормальная работа нарушится.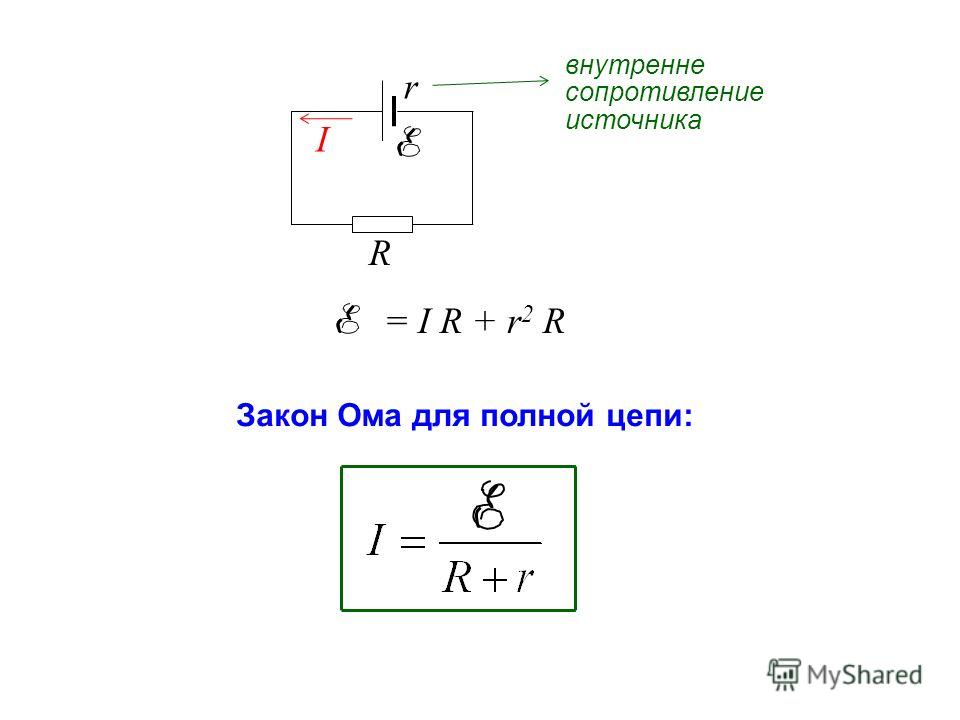 Так, например, при чрезмерном падении напряжения на зажимах электрической лампы сила ее света значительно уменьшится.

Из основной формулы закона Ома следует также, что r = U/I, т. е. что сопротивление равно частному от деления напряжения на зажимах участка цепи на ток, протекающий в этом участке.

Единицей сопротивления служит Ом, равный сопротивлению линейного проводника, в котором устанавливается ток в 1 а при напряжении 1 в.

Величина сопротивления любого тела зависит от температуры. С повышением температуры металлических проводников их сопротивление увеличивается.

Это увеличение сопротивления связано с усилением хаотического теплового движения элементарных частиц, затрудняющего направленное движение электронов.

В диэлектриках увеличение температуры приводит к уменьшению сопротивления вследствие увеличения количества свободных зарядов при нагреве.
Зависимость сопротивления проводника от температуры может быть представлена приближенной формулой:

в которой r₁ — сопротивление проводника при температуре t₁ нагрева;
r₀ — сопротивление проводника при начальной температуре t^оС;
а (альфа) — температурный коэффициент сопротивления; у всех чистых металлов температурный коэффициент сопротивления приблизительно равен 0,004 1/1^оС.
В некоторых приборах и измерительных схемах применяются сплавы, имеющие весьма малые температурные коэффициенты: манганин, константан и др. Температурный коэффициент сопротивления константана равен +0,000003 1/1^оС.

Следует отметить, что сопротивление угля и диэлектриков при нагреве уменьшается, т. е. они имеют отрицательный температурный коэффициент сопротивления.

Сопротивление и закон Ома | Абсолютная книга по электронике

Ultimate Electronics: практическое проектирование и анализ схем

---

Как решить задачи по закону Ома для резисторов. Микроскопические причины, по которым закон Ома является макроскопически линейным. 11 минут чтения

В разделе «Электроны в движении» мы обсуждали, как электрические поля вызывают силу →F=qe→E на электрон. Как и в случае с любым объектом, на который действует результирующая сила, электрон будет ускоряться →Fnet=me→a в ответ на эту силу.Со временем это ускорение вызывает увеличение скорости: →a=d→vdt . Скорость носителей заряда можно описать как электрический ток.

Для свободных электронов, летающих в вакууме, это конец истории.

Однако для электронов, движущихся в материале — обычно, но не всегда в твердом теле — столкновения между электроном и самим материалом являются невероятно доминирующим фактором в общем движении электрона.

Хотя электрон все еще ускоряется электрическим полем, он часто теряет энергию из-за столкновений с материалом.Каждое столкновение рассеивает кинетическую энергию , накопленную электроном в материале, который становится теплом.

В результате, чтобы электроны двигались через материал с постоянной средней скоростью (нулевое среднее ускорение), нам по-прежнему необходимо добавлять энергию для компенсации кинетической энергии, теряемой при столкновениях с неподвижным материалом. Это свойство называется сопротивлением .

(Изучая механику и кинематику, существует спектр между упругими столкновениями, которые сохраняют полную кинетическую энергию, и неупругими столкновениями, которые не сохраняют полную кинетическую энергию, потому что часть этой энергии преобразуется в тепло, звук, деформацию материал и т. д.В случае трения или омического сопротивления мы имеем в виду неупругие столкновения.)

---

Электрическое сопротивление при столкновениях аналогично сопротивлению воздуха.

Представьте себе мячик для пинг-понга, упавший с башни. Под действием силы тяжести мяч летит к земле. Если бы не было сопротивления воздуха, скорость мяча продолжала бы увеличиваться и возрастать без ограничений. Но в воздухе между мячом и молекулами воздуха происходят столкновения, поэтому мяч достигает некоторой стационарной скорости, которую в этой ситуации часто называют «конечной скоростью».При этой установившейся скорости энергия, полученная при движении вниз в гравитационном поле потенциальной энергии, равна энергии, потерянной при столкновениях при отталкивании воздуха с пути. Когда мы усредняем многие из этих микроскопических столкновений, оказывается, что мяч не ускоряется и не замедляется, а вместо этого продолжает падать с постоянной скоростью.

Это действительно рассеивание кинетической энергии. Если бы это было не так, то добавление энергии вызвало бы дальнейшее ускорение, а не просто поддержание постоянной скорости.

Аналогия с жидкостью тоже уместна. Проталкивание жидкости через трубу требует энергии (обычно определяемой как разность давлений) для поддержания постоянной скорости (обычно определяемой как расход), потому что поток постоянно теряет энергию из-за сопротивления внутренних стенок трубы, а также к вязким взаимодействиям между молекулами жидкости. Эти силы сопротивления действительно рассеиваются в виде тепла. (Однако из-за такой высокой удельной теплоемкости воды мы обычно не замечаем этого повышения температуры в повседневной жизни!)

Автомобиль, движущийся с постоянной скоростью по ровному шоссе, демонстрирует оба этих явления: чтобы поддерживать постоянную скорость, по-прежнему необходимо добавлять энергию за счет сопротивления воздуха, а также сопротивления жидкостей внутри двигателя и трансмиссии, трения в колесе. подшипников, неупругая деформация резиновых покрышек и т. д.Если бы это было не так, мы могли бы просто поставить машину на нейтраль и заглушить двигатель, как только наберем крейсерскую скорость.

Когда мы движемся через что-либо, кроме вакуума без трения (или сверхпроводника!), материалы будут взаимодействовать, сталкиваться, деформироваться и вызывать потери кинетической энергии. Независимо от того, движется ли это автомобиль по шоссе или электрон в металле, результат один и тот же: нужно постоянно добавлять больше энергии просто для поддержания постоянной средней кинетической энергии.

---

Закон Ома обычно рассматривается как:

В=ИК

где Р – сопротивление резистора, В – падение напряжения на резисторе, а I это ток через резистор. (См. оставшуюся часть этой главы, в том числе Закон Кирхгофа о напряжении (KVL) и Закон Кирхгофа о токе (KCL), Обозначение напряжений, токов и узлов, а также Решение систем цепей для получения дополнительной информации о правильном указании напряжения и тока!)

Поскольку напряжение является мерой работы на единицу заряда, закон Ома означает, что для материалов с более высоким сопротивлением требуется больше работы, чтобы пропустить тот же поток тока.

Закон Ома утверждает, что сопротивление является линейной функцией, но это правило не является универсальным ; на самом деле это эмпирических (основанных на наблюдениях, а не на теории). На самом деле это линеаризованная модель триллионов или более взаимодействий атомарного масштаба внутри материала, и оказывается, что в среднем , агрегированное поведение выглядит примерно линейным.

---

Если мы знаем любые два из V, I или R , мы можем решить для третьей переменной:

В=I⋅RI=VRR=VI

Это одно из самых основных практических уравнений в электронике, поэтому мы выделяем его во всех его формах.

Эти соотношения можно рассматривать с теоретической точки зрения при установлении связи между токами и напряжениями в цепи, но они также имеют практическое значение:

• Если у нас есть известных токов, протекающих через известных сопротивлений, мы можем умножить два, чтобы получить напряжение: V=I⋅R .
• Если у нас есть известных напряжений на сопротивлении известных , мы можем разделить два значения, чтобы получить ток: I=VR .
• Наконец, если у нас есть известное напряжение и известный ток , мы можем разделить их, чтобы получить сопротивление: R=VI .

В математическом смысле, когда мы используем слово известное , мы противопоставляем его неизвестной переменной , которую ищем. (См. Системы уравнений.)

Но в практическом смысле известный может означать две немного разные вещи:

• «Известный» может означать внешне контролируемый или фиксированный . Например, если у нас есть источник тока, который всегда выдает 2 ампера, то этот ток известен, потому что он контролируется и устанавливается на определенное значение.
• «Известно» может означать измеренное . Например, мы можем измерить напряжение 6 вольт на выходе источника тока. Это напряжение известно, потому что оно измеряется, а не фиксируется каким-либо процессом.

В большинстве вопросов, связанных с законом Ома, мы комбинируем два типа «известных». Чтобы объединить два приведенных выше примера, если наши 2 A источник тока подключен к какому-то неизвестному сопротивлению, и мы измеряем 6 В на выходе мы можем определить, что неизвестное сопротивление равно:

R=VI=62=3 Ом

Линейность закона Ома чрезвычайно полезна при проведении измерений.Резисторы — это компоненты, которые линейно преобразуют разность напряжений в ток и наоборот, и это полезный эффект во многих аналоговых схемах. Подробнее о вольтметрах, амперметрах и омметрах мы поговорим в разделе «Мультиметры и измерения».

---

Наш первый пример — одиночный 100 Ом резистор R1, подключенный к источнику напряжения:

Упражнение Нажмите на схему, затем нажмите «Симуляция» и нажмите «Запустить решатель постоянного тока». Это покажет расчетный ток:

I=VR=5 V100 Ом=0.05 А=50 мА

Затем нажмите «Запустить DC Sweep». Это настроено для регулировки значения источника напряжения от -5 до +5. Симулятор мгновенно построит график с настройкой напряжения по оси x и результирующим током по оси y.

Вместо того, чтобы управлять сопротивлением с источником напряжения, мы можем вместо этого подключить его к фиксированному источнику тока:

Упражнение Нажмите на схему, нажмите «Симуляция» и «Запустить решатель постоянного тока». Это покажет рассчитанное напряжение:

ВА=I⋅R=(1 А)⋅(100 Ом)=100 В

Затем нажмите «Запустить DC Sweep».Это настроено для настройки значения текущего источника. Симулятор мгновенно построит график с текущими настройками по оси x и результирующим напряжением по оси y.

Использование симулятора CircuitLab для изменения токов и напряжений и построения графика развертки постоянного тока является очень простой функцией. Чуть более продвинутый случай — изменение сопротивления:

.

Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током». Теперь симулятор подключает различные резисторы от 1 до 1000 Ом и строит результирующую кривую тока с сопротивлением в Омах по оси x и током по оси y.

Это работает, устанавливая DC Sweep для изменения «R1.R», что означает «сопротивление резистора с именем R1». Просмотр параметров компонента — мощный инструмент моделирования цепей.

---

Сопротивление зависит от выбора материала (например, алюминия или меди) и его физических размеров. Для твердого тела постоянной площади поперечного сечения A и длина L , сопротивление:

Р=ρLA

Размеры имеют смысл: если мы сделаем резистор в два раза длиннее, то расстояние для столкновений и отвода энергии будет в два раза больше, как у резисторов, соединенных последовательно.Вместо этого, если мы увеличим площадь поперечного сечения, средняя скорость дрейфа будет ниже при той же величине тока, поэтому при каждом столкновении теряется меньше энергии.

Удельное сопротивление ρ является свойством материала, а также функцией температуры: см. Практические резисторы: температурный коэффициент для получения дополнительной информации.

---

Почему ток линейно пропорционален напряжению в резистивном материале?

Это часто воспринимается как должное, но на самом деле это не очевидно. В свободном пространстве заряд в постоянном электрическом поле имел бы линейно возрастающую скорость , а не (в среднем) постоянную скорость в резистивном материале.

Вот одна из возможных моделей:

Даже при нулевом приложенном электрическом поле (то есть при нулевом напряжении) заряды не покоятся. Из-за теплового движения они постоянно толкаются.

Теперь давайте применим электрическое поле (т.е. ненулевое напряжение). Это поле →E поле вызывает силу на заряд:

→F=q→E=m→a

Эта сила немного ускоряет заряд в направлении поля. Однако, прежде чем он начнет двигаться особенно быстро, заряд сталкивается с другими зарядами внутри материала.Это столкновение вызывает потерю кинетической энергии (превращающейся в тепло в материале), и заряд должен снова стартовать с нулевой скоростью. Оттуда он начинает ускоряться за счет поля, и цикл ускорения и столкновения повторяется.

Предположим, что среднее время между столкновениями равно tcollision . В этом случае в промежутках между столкновениями →E поле может ускорить заряд от v=0 до некоторой скорости vmax до столкновения. В этом случае (с фиксированным tcollision ), средняя скорость частицы будет пропорциональна ускорению, обусловленному полем.(Если это неясно, нарисуйте график зависимости скорости заряда от времени. Это будет иметь вид пилообразной формы: увеличение от 0 до vmax во время tcollision , затем внезапно падает до 0 и повторяется снова. Средняя скорость ¯¯¯¯¯vd=vmax2 .)

Для получения более подробной информации о том, как все это проявляется со случайными тепловыми колебаниями в трех измерениях, посмотрите модель Drude .

Вы можете задаться вопросом, почему у нас есть среднее время между столкновениями, а не среднее расстояние между столкновениями.Это связано с тем, что тепловая скорость намного больше, чем скорость дрейфа, поэтому эти случайные тепловые скорости в основном определяют, когда происходит столкновение, а не скорость дрейфа, которая важна для определения частоты столкновений.

Для большинства материалов более высокая температура означает более высокие тепловые скорости и более короткое время столкновения. , поэтому более высокое сопротивление. Дополнительные сведения о взаимосвязи между сопротивлением и температурой см. в разделе Практические резисторы: температурный коэффициент.

---

Резисторы типа

обычно имеют линейную линейность на много порядков величины тока — в отличие от полупроводникового перехода, как мы увидим позже.

Резисторы обычно линейны независимо от того, в каком направлении течет ток – также в отличие от полупроводникового перехода.

Представьте себе механическую цилиндрическую пружину: сила линейна для малых и больших толчков, но в какой-то момент вы начинаете постоянно деформировать металл (пластическая деформация) и получаете нелинейное поведение.

Таким же образом, если вы превысите пределы резистора, вы можете навсегда заменить его, как правило, из-за перегрева. Дополнительные сведения см. в нескольких следующих разделах, посвященных мощности и практическим резисторам: номинальная мощность (мощность).

---

Сверхпроводники когда-то были экзотическими материалами, но становятся все более и более распространенными, поскольку их цена снижается, а диапазон рабочих температур растет. В настоящее время нет известных материалов, которые являются сверхпроводниками при комнатной температуре и давлении, но исследования в этой области находят материалы, которые работают при все более и более высоких температурах.

Сверхпроводники имеют не только низкое сопротивление, но и предлагают действительно нулевое сопротивление при протекании тока.

В сверхпроводнике нет внутренних неупругих столкновений между носителями заряда и веществом.

Существуют практические ограничения на сверхпроводники в нескольких измерениях:

1. Текущий. Сверхпроводник может поддерживать только определенную максимальную плотность тока, известную как критический ток .
2. Магнитное поле. Сверхпроводящие материалы имеют ограничения на напряженность магнитного поля, в котором они могут работать.
3. Рабочая температура. Сверхпроводящие материалы перестают быть сверхпроводящими при превышении некоторого максимального предела температуры.

В дополнение к этому, сверхпроводники и сверхпроводящие провода по-прежнему относительно сложны в работе с производственной точки зрения. Материалы часто хрупкие, их необходимо охлаждать до чрезвычайно низких температур, и их трудно соединять и соединять с другими компонентами.

---

В следующем разделе «Мощность» мы поговорим о том, куда уходит тепло от этих резистивных столкновений, и подумаем больше о потоке энергии и мощности в целом.

---

Роббинс, Майкл Ф. Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.com. Доступ . (Авторское право © 2021 CircuitLab, Inc. )

Электрическое сопротивление и закон Ома | Базовая теория постоянного тока (DC)

Для обзора, напряжение является мерой потенциальной энергии, доступной для электрических зарядов. Ток — это равномерный дрейф электрических зарядов в ответ на напряжение.Мы можем иметь напряжение, не имея тока, но мы не можем иметь ток, не имея сначала напряжения, которое его мотивирует. Ток без напряжения был бы эквивалентен движению без движущей силы.

Когда электрические заряды проходят через такой материал, как металл, они, естественно, сталкиваются с некоторым трением, так же как жидкость, движущаяся по трубе, неизбежно сталкивается с трением. У нас есть название для этого трения по отношению к движению электрического заряда: сопротивление . Подобно напряжению и току, сопротивление имеет свою особую единицу измерения: Ом , названную в честь немецкого физика Георга Симона Ома.

На этом этапе было бы неплохо обобщить и сравнить символы и единицы, которые мы используем для обозначения напряжения, тока и сопротивления:

 

реалов

Количество	Алгебраический символ	Блок и сокращение блока
Напряжение	$V$ (или $E$)	Вольт	В
Текущий	$I$	Ампер (или Ампер)	А
Сопротивление		Ом	$\Омега$

Ом определяет сопротивление как математическое соотношение между приложенным напряжением и результирующим током. Эта формула стала известна как Закон Ома , возможно, самая основная формула во всей электротехнике (показана здесь в трех разных формах, каждая из которых относится к разным переменным):

\[R = {V \over I} \hskip 30pt V = IR \hskip 30pt I = {V \over R}\]

Условно выражаясь, сопротивление — это напряжение, необходимое для протекания тока определенной силы через проводящий материал. Многие материалы имеют относительно стабильное сопротивление, а другие нет. Продаются устройства, называемые резисторами , которые изготавливаются с очень точным значением сопротивления для ограничения тока в цепях (среди прочего).

Вот пример закона Ома в действии: рассчитайте величину тока в цепи с источником напряжения 25 В и общим сопротивлением 3500 \(\Омега\). Взяв 25 вольт и разделив на 3500 Ом, вы должны получить результат 0,007143 ампера, или 7,143 миллиампер (7,143 мА).

Один из самых сложных аспектов закона Ома — не забывать хранить все переменные в контексте . Это общая проблема для многих студентов, изучающих физику: ни одно из уравнений, изученных на уроках физики, не даст правильных результатов, если все переменные не относятся к одному и тому же объекту или ситуации.2\)). Точно так же с законом Ома мы должны убедиться, что используемые нами значения напряжения, тока и сопротивления относятся к одной и той же части одной и той же цепи.

Если рассматриваемая цепь имеет только один источник напряжения, одно сопротивление и один путь для тока, мы не можем неправильно применить закон Ома. Выражение предыдущего примера в схематической диаграмме:

Однако, если мы посмотрим на более сложную цепь, мы столкнемся с возможностью неправильного применения закона Ома, потому что в цепи есть несколько сопротивлений, а не одно сопротивление:

Какое сопротивление мы используем для расчета тока в этой цепи? Делим ли мы наши 25 вольт на 3500 Ом, как в прошлый раз, или делим на 1500 Ом, или что-то совершенно другое? Ответ на этот вопрос заключается в отождествлении напряжений и токов. Мы знаем, что потенциал 25 вольт будет приложен к 90 240 общим 90 241 из двух сопротивлений \(R_1\) и \(R_2\), и, поскольку есть только один путь для тока, они должны иметь один и тот же ток. Таким образом, мы фактически имеем три напряжения (\(V_1\), \(V_2\) и \(V_{общий}\)), три сопротивления (\(R_1\), \(R_2\), и \(R_{total}\)), и только один ток (\(I\)):

Используя \(V = IR\) форму закона Ома, чтобы связать эти три напряжения (\(V_1\), \(V_2\) и \(V_{общий}\)) с одним током (\(I \)), мы получаем три уравнения для этой схемы:

\[V_{1} = I R_{1}\]

\[V_{2} = I R_{2}\]

\[V_{всего} = I R_{всего} = I (R_1 + R_2)\]

Мы можем решить только одну неизвестную переменную за один раз в любом уравнении.Это означает, что мы пока не можем найти \(V_1\), потому что, хотя мы знаем значение резистора \(R_1\) (3500 Ом), мы еще не знаем ток в цепи (\(I\)). То же самое для \(V_2\), потому что мы еще не знаем значение \(I\). Однако третье уравнение разрешимо, поскольку мы знаем как общее напряжение, так и значения обоих резисторов, оставляя ток цепи \(I\) как единственную неизвестную переменную. Манипуляции с этим уравнением и решение для \(I\):

\[I = {V_{total} \over R_{total}} = {V_{total} \over R_1 + R_2} = {25 \hbox{ V}\over 3500 \> \Omega + 1500 \> \Omega } = 0.005 \hbox{ А} = 5 \hbox{ мА}\]

Теперь, когда мы знаем величину тока в этой цепи, мы можем решить для \(V_1\) и \(V_2\) в других уравнениях, чтобы найти, что напряжение на резисторе \(R_1\) составляет 17,5 вольт, и что напряжение на резисторе \(R_2\) 7,5 вольт.

Закон Ома

Электрические схемы используются во всей аэрокосмической технике, от систем управления полетом, до приборной панели, до двигателя системы управления, чтобы аэродинамическая труба аппаратура и эксплуатация.В самой простой схеме используется один резистор . и источник электрического потенциала или напряжения . Электроны проходят через схема, производящая токов электричества. Сопротивление, напряжение и ток связаны между собой соотношением Закон Ома , как показано на рисунке. Если обозначить сопротивление через R , ток через i , а напряжение через V , то закон Ома гласит:

В = я Р

Сопротивление – это свойство цепи, которое противодействует потоку электронов. через провод.Это аналогично трению в механической системе или аэродинамической системе. тяга. Сопротивление измеряется в Ом и зависит от геометрия резистора и материал, из которого изготовлен резистор. На атомном уровне, свободные электроны в материале находятся в постоянном беспорядочном движении, постоянно сталкиваясь друг с другом и с окружающими атомами материала. При приложении электрического поля электроны преимущественно движутся в направлении, противоположном полю.Атомы образуют матрицу, через которую электроны переехать. В зависимости от расстояния, размера и ориентации матрицы скорость потока электронов будет меняться. Различные материалы имеют разные значения электропроводности . Удельное сопротивление материала является обратной величиной проводимости и обозначается как rho . Если материал имеет длину l и площадь поперечного сечения A , сопротивление равно предоставлено:

R = (ро * л) / А

Когда электроны движутся через материал, сталкиваясь друг с другом и с атомной матрицей, электроны генерируют случайную тепловую энергию или тепло.2 Р

Таким образом, резистор имеет два номинала: 1) его омическое значение и 2) его способность рассеивать мощность.

Поскольку сопротивление зависит от геометрии резистора или провода, а геометрия можно изменить приложенной силой, мы можем построить электрическую цепь для обнаружения сил по изменению сопротивления. Электрический тензорезисторы являются одним из самых распространенных типов инструментов, используемых в испытания в аэродинамической трубе.При построении практической схемы обычно используется более одного резистора. Резисторы может быть подключен в параллельно или в серия с источником питания. Специальная схема, называемая Мост Уитстона используется при испытаниях в аэродинамической трубе для исключить температурную погрешность в тензодатчиках.

---

Деятельность:

---

Навигация ..

Домашняя страница руководства для начинающих

20.2. Закон Ома: сопротивление и простые схемы – College Physics

Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, к нему прикладывается разность потенциалов ВВ величиной 12{В}{}, создающая электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Закон Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению ВВ размером 12{В}{}. Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлическом проводе прямо пропорционален приложенному напряжению :

I∝V.I∝V. size 12{I prop V.} {}

20,12

Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием.Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Сопротивление и простые схемы

Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением RR размером 12{R} {}. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток.Сопротивление определяется как обратно пропорциональное току, или

I∝1R. I∝1R. size 12{I prop { {1} over {R} } “.”} {}

20,13

Таким образом, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

Я=ВР. Я=ВР. size 12{I = {{V} over {R} } “.”} {}

20,14

Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов.Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление RR размер 12{R}{}, которое не зависит от напряжения ВВ размера 12{V}{} и тока II размера 12{I}{}. Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является ом, и он обозначается символом ΩΩ размера 12{ %OMEGA} {} (греческая омега в верхнем регистре).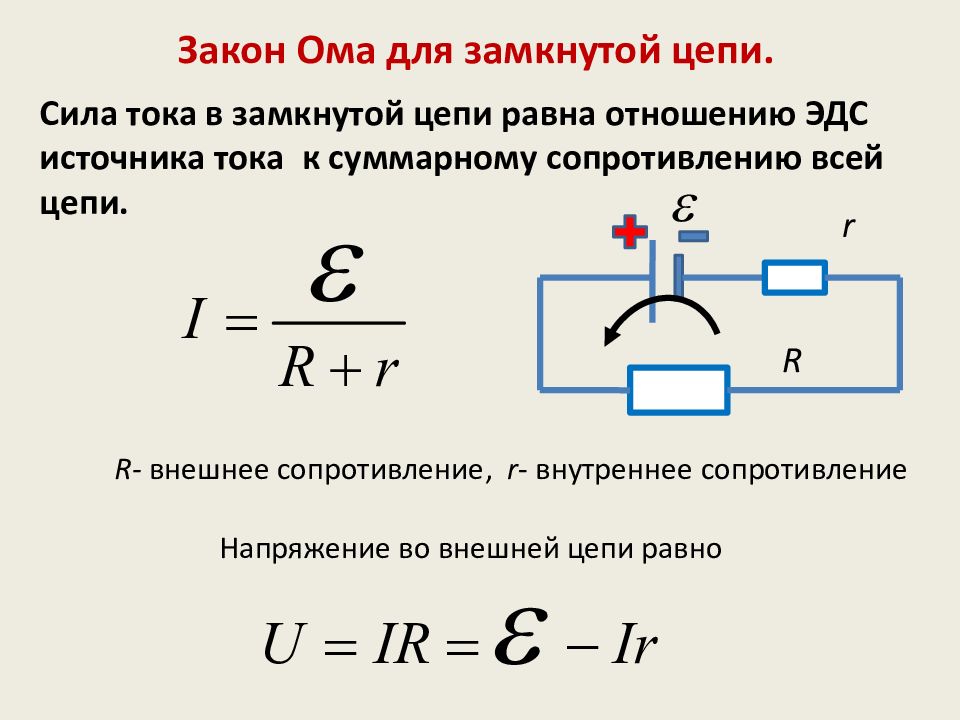 Перестановка I=V/RI=V/R размера 12{I = итал. “V/R”} {} дает R=V/IR=V/I размера 12{R= итал. “V/I”} {}, и поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

1 Ом = 1 ВА. 1 Ом = 1 ВА. size 12{“1 ” %OMEGA =” 1 ” { {V} over {A} } “.”} {}

20.15

На рис. 20.8 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно принять с пренебрежимо малым сопротивлением, либо их сопротивление включить в РР размер 12{R} {}.

Рис. 20.8 Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример 20.4

Расчет сопротивления: автомобильная фара

Чему равно сопротивление автомобильной фары, через которую 2. 50 А протекает при подаче на него 12,0 В?

Стратегия

Мы можем преобразовать закон Ома в соответствии с формулой I=V/RI=V/R размер 12{I = итал. “V/R”} {} и использовать его для определения сопротивления.

Решение

Изменение размера I=V/RI=V/R 12{I = ital “V/R”} {} и подстановка известных значений дает

R=VI=12,0 В2,50 A= 4,80 Ом. R=VI=12,0 В2,50 A= 4,80 Ом. размер 12{R = {{V} над {I} } = {{“12” “.” “0 В”} свыше {2 “.” “50 А”} } =” 4″ “.” “80 ” %OMEGA “.”} {}

20.16

Обсуждение

Это относительно небольшое сопротивление, но оно больше, чем холодостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.

Диапазон сопротивлений превышает многие порядки.Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012Ω1012Ω размер 12{“10” rSup { размер 8{“12”} } `%OMEGA} {} или более. У сухого человека сопротивление между ладонями и ногами может составлять 105 Ом 105 Ом размер 12 {“10” rSup { размер 8 {5} } ` %OMEGA } {}, тогда как сопротивление человеческого сердца составляет около 103 Ом 103 Ом размер 12 {“10″. ” rSup {размер 8{3}} `%OMEGA} {}. Кусок медной проволоки большого диаметра метровой длины может иметь сопротивление 10-5 Ом 10-5 Ом размер 12{“10” rSup { размер 8{ – 5} } ` %OMEGA } {}, а сверхпроводники вообще не имеют сопротивления. (они неомические).Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».

Дополнительную информацию можно получить путем решения I=V/RI=V/R размера 12{I = ital “V/R”} {} для V,V, размера 12{V} {}, что дает

V=IR. V =ИК. размер 12{V = итал. “IR.”} {}

20.17

Это выражение для размера VV 12{V} {} можно интерпретировать как падение напряжения на резисторе, создаваемое протеканием тока II размера 12{ я} {}. Для этого напряжения часто используется фраза IRIR size 12 {ital “IR”} {} drop .Например, фара в примере 20.4 имеет размер IRIR 12{ ital “IR”} {} падение 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается в источнике напряжения и уменьшается в резистор. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия.Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE=qΔVPE=qΔV размер 12{“PE”=qΔV} {}, и тот же размер qq 12{q} {} проходит через каждый. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 20.9.)

Рисунок 20.9 Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Установление связей: сохранение энергии

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

PhET Explorations

Закон Ома

Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.

Закон Ома и схемы

Основной закон Ома и схемы

В этой лабораторной работе мы обнаружим взаимосвязь между напряжением, сопротивлением и током, а затем изучим правила которые управляют различными конфигурациями цепей.

Начнем с блока питания. Для сегодняшней лаборатории мы можем рассматривать его как источник напряжения, то есть его работа для вывода определенного напряжения независимо от того, что к нему подключено. Думайте об этом как о причудливой батарее, которую вы можете подключить в стену. Следующее, на что нужно обратить внимание, это резистор. Мы рассмотрели их в некоторых вводных лабораторных работах и мы вернемся и посмотрим на них снова сегодня. Как следует из названия, резистор с большим значением будет очень полезен. хорошая работа по сопротивлению потоку электричества.Этот поток тоже имеет название, его называют током.

Настройте источник напряжения на четыре вольта. Установите цифровой мультиметр на напряжение и выполните прямое измерение. Когда ты проверьте 4 вольта, снимите цифровой мультиметр и настройте его на измерение тока (мА). Возьмите на выбор 6 или 7 резисторов, не менее 100 Ом. Подключите один резистор к источнику питания и цифровому мультиметру. Один провод должен идти от блока питания к резистору, то другой конец резистора должен идти к цифровому мультиметру, а цифровой мультиметр должен замыкать петлю и возвращаться обратно к источнику питания.Преподаватель лаборатории покажет вам одну из этих схем на лекции перед лабораторией. Измерьте ток через резистор на четыре вольта. Включите остальные резисторы один за другим. Вы видите подтверждение название? Когда вы получаете более высокие сопротивления, вы получаете более низкие токи?

Постройте кривую зависимости токов от сопротивления, как будет выглядеть график? Надеюсь, это подтверждает следующее уравнение:

ΔV = I R

Это известно как закон Ома. Мы можем проверить это, выбрав три резистора, каждый из которых больше 1000 Ом, а затем начертить I, как мы варьировать ΔV. Это должны быть красивые прямые линии. Склоны соответствуют вашим ожиданиям?

Цепи с несколькими резисторами
Следующее, на что следует обратить внимание, это то, что происходит с ситуацией, когда мы добавляем больше или больше резисторов к тому, что у нас уже есть. Начните с самой основной проблемы, как второй резистор влияет на схему? Оказывается, это более сложный проблема, чем можно подумать, так как есть два способа добавить второй резистор.Давайте рассмотрим каждый из них по очереди.

В нашей исходной схеме с одним резистором источник питания подключен к резистору. Давайте решим, что мы хотим измерить ток, выходящий из источника питания, поэтому мы вставляем цифровой мультиметр в качестве амперметра между источником питания и резистором. Теперь добавим второй резистор и посмотрим, как это повлияет на ток в цепи. Как подключить второй резистор? Подключите второй резистор так, чтобы кончики двух резисторов были соединены друг с другом, а хвосты — с друг с другом.Поскольку это приведет к тому, что резисторы выстроятся бок о бок, это называется параллельной схемой. Текущий от источника питания подниматься, опускаться или оставаться на прежнем уровне? Означает ли это, что сопротивление в цепи то увеличивалось, то уменьшалось, или остался прежним?

Это еще один способ подключения второго резистора. Отсоедините первую цепь и вместо этого подключите «наконечник» второй. резистор и к «хвосту» первого. Это называется последовательным соединением. Ваш ток идет вверх или вниз, или остается такой же? Означает ли это, что сопротивление в цепи увеличилось, уменьшилось или осталось прежним?

Теперь мы должны исследовать эти случаи более подробно.Поскольку в настоящее время у нас подключена последовательная цепь, мы можем начать с нее. Удалите цифровой мультиметр из схемы, чтобы использовать его в качестве измерителя напряжения. После того, как цепь будет пересоединена, измерьте напряжение на источник питания. Затем измерьте напряжение на каждом резисторе. Сделайте ваши результаты напряжений через комбинацию резисторы имеет смысл сравнивать с напряжением на блоке питания? Имеют ли значение напряжения на каждом резисторе? по сравнению с током в цепи? Объяснять.Добавьте последовательно третий резистор, и прежде чем делать какие-либо измерения, предсказать, что вы найдете. Соответствуют ли ваши измерения вашим прогнозам? Можете ли вы определить правило поведения напряжения? Как работает ток в цепи? Как сопротивления объединяются, чтобы сформировать общее сопротивление цепи?

Рис. 1. Измерение тока в последовательной цепи

Теперь давайте вернемся и применим ту же логику к параллельной схеме.Соберите параллельную цепь с двумя резисторами. Возьмите Цифровой мультиметр и проверьте напряжение на источнике питания и на каждом из резисторов. Что такое шаблон? Используйте закон Ома для предсказания ток через каждый резистор.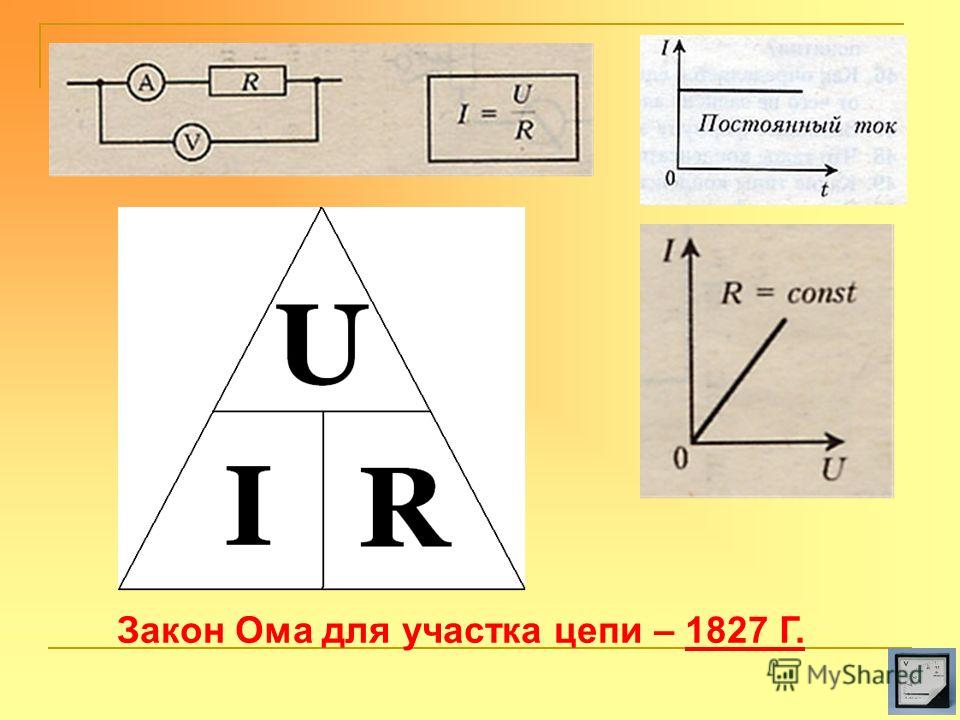 Измерьте ток, подключив цифровой мультиметр в качестве амперметра после каждого резистора (следя за тем, чтобы измерять ток только от этого резистора, а не от комбинации). Имеет ли ответ смысл? Теперь измерьте ток от блока питания, это тоже имеет смысл учитывая токи через каждый резистор? Добавьте третий резистор в параллели? Какое напряжение на нем будет? Какой будет ток через него? Можете ли вы найти правила, описывающие напряжение, ток и комбинированное сопротивление в параллельных цепях?

Рис. 2. Измерение тока в параллельной цепи

Запишите свои наблюдения и выводы в лабораторную тетрадь.

Закон

Ом (сопротивление) – Engineer-Educators.com

Два фундаментальных свойства тока и напряжения связаны третьим свойством, известным как сопротивление. В любой электрической цепи при приложении к ней напряжения возникает ток. Сопротивление проводника будет определять величину тока, протекающего при заданном напряжении. В большинстве случаев чем больше сопротивление цепи, тем меньше ток. Если сопротивление уменьшить, то ток увеличится.Эта зависимость носит линейный характер и известна как закон Ома.

Рис. 38. Зависимость напряжения от тока в цепи постоянного сопротивления.

Под линейно-пропорциональной характеристикой подразумевается, что если одна единица отношения увеличивается или уменьшается на определенный процент, другие переменные отношения увеличиваются или уменьшаются на тот же процент. Например, если напряжение на резисторе удвоится, то ток через резистор удвоится.Следует добавить, что это соотношение справедливо только в том случае, если сопротивление в цепи остается постоянным. Ведь видно, что при изменении сопротивления меняется и ток. График этой зависимости показан на рис. 38, где используется постоянное сопротивление 20 Ом. Соотношение между напряжением и током в этом примере показывает напряжение, отложенное горизонтально по оси X в значениях от 0 до 120 вольт, а соответствующие значения тока отложены вертикально в значениях от 0 до 6. 0 ампер по оси Y. Прямая линия, проведенная через все точки пересечения линий напряжения и тока, представляет уравнение
I = E⁄20 и называется линейной зависимостью.

Закон Ома может быть выражен в виде следующего уравнения:

Уравнение 1

Где I — ток в амперах, E — разность потенциалов, измеренная в вольтах, а R — сопротивление, измеренное в омах. Если известны любые две из этих схемных величин, третью можно найти простым алгебраическим преобразованием.С помощью этого уравнения мы можем рассчитать ток в цепи, если известны напряжение и сопротивление. Эту же формулу можно использовать для расчета напряжения. Умножая обе части уравнения 1 на R, мы получаем эквивалентную форму закона Ома:

Все три формулы, представленные в этом разделе, эквивалентны друг другу и представляют собой просто разные способы выражения закона Ома.

Различные уравнения, которые можно вывести путем перестановки основного закона, можно легко получить, используя треугольники на рисунке 39.

Треугольники, содержащие E, R и I, разделены на две части, где E над линией и I × R под ним. Чтобы определить неизвестную величину цепи, когда известны две другие, закройте неизвестную величину большим пальцем. Расположение оставшихся непокрытых букв в треугольнике укажет на выполняемую математическую операцию.Например, чтобы найти I, обратитесь к рисунку 39A и закройте I большим пальцем. Незакрашенные буквы означают, что E нужно разделить на R, или I = E/R. Чтобы найти R, обратитесь к Рисунку 39B и закройте R большим пальцем. Результат показывает, что E нужно разделить на I, или R = E/I. Чтобы найти E, обратитесь к рисунку 39C и закройте E большим пальцем. Результат показывает, что I следует умножить на R, или E = I × R.

Эта таблица полезна при изучении закона Ома. Его следует использовать для дополнения знаний новичка об алгебраическом методе.

Физика для науки и техники II

6.5 Закон Ома из Office of Academic Technologies на Vimeo.

6.05 Закон Ома

Мы видели, что сопротивление определяется как разность потенциалов между двумя точками, деленная на величину тока, проходящего через эти точки. А также удельное сопротивление определялось как отношение напряженности электрического поля в интересующей области к плотности тока в этой области.Эти соотношения в физике известны как законы Ома.

Здесь мы можем выразить разность потенциалов между двумя точками как ток, умноженный на сопротивление. Если мы построим разность потенциалов между двумя точками в зависимости от тока, проходящего через эти точки, для различных типов компонентов типичной электрической цепи, мы можем получить два разных случая. Один случай состоит в том, что зависимость между разностью потенциалов и током является линейной, так что это отношение, другими словами, В на i , всегда становится постоянным.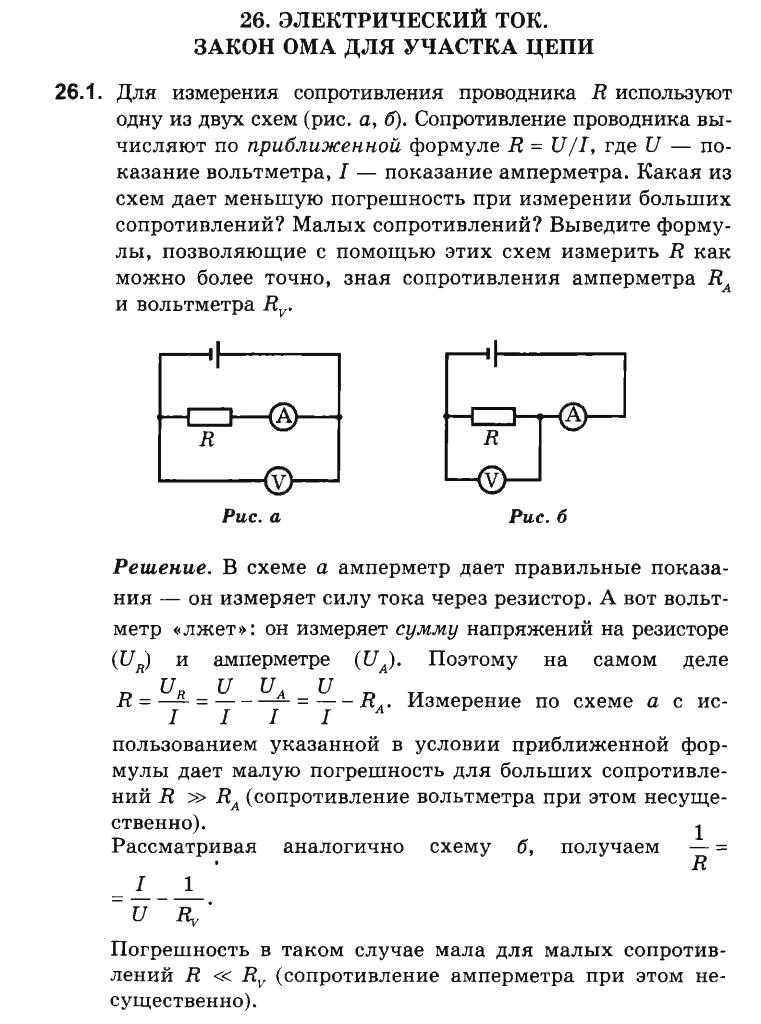

Конечно, ко второй категории относится тот случай, когда это отношение не является постоянным, и в результате мы получаем кривую. Например, что-то вроде этого, как в случае с диодами pn . Итак, вот пример поведения резистора, например, в случае диода pn .

Теперь говорят, что проводящее устройство подчиняется закону Ома, если его сопротивление между любыми двумя точками не зависит от величины и полярности разности потенциалов, приложенной между этими точками.Итак, если мы сделаем это заявление, то проводящее устройство подчиняется закону Ома, если его сопротивление между любыми двумя точками не зависит от величины и полярности разности потенциалов, приложенной между этими точками. Другими словами, отношение В к к или к к В остается все время постоянным, так что наклон кривой остается постоянным. Другими словами, мы получаем прямую линию, когда строим i против V или V против i .

Теперь V равно i умножить на R .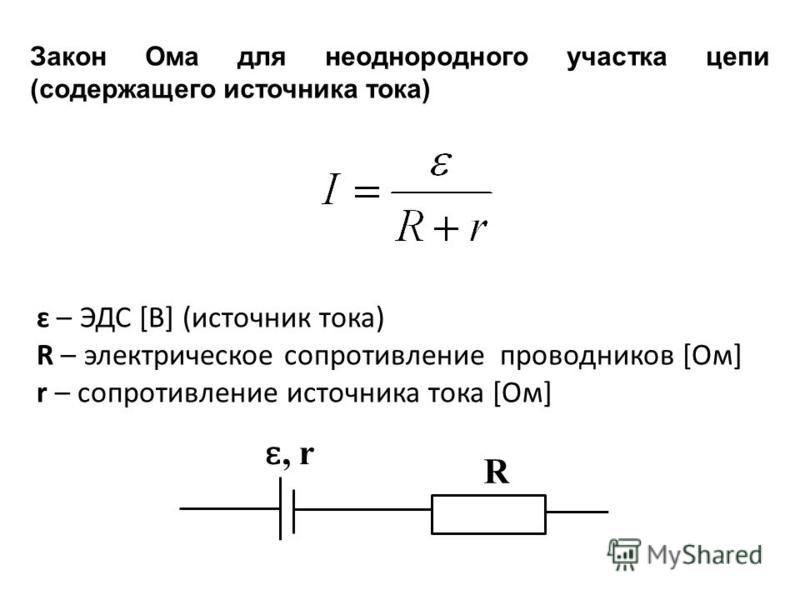 Верно для всех проводящих устройств. Мы просто разделяем эти устройства независимо от того, подчиняются они закону Ома или нет, просто наблюдая за сопротивлением, остается ли оно постоянным или нет. Другими словами, отношение В к i , тока к разности потенциалов к току, остается постоянным или нет.

Если это отношение остается постоянным, то мы говорим, что компонент подчиняется закону Ома. Если это не так, то мы говорим, что этот компонент не подчиняется закону Ома.Итак, если i против V линейно, то это соответствует случаю подчинения закону Ома. С другой стороны, если i против V , разность потенциалов нелинейна, то этот случай мы называем неподчинением закону Ома.

Теперь, конечно, локальный аналог закона Ома связан с определением удельного сопротивления, которое определялось как отношение напряженности электрического поля к плотности тока. И отсюда мы можем выразить E как ρ , умноженное на J . Конечно, это справедливо только для изотропных материалов. Материалы, электрические свойства которых одинаковы во всех направлениях. И здесь снова аналогичным образом, если отношение электрического поля к плотности тока остается все время постоянным, иначе говоря, если удельное сопротивление среды постоянно, то эта среда подчиняется закону Ома. С другой стороны, если это отношение, электрическое поле к плотности тока, непостоянно или E по сравнению с J не является линейной кривой, то в итоге мы говорим, что эта среда не подчиняется закону Ома.

Итак, до сих пор мы ввели два разных набора величин, в основном микроскопических величин, и это были электрические поля, плотность тока, удельное сопротивление. Эти величины важны, когда мы изучаем фундаментальное электрическое поведение материи. Итак, скажем, что они важны, когда мы ищем фундаментальные электрические свойства материи.

С другой стороны, макроскопические свойства или макроскопические величины, такие как разность потенциалов, ток и сопротивление, и эти величины важны, когда мы изготавливаем электрические приборы из конкретных проводников.