Закон Ома для цепи переменного тока. Мощность в цепи переменного тока. Резонанс в электрической цепи.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Закон Ома для цепи переменного тока. Мощность в…
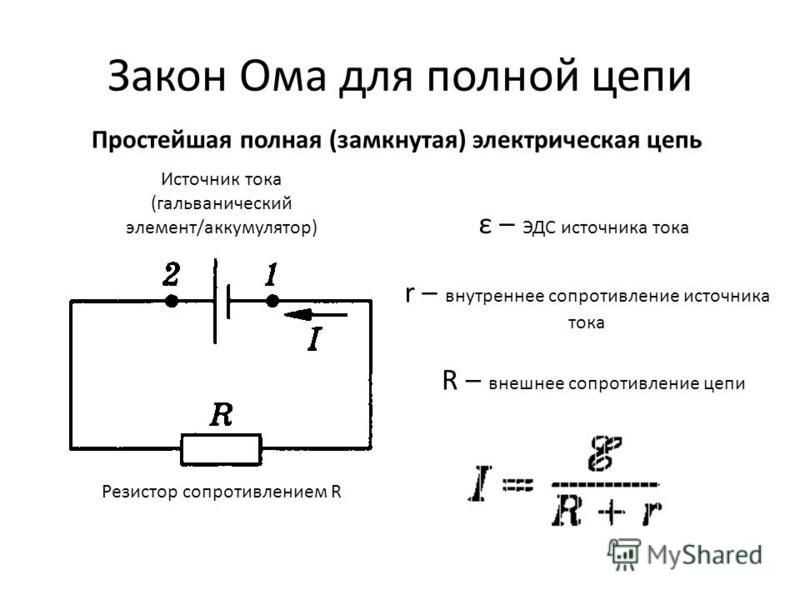
Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: – полное сопротивление переменному току. | |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: . | |
Сдвиг фаз в цепи переменного тока определяется характером нагрузки: или . |
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): | |
или, переходя к действующим значениям, . | |
Величина наз. | коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии или .
| |
Следовательно, – т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. | |
Амплитуды колебаний напряжения на индуктивности и емкости будут равны
и – т. |
|
Следовательно, . |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
При этом если величина , то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! | |
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа . | |
В случае резонанса . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов. |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т. |
|
Теги:
конспект
Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. – Объяснение нового материала.
Комментарии преподавателяЗакон Ома для участка цепиСила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару.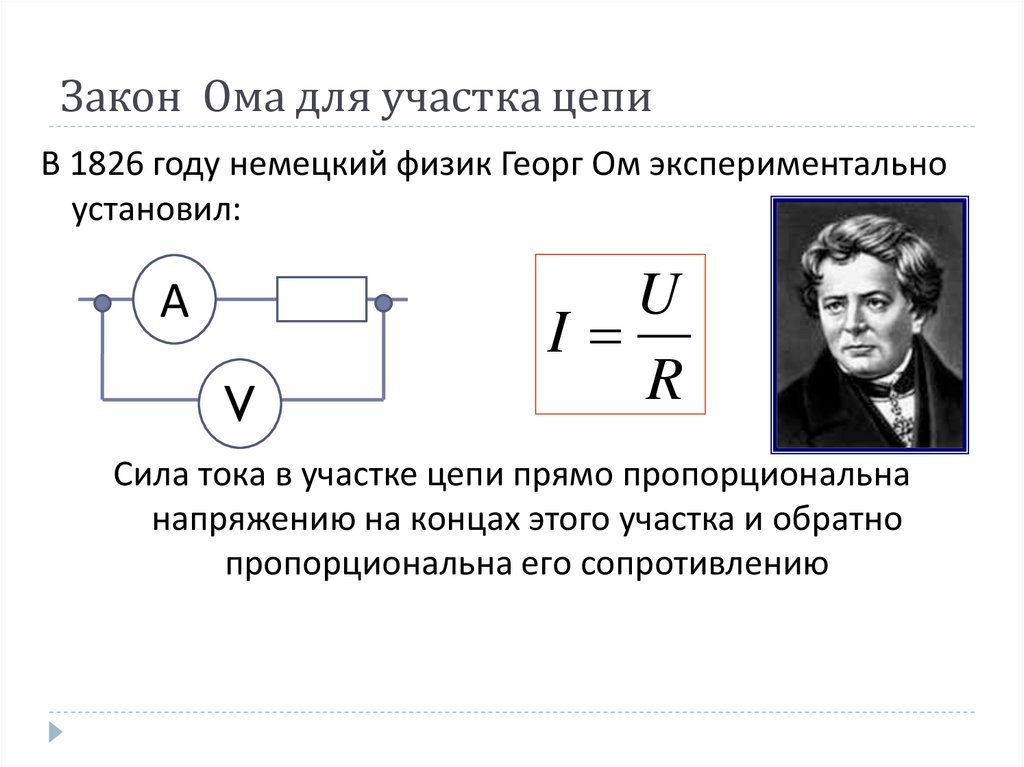 Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.
Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.
Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.
Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.
Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника.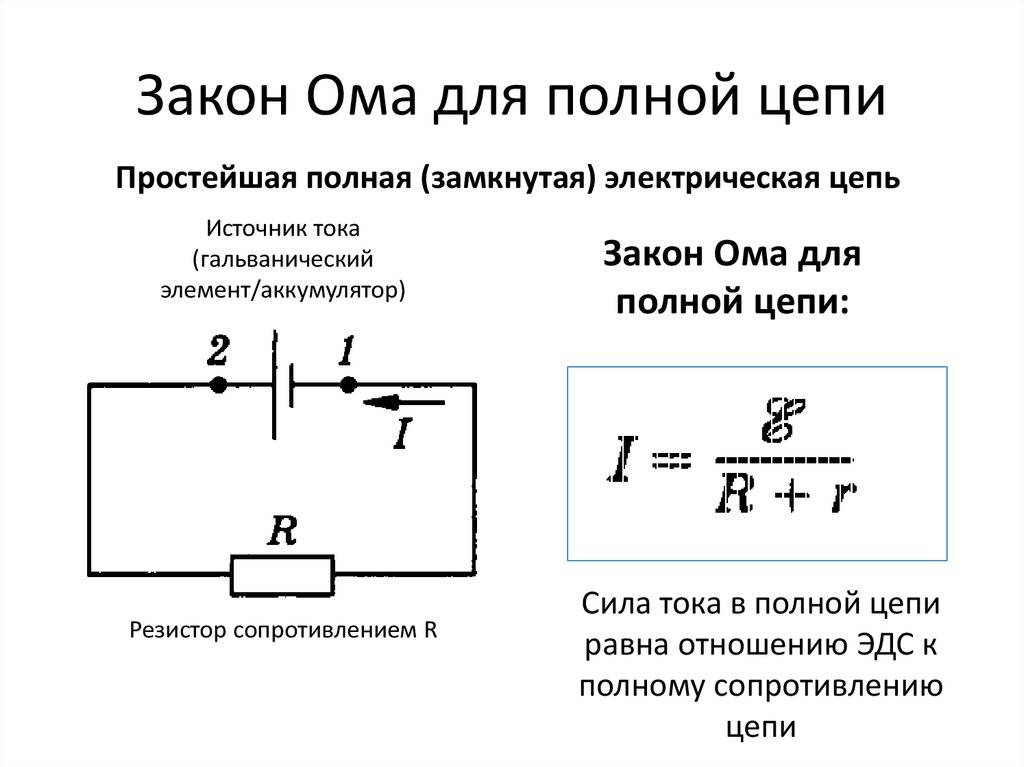 Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R – сопротивление проводника,
1/R – электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
работа электрического тока в цепи, состоящей из параллельно соединенных участков,
A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.

- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2.Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
К занятию прикреплен файл «Это интересно». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://www.youtube.com/watch?v=cVKE9NItreo
- http://znaika.ru/catalog/10-klass/physics/
- http://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- http://www.youtube.com/watch?v=EDI8DzWSSWY
- http://www.youtube.com/watch?v=bH_-qGnjJqc
формула взаимосвязи между электрическими величинами, порядок расчета
Фундаментальным положением, описывающим зависимость тока, сопротивления и напряжения друг от друга является закон Ома для цепи переменного тока. Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность.
- Основные понятия
- Определение напряжения
- Импеданс цепи
- Закон для переменного тока
- Использование формулы
Основные понятия
Вся наука электротехника построена на оперировании такими понятиями, как заряд и потенциал. Кроме этого, важными явлениями в цепи являются электрические и магнитные поля. Для того чтобы разобраться в сущности закона Ома, необходимо понимать, что представляют собой эти величины, и от чего зависят те или иные электромагнитные процессы.
Электричеством называется явление, обусловленное взаимодействием зарядов между собой и их движением. Это слово было введено в обиход Уильямом Гилбертом в 1600 году после открытия им способности некоторых тел наэлектризовываться. Так как свои эксперименты он проводил с кусочками янтаря, то и свойство притягивать или отталкивать ими другие вещества им было названо «янтарностью», что в переводе с греческого звучит как электричество.
В дальнейшем различными ученными, такими как Эрстед, Ампер, Джоуль, Фарадей, Вольт, Ленц и Ом был открыт ряд явлений. Благодаря их исследованиям в обиходе появились понятия: электромагнитная индукция и поле, гальванический элемент, ток и потенциал. Ими была открыта связь между электричеством и магнетизмом, что привело к появлению науки, изучающей теорию электромагнитных явлений.
В 1880 году русский инженер Лачинов теоретически указал, какие условия необходимы для передачи электричества на расстояния. А через 8 лет Генрих Рудольф Герц во время экспериментов зарегистрировал электромагнитные волны.
Таким образом было установлено, что электрические заряды способны создавать вокруг себя электрическое излучение. Условно их разделили на частицы с положительным и отрицательным знаком заряда. Было установленно, что одноимённого знака заряды притягиваются, а разноимённого — отталкиваются. Для возникновения их движения к физическому телу необходимо приложить какую-либо энергию. При их перемещении возникает магнитное поле.
При их перемещении возникает магнитное поле.
Свойство материалов обеспечивать движение зарядов получило название проводимость, а величина, обратная ей, — сопротивление. Способность пропускать через себя заряды зависит от структуры кристаллической решётки вещества, её связей, дефектов и содержания примесей.
Определение напряжения
Учёными было установлено, что существует два вида перемещения зарядов — хаотичное и направленное. Первый тип не приводит ни к каким процессам, так как энергия находится в сбалансированном состоянии. Но если к телу приложить силу, заставляющую заряды следовать в одну сторону, то возникнет электрический ток. Существует два вида:
- Постоянный — сила и направление которого остаются постоянными во времени.
- Переменный — имеющий разную величину в определённой точке времени и изменяющий своё движение, при этом повторяющий через равные интервалы времени своё изменение (цикл).
 Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Заряд характеризуется таким понятием, как потенциал, то есть количеством энергии, которой он обладает. Необходимая сила для перемещения заряда из одной точки тела в другую называется напряжением.
Определяется она относительно изменения потенциала заряда. Сила тока определяется отношением количества заряда, прошедшего через тело за единицу времени, к величине этого периода. Математически она описывается выражением: Im = ΔQ/ Δt, измеряется в амперах (A).
Относительно переменного сигнала вводится дополнительная величина — частота f, которая определяет цикличность прохождения сигнала f = 1/T, где T — период. За её единицу измерения принят герц (Гц). Исходя из этого синусоидальный ток выражается формулой:
I = Im * sin (w*t+ Ψ), где:
- Im — это сила тока в определённый момент времени;
- Ψ — фаза, определяемая смещением волны тока по отношению к напряжению;
- w — круговая частота, эта величина зависит от периода и равна w = 2*p*f.

Напряжение же характеризуется работой, которую совершает электрическое поле для переноса заряда из одной точки в другую. Определяется она как разность потенциалов: Um = φ1 — φ2. Затрачиваемая работа же складывается из двух сил: электрических и сторонних, называется электродвижущей (ЭДС). Зависит она от магнитной индукции. Потенциал же равен отношению энергии взаимодействия заряда окружающего поля к значению его величины.
Поэтому для гармонического изменения сигнала значение напряжения выражается как:
U = Um * sin (w*t + Ψ).
Где Um — амплитудное значение напряжения. Измеряется переменное напряжение в вольтах (В).
Импеданс цепи
Каждое физическое тело имеет своё сопротивление. Обусловлено оно внутренним строением вещества. Характеризуется эта величина свойством проводника препятствовать прохождению тока и зависит от удельного электрического параметра. Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м2. Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.
Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.
В то же время импеданс, полное сопротивление, находится как сумма пассивной и реактивной составляющей. Первая определяется только активным сопротивлением, состоящим из резистивной нагрузки источника питания и резисторов: R = R0 + r. Вторая находится как разность между ёмкостным и индуктивным сопротивлением: X = XL-Xc.
Если в электрическую цепь поместить идеальный конденсатор (без потерь), то после того, как на него поступит переменный сигнал, он зарядится. Ток начнёт поступать далее, в соответствии с периодами его заряда и разряда. Количество электричества, протекающее в цепи, равно: q = C * U, где С — ёмкость элемента, Ф; U — напряжение источника питания или на обкладках конденсатора, В.
Так как скорости изменения тока и напряжения прямо пропорциональны частоте w, то будет справедливым следующее выражение: I = 2* p * f * C * U. Отсюда получается, что ёмкостной импеданс вычисляется по формуле:
Xc = 1/ 2* p * f * C = 1/ w * C, Ом.
Индуктивное же сопротивление возникает вследствие появления в проводнике собственного поля, называемого ЭДС самоиндукции EL. Зависит она от индуктивности и скорости изменения тока. В свою очередь индуктивность зависит от форм и размеров проводника, магнитной проницаемости среды: L =Ф / I, измеряется в теслах (Тл). Поскольку напряжение, приложенное к индуктивности, по своей величине равно ЭДС самоиндукции, то справедливо EL = 2* p * f * L * I. При этом скорость изменения тока пропорциональна частоте w. Исходя из этого индуктивное сопротивление равно:
Xl = w * L, Ом.
Таким образом, импеданс цепи рассчитывается как: Z = (R 2 +(X c-X l) 2) ½, Ом.
com/embed/y8djn-Zmolc”>То есть он зависит от частоты переменного сигнала, индуктивности и ёмкости цепи, а также активного сопротивления источника и электрической линии. При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.
Закон для переменного тока
Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.
Математически закон Ома был описан как:
I = U / R, А.
Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.
Поэтому закон Ома для переменного тока описывается формулой:
I = U / Z, где:
- I — сила переменного тока, А;
- U — разность потенциалов, В;
- Z — полное сопротивление цепи, Ом.

Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:
Z = ((R+r)2 + (w*L — 1/w*C)2)½ = ((R+r)2+X2)½.
При прохождении тока переменной величины электромагнитное поле совершает работу, при этом из-за сопротивления, оказываемого в цепи, выделяется тепло. То есть электрическая энергия переходит в тепловую. Мощность же пропорциональна току и напряжению. Формула, описывающая мгновенное значение, выглядит как: P = I*U.
В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:
P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.
Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.
Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * ej*Ψ.
Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 900, то комплексное число можно не учитывать.
Использование формулы
Использование закона Ома позволяет построить временные характеристики различных элементов. С помощью него несложно рассчитать нагрузки для электрических схем, выбрать нужное сечение проводов, правильно подобрать защитные автоматы и предохранители. Понимание закона даёт возможность применить правильный источник питания.
Использование Закона Ома можно применить на практике для решения задачи. Например, пускай есть электрическая линия, состоящая из последовательно соединённых элементов, таких как: ёмкость, индуктивность и резистор. При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .
При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .
Вначале необходимо рассчитать реактивное сопротивление в цепи переменного тока. Так, ёмкостное сопротивление находится из выражения: Xc = 1/ (2 *p *F*C) и на частоте 200 Гц оно равно: Xc = 588 Ом.
Индуктивное сопротивление находится из выражения: XL = 2*p*F* L. На f = 200 Гц и оно оставляет: X*L = 1,25 Ом. Полное сопротивление RLC цепи будет: Z = ((10 *10 3 +1*10 3 ) 2 + (588−1,25) 2 ) ½ = 11 кОм.
Разность потенциалов, изменяющаяся по гармоническому закону синуса, будет определяться: U (t) = U * sin (2* p *f*t) = 120*sin (3,14*t). Ток будет равен: I (t) = 10* 10 −3 + sin (3,14*t+p/2).
По рассчитанным данным можно построить график тока, соответствующий частоте 100 Гц. Для этого в декартовой системе координат отображается зависимость тока от времени.
Следует отметить, закон Ома для переменного сигнала отличается от использующегося для классического расчёта лишь учётом полного сопротивления и частоты сигнала. А учитывать их важно, так как любой радиокомпонент обладает как активным, так и реактивным сопротивлением, что в итоге сказывается на работе всей схемы, особенно на высоких частотах. Поэтому при проектировании электронных конструкций, в частности импульсных устройств, для расчётов используется именно полный закон Ома.
3.2 Закон Ома: сопротивление и простые схемы
Цели обученияЗакон Ома Сопротивление и простые схемы
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Объясните происхождение закона Ома
- Расчет напряжений, токов и сопротивлений по закону Ома
- Объясните разницу между омическими и неомическими материалами
- Опишите простую схему
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 4.
 E.4.1 Учащийся может делать прогнозы относительно свойств резисторов и/или конденсаторов, помещенных в простую цепь, на основе геометрии элемента цепи и при поддержке научных теорий и математических соотношений. (СП 2.2, 6.4)
E.4.1 Учащийся может делать прогнозы относительно свойств резисторов и/или конденсаторов, помещенных в простую цепь, на основе геометрии элемента цепи и при поддержке научных теорий и математических соотношений. (СП 2.2, 6.4)
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, к нему прикладывается разность потенциалов ВВ величиной 12{В}{}, создающая электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению VV размером 12{V}{}. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению .
3.12 И∝ВИ∝В
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R.R. Размер 12{R} {} Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
3.13 И∝1Р.И∝1Р. размер 12 {I prop { {1} over {R} } “.”} {}
Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает
3.14 I=VR. I=VR. размер 12{I = {{V} над {R} } “.”} {}
I=VR. размер 12{I = {{V} над {R} } “.”} {}
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление RR размер 12{R}{}, не зависящее от напряжения ВВ размера 12{V}{} и тока I.I. size 12{I} {} Объект с простым сопротивлением называется резистор , даже если его сопротивление мало. Единицей измерения сопротивления является ом, и он обозначается символом ΩΩ размера 12{ %OMEGA} {} (греческая омега в верхнем регистре). Перестановка I=V/RI=V/R размера 12{I = итал. “V/R”} {} дает R=V/IR=V/I размера 12{R= итал. “V/I”} {}, и поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер.
3,15 1 Ом=1 ВА1 Ом=1 ВА
На рис. 3.8 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Сопротивление проводов, соединяющих источник напряжения с резистором, можно принять пренебрежимо малым, либо их сопротивление можно включить в размер R.R. 12{R} {}
Рисунок 3.8 Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Установление соединений: соединения в реальном мире
Закон Ома (V=IRV=IR) представляет собой фундаментальную зависимость, которая может быть представлена линейной функцией, где наклон линии представляет собой сопротивление. Сопротивление представляет собой напряжение, которое необходимо приложить к резистору, чтобы создать ток силой 1 А в цепи. График (на рисунке ниже) показывает это представление для двух простых цепей с резисторами, которые имеют разные сопротивления и, следовательно, разные наклоны.
График (на рисунке ниже) показывает это представление для двух простых цепей с резисторами, которые имеют разные сопротивления и, следовательно, разные наклоны.
Рисунок 3.9 На рисунке показано соотношение между током и напряжением для двух разных резисторов. Наклон графика представляет значение сопротивления, которое составляет 2 Ом и 4 Ом для двух показанных линий.
Создание соединений: соединения в реальном мире
Материалы, которые следуют закону Ома, имея линейную зависимость между напряжением и током, известны как омические материалы. С другой стороны, некоторые материалы демонстрируют нелинейную зависимость напряжения от тока и поэтому известны как неомические материалы. На рисунке ниже показаны соотношения тока и напряжения для двух типов материалов.
Рисунок 3.10 Показана зависимость между напряжением и током для омических и неомических материалов.
Очевидно, что сопротивление омического материала, показанное на (а), остается постоянным и может быть рассчитано путем нахождения наклона графика, но это неверно для неомического материала, показанного на (б).
Пример 3.4 Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее 12,0 В?
Стратегия
Мы можем преобразовать закон Ома, как указано в I=V/RI=V/R size 12{I = ital “V/R”} {}, и использовать его, чтобы найти сопротивление.
Решение
Изменение размера I=V/RI=V/R 12{I = ital “V/R”} {} и подстановка известных значений дает
3,16 R=VI=12,0 V2,50 A= 4,80 Ом.R=VI=12,0 В2,50 А= 4,80 Ом. размер 12{R = {{V} над {I} } = {{“12” “.” “0 В”} более {2 “.” “50 А”} } =” 4″ “.” “80 ” %OMEGA “.”} {}
Обсуждение
Это относительно небольшое сопротивление, но оно больше, чем холодостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.
Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012 Ом 1012 Ом и более. У сухого человека сопротивление между руками и ногами может составлять 105 Ом, 105 Ом, тогда как сопротивление человеческого сердца составляет около 103 Ом.103 Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10-5 Ом, 10-5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».
Дополнительная информация получена путем решения I=V/RI=V/R размера 12{I = ital “V/R”} {} для V,V, размера 12{V} {}, что дает
3,17 В=ИК.В=ИК. размер 12{V = итал. “IR.”} {}
Это выражение для ВН типоразмера 12{В} {} можно интерпретировать как падение напряжения на резисторе, создаваемое током И. И. size 12{I} {} Фраза IRIR size 12{ ital “IR”} {} drop часто используется для обозначения этого напряжения. Например, фара в примере 3.4 имеет размер IRIR 12{ ital “IR”} {} падение 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается в источнике напряжения и уменьшается в резистор. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE=qΔVPE=qΔV размер 12{“PE”=qΔV} {}, и тот же размер qq 12{q} {} проходит через каждый.
И. size 12{I} {} Фраза IRIR size 12{ ital “IR”} {} drop часто используется для обозначения этого напряжения. Например, фара в примере 3.4 имеет размер IRIR 12{ ital “IR”} {} падение 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается в источнике напряжения и уменьшается в резистор. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE=qΔVPE=qΔV размер 12{“PE”=qΔV} {}, и тот же размер qq 12{q} {} проходит через каждый.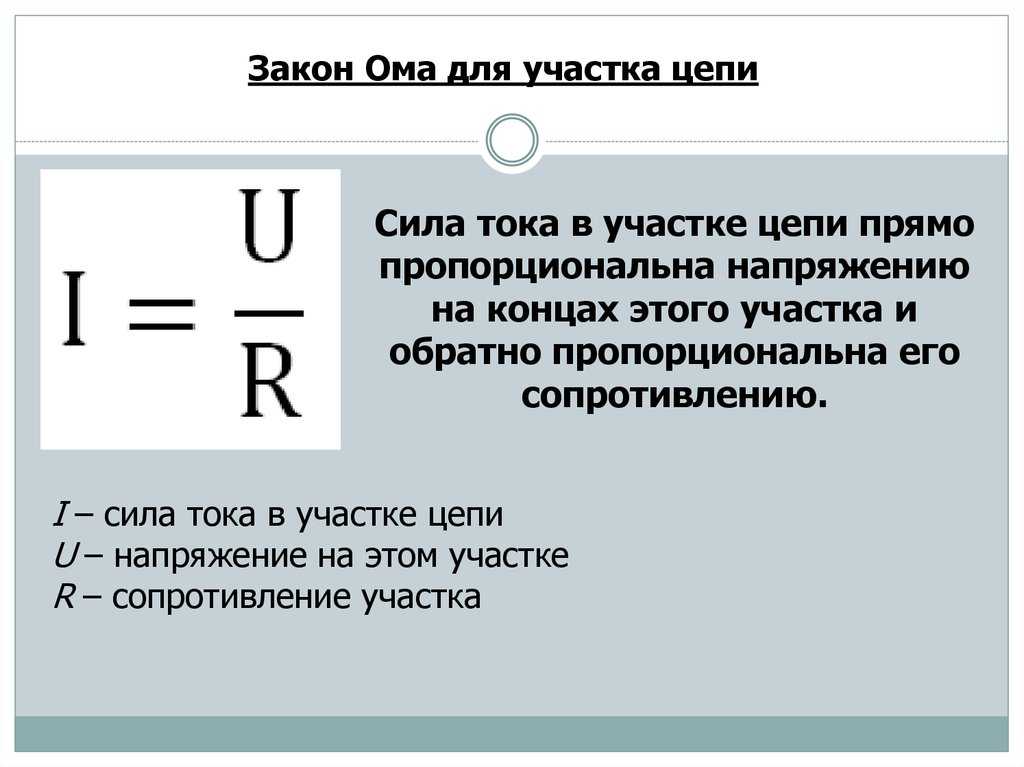 Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 3.11.)
Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 3.11.)
Рис. 3.11 Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Соединения: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
PhET Исследования: Закон Ома
Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Рисунок 3.12 Закон Ома
- Печать
- Поделиться
20.
 2 Закон Ома: Сопротивление и простые цепи – Колледж Физика 2e
2 Закон Ома: Сопротивление и простые цепи – Колледж Физика 2eЦели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.
- Расчет напряжения, тока или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов VV, которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению VV. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
I∝V.I∝V.
20.12
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением RR. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
I∝1R. I∝1R.
I∝1R.
20.13
Так, например, ток уменьшится вдвое, если сопротивление удвоится. Сочетание отношений тока к напряжению и тока к сопротивлению дает
I=VR.I=VR.
20.14
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление RR, не зависящее от напряжения VV и тока II. Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей измерения сопротивления является ом и обозначается символом ΩΩ (греческая омега в верхнем регистре). Перестановка I=V/RI=V/R дает R=V/IR=V/I, поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
1 Ом = 1 ВА. 1 Ом = 1 ВА.
1 Ом = 1 ВА.
20,15
На рис. 20.8 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Сопротивление проводов, соединяющих источник напряжения с резистором, можно принять пренебрежимо малым, либо их сопротивление включить в RR.
Рисунок 20,8 Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 20,4
Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
Стратегия
Мы можем преобразовать закон Ома в формулу I=V/RI=V/R и использовать его для определения сопротивления.
Решение
Перестановка I=V/RI=V/R и подстановка известных значений дает
R=VI=12,0 V2,50 A= 4,80 Ом. R=VI=12,0 V2,50 A= 4,80 Ом.
20.16
Обсуждение
Это относительно небольшое сопротивление, но оно больше морозостойкости фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.
Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012 Ом 1012 Ом и более. У сухого человека сопротивление между руками и ногами может составлять 105 Ом 105 Ом, тогда как сопротивление человеческого сердца составляет около 103 Ом 103 Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10-5 Ом 10-5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».
Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».
Дополнительная информация получена путем решения I=V/RI=V/R для V,V, что дает
V=IR.V=IR.
20,17
Это выражение для VV можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока II. Фраза IRIR drop часто используется для обозначения этого напряжения. Например, у фары в примере 20.4 падение IRIR составляет 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия.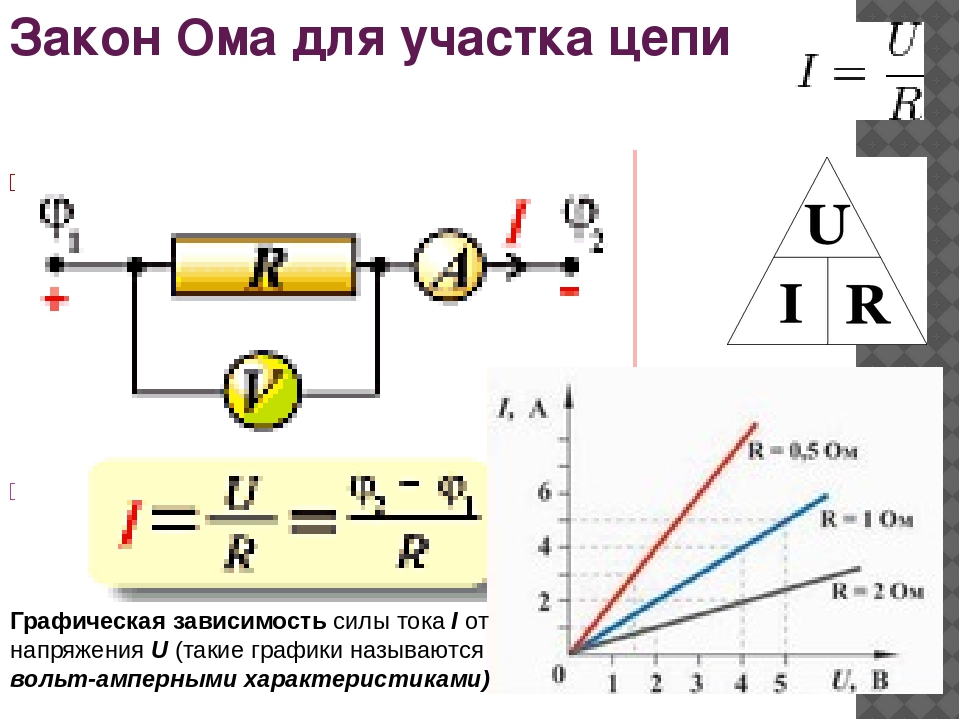 Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE=qΔVPE=qΔV, и через каждый протекает одно и то же qq. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 20.9..)
Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE=qΔVPE=qΔV, и через каждый протекает одно и то же qq. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 20.9..)
Рисунок 20,9 Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Исследования ФЕТ
Установление связей: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Исследования ФЕТ
Закон Ома
Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Закон Ома и электрические цепи
Введение
В этом эксперименте вы измерите вольт-амперные характеристики резистора и проверите, чтобы
проверьте, удовлетворяет ли резистор закону Ома. В процессе вы научитесь пользоваться мультиметром для
измерять напряжение, силу тока и сопротивление. Затем вы проверите некоторые законы теории цепей. Если разность потенциалов В , прикладывается к проводнику, электрический ток I , потечет
от конца с высоким потенциалом к концу с низким потенциалом. В общем, ток будет увеличиваться с
приложенное напряжение (разность потенциалов).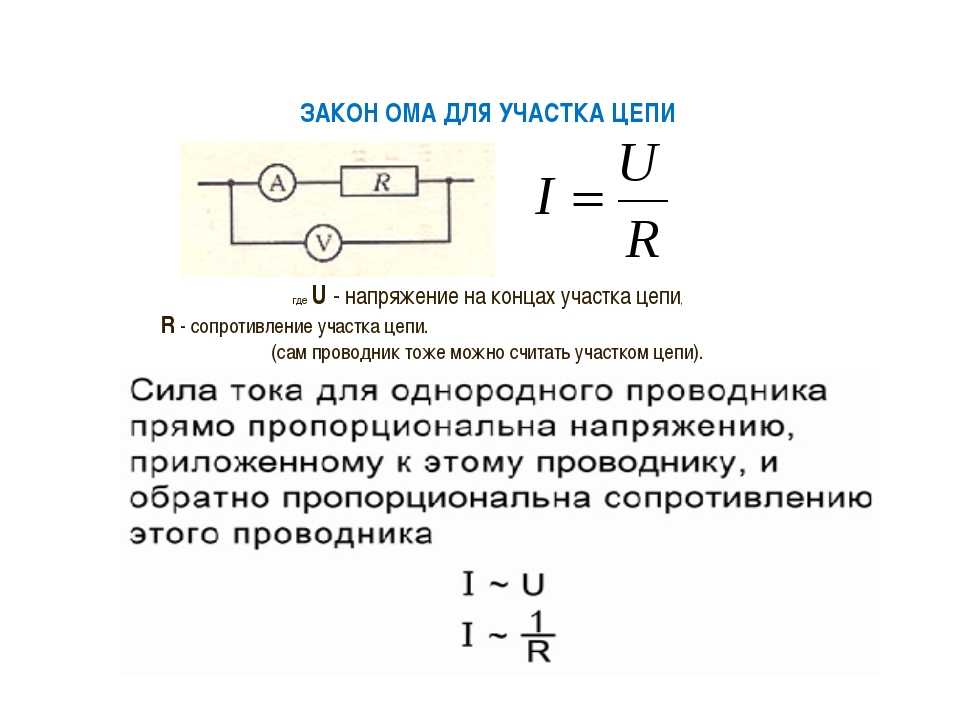 График зависимости тока от напряжения называется
вольт-амперная ( I – V ) характеристика. Если характеристика I – V представляет собой прямую линию, как на рис. 1, то говорят
что кусок проводника удовлетворяет закону Ома: V = IR , где R — константа, определенная как
сопротивление и измеряется в вольтах/амперах или Ω (Ом).
График зависимости тока от напряжения называется
вольт-амперная ( I – V ) характеристика. Если характеристика I – V представляет собой прямую линию, как на рис. 1, то говорят
что кусок проводника удовлетворяет закону Ома: V = IR , где R — константа, определенная как
сопротивление и измеряется в вольтах/амперах или Ω (Ом).
Рисунок 1 : ВАХ для омического материала
В электрической цепи провода, которые используются для соединения элементов цепи, имеют сопротивление.
Однако сопротивления проводов обычно пренебрежимо малы по сравнению с сопротивлениями проводов.
элементы цепи. Существуют специальные элементы, называемые резисторами, которые контролируют распределение токов.
в цепи введением в цепь известных сопротивлений. Токи и напряжения при разных
части схемы можно рассчитать, используя теорию цепей, которая будет обсуждаться позже. Существует много видов резисторов, но наиболее распространенными являются резисторы из углеродного композита.
показано ниже. Эти резисторы представляют собой маленькие коричневые цилиндры с цветными полосами. Цветные полосы следуют
цветовой код, указывающий сопротивление в пределах указанного производственного допуска.
Существует много видов резисторов, но наиболее распространенными являются резисторы из углеродного композита.
показано ниже. Эти резисторы представляют собой маленькие коричневые цилиндры с цветными полосами. Цветные полосы следуют
цветовой код, указывающий сопротивление в пределах указанного производственного допуска.
Рисунок 2
В этой лабораторной работе вы будете изучать только простые схемы DC , состоящие из источника питания и одного или больше резисторов, соединенных с проводами, сопротивления которых пренебрежимо малы по сравнению с сопротивлениями резисторы. Основная теория анализа цепи резюмируется двумя законами, известными как закон Кирхгофа. Правила:
1
Правило петли Кирхгофа- Общее изменение напряжения вокруг любого замкнутого контура равно нулю. Это очевидно, когда вы
считать, что напряжение есть разность потенциалов.
 Это правило просто говорит о том, что разность потенциалов
из одной точки в эту же точку равно нулю, как бы вы ни шли по кругу.
Это правило просто говорит о том, что разность потенциалов
из одной точки в эту же точку равно нулю, как бы вы ни шли по кругу. 2
Правило соединения Кирхгофа- Величина тока, протекающего в любой точке провода (или в месте соединения проводов), всегда равно количеству тока, вытекающего из него.
В цепи обычно встречаются два типа соединения резисторов: последовательное и параллельное. соединение показано на рис. 3.
Рисунок 3
Используя правила Кирхгофа, можно показать, что три последовательных резистора эквивалентны одному резистор с эквивалентным сопротивлением, Ом , определяемый по формуле:
( 1 )
Р = Р 1 + Р 2 + R 3 (резисторы последовательно)
Точно так же три резистора, соединенные параллельно, эквивалентны одному резистору с эквивалентное сопротивление, R , определяемое по формуле:
( 2 )
= + + (параллельные резисторы)
Аппаратура
Аппаратура для этого эксперимента состоит из регулируемого источника питания и двух мультиметров.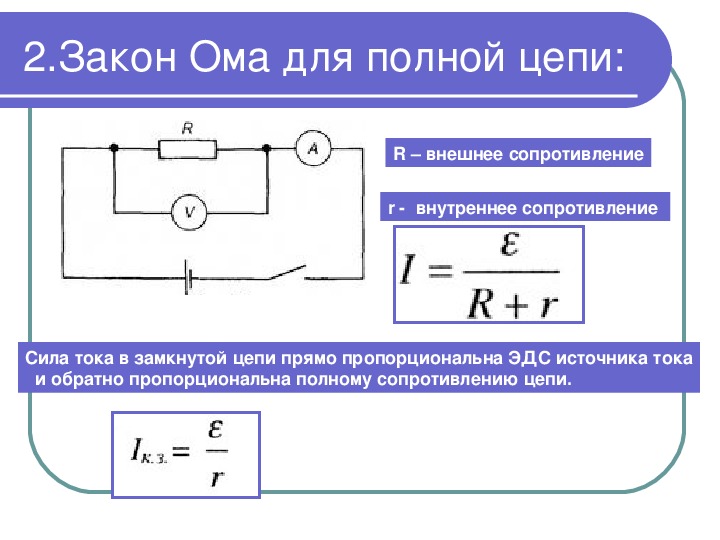 Эти части оборудования описаны ниже.
Эти части оборудования описаны ниже.
Регулируемый блок питания
Рисунок 4
Выше показан регулируемый источник питания и его условное обозначение на схеме. Этот блок питания преобразует выход из обычной розетки 110 В, 60 Гц AC в постоянный источник питания DC с переменное напряжение от 0 до 20 В. Выдает максимальный ток 0,5 А. Поворот ручки управления на устройстве может варьироваться выходное напряжение. Рекомендуется всегда начинать с нулевого напряжения и постепенно увеличивайте его до нужного значения. Выход получается через красный и черный разъемы. По по соглашению, красный разъем — это положительный терминал, а черный разъем — отрицательный.
Измерение токов, напряжений и сопротивлений
Когда мультиметр настроен на измерение тока, он служит амперметром, когда он настроен на измерение
напряжения он служит вольтметром, а когда настроен на измерение сопротивлений, служит омметром.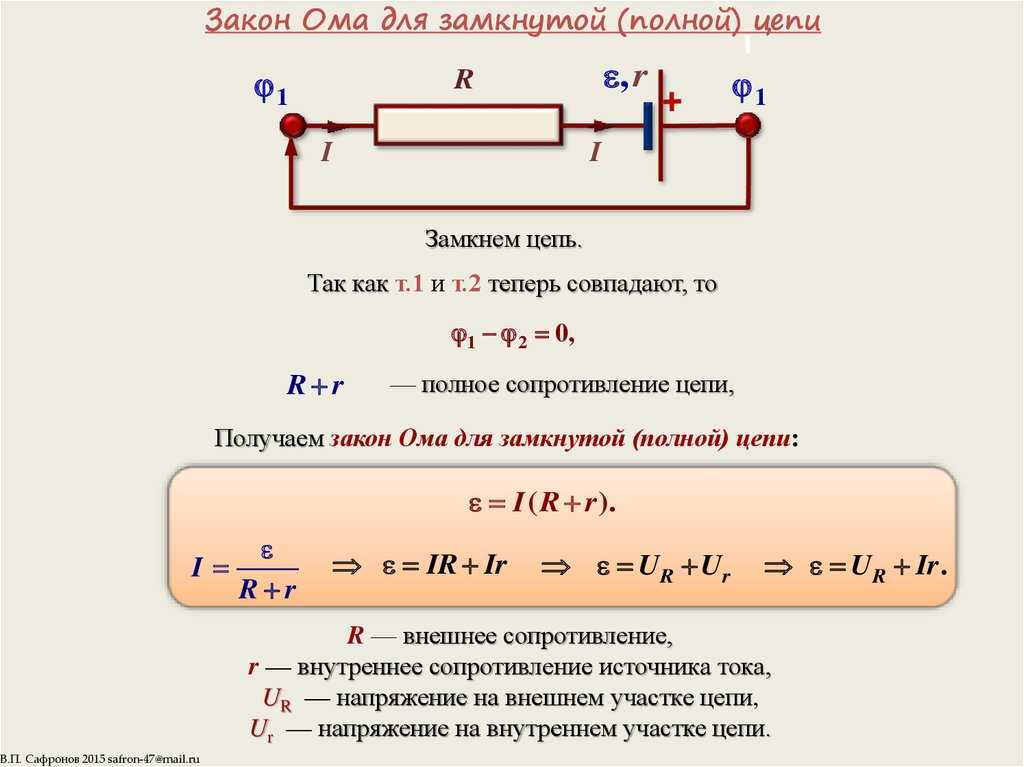 Ниже приведены символы амперметра, вольтметра и омметра.
Ниже приведены символы амперметра, вольтметра и омметра.
Рисунок 5
Чтобы измерить ток, протекающий через такой объект, как резистор, амперметр подключают к
серии с объектом, как показано на рис. 6а. Амперметры имеют очень низкое сопротивление так что когда они
помещенные в цепь, они не оказывают существенного влияния на общее сопротивление цепи и, следовательно, на ток,
измеряться. Для измерения напряжения на объекте, таком как резистор, вольтметр подключается параллельно
с объектом, как показано на рис. 6б. Вольтметры имеют очень большое сопротивление так что только небольшая часть
часть тока цепи будет отведена через вольтметр. Для измерения сопротивления объекта, например резистора, омметр подключается к объекту.
как показано на рис. 6в. Если резистор подключен к цепи, то один конец резистора должен быть
отключен от цепи во время измерения. Батарейка в мультиметре поставляет
ток, необходимый для измерения сопротивления, чтобы внешний источник питания не требуется.
Рисунок 6
Выполнение одновременных измерений тока и напряжения
Рисунок 7
Существует два способа проведения одновременных измерений A и V , как показано на рис. 7а и
Рис. 7б. На рис. 7а амперметр измеряет ток в резисторе R , а вольтметр не
измерить напряжение на резисторе, В Р . Вместо этого он измеряет напряжение на резисторе плюс
напряжение на амперметре, В А . Since V R + V A = I R + IR A , where R A is the resistance of the ammeter ,
показания вольтметра будут примерно равны В R , если R намного больше сопротивления
амперметр. Амперметры обычно имеют сопротивление 0,001 Ом или меньше. Использование метода (а) для измерения
напряжение на резисторе с малым сопротивлением, скажем, 0,1 Ом, даст ошибку в напряжении IR A / IR = 0,001/0,1 или ошибку 1%. С другой стороны, при большом сопротивлении, скажем, R = 1000 Ом, ошибка
уменьшается до
Использование метода (а) для измерения
напряжение на резисторе с малым сопротивлением, скажем, 0,1 Ом, даст ошибку в напряжении IR A / IR = 0,001/0,1 или ошибку 1%. С другой стороны, при большом сопротивлении, скажем, R = 1000 Ом, ошибка
уменьшается до
IR A / IR = 0,001/1000 или 0,0001%.
Поэтому метод, показанный на рис. 7а, следует использовать для измерения больших сопротивлений. На рис. 7б вольтметр измеряет напряжение на резисторе R , а амперметр не измерить ток через резистор I . Вместо этого он измеряет ток через резистор плюс ток через вольтметр, I В . Сумма этих токов определяется выражением:
( 3 )
я + я В = +
где R V сопротивление вольтметра. Следовательно, измерение амперметра будет приблизительно равно I , если R намного меньше, чем R V . Вольтметры обычно имеют сопротивления
100 000 Ом или более. Используя метод (б) для измерения тока на резисторе с большим сопротивлением, скажем
1000 Ом, погрешность измерения тока составит I V / I = R / R V = 1000/100000 или ошибка 1%.
Для небольшого сопротивления, скажем, Ом = 0,1 Ом, ошибка уменьшается до
Вольтметры обычно имеют сопротивления
100 000 Ом или более. Используя метод (б) для измерения тока на резисторе с большим сопротивлением, скажем
1000 Ом, погрешность измерения тока составит I V / I = R / R V = 1000/100000 или ошибка 1%.
Для небольшого сопротивления, скажем, Ом = 0,1 Ом, ошибка уменьшается до
Ом/Ом В = 0,1/100 000 или 0,0001%.
Поэтому метод, показанный на рис. 7b, следует использовать для измерения малых сопротивлений.
Процедура
Измерение сопротивления
1
Используя мультиметр в качестве омметра, измерьте и запишите сопротивления каждого из трех предусмотрены резисторы. Не забудьте включить оценки неопределенности, основанные на точности метр.2
Соедините три резистора последовательно. Запишите эквивалентное сопротивление, определенное с помощью омметр.
3
Соедините три резистора параллельно. Запишите эквивалентное сопротивление, определенное с помощью омметр.
Вольт-амперные характеристики резистора
Эта часть эксперимента требует, чтобы вы одновременно измеряли ток и напряжение на резистор. Резисторы, используемые в этом эксперименте, имеют сопротивление около 1000 Ом. Следовательно метод, показанный на рис. 7а, следует использовать для одновременного измерения I и V .
1
Выберите резистор с сопротивлением около 600 Ом. Подключите блок питания (не включайте его еще), вольтметр, амперметр и резистор в соответствии с принципиальной схемой, показанной на рис. Рис. 7а. Вы можете использовать Fluke 77 в качестве амперметра и Micronta в качестве вольтметра. Поскольку напряжение блока питания около 10 В, ток будет порядка миллиампер. Таким образом, клеммы «300 мА» и «COM» на Fluke 77 следует использовать для амперметра. связь.
связь.2
Попросите инструктора лаборатории проверить вашу схему, прежде чем включать источник питания.3
С ручкой управления в минимальном положении (полностью против часовой стрелки) включите питание. питание включено. Поверните ручку управления вверх, пока вольтметр не покажет около одного вольта. Запишите тока и напряжения.4
Увеличивайте напряжение с шагом 2 В. Измерьте и запишите ток и напряжение. Останавливаться когда напряжение достигает примерно 15 Вольт.5
Полностью поверните ручку управления на блоке питания против часовой стрелки и поверните выключатель питания. выключенный.6
Проверьте свои данные, построив приблизительный график V против I на листе технических данных или на листе миллиметровой бумаги. Проверьте, согласуется ли ваш график с законом Ома. Проверьте, дает ли наклон вашего участка правильный сопротивление.7
Повторите вышеуказанные шаги, чтобы измерить V vs. I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА.
I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА.
Правила Кирхгофа
В этом эксперименте вы проверите правила Кирхгофа на простой схеме, показанной ниже.
Рисунок 8
1
Подключите три резистора и блок питания в соответствии с приведенной выше схемой. Быть Обязательно определите и запишите значения трех резисторов.2
Попросите инструктора лаборатории проверить вашу схему, прежде чем включать источник питания.3
Включите источник питания и регулируйте ручку управления до тех пор, пока напряжение источника питания не станет равным 10 В. Запишите выходное напряжение 90 245 В 90 034 и сохраните его до конца эксперимента.4
Измерить и записать напряжения В 1 , В 2 и В 3 на каждом из резисторов. Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.
Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.5
Измерьте и запишите токи I 1 , I 2 и I 3 через каждый из резисторов вместе с соответствующие значения неопределенности. Поскольку для этого измерения источник питания всегда включен, легко перегореть предохранитель на мультиметре, если он не подключен должным образом. Выключить мультиметр при подключении. Убедитесь, что мультиметр подключен последовательно с резистором, который вы измеряете, прежде чем включать его. Если вы не уверены, уточните у своего инструктор.6
Выключите мультиметр и источник питания, когда закончите эксперимент.
Когда вы закончите эксперимент, очистите свое рабочее место и верните все
провода и зажимы в свои бункеры для хранения. Убедитесь, что вы и ваш инструктор поставили свои подписи на листах данных и передали копию
свои данные, прежде чем покинуть лабораторию.
Анализ данных
Измерение сопротивления
Для этой части мы будем обозначать рассчитанное эквивалентное сопротивление через R T , а измеренное эквивалентное сопротивление через R .
1
Рассчитайте сумму R T сопротивлений трех резисторов R 1 , R 2 и R 3 подключены серии.2
Каковы погрешностиu R 1 , u R 2 , u R 3
в ваших измерениях сопротивлений? Что это источник неопределенности?3
Используя ваши значения погрешностей трех резисторов, рассчитайте погрешность сумма u R T с помощью формулы распространения неопределенности для суммы.
4
Суммируйте ваши значения R и R T , включая неопределенности.5
Рассчитайте общее сопротивлениеR T
для параллельного соединения.6
Используя формулу распространения неопределенности для отношения, покажите, что дробная неопределенность из f совпадает с дробной неопределенностью 1/ f , т.е. показывает=
u 1/f 1/f 7
Используя уравнение шага 6, вычислите неопределенности 1/ R 1 , 1/ R 2 и 1/ R 3 . Затем с помощью распространения неопределенности для суммы, рассчитать неопределенность 1/ R T от неопределенностей из 1/ Р 1 , 1/ Р 2 и 1/ Р 3 . Наконец, снова используя уравнение шага 6, рассчитайте неопределенность R T от неопределенности 1/ R T .
8
Суммируйте ваши значения R и R T , включая неопределенности.Характеристики тока и напряжения резистора и лампочки
1
Подготовьте две таблицы (одну для резистора и одну для лампочки) токов и напряжений. из полученных данных.2
Сделайте график рассеяния В против I для данных резистора.3
Создайте линейную подгонку вашего графика по закону Ома по методу наименьших квадратов: В = ИК . Чему соответствуют параметры наклона и пересечения в подгонке?4
Суммируйте значение R (измеренное мультиметром) и подогнанное значение R , включая неопределенности.5
Постройте диаграмму рассеяния В против I для данных об лампочке.
Петля Кирхгофа и правила соединений
1
Каковы погрешности ваших измерений токов I 1 , I 2 и I 3 ? На основе этих неопределенностей проверьте, удовлетворяют ли измеренные токи правилу перехода, т. е.
е.I 1 = I 2 + I 3 .
2
В схеме, используемой в этой части, три петли. Запишите уравнение, данное правило цикла для каждого цикла. На основании погрешностей в ваших измерениях В 1 , В 2 , и В 3 , убедитесь, что измеренные вами напряжения удовлетворяют уравнениям, полученным из правила контура.
Обсуждение
Обобщите результаты для раздела, посвященного измерению сопротивления. Какое из соединений, последовательное или параллельное, дало наименьшую суммарную сопротивление? Почему? Соответствует ли ваше измеренное значение общего сопротивления последовательного соединения и параллельное соединение соответствует расчетному эквивалентному сопротивлению? Дайте характеристику вольт-амперной характеристики резистора, изучаемого в разделе «Вольт-амперная характеристика резистора».




 е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p).
е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p).

 Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Эта переменчивость описывается по гармоническому закону синуса или косинуса.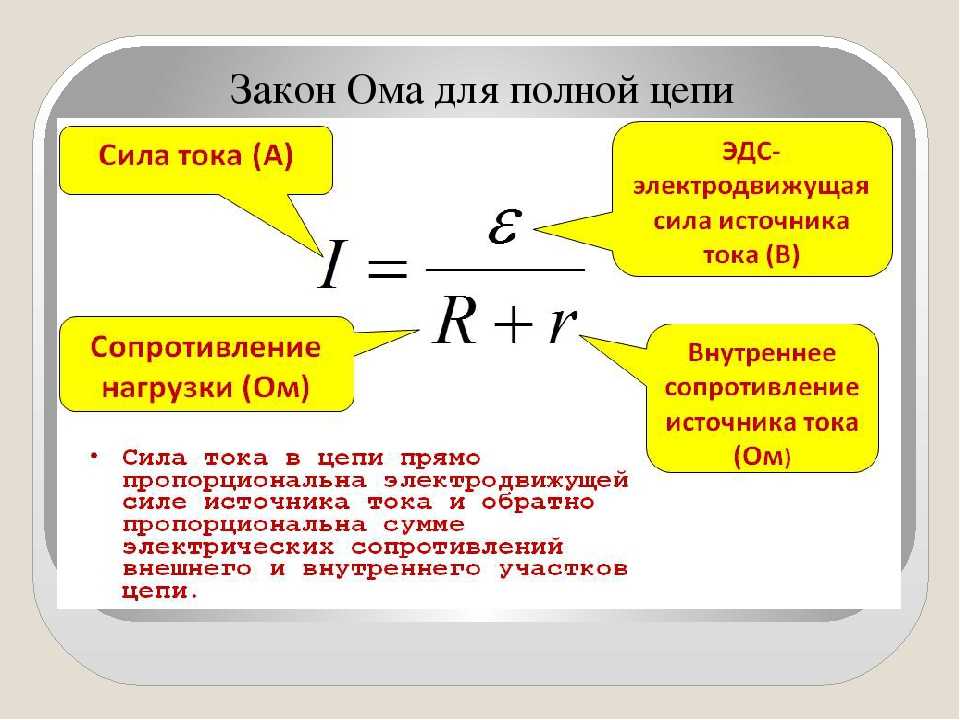

 E.4.1 Учащийся может делать прогнозы относительно свойств резисторов и/или конденсаторов, помещенных в простую цепь, на основе геометрии элемента цепи и при поддержке научных теорий и математических соотношений. (СП 2.2, 6.4)
E.4.1 Учащийся может делать прогнозы относительно свойств резисторов и/или конденсаторов, помещенных в простую цепь, на основе геометрии элемента цепи и при поддержке научных теорий и математических соотношений. (СП 2.2, 6.4)  Это правило просто говорит о том, что разность потенциалов
из одной точки в эту же точку равно нулю, как бы вы ни шли по кругу.
Это правило просто говорит о том, что разность потенциалов
из одной точки в эту же точку равно нулю, как бы вы ни шли по кругу.
 связь.
связь. I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА.
I характеристики лампочки (#53, 120 мА при
14 В). Используйте ту же схему, но замените резистор лампочкой. Возьмите показания данных в
шаг тока от 10 мА до максимум 100 мА. Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.
Запомни
включите оценки неопределенности для каждого из ваших измерений на основе рейтинга точности
метр.

 е.
е.