Закон ома выражается формулой: Какая формула выражает закон Ома?

Обобщенный закон Ома.

Закон Ома выражаемый формулой, определяет зависимость между током и напряжением на пассивном участке электрической цепи.

Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).

Из формулы 15 следует:

_a-_b=I(R₁+R₂)- E₁+E₂ (16)

На положительное напряжение на участке a – b Uab=_a-_b

Следовательно, Uab= I(R₁+R₂)- E₁+E₂ (17)

(18)

Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.

Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».

Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.

Пример № 1 построения потенциальной диаграммы:

Построить потенциальную диаграмму для одноконтурной схемы:

E₁=25В; E₂=5В; E₃=20В; E₄=35В,

R₁=8 Ом; R₂=24 Ом; R₃=40 Ом; R₄=4 Ом,

r₁=2 Ом; r₂=6 Ом; r₃=2 Ом; r₄=4 Ом.

Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r

1– r₄) за их пределы; обозначим точки контура.

Рис.2

2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:

3. За базисную точку примем точку a. Найдем потенциалы остальных точек:

_b= _a– IR_{1 =} – 4В _e= _d– IR_{2 =} 8В

_c= _b– Ir_{1 =} – 5В _f= _e+ E_{2 =} 13В

_d= _c+ E_{1 =} 20В _q= _f– Ir_{2 =} 10В

_k= _q– IR_{3 =} – 10В _n= _m– IR_{4 =} – 33В

_e = _k – E_{3 =} – 30В _o = _n – Ir_{4 =} – 35В

_m = _e

– Ir_{3 =} – 31В _a = _o + E_{4 =} 0

4. В системе координат строим потенциальную диаграмму:

Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.

Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.

Первый закон Кирхгофа:

Алгебраическая сумма токов в узле равна нулю:

_i = 0 (19)

Где i – число ветвей, сходящихся в данном узле.

Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.

Рис.17. Иллюстрация к первому закону Кирхгофа.

Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:

Nуp = Nу – 1,

Где Nу – число узлов в рассматриваемой цепи.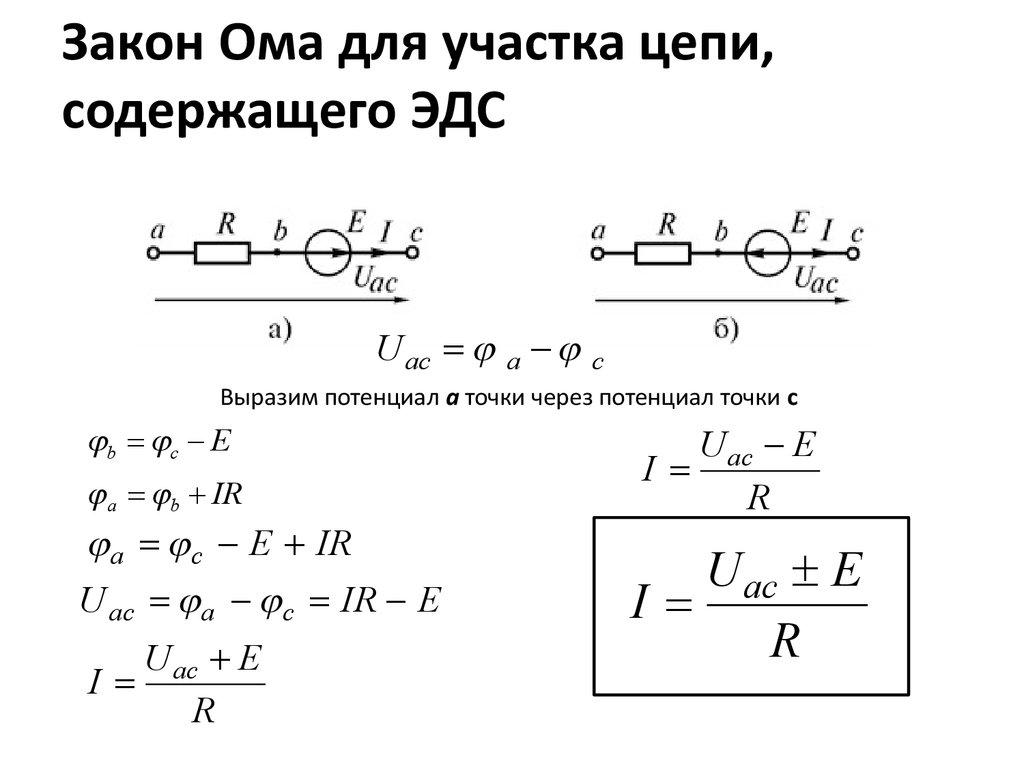

Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.

Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».

Тогда уравнение по первому закону Кирхгофа запишется так:

I₁ – I₂ + I₃ – I₄ = 0.

Уравнения, составленные по первому закону Кирхгофа, называются узловыми.

Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.

Второй закон Кирхгофа:

Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:

 Ui =  Ei

 IiRi=Ei(20)

Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.

**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:

Nуp = Nb – Nу + 1 – Nэ.д.с.

Где Nb – число ветвей электрической цепи;

Nу – число узлов;

Nэ.д.с. – число идеальных источников э.д.с.

Рис.18. Иллюстрация ко второму закону Кирхгофа.

Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:

1. произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).

2. э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».

Например, для контура рис. 18, второй закон Кирхгофа запишется следующим образом:

U₁ – U₂ + U₃ = E₁ – E₃ – E₄ (21)

Уравнение (20) можно переписать в виде:

 (Ui – Ei) = 0 (22)

Где (U – E) – напряжение на ветви.

Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:

Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.

Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.

Задача №1.

В схеме рис.1 заданы токи I₁ и I₃, сопротивления и э.д.с. Определить токи I₄, I₅, I₆ ; напряжение между точками a и b, если I₁ = 10мA, I₃ = -20 мA, R₄ = 5kОм, E₅ = 20B, R₅ = 3kОм, E₆ = 40B, R₆ = 2kОм.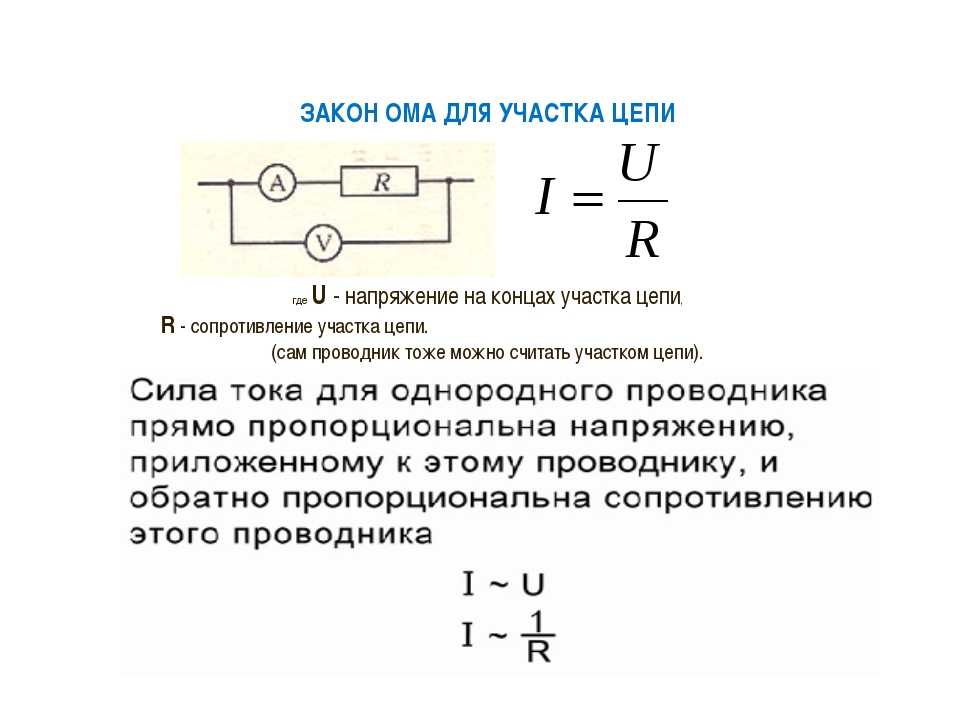

.

Рис.1

Решение:

1. Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.

В результате решения получаем: I₆ = 0; I₄ = 10мA; I₅ = -10мA

2. зададим направление напряжения между точками a и b от точки «a» к точке «b» – U_ab. Это напряжение найдем из уравнения по второму закону Кирхгофа:

I₄R₄ + U_ab + I₆

R₆ = 0

U_ab = – 50B.

Задача №2.

Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.

Дано: I₁ = 20мA; I₂ = 10мA

R₁ = 5kОм, R₃ = 4kОм, R₄ = 6kОм, R₅ = 2kОм, R₆ = 4kОм.

Рис.2

Решение:

Число узловых уравнений – 3, число контурных уравнений – 1.

Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.

В данной цепи известны токи ветвей I₁ и I₂. Неизвестные токи I₃, I₄, I₅, I₆.

Решая систему, получаем: I₃ = 13,75 мA; I₄ = -3,75мA; I₅ = 6,25мA; I₆ = 16,25мA.

1. Фотометрия.

%PDF-1.6 % 1 0 obj > /Metadata 4 0 R /OCProperties > > > ] /ON [ 5 0 R ] /Order [ ] /RBGroups [ ] >> /OCGs [ 5 0 R ] >> /Pages 7 0 R /StructTreeRoot 30 0 R /Type /Catalog >> endobj 2 0 obj /CreationDate (D:20130711143933+03’00’) /Creator (Microsoft Word 2013) /ModDate (D:20130711144145+03’00’) /Producer (Microsoft Word 2013) /Title >> endobj 3 0 obj > /Font > >> /Fields 278 0 R >> endobj 4 0 obj > stream application/pdf

Юра

1. Фотометрия.

2013-07-11T14:39:33+03:00Microsoft® Word 20132013-07-11T14:41:45+03:002013-07-11T14:41:45+03:00Microsoft® Word 2013uuid:1de896c6-a96d-42d9-8387-15f71bdb6931uuid:3aabc18f-2ed0-4035-a986-9c36ba79138b endstream endobj 5 0 obj > /PageElement > /Print > /View > >> >> endobj 6 0 obj > stream x͙oFW_Pݑ_@KaAC10d@V/gYĒO r%S#Re$eBT&C!yN!j^B;Rd;I*0d *)y|),U0O߫K_՟Vwq. &/%;1d/@d/@d/TԪ~wW777]|rJs>?c|l}\wTrVvֻܨ>J&sĒw鋝Q5~[s(ZtwnյBs°:]C_|f!2XNm׋`|}Rv=~Mׁ;knr{>,Wzo87HgωVJ6{nXWSAuuz=Pk4355⠮ᔮlQ*ހ(Ocvn;z+N׹ H.P3″PoE]`?*,PbCXZP QfxhHG7 uD)Q6J0x̬/B}پqC

Закон

Ома (сопротивление) – Mypdh.engineer

Два фундаментальных свойства тока и напряжения связаны третьим свойством, известным как сопротивление. В любой электрической цепи при приложении к ней напряжения возникает ток. Сопротивление проводника будет определять величину тока, протекающего при заданном напряжении. В большинстве случаев чем больше сопротивление цепи, тем меньше ток. Если сопротивление уменьшить, то ток возрастет. Эта зависимость имеет линейный характер и известна как закон Ома.

Рис. 38. Зависимость напряжения от тока в цепи постоянного сопротивления.

Под линейно-пропорциональной характеристикой подразумевается, что если одна единица отношения увеличивается или уменьшается на определенный процент, другие переменные отношения увеличиваются или уменьшаются на тот же процент. Например, если напряжение на резисторе удвоится, то ток через резистор удвоится. Следует добавить, что это соотношение справедливо только в том случае, если сопротивление в цепи остается постоянным. Ведь видно, что при изменении сопротивления меняется и ток. График этой зависимости показан на рис. 38, где используется постоянное сопротивление 20 Ом. Зависимость между напряжением и током в этом примере показывает напряжение, отложенное горизонтально по оси X в значениях от 0 до 120 вольт, а соответствующие значения тока отложены вертикально в значениях от 0 до 6,0 ампер по оси Y. Прямая линия, проведенная через все точки пересечения линий напряжения и тока, представляет собой уравнение 9.0011 I = E⁄20 и называется линейной зависимостью.

Закон Ома может быть выражен в виде следующего уравнения:

Уравнение 1

Где I — ток в амперах, E — разность потенциалов, измеренная в вольтах, а R — сопротивление, измеренное в омах. Если известны любые две из этих схемных величин, третью можно найти простым алгебраическим преобразованием. С помощью этого уравнения мы можем рассчитать ток в цепи, если известны напряжение и сопротивление. Эту же формулу можно использовать для расчета напряжения. Умножая обе части уравнения 1 на R, мы получаем эквивалентную форму закона Ома, а именно:

Уравнение 2 Уравнение 3 Рисунок 39. Диаграмма закона Ома.

Все три формулы, представленные в этом разделе, эквивалентны друг другу и представляют собой просто разные способы выражения закона Ома.

Различные уравнения, которые можно вывести путем перестановки основного закона, можно легко получить, используя треугольники на рис. 39.

Треугольники, содержащие E, R и I, разделены на две части, причем E над линией и I × R под ним. Чтобы определить неизвестную величину цепи, когда известны две другие, закройте неизвестную величину большим пальцем. Расположение оставшихся непокрытых букв в треугольнике укажет на выполняемую математическую операцию. Например, чтобы найти I, обратитесь к рисунку 39.А и прикрыть I большим пальцем. Незакрашенные буквы означают, что E нужно разделить на R, или I = E/R. Чтобы найти R, обратитесь к Рисунку 39B и закройте R большим пальцем. Результат показывает, что E нужно разделить на I, или R = E/I. Чтобы найти E, обратитесь к рисунку 39C и закройте E большим пальцем. Результат показывает, что I следует умножить на R, или E = I × R.

Эта таблица полезна при изучении закона Ома. Его следует использовать для дополнения знаний новичка об алгебраическом методе.

Что такое закон Ома? (с картинками)

`;

Наука

Факт проверен

Каризе Уй

Дата последнего изменения: 22 ноября 2022 г.

Закон Ома — это закон, используемый в физике, который в основном объясняет, как электричество работает правильно в простой цепи. Чтобы объяснить электрический процесс, закон показывает, как три элемента электричества — ампер, сопротивление и напряжение — работают вместе, чтобы создать функционирующую электрическую цепь. Закон гласит, что количество электрического тока, измеряемого в амперах, протекающего через проводник, пропорционально или равно напряжению, но обратно пропорционально сопротивлению в проводнике.

Инициатором и тезкой закона был Джордж Симон Ом, известный немецкий физик начала 1800-х годов. Работая профессором в иезуитской гимназии Кельна в Германии, он экспериментировал и наблюдал за поведением электричества в простых цепях с проводами разной длины. Он описал и задокументировал все результаты в книге «Гальваническая цепь, исследованная математически», которая сначала была отвергнута, но позже признана, что привело к установлению закона Ома.0003

Закон Ома можно записать в виде простого математического уравнения: I = V/R, где I — электрический ток, измеряемый в амперах, V — напряжение, а R — сопротивление. В этом уравнении сопротивление обычно является постоянной величиной, поскольку его значение зависит не от величины электрического тока, а скорее от материалов, используемых для изготовления цепи, таких как металлические провода и сам резистор. Формула может быть выражена в других обратных формах, таких как V = IR или R = V/I. Эти обратные формулы могут помочь найти значение одного элемента, если значения двух других элементов уже определены.

По сути, есть три «истинных» утверждения, которые следует помнить в отношении закона Ома. Первое утверждение состоит в том, что значение I будет увеличиваться или уменьшаться, если значение V соответственно увеличивается или уменьшается. Второе утверждение состоит в том, что значение I уменьшится, если значение R увеличится, а значение V не изменится. Третье утверждение состоит в том, что значение I увеличится, если значение R уменьшится, а значение V останется прежним.

Принцип закона Ома может быть практически применен в приборах и любом оборудовании, работающем от электричества или батареи. Например, простому светоизлучающему диоду (LED) требуется всего 2 вольта и 0,02 ампера, чтобы загореться, но он подключен к 6-вольтовой батарее. Это может привести к короткому замыканию светодиода, и для уменьшения тока необходим резистор. Используя формулу R = V/I, можно определить, что резистор, содержащий 200 Ом, необходим для управления током, поступающим в светодиод.