Закон эдс индукции фарадея для трансформаторов. Закон электромагнитной индукции формула
Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.
Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
где – индукция поля, – площадь контура, – угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см.
Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока
Здесь – изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи
Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи
где – сила тока в цепи, – коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А.
Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
где – индуктивность контура, – сила тока в нем.
Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Рассмотрим теперь задачи.
Из перечисленных в задаче 23.1.1
Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2 ), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2 ).
Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3 ) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом.
Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в
При вращении рамки 1 (задача 23.1.5 ) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота – будет равен , где – индукция, – площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ
формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота – будет равен , где – индукция, – площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ
В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2 ). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7 ) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче – 2 .
Поэтому пока магнит покоится около кольца (задача 23.1.7 ) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче – 2 .
Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ
В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4 ). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1 ).
При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1 ), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1 ). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 – ответ 3 ).
Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4 ).
Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4 ) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) – ответ 3 .
Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23. 2.5 ) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2 ).
2.5 ) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2 ).
Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2 ).
Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7 ), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1 ).
При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8 ). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина – увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2 ). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина – приближение магнита, кольцо будет отталкиваться от него (ответ 2 ). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина – приближение магнита, кольцо будет отталкиваться от него (ответ 2 ). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
Задача 23.2.10 – единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4 ).
Эмпирически М. Фарадей показал, что сила тока индукции в проводящем контуре прямо пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность ограниченную рассматриваемым контуром. Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S – это величина, равная:
Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S – это величина, равная:
где модуль вектора магнитной индукции; – угол между вектором магнитной индукции и нормалью к плоскости контура. Магнитный поток трактуют как величину, которая пропорциональна количеству линий магнитной индукции, проходящих сквозь рассматриваемую поверхность площади S.
Появление тока индукции говорит о том, что в проводнике возникает определенная электродвижущая сила (ЭДС). Причиной появления ЭДС индукции является изменение магнитного потока. В системе международных единиц (СИ) закон электромагнитной индукции записывают так:
где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур.
Знак магнитного потока зависит от выбора положительной нормали к плоскости контура. При этом направление нормали определяют при помощи правила правого винта, связывая его с положительным направлением тока в контуре. Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.
Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.
На рис.1 изображен замкнутый контур. Допустим, что положительным является направление обхода контура против часовой стрелки, тогда нормаль к контуру () составляет правый винт в направлением обхода контура. Если вектор магнитной индукции внешнего поля сонаправлен с нормалью и его модуль увеличивается со временем, тогда получим:
Title=”Rendered by QuickLaTeX.com”>
При этом ток индукции создаст магнитный поток (Ф’), который будет меньше нуля. Линии магнитной индукции магнитного поля индукционного тока () изображены на рис. 1 пунктиром. Ток индукции будет направлен по часовой стрелке. ЭДС индукции будет меньше нуля.
Формула (2) – это запись закона электромагнитной индукции в наиболее общей форме. Ее можно применять к неподвижным контурам и движущимся в магнитном поле проводникам. Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.
Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.
В том случае, если магнитный поток изменяется за равные промежутки времени на одну и ту же величину, то закон электромагнитной индукции записывают как:
Если в переменном магнитном поле рассматривается контур, состоящий из N витков, то закон электромагнитной индукции примет вид:
где величину называют потокосцеплением.
Примеры решения задач
ПРИМЕР 1
| Задание | Какова скорость изменения магнитного потока в соленоиде, который имеет N=1000 витков, если в нем возбуждается ЭДС индукции равная 200 В? |
| Решение | Основой для решения данной задачи служит закон электромагнитной индукции в виде: где – скорость изменения магнитного потока в соленоиде. Следовательно, искомую величину найдем как: Проведем вычисления: |
| Ответ |
ПРИМЕР 2
| Задание | Квадратная проводящая рамка находится в магнитном поле, которое изменяется по закону: (где и постоянные величины). Нормаль к рамке составляет угол с направлением вектора магнитной индукции поля. Стона рамки b. Получите выражение для мгновенного значения ЭДС индукции (). Нормаль к рамке составляет угол с направлением вектора магнитной индукции поля. Стона рамки b. Получите выражение для мгновенного значения ЭДС индукции (). |
| Решение | Сделаем рисунок. За основу решения задачи примем основной закон электромагнитной индукции в виде: |
Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого контура в нем возникает электрический ток, который называютиндукционным током. Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 24). Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 25). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.
25). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.
Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием магнитный поток.Магнитным потоком через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции В на площадь контура S и на косинус угла а между направлением вектора магнитной индукции и нормалью к площади контура. Ф = BS cos α (рис. 26).
Опытным путем был установлен основной закон электромагнитной индукции:ЭДС индукции в замкнутом контуре равна по величине скорости из-менения магнитного потока через контур. ξ = ΔФ/t..
Если рассматривать катушку, содержащую п витков, то формула основного закона электромагнитной индукции будет выглядеть так: ξ = n ΔФ/t.
Единица измерения магнитного потока Ф – вебер (Вб): 1В6 =1Β c.
Из основного закона ΔФ =ξ t следует смысл размерности: 1 вебер – это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.
Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.
Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур. Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло. (рис. 27). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
(рис. 27). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E i пропорционально скорости изменения магнитного потока:
E i = -К , (27.1)
где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.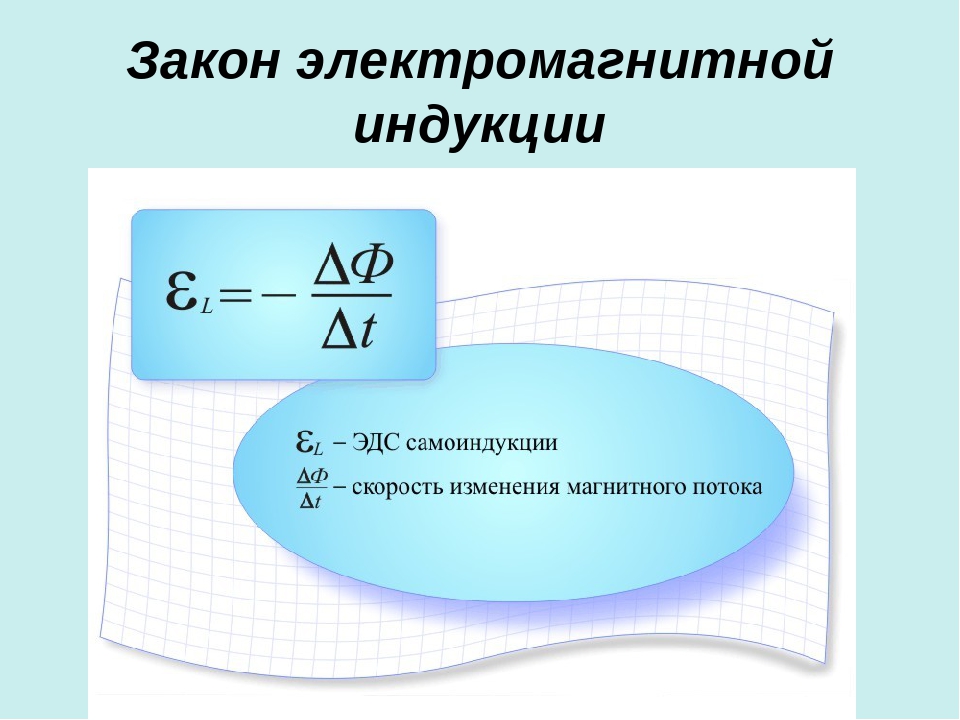
В системе единиц СИ коэффициент К = 1, т.е.
E i = – . (27.2)
Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.
Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции E i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E i не зависит от способа изменения магнитного потока.
Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС E i 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца – общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:
Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то E i будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:
E i = -N× , (27.3)
Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.
Рассмотрим некоторые примеры применения этого закона.
Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.
Если мгновенное значение скорости проводника есть v , то за время dt он опишет площадь dS = l×v ×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = B n ×l×v ×dt. Здесь B n – составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:
E i = B n ×l×v . (27.4)
Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).
В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).
Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v = 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10 -5 Тл, по формуле (27.4) находим
U = B n ×l×v = 2×10 -5 ×2×20 = 0,8×10 -3 В,
т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз.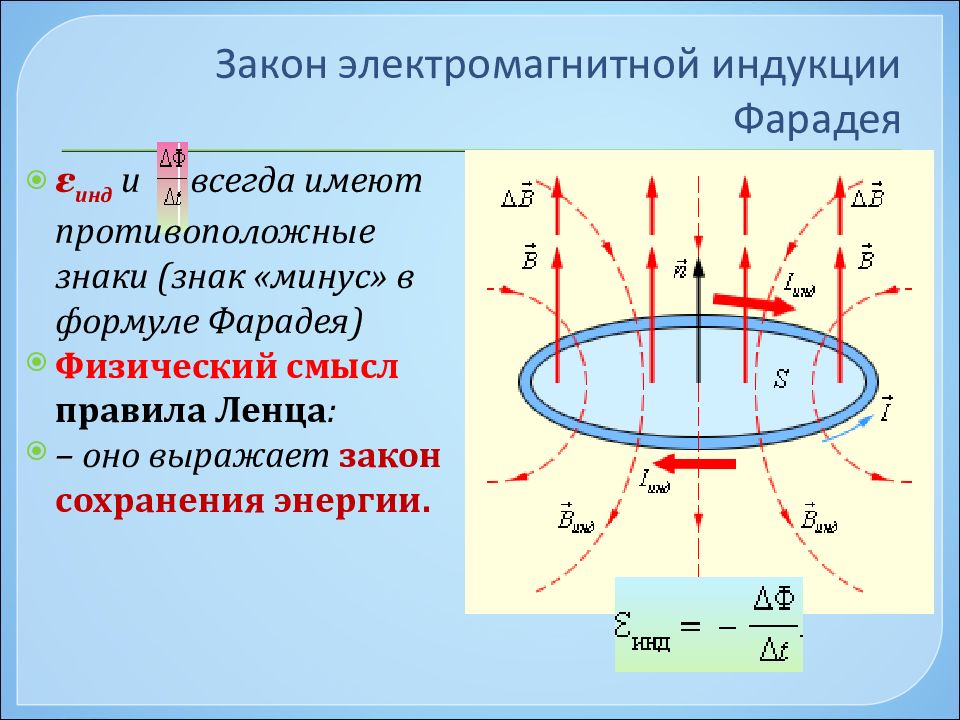 Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).
Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).
Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть
где R – полное сопротивление цепи.
Величина прошедшего заряда равна
q = = – = . (27.6)
Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф 1 -Ф 2), и обратно пропорциональна сопротивлению цепи R. Соотношение (27. 6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.
6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
E i = = – . (27.7)
Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.
В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.
После того, как было установлено, что магнитное поле создаётся электрическими токами, учёные пытались решить обратную задачу – при помощи магнитного поля создать электрический ток. Эту задачу в 1831 г. успешно решил М. Фарадей , который открыл явление электромагнитной индукции. Суть этого явления заключается в том, что в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего этот контур, возникает электрически ток, который называется индукционным . Схема некоторых опытов Фарадея показана на рис. 3.12.
При изменении положения постоянного магнита относительно катушки, замкнутой на гальванометр, в последней возникал электрический ток, причём направление тока оказывалось различным – в зависимости от направления перемещения постоянного магнита. Аналогичный результат достигался и при перемещении другой катушки, по которой шёл электрический ток. Более того, в большой катушке возникал ток даже при неизменном положении меньшей катушки, но при изменении тока в ней.
Более того, в большой катушке возникал ток даже при неизменном положении меньшей катушки, но при изменении тока в ней.
На основании подобных опытов М. Фарадей пришёл к выводу, что в катушке всегда возникает электрический ток при изменении магнитного потока, сцепленного с этой катушкой. Величина тока зависит от скорости изменения магнитного потока. Сейчас мы формулируем открытия Фарадея в виде закона электромагнитной индукции : при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ЭДС индукции, которая определяется как
Знак “-” в выражении (3.53) означает, что при увеличении магнитного потока магнитное поле, созданное индукционным током, направлено против внешнего магнитного поля. Если же магнитный поток уменьшается по величине, то магнитное поле индукционного тока совпадает по направлению с внешним магнитным полем. Русский учёный Х. Ленц таким образом определил появление знака минус в выражении (3.53) – индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле имеет такое направление, что препятствует изменению магнитного потока, вызвавшего возникновение индукционного тока .
Дадим ещё одну формулировку закона электромагнитной индукции : ЭДС индукции в замкнутом проводящем контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего этот контур.
Немецкий физик Гельмгольц показал, что закон электромагнитной индукции можно получить из закона сохранения энергии. В самом деле, энергия источника ЭДС по перемещению проводника с током в магнитном поле (см.рис.3.37) будет затрачена как на Джоулев разогрев проводника сопротивлением R, так и на работу по перемещению проводника:
Тогда из уравнения (3.54) сразу же следует, что
В числителе выражения (3.55) стоит алгебраическая сумма ЭДС, действующих в контуре. Следовательно,
Какова же физическая причина возникновения ЭДС? На заряды в проводнике АВ действует сила Лоренца при движении проводника вдоль оси x. Под действием этой силы положительные заряды будут смещаться вверх, в результате чего электрическое поле в проводнике будет ослаблено. Другими словами, в проводнике появится ЭДС индукции. Следовательно, в рассмотренном нами случае физической причиной возникновения ЭДС является сила Лоренца. Однако, как мы уже отмечали, и в неподвижном замкнутом контуре может появиться ЭДС индукции, если будет изменяться магнитное поле, пронизывающее этот контур.
Другими словами, в проводнике появится ЭДС индукции. Следовательно, в рассмотренном нами случае физической причиной возникновения ЭДС является сила Лоренца. Однако, как мы уже отмечали, и в неподвижном замкнутом контуре может появиться ЭДС индукции, если будет изменяться магнитное поле, пронизывающее этот контур.
В этом случае заряды можно считать неподвижными, а на неподвижные заряды сила Лоренца не действует. Чтобы объяснить возникновение ЭДС в этом случае, Максвелл предположил, что всякое изменяющееся магнитное поле порождает в проводнике изменяющееся электрическое поле, которое и является причиной возникновения ЭДС индукции. Циркуляция вектора напряжённости, действующей в этом контуре, таким образом, будет равна ЭДС индукции, действующей в контуре:
. (3.56)
Явление электромагнитной индукции используется для превращения механической энергии вращения в электрическую – в генераторах электрического тока. Обратный процесс – превращение электрической энергии в механическую, основанный на вращательном моменте, действующем на рамку с током в магнитном поле, используется в электродвигателях.
Рассмотрим принцип действия генератора электрического тока (рис. 3.13). Пусть у нас проводящая рамка вращается между полюсами магнита (это может быть и электромагнит) с частотой w. Тогда угол между нормалью к плоскости рамки и направлением магнитного поля изменяется по закону a = wt . В этом случае магнитный поток, сцепленный с рамкой, будет изменяться в соответствии с формулой
где S – площадь контура. В соответствии с законом электромагнитной индукции в рамке будет индуцироваться ЭДС
с e max = BSw. Таким образом, если в магнитном поле вращается с постоянной угловой скоростью проводящая рамка, то в ней будет индуцироваться ЭДС, изменяющаяся по гармоническому закону. В реальных генераторах вращают много витков, соединенных последовательно, а в электромагнитах, для увеличения магнитной индукции, используют сердечники с большой магнитной проницаемостью m ..
Индукционные токи могут возникать и в толще проводящих тел, помещённых в переменное магнитное поле. В этом случае эти токи называются токами Фуко. Эти токи вызывают разогрев массивных проводников. Это явление используется в вакуумных индукционных печах, где сильные токи разогревают металл до плавления. Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.
В этом случае эти токи называются токами Фуко. Эти токи вызывают разогрев массивных проводников. Это явление используется в вакуумных индукционных печах, где сильные токи разогревают металл до плавления. Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.
Формулы электромагнитной индукции 11. Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (з.Фарадея-Максвелла). Правила Ленца
Обобщая результат опытов, Фарадей сформулировал закон электромагнитной индукции. Он показал, что при всяком изменении магнитного потока в замкнутом проводящем контуре возбуждается индукционный ток. Следовательно, в контуре возникает ЭДС индукции.
ЭДС индукции прямо пропорциональна скорости изменения магнитного потока во времени . Математическую запись этого закона оформил Максвелл и поэтому он называется законом Фарадея-Максвелла (законом электромагнитной индукции).
4.2.2. Правило Ленца
В законе электромагнитной индукции не говорится о направлении индукционного тока. Этот вопрос решил Ленц в 1833г. Он установил правило, позволяющее определить направление индукционного тока.
Этот вопрос решил Ленц в 1833г. Он установил правило, позволяющее определить направление индукционного тока.
Индукционный ток имеет такое направление, что созданное им магнитное поле препятствует изменению магнитного потока, пронизывающего данный контур, т.е. индукционный ток. Он направлен так, чтобы противодействовать причине, его вызывающей. Например, пусть в замкнутый контур вдвигается постоянный магнит NS (рис.250).
| |
| Рис.250 Рис.251 |
Число силовых линий, пересекающих замкнутый контур увеличивается, следовательно, увеличивается магнитный поток. В контуре возникает индукционный ток I i , который создает магнитное поле, силовые линии которого (пунктирные линии, перпендикулярные плоскости контура) направлены против силовых линий магнита. При выдвижении магнита магнитный поток, пронизывающий контур, уменьшается (рис.251), а индукционный ток I i создает поле, силовые линии которого направлены в сторону линии индукции магнита (на рис. 251 пунктирные линии).
251 пунктирные линии).
С учетом правила Ленца, закон Фарадея-Максвелла запишется в виде
Для решения физической задачи используют формулу (568).
Среднее по времени значение ЭДС индукции определяется формулой
Выясним способы изменения магнитного потока.
Первый способ . В=const и α=const . Изменяется площадь S .
Пример. Пусть в однородном магнитном поле В=const перпендикулярно силовым линиям движется проводник длиной l со скоростью (рис.252) Тогда на концах проводника возникает разность потенциалов , равная ЭДС индукции. Найдем её.
Изменение магнитного потока равно
В формуле (570) α – это угол между нормалью плоскости, омываемой при движении проводника, и вектором индукции .
После того, как было установлено, что магнитное поле создаётся электрическими токами, учёные пытались решить обратную задачу – при помощи магнитного поля создать электрический ток. Эту задачу в 1831 г. успешно решил М. Фарадей , который открыл явление электромагнитной индукции. Суть этого явления заключается в том, что в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего этот контур, возникает электрически ток, который называется индукционным . Схема некоторых опытов Фарадея показана на рис. 3.12.
Фарадей , который открыл явление электромагнитной индукции. Суть этого явления заключается в том, что в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего этот контур, возникает электрически ток, который называется индукционным . Схема некоторых опытов Фарадея показана на рис. 3.12.
При изменении положения постоянного магнита относительно катушки, замкнутой на гальванометр, в последней возникал электрический ток, причём направление тока оказывалось различным – в зависимости от направления перемещения постоянного магнита. Аналогичный результат достигался и при перемещении другой катушки, по которой шёл электрический ток. Более того, в большой катушке возникал ток даже при неизменном положении меньшей катушки, но при изменении тока в ней.
На основании подобных опытов М. Фарадей пришёл к выводу, что в катушке всегда возникает электрический ток при изменении магнитного потока, сцепленного с этой катушкой. Величина тока зависит от скорости изменения магнитного потока. Сейчас мы формулируем открытия Фарадея в виде закона электромагнитной индукции : при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ЭДС индукции, которая определяется как
Сейчас мы формулируем открытия Фарадея в виде закона электромагнитной индукции : при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ЭДС индукции, которая определяется как
Знак “-” в выражении (3.53) означает, что при увеличении магнитного потока магнитное поле, созданное индукционным током, направлено против внешнего магнитного поля. Если же магнитный поток уменьшается по величине, то магнитное поле индукционного тока совпадает по направлению с внешним магнитным полем. Русский учёный Х. Ленц таким образом определил появление знака минус в выражении (3.53) – индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле имеет такое направление, что препятствует изменению магнитного потока, вызвавшего возникновение индукционного тока .
Дадим ещё одну формулировку закона электромагнитной индукции : ЭДС индукции в замкнутом проводящем контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего этот контур.
Немецкий физик Гельмгольц показал, что закон электромагнитной индукции можно получить из закона сохранения энергии. В самом деле, энергия источника ЭДС по перемещению проводника с током в магнитном поле (см.рис.3.37) будет затрачена как на Джоулев разогрев проводника сопротивлением R, так и на работу по перемещению проводника:
Тогда из уравнения (3.54) сразу же следует, что
В числителе выражения (3.55) стоит алгебраическая сумма ЭДС, действующих в контуре. Следовательно,
Какова же физическая причина возникновения ЭДС? На заряды в проводнике АВ действует сила Лоренца при движении проводника вдоль оси x. Под действием этой силы положительные заряды будут смещаться вверх, в результате чего электрическое поле в проводнике будет ослаблено. Другими словами, в проводнике появится ЭДС индукции. Следовательно, в рассмотренном нами случае физической причиной возникновения ЭДС является сила Лоренца. Однако, как мы уже отмечали, и в неподвижном замкнутом контуре может появиться ЭДС индукции, если будет изменяться магнитное поле, пронизывающее этот контур.
В этом случае заряды можно считать неподвижными, а на неподвижные заряды сила Лоренца не действует. Чтобы объяснить возникновение ЭДС в этом случае, Максвелл предположил, что всякое изменяющееся магнитное поле порождает в проводнике изменяющееся электрическое поле, которое и является причиной возникновения ЭДС индукции. Циркуляция вектора напряжённости, действующей в этом контуре, таким образом, будет равна ЭДС индукции, действующей в контуре:
. (3.56)
Явление электромагнитной индукции используется для превращения механической энергии вращения в электрическую – в генераторах электрического тока. Обратный процесс – превращение электрической энергии в механическую, основанный на вращательном моменте, действующем на рамку с током в магнитном поле, используется в электродвигателях.
Рассмотрим принцип действия генератора электрического тока (рис. 3.13). Пусть у нас проводящая рамка вращается между полюсами магнита (это может быть и электромагнит) с частотой w. Тогда угол между нормалью к плоскости рамки и направлением магнитного поля изменяется по закону a = wt . В этом случае магнитный поток, сцепленный с рамкой, будет изменяться в соответствии с формулой
Тогда угол между нормалью к плоскости рамки и направлением магнитного поля изменяется по закону a = wt . В этом случае магнитный поток, сцепленный с рамкой, будет изменяться в соответствии с формулой
где S – площадь контура. В соответствии с законом электромагнитной индукции в рамке будет индуцироваться ЭДС
с e max = BSw. Таким образом, если в магнитном поле вращается с постоянной угловой скоростью проводящая рамка, то в ней будет индуцироваться ЭДС, изменяющаяся по гармоническому закону. В реальных генераторах вращают много витков, соединенных последовательно, а в электромагнитах, для увеличения магнитной индукции, используют сердечники с большой магнитной проницаемостью m ..
Индукционные токи могут возникать и в толще проводящих тел, помещённых в переменное магнитное поле. В этом случае эти токи называются токами Фуко. Эти токи вызывают разогрев массивных проводников. Это явление используется в вакуумных индукционных печах, где сильные токи разогревают металл до плавления. Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.
Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.
Вектор магнитной индукции \(~\vec B\) характеризует силовые свойства магнитного поля в данной точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величина называется магнитным потоком и обозначается греческой буквой Φ (фи).
- Магнитный поток Φ однородного поля через плоскую поверхность – это скалярная физическая величина, численно равная произведению модуля индукции B магнитного поля, площади поверхности S и косинуса угла α между нормалью \(~\vec n\) к поверхности и вектором индукции \(~\vec B\) (рис. 1):
В СИ единицей магнитного потока является вебер (Вб):
1 Вб = 1 Тл ⋅ 1 м 2 .
- Магнитный поток в 1 Вб – это магнитный поток однородного магнитного поля с индукцией 1 Тл через перпендикулярную ему плоскую поверхность площадью 1 м 2 .

Из формулы (1) следует, что магнитные поток может изменяться:
- или только за счет изменения модуля вектора индукции B магнитного поля, тогда \(~\Delta \Phi = (B_2 – B_1) \cdot S \cdot \cos \alpha\) ;
- или только за счет изменения площади контура S , тогда \(~\Delta \Phi = B \cdot (S_2 – S_1) \cdot \cos \alpha\) ;
- или только за счет поворота контура в магнитном поле, тогда \(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 – \cos \alpha_1)\) ;
- или одновременно за счет изменения нескольких параметров, тогда \(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 – B_1 \cdot S_1 \cdot \cos \alpha_1\) .
Электромагнитная индукция (ЭМИ)
Открытие ЭМИ
Вам уже известно, что вокруг проводника с током всегда существует магнитное поле.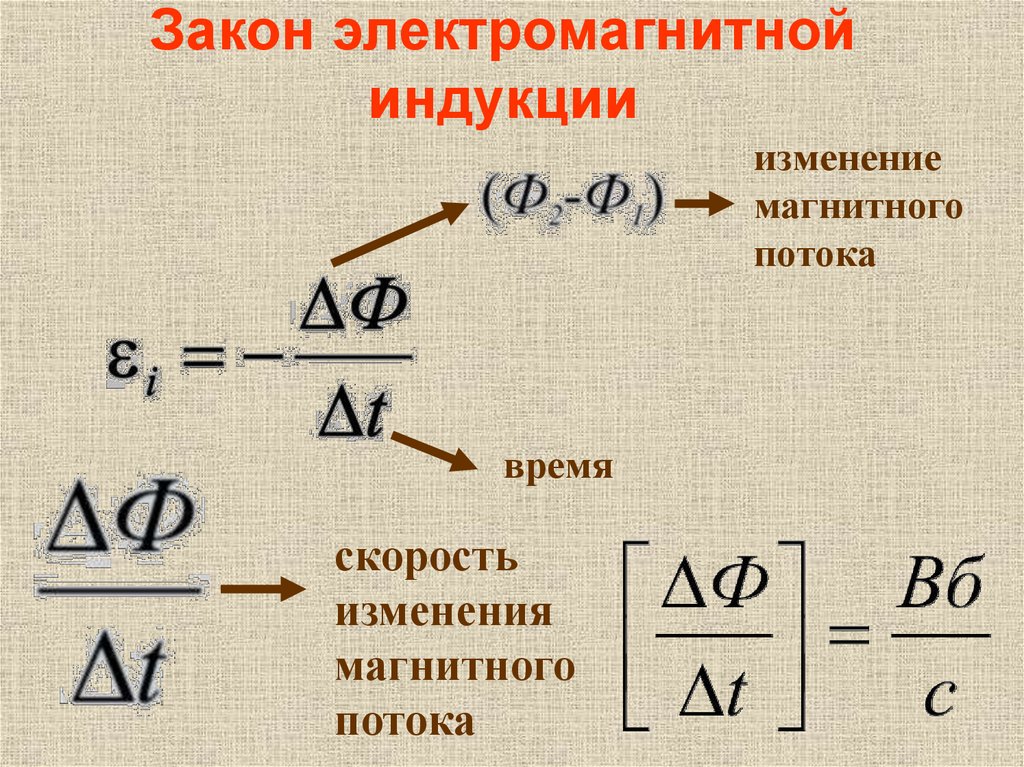 А нельзя наоборот, с помощью магнитного поля создать ток в проводнике? Именно такой вопрос заинтересовал английского физика Майкла Фарадея, который в 1822 г. записал в своем дневнике: «Превратить магнетизм в электричество». И только через 9 лет эта задача была им решена.
А нельзя наоборот, с помощью магнитного поля создать ток в проводнике? Именно такой вопрос заинтересовал английского физика Майкла Фарадея, который в 1822 г. записал в своем дневнике: «Превратить магнетизм в электричество». И только через 9 лет эта задача была им решена.
Открытие электромагнитной индукции , как назвал Фарадей это явление, было сделано 29 августа 1831 г. Первоначально была открыта индукция в неподвижных друг относительно друга проводниках при замыкании и размыкании цепи. Затем, ясно понимая, что сближение или удаление проводников с током должно приводить к тому же результату, что и замыкание и размыкание цепи, Фарадей с помощью опытов доказал, что ток возникает при перемещении катушек относительно друг друга (рис. 2).
17 октября, как зарегистрировано в его лабораторном журнале, был обнаружен индукционный ток в катушке во время вдвигания (или выдвигания) магнита (рис. 3).
В течение одного месяца Фарадей опытным путем открыл, что в замкнутом контуре возникает электрический ток при любом изменении магнитного потока через него. Полученный таким способом ток называется индукционным током I i .
Полученный таким способом ток называется индукционным током I i .
Известно, что в цепи возникает электрический ток в том случае, когда на свободные заряды действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы, действие которых характеризуется ЭДС, которую называют ЭДС индукции и обозначают E i .
Индукционный ток I i в контуре и ЭДС индукции E i связаны следующим соотношением (законом Ома):
\(~I_i = -\dfrac {E_i}{R},\)
где R – сопротивление контура.
- Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции .
Если контур замкнут, то вместе с ЭДС индукции возникает и индукционный ток.
Джеймс Клерк Максвелл предложил такую гипотезу: изменяющееся магнитное поле создает в окружающем пространстве электрическое поле, которое и приводит свободные заряды в направленное движение, т.
 е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое .
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами .
е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое .
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами .
История
Вот краткое описание первого опыта, данное самим Фарадеем.
«На широкую деревянную катушку была намотана медная проволока длиной в 203 фута (фут равен 304,8 мм), и между витками ее намотана проволока такой же длины, но изолированная от первой хлопчатобумажной нитью. Одна из этих спиралей была соединена с гальванометром, а другая – с сильной батареей, состоящей из 100 пар пластин… При замыкании цепи удалось заметить внезапное, но чрезвычайно слабое действие на гальванометр, и то же самое замечалось при прекращении тока. При непрерывном же прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого-либо индукционного действия на другую спираль, не смотря на то что нагревание всей спирали, соединенной с батареей, и яркость искры, проскакивающей между углями, свидетельствовали о мощности батареи».
См. так же
- Васильев А. Вольта, Эрстед, Фарадей //Квант. – 2000. – № 5. – С. 16-17
Правило Ленца
Русский физик Эмилий Ленц в 1833 г. сформулировал правило (правило Ленца ), которое позволяет установить направление индукционного тока в контуре:
- возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится препятствовать тому изменению внешнего магнитного потока, вызвавшее данный ток.
- индукционный ток имеет такое направление, что препятствует причине его вызывающей.
Например, при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки, т.е. вектор индукции \({\vec{B}}”\) этого поля направлен против вектора индукции \(\vec{B}\) внешнего магнитного поля. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с индукцией \({\vec{B}}”\), увеличивающее магнитный поток через витки катушки.
См. так же
Закон ЭМИ
Опыты Фарадея показали, что ЭДС индукции (и сила индукционного тока) в проводящем контуре пропорциональна скорости изменения магнитного потока. Если за малое время Δt магнитный поток меняется на ΔΦ, то скорость изменения магнитного потока равна \(\dfrac{\Delta \Phi }{\Delta t}\). С учетом правила Ленца Д. Максвелл в 1873 г. дал следующую формулировку закона электромагнитной индукции:
- ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, пронизывающего этот контур, взятой с противоположным знаком
- Эту формулу можно применять только при равномерном изменении магнитного потока.
- Знак «минус» в законе следует из закона Ленца. При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (E i i > 0) (рис. 4, б).
В Международной системе единиц закон электромагнитной индукции используют для установления единицы магнитного потока. Так как ЭДС индукции E i выражают в вольтах, а время в секундах, то из закона ЭМИ вебер можно определить следующим образом:
Так как ЭДС индукции E i выражают в вольтах, а время в секундах, то из закона ЭМИ вебер можно определить следующим образом:
- магнитный поток через поверхность, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции равная 1 В:
ЭДС индукции в движущемся проводнике
При движении проводника длиной l со скоростью \(\vec{\upsilon}\) в постоянном магнитном поле с вектором индукции \(\vec{B}\) в нем возникает ЭДС индукции
\(~E_i = B \cdot \upsilon \cdot l \cdot \sin \alpha,\)
где α – угол между направлением скорости \(\vec{\upsilon}\) проводника и вектором магнитной индукции \(\vec{B}\).
Причиной появления этой ЭДС является сила Лоренца, действующая на свободные заряды в движущемся проводнике. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.
С учетом этого можно сформулировать следующее для определения направления индукционного тока в движущемся проводнике (правило левой руки ):
- нужно расположить левую руку так, чтобы вектор магнитной индукции \(\vec{B}\) входил в ладонь, четыре пальца совпадали с направлением скорости \(\vec{\upsilon}\)проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис.
 5).
5).
Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C.344- 351.
- Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учрежде-ний с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. – Мн.: Нар. асвета, 2008. – С. 170-182.
- Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – С. 399-408, 412-414.
На данном уроке, тема которого: «Правило Ленца. Закон электромагнитной индукции», мы узнаем общее правило, позволяющее определить направление индукционного тока в контуре, установленное в 1833 г. Э.X. Ленцем. Также рассмотрим опыт с алюминиевыми кольцами, наглядно демонстрирующий это правило, и сформулируем закон электромагнитной индукции
Э.X. Ленцем. Также рассмотрим опыт с алюминиевыми кольцами, наглядно демонстрирующий это правило, и сформулируем закон электромагнитной индукции
Приближением или удалением магнита от сплошного кольца мы меняем магнитный поток, который пронизывает площадь кольца. Согласно теории явления электромагнитной индукции, в кольце должен возникнуть индукционный электрический ток. Из опытов Ампера известно, что там, где проходит ток, возникает магнитное поле. Следовательно, замкнутое кольцо начинает вести себя как магнит. То есть происходит взаимодействие двух магнитов (постоянный магнит, который мы двигаем, и замкнутый контур с током).
Так как система не реагировала на приближение магнита к кольцу с разрезом, то можно сделать вывод, что индукционный ток в незамкнутом контуре не возникает.
Причины отталкивания или притягивания кольца к магниту
1. При приближении магнита
При приближении полюса магнита кольцо отталкивается от него. То есть оно ведет себя как магнит, у которого с нашей стороны такой же полюс, как у приближающегося магнита. Если мы приближаем северный полюс магнита, то вектор магнитной индукции кольца с индукционным током направлен в противоположную сторону относительно вектора магнитной индукции северного полюса магнита (см. Рис. 2).
Если мы приближаем северный полюс магнита, то вектор магнитной индукции кольца с индукционным током направлен в противоположную сторону относительно вектора магнитной индукции северного полюса магнита (см. Рис. 2).
Рис. 2. Приближение магнита к кольцу
2. При удалении магнита от кольца
При удалении магнита кольцо тянется за ним. Следовательно, со стороны удаляющегося магнита у кольца образовывается противоположный полюс. Вектор магнитной индукции кольца с током направлен в ту же сторону, что и вектор магнитной индукции удаляющегося магнита (см. Рис. 3).
Рис. 3. Удаление магнита от кольца
Из данного опыта можно сделать вывод, что при движении магнита кольцо ведет себя также подобно магниту, полярность которого зависит от того, увеличивается или уменьшается магнитный поток, пронизывающий площадь кольца. Если поток возрастает, то векторы магнитной индукции кольца и магнита противоположны по направлению. Если магнитный поток сквозь кольцо уменьшается со временем, то вектор индукции магнитного поля кольца совпадает по направлению с вектором индукции магнита.
Направление индукционного тока в кольце можно определить по правилу правой руки. Если направить большой палец правой руки по направлению вектора магнитной индукции, то четыре согнутых пальца укажут направление тока в кольце (см. Рис. 4).
Рис. 4. Правило правой руки
При изменении магнитного потока, пронизывающего контур, в контуре возникает индукционный ток такого направления, чтобы своим магнитным потоком компенсировать изменение внешнего магнитного потока.
Если внешний магнитный поток возрастает, то индукционный ток своим магнитным полем стремится замедлить это возрастание. Если магнитный поток убывает, то индукционный ток своим магнитным полем стремится замедлить это убывание.
Эта особенность электромагнитной индукции выражается знаком «минус» в формуле ЭДС индукции.
Закон электромагнитной индукции
При изменении внешнего магнитного потока, пронизывающего контур, в контуре возникает индукционный ток. При этом значение электродвижущей силы численно равно скорости изменения магнитного потока, взятой со знаком «-».
Правило Ленца является следствием закона сохранения энергии в электромагнитных явлениях.
Список литературы
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.
Домашнее задание
- Вопросы в конце параграфа 10 (стр. 33) – Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы)
- Как формулируется закон электромагнитной индукции?
- Почему в формуле для закона электромагнитной индукции стоит знак «-»?
- Интернет-портал Festival.1september.ru ().
- Интернет-портал Physics.kgsu.ru ().
- Интернет-портал Youtube.com ().
Эмпирически М. Фарадей показал, что сила тока индукции в проводящем контуре прямо пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность ограниченную рассматриваемым контуром. Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S – это величина, равная:
Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S – это величина, равная:
где модуль вектора магнитной индукции; – угол между вектором магнитной индукции и нормалью к плоскости контура. Магнитный поток трактуют как величину, которая пропорциональна количеству линий магнитной индукции, проходящих сквозь рассматриваемую поверхность площади S.
Появление тока индукции говорит о том, что в проводнике возникает определенная электродвижущая сила (ЭДС). Причиной появления ЭДС индукции является изменение магнитного потока. В системе международных единиц (СИ) закон электромагнитной индукции записывают так:
где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур.
Знак магнитного потока зависит от выбора положительной нормали к плоскости контура. При этом направление нормали определяют при помощи правила правого винта, связывая его с положительным направлением тока в контуре. Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.
Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.
На рис.1 изображен замкнутый контур. Допустим, что положительным является направление обхода контура против часовой стрелки, тогда нормаль к контуру () составляет правый винт в направлением обхода контура. Если вектор магнитной индукции внешнего поля сонаправлен с нормалью и его модуль увеличивается со временем, тогда получим:
Title=”Rendered by QuickLaTeX.com”>
При этом ток индукции создаст магнитный поток (Ф’), который будет меньше нуля. Линии магнитной индукции магнитного поля индукционного тока () изображены на рис. 1 пунктиром. Ток индукции будет направлен по часовой стрелке. ЭДС индукции будет меньше нуля.
Формула (2) – это запись закона электромагнитной индукции в наиболее общей форме. Ее можно применять к неподвижным контурам и движущимся в магнитном поле проводникам. Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.
Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.
В том случае, если магнитный поток изменяется за равные промежутки времени на одну и ту же величину, то закон электромагнитной индукции записывают как:
Если в переменном магнитном поле рассматривается контур, состоящий из N витков, то закон электромагнитной индукции примет вид:
где величину называют потокосцеплением.
Примеры решения задач
ПРИМЕР 1
| Задание | Какова скорость изменения магнитного потока в соленоиде, который имеет N=1000 витков, если в нем возбуждается ЭДС индукции равная 200 В? |
| Решение | Основой для решения данной задачи служит закон электромагнитной индукции в виде: где – скорость изменения магнитного потока в соленоиде. Следовательно, искомую величину найдем как: Проведем вычисления: |
| Ответ |
ПРИМЕР 2
| Задание | Квадратная проводящая рамка находится в магнитном поле, которое изменяется по закону: (где и постоянные величины).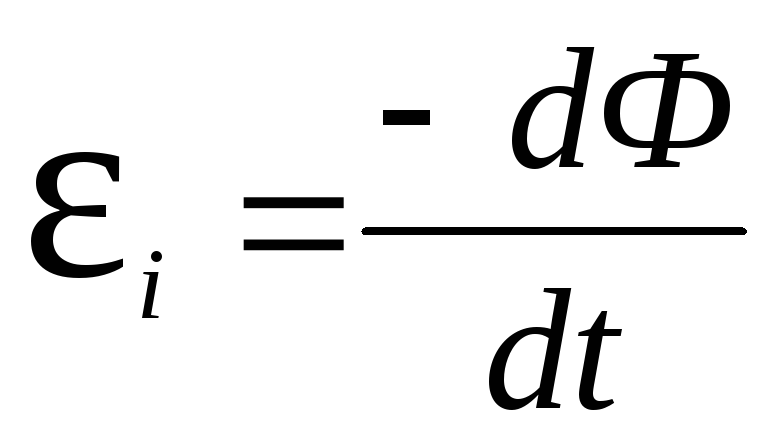 Нормаль к рамке составляет угол с направлением вектора магнитной индукции поля. Стона рамки b. Получите выражение для мгновенного значения ЭДС индукции (). Нормаль к рамке составляет угол с направлением вектора магнитной индукции поля. Стона рамки b. Получите выражение для мгновенного значения ЭДС индукции (). |
| Решение | Сделаем рисунок. За основу решения задачи примем основной закон электромагнитной индукции в виде: |
закон электромагнитной индукции — формула явления
Сегодня мы раскроем такой феномен физики, как «закон электромагнитной индукции». Расскажем, почему Фарадей провел опыты, приведем формулу и объясним важность явления для повседневной жизни.
Древние боги и физика
Древние люди поклонялись неведомому. И сейчас человека страшит пучина моря и даль космоса. Но наука может объяснить, почему. Субмарины снимают невероятную жизнь океанов на глубине свыше километра, космические телескопы изучают объекты, которые существовали всего лишь через считанные миллионы лет после большого взрыва.
Но тогда люди обожествляли все, что их завораживало и тревожило:
- восход солнца;
- пробуждение растений весной;
- дождь;
- рождение и смерть.

В каждом предмете и явлении жили неведомые силы, которые управляли миром. До сих пор дети склонны очеловечивать мебель и игрушки. Оставаясь без присмотра взрослых, они фантазируют: одеяло обнимет, табуретка подойдет, окно откроется само по себе.
Пожалуй, первым эволюционным шагом человечества стало умение поддерживать огонь. Антропологи предполагают, что самые ранние костры зажглись от дерева, в которое ударила молния.
Таким образом, электричество сыграло в жизни человечества огромную роль. Первая молния дала толчок к развитию культуры, основной закон электромагнитной индукции привел человечество к современному состоянию.
От уксуса до ядерного реактора
В пирамиде Хеопса были найдены странные керамические сосуды: горлышко запечатано воском, в глубине скрыт металлический цилиндр. На внутренней стороне стенок обнаружили остатки уксуса или кислого вина. Ученые пришли к сенсационному выводу: этот артефакт – батарейка, источник электричества.
Но до 1600 года изучать этот феномен никто не брался. До движущихся электронов исследовали природу статического электричества. О том, что янтарь дает разряды, если его потереть о мех, знали еще древние греки. Цвет этого камня напоминал им свет звезды Электры из Плеяд. А название минерала стало, в свою очередь, поводом окрестить физическое явление.
До движущихся электронов исследовали природу статического электричества. О том, что янтарь дает разряды, если его потереть о мех, знали еще древние греки. Цвет этого камня напоминал им свет звезды Электры из Плеяд. А название минерала стало, в свою очередь, поводом окрестить физическое явление.
Первый примитивный источник постоянного тока был построен в 1800 году
Естественно, как только появился достаточно мощный конденсатор, ученые принялись изучать свойства подключенного к нему проводника. В 1820 году датский ученый Ханс Кристиан Эрстед обнаружил, что магнитная стрелка отклоняется рядом с включенным в сеть проводником. Данный факт дал толчок к открытию закона электромагнитной индукции Фарадеем (формула будет приведена чуть ниже), который позволил человечеству добывать электричество из воды, ветра и ядерного топлива.
Примитивное, но современное
Физическая основа опытов Макса Фарадея была заложена Эрстедом. Если включенный проводник влияет на магнит, то верно и обратное: намагниченный проводник должен вызывать ток.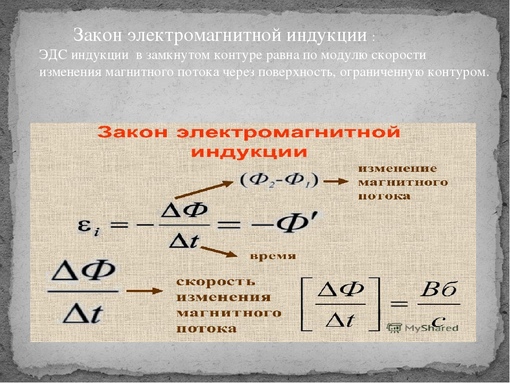
Структура опыта, который помог вывести закон электромагнитной индукции (ЭДС как понятие мы рассмотрим чуть позже), была весьма проста. Смотанную в пружину проволоку подключили к прибору, который регистрирует ток. К виткам ученый поднес большой магнит. Пока магнит двигался рядом с контуром, прибор регистрировал поток электронов.
С тех пор техника усовершенствовалась, но основной принцип создания электричества на огромных станциях пока что тот же: движущийся магнит возбуждает ток в смотанном пружиной проводнике.
Развитие идеи
Самый первый опыт убедил Фарадея, что электрическое и магнитное поля взаимосвязаны. Но требовалось выяснить, как именно. Возникает ли вокруг проводника с током еще и магнитное поле или они просто способны влиять друг на друга? Поэтому ученый пошел дальше. Он смотал одну проволоку, подвел к ней ток, и эту катушку вдвинул в другую пружину. И тоже получил электричество. Этот опыт доказал, что движущиеся электроны создают не только электрическое, но и магнитное поле.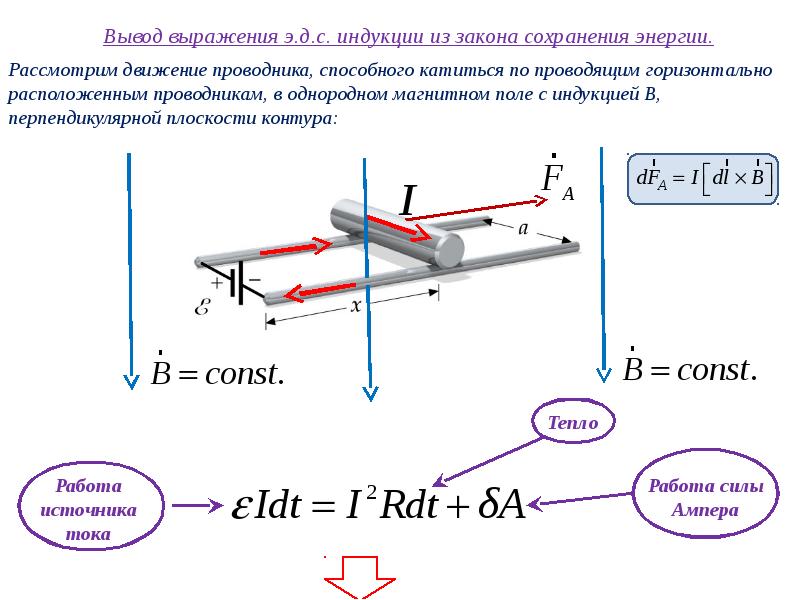 Позже ученые выяснили, как они располагаются в пространстве относительно друг друга. Электромагнитное поле – это и та причина, по которой существует свет.
Позже ученые выяснили, как они располагаются в пространстве относительно друг друга. Электромагнитное поле – это и та причина, по которой существует свет.
Экспериментируя с разными вариантами взаимодействия проводников под напряжением, Фарадей выяснил: ток передается лучше всего, если и первую, и вторую катушки намотать на один общий металлический сердечник. Формула, выражающая закон электромагнитной индукции, была выведена именно на этом приборе.
Формула и ее составляющие
Теперь, когда история изучения электричества доведена до эксперимента Фарадея, пора написать формулу:
Расшифруем:
ε – это электродвижущая сила (сокращенно ЭДС). В зависимости от величины ε электроны перемещаются в проводнике интенсивнее или слабее. На ЭДС влияет мощность источника, а на нее – напряженность электромагнитного поля.
Φ – величина магнитного потока, который проходит в данный момент через заданную площадь. Фарадей сворачивал проволоку в пружину, так как ему требовалась определенное пространство, сквозь которое проходил бы проводник. Конечно, можно было бы изготовить очень толстый проводник, но это было бы дорого. Форму круга ученый выбрал потому, что у этой плоской фигуры соотношение площади к длине поверхности наибольшее. Это самая энергетически эффективная форма. Поэтому капли воды на плоской поверхности становятся круглыми. К тому же пружину с круглым сечением гораздо проще получить: достаточно лишь намотать проволоку на какой-то круглый предмет.
Конечно, можно было бы изготовить очень толстый проводник, но это было бы дорого. Форму круга ученый выбрал потому, что у этой плоской фигуры соотношение площади к длине поверхности наибольшее. Это самая энергетически эффективная форма. Поэтому капли воды на плоской поверхности становятся круглыми. К тому же пружину с круглым сечением гораздо проще получить: достаточно лишь намотать проволоку на какой-то круглый предмет.
t – время, за которое поток прошел сквозь контур.
Приставка d в формуле закона электромагнитной индукции означает, что величина дифференциальная. То есть маленький магнитный поток надо продифференцировать по небольшим отрезкам времени, чтобы получить конечный результат. Это математическое действие требует от людей некоторой подготовленности. Чтобы лучше понять формулу, мы настоятельно рекомендуем читателю вспомнить дифференцирование и интегрирование.
Следствия из закона
Сразу после открытия стали исследовать явление электромагнитной индукции. Закон Ленца, например, был выведен экспериментально российским ученым. Именно это правило добавило минус в конечную формулу.
Именно это правило добавило минус в конечную формулу.
Вид у него такой: направление индукционного тока не случайно; поток электронов во второй обмотке как бы стремится уменьшить действие тока в первой обмотке. То есть возникновение электромагнитной индукции – это фактически сопротивление второй пружины вмешательству в «личную жизнь».
Правило Ленца имеет и другое следствие.
- если ток в первой катушке будет возрастать, то ток второй пружины тоже будет стремиться к увеличению;
- если ток в индуцирующей обмотке будет падать, то уменьшится и ток во второй.
Согласно этому правилу, проводник, в котором возникает индуцированный ток, фактически стремится скомпенсировать действие изменяющегося магнитного потока.
Зерно и осел
Использовать простейшие механизмы себе на благо люди стремились давно. Помол муки – дело сложное. Некоторые племена растирают зерно вручную: кладут пшеницу на один камень, накрывают другим плоским и круглым камнем, и вертят жернов. Но если надо смолоть муку на целую деревню, то одним мускульным трудом не обойтись. Сначала люди догадались привязать к жернову тягловое животное. Ослик тянул за веревку – камень вращался. Потом, вероятно, люди подумали: «Река течет все время, она толкает всякие предметы вниз по течению. Почему бы нам не использовать это на благо?» Так появились водяные мельницы.
Но если надо смолоть муку на целую деревню, то одним мускульным трудом не обойтись. Сначала люди догадались привязать к жернову тягловое животное. Ослик тянул за веревку – камень вращался. Потом, вероятно, люди подумали: «Река течет все время, она толкает всякие предметы вниз по течению. Почему бы нам не использовать это на благо?» Так появились водяные мельницы.
Колесо, вода, ветер
Конечно, первые инженеры, которые строили эти сооружения, ничего не знали ни о силе тяготения, из-за которой вода стремится всегда вниз, ни о силе трения или поверхностного натяжения. Но они видели: если поставить в ручей или речку колесо с лопастями на диаметре, то оно не только будет вращаться, но и сможет делать полезную работу.
Но и этот механизм был ограничен: не везде есть проточная вода с достаточно силой течения. Поэтому люди пошли дальше. Они построили мельницы, которые работали от ветра.
Уголь, мазут, бензин
Когда ученые поняли принцип возбуждения электричества, была поставлена техническая задача: получать его в промышленных масштабах. На тот момент (середина девятнадцатого века) мир был охвачен лихорадкой машин. Всю сложную работу стремились поручить расширяющемуся пару.
На тот момент (середина девятнадцатого века) мир был охвачен лихорадкой машин. Всю сложную работу стремились поручить расширяющемуся пару.
Но тогда нагреть большие объемы воды умели только ископаемым топливом – углем и мазутом. Поэтому те которые были богаты древними углеродами, сразу привлекли внимание инвесторов и рабочих. А перераспределение людей привело к промышленной революции.
Голландия и Техас
Однако такое положение вещей плохо отразилось на экологии. И ученые задумались: как получать энергию, не разрушая природу? Выручило хорошо забытое старое. Мельница использовала крутящий момент для совершения непосредственно грубой механической работы. Турбины гидроэлектростанций вращают магниты.
На данный момент самое чистое электричество получают из энергии ветра. Инженеры, которые строили первые генераторы Техаса, опирались на опыт ветряных мельниц Голландии.
Федун В.И. Конспект лекций по физике Электромагнетизи
Лекция 26.
Электромагнитная
индукция. Открытие Фарадея .
Открытие Фарадея .
В 1831 г. М. Фарадеем было сделано одно из важнейших фундаментальных открытий в электродинамике – обнаружено явлениеэлектромагнитной индукции .
В замкнутом проводящем контуре при изменении магнитного потока (потока вектора ), охватываемого этим контуром, возникает электрический ток .
Этот ток получил название индукционного .
Появление индукционного тока означает, что при изменении магнитного
Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами, которые удобно объяснить с помощью рисунка.
1-й способ: перемещение рамки в магнитном поле неподвижной катушки(см. рис.26.1).
2-й способ: изменение магнитного поля , создаваемого катушкой, за счет ее движения или вследствие изменения силы токав ней (или того и другого вместе). Рамкапри этом неподвижна.
В обоих этих случаях гальванометр будет показывать наличие индукционного
тока в рамке.
Направление индукционного тока и, соответственно, знак э.д.с. индукции определяются правилом Ленца.
Правило Ленца.
Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей .
Правило Ленца выражает важное физическое свойство – стремление системы противодействовать изменению ее состояния. Это свойство называют электромагнитной инерцией .
Какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции определяется формулой
Природа электромагнитной индукции .
С целью выяснения физических причин, которые приводят к возникновению э.д.с. индукции, последовательно рассмотрим два случая.
1. Контур движется в постоянном магнитном поле.
действовать сила
Электродвижущая сила,
создаваемая этим полем, называется электродвижущей
силой индукции .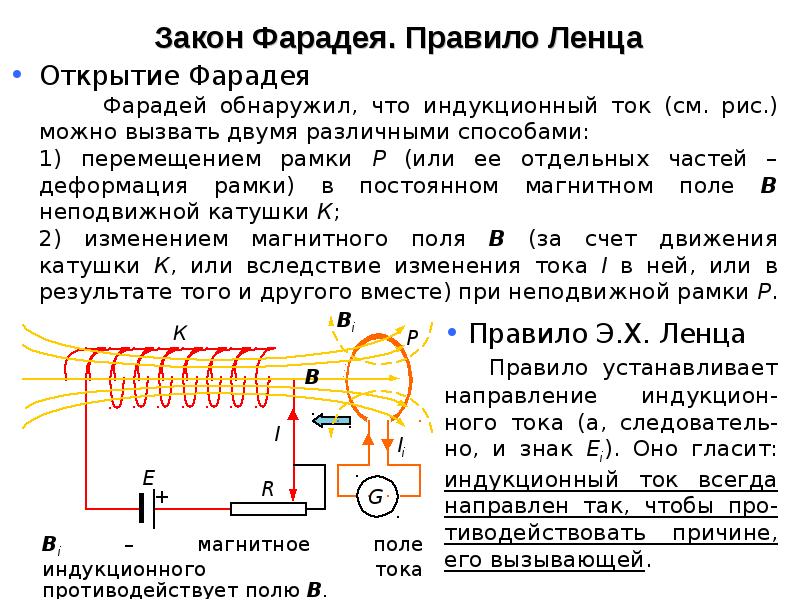 В нашем случае
В нашем случае
. |
Здесь знак «минус» поставлен потому, что стороннее поле направлено против положительного обхода контура, определяемого правилом правого винта. Произведениеесть скорость приращения площади контура (приращение площади в единицу времени), поэтому
, |
где
– приращение магнитного потока сквозь
контур.
. |
Полученный результат можно обобщить на случай произвольной ориентации вектора индукции магнитного поля относительно плоскости контура и на любой контур, движущийся (и/или деформируемый) произвольным образом в постоянном неоднородном внешнем магнитном поле.
Итак, возбуждение э.д.с. индукции при
движении контура в постоянном магнитном
поле объясняется действием магнитной
составляющей силы Лоренца, пропорциональной
,
которая возникает при перемещении
проводника.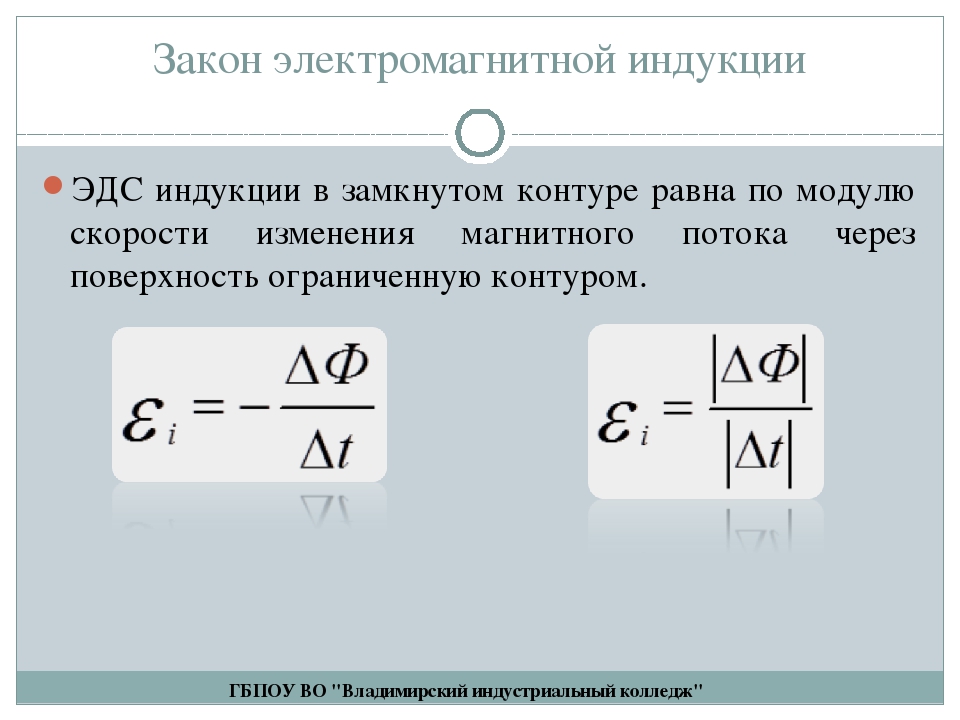
2. Контур покоится в переменном магнитном поле.
Наблюдаемое на опыте возникновение индукционного тока свидетельствует о том, что и в этом случае в контуре появляются сторонние силы, которые теперь связаны с изменяющимся во времени магнитным полем. Какова же их природа? Ответ на этот принципиальный вопрос был дан Максвеллом.
Поскольку проводник покоится, то скорость
упорядоченного движения электрических
зарядов
и, следовательно, магнитная сила,
пропорциональная
,
также равна нулю и уже не может привести
заряды в движение. Однако кроме магнитной
силы на электрический заряд может
действовать только сила со стороны
электрического поля, равная.
Поэтому остается заключить, чтоиндукционный ток обусловлен
электрическим полем
,
возникающим при изменении во времени
внешнего магнитного поля . Именно
это электрическое поле и ответственно
за появление э.д.с. индукции в неподвижном
контуре. Согласно Максвеллу,изменяющееся
во времени магнитное поле порождает в
окружающем пространстве электрическое
поле . Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
Формулировка закона электромагнитной индукции , данная Максвеллом, принадлежит к числу наиболее важных обобщений электродинамики.
Всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле .
Математическая формулировка закона электромагнитной индукции в понимании Максвелла имеет вид:
Циркуляция вектора напряженности этого поля по любому неподвижному замкнутому контуруопределяется выражением
, |
где – магнитный поток, пронизывающий контур.
Используемый для обозначения скорости изменения магнитного потока знак частной производной указывает на то, что контур является неподвижным.
Поток вектора
через поверхность, ограниченную контуром,
равен
,
поэтому выражение закона электромагнитной
индукции можно переписать следующим
образом:
Это одно из уравнений системы уравнений
Максвелла.
Тот факт, что циркуляция электрического поля, возбуждаемого переменным во времени магнитным полем, отлична от нуля, означает, что рассматриваемое электрическое поле не потенциальное .Оно, как и магнитное поле, являетсявихревым .
В общем случае электрическое поле может быть представлено векторной суммой потенциального (поля статических электрических зарядов, циркуляция которого равна нулю) и вихревого (обусловленного изменяющимся во времени магнитным полем) электрических полей.
В основе рассмотренных нами явлений,
объясняющих закон электромагнитной
индукции, не просматривается общего
принципа, позволяющего установить
общность их физической природы. Поэтому
эти явления следует рассматривать как
независимые, а закон электромагнитной
индукции – как результат их совместного
действия. Тем более удивительным
оказывается тот факт, что э.д.с. индукции
в контуре всегда равна скорости изменения
магнитного потока сквозь контур. В тех
случаях, когда меняется и поле
и расположение или конфигурация контура
в магнитном поле, э. д.с. индукции следует
рассчитывать по формуле
д.с. индукции следует
рассчитывать по формуле
Выражение, стоящее в правой части этого равенства, представляет собой полную производную магнитного потока по времени: первое слагаемое связано с изменением магнитного поля во времени, второе – с движением контура.
Можно сказать, что во всех случаях индукционный ток вызывается полной силой Лоренца
. |
Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца – зависит от выбора системы отсчета .
О работе сил Лоренца и Ампера .
Из самого определения работы следует, что сила, действующая в магнитном поле на электрический заряд и перпендикулярная его скорости, не может совершать работы. Однако при движении проводника с током, увлекающего за собой заряды, сила Ампера все же работу совершает. Наглядным подтверждением этого служат электромоторы.
Это противоречие исчезает, если принять
во внимание, что движение проводника в
магнитном поле неизбежно сопровождается
явлением электромагнитной индукции. Поэтому наряду с силой Ампера работу
над электрическими зарядами совершает
и возникающая в проводнике электродвижущая
сила индукции. Т.о., полная работа сил
магнитного поля складывается из
механической работы, обусловленной
силой Ампера, и работы э.д.с., индуцируемой
при движении проводника. Обе работы
равны по модулю и противоположны по
знаку, поэтому их сумма равна нулю.
Действительно, работа амперовой силы
при элементарном перемещении проводника
с током в магнитном поле равна
Поэтому наряду с силой Ампера работу
над электрическими зарядами совершает
и возникающая в проводнике электродвижущая
сила индукции. Т.о., полная работа сил
магнитного поля складывается из
механической работы, обусловленной
силой Ампера, и работы э.д.с., индуцируемой
при движении проводника. Обе работы
равны по модулю и противоположны по
знаку, поэтому их сумма равна нулю.
Действительно, работа амперовой силы
при элементарном перемещении проводника
с током в магнитном поле равна
,
за это же время э.д.с. индукции совершает
работу
, |
тогда полная работа
.
Силы Ампера совершают работу не за счет энергии внешнего магнитного поля, которое может оставаться постоянным, а за счет источника э.д.с., поддерживающего ток в контуре.
Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого контура в нем возникает электрический ток, который называютиндукционным током. Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 24). Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 25). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.
Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 24). Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 25). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.
Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием магнитный поток.Магнитным потоком через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции В на площадь контура S и на косинус угла а между направлением вектора магнитной индукции и нормалью к площади контура. Ф = BS cos α (рис. 26).
Ф = BS cos α (рис. 26).
Опытным путем был установлен основной закон электромагнитной индукции:ЭДС индукции в замкнутом контуре равна по величине скорости из-менения магнитного потока через контур. ξ = ΔФ/t..
Если рассматривать катушку, содержащую п витков, то формула основного закона электромагнитной индукции будет выглядеть так: ξ = n ΔФ/t.
Единица измерения магнитного потока Ф – вебер (Вб): 1В6 =1Β c.
Из основного закона ΔФ =ξ t следует смысл размерности: 1 вебер – это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.
Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.
Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур. Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло. (рис. 27). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур. Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло. (рис. 27). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
В 1831 году английский ученый физик в своих опытах М.Фарадей открыл явление электромагнитной индукции . Затем изучением этого явления занимались русские ученый Э. Х. Ленц и Б.С.Якоби.
Х. Ленц и Б.С.Якоби.
В настоящее время, в основе многих устройств лежит явление электромагнитной индукции, например в двигателе или генераторе электрического тока тока, в трансформаторах, радиоприемниках, и многих других устройствах.
Электромагнитная индукция – это явление возникновения тока в замкнутом проводнике, при прохождении через него магнитного потока. То есть, благодаря этому явлению мы можем преобразовывать механическую энергию в электрическую – и это замечательно. Ведь до открытия этого явления люди не знали о методах получения электрического тока , кроме гальваники.
Когда проводник оказывается под действием магнитного поля, в нем возникает ЭДС, которую количественно можно выразить через закон электромагнитной индукции.
Закон электромагнитной индукции
Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром.
В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n:
Но в общем случае, применяют формулу ЭДС с общим потокосцеплением:
ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в проводнике является катушка, через которую проходит постоянный магнит . Направление индуцируемого тока можно определить с помощью правила Ленца .
Наиболее простым примером появления тока в проводнике является катушка, через которую проходит постоянный магнит . Направление индуцируемого тока можно определить с помощью правила Ленца .
Правило Ленца
Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.
В том случае, когда мы вводим магнит в катушку, магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца, направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.
В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.
Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.
Для описания процессов в физике и химии есть целый ряд законов и соотношений, полученных экспериментальным и расчетным путем. Ни единого исследования нельзя провести без предварительной оценки процессов по теоретическим соотношениям. Законы Фарадея применяются и в физике, и в химии, а в этой статье мы постараемся кратко и понятно рассказать о всех знаменитых открытиях этого великого ученого.
История открытия
Закон Фарадея в электродинамике был открыт двумя ученными: Майклом Фарадеем и Джозефом Генри, но Фарадей опубликовал результаты своих работ раньше – в 1831 году.
В своих демонстрационных экспериментах в августе 1831 г. он использовал железный тор, на противоположные концы которого был намотан провод (по одному проводу на стороны). На концы одного первого провода он подал питание от гальванической батареи, а на выводы второго подключил гальванометр. Конструкция была похожа на современный трансформатор. Периодически включая и выключая напряжение на первом проводе, он наблюдал всплески на гальванометре.
Конструкция была похожа на современный трансформатор. Периодически включая и выключая напряжение на первом проводе, он наблюдал всплески на гальванометре.
Гальванометр — это высокочувствительный прибор для измерения силы токов малой величины.
Таким образом было изображено влияние магнитного поля, образовавшегося в результате протекания тока в первом проводе, на состояние второго проводника. Это воздействие передавалось от первого ко второму через сердечник – металлический тор. В результате исследований было обнаружено и влияние постоянного магнита, который двигается в катушке, на её обмотку.
Тогда Фарадей объяснял явление электромагнитной индукции с точки зрения силовых линий. Еще одной была установка для генерирования постоянного тока: медный диск вращался вблизи магнита, а скользящий по нему провод был токосъёмником. Это изобретение так и называется — диск Фарадея.
Ученные того периода не признали идеи Фарадея, но Максвелл взял исследования для основы своей магнитной теории. В 1836 г. Майкл Фарадей установил соотношения для электрохимических процессов, которые назвали Законами электролиза Фарадея. Первый описывает соотношения выделенной на электроде массы вещества и протекающего тока, а второй соотношения массы вещества в растворе и выделенного на электроде, для определенного количества электричества.
В 1836 г. Майкл Фарадей установил соотношения для электрохимических процессов, которые назвали Законами электролиза Фарадея. Первый описывает соотношения выделенной на электроде массы вещества и протекающего тока, а второй соотношения массы вещества в растворе и выделенного на электроде, для определенного количества электричества.
Электродинамика
Первые работы применяются в физике, конкретно в описании работы электрических машин и аппаратов (трансформаторов, двигателей и пр.). Закон Фарадея гласит:
Для контура индуцированная ЭДС прямо пропорциональна величине скорости магнитного потока, который перемещается через этот контур со знаком минус.
Это можно сказать простыми словами: чем быстрее магнитный поток движется через контур, тем больше на его выводах генерируется ЭДС.
Формула выглядит следующим образом:
Здесь dФ – магнитный поток, а dt – единица времени. Известно, что первая производная по времени – это скорость. Т.е скорость перемещения магнитного потока в данном конкретном случае. Кстати перемещаться может, как и источник магнитного поля (катушка с током – электромагнит, или постоянный магнит), так и контур.
Кстати перемещаться может, как и источник магнитного поля (катушка с током – электромагнит, или постоянный магнит), так и контур.
Здесь же поток можно выразить по такой формуле:
B – магнитное поле, а dS – площадь поверхности.
Если рассматривать катушку с плотнонамотанными витками, при этом в количестве витков N, то закон Фарадея выглядит следующим образом:
Магнитный поток в формуле на один виток, измеряется в Веберах. Ток, протекающий в контуре, называется индукционным.
Электромагнитная индукция – явление протекания тока в замкнутом контуре под воздействием внешнего магнитного поля.
В формулах выше вы могли заметить знаки модуля, без них она имеет слегка иной вид, такой как было сказано в первой формулировке, со знаком минус.
Знак минус объясняет правило Ленца. Ток, возникающий в контуре, создает магнитное поле, оно направлено противоположно. Это является следствием закона сохранения энергии.
Направление индукционного тока можно определить по правилу правой руки или , мы его рассматривали на нашем сайте подробно.
Как уже было сказано, благодаря явлению электромагнитной индукции работают электрические машины трансформаторы, генераторы и двигатели. На иллюстрации показано протекание тока в обмотке якоря под воздействием магнитного поля статора. В случае с генератором, при вращении его ротора внешними силами в обмотках ротора возникает ЭДС, ток порождает магнитное поле направленное противоположно (тот самый знак минус в формуле). Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.
И наоборот — при протекании тока в роторе возникает поле, которое взаимодействует с полем статора и ротор начинает вращаться. При нагрузке на вал ток в статоре и в роторе повышается, при этом нужно обеспечить переключение обмоток, но это уже другая тема, связанная с устройством электрических машин.
В основе работы трансформатора источником движущегося магнитного потока является переменное магнитное поле, возникающее в следствие протекания в первичной обмотке переменного тока.
Если вы желаете более подробно изучить вопрос, рекомендуем просмотреть видео, на котором легко и доступно рассказывается Закон Фарадея для электромагнитной индукции:
Электролиз
Кроме исследований ЭДС и электромагнитной индукции ученный сделал большие открытия и в других дисциплинах, в том числе химии.
При протекании тока через электролит ионы (положительные и отрицательные) начинают устремляться к электродам. Отрицательные движутся к аноду, положительные к катоду. При этом на одном из электродов выделяется определенная масса вещества, которое содержится в электролите.
Фарадей проводил эксперименты, пропуская разный ток через электролит и измеряя массу вещества отложившегося на электродах, вывел закономерности.
m – масса вещества, q – заряд, а k – зависит от состава электролита.
А заряд можно выразить через ток за промежуток времени:
I=q/t , тогда q = i*t
Теперь можно определить массу вещества, которое выделится, зная ток и время, которое он протекал. Это называется Первый закон электролиза Фарадея.
Это называется Первый закон электролиза Фарадея.
Второй закон:
Масса химического элемента, который осядет на электроде, прямо пропорциональна эквивалентной массе элемента (молярной массе разделенной на число, которое зависит от химической реакции, в которой участвует вещество).
С учетом вышесказанного эти законы объединяются в формулу:
m – масса вещества, которое выделилось в граммах, n – количество переносимых электронов в электродном процессе, F=986485 Кл/моль – число Фарадея, t – время в секундах, M молярная масса вещества г/моль.
В реальности же из-за разных причин, масса выделяемого вещества меньше чем расчетная (при расчетах с учетом протекающего тока). Отношение теоретической и реальной масс называют выходом по току:
B т = 100% * m расч /m теор
Законы Фарадея внесли существенный вклад в развитие современной науки, благодаря его работам мы имеем электродвигатели и генераторы электроэнергии (а также работам его последователей). Работа ЭДС и явления электромагнитной индукции подарили нам большую часть современного электрооборудования, в том числе и громкоговорители и микрофоны, без которых невозможно прослушивание записей и голосовая связь. Процессы электролиза применяются в гальваническом методе покрытия материалов, что несет как декоративную ценность, так и практическую.
Работа ЭДС и явления электромагнитной индукции подарили нам большую часть современного электрооборудования, в том числе и громкоговорители и микрофоны, без которых невозможно прослушивание записей и голосовая связь. Процессы электролиза применяются в гальваническом методе покрытия материалов, что несет как декоративную ценность, так и практическую.
Похожие материалы:
Нравится(0 ) Не нравится(0 )
НАЧАЛА ФИЗИКИ
Майкл Фарадей (1791–1867) – великий английский физик. Автор ряда фундаментальных и прикладных открытий, в том числе закона электромагнитной индукции, законов электролиза (законы Фарадея), явления вращения плоскости поляризации света в магнитном поле (эффект Фарадея). В 1821 г. впервые осуществил вращение магнита вокруг проводника с током и проводника с током вокруг магнита, создав первую лабораторную модель электродвигателя. 29 августа 1831 г. Фарадей открыл явление электромагнитной индукции — возникновение электрического поля при изменении магнитного поля. В последующем Фарадей всесторонне исследовал это явление, которое без преувеличения можно назвать краеугольным камнем современной электродинамики и ее практического приложения – электротехники. В 1835 г. открыл так называемые экстратоки, которые возникают при замыкании и размыкании электрической цепи, и установил их направление.
В последующем Фарадей всесторонне исследовал это явление, которое без преувеличения можно назвать краеугольным камнем современной электродинамики и ее практического приложения – электротехники. В 1835 г. открыл так называемые экстратоки, которые возникают при замыкании и размыкании электрической цепи, и установил их направление.
Однако главной заслугой Фарадея является разработка концепции электромагнитного поля (сам этот термин впервые употребил Фарадей). Если до него господствовало представление о прямом и мгновенном взаимодействии зарядов и токов через пустое пространство, то Фарадей последовательно развивал идею о том, что существует материальный переносчик этого взаимодействия – электромагнитное поле. Концепция поля является фундаментом современной физики. При этом Фарадей категорически не любил формулы – физику он понимал «на пальцах», видя за проводимыми им экспериментами взаимосвязи причин и явлений. Именно этот взгляд и позволил ему сформулировать концепцию электромагнитного поля (да и сам термин – поле – впервые употребил Фарадей).
Фарадей прославился не только многочисленными открытиями. Он был блестящим популяризатором науки. С 1826 г. и почти до самой кончины он читал научно-популярные публичные лекции. Одна из них – «История свечи с точки зрения химии» – стала самой известной научно-популярной лекцией в истории науки. Позже она была издана отдельной книгой и переведена на многие языки (в том числе и русский).
ЭДС (29.2) называют ЭДС индукции. С законом электромагнитной индукции можно связать определенное правило знаков, т.е. и поток и ЭДС считать алгебраическими величинами (тогда в формуле (29.2) должен быть знак «минус»). В этом случае закон (29.2) автоматически даст направление ЭДС (направление индукционного тока). Можно, однако, считать все величины в законе (29.2) положительными, а направление индукционного тока определять независимо из правила Ленца.
446/597
Закон Ленца — College Physics: OpenStax
Закон индукции Фарадея имеет множество применений, которые мы рассмотрим в этой и других главах. На этом этапе давайте упомянем несколько, которые связаны с хранением данных и магнитными полями. Очень важное применение связано с аудио и видео записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, на которое намотана катушка проволоки — электромагнит (рис. 2).Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые зависят от амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, что приводит к записи сигнала. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения.
На этом этапе давайте упомянем несколько, которые связаны с хранением данных и магнитными полями. Очень важное применение связано с аудио и видео записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, на которое намотана катушка проволоки — электромагнит (рис. 2).Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые зависят от амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, что приводит к записи сигнала. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Аналогичные принципы применимы к жестким дискам компьютеров, но с гораздо большей скоростью. Здесь записи на вращающемся диске с покрытием. Считывающие головки исторически заставляли работать по принципу индукции. Однако входная информация передается в цифровой, а не в аналоговой форме — на вращающемся жестком диске записывается последовательность нулей или единиц. Сегодня большинство устройств считывания с жестких дисков не работают по принципу индукции, а используют технику, известную как гигантское магнитосопротивление .(Открытие того, что слабые изменения магнитного поля в тонкой пленке железа и хрома могут вызвать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти в магнитной полосе на магнитной полосе. оборотная сторона вашей личной кредитной карты, используемой в продуктовом магазине или банкомате.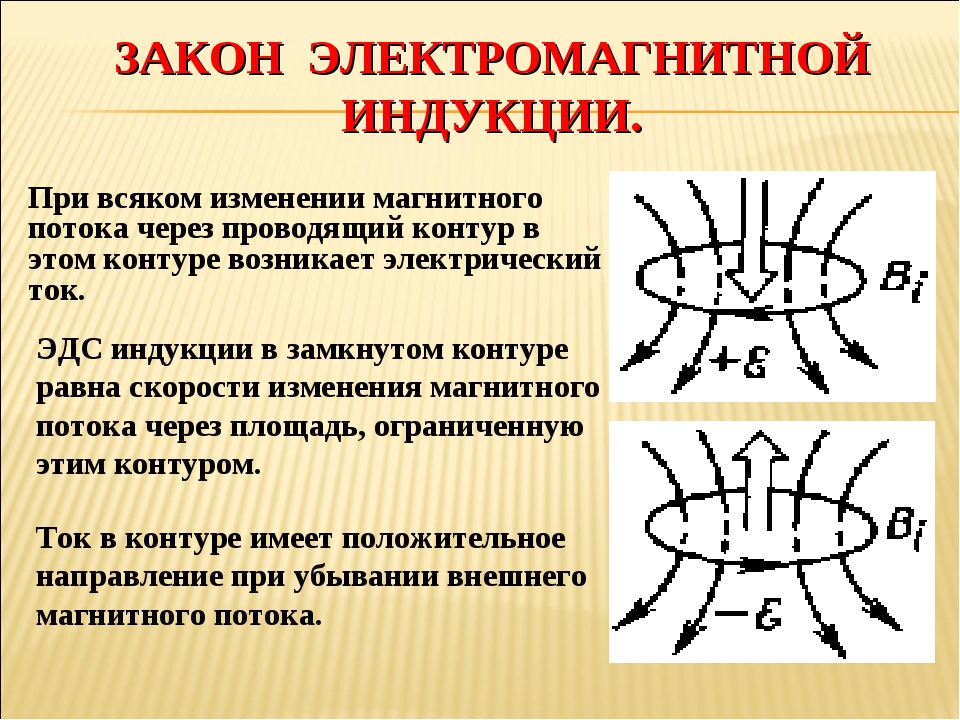 Это работает по тому же принципу, что и упомянутая в последнем абзаце аудио- или видеокассета, в которой голова считывает личную информацию с вашей карты.
Это работает по тому же принципу, что и упомянутая в последнем абзаце аудио- или видеокассета, в которой голова считывает личную информацию с вашей карты.
Еще одним применением электромагнитной индукции является передача электрических сигналов через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном снаружи черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе. Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы необходимо передавать через различные среды.
Еще одной современной областью исследований, в которой электромагнитная индукция успешно реализуется (и имеет значительный потенциал), является транскраниальное магнитное моделирование. Множество расстройств, включая депрессию и галлюцинации, можно отнести к нерегулярной локальной электрической активности в головном мозге. В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозге. В выявленных местах индуцируются слабые электрические токи, что может привести к восстановлению электрических функций в тканях головного мозга.
В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозге. В выявленных местах индуцируются слабые электрические токи, что может привести к восстановлению электрических функций в тканях головного мозга.
Апноэ во сне («остановка дыхания») поражает как взрослых, так и младенцев (особенно недоношенных детей и может быть причиной внезапной детской смерти [SID]). У таких людей дыхание может неоднократно останавливаться во время сна. Прекращение более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию.Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль. В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль. В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Установление связей: сохранение энергии
Закон Ленца является проявлением закона сохранения энергии.ЭДС индукции создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
Пример 1. Расчет ЭДС: насколько велика ЭДС индукции?
Рассчитайте величину ЭДС индукции, когда магнит на рисунке 1(а) вталкивается в катушку, учитывая следующую информацию: катушка с одним контуром имеет радиус 6.00 см, а среднее значение [латекс]\boldsymbol{B \;\textbf{cos} \;\theta}[/latex] (данное, поскольку поле стержневого магнита комплексное) увеличивается с 0,0500 Тл до 0,250 Тл. за 0,100 с.
Стратегия
Чтобы найти величину ЭДС, мы используем закон индукции Фарадея, сформулированный как [латекс]\boldsymbol{\textbf{ЭДС} = -N \frac{\Delta \phi}{\Delta t}}[ /latex], но без знака минус, указывающего направление:
[латекс]\boldsymbol{\textbf{emf} = N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta t}}[/latex]
Раствор
Нам дано, что [латекс]\boldsymbol{N = 1}[/латекс] и [латекс]\boldsymbol{\Delta t=0.100 \;\textbf{s}}[/latex], но мы должны определить изменение потока [latex]\boldsymbol{\Delta \phi}[/latex], прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
Поскольку площадь петли фиксирована, мы видим, что
[латекс]\boldsymbol{\Delta \phi = \Delta (BA \;\textbf{cos} \theta) = A \Delta(B \;\textbf{cos} \;\theta)}[/latex]
Теперь [латекс]\boldsymbol{\Delta (B \;\textbf{cos} \;\theta) = 0,200 \;\textbf{T}}[/latex], поскольку было дано, что [латекс]\boldsymbol{ B \;\textbf{cos} \;\theta}[/latex] меняется с 0.2)(0,200 \;\textbf{T})}{0,100 \;\textbf{s}}}[/latex] [латекс]\boldsymbol{= 22,6 \; \textbf{мВ}}[/латекс]
Обсуждение
Хотя это легко измеряемое напряжение, оно явно недостаточно велико для большинства практических применений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.
Закон Фарадея: формулировка, уравнение и приложения
Что такое закон Фарадея
Закон электромагнитной индукции Фарадея гласит, что напряжение индуцируется в проводнике всякий раз, когда существует относительное движение между проводником и внешним магнитным полем. Величина этого напряжения пропорциональна скорости изменения магнитного потока. Таким образом, закон устанавливает количественную связь между изменяющимся магнитным потоком и наведенным напряжением в электромагнитной цепи.
Величина этого напряжения пропорциональна скорости изменения магнитного потока. Таким образом, закон устанавливает количественную связь между изменяющимся магнитным потоком и наведенным напряжением в электромагнитной цепи.
История
Этот закон приписывают английскому ученому Майклу Фарадею, внесшему значительный вклад в развитие электромагнетизма и электрохимии. В 1831 году Фарадей впервые продемонстрировал электромагнитную индукцию, обернув два провода вокруг противоположных сторон железного кольца.Один провод был подключен к батарее, которая давала ток, а другой провод к гальванометру. Ток в первом проводе создавал магнитное поле, которое проходило по второму проводу. При изменении магнитного потока во втором проводе индуцировался ток, регистрируемый гальванометром.
Уравнение закона Фарадея
Рассмотрим пример проводящего провода, намотанного на катушку. Предположим, эта катушка помещена во внешнее магнитное поле, представленное магнитными силовыми линиями. Количество линий, проходящих через данную площадь поперечного сечения, определяется как магнитный поток. Есть несколько способов изменить этот поток.
Количество линий, проходящих через данную площадь поперечного сечения, определяется как магнитный поток. Есть несколько способов изменить этот поток.
Согласно закону Фарадея, изменение магнитного потока вызывает индуцированное напряжение, называемое электродвижущей силой (ЭДС). Математически закон задается следующей формулой.
ε = – Н dφ/dt
Где,
ε = ЭДС индукции
Н = количество витков катушки
dφ/dt = мгновенное изменение магнитного потока во времени
СИ Единица ЭДС : Вольт
Знак минус потому, что ЭДС индукции противодействует магнитному полю.Величина ЭДС определяется выражением
.|ε| = N dφ/dt
Если N = 1 и dφ/dt = 1 Втб/с, то |ε| = 1 В
Таким образом, ЭДС индукции представляет собой напряжение, создаваемое на катушке из одного витка при скорости потока 1 Втб/с. Закон Ленца определяет направление индукционного тока.
Закон ФарадеяДифференциальная форма закона Фарадея
Шотландский математик Джеймс Клерк Максвелл разработал набор дифференциальных уравнений в частных производных, которые описывают, как электрические и магнитные поля генерируются зарядами, токами и изменениями полей. Сегодня эти уравнения известны под общим названием уравнения Максвелла. Более ранняя версия уравнений была впервые опубликована в 1861 году. Уравнение Максвелла-Фарадея имеет вид
Сегодня эти уравнения известны под общим названием уравнения Максвелла. Более ранняя версия уравнений была впервые опубликована в 1861 году. Уравнение Максвелла-Фарадея имеет вид
∇ X E = -∂ B /∂t
Где,
E : Электрическое поле
B : Магнитное поле
Применение закона Фарадея
Закон Фарадея — один из самых фундаментальных законов электромагнетизма.Этот закон находит свое применение в большинстве электрических устройств. Он может объяснить принцип работы трансформаторов, генераторов, катушек индуктивности и двигателей. Вот несколько вариантов использования и приложений, в том числе в повседневной жизни.
- Трансформатор : Он состоит из пары катушек, намотанных на квадратный сердечник. Переменный ток, проходящий через одну катушку, создает изменяющееся магнитное поле, в результате чего во второй катушке возникает индуцированный ток.

- Генератор : Устройство, преобразующее механическую энергию в электрическую, используемую во внешней цепи.Катушка проводника быстро вращается между полюсами подковообразного магнита. Вращающаяся катушка перехватывает магнитное поле, и в ней индуцируется ток.
- Индукционная плита : Используется для нагрева посуды с помощью индукции вместо пламени или электрической катушки. В нем используется понятие взаимной индуктивности, основанное на принципе взаимной индукции.
- Электрические звонки : Устройство, работающее от электромагнита. Молоток с электромагнитным приводом ударяет по колоколу, что приводит к звуку.
- Электромагнитный расходомер : Устройство, используемое для измерения скорости проводящих жидкостей с помощью приложения магнитного поля. ЭДС индукции пропорциональна скорости жидкости.
Последний раз статья рецензировалась в четверг, 30 сентября 2021 г.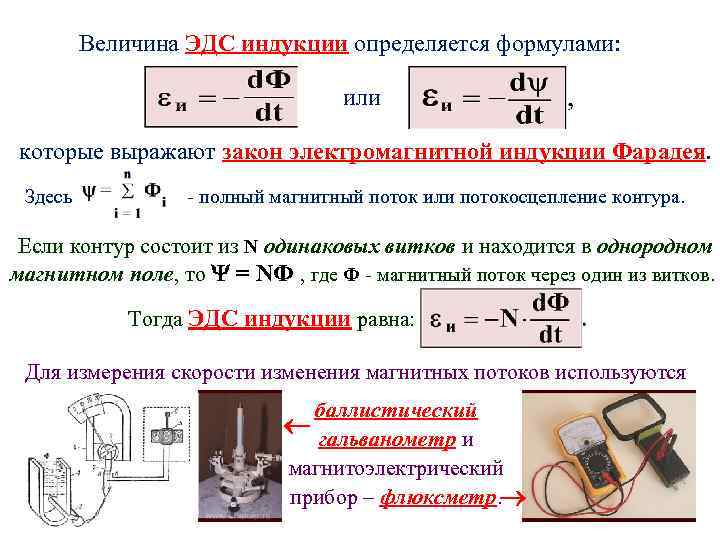
6.2 Закон индукции Фарадея: Закон Ленца
Применение электромагнитной индукции
Существует множество применений закона индукции Фарадея, которые мы рассмотрим в этой и других главах.На этом этапе давайте упомянем несколько, которые связаны с хранением данных и магнитными полями. Очень важное применение связано с аудио и видео записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, на которое намотана катушка проволоки — электромагнит (рис. 6.8). Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы, которые являются функцией амплитуды и частоты сигнала, создают переменные магнитные поля на записывающей головке.Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, что приводит к записи сигнала. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Рисунок 6.8 Головки записи и воспроизведения, используемые с аудио- и видеомагнитофонами.(Стив Юрветсон)
Аналогичные принципы применимы и к жестким дискам компьютеров, но с гораздо большей скоростью. Здесь записи на вращающемся диске с покрытием. Считывающие головки исторически заставляли работать по принципу индукции. Однако входная информация передается в цифровой, а не в аналоговой форме — на вращающемся жестком диске записывается последовательность нулей или единиц. Сегодня большинство считывающих устройств с жестких дисков не работают по принципу индукции, а используют технику, известную как гигантское магнитосопротивление — открытие, что слабые изменения магнитного поля в тонкой пленке железа и хрома могут вызвать гораздо большие изменения в магнитном поле. электрическое сопротивление было одним из первых крупных успехов нанотехнологии.Еще одно применение индукции можно найти на магнитной полосе на обратной стороне вашей личной кредитной карты, используемой в продуктовом магазине или банкомате. Это работает по тому же принципу, что и аудио- или видеокассета, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.
электрическое сопротивление было одним из первых крупных успехов нанотехнологии.Еще одно применение индукции можно найти на магнитной полосе на обратной стороне вашей личной кредитной карты, используемой в продуктовом магазине или банкомате. Это работает по тому же принципу, что и аудио- или видеокассета, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.
Еще одним применением электромагнитной индукции является передача электрических сигналов через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном снаружи черепа и используется для создания переменного магнитного поля.Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе. Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы необходимо передавать через различные среды.
Рис. 6.9 Электромагнитная индукция, используемая для передачи электрических токов через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (Бьорн Кнетч)
Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (Бьорн Кнетч)
Еще одной современной областью исследований, в которой электромагнитная индукция успешно реализуется со значительным потенциалом, является транскраниальная магнитная стимуляция.В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозге. В выявленных местах индуцируются слабые электрические токи, что может привести к восстановлению электрических функций в тканях головного мозга.
Апноэ во сне ( остановка дыхания ) поражает как взрослых, так и младенцев, особенно недоношенных детей, и может быть причиной внезапной детской смерти (ВСН). У таких людей дыхание может неоднократно останавливаться во время сна.Прекращение более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль.В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль.В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Установление связей: сохранение энергии
Закон Ленца является проявлением закона сохранения энергии. ЭДС индукции создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
Пример 6.1 Расчет ЭДС: насколько велика ЭДС индукции?
Рассчитайте величину ЭДС индукции, когда магнит на рис. 6.7(а) вталкивается в катушку, учитывая следующую информацию: катушка с одним контуром имеет радиус 6.00 см, а среднее значение BcosθBcosθ размером 12{B”cos”θ} {} (данное, поскольку поле стержневого магнита комплексное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.
Стратегия
Чтобы найти величину ЭДС, мы используем закон индукции Фарадея, сформулированный как ЭДС=-NΔΦΔt, ЭДС=-NΔΦΔt, но без знака минус, указывающего направление.
Раствор
Нам дано, что N=1N=1 размер 12{N=1} {} и Δt=0.100 с, Δt=0,100 с, но мы должны определить изменение потока ΔΦΔΦ размером 12{ΔΦ} {}, прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
6.4 ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ).ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ). размер 12{ΔΦ=Δ \( BA”cos”θ \) =AΔ \( B”cos”θ \) } {}Сейчас Δ(Bcosθ)=0,200 Тл, Δ(Bcosθ)=0,200 Тл, размер 12{Δ \( B”cos”θ \)=0 “.” “200”`T} {}, так как было задано, что BcosθBcosθ размер 12{B”cos”θ} {} изменяется от 0,0500 до 0,250 Тл. Площадь петли A=πr2=(3,14…)(0,060 м)2=1,13×10-2м2.A=πr2=(3,14…)(0,060 м)2=1,13×10-2 м2. size 12{A=πr rSup { size 8{2} } = \( 3 “.” “14” “.” “.” “.” \) \( 0 “.” “060”`m \) rSup { размер 8{2} } =1 “.” “13” умножить на “10” rSup { size 8{ – 2} } `m rSup { size 8{2} } } {} Таким образом,
6,5 ΔΦ=(1,13×10–2 м2)(0,200 Тл).ΔΦ=(1,13×10–2 м2)(0,200 Тл). размер 12{ΔΦ= \( 1 “.” “13” умножить на “10” rSup { размер 8{ – 2} } “m” rSup { размер 8{2} } \) \( 0 “. ” “200”” Т” \) } {}
” “200”” Т” \) } {}Ввод определенных значений в выражение для ЭДС дает
6.6 ЭДС=NΔΦΔt=(1.13×10-2 м2)(0,200Тл)0,100с=22,6мВ.Эдс=NΔΦΔt=(1,13×10-2 м2)(0,200Тл)0,100с=22,6мВ. размер 12{E=N {{ΔΦ} над {Δt} } = { { \( 1 “.” “13” умножить на “10” rSup {размер 8{- 2} } “m” rSup {размер 8{2} } \) \( 0 “.” “200”” T” \) } более {0 “.” “100”” с”} } =”22″ “.” 6″ мВ”} {}Обсуждение
Хотя это легко измеряемое напряжение, оно явно недостаточно велико для большинства практических применений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.
Магнитный поток и закон Фарадея
Простейшим примером индуцированного электрического поля является поле, генерируемое внутри небольшой круглой проводящей петли из-за изменяющегося магнитного поля и ответственное за последующий ток. Вообще говоря, индуцированное электрическое поле зависит не только от того, как магнитное поле B \mathbf{B}B изменяется со временем, но и от того, как может измениться геометрическое соотношение между контуром и магнитным полем. Например, даже в однородном и постоянном магнитном поле изменение формы проводящего контура или его ориентации относительно силовых линий магнитного поля будет создавать электрическое поле и, следовательно, ток.Подходящая комбинация геометрии и магнитного поля, необходимая для описания индуцированного электрического поля, когда одно из них изменяется, называется магнитным потоком. Самое основное определение – это магнитный поток через плоскую фигуру из-за однородного магнитного поля. Рассмотрим плоскую область площадью AAA и выберите единичный вектор n \mathbf{n}n, перпендикулярный поверхности. Для удобства вектор площади A \mathbf{A}A определяется как A \mathbf{A}A === AAAn \mathbf{n}n. В общем случае A \mathbf{A}A будет наклонен под некоторым углом θ \theta θ с силовыми линиями магнитного поля, т.е.е., θ \theta θ будет меньшим углом между A \mathbf{A}A и B \mathbf{B}B. (См. рисунок ниже.)
Например, даже в однородном и постоянном магнитном поле изменение формы проводящего контура или его ориентации относительно силовых линий магнитного поля будет создавать электрическое поле и, следовательно, ток.Подходящая комбинация геометрии и магнитного поля, необходимая для описания индуцированного электрического поля, когда одно из них изменяется, называется магнитным потоком. Самое основное определение – это магнитный поток через плоскую фигуру из-за однородного магнитного поля. Рассмотрим плоскую область площадью AAA и выберите единичный вектор n \mathbf{n}n, перпендикулярный поверхности. Для удобства вектор площади A \mathbf{A}A определяется как A \mathbf{A}A === AAAn \mathbf{n}n. В общем случае A \mathbf{A}A будет наклонен под некоторым углом θ \theta θ с силовыми линиями магнитного поля, т.е.е., θ \theta θ будет меньшим углом между A \mathbf{A}A и B \mathbf{B}B. (См. рисунок ниже.)
Вектор, помеченный как «нормальный», является нашим единичным вектором n \mathbf{n}n, а магнитный поток через плоскую область AAA определяется как
Ф=В⋅А. \Phi = \mathbf{B} \cdot \mathbf{A}. Ф=В⋅А.
\Phi = \mathbf{B} \cdot \mathbf{A}. Ф=В⋅А.
По сути, скалярное произведение проецирует нашу исходную площадь AAA на плоскость, перпендикулярную B \mathbf{B}B.
Магнитный поток через поверхность, склеенную вместе с небольшими плоскостями (подумайте о чем-то вроде геодезического купола), представляет собой просто сумму магнитного потока через каждый «участок».’ Участку поверхности назначается вектор ai \mathbf{a}_i ai, который указывает нормаль (перпендикуляр) к поверхности. Кроме того, величина каждого ai \mathbf{a}_i ai определяется как площадь соответствующего участка.
Магнитный поток Φi \Phi_{i} Φi, проходящий через участок, определяется скалярным произведением, которое вычисляет компонент Bi \mathbf{B}_i Bi, параллельный ai \mathbf{a}_i ai:
Φi=Bi⋅ai \Phi_{i} = \mathbf{B}_i \cdot \mathbf{a}_i Φi=Bi⋅ai
Таким образом, общий магнитный поток через поверхность, состоящую из множества маленьких пятен, ai \mathbf{a}_i ai, представляет собой сумму всех пятен:
Φ=∑iBi⋅ai. \Phi = \sum_i \mathbf{B}_i \cdot \mathbf{a}_i .Φ=i∑Bi⋅ai.
\Phi = \sum_i \mathbf{B}_i \cdot \mathbf{a}_i .Φ=i∑Bi⋅ai.
Поскольку ai \mathbf{a}_i ai становится исчезающе малым, как в случае гладкой поверхности, сумма заменяется поверхностным интегралом :
Φ=∫SB⋅да. \Phi = \int_S \mathbf{B} \cdot d\mathbf{a}. Φ=∫SB⋅да.
К счастью, магнитный поток часто можно вычислить, не прибегая к явному вычислению интеграла. Как правило, расчет магнитного потока довольно прост, поскольку в основном рассматриваются плоские петли.Однако после обсуждения следующей темы, закона Фарадея, необходимо будет допустить, что SSS гладкой поверхности может быть произвольным, чтобы определить дифференциальную форму закона Фарадея в следующем разделе.
Небольшая плоская проволочная петля площадью A A A ориентирована перпендикулярно однородному магнитному полю внутри цилиндрического соленоида с числом витков на единицу длины n n n и током I I I. Каков поток через петлю?
В этом случае B⋅da \mathbf{B} \cdot d\mathbf{a} B⋅da постоянна, поэтому поток равен просто Φ=BA=µ0nIA \Phi = BA = \mu_0 n IA Φ=BA =μ0nIA.



 е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое .
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами .
е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое .
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами . 5).
5).

