Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме
Фарадей был первым, кто обнаружил явление электромагнитной индукции. Это случилось в ходе опыта, когда он исследовал изменение потока магнитной индукции в замкнутом проводнике и выявил, что при этом вырабатывается электрический ток. Определение направления ЭДС индукции осуществляется согласно правилу, сформулированному Ленцем.
Определение 1Направление индукционного потока препятствует изменению магнитного потока через создаваемое им поле.
Определение 2Нейман определил закон электромагнитной индукции математически, и этой формулировкой мы пользуемся по сей день: εi=-dΦdt.
В нем не учитываются возможные движения контура. Соотношение dΦdt является выражением полной скорости изменения потока индукции, который охватывается проводником при его движении и деформации, а также при изменениях магнитного поля.
Закон Фарадея для электромагнитной индукции очень важен, поскольку он является выражением нового физического явления: когда магнитное поле изменяется, оно порождает электрическое, т.
Движение магнитов может порождать электрический ток даже при неподвижных проводниках.
Электромагнитная индукция является одним из фундаментальных природных законов, устанавливающим связь между магнитным или электрическим полями.
Закон Фарадея в дифференциальной форме
Чтобы сформулировать закон Фарадея в такой форме, нам потребуется вспомнить несколько базовых формул.
- ЭДС индукции: εi=-υBl.
- Магнитный поток: Φ=∫SBndS.
- Теорема Стокса: ∮l=a→dl=∫Srotna→dS.
Используя данные выражения, мы можем записать следующую формулу:
∮C(Edl)=∫S(n rot E)dS=-1c∫Sn∂B∂tdS.
Здесь S обозначает поверхность, натянутую на контур S. Поскольку значение S является произвольным, то мы можем записать:
Определение 4rot E=-1c∂B∂t.
Это и есть дифференциальная форма закона Фарадея, которая описывает возникновение электрического поля в точке при изменении магнитного поля в том же месте. Само поле при этом называется индукционным.
Само поле при этом называется индукционным.
Индукционное поле не является потенциальным, в отличие от электростатического, а работа по перемещению заряда в нем по замкнутому контуру не является нулевой.
Задачи на применение закона Фарадея
Пример 1Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный Φ1 и уменьшающийся после этого до 0. Найдите величину заряда, проходящего по цепи.
Решение
Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:
εi=-dΦdt.
Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:
I=-1RdΦdt.
Полное сопротивление цепи здесь обозначено буквой R.
Для нахождения заряда, идущего по цепи, нам пригодится выражение:
q=∫Idt.
Поставим эти выражения в нужную формулу и получим:
q=-1R∫Φ10dΦ=ΦR.
Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.
Ответ: q=ΦR.
Пример 2Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна l. Она движется поступательно с постоянной скоростью v в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию εi от расстояния x.
Рисунок 1
Решение
Найти ответ можно с помощью закона Фарадея.
εi=-dΦdt.
Для получения искомой функции Ei(x) нам нужно построить функцию Ф(x). Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:
B=μ0I2πr.
Расстояние до точки рассмотрения здесь обозначено буквой r.
Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:
Выразим ее такой формулой:
dS=adr.
С учетом приведенных выше выражений, а также того факта, что B→⊥S→, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:
dΦ=BdS=μ0I2πradr.
Далее вычисляем величину полного потока, учитывая, что x≤r≤x+a:
Φ=∫xx+aμ0I2πradr=μ0Ia2πlnx+ax.
После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее:
εi=-dΦdx·dxdt=-μ0Ia2π·xx+a(x-1-(x+a)x-2)·υ==-μ0Ia2π·xx+ax-x-ax2=μ0Ia2υ2π(x+a)x.
Ответ: εi=μ0Ia2υ2π(x+a)x.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Автор: Роман Адамчук
Преподаватель физики
Закон электромагнитной индукции Фарадея
Если взять замкнутую проводящую систему и создать в ней условия для того чтобы магнитный поток изменился в магнитном поле, то в результате этих движений появится электрический ток.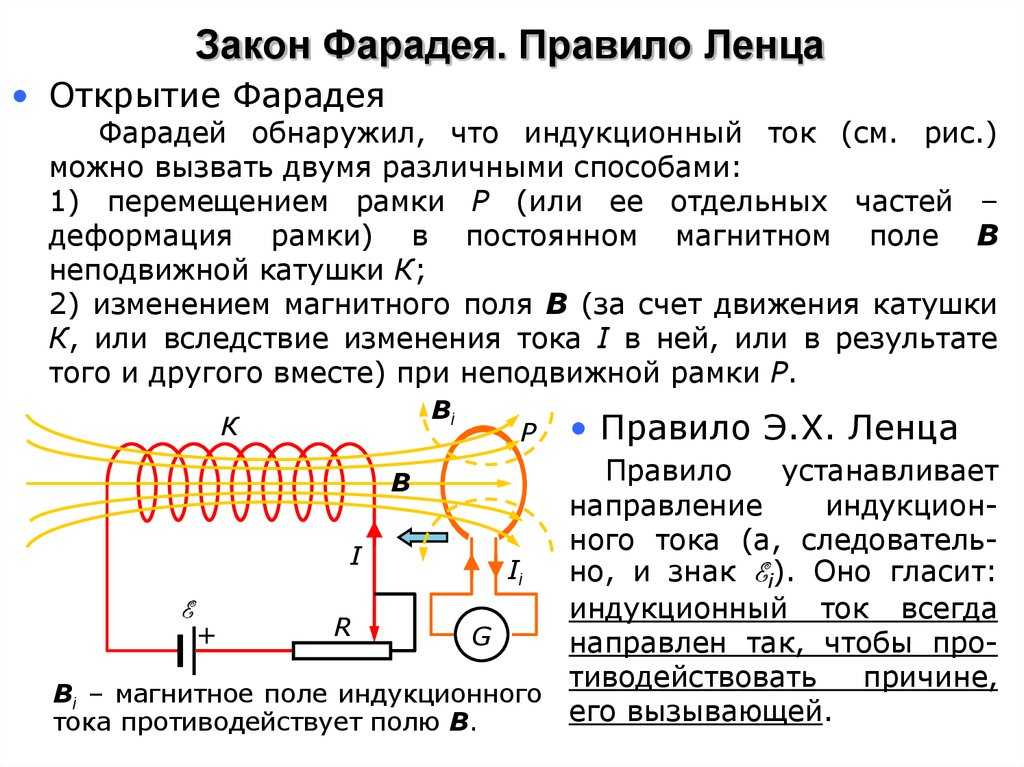 Данное обстоятельство описывает закон электромагнитной индукции Фарадея – английского ученого, который при проведении опытов добился превращения магнитной энергии в электричество. Оно получило название индукционного, поскольку до того времени его можно было создать лишь гальваническим путем.
Данное обстоятельство описывает закон электромагнитной индукции Фарадея – английского ученого, который при проведении опытов добился превращения магнитной энергии в электричество. Оно получило название индукционного, поскольку до того времени его можно было создать лишь гальваническим путем.
История открытия
Явление электромагнитной индукции было открыто сразу двумя учеными. Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС.
Для демонстрации явления использовался железный тор, напоминающий конфигурацию современного трансформатора. Противоположные стороны его были обмотаны двумя проводниками с целью использования электромагнитных свойств.
К одному из проводов подключался ток, вызывающий своеобразную электрическую волну при прохождении сквозь тор, и некоторый электрический всплеск с противоположной стороны. Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода.
Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода.
Постепенно были обнаружены и другие формы проявления электромагнитной индукции. Кратковременное возникновение тока наблюдалось во время генерации его на медном диске, вращающемся возле магнита. На самом диске был установлен скользящий электропровод.
Наибольшие представление о том, что такое индуктивность, дал эксперимент с двумя катушками. Одна из них, с меньшими размерами, подключена к жидкостной батарее, расположенной на рисунке с правой стороны. Таким образом, через эту катушку начинает протекать электрический ток, под действием которого возникает магнитное поле.
Когда обе катушки находятся в неподвижном положении относительно друг друга, никаких явлений не происходит. Когда небольшая катушка начинает двигаться, то есть выходить из большой катушки или входить в нее, наступает изменение магнитного потока. В результате, в большой катушке наблюдается появление электродвижущей силы.
Открытие Фарадея доработал другой ученый – Максвелл, который обосновал его математически, отображая данное физическое явление дифференциальными уравнениями. Еще одному ученому-физику – Ленцу удалось определить направление электротока и ЭДС, полученных под действием электромагнитной индукции.
Законы электромагнитной индукции
Сущность электромагнитной индукции определяется замкнутым контуром с электропроводностью, площадь которого пропускает через себя изменяющийся магнитный поток. В этот момент под влиянием магнитного потока появляется электродвижущая сила Еi и в контуре начинает течь электрический ток.
Закон Фарадея для электромагнитной индукции заключается в прямой зависимости ЭДС и скорости, составляющих пропорцию. Данная скорость представляет собой время, в течение которого магнитный поток подвергается изменениям.
Данный закон выражается формулой Еi = — ∆Ф/∆t, в которой Еi – значение электродвижущей силы, возникающей в контуре, а ∆Ф/∆t является скоростью изменения магнитного потока. В этой формуле не совсем понятным остается знак «минус», но ему тоже имеется свое объяснение. В соответствии с правилом русского ученого Ленца, изучавшего открытия Фарадея, этот знак отображает направление ЭДС, возникающей в контуре. То есть, направление индукционного тока происходит таким образом, что создаваемый им магнитный поток на площади, ограниченной контуром, препятствует изменениям, вызванным этим током.
В этой формуле не совсем понятным остается знак «минус», но ему тоже имеется свое объяснение. В соответствии с правилом русского ученого Ленца, изучавшего открытия Фарадея, этот знак отображает направление ЭДС, возникающей в контуре. То есть, направление индукционного тока происходит таким образом, что создаваемый им магнитный поток на площади, ограниченной контуром, препятствует изменениям, вызванным этим током.
Открытия Фарадея были доработаны Максвеллом, у которого теория электромагнитного поля получила новые направления. В результате, появился закон Фарадея и Максвелла, выраженный в следующих формулах:
- Edl = -∆Ф/∆t – отображает электродвижущую силу.
- Hdl = -∆N/∆t – отображает магнитодвижущую силу.
В этих формулах Е соответствует напряженности электрического поля на определенном участке dl, Н является напряженностью магнитного поля на этом же участке, N – поток электрической индукции, t – период времени.
Оба уравнения отличаются симметричностью, позволяющей сделать вывод, что магнитные и электрические явления связаны между собой. С физической точки зрения эти формулы определяют следующее:
С физической точки зрения эти формулы определяют следующее:
- Изменениям в электрическом поле всегда сопутствует образование магнитного поля.
- Изменения в магнитном поле всегда происходят одновременно с образованием электрического поля.
Изменяющийся магнитный поток, проходящий сквозь замкнутую конфигурацию проводящего контура, приводит к возникновению в этом контуре электрического тока. Это основная формулировка закона Фарадея. Если изготовить проволочную рамку и поместить ее внутри вращающегося магнита, то в самой рамке появится электричество.
Это и будет индукционный ток, в полном соответствии с теорией и законом Майкла Фарадея. Изменения магнитного потока, проходящего через контур, могут быть произвольными. Следовательно, формула ∆Ф/∆t бывает не только линейной, а в определенных условиях принимает любую конфигурацию. Если изменения происходят линейно, то ЭДС электромагнитной индукции, возникающей в контуре, будет постоянной. Временной интервал t становится каким угодно, а отношение ∆Ф/∆t не будет зависеть от его продолжительности.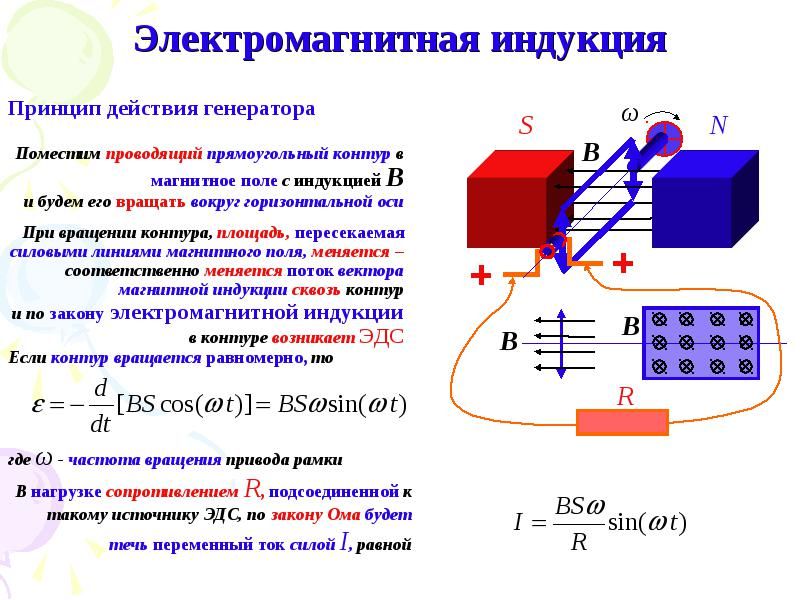
Если же изменения магнитного потока принимают более сложную форму, то ЭДС индукции уже не будет постоянной, а будет зависеть от данного промежутка времени. В этом случае временной интервал рассматривается в качестве бесконечно малой величины и тогда соотношение ∆Ф/∆t с точки зрения математики станет производной от изменяющегося магнитного потока.
Существует еще один вариант, трактующий закон электромагнитной индукции Фарадея. Его краткая формулировка объясняет, что действие переменного магнитного поля вызывает появление вихревого электрического поля. Этот же закон можно трактовать как одну из характеристик электромагнитного поля: вектор напряженности поля может циркулировать по любому из контуров со скоростью, равной скорости изменения магнитного потока, проходящего через тот или иной контур.
Закон Фарадея для электромагнитной индукции и для электролиза
Для описания процессов в физике и химии есть целый ряд законов и соотношений, полученных экспериментальным и расчетным путем. Ни единого исследования нельзя провести без предварительной оценки процессов по теоретическим соотношениям. Законы Фарадея применяются и в физике, и в химии, а в этой статье мы постараемся кратко и понятно рассказать о всех знаменитых открытиях этого великого ученого.
Ни единого исследования нельзя провести без предварительной оценки процессов по теоретическим соотношениям. Законы Фарадея применяются и в физике, и в химии, а в этой статье мы постараемся кратко и понятно рассказать о всех знаменитых открытиях этого великого ученого.
- История открытия
- Электродинамика
- Электролиз
История открытия
Закон Фарадея в электродинамике был открыт двумя ученными: Майклом Фарадеем и Джозефом Генри, но Фарадей опубликовал результаты своих работ раньше – в 1831 году.
В своих демонстрационных экспериментах в августе 1831 г. он использовал железный тор, на противоположные концы которого был намотан провод (по одному проводу на стороны). На концы одного первого провода он подал питание от гальванической батареи, а на выводы второго подключил гальванометр. Конструкция была похожа на современный трансформатор. Периодически включая и выключая напряжение на первом проводе, он наблюдал всплески на гальванометре.
Гальванометр — это высокочувствительный прибор для измерения силы токов малой величины.
Таким образом было изображено влияние магнитного поля, образовавшегося в результате протекания тока в первом проводе, на состояние второго проводника. Это воздействие передавалось от первого ко второму через сердечник – металлический тор. В результате исследований было обнаружено и влияние постоянного магнита, который двигается в катушке, на её обмотку.
Тогда Фарадей объяснял явление электромагнитной индукции с точки зрения силовых линий. Еще одной была установка для генерирования постоянного тока: медный диск вращался вблизи магнита, а скользящий по нему провод был токосъёмником. Это изобретение так и называется — диск Фарадея.
Ученные того периода не признали идеи Фарадея, но Максвелл взял исследования для основы своей магнитной теории. В 1836 г. Майкл Фарадей установил соотношения для электрохимических процессов, которые назвали Законами электролиза Фарадея. Первый описывает соотношения выделенной на электроде массы вещества и протекающего тока, а второй соотношения массы вещества в растворе и выделенного на электроде, для определенного количества электричества.
Электродинамика
Первые работы применяются в физике, конкретно в описании работы электрических машин и аппаратов (трансформаторов, двигателей и пр.). Закон Фарадея гласит:
Для контура индуцированная ЭДС прямо пропорциональна величине скорости магнитного потока, который перемещается через этот контур со знаком минус.
Это можно сказать простыми словами: чем быстрее магнитный поток движется через контур, тем больше на его выводах генерируется ЭДС.
Формула выглядит следующим образом:
Здесь dФ – магнитный поток, а dt – единица времени. Известно, что первая производная по времени – это скорость. Т.е скорость перемещения магнитного потока в данном конкретном случае. Кстати перемещаться может, как и источник магнитного поля (катушка с током – электромагнит, или постоянный магнит), так и контур.
Здесь же поток можно выразить по такой формуле:
B – магнитное поле, а dS – площадь поверхности.
Если рассматривать катушку с плотнонамотанными витками, при этом в количестве витков N, то закон Фарадея выглядит следующим образом:
Магнитный поток в формуле на один виток, измеряется в Веберах. Ток, протекающий в контуре, называется индукционным.
Ток, протекающий в контуре, называется индукционным.
Электромагнитная индукция – явление протекания тока в замкнутом контуре под воздействием внешнего магнитного поля.
В формулах выше вы могли заметить знаки модуля, без них она имеет слегка иной вид, такой как было сказано в первой формулировке, со знаком минус.
Знак минус объясняет правило Ленца. Ток, возникающий в контуре, создает магнитное поле, оно направлено противоположно. Это является следствием закона сохранения энергии.
Направление индукционного тока можно определить по правилу правой руки или буравчика, мы его рассматривали на нашем сайте подробно.
Как уже было сказано, благодаря явлению электромагнитной индукции работают электрические машины трансформаторы, генераторы и двигатели. На иллюстрации показано протекание тока в обмотке якоря под воздействием магнитного поля статора. В случае с генератором, при вращении его ротора внешними силами в обмотках ротора возникает ЭДС, ток порождает магнитное поле направленное противоположно (тот самый знак минус в формуле). Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.
Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.
И наоборот — при протекании тока в роторе возникает поле, которое взаимодействует с полем статора и ротор начинает вращаться. При нагрузке на вал ток в статоре и в роторе повышается, при этом нужно обеспечить переключение обмоток, но это уже другая тема, связанная с устройством электрических машин.
В основе работы трансформатора источником движущегося магнитного потока является переменное магнитное поле, возникающее в следствие протекания в первичной обмотке переменного тока.
Если вы желаете более подробно изучить вопрос, рекомендуем просмотреть видео, на котором легко и доступно рассказывается Закон Фарадея для электромагнитной индукции:
Электролиз
Кроме исследований ЭДС и электромагнитной индукции ученный сделал большие открытия и в других дисциплинах, в том числе химии.
При протекании тока через электролит ионы (положительные и отрицательные) начинают устремляться к электродам. Отрицательные движутся к аноду, положительные к катоду. При этом на одном из электродов выделяется определенная масса вещества, которое содержится в электролите.
Фарадей проводил эксперименты, пропуская разный ток через электролит и измеряя массу вещества отложившегося на электродах, вывел закономерности.
m=k*Q
m – масса вещества, q – заряд, а k – зависит от состава электролита.
А заряд можно выразить через ток за промежуток времени:
I=q/t, тогда q = i*t
Теперь можно определить массу вещества, которое выделится, зная ток и время, которое он протекал. Это называется Первый закон электролиза Фарадея.
Второй закон:
Масса химического элемента, который осядет на электроде, прямо пропорциональна эквивалентной массе элемента (молярной массе разделенной на число, которое зависит от химической реакции, в которой участвует вещество).
С учетом вышесказанного эти законы объединяются в формулу:
m – масса вещества, которое выделилось в граммах, n – количество переносимых электронов в электродном процессе, F=986485 Кл/моль – число Фарадея, t – время в секундах, M молярная масса вещества г/моль.
В реальности же из-за разных причин, масса выделяемого вещества меньше чем расчетная (при расчетах с учетом протекающего тока). Отношение теоретической и реальной масс называют выходом по току:
Bт = 100% * mрасч/mтеор
Ну и напоследок рекомендуем просмотреть подробное объяснение закона Фарадея для электролиза:
Законы Фарадея внесли существенный вклад в развитие современной науки, благодаря его работам мы имеем электродвигатели и генераторы электроэнергии (а также работам его последователей). Работа ЭДС и явления электромагнитной индукции подарили нам большую часть современного электрооборудования, в том числе и громкоговорители и микрофоны, без которых невозможно прослушивание записей и голосовая связь.
Похожие материалы:
- Закон Джоуля-Ленца
- Зависимость сопротивления проводника от температуры
- Закон Ома простыми словами
Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме
Содержание статьи
1. Закон Фарадея
2. Дифференциальная формулировка закона Фарадея
Закон Фарадея
Явление электромагнитной индукции было открыто Фарадеем экспериментально. Фарадей определил, что в замкнутом проводнике при изменении потока магнитной индукции возникает электрический ток. Правило, по которому определяют направление ЭДС индукции, сформулировал Ленц (индукционный ток направлен так, что создаваемое им поле препятствует изменению магнитного потока). Нейман дал математическое определение закона электромагнитной индукции в современной форме:
при этом контур считается неподвижным. Под $\frac{dФ}{dt}$ понимают полную скорость изменения потока индукции, охватываемого проводником в результате движения и деформации проводника и изменения магнитного поля. Закон Фарадея выражает новое физическое явление: изменяющееся магнитное поле порождает электрическое поле. Следовательно, электрическое поле порождается не только электрическими зарядами, но и изменяющимся магнитным полем.
Под $\frac{dФ}{dt}$ понимают полную скорость изменения потока индукции, охватываемого проводником в результате движения и деформации проводника и изменения магнитного поля. Закон Фарадея выражает новое физическое явление: изменяющееся магнитное поле порождает электрическое поле. Следовательно, электрическое поле порождается не только электрическими зарядами, но и изменяющимся магнитным полем.
Замечание
Электрический ток может генерироваться движением магнитов, а проводники могут оставаться неподвижными.
Электромагнитная индукция является фундаментальным законом природы, который устанавливает связь между электрическими и магнитными полями.
Дифференциальная формулировка закона Фарадея
Используем определения ЭДС индукции вида:
потока:
где $L$ – контур, $S$ – поверхность, натянутая на контур $L$, $\overrightarrow{s}$ – вектор перемещения. Тогда закон Фарадея можно записать в виде:
Согласно формуле Стокса, имеем:
Подставим правую часть выражения (5) вместо левой части уравнения (4), получим:
где производная по времени – под знаком интеграла, так как площадь интегрирования не зависит от времени. Так как $S$ произвольна, то из (6) следует, что:
Так как $S$ произвольна, то из (6) следует, что:
Уравнение (7) – дифференциальная форма записи закона электромагнитной индукции Фарадея. Это уравнение описывает закон возникновения электрического поля в точке за счет изменения магнитного поля в этой же точке. При этом поле $\overrightarrow{E}$ называют индукционным. Индукционное электрическое поле (в отличие от электростатического поля) не является потенциальным. В общем случае работа по перемещению заряда $q$ в индукционном электрическом поле по замкнутому контуру не равна нулю:
Пример 1
Задание: Вычислите полный заряд, который проходит по цепи, если в магнитном поле находится замкнутый проволочный контур, который в начальный момент времени пронизывает поток магнитной индукции, равный $Ф_1$. Поток уменьшается до нуля.
Решение:
Мгновенное значение ЭДС можно определить формулой:
\[{{\mathcal E}}_i=-\frac{dФ}{dt}\left(1. 0_{Ф_1}{dФ}=\frac{Ф}{R}.\]
0_{Ф_1}{dФ}=\frac{Ф}{R}.\]
Данное выражение было получено Фарадеем. Он эмпирически заключил, что заряд, который проходит по цепи, пропорционален полному числу линий магнитной индукции, которые пересекает проводник, и обратно пропорционален сопротивлению цепи.
Ответ: $q=\frac{Ф}{R}.$
Пример 2
Задание: Найдите ЭДС индукции как функцию ${{\mathcal E}}_i$ от расстояния $x$ для квадратной рамки с током. Рамка имеет сторону $a$ и находится в одной плоскости с проводников с током силы $I$. Рамка движется поступательно с постоянной скоростью $v$. Направление движения указано на рис.1.
Рисунок 1.
Решение:
В качестве основания для решения задачи используем закон Фарадея:
\[{{\mathcal E}}_i=-\frac{dФ}{dt}\left(2.1\right).\]
Для того чтобы получить искомую функцию ${{\mathcal E}}_i(x)$, построим функцию $Ф(x)$. Магнитное поле, в котором находится рамка, создается бесконечным проводником с током, оно может быть представлено как:
\[B=\frac{{\mu }_0I}{2\pi r}\left(2. 2v}{2\pi \left(x+a\right)x}.$
2v}{2\pi \left(x+a\right)x}.$
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 03.03.2022
Выполнение любых типов работ по физике
Онлайн помощь по физике Заказать решение задач по термодинамике Отчет по практике по физике Контрольная работа по теме кинематика Презентация на тему термодинамика Реферат на тему термодинамика Контрольная работа на тему термодинамика Контрольная работа по физике на тему термодинамика Презентация на тему физика атомного ядра Презентация на тему атомная физика
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Закон электромагнитной индукции Фарадея
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Нижегородский Государственный Технический Университет
Выксунский филиал
Кафедра ОиОПД
Закон электромагнитной индукции Фарадея
Лабораторная работа № 2-8
г. Выкса
Выкса
2006 г.
Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.
Даны сведения по закону индукции Фарадея, принципы действия генератора, трансформатора, методика и описание установки по измерению взаимной индукции.
Научный редактор А.А. Радионов
Цель работы: ознакомиться с законом электромагнитной индукции, принципом действия генератора, трансформатора, методикой измерения взаимной индуктивности.
Приборы и оборудование: две катушки (неподвижная и подвижная), звуковой генератор, электронный осциллограф, вольтметр.
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Пусть
прямой проводник длиной l движется со скоростью в однородном магнитном поле с индукцией
,
как показано на рис.1. Вместе с ним
движутся с той же скоростью все его
заряды – положительные и отрицательные.
Под действием сил Лоренца свободные
заряды начинают перераспределяться,
что ведет к появлению электрического
поля. Силы Лоренца являются сторонними
силами. Электрическое
поле, в свою очередь, начинает действовать
на заряды силой
.
Когда силы, действующие на каждый заряд,
уравновесятся, ЭДС индукции перестанет
расти. Наведение ЭДС на проводнике,
движущемся в магнитном поле, называется
электромагнитной
индукцией.
Силы Лоренца являются сторонними
силами. Электрическое
поле, в свою очередь, начинает действовать
на заряды силой
.
Когда силы, действующие на каждый заряд,
уравновесятся, ЭДС индукции перестанет
расти. Наведение ЭДС на проводнике,
движущемся в магнитном поле, называется
электромагнитной
индукцией.
Работа сил Лоренца (сторонних сил) в расчете на единичный заряд равна ЭДС индукции:
(1)
Физический смысл знака минус выяснится ниже.
Для прямого проводника, движущегося прямолинейно и равномерно в однородном поле так, что его длина перпендикулярна векторам и (см. рис.1).
(2)
– закон электромагнитной индукции в формулировке Фарадея.
Рассмотрим еще одно движение проводника в магнитном поле (рис. 2) – движение колесной пары 1—2 в однородном поле индукции (вид сверху). Так как , a , по формуле (2) можно написать:
,
где – элементарное изменение магнитного
потока через поверхность, ограниченную
контуром определения ЭДС.
По определению, магнитным потоком через данную поверхность называется число линий индукции магнитного поля, проходящих через эту поверхность.
(3)
– это математическая запись закона электромагнитной индукции в формулировке Максвелла.
ЭДС индукции, возникающая в контуре, равна скорости изменения магнитного потока через поверхность, опирающуюся на этот контур.
Движение проводника, в котором создается э. д. с. индукции, требует затраты механической энергии, которая по закону сохранения переходит в энергию электрического поля.
Пусть
замкнутый проводник, сечение которого
изображено на рис.3, движется в однородном
магнитном поле.
По закону электромагнитной индукции в
нем возникает индукционный ток
.
Если бы индукционный ток был направлен
на нас (возможны всего два направления,
перпендикулярных плоскости чертежа),
то сила Ампера Fa,
действующая
на проводник, была бы направлена вдоль
скорости,
проводник двигал бы сам себя и при этом
индуцировался ток, т. е. был бы нарушен
закон сохранения энергии. Остается лишь
одна возможность: индукционный ток
направлен в плоскость чертежа, сила
Ампера препятствует движению, и необходимо
совершить работу против этой силы, чтобы
получить индукционный ток.
е. был бы нарушен
закон сохранения энергии. Остается лишь
одна возможность: индукционный ток
направлен в плоскость чертежа, сила
Ампера препятствует движению, и необходимо
совершить работу против этой силы, чтобы
получить индукционный ток.
Мы
получили правило
Ленца –
индукционный ток, возникающий в
проводнике, имеет такое направление,
что своим магнитным действием препятствует
наводящему его движению. Это правило,
говорящее как будто лишь о направлении
индукционного тока, по существу является
одним из наиболее общих выражений закона
сохранения и превращения энергии. Его
можно трактовать так: индукционный ток
магнитным действием препятствует любой
причине своего появления. Пусть какой-либо
контур пронизывается возрастающим
магнитным потоком (рис.4), т. е.
>0.
Индукционный ток
,
возникающий в контуре, по правилу Ленца
имеет такое направление, при котором
его магнитный поток мешает возрастанию
наводящего магнитного потока. Индукционный
ток, таким образом, связан с изменением
магнитного потока правилом
левого винта.
ЭДС, возникающая в контуре, направлена так, что магнитный поток индукционного тока (если контур замкнут) противоположен по знаку изменению магнитного потока, наводящего ЭДС. Таков физический смысл знака минус, содержащегося во всех формулировках закона электромагнитной индукции.
Если в контуре сопротивлением R изменяется магнитный поток на величину , то по данному контуру протекает определенный заряд ΔQ, который можно подсчитать:
.
Интегрируя почленно, получаем (без учета знака):
(4)
Рассмотрим контур, помещенный в магнитное; поле с индукцией (рис. 5). При всяком изменении магнитного потока Ф через площадь S поверхности, ограниченной контуром, в последнем возникает ЭДС индукции
, (5)
где – магнитный поток, – проекция на нормаль к
площадке
dS;
N – число
витков в контуре;
потокосцепление.
Соотношение (5) – закон электромагнитной
индукции Фарадея. Знак минус в формуле
соответствует правилу Ленца: индукционный
ток всегда имеет такое направление, что
он препятствует причине, его вызывающей.
Знак минус в формуле
соответствует правилу Ленца: индукционный
ток всегда имеет такое направление, что
он препятствует причине, его вызывающей.
Универсальность закона Фарадея в том, что ЭДС индукции не зависит от причины изменения магнитного потока, а они могут быть весьма различными. Приведем три примера. В электрогенераторе магнитный поток через витки катушки статора (рис.8) меняется вследствие того, что около катушки вращается электромагнит. В трансформаторе (рис. 9) напряжение первичной обмотки в соответствии с (5) изменяет поток, вследствие чего во вторичной обмотке возникает индукционный ток. Если разряжать конденсатор С после замыкания ключа К через сопротивление R и катушку индуктивности L, то поток уменьшается в катушке просто потому, что падает ток I в катушке. Возникающую ЭДС ε=-LdI/dt называют ЭДС самоиндукции, L – индуктивностью катушки (рис. 6).
Рассмотрим
два контура 1 и 2, расположенных на
некотором расстоянии друг от друга
(рис. 7). Если по контуру 1 пропустить ток
I1 то он создает поток магнитной индукции
через контур 2:
7). Если по контуру 1 пропустить ток
I1 то он создает поток магнитной индукции
через контур 2:
(6)
Коэффициент пропорциональности М21 называют коэффициентом взаимной индукции контуров (взаимной индуктивностью контуров). Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды.
При изменении силы тока в первом контуре магнитный поток сквозь второй контур изменяется. Следовательно, в нем наводится ЭДС взаимной индукции:
. (7)
Если поменять местами контуры 1 и 2 и повторить все предыдущие рассуждения, то получим:
. (8)
Можно показать, что коэффициенты взаимной индукции равны
.
ПРИНЦИП ДЕЙСТВИЯ ГЕНЕРАТОРА ПЕРЕМЕННОГО ТОКА
Закон
индукции Фарадея лежит в основе
электроэнергетики: на этом принципе
действуют генераторы – источники
электроснабжения промышленности и
населения, трансформаторы. Простейший
электрогенератор содержит вращающийся
магнит (либо электромагнит) – ротор и
неподвижную катушку статора (рис. 8). При
вращении ротора в витках обмотки статора
магнитный поток меняется по закону:
,
и возникает ЭДС индукции
Простейший
электрогенератор содержит вращающийся
магнит (либо электромагнит) – ротор и
неподвижную катушку статора (рис. 8). При
вращении ротора в витках обмотки статора
магнитный поток меняется по закону:
,
и возникает ЭДС индукции
,
обеспечивающая ток в нагрузке R.
ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
Трансформатор
(рис.9) содержит ферромагнитный сердечник,
на котором две обмотки, первичная с
числом витков n1 и
вторичная с n2.
К вторичной подключена нагрузка R,
к
первичной – источник напряжения U1.
В
соответствии с законом Фарадея, U1 вызывает
рост магнитного потока Ф, ().
Сердечник,
имеющий большую магнитную проницаемость
(μ=400÷10000), выполняет две функции. Во-первых,
он концентрирует магнитный поток так,
что поток Ф
через
первичную и вторичную обмотки практически
одинаков. Во-вторых, большое значение
μ
обеспечивает
малый ток через первичную обмотку, когда
нагрузка не подключена (ток холостого
хода), т. е. снижает потери энергии при
трансформации.
е. снижает потери энергии при
трансформации.
В соответствии с (5) на вторичной обмотке возникает напряжение , так что напряжение изменяется:
,
где n2/n1 – коэффициент трансформации.
СОСТАВ УСТАНОВКИ
В данной работе определяют взаимную индуктивность двух катушек (длинной катушки – L1 и короткой катушки – L2, которую надевают на катушку L1 и могут перемещать вдоль ее оси). Схема установки представлена на рис.10. Питание одной из катушек (например L1) осуществляется от генератора звуковой частоты, напряжение
(9)
с которого подается через резистор с сопротивленцем R. Вольтметр, расположенный на панели PQ, измеряет действующее напряжение.
Сопротивление выбирается таким, чтобы выполнялось неравенство
, (10)
где
L1 –
индуктивность катушки L1,
R1 –
ее активное сопротивление. В этом случае
силу тока, протекающего через катушку
L1,
можно
определить по формуле
В этом случае
силу тока, протекающего через катушку
L1,
можно
определить по формуле
. (11)
Переменный ток в катушке L1 создает ЭДС индукции в катушке L2:
. (12)
Для измерения ε2 в данной работе используют осциллограф. Амплитуда ЭДС индукции
, (13)
где ν – частота звукового генератора. Из (13) имеем
. (14)
Если поменять местами катушки L1 и L2, то можно определить
(15)
ИЗМЕРЕНИЯ
Собрать установку, состоящую из звукового генератора, электронного осциллографа и двумя соосно расположенными катушками L1 и L2. Ознакомиться с работой звукового генератора и электронного осциллографа (см. описание), включить их в сеть 220 В, подготовить к работе.
УКАЗАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ
1. Приборы питаются от сети 220 В. Включение
в сеть приборов должно проводиться
только в присутствие лаборанта или
преподавателя.
Приборы питаются от сети 220 В. Включение
в сеть приборов должно проводиться
только в присутствие лаборанта или
преподавателя.
2. Все корпусные клеммы приборов должны быть надежно заземлены (для заземления должен применяться провод без изоляции).
3. Запрещается работать в помещении одному.
Задание 1
Измерение взаимной индуктивности М21 и М12 и исследование их зависимости от взаимного расположения катушек
1. Напряжение сигнала со звукового генератора установите в диапазоне 1-4 В, а его частоту – в пределах 30-200 кГц.
2. Подайте напряжение на катушку L1, а ЭДС с катушки L2 на осциллограф.
3.
Установите подвижную катушку L1 в
крайнее положение. Перемещая ее в
противоположное крайнее положение,
через каждый сантиметр запишите значение
ЭДС магнитной индукции в цепи катушки
L2.
4. По формуле (14) рассчитайте М21. Данные измерений и вычислений занесите в табл.1.
5. Поменяв местами катушки L1 и L2, повторите измерения по п.п. 1-4.
6. Постройте графики зависимости М21 и М12 как функции координаты z (z – расстояние между центрами катушек L1 и L2).
Таблица 1
z, см | ε02, В | М21 Гн | z, см | ε01, В | M21, Гн |
UД= | ν= | ||||
Задание 2
Определение М21 для различных напряжений питания
1. Поставьте катушку L1 в
среднее положение относительно катушки
L2.
Поставьте катушку L1 в
среднее положение относительно катушки
L2.
2. Установите частоту звукового генератора 104 Гц.
3. Изменяя напряжение UД в цепи катушки L1 снимите зависимость амплитуды ЭДС магнитной индукции от UД: ε02=f(UД). Измерения провести в интервале 0-5 В через 0,5 В.
4. По формуле (14) рассчитайте M21. Данные измерений и вычислений занесите в табл.2
Таблица 2
U0, В | ||
ε02, В | ||
М21, Гн | ||
ν= | R=104 Ом | |
5. По
данным табл. 2 найдите среднее значение
М21.
По
данным табл. 2 найдите среднее значение
М21.
Задание 3
Определение М21 для различных частот генератора
1. Поставьте катушку L1 в среднее положение относительно катушки L2.
2. Установите амплитуду напряжения звукового генератора 2 В.
3. Изменяя частоту генератора от 5 до 20 кГц (не менее 10 точек), снимите зависимость амплитуды ЭДС индукции ε02 от частоты подаваемого напряжения.
4. По формуле (14) рассчитайте M21. Данные измерений и вычислений занесите в табл.3.
Таблица 3
ν, Гц | ||
ε02, В | ||
М21, Гн | ||
UД= | R=104 Ом | |
5. По
данным табл. 3 найдите среднее значение
М21.
По
данным табл. 3 найдите среднее значение
М21.
6. Для одного из полученных значений М21 рассчитайте абсолютную и относительную погрешности ΔМ21 и ΔМ21/М21.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте закон электромагнитной индукции (закон Фарадея) и правило Ленца.
2. В чем состоит явление электромагнитной индукции? Приведите примеры.
3. Принцип действия генератора переменного тока.
4. Принцип действия трансформатора.
5. В чем состоит явление взаимной индукции? От чего зависит взаимная индуктивность?
6. На замкнутом железном сердечнике с магнитной проницаемостью μ намотаны две катушки с числом витков n1 и n2. Вывести формулу для взаимной индуктивности, если длина сердечника l, a площадь поперечного сечения S.
12
формулировка закона Фарадея, физическая формула
Содержание
- 1 История
- 2 Формулирование закона электромагнитной индукции
- 3 ЭДС индукции в проводнике
- 4 Законы электролиза
- 5 Видео
Возникновение электродвижущей силы индукции было важнейшим открытием в области физики. Оно явилось основополагающим для развития технического применения этого явления.
Оно явилось основополагающим для развития технического применения этого явления.
Майкл Фарадей
История
В 20-е годы 19-го века датчанин Эрстед наблюдал за отклонением магнитной стрелки при расположении ее рядом с проводником, по которому протекал электроток.
Это явление захотел исследовать ближе Майкл Фарадей. С большим упорством он преследовал свою цель – преобразовать магнетизм в электричество.
Первые опыты Фарадея принесли ему ряд неудач, так как он изначально считал, что значительный постоянный ток в одном контуре может сгенерировать ток в рядом находящемся контуре при условии отсутствия электрической связи между ними.
Исследователь видоизменил эксперименты, и в 1831 году они увенчались успехом. Опыты Фарадея начинались с наматывания медной проволоки вокруг бумажной трубки и соединения ее концов с гальванометром. Затем ученый погружал магнит внутрь катушки и замечал, что стрелка гальванометра давала мгновенное отклонение, показывая, что в катушке был индуцирован ток. После вынимания магнита наблюдалось отклонение стрелки в противоположном направлении. Вскоре в ходе других экспериментов он заметил, что в момент подачи и снятия напряжения с одной катушки появляется ток в рядом находящейся катушке. Обе катушки имели общий магнитопровод.
После вынимания магнита наблюдалось отклонение стрелки в противоположном направлении. Вскоре в ходе других экспериментов он заметил, что в момент подачи и снятия напряжения с одной катушки появляется ток в рядом находящейся катушке. Обе катушки имели общий магнитопровод.
Опыты Фарадея
Многочисленные опыты Фарадея с другими катушками и магнитами были продолжены, и исследователь установил, что сила индуцированного тока зависит от:
- количества витков в катушке;
- силы магнита;
- скорости, с которой магнит погружался в катушку.
Термин «электромагнитная индукция» (эми) относится к явлению, что ЭДС генерируется в проводнике переменным внешним магнитным полем.
Формулирование закона электромагнитной индукции
Словесная формулировка закона электромагнитной индукции: индуцированная электродвижущая сила в любом замкнутом контуре равна отрицательной временной скорости изменения магнитного потока, заключенного в цепь.
Явление электромагнитной индукции
Это определение математически выражает формула:
Е = — ΔΦ/ Δt,
где Ф = В х S, с плотностью магнитного потока В и площадью S, которую пересекает перпендикулярно магнитный поток.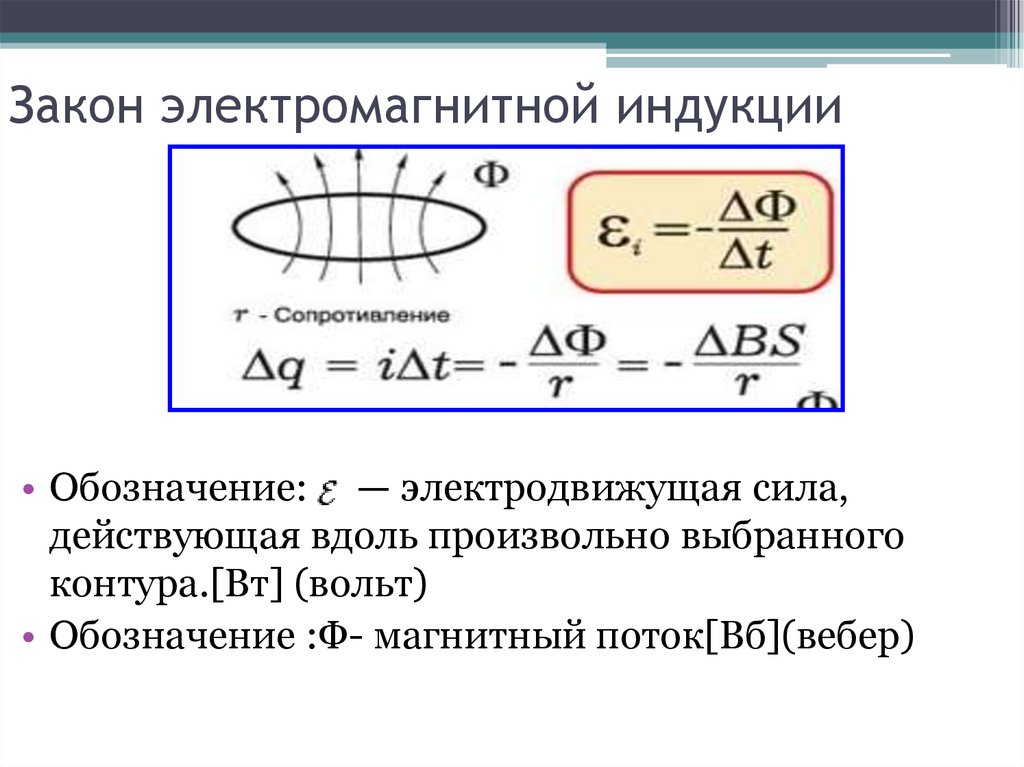
Дополнительная информация. Существуют два разных подхода к индукции. Первый – объясняет индукцию с помощью силы Лоренца и ее действия на движущийся электрозаряд. Однако в определенных ситуациях, таких как магнитное экранирование или униполярная индукция, могут возникнуть проблемы в понимании физического процесса. Вторая теория использует методы теории поля и объясняет процесс индукции с помощью переменных магнитных потоков и связанных с ними плотностей этих потоков.
Физический смысл закона электромагнитной индукции формулируется в трех положениях:
- Изменение внешнего МП в катушке провода индуцирует в ней напряжение. При замкнутой проводящей электроцепи индуцированный ток начинает циркулировать по проводнику;
- Величина индуцированного напряжения соответствует скорости изменения магнитного потока, связанного с катушкой;
- Направление индукционной ЭДС всегда противоположно причине, ее вызвавшей.
Закон электромагнитной индукции
Важно! Формула для закона электромагнитной индукции применяется в общем случае. Не существует известной формы индукции, которая не может быть объяснена изменением магнитного потока.
Не существует известной формы индукции, которая не может быть объяснена изменением магнитного потока.
ЭДС индукции в проводнике
Для расчета индукционного напряжения в проводнике, который движется в МП, применяют другую формулу:
E = — B x l x v х sin α, где:
- В – индукция;
- l – протяженность проводника;
- v – скорость его движения;
- α – угол, образованный направлением перемещения и векторным направлением магнитной индукции.
Важно! Способ определения, куда направлен индукционный ток, создающийся в проводнике: располагая правую руку ладонью перпендикулярно вхождению силовых линий МП и, отведенным большим пальцем указывая направление перемещения проводника, узнаем направление тока в нем по распрямленным четырем пальцам.
Правило правой руки
Законы электролиза
Формула ЭДС индукции
Исторические опыты Фарадея в 1833 году были связаны и с электролизом. Он брал пробирку с двумя платиновыми электродами, погруженными в растворенный хлорид олова, нагретый спиртовой лампой. Хлор выделялся на положительном электроде, а олово – на отрицательном. Затем он взвешивал выделившееся олово.
Хлор выделялся на положительном электроде, а олово – на отрицательном. Затем он взвешивал выделившееся олово.
В других опытах исследователь соединял емкости с разными электролитами последовательно и замерял количество осаждающегося вещества.
На основании этих экспериментов формулируются два закона электролиза:
- Первый из них: масса вещества, выделяемого на электроде, прямо пропорциональна количеству электричества, пропускаемого через электролит. Математически это записывают так:
m = K x q, где К – константа пропорциональности, называемая электрохимическим эквивалентом.
Сформулируйте его определение, как масса вещества в г, высвобождаемая на электроде при прохождении тока в 1 А за 1 с либо при прохождении 1 Кл электричества;
Первый закон электролиза
- Второй закон Фарадея гласит: если одинаковое количество электричества пропускается через разные электролиты, то количество веществ, высвобождаемых на соответствующих электродах, прямо пропорционально их химическому эквиваленту (химический эквивалент металла получается путем деления его молярной массы на валентность – M/z).

Для второго закона электролиза используется запись:
К = 1/F x M/z.
Здесь F – постоянная Фарадея, которая определяется зарядом 1 моля электронов:
F = Na (число Авогадро) х e (элементарный электрозаряд) = 96485 Кл/моль.
Запишите другое выражение для второго закона Фарадея:
m1/m2 = К1/К2.
Второй закон электролиза
Например, если взять две соединенных последовательно электролитических емкости, содержащие раствор AgNO 3 и CuSO 4, и пропустить через них одинаковое количество электричества, то соотношение массы осажденной меди на катоде одной емкости к массе осажденного серебра на катоде другой емкости будет равно отношению их химических эквивалентов. Для меди это – 63,5/2, для серебра – 108/1, значит:
m1/m2 = 63,5/(2 х 108).
Теория электромагнетизма со времен Фарадея продолжала развиваться. В середине 20-го века для закона индукции была применена формулировка в рамках квантовой теории электромагнитных полей – квантовой электродинамики. Сегодня, благодаря большой технической области использования, она представляет собой одну из наиболее точных физических теорий, проверенных посредством экспериментов.
В середине 20-го века для закона индукции была применена формулировка в рамках квантовой теории электромагнитных полей – квантовой электродинамики. Сегодня, благодаря большой технической области использования, она представляет собой одну из наиболее точных физических теорий, проверенных посредством экспериментов.
Видео
Линии магнитной индукции
Оцените статью:
электромагнетизм – Закон Фарадея и электромагнитная индукция
Задавать вопрос
Спросил
Изменено 2 года, 2 месяца назад
Просмотрено 871 раз
$\begingroup$
Закон электромагнитной индукции Фарадея гласит, что скорость изменения магнитного потокосцепления пропорциональна индуцированной $\mathcal{ЭДС}$. Для проводника формула идет
$$\mathcal{ЭДС}=N\frac{\Delta\Phi}{\Delta t}$$
Где $N$ — количество витков в проводе, $\Phi$ — потокосцепление , а $t$ — время.
Однако я не понимаю, как $N$ становится переменной в формуле. Принципом, лежащим в основе электромагнитной индукции, является скорость изменения потокосцепления, но $N$ не зависит от площади, хотя и связана с $B$, плотностью магнитного потока.
Через отношение
$$\Phi=NBA$$
Это становится интуитивно понятным, если $N$ относится к числу витков соленоида $X$, создающего магнитное поле, а $B$ — это плотность магнитного потока, обеспечиваемая единичной катушкой соленоида $X$, но I не совсем понимаю, как понимать формулу, если обстоятельства обратные,
Где $N$ становится числом витков соленоида $Y$, в котором будет индуцирована $\mathcal{ЭДС}$, а $B$ обозначает плотность магнитного потока соленоида $X$, индуцирующего $\mathcal{ЭДС}.$
Я хочу пояснить переменную $N$ в этих типах явлений, потому что я не вижу интуитивного способа связать с ней концепцию магнитного потокосцепления и индуцированной $\mathcal{ЭДС}$.
- электромагнетизм
- электричество
- электромагнитная индукция
$\endgroup$
1
$\begingroup$
Я думаю, ваша проблема в том, почему ЭДС зависит от количества витков в катушке, не так ли?
Представьте себе такую ситуацию (извините за неточности). Я попытался сделать катушку из проволоки с N витками в сумме (все витки соединены, но если бы я сделал это, то изображение стало бы беспорядочным), а красные стрелки представляют линии магнитного поля. Поскольку каждая петля имеет одинаковую площадь, магнитный поток будет одинаковым во всех петлях (я считаю, что магнитное поле B однородно внутри катушки) и любое изменение магнитного поля B вызовет одинаковое изменение магнитного потока во всех контурах. Таким образом, ЭДС , развиваемая в каждом контуре, определяется Законом Фарадея как $$ \mathcal{ЭДС} = -\frac{d\phi}{dt}~~~~~~~(1)$$ Теперь, так как у нас есть $N$ петель и в каждой петле ЭДС равна $-\frac{d\phi}{dt}$ поэтому общая ЭДС от А до В есть сумма этих ЭДС и, следовательно, $$ \mathcal{emf_{A ~to~ B} } = -N \frac{d\phi}{dt}$$
Ваша интуитивная проблема заключалась в том, почему emf зависит от числа витков, когда экспериментально было установлено, что ЭДС зависит только от магнитного потока, который в свою очередь зависит от площади петли, ну как вы видели из математики сделанной выше, ЭДС вызывается в каждый виток по закону Фарадея но благодаря связности мы получили в сумме все ЭДС от одного конца до другого.
Я попытался сделать катушку из проволоки с N витками в сумме (все витки соединены, но если бы я сделал это, то изображение стало бы беспорядочным), а красные стрелки представляют линии магнитного поля. Поскольку каждая петля имеет одинаковую площадь, магнитный поток будет одинаковым во всех петлях (я считаю, что магнитное поле B однородно внутри катушки) и любое изменение магнитного поля B вызовет одинаковое изменение магнитного потока во всех контурах. Таким образом, ЭДС , развиваемая в каждом контуре, определяется Законом Фарадея как $$ \mathcal{ЭДС} = -\frac{d\phi}{dt}~~~~~~~(1)$$ Теперь, так как у нас есть $N$ петель и в каждой петле ЭДС равна $-\frac{d\phi}{dt}$ поэтому общая ЭДС от А до В есть сумма этих ЭДС и, следовательно, $$ \mathcal{emf_{A ~to~ B} } = -N \frac{d\phi}{dt}$$
Ваша интуитивная проблема заключалась в том, почему emf зависит от числа витков, когда экспериментально было установлено, что ЭДС зависит только от магнитного потока, который в свою очередь зависит от площади петли, ну как вы видели из математики сделанной выше, ЭДС вызывается в каждый виток по закону Фарадея но благодаря связности мы получили в сумме все ЭДС от одного конца до другого.
Надеюсь, это поможет.
$\endgroup$
$\begingroup$
ЭДС замкнутого контура равна $$\mathscr E = -\frac {d\Phi}{dt}$$ в котором $$\Phi =\int_S \vec B.d\vec S$$ поверхностный интеграл вычисляется по любой поверхности, ограниченной петлей.
Вполне возможно применить этот так как он стоит на катушку N витков. Площадь S , ограниченная спиралью, образованной проводом катушки, почти равна N , умноженной на площадь одного витка, рассматриваемого как бы в одной плоскости. Таким образом, $$S=NA_{поворот}.$$ Преимущество написания уравнений в том виде, как я это сделал в начале, без явного появления $N$, заключается в том, что они формально правильны для ситуаций, в которых разные величины потока могут быть связаны с разными витками, как это может быть в случае соленоида. Интеграция позаботится об этом.
Если один и тот же поток $\phi$ связан с каждым витком катушки, мы можем написать
$$\Phi =N\int_{A_{поворот}} \vec B. d\vec A_{поворот}$$
в сочетании с
$$\mathscr E = -\frac {d\Phi}{dt}$$
Здесь мы по-прежнему рассматриваем поток как увеличивающийся с числом витков в соответствии с топологической точкой зрения, объясненной ранее.
d\vec A_{поворот}$$
в сочетании с
$$\mathscr E = -\frac {d\Phi}{dt}$$
Здесь мы по-прежнему рассматриваем поток как увеличивающийся с числом витков в соответствии с топологической точкой зрения, объясненной ранее.
Альтернативный подход заключается в записи
$$\mathscr E = N\frac {d\phi}{dt}.$$ $\phi$ — это поток, связанный с одним витком, как указано в $\phi =\int_{A_{turn}} \vec B.d\vec A_{turn}$, и можно думать о $N$ витках как находясь последовательно, поэтому их ЭДС складываются.
$\endgroup$
$\begingroup$
N постоянна для данной системы, но она может меняться от системы к системе. Однако изменение площади и скорости изменения магнитного поля влияет на ЭДС индукции в данной системе.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Законы электромагнитной индукции Фарадея
Закон электромагнитной индукции Фарадея показывает взаимосвязь между магнитным полем, электрическим током и электродвижущей силой (ЭДС).
В природе есть два взаимозависимых явления, а именно электричество и магнетизм . Электромагнетизм — это раздел физики, который занимается изучением эффектов электричества и магнетизма и их зависимости друг от друга.
В настоящее время хорошо известен тот факт, что изменяющееся магнитное поле может создавать ЭДС (электродвижущую силу), а движущийся заряд (или электрический ток) может создавать магнитное поле. Однако эти концепции являются результатом нескольких экспериментов, проведенных многими физиками и инженерами.
Один из них Майкл Фарадей , который разработал два основных закона электромагнитной индукции в 1831 году. Эти законы широко известны как Первый закон Фарадея и Второй закон Фарадея электромагнитной индукции . Эти два закона объясняют, как изменяющееся магнитное поле создает ЭДС в движущемся проводнике.
Эти два закона объясняют, как изменяющееся магнитное поле создает ЭДС в движущемся проводнике.
При изменении магнитного поля, связанного с проводником, в проводнике индуцируется электродвижущая сила (ЭДС), это явление известно как электромагнитная индукция . Электромагнитная индукция является наиболее фундаментальным принципом, на котором сегодня работают многие электрические устройства, такие как двигатели, генераторы, измерительные приборы и т. д.
Закон электромагнитной индукции ФарадеяПервый закон электромагнитной индукции Фарадея описывает индукцию электродвижущей силы в проводнике, а второй закон Фарадея определяет величину электродвижущей силы, индуцированной в проводнике.
Два физика Майкл Фарадей и Джозеф Генри провели длинную серию экспериментов. Из наблюдений за этими экспериментами Фарадей описал, что когда изменяющееся магнитное поле соединяется с проводником, в проводнике индуцируется ЭДС.
Первый закон Фарадея электромагнитной индукции гласит, что « Всякий раз, когда магнитное поле, связанное с проводником, изменяется, в проводнике индуцируется электродвижущая сила (ЭДС) ».
Если цепь проводника замкнута, по проводнику начинает течь ток, называемый индуктивным током.
Изменение магнитного поля, связанного с проводником, можно вызвать двумя способами:
- Путем перемещения проводника относительно стационарного магнитного поля.
- Путем перемещения магнитного поля, когда проводник удерживается неподвижно.
Второй закон Фарадея утверждает, что « величина ЭДС индукции в проводнике равна скорости изменения магнитного потока, связанного с проводником ».
Вывод закона ФарадеяРассмотрим катушку с N проводниками и магнит движется к катушке, затем
В начальном положении потокосцепление с катушкой равно
В конечном состоянии потокосцепление с катушкой
Отсюда изменение потокосцепления равноТеперь скорость изменения потокосцепления равна
Согласно второму закону электромагнитной индукции Фарадея, ЭДС, индуцируемая в проводнике, равна скорости изменения потокосцепления.
В дифференциальной форме,
Где, 𝜙 = 2 – 1 , полное изменение магнитного потока.
Применение законов электромагнитной индукции ФарадеяЗаконы Фарадея являются наиболее фундаментальными законами электромагнетизма. Эти законы широко используются во многих областях электротехники, таких как электрические машины, измерительные приборы, в медицине для диагностики заболеваний и т. д. Вот некоторые распространенные применения законов Фарадея:
- Трансформатор работает по принципу электромагнитной индукции. Поэтому закон Фарадея может служить для его анализа.
- Производство электроэнергии генератором также основано на законах электромагнитной индукции Фарадея.
- Законы Фарадея также лежат в основе работы многих других приборов, таких как индукционные плиты, электромагнитные расходомеры, электрогитары, электрические скрипки и т. д.
Катушка с 700 витками развивает среднее индуцируемое напряжение 50 В. Каким должно быть изменение магнитного потока, чтобы возникло такое напряжение, если интервал времени для этого изменения составляет 0,7 секунды.
Каким должно быть изменение магнитного потока, чтобы возникло такое напряжение, если интервал времени для этого изменения составляет 0,7 секунды.
Данные :
Теперь по закону Фарадея получаем
Магнитный поток, связанный с катушкой, имеющей 250 витков, изменяется с 1,4 Вб до 2 Вб за 0,45 секунды. Вычислите ЭДС индукции в катушке.
Данные данные,
Теперь, согласно закону Фарадея, у нас есть,
Читать далее
Похожие сообщения:
Подпишитесь на нас и поставьте лайк:
Закон индукции Фарадея для чайников
Электричество и магнетизм
Закон индукции Фарадея был открыт в результате экспериментов, проведенных Майклом Фарадеем в Англии в 1831 году и Джозефом Генри в Соединенных Штатах примерно в то же время.
Несмотря на то, что Фарадей опубликовал свои результаты первым, что дает ему приоритет открытия, единица индуктивности в СИ называется Генри (аббревиатура H) . С другой стороны, единица измерения емкости в системе СИ, как мы видели, называется фарад (сокращение F) .
С другой стороны, единица измерения емкости в системе СИ, как мы видели, называется фарад (сокращение F) .
В главе, где речь идет о колебаниях в емкостно-индуктивных цепях, мы видим, как уместно связать в едином контексте имена этих двух талантливых современников.
*Помимо их независимого одновременного открытия закона индукции, Фарадей и Генри имеют несколько других сходств в их жизнях. Оба были учениками в раннем возрасте. Фарадей в возрасте 14 лет поступил в ученики к лондонскому переплетчику. Генри в возрасте 13 лет поступил в ученики к часовщику в Олбани, штат Нью-Йорк. В последующие годы Фарадей был назначен директором королевского учреждения в Лондоне, основанием которого в значительной степени обязан американец Бенджамин Томсон (граф Румфорд). Генри, с другой стороны, потому что секретарь Смитсоновского института в Вашингтоне, округ Колумбия, который был найден благодаря пожертвованию англичанина Джеймса Смитсона.
Фарадей заметил, что если магнит перемещать к катушке с проволокой (соленоиду), соединенной последовательно с гальванометром, в токе возникает электрический ток. При перемещении магнита к соленоиду гальванометр показывает отклонение в одном направлении, а при удалении магнита от соленоида гальванометр показывает отклонение в противоположном направлении. Когда магнит неподвижен, в гальванометре нет отклонения. Аналогичные результаты получаются, когда магнит остается неподвижным, а катушка перемещается. При перемещении магнита отклонение в гальванометре велико, а при медленном перемещении — отклонение мало. Было также обнаружено, что если в непосредственной близости находятся две замкнутые цепи, одна из которых содержит батарею, а другая – гальванометр, и цепь батареи замыкается нажатием кнопки К, а затем размыкается, то гальванометр во вторичной цепи показывает неисправность. отклонение сначала в одну сторону, а затем в другую.
При перемещении магнита к соленоиду гальванометр показывает отклонение в одном направлении, а при удалении магнита от соленоида гальванометр показывает отклонение в противоположном направлении. Когда магнит неподвижен, в гальванометре нет отклонения. Аналогичные результаты получаются, когда магнит остается неподвижным, а катушка перемещается. При перемещении магнита отклонение в гальванометре велико, а при медленном перемещении — отклонение мало. Было также обнаружено, что если в непосредственной близости находятся две замкнутые цепи, одна из которых содержит батарею, а другая – гальванометр, и цепь батареи замыкается нажатием кнопки К, а затем размыкается, то гальванометр во вторичной цепи показывает неисправность. отклонение сначала в одну сторону, а затем в другую.
Замечено, что в гальванометре не возникает отклонений, если ток в первичной цепи протекает непрерывно. Отклонение в гальванометре производится только при включении или отключении тока в первичной цепи. Фарадей суммировал эти экспериментальные результаты в виде следующих законов:
- 1: Всякий раз, когда происходит изменение магнитных силовых линий или магнитного потока, в цепи возникает индуцированный ток.

- 2:Индуцированный ток или ЭДС существует только в течение того времени, в течение которого силовые линии или магнитный поток фактически меняются.
- 3: Величина индуцированной ЭДС зависит от скорости изменения магнитных силовых линий или магнитного потока.
На рисунке (1) показана катушка провода как часть цепи, содержащей амперметр. Обычно мы ожидаем, что амперметр не покажет ток в цепи, потому что электродвижущая сила отсутствует. Однако если мы подтолкнем стержневой магнит к катушке так, чтобы его северный полюс был обращен к катушке, произойдет замечательная вещь. Пока магнит движется, амперметр отклоняется, показывая, что в катушке установился ток. Если мы удерживаем магнит неподвижно относительно катушки, амперметр не отклоняется. Если мы отодвинем магнит от катушки, счетчик снова отклонится, но уже в другую сторону, а значит, ток в катушке будет противоположного направления. Если мы используем конец магнита с северным полюсом вместо конца с северным полюсом, эксперимент работает, как описано, но отклонения меняются на противоположные. Чем быстрее перемещается магнит, тем больше показания счетчика. Дальнейшие эксперименты показывают, что имеет значение относительное движение магнита и катушки. Нет никакой разницы, перемещаем ли мы магнит к катушке или катушку к магниту.
Чем быстрее перемещается магнит, тем больше показания счетчика. Дальнейшие эксперименты показывают, что имеет значение относительное движение магнита и катушки. Нет никакой разницы, перемещаем ли мы магнит к катушке или катушку к магниту.
«ЭДС индукции в цепи равна отрицательной скорости изменения магнитного потока через цепь со временем». как помогает нам визуализировать метод линий поля Фарадея, именно изменение числа линий поля, проходящих через петлю цепи, индуцирует ЭДС в петле. В частности, именно скорость изменения числа силовых линий, проходящих через петлю, определяет ЭДС индукции.
Чтобы сделать это утверждение количественным, мы вводим магнитный поток Φ B , который определяется как «Число магнитных силовых линий, проходящих нормально через определенную область, называется магнитным потоком». Он обозначается как Φ B. Это скалярная величина, и ее единицей в системе СИ является Вебер (Вб). Он измеряется произведением напряженности магнитного поля на составляющую площади вектора, параллельную магнитному полю. Математически это представляется как:
Математически это представляется как:
Φ B = B.A
Φ B =BA cosθ
направления векторов B и A.
При перемещении магнита в сторону петли стрелка амперметра отклоняется в одном направлении, как показано на рисунке (а). Когда магнит останавливается и удерживается неподвижно относительно фигуры петли (b), отклонения не наблюдается. При удалении магнита от петли игла отклоняется в противоположную сторону, как показано на рисунке (в). Наконец, если магнит удерживать неподвижно, а петлю перемещать либо к нему, либо от него, игла отклоняется. Из этих наблюдений мы делаем вывод, что петля обнаруживает, что магнит движется относительно нее, и связываем это обнаружение с изменением магнитного поля. Таким образом, кажется, что существует связь между текущим и изменяющимся магнитным полем.
Эти результаты весьма примечательны, учитывая тот факт, что ток устанавливается, даже если в цепи нет батарей. Мы называем такой ток индукционным током, который создается ЭДС индукции. Это явление называется электромагнитной индукцией.
Мы называем такой ток индукционным током, который создается ЭДС индукции. Это явление называется электромагнитной индукцией.
- https://en.wikipedia.org/wiki/Faraday%27s_law_of_induction
- https://www.daenotes.com/electronics/basic-electronics/faraday-laws-of-electromagnetic-induction
Статьи по теме
Проверить также
Закрыть
Законы электромагнитной индукции – 1095 слов
Центральной темой этого доклада было изучение принципов, лежащих в основе физики электромагнитной индукции. В докладе рассмотрены закон Фарадея, характеризующий генерацию ЭДС в замкнутой цепи при наведении внешнего магнитного поля, и закон Ленца, иллюстрирующий способность цепи сопротивляться внешнему индуктивному воздействию. Обобщающим принципом для двух правил были мнемонические законы Флеминга, которые позволяют определять направления электромагнитных векторных величин двумя руками.
Введение
Глубокое понимание природы электрофизических процессов является основой для успешного и вдумчивого понимания предмета. Если рассматривать физические законы по отдельности, то они представляют собой посредственную математическую конструкцию, но изучение взаимосвязи явлений позволяет расширить академические рамки. В этой статье рассматриваются три важных закона электричества: закон Фарадея, закон Ленца и правила Флеминга. Каждый закон относится к области физики электромагнитной индукции. В частности, общее представление об индукции сводится к тому, что при прохождении через проводник магнитного потока, излучаемого источником магнитного поля, в цепи возникает электрический ток. Отсюда следует, что если проводник поместить в магнитное поле и привести в движение, то в проводнике возникнет собственная ЭДС.
Обзор законов
Закон Фарадея
Одним из первых принципов электродинамики, определяющих взаимосвязь между внешним магнитным полем и генерацией ЭДС, является закон Фарадея. В общем виде закон Фарадея следует сформулировать как пропорциональность генерируемой ЭДС скорости изменения магнитного потока, как показано в уравнении [1] . Другими словами, изменение напряженности магнитного потока (при движении магнита) вблизи замкнутого контура приводит к ЭДС индукции, противоположной по направлению и равной по величине потоку. Следовательно, чем быстрее меняется магнитное поле, тем большее напряжение будет проявляться в цепи. Уравнение [1] указано, что ЭДС в цепи прямо пропорциональна скорости изменения магнитного потока в зависимости от времени, и в случае большого числа витков катушки индуктора их количество добавляется к формула, Н.
В общем виде закон Фарадея следует сформулировать как пропорциональность генерируемой ЭДС скорости изменения магнитного потока, как показано в уравнении [1] . Другими словами, изменение напряженности магнитного потока (при движении магнита) вблизи замкнутого контура приводит к ЭДС индукции, противоположной по направлению и равной по величине потоку. Следовательно, чем быстрее меняется магнитное поле, тем большее напряжение будет проявляться в цепи. Уравнение [1] указано, что ЭДС в цепи прямо пропорциональна скорости изменения магнитного потока в зависимости от времени, и в случае большого числа витков катушки индуктора их количество добавляется к формула, Н.
Этот основной закон важен для понимания электродинамических процессов в замкнутом контуре. В частности, его используют для определения работы трансформаторов, генераторов, электродвигателей и дросселей ( Закон индукции Фарадея , 2018). Таким образом, трансформаторы переносят энергию переменного электромагнитного поля за счет явления взаимной индукции, преобразуя таким образом величину напряжения на разных клеммах. Если обратить внимание на уравнение [1] , то в уравнении есть минус, что вполне оправдано законом Ленца.
Если обратить внимание на уравнение [1] , то в уравнении есть минус, что вполне оправдано законом Ленца.
Закон Ленца
Закон Ленца постулирует второе важное электродинамическое свойство цепи, связанное с направлением индукционного тока. Стоит уточнить, что индукционный ток, возникающий в замкнутой цепи в результате изменения магнитного потока, всегда имеет определенное направление. Более того, как известно, сам поток тока создает уникальное своим направлением магнитное поле. Это означает, что силовые линии магнитного поля от магнита имеют определенное направление, согласно которому по правилу правой руки ток в цепи должен течь по часовой стрелке ( Три правила правой руки , 2018). Однако в действительности закон Ленца отражает противоположный эффект: электрический ток, генерируемый в цепи, имеет другое направление, чем ожидалось. Объяснение этого парадокса заключается в стремлении цепи сопротивляться изменению магнитного потока, чтобы ослабить действие причины, инициировавшей генерацию индукционного тока.
Следует признать, что закон Ленца действует независимо от типа цепи или направления движения силовых линий магнитного поля. В частности, при изменении площади цепи индукционный ток индуцируется силой Лоренца, но индукционный ток ослабляет действие внешнего магнитного поля. С другой стороны, величина магнитного потока может быть увеличена, и в этом случае эффект вихревого электрического поля индуцирует индукционный ток. Однако и в этом случае ток будет направлен на подавление действия внешнего поля. Примечательно, что магнитное поле может создаваться протеканием тока в соседней цепи. Тогда в рассматриваемой цепи индукционный ток может иметь то же направление, что и линии этого поля. В частности, если внешний ток численно увеличивается, то наблюдается новый ток, уменьшающий это увеличение, и наоборот.
Правила Флеминга
Более глубокое понимание связи между направлениями силовых линий, током и результирующей магнитной силой возможно с помощью двух мнемонических правил Флеминга. При работе с электрическими машинами это необходимые правила, будь то генераторы (правая рука) или электродвигатели (левая рука). В частности, взаимодействие внешнего магнитного поля с электромагнитным полем цепи создает вектор физической силы, направление которой можно определить с помощью мнемотехники. Примечательно, что результирующая магнитная сила всегда перпендикулярна двум полям, образуя трехосную плоскость. Для применения этих правил средний палец должен указывать в направлении тока, указательный — в направлении силовых линий, а большой палец будет описывать вектор конечной магнитной силы. Наглядным примером применения правил Флеминга может быть рассмотрение принципиальной схемы стандартного электродвигателя, имеющего ротор и статор. Базовые модели простых двигателей состоят из кольцеобразного металлического статора, в котором вращается ротор, обмотанный медной проволокой. В ротор подается электрический ток от внешнего источника, создающий электромагнитное поле. Это поле, в свою очередь, взаимодействует с магнитными полями двух постоянных магнитов в статоре, создавая новую физическую силу.
При работе с электрическими машинами это необходимые правила, будь то генераторы (правая рука) или электродвигатели (левая рука). В частности, взаимодействие внешнего магнитного поля с электромагнитным полем цепи создает вектор физической силы, направление которой можно определить с помощью мнемотехники. Примечательно, что результирующая магнитная сила всегда перпендикулярна двум полям, образуя трехосную плоскость. Для применения этих правил средний палец должен указывать в направлении тока, указательный — в направлении силовых линий, а большой палец будет описывать вектор конечной магнитной силы. Наглядным примером применения правил Флеминга может быть рассмотрение принципиальной схемы стандартного электродвигателя, имеющего ротор и статор. Базовые модели простых двигателей состоят из кольцеобразного металлического статора, в котором вращается ротор, обмотанный медной проволокой. В ротор подается электрический ток от внешнего источника, создающий электромагнитное поле. Это поле, в свою очередь, взаимодействует с магнитными полями двух постоянных магнитов в статоре, создавая новую физическую силу. Используя правило левой руки Флеминга, можно определить результирующее направление этой силы.
Используя правило левой руки Флеминга, можно определить результирующее направление этой силы.
Заключение
В этом отчете подробно рассмотрена природа законов электромагнитной индукции. Подводя итог, можно сказать, что эти законы являются фундаментальными принципами, объясняющими электродинамические процессы при воздействии внешнего магнитного поля на замкнутую цепь. Закон Фарадея определяет равенство между ЭДС индукции и изменяющимся во времени магнитным потоком. Закон Ленца показывает, что индуктивный ток имеет направление, противоположное внешнему полю, что обусловлено стремлением подавить действие цепи. Мнемонические правила Флеминга применяются для определения направления результирующей магнитной силы, возникающей в результате взаимодействия магнитного и электромагнитного полей. В докладах показаны реальные примеры применимости этих законов и определена их взаимосвязь.
Список литературы
Altium Designer (2018) Что такое закон Ленца и как он влияет на проектирование печатных плат? Интернет.
Corbac40 (2019) Regra da mão esquerda . Веб.
Electrical4U (2021) Законы электромагнитной индукции Фарадея: первый и второй закон . Веб.
Закон индукции Фарадея: как работают трансформаторы (2018). Веб.
Три правила правой руки электромагнетизма (2018). Веб.
Этот отчет о законах электромагнитной индукции был написан и представлен вашим коллегой ученик. Вы можете использовать его для исследовательских и справочных целей, чтобы написать свою собственную статью; однако ты должны цитировать его соответственно.
Запрос на удаление
Если вы являетесь владельцем авторских прав на эту статью и больше не хотите, чтобы ваша работа публиковалась на IvyPanda.
Запросить удаление
Как они управляют перекрестными помехами и электромагнитными помехами?
Ключевые выводы
Закон Ленца и закон Фарадея сообщают нам две важные вещи о том, как изменяющееся магнитное поле взаимодействует с петлей проводника.

Эти два фундаментальных физических закона объединяются, чтобы управлять тем, как магнитные поля генерируются проводниками, по которым течет постоянный или переменный ток.
Закон Ленца устанавливает направление индуцированного тока, а закон Фарадея связывает величину индуцированной противоЭДС со скоростью изменения индуцирующего магнитного поля.
Магнитная индукция в трансформаторе подчиняется закону Ленца и закону Фарадея.
Катушки индуктивности и трансформаторы не работали бы, если бы не существовали фундаментальные законы электромагнетизма. У нас было бы только электрическое поле и никаких магнитных эффектов, создаваемых движущимися токами. Двумя основными электромагнитными законами, описывающими взаимосвязь между индуцированными напряжениями и магнитным полем, являются закон Ленца и закон Фарадея. На уровне печатной платы эти два закона объединяются для создания индуктивной связи между различными цепями.
На уровне печатной платы эти два закона объединяются для создания индуктивной связи между различными цепями.
Поток и магнитный поток напрямую влияют на электромагнетизм, и чтобы понять взаимосвязь таких вопросов, как закон Фарадея и закон Ленца, вы будете рассматривать такие основные темы, как электромагнитная индукция или индуцированная ЭДС, потокосцепление, электрический ток и индуцированное электрическое поле, сила Лоренца и силовые линии магнитного поля. Независимо от того, имеет ли место однородное магнитное поле или переменный магнитный поток в вашей проволочной петле или электрическое поле в целом, вы должны быть уверены, что у вас есть хороший датчик плотности потока и напряженности магнитного поля.
Независимо от того, имеет ли место однородное магнитное поле или переменный магнитный поток в вашей проволочной петле или электрическое поле в целом, вы должны быть уверены, что у вас есть хороший датчик плотности потока и напряженности магнитного поля.
Если термин «индуктивная связь» звучит расплывчато, просто помните, что мы говорим о перекрестных помехах, электромагнитных помехах, передаче шума и любых других способах, которыми магнитное поле может индуцировать шум в электрической цепи. Чтобы лучше увидеть и предсказать, когда сигнал в одной области печатной платы может вызвать шум в другой области печатной платы, полезно знать кое-что о разнице между законом Ленца и законом Фарадея. Вот чем они отличаются и где они приводят к перекрестным помехам в топологии печатной платы.
Закон Ленца против закона Фарадея
Эти два фундаментальных физических закона определяют, как магнитное поле взаимодействует с контуром проводника. Учтите, что у нас есть две петли проводника, обращенные друг к другу. По одной петле течет ток, который мы назовем индукционным током, а по другой петле ток не течет. По закону Ампера мы знаем, что ток в одном контуре создает магнитное поле. Как это магнитное поле взаимодействует с другой петлей? Чтобы получить ответ, нам нужно посмотреть на разницу между законом Ленца и законом Фарадея.
По одной петле течет ток, который мы назовем индукционным током, а по другой петле ток не течет. По закону Ампера мы знаем, что ток в одном контуре создает магнитное поле. Как это магнитное поле взаимодействует с другой петлей? Чтобы получить ответ, нам нужно посмотреть на разницу между законом Ленца и законом Фарадея.
Закон Фарадея
Проще говоря, закон Фарадея гласит следующее:
Это говорит нам кое-что важное об условиях, необходимых для индукции: Магнитное поле, создаваемое током, должно изменяться во времени (колебаться, возрастать или падать) чтобы индуцировать ток во втором витке проводника. Обычно это видно в базовом эксперименте по перемещению магнитного поля к контуру проводника и от него, как показано на изображении ниже.
Напряжение и ток индуцируются в цепи только изменяющимся магнитным полем.
Поскольку изменяющееся магнитное поле индуцирует напряжение, оно также индуцирует ток. В каком направлении течет этот ток? Для этого нам понадобится закон Ленца.
В каком направлении течет этот ток? Для этого нам понадобится закон Ленца.
Закон Ленца
Понимание электрической энергии означает понимание направления тока и контура проводимости, а также любого изменяющегося потока, механической энергии или переменного магнитного поля в вашем изделии. Закон Ленца на самом деле является аналогом закона Фарадея в том смысле, что он говорит вам направление индуцированного тока, но не явно.
Это имеет важное следствие: направление индукционного тока противоположно направлению индукционного тока. Если индуцирующее и индуцируемое поля направлены в противоположные стороны, то и токи также должны быть направлены в противоположные стороны благодаря определению правила правой руки. Направление индуцированного магнитного поля показано на изображении ниже, где индуцированное магнитное поле, создаваемое индуцированным током, определяется по правилу правой руки.
Закон Ленца определяет направление индуцированного тока и напряжения в контуре проводника.
Вместе эти два закона говорят нам все, что нам нужно знать о поведении электромагнитного поля в печатной плате. Собрав их вместе, мы теперь можем лучше понять, как возникают перекрестные помехи, электромагнитные помехи и шумовая связь между различными областями печатной платы.
Как эти законы управляют индуктивными перекрестными помехами и электромагнитными помехами в печатной плате
Очевидно, что мы имеем дело с поведением индуктивного сигнала, а это означает, что нам необходимо рассмотреть два возможных эффекта, связанных с индукцией в печатной плате:
Перекрёстные помехи : Когда сигнал переключается, магнитное поле, создаваемое переключающим током, индуцирует сигнал в трассе-жертве, который затем может распространяться по межсоединению и достигать приемника.
Шумовая связь : Это в основном форма перекрестных помех, когда колебательный сигнал индуцируется в проводнике; одной из распространенных форм является шумовая связь между переходными отверстиями.

Когда возникают эти эффекты, закон Ленца гласит, что индуцированный сигнал создает свое собственное магнитное поле, и направление индуцированного магнитного поля указывает в направлении, противоположном направлению индуцированного магнитного поля. Между тем, закон Фарадея гласит, что величина индуцированной обратной ЭДС тем больше, чем выше частота индуцирующего сигнала. Эти два закона вместе с законом Ома полностью описывают поведение индуктивных перекрестных помех.
Вышеупомянутые пункты относятся к индуцированным перекрестным помехам между дорожками агрессора и жертвы, а также к электромагнитным помехам, индуцированным в токовой петле на реальной печатной плате. Всякий раз, когда есть изменяющееся магнитное поле, падающее параллельно петле проводника, тогда будет индуцированный ток. Чтобы уменьшить величину обоих эффектов, у вас есть два варианта настройки геометрии трассы:
Используйте немного более широкие дорожки
Разместите трассы ближе к их опорной плоскости (т.
 е. используйте более тонкий ламинат для микрополосковых или полосковых трасс)
е. используйте более тонкий ламинат для микрополосковых или полосковых трасс)
Правильный набор инструментов для трассировки и проектирования трасс поможет вам поддерживать желаемый импеданс, а также поможет отрегулировать размеры трассы, чтобы оставаться в пределах требуемых допусков. У вас также будут инструменты, необходимые для анализа перекрестных помех в готовой разводке печатной платы. Вы также должны быть уверены, что найдете правильную дифференциальную форму в своих уравнениях, чтобы справиться с любой проблемой, такой как взаимная индукция или аномальные состояния электромагнитной индукции, электролиз и ваша различная индуцированная электродвижущая сила. Определение электродвижущей силы, наведенного напряжения и положения ваших цепей в вихревых токах — все это жизненно важно для целостности вашего продукта, от его медного провода до платы и самой упаковки.
Если вас беспокоит закон Ленца или закон Фарадея, лучшее программное обеспечение для компоновки и проектирования печатных плат, а также полный набор инструментов анализа помогут вам понять, как эти два эффекта влияют на электромагнитное поведение вашей печатной платы. Allegro PCB Editor включает в себя функции, необходимые для планирования компоновки платы для любого приложения, а также расширенные инструменты проверки проекта и утилиты полевого решателя для анализа поведения вашей высокоскоростной и высокочастотной электроники.
Allegro PCB Editor включает в себя функции, необходимые для планирования компоновки платы для любого приложения, а также расширенные инструменты проверки проекта и утилиты полевого решателя для анализа поведения вашей высокоскоростной и высокочастотной электроники.
Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов. Чтобы посмотреть видео по связанным темам или узнать, что нового в нашем наборе инструментов для проектирования и анализа, подпишитесь на наш канал YouTube.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка – что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Закон электромагнитной индукции Фарадея, вывод и заблуждения.

Часть 1
Это часть 1 двух статей о законе Фарадея. В первой части я попытаюсь прояснить некоторые недоразумения, связанные с различными формами закона Фарадея, и предоставить простой вывод закона Фарадея. Во второй части мы исследуем некоторые причуды и «исключения» закона Фарадея.
Содержание
Часть 1
- 3 Стучающие формы Закон Фарадея
- Законодательство Фарадея и Движение ЭМС
- и последнее мысли
4.ship 2
Закон Фарадея
См. Уравнения Максвелла для краткого и интуитивно понятного введения во все уравнения Максвелла и закон силы Лоренца.
Я прочитал 3 разных учебника по электромагнетизму. Каждый дал свое описание того, что он определяет как закон Фарадея.
Определения
Первое определение:
\(\mathcal{E}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}\), или, другими словами, чистая ЭДС равна отрицательной величине количества «линий магнитного поля» , пересекаемых «проводом» в единицу времени.
Второе определение:
$\mathcal{E}=-\frac{\partial \phi_{B\space closed}}{\partial t}$, или чистая ЭДС равна отрицательной величине изменения магнитного потока в единицу времени на некоторой «замкнутой поверхности» .
Третье определение:
Это похоже на первое. $\mathcal{E_{motional}}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}$, или, другими словами, движущая ЭДС равна отрицательной сумме «магнитное поле» проходит по «проводу» в единицу времени.
Четвертое определение:
На самом деле это называется законом Максвелла-Фарадея, который является отдельной штукой, но люди до сих пор смешивают его с законом Фарадея. $\nabla \times E=-\frac{\partial B}{\partial t}$ или в более знакомой интегральной форме $\oint\limits_{\partial \sigma}E\cdot dl=-\iint\limits_{ \sigma} \frac{\partial B}{\partial t}\cdot dA$. Обратите внимание, что это утверждение относительно поля $B$ и самого поля $E$ , и не имеет ничего общего с формой проволоки или скоростью проволоки.
Все это кажется запутанным. И чтобы еще больше вас запутать, эти четыре определения не эквивалентны. Некоторые применимы в большем количестве случаев, чем другие.
Например, первое определение очень расплывчато (хотя оно может быть самым оригинальным из того, что придумал Фарадей). Он ошибочен во многих случаях. Второе определение справедливо до тех пор, пока понятие «замкнутая поверхность» не потеряет смысла. Третье определение справедливо, если понятие «провод» не определено. Четвертый – это опять же отдельный закон. Это одно из четырех уравнений Максвелла. Поэтому он фундаментален и работает во всех случаях (где работает электромагнетизм Максвелла). Я объясню все это позже.
ЭДС движения и ЭДС индукции
ЭДС определяется следующим образом: дурное имя) длинный путь $s$ определяется как работа на единицу заряда на этом пути. Другими словами, если вы двигаете воображаемую заряженную частицу с зарядом $q$ по пути $s$, вычислите работу, совершаемую над зарядом $q$ электромагнитной силой , тогда вы можете разделить ее на $q$, чтобы получить ЭДС по этому пути.
Электродвижущая сила (ЭДС), которую мы определили здесь, представляет собой результирующую ЭДС .
Поскольку $F$ состоит из двух частей, а именно $F=F_E+F_B$, мы можем разделить электромагнитную силу на электростатическую и магнитную.
$\mathcal{E}_s = \frac{1}{q}\int\limits_s F\cdot dl$ $=\frac{1}{q}\int\limits_s F_E\cdot dl + \frac{1 }{q}\int\limits_s F_B\cdot dl$
Вспомним закон силы Лоренца, $F_B=qv\times B, \space F_E=qE$ (обратите внимание, что все $v,B,E$ являются векторами, а $ F_B, F_E$). Мы подключаем это, замечаем, что $q$ отменяется (так и должно быть, потому что это точка $\frac{1}{q}$ в определении)
$\mathcal{E}_s = \int\limits_s E\cdot dl + \int\limits_s (v\times B)\cdot dl$
Первая часть, $\int\limits_s E\cdot dl$ называется ЭДС индуцирования , вторая часть $\int\limits_s (v\times B)\cdot dl$ называется ЭДС движения .
По-видимому, $E\cdot dl$ может генерироваться (предположим, что это все из-за магнитных взаимодействий) только при наличии изменяющегося поля $B$. Это связано с тем, что изменение поля $B$ создает завиток в $E$, а без него и без какого-либо заряда (как в цепи) $E=0$. Так 9ЭДС 0053, индуцированная ЭДС , названа так потому, что она индуцируется изменяющимся магнитным полем.
Это связано с тем, что изменение поля $B$ создает завиток в $E$, а без него и без какого-либо заряда (как в цепи) $E=0$. Так 9ЭДС 0053, индуцированная ЭДС , названа так потому, что она индуцируется изменяющимся магнитным полем.
С другой стороны, вторая половина не имеет ничего общего с изменяющимся магнитным полем. Вместо этого требуется движение пути или провода , поэтому он называется движущаяся ЭДС .
Первая часть также дает вам электростатическое напряжение на пути $s$. Как видите, форма ЭДС , индуцированная , близка к форме закона Максвелла-Фарадея, поэтому мы можем использовать закон Максвелла-Фарадея для вычисления ЭДС индуцирования для 9054.0053 замкнутый контур (поскольку интегральная форма закона Максвелла-Фарадея работает только в замкнутом контуре).
Вторая часть сложнее, мы выведем непосредственно из нее то, что я назвал Законом Фарадея о движении, по сути, третье определение закона Фарадея
Вывод закона Фарадея
Мы хотим вывести $\mathcal{E}=-\ frac{\partial \phi_{B\spaceclosed}}{\partial t}$ (наше второе определение). Давайте сначала получим ЭДС движения и объединим ее с ЭДС индуцирования, чтобы получить результирующую ЭДС.
Давайте сначала получим ЭДС движения и объединим ее с ЭДС индуцирования, чтобы получить результирующую ЭДС.
Моторная часть вывода закона Фарадея
Мы хотим получить $\mathcal{E_{motional}}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}$.
Начнем с определения ЭДС движения
$\int\limits_s (v\times B)\cdot dl$
На первый взгляд кажется, что это должно равняться 0, потому что $v\parallel dl$, правильно ?
$v\parallel dl$, когда проводник/путь неподвижен! Но весь смысл движущейся ЭДС в том, что теперь провод и путь не стационарны.
Например, провод может двигаться вправо, в то время как заряженная частица движется вверх по проводу.
$v$ обозначает полное движение относительно магнитного поля (вправо и вверх). $dl$ просто указывает вверх. То же самое можно сказать о концепции пути , в то время как путь относительно магнитного поля направлен вправо и вверх, нас интересует только ЭДС вдоль восходящего направления (мы рассмотрим, почему это так, в следующих статьях), поэтому $dl$ снова указывает вверх.
Следовательно, $v=v_{вдоль}+v_{из}$, или результирующая скорость = скорость вдоль провода или предопределенное направление пути + скорость провода или предопределенный путь в этой точке.
$v_{вдоль}\parallel dl$, но $v_{of}\not\parallel dl$!
нам нужно учитывать только $v_{of}$, поэтому $\mathcal{E_{motional}}=\int\limits_s (v_{of}\times B)\cdot dl$
Обратите внимание, что $(v_{ of}\times B)\cdot dl$ — это коробочный продукт.
Представляет объем параллелепипеда, образованного тремя векторами $v_{of}, B, dl$; поэтому возникает естественный вопрос: каково физическое значение этого тома? Я оставлю это читателям для жонглирования.
Чтобы вычислить тот же объем, мы также можем немного поменять порядок векторов.
$(v_{of}\times B)\cdot dl=(dl\times v_{of})\cdot B$
Теперь эту величину гораздо легче понять. $(dl\times v_{of})$ представляет собой скорость, с которой область заметается сегментом $dl$, когда он движется со скоростью $v_{of}$! Итак, $dl\times v_{of}=-d\frac{dA_{of \space dl}}{dt}$. Впереди небольшая буква $d$, обозначающая, что эта скорость очистки области бесконечно мала, потому что $dl$ бесконечно мала. Отрицательный знак не имеет большого значения. Это связано с определением направления площади по правилу правой руки. 92 A}{\Delta t}=-\Delta \frac{\Delta A}{\Delta t}$. Опять же, двойной $\Delta$ указывает на малость площади.
Впереди небольшая буква $d$, обозначающая, что эта скорость очистки области бесконечно мала, потому что $dl$ бесконечно мала. Отрицательный знак не имеет большого значения. Это связано с определением направления площади по правилу правой руки. 92 A}{\Delta t}=-\Delta \frac{\Delta A}{\Delta t}$. Опять же, двойной $\Delta$ указывает на малость площади.
Видимо, $-\frac{dA_{of \space dl}}{dt}\cdot B=-\frac{dA_{of\space dl}\cdot B}{dt}=-\frac{d\phi_B {dt}$, или, другими словами, скорость, с которой мы сканируем площадь, умноженную на поле $B$, равна скорости, с которой мы сканируем магнитный поток.
Итак, подключив его обратно к интегралу,
$\mathcal{E_{motional}}=\int\limits_s -d \frac{d\phi_B}{dt} = -\frac{d\phi_{B\ пробел заметен \space by \space s}}{dt}$
Таким образом, мы получили третье определение закона Фарадея, которое мне нравится называть Законом Фарадея о движении.
Последнее замечание: единственная фундаментальная теорема электромагнетизма, которую мы использовали выше, — это закон силы Лоренца.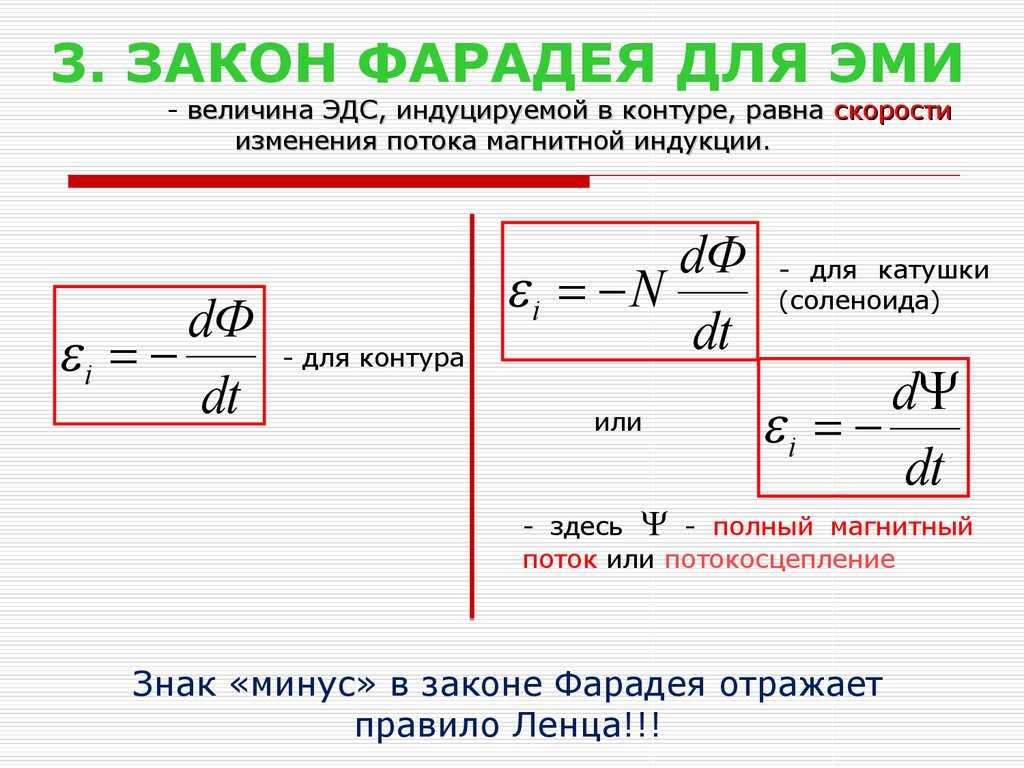 Таким образом, другими словами, этот Закон Фарадея о движении должен иметь такую же предсказательную силу, как и Закон силы Лоренца. Все вещи, предсказуемые законом Фарадея о движении, должны предсказываться законом силы Лоренца, и наоборот. В некоторых случаях закон силы Лоренца намного проще (как в «исключениях» закона Фарадея о движении)
Таким образом, другими словами, этот Закон Фарадея о движении должен иметь такую же предсказательную силу, как и Закон силы Лоренца. Все вещи, предсказуемые законом Фарадея о движении, должны предсказываться законом силы Лоренца, и наоборот. В некоторых случаях закон силы Лоренца намного проще (как в «исключениях» закона Фарадея о движении)
Вывод петлевой формы закона Фарадея
Теперь мы можем легко вывести петлевую форму закона Фарадея из этой «подметающей» формы. Это включено во многие учебники. Основная идея состоит в том, чтобы отметить, что когда мы проходим $s$, все $\phi_B$, через которые мы проходим, перемещаются либо из $\phi_{inside\space loop}\rightarrow \phi_{outside \space loop}$, либо из $\phi_ {outside\space loop}\rightarrow \phi_{inside \space loop}$
Таким образом, если $s$ является частью цикла, $\frac{d\phi_{B\space заметается \space by \space s} }{dt}$ просто переходит в $\frac{d\phi_{B\space inside\space loop\space due\space to\space change\space in\space \sigma}}{dt}$; дедукция знака требует некоторой осторожности, поэтому я не буду утомлять вас этим. Важность «из-за изменения $\sigma$» станет очевидной позже.
Важность «из-за изменения $\sigma$» станет очевидной позже.
Теперь мы получаем:
$\mathcal{E_{motional\space in\space \sigma}}= -\frac{d\phi_{B\space inside\space loop\space due\space to\space change \space in\space \sigma}}{dt}$
Что близко к полной петлевой версии закона Фарадея (определение 2)
Чтобы получить полную петлевую версию закона Фарадея, мы должны проанализировать $\mathcal{E }_{induced}$, или индуцированная ЭДС .
К счастью, это дается просто законом Максвелла-Фарадея.
Напомним $\mathcal{E_{индуцированный}}=\oint\limits_{\partial \sigma}E\cdot dl$
$=-\iint\limits_{\sigma} \frac{\partial B}{\partial t}\cdot dA$
$=-\frac{\partial \phi_{B\space due \space to \space change\space in\space B}}{\partial t}$
Теперь добавим $\ mathcal{E_{двигательный}}, \space \mathcal{E_{индуцированный}}$.
$\mathcal{E_{net}}=\mathcal{E_{motional}}+\mathcal{E_{induced}}$
$=-\frac{\partial\phi_{B\space inside\space loop \пространство из-за\пространство до\изменение пространства\пространство в\пространство \sigma}}{\partial t}-\frac{\partial \phi_{B\пробел из-за \пространство до \изменение пространства\пространство в\пространство B}} {\ парциальное т} $
Обратите внимание на две тонкости:
Я заменил полную производную на частную, чтобы сделать ее более точной, поскольку другие переменные, такие как местоположение, также могут влиять на $\phi_B$. Если вы не знаете, о чем я говорю, пусть это вас не беспокоит.
Если вы не знаете, о чем я говорю, пусть это вас не беспокоит.
Две $\frac{\partial \phi_B}{\partial t}$ исключают друг друга, потому что они вызваны разными причинами. На самом деле «изменение $B$» и «изменение $\sigma$» — единственные возможные причины изменения потока. Изменение «угла» является частью либо изменения $B$, либо изменения $\sigma$. Таким образом, они складываются в $\frac{\partial \phi_{B\space net}}{\partial t}$
Отлично, теперь созерцайте всю прелесть закона Фарадея в том виде, в каком мы его вывели :
$\mathcal{E_{net}}=-\frac{\partial \phi_{B\space net}}{\partial t}$
Заключение
Резюмируя, что только что произошло. Сначала мы объяснили разницу ЭДС движения и ЭДС индукции. ЭДС движения — это ЭДС, создаваемая движением провода/дорожки в магнитном поле. Индуцированная ЭДС – это ЭДС, возникающая в результате изменения магнитного поля.
Другой способ представить это так: ЭДС движения возникает из-за $v\times B$ части силы, а ЭДС индукции возникает из-за части электромагнитной силы в размере $E$.
Существует несколько определений закона Фарадея. Четвертое определение, которое мы дали, на самом деле называется законом Максвелла-Фарадея. Его не следует путать с законом Фарадея, поскольку он более фундаментален и имеет дело только с индуцированной ЭДС.
Некоторые версии закона Фарадея имеют дело с ЭДС движения, как в третьем определении. Закон Фарадея, касающийся движущихся ЭДС, может иметь 2 разновидности: «вариант подметающей проволоки» и «вариант замкнутого контура». Они фактически эквивалентны. Другие версии объединяют третью версию с законом Максвелла-Фарадея, чтобы создать утверждение, которое обрабатывает как ЭДС движения, так и ЭДС индуцирования. Эта версия относится к «замкнутому циклу», потому что законом Максвелла-Фарадея трудно манипулировать, когда нет замкнутого цикла.
Первое определение, включающее линию магнитного поля, проблематично (рассмотрено в части 2), но, вероятно, оно ближе к первоначальному предложению Фарадея.
И последнее, но не менее важное: я предложил простое доказательство закона Фарадея с использованием закона силы Лоренца и закона Максвелла-Фарадея.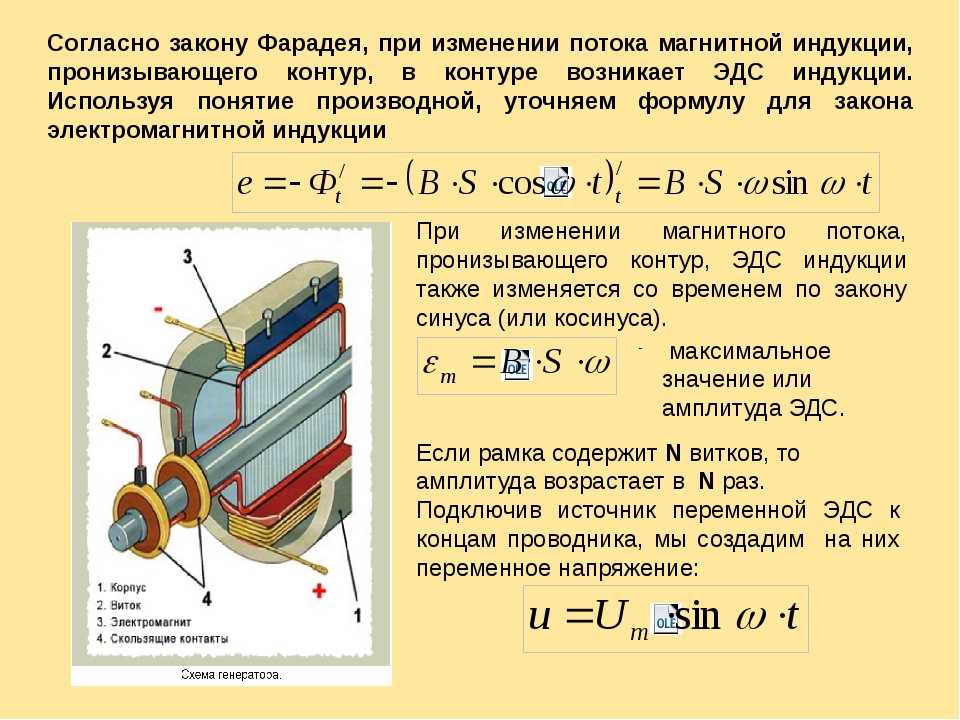





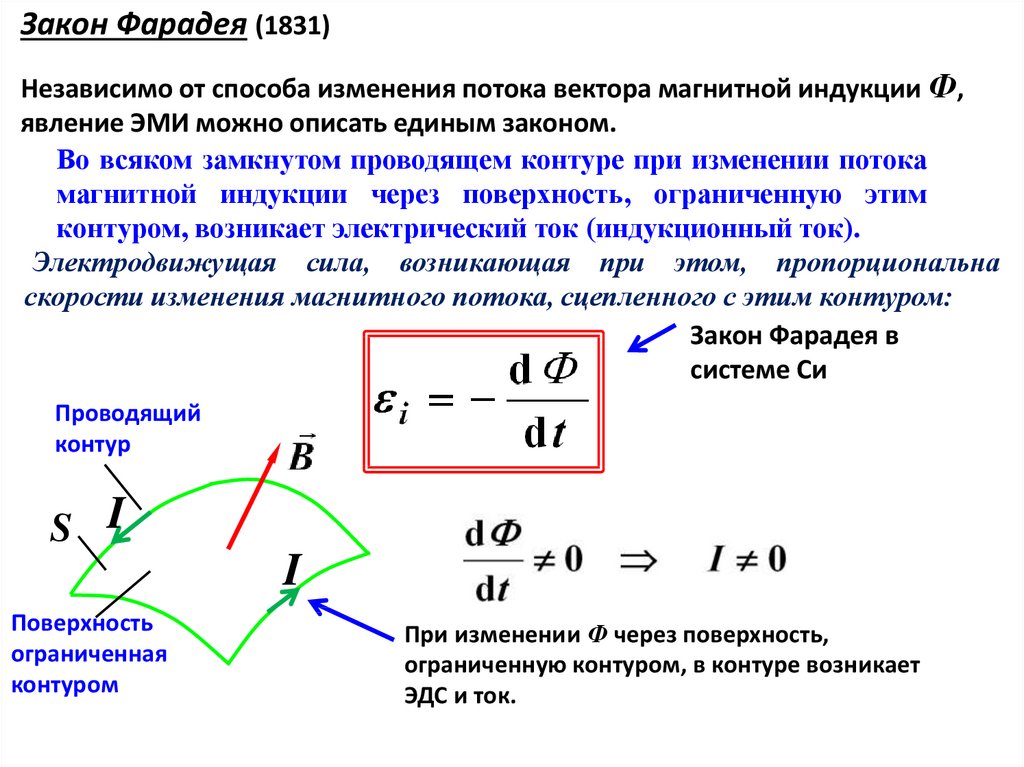 е. используйте более тонкий ламинат для микрополосковых или полосковых трасс)
е. используйте более тонкий ламинат для микрополосковых или полосковых трасс)