Импульс тела. Другая формулировка второго закона Ньютона
Не так давно мы изучали второй закон Ньютона. Напомним, что он гласит следующее: равнодействующая сила, действующая на тело равна произведению массы тела и ускорения, сообщаемого этой силой:
Из кинематики мы знаем, что ускорение легко можно представить, как отношение изменения скорости к промежутку времени:
После преобразований получаем:
В правой части у нас появилась величина, равная произведению массы и скорости. Эта физическая величина называется импульсом. В общем и целом, можно сказать, что импульс — это мера механического движения. Более подробно с физическим смыслом импульса мы познакомимся при изучении закона сохранения импульса.
Исходя из полученного уравнения, мы можем иначе сформулировать второй закон Ньютона: сила, приложенная к телу равна отношению изменения импульса к промежутку времени, за который это изменение произошло:
Кстати,
именно так Ньютон изначально сформулировал свой закон (за исключением того, что
он был записан в дифференциальной форме, но мы, на данном этапе, не затрагиваем
высшую математику).
Итак, давайте обратимся к определению импульса. Импульс тела (или материальной точки) — это физическая величина, равная произведению массы тела и его скорости:
Поскольку скорость является векторной величиной, импульс имеет направление. Это направление совпадает с направлением скорости тела.
Единица измерения импульса: .
Необходимо отметить, что импульс тела складывается из импульсов материальных точек, из которых состоит тело. Как правило, любое движущееся тело обладает импульсом. Есть лишь одно исключение — это некоторые виды вращательного движения. Например, если мы рассмотрим вращение однородного диска вокруг оси, проходящей через его центр, то убедимся, что импульс диска равен нулю.
Рассмотрим
две диаметрально противоположные точки 1 и 2.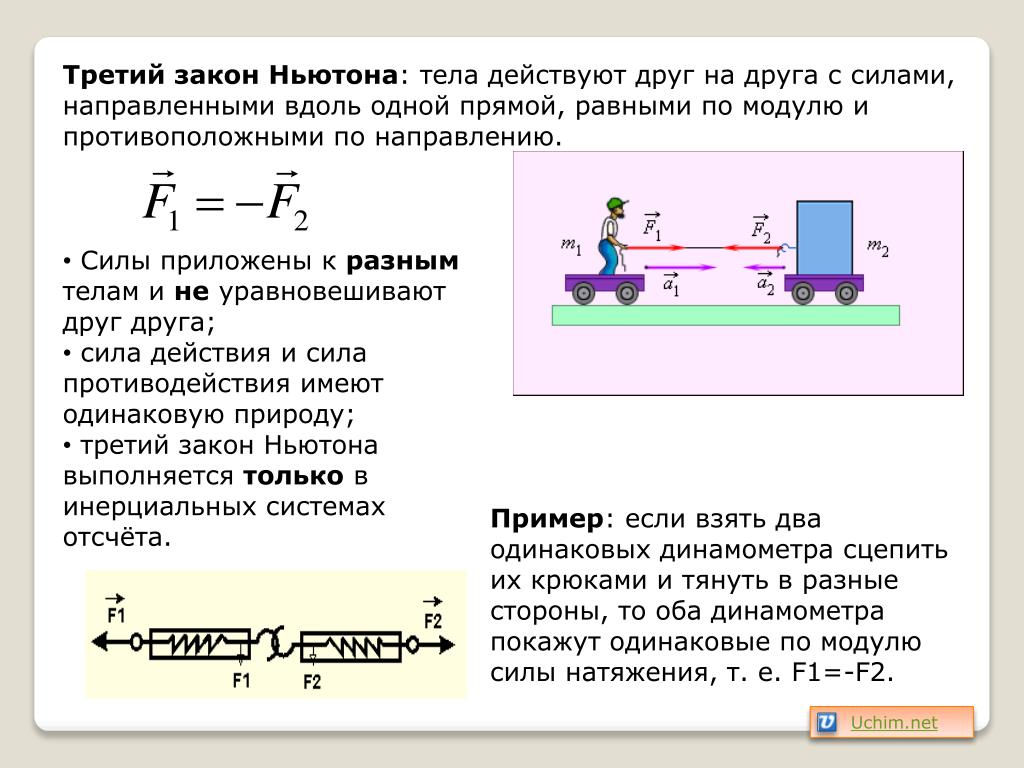
Пример решения задачи.
Задача.
Автомобиль
едет по дороге со скоростью 65 км/ч, а сзади него едет другой автомобиль с той
же скоростью. Из-под колеса впереди идущего автомобиля вылетает кусочек грязи
под углом 30° к направлению движения обеих машин. С какой силой этот кусочек
массой 50 г отлетит в лобовое стекло идущего сзади автомобиля? Время удара
грязи о стекло составляет 0,2 с.
В первую очередь заметим, что грязь вылетит из-под колеса с той же скоростью, с которой вращается колесо. Поскольку в задаче сказано пренебречь изменением скорости грязи в процессе полета, мы можем считать скорость постоянной до удара о стекло. Заметим, что другой автомобиль тоже двигается, поэтому нам необходимо вычислить скорость движения кусочка грязи, относительно второго автомобиля.
Российские физики изучили условия, при которых не выполняется третий закон Ньютона
«Третий закон Ньютона, который все помнят из школьной программы, утверждает, что сила действия равняется силе противодействия. Однако для некоторых открытых и неравновесных дисперсных систем – частиц в среде – симметрия эффективной силы межчастичного взаимодействия может нарушаться, и возникает очень интересная физика: например, частицы самоорганизуются в сложные структуры, система аномально разогревается, появляются необычные неравновесные фазовые переходы», ― комментирует Евгений Лисин, заведующий лабораторией диагностики пылевой плазмы ОИВТ РАН.
Впервые такую систему с несимметричным взаимодействием частиц удалось получить в конце 90-х гг прошлого века в Германии: ученые изучали поведение пылевых частиц в газоразрядной плазме, воздействуя на них лазером по очереди, и обнаружили, что частицы откликаются по-разному в зависимости от их расположения в системе. С тех пор, как были опубликованы первые теории и модели несимметричного взаимодействия между микрочастицами в пылевой плазме, в теоретическом развитии этой темы было проведено множество исследований. Однако, несмотря на богатую теоретическую базу, одной из важных нерешенных проблем оставалось прямое экспериментальное исследование особенностей несимметричного взаимодействия между частицами. Точно измерить силу межчастичного взаимодействия и определить степень нарушения симметрии в зависимости от условий среды ранее не удавалось. Решение этой проблемы стало возможным благодаря оригинальному спектральному методу измерения, который был разработан учеными ОИВТ РАН и МФТИ при поддержке Российского научного фонда.
В ходе экспериментов в плазму газового электрического разряда помещались две твердые сферические частицы (пылинки) размером в несколько микрон. В разряде частицы приобретали значительный отрицательный заряд (в 10000 раз превышающий элементарный заряд электрона). В сильном электрическом поле разряда заряженные частицы могли левитировать, а для удержания одноименно заряженных частиц на близком расстоянии друг к другу ученые дополнительно использовали специальную потенциальную ловушку. Наличие сильного электрического поля приводило к формированию направленного потока ионов. Заряженные микрочастицы этот поток возмущали, образуя за собой ионный кильватерный след (наподобие следа от быстро идущего по воде корабля). Таким образом на микрочастицу, находящуюся в кильватерном следе второй частицы, действовала не только сила электростатического отталкивания от второй частицы, но и сила притяжения к её следу.
«Формальное невыполнение третьего закона Ньютона может возникать в системах взаимодействующих частиц, когда среда, в которой находятся частицы, является своеобразным переносчиком взаимодействия, и способна воспринять недостаток или избыток импульса, так как закон сохранения импульса нарушить нельзя. Кроме газоразрядной пылевой плазмы примерами таких систем являются некоторые виды коллоидных суспензий и активной материи», ― комментирует Михаил Васильев, ведущий научный сотрудник лаборатории активных сред и систем МФТИ.
Полученные результаты открывают новые перспективы исследования дисперсных систем с нарушенной симметрией межчастичного взаимодействия. Изучение таких систем – это сравнительно новое направление исследований, которое стало активно развиваться последние несколько лет. Хотя детали несимметричного взаимодействия частиц удобнее изучать на примере плазменно-пылевых систем из-за относительной малости действующих в них диссипативных сил, практического применения можно ожидать скорее в области активных коллоидов, которые интенсивно изучаются разными научными группами по всему миру. Коллективное поведение частиц в синтетических активных коллоидах имеет общие закономерности с поведением колоний бактерий, косяков рыб, стай птиц и т.д. Коллоидное активное вещество привлекает значительное внимание со стороны материаловедения в контексте разработки новых материалов с «программируемым» откликом на механические напряжения, магнитные и тепловые поля. Появляются также перспективные приложения, связанные с сепарацией вещества, коллективной адресной доставкой микрогруза (например, лекарств) и преобразованием механической энергии хаотического движения.
Изучение таких систем – это сравнительно новое направление исследований, которое стало активно развиваться последние несколько лет. Хотя детали несимметричного взаимодействия частиц удобнее изучать на примере плазменно-пылевых систем из-за относительной малости действующих в них диссипативных сил, практического применения можно ожидать скорее в области активных коллоидов, которые интенсивно изучаются разными научными группами по всему миру. Коллективное поведение частиц в синтетических активных коллоидах имеет общие закономерности с поведением колоний бактерий, косяков рыб, стай птиц и т.д. Коллоидное активное вещество привлекает значительное внимание со стороны материаловедения в контексте разработки новых материалов с «программируемым» откликом на механические напряжения, магнитные и тепловые поля. Появляются также перспективные приложения, связанные с сепарацией вещества, коллективной адресной доставкой микрогруза (например, лекарств) и преобразованием механической энергии хаотического движения.
Закон Ньютона второй – Энциклопедия по машиностроению XXL
Следует отметить, что точность воспроизведения единицы массы при таком ее определении была бы весьма низкой. Поэтому, принимая во внимание второй, четвертый и пятый критерии выбора единиц ФВ, ввели лишнюю основную единицу — килограмм (единицу массы). При этом в одном из законов Ньютона — втором или всемирного тяготения, требовалось сохранить коэффициент пропорциональности. Он был оставлен в менее широко применяемом на практике законе всемирного тяготения. Мировая константа — гравитационная постоянная у = (6,6720 0,041)-10 ” (Н м )/кН. Полученная система единиц ФВ не оптимальна с точки зрения первого критерия, но с точки зрения практического удобства — оптимальна.I, В классической механике большинство количественных результатов, характеризующих важнейшие свойства наблюдаемых движений, получено на основании законов Ньютона.
 Второй закон Ньютона (или вторая аксиома механического движения), устанавливающий простое соотношение между ускорением движущейся точки данной массы и действующими силами, является фундаментом для численного решения разнообразных частных задач. Однако второй закон Ньютона справедлив, вообще говоря, только для точек постоянной массы. Если масса точки изменяется, то основной закон движения в форме Ньютона, на котором должны строиться все ма-
[c.107]
Второй закон Ньютона (или вторая аксиома механического движения), устанавливающий простое соотношение между ускорением движущейся точки данной массы и действующими силами, является фундаментом для численного решения разнообразных частных задач. Однако второй закон Ньютона справедлив, вообще говоря, только для точек постоянной массы. Если масса точки изменяется, то основной закон движения в форме Ньютона, на котором должны строиться все ма-
[c.107]Закон Ньютона второй 32 [c.422]
Однако вместо формул аналитической механики за исходное уравнение можно взять второй закон Ньютона. [c.414]
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью (например, ударные нагрузки). Действие таких нагрузок сопровождается возникновением колебаний сооружений. При колебании же вследствие изменения скорости колеблющихся масс возникают силы инерции, пропорциональные (по второму закону Ньютона) колеблющимся мас-са. м п ускорениям. Эти силы инерции могут во много раз превосходить те же нагрузки, приложенные статически.
[c.11]
м п ускорениям. Эти силы инерции могут во много раз превосходить те же нагрузки, приложенные статически.
[c.11]
Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом де/ю, второй закон Ньютона для рассматриваемой точки дает ma=f +jV. Перенося здесь величину та в правую часть равенства и учитывая обозначение (84), придем к соотношению (85). Наоборот, перенося в уравнении (85) величину f в другую часть равенства и учитывая обозначение (84), получим выражение второго закона Ньютона. [c.345]
Это утверждение, новое в том смысле, что оно не вытекает из всех введенных выше исходных определений, и должно быть добавлено к ним в качестве самостоятельного постулата. Такой постулат был введен Ньютоном и называется вторым постулатом (законом) Ньютона. [c.53]
Именно это равенство (используя термин сила ) обычно называют вторым законом Ньютона. [c.55]
[c.55]
Тогда в соответствии со вторым законом Ньютона в некоторой инерциальной системе отсчета имеют место /V равенств [c.62]
Поэтому в соответствии со вторым законом Ньютона [c.69]
Но равенство (13) выражает второй закон Ньютона для материальной точки, помещенной в центре инерции и движущейся вместе с ним, если масса этой точки равна М и если к ней приложена сила / внеш- Отсюда следует, что теорему сб изменении количества движения можно сформулировать так [c.71]
Мы установили таким образом, что второй закон Ньютона может быть применен и в неинерциальной системе отсчета, если к силам, действующим на каждую точку, добавить переносную и кориолисову силы инерции. [c.104]
Движение системы, состоящей из N материальных точек, в инерциальной системе отсчета, в соответствии со вторым законом Ньютона, описывается дифференциальными уравнениями
[c. 121]
121]
Если представить второй закон Ньютона в ЗЛ/-мерной записи [c.128]
В этом смысле уравнения (22) представляют собой просто запись второго закона Ньютона в проекциях на оси qj. [c.128]
При выводе уравнений Лагранжа мы исходим из записи второго закона Ньютона. Для систем, содержащих голономные механические связи, этот закон имеет вид [c.155]
Естественно поставить вопрос почему нельзя было с самого начала постулировать уравнения (22) либо (29), если они являются лишь ковариантной записью второго закона Ньютона Действительно, такой постулат мог бы быть положен в основу механики (голономных систем). Именно, в наше время построение новых систем механики, в частности, релятивистской механики. [c.164]
Равенство (14) по форме напоминает второй закон Ньютона для точки [c.173]
Это последнее утверждение играет важную роль потому, что оно позволяет положить в основу классической механики в качестве исходного постулата не второй закон Ньютона (или его ко-вариантную запись — уравнения Лагранжа), а вариационный принцип Гамильтона. Действительно, по крайней мере Для движений в потенциальных полях, постулируя вариационный принцип Гамильтона, можно получить из него как следствие уравнения Лагранжа. В теоретической физике иногда оказывается удобным вводить исходную аксиоматику в форме соответствующего вариационного принципа, устанавливающего общие свойства движения в глобальных терминах, и уже из этого принципа получать уравнения движения.
[c.280]
Действительно, по крайней мере Для движений в потенциальных полях, постулируя вариационный принцип Гамильтона, можно получить из него как следствие уравнения Лагранжа. В теоретической физике иногда оказывается удобным вводить исходную аксиоматику в форме соответствующего вариационного принципа, устанавливающего общие свойства движения в глобальных терминах, и уже из этого принципа получать уравнения движения.
[c.280]
Если в известную из физики формулу второго закона Ньютона [c.29]
Основным законом динамики является второй закон Ньютона производная по времена от количества движения материальной точки равна действующей на нее силе, т. е. [c.319]
Рассмотрим теперь одну материальную точку с массой т, подверженную внешнему воздействию. В соответствии с принципом детерминированности ускорение этой точки есть функция от радиуса-вектора и скорости этой точки, а также, быть может, времени Г Математическим выражением этого служит второй закон Ньютона
[c.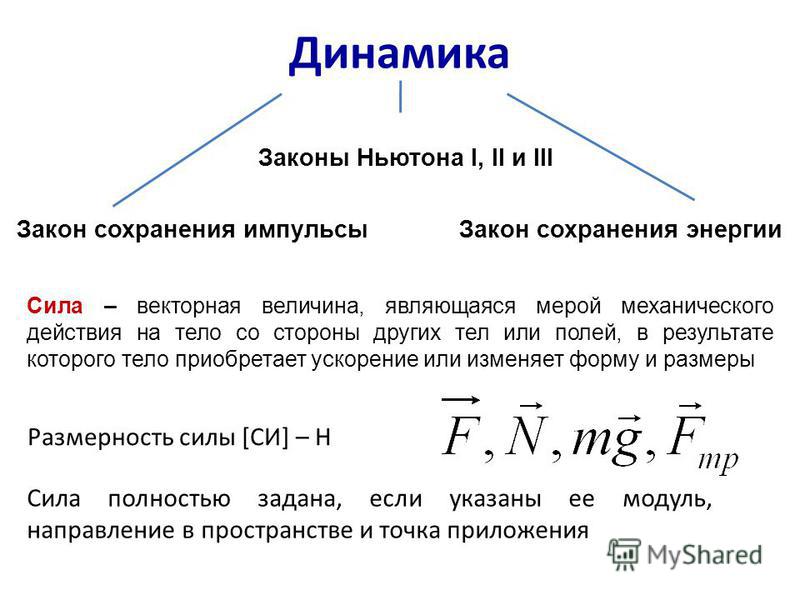 160]
160]
Второй закон Ньютона утверждает, что производная по времени от количества движения материальной точки равна действующей на точку силе. [c.161]
Обратимся к прямой задаче динамики и рассмотрим уравнение, выражающее второй закон Ньютона [c.170]
Доказательство получается посредством проектирования векторного уравнения второго закона Ньютона (см. стр. 160) на естественные оси.О [c.184]
С учетом этого определения второй закон Ньютона может быть представлен в виде [c.190]
Доказательство. Умножим уравнение, выражающее второй закон Ньютона, скалярно на V. Будем иметь [c.195]
Пусть N — реакция связи. При освобождении от связи второй закон Ньютона следует записать в виде [c.198]
Замечание 3.11.3. Этапы, выделенные в доказательстве теоремы 3.11.4, имеют самостоятельную ценность. Вспомним, что закон электростатического взаимодействия точечных зарядов имеет вид закона Ньютона, когда вместо масс используются заряды, а вместо гравитационной постоянной — диэлектрическая проницаемость. Пусть точечный положительный заряд у находится между бесконечными противоположно заряженными пластинами. Примем, что первая пластина заряжена отрицательно с плотностью заряда —первой пластины обозначим у, а до второй пластины — 1/2 Цилиндром с осью, перпендикулярной к пластинам и проходящей через точечный заряд, вырежем в этих пластинах два круга радиуса I. В соответствии с этапом 2 доказательства теоремы 3.11.4 силовая функция от воздействия кругов на точечный заряд будет выражаться формулой
[c.268]
Пусть точечный положительный заряд у находится между бесконечными противоположно заряженными пластинами. Примем, что первая пластина заряжена отрицательно с плотностью заряда —первой пластины обозначим у, а до второй пластины — 1/2 Цилиндром с осью, перпендикулярной к пластинам и проходящей через точечный заряд, вырежем в этих пластинах два круга радиуса I. В соответствии с этапом 2 доказательства теоремы 3.11.4 силовая функция от воздействия кругов на точечный заряд будет выражаться формулой
[c.268]
П2.2.2. Обобщенный закон Ньютона. Второй закон Ньютона (П2.9), записанный для трехмерных векторов скорости у и силы /, можно обобщить на введенный ранее четырехмерный континуум. Естественно считать при этом, что 1) сила, как и в трехмерном пространстве, должна быть равна нулю, если вектор скорости постоянен, и 2) сила пропорциональна массе точки. Домножим уравнение (П2.9) на множитель 1/д/1 — [c.433]
Следует отметить, что точность воспроизведения единицы маС сы при таком ее определении была бы весьма низкой.
 Поэтому, прИ нимая во внимание второй, четвертый и пятый критерии выбора единиц ФВ, ввели лишнюю основную единицу — килограмм (еДИ ницу массы). При этом в одном из законов Ньютона — втором, всемирного тэтотения, требовалось сохранить коэффициент пропор
[c.24]
Поэтому, прИ нимая во внимание второй, четвертый и пятый критерии выбора единиц ФВ, ввели лишнюю основную единицу — килограмм (еДИ ницу массы). При этом в одном из законов Ньютона — втором, всемирного тэтотения, требовалось сохранить коэффициент пропор
[c.24]Реакции в кинематических парах обозначим двумя цифрами первая показывает номер звена, на которое действует сила, вторая — номер звена, со стороны которого действует сила. Наирнмер, реакция р2 — сн ча, действующая со стороны звена 1 иа звено 2. Причем по третьему закону Ньютона реакции / 21 и -F12 равны по значению, но противоположны по направлению [c.142]
Б. Уравнение массы (уравнение второго закона Ньютона) F = та = u(dVjdt), где а = dV/dt — ускорение Стл = т — аналог электрической емкости (масса элемента). [c.68]
Вспомним теперь, что при выводе всех основных теорем механики в 2—4 этой главы мы опирались лишь на второй закон Ньютона. Следовательно, асе теоремы механики, сформулированные нами выиш, будут верны и в неинерциальных системах отсчета, если к силам, действуюш,им на точки системы, добавить перенскные и кориолисовы силы инерции.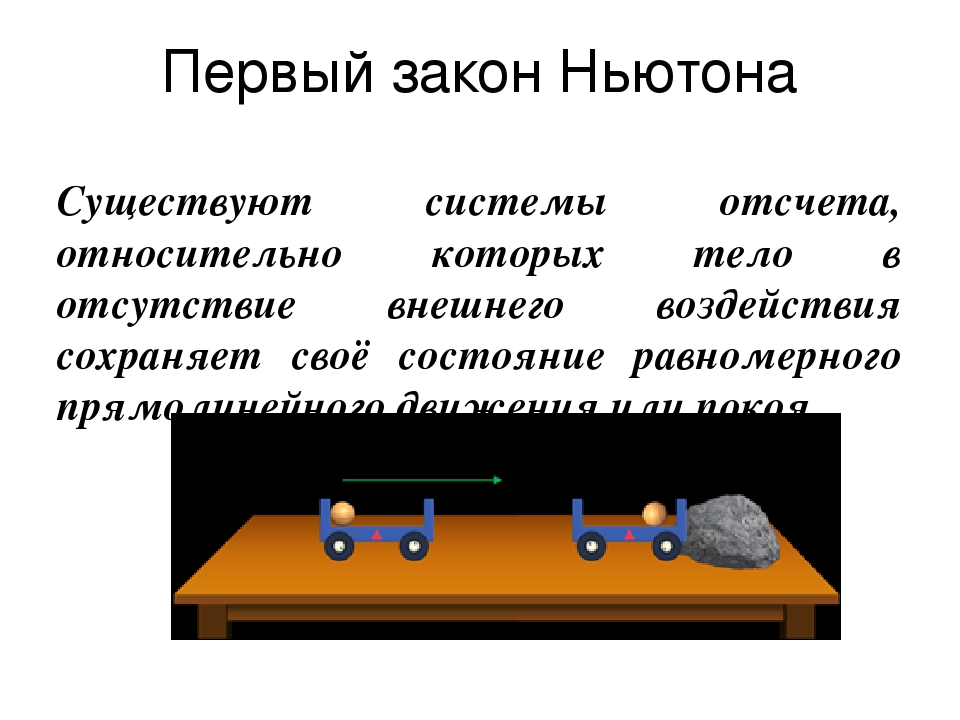 Если силы делятся на
[c.104]
Если силы делятся на
[c.104]
Идеальные связи. Для того чтобы записать второй закон Ньютона для материальной точки, движение которой стеснено механической удерживающей связью, надо к действующим на точку силам добавить реакции связи. Эти реакции сами зависят от характера движения точки, т. е. являются функциями ее скоростей и ускорений. Используя лагранжев формализм для систем, содержащих механические связи, часто удается описать дьижения системы, не вводя в рассмотрение эти функции — реакции связи. [c.154]
Сделаем предварительно следующее замечание об использовании уравнений Лагранжа для описания относительного движения в неинерциальной системе отсчета. В гл. И было установлено, что второй закон Ньютона (а значит, и основные теоремы динамики) может быть использован и в неинерциальной системе отсчета, если к /-Й точке системы (/=],. .., N) помимо действующих сил приложить силы инерции — переносную, Ji ep = = — miWi ер. и кориолисову, Ji кор = — 2т,- (ш х / o, )-
[c. 160]
160]
Второй путь. Неинерциальный наблюдатель мог бы с самого начала добавить к исходным (приложенным) силам переносные и кориолисоры силы инерции. Относительные скорости, входящие в Еыражения для кориолисовых сил, рассматривались бы при этом как неизвестные функции. Далее такой наблюдатель мог бы рассуждать так Теперь, после добавления сил инерции, в моей системе отсчета верен второй закон Ньютона значит, в этой системе верны и уравнения Лагранжа, если в них входит кинетическая энергия видимого мной (т. е. относительного ) движения и если обобщенные силы подсчитываются, исходя из виртуальных перемещений в относительном движении . Поэтому такой наблюдатель мог бы сразу выписать уравнение Лагранжа в своей системе отсчета, подсчитывая кинетическую энергию через свои , т. е. относительные скорости. Но при подсчете обобщенных сил ему пришлось бы принять во внимание и работу сил инерции на виртуальных перемещениях в относительном движении. [c.164]
До сих пор в основе всех наших рассуждений лежали некоторые исходные представления, играющие во всем последующем построении роль аксиом. Мы постулировали, в частности, второй закон Ньютона и при гыводе основ ых законов и теорем механики всегда исходили из него. В настоящей главе, выводя уравнения движения в форме, ковариантной по отношению к любым точечным преобразованиям координат, мы также положили в основу рассуждений второй закон Ньютона и в конечном результате придали ему форму уравнений Лагранжа. В этом смысле второй закон Ньютона оказывается эквивалентным утверждению о том, что движение может быть описано уравнениями (22), а движение в потенциальном поле — уравнениями (29), где L = T—К.
[c.164]
Мы постулировали, в частности, второй закон Ньютона и при гыводе основ ых законов и теорем механики всегда исходили из него. В настоящей главе, выводя уравнения движения в форме, ковариантной по отношению к любым точечным преобразованиям координат, мы также положили в основу рассуждений второй закон Ньютона и в конечном результате придали ему форму уравнений Лагранжа. В этом смысле второй закон Ньютона оказывается эквивалентным утверждению о том, что движение может быть описано уравнениями (22), а движение в потенциальном поле — уравнениями (29), где L = T—К.
[c.164]
До сих пор в этом курсе изучение движения сводилось к составлению и исследованию дифференциальР ых уравнений, описывающих это движение. Исходным для дифференциальных уравнений любого вида был второй закон Ньютона, устанавливающий связь между ускорением и величиной действующей силы в этот же момент. Поэтому в основе дифференциальных уравнений, которыми мы пользовались до сих пор, всегда лежали локальные
[c. 271]
271]
Пример 3.9.1. Ареометр — это цилиндрический сосуд с делениями, по глубине погружения которого в жидкость можно судить о ее плотности. Пусть го — уровень равновесного положения, Р — вес, 5 — площадь поперечного сечения ареометра, р — плотность жидкости. В положении равновесия вес ареометра уравновешен силой Архимеда Р = хоЗрд. Если ареометр имеет меньший уровень погружения г — 2а — X, то архимедова сила станет меньше веса. Без учета сил трения прибора о жидкость проекция уравнения второго закона Ньютона на вертикальное направление примет вид [c.211]
В соответствии с принципами относительности и детерминированности (см. 3.2, 3.3) второй закон Ньютона, связывающий ускорение материальной точки с действующими на нее от других объектов силами, справедлив и имеет одинаковое выражение для всех инерциальных систем отсчета. Если система отсчета неинерциаичьна, то связь между относительным ускорением материальной точки и приложенными к ней силами будет более сложной. [c.274]
[c.274]
Теорема 5.1.1. (Приыщш Даламбера-Лагранжа). Для того чтобы ускорения Ги материальных точек (ш,у,г ), I/ = удовлетворяли второму закону Ньютона в инерциальной системе отсчета под действием активных сил и идеальных двусторонних связей (см. 3.8), необходимо и достаточно выполнение общего уравнения динамики [c.378]
Классическая механика (1980) — [ c.53 , c.55 ]
Основные законы механики (1985) — [ c.40 ]
Курс теоретической механики. Т.1 (1972) — [ c.228 ]
Курс теоретической механики. Т.1 (1982) — [ c.9 , c.16 ]
Курс теоретической механики. Т.2
(1983) — [
c.13
]
Т.2
(1983) — [
c.13
]
Теоретическая механика (1990) — [ c.72 ]
Методы подобия и размерности в механике (1954) — [ c.21 ]
Теоретическая механика (1999) — [ c.87 ]
Курс теоретической механики Том2 Изд2 (1979) — [ c.12 , c.13 , c.152 , c.153 ]
Газовая динамика (1988) — [ c.32 ]
Механика сплошной среды Т.1 (1970) — [ c.136 ]
Справочное руководство по физике (0) — [ c.44 ]
Закон Ньютона – первый, второй, третий.
 Несколько определений
Несколько определенийПервый закон Ньютона
Тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называют свободным. Движение такого тела называется свободным движением или движением по инерции.
Существует система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно
ИЛИ
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго
Такие системы называется инерциальными системами отсчёта — Первый закон Ньютона.
Второй закон Ньютона
Всякое тело оказывает сопротивление при попытке привести его в движение, т.е. придать ему некоторое ускорение. Такое свойство тел называется инертностью. Мера инертности — масса.
Мера инертности — масса.
Система тел, на которую не оказывают влияние другие тела, называется замкнутой системой или изолированной системой. В таких системах тела могут взаимодействовать только друг с другом.Пусть замкнутая система состоит из двух тел (двух материальных точек). Скорость тел и , а и приращение этих скоростей за один и тот же промежуток времени . Векторы и имеют противоположные направления и связаны соотношением . Коэффициенты и постоянны и имеют одинаковые знаки и называются массами или инертными массами тел 1 и 2.
Импульс или количество движения материальной точки — вектор, равный произведению массы точки на её скорость.
Импульс системы — векторная сумма импульсов отдельных материальных точек, из которых состоит система: для системы состоящей из материальных точек.
Импульс изолированной системы остаётся постоянным во времени — Закон сохранения импульса.
Сила (в механике) — всякая причина, которая меняет импульс тела (это качественная характеристика). Количественная характеристика выражается уравнением:
Это уравнение справедливо только в том случае, если m не зависит от скорости.
В инерциальной системе отсчёта производная импульса материальной точки по времени равна действующей на неё силе.
ИЛИ
В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе
Приведённые выше высказывания есть ничто иное как две формулировки второго закона Ньютона. Соответствующее определению закона уравнение — уравнение движения материальной точки.
Третий закон Ньютона
Силы взаимодействия двух материальных точек равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.
ИЛИ
Всякому действию соответствует равное и противоположно направленное противодействие.
ИЛИ
Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: . Или, если система состоит множества материальных точек, то , т.е. материальные точки взаимодействуют попарно. Обе силы направлены вдоль прямой, соединяющей эти точки.
Три этих выражения — различные формулировки Третьего закона Ньютона.
Любая система, движущаяся с ускорением относительно инерциальной системы отсчёта, является неинерциальной.
Post Views: 3 352
Похожее| МЕТЕОРОЛОГ ДЖЕФФ ХЭБИ Законы Ньютона состоят из трех законов, которые помогают описывать и объяснять движение.  Первый закон заключается в том, что движение объектов равномерно, пока не будет выполнено
на другой силой. Этот закон противоречит повседневному опыту, поскольку в повседневном опыте кажется, что естественная склонность к
объекты для замедления и остановки. Например, катание мяча по земле приведет к тому, что мяч замедлится, а затем, в конечном итоге, упадет.
где-нибудь отдохнуть.Причина, по которой он приходит в состояние покоя, заключается в замедлении силы трения. Трение мешает шарику катиться
при равномерном движении. Если на мяч не действуют силы, такие как трение, то он продолжал бы двигаться с постоянной скоростью с течением времени.
Таким образом, согласно первому закону, естественное движение должно двигаться равномерно, пока не будет действовать другая сила. Примеры сил и процессов, которые
Силы размещения, действующие на объект, включают гравитацию, магнетизм, электрические, трение, нормальные, толкающие, тянущие и столкновения. Первый закон заключается в том, что движение объектов равномерно, пока не будет выполнено
на другой силой. Этот закон противоречит повседневному опыту, поскольку в повседневном опыте кажется, что естественная склонность к
объекты для замедления и остановки. Например, катание мяча по земле приведет к тому, что мяч замедлится, а затем, в конечном итоге, упадет.
где-нибудь отдохнуть.Причина, по которой он приходит в состояние покоя, заключается в замедлении силы трения. Трение мешает шарику катиться
при равномерном движении. Если на мяч не действуют силы, такие как трение, то он продолжал бы двигаться с постоянной скоростью с течением времени.
Таким образом, согласно первому закону, естественное движение должно двигаться равномерно, пока не будет действовать другая сила. Примеры сил и процессов, которые
Силы размещения, действующие на объект, включают гравитацию, магнетизм, электрические, трение, нормальные, толкающие, тянущие и столкновения. Второй закон дает математическую связь между силой, массой и ускорением. Третий закон гласит, что для каждого действия существует равная и противоположная реакция. Примером может служить ракета, движущаяся в одном направлении, в то время как выхлоп движется в обратном направлении. Другой пример – толкание воды назад, чтобы двигаться вперед при плавании. |
Как работают законы движения Ньютона
Рядом с E = mc² , F = ma – самое известное уравнение во всей физике.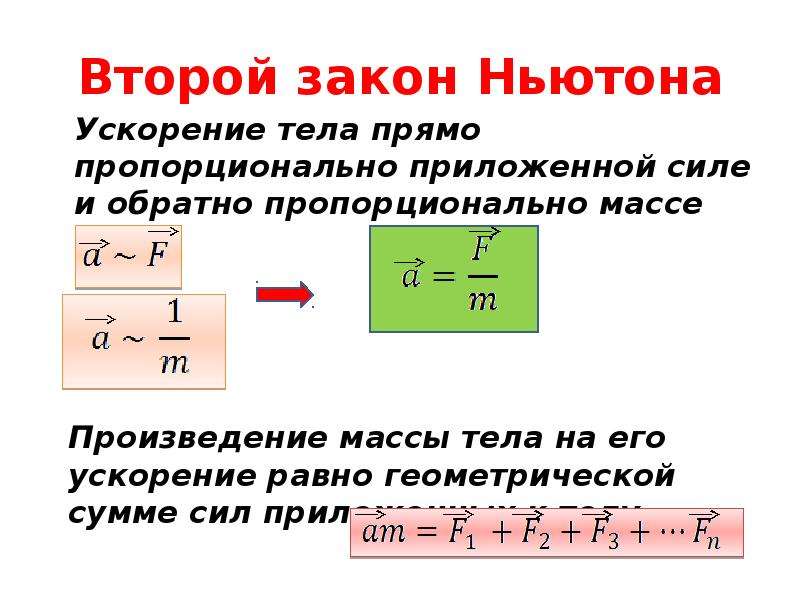 Тем не менее, многие люди остаются озадаченными этим довольно простым алгебраическим выражением. На самом деле это математическое представление второго закона движения Исаака Ньютона, одного из самых важных вкладов великого ученого. «Второй» подразумевает, что существуют другие законы, и, к счастью для студентов и любителей мелочей, есть только два дополнительных закона движения. Все три представлены здесь, используя собственные слова Ньютона:
Тем не менее, многие люди остаются озадаченными этим довольно простым алгебраическим выражением. На самом деле это математическое представление второго закона движения Исаака Ньютона, одного из самых важных вкладов великого ученого. «Второй» подразумевает, что существуют другие законы, и, к счастью для студентов и любителей мелочей, есть только два дополнительных закона движения. Все три представлены здесь, используя собственные слова Ньютона:
- Каждый объект остается в своем состоянии покоя или равномерного движения – по прямой линии, если только он не вынужден изменить это состояние под действием приложенных к нему сил.
- Сила равна изменению количества движения за изменение во времени. Для постоянной массы сила равна массе, умноженной на ускорение.
- На каждое действие есть равная и противоположная реакция.
Эти три закона составляют основу так называемой классической механики или науки о движении тел, на которые действуют силы. Движущиеся тела могут быть большими объектами, такими как вращающиеся луны или планеты, или они могут быть обычными объектами на поверхности Земли, такими как движущиеся транспортные средства или летящие пули. Даже тела в покое – это честная дичь.
Даже тела в покое – это честная дичь.
Классическая механика начинает разваливаться, когда она пытается описать движение очень маленьких тел, таких как электроны. Физикам пришлось создать новую парадигму, известную как квантовая механика , для описания поведения объектов на атомном и субатомном уровне.
Но квантовая механика выходит за рамки этой статьи. В центре нашего внимания будет классическая механика и три закона Ньютона. Мы подробно рассмотрим каждый из них как с теоретической, так и с практической точки зрения.Мы также обсудим историю этих законов, потому что то, как Ньютон пришел к своим выводам, так же важно, как и сами выводы. Лучше всего начинать с самого начала – с первого закона Ньютона.
Законы Ньютона о браке | The New Yorker
ФОТО: Дж.Я хотел бы, чтобы мы могли вывести остальные явления природы с помощью тех же рассуждений из механических принципов.
– Сэр Исаак Ньютон, «Математические основы естественной философии»
 R. EYERMAN / LIFE / GETTY
R. EYERMAN / LIFE / GETTYЗАКОН I: Движущееся тело будет оставаться в движении. Тело в состоянии покоя спросят, каковы его планы на день.
Первый закон касается прежде всего инерции, которую часто ошибочно называют «расслабляющей», и различных способов, которыми одно тело может воздействовать на другое инертное (и совершенно удовлетворенное) тело. И наоборот, он утверждает, что движущееся тело будет удерживаться в движении со списком поручений, написанным на обратной стороне конверта, прежде чем это тело «станет одним целым с диваном до конца дня», что кажется ненужной характеристикой.Также известен как «Принцип субботы».
Покоящийся объект не начнет двигаться, если на него не действует неуравновешенная сила. Но определенно не используйте слово «неуравновешенный». Это не сработает для объекта. Кроме того, любую силу, которая заставляет другое тело переходить из состояния инерции в «попытку, может быть, чего-то достичь сегодня», технически можно измерить, описав ее величину и направление , но никогда не описать величину силы.
Когда движущийся объект наконец останавливается (на много часов позже, чем хотелось) и становится ясно, что объект забыл один элемент (I), который был написан на другой стороне конверта (E), он получит ноль (0) баллов за то, что он запомнил и ожидал в пробке (T), благодаря провалу с Waze (W), мы можем сказать, что (E – I) ( T + W) = 0 .
ЗАКОН II: Чем тяжелее объект, тем больше сила, необходимая для его перемещения, особенно если он отказывается двигаться, из-за ошибочной попытки поставить какую-то точку.
Второй закон гласит, что чем тяжелее объект физически, умственно и эмоционально, тем сильнее на него действует инерция, и тем больше объект может ожидать, что объект будет брошен ему в лицо, если, не дай Бог, объект откажется. вставать с постели на три дня после потери единственной работы, которую объект когда-либо любил.
Противодействующая сила, создаваемая инертным объектом, зависит не только от его буквальной массы, которая увеличивается из-за сил тяжести, времени, слишком большого выноса и слабой депрессии, но также из-за его тенденции активно сопротивляться изменениям. Эта тенденция связана либо с постоянным и необоснованным характером сил, действующих на него, либо с психологическим отвращением к тому, чтобы ему говорили, что делать, из-за какой-то странной вещи с его отцом, в зависимости от того, кого вы спрашиваете.
Эта тенденция связана либо с постоянным и необоснованным характером сил, действующих на него, либо с психологическим отвращением к тому, чтобы ему говорили, что делать, из-за какой-то странной вещи с его отцом, в зависимости от того, кого вы спрашиваете.
Чем больше сопротивления предоставляется, тем сильнее сила, необходимая для его преодоления, что часто приводит к взаимному структурному повреждению, также известному как «высказывание вещей, которые вы не можете вернуть» и «хлопанье ящика для столового серебра с такой силой, что вы сломаете его. функция мягкого закрытия.”
Неизбежность этого закона и его последствия могут быть выражены в виде математического уравнения F = ML , где F = Fuck и ML = My Life.
ЗАКОН III: На каждое действие существует противоположная и приводящая в замешательство реакция.
Третий закон гласит, что один объект всегда будет иметь совершенно непропорциональную отрицательную реакцию на действие другого. Это называется заблуждением из ниоткуда и основано на иллюзии, что реакции являются ответами только на действию под рукой, а не к каждому аналогичному действию, которое произошло во всех предыдущих взаимодействиях между двумя объектами.Это часто называют кумулятивным индексом усталости от вашей чуши.
Это называется заблуждением из ниоткуда и основано на иллюзии, что реакции являются ответами только на действию под рукой, а не к каждому аналогичному действию, которое произошло во всех предыдущих взаимодействиях между двумя объектами.Это часто называют кумулятивным индексом усталости от вашей чуши.
Возьмем, к примеру, движущийся объект, который пытается на мгновение отдохнуть, чтобы не плакать перед детьми, как однажды, и случайно запирает дверь в ванную со звуком. Хотя кажется математически невозможным, что это вызовет двух с половиной часовую драку, реакция уместна, если исправить тот факт, что это вызывает проблемы с доверием с момента обнаружения секретной контрольной учетной записи, даже если это было миллион лет назад, или 10 6 (y) .
Хотя действие встречается гораздо реже, оно также может вызвать неожиданную положительную реакцию. Рассмотрим автомобиль, путешествующий из ресторана в дом: на ускорение влияют масса и внешнее трение, но на него также влияют силы внутри автомобиля.
Если два тела покоятся внутри – одно по аномалии расписания; удерживается вместе временем, взаимным расширением массы и неопределимой константой любви – одно тело может замечать что-то в другом теле, например, как оно притворяется, что знает слова песни по радио, и это может занять другое тело. за руку, улыбнитесь и предложите сменить направление, потому что натурщик не ждет их в течение часа, а сегодня вечером, на этот раз, ни одно тело вообще не толкает и не тянет.
Учимся жить по законам движения
Освободившись от тисков земного притяжения, космонавты попадают в живой учебник физики. Законы движения ускользали от лучших умов мира на протяжении тысячелетий, пока Исаак Ньютон не открыл их в семнадцатом веке. Но в условиях невесомости орбиты эти законы очевидны – и часто очень неприятны.
Российский космонавт Юрий Гагарин во время своего первого обращения вокруг Земли в 1961 году был первым, кто испытал на себе практические эффекты.Он отложил карандаш, пока писал свой журнал. Повинуясь первому закону Ньютона – тому же принципу равномерного движения, который заставляет планеты вращаться вокруг нашего Солнца – карандаш парил вне досягаемости: Гагарин должен был завершить свой журнал, говоря в магнитофон. В настоящее время космонавты держат оборудование на липучках или эластичных ремнях.
Повинуясь первому закону Ньютона – тому же принципу равномерного движения, который заставляет планеты вращаться вокруг нашего Солнца – карандаш парил вне досягаемости: Гагарин должен был завершить свой журнал, говоря в магнитофон. В настоящее время космонавты держат оборудование на липучках или эластичных ремнях.
Второй закон Ньютона гласит, что сила необходима для ускорения или замедления тела. На практике это означает, что космонавты должны научиться осторожно перемещаться по космическому кораблю, иначе они будут просто беспомощно парить в воздухе.И как только астронавты начинают двигаться, они должны не забывать останавливаться, когда они приближаются к тому месту, где они хотят быть. В противном случае они будут продолжать, пока не ударит что-нибудь – или кого-нибудь. Новички, как правило, собирают много синяков. Некоторые животные, летавшие в космос, так и не научились – одна пара новорожденных перепелов не могла адаптироваться к жизни на российской космической станции «Мир» и умерла всего через несколько дней.
Третий закон Ньютона гласит, что на каждое действие существует равное и противоположное противодействие. Это также имеет очень очевидные последствия для космонавтов: если они попытаются повернуть винт, не прикрепляясь к стене, вместо этого они обнаружат, что скручивают.Реакция даже на самые легкие действия – например, набор текста на клавиатуре компьютера – заставит космонавта уплыть. Вот почему рабочие места на МКС щедро снабжены удерживающими петлями, где экипаж может закрепить ноги.
Дело не в том, что законы движения на Земле отличаются от законов движения в космосе. Но гравитационное поле Земли обладает такой подавляющей силой, что маскирует их точное воздействие. А гравитация является неотъемлемой частью всех видов явлений, которые мы принимаем как должное.Например, воздух в наших домах циркулирует естественным образом: горячий воздух поднимается вверх, потому что он легче холодного, и образуются конвекционные потоки. На орбите нет ничего легче, чем что-либо другое, поэтому обычные конвекционные потоки существовать не могут. Без вентилятора спящие космонавты задохнулись бы от углекислого газа, который скапливается вокруг их лиц.
Без вентилятора спящие космонавты задохнулись бы от углекислого газа, который скапливается вокруг их лиц.
Точно так же невесомое пламя ведет себя совсем не так, как его земные аналоги. Вместо мерцающего столба горячего газа, различающегося по цвету и составу за счет гравитационных эффектов, пламя на орбите представляет собой небольшую синюю сферу.(И лучше всего было ограничиться лабораторным экспериментом: настоящий пожар на борту космического корабля – это то, чего опасаются все астронавты.)
Сама МКС, конечно же, является прекрасным выражением законов движения. Борясь с веками интуиции и здравого смысла, Ньютон понял, что пуля, выпущенная из ружья, должна продолжать двигаться бесконечно. Конечно, на Земле сила тяжести вскоре притягивает его к земле, и трение атмосферы в любом случае замедлит снаряд. Но чем быстрее вы выстрелите, тем дальше она пролетит, прежде чем упадет на землю.И если вы можете разогнать свою пулю – или, что более полезно, ваш космический корабль – до скорости около 8 км / с, она никогда не завершит свою траекторию. Вместо этого он будет вращаться вокруг Земли в состоянии постоянного свободного падения. Его скорость в точности нейтрализует притяжение Земли: это создает одновременно неприятный и волнующий мир, с которым астронавты борются и наслаждаются.
Вместо этого он будет вращаться вокруг Земли в состоянии постоянного свободного падения. Его скорость в точности нейтрализует притяжение Земли: это создает одновременно неприятный и волнующий мир, с которым астронавты борются и наслаждаются.
Спасибо за лайк
Вам уже понравилась эта страница, вам может понравиться только один раз!
Законы Ньютона – Физика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Миссис Лигон – Наука 7/8 / Законы движения Ньютона
Сэр Исаак Ньютон жил в 1600-х годах. Как и все ученые, он наблюдал за окружающим миром. Некоторые из его наблюдений касались движения. Его наблюдения со временем подкреплялись большим количеством данных; и теперь мы называем это законами движения Ньютона. Его законы движения объясняют покой, постоянное движение, ускоренное движение и описывают, как уравновешенные и неуравновешенные силы действуют, вызывая эти состояния движения.
Некоторые из его наблюдений касались движения. Его наблюдения со временем подкреплялись большим количеством данных; и теперь мы называем это законами движения Ньютона. Его законы движения объясняют покой, постоянное движение, ускоренное движение и описывают, как уравновешенные и неуравновешенные силы действуют, вызывая эти состояния движения.
Просмотрите три закона движения:
Первый закон движения Ньютона гласит, что объект в состоянии покоя будет оставаться в состоянии покоя, а объект в движении будет оставаться в движении, пока на него не воздействует внешняя, неуравновешенная внешняя сила.
Объект не изменит своего движения, если на него не действует сила.
Неподвижный объект остается неподвижным, пока что-нибудь не толкнет или не потянет его.
Движущийся объект продолжает двигаться с той же скоростью, пока что-то не толкает или не тянет его, чтобы изменить его скорость или направление.

Все объекты сопротивляются изменению своего движения.
Эта тенденция сопротивляться изменению движения называется инерцией.
Чем больше масса объекта, тем больше его инерция.
Что делать:
Создание слайд-шоу: заголовок + 3 слайда (по одному для каждого закона)
Выберите вид спорта из утвержденного учителем списка
Включите объяснение того, как спорт демонстрирует или описывает закон движения. Включите изображение (с правильными атрибутами), иллюстрирующее объяснение.
Как вас будут оценивать:
Это считается ТЕСТОВОЙ оценкой!
Ваше слайд-шоу будет проверяться на следующие вещи:
Точность и завершенность (62,5% оценки).
 Неполное слайд-шоу или объяснение не будут полностью точными.
Неполное слайд-шоу или объяснение не будут полностью точными.Визуальное обращение (25% оценки). Это включает в себя цвет и тип шрифта, а также организацию слайдов. Правильное написание и грамматика также являются ключом к визуальной привлекательности.
Соответствующие ссылки на фотографии (12.5% от оценки). Изображения должны быть правильно указаны или процитированы с использованием commons.wikimedia.org или search.creativecommons.org
Бонусные баллы будут начислены за совместное использование презентации с классом в установленный срок.
Рубрика будет использоваться 3 раза / один раз для каждого закона движения
| | Эксперт 10 баллов | Квалифицированный Новичок 6 баллов | Новичок 4 балла | |||||
Содержание и точность |
|
|
|
| ||||
| | Эксперт 4 балла | Квалифицированный 3 балла | Новичок 2 балла | Новичок 1 балл | ||||
| | Эксперт 2 балла | | Новичок 1 балл | Новичок
 |


 Уравнение F = m * a. Масса – это количество вещества
объект содержит. Часто это выражается в граммах или килограммах. Ускорение – это изменение скорости. Примеры ускорений
включают ускорение свободного падения, более сильное нажатие на объект, использование топлива для ускорения движения, замедление из-за трения и
круговое движение. Термин чистая сила означает результат действия всех сил на объект в один момент.Перемещение объекта вверх
рампа будет включать в себя несколько сил, таких как гравитация, нормаль, трение и толкание объекта.
Уравнение F = m * a. Масса – это количество вещества
объект содержит. Часто это выражается в граммах или килограммах. Ускорение – это изменение скорости. Примеры ускорений
включают ускорение свободного падения, более сильное нажатие на объект, использование топлива для ускорения движения, замедление из-за трения и
круговое движение. Термин чистая сила означает результат действия всех сил на объект в один момент.Перемещение объекта вверх
рампа будет включать в себя несколько сил, таких как гравитация, нормаль, трение и толкание объекта.
 Неполное слайд-шоу или объяснение не будут полностью точными.
Неполное слайд-шоу или объяснение не будут полностью точными.