Вопрос 4
Равнопеременное движение. Уравнения скорости и перемещения при равнопеременном движении. Графическое представление равнопеременного движения.
Краткий ответ
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Скорость при равноускоренном движении по прямой — это начальная скорость тела плюс ускорение данного тела умноженное на время в пути
Перемещение при равноускоренном движении по прямой — это расстояние пройденное телом по прямой (расстояние между начальной и конечной точками движения)
Обозначения:
— Перемещение тела при равноускоренном движении по прямой
— Начальная скорость тела
— Скорость тела при равноускоренном движении по прямой
— Ускорение тела
— Время движения тела
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом.
Зависимость физических величин выражают при помощи функций. Обозначают:
(t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени.
При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.
Для характеристики неравномерного движения вводится понятие средней скорости:
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.В физике наибольший интерес представляет не средняя, а мгновенная скорость
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.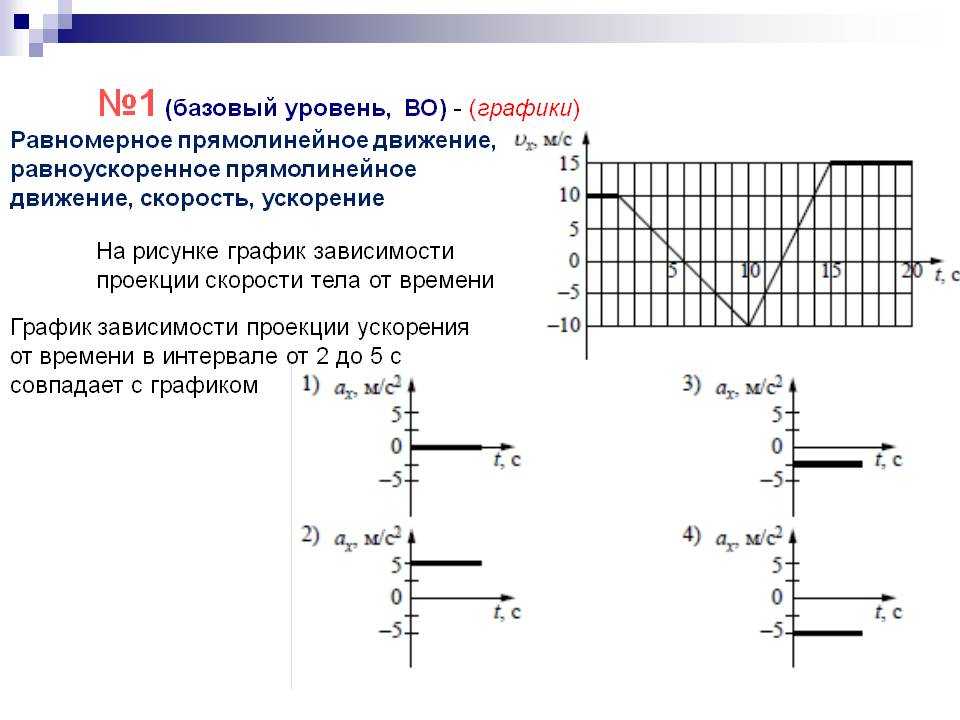
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным
Скорость при равноускоренном движении по прямой — это начальная скорость тела плюс ускорение данного тела умноженное на время в пути
Перемещение при равноускоренном движении по прямой — это расстояние пройденное телом по прямой (расстояние между начальной и конечной точками движения)
Обозначения:
— Перемещение тела при равноускоренном движении по прямой
— Начальная скорость тела
— Скорость тела при равноускоренном движении по прямой
— Ускорение тела
— Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
– если известны начальная, конечная скорости движения и ускорение.
– если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
(t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
§ 4. Ускорение
Скорость частицы может изменяться со временем как по величине, так и по направлению. Физическая величина, характеризующая быстроту изменения скорости по модулю и направлению, называется ускорением частицы.
Рассмотрим
движение, при котором все участки
траектории частицы лежат в одной
плоскости. Пусть вектор
задает скорость частицы в момент времени
.
Через промежуток времени
частица оказалась в другой точке
траектории и приобрела скорость ,
отличную от
как по модулю, так и по направлению
(рис.
4.1).
Средним ускорением неравномерного движения в интервале времени от до называется векторная величина, равная отношению изменения скорости к интервалу времени :
(4.1)
Рис. 4.1
Мгновенным ускорением точки (ускорением в данный момент времени) называется предел среднего ускорения при стремлении промежутка к нулю ( ).
(4.2)
Таким образом, ускорение частицы в момент времени равно производной от вектора скорости по времени. Вектор направлен так же, как и вектор . Зная кинематические уравнения движения частицы (2.5) или (2.6), можно найти зависимость скорости от времени , а затем ускорение в любой момент времени.
С
учетом выражений (2.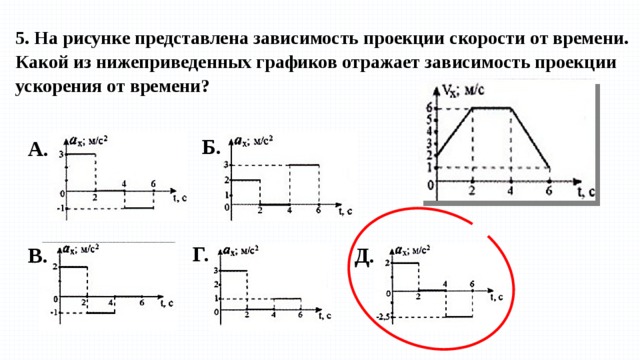
9) и (4.2)
(4.3)
где – проекции вектора скорости на неподвижные координатные оси. Таким образом, проекция ускорения на координатную ось равна первой производной по времени проекции скорости на эту ось.
Модуль ускорения
(4.4)
Если известна траектория частицы, то через любую точку можно провести две оси: , направленную по касательной к траектории в сторону вектора , и ось , направленную по нормали к траектории к центру кривизны траектории в данной точке (т.е. центру окружности, дугой которой является элементарный отрезок траектории частицы, содержащий данную точку) (рис. 4.2). Тогда вектор можно представить в виде суммы двух составляющих и :
(4.5)
где – орты осей
и
,
и
– проекции векторов
и
на эти оси.
Рис. 4.2
Вектор
называют тангенциальным или касательным ускорением, вектор
–
Можно показать, что тангенциальная составляющая ускорения
(4.6)
т.е. равна первой производной по времени от модуля скорости. Т.о., тангенциальное ускорение характеризует быстроту изменения модуля скорости частицы. При ускоренном движении , проекция положительна, вектор совпадает по направлению со скоростью частицы. При замедленном движении , проекция отрицательна, вектор противоположен по направлению . При равномерном движении тангенциальное ускорение равно нулю.
Нормальная составляющая ускорения
,
(4.
7)
где – радиус кривизны траектории в данной точке. Нормальное ускорение характеризует быстроту изменения направления скорости частицы. Проекция всегда положительна, вектор всегда направлен к центру кривизны. При прямолинейном движении нормальное ускорение отсутствует.
Таким образом, вектор полного ускорения определяется формулой (4.5), а модуль – соотношением
(4.8)
Пример 4.1. Частица движется в положительном направлении оси так, что ее скорость меняется по закону , где – положительная постоянная. Имея в виду, что в момент она находится в точке , найти зависимость от времени ускорения частицы.
Решение. По определению
Так как по условию задачи ускорение и элементарное приращение скорости направлены по оси , можно написать, что модуль ускорения
(4.
9)
Найдем зависимость модуля скорости частицы от времени .
Поскольку движение частицы происходит вдоль оси , то учитывая закон изменения ее скорости
, (4.10)
разделяем переменные
(4.11)
Проинтегрировав выражение (4.11), найдем зависимость координаты частицы от времени :
(4.12)
Подставив выражение (4.12) в соотношение (4.10), получаем
(4.13)
Подставляя выражение (4.13) в соотношение (4.9), получаем окончательно
откуда
видно, что ускорение частицы не зависит
от времени.
Ответ:
Вопросы:
1. Дать определения векторов средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения. Каковы направления этих векторов?
2. Что характеризует тангенциальное ускорение? Каков его модуль?
3. Что характеризует нормальное ускорение? Каковы его направление и модуль?
4. При каком движении отсутствует нормальное ускорение? тангенциальное?
Лекция 3. Кинематика вращательного движения твердого тела
Графики скорости-времени: значение формы
Наше исследование одномерной кинематики было связано с многочисленными средствами, с помощью которых может быть представлено движение объектов. К таким средствам относятся использование слов, использование диаграмм, использование чисел, использование уравнений и использование графиков. Урок 4 посвящен использованию графиков зависимости скорости от времени для описания движения.
Как мы узнаем, особенности движения объектов демонстрируются формой и наклоном линий на графике зависимости скорости от времени. Первая часть этого урока включает в себя изучение взаимосвязи между формой v-t графика и движением объекта.
Постоянная скорость в сравнении с изменяющейся скоростью
Рассмотрим автомобиль, движущийся с постоянной скоростью вправо (+), скажем, +10 м/с. Как вы узнали из предыдущего урока, автомобиль, движущийся с постоянной скоростью, — это автомобиль с нулевым ускорением.
Если построить график зависимости скорости от времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как постоянная положительная скорость, приводит к линии с нулевым наклоном (горизонтальная линия имеет нулевой наклон) при построении графика зависимости скорости от времени. Кроме того, на график наносятся только положительные значения скорости, соответствующие движению с положительной скоростью.
Теперь рассмотрим автомобиль, движущийся вправо (+) с изменяющейся скоростью, то есть автомобиль, который движется вправо, но ускоряется или ускоряется . Поскольку автомобиль движется в положительном направлении и ускоряется, говорят, что автомобиль имеет положительное ускорение .
Если построить график зависимости скорости от времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как изменение положительной скорости, приводит к наклонной линии при построении графика зависимости скорости от времени. Наклон линии положительный, что соответствует положительному ускорению. Кроме того, на график наносятся только положительные значения скорости, соответствующие движению с положительной скоростью.
Графики зависимости скорости от времени для двух типов движения — постоянной скорости и изменяющейся скорости (ускорения) — можно обобщить следующим образом.
| Положительная скорость Нулевое ускорение | Положительная скорость Положительное ускорение |
|---|---|
Значение уклона
Формы графиков зависимости скорости от времени для этих двух основных типов движения — движения с постоянной скоростью и движения с ускорением (т.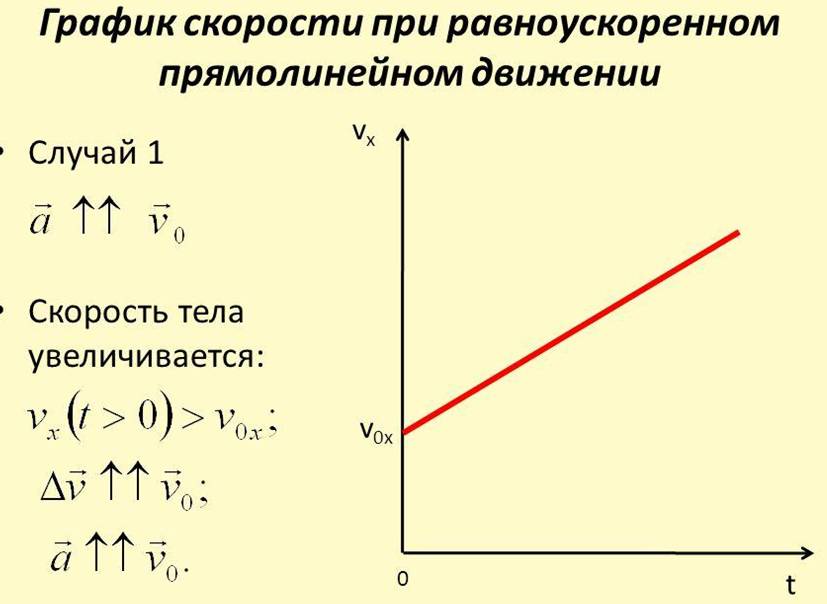
е. с изменением скорости) — раскрывают важный принцип. Принцип заключается в том, что наклон линии на графике скорость-время дает полезную информацию об ускорении объекта. Если ускорение равно нулю, то наклон равен нулю (т. Е. Горизонтальная линия). Если ускорение положительное, то и наклон положительный (т. е. линия с наклоном вверх). Если ускорение отрицательное, то и наклон отрицательный (т. е. линия с наклоном вниз). Этот самый принцип может быть распространен на любое мыслимое движение.
Наклон графика зависимости скорости от времени дает информацию об ускорении объекта. Но как определить, движется ли объект в положительном направлении (т. е. с положительной скоростью) или в отрицательном направлении (т. е. с отрицательной скоростью)? И как определить, ускоряется объект или замедляется?
Ответы на эти вопросы зависят от способности человека читать график. Поскольку график представляет собой график зависимости скорости от времени, скорость будет положительной всякий раз, когда линия лежит в положительной области (над осью X) графика.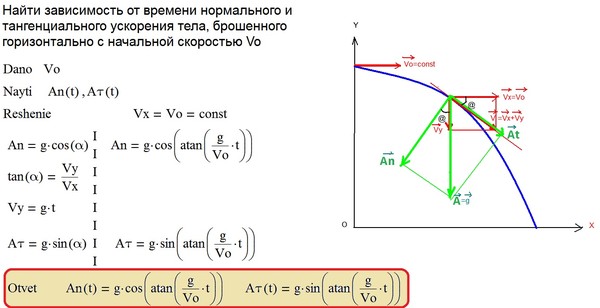
Точно так же скорость будет отрицательной всякий раз, когда линия лежит в отрицательной области (ниже оси x) графика. Как вы узнали из Урока 1, положительная скорость означает, что объект движется в положительном направлении; а отрицательная скорость означает, что объект движется в отрицательном направлении. Таким образом, известно, что объект движется в положительном направлении, если линия расположена в положительной области графика (независимо от того, имеет ли она наклон вверх или вниз). А известно, что объект движется в отрицательном направлении, если линия расположена в отрицательной области графика (независимо от того, идет ли она с наклоном вверх или вниз). И, наконец, если линия пересекает ось абсцисс из положительной области графика в отрицательную (или наоборот), то объект изменил направление.
Ускорение или замедление
Как теперь определить, ускоряется объект или замедляется? Ускорение означает, что величина (или числовое значение) скорости становится большой.
Например, ускоряется объект, скорость которого изменяется от +3 м/с до +9 м/с. Точно так же ускоряется и объект, скорость которого изменяется от -3 м/с до -9 м/с. В каждом случае величина скорости (само число, а не знак или направление) увеличивается; скорость становится больше. Учитывая этот факт, можно было бы предположить, что объект ускоряется, если линия на графике скорость-время изменяется от точки, близкой к точке с нулевой скоростью, к точке, расположенной дальше от точки с нулевой скоростью. То есть, если линия удаляется дальше от оси x (точка нулевой скорости), то объект ускоряется. И наоборот, если линия приближается к оси x, то объект замедляется.
См. анимацию различных движений с сопровождающими графиками
Проверьте свое понимание
1. Рассмотрите график справа. Объект, движение которого представлено на этом графике, это .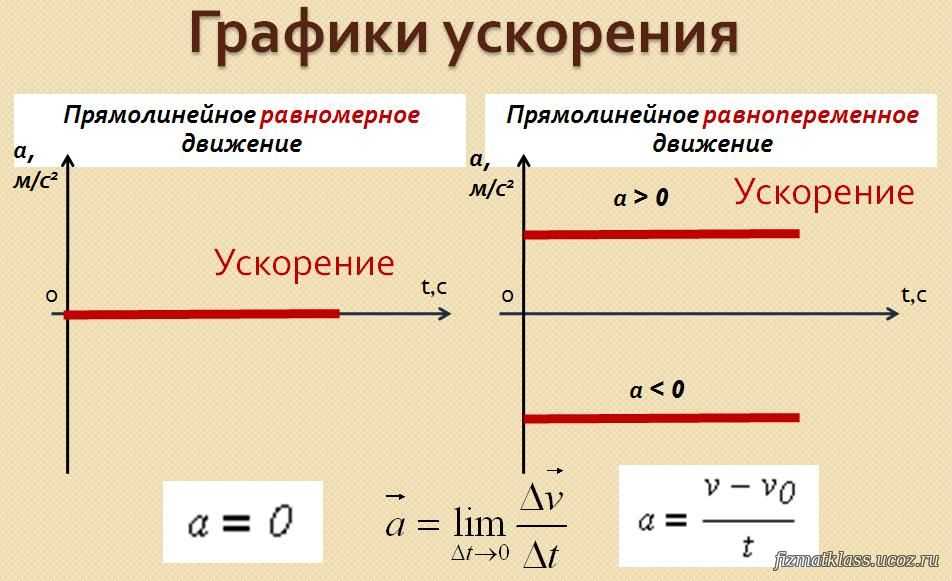
.. (включая все верные):
- , движущиеся в положительном направлении.
- движется с постоянной скоростью.
- движется с отрицательной скоростью.
- замедляется.
- изменение направления.
- ускоряется.
- движется с положительным ускорением.
- движется с постоянным ускорением.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Graph That Motion или наших Graphs and Ramps Interactives. Каждый из них находится в разделе Physics Interactives на нашем веб-сайте и позволяет учащимся применять концепции кинематических графиков (как положение-время, так и скорость-время) для описания движения объектов.
Посетите: Постройте график этого движения || Графики и линейные изменения
Следующий раздел:
Перейти к следующему уроку:
Разница между скоростью и ускорением (со сравнительной таблицей)
Скорость и ускорение — два ключевых понятия, которые всегда обсуждаются при изучении движения. Скорость можно понимать как скорость тела, движущегося в определенном направлении, тогда как ускорение — любое изменение скорости объекта во времени.
Движение подразумевает движение; это акт движения или, точнее, изменение положения тела во времени. Всякий раз, когда вы идете, бежите или едете, вы на самом деле находитесь в движении, и не только это, полет птиц, плавание рыб, вытекание воды из реки, падение листьев с деревьев, вращение и обращение земли — это тоже движение.
Для неспециалиста эти два термина — одно и то же, но в физике между скоростью и ускорением есть тонкая разница.
Содержание: Скорость и ускорение
- Сравнительная таблица
- Определение
- Ключевые отличия
- Сходства
- Заключение
Сравнительная таблица
| База для сравнения | Скорость | Ускорение |
|---|---|---|
| Значение | Скорость означает скорость объекта в заданном направлении. | Ускорение относится к любому изменению скорости объекта во времени. 92 |
Определение скорости
В физике скорость описывается как векторное измерение, поскольку она имеет как величину, так и направление, где величина представляет скорость, а направление показывает направление движения.
Скорость — это физическая величина, описывающая скорость, с которой движется объект, а также его направление. Он подразумевает скорость изменения положения кого-либо или чего-либо во времени, т. е. насколько быстро объект с течением времени перемещается из одной точки в другую.
Можно изменить скорость движущегося тела, изменив его скорость, направление или и то, и другое. В любой точке скорость тела касается его пути в этой точке.
Определение ускорения
Мера изменения скорости во времени называется ускорением. Всякий раз, когда объект меняет свою скорость, говорят, что он ускоряется. Это векторное выражение, которое имеет как величину, так и направление. Говорят, что объект ускоряется, когда его скорость увеличивается или уменьшается, или изменяется направление движения, или и то, и другое. Он связан с тем, как движение тела изменяется во времени.
Изменение скорости и направления объекта указывается компонентом ускорения, т.е. направлением. Когда направление ускорения параллельно скорости, считается, что объект ускоряется или его скорость увеличивается. Однако, когда направление ускорения антипараллельно скорости, объект замедляется или его скорость замедляется. Более того, если составляющая ускорения перпендикулярна скорости, то она отражает степень изменения направления объекта. Может быть два типа ускорения, а именно:
- Центростремительное ускорение : Когда объект движется с постоянной скоростью по кругу, подобно вращению Земли, это ускорение называется центростремительным ускорением, потому что происходит изменение направления объекта.
- Тангенциальное ускорение : Когда направление движения не изменяется, но скорость меняется со временем, это называется тангенциальным ускорением.
Ключевые различия между скоростью и ускорением
Разницу между скоростью и ускорением можно четко определить по следующим основаниям:
- Скорость объекта относится к скорости в определенном направлении. Ускорение подразумевает любое изменение скорости объекта по отношению ко времени.
- Скорость есть не что иное, как скорость изменения смещения. С другой стороны, ускорение — это скорость изменения скорости во времени.
- Скорость определяет скорость движущегося объекта вместе с направлением движения.
