График постоянного ускорения: скорость в зависимости от времени: подробная информация –
В этой статье мы изучим зависимость скорости графика постоянного ускорения от времени, что является одним из важных аспектов определения значения ускорения.
Поскольку термин «константа» указывает на устойчивость, график зависимости скорости от времени на графике постоянного ускорения указывает на то, что ускорение остается постоянным на протяжении всего движения, только мы можем найти изменение скорости тела в течение определенного периода, измеряя наклон построенной кривой график VT .
Теперь давайте сосредоточимся на различных аспектах графика зависимости скорости от времени на графике постоянного ускорения, что является основным моментом.
Как выглядит постоянное ускорение на графике зависимости скорости от времениГрафик постоянного ускорения будет линейным.
Термин «константа» указывает на то, что во время определенного движения не будет изменения ускорения. Если объект подвергается этому типу ускорения, то построенный график будет линейным с наклоном; эти кривые используются для определения значения только переменной скорости.
Теперь давайте знать о скорости и постоянной отношение ускорения.
Что происходит со скоростью при постоянном ускоренииИзвестно, что если тело ускоряется, происходит изменение скорости.
- Ускоряющееся тело меняет скорость на равную величину за каждую секунду. Известно, что это постоянное ускорение, поскольку скорость изменяется на одинаковую величину в течение определенного периода. Не следует сравнивать это с телом, имеющим постоянную скорость.
- Если мы рассмотрим график VT, это ускорение рассчитывается, зная наклон линии. Если эта линия горизонтальна, эта скорость будет постоянной, а ускорение будет нулевым.
Пора изучить график постоянного ускорения.
Чтобы узнать, как найти среднюю скорость на графике AT, проверьте здесь.
- Как найти среднюю скорость на графике времени разгона
Мы можем интерпретировать график скорость-время или график VT, наблюдая за формой кривой на его графике.
- Если график VT имеет параболическую кривую положения, он имеет постоянное ускорение.
- Это называется графиком постоянного ускорения.
- Кроме того, это достигается, когда постоянное ускорение указывает на непрерывное изменение скорости движения.
- При построении графика наклон будет постепенно увеличиваться.
- Константа также гарантирует, что график VT имеет постоянный наклон.
Постоянное ускорение может быть прямым или параболическим, в зависимости от значений.
Как вы интерпретируете график зависимости ускорения от времениМы можем измерить величину изменения скорости по графику зависимости ускорения от времени.
Когда мы используем значения наблюдаемого движения и наносим его на график постоянного ускорения От времени площадь под полученной кривой говорит об изменении скорости объекта. Другими словами, мы можем сказать, что площадь под кривой для периода будет равна изменению скорости в течение этого интервала.
График AT предназначен для определения изменения скорости.
Как вы изобразите скорость против времениЕсть две возможности построить график VT, которые кратко описаны ниже.
- Когда значения нанесены на график VT, будет два типа движения, которые классифицируются как постоянные и переменные скорость.
- Наклон графика зависимости скорости от времени дает ускорение. Это означает, что наклон в определенный период указывает значение ускорения тела в этой точке.
- Если склон крутой или крутой, тело будет иметь быструю переменную скорость.
- Если склон пологий, то будет постоянная скорость.
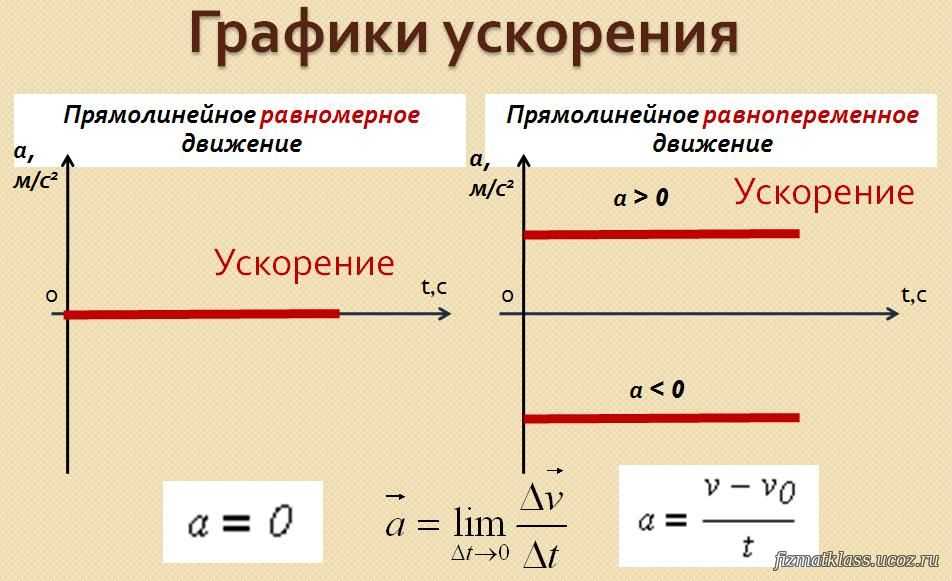
- Два других случая заключаются в том, что если наклон положительный и восходящий, то ускорение положительное.
- Если значение наклона графика VT отрицательное и построено вниз, ускорение будет отрицательным. Следующее изображение может быть примером движения.
Бесплатные изображения Pixabay
Теперь давайте получим некоторую информацию о графике постоянного ускорения в зависимости от времени.
Важные случаи зависимости скорости от времени на графике постоянного ускоренияТри основных случая, касающихся зависимости скорости от времени на графике ускорения, приведены ниже.
Случай 1: графики VT с постоянной скоростью для случая нулевого ускорения- На графике VT ось Y обозначает скорость, а ось X обозначает время.
- Из графика, показанного ниже, мы можем интерпретировать, что V постоянна на всем временном интервале.
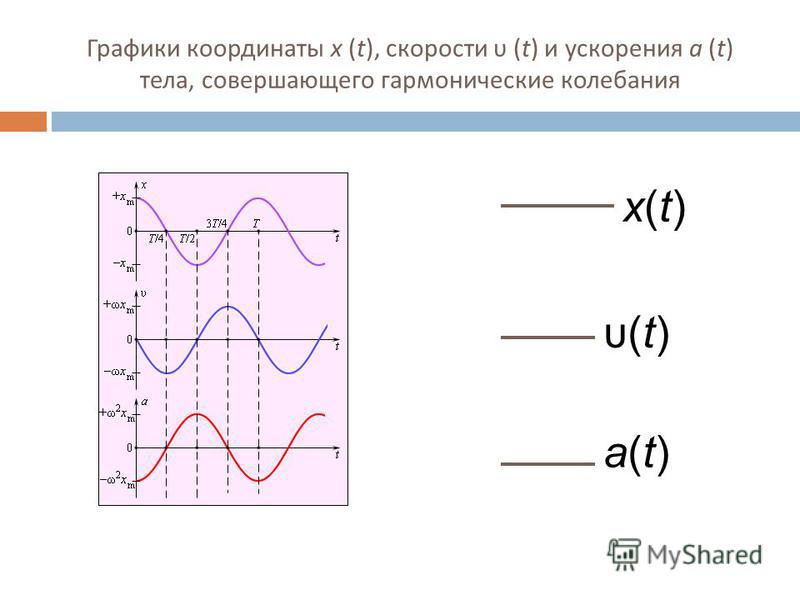
- Несмотря на то, что время меняется, скорость будет постоянной в каждой точке графика.
- Здесь начальная скорость положительна, потому что мы получаем другой график, когда выбираем отрицательную начальную скорость.
- Пример: ускорение объекта равно нулю, а скорость постоянна со скоростью 6 м / с при t = 0, тогда она остается постоянной на протяжении всего интервала.
Другими словами, предположим, что ускорение и константа будут положительными, а начальное V равно нулю. В этом случае скорость объекта увеличивается, и мы получаем линейную кривую значений при вычислении с помощью следующего уравнения.
V = u + при
Здесь u = 0, то приведенное выше уравнение принимает вид
V = а * т
Изображение: постоянное ускорениеКак показано ниже, наклон области под графиком будет измерять величину ускорения.
Когда происходит увеличение ускорения, полученный график VT будет кривой, которую можно измерить, используя формулу, как показано ниже:
V = и + (а * т)
Здесь u = 0, то приведенное выше уравнение принимает вид
V = а * т
- Мы знаем, что ускорение – это функция времени; поэтому мы получаем кривую на графике VT.
- Речь шла только об увеличении ускорения; график замедления будет отличаться от положительное ускорение график зависимости от времени.
- Например, если ускорение тела является функцией t и начальной скоростью U = 0, график будет кривой. Наклон графика VT в любой момент периода дает ускорение в этот момент.
Поскольку ускорение непрерывно увеличивается с увеличением t, величина его наклона также будет увеличиваться.
Площадь, которую мы получаем, когда строим график зависимости скорости от времени, представляет собой изменение положения тела.
Когда мы хотим вычислить ускорение на графике скорость-время, мы наносим его значения. После нанесения значений на график мы получаем определенную область под графиком, которая обозначает смещение, которое может даже быть известно как изменение положения тела, когда оно находится в движении.
Каков наклон графика скорость-время?Мы знаем, что можем рассчитать значение ускорения по типичному графику скорость-время.
Когда мы строим график зависимости скорости от времени, мы найдем значение ускорения тела, движущегося по пути; поэтому наклон графика VT представляет собой ускорение тела. Когда мы вычисляем уклон в определенное время, это указывает на ускорение тела в этой точке.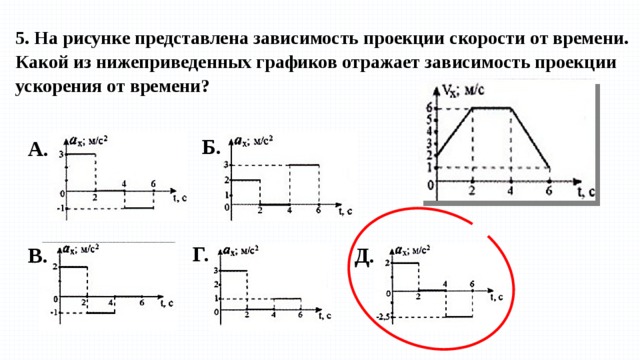
Мы можем интерпретировать график ускорения в зависимости от времени, найдя область под построенным графиком.
Область на графике времени ускорения показывает изменение скорости движущегося тела за определенный период. Исходя из этого, мы можем сказать, что площадь под кривой графика AT примерно равна изменению скорости тела.
Как узнать, что у графика постоянная скорость?Вы должны увидеть много Графики скорость-время интерпретировать его значения.
Если вы рассмотрите любой из графиков VT, и если это прямая или горизонтальная линия, мы можем считать, что он имеет постоянную скорость. Если график отличается от горизонтального, тогда скорость является переменной, а если вы рассматриваете график AT, и он будет равен нулю, то даже в этом случае скорость будет постоянной.
Что происходит со скоростью при постоянном ускорении?Скорость не будет постоянной при постоянном ускорении.
В частности пример движения, если ускорение движения постоянно, то постоянной скорости не будет, потому что постоянное количество в секунду изменит скорость объекта в конкретном движении.
Как изменяется скорость при постоянном ускорении?Скорость будет изменяться, когда тело движется с постоянным ускорением.
Если тело испытывает постоянное ускорение, то скорость этого тела будет постоянно изменяться. Если и скорость, и ускорение находятся в одном направлении, то траектория этого графика будет аналогична графику, построенному без ускорения.
Как вы можете интерпретировать постоянство ускорения на основе графика зависимости скорости от времени?Мы можем интерпретировать значение ускорения, наблюдая за типом кривой на графике.
Когда тело подвергается постоянному ускорению, график будет линейным, то есть прямым и наклонным. Эти линии на графиках VT представляют изменение скорости во время движения, но не в случае постоянного ускорения и замедления.
§2.7 Определение закона движения по известной зависимости скорости от времени
§2.7 Определение закона движения по известной зависимости скорости от времени
|
Таким
образом, нахождение закона движения сводится к утомительной математической
процедуре. К счастью, давно разработаны методы вычисления подобных сумм для
произвольных зависимостей скоростей от времени. Эти методы составляют суть
интегрального исчисления. Примененный нами графический метод определения закона
движения фактически является одним из способов вычисления подобных сумм.
Подчеркнем, что проблема вычисления подобных сумм является математической,
физический смысл которой вполне очевиден – на бесконечно малом интервале времени
движение приблизительно равномерное.
Таким образом, нахождение закона движения сводится к утомительной
математической процедуре.домашнее задание и упражнения – Связь между временем, скоростью и ускорением
спросил
Изменено 9 лет, 9 месяцев назад
Просмотрено 4к раз
$\begingroup$
Это вопрос от И.Е. Общая физика Иредова:
$1.22$ : Скорость частицы, движущейся в положительном направлении оси $x$, изменяется как $v = α \sqrt x$, где $α$ — положительная постоянная.
2 x$$ 92}{4} $$ для заданных начальных условий.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Понимание независимых и зависимых переменных
Все ресурсы по физике для средней школы
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
Справка по физике для старших классов » Вводные принципы » Понимание независимых и зависимых переменных
Ученый измеряет расстояние, которое частица проходит за заданный промежуток времени. Каждую секунду она измеряет, как далеко он продвинулся, и создает график своих результатов. Что является независимой переменной в этом эксперименте?
Возможные ответы:
Это будет зависеть от формы графика
Ни одна из них не является независимой
Время
Обе переменные являются независимыми
Расстояние
Правильный ответ:
Время
0 .Правильный ответ:
0
Объяснение:
Экспериментатор манипулирует независимой переменной. Любые вносимые изменения предсказуемы. Зависимая переменная реагирует на изменения, внесенные в независимую переменную. Его изменения не контролируются экспериментатором и их трудно предсказать.
В этом конкретном эксперименте ученый измеряет, как изменяется расстояние до частицы за заданное время. Она может контролировать количество времени, которое измеряет, но может наблюдать только за пройденным расстоянием.
На графике независимая переменная будет отображаться на оси x.
Сообщить об ошибке
Что является независимой переменной при рассмотрении скорости через расстояние и время?
Возможные ответы:
Ускорение
Время
Перемещение
Расстояние
Скорость
Правильный ответ:
Время
Объяснение: Есть несколько способов ответить на этот вопрос.
Во-первых, представьте, что вы строите график скорости. Поскольку уравнение имеет вид , смещение будет отложено по оси y, а время будет отложено по оси x. Ось X будет там, где мы поместим нашу независимую переменную.
Другой способ думать об этом — спросить себя, какими были бы наши «входы» и «выходы», если бы мы измеряли скорость. Представьте, что вы идете по улице и записываете, какое расстояние вы проходите каждую секунду. Время — это то, что вы «вводите», а пройденное расстояние — это ваш «выход».
Сообщить об ошибке
Вы смотрите на график движения автомобиля. По оси у отложено перемещение, по оси абсцисс время. Что из перечисленного является независимой переменной?
Возможные ответы:
Смещение
Время
Расстояние
Ускорение
Скорость
Правильный ответ:
Время
Объяснение:
Независимые переменные задаются экспериментатором заранее, и ими можно манипулировать, чтобы изменить измеряемую зависимую переменную.
Независимые переменные обычно изображаются на оси x, а зависимые переменные — на оси y.
В этом вопросе время является независимой переменной, а смещение является зависимой переменной. Экспериментатор может выбрать время выборки, но не обязательно может предсказать смещение, которое будет измерено в каждой точке. Это определяет время как независимую переменную.
Сообщить об ошибке
Где чаще всего на графике отображается независимая переменная?
Возможные ответы:
Независимая переменная не отображается
По осям х и у
По оси у
По оси х
Иногда по оси х, иногда по оси у
Правильный ответ:
По оси ось x
Объяснение:
Независимая переменная контролируется экспериментатором, а зависимая переменная будет колебаться в зависимости от входных данных независимой переменной.
