Зависимость силы тока от напряжения. Сопротивление
На прошлых уроках мы с вами познакомились с понятиями «сила электрического тока» и «напряжение». Давайте вспомним, что силой тока называется физическая величина, численно равная электрическому заряду, протекающему через поперечное сечение проводника за единицу времени.
Напряжение — это физическая величина, характеризующая работоспособность электрического поля.
Таким образом, сила тока и напряжение характеризуют электрический ток и его действия. Значит, сила тока должна каким-то образом зависеть от напряжения. Давайте установим эту зависимость. Для чего воспользуемся установкой, представленной на рисунке.
В качестве потребителя тока в цепи используется резистор — это металлический проводник в виде спирали. Параллельно резистору подключён вольтметр, измеряющий напряжение
на этом участке цепи.
Будем изменять напряжение на резисторе и следить за соответствующими изменениями силы тока в цепи, а все измерения заносить в таблицу:
Уже из этих данных следует, что сила тока в проводнике прямо пропорциональна напряжению на проводнике: I ~ U.
Подключим теперь к источнику тока другую спираль, например, спираль осветительной лампы и повторим опыт.
Как видим, при тех же значениях напряжения, что и в первом случае, мы получили другие значения силы тока. Однако и в этом проводнике
Наблюдаемую
нами зависимость силы тока в проводнике от напряжения между концами этого
проводника можно изобразить графически. На таком графике в условно выбранном
масштабе по оси абсцисс откладывается напряжение, а по оси ординат — сила тока.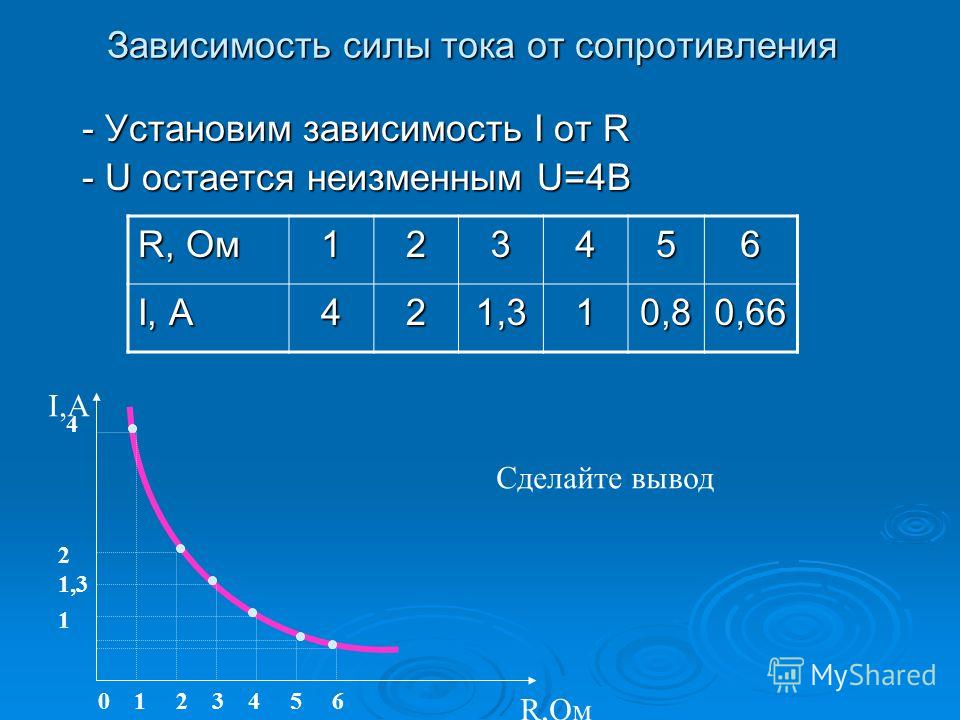
Такой график в физике называют вольт-амперной характеристикой проводника.
Теперь, по результатам проведённых опытов, вычислим отношение напряжения к силе тока для каждого из измерений:
Как видим, оно постоянно для каждого из проводников, но имеет разное значение для разных проводников.
Следовательно, существует физическая величина, характеризующая свойства проводника, по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника или просто сопротивлением. Обозначают сопротивление латинской буквой R.
За единицу сопротивления принимают ом. Она получила своё название в честь немецкого учёного Г. Ома, открывшего основной закон электрической цепи.
1 Ом — это сопротивление проводника, в котором при напряжении 1 В проходит ток силой 1 А.
Это небольшое сопротивление. У спиралей обычных электроламп оно составляет сотни ом, поэтому сопротивление часто выражают в кратных единицах:
Попытаемся
теперь объяснить, почему проводник обладает электрическим сопротивлением. Вспомните, что электрический ток в металлах представляет собой направленное
движение свободных электронов. Движущиеся под действием электрического поля
электроны взаимодействуют с атомами и ионами кристаллической решётки металла. Следовательно,
атомы и ионы препятствуют движению электронов
Вспомните, что электрический ток в металлах представляет собой направленное
движение свободных электронов. Движущиеся под действием электрического поля
электроны взаимодействуют с атомами и ионами кристаллической решётки металла. Следовательно,
атомы и ионы препятствуют движению электронов
Электрическое сопротивление можно сравнить с трением, которое всегда препятствует движению. Как мы знаем, любое тело быстрее скатится с гладкой поверхности, чем с шершавой.
Подобно этому, электроны в плохом проводнике двигаются медленнее, чем в хорошем. В диэлектриках, электрическое сопротивление бесконечно большое, поэтому они и не проводят ток.
Таким
образом, новая величина — сопротивление — отражает противодействие среды
движению в ней свободных носителей заряда.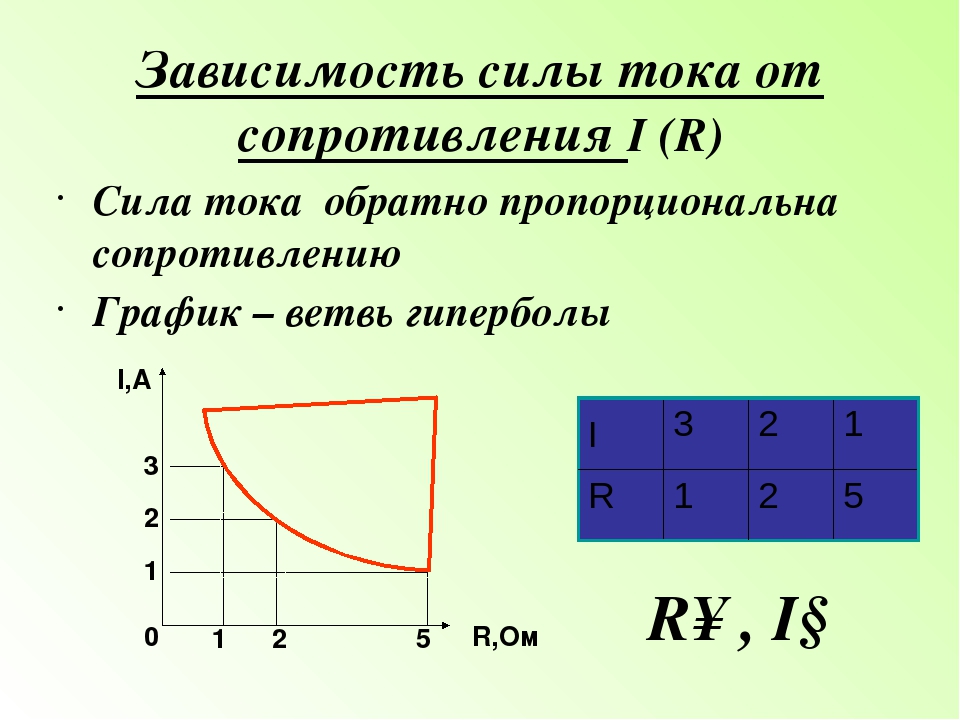
Определённым сопротивлением обладают и измерительные приборы. При включении последовательно в цепь амперметра его сопротивление добавляется к полному сопротивлению цепи. Это вызывает нежелательное уменьшение силы тока. Чтобы этого не случилось, сопротивление амперметра должно быть мало́. Идеальным был бы амперметр без сопротивления. Именно таким мы и будем считать сопротивление амперметра в задачах.
Наоборот, добавление вольтметра параллельно некоторому прибору создаёт току ещё один «обходной» путь, что также резко изменяет параметры цепи. Чтобы избежать этих нежелательных последствий, надо применять вольтметры с максимально больши́м сопротивлением.
И
ещё об очень важном. При слишком малом сопротивлении цепи сила тока в ней может
принять недопустимо большое значение.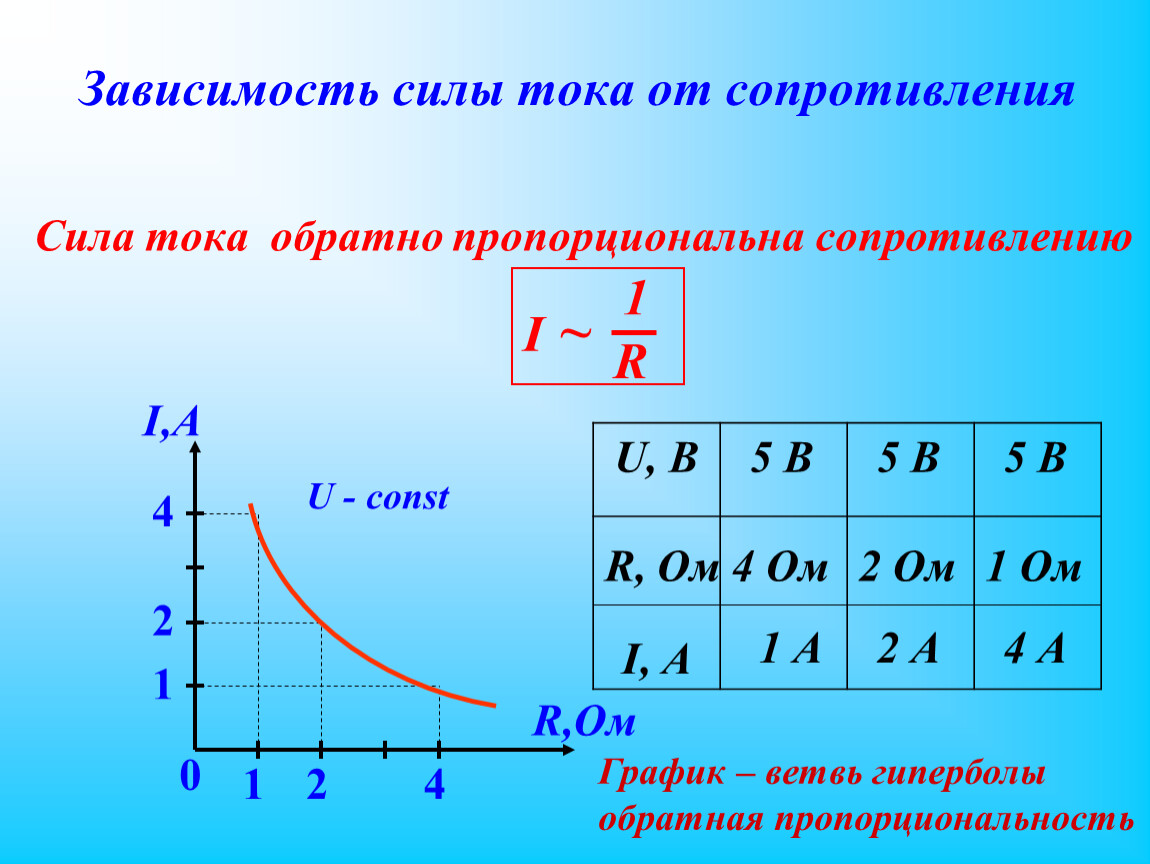 При замыкании цепи, представленной на
рисунке, ток в ней пройдёт, фактически не испытывая сопротивления. Это — короткое
замыкание.
При замыкании цепи, представленной на
рисунке, ток в ней пройдёт, фактически не испытывая сопротивления. Это — короткое
замыкание.
В таком режиме могут быть испорчены и прибор, и источник тока, а перегрев проводов может привести к пожару.
Пример решения задачи.
Задача. Когда напряжение увеличили на 3 В, сила тока в цепи возросла вдвое, и ток за 1 с совершил работу 3 Дж. Найдите значения силы тока после увеличения напряжения.
Урок физики в 8-м классе по теме “Зависимость силы тока от напряжения. Закон Ома для участка цепи”
Тема урока: Зависимость силы тока от напряжения. Закон Ома для участка цепи.
Цель урока: Установить зависимость между силой тока, напряжением на однородном участке электрической цепи и сопротивлением этого участка.
Задачи урока:
- Выяснить, что сила тока в участке цепи обратно пропорциональна его сопротивлению, если при этом напряжение остается постоянным
- выяснить, что сила тока прямо пропорциональна
напряжению на концах проводника, если при этом
сопротивление не меняется.

- научиться применять закон Ома для участка цепи при решении задач.
- научиться определять силу тока, напряжение по графику зависимости между этими величинами, а также сопротивление.
Оборудование: Экран, демонстрационные амперметр и вольтметр, источник тока, ключ, соединительные провода, демонстрационный магазин сопротивлений, ТСО, портреты ученых.
План урока
- Организационный момент.
- целью подготовки к восприятию нового материала.
- Изучение нового материала.
- Закрепление знаний, умений и навыков.
- Домашнее задание.
- Подведение итогов урока.
ХОД УРОКА
1. Организационный момент
Учитель: По словам русского поэта ХIХ века Якова Петровича Полонского,
Царство науки не знает предела –
Всюду следы ее вечных побед,
Разума слово и дело,
Сила и свет.
Эти слова по праву можно отнести к теме,
которую мы сейчас изучаем – электрические
явления. Они подарили нам много открытий,
осветивших нашу жизнь в прямом и переносном
смысле. А сколько еще неопознанного вокруг! Какое
поле деятельности для пытливого ума, умелых рук и
любознательной натуры. Так что запускайте свой
«вечный двигатель», и вперед!
Вспомним, что изучая тему «Электрические
явления», вы узнали основные величины,
характеризующие электрические цепи.
2. Актуализация знаний учащихся
Учитель: В начале, пожалуйста, перечислим основные величины, характеризующие электрические цепи.
Ученики: Сила тока, напряжение и сопротивление.
Учитель: А теперь, дайте небольшую характеристику каждой из этих величин, по следующему плану:
- Название величины.
- Что характеризует данная величина?
- По какой формуле находится?
- В каких единицах измеряется?
- Каким прибором измеряется или изменяется?
Ученики:
Сила тока

– формула для нахождения силы тока, где q-заряд, проходящий через поперечное сечение проводника, t-время прохождения заряда. Единица измерения – ампер. Измеряется сила тока – амперметром.
Напряжение-величина, которая характеризует электрическое поле.
– формула для нахождения напряжения, где А- работа по переносу заряда через поперечное сечение проводника, q-заряд. Единица измерения – вольт. Напряжение измеряется вольтметром.
Сопротивление характеризует сам проводник, обозначается – R, единица измерения 1Ом.
Учитель: на доске заполняем таблицу 1:
Таблица 1
Физическая величина |
Сила тока |
Напряжение |
Сопротивление |
| Обозначение | |||
| Единица измерения | |||
| Прибор для измерения или изменения |
Правильно, заполненная таблица 1:
Таблица 1
Физическая величина |
Сила тока |
Напряжение |
Сопротивление |
| Обозначение | I |
U |
R |
| Единица измерения | 1 А |
1 В |
1 Ом |
| Прибор для измерения или изменения | Амперметр |
Вольтметр |
Проводник |
Учитель: Ребята, а что вы знаете об ученых, открывших силу тока, напряжение, сопротивление?
(Ученики приготовили сообщения об ученых физиках)
Ученики: Единицы измерения физических
величин силы тока, напряжения и сопротивления,
названы в честь ученых открывших их. Ампер, Вольт
и Ом.
Ампер, Вольт
и Ом.
Андре-Мари Ампер – на его памятнике высечена надпись: «Он был также добр и также прост, как и велик». Славился своей рассеянностью. Про него рассказывали, что однажды он с сосредоточенным видом варил в воде свои часы 3 минуты, держа яйцо в руке.
Алессандро Вольта – был рыцарем почетного легиона, получил звание сенатора и графа. Наполеон не упускал случая посетить заседания Французской академии наук, где он выступал. Изобрел электрическую батарею, пышно названную «короной сосудов».
Георг Ом – немецкий физик. Опыты и теоретические доказательства были описаны им в главном труде «Гальваническая цепь, разработанная математически», вышедшем в 1827 г.
Разноуровневые задания:
Задание №1
1. Сколько ампер в 250 мА?
А) 250 А;
Б) 25 А;
В) 2,5 А;
Г) 0,25 А.
2. Вставьте пропущенное определение:
Величина, равная … называется электрическим напряжением.
А) произведению мощности на силу тока;
Б) отношению мощности к силе тока;
В) отношению работы к величине электрического заряда.
3. Начертите схему электрической цепи: источник тока, ключ, амперметр, соединительные провода, две лампочки и вольтметр, измеряющий напряжение на одной из лампочек.
Ответ: (1 – Г; 2 – В; 3 – Рис.1)
Рис. 1
Задание №2
1. Сколько киловольт в 750 В?
А) 750000 кВ;
Б) 0,75 кВ;
В) 75 кВ;
Г) 7,5 кВ.
2. Вставьте пропущенное определение:
Величина, равная … называется силой тока.
А) отношению работы к величине электрического заряда;
Б) отношению электрического заряда ко времени;
В) произведению работы на время.
3. Начертите схему электрической цепи: источник тока, ключ, амперметр, соединительные провода, две лампочки и вольтметр, измеряющий напряжение на двух лампочках.
Ответ: (1 – Б; 2 – Б; 3 – Рис.2)
Рис. 2
3. Изучение нового материала
Учитель: На прошлых уроках ребята, мы
изучали силу тока, напряжение и сопротивление в
отдельности. Сегодня мы перед собой поставили
цель: раскрыть взаимозависимость силы тока,
напряжения и сопротивления на участке
электрической цепи. Выясним, как зависит сила
тока от сопротивления, если напряжение остается
постоянным.
Обратимся к опыту:
1. Соберем цепь, состоящую: источника тока, амперметра, вольтметра, проводников сопротивлением 1 Ом, 2 Ом, 4 Ом.
2. В цепь по очереди включаем проводники,
обладающие различным сопротивлением. Напряжение
на концах проводника во время опыта
поддерживается постоянным. Силу тока в цепи
измеряем амперметром.
Силу тока в цепи
измеряем амперметром.
Результаты измерений поместим в таблицу 2:
Таблица 2
| № опыта | Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
1 |
2 |
1 |
2 |
2 |
2 |
2 |
1 |
3 |
2 |
4 |
0,5 |
Учитель: Что вы наблюдали?
Ученики: С увеличением сопротивления
сила тока уменьшается.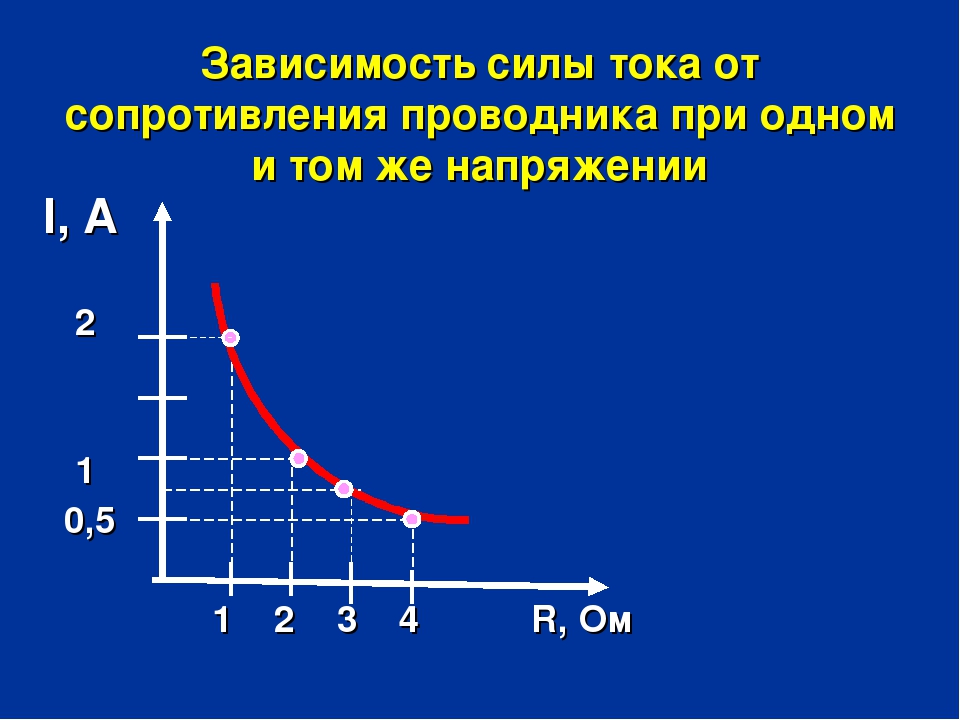
Учитель: Какой вывод можно сделать из этого?
Ученики: Сила тока в проводнике обратно пропорциональна сопротивлению проводника.
Учитель: Выясним, как зависит сила тока от напряжения, если при этом сопротивление не меняется. Обратимся к опыту:
1. Соберем цепь, состоящую из источника тока - аккумулятора, амперметра, спирали из никелиновой проволоки (проводника), ключа и параллельно присоединенного к спирали вольтметра.
2. Присоединяем к первому аккумулятору второй, затем третий такой же, замыкаем цепь и отмечаем показание приборов при каждом подключении дополнительного аккумулятора.
Результаты измерений поместим в таблицу 3:
Таблица 3
| № опыта | Напряжение на концах проводника, В |
Сопротивление проводника, Ом | Сила тока в цепи, А |
1 |
2 |
4 |
0,5 |
2 |
4 |
4 |
1 |
3 |
6 |
4 |
1,5 |
Учитель: Что вы наблюдали?
Ученики: При увеличении напряжения
в два раза, сила тока увеличилась вдвое. При трех
аккумуляторах напряжение на спирали увеличилось
втрое, во столько же раз увеличилась сила
тока.
При трех
аккумуляторах напряжение на спирали увеличилось
втрое, во столько же раз увеличилась сила
тока.
Учитель: Какой вывод из этого можно сделать?
Ученики: Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.
Учитель: Используя результаты опытов, и выводы сделанные из них, установим зависимость силы тока, напряжения и сопротивления.
Такая запись носит название закона Ома для участка цепи.
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Учитель:
Историческая справка: Этот закон
открыл немецкий физик Георг Ом в 1827 году.
Французские школьники изучают этот закон под
именем Пуйе – французского физика, установившего
этот же закон, но спустя 10 лет.
Учитель: Для того, чтобы вам было легче запомнить
формулу закона Ома можно воспользоваться
следующим способом её записи. (рис. 3)
Рис. 3
; ; U = I * R
Физическая пауза
Учитель: Прежде чем приступить к решению задач проведем физическую паузу. Представим, что мы с вами пассажиры автобуса…
- автобус резко трогается с места – ученики должны наклониться назад.
- автобус тормозит – отклонится вперед.
- автобус поворачивает направо – наклоняются влево.
- автобус поворачивает налево – наклоняются вправо.
Учитель: Какое физическое явление вы изображали?
Ученики: Инерция – явление сохранения
скорости тела, когда на это тело не действуют
внешние силы.
4. Закрепление умений и навыков
Используя закон Ома для участка цепи, решим задачу.
Задача 1.
Напряжение на зажимах электрического утюга 220 В, сопротивление нагревательного элемента утюга 50 Ом. Чему равна сила тока в нагревательном элементе?
| Дано: U = 220 В I – ? |
Решение:
Ответ: 4,4 А |
Задача 2.
На рис.4 изображен график зависимости силы тока от напряжения для двух проводников А и В. Определите сопротивление каждого из проводников. Какой из этих проводников обладает большим сопротивлением?
Рис. 4
Учитель: Решаем эту задачу по
вариантам. Вариант 1 – находит сопротивления
проводника А. Вариант 2 – находит сопротивление
проводника В.
Вариант 1 – находит сопротивления
проводника А. Вариант 2 – находит сопротивление
проводника В.
Вариант 1.
| Дано: U = 6B RA – ? |
Решение: ; Ответ: 2 Ом |
Вариант 2.
| Дано: U = 4B RB – ? |
Решение: ; ; Ответ: 4 Ом. |
Ученики: 2 Ом < 4 Ом , значит RA < RB, сопротивление проводника А меньше, чем сопротивление проводника В.
5. Домашнее задание: п.42–44, упр.19 № 3,4
6. Подведение итогов урока, оценки работы
учащихся
Подведение итогов урока, оценки работы
учащихся
Учитель: Молодцы ребята, очень хорошо потрудились, хорошо решали задачи, внимательно слушали и принимали активное участие в выводе закона Ома. Как для каждого прошел урок, мы сейчас увидим по результатам самодиагностики.
Самодиагностика (учащиеся поднимают одну из трех карточек, лежащих у них на парте).
- Красная карточка – удовлетворен уроком, урок полезен для меня, я работал и получил заслуженную оценку; я понимал все, о чем говорилось.
- Желтая карточка – урок был интересен, я отвечал с места, сумел выполнить ряд заданий. Мне на уроке достаточно комфортно.
- Зеленая карточка – пользы от урока я получил мало, я не очень понимал, о чем идет речь, к ответу на уроке я был не готов.
Выразите зависимость силы тока от сопротивления проводника при постоянном напряжении!!! пж
Заменив человека с мотоциклом на однородный тонкий равнобедренный треугольник, скользящий углами основания по внутренней поверхности цилиндра, найти у
… гол наклона треугольника к горизонтальной плоскости. Высота треугольника, проведенная к его основанию равна a=1,7 м, а основание треугольника шириной b=1,8 м расположено горизонтально. Скорость углов основания треугольника равна скорости мотоцикла(15 м/с). Ускорение свободного падения g=10 Н/кг.
Высота треугольника, проведенная к его основанию равна a=1,7 м, а основание треугольника шириной b=1,8 м расположено горизонтально. Скорость углов основания треугольника равна скорости мотоцикла(15 м/с). Ускорение свободного падения g=10 Н/кг.
Найти путь мотоцикла от основания до вершины цилиндра по винтовой линии с шагом между витками (по вертикали) h=0,5 м. Высота цилиндра 8 метров, радиус … 6.
26. На примусе нагрели 2 л воды от 12 до 100 °С. При этом сгорело 50 г керосина. Какое количество теплоты по- лучила вода и сколько его выделилось при … сгорании ке- росина? Почему не равны друг другу эти количества те- плоты? Какую часть составляет количество теплоты, использованное на нагревание воды, от количества те- плоты, выделившегося при сгорании керосина?
241, 242, очень срочно
Тело движется по окружности радиусом 10 м. Период его вращения равен 20 с. Чему равна скорость тела (ответ в мм/с)?
Тело движется по окружности радиус
… ом 4 м со скоростью 25,12 м/с. Чему равна частота вращения (ответ в с-1)?
Чему равна частота вращения (ответ в с-1)?
Рассчитайте, какое количество теплоты выделится при сгорании 1,5 кг каменного угля помогите пожалуйст
Во сколько раз вес автомобилей Камаз и Лада различается, если их массы равны 16 тонн и 800кг. Запишите с формулой и ответом
В балоні об`ємом 12 л знаходиться гелій під тиском 10 атм. при температурі 25 0С. Після того, як з балона взяли 10 г гелію, температура в балоні пониз … илась до 150С. Визначити тиск гелію, який залишився в балоні.
Рассчитайте время движения велосипедиста, если он 1,5 км ехал со скоростью 15 м/с. Укажите правильный вариант ответа: 100 с 0,01 с 225 с Пжжжж
4. Определите путь, пройденный туристом в течение
10 мин, средняя скорость движения которого равна
6 км/ч. Ответ запишите в СИ.
5. Известно, средняя
… скорость роста кедра
составляет около 10 см в год. За сколько лет дерево
достигнет своей максимальной высоты 40 м? Где
растет это дерево, как используется человеком?
6. Начальная координата пешехода хо
100 м. Опреде-
лите координату пешехода через 2 мин, если он
перемещался по прямолинейному участку пути со
M
скоростью v = :-2
Поясните полученный ре-
зультат, изобразите местонахождение пешехода
на координатной оси.
.
с
Начальная координата пешехода хо
100 м. Опреде-
лите координату пешехода через 2 мин, если он
перемещался по прямолинейному участку пути со
M
скоростью v = :-2
Поясните полученный ре-
зультат, изобразите местонахождение пешехода
на координатной оси.
.
с
Исследование зависимости силы тока в цепи от напряжения и сопротивления.
Цель работы: установить на опыте зависимость силы тока от напряжения и сопротивления.
Оборудование: амперметр лабораторный, вольтметр лабораторный, источники питания с выходным напряжением
1,5 В, 4,5 В, 9 В, 12 В, набор из трёх резисторов сопротивлениями 3 Ом, 9 Ом, 15 Ом, лампа накаливания, ключ замыкания тока, соединительные провода.
Ход работы.
Краткие теоретические сведения
- В Международной системе единиц СИ сила тока измеряется в амперах [А].

- U – напряжение. Единица напряжения – Вольт [В] [1B=1Дж/1Кл]
- R-электрическое сопротивление. В СИ единицей электрического сопротивления проводников служит Ом [Ом]. Сопротивление измеряется омметром.
[1A=1Кл/1с]. Прибор для измерения силы тока Амперметр. Включается в цепь последовательно
На схемах электрических цепей амперметр обозначается .
Прибор для измерения напряжения – Вольтметр. Подключается в цепь параллельно тому участку цепи, на котором измеряется разность потенциалов.
Графическая зависимость силы тока I от напряжения U – вольт-амперная характеристика
4.Закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
5. Напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка: U = IR
Напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка: U = IR
6. Сопротивление R участка цепи равно напряжению, приложенному к данному участку, поделенному на силу тока на этом участке, т. е. R = U / I
Лабораторная работа
Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи при неизменном сопротивлении .
В качестве источника тока можно выбрать любые устройства, дающие выходноенапряжение 1.5В; 4.5В; 9В; 12В.
1. В качестве источника тока выберем батарею с выходным напряжением 1,5 В.Мышкой перетаскиваем батарею к клеммам, согласно схеме.
–Замкнём цепь, нажав мышкой на ключ, снимем показания амперметра и вольтметра и запишем полученный результат
I =A,U=B.
Вычислить сопротивление на участке цепи при помощи закона Ома:
R=U/I , R=Ом.
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 1.
–Затем мышкой кликнуть «ввод», «готово».
2. Подсоединим источник тока напряжением 4.5В.Замкнём цепь, нажав мышкой на ключ, снимем показания амперметра и вольтметра и запишем полученный результат
I =A,U=B.
Вычислить сопротивление на участке цепи при помощи закона Ома:
R=U/I , R=Ом.
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 1.
–Затем мышкой кликнуть «ввод», «готово».
3. Подсоединим источник тока напряжением 9В.Замкнём цепь, нажав мышкой на ключ, снимем показания амперметра и вольтметра и запишем полученный результат
I =A,U=B.
Вычислить сопротивление на участке цепи при помощи закона Ома:
R=U/I , R=Ом.
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 1.
–Затем мышкой кликнуть «ввод», «готово».
4. Подсоединим источник тока напряжением 12В.Замкнём цепь, нажав мышкой на ключ, снимем показания амперметра и вольтметра и запишем полученный результат
Подсоединим источник тока напряжением 12В.Замкнём цепь, нажав мышкой на ключ, снимем показания амперметра и вольтметра и запишем полученный результат
I =A,U=B.
Вычислить сопротивление на участке цепи при помощи закона Ома:
R=U/I , R=Ом.
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 1.
–Затем мышкой кликнуть «ввод», «готово».
Таблица 1. Сопротивление участка Ом
- По полученным данным опыта постройте график зависимости силы тока от напряжения.
- По полученным данным опыта постройте график зависимости силы тока от сопротивления.

— Для этого мышкой поставьтесоответствующие точки, ориентируясь на таблицу. Смотрим масштаб по оси U и по оси I. Нажмём «проверить».
– Сделайте вывод.
Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах.
Для этого в цепь будим включать проводники, обладающие различным сопротивлением согласно схеме
1.Включите в цепь по той же схеме вместо электрической лампы проводник сначала сопротивлением 3 Ом. Замкнём цепь, нажав мышкой на ключ, запишем полученный результат и посчитаем силу тока согласно закона Ома
R=Om,U=B,I=U/RI=A
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 2. Далее нажмём «ввод» и «готово»
Далее нажмём «ввод» и «готово»
2. Включите в цепь по той же проводник сопротивлением 9 Ом. Замкнём цепь, нажав мышкой на ключ, запишем полученный результат и посчитаем силу тока согласно закона Ома
R=Om,U=B,I=U/RI=A
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 2.Далее нажмём «ввод» и «готово»
3. Включите в цепь проводник сопротивлением 15 Ом. Замкнём цепь, нажав мышкой на ключ, запишем полученный результат и посчитаем силу тока согласно закона Ома
R=Om,U=B,I=U/RI=A
–Нажмём мышкой на тетрадь и занесём результаты в таблицу, затем в бланк лабораторной работы таблица 2. Далее нажмём «ввод» и «готово»
Далее нажмём «ввод» и «готово»
Таблица 2. Постоянное напряжение на участке В
– Для этого мышкой поставьтесоответствующие точки ориентируясь на таблицу. Нажмите мышкой «проверить».
– Сделайте вывод.
Распространённые ошибки при термоэлектрических расчётах
При моделировании различных электротехнических приборов важную роль играет правильный расчёт электромагнитного нагрева материалов, электропроводность и теплопроводность которых нелинейно зависят от температуры. При моделировании таких нелинейностей даже у опытных инженеров могут возникать некоторые трудности и неожиданные результаты расчетов при комплексных сочетаниях нелинейных свойств материалов, граничных условий и геометрии. Давайте на простом примере разберём, почему это происходит.
Закон Ома и резистивный нагрев
Одним из первых физических законов, с которым сталкиваемся и который используем мы как инженеры, является закон Ома: Ток, протекающий через устройство равен приложенному напряжению (разности потенциалов), делённому на электрическое сопротивление или I = V/Re, где Re — электрическое сопротивление, которое является функцией от геометрии и электропроводности материала.
Далее мы узнаём о рассеиваемой мощности, которая равна произведению приложенного напряжения и тока, или Q = IV, что можно также записать, как Q = I2Re или Q = V2/Re. Немного позже мы сталкиваемся с такими свойствами, как теплопроводность и эквивалентное термическое сопротивление устройства, Rt, которые позволяют нам рассчитать повышение температуры устройства (относительно условий окружающей среды) по формуле ΔT = QRt.
Теперь мы можем определить абсолютное значение температуры устройства по формуле T = T_ {ambient} + QR_t. С этого момента мы и начнём наше обсуждение. Рассмотрим полностью дискретную модель. Да, пример в данной статье настолько прост, что нам даже не придётся использовать программное обеспечение COMSOL Multiphysics® для этой части. Итак, у нас есть модель с сосредоточенными параметрами, электрическое сопротивление которого равно Re = 1 Ω, а тепловое сопротивление — Rt = 1 K/W.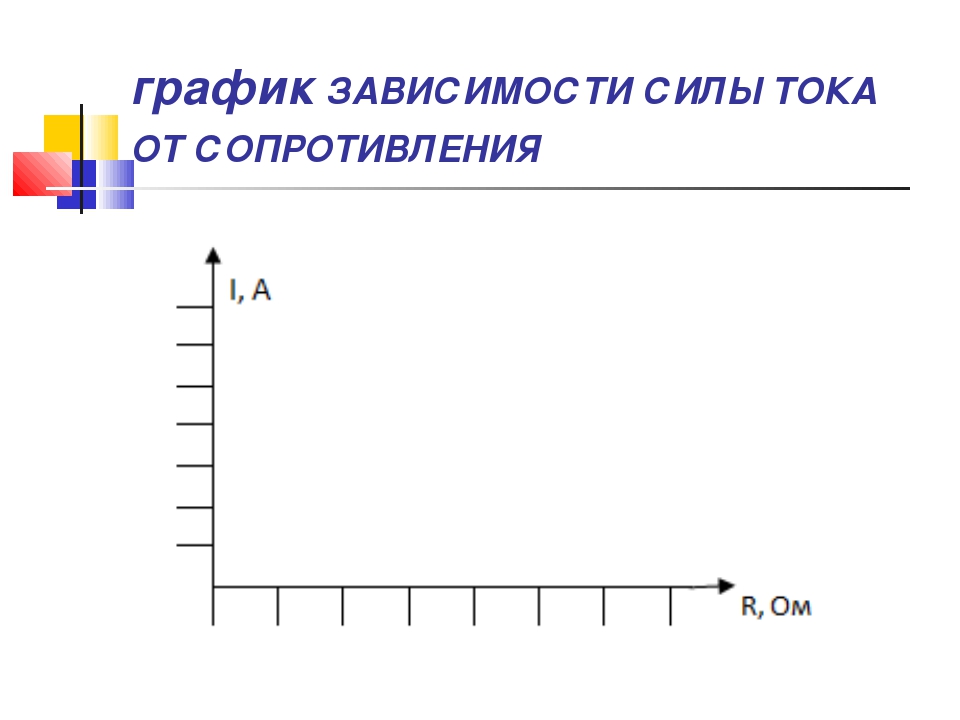 2 R_e R_t.
2 R_e R_t.
Температуру окружающей среды примем равной 300 K или 27°C, что является примерной комнатной температурой. Теперь давайте рассчитаем температуру нашего устройства, как функцию от напряжения (от 0 до 10 В) и тока (от 0 до 10 А), как показано на рисунке ниже. Неудивительно, что мы видим квадратичную зависимость.
Зависимость температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) при постоянных свойствах материала.
Можно предположить, что возможно использовать кривую для расчёта более широкого диапазона рабочих параметров. Поставим задачу нагреть устройство до критической температуры, при которой материал начнёт плавиться и испаряться. Предположим, что он начнёт испаряться при температуре 700 K (427°C). Основываясь на графиках выше и проведя простые математические вычисления можно рассчитать, что максимальное напряжение будет равно 20 В, а ток — 20 А, однако это совершенно неправильно!
Учет нелинейных свойств материала для сосредоточенной модели
На данном этапе вы можете заметить, что допущена ошибка: Электрическое сопротивление непостоянно и зависит от температуры.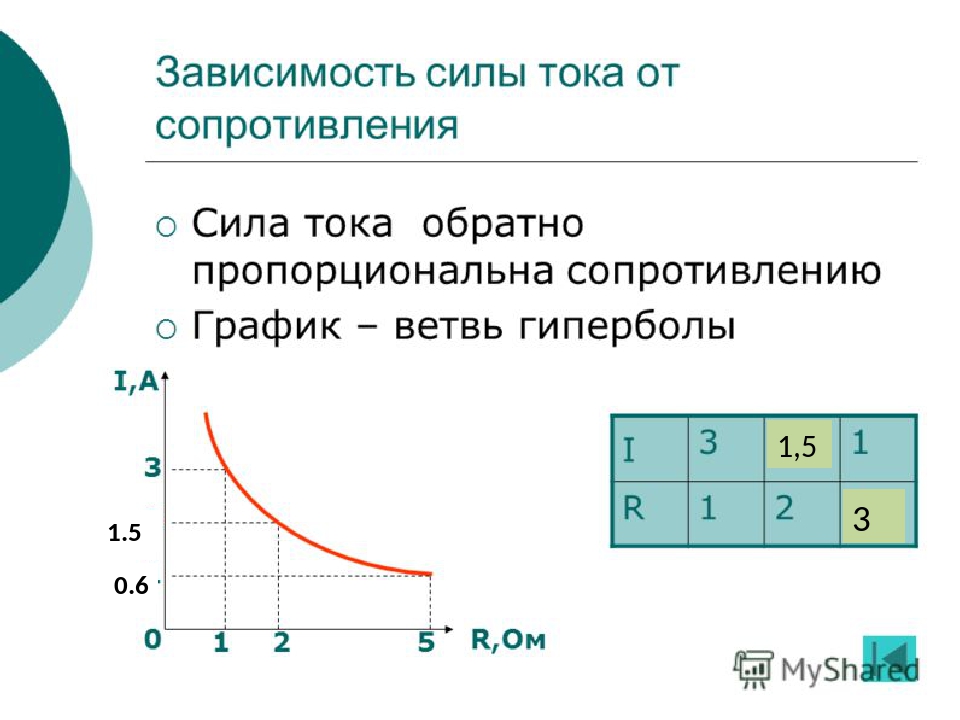 e_0)) R_t
e_0)) R_t
Эти уравнения уже немного сложнее (первое — квадратичное уравнение относительно T), но их ещё можно решить вручную. Графики зависимости температуры от приложенного напряжения и тока показаны ниже.
Зависимости температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) для случая зависимости электрического сопротивления от температуры.
Для варианта с напряжением мы видим, что при увеличении температуры, сопротивление также возрастает. Так как в этом случае сопротивление в уравнении для температуры находится в знаменателе, с его увеличением прирост температуры будет уменьшаться: мы видим, что график температуры лежит ниже, чем для случая с постоянным удельным сопротивлением. Если рассматривать вариант с постоянным током, то зависящее от температуры сопротивление будет в числителе.
По мере увеличения тока резистивный нагрев будет, наоборот, больше, чем в первом случае. На данном этапе мы опять-таки можем вычислить максимальное рабочее напряжение и ток, однако, вы, вероятно, уже видите вторую ошибку, которую мы допустили: необходимо также учитывать температурную зависимость теплового сопротивления. t_0 = 300 K), можно построить зависимости температуры устройства, как показано ниже.
t_0 = 300 K), можно построить зависимости температуры устройства, как показано ниже.
Зависимости температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) для случая зависимости электрического и термического сопротивлений от температуры.
Заметим, что для варианта с током температура возрастает асимптотически. Поскольку электрическое и тепловое сопротивление увеличиваются с повышением температуры, температура устройства возрастает очень резко по мере увеличения тока. При повышении температуры до бесконечности, задача становится нерешаемой. На самом деле, это полностью ожидаемо. Так работает предохранитель в вашем автомобиле. Если решать данную задачу в COMSOL Multiphysics, то можно использовать исследование во временной области (введя термальную массу как функцию от от плотности материала и теплоемкости), с помощью которого можно рассчитать время, в течение которого произойдет отказ устройства.
Для варианта с напряжением всё намного проще. Здесь мы также видим вполне предсказуемое поведение системы. С увеличением сопротивления температура растёт быстрее, чем в предыдущем случае. Однако заметьте, что относительно самого первого случая с постоянным сопротивлением, температура всё же ниже. Иногда это может запутать, но просто отметьте для себя, что одна из нелинейностей приводит к уменьшению температуры, а другая — к увеличению. В целом, если составлять более комплексную модель (например, которую можно сделать и рассчитать в COMSOL Multiphysics), то сложно предугадать, какая из нелинейностей будет преобладать.
Здесь мы также видим вполне предсказуемое поведение системы. С увеличением сопротивления температура растёт быстрее, чем в предыдущем случае. Однако заметьте, что относительно самого первого случая с постоянным сопротивлением, температура всё же ниже. Иногда это может запутать, но просто отметьте для себя, что одна из нелинейностей приводит к уменьшению температуры, а другая — к увеличению. В целом, если составлять более комплексную модель (например, которую можно сделать и рассчитать в COMSOL Multiphysics), то сложно предугадать, какая из нелинейностей будет преобладать.
Какую ещё ошибку можно допустить на этом этапе? В данном случае мы использовали положительный температурный коэффициент теплового сопротивления. Это справедливо для большинства металлов, однако для изоляторов, к примеру для стекла, этот коэффициент будет противоположным. Обычно термическое сопротивление всего устройства в основном зависит как раз от изоляторов, а не от электропроводящих доменов. Кроме того, при расчёте термического сопротивления устройства необходимо учитывать естественное охлаждение. То есть термического сопротивление также будет зависеть от эффектов свободной конвекции (которая возрастает с разницей температур) и излучения (которое пропорционально четвёртой степени разницы температур). Теперь давайте закончим рассмотрение нашей относительно простой задачи и изменим знак температурного коэффициента, αt = 1/400 K, а затем также сравним два варианта — с питающим напряжением (от 0 до 100 В) и протекающим током (от 0 до 100 А).
Кроме того, при расчёте термического сопротивления устройства необходимо учитывать естественное охлаждение. То есть термического сопротивление также будет зависеть от эффектов свободной конвекции (которая возрастает с разницей температур) и излучения (которое пропорционально четвёртой степени разницы температур). Теперь давайте закончим рассмотрение нашей относительно простой задачи и изменим знак температурного коэффициента, αt = 1/400 K, а затем также сравним два варианта — с питающим напряжением (от 0 до 100 В) и протекающим током (от 0 до 100 А).
Зависимости температуры устройства от приложенного напряжения (розовым) и протекающего тока (голубым) при отрицательном температурном коэффициенте термического сопротивления.
Мы видим, что результаты теперь совершенно другие. Обратите внимание, что в обоих случаях при низких значениях сопротивления кривые возрастают квадратично, а при увеличении сопротивления они уже имеют менее резкий характер, так как термическое сопротивление уменьшается. Тангенс угла наклона всегда положителен, но его величина постепенно уменьшается. В случае с током, кривая начинает асимптотически приближаться к значению T = 700 K, а в варианте с напряжением это значение меньше.
Тангенс угла наклона всегда положителен, но его величина постепенно уменьшается. В случае с током, кривая начинает асимптотически приближаться к значению T = 700 K, а в варианте с напряжением это значение меньше.
Это достаточно важный результат, и он позволяет обратить внимание на ещё одну распространённую ошибку. Нелинейные модели материалов, которые мы здесь используем для электрического и термического сопротивлений, являются приближёнными. Они становятся неэффективными при значениях температур около 700 К. Если мы знаем, что устройство будет работать как раз в этом режиме, то нужно найти более сложную материальную модель. Несмотря на то, что существующие модели позволяли получить какой-то результат, всегда стоит проверять адекватность расчёта на действующей рабочей температуре. Конечно, если наши условия эксплуатации далеки от таких температур, можно воспользоваться линеаризованной моделью резистивности (одной из встроенных материальных моделей в COMSOL Multiphysics). Тогда наша модель будет корректной.
Тогда наша модель будет корректной.
Подводя некоторые итоги, мы видим, что температура имеет очень сложную зависимость от питающего напряжения и тока. При рассмотрении нелинейных материалов температура может быть выше или ниже, чем при постоянных свойствах, угол наклона температурной кривой может быть как довольно резким, так и плавным, в зависимости от условий работы.
Запутали ли вас результаты в последнем варианте ещё больше? Что, если мы вернёмся к выражению для сопротивления и изменим один из коэффициентов? У некоторых материалов отрицательный знак температурных коэффициентов для электрического и термического сопротивлений. Что, если бы мы использовали более комплексные нелинейности? Вы все также будете пытаться предсказать ожидаемую температуру на основании сосредоточенной модели, или вы бы скорее положились на полноценный детальный расчёт?
Выводы о распространённых ошибках при электротермических расчётах
Как насчёт случая реального устройства? В нём будет несколько материалов, различные зависимости электро- и теплопроводностей как функции температуры, а также и сложная геометрия. Какой решатель при моделировании вы бы выбрали: стационарный или временной, чтобы узнать, сколько времени потребуется для повышения температуры? Скорее всего, в модели также будут нелинейные граничные условия такие, как условие излучения и свободная конвекция, которые неправильно будет аппроксимировать только одним приближённым тепловым сопротивлением. Что же в таком случае можно ожидать? Да практически всё! И как же рассчитывать такие сложные задачи? Конечно же с помощью COMSOL Multiphysics!
Какой решатель при моделировании вы бы выбрали: стационарный или временной, чтобы узнать, сколько времени потребуется для повышения температуры? Скорее всего, в модели также будут нелинейные граничные условия такие, как условие излучения и свободная конвекция, которые неправильно будет аппроксимировать только одним приближённым тепловым сопротивлением. Что же в таком случае можно ожидать? Да практически всё! И как же рассчитывать такие сложные задачи? Конечно же с помощью COMSOL Multiphysics!
Следующий шаг
Узнайте, как COMSOL Multiphysics может помочь вам в мультифизическом моделировании при решении поставленных задач. Не стесняйтесь написать нам и задать все интересующие вопросы!
Исследование силы тока в электрической цепи
В индивидуальной ученической работе по физике на тему «Исследование силы тока в электрической цепи» автор проводит исследование электрического тока, опытным путем проводит проверку справедливости закона Ома, устанавливая зависимость силы тока от напряжения и от возрастающего сопротивления в электрической цепи.
Подробнее о работе:
В рамках исследовательской работы по физике о силе тока в электрической цепи дается справочная информация об электрическом токе, объясняется принцип Закона Ома, изучается информация о величинах, связанных с электричеством, проводится работа по сбору простейших электрических цепей и выясняется, как рисуют схемы электрических цепей.
В ходе учебного исследовательского проекта по физике «Исследование силы тока в электрической цепи» учащийся школы провел эксперимент по определению зависимости силы тока от электрического сопротивления и подаваемого напряжения, изучил влияние силы тока на работу электроприборов и построил и проанализировал графики I(R), I(U). Предложенный проект актуален, так как каждый человек должен обладать минимальными знаниями в области электричества, чтобы обеспечить свою безопасность при взаимодействии с элекрическим током даже в бытовых условиях.
Оглавление
Введение
1. Электрический ток.
2. Закон Ома.
3. Применение Закона Ома.
4. Опыт № 1. Исследование зависимости силы тока от напряжения.
5. Опыт № 2. Исследование зависимости силы тока от сопротивления .
Заключение
Список используемой литературы
Приложения
Введение
Физика электричества – это то, с чем приходится сталкиваться каждому из нас. Современная наша жизнь без электричества невозможна. Это и любимый компьютер, и телефон, и телевизор. Взрослые,конечно, назовут другие электроприборы, без которых сейчас мы не представляем свою жизнь. Иногда они перегорают, и мы здорово огорчаемся. И, все-таки, как сделать, чтобы приборы не перегорали? Отчего это зависит?
Проблема исследования: какие физические величины влияют на значение силы тока.
Пролистывая учебную литературу мне встретились множество физических законов, которые связаны с электрическими явления. Например, закон Кулона, закон Джоуля-Ленца, закон Фарадея, закон Ома для полной цепи.
Все они очень важные и нужные для человеческой деятельности. Но я решил остановиться на законе Ома для участка цепи, так как из всего разнообразия он мне показался самым простым и понятным.
Но я решил остановиться на законе Ома для участка цепи, так как из всего разнообразия он мне показался самым простым и понятным.
Объект исследования: электрическая цепь.
Предмет исследования: зависимость силы тока от напряжения и от возрастающего сопротивления.
Цель работы: проверка опытным путем справедливости закона Ома.
Гипотеза: чем больше сопротивление в цепи, тем меньше сила тока; чем больше напряжение, тем сила тока становиться больше.
Задачи исследования:
- Рассмотреть понятие электрический ток.
- Найти и изучить информацию о величинах, связанных с электричеством.
- Выбрать информацию, необходимую для исследования.
- Научиться собирать простейшие электрические цепи и узнать, как рисуют схемы электрических цепей.
- Провести эксперимент по определению зависимости силы тока от электрического сопротивления и подаваемого напряжения.
- Изучить влияние силы тока на работу электроприборов.

- Построить и проанализировать графики I(R),I(U).
- Сделать выводы.
Тема исследования актуальна, т.к. закон Ома является одним из важнейших законов энергетики. В быту, например, при включении в цепь несколько потребителей необходимо учитывать выдержит ли нагрузку проводка и не возникнет ли пожар. Но, несмотря на всю свою значимость любой контакт человека с электрическими проводами, находящимися под напряжением, является смертельно опасным. По этому, я считаю, что каждый человек должен обладать минимальными знаниями в области электричества.
Практическая значимость подтверждается проведенными исследованиями, которые позволяют наглядно показать зависимость силы тока от напряжения и сопротивления, что может поспособствовать лучшему усвоению учебного материала.
Этапы исследования:
Первый этап (январь, 2019г.): Подготовительный. (Создание проблемной ситуации, выбор темы, постановка цели)
Второй этап (январь-февраль 2019г. ): Практический. (Сбор информации по выбранной теме, систематизация материалов, подготовка и оформление результатов работы.)
): Практический. (Сбор информации по выбранной теме, систематизация материалов, подготовка и оформление результатов работы.)
Третий этап (март-апрель 2019 г.) Заключительный. (Защита и презентация проекта).
В ходе работы мы использовали следующие методы: сбор, изучение, обобщение теоретического и практического материала, наблюдение, опыт, эксперимент, теоретические методы (анализ, сравнение).
Электрический ток
Что такое электричество? Для человека непосвященного оно ассоциируется со вспышкой молнии или с энергией, питающей телевизор и стиральную машину. Он знает, что электропоезда используют электрическую энергию. О нашей зависимости от электричества ему напоминают линии электропередач.
Однако с электричеством связано немало других, не столь очевидных, но повседневных явлений. Со всеми ними, нас будет знакомить физика, но я еще в 6 классе и сейчас мне об этом хочется узнать. Читая, энциклопедии я выяснил, что, бьющееся сердце, бегущий спортсмен, спящий ребенок и плавающая рыба – все вырабатывает электрическую энергию.
Физика электричества связана с движением электронов и других заряженных частиц в различных веществах. Электрический ток – это направленное движение электронов в металле. Почему электроны покидают атомы? Это объясняется несколькими причинами; под воздействием импульса светаили тепло заставляет атомы колебаться быстрее. Это означает, что электроны могут вылететь из своего атома. При химических реакциях они также перемещаются от атома к атому.
Электрический ток — это течение потока электронов по нити лампочки. Вы могли слышать слово течение применительно к реке: “У этой реки сильное течение”. Это значит, что по реке протекает много воды. Электрический ток подобен этому течению: если говорят “сильный ток”, это значит, что по проволоке протекает много электронов. Сила тока измеряется в амперах (А).
Электрический ток обусловлен движением электрических зарядов. Когда электрическая лампа, соединенная с батареей, включена, ток течет по проводу от одного полюса батареи к лампе, затем через ее волосок, вызывая его свечение, и возвращается назад по второму проводу к другому полюсу батареи. Если выключатель повернуть, то цепь разомкнется – движение тока прекратится, и лампа погаснет.
Если выключатель повернуть, то цепь разомкнется – движение тока прекратится, и лампа погаснет.
Напряжение заставляет электроны двигаться. Эта физическая величина обозначается латинской буквой U и измеряется в вольтах. Присоединив к лампочке батарейку, мы подаем на нить лампочки напряжение. Оно толкает электроны в одном направлении, заставляет их двигаться по нити. Чем оно выше, тем больше электронов будет передвигаться по нити.
Представьте себе нить в виде трубы, целиком заполненной шариками. Если с одного конца трубы втолкнуть шарик, с ее противоположного конца тут же без всякой задержки выпадет другой шарик.Чем больше шариков мы будем заталкивать в один конец трубы, тем больше их будет выпадать из другого. Именно так ведут себя электроны в нити накаливания лампочки, когда на нее подается напряжение.
Закон Ома
Напряжение заставляет электроны двигаться и тем самым создавать электрический ток, а сопротивление препятствует этому току.
 Это подобно игре с садовым шлангом: если сжать его, сопротивление потоку воды увеличится и поток ослабнет, т. е. воды станет протекать меньше. Сопротивление в электричестве действует подобно сжатию шланга, электрическое сопротивление измеряется в омах (Ом), обозначается R. Зависимость между этими физическими величинами отражена в законе Ома.
Это подобно игре с садовым шлангом: если сжать его, сопротивление потоку воды увеличится и поток ослабнет, т. е. воды станет протекать меньше. Сопротивление в электричестве действует подобно сжатию шланга, электрическое сопротивление измеряется в омах (Ом), обозначается R. Зависимость между этими физическими величинами отражена в законе Ома.Для любого проводника или системы проводников и приборов соотношение между напряжением, током и сопротивлением задается формулой:
напряжение = ток × сопротивление.
Это математическое выражение закона Ома, названного так в честь Георга Ома (1787-1854 гг.), который первым установил взаимосвязь этих трех параметровв 1820-е годы именно поэтому этот закон и получил такое название.
Закон Ома – один из самых применяемых законов в электротехнике.
Формулировка закона Ома следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.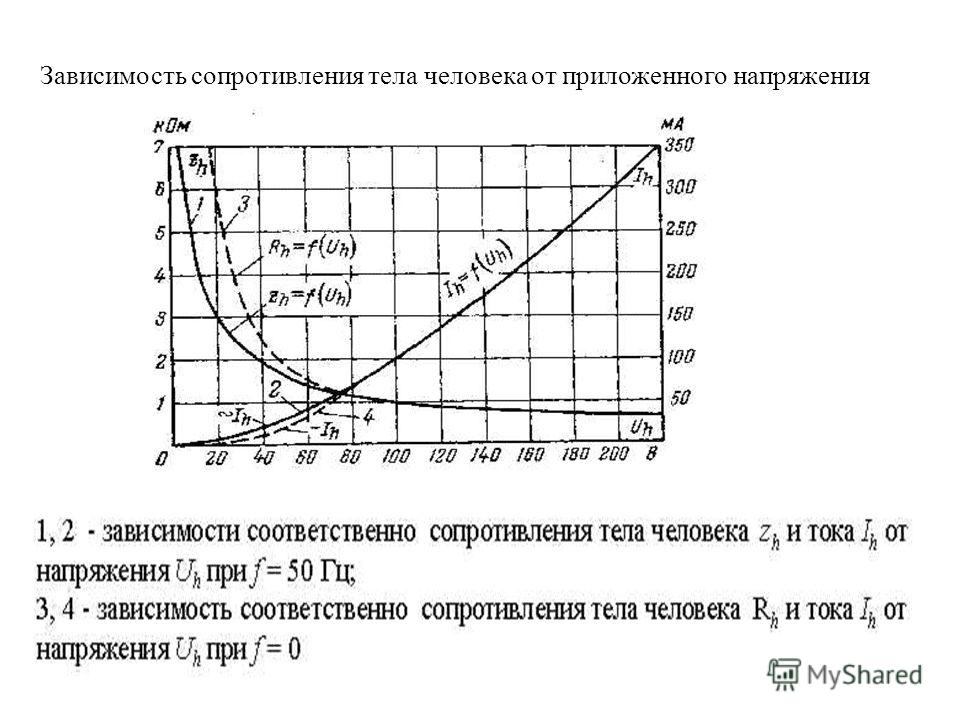
Эту зависимость можно выразить формулой: I=U/R
Где I – сила тока, U — напряжение, приложенное к участку цепи, а R — электрическое сопротивление участка цепи.
Теперь я объясню вам, как электроны, ток, напряжение и сопротивление действуют вместе, заставляя светиться лампочку карманного фонаря.
Чтобы батарейка могла заставить электроны двигаться, цепь между ее выводами не должна иметь разрывов, т. е. должна быть замкнутой. Напряжение, создаваемое батарейкой, постоянно. Оно заставляет электроны двигаться по цепи, частью которой является и нить накаливания лампочки. Нить, сделанная из тугоплавкого металла, обладает сопротивлением, ограничивающим силу тока в цепи. Когда электроны преодолевают сопротивление нити, она накаляется и начинает светиться.
Применение Закона Ома
Электрический ток это опасное физическое явление. Его невозможно увидеть, почувствовать, а тела, находящиеся под напряжением, ничем не отличаются по внешнему виду. Но стоит включить в розетку пылесос или телевизор, щелкнуть выключателем – и энергия словно берется из ниоткуда, он начинает работать.
Но стоит включить в розетку пылесос или телевизор, щелкнуть выключателем – и энергия словно берется из ниоткуда, он начинает работать.
Рассмотрим один из немногих, примеров проявления закона Ома. У нас у каждого в квартирах есть напряжение в розетках 220 вольт. Значит, ток в цепи зависит только от сопротивления электроприборов. Если оно будет очень мало, то может случиться короткое замыкание. Проводка, по которой течет ток в квартире, не справится с возросшей силой тока, нагреется, расплавится и вызовет пожар.
Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Например, вентилятор, который в жаркую погоду является незаменимым средством. Из-за заклинивания лопастей обмотка двигателя подвергнется перегреву. Изоляция обмотки двигателя не рассчитана на серьезный нагрев, она быстро расплавится.
В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока. Такая ситуация может возникнуть практически с любым электроприбором. Для того чтобы избежать перегрева в бытовой технике используют различного рода предохранители.
Такая ситуация может возникнуть практически с любым электроприбором. Для того чтобы избежать перегрева в бытовой технике используют различного рода предохранители.
Для защиты бытовых электрических цепей обычно используются автоматические выключатели. При повышении силы тока они размыкают цепь, и обесточивается вся квартира. Компактность, легкость монтажа и замены, в случае необходимости, объясняет их широкое распространение.
Экспериментальная часть
Для определения зависимости силы тока от электрического напряжения при постоянном сопротивлении я собрал электрическую цепь. Она состояла из источника питания, ключа, резистора в 4 Ом и амперметра. Схема цепи представлена на рисунке 1. Но, для этого мне пришлось познакомиться с этим новым понятием и как обозначаются различные элементы на ней.
Папа помог с этой задачей справиться. Тут меня поджидала еще одна сложность – шкала приборов, которая состояла из больших и маленьких делений, лишь над некоторыми из них стояли числа. Чтобы правильно научиться определять значения величин, нужно верно определить цену деления шкалы прибора. С учителем мы справились с этой трудностью.
Чтобы правильно научиться определять значения величин, нужно верно определить цену деления шкалы прибора. С учителем мы справились с этой трудностью.
Опыт № 1. Исследование зависимости силы тока от напряжения
Цель: проверить на опыте, каксила тока в цепи зависит от напряжения.
Оборудование: источник питания, амперметр, вольтметр, резистор на 3 Ом, провода.
Применяя новые навыки, я периодически изменял напряжение на источнике, смотрел на показания амперметра. Результаты приведены в таблице 1.
Таблица 1. Зависимость силы тока от напряжения
U,B | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
I,A | 0,16 | 0,32 | 0,48 | 0,64 | 0,8 | 0,96 |
R,Ом | 3 | 3 | 3 | 3 | 3 | 3 |
По итогам эксперимента можно сделать вывод: с увеличением напряжения в 2 раза, сила тока тоже увеличивается в 2 раза, т. е. сила тока прямо пропорциональна напряжению на резисторе.
е. сила тока прямо пропорциональна напряжению на резисторе.
По полученным данным построили с руководителем в программе MicrosoftExcel 2007 график, который наглядно отражает прямую зависимость между силой тока и напряжением.
Проверим закон Ома для участка цепи, подставив значения в формулу.
| I1 = 0,5B /3 Ом ≈ 0,17А I2 = 1В/3 Ом ≈ 0,33А I3 = 1,5B /3 Ом = 0,5А | I4 = 2B/3 Ом ≈ 0,67А I5 = 2,5B /3 Ом ≈ 0,83А I6 = 3B /3 Ом = 1А |
Расхождение графиков обусловлено погрешностью измерений.
Опыт № 2. Исследование зависимости силы тока от сопротивления
Цель опыта: проверить на опыте, как сила тока в цепи зависит от сопротивления.
Оборудование: источник питания, амперметр, вольтметр, резисторы(1 Ом, 2 Ом, 3 Ом, 5 Ом, 10 Ом, 15 Ом), реостат, провода.
Для определения зависимости силы тока от сопротивления при постоянном напряжении я собрал электрическую цепь. Схема цепи представлена на рисунке 2 (Приложение 1).Для достижения стабильного напряжения нам пришлось в цепь добавить реостат. Реостат –устройство, с изменяемым сопротивлением для регулирования силы тока и напряжения.
Схема цепи представлена на рисунке 2 (Приложение 1).Для достижения стабильного напряжения нам пришлось в цепь добавить реостат. Реостат –устройство, с изменяемым сопротивлением для регулирования силы тока и напряжения.
По очереди, меняя резисторы, мы смотрели за тем, как изменяется сила тока. Результаты эксперимента представлены в таблице 2. По ним мы построили график в MicrosoftExcel2007. По графику видно, что зависимость силы тока от сопротивления – обратная, т.е. при самом большом сопротивлении сила тока имеет самое минимальное значение.
Таблица 2. Зависимость силы тока от сопротивления.
U, B | 1 | 1 | 1 | 1 | 1 | 1 |
R,Ом | 1 | 2 | 3 | 5 | 10 | 15 |
I,A | 1,05 | 0,55 | 0,34 | 0,2 | 0,1 | 0,05 |
Проверим закон Ома для участка цепи в теории
| I1 = 1B/1 Ом = 1А | I4 = 1B/5 Ом = 0,2А |
| I2 = 1В/2 Ом = 0,5А | I5 = 1B/10 Ом = 0,1А |
| I3 = 1B/3 Ом ≈ 0,33А | I6 = 1B/15 Ом ≈ 0,07А |
Вывод: по результатам проведенных экспериментов мы выяснили, что сила в цепи напрямую зависит от напряжения. Во сколько раз мы увеличиваем напряжение в сети, во столько же раз увеличивается сила тока. Кроме напряжения сила тока еще зависит и от сопротивления. Чем больше сопротивление в цепи, тем меньше сила тока. Эти опыты позволяют проверить на практике закон Ома.
Во сколько раз мы увеличиваем напряжение в сети, во столько же раз увеличивается сила тока. Кроме напряжения сила тока еще зависит и от сопротивления. Чем больше сопротивление в цепи, тем меньше сила тока. Эти опыты позволяют проверить на практике закон Ома.
Заключение
Исследовательская работа была для меня увлекательной и познавательной, я узнал много нового для себя. Изучив теоретически закон Ома, причины возникновения электрического тока и выяснив, что является электрическим током, я понял, что закон Ома для участка цепи является основным законом электричества и находит широкое применение в жизни людей.
Он является очень полезным в технике, так как связывает три основные электрические величины: силу тока, напряжение и сопротивление. Опытным путем мы проверили зависимость силы тока от напряжения и сопротивления, и пришли к выводу: чем больше напряжение при постоянном сопротивлении, тем больше сила тока в цепи, чем больше сопротивление участка цепи, тем меньше сила тока.
Доказали, что закон Ома справедлив. Я узнал, что перегружать электроприборами сеть в доме, где провода не рассчитаны на большую силу тока, нельзя. Всегда необходимо соблюдать технику безопасности.
В процессе исследования у меня возникли такие вопросы. Почему резисторы, которые внешне почти ничем не отличаются, имеют разное сопротивление? Что влияет на его величину? Ответы на эти вопросы я планирую найти в будущем, т.е. продолжу изучать электрические явления.
Таким образом, цель и задачи, поставленные в начале исследования, полностью выполнены.
Список используемой литературы
- Значение [Электронный ресурс].
- Коротун В. Что такое перегрузка электросети и ее последствия [Электронный ресурс].
- Cемейный портал «Дом и семья» [Электронный ресурс].
- Учебник «Физика» для 8 класса А.В. Перышкин, 12-е изд., дораб.- М.: Дрофа, 2018.
- Физика: Энциклопедия. Прохоров А., ред. М.: Дрофа, 2006
Если страница Вам понравилась, поделитесь в социальных сетях:
Закон Ома.
 Онлайн расчёт для постоянного и переменного тока.
Онлайн расчёт для постоянного и переменного тока.
Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи
с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.
Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области
электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное
сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи – физическая величина, значение которой равно работе эффективного
электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии
постоянного тока.
Теперь можно переходить к закону Ома.
Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.
Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы
электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо
пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника
и записана в следующем виде:
I=U/R,
где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.
Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности,
рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам,
также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I2(А)×R(Ом) =
U2(В)/R(Ом)
Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной
крупной статьи на страницах уважающего себя сайта.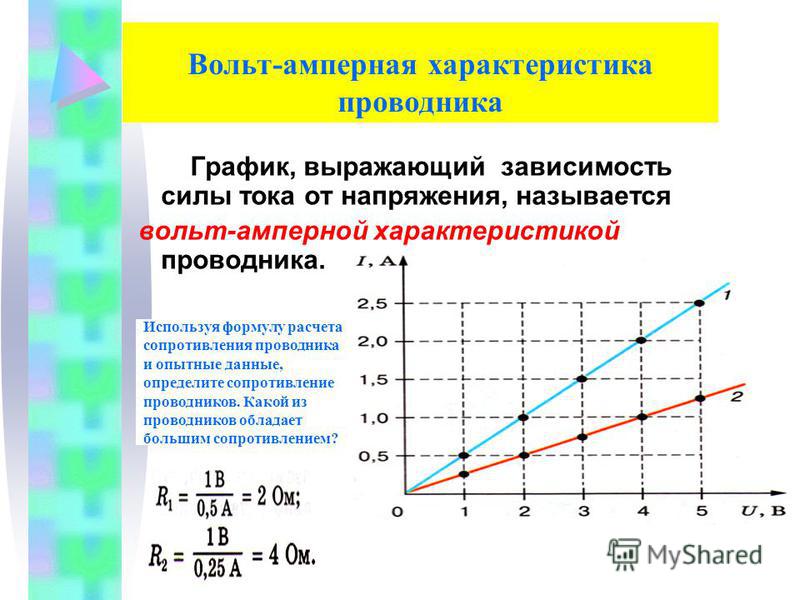
Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.
Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.
Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр.

Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название – закон Ома для полной цепи:
I=U/(R+r) .
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов
определяются исходя из формулы:
1/Rll = 1/R4+1/R5.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице
ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше,
остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует
понимать действующее (эффективное) значение амплитуды переменного сигнала.
А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2),
сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает
амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.
Рассчитываем действующее значение напряжение интересующей нас формы:
Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.
С этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости
в цепи переменного тока.
В общем случае смотреться это будет так:
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z,
состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих
трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице
ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока
и описываются формулами:
XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии
индуктивного или емкостного элемента – необходимо указать значение частоты
f !
КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем
простенький бестрансформаторный источник питания.
Токозадающими цепями в данной схеме являются элементы R1 и С1.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока
нагрузки.
Зададимся номиналами R1 – 30 Ом, С1 – 1 Мкф, частотой сети f – 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет – надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.
Всё – закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!
11,2 Закон Ома | Электрические цепи
11,2 Закон Ома (ESBQ6)
temp textТри основные величины для электрических цепей: ток, напряжение (потенциал разница) и сопротивление . Резюме:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разница потенциалов или напряжение \ (В \) – это количество энергии на единицу заряда, необходимое для перемещения этого заряд между двумя точками в цепи.

Сопротивление, \ (R \), является мерой того, насколько “трудно” протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Георг обнаружил важную взаимосвязь между током, напряжением и сопротивлением в цепи. Саймона Ома, и он называется Закон Ома .
- Закон Ома
Количество электрического тока, протекающего через металлический проводник при постоянной температуре в цепи, составляет пропорциональна напряжению на проводнике и может быть описана как
\ (I = \ frac {V} {R} \)где \ (I \) – ток через проводник, \ (V \) – напряжение через проводник, а \ (R \) сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводник постоянен, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на По оси X графика и тока по оси Y графика мы получим прямую.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R} \] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I} \]
временный текстЗакон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и потенциалом разность (напряжение) на одном и том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное напряжение на резисторе.
и измерить результирующий ток в цепи. Во второй части мы будем варьировать ток
в цепи и измерьте полученное напряжение на резисторе.После получения обоих наборов
измерений, мы рассмотрим взаимосвязь между током и напряжением на
резистор.
В первой части мы будем изменять приложенное напряжение на резисторе.
и измерить результирующий ток в цепи. Во второй части мы будем варьировать ток
в цепи и измерьте полученное напряжение на резисторе.После получения обоих наборов
измерений, мы рассмотрим взаимосвязь между током и напряжением на
резистор.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Кол-во ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.

Измерьте напряжение на резисторе с помощью вольтметра, а ток в схему с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная только с 1 резистора в схема.

Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.

Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте в цепь еще один резистор и измерьте ток и напряжение снова только на исходном резисторе. Продолжайте добавлять резисторы, пока не получите четыре последовательно, но не забывайте измерять напряжение только на исходном резистор каждый раз.Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения. С напряжение – это переменная, которую мы изменяем напрямую, это независимая переменная.
 и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \).
и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \).Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом в случае, если независимая переменная – это ток, который должен быть нанесен на ось \ (x \), и напряжение является зависимой переменной и должно быть отложено по оси \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы.
 Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?
Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление оригинальный резистор. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как бы вы попытались найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_0 \)?
Закон Ома
Учебное упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) – это изменение тока, деленное на изменение напряжение:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) – (\ text {0,4})} {(\ text {12}) – (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как бы вы попытались найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания.Теперь ваша очередь Считайте напряжение источника питания и запишите это.
Затем вы последовательно подключаете два резистора. Теперь вы можете проводить измерения напряжения. для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток такой же везде в цепи мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление при изменении напряжения на них или ток через них увеличивается.Эти проводники называются омическими проводниками . График ток в зависимости от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических жилы – резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Этот происходит потому, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводники называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка распространенный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается из комнаты. температура до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, в результате увеличение тока вызывает повышение температуры нити, что увеличивает ее сопротивление.Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не изменяются. подчиняться закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорируется. При применении металлических ламп накаливания, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \), и начиная с комнатной температуры) изменение довольно велико.
Как правило, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определяют, какой из них подчиняется закону Ома. Вы будете нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр.Учащимся следует обнаружите, что резистор подчиняется закону Ома, а лампочка – нет.
Проводники омические и неомические
Цель
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, провода соединительные, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой резистор, а во втором – лампочка.Настройте обе схемы, указанные выше, начиная с 1 клетка. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметр.
Измерьте ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом. У вас должна быть одна таблица для измерения первой цепи с резистором и еще одна таблица для второй схемы измерения с помощью лампочки.
Кол-во ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) – ось) vs.\ (V \) (\ (x \) – ось), одна для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка резистору Ома? Закон?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа цепей.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \) и напряжение на резисторе \ (\ text {5} \) \ (\ text {V} \), тогда мы можем использовать сопротивление Ома. Закон для расчета тока, протекающего через резистор. Наша первая задача – нарисовать схему диаграмма. При решении любой проблемы с электрическими цепями очень важно составить схему схему перед выполнением любых расчетов.Принципиальная схема этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно изменить на: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
временный текстРабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор – \ (\ text {4} \) \ (\ text {A} \).Какова разность потенциалов (напряжение) на резистор?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят рассчитать напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).\ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Закон Ома
Учебное упражнение 11.2Рассчитайте сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) через него, когда через него протекает ток \ (\ text {2} \) \ (\ text {A} \). Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при наличии разность потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Нарисуйте схему диаграмму перед расчетом.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет через него? Нарисуйте принципиальную схему перед выполнением расчет.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Переплет резисторов последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены в последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. Параллельно В цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общую суммарную сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление равно сумме сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
. \ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {выровнять *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется как следующее определение.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \Правильно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text {1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text { Ω}} {\ text {10} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {выровнять *}Последовательное и параллельное сопротивление
Учебное упражнение 11.3Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}Два резистора соединены последовательно.Эквивалентное сопротивление \ (\ text {100} \) \ (\ текст {Ω} \). Если один резистор \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} – R_ {1} \\ & = \ text {100} \ text {Ω} – \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}Два резистора подключены параллельно.Эквивалентное сопротивление \ (\ text {3,75} \) \ (\ текст {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), какое сопротивление у второго резистора?
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} – \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} – \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ текст {1} \ текст {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими настройками.
Последовательные цепи
Рассмотрим схему, состоящую из трех резисторов и одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова. через любой компонент в цепи. Это потому, что существует только один путь для движения электронов. в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении ток будет течь.Мы знаем, что ток по условию течет от положительного к отрицательному. Общепринятый ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к А.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений по всем три резистора.Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов в серии, мы можем подойти к некоторым проблемам схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора омические по своей природе.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.
Найдите полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найди сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ текст {V} \).\ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.
Найдите полное сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ text {1} \ text {Ω} \]с
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R – R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \), и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета напряжения падение через известные резисторы. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \).Теперь мы можем использовать эту информацию для найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Так как падение напряжения на всех резисторах вместе должно быть таким же, как и падение напряжения через ячейку в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V – V_1 – V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_3 \)
Мы знаем напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома, чтобы рассчитать значение сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
temp textПараллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это потому, что есть только два набора электрически общие точки в параллельной цепи и напряжение, измеренное между наборами общих точек всегда должны быть одинаковыми в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}.\]Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны складываться. до полного тока в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}. \]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельной резисторов, теперь мы можем подойти к некоторым схемам, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная схема
Вычислите ток (I) в этой цепи, если оба резистора омические по своей природе.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.
Найдите эквивалентное сопротивление в цепи
.Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {выровнять *}Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная схема
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найди сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Так как резисторы омические и нам даны напряжение на ячейке и ток через ячейку мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}
Рассчитайте значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для резисторов, включенных параллельно, найти сопротивление \ (R_2 \).\ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} – \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} – \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
temp textРабочий пример 7: Закон Ома, параллельная схема
Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. У нас есть была задана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для вычисления силы тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалент сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через клетка: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I – I_1 \\ & = 6 – 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Учебное упражнение 11.4Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}Теперь мы можем найти неизвестное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} – R_ {1} – R_ {2} – R_ {3} \\ & = 9 – 3 – 3 – 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены в серия с \ (\ text {12} \) \ (\ text {V} \) батареей.Рассчитайте значение тока в схема.
Рисуем принципиальную схему:
Теперь мы находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}Рассчитайте ток через ячейку, если оба резистора омические по своей природе.
Сначала находим общее сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} – \ frac {1} {R_ {2}} – \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} – \ frac {1} {\ text {120}} – \ frac {1} {\ text {40}} – \ frac {1} {\ text {60}} \\ & = \ frac {10 – 1 – 3 – 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}значение тока через аккумулятор
Рисуем принципиальную схему:
Чтобы вычислить значение тока через аккумулятор, нам сначала нужно вычислить эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}Теперь можем посчитать ток через батарею:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}значение тока в каждом из трех резисторов.
Для параллельной цепи напряжение на ячейке такое же, как и напряжение на каждой резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}Вы можете проверить, что они в сумме составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы к работе со схемами. которые объединяют эти две схемы, например, следующую схему:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.Проработать такие схемы относительно легко, потому что вы используете все, что у вас уже есть. узнал о последовательных и параллельных цепях. Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из двух параллельных частей. которые затем последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начнете с вычислить общее сопротивление каждой из параллельных частей, а затем сложить эти сопротивления в серии. {- 1} \\ & = \ текст {5} \, \ Omega \ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}
Эквивалентное сопротивление цепи на Рисунке 11.1 это \ (\ текст {10} \) \ (\ текст {Ω} \).
временный текстПоследовательные и параллельные сети
Учебное упражнение 11.5Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем рассчитать эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Мы начинаем путем вычисления эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ текст {A} \). (Сила тока одинакова при последовательной комбинации резисторов и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов. (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалент сопротивление цепи):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это также является напряжением на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {A} \ end {выровнять *}Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы являются омическими, рассчитайте напряжение на ячейке и на каждом из резисторов \ (R_1 \), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}Итак, напряжение на ячейке:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательной комбинации резисторов, и мы можем рассмотреть весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с поиска напряжение на \ (R_ {1} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}Теперь находим напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).
ток через ячейку
Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2,5}) (\ текст {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение равно то же самое на каждом резисторе в параллельной комбинации:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *}2.2.4 Закон Ома и почему мы заботимся о сопротивлении
2.2.4 Закон Ома и почему мы заботимся о сопротивлении
Устройство, известное нам как тостер, на удивление простое. Он состоит в основном из провода, по которому пропускается ток. Проволока нагревается, поджаривая хлеб. Вот и все!
а почему нагревается провод? Ответ в том, что провод имеет некоторое сопротивление. Когда ток проходит через материал с некоторым сопротивлением, материал нагревается. Это тепло в первую очередь является рассеянием некоторой части электроэнергии, проходящей через материал.Это рассеяние мощности в виде тепла называется «потерями» в электросети.
Сопротивление материала, через который проходит ток, помогает определить потери, но это не единственный фактор. Напряжение, при котором энергия проходит через материал, также имеет значение, как и величина тока.
Это соотношение четко резюмируется в законе Ома, который гласит, что напряжение равно произведению тока и сопротивления, или V = I × R.Закон Ома используется для определения величины напряжения, необходимого для перемещения заданного количества тока (I) через некоторый материал с заданным сопротивлением (R).
Между тем, вспомните наше определение мощности: P = I × V. По сути, это количество мощности, передаваемой в цепи, подобной той, что была в нашем последнем упражнении.
Мы можем включить закон Ома в наше определение мощности, чтобы получить:
P = I × V = I × (I × R) = I2 × R
Это уравнение описывает количество мощности, рассеиваемой в цепи.Он также описывает количество потерь. Таким образом, закон Ома говорит нам, что потери будут увеличиваться пропорционально квадрату тока. Таким образом, если мы сохраним постоянное напряжение и удвоим ток, потери увеличатся в четыре раза.
Чтобы понять важность этого, предположим, что мы пропускаем 1000 ампер тока через цепь с падением напряжения 100 В. Итак, у нас есть мощность 100 кВт. Потери в цепи будут пропорциональны I2 × R, или 10002 × R в этом случае.
Но, если бы нам нужно было 100 кВт мощности, мы могли бы сделать это по-другому, пропустив через цепь 100 А при напряжении 1000 В.Сопротивление в цепи не изменится, но потери в цепи теперь будут пропорциональны 100 2 × R.
Таким образом, увеличивая напряжение (и уменьшая ток) в 10 раз, мы уменьшили наши потери в 100 раз. Это объясняет причину того, что у нас есть сеть переменного тока вместо сети постоянного тока. Помните, что в технологии питания постоянного тока Эдисона напряжение в источнике должно быть близко к напряжению в точке потребления.Но с помощью технологии переменного тока, разработанной Tesla и Westinghouse, мощность может генерироваться и передаваться при очень высоких напряжениях, а затем снижаться до более низких напряжений в точке потребления. Это имело два больших преимущества: во-первых, можно было существенно снизить потери при передаче, а во-вторых, для домов и предприятий было намного безопаснее использовать электроэнергию низкого напряжения, а не высокого напряжения.
9.5: Закон Ома – Физика LibreTexts
До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление.Оказывается, многие материалы демонстрируют простую взаимосвязь между значениями этих свойств, известную как закон Ома. Многие другие материалы не демонстрируют эту взаимосвязь, поэтому, несмотря на то, что они называются законом Ома, они не считаются законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Описание закона Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В .Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
.\ [I \ propto V. \]
Это важное соотношение лежит в основе закона Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток – следствием. Это эмпирический закон, который означает, что это экспериментально наблюдаемое явление, подобное трению.Такая линейная зависимость возникает не всегда. Любой материал, компонент или устройство, которые подчиняются закону Ома, где ток через устройство пропорционален приложенному напряжению, известен как омический материал или омический компонент . Любой материал или компонент, который не подчиняется закону Ома, известен как неомический материал или неомический компонент.
Эксперимент Ома
В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины.Похожий эксперимент показан на рисунке \ (\ PageIndex {1} \). Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор включен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо разместить на резисторе (параллельно резистору). Ток измеряется амперметром, который должен быть на одной линии с резистором (последовательно с резистором).
Рисунок \ (\ PageIndex {1} \): экспериментальная установка, используемая для определения того, является ли резистор омическим или неомическим устройством.(a) Когда батарея подключена, ток течет по часовой стрелке, а вольтметр и амперметр показывают положительные значения. (b) Когда выводы батареи переключаются, ток течет против часовой стрелки, а вольтметр и амперметр показывают отрицательные показания.В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких различных напряжений. Когда батарея была подключена, как показано на рисунке \ (\ PageIndex {1a} \), ток протекал по часовой стрелке, и показания вольтметра и амперметра были положительными.Изменится ли поведение тока, если ток течет в обратном направлении? Чтобы заставить ток течь в обратном направлении, выводы батареи можно переключить. При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в обратном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {1} \): резистор вставлен в цепь с батареей.Приложенное напряжение изменяется от -10,00 В до +10,00 В с шагом 1,00 В. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора.В этом эксперименте напряжение, приложенное к резистору, изменяется от -10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Построен график зависимости напряжения от тока, и результат будет приблизительно линейным. Наклон линии – это сопротивление или напряжение, деленное на ток.Этот результат известен как закон Ома :
.\ [V = IR \ label {Ohms} \]
, где В – напряжение, измеренное в вольтах на рассматриваемом объекте, I – ток, измеренный через объект в амперах, а R – сопротивление в единицах Ом. Как указывалось ранее, любое устройство, которое показывает линейную зависимость между напряжением и током, известно как омическое устройство. Следовательно, резистор – это омическое устройство.
Пример \ (\ PageIndex {1} \): измерение сопротивления
Угольный резистор при комнатной температуре \ ((20 ° C) \) присоединен к 9.oC \) при нагревании резистора какой ток через резистор?
Стратегия
(а) Сопротивление можно найти с помощью закона Ома. Закон Ома гласит, что \ (V = IR \), поэтому сопротивление можно найти с помощью \ (R = V / I \).
(b) Во-первых, сопротивление зависит от температуры, поэтому новое сопротивление после нагрева резистора можно найти с помощью \ (R = R_0 (1 + \ alpha \ Delta T) \). Ток можно найти с помощью закона Ома в виде \ (I = V / R \).
Решение
- Использование закона Ома и решение для сопротивления дает сопротивление при комнатной температуре: \ [R = \ dfrac {V} {I} = \ dfrac {9.oC \) привело к изменению тока на 2,00%. Это может показаться не очень большим изменением, но изменение электрических характеристик может сильно повлиять на цепи. По этой причине многие электронные устройства, такие как компьютеры, содержат вентиляторы для отвода тепла, рассеиваемого компонентами электрических цепей.
Упражнение \ (\ PageIndex {1} \)
Напряжение, подаваемое в ваш дом, изменяется как \ (V (t) = V_ {max} sin \, (2 \ pi \, ft) \). Если к этому напряжению подключить резистор, будет ли по-прежнему действовать закон Ома \ (V = IR \)?
- Ответ
Да, закон Ома все еще в силе.В каждый момент времени ток равен \ (I (t) = V (t) / R \), поэтому ток также является функцией времени, \ (I (t) = \ dfrac {V_ {max} } {R} \, sin \, (2 \ pi \, ft) \).
Моделирование: PhET
Посмотрите, как закон Ома (Equation \ ref {Ohms}) соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Неомные устройства не показывают линейной зависимости между напряжением и током.Одним из таких устройств является элемент полупроводниковой схемы, известный как диод . Диод – это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой схемы, состоящей из батареи, диода и резистора, показана на рисунке \ (\ PageIndex {3} \). Хотя мы не рассматриваем теорию диода в этом разделе, диод можно протестировать, чтобы определить, является ли он омическим или неомическим устройством.
Рисунок \ (\ PageIndex {3} \): Диод – это полупроводниковое устройство, которое пропускает ток, только если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.График зависимости тока от напряжения показан на рисунке \ (\ PageIndex {4} \). Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод находится под отрицательным потенциалом, а катод – под положительным потенциалом, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток – практически нулевой ток.Когда напряжение, приложенное к цепи, увеличивается, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не будет проводить ток. Когда аккумулятор и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит, и ток течет через диод, если напряжение больше 0,7 В. Сопротивление диода близко к нулю. (Это причина наличия резистора в цепи; если бы его не было, ток стал бы очень большим.) Из графика на рисунке \ (\ PageIndex {4} \) видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером безомного устройства.
Рисунок \ (\ PageIndex {4} \): Когда напряжение на диоде отрицательное и небольшое, через диод протекает очень небольшой ток. Когда напряжение достигает напряжения пробоя, диод проводит. Когда напряжение на диоде положительное и превышает 0,7 В (фактическое значение напряжения зависит от диода), диод проводит.По мере увеличения приложенного напряжения ток через диод увеличивается, но напряжение на диоде остается примерно 0,7 В.Закон Ома обычно формулируется как \ (V = IR \), но первоначально он был заявлен как микроскопический вид, в с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность \ (V \ propto I \) происходит от скорости дрейфа свободных электронов в металле, возникающей в результате приложенного электрического поля. Как было сказано ранее, плотность тока пропорциональна приложенному электрическому полю.Переформулировка закона Ома приписывается Густаву Кирхгофу, имя которого мы снова увидим в следующей главе.
Описание лаборатории: лаборатория закона Ома
Вопрос исследования:
Как увеличение напряжения (v) до 5v, 10v, 20v, 35v, а затем 50v повлияет на величину тока (Amps), измеряемого амперметром, при сохранении сопротивления (Ом) на уровне 12 Ом и длины провода 10 см постоянной , в последовательной цепи, чтобы доказать закон Ома?
Справочная информация о законе Ома:
ЗаконОм можно использовать для определения взаимосвязи между напряжением, током и сопротивлением в любой электрической цепи постоянного тока, обнаруженной немецким физиком Георгом Омом.Этот закон гласит, что напряжение равно произведению полного тока на полное сопротивление.
Уравнение этого закона часто представляется в виде треугольника, где напряжение находится вверху, ток и сопротивление внизу, а их разделяет только линия;
Чтобы найти напряжение, вы должны умножить ток и сопротивление, чтобы найти ток или сопротивление, вы должны разделить напряжение либо на ток (чтобы найти сопротивление), либо на сопротивление (чтобы найти ток).
Гипотеза:
Я предсказываю, что чем выше напряжение, тем выше будет сила тока. Я думаю, это потому, что в последовательной цепи будет больше мощности из-за более высокого напряжения, что указывает на то, что ток будет протекать в более быстром темпе даже при сопротивлении 12 Ом.
Если напряжение равно 5, а сопротивление 12 Ом, ток будет двигаться медленнее и уменьшаться, потому что сопротивление вызывает этот более медленный темп в результате использования большего количества энергии от батареи / напряжения.
Переменных:
Независимая переменная: Независимая переменная – величина напряжения; 5В, 10В, 20В, 35В и 50В.
Зависимая переменная: Зависимая переменная – это величина тока, протекающего в последовательной цепи, измеренная в AMPS или A.Управляемая переменная:
Что останется прежним Почему он останется прежним Как он останется прежним Я сохраню сопротивление тем же. Я сохраню сопротивление то же самое, чтобы провести точный эксперимент. Я сохраню сопротивление таким же выставив резистор на 12 Ом. Я сохраню длину проводов тем же. Я сохраню длину проводов то же самое справедливое судебное разбирательство. Я сохраню длину проводов То же самое, только провода длиной 10 см. Я сохраню место амперметра в схема такая же. Я сохраню место амперметра в схема такая же, потому что показания могут измениться в разных позиции и получить точные результаты. Я сохраню место амперметра в схема такая же, построив схему и не добавив к ней ничего лишнего это изменит точку амперметра. Аккумулятор буду держать такой же. Я оставлю батарею такой же, чтобы иметь справедливое судебное разбирательство, потому что, если используются разные батареи, выход может быть другим даже при одинаковом напряжении. Батарею буду держать такой же не вынимая его из цепи, когда он включен, и изменяйте напряжение только тогда, когда нужный. Я оставлю резистор на месте тем же. Я оставлю резистор на месте то же самое, потому что результаты могут быть скомпрометированы, поэтому, чтобы избежать этого и получить точные результаты буду держать резистор на том же месте в серии схема. Я оставлю резистор на месте то же самое, построив схему и не добавив ничего лишнего в схему это могло изменить пятно резистора. Материалы:
- Батарея X1
- Резистор X1
- Амперметр X1
- Провода X7 (при необходимости используйте больше)
- Переключатель X1 (опционально, я не использовал используйте один, поскольку это не обязательно)
Безопасность:
При проведении этого эксперимента обязательно примите меры предосторожности, чтобы быть в безопасности и избегать любой опасности. Во-первых, не допускайте попадания жидкости вокруг контура, потому что, если она разольется, это может вызвать серьезные проблемы с контуром, такие как образование искр и / или возможное возгорание, потому что жидкости увеличивают проводимость электрического потока.
Убедитесь, что все незакрепленные предметы не свисают с любого места вашего тела, как галстук, а если у вас длинные волосы, завяжите их назад, чтобы ничто не касалось цепи, так как это может раздражать вас и быть опасным.
Наконец, проверьте, что все материалы находятся в идеальном состоянии, чтобы избежать любых опасностей, которые могут возникнуть, особенно проверьте батарею, потому что, если она не в идеальном состоянии, она может взорваться и стать очень опасной.
Метод:
График
Таблица результатов:
Напряжение (v) Сопротивление (Ом) Ток (амперы / год) 5 12 0.42 10 12 0,83 20 12 1,67 35 год 12 2,92 50 12 4,17 Заключение эксперимента:
Данные показывают, что чем выше напряжение, тем выше ток, а это означает, что напряжение прямо пропорционально току, что и указано в законе об Омах.Это означает, что при увеличении напряжения ток всегда будет увеличиваться до тех пор, пока нет сопротивления или если сопротивление остается неизменным.
Например, в моем эксперименте я увеличил напряжение с 5 В, 10 В, 20 В, 35 В до 50 В, сохраняя при этом сопротивление таким же, чтобы ток увеличивался каждый раз при увеличении напряжения.
Закон был подтвержден для каждого испытания, которое я проводил, и это можно увидеть, поделив напряжение на ток, чтобы получить сопротивление. Моя гипотеза была верной, в моей гипотезе я утверждал, что чем выше напряжение, тем выше ток.Как показано выше, напряжение прямо пропорционально току.
Один из примеров из моих результатов: когда я увеличил напряжение до 50 В, я разделил это число на ток, равный 4,17, чтобы получить величину сопротивления, равную 12 Ом.
Оценка эксперимента:
В целом эксперимент прошел хорошо, и цель испытания состояла в том, как изменение напряжения могло повлиять на величину тока, протекающего в последовательной цепи, при этом можно было доказать закон Ома.Слабым местом моего эксперимента является график результатов.
Мой график был моей слабостью в этом эксперименте, потому что на графике должно было быть указано сопротивление, поскольку это ключевой факт при доказательстве закона Ома.
Одно улучшение, которое я мог бы сделать, чтобы сделать эксперимент лучше и получить более точные результаты, как если бы я добавил в последовательную цепь вольтамперометр.
Вольтамперометр будет считывать величину напряжения, которое выдается из используемой батареи, поэтому, если бы я использовал вольтамперметр, я мог бы убедиться, что величина напряжения, выдаваемого из батареи, была правильной, и результаты были бы более точными. .
Если мы помогли вам, пожалуйста, помогите нам исправить его улыбку своими старыми эссе … это займет секунды!
-Мы ищем предыдущие эссе, лабораторные работы и задания, которые вы выполнили!
-Мы рассмотрим и разместим их на нашем сайте.
– Доход от рекламы используется для поддержки детей в развивающихся странах.
-Мы помогаем оплатить операции по восстановлению расщелины неба через операцию «Улыбка и поезд улыбки».калькулятор расчета закона Ома рассчитать формулы мощности математический закон Ома круговая диаграмма падение электрического напряжения формула сопротивления электрического тока закон Ватта ЭДС магический треугольник уравнение подсказка онлайн напряжение вольт сопротивление резистора амперы аудиотехника EV = IR – P = VI вычисление зависимости удельного сопротивления проводимости
Ом закон вычисление калькулятор вычислить формулы мощности математический закон Ома круговая диаграмма электрическое падение напряжения электрический ток формула сопротивления закон Ватта ЭДС магический треугольник уравнение подсказка онлайн напряжение вольт сопротивление резистора амперы амперы аудиотехника EV = IR – P = VI calc проводимость связь удельное сопротивление связь – sengpielaudio Sengpiel Berlin
= сбросить.Формулы: V = I R I = V / R R = V / I
Математические формулы закона Ома
ЗаконОма можно переписать тремя способами для вычисления тока, сопротивления и напряжения.
Если через резистор R должен протекать ток I , можно рассчитать напряжение В .
Первая версия формулы (напряжения): V = I × RЕсли есть напряжение В на резисторе R , через него протекает ток I . I можно рассчитать.
Вторая версия (текущей) формулы: I = V / RЕсли через резистор протекает ток I , а на резисторе имеется напряжение В . R можно рассчитать.
Третья версия формулы (сопротивления): R = V / IВсе эти вариации так называемого «закона Ома» математически равны друг другу.
Имя Знак формулы Блок Символ напряжение V или E вольт В текущий я ампер (ампер) А сопротивление р Ом Ом мощность п. ватт Вт Какая формула для электрического тока?
При постоянном токе:
I = Δ Q / Δ t
I – ток в амперах (А)
Δ Q – электрический заряд в кулонах (C),
, который течет в течение времени Δ t в секундах (с).
Напряжение В = ток I × сопротивление R
Мощность P = напряжение В × ток IВ электрических проводниках, в которых ток и напряжение пропорциональны
друг другу, применяется закон Ома: В ~ I или В ⁄ I = const.
Проволока из константана или другая металлическая проволока, выдерживаемая при постоянной температуре, хорошо соответствует закону Ома.
“ V ⁄ I = R = const.” ist не закон Ома. Это определение сопротивления.
После этого в каждой точке, даже с изогнутой кривой, можно рассчитать значение сопротивления.
На многие электрические компоненты, например диоды, закон Ома не распространяется.«Закон Ома» не был изобретен господином Омом
“ U ⁄ I = R = конст.”- это , а не закон Ома или закон Ома. Это определение сопротивления.
После этого в каждой точке – даже с изогнутой кривой – значение сопротивления может быть вычислено.
Закон Ома” постулирует “следующие отношения: Когда к объекту прикладывается напряжение, электрический ток
, протекающий через него, изменяет силу, пропорциональную напряжению. Другими словами, электрическое сопротивление
, определяемое как отношение напряжения к току, является постоянным, и оно равно
независимо от напряжения. и ток.Название закона «почитает» Георга Симона Ома, который смог
доказать эту взаимосвязь для некоторых простых электрических проводников в качестве одного из первых исследователей.
«Закон Ома» действительно не был изобретен Омом.
Обозначение I или J = латиница: приток, международный ампер и R = сопротивление. В = напряжение илиСовет: магический треугольник Ома Магический треугольник V I R можно использовать для расчета всех формулировок закона Ома.
Используйте палец, чтобы скрыть вычисляемое значение. Затем два других значения показывают
, как производить расчет.
разность электрических потенциалов, также называемая падением напряжения, или E = электродвижущая сила (ЭДС = напряжение).Расчет падения напряжения – постоянный / однофазный расчет
Падение напряжения В в вольтах (В) равно току в проводе I в амперах (А), умноженном на удвоение
длина провода L в футах (футах), умноженном на сопротивление провода на 1000 футов R в омах (Ω / kft)
деленное на 1000:
V падение (V) = I провод (A) × R провод (Ом)
= I провод (A) × (2 × L (фут) × R провод (Ом / kft) / 1000 (ft / kft))Падение напряжения В в вольтах (В) равно току провода I в амперах (А), умноженному на два
, длина провода L в метрах (м), умноженная на сопротивление провода на 1000 метров R в омах
(Ом / км) разделить на 1000:
В падение (В) = I провод (A) × R провод (Ом)
= I провод (A) × (2 × L (м) × R провод (Ом / км) / 1000 (м / км))Если требуется блок power P = I × V и напряжение V = I · R ,
ищите ” Формулы большой мощности »:
Расчеты: мощность (ватт), напряжение, ток, сопротивлениеНекоторые думают, что Георг Симон Ом рассчитал «удельное сопротивление».
Поэтому они думают, что только следующее может быть истинным законом Ома.Количество сопротивлений R = сопротивление Ом ρ = удельное сопротивление Ом × м l = двойная длина кабеля м A = поперечное сечение мм 2 Электропроводность (проводимость) σ (сигма) = 1/ ρ
Удельное электрическое сопротивление (удельное сопротивление) = 1/ σРазница между удельным электрическим сопротивлением и электропроводностью
Проводимость в сименсах обратно пропорциональна сопротивлению в омах. Просто введите значение слева или справа.
Калькулятор работает в обоих направлениях знака ↔ .Значение электропроводности (проводимости) и удельного электрического сопротивления 91929291 92 991 σ × A )
(удельное сопротивление) зависит от температуры материала постоянной. Чаще всего его дают при 20 или 25 ° C.
Сопротивление R = ρ × ( l / A ) или RДля всех проводников удельное сопротивление изменяется в зависимости от температуры.В ограниченном диапазоне температур
это примерно линейно:
где α – температурный коэффициент, T – температура, а T 0 – любая температура,
например T 0 = 293,15 K = 20 ° C, при котором удельное электрическое сопротивление ρ ( T 0 ) известен.Площадь поперечного сечения – поперечное сечение – плоскость среза
Теперь возникает вопрос:
Как можно рассчитать площадь поперечного сечения (плоскость среза) A
по диаметру проволоки d и наоборот?Расчет поперечного сечения A (плоскость среза) от диаметра d :
r = радиус проволоки
d = диаметр проволокиРасчетный диаметр d из поперечного сечения A (плоскость среза ) :
Поперечное сечение A провода в мм 2 , вставленные в эту формулу, дают диаметр d в мм.Расчет – Круглые кабели и провода:
Электрическое напряжение В = I × R (закон Ома VIR)
• Диаметр к поперечному сечению и наоборот •
Электрическое напряжение = сила тока × сопротивление (закон Ома)
Введите два значения , будет рассчитано третье значение.
Электроэнергия P = I × В (степенной закон PIV)
Электроэнергия = сила тока × напряжение (закон Ватта)
Введите два значения , будет рассчитано третье значение.Закон Ома. В = I × R , где В, – потенциал на элементе схемы, I – ток
через него, а R – его сопротивление. Это не общеприменимое определение сопротивления
. Это применимо только к омическим резисторам, сопротивление которых R равно
постоянной во всем интересующем диапазоне, а В подчиняется строго линейной зависимости от I . Материалы
считаются омическими, если V линейно зависит от R .Металлы являются омическими, пока один
поддерживает постоянную температуру. Но изменение температуры металла немного меняет R
. Когда ток изменяется быстро, например, при включении света или при использовании источников переменного тока
, может наблюдаться слегка нелинейное и неомическое поведение. Для неомических резисторов
R зависит от тока, и определение R = d V / d I гораздо более полезно. Это значение
иногда называют динамическим сопротивлением.Твердотельные устройства, такие как термисторы,
являются неомическими и нелинейными. Сопротивление термистора уменьшается по мере его нагрева, поэтому его динамическое сопротивление
отрицательно. Туннельные диоды и некоторые электрохимические процессы
имеют сложную кривую от I до В с областью действия отрицательного сопротивления. Зависимость сопротивления
от тока частично связана с изменением температуры устройства
с увеличением тока, но другие тонкие процессы также способствуют изменению сопротивления
в твердотельных устройствах.Расчет: калькулятор параллельного сопротивления (резистора)
Калькулятор цветового кода для резисторов
Электрический ток, электрическая мощность, электричество и электрический заряд
Колесо формул – формулы электротехники
In acoustics используйте «закон Ома в качестве акустического эквивалента »
Как работает электричество.
Закон Ома ясно объяснен.[начало страницы]
Согласно закону Ома, I ∝ V, но I 1 / V в уравнении мощности. Как?
In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?
Это еще один запутанный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.
Согласно закону Ома, ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как объяснить?
, т.е.
- Согласно закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
- Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)
Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.
Давайте проясним путаницу, связанную с утверждением.
P = V x I
На самом деле, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной или она меняется.
- Если мощность источника постоянна, ток будет уменьшаться при увеличении напряжения.
- Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при увеличении напряжения, поскольку мощность больше не постоянна i.е. мощность также была увеличена.
В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).
В = I x R
По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.
Согласно формуле мощности, в ней говорится, что ток обратно пропорционален напряжению, если мощность остается прежней.
Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение власть). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.
Та же история и с генерирующей станцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.
Вкратце:
- Если мощность постоянна = Напряжение обратно пропорционально току , т.е. В ∝ 1 / I в P = VxI .
- Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , т. Е. В I в В = IxR .
Это точная причина , почему по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.
Связанные вопросы / ответы:
Электрическое сопротивление – Гипертекст по физике
Обсуждение
введение
Йех! Что за беспорядок.
Проводимость: С. Грей, 1729 – Сопротивление: Георг Симон Ом, 1827.
Обычная версия…
I ∝ V
I = В ⇒ .В = ИК ⇒ .R = В р Я Variableogy…
- количество: сопротивление R
единица: Ом [Ом] Георг Ом (1787–1854) Германия
Причудливая версия (магнитогидродинамическая версия?)…
J ∝ E
J = σ E ⇐ ⇒ .E = ρ J Добро пожаловать в символ ада…
Электрические характеристики количество символ единица СИ символ собственность… сопротивление R Ом Ом объектов проводимость г siemens S удельное сопротивление ρ омметр Ом · м материалов проводимость σ сименс на метр См / м Закон Ома не является серьезным законом.Это непростая физика. Разумные материалы и устройства подчиняются ему, но есть множество мошенников, которые этого не делают.
резисторы
Плохая выпивка портит наши молодые кишки, но водка идет хорошо.
Лучше постройте крышу над гаражом, пока фургон не намок.
Коды маркировки резисторов и конденсаторов цвет цифра множитель допуск tcr (10 −6 / К) нет ± 20% розовый 10 −3 серебро 10 −2 ± 10% золото 10 -1 ± 5% черный 0 10 0+ ± 250 коричневый 1 10 1+ ± 1% ± 100 красный 2 10 2+ ± 2% ± 50 оранжевый 3 10 3+ ± 0.05% ± 15 желтый 4 10 4+ ± 0,02% ± 25 зеленый 5 10 5+ ± 0,50% ± 20 синий 6 10 6+ ± 0,25% ± 10 фиолетовый 7 ± 0.10% ± 5 серый 8 ± 0,01% ± 1 белый 9 материалы
Сопротивление и удельное сопротивление. Факторы, влияющие на сопротивление в проводящем проводе.
Проводники и изоляторы
Лучшие электрические проводники: серебро, медь, золото, алюминий, кальций, бериллий, вольфрам
Удельное сопротивление и проводимость взаимны.
Электропроводность металлов – это статистическая / термодинамическая величина.
Удельное сопротивление определяется рассеянием электронов. Чем больше рассеяние, тем выше сопротивление.
, где…
σ = Электропроводность [См / м] n = плотность свободных электронов [э / м 3 ] e = заряд электрона (1,60 × 10 −19 Кл) м e = масса электрона (9.11 × 10 −31 кг) v среднеквадратичное значение = Среднеквадратичная скорость электронов [м / с] ℓ = средняя длина свободного пробега [м] Графит
Кому принадлежит эта идея? Нихром был изобретен в 1906 году, что сделало возможным электрические тостеры.
Проводящие полимеры.
Удельное сопротивление выбранных материалов (~ 300 K)
(Обратите внимание на разницу в единицах измерения между металлами и неметаллами.)металлы ρ (нОм м) алюминий 26,5 латунь 64 хром 126 медь 17,1 золото 22,1 утюг 96,1 свинец 208 литий 92.8 ртуть (0 ° C) 941 марганец 1440 нихром 1500 никель 69,3 палладий 105,4 платина 105 плутоний 1414 серебро 15,9 припой 150 сталь, гладкая 180 сталь, нержавеющая 720 тантал 131 банка (0 ° C) 115 титан (0 ° C) 390 вольфрам 52.8 уран (0 ° C) 280 цинк 59 неметаллы ρ (Ом м) оксид алюминия (14 ° C) 1 × 10 14 оксид алюминия (300 ° C) 3 × 10 11 оксид алюминия (800 ° C) 4 × 10 6 углерод аморфный 0.35 карбон, алмаз 2,7 углерод, графит 650 × 10 −9 Оксид индия и олова, тонкая пленка 2000 × 10 −9 германий 0,46 пирекс 7740 40 000 кварц 75 × 10 16 кремний 640 диоксид кремния (20 ° C) 1 × 10 13 диоксид кремния (600 ° C) 70 000 диоксид кремния (1300 ° C) 0.004 вода, жидкость (0 ° C) 861 900 вода, жидкость (25 ° C) 181 800 вода, жидкость (100 ° C) 12 740 температура
Общее правило – удельное сопротивление увеличивается с увеличением температуры в проводниках и уменьшается с увеличением температуры в изоляторах. К сожалению, не существует простой математической функции для описания этих отношений.
Температурную зависимость удельного сопротивления (или обратной проводимости) можно понять только с помощью квантовой механики. Точно так же, как материя представляет собой совокупность микроскопических частиц, называемых атомами, а луч света – это поток микроскопических частиц, называемых фотонами, тепловые колебания в твердом теле представляют собой рой микроскопических частиц, называемых фононами . Электроны пытаются дрейфовать к положительному полюсу батареи, но фононы продолжают врезаться в них.Случайное направление этих столкновений нарушает попытку организованного движения электронов против электрического поля. Отклонение или рассеяние электронов на фононах – один из источников сопротивления. С повышением температуры количество фононов увеличивается, а вместе с ним и вероятность столкновения электронов и фононов. Таким образом, когда температура повышается, сопротивление повышается.
Для некоторых материалов удельное сопротивление линейно зависит от температуры.
ρ = ρ 0 (1 + α ( T – T 0 ))
Удельное сопротивление проводника увеличивается с температурой.В случае меди зависимость между удельным сопротивлением и температурой примерно линейна в широком диапазоне температур.
Для других материалов лучше работает соотношение сил.
ρ = ρ 0 ( T / T 0 ) μ
Удельное сопротивление проводника увеличивается с температурой. В случае вольфрама зависимость между удельным сопротивлением и температурой лучше всего описывается соотношением мощности.
см. Также: сверхпроводимость
разное
магнитосопротивление
фотопроводимость
жидкости
электролиты
газы
пробой диэлектрика
плазма
микрофоны
Угольный микрофон – ничто задом наперед
.Микрофоны и принцип их работы тип звук дает
изменение в…, что вызывает
изменение…, что приводит к
изменению…углерод Плотность гранул сопротивление напряжение конденсатор разделительная пластина емкость напряжение динамический Расположение змеевика флюс напряжение пьезоэлектрический компрессия поляризация напряжение



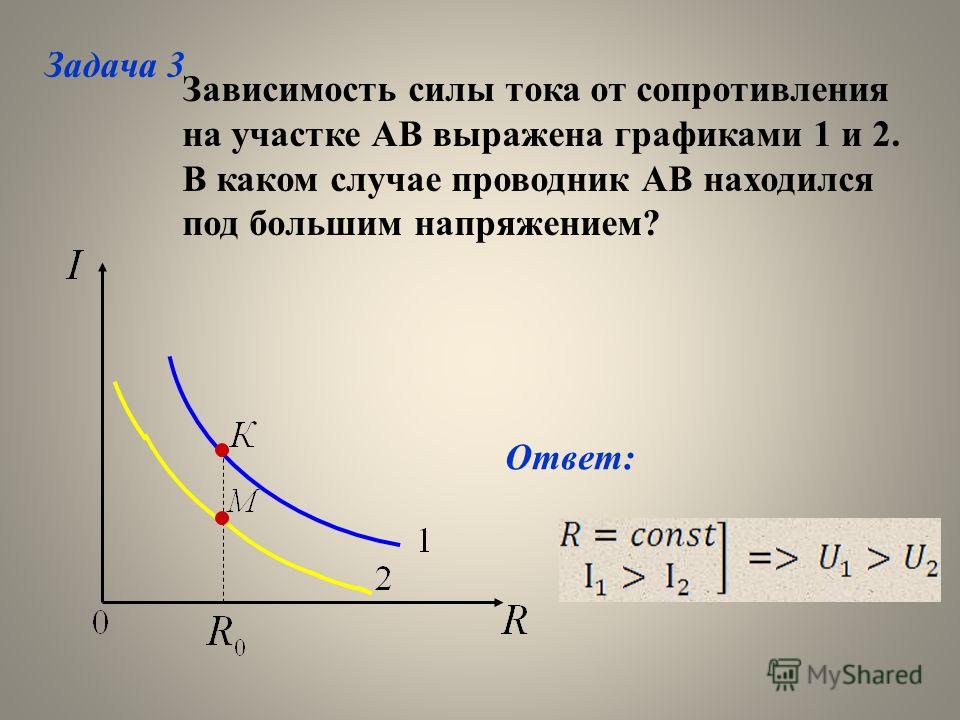
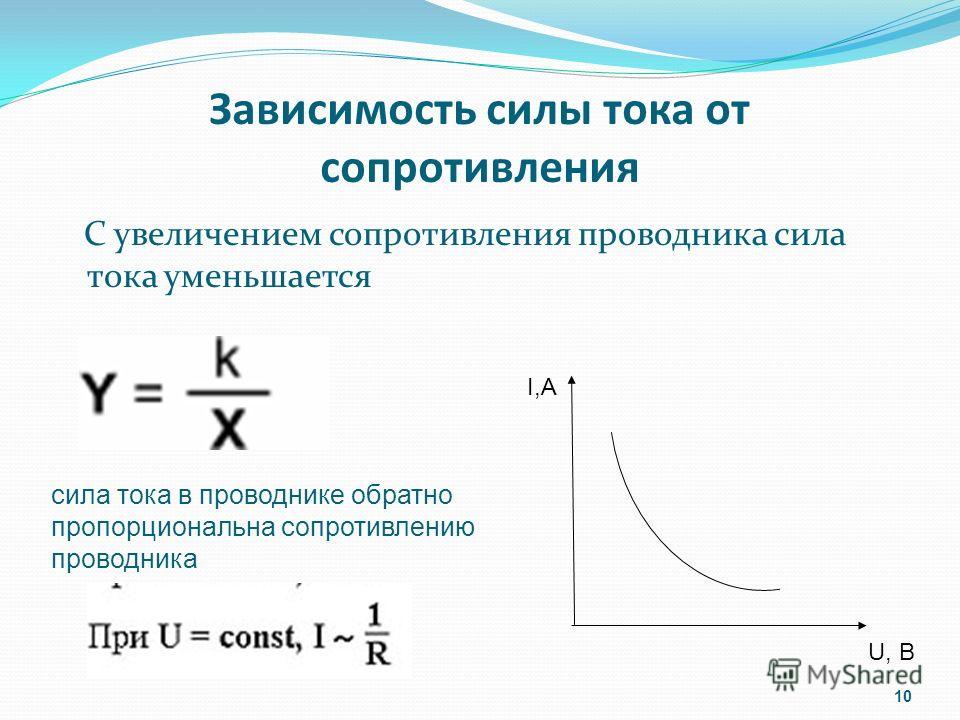







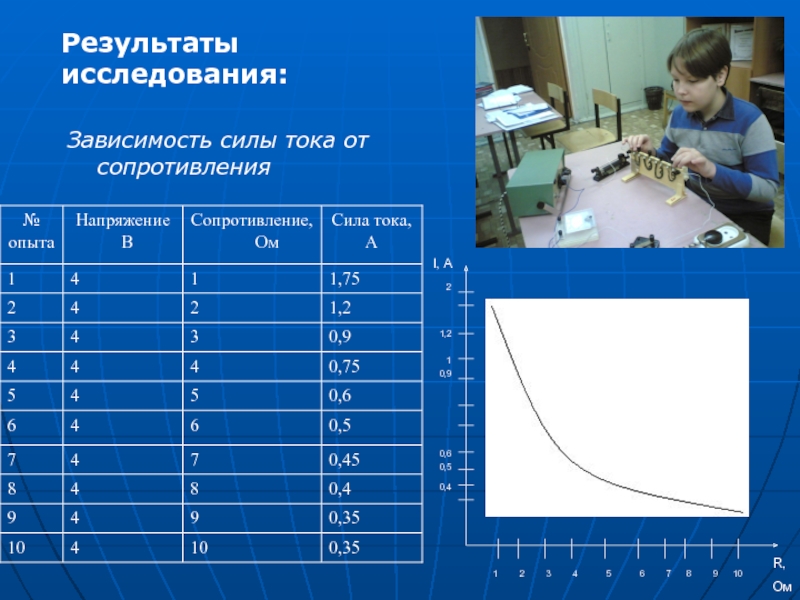
 и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \).
и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \). Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?
Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?