Зависимость ускорения от времени и скорости: Что представляют собой графики, на которых обозначена зависимость ускорения от времени? (статья)

Решение Чертов бесплатно

Поиск:

HOME | § 1   § 2   § 3   § 4   § 5   § 6   § 7   § 8   § 9   § 10   § 11   § 13   § 14   § 15   § 16   § 17   § 18   § 19   § 20   § 21   § 22   § 23   § 24   § 25   § 26   § 27   § 28   § 29   § 30   § 31   § 32   § 33   § 34   § 35   § 36   § 37   § 38   § 39   § 40   § 41   § 105

1. Кинематика Задача # 1.16. Две материальные точки движутся согласно уравнениям; x1=A1t+B1t2+C1t3, x2=A2t+B2t2+C2t3, где A1=4 м/c, B1=8 м/с2, C1= — 16 м/с3, A2=2 м/с, B2= – 4 м/с2, С2=1м/с3 В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v1 и v2 точек в этот момент. Задача # 1.15. Движения двух материальных точек выражаются уравнениями: x1=A1+B1t+C1t2, x2=A2+B2t+C2t2, где A1=20 м, A2=2 м, B1=B2=2 м/с, C1= — 4 м/с2, С2=0,5 м/с2. В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v1 и v2 и ускорения a1 и а2 точек в этот момент: Задача # 1.14. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью v1==l м/с и ускорением a1=2 м/с2, вторая — с начальной скоростью v2=10 м/с и ускорением а2=1 м/с2. Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую? Задача # 1.13. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а=0,1 м/с2, человек начал идти в том же направлении со скоростью v=1,5 м/с. Через какое время t поезд догонит человека? Определить скорость v1 поезда в этот момент и путь, пройденный за это время человеком. Задача # 1.12. Прожектор О (рис. 1.7) установлен на расстоянии l==100 м от стены АВ и бросает светлое пятно на эту стену. Прожектор вращается вокруг вертикальной оси, делая один оборот за время Т=20 с. Найти: 1) уравнение движения светлого пятна по стене в течение первой четверти оборота; 2) скорость v, с которой светлое пятно движется по стене, в момент времени t=2 с. За начало отсчета принять момент, когда направление луча совпадает с ОС. Задача # 1.11. Написать кинематическое уравнение движения x=f(t) точки для четырех случаев, представленных на рис. 1.6. На каждой Задача # 1.10. Движение материальной точки задано уравнением x=At+Bt2, где A =4 м/с, В=—0,05 м/с2. Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени. Задача # 1.9. На рис. 1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось. Задача # 1.8. Уравнение прямолинейного движения имеет вид x=At+Bt2, где A=3 м/с, B=—0,25 м/с2. Построить графики зависимости координаты и пути от времени для заданного движения. Задача # 1.7. Зависимость ускорения от времени при некотором движении тела представлена на рис. 1.5. Определить среднюю путевую скорость <v> за время t=8 с. Начальная скорость v0=0. Задача # 1.6. -Зависимость скорости от времени для движения некоторого тела представлена на рис. 1.4. Определить среднюю путевую скорость <v> за время t=14 с. Рис. 1.4 Рис. 1.5 Задача # 1.5. Тело прошло первую половину пути за время t1=2 с, вторую — за время t2=8 с. Определить среднюю путевую скорость <v> тела, если длина пути s=20 м. Задача # 1.4. Первую половину пути тело двигалось со скоростью v1=2 м/с, вторую — со скоростью v2=8 м/с. Определить среднюю путевую скорость <v> . Задача # 1.3. Три четверти своего пути автомобиль прошел со скоростью v1=60 км/ч, остальную часть пути — со скоростью v2=80 км/ч. Какова средняя путевая скорость <v> автомобиля? Задача # 1.2. Точка двигалась в течение t1=15 c со скоростью v1=5 м/с, в течение t2=10 с со скоростью v2=8 м/с и в течение t3=6 с со скоростью v3=20 м/с. Определить среднюю путевую скорость <v> точки. 1 2 3 4 5

Решения по Физике МИРЭА. sm

График зависимости VX от времени .

С точки зрения математической записи определения скорости и ускорения подобны. Поэтому из графика скорости можно получить график изменения координаты аналогично тому, как мы получали из графика ускорения изменение скорости.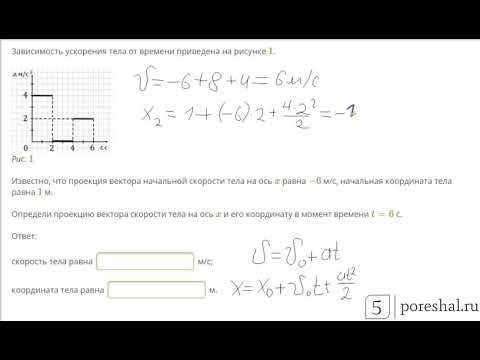

Из определения скорости (5) следует, что по заданной зависимости v

x(t), можно найти изменение координаты (проекции перемещения) x = x  x₀ за промежуток времени t = t  t₀:

. (13)

Аналогично тому, как мы искали изменение проекции скорости v_x по графику a_x(t), поиск изменения координаты x по графику v_x(t) сводится к определению площади под кривой v_x(t).

Н

Рис. 3

апример, для графика на рис. 3 за первые 2 секунды движения 

x будет равно площади треугольника 0.5×2 с×2 м/с=2 м, а за первые 3 секунды будет равно 3 м.

Если v_х > 0, то площадь берется со знаком плюс (x > 0), если v_х < 0 – то со знаком минус (x < 0). Если за время движения проекция скорости принимает как положительные, так и отрицательные значения, то для нахождения изменения координаты за этот промежуток времени нужно провести алгебраическое суммирование соответствующих величин. Например, для графика на рис. 3 перемещение x за промежуток времени со 2-й по 4-ю секунды будет равно нулю.

Если x есть интеграл от проекции скорости (см. выражение (13)), то пройденный путь , согласно определению (7), есть интеграл от модуля скорости. Т.е. для определения пройденного пути площади под графиком v_x(t) нужно всегда складывать независимо от знака проекции скорости. Например, для графика на рис. 3 за первые 3 секунды движения пройденный путь будет совпадать с проекцией перемещения x и будет равен 3 м, а за промежуток времени со 2-й по 4-ю секунды пройденный путь будет равен 2 м.

По графику v_x(t) можно найти среднюю скорость за некий промежуток времени.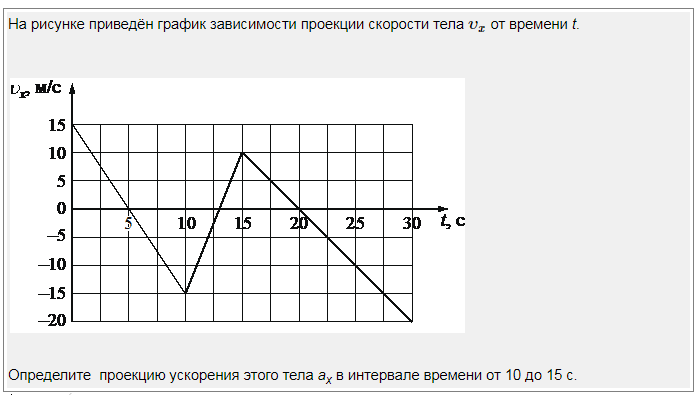

Из определения средней скорости (3) следует, что , а как показано выше, перемещение x численно равно площади под графиком v_x(t). Таким образом, например, для рис. 3 за первые 3 секунды движения средняя скорость равняется 3 м / 3 с=1 м/с.

По графику скорости v_x(t) можно определить проекцию ускорения. Из определения ускорения (10) следует, что ускорение есть производная от скорости по времени, то есть . Геометрический смысл производной есть тангенс угла наклона касательной к кривой в данной точке. Следовательно, тангенс угла наклона касательной к графику скорости v_x(t) численно равен ускорению точки в данный момент времени. В частном случае, когда график v

x(t) представляет прямую линию, тангенс угла наклона этой прямой к оси времени численно равен ускорению, т.е. . Например, для графика на рис. 3 в первые две секунды движения ускорение равнялось , а со 2-й по 4-ю секунды

Качественно: в случае движения с положительным ускорением касательная к графику скорости образует с осью времени острый угол, а если ускорение отрицательное – тупой угол (принято отсчет угла проводить от оси абсцисс против часовой стрелки).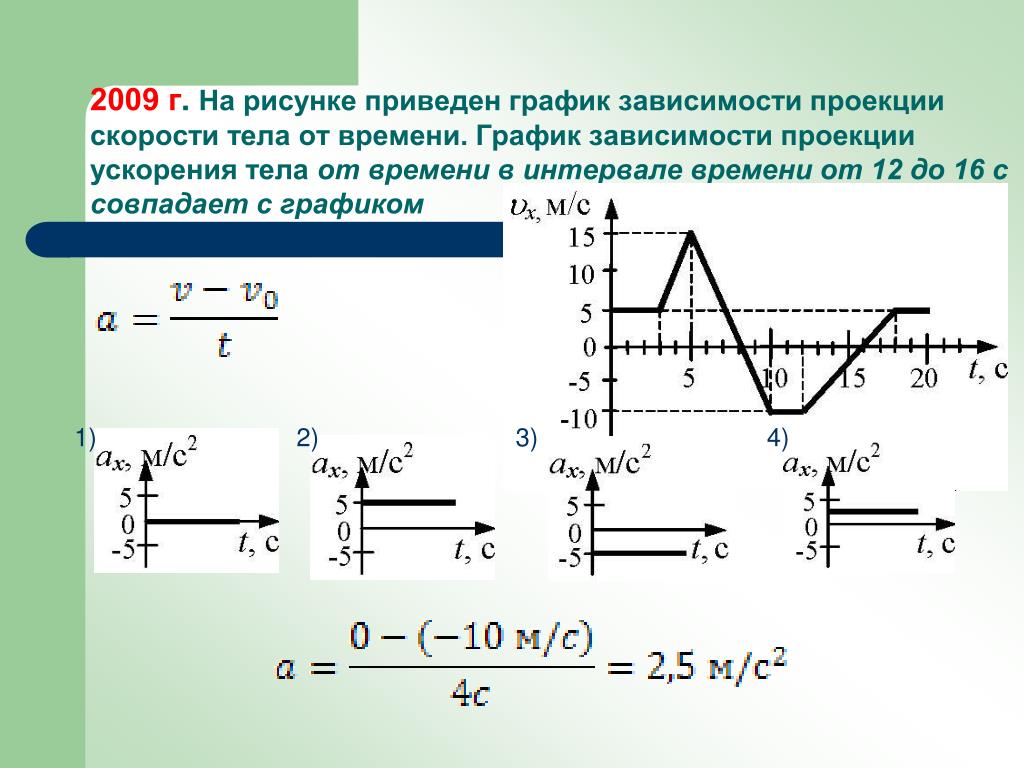 Величина же ускорения (его модуль) определяется крутизной графика скорости.

Задания для самостоятельной работы по графику v_x(t) на рис. 3:

1) Определите x с 3-й по 8-ю секунду, с 8-й по 9-ю секунду, с 9-й по 10-ю. За всё время движения точки.

2) Постройте график координаты x(t), если в начальный момент времени t₀ = 0 x₀ = 0.

3) Постройте график a_x(t).

4) Постройте график пройденного точкой пути как функцию времени.

5) Найдите среднюю скорость точки за следующие промежутки времени: со 2-й по 4-ю секунду; со 2-й по 9-ю секунду; за всё время движения.

6) Определите, в какой момент времени точка удалится от начала координат на максимальное расстояние?

7) Считая, что при t₀ = 0 x₀ = 0, определите, в какой момент времени координата точки снова окажется равной нулю.

8) Определите перемещение x и пройденный точкой путь на участке, на котором она двигалась с максимальным по величине ускорением.

9) Определите перемещение x и пройденный точкой путь на участке, на котором она двигалась с минимальным по величине ускорением.

ньютоновская механика – Почему сила зависит от ускорения, а не от скорости?

Задавать вопрос

спросил 8 лет, 11 месяцев назад

Изменено 5 лет, 1 месяц назад

Просмотрено 14 тысяч раз

$\begingroup$

Согласно $F = ma$, сила есть результат ускорения и массы, верно?

Однако я не понимаю, почему вместо ускорения не используется скорость. Поезд, движущийся со скоростью 100 миль в час, все равно будет воздействовать на вас с большой силой, даже если у него нет ускорения. Кроме того, падение книги с высоты 10 футов вызовет большую силу на горунде, чем падение ее с высоты 1 фут. Таким образом, кажется, что скорость будет влиять на силу больше, чем ускорение.

Почему это не так?

• ньютоновская механика
• ускорение

$\endgroup$

2

$\begingroup$

$F$ в уравнении $F=ma$ — это не сила, которую приложил бы объект, если бы он столкнулся с чем-то другим. Вместо этого $F$ представляет результирующую силу, действующую на объект, которая должна присутствовать, чтобы произвести текущее ускорение объекта $a$. Второй закон Ньютона лучше записать так: $$F_\text{net}=ма,$$ поскольку он явно показывает, какая сила представлена ​​​​в левой части уравнения.

В вашем примере с поездом, если поезд движется с постоянной скоростью 100 миль в час, ускорение равно нулю, и по второму закону Ньютона результирующая сила также равна нулю. Но это не имеет никакого отношения к тому, какую силу поезд приложит к чему-либо в случае столкновения.

$\endgroup$

4

$\begingroup$

Это так просто…..

Два поезда, движущиеся со скоростью 100 миль в час = без ускорения – согласовано.

Результирующая сила указанного поезда будет зависеть от Масса/плотность встречного объекта – второй закон Ньютона.

Так как мы не знаем скорость противостоящего объекта, можно только предположить, что противодействующая сила равна…..морк зовет орсона, входите орсон

$\endgroup$

1

$\begingroup$

ЗДЕСЬ СИЛА ОБОЗНАЧАЕТ СИЛУ, ДЕЙСТВУЮЩУЮ НА ПОЕЗД ДЛЯ ПРОИЗВОДСТВА УСКОРЕНИЯ. ПОСКОЛЬКУ ОН НЕ ИМЕЕТ УСКОРЕНИЯ, НЕ ТРЕБУЕТСЯ НИКАКАЯ СИЛА ДЛЯ ПОДДЕРЖАНИЯ ЕГО ДВИЖЕНИЯ (БЕЗ УЧЕТА СОПРОТИВЛЕНИЯ ВОЗДУХА). ЭТО НЕ ОЗНАЧАЕТ, ЧТО ЭТО БУДЕТ ПРОИЗВОДИТЬ СИЛУ.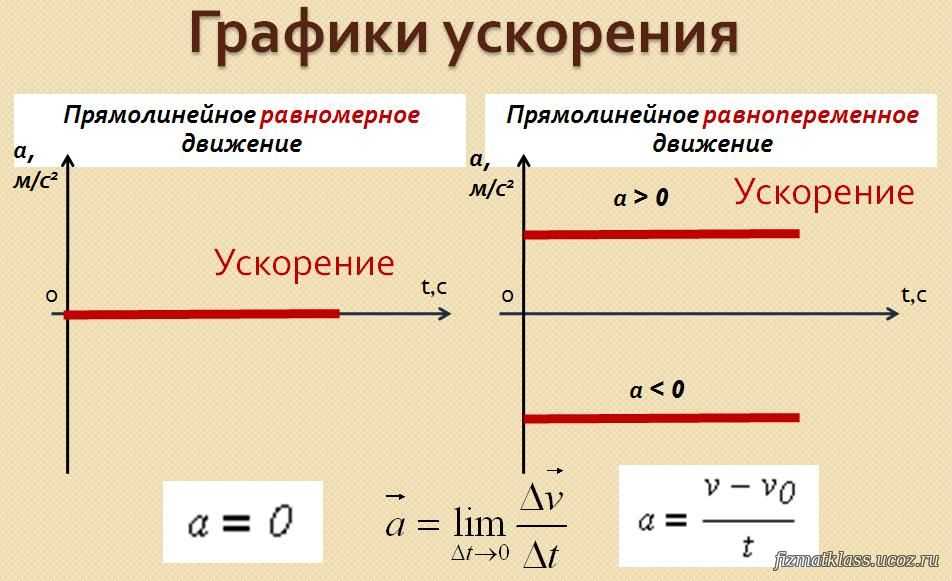 ЭТО НЕ ИМЕЕТ НИЧЕГО СВЯЗАННОГО С СТОЛКНОВЕНИЯМИ. ДЛЯ СТОЛКНОВЕНИЙ ВЫ ДОЛЖНЫ УЧИТЫВАТЬ ИМПУЛЬС (MV)…. НАДЕЮСЬ, ЭТО ПОЛЕЗНО

$\endgroup$

Ньютоновская механика – Силы, зависящие от расстояния, найти производные от положения, зависящие от времени

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 102 раза

$\begingroup$ 92}\hat{r}$$

Которую очень легко получить; но это дает нам систему трех дифференциальных уравнений, которые описывают ускорение в любое время и фактически не дают ускорение как функцию времени. Таким образом, определение ускорения как функции времени, как и определение положения как функции времени, становится задачей решения дифференциальных уравнений.