Зависимость времени от ускорения: Найти зависимость скорости от времени, скорость и ускорение точки через 4 секунды после начала движения…

Элементарный учебник физики Т1

Ландсберг Г.С. Элементарный учебник физики. Т.1. Механика. Теплота. Молекулярная физика. – М.: Наука, 1985. – 606 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ОТ ИЗДАТЕЛЬСТВА ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17. Скорость прямолинейного равноускоренного движения § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22. 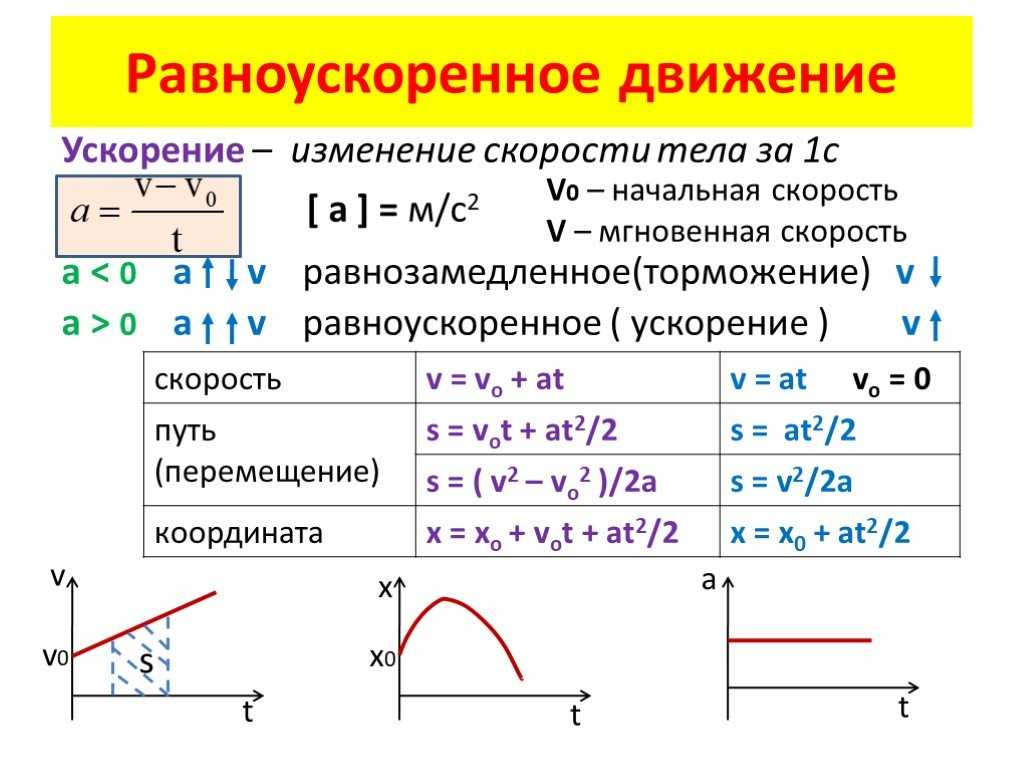Путь, пройденный при равнопеременном движении § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49. Импульс тела § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи. Силы реакции связей. Тело, закрепленное на оси § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177. Закон Архимеда для газов § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. 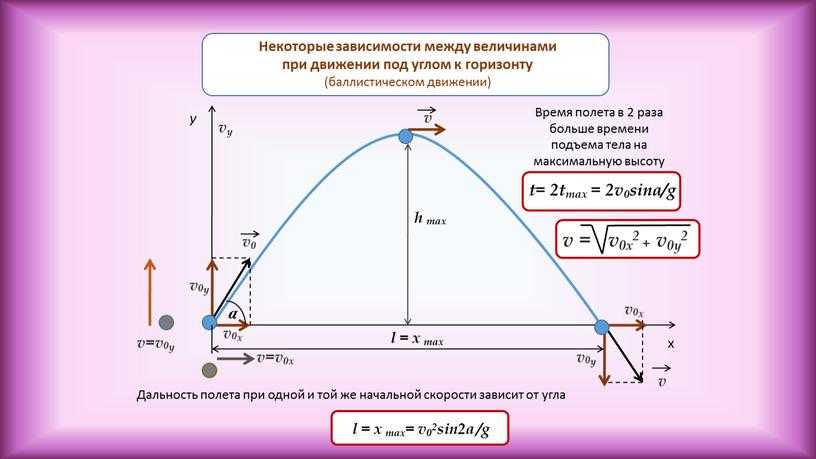Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель

Движение — что это, определение и ответ

Движением тела называется изменение его положения в пространстве относительно других.

Координата — величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.

Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.

Траектория — это линия, вдоль которой движется тело.

Путь — это длина траектории, вдоль которой движется тело.

Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела \(\overrightarrow{S}\) к времени t, за которое это перемещение произошло:

\(\overrightarrow{v} = \frac{\overrightarrow{S}}{t}\)

Скорость ― это векторная величина!

В заданиях, где дана зависимость скорости тела от времени.

Пройденный путь можно вычислить как площадь под графиком. {2}}{2}\)

Где x₀ ― начальная координата тела;

v₀ ― проекция начальная скорость на ось x;

a ― проекция ускорения на ось x;

t ― время движения.

Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получив взяв производную по времени от этой зависимости.

Скорость ― это производная координаты тела по времени v_x(t) = x^‘(t). Например, если зависимость координаты тела при равноускоренном движении имеет вид x(t) = 6 – 2t + 12t², то, взяв первую производную от координаты мы получим зависимость скорости тела от времени v_x(t) = –2 + 12 ∙ 2t = –2 + 24t.

Точно так же, ускорение ― это производная от скорости тела. a_x(t) = v_x^‘(t).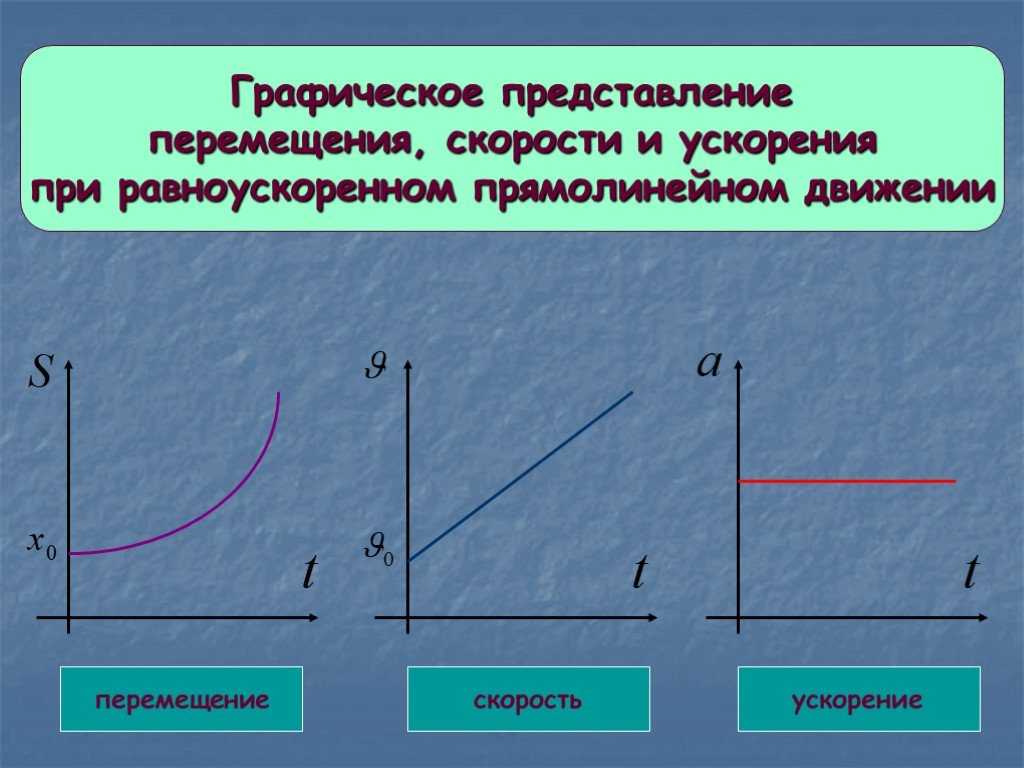 {2}}{2}\),

Где:

H(t) — высота тела над нулевым уровнем в момент времени t [м],

h — начальная высота тела над нулевым уровнем [м],

v₀ — начальная скорость тела [м/с]

α — угол, под которым бросили тело [°],

t — время движения тела [c],

g — ускорении свободного падения [м/с²].

Зависимость горизонтальной координаты от времени при движении под углом к горизонту:

S(t) = v₀ ‧ cos a ‧ t, где:

S(t) — путь, пройденный телом за время t [м]

Угол между вектором скорости тела и горизонтом в любой момент времени может быть выражен из геометрических соображений как:

\(\alpha\left( t \right) = arctg(\frac{v_{y}}{v_{x}})\),

Где:

α(t) — угол между скоростью и горизонтом в момент времени t [°],

v_y = v₀ ∙ sin α – gt — вертикальная проекция скорости тела в момент времени t [м/с],

v_х = v₀ ∙ cos α — горизонтальная проекция скорости тела [м/с].

Работа силы тяжести при падении тела на тот же уровень, с которого тело взлетело (с Земли на Землю, с балкона на балкон и т.д.) равна нулю.

В этом случае выполняется симметрия полета:

• угол, под которым тело упадет, равен углу, под которым тело бросили;

• скорость, с которой тело упадет, равна скорости, с которой тело бросили;

• время взлета тела до максимальной высоты равно времени падания с неё обратно.

Если работа силы тяжести не равна нулю (бросок с Земли на балкон, с балкона на Землю и так далее), симметрия полета не выполняется.

Время взлета на максимальную высоту:

\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\). {2}\sin{2\alpha}}{g}\).

Выводится с помощью подставления прошлой формулы в уравнения равномерного движения вдоль горизонтальной оси:

S = v₀ ‧ cos a ‧ t _полета

Здесь используются формула синуса двойного угла и свойство симметрии полета: время взлета равно времени падения, или полное время движения равно удвоенному времени взлета: t_полета = 2t_взлета

Очевидно, что формула применима только при падении тела на тот же уровень, с которого оно взлетело.

Время падения тела с балкона (без начальной скорости) или при броске горизонтально:

\(t_{падения} = \sqrt{\frac{2H}{g}}\)

Формула выводится при проецировании уравнения координаты при равноускоренном движении на ось OY:

\(H\left( t \right) = h + v_{0}\sin a \cdot t – \frac{gt^{2}}{2}\)

с учетом, что проекция начальной скорости на эту ось равна нулю, а конечная координата — тоже ноль:

\(0 = h – \frac{gt_{падения}^{2}}{2}\)

Максимальная высота подъема тела над Землей:

\(\ h = \frac{v_{0}^{2}\sin^{2}\alpha}{2g}\)

Формулу легко получить объединением уравнения координаты при равноускоренном движении на ось OY с поверхности Земли:

\(\left( t \right) = h + v_{0} \cdot \sin a \cdot t – \frac{gt^{2}}{2}\)

с формулой времени подъема тела на максимальную высоту:

\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\)

Все представленные выше формулы могут быть использованы без вывода в задачах первой части, но в задачах второй части за это будут снимать баллы.

При движении по окружности часто удобно использовать не обычную скорость, а угловую скорость.

Угловая скорость численно равна углу поворота радиуса за единицу времени.

Угловая скорость для тела, двигающегося из точки 1 в точку 2, будет равна:

\(\omega = \frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t}\), где

∆φ ― угол поворота [рад],

∆t ― промежуток времени [с],

ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).

Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как: v = ωR.

Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.

Период — время, за которое тело делает полный оборот по окружности.

\(T = \frac{2\pi R}{v}\), где

T ― период [с],

R ― радиус окружности [м],

v ― скорость [м/с]. {2}R\), где

R ― радиус окружности [м],

a_n ― нормальное ускорение [м/с²],

v ― скорость [м/с],

ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).

02. Силы, зависящие от времени – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

450

• Paul D’Alessandris
• Общественный колледж Монро

1. Силы, зависящие от времени

Игрушечная ракета массой 2,0 кг оснащена двигателем, обеспечивающим тягу, грубо моделируемую функцией F(t) = (60 Н/с) t – (15 Н/с ² ) t ² , для 0 < t < 4,0 с, а затем ноль. Ракета запускается прямо вверх.

Конечно, первым шагом к анализу любой ситуации, связанной с силами, является построение диаграммы свободного тела. Ниже представлена ​​диаграмма свободного тела ракеты в интервале времени 0 < t < 4,0 с.

Учитывая, что вам не предоставлена ​​информация о силе трения, действующей на ракету, вы должны проанализировать траекторию ракеты в гипотетической среде без трения.

Из второго закона Ньютона:

Таким образом, ускорение ракеты непостоянно, и скорость и положение ракеты необходимо определять интегрированием ускорения.

Прежде чем мы это сделаем, обратите внимание, что ускорение ракеты изначально направлено вниз. (При t = 0 с, а = -90,8 м/с ² .) Это связано с тем, что не учитывалась поддерживающая сила, действующая на ракету со стороны стартовой платформы. Эта сила будет удерживать ракету на месте до тех пор, пока сила выхлопных газов, действующих на ракету, не станет равной, а затем превысит силу тяжести ракеты. В действительности ускорение ракеты равно нулю до тех пор, пока F _выхлоп = F _{гравитация} . Это происходит, когда:

Правильная информация о движении приведена в таблице ниже.

Между событиями 2 и 3 ускорение ракеты определяется приведенной выше функцией:

Мы можем интегрировать ускорение, чтобы определить скорость,

Поскольку мы знаем, что v = 0 м/с при t = 0,36 с , можем определить постоянную интегрирования:

Следовательно,

и когда тяга закончится, при t ₃ = 4,0 с, v ₃ = 42,5 м/с.

Чтобы найти положение ракеты в момент прекращения действия тяги, проинтегрируйте функцию скорости:

Так как мы знаем r = 0 м при t = 0,36 с, то можем определить постоянную интегрирования:

Следовательно,

и когда тяга закончится, при t ₃ с, 4,0059 = 4 ₃ = 87,2 м.

Между событиями 3 и 4 ускорение постоянно, поэтому мы можем использовать наши кинематические уравнения постоянного ускорения:

Таким образом, ракета достигнет максимальной высоты 180 м в среде без трения.

Пол Д’Алессандрис (Общественный колледж Монро)

---

Эта страница под названием 02. Time-Dependent Forces распространяется по лицензии CC BY-NC-SA, автором, ремиксом и/или куратором является Пол Д’Алессандрис.

1. Наверх

• Была ли эта статья полезной?

1. Тип артикула

   Раздел или Страница

   Автор

   Поль Д’Алессандрис

   Лицензия

   CC BY-NC-SA

   Показать оглавление

   нет

2. Теги

   На этой странице нет тегов.

ньютоновская механика – Всегда ли ускорение $a$ является функцией времени, даже для силы, зависящей от скорости?

спросил 5 лет, 9 месяцев назад

Изменено 5 лет, 9 месяцев назад

Просмотрено 664 раза

$\begingroup$

Предположим, что частица массы $m$ движется под действием тормозящей силы, зависящей от скорости, $F(v) = – \alpha \sqrt{v}$, и я хотел найти ускорение как функцию времени, $а(т)$.

Могу я сделать следующее?

$$F(v) = – \alpha \sqrt{v} \подразумевается ma(t) = -\alpha \sqrt{v} \подразумевается a(t) = -\frac{\alpha}{m}\ sqrt{v} \qquad (1)$$

Это то, что сделано в одной из моих лекций. Однако я думаю, что это должно быть неправильно, потому что если $F(v)$ является функцией времени, то, конечно же, ускорение также должно быть функцией скорости $a(v)$ и, таким образом, в свою очередь функцией времени следующим образом $а(v(t))$.

Если $(1)$ действительно правильно, не могли бы вы объяснить, почему это правильно и почему это можно сделать?

• ньютоновская механика
• силы
• ускорение
• время
• скорость

$\endgroup$

1

$\begingroup$

Вам просто нужно решить второй закон Ньютона, и он даст скорость частицы как функцию времени. Поскольку ускорение не равно нулю, ясно, что скорость не постоянна. С другой стороны, поскольку ускорение зависит от скорости, ускорение также непостоянно. 92}t.$$

Такое ускорение, зависящее от квадратного корня из скорости, может быть вызвано силой сопротивления. Предположим, что частица была оставлена ​​с некоторой начальной скоростью и далее находится под действием только этой силы сопротивления. Сопротивление будет тормозить частицу, и, следовательно, сама сила сопротивления будет зависеть от времени.

$\endgroup$

5

$\begingroup$

Вы можете написать

F(v)=−α√v как ma(v)=-α√v

a(v)=-α√v/m —–(1)

dv/dt=-α√v/m

dv/√v=- αdt/м интегрирование,

2√v =-αt/m + c ( примените соответствующие ограничения в соответствии с вашим вопросом во время интегрирования, чтобы избежать интегральной константы.

так что здесь, √v = (−αt/m + c)/2 —–(2)

по вашему вопросу, из (1)

a(v)= −α√v/m

из (2 )

a(t)= −α(−αt/m + c)/2m

и предположим, что скорость равна нулю в момент t=0, тогда , c=0

Обратите внимание: я просто взял v=0 при t=0, чтобы упростить уравнение. Но в этом нет никакой логики (поскольку вы упомянули, что F (v) – единственная сила, действующая на тело), ​​поскольку сама F является функцией скорости. Итак, если v = 0, то F также = 0 при t = 0. Это остается таковым, если какая-либо другая сила не приводит тело в движение 🙂

вы получаете,

a(t)= −α(−αt/m)/2m

, то есть

a(t)= α( в квадрате)т/2м(в квадрате)

так что здесь ускорение как функция времени 🙂

$\endgroup$

$\begingroup$

Как вы указали

$$ а = а (v (т)) = а (т) $$

Возможно, вы думаете что-то вроде $a = a(v, t)$, но тогда

$$ а = а(v, t) = а(v(t),t) = а(t) $$

Идея заключается в том, что $a$ явно зависит от $v$, но так как $v$ зависит от времени, то $a$ зависит неявно зависит от $t$

$\endgroup$

$\begingroup$

Из уравнения \begin{уравнение} F(v)=-\альфа\sqrt{v}, \end{уравнение} мы можем получить \begin{уравнение} ма=-\альфа\sqrt{v} \end{уравнение} и поэтому \begin{уравнение} a (v) = – \ frac {\ alpha} {m} \ sqrt {v}, \end{уравнение} что означает, что ускорение является функцией скорости. Но $a(v)\neq a(t)$, потому что мы не знаем, зависит ли $v$ от времени или нет ($v$ может быть постоянным и, следовательно, независимым от времени). Таким образом, мы не можем получить $a(t)=-\frac{\alpha}{m}\sqrt{v}$ в общем случае.

$\endgroup$

4

$\begingroup$

Вы наткнулись на одну из самых распространенных путаниц в классической механике, хотя она обычно не всплывает до второго курса: вы можете рассматривать все либо как функцию конфигурации, либо как функцию траектории.

Когда они говорят $F = F(v)$, они имеют в виду, что сила вообще может зависеть от всего, что касается текущей конфигурации частицы, которая в данном случае является ее положением и скоростью, но в данном конкретном случае сила возникает только зависеть от текущей скорости.

Однако когда мы говорим о траектории частицы, все можно записать как функцию времени $t$; вы всегда можете спросить, какова сила, скорость и т.