Определение давления
До сих пор мы изучали случаи, когда сила, действующая на тело, была приложена к нему в одной точке. Мы так и говорили про неё: «точка приложения силы» . Настало время ситуаций, когда сила приложена к телу во множестве точек, то есть действует на некоторую площадь поверхности. В каждом из таких случаев говорят не только о самой силе, но и о создаваемом ею давлении.
Как приятна зимняя прогулка на лыжах! Однако стоит выйти на снег без них, как ноги будут глубоко проваливаться при каждом шаге, идти будет трудно, и удовольствие будет испорчено.
На этом рисунке вес лыжника примерно равен весу «пешехода». Поэтому силы, с которыми мальчики давят на снег, будем считать равными. Но заметьте: они действуют не на одну точку, а «распределяются» по некоторым поверхностям. У лыжника – по площади касания снега и лыж, а у пешехода – снега и подошв.
Понятно, что Sлыж > Sподошв.
– перпендикулярно приложенная сила, Н.
S – площадь поверхности, м2
Единица давления – 1 паскаль (обозначается: 1 Па). Из формулы-определения видно, что 1 Па = 1 Н/м2
Числовое значение давления показывает силу, приходящуюся на единицу площади её приложения. Например, при давлении 5 паскалей на каждый 1 м2 будет действовать сила 5 ньютонов.
Вернёмся к примеру с мальчиками. На рисунке не указаны числовые значения F и S. Значит, мы не можем количественно сравнить давления, которое оказывают мальчики (с лыжами и без лыж) на снег. Однако мы можем сравнить их качественно, используя слова «больше» и «меньше». Сделаем это.
Сначала запишем исходные данные: силы, с которыми мальчики давят на снег, равны, и площадь лыж больше площади подошв (см. столбик слева):
После знака «Ю», который значит «следовательно», мы составили две дроби.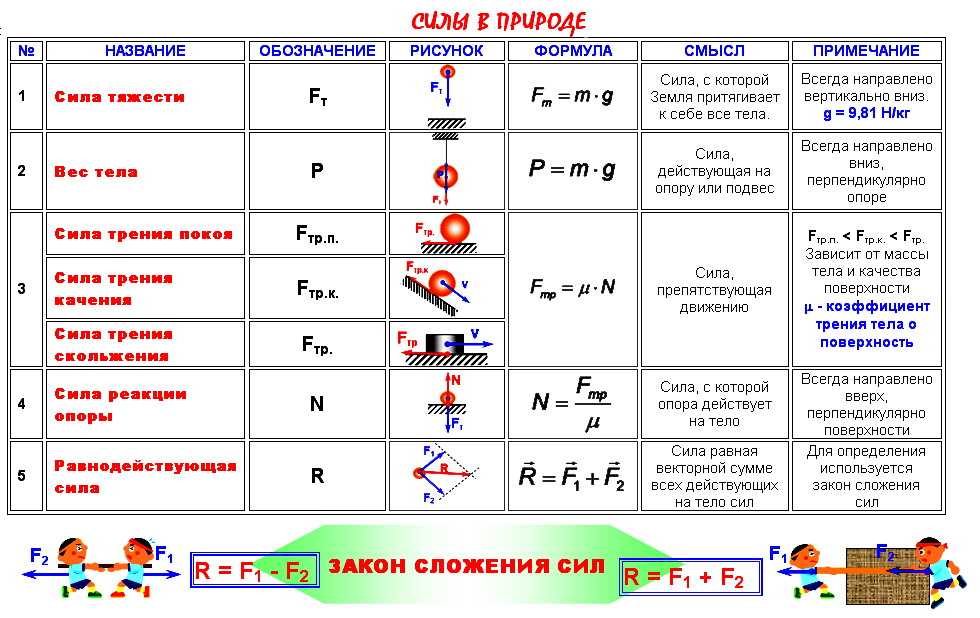
Обратите внимание: знак «больше», присутствовавший в исходных данных, изменился на знак «меньше». Почему? Поскольку знаменатель левой дроби больше знаменателя правой, значит, согласно свойству дроби, сама левая дробь меньше правой. Вспомнив, что каждая дробь в этом неравенстве является давлением, получим: давление лыжника меньше давления пешехода. Этим и объясняется то, что лыжник меньше проваливается в снег, чем пешеход.
Формула-определение давления подсказывает нам, как его можно изменять: чтобы увеличить давление, нужно увеличить силу или уменьшать площадь её приложения. И наоборот: чтобы уменьшить давление, нужно уменьшить силу или увеличить площадь, на которую эта сила действует.
Опубликовано в разделах: 7 класс, Давление телДАВЛЕНИЯ ВЫСОКИЕ • Большая российская энциклопедия
ДАВЛЕ́НИЯ ВЫСО́КИЕ в физике, область давлений, обусловленных сжатием и/или нагреванием вещества, в которой физич. и химич. свойства вещества существенно отличны от его свойств в нормальных условиях.
Состояние вещества при таких давлениях называют экстремальным. Значения давлений, которые принято считать Д. в., зависят от рассматриваемых физич. явлений или конкретных задач. Так, свойства газов с ростом давления до ок. 0,1 ГПа при нормальной темп-ре приближаются к свойствам жидкости, и для газов такие и более высокие давления считают Д. в. Для жидкостей вследствие их малой сжимаемости область Д. в. начинается от единиц ГПа. Такие же значения давлений считаются высокими и для твёрдых тел, однако в некоторых случаях существенные изменения их свойств могут происходить и при более низких давлениях. Напр., при одноосном сжатии металлов происходят необратимые деформации при давлениях (напряжениях) в десятки и сотни МПа. С ростом давления уменьшаются межатомные и межмолекулярные расстояния в веществе, и иногда к Д. в. относят давления, при которых изменение этих расстояний сопоставимо с их значениями, т.
е. давления порядка модулей упругости. В природе наиболее высокие значения имеют давления в центрах планет и звёзд. Напр., в центре Земли они ок. 360 ГПа, Юпитера – порядка 2·104 ГПа, Солнца – 2·107 ГПа, белых карликов – 109–1011 ГПа (по теоретич. оценкам).
С увеличением давления изменяются механич., электрич. и магнитные свойства веществ, взаимная растворимость контактирующих компонент и фаз, происходят фазовые переходы. Большинство жидкостей затвердевает при комнатной темп-ре и Д. в. до 3–6 ГПа. При изотермич. сжатии твёрдое тело может перейти из парамагнитного в ферромагнитное состояние, диэлектрик или полупроводник может стать проводником. Напр., молекулярный кристалл водорода становится металлом при давлении ок. 350 ГПа. По теоретич. оценкам, при давлениях ок. 400 ГПа металлич. фаза водорода становится атомным кристаллом.
Схемы аппаратов высокого давления: а – аппарат “цилиндр – поршень”; б – камера с криволинейными пуансонами; в – многопуансонная камера; 1 – поршень или пуансон; 2 –…
При достаточно сильном повышении давления путём сжатия без существенного повышения темп-ры происходят полиморфные превращения с образованием более плотных кристаллич. модификаций. Фазы, область термодинамич. устойчивости которых соответствует Д. в., называют фазами высоких давлений. Примеры таких фаз – коэсит и стишовит – кристаллич. модификации кремнезёма (SiO2), существуют как метастабильные фазы и в нормальных условиях, в которых стабильная фаза SiO2 – кристаллич. кварц. Плотности кварца, коэсита и стишовита в нормальных условиях равны соответственно 2,65; 3,1 и 4,3 г/см3. Др. пример фазы Д. в. – алмаз (кристаллич. модификация углерода). В нормальных условиях он сохраняется как метастабильная фаза, не переходя в устойчивую фазу – графит.
Решётки молекулярных кристаллов, имеющих относительно рыхлые (ажурные) структуры (кристаллы кварца, льда), при сильном статич. сжатии без нагревания теряют механич. устойчивость и, не переходя в новую равновесную фазу, разрушаются – аморфизуются. При комнатной темп-ре аморфизация кварца начинается примерно при 25 ГПа и заканчивается примерно при 30 ГПа.
Теоретич. расчёты термодинамич. и др. свойств жидкостей и твёрдых тел при Д. в. выполняются на основе классич. и квантовой механики, как правило, с использованием ряда упрощающих приближений и моделей и нуждаются в эксперим. проверке. Исключение составляют сверхвысокие сжатия огромными давлениями, при которых для электронных оболочек уже нет достаточного объёма и они разрушаются, а электроны образуют вырожденный идеальный ферми-газ, свойства которого, в т.
2$ ГПа.
Статические методы
создания в лабораторных условиях Д. в. основаны на нагревании образца, заключённого в прочную жёсткую оболочку, или на гидростатич. сжатии образца внешними силами в прессах спец. конструкций с сохранением всей или почти всей его массы. В механич. методах используют насосы и компрессоры (гидравлические и газовые), позволяющие достигать значений давления до 1–1,5 ГПа. В установках типа «цилиндр – поршень» (рис., а), применяемых для сжатия газов, жидкостей и твёрдых тел, величина Д. в. ограничена прочностью поршней на сжатие. При использовании для их изготовления твёрдых сплавов максимально достижимые давления составляют 5–6 ГПа. Прочность конструкций повышают, напр., искривляя профиль деталей камеры (рис., б) или разделяя стенки камеры на сегменты для того, чтобы не было круговых растягивающих напряжений (т.
н. многопуансонные аппараты; рис., в). В многоступенчатых аппаратах камера Д. в. помещается внутри большего сосуда с меньшим давлением, при этом достигается бóльшая прочность деталей. Использование природных или синтетич. алмазов в аппаратах Д. в. позволило достигать давлений ок. 100 ГПа. Однако в технике статич. экспериментов повышение Д. в. связано с уменьшением объёма рабочей камеры. Так, объём алмазных камер уменьшают до десятых или сотых долей мм3. Др. недостатком статич. методов является ограниченность области допустимых высоких темп-р, при которых детали установок не испаряются, не плавятся и не теряют прочности. Низкотемпературные исследования выполняют с использованием криогенной техники, а исследования в интервале темп-р от –196 °C до 400 °C – в термостатах. Темп-ры до 1500–3000 °C в стационарном режиме получают с помощью электрич.
нагревателей, помещённых внутри камеры. Нагревание образцов через прозрачные алмазные стенки осуществляют лазерным излучением. Для мн. науч. и практич. целей фазу вещества, полученную при Д. в., нужно сохранять в нормальных условиях, однако, как правило, при снижении давления происходит обратный переход. Иногда всё же удаётся сохранить фазу Д. в. в метастабильном состоянии, для этого снижают сначала темп-ру сжатого вещества, а затем давление.
Динамические методы
В кратковременных процессах взрывного типа (взрыв конденсированного ВВ – тротила, гексогена и др., столкновение тел при большой скорости относительного движения и др.) образуются сильные ударные волны, сжимающие и нагревающие вещество, по которому они распространяются. Соответственно в нём развиваются Д. в., которые в отличие от статических Д. в. называют динамическими.
При детонации конденсированных ВВ возникают ударные волны с давлением до нескольких десятков ГПа. Такие волны переходят затем в исследуемое вещество, контактирующее с ВВ. С помощью кумулятивных зарядов достигают давлений порядка сотен ГПа. Образцы, помещённые в ближней зоне подземного ядерного взрыва, подвергаются давлениям ок. 4–5 ТПа. Для получения динамических Д. в. используются также спец. газовые и др. одноступенчатые и двухступенчатые пушки, которые разгоняют снаряды – пластины, ударяющие затем по преграде из исследуемого вещества. Относит. скорость столкновения пластины и мишени достигает в двухступенчатых пушках 10 км/с; давления, развиваемые при ударе, составляют от нескольких десятков до 100 ГПа.
Три уравнения, выражающие законы сохранения массы, импульса и энергии в ударной волне, связывают пять величин – скорость ударной волны $D$, давление $p$, плотность вещества $\rho$, скорость его движения $u$ и внутр.
энергию $\varepsilon$ за ударно-волновым разрывом. Измерив скорости $D$ и $u$ и зная состояние вещества перед волной, можно вычислить $p$ и $\varepsilon$ как функции от $\rho$ (см. Ударная волна), т. е. получить данные об уравнении состояния.
Результат динамич. сжатия вещества зависит от времени сжатия. Если время $\tau$ удержания вещества при динамическом Д. в. больше времени установления термодинамич. равновесия $\tau_p$ в сжатом веществе, то его воздействие во многих случаях даёт такие же (или близкие) результаты, что и действие на это вещество статич. давлений при одинаковых конечных плотности и темп-ре. Если же $\tau \lt\tau_p$, то вещество при динамич. действии Д. в. либо сохраняет свою исходную структуру, либо находится в неравновесном состоянии и имеет соответственно др. свойства по сравнению с результатом статич. сжатия.
Существуют два осн.
кинетич. механизма перестройки кристаллич. структуры вещества – т. н. диффузионный механизм (с активацией отд. атомных частиц и преодолением активационных барьеров каждым атомом или молекулой индивидуально) и мартенситный (характеризующийся кооперативной, когерентной перестройкой кристаллич. решётки). Если мартенситный переход геометрически возможен, то его время достаточно малó. Полиморфные превращения, наблюдаемые при статическом и ударном сжатии мн. металлов (напр., железа, висмута, натрия, калия), а также германия и некоторых соединений, имеют, как правило, мартенситную природу. Диффузионный механизм при сравнительно низких темп-рах кинетически запрещён как при динамических, так и при статических Д. в. (требует практически бесконечного времени), но при высоких темп-рах он может быть достаточно быстрым. Пример – плавление в ударной волне.
Темп-ра при сжатии в ударной волне возрастает быстрее, чем при адиабатич. сжатии. Однако разгрузка (снятие Д. в.) происходит адиабатически, и вещество после разгрузки имеет повышенную темп-ру по сравнению с исходным состоянием до ударного сжатия. Возвращение к нормальной темп-ре после снятия давления происходит при медленном остывании образца в окружающей среде. Это способствует возвращению к исходному равновесному состоянию (отжиг). Тем не менее образовавшиеся при динамич. нагрузках (в ударной волне) кристаллич. и аморфные структуры после снятия давления нередко сохраняются сколь угодно долго в метастабильных состояниях. Многообразие начальных состояний вещества, интенсивностей ударных волн, возможность вариаций длительности фаз сжатия и разгрузки используются при динамич. нагрузках для получения известных и новых модификаций с уникальными физико-химич.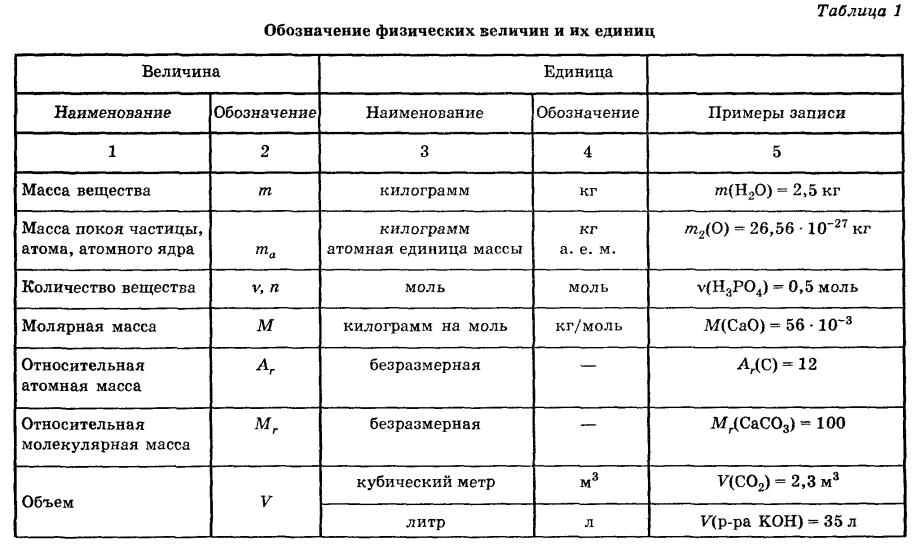
и механич. свойствами. Уникальность свойств метастабильных веществ, получаемых при динамических Д. в., обусловлена тем, что действие динамич. нагрузки не эквивалентно медленному сжатию и нагреву: важна кинетика процессов при нагрузке и разгрузке. Напр., в ударной волне возможен процесс полимеризации и в том случае, когда в отсутствии динамич. сжатия при тех же $p$ и $T$ она не происходит.
Особенности процесса изменения свойств вещества и их исследования при воздействии динамических Д. в. заключаются в том, что определённые значения давления $p$ и темп-ры $T$ наблюдаются только лишь на отд. линии – на ударной адиабате $p(T)$. Для распространения этих данных на всё поле $p$, $T$ привлекают теоретич. расчёты, исходя из уравнения состояния, содержащего неопределённые параметры, которые затем вычисляют, используя данные ударной адиабаты.
История развития физики высоких давлений
Начало систематич. эксперим. исследований твёрдых тел при Д. в. было положено работами П. У. Бриджмена в 1920-х гг. Разработанные им методы позволили исследовать свойства веществ при статич. давлениях в несколько ГПа. Стимулом для дальнейших исследований явились развитие физики твёрдого тела и необходимость получения данных для теории внутр. строения Земли. В 1940–50-х гг., когда были разработаны методы получения и диагностики ударных волн и методы высокоточных измерений скорости $u$, ударные волны стали важнейшим, часто незаменимым средством эксперим. исследования веществ в экстремальных условиях. Диапазон Д. в. с надёжными, имеющими высокую точность количественными данными об уравнениях состояния увеличился примерно на два порядка, что создало условия для мощного скачка в изучении физич.
и химич. свойств вещества и создания новой области науки – физики высоких давлений. Были получены широкодиапазонные уравнения состояния мн. химич. элементов и соединений – металлов, сплавов, минералов, горных пород, полимеров, воды и др. жидкостей. Полученные данные нашли широкое применение в науке о Земле и др. планетах Солнечной системы.
Применения высоких давлений
Во 2-й пол. 20 в. с помощью статических Д. в. получены важные науч. результаты, многие из которых нашли широкое практич. применение: синтезированы алмаз (в Ин-те физики высоких давлений АН СССР под рук. Л. Ф. Верещагина, 1960) и алмазоподобные модификации нитрида бора (боразон, $p \geq5$ ГПа и $T \geq 1350$ °C), получены плотные кристаллич. модификации важных породообразующих минералов (кремнезёма, оливина), зафиксирован переход диэлектриков в проводящее и сверхпроводящее состояния, установлены диаграммы состояний для многих одно- и многокомпонентных систем.
Д. в. используются при механич. обработке металлов и при полимеризации. Под воздействием динамических Д. в. (в детонационной ударной волне) получены алмаз, боразон, а также тугоплавкий сплав W и Mn, который др. методами получить не удаётся. Статические и динамические Д. в. широко применяются в науке и технике для исследования веществ, изменения их свойств в нужном направлении и разработки новых наукоёмких технологич. процессов. В частности, статич. и динамич. прессованием порошков получают новые материалы; детонационные и ударные волны используются для упрочнения машиностроительных деталей, резки и сварки металлов, прессования порошков и др. Успешно развивается новый раздел химии – механохимия с химич. твердофазными превращениями под действием деформаций сжатия и сдвига.
Давление – Citizendium
| | Основной артикул | Обсуждение | Статьи по теме [?] | Библиография [?] | Внешние ссылки [?] | Версия для цитирования [?] |
| ||||||||||||
Эта редактируемая основная статья находится в разработке и подлежит отказу от ответственности . [изменить введение] | |||||||||||||||||||
(CC) Диаграмма: Brant Carlson
Иллюстрация сил, действующих на атомы или молекулы, сталкивающиеся с внутренними стенками контейнера. Столкновения и результирующие силы показаны красным цветом. Давление есть сумма сил столкновения.
Давление (обозначение: p ) — это сила, прикладываемая к площади в направлении, перпендикулярном поверхности этой области.
Давление — это естественное физическое явление. Это скалярная величина и фундаментальный параметр термодинамики.
Содержание
- 1 Математическое определение
- 2 Различные единицы измерения давления
- 3 Зависимость абсолютного давления от избыточного давления
- 4 Отрицательное или вакуумметрическое давление
- 5 Пример воздействия давления
- 6 Каталожные номера
Математическое определение
Математически давление может быть выражено как: [1]
- p=FA{\displaystyle p={\frac {F}{A}}}
где:
- p{\displaystyle p} — давление
- F{\displaystyle F} – перпендикулярная сила
- A{\displaystyle A} — это площадь.
Единицей давления в СИ является паскаль (Па), равный одному ньютону на квадратный метр (Н·м
Различные единицы давления
| паскаль (Па) | бар (бар) | атмосфера (атм) | торр (торр) | фунт-сила на квадратный дюйм (psi) | килограмм-сила на квадратный сантиметр (кгс/см 2 ) | |
|---|---|---|---|---|---|---|
| 1 Па | ≡ 1 Н/м 2 | 10 −5 | 9,8692×10 | 7,5006×10 −3 | 145,04×10 −6 | 1,01972×10 −5 |
| 1 бар | 100 000 | ≡ 10 6 дин/см 2 | 0,98692 | 750. 06 | 14.504 | 1.01972 |
| 1 атм | 101 325 | 1.01325 | ≡ 1 атм | 760 | 14.696 | 1.03323 |
| 1 торр | 133.322 | 1,3158×10 −3 | ≡ 1 торр ≈ 1 мм рт.ст. | 19,337×10 −3 | 1,35951×10 −3 | |
| 1 psi | 6 894,76 | 68,948×10 −3 | 68,046×10 −3 | 51.715 | ≡ 1 фунт-сила/дюйм 2 | 7,03059×10 −2 |
| 1 кгс/см 2 | 98 066,5 | 0,980665 | 0,967838 | 735.5576 | 14.22357 | ≡ 1 кгс/см 2 |
Пример чтения: 1 Па = 1 Н/м 2 = 10 
д.
Примечание: мм рт. ст. — это сокращение от миллиметра ртутного столба
О торре: В технической литературе нет единого мнения о том, должно ли торр называться «торр» или «торр». Также нет единого мнения о том, должен ли символ для этой единицы давления быть «торр» или «торр». И Национальная физическая лаборатория Соединенного Королевства (см. Единицы давления), и Лаборатория эталонов измерений Новой Зеландии (см. Единицы барометрического давления) используют «торр» в качестве названия и символа. Обширный поиск на веб-сайте Национального института стандартов и технологий США не нашел таких четких определений. Поэтому в этой таблице «торр» используется как в качестве имени, так и в качестве символа.
Абсолютное давление в зависимости от манометрического давления
(CC) Диаграмма: Милтон Бейчок
атмосферное давление, что означает, что они измеряют давление выше атмосферного давления. Однако абсолютное давление равно нулю по отношению к полному вакууму.
Таким образом, абсолютное давление любой системы равно манометрическому давлению системы плюс местное атмосферное давление или давление окружающей среды . Рисунок 1 иллюстрирует взаимосвязь между манометрическим и абсолютным давлением для любых давлений выше атмосферного.
Примером разницы между манометрическим и абсолютным давлением является давление воздуха в шине автомобиля. Датчик давления в шинах может показывать 220 кПа как манометрическое давление, но это означает, что давление на 220 кПа выше атмосферного давления. Поскольку атмосферное давление на уровне моря составляет около 101 кПа, абсолютное давление в шине составляет около 321 кПа.
В техническом письме это будет записано как манометрическое давление 220 кПа или как абсолютное давление 321 кПа . Там, где место ограничено, например, на циферблатах манометров, заголовках таблиц или подписях к графикам, использование модификатора в скобках, например,
[2] [3] Манометрическое давление также иногда пишется избыточное давление . Это обсуждение модификаторов также относится к другим единицам давления, таким как бар, торр, атмосфера и т. д.Отрицательное или вакуумметрическое давление
Хотя давление, как правило, положительное, при описании системы, работающей при давлении ниже атмосферного (частичный вакуум), давление (как показано на рис. 1) может быть выражено в единицах его ниже атмосферного давления или с точки зрения того, насколько оно выше полного вакуума. Например, если атмосферное давление составляет 101 кПа, точка B на рисунке 1 может быть выражена как 45 кПа вакуума, что означает, что давление на 45 кПа ниже атмосферного. Его также можно выразить как 56 кПа (абсолютное значение), что означает, что давление на 56 кПа выше нуля. В технической документации очень важно четко указать, как выражаются любые давления ниже атмосферного.
Такое утверждение, как система работает при вакууме 100 торр приведет к путанице, поскольку может означать абсолютное давление 100 торр или давление -100 торр (т.
Пример воздействия давления
Палец можно прижать к стене, не оставив длительного впечатления; однако тот же палец, нажимающий кнопку, может легко сделать маленькую дырку в стене. Хотя сила, приложенная к поверхности, одинакова, кнопка оказывает большее давление, потому что острие концентрирует эту силу на меньшей площади.
Другой пример — обычный нож. Плоской стороной ножа яблоко не разрежешь. Но если мы будем использовать тонкую сторону, она легко разрежет яблоко. Когда мы используем тонкую сторону, на нее оказывается большее давление, потому что площадь поверхности уменьшается, и поэтому она легко режет яблоко.
Если человек находится на дне глубокого бассейна с водой, давление воды вызовет боль в ушах. Эту боль нельзя облегчить, повернув голову. Сила воздействия воды на барабанную перепонку всегда одинакова и всегда перпендикулярна поверхности, где барабанная перепонка соприкасается с водой.
Ссылки
- ↑ определение IUPAC
- ↑ Результаты поиска 1 и 2 (с сайта Национальной физической лаборатории, Великобритания)
- ↑ Арнольд Иван Джонс и Корнелиус Вандмахер (2007). Метрические единицы в машиностроении: Going SI , исправленное издание. Американское общество инженеров-строителей, стр. 147. ISBN 0-7844-0070-9.
Метрические единицы в машиностроении: Going SI , исправленное издание. Американское общество инженеров-строителей, стр. 147. ISBN 0-7844-0070-9. Что такое “давление” и каково его отношение к силе?
Честно говоря, я думаю, что уроки физики тщательно формулируют вещи, чтобы не свернуть в том направлении, в котором вы пытаетесь. Потому что все будет усложняться.
Позвольте мне начать с утверждения:
ограничители давления при твердой массе
Это неправильно, но это очень умная попытка объяснить мир. Что-то меняется на поверхности твердого вещества. Однако сила все равно передается.
Существует измеримая разница в свойствах твердого блока материи при атмосферном давлении. У вас может быть (гипотетически) материал, который меняет цвет при нагрузке. На самом деле у нас есть вещи, которые делают очень похожие вещи. Я хочу сказать, что влияние поверхностного давления имеет физический смысл.
Твердое тело представляет собой решетку атомов, которые сохраняют свое относительное положение за счет электронных связей. Давление на поверхность твердого тела уменьшает расстояние между атомами.
Тем не менее, вы можете полностью снять давление, и твердое тело не развалится. Это связано с тем, что химические связи представляют собой примерно потенциал Леннарда-Джонса. Это не точно и зависит от конкретной связи, но для наших целей этого более чем достаточно. Этот потенциал:
Это график «потенциала» для химической связи. Здесь «потенциал» — это математическое понятие. Это антипроизводная силы. Опять же, я говорю довольно конкретно о твердых телах. Но я хочу, чтобы вы рассмотрели здесь несколько моментов, которые важны для получения ПОЛНОЙ молекулярной картины давления, о чем на самом деле и просит ваш вопрос:
- Небольшой кристалл при нормальном земном давлении имеет положение атомов, сдвинутое чуть влево от самого минимума этого графика
- Возьмите этот маленький кристалл в космос. Теперь их атомные позиции равны точно на минимуме этого графа .
- Подумайте о ядре Земли. Мы считаем, что из-за физики высокого давления у него все еще может быть некоторая решетчатая структура. В этом случае позиции атомов были бы левее минимума, но далеко на выше 0 по оси Y . Это очень круто, потому что демонстрирует, что давление там превышает максимальную прочность на растяжение, которую может иметь материал.
Теперь их атомные позиции равны точно на минимуме этого графаЭто то, что я бы использовал, чтобы ввести абсолютное давление . В космосе нулевое давление. Твердое вещество ведет себя как пружина. При нулевом давлении твердое вещество представляет собой пружину в точке покоя.
Теперь поговорим о относительном давлении (иногда манометрическом давлении). Это форма давления, которой вас хотят научить на уроках физики. Это потому, что ньютоновская физика (даже большая часть жидкостей) может быть очень хорошо концептуализирована без какого бы то ни было упоминания об атомах.
Когда вы нажимаете рукой на стену или ногой на землю, сила мала по сравнению с давлением окружающей среды, но давление окружающей среды одинаково проникает во все. В этих случаях мы имеем дело с неизотропные сил – и под этим я подразумеваю направленные.
Определение давления на самом деле не имеет значения, является ли оно относительным, абсолютным или изотропным. Это просто сила на единицу площади. Это просто юнит, а юниты постоянно повторяются в разных контекстах.
По сути, любую силу, которую вы рассматриваете в базовой физике, можно представить как давление, просто взяв где-нибудь поперечное сечение. Это верно для натяжения веревкой или толкания палкой. Между «вытягиванием» и «толканием» есть разница в знаках, и в материалах они воспринимаются как «растяжение» и «сжатие», неизотропное напряжение… которое имеет единицы измерения давления.
Надеюсь, это поможет, но я не удивлюсь, если вы еще больше запутаетесь. Следует упомянуть о тензоре напряжений материала.