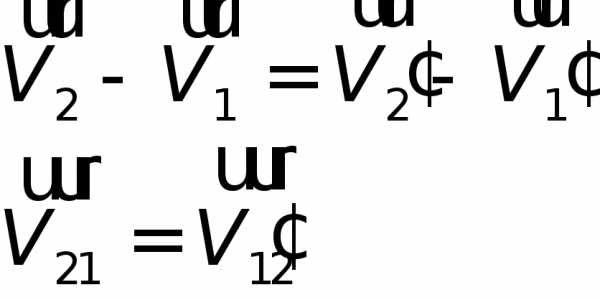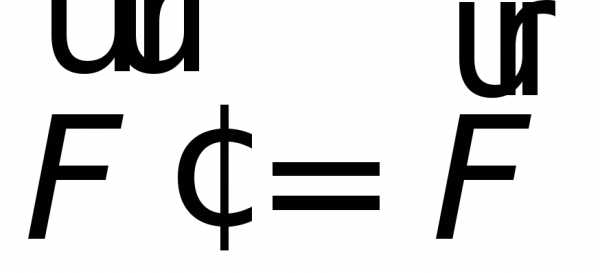Кратко и понятно о первом, втором и третьем законах Ньютона: формулировки, примеры и формулы
 Три закона Ньютона — это основа классической механики. В 1867 году Ньютон опубликовал работу под названием «Математические начала натуральной философии». Там были все знания, накопленные до него другими учёными, а также новые, открытые самим Ньютоном. Его считают одним из самых первых основоположником современной физики. Благодаря систематизированным знаниям, которые были описаны в вышеуказанном труде, он открыл множество законов механики, Закон всемирного тяготения и многое другое.
Три закона Ньютона — это основа классической механики. В 1867 году Ньютон опубликовал работу под названием «Математические начала натуральной философии». Там были все знания, накопленные до него другими учёными, а также новые, открытые самим Ньютоном. Его считают одним из самых первых основоположником современной физики. Благодаря систематизированным знаниям, которые были описаны в вышеуказанном труде, он открыл множество законов механики, Закон всемирного тяготения и многое другое.
Кратко о законах Ньютона
Первый закон Ньютона
- Формулировка. В наше время встречаются несколько формулировок, вот одна из самых современных: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно». Этот закон иногда называют Законом инерции.
- Трактовка. Если описать это утверждение простыми словами, то можно увидеть, что всё достаточно просто: если какое-то тело находится в покое относительно чего-либо, то оно и будет оставаться в покое до тех пор, пока на него не подействует какой-либо предмет. То же самое, если тело движется равномерно прямолинейно, то оно будет продолжать так двигаться, пока на него не подействует какая-либо сила. До Ньютона его открыл Галилео Галилей, но он не совсем точно его описал. Теперь осталось только разобраться, что такое инерциальные системы отсчёта. Проще говоря, это такая система, для которой выполняется Первый закон Ньютона.
- Пример действия. Представьте себе парашютиста, который движется прямолинейно равномерно к Земле. Это будет продолжаться до тех пор, пока притяжение к поверхности Земли будет компенсироваться сопротивлением воздуха. Если же сопротивление станет меньше либо больше, то тогда на тело начнёт действовать сила притяжения, и оно станет двигаться прямолинейно равноускоренно.
- История открытия. Существует легенда об открытии этого утверждения. Когда-то Ньютон сидел под деревом, и рядом с ним упало яблоко. Это подтолкнуло его на размышления о том, почему яблоко упало перпендикулярно земле, каковы были причины данного явления. По крайней мере, так описывал этот эпизод знаменитый биограф Уильям Стьюкли.
- Формулы у него нет.
Это интересно: система отсчета в физике – определение и ее виды.
Второй закон Ньютона
Он описывает поведение тела при действии на него других объектов. Что с ним происходит, как он начинает двигаться и прочее.
- Формулировка. «В инерциальных системах отсчёта ускорение тела с постоянной массой прямо пропорционально равнодействующей всех сил и обратно пропорционально его массе».
- Формула. Математическое описание этого утверждения такое: а = F/m, где a — это ускорение, F — равнодействующая всех сил, приложенных к телу, m — масса тела.
- Трактовка. Из формулы мы видим, что ускорение тела зависит от силы, приложенной к этому телу, и массы. А также можно увидеть, что чем больше равнодействующая всех сил, то тем больше ускорение, и чем больше масса тела, тем ускорение меньше. Говоря простым языком, если равнодействующая всех сил не равна нулю и не меньше нуля, то выполняется данное утверждение. Можно сказать ещё проще, если на тело действует сила, то оно приобретает ускорение.
- Пример действия. Возьмём бейсбольную биту и мяч. Если ударить битой по мячу, и удар будет сильнее действия всех других сил, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.
Это интересно: формула всемирного тяготения – определение закона.
Третий закон Ньютона
- Формулировка. «Тела взаимодействуют друг на друга с силами одинаковой природы, направленными вдоль прямой, которая соединяет центры масс этих тел, а силы равны по модулю и разнонаправленны».
- Трактовка. Это значит, что на каждое действие есть своё противодействие.
- Пример действия. Более понятно это можно рассмотреть на таком примере: представьте пушку, из которой стреляют ядром. Ядро будет действовать на пушку с той же силой, с какой пушка вытолкала ядро. Поэтому при выстреле пушка откатится чуть-чуть назад, это происходит из-за того, что размеры пушки и ядра разные. Примерно то же самое происходит и при падении яблока на землю. Земля действует на яблоко с некой силой и яблоко тоже действует на Землю. Только из-за того, что масса Земли в миллионы раз больше яблока этого действия не видно. Еще один пример действия Третьего закона для закрепления усвоенного. Возьмём довольно сложный пример: притяжение планет. Луна вертится вокруг Земли благодаря тому, что она притягивается к Земле, но по Третьему закону Ньютона Луна тоже притягивает Землю к себе. Однако, из-за того, что их массы разные, Луна не может притянуть Землю, но у неё получается вызвать отливы и приливы в морях и океанах.
- Формула. Математически это утверждение можно записать так: F1 = -F2, где F1 — это сила, с которой первое тело действует на второе, а F2 — сила, с которой второе тело действует на первое.
obrazovanie.guru
Три закона Ньютона краткое определение

Три закона сэра Исаака Ньютона описывают движение массивных тел и как они взаимодействуют. В то время как законы Ньютона могут показаться очевидными для нас сегодня, более трех веков назад они считались революционными.
Ньютон, пожалуй, наиболее известен своей работой по изучению гравитации и движения планет. Призванный астрономом Эдмондом Галлеем после признания того, что за несколько лет до этого он потерял доказательство эллиптических орбит, Ньютон опубликовал свои законы в 1687 году в своей оригинальной работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под воздействием внешних сил.
Формулируя свои три закона, Ньютон упростил обращение к массивным телам, считая их математическими точками без размера или вращения. Это позволило ему игнорировать такие факторы, как трение, сопротивление воздуха, температура, свойства материала и т. Д., И сосредоточиться на явлениях, которые могут быть описаны исключительно по массе, длине и времени. Следовательно, три закона не могут быть использованы для описания точности поведения больших жестких или деформируемых объектов; однако во многих случаях они обеспечивают подходящие точные приближения.
Законы Ньютона
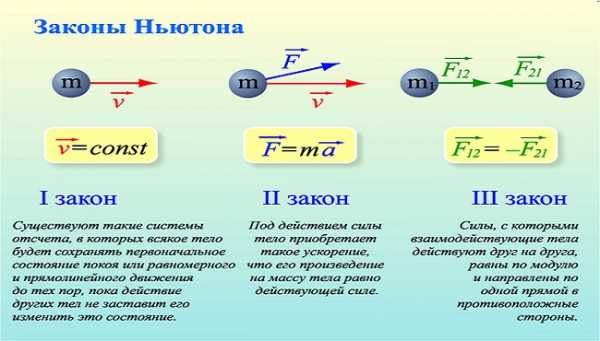 Три закона Ньютона
Три закона НьютонаЗаконы Ньютона относятся к движению массивных тел в инерциальной системе отсчета, иногда называемой ньютоновской системой отсчета, хотя сам Ньютон никогда не описывал такую систему отсчета. Инерциальную систему отсчета можно описать как трехмерную систему координат, которая либо стационарна, либо равномерно линейна, т. е. Не ускоряется и не вращается. Он обнаружил, что движение в такой инерциальной системе отсчета может быть описано тремя простыми законами.
Первый закон движения Ньютона
Первый Закон Движения гласит: Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения. Это просто означает, что вещи не могут начинать, останавливать или изменять направление самостоятельно. Требуется сила, действующая на них извне, чтобы вызвать такое изменение. Это свойство массивных тел сопротивляться изменениям в их движении иногда называют инерцией.
Второй закон движения Ньютона
Второй закон движения описывает, что происходит с массивным телом, когда на него воздействует внешняя сила. В нем говорится: Сила, действующая на объект, равна массе этого объекта своего ускорения. Это написано в математической форме как F = ma, где F — сила, m — масса, a — ускорение. Жирные буквы указывают, что сила и ускорение являются векторными величинами, что означает, что они имеют как величину, так и направление. Сила может быть одной силой, или это может быть векторная сумма более чем одной силы, которая является чистой силой после объединения всех сил.
Когда постоянная сила действует на массивное тело, она заставляет ее ускоряться, т. е. Изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация просматривается из движущейся системы отсчета, это тело может показаться ускоряющимся, замедляющим или изменяющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета перемещается относительно друг друга.
Третий закон движения Ньютона
Третий закон движения гласит: Для каждого действия существует равное противодействие. Этот закон описывает то, что происходит с телом, когда оно оказывает силу на другое тело. Силы всегда встречаются парами, поэтому, когда одно тело толкает другого, второе тело отталкивается так же сильно. Например, когда вы нажимаете тележку, тележка отталкивается от вас; когда вы тянете за веревку, веревка откидывается на вас; когда сила тяжести тянет вас к земле, земля подталкивает вас и когда ракета воспламеняет свое топливо за ним, расширяющийся выхлопной газ толкается на ракете, заставляя его ускоряться.
Если один объект намного, гораздо более массивный, чем другой, особенно в случае привязки первого объекта к Земле, практически все ускорение передается второму объекту, и ускорение первого объекта можно безопасно игнорировать, Например, если вы бросили мяч на запад, вам не нужно было бы считать, что вы на самом деле заставили вращаться Землю быстрее, пока мяч находился в воздухе. Однако, если вы стоите на роликовых коньках, и вы бросили мяч для боулинга, вы начнете двигаться назад с заметной скоростью.
Три закона были проверены бесчисленными экспериментами за последние три столетия, и до сих пор они широко используются для описания видов предметов и скоростей, с которыми мы сталкиваемся в повседневной жизни. Они составляют основу того, что сейчас известно как классическая механика, а именно изучение массивных объектов, которые больше, чем очень мелкие масштабы, рассматриваемые квантовой механикой, и которые движутся медленнее, чем очень высокие скорости, релятивистские механики.
tagweb.ru
Три закона Ньютона | Физика
Раздел механики, в котором изучают, как взаимодействие тел влияет на их движение, называют динамикой.
Основные законы динамики открыли итальянский ученый Галилео Галилей и английский ученый Исаак Ньютон. Вы изучали эти законы в курсе физики основной школы. Напомним их.

1. Первый закон ньютона (закон инерции)
Повторим один из опытов, которые поставил итальянский ученый Галилео Галилей.
Поставим опыт
Будем скатывать шар по наклонной плоскости и наблюдать за его дальнейшим движением по горизонтальной поверхности.
Если она посыпана песком, шар остановится очень скоро (рис. 13.1, а).
Если она покрыта тканью, шар катится значительно дольше (рис. 13.1, б).
А вот по стеклу шар катится очень долго (рис. 13.1, в).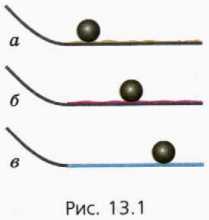
На основании этого и подобных опытов Галилей открыл закон инерции:
Сохранение скорости тела, когда на него не действуют другие тела или действия других тел скомпенсированы, называют явлением инерции.
? 1. Почему при встряхивании мокрого зонта с него слетают капли воды?
Особенно красиво смотрится явление инерции в фигурном катании (рис. 13.2).
Закон инерции называют также первым законом Ньютона, потому что Ньютон включил его в качестве первого закона в систему трех законов динамики, которые называют «тремя законами Ньютона».
Инерциальные системы отсчета
Закон инерции выполняется с хорошей точностью в системе отсчета, связанной с Землей. Но он не выполняется, например, в системе отсчета, связанной с тормозящим автобусом: при резком торможении пассажиры отклоняются вперед, хотя на них не действуют направленные вперед силы.
Инерциальных систем отсчета бесконечно много. Ведь если некоторая система отсчета является инерциальной, то инерциальной будет любая другая система отсчета, движущаяся относительно нее прямолинейно и равномерно.
Сформулируем теперь первый закон Ньютона с указанием систем отсчета, в которых он выполняется.
Существуют системы отсчета (называемые инерциальными), относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы
Изучать влияние взаимодействия тел на их движение удобнее всего именно в инерциальных системах отсчета, потому что в этих системах отсчета изменение скорости тела обусловлено только действием других тел на это тело.
Принцип относительности Галилея
Как показывает опыт, во всех инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях.
Это утверждение называют принципом относительности Галилея.
В справедливости принципа относительности Галилея легко убедиться, сидя в поезде, который плавно движется с постоянной скоростью. В таком случае все опыты с механическими явлениями, поставленные в вагоне, дадут одинаковые результаты независимо от того, едет поезд или стоит: например, лежащее на столе яблоко будет покоиться, а свободно падающие предметы будут падать вертикально вниз (относительно вагона!).
Поэтому пассажир может определить, едет поезд или стоит на станции, только посмотрев в окно (рис. 13.3).
2. Второй закон ньютона
Равнодействующая
Как вы уже знаете из курса физики основной школы, силы – векторные величины: каждая сила характеризуется числовым значением (модулем) и направлением. Силы измеряют с помощью динамометров. Единицей силы в СИ является 1 ньютон (Н). Определение ньютона мы дадим позже.
Если на тело, которое можно считать материальной точкой, действуют несколько сил, то их можно заменить одной силой, которая является векторной суммой этих сил. Ее называют равнодействующей.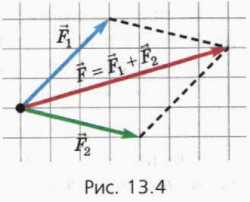
На рисунке 13.4 показано, как найти равнодействующую двух сил: а
? 2. К телу приложены две силы, равные по модулю 1 Н и 2 Н. Отвечая на следующие вопросы, сделайте пояснительные чертежи.
а) Какое наименьшее значение может принимать равнодействующая этих сил? Как направлены силы в этом случае?
б) Какое наибольшее значение может быть у равнодействующей этих сил? Как направлены силы в атом случае?
в) Может ли равнодействующая этих сил быть равной 2 Н?
? 3. К телу приложены две силы, равные по модулю 3 Н и 4 Н. Может ли их равнодействующая быть равной 5 Н? Если да, то чему в этом случае равен угол между приложенными силами?
? 4. К телу приложены три равные по модулю силы по 1 Н каждая. Как они должны быть направлены, чтобы:
а) равнодействующая была равна 1 Н?
б) равнодействующая была равна нулю?
в) равнодействующая была равна 2 Н?
Масса тела
В курсе физики основной школы рассказывалось также об опытах, которые доказывают, что под действием постоянной силы тело движется с постоянным ускорением.
Коэффициент пропорциональности между силой и ускорением характеризует инертные свойства тела и называется массой тела. Чем больше масса тела, тем большую силу надо приложить к телу, чтобы сообщить ему то же ускорение.
Единицей массы в СИ является 1 килограмм (кг). Это масса эталона, хранящегося в Международном бюро мер и весов (Франция). Приближенно можно считать, что одному килограмму равна масса 1 л воды.
Обозначают массу буквой m.
Второй закон Ньютона
Соотношение между равнодействующей всех сил, приложенных к телу, массой тела и его ускорением Ньютон сформулировал как второй из трех основных законов механики.
Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение:
В инерциальной системе отсчета сила является причиной ускорения, поэтому второй закон Ньютона часто записывают так:
Итак, приобретаемое телом ускорение прямо пропорционально равнодействующей приложенных к телу сил, одинаково с ней направлено и обратно пропорционально массе тела.
Заметим, что второй закон Ньютона справедлив только в инерциальных системах отсчета. Напомним: в этих системах отсчета ускорение тела обусловлено только действием на него других тел.
Единицу силы в СИ определяют на основе второго закона Ньютона: сила в 1 ньютон сообщает телу массой 1 кг ускорение 1 м/с2. Поэтому 1 Н = 1 кг * м/с2.
Сила тяжести
Как вы уже знаете, под действием притяжения Земли все тела падают с одинаковым ускорением – ускорением свободного падения . Силу притяжения, действующую на тело со стороны Земли, называют силой тяжести и обозначают т.
Когда тело свободно падает, на него действует только сила тяжести, поэтому она и является равнодействующей всех приложенных к телу сил. При атом тело движется с ускорением , поэтому из второго закона Ньютона получаем:
? 5. С какой силой Земля притягивает:
а) килограммовую гирю?
б) человека массой 60 кг?
Сила, скорость и ускорение – кто «третий лишний»?
Неочевидное следствие второго закона Ньютона состоит в том, что он утверждает: направление ускорения тела совпадает с направлением равнодействующей приложенных телу сил. Скорость же вела может быть при этом направлена как угодно!
Поставим опыт
Бросим шарик вниз, затем – вверх, а потом – под углом к горизонту (рис. 13.5)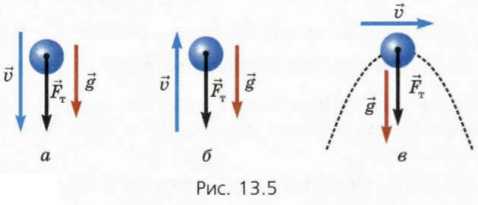
На шарик во время всего движения действует только направленная вниз сила тяжести. Однако в первом случае (а) скорость шарика совпадает по направлению с этой силой, во втором случае (б) – скорость вначале противоположна силе тяжести, а в третьем (в) – скорость направлена под углом к силе тяжести (например, в верхней точке траектории скорость перпендикулярна силе тяжести).
? 6. Тело равномерно движется по окружности. Чему равен угол между скоростью тела и равнодействующей?
? 7. Чему равен угол между скоростью автомобиля и равнодействующей приложенных к нему сил, когда автомобиль:
а) разгоняется на прямой дороге?
б) тормозит на прямой дороге?
в) движется равномерно по дуге окружности?
3. Третий закон ньютона
Поставим опыт
Предложим первокласснику и десятикласснику посоревноваться в перетягивании каната, стоя на скейтбордах: тогда трением между колесами и полом можно пренебречь (схема опыта показана на рисунке 13.6).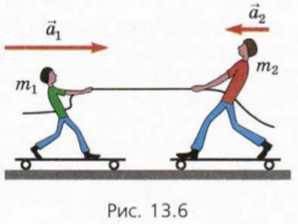
Мы увидим, что оба соперника движутся с ускорением. Значит, на каждого из них действу другого. Ускорения соперников направлено противоположно, причем ускорение первоклассника намного больше ускорения десятиклассника.
Точные опыты, подобные описанном выше, показывают, что модули ускорений обратно пропорциональны массам тел:
a1/a2 = m2/m1.
Поскольку ускорения направлены противоположно,
Согласно второму закону Ньютона m11 = 1 и m22 = 2, где 1 – сила, действующая на первое тело со стороны второго, а 2 – сила, действующая на второе тело со стороны первого.
Из соотношения (5) следует, что 1 = –2. Это и есть третий закон Ньютона.
Тела взаимодействуют друг с другом с силами, равными по модулю и противоположными по направлению.
Свойстве сил, с которыми тела взаимодействуют друг с другом:
– эти силы обусловлены одним и тем же взаимодействием и поэтому имеют одну и ту же физическую природу;
– эти силы направлены вдоль одной прямой;
– эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга.
Примеры проявления третьего закона Ньютона
Когда камень падает на Землю, на него действует сила тяжести 1 со стороны Земли, а на Землю – сила 2 притяжения со стороны камня (рис. 13.7, для наглядности масштаб не соблюден). Обе эти силы относятся к силам всемирного тяготения.
? 8. Согласно третьему закону Ньютона F1 = F2. Почему же ускорение камня заметно, а ускорение Земли – нет?
Когда камень лежит на Земле, на него кроме силы тяжести, которую будем обозначать теперь т, действует еще направленная вверх сила давления со стороны опоры (рис. 13.8, а). Она направлена перпендикулярно поверхности опоры, поэтому ее называют силой нормальной реакции (перпендикуляр называют часто нормалью). (Когда тело можно считать материальной точкой, все действующие на него силы желательно изображать на чертежах приложенными в одной точке.)
Когда камень покоится, его ускорение равно нулю. Значит, согласно второму закону Ньютона равнодействующая приложенных к камню сил и т, равна нулю (будем говорить, что в таком случае силы уравновешивают друг друга):
Отсюда следует:
Опора давит на камень силой , направленной вверх, а камень, по третьему закону Ньютона, давит на опору силан , направленной вниз (рис. 13.8, 6). Обе эти силы – силы упругости.
Силу, с которой тело вследствие действия на него силы тяжести давит на горизонтальную опору или растягивает вертикальный поднес, называют весом тела.
Итак, – это вес камня. По третьему закону Ньютона
Из формул (8) и (9) следует:
Итак, вес покоящегося тела равен действующей на это тело силе тяжести. Однако несмотря на это вес и сила тяжести существенно отличаются друг от друга:
– эти силы приложены к разным телам: вес действует на опору или поднес, а сила тяжести – на само тело;
– эти силы имеют разную физическую природу: вес – это сила упругости, а сила тяжести – проявление сил всемирного тяготения.
Кроме того, как мы увидим несколько позже (§ 16), вес может быть не равен силе тяжести и даже быть равным нулю.
Дополнительные вопросы и задания
9. Ускорение тела в некоторой инерциальной системе отсчета равно 3 м/с2 и направлено вдоль оси x. Чему равно ускорение этого тела в инерциальной системе отсчета, движущейся относительно заданной со скоростью 4 м/с, направленной вдоль оси y? Есть ли здесь лишние данные?
10. Брусок массой 0,5 кг соскальзывает с наклонной плоскости с углом наклона 30º. Скорость бруска увеличивается. Ускорение бруска равно 2 м/с2. Изобразите на чертеже равнодействующую приложенных к бруску сил. Чему она равна? Есть ли в задаче лишние данные?
11. Зависимость координаты x автомобиля от времени выражается в единицах СИ формулой x = 20 – 10t + t2. Ось x направлена вдоль дороги, масса автомобиля 1 т.
а) Чему равна равнодействующая приложенных к автомобилю сил?
б) Как она направлена в начальный момент – в направлении скорости автомобиля или противоположно ей?
12. Автомобиль массой 1 т едет со скоростью 72 км/ч по выпуклому мосту, имеющему форму дуги окружности радиусом 50 м. Сделайте чертеж и ответьте на вопросы.
а) Чему равна и как направлена равнодействующая сил, приложенных к автомобилю в верхней точке моста?
б) Какие силы действуют на автомобиль в этой точке? Как они направлены и чему они равны?
в) Во сколько раз вес автомобиля в верхней точке моста меньше действующей на автомобиль силы тяжести?
phscs.ru
2.3.1. Формулировка третьего закона Ньютона.
ЗАКОН ! | “ Две взаимодействующие материальные точки действуют друг на друга с силами одной природы, которые численно равны и направлены в противоположные стороны вдоль прямой, соединяющие эти точки “. |
Если 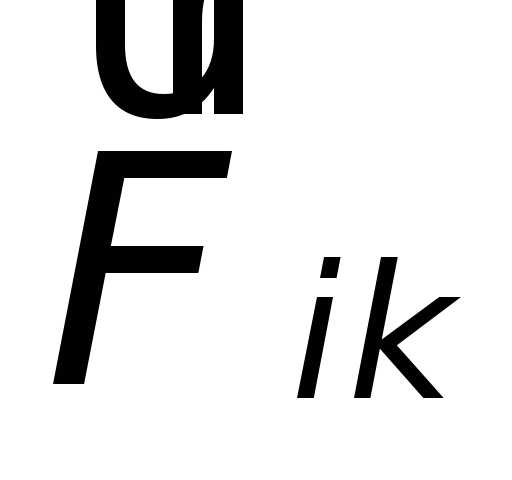 – сила,
действующая на i-тую
материальную точку со стороны k-той
материальной точки, а
– сила,
действующая на i-тую
материальную точку со стороны k-той
материальной точки, а 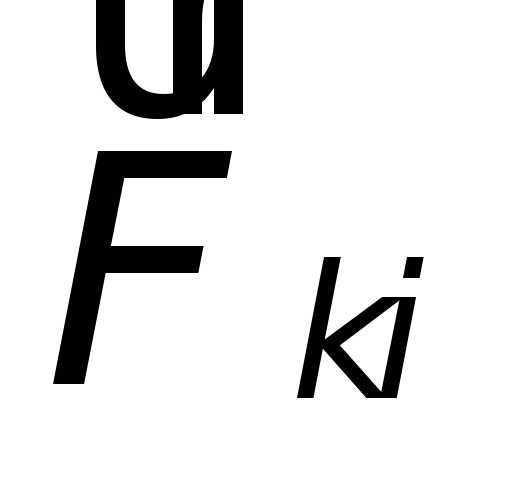 – сила,
действующая на k-тую
материальную точку со стороны i-той,
то согласно третьему закону Ньютона:
– сила,
действующая на k-тую
материальную точку со стороны i-той,
то согласно третьему закону Ньютона:
(2.6) |
Подчеркнем, что силы в третьем законе Ньютона:
приложены к разным материальным точкам;
в любой системе тел действуют парами;
имеют одну природу.
Сам третий закон применим только в рамках классической механики.
Силы 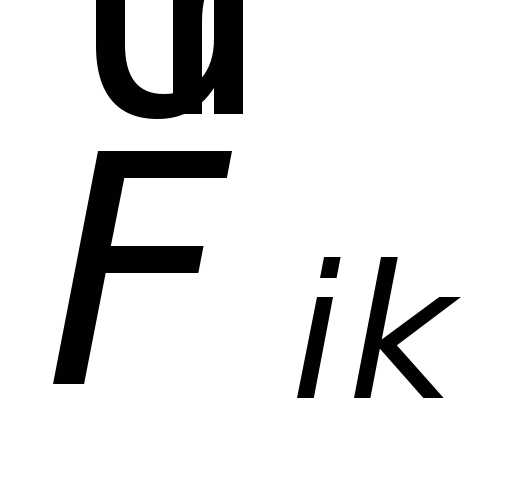 и
и 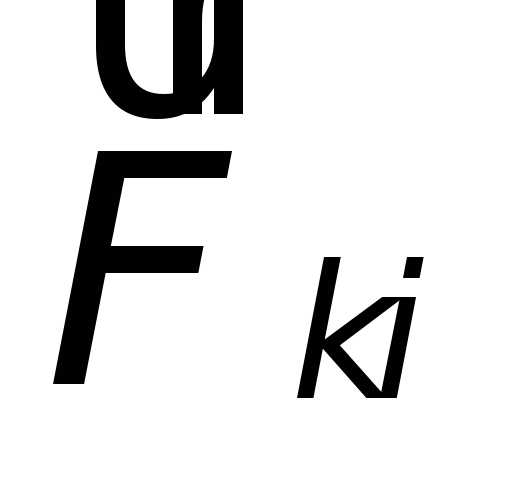 (приложенные
к разным материальным точкам) могут
взаимно уравновешиваться, только если
эти точки принадлежат к одному телу.
(приложенные
к разным материальным точкам) могут
взаимно уравновешиваться, только если
эти точки принадлежат к одному телу.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Второй и третий законы Ньютона справедливы только для инерциальных систем отсчета!!!
2.3.2. Силы инерции.
В неинерциальных системах отсчета возникают силы инерции, которые вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как, если на какое-либо тело действует сила инерции, то нельзя указать со стороны какого тела она действует и, соответственно, не существует противодействующей силы. (Действие есть, а противодействия нет!).
2.4. Преобразования Галилея.
Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно, т.е. не привязав себя к другой инерциальной системе отсчета.
В основу классической механики положен принцип независимости пространства и времени. В качестве аксиом принимается абсолютность промежутков времени и длин:
1) промежуток времени между какими-либо двумя событиями одинаков во всех системах отсчёта; 2) размеры тела не зависят от скорости его движения относительно системы отсчёта. Преобразованиями
Галилея называются преобразования координат
и времени, применяемые в классической
механике при переходе от одной
инерциальной системы отсчёта | |
Рисунок 2.1 |
Если
сходные оси декартовых координат
инерциальных систем отсчёта  и
и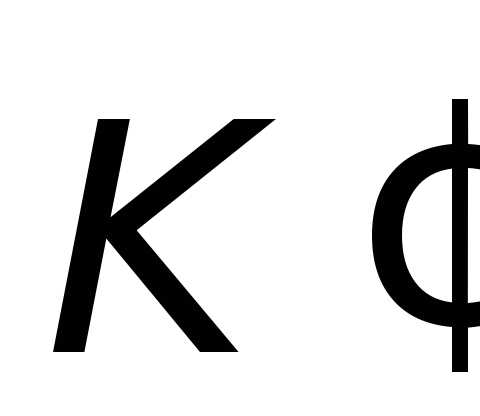 проведены
попарно параллельно друг другу, и если
в начальный момент времени
начала координат
проведены
попарно параллельно друг другу, и если
в начальный момент времени
начала координат и
и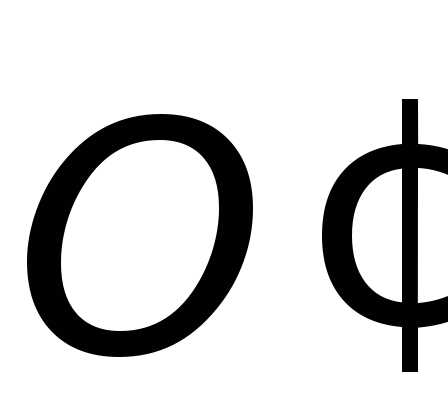 совпадают друг с другом (рис. 2.1), то
преобразования Галилея имеют вид:
совпадают друг с другом (рис. 2.1), то
преобразования Галилея имеют вид:
и | (2.7) |
или:
и | (2.8) |
где:
x,y,z
и 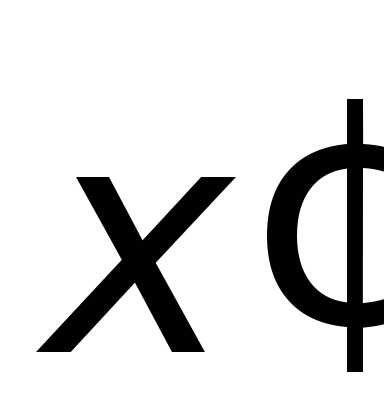 ,
, ,
, – координаты точки М в системах отсчёта
– координаты точки М в системах отсчёта в момент времениt
и
в момент времениt
и 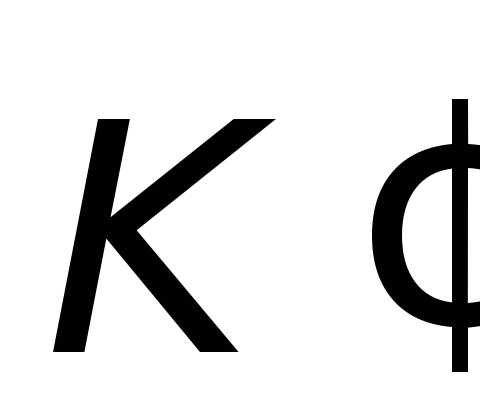 в момент времени
в момент времени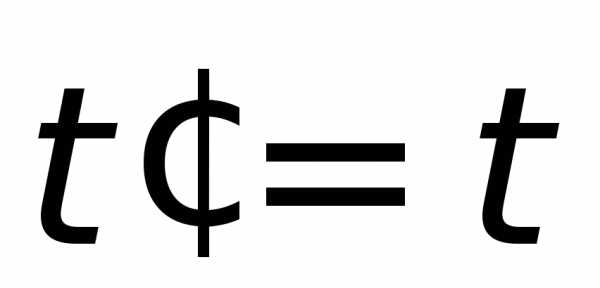 ;
;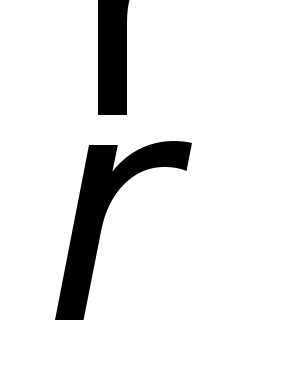 и
и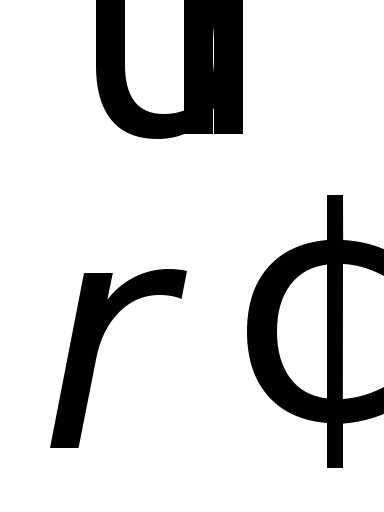 – радиусы – векторы точки М в тех же
системах отсчёта;
– радиусы – векторы точки М в тех же
системах отсчёта;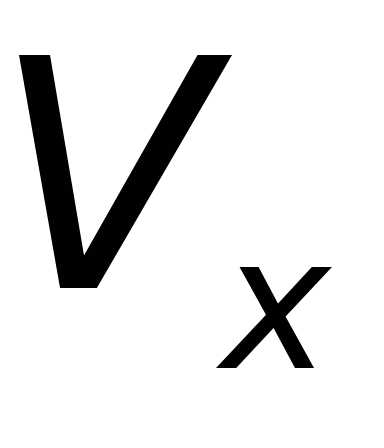 ,
,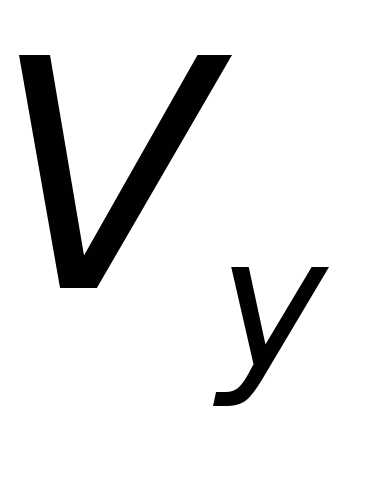 ,
,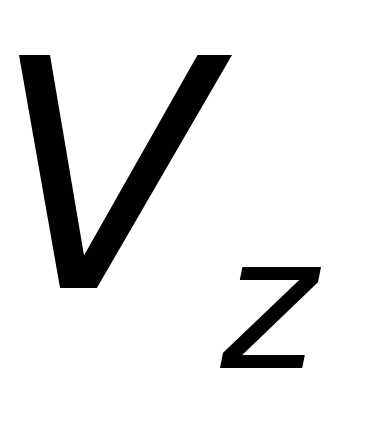 – проекции скорости
– проекции скорости системы
системы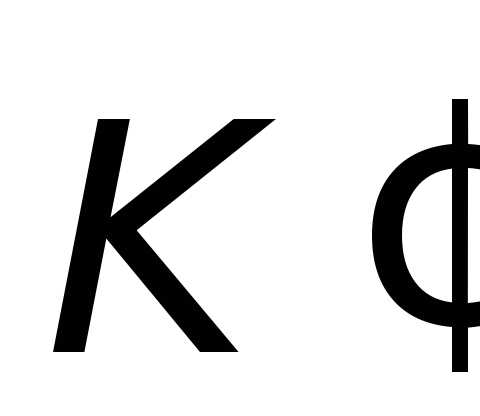 на оси координат системы
на оси координат системы .
.
Обычно
оси координат проводят так, что система | ||
| ||
(2.9) | ||
Рисунок 2.2. | ||
Из
преобразований Галилея вытекает
следующий закон преобразования скорости
произвольной точки М (рис. 2.1.) при переходе
от одной инерциальной системы  к другой
к другой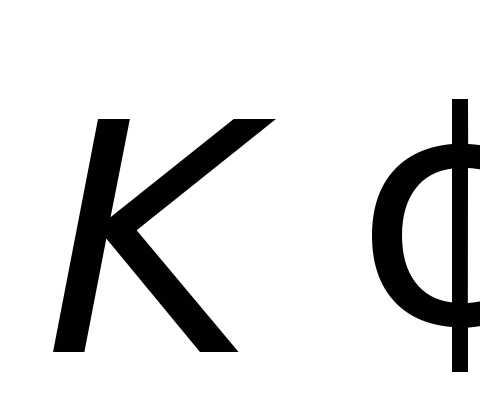 ,
,
(2.10) |
где
скорость точки М – 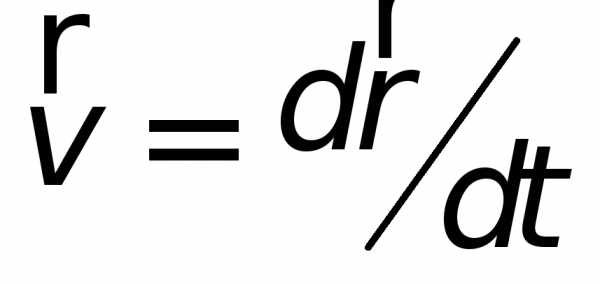 в системе отсчета
в системе отсчета ,
и
,
и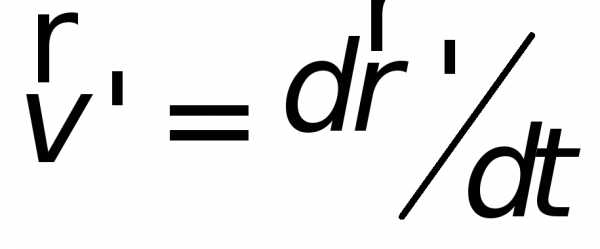 – в системе
– в системе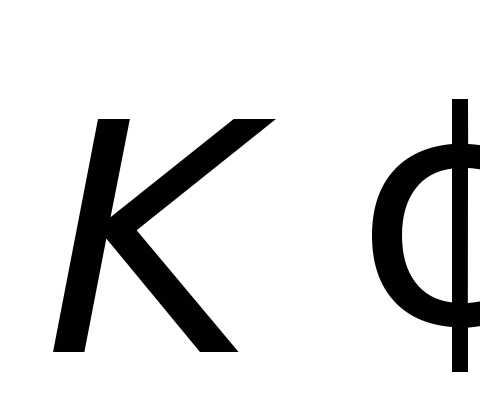 .
.
Соответственно преобразуются и проекции скорости на сходственные оси координат:
(2.11) |
Ускорение точки М в системах отсчёта
одинаковы.
| (2.13) |
Итак, ускорение материальной точки не зависит от выбора инерциальной системы отсчёта, т. е. инвариантно относительно преобразований Галилея.
Силы взаимодействия между материальными точками зависят только от их взаимного расположения и от скорости движения друг относительно друга.
Взаимное
расположение каких-либо двух точек 2 и
1, характеризуется вектором, равным
разности радиусов- векторов этих точек.
В системе  вектором,
а в системе
вектором,
а в системе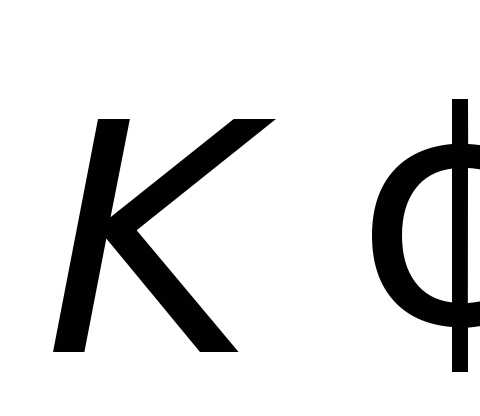 – вектором
– вектором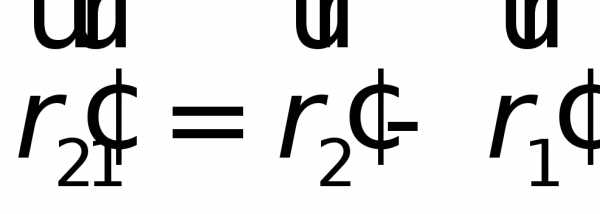 .
.
Согласно аксиоме 2 следует, что расстояния между точками 1 и 2 в системах одинаковы:
| (2.14) |
или:
(2.15) |
Скорость движения точки 2 относительно точки 1 (относительная скорость) равна разности скоростей этих точек
В
системе В
системе | (2.16) |
Из преобразований Галилея следует, что:
| (2.17) |
Итак, взаимное расположение и скорость относительного движения двух любых материальных точек не зависят от выбора инерциальной системы отсчёта, т. е. они инвариантны относительно преобразований Галилея. Соответственно инвариантны и силы, действующие на материальную точку:
| (2.18) |
Уравнения, выражающие законы Ньютона, инвариантны относительно преобразований Галилея, т. е. не изменяют свой вид при преобразовании координат и времени от одной инерциальной системы отсчёта к другой:
где 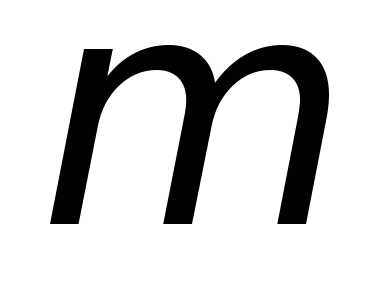 и
и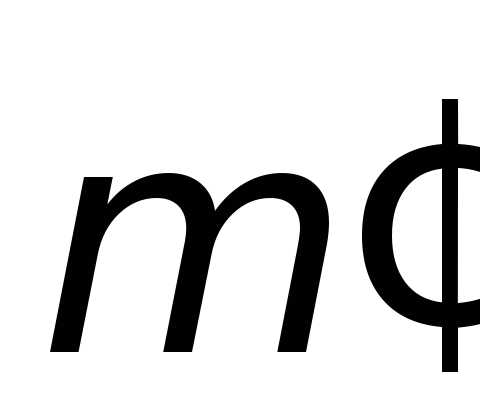 – масса рассматриваемой материальной
точки, одинаковая во всех системах
отсчёта.
– масса рассматриваемой материальной
точки, одинаковая во всех системах
отсчёта.
Т.о., в классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы механики одинаковы во всех инерциальных системах отсчёта.
Это значит, что в разных инерциальных системах отсчёта все механические процессы при одних и тех же условиях протекают одинаково.
Следовательно, с помощью любых механических экспериментов, проведённых в замкнутой системе тел, нельзя установить, покоится эта система или движется равномерно и прямолинейно (относительно какой-либо инерциальной системы отсчёта).
Механический принцип относительности означает, что в классической механике все инерциальные системы отсчёта совершенно равноправны.
Записанные
соотношения справедливы в случае
классической механики, т.е. u,  << c.
<< c.
Для скоростей, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
studfiles.net
Три закона Ньютона (ННН) – Познавательные статьи – Каталог статей
Главными законы классической механики являются три закона Ньютона. Сейчас мы рассмотрим их подробней.
Первый закон Ньютона
Наблюдения и опыт показывают, что тела получают ускорение относительно Земли, т. е. изменяют свою скорость относительно Земли, только при действии на них других тел.
Представим себе, что пробка воздушного «пистолета» приходит в движении под действием газа, сжимаемого выдвигаемым поршнем, т.е. получается такая последовательная цепочка сил:
Сила, приводящая в движение поршень => Сила поршня, сжимающая газ в цилиндре => Сила газа, приводящая в движение пробку.
В этом и других подобных случаях изменение скорости, т.е. возникновение ускорения, есть результат действие сил на данное тело других тел.
Если же на тело не будут действовать силы (или силы будут скомпенсированным, т.е. ), то тело будет оставаться в покое (относительно Земли), либо двигаться равномерно и прямолинейно, т.е. без ускорения.
На основе этого позволило установить первый закон Ньютона, который чаще называют закон инерции:
Существуют такие инерциальные системы отсчета, относительно которых, тело покоится (частный случай движения) или движется равномерно и прямолинейно, если на тело не действуют силы или действия этих сил скомпенсировано.
Проверить простыми опытами данный закон практически невозможно, потому что невозможно полностью устранить действие всех окружающих сил, особенно действие трения.
Тщательные опыты по изучению движения тел были впервые произведены итальянским физиком Галилеем Галилео в конце XVI и начале XVII веков. Позже более подробнее этот закон был описан Исааком Ньютоном, поэтому в честь него и был назван этот закон.
Подобные проявления инерции тел широко используются в быту и технике. Встряхивание пыльной тряпки, «сбрасывания» столбика ртути в термометре.
Второй закон Ньютона
Различные опыты показывают, что ускорения совпадает с направлением силы, вызывающее это ускорение. Поэтому, можно сформулировать закон зависимости сил приложенных к телу от ускорения:
В инерциальной системе отсчёта произведение массы и ускорение равно равнодействующей силы (равнодействующая сила – геометрическая сумма всех сил, приложенных к телу).
Масса тела, является коэффициентом пропорциональности данной зависимости. По определению ускорения () запишем закон в иной форме, а далее получается, что в числители правой части равенства является изменение импульса Δp, поскольку Δp=mΔv
Значит, второй закон можно записать в такой виде:
В таком виде Ньютон и записал свой второй закон.
Данный закон действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.
Третьей закон Ньютона
При соударении двух тел изменяют свою скорость, т.е. получают ускорения оба тела. Земля притягивает Луну и заставляет ее двигаться по криволинейной траектории; в свою же очередь Луна также притягивает Землю (сила всемирного тяготения).
Эти примеры показывают, что силы всегда возникают парами: если одно тело действует с силой на другое, то и второе тело действует на первое с такой же силой. Все силы носят взаимный характер.
Тогда можно сформулировать третий закон Ньютона:
Тела попарно действуют друг на друга с силами, направленными вдоль прямой, равными по модулю и противоположными по направлению.
Часто этот закон называют трудным законом, т.к. не понимают смысл этот закон. Для простоты понимания закона можно переформулировать данный закон («Действие равно противодействию») на «Сила, противодействующая равна силе действующей», так как эти силы приложены к разным телам.
Даже падение тел строго подчиняется закону противодействия. Яблоко надает на Землю оттого, что его притягивает земной шар; но точно с такой же силой и яблоко притягивает к себе всю нашу планету.
Для силы Лоренца третий закон Ньютона не выполняется.
 Основные законы механики Ньютон
сформулировал в своей книге «Математические начала натуральной философии».
Основные законы механики Ньютон
сформулировал в своей книге «Математические начала натуральной философии».
Итак, можно сделать вывод, что все эти три закона Ньютона являются фундаментном классической механики; и каждый из законов вытекает в другой.
www.naukamira.ru
Третий закон Ньютона | Все формулы
Третий закон Ньютона — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
Из 3 закона Ньютона можно вывести отношение масс и ускорений тел:
То получаем, что
Из этого равенства можно сделать отношения масс и ускорений разных тел
Все эти Силы :
— действуют вдоль одной прямой;
— направлены в противоположные стороны;
— равны по величине;
— приложены к разным телам, поэтому не уравновешивают друг друга;
— одинаковой природы.
На картинке показан как действует третий закон Ньютона. Человек воздействует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.
В формуле мы использовали :
— Сила действующая на 2 предмет
— Сила действующая на 1 предмет
— Масса тела
— Ускорение тела
xn--b1agsdjmeuf9e.xn--p1ai
1.2.2. Второй и третий законы ньютона
1.20 Основной закон динамики________________________________________________________
Общая формулировка второго закона Ньютона_____________________________________________________________
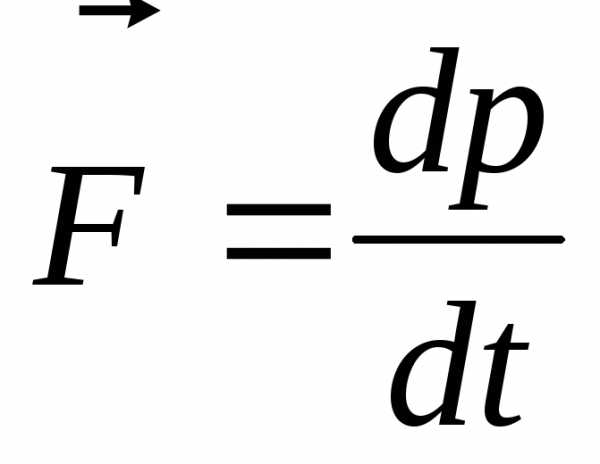
Скорость изменения импульса материальной точки (тела) равна действующей на нее(него) силе.
Записанное уравнение называют еще уравнением движения материальной точки.
Еще одна формулировка второго закона Ньютона__________________________________________________________
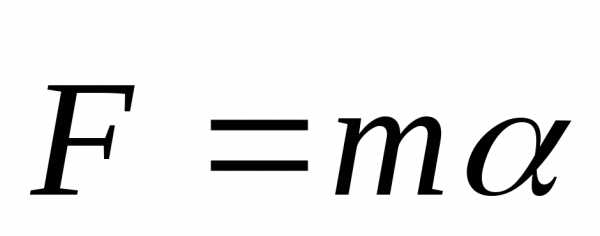
или
Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).
Единица силы________________________________________________________________________________________
1 Н = 1 (кг • м)/с2
1 ньютон — сила, которая массе в 1 кг сообщает ускорение 1м/с2 в направлении действия силы.
♦ Второй закон Ньютона справедлив только в инерциальных системах отсчета 1.18.
1.21 1.21 Принцип независимости действия сил______________________________________
Формулировка принципа независимости действия сил______________________________________________________
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.
Ускорение, приобретаемое точкой под действием нескольких сил___________________________________________
-результирующая сила. Сила может
быть разложена на две составляющие —тангенциальную (
может
быть разложена на две составляющие —тангенциальную (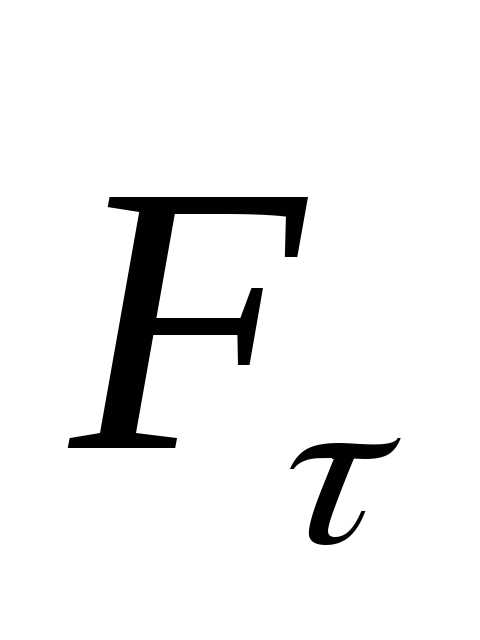 ) и нормальную (см. рисунок).
) и нормальную (см. рисунок).
Тангенциальная и нормальная составляющие силы_________________________________________________________
Р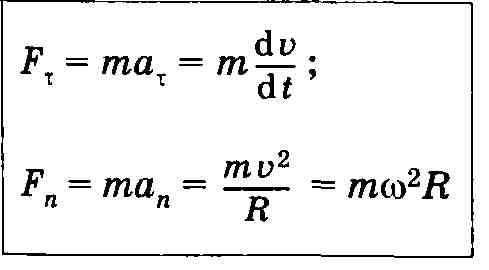
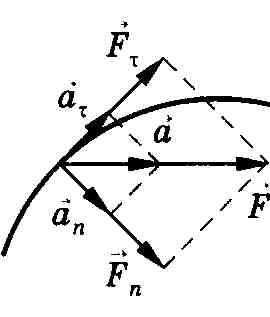 азложение
силы на составляющие приводит к
существенному упрощению решения задач.
Например, на рисунке действующая силаF = та разложена
на два компонента: тангенциальную силу FT (направлена
по касательной к траектории) и нормальную
силу Fn (направлена
по нормали к центру кривизны).
азложение
силы на составляющие приводит к
существенному упрощению решения задач.
Например, на рисунке действующая силаF = та разложена
на два компонента: тангенциальную силу FT (направлена
по касательной к траектории) и нормальную
силу Fn (направлена
по нормали к центру кривизны).
♦ Если на материальную точку действует одновременно несколько
сил, то, согласно принципу независимости действия сил, под F
во втором законе Ньютона понимают результирующую силу.
17
1.22 Третий закон Ньютона_______
Формулировка третьего закона Ньютона____________
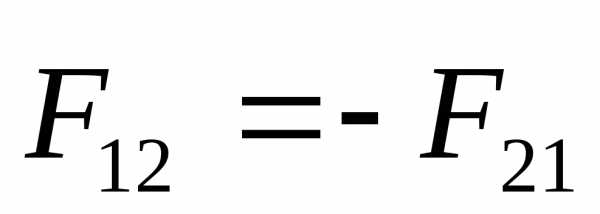 Всякое действие
материальных точек (тел) друг на друга
имеет характер взаимодействия; силы,
с которыми действуют друг на друга
материальные точки, всегда равны по
модулю, противоположно направлены и
действуют вдоль прямой, соединяющей
эти точки.
Всякое действие
материальных точек (тел) друг на друга
имеет характер взаимодействия; силы,
с которыми действуют друг на друга
материальные точки, всегда равны по
модулю, противоположно направлены и
действуют вдоль прямой, соединяющей
эти точки.
[F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой]
Силы в третьем законе Ньютона________________________________________________________________
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
♦ Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
studfiles.net

 (x, y, z, t) к другой
(x, y, z, t) к другой 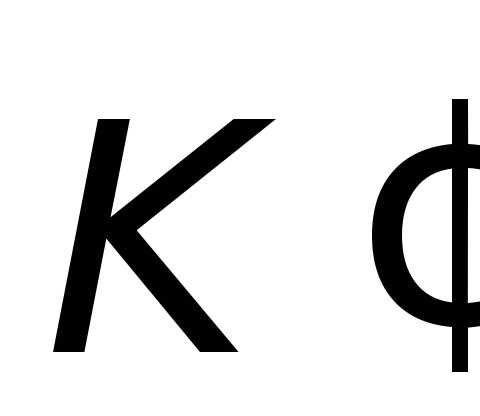 (x’, y’,z’, t’), которая
движется относительно системы
(x’, y’,z’, t’), которая
движется относительно системы  прямолинейно и поступательно с
постоянной скоростью
прямолинейно и поступательно с
постоянной скоростью .
.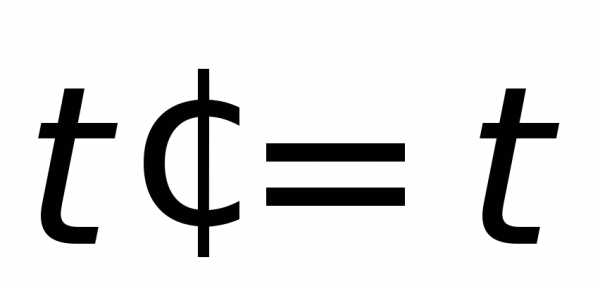
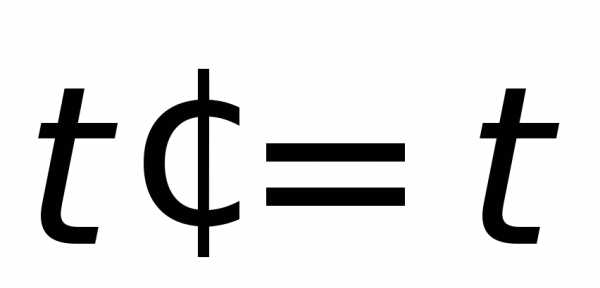
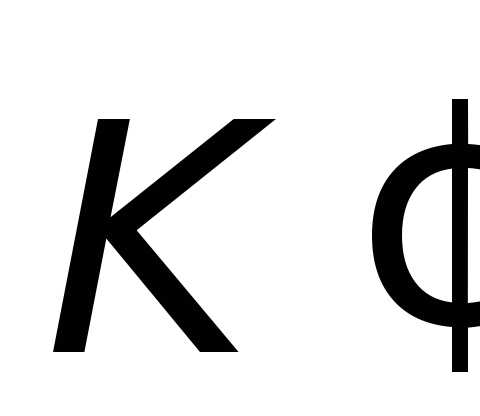 движется вдоль оси ОХ в положительном
направлении (рис. 2.2.). В этом случае
преобразования Галилея имеют более
простой вид:
движется вдоль оси ОХ в положительном
направлении (рис. 2.2.). В этом случае
преобразования Галилея имеют более
простой вид: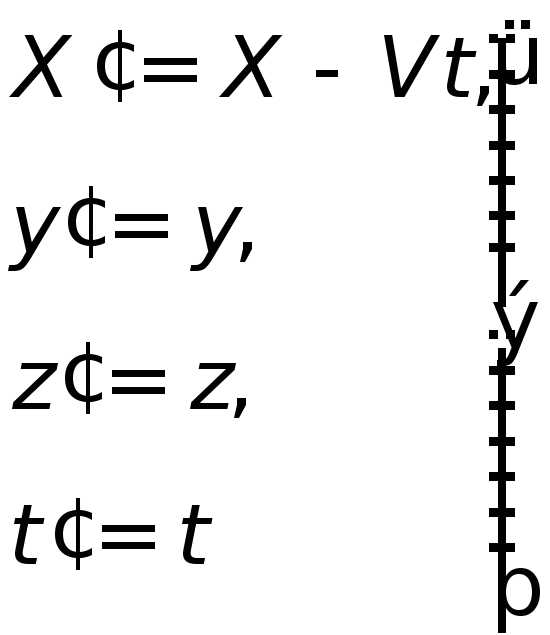
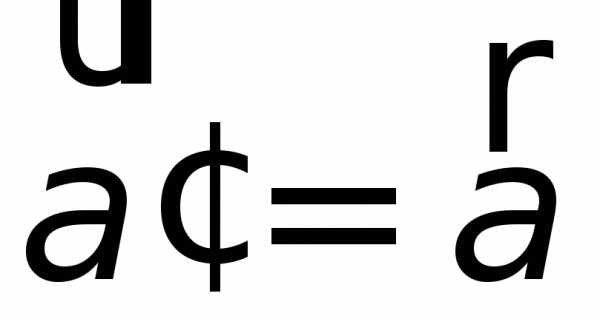
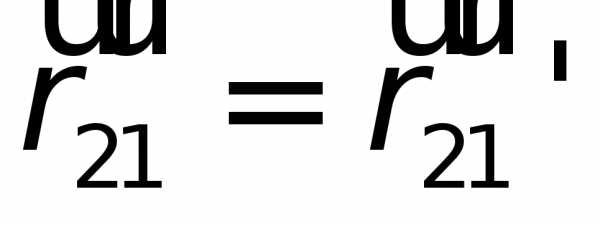
 :
: :
: