1 курс матрицы – тематике БНТУ АТФ 1 курс Матрицы и действия над ними Основные определения линейные операции над матр

Лекция 4. Матрицы и определители

Матрицы и определители. Лекция 4.

Матрицы.

Основные понятия.

Матрицей называется прямоугольная таблица чисел.

Пример 13. , ,,.

В общем случае матрица может содержать строк истолбцов

.

Числа называютсяэлементами матрицы, где – указывает номер строки,– указывает номер столбца.

Элементы образуютглавную диагональ матрицы. Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров называетсяматрицей – го порядка.

Матрицы называются равными, если у них равны элементы, стоящие на соответствующих местах, т. е. тогда и только тогда, когда, для всех,.

Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.

Пример 14. .

Если все элементы матрицы равны нулю, то матрица называется нулевой.

Пример 15. .

Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.

Пример 16. , .

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.

Пример 17

. ,.

Матрица, содержащая одну строку (столбец), называется вектором (вектор-строкой, вектор-столбцом).

Пример 18. ,.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной .

Пример 19. ;

Очевидно, что .

Действия над матрицами.

Матрицы одинаковых размерностей можно складывать и вычитать. Если

, , то, причем

, для всех .

Пример 20

. ,

.

Умножение матрицы на число.

Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.

Пример 21. Пусть , тогда. Матрицаназываетсяпротивоположной к матрице.

Умножение матриц.

Умножение матриц можно только в том случае, когда число столбцов матрицыравно числу строк матрицыВ этом случае справедливо соотношение, причем элементы матрицыравны,,. Другими словами строки матрицыумножаются на столбцы матрицы

Пример 22. Пусть ,. Тогда

,

.

Видим, что в общем случае . Если же выполняется условие, то матрицыиназываютсяперестановочными друг с другом.

Матрица называется ступенчатой, если для её элементов выполняются условия:

1. под первым не нулевым элементом каждой строки находится 0;

2. первый ненулевой элемент любой строки находится правее первого не нулевого элемента любой строки, расположенной выше.

Пример 23. Следующая матрица является ступенчатой.

.

Элементарные преобразования матриц.

Элементарными преобразованиями матриц являются:

1. Перестановка местами двух любых её строк (столбцов).

2. Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.

3. Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Две матрицы называютсяэквивалентными, если одна из них получается из другой с помощью элементарных преобразований

Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.

Определители.

Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.

Пример 24. Если , то. Так.

Если , то.

Так .

Если , то

. Так

.

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.

С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.

Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.

Вычисление определителей более высоких порядков осуществляется путем использования их свойств.

Свойства определителей.

Пусть дана квадратная матрица

Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается

Минором некоторого элемента определителя называют определитель, который получается вычеркиванием из негостроки истолбца. Например

, .

Алгебраическим дополнением элемента определителя называют число. Например

, .

Свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е. .

2. Определитель меняет знак при перестановке любых двух его строк (столбцов).

3. Определитель, имеющий две равные строки (столбца), равен 0.

4. Общий множитель строки (столбца) можно выносить за знак определителя, например

.

5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например

6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.

(I=I+II).

7. Определитель треугольной матрицы равен произведению её диагональных элементов.

8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например

.

Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.

9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.

22

studfiles.net

Лекция 1. Матрицы

Определение и некоторые свойства определителей порядка n. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства этих операций

1.1. Основные понятия

Определение 1. Матрицей называется прямоугольная таблица чисел.

Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:

a11

a12

…

a1n

a11

a12

…

a1n

a

a

…

a

a

a

…

a

A =

21

22

2n

=

21

22

2n

.

… …

…

…

… … … …

as2

…

as1

as2

…

asn

as1

asn

Числа, составляющие матрицу, называются ее элементами,

элемент aij матрицыA расположен в ееi -йстроке и

j -мстолбце.

Числа s иn (число строк и столбцов матрицы) называются ее порядками.

Говорят также, что A – матрица размеромs ×n . Еслиs = n , матрицаA называетсяквадратной.

Для краткой записи используется также обозначение A = (aij ) (илиA = aij ) и далее указывается, в каких пределах изменяютсяi и

j , например,A =	aij	,	i =1,…,s ,j =1,…,n . (Запись	читается так:
матрица A с элементами			aij ,i изменяется от 1 доs ,j	– от 1 до n .)

Среди квадратных матриц отметим диагональные матрицы, у которых все элементы с неравными индексами (i ≠ j ) равны нулю:

	a11	0	0	…	0
	0	a22	0	…	0
	0	0	a33	…	0	.
	… …		… … …
	0	0	0	0	ann
Будем говорить, что		элементы		a11,a22 ,…,ann расположены на

главной диагонали. Диагональная матрица вида

1		0	0	…	0
	0	1	0	…	0
E =	0	0	1	…	0
… …			…	…	…
0		0	0	…	1

называется единичной матрицей.

В дальнейшем будут встречаться матрицы вида

a11	0	0	…	0			a11		a12	a13…
a	a	0	…	0				0	a	a	…
21	22								22	23
a	a	a	…	0		и		0	0	a	…
31	32	33	…	…					…	33
…	…	…					…			… …
a	a	a	…	a				0	0	0 …
n1	n2	n3		nn

которые называются треугольными матрицами, а также матрицы, состоящие из одного столбца:

a1a2…

an

и одной строки:

(a1,a2,…,an )(матрица-столбец и матрица-строка).

Матрица, все элементы которой равны нулю, называется нулевой.

1.2. Определители порядка n

Пусть дана квадратная матрица порядка n :

		a11	a12	…	a1n
		a	a	…	a
	A =	21	22		2n		.	(1.1)
		…	…	…	…
		a	a	…	a
		n1	n2		nn

Составим всевозможные произведения n элементов матрицы, расположенных в разных строках и разных столбцах, т.е. произведения вида

a1α	a2α	2	… anα	n	.	(1.2)
1
Число произведений вида (1.2) равно n!						(примем этот факт без

доказательства).

Будем считать все эти произведения членами определителя порядка n , соответствующего матрице (1.1).

Вторые индексы множителей в (1.2) составляют перестановку

первых n натуральных чисел 1, 2,…,n .
Говорят,	что числа i и		j в перестановке составляютинверсию,
если i > j , а в перестановкеi			расположено раньше		j .
Пример 1. В перестановке шести чисел, 1 2					6	4 5 3 , числа 6
и 4 , 6 и 5 , 6 и 3 ,		4 и 3 , 5 и 3 составляют инверсии.
Перестановка называется четной, если число инверсий в ней
четно, и нечетной, если число инверсий в ней нечетно.
Пример	2.	Перестановка		1 2 6 4 5 3		– нечетная, а

перестановка 1 2 3 4 5 6 – четная ( 0 инверсий).

Определение 2. Определителем порядка n, соответствующим матрице(1.2), называется алгебраическая сумма n! членов, составленная следующим образом: членами определителя служат всевозможные произведения n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем слагаемое берется со знаком”+”, если множество вторых индексов является четной перестановкой чисел1, 2,…, n, и со знаком”–”, если нечетной.

Обозначать определитель матрицы (1.2) принято так:

			a11	a12	…	a1n
A		= detA =	a21	a22	…	a2n.
			…	… … …

an1 an2 … ann

Замечание. Определение 2 дляn = 2 иn = 3 приводит к уже знакомым нам определителям2-гои3-гопорядка:

a11

a12

= a a−a a

21

,

a21

a22

11

22

12

a11

a12

a13

a21

a22

a23

= a11a22a33+ a12a23a31+ a21a32a13−

a31

a32

a33

−a13a22a31−a23a32a11−a12a21a33.

Транспонированием вокруг главной диагонали матрицыA

называется переход к матрице AT , для которой строки матрицыA являются столбцами, а столбцы – строками:

		a11	a21	…	an1
T		a	a	…	a
		12	22		n2
A	=	…	… … …			.
		a	a	…	a
		1n	2n		nn
Будем говорить,	что		определитель			∆T =		AT		получен

транспонированием определителя ∆ .

Свойства определителя порядка п

1.∆T = ∆ (определитель не меняется при транспонировании вокруг главной диагонали).

2.Если одна из строк определителя состоит из нулей, определитель равен нулю.

3.От перестановки двух строк определитель меняет лишь знак.

4.Определитель, содержащий две одинаковые строки, равен нулю.

5.Если все элементы некоторой строки определителя умножить на

число k , определитель умножится наk .

6.Определитель, содержащий две пропорциональные строки, равен нулю.

7.Если все элементы i -йстроки определителя представлены в

виде суммы aij = bj +c j ,j =1,…n , то определитель равен сумме двух

определителей, у которых все строки, кроме i -й,такие же, как в исходном определителе, аi -ястрока в одном определителе состоит изbj , а в другом – изc j .

Определение 3. i-ястрока определителя является линейной

комбинацией	остальных его	строк, если	k j ,j =1,…,i −1,i +1,…,n
такие, что,	умножая j -ю	строку на k j ,	а затем складывая все

строки, кроме i-й, получим i-юстроку.

8.Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9.Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

Замечание. Мы сформулировали свойства определителя для

строк. В силу свойства 1 ( ∆T = ∆)				они справедливы и для столбцов.
Все	приведенные	свойства		были	доказаны	на практических
занятиях	для n = 3 ;	для	произвольного n			примем их	без
доказательства.					n выбрать элементaij
Если	в определителе ∆		порядка				и

вычеркнуть столбец и строку, на пересечении которых расположен aij ,

оставшиеся строки и столбцы образуют определитель порядка n −1 , который называетсяминором определителя∆ , соответствующим элементуaij .

Пример 3. В определителе

∆ =		−1	1	0
		2	3	5
		−4	7	11

минором элемента a = 3 является определительM	22	=		−1	0		.
22				−4	11

Определение 4.

Алгебраическим дополнением Aij элемента

aij

определителя ∆ называется его минор, умноженный на(−1)i+ j ,

где

i – номер строки,

j – номер

столбца, в которых расположен

выбранный элемент aij .

Пример 4. В определителе

∆ =

−1

1

0

2

3

5

−4

7

11

алгебраическое дополнение A

=

−1

0

(−1)2+2 = −11 .

22

−4

11

Теорема 1 (о разложении по строке). Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.

Теорема 1 позволяет свести вычисление определителя порядка n к вычислениюn определителей порядкаn −1 .

Пример 5. Вычислить определитель4-гопорядка:

														2			−3	4				1
										∆ =				4			−2	3				2			.
														3			−1	4				3
															1 −1 2 0
Решение. Воспользуемся теоремой 1 и разложим определитель∆
по 4-йстроке:
			−3		4	1				(−1)4+1 +(−1)													2					4	1				(−1)4+2 +
∆ =1			−2 3 2																				4 3 2
			−1		4	3																	3					4	3
		2			−3	1		(−1)4+3 +0											2				−3						4		(−1)4+4 =
+2		4 −2 2																	4 −2 3
		3			−1	3													3				−1						4
				−3 4 1												2 4 1											2 −3 1
= −				−2 3 2								−				4 3 2					−2						4 −2 2								=
				−1 4 3												3 4 3											3 −1 3

				0	0	1			0	0	1			0	0	1
=		−	4		−5 2			−	0	−5	2		−2	0	4	2	=
свойство 9				8	−8	3			−3−8		3			−3	8	3
	4	−5			0	−5				0 4		= 32−40+15−24=17 .
= −				−				−2
теорема 1	8	−8			−3	−8				−3 8

Замечание. Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядкаn сведется к вычислениювсего одного определителя порядкаn −1 .

Пример 6. Вычислить

	2	−3	4	1
∆ =	4	−2	3	2		.
	3	−1	4	3
	1	−1	2	0

Решение. Прибавим первый столбец ко второму и первый столбец, умноженный на (−2 ), к третьему, в результате получим

	2	−1	0	1
∆ =	4	2	−5	2		.
	3	2	−2	3
	1	0	0	0

Теперь применим теорему 1 и разложим по последней строке:

	−1	0	1		(−1)4+1 ,
∆ =1	2	−5	2
	2	−2	3

вычисление определителя 4-гопорядка свелось к вычислению всего одного определителя3-гопорядка.

Далее аналогично к первому столбцу прибавим третий и полученный определитель разложим по первой строке:

	0	0	1		4	−5
∆ = −	4	−5	2	=			= 8−25= −17 ,
	5	−2	3		5	−2

studfiles.net

Матрицы 1 курс. Задания

Дана квадратная матрица 7*7 с элементами типа INTEGER. Создать функцию поиска индекса максимального элемента главной диагонали. Из строки, содержащей максимальный элемент главной диагонали, сформировать одномерный массив. Вывести исходную матрицу и полученный массив.

Создать процедуру получения из квадратной матрицы n*n (n < 9) минора путем вычеркивания произвольной строки и столбца. С использованием этой процедуры для квадратной матрицы 3*3 составить и вывести 3 минора, полученные путем вычеркивания 1 строки и 1, 2, 3 столбца. Сформировать из определителей этих миноров одномерный массив размерностью 3. Вывести исходную матрицу в виде матрицы и полученный массив.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию поиска индекса минимального по модулю элемента побочной диагонали. Из строки, содержащей этот элемент главной диагонали, сформировать одномерный массив. Вывести исходную матрицу и полученный массив.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию поиска индекса первого отрицательного элемента главной диагонали. Из строки, содержащей этот элемент матрицы, сформировать одномерный массив. Вывести исходную матрицу и полученный массив.

Создать процедуру получения из квадратной матрицы n*n (n < 9) минора путем вычеркивания произвольной строки и столбца. С использованием этой процедуры для матрицы 3х3 составить и вывести 3 минора, полученные путем вычеркивания 1 столбца и 1, 2, 3 строки. Сформировать из определителей этих миноров одномерный массив размерностью 3. Вывести исходную матрицу и полученный массив.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию поиска индексов минимального элемента всей матрицы. Из строки, содержащей минимальный элемент всей матрицы, сформировать одномерный массив. Вывести исходную матрицу и полученный массив.

Создать процедуру получения из квадратной матрицы n*n (n < 9) минора путем вычеркивания произвольной строки и столбца. С использованием этой процедуры из матрицы 3*3 составить и вывести 3 минора, полученные путем вычеркивания строк и столбцов элементов главной диагонали. Сформировать из определителей этих миноров одномерный массив размерностью 3. Вывести исходную матрицу и полученный массив.

Дана исходная матрица m*n (m, n <=7). Сформировать другую матрицу такого же размера, у которой внутренние элементы матрицы есть квадрат разности между средним значением в строке и значением элемента, а наружные элементы оставлены без изменения. Найти максимальное отклонение между соответствующими элементами матриц.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию определения максимального элемента главной диагонали матрицы. Из столбца, содержащего максимальный элемент главной диагонали, сформировать одномерный массив. Отсортировать массив по возрастанию. Вывести исходную матрицу в виде матрицы и полученный массив.

Создать процедуру получения из квадратной матрицы n*n (n < 9) минора путем вычеркивания произвольной строки и столбца. С использованием этой процедуры для квадратной матрицы 3х3 составить и вывести 3 минора, полученные путем вычеркивания строки и столбца элементов, лежащих на побочной диагонали. Сформировать из определителей этих миноров одномерный массив размерностью 3. Вывести исходную матрицу и полученный массив.

Сформировать из квадратной матрицы a[i,j] с элементами типа INTEGER вектор из элементов, начиная с a[1,1], таким образом, чтобы из трех соседних элементов a[i+1,j], a[i,j+1] и a[i+1,j+1], следующим выбирался наибольший. Обход продолжать до тех пор, пока не будет достигнута нижняя или правая граница матрицы.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию поиска максимального элемента главной диагонали матрицы. Из строки, содержащей максимальный элемент главной диагонали, сформировать одномерный массив. Вывести исходную матрицу в виде матрицы и полученный массив.

Из квадратной матрицы n*n (n < 7) с элементами типа INTEGER получить путем вычеркивания элементов главной диагонали матрицу, уплотненную по столбцам, размерностью n*(n-1) за счет сдвига верхней треугольной матрицы влево. Вывести исходную и полученную матрицы.

Из квадратной матрицы n*n (n < 7) с элементами типа INTEGER получить путем вычеркивания элементов главной диагонали матрицу, уплотненную по строкам, размерностью (n-1)*n за счет сдвига верхней треугольной матрицы вниз. Вывести исходную и полученную матрицы.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию определения индексов максимального элемента матрицы. Из строки, содержащей максимальный элемент всей матрицы, сформировать одномерный массив. Вывести исходную матрицу в виде матрицы и полученный массив.

В прямоугольной матрице m*n (m, n < 7) с элементами типа INTEGER вместо строки, содержащей максимальное значение суммы соседних элементов, поместить строку, содержащую максимальный элемент главной диагонали. В основной программе вывести исходную матрицу, индексы строк и результирующую матрицу.

В прямоугольной матрице m*n (m, n < 7) с элементами типа INTEGER поменять местами строки, содержащие максимальное значение произведений соседних элементов и максимальный элемент всей матрицы. В основной программе вывести исходную матрицу, индексы строк и результирующую матрицу.

В прямоугольной матрице m*n (m, n < 7) с элементами типа INTEGER вместо столбца, содержащего максимальное значение произведений соседних элементов, поместить столбец, содержащий максимальный элемент всей матрицы. В основной программе вывести исходную матрицу, индексы столбцов и результирующую матрицу.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию определения индекса строки матрицы, содержащей максимальный элемент в k-том столбце. Из строки, содержащей максимальный элемент 3 столбца, сформировать одномерный массив. Вывести исходную матрицу в виде матрицы и полученный массив.

В прямоугольной матрице m*n (m, n < 7) с элементами типа INTEGER отсортировать строки матрицы по возрастанию суммы квадратов элементов строки. Вывести исходную и результирующую матрицы. После каждой строки результирующей матрицы привести сумму квадратов элементов строки.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать процедуру нахождения индексов максимального элемента матрицы. Сформировать массив, элементы которого являются произведениями элементов строки и столбца, пересекающихся на максимальном элементе всей матрицы. Упорядочить его по возрастанию. Вывести исходную матрицу в виде матрицы и полученный массив.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать процедуру нахождения индексов максимального элемента матрицы. Сформировать массив, элементы которого являются произведениями элементов строки и столбца, пересекающихся на максимальном элементе всей матрицы. Упорядочить его по возрастанию абсолютных значений. Вывести исходную матрицу в виде матрицы и полученный массив.

Сформировать из квадратной матрицы 7*7 с элементами, равными индексам, например a[1,2]=12, одномерный вектор из элементов при обходе по пути в форме буквы «П». Вывести исходную матрицу и вектор.

Сформировать из квадратной матрицы 7*7 с элементами, равными индексам, например a[1,2]=12, одномерный вектор из элементов при обходе по пути в форме буквы «Г». Упорядочить его по возрастанию. Вывести исходную матрицу и два вектора.

Сформировать из квадратной матрицы 7*7 с элементами, равными индексам, например a[1,2]=12, одномерный вектор из элементов при обходе по пути в форме буквы «S». Вывести исходную матрицу и вектор.

Сформировать из квадратной матрицы 7*7 с элементами, равными индексам, например a[1,2]=12, одномерный вектор из элементов при обходе по границам верхней треугольной матрицы. Вывести исходную матрицу и вектор.

Дана квадратная матрица 7х7 с элементами типа INTEGER. Создать функцию определения индекса строки матрицы, содержащей минимальный элемент в k-том столбце. Из строки, содержащей минимальный элемент первого столбца, сформировать одномерный массив. Вывести исходную матрицу в виде матрицы и полученный массив.

Выполнить задание А с применением динамических массивов.

studfiles.net

Высшая математика 1 курс

Замечание 1

Курс высшей математики в вузах различается как продолжительностью изучения, так и наполнением тем для изучения. Но существует определенный неизменяемый перечень тем, обязательных для изучения студентами. Дадим краткую характеристику основным темам, которые изучаются на $1$ курсе вуза.

Линейная алгебра

Матрицы и действия над ними

Рассматриваются матрицы, которые содержат m строк и n столбцов.

Изучаются равные матрицы, квадратные, диагональные, единичные, треугольные и трапецевидные матрицы.

Над матрицами выполняются следующие виды действий:

• сложение матриц одинакового размера;
• умножение матрицы на вектор-столбец;
• умножение матрицы на число;
• умножение матриц, причем вводится понятие согласованности и транспортирования матриц;

Определитель квадратной матрицы

Рассматривается понятие определителя для матриц до 4-го порядка.

Основные свойства определителей:

1. Если А и В являются квадратными матрицами, то $|AB|=|BA|=|A| \times |B|$. Причем $AB \ne BA$.
2. $|A|=|A^T|$.
3. Определитель равен нулю, если он содержит нулевой ряд или $2$ одинаковых параллельных ряда.
4. Для диагональной и треугольной матриц определитель равен произведению чисел главной диагонали.
5. Общий множитель любого ряда определителя можно вынести за его знак.

Рассматривается понятие минора и теорема Лапласа (о разложении определителя).

Обратная матрица

Алгоритм нахождения обратной матрицы при условии, что матрица $A$ – невырожденная и ее определитель не равен нулю:

1. Каждый элемент матрицы заменяется его алгебраическим дополнением, получается союзная матрица.
2. Союзная матрица транспонируется.
3. Выполняется деление каждого элемента союзной матрицы на определитель матрицы.

Ранг матрицы

Ранг матрицы рассматривается как максимальное число линейно-зависимых строк матрицы и наибольшее из порядков отличных от нуля миноров данной матрицы.

Свойства:

1. Ранг матрицы не изменяется при транспонировании.
2. При вычеркивании нулевого ряда ранг не изменяется.
3. Ранг матрицы не изменяется при выполнении элементарных преобразований.
4. Ранг треугольной матрицы равен числу ненулевых элементов, расположенных на главной диагонали.

Метод Крамера решения невырожденных систем СЛАУ

Уравнение $AX=B$, где $|A| \ne 0$ решается так:

$a_k=\frac{|A_k |}{|A|}$ , где $A_k$ можно получить из $A$ заменой какого столбца на столбец свободного члена $B$.

Метод Гаусса

Вводится понятие расширенной матрицы, совместной и определенной системы уравнений, равносильных систем уравнений, однородной системы линейных уравнений.

Правило решения системы уравнений:

Найти ранг основной ($rA$) и расширенной ($r \bar{A}$):

1. Если $rA \ne r \bar{A}$, то система несовместна;
2. Если $rA=r \bar{A}=r$, то система совместна и находят базисный минор порядка $r$:
   • берутся $r$ уравнений, из коэффициентов которых составляется базисный минор, остальные отбрасываются. Неизвестные, коэффициенты которых составляют минор, называются главными. Их записывают слева, а остальные $(n-r)$ – справа;
   • выражают главные неизвестные через свободные и получают общее решение системы;
   • свободным неизвестным дают произвольное значение и получают частные решения.

Элементы векторной алгебры

Векторы

Изучается понятие вектора, длина и направление вектора, противоположный вектор, нулевой вектор, коллинеарные и компланарные векторы.

Операции над векторами

Рассматриваются операции над векторами:

• умножение вектора на число;
• сумма векторов;
• скалярное, векторное и смешанное произведение векторов.

Аналитическая геометрия

Прямая на плоскости

Несколько видов уравнений описывают прямую на плоскости: уравнение с угловым коэффициентом, уравнение прямой через точку и направление, уравнение через 2 точки, уравнение в отрезках, уравнение через данную точку перпендикулярно вектору, нормальное уравнение прямой.

Традиционно рассматривается формула для нахождения угла между прямыми, условия перпендикулярности и параллельности прямых и расстояния от точки до прямой.

Плоскость в пространстве

Плоскость в пространстве задается с помощью различных видов уравнения: уравнение через точку перпендикулярно к вектору, уравнение через 3 точки, нормальное уравнение плоскости, уравнение в отрезках.

Рассматривается угол между плоскостями и расстояние от точки до плоскости.

Прямая в пространстве

Канонические уравнения прямой или уравнения прямой с направляющими коэффициентами, уравнения в параметрическом виде, общее и векторное уравнение прямой, уравнение прямой через 2 точки в пространстве. Формула угла между прямыми.

Взаимное расположение плоскостей, прямых и прямой и плоскости

Для каждого из вариантов расположения предлагается формула для нахождения угла между плоскостями, прямыми и прямой и плоскостью, а также условия параллельности и перпендикулярности плоскостей, прямых, прямой и плоскости.

Отдельно изучается пересечение прямой с плоскостью и условие принадлежности прямой плоскости.

Линии второго порядка

Эллипс

Кроме основного канонического уравнения эллипса изучаются понятия эксцентриситета и директрис.

Гипербола

Изучается каноническое уравнение гиперболы, уравнения асимптот, понятие эксцентриситета, директрисы и фокальных радиусов.

Парабола

Рассматривается понятие полуфокального диаметра параболы и каноническое уравнение параболы.

Замечание 2

Изучение высшей математики на первом курсе, как правило, заканчивается изучением раздела «Линии второго порядка», но может варьироваться в зависимости от учебных планов, программ и специальностей.

spravochnick.ru

21.08.02. МАТРИЦЫ ( 1-курс). | По дороге к источнику …

21/08/2002 Матрицы ( 1-курс).

 

Матрица человека – это универсальное поле, содержащее в себе всю информацию о строении и функциональном устройстве человека вообще. Работа рукой в матрицах, работа с образным содержанием матриц является одним из методов работы с планом причин.

После отработки в полях, негативные образы часто восстановливаются, самосохраняются – почему?

Во-первых, у работающего могут быть недостаточно чувствительные руки, мало опыта. Во-вторых, пациенты не верят в “пасы” руками, не понимают, что происходит.

Стен Гроф пробивается к матрицам через перинатальный уровень сознания. Академик Шипов через науку (1993 г.) выступает за обоснование этих вещей, разделяя мир на уровни:

5                    Хроники Акаши, библиотека событий, план кармы

4              Уровень мыслей, матрицы

3                    Эмоции, астральное тело: по телу эмоций строится тело физическое

2                    Эфирное тело

1              Физическое тело

Перинатальный уровень бессознательного – это уровень пересечения индивидуального бессознательного с коллективным.  Это период в жизни человека от момента зачатия ребенка до момента рождения – 9 месяцев.

Матрица содержит всю информацию о человеке вообще. Любая информация о любом достижении человека в направлении развития сознания автоматически становится элементом человеческой матрицы. Для последующих поколений этот элемент является данностью. Хорошее является достоянием всех. Если принять за поколение срок в 20 лет, то человек, родившийся в 1980 году накопил в матрице около 2800 элементов! У кого много негатива в полях – идет большой отбор энергии. Насыщенность потока возрастает сразу во всех направлениях.

На матрицы можно выходить напрямую. Как происходит работа? Рука принимает и предает нам, как отражение по телевизору, всю информацию из Хроников Акаши – этой всемирной всечеловеческой библиотеки. Надо только успокоиться, убрать все эмоции, задать грамотный вопрос. По анализу потоков выходим на 5-ый уровень.

Ладонь является чакрой, видится в виде желтого шара, сферы. Словно на руке – линза, через которую видим образы, появившиеся н ответ на заданный вопрос.

Убираем в матрице раз за разом негатив, осознаем, основание разрушается, информация о явлении уходит.

Меняя образ, выходящий на руку, мы можем менять образ, который находится в Хрониках Акаши, т.е. реальность. Это возможно потому, что каждый человек есть по образу и подобию и другой человек тоже. Я есть они, они есть я. Я знаю все о о нем.

Мы работаем в матрицах не с самими негативными силами, а с отображением силы (как в зеркале — солнечный зайчик ).

 

 

 

 

 

Входим в матрицу напрямую, решением. Это возможно при использовании динамической системы координат. Это  обеспечивает  безопасность  работы. Проекция образа  на динамическую систему  координат  является    статичной,   неподвижной

и   хорошо      поддается воздействию руки. Зафиксировав  динамичный образ, такая система координат не искажает

его,    проекция   образа  тождественна   самому  образу  и изменения   образа  приводят к изменениям  в реальности.

Связав систему координат с левой ладонью, мы получаем возможность выхода к управляющим матрицам , где находится та информация, которая движет человеком в мире.

На левой руке записана наша судьба. Правая (для правшей) обладает вакуумными свойствами — свойствами улавливать потоки энергии. Наше тело является более фиксированной энергией, более грубой. Мы тоже часть энергии, поэтому мы можем это делать.

 

Каждая из направлений этой системы координат описывает одно из важнейших движений человека.

 

 

Связав систему координат с левой ладонью, мы получаем возможность выхода к управляющим матрицам , где находится та информация, которая движет человеком в мире.

 

На левой руке записана наша судьба. Правая (для правшей) обладает вакуумными свойствами — свойствами улавливать потоки энергии. Наше тело является более фиксированной энергией, более грубой. Мы тоже часть энергии, поэтому мы можем это делать.

 

 

 

Каждая из направлений этой системы координат описывает одно из важнейших движений человека.

 

Координата 1. Все движения над ладонью – это движения в Духе, (ты добр, порядочен, ты сострадателен).

Координата 2. Все движения под ладонью – деградация, Падение ( это зависть, страх, злость, недопустимые действия). Это очень низкие вибрации, грубые, тяжелые, это ощущается, как что-то неприятное.

Третья координата – Путь. Человек проявляет движение познания, учиться или что-то хорошо делает.

Координата 4 – Эго -это творческий потенциал человека. характеризует величину наработки творческого потенциала, который при подъеме к духу проявляется высоким творчеством, а при движении вниз — махровым эгоизмом

Координата 5 включает в себя любое Благо человека. Это духовные наработки, знания, мастерство, эдоровье, все материальные ценности. Чем дальше движение по оси 5, тем больше величина блага. Провалы по этой оси указывают на то, что человек боится что-то потерять.

Координата 6 – Магия, движение в прошлое. Магия — любое движение, осуществляемое человеком  в материи ( пишем, читаем, моем пол…), а не только ритуальные действия. Существуют или духовные движения или движения обычного человека в материи. Любое движение, если оно не в духе, — магическое движение, человек застревает в прошлом, не живет в настоящем. Часто человек говорит : “Как хорошо было раньше!” При этом он теряет все. Координата 6 показывет, как часто человек находится в прошлом и как он живет в будущем. Движение энергии вверх по оси 6 называется белой магией, т.к. такое движение человека в мире – благо, а вниз – черной.

У каждого человека своя граница движений. У кого-то при обследовании рука не дотягивается, выходит много информации, у другого – чуть больше ладони. Провалы под любой осью указывают на протерю определенного вида блага.

Любая сила  в матрице  видится один к одному в том образе и действует в том направлении, в котором она проявляется. Матрица исследуется правой рукой, улавливает потоки энергии и представляет собой квадратное горизонтальное поле, лежащее на левой ладони. Матричное пространство не ограничивается плоскостью, а определяется пределами досягаемости правой руки.

Человек может увидеть приходящую информацию или в шаре на ладони или в квадрате.

Пределы

 

 

 

 

Координата 2. Все движения под ладонью – деградация, Падение ( это зависть, страх, злость, недопустимые действия). Это очень низкие вибрации, грубые, тяжелые, это ощущается, как что-то неприятное.

 

Третья координата – Путь. Человек проявляет движение познания, учиться или что-то хорошо делает.  

 

Координата 4 – Эго -это творческий потенциал человека. характеризует величину наработки творческого потенциала, который при подъеме к духу проявляется высоким творчеством, а при движении вниз — махровым эгоизмом

 

Координата 5 включает в себя любое Благо человека. Это духовные наработки, знания, мастерство, эдоровье, все материальные ценности. Чем дальше движение по оси 5, тем больше величина блага. Провалы по этой оси указывают на то, что человек боится что-то потерять.

 

Координата 6 – Магия, движение в прошлое. Магия — любое движение, осуществляемое человеком  в материи ( пишем, читаем, моем пол…), а не только ритуальные действия. Существуют или духовные движения или движения обычного человека в материи. Любое движение, если оно не в духе, — магическое движение, человек застревает в прошлом, не живет в настоящем. Часто человек говорит : “Как хорошо было раньше!” При этом он теряет все. Координата 6 показывет, как часто человек находится в прошлом и как он живет в будущем. Движение энергии вверх по оси 6 называется белой магией, т.к. такое движение человека в мире – благо, а вниз – черной.

 

У каждого человека своя граница движений. У кого-то при обследовании рука не дотягивается, выходит много информации, у другого – чуть больше ладони. Провалы под любой осью указывают на протерю определенного вида блага.

 

Любая сила  в матрице  видится один к одному в том образе и действует в том направлении, в котором она проявляется. Матрица исследуется правой рукой, улавливает потоки энергии и представляет собой квадратное горизонтальное поле, лежащее на левой ладони. Матричное пространство не ограничивается плоскостью, а определяется пределами досягаемости правой руки.

 

Человек может увидеть приходящую информацию или в шаре на ладони или в квадрате. 

 

 

 

Пределы

Верхний   предел   называется       “небо” – это пространство воздействия на Духовный мир,

нижний —    “дно” ,   оно    отделяет    матричное пространство от астрала.

Боковые стенки,  поднимающиеся от дна к небу, отделяют  пространство организованной  жизни

человека от пространства действия стихий.

Т.е. за этими пределами — пространство стихий.

Взрослый   стихиям  подвержен,  старец — от них уходит, учитель — может управлять.

По “пути”  — стихия   “воды”, на “благе” — стихия    ”земли”,

на “магии” — стихия   ”огня” ( игра с огнем), на “эго” — стихия  ”воздуха” (строительство

воздушных замков ).

 

Пространство над ладонью — область духовного роста,

под ладонью — область влияния низших разрушительных сил.

Сама ладонь — низший необходимый уровень движений человека как Человека.

У каждого человека свои пределы, определяемые кармой.

 

Запись в матрицах представляет собой силовые образования, которые преобрели формы и воздействуют на стороны жизни человека, соответствующие координатам выхода сил.

 

Формы

Если силовые образования незначительной величины, например – 1 по оси эго, то можно говорить только о небольшом эгоизме человека;

 

2 и3 – уже неприемлемо, с этим надо работать;

Если пробивает верхний предел — 4, то мы негативно влияем вообще на кого-то, такого человека могут просто убрать через аварию, травмы

Силовые образования могут быть активные и пассивные. Это искаженные божественные энергии.Стоит их ощутить, как например, холодные потоки, они замирают.

Ученые подсчитали, что на 1993 год в Хрониках Акаши 53% энергий божественных искажено.

Существует 5 план физического вакуума, и что человек туда вкладывает своими действиями и эмоциями, то в обязательном порядке приходит назад. Это и есть работа кармы. На востоке это называют Хрониками Акаши. Что такое Хроники? – это время, т.е. Хроники Акаши хранят любое наше движение во времени. А мы можем их переработать с помощью матриц. Количество физических событий не обязательно должно проходить через нашу физическую жизнь – можно через понимание и осознавание.

Т.к. негатив заброшен в Хроники Акаши моментально чувствами или эмоцией, также, работая мыслью, мы можем это убрать!

 

Что такое ситуация болезни? –

это пришла информация и она рассказывает нам о каком-то событии, когда мы промахнулись. Она словно стучится к нам в дверь и говорит – ты пойми в чем дело.

Если человек не понял, то отброшенная лекарствами сила возвращается назад.

Если человека продолжают упорно лечить, то фантом негативной силы начинает воздействовать на лечащих или ухаживающих за больным – начинает разрушать их генетический аппарат. Он словно отбивает им руки, не давая лечить, т.к. больной не заслужил выздоровления, т.к. он ничего не понимает.

Стоит понять, разобраться, как силовое образование становится все меньше и меньше и уходит. Т.о. при работе с матрицами больного человека для действительного результата человек должен сам осознать причину своей болезни и изменить что-то в жизни. “Да, это неспроста со мной такое твориться, что-то я не так сделал” . А не стонать, за что это мне!

 

Как происходит то, что мы вылавливаем из 2800 возможных негативных обстоятельств, положенных каждому, ту физическую форму, которую мы видим в матрице?

На момент зачатия в человечке 7 поколений папы – мы стоим словно на 7 кирпичиках: здесь мы сеяли, делали добрые дела, сражались, убивали, хитрили.

Если ребенок вырастает, и, например, сильно обижается на кого-то – тонкая энергетическая удочка забрасывается в коллективное бессознательное, ребенок не знает, что предки вели себя также – его обида, как червячок, притянет то, что обернется для ребенка болезнью.

Т.е, наше внутреннее движение вытягивает из библиотеки Хроник Акаши совпадающую по вибрациям энергию, которую врачи называют болезнью.

Эти 2800 могут состоятся, а могут не состояться. Вот почему учиться очень благотворно – вы начинаете за собой присматривать. Во-вторых, вы приходите разбираться, вы разбираетесь, негативная сила (ее отображение на ладони) бледнеет, и негативное событие, для вас записанное, травма или авария не произойдет на физическом уровне, может вы только услышите или прочтете об этом.

Оно не только пройдет мимо, но как бы вынимается из библиотеки и постигнет уже ни вас ни сейчас, ни когда придете в другой раз, ни ваших детей, и вообще — в мире становится на один негатив меньше, вы сделали доброе дело.

Это работа для мноих людей.

 

Любое состояние человека можно посмотреть в матричной форме.

 

Например, матрица грязи.

Эта матрица порождает, поддерживает и воссоздает шлаки в организме.

Матрица – каменный пояс— матрица, ответственная за камни в организме ( отложение солей, камни в почках, в желчном и т.д.)

Матрица – грибы – ответственна за опухоли в организме.

Качественная или злокачественная – задается вопрос. Если на вопрос :“опухоль злокачественная?” следует ответ – “да”, тогда руку подбрасывает вверх, если же матрица просто чистая – не о чем говорить, идет спокойствие  — или доброкачественная или нет опухоли.

 

 

 

Называем матрицу. Вход в матрицу осуществляем решением.

Допускаются в матрицу люди, которые сами занимаются собой, самосовершенствованием. Духовные движения таких людей утоньчают их вибрации, помогая почувствовать, увидеть образы сил в матрицах. Даже если вы до конца не чувствуете, но вас есть намерение помочь человеку, жестами, движениями рук вы все равно взаимодействуете с силами в матрице. Рука владеет энергиями, она ткет пространство. Грубое движение может пробить, порвать поля человека. Движения должны быть плавными, мягкими, хоть и сильными. Движение руки по часовой стрелке увеличивает позитивную энергию, против – выводит образ негативной силы из пространства матрицы и, следовательно, уменьшает ее реальность в Хрониках Акаши.

 

Связка рабочих матриц. Она охватывает весь спектр движений человека в мире.

 

1. Нечистая сила рода. Информация о человеке от момента зачатия до момента рождения, содержащая нароботки семи отцовских родов.  Мы входим в эту информацию, потому что может быть именно в роду причина, почему сейчас человеку плохо. Врачи называют это наследственными заболеваниями.
2. Круг врагов – все негативные воздействия на человека чужих людей и других миров.
3. Терновый венец – круг негативных сил, воздействующих на душу.  На ладони должна быть сфера – ровная, мягкая, теплая, полная света. Это то, что путешествует из воплощения в воплощение.
4. Карма
5. Сознание – на матрице должен быть ровный купол до “неба”. Может быть и сильный световой поток из центра ладони вверх.
6. Свободная дурь – собственная воля человека, искажающая божественное. Это безграмотность, глупость, допущенная по отношению к себе самому.
7. Нечистая плоть – грязь в организме, шлаки, камни, соли, опухоли. Можно рассматривать конкретно: матрицу опухолей.
8. Черная вода – отвечает за очищение всех жидкостей в организме. В организме человека — 70% воды ( кровь, слизистая, суставная жидкость, мозг).
9. Матрица ситуации.

 

Негативные матрицы – 1,2,6,7,8 – совокупность или часть сил, которые необходимо привести в порядок, сделать чистой.

Матрицы 3 и 5 – особые, после устранения негатива требуют созидательной работы ( по часовой стрелке 3 круга ).

Матрица 4 – основная. После ее аккуратной отработки в большинстве случаев все очищается.

 

Порядок работы в матрицах.

1. проверить наличие бреши в боковых пределах – по часовой стрелке. Рука, двигаясь, оставляет энергетические нити от пальцев-чакр, которые потом сливаются в ткань, т.о. рука ткет пространство.
2. исследовать провалы дна и астральные кольца (разорвать щелчком) – проверить целостность дна, наличие разрывов в дне, вдавить вышедшие силы в разрывы, швы от разрывов загладить, грязь против часовой опустить, сжечь на дне ( как масло на сковородке)
3. проверить наличие силовых образований в пространстве матрицы, отщелкать

 

Если нечистая сила достигает неба – рассмотреть матрицу источника этой силы.

Если грязь пассивная – вдавить по часовой стрелке в дно.

Если активная сила, живое существо – спрашиваем, что это, отрабатываем в образе.

Чистые силы – нежные и мягкие, вызывают нежность и тепло.

Ключом к доступу в работе с матрицами является мастерство во всем – в мытье пола, окон, любой работе. Небрежность на жизненном плане не дает результатов и в работе с матрицами.

Матрицы 1-9 – ментальные, они доступны многим для осознанной работы.

 

После отработки в негативной матрице должно быть чисто, не должно быть разрывов и провалов в дне.

Провал    в     дне   —   образуется,  если   человеком начинает управлять  астральная сила.      Женская      сила     с        неба вытягивает     божественную    энергию    и    переводит        в нижние вибрации. В  дне   образуется   воронка,    охваченная кольцом в астрале   —   похоже  на  баскетбольную    корзину, мощный  поток  идет  вниз,  вытягивая  энергию   из   высших планов , и тонкая чистая энергия в ней разлагается. Источник такого   провала —  негативное  чувство, к которому постоянно возвращаемся  ( все время “тянет” на плохое — курение, алкоголь, наркотики, азартные игры).  Человек  через себя,  свою  жизнь  кормит  нижний  план  духовными силами.

Если не  делать  движения  навстречу  такому   негативному чувству, то тяга угасает, если нет духовной подпитки. После обработки человек должен держаться!

Кольцо разрываем, входя пальцем внутрь кольца,  формируем дно — рука ткет просттранство, грязь  убираем ( проверить в образе – чтоб не осталось швов!).

 

Разрывы в дне матрицы образуются при

выплескивании негативных эмоций.

Может прийти образ лисицы ( хитрость ),

медведя (идет по жизни напролом ) и т.п.

Образ надо отработать.

Если долго не убирать разрывы в дне,

по ним могут выйти мертвые поля – энергетика тех людей, которые, умерев, по той или иной причине не смогли уйти из мира живых. Иногда родные своими просьбами держат умерших, не дают им уйти. Или, если человек умер без покаяния. “Мертвые не знают, что они мертвые”. Это привидения, явления полтергейста.

Грязь в матрице чистится щелчками.

Какие это силы пробивают дно? – гнев, обида, желание, ненависть. Поднимается негативная сила. Чем больше негатива на духовный мир оказывает человек, тем ближе к небу поднимается нечистая сила. И тогда высший мир наносит удар. Т.о. человек попадает под удар высшего мира.

Вид удара определяется координатой выхода сил.

Если сила выходит из центра ладони – это духовный рост человека – не путать с ударом неба.

 

 

Если это астральная сила, она может выходить на любой оси. Если такая астральная сила вышла на оси блага, человек потеряет то, к чему стремился, чем дорожил. Потеря денег, человека, пожар, авария – все может случиться.

Если по пути – человек может быть парализован, человек будет в жизни остановлен.

Если по оси магии – это вызовет необходимость лишения свободы человека.

По оси эго – удар по самолюбию.

Если удар неба в матрице кармы. Ситуация в жизни – все плохо, денег нет, ребенок больной родился и т.п. “За что? Почему? Это несправедливо!” — и человек принимает решение: “Я жизнь положу, но отомщу.. Я все за это отдам”. Человек представляет собой опасность для неба – получает удар неба. Если человека убирают, он будет приходить еще и еще, пока не поймет. Если же человек разбереться, поймет, осознает, то такой удар может закончиться для человека только тяжелой болезнью и отработает он свой проступок в этой жизни. И в следующей жизни – придет абсолютно здоровым.

Тяжелую ситуацию несет матрица кармы с пробитым дном. Иногда в матрице вообще дна нет! Ощущаются мертвые холодные поля, проникающие через провалы. Человек в большой опасности. Чаще всего такие провалы возникают при неправильном поведении на похоронах, при посещении могил. У каждого своя судьба, кто-то раньше уходит, кто-то позже, однако часто люди, прожившие вместе много лет, не соглашаются с потерей родного человека, держат его мыслями, плачем, хотят уйти вместе – и, в результате, уходят следом. Бывает, на сеансах спиритизма выстраиваются коридоры для мертвых полей. Такими незакономерными действиями также пробивается дно в матрице кармы.

В матрице могут быть перевозбужденные стихии:

 

 

 

 

Например, нашли в матрице силу перевозбуждения стихий : вода пробивает предел. Предел можно видеть как стеклянную стенку, и из дыры вода льется, например, на “землю”, т.е. вода льется на “благо” — может залить квартиру, человек может утонуть или вымываются деньги. Если вода идет на “эго” — кто -то подмочит репутацию, это – удар  по самолюбию. Если на ось магии — можно ошпариться кипятком из кастрюли и т.д. Вода может пробить дно, поток идет в мир мертвых – на поле выйдут мертвые. Дно должно быть всегда закрыто, как замерзший зимой пруд. Если есть трещина  — соединить края трещины.

Поток огня может тоже возбуждать любую стихию. Возбуждение огнем стихии земли вызывается, например, при разбрасывании мусора, при магических обрядах с ножом. Стихия земли возбуждается, при человеческой жадности, скупости, накопительстве, когда недостойный человек ест хлеб, при осквернении могил. Это дает опухоли, потерю здоровья, жизни. Возбуждение огнем воды происходит, когда ножом мешать в воде, отрезать в воде концы роз.

Любое движение в жизни — магическое и действовать нужно осознанно. Пределы пробиваются, во-первых, нашей попыткой выйти за пределы своих возможностей, и, во-вторых, желанием запретного, незаслуженного. По поступку направляется поток.

Как работать с пробитыми пределами. Сначала по часовой стрелке убираем те источники, которые возмущают стихии, т.е. причину, откуда хлещет, а потом латаем дыры в тех пределах, куда уходит поток — рука “ткет” пространство. Когда пределы в норме, рука должна скользить, как по стене.

Вода возмущается , когда человеку открывается знание, до которого он не дорос. Существует правило : отвечать человеку только по вопросу, в меру, не нагружать неподготовленного человека тайными знаниями. Не плевать в воду, не бросать мусор. Внутренне отмечать увиденную грязь.

Огонь возмущается , когда бросаем, не затушив, спички, при магических действиях с огнем. Нельзя тушить спичку водой, нельзя задувать свечу, а надо притушить. Воздух поддувает огонь. В костре искать картошку надо не выдувая пепел, а палкой. “Посеешь ветер — пожнешь бурю”. Убить в ком-то талант — у нас проявится огнем.

Воздух возбуждается от неблагоприятных перемен, при махровом эгоизме, нереализованных возможностях.

22/08/2002 Матрицы ( практика).

Чем ткется карма – нашими внутренними побуждениями и мыслями. Значит, эмоции и мысли – главные элементы матрицы.

Первый уровень матрицы – ментальное поле на руке, 4-ый уровень тонких тел, ментальное тело. Минимум ее – чистота. Т.е. у человека должны быть чистые мысли.

Все, что над ладонью – это область духа: после ментального тела идет кармическое, выше находится будхиальное тело, потом нирваническое.

Эмоции – это наше третье тонкое тело. Оно находится под ладонью. Обычно вся нечистая сила идет из-под ладони. Это результат наших незакономерных эмоций – ненависти, обиды и т.п.

Область духа – это небо. Если человек соблюдает хотя бы 10 заповедей, он сам себя поднимает над обстоятельствами. И нечистых силовых образований в матрице не записывается. Надо стараться чаше быть в духе.

Рука – матрица, как экран, отображает план кармы, записанный на 5-ом уровне. Шипов называет этот план физическим вакуумом и утверждает, что там на нас вываливается все, что мы заложили. Стен Гроф называет это перинатальным уровнем бессознательного, пересекающимся с коллективным бессознательным. Восток говорит о Хрониках Акаши.

Называем матрицу. Входим в матрицу решением.

По грамотному вопросу ( а слова – это поток энергии) из 5-го плана в матрицу устремляются потоки энергии, которые покажут, что в ней есть.

Необходимо соблюдать порядок работы в матрицах. Матрицы расположены так, что вначале работаем с прошлым человека (род, круг врагов), потом работаем с настоящим (душа, карма, сознание), с тонкими планами, затем только приступаем к работе с физическим телом, самым грубым телом. Если что-то сильно нарушено на тонких планах, только тогда задействуется и физическое тело, начинается болезнь.

Заключительная матрица – матрица ситуации. Если мы хорошо и грамотно отработали все 8 матриц, то в матрице ситуации мало что должно остаться плохого. После отработки негатива в ней, делаем творческую работу – 3 раза по часовой стрелке, если матрица представлена сферой. Может быть и поток, направленный из центра ладони вверх.

Точка сборки. Древние тальтеки отмечали, что существует т.н. точка сборки под правой или левой( у левшей) лопаткой у человека. Это светящийся шарик, который словно выдвигается по вопросу из-за спины и начинает сканировать информацию, выхватывая необходимую и проявляя на ладони человека.

Предварительная работа в матрицах все-равно начинается с диагностики поля человека. Все, что есть в полях человека отражается в матрицах и с этим можно работать. После отработки последней матрицы опять смотрим поля – может вывалиться много грязи в поля. Поля могут быть опущены к ногам, вытянуты вперед. Бывают сильные потоки справа – это означает, что у человека украдена судьба. Тогда это можно увидеть в матрице. После отработки всех рабочих матриц можно смотреть конкретно, например, матрицу опухоли и т.п.

Чтобы справиться с силами астральными надо быть очень спокойными, отрешенными. Если вы волнуетесь и очень хотите помочь – не получится. Надо просто быть уверенным. Т.к. человек когда-то заложил какой-то негатив своим поступком, мыслью, вы можете это исправить тоже мыслью, по подобию. Надо помнить, что вы всего лишь ученики.

Примеры для практикования (смотреть до и после отработки).

1. Владислав 68 лет, его жена Инна 67 лет.

Если “пришла” фотография супругов, то смотрим сначала поля женщины, потом мужчины. У женщины все поля впереди, у мужчины – античакра перед ногами. Античакру закрываем, рука ткет пространство.

Смотрим матрицу отношений. Между двумя полями – трещина, порча. Астральное кольцо расщелкиваем, поля поднимаются. Но у женщины шар на уровне живота не уходит, тогда смотрим по-порядку ее матрицы.

Нечистая сила рода.  Червячок в образе. Силы в матрицах никогда не уничтожются – надо представить белую птицу, которая проглотит его.

Круг врагов. Мертвые поля – ощущения холода. Дно открыто, оттуда – мертвые поля. Дно залатать, загладить. Закрыли откачку энергии. Холод – пропускаем через локоток, медленно опуская руку. Прощелкиваем остатки.

Матрица души. Душа – как в сетях. Сетку снимаем, сжимаем в комочек, вниз проталкиваем, прощелкиваем.

Карма – лежит большое кольцо – большая женская сила. Расщелкиваем. Проговариваем об отношениях этих двух людей – поля поднимаются.

2. Руслан, 43 года, хочет бросить курить.

В поле слева и сзади рука не поднимается

Нечистая сила рода. Эмоционально очень задействован – астральное кольцо на дне. Расщелкиваем, дно латаем. Появляется мыльный пузырь. Ужимаем.

Круг врагов. На матрице временная структура.

Матрица души. Шар высокий, большой. Пределы прогибаются шалашиком. Человек творческий, но самоистязается.

Матрица кармы. Остатки облаков или пыли, прощелкиваем. Пошел столб – карма духовного роста — из самого центра ладони.

Сознание. В порядке. Свободная дурь. Достать нельзя – берем матрицу источников силы. Против часовой стрелки уминаем, возвращаемся в матрицу, очищаем по углам.

Нечистая плоть. Пробита стихия воды, устремляется в землю. Огонь открыт в эго. Рука ткет по часовой стрелке. Матрица полная воды. Воду выливаем – выдернуть пробку.

Черная вода. Разрываем кольцо на астрале.

Матрица ситуации. В порядке.

Поле очень мягкое. Астральную шубку расчищаем пальцами, как расческой. Грязь вниз, прощелкиваем.

Можно посмотреть матрицу курения. До работы она была вся полная.

 

www.pupok.eu

Факультативный курс “Матрицы и определители”

Разделы: Математика

---

Предлагаемый курс преследует цель познакомить учащихся с матричной символикой и основными понятиями алгебры матриц, а также научить их уверенно оперировать с матрицами и определителями как объектами более общего характера по сравнению с числами и функциями. Курс расширяет представления о возможностях математики и легко усваивается данной возрастной группой.

Изучение данного курса способствует формированию абстрактных представлений, развитию логического мышления, осуществлению межпредметных связей.

Курс характеризуется рациональным сочетанием логики и наглядности, увеличивается теоретическая значимость изучаемого материала, учащиеся овладевают приёмами аналитической деятельности при решении задач.

Организация учебно-воспитательного процесса

Изучения курса “Матрицы и определители” в 8-ых классах общеобразовательных учреждений рекомендуется проводить во внеурочное время, 1 раз в неделю в течение учебного года.

Учителю предоставляется право самостоятельно выбирать методические пути и приёмы преподавания данного курса.

При планировании учебных занятий следует ориентироваться не только на теоретическую подготовку учащихся, но и на организацию решения практических задач с учётом дифференциации группы и индивидуальных особенностей детей.

Следует способствовать удовлетворению потребностей школьников, проявляющих склонности и интерес к математики.

Учителю необходимо реализовать сбалансированное сочетание традиционных и новых методов обучения, применять иллюстративные и эвристические методы, рационально сочетать устные и письменные виды работы.

Структура программы

Программа курса “Матрицы и определители” состоит из трёх разделов: “Содержание программы”, “Содержание знаний и умений”, “Список литературы”, “Основные понятия курса”.

Содержание программы

Раздел 1. Основные понятия (4 часа)

1. Введение в предмет
2. Типы и формы матриц
3. Матричная символика

Раздел 2. Операции с матрицами (8 часов)

1. Транспонирование матриц
2. Сложение матриц
3. Умножение матрицы на скаляр
4. Умножение матрицы на матрицу

Раздел 3. Определители (10 часов)

1. Понятие определителя
2. Свойства определителей
3. Миноры и алгебраические дополнения
4. Разложение определителя по Лапласу

Раздел 4. Вычисление определителей (12 часов)

1. Метод элементарных преобразований
2. Метод единственного деления
3. Метод опорного элемента

Содержание знаний и умений

В результате изучения курса “Матрицы и определители” учащиеся узнают:

• Основные формы и типы матриц.
• Матричную символику.
• Особенности матричных операций.
• Свойства определителей.
• Понятия миноров и алгебраических дополнений.
• Основные методы вычисления определителей.

Умеют:

• Складывать, перемножать, транспонировать и обращать матрицы с вещественными элементами.
• Разлагать определители.
• Вычислять определители и применять их к решению задач.

Основные понятия курса

Произвольная система чисел из некоторого множества, расположенная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей.

Две матрицы называются равными, если число строк и столбцов у них соответственно равны.

Если число строк матрицы равно числу её столбцов, то такая матрица называется квадратной, а это число порядком матрицы.

В = - матрица третьего порядка

Пусть даны матрицы

А = и В =

Произведением А на число с называется матрица

С =

Пример

Суммой матриц А и В называется матрица:

С = А + В =

Пример

А = В = А + В =

Для матриц выполняются все свойства действий с рациональными числами.

Произведением матрицы А на матрицу В называется матрица

С = , где

Пример:

Квадратная матрица, все диагональные элементы которой равны 1, а остальные 0 называется единичной.

Е = .

Матрицы, имеющие вид называют диагональными.

Матрица, которая получается из данной матрицы заменой строк столбцами, называется транспонированной по отношению к данной.

Определителем n порядка матрицы А называется алгебраическая сумма n! Слагаемых, каждое из которых представляет собой произведение n множителей, взятых по одному и только по одному из каждой строки и каждого столбца матрицы А.

А = определитель.

Некоторые способы вычислений определителей:

1) Определитель 2-ого порядка

Пример:

2) Определитель 3-его порядка

Данный способ называется правило элементарных преобразований или правило Саррюса. Оно действует и для определителей более высоких порядков, но является очень громоздким.

Пример:

3) Определители n-ого порядка.

Минором элемента определителя называется определитель, который получается из данного вычёркиванием строки и столбца, проходящих через данный элемент.

Алгебраическим дополнением элемента определителя n-ого порядка называется минор этого элемента, взятый со знаком .

Пример. Пусть .

Найдём

Правило 1. Если в определите n-ого порядка все элементы I-ой строки (j-ого столбца), кроме равны нулю, то такой определитель равен произведению элемента на его алгебраическое дополнение.

Пример.

Вычислить определитель

Преобразуем определитель так, чтобы все элементы четвёртого столбца, кроме первого равнялись нулю. Для этого умножим все элементы первой строчки на –1 и сложим со второй и третьей, затем умножим первую строчку на – 3 и сложим с четвёртой. В результате получим

.

Затем, применяя правило, получим:

.

Прибавляя к третьей строчки вторую, получим

Правило 2. Определитель n-ого порядка равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения.

Разложение определителя

Пример. Вычислить

Вычислим определитель, разложив его сначала по элементам третьей строки, затем по элементам второго столбца.

Литература

1. Энциклопедия “Аванта +”, “Математика”, 2003 год.
2. Блох Э. Л. “Основы линейной алгебры” – М., 1979.
3. Хедли Л. “Линейная алгебра” – М., 1992.

xn--i1abbnckbmcl9fb.xn--p1ai

I курс, I семестр Линейная алгебра

1.Матрицы. Виды матриц.

2.Действия над матрицами.

3.Определители.

4.Миноры. Алгебраические дополнения.

5.Обратная матрица.

6.Система линейных уравнений.

7.Метод Крамера.

8.Матричный метод.

9.Метод Гаусса.

Теоретический курс

1.Матрицы. Виды матриц.

Прямоугольная таблица, составленная из действительных чисел, следующего вида

называется матрицей размера m x n, где m – количество строк, n – количество столбцов.

Если m=n, то матрица называется квадратной.

Матрица вида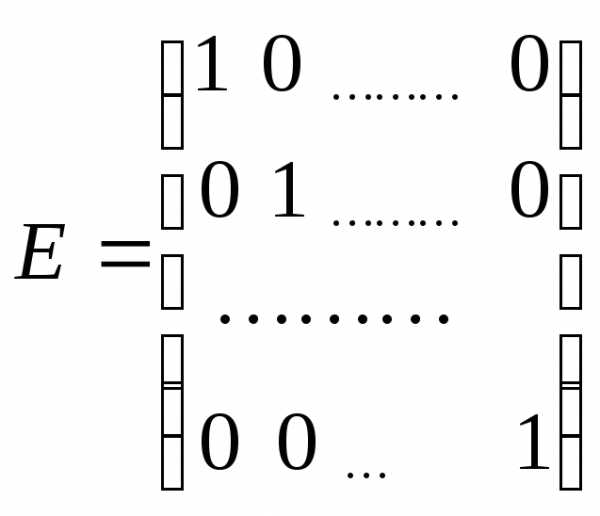

называется единичной.

Матрица, составленная из одного столбца, называется – столбцом. Матрица, составленная из одной строки, называется матрицей- строкой.

Пусть дана матрица

_,

_{тогда матрица вида}

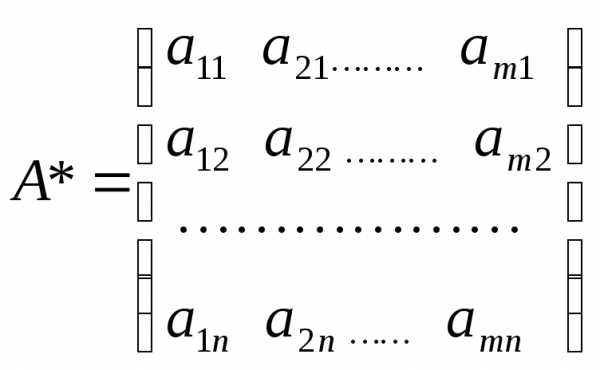
_{называется транпонированной.}

2.Действия над матрицами.

2.1.Сложение. Вычитание.

Суммой матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов данных матриц.

Разностью матриц одинакового размера называется матрица того же размера, каждый элемент которой равен разности соответствующих элементов данных матриц.

2.2.Умножение матриц.

Произведением матрицы на некоторое число называется матрица, полученная из данной умножением всех ее элементов на это число.

Произведением двух матриц – матрицы А размера m x n и матрицы В размера n x k – называется матрица С размера m x k , каждый элемент которой равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-го столбца матрицы В.

3.Определители.

Определителем квадратной матрицы А второго порядка называется число

Определителем квадратной матрицы А третьего порядка называется число

4.Миноры. Алгебраические дополнения.

Минором М_{i j} , соответствующим элементу а_{i j} определителя называется определитель меньшего порядка, полученный из данного вычеркиванием строки и столбца, содержащего элемент а_{i j} .

Алгебраическим дополнением А_{i j} , соответствующим элементу а_{i j} определителя называется минор М_{i j} , умноженный на (- 1)^i+j, т.е.

А_{i j} = (- 1)^i+j М_{i j}

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной в противном случае.

5.Обратная матрица.

Матрица A^-1 называется обратной для квадратной матрицы А,если выполняется равенство:

А^-1× А = А× А^-1=Е

Квадратная матрица имеет обратную тогда и только тогда, когда она невырожденная, т.е. когда

6.Система линейных уравнений.

Линейной системой m уравнений с n неизвестными х₁, х₂,… х_n называется система вида :

Действительные числа а_{i j} называются коэффициентами системы; b_i называются свободными членами системы. Упорядоченный набор чисел c₁, c₂,… c_n называется решением системы, если, будучи подставленным в каждое из уравнений, он обращает их в верные равенства.

Система линейных алгебраических уравнений называется совместной, если она имеет решения, в противном случае она называется несовместной.

Совместная система называется определенной, если она имеет единственное решение, в противном случае она называется неопределенной.

studfiles.net