2.4. Третий закон ньютона
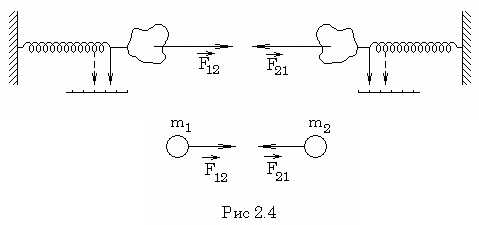
Механическое действие тел друг на друга всегда является их взаимодействием. Если тело 1 действует на тело 2, то при этом обязательно тело 2 действует на тело 1. Так, например, на ведущие колеса электровоза (рис.2.3) действуют со стороны рельсов силы трения покоя, направленные в сторону движения электровоза. Сумма этих сил и есть сила тяги электровоза. В свою очередь, ведущие колеса действуют на рельсы силами трения покоя, направленными в противоположную сторону.
 Количественное
описание механического взаимодействия
было дано Ньютоном в его третьем законе
динамики. Для материальных точек этот
закон формулируется так:
Количественное
описание механического взаимодействия
было дано Ньютоном в его третьем законе
динамики. Для материальных точек этот
закон формулируется так:
Две материальные
точки действуют друг на друга с силами,
равными по величине и направленными
противоположно по прямой, соединяющей
эти точки (рис.2.4): 
Перейдем теперь
от динамики отдельной материальной
точки к динамике механической системы,
состоящей из  материальных точек. Для
материальных точек. Для  -той
материальной точки системы, согласно
второму закону Ньютона (2.5), имеем:
-той
материальной точки системы, согласно
второму закону Ньютона (2.5), имеем:
 .
(2.6)
.
(2.6)
Здесь 
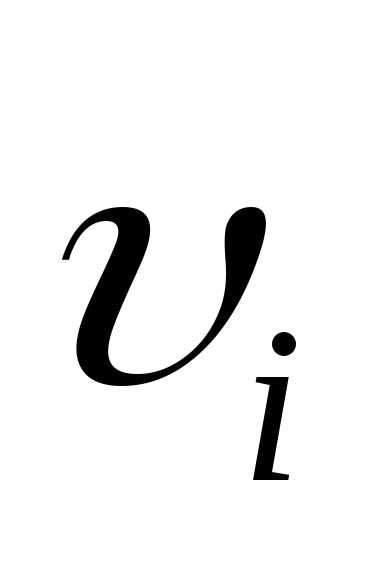 –
масса и скорость
–
масса и скорость -той
материальной точки,
-той
материальной точки, 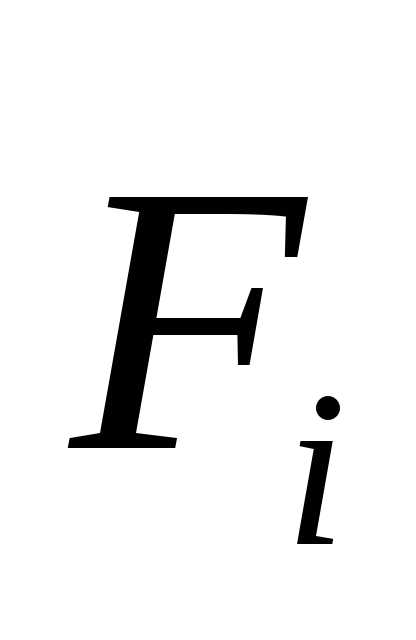 – сумма всех действующих на нее сил.
– сумма всех действующих на нее сил. Силы, действующие
на механическую систему, делятся на
внешние и внутренние. Внешние силы
действуют на точки механической системы
со стороны других, внешних тел. Внутренние
силы действуют между точками самой
системы. Тогда силу  в выражении (2.6) можно представить в виде
суммы внешних и внутренних сил:
в выражении (2.6) можно представить в виде
суммы внешних и внутренних сил:

где 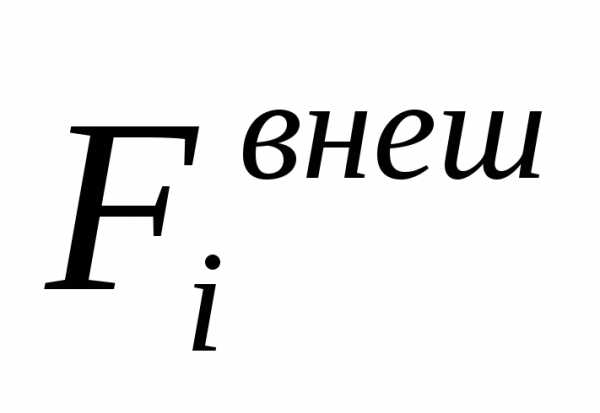 –
результирующая всех внешних сил,
действующих на
–
результирующая всех внешних сил,
действующих на  -тую
точку системы;
-тую
точку системы; 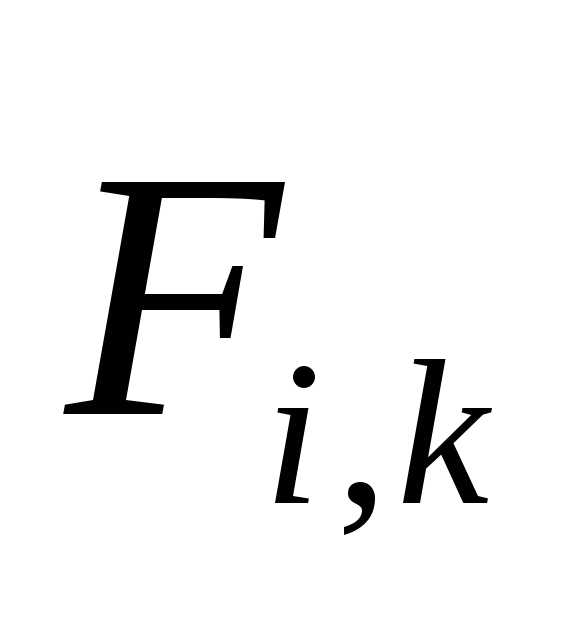 -внутренняя
сила, действующая на эту точку со стороны
-внутренняя
сила, действующая на эту точку со стороны 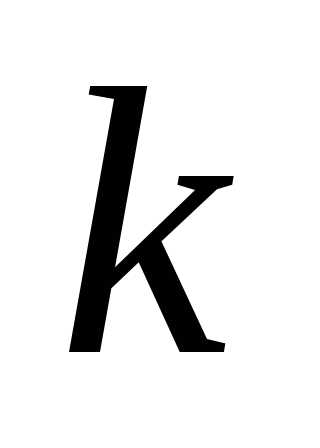 -й.
Подставим выражение (2.7) в (2.6):
-й.
Подставим выражение (2.7) в (2.6):
, (2.8)
просуммировав
левые и правые части уравнений (2.8),
записанных для всех 
. (2.9)
По третьему
закону Ньютона силы взаимодействия  -той
и
-той
и 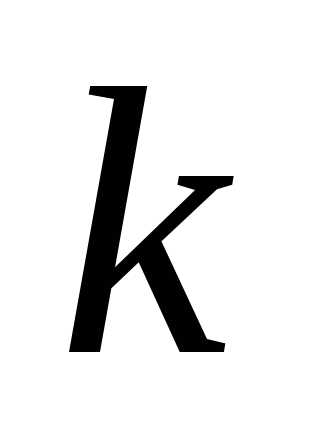 -й точек системы равны по модулю и
противоположны по направлению
-й точек системы равны по модулю и
противоположны по направлению 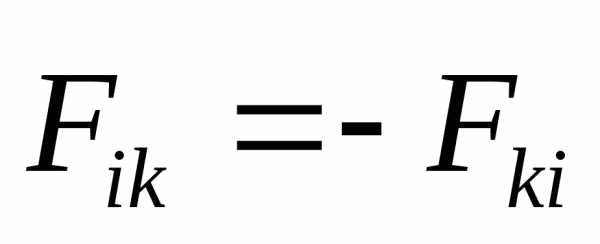 .
.
Поэтому сумма всех внутренних сил в уравнении (2.9) равна нулю:
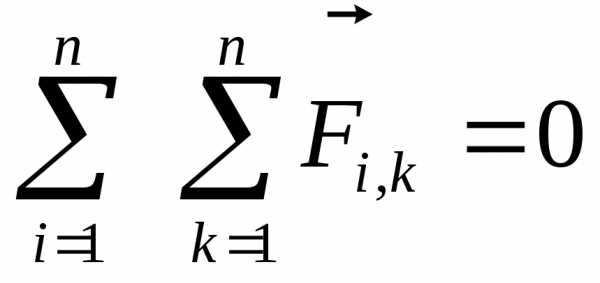 .
(2.10)
.
(2.10)
Векторная сумма всех внешних сил, действующих на систему,
называется главным вектором внешних сил
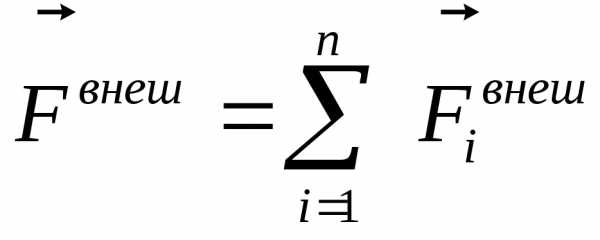 .
(2.11)
.
(2.11)
Поменяв в
выражении (2.9) местами операции суммирования
и дифференцирования и учитывая результаты
(2.10) и (2.11), а также определение импульса
механической системы (2.3), получаем  .
Это основное уравнение динамики
поступательного движения твердого
тела.
.
Это основное уравнение динамики
поступательного движения твердого
тела.
2.5.Центр масс и закон его движения
Центром масс
(инерции) механической системы называется
точке  ,
радиус-вектор которой равен отношению
суммы произведений масс всех материальных
точек системы на их радиус-векторы к
массе всей системы:
,
радиус-вектор которой равен отношению
суммы произведений масс всех материальных
точек системы на их радиус-векторы к
массе всей системы:
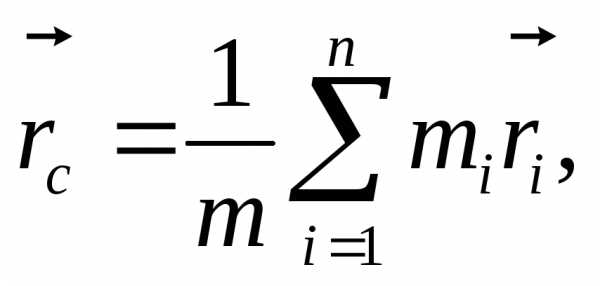 (2.12)
(2.12)
где  и
и  –
масса и радиус-вектор
–
масса и радиус-вектор -той
материальной точки,
-той
материальной точки, 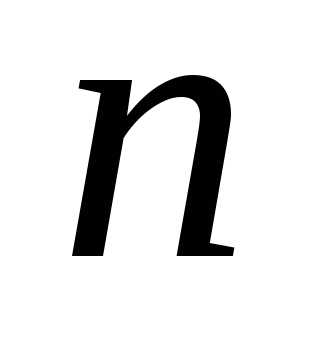 -общее
число этих точек,
– суммарная масса системы. Если радиус-
векторы проведены из центра масс
-общее
число этих точек,
– суммарная масса системы. Если радиус-
векторы проведены из центра масс ,
то
,
то .
.
Таким образом, центр масс – это геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиус-векторы, проведенные из этой точки, равна нулю.
Продифференцировав формулу (2.12) по времени, получаем выражение для скорости центра масс:
Тогда импульс
системы равен произведению ее массы на
скорость центра масс: 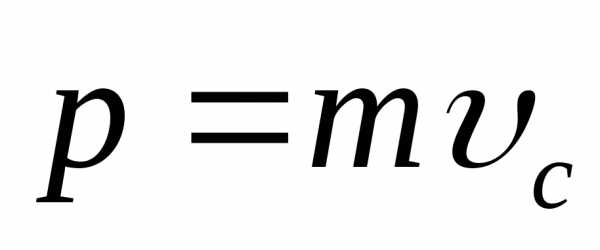 .
Подставив это выражение в основное
уравнение динамики поступательного
движения твердого тела, имеем:
.
Подставив это выражение в основное
уравнение динамики поступательного
движения твердого тела, имеем:
 (2.13)
(2.13)
– центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору приложенных к системе внешних сил.
Уравнение (2.13) показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей, но не могут повлиять на суммарный импульс системы и скорость ее центра масс.
ДЕМОНСТРАЦИЯ 1
Если механическая
система замкнутая, то 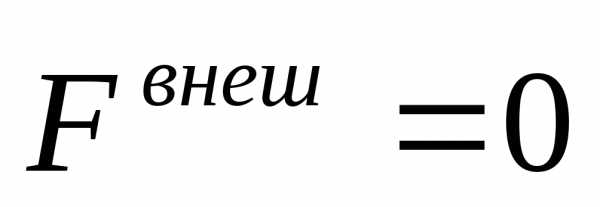 и скорость центра масс не изменяется с
течением времени. Таким образом, центр
масс замкнутой системы либо покоится,
либо движется с постоянной скоростью
относительно инерциальной системы
отсчета. Это означает, что с центром
масс можно связать систему отсчета, и
эта система будет инерциальной.
и скорость центра масс не изменяется с
течением времени. Таким образом, центр
масс замкнутой системы либо покоится,
либо движется с постоянной скоростью
относительно инерциальной системы
отсчета. Это означает, что с центром
масс можно связать систему отсчета, и
эта система будет инерциальной.
studfiles.net
§ 2.3. Третий закон Ньютона
Воздействие тел, друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой F12 , то тело 1 действует на тело 2 с силой F21. Третий закон Ньютона утверждает, что
F12 = F21. (2.6)
Таким образом, силы всегда возникают попарно. Подчеркиваем, что силы, фигурирующие в сотношении (2.6) приложены к разным телам; поэтому они не могут уравновесить друг друга.
Третий закон Ньютона, как и первый два, справедлив лишь в инерциальных системах отсчета. В неинерциальных системах отсчета этот закон оказывается несправедливым.
§ 2.4. Силы
Чтобы свести нахождение закона движения частицы к чисто математической задаче, необходимо прежде всего – в соответствии с уравнением (2.2) – знать действующую на частицу силу, т.е. зависимость силы от определяющих ее величин. Каждая такая зависимость получена в конечном счете на основании обработки результатов опыта и, по существу, всегда опирается на уравнение (2.2), как на определение силы.
Наиболее фундаментальные силы, лежащие в основе всех механических явлений, – это силы гравитационные и электрические. Приведем выражения для этих сил в самом простом виде, когда взаимодействующие массы (заряды) покоятся или движутся с малой (нерелятивистской) скоростью.
Сила гравитационного притяжения, действующая между двумя материальными точками. В соответствии с
 , (2.7)
, (2.7)
где G – гравитационная постоянная.
Фигурирующие в этом законе массы называют гравитационными в отличие от инертной массы, входящей во второй закон Ньютона. Из опыта, однако, установлено, что гравитационная и инертная массы любого тела строго пропорциональны друг другу. Поэтому можно считать их равными (т.е. выбрать один и тот же эталон для измерения обеих масс) и говорить просто о
Кулоновская сила, действующая между двумя точечными зарядами q1 и q2
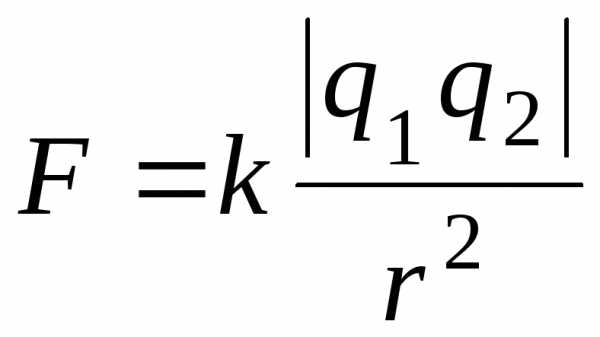 , (2.8)
, (2.8)
где r –расстояние между зарядами,
k – коэффициент
пропорциональности, зависящий от выбора
системы единиц.
В системе
СИ 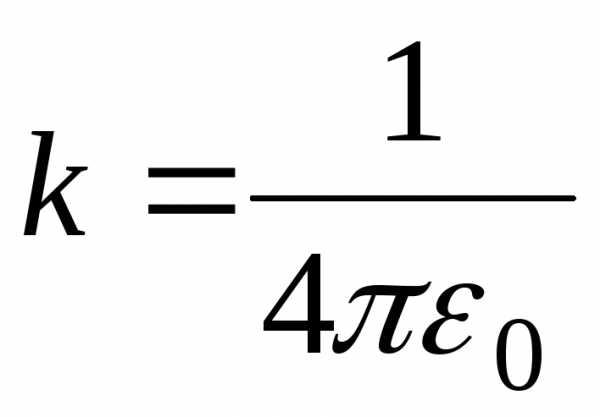 ,
где0 — электрическая
постоянная.
,
где0 — электрическая
постоянная.
В отличие от гравитационной силы кулоновская сила может быть как силой притяжения, так и силой отталкивания.
Заметим, что закон Кулона (2.8) перестает выполняться точно, если заряды движутся. Электрическое взаимодействие движущихся зарядов оказывается сложным образом зависящим от их движения. Одну из частей этого взаимодействия, обусловленную движением, называют магнитной силой (отсюда и другое название данного взаимодействия – электромагнитное). При малых (нерелятивистских) скоростях магнитная сила составляет пренебрежимо малую часть электрического взаимодействия и оно с высокой степенью точности описывается законом (2.8).
Несмотря на то, что гравитационные и электрические взаимодействия лежат в основе всего бесчисленного разнообразия механических явлений, анализ явлений, особенно макроскопических оказался бы весьма сложным, если бы во всех случаях мы исходили из этих фундаментальных взаимодействий. Поэтому удобно ввести другие, приближенные, силы (которые в принципе могут быть получены из фундаментальных сил). Это необходимо для того, чтобы упростить математически задачу настолько, чтобы ее можно было практически решить. С этой целью вводят, например, следующие силы.
studfiles.net
2.3. Второй закон ньютона
Второй закон Ньютона гласит: в инерциальных системах отсчёта произведение массы тела на его ускорение равно векторной сумме сил,действующих на тело. В аналитической форме закон записывается следующим образом:
ma=F.
Не следует воспринимать эту формулировку как определение силы. Смысл её совершенно иной. Второй закон Ньютона утверждает, что в инерциальных системах отсчёта сила, действующая на тело, всегда равна произведению массы этого тела на ускорение, вызванное силой.
С другой стороны, используя эталонную массу, можно ввести единицу измерения силы именно на основе второго закона Ньютона.
Если известны силы, действующие на тело
массой m, можно
рассчитать все кинематические
характеристики движения этого тела.
Действительно, проинтегрировав по
времени выражение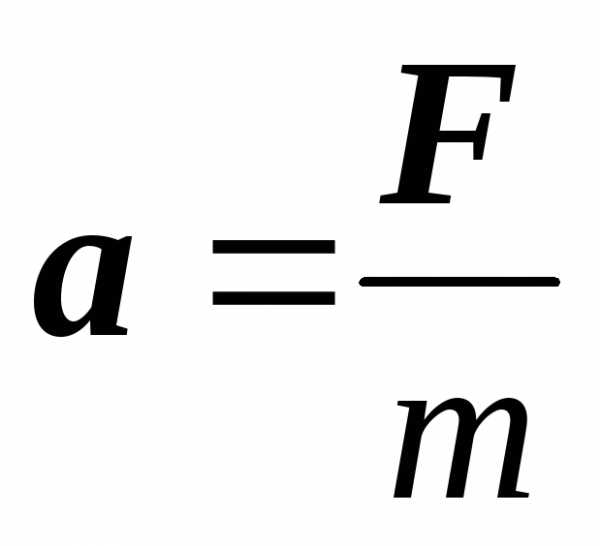 ,
можно получить зависимость скорости
от времени, а проинтегрировав уравнение
зависимости скорости от времени –
выражение, описывающее зависимость
координаты от времени.
,
можно получить зависимость скорости
от времени, а проинтегрировав уравнение
зависимости скорости от времени –
выражение, описывающее зависимость
координаты от времени.
Например, пусть ускорение тела постоянно a=constи направлено вдоль осих; в начальный
момент тело покоится в точке с координатойх=0. По определению ускорение .
Отсюдаdv=adtи
.
Отсюдаdv=adtи .
Взяв интеграл, получаем уравнение
зависимостискорости тела от
времениv=at.
.
Взяв интеграл, получаем уравнение
зависимостискорости тела от
времениv=at.
По определению скорость 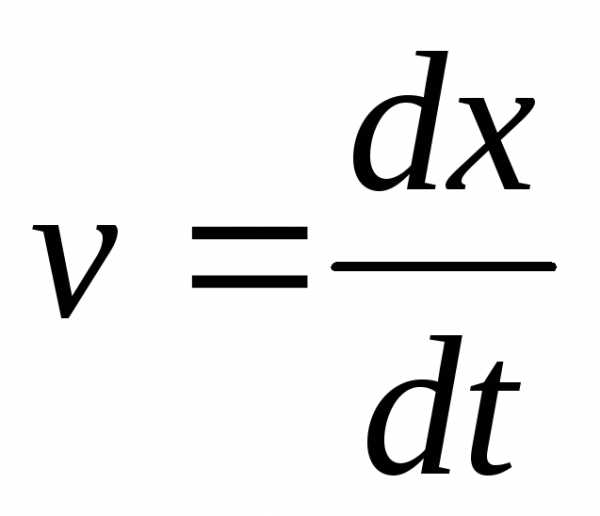 .
Тогдаdx=vdt=atdtи
.
Тогдаdx=vdt=atdtи 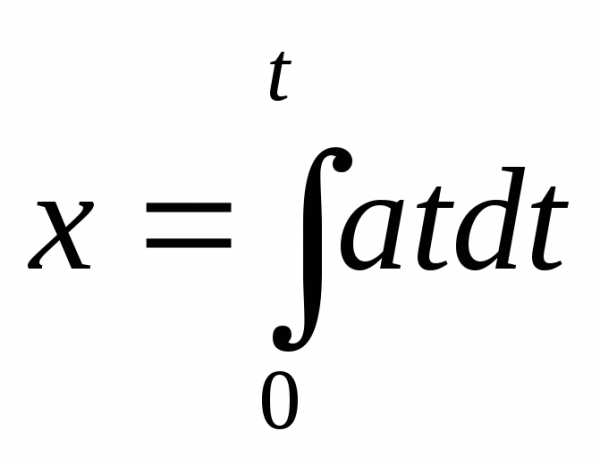 ..
Взяв интеграл, получим уравнение,
..
Взяв интеграл, получим уравнение,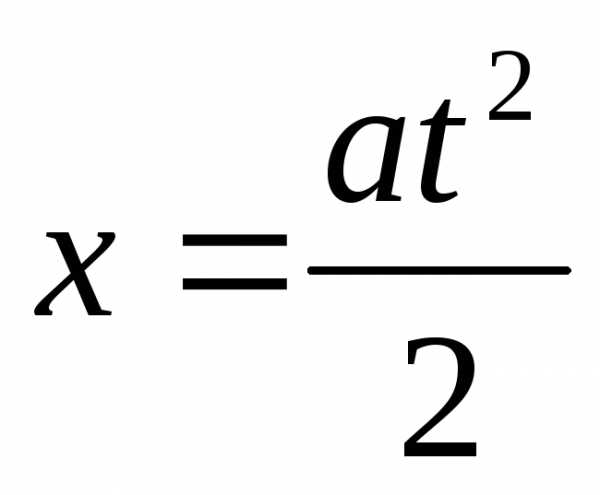 ,
описывающее зависимость координаты
тела от времени.
,
описывающее зависимость координаты
тела от времени.
Таким образом, зная силы, действующие на тело, можно предсказать, как будет двигаться тело под действием этих сил, в какой момент времени тело окажется в нужной точке пространства (кроме сил необходимо также знать начальное положение тела и его начальную скорость).
Второй закон Ньютона можно сформулировать и иначе: скорость изменения импульса тела равна сумме действующих на тело сил:
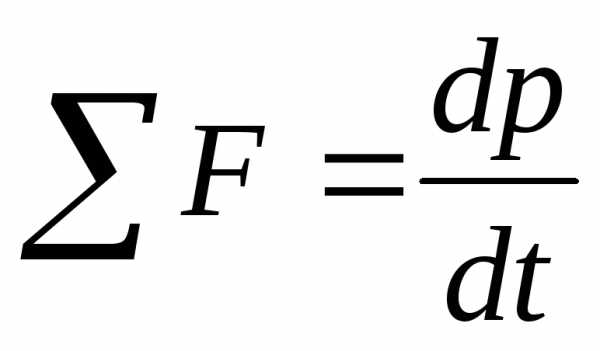 .
.
Эта формулировка не отвергает рассмотренную ранее. Обе формулировки отображают одну и ту же закономерность, они взаимосвязаны, что видно изследующего:
.
Второй закон Ньютона часто называют основным законом динамикипоступательного движения. Именно на основе второго закона решается основная задача динамики – описание движения тел под действием сил, приложенных к телу.
2.4 Третий закон Ньютона
Первый и второй законы Ньютона рассматривают движение тел. Третий закон рассматривает взаимодействие двух тел. Он гласит:силы, с которыми действуют друг на друга два взаимодействующих тела, всегда равны другдругу по величине и направлены в противоположные стороны
F12=-F21
Обратите внимание: силыF12 иF21 приложены к разным телам. Это означает, что эти силы не компенсируют друг друга.
Третий закон справедлив для сил любой природы. Все виды фундаментальных взаимодействий порождают равные по величине и противоположные по направлению силы одной природы.
2.5. Принцип относительности галилея
Как было показано в разд. 2.1, любая система отсчёта, движущаяся равномерно и прямолинейно относительно инерциальной системы отсчёта, является инерциальной.
В разделе 1.6 рассматривалось, что если системы отсчёта движутся друг относительно друга равномерно и прямолинейно, то ускорение тела, измеренное в каждой из систем отсчёта, будет одинаковым.
Это означает, что ускорение какого-либо тела, измеренное в разных инерциальных системах отсчёта, будет одинаковым.
Из второго закона Ньютона следует, что
ускорение тела массой т зависит
от величины силы, приложенной к телу: .
Тогда во всех инерциальных системах
отсчёта на рассматриваемое телодействует одна и та же сила.
.
Тогда во всех инерциальных системах
отсчёта на рассматриваемое телодействует одна и та же сила.
Следовательно, динамические уравнения, составленные в разных системах отсчёта для одного и того же тела, во всех инерциальных системах отсчёта имеют абсолютно одинаковый вид. По виду такого уравнения совершенно невозможно определить, в какой именно инерциальной системе отсчёта производились измерения.
Следовательно, в инерциальных системах отсчёта все механические процессы протекают одинаково; все инерциальные системы по своим свойствам эквивалентны, абсолютной инерциальной системы отсчёта не существует. Эту формулировку и принято называтьпринципом относительности Галилея.
studfiles.net
2.3. Второй и третий законы Ньютона
Сила и ускорение являются векторами. Выражение (2.1) можно переписать в векторном виде
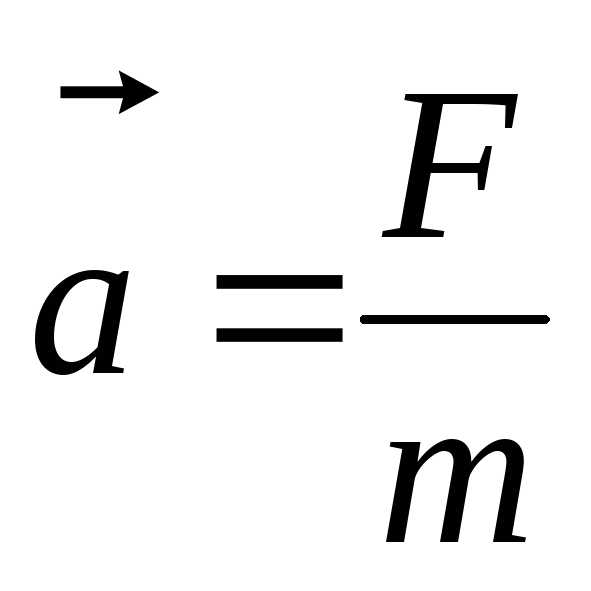 .
(2.2)
.
(2.2)
Это соотношение носит название второго закона Ньютона: в инерциальных системах отсчета ускорение, приобретаемое телом, пропорционально силе, действующей на него, обратно пропорционально массе тела и направлено в сторону действия силы.
Если
на тело действует несколько сил, то в
формуле (2.2) под  надо понимать равнодействующую этих
сил, т.е.
надо понимать равнодействующую этих
сил, т.е.
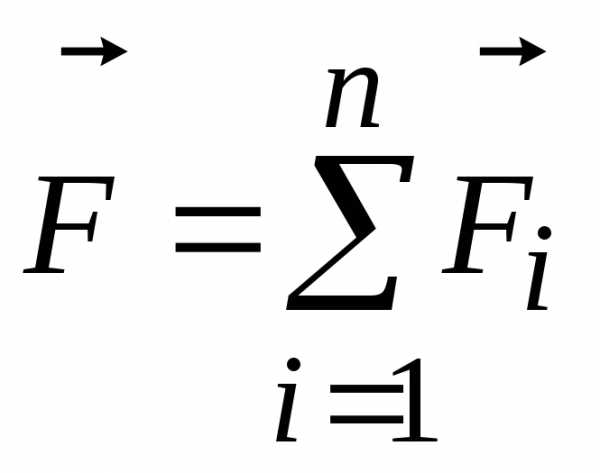 ,
,
где 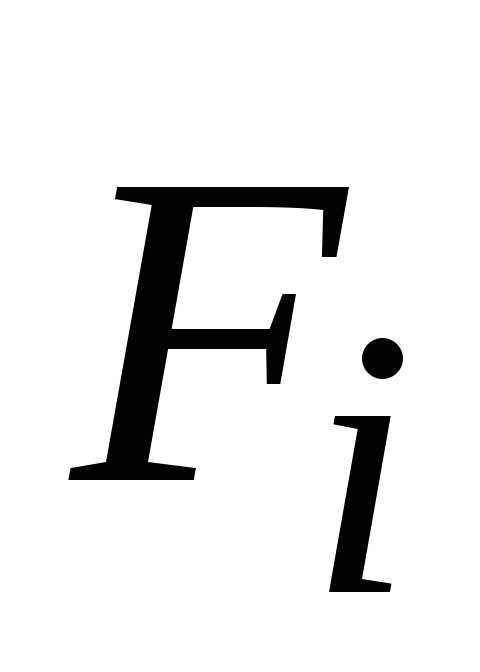
отдельные силы, приложенные к телу.
отдельные силы, приложенные к телу.
Можно
дать иную формулировку второго закона
Ньютона. Из уравнения (2.2), с учетом 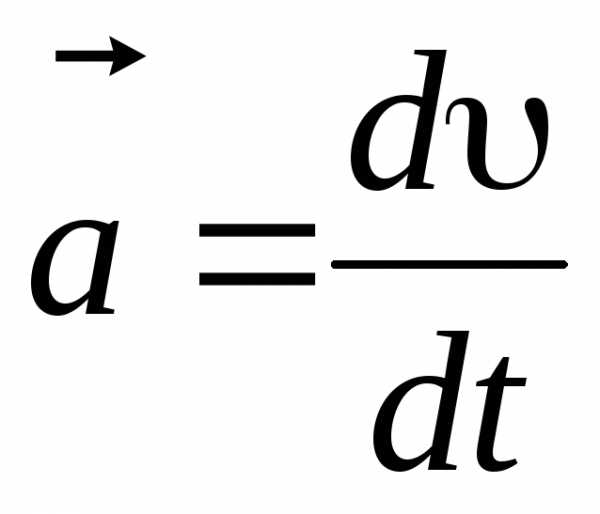 находим
находим
, (2.3)
То есть, равнодействующая сил, действующих на тело, равна производной импульса тела по времени или скорости изменения импульса. Это выражение является более общей формулировкой второго закона Ньютона, поскольку оно применимо и при движении тел со скоростями, сравнимыми со скоростью света.
Единица силы в СИ: 1 Н = 1 кг м/с2 – сила, которая массе в 1 кг сообщает ускорение 1 м/с2.
Принцип независимости действия сил
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.
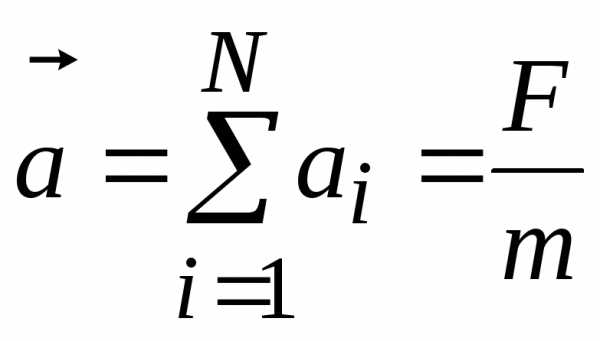 ,
(2.4)
,
(2.4)
где 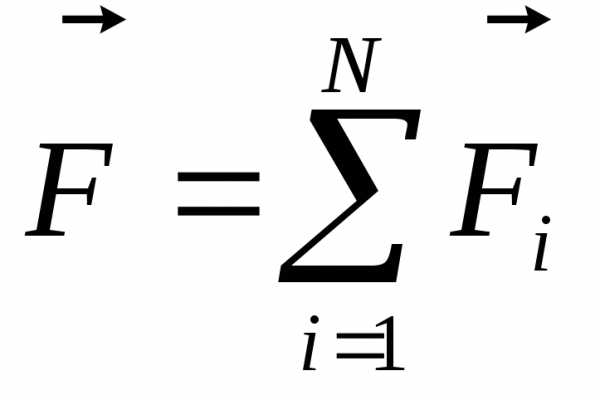
результирующая сила.
результирующая сила.
Сила  может быть разложена на две составляющие
– тангенциальную (
может быть разложена на две составляющие
– тангенциальную (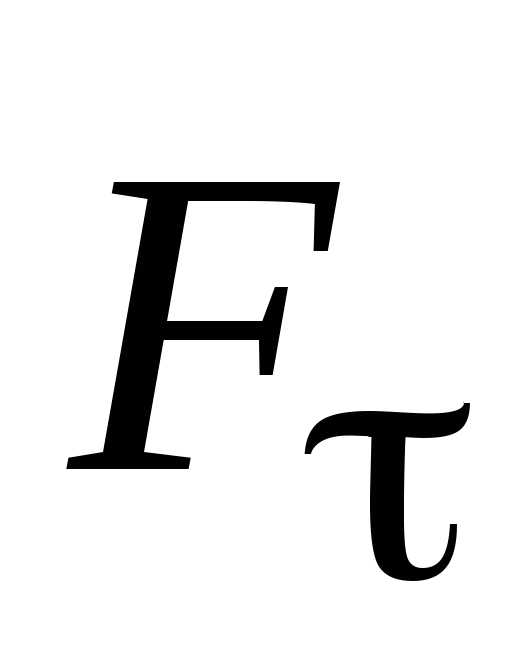 )
и нормальную (
)
и нормальную (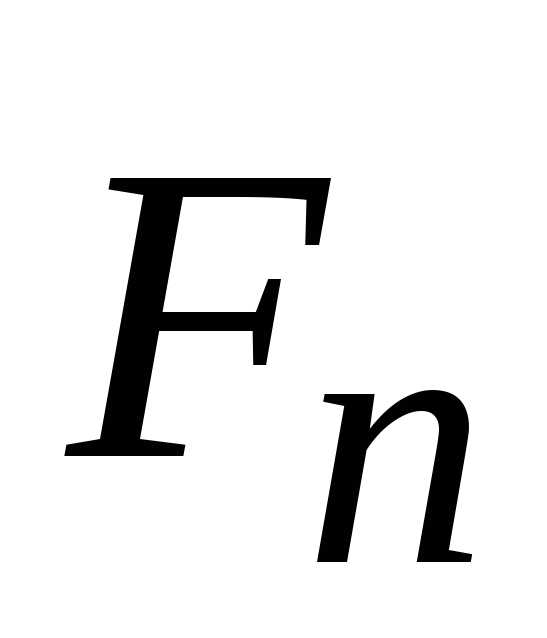 )
:
)
:
;  ;.
(2.5)
;.
(2.5)
Рис.2.1
Вектор 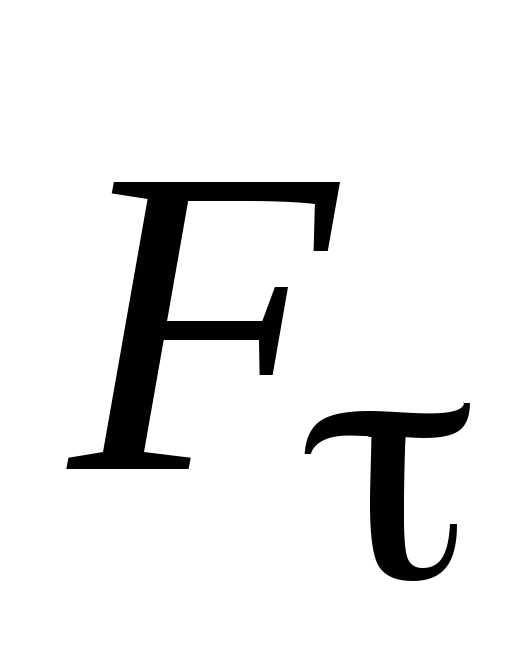
направлен по касательной к траектории;
вектор
направлен по касательной к траектории;
вектор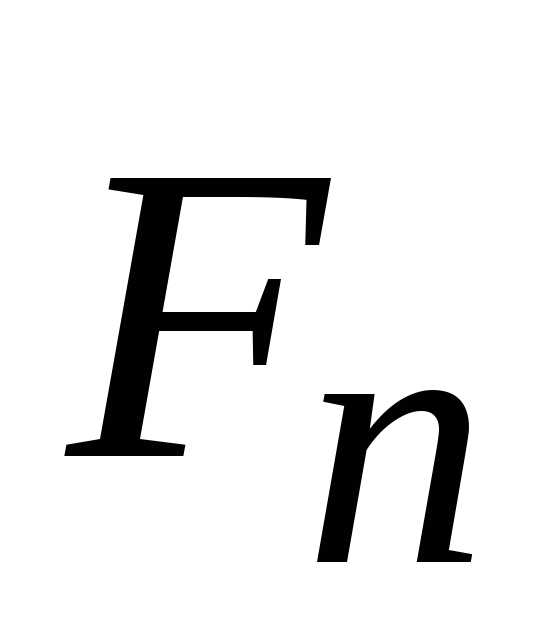
направлен по нормали к центру кривизны
траектории (рис.2.1).
направлен по нормали к центру кривизны
траектории (рис.2.1).
Третий закон Ньютона определяет взаимодействие между телами (материальными точками): в инерциальных системах отсчета силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению
 ,
(2.6)
,
(2.6)
где 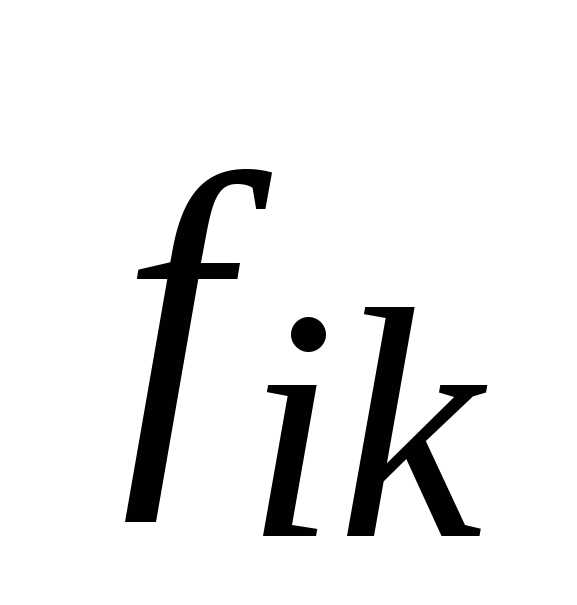 и
и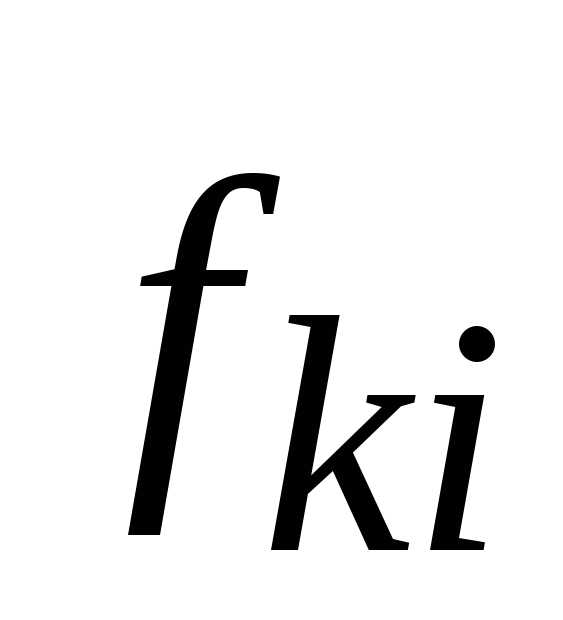
силы, действующие на i-е
тело со стороны k-го
тела и на k-ое
со стороны i-го,
соответственно.
силы, действующие на i-е
тело со стороны k-го
тела и на k-ое
со стороны i-го,
соответственно.
Эти силы приложены к разным телам и всегда возникают попарно, действуют вдоль прямой, соединяющей эти тела.
2.4. Второй закон Ньютона для механической системы. Закон сохранения импульса
Совокупность тел, взаимодействующих между собой и рассматриваемых как единое целое, называется механической системой. Силы, действующие в механической системе, подразделяются на две группы: внутренние и внешние.
1. Внутренние силы – это силы взаимодействия между телами, входящими в систему. Согласно третьему закону Ньютона эти силы попарно равны по модулю и противоположны по направлению, поэтому их векторная сумма равна нулю.
2. Внешние силы – это силы, действующие на тела системы со стороны тел, не принадлежащих ей.
Если на механическую систему не действуют внешние силы или их равнодействующая равна нулю, то такую систему называют замкнутой или изолированной.
Рассмотрим
механическую систему, состоящую только
из двух тел. Обозначим импульсы этих
тел как  и
и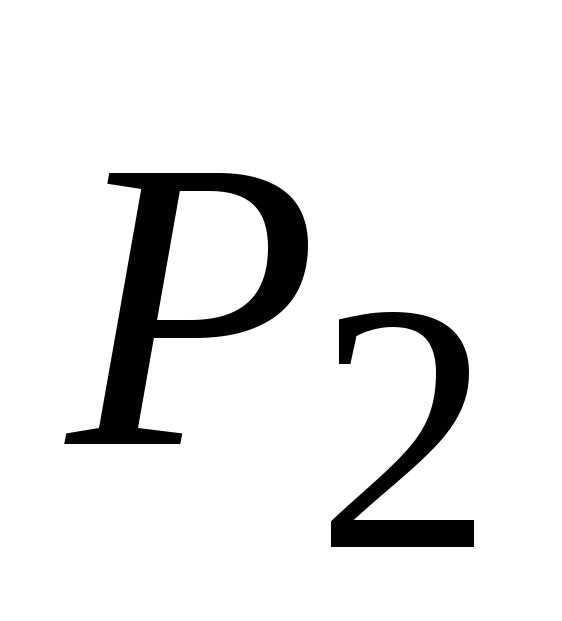 .
Каждое тело данной системы движется
под действием внутренних и внешних сил,
поэтому на основании второго закона
Ньютона для каждого тела можно записать
.
Каждое тело данной системы движется
под действием внутренних и внешних сил,
поэтому на основании второго закона
Ньютона для каждого тела можно записать
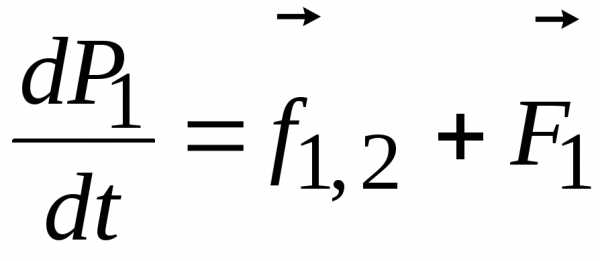 ,
, 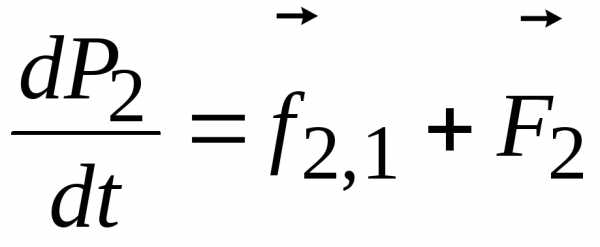 ,
,
где 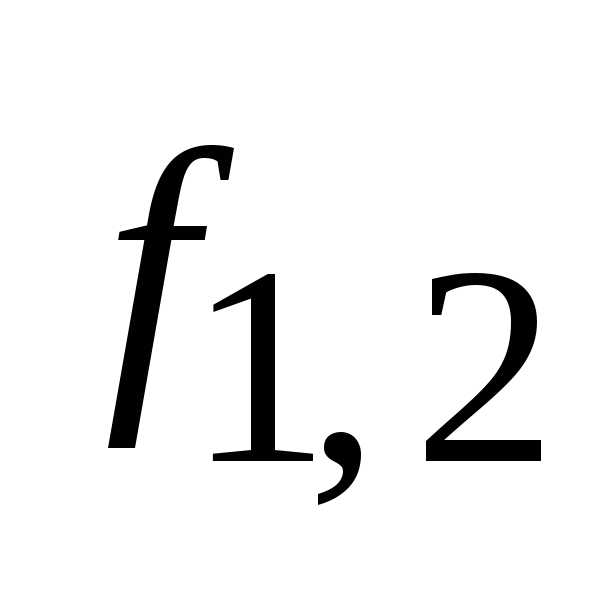 и
и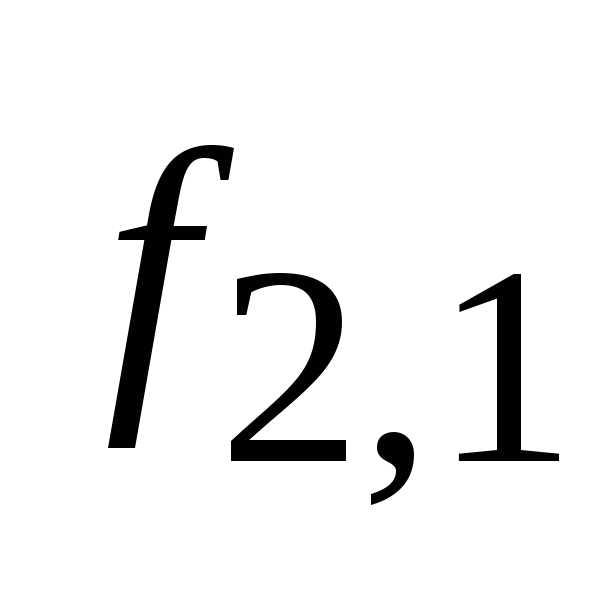
внутренние силы, действующие на первое
тело со стороны второго и на второе тело
со стороны первого, соответственно;
внутренние силы, действующие на первое
тело со стороны второго и на второе тело
со стороны первого, соответственно; 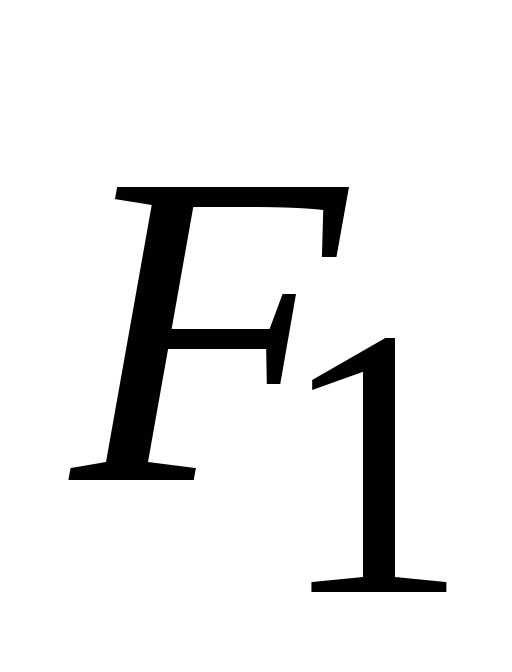 и
и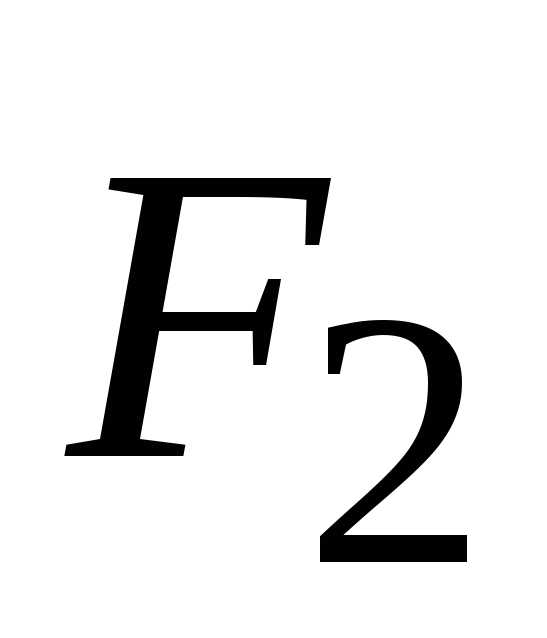
равнодействующие внешних сил, приложенных
к первому и второму телу.
равнодействующие внешних сил, приложенных
к первому и второму телу.
Складывая эти уравнения, получаем
.
Согласно
третьему закону Ньютона  ,
поэтому первая скобка равна нулю.
равнодействующая внешних сил, действующих
на систему и
,
т.к. сумма производных равна производной
от суммы.
,
поэтому первая скобка равна нулю.
равнодействующая внешних сил, действующих
на систему и
,
т.к. сумма производных равна производной
от суммы.
Величину 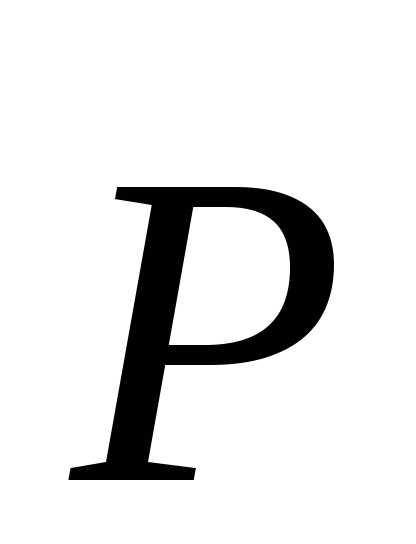 ,
равную векторной сумме импульсов тел,
входящих в механическую систему, называютимпульсом
системы,
т.е.
.
С учетом этого имеем
,
равную векторной сумме импульсов тел,
входящих в механическую систему, называютимпульсом
системы,
т.е.
.
С учетом этого имеем
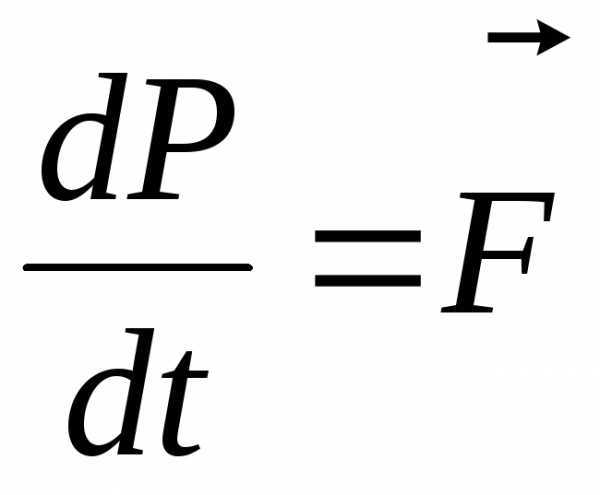 .
(2.7)
.
(2.7)
Получили второй закон Ньютона для механической системы: равнодействующая внешних сил, действующих на механическую систему, равна производной импульса системы по времени (скорости изменения импульса).
В
случае замкнутой механической системы 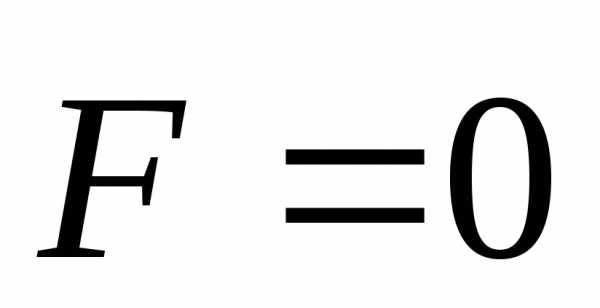 .
Тогда
.
Тогда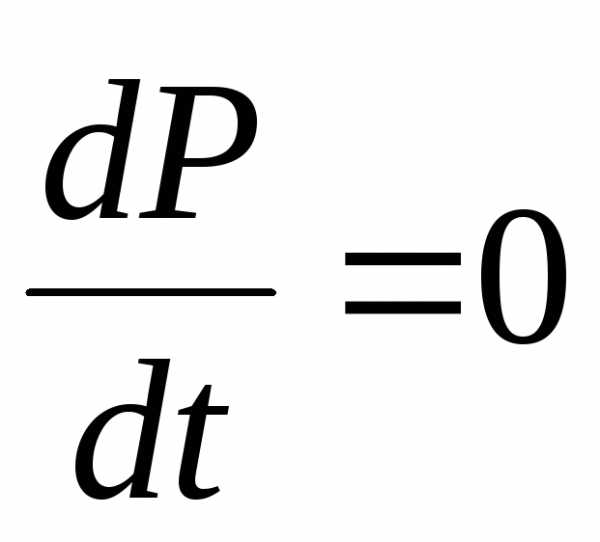 ,
следовательно
,
следовательно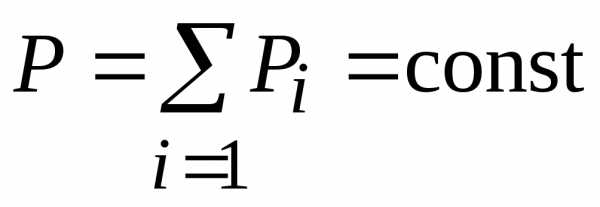 ,
так как производная от постоянной
величины равна нулю. Это соотношение
носит название закона сохранения
импульса: импульс замкнутой механической системы
постоянен при любых взаимодействиях
тел, принадлежащих этой системе.
,
так как производная от постоянной
величины равна нулю. Это соотношение
носит название закона сохранения
импульса: импульс замкнутой механической системы
постоянен при любых взаимодействиях
тел, принадлежащих этой системе.
. (2.8)
Таким образом, импульс замкнутой системы сохраняется, не изменяется с течением времени. Этот закон – фундаментальный закон природы, он универсален и является следствием однородности пространства. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого, ее физические свойства и законы движения не изменяются.
studfiles.net
Законы ньютона 2 – страница 3
2.1.3.
Третий закон Ньютона.
Третий закон Ньютона гласит: действию всегда есть равное и противоположное противодействие, иначе тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по модулю и противоположными по направлению или математически:
Ньютон распространил действие этого закона на случай и столкновения тел, и на случай их взаимного притяжения. Простейшей демонстрацией этого закона может служить тело, расположенное на горизонтальной плоскости, на которое действуют сила тяжести Fт и сила реакции опоры Fо, лежащие на одной прямой, равные по значению и противоположно направленные, равенство этих сил позволяет телу находиться в состоянии покоя (рис. 2).
Из трех фундаментальных законов движения Ньютона вытекают следствия, одно из которых – сложение количества движения по правилу параллелограмма. Ускорение тела зависит от величин, характеризующих действие других тел на данное тело, а также от величин, определяющих особенности этого тела. Механическое действие на тело со стороны других тел, которое изменяет скорость движения данного тела, называют силой. Она может иметь разную природу (сила тяжести, сила упругости и т.д.). Изменение скорости движения тела зависит не от природы сил, а от их величины. Поскольку скорость и сила – векторы, то действие нескольких сил складывается по правилу параллелограмма. Свойство тела, от которого зависит приобретаемое им ускорение, есть инерция, измеряемая массой. В классической механике, имеющей дело со скоростями, значительно меньшими скорости света, масса является характеристикой самого тела, не зависящей от того, движется оно или нет. Масса тела в классической механике не зависит и от взаимодействия тела с другими телами. Это свойство массы побудило Ньютона принять массу за меру материи и считать, что величина ее определяет количество материи в теле. Таким образом, масса стала пониматься как количество материи.
Количество материи доступно измерению, будучи пропорциональным весу тела. Вес – это сила, с которой тело действует на опору, препятствующую его свободному падению. Числено вес равен произведению массы тела на ускорение силы тяжести. Вследствие сжатия Земли и ее суточного вращения вес тела изменяется с широтой и на экваторе на 0,5% меньше, чем на полюсах. Поскольку масса и вес строго пропорциональны, оказалось возможным практическое измерение массы или количества материи. Понимание того, что вес является переменным воздействием на тело, побудило Ньютона установить и внутреннюю характеристику тела – инерцию, которую он рассматривал как присущую телу способность сохранять равномерное прямолинейное движение, пропорциональную массе. Массу как меру инерции можно измерять с помощью весов, как это делал Ньютон.
В состоянии невесомости массу можно измерять по инерции. Измерение по инерции является общим способом измерения массы. Но инерция и вес являются различными физическими понятиями. Их пропорциональность друг другу весьма удобна в практическом отношении – для измерения массы с помощью весов. Таким образом, установление понятий силы и массы, а также способа их измерения позволило Ньютону сформулировать второй закон механики.
Первый и второй законы механики относятся соответственно к движению материальной точки или одного тела. При этом учитывается лишь действие других тел на данное тело. Однако всякое действие есть взаимодействие. Поскольку в механике действие характеризуется силой, то если одно тело действует на другое с определенной силой, то второе действует на первое с той же силой, что и фиксирует третий закон механики. В формулировке Ньютона третий закон механики справедлив лишь для случая непосредственного взаимодействия сил или при мгновенной передаче действия одного тела на другое. В случае передачи действия за конечный промежуток времени данный закон применяется тогда, когда временем передачи действия можно пренебречь.
2.2. Закон всемирного тяготения.
Считается, что стержнем динамики Ньютона является понятие силы, а основная задача динамики заключается в установлении закона из данного движения и, наоборот, в определении закона движения тел по данной силе. Из законов Кеплера Ньютон вывел существование силы, направленной к Солнцу, которая была обратно пропорциональна квадрату расстояния планет от Солнца. Обобщив идеи, высказанные Кеплером, Гюйгенсом, Декартом, Борелли, Гуком, Ньютон придал им точную форму математического закона, в соответствии с которым утверждалось существование в природе силы всемирного тяготения, обусловливающей притяжение тел. Сила тяготения прямо пропорциональна произведению масс тяготеющих тел и обратно пропорционально квадрату расстояния между ними или математически:
, где G – гравитационная постоянная.
Данный закон описывает взаимодействие любых тел – важно лишь то, чтобы расстояние между телами было достаточно велико по сравнению с их размерами, это позволяет принимать тела за материальные точки. В ньютоновской теории тяготения принимается, что сила тяготения передается от одного тяготеющего тела к другому мгновенно, при чем без посредства каких бы то ни было сред. Закон всемирного тяготения вызвал продолжительные и яростные дискуссии. Это не было случайно, поскольку этот закон имел важное философское значение. Суть заключалась в том, что до Ньютона целью создания физических теорий было выявление и представление механизма физических явлений во всех его деталях. В тех случаях, когда это сделать не удавалось, выдвигался аргумент о так называемых “скрытых качествах”, которые не поддаются детальной интерпретации. Бэкон и Декарт ссылки на “скрытые качества” объявили ненаучными. Декарт считал, что понять суть явления природы можно лишь в том случае, если его наглядно представить себе. Так, явления тяготения он представлял с помощью эфирных вихрей. В условиях широкого распространения подобных представлений закон всемирного тяготения Ньютона, несмотря на то, что демонстрировал соответствие произведенных на его основе астрономическим наблюдениям с небывалой ранее точностью, подвергался сомнению на том основании, что взаимное притяжение тел очень напоминало перипатетическое учение о “скрытых качествах”. И хотя Ньютон установил факт его существования на основе математического анализа и экспериментальных данных, математический анализ еще не вошел прочно в сознание исследователей в качестве достаточно надежного метода. Но стремление ограничивать физическое исследование фактами, не претендующими на абсолютную истину, позволило Ньютону завершить формирование физики как самостоятельной науки и отделить ее от натурфилософии с ее претензиями на абсолютное знание.
В законе всемирного тяготения наука получила образец закона природы как абсолютно точного, повсюду применимого правила, без исключений, с точно определенными следствиями. Этот закон был включен Кантом в его философию, где природа представлялась царством необходимости в противоположность морали – царству свободы.
Физическая концепция Ньютона была своеобразным венцом физики XVII века. Статический подход к Вселенной был заменен динамическим. Эксперементально-математический метод исследования, позволив решить многие проблемы физики XVII века, оказался пригодным для решения физических проблем еще в течение двух веков.
2.3. Основная задача механики.
Результатом развития классической механики явилось создание единой механической картины мира, в рамках которой все качественное многообразие мира объяснялось различиями в движении тел, подчиняющемся законам ньютоновской механики. Согласно механической картине мира, если физическое явление мира можно было объяснить на основе законов механики, то такое объяснение признавалось научным. Механика Ньютона, таким образом, стала основой механической картины мира, господствовавшей вплоть до научной революции на рубеже XIX и XX столетий.
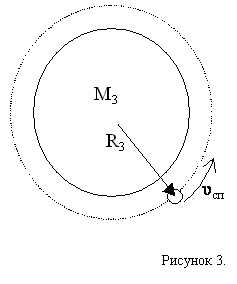 Механика Ньютона, в отличие от предшествующих механических концепций, давало возможность решать задачу о любой стадии движения, как предшествующей, так и последующей, и в любой точке пространства при известных фактах, обусловливающих это движение, а также обратную задачу определения величины и направления действия этих факторов в любой точке при известных основных элементах движения. Благодаря этому механика Ньютона могла использоваться в качестве метода количественного анализа механического движения. Любые физические явления могли изучаться как, независимо от вызывающих их факторов. Например, можно вычислить скорость спутника Земли: Для простоты найдем скорость спутника с орбитой, равной радиусу Земли (рис. 3). С достаточной точностью можно приравнять ускорение спутника ускорению свободного падения на поверхности Земли:
Механика Ньютона, в отличие от предшествующих механических концепций, давало возможность решать задачу о любой стадии движения, как предшествующей, так и последующей, и в любой точке пространства при известных фактах, обусловливающих это движение, а также обратную задачу определения величины и направления действия этих факторов в любой точке при известных основных элементах движения. Благодаря этому механика Ньютона могла использоваться в качестве метода количественного анализа механического движения. Любые физические явления могли изучаться как, независимо от вызывающих их факторов. Например, можно вычислить скорость спутника Земли: Для простоты найдем скорость спутника с орбитой, равной радиусу Земли (рис. 3). С достаточной точностью можно приравнять ускорение спутника ускорению свободного падения на поверхности Земли:
.
С другой стороны центростремительное ускорение спутника .
Поэтому ,
откуда . – Эта скорость называется первой космической скоростью. Тело любой массы, которому будет сообщена такая скорость, станет спутником Земли.
Законы ньютоновской механики связывали силу не с движением, а с изменением движения. Это позволило отказаться от традиционных представлений о том, что для поддержания движения нужна сила, и отвести трению, которое делало силу необходимой в действующих механизмах для поддержания движения, второстепенную роль. Установив динамический взгляд на мир вместо традиционного статического, Ньютон свою динамику сделал основой теоретической физики. Хотя Ньютон проявлял осторожность в механических истолкованиях природных явлений, все равно считал желательным выведение из начал механики остальных явлений природы. Дальнейшее развитие физики стало осуществляться в направлении дальнейшей разработки аппарата механики применительно к решению конкретных задач, по мере решения которых механическая картина мира укреплялась.
2.4. Границы применимости.
Вследствие развития физики в начале XX века определилась область применения классической механики: ее законы выполняются для движений, скорость которых много меньше скорости света. Было установлено, что с ростом скорости масса тела возрастает. Вообще законы классической механики Ньютона справедливы для случая инерциальных систем отсчета. В случае неинерциальных систем отсчета ситуация иная. При ускоренном движении неинерциальной системы координат относительно инерциальной системы первый закон Ньютона (закон инерции) в этой системе не имеет места, – свободные тела в ней будут с течением времени менять свою скорость движения.
Первое несоответствие в классической механике было выявлено, тогда когда был открыт микромир. В классической механике перемещения в пространстве и определение скорости изучались вне зависимости от того, каким образом эти перемещения реализовывались. Применительно к явлениям микромира подобная ситуация, как выявилось, невозможна принципиально. Здесь пространственно-временная локализация, лежащая в основе кинематики, возможна лишь для некоторых частных случаев, которые зависят от конкретных динамических условий движения. В макро масштабах использование кинематики вполне допустимо. Для микро масштабов, где главная роль принадлежит квантам, кинематика, изучающая движение вне зависимости от динамических условий, теряет смысл.
Для масштабов микромира и второй закон Ньютона оказался несостоятельным – он справедлив лишь для явлений большого масштаба. Выявилось, что попытки измерить какую-либо величину, характеризующую изучаемую систему, влечет за собой неконтролируемое изменение других величин, характеризующих данную систему: если предпринимается попытка установить положение в пространстве и времени, то это приводит к неконтролируемому изменению соответствующей сопряженной величины, которая определяет динамическое состояние системы. Так, невозможно точно измерить в одно и то же время две взаимно сопряженные величины. Чем точнее определяется значение одной величины, характеризующей систему, тем более неопределенным оказывается значение сопряженной ей величины. Это обстоятельство повлекло за собой существенное изменение взглядов на понимание природы вещей.
Несоответствие в классической механики исходило из того, что будущее в известном смысле полностью содержится в настоящем – этим и определяется возможность точного предвидения поведения системы в любой будущий момент времени. Такая возможность предлагает одновременное определение взаимно сопряженных величин. В области микромира это оказалось невозможным, что и вносит существенные изменения в понимание возможностей предвидения и взаимосвязи явлений природы: раз значение величин, характеризующих состояние системы в определенный момент времени, можно установить лишь с долей неопределенности, то исключается возможность точного предсказания значений этих величин в последующие моменты времени, т.е. можно лишь предсказать вероятность получения тех или иных величин.
Другое открытие пошатнувшее устои классической механики, было создания теории поля. Классическая механика пыталась свести все явления природы к силам, действующим между частицами вещества, – на этом основывалась концепция электрических жидкостей. В рамках этой концепции реальными были лишь субстанция и ее изменения – здесь важнейшим признавалось описание действия двух электрических зарядов с помощью относящихся к ним понятий. Описание же поля между этими зарядами, а не самих зарядов было весьма существенным для понимания действия зарядов. Вот простой пример нарушения третьего закона Ньютона в таких условиях: если заряженная частица удаляется от проводника, по которому течет ток, и соответственно вокруг него создано магнитное поле, то результирующая сила, действующая со стороны заряженной частицы на проводник с током в точности равна нулю.
Созданной новой реальности места в механической картине мира не было. В результате физика стала иметь дело с двумя реальностями – веществом и полем. Если классическая физика строилась на понятии вещества, то с выявлением новой реальности физическую картину мира приходилось пересматривать. Попытки объяснить электромагнитные явления с помощью эфира оказалось несостоятельными. Эфир экспериментально обнаружить не удалось. Это привело к созданию теории относительности, заставившей пересмотреть представления о пространстве и времени, характерные для классической физики. Таким образом, две концепции – теория квантов и теория относительности – стали фундаментом для новых физических концепций.
3. ЗАКЛЮЧЕНИЕ.
Вклад, сделанный Ньютоном в развитие естествознания, заключался в том, что он дал математический метод обращения физических законов в количественно измеримые результаты, которые можно было подтвердить наблюдениями, и, наоборот, выводить физические законы на основе таких наблюдений. Как он сам писал в предисловии к “Началам”, “… сочинение это нами предлагается как математические основания физики. Вся трудность физики… состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления… Было бы желательно вывести из начал механики и остальные явления природы, рассуждая подобным же образом, ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел вследствие причин, пока неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга. Так как эти силы неизвестны, до сих пор попытки философов объяснить явления природы и оставались бесплодными. Я надеюсь, однако, что или этому способу рассуждения, или другому, более правильному, изложенные здесь основания доставят некоторое освещение”.[1]
Ньютоновский метод стал главным инструментом познания природы. Законы классической механики и методы математического анализа демонстрировали свою эффективность. Физический эксперимент, опираясь на измерительную технику, обеспечивал небывалую ранее точность. Физическое знание все в большей мере становилось основой промышленной технологии и техники, стимулировало развитие других естественных наук. В физике изолированные ранее свет, электричество, магнетизм и теплота оказались объединенными в электромагнитную теорию. И хотя природа тяготения оставалась не выясненной, его действия можно было рассчитать. Утвердилась концепция механистического детерминизма Лапласа, исходившая из возможности однозначно определить поведение системы в любой момент времени, если известные исходные условия. Структура механики как науки казалась прочной, надежной и почти полностью завершенной – т.е. не укладывающиеся в существующие классические каноны феномены, с которыми приходилось сталкиваться, казались вполне объяснимыми в будущем более изощренными умами с позиций классической механики. Складывалось впечатление, что знание физики близко к своему полному завершению – столь мощную силу демонстрировал фундамент классической физики.
4. СПИСОК ЛИТЕРАТУРЫ.
1. Карпенков С.Х. Основные концепции естествознания. М.: ЮНИТИ, 1998.
2. Ньютон и философские проблемы физики XX века. Коллектив авторов под ред. М.Д. Ахундова, С.В. Илларионова. М.: Наука, 1991.
3. Гурский И.П. Элементарная физика. М.: Наука, 1984.
4. Большая Советская Энциклопедия в 30 томах. Под ред. ПрохороваА.М., 3 издание, М., Советская энциклопедия, 1970.
5. ДорфманЯ.Г. Всемирная история физики с начала XIX до середины XX вв. М., 1979.
coolreferat.com
