5 закон ньютона – Законы Ньютона — Википедия. Что такое Законы Ньютона

5. Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие мате­риальных точек (тел) друг на друга носит характер взаимодействия; силы, с которы­ми действуют друг на друга материальные точки, всегда равны по модулю, противо­положно направлены и действуют вдоль прямой, соединяющей эти точки:

F₁₂=-F_2I,

где F₁₂ — сила, действующая на первую материальную точку со стороны второй; F₂₁ — сила, действующая на вторую мате­риальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

При использовании законов динамики иногда допускают следующую ошибку: так как действующая сила всегда вызыва­ет равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая до­лжна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под действием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий же закон Ньютона говорит о равен­стве сил, приложенных к

различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение.

Третий закон Ньютона позволяет осу­ществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

6. Силы, действующие в природе: гравитационные, ядерные, слабо ядерные, электромагнитные.

Силы упругости – силы обусловленные деформациями тела. Деформации связаны с изменением взаимного расположения молекул, образующих рассматриваемое тело, причем силы возникают лишь тогда, когда деформации носят упругий характер. закон Гука Fупр=-kξ

, где  обозначает величину упругой деформации, а к – коэффициент пропорциональности.

7. Деформации твердого тела

Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердо­го тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраня-

ются в теле после прекращения действия внешних сил, называются

пластическими (или остаточными). Деформации реально­го тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать уп­ругие деформации, что мы и будем де­лать.

В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходя­щим деформациям растяжения или сжа­тия и сдвига.

Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы

f₁ и F₂ (F₁=F₂=F), в результате чего длина стер­жня меняется на величину l. Естествен­но, что при растяжении l положительно, а при сжатии — отрицательно.

Сила, действующая на единицу пло­щади поперечного сечения, называется на­пряжением:

=F/S. (21.1)

Если сила направлена по нормали к по­верхности, напряжение называется нор­мальным, если же по касательной к по­верхности — тангенциальным.

Количественной мерой, характеризую­щей степень деформации, испытываемой телом, является его

относительная дефор­мация. Так, относительное изменение дли­ны стержня (продольная деформация)

=l/l, (21.2) относительное поперечное растяжение

(сжатие)

’ = d/d, где d -— диаметр стержня.

Деформации  и ‘ всегда имеют раз­ные знаки (при растяжении l положи­тельно, a Ad отрицательно, при сжатии l отрицательно, a Ad положительно). Из опыта вытекает взаимосвязь  и ’:

’=-,

где  — положительный коэффициент, за­висящий от свойств материала, называе­мый

коэффициентом Пуассона.

Английский физик Р. Гук (1635— 1703) экспериментально установил, что для малых деформаций относительное уд­линение  и напряжение  прямо про­порциональны друг другу:

 = E, (21.3)

где коэффициент пропорциональности Е называется модулем Юнга. Из вы­ражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (21.2), (21.3) и (21.1) вы­текает, что

где k — коэффициент упругости. Выраже­ние (21.4) также задает закон Гука, со­гласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.

Деформации твердых тел подчиняются закону Гука до известного предела. Связь между деформацией и напряжением пред­ставляется в виде диаграммы напряже­ний, которую мы качественно рассмотрим для металлического образца (рис. 35). Из рисунка видно, что линейная зависимость  (), установленная Гуком, выполняется

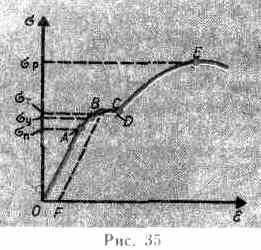
лишь в очень узких пределах до так на­зываемого предела пропорциональности (_п

). При дальнейшем увеличении напря­жения деформация еще упругая (хотя за­висимость  () уже не линейна) и до пре­дела упругости (_у) остаточные деформа­ции не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекра­щения действия силы, изобразится не кри­вой ВО, а параллельной ей — CF. Напря­жение, при котором появляется заметная остаточная деформация (~=0,2 %), назы­вается пределом текучести (_т) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или об­ластью пластических деформаций). Мате­риалы, для которых область текучести значительна, называются вязкими, для ко­торых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется преде­лом прочности (_p).

Диаграмма напряжений для реальных твердых тел зависит от различных факто­ров. Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.

Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, кото­рая равна работе, совершаемой внешними силами при деформации:

где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до l. Согласно закону Гука (21.4), F=kx=ESx/l. Поэтому

т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадра­ту деформации (l)².

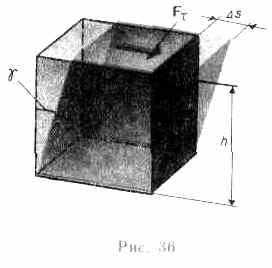
Деформацию сдвига проще всего осу­ществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу F

tau (рис.36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига опре­деляется из формулы

tg = s/h,

где s — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых уг­лов tg).

studfiles.net

Законы Ньютона — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Зако́ны Нью́то́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)

[1]^[2].

Первый закон Ньютона

Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции. Инерция — это свойство тела сохранять скорость своего движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность — это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[3]:

Историческая формулировка

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[4][5][6][7].

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

<math> \vec a = \frac {\vec {F}} {m} ,</math>

где <math> \vec a </math> — ускорение материальной точки;
<math> \vec {F} </math> — равнодействующая всех сил, приложенных к материальной точке;
<math>m</math> — масса материальной точки.

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. <math> \frac {d \vec p} {dt} = \vec{F},</math>

где <math>\vec p=m\vec v</math> — импульс точки, <math>\vec v</math> — её скорость, а <math>t</math> — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени^[8][9][10].

Иногда предпринимаются попытки распространить сферу применения уравнения <math> \frac {d \vec p} {dt} = \vec{F}</math> и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[11][12].

Замечания

Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:

<math>m \vec a = \sum_{i=1}^{n} {\vec{F_i}}</math>

или,

<math> \frac {d \vec p} {dt} = \sum_{i=1}^{n} {\vec{F_i}}.</math>

Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Следует учитывать, что нельзя рассматривать частный случай (при <math> \vec {F} = 0 </math>) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой <math>\vec{F}_{1 \to 2}</math>, а вторая — на первую с силой <math>\vec{F}_{2 \to 1}</math>. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия <math>\vec{F}_{1 \to 2}</math> равна по модулю и противоположна по направлению силе противодействия <math>\vec{F}_{2 \to 1}</math>.

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: <math>\vec{F}_{2 \to 1} = -\vec{F}_{1 \to 2}.</math>

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно^[13].

Историческая формулировка

Ньютон дал следующую формулировку закона^[1]:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[14].

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали друг с другом посредством сил, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел <math>U(|{r}_1 – {r}_2|)</math>, то возникает закон сохранения механической энергии взаимодействующих тел:

<math>{m {v}_1^2 \over 2} + {m {v}_2^2 \over 2} + U(|{r}_1 – {r}_2|) = \operatorname{const}.</math>

Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.

Напишите отзыв о статье “Законы Ньютона”

Комментарии к законам Ньютона

Силы инерции

Помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводят в рассмотрение так называемые силы инерции. Обычно речь идёт о силах инерции двух различных типов^[15]. Сила первого типа (даламберова сила инерции) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой^[13][15].Определяемые таким образом силы инерции силами в смысле законов Ньютона не являются^[16]. Данный факт служит основанием для утверждения о том, что они не являются физическими силами^[13]; ту же мысль выражают, называя их фиктивными^[17], кажущимися^[18] или псевдосилами^[19].

Законы Ньютона и Лагранжева механика

Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Решение уравнений движения

Уравнение <math> \vec {F} = m \vec a </math> является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Исторический очерк

Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде^[1]:

1. Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние.    2. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.    3. Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. Оригинальный текст (лат.)      LEX I Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.    LEX II Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.    LEX III Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi. — [books.google.com/books?id=XJwx0lnKvOgC&printsec=frontcover#PPP2,M1 «Начала», страница 12]

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).

Завершили математизацию основ механики Эйлер и Лагранж.

См. также

Примечания

1. ↑ ^{1 2 3} Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — («Классики науки»). — 5 000 экз. — ISBN 5-02-000747-1.
2. ↑ Тарг С. М. [www.femto.com.ua/articles/part_2/2539.html Ньютона законы механики] // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1992. — Т. 3. — С. 370. — 672 с. — 48 000 экз.
3. ↑ [www.femto.com.ua/articles/part_1/1355.html Инерциальная система отсчёта] // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
4. ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
5. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
6. ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
7. ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
8. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
9. ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
10. ↑ Kleppner D., Kolenkow R. J. [ru.scribd.com/doc/102675075/An-Introduction-to-Mechanics-1973-Daniel-Kleppner-Robert-Kolenkow An Introduction to Mechanics]. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
11. ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
12. ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
13. ↑ ^{1 2 3} Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
14. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
15. ↑ ^{1 2} Тарг С. М. [www.femto.com.ua/articles/part_2/3621.html Сила инерции] // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1994. — Т. 4. — С. 494-495. — 704 с. — 40 000 экз.
16. ↑ «”Силы инерции” — не силы». Журавлёв В. Ф. [bookre.org/reader?file=475187 Основания механики. Методические аспекты]. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
17. ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
18. ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
19. ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.

Ссылки

• [interneturok.ru/video/fizika/9_klass/zakony_vzaimodejstviya_i_dvizheniya_tel/inercialnye_sistemy_otscheta_pervyj_zakon_nyutona/ Первый закон Ньютона] (видеоурок, программа 9 класса)

Литература

• Лич Дж. У. [eqworld.ipmnet.ru/ru/library/books/Lich2961ru.djvu Классическая механика.] М.: Иностр. литература, 1961.
• Спасский Б. И.. История физики. М., «Высшая школа», 1977.
  • [osnovanija.narod.ru/History/Spas/T1_1.djvu Том 1. Часть 1-я;] [osnovanija.narod.ru/History/Spas/T1_2.djvu Часть 2-я]
  • [osnovanija.narod.ru/History/Spas/T2_1.djvu Том 2. Часть 1-я;] [osnovanija.narod.ru/History/Spas/T2_2.djvu Часть 2-я]
• Кудрявцев П. С. [www.edu.delfa.net/Interest/biography/biblio.htm Курс истории физики]. — М.: Просвещение, 1974.

Отрывок, характеризующий Законы Ньютона

Пьер смотрел в глаза княжне Марье.
– Ну, ну… – говорил он.
– Я знаю, что она любит… полюбит вас, – поправилась княжна Марья.
Не успела она сказать эти слова, как Пьер вскочил и с испуганным лицом схватил за руку княжну Марью.
– Отчего вы думаете? Вы думаете, что я могу надеяться? Вы думаете?!
– Да, думаю, – улыбаясь, сказала княжна Марья. – Напишите родителям. И поручите мне. Я скажу ей, когда будет можно. Я желаю этого. И сердце мое чувствует, что это будет.
– Нет, это не может быть! Как я счастлив! Но это не может быть… Как я счастлив! Нет, не может быть! – говорил Пьер, целуя руки княжны Марьи.
– Вы поезжайте в Петербург; это лучше. А я напишу вам, – сказала она.
– В Петербург? Ехать? Хорошо, да, ехать. Но завтра я могу приехать к вам?
На другой день Пьер приехал проститься. Наташа была менее оживлена, чем в прежние дни; но в этот день, иногда взглянув ей в глаза, Пьер чувствовал, что он исчезает, что ни его, ни ее нет больше, а есть одно чувство счастья. «Неужели? Нет, не может быть», – говорил он себе при каждом ее взгляде, жесте, слове, наполнявших его душу радостью.
Когда он, прощаясь с нею, взял ее тонкую, худую руку, он невольно несколько дольше удержал ее в своей.
«Неужели эта рука, это лицо, эти глаза, все это чуждое мне сокровище женской прелести, неужели это все будет вечно мое, привычное, такое же, каким я сам для себя? Нет, это невозможно!..»
– Прощайте, граф, – сказала она ему громко. – Я очень буду ждать вас, – прибавила она шепотом.
И эти простые слова, взгляд и выражение лица, сопровождавшие их, в продолжение двух месяцев составляли предмет неистощимых воспоминаний, объяснений и счастливых мечтаний Пьера. «Я очень буду ждать вас… Да, да, как она сказала? Да, я очень буду ждать вас. Ах, как я счастлив! Что ж это такое, как я счастлив!» – говорил себе Пьер.

В душе Пьера теперь не происходило ничего подобного тому, что происходило в ней в подобных же обстоятельствах во время его сватовства с Элен.
Он не повторял, как тогда, с болезненным стыдом слов, сказанных им, не говорил себе: «Ах, зачем я не сказал этого, и зачем, зачем я сказал тогда „je vous aime“?» [я люблю вас] Теперь, напротив, каждое слово ее, свое он повторял в своем воображении со всеми подробностями лица, улыбки и ничего не хотел ни убавить, ни прибавить: хотел только повторять. Сомнений в том, хорошо ли, или дурно то, что он предпринял, – теперь не было и тени. Одно только страшное сомнение иногда приходило ему в голову. Не во сне ли все это? Не ошиблась ли княжна Марья? Не слишком ли я горд и самонадеян? Я верю; а вдруг, что и должно случиться, княжна Марья скажет ей, а она улыбнется и ответит: «Как странно! Он, верно, ошибся. Разве он не знает, что он человек, просто человек, а я?.. Я совсем другое, высшее».
Только это сомнение часто приходило Пьеру. Планов он тоже не делал теперь никаких. Ему казалось так невероятно предстоящее счастье, что стоило этому совершиться, и уж дальше ничего не могло быть. Все кончалось.
Радостное, неожиданное сумасшествие, к которому Пьер считал себя неспособным, овладело им. Весь смысл жизни, не для него одного, но для всего мира, казался ему заключающимся только в его любви и в возможности ее любви к нему. Иногда все люди казались ему занятыми только одним – его будущим счастьем. Ему казалось иногда, что все они радуются так же, как и он сам, и только стараются скрыть эту радость, притворяясь занятыми другими интересами. В каждом слове и движении он видел намеки на свое счастие. Он часто удивлял людей, встречавшихся с ним, своими значительными, выражавшими тайное согласие, счастливыми взглядами и улыбками. Но когда он понимал, что люди могли не знать про его счастье, он от всей души жалел их и испытывал желание как нибудь объяснить им, что все то, чем они заняты, есть совершенный вздор и пустяки, не стоящие внимания.
Когда ему предлагали служить или когда обсуждали какие нибудь общие, государственные дела и войну, предполагая, что от такого или такого исхода такого то события зависит счастие всех людей, он слушал с кроткой соболезнующею улыбкой и удивлял говоривших с ним людей своими странными замечаниями. Но как те люди, которые казались Пьеру понимающими настоящий смысл жизни, то есть его чувство, так и те несчастные, которые, очевидно, не понимали этого, – все люди в этот период времени представлялись ему в таком ярком свете сиявшего в нем чувства, что без малейшего усилия, он сразу, встречаясь с каким бы то ни было человеком, видел в нем все, что было хорошего и достойного любви.
Рассматривая дела и бумаги своей покойной жены, он к ее памяти не испытывал никакого чувства, кроме жалости в том, что она не знала того счастья, которое он знал теперь. Князь Василий, особенно гордый теперь получением нового места и звезды, представлялся ему трогательным, добрым и жалким стариком.
Пьер часто потом вспоминал это время счастливого безумия. Все суждения, которые он составил себе о людях и обстоятельствах за этот период времени, остались для него навсегда верными. Он не только не отрекался впоследствии от этих взглядов на людей и вещи, но, напротив, в внутренних сомнениях и противуречиях прибегал к тому взгляду, который он имел в это время безумия, и взгляд этот всегда оказывался верен.
«Может быть, – думал он, – я и казался тогда странен и смешон; но я тогда не был так безумен, как казалось. Напротив, я был тогда умнее и проницательнее, чем когда либо, и понимал все, что стоит понимать в жизни, потому что… я был счастлив».
Безумие Пьера состояло в том, что он не дожидался, как прежде, личных причин, которые он называл достоинствами людей, для того чтобы любить их, а любовь переполняла его сердце, и он, беспричинно любя людей, находил несомненные причины, за которые стоило любить их.

С первого того вечера, когда Наташа, после отъезда Пьера, с радостно насмешливой улыбкой сказала княжне Марье, что он точно, ну точно из бани, и сюртучок, и стриженый, с этой минуты что то скрытое и самой ей неизвестное, но непреодолимое проснулось в душе Наташи.
Все: лицо, походка, взгляд, голос – все вдруг изменилось в ней. Неожиданные для нее самой – сила жизни, надежды на счастье всплыли наружу и требовали удовлетворения. С первого вечера Наташа как будто забыла все то, что с ней было. Она с тех пор ни разу не пожаловалась на свое положение, ни одного слова не сказала о прошедшем и не боялась уже делать веселые планы на будущее. Она мало говорила о Пьере, но когда княжна Марья упоминала о нем, давно потухший блеск зажигался в ее глазах и губы морщились странной улыбкой.
Перемена, происшедшая в Наташе, сначала удивила княжну Марью; но когда она поняла ее значение, то перемена эта огорчила ее. «Неужели она так мало любила брата, что так скоро могла забыть его», – думала княжна Марья, когда она одна обдумывала происшедшую перемену. Но когда она была с Наташей, то не сердилась на нее и не упрекала ее. Проснувшаяся сила жизни, охватившая Наташу, была, очевидно, так неудержима, так неожиданна для нее самой, что княжна Марья в присутствии Наташи чувствовала, что она не имела права упрекать ее даже в душе своей.
Наташа с такой полнотой и искренностью вся отдалась новому чувству, что и не пыталась скрывать, что ей было теперь не горестно, а радостно и весело.
Когда, после ночного объяснения с Пьером, княжна Марья вернулась в свою комнату, Наташа встретила ее на пороге.
– Он сказал? Да? Он сказал? – повторила она. И радостное и вместе жалкое, просящее прощения за свою радость, выражение остановилось на лице Наташи.
– Я хотела слушать у двери; но я знала, что ты скажешь мне.
Как ни понятен, как ни трогателен был для княжны Марьи тот взгляд, которым смотрела на нее Наташа; как ни жалко ей было видеть ее волнение; но слова Наташи в первую минуту оскорбили княжну Марью. Она вспомнила о брате, о его любви.
«Но что же делать! она не может иначе», – подумала княжна Марья; и с грустным и несколько строгим лицом передала она Наташе все, что сказал ей Пьер. Услыхав, что он собирается в Петербург, Наташа изумилась.
– В Петербург? – повторила она, как бы не понимая. Но, вглядевшись в грустное выражение лица княжны Марьи, она догадалась о причине ее грусти и вдруг заплакала. – Мари, – сказала она, – научи, что мне делать. Я боюсь быть дурной. Что ты скажешь, то я буду делать; научи меня…
– Ты любишь его?
– Да, – прошептала Наташа.
– О чем же ты плачешь? Я счастлива за тебя, – сказала княжна Марья, за эти слезы простив уже совершенно радость Наташи.
– Это будет не скоро, когда нибудь. Ты подумай, какое счастие, когда я буду его женой, а ты выйдешь за Nicolas.
– Наташа, я тебя просила не говорить об этом. Будем говорить о тебе.
Они помолчали.
– Только для чего же в Петербург! – вдруг сказала Наташа, и сама же поспешно ответила себе: – Нет, нет, это так надо… Да, Мари? Так надо…

Прошло семь лет после 12 го года. Взволнованное историческое море Европы улеглось в свои берега. Оно казалось затихшим; но таинственные силы, двигающие человечество (таинственные потому, что законы, определяющие их движение, неизвестны нам), продолжали свое действие.
Несмотря на то, что поверхность исторического моря казалась неподвижною, так же непрерывно, как движение времени, двигалось человечество. Слагались, разлагались различные группы людских сцеплений; подготовлялись причины образования и разложения государств, перемещений народов.
Историческое море, не как прежде, направлялось порывами от одного берега к другому: оно бурлило в глубине. Исторические лица, не как прежде, носились волнами от одного берега к другому; теперь они, казалось, кружились на одном месте. Исторические лица, прежде во главе войск отражавшие приказаниями войн, походов, сражений движение масс, теперь отражали бурлившее движение политическими и дипломатическими соображениями, законами, трактатами…
Эту деятельность исторических лиц историки называют реакцией.
Описывая деятельность этих исторических лиц, бывших, по их мнению, причиною того, что они называют реакцией, историки строго осуждают их. Все известные люди того времени, от Александра и Наполеона до m me Stael, Фотия, Шеллинга, Фихте, Шатобриана и проч., проходят перед их строгим судом и оправдываются или осуждаются, смотря по тому, содействовали ли они прогрессу или реакции.
В России, по их описанию, в этот период времени тоже происходила реакция, и главным виновником этой реакции был Александр I – тот самый Александр I, который, по их же описаниям, был главным виновником либеральных начинаний своего царствования и спасения России.
В настоящей русской литературе, от гимназиста до ученого историка, нет человека, который не бросил бы своего камушка в Александра I за неправильные поступки его в этот период царствования.
«Он должен был поступить так то и так то. В таком случае он поступил хорошо, в таком дурно. Он прекрасно вел себя в начале царствования и во время 12 го года; но он поступил дурно, дав конституцию Польше, сделав Священный Союз, дав власть Аракчееву, поощряя Голицына и мистицизм, потом поощряя Шишкова и Фотия. Он сделал дурно, занимаясь фронтовой частью армии; он поступил дурно, раскассировав Семеновский полк, и т. д.».
Надо бы исписать десять листов для того, чтобы перечислить все те упреки, которые делают ему историки на основании того знания блага человечества, которым они обладают.
Что значат эти упреки?
Те самые поступки, за которые историки одобряют Александра I, – как то: либеральные начинания царствования, борьба с Наполеоном, твердость, выказанная им в 12 м году, и поход 13 го года, не вытекают ли из одних и тех же источников – условий крови, воспитания, жизни, сделавших личность Александра тем, чем она была, – из которых вытекают и те поступки, за которые историки порицают его, как то: Священный Союз, восстановление Польши, реакция 20 х годов?
В чем же состоит сущность этих упреков?
В том, что такое историческое лицо, как Александр I, лицо, стоявшее на высшей возможной ступени человеческой власти, как бы в фокусе ослепляющего света всех сосредоточивающихся на нем исторических лучей; лицо, подлежавшее тем сильнейшим в мире влияниям интриг, обманов, лести, самообольщения, которые неразлучны с властью; лицо, чувствовавшее на себе, всякую минуту своей жизни, ответственность за все совершавшееся в Европе, и лицо не выдуманное, а живое, как и каждый человек, с своими личными привычками, страстями, стремлениями к добру, красоте, истине, – что это лицо, пятьдесят лет тому назад, не то что не было добродетельно (за это историки не упрекают), а не имело тех воззрений на благо человечества, которые имеет теперь профессор, смолоду занимающийся наукой, то есть читанном книжек, лекций и списыванием этих книжек и лекций в одну тетрадку.
Но если даже предположить, что Александр I пятьдесят лет тому назад ошибался в своем воззрении на то, что есть благо народов, невольно должно предположить, что и историк, судящий Александра, точно так же по прошествии некоторого времени окажется несправедливым, в своем воззрении на то, что есть благо человечества. Предположение это тем более естественно и необходимо, что, следя за развитием истории, мы видим, что с каждым годом, с каждым новым писателем изменяется воззрение на то, что есть благо человечества; так что то, что казалось благом, через десять лет представляется злом; и наоборот. Мало того, одновременно мы находим в истории совершенно противоположные взгляды на то, что было зло и что было благо: одни данную Польше конституцию и Священный Союз ставят в заслугу, другие в укор Александру.
Про деятельность Александра и Наполеона нельзя сказать, чтобы она была полезна или вредна, ибо мы не можем сказать, для чего она полезна и для чего вредна. Если деятельность эта кому нибудь не нравится, то она не нравится ему только вследствие несовпадения ее с ограниченным пониманием его о том, что есть благо. Представляется ли мне благом сохранение в 12 м году дома моего отца в Москве, или слава русских войск, или процветание Петербургского и других университетов, или свобода Польши, или могущество России, или равновесие Европы, или известного рода европейское просвещение – прогресс, я должен признать, что деятельность всякого исторического лица имела, кроме этих целей, ещь другие, более общие и недоступные мне цели.
Но положим, что так называемая наука имеет возможность примирить все противоречия и имеет для исторических лиц и событий неизменное мерило хорошего и дурного.
Положим, что Александр мог сделать все иначе. Положим, что он мог, по предписанию тех, которые обвиняют его, тех, которые профессируют знание конечной цели движения человечества, распорядиться по той программе народности, свободы, равенства и прогресса (другой, кажется, нет), которую бы ему дали теперешние обвинители. Положим, что эта программа была бы возможна и составлена и что Александр действовал бы по ней. Что же сталось бы тогда с деятельностью всех тех людей, которые противодействовали тогдашнему направлению правительства, – с деятельностью, которая, по мнению историков, хороша и полезна? Деятельности бы этой не было; жизни бы не было; ничего бы не было.
Если допустить, что жизнь человеческая может управляться разумом, – то уничтожится возможность жизни.

Если допустить, как то делают историки, что великие люди ведут человечество к достижению известных целей, состоящих или в величии России или Франции, или в равновесии Европы, или в разнесении идей революции, или в общем прогрессе, или в чем бы то ни было, то невозможно объяснить явлений истории без понятий о случае и о гении.
Если цель европейских войн начала нынешнего столетия состояла в величии России, то эта цель могла быть достигнута без всех предшествовавших войн и без нашествия. Если цель – величие Франции, то эта цель могла быть достигнута и без революции, и без империи. Если цель – распространение идей, то книгопечатание исполнило бы это гораздо лучше, чем солдаты. Если цель – прогресс цивилизации, то весьма легко предположить, что, кроме истребления людей и их богатств, есть другие более целесообразные пути для распространения цивилизации.
Почему же это случилось так, а не иначе?
Потому что это так случилось. «Случай сделал положение; гений воспользовался им», – говорит история.
Но что такое случай? Что такое гений?
Слова случай и гений не обозначают ничего действительно существующего и потому не могут быть определены. Слова эти только обозначают известную степень понимания явлений. Я не знаю, почему происходит такое то явление; думаю, что не могу знать; потому не хочу знать и говорю: случай. Я вижу силу, производящую несоразмерное с общечеловеческими свойствами действие; не понимаю, почему это происходит, и говорю: гений.
Для стада баранов тот баран, который каждый вечер отгоняется овчаром в особый денник к корму и становится вдвое толще других, должен казаться гением. И то обстоятельство, что каждый вечер именно этот самый баран попадает не в общую овчарню, а в особый денник к овсу, и что этот, именно этот самый баран, облитый жиром, убивается на мясо, должно представляться поразительным соединением гениальности с целым рядом необычайных случайностей.
Но баранам стоит только перестать думать, что все, что делается с ними, происходит только для достижения их бараньих целей; стоит допустить, что происходящие с ними события могут иметь и непонятные для них цели, – и они тотчас же увидят единство, последовательность в том, что происходит с откармливаемым бараном. Ежели они и не будут знать, для какой цели он откармливался, то, по крайней мере, они будут знать, что все случившееся с бараном случилось не нечаянно, и им уже не будет нужды в понятии ни о случае, ни о гении.
Только отрешившись от знаний близкой, понятной цели и признав, что конечная цель нам недоступна, мы увидим последовательность и целесообразность в жизни исторических лиц; нам откроется причина того несоразмерного с общечеловеческими свойствами действия, которое они производят, и не нужны будут нам слова случай и гений.
Стоит только признать, что цель волнений европейских народов нам неизвестна, а известны только факты, состоящие в убийствах, сначала во Франции, потом в Италии, в Африке, в Пруссии, в Австрии, в Испании, в России, и что движения с запада на восток и с востока на запад составляют сущность и цель этих событий, и нам не только не нужно будет видеть исключительность и гениальность в характерах Наполеона и Александра, но нельзя будет представить себе эти лица иначе, как такими же людьми, как и все остальные; и не только не нужно будет объяснять случайностию тех мелких событий, которые сделали этих людей тем, чем они были, но будет ясно, что все эти мелкие события были необходимы.

wiki-org.ru

5. Третий закон Ньютона

Современная формулировка третьего закона Ньютона:

силы взаимодействия двух частиц равны по величине, противоположны по направлению и направлены по прямой, соединяющей частицы, т.е.

.

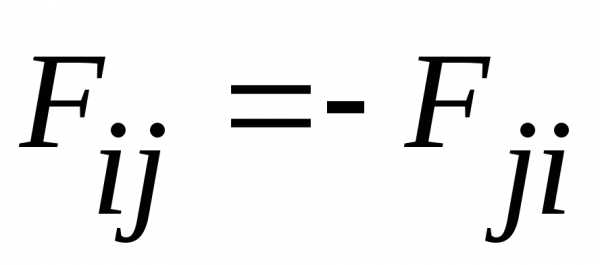Строго говоря, третий закон выполняется для тел, взаимодействующих

контактно, или для покоящихся тел, взаимодействующих на расстоянии.

Опыты показали, что законы классической механики (законы Ньютона) справедливы для макротел (тел с достаточно большими по сравнению с томами

размерами и массой), движущихся с малыми скоростями (по сравнению со

скоростью света).

6. Классический принцип относительности

Основным принципом классической механики является классический

(галилеевский) принцип относительности.

Уравнения динамики не меняются при переходе от одной ИСО к другой, т.е. все ИСО эквивалентны (равноправны) по отношению к механическим явлениям. Или иначе: никакими механическими опытами, проведенными внутри ИСО, нельзя установить движется ли эта ИСО равномерно и прямолинейно или находится в относительном покое.

Работа и энергия

1. Работа переменной силы

Обычно приходится иметь дело с переменной как по величине, так и по направлению силой. Пусть на частицу, движущуюся по криволинейной траектории, действует сила , направление которой составляет с траекторией угол (вообще говоря, переменный). Тогда за время dt частица переместится на 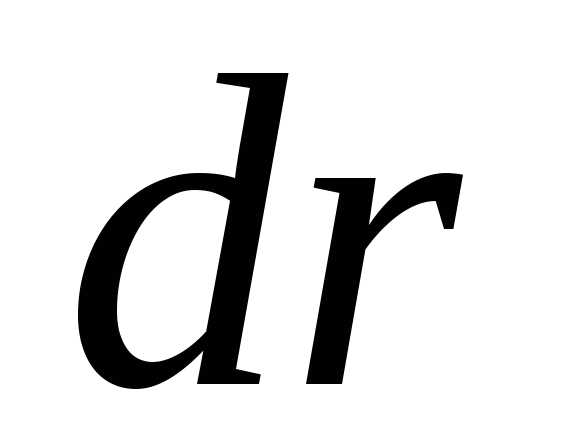, и сила совершит над ней работу

.

Формула является определением элементарной (бесконечно малой)

работы. Ее можно записать и по-другому:

,

где F_l — проекция силы на направление касательной к траектории.

Выражение для работы при конечном перемещении из точки 1 в точку 2

будет выражаться интегралом:

.

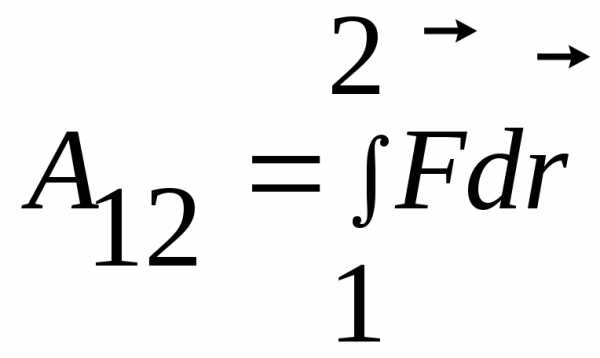Если же на тело одновременно действуют несколько сил, то их суммарная работа равна алгебраической сумме работ каждой силы, или, иначе, равна работе результирующей силы

.

Заметим, что здесь сумма работ — алгебраическая, т.е. каждое слагаемое

в ней имеет знак “плюс” (сила направлена по движению) или “минус” (сила

направлена против движения). К тому же, 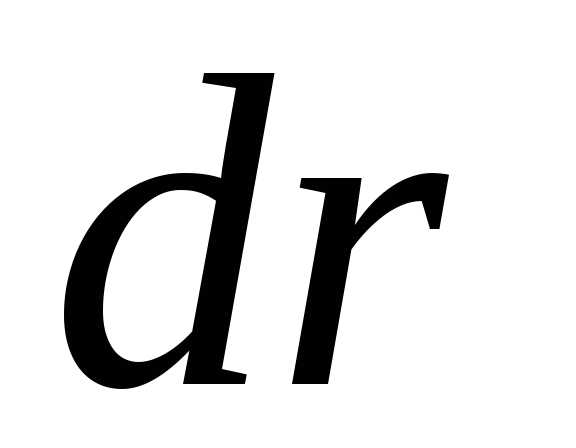— этоперемещение

точки приложения силы.

2. Кинетическая энергия частицы

Пусть на движущуюся частицу действует некоторая сила; в результате движение частицы изменяется (меняется скорость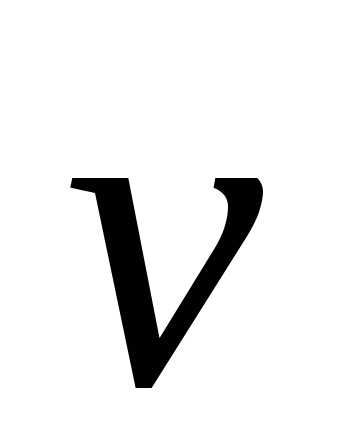). Найдем, чему равна работа силы по изменению скорости частицы. Для этого запишем второй закон Ньютонаи умножим каждую его часть скалярно на элементарное перемещение. В результате получим:

.

.

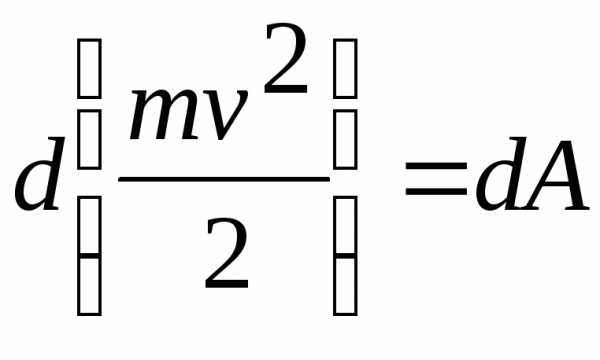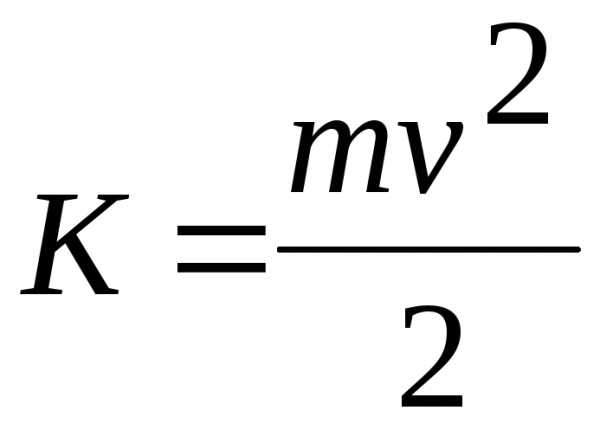называется кинетической энергией частицы. Таким образом, работа всех сил, действующих на частицу, идет на изменение ее кинетической энергии, т.е.

dK=dA или .

3. Консервативные силы и потенциальная энергия

Сила, работа которой не зависит от формы и длины пути (от траектории точки приложения силы), называется консервативной силой.

Математически условие консервативности силы выражается в виде:

.

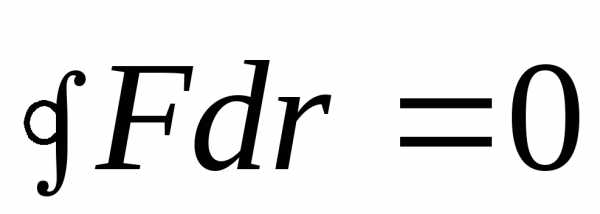Действительно, работа консервативной силы на замкнутом пути в силу определения будет: . Величина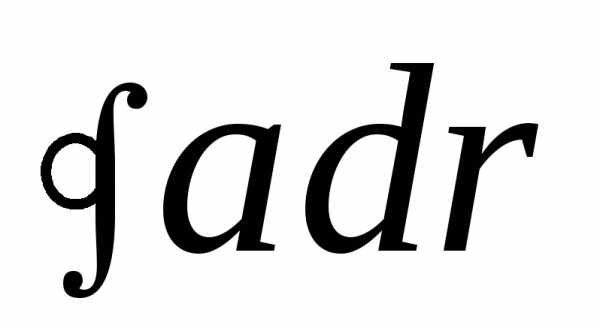называетсяциркуляцией вектора . Поэтомуциркуляция консервативной силы по любому замкнутому контуру равна нулю.

Из определения консервативной силы вытекает и еще одно важнейшее свойство: работа консервативной силы равна изменению (убыли) некоторой скалярной функции , зависящей только от положения частицы (тела) и

называемой потенциальной энергией:

или

.

Последняя из формул являются определением потенциальной энергии.

Как следует из нее, потенциальная энергия определена с точностью до

произвольной постоянной.

studfiles.net

2.5. Второй закон Ньютона

Итак, импульс замкнутой физической системы сохраняется. Причина изменения импульса тела (и отклонения от режима равномерного прямолинейного движения)  внешнее воздействие, мерой которого является сила.

Основным законом динамики поступательного движения является второй закон Ньютона. В самой общей формулировке он читается так: скорость изменения импульса тела равна действующей на него силе.

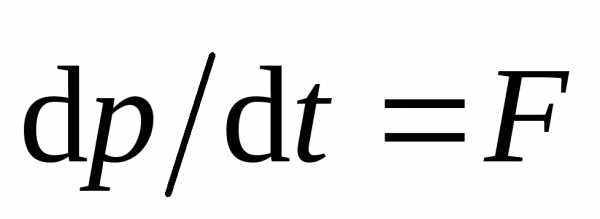. (2.5)

Если масса тела в процессе движения не меняется, то можно записать

,

так что получаем

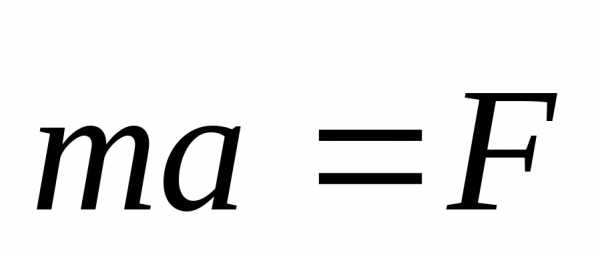. (2.5а)

В уравнениях (2.5) и (2.5а) под следует понимать равнодействующую всех приложенных к телу сил.

Перепишем уравнение (2.5) в следующем виде:

. (2.5б)

Величина 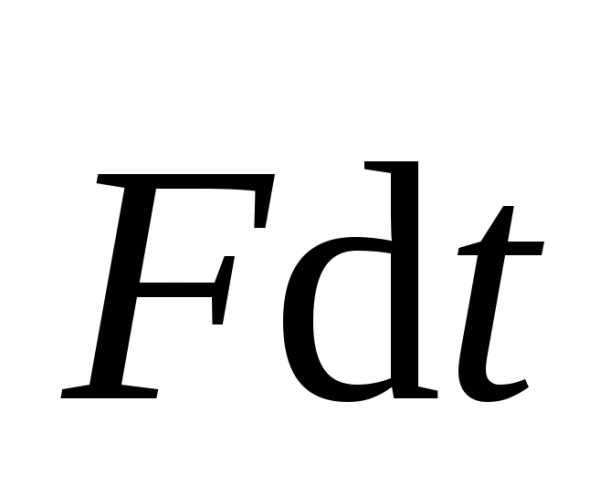, численно равная произведению силы на время ее действия и направленная по направлению силы, называется импульсом силы.

Заметим, что уравнение (2.5) является, по сути, количественным определением понятия силы: если физическая система не является замкнутой, то ее импульс характеризует меру действующей силы (сравните с уравнением (2.4а) и законом сохранения импульса). Иначе действующая сила есть мера незамкнутости системы.

2.6. Третий закон Ньютона и закон сохранения импульса

Опыт показывает, что воздействие тел друг на друга всегда является взаимным,парными силы всегда возникают парами. Если тело1действует на тело2с силой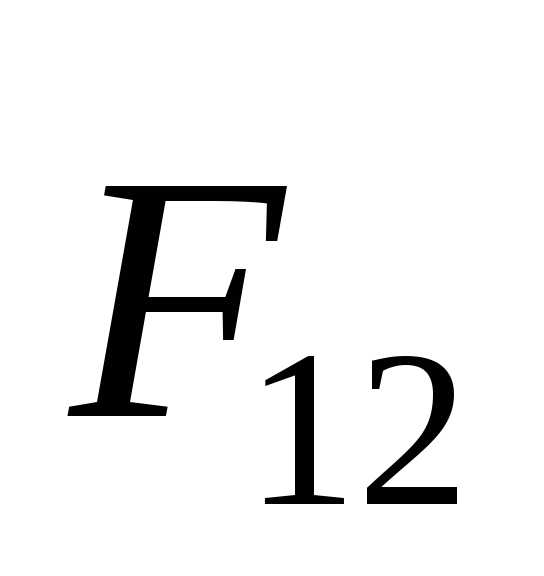, то, в свою оче­редь, тело 2действует на тело1с силой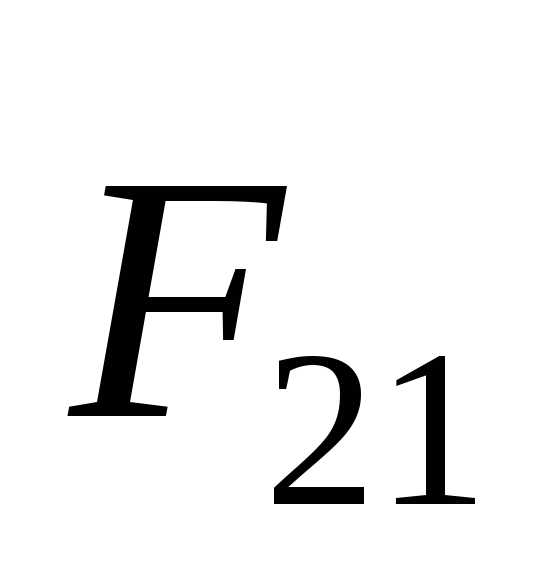, при­чем силы взаимодействия равны по величине и противоположны по направлению (рис. 2.2).

В этом заключается суть третьего закона Ньютона: всякому действию есть равное и противоположное противодействие; иначе,силы, с которыми взаимодействуют тела, равны по величине и противоположны по направлению:

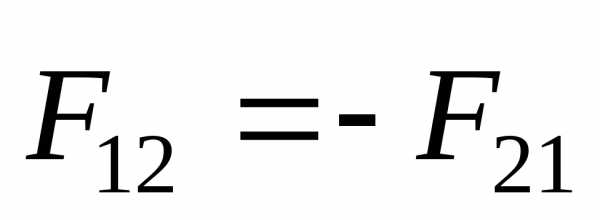. (2.6)

Этот закон является следствием закона сохранения импульса для пары тел. В самом деле, если от выражающего этот закон уравнения взять производную по времени, получим

,

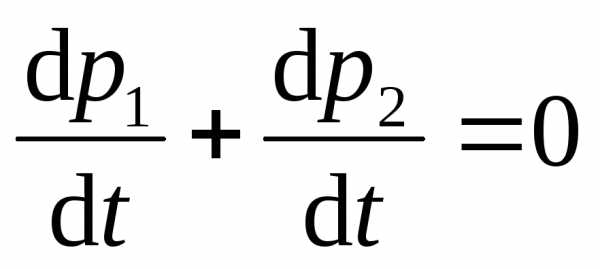что с учетом (2.5а) дает уравнение (2.6).

2.7. Преобразования и принцип относительности Галилея

Уравнение 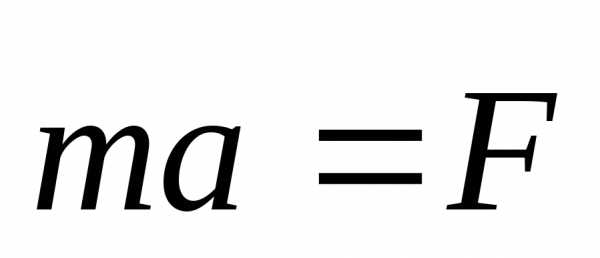, выражающее второй закон Ньютона, показывает, что этот закон не может быть справедлив в любой системе отсчета. Действительно, ускорение тела различно в системах отсчета, движущихся друг относительно друга с ускорением. В то же время действующая на тело сила определяется только взаимным расположением и скоростями тел физической системы, а значит, от выбора системы отсчета не зависят.

Второй закон Ньютона выполняется в инерциальных системах отсчета. Их множественность и равноправие при описании движения тел, а вследствие этого эквивалентность состояния покоя и прямолинейного равномерного движения доказываются так называемыми преобразованиями Галилея, связывающими значения характеристик тела в различных системах отсчета.

При описании движения тел в ряде случаев бывает удобно использовать несколько различных систем отсчета. Обычно одну из них, условно неподвижную, называют лабораторной системой отсчета (ЛСО), другую – движущейся (ДСО).

Пусть ЛСО является инерциальной. Докажем, что если ДСО не имеет относительно нее ускорения, то она также инерциальная.

Положение тела в ЛСО зададим радиусом-вектором , в ДСО – радиусом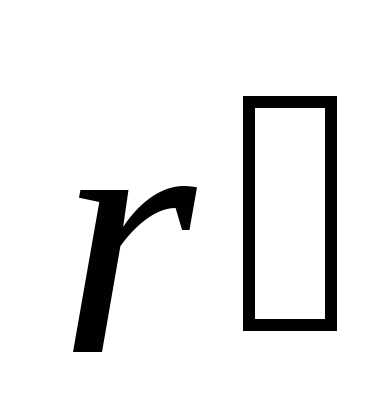-вектором(рис. 2.3). Положение начала отсчета ДСО – точкиО‘ – описывается в ЛСО вектором . Из геометрических соображений очевидно, что

.

В классической механике постулируется, что время во всех системах отсчета течет одинаково: t = t’.

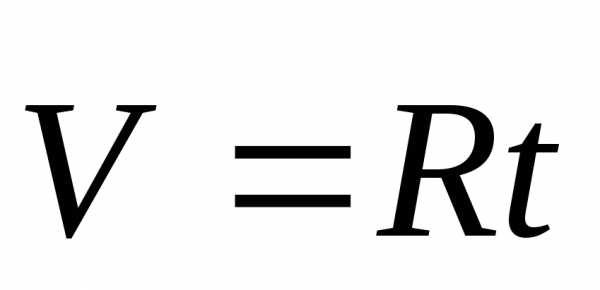Если ДСО движется равномерно вдоль оси х ЛСО со скоростью , то, так что

. (2.7)

В координатной форме это выражение можно записать так:

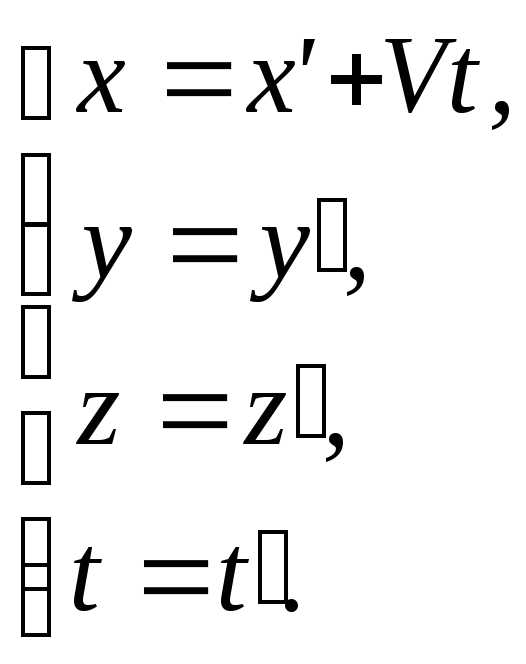(2.7а)

Эти соотношения и называются преобразованиями Галилея для координат.

Возьмем от уравнения (2.7) производную по времени:

,

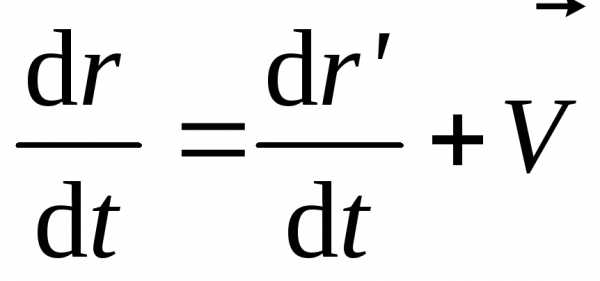т.е.

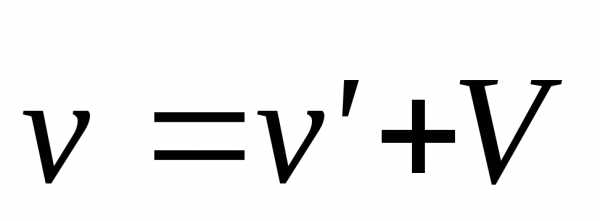. (2.8)

Это уравнение связывает скорости тела в ЛСО и ДСО и носит название классического закона сложения скоростей.

Возьмем еще раз производную по времени:

,

что дает

.

Таким образом, ускорение тела в рассматриваемых системах отсчета одинаково, а потому система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной системы отсчета, также является инерциальной. Поскольку масса тела считается в классической механике одинаковой во всех системах отсчета, то это означает, что закон движения (второй закон Ньютона) во всех инерциальных системах отсчета имеет одинаковый вид.

В результате Галилей сформулировал принцип относительности: во всех инерциальных системах отсчета все механические процессы описываются одинаковыми законами и происходят одинаково.

Иначе говоря, уравнения механики Ньютона, описывающие движение физических тел инвариантны относительно преобразований Галилея.

А. Эйнштейн обобщил этот принцип: во всех инерциальных системах отсчета все физические процессы описываются одинаковыми законами и происходят одинаково.

studfiles.net

§5. Второй и третий законы Ньютона.

Второй закон сформулирован И. Ньютоном следующим образом [6, с.233]: “Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует”.
Чтобы представить этот закон в математическом виде, Ньютону пришлось ввести понятие массы, характеризующей количество материи, содержащейся в теле.
Если следовать приведенному определению, то второй закон Ньютона должен иметь следующее математическое выражение:
,                                                                                    (1)
где – изменение количества движения mV, k – коэффициент пропорциональности, F– приложенная к телу сила. Вполне очевидно, что данная формулировка не соответствует общепринятой формулировке второго закона, устанавливающего связь между силой и ускорением:
,                                                    (2)
так как время нельзя считать коэффициентом пропорциональности, поскольку оно изменяется и, следовательно, не является постоянной величиной.
Предполагается, что форму (2) второму закону Ньютона впервые придал Д. Бернулли [10, с.89].
В таком же виде выше нами было получено соотношение между мгновенным воздействием и изменением скорости при взаимодействии материальных объектов (см. главу I):
,                                                                                        (3)
где – фактор мгновенного воздействия, представляющий силу F, действующую на рассматриваемый материальный объект, – мгновенное изменение скорости в функции времени (ускорение).
Следует отметить, что соотношение (3) нельзя считать строгим доказательством второго закона Ньютона, это скорее результат, вытекающий из здравого смысла, поэтому его можно рассматривать просто в качестве гипотезы.
Ньютон нигде не дает доказательства второго закона, он его просто постулирует. Можно даже сказать, что он просто угадан Ньютоном и то неточно. И после Ньютона никто не смог вывести этот закон из каких-то более общих предпосылок. Таким образом, второй закон Ньютона следует считать одной из аксиом или гипотез, лежащих в основе механики. И тем не менее открытие этого закона является величайшим достижением человеческого ума, позволившим механике стать настоящей наукой и давшим ей основу для дальнейшего развития.
Мы показали, что второй закон Ньютона характеризует мгновенное локальное взаимодействие тел и устанавливает связь между силой и ускорением, возникающим при взаимодействии в данной точке пространства. Понятие мгновенного взаимодействия не устанавливает физической сущности силы, то есть не является ее определением. Поэтому нельзя говорить, что сила это произведение массы тела на его ускорение. Это соотношение определяет величину силы, но не ее физическую сущность. Физическая сущность силы может быть понята из соотношений, полученных нами в первой главе:
,                                                                                             (4)
,                                                                                   (5)
где первое выражение может трактоваться как силовая характеристика поля кинетической энергии для сплошной среды, а второе – выражение силы для дискретного тела, энергия которого изменяется при движении в пространстве. Именно изменение энергии в пространстве, а точнее скорость ее изменения по пространственной координате, и характеризует физическую сущность силы. Чем быстрее будет изменяться энергия, тем больше будет сила, и наоборот. Это объясняется тем, что именно кинетическая энергия является тем свойством движущейся материи, которым обмениваются при взаимодействии материальные объекты.
Выражения (4) и (5) имеют более широкую область применения, чем второй закон Ньютона в форме (2). Это объясняется тем, что мгновенное взаимодействие материальных объектов можно рассматривать не только в виде дискретных тел, но и в виде сплошных сред, что приводит к полевой форме взаимодействия. Поэтому второй закон Ньютона можно считать частным случаем выражений (4) и (5).
Однако, следует обратить внимание на следующее важное обстоятельство. При выводе соотношения (3) мы считали, что изменение скорости от внешнего воздействия будет одинаково и происходит одновременно для всех точек тела. Такое предположение для реальных тел не всегда будет точно выполняться, так как все материальные объекты деформируются из-за конечной скорости распространения воздействия. Исключение могут составлять только воздействия, осуществляющиеся одновременно по всему объему тела, как, например, при действии сил тяготения. Поэтому второй закон Ньютона будет в определенной степени приближенным при использовании его для исследования движения реальных тел. Ниже будет показано, как можно учесть влияние деформации тел на характер их движения.
Следует иметь в виду также и то, что выражение силы через кинетическую энергию будет справедливо только для энергии, связанной с упругой деформацией тел. Энергия же, затраченная на структурные преобразования и нагрев тел, учитываться не должна. Это будут так называемые потери энергии, изменяющие энергию составляющих тело частиц, но не механическую энергию движения тела в целом.
Переходим теперь к рассмотрению третьего закона Ньютона, который гласит [6, с.233]: “Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга равны и направлены в противоположные стороны”.
Этот закон находится как бы в стороне от двух первых законов Ньютона и не связан с ними. Если закон инерции можно вывести из второго закона Ньютона, устранив внешнее воздействие на тело, то есть приняв силу равной нулю, то третий закон существует как бы сам по себе. Ньютон пришел к необходимости этого закона по следующим причинам (цитируем [6, с.234]): “Третий закон динамики был подтвержден опытами Рена и Мариотта над ударами шаров. Сам Ньютон повторил эти опыты с большей точностью, введя поправку на сопротивление воздуха. Он нашел, что “третий закон по отношению к удару и отражению подтверждается теорией, вполне согласующейся с опытом”.
Подтверждается третий закон и для взаимодействий на расстоянии. Если бы эти взаимодействия не были бы равны, то поместив между взаимно притягивающимися телами препятствие, мешающее их сближению, можно было бы обнаружить, как это препятствие уступает действию большей силы. “Я производил подобный опыт с магнитом и железом; если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии”. Точно так же, если бы взаимные притяжения частей Земли не уравновешивались, то Земля ушла бы ускоренным движением в бесконечность”.
И, тем не менее, этот закон Ньютона можно считать только полуэмпирическим, так как он не имеет строгого теоретического доказательства, и поэтому его следует рассматривать только в качестве гипотезы или аксиомы.
Однако между двумя гипотезами, лежащими в основе второго и третьего закона Ньютона, существует достаточно тесная связь, которую мы сейчас и попытаемся установить. Для этого сперва используем второй закон в форме (3):

Так как характеризует величину мгновенного воздействия на тело, то есть воздействия на тело при данном его положении в пространстве, то, суммируя все мгновенные воздействия при перемещении тела в пространстве, получим следующее соотношение (см. формулу (1.5.8)):
,                                              (6)
где – проекция силы F на направление движения тела, V и – скорости движения тела в конце и в начале движения, – изменение кинетической энергии тела на перемещении s.
Выражение (6) говорит о том, что работа внешних сил затрачивается на изменение кинетической энергии движущегося тела. Из выражения (6) вытекает также необходимость понятия самой кинетической энергии.
Теперь рассмотрим сам факт мгновенного взаимодействия с другой стороны. Если на данный материальный объект со стороны других дискретных материальных объектов или материальной среды существует какое-то воздействие в данном месте пространства, то будет вполне логичным предположить, что такое же воздействие будет и со стороны данного тела на контактирующие с ним материальные объекты, так как при взаимодействии материальных объектов обязательно должен быть непосредственный контакт между ними. Это утверждение, кстати, будет относиться ко всем видам взаимодействий, существующим в природе. И если даже тела взаимодействуют друг с другом на каком-то расстоянии, то это значит, что взаимодействие происходит с помощью промежуточной среды, когда воздействие передается от частицы к частице. Правомерность такого утверждения будет нами доказана в последующих главах.
Следует отметить, что, когда мы говорим о равенстве мгновенных взаимодействий, то имеем в виду полные мгновенные взаимодействия F, отнесенные к взаимодействующим объектам в целом, а не к единице их массы.
Если считать такое предположение верным, то для внешних по отношению к данному телу материальных объектов будет справедливо выражение (6), представленное в следующем виде:
,                                         (7)
где изменение скоростей и энергий будет иметь противоположное значение по сравнению с данным объектом, что и характеризуется знаком минус.
Так как силы , характеризующие мгновенное воздействие, для обоих объектов будут по величине одинаковыми, то их работы на одном и том же перемещении, определяемые интегралами в левой части выражения (7), также будут одинаковыми, а это значит, что будут равны и правые части, то есть:
(8)
Отсюда следует, что какую энергию приобретет тело при внешнем воздействии на него, точно такую же энергию потеряют действующие на него материальные объекты, а это и есть не что иное, как закон сохранения энергии.
Таким образом, закон сохранения энергии получается как следствие закона равенства действия и противодействия, то есть третьего закона Ньютона, рассматриваемого совместно со вторым его законом. И если учесть то обстоятельство, что все взаимодействия, как мы покажем это ниже, имеют механическую природу, то можно считать, что второй и третий законы Ньютона являются основными законами природы.
Хотя эти законы и не имеют строгого обоснования, то с точки зрения здравого смысла и их практического использования они вполне достоверны. Действительно, если вдуматься в процесс взаимодействия материальных объектов, то сам факт взаимодействия за счет непосредственного контакта между материальными объектами в одном и том же месте пространства не должен вызывать сомнения. Взаимное действие материальных объектов при их непосредственном контакте вряд ли может быть различным, поскольку оно осуществляется в одном и том же месте пространства в одно и то же время. Несомненно также, что мгновенные взаимодействия будут являться причиной всех материальных процессов и явлений, происходящих в природе. Этот факт лежит в основе принципа причинности и детерминизма. На наш взгляд, такое объяснение будет вполне естественным и логичным.
Ниже будет показано, что закон сохранения энергии лежит в основе многих законов механики. Поскольку мы его получили из двух законов Ньютона, то тем самым мы исключили одну гипотезу, каковой до настоящего времени являлся закон сохранения энергии, то есть число недоказанных гипотез стало меньше. Тем самым мы привели основания механики к более строгому виду.
Однако, на рассматриваемую ситуацию можно взглянуть и с другой точки зрения. Мы предполагали, что при взаимодействии материальных объектов должны выполняться две гипотезы в форме второго и третьего законов Ньютона, из которых вытекает закон сохранения кинетической энергии, причем в гипотезе о втором законе Ньютона, характеризуемой выражением (3), использование массы является чисто эмпирическим фактом и, кроме того, эта характеристика взаимодействия не может быть отнесена к тем случаям, когда отсутствует движение в направлении взаимодействия материальных объектов. Для таких случаев следует использовать условие взаимодействия в форме выражений (4) или (5), по отношению к которым условие (3) можно считать частным случаем. Выражения (4) и (5) представляют собой скорость изменения кинетической энергии по пространственной координате, они могут быть получены, как будет показано в следующем параграфе, из закона сохранения кинетической энергии при взаимодействии материальных объектов. Тогда в качестве основной характеристики взаимодействия в качестве гипотезы можно использовать закон сохранения кинетической энергии, при этом исключается гипотеза о равенстве действия и противодействия, а второй закон Ньютона будет являться просто математической формулой, устанавливающей связь между силой и скоростью изменения кинетической энергии. В итоге, вместо двух гипотез, положенных нами в основу законов механики, останется всего одна, причем масса тел органично входит в выражение кинетической энергии. Такое использование закона сохранения кинетической энергии в качестве основной и единственной гипотезы представляется нам целесообразным. Это свойство закона сохранения кинетической энергии отображено в таблице иерархии основных понятий, законов и принципов механики.
При рассмотрении третьего закона Ньютона следует обратить внимание на одно важное обстоятельство, связанное с наличием сил инерции. До сих пор под равенством действия и противодействия понималось равенство сил, с которыми взаимодействующие тела действуют друг на друга. Но ведь при взаимодействии возникают и силы инерции, которые, как мы показали, тоже являются реальными силами. Сила инерции является реакцией со стороны тела на внешнее воздействие. Она в точности равна действующей на тело внешней силе и направлена ей навстречу. Отсюда следует, что сила инерции будет уравновешивать движущую силу, то есть система действующих на тело сил с учетом силы инерции будет уравновешена. Таким образом, мы получили доказательство принципа Даламбера в его современной формулировке, сущность которого будет подробно рассмотрена в §7.
Третий закон Ньютона имеет и еще одно важное следствие, на которое до сих пор не обращали внимания. Так, если тело движется, преодолевая какое-либо сопротивление среды или силы трения, то на него будет действовать, уравновешиваясь попарно, уже четыре силы: движущая сила и сила инерции (упругая сила деформации) с одной стороны и сила инерции и сила сопротивления с другой стороны, причем силы инерции в обоих случаях будут направлены в разные стороны (рис.1), навстречу действующим на тело внешним силам. То же самое будет происходить и в случае неподвижного тела, когда действие внешней силы уравновешивается реакцией опоры (рис.2). Таким образом, в этих случаях движущая сила и сила сопротивления будут уравновешиваться не непосредственно друг другом, а через посредство силы инерции, являющейся упругой силой деформации. И вообще, следует обратить внимание на то, что силы, действующие на тело, включая и силы инерции, должны существовать попарно, образуя уравновешенную систему, независимо от состояния тела или характера его движения. Поэтому утверждение о том, что центростремительная сила может существовать без центробежной силы инерции, которое некоторые ученые используют для объяснения фиктивности сил инерции, и с этой точки зрения неверно. Сила может уравновешиваться только силой, и ничем больше.

 

energy-source.ru

Пятый закон Ньютона | Bigital.ru

Александр Альбов (С.-Петербург)

Эта история началась в марте 1697 года, когда  начался визит Петра I в Западную Европу. Длился он более года и получил название Великого посольства. Дипломатичской целью визита было стремление Петра заручиться поддержкой европейских стран в борьбе против Турции и Швеции. И, главное, молодой русский царь хотел лично познакомиться с жизнью и порядками Европы, лучшую часть которых он хотел перенести в Россию.

Прежде всего Петра интересовало, конечно, кораблестроение, А потому в Голландии он устроился под именем плотника Петра Михайлова на верфь и своими руками построил корабль и под руководством мастера Поля, при этом  усвоил все то, что «подобало доброму плотнику знать». Однако на все вопросы «Почему именно так?» он слышал одно и то же: «Потому что так строили наши деды и прадеды». Вскоре Петр понял, что «не только руками надлежит будущие великие дела творить, но знать нужно и весьма глубоко всякую теорию, и в том числе корабельную». В Голландии же теорию не почитали, почему Петру «зело стало противно, что такой дальний путь для сего воспринял, а желаемого конца не достиг». Петр считал, что в Англии «архитектура сия так в совершенстве, как и другие, и что кратким временем научиться мочно».

Английский король Вильгельм III (по совместительству правитель Голландии) познакомился с Петром в Гааге. Вильгельму понравился оригинальный ум молодого царя, ему импонировала его энергия, страсть к наукам и в особенности к кораблестроению. Он желал привлечь Петра на свою сторону и по возвращении в Лондон решил подарить ему только что построенную, новейшую по тем временам, легкую и красивую 20-пушечную яхту «Транспорт-Ройял». Петр сразу полюбил морскую красавицу и послал поблагодарить. Посланцу было также сказано, чтобы он сообщил королю о намерении Петра «посетить английскую землю незнатным иностранцем, чтобы видеть корабли и морское поведение». Вильгельм был в восторге от этой идеи, видя в ней большой политический смысл, и тут же выслал для сопровождения царя королевскую яхту и три линейных корабля.

Взяв с собой шестнадцать «волонтеров», включая Меншикова, Петр 7 января 1698 года покинул Амстердам. Уже через три дня яхта бросила якорь у лондонских доков. Через три дня король посетил Петра и разговаривал с ним на голландском языке. Петру в то время исполнилось двадцать шесть лет. Он был молод и любознателен, полон великих планов. Петр посетил корабельные верфи в Дептфорде, Портсмуте и Чатаме, Вулвичский арсенал, лондонские фабрики и мастерские. В начале марта Петр ездил в Гринвичскую астрономическую обсерваторию. Там он проводил наблюдения неба. К тому же в Англии к тому времени уже появились зачатки основной кораблестроительной дисциплины – теории корабля. Повсюду Петр старался получить какие-нибудь чертежи, рисунки, модели. У него завязались прочные отношения с математиками, астрономами и другими учеными.

О поездке  Петра в Оксфорд упоминается в университетском архиве. Главной целью посещения Оксфордского университета было знакомство с профессорами геометрии, астрономии и географии — предметов, связанных с мореплаванием и навигацией и в связи с этим особо интересовавших Петра.

Так Петр встал у колыбели возникающей российской науки. Как же естественна была встреча Петра с Ньютоном! К сожалению, документов о том, как  Петр встречался с Ньютоном, не сохранилось. Единственным документом, способным пролить хоть немного света на пребывание Петра в Англии, приходится признать «Юрнал» — тайный дневник, который вел Петр в Лондоне.  Встреча с Ньютоном произошла, когда Петр посещал Тауэр и расположенный там Монетный двор, хранителем которого был Ньютон (это было два раза, 27 января и 3 апреля 1698 года). Посещение Петром Тауэра 27 января описано в «Юрнале» относительно подробно: «Проехали на правой стороне Темзы здание, именуемое Тур, где английския честных людей сажают за караул». И, чуть ниже, «был в Туре, где денги делают».  В первый свой визит Петр подробно ознакомился с деньгоделательными машинами – станками для механической чеканки монет (в России монеты чеканили вручную). Дело в том, что Англию в то время захлестнул бум массовой порчи и подделки серебряных монет – шиллингов. Предпосылками порчи (срезания части монеты) и подделки денег были несовершенство чеканки монет, а также слабость режима конституционной монархии, установившегося в Англии после «Славной революции» 1688 года, приведшей к свержению короля Якова II.

А вот по поводу второй встречи, 3 апреля 1698 года, за три недели до отъезда Петра из Англии, не сохранилось ни одного документа  ни в английских, ни в российских архивах.

А было вот что. Разговор на этот раз шел не о деньгах, а о том, что интересовало Ньютона как ученого. Речь шла о фундаментальном труде Ньютона, в котором он сформулировал закон всемирного тяготения и три закона движения, ставшие основой классической механики и названные его именем. Труд назывался «Математические начала натуральной философии» или, на современном языке, «Математические основы физики». 28 апреля 1686 года первый том «Математических начал» был представлен Королевскому обществу. Все три тома, после некоторой авторской правки, вышли в 1687 году.

В августе 1684 года астроном Галлей приехал в Кембридж и рассказал Ньютону, что он и Гук обсуждали, как из формулы закона тяготения вывести эллиптичность орбиты планет, но не знали, как подступиться к решению. Ньютон сообщил, что у него уже есть такое решение, и вскоре прислал его Галлею. Тот сразу оценил значение результата и метода доказательства, в ноябре снова навестил Ньютона и на этот раз стал уговаривать его опубликовать свои открытия…

* * *

Все это время Петр I смотрел на Ньютона восхищенными глазами.

– А теперь, государь, спустимся в мою тайную кладовую. Прошу Вас следовать за мной.

– Охотно.

– Однажды я спустился в один из подвалов, коих в Тауэре великое множество, где обнаружил старинные книги по черной магии, Я задержался там до полуночи, — рассказывал Ньютон. – Сумерки опустились быстро, и мне показалось странным голубое свечение, исходящее из большого центрального зала. Когда я вошел туда, в лицо мне ударил яркий голубовато-серый сноп света, исходящий от висящей в воздухе модели солнечной системы. Эту систему, где Солнце является центральным небесным телом, вокруг которого обращается Земля и другие планеты, первым предложил еще в III веке до нашей. эры Аристарх Самосский, но широкое распространение она получила лишь два века назад, когда польский астроном Николай Коперник опубликовал свою книгу “О вращениях небесных сфер“, Церковь за аналогичные взгляды в 1600 году сожгла на костре итальянского монаха Джордано Бруно, она еще многие столетия считала, что в центре мироздания находится Земля, а вокруг нее вращаются Солнце, Луна и другие планеты.

Я подошел ближе, чтобы рассмотреть модель, и вскоре понял, что ошибся – это была не модель солнечной системы, а модель строения атома.

– А что есть атом? — Спросил Петр.

– Атом, по-гречески «неделимый»,– это мельчайшая частица вещества. Древние считали его неделимым, но вскоре оказалось, что атом состоит из ядра и электронной оболочки.  Электронная оболочка атома – это совокупность всех электронов в данном атоме. Ваш будущий соотечественник, русский химик Дмитрий Менделеев, в 1869—1871 годах установит зависимость свойств химических элементов от их атомного веса и свел все известные на ту пору элементы в двумерную таблицу, в которой каждый столбец определяет основные физико-химические свойства, а строки представляют собой периоды, в определенной мере подобные друг другу.

– Вы сказали в 1869—1871 годах, то есть через два века после нас? – переспросил Петр.

– Да, именно так. Запаситесь терпением, государь, Сейчас истина откротся Вам.

По легенде, мысль о системе химических элементов пришла к Менделееву во сне, однако однажды на вопрос, как он открыл периодическую систему, ученый ответил: «Я над ней, может быть, двадцать лет думал, а вы думаете: сидел и вдруг… готово».

В 1913 году датский физик Нильс Бор завершит картину микромира, предложив модель строения атома. В ней электроны вращаются вокруг ядра подобно планетам вокруг Солнца. В этой модели ядро атома состояло из нейтронов, положительно заряженных протонов и некоторого числа электронов, нейтрализующих их заряд; суммарный заряд электронов был равен положительному заряду ядра.

— Значит, Вы, сэр, объяснили картину макромира, а Менделеев и Бор объяснили строение микромира?

— Все немного сложнее, друг мой. Пройдет более 10 лет, и эта модель подвергнется пересмотру. В 1930 году немец Вальтер объявит об открытии нового вида радиоактивного излучения с применением элементарных частиц. Немецкие ученые установят, что при расщеплении ядра атома урана выделяются несколько нейтронов, каждый из которых, в свою очередь, способен инициировать распад атомов урана, вызвать цепную реакцию с выделением огромного количества энергии. На горизонте замаячила перспектива создать бомбу колоссальной разрушительной силы – атомную бомбу. Немцы назовут это оружие «Wunderwaffe».

– «Чудо-оружие»?

– Да. Но, к счастью, они не успеют воплотить это дьявольское изобретение. Раньше русская армия положит конец этой войне.

– Слава богу – Петр широким жестом перекрестился. И добавил:

– Однако, сударь, я ничего не понял в этих протонах, нейтронах и прочих элементарных частицах.

– А Вам и не надо ничего понимать. Я уже подошел к главному. Вы обратили внимание на мои слова «электроны вращаются вокруг ядра подобно планетам вокруг Солнца»?

– Да – неуверенно ответил Петр.

– Так вот, я не знаю, когда, но ученые установят, что и элементарные частицы имеют строение, схожее с Солнечной системой. И, напротив, вполне может статься, что вся наша Солнечная система – всего лишь атом в каком-то другом супермакромире. Получается что-то вроде русской игрушки, которую у вас называют «Матрёшка» — система вложенных друг в друга миров. В этом и только в этом смысле наша Вселенная бесконечна. Эти миры я назвал «параллельными мирами». Первым о параллельных мирах в 1895 году сообщит английский писатель-фантаст Герберт Уэллс в рассказе «Дверь в стене». Физика параллельного мира не обязательно аналогична физике нашего мира.

Параллельные миры – это и есть суть моего пятого закона. Но, как Вы понимаете, заявить об этом открыто я не могу – Церковь все еще очень сильна. Конечно, меня навряд ли сожгут на костре, но Святые отцы придерживались геоцентрической системы очень долго и признали ее ошибочность только в 1963 году, спустя два года после первого космического полета Юрия Гагарина вокруг Земного шара.

– Гагарин – тоже русский?

– Да, его имя облетело весь мир. В знак признания ошибки во внутреннем дворике Ватиканского дворца будет установлен памятный знак – большая полусфера из начищенной до блеска меди.

– Как вы можете знать о том, что будет через триста-четыреста лет?

– А я был там и тогда. И видел все это своими глазами. Только в параллельном мире. Время там течет быстрее, чем у нас, и тем быстрее, чем ниже уровень вложенности. А порталом для перехода в параллельный мир и служит вот эта самая модель строения атома. Хотите испробовать?

– Нет уж, увольте, сэр. – Петр замахал руками. – Скажите только, какая судьба ждет лично меня?

– О, не волнуйтесь, Ваше величество. Вы поставите всю свою страну «на дыбы» и, благодаря этому, одержите целый ряд блистательных побед на суше и на море и закончите жизнь в своей  постели Петром Великим.

* * *

А через три недели, 25 апреля 1698 года, Петр отдал Англии прощальный салют.

Ньютон еще долго помнил Петра. Когда он составлял список рассылки дарственных экземпляров второго издания «Начал» — а это было через десяток с лишним лет, — первым в этом списке он поставил имя русского царя…  Петр, получив дарственный экземпляр, пролистал его и обнаружил в конце книги целый ряд пустых, ничем не запечатанных страниц. Он сразу понял, что это место Ньютон оставил для своего пятого закона.

К сожалению, этот экземпляр не сохранился для истории. Правда, в годы войны, 1943 году, один экземпляр этого редчайшего издания Королевское общество подарило Академии наук СССР на празднование 300-летнего юбилея Ньютона. Однако незапечатанных страниц в нем уже не было.

bigital.ru

2.5. Второй закон Ньютона

Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело силе F:

dp/dt=F. (2.4)

Заменив в уравнении (6) р на mV получим:

d(mV)/dt = m (dV/dt) = m(d²r)/dt² = F. (2.5)

Таким образом, зная силу, действующую на тело, можно определить характер его движения r(t). Поэтому второй закон Ньютона в виде (2.5) называют уравнением движения.

Если в (2.5) заменить dV/dtна ускорение телаа, получится еще один вид закона:

d(mV)/dt=mа=F, (2.6)

или словами: произведение массы тела на его ускорение равно действующей на тело силе.

В частном случае, когда F= 0 (т. е. при отсутствии воздействия на тело со стороны других тел), ускорение, как следует из (2.6),также равно нулю. Этот вывод совпадает с утверждением первого закона Ньютона. Поэтому первый закон входит во второй как его частный случай. Несмотря на это, первый закон формулируется независимо от второго, так как в нем, кроме того, заключается постулат о существовании инерциальных систем отсчета.

2.6. Третий закон Ньютона

Всякое действие тел друг на друга в природе носит характер взаимодействия: если тело 1 действует на тело 2 с силой F₁₂ то и тело 2 в свою очередь действует на тело 1 с силойF₂₁.Третий закон Ньютона при этом утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Используя приведенные выше обозначения сил, содержание третьего закона можно представить в виде равенства:

F₁₂ = – F₂₁. (2.7)

Из третьего закона Ньютона вытекает, что силы возникают попарно: всякой силе, приложенной к какому-то телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу, взаимодействующему с данным.

На рис. 2.2 в качестве примера приведены гравитационные силы, действующие между двумя телами массами m₁ и m₂, находящимися на расстоянии r друг от друга.

2.7. Преобразования Галилея. Принцип относительности Галилея

Преобразования Галилея связывают значения координат и скоростей материальной точки в двух системах отсчета, движущиеся друг относительно друга с постоянной скоростью V₀. Одну из этих систем, обозначенную на

рис. 2.3 буквой К,будем считать неподвижной. Тогда вторая система К будет двигаться прямолинейно и равномерно относительно К. Выберем координатные осиx,y,z системыK и осиx,y, иz системы К так, чтобы осиxиx, совпадали, а осиy, иy, атакжеzи z были параллельны друг другу. Найдем связь между координатамиx,y,z некоторой точки Р в системе К и координатамиx,y, иz той же точки в системе К.Если начать отсчет времени

с того момента, когда начала координат обеих систем совпадали, то, как видно из рис. 3, x = x+V₀t, y = y,z=z. Добавив к этим соотношениям принятое в классической механике предположение, чтовремя в обеих системах течет одинаковым образом, то есть t = t, получим совокупность четырех уравнений:

x = x +V₀t, y = y, z = z, t = t, (2.8)

называемых преобразованиями Галилея для координат и времени.

Первое и последнее из соотношений (10) оказываются справедливыми лишь при значениях V₀ , малых по сравнению со скоростью света в вакууме, которую мы будем обозначать буквой С (V₀<<C).При V₀ сравнимых c C преобразования Галилея должны быть заменены более общими преобразованиями Лоренца. Продифференцировав соотношения (2.8) по времени, найдем связь между скоростями точки P по отношению к системам отсчетаK иK:

dx/dt=dx/dt+V₀илиV_x=V_x+V₀,

dy/dt = dy/dt или V_y = V_y , (2.9)

dz/dt = dz/dt или V_z = V_z .

Три скалярных соотношения (2.9) эквивалентны следующему соотношению между вектором скорости V по отношению к системе K и вектором скоростиVпо отношению к системеK.

V=V+V₀(2.10)

Формулы (2.9) и (2.10) дают правило сложения скоростей в классической механике. Следует иметь в виду, что соотношение(2.10), как и любое другое векторное соотношение, остается справедливым при произвольном выборе взаимных направлений координатных осей систем K и K. Соотношения же (2.9) выполняются только при выборе осей, показанном на рис. 2.3.

Как уже отмечалось, любая система отсчета, движущаяся относительно некоторой инерциальной системы с постоянной скоростью, будет также инерциальной. Теперь мы имеем возможность доказать это утверждение. Для этого продифференцируем по времени соотношение (2.10). Учтя, чтоV₀постоянна, получим:

dV/dt=dV/dtилиa=a.(2.11)

Отсюда следует, что ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, оказывается одним и тем же. Поэтому если одна изэтих систем инерциальна (это значит, что при отсутствии сил a = 0), то и остальные будут инерциальными (aтакже равно нулю).

Сила F, действующая на частицу в системе К, совпадает с силойF, действующей на частицу в системе К: F = F. Это следует из того, что сила зависит от расстояний между данной частицейи действующими на нее частицами (и, возможно, от относительных скоростей частиц), а эти расстояния (и скорости) полагаются в ньютоновской механике одинаковыми во всех инерциальных системах. Масса также одинакова во всех системах.

Из всего сказанного следует вывод, что уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой. С механической точки зрения все инерциальные системы отсчета совершенно эквивалентны:ни одной из них нельзя отдать предпочтение перед другими. Практически это проявляется в том, что никакими механическими опытами, проведенными в пределах данной системы отсчета, нельзя установить, находится ли она в состоянии покоя или в состоянии равномерного и прямолинейного движения. Находясь, например,в вагоне поезда, движущегося без толчков прямолинейно и равномерно, мы, не выглянув в окно, не сможем определить, движетсявагон или покоится. Свободное падение тел, движение брошенных нами тел и все другие механические процессы будут в этом случае происходить так же, как и в случае, если бы вагон был неподвижен. Указанные обстоятельства были выяснены еще Галилеем. Положение о том, что все механические явления в различных инерциальных системах отсчета протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно, носит название принципа относительности Галилея.

studfiles.net