Лекция 19. Алгебра матриц
Лекции по алгебре и геометрии. Семестр 2.
Лекция 19. Алгебра матриц.
Краткое содержание: Основные определения, действия с матрицами и их свойства, нулевая и единичная матрицы, обратная матрица и ее свойства, обратимые матрицы.
Глава 1. Алгебра матриц.
п.1. Основные определения.
Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.
Определение.
Матрицей размера 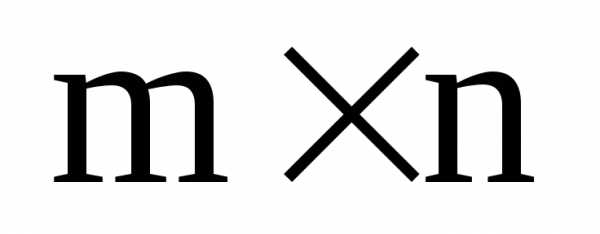 над полем К называется таблица элементов
поля К, имеющую
над полем К называется таблица элементов
поля К, имеющую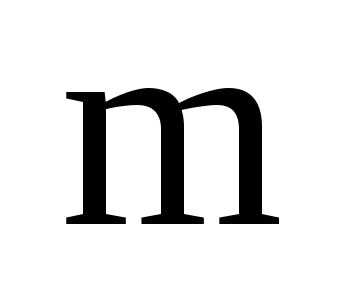 строк и
строк и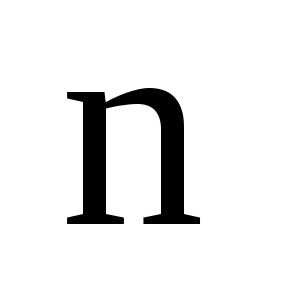 столбцов.
столбцов.
Обозначение:
.
Определение.
Элементы 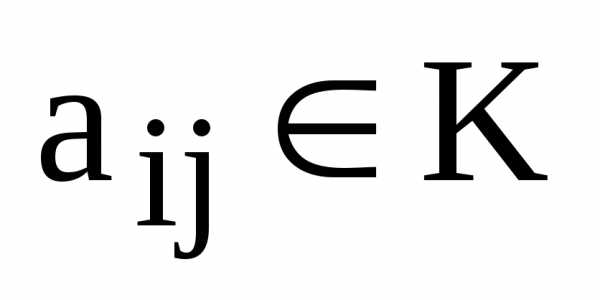 называются элементами матрицы, гдеi– номер строки, в которой находится
элемент
называются элементами матрицы, гдеi– номер строки, в которой находится
элемент
Определение.
Матрица размеров 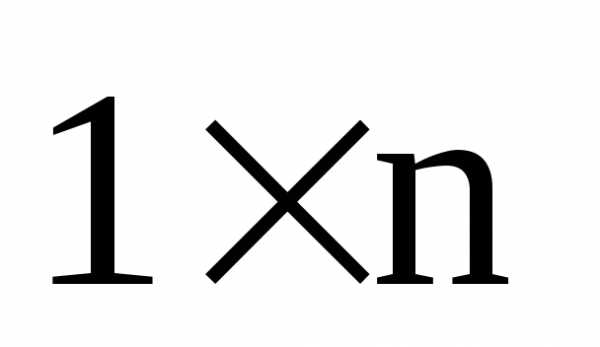 :
:
называется строкой
длины 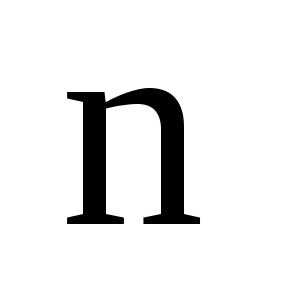 .
.
Определение.
Матрица размеров 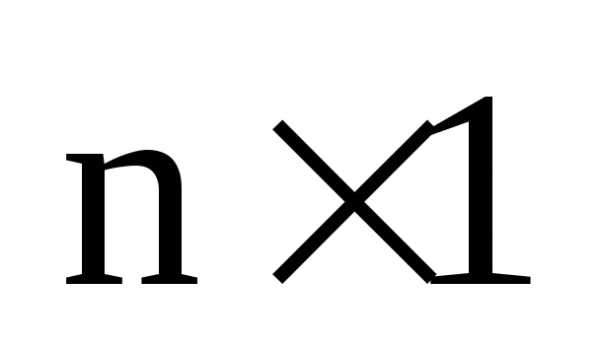 :
:
 называется столбцом
высоты
называется столбцом
высоты 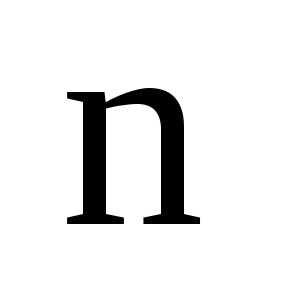 .
.
Определение.
Матрица размеров 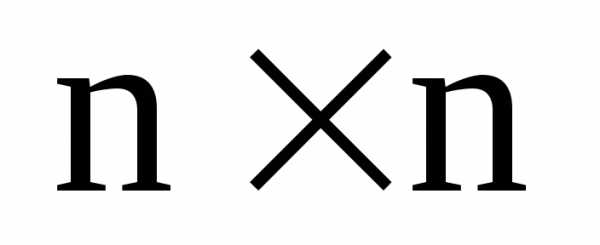 называется квадратной матрицей
называется квадратной матрицей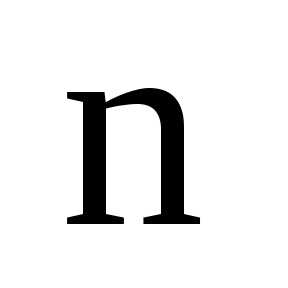
Определение. Матрица, все элементы которой равны нулю, называется нулевой.
В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.
Главную диагональ образуют элементы , т.е. элементы с одинаковыми нижними индексами.
Побочную диагональ образуют элементы .
Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:
 .
.
Определение.
Матрица В размера 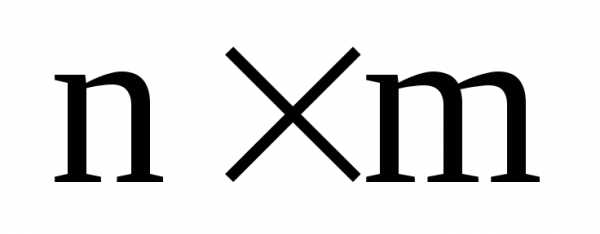 называется транспонированной по
отношению к матрице А размера
называется транспонированной по
отношению к матрице А размера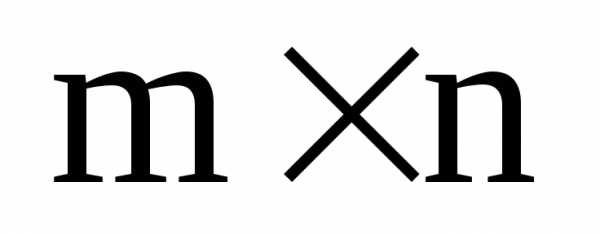
Обозначение: 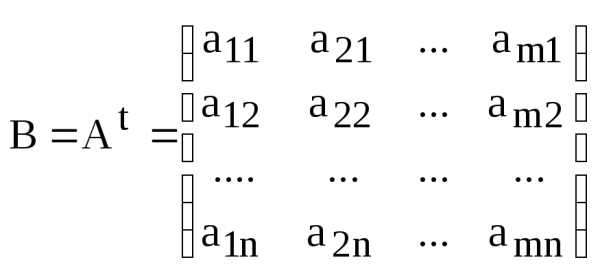 .
.
Определение. Процесс (процедура) получения транспонированной матрицы из данной называется транспонированием матрицы.
Пример:
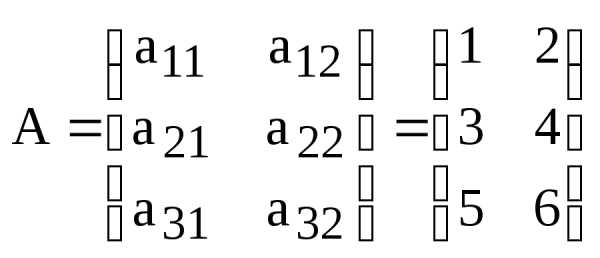 ,
.
,
.
Определение. Две
матрицы  и
и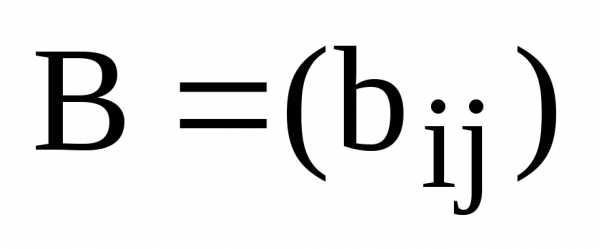 называются равными, если они имеют
одинаковые размеры и для всех значений
индексов выполняется равенство
называются равными, если они имеют
одинаковые размеры и для всех значений
индексов выполняется равенство
п.2. Сложение матриц.
Определение. Суммой
матриц 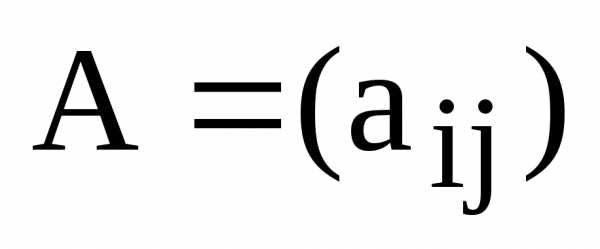 и
и одинаковой размерности
одинаковой размерности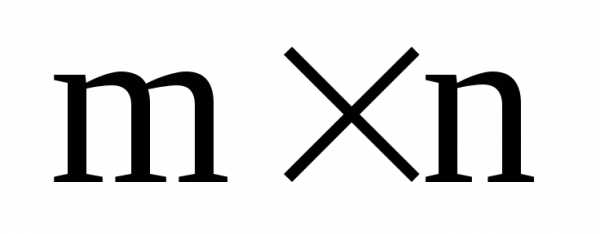 называется третья матрица
называется третья матрица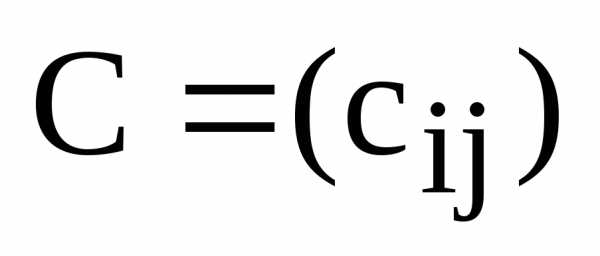 такой же размерности
такой же размерности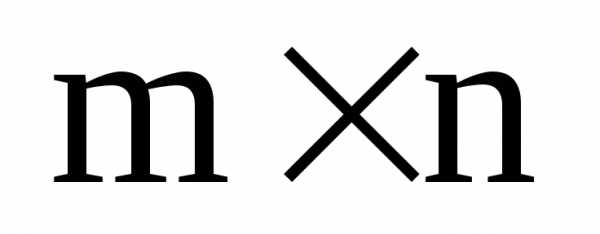 ,
где ее элементы
,
где ее элементы определяются равенствомдля всех значений индексов.
определяются равенствомдля всех значений индексов.
Обозначение: .
Другими словами, для того, чтобы найти сумму двух матриц одинаковой размерности, нужно сложить соответствующие элементы (т.е. элементы, имеющие одинаковые нижние индексы) этих матриц.
Замечание. Сложение матриц различных размеров не определено. (Их нельзя складывать!)
Пример: ,,
.
Определение. Матрица В называется противоположной матрице А, если она удовлетворяет равенству , где 0 – нулевая матрица.
Обозначение: 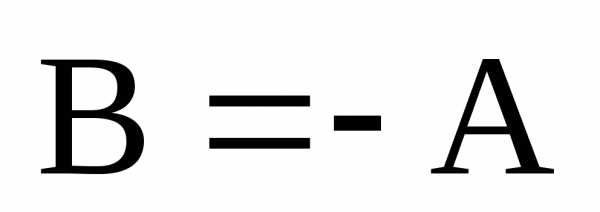 .
.
Множество всех
матриц размера 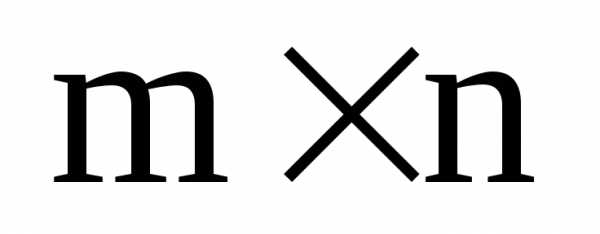 над полемKобозначим
через
над полемKобозначим
через
Теорема. (Свойства сложения матриц.)
Множество  относительно сложения является абелевой
группой.
относительно сложения является абелевой
группой.
Другими словами, сложение матриц подчиняется следующим законам:
1) ассоциативность: справедливо равенство;
2) существование нулевой матрицы:
–нулевая матрица, такая, что верны равенства;
3) существование противоположной матрицы:
,  :;
:;
4) коммутативность:
.
п.3. Умножение матрицы на скаляр.
Определение.
Произведением скаляра 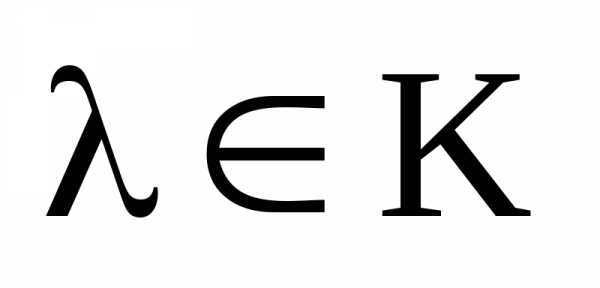 на матрицу
на матрицу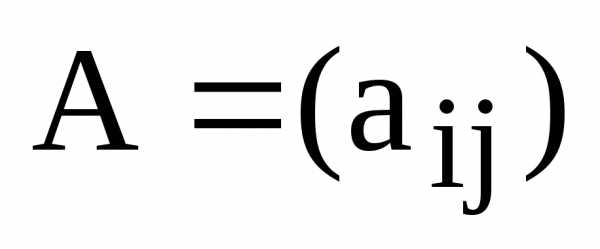 называется матрица
называется матрица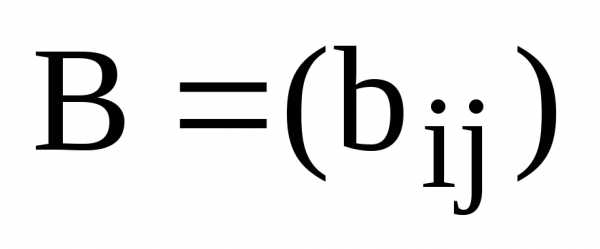 тех же размеров, что и матрица А, где
элементы
тех же размеров, что и матрица А, где
элементы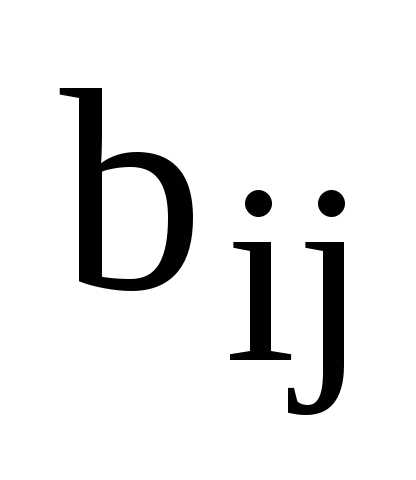
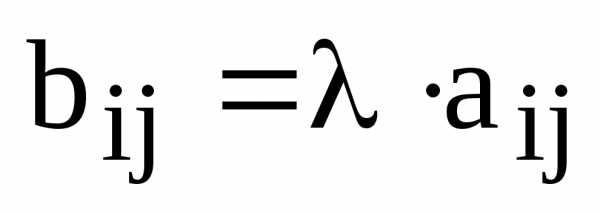 ,
для всех значений индексов.
,
для всех значений индексов. Обозначение:  .
.
Другими словами, для того, чтобы умножить матрицу на скаляр, нужно каждый элемент матрицы умножить на данный скаляр.
Пример:
,
.
Замечание. Легко видеть, что умножив матрицу на (–1) мы получаем противоположную матрицу: .
Теорема. (Свойства умножения матрицы на скаляр.)
Умножение матрицы на скаляр подчиняется законам:
5) ассоциативность: и
;
6) если 1 – единица поля K, тогда
;
7) дистрибутивность умножения относительно сложения скаляров: и
;
8) Дистрибутивность
умножения относительно сложения матриц: 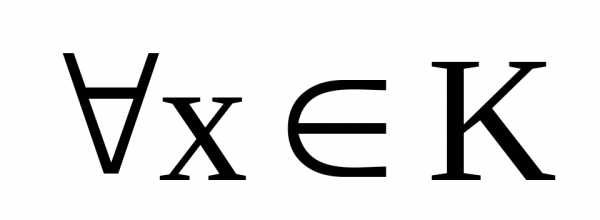 и
и
.
Следствие. Множество 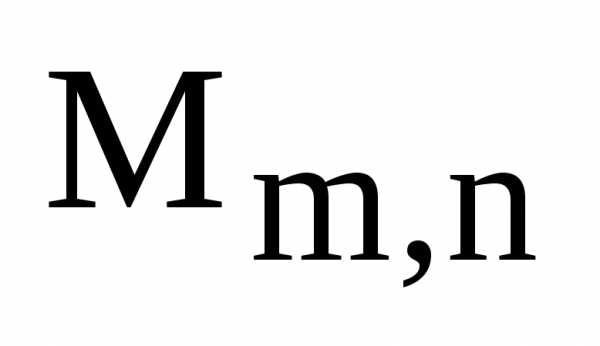 относительно сложения матриц и умножения
матриц на скаляр является векторным
пространством над полем К.
относительно сложения матриц и умножения
матриц на скаляр является векторным
пространством над полем К.
Обозначим через  множество всех столбцов высотыnс элементами из поляK.
множество всех столбцов высотыnс элементами из поляK.
Следствие. Множество 
Определение.
Векторное пространство  называется арифметическим векторным
пространством столбцов высотыn.
называется арифметическим векторным
пространством столбцов высотыn.
п.4. Умножение матриц.
Определение. Произведением строки длины nна столбец высотыnназывается скаляр, вычисляемый по правилу:
.
Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.
Пример.
Определение.
Произведением матрицы 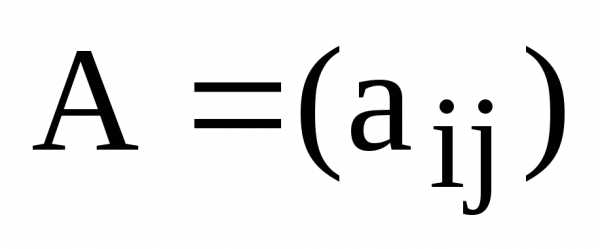
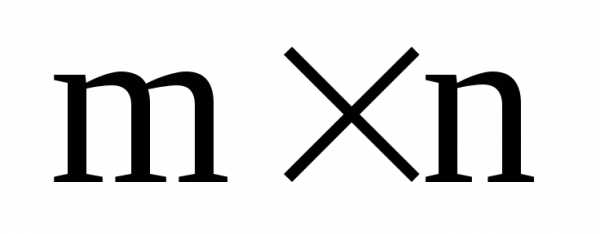 на матрицу
на матрицу размера
размера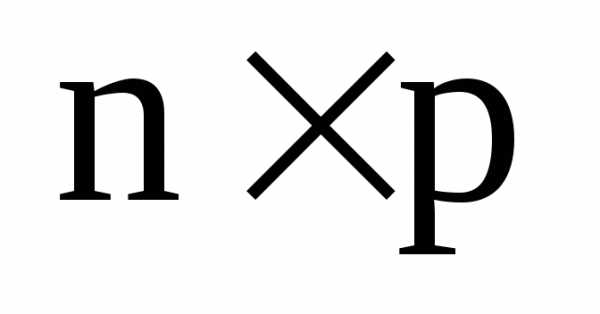 называют матрицу
называют матрицу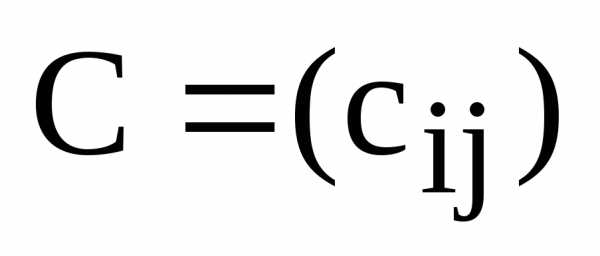 размера
размера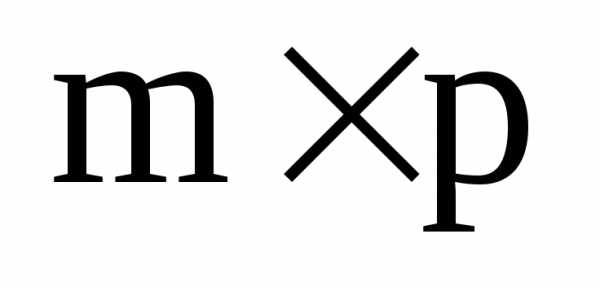 ,
где элемент
,
где элемент является результатом произведения–
й строки матрицы А на
является результатом произведения–
й строки матрицы А на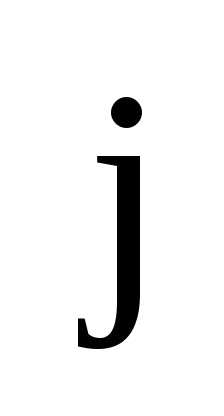 –
й столбец матрицы В для всех значений
индексов,,
т.е.
–
й столбец матрицы В для всех значений
индексов,,
т.е.или
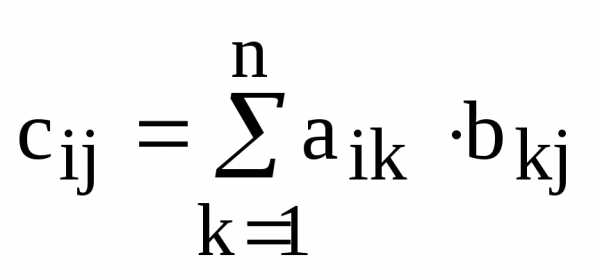 .
.
Обозначение: .
Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)
Пример.
 .
.
Определение.
Квадратную матрицу 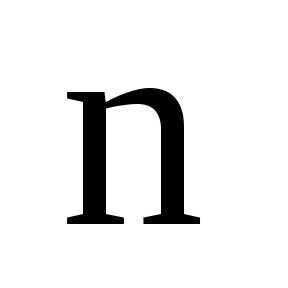 –
го порядка называют единичной матрицейn-го порядка и обозначают
буквой Е, если для любой квадратной
матрицы А
–
го порядка называют единичной матрицейn-го порядка и обозначают
буквой Е, если для любой квадратной
матрицы А
Множество всех квадратных матриц n-го порядка будем обозначать через.
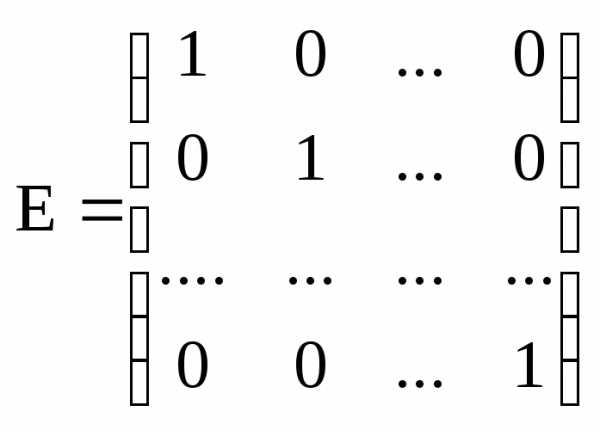
Теорема. Множество 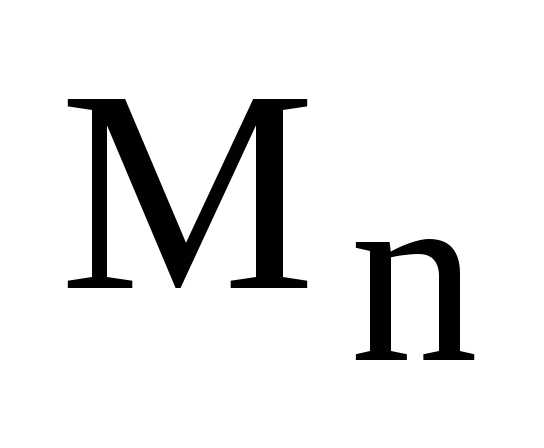 содержит единичную матрицуn-го
порядка, которой является матрица
содержит единичную матрицуn-го
порядка, которой является матрица
 .
.
Доказательство этой теоремы предоставляется читателю.
Теорема. Единичная
матрица Е является единственной в
множестве 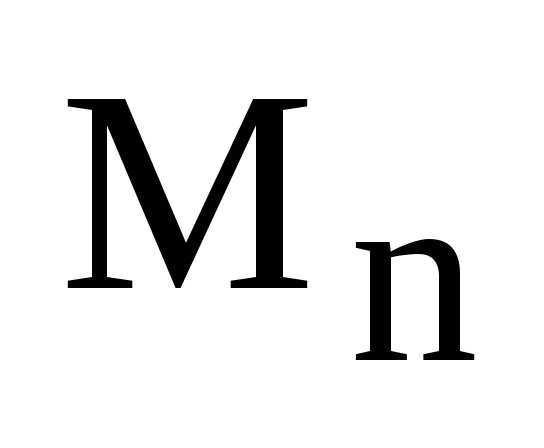 .
.
Доказательство.
Пусть 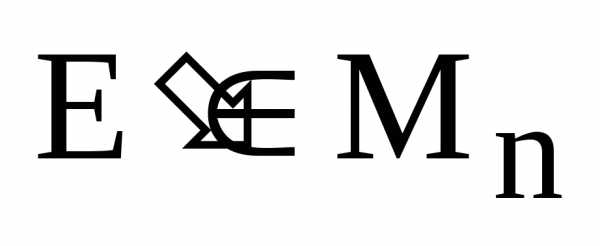
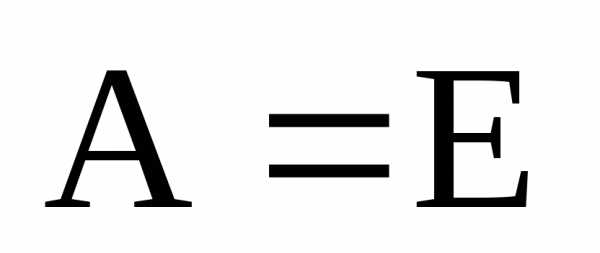 ,
тогда.
Далее, по определению,.
Положим здесь
,
тогда.
Далее, по определению,.
Положим здесь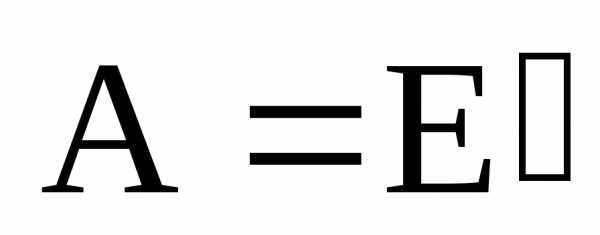 .
Получаем равенство,
отсюда имеем,
ч.т.д.
.
Получаем равенство,
отсюда имеем,
ч.т.д.Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.
Теорема доказана.
Из теоремы
следует, что никакая другая матрица,
кроме матрицы 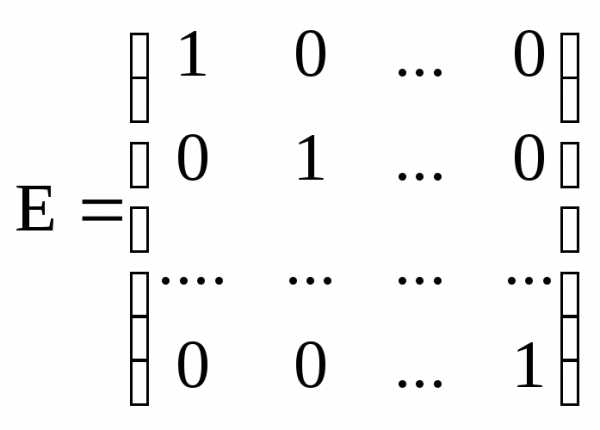 не является единичной.
не является единичной.
Теорема. (Свойства умножения матриц.)
Умножение матриц подчиняется следующим законам:
9) ассоциативность:
;
10) существование единичной матрицы:
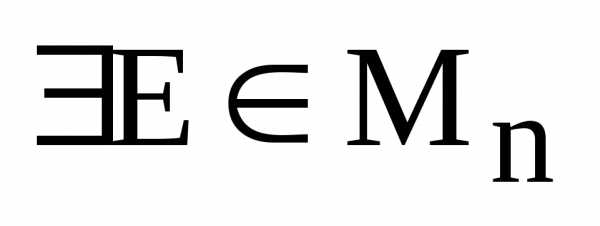 :
: 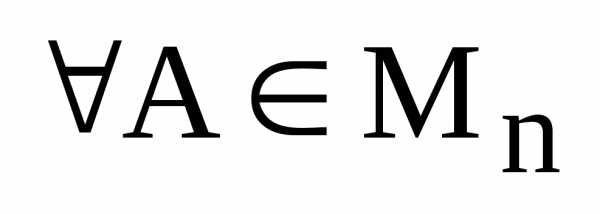 ;
;
дистрибутивность умножения относительно сложения матриц:
11) дистрибутивность умножения относительно сложения матриц:
и
12) умножение матриц
связано с умножением матрицы на число
естественным законом: 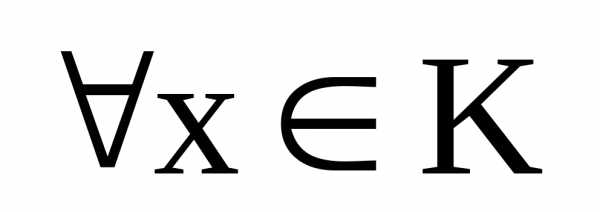 иверно равенство:
иверно равенство:
.
Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.
Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.
Пусть  ,
,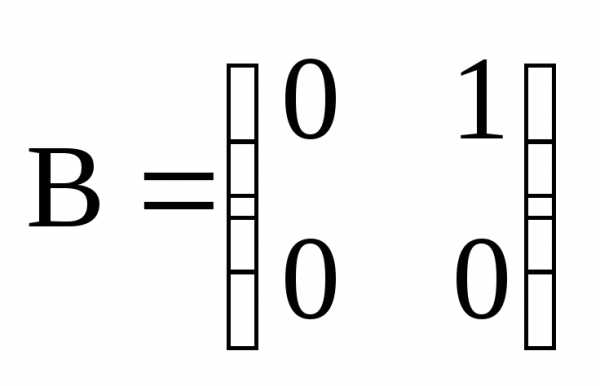 .
Тогда
.
Тогда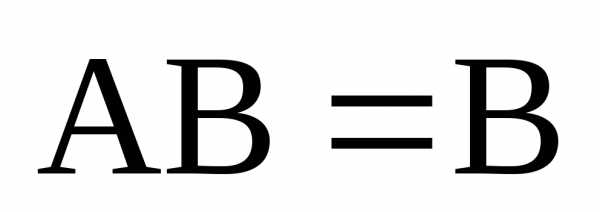 ,
,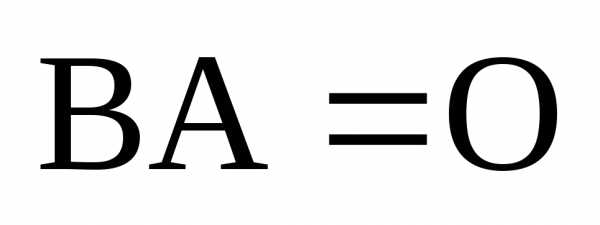 .
.
Аналогичный пример можно привести для квадратных матриц любого порядка.
Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.
Следствие. Множество всех квадратных матриц n-го порядка над полемKявляется некоммутативным кольцом с единицей и с делителями нуля.
Доказательство.
На множестве  всех квадратных матрицn-го
порядка над полемKопределены две операции: сложение матриц
и их умножение, которые подчиняются
законам 1) – 4) и 9) – 11), откуда и следует,
по определению, что
всех квадратных матрицn-го
порядка над полемKопределены две операции: сложение матриц
и их умножение, которые подчиняются
законам 1) – 4) и 9) – 11), откуда и следует,
по определению, что является кольцом с единицей (см. лекцию
1, п.14 и п.15). Пример, приведенный перед
формулировкой данного следствия,
показывает, что кольцо
является кольцом с единицей (см. лекцию
1, п.14 и п.15). Пример, приведенный перед
формулировкой данного следствия,
показывает, что кольцо имеет делители нуля.
имеет делители нуля.
Следствие доказано.
Определение.
Натуральной степенью квадратной матрицы
А называется матрица 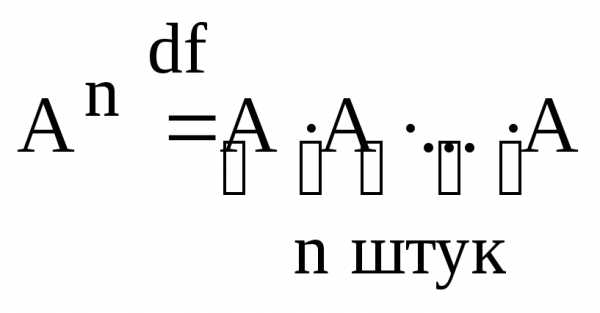 .
.
Нулевую степень
квадратной матрицы А 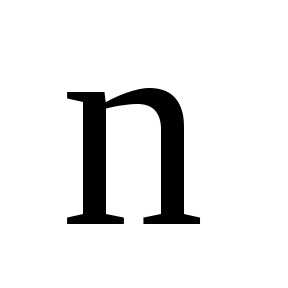 –
го порядка по определению полагают
равной единичной матрице того же порядка:
–
го порядка по определению полагают
равной единичной матрице того же порядка: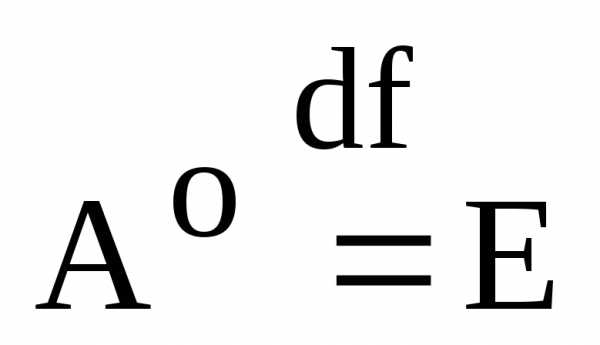 .
.
п.5. Обратная матрица.
Определение. Матрица В называется обратной по отношению к матрице А, если
.
Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.
Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.
Определение. Матрица имеющая обратную матрицу называется обратимой.
Теорема. Если квадратная матрица А имеет обратную, то она единственная.
Доказательство. Пусть В и С – две матрицы обратные к матрице А. Тогда и. Имеем,
, ч.т.д.
Теорема доказана.
Заметим, что точно также доказывается единственность симметричного элемента в любой полугруппе при условии его существования.
Обозначение: если
матрица А обратимая, то обратная к ней
обозначается (мы можем это сделать в
силу ее единственности) через  .
.
Заметим, что если
матрица А обратимая, то обратная к ней
матрица  также является обратимой.
также является обратимой.
Обозначение. Множество всех обратимых матриц n-го порядка над полемKобозначается через
.
Теорема. (Свойства обратных матриц.)
1. Произведение обратимых матриц одного и того же порядка является обратимой матрицей:
, и.
2. Единичная матрица является обратимой, т.е. если Е – единичная матрица n-го порядка, то
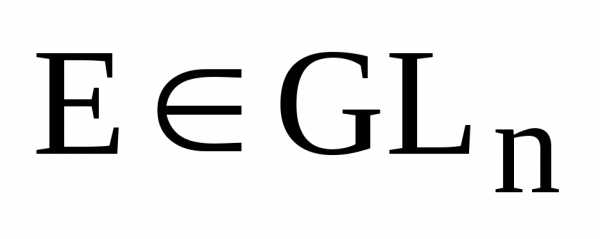 и
и  .
.
3. Если А обратимая,
то и  также является обратимой, т.е. если
также является обратимой, т.е. если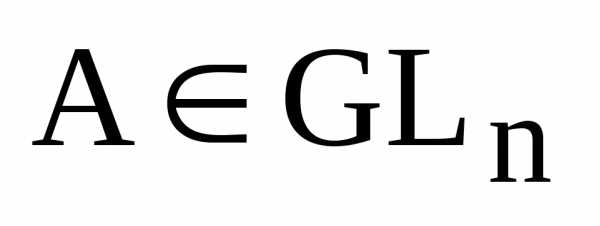 ,
то
,
то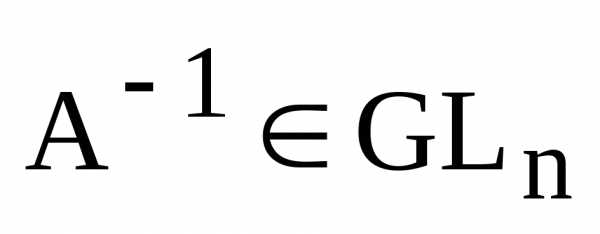 и.
и.
Доказательство.
1) Пусть А и В – обратимые матрицы и 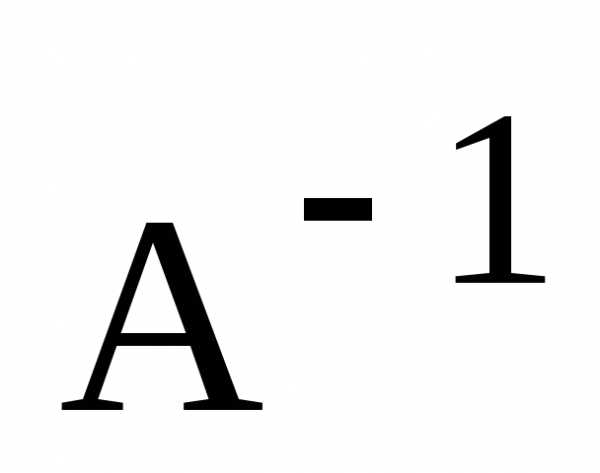 ,
,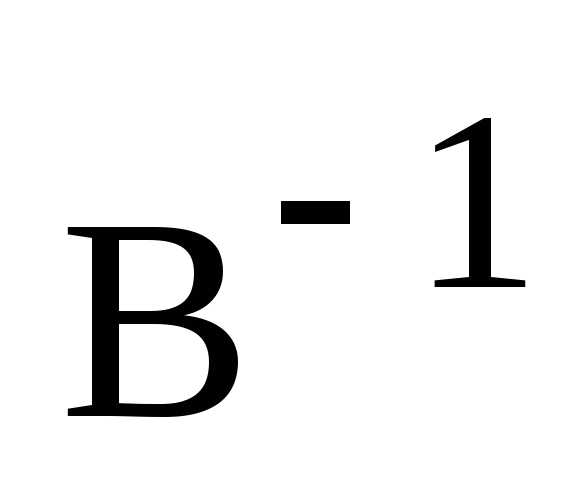 – обратные к ним. Покажем, что произведение
– обратные к ним. Покажем, что произведение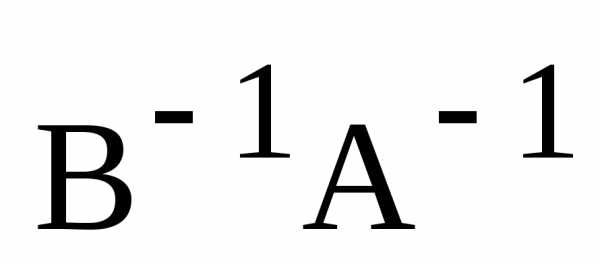 является матрицей обратной к произведению
является матрицей обратной к произведению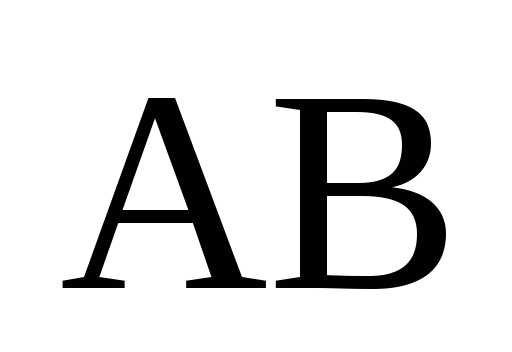 :
:
.
Аналогично получаем . Следовательно, матрица АВ имеет обратную и. Отсюда следует, что матрица АВ является обратимой, т.е., ч.т.д.
2) Так как  ,
то по определению,
,
то по определению, ,
т.е. единичная матрица имеет обратную
и, следовательно, единичная матрица
является обратимой и
,
т.е. единичная матрица имеет обратную
и, следовательно, единичная матрица
является обратимой и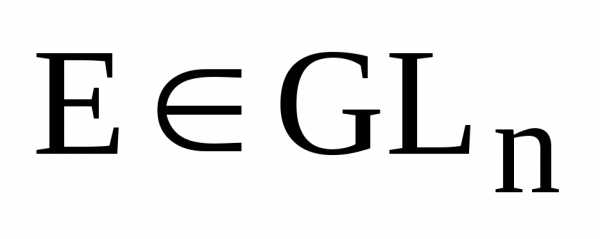 .
.
3) Действительно,
из определения следует, что матрица А
является обратной по отношению к матрице  ,
следовательно, матрица
,
следовательно, матрица обратимая и
обратимая и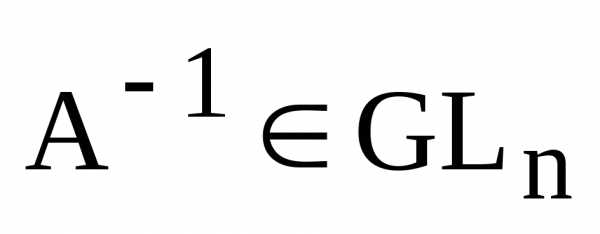 .
Более того, в силу единственности
обратной матрицы следует, что
.
Более того, в силу единственности
обратной матрицы следует, что
.
Теорема доказана.
Следствие. Множество  является некоммутативной группой
относительно умножения.
является некоммутативной группой
относительно умножения.
Доказательство.
На множестве  умножение матриц является внутренней
бинарной алгебраической операцией,
поэтому осталось лишь проверить аксиомы
группы.
умножение матриц является внутренней
бинарной алгебраической операцией,
поэтому осталось лишь проверить аксиомы
группы.
1) Ассоциативность
умножения в множестве 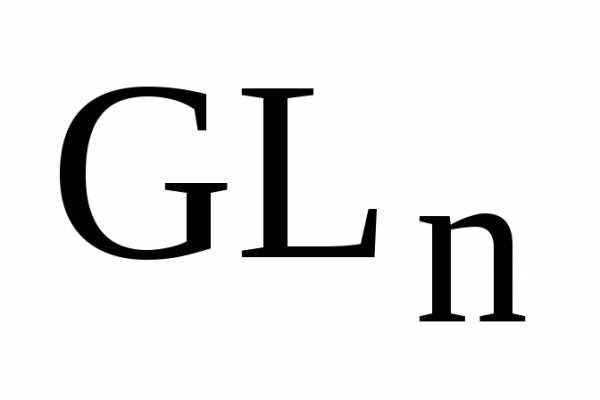 выполняется потому что умножение
квадратных матриц ассоциативно (см
теорему о свойствах умножения матриц).
выполняется потому что умножение
квадратных матриц ассоциативно (см
теорему о свойствах умножения матриц).
Далее, в предыдущей теореме доказано, что:
2) единичная матрица 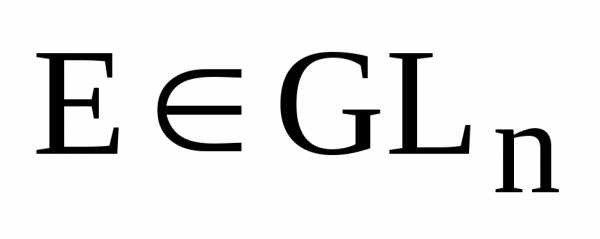 ;
;
3)
существует обратная ей .
.
Следствие доказано.
Определение. Обратимая квадратная матрица называется также неособой или невырожденной. Если квадратная матрица не имеет обратной, то она называется особой или вырожденной.
Замечание. Легко доказать существование особых матриц. Например, матрица
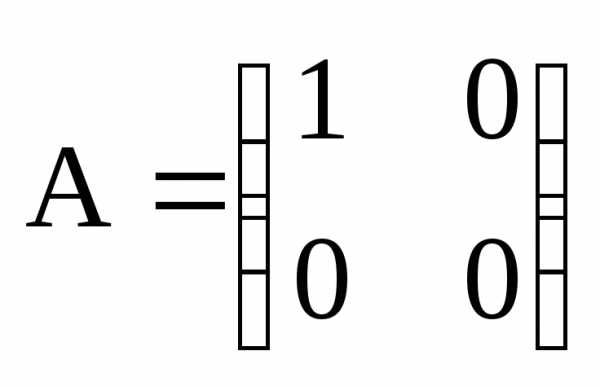
является особой
(вырожденной, необратимой). Действительно,
если бы она была обратимой, то существовала
бы обратная к ней
и.
Пусть далее,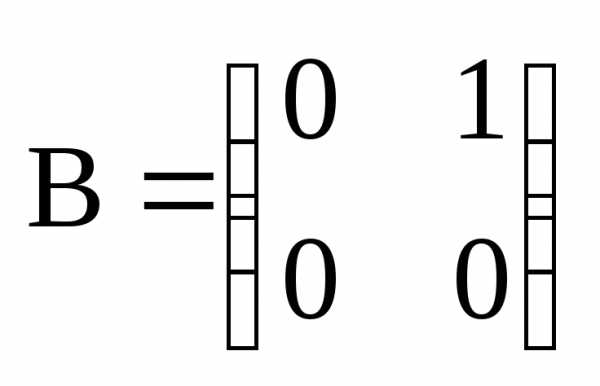 .
Тогда
.
Тогда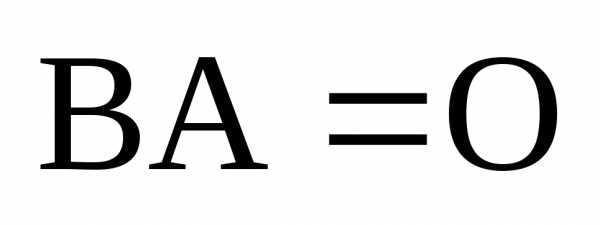 и отсюда получаем
и отсюда получаем
или , т.е. получаем противоречие.
Аналогично, легко показать существование особых матриц любого порядка. Отсюда следует вывод, что не все квадратные матрицы являются обратимыми.
В дальнейшем, мы найдем необходимое и достаточное условие обратимости квадратной матрицы любого порядка и не только докажем существование обратимых матриц, отличных от единичной матрицы, но и выведем формулу для ее вычисления.
studfiles.net
Линейная алгебра Матрицы
42
Линейная алгебра 1
Матрицы 1
Операции над матрицами 2
Определители матриц 6
Обратная матрица 13
Ранг матрицы 16
Линейная независимость 21
Системы линейных уравнений 24
Методы решения систем линейных уравнений 27
Метод обратной матрицы 27
Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера 29
Метод Гаусса (метод последовательного исключения переменных) 31
Матрицаразмераmхn– это прямоугольная таблица чисел, содержащаяmстрок иnстолбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.
Например, рассмотрим матрицу А размерности 2 х 3:
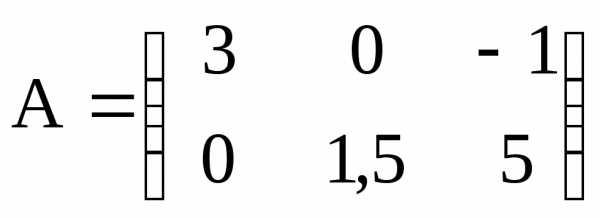
В этой матрице две строки (m= 2) и три столбца (n= 3), т.е. она состоит из шести элементовaij, гдеi- номер строки, j – номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается). А именно,a11= 3;a12= 0;a13= -1;a21= 0;a22= 1,5;a23= 5.
Матрицы А и В одного размера (mхn) называютравными, если они поэлементно совпадают, т.е.aij=bijдля, т.е. для любыхiиj(можно записатьi,j).
Матрица-строка– это матрица, состоящая из одной строки, аматрица-столбец– это матрица, состоящая из одного столбца.
Например,
–
матрица-строка, а .
.
Квадратная матрицаn-го порядка – это матрица, в число строк равно числу столбцов и равно n.
Например,  –
квадратная матрица второго порядка.
–
квадратная матрица второго порядка.
Диагональныеэлементы матрицы – это элементы, у которых номер строки равен номеру столбца (aij,i=j). Эти элементы образуютглавную диагональматрицы. В предыдущем примере главную диагональ образуют элементыa11= 3 иa22= 5.
Диагональная матрица– это квадратная матрица, в которой все
недиагональные элементы равны нулю.
Например,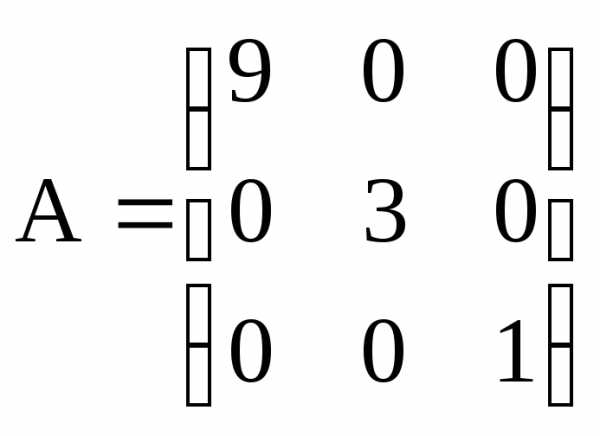 –
диагональная матрица третьего порядка.
Если при этом все диагональные элементы
равны единице, то матрица называетсяединичной(обычно обозначаются
буквой Е). Например,
–
диагональная матрица третьего порядка.
Если при этом все диагональные элементы
равны единице, то матрица называетсяединичной(обычно обозначаются
буквой Е). Например,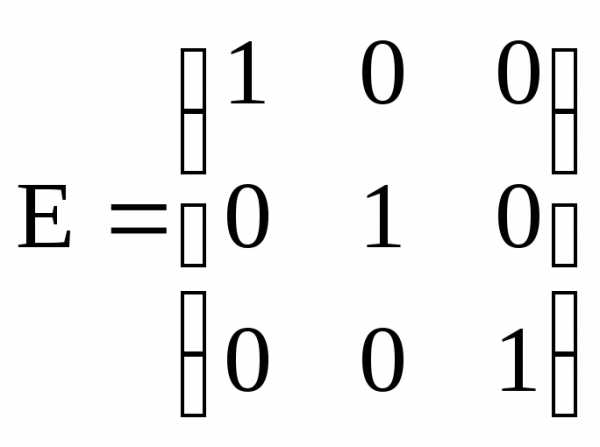 –
единичная матрица третьего порядка.
–
единичная матрица третьего порядка.
Матрица называется нулевой, если все ее элементы равны нулю.
Квадратная матрица
называется треугольной, если все
ее элементы ниже (или выше) главной
диагонали равны нулю. Например,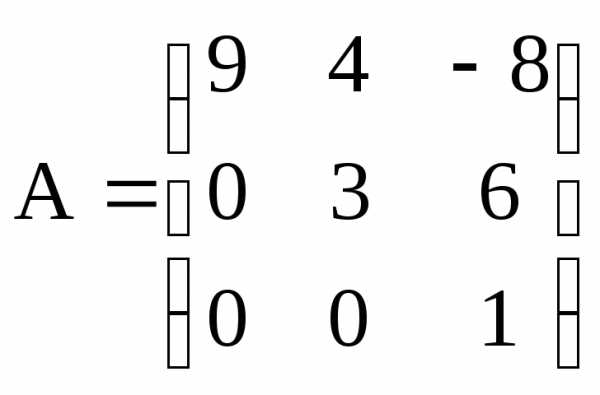 –
треугольная матрица третьего порядка.
–
треугольная матрица третьего порядка.
Операции над матрицами
Над матрицами можно производить следующие операции:
1. Умножение матрицы на число. Произведением матрицы А на числоназывается матрица В =А, элементы которойbij=aijдля любыхiиj.
Например, если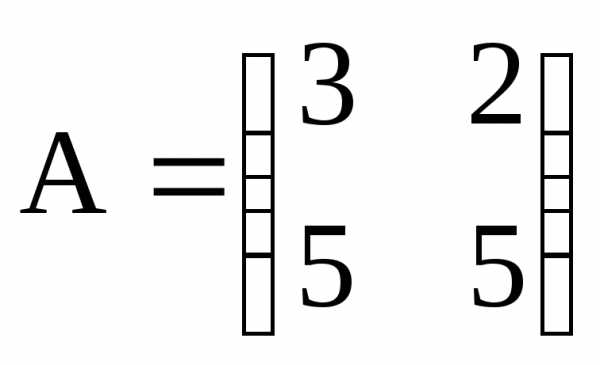 ,
то.
,
то.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой сij=aij+bijдляi,j.
Например, если то
.
Отметим, что через предыдущие операции можно определить вычитание матрицодинакового размера: разность А-В = А + (-1)*В.
3. Умножение матриц. Произведением матрицы А размераmxnна матрицу В размераnxpназывается такая матрица С, каждый элемент которой сijравен сумме произведений элементов i-й строки матрицы А на соответствующие элементыj-го столбца матрицы В, т.е..
Например, если
, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид:
В этом случае матрица А называется согласованной с матрицей В.
На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью Аm(m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.
Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными).
Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами.
1) Коммутативный (переместительный) закон сложения:
А + В = В + А
2) Ассоциативный (сочетательный) закон сложения:
(А + В) + С = А + (В + С)
3) Дистрибутивный (распределительный) закон умножения относительно сложения:
(А + В) = А +В
А (В + С) = АВ + АС
(А + В) С = АС + ВС
5) Ассоциативный (сочетательный) закон умножения:
(АВ) = (А)В = А(В)
A(BС) = (АВ)С
Подчеркнем, что переместительный закон умножения для матриц в общем случае НЕ выполняется, т.е. AB BA. Более того, из существования AB не обязательно следует существование ВА (матрицы могут быть не согласованными, и тогда их произведение вообще не определено, как в приведенном примере умножения матриц). Но даже если оба произведения существуют, они обычно разные.
В частном случае коммутативным законом обладает произведение любой квадратной матрицы А на единичную матрицу того же порядка, причем это произведение равно А (умножение на единичную матрицу здесь аналогично умножению на единицу при умножении чисел):
АЕ = ЕА = А
В самом деле,
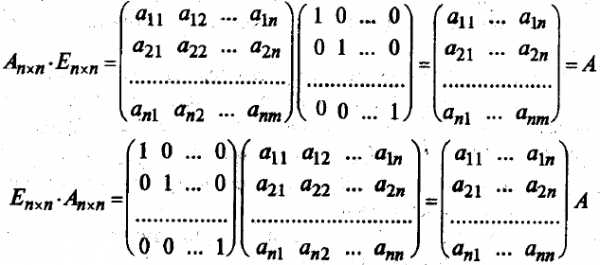
Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,
Продолжим рассмотрение операций над матрицами.
4. Транспонирование матрицыпредставляет собой операцию перехода от матрицы А размераmxnк матрице АТразмераnxm, в которой строки и столбцы поменялись местами:
%.
Свойства операции транспонирования:
1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (AT)T= A.
2) Постоянный множитель можно вынести за знак транспонирования: (А)T=АT.
3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB)T=BTATи (A+B)T=BT+AT.
studfiles.net
Глава 1. Алгебра матриц
1.1. Матрицы. Основные определения
Матрицей А= ( )
) называется прямоугольная таблица чисел,
содержащаяm строк
иn столбцов:
называется прямоугольная таблица чисел,
содержащаяm строк
иn столбцов:

Числа  (),
составляющие данную матрицу, называются
её элементами;i–
номер строки матрицы,j– номер столбца.
(),
составляющие данную матрицу, называются
её элементами;i–
номер строки матрицы,j– номер столбца.
Если m=n, то матрица называется квадратной порядкаn.
Например, 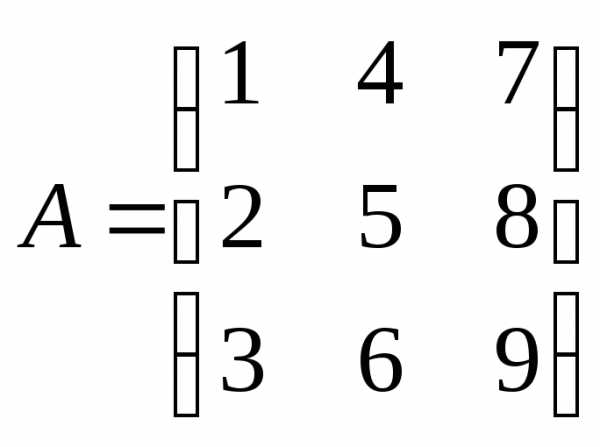 – квадратная матрица третьего порядка.
– квадратная матрица третьего порядка.
Про элементы  такой матрицы говорят, что они стоят на
главной диагонали.
такой матрицы говорят, что они стоят на
главной диагонали.
Треугольная матрица – квадратная матрица, у которой все элементы, стоящие по одну из сторон главной диагонали, равны нулю:
 ,
,
например, 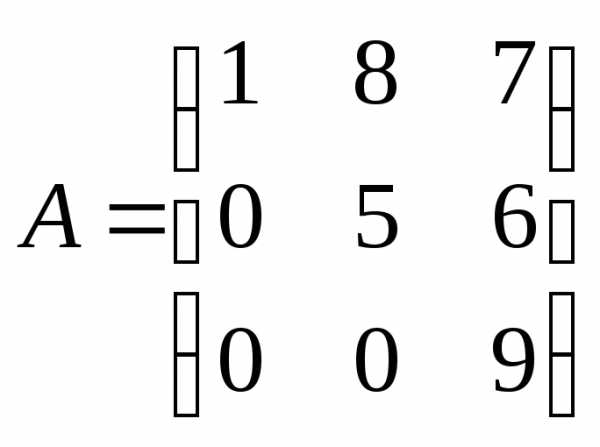 – треугольная матрица третьего порядка
– треугольная матрица третьего порядка
Квадратная матрица вида

называется диагональной матрицей. Диагональные матрицы, в которых все диагональные элементы равны, т.е. ,, называются скалярными матрицами.
Если 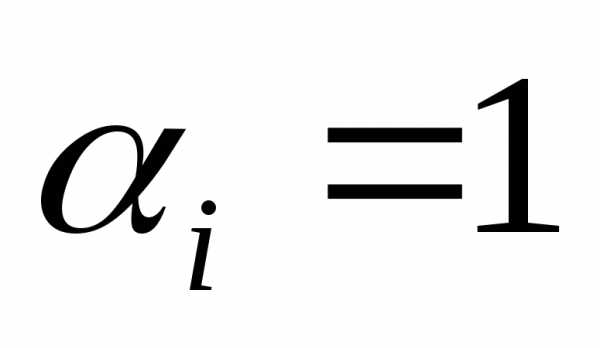
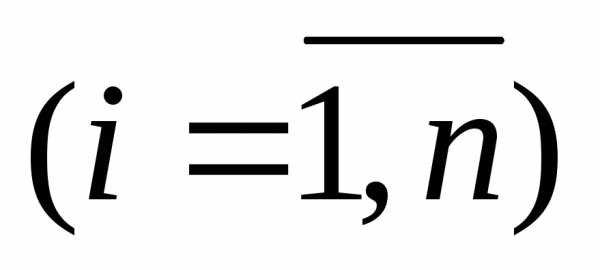 ,
то скалярная матрица называется единичной
и обозначается буквойЕ, т.е.:
,
то скалярная матрица называется единичной
и обозначается буквойЕ, т.е.:
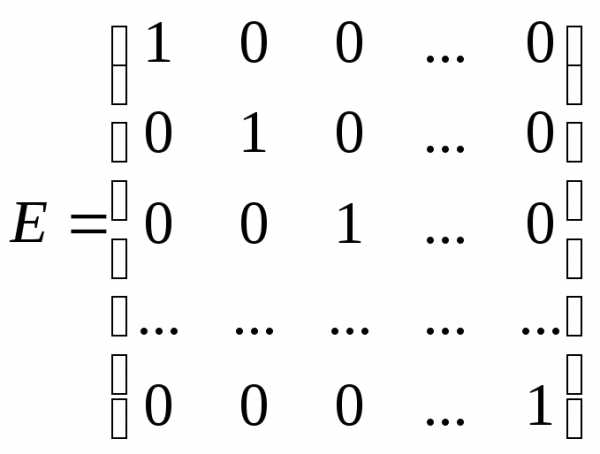 .
.
Например, матрицы А,B,Eявляются соответственно диагональной, скалярной и единичной третьего порядка.
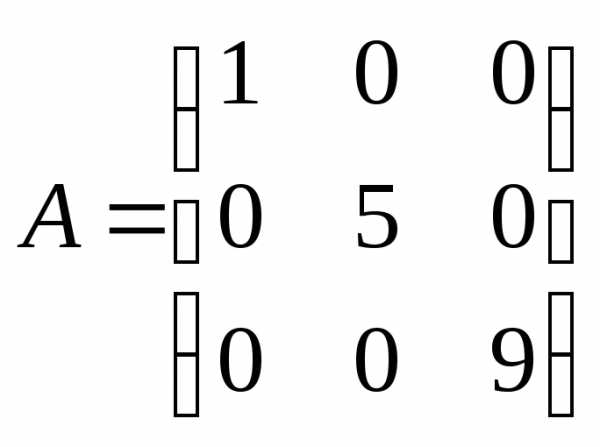 ,
, ,
,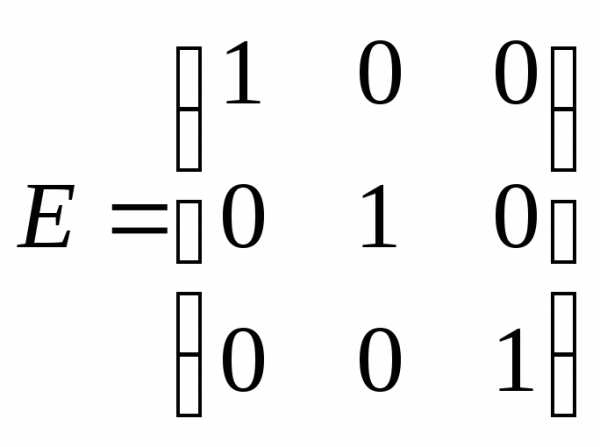 .
.
Симметрической называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны, т.е.
Например, 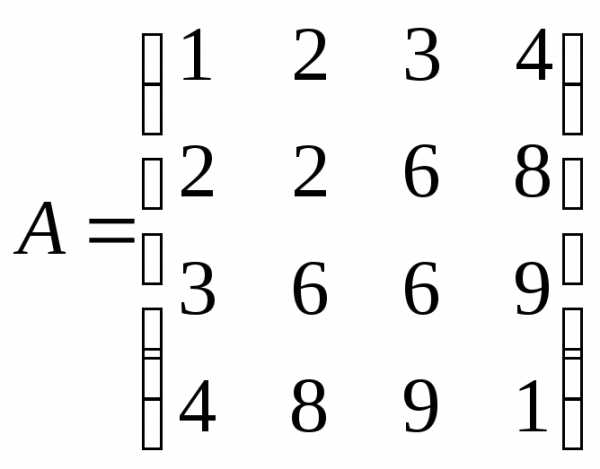 – симметрическая матрица четвертого
порядка.
– симметрическая матрица четвертого
порядка.
Матрица, состоящая из одной строки, называется вектором-строкой, а матрица, состоящая из одного столбца, – вектором-столбцом.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается О.
Например, О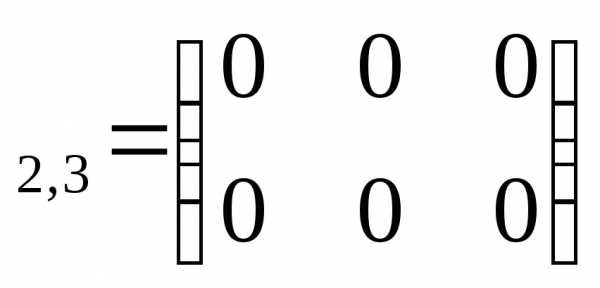 –нулевая матрица размера два на три.
–нулевая матрица размера два на три.
1.2 Действия над матрицами
Две матрицы 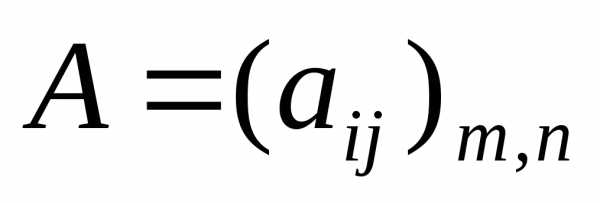 и
и
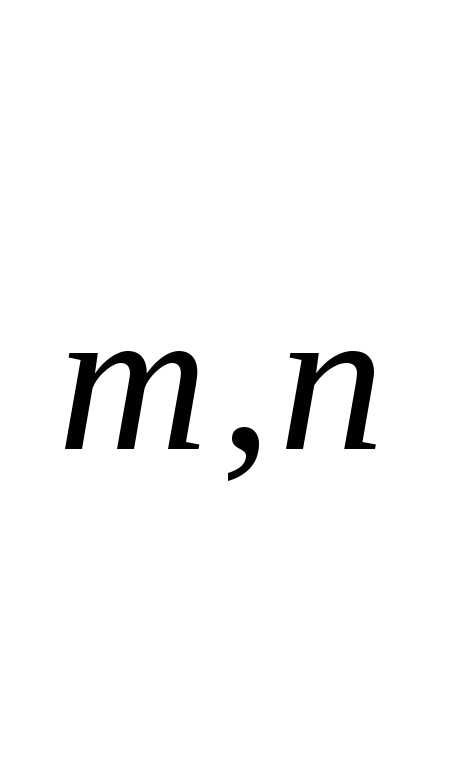 называются равными,А=В, если их
соответствующие элементы равны, т.е.
называются равными,А=В, если их
соответствующие элементы равны, т.е. =
=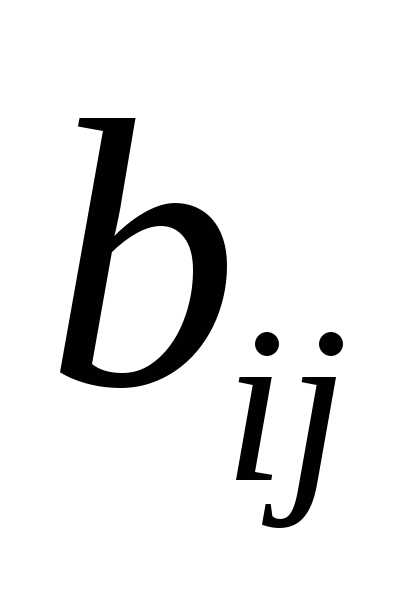 ,
,
Суммой двух матриц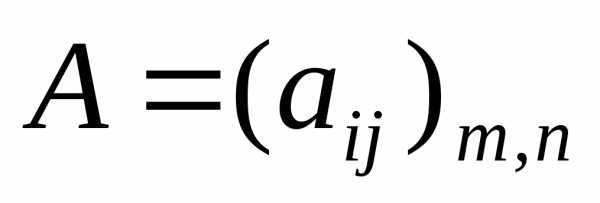 и
и называется матрицаC=A+B,
элементы которойсijравны
сумме соответствующих элементовaijиbijматрицAиB, т.е..
Например,
называется матрицаC=A+B,
элементы которойсijравны
сумме соответствующих элементовaijиbijматрицAиB, т.е..
Например,
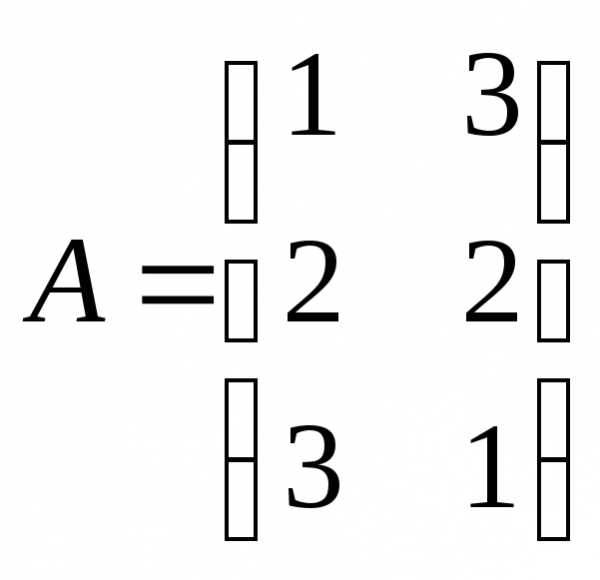 ,
,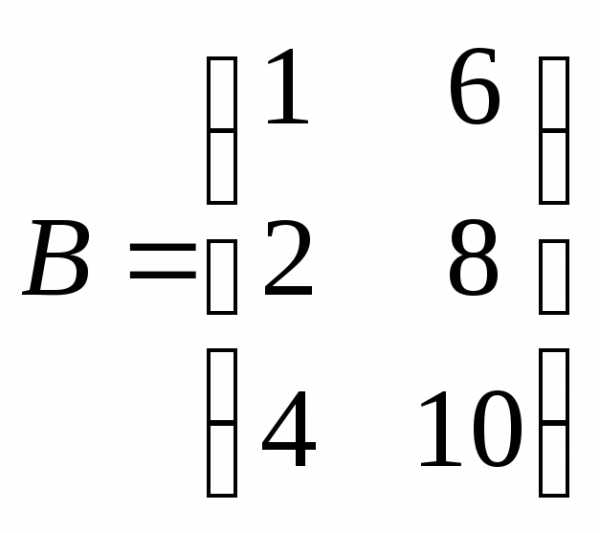 ,
,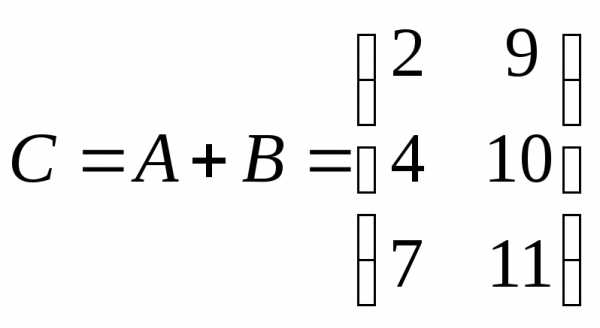 .
.
Для суммы матриц справедливы следующие свойства:
A+B=B+A– коммутативность;
A+(B+C)=(A+B)+C– ассоциативность;
A+О=A.
Произведениемматрицы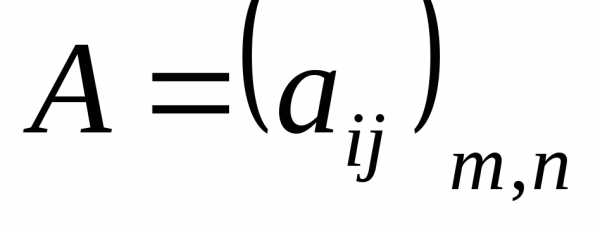 на число
на число  называется матрица
называется матрица ,
элементы которой равны произведению
соответствующих элементов матрицыAна число
,
элементы которой равны произведению
соответствующих элементов матрицыAна число ,
т.е.
,
т.е.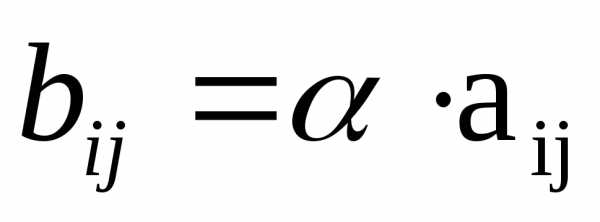 .
Например, если
.
Например, если ,
а матрица
,
а матрица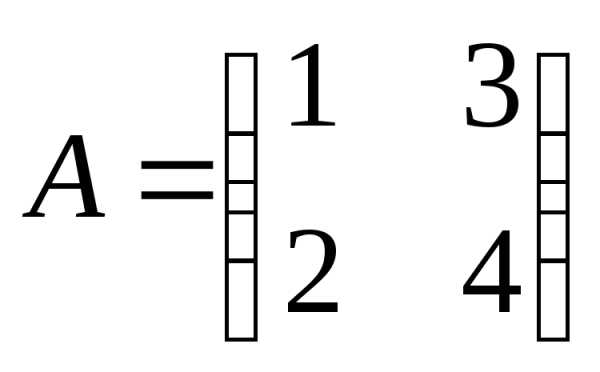 ,
то
,
то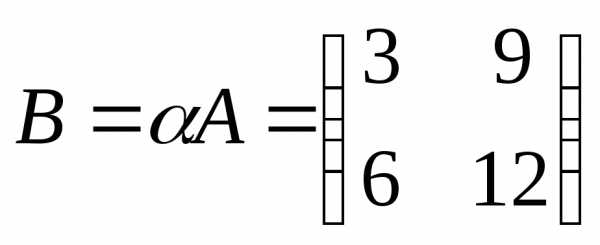 .
.
Пусть A, B, C – матрицы, 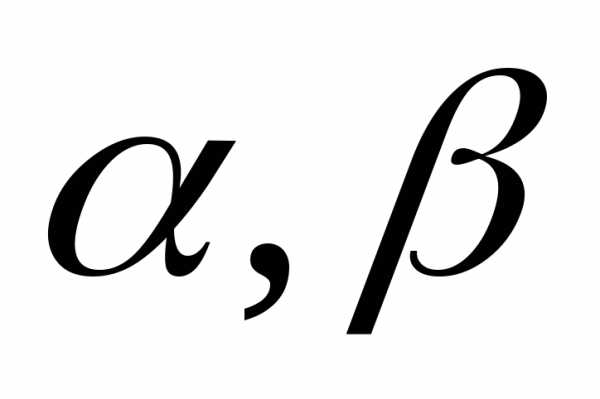 – числа. Из определения произведения
матрицы на число вытекают следующие
свойства:
– числа. Из определения произведения
матрицы на число вытекают следующие
свойства:
1. , 4. ,
2. , 5. ,
3.  О, 6.
.
О, 6.
.
Матрица называется противоположной матрицеA.
Если матрицы AиBодинаковых размеров, то их разность равна.
Произведением матрицыA=(aij)порядка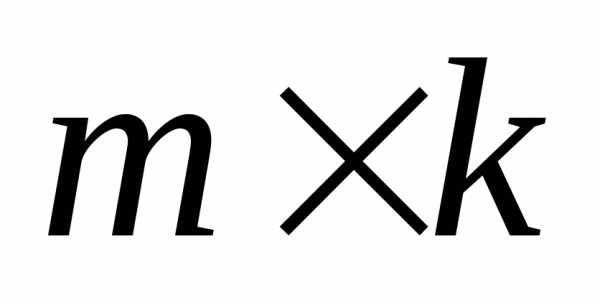 на матрицу
на матрицу порядка
порядка называется матрицапорядка
называется матрицапорядка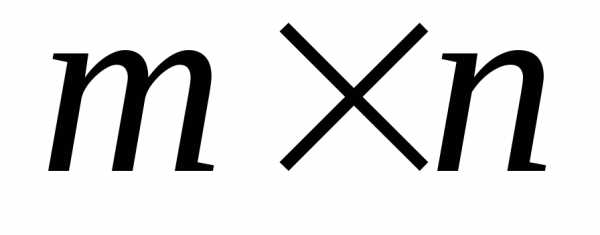 ,
элементы которойс
,
элементы которойс равны:
равны:
, ( ;
; 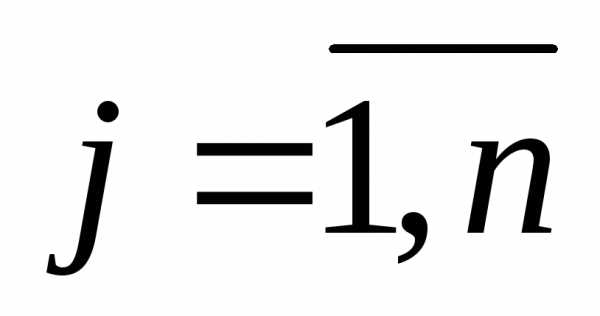 ).
).
Из определения произведения матриц следует: чтобы получить элемент, стоящий на пересечении i-ой строки иj-го столбца матрицыС, необходимо элементыi-ой строки матрицыАумножить на соответствующие элементыj-го столбца матрицыВи полученные произведения сложить.
Произведение АВимеет смысл тогда и только тогда, когда число столбцов матрицыАравно числу строк матрицыВ.
В результате получится матрица, у которой число строк совпадает с числом строк первого сомножителя, а число столбцов – с числом столбцов второго сомножителя.
Для произведения матриц справедливы следующие свойства:
1. A(BC) = (AB)C | 3. (A + B)C = AC + BC |
2. | 4. C(A+B) = CA + CB |
Эти свойства легко доказываются на основе соответствующих определений.
Произведение двух матриц некоммутативно,
т.е. в общем случае АВ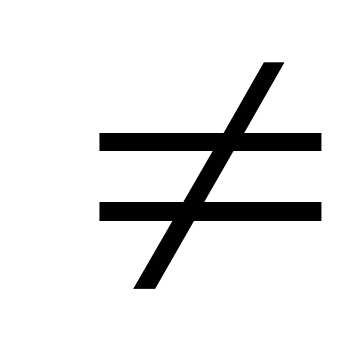 ВА.
В случае прямоугольных матриц легко
подобрать примеры, когда одно из этих
произведений не будет существовать
из-за невыполнения условия равенства
числа столбцов сомножителя, стоящего
первым, числу строк второго сомножителя.
Очевидно, что для квадратных матриц
порядкаnсуществуютАВиВА.
Однако для всехn, начиная сn=2,
можно привести примеры некоммутативных
(неперестановочных) матриц.
ВА.
В случае прямоугольных матриц легко
подобрать примеры, когда одно из этих
произведений не будет существовать
из-за невыполнения условия равенства
числа столбцов сомножителя, стоящего
первым, числу строк второго сомножителя.
Очевидно, что для квадратных матриц
порядкаnсуществуютАВиВА.
Однако для всехn, начиная сn=2,
можно привести примеры некоммутативных
(неперестановочных) матриц.
Пример.Найти произведениеАВиВАматриц:
А=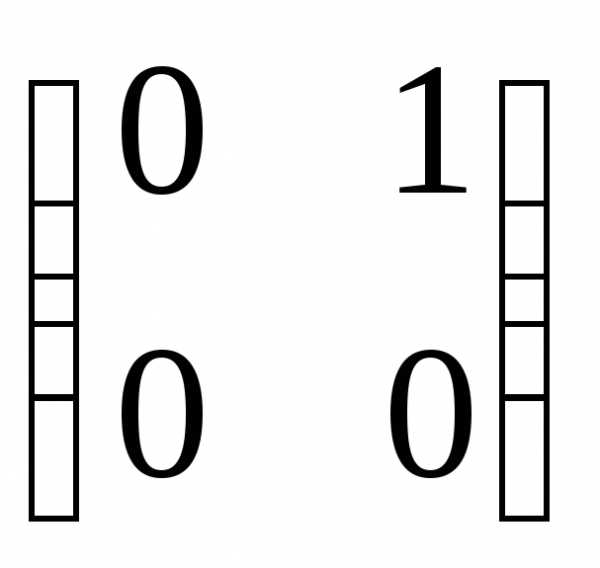 ,В=
,В= .
.
Решение.
;
Пример.Найти произведение матриц А и В.
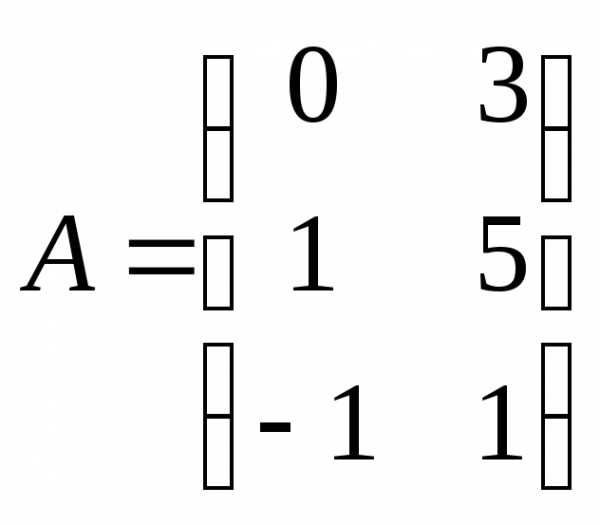 ,
,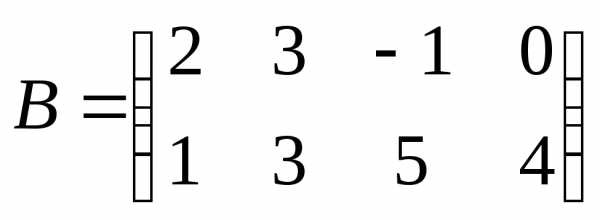 .
.
Решение.
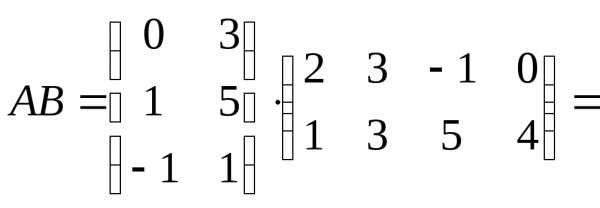
Если АВ=ВА, то матрицы иВназываются коммутативными. Так, например, единичная матрица Е коммутативна с любой квадратной матрицей того же порядка, причемАЕ=ЕА=А.
Скалярная матрица может быть представлена в виде произведения элемента матрицы, стоящего на ее главной диагонали, на единичную матрицу того же порядка:
А= Е.
Е.
Легко видеть, что произведение любой квадратной матрицы на скалярную матрицу того же порядка коммутативно.
Квадратную матрицу Аможно возвести в степеньn, для чего ее надо умножить на саму себяnраз, т.е..
Транспонирование матрицы– это такое преобразование, при котором строки заменяются соответствующими столбцами:

Транспонированная матрица обладает следующими свойствами, которые следуют из определения:
(А)=А;
(А+В)=А+B;
(AB)=BA.
Если матрица А – симметрическая, то А=А, т.е. симметрическая матрица совпадает со своей транспонированной.
Очевидно, что произведение С=ААпредставляет собой симметрическую матрицу. Действительно,
С= (АА)=(А)А=АА=С.
При этом А может быть и прямоугольной матрицей произвольного порядка, С же будет квадратной, порядка, соответствующего числу строк матрицы А.
В различных приложениях используется понятие нормы матрицы.
Под нормой матрицы А=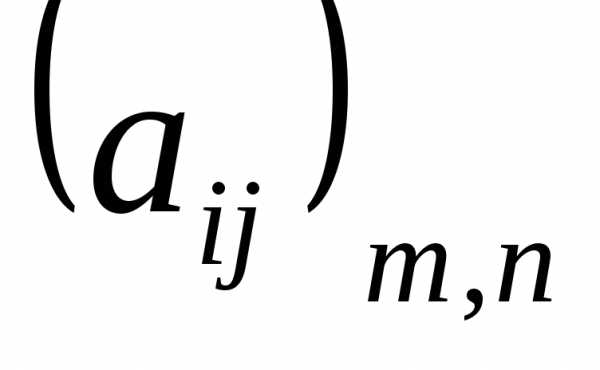 понимается действительное число ||A||,
удовлетворяющее условиям:
понимается действительное число ||A||,
удовлетворяющее условиям:
а) ||A||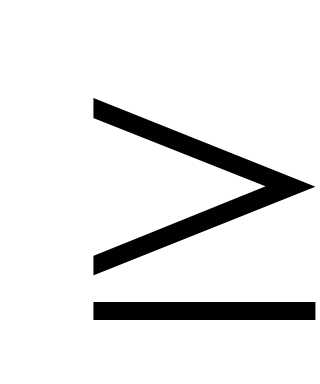 0,
причем ||A|| = 0 тогда и только тогда, когда
А=О;
0,
причем ||A|| = 0 тогда и только тогда, когда
А=О;
б) || A||=|
A||=| |
| ||A||,
(
||A||,
( – число) и, в частности ||-A||=||A||;
– число) и, в частности ||-A||=||A||;
в) ||A+B|| ||A||+||B||;
||A||+||B||;
г) ||AB||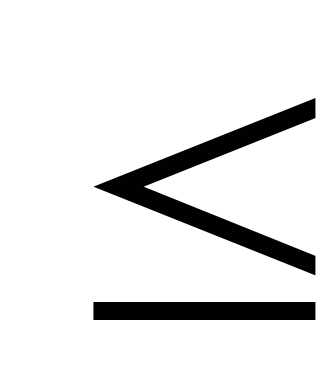 ||A||
||A|| ||B||,
||B||,
где А и В – матрицы, для которых соответствующие операции имеют смысл.
Для матрицы А=(а )
) произвольного типа рассматриваются
главным образом три вида норм:
произвольного типа рассматриваются
главным образом три вида норм:
Все они удовлетворяют перечисленным выше условиям.
studfiles.net
2. Алгебра матриц.. Матрицы и определители
Похожие главы из других работ:
Алгебраические группы матриц
1. Алгебраические группы матриц
…
Алгебраические группы матриц
3.2 Произведение матриц
Соотношения (5) и (6) выражают согласованность действий сложения и умножения на скаляры в множествах матриц размера и отображений . В случае произвольных множеств имеется еще важное понятие произведения (композиции) отображений…
Математическая модель цифрового устройства для интерпретации кода Морзе
Булева Алгебра
Булевой алгеброй называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a…
Матрицы и определители
2. Алгебра матриц.
Ключевые понятия Диагональная матрица. Единичная матрица. Нулевая матрица. Симметричная матрица. Согласованность матриц. Транспонирование. Треугольная матрица. 1. ПОНЯТИЕ МАТРИЦЫ. ТИПЫ МАТРИЦ Прямоугольную таблицу А=…
Матрицы и определители
2. АЛГЕБРА МАТРИЦ
Рассмотрим действия над матрицами, но вначале введем несколько новых понятий. Две матрицы А и В называются матрицами одного порядка, если они имеют одинаковое количество строк и одинаковое количество столбцов. Пример…
Методы решения уравнений, содержащих параметр
2.1. Макарычев Ю.Н. и др. «Алгебра. 7 – 9 класс»
Алгебра. 7 класс. При изучении уравнений представлено два задания с параметром (№№236, 243). Рассматриваются простейшие линейные уравнения…
Методы решения уравнений, содержащих параметр
2.2. Мордкович. А. Г. «Алгебра 7 по 9 класс» и «Алгебра и начала анализа 10 – 11 класс»
Надо отметить, что данное учебное пособие состоит из двух частей: из учебника и задачника (см. [30], [31]). При изучении линейной функции (7 класс глава 6 §28) рассматривается линейное уравнение с двумя переменными и его график…
Методы решения уравнений, содержащих параметр
2.3. Алимов Ш.А. и др. «Алгебра с 7 по 9 класс» и «Алгебра и начала анализа 10 – 11 класс»
Начнем анализ этой группы учебников с 7 класса. Уже при изучении темы «Уравнения с одним неизвестным» предлагаются задания, которые содержит задачи с параметром (№№123-125)…
Основные положения дискретной математики
2 МАТЕМАТИЧЕСКАЯ ЛОГИКА. АЛГЕБРА ЛОГИКИ.
В булевой алгебре рассматривается двухэлементное множество В, элементы которого обозначаются как 0 и 1 и рассматривают их как формальные символы, не имеющие арифметического смысла…
Основные положения дискретной математики
3. БУЛЕВА АЛГЕБРА
Множество В, на котором определены две бинарные операции (конъюнкция и дизъюнкция) и одна унарная операция (отрицание ) и выделены два элемента 0 и 1 называется булевой алгеброй…
Основы высшей математики
2 Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm?n на матрицу Вn?p, называется матрица Сm?p такая, что сik = ai1 ? b1k + ai2 ? b2k + … + ain ? bnk…
Решение математических задач средствами Excel
1.2 Линейная алгебра
…
Численные методы линейной алгебры
5. Вычисление обратных матриц
Обратную матрицу А-1 имеет любая квадратная матрица А, для которой detA 0. Пусть дана матрица А = [aij]nn. Для вычисления элементов обратной матрицы используется соотношение A A-1 = A-1 A = E, где E – единичная матрица. Обозначим обратную матрицу A-1 = X = [xij]nn…
Элементы высшей математики
1.1 Матрицы, виды матриц
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. Для записи матрицы используется следующее обозначение: Для любого элемента первый индекс означает номер строки…
Элементы математической логики. Исчисление высказываний
2. АЛГЕБРА ВЫСКАЗЫВАНИЙ
Любая формула алгебры высказываний рассматривается как сложное высказывание, принимающее значение 0,1…
math.bobrodobro.ru
Алгебра матриц – часть 2
, = 12-12 = 0; А – вырожденная матрица.Теорема. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из множителей есть вырожденная матрица.
Необходимость. Пусть АВ – вырожденная матрица, т.е.
=0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем Это значит, что хотя бы одна из матриц А или В является вырожденной.Достаточность. Пусть в произведении АВ матрица А вырожденная, т.е.
=0. Найдем , т.к. =0; итак, =0; АВ – вырожденная матрица.Замечание. Доказанная теорема справедлива для любого числа множителей.
Обратная матрица
Определение. Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если
АВ = ВА = Е. (1)
Пример.
, .В – матрица обратная к А.
Теорема. Если для данной матрицы обратная существует, то она определяется однозначно.
Предположим, что для матрицы А существуют матрицы Х и У, такие, что
АХ = ХА = Е (2)
АУ = УА = Е (3)
Умножая одно из равенств, например, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Поскольку УА = Е, то ЕХ = УЕ, т.е. Х = У. Теорема доказана.
Теорема (необходимое и достаточное условие существования обратной матрицы).
Обратная матрица А-1 существует тогда и только тогда, когда исходная матрица А невырожденная.
Необходимость. Пусть для матрицы А существует обратная А-1 , т.е. А
А-1 = А-1А = Е. Тогда, ½А А-1 ½= ½А½½А-1 ½=½Е½=1, т.е. ½А½0 и ½А-1 ½0; А – невырожденная.Достаточность. Пусть дана невырожденная матрица порядка n
,так что ее определитель
0. Рассмотри матрицу, составленную из алгебраических дополнений к элементам матрицы А: ,ее называют присоединенной к матрице А.
Следует обратить внимание на то, что алгебраические дополнения к элементам i-ой строки матрицы А стоят в i-ом столбце матрицы А* , для
. Найдем произведения матриц АА* и А* А. Обозначим АА* через С, тогда по определению произведения матриц имеем: Сij = аi1 А 1j + аi2 А 2j + … + аin Аnj ; i = 1, n: j = 1, n.При i = j получим сумму произведений элементов i – ой строки на алгебраические дополнения этой же строки, такая сумма равняется значению определителя. Таким образом Сij = |А| = D – это элементы главной диагонали матрицы С. При i
j, т.е. для элементов Сij вне главной диагонали матрицы С, имеем сумму произведений всех элементов некоторой строки на алгебраические дополнения другой строки, такая сумма равняется нулю. Итак, = АА*Аналогично доказывается, что произведение А на А* равно той же матрице С. Таким образом, имеем А* А = АА* = С. Отсюда следует, что
Поэтому, если в качестве обратной матрицы взять
, то Итак, обратная матрица существует и имеет вид: .Пример. Найдем матрицу, обратную к данной:
Находим D = |А| = -1 ¹ 0, А
существует. Далее находим алгебраические дополнения элементов матрицы А:А
= = 0 ; А = = -1; А = = 3;А
= = -3; А = = 3; А = = -4;А
= = 1; А = = -1; А = = 1;А
=mirznanii.com
Алгебра матриц основные понятия
АЛГЕБРА МАТРИЦ
ОСНОВНЫЕ ПОНЯТИЯ
Определение. Прямоугольная таблица из m строк и n столбцов, заполненная некоторыми математическими объектами, называется – матрицей.
Мы будем рассматривать числовые матрицы. Числа, составляющие матрицу, называются ее элементами. Для обозначения матрицы, как правило, используются круглые скобки. При записи, в общем виде элементы матрицы обозначаются одной буквой с двумя индексами, из которых первый указывает номер строки, а второй – номер столбца матрицы. Например, матрица
.
.
В сокращенной записи: А=(аij); где аij – действительные числа, i=1,2,…m;
j=1,2,…,n (кратко , . ). Произведение называют размером матрицы.
Матрица называется квадратной порядка n, если число ее строк равно числу столбцов и равно n:
Упорядоченный набор элементов а11,а22,…,аnn называется главной диагональю, в свою очередь, а1n,а2,n-1,…,аn1– побочной диагональю матрицы. Квадратная матрица, элементы которой удовлетворяют условию:
называется диагональной, т.е. диагональная матрица имеет вид:
Диагональная матрица порядка n называется единичной, если все элементы ее главной диагонали равны 1. Матрица любого размера называется нулевой или нуль матрицей, если все ее элементы равны нулю.
Единичная матрица обозначается буквой Е, нулевая – О. Матрицы имеют вид:
.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Определение. Суммой матриц А=(аij) и B=(bij) одинаковых размеров называется матрица С=(сij) тех же размеров, такая что cij=aij+bij для всех i и j.
.
Таким образом, чтобы сложить матрицы А и В, надо сложить их элементы, стоящие на одинаковых местах. Например,
A + B = = C
Определение. Произведение матрицы А на число называется матрица А=( аij), получаемая умножением всех элементов матрицы А на число .
Например, если и =5, то
Разность матриц А и В можно определить равенством А-В=А+(-1)В.
Рассмотренные операции называются линейными.
Отметим некоторые свойства операций.
Пусть А,В,С – матрицы одинакового размера; , – действительные числа.
А+В = В+А – коммутативность сложения.
(А+В)+С = А+(В+С) – ассоциативность сложения.
Матрица О, состоящая из нулей, играет роль нуля: А+О=А.
Для любой матицы А существует противоположная –А, элементы которой отличаются от элементов А знаком, при этом А+( -А)=О.
(А) = ()А = (А). 6. (+)А = А+А.
7. (А+В) = А+В. 8. 1* А = А. 9. 0 * А = 0.
УМНОЖЕНИЕ МАТРИЦ
В матричной алгебре важную роль играет операция умножения матриц, это весьма своеобразная операция.
Определение. Произведением матрицы А=(аij) размера и прямоугольной матрицы B=(bij) размера называется прямоугольная матрица С=(сij) размера , такая что cij=ai1+b1j+ ai2+b2j+…+ aik+bkj; , .
Таким образом, элемент произведения матриц А и В, стоящий в i-ой строке и j-ом столбце, равен сумме произведений элементов i-ой строки первой матрицы А на соответствующие элементы j-ого столбца второй матрицы В т.е.
.
Произведение С=АВ определено, если число столбцов матрицы А равно числу строк матрицы В. Это условие, а также размеры матриц можно представить схемой:
Очевидно, что операция умножения квадратных матриц всегда определена.
Примеры. Найдем произведения матриц АВ и ВА, если они существуют.
1. , .
2. , .
Таким образом, коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, т.е. В частном случае коммутативным законом обладает произведение любой квадратной матрицы А n-го порядка на единичную матрицу Е такого же порядка, т.е.
3. , .
Для этих матриц произведение как АВ ,так и ВА не существует.
,
Получим , ВА – не существует.
Свойства умножения матриц.
Пусть А,В,С – матрицы соответствующих размеров (т.е. произведения матриц определены), – действительное число. Тогда на основании определений операций и свойств действительных чисел имеют место следующие свойства:
(АВ)С = А(ВС) – ассоциативность.
(А+В)С = АС+ВС – дистрибутивность.
А(В+С) = АВ+АС – дистрибутивность.
(АВ) = (А)В = А(В).
ЕА = АЕ = А, для квадратных матриц единичная матрица Е играет роль единицы.
Приведем пример доказательства лишь одного свойства. Докажем, например, свойство 3.
Пусть для А=(аij), B=(bij), C=(cij) произведения матриц определены. Найдем элемент i-ой строки и j-го столбца матрицы А(В+С). Это будет число
аi1(b1j+c1j)+ аi2(b2j+c2j)+…+аin(bnj+cnj) =
(аi1b1j+ai2b2j+…+ainbnj)+ (аi1c1j+ai2c2j+…+aincnj).
Первая сумма в правой части равенства равна элементу из i-ой строки и j-го столбца матрицы АВ, а вторая сумма равна элементу из i-ой строки и j-го столбца матрицы АС. Рассуждение верно при любых i и j, то свойство 3 доказано.
Упражнение 1. Проверьте свойство ассоциативности 1 для матриц:
, , .
Упражнение 2. Проверьте свойство дистрибутивности 2 для матриц:
, , .
Упражнение 3. Найти матрицу А3, если .
ВЫРОЖДЕННЫЕ И НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
Определение. Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.
Пример. , = 16-15 = 1 0; А – невырожденная матрица.
, = 12-12 = 0; А – вырожденная матрица.
Теорема. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из множителей есть вырожденная матрица.
Необходимость. Пусть АВ – вырожденная матрица, т.е. =0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем Это значит, что хотя бы одна из матриц А или В является вырожденной.
Достаточность. Пусть в произведении АВ матрица А вырожденная, т.е. =0. Найдем , т.к. =0; итак, =0; АВ – вырожденная матрица.
Замечание. Доказанная теорема справедлива для любого числа множителей.
ОБРАТНАЯ МАТРИЦА
Определение. Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если
АВ = ВА = Е. (1)
Пример. , .
В – матрица обратная к А.
Теорема. Если для данной матрицы обратная существует, то она определяется однозначно.
Предположим, что для матрицы А существуют матрицы Х и У, такие, что
АХ = ХА = Е (2)
АУ = УА = Е (3)
Умножая одно из равенств, например, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Поскольку УА = Е, то ЕХ = УЕ, т.е. Х = У. Теорема доказана.
Теорема (необходимое и достаточное условие существования обратной матрицы).
Обратная матрица А-1 существует тогда и только тогда, когда исходная матрица А невырожденная.
Необходимость. Пусть для матрицы А существует обратная А-1, т.е. А А-1 = А-1А = Е. Тогда, А А-1= АА-1=Е=1, т.е. А0 и А-10; А – невырожденная.
Достаточность. Пусть дана невырожденная матрица порядка n
,
так что ее определитель 0. Рассмотри матрицу, составленную из алгебраических дополнений к элементам матрицы А:
,
ее называют присоединенной к матрице А.
Следует обратить внимание на то, что алгебраические дополнения к элементам i-ой строки матрицы А стоят в i-ом столбце матрицы А*, для .
Найдем произведения матриц АА* и А*А. Обозначим АА* через С, тогда по определению произведения матриц имеем: Сij= аi1А 1j + а i2А 2j + … + а inАnj; = 1, n: j = 1, n.
При = j получим сумму произведений элементов – ой строки на алгебраические дополнения этой же строки, такая сумма равняется значению определителя. Таким образом Сij = |А| = – это элементы главной диагонали матрицы С. При j, т.е. для элементов Сij вне главной диагонали матрицы С, имеем сумму произведений всех элементов некоторой строки на алгебраические дополнения другой строки, такая сумма равняется нулю. Итак, = АА*
Аналогично доказывается, что произведение А на А* равно той же матрице С. Таким образом, имеем А*А = АА* = С. Отсюда следует, что
Поэтому, если в качестве обратной матрицы взять , то Итак, обратная матрица существует и имеет вид:
.
Пример. Найдем матрицу, обратную к данной:
Находим = |А| = -1 0, А существует. Далее находим алгебраические дополнения элементов матрицы А:
А = = 0 ; А = = -1; А = = 3;
А = = -3; А = = 3; А = = -4;
А = = 1; А = = -1; А = = 1;
А =
podelise.ru
МАТРИЦ АЛГЕБРА – это… Что такое МАТРИЦ АЛГЕБРА?
матричная алгебра,- подалгебра полной матричной алгебры Fn всех -матриц над полем F. Операции в Fn определяются следующим образом:
для
Алгебра Fn изоморфна алгебре всех эндоморфизмов n-мерного линейного пространства над F. Размерность Fn ‘ над Fравна n2. Любая ассоциативная алгебра с единицей, размерность к-рой над Fне больше п, изоморфна нек-рой подалгебре в Fn. Ассоциативная алгебра без единицы, размерности меньше пнад F, также изоморфно вкладывается в F п. В силу теоремы Веддерберна алгебра Fn проста, т. е. имеет лишь тривиальные двусторонние идеалы. Центр алгебры Fn состоит из всех скалярных -матриц над F. Группа обратимых элементов алгебры Fn есть полная линейная группа Каждый автоморфизм hалгебры Fn является внутренним:
Неприводимая М. а. проста. Если М. а. Аабсолютно неприводима (напр., когда поле Fалгебраически замкнуто), то A = Fn при n>1 (теорема Бёрнсайда). М. а. полупроста тогда и только тогда, когда она вполне приводима.
С точностью до сопряженности в Fn имеется единственная максимальная нильпотентная подалгебра – алгебра всех верхних треугольных матриц с нулевой диагональю. В алгебре F п тогда и только тогда имеется коммутативная подалгебра размерности r, когда
(теорема – Шура). Для поля комплексных чисел С множество классов сопряженных максимальных коммутативных подалгебр алгебры при конечно, а при n>6 бесконечно.
В алгебре Fn выполняется стандартное тождество степени 2n:
где S2n– симметрич. группа, и никакое тождество меньшей степени не выполняется.
Лит.:[l] Вейль Г., Классические группы, их инварианты и лредставленип, пер. с англ., М., 1947; [2] Джекобсон Н., Строение колец, пер. с англ., М.. 1961; [3] Херстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [4] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [5] Супруненко Д. А., Тышкевич Р. И., Перестановочные матрицы, Минск, 1966.
Д. Л. Супруненко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru

 (AB)
= (
(AB)
= ( A)B
A)B