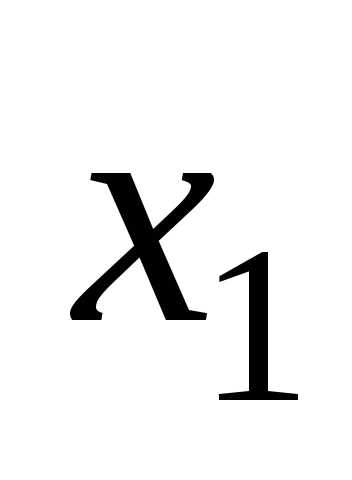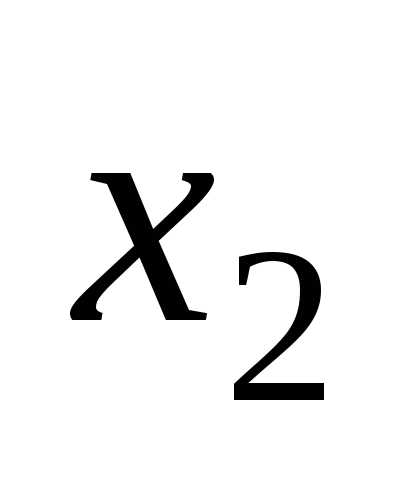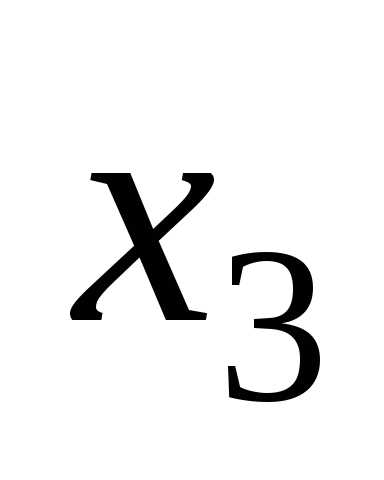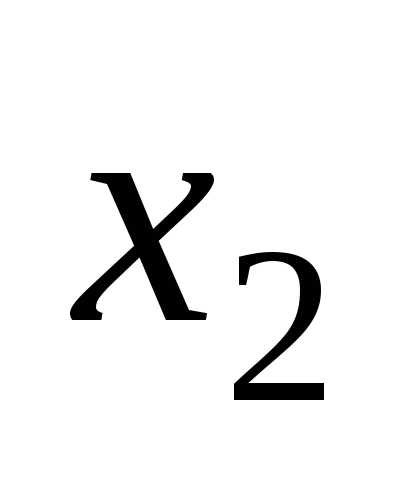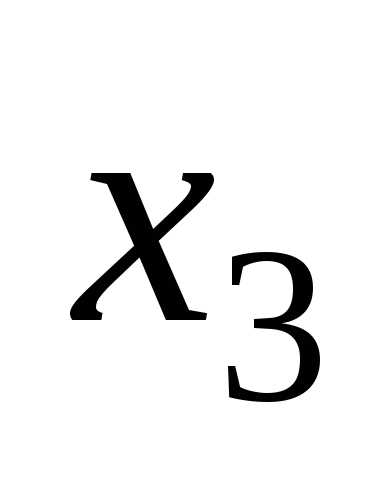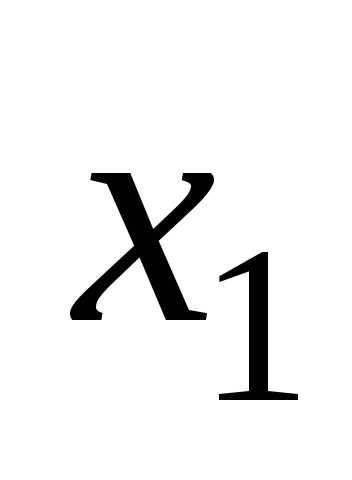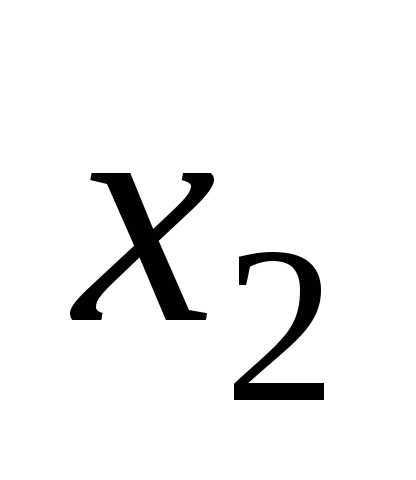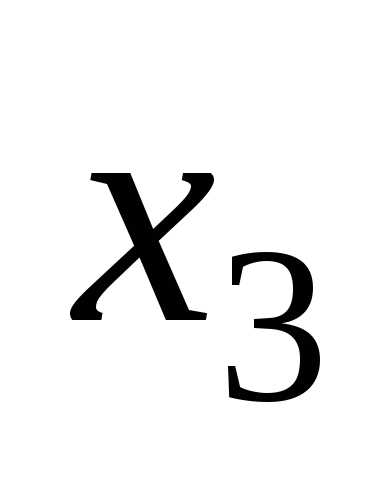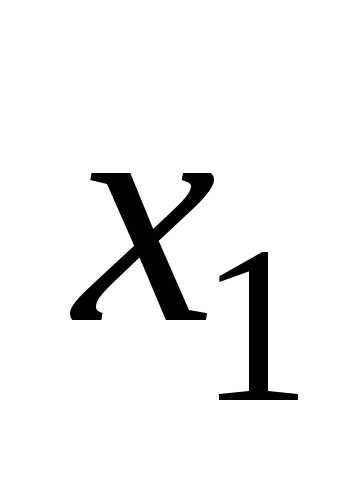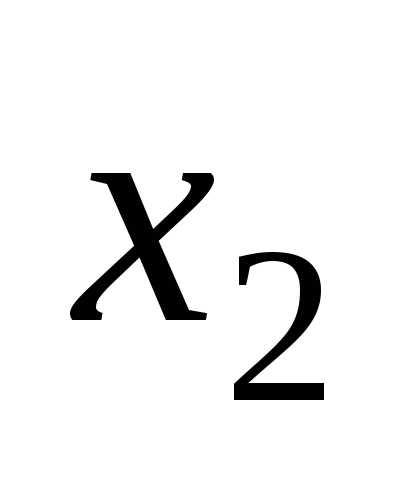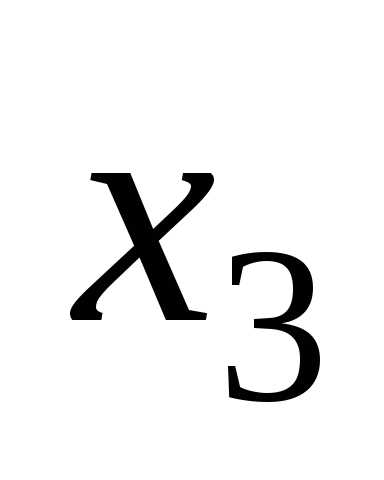7 Предоставление логических функций в базисах и-не, или-не
Логические функции образуют базис, если с их использованием можно реализовать любую логическую функцию.
Логическая функция ИЛИ-НЕ (функция Вебба) образует базис, т. е. для любой логической функции можно реализовать схему, используя только функцию ИЛИ-НЕ. Соответственно и логический элемент реализующий эту функцию – элемент ИЛИ-НЕ.
Логические элементы ИЛИ-НЕ могут быть двухвходовые (2ИЛИ-НЕ), трехвходовые (3ИЛИ-НЕ), четырехвходовые (4ИЛИ-НЕ) (рисунок 12, а, б, в)
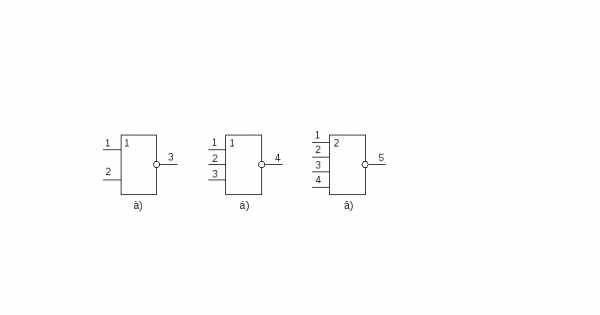
Рисунок 12 – Элементы ИЛИ-НЕ
В базисе 2ИЛИ-НЕ справедливы следующие основные свойства:
Связь в базисе 2ИЛИ-НЕ с конъюнкцией реализуется как:
(рисунок 13, а) (1)
В общем случае, для n входных переменных:
Связь в базисе 2ИЛИ-НЕ с дизъюнкцией реализуется как:
(рисунок 13, б) (2)
В общем случае для n переменных:
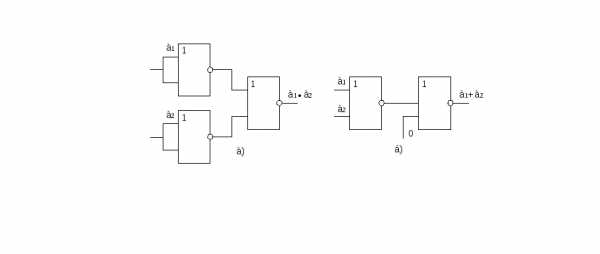
Рисунок 13 – Реализация конъюнкции и дизъюнкции на элементах 2ИЛИ-НЕ
Для представления логической функции в базисе Вебба в общем случае необходимо:
– исходную логическую функцию представить в виде КНФ;
– в элементарных дизъюнкциях знак «+» заменить на и между скобками поставитьвместо «»
Пример:
Логическая функция в базисе Вебба может быть записана с учетом закона двойной инверсии или закона де Моргана (рисунок 14)
Например:
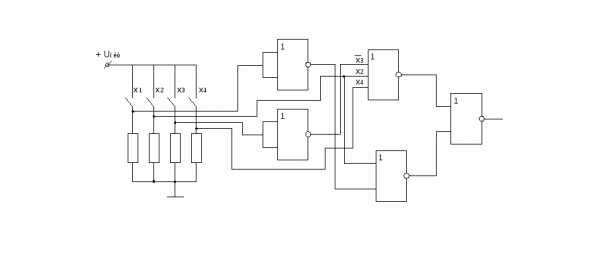
Рисунок 14 – Реализация в базисе Вебба
Если логическая функция должна быть записана только в базисе 2ИЛИ-НЕ, а количество логических переменных у нее больше двух, то необходимо использовать принцип суперпозиции и преобразования 1 и 2.
Например: , здесь
К полученному выражению применяем преобразование 1
Подставляем запись для A в базисе Вебба в выражение и получим:
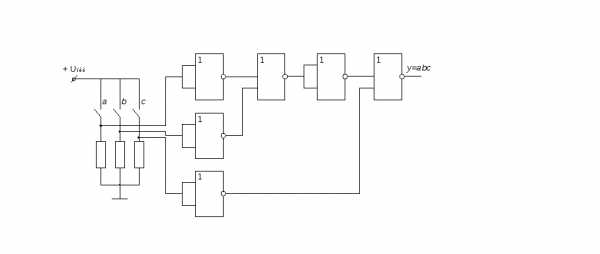
Рисунок 15 – Реализация в базисе 2ИЛИ-НЕ
Логическая функция И-НЕ (функция Шеффера) образует базис, т. е. для любой логической функции можно реализовать схему, используя только функцию И-НЕ. Соответственно и логический элемент реализующий эту функцию – элемент И-НЕ.
Логические элементы И-НЕ могут быть двухвходовые (2И-НЕ), трехвходовые (3И-НЕ), четырехвходовые (4И-НЕ) (рисунок 16, а, б, в)
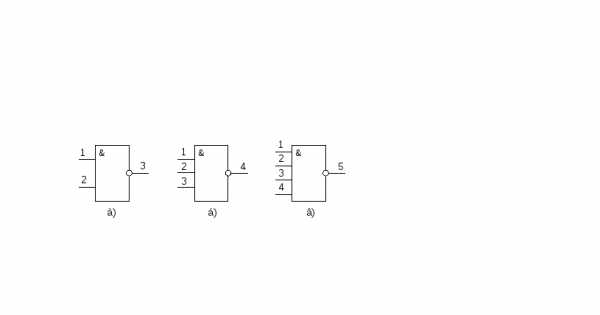
Рисунок 16 – Элементы И-НЕ
Основные свойства в базисе 2И-НЕ для логической функции 2И-НЕ следующие
здесь – определяет операцию И-НЕ
Связь в базисе 2И-НЕ с конъюнкцией реализуется как:
(рисунок 17, а) (3)
В общем случае, для n входных переменных:
Связь в базисе 2И-НЕ с дизъюнкцией реализуется как:
(рисунок 17, б) (4)
В общем случае:
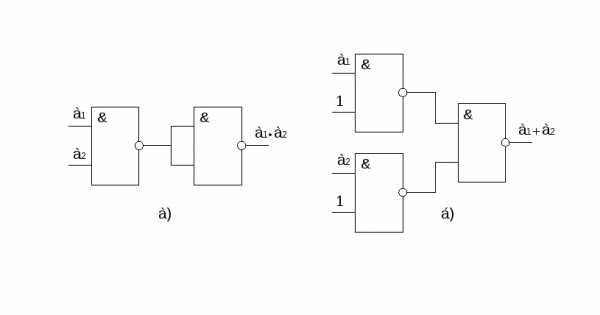
Рисунок 17 – Реализация конъюнкции и дизъюнкции на элементах 2И-НЕ
Для представления логической функции в базисе Шеффера в общем случае необходимо:
– исходную логическую функцию представить в виде ДНФ;
– все элементарные конъюнкции заключить в скобки;
– заменить все знаки + и на
Пример:
Логическая функция в базисе Шеффера может быть записана с учетом закона двойной инверсии или закона де Моргана (рисунок 18)
Например:
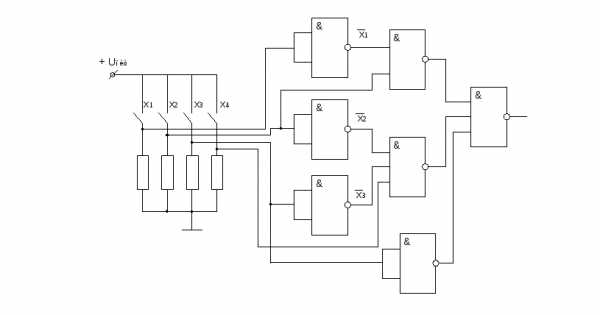
Рисунок 18 – Реализация в базисе Шеффера
Если логическая функция должна быть записана только в базисе 2И-НЕ, а количество логических переменных у нее больше двух, то необходимо использовать принцип суперпозиции и преобразования 3 и 4.
Например: , здесь
К полученному выражению применяем преобразование 3
Подставляем запись для A в базисе Шеффера в выражение и получим:
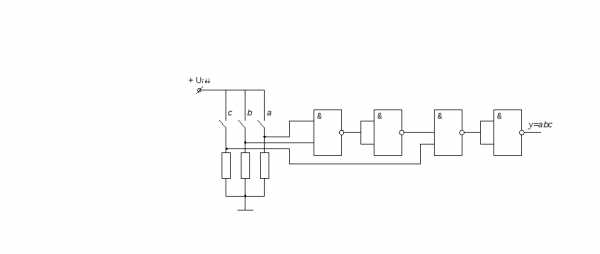
Рисунок 19 – Реализация в базисе 2И-НЕ
7Абсолютно минимальные представления
Задача о нахождении такого аналитического представления ФАЛ, при котором число букв в представлении минимально в классе ДНФ, может быть решена с использованием скобочного представления ФАЛ.
Определение
7-1. Q представляет собой минимальное
представление для функции f,
если не существует в базисе {-, &, }
представления более минимального , чемQ,
каким бы способом ни получилось это
выражение.
}
представления более минимального , чемQ,
каким бы способом ни получилось это
выражение.
Дальнейшая минимизация МДНФ за счет вынесения за скобки является практически наиболее подходящим приемом получения абсолютно минимального представления ФАЛ в классе ДНФ.
Пример 1-7. Для функции
найдена МДНФ вида: .
Если вынести за скобки x1, то получим абсолютно минимальное представление: .
Замечание 1-4. Отметим, что МДНФ зачастую не дает абсолютно минимального представления. В ряде случаев МКНФ оказывается “меньше” МДНФ. Поэтому для получения абсолютно минимальных представлений ФАЛ необходимо из них выбрать наименьшее.
Методы получения МКНФ двойственны методам получения МДНФ.
Глава 2.Преобразования и минимизация в базисе состоящем из функции вебба или из функции шеффера.1
Проблема минимизации ФАЛ может быть сформирована и для случая любого другого базиса. Функции Вебба (Пирса) и Шеффера образуют базисы, состоящие только из одной функции. Будем называть такие базисы монофункциональными.
В
последнее время возник большой интерес
к моно-функциональным базисам. Поэтому
рассмотрим их более подробно. Оба базиса
обладают одинаковыми свойствами, поэтому
рассмотрим задачу минимизации ФАЛ лишь
для одного из них – базиса из функции
Вебба. Для упрощения записи в дальнейшем
будем использовать знак
Все сказанное о базисе Вебба практически без всяких изменений может быть использовано и для базиса, состоящего из функции Шеффера.
По аналогии с двуместными, введем с помощью таблицы n-местные функции Вебба и Шеффера:
x1 | x2 | x3 | . | . | . | xn-1 | Xn | Wn | Sn |
0 | 0 | 0 | . | . | . | 0 | 1 | 1 | |
0 | 0 | 0 | . | . | . | 0 | 1 | 0 | 1 |
0 | 0 | 0 | . | . | . | 1 | 0 | 0 | 1 |
– | – | – | – | – | – | – | – | – | – |
– | – | – | – | – | – | – | – | – | |
1 | 1 | 1 | . | . | . | 0 | 1 | 0 | 1 |
1 | 1 | 1 | . | . | . | 1 | 0 | 0 | 1 |
1 | 1 | 1 | . | . | . | 1 | 1 | 0 | 0 |
При n=2
из этой таблицы получаются двухместные
функции Вебба и Шеффера, а при n=1
обе функции вырождаются в функцию
отрицания. Поэтому в дальнейшем будем
вместо 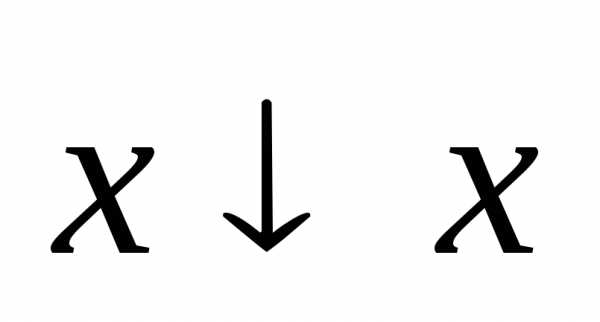 иx/x писать
соответственно
иx/x писать
соответственно  .
.
Для введенных функций справедлив переместительный закон и несправедлив сочетательный закон.
Справедливы следующие соотношения:

(2-1)
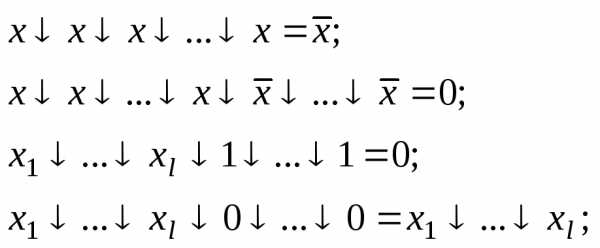
При раскрытии скобок получим:
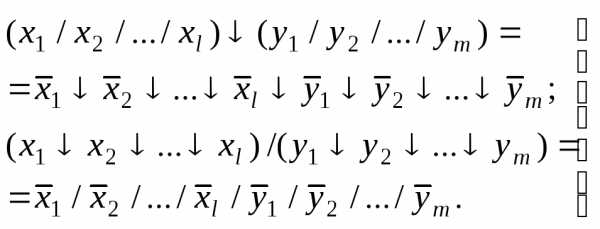
(2-2)
Заметим, что если l или m равны единице, то эти соотношения выразятся несколько иначе. Например, при l=1:
(2-3)
Наконец, приведем соотношения, показывающие связь между многоместными функциями Вебба и Шеффера и являющиеся аналогами формул де Моргана:
(2-4).
Справедливость всех вышеприведенных соотношений можно установить при помощи таблиц истинности ФАЛ.
В дальнейшем в основном будем рассматривать базис, построенный на основе многоместной функции Вебба.
Известно [11], что любую ФАЛ можно представить:
,
если
выбрать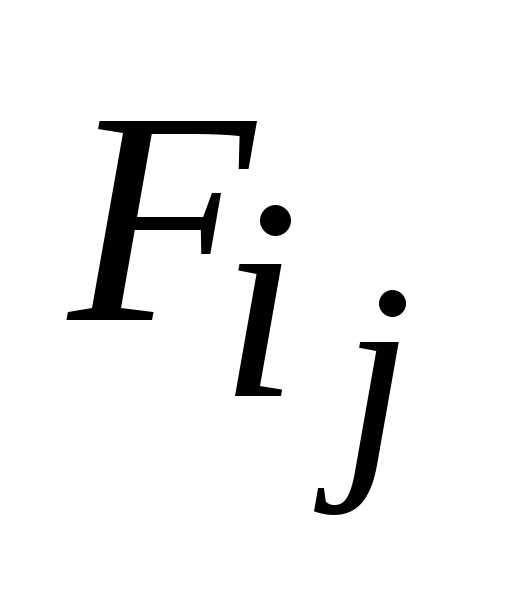 -характеристические
функции единицы для множества Т0 номеров
наборов, на которых функция f обращается в нуль:
-характеристические
функции единицы для множества Т0 номеров
наборов, на которых функция f обращается в нуль:
Применяя последнееиз соотношений (2-1), получаем одну из двух совершенных нормальных форм в базисе Вебба:
(2-5)
Если использовать характеристические функции единицы для множества T1 номеров наборов, на которых функция f обращается в единицу, то получится другая совершенная нормальная форма. Она проще предыдущей, если у функции в таблице истинности нулей больше, чем единиц:
(2-6)
Для получения аналогичных нормальных форм в базисе Шеффера можно использовать характеристические функции нуля.
Перейдем
теперь к аналитическому выражению
характеристических функций единицы в
базисе Вебба. Для любой характеристическойфункцииединицы
в базисе {-, &, }
может быть
получено выражение через конституенту
единицы:
}
может быть
получено выражение через конституенту
единицы:
Если применить последнее из соотношений (2-1), то
(2-7)
и мы можем написать, что

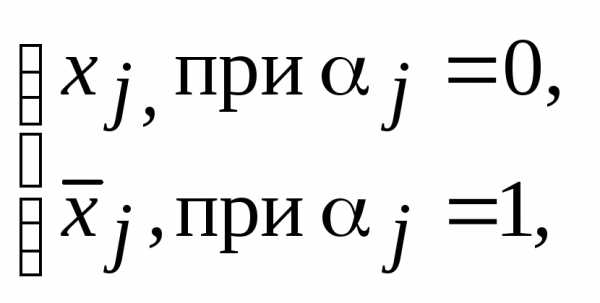
и получить выражение для характеристической функции единицы:
(2-8)
при условии, что
.
Теперь мы можем сформулировать алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Вебба вида, например, (2-5):
Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в нуль.
Выписать термы типа (2-8), соответствующие этим наборам аргументов. При этом, если аргумент
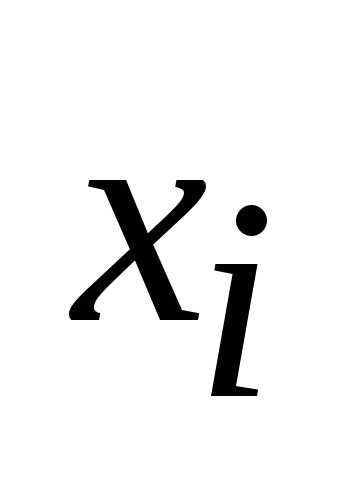 входит в данный набор как нуль, он
вписывается без изменения. Если же
входит в данный набор как нуль, он
вписывается без изменения. Если же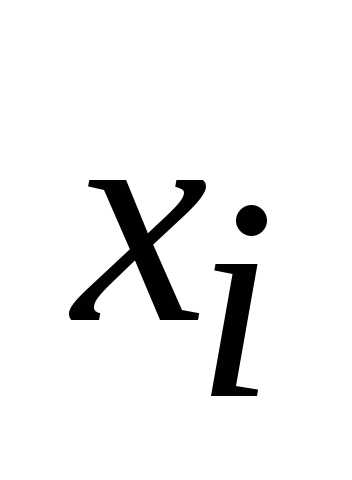 входит в данный набор как единица, то
вписывается его отрицание.
входит в данный набор как единица, то
вписывается его отрицание.Все полученные выражения характеристических функций объединяются k-местной операцией Вебба, где k – количество нулей заданной функции.
Пример 2-1. Построить совершенную нормальную форму вида (2-5) для следующей таблично заданной функции:
|
|
|
|
|
| ||
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
в соответствии с алгоритмом получаем:
Проблема минимизации в монофункциональных базисах.
Существует два подхода к проблеме минимизации: либо по аналогии с минимизацией в классе ДНФ строится специальный метод минимизации для монофункционального базиса, либо минимизация производится в классе ДНФ, а затем строится специальный метод перехода от базиса конъюнкция, дизъюнкция, отрицание к монофункциональному базису. Рассмотрим сначала первый подход на примере минимизации в базисе , состоящем из функции Вебба.
Все
определения для ФАЛ в базисе {-, &, },
введенные в главе 1, имеют свои аналоги
и для рассматриваемого базиса. Совершенной
нормальной формой в дальнейшем будем
считать выражение (2-5), операнды которого
будут иметь наибольший возможный для
данной функции ранг. Определение
минимальной нормальной формы вполне
аналогично определению МДНФ в классе
ДНФ.
},
введенные в главе 1, имеют свои аналоги
и для рассматриваемого базиса. Совершенной
нормальной формой в дальнейшем будем
считать выражение (2-5), операнды которого
будут иметь наибольший возможный для
данной функции ранг. Определение
минимальной нормальной формы вполне
аналогично определению МДНФ в классе
ДНФ.
Понятиям интервал и максимальный интервал из геометрической интерпретации области определения функции алгебры логики соответствовали понятия импликанта и простая импликанта при минимизации в классе ДНФ. В базисе Вебба соответствующие понятия будем называть инверсантой и простой инверсантой .
Инверсанта и функции f характеризуется
тем, что всегда из и=1
следует f=0.
Очевидно, что все Fi из (2-5) являются инверсантами заданной
функции f. Отметим, что 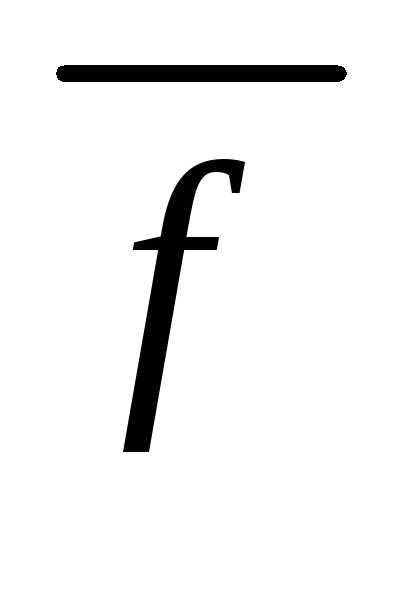 тоже является инверсантой функцииf.
тоже является инверсантой функцииf.
По
аналогии с классическим базисом будем
говорить, что выражение в базисе Вебба,
операндами которого являются все простые
инверсанты заданной функции, является сокращенной
нормальной формой функции. Минимальная
нормальная форма будет
получаться из сокращенной выбрасыванием
некоторых инверсантов. Определение
тупиковой формы в рассматриваемом
базисе Вебба формулируется по аналогии
с классическим базисом {-, &, }.
}.
Тупиковой ДНФ функции f называется дизъюнкция простых импликантов, из которых ни один простой импликант нельзя удалить так, чтобы полученная ДНФ все еще представляла функцию. Получение МДНФ можно разбить на два этапа. На первом находят сокращенную ДНФ. На втором строят тупиковые ДНФ функции, удаляя подмножества элементарных конъюнкций из сокращенной ДНФ. Из полученных тупиковых ДНФ выбирают МДНФ.
Прежде чем перейти к рассмотрению применения в базисе Вебба некоторых известных из классического базиса методов минимизации, укажем эквивалентные преобразования, приводящие к операциям склеивания и поглощения в алгебре Вебба.
Введем теперь операции следующих типов:
склеивания
(2-9)
неполного склеивания
(2-10)
и поглощения
(2-11)
В этих выражениях включен произвольный терм A, указывающий на то, что операции производятся между операндами внутри многоместного терма. Отсутствие А привело бы к двухместным операциям и к вырождению некоторых операндов.
Для двухместного случая аналоги операций склеивания и поглощения имеют вид:
(2-12)
(2-13)
Справедливость всех этих соотношений легко доказать, построив таблицу истинности ФАЛ.
Рассмотрим теперь аналоги методов минимизации, рассмотренных нами для базиса конъюнкция, дизъюнкция, отрицание.
studfiles.net
2.3.1. Элемент и-не (штрих Шеффера)
Алгебраическая форма: | |
Таблица истинности для двух переменных: | |
Условное графическое изображение: |
Функция И-НЕ принимает значение 1 при нулевом значении хотя бы одного аргумента.
2.3.2. Элемент или-не (стрелка Пирса)
Алгебраическая форма: | |
Таблица истинности: | |
Условное графическое изображение: |
Функция ИЛИ-НЕ принимает значение 0, если хотя бы один аргумент принимает значение 1.
Элементы И-НЕ, ИЛИ-НЕ называются функционально-полными, т. к. на основе базиса каждого из них можно выполнить любую элементарную логическую функцию: НЕ, И, ИЛИ. Покажем это на примере элемента И-НЕ. С учетом правила логического умножения операцию НЕ можно представить в виде или .Таким образом, получаем схемы инверторов в базисе И-НЕ (рис. 2.8).
Рис. 2.8. Схемы инверторов в базисе И-НЕ
Применяя последовательно операции двоичного отрицания и теоремы де Моргана, можно операцию ИЛИ представить в виде
,
отсюда получаем элемент ИЛИ в базисе И-НЕ (рис. 2.9).
Рис. 2.9. Элемент ИЛИ в базисе И-НЕ
На основе правила двоичного отрицания имеем и соответственно элемент И в базисе И-НЕ (рис. 2.10).
Рис. 2.10. Элемент И в базисе И-НЕ
2.4. Синтез логических устройств
Под синтезом логических устройств понимается переход от логической функции, заданной любым способом, к электрической схеме, реализующей эту функцию.
Если исходная логическая функция задана в виде таблицы, то синтез начинается с алгебраической записи функции, которая может быть представлена в двух вариантах – совершенной нормальной дизъюнктивнойформе (СДНФ) или совершеннойконъюнктивнойнормальной форме (СКНФ).
Получение СДНФ покажем на примере некоторой логической функции трех переменных, заданной таблицей истинности (табл. 2.1). Для каждого набора переменных, где функция принимает значение 1, в данном случае это наборы № 1, 3, 5, 7, записывается логическое произведение аргументов (минтерм), причем если аргумент имеет значение 0, то в произведении берется его отрицание. Так, для n=1 можно записать, что , дляn = 3 и т. д. Полученные таким образом произведения объединены логическим сложением. В результате для функции по табл. 2.1 получим СДНФ в виде
. (2.1)
Электрическая схема, реализующая функцию (2.1), должна содержать два элемента НЕ, четыре трехвходовых элемента И и один четырехвходовый элемент ИЛИ (рис. 2.11).
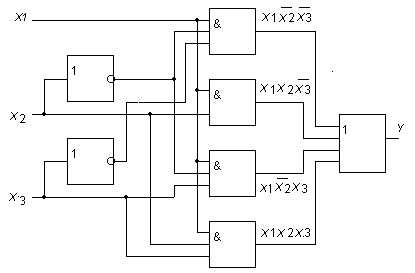
Рис. 2.11. Электрическая схема, реализующая логическую функцию, заданную табл. 2.1
Для замены в СКНД используются наборы переменных, где функция принимает значение «0». В данном случае это набор с номерами 0, 2, 4, 6. Для этих наборов записывается сумма аргументов, причем если аргумент имеет значение 0, то записывается сам аргумент, а если 1 – его отрицание. Полученные таким образом суммы (макстермы) объединяются логическим умножением. Для рассматриваемой функции по табл. 2.1 получим логическое уравнение в СКНФ форме в виде
. (2.2)
Для реализации структурной схемы потребуется два инвертора, четыре элемента ИЛИ на три входа и один четырехвходовый элемент И.
studfiles.net
7Абсолютно минимальные представления
Задача о нахождении такого аналитического представления ФАЛ, при котором число букв в представлении минимально в классе ДНФ, может быть решена с использованием скобочного представления ФАЛ.
Определение
7-1. Q представляет собой минимальное
представление для функции f,
если не существует в базисе {-, &, }
представления более минимального , чемQ,
каким бы способом ни получилось это
выражение.
}
представления более минимального , чемQ,
каким бы способом ни получилось это
выражение.
Дальнейшая минимизация МДНФ за счет вынесения за скобки является практически наиболее подходящим приемом получения абсолютно минимального представления ФАЛ в классе ДНФ.
Пример 1-7. Для функции
найдена МДНФ вида: .
Если вынести за скобки x1, то получим абсолютно минимальное представление: .
Замечание 1-4. Отметим, что МДНФ зачастую не дает абсолютно минимального представления. В ряде случаев МКНФ оказывается “меньше” МДНФ. Поэтому для получения абсолютно минимальных представлений ФАЛ необходимо из них выбрать наименьшее.
Методы получения МКНФ двойственны методам получения МДНФ.
Глава 2.Преобразования и минимизация в базисе состоящем из функции вебба или из функции шеффера.1
Проблема минимизации ФАЛ может быть сформирована и для случая любого другого базиса. Функции Вебба (Пирса) и Шеффера образуют базисы, состоящие только из одной функции. Будем называть такие базисы монофункциональными.
В
последнее время возник большой интерес
к моно-функциональным базисам. Поэтому
рассмотрим их более подробно. Оба базиса
обладают одинаковыми свойствами, поэтому
рассмотрим задачу минимизации ФАЛ лишь
для одного из них – базиса из функции
Вебба. Для упрощения записи в дальнейшем
будем использовать знак (стрелка Пирса) взамен знака для
обозначения функции Вебба (о).
(стрелка Пирса) взамен знака для
обозначения функции Вебба (о).
Все сказанное о базисе Вебба практически без всяких изменений может быть использовано и для базиса, состоящего из функции Шеффера.
По аналогии с двуместными, введем с помощью таблицы n-местные функции Вебба и Шеффера:
x1 | x2 | x3 | . | . | . | xn-1 | Xn | Wn | Sn |
0 | 0 | 0 | . | . | . | 0 | 0 | 1 | 1 |
0 | 0 | 0 | . | . | . | 0 | 1 | 0 | 1 |
0 | 0 | 0 | . | . | . | 1 | 0 | 0 | 1 |
– | – | – | – | – | – | – | – | – | – |
– | – | – | – | – | – | – | – | – | – |
1 | 1 | 1 | . | . | . | 0 | 1 | 0 | 1 |
1 | 1 | 1 | . | . | . | 1 | 0 | 0 | 1 |
1 | 1 | 1 | . | . | . | 1 | 1 | 0 | 0 |
При n=2
из этой таблицы получаются двухместные
функции Вебба и Шеффера, а при n=1
обе функции вырождаются в функцию
отрицания. Поэтому в дальнейшем будем
вместо 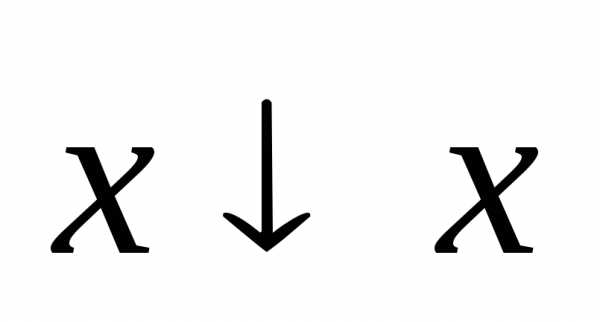 иx/x писать
соответственно
иx/x писать
соответственно 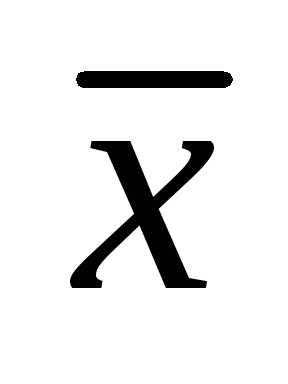 .
.
Для введенных функций справедлив переместительный закон и несправедлив сочетательный закон.
Справедливы следующие соотношения:
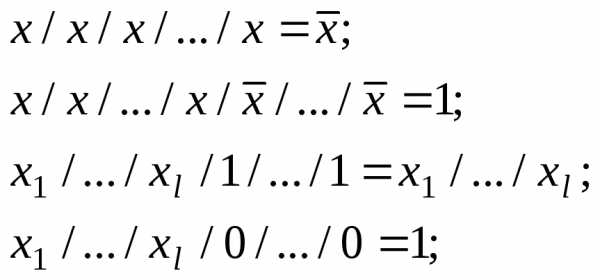
(2-1)
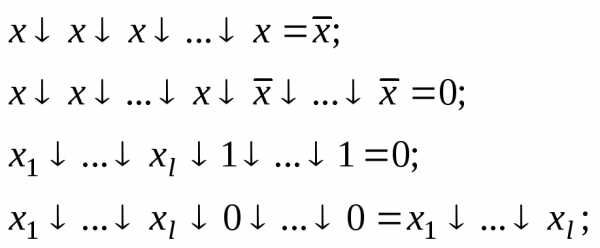
При раскрытии скобок получим:
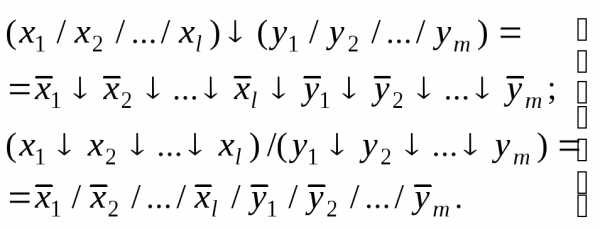
(2-2)
Заметим, что если l или m равны единице, то эти соотношения выразятся несколько иначе. Например, при l=1:
(2-3)
Наконец, приведем соотношения, показывающие связь между многоместными функциями Вебба и Шеффера и являющиеся аналогами формул де Моргана:
(2-4).
Справедливость всех вышеприведенных соотношений можно установить при помощи таблиц истинности ФАЛ.
В дальнейшем в основном будем рассматривать базис, построенный на основе многоместной функции Вебба.
Известно [11], что любую ФАЛ можно представить:
,
если
выбрать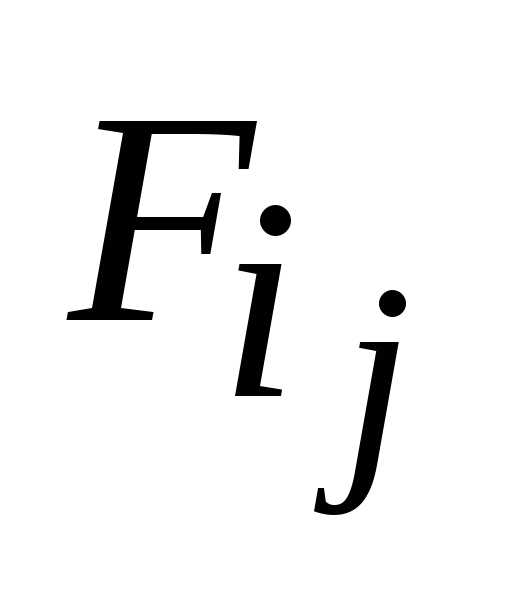 -характеристические
функции единицы для множества Т0 номеров
наборов, на которых функция f обращается в нуль:
-характеристические
функции единицы для множества Т0 номеров
наборов, на которых функция f обращается в нуль:
Применяя последнееиз соотношений (2-1), получаем одну из двух совершенных нормальных форм в базисе Вебба:
(2-5)
Если использовать характеристические функции единицы для множества T1 номеров наборов, на которых функция f обращается в единицу, то получится другая совершенная нормальная форма. Она проще предыдущей, если у функции в таблице истинности нулей больше, чем единиц:
(2-6)
Для получения аналогичных нормальных форм в базисе Шеффера можно использовать характеристические функции нуля.
Перейдем
теперь к аналитическому выражению
характеристических функций единицы в
базисе Вебба. Для любой характеристическойфункцииединицы
в базисе {-, &, }
может быть
получено выражение через конституенту
единицы:
}
может быть
получено выражение через конституенту
единицы:
Если применить последнее из соотношений (2-1), то
(2-7)
и мы можем написать, что
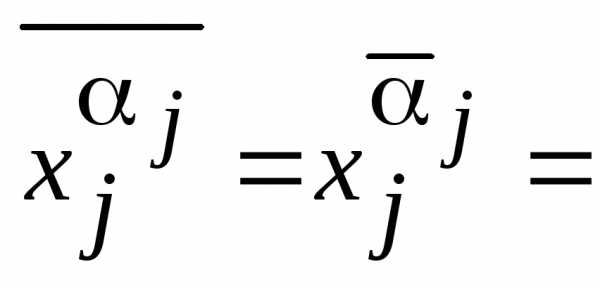
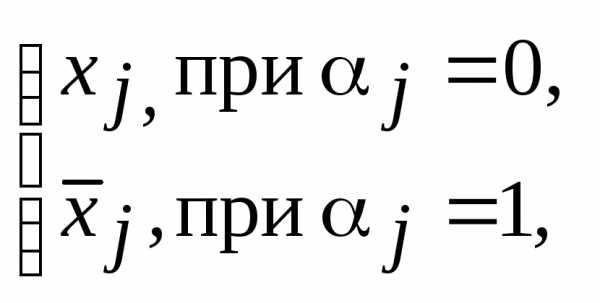
и получить выражение для характеристической функции единицы:
(2-8)
при условии, что
.
Теперь мы можем сформулировать алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Вебба вида, например, (2-5):
Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в нуль.
Выписать термы типа (2-8), соответствующие этим наборам аргументов. При этом, если аргумент
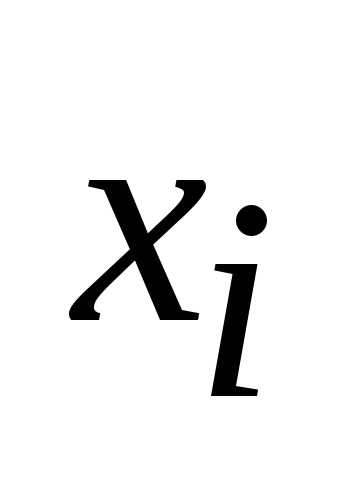 входит в данный набор как нуль, он
вписывается без изменения. Если же
входит в данный набор как нуль, он
вписывается без изменения. Если же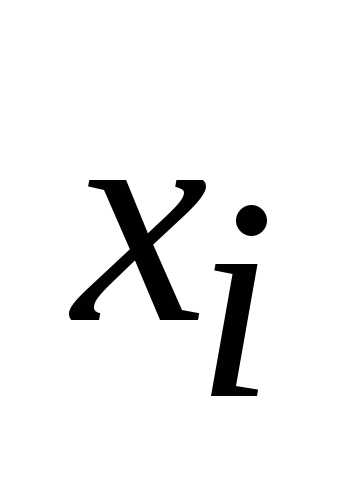 входит в данный набор как единица, то
вписывается его отрицание.
входит в данный набор как единица, то
вписывается его отрицание.Все полученные выражения характеристических функций объединяются k-местной операцией Вебба, где k – количество нулей заданной функции.
Пример 2-1. Построить совершенную нормальную форму вида (2-5) для следующей таблично заданной функции:
|
|
|
|
|
| ||
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
в соответствии с алгоритмом получаем:
Проблема минимизации в монофункциональных базисах.
Существует два подхода к проблеме минимизации: либо по аналогии с минимизацией в классе ДНФ строится специальный метод минимизации для монофункционального базиса, либо минимизация производится в классе ДНФ, а затем строится специальный метод перехода от базиса конъюнкция, дизъюнкция, отрицание к монофункциональному базису. Рассмотрим сначала первый подход на примере минимизации в базисе , состоящем из функции Вебба.
Все
определения для ФАЛ в базисе {-, &, },
введенные в главе 1, имеют свои аналоги
и для рассматриваемого базиса. Совершенной
нормальной формой в дальнейшем будем
считать выражение (2-5), операнды которого
будут иметь наибольший возможный для
данной функции ранг. Определение
минимальной нормальной формы вполне
аналогично определению МДНФ в классе
ДНФ.
},
введенные в главе 1, имеют свои аналоги
и для рассматриваемого базиса. Совершенной
нормальной формой в дальнейшем будем
считать выражение (2-5), операнды которого
будут иметь наибольший возможный для
данной функции ранг. Определение
минимальной нормальной формы вполне
аналогично определению МДНФ в классе
ДНФ.
Понятиям интервал и максимальный интервал из геометрической интерпретации области определения функции алгебры логики соответствовали понятия импликанта и простая импликанта при минимизации в классе ДНФ. В базисе Вебба соответствующие понятия будем называть инверсантой и простой инверсантой .
Инверсанта и функции f характеризуется
тем, что всегда из и=1
следует f=0.
Очевидно, что все Fi из (2-5) являются инверсантами заданной
функции f. Отметим, что 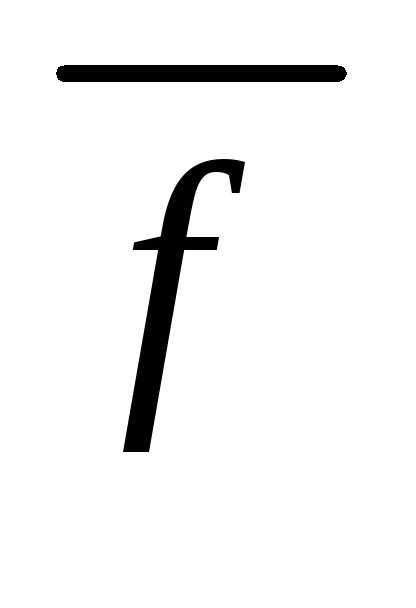 тоже является инверсантой функцииf.
тоже является инверсантой функцииf.
По
аналогии с классическим базисом будем
говорить, что выражение в базисе Вебба,
операндами которого являются все простые
инверсанты заданной функции, является сокращенной
нормальной формой функции. Минимальная
нормальная форма будет
получаться из сокращенной выбрасыванием
некоторых инверсантов. Определение
тупиковой формы в рассматриваемом
базисе Вебба формулируется по аналогии
с классическим базисом {-, &, }.
}.
Тупиковой ДНФ функции f называется дизъюнкция простых импликантов, из которых ни один простой импликант нельзя удалить так, чтобы полученная ДНФ все еще представляла функцию. Получение МДНФ можно разбить на два этапа. На первом находят сокращенную ДНФ. На втором строят тупиковые ДНФ функции, удаляя подмножества элементарных конъюнкций из сокращенной ДНФ. Из полученных тупиковых ДНФ выбирают МДНФ.
Прежде чем перейти к рассмотрению применения в базисе Вебба некоторых известных из классического базиса методов минимизации, укажем эквивалентные преобразования, приводящие к операциям склеивания и поглощения в алгебре Вебба.
Введем теперь операции следующих типов:
склеивания
(2-9)
неполного склеивания
(2-10)
и поглощения
(2-11)
В этих выражениях включен произвольный терм A, указывающий на то, что операции производятся между операндами внутри многоместного терма. Отсутствие А привело бы к двухместным операциям и к вырождению некоторых операндов.
Для двухместного случая аналоги операций склеивания и поглощения имеют вид:
(2-12)
(2-13)
Справедливость всех этих соотношений легко доказать, построив таблицу истинности ФАЛ.
Рассмотрим теперь аналоги методов минимизации, рассмотренных нами для базиса конъюнкция, дизъюнкция, отрицание.
studfiles.net
Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 19
Заметим, что булев базис не является минимальным, т.к. из него можно удалить либо функцию И, либо функцию ИЛИ.
Аналитическая запись булевых функций в базисе Пирса.
Будем использовать следующее обозначение:
.
Вспомним запись булевой функции в совершенной дизъюнктивной нормальной форме: . Символ означает, что дизъюнкция берется только для таких наборов на которых функция равна единице: . Попробуем записать эту функцию таким образом, чтобы оно содержало только функции Пирса и отрицания (отрицание также реализуется функцией Пирса: ). Просуммируем конституенты единицы наборов, где функция равно нулю. Мы получили новую функцию, значения которой противоположны исходной функции, поэтому: . Но последнее выражение есть не что иное, как функция Пирса: . Однако конституенты единицы представляют собой конъюнкции переменных и от конъюнкций нужно также избавиться. Для этого преобразуем конституенты единицы: .
Таким образом, алгоритм перехода от табличного задания функции к аналитической записи в базисе Пирса таков:
1) выбрать в таблице все наборы аргументов, на которых функция равна нулю;
2) аргументы каждого из этих наборов объединяются функцией Пирса. Причем, если аргумент равен 1, то он записывается с отрицанием; если – 0, то без отрицания;
3) все полученные составляющие (термы) объединяются функцией Пирса.
Пример:
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Выбираем наборы 010, 101, 111;
, , ;
3) .
По аналитической записи функции можно нарисовать схему её реализующую:
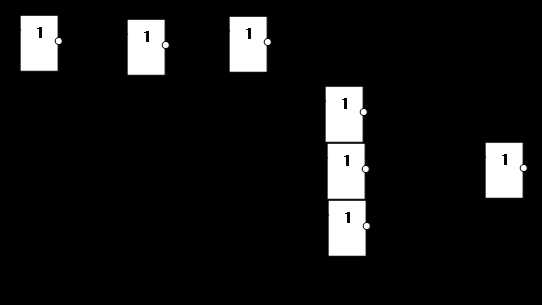
Запись функций в базисе Шеффера.
Конституента нуля для набора записывается так:
. Действительно, в силу определения конституенты нуля она равна нулю на этом наборе, следовательно все слагаемые в конституенте должны быть равны нулю. Отсюда следует правило, если в наборе аргумент равен единице, то в конституенту нуля он записывается с отрицанием, если нулю – без отрицания.
Известно, что любую функцию можно записать в совершенной конъюнктивной нормальной форме в виде произведения конституент нуля. Однако ее можно записать и как инверсию функции значения которой противоположны исходной функции:
Символы () обозначают, что конъюнкциями связываются конституенты нуля наборов на которых исходная функция равна нулю (единице). Действительно, если на наборе функция равна единице, то можно указать для этого набора конституенту нуля равную нулю на этом наборе и единице – на остальных наборах. Конъюнкция этих конституент представляет собой новую функцию равную нулю на тех наборах, где функция равна единице, т.е. и . Полученное выражение – это функция Шеффера над конституентами нуля: . Для получения окончательной записи функции преобразуем конституенты нуля:
Окончательное представление функции: . Следовательно, алгоритм перехода от таблицы истинности к аналитической записи в базисе Шеффера таков:
Выбрать в таблице все наборы аргументов на которых функция равна единице;
Аргументы каждого из этих наборов связать операцией Шеффера, причем, если аргумент равен 1, то он записывается без отрицания, если нулю – с отрицанием.
Все полученные выражения также связываются операцией Шеффера.
Пример:
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
vunivere.ru
Синтез переключательных функций в одноэлементном базисе Операция (стрелка) Пирса
f8(x1,x2)
x1 | 0 | 0 | 1 | 1 |
x2 | 0 | 1 | 0 | 1 |
f8 | 1 | 0 | 0 | 0 |
Эту функцию можем представить, записав по “единицам”:
f8(x1,x2) = x1x2= x1x2
или
x1x2= x1x2
На основе принципа суперпозиции:
f(x1,x2,…xn) = x1x2x3. . .xn= x1x2x3. . .xn
Применяя правило де Моргана:
x1x2x3. . .xn= x1x2x3. . .xn= x1x2x3. . .xn
или:
x1x2x3. . .xn= x1x2x3. . .xn
т.е.
x1x2x3. . .xn= x1x2x3. . .xn
Рассмотрим некоторые соотношения для операции Пирса:
xx = xx = x
x1x2= x1x2= x2x1= x2x1
x1x2x3= (x1x2)x3= x1x2x3x1(x2x3),
т.е. операция Пирса не обладает свойством ассоциативности
x1x2x3= (x1x2)x3= x1(x2x3)
x1x2x3x4= (x1x2)(x3x4)
При этом порядок выполнения операций в формулах, где есть операции Пирса такой:
раскрываются скобки
выполняются операции инверсии
выполняются операции Пирса
Синтез логических функций в базисе Пирса удобно производить, имея запись функции в КНФ.
Допустим, что ФАЛ задана в конъюктивной форме
f = Q1Q2Q3. . . Qn
Подставим член Qiв виде:
Qi= (xrxpxq. . .xwxfxe. . .xz)
Возьмем двойное отрицание от обеих частей этого равенства, применив правило де Моргана
Qi= (xrxpxq. . .xwxfxe. . .xz) = (xr* xp* xq* . . .xw* xf* xe* . . . * xz)
Применяя соотношение, полученное на основе принципа суперпозиции:
Qi= (xrxpxq. . .xwxfxe. . .xz)
Или, применяя это преобразование к исходной форме, получим:
f = Q1Q2Q3. . .Qn
Итак: чтобы от КНФ перейти к базису Пирса и инверсии необходимо:
заменить операции дизъюнкции операциями Пирса
заменить операции конъюнкции операциями Пирса
заключить в скобки все те группы букв, которые соответсвуют конъюнктивным членам.
Пример:
f(x1x2x3) = (x1x2x3) (x1x4) (x2x4) = (x1x2x3)(x1x4) (x2x4)
Замечание. Так как в этих произведениях число букв не увеличивается, и если исходная форма функции была минимальной, то вновь полученная также будет минимальной (в действительности дело обстоит сложнее, поскольку мы рассматриваем не базис “”, а другой, то есть “” и “-” – операцию Пирса и инверсию).
Принципиально можно избавиться от отрицаний, применив соотношение: xi= xixi, но тогда нельзя будет утверждать, что полученная форма будет минимальной!
Операция штрих Шеффера
x1 | 0 | 0 | 1 | 1 |
x2 | 0 | 1 | 0 | 1 |
f14 | 1 | 1 | 1 | 0 |
Заметим, что эта функция дуальна по отношению к f8, поэтому все свойства являются по существу дуально вытекающими из рассмотренных.
f14(x1,x2) = x1x2(запись функций по нулям)
x1| x2= x1x2= x1x2= x1x2= x1x2
на основе принципа суперпозиции:
x1| x2| . . . | xn= x1x2…xn
Рассмотрим некоторые эквивалентности:
x | x = x x = x
x1| x2| x3= (x1x2)| x3= x1| (x2x3)
x1| x2| x3| x4= (x1x2)| (x3x4)
Сформулируем правила перехода от ДНФ функции к выражению с использованием операции “Штрих Шеффера”.
заменить все операции дизъюнкции на операции Шеффера
заменить все операции конъюнкции на операции Шеффера
группы букв, которые соответствуют дизъюнктивным членам, заключить в скобки.
Пример:
f(x1x2x3) = x1x2x3x1x2x1x2x3= = (x1|x2|x3)|(x1|x2)|(x1|x2|x3)
То же самое можно утверждать относительно минимальной формы.
В заключение необходимо отметить, что в настоящее время вопросы синтеза функций в одноэлементном базисе приобретают большое значение, так как соответствующие элементы используют операцию Пирса и Шеффера. Однако в полной мере теоретически методы синтеза разработаны не столь детально, как это сделано в базисе “и”, “или”, “инверсия”.
studfiles.net
| Штрих Шеффера | |
|---|---|
| И-НЕ, NAND | |
| Диаграмма Венна | |
| Определение | x⋅y¯{\displaystyle {\overline {x\cdot y}}} |
| Таблица истинности | (1110){\displaystyle (1110)} |
| Логический вентиль | |
| Нормальные формы | |
| Дизъюнктивная | x¯+y¯{\displaystyle {\overline {x}}+{\overline {y}}} |
| Конъюнктивная | x¯+y¯{\displaystyle {\overline {x}}+{\overline {y}}} |
| Полином Жегалкина | 1⊕xy{\displaystyle 1\oplus xy} |
www.wikiplanet.click