Черчение сечение и разрезы – Сечения. Определение. Виды сечений. Изображение сечений на чертежах

Чем отличается разрез от сечения

Принцип обозначения на чертеже разрезов и сечений одинаковый, посему на черчении этому вопросу уделяется особое внимание. Очень далекий от этой тематики человек вообще не найдет отличий между сечением и разрезом, особенно если говорить о теоретической составляющей вопроса. Между двумя рассматриваемыми понятиями разница имеется, и наша задача – донести ее до читателя.

Определение

Разрезом именуют изображение, которое получают путем мысленного рассечения деталей секущей  плоскостью. Простой разрез отличается от сложного тем, что у него лишь одна секущая плоскость, в то время как во втором случае их несколько. В черчении существует три вида разрезов: фронтальный, горизонтальный и профильный. Разрезы имеют свои правила выполнения и обозначения, которые необходимо знать и учитывать при работе с чертежом.

Сечения необходимы для показа поперечной формы деталей. Сечение получают следующим образом: воображаемая секущая плоскость мысленно рассекает деталь в месте, необходимом для выявления ее формы. Стоит обратить внимание на некоторые нюансы: например, на сечении показано лишь то, что получено в секущей плоскости, не более. Чтобы чертеж был более ясный и понятный, все сечения выделяются штриховкой (допустим, наклонные параллельные линии проводят под углом в 45 градусов). Сечения принято разделять на два вида: вынесенные и наложенные. В первом случае сечение расположено вне контура, во втором – на видах чертежа.

к содержанию ↑

Отличие

Сразу же стоит выделить, что разрез от сечения отличается не только правилом построения, как путают многие люди, имеющие дело непосредственно с чертежами. Признаков отличия несколько, и некоторые из них весьма существенные:

• Главное отличие кроется в том, что разрез показывает то, что расположено в секущей плоскости, а также за ней, в то время сечение показывает то, что внутри секущей плоскости.
• В некоторых случаях обозначение разреза не наносится на чертеж. Например, при совпадении секущей плоскости с плоскостью симметрии детали.
• Сечение имеет несколько нюансов при построении. Например, если несколько одинаковых сечений относятся к одному и тому же предмету, то его линии необходимо обозначать одинаковыми буквами. При этом вычеркивается одно сечение. Данное правило довольно часто не соблюдается, хотя является довольно важным при построении чертежа.

к содержанию ↑

Выводы TheDifference.ru

Несмотря на то, что разрез и сечения имеют очень много общего, TheDifference.ru определил, что разница между ними есть. Сечение и разрез отличают друг от друга по следующим признакам:

1. Правило построения.
2. Разрез показывает расположение как в секущей плоскости, так и вне нее. Сечение же только то, что внутри.
3. Сечения необходимы для показа поперечной формы деталей. Предмет мысленно рассекается одной или несколькими плоскостями. Сечение обозначается штриховкой для более ясного понимания.
4. Разрез в отдельных случаях можно не наносить на чертеж.

thedifference.ru

Разрезы. Сечения

Лекция 12

Разрезы. Сечения.

Введение

 

            Разрезы и сечения применяются для изображения внутренних, невидимых наблюдателю, поверхностей предметов. Для выявления этих поверхностей применяют искусственный прием, заключающийся в том, что предмет условно рассекают плоскостью, называемой секущей, и удаляют часть предмета, находящуюся перед секущей плоскостью. Таким образом становятся видимыми внутренние очертания предмета.

            Разрезом называется изображение предмета, мысленно рассеченного одной или несколькими плоскостями. На разрезе изображается то, что получается в секущей плоскости в результате её пересечения с поверхностями предмета (сечение, входящее в состав разреза) и что расположено за ней.

            Сечение представляет собой изображение плоской фигуры, получающейся в секущей плоскости при мысленном рассечении предмета.

 

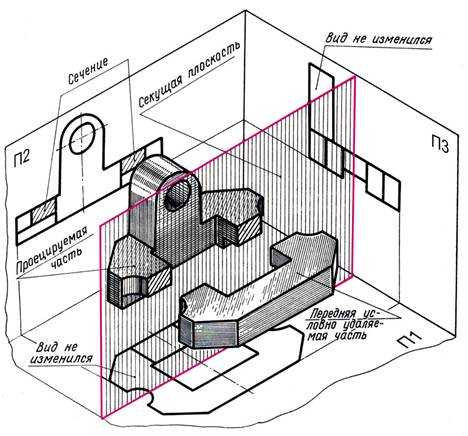
Рис. 12.1

 

            На рис 12.1. показано образование разреза детали. Для выяснения внутренней формы деталь целесообразно рассечь фронтальной секущей плоскостью, походящей через выемки, расположенные в основании этой детали. Сечение получено в результате пересечения этой плоскости с поверхностями, ограничивающими деталь. Оно представляет собой плоский контур (два прямоугольника), заштриховано и отмечено надписью «сечение».

            На рис 12.1. изображены передняя, находящаяся перед секущей плоскостью, мысленно удаляемая и оставшаяся (проецируемая) часть детали. Разрез расположен на фронтальной плоскости проекции, параллельно секущей плоскости и представляет собой ортогональную проекцию оставшейся части детали. Для получения неискаженных изображений секущая плоскость всегда должна быть параллельна плоскости изображения. Если секущая плоскость не параллельна плоскости изображения (наклонные разрезы и сечения), для достижения параллельности следует применять способы преобразования чертежа.

            Мысленное рассечение предмета секущей и плоскостью относятся только к данному разрезу и не влечет за собой изменения других изображений (видов, разрезов) того же предмета. Так, на рис. 12.1. виды сверху и слева не изменились от того, что на месте главного вида выполнен разрез.

            Для выяснения внутренней формы детали выполним ещё один разрез, изображенный на рис. 12.2а. Этот разрез выполняется независимо от первого новой секущей плоскостью (профильной), проходящей через ось цилиндрического отверстия. Разрез расположен на профильной плоскости проекции, параллельно секущей плоскости. На рис. 12.2б выполнен чертеж детали с рассмотренными выше разрезами.

 

Рис. 12.2а, б

 

Классификация разрезов

 

            В зависимости от секущей плоскости относительно горизонтальной плоскости проекций разреза разделяются на горизонтальные, вертикальные и наклонные.

            Горизонтальными разрезами называются разрезы, выполненные горизонтальной секущей плоскостью (см. рис. 12.4)

            Вертикальными разрезами называются разрезы, выполненные секущей плоскостью, перпендикулярной горизонтальной плоскости проекций. Если вертикальный разрез выполнен фронтальной секущей плоскостью, его называют фронтальным; профильной секущей плоскостью – профильными.

            Наклонными называются разрезы, у которых секущая плоскость составляет с горизонтальной плоскостью проекций, угол отличный от прямого (рис. 12.5).

            В зависимости от числа секущих плоскостей разрезы разделяются на простые и сложные. Простые разрезы выполняются одной секущей плоскостью, сложные – несколькими.

            Разрезы делятся на  продольные и поперечные в зависимости от положения секущей плоскости относительно измерений самого предмета.

            Продольными называются разрезы, секущие плоскости которых направлены вдоль длины или высоты предмета (см. рис.12.5).

            Поперечными называются разрезы, у которых секущие плоскости направлены перпендикулярно к длине или высоте предмета (см. рис. 12.6).

           

12.1 Обозначения разрезов

 

            Положение секущей плоскости на чертеже указывают линии сечения. Для горизонтальных разрезов линии сечения указываются на главном виде или виде слева, для фронтальных – на виде сверху и слева; для профильных на главном виде и виде сверху. Для линии сечения применяется разомкнутая линия толщиной от S до 1,5S (см. ГОСТ 2.303-68).

            Для простых разрезов вычерчиваются начальный и конечный штрихи (рис. 12.2), а для сложных – начальный, у перегибов и конечный штрихи (рис. 12.12). Начальный и конечный штрихи линий сечения не должны пересекать контур соответствующего изображения. На этих штрихах перпендикулярно к нам следует ставить стрелки, указывающие направление взгляда. Стрелки находятся на расстоянии 2-3 мм от конца штриха (рис. 12.3)

 

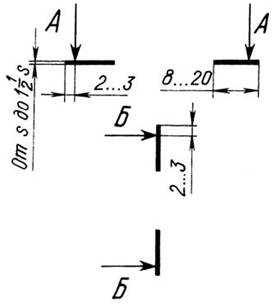
Рис. 12.3.

 

            У начала и конца линии сечения, а при необходимости и у перегибов этой линии (для сложных разрезов), ставят одну и ту же прописную букву русского алфавита.

            Буквы наносят около стрелок, указывающих направления взгляда, и в местах перегиба (в случае необходимости) со стороны внешнего угла, образованного линией сечения и стрелкой. Располагают их параллельно основной подписи чертежа.

            Разрезы простые и сложные отмечаются надписью типа «А-А», теми же буквами, что и у линии сечения, написанными над разрезом через тире.  Их располагают параллельно основной надписи чертежа.

            Если секущая плоскость совпадает с плоскостью симметрии предмета в целом (его наружной и внутренней формой) и соответствующие изображения расположены на одном и том же месте в непосредственной проекционной связи и не разделены какими-либо другими изображениями, на простых горизонтальных, фронтальных и продольных разрезах не отмечают положение секущей плоскости и разрез надписью не сопровождают.

            Примеры разрезов, не требующих надписей, приведены на рис. 12.6.

12.2 Простые разрезы

 

            Горизонтальные разрезы. Горизонтальные разрезы могут быть расположены на месте видов сверху или снизу в том случае, если эти виды не нужны для выяснения формы наружных очертаний предметов. Если эти виды необходимы, горизонтальный разрез следует располагать на свободном месте поля чертежа в соответствии с направлением, указанным стрелками. В этом случае должно быть отмечено положение секущей плоскости и надписан разрез.

            Так, на рис. 12.4 вид сверху необходим для выяснения формы верхнего профиля детали, поэтому горизонтальный разрез помещен на свободном месте поля чертежа и надписан (А-А).

 

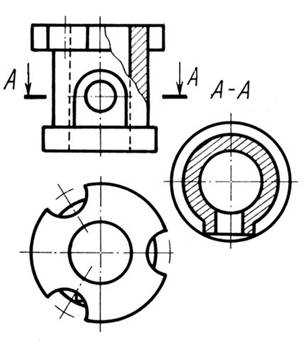
Рис. 12.4

 

            На рис. 12.5 горизонтальный разрез расположен на месте вида сверху, что не нарушило представления о наружной форме детали и дало возможность выполнить чертежи с  наименьшим количеством изображений.

 

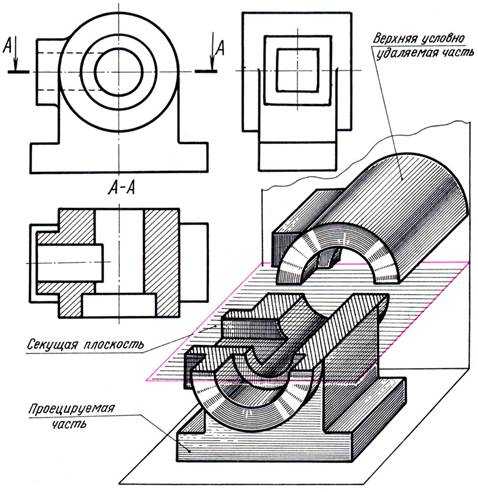
Рис. 12.5

 

            Из чертежа видно, что фронтальная проекция секущей плоскости (линия сечения А-А) не является осью симметрии изображения. В этом случае положение секущей плоскости следует отметить и над разрезом сделать надпись, что и выполнено на рис. 12.5.

            Вертикальные разрезы. Фронтальные разрезы могут быть расположены на месте главного вида. В том случае, если этот вид является необходимым для выяснения формы наружных  очертаний предмета, разрезы помещают на свободное место поля чертежа.

 

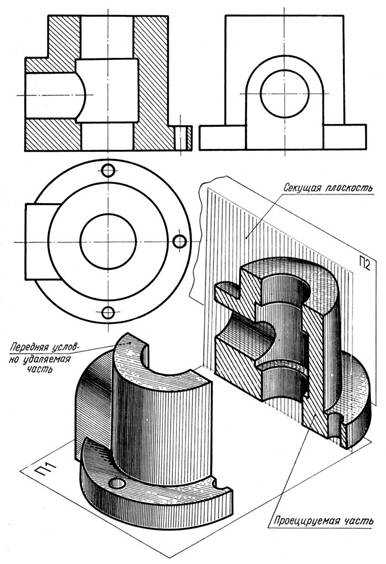
Рис. 12.6

 

            Выполненный на рис. 12.6 фронтальный разрез помещен на месте главного вида. Положение его секущей плоскости не отмечено, и сам разрез не надписан, так как в данном случае секущая плоскость совпадает с плоскостью симметрии детали, а разрез расположен в непосредственной проекционной связи с остальными изображениями.

            Для выяснения формы детали, изображенной на рис. 12.7, выполнено два профильных разреза. Разрезы расположены на месте вида слева (Б-Б) и вида справа (А-А).

 

 

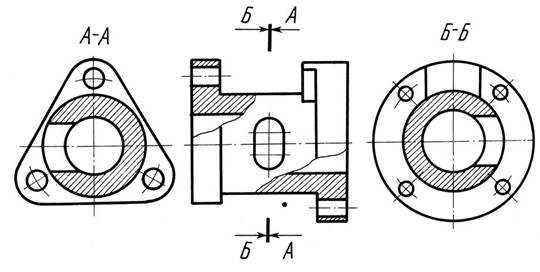
Рис. 12.7

 

            Наклонные разрезы. Вертикальный разрез, когда секущая плоскость не параллельна фронтальной или профильной плоскости проекций, а также наклонный разрез должны строиться и располагаться в соответствии с направлением, указанным стрелками на линии сечения (рис. 12.8).

 

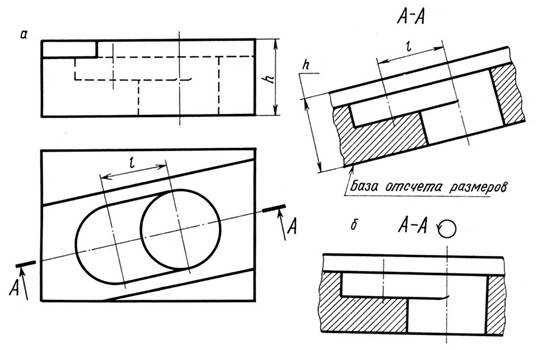
Рис. 12.8

 

            При выполнении вертикального разреза детали, изображенной на рис. 12.8 для получения неискаженного сечения фронтальную плоскость П2 заменяют дополнительной плоскостью, которая перпендикулярна к горизонтальной плоскости проекций П1 и параллельна секущей плоскости, отмеченной линией сечения А-А.

            Подобные разрезы, а так же наклонные допускается располагать с поворотом до положения, соответствующего принятому для данного предмета на главном изображении. В этом случае к надписи добавляется знак «…», означающий повернутое изображение.

 

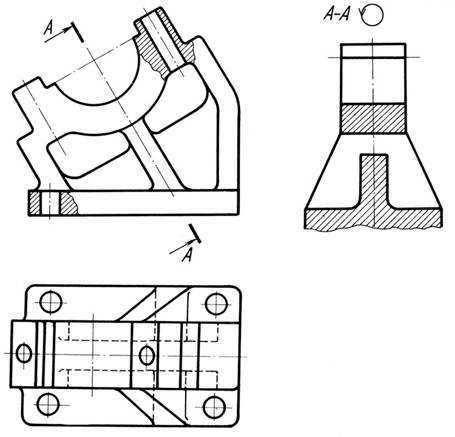
Рис. 12.9

 

            На рис. 18.9 изображен корпус подшипника, наклоненный к горизонтальной плоскости проекций. Для выявления его формы целесообразно выполнить наклонный разрез фронтально-проецирующей плоскостью (линия сечения А-А).

            Наклонный разрез помещен на свободном месте поля чертежа и надписан. Секущая плоскость разрезает одно ребро детали вдоль длинной стороны, оно не заштриховано.

18.3 Совмещение вида с разрезом

 

            Для уменьшения количества изображений целесообразно во многих случаях соединять часть вида и часть соответствующего разреза. Это сочетание даёт возможность при наименьшем количестве изображений получить исчерпывающее представление о внешней и внутренней форме изображенного предмета.

            Соединение части вида  с частью соответствующего разреза выполняется на изображениях,  расположенных на местах основных видов (в проекционной связи). Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистой линией. Такое соединение выполняется для несимметричных фигур (рис. 12.7).

            Если соединяются половина вида и половина разреза, каждый из которых является симметричной фигурой, разделяющей линией служит ось симметрии  – штрихпунктирная тонкая линия. Разрезы рекомендуется располагать справа и снизу от оси симметрии.

 

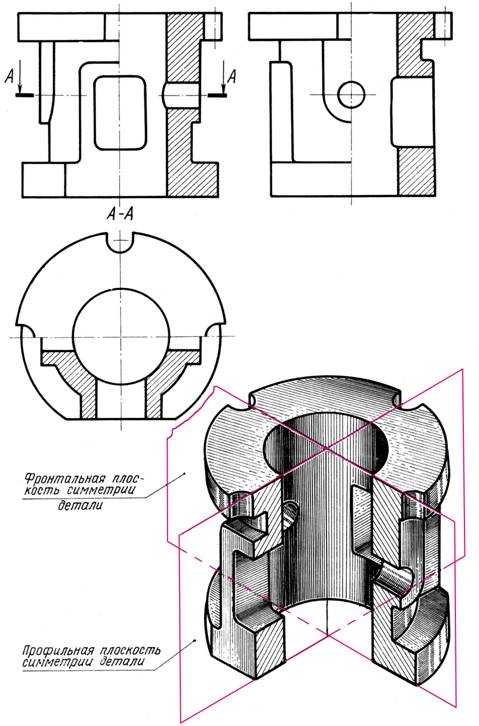
Рис. 12.10

 

            Для выявления наружных и внутренних очертаний детали, изображенной на рис. 12.10 разрезы выполнены в соединении с соответствующими видами, что обусловлено формой данной детали. На представленных изображениях соединяются половина вида и половина разреза, каждый из которых есть симметричная фигура, свидетельством чему являются оси симметрии всех изображений.

            На половине вида не следует проводить штриховых линий проекции внутренних очертаний предмета (они изображены на разрезе), а на половине разреза не следует повторять штриховыми линиями изображения наружных очертаний предмета так, как они показаны на половине вида.

 

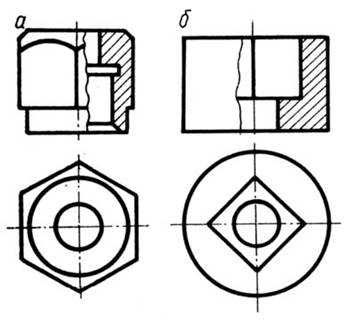
Рис. 12.11

 

            Если линия оси симметрии изображения совпадает со сплошной основной линией, принадлежащей проекции предмета (например, ребра), следует соединять части вида и разреза, разделяя их сплошной волнистой линией. Эту линию можно проводить справа (рис. 12.11а) или слева (рис. 12.11б) ось фронтальной проекции ребра в зависимости от того, что необходимо показать на виде и на разрезе.

12.4 Сложные разрезы

 

            Выполнение сложных разрезов дает возможность уменьшить количество изображений, так как на одном изображении при помощи нескольких секущих плоскостей можно выявить внутреннюю форму предмета в разных его местах.

            В зависимости от взаимного положения секущих плоскостей сложные разрезы делятся на ступенчатые и ломаные.

            Ступенчатые разрезы выполняются параллельными секущими плоскостями. Они могут быть горизонтальными, фронтальными, профильными и наклонными.

            На рис. 12.12а изображен фронтальный ступенчатый разрез детали, выполненный двумя фронтальными секущими плоскостями. При построении разреза секущие плоскости совмещаются в одну плоскость, параллельную плоскостям изображения. На разрезе не отображается то,  что он выполнен несколькими секущими плоскостями.

 

Рис. 12.12

 

            Переход от одной секущей плоскости к другой осуществляется плоскостью, перпендикулярной к секущим плоскостям, так называемой плоскостью перехода. В некоторых случаях переход от одной секущей плоскости к другой выполняют плоскостью, проходящей по оси симметрии отверстия, как это показано на рис. 12.12б. На рис. 12.12в выполнен наклонный ступенчатый разрез.

            Ломаные разрезы выполняются пересекающимися секущими плоскостями (их линия сечения является ломаной линией).

            Для получения неискаженных изображений секущие плоскости этих разрезов способом вращения вокруг проецирующих прямых (линии пересечения секущих плоскостей) совмещаются в одну плоскость, параллельную плоскости изображения. Если совмещенные секущие плоскости окажутся параллельными одной из основных плоскостей проекций, ломаный разрез помещают на месте соответствующего вида. Выбор плоскости совмещения зависит от заданных условий (конструктивных особенностей предмета, удобства размещения и т.д.)

            На рис 12.13 изображен ломаный разрез, образованный двумя пересекающимися горизонтально-проецирующими плоскостями, одна из которых фронтальная. Для построения разреза левую секущую плоскость вместе с расположенным в ней сечением поворачивают вокруг линии её пересечения с фронтальной секущей плоскостью до совмещения с последней.

 

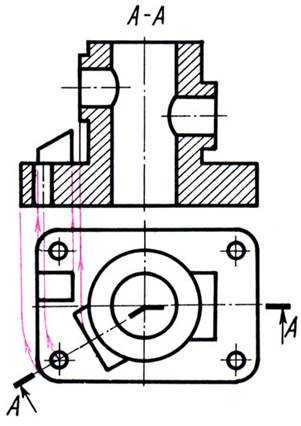
Рис. 12.13

 

            В данном примере направление совмещения секущей плоскости (поворота) совпадает с направлением взгляда, указанного стрелкой на линии сечения (у буквы А).

            Направление взгляда может и не совпадать с направлением поворота секущих плоскостей до совмещения их в одну плоскость, как это выполнено на рис. 12.14, где направление совмещения и стрелки у буквы А противоположны.

            При построении ломаных разрезов следует обращать внимание на изображение элементов предмета, расположенных за секущей плоскостью, которые при выполнении разреза поворачивать не следует. Так спроецирован выступ детали на рис. 12.13, расположенный за секущей горизонтально-проецирующей плоскостью, он не участвует в повороте.

 

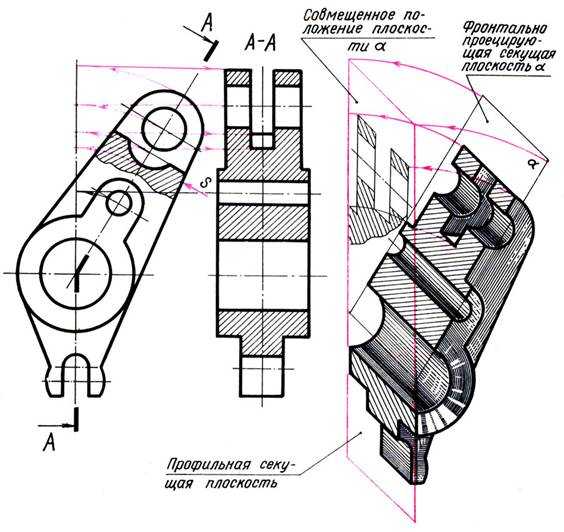
Рис. 12.14

 

12.5 Местный разрез

 

            Местным разрезом называется разрез, служащий  для выяснения устройства предмета лишь в отдельном, ограниченном месте. Местные разрезы применяются в тех случаях, когда для выяснения внутренней формы предмета целесообразно показать разрез лишь на некоторой части проекции, вскрывая интересующие нас выемки, отверстия и т.д.

            Местный разрез выделяется на виде сплошной волнистой линией. Эта линия не должна совпадать с какими-либо другими линиями изображения. На рис. 12.9 для изображения цилиндрических отверстий детали выполнены местные разрезы. На чертежах местные разрезы не обозначаются.  

 

12.6 Сечения

 

            Для изображения большой группы деталей применяются нормальные сечения, которые изображаются самостоятельно, т.е. не входят в состав разреза. Такие сечения в большинстве случаев выявляют форму предметов в их поперечных измерениях.

            Сечением называется изображение, полученное при мысленном пересечении предмета одной или несколькими плоскостями.

            В сечении показывают лишь то, что получается в секущей плоскости. Часть предмета, находящуюся за этой плоскостью в сечении не изображают. Следовательно, для получения сечения нужно:

а) в определённом месте детали провести секущую плоскость;

б) фигуру, полученную в сечении повернуть в положение, параллельное плоскости проекций;

в) на свободном месте поля чертежа вычертить сечение и, в случае необходимости, оформить его надписью.

12.6.1 Классификация сечений

 

            Сечение, как разрез,  – изображение условное. Условность заключается, во-первых, в том, что секущую плоскость проводят мысленно, а во-вторых, – в том, что фигура, образованная в сечении, отдельно от предмета не существует: её мысленно отрывают и изображают на свободном месте поля чертежа.

Сечения разделяют на входящие в состав разреза и существующие  как самостоятельные изображения. Последние, в свою очередь, разделяются на вынесенные и наложенные. 

Сечение называют вынесенным, если оно выполнено отдельно от основного изображения. Их допускается располагать в разрыве между частями одного и того же вида. Вынесенные сечения предпочтительнее наложенных, которые затемняют чертежи. Вынесенные сечения обводят сплошной основной линией и заштриховывают под углом 45° к основной надписи чертежа.

Правила и обозначения линии сечения, т.е. следа секущей плоскости, те же, что и для разрезов.

Рассмотрим некоторые случаи выполнения вынесенных сечений:

1. Сечение представляет собой симметричную фигуру, размещенную на продолжении следа секущей плоскости. В этом случае линию сечения, совпадающую с осью симметрии самого сечения, изображают тонкой штрихпунктирной линией без обозначения буквами и стрелками (рис. 12.15а). Так же выполняют симметричные сечения, располагаемые в разрыве между частями самого изображения (рис. 12.15в)

 

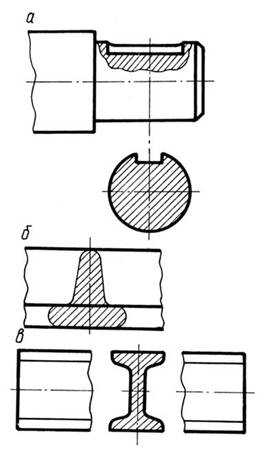
Рис. 12.15.

 

2. Сечение представляет несимметричную фигуру, размещенную на свободном месте поля чертежа. В этом случае линию сечения обозначают и само сечение подписывают (рис. 12.16)

 

 

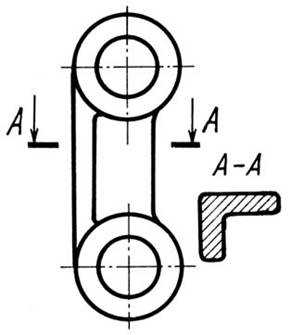
Рис. 12.16.

 

3. Сечение располагают на месте вида слева в непосредственной проекционной связи (рис. 12.17)

 

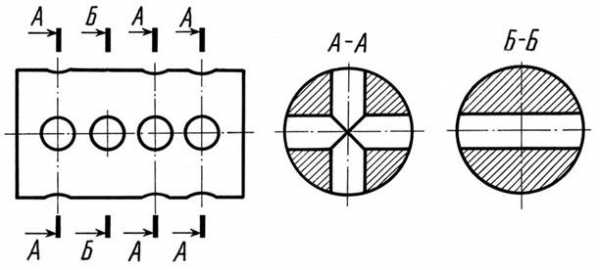
Рис. 12.17.

 

Наложенным сечением называется сечение, расположенное непосредственно на виде предмета. Контур наложенного сечения изображают сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают (рис. 12.15б). если фигура сечения симметрична положение секущей плоскости указывают штрихпунктирной тонкой линией без обозначения буквами и стрелками и линию сечения не проводят (рис. 12.15б)

Во всех остальных случаях для линии сечения применяют разомкнутую линию с указанием стрелками направления взгляда, обозначают её одинаковыми прописными буквами русского алфавита. Сечение сопровождают надписью по типу «А-А»; размеры букв, величина стрелок и другие данные такие же, как и для разрезов.

Построение и расположение сечения должно соответствовать направлению, указанному стрелками. Допускается располагать сечение на любом месте поля чертежа.

            Для несимметричных сечений, расположенных в разрыве (рис. 12.18а) или наложенных рис. (12.18б), линию сечения проводят со стрелками, но буквы не обозначают.

 

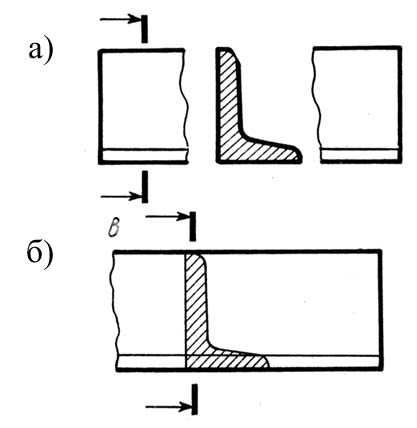
Рис. 12.18.

 

            Для нескольких одинаковых сечений, относящихся к одному предмету, линию сечения обозначают одной буквой и вычерчивают одно сечение (рис. 12.17).

 

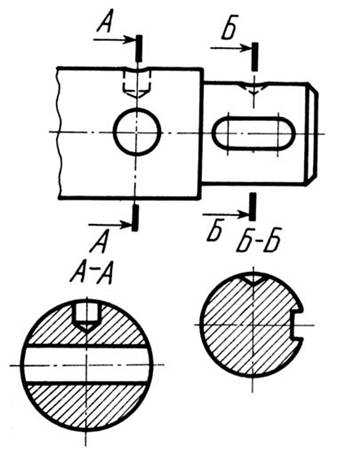
Рис. 12.19.

 

            Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубление показывают полностью как на разрезе  (рис .12.19.). На этом чертеже контур призматического отверстия (шпоночного паза) показан не полностью, а контур цилиндрических отверстий и конического углубления – полностью.

 

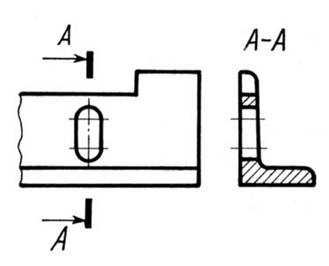
Рис. 12.20.

 

            Если секущая плоскость проходит через некруглое отверстие и сечение состоит из отдельных самостоятельных частей, следует применять разрезы  (рис. 12.20). При необходимости допускается в качестве секущей применять цилиндрическую поверхность, развертываемую затем в плоскость (рис. 12.21.)

Рис. 12.21.

 

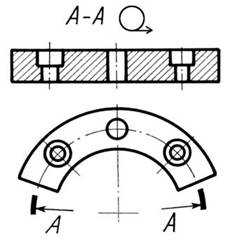
Рис. 12.22.

12.6.3 Наклонные сечения

 

            Секущие плоскости могут быть направлены по отношению к плоскостям проекций под различными углами. В этом случае допускается располагать сечения с поворотом, добавляя соответствующий знак , означающий, что изображение повернуто (рис. 12.22а).

            Если на чертеже несколько секущих плоскостей, наклоненных под

разными углами, то знак  не наносят (рис. 12.22б).

 

Рис. 12.22.

 

            Секущие плоскости следует выбирать, чтобы получать нормальные поперечные сечения. Если элементы предмета наклонены к плоскостям проекций, секущие плоскости для получения нормальных сечений располагают перпендикулярной к этим элементам (рис. 12.23)

 

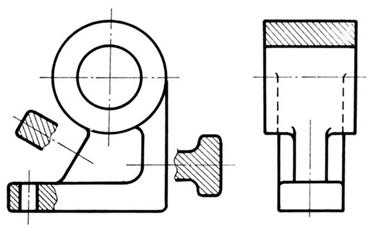
Рис. 12.23

 

refleader.ru

ЧЕРЧЕНИЕ. Школьный интернет-учебник – Сечения и разрезы 4-5

 

Форма многих деталей не может быть выявлена только разрезом или видом. Выполнять же два изображения – вид и разрез нерационально. Согласно ГОСТ 2.305-68 допускается соединять на одном изображении часть вида и часть соответствующего разреза.

Местный  разрез

Если требуется выяснить устройство предмета лишь в отдельном, ограниченном месте, можно применить разрез, называемый местным (рис.1).

 

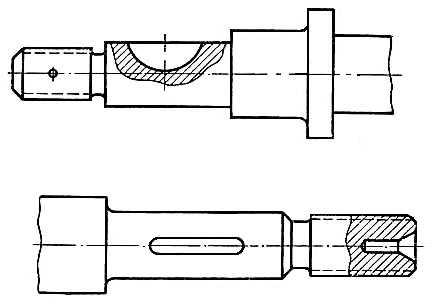
Рис. 1. Местный разрез

Местный разрез выделяется на виде сплошной волнистой линией (толщина от s/2 до s/3, линию проводят от руки), не совпадающей с какими-либо линиями изображения.

Если местный разрез выполняется на части предмета, представляющей собой тело вращения и, следовательно, изображенной с осевой линией, то местный разрез с видом могут разделяться этой осевой линией.

Соединение половины вида и половины разреза

Если изображения внешнего вида и его внутреннего строения имеют ось симметрии, то для сокращения графических построений и экономии площади чертежа допускается совмещать половину вида и половину разреза.

На рис. 2.а приведен чертеж детали без разреза, а на  рис. 2,б с разрезом.

 

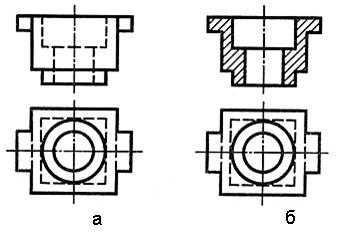
Рис. 2. Чертеж детали без разреза (а) и с разрезом (б).

На рис. 3. даны половина главного вида и половина разреза той же детали. Понятна ли форма отсутствующих половины вида и половины разреза, на месте которых стоят крестики?

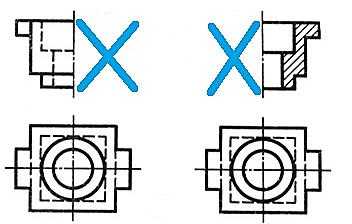
Рис. 3. Половина главного вида и половина разреза той же детали.

Так как и вид, и разрез – фигуры симметричные, то по половине вида можно судить о второй его половине. То же можно сказать и о разрезе. Поэтому рекомендуется, в целях сокращения размера чертежа и времени на его выполнение, соединять половину вида и половину соответствующего разреза при симметричных виде и разрезе. Получается изображение, приведенное на рис. 4.

Рис. 4. Соединение половины вида и половины разреза

Границей между половиной вида и половиной разреза служит осевая (штрихпунктирная) линия (рис. 4). На половине вида внутренние очертания детали не показывают; штриховые линии только повторили бы очертания внутреннего контура, выявленные разрезом. Размерные линии для внутренних очертаний предмета, которые изображены лишь до оси симметрии, обрывают, проводя несколько дальше оси; стрелку ставят с одной стороны, а размер наносят полный (см. рис. 4).

При этом разрез должен располагаться правее или ниже оси симметрии, разделяющей половину вида с половиной разреза (рис. 5).

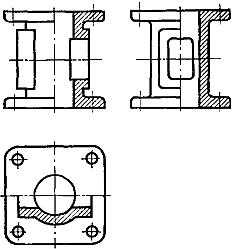
Рис. 5. Расположение разреза на чертеже.

Допускается разделение вида и разреза осевой (штрихпунктирной) линией при разрезании части предмета, представляющее собой тело вращения (рис. 6).

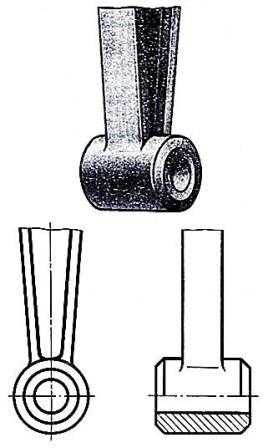
Рис.6. Выполнение разреза предмета, части которого симметричная фигура.

Соединение части вида и части разреза

Не для всех симметричных изображений можно применять соединение половины вида и половины разреза. Детали (рис. 7), имеют элементы (квадратное отверстие, поверхность в виде шестиугольной призмы), ребра которых совпадают с осью симметрии. Если соединить половину вида и половину разреза, границей между которыми является осевая (штрихпунктирная) линия, то ребра, совпадающие с ней, не изобразятся. В таких случаях показывают часть вида и часть разреза (см. рис. 7). Волнистую линию, разделяющую часть вида и часть разреза, проводят так, чтобы было показано ребро. Если ребро, совпадающее с осью симметрии, расположено в отверстии, то показывают больше половины разреза (рис. 7, а). Если ребро расположено на наружной поверхности, то показывают больше половины вида (рис. 7, б).

 

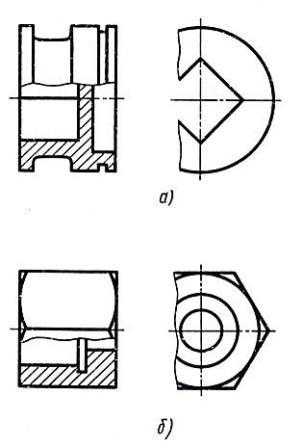
Рис. 7. Соединение части вида и части разреза при совпадении проекции ребра с осью симметрии

Примеры выполнения других деталей с соединением части вида и части разреза показаны на рисунках 8 и 9.

 

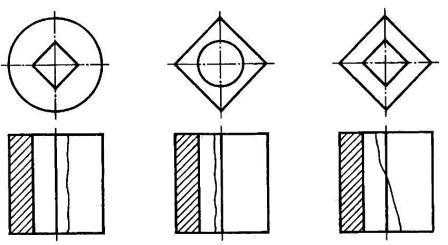
Рис. 8. Соединение частей вида и разреза

Рис.9. Наложение оси симметрии на линию контура: а) разреза; б) вида.

Если форму детали отобразить только видами спереди и сверху, то не будет определено внутреннее устройство детали и глубина выемки. Если выполнить фронтальный разрез и вид сверху детали, то невозможно будет уяснить высоту элемента верхней части детали (рис. 10).

 

Рис.10.Аксонометрическая проекция детали

 Если дать полный фронтальный разрез (рис. 11), то по одному виду сверху нельзя будет судить о форме и высоте верхнего ушка.

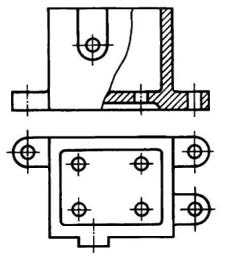
Рис.11. Соединение вида и разреза

Этот элемент на фронтальном разрезе не будет показан. Чтобы иметь полное представление о форме детали, целесообразно соединить часть вида и часть разреза. Разделяют их тоже сплошной волнистой линией. Данный пример характеризует рациональный способ построения чертежа.

cherch-ikt.ucoz.ru

ЧЕРЧЕНИЕ. Школьный интернет-учебник – Сечения и разрезы 4-7

В целях сокращения количества изображений на чертеже установлен ряд условностей и упрощений, облегчающих их выполнение.

1. Условные знаки.  Для того чтобы сократить количество видов на чертеже, при вычерчивании деталей имеющих квадратное или круглое сечение пользуются условными знаками  ø  и  □.

Рис. 1. Обозначение диаметра и стороны квадратного элемента

Обозначение толщины (например, s2) позволяет плоские предметы изображать также в одной проекции. Для этого чертят линию с полкой-выноской на которой пишут s2, другой конец линии заканчивают утолщенной точкой.



Рис. 2. Толщина  детали

При изображении предмета в одной проекции допускается условно обозначать его длину. В этом случае перед размерным числом пишут латинскую строчную букву L (рис. 3).

Рис. 3. Длина  детали

2. Разрыв детали. Чтобы сделать короче изображение длинной детали, не меняя масштаба, применяют разрыв, используя для этого сплошные волнистые линии. Размерную линию при этом не разрывают. Разрыв применяют для деталей с одинаковым или равномерно меняющимся поперечным сечением.



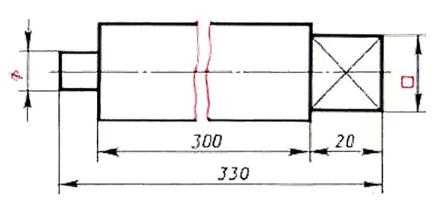
Рис. 4. Разрыв детали

Длинные детали, имеющие закономерно изменяющееся поперечное сечение, тоже можно показывать с разрывом. Размерную линию при этом не прерывают, размерное число должно соответствовать действительному размеру детали. Следует иметь в виду, что частичные изображения с разрывом ограничивают либо сплошной волнистой линией, либо сплошной тонкой линией с изломом, которая выходит за контур изображения на длину 2…4 мм.



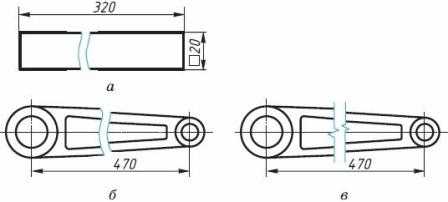
Рис. 5. Разрыв детали

3. Одинаковые элементы.  Если на детали имеются симметрично или равномерно расположенные элементы (например, отверстия), то на чертежах допускается показывать один или два из них, а для остальных – намечать лишь центры (рис. 6). Перед размерным числом указывают их количество.

Рис. 6. Изображение одинаковых элементов

4. Неполные изображения. При выполнении на чертеже видов и разрезов разрешается применять неполные изображения. Так, если вид или разрез представляют собой симметричную фигуру, то допускается вычерчивать половину детали до осевой линии (вид сверху на рис. 7, a) или несколько больше половины с проведением линии обрыва (рис. 7, б).



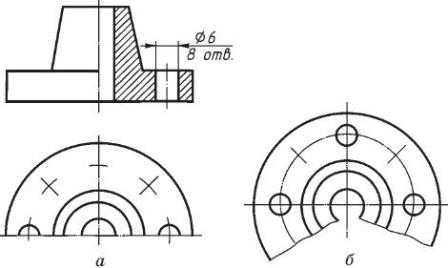
Рис. 7. Неполные изображения

Разрешается вместо полного вида показывать на чертеже лишь отдельные элементы детали, если при этом хорошо читается ее форма. На рисунке 8 вместо вида сверху приведено изображение только шпоночной канавки.

Рис. 8. Неполное изображение детали со шпоночной канавкой

На рисунке 9 приведен чертеж, на котором условно показано лишь несколько элементов (зубьев) шестеренки, а остальные не изображены.

Рис. 9. Неполное изображение шестеренки

5. Линии взаимного пересечения поверхностей. На технических чертежах линии взаимного пересечения поверхностей, если не требуется точного их построения, допускается показывать упрощенно. Так, линию пересечения двух цилиндров (рис. 10, а)  на чертеже можно не строить по точкам для проведения ее по лекалу, а выполнить с помощью циркуля (рис. 10, б). В этом случае лекальную кривую заменяют дугой окружности. В отдельных случаях кривые линии заменяют прямыми (рис. 10, в).



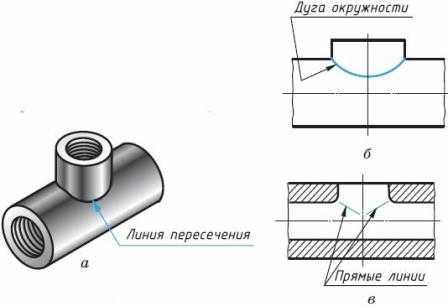
Рис. 10. Линии взаимного пересечения двух цилиндров

На чертеже плавный переход одной поверхности в другую можно изображать сплошной тонкой линией, не доводя ее до контура поверхности (см. рис. 10, в). Плавный переход иногда можно не показывать совсем (рис. 11).

Рис. 11

6. Дополнительные виды. Стандарт разрешает использовать кроме основных плоскостей проекций (грани куба) и дополнительные – для изображения таких элементов деталей, которые проецируются на основные плоскости с искажением (рис. 12, а). Дополнительную плоскость располагают параллельно поверхности элемента детали, изображение которого необходимо выполнить (рис. 12, б). Затем ее совмещают с основной плоскостью проекций. Полученное на этой плоскости изображение называют дополнительным видом.

На рисунке 12, в левой часть детали на виде сверху условно не показана, так как при проецировании на горизонтальную плоскость она изображается искаженной. Дополнительный вид дает неискаженное представление о форме и размерах этой части детали.



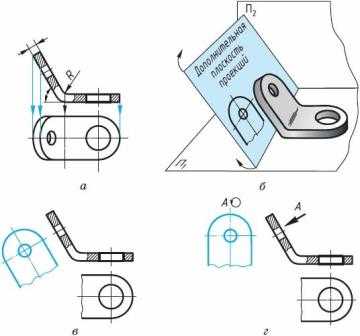
Рис. 12

На чертеже дополнительный вид отмечают надписью типа А, а направление взгляда указывают на чертеже стрелкой с тем же буквенным обозначением.

Разрешается поворачивать дополнительный вид (рис. 12, г).

При этом к надписи добавляют знак – «повернуто», располагая его рядом с буквой.

В том случае, когда дополнительный вид расположен в проекционной связи, как это сделано на рисунке 12, в, его не обозначают и не подписывают.

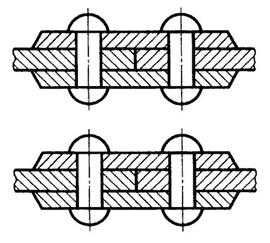
7. Штриховка смежных сечений. Для смежных сечений двух деталей следует брать наклон линий штриховки для одного сечения вправо, для другого – влево (встречная штриховка).

При штриховке «в клетку» для смежных сечений двух деталей расстояние между линиями штриховки в каждом сечении должно быть разным.

В смежных сечениях со штриховкой одинакового наклона и направления следует изменять расстояние между линиями штриховки (рис. 13) или сдвигать эти линии в одном сечении по отношению к другому, не изменяя угла их наклона (рис. 14).

Рис. 13.

Рис. 14.

8. Большие площади сечений. При больших площадях сечений, а также при указании профиля грунта на строительных чертежах допускается наносить обозначение лишь у контура сечения узкой полоской равномерной ширины (рис. 15).



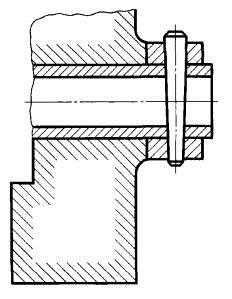
Рис. 15. Штриховка при больших площадях сечений

9. Узкие площади сечений, ширина которых на чертеже менее 2 мм, допускается показывать зачерненными с оставлением просветов между смежными сечениями не менее 0,8 мм (рис. 16).

Рис. 16. Зачерненные узкие площади сечений

10. Плоские поверхности выделяют на чертеже диагоналями, выполненными сплошными тонкими линиями (рис.17).

 

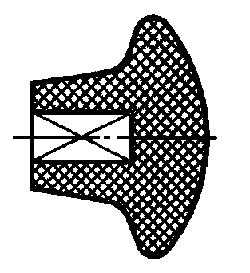
Рис. 17

11. Сплошная сетка, рифление. На чертежах предметов, имеющих сплошную сетку, рифление, орнамент и т. д., допускается изображать эти эле­менты частично, с упрощением (рис.18).

 

Рис. 18. Рифление на детали

 

cherch-ikt.ucoz.ru

ЧЕРЧЕНИЕ. Школьный интернет-учебник – Сечения и разрезы 4-4

Приложения    Ботвинников А.Д. § [1] Степакова В. В. § [3] Вышнепольский И.С. § [8]         Это интересно!

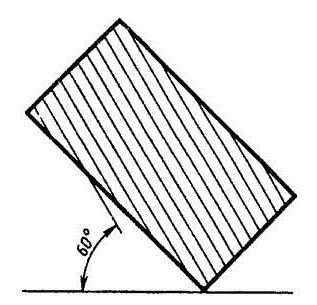
Вам известно, что фигуру сечения на чертеже выделяют штриховкой. Это – общее графическое обозначение материалов в сечениях независимо от их вида. Если на сечении хотят показать, из какого материала деталь изготовлена, то пользуются их графическими обозначениями. Некоторые из них показаны в таблице. Графическое обозначение материалов в сечениях должно способствовать легкому различению деталей, а также показывать вид материала детали, не затрудняя чтение чертежа. Правила графического обозначения и нанесения материалов в сечениях на чертежах для всех отраслей промышленности и строительства устанавливает ГОСТ 2.306—68 (СТ СЭВ 860—78). Согласно этому стандарту, допускается применять дополнительные графические обозначения материалов, поясняя их на чертеже. 1. Штриховку выполняют сплошными тонкими линиями. Наклонные параллельные линии штриховки должны проводиться под углом 45° или к линиям рамки чертежа, или к линии контура изображения, или к его оси (рис.1).   Рис. 1. Наклонные параллельные линии штриховки 2. Если линии штриховки, проведенные под углом 45° к линиям рамки чертежа, оказываются параллельными линиям контура или осевым линиям, следует вместо угла 45° выбирать угол 30° или 60° (рис. 2). Рис. 2. Линии штриховки, если линии контура расположены под углом 45° к линиям рамки чертежа 3. Линии штриховки можно наносить с наклоном как в правую, так и в левую сторону, но, как правило, в одну и ту же сторону на всех сечениях одной и той же детали, независимо от количества листов чертежа, на которых эти сечения выполнены.   4. Частота нанесения линий штриховки должна быть одинаковой для всех сечений данной детали, выполняемых в одном масштабе. Расстояние между штрихами принимают от 1 до 10 мм в зависимости от площади штриховки и необходимости разнообразить штриховку смежных областей. 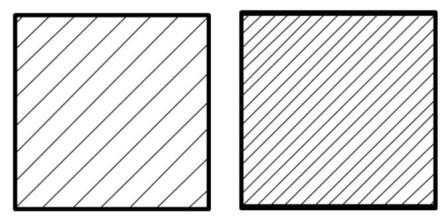  5. В смежных сечениях следует применять встречную штриховку (наклон штриховки одного сечения вправо, другого — влево) или сдвигать линии штриховки в одном сечении по отношению к другому, когда наклон штриховки обоих сечений одинаков. Можно также изменять расстояние между линиями штриховки. При штриховке «в клетку» расстояние между линиями штриховки в каждом сечении должно быть разным (рис.3). Рис. 3. Линии штриховки в смежных сечениях 6. Узкие площади сечений толщиной менее 2 мм показывают зачерненными, оставляя просветы между смежными сечениями не менее 0,8 мм. (рис.4). Рис. 4. Зачернённая штриховка в смежных сечениях, толщиной менее 2 мм

Практические задания, тесты и домашние работы Графическая работа     Вопросы для повторения pdf  Вопросы   Тест   Домашняя работа     Черчение с увлечением!

cherch-ikt.ucoz.ru

ЧЕРЧЕНИЕ. Школьный интернет-учебник – Сечения и разрезы 4-2

Приложения    Ботвинников А.Д. § [1] Степакова В. В. § [3] Вышнепольский И.С. § [8]         Это интересно! pdf   Сечение тора

Задание: По чертежу выполните необходимые сечения одного из валиков. Проставьте размеры.

Практические задания, тесты и домашние работы Графическая работа     docx  Графическая работа  “Выполнить необходимое сечение”    12 вариантов (Степакова В.В.)   Тест   Домашняя работа     Черчение с увлечением! pdf  pdf

cherch-ikt.ucoz.ru

IX. Разрезы и сечения

Приступая к выполнению листа «Проекционное черчение», вы ознакомились с содержанием ГОСТ 2.305-68 («Изображе­ния— виды, разрезы — сечения»). Перед вычерчиванием раз­резов еще раз детально изучите разделы 3, 4 и 6 данного

ГОСТа.

Содержание раздела VII и некоторых пунктов разделов III и IV в данной работе используется неполностью, но про­граммой предусмотрено изучение ГОСТ 2.305-68 во всем его объеме при выполнении данного листа и проверка знания этого ГОСТа на зачете. Поскольку в разрезах и сечениях используется штриховка, изучите ГОСТ 2.306-68, знание кото­рого также проверяется на зачете.

Обратите внимание на следующее:

разрезы классифицируются в зависимости от положения секущей плоскости (горизонтальные, вертикальные — фрон­тальные и профильные, наклонные) и от количества и взаи­моположения секущих плоскостей (простые, сложные — сту­пенчатые, ломаные и т.д.). Классификация эта приводится в ГОСТ 2.305-68.

В задаче 3-й некоторых заданий придется использовать ступенчатый разрез. Обратите внимание, что из всех плоско­стей, составляющих «ступеньки», в образовании изображе­ния такого разреза участвуют только плоскости, параллель­ные соответствующей плоскости проекций. Так, в изображе­нии А—А на рис. 16 участвуют только профильные плоско­сти Σ и .

При соединении половины симметричного вида с полови­ной симметричного разреза границей между ними может служить ось симметрии (рис. 11, 12, 14, 15).

Если с осью симметрии ‘совпадает линия видимого кон­тура, граница между видом и разрезом отмечается сплошной волнистой линией, смещенной в сторону от оси. При этом увеличивается площадь вида за счет разреза, если линия ви­димого контура имеется на наружном виде (рис. 10), или площадь разреза за счет наружного вида, если такая линия имеется на разрезе (рис. 13). В любом случае линия види­мого контура границей между видом и разрезам служить не может.

Если разрез проходит вдоль какого-либо плоского эле­мента детали (например — ребра), участок разреза в преде­лах этого элемента условно не штрихуется. Если же разрез проходит поперек такого элемента, этот участок штрихуется, как и все остальные (рис. 15, 16).

Расстояние между прямыми линиями штриховки выби­рается в пределах от 2 до 10 мм, в зависимости от площади штрихуемого участка. На данном листе рекомендуется брать интервал между штрихами 2 мм.

В задаче 3-ей каждого задания предусмотрено выполне­ние наклонного- сечения, для которого положение секущей плоскости задано с помощью засечек по краям проекции в соответствии с ГОСТом. Следует твердо помнить, что сече­ние— плоская фигура, изображающая участок тела, непо­средственно соприкоснувшийся с «режущей» плоскостью. Рас­смотрим метод построения наклонного сечения на примере рис. 15.



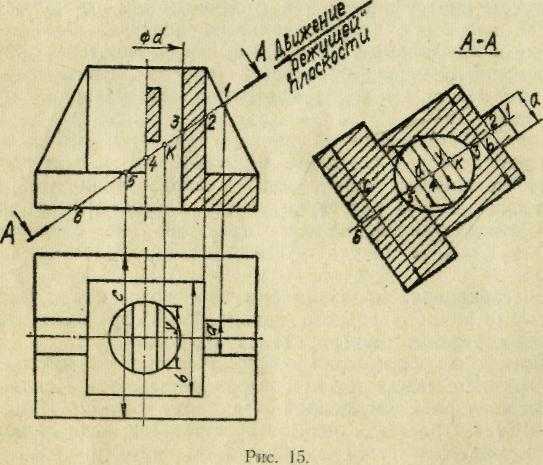
Если в сечении намечается симметричная фигура, базой для его построения служит ось симметрии. Ее располагают параллельно заданному следу секущей плоскости или параллельно одной из сторон рамки чертежи. В последнем случае под обозначением сечения указывается «повернуто» (При отсутствии симметрии на чертеже условно проводится какая-либо прямая, параллельная проекция секущей плоскости лежащая в этой плоскости. Эта прямая и служит базой для построения сечения).

Фигуру сечения рекомендуется строить в таком порядке, в каком секущая плоскость, двигаясь вдоль направления сле­да как реальный «режущий» нож, пересекает отдельные эле­менты тела, (например, справа налево, как показано на рис. 15). Причем, сначала очерчивается наружный контур, а затем внутренний, если он имеется.



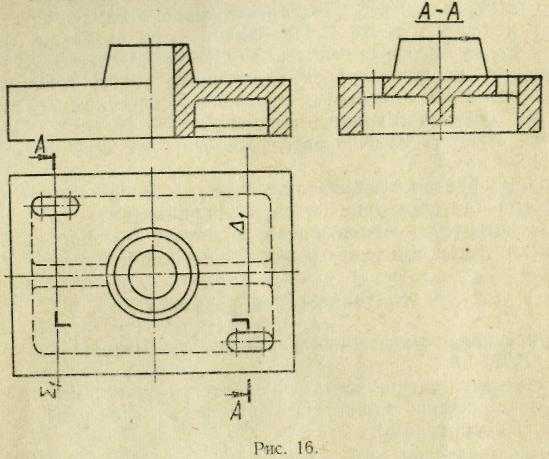
На участке 1—2 «режущая» плоскость пересекает ребро на ширине «о». По длине участка 1—2, измеренной вдоль следа, и по его ширине «а», измеренной на горизонтальной проекции и направлении, перпендикулярном фронтальной плоскости проекций, построим этот участок. Таким же обра­зом строим участки 2—5 и 5—6. Они также прямоугольные, так как секущая плоскость пересекает параллелепипеды. С помощью линий проекционной связи, опущенных на гори­зонтальную проекцию из точек 2 и 5, измеряем ширину «b» (для участка 2—5) и «с» (для участка 5—6).

На этом построение замкнутого наружного контура сече­ния закончено.

Внутри данного тела на пути «режущей» плоскости встре­чается вертикальное цилиндрическое отверстие диаметра «d». В его пересечении с (наклонной секущей плоскостью обра­зуется эллипс, большая ось которого (3—4) измеряется вдоль следа плоскости. Малая ось всегда равна диаметру отвер­стия.

Передвигаясь вдоль следа, «режущая» плоскость встре­чает пустоту в точке 3. Двигаясь дальше, она образует эл­липс с центром в точке 4. Положение этих, а также любых других точек на оси симметрии может быть отмечено на рас­стоянии от любой из ранее отмеченных точек, измеренном вдоль проекции плоскости, отмеченной засечками. Так, на уровне точки К ширина эллипса — «Y». Поэтому эллипс можно построить или по размерам его осей, или по точкам, подобным точке К.

Таким образом, любая точка контура сечения может быть построена или проверена по двум координатам, одна из ко­торых измеряется вдоль следа, а другая — в направлении, перпендикулярном к следу секущей плоскости.

studfiles.net