Дифференциальные уравнения Основные понятия
Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.
Общий вид дифференциальных уравнений: F (x,y,y’,y’’..y’’’) = 0
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения.
Процесс отыскания решения ДУ называется его интегрированием.
Дифференциальные уравнения первого порядка
Обыкновенным
дифференциальным уравнением первого
порядка называется уравнение вида F(x,
y, y‘
)=0, где F — известная функция трех переменных, x —
независимая переменная, y(
Уравнение y‘=f(x, y) устанавливает связь между координатами точки (x, y) и угловым коэффициентом y‘ касательной к интегральной кривой, проходящей через эту точку.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
P(x;y)dx+Q(x;y)
Где P(x;y) и Q(x;y) – известные функции. Уравнение P(x;y)dx+Q(x;y)dy=0 удобно тем, что переменные в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.
Если дифференциальное уравнение первого порядка y‘=f(x, y), имеет решение, то решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=φ(x,C), где C — произвольная константа.
Функция y=φ
Функция y=φ(x,C) является решением ДУ при каждом фиксированном значении С.
Каково бы ни было начальное условие y(x0)= y0, можно найти такое значение постоянной С=С0 , что функция y=φ(x,C0) удовлетворяет данному начальному условию.
Частным решением
Задача отыскания решения ДУ первого порядка P(x;y)dx+Q(x;y)dy=0, удовлетворяющего заданному начальному условию y(x0)= y0 , называется задачей Коши.
Теорема(существования и единственности решения задачи Коши).
Если
в уравнении
Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнение вида
P(x)dx+Q(y
В нем одно слагаемое зависит только от x, а другое – от y. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:
∫ P(x)dx+∫Q(y)dy=с – его общий интеграл.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:
P1(x) . Q1(y) . dx+ P2(x) . Q2
Особенность этого уравнения в том, что коэффициенты представляют собой произведения двух функций, одна из которых зависит только от х другая – только от у.
Уравнение P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0 легко сводится к уравнению P(x)dx+Q(y)dy=0. путем почленного деления его на
, – общий интеграл.
studfiles.net
Основные понятия и определения дифференциальных уравнений
Дифференциальным уравнением называется уравнение, связывающее независимую переменную [cbm]x[/cbm] , искомую функцию [cbm]y=f(x)[/cbm] и её производные [cbm]y’,y”,\ldots,y^{(n)}[/cbm] , т. е. уравнение вида
[cbm]F(x,y,y’,y”,\ldots,y^{(n)})=0.[/cbm]
Если искомая функция [cbm]y=y(x)[/cbm] есть функция одной независимой переменной [cbm]x[/cbm] , дифференциальное уравнение называется обыкновенным; например,
[cbm]\mathsf{1)}~\frac{dy}{dx}+xy=0, \quad \mathsf{2)}~y”+y’+x=\cos{x}, \quad \mathsf{3)}~(x^2-y^2)\,dx-(x+y)\,dy=0.[/cbm]
Когда искомая функция [cbm]y[/cbm] есть функция двух и более независимых переменных, например, если [cbm]y=y(x,t)[/cbm] , то уравнение вида
[cbm]F\!\left(x,t,y,\frac{\partial{y}}{\partial{x}},\frac{\partial{y}}{\partial{t}},\ldots,\frac{\partial^m{y}}{\partial{x^k}\partial{t^l}}\right)=0[/cbm]
называется уравнением в частных производных. Здесь [cbm]k,l[/cbm] — неотрицательные целые числа, такие, что [cbm]k+l=m[/cbm] ; например
[cbm]\frac{\partial{y}}{\partial{t}}-\frac{\partial{y}}{\partial{x}}=0, \quad \frac{\partial{y}}{\partial{t}}=\frac{\partial^2y}{\partial{x^2}}.[/cbm]
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение [cbm]y’+xy=e^x[/cbm] — уравнение первого порядка, дифференциальное уравнение [cbm]y”+p(x)y=0[/cbm] , где [cbm]p(x)[/cbm] — известная функция, — уравнение второго порядка; дифференциальное уравнение [cbm]y^{(9)}-xy”=x^2[/cbm] — уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на интервале [cbm](a,b)[/cbm] называется функция [cbm]y=\varphi(x)[/cbm] , определенная на интервале [cbm](a,b)[/cbm] вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции [cbm]y=\varphi(x)[/cbm] в дифференциальное уравнение превращает последнее в тождество по [cbm]x[/cbm] на [cbm](a,b)[/cbm] . Например, функция [cbm]y=\sin{x}+\cos{x}[/cbm] является решением уравнения [cbm]y”+y=0[/cbm] на интервале [cbm](-\infty,+\infty)[/cbm] . В самом деле, дифференцируя функцию дважды, будем иметь
[cbm]y’=\cos{x}-\sin{x}, \quad y”=-\sin{x}-\cos{x}.[/cbm]
Подставляя выражения [cbm]y”[/cbm] и [cbm]y[/cbm] в дифференциальное уравнение, получим тождество
[cbm]-\sin{x}-\cos{x}+\sin{x}+\cos{x}\equiv0[/cbm]
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Общий вид уравнения первого порядка
[cbm]F(x,y,y’)=0.[/cbm](1)

Если уравнение (1) удается разрешить относительно [cbm]y'[/cbm] , то получится уравнение первого порядка, разрешенное относительно производной.
[cbm]y’=f(x,y).[/cbm](2)
Задачей Коши называют задачу нахождения решения [cbm]y=y(x)[/cbm] уравнения [cbm]y’=f(x,y)[/cbm] , удовлетворяющего начальному условию [cbm]y(x_0)=y_0[/cbm] (другая запись [cbm]y|_{x=x_0}=y_0[/cbm] ).
Геометрически это означает, что ищется интегральная кривая, проходящая через заданную
точку [cbm]M_0(x_0,y_0)[/cbm] плоскости [cbm]xOy[/cbm] (рис. 1).
Теорема существования и единственности решения задачи Коши
Пусть дано дифференциальное уравнение [cbm]y’=f(x,y)[/cbm] , где функция [cbm]f(x,y)[/cbm] определена в некоторой области [cbm]D[/cbm] плоскости [cbm]xOy[/cbm] , содержащей точку [cbm](x_0,y_0)[/cbm] . Если функция [cbm]f(x,y)[/cbm] удовлетворяет условиям
а) [cbm]f(x,y)[/cbm] есть непрерывная функция двух переменных [cbm]x[/cbm] и [cbm]y[/cbm] в области [cbm]D[/cbm] ;
б) [cbm]f(x,y)[/cbm] имеет частную производную [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] , ограниченную в области [cbm]D[/cbm] , то найдется интервал [cbm](x_0-h,x_0+h)[/cbm] , на котором существует единственное решение [cbm]y=\varphi(x)[/cbm] данного уравнения, удовлетворяющее условию [cbm]y(x_0)=y_0[/cbm] .
Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения [cbm]y’=f(x,y)[/cbm] , но эти условия не являются необходимыми. Именно, может существовать единственное решение уравнения [cbm]y’=f(x,y)[/cbm] , удовлетворяющее условию [cbm]y(x_0)=y_0[/cbm] , хотя в точке [cbm](x_0,y_0)[/cbm] не выполняются условия а) или б) или оба вместе.
Рассмотрим примеры.
1. [cbm]y’=\frac{1}{y^2}[/cbm] . Здесь [cbm]f(x,y)=\frac{1}{y^2},~\frac{\partial{f}}{\partial{y}}=-\frac{2}{y^3}[/cbm] . В точках [cbm](x_0,0)[/cbm] оси [cbm]Ox[/cbm] условия а) и б) не выполняются (функция [cbm]f(x,y)[/cbm] и её частная производная [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] разрывны на оси [cbm]Ox[/cbm] и неограниченны при [cbm]y\to0[/cbm] ), но через каждую точку оси [cbm]Ox[/cbm] проходит единственная интегральная кривая [cbm]y=\sqrt[3]{3(x-x_0)}[/cbm] (рис. 2).
2. [cbm]y’=xy+e^{-y}[/cbm] . Правая часть уравнения [cbm]f(x,y)=xy+e^{-y}[/cbm] и ее частная производная [cbm]\frac{\partial{f}}{\partial{y}}=x-e^{-y}[/cbm] непрерывны по [cbm]x[/cbm] и [cbm]y[/cbm] во всех точках плоскости [cbm]xOy[/cbm] . В силу теоремы существования и единственности областью, в которой данное уравнение имеет единственное решение
является вся плоскость [cbm]xOy[/cbm] .
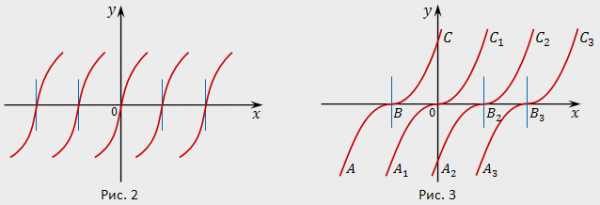
3. [cbm]y’=\frac{3}{2}\sqrt[3]{y^2}[/cbm] . Правая часть уравнения [cbm]f(x,y)=\frac{3}{2}\sqrt[3]{y^2}[/cbm] определена и непрерывна во всех точках плоскости [cbm]xOy[/cbm] . Частная производная [cbm]\frac{\partial{f}}{\partial{y}}=\frac{1}{\sqrt[3]{y}}[/cbm] обращается в бесконечность при [cbm]y=0[/cbm] , т.е. на оси [cbm]Ox[/cbm] , так что при [cbm]y=0[/cbm] нарушается условие б) теоремы существования и единственности. Следовательно, в точках оси [cbm]Ox[/cbm] возможно нарушение единственности. Легко проверить, что функция [cbm]y=\frac{(x+c)^3}{8}[/cbm] есть решение данного уравнения. Кроме этого, уравнение имеет очевидное решение [cbm]y\equiv0[/cbm] . Таким образом, через каждую точку оси [cbm]Ox[/cbm] проходит по крайней мере две интегральные линии и, следовательно, действительно в точках этой оси нарушается единственность (рис. 3).
Интегральными линиями данного уравнения будут также линии, составленные из кусков кубических парабол [cbm]y=\frac{(x+c)^3}{8}[/cbm] и отрезков оси [cbm]Ox[/cbm] , например, [cbm]ABOC_1,[/cbm] [cbm]ABB_2C_2,[/cbm] [cbm]A_2B_2x[/cbm] и др., так что через каждую точку оси [cbm]Ox[/cbm] проходит бесконечное множество интегральных линий.
Условие Липшица
Замечание. Условие ограниченности производной [cbm]\partial{f}/\partial{y}[/cbm] , фигурирующее в теореме существования и единственности решения задачи Коши, может быть несколько ослаблено и заменено так называемым условием Липшица.
Говорят, что функция [cbm]f(x,y)[/cbm] , определенная в некоторой области [cbm]D[/cbm] , удовлетворяет в [cbm]D[/cbm] условию Липшица по [cbm]y[/cbm] , если существует такая постоянная [cbm]L[/cbm] (постоянная Липшица), что для любых [cbm]y_1,y_2[/cbm] из [cbm]D[/cbm] и любого [cbm]x[/cbm] из [cbm]D[/cbm] справедливо неравенство
[cbm]|f(x,y_2)-f(x,y_1)| \leqslant L|y_2-y_1|.[/cbm]
Существование в области [cbm]D[/cbm] ограниченной производной [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] достаточно для того, чтобы функция [cbm]f(x,y)[/cbm] удовлетворяла в [cbm]D[/cbm] условию Липшица. Напротив, из условия Липшица не вытекает условие ограниченности [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] ; последняя может даже не существовать. Например, для уравнения [cbm]y’=2|y|\cos{x}[/cbm] функция [cbm]f(x,y)=2|y|\cos{x}[/cbm] не дифференцируема по [cbm]y[/cbm] в точке [cbm](x_0,0),x_0\ne\frac{\pi}{2}+k\pi,k\in\mathbb{Z}[/cbm] , но условие Липшица в окрестности этой точки выполняется. В самом деле,
[cbm]{|f(x,y_2)-f(x,y_1)|=L|2|y_2|\cos{x}-2|y_1|\cos{x}|=2|\cos{x}|\,||y_2|-|y_1||\leqslant2|y_2-y_1|.}[/cbm]
поскольку [cbm]|\cos{x}|\leqslant1,[/cbm] а [cbm]||y_2|-|y_1||\leqslant|y_2-y_1|[/cbm] . Таким образом, условие Липшица выполняется с постоянной [cbm]L=2[/cbm] .
Теорема. Если функция [cbm]f(x,y)[/cbm] непрерывна и удовлетворяет условию Липшица по [cbm]y[/cbm] в области [cbm]D[/cbm] , то задача Коши
[cbm]\frac{dy}{dx}=f(x,y), \quad y|_{x=x_0}=y_0, \quad (x_0,y_0)\in{D}.[/cbm]
имеет единственное решение.
Условие Липшица является существенным для единственности решения задачи Коши. В качестве примера рассмотрим уравнение
[cbm]\frac{dy}{dx}=\begin{cases}\dfrac{4x^3y}{x^4+y^4},&x^2+y^2>0,\\0,&x=y=0.\end{cases}[/cbm]
Нетрудно видеть, что функция [cbm]f(x,y)[/cbm] непрерывна; с другой стороны,
[cbm]f(x,Y)-f(x,y)=\frac{4x^3(x^4+yY)}{(x^4+y^2)(x^4+Y^2)}(Y-y).[/cbm]
Если [cbm]y=\alpha x^2,~Y=\beta x^2,[/cbm] то
[cbm]|f(x,Y)-f(x,y)|=\frac{4}{|x|}\frac{1-\alpha\beta}{(1+\alpha^2)(1+\beta^2)}|Y-y|,[/cbm]
и условие Липшица не удовлетворяется ни в одной области, содержащей начало координат [cbm]O(0,0)[/cbm] , так как множитель при [cbm]|Y-y|[/cbm] оказывается неограниченным при [cbm]x\to0[/cbm] .
Данное дифференциальное уравнение допускает решение [cbm]y=C^2-\sqrt{x^4+C^4},[/cbm] где [cbm]C[/cbm] — произвольная постоянная. Отсюда видно, что существует бесконечное множество решений, удовлетворяющих начальному условию [cbm]y(0)=0.[/cbm]
Общим решением дифференциального уравнения (2) называется функция
[cbm]y=\varphi(x,C),[/cbm](3)
зависящая от одной произвольной постоянной [cbm]C[/cbm] , и такая, что
1) она удовлетворяет уравнению (2) при любых допустимых значениях постоянной [cbm]C;[/cbm]
2) каково бы ни было начальное условие
[cbm]\Bigl.{y}\Bigr|_{x=x_0}=y_0,[/cbm](4)
можно подобрать такое значение [cbm]C_0[/cbm] постоянной [cbm]C[/cbm] , что решение [cbm]y=\varphi(x,C_0)[/cbm] будет удовлетворять заданному начальному условию (4). При этом предполагается, что точка [cbm](x_0,y_0)[/cbm] принадлежит области, где выполняются условия существования и единственности решения.
Частным решением дифференциального уравнения (2) называется решение, получаемое из общего решения (3) при каком-либо определенном значении произвольной постоянной [cbm]C[/cbm] .
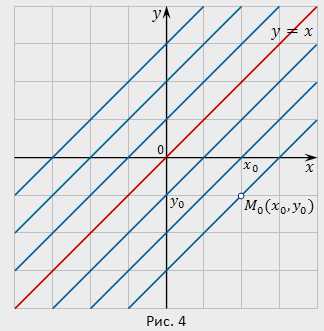
Пример 1. Проверить, что функция [cbm]y=x+C[/cbm] есть общее решение дифференциального уравнения [cbm]y’=1[/cbm] и найти частное решение, удовлетворяющее начальному условию [cbm]y|_{x=0}=0[/cbm] . Дать геометрическое истолкование результата.
Решение. Функция [cbm]y=x+C[/cbm] удовлетворяет данному уравнению при любых значениях произвольной постоянной [cbm]C[/cbm] . В самом деле, [cbm]y’=(x+C)’=1.[/cbm]
Зададим произвольное начальное условие [cbm]y|_{x=x_0}=y_0[/cbm] . Полагая [cbm]x=x_0[/cbm] и [cbm]y=y_0[/cbm] в равенстве [cbm]y=x+C[/cbm] , найдем, что [cbm]C=y_0-x_0[/cbm] . Подставив это значение [cbm]C[/cbm] в данную функцию, будем иметь [cbm]y=x+y_0-x_0[/cbm] . Эта функция удовлетворяет заданному начальному условию: положив [cbm]x=x_0[/cbm] , получим [cbm]y=x_0+y_0-x_0=y_0[/cbm] . Итак, функция [cbm]y=x+C[/cbm] является общим решением данного уравнения.
В частности, полагая [cbm]x_0=0[/cbm] и [cbm]y_0=0[/cbm] , получим частное решение [cbm]y=x[/cbm] .
Общее решение данного уравнения, т.е. функция [cbm]y=x+C[/cbm] , определяет в плоскости [cbm]xOy[/cbm] семейство параллельных прямых с угловым коэффициентом [cbm]k=1[/cbm] . Через каждую точку [cbm]M_0(x_0,y_0)[/cbm] плоскости [cbm]xOy[/cbm] проходит единственная интегральная линия [cbm]y=x+y_0-x_0[/cbm] . Частное решение [cbm]y=x[/cbm] определяет одну из интегральных кривых, а именно прямую, проходящую через начало координат (рис.4).
Пример 2. Проверить, что функция [cbm]y=Ce^x[/cbm] есть общее решение уравнения [cbm]y’-y=0[/cbm] и найти частное решение, удовлетворяющее начальному условию [cbm]y|_{x=1}=-1.[/cbm] .

Решение. Имеем [cbm]y=Ce^x,~y’=Ce^x[/cbm] . Подставляя в данное уравнение выражения [cbm]y[/cbm] и [cbm]y'[/cbm] , получаем [cbm]Ce^x-Ce^x\equiv0[/cbm] , т. е. функция [cbm]y=Ce^x[/cbm] удовлетворяет данному уравнению при любых значениях постоянной [cbm]C[/cbm] .
Зададим произвольное начальное условие [cbm]y|_{x=x_0}=y_0[/cbm] . Подставив [cbm]x_0[/cbm] и [cbm]y_0[/cbm] вместо [cbm]x[/cbm] и [cbm]y[/cbm] в функцию [cbm]y=Ce^x[/cbm] , будем иметь [cbm]y_0=Ce^{x_0}[/cbm] , откуда [cbm]C=y_0e^{-x_0}[/cbm] . Функция [cbm]y=y_0e^{x-x_0}[/cbm] удовлетворяет начальному условию. Действительно, полагая [cbm]x=x_0[/cbm] , получим [cbm]y=y_0e^{x_0-x_0}=y_0[/cbm] . Функция [cbm]y=Ce^x[/cbm] есть общее решение данного уравнения.
При [cbm]x_0=1[/cbm] и [cbm]y_0=-1[/cbm] получим частное решение [cbm]y=-e^{x-1}[/cbm] .
С геометрической точки зрения общее решение определяет семейство интегральных кривых, которыми являются графики показательных функций; частное решение есть интегральная кривая, проходящая через точку [cbm]M_0(1;-1)[/cbm] (рис.5).
Соотношение вида [cbm]\Phi(x,y,C)=0[/cbm] , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.
Соотношение, получаемое из общего интеграла при конкретном значении постоянной [cbm]C[/cbm] , называется частным интегралом дифференциального уравнения.
Задача решения или интегрирования дифференциального уравнения состоит в нахождении общего решения или общего интеграла данного дифференциального уравнения. Если дополнительно задано начальное условие, то требуется выделить частное решение или частный интеграл, удовлетворяющие поставленному начальному условию.
Так как с геометрической точки зрения координаты [cbm]x[/cbm] и [cbm]y[/cbm] равноправны, то наряду с уравнением [cbm]\frac{dx}{dy}=f(x,y)[/cbm] мы будем рассматривать уравнение [cbm]\frac{dx}{dy}=\frac{1}{f(x,y)}[/cbm] .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
calcsbox.com
Понятие дифференциального уравнения и его решения — Мегаобучалка
Лекция 9. Дифференциальные уравнения первого порядка
Понятие дифференциального уравнения и его решения
Уравнение вида: , (9.1)
которое связывает аргумент , неизвестную функцию и ее производные, называется дифференциальным уравнением.
Порядком дифференциального уравнения называют порядок наивысшей производной, которую содержит в себе уравнение, а ее степень называется степенью дифференциального уравнения.
Если неизвестная функция, которая входит в дифференциальное уравнение, является функцией более чем одной переменной, то дифференциальное уравнение называется уравнением в частных производных. Решением дифференциального уравненияназывают функцию , подстановка которой в уравнение превращает его в тождество. График решения называется интегральной кривой. Решить или проинтегрировать данное дифференциальное уравнение значит найти все его решения. Уравнение (9.1) имеет множество решений.
Пример 1. Показать, что функция является решением уравнения
Решение. Находим Подставляем в заданное уравнение то есть функция действительно является решением заданного дифференциального уравнения.
Общим решением дифференциального уравнения -го порядка называется его решение:
, (9.2)
которое содержит независимых произвольных постоянных .
Если общее решение задано в неявном виде:
, (9.3)
то оно называется общим интегралом.
Частным решением дифференциального уравненияназывается решение, которое получается из общего решения, если свободным постоянным придавать некоторые значения.
Дифференциальным уравнением первого порядка называется уравнение вида:
, (9.4)
или
. (9.5)
Уравнение (9.5) – уравнение первого порядка, разрешенное относительно производной. Общее решение этого уравнения имеет вид:
, (9.6)
где – произвольная постоянная.
Задача решения дифференциального уравнения, которое удовлетворяет начальному условию: , имеет название задачи Коши. Решение дифференциального уравнения (9.5) существует не для любой функции и не при любом начальном условии.
Теорема.Если в уравнении функция и ее частная производная непрерывны в некоторой замкнутой области и точка , то существует единственное решение этого уравнения, которое удовлетворяет начальному условию при .
Геометрический смысл задачи Коши состоит в том, что график функции , то есть интегральная кривая, которая проходит через точку , единственная.
Если в точке условия теоремы Коши выполняются, то начальное условие будем называть допустимым.
Для решения задачи Коши в общее решение уравнения (9.6) нужно подставить начальное условие и решить уравнение относительно постоянной . Тогда частное решение будет решением задачи.
Пример 2. Решить уравнение: ; .
Решение. Запишем уравнение в дифференциалах и интегрируем его правую и левую части: .
Используем начальное условие: .
Следовательно, .
Таким образом, является решением задачи Коши.
megaobuchalka.ru
Общий интеграл дифференциального уравнения
Определение и формула общего интеграла дифференциального уравнения
Рассмотрим дифференциальное уравнение первого порядка
Если продифференцировать равенство (2) по переменной x при условии, что :
и исключить постоянную C из уравнений (2), (3), то получим дифференциальное уравнение, эквивалентное уравнению (1).
В этом случае говорят, что уравнение (1) есть дифференциальным уравнением семейства функций (2), зависящих от параметра C.
Примеры решения задач
Частным интегралом дифференциального уравнения (1) есть общий интеграл (2) этого уравнения при заданном (известном) значении постоянной C.
Например: Частным интегралом для дифференциального уравнения из прошлого примера есть функция
полученная из общего интеграла этого уравнения для значения .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Дифференциальные уравнения первого порядка. Задача Коши. Общее, частное и особое решения дифференциального уравнения
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
Определение. Задачей Коши(Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
Теперь интегрируем:
– это общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
Определение. Интегральной кривойназывается график y = j(x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решениемдифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
– это так называемая дифференциальная формауравнения первого порядка.
23.Теорема Коши существования и единственности решения дифференциального уравнения первого порядка (без доказательства).
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х
24.Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные, линейные.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
– это так называемая дифференциальная формауравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
megaobuchalka.ru
Неоднородные дифференциальные уравнения 2ого порядка
Определение и формулы неоднородных ДУ второго порядка
Нахождение решения однородного уравнения (2) можно посмотреть тут — решение дифференциальных уравнений второго порядка и линейные неоднородные дифференциальные уравнения второго порядка.
Методы нахождения частного решения неоднородных ДУ второго порядка
Существует несколько методов нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (1). Эти методы выбираются в зависимости от вида правой части – функции .
1) Если функция представляет собой многочлен n-ой степени
то частное решение уравнения (1) ищется в виде
Здесь – многочлен степени n с неопределенными коэффициентами (которые подлежат определению), а s – кратность корня характеристического уравнения однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных нулю).
Так как – частное решение уравнения (1), то коэффициенты, определяющие многочлен , можно найти методом неопределенных коэффициентов из равенства
использовав тот факт, что два многочлена равны, если равны коэффициенты при соответствующих степенях независимой переменной.
2) Если функция , стоящая в правой части уравнения (1), имеет вид
то есть представляет собой произведение многочлена степени n и экспоненты, то частное решение этого уравнения ищется в виде
где – многочлен степени n с неопределенными коэффициентами, а s – кратность корня в характеристическом уравнении соответствующего однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных a). Коэффициенты многочлена определяются подстановкой частного решения в исходное уравнение (так как является решением, то оно должно удовлетворять уравнению). Таким образом, должно выполняться равенство (3).
3) Если правая часть неоднородного дифференциального уравнения (1) имеет вид:
то частное решение в этом случае ищем в виде:
Здесь s – число комплексно сопряженных пар корней характеристического уравнения – многочлены степени k с неизвестными коэффициентами. Коэффициенты этих многочленов определяются из равенства (3).
Если правая часть имеет отличную, от описанных выше, структуру, то для нахождение решения уравнения (1) применяют метод вариации произвольной постоянной:
1) находится общее решение соответствующего линейного однородного уравнения (2) в виде
где – линейно независимые частные решения линейного однородного дифференциального уравнения (2), – некоторые произвольные постоянные;
2) варьируются произвольные постоянные, то есть считается, что они являются функциями независимой переменной x:
А в качестве общего решения исходного дифференциального уравнения (1) рассматривается функция
Функции (точнее их производные ) являются решением системы
Тогда сами неизвестные функции находятся с помощью интегрирования.
ru.solverbook.com
