Момент инерции тела относительно оси
П усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами
,
находящиеся от оси на расстоянии
соответственно.
усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами
,
находящиеся от оси на расстоянии
соответственно.
Моментом инерции материальной точки относительно оси (OO) называется произведение массы материальной точки на квадрат ее расстояния до этой оси:

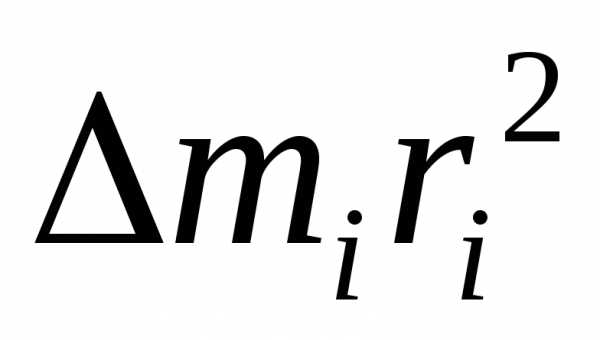 . (6.1)
. (6.1)
Моментом инерции (МИ) тела относительно оси (OO) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:
 . (6.2)
. (6.2)
Как видно момент инерции тела есть величина аддитивная – момент инерции всего тела относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.
В данном случае
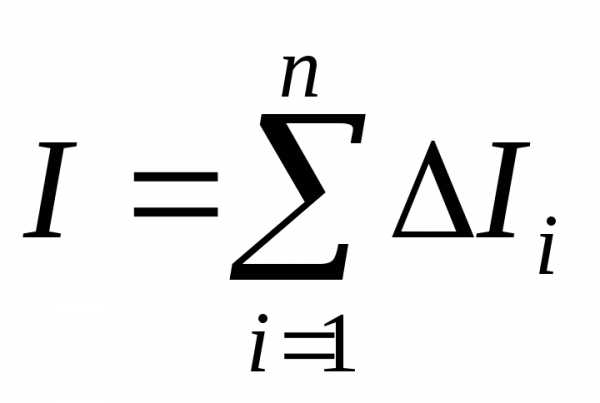 .
.
Измеряется момент инерции в кгм2. Так как
, (6.3)
где
–
плотность вещества,  – объемi – го участка, то
– объемi – го участка, то
 ,
,
или, переходя к бесконечно малым элементам,
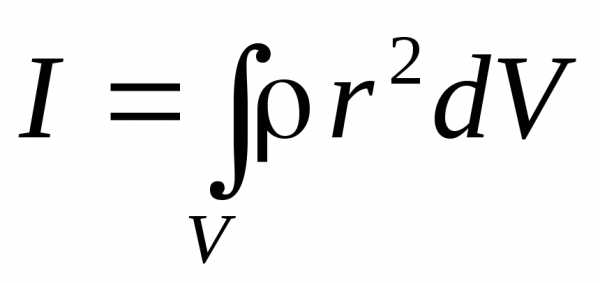 . (6.4)
. (6.4)
Формулу (6.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает
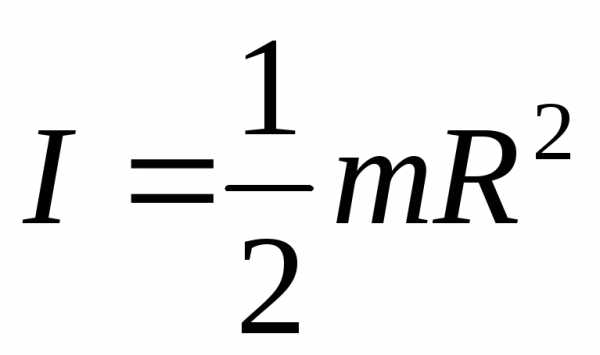 ,
,
где т
Большую помощь при вычислении МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела Ic относительно оси, проходящей через центр масс тела и параллельной данной, и произведения массы тела на квадрат расстояния d между указанными осями:
. (6.5)
Момент силы относительно оси
Пусть на тело действует сила F. Примем для простоты, что сила F лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.6.2,а), которую назовем осью (например, это ось вращения тела). На рис. 6.2,а А – точка приложения силы
 – точка пересечения оси с плоскостью, в
которой лежит сила;r–
радиус-вектор, определяющий положение
точки А относительно точки О‘; O‘B = b – плечо
силы. Плечом силы относительно оси
называется наименьшее расстояние от
оси до прямой, на которой лежит вектор
силы F (длина перпендикуляра, проведенного из
точки
– точка пересечения оси с плоскостью, в
которой лежит сила;r–
радиус-вектор, определяющий положение
точки А относительно точки О‘; O‘B = b – плечо
силы. Плечом силы относительно оси
называется наименьшее расстояние от
оси до прямой, на которой лежит вектор
силы F (длина перпендикуляра, проведенного из
точки  к
этой прямой).
к
этой прямой).Моментом силы относительно оси называется векторная величина, определяемая равенством

Модуль этого вектора . Иногда, поэтому говорят, что момент силы относительно оси – это произведение силы на ее плечо.
Если
сила F направлена произвольно, то ее можно
разложить на две составляющие;  и
и (рис.6.2,б),
т.е.
(рис.6.2,б),
т.е. 

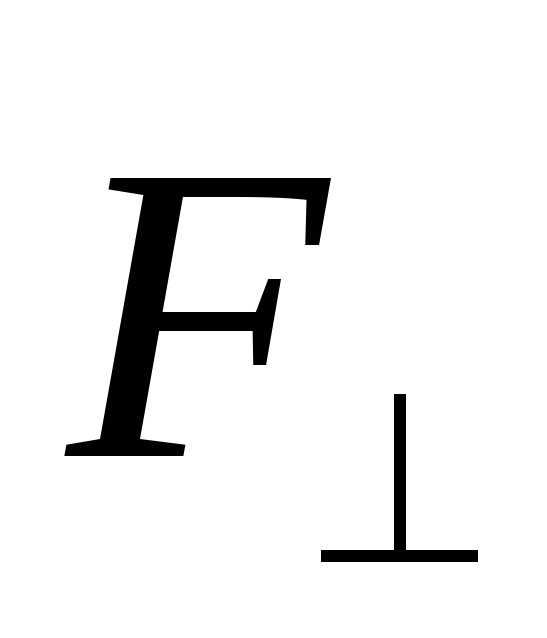 ,
где
,
где –
составляющая, направленная параллельно
оси ОО, а
–
составляющая, направленная параллельно
оси ОО, а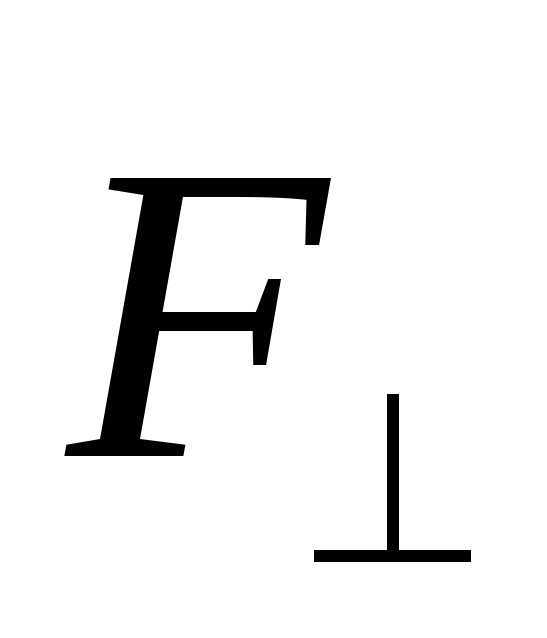 лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор
лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор. (6.7)
В соответствии с выражениями (6.6) и (6.7) вектор М направлен вдоль оси (см. рис.6.2, а,б).
Момент импульса тела относительно оси вращения
П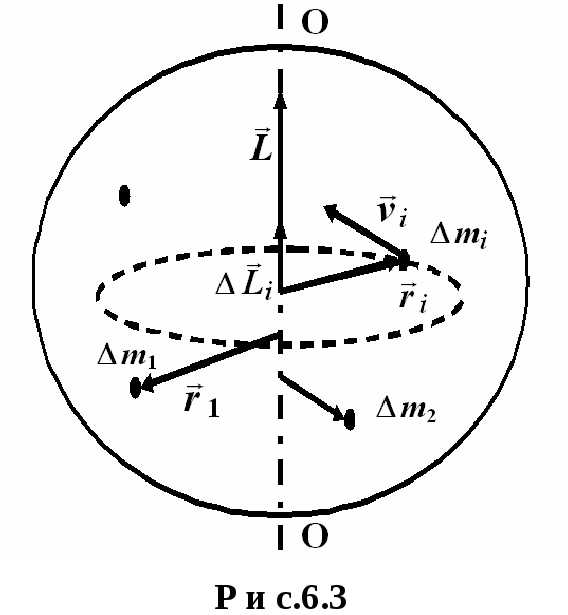
 .
Разобьем это тело мысленно на элементарные
участки с массами
,
которые находятся от оси соответственно
на расстояниях
и вращаются по окружностям, имея линейные
скоростиИзвестно, что величина равная- есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор)
.
Разобьем это тело мысленно на элементарные
участки с массами
,
которые находятся от оси соответственно
на расстояниях
и вращаются по окружностям, имея линейные
скоростиИзвестно, что величина равная- есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор), (6.8)
где ri– радиус-вектор, определяющий положение i – участка относительно оси.
Моментом импульса всего тела относительно оси вращения называют вектор
(6.9)
модуль
которого  .
.
В
соответствии с выражениями (6.8) и (6.9)
векторы  и
и направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
 . (6.10)
. (6.10)
studfiles.net
Момент инерции тела относительно оси
П усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами
,
находящиеся от оси на расстоянии
соответственно.
усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами
,
находящиеся от оси на расстоянии
соответственно.
Моментом инерции материальной точки относительно оси (OO) называется произведение массы материальной точки на квадрат ее расстояния до этой оси:

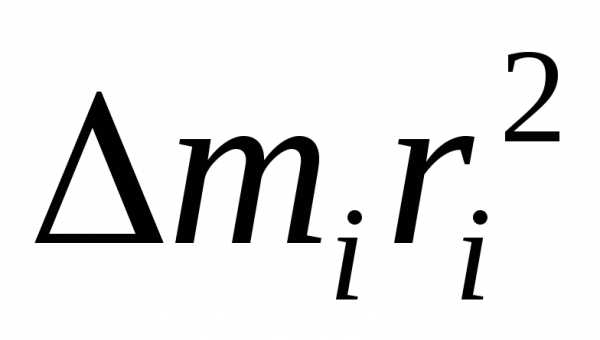 . (6.1)
. (6.1)
Моментом инерции (МИ) тела относительно оси (OO) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:
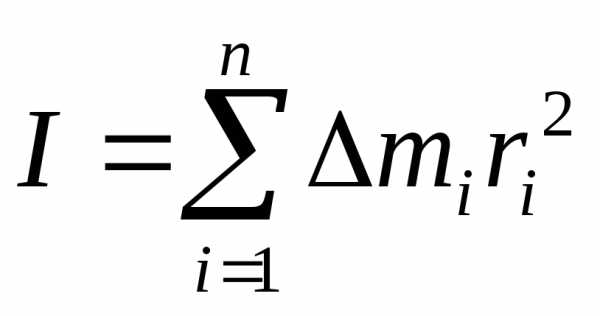 . (6.2)
. (6.2)
Как видно момент инерции тела есть величина аддитивная – момент инерции всего тела относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.
В данном случае
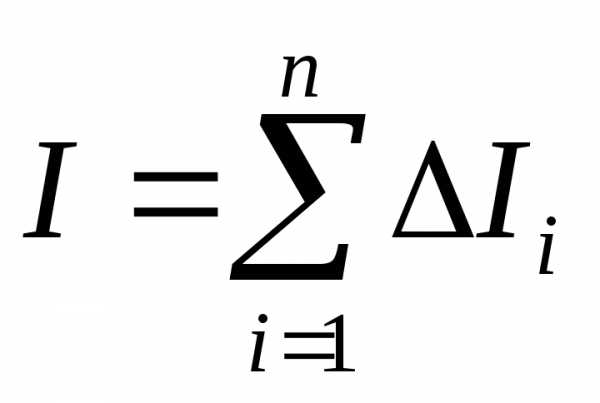 .
.
Измеряется момент инерции в кгм2. Так как
, (6.3)
где
–
плотность вещества,  – объемi – го участка, то
– объемi – го участка, то
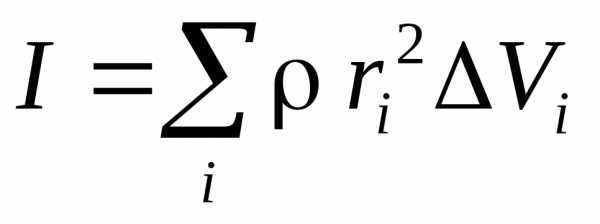 ,
,
или, переходя к бесконечно малым элементам,
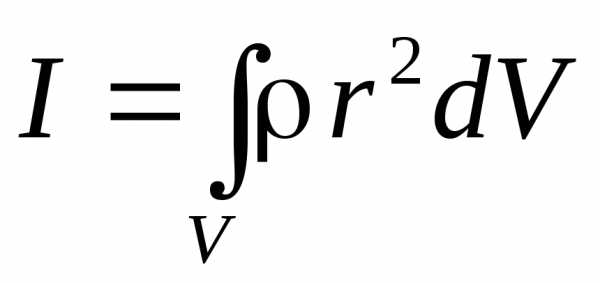 . (6.4)
. (6.4)
Формулу (6.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает
 ,
,
где т – масса; R – радиус цилиндра.
Большую помощь при вычислении МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела
. (6.5)
Момент силы относительно оси
Пусть
на тело действует сила F.
Примем для простоты, что сила F лежит в плоскости, перпендикулярной
некоторой прямой ОО (рис.6.2,а),
которую назовем осью (например, это ось
вращения тела). На рис. 6.2,а А – точка приложения силы F,  – точка пересечения оси с плоскостью, в
которой лежит сила;r–
радиус-вектор, определяющий положение
точки А относительно точки О‘; O‘B = b – плечо
силы. Плечом силы относительно оси
называется наименьшее расстояние от
оси до прямой, на которой лежит вектор
силы F (длина перпендикуляра, проведенного из
точки
– точка пересечения оси с плоскостью, в
которой лежит сила;r–
радиус-вектор, определяющий положение
точки А относительно точки О‘; O‘B = b – плечо
силы. Плечом силы относительно оси
называется наименьшее расстояние от
оси до прямой, на которой лежит вектор
силы F (длина перпендикуляра, проведенного из
точки  к
этой прямой).
к
этой прямой).
Моментом силы относительно оси называется векторная величина, определяемая равенством
. (6.6)

Модуль этого вектора . Иногда, поэтому говорят, что момент силы относительно оси – это произведение силы на ее плечо.
Если
сила F направлена произвольно, то ее можно
разложить на две составляющие;  и
и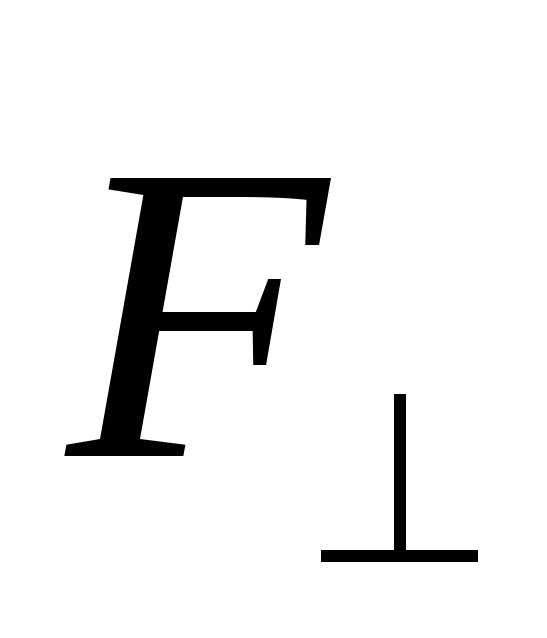 (рис.6.2,б),
т.е.
(рис.6.2,б),
т.е. 
 +
+ ,
где
,
где –
составляющая, направленная параллельно
оси ОО, а
–
составляющая, направленная параллельно
оси ОО, а лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор
лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор
. (6.7)
В соответствии с выражениями (6.6) и (6.7) вектор М направлен вдоль оси (см. рис.6.2, а,б).
Момент импульса тела относительно оси вращения
П усть
тело вращается вокруг некоторой оси ОО
с угловой скоростью
усть
тело вращается вокруг некоторой оси ОО
с угловой скоростью .
Разобьем это тело мысленно на элементарные
участки с массами
,
которые находятся от оси соответственно
на расстояниях
и вращаются по окружностям, имея линейные
скоростиИзвестно, что величина равная- есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор)
.
Разобьем это тело мысленно на элементарные
участки с массами
,
которые находятся от оси соответственно
на расстояниях
и вращаются по окружностям, имея линейные
скоростиИзвестно, что величина равная- есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор)
, (6.8)
где ri– радиус-вектор, определяющий положение i – участка относительно оси.
Моментом импульса всего тела относительно оси вращения называют вектор
(6.9)
модуль
которого  .
.
В
соответствии с выражениями (6.8) и (6.9)
векторы  и
и направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
 . (6.10)
. (6.10)
studfiles.net
15.. Момент инерции материальной точки. Момент инерции тела. Теорема Штейнера.
Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси.Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
J=J_C+md^2
J_C — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.
16. Момент импульса материальной точки. Момент импульса твердого тела относительно неподвижной оси вращения.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам ~\mathbf r и ~\mathbf p. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
17.Основное уравнение динамики вращательного движения.
Основое уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
studfiles.net
1.10
1.10. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Твердое тело как система материальных точек. Движение центра инерции твердого тела. Кинетическая энергия вращающегося тела. Понятие момента инерции относительно неподвижной оси. Теорема Штейнера. Моменты инерции некоторых простейших тел. Уравнение динамики вращательного движения относительно неподвижной оси.
Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них – уравнение движения центра масс (4.11), другое-уравнение моментов вС-системе (6.24):
(10.1) |
Зная законы действующих внешних сил, точки их приложения и начальные условия, можно с помощью этих уравнений найти как скорость, так и положение каждой точки твердого тела в любой момент времени, т. е. полностью решить задачу о движении тела. Однако, несмотря на кажущуюся простоту уравнений (10.1), решение их в общем случае представляет собой весьма трудную задачу. Это прежде всего обусловлено тем обстоятельством, что связь между собственным моментом импульса и скоростями отдельных точек твердого тела в С-системе оказывается сложной, за исключением немногих частных случаев. Мы не будем рассматривать эту задачу в общем виде (она решается в курсе теоретической механики) и ограничимся в дальнейшем только отдельными частными случаями.
Если перенести силы вдоль направления их действия, то ясно, что не изменятся ни их результирующая , ни их суммарный момент . При этом уравнения (10.1)тоже не изменятся, а следовательно не изменится и движение твердого тела. Поэтому точки приложения внешних сил можно переносить вдоль направления действия сил – удобный прием решения задач, которым постоянно пользуются.
Рассмотрим теперь понятие равнодействующей силы. В тех случаях, когда суммарный момент всех внешних сил оказывается перпендикулярным результирующей силе, т. е. , все внешние силы могут быть сведены к одной силе , действующей вдоль определенной прямой. В самом деле, если относительно некоторой точки О суммарный момент , то всегда можно найти такой вектор (рис. 10.1), что при заданных и
При этом выбор неоднозначен: прибавление к нему любого вектора ,
|
Рис. 10.1. Введение понятия равнодействующей силы |
параллельного , не изменит последнего равенства. А это означает, что данное равенство определяет не точку “приложения” силы , а линию ее действия. Зная модули M и F соответствующих векторов, можно найти плечо l силы (рис.6.14): .
Таким образом, если , систему сил, действующих на отдельные точки твердого тела, можно заменить одной равнодействующей силой – силой, которая равна результирующей и создает момент, равный суммарному моменту всех внешних сил.
Таким случаем является действие однородного силового поля, например поля тяжести, в котором действующая на каждую частицу сила имеет вид . В этом случае суммарный момент сил тяжести относительно любой точки О равен
Стоящая в круглых скобках сумма, равна где масса тела радиус-вектор его центра масс относительно точки O. Поэтому
Это означает, что равнодействующая сил тяжести проходит через центр масс тела. Обычно говорят, что равнодействующая сил тяжести приложена к центру масс тела или к его центру тяжести. Момент этой силы относительно центра масс тела равен нулю.
Теперь перейдем к рассмотрению частных случаев движения твердого тела.
Вращение вокруг неподвижной оси.
Рассмотрим вращение твердого тела вокруг неподвижной оси. Найдем выражение для момента импульса твердого тела относительно оси 00′ (рис. 6.15). Момент импульса частицы можно записать в виде
где и – масса и расстояние от оси вращения частицы твердого тела, – его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим
(10.2) |
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат кратчайшего расстояния от оси.
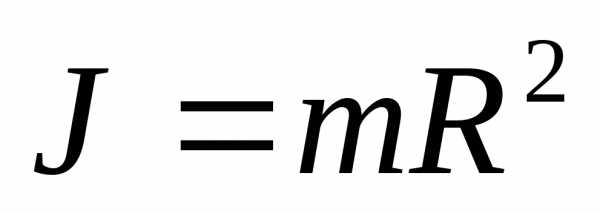
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.
(10.3) | ||
| ||
Рис. 10.2. Вращение твердого тела вокруг оси | ||
Момент инерции твердого тела зависит от распределения масс относительно интересующей нас оси и является величиной аддитивной. Вычисление момента инерции тела проводится по формуле
где dm и dV – масса и объем элемента тела, находящегося на расстоянии от интересующей нас оси z, – плотность тела в данной точке.
Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в следующей таблице (здесь т – масса тела):
Вид твердого тела | Положение оси | Момент инерции |
Тонкий стержень длины L | Перпендикулярно стержню | |
Сплошной цилиндр радиуса R | Совпадает с осью цилиндра | |
Тонкий диск радиуса R | Совпадает с диаметром диска | |
Шар радиуса R | Проходит через центр шара |
Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси z равен моменту инерции относительно оси параллельной данной и проходящей через центр масс С тела, плюс произведение массы т тела нa квадрат расстояния а между осями:
(10.4) |
Таким образом, если известен момент инерции то нахождение момента инерции I элементарно. Например, момент инерции тонкого стержня (массы т и длины l) относительно оси, перпендикулярной стержню и проходящей через его конец, равен
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.Получим выражение для кинетической энергии вращающегося твердого тела с неподвижной осью вращения. Учитывая связь скорости частицы вращающегося твердого тела с угловой скоростью запишем
,
или, более коротко
, | (10.5) |
где I – момент инерции тела относительно оси вращения, – его угловая скорость.
Запишем выражение для кинетической энергии твердого тела при плоском движении, когда тело участвует как во вращетельном, так и в поступательном движении. В этом случае
(10.6) |
где – момент инерции тела относительно оси вращения, проходящей через его центр масс, -угловая скорость тела, т – его масса, – скорость центра инерции тела в K-системе отсчета. Таким образом, кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в С-системе и энергии, связанной с движением центра масс.
Запишем основное уравнение динамики вращения твердого тела с неподвижной осью вращения. Это уравнение легко получить, как следствие как следствие уравнения моментов для материальной точки, если продифференцировать (10.2)по времени, тогда
(10.7) |
где – суммарный момент всех внешних сил относительно оси вращения, проекция углового ускорения на ось вращения. Из этого уравнения, в частности, видно, что момент инерции I определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил тело с большим моментом инерции приобретает меньшее угловое ускорение. Моменты сил относительно оси – величины алгебраические: их знаки зависят как от выбора положительного направления оси z, совпадающей с осью вращения, так и от направления
|
Рис. 10.3. Выбор положительного направления вращения (правый винт) |
“вращения” соответствующего момента силы. Например, выбрав положительное направление оси z, как показано на рис. 10.3, мы тем самым задаем и положительное направление отсчета угла – оба эти направления связаны правилом правого винта. Полагают, что если некоторый момент “вращает” в положительном направлении угла, то он считается положительным, и наоборот. А знак суммарного момента в свою очередь определяет знак – проекции вектора углового ускорения на ось z.
Интегрирование уравнения (10.7)с учетом начальных условий -значений угловой скорости и угла и начальный момент времени – позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси, т. е. найти зависимость от времени угловой скорости и угла поворота.
Заметим, что уравнение (10.7)справедливо влюбой системе отсчета, жестко связанной с осью вращения. Однако если система отсчета неинерциальная, то необходимо помнить, что момент сил включает в себя не только моменты сил взаимодействия с другими телами, но и моменты сил инерции.
6
studfiles.net
9.Момент инерции тела относительно оси.Радиус инерции тела.
Моментом инерции тела относительно данной оси Оz (или осевым моментом инерции) называется скалярная величина равная сумме произведений масс всех точек тела на квадраты их расстояний от этой оси: . Из определения следует что момент инерции тела относительно любой оси является величиной положительной и не равной нулю.Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси.Для одной мат.точки,находящейся на расстоянииh от оси : .Моменты инерции относительно осей опр. Формулами:+,+,+.
Радиус инерции тела относ.оси Oz называется ленейная вел-на определяемая равенством,
M-масса тела.Радиус инерции геометрически равен расстоянию от оси OZ той точки,в которой надо сосредоточить муссу всего тела,чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
10.Теорема о моментах инерции тела относительно параллельных осей.Теорема Гюйгенса: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси,ей параллельной, проходящей через центр масс тела,сложенному с произведением массы всего тела на квадрат расстояния между осями. Если— момент инерции тела относительно оси, проходящей черезцентр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен.
11(12).Моменты инерции простых тел относительно главных центральных осей:однородного тонкого стержня,сплошного круглого цилиндра.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции.Момент инерции стержня относительно оси, проходящей через его конец, равен: . Ось перпендикулярна к стержню и проходит через его середину:
Сплошного круглого диска:
12.Диф.Уравнения движения механической системы.
Рассмотрим сис.,состоящую из n мат.точек.Выделим какую-нибудь точку системы с массой .Обозначим равнодействующую всех приложенных к точке внешних сил через,а внутренних сил через.Если точка имеет при этом ускорение, то по основному закону динамики.Аналогичный результат получим для любой точкиУравнения представляют собой диф. Уравнения движения системы в векторной форме.Входящие в правые части уравнений силы могут в общем случае зависить от времени,координат точек системы и скоростей.Полное решение основной задачи динамики для системы будет состоять в том,чтобы,зная заданные силы и наложенные связи,проинтегрировать соответствующие диф. Уравнения и определить в результате закон движ. Каждой из точек системы и реакции связи.
13.Теорема о движении центра масс механической системы.
Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением движения материальной точки, получаем другое выражение теоремы: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Проектируя обе части равенства на координатные оси, получим:
Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.Значение доказанной теоремы состоит в следующем.1) Теорема дает обоснование методам динамики точки. Из уравнений видно, что решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т. е. имеют вполне конкретный смысл.2) Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все наперед неизвестные внутренние силы. В этом состоит ее практическая ценность.
studfiles.net
9. Понятие о моменте инерции тела. Радиус инерции.
Моментом инерции твердого тела относительно какой – либо осиz (осевым моментом инерции) называется скалярная величина, равная сумме, составленной из произведений массы mk каждой точки тела на квадрат ее расстояния rk до данной оси.
Момент инерции бесконечно тонкого кольца (материальной окружности) относительно его оси вращения равен произведению его массы на квадрат радиуса:
Момент инерции тела относительно оси представить в виде произведения массы тела на квадрат длины некоторого отрезка , называемого радиусом инерции тела относительно соответствующей оси:
Под радиусом инерции тела относительно какой – либо оси можно понимать радиус такого бесконечно тонкого кольца, в котором нужно сосредоточить всю массу М тела, чтобы получить момент инерции кольца, равный моменту инерции тела относительно этой оси.
10. Момент инерции относительно параллельных осей (теорема Гюйгенса – Штейна).
Момент инерции тела относительно какой – либо оси равен моменту инерции этого тела относительно центральной оси, параллельной данной оси, сложенному с произведением массы тела на квадрат расстояния между этими осями.
– теорема Гюйгенса – Штейна.
11. Осевые моменты инерции однородных тел: стержень, полый и сплошной цилиндры, шар.
– момент инерции тонкого прямого стержня постоянного сечения
Момент инерции однородного прямого тонкого стержня относительно его центральной оси симметрии равен 1/12 произведения массы стержня на квадрат его длины.
– момент инерции сплошного
круглого цилиндра.
Момент инерции однородного сплошного круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на квадрат его радиуса.
– момент инерции полого круглого цилиндра.
Момент инерции однородного полого круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на сумму квадратов его наружного и внутреннего радиусов.
12. Динамическое уравнение вращения твердого тела вокруг неподвижной оси.
(1), где
Произведение момента инерции тела относительно его оси вращения на угловое ускорение тела равно главному моменту всех приложенных к телу внешних сил относительно той же оси.
Уравнение (1) называется динамическим уравнением вращательного движения твердого тела.
13. Теорема об изменении кинетической энергии материальной системы.
Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.
, где Т – кинетическая энергия в конечный момент времени
Т0 – кинетическая энергия в начальный момент времени
∑Аiе +∑Аij – сумма работ внешних и внутренних сил
Условие: необходимо начальное и конечное положения.
14. Кинетическая энергия материальной системы. Теорема Кенига.
Механическая система – совокупность тел, связанных между собой различными связями.
Положения и движение каждого из тел взаимно обусловлено. Кинетическая энергия механической системы определяется как арифметическая сумма кинетических энергий i-го тела, входящего в систему.
Теорема Кенига:
Кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии этой системы в ее относительном движении относительно центра масс.
studfiles.net
Момент инерции – это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
Осевые моменты инерции некоторых тел.Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
med.academic.ru



