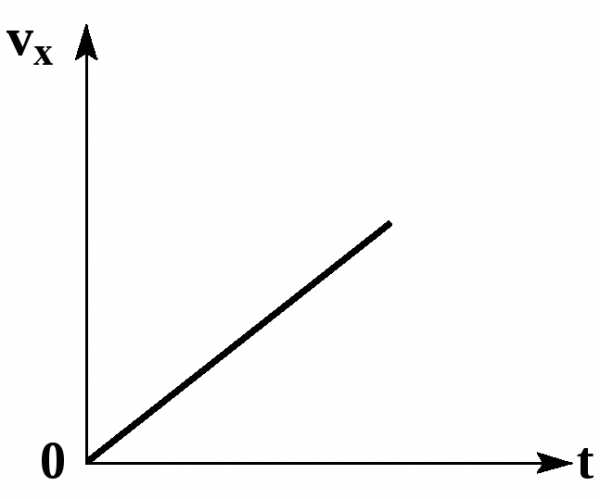
Проекции скорости и ускорения
Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной
скорости  и ускорения
и ускорения могут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.
могут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.
Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.
График скорости
Из уравнения следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.
|
|
Основные виды движения
аn = 0, a = 0 – прямолинейное равномерное движение;
аn = 0, a
аn = 0, a 0 – прямолинейное с переменным ускорением;
аn = const, a = 0 – равномерное по окружности
аn = const, a = const – равнопеременное по окружности
аn
Вращательное движение твердого тела.
Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Равномерное движение по окружности
Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.
При равномерном
движении по окружности значение скорости
остается постоянным, а направление
вектора скорости 

Из подобия треугольников OAB и BCD следует

Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.
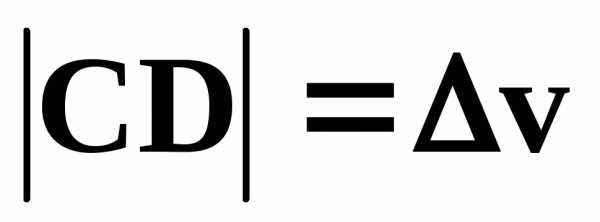 ,
то получаем
,
то получаем 
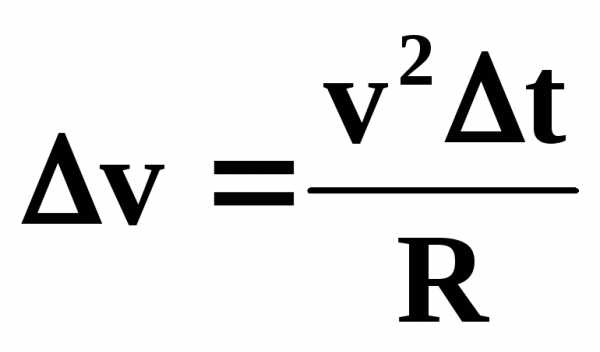 .
.
Поскольку 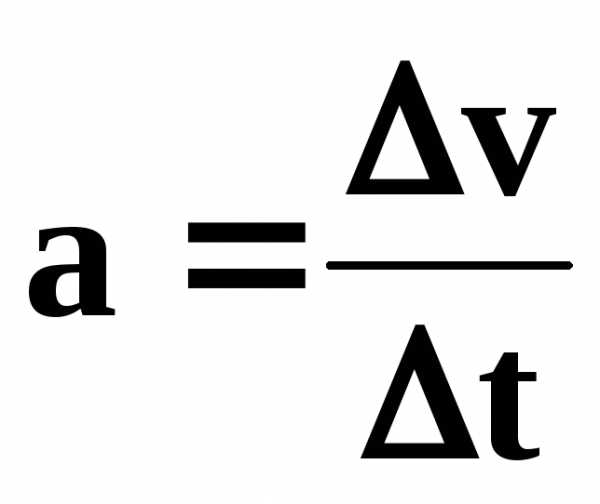 ,
то получаем
,
то получаем
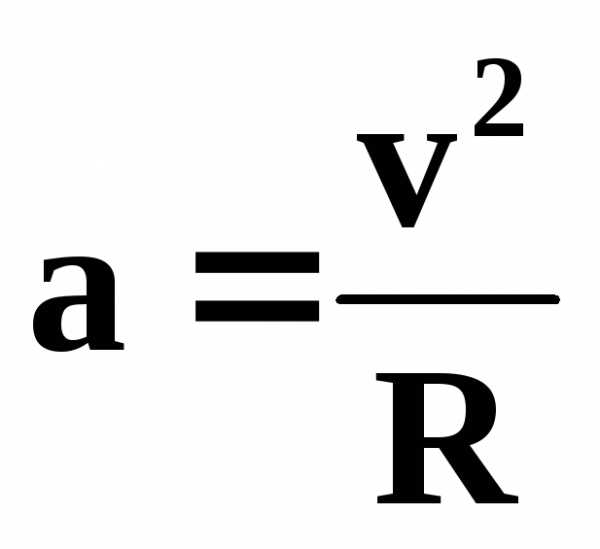
Период и частота
Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т). Т.к. длина окружности равна 2R, период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется:

Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
 (с-1)
(с-1)studfiles.net
§ 5. Понятие ускорения точки
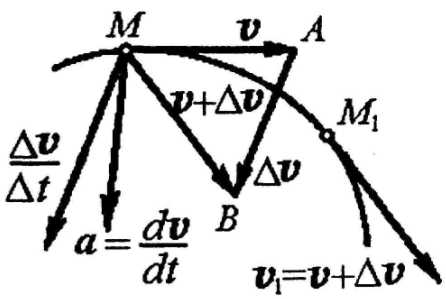
Ускорение точки характеризует быстроту изменения ее скорости. Положим,
что точка движется по криволинейной траектории (рис. 2.7). В момент времени
она занимает положение
и имеет скорость . В момент времени
точка занимает положение
и имеет скорость
в точку и соединяя концы векторов и и , получим вектор , выражающий приращение вектора скорости за время .
Отношение приращения вектора скорости промежутку времени , в течение которого произошло это приращение, называется средним ускорением
. (2.11)
Рассмотрим предел выражения (2.11) при приближении
к нулю. Получим истинное ускорение точки в момент времени , т. е. в положении
;
. (2.12)
Таким образом, вектор ускорения равен первой производной от вектора скорости по времени или второй производной от радиуса-вектора по времени.
Заметим, что вектор
находится в плоскости
(рис. 2.7), проходящей через касательную к траектории в точке
и параллельной касательной в точке . При ,
стремящемся к нулю, плоскость
вращается вокруг касательной , будучи все время параллельной
вектору . Плоскость, с которой
совпадает предельное положение плоскости
§ 6. Определение ускорения при координатном
способе задания движения
При определении ускорения в случае задания движения в прямоугольных координатах, т. е. в виде
; ; ,
последовательность операций аналогична действиям, описанным в § 5. Сначала найдем проекции вектора ускорения на координатные оси:
; ; . (2.13)
Проекции ускорения точки на координатные оси равны вторым производным от соответствующих координат по времени или первым производным по времени от проекций скорости на соответствующие оси.
Модуль ускорения определяется по формуле
. (2.14)
Направление вектора ускорения определяется направляющими косинусами:
; ; . (2.15)
Задача 2.5. Движение точки задано уравнениями:
; ,
где – в , – в . Определить величину и направление ускорения при .
Решение. Находим проекции ускорения на координатные оси:
; .
Как видно, проекции ускорения не зависят от времени движения, значит ускорение тоже постоянно
и его направление
; .
§ 7. Разложение вектора ускорения по естественным
осям траектории
Проведем в точке кривой соприкасающуюся плоскость (рис.2.8), определение которой дано в разделе § 6, и плоскость, перпендикулярную к касательной. Эта плоскость называется нормальной плоскостью. Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью кривой. Прямая, перпендикулярная к главной нормали и касательной, называется бинормалью.
Рассмотрим три взаимно перпендикулярные оси: касательную, направленную в сторону возрастания дуговой координаты; главную нормаль, направленную в сторону вогнутости кривой; бинормаль, направленную по отношению к двум другим осям подобно тому, как ось направлена по отношению к осям и . Эти три оси называются естественными осями кривой. Единичные векторы этих осей принято обозначать соответственно , и .
Из курса высшей математики известно, что угол поворота касательной при переходе точки из одного положения в другое называется углом смежности. Предел отношения угла смежности к приращению дуговой координаты , когда она стремится к нулю, называется кривизной кривой в точке
. (2.16)
Величина , обратная кривизне кривой, называется радиусом кривизны:
. (2.17)
Представим вектор скорости в виде произведения его проекции на
касательную и единичного вектора . Тогда
.
Величина единичного вектора постоянна, направление же его при движении точки вдоль ее траектории меняется. Поэтому вектор нельзя рассматривать как постоянный и его производная по времени не равна нулю. Дифференцируя последнее выражение как произведение двух функций времени, получим
. (2.18)
Выясним, чему равна производная . Возьмем на кривой (рис. 2.9) два положения движущейся точки и , соответствующие моментам времени и . Орты касательной в этих точках соответственно и . Перенося в точку , определим приращение орта . Как видно из рисунка,
;
.
Следовательно,
.
Из рис. 2.9 видно, что угол, образованный вектором и касательной, . При и поэтому . Это значит, что вектор направлен по нормали к траектории, а так как он лежит в соприкасающейся плоскости, то эта нормаль является главной нормалью.
Значит,
,
и равенство (2.18) примет вид
. (2.19)
Первое слагаемое суммы (2.19) называется касательным ускорением
точки , второе – нормальным ускорением . Тогда
. (2.20)
Проекции ускорения на касательную и главную нормаль соответственно равны:
; (2.21)
. (2.22)
Проекция ускорения на бинормаль всегда равна нулю.
Модуль полного ускорения точки определяется через ее касательное и
нормальное ускорения
. (2.23)
Задача 2.5. Уравнения движения пальца кривошипа дизеля в период пуска имеют вид:
; ,
где – в , – в . Найти скорость, касательное и нормальное ускорения пальца.
Решение. Находим проекции скорости точки на координатные оси. Так как
;
,
получаем
;.
Определяем модуль вектора скорости
Находим проекции ускорения на координатные оси:
.
Определяем модуль вектора ускорения. Так как
то
.
Определяем модуль касательного ускорения:
,
тогда модуль нормального ускорения:
§ 8. Некоторые частные случаи движения точки
Пользуясь полученными результатами, исследуем зависимость значений ее нормального и касательного ускорений от характера движения точки.
При равномерном движении, когда численное значение скорости постоянно, касательное ускорение обращается в нуль. Оно отлично от нуля только при неравномерном движении и поэтому характеризует изменение скорости по величине.
При прямолинейном движении, когда радиус кривизны траектории равен бесконечности, нормальное ускорение обращается в нуль. Оно отлично от нуля только при криволинейном движении и, следовательно, характеризует изменение скорости по направлению.
Обе составляющие ускорения обращаются в нуль только при равномерном и прямолинейном движении.
Неравномерное движение точки называется ускоренным, если модуль скорости возрастает, и замедленным – в противоположном случае. Легко доказать, что движение является ускоренным, если знаки величин и одинаковы, и замедленным, если эти знаки различны. При ускоренном движении вектор касательного ускорения направлен в ту же сторону, что и скорость, при замедленном – в противоположную сторону.
Движение называется равнопеременным в том случае, если касательное
ускорение постоянно, т. е.
, (2.24)
откуда
.
Интегрируя последнее выражение и имея в виду, что при , получим
. (2.25)
Формула (2.25) определяет скорость равнопеременного движения. Подставляем в нее значение . Интегрируя и имея в виду, что при , получим
. (2.26)
Выражение (2.26) называют уравнением равнопеременного движения точки по траектории.
nwpi-fsap.narod.ru
Проекции скорости и ускорения
Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной скорости и ускорения могут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.
Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.
График скорости
Из уравнения следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.
Основные виды движения
1. аn = 0, at = 0 – прямолинейное равномерное движение;
2. аn = 0, at = const – прямолинейное равнопеременное движение;
3. аn = 0, at ¹ 0 –прямолинейное с переменным ускорением;
4. аn = const, at = 0 –равномерное по окружности
5. аn = const, at = const – равнопеременное по окружности
6. аn ¹ const, at ¹ const – криволинейное с переменным ускорением.
Вращательное движение твердого тела.
Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Равномерное движение по окружности
Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.
При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения.
Из подобия треугольников OAB и BCD следует
Если интервал времени ∆t мал, то мал и угол a. При малых значениях угла a длина хорды AB примерно равна длине дуги AB, т.е. . Т.к. , , то получаем
.
Поскольку , то получаем
Период и частота
Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т). Т.к. длина окружности равна 2pR, период обращения при равномерном движении тела со скоростью v по окружности радиусом Rравняется:
Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
(с-1)
Кинематика вращательного движения
| При вращении твердого тела вокруг неподвижной оси OO’ точка M этого тела с радиус-вектором за время Dt пройдет путь равный длине дуги DS, а радиус вектор повернется на угол Dj. Величина называется углом поворота радиус-вектора выбранной точки от некоторого начального положения или модулем углового перемещения. |
Для указания направления вращения малым углам поворота приписывают направление: направлен по оси вращения так, чтобы рассматриваемое с его конца вращение происходило против часовой стрелки (правило правого винта). Если тело сделало N поворотов: . Средняя угловая скорость:
(11)
Мгновенная угловая скорость:
(12)
| Направление связано с углом поворота правилом правого винта. Размерность – рад/с. Если тело делает n оборотов в сек, то его угловая скорость . Связь линейной и угловой скоростей: ; |
или
(13)
в векторной форме:
(14)
Угловое ускорение вращающегося тела
Отношение называется средним угловым ускорением.
infopedia.su
KINEMATIKA_prostaye
14
Какие способы задания движения точки применяются в кинематике и в чем они состоят? Как определить траекторию при координатном способе задания точки?
Движение точки в пространстве определяется тремя основными способами: векторным, координатным и естественным.
Векторный:выберем некоторый неподвижный центр О и проведём из центра в точку М, движение которой изучаем, радиус-векторr. При движении точки М радиус-вектор изменяется по величине и направлению. Каждому моменту времениtсоответствует определённое значениеr. Следовательно, радиус-вектор однозначно определяет положение точки М. таким образом, чтобы определить движение точки, нужно задать её радиус-вектор в виде однозначной и непрерывной функции времениr:r=r(t).
Координатный:Если координаты точки заданы как однозначные функции времени:x=x(t),y=y(t),z=z(t), то положение точки М в пространстве известно в каждый момент времени. Эти уравнения определяют закон движение точки и называются уравнениями её движения.
Естественный:этот способ задания движения применяется в том случае, когда траектория точки, относительно выбранной системы отсчёта, известна. При движении точки М криволинейная координатаsбудет изменяться с течением времени, то есть:s=s(t). Зная это уравнение, можно определить положение точки в каждый момент времени. Его называют уравнением движение или законом движения вдоль заданной траектории.
Зададим положение точки в пространстве
координатным особом: x=x(t),y=y(t),z=z(t)
(*). Чтобы определить положение точки в
начальный момент времени (t=0)
необходимо в уравнения (*) подставитьt=0. Теперь, для определения
траектории точки:s=s(t)
воспользуемся формулой длины дуги
кривой:или, с учётом того, что дифференцирование
производиться по времени, можно переписать
так: .
Знак «+» берётся в том случае, когда
точка движется в сторону с положительного
отсчёта криволинейной координатыs.
.
Знак «+» берётся в том случае, когда
точка движется в сторону с положительного
отсчёта криволинейной координатыs.
Какая зависимость существует между радиус-вектором движущейся точки и вектором скорости этой точки? Как направлен вектор скорости криволинейного движения точки по отношению к её траектории?
Разложим радиус вектор  по ортам декартовой системы координат:.
Теперь продифференцируем равенство по
времени. В результате получим разложение
скорости по ортам
по ортам декартовой системы координат:.
Теперь продифференцируем равенство по
времени. В результате получим разложение
скорости по ортам :,
разложение можно представить так:,
где
:,
разложение можно представить так:,
где ,
, ,
, – проекции вектора скорости на оси
координат. Таким образом, проекции
скорости на неподвижные декартовы оси
координат равны первым производным по
времени соответствующих координат
движущейся точки.
– проекции вектора скорости на оси
координат. Таким образом, проекции
скорости на неподвижные декартовы оси
координат равны первым производным по
времени соответствующих координат
движущейся точки.
При векторном:Для того, чтобы точно
вычислить скорость точки в данный момент
времени, необходимо перейти в формуле перейти к пределу при стремлении
промежутка времени к нулю, то есть:
перейти к пределу при стремлении
промежутка времени к нулю, то есть: .
Этот предел представляет собой первую
векторную производную по времени от
радиус-вектора точки по времени
.
Этот предел представляет собой первую
векторную производную по времени от
радиус-вектора точки по времени .
Как следует из этих формул, вектор
скорости направлен по касательной к
траектории точки в сторону её движения.
.
Как следует из этих формул, вектор
скорости направлен по касательной к
траектории точки в сторону её движения.
При координатном:Найдём модуль скорости, зная её проекции:. Для определения направления вектора скорости воспользуемся направляющими косинусами:
, ,
, .
В итоге мы всё же прижжем к выводу, что
вектор скорости направлен по касательной
к траектории.
.
В итоге мы всё же прижжем к выводу, что
вектор скорости направлен по касательной
к траектории.
При естественном:,
известно, что .
Вектор
.
Вектор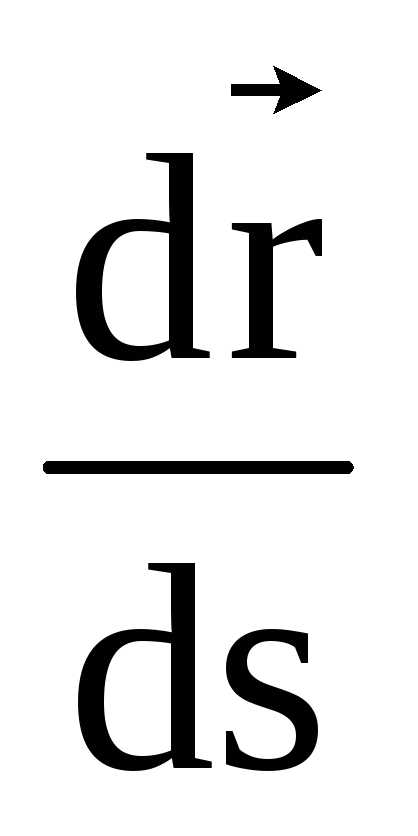 есть единичный вектор касательной к
траектории (её орт), направленный в
сторону возрастания криволинейной
координатыs. Обозначая
орт касательной
есть единичный вектор касательной к
траектории (её орт), направленный в
сторону возрастания криволинейной
координатыs. Обозначая
орт касательной запишем начальную формулу так:
запишем начальную формулу так: ,
домножим левую и правую часть уравнения
на единичный вектор
,
домножим левую и правую часть уравнения
на единичный вектор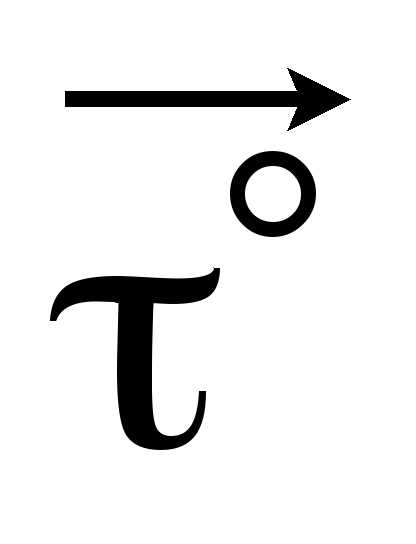 :
: .
Перепишет выражение так:
.
Перепишет выражение так: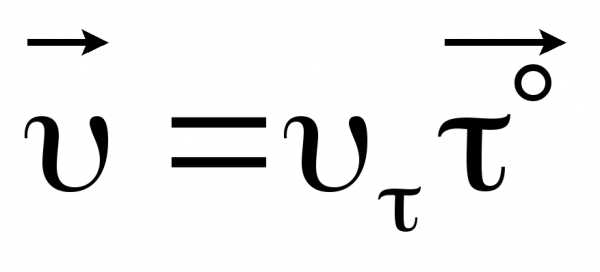 .
Таким образом, видно, что вектор скорости
направлено по касательной к траектории
точки.
.
Таким образом, видно, что вектор скорости
направлено по касательной к траектории
точки.
Как определяется модуль и направление скорость точки при координатном способе задания движения?
 ,
,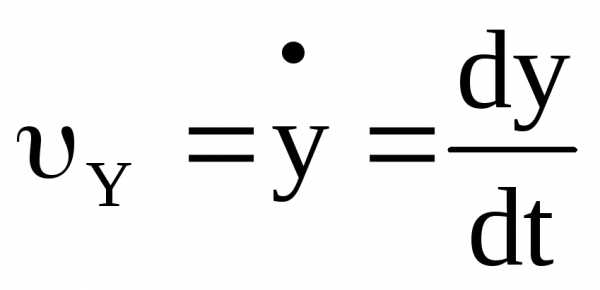 ,
, Таким образом, проекции скорости на
неподвижные декартовы оси координат
равны первым производным по времени от
соответствующих координат движущейся
точки. Из равенств следует, что проекции
скорости точки на координатные оси
равны скорости проекций этой точки на
те же оси. Зная проекции вектора скорости
точки, найдём его модуль:.
Таким образом, проекции скорости на
неподвижные декартовы оси координат
равны первым производным по времени от
соответствующих координат движущейся
точки. Из равенств следует, что проекции
скорости точки на координатные оси
равны скорости проекций этой точки на
те же оси. Зная проекции вектора скорости
точки, найдём его модуль:.
Для определения направления вектора скорости воспользуемся направляющими косинусами:
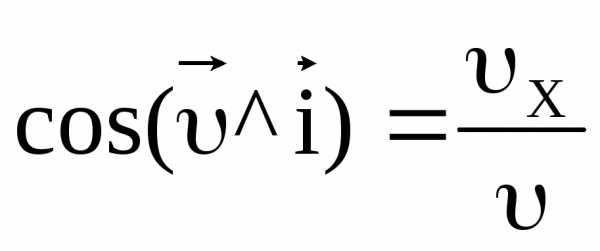 ,
,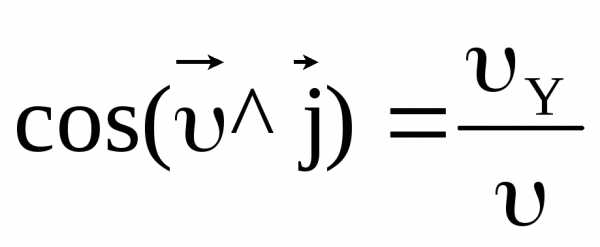 ,
, .
.
Какая зависимость существует между радиус-вектором движущейся точки и вектором ускорения точки? Как направлен вектор ускорения криволинейного движения точки по отношению к её траектории, в какой плоскости он лежит?
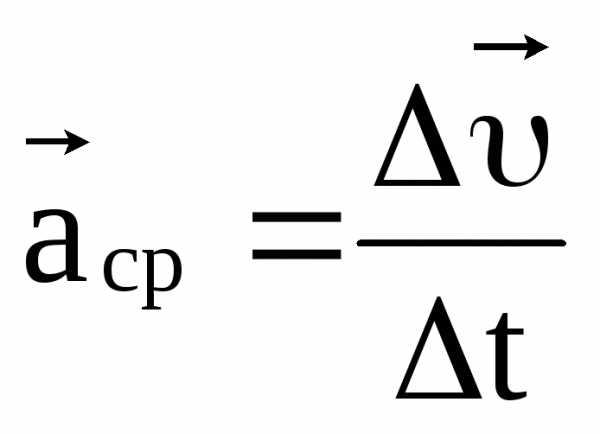
 ,
при стремлении
,
при стремлении к нулю получаем следующий предел:
к нулю получаем следующий предел: ,
этот предел называют ускорение точки
в данный момент времени. Так как вектор
скорости есть первая производная
радиус-вектора точки по времени, то:
,
этот предел называют ускорение точки
в данный момент времени. Так как вектор
скорости есть первая производная
радиус-вектора точки по времени, то: .
Таким образом, ускорение точки в данный
момент времени, есть векторная величина,
равная первой производной от вектора
скорости или второй производной от
радиус-вектора по времени.
.
Таким образом, ускорение точки в данный
момент времени, есть векторная величина,
равная первой производной от вектора
скорости или второй производной от
радиус-вектора по времени.
Установим теперь положение вектора  относительно траектории. Отметим, что
плоскость треугольника МАВ, образованного
векторами
относительно траектории. Отметим, что
плоскость треугольника МАВ, образованного
векторами ,
,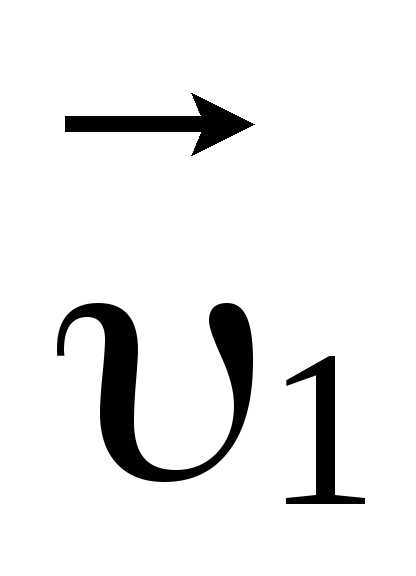 и
и ,
при
,
при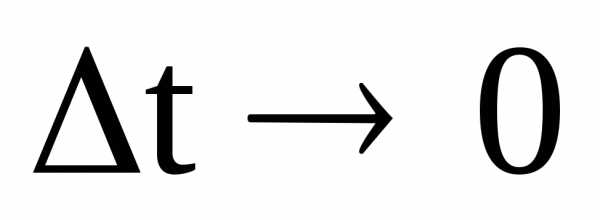 будет поворачиваться вокруг вектора
будет поворачиваться вокруг вектора ,
т.е. вокруг касательной к траектории в
точке М, и займёт в пределе определённое
предельной положение. Это предельное
положение плоскости МАВ называется
соприкасающейся плоскостью в точке М
траектории. Вектор среднего ускорения
,
т.е. вокруг касательной к траектории в
точке М, и займёт в пределе определённое
предельной положение. Это предельное
положение плоскости МАВ называется
соприкасающейся плоскостью в точке М
траектории. Вектор среднего ускорения направлен так же, как и
направлен так же, как и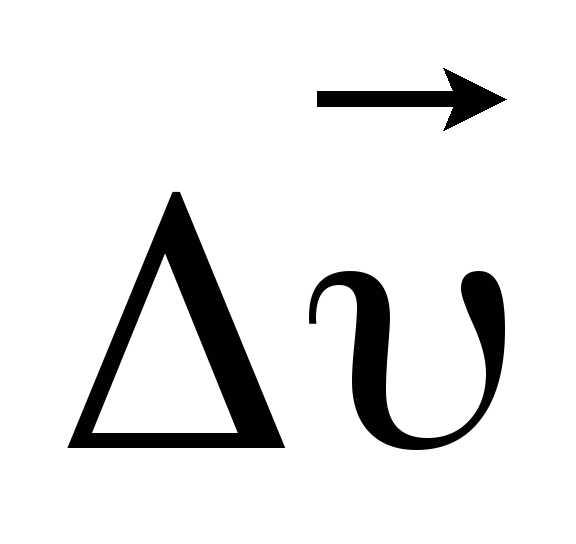 ,
т.е. в сторону вогнутости кривой, и всё
время находиться в плоскости треугольника
МАВ. Предел вектора
,
т.е. в сторону вогнутости кривой, и всё
время находиться в плоскости треугольника
МАВ. Предел вектора при
при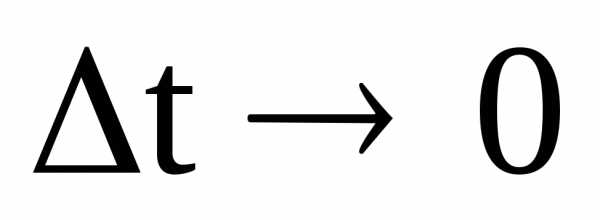 есть вектор
есть вектор ,
который расположен в предельном положении
треугольника МАВ, т.е. в соприкасающейся
плоскости траектории точки М. Итак,
вектор полного ускорения точки находиться
в соприкасающейся плоскости траектории
точки М направлен в сторону вогнутости
траектории.
,
который расположен в предельном положении
треугольника МАВ, т.е. в соприкасающейся
плоскости траектории точки М. Итак,
вектор полного ускорения точки находиться
в соприкасающейся плоскости траектории
точки М направлен в сторону вогнутости
траектории.
Как определяется модуль и ускорение точки при координатном способе задания движения?
Разложим радиус вектор  по ортам декартовой системы координат:.
Теперь дважды дифференцируем равенство
по времени. В результате получим
разложение ускорения по ортамi,j,k:,
разложение можно представить так:,
где
по ортам декартовой системы координат:.
Теперь дважды дифференцируем равенство
по времени. В результате получим
разложение ускорения по ортамi,j,k:,
разложение можно представить так:,
где ,
, ,
,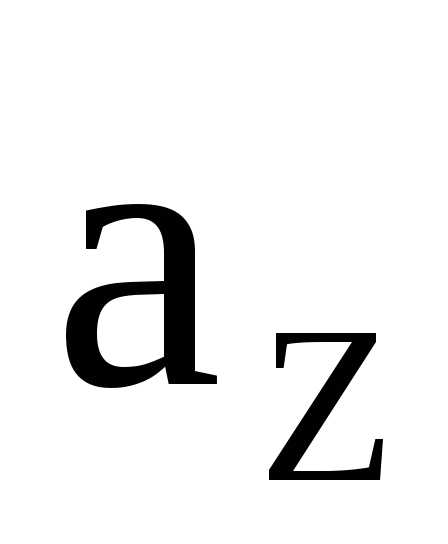 – проекции вектора ускорения на оси
координат. То есть, проекции вектора
ускорения на неподвижные оси координат
равны первым производным по времени от
соответствующих проекций вектора
скорости или вторым производным от
соответствующих координат точки. По
этим проекциям определяем величину
вектора ускорения:.
– проекции вектора ускорения на оси
координат. То есть, проекции вектора
ускорения на неподвижные оси координат
равны первым производным по времени от
соответствующих проекций вектора
скорости или вторым производным от
соответствующих координат точки. По
этим проекциям определяем величину
вектора ускорения:.
Какие оси называются естественными осями? Дайте из определения и приведите соответствующий рисунок.

Единичный вектор касательной –  ,
нормали –
,
нормали – ,
бинормали –
,
бинормали – .
Через эти векторы проходят плоскости:
(
.
Через эти векторы проходят плоскости:
( ,
,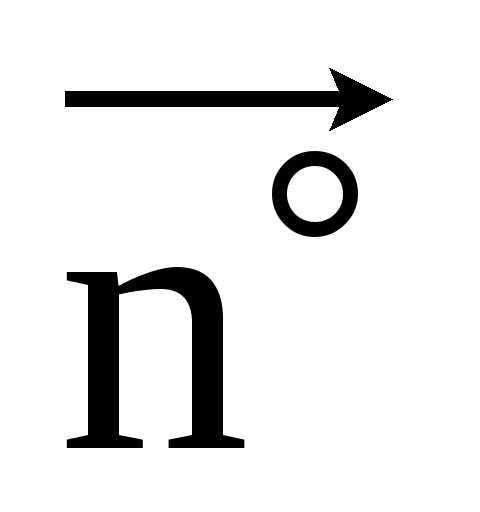 )
– соприкасающаяся, (
)
– соприкасающаяся, ( ,
, )
– нормальная, (
)
– нормальная, (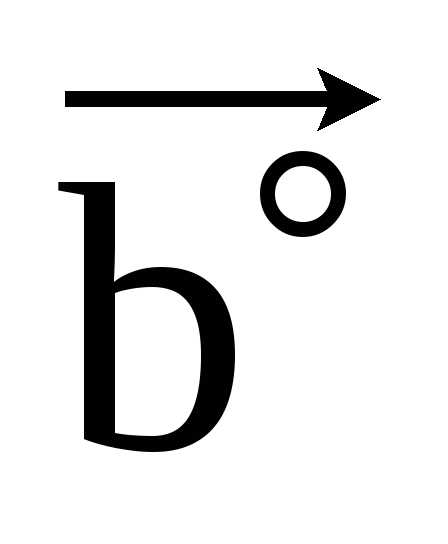 ,
, )
– спрямляющая. Три взаимно перпендикулярных
направления, которые определяются
векторам
)
– спрямляющая. Три взаимно перпендикулярных
направления, которые определяются
векторам ,,
,, ,
образуют естественную систему координат,
или так называемый естественный
(подвижный) трёхгранник. Оси этой системы
координат называются естественными
осями (касательная, нормаль, бинормаль).
,
образуют естественную систему координат,
или так называемый естественный
(подвижный) трёхгранник. Оси этой системы
координат называются естественными
осями (касательная, нормаль, бинормаль).
– Единичный вектор 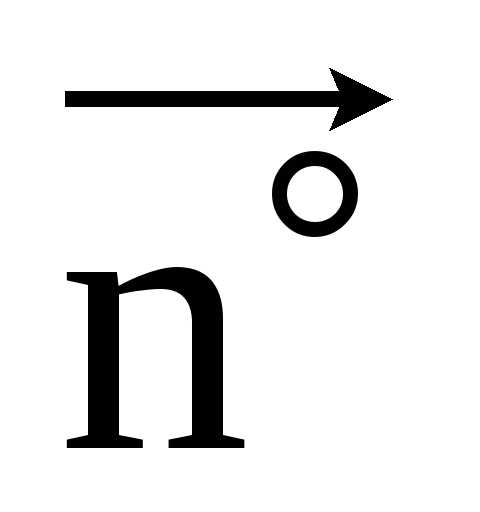 всегда направлен в сторону вогнутости
кривой.
всегда направлен в сторону вогнутости
кривой.
– Предельное положение секущей, проходящей
через две точки кривой Mи ,
когда
,
когда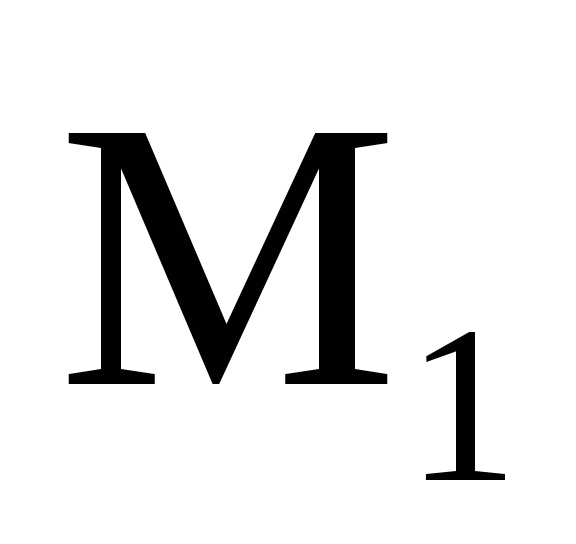 стремиться кM, называется
касательной к кривой в точкеM.
Единичным вектором этой касательной
является вектор
стремиться кM, называется
касательной к кривой в точкеM.
Единичным вектором этой касательной
является вектор .
Плоскость, образованная взаимно
перпендикулярными векторами
.
Плоскость, образованная взаимно
перпендикулярными векторами и
и называется соприкасающейся.
называется соприкасающейся.
– Единичный вектор нормали 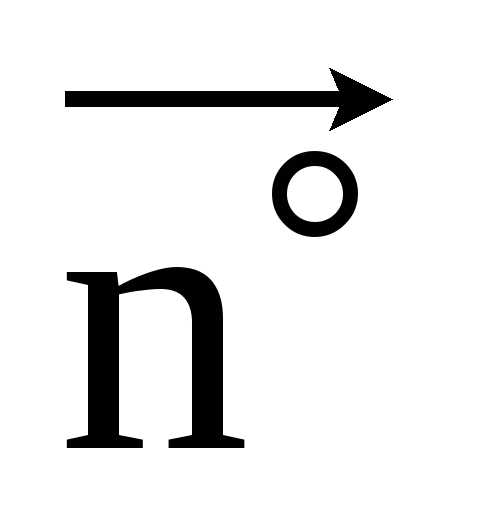 всегда направлен в сторону вогнутости
кривой, а геометрическое место нормалей
к данной кривой называют нормальной
плоскостью.
всегда направлен в сторону вогнутости
кривой, а геометрическое место нормалей
к данной кривой называют нормальной
плоскостью.
Чему равны проекции вектора скорости точки на естественные оси? Запишите соответствующие формулы.
 ,
, ,
,
Чему равны проекции вектора ускорения точки на естественные оси? Запишите соответствующие формулы.
 Формула представляет собой разложение
ускорения точки М по ортам естественного
трёхгранника. Составляющие вектора
ускорения по направлениям
Формула представляет собой разложение
ускорения точки М по ортам естественного
трёхгранника. Составляющие вектора
ускорения по направлениям и
и соответственно равны:
соответственно равны: ,
, .
Проекция ускорения на направление
касательной:
.
Проекция ускорения на направление
касательной: ,
называется касательным или тангенциальным
ускорением. Проекция ускорения на
главную нормаль:
,
называется касательным или тангенциальным
ускорением. Проекция ускорения на
главную нормаль: ,
называется нормальным ускорением. Так
как ускорение точки лежит в соприкасающейся
плоскости, то проекция ускорения точки
на бинормаль равна нулю.
,
называется нормальным ускорением. Так
как ускорение точки лежит в соприкасающейся
плоскости, то проекция ускорения точки
на бинормаль равна нулю.
Напишите формулу для определения касательного ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю?
Касательное ускорение характеризует
изменение скорости по величине.
Касательное ускорение равно нулю, при
движении точки с постоянной по модулю
скоростью и в моменты времени, когда
скорость достигает экстремальных
значений. При 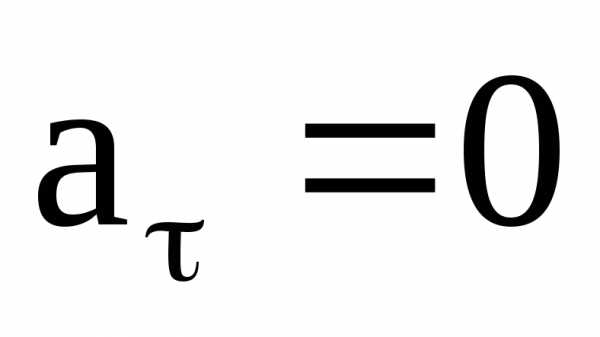 движение равномерное.
движение равномерное.
Формула для определения касательного
ускорения (проекция ускорения на
направление касательной):  .
Или, если единичный вектор касательной
определяем формулой:
.
Или, если единичный вектор касательной
определяем формулой: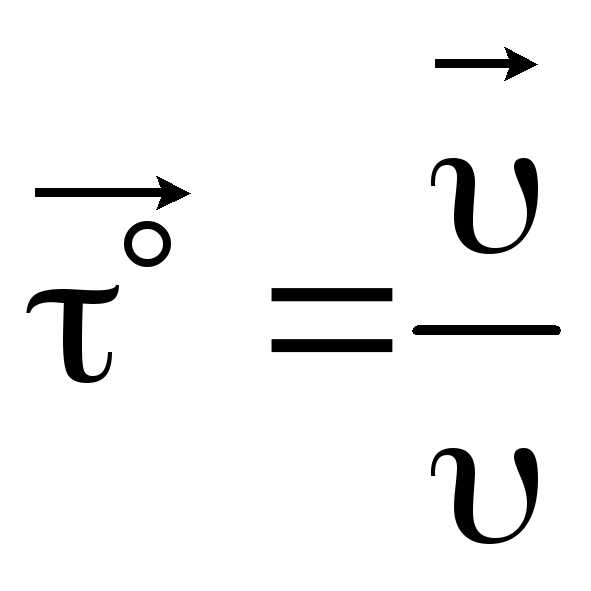 ,
то запишем:
,
то запишем:
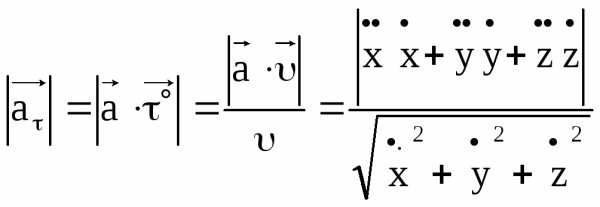
Напишите формулу для определения нормального ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю?
Нормальное ускорение характеризует
изменение скорости по направлению.
Нормальное ускорение равно нулю при
прямолинейном движении (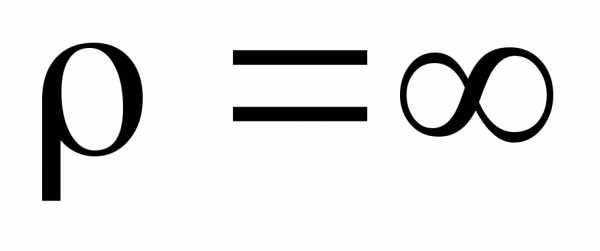 ),
в точках перегиба криволинейной
траектории и с в моменты, когда скорость
точки обращается в нуль.
),
в точках перегиба криволинейной
траектории и с в моменты, когда скорость
точки обращается в нуль.
Формула для определения нормального
ускорения (проекция ускорения на
направление нормали): 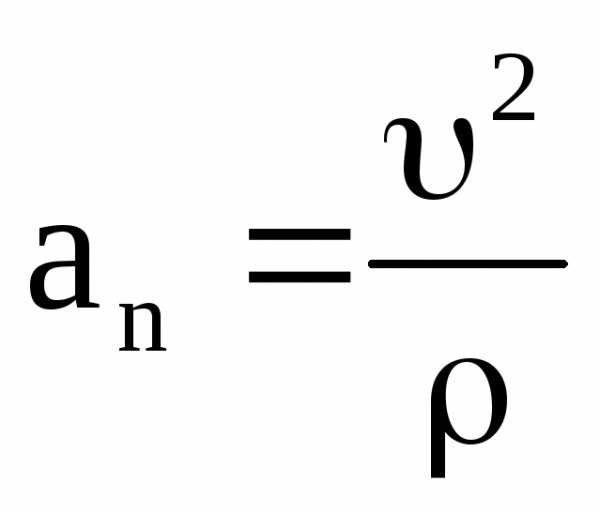 .
Или, если единичный вектор касательной
определяем формулой:
.
Или, если единичный вектор касательной
определяем формулой: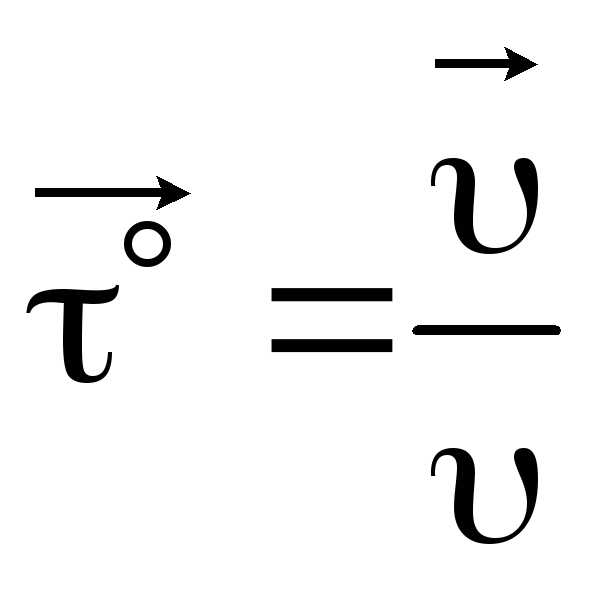 ,
то запишем:
,
то запишем:
Чему равно ускорение точки при равномерном криволинейном движении. Как это ускорение направлено и по какой формуле вычисляется?
Ф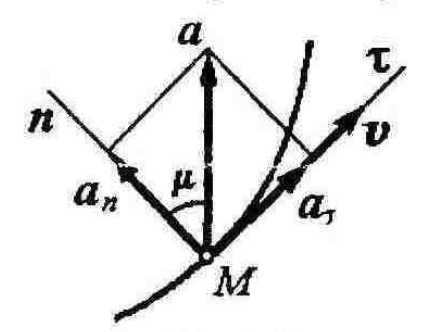 ормула
для определения касательного ускорения
(проекция ускорения на направление
касательной):
ормула
для определения касательного ускорения
(проекция ускорения на направление
касательной): .
Формула для определения нормального
ускорения (проекция ускорения на
направление нормали):
.
Формула для определения нормального
ускорения (проекция ускорения на
направление нормали):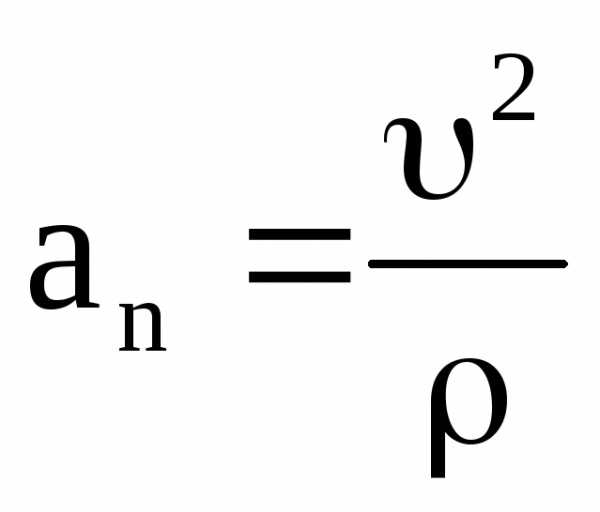 .
Модуль полного ускорение точки вычисляется
по теореме Пифагора:
.
Модуль полного ускорение точки вычисляется
по теореме Пифагора: .
Определим направление вектора
.
Определим направление вектора :
: – угол между вектором полного ускорения
и нормалью.
– угол между вектором полного ускорения
и нормалью.
Какое движение твердого тела называется поступательным? Перечислите свойства поступательного движения твёрдого тела.
– Поступательным движением твёрдого тела называется такое движение, при котором любая прямая, проведённая в теле во всё время движения, остаётся параллельной своему первоначальному направлению.
СВ1:При поступательном движении твёрдого тела всё его точки описывают одинаковые траектории, которые при параллельном переносе совпадают.
СВ2:При поступательном движении всё точки твёрдого тела движутся с одинаковыми скоростями и ускорениями для любого момента времени.
Какое движение твердого тела называется движением вокруг неподвижной оси? Запишите уравнение вращательного движения. Сделайте соответствующий рисунок.
В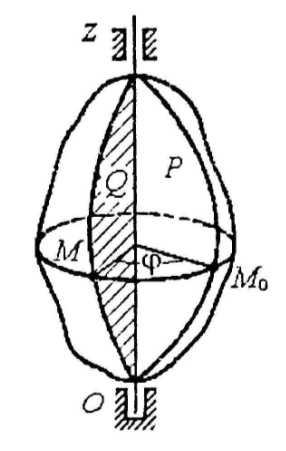 ращательное
движение. Это такое движение твёрдого
тела, при котором все точки этого тела
описывают концентрические окружности,
центры которых лежат на одной прямой,
называемой осью вращения. Уравнение
или закон вращательного движения вокруг
неподвижной оси:
ращательное
движение. Это такое движение твёрдого
тела, при котором все точки этого тела
описывают концентрические окружности,
центры которых лежат на одной прямой,
называемой осью вращения. Уравнение
или закон вращательного движения вокруг
неподвижной оси: .
.
Что называется угловой скоростью и угловым ускорением тела? Напишите формулы для их определения.
Угловой скоростьютела называется
физическая величина, характеризующая
быстроту изменения угла поворота тела во времени, то есть:
тела во времени, то есть: .
Угловая скорость равна первой производной
по времени от угла поворота тела.
.
Угловая скорость равна первой производной
по времени от угла поворота тела.
Угловым ускорениемназывается такая физическая величина, характеризующая быстроту изменения угловой скорости тела во времени:. Угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота.
Какое вращение твердого тела называется равномерным, какое равномерно-переменным? Запишите уравнения равномерного и равнопеременного вращательного движения.
– Вращение тела называют равномерным,
если угловая скорость тела постоянна,
то есть угловое ускорение равно нулю:
,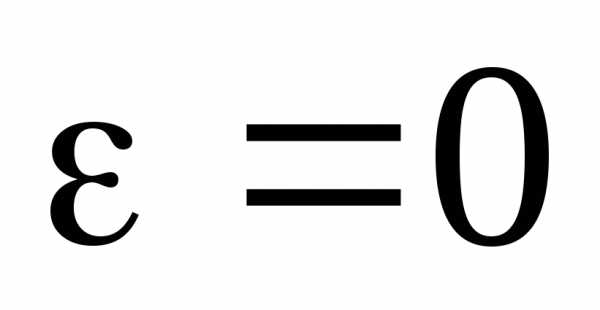 .
.
– Равнопеременным вращением называется такое вращательное движение тела, при котором его угловое ускорение постоянно (угловая скорость с каждым одинаковым промежутком времени изменяется да одну и ту же величину): ,.
Равномерное: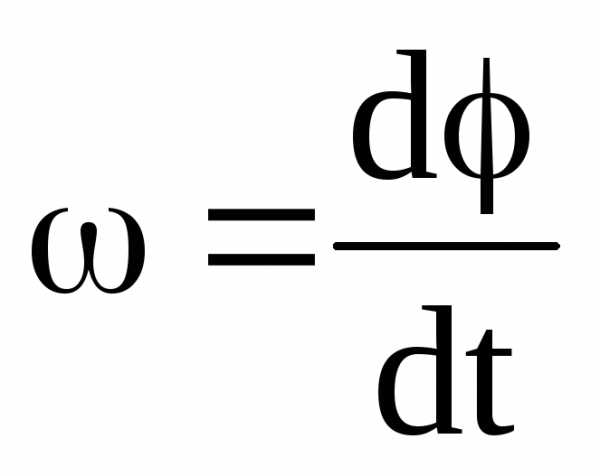 =>
=>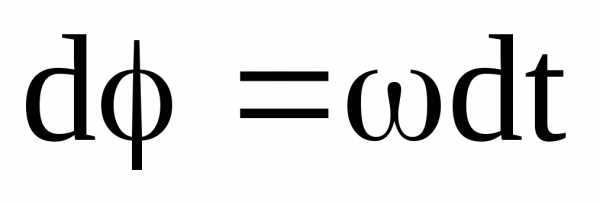 =>.
Произвольную константу С определяем
из начального условия:
=>.
Произвольную константу С определяем
из начального условия: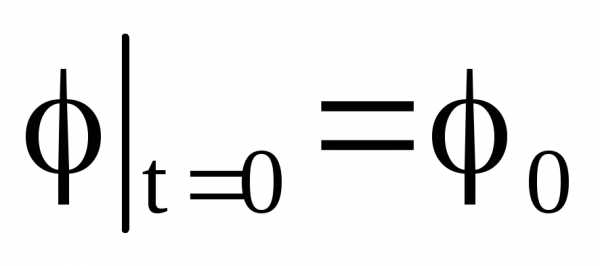 .
В результате находим:
.
В результате находим: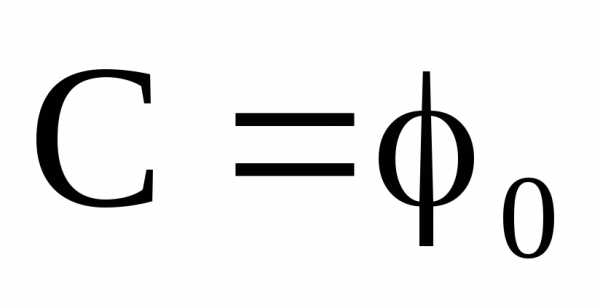 .
Тогда:- з-н равномерного вращательного движение
твёрдого тела.
.
Тогда:- з-н равномерного вращательного движение
твёрдого тела.
Равнопеременное: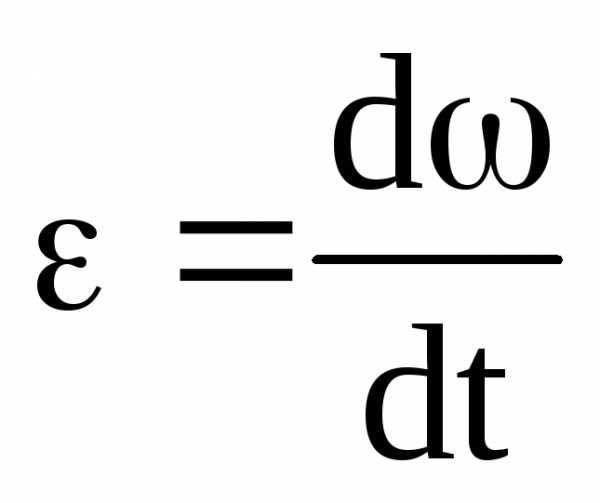 =>=>.
Произвольную константу С определяем
из начального условия:
=>=>.
Произвольную константу С определяем
из начального условия: .
Тогда:- з-н изменения угловой скорости при
равнопеременном вращательном движении
твёрдого тела.
.
Тогда:- з-н изменения угловой скорости при
равнопеременном вращательном движении
твёрдого тела.
Далее:  =>=>
=>=> .
Произвольную константу С определяем
из начального условия:
.
Произвольную константу С определяем
из начального условия: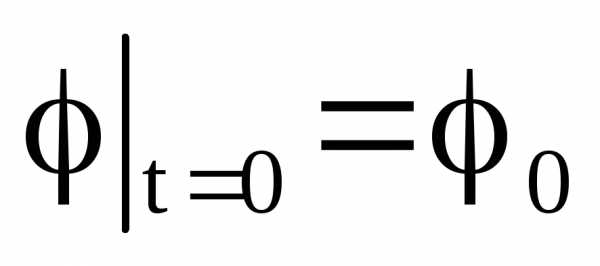 .
В результате находим:
.
В результате находим: .
Окончательно:
.
Окончательно: – з-н равнопеременного вращательного
движения твёрдого тела.
– з-н равнопеременного вращательного
движения твёрдого тела.
Какая зависимость существует между угловой скоростью вращающегося тела и числом его оборотов в минуту?
 ,n– число оборотов в минуту
[об/мин],
,n– число оборотов в минуту
[об/мин], – угловая скорость [
– угловая скорость [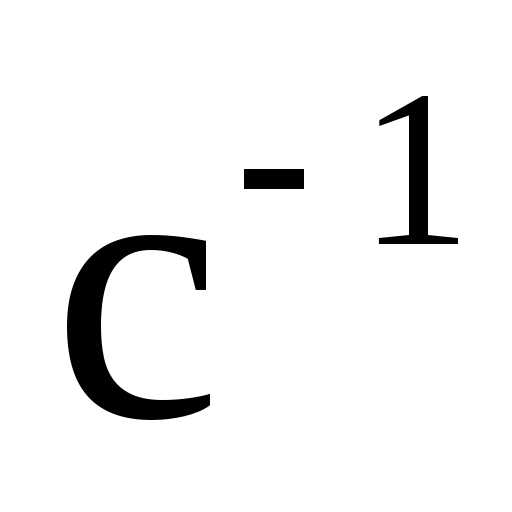 ].
].
Пример: n=23 об/мин, найти
угловую скорость тела. Решение:.
тела. Решение:.
Как изображается угловая скорость тела в виде вектора, как определить направление этого вектора?
Вектор угловой скорости тела направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца видел вращение тела против хода часовой стрелки.
Как выражается зависимость между угловой скоростью вращающегося тела и линейной скоростью какой-нибудь точки этого тела?
Линейная скорость какой-либо точки вращающегося твёрдого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения.
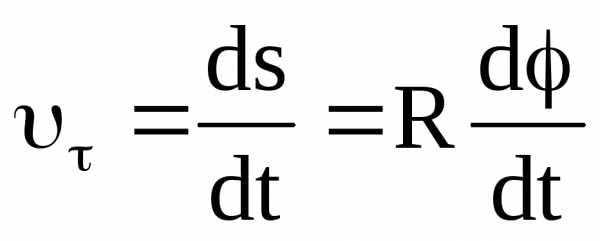 ,
то есть:
,
то есть: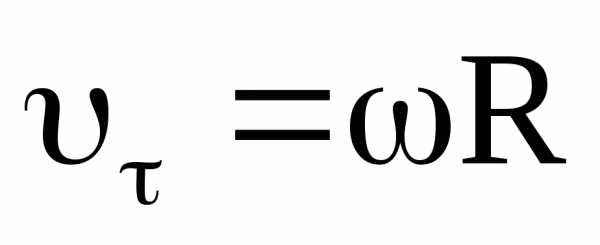 .
Модуль
.
Модуль ,
вектора
,
вектора равен:.
равен:.
Напишите формулы для определения касательного и нормального ускорения точки твёрдого тела, вращающегося вокруг неподвижной оси.
Определим тангенциальное и нормальное ускорения точки во вращательном движении вокруг неподвижной оси: ,. Модуль полного ускорения точки равен:.
Напишите векторные формулы для скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси.
Твёрдое тело вращается вокруг неподвижной
оси Оzс угловой скоростью .
.
– Определим скорость произвольной точки М этого тела:
Угловая
 – вектор угловой скорости.
– вектор угловой скорости.
Линейная

Вектор скорости любой точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведённый из произвольного центра, взятого на оси вращения.
– Определим ускорения произвольной точки М этого тела:
Угловое
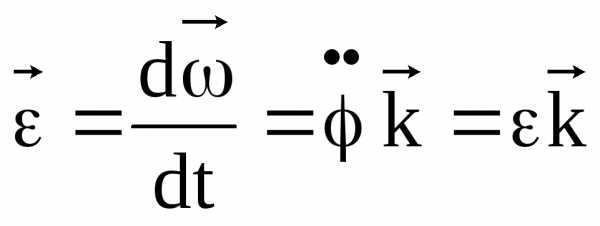 – вектор углового ускорения.
– вектор углового ускорения.
Вектор углового ускорения 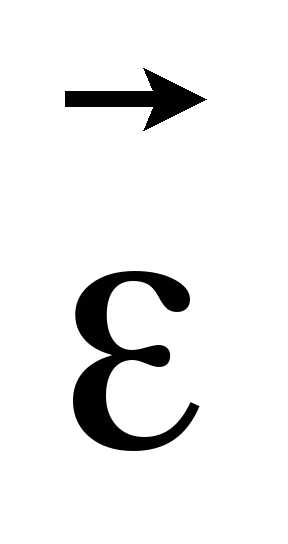 ,
так же как и вектор угловой скорости
,
так же как и вектор угловой скорости ,
лежит на си вращения. При этом в случае
ускоренного вращения вектор
,
лежит на си вращения. При этом в случае
ускоренного вращения вектор направлен в ту же сторону, что и вектор
направлен в ту же сторону, что и вектор ,
в случае же замедленного вращения вектор
,
в случае же замедленного вращения вектор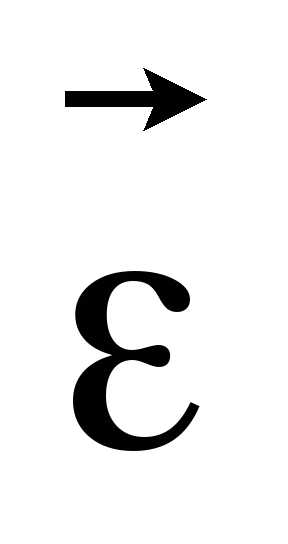 направлен в сторону, противоположную
вектору
направлен в сторону, противоположную
вектору .
.
Полоное
или
Найдём модули ускорений:
Какое движение твердого тела называется плоским, или плоскопараллельным? Запишите уравнения плоскопараллельного движения твёрдого тела, пояснив их на рисунке.
Д вижение
абсолютно твёрдого тела называется
плоскопараллельным (или плоским), если
всё точки этого тела движутся в плоскостях,
параллельных некоторой неподвижной
плоскости.
вижение
абсолютно твёрдого тела называется
плоскопараллельным (или плоским), если
всё точки этого тела движутся в плоскостях,
параллельных некоторой неподвижной
плоскости.
,,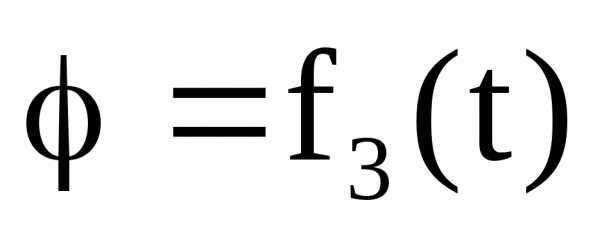 .
Уравнения, полностью определяющие
положение плоской фигуры в любой момент
времени, называются уравнениями
плоскопараллельного движения твёрдого
тела.
.
Уравнения, полностью определяющие
положение плоской фигуры в любой момент
времени, называются уравнениями
плоскопараллельного движения твёрдого
тела.
Сформулируйте теоремы о перемещениях плоской фигуры. Сделайте соответствующие рисунки.
Т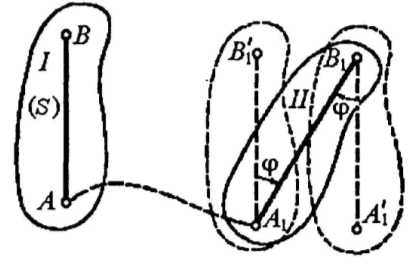 1:Всякое перемещение плоской фигуры в её
плоскости можно осуществлять посредством
поступательного перемещения вместе с
произвольной точкой (полюсом) и вращением
вокруг этого полюса.
1:Всякое перемещение плоской фигуры в её
плоскости можно осуществлять посредством
поступательного перемещения вместе с
произвольной точкой (полюсом) и вращением
вокруг этого полюса.
Т 2
(Эйлера-Шаля):Всякое непоступательное
перемещение плоской фигуры в её плоскости
может быть осуществлено посредством
одного вращения вокруг некоторого
центра, называемого центром конечного
вращения.
2
(Эйлера-Шаля):Всякое непоступательное
перемещение плоской фигуры в её плоскости
может быть осуществлено посредством
одного вращения вокруг некоторого
центра, называемого центром конечного
вращения.
З
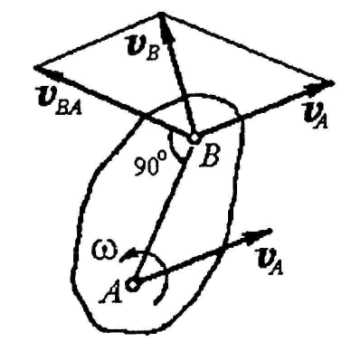 апишите
формулу распределения скоростей точек
плоской фигуры. Как определить скорость
точки плоской фигуры с помощью формулы?
Сделайте соответствующий рисунок.
апишите
формулу распределения скоростей точек
плоской фигуры. Как определить скорость
точки плоской фигуры с помощью формулы?
Сделайте соответствующий рисунок.
studfiles.net
Равнопеременное прямолинейное движение | Физика для всех
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
av-mag.ru
Кинематика
Кинематика – это раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Кинематика точки
Выберем неподвижную систему координат Oxyz с центром в неподвижной точке O. Тогда положение точки M однозначно определяются ее координатами (x, y, z). Таким образом, положение точки определяется вектором, проведенным из начала координат O в точку M. Такой вектор называют радиус-вектором:
,
где – единичные векторы в направлении осей x, y, z.
Скорость точки – это производная радиус-вектора по времени:
.
Вектор скорости направлен по касательной к траектории точки. Модуль скорости:
.
Ускорение точки – это производная вектора скорости по времени:
.
Модуль ускорения:
.
Касательное (тангенциальное) ускорение – это проекция вектора ускорения на направление вектора скорости:
;
.
Оно вызывает изменение модуля скорости:
.
При скорость, по абсолютной величине, возрастает, и вектор направлен вдоль скорости. При скорость убывает, и вектор направлен противоположно скорости.
Нормальное ускорение перпендикулярно вектору скорости и направлено к центру кривизны траектории:
.
Оно вызывает изменение направления скорости и связано с радиусом кривизны траектории ρ:
.
Отсюда
.
Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, , то
.
См. подробнее: Кинематика материальной точки > > >
Кинематика твердого тела
Чтобы однозначно определить положение твердого тела, нужно указать три координаты (xA, yA, zA) одной из точек A тела и три угла поворота. Таким образом, положение твердого тела определяется шестью координатами. То есть твердое тело имеет шесть степеней свободы.
В общем случае, зависимость координат точек твердого тела относительно неподвижной системы координат определяется довольно громоздкими формулами. Однако скорости и ускорения точек определяются довольно просто. Для этого нужно знать зависимость координат от времени одной, произвольным образом выбранной, точки A и вектора угловой скорости . Дифференцируя по времени, находим скорость и ускорение точки A и угловое ускорение тела :
; ; .
Тогда скорость и ускорение точки тела с радиус вектором определяется по формулам:
(1) ;
(2) .
Здесь и далее, произведения векторов в квадратных скобках означают векторные произведения.
Отметим, что вектор угловой скорости одинаков для всех точек тела. Он не зависит от координат точек тела. Также вектор углового ускорения одинаков для всех точек тела.
См. вывод формул (1) и (2) на странице: Скорость и ускорение точек твердого тела > > >
Поступательное движение твердого тела
При поступательном движении, угловая скорость равна нулю. Скорости всех точек тела равны. Любая прямая, проведенная в теле, перемещается, оставаясь параллельной своему начальному направлению. Таким образом, для изучения движения твердого тела при поступательном движении, достаточно изучить движение одной любой точки этого тела. См. раздел Кинематика точки.
Равноускоренное движение
Рассмотрим случай равноускоренного движения. Пусть проекция ускорения точки тела на ось x постоянна и равна ax . Тогда проекция скорости vx и x – координата этой точки зависят от времени t по закону:
vx = vx0 + axt;
,
где vx0 и x0 – скорость и координата точки в начальный момент времени t = 0.
Вращательное движение твердого тела
Рассмотрим тело, которое вращается вокруг неподвижной оси. Выберем неподвижную систему координат Oxyz с центром в точке O. Направим ось z вдоль оси вращения. Считаем, что z – координаты всех точек тела остаются постоянными. Тогда движение происходит в плоскости xy. Угловая скорость ω и угловое ускорение ε направлены вдоль оси z:
; .
Пусть φ – угол поворота тела, который зависит от времени t. Дифференцируя по времени, находим проекции угловой скорости и углового ускорения на ось z:
;
.
Рассмотрим движение точки M, которая находится на расстоянии r от оси вращения. Траекторией движения является окружность (или дуга окружности) радиуса r.
Скорость точки:
v = ω r .
Вектор скорости направлен по касательной к траектории.
Касательное ускорение:
aτ = ε r .
Касательное ускорение также направлено по касательной к траектории.
Нормальное ускорение:
.
Оно направлено к оси вращения O.
Полное ускорение:
.
Поскольку векторы и перпендикулярны друг другу, то модуль ускорения:
.
Равноускоренное движение
В случае равноускоренного движения, при котором угловое ускорение постоянно и равно ε, угловая скорость ω и угол поворота φ изменяются со временем t по закону:
ω = ω0 + ε t;
,
где ω0 и φ0 – угловая скорость и угол поворота в начальный момент времени t = 0.
Плоскопараллельное движение твердого тела
Плоскопараллельным или плоским называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости. Выберем прямоугольную систему координат Oxyz. Оси x и y расположим в плоскости, в которой происходит перемещение точек тела. Тогда все z – координаты точек тела остаются постоянными, z – компоненты скоростей и ускорений равны нулю. Векторы угловой скорости и углового ускорения наоборот, направлены вдоль оси z. Их x и y компоненты равны нулю.
Теорема о проекциях скоростей двух точек тела
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
vAcos α = vBcos β.
См. подробнее: Теорема о проекциях скоростей двух точек твердого тела на прямую >>>
Мгновенный центр скоростей
Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент равна нулю.
Чтобы определить положение мгновенного центра скоростей P плоской фигуры, нужно знать только направления скоростей и двух его точек A и B. Для этого через точку A проводим прямую, перпендикулярную направлению скорости . Через точку B проводим прямую, перпендикулярную направлению скорости . Точка пересечения этих прямых есть мгновенный центр скоростей P. Угловая скорость вращения тела:
.
Если скорости двух точек параллельны друг другу, то ω = 0. Скорости всех точек тела равны друг другу (в данный момент времени).
Разложение скорости на поступательную и вращательную компоненты
Если известна скорость какой либо точки A плоского тела и его угловая скорость ω, то скорость произвольной точки M определяется по формуле (1), которую можно представить в виде суммы поступательного и вращательного движения:
,
где – скорость вращательного движения точки M относительно точки A. То есть скорость, которую имела бы точка M при вращении по окружности радиуса |AM| с угловой скоростью ω, если бы точка A была неподвижной.
Модуль относительной скорости:
vMA = ω |AM|.
Вектор направлен по касательной к окружности радиуса |AM| с центром в точке A.
Определение ускорений точек плоского тела
Определение ускорений точек плоского тела выполняется с применением формулы (2). Ускорение любой точки M равно векторной сумме ускорения некоторой точки A и ускорения точки M при вращении вокруг точки A, считая точку A неподвижной:
.
можно разложить на касательное и нормальное ускорения:
.
Касательное ускорение направлено по касательной к траектории. Нормальное ускорение направлено из точки M к точке A. Здесь ω и ε – угловая скорость и угловое ускорение тела.
Сложное движение точки
Пусть O1x1y1z1 – неподвижная прямоугольная система координат. Скорость и ускорение точки M в этой системе координат будем называть абсолютной скоростью и абсолютным ускорением .
Пусть Oxyz – подвижная прямоугольная система координат, скажем, жестко связанная с неким твердым телом, движущимся относительно системы O1x1y1z1. Скорость и ускорение точки M в системе координат Oxyz будем называть относительной скоростью и относительным ускорением . Пусть – угловая скорость вращения системы Oxyz относительно O1x1y1z1.
Рассмотрим точку, совпадающую, в данный момент времени, с точкой M и неподвижной, относительно системы Oxyz (точка, жестко связанная с твердым телом). Скорость и ускорение такой точки в системе координат O1x1y1z1 будем называть переносной скоростью и переносным ускорением .
Теорема о сложении скоростей
Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Теорема о сложении ускорений (теорема Кориолиса)
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.
См. подробнее: Сложное движение точки, теорема Кориолиса >>>
Сложное движение точки. Пример решения задачи >>>
Использованная литература:
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Движение с постоянным ускорением | Учеба-Легко.РФ
Равноускоренным называют движение с постоянным ускорением. Простейшим примером такого движения является свободное падение тел, изучением которых занимался ещё Галилео Галилей. Скорость движения при этом не остаётся постоянной: в общем случае она меняется и по модулю, и по направлению. Описание данного движения значительно сложнее по сравнению с равномерным прямолинейном. Действия с числами здесь заменяют на действия с векторами, так как векторы содержат в себе информацию о направлений величин, характеризующих движение (о скорости, ускорений, перемещений).
Ускорение при равноускоренном движений показывает, на сколько изменяется скорость тела за каждую секунду движения:
(1)
Где V0 – начальная скорость тела, а V скорость того же тела спустя некоторое время t.
Ускорение показывает изменение скорости за единицу времени.
Из определения ускорения следует, что мгновенная скорость тела при равноускоренном движении изменяется с течением времени по линейному закону:
(2)
Эта формула позволяет по начальной скорости и ускорению тела вычислить его скорость в любой момент времени t. Между тем основная задача механики заключается в определении того, где будет находиться тело спустя заданное время. Для её решения необходимо знать перемещение, совершённое телом за это время. Перемещение можно найти, умножив среднюю скорость на время движения:
s=vcpt
При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей движения:
Поэтому:
Подставляя сюда выражения (2), получаем:
s=v0t +at2/2(3)
Именно это уравнение является обобщением формулы:s=vt на случай движения с постоянным ускорением.
Уравнения (1),(2),(3) – векторные. Действия с векторами отличаются от действий с числами, поэтому никакие числовые значения перемещения, скорости и ускорения в такие уравнения подставлять нельзя. Между тем любые расчёты требуют проведений операций именно с числами. Чтобы это стало возможным, необходимо от векторного способа описания движения перейти к координатному. При координатном описаний движения вместо векторов используют проекций на оси координат. Поскольку любой вектор характеризуется тремя проекциями на оси X,Y и Z, следовательно каждому вектору уравнению в общем случае будут соответствовать три уравнения в координатной форме. Для плоского (двухмерного) движения таких уравнений только два. Если же движение является прямолинейным, то для его описания достаточно одного уравнения в проекций на ось X(при условии, что эта ось направлена параллельно вектору скорости частицы). Тогда уравнения (2) и (3).например, можно записать следующим образом:
vx=v0x+axt
sx=v0xt+axt2/2(4)
При координатном описаний движения, координота тела будет равна:
x=x0+v0xt+axt2/2(5)
В заключение хотим предоставить Вашему вниманию шпаргалку:
uclg.ru