Действия с матрицей – умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Действия с матрицами

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можетебесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Начнем.

Матрица – это прямоугольная таблица каких-либо 

элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами 

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов: Все числа (элементы) внутри матрицы  существуют сами по себе, то есть ни о каком вычитании речи не идет:Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки: и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».

Если в матрице один столбец или одна строка, то такие матрицы также называютвекторами.

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точкизаписаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение:и– это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:  У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

 – умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО

: Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если– окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.  

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и 

НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример: Транспонировать матрицу 

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

 – транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример: Транспонировать матрицу 

Сначала переписываем первую строку в первый столбец:

 

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.  НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример: Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример: Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

 

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

Чтобы матрицу  можно было умножить на матрицунеобходимо,чтобы число столбцов матрицы равнялось числу строк матрицы.

Пример:  Можно ли умножить матрицу на матрицу?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно, и вообще, такая запись 

не имеет смысла 

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.  Например, для матриц, ивозможно как умножение, так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример: Умножить матрицу на матрицуЯ буду сразу приводить формулу для каждого случая:

 – попытайтесь сразу уловить закономерность.

Пример сложнее:

Умножить матрицу на матрицу

Формула: 

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение (правильный ответ).

Обратите внимание, что ! Это почти всегда так!

Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу на матрицу, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Будет время, распишу подробнее

6) Действие шестое. Нахождение обратной матрицы.

Данная тема достаточно обширна, и вынес даннай вопрос на отдельную страницу.

А пока спектакль закончен.

studfiles.net

1.1. Матрицы. Действия над матрицами

Матрицей размерности называется прямоугольная таблица, состоящая изэлементов, расположенных вm строках и

n столбцах.

Элементы матрицы (первый индексi − номер строки, второй индекс j − номер столбца) могут быть числами, функциями и т. п. Матрицы обозначают заглавными буквами латинского алфавита.

Матрица называется квадратной, если у нее число строк равно числу столбцов (m = n). В этом случае число n называется порядком матрицы, а сама матрица называется матрицей n-го порядка.

Элементы с одинаковыми индексами образуютглавную диагональ квадратной матрицы, а элементы (т.е. имеющие сумму индексов, равнуюn+1) − побочную диагональ.

Единичной матрицей называется квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0. Она обозначается буквой Е.

Нулевая матрица − это матрица, все элементы которой равны 0. Нулевая матрица может быть любого размера.

К числу линейных операций над матрицами относятся:

1) сложение матриц;

2) умножение матриц на число.

Операция сложения матриц определена только для матриц одинаковой размерности.

Суммой двух матриц А и В называется матрица С, все элементы которой равны суммам соответствующих элементов матриц А и В:

.

Произведением матрицы А на число k называется матрица В, все элементы которой равны соответствующим элементам данной матрицы А, умноженным на число k:

.

Операция умножения матриц вводится для матриц, удовлетворяющих условию: число столбцов первой матрицы равно числу строк второй.

Произведением матрицы А размерности на матрицу В размерности называется матрицаС размерности , элементi-ой строки и j-го столбца которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

.

Произведение матриц (в отличие от произведения действительных чисел) не подчиняется переместительному закону, т.е. в общем случае А В В А.

1.2. Определители. Свойства определителей

Понятие определителя вводится только для квадратных матриц.

Определителем матрицы 2-го порядка называется число, вычисляемое по следующему правилу

.

Определителем матрицы 3-го порядка называется число, вычисляемое по следующему правилу:

Первое из слагаемых со знаком «+» представляет собой произведение элементов, расположенных на главной диагонали матрицы (). Остальные два содержат элементы, расположенные в вершинах треугольников с основанием, параллельным главной диагонали (и). Со знаком «-» входят произведения элементов побочной диагонали () и элементов, образующих треугольники с основаниями, параллельными этой диагонали (и).

Это правило вычисления определителя 3-го порядка называется правилом треугольников (или правилом Саррюса).

Свойства определителей рассмотрим на примере определителей 3-го порядка.

1. При замене всех строк определителя на столбцы с теми же номерами, что и строки, определитель своего значения не меняет, т.е. строки и столбцы определителя равноправны

.

2. При перестановке двух строк (столбцов) определитель меняет свой знак.

3. Если все элементы некоторой строки (столбца) нули, то определитель равен 0.

4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

5. Определитель, содержащий две одинаковые строки (столбца), равен 0.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

7. Если каждый элемент некоторого столбца (строки) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце (строке) стоят первые слагаемые, а в другом − вторые. Остальные элементы у обоих определителей одинаковые. Так,

.

8. Определитель не изменится, если к элементам какого-либо его столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число.

Следующее свойство определителя связано с понятиями минора и алгебраического дополнения.

Минором элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, на пересечении которых этот элемент расположен.

Например, минором элемента определителя называется определитель .

Алгебраическим дополнением элементаопределителя называется его минор, умноженный на, гдеi − номер строки, j − номер столбца, на пересечении которых находится элемент . Алгебраическое дополнение обычно обозначается. Для элементаопределителя 3-го порядка алгебраическое дополнение

9. Определитель равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения.

Например, определитель можно разложить по элементам первой строки

,

или второго столбца

.

Свойства определителей применяются для их вычисления.

studfiles.net

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел – матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин “матрица” появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m – строк и n – столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,…, a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц – поэлементная операция

2. Вычитание матриц – поэлементная операция

3. Произведение матрицы на число – поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ijматрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

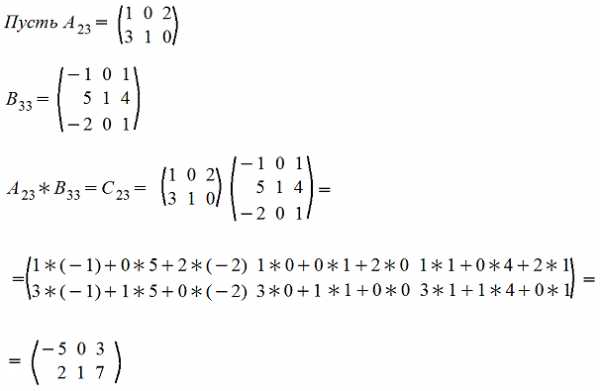
5. Возведение в степень

m>1 целое положительное число. А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A’

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n – произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) – во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji– комплексно – сопряженное к a_ji, т.е. если A=3+2i, то комплексно – сопряженное Ã=3-2i)

Пример

tehtab.ru

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Начнем.

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов: Все числа (элементы) внутри матрицы  существуют сами по себе, то есть ни о каком вычитании речи не идет:Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки: и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».

Если в матрице один столбец или одна строка, то такие матрицы также называютвекторами.

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точкизаписаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение:и– это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

–умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО: Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если– окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.  

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример: Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

–транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример: Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

 

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример: Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример: Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

 

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

Чтобы матрицу  можно было умножить на матрицунеобходимо,чтобы число столбцов матрицы  равнялось числу строк матрицы .

Пример: Можно ли умножить матрицу  на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так. Например, для матриц, ивозможно как умножение, так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример: Умножить матрицу  на матрицу Я буду сразу приводить формулу для каждого случая:

–попытайтесь сразу уловить закономерность.

Пример сложнее:

Умножить матрицу на матрицу

Формула:

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение (правильный ответ).

Обратите внимание, что ! Это почти всегда так!

Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу на матрицу, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Будет время, распишу подробнее

6) Действие шестое. Нахождение обратной матрицы.

Данная тема достаточно обширна, и вынес даннай вопрос на отдельную страницу.

А пока спектакль закончен.

Желаю успехов!

studfiles.net

Действия с матрицами

Матрицы и действия с ними, определители

Сложение матриц

Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц \(A=\{A_{ik}\}\) и \(B=\{B_{ik}\}\), матрица \(A+B\), определяется следующим образом: \((A+B)_{ik}=A_{ik}+B_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq n\). Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , \] \[ B=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 3 & 4 \end{array} \right) , \] тогда \[ A+B=\left( \begin{array}{ccc} 3 & 5 & -1 \\ 4 & -3 & 11 \end{array} \right) . \]

Умножение матрицы на число

Пусть \(A=\{a_{ik}\}\) – матрица типа \((m,n)\), \(\lambda\) – произвольное число. Тогда матрица \(\{\lambda a_{ik}\}\) называется произведением числа \(\lambda \) на матрицу \(A\) и обозначается \(\lambda \cdot A\).

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) . \]

Замечание.

Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения \(c\cdot A\) и \(cA\) равноправны.

Пусть \[ A=\left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right), B=\left( \begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array} \right). \]

Вычислить \(3A-2B\).

Проверить ответ

\[3A-2B=\left( \begin{array}{cc} 4 & 13 \\ 6 & 7 \end{array} \right)\]

Транспонирование матриц

Если для заданной матрицы \(A\) ее строки записать как столбцы, получим новую матрицу, которая называется транспонированной исходной, и обозначается \(A^T\).

Пример. Пусть \[ A=\left( \begin{array}{cccc} 1 &4 & -1 & 4 \\ 7 & 5 & 2 & 2\\ 3 & -6 & 7 & 8 \end{array} \right), \] тогда \[ A^T=\left( \begin{array}{ccc} 1 &7 & 3 \\ 4 & 5 & -6 \\ -1 & 2 & 7 \\ 4 &2 &8 \end{array} \right) . \]

Подчеркнем, если матрица \(A\) имеет тип (\(m,n)\), то \(A^T\) имеет тип \((n,m)\), так что эта операция, вообще говоря, меняет тип матрицы. В частности, если \(A\) была матрицей-столбцом, \(A^T\) будет матрицей-строкой той же длины. Поэтому из типографских соображений матрицу-столбец часто представляют в виде \((a_1,a_2,a_3,….,a_n)^T\) (это выражение занимает меньше места).

Элементарные свойства операций с матрицами

Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.

1. Для любых матриц \(A,B,C\) одного типа \((A+B)+C=A+(B+C)\)(ассоциативность сложения).

2. Для любых матриц \(A,B\) одного типа \(A+B=B+A\) (коммутативность сложения).

3. Пусть \((m,n)\)-матрица \(O\) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа \((m,n)\), \(A+O=A\), \(0\cdot A=O\) для любой матрицы \(A\) того же типа.

4. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1+c_2)A=c_1A+c_2A\).

5. Для любых матриц \(A,B\) одного типа и любого числа \(c\) верно \(c(A+B)=cA+cB\).

6. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1c_2)A=c_1(c_2A)\).

7. Для любой матрицы \(A\) верно \(1\cdot A=A\).

8. Для любых матриц \(A,B\) одного типа \((A+B)^T=A^T+B^T\).

9. Для любого числа \(c\) и любой матрицы \(A\) верно: \((cA)^T=cA^T\).

10. Для любой квадратной матрицы \(detA=detA^T\).

11. Для любой матрицы \((A^T)^T=A\).

Умножение матриц

Рассмотрим сначала умножение матрицы-строки на матрицу столбец. Пусть \(A=(a_1,a_2,…,a_n)\), \(B=(b_1,b_2,…,b_n)^T\). Тогда

\[ AB=a_1b_1+a_2b_2+….+a_nb_n=\sum _{m=1}^na_mb_m. \quad \quad(9) \]

Для того, чтобы было определено умножение между \(A\) и \(B\), необходимо, чтобы длина строки была равна длине столбца. Это условие называют условием согласования типов. Формулу (9) называют правилом умножения строчки на столбец.

Теперь обсудим общий случай. Пусть матрица \(A\) имеет тип \((m,n)\), а матрица \(B\) имеет тип \((n,p)\) (так что длина строки матрицы \(A\) совпадает с длиной столбца матрицы \(B\)). Тогда можно определить их произведение, матрицу \(C\), следующим образом: матрица \(C\) будет иметь тип \((m,p)\), причем для вычисления ее элемента \(C_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq p\), следует взять строку с номером \(i\) матрицы \(A\) и умножить на столбец с номером \(k\) матрицы \(B\), \[ c_{ik}=a_{i1}b_{1k}+a_{i2}b_{2k}+…+a_{in}b_{nk}=\sum _{m=1}^na_{im}b_{mk}. \] Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]

В данном случае матрица \(A\) имеет тип (2,3), матрица \(B\) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения \(A\) на \(B\) получим матрицу типа \((2,2)\). Получаем: \[ AB=\left ( \begin{array}{cc} 1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\ 3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5 \end{array} \right )= \left( \begin{array}{cc} 9 & 8\\ -21 & 20 \end{array} \right). \]

Замечание. Для приведенных матриц произведение \(BA\) не определено – типы матриц \(B\) и \(A\)не согласованы. Это отражает общую ситуацию: результат произведения матриц зависит от порядка сомножителей (в отличие от обычной арифметики) – и даже может не существовать для одного выбора порядка сомножителей, существуя для другого.

Элементарные свойства операций с матрицами (продолжение)

Операция умножения матриц также обладает рядом естественных свойств. (Ниже считается, что типы матриц \(A,B\) согласованы, так что их можно перемножать).

1. \((cA)B=A(cB)=cAB\).

2. \((A_1+A_2)B=A_1B+A_2B\).

3. \(A(B_1+B_2)=AB_1+AB_2\).

4. \((AB)C=A(BC)\).

5. \((AB)^T=B^TA^T\).

6. Для квадратных матриц \(A,B\) одного типа \(det(AB)=detA \cdot detB\).

7. Рассмотрим квадратную матрицу порядка \(n\), \(E=diag\{1,1,1,…,1\}\). Такая матрица играет выделенную роль в умножении матриц: для любых матриц \(A,B\) имеем \(EA=A\), \(BE=B\). Матрица \(E\) называется единичной матрицей порядка \(n\). Согласно описанным выше результатам, \(detE=1\).

1. Умножить матрицы:

а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]

б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]

2. Вычислить \[ \left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5. \]

3. Вычислить \(AB-BA\), если

а) \[ A=\left( \begin{array}{ccc} 1 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right), B=\left( \begin{array}{ccc} 4 & 2 & 3 \\ – 1 & 1 & 3 \\ 1 & 2 & 1 \end{array} \right). \]

б) \[ A=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right), B=\left( \begin{array}{ccc} 3 & 1 & -2 \\ 1 & -1 & 3 \\3 & 5 & 1 \end{array} \right). \]

4. Вычислить

а) \(f(A)\), если \(f(x)=x^2-3x+3\), \[ A=\left( \begin{array}{ccc} -1 & 3 & 2 \\ 1 & -1 & 3 \\ -1 & 2 & 1 \end{array} \right). \]

б) \(f(A)\), если \(f(x)=x^2+4x-2\), \[ A=\left( \begin{array}{ccc} 2 & 1 & 1 \\ 3 & -1 & 2 \\ -1 & 2 & 0 \end{array} \right). \]

5. Показать, что каждая матрица второго порядка \[ A=\left( \begin{array}{cc} a & b \\ c & d \end{array} \right) \]

удовлетворяет уравнению \[ x^2-(a+d)x+(ad-bc)=0. \]

Обратная матрица

В рамках обычной арифметики обсуждается решение числового уравнения \[ ax=1, \] где \(a\) – заданное число. Если \(a \neq 0\), это уравнение имеет единственное решение, которое обозначается \(x=a^{-1}\) и называется обратным к \(a\) числом.

Пусть \(A\) – заданная квадратная матрица порядка \(n\), можно рассмотреть матричное уравнение \[ AX=E. \quad \quad(10) \]

Определение. Если \(detA \neq 0\), матрица \(A\) называется невырожденной.

Определение. Решение уравнения (\ref{obr}) называется матрицей, обратной \(A\).

Теорема. Для того, чтобы существовала обратная \(A\) матрица, небходимо и достаточно, чтобы матрица \(A\) была невырожденной.

Обратную матрицу обозначают \(A^{-1}\).

Основные свойства обратной матрицы.

1. $$AA^{-1}=A^{-1}A=E.$$

2. $$det(A^{-1})=(detA)^{-1}.$$

3. Если квадратные матрицы порядка \(n\) \(A\) и \(B\) невырождены, то \(AB\) тоже невырождена, у нее существует обратная матрица, причем \((AB)^{-1}=B^{-1}A^{-1}\).

4. Для невырожденной квадратной матрицы \(A\) верно: \((A^{-1})^{-1}=A\).

5. Для невырожденной квадратной матрицы \(A\) верно: \((A^T)^{-1}=(A^{-1})^T\).

Докажите эти свойства обратной матрицы.

Для вычисления эелементов обратной матрицы существуют явные формулы.

Пусть \(A\) – квадратная невырожденная матрица порядка \(n\). Вычислим матрицу \(D\) – матрицу алгебраических дополнений, согласно соотношениям

\[ D_{ik}=(-1)^{i+k}det(\widetilde{A}_{ik}), 1 \leq i,k \leq n, \quad \quad(11) \]

где \(\widetilde{A}_{ik} \)- матрица, которая получается из матрицы \(A\) после вычеркивания \(i\)-ой строки и \(k\)-того столбца. Тогда \[ A^{-1}=\frac{D^T}{detA}. \]

Пример. Пусть \(n=2\), \[ A=\left( \begin{array}{cc} a & b \\ c & d \end{array} \right), \] \(detA=ad-bc \neq 0\). Следуя (11), получаем: \[ D=\left( \begin{array}{cc} d & -c \\ -b & a \end{array} \right), \] так что \[ A^{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right). \]

Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.

Найти обратную матрицу для матрицы

1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]

2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]

3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]

Матричные уравнения

Матричными уравнениями называются уравнения вида \[ AX=G, \quad \quad(12)\] \[ XB=G, \quad \quad(13)\] \[ AXB=G, \quad \quad(14)\] где матрицы \(A,B,G\) заданы и требуется построить матрицу \(X\). Мы будем здесь считать, что матрицы \(A,B,G\) – квадратные одного порядка. Решение этих уравнений нетрудно построить, если матрицы \(A,B\) невырождены, так что существуют их обратные \(A^{-1}, B^{-1}\). Умножая, например, уравнение (12) слева на матрицу \(A^{-1}\), получаем: \[ A^{-1}(AX)=(A^{-1}A)X=EX=X=A^{-1}G. \] Умножая уравнение (13) справа на \(B^{-1}\), получаем: \[ (XB)B^{-1}=X(BB^{-1})=XE=X=GB^{-1}. \] Аналогично, умножая (14) слева на \(A^{-1}\) и справа на \(B^{-1}\), получим: \[ X=A^{-1}GB^{-1}. \]

1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]

2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]

3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]

4. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) , G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]

5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]

6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]

publish.sutd.ru

Действия с матрицами

⇐ ПредыдущаяСтр 2 из 8Следующая ⇒

 

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовала для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов:

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».

Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО:

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример:

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:

Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример:

Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

mykonspekts.ru

Примеры действий с матрицами

Примеры действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: 

Обратный пример: .

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

2) Действие второе. Умножение матрицы на число.

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

 – умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО:

Вносить дробь в матрицу НЕ НУЖНО. И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка.

3) Действие третье. Транспонирование матрицы

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:
Транспонировать матрицу 

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

 – транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом  или штрихом справа вверху.

Пошаговый пример:
Транспонировать матрицу 

Сначала переписываем первую строку в первый столбец:

 

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное. 

НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:
Сложить матрицы  и 

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример:
Найти разность матриц , 

А Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

 

5) Действие пятое. Умножение матриц.

Чтобы матрицу   можно было умножить на матрицу  необходимо, чтобы число столбцов матрицы  равнялось числу строк матрицы .

Пример: 
Можно ли умножить матрицу  на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла 

Как умножить матрицы?

Пример:
Умножить матрицу  на матрицу 
 

Пример сложнее:

Умножить матрицу  на матрицу 

Формула: 

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение  (правильный ответ ).

Обратите внимание, что ! Это почти всегда так!

Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу  на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу  на матрицу 

Формула очень похожа на предыдущие формулы:

umotnas.ru