Деление матрицы на число – Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя) – Преподавание математики – Преподавание – Образование, воспитание и обучение

Просто и доступно о матрицах. IV

 

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

 

Назад    Вперёд

6. Произведение матриц.

Пусть даны последовательно выполняемые однородные линейные преобразования

Т.е. в конечном итоге пара    переходит в пару .

Такая операция называется произведением линейных преобразований, а соответствующее преобразование матриц называется произведением матриц.

Непосредственно убеждаемся, что

Соответствующая матрица такова:

И, окончательно:

Возникает вопрос, как сконструировать произведение матриц из исходных? Неужели  всегда нужно будет переходить к линейным преобразованиям, выполнять необходимые алгебраические вычисления, и только потом получать искомое произведение?

— Нет, конечно. Вот самый простой приём умножения матриц:

1. Левую матрицу транспонируем.

2. Тогда искомые матричные элементы получаются как всевозможные взаимные произведения столбцов левой матрицы на столбцы правой матрицы.

3. Место каждого полученного матричного элемента в искомой матрице определяется согласно правилу:

— номер столбца левой матрицы приписывается матричному элементу в качестве номера строки,

— номер столбца правой матрицы приписывается матричному элементу в качестве номера столбца.

Рассмотрим один пример очень подробно.

Ищем произведение:

Сначала транспонируем левую матрицу:

Все необходимые вычисления приведены в  таблице:

№ столбца левой матрицы = № строки результата	№ столбца правой матрицы = № столбца результата	Вычисление матричных элементов
1	1	1∙2+(-2)∙(-2)+3∙0+(-4)∙(-1)=10
1	2	1∙(-1)+(-2)∙3+3∙4+(-4)∙3= –7
2	1	4∙2+(-3)∙(-2)+2∙0+(-1)∙(-1)=15
2	2	4∙(-1)+(-3)∙3+2∙4+(-1)∙3= –8

В итоге получаем:

В дальнейшем произведение матриц будет приводиться без каких-либо подробностей. Потому что это очень просто! Если убрать всё лишнее, то умножение матрицы сводится к применению простенькой схемы:

Ещё примеры умножения матриц-строк и матриц-столбцов:

7. Общее правило умножения матриц.

Пусть даны две матрицы А и В с матричными элементами а_{ikи bkj, здесь i, k, j — некоторые натуральные числа, тогда матричные элементы матрицы С =  АВ, вычисляются по формуле:}

 

с_{ij= аi1· b1 j  + аi2 · b 2j  + …=}

.

 

Здесь знак Σ означает, что выполняется суммирование по всем слагаемым, где индекс k пробегает значения от 1 до n. Но если n =1, то суммирование пропадает, и остаётся только произведение.

Это правило согласуется с вышеприведённым правилом.  

В самом деле,  означает, что строка левой матрицы умножается на столбец правой матрицы. После транспонирования левой матрицы точно такие же результаты будут получаться после умножения столбца одной матрицы на столбец другой. Наконец, от левой матрицы получаем номер строки результата, а от правой — номер столбца.

 

8. Возникает вопрос, всегда ли возможно произведение матриц?

Обратимся к линейным преобразованиям.

Произведение линейных преобразований, т.е. подстановка одного преобразования в другое, возможно, если число функций в первом преобразовании в точности равно числу аргументов во втором преобразовании.

На языке матриц это означает следующее:

Произведение матриц возможно, если число строк в правой матрице равно числу столбцов в левой матрице.

Теперь обратимся к приведённому выше правилу умножения матриц. Понятно, что матрицы можно умножать, если окажется, что у левой (транспонированной) и правой матрицы число строк одинаково.

9. Произведение матриц неперестановочно.

Результат произведения матриц зависит от их порядка, иначе говоря, произведение матриц в общем случае некоммутативно, т. е. неперестановочно.

Более того, может оказаться так, что до перестановки произведение матриц было возможным, а после перестановки произведение этих же матриц не существует.

Две матрицы можно перемножать в любом порядке лишь тогда, когда их размерности равны mxn и nxm. — Именно при выполнении этого условия число столбцов в левой матрице всегда будет равно числу строк в правой матрице независимо от порядка их умножения. Результатом умножения будут квадратные матрицы размерностью mxm  или nxn. Очевидно, что если m≠n, результатом будут совершенно разные матрицы, которые не могут быть равными.

Если же m=n, т.е. если перемножаются две квадратные матрицы с одинаковым числом строк и столбцов, то произведение таких матриц возможно в любом порядке, тем не менее, чаще всего, результат тоже зависит от порядка сомножителей.

Например:

И лишь в исключительных случаях произведение матриц коммутирует, например: 

Пусть вас не удивляет то обстоятельство, что произведение двух матриц после перестановки может не существовать, а если и существует, то результат чаще всего зависит от порядка сомножителей.

В самом деле, матрицы определяют то или иное линейное преобразование, а линейное преобразование, в свою очередь, есть не что иное, как действие, состоящее в том, что одной группе чисел по определённым  правилам ставится в соответствие другая группа чисел.

Так вот, устройство нашего мира таково, что результат зависит от порядка действий.

Например, можно сначала поймать рыбу, а потом сварить уху, а наоборот не получится.

И ещё пример. Можно сначала что-то выпить из стакана, а затем его помыть, или, наоборот, можно сначала его помыть, и только потом что-то выпить из него. — Результат очень разный!

10. Деление матрицы на матрицу не имеет смысла, поэтому не определено.

Возможно лишь деление матрицы на число, что эквивалентно умножению матрицы на число, обратное данному.

М : α = α^{–1∙ М.}

11. Особые матрицы.

Нулевая матрица. Это матрица, у которой все матричные элементы являются нулями.

Единичная матрица. Это квадратная матрица, у которой диагональные элементы, т.е. те у которых номер строки равен номеру столбца, равны единице, а остальные, недиагональные равны нулю.

Например:

Назад      Вперёд

 

©   А.А.Дмитриевский.

 

vestishki.ru

Действия над матрицами

1. Сложение матриц

Пусть матрицы A и B имеют одинаковый размер mn, т.е.

,

.

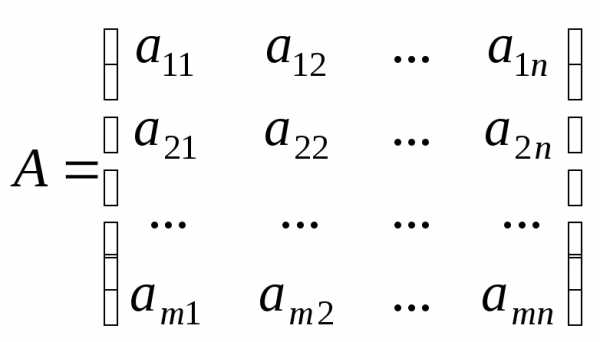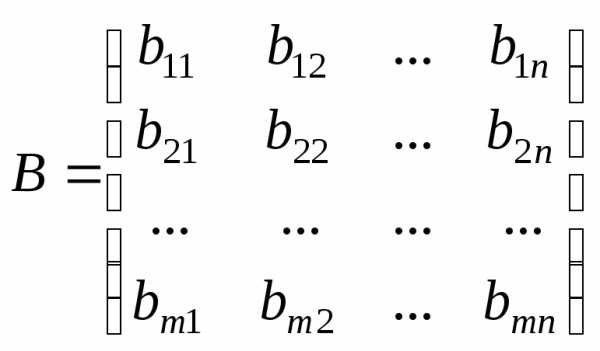
Матрица C размера mn называется суммой матриц A и B, если

, ,

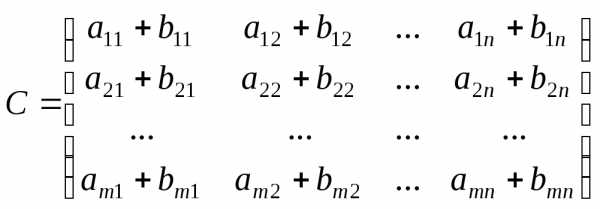то есть чтобы сложить матрицы одинакового размера, необходимо сложить их соответствующие элементы.

2. Умножение матрицы на число

Чтобы умножить матрицу на число, необходимо каждый элемент матрицы умножить на это число.

, , .

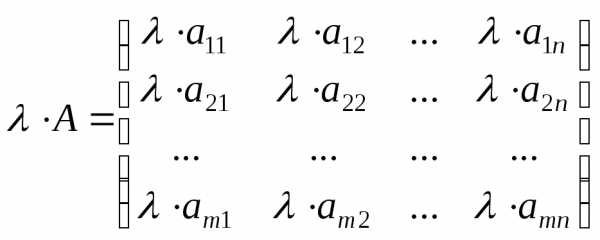3. Умножение матриц

Произведением матрицы A размера mn и матрицы B размера nk называется матрица C размера mk

, имеющая следующий вид:

,

где , , .

Замечание II.1. Отметим, что умножение матриц определено, если число столбцов первой матрицы равно числу строк второй матрицы.

Замечание II.2. Из правила умножения матриц следует, что, вообще говоря, , то есть умножение матриц не коммутативно.

Пример II.1. Заданы матрицы

,

.

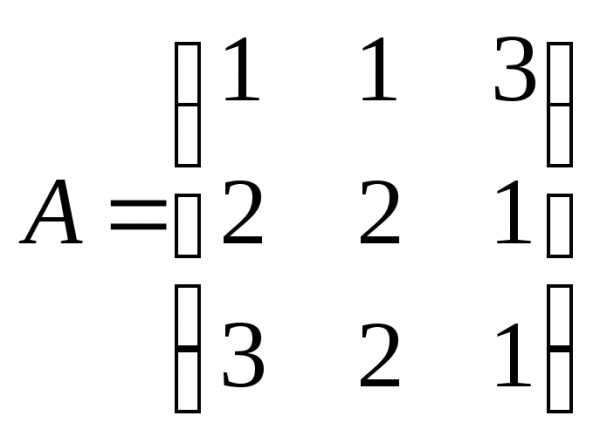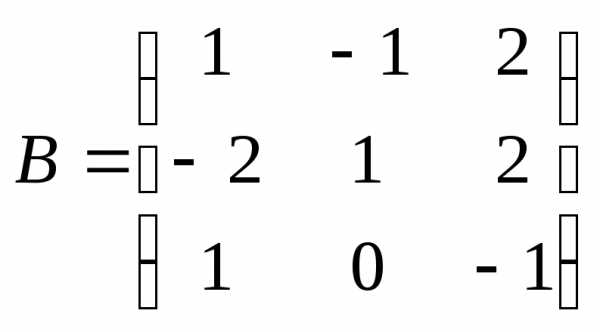
Найти, если это имеет смысл, А+В, АВ, В^Т.

Решение. Так как матрицы квадратные, то для них все эти операции выполняются. Определим сумму матриц A и B, для этого вычислим суммы соответствующих элементов:

.

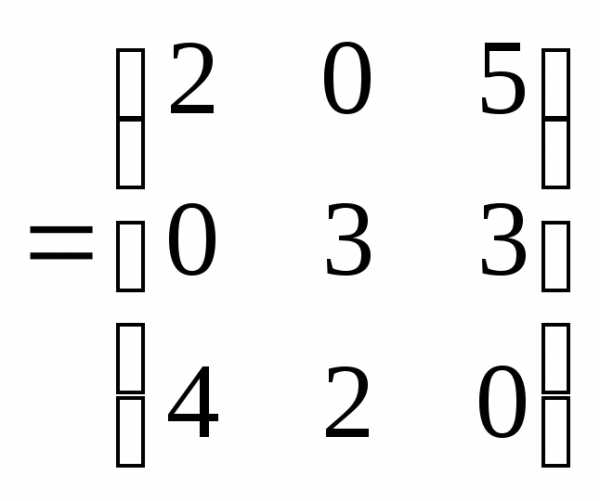Вычислим произведение:

.

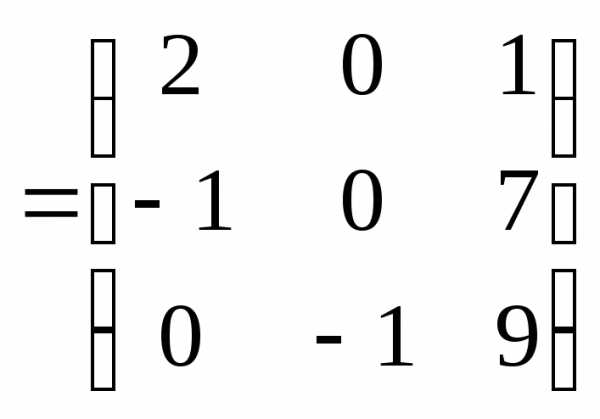Для транспонирования матрицы B необходимо поменять местами соответствующие строки и столбцы:

.

Упражнение. Выяснить, какие из предложенных операций примера 1.1 выполнимы, если размерность матрицы A – mn, а матрицы B – nk.

Определитель матрицы

Если числовая матрица квадратная, то ее можно оценить (определить), то есть поставить в соответствие число.

Определение. Определителем  (или det A) матрицы A порядка n называется многочлен элементов этой матрицы.

Для матрицы порядка n определитель записывается в виде

.

Если матрица числовая, то значение определителя есть число, которое находят по известным правилам.

Свойства определителей

1. Определитель матрицы не меняется при транспонировании матрицы.

.

2. Определитель матрицы равен нулю, если он содержит строку (столбец), все элементы которой равны нулю.

3. Определитель матрицы равен нулю, если элементы двух строк (столбцов) одинаковые.

4. Определитель матрицы равен нулю, если элементы двух строк (столбцов) пропорциональны.

5. Определитель матрицы меняет свой знак на противо-положный при перестановке местами любых двух строк (столбцов).

6. Если все элементы некоторой строки (столбца) имеют общий множитель, то он выносится за знак определителя как сомножитель.

7. Если к одной строке (столбцу) определителя прибавить другую строку (столбец), умноженную на число, то определи-тель не изменится.

8. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

.

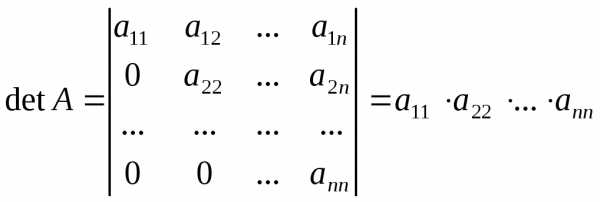Вычисление определителей

Определитель 2-го порядка равен разности произведений элементов главной и побочной диагоналей, то есть

.

Пример II.2. Вычислить определители:

1. ;

;

.

Определитель 3-го порядка вычисляется по формуле:

(II.1)

Для запоминания используется мнемоническое правило – правило треугольников. Оно состоит в изображении (явном или мысленном) элементов матрицы точками. Точки, соответствующие произведениям, которые входят в формулу определителя, соединяются отрезками.

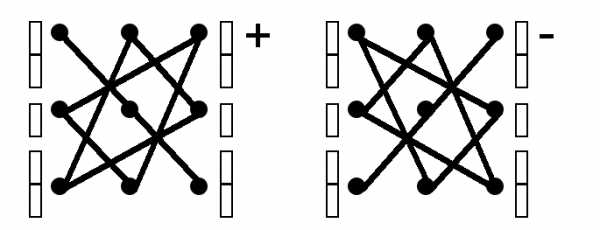
Главной диагонали и двум треугольникам, основания которых параллельны главной диагонали, соответствуют произведения со знаком “+”, а побочной диагонали и треугольникам, основания которых ей параллельны, соответствуют произведения со знаком “”.

Определение. Минором k-го порядка матрицы порядка n называется определитель, полученный из исходного вычеркиванием n–k строк и n–k столбцов. Определитель, составленный из элементов, стоящих на пересечении вычеркнутых n–k строк и столбцов, называется дополнительным минором к минору k–го порядка, .

Определение. Минором 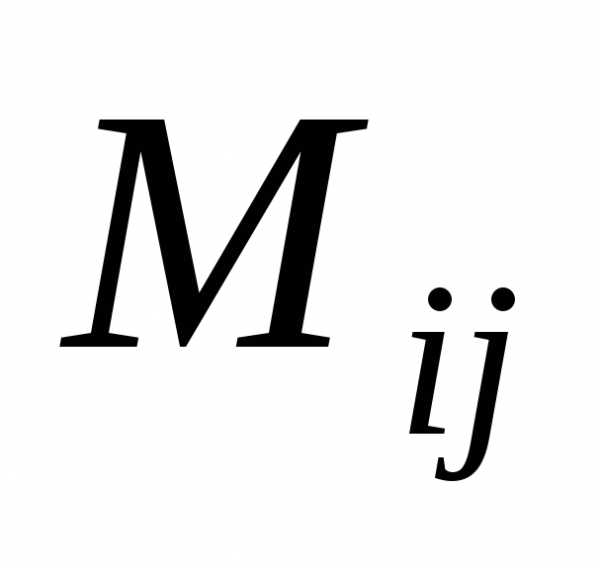элемента матрицы порядка n называется определитель порядка n-1, полученный вычеркиванием i–ой строки и j–го столбца из определителя  исходной матрицы. Элемент и его минор 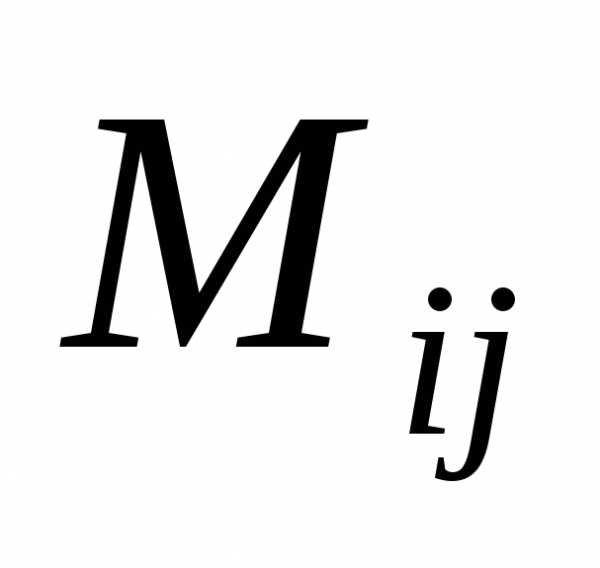являются взаимнодополнительными минорами, .

Определение. Алгебраическим дополнением элемента матрицы порядка n называется минор 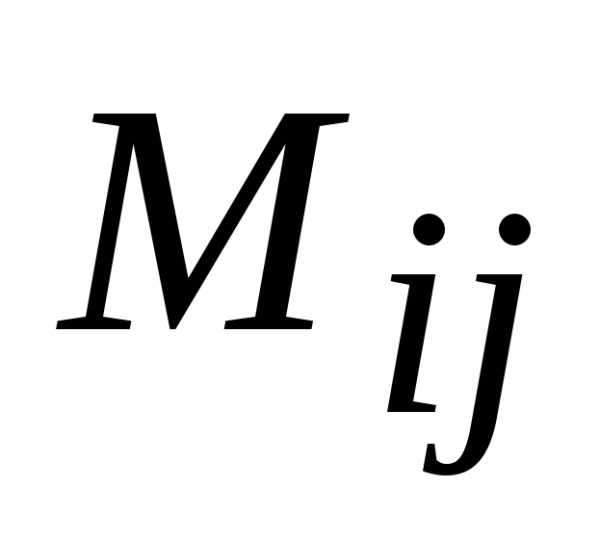этого элемента взятый со знаком «+», если сумма i+j четная, и со знаком «», если сумма i+j нечетная, то есть

, . (II.2)

Определитель n–го порядка можно вычислить разложением по i-ой строке (j-ому столбцу). Например, для определителя 3-го порядка получаются следующие равенства:

,

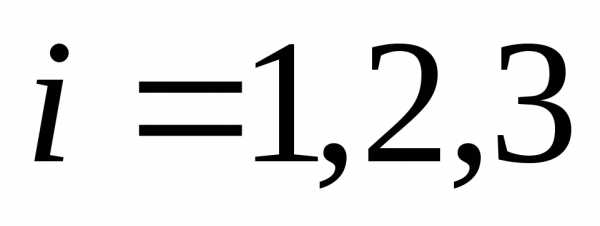
или

, .

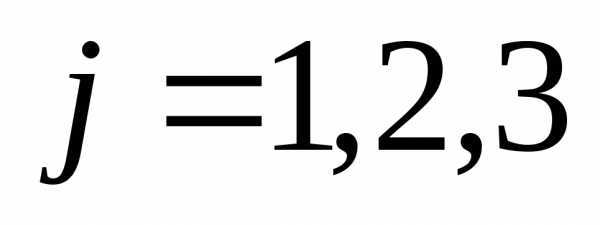Пример II.3.

1. Вычислим определитель по правилу треугольников:

.

2. Вычислим определитель разложением по третьему столбцу. Определим алгебраические дополнения элементов третьего столбца:

,

,

.

Далее, по формуле (II.2), имеем

.

studfiles.net

Как делить матрицы

2 методика:Деление матрицы на числоДеление матрицы на матрицу Матрицы — это векторные математические объекты, содержащие 2 или более скалярных элемента. Матрицы используются для нахождения многих неизвестных в системах скалярных уравнений, и для операций с большими массивами чисел. Как и со скалярными величинами (например, числами 1, 2, 3, 4), с векторами можно производить математические вычисления, такие как сложение, вычитание и умножение. Однако матрицы нельзя непосредственно разделить одну на другую. Для деления матриц необходимо произвести действие, состоящее из двух этапов. Вначале определяется матрица, обратная делителю (знаменателю). Затем на эту матрицу умножается та, которую делят, или матрица-числитель. Такой метод позволяет получить искомый результат, не производя деление непосредственно. В этой статье рассказывается, как делить матрицы. Шаги Метод 1 из 2: Деление матрицы на число 1 Поделите матрицу на скалярную величину. Хотя деление матрицы на другую матрицу не определено строго, матрицу всегда можно разделить на скалярную величину. Такое деление заключается в делении каждого элемента матрицы на данное число. Метод 2 из 2: Деление матрицы на матрицу 1 Определите матрицу, обратную матрице-знаменателю. Методы нахождения обратных матриц и других действий с матрицами можно найти в учебниках и справочниках по математике. Вычислите детерминант матрицы-знаменателя. Процедура нахождения детерминанта матрицы описана в математических учебниках. Цель данного шага заключается в том, чтобы определить, отличен ли детерминант матрицы от нуля. Если детерминант матрицы-делителя равен нулю, это означает, что данная матрица необратима, то есть для нее не существует обратной матрицы. В этом случае прекратите дальнейшие действия. Если матрица, обратная матрице-делителю не существует, дальше можно не продолжать. Такая ситуация подобна делению на ноль, не допустимому для скалярных величин. Если детерминант не равен нулю, найдите матрицу, обратную матрице-знаменателю. Наиболее распространенные способы нахождения обратной матрицы — метод Гаусса-Жордана и процедура нахождения матрицы алгебраических дополнений. Проверьте, правильно ли вы нашли обратную матрицу. Умножьте обратную матрицу на пряму, в результате вы должны получить единичную матрицу. Единичная матрица — это такая, все элементы которой равны нулю, кроме диагональных, которые равны единице. 2 Умножьте матрицу-числитель на обратную знаменателю матрицу. Учтите, что, в отличие от умножения скалярных величин, в данном случае порядок множителей имеет значение. При умножении чисел 2, умноженное на 4 дает тот же результат, что и 4, умноженное на 2. В векторной математике умножение матрицы-числителя на обратную знаменателю матрицу дает результат, отличный от того, если бы обратная матрица была помножена на матрицу-числитель. 3 Заметьте, что результат умножения матриц соответствует искомому. Матрица, не определенная строго в матричной алгебре, вычисляется путем нахождения обратной матрицы и умножения на нее делимой матрицы.

ves-mir.3dn.ru

Как делить матрицы Как? Так!

Содержимое:

3 части:

Если вы знаете, как перемножить две матрицы, можно приступить к «делению» матриц. Слово «деление» заключено в кавычки, потому что на самом деле матрицы делить нельзя. Операция деления заменяется операцией умножения одной матрица на матрицу, которая обратна второй матрице. Для простоты рассмотрим пример с целыми числами: 10 ÷ 5. Найдем число, обратное 5: 5^-1 или ¹/₅, а затем деление заменим умножением: 10 x 5^-1; при этом результат деления и умножения будет одним и тем же. Поэтому считается, что деление можно заменить умножением на обратную матрицу. Как правило, такие вычисления применяются для решения систем линейных уравнений.

Краткое резюме

1. Делить матрицы нельзя. Вместо деления одну матрицу умножают на матрицу, обратную второй матрице. «Деление» двух матриц [A] ÷ [B] записывается так: [A] * [B]^-1 или [B]^-1 * [A].
2. Если матрица [B] не является квадратной или если ее определитель равен 0, запишите «однозначного решения нет». В противном случае найдите определитель матрицы [B] и перейдите к следующему шагу.
3. Найдите обратную матрицу: [B]^-1.
4. Перемножьте матрицы, чтобы найти [A] * [B]^-1 или [B]^-1 * [A]. Имейте в виду, что порядок перемножения матриц влияет на конечный результат (то есть результаты могут быть разными).

Шаги

Часть 1 Проверка «делимости» матриц

1. 1 Разберитесь с «делением» матриц. На самом деле матрицы делить нельзя. Нет такой математической операции, как «деление одной матрицы на другую». Деление заменяется умножением одной матрицы на матрицу, обратную второй матрице. То есть запись [A] ÷ [B] не верна, поэтому ее заменяют такой записью: [A] * [B]^-1. Так как обе записи являются равнозначными в случае скалярных величин, теоретически можно говорить о «делении» матриц, но все-таки лучше пользоваться правильной терминологией.
   • Обратите внимание, что [A] * [B]^-1 и [B]^-1 * [A] – это разные операции. Может быть, придется выполнить обе операции, чтобы найти все возможные решения.
   • Например, вместо (13263913)÷(7423) 2 Убедитесь, что матрица, на которую вы «делите» другую матрицу, является квадратной. Чтобы инвертировать матрицу (найти обратную матрицу), она должна быть квадратной, то есть с одинаковым количеством строк и столбцов. Если инвертируемая матрица не является обратной, однозначного решения нет.
     • Опять же, здесь матрицы не «делятся». В операции [A] * [B]^-1 описанное условие относится к матрице [B]. В нашем примере это условие относится к матрице (7423) 3 Проверьте, можно ли перемножить две матрицы. Чтобы перемножить две матрицы, количество столбцов первой матрицы должно равняться количеству строк второй матрицы. Если это условие не соблюдается в записи [A] * [B]^-1 или [B]^-1 * [A], решения нет.
       • Например, если размер матрицы [А] равен 4 х 3, а размер матрицы [B] равен 2 х 2, решения нет. Нельзя перемножить [A] * [B]^-1, потому что 4 ≠ 2, и нельзя перемножить [B]^-1 * [A], так как 2 ≠ 3.
       • Обратите внимание, что у обратной матрицы [B]^-1 всегда то же количество строк и столбцов, что и у исходной матрицы [B]. Нет необходимости находить обратную матрицу, чтобы проверить, что две матрицы можно перемножить.
       • В нашем примере размер обеих матриц 2 х 2, поэтому их можно перемножить в любом порядке.
     • 4 Найдите определитель матрицы 2 × 2. Запомните: инвертировать матрицу можно только в том случае, если ее определитель не равен нулю (в противном случае инвертировать матрицу нельзя). Вот как найти определитель матрицы 2 х 2:
       • Матрица 2 х 2: определитель матрицы (abcd) То есть из произведения элементов главной диагонали (проходит через верхний левый и нижний правый углы) вычтите произведения элементов другой диагонали (проходит через верхний правый и нижний левый углы).
       • Например, определитель матрицы (7423) 5 Найдите определитель большей матрицы. Если размер матрицы равен 3 х 3 или больше, вычисление определителя немного усложняется.
         • Матрица 3 х 3: выберите любой элемент и зачеркните строку и столбец, в которых он находится. Найдите определитель получившееся матрицы 2 × 2, а затем умножьте его на выбранный элемент; знак определителя уточните в специальной таблице. Повторите описанный процесс для двух других элементов, которые находятся в одной строке или столбце с выбранным элементом. Затем найдите сумму полученных (трех) определителей. Прочитайте , чтобы получить дополнительную информацию о том, как находить определитель матрицы 3 х 3.
         • Большие матрицы: определитель таких матриц лучше искать при помощи графического калькулятора или программного обеспечения. Метод аналогичен методу нахождения определителя матрицы 3 × 3, но применять его вручную довольно утомительно. ^{Например, чтобы найти определитель матрицы 4 х 4, нужно найти определители четырех матриц 3 х 3.}
       • 6 Продолжите вычисления. Если матрица не является квадратной или если ее определитель равен нулю, напишите «однозначного решения нет», то есть процесс вычисления завершен. Если же матрица является квадратной и ее определитель не равен нулю, перейдите к следующему разделу.

Часть 2 Нахождение обратной матрицы

1. 1 Поменяйте местами элементы главной диагонали матрицы 2 х 2. Если дана матрица 2 × 2, воспользуйтесь быстрым методом нахождения обратной матрицы. Для начала поменяйте местами верхний левый элемент и нижний правый элемент. Например:
   • (7423) 2 Оставшиеся два элемента местами не меняйте, но измените их знак. То есть верхний правый элемент и нижний левый элемент умножьте на -1:
     • (3427) 3 Найдите число, обратное значению определителя. Определитель этой матрицы был найден в предыдущем разделе, поэтому не будем вычислять его еще раз. Обратное значение определителя записывается так: 1 / (определитель):
       • В нашем примере определитель равен 13. Обратное значение: 113 4 Полученную матрицу умножьте на обратное значение определителя. Каждый элемент новой матрицы умножьте на обратное значение определителя. Конечная матрица будет обратна исходной матрице 2 х 2:
         • 113∗(3−4−27) 5 Проверьте правильность вычислений. Для этого умножьте исходную матрицу на обратную. Если вычисления правильные, произведение исходной матрицы на обратную даст единичную матрицу: (1001).
         • Примечание: операция перемножения матриц не является коммутативной, то есть важен порядок расположения матриц. Но при умножении исходной матрицы на обратную любой порядок приводит к единичной матрице.
       • 6 (или большего размера). Если вы уже знакомы с этим процессом, лучше воспользоваться графическим калькулятором или специальным программным обеспечением. Если нужно найти обратную матрицу вручную, ниже приводится краткое описание процесса:
         • Присоедините единичную матрицу I с правой стороны исходной матрицы. Например, [B] → [B | I ]. У единичной матрицы все элементы главной диагонали равны 1, а все остальные элементы равны 0.
         • Упростите матрицу так, чтобы привести ее левую сторону к ступенчатому виду; продолжите упрощение, чтобы левая сторона превратилась в единичную матрицу.
         • После упрощения матрица примет следующий вид: [I | B^-1]. То есть ее правая сторона является матрицей, обратной исходной матрице.

Часть 3 Перемножение матриц

1. 1 Запишите два возможных выражения. Операция умножения двух скаляров коммутативна, то есть 2 х 6 = 6 х 2. Это не так в случае умножения матриц, поэтому, возможно, придется решить два выражения:
   • x = [A] * [B]^-1 – это решение уравнения x[B] = [A].
   • x = [B]^-1 * [A] – это решение уравнения [B]x = [A].
   • Каждую математическую операцию выполняйте с обеих сторон уравнения. Если [A] = [C], то [B]^-1[A] ≠ [C][B]^-1, потому что [B]^-1 находится слева от [A], но справа от [C].
2. 2 Определите размер конечной матрицы. Размер конечной матрицы зависит от размеров перемножаемых матриц. Количество строк конечной матрицы равно количеству строк первой матрицы, а количество столбцов конечной матрицы равно количеству столбцов второй матрицы.
   • В нашем примере размер обеих матриц (13263913) 3 Найдите значение первого элемента. Прочитайте или вспомните следующие основные действия:
     • Чтобы найти первый элемент (первая строка, первый столбец) конечной матрицы [A][B]^-1, вычислите скалярное произведение элементов первой строки матрицы [A] и элементов первого столбца матрицы [B]^-1. В случае матрицы 2 x 2 скалярное произведение вычисляется так: a1,1∗b1,1+a1,2∗b2,1 4 Продолжите вычислять скалярные произведения, чтобы найти каждый элемент конечной матрицы. Например, элемент, расположенный во второй строке и первом столбце, равен скалярному произведению второй строки матрицы [A] и первого столбца матрицы [B]^-1. Попробуйте самостоятельно найти оставшиеся элементы. Вы должны получить следующие результаты:
       • (13263913)∗(313−413−213713)=(−1107−5)

Прислал: Волкова Александра . 2017-11-06 10:59:21

kak-otvet.imysite.ru

Умножение матрицы на число – Энциклопедия по машиностроению XXL

В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.  [c.41]

Умножение матрицы на число. Если к—вещественное или комплексное число, то произведение ХА матрицы А на число к определяется формулой  [c.95]

Умножение матрицы на число I (которое можно записать справа, так и слева матрицы) эквивалентно умножению на I кв дого элемента этой матрицы если  [c.40]

При умножении матрицы на некоторое число необходимо умножить на это число все элементы матрицы, т. е.  [c.144]

Умножение (деление) матрицы на число. Для этого необходимо каждый элемент матрицы умножить (разделить) на это число.  [c.181]

Определение 4. Произведением матрицы Л размера тХп на число а называется матрица С тех же размеров, элементы которой получаются из соответствующих элементов матрицы Л умножением их на число а, т. е.  [c.41]

Л]- -[В] умножение тензора на число Тв=%ТА, гле матрица [В]—%[А умножение тензора на тензор (скаляр-ное) Тс=Гл7 в, где матрица [С]=[А][В].  [c.61]

Еще большее число показателей требует для своего расчета применение умножения матриц на векторы. Вектор — это матрица с одной строкой или одним столбцом. Данная операция, таким образом, есть частный случай умножения матриц. Ее результатом является вектор. Примером такой операции является вычисление потребностей в материалах.  [c.53]

В табл. 7.1 приведена скорость выполнения операции умножения матрицы на вектор. В первой колонке представлены выражения для числа тактовых циклов, необходимых для завершения одной операции умножения. Умножение матрицы тХп на вектор /гХ1 требует 2тп операций сложения и умножения. Если предположить, что биты данных проходят в системе с частотой 10 МГц (величина 0,1 мкс/бит является достаточно обоснованной для существующих электронных устройств), то можно вычислить скорость выполнения операций. Представлены два случая. Первый из них соответствует п = т = 32, при /=16 (I эквивалентно точности вычислений), а второй случай относится к п = т=128, / = 32. В табл. 7.2 представлены аналогичные данные для умножителей, выполняющих умножение матрицы на матрицу с точностью I цифр. В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-  [c.207]

В символьных вычислениях центральное место занимает операция вычисления внутреннего произведения, эквивалентная умножению составляющих элементов на вектор (векторное умножение), на матрицу (умножение матрицы на матрицу) или на корреляционную функцию. В предыдущих разделах была установлена общность процедур вычисления внутреннего произведения для большого числа алгоритмов из области цифровых вычислений. В одном типичном представлении символьных вычислений отношения знаний выражаются в терминах логического сопоставления с образцом, процедура которого определяется поиском соглашения по предпосылке-условию (с левой стороны) соотношения если [А], тогда [В] (см. разд. 10.3.5). Здесь [А] является подпространством Л -мерного векторного пространства  [c.354]

Умножение матрицы на скаляр р равносильно умножению всех ее элементов на это число Ьу = р ау 1 = 1,2,] =1,2,…,11.  [c.156]

Умножение матрицы [Aij] на скаляр X дает матрицу [КАц. Произведение двух матриц [Aij] и определено только в том случае, если число столб-  [c.18]

Суммой двух матриц А и В одинакового порядка (тХп) называется матрица того же порядка, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц. Перемножать можно только матрицы, у которых число столбцов в первой матрице совпадает с числом строк во второй. Каждый элемент матрицы — произведения С=ВА — определяется по правилу умножения строки на столбец, которое для квадратных матриц приводит к формуле  [c.46]

Мы уже говорили, что, записывая уравнение (4.19) в виде г = кг, мы просто пользуемся символическим обозначением для указания определенной операции А, совершаемой над координатной системой (или над вектором). Но, расширяя наше понятие о матрицах, можно сделать так, что эта запись будет указывать на действительное умножение на умножение матриц. Матрицы, рассматривавшиеся нами до сих пор, были квадратными, т. е. число их строк равнялось числу столбцов. Однако можно рассматривать также матрицы, состоящие всего лишь из одного столбца, такие, как  [c.119]

Любую матрицу при помощи элементарных преобразований строк и столбцов, заключающихся в перестановке строк (столбцов), умножении строки (столбца) на число и сложении строк (столбцов) между собой, можно привести к каноническому виду. Ранг канонической матрицы равен числу единиц на ее главной диагонали.  [c.16]

Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются замена строк столбцами, а столбцов соответствующими строками перестановка строк матрицы вычеркивание строки, все элементы которой равны нулю умножение какой-либо строки на число, отличное от нуля прибавление к элементам одной строки соответствующих элементов другой строки.  [c.53]

Г. Умножение матриц. Рассмотрим (т X Р) Матрицу а и (/ X ) Матрицу Ъ—число столбцов а равно числу строк Ъ. Такие матрицы, взятые в указанной последовательности а, Ь, называются конформными. Действие умножения определено для конформных матриц. Произведением их с — аЬ называется (т X )”Матрица, элемент /-Й строки и /г-го столбца которой ра ен сумме произведений элементов /-й строки матрицы а на элементы /г-го столбца матрицы Ь  [c.762]

Матрицы, имеющие одинаковое число строк и столбцов, можно складывать (или вычитать) поэлементно. Умножение матрицы [Л,/] на скаляр X дает матрицу [М,у]. Произведение двух матриц определено только в том случае, когда число столбцов в первом множителе Л равно числу строк во втором множителе Произведением (М X Р)-матрицы на (Р X Л )-матрицу будет (М х Ы)-матрица. Умножение матриц обычно обозначается простым написанием их символов один за другим, например  [c.32]

Гамильтониан (2.8), (2.9) зависит от 21 параметра. Существует три типа простейших преобразований, которые изменяют (в частности, исключают) параметры в гамильтониане без изменения уравнений движения. К первому типу относятся групповые преобразования 30(3) х 30(3). С их помощью в представлении (2.9) матрицы А и С могут быть одновременно приведены к диагональному виду. Добавление к гамильтониану произвольной линейной комбинации функций Казимира Рг,Р2, которые являются однородными квадратичными функциями, позволяет исключить еще два параметра. Умножение гамильтониана на произвольную константу Н аН с заменой времени t 1, также позволяет уменьшить число параметров на единицу. Таким образом, квадратичное семейство гамильтонианов (2.8) либо (2.9)) определяется двенадцатью параметрами.  [c.181]

Второй способ состоит в умножении соответствующего диагонального элемента матрицы на некоторое большое число, скажем 10 , перед модификацией соответствующего коэффициента нагрузки. В рассматриваемом случае мы бы получили  [c.486]

Матрица рассеяния 5(Л) не зависит от Л и также сводится к умножению на число (б).  [c.109]

Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -.  [c.63]

Однако этот критерий, строго говоря, не имеет смысла. Путем почленного умножения уравнений на числа, большие единицы, определитель системы линейных алгебраических уравнений можно сделать сколь угодно большим. Обусловленность системы при этом не изменится. В теории матриц вводятся числа обусловленности, инвариантные относительно подобных преобразований. К таким числам относятся числа Тюринга и Тодда.  [c.181]

SUBROUTINE SKM (А, S, М, N) — программа умножения матрицы на скаляр. А — исходная и результирующая матрица S — скалярная величина М, N — целые числа, определяющие размер матрицы.  [c.251]

Рассмотрение данного примера было вызвано необходимостью обеспечить высокую скорость при выполнении операции внутреннего произведения в линейной алгебре (например, для умножения матрицы на вектор или матрицы на матрицу), в противном случае эти операции становятся бессысленными. Операции внутреннего произведения включают умножение двух чисел и сложение результата с третьим числом. Например, 2-разрядный умножитель-сумматор умножает два 2-раз-рядных числа М ц Ы, прибавляет результат к 5-разрядному входному числу X и выводит результаты в виде 5-разрядного числа У. В синхронизированном режиме работы выходной сигнал У мог бы подаваться по цепи обратной связи на вход X для того, чтобы достичь эффекта многократного накопления результата (если имеется возможность накопления до трех произведений и при этом не возникает переполнение).  [c.155]

Одна из целей цифровых оптических вычислений состоит в достижении большей гибкости системы, чем у их аналоговых предшественников. Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,  [c.183]

Разновидности основной архитектуры. Сообщалось и о других способах преобразования схем вычисления свертки в схемы умножителей матрицы на матрицу. В [16] для получения промежуточного произведения при вычислении внутреннего произведения двух векторов используется основная схема вычисления свертки с интегрированием по времени. Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.  [c.200]

Правильный результат получают уже в смешанном формате, путем умножения исходной матрицы на дополненный вектор. Эта процедура может быть выполнена с помощью любого из обсуждавшихся выше вариантов умножения матрицы на матрицу. Ценой этого будет служить увеличение объема памяти, необходимое для записи вектора, и задача класса умножение матрицы на вектор оказывается отданной в уплату за задачу класса матрица — матрица. В целом же кажется более выгодным использовать оптические методы для выполнения суммирования вдоль противодиагоналей. В число возможных оптических способов решения такой задачи входит сегментация цилиндрических линз, сегментация голографических линз или применение матриц оптических волокон, соединяющих соответствующие элементы с детекторами, на которых происходит суммирование.  [c.203]

В работе [20] предлолсхемы построения процессоров внешнего произведения. В первом случае используется перекрестное включение одномерных входных модуляторов (рис. 7.14). Для умножения матрицы на вектор в один из модуляторов вводят целый столбец матрицы, а элементы вектора размещаются в другом модуляторе. Матричный модулятор должен обладать т1 разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице пг1х1 интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только т(21—1) детекторов. Каждое промежуточное произведение может быть накоплено на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным т1. Полное число тактовых импульсов для операции умножения матрицы на вектор составляет пт1. Для умножения матрицы на матрицу требуется кт 21—1) детекторов, при этом необходимое число тактовых циклов составляет лишь пт1 (если т>к).  [c.203]

Все процессоры характеризуются тем, что чем больше объем задачи, тем быстрее они работают. Например, умножители матрицы на вектор (за одним исключением) работают со скоростью в десятки мегаопераций в секунду, характерной для небольших по объему задач. Процессоры умножения матрицы на матрицу работают со скоростями порядка гигаопераций в секунду, что характерно для задач большего масштаба. Очевиден выигрыш в быстродействии, получаемый для параллельной обработки. Более неопределенной характеристикой является абсолютная величина быстродействия. Представленные здесь цифры являются лишь оценками, но они действительно отражают общие свойства оптических вычислений. За небольшим числом исключений имеется очень небольшая разница (менее чем на порядок по величине) между разными видами оптических процессоров, используемых для решения заданной задачи. Возможности оптических процессоров, как представляется, достаточно жестко ограничены определенными скоростями. При сравнении с возможностями электронных процессоров скорости вряд ли произведут на читателя глубокое впечатление. На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.  [c.208]

Матрица S обладает рядом универсальных свойств, вытекаюших из симметрии задачи и закона сохранения энергии. Отметим одно из них. Известно, что при умножении столбца или строки матрицы на число q ее детерминант увеличивается в q раз. Умножая первый и третий столбец мат-  [c.96]

Поэтому математической моделью излучающей системы может служить соотношение (2.24) или (2.27), т. е. систему излучателей можно описывать матрицей как [/)], так и [/)] . Размерности матриц [ )] и [/)] одинаковы, и для хранения их в ЭВМ требуются одинаковые объемы памяти. В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.  [c.62]

В АР с большим числом излучателей матрица [ )] содержит много элементов с малой абсолютной величиной, которые соответствуют излучателям, далеко отстоящим друг от друга. Поскольку в итерационных методах умножение матрицы на вектор является единственной операцией с матрицей, то это позволяет легко исключить операции с элементами матрицы [О], имеющими малое значение. Сохраняя в матрице [1>] только те элементы, которые соответствуют учету взаимодействия не более чем с Ь ближайшими излучателями, можно существенно уменьшить затраты машинного времени (8, 9 в табл. 3.1). Например, расчет токов АР из 21X21 полуволновых вибраторов над экраном ( =с у=0,6Я,) методом сопряженных градиентов с учетом взаимодействия  [c.110]

Умножение двух матриц возможно, если число столбцов первой равно числу строк второй матрицы. Произведением матрицы А = = [aij] размера тХР на матрицу В = [Ьр,] размера рХп является матрица С = [с,/,] размера тХп, в которой каждый элемент iu определяется по правилу умножения строки на столбец элементы /-Н строки первой матрицы умножаются на соответствуюн не элементы kio столбца второй матрицы и полученные произведения складываются  [c.104]

В случае, когда элементами матрицы являются матрицы-блоки, умножение выполняется по тем же правилам, как если бы элементами матриц были числа, т. е. строки первой матрицы-сомно-жителя умножаются на столбцы второй матрицы-сомножителя (см., например, Г а н т м а х е р Ф. Р., Теория матриц, 5),  [c.184]

Умножение на скаляр а тензора Т ь любого ранга вследствие инва-риашносга первого можно выполнять в любом множестве координат. Для этого необходамо каждую компоненту матрицы тензора в выбранной множестве координат умножить на число, характеризующее скал ф. Ранг тензора, получаемого в результате такого умножения, равен рангу тензора, участвующему в этом действии  [c.242]

Произведением матрицы [A]—[aik]m,n на число а называется матрица a,[A]=[aaik]m.n, полученная умножением всех элементов матрицы [Л] на число сг. пример  [c.37]

Быстродействие оптических матричных умножителей было уже описано в табл. 7.1 и 7.2. При вычислении отношения Псалтиса числа в табл. 7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.  [c.210]

Полученный результат справедлив при любом выборе ортонор-мированной системы функций Если система // выбрана произвольно, то для построения матрицы гамильтониана потребуется большое число функций //, и соответствующее представление группы симметрии будет иметь очень высокую размерность. Если, с другой стороны, взять в качестве функций /г собственные состояния гамильтониана, то действие на них гамильтониана сведется к умножению их на некоторое число (собственное значение энергии), и матрица гамильтониана окажется диагональной. Любое преобразование симметрии должно поэтому переводить либо в себя, либо в вырожденное состояние. Размерность представления, порожденного данной функцией / , не может превышать степень вырождения состояния. Таким образом, между размерностью представления группы и степенью вырождения состояния, породившего это представление, существует тесная связь. В частности, если под действием неприводимого представления все состояния некоторой совокупности преобразуются друг через друга, то это означает, что и под действием операции симметрии эти состояния будут преобразовываться друг через друга, т. е. мы не можем найти никакой линейной комбинации (никакого унитарного преобразования), представляющей исключение. Из симметрии гамильтониана поэтому следует, что эти состояния должны быть вырожденными. Мы пришли тем самым, правда с помощью интуитивных соображений, к одному из важных результатов теории групп. Если группа симметрии гамильтониана имеет многомерные неприводимые представления, это означает, что собственные состояния гамильтониана должны быть вырожденными.  [c.38]

---

mash-xxl.info

Алгоритм нахождения обратной матрицы

Действия над матрицой

1. Сложение и вычитание матриц:

Сложение и вычитание матриц – одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:

Сумма двух матриц:

Разность двух матриц:

2. Умножение матрицы на число:

Умножение матрицы на число – процесс, заключающийся в умножении числа на каждый элемент матрицы.

Например, пусть дана матрица А:

Умножим число 3 на матрицу А:

3. Умножение двух матриц:

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.

Можно представить все это в виде схемы:

После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц,  можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.

Посмотрим как это выглядит на схеме:

Посмотрим как это выглядит на примере:

Даны две матрицы:

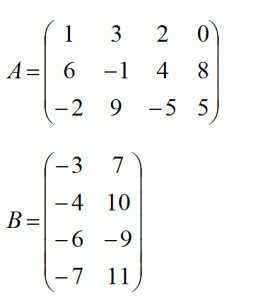
Найдем произведение этих матриц:

4. Деление матриц:

Деление матриц – действие над матрицами, которое в этом понятии не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней:

Согласно этому свойству разделим матрицу А на матрицу В:

В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.

Обратная матрица

Пусть имеется квадратная матрица n-го порядка

Матрица А^-1 называется обратной матрицей по отношению к матрице А, если А*А^-1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.

Теорема условия существования обратной матрицы

Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.

Матрица А = (А1, А2,…А_n) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.

1. Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.

2. Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.

3. Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.

4. Записать обратную матрицу А^-1, которая находится в последней таблице под матрицей Е исходной таблицы.

Пример 1

Для матрицы А найти обратную матрицу А^-1

Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.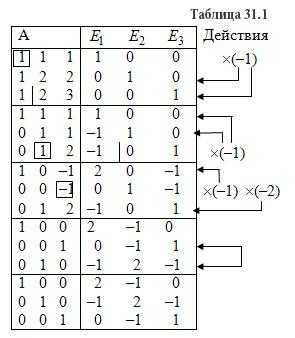

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А^-1.

В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.

Ответ:

Определители матриц (Детерминанты) Определители матриц (Детерминанты)

Определители матриц, способ № 1:

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

, где М_1k – определитель матрицы (детерминант), полученной из исходной матрицывычеркиванием первой строки и k – oго столбца. Следует обратить внимание на то, чтоопределители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Первая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя матрицы по первому столбцу:

Вообще говоря, определитель матрицы может вычисляться по любой строке или столбцуматрицы, т.е. справедлива формула:

Очевидно, что различные матрицы могут иметь одинаковые определители. Определитель единичной матрицы равен 1. Для указанной матрицы А число М_1k называется дополнительным минором элемента матрицы a_1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Дополнительный минор произвольного элемента квадратной матрицы a_ij равенопределителю матрицы, полученной из исходной матрицы вычеркиванием i-ой строки и j-го столбца.

Определители матриц, способ № 2:

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент а₁₁:

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Замечание:

Вычисление определителей матриц четвертого и более высокого порядка приводит к большим вычислениям, так как:

• для нахождения определителя матрицы первого порядка мы находим одно слагаемое, состоящее из одного сомножителя;

• для нахождения определителя матрицы второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей;

• для нахождения определителя матрицы третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей;

• для нахождения определителя матрицы четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т.д.

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 1!=1 2!=1×2=2 3!=1×2×3=6 4!=1×2×3×4=24 5! = 1 × 2 × 3 × 4 × 5 = 120 …

studfiles.net

Как делить матрицы | Сделай все сам

Матричная алгебра – раздел математики, посвященный постижению свойств матриц, их использованию для решения трудных систем уравнений, а также правилам действий над матрицами, включая деление.

Инструкция

1. Существует три действия над матрицами: сложение, вычитание и умножение. Деление матриц, как таковое, действием не является, но его дозволено представить в виде умножения первой матрицы на матрицу, обратную ко 2-й:A/B = A·B^(-1).

2. Следственно операция деления матриц сводится к двум действиям: поиску обратной матрицы и умножению ее на первую. Обратной именуется такая матрица A^(-1), которая при умножении на A дает единичную матрицу.

3. Формула обратной матрицы: A^(-1) = (1/?)•B, где ? — определитель матрицы, тот, что должен быть хорош от нуля. Если это не так, то обратная матрица не существует. B – матрица, состоящая из алгебраических дополнений начальной матрицы А.

4. Скажем, исполните деление заданных матриц.

5. Обнаружьте матрицу, обратную ко 2-й. Для этого вычислите ее определитель и матрицу алгебраических дополнений. Запишите формулу определителя для квадратной матрицы третьего порядка:? = a11·a22·a33 + a12·a23·a31 + a21·a32·a13 – a31·a22·a13 – a12·a21·a33 – a11·a23·a32 = 27.

6. Определите алгебраические дополнения по указанным формулам:A11 = a22•a33 — a23•a32 = 1•2 – (-2)•2 = 2 + 4 = 6;A12 = -(a21•a33 — a23•a31) = -(2•2 – (-2)•1) = -(4 + 2) = -6;A13 = a21•a32 — a22•a31 = 2•2 – 1•1 = 4 – 1 = 3;A21 = -(a12•a33 — a13•a32) = -((-2)•2 — 1•2) = -(-4 — 2) = 6;A22 = a11•a33 — a13•a31 = 2•2 – 1•1 = 4 – 1 = 3;A23 = -(a11•a32 — a12•a31) = -(2•2 – (-2)•1) = -(4 + 2) = -6;A31 = a12•a23 — a13•a22 = (-2)•(-2) – 1•1 = 4 – 1 = 3;A32 = -(a11•a23 — a13•a21) = -(2•(-2) — 1•2) = -(-4 — 2) = 6;A33 = a11•a22 — a12•a21 = 2•1 – (-2)•2 = 2 + 4 = 6.

7. Поделите элементы матрицы алгебраических дополнений на величину определителя, равную 27. Таким образом, вы получили матрицу, обратную ко 2-й. Сейчас задача сводится к умножению первой матрицы на новую.

8. Исполните умножение матриц по формуле C = A*B:c11 = a11•b11 + a12•b21 + a13•b31 = 1/3;c12 = a11•b12 + a12•b22 + a13•b23 = -2/3;c13 = a11•b13 + a12•b23 + a13•b33 = -1;c21 = a21•b11 + a22•b21 + a23•b31 = 4/9;c22 = a21•b12 + a22•b22 + a23•b23 = 2/9;c23 = a21•b13 + a22•b23 + a23•b33 = 5/9;c31 = a31•b11 + a32•b21 + a33•b31 = 7/3;c32 = a31•b12 + a32•b22 + a33•b23 = 1/3;c33 = a31•b13 + a32•b23 + a33•b33 = 0.

Разделять на ноль невозможно, это вестимо всем школьнику, но многим идеально неясно отчего. Поводы этого правила дозволено узнать только в высшем учебном заведении, и то только если вы будете постигать математику. В реальности, основание того, что на ноль разделять невозможно, не такое уж трудное. Узнать это было бы дюже увлекательно многим школьникам.

Повод того, что невозможно разделять на ноль , лежит в математике. В то время как в арифметике есть четыре основные операции над числами (это сложение, вычитание, умножение и деление), в математике таких только две из них (это сложение и умножение). Именно они включены в определение числа. Дабы определить, что такое вычитание и деление, необходимо воспользоваться сложением и умножением и вывести новые операции из них. Дабы осознать данный момент, благотворно разглядеть несколько примеров. Скажем, операция 10-5, с точки зрения ученика школы, обозначает, что от числа 10 отнимается число 5. Но математика ответила бы на вопрос о том, что тут происходит, напротив. Данная операция была бы сведена к уравнению x+5=10. Незнакомое в данной задаче это x, именно оно и является итогом так называемого вычитания. С делением все происходит подобно. Оно каждого лишь верно также выражается через умножение. При этом, итог – это примитивно подходящее число. Скажем, 10:5 математик записал бы как 5*x=10. Данная задача имеет однозначное решение. Учтя все это, дозволено осознать, отчего невозможно разделять на ноль . Запись 10:0 превратилась бы в 0*x=10. То есть, итогом стало бы число, которое при умножении на 0 дает другое число. Но каждому знаменито правило о том, что всякое число, умноженное на ноль , дает ноль . Это качество включено в представление о том, чем является ноль . Следственно получается, что задача о том, как поделить число на ноль , не имеет решения. Это типичная обстановка, много задач в математике не имеют решения. Но как может показаться, из этого правила есть одно исключение. Да, ни одно число невозможно разделять на ноль , но чай сам ноль дозволено? Скажем, 0*x=0. Это чай правильное равенство. Но загвоздка в том, что на месте x может быть идеально всякое число. Следственно итогом такого уравнения стала бы идеальная неясность. Нет причин выбрать какой-нибудь один итог. Следственно ноль на ноль разделять тоже невозможно. Правда, в математическом обзоре с сходственными неопределенностями умеют справляться. Выясняют, нет ли в задаче дополнительных условий, вследствие которым становится допустимым «раскрыть неясность» — так это именуется. Но в арифметике так не делают.

Видео по теме

Для вычисления значений матрицы либо выполнения других математических расчетов используйте программу Microsoft Office Excel. Также вы можете воспользоваться и бесплатными ее аналогами, правило действия тут будет фактически идентичным.

Вам понадобится

• — программа Microsoft Office Excel.

Инструкция

1. Запустите программу Microsoft Office Excel. В меню ввода данных впишите данную вам матрицу для дальнейшего вычисления ее определителя. Выделите одну из незанятых ячеек таблицы, позже чего введите следующую формулу: “=МОПРЕД(ak:fg)”. В данном случае ak будет обозначать координаты, соответствующие левому верхнему углу заданной матрицы, а fg – нижнему правому. Для приобретения определителя нажмите клавишу Enter. Надобное значение будет отображено в выбранной вами пустой ячейке.

2. Используйте функционал Excel для вычисления и других значений. В случае если вы не умеете применять формулы в Microsoft Office Excel, скачайте особую тематическую литературу, и позже прочтения вам будет довольно легко сориентироваться по данной программе.

3. Наблюдательно изучите названия значений формул в данном программном обеспечении, от того что при неправильном их вводе у вас могут испортиться сразу все итоги, в особенности это касается тех, кто исполняет сразу несколько идентичных вычислений по одной формуле единовременно.

4. Время от времени исполняйте проверку полученных в Microsoft Office Excel итогов вычисления. Это связано с тем, что в системе могли случиться какие-нибудь метаморфозы со временем, в частности это относится к тем, кто исполняет работу по образца. Неизменно нелишним будет ненужный раз сверить итоги сразу нескольких нынешних вычислений.

5. Также при работе с формулами будьте весьма осмотрительны и не допускайте происхождения в вашем компьютере вирусов. Даже в случае если операции с формулами в Microsoft Office Excel потребуется вам единоразово, изучите функционал данной программы в большей степени, от того что эти навыки помогут вам в будущем отменнее понимать автоматизацию учета и использовать Excel для выполнения определенных заданий.

jprosto.ru