Дифференциальные уравнения высших порядков без y
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Дан подробный пример решения такого уравнения.
Рассмотрим уравнение, не содержащие функцию в явном виде:
(1)
Порядок этого уравнения понижается на единицу с помощью подстановки:
Действительно, тогда:
…
И мы получили уравнение, в котором порядок понижен на единицу:
Пример
Решить уравнение:
Решение
Делаем подстановку:
Тогда:
Подставляем:
Разделяем переменные:
При u ≠ 0 имеем:
Интегрируем:
Или:
Отсюда:
Интегрируем:
Интегрируем еще раз:
Интегрируем по частям:
Окончательно имеем:
Заменим постоянную:
Теперь рассмотрим случай:
u = 0 также является решением исходного уравнения. Интегрируем:
Ответ
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Диф.уравнения
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Основные понятия
Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.
Общий вид дифференциальных уравнений: F (x,y,y’,y’’..y’’’) = 0
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения.
Процесс отыскания решения ДУ называется его интегрированием.
Дифференциальные уравнения первого порядка
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида F(x, y, y‘ )=0, где F
Уравнение y‘=f(x, y) устанавливает связь между координатами точки (x, y) и угловым коэффициентом y‘ касательной к интегральной кривой, проходящей через эту точку.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
P(x;
Где P(x;y) и Q(x;y) – известные функции. Уравнение P(x;y)dx+Q(x;y)dy=0 удобно тем, что переменные в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.
Если
дифференциальное уравнение первого
порядка y‘=f(x,
y),
имеет решение, то решений у него,
вообще говоря, бесконечно много и эти
решения могут быть записаны в виде y=φ(x,C),
где
Функция y=φ(x,C) называется общим решением дифференциального уравнения 1-го порядка. Она содержит одну произвольную постоянную и удовлетворяет условиям:
Функция y=φ(x,C) является решением ДУ при каждом фиксированном значении С.
Каково бы ни было начальное условие y(x0)= y0, можно найти такое значение постоянной С=С0 , что функция y=φ(x,C0) удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция y=φ(x,C0), полученная из общего решения y=φ(x,C) при конкретном значении постоянной С=С0.
Задача отысканиярешения ДУ первого порядка P(x;y)dx+Q(x;y)dy=0, удовлетворяющего заданному начальному условию y(x0)= y0 , называется задачей Коши.
Теорема (существования и единственности решения задачи Коши).
Если в уравнении y‘=f(x, y) функция f(x, y) и ее частная производная f‘y(x, y) непрерывны в некоторой области D, содержащей точку (x0 ; y0 ), то существкет единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию y(x0)= y0 . (без доказательства)
Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнение вида
В нем одно слагаемое зависит только от x, а другое – от y. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:
∫ P(x)dx+∫Q(y)dy=с – его общий интеграл.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:
P1(x) . Q1(y) . dx+ P
Особенность этого уравнения в том, что коэффициенты представляют собой произведения двух функций, одна из которых зависит только от х другая – только от у.
Уравнение P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0 легко сводится к уравнению P(x)
, – общий интеграл.
Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.
Функция y=φ(x,у) называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на λn, т.е.
f(λ
Дифференциальное уравнение y’= f(x, y) называется однородным, если функция f(x, y) есть однородная функция нулевого порядка.
Покажем, что однородное ДУ y’= f(x, y) можно записать в виде
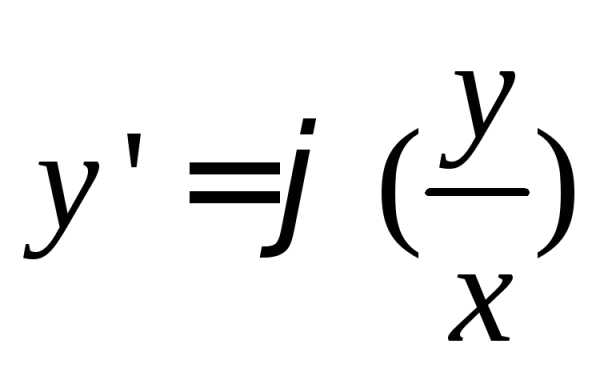
Если f(x, y)- функция нулевого порядка, то, по определению, f(x, y)= f
Положив  ,
получаем:
,
получаем:

Однородное
уравнение 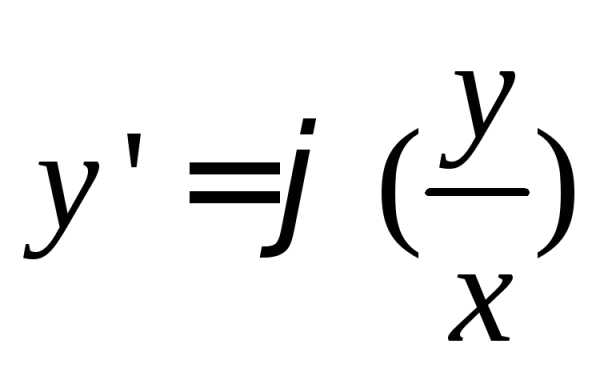 преобразуется в уравнение с разделяющимися
переменными при помощи замены переменной
(подстановки).
преобразуется в уравнение с разделяющимися
переменными при помощи замены переменной
(подстановки).
 или,
что то же самое, y=ux.
или,
что то же самое, y=ux.
Действительно,
подставив y=ux и y’=u’x+u в уравнение  ,
получаемu’x+
,
получаемu’x+
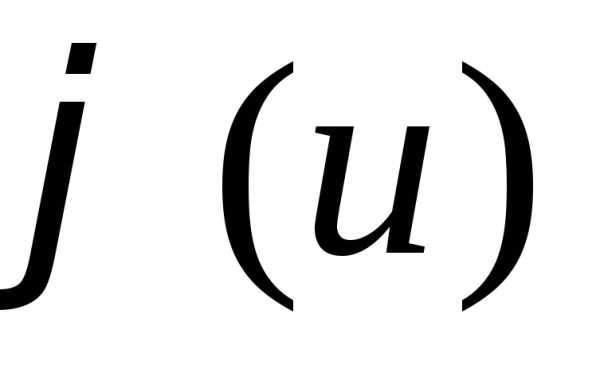 или
или 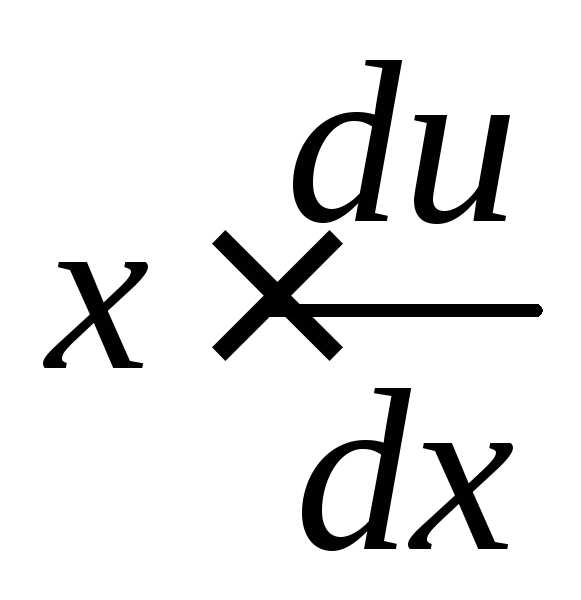 =
=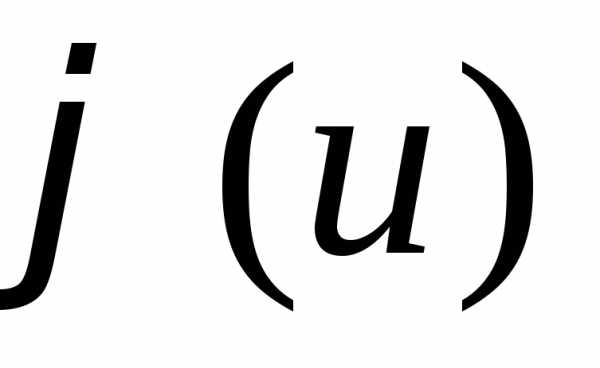 –u, т.е. уравнение с разделяющимися
переменными.
–u, т.е. уравнение с разделяющимися
переменными.Найдя
его общее решение (или общий интеграл),
следует заменить в нем u на 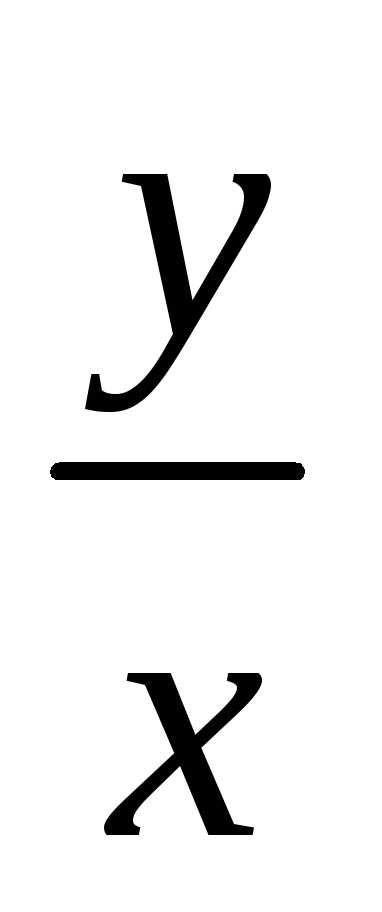 .
Получим общее решение (интеграл) исходного
уравнения.
.
Получим общее решение (интеграл) исходного
уравнения.
Однородное уравнение часто задается в дифференциальной форме:
P(x, y) dx + Q(x, y) dy = 0 Оно будет однородным, если P(x, y)
Переписав
уравнение P(x, y) dx + Q(x, y) dy = 0 в
виде  и применив в правой части рассмотренное
выше преобразование, получим уравнение
и применив в правой части рассмотренное
выше преобразование, получим уравнение .
.
Линейные уравнения. Уравнения Бернулли.
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде
y’+p(x) y
где p(x) и g(x) – заданные функции, в частности – постоянные.
Особенность ДУ y’+p(x) y=g(x): искомая функция y и ее производная y’ входят в уравнение в первой степени, не перемножаясь между собой.
Рассмотрим 2 метода интегрирования ДУ– метод Бернулли и метод Лагранжа.
Метод И.Бернулли
Решение уравнения y’+p(x) y=g(x) ищется в виде произведения двух других функций, т.е. с помощью подстановки y=uv, где u=u(x) и v=v(x) – неизвестные функции от x, причем одна из них произвольна (но не равна 0 – действительно любую функцию y(x) можно записать как
,
где 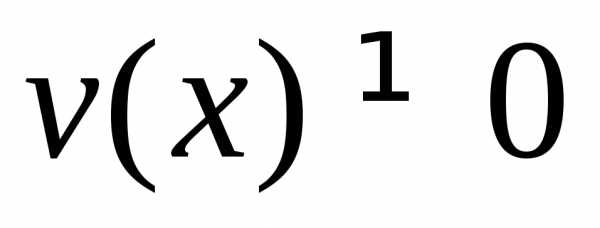 ).
Тогдаy’=u’ v+u v’.
Подставляя выражения y и y’ в уравнение y’+p(x) y=g(x), получаем: u’ v+u v’+p(x) u v=g(x) или
).
Тогдаy’=u’ v+u v’.
Подставляя выражения y и y’ в уравнение y’+p(x) y=g(x), получаем: u’ v+u v’+p(x) u v=g(x) или
u’ v+u (v’+p(x)v)=g(x).
Подберем функцию v=v(x) так, чтобы выражение в скобках было равно 0, т.е. решим ДУ v’+p(x) v=0.
Итак,  +p(x) v=0,
т.е.
+p(x) v=0,
т.е.  =-p(x) dx.
=-p(x) dx.
Интегрируя, получаем:
Ввиду свободы выбора функции v(x), можно принять с=1.
Отсюда 
Подставляя найденную функцию v в уравнение u’ v+u (v’+p(x)v)=g(x), получаем
u’ =g(x).
=g(x).
Получено уравнение с разделяющимися переменными. Решаем его:
, ,
Возвращаясь к переменной y, получаем решение
исходного ДУ y’+p(x) y=g(x).
Метод Лагранжа(метод вариации произвольной постоянной)
Уравнение y’+p(x) y=g(x) интегрируется следующим образом.
Рассмотрим соответствующее уравнение без правой части, т.е. уравнение y’+p(x) y=0. Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся:
 и
.
и
.
Таким
образом,  ,
т.е.
,
т.е.
или
,где
с= 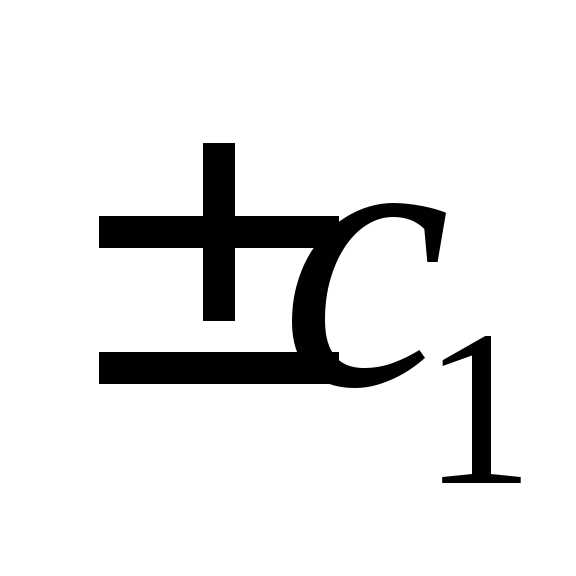
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяем функцией с(х), т.е. полагаем с=с(х).
Решение уравнения y’+p(x) y=g(x) ищем в виде
Уравнение Я.Бернулли
Уравнение вида
называется уравнением Бернулли. Покажем, что его можно привести к линейному.
Если n=0, то ДУ – линейное, а при n=1 – с разделяющимися переменными.
В
общем случае, разделив уравнение
на ,
получим:
,
получим:
.
Обозначим  =z.
Тогда z’=
=z.
Тогда z’=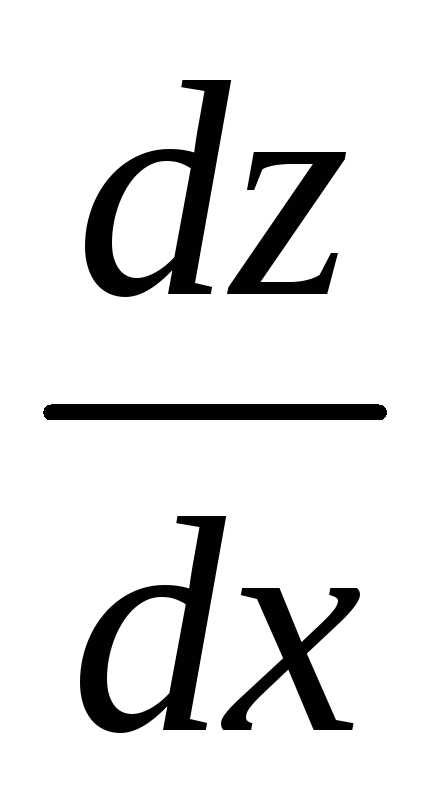 =(1-n)
=(1-n) 
 . Отсюда находим
. Отсюда находим 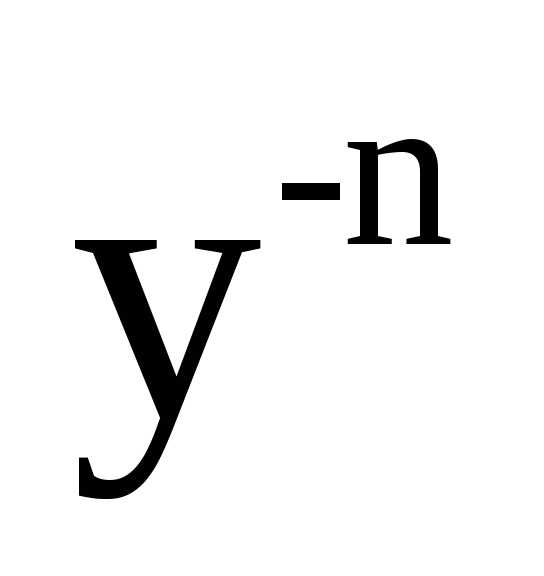
 =
= . Уравнение
принимает
вид
. Уравнение
принимает
вид
.
Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка
z= сводит уравнение
к линейному.
сводит уравнение
к линейному.
Уравнение в полных дифференциалах.
Уравнение P(x;y)dx+Q(x;y)dy=0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x;y), т.е. P(x;y)dx+Q(x;y)dy=du(x;y).
В этом случае ДУ P(x;y)dx+Q(x;y)dy можно записать в виде du(x;y)=0, а его общий интеграл будет:
u(x;y)=c.
Приведем условие, по которому можно судить, что выражение
Δ= P(x;y)dx+Q(x;y)dy
Есть полный дифференциал.
Теорема.
Для
того, чтобы выражение Δ= P(x;y)dx+Q(x;y)dy,
где функции P(x;y) и Q(x;y) и их частные производные  и
и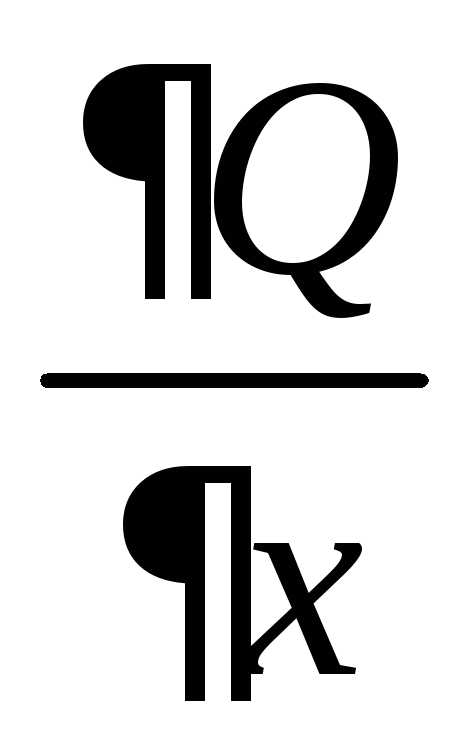 непрерывны в некоторой областиD плоскости Оху,
было полным дифференциалом, необходимо
и достаточно выполнение условия
непрерывны в некоторой областиD плоскости Оху,
было полным дифференциалом, необходимо
и достаточно выполнение условия
 =
= 
Необходимость
Пусть Δ есть полный дифференциал, т.е. P(x;y)dx+Q(x;y)dy=du(x;y).
Учитывая,
что du(x;y)=  dx+
dx+ 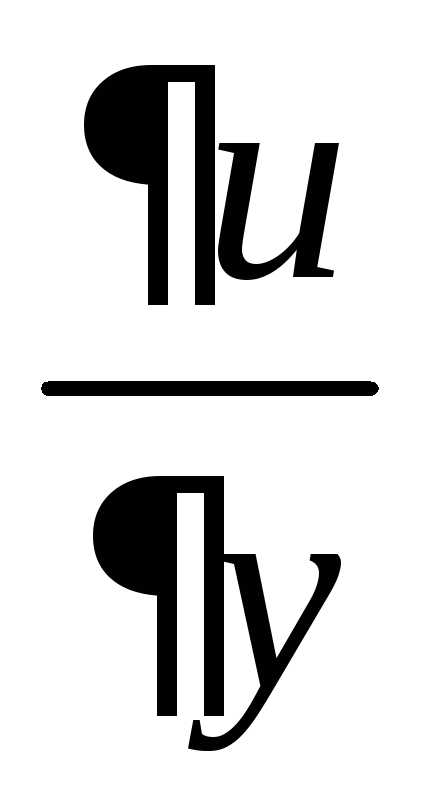 dy,
имеем:
dy,
имеем:
P(x;y)=  ;Q(x;y)=
;Q(x;y)= 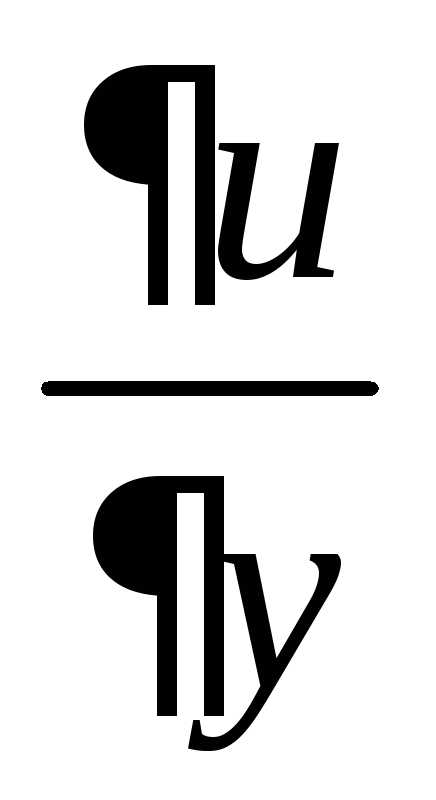 .
.
Дифференцируя эти равенства по у и по х соответственно, получаем
 =
= и
и =
= .
.
А
так как смешанные частные производные 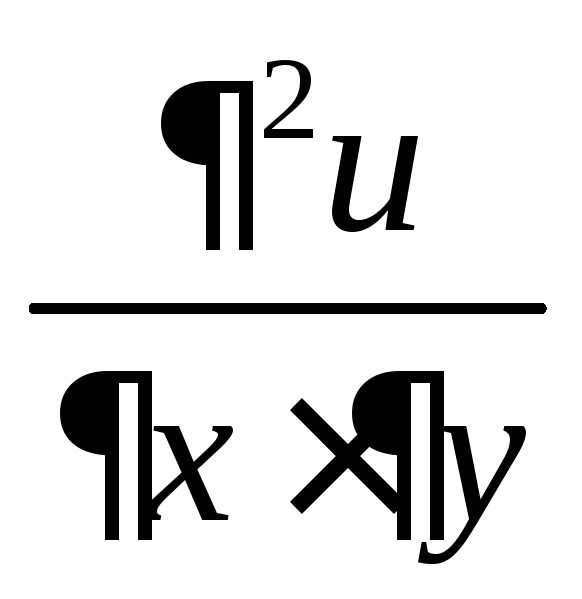 и
и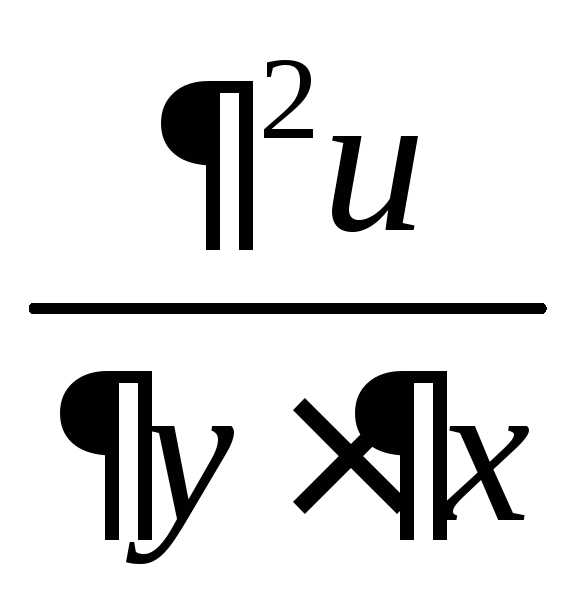 равны между собой, получаем
равны между собой, получаем =
= .
.
Достаточность
Пусть
в области D выполняется условие  =
= .
Покажем, что существует функцияu(x;y) в области D такая, что
.
Покажем, что существует функцияu(x;y) в области D такая, что
du(x;y)=P(x;y)dx+Q(x;y)dy.
Найдем эту функцию. Искомая функция должна удовлетворять требованиям:
 =P(x;y) и
=P(x;y) и  =Q(x;y).
=Q(x;y).
Если
в уравнении  =P(x;y) зафиксировать у и проинтегрировать его по х,
то получим:
=P(x;y) зафиксировать у и проинтегрировать его по х,
то получим:
u(x;y)= .
Здесь
произвольная постоянная с=  зависит
от у . В решении
зависит
от у . В решении
u(x;y)= не
известна лишь  .
Для ее нахождения продифференцируем
данную функцию поу:
.
Для ее нахождения продифференцируем
данную функцию поу:
.
Используя
второе равенство  =Q(x;y), можно записать:
=Q(x;y), можно записать:
.
Отсюда .
В этом равенстве левая часть зависит от у. Покажем, что и правая часть равенства зависит только от у.
Для этого продифференцируем правую часть по х и убедимся, что производная равна 0. Действительно,
= =
=в силу условия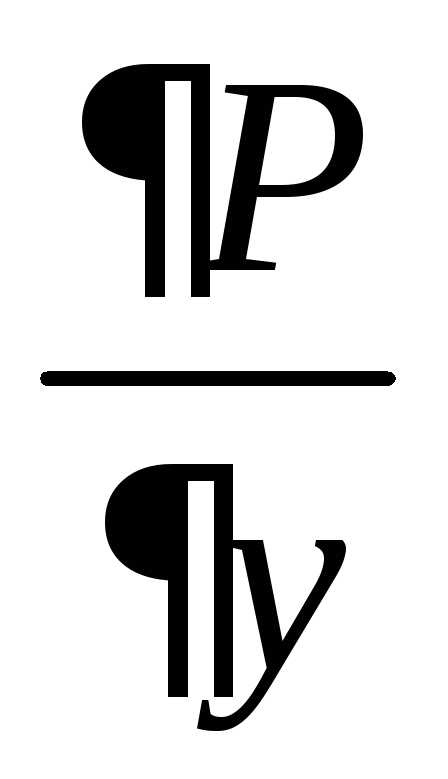 =
= .
.
Из
равенства
находим :
:
, с-const.
Подставляя
найденное значение для  в равенствоu(x;y)= ,
находим функциюu(x;y) такую, что du(x;y)=P(x;y)dx+Q(x;y)dy.
в равенствоu(x;y)= ,
находим функциюu(x;y) такую, что du(x;y)=P(x;y)dx+Q(x;y)dy.
Таким
образом, при решении ДУ вида P(x;y)dx+Q(x;y)dy=0 сначала проверяем выполнение условия  =
= .
Затем, используя равенства
.
Затем, используя равенства =P(x;y) и
=P(x;y) и  =Q(x;y), находим функцию u(x;y). Решение записываем в виде u(x;y)=с.
=Q(x;y), находим функцию u(x;y). Решение записываем в виде u(x;y)=с.
Дифференциальные уравнения высших порядков.
Основные понятия.
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде
F(x;y;y’;y’’)=0
Или, если это возможно, в виде, разрешенном относительно старшей производной:
y’’=f(x;y;y’).
РешениемДУ y’’=f(x;y;y’)называется всякая функцияу=  ,которая при подстановке в уравнение
обращает его в тождество.
,которая при подстановке в уравнение
обращает его в тождество.
Общим
решением ДУ y’’=f(x;y;y’) называется
функция у=  ,где
,где  и
и – не зависящие отх произвольные постоянные.
– не зависящие отх произвольные постоянные.
Аналогичные
понятия и определения имеют место для
ДУ n-го
порядка,
которое в общем виде записывается как F(x;y;y’;y’’;…; 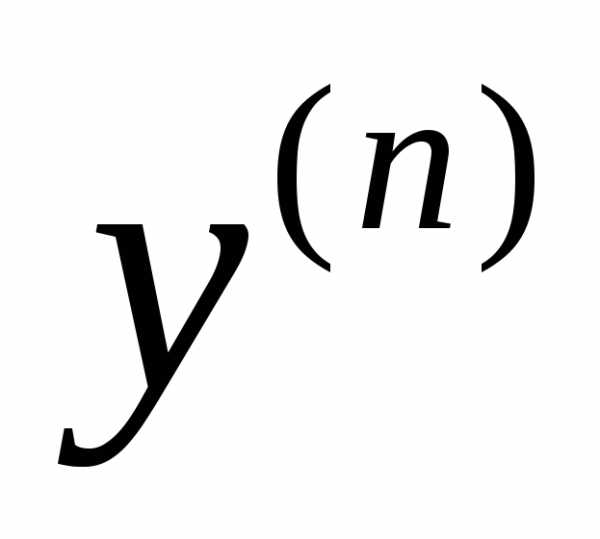 )=0.
)=0.
Уравнения, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим 3 типа уравнений, допускающих понижение порядка.
Пусть дано уравнение y’’=f(x). Порядок можно понизить, введя новую функцию p(x), положив y’=p(x). Тогда y’’=p’(x) и получаем ДУ первого порядка: p’=f(x). Решив его, т.е. найдя функцию р=р(х), решим уравнение у’=р(х). Получим общее решение заданного уравнения y’’=f(x).
Пусть дано уравнение y’’=f(x;y’), не содержащее явно искомой функции у.
Обозначим у’=р,
где р=р(х) – новая неизвестная функция. Тогда у’’=p’ и уравнение y’’=f(x;y’) принимает
вид р’=f(x;p). Пусть р= 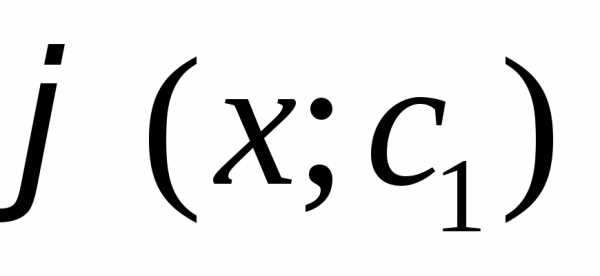 –
общее решение полученного
ДУ первого порядка. Заменяя функцию р на у’,
получаем ДУ: y’=
–
общее решение полученного
ДУ первого порядка. Заменяя функцию р на у’,
получаем ДУ: y’= 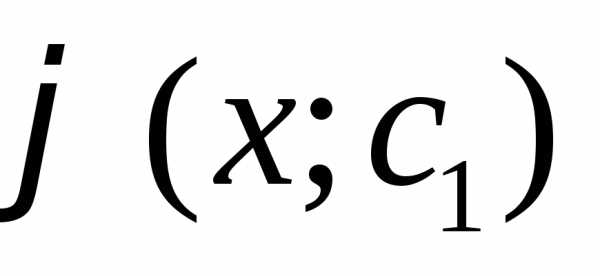 . Оно имеет вид y’’=f(x). Для отыскания у достаточно проинтегрировать
последнее уравнение. Общее решение
уравнения y’’=f(x;y’) будет иметь вид
. Оно имеет вид y’’=f(x). Для отыскания у достаточно проинтегрировать
последнее уравнение. Общее решение
уравнения y’’=f(x;y’) будет иметь вид
у= .
Частным
случаем уравнения y’’=f(x;y’) является уравнение y’’=f(y’), не содержащее также и независимую
переменную х.
Оно интегрируется тем же способом: y’=p(x), y’’=p’=  . Получаем уравнение p’=f(p) с
разделяющимися переменными.
. Получаем уравнение p’=f(p) с
разделяющимися переменными.
Рассмотрим уравнение y’’=f(y;y’), которое не содержит явно
независимой переменной х.
Для понижения порядка уравнения введем новую функцию р=р(у), зависящую от переменной у, полагая y’=p. Дифференцируем это равенство по х, учитывая, что р=р(у(х)):
,
т.е.  =
= .
Теперь уравнениеy’’=f(y;y’) запишется
в виде
.
Теперь уравнениеy’’=f(y;y’) запишется
в виде  =f(y;p).
=f(y;p).
Пусть р=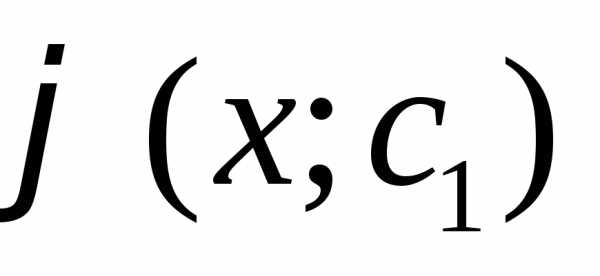 является общим решением этого ДУ первого
порядка. Заменяя функцию р(у) на y’,
получаем y’=
является общим решением этого ДУ первого
порядка. Заменяя функцию р(у) на y’,
получаем y’= – ДУ с разделяющимися переменными.
Интегрируя его, находим общий интеграл
уравнения y’’=f(y;y’):
– ДУ с разделяющимися переменными.
Интегрируя его, находим общий интеграл
уравнения y’’=f(y;y’):
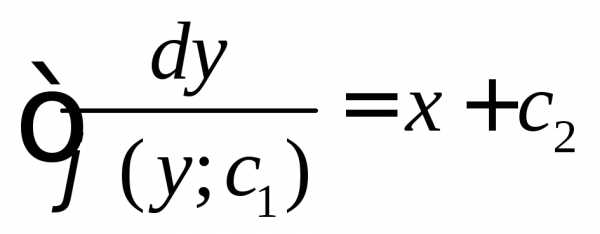 .
.
Частным
случаем уравнения y’’=f(y;y’) является ДУ y’’=f(y). Такое уравнение решается при помощи
аналогичной подстановки: y’=p(y), y’’= .
.
Линейные дифференциальные уравнения высших порядков.
Основные понятия
Уравнения вида
,
где – заданные функции (отх), называется линейным дифференциальным уравнением n-го порядка.
Оно содержит искомую функцию у и все ее производные лишь в первой степени. Функции называютсякоэффициентами уравнения, а функция g(x) – его свободным членом.
Если свободный член g(x)=0, то уравнение называетсялинейным однородным уравнением, иначе – неоднородным.
Разделив
уравнение
на и
обозначив
и
обозначив
запишем уравнение в видеприведенного:
Линейные однородные дифференциальные уравнения второго порядка
Рассмотрим ЛОДУ второго порядка:
И установим некоторые свойства его решений.
Теорема:
Если
функции  и
и являются частными решениями уравнения,
то решением этого уравнения является
также функция
являются частными решениями уравнения,
то решением этого уравнения является
также функция
studfiles.net
Дифференциальные уравнения Лекция 19. Дифференциальные уравнения первого порядка
План лекции
19.1. Задачи, приводящие к дифференциации уравнениям.
19.2. Основные понятия о дифференциальных уравнениях.
19.3. Уравнение первого порядка с разделяющимися переменными.
19.4. Однородные уравнения.
19.5. Дифференциальные уравнения, приводящиеся к однородным.
19.6. Линейные уравнения и уравнения Бернулли.
19.7. Дифференциальные уравнения в полных дифференциалах.
19.1
В различных областях науки и техники весьма часто выражаются задачи, для решения которых требуется решить одно или несколько уравнений, содержащих производные искомых функций. Такие уравнения называются дифференциальными. Рассмотрим несколько задач, приводящих к дифференциальным уравнениям.
Задание 1.на плоскости ХОУ найти кривую, проходящую через О(0;0), у которой угловой коэффициент касательной, проведен к любой точке кривой, равен удвоенной абсциссе точки касания.
Пусть у = f(x) – уравнение искомой кривой. По условию известно, что в каждой точке M(x;f(x)) есть касательная к этой кривой, угловой коэффициент которой, то есть f/(x) равняется 2х. Найти уравнение кривой.
Таким
образом, имеем 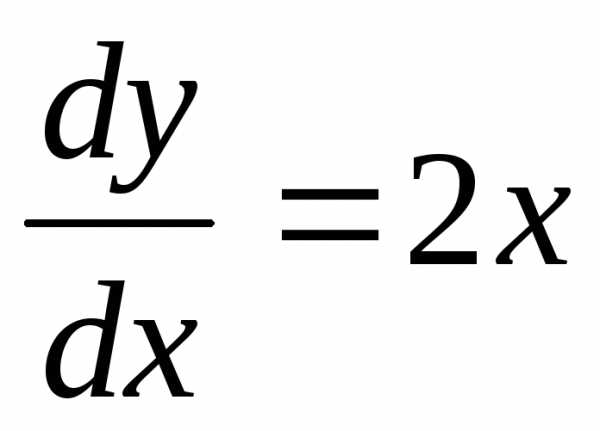 (1).
(1).
Из (1) следует, что y = f(x) есть первообразная для 2х. Следовательно, (2).
Из
(2) следует, что дифференциальное уравнение
(1) имеет бесконечное множество решений,
то есть уравнению (1) удовлетворяет не
одна кривая, а бесконечное множество
парабол. Чтобы из этого множества кривых
выбрать нужную кривую, надо воспользоваться
тем, что искомая кривая проходит через
точку О(0;0). Следовательно, координаты
О должны удовлетворять (2). Поэтому О
= О + С, то
есть С = О.
Значит, искомая кривая будет  .
.
Задание
2. Найти закон
уравнения свободного падающего в пустоте
тела, если пройденный путь начинает
отсчитываться от момента времени t = 0 и начальная
скорость падения равна нулю. Скорость
в этом случае выражается, как известно,
формулой 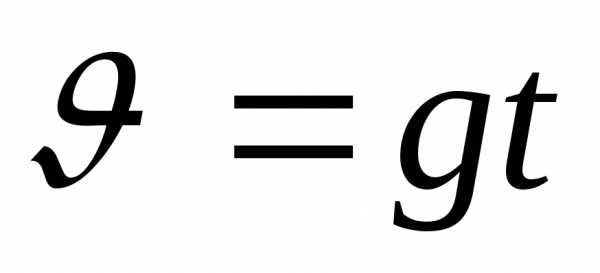 .
.
Решение.
 (3)
следовательно, S
– первообразная для gt,
следовательно
(3)
следовательно, S
– первообразная для gt,
следовательно 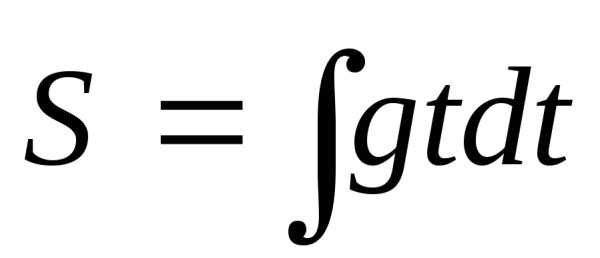 .
Имеем
.
Имеем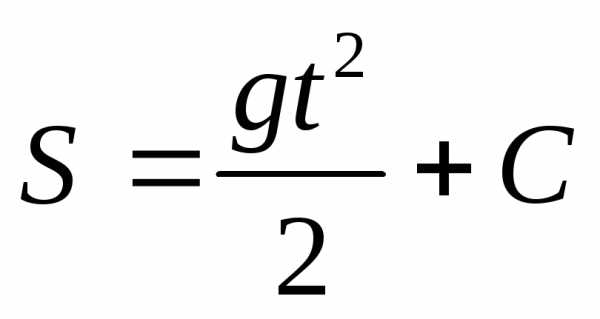 .следовательно,
то
.следовательно,
то ,
то есть
,
то есть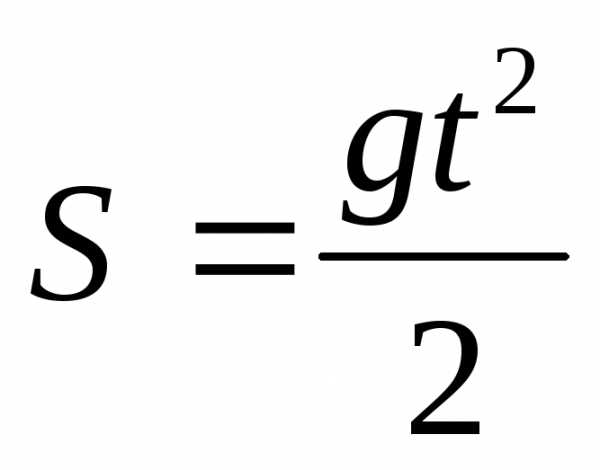 .
.
Задание 3. Пусть тело имеющее температуру Q0 в момент времени t=0, помещено в среду температуры Q(Q0>Q). Требуется найти закон, по которому изменяется температура тела в зависимости от времени. Искомая температура есть функция от времени, которую обозначают через Q(t).
Из функции известно, что скорость движения тела пропорциональна разности температур тела и окружающей среды. Учитывая, что функция Q(t) убывает, в силу максимального смысла произведения получаем , гдеk – коэффициент пропорциональности. ,.
Заметим, что уравнение (4) при Q=0 так же записывает радиоактивный распад.
В
рассмотренных задачах мы приходим к
дифференциации уравнения вида 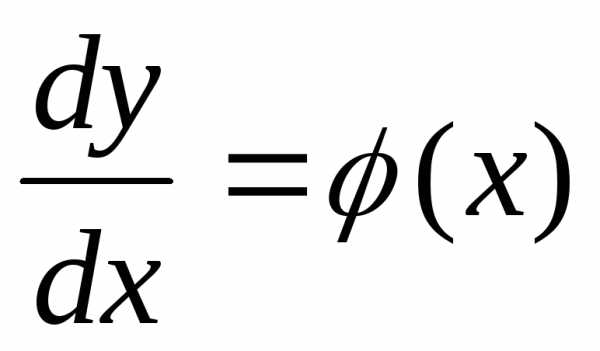 .
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются
гораздо более общими и сложными
дифференциальными уравнениями.
.
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются
гораздо более общими и сложными
дифференциальными уравнениями.
19.2.
Дифференциальным уравнением называется соотношение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного уравнения.
Общий вид дифференциального уравнения: F(x,y.y/,…y(n)) = 0 (1).
Причем F(x,y.y/,…y(n)) может не зависеть от некоторых величин x,y.y/,… Но если это уравнение n-го порядка, то от y(n) обязательно зависит.
Например, у/ + ху = 0, у//+2у/ = 1, 
1-го порядка 2-го порядка 1-го порядка.
Всякая
функция 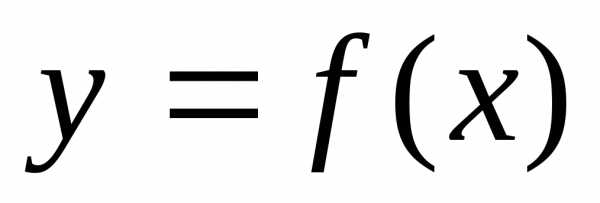 ,
которая, будучи подставлена в уравнение
(1), обращает его в тождество, называетсярешением
этого уравнения.
,
которая, будучи подставлена в уравнение
(1), обращает его в тождество, называетсярешением
этого уравнения.
График решения обыкновенного дифференциального уравнения n-го порядка будем называть интегральной кривой этого уравнения.
Например, является ли функция y = 1+2e-4x решением дифференциального уравнения а) , б). Найдему/ и у// и подставим у, у/, у// в данные уравнения:
,
а) б)
0 = 0 – верно – ложно.
Следовательно, данная функция решения дифференциального уравнения а) не является решением дифференциального уравнения б).
Дифференциальное уравнение первого порядка называется соотношение вида F(x,y,y/) = 0 (2) – в полном виде.
Относительно y/: – в явном или естественном его можно разрешить. (2/).
Решением дифференциального уравнения первого порядка называется функция , зависящая от переменойx и от произвольной постоянной C, обращающая уравнение (2) в верное равенство.
Иногда решение уравнения может быть получено и неявной форме: Ф(х,у,с) = 0 или Ф(х,у) = С.
Решить данное дифференциальное уравнение – значит найти его общее решение в той или иной форме.
Решение, которое получается из общего решения при котором фиксированном значение произвольной постоянной C, называется частным решением.
Частное решение выделяется из общего с помощью так называемого начального условия.
Условие, что при х = х0 функция у должна равняться заданному числу у0 называется начальным условием.
Пример. По общему решению дифференциального уравнения у = сх2 + х2sinx. Найти частное решение удовлетворяющее начальному условию
Тогда частное решение имеет вид: .
Общим решением дифференциального уравнения n-го порядка F(x,y,…y/) = 0(1) называется функция , зависящая отn произвольных постоянных и образующая уравнение (1) в тождество.
Решение, получаемое из общего при закреплении постоянных С1, С2,,….Сn называются частными.
Пусть при заданном значении х = х0 функция у и ее первые (n-1) производная принимают значения: . Эти условия называются начальными. С их помощью можно выделить из общего решения единственное частное решения.
Пример. По общему решению дифференциального уравнения . Найти частное отвечающее условию(так как в общем решении 2 постоянных, то это решение дифференциального уравнения 2-го порядка).
, ,
 ,
, ,
,
 –
частное решение.
–
частное решение.
Остановимся далее на отдельных видах дифференциальных уравнений и методах их решения.
19.3.
studfiles.net
