Дифференциал функции.
Дифференциалом аргумента называется его приращение dx = ∆x.
Дифференциалом функции называется произведение производной на приращение аргумента dy = f′(x)∙∆x или dy = f′(x)∙dx.
Замечание:
Сравнение дифференциала с приращением.
Пусть 
 ∆
∆
.dyи ∆xодного порядка малости, т. е.dyи ∆yодного порядка малости.
α∙∆x– бесконечно малая более высокого порядка малости, чем ∆x.
.Дифференциал есть главная часть приращения функции.
Дифференциал функции отличается от приращения функции на бесконечно малую
более высокого порядка, чем приращение аргумента.
Геометрический смысл дифференциала функции.
dy =f′(x)∙∆x=tgφ∙∆x=NT.
Дифференциал равен приращению ординаты касательной.
Свойства дифференциала.
Дифференциал суммы равен сумме дифференциалов.
d(u + v) = du + dv.
Дифференциал произведения d(u v) = du∙ v + u dv.
Дифференциал сложной функции.
y = f(u), u = φ(x), dy = y′xdx =
dy = f ′(u
Дифференциалы высших порядков.
dy = f ′(x)∙dx,
отсюда 

Гиперболические функции.
Во многих приложениях математического анализа встречаются комбинации показательных функций.
Определения.
Из определений гиперболических функций следуют соотношения:
ch2x–sh2x= 1,sh3x= 2shx∙chx,ch3x=ch2x+sh2x,sh(α±β) =shαchβ±chαshβ.Производные от гиперболических функций.
Теорема Ролля.
Если функция f(x) определена и непрерывна на замкнутом промежутке [a, b], имеет производную во всех внутренних точках этого промежутка и принимает на концах промежутка равные значения, то внутри промежутка найдется, по крайней мере, одна такая точка x = ξ, что
Геометрический смысл.
y
f(a) = f(b), kкас= 0.
A C B На гладкой дуге [a, b] найдется такая точка
f(a) f(b) С, в которой касательная параллельна хорде.
a ξ b x
Теорема Лагранжа (1736-1813, Франция).
Геометрический смысл теоремы Лагранжа.
Имеем гладкую дугу АВ.
На гладкой дуге АВ найдется такая точка С, в которой касательная параллельна хорде АВ.
Доказательство. Рассмотрим функциюF(x) = f(x) – λx. Подберем λ так, чтобы выполнялись условия теоремы Ролля.
F(x) – определена и непрерывна на [a, b], т.к. определена и непрерывна функцияf(x),.
F′(x)= f ′(x) – λ − существует,
Подберем λ так, чтобы выполнялись условия F(a) = F(b), т.е.
По теореме Ролля найдется такая точка x =ξЄ (a, b), чтоF′(ξ) = 0, т.е.
Возрастание и убывание функции.
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции.
Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции.
y y
f(x1) f(x2)f(x2)
x1 x2 x x1 x2 x
x1 < x2, f(x1) < f(x2) x1 < x2, f(x1) > f(x2)
возрастающая функция, убывающая функция.
Признаки возрастания и убывания.
Если
Если f′(x) < 0 всех x, принадлежащих интервалу (a, b), то f(x) убывает на этом интервале.
Доказательство. .
Причем x1<x2.
По теореме Лагранжа имеемf(x2)
–f(x
Аналогично для убывающей функции.
studfiles.net
Дифференциал функции
Если дана дифференцируемая функция $y = f(x)$, то ее приращение
Где $\alpha \to 0$ при $\Delta x\to 0$.
При $\Delta x\to 0$ величина $\alpha $$\Delta $х – бесконечно малая порядка выше, чем $\Delta $х. Из равенства $\Delta $y следует, что приращение функции, которая имеет производную в точке х, не равную нулю, может быть представлено в виде суммы двух слагаемых. В первое слагаемое f`(х) приращение $\Delta $х является приращением первой степени. Именно это слагаемое является главной частью приращения функции и называется ее дифференциалом.
Второе слагаемое выражения$\Delta y=f'(x)\Delta x+\alpha \Delta x$ при $\Delta x\to 0$ – бесконечно малая высшего порядка величина. Таким образом, разность $\Delta $y — dy между приращением функции и ее дифференциалом равная $\alpha $$\Delta $х — бесконечно малая величина высшего по сравнению с $\Delta $х порядка.
Для вычисления дифференциала функции необходимо задать начальное значение независимой переменной x и ее приращение. Если приращение слишком мало, а f `(x) не равно нулю, то величина $\alpha $$\Delta $х значительно меньше дифференциала функции, причем тем меньше, чем меньше $\Delta $х.
Поэтому в ряде случаев вычисление приращения функции заменяется вычислением дифференциала функции с некоторым приближением. Дифференциал функции вычисляется проще, т.к. требует нахождения лишь ее производной для расчета произведения с независимой переменной:
\[\Delta y\approx dy\]Поскольку
\[\Delta y=f(x+\Delta x)-f(x)\] \[dy=f'(x)\Delta x\]Наращенное значение функции имеет вид:
\[f(x+\Delta x)-f(x)\approx f'(x)\Delta x\]С помощью этой приближенной формулы можно находить приближенное значение функции в точке x + $\Delta $х ,близкой к х по известному значению функции.
Дифференцирование основных элементарных функций получается путем нахождения производной и добавления к ней переменной dx.
\[d(cu)=cdu\] \[d(u\pm v)=du\pm dv\] \[d(uv)=udv+vdu\] \[d\left(\frac{u}{v} \right)=\frac{vdu-udv}{v^{2} } \]Пример 2
Показать, что при $\Delta x\to 0$ с точностью до бесконечно малой высшего порядка имеет место приближенное равенство
\[(1+\Delta x)^{n} \approx 1+n\Delta x\]Решение.
Рассмотрим функцию $f(x) = x^n$. Тогда
\[\Delta y=(x+\Delta x)^{n} -x^{n} \] \[dy=nx^{n-1} \Delta x\]Поскольку $\Delta y\approx dy$, то:
\[(x+\Delta x)^{n} -x^{n} \approx nx^{n-1} \Delta x\] \[(x+\Delta x)^{n} \approx x^{n} +nx^{n-1} \Delta x\]Полагая, что х = 1, для достаточно малых приращений имеет место приближенное равенство
\[(1+\Delta x)^{n} \approx 1+n\Delta x\]Формула, полученная в примере 2, широко используется для приближенных вычислений.
\[(1+\Delta x)^{n} \approx 1+n\Delta x\]Например:
- Приближенно вычислить $(1,02)^3$
- Приближенно вычислить $\sqrt{1,005} $
Где $\Delta х = 0,03, n = 5$
\[(1,02)^{3} \approx 1+0,02\cdot 3\]Где $\Delta $х = 0,03, n = 5
\[(1,02)^{3} \approx 1,06\]Где $\Delta х = 0,005, n =0,5$
\[\sqrt{1,005} \approx 1+0,5\cdot 0,005\] \[\sqrt{1,005} \approx 1,0025\]Пример 3
При нагревании объем твердого тела растет пропорционально кубу его линейного расширения. Если $\alpha $ — коэффициент объемного расширения, а t — температура, то имеет место формула
\[1+\beta t=(1+\alpha t)^{3} \]Доказать, что
\[\beta \approx 3\alpha \]Доказательство.
При малых $\alpha $
\[(1+\alpha t)^{3} \approx 1+3\alpha t\]Значит, $1+\beta t=1+3\alpha t$ и $\beta \approx 3\alpha $
spravochnick.ru
Дифференциал (математика) — Википедия РУ
Обозначения
Использование знака дифференциала
Определения
Для функций
Дифференциал функции f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } в точке x0∈R{\displaystyle x_{0}\in \mathbb {R} } может быть определён как линейная функция
- dx0f(h)=f′(x0)h,{\displaystyle d_{x_{0}}f(h)=f'(x_{0})h,}
где f′(x0){\displaystyle f'(x_{0})} обозначает производную f{\displaystyle f} в точке x0{\displaystyle x_{0}} , а h{\displaystyle h} — приращение аргумента при переходе от x0{\displaystyle x_{0}} к x0+h{\displaystyle x_{0}+h} .
Таким образом df{\displaystyle df} есть функция двух аргументов df:(x0,h)↦dx0f(h){\displaystyle df\colon (x_{0},h)\mapsto d_{x_{0}}f(h)} .
Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция dx0f(h){\displaystyle d_{x_{0}}f(h)} , линейно зависящая от h{\displaystyle h} , и для которой верно следующее соотношение
- dx0f(h)=f(x0+h)−f(x0)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}
Для отображений
Дифференциалом отображения f:Rn→Rm{\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} в точке x0∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} называют линейный оператор dx0f:Rn→Rm{\displaystyle d_{x_{0}}f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} такой, что выполняется условие
- dx0f(h)=f(x0+h)−f(x0)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}
Связанные определения
- Отображение f:Rn→Rm{\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} называется дифференцируемым в точке x0∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} если определён дифференциал dx0f:Rn→Rm{\displaystyle d_{x_{0}}f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} .
Свойства
История
Термин «дифференциал» введён Лейбницем. Изначально dx{\displaystyle dx} применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.
Вариации и обобщения
Понятие дифференциала содержит в себе больше, чем просто дифференциал функции или отображения. Его можно обобщать получая различные важные объекты в функциональном анализе, дифференциальной геометрии, теории меры, нестандартном анализе, алгебраической геометрии и так далее.
Литература
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления»
http-wikipediya.ru
Как найти дифференциал. Типовые задачи дифференциирования
Дифференциал… Для одних это прекрасное далёкое, а для других – непонятное слово, связанное с математикой. Но если это ваше суровое настоящее, наша статья поможет узнать, как правильно “приготовить” дифференциал и с чем его “подавать”.
1
Под дифференциалом в математике понимают линейную часть приращения функции. Понятие дифференциала неразрывно связано с записью производной согласно Лейбница f′(x0) = df/dx·x0. Исходя из этого, дифференциал первого порядка для функции f, заданной на множестве X, имеет такой вид: dx0f = f′(x0)·dx0x. Как видите, для получения дифференциала нужно уметь свободно находить производные. Поэтому нелишним будет повторить правила вычисления производных, дабы понимать, что будет происходить в дальнейшем.
2
Итак, рассмотрим дифференцирование поближе на примерах. Нужно найти дифференциал функции, заданной в таком виде: y = x3-x4. Сначала найдём производную от функции: y′= (x3-x4)′ = (x3)′-(x4)′ = 3x2-4x3. Ну, а теперь получить дифференциал проще простого: df = (3x3-4x3)·dx. Сейчас мы получили дифференциал в виде формулы, на практике зачастую также интересует цифровое значение дифференциала при заданных конкретных параметрах х и ∆х.
3
Бывают случаи, когда функция выражена неявно через х. Например, y = x²-yx. Производная функции имеет такой вид: 2x-(yx)′. Но как получить (yx)′? Такая функция называется сложной и дифференцируется согласно соответствующего правила: df/dx = df/dy·dy/dx. В данном случае: df/dy = x·yx-1, а dy/dx = y′. Теперь собираем всё воедино: y′ = 2x-(x·yx-1·y′). Группируем все игреки в одной стороне: (1+x·yx-1)·y′ = 2x, и в итоге получаем: y′ = 2x/(1+x·yx-1) = dy/dx. Исходя из этого, dy = 2x·dx/(1+x·yx-1). Конечно, хорошо, что такие задания встречаются нечасто. Но теперь вы готовы и к ним.
4
Кроме рассмотренных дифференциалов первого порядка, ещё существуют дифференциалы высшего порядка. Попробуем найти дифференциал для функции d/d(x3)·(x3–2x6–x9), который и будет дифференциалом второго порядка для f(x). Исходя из формулы f′(u) = d/du·f(u), где u = f(x), примем u = x3. Получаем: d/d(u)·(u-2u2-u3) = (u-2u2-u3)′ = 1-4u-3u2. Возвращаем замену и получаем ответ – 1–x3–x6, x≠0.
5
Помощником в нахождении дифференциала также может стать онлайн-сервис. Естественно, что на контрольной или экзамене им не воспользуешься. Но при самостоятельной проверке правильности решения его роль сложно переоценить. Кроме самого результата, он также показывает промежуточные решения, графики и неопределённый интеграл дифференциальной функции, а также корни дифференциального уравнения. Единственный недостаток – это запись в одну строку функции при вводе, но со временем можно привыкнуть и к этому. Ну, и естественно, такой сервис не справляется со сложными функциями, но всё, что попроще, ему по зубам.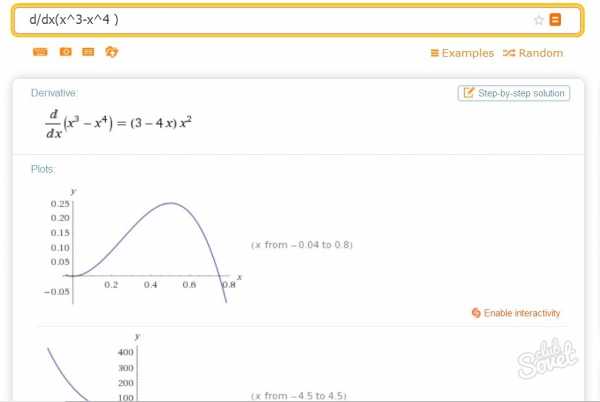
6
Практическое применение дифференциал находит в первую очередь в физике и экономике. Так, в физике зачастую дифференцированием решаются задачи, связанные с определением скорости и её производной – ускорения. А в экономике дифференциал является неотъемлемой частью расчёта эффективности деятельности предприятия и фискальной политики государства, например, эффекта финансового рычага.
В этой статье рассмотрены типовые задачи дифференцирования. Курс высшей математики учащихся ВУЗов зачастую содержит ещё задания на использование дифференциала в приближенных вычислениях, а также поиск решений дифференциальных уравнений. Но главное – при чётком понимании азов вы с лёгкостью расправитесь со всеми новыми задачами.
sovetclub.ru
Дифференциал (математика)
Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.
Содержание
- 1 Обозначения
- 2 Использование знака дифференциала
- 3 Определения
- 3.1 Для функций
- 3.2 Для отображений
- 4 Связанные определения
- 5 Свойства
- 6 История
- 7 Вариации и обобщения
- 8 Литература
Обозначения
Обычно дифференциал функции обозначается . Некоторые авторы предпочитают обозначать шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.
Дифференциал в точке обозначается , а иногда или , а также , если значение ясно из контекста.
Соответственно, значение дифференциала в точке от может обозначаться как , а иногда или , а также , если значение ясно из контекста.
Использование знака дифференциала
- Знак дифференциала используется в выражении для интеграла . При этом иногда (и не вполне корректно) дифференциал вводится как часть определения интеграла.
- Также знак дифференциала используется в обозначении Лейбница для производной . Это обозначение мотивировано тем, что для дифференциалов функции и тождественной функции верно соотношение
Определения
Для функций
Дифференциал функции в точке может быть определён как линейная функция
где обозначает производную в точке .
Таким образом есть функция двух аргументов .
Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция , линейно зависящая от , и для которой верно следующее соотношение
Для отображений
Дифференциалом отображения в точке называют линейный оператор такой, что выполняется условие
Связанные определения
- Отображение называется дифференцируемым в точке если определён дифференциал .
Свойства
- Матрица линейного оператора равна матрице Якоби; её элементами являются частные производные .
- Отметим, что матрица Якоби может быть определена в точке, где дифференциал не определён.
- Дифференциал функции связан с её градиентом следующим определяющим соотношением
История
Термин «дифференциал» введён Лейбницем. Изначально применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.
Вариации и обобщения
- Дифференциалы высших порядков
- Внешний дифференциал
- Дифференциал (дифференциальная геометрия)
- Производная Пеано
- Производная Фреше
Литература
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления»
| Дифференциальное исчисление | |||||||
|---|---|---|---|---|---|---|---|
| Основное | Производная • Дифференциал • Производная по направлению • Частная производная • Полная производная функции • Логарифмическая производная • Матрица Якоби • Матрица Гессе • Дифференциальная форма • Дифференциальное уравнение | ||||||
| Частные виды | Абелев дифференциал • Производная Ли • Производная Дини • Производная Пинкерля • Производная Римана • Ковариантная производная • Производная Пеано • Производная Радона — Никодима | ||||||
| Дифференциальные операторы (в различных координатах) |
| ||||||
| Связанные темы | Численное дифференцирование • Вариационное исчисление • Интеграл • Ряд Тейлора | ||||||
Дифференциал (математика) Информацию О
Дифференциал (математика) Комментарии
Дифференциал (математика)
Дифференциал (математика)
Дифференциал (математика) Вы просматриваете субъект
Дифференциал (математика) что, Дифференциал (математика) кто, Дифференциал (математика) описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Дифференциал – это… Что такое Дифференциал?
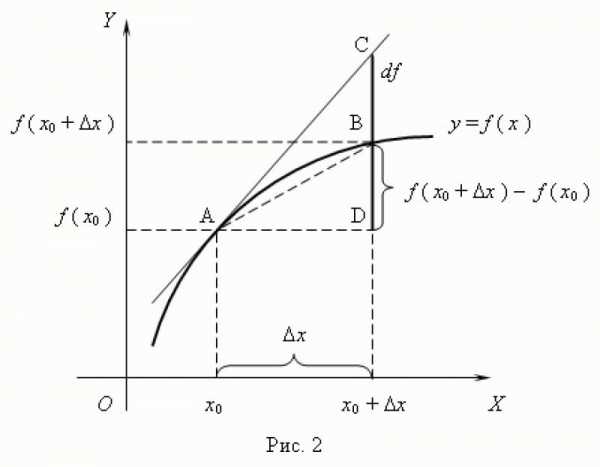
в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0 производную, то приращение
Δy = f (x0 + Δx) – f (x0)
функции f (x) можно представить в виде
Δy = f’ (x0) Δx + R,
где член R бесконечно мал по сравнению с Δх. Первый член
dy = f’ (x0) Δх
в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство
Δy = dy + R
показывает, в каком смысле Д. dy является главной частью приращения Δy.
Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало которому положили в начале 20 в. французские математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия «дифференциал» для функций нескольких переменных, а в применении к Функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления (См. Вариационное исчисление).Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L (x) векторного аргумента х называется линейной, если она непрерывна и удовлетворяет равенству
L (x’ + х “) = L (x’) + L (x “)
для любых х’ и х “ из области определения. Линейная функция n-мерного аргумента х = {x1,…, xn} всегда имеет вид
L (x) = a1x1 +… + anxn,
где a1,…, an — постоянные. Приращение
ΔL = L (x + h) – L (x)
линейной функции L (x) имеет вид
ΔL = L (h),
т. е. зависит только от векторного приращения h, и притом линейно. Функция f (x) называется дифференцируемой при значении аргумента х, если её приращение Δf = f (x + h) – f (x), рассматриваемое как функция от h, имеет главную линейную часть L (h), т. е. выражается в виде
Δf = L (h) + R (h),
где остаток R (h) при h → 0 бесконечно мал по сравнению с h. Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.
В случае f (x) ≡ x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента x и обозначать dx.
Если сделать теперь переменной точку x, в которой определяется Д. df, то он будет функцией двух переменных:
df (x; h).
Далее, считая h = h1 постоянным, можно найти Д. от дифференциала df (x; h1) как главную часть приращения
df (x + h2; h1) — df (x; h1),
где h2 — некоторое второе, не связанное с h1 приращение x. Получаемый таким образом второй дифференциал d2f = d2f (x; h1, h2) является функцией трёх векторных аргументов x, h1 и h2, линейной по каждому из двух последних аргументов. Если d2f непрерывно зависит от x, то он симметричен относительно h1 и h2:
d2f (x; h1, h2) = d2f (x; h2, h1).
Аналогично определяется дифференциал dnf = dnf (x; h1,…, hn) любого порядка n.
В вариационном исчислении сам векторный аргумент x является функцией x (t), а дифференциалы df и d2f функционала f [x (t)] называются его первой и второй вариациями и обозначаются δf и δ2f.
Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
А. Н. Колмогоров.
dic.academic.ru
Дифференциал, Свойства дифференциала | univer-nn.ru
Основные дифференциалы
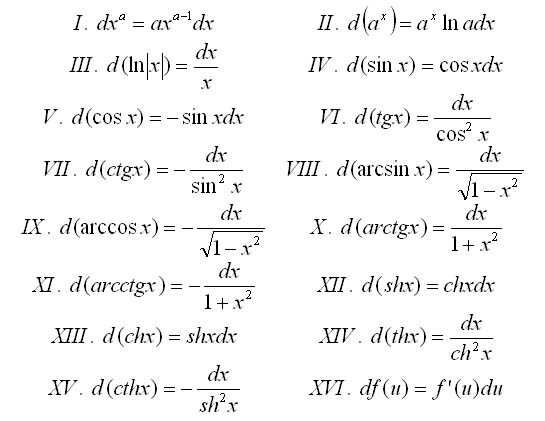 Дифференциал функции обладает свойствами, аналогичными свойствам производной.
Дифференциал функции обладает свойствами, аналогичными свойствам производной.- Дифференциал постоянной равен нулю:dc = 0, с = const.
- Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
d(u+v)=du + dv
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
d(u+c) = du (c= const). - Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
d(uv) = udv + vdu.
Следствие. Постоянный множитель можно выносить за знак дифференциала
d(cu) = cdu (с = const). - Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
- Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Дифференциалы высших порядков.
Если х — независимая переменная и y = f(x) — дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом).
Считая dx постоянной, получаем, что df(x) — функция одной переменной. Предположим, что функция у = f(x) имеет не только первую производную, но и n последовательных производных y» = f»(x), y’” = f”’(x).
Дифференциал от дифференциала функции у = f{x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y = d(dy), причем
Дифференциалом n-го порядка Смотрите пример вычисления дифференциалов первого и второго порядковПомощь в решении задач по математике Вам окажут тут
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
univer-nn.ru
