Дифракция атомов и молекул – это… Что такое Дифракция атомов и молекул?
- Дифракция атомов и молекул
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Дифракция
- Дифракция нейтронов
Смотреть что такое “Дифракция атомов и молекул” в других словарях:
ДИФРАКЦИЯ ЧАСТИЦ — упругое когерентное рассеяние микрочастиц объектами (т. е. рассеяние, происходящее без изменения рассеивающего объекта), при к ром из нач. пучка частиц возникают отклонённые от него дифракц. пучки. Д. ч. имеет место при рассеянии нейтронов,… … Физическая энциклопедия
Дифракция волн — (лат. diffractus буквально разломанный, переломанный) явление, которое можно рассматривать как отклонение от законов геометрической оптики при распространении волн. Первоначально понятие дифракции относилось только к огибанию волнами… … Википедия
ДИФРАКЦИЯ МИКРОЧАСТИЦ — рассеяние эл нов, нейтронов, атомов и др. микрочастиц кристаллами или молекулами жидкостей и газов, при к ром из нач. пучка ч ц возникают дополнительные отклонённые пучки этих ч ц. Направление и интенсивность таких отклонённых пучков зависят от… … Физическая энциклопедия
Дифракция частиц — рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц; направление и… … Большая советская энциклопедия
МОЛЕКУЛ СТРОЕНИЕ
Дифракция рентгеновских лучей — рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских… … Большая советская энциклопедия
Дифракция — первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных макси … Википедия
Дифракция электронов — Дифракция электронов процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет волновые свойства. Данное явление называется корпускулярно волновым дуализмом, в том смысле, что частица вещества(в данном… … Википедия
ДИФРАКЦИЯ ЧАСТИЦ — рассеяние потока микрочастиц (электронов, нейтронов, атомов, молекул и др.) кристаллами или молекулами жидкостей и газов с образованием чередующихся максимумов и минимумов в интенсивности рассеянного пучка. Дифракция частиц аналогична дифракции… … Большой Энциклопедический словарь
ДИФРАКЦИЯ — явление, наблюдаемое при прохождении любых волн (световых, электромагнитных, рентгеновских, звуковых) через отверстия в преградах (или возле краёв последних) и заключающееся в огибании волнами преград, при этом происходит проникновение волны в… … Большая политехническая энциклопедия
dic.academic.ru
Дифракция | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Дифракция — это огибание волнами препятствий. В случае света
Дифракция — это любые отклонения в распространении световых волн от законов геометрической оптики, в частности это проникновение света в область геометрической тени.
Иногда используют более широкое определение:
Дифракцией называется совокупность явлений, которые наблюдаются при распространении волн в среде с резкими неоднородностями.
Классический пример дифракции — прохождение сферической световой волны через маленькое круглое отверстие, когда на экране вместо освещенного круга с четкими границами наблюдается светлый круг с размытыми границами, испещренный чередующимися темными и светлыми кольцами.
Изменяя диаметр отверстия, мы увидим, что картинка на экране будет меняться, в частности, в центре освещенного круга будет появляться и исчезать темное пятно. Объяснение этому явлению дал Френель. Он разбил волновой фронт на зоны так, что расстояния от соседних зон до точки наблюдения отличаются на полдлины волны. Тогда вторичные волны, приходящие от соседних зон, гасят друг друга. Поэтому если в отверстии помещается четное число зон, то в центре освещенного круга будет темное пятно, если нечетное — светлое.
| Каждая точка волнового фронта в момент времени t является источником вторичных волн, огибающая которых является фронтом волны в момент времени t + Δt |
Дифракционная решетка — это оптический прибор, представляющий собой пластину, на которую нанесено большое количество регулярно расположенных штрихов. Вместо штрихов на пластине могут быть регулярно расположенные щели, или канавки, или выступы.
Дифракционная картинка, получающаяся на таких периодических структурах, имеет вид чередующихся максимумов и минимумов различной интенсивности. Материал с сайта http://worldofschool.ru
| В результате дифракции на щели AB плоский фронт волны приобретает кривизну |
Дифракционные решетки используются в спектральных приборах. Их назначение — изучение спектрального состава электромагнитного излучения. Для работы в ультрафиолетовой области применяются решетки, у которых на 1 мм приходится 3600—1200 штрихов, в видимой — 1200—600 штрихов/мм, в инфракрасной — 300 и меньше штрихов/мм. Для ультракоротких рентгеновских волн дифракционную решетку создала природа — это кристаллическая решетка твердых тел.
Волны с большей длиной дифрагируют сильнее, поэтому при прохождении препятствия красные лучи больше отклоняются от прямолинейного пути, чем синие. При падении белого света на призму лучи в результате дисперсии отклоняются в обратном порядке. Скорость света красных лучей в стекле больше, а соответственно и коэффициент преломления меньше, чем синих. В результате красные лучи меньше отклоняются от первоначального направления.
Дифракция клетки
Дифракция краткое сообщение по физики
Физика оптика кратко
Дифракция сообщение
Дифракция краткое определение
worldofschool.ru
Дифракция – Всё для чайников
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Экология
- Обществознание – как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Естествознание
forkettle.ru
Дифракция – Справочник химика 21
Приборы, регистрирующие дифракцию рентгеновских лучей. В настоящее время применяются два метода регистрации рентгеновских лучей фотографический метод, использующий специальную фотопленку типа РТ, [c.115]Информацию о строении вещества получают на основании изучения его физических и химических свойств. Особую роль при изучении структуры играют исследования спектров поглощения и испускания, дифракции различных излучений, магнитных и электрических взаимодействий, механических, термических, электрических и других характеристик веществ. [c.140]
Рис 63, Дифракция рентгеновских лучей [c.112]
В последнее время созданы рентгеновские установки, автоматически расшифровывающие рентгенограммы и даже воспроизводящие стереоскопический чертеж структуры исследуемого вещества. Для этого с помощью фотоэлемента регистрируются рентгеновские лучи, претерпевшие дифракцию на кристаллической решетке исследуемого вещества. Импульсы фотоэлемента автоматически кодируются и вводятся в электронно-вычислительную машину. На основании этой информации машина создает модель одной из возможных структур и затем делает обратный расчет, т. е. по структуре рассчитывает рентгенограмму. В случае несовпадения рассчитанной и эксперимен- [c.151]
Прохождение рентгеновских лучей через кристаллическое вещество сопровождается отклонением их от первоначального направления. Это явление называется дифракцией рентгеновских лучей. [c.111]
Явления дифракции и интерференции электромагнитного излучения (света, радиоволн, у-лучей, рентгеновских лучей и пр.) убедительно доказывают его волновую природу. В то же время электромагнитное излучение обладает энергией, массой, производит давление и т. д. Так, вычислено, что за год масса Солнца уменьшается за счет излучения на J,5-10 кг. [c.11]
Со1 ласно соотношению (2) с движением электрона (масса 9,1 х X Ю З кг, скорость порядка 10 м/с) ассоциируется волна длиной порядка 10″ м, т. е. ее длина соизмерима с размерами атомов. Поэтому при рассеянии электронов кристаллами наблюдается дифракция, причем кристаллы выполняют роль дифракционной решетки, [c.11]
Встречаясь с молекулами, электроны дифрагируют. Результат дифракции регистрируется на фотографической пластинке в виде электронограммы. [c.153]
Изучение дифракции рентгеновских лучей дает информацию о пространственной решетке вещества. Количественно они дают внутриатомное расстояние в кристаллах и более грубо — в жидкостях. Кроме того, на регулярность ориентации указывает разность линий и колец. Дифракционные спектры рентгеновских лучей жидкостей показывают лишь расстояние, при которых молекулы размещены более регулярно — с некоторым указанием на основную молекулярную структуру. Испытание некоторых простых [c.187]
Судя по данным электронной дифракции [71] и некоторым другим, циклобутановое кольцо также неплоское [c.43]
С другой стороны, результаты рентгенографических исследований кристал-лического парафина [35, 30, 22, 61, 66] и данные по дифракции [c.227]
Следовательно, отражения от данного семейства атомных плоскостей каждого кристаллика, находящегося в пучке рентгеновских лучей, будут сливаться в одну сплошную конусную поверхность (конус дифракции), количество таких конусов будет соответствовать количеству семейств атомных плоскостей (рис. 65). [c.114]
Применение дифракции рентгеновских лучей для изучения твердых катализаторов. [c.417]
III-7. Дифракция рентгеновских лучей абсорбционный и эмиссионный спектры (приблизительная длина волны 10 — 10 см) [c.187]
Изменение расстояний при дифракции от скорости охлаждения в интервале плавления было впервые отмечено Кларком [41]. [c.517]
Оказалось также, что уравнение де Бройля справедливо не только для электронов и фотонов, но и для любых других микрочастиц. Так, для определения структуры веществ используется явление дифракции нейтронов (об этих элементарных частицах см, 35), [c.70]
Исследовать внутреннюю структуру кр [ сталлов удалось в XX веке, после того, как в 1912 г. была открыта дифракция рентгеновских лучей, на которой основан р е и т г е и о с т р у к т у р и ы й анализ. [c.160]
ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ [c.111]
Какие из описанных ниже экспериментов самым непосредственным образом подтверждают гипотезу де Бройля о волновых свойствах материи а) дифракция рентгеновских лучей б) фотоэлектрический эффект в) рассеяние альфа-частиц при прохождении через металлическую фольгу г) излучение абсолютно черного тела д) дифракция электронов [c.380]
Наиболее удобными методами изучения кластеров (НгО) (л>2) являются различные варианты масс-спектроскопической техники [363]. Естественно, что чем ниже температура эксперимента, тем более крупные кластеры (с большим п) удается наблюдать. Так, удалось зарегистрировать в спектре пик, соответствующий п= [368] и /г = 36 (температура 77 К) [369]. При температуре жидкого азота были зарегистрированы положительно заряженные кластеры с л от 1 до 40 [370]. В работе [371] удалось наблюдать отрицательно заряженные кластеры, содержащие вплоть до 50 молекул воды. В этой работе была сделана попытка изучить структуру этих кластеров методом электронной дифракции. Авторы приходят к выводу, что по своей структуре эти кластеры не являются фрагментами кристаллов льда, а аморфны. Были также оценены дипольные моменты кластеров с л от 2 до 6 дипольные моменты кластеров с п = = 3- 6 близки к нулю, что, по мнению авторов, свидетельствует о циклическом характере их структуры [361]. Много экспериментальных данных о существовании и свойствах кластеров, состоящих из нескольких десятков молекул воды, приводится в работе [372]. [c.133]
В 1927 г. Дэвиссон и Джермер продемонстрировали, что при прохождении металлической фольги электроны дают точно такую же дифракционную картину, как и рентгеновские лучи, и что соотношение де Бройля правильно определяет длину волны пучка электронов (рис. 8-16). В настоя-шее время электронная дифракция превратилась в распространенный способ исследования строения молекул. [c.355]
Исследования дифракции электронов обычно проводятся с ускорением электронов в поле с разностью потенциалов 40000 В, в результате чего электроны приобретают энергию 40000 эВ. Какую длину волны имеют такие электроны [c.356]
Полинг считал, что предложенную им спиральную модель молекулы можно распространить и на нуклеиновые кислоты. В начале 50-х годов английский физик Морис Хью Фредерик Уилкинс (род. в 1916 г.) изучал нуклеиновые кислоты методом дифракции рентгеновских лучей, и результаты его работы можно было использовать для проверки справедливости предположения Полинга. Английский физик Фрэнсис Гарри Комптон Крик (род. в 1916 г.) и американский химик Джеймс Дьюи Уотсон (род. в 1928 г.) установили, что удовлетворительно объяснить результаты дифракционных исследований можно, лишь несколько усложнив модель молекулы. Каждая молекула нуклеиновой кислоты должна представлять собой двойную спираль, образованную навитыми вокруг общей оси цепями. Эта модель Уотсона — Крика, предложенная ими впервыев 1953г., сыграла важную роль в развитии генетики . [c.131]
Гипотеза де Бройля была экспериментально подтверждена обнаружением у потока электронов дифракционного и интерференционного эффектов. В настоящее время дифракция потоков электронов, нейтронов, протонов широко используется для изучения структуры вещес гв (см. раздел IV). [c.11]
Именно в связи с этой задачей наблюдается постоянно возобновляю-ш ийся интерес к феноменологическому изучению кинетических закономерностей в последние десятилетия. Молекулярная интерпретация кинетики химических процессов в свою очередь проливает свет па химическое строение реагируюп1,их молекул. Полученные таким образом выводы о молекулярной структуре вещества необходимо приводить в соответствие с различными характеристиками строения вещества, например величиной дипольпого момента данными по дифракции электронов и рентгеновских лучей, законами стереохимии. [c.15]
Соморджай и соавт. [236—239] для выяснения механизма каталитических превращений углеводородов на ступенчатых поверхностях платины пытались идентифицировать атомные центры монокристаллов Р1, ответственных за разрыв связей С—С, С—Н и Н—Н. Структура и состав поверхности монокристаллов Р1 были исследованы методами Оже-спектроскопии и дифракции медленных электронов. Полученные результаты сопоставлены с каталитическими свойствами Р1 ь реакциях О—Н-обмена, дегидрирования циклогексана в бензол и гидрогенолиза циклогексана с образованием н-гексана. [c.165]
Несомненный интерес представляет цикл работ Со-морджая и сотр. [174—177] по исследованию кинетики различных реакций (в том числе дегидроциклизации) на монокристаллах металлов (Р1, 1г, N1, Ag) с одновременным определением структуры и состава поверхности методом дифракции медленных электронов и Оже-спект-роскопии. Показано, что атомные ступеньки на поверхности монокристалла Р1 являются активными центрами процессов разрыва связей С—Н и Н—Н. Зависимость скоростей реакций дегидрирования и гидрогенолиза циклогексана и циклогексена от структуры поверхности Р1 свидетельствует о существовании изломов и выступов на атомных ступеньках. Такие дефекты структуры являются особенно активными центрами процесса расщепления С—С-связей. Установлено, что активная поверхность Р1 в процессе реакции покрывается слоем углеродистых отложений свойства этого слоя существенно влияют на скорость и распределение продуктов каталитических реакций. Показано, что дегидрирование циклогексана до циклогексена не зависит от структуры поверхности (структурно-нечувствительная реакция). В то же время дегидрирование циклогексена и гидрогенолиз циклогексана являются структурно-чувствительными реакциями. Полученные результаты позволили расширить классификацию реакций, зависящих от первичной структуры поверхности катализатора и от вторичных изменений поверхности, возникающих в процессе реакции. При проведении реакций на монокристаллах 1г показано, что ступенчатая поверхность 1г в 3—5 раз более активна в [c.252]
Обычно хлорирование не изменяет углов между связями в молекуле, дифракция, например, показывает,, что даже в полихлорсоединеииях сохраняются тетраэдрические углы. Простые алкилхлориды имеют ди-нольные моменты порядка 1,8—2,1D. Б симметричных соединениях, как четыреххлористый углерод, гексахлорэтан и октахлорпропан дипольный момент равен нулю. 1,2-дихлорэтан теоретически может существовать в нс-форме с большим дипольным моментом и в транс-фо-рме с дипольным моментом, равным нулю. [c.66]
Углеводороды, полученные по процессу Фишера-Тропша, очевидно, также имеют в основном линейную структуру их температура плавления от 126 до 129° [13] и 134° [24]. Все эти вещества, в осповном линейного строения, имеют плотности, приблизительно равные 0,96—0,98 г1мл, приближающиеся к вычисленной величине плотности 1,0 для кристаллитов полиэтилена, полученной па основе определения дифракции Х-лучей [c.168]
Два последних высокомолекулярных алифатических углеводорода (полиэтилен и гидрированный полибутадиен) уникальны в том отношении, что они представляют собой примеры нерегулярно разветвленных структур. Фокс и Мертин при изучении инфракрасных снектров углеводородов в области 3—4 [л обнаружили полосу поглощения при 3,38 ц в спектре полиэтилена, которая является характеристической областью колебаний связи С—Н в метильных группах. Было определено, что соотношение СНз составляет от 1/д до 1/70- Все эти величины значительно превышают частоты, которых следовало ожидать, если бы полимеры представляли собой линейные углеводороды. Многие исследователи с тех пор способствовали детальной расшифровке инфракрасных спектров полиэтилена. Наиболее полные и точные исследования провели Рагг [28] и Кросс [9]. Последняя работа представляет особый интерес, поскольку в ней была определена зависимость между интенсивностью поглощения метильных групп и плотностью полимера. Степень кристалличности полиэтилена была определена при помощи нескольких различных методов, основанных, например, на измерениях плотности инфракрасных спектров, дифракции Х-лучей и теплоемкости. Ни один из этих методов не принимался за абсолютный, но метод, основанный на определении плотпости полимера, по-видимому, один из дающих наиболее достоверные данные. Поэтому Кросс впервые установил, что существует тесная зависимость между числом метильных групп в нолиэтиленах и их кристалличностью. [c.169]
Мз квантовой теории света следует, что фотон неспособен дро биться он взаимодейстпует как целое с электроном металла, вы бивая его из пластинки как целое он взаимодействует и со светочувствительным веществом фотографической пленки, вызывая ес потемнение в определенной точке, н т. д. В этом смысле фотон ведет себя подобно частице, т. е. проявляет к о р н у с к у л я р ы с свойства. Однако фотон обладает и волновыми свойствами это проявляется в волновом. характере распространения света, в способности фотона к интерференции и дифракции. Фотом отличается от частицы в классическом понимании этого термина тем, что его точное положение в пространстве, как и точное положение любой волны, не может быть указано. Но он отличается и от классической волны — неспособностью делиться на части. Объединяя в себе корпускулярные и волновые свойства, фотон не является, строго говоря, ни частицей, ни волной, — ему присунда корпускулярно-волновая двойственность. [c.66]
Предположение де Бронля о наличии у электрона волновых свойств получило экспериментальное подтверждение уже в 1927 г., когда К- Д. Девиссоном и Л. X. Джермером в США, Дж. П. Томсоном в Англин и П. С. Тартаковским в СССР независимо друг от друга было установлено, что прн взаимодействии пучка электронов с дифракционной решеткой (в качестве которой использовались кристаллы металлов) наблюдается такая же дифракпион-ная картина, как и при действии на кристаллическую решетку металла пучка рентгеновских лучей в этих опытах электро вел себя как волна, длпна которой в точности совпадала с вычисленной по уравнению де Бройля. В настоящее время волновые свойства электронов подтверждены большим числом опытов и широко используются в электронографии — методе изучения структуры веществ, основанном на дифракции электронов. [c.70]
Итак, электронам, как и фотонам, присуща, корпускулярноволновая двойственность. Корпускулярные свойства электрона вы-рал аются в его способности проявлять свое действие только к.чк це. юго. Волновые свойства электрона проявляются в особенностя.ч его движения, в дифракции п интерференции электронов. [c.71]
Действие интерферометра основано па дифракции двойной щели. Параллельный пучок лучей, вышедший из коотлиматора I (рис. 42), проходит через две параллельные щелн 2 и конденсируется объекти- [c.85]
Но вот произошло открытие рентгеновских лучей и радиоактивности. В 1895 г. Вильгельм Рентген (1845-1923) проводил опыты с сильно ваку-умированными круксовыми трубками (см. рис. 1-11), что позволяло катодным лучам соударяться с анодом без препятствий, создаваемых молекулами газа. Рентген обнаружил, что при этих условиях анод испускает новое излучение, обладающее большой проникающей способностью. Это излучение, названное им х-лучами (впоследствии его стали также называть рентгеновскими лучами), легко проходит через бумагу, дерево и мышечные ткани, но поглощается более тяжелыми веществами, например костными тканями и металлами. Рентген обнаружил, что х-лучи не отклоняются в электрическом и магнитном полях и, следовательно, не являются пучками заряженных частиц. Другие ученые предположили, что эти лучи могут представлять собой электромагнитное излучение, подобное свету, но с меньшей длиной волны. Немецкий физик Макс фон Лауэ доказал эту гипотезу спустя 18 лет, когда ему удалось наблюдать дифракцию рентгеновских лучей на кристаллах. [c.329]
Физикохимия полимеров (1968) — [ c.99 , c.105 ]
Нефтяные битумы (1973) — [ c.36 ]
Химия (1978) — [ c.0 ]
Химическая связь (0) — [ c.0 ]
Биохимия природных пигментов (1986) — [ c.15 ]
Химия твердого тела Теория и приложения Ч.2 (1988) — [ c.2 , c.2 , c.4 , c.7 , c.8 , c.8 , c.71 , c.72 , c.90 , c.148 , c.154 , c.155 , c.177 , c.182 , c.184 , c.187 , c.201 , c.220 , c.304 ]
Искусственные драгоценные камни (1986) — [ c.116 ]
Искусственные драгоценные камни (1986) — [ c.116 ]
Химия справочное руководство (1975) — [ c.391 ]
Рефрактометрические методы химии (1960) — [ c.0 ]
Современная общая химия Том 3 (1975) — [ c.0 ]
Основы органической химии (1968) — [ c.0 ]
Нестехиометрические соединения (1971) — [ c.0 ]
История химии (1975) — [ c.419 ]
Курс химии Часть 1 (1972) — [ c.143 ]
Возможности химии сегодня и завтра (1992) — [ c.0 ]
Курс общей химии (1964) — [ c.134 , c.135 ]
Основы органической химии (1983) — [ c.0 ]
Теоретическая неорганическая химия Издание 3 (1976) — [ c.16 , c.290 ]
Неорганическая химия (1974) — [ c.44 ]
Неорганическая химия Издание 2 (1976) — [ c.49 ]
Основы органической химии 1 Издание 2 (1978) — [ c.0 ]
Основы органической химии Часть 1 (1968) — [ c.0 ]
Гетерогенный катализ (1969) — [ c.0 ]
Курс коллоидной химии (1964) — [ c.37 ]
Неорганическая химия (1987) — [ c.0 ]
Общая химия (1974) — [ c.769 ]
Современная общая химия (1975) — [ c.0 ]
Основы стереохимии и конформационного анализа (1974) — [ c.0 ]
Сверхвысокомодульные полимеры (1983) — [ c.74 ]
Теоретическая неорганическая химия (1969) — [ c.16 , c.41 , c.193 ]
Теоретическая неорганическая химия (1971) — [ c.16 , c.40 , c.186 , c.187 ]
Применение спектров комбинационного рассеяния (1977) — [ c.0 ]
Кристаллические полиолефины Том 2 (1970) — [ c.16 ]
Рефрактометрические методы химии Издание 2 (1974) — [ c.0 ]
Рефрактометрические методы химии Издание 3 (1983) — [ c.0 ]
Теоретическая неорганическая химия (1969) — [ c.16 , c.41 , c.193 ]
Химическая связь (1980) — [ c.0 ]
Строение материи и химическая связь (1974) — [ c.0 ]
Органическая химия Том 1 (1963) — [ c.0 ]
Новейшие методы исследования полимеров (1966) — [ c.0 ]
История химии (1966) — [ c.399 ]
Физическая химия Книга 2 (1962) — [ c.129 , c.162 ]
Основы общей химии Том 2 (1967) — [ c.0 ]
Основы общей химии Том 2 Издание 3 (1973) — [ c.0 ]
Органическая химия Том 1 (1962) — [ c.0 ]
Высокомолекулярные соединения Издание 2 (1971) — [ c.325 , c.326 ]
Практические работы по физической химии Изд4 (1982) — [ c.355 ]
Физическая химия (1967) — [ c.0 ]
Биологические мембраны Структурная организация, функции, модификация физико-химическими агентами (2000) — [ c.0 ]
Теоретическая неорганическая химия (1971) — [ c.16 , c.40 , c.186 , c.187 ]
chem21.info
Дифракция – это… Что такое Дифракция?
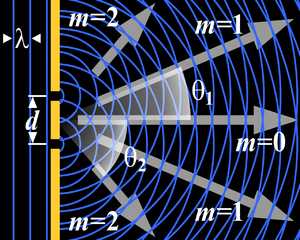 Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумов
Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумовДифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн.[1]
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.
Дифракция волн может проявляться:
- в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;
- в разложении волн по их частотному спектру;
- в преобразовании поляризации волн;
- в изменении фазовой структуры волн.
Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).
Тонкости в толковании термина «дифракция»
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.
Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).
Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.
Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.
Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.
При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.
Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)
Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.
Частные случаи дифракции
Исторически в проблеме дифракции сначала рассматривались два крайних случая, связанных с ограничением препятствием (экраном с дыркой) сферической волны и это была дифракция Френеля, либо плоской волны на щели или системе отверстий – дифракция Фраунгофера
Дифракция на щели
Распределение интенсивности света при дифракции на щели
В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.
Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.
Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.
Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:
Используя формулу Эйлера и её производную: и .
где ненормированная синкус функция определена как .
Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:
См. также Дифракция на N-щелях
Дифракция на отверстии
Дифракция лазерного луча с длиной волны 650 нм, прошедшего через отверстие диаметром 0,2 ммДифракция звука и ультразвуковая локация
Дифракция радиоволн и радиолокация
Исследованием дифракции радиоволн занимается геометрическая теория дифракции[2]
Дифракционная решётка
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ
Дифракция света на ультразвуке
Одним из наглядных примеров дифракции света на ультразвуке является дифракция света на ультразвуке в жидкости. В одной из постановок такого эксперимента в оптически-прозрачной ванночке в форме прямоугольного параллелепипеда с оптически-прозрачной жидкостью с помощью пластинки из пьезоматериала на частоте ультразвука возбуждается стоячая волна. В её узлах плотность воды ниже, и как следствие ниже её оптическая плотность, в пучностях — выше. Таким образом, при этих условиях ванночка с водой становится для световой волны фазовой дифракционной решёткой, на которой осуществляется дифракция в виде изменения фазовой структуры волн, что можно наблюдать в оптический микроскоп методом фазового контраста или методом тёмного поля.
Дифракция электронов
Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет свойства, аналогичные свойствам волны. При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.
Брегговская дифракция
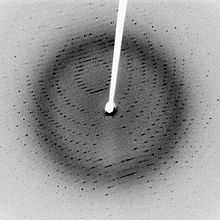 Согласно Закону Брэгга каждая точка (или отражение) в этой дифракционной картине формируется конструктивной интерференцией рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристаллов.
Согласно Закону Брэгга каждая точка (или отражение) в этой дифракционной картине формируется конструктивной интерференцией рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристаллов.Дифракция от трехмерной периодической структуры, такой как атомы в кристалле называется дифракцией Брегга. Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решётке. Брегговская дифракция является следствием интерференции между волнами, отражёнными от кристаллических плоскостей. Условие возникновения интерференции определяется законом Вульфа-Брегга:
- ,
где
- d — расстояние между кристаллическими плоскостями,
- θ угол скольжения — дополнительный угол к углу падения,
- λ — длина волны,
- n (n = 1,2…) — целое число называемое порядком дифракции.
Брегговская дифракция может осуществляться при использовании света с очень маленькой длиной волны, такого как рентгеновское излучение, либо волны материи, такие как нейтроны и электроны, длины волн которых сравнимы или много меньше, чем межатомное расстояние.[3] Получаемые данные дают информацию о межплоскостных расстояния, что позволяет вывести кристаллическую структуру. Дифракционный контраст, в электронных микроскопах и рентгеновских топографических устройствах, в частности, также является мощным инструментом для изучения отдельных дефектов и локальных полей деформации в кристаллах.
Дифракция частиц (нейтронов, атомов, молекул)
История исследований
Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга и Френеля. Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).
Обнаружение дифракции частиц (электронов) в 1927 году (опыт Дэвиссона и Джермера) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.
Дифракция в фотографии
Дифракцию можно наблюдать в фотографии: чрезмерное закрытие диафрагмы (относительного отверстия) приводит к падению резкости. Поэтому для сохранения оптимально резкого изображения на фотографии не рекомендуется полностью закрывать диафрагму. Нужно отметить, что для каждого объектива существует свои границы до которых стоит закрывать диафрагму, в большинстве случаев они равны f/11.[4]
См. также
Примечания
- ↑ В явлении рассеяния на мелких неоднородностях среды сказывается не только экранирование фронта волны, но и свойства самой неоднородности (скажем, водяной капли), определяющие индикатрису рассеяния, что рассматривается, например, в научной дисциплине «Оптика атмосферы» в разделе, связанном с аэрозолем.
- ↑ Боровиков В. А., Кинбер Б. Е. Геометрическая теория дифракции. М.: Связь, 1978, 247 с.
- ↑ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6
- ↑ Что такое дифракция в фотографии. «Про Фото»
Литература
- Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- И. Г. Кондратьев, Г. Д. Малюжинец Дифракция волн // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
Ссылки
dic.academic.ru
Твердые вещества Рентгеноструктурный анализ Дифракция.
Твердые вещества состоят из плотноупакованных частиц. Этими частицами могут быть атомы, молекулы либо ионы. Большинство твердых веществ находится в кристаллической форме. Это означает, что образующие их частицы предельно упорядочены в регулярной пространственной структуре.
Существуют, однако, и такие твердые вещества, в которых частицы не настолько упорядочены, чтобы образовывать регулярную кристаллическую структуру. Такие твердые вещества называются аморфными. Примером аморфного вещества является стекло. Его атомы имеют беспорядочное расположение. К аморфным веществам относится большинство полимеров. Полимеры имеют макромолекулярную цепочечную структуру, образуемую звеньями из небольших молекул, которые называются мономерами (см. гл. 20). Полимерные макромолекулы имеют неодинаковые размеры и поэтому не могут плотно упаковываться, образуя упорядоченное расположение.
Одно время считалось, что древесный уголь, кокс и сажа-разные формы углерода-являются аморфными веществами. Однако рентгеноструктурный анализ показал, что все эти формы углерода состоят из мелких графитоподобных кристаллов.
Рентгеноструктурный анализ
Дифракция
Описанием структуры кристаллов занимается наука кристаллография, самым действенным экспериментальным методом которой является рентгеноструктурный анализ. Этот метод основан на изучении рассеяния рентгеновских лучей, направляемых на исследуемые кристаллы.
Когда распространяющийся плоский фронт волн на поверхности воды достигает перегородки, в которой есть узкая щель, волны выходят из нее кругами (рис. 3.15). Это явление называется дифракцией. Дифракция присуща всем видам излучения, включая радиоволны, световые волны и рентгеновские лучи. При наличии в перегородке нескольких щелей каждая из них оказывается источником круговых или сферических волн. Эти волны интерферируют (взаимодействуют) друг с другом, взаимно уничтожаясь в одних местах и усиливаясь в других местах. Возникает своеобразная дифракционная картина.
Если направить рентгеновские лучи на кристалл, они частично поглотятся кристаллом, а частично пройдут его насквозь. Поглощаемые рентгеновские лучи вызывают возбуждение электронов в атомах кристалла. Когда электроны возвращаются на более низкие энергетические уровни, атомы вновь испускают рентгеновские лучи. Те из них, которые имеют совпадающую фазу, усиливают друг друга и могут быть обнаружены. Те же лучи, которые имеют противоположную фазу друг по отношению к другу, взаимно уничтожаются и не могут быть обнаружены (рис. 3.16). Таким образом, вновь испускаемые рентгеновские лучи образуют дифракционную картину.
Уильям Генри Брэгг (1862-1942) Уильям Лоуренс Брэгг (1890 1971).
В 1912 г. немецкий физик Макс фон Лауэ предположил, что кристаллы могут служить дифракционными решетками для рентгеновских лучей. Ему удалось получить дифракционную картину от кристалла пентагидрата сульфата меди(II) CuSO4 5h3O.
Вслед за этим открытием английские ученые Уильям Генри Брэгт и его сын Уильям Лоуренс Брэгг разработали методику рентгеноструктурного анализа на основе изучения дифракции и стали применять ее для определения структуры кристаллов. Они были совместно награждены Нобелевской премией по физике в 1915 г. Первая структура, которую они определили, была структура сульфида цинка, имеющего кубическую форму. В последующие годы Брэгги определили кристаллическую структуру многочисленных неорганических соединений, минералов, металлов и белков.
Оглавление:
www.himikatus.ru
Дифракция света
7
Л3-4Дифракция света
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшое отверстие в экранах и т.д.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн. Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света Sи точка наблюденияPрасположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точкуP, образуют практически параллельные пучки, говорят одифракции в параллельных лучахили одифракции Фраунгофера. В противном случае говорят одифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником светаSи перед точкой наблюденияPпо линзе так, чтобы точкиSиPоказались в фокальной плоскости соответствующей линзы (рис.).
Принципиально дифракция Фраунгофера
не отличается от дифракции Френеля.
Количественный критерий, позволяющий
установить, какой вид дифракции имеет
место, определяется величиной безразмерного
параметра 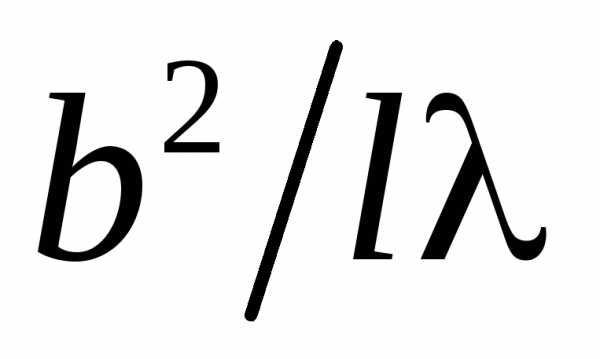 ,
гдеb– характерный
размер препятствия,l– расстояние между препятствием и
экраном, на котором наблюдается
дифракционная картина,– длина волны. Если
,
гдеb– характерный
размер препятствия,l– расстояние между препятствием и
экраном, на котором наблюдается
дифракционная картина,– длина волны. Если
Явление дифракции качественно объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Для монохроматической волны волновая поверхность есть поверхность, на которой колебания совершаются в одинаковой фазе.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. огибает края отверстия.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности на фронте волны. Из повседневного опыта известно, что в большом числе случаев лучи света не отклоняются от их прямолинейного распространения. Так, предметы, освещенные точечным источником света, дают резкую тень. Таким образом, принцип Гюйгенса нуждается в дополнении, позволяющем определять интенсивность волны.
Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источникомS, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой замкнутой поверхности, охватывающей источникS. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому источники вторичных волн действуют синфазно. В аналитическом виде для точечного источника этот принцип записывается в виде
, (1)
гдеE– световой
вектор, включающий в себя временную
зависимость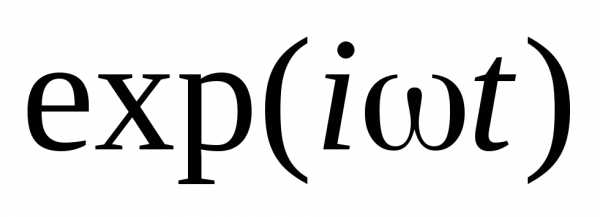 ,k– волновое число,r– расстояние
от точкиPна
поверхности Sдо точкиP,K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точкеP. Правомерность
формулы (1) и вид функцииKустанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
,k– волновое число,r– расстояние
от точкиPна
поверхности Sдо точкиP,K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точкеP. Правомерность
формулы (1) и вид функцииKустанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
В том случае, когда между источником Sи точкой наблюденияPимеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. На поверхности непрозрачных экранов амплитуды вторичных источников считаются равными нулю; в области отверстий амплитуды источников такие же, как при отсутствии экрана (так называемое приближение Кирхгофа).
Метод зон Френеля.Учет амплитуд и фаз вторичных волн позволяет в принципе найти амплитуду результирующей волны в любой точке пространства и решить задачу о распространении света. В общем случае расчет интерференции вторичных волн по формуле (1) довольно сложный и громоздкий. Однако ряд задач можно решить, применив чрезвычайно наглядный прием, заменяющий сложные вычисления. Метод этот получил название методазон Френеля.
Суть метода разберем на примере точечного
источника света S.
Волновые поверхности представляют
собой в этом случае концентрические
сферы с центром в S.Разобьем изображенную на рисунке
волновую поверхность на кольцевые зоны,
построенные так, что расстояния от краев
каждой зоны до точкиPотличаются на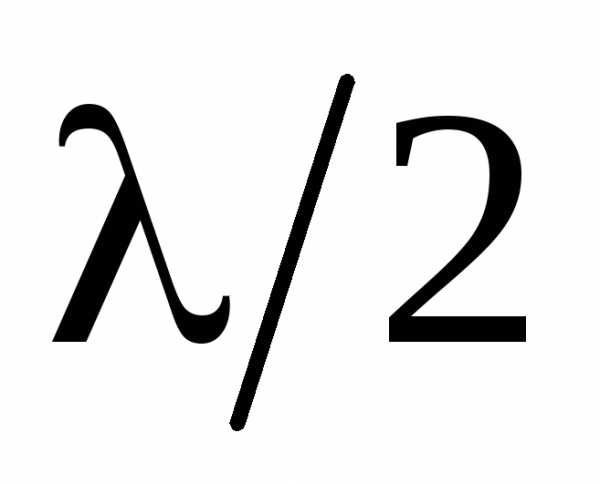 .
Обладающие таким свойством зоны
называютсязонами Френеля. Из рис.
видно, что расстояние
.
Обладающие таким свойством зоны
называютсязонами Френеля. Из рис.
видно, что расстояние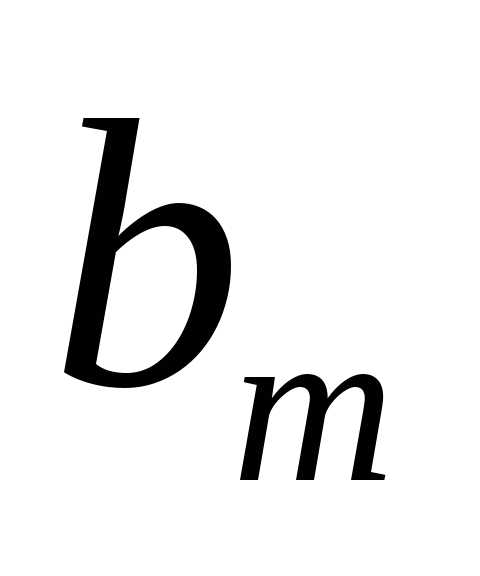 от внешнего края – m-й
зоны до точкиPравно
от внешнего края – m-й
зоны до точкиPравно
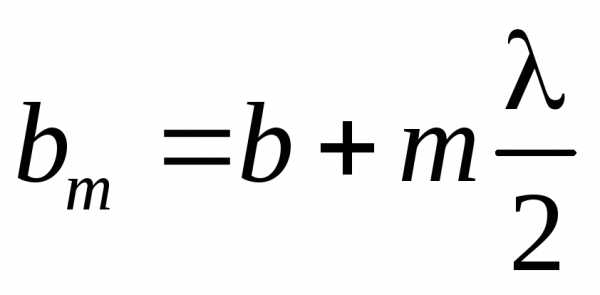 ,
гдеb– расстояние
от вершины волновой поверхностиOдо точкиP.
,
гдеb– расстояние
от вершины волновой поверхностиOдо точкиP.
Колебания, приходящие в точку Pот аналогичных точек двух соседних зон (например, точек, лежащих в середине зон или у внешних краев зон), находятся в противофазе. Поэтому колебания от соседних зон будут взаимно ослаблять друг друга и амплитуда результирующего светового колебания в точкеP
, (2)
где ,
, ,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
Для оценки амплитуд колебаний найдем
площади зон Френеля. Пусть внешняя
граница m-й
зоны выделяет на волновой поверхности
сферический сегмент высоты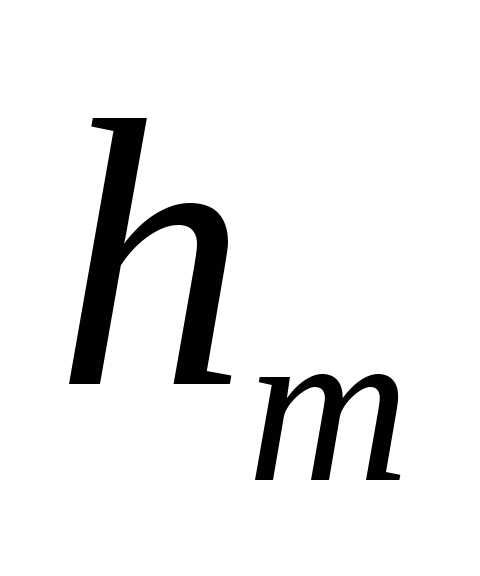 .
Обозначив площадь этого сегмента через
.
Обозначив площадь этого сегмента через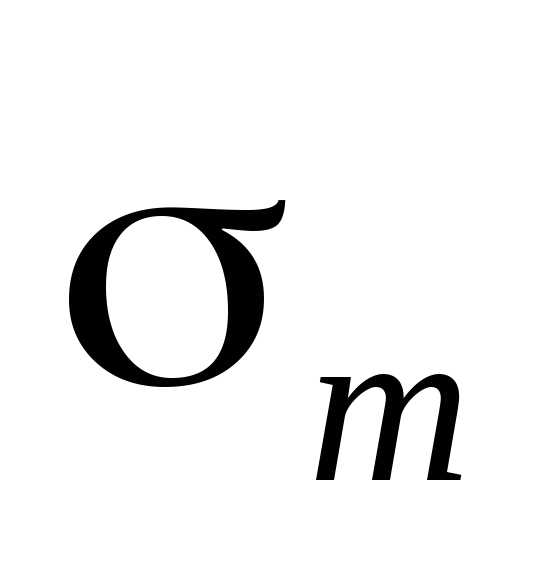 ,
найдем, что, площадьm-й
зоны Френеля равна.
Из рисунка видно, что.
После несложных преобразований,
учитывая
,
найдем, что, площадьm-й
зоны Френеля равна.
Из рисунка видно, что.
После несложных преобразований,
учитывая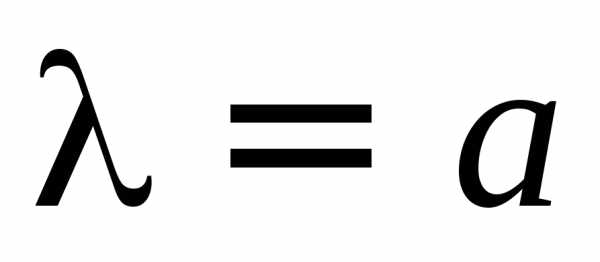 и
и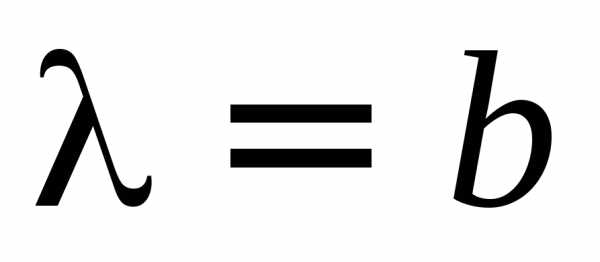 ,
получим
,
получим
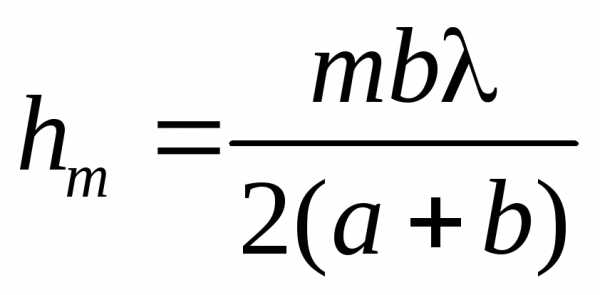 .
Площадь сферического сегмента и
площадьm-й
зоны Френеля соответственно равны
.
Площадь сферического сегмента и
площадьm-й
зоны Френеля соответственно равны
,. (3)
Таким образом, при не слишком
большихmплощади зон
Френеля одинаковы. Согласно предположению
Френеля, действие отдельных зон в точкеPтем меньше, чем больше
угол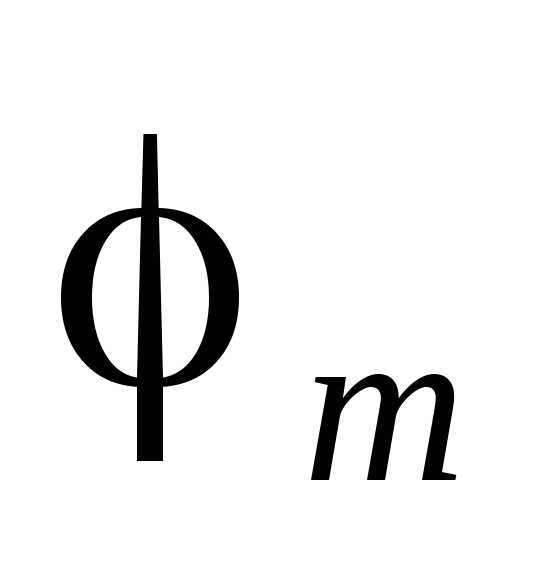 между нормальюn к поверхности зоны и направлением
наP, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точкиPуменьшается с ростомmи вследствие увеличения расстояния от
зоны до точкиP.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
между нормальюn к поверхности зоны и направлением
наP, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точкиPуменьшается с ростомmи вследствие увеличения расстояния от
зоны до точкиP.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
.
Общее число зон Френеля, умещающихся на полусфере, очень велико; например, при ичисло зон достигает~106. Это означает, что амплитуда убывает очень медленно и поэтому можно приближенно считать
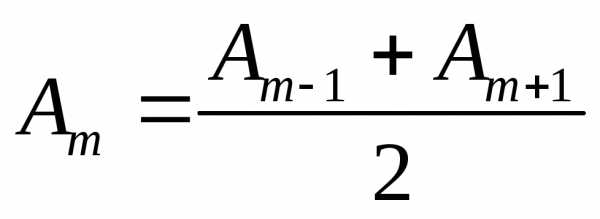 . (4)
Тогда выражение (2) после перегруппировки
суммируется
. (4)
Тогда выражение (2) после перегруппировки
суммируется
, (5) так как выражения в скобках, согласно (4), равны нулю, а вклад последнего слагаемого ничтожно мал. Таким образом, амплитуда результирующих колебаний в произвольной точкеPопределяется как бы половинным действием центральной зоны Френеля.
При не слишком больших mвысота сегмента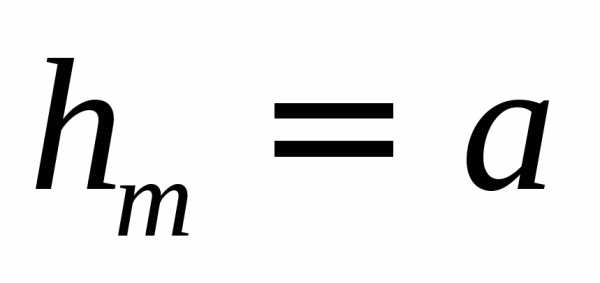 ,
поэтому можно считать, что
,
поэтому можно считать, что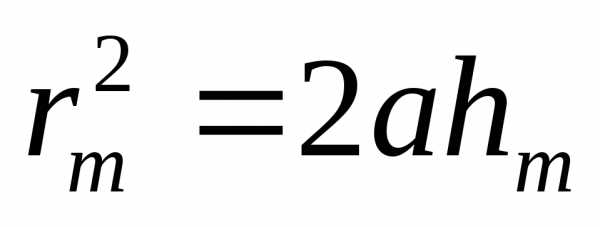 .
Подставив значение для
.
Подставив значение для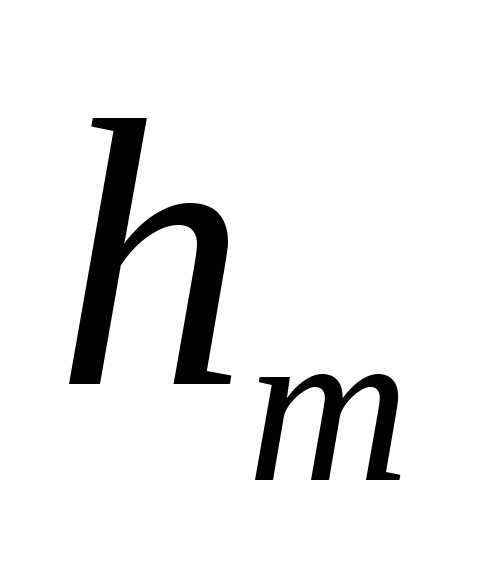 ,
получим для радиуса внешней границыm-й
зоны
,
получим для радиуса внешней границыm-й
зоны
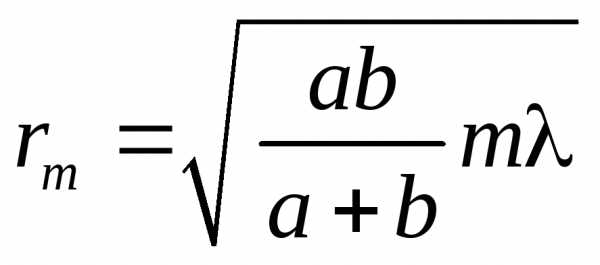 . (6)
Приирадиус первой (центральной) зоны.
Следовательно, распространение света
отSкPпроисходит так, как если бы световой
поток шел внутри очень узкого канала
вдольSP, т.е. прямолинейно.
. (6)
Приирадиус первой (центральной) зоны.
Следовательно, распространение света
отSкPпроисходит так, как если бы световой
поток шел внутри очень узкого канала
вдольSP, т.е. прямолинейно.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонная пластинка – в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрических колец, с радиусами зон Френеля заданной конфигурации. Если поместить зонную пластинку в строго определенном месте (на расстоянии aот точечного источника и на расстоянииbот точки наблюдения), то результирующая амплитуда будет больше, чем при полностью открытом волновом фронте.
Дифракция Френеля на круглом отверстии.Дифракция Френеля наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, в данном случае экрана с отверстием. Сферическая волна, распространяющаяся от точечного источникаS, встречает на своем пути экран с отверстием. Дифракционная картина наблюдается на экране, параллельном экрану с отверстием. Ее вид зависит от расстояния между отверстием и экраном (для данного диаметра отверстия). Проще определить амплитуду световых колебаний в центре картины. Для этого разобьем открытую часть волновой поверхности на зоны Френеля. Амплитуда колебания, возбуждаемая всеми зонами равна
, (7) где знак плюс отвечает нечетнымmи минус – четнымm.
Когда отверстие открывает нечетное
число зон Френеля, то амплитуда
(интенсивность) в центральной точке
будет больше, чем при свободном
распространении волны; если четное то
амплитуда (интенсивность) будет равна
нулю. Например, если отверстие открывает
одну зону Френеля, амплитуда 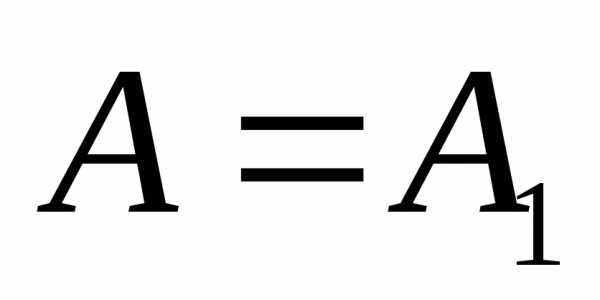 ,
то интенсивность (
,
то интенсивность (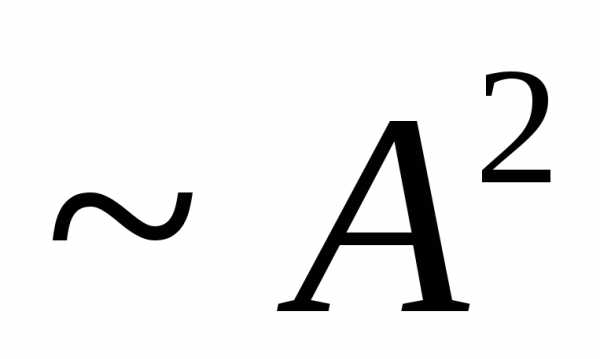 )
больше в четыре раза.
)
больше в четыре раза.
Расчет амплитуды колебания на внеосевых участках экрана более сложен, так как соответствующие зоны Френеля частично перекрываются непрозрачным экраном. Качественно ясно, что дифракционная картина будет иметь вид чередующихся темных и светлых колец с общим центром (если mчетное, то в центре будет темное кольцо, еслиmнечетное – то светлое пятно), причем интенсивность в максимумах убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим светом, а белым светом, то кольца окрашены.
Рассмотрим предельные случаи. Если
отверстие открывает лишь часть
центральной зоны Френеля, на экране
получается размытое светлое пятно;
чередования светлых и темных колец в
этом случае не возникает. Если отверстие
открывает большое число зон, то 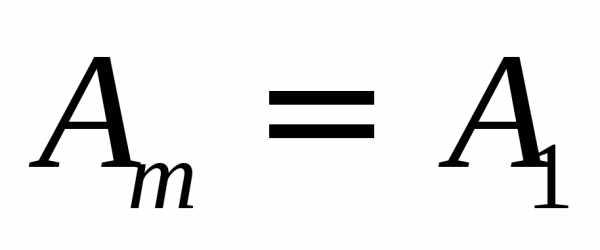 и амплитуда в центре
и амплитуда в центре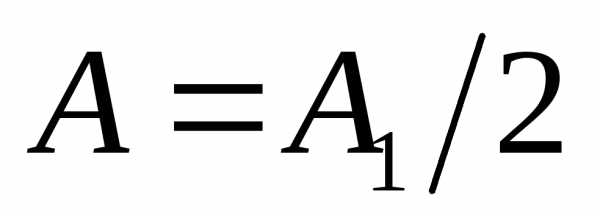 ,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
Дифракция Френеля на диске.Сферическая волна, распространяющаяся от точечного источникаS, встречает на своем пути диск (рис.). Дифракционная картина, наблюдаемая на экране, является центрально симметричной. Определим амплитуду световых колебаний в центре. Пусть диск закрываетmпервых зон Френеля. Тогда амплитуда колебаний равна
или, (8)
так как выражения, стоящие в скобках,
равны нулю. Следовательно, в центре
всегда наблюдается дифракционный
максимум (светлое пятно), соответствующий
половине действия первой открытой зоны
Френеля. Центральный максимум окружен
концентрическими с ним темными и светлыми
кольцами. При небольшом числе закрытых
зон амплитуда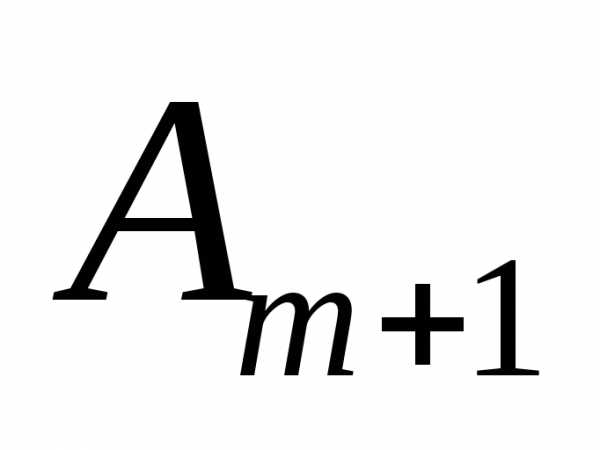 мало отличается от
мало отличается от .
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
.
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
Рассмотрим предельные случаи. Если диск
закрывает лишь небольшую часть центральной
зоны Френеля, он совсем не отбрасывает
тени – освещенность экрана всюду
остается такой же, как при отсутствии
диска. Если диск закрывает много зон
Френеля, чередование светлых и темных
колец наблюдается только в узкой области
на границе геометрической тени. В этом
случае 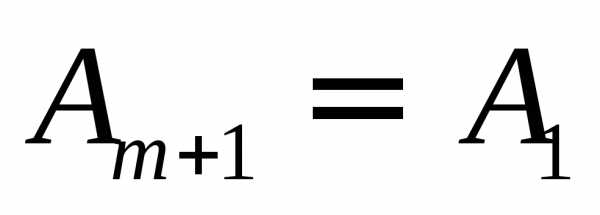 ,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
Дифракция Фраунгофера на одной щели.Пусть плоская монохроматическая волна падает нормально плоскости узкой щели ширинойa. Оптическая разность хода между крайними лучами, идущими от щели в некотором направлении
.
Разобьем открытую часть волновой
поверхности в плоскости щели на зоны
Френеля, имеющие вид равновеликих полос,
параллельных щели. Так как ширина каждой
зоны выбирается такой, чтобы разность
хода от краев этих зон была равна 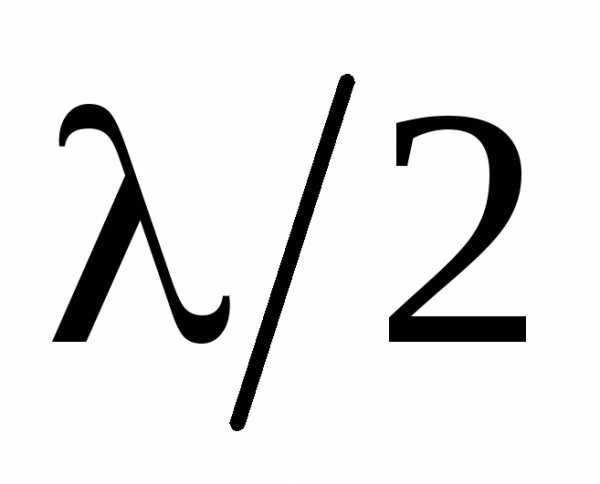 ,
то на ширине щели уместится
,
то на ширине щели уместится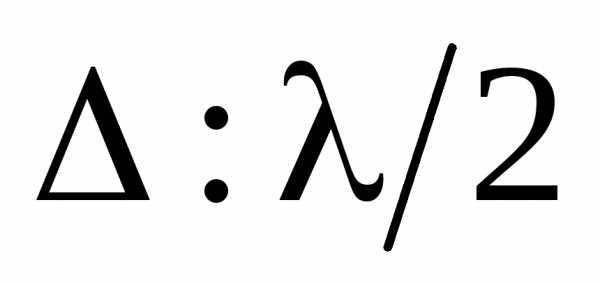 зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
Если число зон Френеля четное, то
, (9а) и в точкеBнаблюдается минимум освещенности (темный участок), если же число зон Френеля нечетное, то
(9б)
и
наблюдается близкая к максимуму
освещенность, соответствующей действию
одной нескомпенсированной зоны Френеля.
В направлении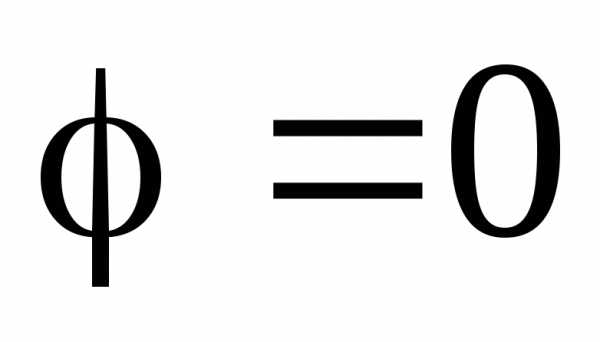 щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке
щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке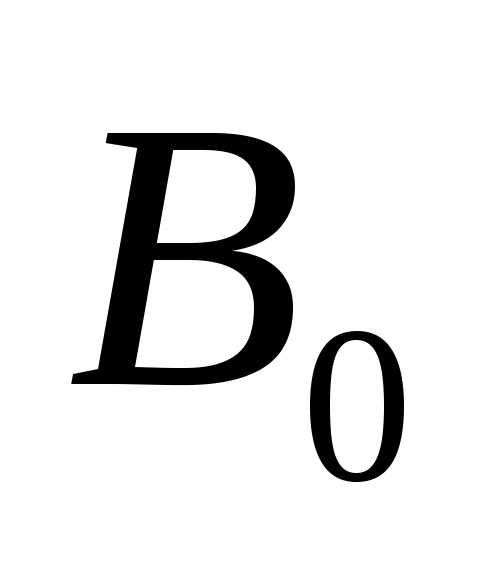 соответствует центральный или главный
максимум освещенности.
соответствует центральный или главный
максимум освещенности.
Расчет освещенности в зависимости от направления дает
, (10)
где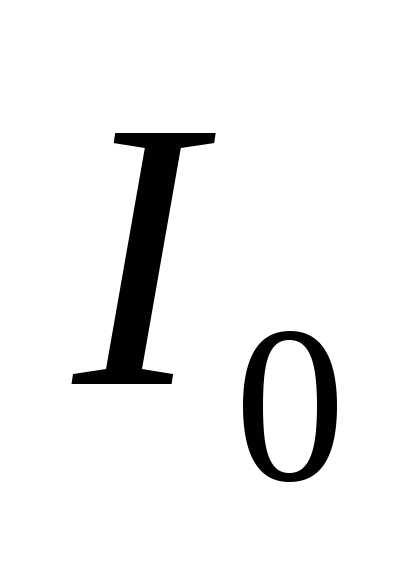 – освещенность в середине дифракционной
картины (против центра линзы),
– освещенность в середине дифракционной
картины (против центра линзы),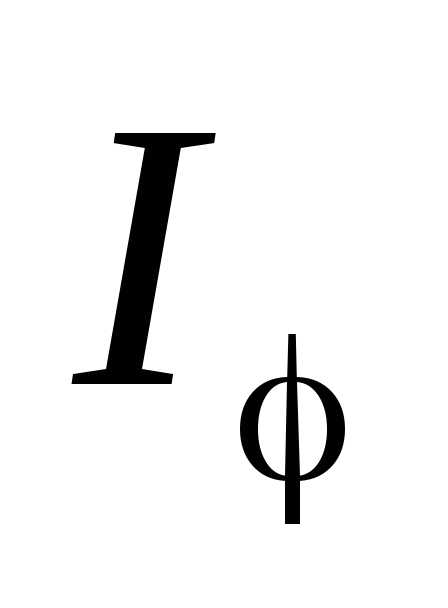 – освещенность в точке, положение
которой определяется направлением.
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям,
удовлетворяющие условиям
– освещенность в точке, положение
которой определяется направлением.
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям,
удовлетворяющие условиям
,,и т.д. Вместо этих условий для максимумов приближенно можно пользоваться соотношением (9б), дающим близкие значения углов. Величина вторичных максимумов быстро убывает. Численные значения интенсивностей главного и следующих максимумов относятся как
и т.д., т.е. основная часть световой энергии, прошедшей через щель, сосредоточена в главном максимуме.
Сужение щели приводит к тому, что
центральный максимум расплывается, а
его освещенность уменьшается. Наоборот,
чем щель шире, тем картина ярче, но
дифракционные полосы уже, а число самих
полос больше. При  в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
studfiles.net
