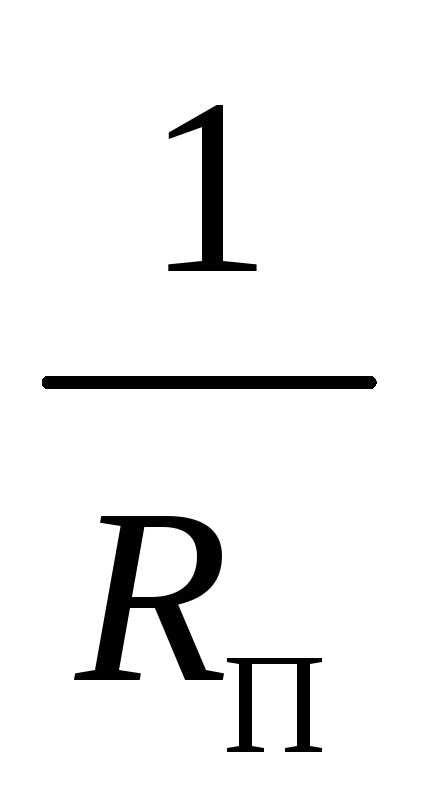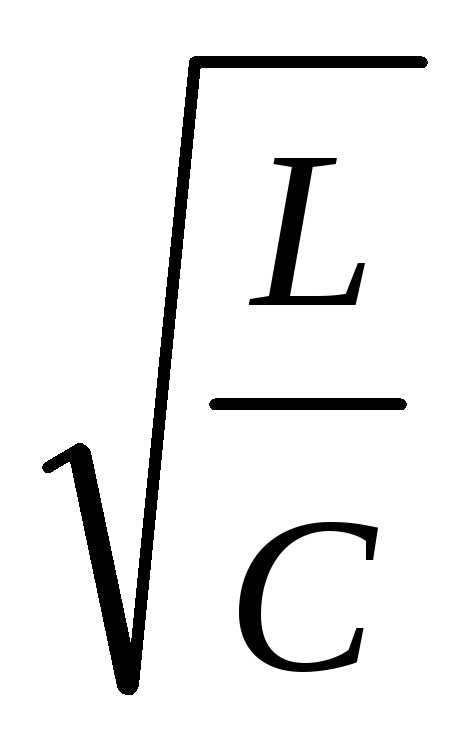Добротности контура формула – Добротность — Википедия - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Что такое добротность колебательного контура?как измерить добротность в радиолюбительских условиях.

«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы, который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания» – авторитетно учит нас Википедия.

Да уж. Напустили тумана ироды – без поллитры не разберёшься. А ведь придётся, раз впряглись.

Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что “quality factor” – это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле – добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её выпуклости меня восхищают, её впуклости сводят с ума».

Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный конденсатор с низким током утечки, и катушку индуктивности – крепкую, добротную и красивую, словно выпавшую из картины венецианского мастера в Пушкинском музее.

Приведём эквивалентную схему колебательного контура.

Здесь L и C – собственные индуктивность и ёмкость компонентов, входящих в состав колебательного контура,

rL – сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,

Rш – сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности, а также потерями, вызванные наличием токов утечки в конденсаторе.

Рис.1

При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.

По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо учитывать и суммировать со значением основной ёмкости С.

Теперь давайте разберёмся, что такое “скорость затухания собственных колебаний в системе” и, каким боком она связана с добротностью.

Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).

Конденсатор С зарядится до уровня, равного напряжению питания.

Теперь перещёлкнем переключатель в правое по схеме положение.

Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель – свободные колебания затухают, причём скорость затухания зависит от потерь в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в е

π = 23,14 раза, как раз и будет числено равняться добротности контура Q.

Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность колебательного контура, генератор сигналов в этом случае не нужен.

Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.

Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».

Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.

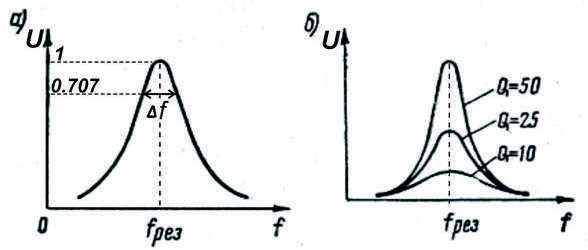
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид: Q = f _рез/Δf .
Рис.2

Из формулы естественным образом вытекает, что чем выше добротность – тем уже полоса пропускания резонансного контура, соответственно, чем ниже – тем шире.

А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?

1. Если речь идёт о низких (звуковых) частотах

, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления) к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих существенных потерь в работу колебательного контура.

2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.

В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с контуром.

Спаяем пару резисторов.

Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.

В нашем случае Q = 250 x V₂/V₁ .
Рис.3

Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать это значение как минимум на порядок.

Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.

Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле: Q = Q₀x R_ш/(R_ш+R_о) , где
Q₀ – добротность ненагруженного контура,
R_ш – шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
R_о – эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте, значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.

А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.

vpayaem.ru

7.5. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с

Любой резонансный контур, в том числе и последовательный принято характеризовать добротностью Q и характеристическим сопротивлением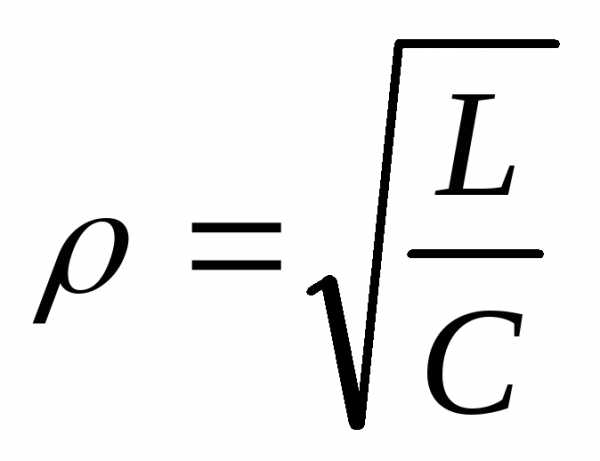

Напомним, что в данном случае будем рассматривать определение добротности контура при изменении частоты источника питания.

При резонансе .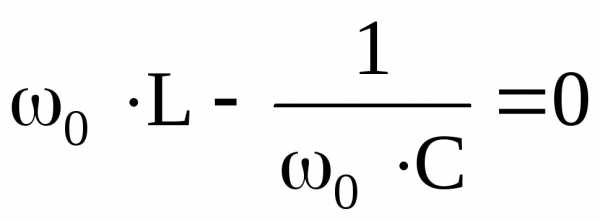

Добротность контура определяет кратность превышения напряжения на зажимах индуктивного или емкостного элемента сопротивления при резонансе над напряжением всей цепи U = U_R.

В электротехнических и радиотехнических установках добротности могут быть любого порядка, вплоть до десятков тысяч. При больших добротностях (50–500) U_L₀ >> U_R, U_R = U_ВХ = U, т. е. напряжение на индуктивности (или на емкости) во много раз больше приложенного напряжения.

Выясним влияние добротности на резонансные кривые при последовательном соединении

R, L, С. Ток в цепи равен

Относительное значение тока: 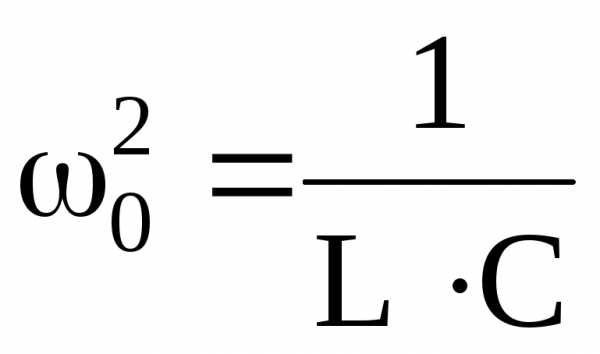, т.е..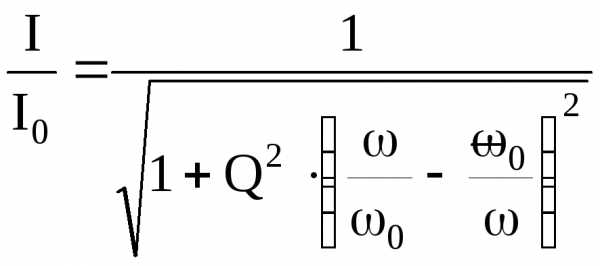

Пои выводе этой формулы учитывалось, что .

Иногда вводят понятие относительной частоты .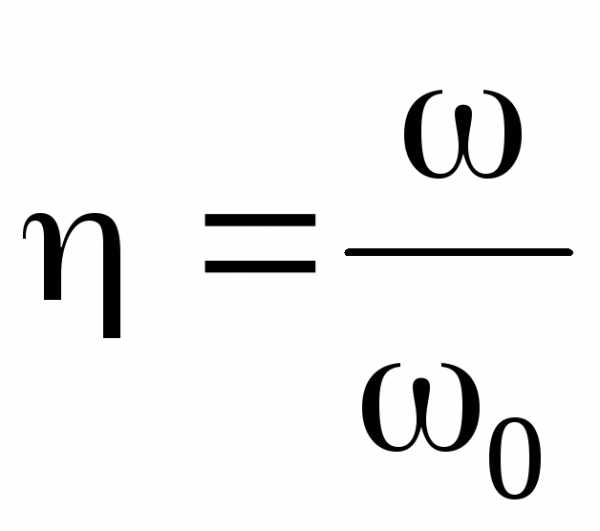

Тогда предыдущая формула запишется так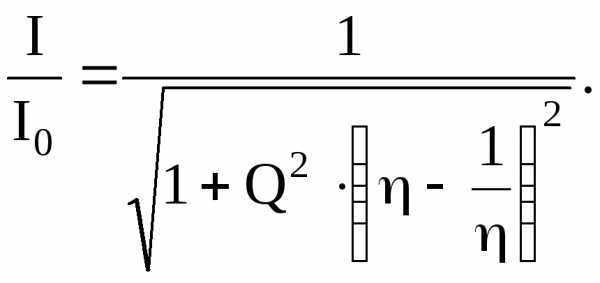

Построим резонансные кривые в относительных (по току) единицах (рис. 7.8) для трех добротностей. Рассматривая три резонансные кривые, видим, что чем больше добротность, тем острее получается резонансная кривая. Полоса пропускания контура определяется разностью частот, которые получатся при пересечении резонансной кривой горизонтальной линией на уровне .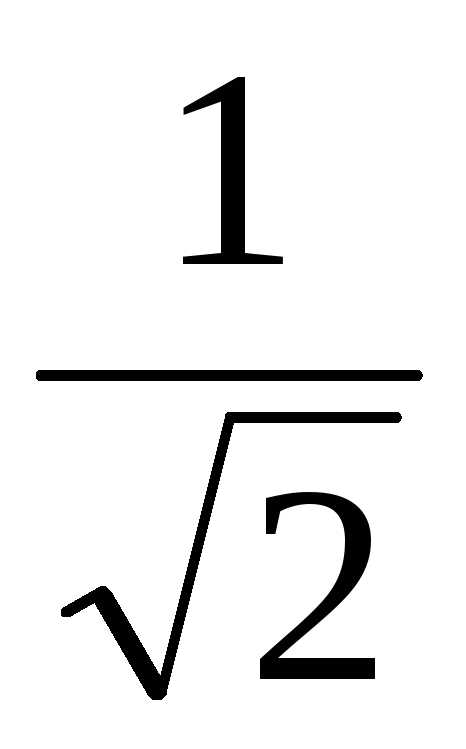

Из рис. 7.8 видно, что чем меньше добротность, тем шире полоса пропускания. В радиоприемниках колебательные контуры имеют большие добротности (500–1000), поэтому эти контуры обладают достаточно узкими полосами пропускания, что способствует избирательному радиоприему только одной станции.

7.6. Определение добротности по резонансной кривой

На практике резонансные частотные характеристики реальных контуров можно получать, изменяя частоту генератора в определенных пределах и снимая показания вольтаметра, подключенного параллельно резистору (см. рис. 7.9 а). Строят экспериментальную резонансную кривую и по этой кривой определяют полосу пропускания. Выведем соответствующую формулу для расчета добротности по резонансной кривой, снятой экспериментально.

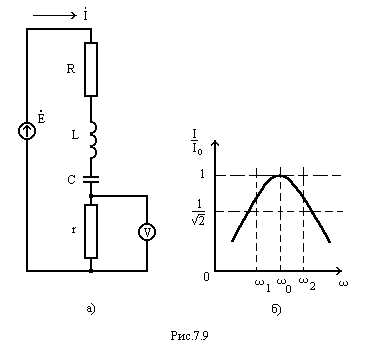
Из рис. 7.9 б следует:

В этом равенстве знаменатели равны, поэтому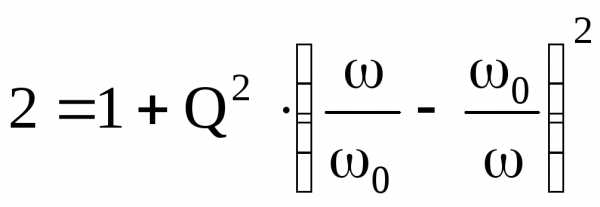

Отсюда .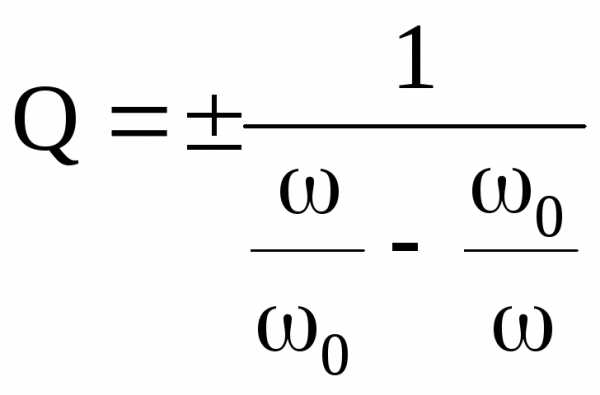

Запишем дважды: при итакие выражения;.

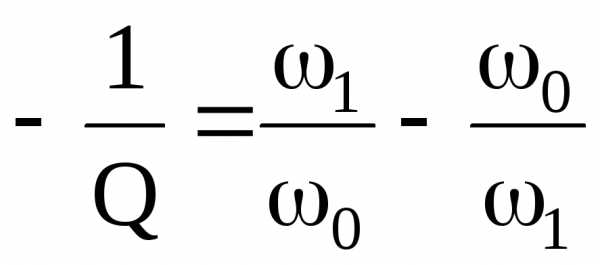После сложения последних выражений получим

или

Отсюда

И далее .

Очень важно: добротность обратно пропорциональна .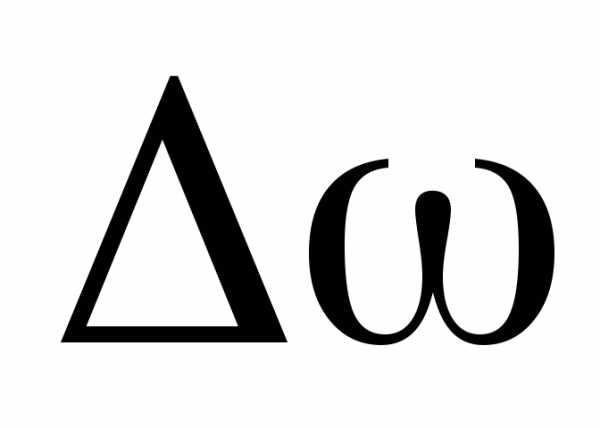

Для последовательного контура R, L, С построена резонансная кривая тока при изменении

емкости С (рис. 7.10).

Пользуясь этой кривой, определим добротность контура. Выражение для тока

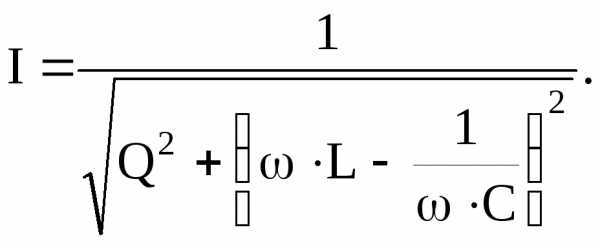
Выполним ряд преобразований последней формулы

;

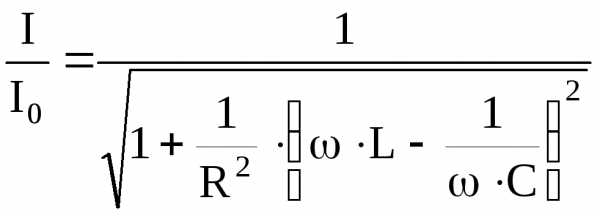Проведем горизонтальную прямую на уровне .

Отметим значения емкости C₁ и С₂.

Далее сделаем ряд очевидных выкладок. Выразим добротность Q через значения

емкости С₁ и С₂. Запишем

Найдем сумму и разность емкостей

Запишем отношение .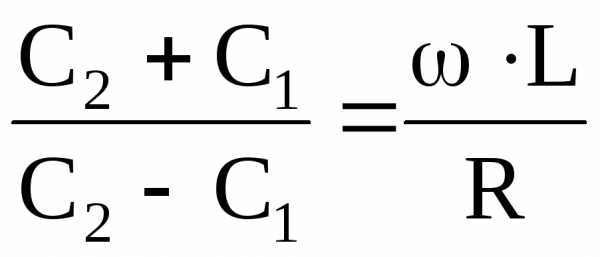

Напомним, что добротность контура определяется превышением напряжения на индуктивном (или емкостном) сопротивлении при резонансе над напряжением всей цепи (или напряжением на активном сопротивлении), т. е.

Таким образом,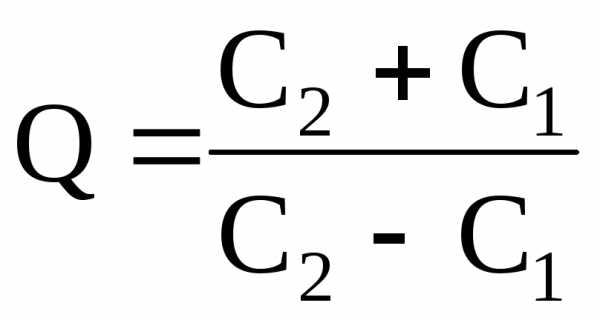

Кроме этого результата, представляется возможным получить значения параметров катушки индуктивности (L и R)

Откуда ;.

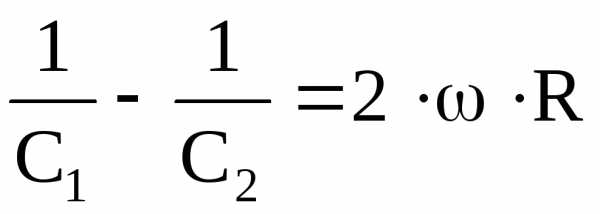Откуда .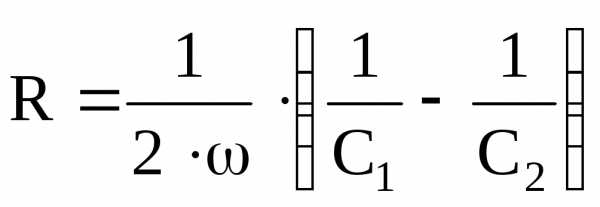

Величина емкости С₀, при которой наступает резонанс, определится так:

; ;;.

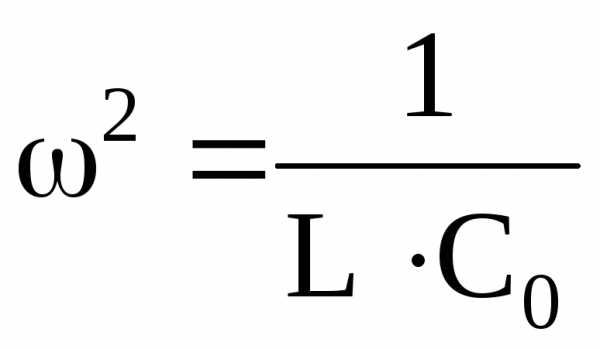Откуда .

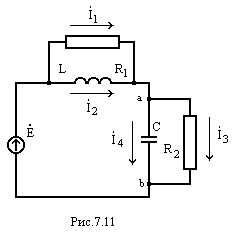
Резонанс напряжений может наблюдаться в схеме, показанной на рис. 7.11.

Входное сопротивление такой схемы

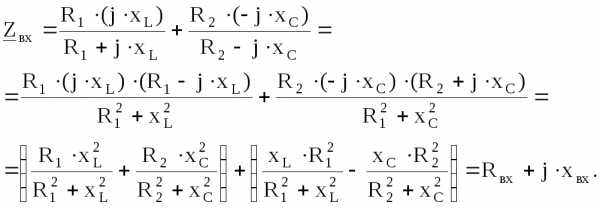
При резонансе реактивная составляющая входного сопротивления должна быть равна нулю, т. е.

studfiles.net

Методы определения добротности

Пользуясь определением добротности, можно показать, что

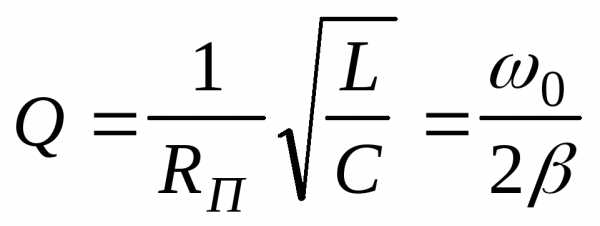, (9)

R_П = r + R + R_L,

где R_П – полное сопротивление цепи; r – внутреннее сопротивление источника тока; R – сопротивление, включенное в контур; R_L – активное сопротивление катушки индуктивности.

1. Расчет теоретического значения добротности. Добротность контура Q_теор можно рассчитать по формуле (9), зная параметры электрической цепи R_П, L и C.

2. Определение добротности по измерениям резонансного напряжения U₀_рез и амплитуды вынуждающей ЭДС ₀. Соотношение (8) при малых коэффициентах затухания принимает вид

откуда

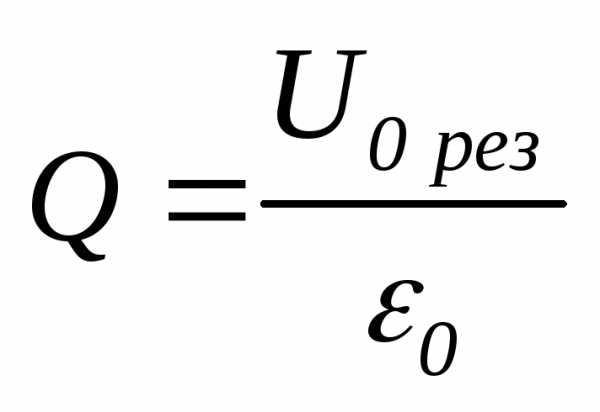. (10)

3. Определение добротности по ширине резонансной кривой. Шириной резонансной кривой называется разность частот, при которых достигается эффективное значение резонансного напряжения на конденсаторе, равное (см. рис. 3) .

Разность этих частот  = ₂ – ₁ является полосой пропускания контура.

Энергия, запасенная в контуре при резонансе, на границах полосы пропускания уменьшается в два раза.

Пользуясь соотношениями (9) и (10) и преобразуя уравнение (5), получаем, что с достаточной степенью точности

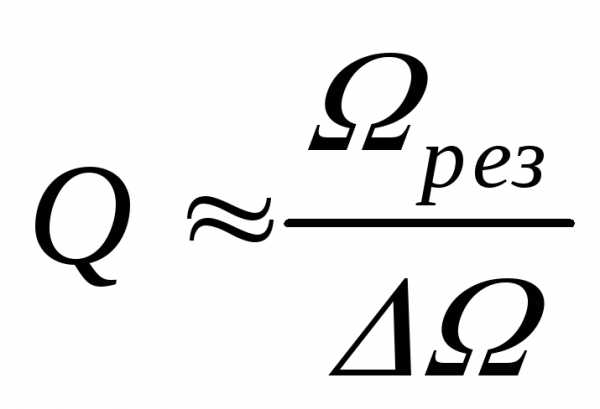. (11)

Таким образом, зная  и _рез, можно вычислить добротность контура.

Расчет добротности этим методом производится с помощью полученной экспериментально резонансной кривой в координатах U₀, . По ней определяются для значения ₁ и ₂ слева и справа от _рез.

Вместо _рез и циклических частот ₁ и ₂ используются соответствующие частоты генератора

. (12)

Метод измерения и описание аппаратуры

Для выполнения работы используется простейший колебательный контур из последовательно соединенных катушки индуктивности L, конденсатора C и сопротивления R. Резонансные кривые снимают при различных сопротивлениях, включенных в контур. Наблюдение за изменением амплитуды колебаний на конденсаторе производится с помощью электронного осциллографа. Для этого сигнал с конденсатора подается на вход осциллографа, и при изменении частоты генератора измеряется амплитуда напряжения. При этом диапазон частот выбирается достаточно широким в обе стороны по отношению к резонансной частоте. Резонансная частота соответствует наибольшей амплитуде измеряемого напряжения при заданном сопротивлении контура. Определение добротности контура производится двумя из вышеописанных способов: по ширине резонансной кривой и по отношению резонансного напряжения к амплитуде вынуждающей ЭДС. Полученные результаты позволяют вычислить омическое сопротивление контура и оценить значение внутреннего сопротивления генератора.

Порядок выполнения работы

Включите генератор синусоидальных колебаний и электронный осциллограф и соберите схему для измерений в соответствии с указаниями на стенде.
Рассчитайте собственную частоту контура по формуле

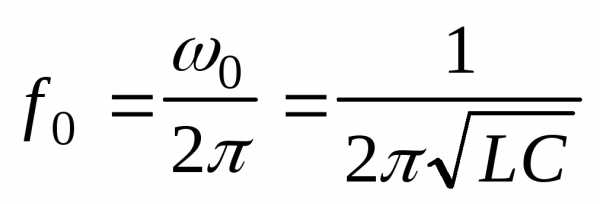Параметры L, C, R_L, r контура даны на стенде. Значения L, C и f₀ запишите в табл. 1.

Определите по осциллографу амплитуды вынужденных колебаний напряжения U₀, снимаемого с конденсатора в делениях масштабной сетки на экране осциллографа, при фиксированных значениях частоты F генератора в выбранном диапазоне частот при R₁. Полученные данные занесите в табл. 1.
Повторите опыт (пункт 3) при другом сопротивлении R₂, включенном в контур.
Не изменяя настройки генератора определите амплитуду колебаний ЭДС генератора, соответствующую резонансной частоте, полученной экспериментально в п. 3,4. Для этого установите на генераторе резонансную частоту, выход генератора подключите непосредственно к входу электронного осциллографа с помощью переключателя на стенде, и зафиксируйте амплитуду сигнала ₀. Результат занесите в табл. 1 и табл. 2.
По данным табл. 1 постройте резонансные кривые при различных сопротивлениях контура R₁ и R₂.
На каждой резонансной кривой отметьте уровень, соответствующий 0,7U₀_рез.

Таблица 1

№

Частота

U₀, В

п/п

F, МГц

R₁ = … Ом

R₂ = … Ом

…

С = … Ф; f₀ = … КГц;

L = … Гн; ₀ = … В.

studfiles.net

Расчет добротности контура

8. По резонансным кривым, снятым экспериментально, определите частоты f₁ и f₂, соответствующие границам полосы пропускания контура и их разность f  f₂  f₁. Результаты измерений занесите в табл. 2.

Таблица 2

Сопротивление контура, Ом	R₁	R₂
U_{0 РЕЗ}, В
0,7U_{0 РЕЗ}, В
f_РЕЗ, МГц
f₁, МГц
f₂, МГц
f, МГц
Q₁
E₀, В
Q₂
Q_СР(Q₁  Q₂)/2
Q_ТЕОРQ

9. Вычислите значения добротности Q₁ и Q₂ по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.

10. Определите среднее арифметическое значение добротности при различных фиксированных значениях сопротивлений контура:

Q_СР  (Q₁  Q₂)/2.

11. Оцените относительную погрешность определения добротности по косвенным измерениям:

Q₁     ,

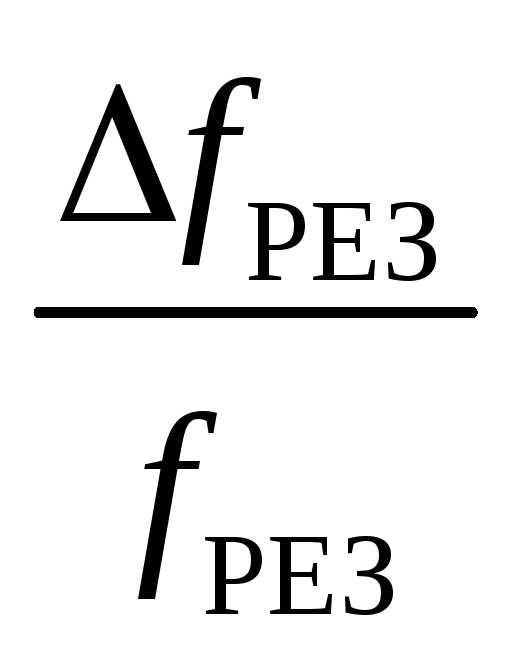
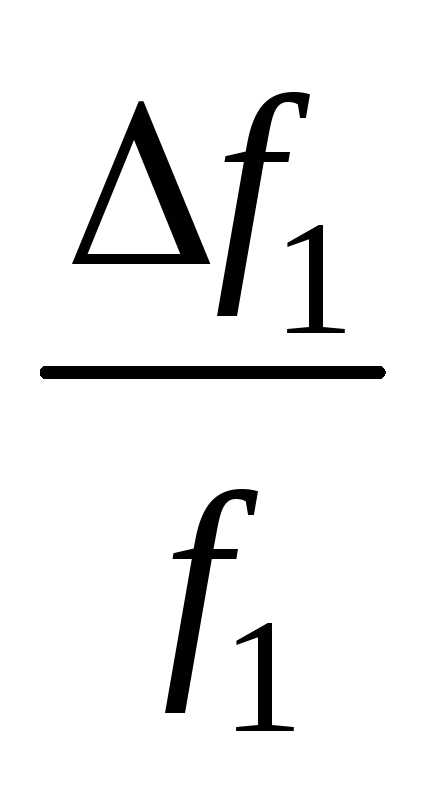
Q₂   ,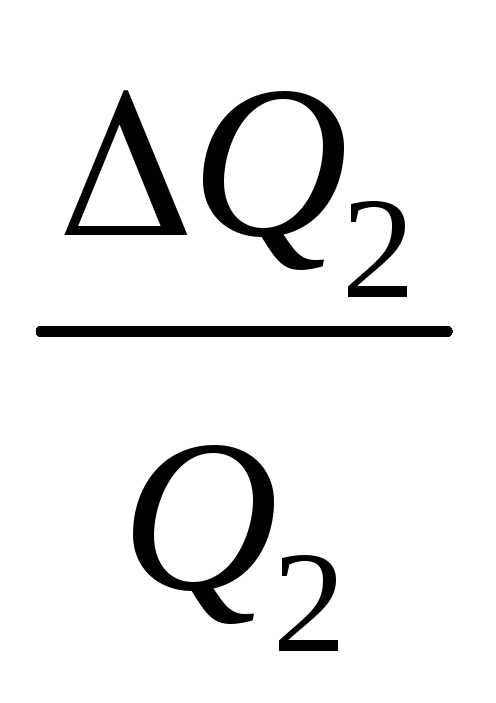

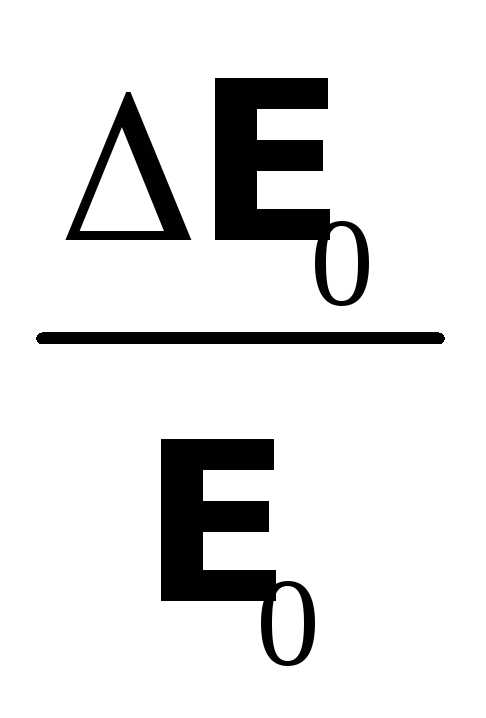где f_РЕЗ, f₁, f₂, U₀_РЕЗ, E₀ – ошибки в определении соответствующих значений f_РЕЗ, f₁, f₂, U₀_РЕЗ, E₀.

Вычислите теоретическое значение добротности контура по формуле (9) и сравните его с результатами расчета по формулам (10) и (12). Объясните возможные причины расхождения результатов измерений и расчета.

Контрольные вопросы

1. Какие колебания называются вынужденными?

2. В чем заключается явление резонанса?

3. От чего зависит добротность контура?

4. Перечислите методы определения добротности контура.

5. Дайте определение полосы пропускания контура.

6. Чему равна частота вынуждающей э. д. с. в момент резонанса?

7. Каким образом снимается резонансная кривая в данной работе?

Список литературы

Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.
Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 129

Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа

Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.

Введение

На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор емкостью C, катушку индуктивностью L и активное сопротивление R.

Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э.д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R  0 при сообщении конденсатору заряда q₀.

Вначале энергия электрического поля конденсатора емкостью C равна:

W_C q₀²/2C  CU₀²/2,

где U₀  q₀/С – максимальная разность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:

I(t)   dq(t)/dt, (1)

где dq(t) – изменение заряда на обкладках конденсатора. Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).

Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции Et), препятствующей изменению тока (E < 0):

E(t)  – L(dI/dt).

При полном разряде конденсатора его электрическое поле исчезает, а ток в контуре, наоборот, достигает максимального значения I₀. Максимального значения достигает и энергия магнитного поля в катушке:

W_L  LI₀²/2.

С этого момента начинается перезарядка конденсатора под действием э. д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.

Интервал времени между двумя последовательными максимальными значениями колеблющейся величины называется периодом колебаний T.

Заметим, что описанные выше колебания происходили бы бесконечно долго лишь при отсутствии испускания таким контуром электромагнитного излучения.

Если колебательный контур содержит активное сопротивление R, то при протекании по нему тока часть общей энергии контура W выделяется в виде тепла:

Q = W_R  I²Rt.

При этом уменьшаются с течением времени амплитудные значения тока в контуре и разности потенциалов на обкладках конденсатора. Колебания затухают.

Временная зависимость разности потенциалов на обкладках конденсатора U(t)  ₁ ₂ наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э. д. с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:

IR  ₁ – ₂  E  U – L(dI/dt). (2)

Преобразуем это уравнение, используя формулу (1) и соотношение q  CU. Тогда уравнение (2) примет вид:

LC(d²U/dt²)  RC(dU/dt)  U  0. (3)

Разделив обе части уравнения (3) на LC и введя обозначения

R/2L = , 1/LC  ₀²,

где ₀ называется собственной циклической (круговой) частотой контура, а  – коэффициентом затухания, получим дифференциальное уравнение:

d²U/dt²  2(dU/dt)  ₀²U  0, (4)

решение которого дает искомую зависимость U(t).

Следует отметить, что аналогичные дифференциальные уравнения могут быть получены для различного рода механических, электромеханических и других колебательных систем, в которых отсутствуют внешние вынуждающие воздействия, а силы сопротивления при малых скоростях движения (скоростях изменения параметра системы, совершающей колебания) линейно зависят от скорости.

При этом энергия, внесенная в сиcтему извне, непрерывно уменьшается в процессе колебаний, переходя, в конечном счете, в тепловую энергию. Уравнение (4) есть линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для частного случая, когда  < ₀, его решение имеет вид:

U(t)  U₀e^^β^tcos(t  ₀), (5)

где ₀ – начальная фаза колебаний;  – циклическая частота затухающих колебаний:

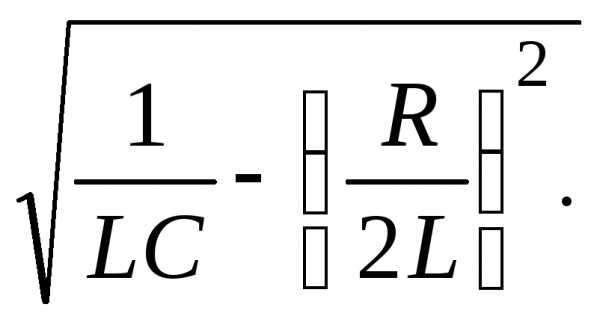= (6)

На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.

Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний

T 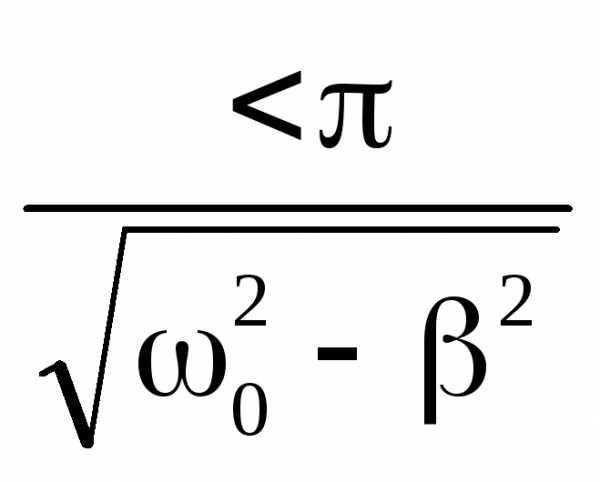 . (7)

Амплитудой затухающих колебаний называют величину

A(t)  U₀e^^^t, (8)

где U₀ – максимально возможное значение амплитуды напряжения:

U₀  A(t  0).

Вообще говоря, при  0 разность потенциалов U(t) не является строго периодической функцией времени: U(t)U(t  T). Периодом колебаний в этом случае принято считать минимальные промежутки времени между наибольшими значениями напряжения одного знака.

Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания . Согласно (8) коэффициент затухания есть физическая величина, обратная времени , в течение которого амплитуда колебаний уменьшается в е раз:

U₀/A()  e при t    1/.

Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при   0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а):

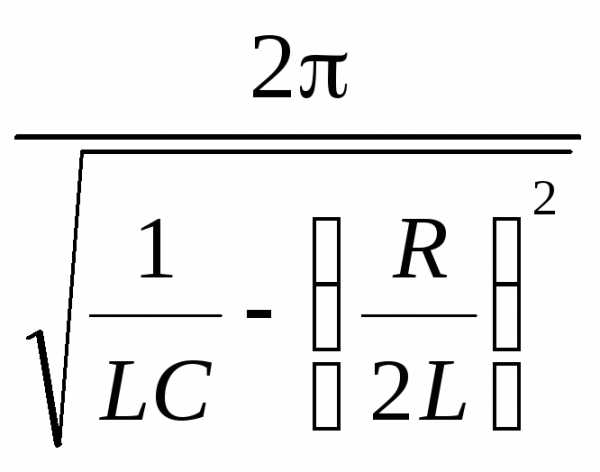
U(t)  U₀cos(₀t  ₀)

с периодом T₀  2/₀  2(формула У.Томсона).

При критическом сопротивлении (см. формулы (6) и (7))

R  R_КР  2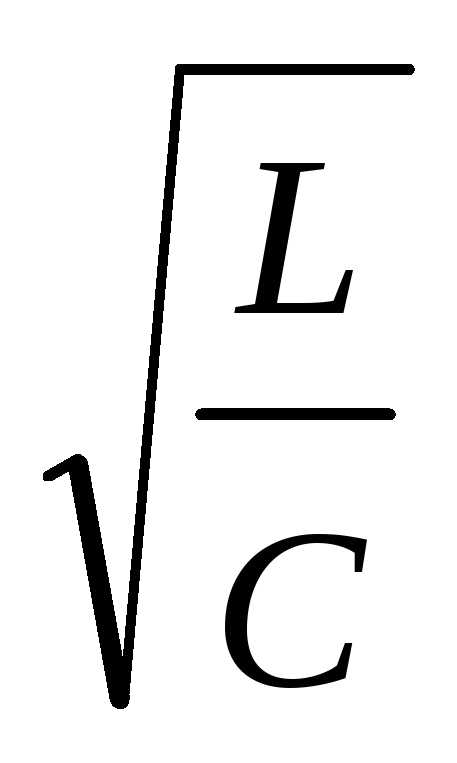

  ₀, и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).

При R < R_КР (т. е. при  < ₀) в контуре реализуется затухающий колебательный процесс (рис. 2б).

При R > R_КР (  ₀) циклическая частота  и период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).

Для характеристики затухающих колебаний наряду с коэффициентом затухания  используются и другие параметры: логарифмический декремент  и добротность контура Q.

Логарифмический декремент вводится как натуральный логарифм отношения амплитуд колебаний, разделенных во времени на период Т (рис. 2):

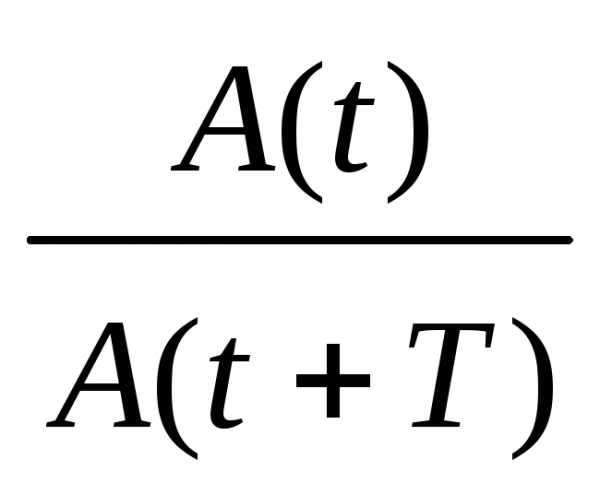  ln ln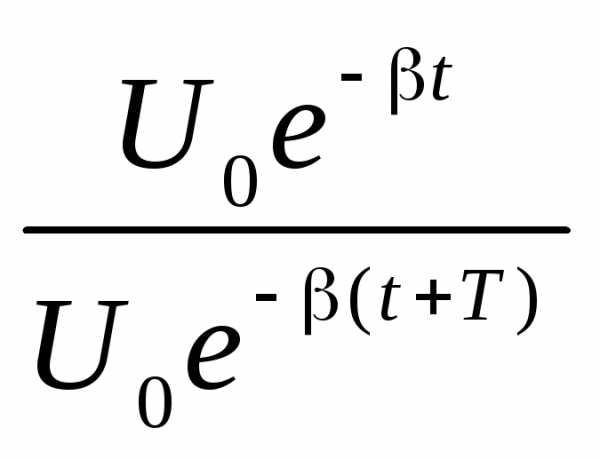 T  T/  1/N, (9)

т.е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N  ).

Из соотношения между  и 

  T  RT/(2L) (10)

при малых затуханиях (  ₀): T  T₀  2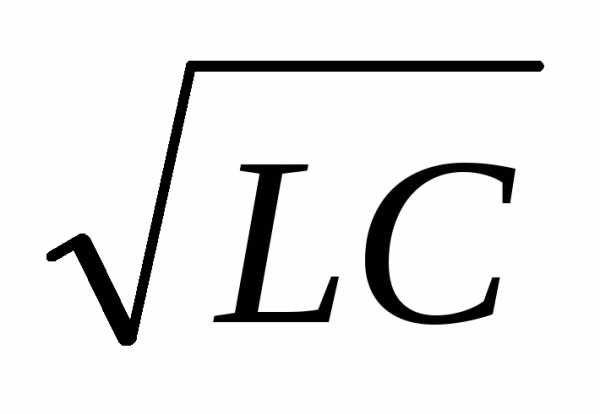можно, зная , определить коэффициент затухания :

  /T₀  /(2 

Добротность контура Q – важный параметр, характеризующий быстроту потери энергии, запасенной в контуре. Добротность контура показывает, во сколько раз амплитуда вынужденных колебаний напряжения на конденсаторе при резонансе превышает амплитуду внешней прикладываемой электродвижущей силы, и определяется формулой:

Q  ₀/2.

Для колебаний при малых  частота затухающих колебаний ω приблизительно равна собственной частоте колебаний ₀ (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:

Q  ₀/2 ≈ /2 = 2/2βT  /. (12)

Для колебательного контура:

R/2L, и ₀  1/.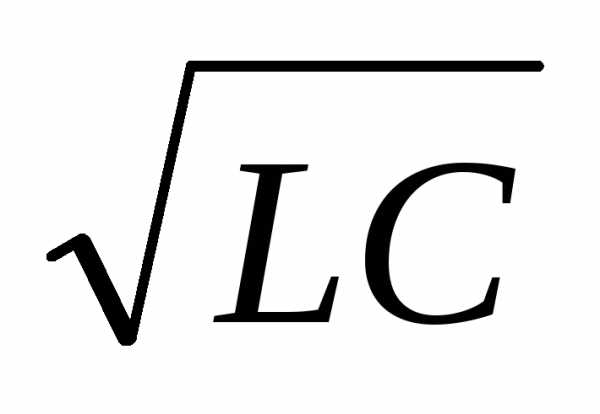

Добротность в этом случае:

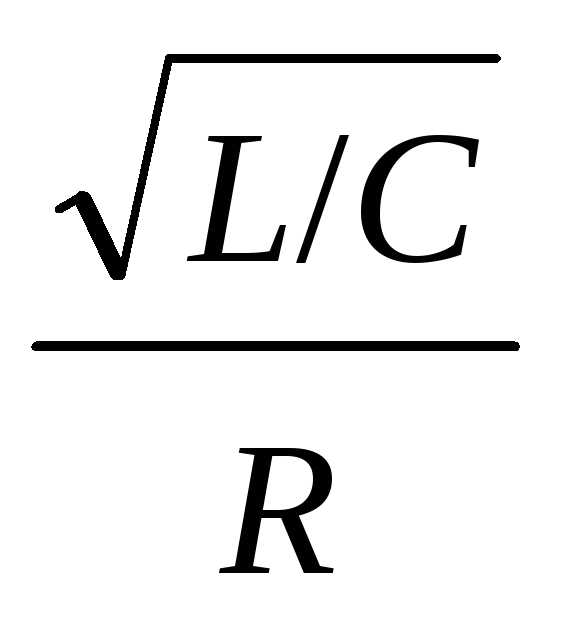
Q  ₀/2   /R. (13)

Физическую величину 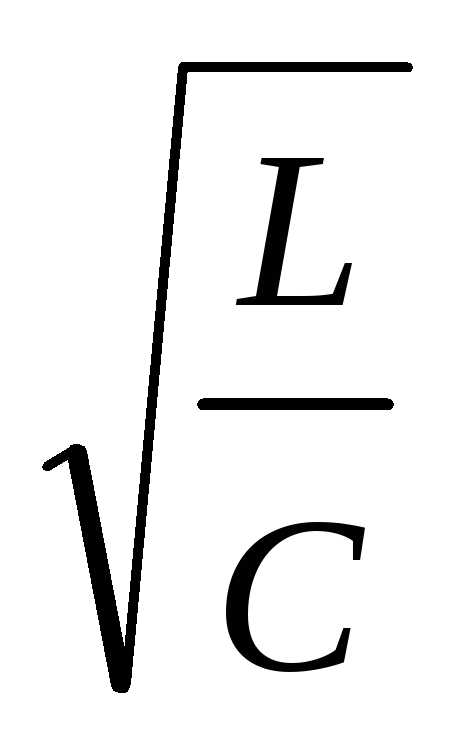  называют волновым или характеристическим сопротивлением колебательного контура.

Из соотношения (13) следует, что контур, имеющий большое активное сопротивление, обладает малой добротностью и интенсивно теряет электромагнитную энергию, колебания быстро затухают.

Все рассмотренные процессы относятся к колебательному контуру с сосредоточенными параметрами R, L и C. В реальных колебательных контурах нельзя выделить ни одного участка цепи, не обладающего активным сопротивлением, индуктивностью и емкостью, т. е. параметры R, L и С не являются сосредоточенными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При этом также необходимо учитывать входные электрические параметры измерительных приборов.

studfiles.net

Резонансная частота, добротность последовательного контура

Выведем формулу резонансной частоты:

Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура .

Настроить контур в резонанс можно:

1) изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;

2) можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.

Т. к. , то можно записать, что .

Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.

Формула добротности:

Вывод:добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.

Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной

Расстройка — отклонение частоты от резонансной. Различают:

1) Абсолютная расстройка — разность текущей частоты и резонансной:

Расстройка может и положительной и отрицательной.

2) Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:

3) Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:

Обычно входные характеристики строят от расстройки.

Входные АЧХ и ФЧХ последовательного контура

, где

— формула входной АЧХ последовательного контура

(на резонансной частоте все расстройки равны 0)

Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение . По мере увеличения расстройки сопротивление контура возрастает.

ФЧХ:

— формула входной ФЧХ последовательного контура

Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: . На частотах меньше резонансной характер сопротивления активно-емкостной, т. к. . На частотах больше резонансной характер сопротивления активно-индуктивный: .

Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы

Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать

— передаточная АЧХ последовательного контура в абсолютных координатах

Вывод: на резонансной частоте коэффициент передачи последовательного контура максимальный: .

ФЧХ:

На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол практически равен углу выходного напряжения, поэтому характеристику сдвигаем на 90° вниз:

Передаточная ФЧХ имеет линейный участок при расстройках от до .

Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура

Избирательность — способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.

На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. , и на этой частоте самый большой коэффициент передачи.

Вывод: последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.

Полоса пропускания контура — область частот, на границах которой модуль комплексного коэффициента передач уменьшается в раз по сравнению с резонансным.

На уровне полосы пропускания коэффициент обозначается :

Нарисуем передаточную характеристику :

Вывод: чем выше добротность, тем уже полоса пропускания контура.

Кривые тока и напряжения такого вида называются резонансными.

Примечание:

При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:

Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность

Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.

В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе: .

— условие резонанса токов

Проводимость индуктивная равна проводимости емкостной.

При резонансе токов сопротивление параллельного контура максимально.

Свойства цепи при резонансе токов:

1. Ток в момент резонанса:

При резонансе токов общий ток минимальный.

2. На практике ,

При резонансе токов токи ветвей приблизительно равны.

3. Построим векторную диаграмму для резонанса токов:

Если бы (контур идеальный), то токи , и общий ток был бы равен 0, но т. к. есть небольшое , то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.

4. Выведем формулу резонансной частоты. Для этого

Вывод: резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.

Получить резонанс токов можно, изменяя L или C, или частоту питающего напряжения.

5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:

Рассчитаем токи в момент резонанса:

Вывод: добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.

infopedia.su

Добротность контура | Шаг за шагом

С течением времени амплитуды напряжения и тока в контуре уменьшаются – электромагнитные колебания затухают, подобно тому, как затухают колебания маятника или струны (рис. 48, 49).

Затухание электромагнитных колебаний в контуре связано с тем, что всякий раз при «перекачивании» энергии из конденсатора в катушку и обратно часть этой энергии безвозвратно теряется. Основные потери энергии в контуре – это потери в проводе катушки, в соединительных проводах, в изоляции проводов, потери в диэлектрике конденсатора и каркасе катушки, а также на излучение электромагнитных волн.

Таким образом, если мы хотим нарисовать реальную схему контура, то, помимо контурной катушки _Lк и конденсатора С_к, мы должны включить в нее и сопротивления, которые будут характеризовать потери энергии (лист 76). В действительности никаких сопротивлений (имеется в виду отдельная деталь) в контуре, конечно, нет. Но потери энергии в катушке, конденсаторе и т. д. существуют реально. Для того чтобы не забывать об этом, мы и рисуем на схеме не только катушку L_к и конденсатор С_к, но и условные сопротивления, которые отображают фактически существующие потери энергии.

Основные виды потерь – потери в катушке, потери на излучение и другие – условно характеризуются сопротивлением R_к, включенным последовательно, с L_к и С_к (лист 76, упрощенные схемы). Во время колебаний по сопротивлению R_к проходит весь контурный ток и, чем больше R_к, тем больше энергии на нем теряется.

Для учета некоторых видов потерь (потери в конденсаторе, в каркасе и др.) иногда приходится считать, что в контуре имеется еще одно сопротивление R_ш, шунтирующее (лист 32) конденсатор С_к или катушку L_к. Во время разряда конденсатора ток разветвляется: часть его проходит через катушку и создает там запасы энергии в виде магнитного поля. Другая часть разрядного тока проходит через сопротивление R_ш и создает там безвозвратные потери энергии. Чем меньше тем больший ток через него проходит, тем больше энергии теряется на этом сопротивлении.

Таким образом, для того чтобы уменьшить потери в контуре, нужно стремиться к тому,чтобы сопротивление R_к было как можно меньше, а сопротивление R_ш как можно больше (рис 50, 51). Сопротивления R_к и R_ш на схемах радиоаппаратуры не изображаются, так как они не представляют собой самостоятельных деталей. Однако эти сопротивления реально существуют и, потребляя энергию, приводят к затуханию колебаний.

Для характеристики затухания колебаний существует специальная величина, называемая добротностью (лист 77).

Добротность обозначается буквой «Q» и представляет собой относительное число, показывающее, во сколько раз энергия, запасаемая в конденсаторе или катушке за четверть периода, больше, чем энергия, теряемая на сопротивлениях R_ки R_ш за то же время. Совершенно очевидно, что, чем выше добротность Q, тем медленнее будут затухать колебания в контуре (лист 78). Добротность реальных колебательных контуров обычно лежит в пределах от 30 (в контуре каждый раз теряется одна тридцатая часть, то есть около 3 % перекачиваемой энергии) до 300 (потери около 0,3% от запасенной энергии). Добротность специальных колебательных систем (кварцевые пластины, объемные резонаторы) достигает нескольких десятков и даже сотен тысяч.

Ухудшить добротность контура (иногда возникает и такая необходимость) можно очень просто: достаточно увеличить потери в контуре, увеличив Rк или уменьшив R_ш. Для этого можно, например, включить в контур обычные сопротивления.

oldradiogid.ru

Расчет добротности контура

8. По резонансным кривым, снятым экспериментально, определите частоты f₁ и f₂, соответствующие границам полосы пропускания контура и их разность Df = f₂ – f₁. Результаты измерений занесите в табл. 2.

Таблица 2

Сопротивление контура, Ом	R₁	R₂
U_{0 РЕЗ}, В
0,7U_{0 РЕЗ}, В
f_РЕЗ,МГц
f₁, МГц
f₂, МГц
Df, МГц
Q₁ =
E₀, В
Q₂ =
Q_СР = (Q₁ + Q₂)/2
Q_ТЕОР = Q =

Q_СР = (Q₁ + Q₂)/2.

11. Оцените относительную погрешность определения добротности по косвенным измерениям:

dQ₁ = = + + ,

dQ₂ = = + ,

где Df_РЕЗ, Df₁, Df₂,DU₀_РЕЗ, DE₀ – ошибки в определении соответствующих значений f_РЕЗ, f₁, f₂, U₀_РЕЗ, E₀.

Контрольные вопросы

1. Какие колебания называются вынужденными?

2. В чем заключается явление резонанса?

3. От чего зависит добротность контура?

4. Перечислите методы определения добротности контура.

5. Дайте определение полосы пропускания контура.

6. Чему равна частота вынуждающей э. д. с. в момент резонанса?

7. Каким образом снимается резонансная кривая в данной работе?

Список литературы

3. Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

4. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 129

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

Введение

Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R = 0 при сообщении конденсатору заряда q₀.

Вначале энергия электрического поля конденсатора емкостью C равна:

W_C = q₀²/2C = CU₀²/2,

где U₀ = q₀/С – максимальнаяразность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:

I(t) = – dq(t)/dt, (1)

Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции E(t), препятствующей изменению тока (E < 0):

E(t) = – L(dI/dt).

W_L = LI₀²/2.

Q = W_R = I²Rt.

Временная зависимость разности потенциалов на обкладках конденсатора U(t) = j₁ – j₂ наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э. д. с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:

IR =j₁ – j₂ + E = U – L(dI/dt). (2)

Преобразуем это уравнение, используя формулу (1) и соотношение q = CU. Тогда уравнение (2) примет вид:

LC(d²U/dt²) + RC(dU/dt) + U = 0. (3)

Разделив обе части уравнения (3) на LC и введя обозначения

R/2L = b, 1/LC = w₀²,

где w₀ называется собственной циклической (круговой) частотой контура, а b – коэффициентом затухания, получим дифференциальное уравнение:

d²U/dt² + 2b(dU/dt) + w₀²U = 0, (4)

решение которого дает искомую зависимость U(t).

U(t) = U₀e^–^βtcos(wt + j₀), (5)

где j₀ – начальная фаза колебаний; w – циклическая частота затухающих колебаний:

w = = (6)

На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.

Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний

T = = . (7)

Амплитудой затухающих колебаний называют величину

A(t) = U₀e^–^b^t, (8)

где U₀ – максимально возможное значение амплитуды напряжения:

U₀= A(t = 0).

Вообще говоря, при b¹ 0 разность потенциалов U(t) не является строго периодической функцией времени: U(t) ¹ U(t + T). Периодом колебаний в этом случае принято считать минимальные промежутки времени между наибольшими значениями напряжения одного знака.

Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания b. Согласно (8) коэффициент затухания есть физическая величина, обратная времени t, в течение которого амплитуда колебаний уменьшается в е раз:

U₀/A(t) = e при t = t= 1/b.

Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при b = 0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а):

U(t) = U₀cos(w₀t + j₀)

с периодом T₀ = 2p/w₀ = 2p (формула У.Томсона).

При критическом сопротивлении (см. формулы (6) и (7))

R = R_КР = 2

b = w₀, и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).

При R < R_КР (т. е. при b < w₀) в контуре реализуется затухающий колебательный процесс (рис. 2б).

При R > R_КР (b > w₀) циклическая частота wи период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).

Для характеристики затухающих колебаний наряду с коэффициентом затухания b используются и другие параметры: логарифмический декремент d и добротность контура Q.

d = ln = ln = bT = T/t = 1/N, (9)

т.е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N = t/T).

Из соотношения между d и b

d = bT = RT/(2L) (10)

при малых затуханиях (b << w₀): T » T₀ = 2p можно, зная d, определить коэффициент затухания b:

b = d/T₀ = d/(2p ). (11)

Q = w₀/2b.

Для колебаний при малых b частота затухающих колебаний ω приблизительно равна собственной частоте колебаний w₀ (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:

Q = w₀/2b ≈ w/2b = 2p/2βT = p/d. (12)

Для колебательного контура:

b = R/2L, и w₀ = 1/ .

Добротность в этом случае:

Q = w₀/2b = = r/R. (13)

Физическую величину r = называют волновым или характеристическим сопротивлением колебательного контура.

studopedya.ru

Что такое добротность колебательного контура?как измерить добротность в радиолюбительских условиях.

7.5. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с

7.6. Определение добротности по резонансной кривой

Методы определения добротности

Метод измерения и описание аппаратуры

Порядок выполнения работы

Расчет добротности контура

Контрольные вопросы

Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа

Введение

Резонансная частота, добротность последовательного контура

Добротность контура | Шаг за шагом

Расчет добротности контура

Оставить комментарий Отменить ответ