Решение ДУ с разделяющимися переменными, примеры, формула
Определение
Дифференциальное уравнение вида:называют дифференциальным уравнением 1-го порядка с разделяющимися переменными. В данном разделе математики эти уравнения самые лёгкие в решении.
Формула
Для решения существует универсальный алгоритм:
- Суть его состоит в том, чтобы обе части ду разделить на произведение функций, зависящих от разных переменных:
- Таким образом мы приводим исходное уравнение, заданное по условию, к виду:
- Далее необходимо проинтегрировать обе части уравнения, из которых мы получим функцию y(x):
Примеры решений
| Пример 1 |
| Решить уравнение: |
| Решение |
Решение как всегда начнем с анализа типа дифференциального уравнения. Данное уравнение попадает под определение ДУ первого порядка с разделяющимися переменными. А значит, начнем действовать по алгоритму решения. Распишем подробно: Далее разделим обе части уравнения на произведение двух функций: Получаем: Возьмем интеграл от обеих частей последнего равенства: Используя формулы и методы интегрирования, получаем: Общее решение: Как видим ответ легко получен и записан в последней строчке. |
| Ответ |
| Пример 2 |
| Решить ДУ первого порядка с разделяющимися переменными: |
| Решение |
Перенесем первое слагагаемое, содержащее dx в правую часть для удобства решения: Разделим обе части на выражение: Получаем: Искомое решение: Получаем ответ, в виде: |
| Ответ |
| Пример 3 |
| Решить ДУ 1-го порядка разделяя переменные: |
| Решение |
Решаем: |
| Ответ |
| Пример 4 |
| Найти общее решение ДУ с разделяющимися переменными: |
| Решение |
Решать начнем с того, что воспользуемся свойством: Получаем, Разделяем переменные, Спокойно интегрируем уравнение, Отсюда ответ, |
| Ответ |
| Пример 5 |
| Решить задачу Коши: |
| Решение |
Найдем для начала общее решение ДУ: Отсюда получается общее решение: Решить задачу Коши это значит, найти постоянную из дополнительного условия . Чтобы это проделать нужно подставить в общее решение и . Теперь, подставляя найденное в общее решение, записываем ответ: |
| Ответ |
xn--24-6kcaa2awqnc8dd.xn--p1ai
Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения, в которых выражение, зависящее от y, входит только в левую часть, а выражение, зависящее от x – только в правую часть, это дифференциальные уравнения с разделяющимися переменными, в которых переменные уже разделены.
В левой части уравнения может находиться производная от игрека и в этом случае решением дифференциального уравнения будет функция игрек, выраженная через значение интеграла от правой части уравнения. Пример такого уравнения – .
В левой части уравнения может быть и дифференциал функции от игрека и тогда для получения решения уравнения следует проинтегрировать обе части уравнения. Пример такого уравнения – .
Пример 1. Найти общее решение дифференциального уравнения
Решение. Пример очень простой. Непосредственно находим функцию по её производной, интегрируя:
Таким образом, получили функцию – решение данного уравнения.
Пример 2. Найти общее решение дифференциального уравнения
Решение. Интегрируем обе части уравнения:
.
Оба интеграла – табличные. Идём к решению:
Функция – решение уравнения – получена. Как видим, нужно только уверенно знать табличные интегралы и неплохо расправляться с дробями и корнями.
Дифференциальные уравнения с разделяющимися переменными, в которых требуется разделить переменные, имеют вид
.
В таком уравнении и
– функции только переменной x,
а и –
функции только переменной
Поделив члены уравнения на произведение , после сокращения получим
.
Как видим, левая часть уравнения зависит только от x, а правая только от y, то есть переменные разделены.
Левая часть полученного уравнения – дифференциал некоторой функции переменной x, а правая часть – дифференциал некоторой функции переменной y. Для получения решения исходного дифференциального уравнения следует интегрировать обе части уравнения. При этом при разделении переменных не обязательно переносить один его член в правую часть, можно почленно интегрировать без такого переноса.
Пример 3. Найти общее решение дифференциального уравнения
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение почленно на произведение и получим
.
Почленно интегрируем:
,
откуда, используя метод замены переменной (подстановки), получаем
или ,
поскольку левая часть равенства есть сумма арифметических значений корней. Таким образом, получили
общий интеграл данного уравнения. Выразим из него
.
Есть задачи, в которых для разделения переменных уравнение нужно не делить почленно на произведение некоторых функций, а почленно умножать. Таков следующий пример.
Пример 4. Найти общее решение дифференциального уравнения
.
Решение. Бывает, что забвение элементарной (школьной) математики мешает даже близко подойти к началу решения, задача выглядит абсолютно тупиковой. В нашем примере для начала всего-то нужно вспомнить свойства степеней.
Так как , то перепишем данное уравнение в виде
.
Это уже уравнение с разделяющимися переменными. Умножив его почленно на произведение , получаем
.
Почленно интегрируем:
Первый интеграл находим интегрированием по частям, а второй – табличный. Следовательно,
.
Логарифимруя обе части равенства, получаем общее решение уравнения:
.
Пример 5. Найти общее решение дифференциального уравнения
.
Это уравнение с разделяющимися переменными
.
Чтобы найти y, требуется найти интеграл. Интегрируем по частям.
Пусть , .
Тогда , .
Находим общее решение уравнения:
Пример 6. Найти частное решение дифференциального уравнения
,
удовлетворяющее условию .
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение почленно на и получим
или
.
Записываем производную y в виде и получаем
Разделяем dy и dx и получаем уравнение:
, которое почленно интегрируя:
,
находим общее решение уравнения:
.
Чтобы найти частное решение уравнения, подставляем в общее решение значения y и x из начального условия:
.
Таким образом частное решение данного дифференциального уравнения:
.
В некоторых случаях ответ (функцию) можно выразить явно. Для этого следует воспользоваться тем свойством логарифма, что сумма логарифмов равна логарифму произведения логарифмируемых выражений. Обычно это следует делать в тех случаях, когда слева искомая функция под логарифмом находится вместе с каким-нибудь слагаемым. Рассмотрим два таких примера.
Пример 7. Найти общее решение дифференциального уравнения
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных запишем производную “игрека” в виде и получим
.
Разделяем “игреки” и “иксы”:
.
Почленно интегрируем и, так как в левой части “игрек” присутствует со слагаемым, в правой части константу интегрирования записываем также под знаком логарифма:
.
Теперь по свойству логарифма имеем
.
Находим общее решение уравнения:
Пример 8. Найти частное решение дифференциального уравнения
,
удовлетворяющее условию .
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение почленно на и получим
или
.
Разделяем dy и dx и получаем уравнение:
которое почленно интегрируя:
находим общее решение уравнения:
.
Чтобы найти частное решение уравнения, подставляем в общее решение значения y и x из начального условия:
.
Таким образом частное решение данного дифференциального уравнения:
.
Выводы. В дифференциальных уравнениях с разделяющимися переменными, как в тех, в которых переменные уже разделены, так и в тех, где переменные требуется разделить, существуют однозначные способы решения, на основе которых может быть построен простой алгоритм. Если недостаточно уверенно освоен материал по нахождению производной и решению интегралов, то требуется его повторить. Во многих задачах на путь к решению уравнения наводят знания и приёмы из элементарной (школьной) математики.
Всё по теме “Дифференциальные уравнения”
Поделиться с друзьями
function-x.ru
Дифференциальные уравнения с разделенными переменными
Многие студенты спрашивают “Как найти решение дифференциального уравнения?” Ответ возможно неординарен, но что Вы знаете о дифференциальных уравнениях (ДУ), их типах, какие распространенные схемы вычислений ДУ? С этого нужно начинать.
Сферы применения дифференциальных уравнений были в общем очерчены на предыдущем уроке. Здесь речь пойдет об одном из самых простых (в плане вычислений) типов ДУ первого порядка среди всех возможных уравнений что Вас ждут. Начнем с базовых понятий теории которые Вы должны знать и мы будем использовать в терминологии. Для одних это не нужно, потому что они ищут готовые ответы по дифференциальным уравнениям и думают, что таким образом решат все проблемы. Но это ошибка, потому что не знание элементарных понятий по теории ДУ сравнимо с тем, что Вы пытаетесь говорить, предварительно не изучив звуки и алфавит.
Дифференциальное уравнение первого порядка, которое можно записать формулой
N(х)dx+М(у)dy=0 (1)
называют уравнением с разделенными переменными.
Их не трудно обнаружить среди других уравнений, основной признак – множители при dx и dy являются функциями (константами), которые зависят только от х при множителе dx и у при dy.
Чтобы найти общее решение (общий интеграл) уравнения с разделенными переменными необходимо проинтегрировать уравнение (1)
Int(N(x), x) + Int(M(y),y) = С,
Для понимания дифференциальное уравнение (1) можно принимать, как условие равенства нулю полного дифференциала некоторой функции двух переменных U(x,y)
Отсюда следует что функция U(x,y)=С=const равна постоянной.
Дифференциальное уравнение вида
f1(x)*g1(y)dx+f2(x)*g2(y)dy=0 (2)
называют дифференциальным уравнением с разделяющимися переменными в симметричной форме.
В уравнении (2) коэффициенты при дифференциалах dx и dy является произведениями двух функций: одна зависит только от x, а вторая – от y. В области, где g1(y), f2(x) принимают отличные от нуля значения в уравнение с разделяющимися переменными (2) сводится к уравнению с разделенными переменными
Звучит как игра слов: разделенными, разделяющимися, однако между ними как видите есть маленькая разница, и теперь Вы ее знаете.
Рассмотрим типичные для практики задания на диф. уравнения первого порядка, которые в достаточно простой способ можно свести к уравнениям с разделенными переменными.
Пример 1 Решить дифференциальное уравнение
Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства
Далее выделим общие множители для каждой суммы и перепишем уравнение в дифференциалах в форме
После этого все, что содержит y переносим к dy, то же самое проделываем с множителями которые содержат переменную x.
В результате придем к дифференциальному уравнению с разделенными переменными
Теперь посмотрите почему данное уравнение называется уравнением с разделенными переменными? – Возле dx имеем функцию зависимую только от “икс”, у dy – только от y.
Проинтегрируем дифференциальное уравнение
Выносим множители, чтобы при переменной в знаменателе стояли единицы. Также, чтобы в числителе получить дифференциалы знаменателя умножаем обе части на 2
Это позволяет упростить вычисления интеграла ДУ (после интегрирования получить логарифмы)
Константу рекомендуем внести в логарифм, для этого записывайте всегда ее в виде C1=ln(C)
Чтобы раскрыть логарифмическое уравнение экспонируем (находим экспоненту) правую и левую сторону зависимости
(3)
Также выделяем значение функции
Конечная запись имеет двойной корень и является общим решением уравнения с разделяющимися переменными. Это не совсем хороший тон подавать ответ, лучше решение оставить в виде формулы (3), только тройку перенести в правую сторону.
Пример 2 Найти общий интеграл дифференциального уравнения
Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства
С первых скобок выносим общий для двух слагаемых множитель y за скобки
Далее разделим множители так, чтобы при dy получить функцию только от y, а при dx – функцию аргумента x. В результате получим дифференциальное уравнение с разделенными переменными
После интегрирования
получим корневую зависимость для y и арктангенс в результате вычисления интеграла по аргументу (правая сторона).
Общий интеграл можем оставить в такой форме или перенести артангенс в левую часть зависимости.
Так же можем записать решение дифференциального уравнения в виде зависимости y(x) (явном виде). Для этого возведем обе части к квадрату
и перенеся сталую в правую сторону, вычислим корень квадратный
Это и есть искомое решение дифференциального уравнения.
Пример 3 Решить дифференциальное уравнение
Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства
и разделяем переменные
Проинтегрируем левую и правую сторону зависимости
В результате придем к логарифмическому уравнению вида
И снова обращаем Ваше внимание на то что в таком виде как правило не записывают.
Целесообразно, для компактности конечного решения, постоянную вносить под логарифм, то есть в форме
Взяв экспоненту от правой и левой части формулы придем к конечному виду решения дифференциального уравнения
Как Вы могли убедиться примеры достаточно просты, методика вычислений ДУ з разделенными переменными легкая для изучения.
Пример 4 Решить дифференциальное уравнениеРешение: Одно из слагаемых (не содержит производной) переносим за знак равенства
и записываем уравнение в дифференциалах..
Следующим шагом сводим зависимость к дифференциальному уравнению с разделенными переменными.
Для заданного уравнения всего лишь перекрестным делением записываем корни в знаменатели
В таком виде можем интегрировать уравнения
Левая сторона содержит функцию которая при иртегрировании даст корневую зависимость, для правой стороны по формулам получим арксинус.
Выполняем манипуляции с корнем, чтобы получить зависимость вида y=y(x)
Решение дифференциального уравнения будет иметь вид
На этом вводный урок закончен и основные выводы Вы должны сделать самостоятельно.
Для закрепления темы рекомендуем самостоятельно решить несколько из следующих примеров.
 Хотите верьте, а хотите – нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Хотите верьте, а хотите – нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Схему вычислений должны заучить и знать на зубок – это один из основных методов решения сложных примеров на диф. уравнения.
yukhym.com
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение с разделенными переменными записывается в виде: (1).В этом уравнении одно слагаемое зависит только от x, а другое – от y. Проинтегрировав почленно это уравнение, получаем: – его общий интеграл.
Пример: найти общий интеграл уравнения: .
Решение: данное уравнение
– дифференциальное уравнение с
разделенными переменными. Поэтому
или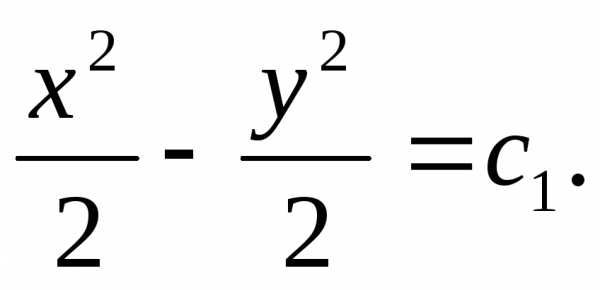 Обозначим
Обозначим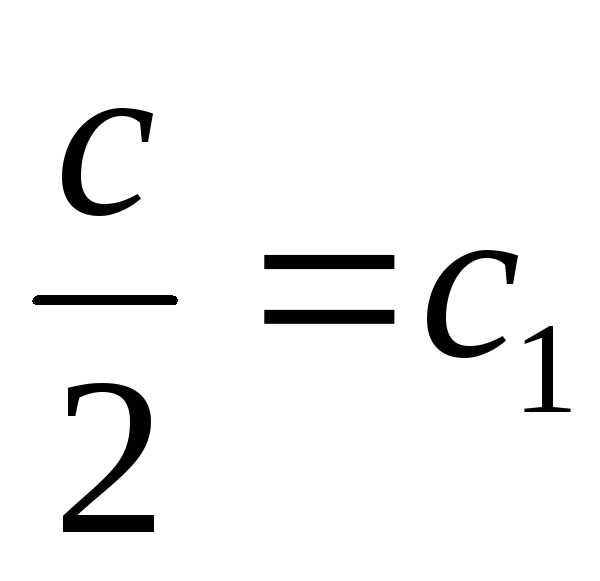 .
Тогда–
общий интеграл дифференциального
уравнения.
.
Тогда–
общий интеграл дифференциального
уравнения.
Уравнение с разделяющимися переменными имеет вид (2).Уравнение (2) легко сводиться к уравнению (1) путем почленного деления его на . Получаем:– общий интеграл.
Пример: Решить уравнение .
Решение: преобразуем левую
часть уравнения:
.
Делим обе части уравнения на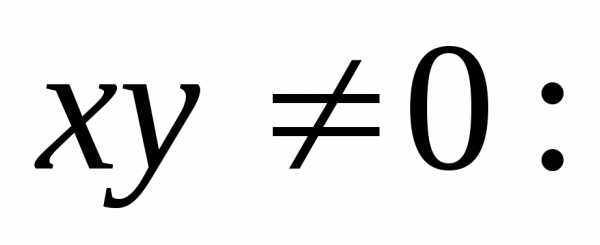 Решением является выражение:т.е.
Решением является выражение:т.е.
Однородные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения первого порядка.
Уравнение вида
называетсяоднородным,
если  и
и –
однородные функции одного порядка
(измерения). Функция
–
однородные функции одного порядка
(измерения). Функция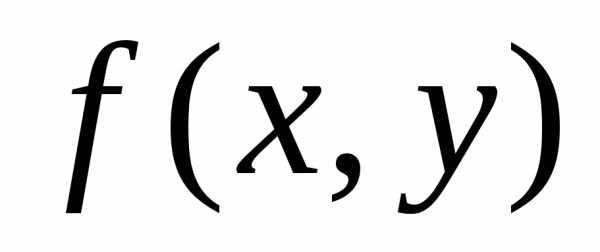 называется
однородной функцией первого порядка
(измерения), если при умножении каждого
ее аргумента на произвольный множитель
называется
однородной функцией первого порядка
(измерения), если при умножении каждого
ее аргумента на произвольный множитель вся функция умножиться на
вся функция умножиться на ,
т.е.=
,
т.е.=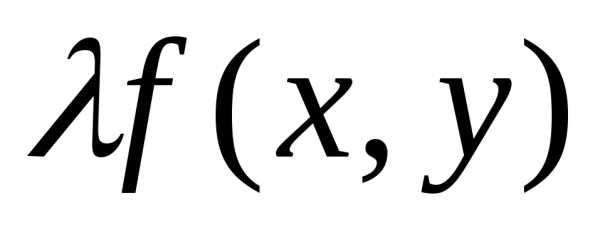 .
.
Однородное уравнение может быть приведено
к виду 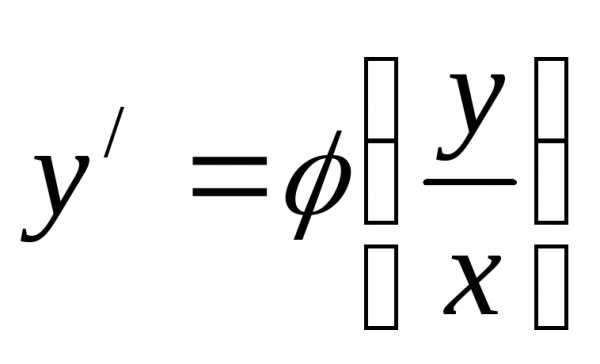 .
С помощью подстановки
.
С помощью подстановки (
(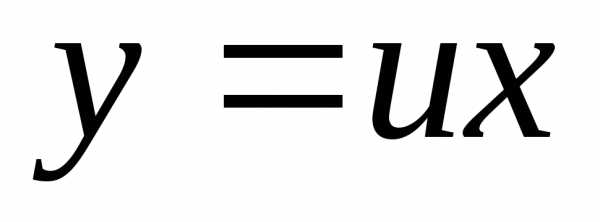 )однородное
уравнение приводится к уравнению с
разделяющимися переменными по отношению
к новой функции
)однородное
уравнение приводится к уравнению с
разделяющимися переменными по отношению
к новой функции .
.
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде.
Метод Бернулли
Решение уравнения ищется в виде произведения двух других функций, т.е. с помощью подстановки().
Пример: проинтегрировать уравнение .
Полагаем
.
Тогда
,
т.е.
.
Сначала решаем уравнение=0:
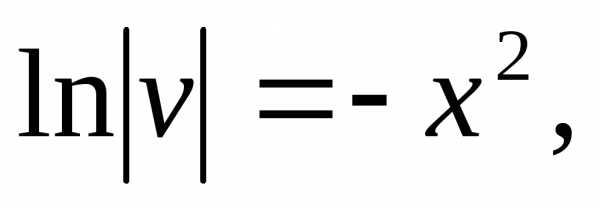
 .
.
Теперь решаем уравнение
т.е. .
Итак, общее решение данного уравнения
естьт.е.
.
Итак, общее решение данного уравнения
естьт.е.
Уравнение Я. Бернулли
Уравнение вида , гденазываетсяуравнением Бернулли.Данное уравнение решается с помощью метода Бернулли.
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Однородным линейным дифференциальным
уравнением второго порядка называется
уравнение вида (1), где и
и постоянны.
постоянны.
Частные решения уравнения (1) будем
искать в виде  ,
гдек – некоторое число. Дифференцируя
эту функцию два раза и подставляя
выражения для
,
гдек – некоторое число. Дифференцируя
эту функцию два раза и подставляя
выражения для в
уравнение (1), получимт.е.или(2)(
в
уравнение (1), получимт.е.или(2)( ).
).
Уравнение 2 называется характеристическим уравнением дифференциального уравнения.
При решении характеристического уравнения (2) возможны три случая.
Случай 1.Корни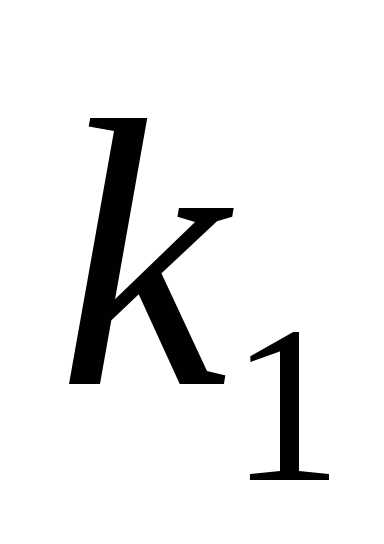 и
и уравнения (2) действительные и различные:
уравнения (2) действительные и различные: .
В этом случае частными решениями
уравнения (1) являются функции
.
В этом случае частными решениями
уравнения (1) являются функции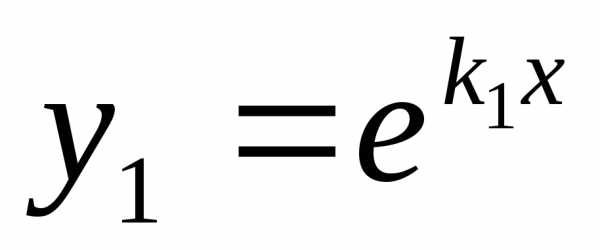 и
и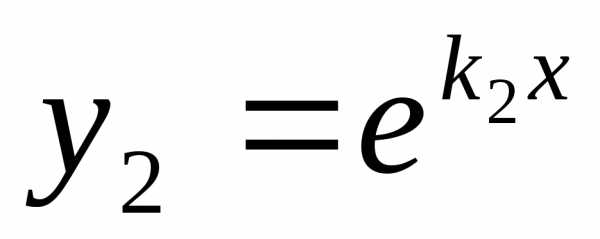 .
Следовательно, общее решение уравнения
(1) имеет вид.
.
Следовательно, общее решение уравнения
(1) имеет вид.
Случай 2.Корни и
и уравнения (2) действительные и равные:
уравнения (2) действительные и равные: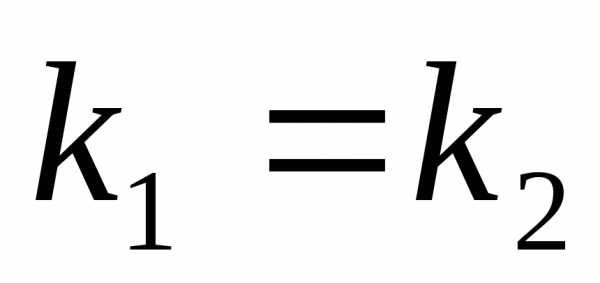 .
В этом случае частными решениями
уравнения (1) являются функции
.
В этом случае частными решениями
уравнения (1) являются функции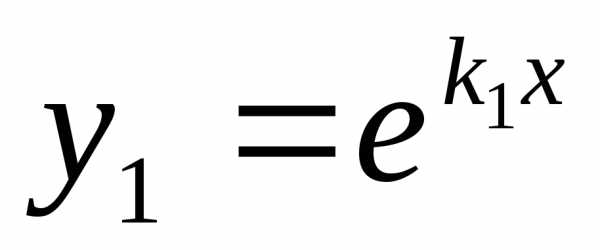 и
и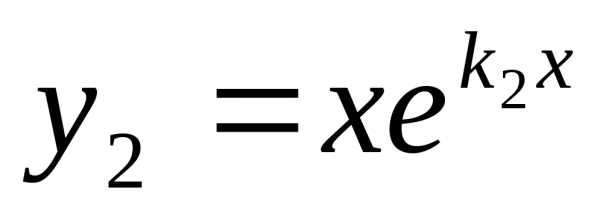 .
Следовательно, общее решение уравнения
(1) имеет вид.
.
Следовательно, общее решение уравнения
(1) имеет вид.
Случай 3.Корни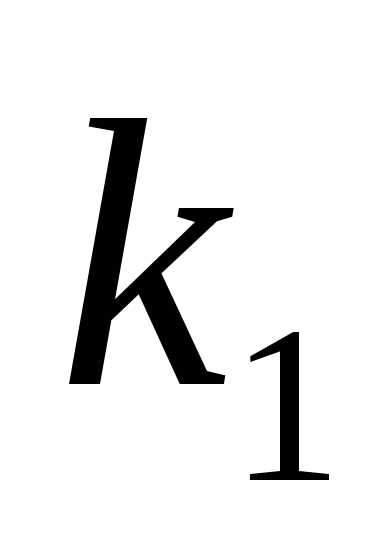 и
и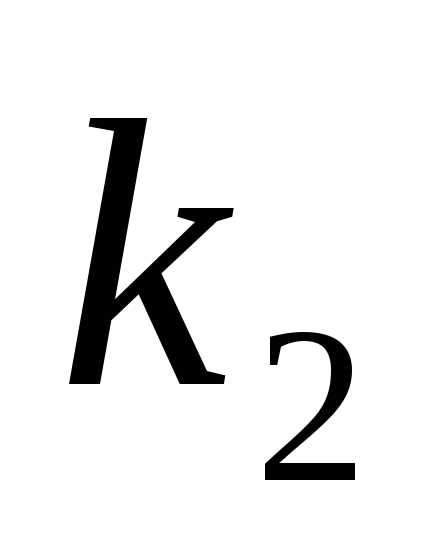 уравнения (2) комплексные:,.
В этом случае частными решениями
уравнения (1) являются функциии.
Следовательно, общее решение уравнения
(1) имеет вид
уравнения (2) комплексные:,.
В этом случае частными решениями
уравнения (1) являются функциии.
Следовательно, общее решение уравнения
(1) имеет вид
Пример. Решить уравнение .
Решение: составим характеристическое уравнение:. Тогда. Общее решение данного уравнения.
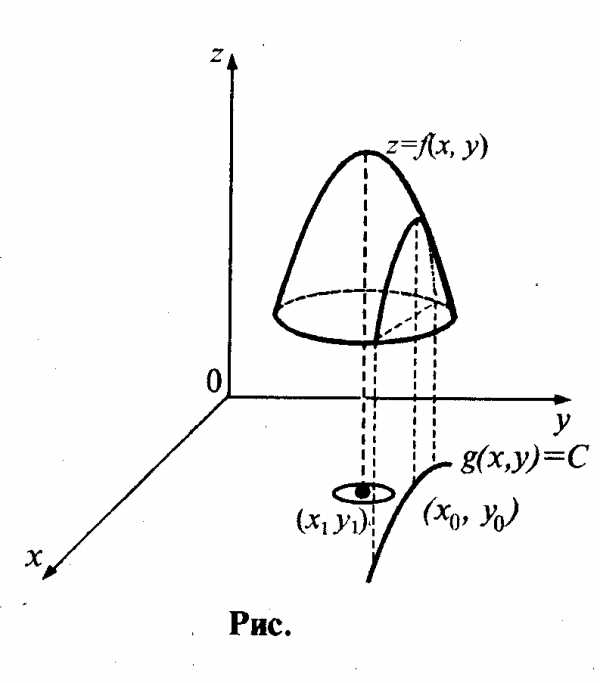
Экстремум функции нескольких переменных. Условный экстремум.
Экстремум функции нескольких переменных
Определение. Точка М (хо,уо) называется точкой максимума (минимума) функции z=f(x, у), если существует окрестность точки М, такая, что для всех точек {х, у) из этой окрестности выполняется неравенство ()
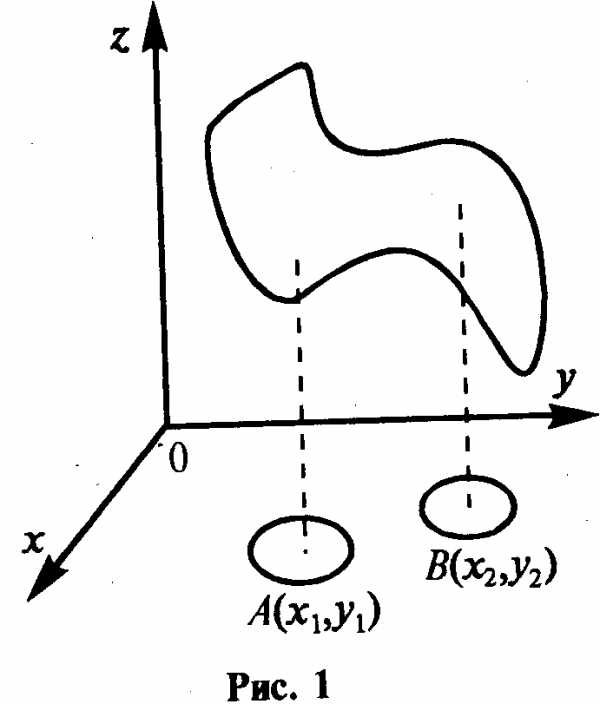
На рис. 1 точка А —
есть точка минимума, а точка В—точка максимума.
—
есть точка минимума, а точка В—точка максимума.
Необходимое условие экстремума — многомерный аналог теоремы Ферма.
Теорема. Пусть
точка  –
есть точка экстремума дифференцируемой
функцииz=f(x,
у). Тогда частные производные
–
есть точка экстремума дифференцируемой
функцииz=f(x,
у). Тогда частные производные 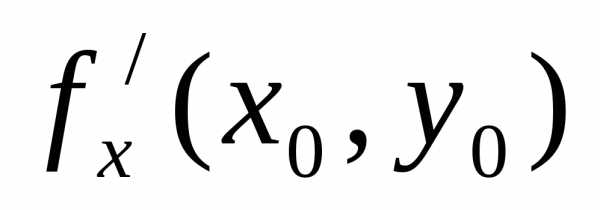 и
и 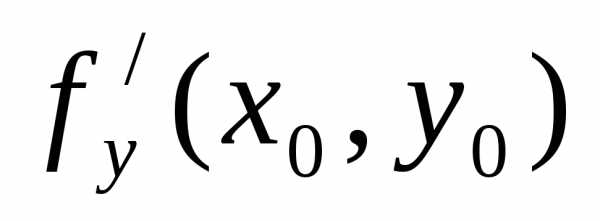 в этой точке равны нулю.
в этой точке равны нулю.
Точки, в которых выполнены необходимые условия экстремума функции z=f(x, у), т.е. частные производные z‘x и z‘y равны нулю, называются критическими или стационарными.
Равенство частных производных нулю выражает лишь необходимое, но недостаточное условие экстремума функции нескольких переменных.
На рис. изображена так
называемая седловая
точка М (хо,уо). Частные производные 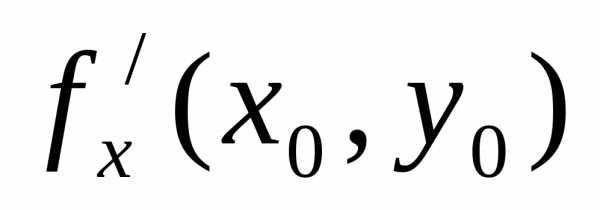 и
и 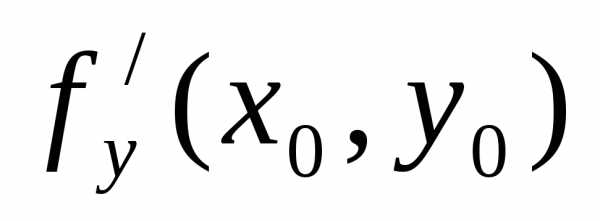 равны
нулю, но, очевидно, никакого экстремума
в точке М(хо,уо) нет.
равны
нулю, но, очевидно, никакого экстремума
в точке М(хо,уо) нет.

Такие седловые точки являются двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными словами, требуется знать достаточное условие экстремума.
Теорема (достаточное
условие экстремума функции двух
переменных). Пусть
функция z=f(x,
у): а) определена
в некоторой окрестности критической
точки (хо,уо),
в которой =0
и 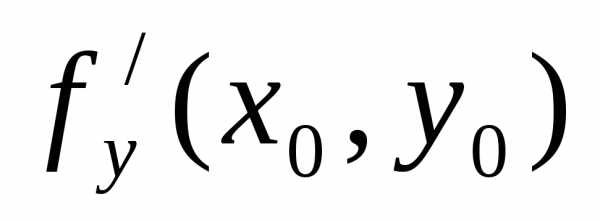 =0;
=0;
б) имеет в этой точке непрерывные частные производные второго порядка;;Тогда, если ∆=АС— В2 >0, то в точке (хо,уо) функция z=f(x, у) имеет экстремум, причем если А<0 — максимум, если А>0 — минимум. В случае ∆=АС— В2<0, функция z=f(x, у) экстремума не имеет. Если ∆=АС— В2=0, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
Найти частные производные функции z‘x и z‘y.
Решить систему уравнений z‘x =0, z‘y =0 и найти критические точки функции.
Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
Найти экстремумы (экстремальные значения) функции.
Пример. Найти экстремумы функции
Решение. 1. Находим частные производные

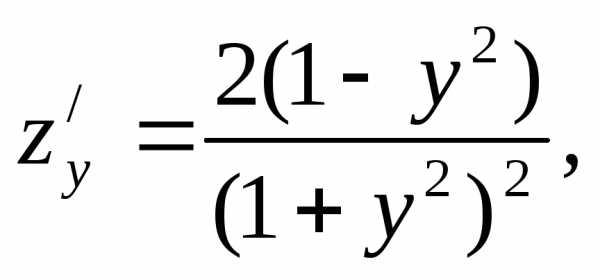
2. Критические точки функции находим из системы уравнений:
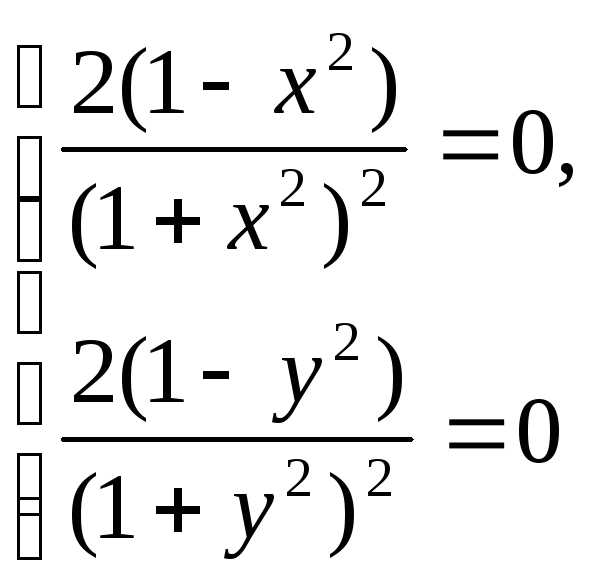
имеющей четыре решения (1; 1), (1; —1), (—1; 1) и (—1; -1).
3. Находим частные производные второго порядка:
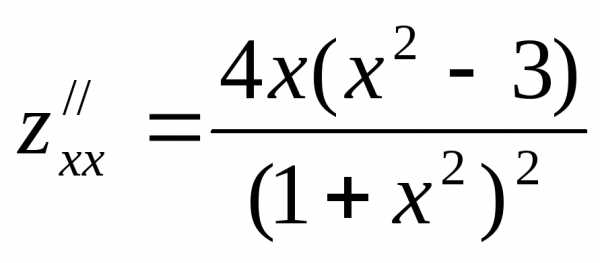 ;;
;; ,
вычисляем их значения в каждой критической
точке и проверяем в ней выполнение
достаточного условия экстремума.
,
вычисляем их значения в каждой критической
точке и проверяем в ней выполнение
достаточного условия экстремума.
Например, в точке (1; 1) A=z“(1; 1)= -1; В=0; С= -1. Так как ∆= АС— В2 = (-1)2-0=1 >0 и А=-1<0, то точка (1; 1) есть точка максимума.
Аналогично устанавливаем, что (-1; -1) — точка минимума, а в точках (1; —1) и (—1; 1), в которых ∆=АС— В2 <0, — экстремума нет. Эти точки являются седловыми.
4. Находим экстремумы функции zmax = z(l; 1) = 2, zmin = z(-l; -1) = -2,
Условный экстремум. Метод множителей Лагранжа.
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g (х,у) = С, называемому уравнением связи.
Определение. Точка  называется точкойусловного
максимума (минимума), если
существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности удовлетворяющих условию g (x,y)
= С, выполняется неравенство
называется точкойусловного
максимума (минимума), если
существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности удовлетворяющих условию g (x,y)
= С, выполняется неравенство
().
На рис. изображена точка
условного максимума  .Очевидно, что она не
является точкой безусловного экстремума
функции z
= f(x,y) (на рис. это точка
.Очевидно, что она не
является точкой безусловного экстремума
функции z
= f(x,y) (на рис. это точка  ).
).
Наиболее простым способом
нахождения условного экстремума
функции двух переменных является
сведение задачи к отысканию экстремума
функции одной переменной. Допустим
уравнение связи g (x,y) = С удалось разрешить
относительно одной из переменных,
например, выразить у через х: 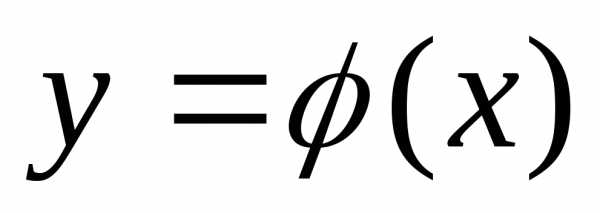 .Подставив полученное
выражение в функцию двух переменных,
получим z
= f(x,y) =, т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции z = f(x,y).
.Подставив полученное
выражение в функцию двух переменных,
получим z
= f(x,y) =, т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции z = f(x,y).
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11.
Решение. Выразим из уравнения
3х +2у = 11
переменную y
через переменную x
и подставим полученное  в функциюz.
Получим z=x2+2
в функциюz.
Получим z=x2+2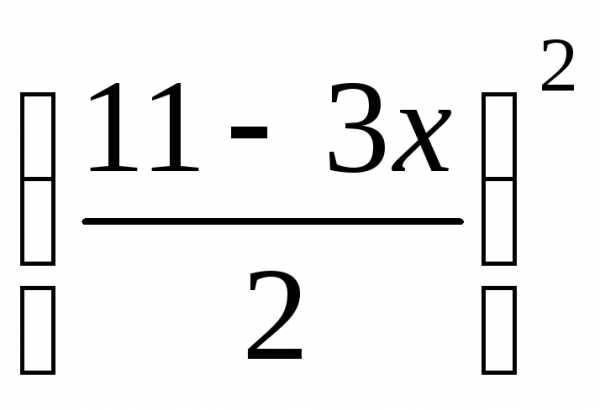 илиz =
илиz =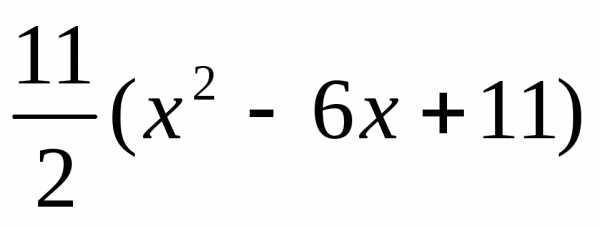 .Эта функция имеет
единственный минимум при
.Эта функция имеет
единственный минимум при 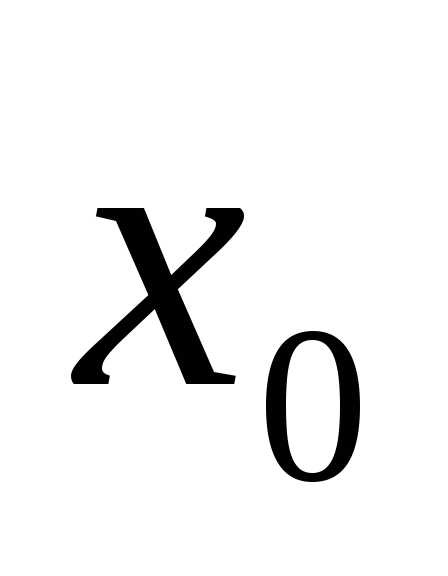 = 3. Соответствующее
значение функции
= 3. Соответствующее
значение функции 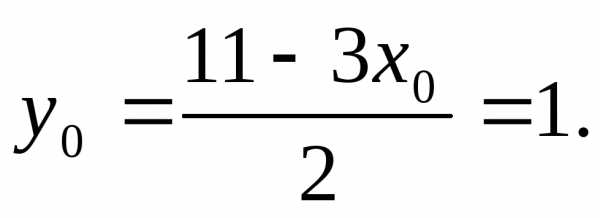 Таким образом, (3; 1) — точка условного
экстремума (минимума).
Таким образом, (3; 1) — точка условного
экстремума (минимума).
В рассмотренном примере уравнение связи g(x, у) = С оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
Эта функция называется функцией Лагранжа, а  —
множителем Лагранжа. Верна
следующая теорема.
—
множителем Лагранжа. Верна
следующая теорема.
Теорема. Если
точка 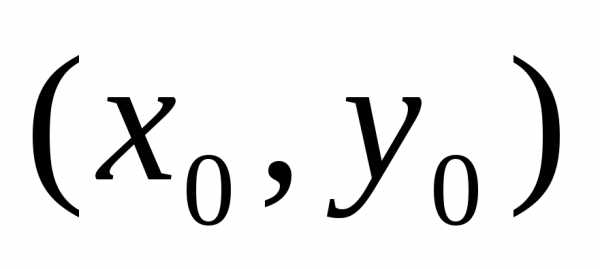 является
точкой условного экстремума функцииz = f(x,y)
при условии g (x,y)
= С, то существует значение
является
точкой условного экстремума функцииz = f(x,y)
при условии g (x,y)
= С, то существует значение 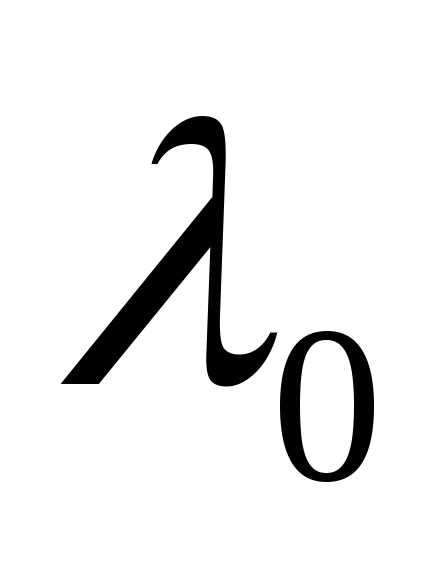 такое,
что точкаявляется
точкой экстремума функцииL{x,y,
такое,
что точкаявляется
точкой экстремума функцииL{x,y,  ).
).
Таким образом, для нахождения условного экстремума функции z = f(х,у) при условии g(x,y) = С требуется найти решение системы
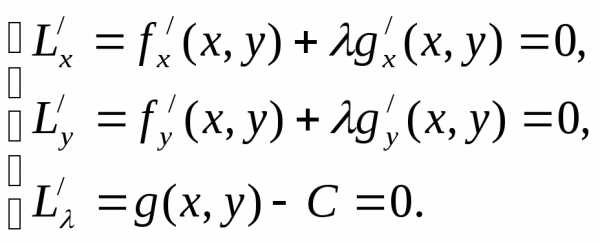
На рис. показан геометрический смысл условий Лагранжа. Линия g (х,у) = С пунктирная, линия уровня g(x,y) = Q функции z = f(x,y) сплошные.
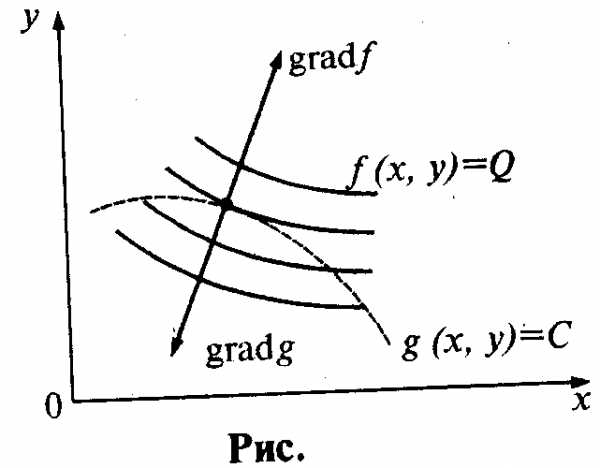
Из рис. следует, что в точке условного экстремума линия уровня функции z = f(x,y) касается линии g(x,y) = С.
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11, используя метод множителей Лагранжа.
Решение. Составляем функцию Лагранжа L = х2 + 2у2 +
Приравнивая к нулю ее частные производные, получим систему уравнений
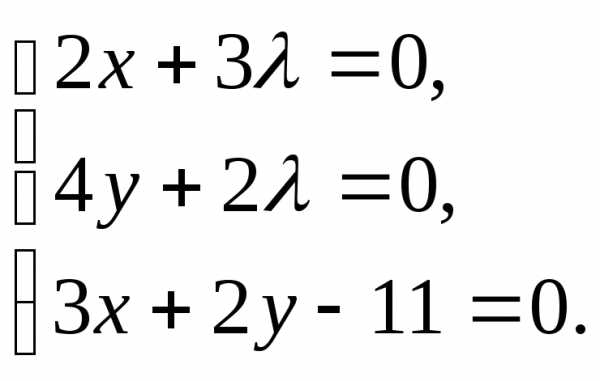
Ее единственное решение
(х=3, у=1,  =—2). Таким образом, точкой
условного экстремума может быть только
точка (3;1). Нетрудно убедиться в том,
что в этой точке функция z=f(x,y) имеет условный минимум.
=—2). Таким образом, точкой
условного экстремума может быть только
точка (3;1). Нетрудно убедиться в том,
что в этой точке функция z=f(x,y) имеет условный минимум.
studfiles.net
Уравнения с разделяющимися переменными
Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
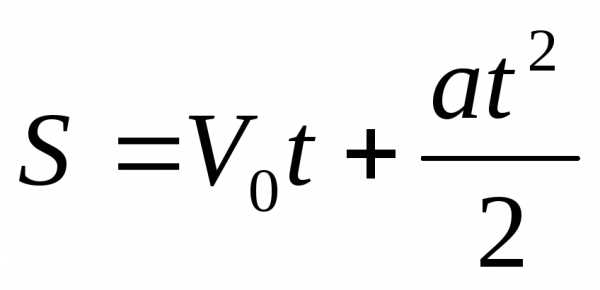
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
Тогда получаем: – уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
– обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .
– обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается
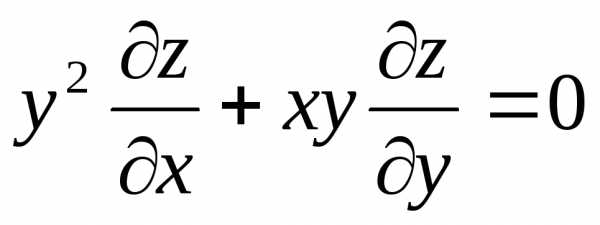 –
дифференциальное уравнение в частных
производных первого порядка.
–
дифференциальное уравнение в частных
производных первого порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если
функция f(x, y)
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную
частную производную
,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение 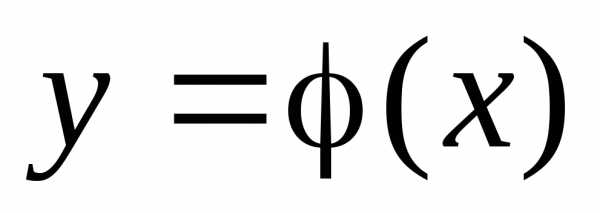 уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:


Теперь
интегрируем: 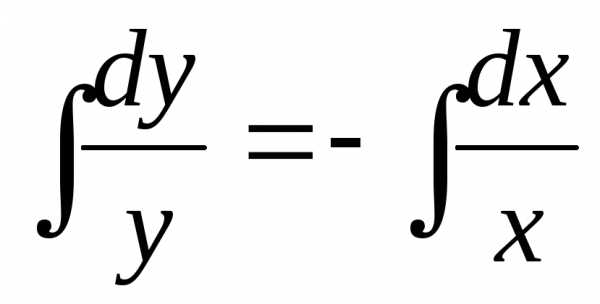
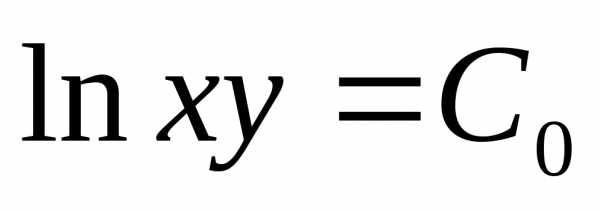
 –
это общее решение исходного дифференциального
уравнения.
–
это общее решение исходного дифференциального
уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
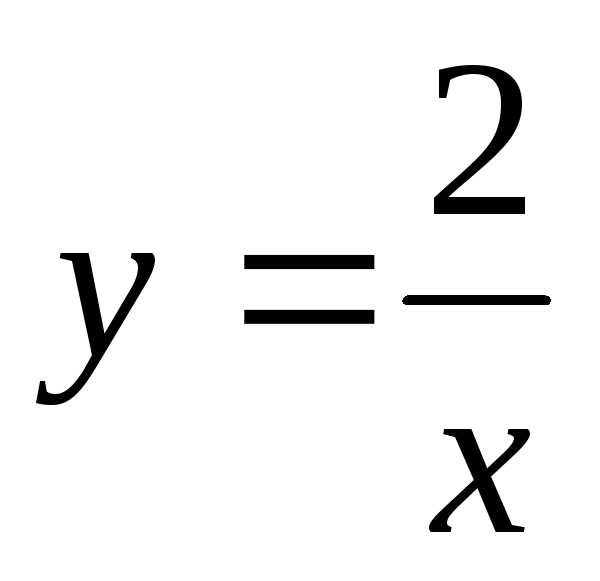
Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения: Найти особое решение, если оно существует.
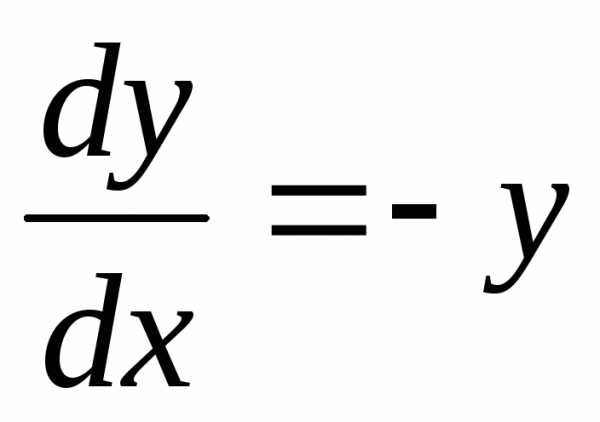
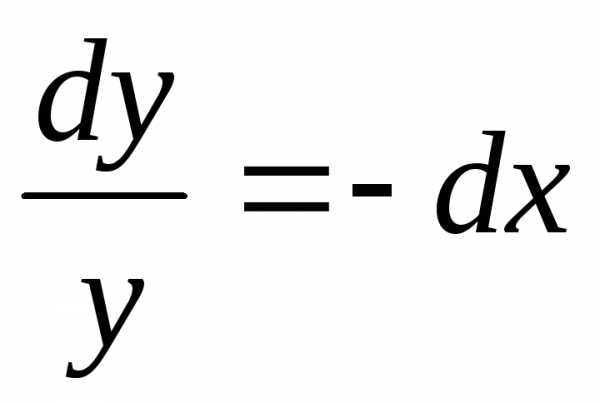

Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC 0.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением,разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
Определение. Дифференциальное уравнение называетсяуравнением с разделяющимися переменными, если его можно записать в виде
.
Такое уравнение можно представить также в виде:
Перейдем к новым обозначениям
Получаем:
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального
уравнения: 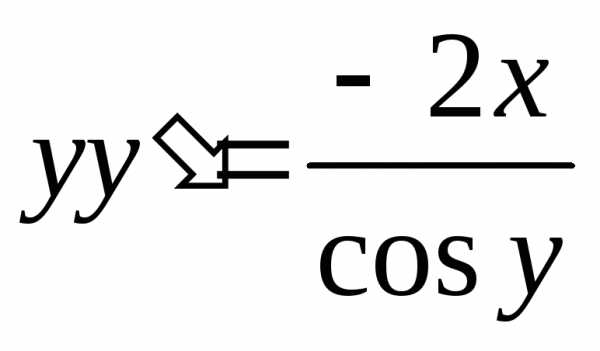
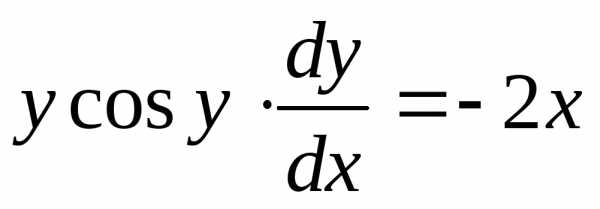
Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):

это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
 –
верно
–
верно
Пример. Найти решение дифференциального
уравнения 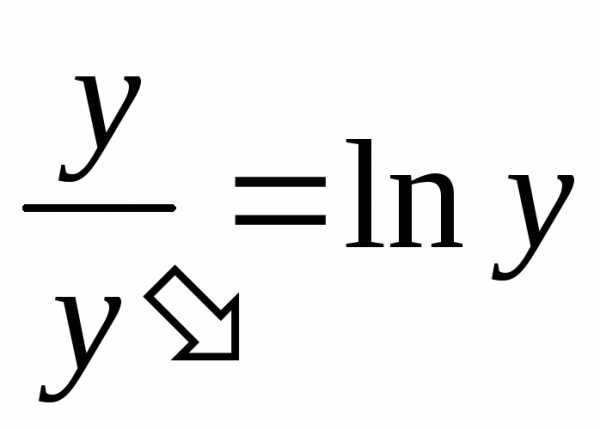 при условии у(2) = 1.
при условии у(2) = 1.
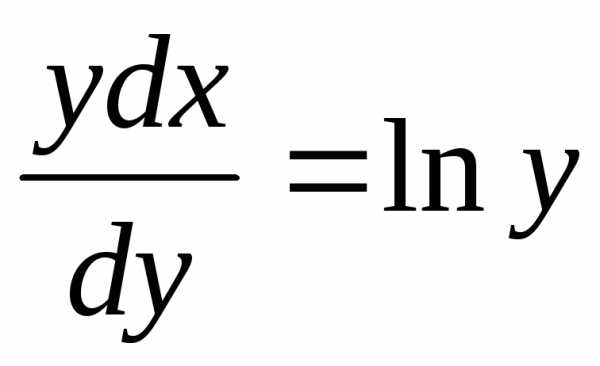


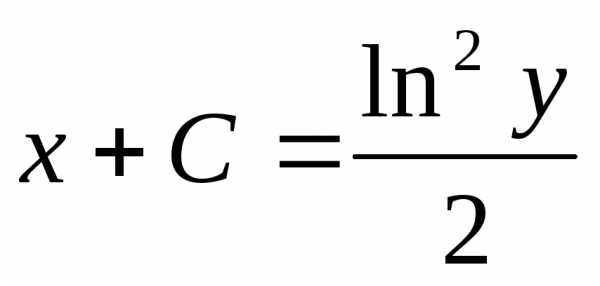
при у(2) = 1 получаем
Итого: или  – частное решение;
– частное решение;
Проверка: , итого
– верно.
Пример. Решить уравнение 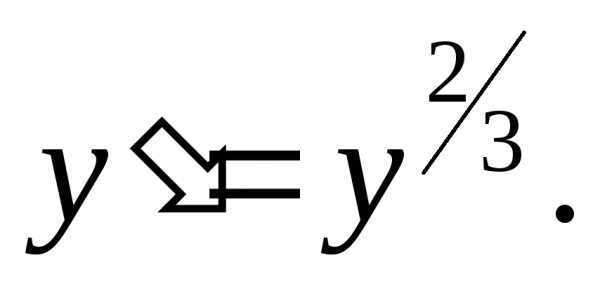
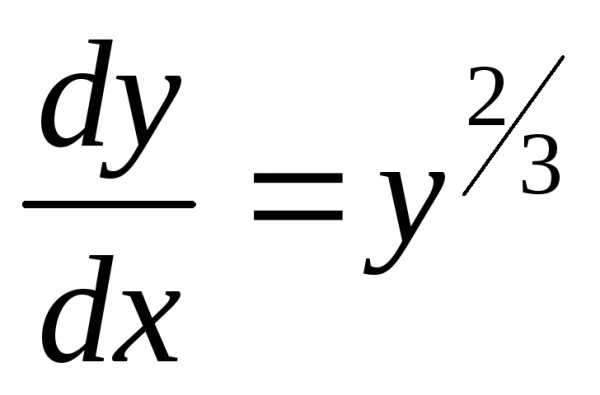
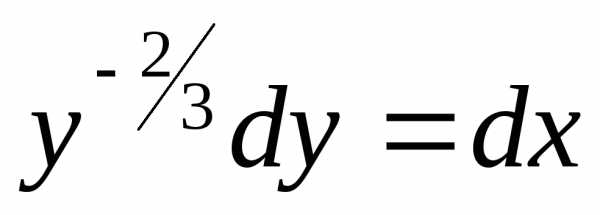
– общий интеграл
 –
общее решение
–
общее решение
Пример. Решить уравнение
Пример. Решить уравнение 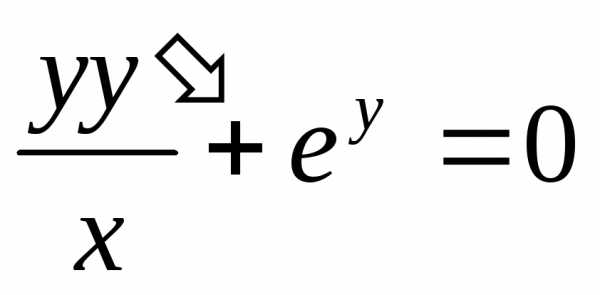 при
условии у(1) = 0.
при
условии у(1) = 0.
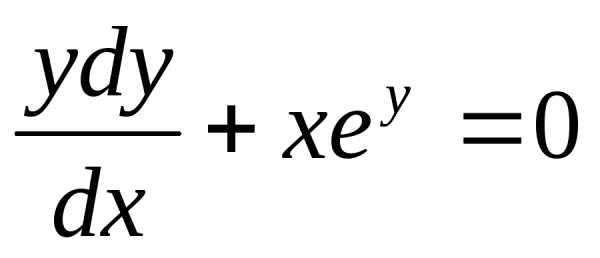
Интеграл, стоящий в левой части будем брать по частям (см. Интегрирование по частям. ).
Если у(1) = 0, то
Итого, частный интеграл: .
Пример. Решить уравнение .
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. п.16. Получаем общий интеграл:
Пример. Решить уравнение 
Преобразуем заданное уравнение:
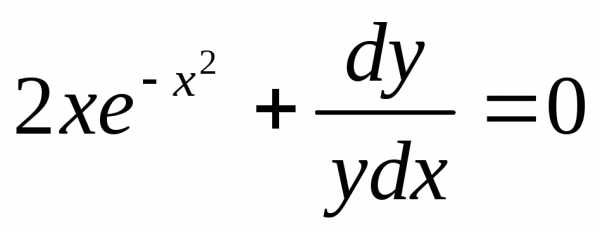
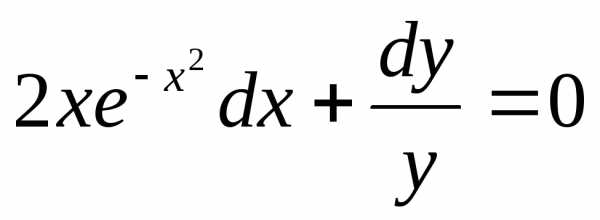
 Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Пример. Решить уравнение .
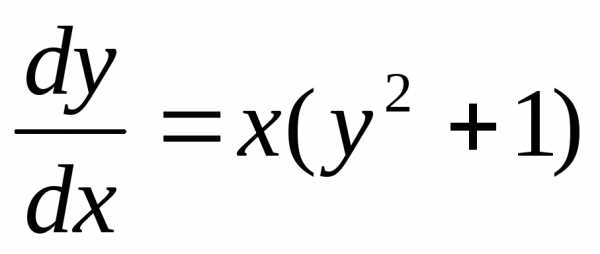
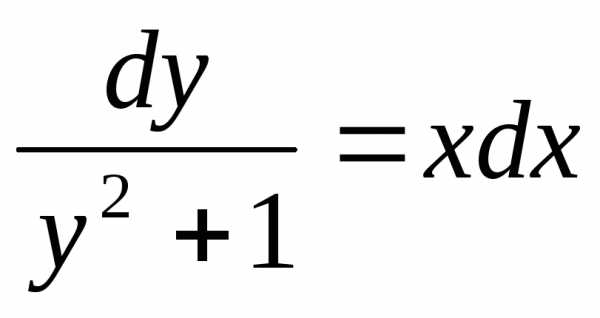
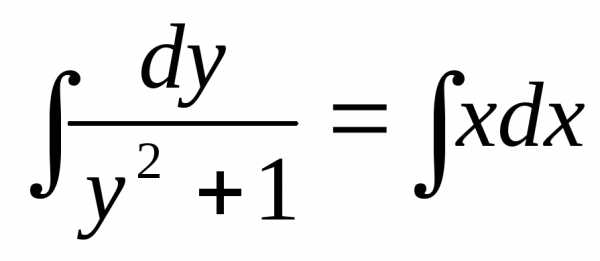 ;
; 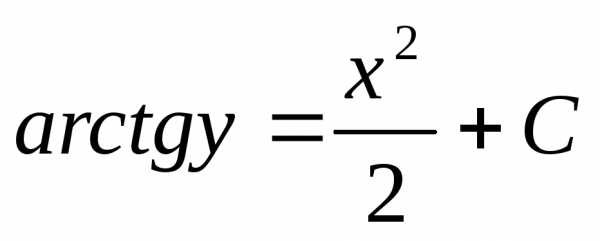 ;
;
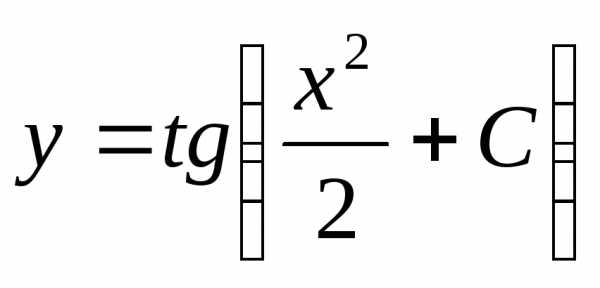
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:
Получаем частное решение
Однородные уравнения.
Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:
Пример. Является ли однородной функция
Таким образом, функция f(x, y) является однородной 3- го порядка.
Определение. Дифференциальное уравнение вида называетсяоднородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида является однородным, если функцииP(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:
Т.к.
параметр t
вообще говоря произвольный, предположим,
что 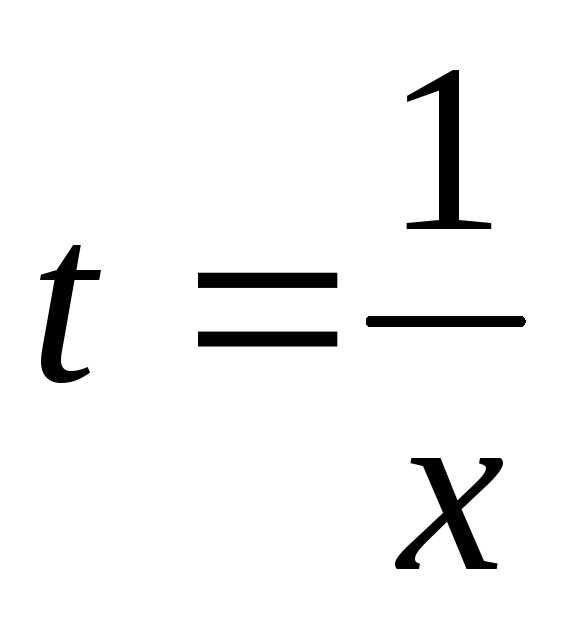 .
Получаем:
.
Получаем:

Правая
часть полученного равенства зависит
фактически только от одного аргумента  ,
т.е.
,
т.е.
Исходное дифференциальное уравнение таким образом можно записать в виде:
Далее заменяем y = ux, .
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Пример. Решить уравнение 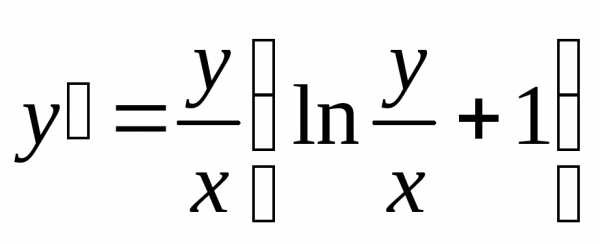 .
.
Введем вспомогательную функцию u.
.
Отметим,
что введенная нами функция u всегда положительна, т.к. в противном
случае теряет смысл исходное
дифференциальное уравнение, содержащее 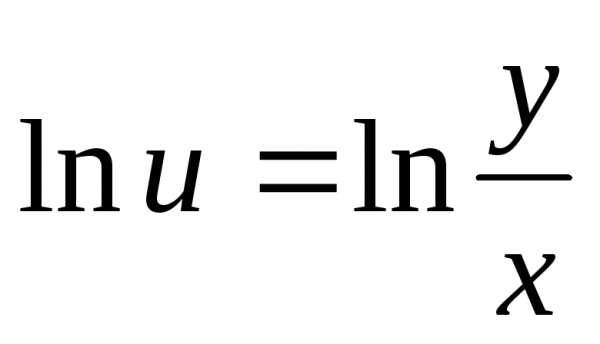 .
.
Подставляем в исходное уравнение:
Разделяем переменные:
Интегрируя, получаем:
Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

Уравнения, приводящиеся к однородным.
Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.
Это
уравнения вида 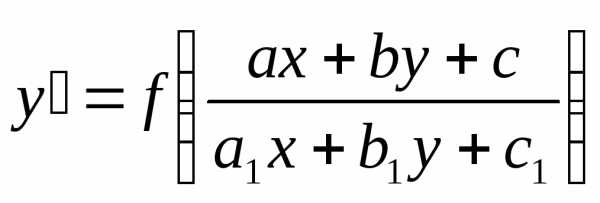 .
.
Если
определитель 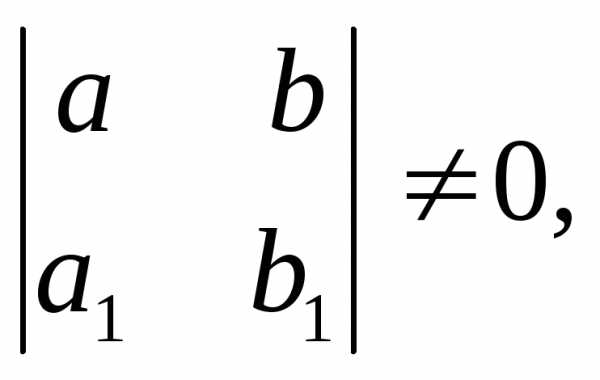 то переменные могут быть разделены
подстановкой
то переменные могут быть разделены
подстановкой
где
и
– решения системы уравнений 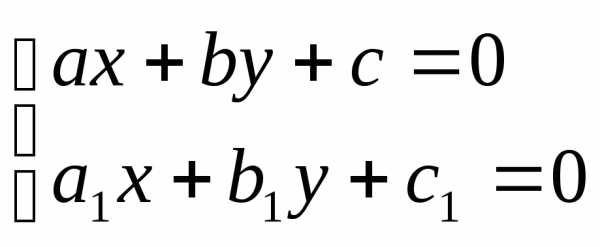
Пример. Решить уравнение
Получаем
Находим значение определителя .
Решаем систему уравнений
Применяем подстановку в исходное уравнение:
Заменяем переменную при подстановке в выражение, записанное выше, имеем:
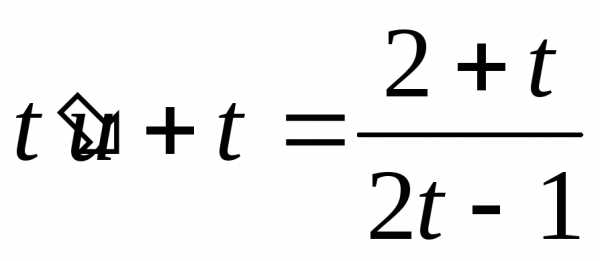
studfiles.net
ДУ с разделяющимися переменными
К дифференциальным уравнениям с разделяющимися переменными относятся пять видов дифференциальных уравнений:
1. Уравнение вида , не содержащее (явно) искомую функцию. Запишем его с помощью дифференциалов или , откуда получим общее решение .
Пример. Найти решение задачи Коши , .
Решение. Найдем сначала общее решение
.
Используя начальное условие , получим
.
Ответ: .
2. Уравнение вида , не содержащее (явно) независимую переменную. Имеем или , откуда общий интеграл: .
Пример. Найти решение задачи Коши , .
Решение. Найдем сначала общее решение
.
Используя начальное условие , получим
.
Ответ: .
3. Уравнение вида или , в котором правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от .
Интегрируется после “разделения переменных”, т.е. приведения путем умножения и деления к виду .
В одну часть входят только функции от и дифференциал , а в другую – функция от и . Общий интеграл: .
4. Уравнение вида .
Интегрируется также после “разделения переменных”, т.е. приведения путем умножения и деления к виду .
В одну часть входят только функции от и дифференциал , а в другую – функция от и . Общий интеграл: .
Пример. Найти общий интеграл .
Решение. Разделяем переменные
.
Получили семейство окружностей.
Ответ: .
5. Иногда к уравнениям с разделяющимися переменными относят уравнение вида , где , , – постоянные. Заменой переменной на : , получим уравнение , т.е. уравнение вида 2.
Пример. Найти общий интеграл .
Решение. Полагаем , получим уравнение , т.е. уравнение вида 2. Отсюда
.
Найти общий интеграл:
1. 1. . 1.2. . 1.3. .
1.4. . 1.5. . 1.6. .1.7. . 1.8. . 1.9. . 1.10. .
Задачи для самостоятельного решения:
2.1. . 2.2. . 2.3. , .
2.4. . 2.5. , . 2.6. , . 2.7. , . 2.8. , . 2.9. . 2.10. .
Ответы: 2.1. .2. 2. . 2.3. .
2.4. . 2.5. . 2.6. .
2.7. . 2.8. . 2.9. .
2.10. .
Однородные ДУ. Уравнения, приводимые к однородным уравнениям
I.Функция называется однородной функцией -го измерения, если для всех выполняется неравенство .
Однородным дифференциальным уравнением называется уравнение вида
(1)
или , где , – однородные функции одного измерения.
Однородное уравнение приводится с помощью замены
(2)
к уравнению с разделяющимися переменными.
Действительно, из (2) следует, что . Из (1) получаем , т.е. уравнение с разделяющимися переменными, решение которого
. (3)
Замечание. Если , то уравнение (1) имеет вид , т.е. изначально является уравнением с разделяющимися переменными. Если при значении , то кроме решений, задаваемых формулой (3), существует также особоерешение .
Пример. Найти общий интеграл .
Решение. Данное уравнение однородное, так как -однородная функция нулевого измерения. Полагаем . Из уравнения получаем .
Находим общее решение, вычисляя интеграл в левой части методом неопределенных коэффициентов:
, ,
где . Получили семейство окружностей, касающихся оси в начале координат. Кроме того, существует особое решение .
II.Рассмотримуравнение
. (4)
Пусть , тогда строки пропорциональны и . Такое уравнение заменой сводится к уравнению с разделяющимися переменными.
Пример. Найти общий интеграл уравнения .
Решение. Вычисляем . Вводим новую зависимую переменную .
Из уравнения получим
.
Далее решаем уравнение с разделяющимися переменными:
.
В результате
.
III.Пусть и, по крайней мере, одно из чисел или не равно нулю. Тогда уравнение (4) не является однородным, однако это уравнение можно привести к однородному путем введения новых переменных и , где , . Подставляя в (4), получим
.
Таким образом, будем иметь однородное уравнение, если и являются решением системы:
.
Пример. Найти общий интеграл уравнения .
Решение. Вычисляем . Вводим новые переменные и , где , .
Из уравнения получим
.
Таким образом, будем иметь однородное уравнение, если и являются решением системы:
.
Находим решение однородного уравнения:
.
Следовательно,
.
В результате
.
Решить уравнения:
1.1. . 1.2. . 1.3. . 1.4. .
1.5. , . 1.6. .1.7. .
1.8. , . 1.9. .
1.10. .
Задачи для самостоятельного решения:
2.1. ; 2.2. ; 2.3. ;
2.4. ; 2.5. ; 2.6. ;
2.7. ; 2.8. ; 2.9. ;
2.10. ; 2.11. ; 2.12. ;
2.13. ; 2.14. ;
2.15. ; 2.16. ; 2.17. ;
2.18. ; 2.19. ; 2.20. .
Ответы:2.1. ; 2.2. ; 2.3. ;
2.4. ; 2.5. ; 2.6. ; 2.7. ; 2.8. ; 2.9. ; 2.10. ; 2.11. ; 2.12. ; 2.13. ; 2.14. ; 2.15. ; 2.16. ; 2.17. ; 2.18. ; 2.19. ;2.20. .
ЛДУ. Уравнения Бернулли
Пусть , – непрерывные функции на заданном интервале . Тогда уравнение
(1)
называется линейным дифференциальным уравнением (ЛДУ) первого порядка, а уравнение
, (2)
где и называется уравнением Бернулли.
По методу Бернулли решение ищем в виде произведения двух неизвестных функций: . Тогда из (1) следует
а из (2)
В обоих случаях получаем уравнения с разделяющимися переменными.
Заметим, что при уравнение Бернулли имеет решение .
Пример. Решить уравнение .
Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка. По методу Бернулли решение ищем в виде произведения двух неизвестных функций: . Тогда из уравнения следует
Поэтому , .
Ответ: .
Пример. Решить уравнение .
Решение. Это уравнение Бернулли с . По методу Бернулли решение ищем в виде произведения двух неизвестных функций: . Тогда из уравнения следует
Ответ: .
Решить уравнения:
1. 1. . 1.2. . 1.3. . 1.4. . 1.5. . 1.6. . 1.7. .
1.8. .1.9. . 1.10. , .
Задачи для самостоятельного решения:
2.1. . 2.2. . 2.3. , .
2.4. . 2.5. . 2.6. .
2.7. . 2.8. .
Ответы: 2.1. . 2.2. . 2.3. .
2.4. . 2.5. . 2.6. .
2.7. . 2.8. .
infopedia.su
Дифференциальные уравнения с разделяющимися переменными
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. Научно-издательский центр “Регулярная и хаотическая динамика”. 2000.
Уравнения с разделяющимися переменными.
Уравнения с разделяющимися переменными могут быть записаны в виде $$y’=f(x)g(y),\qquad\qquad\qquad(1)$$ а также в виде $$M(x)N(y)dx+P(x)Q(y)dy=0.\qquad\qquad\qquad(2)$$ Для решения этого уравнения его нужно преобразовать таким образом, чтобы в одну часть уравнения входило только $x,$ а в другую только $y,$ а затем проинтегрировать обе части.
При делении обеих частей уравнения на выражение, содержащее неизвестные $x$ и $y,$ могут быть потеряны решения, обращающие это выражение в нуль.
Пример. Решить уравнение $$x^2y^2y’+1=y.$$
Решение.
Преобразуем заданное уравнение к виду (2).
$$x^2y^2\frac{dx}{dy}=y-1;\qquad\qquad x^2y^2dy=(y-1)dx.$$
Делим обе части уравнения на $x^2(y-1):$
$$\frac{y^2}{y-1}dy=\frac{dx}{x^2}.$$
Переменные разделены. Интегрируем обе части уравнения:
$$\int\frac{y^2}{y-1}dy=\int\frac{dx}{x^2}.$$
$$\int\frac{y^2}{y-1}dy=\int\frac{y^2-1+1}{y-1}dy=\int\left(y+1+\frac{1}{y-1}\right)dy=\frac{y^2}{2}+y+\ln|y-1|+C.$$
$$\int\frac{dx}{x^2}=-\frac{1}{x}+C.$$
Таким образом,
$$\frac{y^2}{2}+y+\ln|y-1|=-\frac{1}{x}+C.$$
При делении на $x^2(y-1)$ могли быть потеряны решения $x=0$ и $y-1=0,$ то есть $y=1.$ Если подставить эти значения в условие, то становится очевидно, что $y=1$ – решение заданного уравнения, а $x=0$ – нет.
Ответ: $\frac{y^2}{2}+y+\ln|y-1|=-\frac{1}{x}+C,$ $y=1.$
Уравнения сводящиеся к уравнениям с разделяющимися переменными.
Уравнения вида $y’=f(ax+by)$ приводится к уравнениям с разделяющейся переменной заменой $z=ax+by$ (или $z=ax+by+c,$ где $c- $ любое).
Примеры.
65. $y’=\sqrt{4x+2y-1}.$
Решение.
Сделаем замену переменных.
$z=4x+2y-1.$ Отсюда $y=\frac{1}{2}(z-4x+1)\Rightarrow y’=\frac{1}{2}z’-2$
Получаем $$\frac{1}{2}z’-2=\sqrt{z}$$
Преобразуем данное уравнение к виду (2).
$$\frac{dz}{2dx}=\sqrt{z}+2\Rightarrow \frac{dz}{\sqrt z+2}=2dx$$
Интегрируем обе части уравнения:
$$\int\frac{dz}{\sqrt z+2}=\int 2dx$$
$$\int\frac{dz}{\sqrt z+2}=[z=t^2\qquad dz=2tdt]=\int\frac{2tdt}{t+2}=2\int\frac{t+2-2}{t+2}dt=2(t-2\ln|t+2|)+C=$$ $$=2(\sqrt z-2\ln|\sqrt z+2|)+C=2(\sqrt{4x+2y-1}-2\ln|\sqrt{4x+2y-1}+2|)+С.$$
$$\int 2dx=2x+C.$$
Таким образом, получили
$$2(\sqrt{4x+2y-1}-2\ln|\sqrt{4x+2y-1}+2|)=2x+C\Rightarrow \sqrt{4x+2y-1}-\ln(\sqrt{4x+2y-1}+2)=x+C.$$
Ответ: $$\sqrt{4x+2y-1}-\ln(\sqrt{4x+2y-1}+2)=x+C..$$
mathportal.net
