Двойной интеграл, формулы и примеры
Определение двойного интеграла
Пусть в замкнутой области , принадлежащей плоскости , задана непрерывная функция . Разобьем эту область на элементарных областей , площади которых будем обозначать как , а наибольшее расстояние между точками соответствующей области – через (рис. 1).
В каждой элементарной области выберем произвольную точку . Значение функции в этой точке умножим на площадь соответствующей элементарной области и все такие произведения просуммируем:
Полученная сумма называется интегральной суммой функции в области .
Найдем предел указанной интегральной суммы при таким образом, чтобы . Если такой предел существует и не зависит ни от способа разбиения области на элементарные области, ни от способа выбора в них точек , то он называется двойным интегралом от функции по области и обозначается . Итак, двойной интеграл определяется равенством
Область называется областью интегрирования, и – переменные интегрирования, функция – подынтегральной функцией, которая является интегрируемой в области ; – элементом площади.
Свойства двойного интеграла
1. Константу можно выносить за знак двойного интеграла:
где
2. Двойной интеграл суммы/разности двух функций равен сумме/разности интегралов от каждой из них:
3. Если область интегрирования можно разбить на две области и , например, как это показано на рисунке 2, то
4. Если в области интегрирования функция , то и двойной интеграл .
5. Если функции и в области удовлетворяют неравенству , то справедливо и неравенство
6. , где – это площадь области .
где и – наименьшее и наибольшее значения подынтегральной функции в области соответственно.
8. Если функция непрерывна в замкнутой области , площадь которой равна , то в этой области существует такая точка , что имеет место равенство:
Величина называется средним значением функции в област .
Пусть область интегрирования – это прямоугольник со сторонами, параллельными координатным осям и которые определяются уравнениями , ; , (рис. 3). В этом случае двойной интеграл вычисляется по одной из формул:
или
Интегралы, стоящие в правых частях этих формул, называются
После того, как эта функция определена, нужно выполнить внешнее интегрирование – проинтегрировать полученную функцию по переменной . В результате второго интегрирования получаем уже число.
Примеры решения задач
Как вычислить двойной интеграл
Как вычислить двойной интеграл? Примеры решений
Прозвучал удар гонга, который открывает второй раунд в бою с двойными интегралами. Если вы недавно надели перчатки или вообще боксируете с грушей, то, пожалуйста, начните с первого раунда Двойные интегралы для чайников. Настоятельно рекомендую разобраться со всеми примерами вводного урока без халтуры, это очень важно. К тому же, добрый дядя Саша нарисовал много картинок, которые можно распечатать и наклеить у себя в туалете. Помните, что Коперник свои блестящие открытия в астрономии делал именно там.
Однако задорное получилось вступление…. Задумался вот… почему? Да потому что мне хорошо. А отчего хорошо, поясню в конце статьи.
Вспоминаем общую запись двойного интеграла:
В первой статье Двойные интегралы для чайников я очень подробно рассмотрел понятие двойного интеграла, алгоритм его решения, важнейшие задачи на обход области интегрирования. Также были прорешаны простейшие двойные интегралы в примерах на нахождение площади плоской фигуры.
Снова
посмотрим на общую запись двойного
интеграла и заметим, что в нём притаилась
функция двух переменных .
А когда речь заходит о функции двух
переменных, то это часто
попахивает сероводородом
В большинстве практических задач требуется формально вычислить двойной интеграл, но, помимо этого, он обладает отличным геометрическим смыслом – с помощью двойного интеграла помимо площади можно вычислить еще и объём. Геометрический смысл двойного интеграла поясню ниже на конкретных примерах.
Начинаем набивать наш двойной интеграл разнообразной начинкой:
Пример 1
Вычислить двойной интеграл , Изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Решение: Изобразим
область интегрирования на
чертеже: 
Напоминаю, что выполнение чертежа – необходимый начальный этап решения. Чертёж крайне важно выполнить правильно и точно, поскольку ошибка в графике незамедлительно запорет всё задание.
Выберем следующий порядок обхода:
Вопросы порядка обхода области интегрирования, я комментировать практически не буду, пожалуйста, смотрите статью Двойные интегралы для чайников.
Таким образом:
Обратите внимание на следующее действие: в данном случае можно вынести «икс» из внутреннего интеграла во внешний интеграл. Почему? Во внутреннем интеграле
С интегралами настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
Вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл , при этом ни в коем случае не забываем про «икс», который там уже находится:
Готово.
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
Для
наглядности еще раз приведу чертёж, он
будет точно таким же, но с другими
обозначениями графиков: 
Второй способ обхода области:
Таким образом:
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
Вместо «икса» подставляются функции! Всегда проявляйте повышенное внимание при подстановке пределов интегрирования.
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
Результаты совпали, значит, задание выполнено верно.
Если есть время, постарайтесь всегда проводить проверку, даже если этого не требуется в условии: вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Ответ:
Пример 2
Вычислить двойной интеграл , Выполнить проверку: изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Это пример для самостоятельного решения. Обратите внимание, что в двойном интеграле изначально присутствует константа. А константу можно вынести за знак двойного интеграла, в данном случае: В ходе решения вынесение константы целесообразно проводить в момент перехода к повторным интегралам.
Как видите, свойство линейности справедливо не только для «обычных», но и для кратных интегралов. Интеграл от интеграла недалеко падает.
Самое главное потом при вычислениях вынесенную константу не потерять. А забывают о ней часто.
Примерный образец чистового оформления примера в конце урока.
Двойной интеграл как объем тела
Рассмотрим основной геометрический смысл двойного интеграла . Предполагаем, что функция существует в каждой точке плоской области .
Геометрически функция двух переменных задаёт некоторую поверхность в трехмерном пространстве. Для определенности считаем, что , то есть поверхность располагается над плоскостью .
Тогда
двойной интеграл численно равен
объёму цилиндрического
бруса : 
Что такое цилиндрический брус, думаю, всем понятно из чертежа. Плоская фигура (заштрихована на чертеже) полностью лежит в плоскости и брус ограничен областью снизу. Сверху брус как раз ограничен поверхностью , которая представляет собой такую шапку. Образно говоря, плоская область по своей границе перпендикулярными лучами вырезает из поверхности эту шапочку.
Дополнительно
поясню геометрический смысл на Примере
1. В нём мы рассматривали двойной
интеграл ,
причём область интегрирования имела
следующий вид: 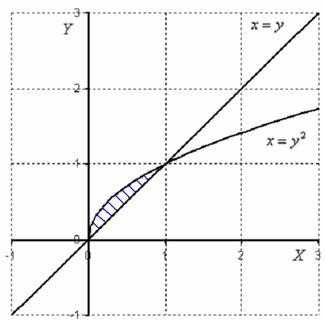
Подынтегральная функция задаёт плоскость в пространстве. Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси . В данном примере плоскость располагается в пространстве над областью , поэтому объем тела получился положительным: . Возможно, не всем до конца понятно, о каком объеме идёт речь: из границы области направьте на себя лучи. Эти лучи вырежут кусочек из плоскости , которая лежит над областью .
Двойной интеграл может быть и отрицательным, в таких случаях график функции полностью (или бОльшей частью) лежит под областью . Это тоже объем тела, только со знаком минус, поскольку поверхность полностью (или бОльшей частью) лежит подкоординатной плоскостью .
Прошу прощения, пока не подыскал программы для построения трехмерных чертежей, которая бы меня устраивала, пришлось объяснять на пальцах.
Однако на практике почти всегда встречаются задачи на формальное вычисление двойных интегралов, поэтому мы продолжим совершенствовать технику вычислений:
Пример 3
Вычислить двойной интеграл ,
Решение: Изобразим
область интегрирования на чертеже: 
После того, как корректно выполнен чертеж и правильно найдена область интегрирования, самое время разобраться с порядком обхода.
Согласно первому способу обхода, область придется разделить на две части, при этом необходимо будет вычислить следующие интегралы:
Энтузиазма, прямо скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным функциям, переход здесь элементарен:
Порядок обхода области:
Таким образом:
Ну вот, совсем другое дело. И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу можно сразу вынести во внешний интеграл
1) Найдём внутренний интеграл:
Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначалавместо «икса» мы подставили верхний предел интегрирования , затем вместо «икса» подставили нижний предел интегрирования . Будьте внимательны при подстановках!
2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про , который там уже находится:
Ответ:
Для тренировки можете попробовать вычислить двойной интеграл менее рациональным способом: . Результаты должны совпасть.
Пример 4
Вычислить двойной интеграл ,
Это пример для самостоятельного решения. Постройте область и проанализируйте, какой способ обхода области выгоднее использовать. Полное решение и ответ в конце урока.
Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов:
Пример 5
Вычислить двойной интеграл ,
Решение: Сначала рассмотрим то, чего делать не нужно – в данном случае не следует использовать свойства линейности кратного интеграла и представлять его в виде: Почему? Вычислений заметно прибавится!
Решение,
как обычно, начинаем с построения области
интегрирования: 
Область незамысловата, даже штриховать не буду. В данном примере, как легко заметить, не имеет особого значения порядок интегрирования, поэтому выберем первый, более привычный вариант обхода области:
Таким образом:
Здесь, в отличие от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является сумма.
С повторными интегралами опять разбираемся по отдельности. Да, кстати, кто хочет посмотреть, как решать повторные интегралы одной строкой, пожалуйста, зайдите на страницу Готовые решения по высшей математике и закачайте архив с примерами решений кратных интегралов.
1) Сначала берём внутренний интеграл:
Хотелось бы остановиться на нескольких существенных моментах. Во-первых, о частном интегрировании. О нём я уже подробно рассказывал в статье Дифференциальные уравнения в полных дифференциалах. Вкратце повторюсь:
Если интегрирование проводится по «игрек», то переменная «икс» считается константой. И наоборот.
Тем не менее, вот нашли вы первообразную и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»: Получена исходная подынтегральная функция, значит, всё в порядке.
Момент второй, подстановка пределов интегрирования. По стандартной формуле Ньютона-Лейбница сначала вместо «игреков» мы подставили , а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
И, наконец, может показаться странным результат: Ведь можно раскрыть скобки и привести подобные слагаемые! В данном случае это сделать несложно, и чайникам, вероятно, лучше так и поступить. Но если будет не вторая, а 3-я или 4-ая степень? На самом деле линейную функцию в степени выгоднее проинтегрировать, не раскрывая скобок! Данный прием я уже применял и подробно комментировал во втором параграфе урока Как вычислить объем тела вращения? Ещё раз посмотрим, как он работает:
2) Берём оставшийся внешний интеграл:
При нахождении интеграла использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
Ответ:
Пример 6
Вычислить двойной интеграл ,
Это пример для самостоятельного решения. В образце решения, как и в разобранном примере, использован первый способ обхода области.
На практике немало примеров, где трудно (а то и невозможно) обойтись без микрокалькулятора-«дробовика». Рассмотрим практический пример на данную тему:
Пример 7
Вычислить двойной интеграл по области
Задача будет решена двумя способами, так как готовое решение у меня уже есть =) А если серьезно, второй способ будет нужен для дополнительных важных комментариев.
Решение: Изобразим область интегрирования на чертеже:
Область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях.
Выберем следующий порядок обхода области: Таким образом:
1)
Начинающим чайникам всегда рекомендую выполнять проверку, особенно в подобных примерах: возьмите частную производную по «игрек» от первообразной и получите подынтегральную функцию .
Будьте предельно внимательны в подстановке пределов интегрирования: сначала вместо«игреков» подставляем , затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
2) Второй шаг прост:
Перейдём к обратной функции и изменим порядок обхода области:
Таким образом:
1) Вычислим внутренний интеграл:
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Не лишней будет и промежуточная проверка, возьмём частную производную по «икс» от найденной первообразной: Получена подынтегральная функция, что и хотелось увидеть.
Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем вместо «иксов» подставляем . После подстановки должны остаться только «игреки».
Степени рекомендую оставить в виде , а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
2)
Результаты совпали, как оно и должно быть.
Легко заметить, что первый способ решения был заметно проще. Всегда перед решением анализируйте – какой путь легче и короче.
Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю вручную. Но не удивляйтесь, если на практике получится ответ вроде , по крайне мере, в своей коллекции я нашел немало диких примеров, где без микрокалькулятора-«дробовика» фактически не обойтись.
Ответ:
Ответ получился отрицательным. Геометрически это обозначает, что график подынтегральной функции (поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования под плоскостью .
Пример 8
Вычислить двойной интеграл по области
Это пример для самостоятельного решения. Ответ будет целым – чтобы от своего хорошего настроения не запугать вас окончательно =). Похожие двойные интегралы встречаются в известном задачнике Кузнецова, и по этой причине пример тоже уместен. Полное решение и ответ в конце урока.
Студенты-заочники почти всегда сталкиваются с двойными интегралами наподобие тех, которые уже рассмотрены, но никто не застрахован от творческих примеров, где в подынтегральной функции есть какие-нибудь синусы, косинусы, экспоненты и т.п.
Рассмотрим заключительные примеры на данную тему:
Пример 9
Вычислить двойной интеграл по области
Решение: В ходе выполнения чертежа может возникнуть трудность с построением прямой , которая параллельна оси . Ничего сложного: если , то – примерно на этом уровне и следует провести прямую.
Выполним чертёж:
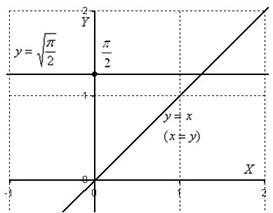
После выполнения чертежа нужно выяснить, какой порядок обхода области выгоднее применить.
Рассмотрим первый способ обхода: Тогда:
Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл придётся дважды брать по частям.
Но есть еще и второй способ обхода области: Следовательно:
Выглядит гораздо привлекательнее, начинаем вычисления:
1) По формуле Ньютона-Лейбница разберемся с внутренним интегралом:
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Если возникают трудности с интегрированием, можно прибегнуть даже к такому способу: временно замените «игрек» конкретным числом, например, «пятёркой»: . Теперь замените «пятёрку» обратно – «игреком»:
И, конечно же, лучше сделать проверку, продифференцировав первообразную по «икс»:
Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем , затем – ноль. После подстановки должны остаться только «игреки».
2) Полученный результат перемещаем во внешний интеграл, не забывая, что там уже есть и константа 4:
Второй интеграл взят методом подведения функции под знак дифференциала.
Ответ:
Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от подынтегральной функции.
Пример 10
Вычислить двойной интеграл по области
Это пример для самостоятельного решения.
Хочется привести ещё примеры, но в первом раунде я обещал не маньячить, поэтому скрепя сердце, заканчиваю статью. Множество других примеров на вычисление двойных интегралов можно найти в соответствующем архиве на странице Готовые решения по высшей математике. Если тема проработана качественно, то рискну предположить, что многие читатели самостоятельно смогут разобраться и в тройных интегралах – принципы решения очень похожи!
Раскрою секрет хорошего настроения – в аккурат перед вторым раундом на ринг вышла симпатичная девушка с табличкой 222. С вашего позволения, заключительное мудрое пожелание:
Хорошо должно быть каждый день!
Решения и ответы:
studfiles.net
Как вычислить двойной интеграл? Примеры решений
Прозвучал удар гонга, который открывает второй раунд в бою с двойными интегралами. Если вы недавно надели перчатки или вообще боксируете с грушей, то, пожалуйста, начните с первого раунда Двойные интегралы для чайников. Настоятельно рекомендую разобраться со всеми примерами вводного урока без халтуры, это очень важно. К тому же, добрый дядя Саша нарисовал много картинок, которые можно распечатать и наклеить у себя в туалете. Помните, что Коперник свои блестящие открытия в астрономии делал именно там.
Однако задорное получилось вступление…. Задумался вот… почему? Да потому что мне хорошо. А отчего хорошо, поясню в конце статьи.
Вспоминаем общую запись двойного интеграла:
В первой статье Двойные интегралы для чайников я очень подробно рассмотрел понятие двойного интеграла, алгоритм его решения, важнейшие задачи на обход области интегрирования. Также были прорешаны простейшие двойные интегралы в примерах на нахождение площади плоской фигуры.
Снова посмотрим на общую запись двойного интеграла и заметим, что в нём притаилась функция двух переменных . А когда речь заходит о функции двух переменных, то это часто попахивает сероводородом частными производными второго порядка. Поэтому для освоения примеров вам необходимо уметь более или менее уверенно их находить.
В большинстве практических задач требуется формально вычислить двойной интеграл, но, помимо этого, он обладает отличным геометрическим смыслом – с помощью двойного интеграла помимо площади можно вычислить еще и объём. Геометрический смысл двойного интеграла поясню ниже на конкретных примерах.
Начинаем набивать наш двойной интеграл разнообразной начинкой:
Пример 1
Вычислить двойной интеграл
,
Изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Решение: Изобразим область интегрирования на чертеже:
Напоминаю, что выполнение чертежа – необходимый начальный этапрешения. Чертёж крайне важно выполнить правильно и точно, поскольку ошибка в графике незамедлительно запорет всё задание.
Выберем следующий порядок обхода:
Вопросы порядка обхода области интегрирования, я комментировать практически не буду, пожалуйста, смотрите статью Двойные интегралы для чайников.
Таким образом:
Обратите внимание на следующее действие: в данном случае можно вынести «икс» из внутреннего интеграла во внешний интеграл. Почему? Во внутреннем интеграле интегрирование проводится по «игрек», следовательно, «икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
С интегралами настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
Вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл , при этом ни в коем случае не забываем про «икс», который там уже находится:
Готово.
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
Для наглядности еще раз приведу чертёж, он будет точно таким же, но с другими обозначениями графиков:
Второй способ обхода области:
Таким образом:
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
Вместо «икса» подставляются функции!
Всегда проявляйте повышенное внимание при подстановке пределов интегрирования.
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
Результаты совпали, значит, задание выполнено верно.
Если есть время, постарайтесь всегда проводить проверку, даже если этого не требуется в условии: вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Ответ:
Пример 2
Вычислить двойной интеграл
,
Выполнить проверку: изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Это пример для самостоятельного решения. Обратите внимание, что в двойном интеграле изначально присутствует константа. А константу можно вынести за знак двойного интеграла, в данном случае:
В ходе решения вынесение константы целесообразно проводить в момент перехода к повторным интегралам.
Как видите, свойство линейности справедливо не только для «обычных», но и для кратных интегралов. Интеграл от интеграла недалеко падает.
studopedya.ru
Двойные интегралы для чайников – страница 11
Ответ:
Вот такая вот глупая и наивная задача.
Любопытный пример для самостоятельного решения:
Пример 10
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями , ,
Примерный образец чистового оформления решения в конце урока.
В Примерах 9-10 значительно выгоднее использовать первый способ обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в заключение курса молодого ботана рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями ,
Решение: нас с нетерпением ждут две параболы с бзиком, которые лежат на боку. Улыбаться не нужно, похожие вещи в кратных интегралах встречаются частенько.
Как проще всего сделать чертёж?
Представим параболу в виде двух функций:
– верхняя ветвь и – нижняя ветвь.
Аналогично, представим параболу в виде верхней
fizich.ru
Вычисление двойных интегралов.
Литература: Б.П. Демидович Сборник задач и упражнений по математическому анализу 624 стр. М.: “ЧеРо”, 1997
Определение: Двойным интегралом от непрерывной функции $f(x, y)$ распространенным на ограниченную замкнутую квадрируемую область $\Omega$, называется число $$\iint\limits_{\Omega}f(x,y)dxdy=\lim\limits_{max|\Delta x_i|\rightarrow 0\quad max|\Delta y_i|\rightarrow 0}\sum\limits_i\sum\limits_j f(x_i, y_j)\Delta x_i\Delta y_j ,$$ где $\Delta x_i=x_{i+i}-x_i,$ $\Delta y_j=y_{j+1}-y_j$ и сумма распространяется на те значения $i$ и $j$ для которых $(x_i, y_j)\in\Omega.$
Непосредственное вычисление двойного интеграла.
Если область $\Omega$ задана неравенствами $$a\leq x\leq b,\qquad y_1(x)\leq y\leq y_2 (x),$$ где $y_1(x)$ и $y_2(x) -$ непрерывные функции на сегменте $[a, b],$ то соответствующий двойной интеграл может быть вычислен по формуле $$\iint\limits_{\Omega}f(x, y)dxdy=\int\limits_a^bdx\int\limits_{y_1(x)}^{y_2(x)}f(x, y)dy.$$
Замена переменных в двойном интеграле.
Если непрерывно дифференцируемые функции $$x=x(u, v),\quad y=y(u, v)$$ осуществляют взаимно однозначное отображение ограниченной и замкнутой области $\Omega$ в плоскости $Oxy$ на область $\Omega’$ в плоскости $Ouv$ и якобиан $$I=\frac{D(x, y)}{D(u, v)}$$ сохраняет постоянный знак в $\Omega$ за исключением, быть может, множества меры ноль, то справедлива формула $$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega’}f(x(u, v), y(u, v))|I|dudv.$$
В частности, для случая перехода к полярным $r$ и $\varphi$ координатам и по формулам имеем $$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega’}f(r\cos\varphi,\, r\sin\varphi)r drd\varphi.$$
Примеры:
Вычислить интегралы.
3906. $\int\limits_0^1dx\int\limits_0^1(x+y)dy.$
Решение.
$$\int\limits_0^1dx\int\limits_0^1(x+y)dy=\int\limits_0^1\left(\left.\left(xy+\frac{y^2}{2}\right)\right|_0^1\right)dx=\int\limits_0^1\left(x+\frac{1}{2}-0\right)dx=\left.\left(\frac{x^2}{2}+ \frac{1}{2}x\right)\right|_0^1= \frac{1}{2}+\frac{1}{2}-0=1.$$
Ответ: 1.
3908. $\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr.$
Решение.
$$\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr=\int\limits_0^{2\pi}\left(\int\limits_0^a r^2\sin^2\varphi\,dr\right)d\varphi=\int\limits_0^{2\pi}\left(\sin^2\varphi\left.\frac{r^3}{3}\right|_0^a\right)d\varphi=\int\limits_0^{2\pi}\sin^2\varphi\left(\frac{a^3}{3}-0\right)d\varphi=$$
$$=\frac{a^3}{3}\int\limits_0^{2\pi}\frac{1-cos2\varphi}{2}d\varphi=\frac{a^3}{3}\left.\left(\frac{1}{2}\varphi-\frac{1}{4}\sin2\varphi\right)\right|_0^{2\pi}=\frac{a^3}{3}\left(\frac{1}{2}2\pi-\frac{1}{4}\sin4\varphi-0\right)=\frac{a^3\pi}{3}.$$
Ответ: $\frac{a^3\pi}{3}.$
3912 а) Какой знак имеет интеграл $\iint\limits_{|x|+|y|\leq 1}\ln(x^2+y^2)\,dxdy;$
Изменить порядок интегрирования в следующих интегралах:
3924. $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy.$
Решение.
Сделаем рисунок интегрируемой области:
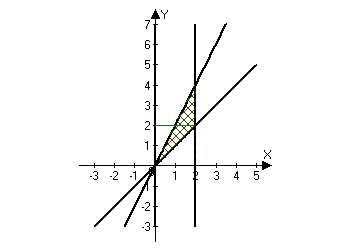
Область интегрирования ограничена прямыми $y=x, y=2x$ и $x=2.$ Заметим, что в этой области если $y$ меняется от $0$ до $2,$ то координата $x$ меняется от прямой $y=2x$ (или $x=\frac{y}{2}$) до $y=x.$ Если же $y$ меняется от $2$ до $4,$ то координата $x$ меняется от прямой $y=2x$ ($x=\frac{y}{2}$) до $x=2.$ Таким образом,
$$\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$$
Ответ: $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$
3928. $\int\limits_1^2dx\int\limits_{2-x}^{\sqrt{2x-x^2}}f(x, y)dy.$
3932. Вычислить интеграл $\iint\limits_{\Omega}xy^2dxdy,$ если область $\Omega$ ограничена параболой $y^2=2px$ и прямой $x=p/2\quad (p>0).$
3939. В двойном интеграле $\iint\limits_{\Omega}f(x,y)dxdy$ перейти к полярным координатам $r$ и $\varphi,$ полагая $x=r\cos\varphi$ и $y=r\sin\varphi,$ расставить пределы интегрирования, если $\Omega -$ кольцо $a^2\leq x^ 2+y^2\leq b^2.$
3944. Перейти к полярным координатам, $r$ и $\varphi,$ полагая $x=r\cos\varphi$ и $y=r\sin\varphi,$ и расставить пределы интегрирования в том и другом порядке в следующем интеграле: $\int\limits_0^1dx\int\limits_{1-x}^{\sqrt{1-x^2}}f(x, y)dy.$
3948. Предполагая, что $r$ и $\varphi,$ – полярные координаты, изменить порядок интегрирования в следующих интегралах: $\int\limits_{-\pi/2}^{\pi/2}d\varphi\int\limits_0^{a\cos\varphi}f(\varphi,r)dt\quad (a>0).$
3954. Переходя к полярным координатам, вычислить двойной интеграл $\iint\limits_{x^2+y^2\leq a^2}\sqrt{x^2+y^2}dxdy.$
3958. Вместо $x$ и $y$ ввести новые переменные $u$ и $v$ определить пределы интегрирования в следующих двойных интегралах $\int\limits_0^2dx\int\limits_{1-x}^{2-x}f(x, y)dy,$ если $u=x+y,\,\, v=x-y.$
3964. Произведя соответствующие замены переменных, свести двойные интегралы к однократным: $\iint\limits_{\Omega}f(xy)dxdy,$ где область $\Omega$ ограничена кривыми $xy=1,\,\, xy=2,\,\, y=x,\,\, y=4x\,\, (x>0, y>0).$
mathportal.net
Двойные интегралы для чайников – страница 20
Вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл , при этом ни в коем случае не забываем про «икс», который там уже находится:
Готово.
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
Для наглядности еще раз приведу чертёж, он будет точно таким же, но с другими обозначениями графиков:
Второй способ обхода области:
Таким образом:
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
fizich.ru
Откуда взять пределы интегрирования? – Двойные интегралы для чайников
Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область . Область представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры иливычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.
После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
Грубо говоря, задача сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?!
Второй способ перехода к повторным интегралам встречается несколько реже:
Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками –будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции , зависящие от «игрек».
Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:
Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения.
Алгоритм решения двойного интеграла:
Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу?
1) Необходимо выполнить чертёж. Без чертежа задачу не решить. Точнее, решать-то она решается, но это будет похоже на игру в шахматы вслепую. На чертеже следует изобразить область , которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т.д. Грамотную и быструю технику построения чертежей можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков. Итак, этап первый – выполнить чертёж.
2) Расставить пределы интегрирования и перейти к повторным интегралам.
3) Взять внутренний интеграл
4) Взять внешний интеграл и получить ответ (число).
Область интегрирования. Порядок обхода области интегрирования.
Как изменить порядок обхода?
В данном параграфе мы рассмотрим важнейший вопрос – как перейти к повторным интегралам и правильно расставить пределы интегрирования. Как было сказано выше, сделать это можно так:
И так:
На практике эта вроде бы несложная задача вызывает наибольшие затруднения, и студенты часто путаются в расстановке пределов интегрирования. Рассмотрим конкретный пример:
Пример 1
Дан двойной интеграл с областью интегрирования . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
fizich.ru
