Эксперимент Белла. Квантовый ум [Грань между физикой и психологией]
Эксперимент Белла
Эксперимент, демонстрирующий квантовую сцепленность или взаимосвязанность, иногда называют «единством мира» или экспериментом Белла[17]. Этот эксперимент показал, что фотоны от данного источника света взаимосвязаны.
Подобно всем другим квантовым феноменам, свет иногда ведет себя как частицы, а иногда как волны. Например, представьте себе неоновую лампу, испускающую фотоны во все стороны. Один фотон идет в одном направлении, а другой – в противоположном. Удивительный эксперимент, проводившийся с этими фотонами, показал, что все, что бы ни происходило с одной частицей, оказывалось связанным с тем, что происходило с другой, независимо от разделявшего их расстояния1.
Результаты показывают, что измерения движения одной частицы неразрывно связаны с измерениями движения другой даже после того, как они были разделены во времени и пространстве. Точнее, измерения спина частицы A в одном месте дают информацию о спине частицы-двойника B, находящейся в другой точке пространства-времени. Если я двумя руками бросаю два шарика, один налево, а другой направо, то через 10 минут измерения вращения одного шарика мало что скажут о вращении другого. Как могут быть связанными два разделенных квантовых объекта, если нельзя вообразить ничего, что бы их соединяло?
На самом деле, субатомные частицы, например фотоны, вовсе не похожи на маленькие вращающиеся шарики. По существу, понятие «спин», подобно понятию «частица», – это термин ОР, полезный для описания «псевдовращательных» характеристик квантовых объектов. Понятие спина просто характеризует присущий частице угловой момент, который, подобно угловому моменту вращения шарика, противится изменениям.
Если измерения спина частицы A показывают, что ее момент направлен вверх, мы можем догадываться, что спин частицы B будет направлен вниз. Если мы обнаруживаем, что спин A направлен вниз, то можем предсказывать, что спин B будет направлен вверх. A + B в некотором смысле компенсируют друг друга – они взаимосвязаны, их суммарный спин уравновешен.
Теперь подумаем об этом феномене с более личной точки зрения. Допустим, что вы и я парные фотоны, в некоторый момент покидающие неоновую лампу (см. рис. 19.1). Пусть вы со скоростью света двигаетесь в Москву, в то время как я свечу в направлении Лос-Анджелеса.
Рис. 19.1. Эксперимент Белла
Теперь допустим, что люди в Москве и в Лос-Анджелесе (Л. А.) смотрят на наши головы. Если в данный момент они обнаруживают, что моя голова смотрит вниз, то могут правильно предсказывать, что ваша голова в Москве будет смотреть вверх. Если кто-нибудь в Москве это проверит, то действительно обнаружит, что ваша голова смотрит вверх! Если люди в Л.А. видят, что моя голова смотрит вверх, то москвичи обнаружат, что ваша голова смотрит вниз. Эксперимент Белла показывает, что мы двое, остаемся каким-то неизвестным образом связанными через пространство и время.
В этом суть эксперимента Белла, которую нам нужно знать в настоящий момент. Результаты показывают, что две квантовые сущности, которые первоначально были частями одной и той же системы, совершенно необъяснимым образом остаются взаимосвязанными. Они считаются «сцепленными»
Эксперимент показывает, что, зная движения одного из сцепленных фотонов, вы знаете движения другого. Аналогия этой сцепленности на человеческом уровне может быть более чем метафорической. Поскольку все человеческие существа происходят от одного и того же источника, называем ли мы его Землей, или богом, или чем-то еще, и поскольку многие из нас ощущают себя происходящими из одной и той же семьи, нас тоже можно считать «спаренными». Чем ближе наше родство или чем больше мы чувствуем, что происходим из одного и того же источника, тем больше мы оказываемся сцеплены связями, которые кажутся выходящими за пределы законов случайности. Опыт связи представляет собой феномен НОР и его, как и все чувство взаимосвязанности, трудно обосновать в терминах ОР.
Тем не менее, многие люди чувствуют себя связанными паранормальным образом. Я часто видел, что если один человек в группе знает, что происходит внутри него, то он многое знает о том, что происходит или вот-вот произойдет в окружающих его других людях. Справедливо и обратное. Если вы знаете меня, то знаете себя. Многие люди всегда чувствовали себя в определенном смысле взаимосвязанными, подобно фотонам в экспериментах Белла. Кажется, будто мы знаем друг друга.
Наши отношения симметричны в том смысле, что мы компенсируем поведение друг друга. Теоретически, эта компенсация существует независимо от того, насколько далеко мы разделены в пространстве или времени. По-другому можно сказать, что не существует никакого определенного местоположения, или что существует «нелокальность».
Если мы будем далее рассматривать наши частицы, оказывается, что если вы знаете поведение одной частицы, скажем, в 2001 году, то будете знать, что будет делать эта частица в 2025 году! Что еще более странно, если вы знаете, что делала одна частица в 2025 году, то можете идти назад во времени и будете знать, что другая частица делала в 1920 году. Более того, связь между двумя сцепленными фотонами так же сильна, когда они находятся на противоположных концах Земли, какой она была бы, если бы их разделяло 3 метра.
Существуют ли скрытые силы, которые соединяют частицы?[18] Никто не знает. На данный момент в квантовой физике причины этого взаимодействия остаются не объясненными. Некоторые люди предполагают, что фотоны связаны посредством сигналов, идущих быстрее скорости света, – так называемых тахионных сигналов. Тахион – это (гипотетическая) частица, способная двигаться быстрее света и не подчиняющаяся теории относительности, которая утверждает, что ничто не может двигаться быстрее скорости света. Слово тахион означает «быстрый».
Если бы тахионы существовали и могли двигаться быстрее скорости света, то они могли бы идти назад во времени, так что будущее могло бы влиять на настоящее и поведение частицы в 2022 году могло бы влиять на поведение другой частицы в 1970 году.
Некоторые физики думают, что между фотонами может быть тахионная коммуникация: тот, что находится в Москве, посылает сигналы вперед и назад во времени тому, что находится в Лос-Анджелесе, – что объясняло бы, как один фотон «знает», что делает другой. Но эту тахионную теорию запрещает один из результатов теории относительности, разработанной Альбертом Эйнштейном. Согласно теории относительности, ничто измеримое не может двигаться быстрее света[19].
Все, что можно сказать в настоящее время, – это то, что локальность или пространственная разделенность частиц перестала быть содержательным понятием. Частицы больше не имеют раздельного местонахождения[20]. В повседневной жизни нет никакой простой аналогии этой «нелокальности» сцепленных квантовых объектов – за исключением того, что никто из нас не живет в отдельной реальности. Утверждать, что спин одной частицы рассказывает нам о другой частицы, – это почти все равно, что утверждать: если вам известно нечто обо мне, то мы можем понимать моего партнера, независимо от того, где он или она находится, независимо от разницы во времени или разделения в пространстве. Если я знаю что-то о своем поведении, то знаю что-то и о вашем. На уровне наших глубочайших, самых чувственных, тонких переживаний мы взаимосвязаны. Как это происходит?
fil.wikireading.ru
Первый эксперимент, который корректно доказывает нарушение неравенства Белла

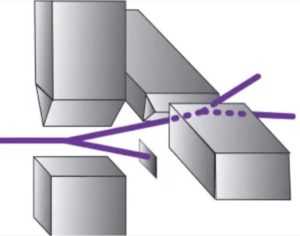
Ведущий автор научной работы Бас Хенсен (Bas Hensen) и профессор Рональд Хансон (Ronald Hanson) настраивают установку для эксперимента Белла в точке А, откуда эмитируются электроны
В 1935 году Альберт Эйнштейн поставил под сомнение принцип квантовой теории о том, что наблюдение одной частицы мгновенно влияет на состояние связанной с ней частицы, где бы она ни находилась. Это означает, что информация от частицы к частице передаётся быстрее скорости света, что Эйнштейн считал невозможным и несовместимым с теорией относительности.
Физики с 70-х гг пытались проверить данное свойство частиц. Для этого были сформулированы так называемые неравенства Белла и условия эксперимента Белла. Но учёным никак не удавалось избавиться от проблем экспериментальной установки или «лазеек» (loopholes), которые не позволяли назвать эксперимент чистым и корректным, действительно опровергающим теорию относительности и демонстрирующим передачу информации быстрее скорости света. Эти лазейки позволяли объяснить передачу информации якобы быстрее скорости света другими локальными факторами.
Только сейчас исследователям из технологического университета Делфта (Нидерланды) удалось впервые в истории провести корректный эксперимент Белла, избавленный от обеих известных проблем экспериментальной установки: лазейки местоположения (locality loophole) и лазейки обнаружения (detection loophole).
Экспериментаторы из технологического университета Делфта проверили состояние частиц на расстоянии 1,3 км (на территории кампуса) и зарегистрировали совпадение ~96%. Это больше, чем предсказано теоремой Белла.
Результаты и техника эксперимента опубликованы в статье “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres”, журнал Nature, дата публикации 21 октября 2015 года (pdf).
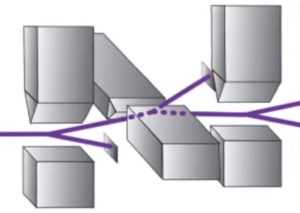
На иллюстрации: слева точка А с одним из двух алмазов, другой алмаз находится на противоположном конце кампуса справа. Между ними — точка С, где располагается сплитер (разделитель) луча.
Теорема Белла показывает, что вне зависимости от реального наличия в квантово-механической теории неких скрытых параметров, влияющих на любую физическую характеристику квантовой частицы, можно провести серийный эксперимент, статистические результаты которого подтвердят либо опровергнут наличие таких скрытых параметров в квантово-механической теории. Условно говоря, в одном случае статистическое соотношение составит не более 2:3, а в другом — не менее 3:4.
Условия эксперимента Белла объясняются на видео на примере пары «связанных» любовными узами посетителей ресторана, которые должны заказать разное вино в бокале и бутылке. Они могут заранее договориться о стратегии, но не могут обмениваться информацией во время «игры».
Главным достижением группы экспериментаторов в последнем эксперименте является продвинутая техника, которая позволила избавиться от лазеек местоположения и обнаружения. Для этого они использовали два алмазных детектора (в точках А и С на схеме вверху) и разделитель сигнала посередине между ними. Спины электронов измерялись с помощью микроволновых и лазерных импульсов в детекторах на противоположных сторонах кампуса. Архитектура установки с разделением луча и детектированием спина связанных электронов спроектирована таким образом, что связанные электроны не могли обмениваться информацией с помощью никакой из известных лазеек во время измерения.
Эксперимент доказал нарушение концепции локального реализма, который сочетает принцип локальности с «реалистичным» предположением, что все объекты обладают «объективно существующими» значениями своих параметров и характеристик для любых возможных измерений, могущих быть произведенными над этими объектами, перед тем как эти измерения производятся.
В реальности же подтвердился принцип квантовой механики, что у электронов нет характеристик до тех пор, пока их не наблюдают с помощью детектора. До этого момента частицы существуют в нескольких состояниях одновременно.
Правда, некоторые независимые эксперты говорят, что есть ещё третья лазейка, от которой во время эксперимента не избавились. Дело в том, что случайное разделение электронов с разными спинами может быть не совсем случайным, а происходить с некоей скрытой закономерностью. Так что о нарушении теории относительности и неправоте Эйнштейна пока рано говорить с полной уверенностью.
В следующем году в Массачусетском технологическом институте пройдёт более продвинутый эксперимент, в котором детекторы будут проверять характеристики фотонов с разных частей Галактики — там уже наверняка не будет действовать никакая из трёх лазеек.
habr.com
Спин электрона. Эксперимент Штерна-Герлаха. | LightCone
Спин (spin – вращение) это наиболее простая вещь на которой можно продемонстрировать отличия квантовой механики от классической. Из определения кажется, что связан он с вращением, но не надо представлять себе электрон или протон вращающимися шариками. Как и в случае многих других устоявшихся научных терминов было доказано что это не так, но терминология уже устоялась. Электрон – точечная частица (нулевого радиуса). А спин отвечает за магнитные свойства. Если электрически заряженная частица движется по кривой траектории (в том числе вращается), то образуется магнитное поле. Электромагниты так работают – электроны движутся по проводам катушки. Но спин отличается от классического магнита. Вот неплохая анимация:
Если магнитики пропускать через неоднородное магнитное поле (обратите внимание на различную форму северного и южного полюсов магнита, задающего поле), то в зависимости от ориентации магнитика (его вектора магнитного момента) они будут притягиваться (отталкиваться) от полюса с большей концентрацией силовых линий магнитного поля (заостренный полюс магнита). В случае перпендикулярной ориентации магнитик вообще никуда не отклонится и попадет в центр экрана.
Пропуская электроны мы будем наблюдать только отклонение вверх или вниз на одно и то же расстояние. Это пример квантования (дискретности). Спин электрона может принимать только одно из двух значений относительно заданной оси ориентации магнита – «вверх» или «вниз». Поскольку электрон мысленно представить себе нельзя (у него нет ни цвета, ни формы, ни даже траектории движения), как и во всех подобных анимациях цветные шарики не отражают реальность, но суть думаю понятна.
Если электрон отклонился вверх, то говорят, что его спин направлен «вверх» (+1/2 условно обозначают) относительно оси магнита. Если вниз, то -1/2. И казалось бы спин можно описать обычным вектором, указывающим направление. У тех электронов, где он был направлен вверх, они и отклонятся вверх в магнитном поле, а у которых вниз – те соответственно вниз. Но не все так просто! Электрон отклоняется вверх (вниз) на одно и тоже расстояние относительно любой ориентации магнита. На видео выше можно было бы менять не ориентацию пропускаемых магнитиков, а поворачивать сам магнит, создающий магнитное поле. Эффект в случае обычных магнитиков был бы тот же. Что будет в случае электронов – в отличие от магнитиков они всегда будут отклонятся на одно и тоже расстояние вверх или вниз.
Если, например, пропустить вертикально расположенный классический магнитик через два перпендикулярно ориентированных друг относительно друга магнита, то отклоняясь вверх в первом, он не отклонится во втором вообще никак – его вектор магнитного момента будет перпендикулярен линиям магнитного поля. На видео выше это тот случай когда магнитик попадает в центр экрана. Электрон же обязан куда-нибудь отклонится.
Если мы будем пропускать через второй магнит только электроны со спином вверх, как на рисунке, то окажется что часть из них оказались еще и со спином вверх (вниз) относительно другой перпендикулярной оси. Вправо и влево фактически, но спин измеряют относительно выбранной оси, поэтому «вверх» и «вниз» общепринятая терминология вместе с указанием оси. Вектор не может быть направлен сразу вверх и вправо. Делаем вывод, что спин – это не классический вектор, прикрепленный к электрону наподобие вектора магнитного момента магнитика. Более того, зная, что спин электрона направлен вверх после прохождения первого магнита (отклоняющиеся вниз блокируем), невозможно предсказать куда он отклонится во втором случае: вправо или влево.
Ну и можно еще чуть-чуть усложнить эксперимент – блокировать электроны, отклонившиеся влево и пропустить через третий магнит, ориентированный как и первый.
И мы увидим, что электроны будут отклонятся как вверх, так и вниз. То есть электроны, попадающие во второй магнит все имели спин вверх относительно ориентации первого магнита, а потом часть из них стала вдруг со спином вниз относительно той же самой оси.
Странно! Если через такую конструкцию пропускать классические магнитики, повернутые под одним и тем же произвольно выбранным углом, то они всегда будут попадать в конце в одну и ту же точку экрана. Это называется детерминизмом. Повторив эксперимент при полном соответствии начальных условий мы должны получить тот же результат. В этом заключается основа предсказательной силы науки. Даже наша интуиция основана на повторяемости результатов в схожих ситуациях. В квантовой механике предсказать куда отклонится конкретно взятый электрон в общем случае невозможно. Хотя в некоторых ситуациях есть исключения: если поставить два магнита с одинаковой ориентацией, то если электрон отклонится вверх в первом, то он точно отклонится вверх и во втором. А если магниты повернуты на 180 градусов друг относительно друга и в первом электрон отклонился, например, вниз, то во втором он точно отклонится вверх. И наоборот. Сам по себе спин не меняется. Это уже хорошо)
Какие из всего этого можно сделать общие выводы.
- Многие величины, которые могли принимать любые значения в классической механике, могут иметь только некоторые дискретные (квантованные) значения в квантовой теории. Помимо спина энергия электронов в атомах является ярким примером.
- Объектам микромира нельзя приписать никакие классические характеристики до момента измерения. Нельзя полагать, что спин имел какое-то определенное направление до того как мы посмотрели куда отклонился электрон. Это общее положение и оно касается всех измеряемых величин: координат, скорости и т.п. Квантовая механика субъективна. Она утверждает, что объективный, не зависимый ни от кого классический мир, просто не существует. Теорема Белла наиболее наглядно демонстрирует данный факт. Роль субъекта (наблюдателя) в квантовой механике чрезвычайно важна.
- Процесс измерения затирает (делает неактуальной) информацию о предыдущем измерении. Если спин оказался направлен вверх относительно оси y, то неважно, что раньше он был направлен вверх относительно оси x, он может оказаться и спином вниз относительно той же самой оси x впоследствии. Опять же данное обстоятельство касается не только спина. Например, если электрон обнаружен в точке с координатами (x, y, z) это в общем случае не значит, что он был в этой точке до этого. Данный факт известен под названием «коллапс волновой функции».
- Есть такие физические величины значения которых невозможно знать одновременно. Например, нельзя измерить спин относительно оси x и одновременно относительно перпендикулярной ей оси y. Если мы попытаемся сделать это одновременно, то магнитные поля двух повернутых магнитов наложатся и мы вместо двух разных осей получим одну новую и измерим спин относительно нее. Последовательно измерять тоже не удастся вследствие предыдуще изложенного вывода №3. Это тоже общий принцип. Например, координату и импульс (скорость) тоже нельзя измерить одновременно с большой точностью — знаменитый принцип неопределенности Гейзенберга.
- Предсказать результат единичного измерения невозможно в принципе. Квантовая механика позволяет лишь вычислять вероятности того или иного события. Например, можно посчитать, что в опыте на первой картинке при ориентации магнитов 90° друг к другу 50% отклонится влево и 50% вправо. Предсказать куда отклонится конкретно взятый электрон нельзя. Данное общее обстоятельство известно как «правило Борна» и является центральным в Копенгагенской интерпретации.
- Детерминированные классические законы выводятся из вероятностных квантовомеханических за счет того, что в макроскопическом объекте очень много частиц и вероятностные флуктуации усредняются. Например, если в опыте на первой картинке пропускать вертикально ориентированный классический магнитик, то 50% составляющих его частиц будут «тянуть» его вправо, а 50% влево. В итоге он никуда не отклонится. При других ориентациях углов магнита меняется процентное соотношение, что в итоге и влияет на отклоняемое расстояние. Квантовая механика позволяет рассчитать конкретные вероятности и как следствие из нее можно вывести формулу для отклоняемого расстояния в зависимости от угла ориентации магнитика, получаемую обычно из классической электродинамики. Так классическая физика выводится и является следствием квантовой.
Да, описанные действия с магнитиками называются эксперимент Штерна-Герлаха.
Существует видеоверсия данного поста в части 2 и части 3 элементарного введения в квантовую механику.
Вторая статья цикла про спин электрона: Электроны в магнитном поле.
lightcone.ru
5 знаменитых квантовых экспериментов — T&P
Никто в мире не понимает квантовую механику — это главное, что нужно о ней знать. Да, многие физики научились пользоваться ее законами и даже предсказывать явления по квантовым расчетам. Но до сих пор непонятно, почему присутствие наблюдателя определяет судьбу системы и заставляет ее сделать выбор в пользу одного состояния. «Теории и практики» подобрали примеры экспериментов, на исход которых неминуемо влияет наблюдатель, и попытались разобраться, что квантовая механика собирается делать с таким вмешательством сознания в материальную реальность.
Кот Шредингера
Сегодня существует множество интерпретаций квантовой механики, самой популярной среди которых остается копенгагенская. Ее главные положения в 1920-х годах сформулировали Нильс Бор и Вернер Гейзенберг. А центральным термином копенгагенской интерпретации стала волновая функция — математическая функция, заключающая в себе информацию обо всех возможных состояниях квантовой системы, в которых она одновременно пребывает.
По копенгагенской интерпретации, доподлинно определить состояние системы, выделить его среди остальных может только наблюдение (волновая функция только помогает математически рассчитать вероятность обнаружить систему в том или ином состоянии). Можно сказать, что после наблюдения квантовая система становится классической: мгновенно перестает сосуществовать сразу во многих состояниях в пользу одного из них.
У такого подхода всегда были противники (вспомнить хотя бы «Бог не играет в кости» Альберта Эйнштейна), но точность расчетов и предсказаний брала свое. Впрочем, в последнее время сторонников копенгагенской интерпретации становится все меньше и не последняя причина тому — тот самый загадочный мгновенный коллапс волновой функции при измерении. Знаменитый мысленный эксперимент Эрвина Шредингера с бедолагой-котом как раз был призван показать абсурдность этого явления.
Итак, напоминаем содержание эксперимента. В черный ящик помещают живого кота, ампулу с ядом и некий механизм, который может в случайный момент пустить яд в действие. Например, один радиоактивный атом, при распаде которого разобьется ампула. Точное время распада атома неизвестно. Известен лишь период полураспада: время, за которое распад произойдет с вероятностью 50%.
Получается, что для внешнего наблюдателя кот внутри ящика существует сразу в двух состояниях: он либо жив, если все идет нормально, либо мертв, если распад произошел и ампула разбилась. Оба этих состояния описывает волновая функция кота, которая меняется с течением времени: чем дальше, тем больше вероятность, что радиоактивный распад уже случился. Но как только ящик открывается, волновая функция коллапсирует и мы сразу видим исход живодерского эксперимента.
Выходит, пока наблюдатель не откроет ящик, кот так и будет вечно балансировать на границе между жизнью и смертью, а определит его участь только действие наблюдателя. Вот абсурд, на который указывал Шредингер.
Дифракция электронов
По опросу крупнейших физиков, проведенному газетой The New York Times, опыт с дифракцией электронов, поставленный в 1961 году Клаусом Йенсоном, стал одним из красивейших в истории науки. В чем его суть?
Есть источник, излучающий поток электронов в сторону экрана-фотопластинки. И есть преграда на пути этих электронов — медная пластинка с двумя щелями. Какой картины на экране можно ожидать, если представлять электроны просто маленькими заряженными шариками? Двух засвеченных полос напротив щелей.
В действительности на экране появляется гораздо более сложный узор из чередующихся черных и белых полос. Дело в том, что при прохождении через щели электроны начинают вести себя не как частицы, а как волны (подобно тому, как и фотоны, частицы света, одновременно могут быть и волнами). Потом эти волны взаимодействуют в пространстве, где-то ослабляя, а где-то усиливая друг друга, и в результате на экране появляется сложная картина из чередующихся светлых и темных полос.
При этом результат эксперимента не меняется, и если пускать электроны через щель не сплошным потоком, а поодиночке, даже одна частица может быть одновременно и волной. Даже один электрон может одновременно пройти через две щели (и это еще одно из важных положений копенгагенской интерпретации квантовой механики — объекты могут одновременно проявлять и свои «привычные» материальные свойства, и экзотические волновые).
Но при чем здесь наблюдатель? При том, что с ним и без того запутанная история стала еще сложнее. Когда в подобных экспериментах физики попытались зафиксировать с помощью приборов, через какую щель в действительности проходит электрон, картинка на экране резко поменялась и стала «классической»: два засвеченных участка напротив щелей и никаких чередующихся полос.
Электроны будто не захотели проявлять свою волновую природу под пристальным взором наблюдателя. Подстроились под его инстинктивное желание увидеть простую и понятную картинку. Мистика? Есть и куда более простое объяснение: никакое наблюдение за системой нельзя провести без физического воздействия на нее. Но к этому вернемся еще чуть позже.
Нагретый фуллерен
Опыты по дифракции частиц ставили не только на электронах, но и на куда больших объектах. Например, фуллеренах — крупных, замкнутых молекулах, составленных из десятков атомов углерода (так, фуллерен из шестидесяти атомов углерода по форме очень похож на футбольный мяч: полую сферу, сшитую из пяти- и шестиугольников).
Недавно группа из Венского университета во главе с профессором Цайлингером попыталась внести элемент наблюдения в подобные опыты. Для этого они облучали движущиеся молекулы фуллерена лазерным лучом. После, нагретые внешним воздействием, молекулы начинали светиться и тем неминуемо обнаруживали для наблюдателя свое место в пространстве.
Вместе с таким нововведением поменялось и поведение молекул. До начала тотальной слежки фуллерены вполне успешно огибали препятствия (проявляли волновые свойства) подобно электронам из прошлого примера, проходящим сквозь непрозрачный экран. Но позже, с появлением наблюдателя, фуллерены успокоились и стали вести себя как вполне законопослушные частицы материи.
Охлаждающее измерение
Одним из самых известных законов квантового мира является принцип неопределенности Гейзенберга: невозможно одновременно установить положение и скорость квантового объекта. Чем точнее измеряем импульс частицы, тем менее точно можно измерить ее положение. Но действие квантовых законов, работающих на уровне крошечных частиц, обычно незаметно в нашем мире больших макрообъектов.
Потому тем ценнее недавние эксперименты группы профессора Шваба из США, в которых квантовые эффекты продемонстрировали не на уровне тех же электронов или молекул фуллерена (их характерный диаметр — около 1 нм), а на чуть более ощутимом объекте — крошечной алюминиевой полоске.
Эту полоску закрепили с обеих сторон так, чтобы ее середина была в подвешенном состоянии и могла вибрировать под внешним воздействием. Кроме того, рядом с полоской находился прибор, способный с высокой точностью регистрировать ее положение.
В результате экспериментаторы обнаружили два интересных эффекта. Во-первых, любое измерение положения объекта, наблюдение за полоской не проходило для нее бесследно — после каждого измерения положение полоски менялось. Грубо говоря, экспериментаторы с большой точностью определяли координаты полоски и тем самым, по принципу Гейзенберга, меняли ее скорость, а значит и последующее положение.
Во-вторых, что уже совсем неожиданно, некоторые измерения еще и приводили к охлаждению полоски. Получается, наблюдатель может лишь одним своим присутствием менять физические характеристики объектов. Звучит совсем невероятно, но к чести физиков скажем, что они не растерялись — теперь группа профессора Шваба думает, как применить обнаруженный эффект для охлаждения электронных микросхем.
Замирающие частицы
Как известно, нестабильные радиоактивные частицы распадаются в мире не только ради экспериментов над котами, но и вполне сами по себе. При этом каждая частица характеризуется средним временем жизни, которое, оказывается, может увеличиваться под пристальным взором наблюдателя.
Впервые этот квантовый эффект предсказали еще в 1960-х годах, а его блестящее экспериментальное подтверждение появилось в статье, опубликованной в 2006 году группой нобелевского лауреата по физике Вольфганга Кеттерле из Массачусетского технологического института.
В этой работе изучали распад нестабильных возбужденных атомов рубидия (распадаются на атомы рубидия в основном состоянии и фотоны). Сразу после приготовления системы, возбуждения атомов за ними начинали наблюдать — просвечивать их лазерным пучком. При этом наблюдение велось в двух режимах: непрерывном (в систему постоянно подаются небольшие световые импульсы) и импульсном (система время от времени облучается импульсами более мощными).
Полученные результаты отлично совпали с теоретическими предсказаниями. Внешние световые воздействия действительно замедляют распад частиц, как бы возвращают их в исходное, далекое от распада состояние. При этом величина эффекта для двух исследованных режимов также совпадает с предсказаниями. А максимально жизнь нестабильных возбужденных атомов рубидия удалось продлить в 30 раз.
Электроны и фуллерены перестают проявлять свои волновые свойства, алюминиевые пластинки охлаждаются, а нестабильные частицы замирают в своем распаде: под всесильным взором наблюдателя мир меняется. Чем не свидетельство вовлеченности нашего разума в работу мира вокруг? Так может быть правы были Карл Юнг и Вольфганг Паули (австрийcкий физик, лауреат Нобелевской премии, один из пионеров квантовой механики), когда говорили, что законы физики и сознания должны рассматриваться как взаимодополняющие?
Но так остается только один шаг до дежурного признания: весь мир вокруг суть иллюзорное порождение нашего разума. Жутковато? («Вы и вправду думаете, что Луна существует лишь когда вы на нее смотрите?» — комментировал Эйнштейн принципы квантовой механики). Тогда попробуем вновь обратиться к физикам. Тем более, в последние годы они все меньше жалуют копенгагенскую интерпретацию квантовой механики с ее загадочным коллапсом волной функции, на смену которому приходит другой, вполне приземленный и надежный термин — декогеренция.
Дело вот в чем — во всех описанных опытах с наблюдением экспериментаторы неминуемо воздействовали на систему. Подсвечивали ее лазером, устанавливали измеряющие приборы. И это общий, очень важный принцип: нельзя пронаблюдать за системой, измерить ее свойства не провзаимодействовав с ней. А где взаимодействие, там и изменение свойств. Тем более, когда с крошечной квантовой системой взаимодействуют махины квантовых объектов. Так что вечный, буддистский нейтралитет наблюдателя невозможен.
Как раз это объясняет термин «декогеренция» — необратимый с точки зрения термодинамики процесс нарушения квантовых свойств системы при ее взаимодействии с другой, крупной системой. Во время такого взаимодействия квантовая система утрачивает свои изначальные черты и становится классической, «подчиняется» системе крупной. Этим и объясняется парадокс с котом Шредингера: кот представляет собой настолько большую систему, что его просто нельзя изолировать от мира. Сама постановка мысленного эксперимента не совсем корректна.
В любом случае, по сравнению с реальностью как актом творения сознания, декогеренция звучит куда более спокойно. Даже, может быть, слишком спокойно. Ведь с таким подходом весь классический мир становится одним большим эффектом декогеренции. А как утверждают авторы одной из самых серьезных книг в этой области, из таких подходов еще и логично вытекают утверждения вроде «в мире не существует никаких частиц» или «не существует никакого времени на фундаментальном уровне».
Созидающий наблюдатель или всесильная декогеренция? Приходится выбирать из двух зол. Но помните — сейчас ученые все больше убеждаются, что в основе наших мыслительных процессов лежат те самые пресловутые квантовые эффекты. Так что где заканчивается наблюдение и начинается реальность — выбирать приходится каждому из нас.
theoryandpractice.ru
Квантовая реальность – Часть 1
Шаг назад
Часть 1. Спин.
Физические эксперименты всегда подразумевают измерение каких-либо величин. В экспериментах по схеме Белла, мы будем измерять спин элементарных частиц, поэтому нам следует разобраться, что же это за штука такая.
В классической механике есть такая величина: момент импульса. Так же, как и просто импульс, момент импульса характеризует количество движения. Разница вот в чём: импульс характеризует поступательное движение тела в определённой системе отсчёта, а момент импульса – вращательное движение тела вокруг определённой оси вращения.
Вы знаете, конечно, что импульс определяется как произведение массы тела на его линейную скорость. А момент импульса определяется как произведение момента инерции тела на его угловую скорость, ту, которая измеряется в оборотах в секунду. Что такое момент инерции – я тут объяснять не буду, для нашей задачи это несущественно. Зато очень существенно вот что: момент импульса является величиной векторной, то есть, характеризуется не только абсолютным значением, но и направлением, которое всегда совпадает с направлением оси вращения. Тут вы можете спросить: но ведь у оси вращения два направления. Например, куда направлен вектор момента импульса вращающейся юлы-волчка, вверх или вниз? Отвечу: принято определять направление вектора момента импульса по “правилу буравчика”. При вращении тела этот вектор направлен туда, куда вкручивался бы штопор, вращай мы его также. Так что, если юла раскручена по часовой стрелке, то считается, что вектор момента импульса направлен вниз. А если против часовой – тогда вверх.
Момент импульса, как и импульс, подчиняется закону сохранения. То есть, если вращающееся тело не взаимодействует ни с какими другими телами, его момент импульса остаётся неизменным, что бы там не происходило внутри самого тела. Даже если тело самопроизвольно развалится на несколько частей, то суммарный момент импульса всех осколков будет равен моменту импульса развалившегося тела. Причём, момент импульса не меняется не только по абсолютной величине, но и по направлению. Это можно наблюдать на примере той же юлы: пока она достаточно быстро крутится, её ось вращения направления не меняет. Повторяю: если тело ни с чем не взаимодействует, то его момент импульса сохраняется. Но если на тело воздействовать извне, то его момент импульса изменить можно, как по абсолютной величине , так и по направлению.
Спин элементарной частицы – это её момент импульса. Можно считать, что частица – это шарик, который вращается вокруг собственной оси, как, например, наша планета. Такое представление, вообще-то, довольно примитивно, но для нашей задачи сгодится. Надо только понимать, что спин, в отличие от классического момента импульса – величина квантовая, и поэтому обладает некоторыми специфическими особенностями, которые мы ниже рассмотрим.
Момент импульса тела может быть любым как по направлению, так и по абсолютной величине. Спин частицы по абсолютной величине может принимать только одно из небольшого набора значений (количество возможных значений определяется типом частицы). Иными словами, спин квантуется. А вот направление спина частицы может быть любым. Стало быть, измерять мы будем именно направление спина.
Ну что же, перейдём к “практической” части. Нет, это ещё не белловские эксперименты, для начала мы проделаем несколько простых опытов, чтобы лучше понять свойства спина и поупражняться с его измерением.
Для измерения спина частиц используют устройство, которое называется “прибор Штерна-Герлаха”, по фамилиям его изобретателей. Дальше мы будем называть это устройство сокращено: “ПШГ”. Кратко рассмотрим принцип действия прибора.
Элементарная частица имеет электрический заряд* и вращается, а значит, она представляет собой маленький магнит. Другими словами, если у частицы есть спин, значит, у неё есть и магнитные свойства, или, говоря более научно – магнитный момент. Вот этот-то магнитный момент вращающейся частицы и использует ПШГ. Устройство ПШГ, а также прочее оборудование, необходимое для опытов, показаны на рисунке 1.1.

Собственно, сам ПШГ состоит из двух магнитов. Верхний и нижний магниты имеют различную форму, благодаря чему магнитное поле в промежутке между ними неоднородно. Также на рисунке изображены источник частиц, (надо же их откуда-то брать?) и экран, который регистрирует точку попадания частицы. Например, в качестве экрана может использоваться фотопластинка: попавшая в неё частица “засвечивает” точку попадания.
Для наших дальнейших опытов решающее значение будет иметь ориентация самого прибора, а также спинов частиц в пространстве. Поэтому на рисунке показана система координат XYZ. Ориентацию ПШГ мы будем показывать толстой серой стрелкой. В данном случае прибор ориентирован вдоль положительного направления оси Z. Направление векторов спинов (для компактности будем говорить просто «направление спинов») частиц будем показывать тонкой черной стрелкой. На рисунке спин «красной» частицы направлен вверх, в направлении +Z, а спин «синей» частицы направлен вниз, в направлении –Z .
Итак, источник выпускает частицу в направлении оси X. Затем частица попадает в ПШГ и проходит через зазор между магнитами. Если частица не обладает спином, то магнитное поле на неё никак не влияет, она движется по прямой и попадает в центр экрана – его мы приняли за начало координат. Траектория такой частицы показана на рисунке зелёной линией. На самом деле мы тут будем «работать» только с частицами, обладающими ненулевым спином, так что зелёную траекторию я нарисовал чисто для того, чтобы обозначить центр экрана.
Если спин направлен вверх, то неравномерное магнитное поле в зазоре отклоняет частицу вверх (красная траектория). Если спин направлен вниз, то частица отклоняется вниз (синяя траектория). Таким образом, наблюдая на экране точку попадания частицы, мы определяем, как был направлен её спин – вверх или вниз.
Мы рассмотрели случаи, когда спин частицы направлен вдоль оси Z. То есть, направление спина совпадает с ориентацией прибора или строго противоположно ей. Но ведь спин частицы может быть ориентирован в пространстве как угодно. Возникает вопрос: а что же будет с частицей, если её спин и ориентация ПШГ не совпадают? Тут классическая физика и квантовая механика дают разные ответы.
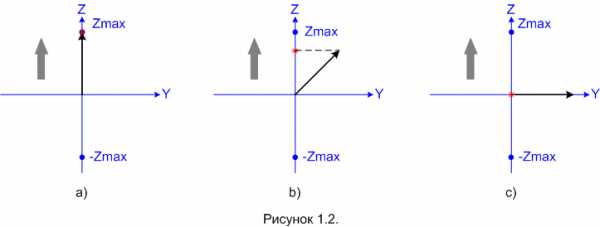
Если рассматривать ситуацию чисто «классически», и представлять себе частицу как вращающийся заряженный шарик, то ответ будет такой: отклонение частицы пропорционально проекции её спина на направление ориентации прибора (в нашем случае это то же самое, что ось Z). То есть, максимальное отклонение точки попадания от центра экрана будет у тех частиц, у которых спин направлен параллельно оси Z (Рисунок 1.2-a, точка «Zmax»). Разумеется, если спин параллелен оси Z, но направлен в противоположную сторону, то частица попадёт в точку «–Zmax».
Если спин частицы направлен под углом у оси Z, частица должна попасть в точку где-то между «–Zmax» и «Zmax» (Рисунок 1.2-b). Если же спин частицы ориентирован перпендикулярно оси Z, например, вдоль оси Y, то частица вообще не должна отклоняться от центра (Рисунок 1.2-c).
Отклонения частицы по оси Y при такой ориентации прибора (напоминаю – она показана толстой серой стрелкой) быть не должно.
Ось X на рисунке 1.2 и на следующих рисунках не показана, чтобы не загромождать. Можете считать, что она направлена от нас прямо вглубь рисунка. Места попадания частиц в регистрирующий экран показаны красной звёздочкой. Направление спина показано так, как мы условились раньше: тонкой чёрной стрелкой.
Квантовая механика предсказывает совершенно другой результат: все частицы будут отклоняться на максимально возможное расстояние и попадать только в одну из двух точек, причём, линия, походящая через эти две точки и центр экрана, будет параллельна ориентации прибора. В нашем случае, когда ПШГ ориентирован параллельно оси Z, это будут точки либо «Zmax», либо «–Zmax». В этом, собственно, и заключается «квантовость». Если в «классике» мы можем намерять любое отклонение, а значит и направление момента импульса, то в квантовой механике направление спина «квантуется»: есть только два возможных результата измерения.
Тут, чтобы вас не запутать на будущее, я должен оговорить вот что: на самом деле два результата измерения мы получим только на частицах со спином 1/2. К таким частицам относятся, в частности, электроны, протоны, нейтроны и некоторые другие. Для прочих частиц возможны три результата, четыре, пять и так далее, но в любом случае число возможных результатов будет конечным. Чтобы не делать в дальнейшем таких оговорок, давайте определимся: мы будем в наших экспериментах работать только с протонами.
Итак, классическая физика и квантовая механика предсказывают разные результаты опытов с протонами. Ну что же, вооружившись банальностью «опыт – критерий истины» приступим к экспериментальной проверке.
Установка для опыта у нас уже есть, она показана на рисунке 1.1. Только там у нас был «источник частиц», теперь это будет источник конкретно протонов.
Предполагаем, что источник выпускает протоны со случайно ориентированным спином. Значит, если права классическая физика, то протоны должны попадать в экран со случайным отклонением по оси Z в диапазоне от «–Zmax» до «Zmax». Тогда, если мы выпустим достаточно много протонов, то картинка на экране должна будет выглядеть так, как показано на рисунке 1.3-a. То есть, будет сплошная полоса попаданий.
Ну а если права квантовая механика, то после серии «выстрелов» на экране будет картинка как на рисунке 1.3-b: только два варианта попаданий. Причём, попадания распределятся примерно пополам: половина вверх, половина вниз.
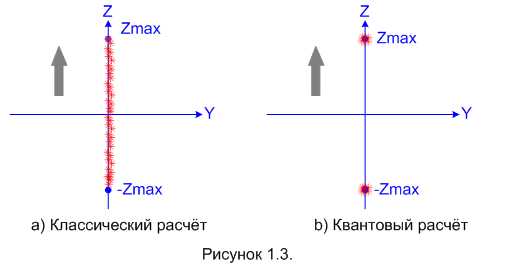
В реальности такой эксперимент даёт картинку в полном соответствии с предсказаниями квантовой механики, как на рисунке 1.3-b. Это один из тех экспериментов, о которых я говорил во введении: с точки зрения классической физики его результаты объяснить не удаётся, а квантовая механика объясняет их «на раз».
Сторонники классического подхода тут могут «уцепиться за соломинку»: мол, мы предположили, что спин протонов, испускаемых источником, ориентирован случайно, а вдруг это не так? Возможно, источник выпускает протоны, ориентированные только вертикально, вдоль оси Z. В таком случае «классический» расчёт даст такую же картину распределения попаданий, как и квантовый (рисунок 1.3-b).
Хорошо, мы это можем легко проверить. Повернём ПШГ на некоторый угол вокруг оси X и проделаем опять длинную серию «выстрелов». Если версия «классиков» верна, то мы увидим на экране картинку типа 1.4-a. Ну а если всё же правда на «квантовой» стороне, то картинка будет как 1.4-b.
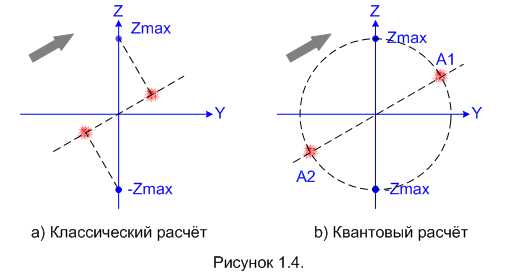
Я пока не буду объяснять, почему классический (a) и квантовый (b) расчёты дадут при такой ориентации прибора именно эти картины распределения попаданий. Если вам непонятно, то предлагаю тут притормозить и разобраться самостоятельно. Вся необходимая для этого информация изложена выше и даже выделена жирным курсивом. Также вам помогут, надеюсь, дополнительные построения, нарисованные пунктирными линиями.
Разобрались? Отлично, тогда едем дальше. Проделав эксперимент с «повёрнутым» ПШГ (на рисунке 1.4 он повёрнут вокруг оси X на 60 градусов вправо), убеждаемся, что результаты опыта совпадают с квантовыми предсказаниями: половина (приблизительно) протонов попадает в точку A1, половина – в точку A2. Для верности можем провести эксперименты с разными углами поворота ПШГ и убедиться: результат всегда таков, как предсказывает квантовая механика. Заодно мы убедимся в том, что наше предположение о случайной ориентации спинов на входе прибора было правильным.
Итак, констатируем важный вывод, на который мы будем ссылаться в дальнейших рассуждениях:
Утверждение 1.1.
Вне зависимости от того, с каким направлением спина протон входит в измерительный прибор, мы получим только один из двух возможных результатов измерения: направление спина протона либо совпадает с ориентацией прибора, либо строго противоположно ему.
Для порядка отмечу, что в нашем случае измерительным прибором является устройство, включающее ПШГ и регистрирующий экран. Однако, утверждение 1.1. верно и для любого другого устройства, измеряющего направление спина. Но мы будем и дальше пользоваться прибором Штерна-Герлаха. Только вот, в свете утверждения 1.1., регистрирующий экран нам больше не нужен. Поскольку из ПШГ все протоны выходят только по одной из двух возможных траекторий, мы можем вместо экрана поставить на каждой траектории детектор протонов. Теперь схема эксперимента, показанного на рисунке 1.1, будет выглядеть так, как на рисунке 1.5-a.
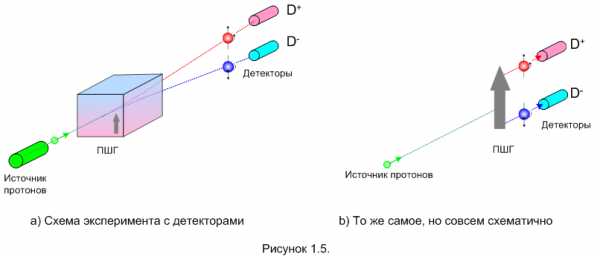
Детекторы обозначены как D+ (плюс – детектор) и D– (минус – детектор). В плюс – детектор будут попадать все протоны, направление спина которых совпадает с ориентацией прибора. В минус – детектор попадут все протоны с противоположной прибору ориентацией.
Разумеется, если мы теперь захотим покрутить ПШГ вокруг «линии выстрела», показанной на рисунке зелёным пунктиром, то мы должны будем соответствующим образом переместить и детекторы, иначе все «выстрелы» уйдут в «молоко». Чтобы не мучится с определением нового положения детекторов, мы можем просто объединить ПШГ и детекторы в единую конструкцию и вращать её всю целиком так, как нам требуется. Дальше при описании опытов я буду эту измерительную конструкцию изображать так, как показано на рисунке 1.5-b.
Итак, мы выяснили, что ПШГ направляет входные протоны по одной и из двух возможных траекторий. Дальше эти траектории будем называть так: “плюс-канал” и “минус-канал”. Выше, на рисунках 1.1, 1.5, протон в плюс-канале (красный) я изобразил со спином вверх, а протон в минус-канале (синий) со спином вниз. Но это было сделано, так сказать, “авансом”, на самом деле мы пока не уверены, что протоны выходят из прибора именно в таких состояниях. Есть ведь серьёзные поводы для сомнений.
Во-первых, может быть, вообще никакого спина у протона не существует, а ПШГ просто разбрасывает протоны по каналам каким-то случайным или псевдослучайным образом, как, например, фонтан разбрасывает водяные брызни?
Во-вторых, в “классическом” случае, если бы мы действительно имели дело с вращающимися заряженными шариками без всяких квантовых свойств, шарик отклонялся бы в неравномерном магнитном поле, но его момент импульса при этом бы не изменился: какой на входе, такой и на выходе. Другими словами, “классическое” измерение не меняет измеряемой величины. Может быть и в квантовом случае такая картина: с каким протон спином вошел в прибор, с таким и вышел?
Для начала проведём эксперимент, который должен развеять наши сомнения на счёт “во-первых” (рисунок 1.6).
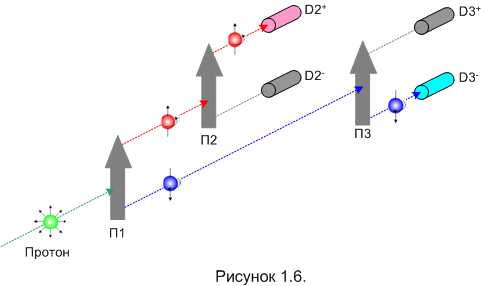
Теперь у нас в схеме три ПШГ, они обозначены как П1, П2, П3. Обратите внимание: на выходах П1 детекторов нет. Протоны, прошедшие через плюс-канал П1, сразу попадают в П2, и далее в один из двух детекторов: D2+ или D2–. Аналогично, протоны из минус-канала П1 попадают в П3, а затем в D3+ или D3–.
“Отстреляем” серию протонов и убедимся, что в такой конфигурации опыта на каждый “выстрел” срабатывает только один из двух детекторов: либо D2+, либо D3–. Детекторы D2– и D3+ не срабатывают никогда. Получается вот что: если протон оказался в плюс-канале П1, то он гарантировано попадает и в плюс-канал П2. Аналогично, из минус-канала П1 протон гарантировано попадает в минус-канал П3. Очевидно, что если бы ПШГ действительно разбрасывал протоны по каналам беспорядочно, то такого результата мы бы не получили. Протоны на выходах П1 были бы ориентированы так же случайно, как и на его входе, и регистрировались бы с равной вероятностью всеми четырьмя детекторами. Так что мы можем уверенно утверждать: протон несёт в себе какой-то параметр состояния, согласно которому ПШГ “сортирует” протон в плюс- или минус-канал. Учитывая результаты предыдущих экспериментов, мы констатируем некоторое сходство это параметра с классическим моментом импульса. Поэтому продолжаем называть этот параметр спином и рисовать протон со стрелочкой. Да, а вот эта куча стрелочек, проткнувшая на рисунке 1.6 зелёный протон, будет означать, что спин протона не определён.
Чтобы дальше исследовать свойства спина, проделаем следующий эксперимент. (рисунок 1.7).
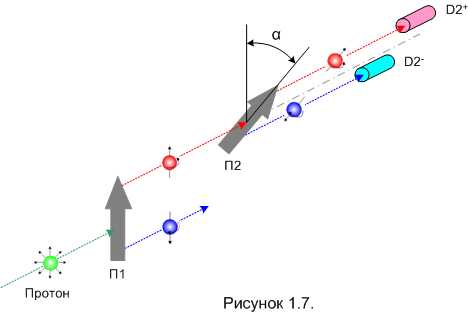
Прибор П1 у нас жестко зафиксирован и работает в качестве источника упорядоченных протонов. Так что в П2 попадают только такие протоны, которые гарантированно пройдут через ПШГ с вертикальной ориентацией. Ну а П2 может поворачиваться вокруг оси, показанной на рисунке штрихпунктирной линией на любой угол α. Теперь посмотрим, как будут срабатывать детекторы при разных значениях угла α. Разумеется, в зачёт пойдут только те попытки, когда срабатывает хотя бы один детектор. Если не ни один не срабатывает, значит, протон в П1 ушел в минус-канал, этот случай нас сейчас не интересует.
Для угла в 0° срабатывать будет только плюс-детектор D2+ (это мы уже видели в предыдущем эксперименте, рисунок 1.6). Теперь повернём измеритель на 1° и произведём серию “выстрелов”. Здесь мы увидим, что иногда, очень редко, срабатывает минус-детектор D2–. Но “иногда” нас не устраивает, нам нужно определить вероятности срабатывания плюс-детектора или минус-детектора. Мы их легко посчитаем по следующим формулам.
Вероятность срабатывания плюс-детектора D2+:
где:
N(+) – количество срабатываний детектора D2+;
N(–) – количество срабатываний детектора D2–.
Соответственно, вероятность срабатывания минус-детектора D2–:
Как не трудно догадаться, вероятности P(+) и P(–) в сумме всегда дают единицу
Итак, мы получили вероятности срабатывания того или иного детектора при α = 1°. Аналогичным образом мы можем проделать опыт для любых значений угла, и получить графики зависимости вероятностей P(+) и P(–) от угла α. Эти графики будут выглядеть так (рисунок 1.8).
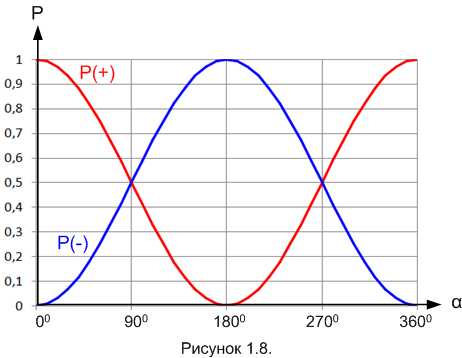
А вот формулы этих зависимостей:
Утверждение 1.2:
Как видите, утверждение 1.2. сформулировано без слов. Тем не менее, смысл его вполне ясен, а кому не ясен – смотрите на графики.
Отметим «особые» случаи:
Если угол между ориентациями приборов П1 и П2 равен 0° (направления совпадают), то протон гарантировано попадает в плюс-детектор (вероятность этого события равна единице) и никогда не попадёт в минус-детектор.
Если угол равен 180° (направления противоположны), то ситуация обратная: будет срабатывать только минус-детектор.
Если угол равен 90° или 270° градусов (ориентации приборов перпендикулярны), то вероятности срабатывания плюс-детектора и минус-детектора одинаковы и равны 0,5.
При всех прочих значениях углов вероятности срабатывания плюс-детектора и минус-детектора будут различными, но в сумме они всё равно дадут единицу.
Для объяснения этих результатов можно предложить две версии.
Версия 1. Спин протона влияет на его “сортировку” при прохождении ПШГ. Но сам спин при этом не меняется.
Версия 2. Спин протона не только влияет на его “сортировку” при прохождении ПШГ, но и меняется при этом: в плюс-канале направление спина совпадает с ориентацией ПШГ, а в минус-канале направления противоположны.
Очередной эксперимент (рисунок 1.9) поможет нам выяснить, какая из этих версий правильная.
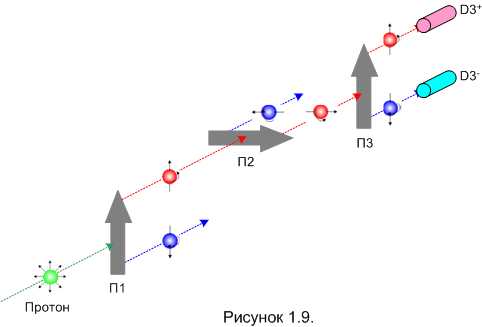
Засчитывать опять будем только результативные “выстрелы”, когда срабатывает хотя бы один детектор. Результативных “выстрелов” будет примерно четверть: половину протонов отсеет в минус канал П1, ещё половину – П2.
Если верна версия 1 (спин протона при прохождении ПШГ не меняется), то будет срабатывать только плюс-детектор. Надо объяснять почему?
Если верна версия 2 (направление спина протона на плюс-выходе ПШГ совпадает с ориентацией ПШГ), то примерно в половине результативных попыток будет срабатывать плюс-детектор, а в половине – минус детектор.
Так вот, если мы реально проведём такой эксперимент, то увидим, что с равной вероятностью срабатывают оба детектора. Значит, верна версия 2.
Вернёмся чуть назад, к предыдущему опыту (рисунок 1.7) и его результатам (рисунок 1.8). Теперь мы точно знаем, что в плюс-канале П1 оказываются только те протоны, направление спина которых совпадает с ориентацией П1. А значит, утверждение 1.2 (формулы (ф. 1.3), (ф. 1.4)) определяют вероятности попадания протона в плюс-канал или в минус-канал в зависимости от угла между направлением спина протона и ориентацией прибора.
Кстати, обращаю внимание: утверждение 1.2. исчерпывающе объясняет результаты всех проделанных нами опытов, а также «поглощает» утверждение 1.1, сделанное в предыдущей части.
Формулы из утверждения 1.2 – типичный пример того, какие предсказания даёт квантовый подход. Как уже было сказано во введении, квантовая теория принципиально не позволяет точно вычислить результат эксперимента, но может точно вычислить вероятность того или иного результата. Вот и в нашем случае невозможно вычислить, какой детектор сработает, если угол α не равен 0° или 180°.
Теперь мы можем сформулировать обозначенную во введении проблему (детерминизм или случайность) на нашем конкретном примере. Посмотрите ещё раз на ситуацию, когда направление спина протона и ориентация прибора не параллельны. В этом случае может сработать либо плюс-детектор, либо минус-детектор. Классический (детерминистский) и квантовый (случайный) подход объясняют эту неопределённость по разному.
Классический подход: в системе, включающей протон и измеритель спина, заключены скрытые параметры, предопределяющие тот или иной результат измерения. Нам же выбор результата кажется случайным только потому, что мы этих параметров не знаем. Или, более философично: в системе протон – измеритель “записан” (или, если угодно, “запрограммирован”) только один вариант будущего состояния системы, именно он и будет реализован.
Квантовый подход: в системе, включающей протон и измеритель спина, предопределено то, что мы получим один из двух результатов измерения. Также предопределена вероятность получения того или иного результата. Но выбор результата абсолютно случаен. Опять же, философично: в системе протон – измеритель “записаны” два варианта будущего состояния системы и вероятности реализации каждого из них. Но какой из них реализуется – это не предопределено.
В самых популярных статейках такой квантовый подход принято «объяснять» ещё следующим образом: протон перед попаданием в измеритель находится в двух состояниях одновременно (погуглите на тему «кот Шредингера»). А в измерителе протон скачкообразно переходит в одно из этих состояний. В более серьёзных статьях говорят, что перед попаданием в измеритель протон находится в суперпозиции состояний. А при измерении происходит разрушение суперпозиции (оно же – коллапс волновой функции, оно же – редукция).
Какой из двух подходов правильный – классический или квантовый? Как раз это мы и будем выяснять в «следующих сериях».
______________
*Некоторые электрически нейтральные частицы, нейтрон, например, тоже обладают магнитным моментом. Но физический механизм этого явления мы тут рассматривать не будем, это к нашей теме не относится.
Шаг вперёд
www.eslitak.com
3. Действительность и мир квантов (Пол Девис)
П.Девис
3. Действительность и мир квантов
Лабиринт парадоксов
Летом 1982 г. в Парижском университете был проведен исторический эксперимент. Французский физик Ален Аспек и его сотрудники решили проверить, не удастся ли им “перехитрить” квант. На карту были поставлены не только наиболее плодотворная научная теория, но и сама основа того, что мы считаем физической реальностью.
Как и многие решающие эксперименты в физике, парижский эксперимент восходил к парадоксу, который озадачивал и интриговал физиков и философов на протяжении почти половины века. Речь идет об одной из принципиальных особенностей квантовой физики — о неопределенности. Знаменитый принцип неопределенности Гейзенберга вынуждает вносить существенные поправки в простую, построенную на интуиции картину мира атомов, согласно которой частицы под действием сил движутся по вполне определенным траекториям. В действительности частица, например электрон, движется сложным, почти непредсказуемым образом, и проследить за ее движением в деталях или хотя бы дать его описание невозможно.
До появления квантовой теории физическую Вселенную рассматривали как огромный часовой механизм, ход которого до мельчайших деталей неукоснительно следовал безупречной логике причины и следствия, воплощенной в законах механики Ньютона, Разумеется, законы Ньютона и поныне справедливы для описания большинства явлений в окружающем нас мире. Они направляют пулю к цели и заставляют планеты двигаться точно по орбитам. Но, как мы теперь уже знаем, в масштабах атома многое обстоит совсем иначе. На смену знакомому упорядоченному движению макроскопических тел приходит беспорядок и хаос. Привычные твердые тела на поверку оказываются призрачной мозаикой, образованной всплесками энергии. Квантовая неопределенность убеждает нас, что невозможно всегда все знать о частице. Если, фигурально говоря, вы попытаетесь “пришпилить” частицу к определенному месту, она ускользнет от вас.
Эта неуловимость квантовых частиц доставила немало хлопот физикам при построении квантовой теории. В 20-х годах нашего столетия новая квантовая механика выглядела лабиринтом парадоксов. Хотя Вернер Гейзенберг и Эрвин Шрёдингер были главными строителями квантовой теории, ее интерпретацию предложили Макс Борн и особенно Нильс Бор. Датский физик Бор первым осознал во всей полноте, что квантовая теория в той же мере применима к веществу, как и к излучению, и в последующие годы стал ведущим авторитетом и лидером среди физиков в области концептуальных основ квантовой механики. Институт Бора в Копенгагене был центром исследований по квантовой физике на протяжении более чем десятилетия. Однажды Бор заметил своим коллегам: “Если у человека при первом знакомстве с квантовой механикой голова не идет кругом, то он не понимает в ней ничего”. В своей книге “Физика и философия” Гейзенберг вспоминает о первых мучительных сомнениях по поводу смысла новой квантовой механики:
Я вспоминаю дискуссии с Бором, длившиеся за полночь, которые приводили меня почти в отчаяние. И когда я после таких обсуждений отправлялся на прогулку в соседний парк, передо мной снова и снова возникал вопрос: действительно ли природа может быть столь абсурдной, какой она предстает перед нами в этих атомных экспериментах?
Самым крупным оппонентом квантовой механики был Эйнштейн. Хотя ему самому довелось приложить руку к формулировке квантовой теории, он никогда полностью не разделял ее идей, считая квантовую теорию либо ошибочной, либо в лучшем случае “истинной наполовину”. Известно его изречение: “Бог не играет в кости”. Эйнштейн был убежден, что за квантовым миром с его непредсказуемостью, неопределенностью и беспорядком скрывается привычный классический мир конкретной действительности, где объекты обладают четко определенными свойствами, такими, как положение и скорость, и детерминировано движутся в соответствии с причинно-следственными закономерностями. “Безумие” атомного мира по утверждению Эйнштейна, не является фундаментальным свойством. Это всего лишь фасад, за которым “безумие” уступает место безраздельному господству разума.
Эйнштейн пытался найти это фундаментальное свойство в нескончаемых дискуссиях с Бором — наиболее ярким выразителем взглядов той группы физиков, которые считали квантовую неопределенность неотъемлемой чертой природы, не сводимой к чему-либо другому. Эйнштейн с завидным упорством продолжал свои атаки на квантовую неопределенность, пытаясь придумать гипотетические (“мысленные”, как принято говорить) эксперименты, которые обнаружили бы логический изъян в официальной версии квантовой теории. Бор каждый раз отражал нападки Эйнштейна, опровергая его аргументы.
Особенно памятен один эпизод на конференции, на которой собрались многие ведущие физики Европы в надежде услышать о последних достижениях новой тогда квантовой теории. Эйнштейн направил свою критику против варианта принципа неопределенности, устанавливающего, с какой точностью можно определить энергию частицы и момент времени, когда частица ей обладает. Эйнштейн предложил необычайно остроумную схему, позволяющую обойти неопределенность энергии—времени. Его идея сводилась к точному намерению энергии с помощью взвешивания: знаменитая формула Эйнштейна E= mc2 сопоставляет энергию E и массу т, а массу можно измерить взвешиванием.
На этот раз Бор был обеспокоен, и те, кто видел, как он провожал Эйнштейна в гостиницу, заметили, что Бор был сильно взволнован. Но на следующий день Бор, проведший бессонную ночь за детальным анализом рассуждений Эйнштейна, торжествуя, обратился к участникам конференции. Развивая свои аргументы против квантовомеханической неопределенности, Эйнштейн упустил из виду один важный аспект созданной им самим теории относительности. Согласно этой теории, гравитация замедляет течение времени. А поскольку при взвешивании без гравитации не обойтись, эффектом замедления времени пренебречь нельзя. Бор продемонстрировал, что при надлежащем учете этого аффекта неопределенность восстанавливается на обычном уровне.
Эксперимент Эйнштейна — Подольского — Розена
Самые важные мысленные эксперименты Эйнштейна, не утратившие своего значения и поныне, были предложены лишь в 1935 г., когда вместе со своими коллегами Борисом Подольским и Натаном Розеном он опубликовал в журнале The Physical Review статью, содержащую наиболее убедительную и по сей день формулировку парадоксальной природы квантовой физики. По существу эксперимент Эйнштейна—Подольского—Розена затрагивал старую проблему: может ли частица одновременно обладать определенным положением и определенным импульсом. Задача, которую поставили перед собой Эйнштейн и его коллеги, состояла в том, чтобы придумать схему мысленного эксперимента, позволяющего (по крайней мере в принципе) сколь угодно точно измерить координаты частицы и ее импульс.
К тому времени было общепризнано, что любая попытка непосредственно измерить положение и импульс частицы обречена на провал по простой причине: когда вы пытаетесь измерить положение частицы, само измерение вносит не поддающиеся контролю изменения в величину импульса частицы. В свою очередь измерение импульса аннулирует всю полученную ранее информацию о положении частицы. Измерение одного типа несовместимо с измерением другого типа и аннулирует его результат. И если Эйнштейн надеялся преуспеть в попытке одновременного измерения координат и импульсов, ему надлежало избрать более тонкую стратегию.
Если отвлечься от второстепенных деталей, то суть работы Эйнштейна, Подольского и Розена сводится к следующему. Пусть установлено, что невозможно непосредственно измерить в одно и то же время положение и импульс одной частицы; тогда возникает мысль взять вторую частицу — “сообщницу”. Располагая двумя частицами, можно одновременно измерять большее число величин. Если бы нам удалось каким-то образом заранее связать движение двух частиц то измерения, выполненные одновременно над обеим частицами, позволили бы экспериментатору проникнуть сквозь завесу квантовой неопределенности, непреодолимую по утверждению Бора,
Использованный Эйнштейном и его коллегами принцип достаточно известен. При игре в бильярд, когда шар, по которому игрок ударяет кием, сталкивается с другим шаром, оба они разлетаются в разные стороны. Но их движения не произвольны, а жестко связаны друг с другом законом действия и противодействия — законом сохранения импульса. Измерив импульс одного шара, можно судить об импульсе другого (который может откатиться далеко в сторону), даже непосредственно не наблюдая за ним- Закон сохранения импульса справедлив и для квантовых частиц. Значит, необходимо лишь, чтобы две квантовые частицы, 1 и 2, столкнувшись между собой, провзаимодействовали и разлетелись на большое расстояние. В этот момент можно измерить импульс частицы 1. Зная его, можно, воспользовавшись законом сохранения импульса, точно вычислить импульс частицы 2, которая, собственно, нас и интересует. Измерение импульса частицы 1, разумеется, внесет неопределенность в ее положение, но это несущественно, так как не влияет на положение частицы 2 (а нас интересует именно она), поскольку та находится далеко; в принципе она могла бы располагаться на расстоянии нескольких световых лет. Если в один и тот же момент непосредственно измерить положение частицы 2, то ее положение и импульс станут известны одновременно. Иначе говоря, мы перехитрим принцип неопределенности!
Рассуждения Эйнштейна—Подольского—Розена основаны на двух допущениях, имеющих принципиальное значение. Во-первых, предполагается, что измерение, проведенное в одном месте, не может мгновенно повлиять на частицу, находящуюся далеко от него. Такое допущение основано на том, что взаимодействие между системами ослабевает с расстоянием. Трудно представить, чтобы два электрона, разделенные расстоянием в несколько метров, а тем более световых лет, каким-то неведомым образом влияли на положение и импульс друг друга. Эйнштейн отвергал подобную мысль, называя ее “призрачным действием на расстоянии”.
Отвергая идею мгновенного дальнодействия, Эйнштейн исходил из своего убеждения, что никакой сигнал или воздействие не могут распространяться быстрее света. Это — ключевой момент теории относительности, и им не следовало пренебрегать. Кроме того, невозможность распространения сигналов со скоростью выше скорости света принципиально важна для общего определения прошлого и будущего во Вселенной. Преодоление светового барьера эквивалентно распространению сигналов назад во времени, а это чревато парадоксами.
Второе фундаментальное допущение, из которого исходил Эйнштейн со своими коллегами, было связано с признанием существования “объективной реальности”. Они предполагали, что такие характеристики, как положение и импульс частицы, существуют объективно, даже если частица удалена и эти характеристики непосредственно не наблюдаемы. Именно в этом Эйнштейн расходился с Бором. По мнению Бора, просто нельзя приписывать частице такие характеристики, как положение или импульс, если нет возможности реально их наблюдать. Измерение, выполненное кем-то еще (“по доверенности”) в счет не идет. Использование частицы-“сообщницы” — просто надувательство.
На этом этапе Эйнштейн и Бор могли признать лишь несовпадение своих позиций. Необходим был такой вариант мысленного эксперимента, который позволил бы проверить, нарушается или нет принцип неопределенности на практике. В 60-х годах Джон Белл из ЦЕРНа придумал, как это сделать. Он использовал два основных допущения Эйнштейна, Подольского и Розена (распространение сигналов со скоростью меньше скорости света и существование объективной реальности) для вывода наиболее общих соотношений между измерениями с частицей 1 и измерениями с частицей 2, причем измерениями не только положения и импульса, но и других характеристик, в частности ориентации спина. Белл обнаружил, что измерения некоторых типов позволяют различить позиции Эйнштейна и Бора, отдавая предпочтение одной из них. Иначе говоря, два упомянутых допущения позволяют сделать определенные экспериментальные предсказания, которые не подтвердились бы, будь справедлива квантовая механика в духе Бора с внутренне присущей ей неопределенностью. Таким образом, если бы удалось выполнить соответствующий реальный эксперимент, то тем самым осуществилась бы прямая проверка наличия квантовой неопределенности.
Белл записал суть различия двух соперничающих теории в форме математического соотношения, получившего название неравенства Белла. Проще говоря, если прав Эйнштейн, то результаты реального эксперимента должны подтвердить неравенство Белла. Если же прав Бор, то это неравенство не будет выполнено. Очередь теперь была за экспериментаторами.
Крушение наивного представления о реальности
Практическую проверку неравенства Белла не удалось осуществить в 60-е годы. Основная проблема заключалась в недостаточной точности оборудования того времени. Чтобы с уверенностью исключить обмен сигналами между двумя частицами, находящимися на некотором расстоянии друг от друга, измерения следовало произвести за столь короткий интервал времени, за который сигналы, распространяющиеся со скоростью света (или медленнее), не успевали бы преодолеть расстояние между частицами. Это означает, что при расстоянии между частицами в несколько метров измерения должны занимать не более нескольких миллиардных долей секунды.
В 70-е годы ряд групп экспериментаторов поставили различного рода эксперименты с двумя частицами, но ни одна из групп не достигла точности, при которой результаты можно было бы считать безупречными. Наконец, Ален Аспек в Париже, внеся ряд усовершенствований в методику, приступил в 1981 г. к серии экспериментов, в которых одновременно измерялись направления поляризации двух фотонов, испущенных одним и тем же атомом и движущихся в противоположные стороны. Кульминационным стал эксперимент, выполненный летом 1982г., который впервые позволил дать окончательный ответ на интересовавший всех вопрос. Результаты не оставляли никакого сомнения: Эйнштейн был неправ. Квантовую неопределенность невозможно обойти. Она — неотъемлемая особенность квантового мира и не может быть сведена к чему-то другому. Наивное представление о реальности частиц, обладающих четко определенными свойствами в отсутствие наблюдений над ними не выдержало испытания. Аспек “забил последний гвоздь” в гроб физики, основанной на здравом смысле.
Небезынтересен способ, которым в эксперименте Аспека выявлено различие между квантовой и альтернативной “реалистической” теориями. Экспериментаторы задались целью выяснить, в какой мере результаты измерений, производимых над одним фотоном, корреллируют с результатами измерений над другим фотоном. Как следует из неравенства Белла, “реалистические” теории предсказывают существование верхнего предела, максимального уровня корреляции. В отличие от них квантовая механика предсказывает более высокую степень корреляции: между двумя частицами как бы существует некая сверхъестественная “телепатическая” связь. Результаты измерений показали, что корреляция превосходит максимум, предусмотренный неравенством Белла, и тем самым подтвердили наличие в квантовой физике внутренней неопределенности.
Эту ситуацию можно сравнить с тем, что происходит, когда два человека, сидя спиной друг к другу, одновременно бросают монеты. Если бросания совершенно случайны, то никакой корреляции между их результатами не будет. “Орлы” при бросаниях одной монеты будут выпадать с одинаковой частотой независимо от того, выпадет при бросании другой монеты “орел” или “решка”. Предположим, однако, что бросания не вполне случайны и выпадение “орла” при бросании одной монеты чаще совпадает с выпадением “орла” при бросании другой; аналогичная картина наблюдается при выпадении “решки”. Эксперименты демонстрируют наличие определенной положительной корреляции между результатами бросания двух монет. В эксперименте с двумя частицами поведение частиц случайно, но не независимо, так как обе они испущены одним и тем же атомом. Следовательно, некоторую корреляцию в поведении частиц можно ожидать заранее. Решающая проверка заключается в определении точной величины этой корреляции.
На первый взгляд может показаться, будто эксперимент Аспека позволяет достигать скорости распространения сигналов, превышающей скорость света. Применительно к бросанию монеты это означает следующее: если у меня “орел” чаще всего совпадает с вашим, то создается впечатление, будто я могу послать вам сигнал (даже если вы не видите моей монеты), пользуясь простым кодом, например, обозначая “орел” точкой, а “решку” — тире. Если корреляция ниже 100 %, то на сигнал накладывается “шум”, но при достаточно большом числе повторений его можно передать без искажений.
Однако, как показывают дальнейшие размышления, подобная возможность передачи сигналов со скоростью выше скорости света иллюзорна. Исход каждого из моих бросаний монеты хотя и коррелирован с исходом ваших, но все же полностью непредсказуем, поскольку я не могу заранее заставить монету выпадать “орлом” или “решкой”. Если при очередном бросании у меня выпадает “орел”, то я знаю, что и у вас, вероятно, выпал “орел”, но от этого мало толку, ибо я не могу управлять последовательностью точек и тире в передаваемом сигнале, и мой сигнал вырождается в сплошной (белый) шум.
Причуды квантовой реальности
Через несколько месяцев после того, как Аспек опубликовал результаты своего эксперимента, мне выпала честь составить для Би-Би-Си документальную радиопередачу о фундаментальных парадоксах квантовой физики. В число участников передачи входили сам Аспек, Джон Белл, Дэвид Бом, Джон Уиллер, Джон Тейлор и Рудольф Пайерлс. Я спросил всех участников передачи, как они оценивают результаты эксперимента Аспека и не кажется ли им, что реальность, основанная на представлениях здравого смысла, теперь мертва. Разнообразие ответов было поразительным.
Один или два участника передачи вообще не выразили удивления по поводу эксперимента Аспека. Их вера в правильность общепринятой точки зрения, давно провозглашенной Бором, была столь сильна, что эксперимент Аспека они восприняли лишь как подтверждение (хотя и весьма желательное) того, что никогда не вызывало серьезных сомнений. Другие участники передачи не разделяли такой точки зрения. Их уверенность в существовании реальности, укладывающейся в рамки здравого смысла, — той объективной реальности, поиском которой занимался Эйнштейн, — осталась непоколебленной. По их мнению, следовало бы отказаться от предположения, что сигналы не могут распространяться со скоростью выше скорости света. В конечном счете должно существовать какое-то “призрачное действие на расстоянии”. Бором уже была разработана теория, включающая подобные “нелокальные” эффекты.
А как быть с парадоксами, связанными с распространением сигналов? Возможно, что-то мешает нам управлять такими сигналами. В этих вопросах достичь полной ясности так и не удалось.
Холя не все физики согласны с ниспровержением наивной реальности, взгляды Бора остаются общепринятыми, и результаты Аспека, несомненно, лишь подкрепили их. Эта точка зрения оказывает глубокое влияние на наши представления об окружающем нас физическом мире.
Во-первых, описанная схема эксперимента с двумя частицами показывает, что свойства, частицы,, находящейся “там”, неразрывно связаны со свойствами частицы, находящейся “здесь”. Упрощающее предположение, что две частицы можно рассматривать как изолированные и независимые физические объекты только потому, что они движутся на большом расстоянии друг от друга, в корне ошибочно. Пока над частицами не производится отдельных измерений, они остаются частью единого целого. То, что мы .понимаем под свойствами частиц, определяется экспериментальной установкой в целом, а она может занимать значительную область пространства. Кроме того, хотя в эксперименте Аспека “целостная” система двух частиц умышленно поставлена в контролируемые условия, частицы продолжают вести себя естественным образом — взаимодействовать и разлетаться. Следовательно, нелокальный характер квантовых систем является общим свойством природы, а не искусственной ситуацией, созданной в лаборатории.
Некоторые ученые подчеркивали, что квантовая физика рисует картину мира, в котором отдельные частицы материи не существуют сами по себе как первичные объекты. Статусом “реальности” обладает здесь только ансамбль частиц, рассматриваемый как единое целое, в том числе и частиц, из которых состоит измерительный прибор.
Совершенно иначе выглядит традиционное представление о реальности, основанное на классической ньютоновской физике. Согласно Ньютону, вещество состоит из частиц, которые рассматриваются, однако, просто как “строительные блоки” для более крупных конструкций. Такая картина, несомненно, привлекательна, поскольку позволяет наглядно представить мириады “элементарных частиц” наподобие твердых шариков, которые, сцепляясь друг с другом, образуют обычные тела, такие, как камень. Все свойства камня в этом случае можно приписать атомам или любым другим элементарным “строительным блокам” в зависимости от последних веяний моды. Камень построен из элементарных частиц, а те в свою очередь — простые части камня и ничего более. Немецкий физик Отто Фриш, открывший деление ядер, так описывает классическую картину мира:
Считается, что заведомо существует внешний мир, который состоит из частиц, обладающих местоположением, размером, твердостью и т.д. Чуть больше сомнений возникает относительно того, имеют ли частицы цвет и запах; однако все они вполне “добропорядочны” и существуют независимо от того, наблюдаем мы их или нет.
Подобный взгляд на природу можно с полным основанием назвать наивным реализмом.
Квантовая физика ниспровергает столь упрощенную классическую взаимосвязь целого и его частей. Квантовый подход требует рассматривать частицы только в их взаимосвязи с целым. Поэтому было бы неверно считать элементарные частицы вещества материальными объектами, которые, соединяясь в ансамбли, образуют более крупные объекты. При более точном описании мир выступает как совокупность отношений.
С точки зрения “наивного реалиста” Вселенная представляет собой совокупность объектов. Для специалиста по квантовой физике это подвижная единая ткань, состоящая из всплесков энергии, и ни одна из частей этой “ткани” не существует независимо от целого, а это целое включает и наблюдателя.
Американский физик Г. П. Стэпп так сформулировал квантовую концепцию частицы:
Элементарная частица не есть нечто независимо существующее и не поддающееся анализу. По существу — это среда, распространяющаяся вовне на другие объекты.
Невольно на память приходит строка из Уильяма Блейка: “Вселенная в песчинке видней …”. Мы должны рассматривать все вещество и энергию в рамках всеобъемлющего единого бытия.
Еще одно следствие квантовой физики затрагивает роль наблюдателя — лица, реально выполняющего измерения. Квантовая неопределенность не переносится на производимые нами реальные наблюдения. Это означает, что в каком-то звене цепи, соединяющей исследуемую квантовую систему с экспериментальной установкой, шкалами и измерительными приборами, нашими органами чувств, нашим мозгом и, наконец, нашим сознанием, должно происходить нечто такое, что рассеивает квантовую неопределенность. Правила квантовой физики вполне определенны в этом отношении. В отсутствие наблюдателя квантовая система каким-то образом существует и развивается. После того как произведено наблюдение, поведение системы становится совершенно иным. Чем именно вызвано изменение в поведении системы, не ясно, но некоторые физики утверждают, что это изменение явно обусловлено вмешательством экспериментатора.
Этим слегка интригующим замечанием мы завершим наш рассказ о проблемах и парадоксах квантовой физики. И какие бы споры ни велись вокруг ее принципиальных основ, подавляющее большинство ученых все же сходится на том, что в своих приложениях квантовая теория работает блестяще. В частности, именно на ней основывается все описание мира элементарных частиц — того самого мира, в недрах которого погребена суперсила.
cyber-ek.ru
Теорема Белла • Джеймс Трефил, энциклопедия «Двести законов мироздания»
«Бог не играет в кости со Вселенной».
Этими словами Альберт Эйнштейн бросил вызов коллегам, разрабатывавшим новую теорию — квантовую механику. По его мнению, принцип неопределенности Гейзенберга и уравнение Шрёдингера вносили в микромир нездоровую неопределенность. Он был уверен, что Создатель не мог допустить, чтобы мир электронов так разительно отличался от привычного мира ньютоновских бильярдных шаров. Фактически, на протяжении долгих лет Эйнштейн играл роль адвоката дьявола в отношении квантовой механики, выдумывая хитроумные парадоксы, призванные завести создателей новой теории в тупик. Тем самым, однако, он делал доброе дело, серьезно озадачивая теоретиков противоположного лагеря своими парадоксами и заставляя глубоко задумываться над тем, как их разрешить, что всегда бывает полезно, когда разрабатывается новая область знаний.
Есть странная ирония судьбы в том, что Эйнштейн вошел в историю как принципиальный оппонент квантовой механики, хотя первоначально сам стоял у ее истоков. В частности, Нобелевскую премию по физике за 1921 год он получил вовсе не за теорию относительности, а за объяснение фотоэлектрического эффекта на основе новых квантовых представлений, буквально захлестнувших научный мир в начале ХХ века.
Больше всего Эйнштейн протестовал против необходимости описывать явления микромира в терминах вероятностей и волновых функций (см. Квантовая механика), а не с привычной позиции координат и скоростей частиц. Вот что он имел в виду под «игрой в кости». Он признавал, что описание движения электронов через их скорости и координаты противоречит принципу неопределенности. Но, утверждал Эйнштейн, должны существовать еще какие-то переменные или параметры, с учетом которых квантово-механическая картина микромира вернется на путь целостности и детерминизма. То есть, настаивал он, нам только кажется, будто Бог играет с нами в кости, потому что мы не всё понимаем. Тем самым он первым сформулировал гипотезу скрытой переменной в уравнениях квантовой механики. Она состоит в том, что на самом деле электроны имеют фиксированные координаты и скорость, подобно ньютоновским бильярдным шарам, а принцип неопределенности и вероятностный подход к их определению в рамках квантовой механики — результат неполноты самой теории, из-за чего она и не позволяет их доподлинно определить.
Теорию скрытой переменной можно наглядно представить примерно так: физическим обоснованием принципа неопределенности служит то, что измерить характеристики квантового объекта, например электрона, можно лишь через его взаимодействие с другим квантовым объектом; при этом состояние измеряемого объекта изменится. Но, возможно, есть какой-то иной способ измерения с использованием неизвестных нам пока что инструментов. Эти инструменты (назовем их «субэлектронами»), возможно, будут взаимодействовать с квантовыми объектами, не изменяя их свойств, и принцип неопределенности будет неприменим к таким измерениям. Хотя никаких фактических данных в пользу гипотез такого рода не имелось, они призрачно маячили на обочине главного пути развития квантовой механики — в основном, я полагаю, по причине психологического дискомфорта, испытываемого многими учеными из-за необходимости отказа от устоявшихся ньютоновских представлений об устройстве Вселенной.
И вот в 1964 году Джон Белл получил новый и неожиданный для многих теоретический результат. Он доказал, что можно провести определенный эксперимент (подробности чуть позже), результаты которого позволят определить, действительно ли квантово-механические объекты описываются волновыми функциями распределения вероятностей, как они есть, или же имеется скрытый параметр, позволяющий точно описать их положение и импульс, как у ньютоновского шарика. Теорема Белла, как ее теперь называют, показывает, что как при наличии в квантово-механической теории скрытого параметра, влияющего на любую физическую характеристику квантовой частицы, так и при отсутствии такового можно провести серийный эксперимент, статистические результаты которого подтвердят или опровергнут наличие скрытых параметров в квантово-механической теории. Условно говоря, в одном случае статистическое соотношение составит не более 2:3, а в другом — не менее 3:4.
(Тут я хочу в скобках заметить, что в том году, когда Белл доказал свою теорему, я был студентом-старшекурсником в Стэнфорде. Рыжебородого, с сильным ирландским акцентом Белла было трудно не заметить. Помню, я стоял в коридоре научного корпуса Стэнфордского линейного ускорителя, и тут он вышел из своего кабинета в состоянии крайнего возбуждения и во всеуслышание заявил, что только что обнаружил по-настоящему важную и интересную вещь. И, хотя доказательств на этот счет у меня нет никаких, мне очень хотелось бы надеяться, что я в тот день стал невольным свидетелем его открытия.)
Однако опыт, предлагаемый Беллом, оказался простым только на бумаге и поначалу казался практически невыполнимым. Эксперимент должен был выглядеть так: под внешним воздействием атом должен был синхронно испустить две частицы, например два фотона, причем в противоположных направлениях. После этого нужно было уловить эти частицы и инструментально определить направление спина каждой и сделать это тысячекратно, чтобы накопить достаточную статистику для подтверждения или опровержения существования скрытого параметра по теореме Белла (выражаясь языком математической статистики, нужно было рассчитать коэффициенты корреляции).
Самым неприятным сюрпризом для всех после публикации теоремы Белла как раз и стала необходимость проведения колоссальной серии опытов, которые в ту пору казались практически невыполнимыми, для получения статистически достоверной картины. Однако не прошло и десятилетия, как ученые-экспериментаторы не только разработали и построили необходимое оборудование, но и накопили достаточный массив данных для статистической обработки. Не вдаваясь в технические подробности, скажу лишь, что тогда, в середине шестидесятых, трудоемкость этой задачи казалась столь чудовищной, что вероятность ее реализации представлялась равной тому, как если бы кто-то задумал посадить за пишущие машинки миллион дрессированных обезьян из пословицы в надежде отыскать среди плодов их коллективного труда творение, равное Шекспиру.
Когда в начале 1970-х годов результаты экспериментов были обобщены, всё стало предельно ясно. Волновая функция распределения вероятностей совершенно безошибочно описывает движение частиц от источника к датчику. Следовательно, уравнения волновой квантовой механики не содержат скрытых переменных. Это единственный известный случай в истории науки, когда блестящий теоретик доказал возможность экспериментальной проверки гипотезы и дал обоснование метода такой проверки, блестящие экспериментаторы титаническими усилиями провели сложный, дорогостоящий и затяжной эксперимент, который в итоге лишь подтвердил и без того господствующую теорию и даже не внес в нее ничего нового, в результате чего все почувствовали себя жестоко обманутыми в ожиданиях!
Однако не все труды пропали даром. Совсем недавно ученые и инженеры к немалому собственному удивлению нашли теореме Белла весьма достойное практическое применение. Две частицы, испускаемые источником на установке Белла, являются когерентными (имеют одинаковую волновую фазу), поскольку испускаются синхронно. И это их свойство теперь собираются использовать в криптографии для шифровки особо секретных сообщений, направляемых по двум раздельным каналам. При перехвате и попытке дешифровки сообщения по одному из каналов когерентность мгновенно нарушается (опять же в силу принципа неопределенности), и сообщение неизбежно и мгновенно самоуничтожается в момент нарушения связи между частицами.
А Эйнштейн, похоже, был неправ: Бог все-таки играет в кости со Вселенной. Возможно, Эйнштейну все-таки следовало прислушаться к совету своего старого друга и коллеги Нильса Бора, который, в очередной раз услышав старый припев про «игру в кости», воскликнул: «Альберт, перестань же ты, наконец, указывать Богу, что ему делать!»
elementy.ru
