Электроцепь и электросхема
Электроцепь и электросхема
- Подробности
- Категория: Электротехника
Paste a VALID AdSense code in Ads Elite Plugin options before activating it.
class=”eliad”>Электрическая цепь. Электрическая схема
Источник тока и потребитель электроэнергии, соединенные между собой проводниками, образуют электрическую цепь. Когда цепь замкнута, по ней идет ток. Если один проводник убрать или разорвать его в любом месте, ток по цепи не пойдет. Потребитель электроэнергии в этом случае работать не будет. Замыкать и размыкать цепь, не снимая и не разрывая проводников, можно с помощью выключателя.
Самая простая электрическая цепь состоит из четырех элементов (рис. справа): источник тока, выключатель, потребитель электроэнергии, проводники.
Нетрудно нарисовать их и показать, как они соединены между собой. Но обычно цепи бывают гораздо сложнее. Например, в учебной мастерской есть электрические цепи, в которые входят несколько ламп, электродвигатели станков, электрические печи и другое электрооборудование. Выполнить рисунки таких цепей сложно. Вот почему в электротехнике принято изображать цепи с помощью
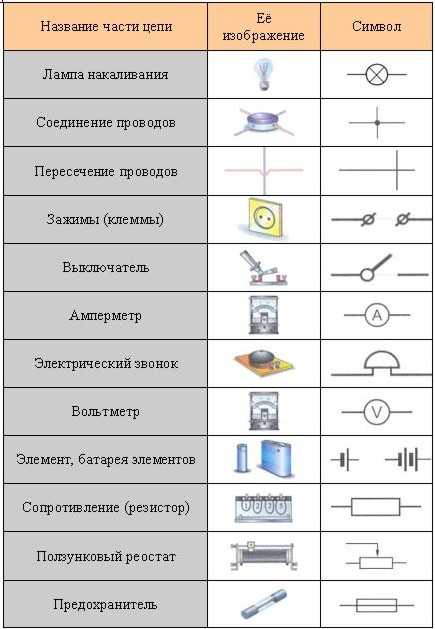
С помощью этих условных обозначений электрическую цепь (см. рис. выше) можно изобразить, как это показано на рисунке слева. Такое изображение электрической цепи с помощью условных знаков называется электрической схемой
Paste a VALID AdSense code in Ads Elite Plugin options before activating it.
class=”eliad”>technologys.info
Схемы электрических цепей и ЭДС | энергетик
Схемы электрической цепи, понятие параметров и элементов электрических цепей:
Для начала вспомним определения:
Параметрами электрической цепи называется величина, связывающая ток и напряжение на конкретном участке цепи (r – сопротивлением, рис. 1 а; L – индуктивностью, рис. 1 б; C – ёмкостью, рис. 1 в. ).
Элементами электрической цепи называют отдельные устройства входящие в электрическую цепь и выполняющие в ней определённую функцию. Пример отдельных элементов и простой схемы электрической цепи:
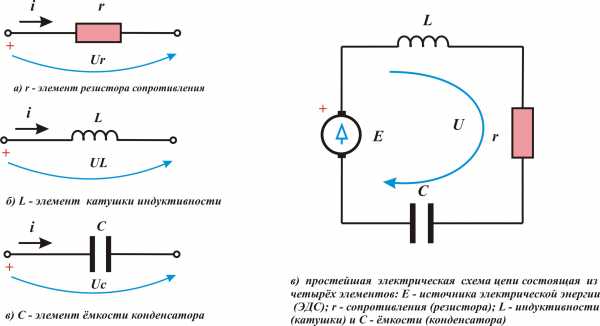
Рис.1
Схемы электрических цепей:
При конструировании, монтаже и работе электрических установок (электрооборудования) нельзя обойтись без электрических схем. Электрические схемы по своему назначению различаются на несколько типов: структурные, функциональные, принципиальные, монтажные, однолинейные, и др.
Принципиальная схема даёт полное представление о работе электроустановки, полный состав элементов и связи между ними.
Схема электрической цепи – это графическое представление изображения электрической цепи, которая содержит условные обозначения элементов и соединение этих элементов. Условные обозначение в электрических схемах установлены стандартами системы ЕСКД. Различают последовательное и параллельное соединение элементов в схемах и электрических цепях. Сложные электрические схемы образуются в результате включения групп элементов соединенных между собой последовательно или параллельно (см. на рис. 2).
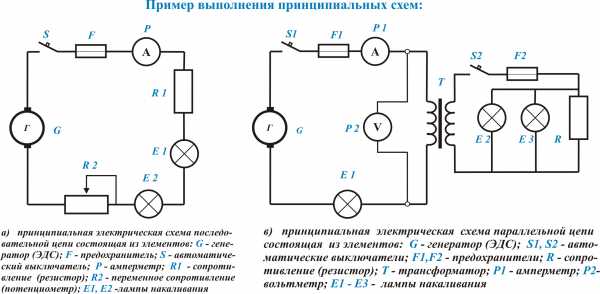
Рис.2
Электродвижущая сила (ЭДС):
Физические процессы получения электрической энергии различаются в зависимости от вида преобразуемой энергии, где главное различие состоит в природе сил, которые разделяют положительный и отрицательный заряды в веществе. На электрически заряженные частицы кроме сил электрического поля при определенных условиях действуют сторонние силы, обусловленные неэлектромагнитными процессами (тепловые процессы, химические реакции и т.д.)
В результате действия сторонних сил в источнике электрической энергии происходит разделение электрических зарядов и образуется электродвижущая сила (ЭДС).
Величина, характеризующая способность стороннего поля и индуцированного электрического поля вызывает электрический ток, называется электродвижущей силой.
Для примера рассмотрим преобразование тепловой энергии в электрическую:
В замкнутой цепи из двух разных металлов при одинаковой температуре (контактов 1 и 2) электрический ток не возникает, так как контактные разности потенциалов в обоих контактах одинаковы, но направлены в противоположные стороны по цепи (см. рис. 3):
Рис.3
energetik.com.ru
Электрическая схема
Главная → Теория электрических цепей → Электрическая схемаЭлектрическая схема, схема электрической цепи, схема замещения электрической цепи
1 Схема электрической цепи и элементы схемы [1, с. 16 – 17]
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения.
Реальные элементы электрической цепи идеализируются для упрощения математического описания элемента электрической цепи. Однако идеализированные уравнения должны правильно отражать основные физические явления в том или ином реальном элементе электрической цепи.
Идеализированному элементу электрической цепи ставят в соответствие его математическую модель —
Каждому схемному элементу соответствует условное геометрическое изображение. Тогда способ соединения элементов реальной цепи легко представить с помощью соответствующего соединения схемных элементов. Геометрическое изображение соединения схемных элементов, отображающее соединение реальных элементов электрической цепи и ее свойства, называют схемой электрической цепи (схемой цепи).
В схеме выделяют ветви — участки, которые характеризуются одним и тем же током в начале и конце в любой момент времени, и
Ветвям и узлам схемы электрической цепи, как правило, соответствуют ветви и узлы реальной электрической цепи. В схемах электрических цепей, содержащих многополюсные элементы, некоторые узлы и ветви могут не отображать узлы и ветви цепи. Кроме того, некоторые ветви схемы вводят для учета конструктивных и монтажных параметров цепи (например, паразитных емкостей между зажимами элемента, емкостей монтажа, индуктивностей выводов).
Применительно к электрической цепи ветвь часто определяют как участок цепи, в любом сечении которого ток имеет одно и то же значение в данный момент времени, а
2 Схема электрической цепи[2, с. 131 – 136]
Электрическую цепь на чертежах изображают в виде схемы электрической цепи, под которой понимают графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее соединения этих элементов. Например, на рис. 2.1 представлена электрическая схема цепи, в которую входят следующие устройства: генератор переменного тока 1, трансформаторы 2 и 5, линии электропередачи 3 и 4, преобразователь переменного тока в постоянный 6, нагрузка 7.
Рис. 2.1
Исследование процессов в электрической цепи требует знания связей между токами и напряжениями отдельных ее участков. Эти связи могут быть определены в виде математических соотношений, например, вида (u = r·i, uL = L·di/dt и др.). Они могут быть заданы и в виде вольтамперных или иных характеристик.
Записанные в аналитической форме соотношения между токами, напряжениями, зарядами, потокосцеплениями элемента электрической цепи являются математической моделью этого элемента электрической цепи.
Так, например, u = r·i есть математическая модель резистора; uL = L·di/dt – математическая модель идеальной индуктивной катушки; u = r·i + L·di/dt – приближенная математическая модель либо реальной катушки при условии пренебрежения токами смещения между витками катушки, либо цепи, содержащей резистор и идеальную индуктивную катушку, включенные последовательно.
Обратно, математическим соотношениям, приведенным выше, могут быть поставлены в соответствие электрические цепи, содержащие идеальные индуктивные катушки и резисторы.
Математическим соотношениям между, токами, напряжениями, потокосцеплениями, зарядами и другими величинами, следовательно, могут быть поставлены в соответствие электрические цепи, содержащие только идеализированные элементы г, L, С, M, E, J и др. Очевидно, схемы таких электрических цепей и сами электрические цепи тождественны, так как каждому элементу схемы электрической цепи соответствует единственный элемент идеализированной электрической цепи.
Таким образом, для расчета процессов в электрической цепи следует определить математические соотношения для отдельных участков исходной цепи, по этим соотношениям построить некую другую (идеализированную) электрическую цепь, анализ процессов в которой заменит анализ процессов в исходной реальной электрической цепи.
Схему этой другой (идеализированной) электрической цепи, отображающей при определенных условиях свойства реальной цепи, называют схемой замещения электрической цепи или кратко – схемой замещения.
Рассмотрим в качестве примера электрическую цепь, схема которой изображена на рис. 2.1. Можно составить некоторую схему замещения (рис. 2.2) этой цепи.
Рис. 2.2
Приведенная на рис. 2.2, а схема замещения электрической цепи, схема которой дана на рис. 2.1, является приближенной в пределах тех допущений, которые сделаны при представлении схем замещений отдельных устройств, входящих в состав цепи.
Для каждого элемента схемы рис. 2.2, а могут быть записаны в аналитическом или графическом виде соотношения между токами, напряжениями, зарядами и потокосцеплениями. Составление математических соотношений, а следовательно, и схем замещений является специфической для инженера задачей, решение которой требует глубокого понимания особенностей электромагнитных процессов, умения решать в общем случае задачи исследования распределения электромагнитного поля.
Обычно термин «электрическая цепь» применяется к цепи с идеализированными элементами, электрическая схема и схема замещения которой тождественны.
Электрическая цепь и соответственно схема цепи имеют в общем случае ветви и узлы.
Ветвью электрической цепи и соответственно ее схемы называют весь участок электрической цепи, в котором в любой момент бремени ток имеет одно и то оке значение вдоль всего участка.
Узлом электрической цепи и соответственно ее схемы называют место соединения ветвей. На схеме узел изображают точкой.
3. Модели и схема электрической цепи[3, с. 22 – 25]
Электрические цепи, используемые в современной радиоэлектронике, образуются, как правило, из связанных друг с другом соединительными проводами ее компонентов: резисторов, конденсаторов, катушек индуктивности и транзисторов, предназначенных для приближенной практической реализации соответственно резистивных сопротивлений, емкостей, индуктивностей и активных элементов электрических цепей.
При анализе колебаний в реальной электрической цепи она заменяется некоторой идеализированной цепью из того или иного числа элементов, колебания в которой пренебрежимо мало отличаются от колебаний в анализируемой электрической цепи. Идеализированную электрическую цепь, свойства которой аппроксимируют (представляют приближенно) свойства реальной электрической цепи, будем называть моделью электрической цепи. Каждой конкретной модели электрической цепи соответствует система уравнений, благодаря решению которой удается оценить те или иные свойства электрической цепи. Эта система уравнений получила название математической модели электрической цепи.
Графическое изображение модели электрической цепи называют схемой замещения цепи, или просто схемой цепи (иногда электрической схемой). Схема электрической цепи отражает как число и характер элементов электрической цепи, из которых состоит модель электрической цепи, так и порядок соединения их между собой.

Рис. 3.1
Различие между понятиями «электрическая цепь» и „модель электрической цепи“ иллюстрирует рис. 3.1. На нем приведены схематическое изображение цепи, составленной из дискретных резисторов, конденсаторов и катушек индуктивности (рис. 3.1, а), и схема модели этой цепи, составленная в предположении, что ее компоненты точно моделируются соответствующими пассивными элементами (рис. 3.1, б).
Понятия «электрическая цепь» и „схема электрической цепи“ часто отождествляются.
Чем полнее и точнее должна отражать модель электрической цепи свойства электрической цепи, тем сложнее она становится, т. е. тем большее число элементов она содержит. Ясно, что в каждом конкретном случае следует применять модель не сложнее той, которая позволяет решить задачу анализа с требуемой точностью.
Необходимо иметь в виду и принципиальную возможность физического осуществления электрической модели исходной электрической цепи, после чего эта модель становится, в свою очередь, электрической цепью. Вместе с тем следует помнить, что переход от реальной электрической цепи к схеме электрической связан с рядом допущений. Схема электрической цепи является схемой модели электрической цепи и может быть использована для изучения ее свойств лишь в границах, в которых модель с достаточной точностью воспроизводит свойства реальной электрической цепи.
Список литературы
1. Теоретические основы электротехники. Т. I. Основы теории линейных цепей. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, переработ. и доп. М., «Высш. школа», 1976. 544 с. с ил.
2. Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники: В 2-х т. Учебник вузов. Том 1. – 3-е изд., перераб. и доп. – Л.: Энергоиздат. Ленингр. отд-ние, 1981. – 536 с., ил.
3. Белецкий А. Ф. Теория линейных электрических цепей: Учебник для вузов. – Радио и связь, 1986. 544 с.: ил.
электрическая схема, схема электрической цепи, схема замещения электрической цепи
18.07.2011, 29496 просмотров.
rgr-toe.ru
Электрическая цепь и ее элементы. Принципиальная схема электрической цепи. Схема замещения электрической цепи
1)Электрическая цепь:
Совокупность устройств для получения в них эл. тока наз. электрической цепью. В основном цепь состоит из источников питания, приёмников энергии, или потребителей, и проводов для передачи эл. энергии.
2) Элемент электричес- кой цепи:
Элементы электрической цепи – устройство или прибор, выполняющий определенные функции. Все элементы электрической цепи принципиально делятся на источники и потребители:
3) монтажная схема электрической цепи.
Монтажная схема -изображает элементы цепи и соединительные провода.
4) принципиальная схема электрической цепи.
Принципиальная схема – на ней показываются условные графические изображения элементов и их соединений.
5) схема замещения электрической цепи.
Схема замещения – расчетная модель электрической цепи, на которой элементы замещаются идеализи -рованными элементами без вспомогательных элементов, не влияющих на результаты расчетов.
6)Иисточники эц:
В качестве источников питания применяются эл. генераторы, аккумуляторы и первичные элементы.
7) Приемники эц:
К приёмникам эл. энергии относятся электродвигате ли, лампы накаливания, нагревательные устройст ва и тд.
8)Классификация эц по роду тока:
. ПО РОДУ ТОКА: – 1. цепи постоянного тока (ток, не меняющ. во времени), 2. цепи переменного тока (синусоидально-измененяющийся ток
I(t)
t
9) Линейные эц:
Линейные – ЭЦ сопротивление каждого эл-та кот. не зависит ни от тока, ни от напряжения. Зависимость напряж. от тока показывается на вольт-амперных хар-ках.
I(t)
t
10)Нелинейные эц:
Нелинейные – если хотя бы один эл-т в цепи имеет сопрот-е, зависящее или от тока или от напряж-я.
I(t)
t
11) Простые эц:
Все элементы соединены последовательно
12)Сложные эц:
Сложнее электрические цепи содержат азветвления
13) Идеальный источник ЭДС:
Ид ист ЭДС – источник, напряжение на зажимах которого не зависит от тока
14) Идеальный источник тока:
Источник энергии, ток через который не зависит от напряжения на его зажимах
15) Схемы замещения реальных источников энергии:
Графическое изображение Эл. цепи, составленное из условных обозначений электротехнич. устройств, наз. принципиальной схемой. Схема замещения эл. цепи является её количественной моделью. Она состоит из совокупности различных идеализированных элементов, выбранных так, чтобы можно было с хорошим приближением описать процессы эл. цепи.
Рассмотрим один из распространённых источников энергии постоянного тока – гальванический элемент. Между разноимённо заряженными пластинами возникает однородное Эл. поле с напряженностью Е [В/м], которое препятствует направленному движению ионов в растворе. Напряжение, при котором накопление зарядов прекращается, служит количественной мерой сторонней силы. Её называют электродвижущей силой (ЭДС, ξ). Если к выводам гальванического элемента подключить приёмник,. То в замкнутой эл. цепи возникнет ток. Заряд каждой из пластин уменьшится и появится направленное движение ионов в растворе кислоты. Направленное движение ионов сопровождается их взаимными столкновениями, что создает внутреннее сопротивление гальванического элемента постоянному току. Т.о., эскизное изображение которого дано на рис.1, а изображение на принципиальных схемах – на рис.2, можно представить в виде схемы замещения (рис.3), состоящей из последовательно включенных источника ЭДС ξ и резистивного элемента с сопротивлением . Равным внутреннему сопротивлению гальванического элемента. Стрелка ЭДС указывает направление движения положительных зарядов внутри источника под действием сторонних сил. Схема замещения рис.3 применяется и для любых других источников эл. энергии постоянного тока.
16) Закон Ома для участ-ка цепи:
Uab = IR => I = Uab/R
17) закон Ома для участка цепи, содержа -щего источник ЭДС:
Uab
a I R c E b
Uab = Uac + Ucb
Uac = IR
Ucb = φc – φb = – E
φb – φc = E
Uab = IR – E
I = (Uab + E)/R
18) Режимы работы источников энергии:
Ист. тока и ЭДС м. раб-ть как в режиме ист. тока так и в режиме потребителей (приемников) эл-ой эн-ии. Источник ЭДС работает в режиме потреб-ля , если напряжения тока ч/з него и ЭДС не совпадают. (рис-1 – потребитель, 2-источник):
Ист. тока раб. в режиме потребителя, если напряж. на зажиме, из кот вытекает ток, выше чем, на зажиме, в котором ток втекает.
19,26) Баланс мощностей в цепи постоянного тока:
Сумме мощностей энергии равна сумме мощностей приёмников энергии
∑ Pист = ∑Pпр
Pпр = I2 R
Pист = EI
Если направление тока и ЭДС через источник тока не совпадает, то исто -чник потребляет энергию
20) первый закон Кирхгофа
закон Кирхгофа: сумма токов, направленных к узлу, равна сумме токов, направленных от него.
Для узла А можно написать:, I1 + I2 – I3 – I4 – I5 = 0 а в общем виде ,т.е.алгебраичеc-кая сумма токов в узле равна нулю. При этом токи, направленные от узла, считаются отрицательными.
21) второй закон Кирхгофа
Рассмотрим источники, работающие в режиме генератора, т.е. аправления токов совпадают с направ -лениями ЭДС. Одинаковое для них напряжение между точками ВА или, что то же, между точками ЖЗ определяется по формуле:
Тогда для замкнутого контура АБВГДА спра -ведливо уравнение
откуда
или в обшей форме
.
 22) расчёт цепей посто- янного тока путём непосредственного
применения законов Кирхгофа.
22) расчёт цепей посто- янного тока путём непосредственного
применения законов Кирхгофа.
По первому зак. Кирхгофа составляется Y – 1 урав- нений. Направления токов выбираются произвольно
По II-му составляется
B – (Y – 1) – T уравнений, где В – кол. ветвей в цепи
Y – кол. узлов в цепи
T – кол. ветвей содерж. источник тока.
23) расчёт цепей постоян -ного тока методом контурных токов
Он снован на предположении, что в каждом независимом контуре, в каждой
vunivere.ru
Электрическая цепь и ее элементы
Электрической цепью называется совокупность электротехнических устройств, предназначенных для передачи, распределения и взаимного преобразования электрической и других видов энергии и информации.
Основными элементами электрической цепи являются источники электрической энергии и приемники электрической энергии.
В источниках механическая, химическая и другие виды энергии преобразуются в электрическую энергию. В приемниках электрическая энергия превращается в механическую, тепловую, световую и другие виды энергии.
В судовых электрических цепях в качестве источников могут использоваться дизель-генераторы, турбогенераторы, валогенераторы, аккумуляторные батареи (в режиме разрядки), гальванические элементы, статистические и машинные преобразователи. Основные приемники электрической энергии на судах – это электродвигатели, нагревательные элементы, светильники, устройства автоматики, аккумуляторные батареи (в режиме зарядки).
Электрические цепи содержат также вспомогательные элементы: соединительные провода (кабельные трассы, линии передачи), коммутационную аппаратуру (выключатели, переключатели), устройства измерения и контроля параметров.
Графическое изображение электрической цепи называется схемой. На рис. 1 приведен пример схемы электрической цепи постоянного тока, состоящей из источника, приемника и соединительных проводов.
Рис. 1. Схема простейшей электрической цепи постоянного тока
Процессы, происходящие в электрической цепи, описываются с помощью таких понятий как ток, напряжение, электродвижущая сила (ЭДС), мощность, энергия. В цепях постоянного тока ЭДС, напряжение, ток, мощность не зависят от времени. Символы этих величин для цепей, постоянного тока принято изображать прописными буквами E, U, I, P. В цепях переменного тока ЭДС, напряжение, ток, мощность являются функциями времени. Для обозначения мгновенных значений этих величин используются строчные буквы e, u, i, p.
Электрический ток (ток проводимости) как явление представляет собой упорядоченное движение носителей зарядов внутри проводника.
Количественно электрический ток (сила тока) определяется как скорость протекания зарядов q через любое поперечное сечение проводника:
Ток измеряется в амперах [А].
За истинное направление тока условно принято движение положительных зарядов. Поэтому во внешней по отношению к источнику цепи ток течет от точки схемы с большим потенциалом к точке схемы с меньшим потенциалом (от зажима «+» к зажиму «–» на рис. 1).
Напряжение на участке электрической цепи – это работа сил электрического поля по перемещению единичного положительного заряда между начальной и конечной точками этого участка. Напряжение равно разности электрических потенциалов начальной и конечной точек участка. Так, для участка ab на рис. 2
,
где φa, φb – потенциалы точек a и b соответственно.
Во внешней по отношению к источнику цепи направления напряжения и тока совпадают (см. рис. 1, 2).
Рис. 2. Участок электрической цепи
Перенос зарядов в электрических цепях в установившемся режиме работы осуществляется под воздействием ЭДС источников электрической энергии. ЭДС источника создается за счет затрат внешней по отношению к электрической цепи энергии: механической энергии приводного двигателя, вращающего генератор, электрохимической энергии аккумуляторной батареи или гальванического элемента, тепловой энергии в термопаре. ЭДС источника E численно равна разности потенциалов между положительным и отрицательным зажимами источника в режиме холостого хода (когда ток источника равен нулю).
Ток внутри источника ЭДС направлен от зажима «–» к зажиму «+», а стрелка внутри окружности, изображающей источник на схеме, направлена в сторону большего потенциала (см. рис. 1).
Напряжение и ЭДС измеряются в вольтах [В].
Электрическая энергия, выделяемая (потребляемая) на участке электрической цепи за время t, равна
Энергия измеряется в джоулях [Дж].
Электрическая мощность характеризует скорость изменения энергии
Мощность измеряется в ваттах [Вт].
Анализ работы электрической цепи значительно упрощается, если элементы считать идеальными. Поэтому на схемах реальные элементы цепи заменяются идеальными элементами схемы. Эти идеальные элементы схемы отражают какие-то определенные свойства реальных элементов цепи. Для отражения нескольких различных свойств реального элемента его схема может компоноваться из нескольких идеальных элементов с различными свойствами.
Для цепей постоянного тока используются понятия двух идеальных элементов: идеального источника и идеального приемника.
Идеальный приемник (см. рис. 1, 2) – это пассивный элемент цепи, в котором энергия электрического тока безвозвратно рассеивается в виде тепла. Свойствами идеального пассивного элемента практически обладает резистор, который характеризуется сопротивлением R или проводимостью g = 1/R. Единица измерения сопротивления называется ом [Ом], а проводимости – сименс [См], причем 1См = 1/Ом.
В соответствии с законом Джоуля-Ленца энергия, выделяющаяся в виде тепла в пассивном элементе, прямо пропорциональна сопротивлению, квадрату тока и времени. Этот закон выражается формулами:
Идеальный источник – это такой активный элемент цепи, который всю выработанную энергию отдает во внешнюю цепь. Коэффициент полезного действия (КПД) идеального источника h = 100 %. В природе такого источника не существует. По своим характеристикам к идеальному приближается источник, у которого потери энергии в виде тела внутри источника пренебрежимо малы по сравнению с энергией, отдаваемой приемнику.
Реальный источник в схеме электрической цепи можно представить, например, в виде совокупности двух идеальных элементов: идеального источника ЭДС Е и внутреннего сопротивления источника Ri (см. рис. 1). Введение в схему внутреннего сопротивления источника Ri позволяет учесть потери энергии в виде тепла внутри самого источника.
Элементы электрических цепей можно подразделить на линейные и нелинейные.
В пассивном линейном элементе отношение напряжения к току постоянно. В качестве пассивного линейного элемента можно рассматривать, например, резистор с постоянным сопротивлением R:
Графическую зависимость напряжения от тока (или тока от напряжения) для пассивных элементов принято называть вольт-амперной характеристикой. Вольт-амперная характеристика резистора приведена на рис. 3. Она представляет собой луч 1, выходящий из начала координат. У пассивного нелинейного элемента отношение напряжения к току непостоянно и вольт-амперная характеристика нелинейна (рис. 3, кривая 2).
Рис. 3. Вольт-амперные характеристики линейного 1
и нелинейного 2 пассивных элементов
Графическую зависимость напряжения от тока для источников электрической энергии принято называть внешней характеристикой. Внешняя характеристика реального линейного источника приведена на рис. 4. Она представляет собой отрезок прямой линии 1 между точкой холостого хода (U = E) и точкой короткого замыкания (U = 0). Пунктирной линией 2, параллельной оси абсцисс, на этом графике изображена внешняя характеристика идеального источника ЭДС. Внешняя характеристика реального нелинейного источника приведена на рис. 4, кривая 3. Цепь называется линейной, если все элементы цепи линейны. Если хотя бы один элемент цепи нелинеен, то цепь будет нелинейной. Практически все цепи нелинейные. Однако при рассмотрении изменений напряжений и токов в ограниченном диапазоне многие цепи можно считать линейными.
В настоящем учебном пособии рассматриваются линейные электрические цепи постоянного тока.
Рис. 4. Внешние характеристики линейного 1, идеального 2
и нелинейного 3 источников ЭДС
Похожие статьи:
poznayka.org
Как упростить схему электрической цепи. 1.9 Методы расчета цепей постоянного тока
Kvant. Преобразование эл. цепей — PhysBook
Зильберман А.Р. Преобразование электрических цепей //Квант. — 2002. — № 3. — С. 30-31,34.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
В этой статье рассказывается о методе, позволяющем упрощать сложные задачи по расчету электрических цепей.
Что мы понимаем под «преобразованием цепи»? Предположим, что у нас есть сложная схема из резисторов, имеющая множество выводов и подключенная к источникам. Заменим эту схему другой, но с тем же числом выводов, причем так, чтобы сопротивления между двумя любыми выводами у новой схемы были такими же, как у старой. Ясно, что источники «ничего не узнают» об этой замене и токи, потребляемые схемой, останутся прежними. Но найти эти токи, возможно, окажется проще.
Итак, если мы хотим подсчитать токи в сложной схеме, ее можно заменить более простой эквивалентной схемой. При этом токи внутри заменяемой части меняются. Поэтому так поступать можно только с той частью схемы, которая нас непосредственно не интересует.
С подобными заменами вы, конечно же, встречались. Пусть, например, в схеме два сопротивления[1]r1 и r2 включены последовательно. Их мы можем заменить одним, равным по величине сумме r1 + r2. Если же два сопротивления включены параллельно, то их также можно заменить одним, величина которого равна \(~\frac{r_1 r_2}{r_1 + r_2}\) . Это — простейшие примеры преобразования цепей. Мы же остановимся на более сложных схемах.
Посмотрим, как преобразуются друг в друга схемы, имеющие по три вывода, – «звезда» и «треугольник» (рис.1).
Рис. 1
Немного непривычные обозначения на рисунке 1,б очень удобны — индексы показывают, между какими точками включено сопротивление. Например, сопротивление R13 включено между точками 1 и 3 и т.д.
Если мы хотим заменить одну из этих схем другой, нужно получить такие соотношения между r и R, чтобы сопротивления между любыми точками были для обеих схем одинаковы.
В схеме «звезда» (см. рис. 1, а) сопротивление между точками 1 и 2 равно r1 + r2, а в схеме «треугольник» оно равно \(~\frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . Следовательно, для того чтобы со- противления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы
\(~r_1 + r_2 = \frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . (1)Аналогично, для точек 2 и 3
\(~r_2 + r_3 = \frac{R_{23} (R_{13} + R_{12})}{R_{12} + R_{13} + R_{23}}\) , (2)и для точек 1 и 3:
\(~r_1 + r_3 = \frac{R_{13} (R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . (3)Система уравнений (1) — (3) легко решается. Сложим все уравнения и поделим обе части на 2:
\(~r_1 + r_2 + r_3 = \frac{R_{12} R_{13} + R_{12} R_{23} + R_{13} R_{23}}{R_{12} + R_{13} + R_{23}}\) .Вычтя теперь из этого уравнения уравнение (2), получим
\(~r_1 = \frac{R_{12} R_{13}}{R_{12} + R_{13} + R_{23}}\) .Аналогично,
\(~r_2 = \frac{R_{12} R_{23}}{R_{12} + R_{13} + R_{23}}\) ,и
\(~r_3 = \frac{R_{13} R_{23}}{R_{12} + R_{13} + R_{23}}\) .Эти результаты легко запомнить – знаменатель всюду один и тот же, а в числителе справа дважды встречается тот же индекс, что и слева\[~r_1 \to R_{12} R_{13}, r_2 \to R_{12} R_{23}, r_3 \to R_{13} R_{23}\] .
Немного сложнее получить формулы для обратного преобразования:
\(~R_{12} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_3}\) , \(~R_{13} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_2}\) , \(~R_{23} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_1}\) ,но их также легко запомнить – числитель всюду один и тот же, а в знаменателе стоит как раз тот индекс, которого недостает слева.
Пользуясь формулами, которые мы только что получили, можно производить замену одной схемы другой. Например, «звезду» с сопротивлениями 1 Ом можно заменить «треугольником» с сопротивлениями 3 Ом (рис.2).
Рис. 2
Решим теперь такую задачу: найдем сопротивление между точками A и B в схеме на рисунке 3.
Рис. 3
Это обычная схема «мостика», но в нашей задаче «мостик» неуравновешен. Такие задачи приходится решать при помощи правил Кирхгофа. В школьной программе их нет, да и вычисления с помощью этих правил очень громоздкие – в нашем случае получилась бы система пяти уравнений с пятью неизвестными. Мы поступим проще: заменим «треугольник» ACD «звездой», как показано на рисунке 4.
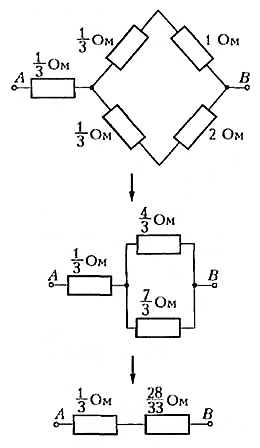
Рис. 4
Теперь ясно, что сопротивление между точками A и B будет равно
\(~R_{AB} = \frac 13 + \frac{28}{33} = \frac{13}{11}\) Ом.Мы заменяли «треугольник» ACD «звездой», но можно было решать задачу иначе – заменяя «звезду» ADB «треугольником» (проделайте зто самостоятельно).
Пусть теперь к точкам A и B подключена батарея с пренебрежимо малым внутренним сопротивлением и ЭДС ε = 1 В. Нужно найти ток через участок СВ. Понятно, что преобразовать схему надо так, чтобы не затронуть интересующее нас сопротивление СВ. Подойдет то преобразование, которое мы делали раньше (см. рис.4). Используя, что \(~R_{AB} = \frac{13}{11}\) Ом , получим
\(~I = \frac{\varepsilon}{R_{AB}} = \frac{11}{13}\) А.После разветвления токи в верхней и в нижней ветвях поделятся в отношении, обратном сопротивлениям ветвей:
\(~\frac{I_1}{I_2} = \frac 74\) .Отсюда находим
\(~I_1 = \frac{7}{13}\) А.Немного сложнее было бы найти ток, идущий через участок CD. Для этого пришлось бы еще найти ток через участок АС, а затем вычесть из него найденный уже ток через участок СВ.
Можно еще немного усложнить задачу — учесть внутреннее сопротивление батареи r. Тогда полный ток равен
\(~I = \frac{\varepsilon}{r + R_{AB}}\) ,а остальные токи находятся так же, как и раньше.
Рис. 5
Рассмотрим более интересную задачу, найдем, при каком соотношении между величинами r и R сопротивление между точками А и В в схеме, показанной на рисунке 5, максимально в крайнем положении движка потенциометра.
Рис. 6
Сначала преобразуем схему, заменив «треугольник» ACD «звездой» (рис.6). Очевидно, что сопротивление r не влияет на соотношение сопротивлений в остальной цепи. Займемся поэтому оставшейся частью схемы. Тут включены параллельно два сопротивления: 5r + R1 и 7r + R2, где R1 и R2 – сопротивления верхней и нижней частей потенциометра соответственно. При этом сумма сопротивлений 5r + R1, и 7r + R2 остается постоянной. Посмотрим, какими они должны быть, чтобы полное сопротивление было максимальным. Обозначим
\(~5r + R_1 = r_1\) и \(~7r + R_2 = r_2\).Тогда общее сопротивление включенных параллельно частей схемы равно
\(~r_0 = \frac{r_1 r_2}{r_1 + r_2}\) .Если учесть, что
\(~r_1 + r_2 = \operatorname{const} = c\) ,то
\(~r_0 = \frac{r_1 (c – r_1)}{c}\) .Это выражение максимально, когда максимален числитель. Но \(~y = cr_1 – r^2_1\) – это уравнение параболы, ветви которой пересекают ось абсцисс в точках 0 и с. Поэтому числитель дроби наибольший при \(~r_1 = \frac c2\). Так как r1 + r2 = с, то это означает, что сопротивление между точками А и В максимально, если r1 = r2, т.е.
\(~5r + R_1 = 7r + R_2\), или \(~R_1 – R_2 = 2r\).Ясно, что это возможно лишь в том случае, если сопротивление всего потенциометра R = R1 + R2 не меньше чем 2r. В противном же случае максимум сопротивления между точками A и B достигается, когда движок потенциометра находится в крайнем положении.
Итак, ответ: R
xn—-7sbeb3bupph.xn--p1ai
1.2.3.Схемы замещения реальных элементов электрической цепи. Элементы схемы электрической цепи
Схемы замещения реальных элементов электрической цепи
26 | 1. Основные положения |
1.2.3.1. Активные элементы
Как видно из рис. 1.11 и1.12 ВАХ идеальных источников ЭДС и тока не пересекают оси тока и напряжения соответственно. Это говорит о том, что идеальный источник ЭДС не может находится в режиме короткого замыкания (в этом случае мы получимiкз = ∞, откудаp =ui = ∞, что не имеет физического смысла), а идеальный источник тока в режиме холостого хода (в этом случае мы получимuхх = ∞, откудаp =ui = ∞, что не имеет физического смысла).
Таким образом, для моделирования источника напряжения (так, обычно, называют реальный источник ЭДС) нам необходимо добавить последовательно включённый с источником ЭДС резистивный элемент с сопротивлением Rвн (который характеризует внутреннее сопротивление источника), ограничивающий ток через источник ЭДС, а для моделирование реального источника тока нам необходимо добавить параллельно включённый с источником тока резистивный элемент с проводимостьюGвн (характеризует внутреннюю проводимость источника), ограничивающий падение напряжения на источнике тока.
Схемы замещения реальных источников напряжения и тока и их ВАХ приведены на рис. 1.13 и1.14.
Источник напряжения используется в качестве схемы замещения источников электрической энергии, внутреннее сопротивление которых много меньше сопротивления нагрузки (Rвн Rн, это наиболее распостранённый случай, соответствующий, например, гальваническим элементам и индуктивным генераторам), противном случае (Rвн Rн, характерно для емкостных генераторов и полупроводниковых устройств, работающих в соответствующих режимах) используется источник тока.
Следует отметить, что при анализе электрической цепи широко практикуется взаимное преобразование источников тока и напряжения. Целью этих преобразований является исключительно упрощение математических расчётов и они не несут в себе физического смысла.
1.2. Элементы электрической цепи замещения | 27 |
1.2.3.2. Пассивные элементы
Схема замещения реального элемента электрической цепи характеризует протекающие в нём физические процессы, т. е. является математической моделью элемента. Сложность схемы замещения определяется необходимой точностью расчётов, конструктивными особенностями реального элемента и характером протекающего тока. Обычно в качестве основного критерия выступает частота тока––чем выше частота, тем выше роль процессов связанных с преобразованием энергии электрического и магнитного полей и сложнее схема замещения. Выбор схемы замещения является весьма сложной задачей, требующей глубокого понимания процессов протекающих не только в самом элементе, но и их влияния на цепь в целом.
Рассмотрим схемы замещения наиболее распространённых пассивных элементов: резистора, конденсатора и катушки индуктивности.
Резистор
Характеристики идеального резистора будут соответствовать резистивному элементу схемы замещения.
Реальные резисторы, в основной массе случаев, достаточно хорошо отвечают этой модели, однако при необходимости более точных расчётов, особенно на высоких частотах, становится необходимым учитывать индуктивность проволоки (для проволочных резисторов), а также её барьерную ёмкость (рис. 1.15). На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов резистора.
Если резистор выполнен в виде катушки, то индуктивная составляющая будет играть значительную роль уже на сравнительно низких частотах.
Конденсатор
Характеристики идеального конденсатора будут соответствовать емкостному элементу схемы замещения.
Реальные конденсаторы, в основной массе случаев, достаточно хорошо отвечают этой модели, однако при необходимости более точных расчётов, особенно на высоких напряжениях, становится необходимым учитывать неидеальность диэлектрика, находящегося между обкладками конденсатора, которая характеризуется током утечки и на схеме
28 |
|
| 1. Основные положения | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.15. Схема замещения резистораа ––на низких частотах;б ––на высоких частотах
Cп иLп ––паразитные емкостная и индуктивная составляющие
замещения представлена в виде резистивного элемента, подключенного параллельно к емкостному (рис. 1.16). На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов конденсатора.
Рис. 1.16. Схема замещения конденсатора
а––на низких частотах;б ––на высоких частотахRп ––паразитная резистивная составляющие
Катушка индуктивности
Характеристики идеальной катушки индуктивности будут соответствовать индуктивному элементу схемы замещения.
Реальные катушки индуктивности намотаны из провода, имеющего ненулевое удельное сопротивление, таким образом, чем больше витков содержит катушка, тем будет выше её активное сопротивление, которое, обычно, необходимо учитывать во всём диапазоне частот (следует отметить, что на постоянном токе индуктивная составляющая катушки будет равна нулю, и в качестве схемы замещения можно ис-
studfiles.net
Электрические цепи и их элементы | Справочник
Электрическая цепь представляет собой совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении. В электрической цепи постоянного тока могут действовать как постоянные токи, так и токи, направление которых остается постоянным, а значение изменяется произвольно во времени или по какому-либо закону.
Электрическая цепь состоит из отдельных устройств или элементов, которые по их назначению можно разделить на 3 группы. Первую группу составляют элементы, предназначенные для выработки электроэнергии (источники питания). Вторая группа — элементы, преобразующие электроэнергию в другие виды энергии (механическую, тепловую, световую, химическую и т. д.). Эти элементы называются приемниками элек
xn—-7sbeb3bupph.xn--p1ai
